Περιεχόμενα ΠΡΟΛΟΓΟΣ... 9 ΕΙΣΑΓΩΓΗ... 11

Transcript

1

2

3 Περιεχόμενα ΠΡΟΛΟΓΟΣ... 9 ΕΙΣΑΓΩΓΗ ΤΑΞΗ Α ΠΟΣΟΣΤΑ ΑΝΑΛΟΓΑ ΠΟΣΑ ΜΕΛΕΤΗ ΑΝΑΛΟΓΑ ΠΟΣΑ ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΕΣΟΚΑΘΕΤΟΙ ΔΙΑΜΕΣΟΙ ΤΡΙΓΩΝΟΥ ΥΨΗ ΜΕΣΟΚΑΘΕΤΟΙ ΤΡΙΓΩΝΟΥ ΤΑΞΗ Β ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΣΥΝΑΡΤΗΣΗ ΕΥΘΕΙΑΣ ΑΝΤΙΣΤΡΟΦΑ ΠΟΣΑ ΣΥΝΑΡΤΗΣΗ ΥΠΕΡΒΟΛΗΣ ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΑΞΟΝΑ ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΣΗΜΕΙΟ ΤΑΞΗ Γ ΣΥΝΑΡΤΗΣΗ ΠΑΡΑΒΟΛΗΣ y=αx 2 & y=αx 2 +β ΣΥΝΑΡΤΗΣΗ ΠΑΡΑΒΟΛΗΣ y=αx 2 +βχ+γ & y=αx 2 +βχ ΘΕΩΡΗΜΑ ΘΑΛΗ ΣΥΧΝΟΤΗΤΑ & ΣΧΕΤΙΚΗ ΣΥΧΝΟΤΗΤΑ ΑΠΛΗΣ ΚΑΤΑΝΟΜΗΣ ΟΜΑΔΟΠΟΙΗΜΕΝΗ ΚΑΤΑΝΟΜΗ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΕΡΩΤΗΜΑΤΑ ΤΩΝ ΦΥΛΛΩΝ ΕΡΓΑΣΙΑΣ ΣΧΕΔΙΑ ΔΙΔΑΣΚΑΛΙΑΣ ΠΑΡΑΡΤΗΜΑ ΟΔΗΓΙΕΣ ΓΙΑ ΤΑ ΛΟΓΙΣΜΙΚΑ ΧΡΗΣΙΜΕΣ ΗΛΕΚΤΡΟΝΙΚΕΣ ΔΙΕΥΘΥΝΣΕΙΣ

4

5 ΤΑΞΗ Β 45

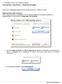
6 46 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ The Egyptians had a rope with 12 evenly spaced knots like this one: that they used to build perfect corners in their buildings and pyramids. Οι Αιγύπτιοι είχαν ένα σχοινί με 12 κόμπους σε ίσα διαστήματα (σε ίσες αποστάσεις), όπως φαίνεται στο σχήμα και το χρησιμοποιούσαν για να κατασκευάζουν τέλειες γωνίες στα κτίρια τους και στις πυραμίδες.

7 TΑΞΗ Β 47

8 48 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομ... ΘΕΜΑ: Το Πυθαγόρειο Θεώρημα Λογισμικό: Internet Explorer Εργαστείτε σε μία από τις παρακάτω ηλεκτρονικές διευθύνσεις, όπως έχει καθοριστεί για κάθε ομάδα. Αν υπάρχει πρόβλημα πρόσβασης εργαστείτε σε κάποια άλλη. Σημειώνετε ό,τι θεωρείτε σημαντικό για συζήτηση ή περαιτέρω επεξεργασία στο κενό χώρο του φύλλου εργασίας σας. Όταν τελειώσετε με τη συγκεκριμένη διεύθυνση, θα ασχοληθείτε όλοι με την τελευταία οπωσδήποτε (γι αυτό ρυθμίστε κατάλληλα το χρόνο σας). Ι) ΙΙ)

9 TΑΞΗ Β 49 ΙΙΙ) IV) V) VI)

10 50 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΣΥΝΑΡΤΗΣΗ ΕΥΘΕΙΑΣ

11 TΑΞΗ Β 51 f = x 1

12 52 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομ... ΘΕΜΑ: Κατασκευή και μελέτη γραφικής παράστασης ευθείας: h=2x+1 Λογισμικό: The function Probe I) Σύνταξη πίνακα τιμών Πληκτρολογήστε τις τιμές που βλέπετε στη στήλη του x (μετά από κάθε νούμερο πατήστε enter ή με τον κέρσορα-ποντίκι πηγαίνετε στην επόμενη σειρά). Μετά πληκτρολογήστε, στην επόμενη στήλη, στην ίδια γραμμή με το x τον τύπο της συνάρτησης (h=2x+1) και κάντε μόνο κλικ του κέρσορα στην κενή στήλη. ΙΙ) Μεταφορά σημείων στο Καρτεσιανό επίπεδο i) της h=2x-1 Επιλέξτε τις τιμές της στήλης του h και ύστερα το send από πάνω και μετά points to graph.

13 TΑΞΗ Β 53 ΙΙΙ) Ένωση σημείων Πηγαίνετε στον πρώτο πίνακα και επιλέξτε Graph και στη συνέχεια connect points. Τι σχήμα είναι η γραφική παράσταση της h;... IV) Άλλα παραδείγματα Επαναλάβετε την ίδια διαδικασία (δηλαδή βήματα ΙΙ, ΙΙΙ), και στους ί- διους πίνακες, για τις συναρτήσεις: ii) z=2x iii) f=x-1 iv) v=2x+3 Προσοχή: Για να επιτευχθεί η αυτόματη εύρεση των τιμών τους, κάντε «κλικ» με το ποντίκι ή «enter» στη στήλη κάτω από τον τύπο. Για το σχεδιασμό μιας παράστασης απαιτείται η μετακίνηση του ψ πάνω από τον τύπο της συνάρτησής της. Για να εμφανιστεί όλη η γραφική παράσταση μιας συνάρτησης και όχι ένα τμήμα της κάντε τα βήματα: Graph/ ew equation και πληκτρολογήστε τον τύπο της συγκεκριμένης συνάρτησης, οπότε εμφανίζεται πλήρη σχεδίαση. Δοκιμάστε και δικά σας παραδείγματα της ίδιας μορφής. V) Τι παρατηρείτε για κάποιες από τις παραστάσεις των συναρτήσεων; α) β) γ)

14 54 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ VI) Που πιστεύετε ότι οφείλονται οι προηγούμενες παρατηρήσεις; α) β) γ) Δώστε δικά σας παραδείγματα για κάθε μία περίπτωση. VII) Εργασία για το σπίτι: 1) Να ολοκληρωθούν τα δύο προηγούμενα βήματα V) και VI). 2) Να γραφούν οι τύποι των συναρτήσεων των ευθειών που προηγούνται αυτού του φύλλου εργασίας από αριστερά προς δεξιά. i) η πρώτη (μώβ) είναι:. ii) η δεύτερη (κόκκινη) είναι: iii) η τρίτη (μπλε) είναι:. iv) η τέταρτη (πράσινη) είναι: f = x-1... Παρατήρηση: Ο τύπος οποιασδήποτε ευθείας εμφανίζεται αμέσως στο επάνω μέρος του πίνακα Graph και κάτω από τη βασική εργαλειοθήκη, όταν αυτή επιλεγεί με το ποντίκι (μία φορά). Για τη ζωγραφική εμφάνιση ενός τύπου μπορείτε να ακολουθήσετε τα βήματα της παρακάτω σημείωσης.

15 TΑΞΗ Β 55 Σημείωση: Αν θέλετε να γράφετε και τον τύπο κάθε συνάρτησης μαζί με τη γραφική της παράσταση, όπως στο σχήμα της σελίδας πριν από το φύλλο εργασίας, τότε πρέπει να ενεργοποιήσετε το γ εικονίδιο του μολυβιού από τον πίνακα του Toolbar και κατόπιν χρησιμοποιώντας το ποντίκι γράφετε τον τύπο όπως και σε απλό χαρτί. Απαιτείται όμως πολύ προσεκτική και αργή κίνηση για ένα καλογραμμένο αποτέλεσμα. Αν γίνει κάποιο λάθος, ενεργοποιήστε πάλι από το Toolbar το α εικονίδιο του βέλους (οπότε γίνεται έντονη η γραφή του τύπου) και επιλέξτε από το Edit του Graph το Clear Selections.

16 56 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΑΝΤΙΣΤΡΟΦΑ ΠΟΣΑ x 0, , y , ,5 x*y x y x*y 0, ,5 5 2, ,5 5 q 0,9 1, s 5 3 0,9 2,5 q*s 4,5 4,5 4,5 37,5

17 TΑΞΗ Β 57 q s q*s 0,9 5 1, ,9 15 2,5 α 0,25 1 2,5 4 5 β α*β m n m*n 0,5 7 3,5 1 3,5 3,5 7 0,5 3,5 14 0,25 3,5 17,5 0,2 3,5

18 58 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομ... ΘΕΜΑ: Αντίστροφα Ποσά Λογισμικό: Ms Excel Α) Περίπτωση Πρώτη I) Καταγραφή των τιμών οριζόντια Στον πίνακα που ακολουθεί έχουν αναγραφεί οι τιμές των ποσών τα οποία πρόκειται να εξεταστούν. ΑΝΤΙΣΤΡΟΦΑ ΠΟΣΑ x 0, , y , ,5 x*y Πληκτρολογήστε όπως βλέπετε τους αριθμούς στις γραμμές x και y. Στη συνέχεια κάντε τους πολλαπλασιασμούς, όπως έχουν σημειωθεί στην επόμενη γραμμή, με τα εξής βήματα: Επιλέξτε το κελί που βρίσκεται δεξιά του x*y και κάτω από τα νούμερα της πρώτης στήλης, το =, το κελί με την πρώτη τιμή του x (το 0,5), την πράξη του πολλαπλασιασμού (*) από το δεξί τμήμα του πληκτρολογίου, την πρώτη τιμή του y (10) και enter, οπότε σε αυτό το επιλεγμένο κελί αναγράφεται το αποτέλεσμα του πολλαπλασιασμού (0,5*10). Ε- παναλάβετε την ίδια διαδικασία και για τα υπόλοιπα 5 κελιά. Τι παρατηρείτε για τις τιμές x*y;... Γιατί συμβαίνει αυτό;... Ποια εξισωτική σχέση συνδέει τα x και y;...

19 TΑΞΗ Β 59 ΙΙ) Καταγραφή των τιμών κατακόρυφα Στον πίνακα που ακολουθεί έχουν αναγραφεί οι τιμές των προηγούμενων ποσών, αλλά κατακόρυφα και θα υπολογισθούν τα γινόμενα αξιοποιώντας τώρα κάποιες ιδιότητες του Excel κατά την εκτέλεση των πράξεων (εδώ του πολλαπλασιασμού). ΑΝΤΙΣΤΡΟΦΑ ΠΟΣΑ x y x*y 0, ,5 2, ,5 Πληκτρολογήστε πάλι, όπως βλέπετε τους αριθμούς στις στήλες x και y. Στη συνέχεια θα γίνουν οι πολλαπλασιασμοί, όπως έχουν σημειωθεί, στην επόμενη στήλη με τα εξής βήματα: i) Υπολογισμός του πρώτου μόνο κελιού Επαναλάβετε την ίδια διαδικασία όπως προηγουμένως, δηλαδή: Επιλέξτε το κελί που βρίσκεται αμέσως δεξιά του 10, το =, το κελί με την πρώτη τιμή του x (το 0,5), την πράξη του πολλαπλασιασμού (*) από το δεξί τμήμα του πληκτρολογίου, την πρώτη τιμή του y (το 10) και enter, οπότε σε αυτό το επιλεγμένο κελί αναγράφεται το αποτέλεσμα του πολλαπλασιασμού (0,5*10). ii) Υπολογισμός των υπόλοιπων κελιών Επιλέξτε το πρώτο κελί δίπλα από το 10, στο οποίο μόλις καταγράφηκε το αποτέλεσμα του πολλαπλασιασμού 0,5*10 και τοποθετήστε τον κέρσορα στην κάτω δεξιά κορυφή του, ώστε να γίνει +. Στη συνέχεια τον σύρετε προς τα κάτω, ώστε να συμπεριληφθούν όλα τα κελιά στα οποία θέλετε να υπολογισθούν οι υπόλοιπες τιμές και πατάτε enter, οπότε αυτομάτως εμφανίζονται όλα τα γινόμενα.

20 60 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ Φυσικά τα αποτελέσματα που βρέθηκαν εδώ είναι ίδια ακριβώς με αυτά που υπολογίσθηκαν στην προηγούμενη περίπτωση του α πίνακα, οπότε ισχύουν και οι ίδιες παρατηρήσεις. Β) Περίπτωση Δεύτερη Εργαστείτε με όποιον από τους δύο τρόπους (οριζόντια ή κατακόρυφα) επιθυμείτε για τις επόμενες τιμές των ποσών q και s. q 0,9 1, s 5 3 0,9 2,5 q*s ή q s q*s 0,9 5 1, ,9 15 2,5 Τι παρατηρείτε;... Γιατί συμβαίνει αυτό;... Ποια εξισωτική σχέση συνδέει τα q και s;... Σημείωση: Για να μη χάνετε χρόνο δεν είναι απαραίτητο να σημειωθούν τα q, s, q*s και ούτε το χρωματιστό περίγραμμα του πίνακα.

21 TΑΞΗ Β 61 Γ) Άλλα παραδείγματα Ελέγξτε με όποιον τρόπο θέλετε, αν είναι αντίστροφα τα ποσά που ακολουθούν (η οριζόντια καταγραφή έχει γίνει μόνο για εξοικονόμηση χώρου στο φύλλο εργασίας σας). i) α 0,25 1 2,5 4 5 β α*β Απάντηση: είναι... δεν είναι... εξίσωση... ii) m n m*n 0, ,5 7 0,5 14 0,25 17,5 0,2 Απάντηση: είναι... δεν είναι... εξίσωση... Δ) Ασκήσεις (εργασία για το σπίτι) i) Να ολοκληρωθούν οι παραπάνω απαντήσεις. ii) Παρατηρώντας τις διάφορες τιμές των αντίστροφων ποσών μπορείτε να βρείτε τη γενική εξισωτική σχέση που τα συνδέει;...

22 62 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΣΥΝΑΡΤΗΣΗ ΥΠΕΡΒΟΛΗΣ

23 TΑΞΗ Β 63

24 64 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομηνία... ΘΕΜΑ: Κατασκευή και μελέτη γραφικής παράστασης υπερβολής: v=2/x Λογισμικό: The function Probe I) Σύνταξη πίνακα τιμών

25 TΑΞΗ Β 65 Πληκτρολογήστε τις τιμές που βλέπετε στη στήλη του x (μετά από κάθε νούμερο πατήστε enter ή με τον κέρσορα-ποντίκι πηγαίνετε στην επόμενη σειρά). Μετά πληκτρολογήστε, στην επόμενη στήλη, στην ίδια γραμμή με το x τον τύπο της συνάρτησης v=2/x και κάντε μόνο κλικ του κέρσορα στην κενή στήλη. ΙΙ) Μεταφορά σημείων στο Καρτεσιανό επίπεδο της v=2/x Mαρκάρετε μαυρίστε τις τιμές της στήλης του v και επιλέξτε από πάνω το send και μετά points to graph. ΙΙΙ) Ένωση σημείων Πηγαίνετε μετά στον κάτω πίνακα και επιλέξτε Graph και στη συνέχεια connect points. Τι σχήμα είναι η γραφική παράσταση της v;... Ονομασία:..... ΙV) Επαναλάβετε την ίδια διαδικασία (δηλαδή βήματα ΙΙ, ΙΙΙ), και στους ίδιους πίνακες, για τις τιμές της στήλης του w της συνάρτησης k=2/w. V) Άλλος τρόπος σχεδίασης γραφικής παράστασης για την y=2/x. Από τον πίνακα του Graph επιλέξτε: Graph / ew Equation. Στη συνέχεια πληκτρολογήστε τον τύπο της συνάρτησης και μετά enter. Τι παρατηρείτε; i).. ii). Στη συνέχεια κάντε τις παραστάσεις των συναρτήσεων q=-3/x, u=-3/w και τις m=x, h=w, s=-x, t=-w, αν δουλεύετε από το table, ή από το graph τις παραστάσεις των y=-3/χ και y=χ, y=-χ Προσοχή: Για να επιτευχθεί η αυτόματη εύρεση των τιμών τους από το table απαιτείται, ως γνωστόν, η μετακίνηση των x και y πάνω από τις αντίστοιχες στήλες. Δοκιμάστε και δικά σας παραδείγματα της ίδιας μορφής.

26 66 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ VI) Εξετάστε προσεκτικά όσες γραφικές παραστάσεις έχετε σχεδιάσει Τι παρατηρείτε για κάποιες από τις παραστάσεις των νέων συναρτήσεων; Ποια η σχέση τους με την αρχή των αξόνων; Ποια η σχέση τους με τις m=x, h=w, s=-x, t=-w; ή τις y=x, y=-x; VII) Που πιστεύετε ότι οφείλονται οι προηγούμενες παρατηρήσεις; Δώστε δικά σας παραδείγματα για κάθε μία περίπτωση. VIII) Εργασία για το σπίτι: Να ολοκληρωθούν τα δύο προηγούμενα βήματα VI) και VII). Σημείωση: Ίσως ήδη παρατηρήσατε ότι όποια γραφική παράσταση υπερβολής και αν σχεδιάστηκε πλησιάζει τους άξονες χχ και ψψ, αλλά καμιά δεν τους τέμνει, γι αυτό και οι χχ και ψψ αποτελούν ο- ριζόντια και κατακόρυφη ασύμπτωτη ευθεία αντίστοιχα για τις γραφικές παραστάσεις των υπερβολών.

27 TΑΞΗ Β 67 ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΑΞΟΝΑ

28 68 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ

29 TΑΞΗ Β 69

30 70 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ

31 TΑΞΗ Β 71 ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομ... ΘΕΜΑ: Κατασκευή συμμετρικών γεωμετρικών σχημάτων ως προς άξονα Λογισμικό: The Cabri Geometry II Α) Κατασκευή συμμετρικού σημείου Αφού κατασκευάσετε ένα σημείο και μία ευθεία, επιλέγοντας τα διπλανά αντίστοιχα εικονίδια με «κλίκ» και μεταφέροντάς τα στη λευκή σελίδα, πάλι με «κλίκ», στη συνέχεια επιλέξτε το σύμβολο της συμμετρίας (το γ κατά σειρά εικονίδιο από πάνω προς τα κάτω). Αν δεν υπάρχει, αναζητήστε το από την εργαλειοθήκη (α επιλογή από τη λίστα του έκτου κατά σειρά εικονιδίου της κάτω από το window) στην ένδειξη reflection. Τώρα, προκειμένου να σχεδιαστεί το συμμετρικό, κάντε τα εξής βήματα: Σύμβολο συμμετρίας / Επιλογή σημείου (εμφανίζεται η ένδειξη reflect this point) / επιλογή ευθείας (εμφανίζεται η ένδειξη with respect to this line). Β) Κατασκευή συμμετρικού ευθυγράμμου τμήματος Επιλέξτε το διπλανό εικονίδιο του τμήματος με την ένδειξη segment. (Είναι στον ίδιο πίνακα με την ευθεία). Μετά κάντε «κλικ» στη σελίδα σχεδιασμού, χαράξτε ένα τμήμα στο μήκος που επιθυμείτε και σταματήστε πάλι με «κλικ». Για να σχεδιαστεί το τμήμα πρέπει ο κέρσορας να έχει το σύμβολο του μολυβιού. Στη συνέχεια επαναλάβετε τα προηγούμενα βήματα: Σύμβολο συμμετρίας / Επιλογή τμήματος / επιλογή της ευθείας Σημείωση: Το τμήμα μπορεί να γίνει με κατασκευή, όπως προηγουμένως, δύο σημείων και ένωσή τους, αφού επιλεγεί το εικονίδιο του τμήματος.

32 72 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ Γ) Κατασκευή συμμετρικού τριγώνου Επιλέγοντας το διπλανό α εικονίδιο (από την ίδια στήλη με το τμήμα) και κάνοντας 3 «κλικ» στη σελίδα εργασίας σχεδιάζεται ένα τρίγωνο. Στη συνέχεια βρείτε το συμμετρικό του τριγώνου ως προς την ίδια ευθεία, με τα γνωστά βήματα: Σύμβολο συμμετρίας / Επιλογή σχήματος (εμφανίζεται η ένδειξη reflect this triangle) / επιλογή της ευθείας (εμφανίζεται η ένδειξη with respect to this line). Παρατήρηση: - Με επιλογή ( «τσίμπημα» - μετατροπή του κέρσορα σε χεράκι) κάποιας κορυφής και συνεχές πάτημα να δημιουργήσετε διάφορες θέσεις (είδη) τριγώνων και να παρακολουθήσετε συγχρόνως και το συμμετρικό σχήμα. Επίσης με επιλογή του β εικονιδίου να πιάσετε το σχήμα και να το μετακινήσετε. Τι παρατηρείτε;... - Αν θέλετε να μετακινηθεί όλο το σχήμα, επιλέγετε πρώτα το β από τα πάρα πάνω εικονίδια και μετά κάνετε τη μετακίνηση. Σημείωση: Ο σχεδιασμός του τριγώνου μπορεί να γίνει επίσης με κατασκευή 3 σημείων και μετά ένωση αυτών. Τώρα όμως για την εύρεση του συμμετρικού του τριγώνου πρέπει να βρεθούν τα συμμετρικά των πλευρών. Δ) Κατασκευή συμμετρικού γωνίας Σημειώστε το σημείο της κορυφής και στη συνέχεια με την ένδειξη του τμήματος (segment) σχεδιάστε τις πλευρές της. Μετά κατασκευάστε το συμμετρικό κάθε τμήματος ως προς την ήδη υπάρχουσα ευθεία με τα γνωστά βήματα: Σύμβολο συμμετρίας / Επιλογή πλευράς / επιλογή της ευθείας. Παρατήρηση: Με επιλογή (τσίμπημα) της κορυφής της γωνίας δημιουργείστε διάφορα είδη της. Τι παρατηρείτε για τα συμμετρικά τους;...

33 TΑΞΗ Β 73 Σημείωση: Ο σχεδιασμός της γωνίας μπορεί να γίνει με κατασκευή 3 σημείων και ένωση του ενός με τ άλλα δύο. Ε) Κατασκευή συμμετρικού κύκλου i) Κατασκευή κύκλου: Επιλέξτε το διπλανό εικονίδιο. Στη συνέχεια κάντε ένα κλικ σημειώνοντας έτσι το κέντρο του. Μετά αρχίστε να απομακρύνεστε αργάαργά, οπότε εμφανίζεται ο κύκλος. Σταματήστε, όταν αυτός έχει το μέγεθος που θέλετε. ii) Κατασκευή του συμμετρικού σχήματος του κύκλου: Κάντε τα βήματα: Σύμβολο συμμετρίας / Επιλογή κύκλου / επιλογή ευθείας. Στη συνέχεια μετακινήστε τον κύκλο και παρακολουθήστε το συμμετρικό του. - Τι παρατηρείτε;... ΣΤ) Άλλα σχήματα Δουλεύοντας με την επιλογή του διπλανού εικονιδίου (polygon είναι στον ίδιο πίνακα με την ευθεία και κάτω από την ένδειξη του τριγώνου), κατασκευάστε διάφορα σχήματα, βρείτε τα συμμετρικά τους και παρατηρήστε τα κατά τη μετακίνηση του άξονα συμμετρίας. Ζ) Μέτρηση και σύγκριση συμμετρικών σχημάτων Επανέλθετε σε κάθε ένα από τα προηγούμενα σχήματα και μετρήστε τα ως εξής: i) Μέτρηση γωνίας: Αφού επιλέξετε το διπλανό εικονίδιο (εμφανίζεται με την ένδειξη angle - γ επιλογή από το τέλος της εργαλειοθήκης) κάντε τα βήματα: Μαρκάρετε μία πλευρά, την κορυφή της και την άλλη πλευρά, ο- πότε εμφανίζεται η τιμή της γωνίας σε μοίρες ( ).

34 74 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ii) Μέτρηση τμήματος: Αφού επιλέξετε το διπλανό εικονίδιο (εμφανίζεται με την ένδειξη distance and length στον ίδιο πίνακα με την ένδειξη angle), κάντε τα βήματα: Μαρκάρετε το τμήμα (εμφανίζεται η ένδειξη Length of the segment) και κάντε «κλικ», οπότε έχουμε αμέσως το μήκος. Σημείωση: Στο τρίγωνο, όταν έχει κατασκευαστεί με την επιλογή του συμβόλου του, η μέτρηση δίνει την περίμετρό του. Όμως η εύρεση του μήκους μιας πλευράς γίνεται με τα βήματα: Μαρκάρετε το ένα άκρο (εμφανίζεται η ένδειξη distance from that point) / Μαρκάρετε και το άλλο άκρο (εμφανίζεται η ένδειξη to that point). Τώρα κάντε το ίδιο για τα αντίστοιχα συμμετρικά. - Τι παρατηρείτε;... iii) Στον κύκλο να μετρήσετε την επιφάνειά του με τα βήματα: Επιλέξτε το διπλανό εικονίδιο με το area από τη στήλη των μετρήσεων και μαρκάρετε με «κλικ» την περιφέρεια, οπότε εμφανίζεται η τιμή του εμβαδού. Αν θέλετε να μετρήσετε την ακτίνα, εργαστείτε όπως στη μέτρηση πλευράς τριγώνου, ενώ για το μήκος του κύκλου, μαρκάρετε ένα σημείο του, αφού πρώτα έχετε επιλέξει το σύμβολο του μήκους. Στη συνέχεια κάντε το ίδιο για το σχήμα του συμμετρικού κύκλου. - Τι παρατηρείτε;... Η) Εργασία για το σπίτι Να κατασκευαστούν στα τετράδια σας τα προηγούμενα σχήματα και να βρεθούν τα συμμετρικά τους.

35 TΑΞΗ Β 75 ΣΥΜΜΕΤΡΙΑ ΩΣ ΠΡΟΣ ΣΗΜΕΙΟ

36 76 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ

37 TΑΞΗ Β 77

38 78 ΠΡΑΓΜΑΤΙΚΕΣ ΔΙΔΑΣΚΑΛΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ Η/Υ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ

39 TΑΞΗ Β 79 ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... Ημερομ... ΘΕΜΑ: Κατασκευή συμμετρικών γεωμετρικών σχημάτων ως προς σημείο (κέντρο) Λογισμικό: The Cabri Geometry II Α) Κατασκευή συμμετρικού σημείου Κατασκευάστε ένα σημείο που θα αποτελέσει το κέντρο συμμετρίας με τα γνωστά βήματα (επιλέγοντας το διπλανό εικονίδιο του σημείου με «κλικ» και μεταφέροντάς το στη λευκή σελίδα, πάλι με «κλικ» ). Μετά φτιάξτε ένα άλλο σημείο για το οποίο θα βρείτε το συμμετρικό. Στη συνέχεια επιλέξτε το σύμβολο της συμμετρίας (το β εικονίδιο από δίπλα). Αν δεν υπάρχει, αναζητείστε το από την εργαλειοθήκη στην ένδειξη symmetry. Τώρα, προκειμένου να σχεδιαστεί το συμμετρικό, κάντε τα εξής βήματα: Σύμβολο συμμετρίας / Επιλογή σημείου (εμφανίζεται η ένδειξη reflect this point) / επιλογή του πρώτου σημείου, του κέντρου συμμετρίας (εμφανίζεται η ένδειξη with respect to this object). Β) Κατασκευή συμμετρικού ευθυγράμμου τμήματος Επιλέξτε το διπλανό εικονίδιο του τμήματος με την ένδειξη segment. (Είναι στον πίνακα κάτω από το γ τετράγωνο της εργαλειοθήκης). Μετά κάντε «κλικ» στη σελίδα σχεδιασμού, χαράξτε ένα τμήμα στο μήκος που επιθυμείτε και σταματήστε πάλι με «κλικ». Για το σχεδιασμό πρέπει ο κέρσορας να έχει το σύμβολο του μολυβιού. Στη συνέχεια επαναλάβετε τα προηγούμενα βήματα: Σύμβολο συμμετρίας / Επιλογή τμήματος / επιλογή του κέντρου συμμετρίας. Σημείωση: Το τμήμα μπορεί να γίνει με κατασκευή και ένωση 2 σημείων.

40