Critical Dynamics in Driven-Dissipative Bose-Einstein Condensation
|
|
|
- ÊΝηρεύς Νικολάκος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Critical Dynamics in Driven-Dissipative Bose-Einstein Condensation Uwe C. Täber 1 and Sebastian Diehl Weigang Li 1 1 Department of Physics, Virginia Tech, Blacsbrg, Virginia, USA Institte of Theoretical Physics, TU Dresden, Germany Renormalization Methods in Statistical Physics and Lattice Field Theories Montpellier, 8 Agst 015 Ref.: Phys. Rev. X 4, (014); arxiv:
2 Otline Experimental Motivation Langevin Description of Critical Dynamics Driven-Dissipative Bose Einstein Condensation Relationship with Eilibrim Critical Dynamics Scaling Laws and Critical Exponents Onsager Machlp Fnctional Janssen De Dominicis Response Fnctional One-Loop Renormalization Grop Analysis Two-Loop Renormalization Grop Analysis Conserved Dynamics Variant Critical Aging and Otloo
3 Experimental Motivation Pmped semicondctor antm wells in optical cavities: driven Bose Einstein condensation of exciton-polaritons J. Kasprza et al., Natre 443, 409 (006); K.G. Lagodais et al., Natre Physics 4, 706 (008) Theoretical approach: I nonlinear Langevin dynamics, mapped to path integral I pertrbatively analyze ltraviolet divergences (d dc = 4) I scale (µ) dependence, flow eations for rnning coplings I emerging symmetry: ξ indces scale invariance I critical RG fixed point scale invariance, infrared scaling laws I loop expansion in ϵ = dc d 1 critical exponents
4 Langevin Description of Critical Dynamics Critical slowing-down as correlated regions grow (τ T T c ): relaxation time t c (τ) ξ(τ) z τ zν, dynamic exponent z coarse-grained description: fast modes random noise mesoscopic Langevin eation for slow variables S α (x, t) Example: prely relaxational critical dynamics ( model A ): S α (x, t) t = D δh[s] δs α (x, t) + ζα (x, t), ζ α (x, t) = 0, ζ α (x, t) ζ β (x, t ) = D B T δ(x x ) δ(t t ) δ αβ Einstein relation garantees that P[S, t] e H[S]/ BT as t non-conserved order parameter: D = const. conserved order parameter: relaxes diffsively, D D Generally: mode coplings to additional conserved, slow fields varios dynamic niversality classes
5 Driven-Dissipative Bose Einstein Condensation Noisy Gross Pitaevsii eation for complex bosonic field ψ: ψ(x, t) [ i = (A id) µ + iχ t + (λ iκ) ψ(x, t) ] ψ(x, t) + ζ(x, t) A = 1/m eff ; D diffsivity (dissipative); µ chemical potential; χ pmp rate - loss; λ, κ > 0: two-body interaction / loss noise correlators: (γ = 4D B T in eilibrim) ζ(x, t) = 0 = ζ(x, t) ζ(x, t ) ζ (x, t) ζ(x, t ) = γ δ(x x ) δ(t t ) r = χ D, r = µ D, = 6κ D, r K = A D, r U = λ κ, ζ iζ time-dependent complex Ginzbrg Landa eation ψ(x, t) t = D [ r + ir (1 + ir K ) + 6 (1 + ir U) ψ(x, t) ] ψ(x, t) + ζ(x, t)
6 Relationship with Eilibrim Critical Dynamics Model A relaxational inetics for non-conserved order parameter: ψ(x, t) t = D δ H[ψ] δψ + ζ(x, t) (x, t) with non-hermitean Hamiltonian [ (r H[ψ] = d d x + ir ) ψ(x, t) + (1 + ir K ) ψ(x, t) + 1 (1 + ir U) ψ(x, t) 4] (1) r = r K = r U = 0: eilibrim model A for non-conserved two-component order parameter, GL-Hamiltonian H[ψ] () r = r U r, r K = r U 0: S 1/ = Re/Imψ, H = (1 + ir K ) H S α (x, t) t = D δh[ S] δs α (x, t) + Dr K β ϵ αβ δh[ S] δs β (x, t) + η α(x, t) η α (x, t) = 0, η α (x, t) η β (x, t ) = γ δ αβ δ(x x ) δ(t t ) effective eilibrim dynamics with detailed balance (FDT)
7 Scaling Laws and Critical Exponents (Bi-)critical point τ, τ = r K τ 0: correlation length ξ(τ) τ ν niversal scaling for dynamic response and correlation fnctions: 1 ( ω ) χ(, ω, τ) η (1 + ia η η ˆχ c ) z (1 + ia η η, ξ c ) 1 ( ω ) C(, ω, τ) Ĉ z, ξ, a η η c +z η five independent critical exponents (three in eilibrim: ν, η, z) Non-pertrbative (nmerical) renormalization grop stdy: d = 3: ν 0.716, η = η 0.039, z.11, η c 0.3 L.M. Sieberer, S.D. Hber, E. Altman, S. Diehl, Phys. Rev. Lett. 88, (013); Phys. Rev. B 89, (014) Thermalization: one-loop scenario (); two-loop model A (1) Critical exponents in ϵ = 4 d expansion: ν = 1 + ϵ 10 + O(ϵ ), η = ϵ 50 + O(ϵ3 ) z = + cη, c = 6 ln O(ϵ) as for eilibrim model A; in addition, novel critical exponent: η c = c η, c = ( 4 ln 4 3 1) + O(ϵ), bt FDT η = η ϵ = 1: ν 0.65, η = η 0.0, z.0145, η c
8 Onsager Machlp Fnctional Copled Langevin eations for mesoscopic stochastic variables: S α (x, t) = F α [S](x, t) + ζ α (x, t), ζ α (x, t) = 0, t ζ α (x, t)ζ β (x, t ) = L α δ(x x ) δ(t t ) δ αβ systematic forces F α [S], stochastic forces (noise) ζ α noise correlator L α : can be operator, fnctional of S α Assme Gassian stochastic process probability distribtion: [ W[ζ] exp 1 tf d d x dt ζ α (x, t) [ (L α ) 1 ζ α (x, t) ]] 4 0 α switch variables ζ α S α : W[ζ] D[ζ] = P[S]D[S] e G[S] D[S], with Onsager-Machlp fnctional providing field theory action: G[S] = 1 d d x dt ( t S α F α [S]) [ (L α ) 1 ( t S α F α [S]) ] 4 α fnctional determinant = 1 with forward (Itô) discrectization normalization: D[ζ]W [ζ] = 1 partition fnction = 1 problems: (L α ) 1, high non-linearities F α [S] (L α ) 1 F α [S]
9 Janssen De Dominicis Response Fnctional Average over noise histories : A[S] ζ D[ζ] A[S(ζ)] W [ζ]: se 1 = D[S] α (x,t) δ( t S α (x, t) F α [S](x, t) ζ α (x, t) ) = D[i S] D[S] exp [ d d x dt S α α ( t S α F α [S] ζ α ) ] [ A[S] ζ D[i S] D[S] exp d d x dt ] S α ( t S α F α [S]) α ( A[S] D[ζ] exp d d x dt α perform Gassian integral over noise ζ α : A[S] ζ = D[S] A[S] P[S], P[S] [ ]) 1 4 ζα (L α ) 1 ζ α S α ζ α D[i S] e A[ S,S], with Janssen De Dominicis response fnctional tf A[ S, S] = d d x dt [ Sα ( t S α F α [S]) S ] α L α Sα 0 α D[i S] D[S] e A[ S,S] = 1; integrate ot S α Onsager Machlp
10 One-Loop Renormalization Grop Analysis Casality: propagator directed line, noise two-point vertex two-point vertex fnction with γ = 4DT, r = r U r, = T : [ Γ ψψ (, ω) = iω+d r(1+ir U )+(1+ir K ) + 3 (1+ir U) + ] 1 r + flctation-indced shift of critical point: τ = r r c, τ = r U τ ( ) = r U r K : β = R 1 + r KR R + R R3 1+rKR R 0 [ ] β = R ϵ R R 3(1+rKR ) R R thermalization; to O(ϵ): ν 1 = 5 ϵ, η = η c = η = 0, z =
11 Two-Loop Renormalization Grop Analysis two-loop Feynman graphs for two-point vertex fnctions Γ ψ ψ (, ω), Γ ψψ (, ω) special case r = 0: T. Risler, J. Prost, and F. Jülicher, Phys. Rev. E 7, (005) RG beta fnction β rk : r KR 0, hence to O(ϵ ): + 9ΒrK R η = η = ϵ 50 + O(ϵ3 ) ( z = + ϵ 50 6 ln 4 3 ( 1) η c = ϵ 50 4 ln 4 3 1) sbleading scaling exponent rkr
12 Conserved Dynamics Variant Complex model B variant for conserved order parameter: t ψ(x, t) = D δ H[ψ] δψ + ζ(x, t), ζ(x, t) = 0 (x, t) ζ (x, t) ζ(x, t ) = 4T D δ(x x ) δ(t t ) non-linear vertex to all orders: Γ ψψ ( = 0, ω) = iω, Γ ψ ψ (, ω = 0) =0 = DT exact scaling relations: η = η, z = 4 η dynamic scaling laws: 1 ( χ(, ω, τ) η (1 + ia η η ˆχ c ) C(, ω, τ) 1 6 η Ĉ ( ω 4 η, ξ, a η ηc ) ω 4 η (1 + ia η η c ), ξ to two-loop order: η c = η + O(ϵ 3 ) = ϵ 50 + O(ϵ3 ) non-eilibrim drive indces no independent critical exponent )
13 Critical Aging and Otloo Qench from random initial conditions onto critical point: time translation invariance broen t c : system always remembers disordered initial state critical aging scaling in limit t /t 0: ( t ) θ χ(, t, t z +η (, τ) t 1 + ia η η ˆχ z ( 1 + ia ) ) η ηc t, ξ c model A: θ = γ 0 /z, γ 0 = 5 ϵ + O(ϵ ) as in eilibrim inetics model B: θ = 0 exactly Crrent and ftre projects: critical ench of driven complex Model A: two-loop analysis coarsening, critical aging in sitable spherical model limit? thermalization and emerging Model E dynamics?
Higher spin gauge theories and their CFT duals
 Higher spin gauge theories and their CFT duals E-mail: hikida@phys-h.keio.ac.jp 2 AdS Vasiliev AdS/CFT 4 Vasiliev 3 O(N) 3 Vasiliev 2 W N 1 AdS/CFT g µν Vasiliev AdS [1] AdS/CFT anti-de Sitter (AdS) (CFT)
Higher spin gauge theories and their CFT duals E-mail: hikida@phys-h.keio.ac.jp 2 AdS Vasiliev AdS/CFT 4 Vasiliev 3 O(N) 3 Vasiliev 2 W N 1 AdS/CFT g µν Vasiliev AdS [1] AdS/CFT anti-de Sitter (AdS) (CFT)
Markov chains model reduction
 Markov chains model reduction C. Landim Seminar on Stochastic Processes 216 Department of Mathematics University of Maryland, College Park, MD C. Landim Markov chains model reduction March 17, 216 1 /
Markov chains model reduction C. Landim Seminar on Stochastic Processes 216 Department of Mathematics University of Maryland, College Park, MD C. Landim Markov chains model reduction March 17, 216 1 /
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
ERG for a Yukawa Theory in 3 Dimensions
 ERG for a Yukawa Theory in 3 Dimensions Hidenori SONODA Physics Department, Kobe University, Japan 14 September 2010 at ERG2010 Abstract We consider a theory of N Majorana fermions and a real scalar in
ERG for a Yukawa Theory in 3 Dimensions Hidenori SONODA Physics Department, Kobe University, Japan 14 September 2010 at ERG2010 Abstract We consider a theory of N Majorana fermions and a real scalar in
([28] Bao-Feng Feng (UTP-TX), ( ), [20], [16], [24]. 1 ([3], [17]) p t = 1 2 κ2 T + κ s N -259-
![([28] Bao-Feng Feng (UTP-TX), ( ), [20], [16], [24]. 1 ([3], [17]) p t = 1 2 κ2 T + κ s N -259- ([28] Bao-Feng Feng (UTP-TX), ( ), [20], [16], [24]. 1 ([3], [17]) p t = 1 2 κ2 T + κ s N -259-](/thumbs/89/98133812.jpg) 5,..,. [8]..,,.,.., Bao-Feng Feng UTP-TX,, UTP-TX,,. [0], [6], [4].. ps ps, t. t ps, 0 = ps. s 970 [0] []. [3], [7] p t = κ T + κ s N -59- , κs, t κ t + 3 κ κ s + κ sss = 0. T s, t, Ns, t., - mkdv. mkdv.
5,..,. [8]..,,.,.., Bao-Feng Feng UTP-TX,, UTP-TX,,. [0], [6], [4].. ps ps, t. t ps, 0 = ps. s 970 [0] []. [3], [7] p t = κ T + κ s N -59- , κs, t κ t + 3 κ κ s + κ sss = 0. T s, t, Ns, t., - mkdv. mkdv.
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Quantum Statistical Mechanics (equilibrium) solid state, magnetism black body radiation neutron stars molecules lasers, superuids, superconductors
 BYU PHYS 73 Statistical Mechanics Chapter 7: Sethna Professor Manuel Berrondo Quantum Statistical Mechanics (equilibrium) solid state, magnetism black body radiation neutron stars molecules lasers, superuids,
BYU PHYS 73 Statistical Mechanics Chapter 7: Sethna Professor Manuel Berrondo Quantum Statistical Mechanics (equilibrium) solid state, magnetism black body radiation neutron stars molecules lasers, superuids,
The Feynman-Vernon Influence Functional Approach in QED
 The Feynman-Vernon Influence Functional Approach in QED Mark Shleenkov, Alexander Biryukov Samara State University General and Theoretical Physics Department The XXII International Workshop High Energy
The Feynman-Vernon Influence Functional Approach in QED Mark Shleenkov, Alexander Biryukov Samara State University General and Theoretical Physics Department The XXII International Workshop High Energy
LTI Systems (1A) Young Won Lim 3/21/15
 LTI Systems (1A) Copyright (c) 214 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
LTI Systems (1A) Copyright (c) 214 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
EE 570: Location and Navigation
 EE 570: Location and Navigation INS Initialization Aly El-Osery Kevin Wedeward Electrical Engineering Department, New Mexico Tech Socorro, New Mexico, USA In Collaboration with Stephen Bruder Electrical
EE 570: Location and Navigation INS Initialization Aly El-Osery Kevin Wedeward Electrical Engineering Department, New Mexico Tech Socorro, New Mexico, USA In Collaboration with Stephen Bruder Electrical
 μ μ μ s t j2 fct T () = a() t e π s t ka t e e j2π fct j2π fcτ0 R() = ( τ0) xt () = α 0 dl () pt ( lt) + wt () l wt () N 2 (0, σ ) Time-Delay Estimation Bias / T c 0.4 0.3 0.2 0.1 0-0.1-0.2-0.3 In-phase
μ μ μ s t j2 fct T () = a() t e π s t ka t e e j2π fct j2π fcτ0 R() = ( τ0) xt () = α 0 dl () pt ( lt) + wt () l wt () N 2 (0, σ ) Time-Delay Estimation Bias / T c 0.4 0.3 0.2 0.1 0-0.1-0.2-0.3 In-phase
Ηλεκτρονικοί Υπολογιστές IV
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Εισαγωγή στα δυναμικά συστήματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές IV Εισαγωγή στα δυναμικά συστήματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics
 Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics Dmitry Bagrets Nucl. Phys. B 9, 9 (06) arxiv: 607.00694 Alexander Altland Univ. zu Köln Alex Kamenev Univ. of Minnesota PCS IBS Workshop, Daejeon,
Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics Dmitry Bagrets Nucl. Phys. B 9, 9 (06) arxiv: 607.00694 Alexander Altland Univ. zu Köln Alex Kamenev Univ. of Minnesota PCS IBS Workshop, Daejeon,
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1
 General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
Geodesic paths for quantum many-body systems
 Geodesic paths for quantum many-body systems Michael Tomka, Tiago Souza, Steve Rosenberg, and Anatoli Polkovnikov Department of Physics Boston University Group: Condensed Matter Theory June 6, 2016 Workshop:
Geodesic paths for quantum many-body systems Michael Tomka, Tiago Souza, Steve Rosenberg, and Anatoli Polkovnikov Department of Physics Boston University Group: Condensed Matter Theory June 6, 2016 Workshop:
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
8.324 Relativistic Quantum Field Theory II
 8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
The Probabilistic Method - Probabilistic Techniques. Lecture 7: The Janson Inequality
 The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
UV fixed-point structure of the 3d Thirring model
 UV fixed-point structure of the 3d Thirring model arxiv:1006.3747 [hep-th] (PRD accepted) Lukas Janssen in collaboration with Holger Gies Friedrich-Schiller-Universität Jena Theoretisch-Physikalisches
UV fixed-point structure of the 3d Thirring model arxiv:1006.3747 [hep-th] (PRD accepted) Lukas Janssen in collaboration with Holger Gies Friedrich-Schiller-Universität Jena Theoretisch-Physikalisches
Non-Gaussianity from Lifshitz Scalar
 COSMO/CosPA 200 September 27, 200 Non-Gaussianity from Lifshitz Scalar Takeshi Kobayashi (Tokyo U.) based on: arxiv:008.406 with Keisuke Izumi, Shinji Mukohyama Lifshitz scalars with z=3 obtain super-horizon,
COSMO/CosPA 200 September 27, 200 Non-Gaussianity from Lifshitz Scalar Takeshi Kobayashi (Tokyo U.) based on: arxiv:008.406 with Keisuke Izumi, Shinji Mukohyama Lifshitz scalars with z=3 obtain super-horizon,
Constitutive Relations in Chiral Media
 Constitutive Relations in Chiral Media Covariance and Chirality Coefficients in Biisotropic Materials Roger Scott Montana State University, Department of Physics March 2 nd, 2010 Optical Activity Polarization
Constitutive Relations in Chiral Media Covariance and Chirality Coefficients in Biisotropic Materials Roger Scott Montana State University, Department of Physics March 2 nd, 2010 Optical Activity Polarization
Bayesian modeling of inseparable space-time variation in disease risk
 Bayesian modeling of inseparable space-time variation in disease risk Leonhard Knorr-Held Laina Mercer Department of Statistics UW May, 013 Motivation Ohio Lung Cancer Example Lung Cancer Mortality Rates
Bayesian modeling of inseparable space-time variation in disease risk Leonhard Knorr-Held Laina Mercer Department of Statistics UW May, 013 Motivation Ohio Lung Cancer Example Lung Cancer Mortality Rates
Major Concepts. Multiphase Equilibrium Stability Applications to Phase Equilibrium. Two-Phase Coexistence
 Major Concepts Multiphase Equilibrium Stability Applications to Phase Equilibrium Phase Rule Clausius-Clapeyron Equation Special case of Gibbs-Duhem wo-phase Coexistence Criticality Metastability Spinodal
Major Concepts Multiphase Equilibrium Stability Applications to Phase Equilibrium Phase Rule Clausius-Clapeyron Equation Special case of Gibbs-Duhem wo-phase Coexistence Criticality Metastability Spinodal
PHASE TRANSITIONS IN QED THROUGH THE SCHWINGER DYSON FORMALISM
 PHASE TRANSITIONS IN THROUGH THE SCHWINGER DYSON FORMALISM Spyridon Argyropoulos University of Athens Physics Department Division of Nuclear Physics and Elementary Particles Supervisor: C.N. Ktorides Athens
PHASE TRANSITIONS IN THROUGH THE SCHWINGER DYSON FORMALISM Spyridon Argyropoulos University of Athens Physics Department Division of Nuclear Physics and Elementary Particles Supervisor: C.N. Ktorides Athens
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
A thermodynamic characterization of some regularity structures near the subcriticality threshold
 Nils Berglund nils.berglund@univ-orleans.fr http://www.univ-orleans.fr/mapmo/membres/berglund/ SPA 2017 Invited Session: Regularity structures A thermodynamic characterization of some regularity structures
Nils Berglund nils.berglund@univ-orleans.fr http://www.univ-orleans.fr/mapmo/membres/berglund/ SPA 2017 Invited Session: Regularity structures A thermodynamic characterization of some regularity structures
The Wilson-Fisher Fixed Point via ERG
 The Wilson-Fisher Fixed Point via ERG Hidenori SONODA Physics Department, Kobe University 24 February 2010 at INT-10-45W RG workshop Abstract I construct the RG flows of the Wilson action for the real
The Wilson-Fisher Fixed Point via ERG Hidenori SONODA Physics Department, Kobe University 24 February 2010 at INT-10-45W RG workshop Abstract I construct the RG flows of the Wilson action for the real
Lifting Entry (continued)
 ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
Connec&ng thermodynamics to sta&s&cal mechanics for strong system-environment coupling
 Connec&ng thermodynamics to sta&s&cal mechanics for strong system-environment coupling Chris Jarzynski Ins&tute for Physical Science and Technology Department of Chemistry & Biochemistry Department of
Connec&ng thermodynamics to sta&s&cal mechanics for strong system-environment coupling Chris Jarzynski Ins&tute for Physical Science and Technology Department of Chemistry & Biochemistry Department of
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
The Spiral of Theodorus, Numerical Analysis, and Special Functions
 Theo p. / The Spiral of Theodorus, Numerical Analysis, and Special Functions Walter Gautschi wxg@cs.purdue.edu Purdue University Theo p. 2/ Theodorus of ca. 46 399 B.C. Theo p. 3/ spiral of Theodorus 6
Theo p. / The Spiral of Theodorus, Numerical Analysis, and Special Functions Walter Gautschi wxg@cs.purdue.edu Purdue University Theo p. 2/ Theodorus of ca. 46 399 B.C. Theo p. 3/ spiral of Theodorus 6
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ä Œμ Ìμ. ±É- É Ê ± μ Ê É Ò Ê É É, ±É- É Ê, μ Ö
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2017.. 48.. 5.. 740Ä744 ˆ Œˆ ƒ Š Œ ˆ Œˆ ˆŸ ˆ ˆ ˆŸ ˆˆ ƒ ˆ Šˆ ˆ.. Œμ Ìμ ±É- É Ê ± μ Ê É Ò Ê É É, ±É- É Ê, μ Ö ±μ³ ² ± ÒÌ ³μ ʲÖÌ Ð É Ò³ ² ³ Š² ËËμ Î É μ - ³ μ É Ò Ë ³ μ Ò ³ Ò Å ²μ ÉÉ. Ì
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2017.. 48.. 5.. 740Ä744 ˆ Œˆ ƒ Š Œ ˆ Œˆ ˆŸ ˆ ˆ ˆŸ ˆˆ ƒ ˆ Šˆ ˆ.. Œμ Ìμ ±É- É Ê ± μ Ê É Ò Ê É É, ±É- É Ê, μ Ö ±μ³ ² ± ÒÌ ³μ ʲÖÌ Ð É Ò³ ² ³ Š² ËËμ Î É μ - ³ μ É Ò Ë ³ μ Ò ³ Ò Å ²μ ÉÉ. Ì
Motion analysis and simulation of a stratospheric airship
 32 11 Vol 32 11 2011 11 Journal of Harbin Engineering University Nov 2011 doi 10 3969 /j issn 1006-7043 2011 11 019 410073 3 2 V274 A 1006-7043 2011 11-1501-08 Motion analysis and simulation of a stratospheric
32 11 Vol 32 11 2011 11 Journal of Harbin Engineering University Nov 2011 doi 10 3969 /j issn 1006-7043 2011 11 019 410073 3 2 V274 A 1006-7043 2011 11-1501-08 Motion analysis and simulation of a stratospheric
Thesis presentation. Turo Brunou
 Thesis presentation Turo Brunou 11.8.2008 Topic System Dynamics Model of Handset Bundling Business. Goal to examine the effect of handset bundling on mobile diffusion and data usage Structure Intro Industry
Thesis presentation Turo Brunou 11.8.2008 Topic System Dynamics Model of Handset Bundling Business. Goal to examine the effect of handset bundling on mobile diffusion and data usage Structure Intro Industry
Dr. D. Dinev, Department of Structural Mechanics, UACEG
 Lecture 4 Material behavior: Constitutive equations Field of the game Print version Lecture on Theory of lasticity and Plasticity of Dr. D. Dinev, Department of Structural Mechanics, UACG 4.1 Contents
Lecture 4 Material behavior: Constitutive equations Field of the game Print version Lecture on Theory of lasticity and Plasticity of Dr. D. Dinev, Department of Structural Mechanics, UACG 4.1 Contents
Distances in Sierpiński Triangle Graphs
 Distances in Sierpiński Triangle Graphs Sara Sabrina Zemljič joint work with Andreas M. Hinz June 18th 2015 Motivation Sierpiński triangle introduced by Wac law Sierpiński in 1915. S. S. Zemljič 1 Motivation
Distances in Sierpiński Triangle Graphs Sara Sabrina Zemljič joint work with Andreas M. Hinz June 18th 2015 Motivation Sierpiński triangle introduced by Wac law Sierpiński in 1915. S. S. Zemljič 1 Motivation
Thermoelectrics: A theoretical approach to the search for better materials
 Thermoelectrics: A theoretical approach to the search for better materials Jorge O. Sofo Department of Physics, Department of Materials Science and Engineering, and Materials Research Institute Penn State
Thermoelectrics: A theoretical approach to the search for better materials Jorge O. Sofo Department of Physics, Department of Materials Science and Engineering, and Materials Research Institute Penn State
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Hartree-Fock Theory. Solving electronic structure problem on computers
 Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
Derivation of Optical-Bloch Equations
 Appendix C Derivation of Optical-Bloch Equations In this appendix the optical-bloch equations that give the populations and coherences for an idealized three-level Λ system, Fig. 3. on page 47, will be
Appendix C Derivation of Optical-Bloch Equations In this appendix the optical-bloch equations that give the populations and coherences for an idealized three-level Λ system, Fig. 3. on page 47, will be
Computing the Gradient
 FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical oundation o the Finite Volume Method (FVM) and its applications in
FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical oundation o the Finite Volume Method (FVM) and its applications in
CorV CVAC. CorV TU317. 1
 30 8 JOURNAL OF VIBRATION AND SHOCK Vol. 30 No. 8 2011 1 2 1 2 2 1. 100044 2. 361005 TU317. 1 A Structural damage detection method based on correlation function analysis of vibration measurement data LEI
30 8 JOURNAL OF VIBRATION AND SHOCK Vol. 30 No. 8 2011 1 2 1 2 2 1. 100044 2. 361005 TU317. 1 A Structural damage detection method based on correlation function analysis of vibration measurement data LEI
Higher Derivative Gravity Theories
 Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Dark matter from Dark Energy-Baryonic Matter Couplings
 Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression. Lu Tian and Richard Olshen Stanford University
 Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Chapter 9 Ginzburg-Landau theory
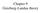 Chapter 9 Ginzburg-Landau theory The liit of London theory The London equation J µ λ The London theory is plausible when B 1. The penetration depth is the doinant length scale ean free path λ ξ coherent
Chapter 9 Ginzburg-Landau theory The liit of London theory The London equation J µ λ The London theory is plausible when B 1. The penetration depth is the doinant length scale ean free path λ ξ coherent
Free Energy and Phase equilibria
 Free Energy and Phase equilibria Thermodynamic integration 7.1 Chemical potentials 7.2 Overlapping distributions 7.2 Umbrella sampling 7.4 Application: Phase diagram of Carbon Why free energies? Reaction
Free Energy and Phase equilibria Thermodynamic integration 7.1 Chemical potentials 7.2 Overlapping distributions 7.2 Umbrella sampling 7.4 Application: Phase diagram of Carbon Why free energies? Reaction
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM. by Zoran VARGA, Ms.C.E.
 DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Fundamentals of Signals, Systems and Filtering
 Fundamentals of Signals, Systems and Filtering Brett Ninness c 2000-2005, Brett Ninness, School of Electrical Engineering and Computer Science The University of Newcastle, Australia. 2 c Brett Ninness
Fundamentals of Signals, Systems and Filtering Brett Ninness c 2000-2005, Brett Ninness, School of Electrical Engineering and Computer Science The University of Newcastle, Australia. 2 c Brett Ninness
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
On the Galois Group of Linear Difference-Differential Equations
 On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
ECON 381 SC ASSIGNMENT 2
 ECON 8 SC ASSIGNMENT 2 JOHN HILLAS UNIVERSITY OF AUCKLAND Problem Consider a consmer with wealth w who consmes two goods which we shall call goods and 2 Let the amont of good l that the consmer consmes
ECON 8 SC ASSIGNMENT 2 JOHN HILLAS UNIVERSITY OF AUCKLAND Problem Consider a consmer with wealth w who consmes two goods which we shall call goods and 2 Let the amont of good l that the consmer consmes
No. 7 Modular Machine Tool & Automatic Manufacturing Technique. Jul TH166 TG659 A
 7 2016 7 No. 7 Modular Machine Tool & Automatic Manufacturing Technique Jul. 2016 1001-2265 2016 07-0122 - 05 DOI 10. 13462 /j. cnki. mmtamt. 2016. 07. 035 * 100124 TH166 TG659 A Precision Modeling and
7 2016 7 No. 7 Modular Machine Tool & Automatic Manufacturing Technique Jul. 2016 1001-2265 2016 07-0122 - 05 DOI 10. 13462 /j. cnki. mmtamt. 2016. 07. 035 * 100124 TH166 TG659 A Precision Modeling and
ΗΜΥ 220: ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Ακαδημαϊκό έτος Εαρινό Εξάμηνο Κατ οίκον εργασία αρ. 2
 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΗΜΥ 220: ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Ακαδημαϊκό έτος 2007-08 -- Εαρινό Εξάμηνο Κατ οίκον εργασία αρ. 2 Ημερομηνία Παραδόσεως: Παρασκευή
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΗΜΥ 220: ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Ακαδημαϊκό έτος 2007-08 -- Εαρινό Εξάμηνο Κατ οίκον εργασία αρ. 2 Ημερομηνία Παραδόσεως: Παρασκευή
A Lambda Model Characterizing Computational Behaviours of Terms
 A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
u = g(u) in R N, u > 0 in R N, u H 1 (R N ).. (1), u 2 dx G(u) dx : H 1 (R N ) R
 2017 : msjmeeting-2017sep-05i002 ( ) 1.. u = g(u) in R N, u > 0 in R N, u H 1 (R N ). (1), N 2, g C 1 g(0) = 0. g(s) = s + s p. (1), [8, 9, 17],., [15] g. (1), E(u) := 1 u 2 dx G(u) dx : H 1 (R N ) R 2
2017 : msjmeeting-2017sep-05i002 ( ) 1.. u = g(u) in R N, u > 0 in R N, u H 1 (R N ). (1), N 2, g C 1 g(0) = 0. g(s) = s + s p. (1), [8, 9, 17],., [15] g. (1), E(u) := 1 u 2 dx G(u) dx : H 1 (R N ) R 2
Φαινόμενο Unruh. Δημήτρης Μάγγος. Εθνικό Μετσόβιο Πολυτεχνείο September 26, / 20. Δημήτρης Μάγγος Φαινόμενο Unruh 1/20
 Φαινόμενο Unruh Δημήτρης Μάγγος Εθνικό Μετσόβιο Πολυτεχνείο September 26, 2012 1 / 20 Δημήτρης Μάγγος Φαινόμενο Unruh 1/20 Outline Σχετικότητα Ειδική & Γενική Θεωρία Κβαντική Θεωρία Πεδίου Πεδία Στον Χωρόχρονο
Φαινόμενο Unruh Δημήτρης Μάγγος Εθνικό Μετσόβιο Πολυτεχνείο September 26, 2012 1 / 20 Δημήτρης Μάγγος Φαινόμενο Unruh 1/20 Outline Σχετικότητα Ειδική & Γενική Θεωρία Κβαντική Θεωρία Πεδίου Πεδία Στον Χωρόχρονο
ΔΗΜΟΣΙΕΥΣΕΙΣ σε περιοδικά με κριτές
 ΔΗΜΟΣΙΕΥΣΕΙΣ σε περιοδικά με κριτές 1. Patsis, P. A. & Zachilas, L.: 1990, Complex Instability Of Simple Periodic-Orbits In A Realistic 2-Component Galactic Potential, Astron. & Astroph., 227, 37 (ISI,
ΔΗΜΟΣΙΕΥΣΕΙΣ σε περιοδικά με κριτές 1. Patsis, P. A. & Zachilas, L.: 1990, Complex Instability Of Simple Periodic-Orbits In A Realistic 2-Component Galactic Potential, Astron. & Astroph., 227, 37 (ISI,
Dong Liu State Key Laboratory of Particle Detection and Electronics University of Science and Technology of China
 Dong Liu State Key Laboratory of Particle Detection and Electronics University of Science and Technology of China ISSP, Erice, 7 Outline Introduction of BESIII experiment Motivation of the study Data sample
Dong Liu State Key Laboratory of Particle Detection and Electronics University of Science and Technology of China ISSP, Erice, 7 Outline Introduction of BESIII experiment Motivation of the study Data sample
 χ (1) χ (3) χ (1) χ (3) L x, L y, L z ( ) ħ2 2 2m x + 2 2 y + 2 ψ (x, y, z) = E 2 z 2 x,y,z ψ (x, y, z) E x,y,z E x E y E z ħ2 2m 2 x 2ψ (x) = E xψ (x) ħ2 2m 2 y 2ψ (y) = E yψ (y) ħ2 2m 2 z 2ψ (z)
χ (1) χ (3) χ (1) χ (3) L x, L y, L z ( ) ħ2 2 2m x + 2 2 y + 2 ψ (x, y, z) = E 2 z 2 x,y,z ψ (x, y, z) E x,y,z E x E y E z ħ2 2m 2 x 2ψ (x) = E xψ (x) ħ2 2m 2 y 2ψ (y) = E yψ (y) ħ2 2m 2 z 2ψ (z)
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Appendix A. Curvilinear coordinates. A.1 Lamé coefficients. Consider set of equations. ξ i = ξ i (x 1,x 2,x 3 ), i = 1,2,3
 Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point
Appendix A Curvilinear coordinates A. Lamé coefficients Consider set of equations ξ i = ξ i x,x 2,x 3, i =,2,3 where ξ,ξ 2,ξ 3 independent, single-valued and continuous x,x 2,x 3 : coordinates of point
ΕΚΠ 413 / ΕΚΠ 606 Αυτόνοµοι (Ροµ οτικοί) Πράκτορες
 ΕΚΠ 413 / ΕΚΠ 606 Αυτόνοµοι (Ροµ οτικοί) Πράκτορες Λήψη Α οφάσεων υ ό Αβεβαιότητα Decision Making under Uncertainty Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Εντο
ΕΚΠ 413 / ΕΚΠ 606 Αυτόνοµοι (Ροµ οτικοί) Πράκτορες Λήψη Α οφάσεων υ ό Αβεβαιότητα Decision Making under Uncertainty Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Εντο
 1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
Symmetries and Feynman Rules for Ramond Sector in WZW-type Superstring Field Theories
 Symmetries and Feynman Rules for Ramond Sector in WZW-type Superstring Field Theories Hiroshi Kunitomo YITP 215/3/5 @Nara Women s U. Nara arxiv:1412.5281, 153.xxxx Y TP YUKAWA INSTITUTE FOR THEORETICAL
Symmetries and Feynman Rules for Ramond Sector in WZW-type Superstring Field Theories Hiroshi Kunitomo YITP 215/3/5 @Nara Women s U. Nara arxiv:1412.5281, 153.xxxx Y TP YUKAWA INSTITUTE FOR THEORETICAL
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
100x W=0.1 W=
 1 2 abstract: 1 [1] 1970 Furstenberg [2] 1 [3] 1979 Anderson [4] 1 2 1 H = NX n=1 jn >V n < nj); fv n g HjΨ >= EΨ > (ffi n =), ffi n+1 + ffi n 1 + V n ffi n = Effi n,
1 2 abstract: 1 [1] 1970 Furstenberg [2] 1 [3] 1979 Anderson [4] 1 2 1 H = NX n=1 jn >V n < nj); fv n g HjΨ >= EΨ > (ffi n =), ffi n+1 + ffi n 1 + V n ffi n = Effi n,
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009
 Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009 1 IV. Hedging of credit derivatives 1. Two default free assets, one defaultable asset 1.1 Two
Credit Risk. Finance and Insurance - Stochastic Analysis and Practical Methods Spring School Jena, March 2009 1 IV. Hedging of credit derivatives 1. Two default free assets, one defaultable asset 1.1 Two
Supplementary Information Chemical Partition of the Radiative Decay Rate of Luminescence of Europium Complexes
 Supplementary Information Chemical Partition of the Radiative Decay Rate of Luminescence of Europium Complexes Nathalia B. D. Lima [a], José Diogo L. Dutra [a,b], Simone M. C. Gonçalves [a], Ricardo O.
Supplementary Information Chemical Partition of the Radiative Decay Rate of Luminescence of Europium Complexes Nathalia B. D. Lima [a], José Diogo L. Dutra [a,b], Simone M. C. Gonçalves [a], Ricardo O.
Optical Feedback Cooling in Optomechanical Systems
 Optical Feedback Cooling in Optomechanical Systems A brief introduction to input-output formalism C. W. Gardiner and M. J. Collett, Input and output in damped quantum systems: Quantum Stochastic differential
Optical Feedback Cooling in Optomechanical Systems A brief introduction to input-output formalism C. W. Gardiner and M. J. Collett, Input and output in damped quantum systems: Quantum Stochastic differential
Variational Wavefunction for the Helium Atom
 Technische Universität Graz Institut für Festkörperphysik Student project Variational Wavefunction for the Helium Atom Molecular and Solid State Physics 53. submitted on: 3. November 9 by: Markus Krammer
Technische Universität Graz Institut für Festkörperphysik Student project Variational Wavefunction for the Helium Atom Molecular and Solid State Physics 53. submitted on: 3. November 9 by: Markus Krammer
d dt S = (t)si d dt R = (t)i d dt I = (t)si (t)i
 d d S = ()SI d d I = ()SI ()I d d R = ()I d d S = ()SI μs + fi + hr d d I = + ()SI (μ + + f + ())I d d R = ()I (μ + h)r d d P(S,I,) = ()(S +1)(I 1)P(S +1, I 1, ) +()(I +1)P(S,I +1, ) (()SI + ()I)P(S,I,)
d d S = ()SI d d I = ()SI ()I d d R = ()I d d S = ()SI μs + fi + hr d d I = + ()SI (μ + + f + ())I d d R = ()I (μ + h)r d d P(S,I,) = ()(S +1)(I 1)P(S +1, I 1, ) +()(I +1)P(S,I +1, ) (()SI + ()I)P(S,I,)
ˆ ˆŠ - Œ ˆ Œˆ Šˆ ˆ ƒˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2005.. 36.. 6 Š 536.1 ˆ ˆŠ - Œ ˆ Œˆ Šˆ ˆ ˆ Œ ˆ ˆ Š Š ˆ Œˆ (Š 100- ˆ ˆ ).. ÊÌ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ. ˆ Ÿ... 1282 ˆ ˆ ˆ Šˆ ˆ : Œ ˆŠˆ Š Œ ˆ ŒˆŠ 1286 Œˆ ˆ Œ ˆ ˆ- Š Œ ˆ ŒˆŠˆ 1299 ˆ ˆ ˆŠ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2005.. 36.. 6 Š 536.1 ˆ ˆŠ - Œ ˆ Œˆ Šˆ ˆ ˆ Œ ˆ ˆ Š Š ˆ Œˆ (Š 100- ˆ ˆ ).. ÊÌ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ. ˆ Ÿ... 1282 ˆ ˆ ˆ Šˆ ˆ : Œ ˆŠˆ Š Œ ˆ ŒˆŠ 1286 Œˆ ˆ Œ ˆ ˆ- Š Œ ˆ ŒˆŠˆ 1299 ˆ ˆ ˆŠ
DuPont Suva 95 Refrigerant
 Technical Information T-95 SI DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Technical Information T-95 SI DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Approximation of dynamic boundary condition: The Allen Cahn equation
 1 Approximation of dynamic boundary condition: The Allen Cahn equation Matthias Liero I.M.A.T.I. Pavia and Humboldt-Universität zu Berlin 6 th Singular Days 2010 Berlin Introduction Interfacial dynamics
1 Approximation of dynamic boundary condition: The Allen Cahn equation Matthias Liero I.M.A.T.I. Pavia and Humboldt-Universität zu Berlin 6 th Singular Days 2010 Berlin Introduction Interfacial dynamics
Supplementary Material for The Cusp Catastrophe Model as Cross-Sectional and Longitudinal Mixture Structural Equation Models
 Supplementary Material for The Cusp Catastrophe Model as Cross-Sectional and Longitudinal Mixture Structural Equation Models Sy-Miin Chow Pennsylvania State University Katie Witkiewitz University of New
Supplementary Material for The Cusp Catastrophe Model as Cross-Sectional and Longitudinal Mixture Structural Equation Models Sy-Miin Chow Pennsylvania State University Katie Witkiewitz University of New
Depth versus Rigidity in the Design of International Trade Agreements. Leslie Johns
 Depth versus Rigidity in the Design of International Trade Agreements Leslie Johns Supplemental Appendix September 3, 202 Alternative Punishment Mechanisms The one-period utility functions of the home
Depth versus Rigidity in the Design of International Trade Agreements Leslie Johns Supplemental Appendix September 3, 202 Alternative Punishment Mechanisms The one-period utility functions of the home
Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog
 J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
