Υπολογιστικά Μαθηματικά (Set 2)
|
|
|
- Ἡσαΐας Χριστόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Υπολογιστικά Μαθηματικά (Set 2) Ζαφειράκογλου Απόστολος 1 Πολυώνυμο Langrange 1.1 Εισαγωγικά Στην υπόθεση της άσκησης δινοταν η συνάρτηση y(x) = 2 3 x sin(πx), x (0, 2). Ζητούμενο ήταν να προσεγγιστεί με ένα πολυώνυμο: i. Lagrange ii. Hermite Δεδομένου ότι η C++, όπως βέβαια και κάθε κλασσική γλώσσα προγραμματισμού, δεν μπορεί να διαχειριστεί πολυώνυμα, αρχικό ζητούμενο ήταν η ανάπτυξη ενός class, που να μπορεί να δουλέψει δίνοντας την αίσθηση ότι μεταχειρίζεται πολυώνυμα. Το class που αναπτύχθηκε σε αυτή την εργασία για το σκοπό αυτό ονομάζεται polynomial και καλείται ως header στην αρχή των προγραμμάτων μέσω της εντολής #include. Οι λόγοι για τους οποίους γίνεται αυτό είναι δύο: i. αφενώς μικραίνει ο κώδικας που πρέπει να ελέγξει κάποιος στο main πρόγραμμά του και ii. αφετέρου γίνεται ευκολότερη η χρήση του ίδιου κομματιού κώδικα, από άλλα προγράμματα Η κλάση που ακολουθεί, έχει προγραμματιστεί ώστε να κάνει τα ακόλουθα: n o βαθμός του πολυωνύμου a[ ] είναι ο πίνακας των συντελεστών. Το στοιχείο του πίνακα a[i] είναι συντελεστής του όρου x i Ορίζονται οι συναρτήσεις add και multiply, οι οποίες add: προσθέτει δύο αντίκειμενα πολυώνυμα multiply: πολλαπλασιάζει ένα πολυώνυμα με ένα μονώνυμο Χάρη στις δύο παραπάνω συναρτήσεις μπορούν πλέον να γραφούν ευκολότερα οι πράξεις τις αφαίρεσης πολυωνύμων και πολλαπλασιασμού δύο πολυωνύμων (prod). 1
2 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange Υπερφορτώνονται οι τελεστές +,-,*,/ για όλους τους δυνατούς συνδιασμούς πράξεων, ακόμη και για αφαίρεση double από polynomial ή για πολλαπλασιασμό double με polynomial Δημιουργήθηκε η μέθοδος της παραγώγισης D() ενός polynomial Η συνάρτηση Show δείχνει το αντικείμενο με μορφή πολυωνύμου, ενώ η συνάρτηση valueon() δείχνει την τιμή του πολυωνύμου σε εκείνο το σημείο. 1.2 Header Polynomial.h 1 #ifndef POLYNOMIAL_H_INCLUDED 2 #define POLYNOMIAL_H_INCLUDED 3 #include <iostream> 4 #include <cmath> 5 #include <cstdlib> 6 7 using namespace std; 8 9 class polynomial 10 { public: 13 int n; 14 double a [30]={0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}; 15 polynomial friend operator+(const polynomial&, const polynomial&); 16 polynomial friend operator+(const polynomial&, const double&); 17 polynomial friend operator (const polynomial&, const polynomial&); 18 polynomial friend operator (const polynomial&, const double&); 19 polynomial friend operator*(const polynomial&, const polynomial&); 20 polynomial friend operator*(const double&, const polynomial&); 21 polynomial friend operator*( const polynomial&,const double&); 22 polynomial friend operator/(const polynomial&,const double&); 23 void show() 24 { 25 short int i=n; 26 while(i>=2) 27 { 28 cout <<"("<< a[i]<<")x^"<<i<<" + "; 29 i ; 30 } 31 cout <<"("<< a[1]<<")x + "<<"("<<a[0]<<")"<<endl; 32 } 33 double valueon(double xx) 34 { 35 int j=n;double val=0; 36 while(j>=0) 37 { 38 val+=a[j]*pow(xx,j); 2
3 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 39 j ; 40 } 41 return val; 42 } 43 }; /* Object polynomial: overloading +,*, */ 46 polynomial add(polynomial p1, polynomial p2) 47 { 48 polynomial result; 49 int i=p1.n; 50 if(p1.n<p2.n) 51 { 52 i=p2.n; 53 } 54 result.n=i; 55 while(i>=0) 56 { 57 result.a[i]=p1.a[i]+p2.a[i]; 58 i ; 59 } return result; 62 } polynomial multiply(int j,double x,polynomial p1) 65 { 66 polynomial result; int i; 67 result.n=p1.n+j; 68 i=p1.n; 69 while(i>=0) 70 { 71 result.a[i+j]=x*p1.a[i]; 72 i ; 73 } 74 /*cout <<"****"<<endl; 75 result.show();*/ 76 return result; 77 } polynomial prod(polynomial p1, polynomial p2) 80 { 81 polynomial result; 82 result.n=p1.n+p2.n; 83 int i=p1.n; while(i>=0) 87 { 3
4 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 88 result=add(result, multiply(i,p1.a[i],p2)); 89 i ; 90 } 91 return result; 92 } polynomial frac(double y,polynomial p1) 95 { 96 int k=p1.n; polynomial result; 97 result.n=p1.n; 98 while(k>=0) 99 { 100 result.a[k]=p1.a[k]/y; 101 k ; 102 } 103 return result; 104 } polynomial D(polynomial p1) 107 { 108 polynomial result; 109 result.n=p1.n 1; 110 int i; 111 i=p1.n; 112 while(i>=1) 113 { 114 result.a[i 1]=i*p1.a[i]; 115 i ; 116 } 117 return result; 118 } polynomial operator+(const polynomial& p1, const polynomial& p2) 121 { 122 return add(p1, p2); 123 } polynomial operator*(const polynomial& p1, const polynomial& p2) 126 { 127 return prod(p1, p2); 128 } 129 polynomial operator*(const double& p1, const polynomial& p2) 130 { 131 return multiply(0,p1, p2); 132 } 133 polynomial operator*( const polynomial& p2,const double& p1) 134 { 135 return multiply(0,p1, p2); 136 } 4
5 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 137 polynomial operator/( const polynomial& p2,const double& y) 138 { 139 return frac(y, p2); 140 } 141 polynomial operator (const polynomial& p1, const polynomial& p2) 142 { 143 polynomial p3=( 1)*p2; 144 return add(p1, p3); 145 } 146 polynomial operator (const polynomial& p1, const double& aa) 147 { 148 polynomial p2; 149 p2.n=0;p2.a[0]= aa; 150 return add(p1, p2); 151 } 152 polynomial operator+(const polynomial& p1, const double& aa) 153 { 154 polynomial p2; 155 p2.n=0;p2.a[0]=aa; 156 return add(p1, p2); 157 } #endif // POLYNOMIAL_H_INCLUDED 1.3 Πολυώνυμο Lagrange Κάνοντας χρήση της παραπάνω κλάσης έγινε ευκολότερος ο προσδιορισμός των συντελεστών Lagrange και του ομόνυμου πολυωνύμου για την συνάρτηση της υπόθεσης y(x) = 2 3 x sin(πx), x (0, 2). Διάγραμμα 1.1: Γραφική παράσταση της συνάρτησης y(x) = 2 3 x sin(πx) Ο κώδικας που χρησιμοποιήθηκε εκμεταλλεύεται όλα τα στοιχεία της κλάσης. Στην αρχή ορί- 5
6 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange ζεται η συνάρτηση της εκφώνησης και έπειτα μια συνάρτηση που επιστρέφει ως αποτέλεσμα το πολυώνυμο lagrange. Στην main γίνεται η άθροιση των συντελεστών lagrange επί τις τιμές της συνάρτησης στα αντίστοιχα σημεία, και παρουσιάζεται το αποτέλεσμα. 1 #include <iostream> 2 #include <cmath> 3 #include <fstream> 4 #include "polynomial.h" 5 6 //Langrange 7 using namespace std; 8 9 /*Startup Functions*/ 10 double x[11];double f[11]; 11 int steps=9; 12 double pi= ; double myfunc(double xx) 15 { 16 return 2 3*xx*sin(pi*xx); 17 } //InitCond 20 void initx() 21 { 22 int i=0;double h=0.2; 23 x[0]=0.2; 24 while( i<=steps) 25 { 26 x[i]=x[0]+i*h; 27 i++; 28 } 29 } 30 void inity() 31 { 32 short int i=0; 33 while(i<=steps) 34 { 35 f[i]= myfunc(x[i]); 36 i++; 37 } 38 } void init() 41 { 42 initx();inity(); 43 } polynomial lagrange(int i) 6
7 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 46 { 47 polynomial result,cur[10]; 48 result.n=0;result.a[0]=1; 49 int k=0,j=0; 50 while(k<=steps) 51 { 52 cur[k].n=1;cur[k].a[0]= x[k];cur[k].a[1]=1; 53 cur[k]=cur[k];//cur[k].valueon(x[k]); 54 k++; 55 } 56 k=0; 57 while(k<=steps) 58 { 59 if(k==i){} 60 else 61 { 62 result=result*cur[k];//cur[k].valueon(x[k]); 63 result=result/result.valueon(x[i]); 64 } 65 k++; 66 } return result; 69 } int main() 72 { 73 init(); 74 polynomial final;final.n=0;int g=0; 75 while(g<=steps) 76 { 77 final=f[g]*lagrange(g) +final; 78 g++; 79 } final.show(); 82 return 0; 83 } Παραθέτω τα πολυώνυμα που έβγαλε ως αποτέλεσμα το πρόγραμμα: x x x 2 125x
8 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange Διάγραμμα 1.2 Το πολυώνυμο 9ου βαθμού και το αντίστοιχο διάγραμμα: x x x x x x x x x
9 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange Διάγραμμα 1.3: Διάγραμμα προσεγγιστικού πολυωνύμου Lagrange 9ου βαθμού 1.4 Πολυώνυμο Hermite Το δεύτερο ερώτημα της ίδιας άσκησης ζητούσε να προσεγγιστεί η ίδια συνάρτηση με ένα πολύωνυμο Hermite. Αυτό έγινε εύκολα με τροποποίηση του παραπάνω κώδικα. Έγινε χρήση τόσο της συνάρτησης Lagrange, όσο και της μεθόδου της παραγώγισης που αναπτύχθηκε στην κλάση polynomial. Προφανώς χρησιμοποιήθηκε και η παράγωγος της συνάρτησης, η οποία ονομάζεται dmyfunc, που έδωσε του τα σημεία του πίνακα df[]. 1 #include <iostream> 2 #include <cmath> 3 #include <fstream> 4 #include "polynomial.h" 5 //Hermite 6 7 using namespace std; /*Startup Functions*/ 11 double x[11];double f[11];double df[11]; 12 int steps=9; 13 double pi= ; double myfunc(double xx) 16 { 17 return 2 3*xx*sin(pi*xx); 18 } 19 double dmyfunc(double xx) 9
10 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 20 { 21 return 3*(xx*cos(pi*xx)*pi + sin(pi*xx)); 22 } //InitCond 25 void initx() 26 { 27 int i=0;double h=0.2; 28 x[0]=0.2; 29 while( i<=steps) 30 { 31 x[i]=x[0]+i*h; 32 i++; 33 } 34 } 35 void inity() 36 { 37 short int i=0; 38 while(i<=steps) 39 { 40 f[i]= myfunc(x[i]); 41 df[i]= dmyfunc(x[i]); 42 i++; 43 } 44 } void init() 47 { 48 initx();inity(); 49 } polynomial lagrange(int i) 52 { 53 polynomial result,cur[10]; 54 result.n=0;result.a[0]=1; 55 int k=0,j=0; 56 while(k<=steps) 57 { 58 cur[k].n=1;cur[k].a[0]= x[k];cur[k].a[1]=1; 59 cur[k]=cur[k];//cur[k].valueon(x[k]); 60 k++; 61 } 62 k=0; 63 while(k<=steps) 64 { 65 if(k==i){} 66 else 67 { 68 result=result*cur[k];//cur[k].valueon(x[k]); 10
11 ΠΜΣ Υπολογιστικη ς Φυσικη ς 1 Πολυω νυμο Langrange 69 result=result/result.valueon(x[i]); 70 } 71 k++; 72 } return result; 75 } polynomial A(int i) 78 { 79 polynomial result,mon,dlang,aa;result.n=0;result.a[0]=0;mon.n=1;mon.a [0]= x[i];mon.a[1]=1; 80 aa.n=0;aa.a[0]=1; 81 dlang=d(lagrange(i)); 82 result=(aa 2*mon*dlang.valueon(x[i]))*lagrange(i)*lagrange(i); return result; 85 } 86 polynomial B(int i) 87 { 88 polynomial result,mon;result.n=0;result.a[0]=0; 89 mon.n=1;mon.a[0]= x[i];mon.a[1]=1; result=mon*lagrange(i)*lagrange(i); return result; 94 } 95 int main() 96 { 97 init(); 98 polynomial final,sum1,sum2;final.n=0;int g=0; 99 while(g<=steps) 100 { 101 sum1=sum1+a(g)*f[g]; 102 sum2=sum2+b(g)*df[g]; 103 g++; 104 } 105 final=sum1+sum2; 106 final.show(); 107 return 0; 108 } Το πολυώνυμο που εξήχθει είναι το ακόλουθο, και όπως φαίνεται από την γραφική του παράσταση, εφαρμόζει με εξαιρετική ακρίβεια πάνω στην πραγματική συνάρτηση, και άρα αποτελεί πολύ ικανοποιητική προσέγγιση της, ακόμα και ένα μικρό διάστημα έξω από αυτό που ζητήθηκε! 11
12 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις x x x x x x x x x x x x x x x x x x x + 2 Διάγραμμα 1.4: Γραφική παράσταση του πολυωνύμου Hermite (μωβ) με την πραγματική γραφική παράσταση της συνάρτησης (πορτοκαλί). 2 Αριθμητικές Ολοκληρώσεις 2.1 Newton-Cotes (Romberg s Improvement) Ζητούμενο της δεύτερης άσκησης ήταν η αριθμητική ολοκλήρωση δύο συναρτήσεων, με διαφορετικούς τρόπους. Όπως είναι αναμενόμενο, οι μέθοδοι για αυτού του είδους τις ολοκληρώσεις, βασίζονται στην ιδέα του συμπτωτικού πολυωνύμου. Χαρακτηριστικοί τύποι είναι αυτοί των Newton-Cotes. Στο κώδικα που ακολουθεί γίνεται σύγκριση των αποτελεσμάτων με τις πραγματικές τιμές των ολοκληρωμάτων, και υπολογίζεται το σφάλμα. Ακόμη γίνεται χρήση της βελτίωσης του Romberg. Για ευκολία ελέγχου των διαφόρων μεθόδων, ο πηγαίος κώδικας έχει μέσα όλες της ρουτίνες που απαιτούνται. Σε αυτό το σημείο πρέπει να σημειωθούν δύο πράγματα: i. Χάρη στο polynomial class, έγινε δυνατή η ανάπτυξη ρουτίνας που υπολογίζει συμπτωτικό 12
13 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις πολυώνυμο, αν της δοθεί μιά διαμέριση. Η ρουτίνα ονομάζεται Psympt. Προφανώς για διαμέριση του πεδίου σε 2, 3 ή 4 σημεία, το αποτέλεσμα είναι οι τύποι των Newton- Cotes. Παρ όλ αυτά δεν γίνεται χρήση της ρουτίνας για τόσα σημεία αλλά εφαρμόζονται απευθείας οι έτοιμες φόρμουλες της θεωρίας. ii. Όπως θα φανεί αργότερα από τα αποτελέσματα των μεθόδων, οι μέθοδοι των Newton- Cotes δεν καταφέρνουν να πιάσουν την επιθυμητή ακρίβεια. Γι αυτό ακριβώς το λόγο, προσεγγίζουμε με μια καλύτερη διαμέριση, και ζητούμε από την Psympt την κατασκευή κάποιων πολυωνύμων μεγαλύτερου βαθμού. Ολοκληρώνοντας τα πολυώνυμα με τη χρήση της ρουτίνας Intergrate, μπορούμε να καταλήξουμε σε μια καλύτερη εκτίμηση της πραγματικής τιμής. 1 #include <iostream> 2 #include <iomanip> 3 #include "polynomial.h" 4 #include <cmath> 5 using namespace std; 6 double pi= ;double eps=pow(10, 6); 7 double h;int n; 8 double *x= new double [n+5]; 9 10 double myfunc(double xx) 11 { 12 // Formula of function 13 return sqrt(xx 0.1); 14 //return exp( xx)*sin(5*xx); 15 } 16 void set(double a,double b,double M) 17 { 18 // a:start X, b:end X, M:How many steps 19 int i=0; h=(b a)/(m); n=m; 20 while (i<=n) 21 { 22 x[i]=a+h*i; 23 i++; 24 } 25 } 26 double NC(short int order,int o) 27 { 28 double answ=0; 29 if(order==1){ 30 answ=(h/2)*(myfunc(x[o]) +myfunc(x[o+1])); 31 } 32 else if (order==2){ 33 answ=(h/3)*(myfunc(x[o]) +4*myfunc(x[o+1])+myfunc(x[o+2])); 34 } 35 else if (order ==3){ 13
14 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 36 answ=(3*h/8)*(myfunc(x[o]) +3*myfunc(x[o+1]) + 3*myfunc(x[o+2])+myfunc(x [o+3])); 37 } 38 return answ; 39 } double trapezoid(int k, int o) 42 { 43 int i=o; double sum=0; 44 while(i<=k 1) 45 { 46 sum+=nc(1,i); 47 i++; 48 } 49 return sum; 50 } double Simpson(int k, int o) 53 { 54 int i=o; double sum=0; 55 while(i<=k 2) 56 { sum+=nc(2,i); 59 i+=2; 60 } 61 return sum; 62 } double Simpson38(int k, int o) 65 { 66 int i=o; double sum=0; 67 while(i<=k 3) 68 { 69 sum+=nc(3,i); 70 i+=3; 71 } 72 return sum; 73 } double Romberg(int k,int o) 76 { 77 double I1,I2; 78 set(1,2,k); 79 I1=Simpson(k,o); 80 set(1,2,2*k); 81 I2=Simpson(2*k,o); 82 //cout <<"I1="<<I1<<" I2="<<I2<<endl; 83 return I2 + (I2 I1)/3; 14
15 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 84 } 85 double factorial(double xx) 86 { 87 int i=1; double answ=1; 88 while(i<=xx) 89 { 90 answ*=i; 91 i++; 92 } 93 return answ; 94 } 95 double delta(int k,int i) 96 { 97 double answ=0; 98 if(k==1) 99 { 100 answ=myfunc(x[i+1]) myfunc(x[i]); 101 } 102 else 103 { 104 answ=delta(k 1,i+1) delta(k 1,i); 105 } return answ; 108 } 109 polynomial Psympt(int n, int o) 110 { 111 polynomial s,ks,answ;int i=1; 112 s.n=1;s.a[1]=1/h;s.a[0]= x[o]/h; answ.n=0;answ.a[0]=myfunc(x[o]); ks. n=0;ks.a[0]=1; 113 while(i<=n) 114 { 115 ks=ks*(s i+1)/i; 116 answ=answ+delta(i,o)*ks; 117 i++; 118 } 119 return answ; 120 } polynomial Intergrate(polynomial p1) 123 { 124 polynomial answ; 125 answ.n=p1.n+1; 126 int i=n; 127 while(i>=0) 128 { 129 answ.a[i+1]=p1.a[i]/(i+1); 130 i ; 131 } 15
16 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 132 return answ; 133 } int main() 136 { 137 int simeia=2; double err; 138 int g; 139 double realvalue=(2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3; cout.precision(15) ; 142 cout <<"\n Newton Cotes 1 "<<endl; 143 set(1,2,simeia); 144 cout << " "<<NC(1,0)<<endl; 145 err=fabs(100*((realvalue) (NC(1,0)))/(realvalue)); 146 cout.precision(2) ; 147 cout <<" Error = "<<err <<"%"<<endl; cout.precision(15) ; 150 cout <<"\n Newton Cotes 2 "<<endl; 151 simeia=3; 152 set(1,2,simeia); 153 cout << " "<<NC(2,0)<<endl; 154 err=fabs(100*((realvalue) (NC(2,0)))/(realvalue)); 155 cout.precision(2) ; 156 cout <<" Error = "<<err <<"%"<<endl; cout.precision(15) ; 159 cout <<"\n Newton Cotes 3 "<<endl; 160 simeia=4; 161 set(1,2,simeia); 162 cout << " "<<NC(3,0)<<endl; 163 err=fabs(100*((realvalue) (NC(3,0)))/(realvalue)); 164 cout.precision(2) ; 165 cout <<" Error = "<<err <<"%"<<endl; cout.precision(15) ; cout <<"\n Romberg \n"<< " "<< Romberg(4,0)<<"\n"<<endl; 170 err=fabs(100*((realvalue) (Romberg(4,0)))/(realvalue)); 171 cout.precision(2) ; 172 cout <<" Error : "<<err <<"%"<<endl; ////Psympt cout.precision(2) ; 176 cout <<"\n\n Symptotical Polynomial 5 points "<<endl; 177 polynomial myp,myintergratedp; 178 simeia=5; 179 set(1,2,simeia); 180 myp=psympt(simeia,0); 16
17 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 181 cout <<" P5(x) = "; 182 myp.show(); 183 myintergratedp=intergrate(myp); 184 cout <<"After Intergration = "; 185 myintergratedp.show(); 186 double myvalue=myintergratedp.valueon(2) myintergratedp.valueon(1); 187 cout.precision(15) ; 188 cout <<"Value of Intergrated Polynomial = "<< myvalue<<endl; 189 err=fabs(100*((realvalue) (myvalue))/(myvalue)); 190 cout.precision(2) ; 191 cout <<" Error = "<<err <<"%"<<endl; 192 cout << "\n"<<endl; 193 ////Psympt cout.precision(2) ; 195 cout <<"\n Symptotical Polynomial 6 points "<<endl; 196 //polynomial myp,myintergratedp; 197 simeia=6; 198 set(1,2,simeia); 199 myp=psympt(simeia,0); 200 cout <<" P6(x) = "; 201 myp.show(); 202 myintergratedp=intergrate(myp); 203 cout <<"After Intergration = "; 204 myintergratedp.show(); 205 myvalue=myintergratedp.valueon(2) myintergratedp.valueon(1); 206 cout.precision(15) ; 207 cout <<"Value of Intergrated Polynomial = "<< myvalue<<endl; 208 err=fabs(100*((realvalue) (myvalue))/(myvalue)); 209 cout.precision(2) ; 210 cout <<" Error = "<<err <<"%"<<endl; 211 cout.precision(15) ; //Simpson 214 cout <<"\n\n Simpson \n"<<endl; g=3; 217 simeia=1; 218 while(g<=24){ 219 simeia=g*simeia; 220 set(1,2,simeia); 221 cout.precision(19) ; 222 cout <<"Running for "<<g<<"points"<<endl; 223 cout << " Simpson = "<<Simpson(simeia,0)<<endl; 224 cout << " Real value = "<<(2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3<<endl; 225 err=100*(((2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3) (Simpson(simeia,0))) /((2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3); 226 cout.precision(3) ; 227 cout<<" Error = "<< fabs(err)<<"%"<<endl; 228 g*=2; 17
18 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 229 } cout <<"\n Simpson38 \n"<<endl; 232 g=4; 233 simeia=1; while(g<=100){ 236 simeia=g*simeia; 237 set(1,2,simeia); 238 cout.precision(15) ; 239 cout <<"Running for "<<g<<"points"<<endl; 240 cout << " Simpson38 = "<<Simpson38(simeia,0)<<endl; 241 cout << " Real value = "<<(2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3<<endl; 242 err=100*(((2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3) (Simpson38(simeia,0))) /((2*pow(2 0.1,1.5) 2*pow(1 0.1,1.5))/3); 243 cout.precision(3) ; 244 cout<<" Error = "<< fabs(err)<<"%"<<endl; 245 g*=3; 246 } 247 return 0; 248 } Κάποια πράγματα που αξίζει ακόμη να σχολιαστούν για τον κώδικα, ειναι ο τρόπος σύνταξης των συναρτήσεων. Έγινε προσπάθεια οι ρουτίνες που γράφτηκαν, να προσομοιάζουν το τρόπο σύνταξης των συμβολικών γλωσσών προγραμματισμού. Αυτή η γενικότητα έγινε σκόπιμα, ώστε τόσο τα κομμάτια του κώδικα να είναι δυνατό να μεταφερθούν από την μια άσκηση στην άλλη, όσο και να γίνει ευκολότερη η απασφαλμάτωση κατά τη συγγραφή. Αν και σε γενικές γραμμές τα ονόματα και ο κώδικας δείχνουν τι κάνει η κάθε συνάρτηση, υπάρχουν κάποια σημεία που κρίθηκε αναγκαίο να εξηγηθούν καλύτερα: NC(τύπος, σημείο εκκίνησης): η συνάρτηση NC ανάλογα με το εάν το πρώτο όρισμα είναι 1, 2 ή 3, επιστρέφει το αποτέλεσμα του αντίστοιχου τύπου των Newton-Cotes, ξεκινώντας από το σημείο που καθορίζεται από δεύτερο όρισμα. Αυτό έγινε για να γραφούν οι συναρτήσεις trapezoid, Simpson, Simpson38 με ομοιόμορφο τρόπο set(αρχή διαμέρισης, τέλος διαμέρισης, πλήθος): η συνάρτηση αυτή δημιουργεί το πίνακα των σημείων της διαμέρισης delta(): συνάρτηση που υπολογίζει τις εμπρόσθιες διαφορές μέσω αναδρομής factorial: υπολογίζει το παραγοντικό ενός αριθμού Στον παραπάνω κώδικα βρίσκονται όλες οι συναρτήσεις αριθμητικής ολοκλήρωσης, καθώς και οι συναρτήσεις που πρέπει να ολοκληρώσουμε. Αλλάζοντας μόνο την προς ολοκλήρωση συνάρτηση μπορούμε να υπολογίσουμε και το δεύτερο ολοκλήρωμα με τις ίδιες μεθόδους. Όπως εύκολα μπορούμε να συμπεράνουμε από τα αποτελέσματα, όσο πιο μεγάλος είναι ο βαθμός του 18
19 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις συμπτωτικού πολυωνύμου, τόσο καλύτερη είναι η προσέγγιση στη πραγματική τιμή. Υπολογιστικά όμως, δεν συμφέρει από την άποψη των πολλών πράξεων που απαιτούνται για την κατασκευή τους. Αξίζει ακόμη να σημειωθεί, ότι σε ίδια τάξη σφάλματος μπορούμε να καταλήξουμε ευκολότερα με τη χρήση της μεθόδου Simpson, και σε ακόμη καλύτερη, και γρηγορότερα, με τη μέθοδο του Simpson 3/8. Αποτελέσματα της εκτέλεσης του κώδικα των μεθόδων όπως αυτά υπολογίστηκαν αυτόματα από τον κώδικα. Οι παρακάτω εικόνες παρουσιάζουν τα σφάλματα 19
20 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 2.2 Filon Method Το ολοκλήρωμα που δόθηκε στο δεύτερο ερώτημα της δεύτερης άσκησης ήταν της μορφής y(x) sin(kx) dx. Από τη θεωρία προβλέπετε να συγκλίνει ταχύτερα με τη μέθοδο του Filon. Στο παρακάτω πηγαίο κώδικα αναπτύσσεται η μέθοδος του Filon, ενώ γίνεται σύγκριση της μεθόδου με άλλες μεθόδους αριθμητικής ολοκλήρωσης, και συγκεκριμένα με την μέθοδο των τραπεζίων, καθώς επίσης και με τη μέθοδο του Simpson. Ο κώδικας δεν έχει ιδιαίτερες διαφορές με τον προηγούμενο στη γενική φιλοσοφία. Όσον αφορά το κομμάτι της μεθόδου Filon, οι διάφοροι συντελεστές (A, B, Ce, Co) είναι και αυτοί συναρτήσεις. 1 #include <iostream> 2 #include <iomanip> 3 #include <cmath> 4 using namespace std; 5 double pi= ;double eps=pow(10, 6); 6 int n=4;double k=5; 7 double *x= new double [n+5]; 8 //double realvalue=(pi/2+1)*log(pi/2+1); 9 double realvalue= exp( 2*pi)*(sin(5*pi*2)+5*cos(5*pi*2))/26 +exp( 0)*(sin (5*0)+5*cos(5*0))/26; 10 double q,a=0,b=2*pi; 11 double h=((b a)/n); 12 double y(double xx) 13 { 14 return exp( xx); 15 } double A() 18 { 19 return 1/q + sin(2*q)/(2*q*q) 2*pow(sin(q),2)/pow(q,3); 20 } 21 double B() 22 { 23 return 1/(q*q) + pow(cos(q),2)/(pow(q,2)) (sin(2*q))/pow(q,3); 24 } 25 double D() 26 { 27 return 4*sin(q)/(q*q*q) 4*cos(q)/(q*q); 28 } 29 double Se() 30 { 31 double sum=0;int i=0; 32 while(i<=n) 33 { 34 sum+=y(a+2*i*h)*sin(k*a+2*i*q); 35 i++; 36 } 20
21 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 37 return 2*sum y(a)*sin(k*a) y(b)*sin(k*b); 38 } 39 double So() 40 { 41 double sum=0;int i=1; 42 while(i<=n) 43 { 44 sum+=y(a+(2*i 1)*h)*sin(k*a+(2*i 1)*q); 45 i++; 46 } 47 return sum ; 48 } double Filon() 51 { 52 q=h*k; 53 return h*(a()*y(a)*cos(k*a) A()*y(b)*cos(k*b)+B()*Se()+D()*So()); 54 } int main() 57 { 58 int g=0; 59 cout.precision(4); 60 while(g<=15) 61 { 62 cout <<"h="<<h<<endl; 63 cout.precision(18); 64 cout << "Real Value = "<<realvalue <<"\nfilon = "<< Filon()<<endl; 65 cout.precision(4); 66 cout <<"Error = "<< fabs(100*(realvalue Filon())/realvalue)<<"%\n"<< endl; 67 n=2*n; 68 h=((b a)/n); 69 g++; 70 } 71 return 0; 72 } Τα αποτελέσματα του παραπάνω προγράμματος έδειξαν ότι ακόμα και για πυκνότερη διαμέριση, το σφάλμα της Filon δεν πέφτει κάτω από ένα σημείο, σε αντίθεση με τη μέθοδο των τραπεζίων ή του Simpson. Πρέπει να σημειωθεί ότι αυτή την ιδιομορφία την παρουσιάζει αυτή η συνάρτηση, και (παρ ότι δεν μπορώ να το αποδείξω) σχετίζεται με τον εκθετικό παράγοντα. Το ίδιο δεν παρατηρήθηκε με άλλες συναρτήσεις που δίνονταν ως παραδείγματα σε διάφορα βιβλία αριθμητικής ανάλυσης, για να δοκιμαστεί ο κώδικας, και άρα είναι ασφαλές να πούμε ότι δεν υπάρχει κάποιο λογικό σφάλμα. 21
22 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις Αποτελέσματα της εκτέλεσης του κώδικα των μεθόδων όπως αυτά υπολογίστηκαν αυτόματα από τον κώδικα. Οι παρακάτω εικόνες παρουσιάζουν τα σφάλματα 22
23 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 23
24 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 2.3 Μέθοδος Gauss Η μέθοδος Gauss αποτελεί προσέγγιση της πραγματικής τιμής ενός ολοκληρώματος της μορφής 1 1 f(x)dx. Το ολοκλήρωμα που ζητούσε η υπόθεση ήταν το π 2 0 log(x + 1)dx. Προφανώς με ένα μετασχηματισμό μπορεί να αλλάξει μορφή, και να γίνει της μορφής Gauss. Επιλέγουμε την αλλαγή μεταβλητής t = 1 2 (b + a)x + 1 (b a), και το ολοκλήρωμα μετασχηματίζεται σε 2 1 π 1 4 log( π (t + 1) + 1)dt. Το πρόγραμμα τρέχει με Gauss δύο σημείων, 4 και 8 σημείων, καθώς επίσης και άλλες μεθόδους ολοκλήρωσης για να γίνει σύγκριση αυτών. Είναι προφανές 4 ότι το σφάλμα της μεθόδου Gauss για 2 μόλις σημεία είναι αισθητά μικρότερο σε σχέση με άλλες αριθμητικές μεθόδους ολοκλήρωσης στα 2 σημεία. Το ίδιο ισχύει και για τα 4 σημεία. 1 #include <iostream> 2 #include <iostream> 3 #include <iomanip> 4 #include <cmath> 5 //Gauss 6 using namespace std; 7 double pi= ;double eps=pow(10, 6); 8 int n=4;double a=0,b=pi/2,h=(b a)/n; 9 10 double x[1000]; 11 double realvalue=(pi/2)*(log(pi/2+1) 1)+log(pi/2+1); double myfunc(double xx) 14 { 15 // Formula of function 16 return log(xx+1); } 24
25 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 19 double myfunc2(double tt) 20 { 21 // Formula of function 22 return log((pi/4)*(tt+1)+1)*pi/4; 23 } 24 void set(double a,double b,double M) 25 { 26 // a:start X, b:end X, M:How many steps 27 int i=0; h=(b a)/(m); n=m; while (i<=n) 31 { 32 x[i]=a+h*i; 33 i++; 34 } 35 } double NC(short int order,int o) 38 { 39 double answ=0; 40 if(order==1){ 41 answ=(h/2)*(myfunc(x[o]) +myfunc(x[o+1])); 42 } 43 else if (order==2){ 44 answ=(h/3)*(myfunc(x[o]) +4*myfunc(x[o+1])+myfunc(x[o+2])); 45 } 46 else if (order ==3){ 47 answ=(3*h/8)*(myfunc(x[o]) +3*myfunc(x[o+1]) + 3*myfunc(x[o+2])+myfunc(x [o+3])); 48 } 49 return answ; 50 } double trapezoid(int k, int o) 53 { 54 int i=o; double sum=0; 55 while(i<=k 1) 56 { 57 sum+=nc(1,i); 58 i++; 59 } 60 return sum; 61 } double Simpson(int k, int o) 64 { 65 int i=o; double sum=0; 66 while(i<=k 2) 25
26 ΠΜΣ Υπολογιστικη ς Φυσικη ς 2 Αριθμητικε ς Ολοκληρω σεις 67 { sum+=nc(2,i); 70 i+=2; 71 } 72 return sum; 73 } 74 double Gauss() 75 { 76 return myfunc2(0.5773)+myfunc2( ); 77 } 78 double Gauss4() 79 { 80 return *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ); 81 } 82 double Gauss8() 83 { 84 return *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ) *myfunc2( ); 85 } 86 int main() 87 { 88 int simeia; 89 cout << "Gauss (2 points)= "<<Gauss()<<endl; 90 cout << "Real Value= "<<realvalue<<endl; 91 cout << "Error on Gauss= "<<fabs(100*(realvalue Gauss())/realvalue)<<"%" <<endl; cout << "\ngauss (4 points)= "<<Gauss4()<<endl; 94 cout << "Real Value= "<<realvalue<<endl; 95 cout << "Error on Gauss= "<<fabs(100*(realvalue Gauss4())/realvalue)<<"% "<<endl; cout << "\ngauss (8 points)= "<<Gauss8()<<endl; 98 cout << "Real Value= "<<realvalue<<endl; 99 cout << "Error on Gauss= "<<fabs(100*(realvalue Gauss8())/realvalue)<<"% "<<endl; simeia=2; 102 set(a,b,simeia); 103 cout <<"\n\trapezoid (2 points)= " <<trapezoid(simeia,0)<<endl; 104 cout << "Error on Trapezoid= "<<fabs(100*(realvalue trapezoid(simeia,0)) /realvalue)<<"%"<<endl; simeia=3; 107 set(a,b,simeia); 26
27 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις 108 cout <<"\n\nsimpson (3 points)= " <<Simpson(simeia,0)<<endl; 109 cout << "Error on Simpson= "<<fabs(100*(realvalue Simpson(simeia,0))/ realvalue)<<"%"<<endl; simeia=6; 113 set(a,b,simeia); 114 cout <<"\n\nsimpson (6 points)= " <<Simpson(simeia,0)<<endl; 115 cout << "Error on Simpson= "<<fabs(100*(realvalue Simpson(simeia,0))/ realvalue)<<"%"<<endl; return 0; 119 } Παραθέτω τα αποτελέσματα του εκτελέσιμου που παρουσιάζουν και τα σχετικά σφάλματα: 3 Διαφορικές Εξισώσεις Οι διαφορικές εξισώσεις αποτελούν ένα από τα πιο ουσιώδη κομμάτια της αριθμητικής ανάλυσης. Η σημασία είναι προφανής, αφού οι περισσότεροι νόμοι στη φυσική περιγράφονται με μια διαφορική εξίσωση, η οποία σπανίως είναι αναλυτικά επιλύσιμη. Συνεπώς για να μπορέσουμε να πάρουμε αριθμητικά δεδομένα, αναγκαζόμαστε να καταφύγουμε σε μεθόδους αριθμητικής ολοκλήρωσης. Στην εργασία αυτή, ζητούμενο ήταν η ολοκλήρωση των εξισώσεων κίνησης του Χαμιλτονιανού συστήματος H = p2 2 cosθ. Οι μέθοδοι που εφαρμόστηκαν και συγκρίθηκαν ήταν οι: i. Runge-Kutta 4ης τάξης ii. Milne 27
28 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις 3.1 Runge-Kutta Η πιο ευρέως διαδεδομένη μέθοδος ολοκλήρωσης είναι η Runge-Kutta. Αυτό έχει να κάνει τόσο με την προγραμματιστική απλότητα που παρουσιάζει, όσο και με την μεγάλη ακρίβεια που μπορεί να δώσει στις αριθμητικές ολοκληρώσεις των διαφορικών εξισώσεων. Από την H = p2 cosθ μπορούμε να πάρουμε τις εξισώσεις κίνησης με τη χρήση των 2 σχέσεων: dp dt = H dθ = sinθ, θ dt = H p = p Θεωρούμε αυτές λοιπόν ως σύστημα διαφορικών εξισώσεων, με αρχικές συνθήκες θ(0) = 0 και p(0) = ± 2E 0 + sinθ 0 για τιμές E 0 = 0 και E 0 = 1.5. Στο ακόλουθo πρόγραμμα αναπτύχθηκε η μέθοδος για προσέγγιση 4ης τάξης (Runge-Kutta 4th Order). 1 #include<iostream> 2 #include<cmath> 3 #include<cstdlib> 4 #include <fstream> 5 #define steps using namespace std; 8 9 double F( double theta, double p){ 10 double z; 11 z=p; 12 return z;} double G( double theta, double p){ 15 double z; 16 z= sin(theta); 17 return z;} int main() 20 { 21 ofstream fout; 22 fout.open ("RKdata.txt"); 23 double theta,theta0,p,p0,h,h,e; 24 double k1,k2,k3,k4; 25 double l1,l2,l3,l4; 26 int i; 27 cout.precision(11); 28 fout.precision(11); 29 h=0.0001; 30 theta0=0; 31 E=1.5; 32 p0=fabs(sqrt(2.*(e+cos(theta0)))); 33 //cout << p0 <<endl; 34 theta=theta0; 35 p=p0; 36 i=0; 28
29 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις 37 fout<<"t"<<" "<<"theta"<<" "<<"p"<<" "<<"H"<<endl<<endl; while(i<steps) 40 { 41 //k1,l1 42 k1=h*f(theta,p); 43 l1=h*g(theta,p); //k2,l2 46 k2=h*f(theta+0.5*k1,p+0.5*l1); 47 l2=h*g(theta+0.5*k1,p+0.5*l1); 48 //k3,l3 49 k3=h*f(theta+0.5*k2,p+0.5*l2); 50 l3=h*g(theta+0.5*k2,p+0.5*l2); //k4,l4 53 k4=h*f(theta+k3,p+l3); 54 l4=h*g(theta+k3,p+l3); //new values of theta,p 57 theta=theta+(k1+2.*k2+2.*k3+k4)/6.; 58 p=p+(l1+2.*l2+2.*l3+l4)/6.; 59 H=(p*p*0.5) cos(theta); 60 cout <<"\n\n Status:\n \n"<<endl; 61 cout <<" Iteration : "<<i<<"\n * theta= "<<theta<<"\n * p= "<<p<<endl; 62 cout <<"\n * Energy H= "<<H<<endl; 63 fout<<i<<" "<<theta<<" "<<p<<" "<<H<<endl; 64 i++; 65 } 66 cout<<"\n\n\n=========================\n Energy at the end \n * H="<<H<< endl; 67 fout.close(); return 0; 70 } Τα αποτελέσματα του εκτελέσιμου αποθηκεύτηκαν σε ένα αρχείο txt και σχεδιάστηκαν με το gnuplot. Όπως εύκολα παρατηρούμε, για ενέργεια Ε 0 = 0, το σύστημα εκτελεί περιοδική κίνηση, καθώς ο γεωμετρικός τόπος των σημείων του, είναι κλειστή κωνική τομή. Αντίθετα, για Ε 0 = 1.5, το φασικό διάγραμμα δείχνει μια ημιτονοειδή μορφή. Σε κάθε περίπτωση, η ενέργεια δείχνει να παραμένει σχετικά σταθερή ακόμη και μετά από 10 6 χρονικές μονάδες. 29
30 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.1: Φασικό διάγραμμα για Ε=1.5 Διάγραμμα 3.2: Ενέργεια σε σχέση με το χρόνο Διάγραμμα 3.3: Φασικό διάγραμμα για Ε=0 30
31 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.4: Εξέλιξη της ενέργειας με το χρόνο 3.2 Milne Μία ακόμα πολύ διαδεδομένη μέθοδος αριθμητικής ολοκλήρωσης διαφορικών είναι η μέθοδος Milne. Δεδομένου ότι η μέθοδος αυτή απαιτεί τη γνώση κάποιων αρχικών συνθηκών παραπάνω, χρησιμοποιείται στην αρχή ένα RK4 ως εκκινητής για να παράξει αυτές τις συνθήκες. Για το ακριβώς ίδιο σύστημα διαφορικών εξισώσεων, γράφτηκε ο ακόλουθος κώδικας: 1 #include<iostream> 2 #include<cmath> 3 #include<cstdlib> 4 #include <fstream> 5 #define steps using namespace std; 8 double parray[4],thetaarray[4],harray[4]; 9 double thetan,thetanp1,thetanp2,thetanp3,pn,pnp1,pnp2,pnp3 ; 10 double k1,k2,k3,k4, l1,l2,l3,l4; double F( double theta, double p){ 13 double z; 14 z=p; 15 return z;} double G( double theta, double p){ 18 double z; 19 z= sin(theta); 20 return z;} int main() 23 { 24 double theta,theta0,p,p0,h,h,e; 25 ofstream fout; 26 fout.open ("Milnedata.txt"); 31
32 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις 27 fout<<"t"<<" "<<"theta"<<" "<<"p"<<" "<<"H"<<endl<<endl; //double k1,k2,k3,k4; 30 //double l1,l2,l3,l4; 31 int i; 32 cout.precision(11); 33 h=0.0001; 34 theta0=0; 35 E=0.; 36 p0=fabs(sqrt(2.*(e+cos(theta0)))); 37 theta=theta0; 38 p=p0; 39 i=0; 40 //Runge Kutta Starter 41 while(i<5) 42 { 43 //k1,l1 44 k1=h*f(theta,p); 45 l1=h*g(theta,p); //k2,l2 48 k2=h*f(theta+0.5*k1,p+0.5*l1); 49 l2=h*g(theta+0.5*k1,p+0.5*l1); 50 //k3,l3 51 k3=h*f(theta+0.5*k2,p+0.5*l2); 52 l3=h*g(theta+0.5*k2,p+0.5*l2); //k4,l4 55 k4=h*f(theta+k3,p+l3); 56 l4=h*g(theta+k3,p+l3); //new values of theta,p 59 theta=theta+(k1+2.*k2+2.*k3+k4)/6.; 60 p=p+(l1+2.*l2+2.*l3+l4)/6.; 61 H=(p*p*0.5) cos(theta); parray[i]=p; 64 thetaarray[i]=theta; 65 Harray[i]=H; 66 fout<<i<<" "<<theta<<" "<<p<<" "<<H<<endl; //cout <<"\n\n Status:\n \n"<<endl; 69 //cout <<" Iteration : "<<i<<"\n * theta= "<<theta<<"\n * p= "<<p<<endl; 70 //cout <<"\n * Energy H= "<<H<<endl; 71 i++; 72 } 73 //InitCond 74 thetan=thetaarray[3]; 75 thetanp1=thetaarray[2]; 32
33 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις 76 thetanp2=thetaarray[1]; 77 thetanp3=thetaarray[0]; 78 pn=parray[3]; 79 pnp1=parray[2]; 80 pnp2=parray[1]; 81 pnp3=parray[0]; while(i<steps) 84 { 85 thetanp3=thetanp2; 86 thetanp2=thetanp1; 87 thetanp1=thetan; 88 thetan=thetanp3 (4*h/3)*(2*F(thetan,pn) F(thetanp1,pnp1)+2*F(thetanp2, pnp2)); pnp3=pnp2; 91 pnp2=pnp1; 92 pnp1=pn; 93 pn=pnp3 (4*h/3)*(2*G(thetan,pn) G(thetanp1,pnp1)+2*G(thetanp2,pnp2)); 94 H=(pn*pn*0.5) cos(thetan); fout<<i<<" "<<thetan<<" "<<pn<<" "<<H<<endl; i++; 99 } cout<<"\n\n\n=========================\n Energy at the end \n * H="<<H<< endl; 102 fout.close(); return 0; 105 } Γραφικές Παραστάσεις h= Οι γραφικές παραστάσεις του χώρου των φάσεων καθώς επίσης και της εξέλιξης της ενέργειας για h = 10 4 για 10 6 βήματα με τη μέθοδο RK4. 33
34 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.5: Φασικό διάγραμμα για E 0 = 0 με RK4 Διάγραμμα 3.6: Φασικό διάγραμμα για E 0 = 1.5 με RK4 Διάγραμμα 3.7: Εξέλιξη της ενέργειας E 0 = 0 με RK4 34
35 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Οι ίδιες γραφικές παραστάσεις για h = 10 4 σε ίδιο αριθμό βημάτων με την Milne Διάγραμμα 3.8: Φασικό διάγραμμα για E 0 = 0 με Milne Διάγραμμα 3.9: Φασικό διάγραμμα για E 0 = 1.5 με Milne 35
36 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.10: Εξέλιξη της ενέργειας E 0 = 1.5 με Milne Διάγραμμα 3.11: Εξέλιξη της ενέργειας E 0 = 0 με Milne Η σύγκριση των διαγραμμάτων των δύο μεθόδων για μικρότερο βήμα h =
37 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.12: Εξέλιξη της ενέργειας RK4 Διάγραμμα 3.13: Εξέλιξη της ενέργειας Milne 3.3 Σύγκριση των δύο μεθόδων Στα επόμενα δύο διαγράμματα παρουσιάζεται το elapsed time of execution σαν συνάρτηση των steps ολοκλήρωσης. Το βήμα διατηρήθηκε στα h = Όπως εύκολα μπορεί να συμπεράνει κανείς, η μέθοδος Milne είναι περίπου 3 φορές πιο αργή για τις ίδιες συνθήκες εργασίας. Επιπλέον μειονέκτημα είναι ότι χρησιμοποιεί ένα RK starter, όμως η ακρίβεια της μεθόδου είναι εξαιρετική. 37
38 ΠΜΣ Υπολογιστικη ς Φυσικη ς 3 Διαφορικε ς Εξισω σεις Διάγραμμα 3.14: Runge-Kutta execution time Διάγραμμα 3.15: Milne execution time 38
Υπολογιστικά Mαθηματικά II
 Υπολογιστικά Mαθηματικά II Ζαφειράκογλου Απόστολος 1 Άσκηση Να υπολογιστεί με τη μέθοδο Monte Carlo το ολοκλήρωμα : I = ˆ1 dx 1 ˆ1 ˆ1 dx 2... (x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 + x 8 + x 9 + x 1
Υπολογιστικά Mαθηματικά II Ζαφειράκογλου Απόστολος 1 Άσκηση Να υπολογιστεί με τη μέθοδο Monte Carlo το ολοκλήρωμα : I = ˆ1 dx 1 ˆ1 ˆ1 dx 2... (x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 + x 8 + x 9 + x 1
Προγραμματισμός Ι. Κλάσεις και Αντικείμενα. Δημήτρης Μιχαήλ. Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο
 Προγραμματισμός Ι Κλάσεις και Αντικείμενα Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Κλάσεις Η γενική μορφή μιας κλάσης είναι η εξής: class class-name { private data and
Προγραμματισμός Ι Κλάσεις και Αντικείμενα Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Κλάσεις Η γενική μορφή μιας κλάσης είναι η εξής: class class-name { private data and
Υπολογιστικά Mαθηματικά II
 Υπολογιστικά Mαθηματικά II Ζαφειράκογλου Απόστολος 1 Μελέτη διασπάσεων με τη μέθοδο Monte Carlo Να προσδιοριστεί ο αριθ-µός των πυρήνων του στοιχείου 134 I 53 ως συνάρτηση του χρόνου, αν είναι γνωστό ότι
Υπολογιστικά Mαθηματικά II Ζαφειράκογλου Απόστολος 1 Μελέτη διασπάσεων με τη μέθοδο Monte Carlo Να προσδιοριστεί ο αριθ-µός των πυρήνων του στοιχείου 134 I 53 ως συνάρτηση του χρόνου, αν είναι γνωστό ότι
Γ7.1 Επανάληψη ύλης Β Λυκείου. Γ Λυκείου Κατεύθυνσης
 Γ7.1 Επανάληψη ύλης Β Λυκείου Γ Λυκείου Κατεύθυνσης Απλά προγράμματα Ένα πρόγραμμα στη C++ που υπολογίζει το άθροισμα 2 ακέραιων αριθμών. // simple program #include using namespace std; int main(){
Γ7.1 Επανάληψη ύλης Β Λυκείου Γ Λυκείου Κατεύθυνσης Απλά προγράμματα Ένα πρόγραμμα στη C++ που υπολογίζει το άθροισμα 2 ακέραιων αριθμών. // simple program #include using namespace std; int main(){
Η εντολή if-else. Η απλή μορφή της εντολής if είναι η ακόλουθη: if (συνθήκη) { Η γενική μορφή της εντολής ifelse. εντολή_1; εντολή_2;..
 Επιλογή - Επανάληψη Η εντολή if-else Ο τελεστής παράστασης συνθήκης H εντολή switch Η εντολές for και while Η εντολή do-while Η εντολές break - continue - goto Μαθηματικές συναρτήσεις Λέξεις κλειδιά στη
Επιλογή - Επανάληψη Η εντολή if-else Ο τελεστής παράστασης συνθήκης H εντολή switch Η εντολές for και while Η εντολή do-while Η εντολές break - continue - goto Μαθηματικές συναρτήσεις Λέξεις κλειδιά στη
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 68 Αριθμητικές Μέθοδοι
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 68 Αριθμητικές Μέθοδοι
Πρόλογος Εισαγωγή στη δεύτερη έκδοση Εισαγωγή... 11
 Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
Περιεχόμενα Πρόλογος... 9 Εισαγωγή στη δεύτερη έκδοση... 0 Εισαγωγή... Ε. Εισαγωγή στην έννοια της Αριθμητικής Ανάλυσης... Ε. Ταξινόμηση των θεμάτων που απασχολούν την αριθμητική ανάλυση.. Ε.3 Μορφές σφαλμάτων...
15 εκεµβρίου εκεµβρίου / 64
 15 εκεµβρίου 016 15 εκεµβρίου 016 1 / 64 Αριθµητική Ολοκλήρωση Κλειστοί τύποι αριθµητικής ολοκλήρωσης Εστω I(f) = b µε f(x) C[a, b], τότε I(f) = F(b) F(a), όπου F(x) είναι το αόριστο ολοκλήρωµα της f(x).
15 εκεµβρίου 016 15 εκεµβρίου 016 1 / 64 Αριθµητική Ολοκλήρωση Κλειστοί τύποι αριθµητικής ολοκλήρωσης Εστω I(f) = b µε f(x) C[a, b], τότε I(f) = F(b) F(a), όπου F(x) είναι το αόριστο ολοκλήρωµα της f(x).
Υπολογιστικά Μαθηματικά
 Υπολογιστικά Μαθηματικά CompMath Set1, Ζαφειράκογλου Απόστολος Εισαγωγή Η φιλοσοφία που χρησιμοποιήθηκε στην παρούσα εργασία ακολουθεί τα πρότυπα του συναρτησιακού προγραμματισμού. Οι κώδικες είναι γραμμένοι
Υπολογιστικά Μαθηματικά CompMath Set1, Ζαφειράκογλου Απόστολος Εισαγωγή Η φιλοσοφία που χρησιμοποιήθηκε στην παρούσα εργασία ακολουθεί τα πρότυπα του συναρτησιακού προγραμματισμού. Οι κώδικες είναι γραμμένοι
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τύποι δεδομένων ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ. Ακέραιοι αριθμοί (int) Πράξεις μεταξύ ακεραίων αριθμών
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ 1 Τύποι δεδομένων Η γλώσσα προγραμματισμού C++ υποστηρίζει τους παρακάτω τύπους δεδομένων: 1) Ακέραιοι αριθμοί (int). 2) Πραγματικοί αριθμοί διπλής ακρίβειας
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ 1 Τύποι δεδομένων Η γλώσσα προγραμματισμού C++ υποστηρίζει τους παρακάτω τύπους δεδομένων: 1) Ακέραιοι αριθμοί (int). 2) Πραγματικοί αριθμοί διπλής ακρίβειας
Αριθµητική Ολοκλήρωση
 Κεφάλαιο 5 Αριθµητική Ολοκλήρωση 5. Εισαγωγή Για τη συντριπτική πλειοψηφία των συναρτήσεων f (x) δεν υπάρχουν ή είναι πολύ δύσχρηστοι οι τύποι της αντιπαραγώγου της f (x), δηλαδή της F(x) η οποία ικανοποιεί
Κεφάλαιο 5 Αριθµητική Ολοκλήρωση 5. Εισαγωγή Για τη συντριπτική πλειοψηφία των συναρτήσεων f (x) δεν υπάρχουν ή είναι πολύ δύσχρηστοι οι τύποι της αντιπαραγώγου της f (x), δηλαδή της F(x) η οποία ικανοποιεί
Εντολές εισόδου - εξόδου. Εισαγωγή στη C++
 Εντολές εισόδου - εξόδου Εισαγωγή στη C++ Το πρώτο πρόγραμμα //my first program #include using namespace std; int main(){ cout
Εντολές εισόδου - εξόδου Εισαγωγή στη C++ Το πρώτο πρόγραμμα //my first program #include using namespace std; int main(){ cout
Πληροφορική 2. Γλώσσες Προγραμματισμού
 Πληροφορική 2 Γλώσσες Προγραμματισμού 1 2 Γλώσσες προγραμματσιμού Επιτρέπουν την κωδικοποίηση των αλγορίθμων Η εκτέλεση ενός προγράμματος θα πρέπει να δίνει τα ίδια αποτελέσματα με την νοητική εκτέλεση
Πληροφορική 2 Γλώσσες Προγραμματισμού 1 2 Γλώσσες προγραμματσιμού Επιτρέπουν την κωδικοποίηση των αλγορίθμων Η εκτέλεση ενός προγράμματος θα πρέπει να δίνει τα ίδια αποτελέσματα με την νοητική εκτέλεση
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Τύποι δεδομένων, μεταβλητές, πράξεις. Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Τύποι δεδομένων, μεταβλητές, πράξεις Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Τύποι δεδομένων, μεταβλητές, πράξεις Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό
Αντικειμενοστραφείς Γλώσσες Προγραμματισμού C++ / ROOT
 = Αντικειμενοστραφείς Γλώσσες Προγραμματισμού Ιωάννης Παπαδόπουλος Τμήμα Φυσικής, Πανεπιστήμιο Ιωαννίνων Δεκέμβριος 2018 1/18 = 2/18 = 1 αντικειμένων Μέθοδοι αντιγράφου (copy constructor) Κατασκευή μέσω
= Αντικειμενοστραφείς Γλώσσες Προγραμματισμού Ιωάννης Παπαδόπουλος Τμήμα Φυσικής, Πανεπιστήμιο Ιωαννίνων Δεκέμβριος 2018 1/18 = 2/18 = 1 αντικειμένων Μέθοδοι αντιγράφου (copy constructor) Κατασκευή μέσω
Αριθµητική Ανάλυση. ιδάσκοντες: Τµήµα Α ( Αρτιοι) : Καθηγητής Ν. Μισυρλής, Τµήµα Β (Περιττοί) : Επίκ. Καθηγητής Φ.Τζαφέρης. 25 Μαΐου 2010 ΕΚΠΑ
 Αριθµητική Ανάλυση Κεφάλαιο 9. Αριθµητική Ολοκλήρωση ιδάσκοντες: Τµήµα Α ( Αρτιοι) : Καθηγητής Ν. Μισυρλής, Τµήµα Β (Περιττοί) : Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 5 Μαΐου 010 ιδάσκοντες:τµήµα Α ( Αρτιοι)
Αριθµητική Ανάλυση Κεφάλαιο 9. Αριθµητική Ολοκλήρωση ιδάσκοντες: Τµήµα Α ( Αρτιοι) : Καθηγητής Ν. Μισυρλής, Τµήµα Β (Περιττοί) : Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 5 Μαΐου 010 ιδάσκοντες:τµήµα Α ( Αρτιοι)
Είναι γνωστό ότι η δύναμη που ασκείται σε ένα ελατήριο και ονομάζεται δύναμη επαναφοράς δίνεται από τη σχέση : F = kx (3.1)
 3.1. Εισαγωγή Είναι γνωστό ότι η δύναμη που ασκείται σε ένα ελατήριο και ονομάζεται δύναμη επαναφοράς δίνεται από τη σχέση : F = kx (3.1) Αν ϑελήσουμε να υπολογίσουμε το έργο της δύναμης αυτής μεταξύ δύο
3.1. Εισαγωγή Είναι γνωστό ότι η δύναμη που ασκείται σε ένα ελατήριο και ονομάζεται δύναμη επαναφοράς δίνεται από τη σχέση : F = kx (3.1) Αν ϑελήσουμε να υπολογίσουμε το έργο της δύναμης αυτής μεταξύ δύο
Αναφορές, είκτες και Αλφαριθμητικά
 Αναφορές, είκτες και Αλφαριθμητικά Ο τελεστής αναφοροποίησης Αναφορές είκτες Πίνακες και δείκτες Ο τελεστής new και delete υναμικοί πίνακες είκτες προς συναρτήσεις Αλφαριθμητικά της C Πίνακες Αλφαριθμητικών
Αναφορές, είκτες και Αλφαριθμητικά Ο τελεστής αναφοροποίησης Αναφορές είκτες Πίνακες και δείκτες Ο τελεστής new και delete υναμικοί πίνακες είκτες προς συναρτήσεις Αλφαριθμητικά της C Πίνακες Αλφαριθμητικών
Στοιχειώδης προγραμματισμός σε C++
 Στοιχειώδης προγραμματισμός σε C++ Σύντομο Ιστορικό. Το πρόγραμμα Hello World. Ο τελεστής εξόδου. Μεταβλητές και δηλώσεις τους. Αντικείμενα, μεταβλητές, σταθερές. Ο τελεστής εισόδου. Θεμελιώδεις τύποι.
Στοιχειώδης προγραμματισμός σε C++ Σύντομο Ιστορικό. Το πρόγραμμα Hello World. Ο τελεστής εξόδου. Μεταβλητές και δηλώσεις τους. Αντικείμενα, μεταβλητές, σταθερές. Ο τελεστής εισόδου. Θεμελιώδεις τύποι.
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τι περιλαμβάνει μια μεταβλητή; ΔΕΙΚΤΕΣ. Διεύθυνση μεταβλητής. Δείκτης
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι περιλαμβάνει μια μεταβλητή; ΔΕΙΚΤΕΣ Πρώτα να δούμε τι ακριβώς συμπεριλαμβάνει μια μεταβλητή τύπος Καθορίζει το μέγεθος στην μνήμη σε Bytes τιμή Η αριθμητική τιμή που αποθηκεύεται στην
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι περιλαμβάνει μια μεταβλητή; ΔΕΙΚΤΕΣ Πρώτα να δούμε τι ακριβώς συμπεριλαμβάνει μια μεταβλητή τύπος Καθορίζει το μέγεθος στην μνήμη σε Bytes τιμή Η αριθμητική τιμή που αποθηκεύεται στην
Υπερφόρτωση τελεστών
 Υπερφόρτωση τελεστών 19 Νοεμβρίου 2012 1 Γενικά Στα προηγούμενα είδαμε ότι ορίζοντας μία κλάση, ορίζουμε ένα νέο τύπο τον οποίο μπορούμε να χρησιμοποιήσουμε για να δηλώσουμε αντικείμενα αυτής της νέας
Υπερφόρτωση τελεστών 19 Νοεμβρίου 2012 1 Γενικά Στα προηγούμενα είδαμε ότι ορίζοντας μία κλάση, ορίζουμε ένα νέο τύπο τον οποίο μπορούμε να χρησιμοποιήσουμε για να δηλώσουμε αντικείμενα αυτής της νέας
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Δομές Επανάληψης. Εισαγωγή στη C++
 Δομές Επανάληψης Εισαγωγή στη C++ Επαναληπτικές δηλώσεις Οι βρόγχοι (loops) αναγκάζουν ένα τμήμα κώδικα να επαναλαμβάνεται. Η επανάληψη συνεχίζεται για όσο μία λογική συνθήκη είναι αληθής. Όταν η συνθήκη
Δομές Επανάληψης Εισαγωγή στη C++ Επαναληπτικές δηλώσεις Οι βρόγχοι (loops) αναγκάζουν ένα τμήμα κώδικα να επαναλαμβάνεται. Η επανάληψη συνεχίζεται για όσο μία λογική συνθήκη είναι αληθής. Όταν η συνθήκη
5269: Υπολογιστικές Μέθοδοι για Μηχανικούς. Ολοκληρώματα.
 69: Υπολογιστικές Μέθοδοι για Μηχανικούς Ολοκληρώματα ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Αριθμητική Ολοκλήρωση συναρτήσεων Χρησιμοποιούμε αριθμητικές μεθόδους για τον
69: Υπολογιστικές Μέθοδοι για Μηχανικούς Ολοκληρώματα ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Αριθμητική Ολοκλήρωση συναρτήσεων Χρησιμοποιούμε αριθμητικές μεθόδους για τον
Ευστρατιάδης Ευστράτιος Γεώργιος ΑΕΜ: ο σετ ασκήσεων Υπολ.Μαθ.2
 Ευστρατιάδης Ευστράτιος Γεώργιος ΑΕΜ: 4261 2 ο σετ ασκήσεων Υπολ.Μαθ.2 Κατασκεύασα και χρονομέτρησα ρουτίνες που δίνουν τυχαίους αριθμούς, οι οποίες χρησιμοποιούν διαφόρων τύπων αριθμητικές (int, unsigned
Ευστρατιάδης Ευστράτιος Γεώργιος ΑΕΜ: 4261 2 ο σετ ασκήσεων Υπολ.Μαθ.2 Κατασκεύασα και χρονομέτρησα ρουτίνες που δίνουν τυχαίους αριθμούς, οι οποίες χρησιμοποιούν διαφόρων τύπων αριθμητικές (int, unsigned
Προγραμματισμός Υπολογιστών με C++
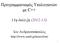 Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 11η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Υπερφόρτωση του τελεστή εκχώρησης. Στατικές μεταβλητές, στατικές σταθερές
Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 11η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Υπερφόρτωση του τελεστή εκχώρησης. Στατικές μεταβλητές, στατικές σταθερές
Συναρτήσεις (Functions) Εισαγωγή στη C++
 Συναρτήσεις (Functions) Εισαγωγή στη C++ 1 Δημιουργία συναρτήσεων Για κάθε συνάρτηση που θα δημιουργούμε θα πρέπει να ορίζουμε τα εξής: Τύπος επιστρεφόμενης τιμής Όνομα συνάρτησης Παράμετροι π.χ. int athrisma(int
Συναρτήσεις (Functions) Εισαγωγή στη C++ 1 Δημιουργία συναρτήσεων Για κάθε συνάρτηση που θα δημιουργούμε θα πρέπει να ορίζουμε τα εξής: Τύπος επιστρεφόμενης τιμής Όνομα συνάρτησης Παράμετροι π.χ. int athrisma(int
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Εντολές for, while, do-while Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Εντολές for, while, do-while Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Εντολές for, while, do-while Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
Aριθμητική Ανάλυση, 4 ο Εξάμηνο Θ. Σ. Παπαθεοδώρου
 Aριθμητική Ανάλυση, 4 ο Εξάμηνο Θ. Σ. Παπαθεοδώρου Άνοιξη 2002 ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑΤΑ 1. Τι σημαίνει f ; f 2 ; f 1 ; Να υπολογισθούν αυτές οι ποσότητες για f(x)=(x-α) 3 (β-x) 3, α
Aριθμητική Ανάλυση, 4 ο Εξάμηνο Θ. Σ. Παπαθεοδώρου Άνοιξη 2002 ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑΤΑ 1. Τι σημαίνει f ; f 2 ; f 1 ; Να υπολογισθούν αυτές οι ποσότητες για f(x)=(x-α) 3 (β-x) 3, α
Προγραμματισμός Υπολογιστών με C++
 Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 2η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Βασικοί αριθμητικοί τύποι, μετατροπές τύπων και σταθερές. Πίνακες. Πίνακες
Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 2η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Βασικοί αριθμητικοί τύποι, μετατροπές τύπων και σταθερές. Πίνακες. Πίνακες
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Κεφ. 6Β: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης). Μέθοδος Euler 3. Μέθοδοι
Εισαγωγή στον Προγραμματισμό με C++
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στον Προγραμματισμό με C++ Ενότητα # 6: Συναρτήσεις Κωνσταντίνος Κουκουλέτσος Τμήμα Αυτοματισμού Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στον Προγραμματισμό με C++ Ενότητα # 6: Συναρτήσεις Κωνσταντίνος Κουκουλέτσος Τμήμα Αυτοματισμού Άδειες Χρήσης Το παρόν
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Ονοματεπώνυμο και ΑΜ: Είχα παραδώσει εργασίες τα εξής ακαδημαϊκά έτη: Διάρκεια: 2,5 ώρες, κλειστά βιβλία και σημειώσεις ΚΑΛΗ ΕΠΙΤΥΧΙΑ!
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Προγραμματισμός Υπολογιστών με C++ Εξεταστική περίοδος: Σεπτεμβρίου 2011. Διδάσκων: Α. Δημάκης Γράψτε όλες τις απαντήσεις σας πάνω σε αυτό το
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Προγραμματισμός Υπολογιστών με C++ Εξεταστική περίοδος: Σεπτεμβρίου 2011. Διδάσκων: Α. Δημάκης Γράψτε όλες τις απαντήσεις σας πάνω σε αυτό το
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 63 Αριθμητικές Μέθοδοι
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2015 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2015 1 / 63 Αριθμητικές Μέθοδοι
Χωρική Βάση δεδοµένων Autocad
 Χωρική Βάση δεδοµένων Autocad Όλοι η πληροφορία σας βρίσκεται σε ένα αρχείο µε κατάληξη.dwg το οποίο αντιπροσωπεύει τη βάση δεδοµένων σας. Αυτό το αρχείο µπορούµε να το επεξεργαστούµε µε διάφορους τρόπους
Χωρική Βάση δεδοµένων Autocad Όλοι η πληροφορία σας βρίσκεται σε ένα αρχείο µε κατάληξη.dwg το οποίο αντιπροσωπεύει τη βάση δεδοµένων σας. Αυτό το αρχείο µπορούµε να το επεξεργαστούµε µε διάφορους τρόπους
5269: Υπολογιστικές Μέθοδοι για Μηχανικούς. Ολοκληρώματα.
 69: Υπολογιστικές Μέθοδοι για Μηχανικούς Ολοκληρώματα ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Αριθμητική Ολοκλήρωση συναρτήσεων Χρησιμοποιούμε αριθμητικές μεθόδους για τον
69: Υπολογιστικές Μέθοδοι για Μηχανικούς Ολοκληρώματα ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Αριθμητική Ολοκλήρωση συναρτήσεων Χρησιμοποιούμε αριθμητικές μεθόδους για τον
Παράδειγµα #11 ΠΡΟΒΛΗΜΑΤΑ ΑΡΧΙΚΩΝ ΤΙΜΩΝ Σ Ε ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης
 Παράδειγµα # ΠΡΟΒΛΗΜΑΤΑ ΑΡΧΙΚΩΝ ΤΙΜΩΝ Σ Ε ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης Άσκηση ίδεται η διαφορική εξίσωση: dy dx y 0 = 0 x = y + e, Να επιλυθεί το πρόβληµα αρχικών τιµών µε τις µεθόδους Euler και Runge-Kutta
Παράδειγµα # ΠΡΟΒΛΗΜΑΤΑ ΑΡΧΙΚΩΝ ΤΙΜΩΝ Σ Ε ΕΠΙΜΕΛΕΙΑ: Ν. Βασιλειάδης Άσκηση ίδεται η διαφορική εξίσωση: dy dx y 0 = 0 x = y + e, Να επιλυθεί το πρόβληµα αρχικών τιµών µε τις µεθόδους Euler και Runge-Kutta
x από το κεντρικό σημείο i: Ξεκινάμε από το ανάπτυγμα Taylor στην x κατεύθυνση για απόσταση i j. Υπολογίζουμε το άθροισμα:
 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 0 05, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #: ΑΡΙΘΜΗΤΙΚΗ ΠΑΡΑΓΩΓΙΣΗ και ΟΛΟΚΛΗΡΩΣΗ Ημερομηνία ανάρτησης εργασίας στην ιστοσελίδα του μαθήματος: 0 Ημερομηνία παράδοσης εργασίας: 9 0 Επιμέλεια απαντήσεων:
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 0 05, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #: ΑΡΙΘΜΗΤΙΚΗ ΠΑΡΑΓΩΓΙΣΗ και ΟΛΟΚΛΗΡΩΣΗ Ημερομηνία ανάρτησης εργασίας στην ιστοσελίδα του μαθήματος: 0 Ημερομηνία παράδοσης εργασίας: 9 0 Επιμέλεια απαντήσεων:
Οντοκεντρικός Προγραμματισμός
 Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Συναρτήσεις - Μεταβλητές ΔΙΔΑΣΚΟΝΤΕΣ: Iωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής Συναρτήσεις / Μεταβλητές
Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Συναρτήσεις - Μεταβλητές ΔΙΔΑΣΚΟΝΤΕΣ: Iωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής Συναρτήσεις / Μεταβλητές
Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση
 ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση ΣΠΟΥΔΑΣΤΗΣ: ΧΑΤΖΗΓΕΩΡΓΙΟΥ ΑΝΤΩΝΗΣ Α.Μ. 09036 Εξάμηνο ΠΤΧ ΚΑΘΗΓΗΤΗΣ: ΔΡ. ΜΠΡΑΤΣΟΣ ΑΘΑΝΑΣΙΟΣ Περιεχόμενα 3.1 Πολυωνυμική παρεμβολή...
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ Εφαρμοσμένα Μαθηματικά 3η εργαστηριακή άσκηση ΣΠΟΥΔΑΣΤΗΣ: ΧΑΤΖΗΓΕΩΡΓΙΟΥ ΑΝΤΩΝΗΣ Α.Μ. 09036 Εξάμηνο ΠΤΧ ΚΑΘΗΓΗΤΗΣ: ΔΡ. ΜΠΡΑΤΣΟΣ ΑΘΑΝΑΣΙΟΣ Περιεχόμενα 3.1 Πολυωνυμική παρεμβολή...
Άσκηση 1. Α. Υπολογίστε χωρίς να εκτελέσετε κώδικα FORTRAN τα παρακάτω: Ποιά είναι η τελική τιμή του Z στα παρακάτω κομμάτια κώδικα FORTRAN:
 Άσκηση 1 Α. Υπολογίστε χωρίς να εκτελέσετε κώδικα FORTRAN τα παρακάτω: Ποιά είναι η τελική τιμή του J στα παρακάτω κομμάτια κώδικα FORTRAN: INTEGER J J = 5 J = J + 1 J = J + 1 INTEGER X, Y, J X = 2 Y =
Άσκηση 1 Α. Υπολογίστε χωρίς να εκτελέσετε κώδικα FORTRAN τα παρακάτω: Ποιά είναι η τελική τιμή του J στα παρακάτω κομμάτια κώδικα FORTRAN: INTEGER J J = 5 J = J + 1 J = J + 1 INTEGER X, Y, J X = 2 Y =
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 5 Ο ΕΞΑΜΗΝΟ, ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΟΣΕΩΝ. Κεφ. 1: Εισαγωγή (διάρκεια: 0.5 εβδομάδες)
 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 5 Ο ΕΞΑΜΗΝΟ, 2016-2017 ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΟΣΕΩΝ Κεφ. 1: Εισαγωγή (διάρκεια: 0.5 εβδομάδες) Κεφ. 2: Επίλυση συστημάτων εξισώσεων (διάρκεια: 3 εβδομάδες) 2.1 Επίλυση εξισώσεων 2.2 Επίλυση
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 5 Ο ΕΞΑΜΗΝΟ, 2016-2017 ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΡΑΔΟΣΕΩΝ Κεφ. 1: Εισαγωγή (διάρκεια: 0.5 εβδομάδες) Κεφ. 2: Επίλυση συστημάτων εξισώσεων (διάρκεια: 3 εβδομάδες) 2.1 Επίλυση εξισώσεων 2.2 Επίλυση
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Πληροφορική II. Ενότητα 3 : Γλώσσες προγραμματισμού. Δρ.
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 3 : Γλώσσες προγραμματισμού Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 3 : Γλώσσες προγραμματισμού Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής
Αντικειμενοστραφείς Γλώσσες Προγραμματισμού C++ / ROOT
 Αντικειμενοστραφείς Γλώσσες Προγραμματισμού Ιωάννης Παπαδόπουλος Τμήμα Φυσικής, Πανεπιστήμιο Ιωαννίνων Οκτώβριος 2018 1/28 1 (implicit) μετατροπές 2 (Functions) 3 (Pointers) 4 (Arrays) 2/28 (implicit)
Αντικειμενοστραφείς Γλώσσες Προγραμματισμού Ιωάννης Παπαδόπουλος Τμήμα Φυσικής, Πανεπιστήμιο Ιωαννίνων Οκτώβριος 2018 1/28 1 (implicit) μετατροπές 2 (Functions) 3 (Pointers) 4 (Arrays) 2/28 (implicit)
Κεφάλαιο 7: Υποπρογράμματα. Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών
 Κεφάλαιο 7: Υποπρογράμματα Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ορισμός Αφαίρεση με χρήση υποπρογραμμάτων (subprogram abstraction) είναι η αντιστοίχιση ενός συνόλου εισόδων σε ένα σύνολο εξόδων
Κεφάλαιο 7: Υποπρογράμματα Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ορισμός Αφαίρεση με χρήση υποπρογραμμάτων (subprogram abstraction) είναι η αντιστοίχιση ενός συνόλου εισόδων σε ένα σύνολο εξόδων
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τι είναι ; Συναρτήσεις. Παράδειγμα #1. double convert ( double cm ) { double inch;
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι είναι ; Συναρτήσεις Αυτόνομα τμήματα κώδικα (υποπρογράμματα) που πραγματοποιούν μια καθορισμένη εργασία. Χρήσιμες για περιπτώσεις που ο ίδιος υπολογισμός επαναλαμβάνεται πολλές φορές
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι είναι ; Συναρτήσεις Αυτόνομα τμήματα κώδικα (υποπρογράμματα) που πραγματοποιούν μια καθορισμένη εργασία. Χρήσιμες για περιπτώσεις που ο ίδιος υπολογισμός επαναλαμβάνεται πολλές φορές
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2014 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2014 1 / 42 Αριθμητικές Μέθοδοι
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Οκτώβριος 2014 Δρ. Δημήτρης Βαρσάμης Οκτώβριος 2014 1 / 42 Αριθμητικές Μέθοδοι
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
f x και τέσσερα ζευγάρια σημείων
 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 014 015, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #: ΑΡΙΘΜΗΤΙΚΗ ΠΑΡΕΜΒΟΛΗ Ημερομηνία ανάρτησης εργασίας στην ιστοσελίδα του μαθήματος: 1 11 014 Ημερομηνία παράδοσης εργασίας: 18 11 014 Επιμέλεια απαντήσεων:
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ, 014 015, 5 Ο ΕΞΑΜΗΝΟ ΕΡΓΑΣΙΑ #: ΑΡΙΘΜΗΤΙΚΗ ΠΑΡΕΜΒΟΛΗ Ημερομηνία ανάρτησης εργασίας στην ιστοσελίδα του μαθήματος: 1 11 014 Ημερομηνία παράδοσης εργασίας: 18 11 014 Επιμέλεια απαντήσεων:
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 7: Υπορουτίνες
 Κεφάλαιο 7: Υπορουτίνες Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ορισμός Αφαίρεση με χρήση υπορουτινών (subroutine abstraction) είναι η αντιστοίχιση ενός συνόλου εισόδων σε ένα σύνολο εξόδων που μπορεί
Κεφάλαιο 7: Υπορουτίνες Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ορισμός Αφαίρεση με χρήση υπορουτινών (subroutine abstraction) είναι η αντιστοίχιση ενός συνόλου εισόδων σε ένα σύνολο εξόδων που μπορεί
2.Τι εννοούμε με βαθμό συνέχειας μιας συνάρτησης; Ποια είναι η χρησιμότητα της από πλευράς εφαρμογών;
 ΗΥ1 ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΣΕΤ ΑΣΚΗΣΕΩΝ 5 1.Tι είναι συνάρτηση; Περιγράψτε τα στοιχεία που την ορίζουν..τι εννοούμε με βαθμό συνέχειας μιας συνάρτησης; Ποια είναι η χρησιμότητα της από πλευράς εφαρμογών;.να
ΗΥ1 ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ ΣΕΤ ΑΣΚΗΣΕΩΝ 5 1.Tι είναι συνάρτηση; Περιγράψτε τα στοιχεία που την ορίζουν..τι εννοούμε με βαθμό συνέχειας μιας συνάρτησης; Ποια είναι η χρησιμότητα της από πλευράς εφαρμογών;.να
Κεφάλαιο 8. Αριθμητικός υπολογισμός ορισμένου ολοκληρώματος
 Κεφάλαιο 8. Αριθμητικός υπολογισμός ορισμένου ολοκληρώματος Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται οι αριθμητικές μέθοδοι τον υπολογισμό των ορισμένων ολοκληρωμάτων. Παρουσιάζονται οι μέθοδοι του παραλληλογράμμου,
Κεφάλαιο 8. Αριθμητικός υπολογισμός ορισμένου ολοκληρώματος Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται οι αριθμητικές μέθοδοι τον υπολογισμό των ορισμένων ολοκληρωμάτων. Παρουσιάζονται οι μέθοδοι του παραλληλογράμμου,
Πιο συγκεκριμένα, η χρήση του MATLAB προσφέρει τα ακόλουθα πλεονεκτήματα.
 i Π Ρ Ο Λ Ο Γ Ο Σ Το βιβλίο αυτό αποτελεί μια εισαγωγή στα βασικά προβλήματα των αριθμητικών μεθόδων της υπολογιστικής γραμμικής άλγεβρας (computational linear algebra) και της αριθμητικής ανάλυσης (numerical
i Π Ρ Ο Λ Ο Γ Ο Σ Το βιβλίο αυτό αποτελεί μια εισαγωγή στα βασικά προβλήματα των αριθμητικών μεθόδων της υπολογιστικής γραμμικής άλγεβρας (computational linear algebra) και της αριθμητικής ανάλυσης (numerical
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τι είναι οι πίνακες; Μονοδιάστατοι πίνακες. Απλές μεταβλητές: Κεντρική μνήμη
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Μονοδιάστατοι πίνακες Τι είναι οι πίνακες; Απλές μεταβλητές: Κεντρική μνήμη 32 10 0001 a e z Ονόματα μεταβλητών 1 2 Τι είναι οι πίνακες; Πίνακες: Κεντρική μνήμη x Όνομα πίνακα 3 Τι είναι
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Μονοδιάστατοι πίνακες Τι είναι οι πίνακες; Απλές μεταβλητές: Κεντρική μνήμη 32 10 0001 a e z Ονόματα μεταβλητών 1 2 Τι είναι οι πίνακες; Πίνακες: Κεντρική μνήμη x Όνομα πίνακα 3 Τι είναι
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Δομή του προγράμματος. Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δομή του προγράμματος Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δομή του προγράμματος Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εισαγωγή στην Αριθμητική Ανάλυση
 Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΚΑΙ ΠΙΝΑΚΕΣ
 ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΚΑΙ ΠΙΝΑΚΕΣ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Βασικοί Τύποι Πίνακες (μέρος 1) Συμβολοσειρές Ο Προεπεξεργαστής Τελευταία ενημέρωση: Σεπτέμβριος 2016 Εισαγωγή - 2 short:
ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΚΑΙ ΠΙΝΑΚΕΣ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Βασικοί Τύποι Πίνακες (μέρος 1) Συμβολοσειρές Ο Προεπεξεργαστής Τελευταία ενημέρωση: Σεπτέμβριος 2016 Εισαγωγή - 2 short:
Δομές Δεδομένων & Αλγόριθμοι
 - Πίνακες 1 Πίνακες Οι πίνακες έχουν σταθερό μέγεθος και τύπο δεδομένων. Βασικά πλεονεκτήματά τους είναι η απλότητα προγραμματισμού τους και η ταχύτητα. Ωστόσο δεν παρέχουν την ευελιξία η οποία απαιτείται
- Πίνακες 1 Πίνακες Οι πίνακες έχουν σταθερό μέγεθος και τύπο δεδομένων. Βασικά πλεονεκτήματά τους είναι η απλότητα προγραμματισμού τους και η ταχύτητα. Ωστόσο δεν παρέχουν την ευελιξία η οποία απαιτείται
Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ
 Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ 1. Εύρεση ρίζας Στο κεφάλαιο αυτό θα ασχοληθούμε με την εύρεση ρίζας μιας συνάρτησης ή αλλιώς με την ευρεση λύσης της εξίσωσης: Πριν αναφερθούμε στην
Β ΜΕΡΟΣ: ΕΦΑΡΜΟΓΗ ΤΟΥ MATLAB ΣΤΗΝ ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ 1. Εύρεση ρίζας Στο κεφάλαιο αυτό θα ασχοληθούμε με την εύρεση ρίζας μιας συνάρτησης ή αλλιώς με την ευρεση λύσης της εξίσωσης: Πριν αναφερθούμε στην
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Δείκτες Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δείκτες Διδάσκοντες: Αν Καθ Δ Παπαγεωργίου, Αν Καθ Ε Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δείκτες Διδάσκοντες: Αν Καθ Δ Παπαγεωργίου, Αν Καθ Ε Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών
 Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ενότητα 7: Υπορουτίνες Καθ. Γιάννης Γαροφαλάκης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Ορισμός Αφαίρεση με χρήση υπορουτινών (subroutine abstraction)
Αρχές Γλωσσών Προγραμματισμού και Μεταφραστών Ενότητα 7: Υπορουτίνες Καθ. Γιάννης Γαροφαλάκης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Ορισμός Αφαίρεση με χρήση υπορουτινών (subroutine abstraction)
Προγραμματισμός Υπολογιστών με C++
 Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 5η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Πίνακες ως ορίσματα συναρτήσεων. Τα ορίσματα argc και argv της main.
Προγραμματισμός Υπολογιστών με C++ ( 2012-13 ) 5η διάλεξη Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Τι θα ακούσετε σήμερα Πίνακες ως ορίσματα συναρτήσεων. Τα ορίσματα argc και argv της main.
α n z n = 1 + 2z 2 + 5z 3 n=0
 Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Η ύλη συνοπτικά... Γεννήτριες συναρτήσεις Τι είναι η γεννήτρια Στην
Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Η ύλη συνοπτικά... Γεννήτριες συναρτήσεις Τι είναι η γεννήτρια Στην
Δομή Προγράμματος C++, Χειρισμός Μεταβλητών και Συναρτήσεις Εισόδου - Εξόδου
 Εργαστήριο 2: Δομή Προγράμματος C++, Χειρισμός Μεταβλητών και Συναρτήσεις Εισόδου - Εξόδου Ο σκοπός αυτής της εργαστηριακής άσκησης είναι η ανάλυση των βασικών χαρακτηριστικών της Γλώσσας Προγραμματισμού
Εργαστήριο 2: Δομή Προγράμματος C++, Χειρισμός Μεταβλητών και Συναρτήσεις Εισόδου - Εξόδου Ο σκοπός αυτής της εργαστηριακής άσκησης είναι η ανάλυση των βασικών χαρακτηριστικών της Γλώσσας Προγραμματισμού
ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, , 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #4: ΟΛΟΚΛΗΡΩΣΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης. με το πολυώνυμο παρεμβολής Lagrange 2 ης τάξης
 ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, 6-7, 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #: ΟΛΟΚΛΗΡΩΣΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης. Διατυπώστε τον 1 ο κανόνα ολοκλήρωσης Smpson b f ( xdx ) ( 1 3 f f f ) a, αντικαθιστώντας τη συνάρτηση f
ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, 6-7, 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #: ΟΛΟΚΛΗΡΩΣΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης. Διατυπώστε τον 1 ο κανόνα ολοκλήρωσης Smpson b f ( xdx ) ( 1 3 f f f ) a, αντικαθιστώντας τη συνάρτηση f
17TimeThis.h function returns reference pointer to same object { return *this; }
 Προαπαιτούµενη Κάθε οµάδα θα πρέπει να εµπλουτίσει το ίδιο πρόγραµµα, που έκανε την προηγούµενη φορά, προσθέτοντας στην κλάση του έναν ή περισσότερους υπερφορτωµένους τελεστές (όπως , ++, +,-,+=..)
Προαπαιτούµενη Κάθε οµάδα θα πρέπει να εµπλουτίσει το ίδιο πρόγραµµα, που έκανε την προηγούµενη φορά, προσθέτοντας στην κλάση του έναν ή περισσότερους υπερφορτωµένους τελεστές (όπως , ++, +,-,+=..)
Ονοματεπώνυμο και ΑΜ: Είχα παραδώσει εργασίες τα προηγούμενα ακαδημαϊκά έτη: ΚΑΛΗ ΕΠΙΤΥΧΙΑ!
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Προγραμματισμός Υπολογιστών με C++ Εξεταστική περίοδος: Φεβρουαρίου 2010. Διδάσκων: Α. Δημάκης Γράψτε όλες τις απαντήσεις σας πάνω σε αυτό το
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Προγραμματισμός Υπολογιστών με C++ Εξεταστική περίοδος: Φεβρουαρίου 2010. Διδάσκων: Α. Δημάκης Γράψτε όλες τις απαντήσεις σας πάνω σε αυτό το
Προγραµµατιστικές Τεχνικές
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Προγραµµατιστικές Τεχνικές Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωµύλος Κορακίτης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Προγραµµατιστικές Τεχνικές Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωµύλος Κορακίτης
Κλήση Συναρτήσεων ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ. Γεώργιος Παπαϊωάννου ( )
 ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Μορφές μεταβίβασης ορισμάτων σε συναρτήσεις (και μεθόδους) και οι επιπτώσεις τους Επιστροφή τιμών από κλήση συναρτήσεων Υπερφόρτωση
ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Μορφές μεταβίβασης ορισμάτων σε συναρτήσεις (και μεθόδους) και οι επιπτώσεις τους Επιστροφή τιμών από κλήση συναρτήσεων Υπερφόρτωση
Οντοκεντρικός Προγραμματισμός
 Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Εισαγωγή στην C++ ΔΙΔΑΣΚΟΝΤΕΣ:Iωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής H Γλώσσα C++ ΙΣΤΟΡΙΑ 1967:
Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Εισαγωγή στην C++ ΔΙΔΑΣΚΟΝΤΕΣ:Iωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής H Γλώσσα C++ ΙΣΤΟΡΙΑ 1967:
Προγραμματισμός Ι. Εισαγωγή στην C++ Δημήτρης Μιχαήλ. Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο
 Προγραμματισμός Ι Εισαγωγή στην C++ Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Η γλώσσα C++ Σχεδιάστηκε το 1979 από τον Bjarne Stroustrup στα Bell Laboratories Βασίζεται
Προγραμματισμός Ι Εισαγωγή στην C++ Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Η γλώσσα C++ Σχεδιάστηκε το 1979 από τον Bjarne Stroustrup στα Bell Laboratories Βασίζεται
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Α.Π.Θ. ΕΡΓΑΣΤΗΡΙΟ C++ ΕΞΑΜΗΝΟ Γ Ακαδηµαϊκό Έτος
 ΠΑΡΑ ΕΙΓΜΑ δυναµικής δέσµευσης και αποδέσµευσης µνήµης στη C++ µέσω των new και delete. // create.cpp #include using namespace std; class values public: values() : value1(0), value2(0) count++;
ΠΑΡΑ ΕΙΓΜΑ δυναµικής δέσµευσης και αποδέσµευσης µνήµης στη C++ µέσω των new και delete. // create.cpp #include using namespace std; class values public: values() : value1(0), value2(0) count++;
Πληροφορική 2. Αλγόριθμοι
 Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Γλώσσα Προγραμματισμού C++ Εισαγωγή - Μια πρώτη ματιά
 Γλώσσα Προγραμματισμού C++ Εισαγωγή - Μια πρώτη ματιά Βασικά χαρακτηριστικά αναπτύχθηκε ως επέκταση της C το 1979 υπερσύνολο της C γλώσσα γενικού σκοπού, γρήγορη, Αντικειμενοστραφής προγραμματισμός (Object
Γλώσσα Προγραμματισμού C++ Εισαγωγή - Μια πρώτη ματιά Βασικά χαρακτηριστικά αναπτύχθηκε ως επέκταση της C το 1979 υπερσύνολο της C γλώσσα γενικού σκοπού, γρήγορη, Αντικειμενοστραφής προγραμματισμός (Object
Υπερφόρτωση τελεστών (operator(
 Υπερφόρτωση τελεστών (operator( overloading) Η υπερφόρτωση τελεστών είναι ένα από τα πιο ενδιαφέροντα χαρακτηριστικά του αντικειμενοστραφούς προγραμματισμού. Αναφέρεται στην πρόσθετη χρήση των συνηθισμένων
Υπερφόρτωση τελεστών (operator( overloading) Η υπερφόρτωση τελεστών είναι ένα από τα πιο ενδιαφέροντα χαρακτηριστικά του αντικειμενοστραφούς προγραμματισμού. Αναφέρεται στην πρόσθετη χρήση των συνηθισμένων
Εισαγωγή στη γλώσσα προγραμματισμού C++
 Εισαγωγή στη γλώσσα προγραμματισμού C++ Ακολουθιακή Δομή Παράδειγμα 1 ex05 2 Να δημιουργήσετε ένα πρόγραμμα το οποίο να διαβάζει την θερμοκρασία σε βαθμούς Φαρενάϊτ και να εμφανίζει την αντίστοιχη θερμοκρασία
Εισαγωγή στη γλώσσα προγραμματισμού C++ Ακολουθιακή Δομή Παράδειγμα 1 ex05 2 Να δημιουργήσετε ένα πρόγραμμα το οποίο να διαβάζει την θερμοκρασία σε βαθμούς Φαρενάϊτ και να εμφανίζει την αντίστοιχη θερμοκρασία
5269: Υπολογιστικές Μέθοδοι για Μηχανικούς.
 569: Υπολογιστικές Μέθοδοι για Μηχανικούς Παρεμβολή ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Παρεµβολή Παρεµβολή interpoltion είναι η διαδικασία µε την οποία βρίσκεται µία
569: Υπολογιστικές Μέθοδοι για Μηχανικούς Παρεμβολή ttp://ecourses.cemeng.ntu.gr/courses/computtionl_metods_or_engineers/ Παρεµβολή Παρεµβολή interpoltion είναι η διαδικασία µε την οποία βρίσκεται µία
3 Αλληλεπίδραση Αντικειμένων
 Αφαίρεση και Αρθρωσιμότητα 3 Αλληλεπίδραση Αντικειμένων Πώς συνεργάζονται τα αντικείμενα που δημιουργούμε Αφαίρεση (abstraction) είναι η δυνατότητα να αγνοούμε τις λεπτομέρειες και να εστιάζουμε την προσοχή
Αφαίρεση και Αρθρωσιμότητα 3 Αλληλεπίδραση Αντικειμένων Πώς συνεργάζονται τα αντικείμενα που δημιουργούμε Αφαίρεση (abstraction) είναι η δυνατότητα να αγνοούμε τις λεπτομέρειες και να εστιάζουμε την προσοχή
Εισαγωγή στον Προγραµµατισµό. Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011
 Εισαγωγή στον Προγραµµατισµό Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011 Τελεστής σύντοµης ανάθεσης Τελεστής σύντοµης ανάθεσης (shorthand assignment operator) µεταβλητή = µεταβλητή τελεστής
Εισαγωγή στον Προγραµµατισµό Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011 Τελεστής σύντοµης ανάθεσης Τελεστής σύντοµης ανάθεσης (shorthand assignment operator) µεταβλητή = µεταβλητή τελεστής
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Εντολές επανάληψης Εντολές επανάληψης while for do-while ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Παράδειγμα #1 Εντολή while
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Εντολές επανάληψης Εντολές επανάληψης Στη C++ υπάρχουν 3 διαφορετικές εντολές επανάληψης: while for do-while 1 2 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Εντολή while Παράδειγμα #1 Κατασκευάστε πρόγραμμα που για
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Εντολές επανάληψης Εντολές επανάληψης Στη C++ υπάρχουν 3 διαφορετικές εντολές επανάληψης: while for do-while 1 2 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Εντολή while Παράδειγμα #1 Κατασκευάστε πρόγραμμα που για
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Συναρτήσεις II Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις II Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις II Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ
 Ασκήσεις ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ για Γενική Επανάληψη Πολυχρόνη Μωυσιάδη, Καθηγητή ΑΠΘ ΟΜΑΔΑ 1. Συναρτήσεις 1. Δείξτε ότι: και υπολογίστε την τιμή 2. 2. Να υπολογισθούν οι τιμές και 3. Υπολογίστε τις τιμές
Ασκήσεις ΜΑΘΗΜΑΤΙΚΩΝ ΔΑΣΟΛΟΓΙΑΣ για Γενική Επανάληψη Πολυχρόνη Μωυσιάδη, Καθηγητή ΑΠΘ ΟΜΑΔΑ 1. Συναρτήσεις 1. Δείξτε ότι: και υπολογίστε την τιμή 2. 2. Να υπολογισθούν οι τιμές και 3. Υπολογίστε τις τιμές
(6,5 μονάδες) Θέμα 1 ο. Τμήμα Πολιτικών Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Διεθνές Πανεπιστήμιο Ελλάδος ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 Τμήμα Πολιτικών Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Διεθνές Πανεπιστήμιο Ελλάδος ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ΕΡΓΑΣΤΗΡΙΟΥ ΑΡΙΘΜΗΤΙΚΗΣ ΑΝΑΛΥΣΗΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔ. ΕΤΟΣ 08-09 ΔΙΔΑΣΚΩΝ : Χ. Βοζίκης ΟΝΟΜΑΤΕΠΩΝΥΜΟ Αριθμός
Τμήμα Πολιτικών Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Διεθνές Πανεπιστήμιο Ελλάδος ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ΕΡΓΑΣΤΗΡΙΟΥ ΑΡΙΘΜΗΤΙΚΗΣ ΑΝΑΛΥΣΗΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔ. ΕΤΟΣ 08-09 ΔΙΔΑΣΚΩΝ : Χ. Βοζίκης ΟΝΟΜΑΤΕΠΩΝΥΜΟ Αριθμός
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 2: Γεννήτριες Συναρτήσεις Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
ΠΟΛΥΜΟΡΦΙΣΜΟΣ. 4.1 Κληρονομικότητα και Αρχή της Υποκατάστασης
 ΠΟΛΥΜΟΡΦΙΣΜΟΣ Λόγω της θεμελιώδους σημασίας της έννοιας του πολυμορφισμού (polymorphism) στην αντικειμενοστρεφή σχεδίαση, κρίνεται σκόπιμο στο σημείο αυτό του βιβλίου να αναλυθεί εκτενέστερα. Ο πολυμορφισμός
ΠΟΛΥΜΟΡΦΙΣΜΟΣ Λόγω της θεμελιώδους σημασίας της έννοιας του πολυμορφισμού (polymorphism) στην αντικειμενοστρεφή σχεδίαση, κρίνεται σκόπιμο στο σημείο αυτό του βιβλίου να αναλυθεί εκτενέστερα. Ο πολυμορφισμός
ΟΝΤΟΚΕΝΤΡΙΚΟΣ ΠΡΟΓΡ/ΣΜΟΣ C++
 Υπερφόρτωση, keywords CONST, STATIC, FRIEND ΟΝΤΟΚΕΝΤΡΙΚΟΣ ΠΡΟΓΡ/ΣΜΟΣ C++ Μ. Ρήγκου (rigou@ceid.upatras.gr) Τι θα συζητήσουμε σήμερα Υπερφόρτωση Συναρτήσεων Τελεστών CONST αντικείμενα, μεταβλητές και συναρτήσεις
Υπερφόρτωση, keywords CONST, STATIC, FRIEND ΟΝΤΟΚΕΝΤΡΙΚΟΣ ΠΡΟΓΡ/ΣΜΟΣ C++ Μ. Ρήγκου (rigou@ceid.upatras.gr) Τι θα συζητήσουμε σήμερα Υπερφόρτωση Συναρτήσεων Τελεστών CONST αντικείμενα, μεταβλητές και συναρτήσεις
Πίνακας Περιεχομένων
 Πίνακας Περιεχομένων Πρόλογος... 11 Κεφάλαιο 1o: Εισαγωγικά... 15 1.1 Με τι ασχολείται η Αριθμητική Ανάλυση... 15 1.2 Πηγές Σφαλμάτων... 17 1.2.1 Εισόδου... 17 1.2.2 Αριθμητικής Υπολογιστών... 18 1.2.3
Πίνακας Περιεχομένων Πρόλογος... 11 Κεφάλαιο 1o: Εισαγωγικά... 15 1.1 Με τι ασχολείται η Αριθμητική Ανάλυση... 15 1.2 Πηγές Σφαλμάτων... 17 1.2.1 Εισόδου... 17 1.2.2 Αριθμητικής Υπολογιστών... 18 1.2.3
Προγραμματισμός Η/Υ 1 (Εργαστήριο)
 Προγραμματισμός Η/Υ 1 (Εργαστήριο) Ενότητα 2: Δομή ενός προγράμματος C Καθηγήτρια Εφαρμογών: Τσαγκαλίδου Ροδή Τμήμα: Ηλεκτρολόγων Μηχανικών Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Προγραμματισμός Η/Υ 1 (Εργαστήριο) Ενότητα 2: Δομή ενός προγράμματος C Καθηγήτρια Εφαρμογών: Τσαγκαλίδου Ροδή Τμήμα: Ηλεκτρολόγων Μηχανικών Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι
 ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι κ. ΠΕΤΑΛΙΔΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΤΕΧΝΟΛΟΓΙΑ ΛΟΓΙΣΜΙΚΟΥ Ι κ. ΠΕΤΑΛΙΔΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΜΗΧΑΝΙΚΗΣ ΕΦΑΡΜΟΓΕΣ ΜΕ ΧΡΗΣΗ MATLAB ΔΕΥΤΕΡΗ ΕΚΔΟΣΗ [ΒΕΛΤΙΩΜΕΝΗ ΚΑΙ ΕΠΑΥΞΗΜΕΝΗ]
![ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΜΗΧΑΝΙΚΗΣ ΕΦΑΡΜΟΓΕΣ ΜΕ ΧΡΗΣΗ MATLAB ΔΕΥΤΕΡΗ ΕΚΔΟΣΗ [ΒΕΛΤΙΩΜΕΝΗ ΚΑΙ ΕΠΑΥΞΗΜΕΝΗ] ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΜΗΧΑΝΙΚΗΣ ΕΦΑΡΜΟΓΕΣ ΜΕ ΧΡΗΣΗ MATLAB ΔΕΥΤΕΡΗ ΕΚΔΟΣΗ [ΒΕΛΤΙΩΜΕΝΗ ΚΑΙ ΕΠΑΥΞΗΜΕΝΗ]](/thumbs/66/55146645.jpg) ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΜΗΧΑΝΙΚΗΣ ΕΦΑΡΜΟΓΕΣ ΜΕ ΧΡΗΣΗ MATLAB ΔΕΥΤΕΡΗ ΕΚΔΟΣΗ [ΒΕΛΤΙΩΜΕΝΗ ΚΑΙ ΕΠΑΥΞΗΜΕΝΗ] Συγγραφείς ΝΤΑΟΥΤΙΔΗΣ ΠΡΟΔΡΟΜΟΣ Πανεπιστήμιο Minnesota, USA ΜΑΣΤΡΟΓΕΩΡΓΟΠΟΥΛΟΣ ΣΠΥΡΟΣ Αριστοτέλειο
ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΓΙΑ ΠΡΟΒΛΗΜΑΤΑ ΜΗΧΑΝΙΚΗΣ ΕΦΑΡΜΟΓΕΣ ΜΕ ΧΡΗΣΗ MATLAB ΔΕΥΤΕΡΗ ΕΚΔΟΣΗ [ΒΕΛΤΙΩΜΕΝΗ ΚΑΙ ΕΠΑΥΞΗΜΕΝΗ] Συγγραφείς ΝΤΑΟΥΤΙΔΗΣ ΠΡΟΔΡΟΜΟΣ Πανεπιστήμιο Minnesota, USA ΜΑΣΤΡΟΓΕΩΡΓΟΠΟΥΛΟΣ ΣΠΥΡΟΣ Αριστοτέλειο
Οντοκεντρικός Προγραμματισμός
 Οντοκεντρικός Προγραμματισμός Ενότητα 7: C++ TEMPLATES, ΥΠΕΡΦΟΡΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΡΕΣΕΙΣ Χειρισμός Εξαιρέσεων ΔΙΔΑΣΚΟΝΤΕΣ: Ιωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ
Οντοκεντρικός Προγραμματισμός Ενότητα 7: C++ TEMPLATES, ΥΠΕΡΦΟΡΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΡΕΣΕΙΣ Χειρισμός Εξαιρέσεων ΔΙΔΑΣΚΟΝΤΕΣ: Ιωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ
Οντοκεντρικός Προγραμματισμός
 Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Δομές Ελέγχου ΔΙΔΑΣΚΟΝΤΕΣ: Ιωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής Δομές Ελέγχου Εισαγωγή Πριν
Οντοκεντρικός Προγραμματισμός Ενότητα 5: H ΓΛΩΣΣΑ C++ Δομές Ελέγχου ΔΙΔΑΣΚΟΝΤΕΣ: Ιωάννης Χατζηλυγερούδης, Χρήστος Μακρής Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ & Πληροφορικής Δομές Ελέγχου Εισαγωγή Πριν
