Ικανή και αναγκαία συνθήκη για να εκτελεί ένα σώµα ή ένα υλικό σηµείο Γ.Α.Τ. είναι: η συνισταµένη των δυνάµεων που ασκούνται στο σώµα να έχει τη
|
|
|
- Μαρία Φλέσσας
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΤΑΛΑΝΤΩΣΕΙΣ (µερικές σηµειώσεις...) Ικανή και αναγκαία συνθήκη για να εκτελεί ένα σώµα ή ένα υλικό σηµείο Γ.Α.Τ. είναι: η συνισταµένη των δυνάµεων που ασκούνται στο σώµα να έχει τη διεύθυνση της κίνησης, µέτρο ανάλογο της αποµάκρυνσης από τη θέση ισορροπίας και φορά αντίθετη της αποµάκρυνσης. ΣFx=-D.x (0) Η ΣFx ονοµάζεται και δύναµη επαναφοράς, και έχει κατεύθυνση πάντα προς τη θέση ισορροπίας. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΜΕΓΕΘΗ ΣΤΗ Γ.Α.Τ. Αποµάκρυνση x Πλάτος A Περίοδος Τ Συχνότητα f Κυκλική συχνότητα ω Φάση φ Τ=1/f f=1/τ ω=2πf=2π/τ φ=ωt+φο όπου φο η αρχική φάση ΕΞΙΣΩΣΕΙΣ Γ.Α.Τ. Οι εξισώσεις της Γ.Α.Τ. µπορούν να προκύψουν από τον κύκλο αναφοράς. Θεωρούµε ότι σώµα Σ µάζας m εκτελεί Ο.Κ.Κ. σε κύκλο ακτίνας A µε σταθερή γωνιακή ταχύτητα ω. Η προβολή Π του Σ σε µια διάµετρο του κύκλου, εκτελεί Γ.Α.Τ.. Αποµάκρυνσης Ταχύτητας επιτάχυνσης δύναµης x=aηµωt (1) u=uοσυνωt (2) a=-aοηµωt (3) F=-maοηµωt (4) u=ωaσυνωt a=-ω²aηµωt F=-mω²Aηµωt u=uοηµ(ωt+π/2) a=aοηµ(ωt+π) F=maοηµ(ωt+π) u=ωaηµ(ωt+π/2) a=ω²aηµ(ωt+π) F=mω²Aηµ(ωt+π) Οι παραπάνω σχέσεις ισχύουν όταν φο=0, δηλαδή όταν η αρχική φάση είναι µηδέν. Αν υπάρχει αρχική φάση, τότε πρέπει να την προσθέσουµε στη φάση ωt, οπότε οι παραπάνω σχέσεις παίρνουν τη µορφή: x=aηµ(ωt+φο) u=uοσυν(ωt+φο) a=-aοηµ(ωt+φο) F=-maοηµ(ωt+φο) Από τις παραπάνω σχέσεις παρατηρούµε ότι: Βαγγέλης Κολτσάκης Σελίδα 1 από 6
2 Η διαφορά φάσης ταχύτητας - αποµάκρυνσης είναι φ=π/2 Η διαφορά φάσης επιτάχυνσης - ταχύτητας είναι φ=π/2 Η διαφορά φάσης επιτάχυνσης -αποµάκρυνσης είναι φ=π Από τις (1) και (2) προκύπτει: u=±ω (A²-x²) (5) Από τις (2) και (3) προκύπτει: a=±ω (uο²-u²), (6) άρα και F=±mω (uο²-u²) (7) Από τις (1) και (3) προκύπτει: a=-ω²x Από τις (1) και (4) προκύπτει: F=-mω²x (8) Από τις (0) και (8) προκύπτει: D=mω² (9) Από την (9) προκύπτει: Τ=2π (m/d) (10) Η D ονοµάζεται σταθερά επαναφοράς (µονάδα µέτρησης: N/m). (Παρατηρούµε από την σχ. 10 ότι η περίοδος της Γ.Α.Τ. εξαρτάται από τη σταθερά επαναφοράς D και από τη µάζα m του ταλαντωτή, ενώ είναι ανεξάρτητη από το πλάτος A της ταλάντωσης). ΕΥΡΕΣΗ ΤΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΜΕΓΕΘΩΝ ΣΤΗΝ Γ.Α.Τ. Όταν γνωρίζουµε την εξίσωση της αποµάκρυνσης: αντιστοιχούµε την εξίσωση που µας δίνεται µε την γενική εξίσωση x=aηµ(ωt+φο). Αν η εξίσωση που έχουµε δεν έχει τέτοια µορφή, τη µετασχηµατίζουµε έτσι ώστε να πάρει τη µορφή αυτή. Με ανάλογο τρόπο δουλεύουµε όταν µας δίνεται όχι η εξίσωση της αποµάκρυνσης, αλλά η εξίσωση κάποιου άλλου χαρακτηριστικού µεγέθους (πχ ταχύτητας, επιτάχυνσης, δύναµης). ΕΛΕΓΧΟΣ ΚΑΙ ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΗΣ ΑΡΧΙΚΗΣ ΦΑΣΗΣ φο. Η αρχική φάση παίρνει τιµές 0 φο 2π. Πιθανώς να αναφέρεται άµεσα ή έµµεσα στην εκφώνηση αν υπάρχει αρχική φάση. Μπορούµε να διαπιστώσουµε ότι υπάρχει αρχική φάση και να την υπολογίσουµε, αν συµβαίνει ένα από τα ακόλουθα: Αναφέρεται άµεσα στην εκφώνηση ότι υπάρχει αρχική φάση. Η εξίσωση κάποιου χαρακτηριστικού µεγέθους σε συνάρτηση µε το χρόνο δεν έχει ακριβώς την ίδια µορφή µε τη γενική µορφή της εξίσωσης του µεγέθους αυτού. Βαγγέλης Κολτσάκης Σελίδα 2 από 6
3 Η αποµάκρυνση δεν είναι µηδέν τη χρονική στιγµή t=0. Στην περίπτωση αυτή µπορεί να δίνεται περιορισµός για κάποιο άλλο µέγεθος, ή ακόµη και κάποια στιγµιαία τιµή κάποιου άλλου µεγέθους. Η επιτάχυνση δεν είναι µηδέν τη χρονική στιγµή µηδέν. Η ταχύτητα δεν είναι µέγιστη τη χρονική στιγµή µηδέν. Η δυναµική ενέργεια του ταλαντωτή δεν είναι µηδέν τη χρονική στιγµή µηδέν. Η κινητική ενέργεια του ταλαντωτή δεν είναι µέγιστη τη χρονική στιγµή µηδέν. Μπορούµε να δουλέψουµε µε δυο τρόπους: α' τρόπος: µε τριγωνοµετρικές εξισώσεις Χρησιµοποιούµε την εξίσωση κάποιου µεγέθους που µας δίνεται η αλγεβρική του τιµή για τη χρονική στιγµή t=0. Προκύπτει έτσι µια τριγωνοµετρική εξίσωση, που µας δίνει όλες τις δυνατές τιµές της αρχικής φάσης φο. Συνήθως υπάρχουν και κάποιοι περιορισµοί (όπως πχ πρόσηµο κάποιου χαρακτηριστικού µεγέθους), τους οποίους λαµβάνουµε υπόψη. Απορρίπτουµε έτσι κάποιες από τις τιµές τις φο και βρίσκουµε µια δεκτή τιµή. Αν δεν υπάρχει περιορισµός για κάποιο άλλο µέγεθος, πρέπει να κάνουµε δεκτές όλες τις τιµές τις φο, και να δουλέψουµε στη συνέχει µε πάνω από µια περιπτώσεις. Μπορεί επίσης να δίνονται οι τιµές δυο χαρακτηριστικών µεγεθών για τη χρονική στιγµή t=0. ουλεύοντας όπως παραπάνω, βρίσκουµε τιµές για τη φο από δυο τριγωνοµετρικές εξισώσεις, οπότε δεκτή τιµή είναι αυτή για την οποία οι δυο εξισώσεις συναληθεύουν. β' τρόπος: µε τον κύκλο αναφοράς Μπορούµε να εφαρµόσουµε τα δεδοµένα στον κύκλο αναφοράς, ως εξής: από µια εξίσωση που µας δίνεται, τοποθετούµε όλες τις πιθανές φο στον κύκλο αναφοράς, και σε συνδυασµό µε τα υπόλοιπα δεδοµένα, απορρίπτουµε κάποιες από αυτές και βρίσκουµε µια δεκτή. ΕΝΕΡΓΕΙΑ ΣΤΗ Γ.Α.Τ. υναµική ενέργεια ταλάντωσης: U=1/2 Dx²=1/2 muο²-1/2 mu²=1/2 DA²ηµ²ωt Κινητική ενέργεια ταλάντωσης: Βαγγέλης Κολτσάκης Σελίδα 3 από 6
4 K=1/2 mu²=1/2 DA²-1/2 Dx²=1/2 muο²συν²ωt Ολική (µηχανική) ενέργεια ταλάντωσης: Εολική (ταλάντωσης) = Εσε τυχαία θέση = Εσε ακραία θέση = Εστη Θ.Ι. = ΣΤΑΘΕΡΗ δηλ. Εολ=U+K=Umax=Kmax = ΣΤΑΘΕΡΗ δηλ. Εολ=1/2 Dx² + 1/2 mu² = 1/2 DA² = 1/2 muο² = ΣΤΑΘΕΡΗ Ρυθµός µεταβολής κινητικής ενέργειας: K/ t=σfu=-dxu Ρυθµός µεταβολής δυναµικής ενέργειας: U/ t=- Εκιν/ t=-σfu=dxu ηλ. Οι δυο ρυθµοί είναι αντίθετοι, αφού U+K=ΣΤΑΘ. Παρατήρηση: η ολική µηχανική ενέργεια ενός σώµατος που εκτελεί Γ.Α.Τ. δεν ταυτίζεται πάντα µε την ενέργεια ταλάντωσης του σώµατος. Η ολική µηχανική ενέργεια µπορεί να είναι µεταβλητή, λόγω της βαρύτητας, ενώ η ενέργεια ταλάντωσης παραµένει σταθερή. Χαρακτηριστικό παράδειγµα είναι το σώµα που ταλαντώνεται κατακόρυφα ενωµένο σε ελατήριο. Η ενέργεια ταλάντωσης του συστήµατος σώµα - ελατήριο παραµένει σταθερή, ενώ η ολική µηχανική ενέργεια του σώµατος µεταβάλλεται, επειδή µεταβάλλεται η λόγω βαρύτητας δυναµική του ενέργεια. Προσοχή, δεν πρέπει να συγχέουµε την δυναµική ενέργεια ταλάντωσης ½ Dx² µε την δυναµική ενέργεια ελατηρίου 1/2K l², αφού αυτές δεν ταυτίζονται πάντα. Στην πρώτη περίπτωση, µε x παριστάνεται η αποµάκρυνση, δηλαδή η απόσταση από τη Θ.Ι, ενώ στην δεύτερη περίπτωση µε l παριστάνεται η επιµήκυνση ή η συσπείρωση του ελατηρίου (διαφορά από το φυσικό του µήκος). Στις ασκήσεις που δουλεύουµε µε Α..Ε. Στις ασκήσεις αυτές χρησιµοποιούµε την Α..Ε. εννοώντας ως ενέργεια την ενέργεια ταλάντωσης (δηλαδή δεν λαµβάνουµε υπόψη άλλες τυχόν µορφές ενέργειας που έχει το ταλαντούµενο σώµα, εκτός και αν µας ζητείται κάτι τέτοιο). Εντοπίζουµε τη Θ.Ι. του σώµατος. Εφαρµόζουµε τη σχέση Εσε τυχαία θέση = Εσε ακραία θέση = Εστη Θ.Ι. Βαγγέλης Κολτσάκης Σελίδα 4 από 6
5 ΠΩΣ ΑΠΟ ΕΙΚΝΥΟΥΜΕ ΟΤΙ ΕΝΑ ΣΩΜΑ ΕΚΤΕΛΕΙ Γ.Α.Τ. (ΚΑΙ ΠΩΣ ΒΡΙΣΚΟΥΜΕ ΤΗΝ ΠΕΡΙΟ Ο) 1. Κάνουµε ένα σχήµα, µε το σώµα σε δυο θέσεις: στη θέση ισορροπίας της ταλάντωσης (Θ.Ι.Τ.) και σε τυχαία θέση, όπου το σώµα που ταλαντώνεται έχει αποµάκρυνση x. Σηµειώνουµε τις δυνάµεις που ασκούνται στο σώµα στη θέση ισορροπίας της ταλάντωσης και στην τυχαία θέση. 2. Αναλύουµε τις δυνάµεις σε άξονες, έτσι ώστε ο άξονας x να έχει τη διεύθυνση της ταλάντωσης (παράλληλος στην τροχιά του σώµατος) και θετική φορά ίδια µε τη φορά της αποµάκρυνσης. 3. Εφαρµόζοντας τη συνθήκη ΣFx=0 στη Θ.Ι.Τ. συνήθως προκύπτει µια σχέση δυνάµεων που τη χρησιµοποιούµε στη συνέχεια. 4. Στην τυχαία θέση προσπαθούµε να δείξουµε ότι ΣFx=-Dx (χρησιµοποιώντας ίσως και τη σχέση που βρήκαµε παραπάνω), όπου D είναι συνάρτηση σταθερών µεγεθών. 5. Έχοντας πλέον αποδείξει ότι το σώµα εκτελεί Γ.Α.Τ., έχουµε συγχρόνως βρει και την σταθερά ταλάντωσης D, οπότε µπορούµε να υπολογίσουµε και την περίοδο της ταλάντωσης από τη σχέση T=2π (m/d). Παρατηρήσεις Όταν έχουµε σώµα δεµένο σε ελατήριο, το σώµα εκτελεί ταλάντωση µε D=κ, όπως και να εκτραπεί το ελατήριο από τη Θ.Ι.Τ.. Όταν έχουµε σύστηµα ελατηρίων, όπου κ χρησιµοποιούµε το κολ του ισοδύναµου ελατήριου. Στην παράλληλη σύνδεση Κολ=Κ1+Κ2+. ενώ στην κατά σειρά σύνδεση 1/Κολ=1/Κ1+1/Κ2+. Όταν έχουµε ταλάντωση για πολύ µικρές τιµές πλάτους, στην απόδειξη του ότι εκτελείται Γ.Α.Τ. πρέπει να κάνουµε κάποιες αναγκαίες προσεγγίσεις, όπως: Αν έχουµε πολύ µικρή γωνία φ, τότε ηµφ 0 και συνφ 1. Αν έχουµε πολύ µικρή αποµάκρυνση x, τότε x² 0 και α+βx α. Η ΠΕΡΙΠΤΩΣΗ ΤΗΣ ΚΡΟΥΣΗΣ Αν έχουµε ελαστική ή ηµιελαστική κρούση χωρίς να µεταβάλλεται η µάζα του ταλαντωτή, τότε η Θ.Ι του συστήµατος παραµένει η ίδια. Αν έχουµε πλαστική κρούση, και γενικότερα αν µεταβάλλεται η µάζα του ταλαντωτή, τότε αλλάζει και η Θ.Ι., εκτός αν έχουµε πλαστική κρούση σε λείο οριζόντιο επίπεδο. Όταν αλλάζει η Θ.Ι., πρέπει και πάλι να εφαρµόσουµε τη σχέση ΣFx=0 για τη νέα Θ.Ι.. Προσοχή, όταν µεταβάλλεται η µάζα του ταλαντωτή, τότε µεταβάλλεται και η περίοδός του. Επίσης η Θ.Ι. αλλάζει και στην περίπτωση που έχουµε διάσπαση συστήµατος σωµάτων. Βαγγέλης Κολτσάκης Σελίδα 5 από 6
6 Γενικά, αν έχουµε κρούση, τότε η στιγµή αµέσως µετά την κρούση είναι η στιγµή t=0 της ΑΑΤ. (πρέπει να δείξω ότι το σώµα θα εκτελέσει ΑΑΤ και να υπολογίσω την D) Από την Α Ο βρίσκω την ταχύτητα του σώµατος τη στιγµή t=0. Βρίσκω την ΘΙΤ, οπότε, αφού γνωρίζω που βρίσκεται το σώµα την t=0 (στη θέση της κρούσης), γνωρίζω και την αποµάκρυνση τη στιγµή t=0. Από τη σχέση 1/2 Dx² + 1/2 mu² = 1/2 DA² βρίσκω το πλάτος της ταλάντωσης. Μπορώ πλέον να βρω την αρχική φάση, τις εξισώσεις κίνησης κλπ. Η ΠΕΡΙΠΤΩΣΗ ΣΩΜΑΤΟΣ ΣΕ ΕΠΑΦΗ ΜΕ ΕΠΙΦΑΝΕΙΑ ***Έστω σώµα πάνω σε δίσκο που ταλαντώνεται κατακόρυφα. Σε κάθε θέση ισχύει ΣF=-Dx N-B=-Dx. Επαφή χάνεται όταν Ν=0. Αυτό µπορεί να συµβεί µόνο όταν το σύστηµα κινείται πάνω από τη θέση ισορροπίας, αφού: πάνω από τη Θ.Ι. ισχύει ΣF=-Dx N-B=-Dx Ν=B-Dx και η επαφή χάνεται όταν Ν=0 Β=Dx x=b/d. κάτω από τη Θ.Ι. ισχύει ΣF=-Dx N-B=-D(-x) Ν=B+Dx και η επαφή δεν χάνεται ποτέ. Επίσης, από τα παραπάνω προκύπτει ότι Nmin=B-DA, Nmax=B+DA. ***Προσοχή, σε περιπτώσεις ως την προηγούµενη, το σώµα, ο δίσκος και όλο το σύστηµα έχουν διαφορετικές σταθερές ταλάντωσης D. Έχουν όµως κοινή περίοδο Τ. Ισχύει: Dσώµατος=mσώµατοςω², Dδίσκου=mδίσκουω², Dσυστήµατος =mσυστήµατοςω², Στις περιπτώσεις αυτές χρησιµοποιούµε τη σχέση ΣF=ma ΣF=mω²x, όπου m η µάζα του σώµατος ή του δίσκου ή όλου του συστήµατος, δηλ. Του σώµατος στο οποίο αναφέρονται οι δυνάµεις. Στην εφαρµογή των παραπάνω θέσεων η θετική φορά επιλέγεται προς τη Θ.Ι.. ***Έστω σώµα πάνω σε επιφάνεια η οποία ταλαντώνεται οριζόντια. Σε κάθε θέση, η δύναµη επαναφοράς για το σώµα είναι η στατική τριβή Τσ, που έχει πάντα κατεύθυνση προς τη Θ.Ι. και µέτρο ΣFx=ma Τσ=mω²x. Η µέγιστη τιµή της είναι Τσ,max=mω²A. Το σώµα χάνει την επαφή του µε την επιφάνεια στη θέση που η στατική τριβή γίνεται ίση µε την οριακή τριβή, η οποία θεωρείται ίση µε την τριβή ολίσθησης. ηλαδή η επαφή χάνεται όταν mω²x=nn. Βαγγέλης Κολτσάκης Σελίδα 6 από 6
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Β.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
Ημερομηνία: Παρασκευή 27 Οκτωβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
Ενδεικτικές Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Α.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
Τηλ./Fax: , Τηλ: Λεωφόρος Μαραθώνος &Χρυσοστόµου Σµύρνης 3, 1
 . 1. Η απλή αρµονική ταλάντωση είναι κίνηση: α. ευθύγραµµη οµαλή β. ευθύγραµµη οµαλά µεταβαλλόµενη γ. οµαλή κυκλική δ. ευθύγραµµη περιοδική. Η φάση της αποµάκρυνσης στην απλή αρµονική ταλάντωση: α. αυξάνεται
. 1. Η απλή αρµονική ταλάντωση είναι κίνηση: α. ευθύγραµµη οµαλή β. ευθύγραµµη οµαλά µεταβαλλόµενη γ. οµαλή κυκλική δ. ευθύγραµµη περιοδική. Η φάση της αποµάκρυνσης στην απλή αρµονική ταλάντωση: α. αυξάνεται
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις. Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 2 Σεπτέµβρη 204 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Σύστηµα ελατηρίου - σώµατος εκτελεί απλή αρµονική ταλάντωση πλάτους Α.
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 2 Σεπτέµβρη 204 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Σύστηµα ελατηρίου - σώµατος εκτελεί απλή αρµονική ταλάντωση πλάτους Α.
Πρόχειρες Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Πρόχειρες Λύσεις Θέµα Α Α.1 Σε µια εξαναγκασµένη ταλάντωση η συχνότητα του διεγέρτη είναι µεγαλύτερη της ιδιοσυχνότητας του ταλαντωτή. Αν µειώνουµε συνεχώς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Πρόχειρες Λύσεις Θέµα Α Α.1 Σε µια εξαναγκασµένη ταλάντωση η συχνότητα του διεγέρτη είναι µεγαλύτερη της ιδιοσυχνότητας του ταλαντωτή. Αν µειώνουµε συνεχώς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Β έκδοση Θέµα Α Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΤΑΛΑΝΤΩΣΗ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ ΜΕ ΔΥΟ ΣΩΜΑΤΑ
 ΤΑΛΑΝΤΩΣΗ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ ΜΕ ΔΥΟ ΣΩΜΑΤΑ Σώμα είναι τοποθετημένο πάνω σε ορίζοντα δίσκο.ο δίσκος τιθεται σε οριζόντια αρμονικη ταλάντωση με συχνότητα f.αν ο συντελεστης μέγιστης στατικης τριβής μεταξύ
ΤΑΛΑΝΤΩΣΗ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ ΜΕ ΔΥΟ ΣΩΜΑΤΑ Σώμα είναι τοποθετημένο πάνω σε ορίζοντα δίσκο.ο δίσκος τιθεται σε οριζόντια αρμονικη ταλάντωση με συχνότητα f.αν ο συντελεστης μέγιστης στατικης τριβής μεταξύ
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
T 4 T 4 T 2 Τ Τ Τ 3Τ Τ Τ 4
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
1 Απλή Αρµονική Ταλάντωση
 ,Θετικής & Τεχνολογικής Κατεύθυνσης Καραδηµητρίου Ε. Μιχάλης http://perifysikhs.wordpress.com mixalis.karadimitriou@gmail.com Πρόχειρες Σηµειώσεις 2011-2012 1 Απλή Αρµονική Ταλάντωση 1.1 Περιοδικά Φαινόµενα
,Θετικής & Τεχνολογικής Κατεύθυνσης Καραδηµητρίου Ε. Μιχάλης http://perifysikhs.wordpress.com mixalis.karadimitriou@gmail.com Πρόχειρες Σηµειώσεις 2011-2012 1 Απλή Αρµονική Ταλάντωση 1.1 Περιοδικά Φαινόµενα
1. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος:
 ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ 0077 -- 00 Θέμα ο. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος: α. έχει την ίδια φάση με την επιτάχυνση α. β. είναι μέγιστη στις ακραίες
ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ 0077 -- 00 Θέμα ο. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος: α. έχει την ίδια φάση με την επιτάχυνση α. β. είναι μέγιστη στις ακραίες
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΑΠΑΝΤΗΣΕΙΣ. Η κινητική ενέργεια του κυλίνδρου λόγω της μεταφορικής του κίνησης δίνεται από την σχέση: Κ μετ = 1 m u 2 cm
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Γ έκδοση Α.1. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου. Ονοματεπώνυμο εξεταζόμενου:.
 Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου Ονοματεπώνυμο εξεταζόμενου:. Καμιά άλλη σημείωση δεν επιτρέπεται στα θέματα τα οποία θα παραδώσετε μαζί με το γραπτό σας. Οι απαντήσεις λοιπόν
Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου Ονοματεπώνυμο εξεταζόμενου:. Καμιά άλλη σημείωση δεν επιτρέπεται στα θέματα τα οποία θα παραδώσετε μαζί με το γραπτό σας. Οι απαντήσεις λοιπόν
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα
 Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις. Ενδεικτικές Λύσεις. Θέµα Α
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθµό της
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθµό της
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
1. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος:
 ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ 33 0077 -- 00 Θέμα ο. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος: α. έχει την ίδια φάση με την επιτάχυνση α. β. είναι μέγιστη στις ακραίες
ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ 33 0077 -- 00 Θέμα ο. Ένα σώμα εκτελεί ΑΑΤ πλάτους Α. Η ταχύτητα του σώματος: α. έχει την ίδια φάση με την επιτάχυνση α. β. είναι μέγιστη στις ακραίες
 ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
Θέμα 1 ο (Μονάδες 25)
 ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση. Θέµα 2ο
 1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση Θέµα 1ο 1.1. Η εξίσωση της αποµάκρυνσης ενός υλικού σηµείου, που εκτελεί απλή αρµονική ταλάντωση πλάτους Α και γωνιακής συχνότητας ω, είναι της µορφής x =
1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση Θέµα 1ο 1.1. Η εξίσωση της αποµάκρυνσης ενός υλικού σηµείου, που εκτελεί απλή αρµονική ταλάντωση πλάτους Α και γωνιακής συχνότητας ω, είναι της µορφής x =
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις ευτέρα 3 Σεπτέµβρη 2018 Θέµα Α
 Α.1. ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις ευτέρα 3 Σεπτέµβρη 2018 Θέµα Α Ακίνητο πυροβόλο όπλο εκπυρσοκροτεί (δ) Η ορµή του συστήµατος
Α.1. ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις ευτέρα 3 Σεπτέµβρη 2018 Θέµα Α Ακίνητο πυροβόλο όπλο εκπυρσοκροτεί (δ) Η ορµή του συστήµατος
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Η απλή αρµονική ταλάντωση είναι κίνηση : (δ) ευθύγραµµη περιοδική Α.2. Σώµα εκτελεί απλή αρµονική
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση ΙΙ - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Η απλή αρµονική ταλάντωση είναι κίνηση : (δ) ευθύγραµµη περιοδική Α.2. Σώµα εκτελεί απλή αρµονική
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Β ΦΑΣΗ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΑΠΑΝΤΗΣΕΙΣ. ΕΡΩΤΗΣΗ Α1 Α2 Α3 Α4 ΑΠΑΝΤΗΣΗ δ β β γ.
 ΤΑΞΗ: ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 06 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 06 ιάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΕΡΩΤΗΣΗ Α Α Α3 Α4 ΑΠΑΝΤΗΣΗ δ β
ΤΑΞΗ: ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 06 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 06 ιάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΕΡΩΤΗΣΗ Α Α Α3 Α4 ΑΠΑΝΤΗΣΗ δ β
Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής
 Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής Σώµα µάζας m=kg ισορροπεί δεµένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=00 N/m, το άλλο άκρο του οποίου είναι στερεωµένο ακλόνητα στο
Ταλάντωση, γραφικές παραστάσεις και ρυθµοί µεταβολής Σώµα µάζας m=kg ισορροπεί δεµένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=00 N/m, το άλλο άκρο του οποίου είναι στερεωµένο ακλόνητα στο
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις. Λύσεις. Θέµα Α
 2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Λύσεις Θέµα Α Α.1. Απλός αρµονικός ταλαντωτής εκτελεί ταλάντωση πλάτους Α. ιατηρούµε σταθερό το πλάτος
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Λύσεις Θέµα Α Α.1. Απλός αρµονικός ταλαντωτής εκτελεί ταλάντωση πλάτους Α. ιατηρούµε σταθερό το πλάτος
ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 1 Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β Ερώτηση 1. ΘΕΜΑ Β Σώμα εκτελεί Α.Α.Τ. με εξίσωση απομάκρυνσης
ΚΕΦΑΛΑΙΟ 1 Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) 1ο σετ - Μέρος Β Ερώτηση 1. ΘΕΜΑ Β Σώμα εκτελεί Α.Α.Τ. με εξίσωση απομάκρυνσης
1. Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα.
 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / ΘΕΜΑ Α Α1. α, Α2. α, Α3. β, Α4. γ, Α5. α. Σ, β. Σ, γ. Λ, δ. Σ, ε. Λ.
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. α, Α2. α, Α3. β, Α4. γ, Α5. α. Σ, β. Σ, γ. Λ, δ. Σ, ε. Λ. ΘΕΜΑ Β Β1. Σωστή απάντηση είναι η γ. Ο αριθμός των υπερβολών ενισχυτικής συμβολής που τέμνουν την
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. α, Α2. α, Α3. β, Α4. γ, Α5. α. Σ, β. Σ, γ. Λ, δ. Σ, ε. Λ. ΘΕΜΑ Β Β1. Σωστή απάντηση είναι η γ. Ο αριθμός των υπερβολών ενισχυτικής συμβολής που τέμνουν την
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΛΑΓΙΑ ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Ημερομηνία: Τετάρτη 26 Οκτωβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ 6/0/06 ΕΩΣ 30/0/06 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τετάρτη 6 Οκτωβρίου 06 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΘΕΜΑ Α. Α.1. Ένα σύστηµα ελατηρίου-µάζας εκτελεί απλή αρµονική ταλάντωση πλάτους Α.
 ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΜΕ ΣΩΜΑΤΑ ΣΕ ΕΠΑΦΗ. Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.
 Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.. Σώμα μάζας = 0,5 g έχει το ένα άκρο στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς = 50 / και το άλλο άκρο του βρίσκεται
Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.. Σώμα μάζας = 0,5 g έχει το ένα άκρο στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς = 50 / και το άλλο άκρο του βρίσκεται
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Μια µικρή σφαίρα προσκρούει ελαστικά στην επίπεδη επιφάνεια ενός κατακόρυφου τοίχου. Αν η σφαίρα κτυπήσει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Μια µικρή σφαίρα προσκρούει ελαστικά στην επίπεδη επιφάνεια ενός κατακόρυφου τοίχου. Αν η σφαίρα κτυπήσει
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις
 1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Οµάδα Β Στις ηµιτελείς
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Οµάδα Β Στις ηµιτελείς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις Σύνολο Σελίδων: οχτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 13 Αυγούστου 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση Ι - Κρούσεις Σύνολο Σελίδων: οχτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 13 Αυγούστου 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ.
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις
 1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Οµάδα Α Στις ηµιτελείς
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Οµάδα Α Στις ηµιτελείς
ΛΥΣΕΙΣ. Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 01-013 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΟΦΟΙΤΟΙ ΗΜΕΡΟΜΗΝΙΑ: /10/1 ΘΕΜΑ 1 ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 01-013 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΟΦΟΙΤΟΙ ΗΜΕΡΟΜΗΝΙΑ: /10/1 ΘΕΜΑ 1 ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση
 Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
1 η χρονική στιγμή της
 ΩΘΗΣΗ ΚΑΙ.ΑΠΟ ΤΟ ΖΕΝΙΘ ΣΤΟ ΝΑΔΙΡ Ένα σώμα μάζας είναι στερεωμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου φυσικού μήκους και σταθεράς σκληρότητας, το πάνω άκρο του οποίου είναι στερεωμένο σε οροφή.
ΩΘΗΣΗ ΚΑΙ.ΑΠΟ ΤΟ ΖΕΝΙΘ ΣΤΟ ΝΑΔΙΡ Ένα σώμα μάζας είναι στερεωμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου φυσικού μήκους και σταθεράς σκληρότητας, το πάνω άκρο του οποίου είναι στερεωμένο σε οροφή.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Β έκδοση Στις ηµιτελείς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Β έκδοση Στις ηµιτελείς
Στα ερωτήματα 1,2.3,4 του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε)
 Ζήτημα ο Στα ερωτήματα,., του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε. Ένα σώμα κάνει απλή αρμονική ταλάντωση στην οποία η απομάκρυνση είναι της μορφής χ=aημωt κάποια στιγμή t η φάση του
Ζήτημα ο Στα ερωτήματα,., του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε. Ένα σώμα κάνει απλή αρμονική ταλάντωση στην οποία η απομάκρυνση είναι της μορφής χ=aημωt κάποια στιγμή t η φάση του
Φυσική Γ Λυκείου Θετικού Προσανατολισμού Σχ. έτος Διαγώνισμα Κρούσεις - Ταλαντώσεις. Δευτέρα 3 Σεπτεμβρίου Θέμα Α
 Διαγώνισμα Κρούσεις - Ταλαντώσεις Δευτέρα 3 Σεπτεμβρίου 2018 Θέμα Α Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και, δίπλα, το γράμμα που αντιστοιχεί στη ϕράση
Διαγώνισμα Κρούσεις - Ταλαντώσεις Δευτέρα 3 Σεπτεμβρίου 2018 Θέμα Α Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και, δίπλα, το γράμμα που αντιστοιχεί στη ϕράση
2 ο Διαγώνισμα Γ Λυκείου
 ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
12ο ΓΕΛ ΠΕΙΡΑΙΑ 12/10/2010 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ
 1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Τρίτη 1 Αυγούστου 2017 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ / ΤΜΗΜΑ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΟΥΛΙΟY 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 3 Αυγούστου 2014 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις. Θέµα Α
 1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 3 Αυγούστου 2014 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια χρονική
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 3 Αυγούστου 2014 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια χρονική
1.1 Κινηματική προσέγγιση
 1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
Ποια μπορεί να είναι η κίνηση μετά την κρούση;
 Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ονοματεπώνυμο: Επιμέλεια διαγωνίσματος: Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Σύνολο Σελίδων: επτά (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Σύνολο Σελίδων: επτά (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς
Physics by Chris Simopoulos
 ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ. ΣΥΣΤΗΜΑΤΑ ΠΟΥ ΕΚΤΕΛΟΥΝ ΓΡΑΜΜΙΚΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ. Για να δείξω ότι ένα σώμα εκτελεί γραμμική αρμονική ταλάντωση ακολουθώ τον εξής τρόπο. Ι. Σχεδιάζω το σχήμα και τοποθετώ τις δυνάμεις
ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ. ΣΥΣΤΗΜΑΤΑ ΠΟΥ ΕΚΤΕΛΟΥΝ ΓΡΑΜΜΙΚΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ. Για να δείξω ότι ένα σώμα εκτελεί γραμμική αρμονική ταλάντωση ακολουθώ τον εξής τρόπο. Ι. Σχεδιάζω το σχήμα και τοποθετώ τις δυνάμεις
[ Απ. α) , β) µατος. Εκτρέπουµε το σύστηµα προς τα κάτω κατά x=0,5 m και το αφήνουµε ελεύθερο.
 47. Σώµα (Σ 1 ) είναι τοποθετηµένο πάνω σε σώµα (Σ ) και το σύστηµα εκτελεί Α.Α.Τ. κατακόρυφα µε περίοδο Τ. α) Να εκφράσετε τη δύναµη αντίδρασης F του σώµατος (Σ ) στο σώµα (Σ 1 ), σε συνάρτηση µε την
47. Σώµα (Σ 1 ) είναι τοποθετηµένο πάνω σε σώµα (Σ ) και το σύστηµα εκτελεί Α.Α.Τ. κατακόρυφα µε περίοδο Τ. α) Να εκφράσετε τη δύναµη αντίδρασης F του σώµατος (Σ ) στο σώµα (Σ 1 ), σε συνάρτηση µε την
5. Ένα σώµα ταλαντώνεται µεταξύ των σηµείων Α και Ε. Στο σχήµα φαίνονται πέντε θέσεις Α,Β,Γ, και Ε, οι οποίες ισαπέχουν µεταξύ 1
 1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
Physics by Chris Simopoulos. Η μάζα m χάνει την επαφή της όταν F=0 A 2. 2 Δεκτή η τιμή με το θετικό πρόσημο (δεύτερο τεταρτημόριο) 5 rad 5.
 . ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ ΛΥΣΕΙΣ. ( ) (f) 8 ) (f ), / sec γ) Τυχαία Θέση: F F B F F B D F B F g D () Η μάζα χάνει την επαφή της όταν F= () g D g. rad / sec U U U U U U U g (f ) D Δεκτή
. ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΣΗΣ ΛΥΣΕΙΣ. ( ) (f) 8 ) (f ), / sec γ) Τυχαία Θέση: F F B F F B D F B F g D () Η μάζα χάνει την επαφή της όταν F= () g D g. rad / sec U U U U U U U g (f ) D Δεκτή
Ταλαντώσεις. =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του.
 Ταλαντώσεις Άσκηση 1 η Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και την χρονική στιγμή t=0s βρίσκεται στην θέση =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του. Για t=0s, =+, υ>0 =+ 2 = =
Ταλαντώσεις Άσκηση 1 η Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και την χρονική στιγμή t=0s βρίσκεται στην θέση =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του. Για t=0s, =+, υ>0 =+ 2 = =
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 3-0-0 ΧΕΙΜΕΡΙΝΑ ΘΕΜΑ ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
3-0-0 ΧΕΙΜΕΡΙΝΑ ΘΕΜΑ ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ - ΑΣΚΗΣΕΙΣ
 ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση
 Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Α ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Τρίτη 5 Ιανουαρίου 016 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από 1-4 να γράψετε στο τετράδιο σας
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Τρίτη 5 Ιανουαρίου 016 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από 1-4 να γράψετε στο τετράδιο σας
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012 ΘΕΜΑ Α A 1. Α 2. Α 3. Α 4. γ β γ γ Α 5. α. Σ β. Σ γ. Λ δ. Λ ε. Σ ΘΕΜΑ Β Β 1. Σωστή η απάντηση γ Αιτιολόγηση: Για την αρχική
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ 2012 ΘΕΜΑ Α A 1. Α 2. Α 3. Α 4. γ β γ γ Α 5. α. Σ β. Σ γ. Λ δ. Λ ε. Σ ΘΕΜΑ Β Β 1. Σωστή η απάντηση γ Αιτιολόγηση: Για την αρχική
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
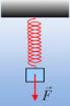 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 2016 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 06 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α δ Α β Α γ Α δ Α5 α Σ, β Σ, γ Λ, δ Λ, ε Σ. ΘΕΜΑ Β Β.α. Σωστό το ii. β.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 06 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α δ Α β Α γ Α δ Α5 α Σ, β Σ, γ Λ, δ Λ, ε Σ. ΘΕΜΑ Β Β.α. Σωστό το ii. β.
m αντίστοιχα, εκτελούν Α.Α.Τ. και έχουν την
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Ερώτηση. ΘΕΜΑ Β Δύο σώματα με μάζες m m και m m αντίστοιχα, εκτελούν Α.Α.Τ.
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Ερώτηση. ΘΕΜΑ Β Δύο σώματα με μάζες m m και m m αντίστοιχα, εκτελούν Α.Α.Τ.
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
Σε πολλές περιπτώσεις έχουμε δύο σώματα που εκτελούν ταλάντωση τα οποία βρίσκονται σε επαφή
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΣΩΜΑΤΑ ΣΕ ΕΠΑΦΗ Σε πολλές περιπτώσεις έχουμε δύο σώματα που εκτελούν ταλάντωση τα οποία βρίσκονται σε επαφή μεταξύ τους. Η επαφή αυτή μπορεί να υπάρχει στη διάρκεια της ταλάντωσης είτε να
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΣΩΜΑΤΑ ΣΕ ΕΠΑΦΗ Σε πολλές περιπτώσεις έχουμε δύο σώματα που εκτελούν ταλάντωση τα οποία βρίσκονται σε επαφή μεταξύ τους. Η επαφή αυτή μπορεί να υπάρχει στη διάρκεια της ταλάντωσης είτε να
