ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ. Τμήμα Ηλεκτρονικής. Πτυχιακή Εργασία
|
|
|
- Πρόκρις Γαλάνης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τμήμα Ηλεκτρονικής Πτυχιακή Εργασία Υλοποίηση σύγχρονων ακολουθιακών κυκλωμάτων σε VHDL για FPGAs/CPLDs και ανάλυση χρονισμών για εύρεση της μέγιστης συχνότητας λειτουργίας. ΠΑΛΥΒΟΣ ΙΩΑΝΝΗΣ Α.Μ Λαμία Αύγουστος
2 Περιεχόμενα 1. Λογικά Κυκλώματα 1.1 Βασικά Ακολουθιακά Κυκλώματα 1.2 Flip Flops Το βασικό FF (SR) Χρονιζόμενα FF τύπου SR FF τύπου D JK Flip Flop FF τύπου Τ 2. Σύγχρονα Ακολουθιακά Κυκλώματα 2.1 Βασικές έννοιες για τα ΣΑΚ 2.2 Ανάλυση ΣΑΚ ΣΑΚ χωρίς εξωτερικές εισόδους και εξόδους ΣΑΚ με εξωτερικές εισόδους ΣΑΚ με εξωτερικές εισόδους και εξόδους 3. Απαριθμητές και καταχωρητές 3.1 Ασύγχρονοι απαριθμητές Ασύγχρονοι δυαδικοί απαριθμητές Ασύγχρονοι μη-δυαδικοί απαριθμητές 3.2 Σύγχρονοι απαριθμητές Σύγχρονοι δυαδικοί απαριθμητές Σύγχρονοι μη-δυαδικοί απαριθμητές 3.3 Καταχωρητές Σειριακής-εισόδου-σειριακής-εξόδου Σειριακής-εισόδου-παράλληλης-εξόδου Παράλληλης-εισόδου-παράλληλης-εξόδου Παράλληλης-εισόδου-σειριακής-εξόδου 2
3 4. VHDL 4.1 Γενικά για την VHDL 4.2 Δομή της VHDL 4.3 FPGA 4.4 Βασικά τμήματα κώδικα VHDL Διεργασίες ακολουθιακού κώδικα Συχνά χρησιμοποιούμενες ακολουθιακές εντολές Καταχωρητής, πακέτο και συστατικό στοιχείο Προκαθορισμένοι τελεστές 5. Αλγόριθμος 6. Ανάλυση Εντολών Αλγορίθμου 7. Ανάλυση χρονισμών 7.1 Clock Setup Time 7.2 Clock Hold Time 7.3 Clock to Output Delay 7.4 Maximum Clock Frequency 7.5 Slack 7.6 Ανάλυση του χρονισμού 7.7 Τρόπος εύρεσης μέγιστης συχνότητας FPGA 8. Βιβλιογραφία 3
4 Λίστα Σχημάτων Σχήμα 1.1 Λογικό 1 και 0 Δυαδικού Σήματος Σελίδα 8 Σχήμα 1.2 Σύμβολο λογικών κυκλωμάτων Σελίδα 9 Σχήμα 1.3 Σήματος εισόδου και εξόδου του σχήματος 1.2 Σελίδα 9 Σχήμα 1.4 Το κύκλωμα Flip και το διάγραμμα χρονισμού του Σελίδα 11 Σχήμα 1.5 SR μανταλωτής κατασκευασμένος με πύλες NOR Σελίδα 12 Σχήμα 1.6 Διάγραμμα χρονισμού του SR μανταλωτή Σελίδα 13 Σχήμα 1.7 Χρονιζόμενο SR FF με πύλες ΝOR και NAND Σελίδα 14 Σχήμα 1.8 Κυματομορφές εισόδου-εξόδου SR μανταλωτή με CLK Σελίδα 15 Σχήμα 1.9 FF τύπου D Σελίδα 16 Σχήμα 1.10 Κυματομορφές εισόδου-εξόδου του μανταλωτή τύπου D Σελίδα 16 Σχήμα 1.11 FF τύπου JK Σελίδα 17 Σχήμα 1.12 FF τύπου T Σελίδα 18 Σχήμα 2.1 Κύκλωμα Moore Mealy Σελίδα 20 Σχήμα 2.2 ΣΑΚ με δυο FFs Σελίδα 21 Σχήμα 2.3 Διάγραμμα κατάστασης του σχήματος 2.2 Σελίδα 23 Σχήμα 2.4 ΣΑΚ με FFs τύπου JK με εξωτερική έξοδο Σελίδα 23 Σχήμα 2.5 Διάγραμμα κατάστασης του σχήματος 2.4 Σελίδα 25 Σχήμα 2.6 ΣΑΚ με Τα FFs και εξωτερική είσοδο και έξοδο Σελίδα 26 Σχήμα 2.7 Διάγραμμα κατάστασης του σχήματος 2.6 Σελίδα 28 Σχήμα 3.1 Ασύγχρονος προσθετικός δυαδικός απαριθμητής mod-8 Σελίδα 30 Σχήμα 3.2 Ασύγχρονος αφαιρετικός δυαδικός απαριθμητής mod-8 Σελίδα 33 Σχήμα 3.3 Ασύγχρονος δεκαδικός απαριθμητής Σελίδα 34 Σχήμα 3.4 Σύγχρονος προσθετικός δυαδικός απαριθμητής mod-8 Σελίδα 35 Σχήμα 3.5 Τύποι Καταχωρητών Σελίδα 37 Σχήμα 3.6 Καταχωρητές ολίσθησης Σειριακής εισόδου Σειριακής εξόδου 4 bit Σελίδα Σχήμα 3.7 Καταχωρητές ολίσθησης Σειριακής εισόδου Παράλληλης εξόδου 4 bit Σελίδα 39 Σχήμα 3.8 Καταχωρητές Παράλληλης εισόδου παράλληλης εξόδου με FF τύπου D Σελίδα 40 Σχήμα 3.9 Καταχωρητές Παράλληλης εισόδου Παράλληλης εξόδου 4 bit με FF τύπου SR Σελίδα 41 Σχήμα 3.10 Καταχωρητές ολίσθησης Παράλληλης εισόδου Παράλληλης εξόδου 4 bit Σελίδα 42 Σχήμα 3.11 Καταχωρητής 8 bit κατασκευασμένος από δυο καταχωρητές 4 bit Σελιδα 43 4
5 Σχήμα 4.1 Δομή της VHDL Σελίδα 44 Σχήμα 4.2 Συνδυαστική λογική Σελίδα 46 Σχήμα 4.3 Καταχωρητής 4-bit Σελίδα 50 Σχήμα 4.4 Θεμελιώδης μονάδες κώδικα VHDL Σελίδα 51 Σχήμα 7.1 Clock Setup Time Σελίδα 67 Σχήμα 7.2 Clock Hold Time Σελίδα 68 Σχήμα 7.3 Clock to Output Delay Σελίδα 69 Σχήμα 7.4 Slack Σελίδα 70 5
6 Λίστα Πινάκων Πίνακας 1.1 Κύρια χαρακτηριστικά Σύγχρονου και Ασύγχρονου Α.Κ. Σελίδα 10 Πίνακας 2.1 Πίνακας καταστάσεων του σχήματος 2.2 Σελίδα 22 Πίνακας 2.2 Πίνακας καταστάσεων του σχήματος 2.4 Σελίδα 25 Πίνακας 2.3 Πίνακας καταστάσεων του σχήματος 2.6 Σελίδα 27 6
7 Περίληψη Στο πρώτο κεφάλαιο της εργασίας κάνουμε μια σύντομη αναφορά στα λογικά κυκλώματα και τα Flip Flop. Συνεχίζουμε με Σύγχρονα ακολουθιακά κυκλώματα και μελετάμε την μεθοδολογία ανάλυσης και σχεδίασης τέτοιων κυκλωμάτων. Στο κεφάλαιο τρία με τους απαριθμητές, σύγχρονους και ασύγχρονους. Οι σύγχρονοι δεν είναι κάτι άλλο παρά σύγχρονα ακολουθιακά κυκλώματα τα οποία σχεδιάζονται έτσι ώστε να βρίσκουν εφαρμογή στη απαρίθμηση παλμών. Στο ίδιο κεφάλαιο αναφερόμαστε στους καταχωρητές για σειριακή και παράλληλη είσοδο δεδομένων καθώς και την σειριακή και παράλληλη έξοδο αυτών. Παρατηρούμε ότι πρόκειται για ΣΑΚ τα οποία κατασκευάζονται από FF τύπου D, SR και JK.Τα κυκλώματα αυτά μπορούμε να τα χρησιμοποιήσουμε για προσωρινή αποθήκευση δεδομένων τα οποία μεταφέρονται παράλληλα ή σειριακά. Τέλος, χρησιμοποιούνται για την υλοποίηση ορισμένων απλών αριθμητικών πράξεων πολλαπλασιασμού ή διαίρεσης αριθμών με πράξεις του δυο. Έπειτα, αναφερόμαστε στη γλώσσα προγραμματισμού VHDL και συνεχίζουμε με τον αλγόριθμο που φτιάξαμε αναλύοντας μια μια εντολή ξεχωριστά. Στο τελευταίο κεφάλαιο μιλάμε για την την μέγιστη συχνότητα λειτουργίας ενός FPGA, πως την βρίσκουμε και από ποια στοιχεία αναλύεται. 7
8 1. ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός αυτής της παραγράφου είναι να μελετήσουμε ένα βασικό κύτταρο μνήμης ενός bit, που είναι το flip flop (FF). Ένα κύκλωμα με flip flop μπορεί να διατηρηθεί σε μια δυαδική κατάσταση επ αόριστον (εφόσον το τροφοδοτούμε με ισχύ), έως ότου κάποιο σήμα εισόδου το κάνει να αλλάξει κατάσταση. Υπάρχουν τέσσερα είδη FFs και οι διαφορές ανάμεσά τους είναι ο αριθμός των εισόδων που έχουν και ο τρόπος με τον οποίο αυτές οι είσοδοι επηρεάζουν την δυαδική τους κατάσταση. Σχήμα 1.1 Λογικό 1 και 0 δυαδικού σήματος Τα ηλεκτρονικά ψηφιακά κυκλώματα λέγοντα επίσης και λογικά κυκλώματα, επειδή με τις κατάλληλες εισόδους παράγουν εξόδους που είναι λογικές συναρτήσεις. Μπορούμε να επεξεργαστούμε οποιαδήποτε πληροφορία 8
9 υπολογισμού ή ελέγχου περνώντας δυαδικά σήματα από διάφορους συνδυασμούς λογικών κυκλωμάτων όπου κάθε σήμα παριστάνει μια μεταβλητή και μεταφέρει ένα bit πληροφορίας. Το σχήμα 1.2 δείχνει τα σύμβολα των κυκλωμάτων που πραγματοποιούν τις λογικές πράξεις ΚΑΙ, Ή, ΌΧΙ (AND, OR, NOT). Αυτά τα κυκλώματα ονομάζονται πύλες (gates) που παράγουν το λογικό 1 ή το λογικό 0 ως σήμα εξόδου (σχήμα 1.1). Σχήμα 1.2 Σύμβολα λογικών κυκλωμάτων Τα δύο σήματα εισόδων x και y στις πύλες δυο εισόδων του σχήματος 1.2 μπορούν να βρίσκονται σε μία από τις τέσσερις δυνατές καταστάσεις: 00, 01, 10, 11. Αυτά τα σήματα φαίνονται στο σχήμα 1.3 μαζί με τα σήματα εξόδου για τις πύλες ΚΑΙ και Ή. Τα χρονικά διαγράμματα δείχνουν την απόκριση κάθε κυκλώματος σε καθέναν από τους τέσσερις δυνατούς δυαδικούς αριθμούς εισόδου. Ο λόγος που η πύλη ΟΧΙ ονομάζεται αντιστροφέας φαίνεται συγκρίνοντας το σήμα x (είσοδός του) και το x (έξοδός του). Το μαθηματικό σύστημα της δυαδικής λογικής είναι γνωστό σαν Άλγεβρα Boole. Οι σχεδιαστές ψηφιακών συστημάτων χρησιμοποιούν την Άλγεβρα Boole για να μετατρέπουν διαγράμματα κυκλωμάτων σε αλγεβρικές φράσεις, και αντίστροφα. Σχήμα 1.3 Σήματα εισόδου εξόδου για τις πύλες του σχήματος 1.2 9
10 1.1 Βασικά ακολουθιακά κυκλώματα Τα λογικά κυκλώματα των ψηφιακών συστημάτων μπορεί να είναι συνδυαστικά (combinational) ή ακολουθιακά (sequential). Ένα συνδυαστικό κύκλωμα αποτελείται από λογικές πύλες των οποίων οι έξοδοι καθορίζονται από τις εισόδους εκείνης της στιγμής και δεν εξαρτώνται καθόλου από προηγούμενες τιμές των εισόδων. Τα κυκλώματα με τα οποία μας ενδιαφέρουν είναι τα ακολουθιακά. Στα ακολουθιακά κυκλώματα, οι έξοδοι σε κάθε χρονική στιγμή εξαρτώνται όχι μόνο από τις τιμές των εισόδων τη χρονική εκείνη στιγμή, αλλά και από τις τιμές των εξόδων την προηγούμενη χρονική στιγμή. Τα ακολουθιακά κυκλώματα χωρίζονται σε δυο μεγάλες κατηγορίες, στα σύγχρονα (synchronous) και στα ασύγχρονα (asynchronous), ανάλογα με το αν αυτά επηρεάζονται σε συγκεκριμένες χρονικές στιγμές ή όχι. Αυτό σημαίνει ότι τα σύγχρονα ακολουθιακά κυκλώματα (ΣΑΚ) λειτουργούν σύμφωνα με κάποιο παλμό χρονισμού (ρολόι, clock). Οποιεσδήποτε αλλαγές στη έξοδο (κατάσταση) ενός ΣΑΚ συμβαίνουν σε συγκεκριμένες (διακριτές) χρονικές στιγμές. Αποτέλεσμα αυτού είναι ότι τα ΣΑΚ δεν παρουσιάζουν προβλήματα αστάθειας και ο χρονισμός τους μπορεί εύκολα να αναλυθεί σε ανεξάρτητα διακριτά βήματα. Αντίθετα, η συμπεριφορά ενός ασύγχρονου ακολουθιακού κυκλώματος εξαρτάται από τη σειρά με την οποία αλλάζουν οι παλμοί εισόδου του και μπορεί να επηρεασθεί σε οποιαδήποτε χρονική στιγμή. Ένα συνδυαστικό κύκλωμα με ανατροφοδότηση (feedback) αποτελεί ουσιαστικά ένα ασύγχρονο ακολουθιακό κύκλωμα. Εξαιτίας της ανατροφοδότησης, ένα τέτοιο κύκλωμα μπορεί να γίνει εύκολα ασταθές (unstable). ΠΙΝΑΚΑΣ 1.1 Κύρια χαρακτηριστικά των σύγχρονων και ασύγχρονων ακολουθιακών κυκλωμάτων 10
11 1.2 Flip Flops (FFs) Για να μπορέσουμε να παρακολουθήσουμε την αλληλουχία κάποιων γεγονότων θα πρέπει να έχουμε ένα κύκλωμα το οποίο να μπορεί να "θυμάται", δηλαδή να έχει μνήμη (memory). Το απλούστερο και πιο διαδεδομένο κύτταρο μνήμης είναι ο δισταθής πολυδονητής (bistable multivibrator), ο οποίος ονομάζεται flip-flop (FF). Σήμα κατατεθέν το FF είναι ότι η έξοδος της μιας τροφοδοτεί την είσοδο της άλλης, διαπιστώνοντας έτσι τον καταλυτικό ρόλο της ανα-τροφοδότησης στην λειτουργία των κυκλωμάτων Το βασικό Flip Flop (SR) Σχήμα 1.4 (α) Το κύκλωμα flip (β) Το διάγραμμα χρονισμού του Έστω ένα κύκλωμα flip flop με πύλη NOR και NOT όπως φαίνεται στο σχήμα 1.4(α) το οποίο έχει θετική ανατροφοδότηση (ανάδραση). Ας θεωρήσουμε ότι θέτοντας το κύκλωμα στην τροφοδοσία (power on) ο διακόπτης είναι γειωμένος (S=0) και η έξοδος Q=0. Η έξοδος της πύλης NOR είναι σε κατάσταση HIGH (Y=1). Το κύκλωμα ηρεμεί στην κατάσταση αυτή μέχρι τη χρονική στιγμή t 1 που ο διακόπτης εισόδου αλλάζει θέση και γίνεται S=1. Τότε γίνεται Y=0 και Q=1. Η νέα κατάσταση του κυκλώματος είναι πλέον και η μόνιμη κατάσταση αυτού. Ακόμη και αν επαναφέρουμε τον διακόπτη στην αρχική του θέση S=0 (τη χρονική στιγμή t 2 ), η έξοδος παραμένει στην κατάσταση Q=1, γιατί το Q αυτό επανατροφοδοτείται στην μία από τις δύο εισόδους της πύλης NOR, κρατώντας την έξοδό της στο λογικό 0 (Υ=0). Με άλλα λόγια, το λογικό αυτό κύκλωμα "θυμάται" ότι η είσοδος S έγινε κάποτε "1" (ΟΝ). Το πρόβλημά του όμως είναι ότι παραμένει στην κατάσταση αυτή για όσο χρόνο είναι στην τροφοδοσία. Δηλαδή, το κύκλωμα άλλαξε κατάσταση (flip) με την αλλαγή της θέσης του διακόπτη, αλλά δεν επανέρχεται. Πρόκειται για απλό κύκλωμα που ονομάζεται "flip" λόγω του τρόπου λειτουργίας του, με περιορισμένες όμως δυνατότητες χρήσης. Το διάγραμμα χρονισμού του δίνεται στο Σχήμα 1.4(β). 11
12 (γ) (δ) Σχήμα 1.5 SR μανταλωτής κατασκευασμένος με πύλες NOR (α) Το κύκλωμα flip (β) λογικό διάγραμμα (γ) πίνακας αληθείας (δ) σύμβολο Ας αντικαταστήσουμε τον αντιστροφέα του προηγούμενου σχήματος με μία πύλη NOR, όπως δείχνεται στο Σχήμα 1.5(α). Το κύκλωμα έχει τώρα δύο εισόδους, τις S και R, όπως φαίνεται και στο Σχήμα 1.5(β), και ονομάζεται SR flip-flop ή πιο σωστά SR μανταλωτής (SR latch). Ο μανταλωτής είναι ένας τύπος flip-flop χωρίς ρολόι ή με ρολόι το οποίο είναι ευαίσθητο στη διάρκεια του παλμού (level-sensitive clock). Οι είσοδοι S και R πήραν την ονομασία τους από τα αρχικά γράμματα των λέξεων SET και RESET αντίστοιχα. Η απόδοση της λέξης SET στην ελληνική γλώσσα θα είναι "ενεργοποίηση" ή "καθορισμός της εξόδου στο λογικό 1", ενώ εκείνη της λέξης RESET θα είναι "απενεργοποίηση" ή "εκκαθάριση" ή "μηδενισμός" ή "επαναφορά" της εξόδου. Με την λέξη έξοδο εννοούμε την Q η οποία αποτελεί και την κατάσταση (state) του FF, ενώ η έξοδος Q είναι συμπληρωματική της Q. Έστω S=1 και R=0. Τότε η έξοδος Q' της πύλης 2 είναι 0, ανεξάρτητα από την τιμή της άλλης εισόδου της πύλης αυτής. Συνεπώς, η πύλη 1 έχει και τις δύο εισόδους της στο λογικό 0 και άρα Q=1. Δηλαδή, για S=1, R=0 πήραμε Q=1 (και Q'=0). Με άλλα λόγια, ενεργοποιήσαμε το FF ή καθορίσαμε την κατάσταση του FF να γίνει 1 (SET). Αν τώρα αλλάξουμε την τιμή της εισόδου S και την κάνουμε 0 (S=0), αυτή η αλλαγή δεν επηρεάζει την κατάσταση του FF, η οποία παραμένει στο λογικό 1 Αυτό συμβαίνει διότι η άλλη είσοδος της πύλης 2 εξακολουθεί να είναι στο λογικό 1. Μπορούμε επομένως να πούμε ότι το FF "θυμάται" την προηγούμενη κατάσταση. Αλλάζοντας αυτή τη φορά την τιμή της εισόδου R και θέτοντας αυτή στο λογικό 1, δηλαδή R=1 και S=0. Για R=1 η έξοδος της πύλης 1 γίνεται 0 (Q=0) και κατά συνέπεια η έξοδος της πύλης 2 γίνεται 1 (Q'=1), αφού και στις δύο εισόδους της εφαρμόζεται το λογικό 0. Άρα, για S=0 και R=1 επιτύχαμε την "εκκαθάριση" ή "μηδενισμό" (RESET) του FF. Αν επαναφέρουμε την είσοδο R στο λογικό 0, οπότε S=0 και R=0, η κατάσταση του FF δεν αλλάζει, δηλαδή Q=0 και Q'=1. Άρα και πάλι μπορούμε να πούμε ότι το FF "θυμάται" την προηγούμενη κατάστασή του. Συνοψίζοντας μέχρι το σημείο αυτό, θα μπορούσαμε να ισχυρισθούμε ότι έχουμε καταφέρει να σχεδιάσουμε ένα βασικό στοιχείο μνήμης στο οποίο έχουμε τη δυνατότητα να αποθηκεύσουμε ένα δυαδικό ψηφίο 1 ή 0 ανάλογα αν S=1 και R=0 ή S=0 και R=1. Στην κανονική του λειτουργία και οι δύο είσοδοι S και R είναι στο 12
13 λογικό 0. Αλλάζουμε κάποια από τις δύο εισόδους μόνο όταν θέλουμε να αποθηκεύσουμε ένα νέο δεδομένο. Μετά την είσοδο του νέου δεδομένου, οι είσοδοι S και R επαναφέρονται στο λογικό 0. Με άλλα λόγια, όταν και οι δύο είσοδοι του FF είναι στο λογικό 0, τότε αυτό "θυμάται" ποια από τις δύο άλλαξε τελευταία. Τι θα συμβεί όμως εάν και οι δύο είσοδοι S και R γίνουν 1 (S=1, R=1); Στην περίπτωση αυτή και οι δύο έξοδοι των πυλών 1 και 2 γίνονται 0 (Q=0, Q'=0). Αυτές οι τιμές εξόδου αντιφάσκουν με το γεγονός της συμπληρωματικότητάς τους, δηλαδή ότι η μία (Q) να είναι συμπληρωματική της άλλης (Q'). Εάν μάλιστα συνεχίσουμε επαναφέροντας τις εισόδους στο λογικό 0 (S=0, R=0) τότε η κατάσταση (έξοδος) του FF θα είναι απροσδιόριστη. Εάν η είσοδος S γίνει 0, αφού ήδη έχει γίνει 0 η είσοδος R, τότε η έξοδος θα γίνει 1 (Q=1). Αν όμως η είσοδος R καθυστερήσει περισσότερο από την S να μεταβεί στο λογικό 0 (οπότε στιγμιαία θα έχουμε S=0 και R=1), τότε η έξοδος Q θα παραμείνει στο λογικό 0 (Q=0). Είναι φανερό ότι η περίπτωση S=R=1 του πίνακα αλήθειας πρέπει να αποφεύγεται. Σχήμα 1.6 Διάγραμμα χρονισμού του SR μανταλωτή του σχήματος 1.5 Σύμφωνα με την κυματομορφή της εξόδου Q του SR μανταλωτή του παραπάνω σχήματος και του σχήματος 1.5 (γ), παρατηρούμε ότι πριν την χρονική στιγμή t 0 έχουμε S=0 και R=1 οπότε Q=0. Την t 0 έχουμε S=0 και R=0, έτσι το Q=0 η κατάσταση του FF δεν αλλάζει επειδή το FF θυμάται την προηγούμενη κατάστασή του. Την t 1 έχουμε S=1 και R=0, τότε το FF ενεργοποιείται (Q=1). Παραμένει σε αυτήν την κατάσταση t 3 για τον ίδιο ακριβώς λόγο που αναφέραμε πιο πριν. Την t 5 η είσοδος R γίνεται και πάλι 1 (S=0, R=1). Αυτό συνεπάγεται μηδενισμό της εξόδου, η οποία όμως ήδη βρίσκεται σε κατάσταση 0. Άρα δεν παρατηρούμε καμία αλλαγή στην έξοδο μέχρι την χρονική στιγμή t 7 οπότε η είσοδος S γίνεται 1 (S=1, R=0). Η έξοδος μεταβαίνει στο λογικό 1 την χρονική στιγμή t 9 (S=0, R=1). Από την t 10 και μετά η έξοδος Q=0. S R Q S R Q t t t t t t t t t t t
14 1.2.2 Χρονιζόμενα FFs τύπου SR Τα FF τύπου SR είναι εξαιρετικά ευαίσθητα στους οποιουσδήποτε ανεπιθύμητους παλμούς μικρού εύρους (αιχμές, glitches) που θα παρουσιασθούν στις εισόδους τους. Αυτοί οι παλμοί θα μπορούσαν να προκύψουν λόγω της διαφορετικής καθυστέρησης που υφίσταται ένας παλμός μέσα από ένα συνδυαστικό κύκλωμα (hazards). Για να αποφύγουμε τέτοια προβλήματα, συγχρονίζουμε τις εισόδους του FF, προσθέτοντας ένα επιπλέον επίπεδο πυλών AND ή NAND, όπως δείχνεται στο Σχήμα 1.7. Σχήμα 1.7 Χρονιζόμενο SR FF (α) με πύλες NOR (β) με πύλες NAND (γ), (δ) πίνακας λειτουργίας (ε) σύμβολο Έτσι, μόνον όταν ο παλμός του ρολογιού (clock, CLK) είναι στο λογικό 1 (CLK=1) επιτρέπεται οι τιμές των S και R να "περάσουν" στις εισόδους SET και RESET και να επηρεάσουν την λειτουργία του FF. Όταν CLK=0, τότε οι είσοδοι S και R δεν μπορούν να επηρεάσουν το FF και το κύκλωμα παραμένει στην προηγούμενή του κατάσταση. Παρατηρούμε συνεπώς, ότι οι επιπλέον πύλες AND ή NAND παίζουν τον ρόλο της πύλης, η οποία ελέγχεται από την είσοδο του ρολογιού CLK. Γι' αυτό και η είσοδος CLK αναφέρεται πολλές φορές και ως πύλη ενεργοποίησης (gate enable). Η όλη λειτουργία των κυκλωμάτων του Σχήματος 1.7 αναλύεται στον πίνακα του Σχήματος 1.7(γ), ο οποίος ονομάζεται πίνακας λειτουργίας του FF. Παρατηρούμε ότι στο αριστερό μέρος του πίνακα έχει συμπεριληφθεί και η κατάσταση του FF πριν εφαρμοσθεί ο ωρολογιακός παλμός. Αυτή συμβολίζεται ως Qt. Δηλαδή, αν γνωρίζουμε την κατάσταση του FF πριν εφαρμοσθεί ο ωρολογιακός παλμός, καθώς και τις τιμές των εισόδων S, R, μπορούμε να βρούμε σε ποιά κατάσταση θα βρεθεί αυτό (Qt+1) μετά την εφαρμογή του παλμού. Έτσι, αν και οι δύο είσοδοι S και R είναι 0 (S=R=0), τότε το κύκλωμα παραμένει ("θυμάται") στην προηγούμενη κατάστασή του, δηλαδή Qt+1=Qt. Αν οι δύο είσοδοι είναι διαφορετικές (S R), τότε η έξοδος θα έχει την ίδια τιμή με αυτή της εισόδου S. Αν και οι δύο είσοδοι S και R είναι στο λογικό 1 (S=R=1), τότε η έξοδος είναι απροσδιόριστη. 14
15 Η κατάσταση αυτή πρέπει να αποφεύγεται. Με βάση αυτές τις παρατηρήσεις, μπορούμε να συμπτύξουμε τον πίνακα του Σχήματος 1.7(γ) στον πιο περιεκτικό πίνακα λειτουργίας του Σχήματος 1.7(δ). Η είσοδος του ρολογιού CLK δεν συμπεριλαμβάνεται στον πίνακα λειτουργίας του κυκλώματος. Μέχρις εδώ, έχουμε καταφέρει να θωρακίσουμε το FF μας από ανεπιθύμητες αιχμές που παρουσιάζονται στα κυκλώματα, συγχρονίζοντας την λειτουργία του σύμφωνα με τους παλμούς ενός ρολογιού. Σχήμα 1.8 Κυματομορφές εισόδου-εξόδου SR μανταλωτή με CLK Σύμφωνα με τις κυματομορφές του σχήματος 1.8 και του 1.5(γ), παρατηρούμε ότι μεταξύ των t 5 και t 6, το S=1 και το R=0, το FF δεν θα επηρεαστεί γιατί στο χρονικό εκείνο διάστημα ο παλμός του ρολογιού ήταν στο λογικό 0 (CLK=0). Αντίθετα, όταν το S=1 και το R=0 μεταξύ των t 7 και t 8, το FF θα επηρεαστεί γιατί στο χρονικό εκείνο διάστημα ο παλμός του ρολογιού ήταν στο λογικό 1 (CLK=1). Το FF επίσης θα επηρεαστεί την χρονική στιγμή μεταξύ t 9 και t 10 για τον ίδιο ακριβώς λόγο όταν το S=0 και το R=1. 15
16 1.2.3 FF τύπου D Αν στο χρονιζόμενο SR FF προσθέσουμε έναν αντιστροφέα μεταξύ των εισόδων του, τότε παίρνουμε το FF τύπου D του Σχήματος 1.9. Ουσιαστικά έχουμε επιτύχει να λειτουργούμε το κύκλωμα μόνο για τις περιπτώσεις της 2ης και 3ης γραμμής του πίνακα λειτουργίας του Σχήματος 1.7(δ). Έτσι, εάν D=0 τότε Q=0, ενώ εάν D=1 τότε Q=1. Αυτά συμβαίνουν υπό την προϋπόθεση ότι G=1 (CLK=1). Σχήμα 1.9 FF τύπου D (α) λογικό κύκλωμα (β) πίνακας λειτουργίας (γ) σύμβολο Είναι σημαντικό να τονισθεί ότι η έξοδος Q ακολουθεί το δεδομένο εισόδου D σε όλη τη διάρκεια που ο ωρολογιακός παλμός είναι στο λογικό 1 (G=1). Όταν ο παλμός αυτός μεταβεί στο 0, στην έξοδο Q παραμένει η τελευταία τιμή που είχε αυτή ακριβώς πριν τη μετάβαση του παλμού CLK από το 1 στο 0. Το FF αυτό ονομάζεται και μανταλωτής D (D latch), παίρνοντας το όνομά του από την δυνατότητα φύλαξης δεδομένων (data) σ' αυτόν. Σχήμα 1.10 Κυματομορφές εισόδου-εξόδου του μανταλωτή τύπου D 16
17 1.2.4 JK Flip-Flop Η απροσδιόριστη κατάσταση του SR FF θα μπορούσε να αποφευχθεί τροποποιώντας το κύκλωμα του Σχήματος 1.7(α), όπως δείχνεται στο Σχήμα 1.11(α), όπου ανατροφοδοτούμε τις εξόδους στις εισόδους. Το νέο αυτό κύκλωμα ονομάζεται JK flip-flop. Η λειτουργία του είναι ακριβώς ίδια με εκείνη του SR, με μόνη διαφορά ότι το κύκλωμα αυτό δεν έχει απροσδιόριστη κατάσταση όταν και οι δύο είσοδοί του είναι στο λογικό 1. Οι είσοδοι J και Κ συμπεριφέρονται όπως οι είσοδοι S και R, δηλαδή όταν αυτές είναι διαφορετικές μεταξύ τους η J ενεργοποιεί (sets) το FF, ενώ η K το απενεργοποιεί (resets). Όταν J=K=1 και φυσικά η είσοδος του ρολογιού είναι 1 (CLK=1), τότε η κατάσταση του FF αντιστρέφεται, δηλαδή από 1 γίνεται 0 και από 0 γίνεται 1. Σχήμα 1.11 FF τύπου JK (α)λογικό κύκλωμα (β) πίνακας λειτουργίας (γ)σύμβολο Έστω ότι Q=0 (οπότε Q'=1), J=1 και K=0. Τότε, κατά την διάρκεια που ο παλμός του ρολογιού είναι 1 (CLK=1), η έξοδος της πρώτης πύλης AND θα είναι 0 και η έξοδος της δεύτερης πύλης AND θα είναι 1. Κατά συνέπεια οι είσοδοι RESET και SET του βασικού FF θα είναι 0 και 1 αντίστοιχα, αναγκάζοντας την έξοδό του να μεταβεί στην κατάσταση Q=1 (και άρα Q'=0). Παρατηρούμε επομένως ότι για J=1 και Κ=0 η κατάσταση του JK FF έγινε Q=1. Είδαμε λοιπόν, ότι για J=1 και K=0 η έξοδος του JK FF έγινε Q=1. Έστω τώρα ότι εφαρμόζουμε και στις δύο εισόδους λογικό 1 (J=K=1). Όταν ο παλμός του ρολογιού γίνει 1, τότε η έξοδος της πύλης 1 θα είναι στο λογικό 1 (άρα RESET=1), ενώ η έξοδος της πύλης 2 θα είναι στο λογικό 0 (άρα SET=0), αφού Q'=0. Η έξοδος του βασικού FF για SET=0 και RESET=1 γίνεται 0 (Q=0). Διαπιστώνουμε επομένως ότι το FF άλλαξε κατάσταση και από Q=1 έγινε Q=0. Συνεχίζοντας την ανάλυση μπορούμε να δούμε ότι αν η κατάσταση του FF είναι Q=0 και οι είσοδοι J=K=1, τότε όταν ο παλμός του ρολογιού είναι 1, θα επιτρέψει στις εξόδους των AND πυλών 1 και 2 να γίνουν 0 και 1 αντίστοιχα. Αποτέλεσμα αυτού θα είναι το βασικό FF να ενεργοποιηθεί, αφού SET=1 και RESET=0, οπότε η έξοδος να γίνει Q=1. Δηλαδή η κατάσταση του JK FF από 0 έγινε 1. Παρατηρούμε επομένως ότι όταν J=K=1 και εφόσον CLK=1, η κατάσταση του JK FF αλλάζει, μεταβαίνοντας κάθε φορά στη συμπληρωματική αυτής στην οποία ήταν. 17
18 1.2.5 FF τύπου T Σχήμα 1.12 FF τύπου Τ (α) λογικό κύκλωμα (β) πίνακας λειτουργίας (γ) σύμβολο Πρόκειται για μία παραλλαγή του JK FF. Προκύπτει άμεσα από το JK FF συνδέοντας μαζί και τις δύο εισόδους του (σχήμα 1.12 (α)). Συνεπώς, ο πίνακας λειτουργίας του Τ FF αποτελείται ουσιαστικά από την πρώτη και τέταρτη γραμμή του αντίστοιχου πίνακα λειτουργίας του JK FF (Σχήμα 1.12(β)). Όταν Τ=0 το FF παραμένει στην προηγούμενη κατάσταση ("θυμάται"), ενώ όταν Τ=1 αυτό μεταβαίνει στην συμπληρωματική της προηγούμενης κατάστασής του. Αυτή ακριβώς η λειτουργία του, δηλαδή της μετάπτωσης από την μία λογική στάθμη στην άλλη (Τoggle), έδωσε και την ονομασία στο συγκεκριμένο FF. 18
19 2. ΣΥΓΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός του κεφαλαίου αυτού είναι η μελέτη των σύγχρονων ακολουθιακών κυκλωμάτων. Τα κυκλώματα αυτά αποτελούνται από Flip Flops (FFs) τα οποία συνδέονται μεταξύ τους και λειτουργούν συγχρονισμένα, η έξοδός τους παίρνει τιμές 0 και 1 ανάλογα με τον παλμό ρολογιού που θα δοθεί στην είσοδο. Η ανάλυση της λειτουργίας, καθώς και η σχεδίαση τέτοιων κυκλωμάτων, είναι ένας ουσιώδους σημασίας τομέας της ψηφιακής σχεδίασης. Τι γίνεται αν σ ένα τέτοιο κύκλωμα επιδρούν κάποιες εξωτερικές είσοδοι για τον έλεγχο αυτού; Και τέλος, τι θα κάναμε αν μας ζητούσαν να σχεδιάσουμε ένα ακολουθιακό κύκλωμα αποτελούμενο από ένα ή περισσότερα FFs. Με ποιό τρόπο θα τα συνδυάζαμε αυτά; Αν όλα τα FFs του κυκλώματος χρονίζονται με το ίδιο ρολόι (clock), τότε αυτό ονομάζεται σύγχρονο ακολουθιακό κύκλωμα. Θα εξετάσουμε τον τρόπο ανάλυσής του. Η ανάλυση ενός κυκλώματος αφορά την περίπτωση που μας δίνεται το όλο κύκλωμα και μας ζητείται να προσδιορίσουμε τον ακριβή τρόπο λειτουργίας του. Θα την δούμε αναλυτικότερα στην ενότητα Βασικές έννοιες για τα ΣΑΚ Πριν όμως ασχοληθούμε διεξοδικά με την ανάλυση και σχεδίαση ΣΑΚ, ας επιχειρήσουμε να διευκρινίσουμε ορισμένες έννοιες σχετικά με την κατάσταση και την έξοδο ενός ΣΑΚ, καθώς και των μοντέλων που υπάρχουν για την μελέτη αυτών, ανάλογα με τον τρόπο που επιδρούν οι τυχόν εξωτερικές είσοδοι του κυκλώματος. Είναι γνωστό ότι για να προσδιορίσουμε την έξοδο ενός συνδυαστικού κυκλώματος σε κάθε χρονική στιγμή απαιτείται να γνωρίζουμε την είσοδο καθώς και την λογική που υλοποιούν οι πύλες του κυκλώματος, δηλαδή τον τρόπο διασύνδεσής τους. Σ ένα ακολουθιακό κύκλωμα όμως, για να βρούμε την έξοδο, πρέπει να γνωρίζουμε την παρούσα κατάσταση των FFs, καθώς και την εξωτερική είσοδο. Με τον όρο κατάσταση (state) εννοούμε όλες τις εξόδους των FFs στη συγκεκριμένη χρονική στιγμή. Αν ένα κύκλωμα αποτελείται από Ν FFs, θα έχει το πολύ 2 Ν διαφορετικές καταστάσεις. οι είσοδοι, όπως και το ρολόι, δεν συμπεριλαμβάνονται στον ορισμό της κατάστασης. Επιπλέον, η κατάσταση δεν είναι το ίδιο πράγμα με την έξοδο του κυκλώματος. Μερικές ή και όλες οι έξοδοι των FFs μπορεί να οδηγούνται κατευθείαν στην έξοδο, αλλά γενικά, η έξοδος ενός ΣΑΚ είναι ένας συνδυασμός των εξόδων (καταστάσεων) των FFs, όπως δείχνεται στο Σχήμα 2.1α. Η έξοδος του κυκλώματος θα αλλάξει μόνο όταν δοθεί παλμός ρολογιού. Ένα τέτοιο κύκλωμα, στο οποίο η έξοδος αλλάζει σε συμφωνία με τους ωρολογιακούς παλμούς ονομάζεται κύκλωμα Moore. Αν στο ΣΑΚ προσθέσουμε κάποιες εξωτερικές εισόδους (εκτός του ρολογιού), τότε και πάλι το κύκλωμα αυτό εξακολουθεί να είναι ένα κύκλωμα Moore, υπό την προϋπόθεση ότι η έξοδος του κυκλώματος λαμβάνεται από τις εξόδους των FFs και άρα οι οποιεσδήποτε αλλαγές στην έξοδο συμβαίνουν μόνο κατά τις αλλαγές των ωρολογιακών παλμών. Αν όμως η εξωτερική είσοδος μπορεί να επηρεάσει την έξοδο του κυκλώματος σε οποιαδήποτε χρονική στιγμή, χωρίς να είναι απαραίτητο να συγχρονιστεί με τους ωρολογιακούς παλμούς (βλ. Σχήμα 2.1β), τότε το κύκλωμα αυτό ονομάζεται κύκλωμα Mealy. Δηλαδή σ ένα τέτοιο κύκλωμα η έξοδος εξαρτάται από την εσωτερική κατάσταση καθώς και από τις εξωτερικές επιρροές (εξωτερικές εισόδους). Οι έξοδοι των FFs αποτελούν και πάλι την εσωτερική κατάσταση. Οι είσοδοι δεν παρεμβαίνουν άμεσα στην κατάσταση, αλλά επηρεάζουν την έξοδο του 19
20 κυκλώματος μέσω του συνδυαστικού κυκλώματος, και μάλιστα σε οποιαδήποτε χρονική στιγμή. Σχήμα 2.1 (α) Κύκλωμα Moore (β) Κύκλωμα Mealy 20
21 2.1 Ανάλυση ενός ΣΑΚ Με τον όρο "ανάλυση" ενός ακολουθιακού κυκλώματος εννοούμε την εύρεση ολόκληρης της χρονικής ακολουθίας των εισόδων, εξόδων και καταστάσεων αυτού. Έτσι, όταν μας δίνεται ένα σύγχρονο ακολουθιακό κύκλωμα (ΣΑΚ), θα θέλαμε να προσδιορίσουμε όλη την αλληλουχία των δυνατών καταστάσεων αυτού, όπως και των πιθανών εξόδων του, σε συνάρτηση με τις τιμές των εξωτερικών εισόδων του κυκλώματος και τους ωρολογιακούς παλμούς. Η διαδικασία της ανάλυσης ενός ΣΑΚ γίνεται πολύ εύκολα σε τρία ξεχωριστά βήματα: συναρτήσεις εισόδου πίνακας καταστάσεων διάγραμμα καταστάσεων. Η όλη παρουσίαση αρχίζει με απλά ακολουθιακά κυκλώματα χωρίς επιπλέον εισόδους ή εξόδους (υποενότητα 2.2.1), και συνεχίζεται με ακολουθιακά κυκλώματα μόνο με εισόδους (υποενότητα 2.2.2) ή με εισόδους και εξόδους (υποενότητα 2.2.3) ΣΑΚ χωρίς εξωτερικές εισόδους και εξόδους Ας περιγράψουμε την όλη διαδικασία επιχειρώντας να αναλύσουμε το απλό κύκλωμα του Σχήματος 2.2(α). Πρόκειται για ένα κύκλωμα με δύο FFs τύπου JK στο οποίο δεν δίνουμε παλμό ρολογιού. Στο κύκλωμα δεν εφαρμόζεται καμιά εξωτερική είσοδος και οι έξοδοι αυτού είναι αυτές των FFs (κατάσταση των FFs). Σχήμα 2.2 Σύγχρονο ακολουθιακό κύκλωμα με δύο FFs 21
22 Κατ' αρχήν παρατηρούμε ότι πράγματι πρόκειται για ένα ΣΑΚ αφού και τα δύο FFs τύπου JK τροφοδοτούνται με τους ίδιους ωρολογιακούς παλμούς CLK, Σχήμα 2.2α. Απαριθμούμε τα FFs αρχίζοντας από το 0, όπως δείχνεται στο Σχήμα 2.2β. Έτσι έχουμε το FF0 με εισόδους J0, K0 και εξόδους Q0, Q 0 και το FF1 με εισόδους J1, K1 και εξόδους Q1, Q 1. Μετά από αυτά, είμαστε πλέον έτοιμοι για να αρχίσουμε την ανάλυση του κυκλώματος. Η όλη ανάλυση επιτυγχάνεται σε τρία βήματα, ως εξής: Βήμα Α1: Γράφουμε τις λογικές συναρτήσεις των εισόδων των FFs. Από το Σχήμα 2.2(β) βλέπουμε ότι: J0 = Q 1 J1 = Q0 Κ0 = 1 Κ1 = 1 Βήμα Α2: Καταστρώνουμε τον πίνακα καταστάσεων. Ο πίνακας καταστάσεων περιέχει ουσιαστικά την παρούσα και την επόμενη κατάσταση του ακολουθιακού κυκλώματος. Αυτό είναι και το ζητούμενο, δηλαδή σε ποιά κατάσταση θα βρεθεί το κύκλωμα στην επόμενη χρονική στιγμή, αν γνωρίζουμε την κατάστασή του στην παρούσα χρονική στιγμή. Ο πίνακας καταστάσεων αποτελείται από τρία τμήματα (Πίνακας 2.1): Το πρώτο τμήμα που περιέχει την παρούσα κατάσταση. Σ' αυτό καταγράφονται όλες οι δυνατές τιμές των καταστάσεων Q. Στην προκειμένη περίπτωση έχουμε 2 FFs και άρα 4 δυνατές τιμές για το ζεύγος Q1, Q0. Στη γενική περίπτωση κυκλώματος που αποτελείται από n FFs, έχουμε συνολικά 2 n δυνατές καταστάσεις. Το δεύτερο τμήμα περιέχει τις τιμές των εισόδων των FFs, όπως αυτές προκύπτουν από τις συναρτήσεις εισόδου του βήματος Α1 και τις τιμές της παρούσας κατάστασης. Έτσι, παρατηρούμε ότι η στήλη J1 είναι ίδια με την στήλη Q0 της παρούσας κατάστασης, αφού J1 = Q0. Επίσης, η στήλη J0 είναι συμπληρωματική της στήλης Q1, αφού J0 = Q 1. Τέλος, οι τιμές των Κ1 και Κ0 είναι όλες ίσες με 1. Το τρίτο τμήμα περιέχει την επόμενη κατάσταση του κυκλώματος. Κάθε τιμή του τμήματος αυτού προκύπτει από τις αντίστοιχες τιμές της παρούσας κατάστασης και των εισόδων, λαμβάνοντας υπόψη τον τρόπο λειτουργίας του FF. Πίνακας 2.1 Πίνακας καταστάσεων του κυκλώματος του σχήματος
23 Έτσι, οι τιμές της στήλης Q1 της επόμενης κατάστασης προκύπτουν από την στήλη Q1 της παρούσας κατάστασης και τις τιμές των στηλών εισόδου J1, Κ1. Για παράδειγμα, η δεύτερη τιμή του Q1 της επόμενης κατάστασης είναι 1, επειδή η αντίστοιχη τιμή του Q1 της παρούσας κατάστασης είναι 0 και οι είσοδοι J1 = 1, Κ1 = 1, που σημαίνει ότι το FF αλλάζει κατάσταση με την έλευση του ενεργού παλμού του ρολογιού (toggle). Βήμα Α3: Σχεδιάζουμε το διάγραμμα καταστάσεων. Το διάγραμμα καταστάσεων (state diagram) δεν είναι τίποτε άλλο από την γραφική απεικόνιση του πίνακα καταστάσεων. Κάθε κατάσταση απεικονίζεται με ένα κύκλο και κάθε μετάβαση δείχνεται με ένα βέλος. Το διάγραμμα καταστάσεων του κυκλώματος που εξετάζουμε, δείχνεται στο Σχήμα 2.3. Σχήμα 2.3 Διάγραμμα καταστάσεως του κυκλώματος του σχήματος 2.2 Το διάγραμμα προέκυψε από τις αντίστοιχες τιμές της παρούσας και επόμενης κατάστασης του πίνακα καταστάσεων του Σχήματος 2.3. Βλέπουμε δηλαδή πως αν η παρούσα κατάσταση (Q1Q0) είναι 00, η επόμενη κατάσταση (τρίτο τμήμα του πίνακα καταστάσεων) είναι 01. Άρα, με την έλευση του ενεργού παλμού το κύκλωμα μεταβαίνει από το 00 στο 01. Όμοια βρίσκουμε ότι με τον επόμενο παλμό του ρολογιού το κύκλωμα αλλάζει κατάσταση και από το 01 μεταβαίνει στο 10, ενώ από το 10 μεταβαίνει στο 00. Δηλαδή, το συγκεκριμένο κύκλωμα με κάθε ενεργό ωρολογιακό παλμό περνά διαδοχικά από τις καταστάσεις 00, 01, 10 ή 0, 1, 2 στο δεκαδικό σύστημα αρίθμησης. Πρόκειται επομένως για ένα κύκλωμα απαρίθμησης παλμών (counter) με δυνατότητα απαρίθμησης 3 παλμών (modulo-3). Αν το κύκλωμα για κάποιο λόγο (π.χ. κατά την έναρξη της τροφοδοσίας του) βρεθεί στην κατάσταση 11 (δηλαδή Q1 = 1, Q0 = 1) τότε με τον πρώτο ενεργό ωρολογιακό παλμό μεταβαίνει στην κατάσταση 00, και από εκεί συνεχίζει, όπως ήδη έχουμε περιγράψει. 23
24 ΣΑΚ με εξωτερικές εισόδους Αν στο κύκλωμα που θέλουμε να αναλύσουμε εφαρμόζονται κάποιες εξωτερικές είσοδοι, τότε πρέπει να τις λάβουμε υπόψη μας στη διαδικασία της ανάλυσης, προσδιορίζοντας την επίδραση που αυτές έχουν στο κύκλωμα. Η διαδικασία της ανάλυσης δεν αλλάζει και εξακολουθεί να γίνεται ακολουθώντας τα τρία βήματα που αναφέραμε στην προηγούμενη παράγραφο. Ας παρακολουθήσουμε την ανάλυση ενός τέτοιου κυκλώματος μέσα από ένα παράδειγμα. Σχήμα 2.4 ΣΑΚ με FFs τύπου JK και με εξωτερική είσοδο Βήμα Α1: Γράφουμε τις συναρτήσεις εισόδου. J1 = K1 = J0 = K0 = 1 Βήμα Α2: Καταστρώνουμε τον πίνακα καταστάσεων. Παρατηρούμε ότι οι είσοδοι J, K των FFs είναι συναρτήσεις όχι μόνο της παρούσας κατάστασης Q, αλλά και της τιμής της εισόδου Χ. Αυτό σημαίνει πως για να προσδιορίσουμε την επόμενη κατάσταση πρέπει να ξέρουμε την παρούσα κατάσταση και την είσοδο Χ. Έτσι, στο πρώτο τμήμα του πίνακα καταστάσεων ενσωματώνουμε και τις τιμές του Χ. Οι δυνατοί συνδυασμοί των τριών μεταβλητών X, Q1, Q0 είναι 8, όπως φαίνεται στον πίνακα 2.2. Κατά τα υπόλοιπα, ο πίνακας καταστάσεων προκύπτει με τον γνωστό πλέον τρόπο. 24
25 Πίνακας 2.2 Πίνακας καταστάσεων του κυκλώματος του σχήματος 2.4 Βήμα Α3: Σχεδιάζουμε το διάγραμμα καταστάσεων. Σε κάθε βέλος (μετάβαση) του διαγράμματος καταστάσεων σημειώνουμε και την αντίστοιχη τιμή της εισόδου Χ (Σχήμα2.5). Έτσι, εύκολα παρατηρούμε ότι όταν η εξωτερική είσοδος Χ = 1 το κύκλωμα απαριθμεί συνολικά (προς τα πάνω), δηλαδή 0, 1, 2, 3, 0, 1,..., ενώ όταν Χ = 0 το κύκλωμα απαριθμεί ανάστροφα (προς τα κάτω), δηλαδή 3, 2, 1, 0, 3, 2,... Συνεπώς πρόκειται για ένα κύκλωμα απαρίθμησης 4 παλμών (modulo-4), η λειτουργία του οποίου εκφράζεται από την εξωτερική είσοδο Χ. Σχήμα 2.5 Διάγραμμα καταστάσεως του κυκλώματος του σχήματος
26 ΣΑΚ με εξωτερικές εισόδους και εξόδους Ένα ΣΑΚ μπορεί να έχει μία ή περισσότερες εξωτερικές εισόδους ή/και εξόδους. Η διαδικασία ανάλυσης του τρόπου λειτουργίας είναι ίδια με αυτή που μάθαμε στις προηγούμενες παραγράφους και γίνεται σε τρία βήματα. Ο πίνακας καταστάσεων στην προκειμένη περίπτωση θα αποτελείται από ένα επιπλέον τμήμα, όπου θα καταγράφονται οι τιμές των εξωτερικών εξόδων για κάθε δυνατή περίπτωση των εισόδων και της παρούσας κατάστασης. Ας παρακολουθήσουμε την διαδικασία ανάλυσης ενός τέτοιου κυκλώματος μέσα από το παράδειγμα που ακολουθεί. Σχήμα 2.6 ΣΑΚ με Τα FFs και εξωτερική είσοδο και έξοδο. Αρχίζουμε την ανάλυση του κυκλώματος ακολουθώντας τα γνωστά τρία βήματα: Βήμα Α1: Γράφουμε τις εξισώσεις εισόδου των FFs. T1= Q 0 Τ0 = Αφού το κύκλωμα διαθέτει και μια εξωτερική έξοδο Υ, είναι σκόπιμο να γράψουμε την λογική συνάρτηση αυτής, ώστε στη συνέχεια να είμαστε έτοιμοι να προσδιορίσουμε την τιμή της για κάθε δυνατό συνδυασμό της παρούσας κατάστασης και της εισόδου. Έτσι έχουμε: Y = X Q1 Q0 Βήμα Α2: Καταστρώνουμε τον πίνακα καταστάσεων. Έχουμε μία εξωτερική είσοδο και δύο FFs, και κατά συνέπεια 8 διαφορετικές περιπτώσεις μπορoύν να υπάρξουν στην παρούσα κατάσταση. Με βάση αυτές τις τιμές και τις συναρτήσεις εισόδου, συμπληρώνουμε το δεύτερο τμήμα του πίνακα καταστάσεων που περιέχει όλες τις δυνατές περιπτώσεις στις οποίες μπορούν να βρεθούν οι είσοδοι Τ0, Τ1 των δύο FFs. Στο σημείο αυτό, και πριν συνεχίσουμε στον προσδιορισμό της επόμενης κατάστασης (δεξιό τμήμα του Πίνακα 2.3) καταγράφουμε τις τιμές εξόδου της Υ. Οι τιμές της προκύπτουν από τις αντίστοιχες τιμές της εξωτερικής εισόδου και της παρούσας κατάστασης. Τέλος, προσδιορίζουμε την επόμενη κατάσταση από την παρούσα κατάσταση και τις τιμές των εισόδων Τ0, Τ1 των FFs με βάση τον πίνακα λειτουργίας τους. 26
27 Πίνακας 2.3 Πίνακας καταστάσεων του κυκλώματος του σχήματος 2.6 Βήμα Α3: Σχεδιάζουμε το διάγραμμα καταστάσεων. Το διάγραμμα καταστάσεων σχεδιάζεται κατά τα γνωστά από την παρούσα και επόμενη κατάσταση του Πίνακα 2.3. Σε κάθε μετάβαση σημειώνουμε τις αντίστοιχες τιμές των εξωτερικών εισόδων και εξόδων με την μορφή Χ/Υ. Έτσι, αν το κύκλωμα βρεθεί στην κατάσταση 10 και είσοδος Χ = 0, τότε έλευση του ενεργού παλμού θα το οδηγήσει στην κατάσταση 00 και η έξοδος θα είναι Υ = 1. Για τον λόγο αυτό στο βέλος από το 10 στο 00 σημειώνουμε 0/1. Αν όμως η είσοδος Χ = 1, τότε η έλευση του ενεργού παλμού θα το οδηγήσει στην κατάσταση 01 και η έξοδος Υ θα ισούται με 0 (Υ=0). Παρατηρούμε ότι αν το κύκλωμα βρεθεί στην κατάσταση 01 και η είσοδος Χ = 1, τότε αυτό εγκλωβίζεται στην ίδια κατάσταση. Αυτό δείχνεται στο διάγραμμα καταστάσεων με ένα βρόχο. Όμοια, αν το κύκλωμα βρεθεί στην κατάσταση 11 και η είσοδος είναι Χ = 0, τότε παραμένει στην ίδια κατάσταση μέχρις ότου γίνει Χ = 1, οπότε και με την έλευση του ενεργού παλμού μεταβαίνει στην κατάσταση
28 Σχήμα 2.7 Διάγραμμα καταστάσεως του κυκλώματος του σχήματος
29 3. ΑΠΑΡΙΘΜΗΤΕΣ Οι απαριθμητές ή μετρητές (counters) είναι ακολουθιακά κυκλώματα αποτελούμενα από FFs και πύλες που έχουν την δυνατότητα απαρίθμησης παλμών (γεγονότων) και χρησιμοποιούνται για την μέτρηση του χρόνου (λειτουργούν σαν ψηφιακά ρολόγια). Ένας απαριθμητής ο οποίος τροφοδοτείται με κάποιους ωρολογιακούς παλμούς μπορεί να χρησιμοποιηθεί για να μετράει αυτούς τους παλμούς. Εφόσον οι παλμοί εμφανίζονται σε τακτά χρονικά διαστήματα, ο απαριθμητής μπορεί να χρησιμοποιηθεί ως όργανο για την μέτρηση του χρόνου και κατά συνέπεια της περιόδου ή της συχνότητας. Υπάρχουν δύο βασικές κατηγορίες απαριθμητών: οι ασύγχρονοι και οι σύγχρονοι. Θα δούμε ότι οι ασύγχρονοι απαριθμητές είναι πιο απλοί στην σχεδίασή τους και συνήθως απαιτείται ο ελάχιστος αριθμός πυλών για την κατασκευή τους. Παρουσιάζουν όμως πρόβλημα στην μέγιστη συχνότητα λειτουργίας που μπορούμε να πετύχουμε, επειδή το κάθε FF πυροδοτείται από την έξοδο του προηγουμένου του. Οι απαριθμητές αυτού του τύπου ονομάζονται ασύγχρονοι (asynchronous) ή σειριακοί (serial) ή κυματώσεως (ripple). Η άλλη κατηγορία απαριθμητών είναι οι λεγόμενοι σύγχρονοι (synchronous) ή παράλληλοι (parallel). Όπως θα δούμε, σ' αυτούς όλα τα FFs πυροδοτούνται ταυτόχρονα, αφού ο ίδιος ωρολογιακός παλμός εφαρμόζεται σε καθένα από αυτά. Με τον τρόπο αυτό πετυχαίνουμε μεγαλύτερες ταχύτητες λειτουργίας, με τίμημα όμως τον μεγαλύτερο αριθμό πυλών του κυκλώματος. Στην πρώτη ενότητα του κεφαλαίου θα γνωρίσουμε τους ασύγχρονους απαριθμητές, τόσο τους δυαδικούς όσο και τους μη δυαδικούς. Στην δεύτερη ενότητα θα ασχοληθούμε με τους σύγχρονους απαριθμητές. Εκτός από την γνωστή μέθοδο σχεδίασης αυτών, θα μάθουμε και μία νέα μέθοδο για την σχεδίαση σύγχρονων κυκλωμάτων κανονικής απαρίθμησης. 3.1 Ασύγχρονοι Απαριθμητές Οι ασύγχρονοι απαριθμητές κατασκευάζονται με FFs καθένα από τα οποία πυροδοτείται από το προηγούμενό του. Όταν λέμε απαριθμητή, εννοούμε ένα ακολουθιακό κύκλωμα με FFs, οι καταστάσεις των οποίων για κάθε νέο ωρολογιακό παλμό αλλάζουν έτσι ώστε ο αριθμός που σχηματίζεται στην έξοδο να διατρέχει κυκλικά ένα σύνολο δυαδικών αριθμών Ν. Αν το πλήθος Ν των αριθμών είναι δύναμη του 2, δηλαδή αν Ν= 2 n, και ο απαριθμητής διατρέχει τους αριθμούς αυτούς κανονικά (τον ένα μετά τον άλλο), τότε αυτός ονομάζεται δυαδικός απαριθμητής (binary counter). Αν το Ν δεν είναι δύναμη του 2, δηλαδή Ν 2 n, τότε ο απαριθμητής ονομάζεται μη-δυαδικός. Θα εξετάσουμε χωριστά την κάθε μία περίπτωση. 29
30 3.1.1 Ασύγχρονοι Δυαδικοί Απαριθμητές Το κύκλωμα του Σχήματος 3.1α μας δείχνει έναν ασύγχρονο δυαδικό απαριθμητή των 3-bits, ο οποίος είναι σχεδιασμένος με FFs τύπου Τ αρνητικής ακμής πυροδότησης. Η είσοδος Τ καθενός FF είναι συνδεδεμένη στο λογικό 1. Σχήμα 3.1 Ασύγχρονος προσθετικός δυαδικός απαριθμητής (mod-8) (α) Λογικό κύκλωμα (β) κυματομορφές εξόδου Αυτό σημαίνει ότι η ενεργός ακμή στην είσοδο CLK του κάθε FF, θα το αναγκάζει να αλλάζει κατάσταση (toggle). Οι έξοδοι του απαριθμητή είναι οι τρεις καταστάσεις Q0, Q1, Q2 των FFs. Παρατηρούμε ότι το κάθε FF πυροδοτείται από την έξοδο του προηγουμένου FF. Ο παλμός εισόδου εφαρμόζεται μόνο στο πρώτο από τα FFs. Οι κυματομορφές της εισόδου και των εξόδων του απαριθμητή δίνονται στο Σχήμα 3.1(β). Ας εξετάσουμε τον τρόπο λειτουργίας του κυκλώματος. Έστω ότι αρχικά όλα τα FFs έχουν μηδενιστεί (reset, εκκαθάριση). Με την πρώτη αρνητική ακμή των ωρολογιακών παλμών το FF0 αλλάζει κατάσταση και από το 0 μεταβαίνει στο 1. Με την επόμενη αρνητική ακμή, αυτό αλλάζει και πάλι κατάσταση και από το 1 μεταβαίνει στο 0. Οι μεταπτώσεις αυτές συνεχίζονται για κάθε αρνητική ακμή των ωρολογιακών παλμών CLK. Η έξοδος όμως του FF0 συνδέεται στην είσοδο ρολογιού του επόμενου FF1. Έτσι, με κάθε αρνητική ακμή του Q0 το FF1 αλλάζει κατάσταση, αφού πρόκειται για FF τύπου Τ με Τ=1. Παρόμοια είναι και η συμπεριφορά του τρίτου FF, του οποίου η είσοδος ρολογιού τροφοδοτείται από την έξοδο Q1 του δεύτερου FF. Αν διαβάζουμε τις εξόδους των τριών FFs με την σειρά Q2Q1Q0, αρχίζοντας από τα αριστερά των κυματομορφών του Σχήματος 3.1β, διατρέχουμε κυκλικά τους αριθμούς 000, 001, 010,..., 111. Σε δεκαδική αναπαράσταση οι αριθμοί αυτοί είναι 0, 1, 2,..., 7. Άρα, πρόκειται για ένα κύκλωμα με κύκλο απαρίθμησης 8 (mod-8). Modulo ή modulus ή mod ενός 30
31 απαριθμητή είναι το πλήθος των καταστάσεων που διατρέχει αυτός. To FF0 αλλάζει κατάσταση σε κάθε αρνητική ακμή του ρολογιού. Πρόκειται δηλαδή για το λιγότερο σημαντικό ψηφίο (LSB, Least Significant Bit). Η περίοδος των παλμών Q0 είναι 2πλάσια της περιόδου των ωρολογιακών παλμών, δηλαδή η συχνότητα των παλμών του Q0 είναι υποδιπλάσια της συχνότητας των ωρολογιακών παλμών. Αντίστοιχα, η περίοδος των παλμών Q1 είναι 2πλάσια της περιόδου των παλμών Q0 και άρα 4πλάσια της περιόδου των ωρολογιακών παλμών. Τέλος, η περίοδος των παλμών Q2 είναι 8πλάσια της περιόδου των ωρολογιακών παλμών. Διαπιστώνουμε επομένως ότι η κάθε έξοδος Q0, Q1, Q2 πετυχαίνει την διαίρεση της συχνότητας των ωρολογιακών παλμών δια 2, 4 και 8 αντίστοιχα. Έχοντας πλέον αναλύσει διεξοδικά το κύκλωμα του απαριθμητή του Σχήματος 3.1 ας προχωρήσουμε σε ορισμένες παρατηρήσεις και γενικεύσεις. Το κύκλωμα του Σχήματος 3.1 αποτελείται από 3 FFs και είναι ένας απαριθμητής 8 διαφορετικών καταστάσεων (mod-8). Στη γενική περίπτωση κατά την οποία έχουμε n FFs, το κύκλωμα θα είναι σε θέση να απαριθμεί Ν= 2 n καταστάσεις, δηλαδή να διατρέχει κυκλικά τους αριθμούς από 0 μέχρι και Ν-1. Τότε λέμε ότι έχουμε έναν απαριθμητή με κύκλο απαρίθμησης Ν (mod-n). Στους ασύγχρονους απαριθμητές το κάθε FF πυροδοτείται από την έξοδο του προηγουμένου του. Έτσι βλέπουμε ότι το FF0 πρέπει να αλλάξει κατάσταση (από 1 σε 0) ώστε αυτό να πυροδοτήσει το FF1 και αυτό με τη σειρά του να αλλάξει κατάσταση (από 1 σε 0) ώστε να πυροδοτήσει το FF2. Η πυροδότηση διαδίδεται από το ένα FF στο άλλο σαν την κυμάτωση στο νερό, γι' αυτό και οι ασύγχρονοι απαριθμητές ονομάζονται και απαριθμητές κυματώσεως (ripple counters). Ο τρόπος αυτός λειτουργίας των απαριθμητών δημιουργεί κάποια προβλήματα εξαιτίας της καθυστέρησης διάδοσης που εισάγει κάθε FF. Ας υποθέσουμε, για παράδειγμα, ότι κάθε FF έχει μια τυπική καθυστέρηση διάδοσης (propagation delay) 10 ns. Τότε, το κύκλωμα του Σχήματος 3.1 το οποίο αποτελείται από 3 FFs, θα παρουσιάζει μια συνολική καθυστέρηση 30 ns. Αυτό σημαίνει ότι η περίοδος των ωρολογιακών παλμών θα πρέπει να είναι μεγαλύτερη από 30 ns ώστε το κύκλωμα να λειτουργεί αξιόπιστα. Με άλλα λόγια, η συχνότητα των παλμών του ρολογιού πρέπει να είναι μικρότερη από 1/30 ns ~ 33 MHz. Ο απαριθμητής του Σχήματος 3.1 είναι ένας προσθετικός δυαδικός απαριθμητής, δηλαδή μετράει προς τα πάνω (count-up). Πόσο εύκολα θα μπορούσε να σχεδιάσει κανείς έναν αφαιρετικό δυαδικό απαριθμητή, δηλαδή έναν απαριθμητή που να μετράει προς τα κάτω (count-down); Η απάντηση στο ερώτημα αυτό είναι πολύ εύκολη. Άμεσα θα λέγαμε, μπορούμε να έχουμε έναν αφαιρετικό απαριθμητή, από την στιγμή που έχουμε το κύκλωμα του προσθετικού στο Σχήμα 3.1. Το μόνο που έχουμε να κάνουμε είναι να πάρουμε ως εξόδους του κυκλώματος τις συμπληρωματικές καταστάσεις Q2, Q1, Q0 των FFs, αντί για τις Q2, Q1, Q0. Από τις κυματομορφές του Σχήματος 3.1(β) φαίνεται ότι με κάθε νέο παλμό του ρολογιού το κύκλωμα θα διατρέχει τις τιμές {(Q2 Q1 Q0 )10}= {7, 6, 5, 4, 3, 2, 1, 0, 7, 6, 5, 4,...}. Υπάρχει όμως και άλλος τρόπος για να σχεδιάσουμε έναν αφαιρετικό δυαδικό απαριθμητή. Αυτός δίνεται στο Σχήμα 3.2(α) και όπως παρατηρούμε πρόκειται για το ίδιο κύκλωμα με εκείνο του Σχήματος 3.1(α), με μόνη διαφορά ότι το κάθε FF πυροδοτείται με την συμπληρωματική κατάσταση του προηγουμένου του. Ως έξοδοι του απαριθμητή θεωρούνται και πάλι οι κανονικές καταστάσεις Q2, Q1, Q0 των FFs. 31
32 Οι κυματομορφές των ωρολογιακών παλμών και των εξόδων του κυκλώματος δείχνονται στο Σχήμα 3.2(β). Σχήμα 3.2 Ασύγχρονος αφαιρετικός δυαδικός απαριθμητής (α) λογικό κύκλωμα (β) κυματομορφές εξόδου Αρχικά θεωρήσαμε ότι όλα τα FFs είχαν εκκαθαριστεί. Με την πρώτη αρνητική ακμή των ωρολογιακών παλμών το FF0 αλλάζει κατάσταση (toggle) και από 0 γίνεται 1. Αυτό σημαίνει ότι η συμπληρωματική κατάσταση Q0 αυτού από 1 γίνεται 0. Συνέπεια αυτού είναι η ενεργοποίηση του επόμενου FF1 με επακόλουθο την αλλαγή της κατάστασης Q1 αυτού από 0 που ήταν σε 1. Άρα, το Q1 από 1 γίνεται 0 και ενεργοποιεί και το τελευταίο FF2, το οποίο με την σειρά του αλλάζει και αυτό κατάσταση. Έτσι το κύκλωμα με την πρώτη ενεργό ακμή του ρολογιού από το 000 που ήταν πήγε στο 111. Με κάθε νέο ωρολογιακό παλμό συνεχίζει την απαρίθμηση προς τα κάτω μέχρις ότου μηδενιστεί και αρχίσει η επανάληψη του ίδιου κύκλου. Σημειώνεται ότι ο κύκλος απαρίθμησης του αφαιρετικού απαριθμητή εξακολουθεί να είναι ο ίδιος και ίσος με 8 (mod-8) στην προκειμένη περίπτωση, αφού το κύκλωμα διατρέχει και πάλι οκτώ διαφορετικές καταστάσεις Ασύγχρονοι Μη-Δυαδικοί Απαριθμητές Είδαμε ότι δυαδικοί απαριθμητές είναι εκείνοι οι οποίοι έχουν κύκλο απαρίθμησης Ν δύναμη του 2, δηλαδή Ν=2 n. Τις περισσότερες όμως φορές θα θέλαμε να μετρούμε κατά δεκάδες, αφού το δεκαδικό είναι το σύστημα αρίθμησης που χρησιμοποιούμε, ή κατά δωδεκάδες ή κατά οποιοδήποτε άλλο αριθμό. Είναι απαραίτητο λοιπόν, να μελετήσουμε τον τρόπο για την σχεδίαση τέτοιων απαριθμητών, δηλαδή μη-δυαδικών απαριθμητών με κύκλο απαρίθμησης Ν 2 n. 32
33 Η σχεδίαση μη-δυαδικών απαριθμητών γίνεται εύκολα με την χρήση μιας πύλης NAND ως αποκωδικοποιητή. Οι είσοδοι της πύλης NAND αποκωδικοποιούν την κατάσταση Ν των FFs, ενώ η έξοδος αυτής τροφοδοτεί τις εισόδους άμεσου μηδενισμού όλων των FFs. Ας εξετάσουμε την περίπτωση των μη-δυαδικών απαριθμητών μέσω ενός παραδείγματος. Σε έναν δεκαδικό ασύγχρονο απαριθμητή παρατηρούμε ότι Ν=10 (2 3 <10<2 4 ) και συνεπώς θα χρειαστούμε 4 FFs για την υλοποίησή του. Θα σχεδιάσουμε λοιπόν έναν δυαδικό απαριθμητή των 4 bits, ο οποίος θα μπορεί να διέρχεται από όλες τις καταστάσεις από 0 μέχρι και 15, αλλά θα αναγκάσουμε αυτόν να αρχίζει την απαρίθμηση από την αρχή κάθε φορά που μετράει τους 10 πρώτους παλμούς. Στο Σχήμα 3.5 δείχνεται το ζητούμενο κύκλωμα. Η πύλη NAND τροφοδοτείται από τις εξόδους Q1 και Q3. Αυτό συμβαίνει επειδή ο αριθμός (10)10 γράφεται στο δυαδικό ως 1010, δηλαδή Ν=(Q3Q2Q1Q0)2=(1010)2. Παρατηρείστε ότι το Q0 είναι το LSB. Άρα, ο απαριθμητής λειτουργεί κανονικά, όπως τον έχουμε γνωρίσει από το Σχήμα 3.1, αρχίζοντας από το 0 και αυξανόμενος κατά 1 με την έλευση κάθε αρνητικού παλμού. Η έξοδος G της πύλης NAND βρίσκεται στη λογική κατάσταση 1 (G= (Q1Q3) =1). Μετά από 10 παλμούς του ρολογιού, ο απαριθμητής έχει φτάσει στην κατάσταση (Q3Q2Q1Q0)2=(1001)2=910. Με τον επόμενο ωρολογιακό παλμό οι έξοδοι των FFs αλλάζουν κατάσταση μεταβαίνοντας στο (1010)2. Σχήμα 3.3 Ασύγχρονος δεκαδικός απαριθμητής (α) λογικό κύκλωμα (β) κυματομορφές εξόδου 33
34 Τότε όμως η έξοδος της πύλης NAND γίνεται 0 (G=(Q3Q1) =0), επιβάλλοντας την εκκαθάριση όλων των FFs. Έτσι, με τον επόμενο ωρολογιακό παλμό η απαρίθμηση αρχίζει και πάλι από την αρχή. 3.2 Σύγχρονοι Απαριθμητές Στην προηγούμενη ενότητα γνωρίσαμε τους ασύγχρονους απαριθμητές και διαπιστώσαμε ότι παρουσιάζεται πρόβλημα κατά την λειτουργία τους σε υψηλές συχνότητες, εξαιτίας της καθυστέρησης που εισάγεται στην πυροδότηση των FFs. Το πρόβλημα αυτό το επιλύουμε εύκολα με την πυροδότηση όλων των FFs με ένα κοινό ρολόι. Στην περίπτωση αυτή έχουμε να κάνουμε με σύγχρονα ακολουθιακά κυκλώματα. Εδώ θα ασχοληθούμε με τους σύγχρονους απαριθμητές (δυαδικούς και μη-δυαδικούς) Σύγχρονοι Δυαδικοί Απαριθμητές Πρόκειται για απαριθμητές των οποίων ο κύκλος απαρίθμησης Ν είναι δύναμη του 2, δηλαδή Ν=2 n. Ένας τέτοιος απαριθμητής αποτελείται από n FFs, τα οποία χρονίζονται από ένα κοινό ωρολογιακό παλμό. Στο Σχήμα 3.4(α) δείχνεται ένας σύγχρονος απαριθμητής με κύκλο απαρίθμησης 8 (mod-8), βασισμένος σε FFs τύπου Τ αρνητικής ακμής πυροδότησης. Οι κυματομορφές εξόδου αυτού δείχνονται στο Σχήμα 3.4(β) και είναι ίδιες με εκείνες του Σχήματος 3.1(β). Σχήμα 3.4 Σύγχρονος προσθετικός δυαδικός απαριθμητής (mod-8) (α) λογικό κύκλωμα (β) κυματομορφές εξόδου Ο τρόπος λειτουργίας του έχει ως εξής: Η είσοδος Τ0=1, γεγονός που σημαίνει ότι το FF0 αλλάζει κατάσταση κάθε φορά που ο ωρολογιακός παλμός μεταβαίνει από 34
35 το 1 στο 0 (αρνητική ακμή). Όταν Τ1=1 και ο ωρολογιακός παλμός μεταβαίνει από το 1 στο 0, τότε το FF1 αλλάζει κατάσταση. Παρόμοια συμβαίνουν και για το FF2, το οποίο αλλάζει κατάσταση κατά την αρνητική ακμή του ρολογιού εφόσον Τ2=1. Παρατηρούμε ότι Τ2=Q1T1=Q1Q0, δηλαδή το FF2 αλλάζει κατάσταση όταν όλα τα προηγούμενα από αυτό FFs βρίσκονται στην κατάσταση 1. Γενικά ισχύει ότι Tn=Qn-1...Q1Q0, όπου Tn η είσοδος του n-οστού FF και Qn-1,..., Q1, Q0 οι έξοδοι όλων των προηγούμενων FFs. Ας σημειωθεί ότι στο κύκλωμα του Σχήματος 3.4(α) Q0 θα είναι το λιγότερο σημαντικό ψηφίο (LSB) της λέξης εξόδου και Q2 το περισσότερο σημαντικό ψηφίο (MSB) αυτής. Στο σημείο αυτό θα ήταν σκόπιμο να παρατηρήσουμε τα εξής σχετικά με τους σύγχρονους δυαδικούς απαριθμητές: Η είσοδος Τ κάθε FF τροφοδοτείται με το γινόμενο των εξόδων Q όλων των προηγούμενων FFs. Για να πάρουμε αφαιρετικό απαριθμητή θα πρέπει να επιλέξουμε τις εξόδους Q ή να τροποποιήσουμε τις εισόδους των FFs, αλλά όχι τις εισόδους του ρολογιού, αφού η αλλαγή της πυροδότησης δεν επηρεάζει την λειτουργία του σύγχρονου ακολουθιακού κυκλώματος. Εφόσον όλα τα FFs πυροδοτούνται από το ίδιο ρολόι, δεν υπάρχουν προβλήματα καθυστέρησης διάδοσης των παλμών πυροδότησης, όπως αυτά που συναντήσαμε στους ασύγχρονους απαριθμητές. Έτσι, ανεξάρτητα από το πλήθος των FFs, η μέγιστη συχνότητα λειτουργίας ενός τέτοιου κυκλώματος καθορίζεται από την καθυστέρηση διάδοσης ενός FF. Για μια τυπική καθυστέρηση των 10ns, ένας τέτοιος απαριθμητής, από οσαδήποτε FFs και αν αποτελείται, θα μπορεί να λειτουργεί με ρολόι μεγίστης συχνότητας 1/10ns=100MHz Σύγχρονοι Μη-Δυαδικοί Απαριθμητές Μη-δυαδικοί απαριθμητές είναι εκείνοι που απαριθμούν πλήθος καταστάσεων Ν, το οποίο δεν είναι δύναμη του 2, δηλαδή Ν 2 n. Για την σχεδίαση τέτοιων απαριθμητών χρησιμοποιούμε τις τεχνικές σχεδίασης σύγχρονων ακολουθιακών κυκλωμάτων που χρησιμοποιήσαμε στο κεφάλαιο
36 3.3 Καταχωρητές Πρόκειται για σύγχρονα ακολουθιακά κυκλώματα τα οποία χρησιμοποιούνται κυρίως για την προσωρινή αποθήκευση δυαδικής πληροφορίας, αλλά και για την εκτέλεση απλών πράξεων, όπως πολλαπλασιασμού και διαίρεσης με δυνάμεις του 2 ή και εύρεσης του συμπληρώματος αριθμού. Στη παρούσα ενότητα θα γνωρίσουμε μια άλλη κατηγορία σύγχρονων ακολουθιακών κυκλωμάτων, τους καταχωρητές. Τονίζουμε ότι πρόκειται και πάλι για σύγχρονα ακολουθιακά κυκλώματα τα οποία βρίσκουν εφαρμογή στην προσωρινή αποθήκευση δυαδικών αριθμών και στην εκτέλεση στοιχειωδών πράξεων σ' αυτούς. Είναι ακριβώς αυτή τους η εφαρμογή η οποία μας οδηγεί να εξετάζουμε αυτά τα σύγχρονα ακολουθιακά κυκλώματα ξεχωριστά στο παρόν κεφάλαιο. Καταχωρητής είναι ένα σύνολο από FFs στα οποία μπορούμε να αποθηκεύσουμε δυαδική πληροφορία. Ας θυμηθούμε ότι σε κάθε FF μπορεί να αποθηκευτεί 1 bit πληροφορίας. Έτσι, σ' έναν καταχωρητή ο οποίος αποτελείται από n FFs μπορούμε να αποθηκεύσουμε n bits πληροφορίας. Η εισαγωγή (φόρτωση, εγγραφή, είσοδος) της δυαδικής πληροφορίας σ' έναν καταχωρητή μπορεί να γίνει είτε σειριακά, δηλαδή 1 bit με κάθε ωρολογιακό παλμό, είτε παράλληλα, δηλαδή και τα n bits με ένα ωρολογιακό παλμό. Το ίδιο ισχύει και για την εξαγωγή (έξοδο, ανάγνωση) της πληροφορίας. Έτσι, διακρίνουμε 4 κατηγορίες καταχωρητών, όπως δείχνονται στο Σχήμα 3.5: καταχωρητές σειριακής εισόδου - σειριακής εξόδου, καταχωρητές σειριακής εισόδου - παράλληλης εξόδου, καταχωρητές παράλληλης εισόδου - σειριακής εξόδου και καταχωρητές παράλληλης εισόδου - παράλληλης εξόδου. Πριν αρχίσουμε την εξέταση καθενός από αυτούς τους τύπους καταχωρητών, θα ήταν χρήσιμο να θυμίσουμε το αποτέλεσμα της ολίσθησης ενός δυαδικού αριθμού προς τα αριστερά ή προς τα δεξιά. Ολίσθηση, λοιπόν, ενός δυαδικού αριθμού Ν προς τα αριστερά κατά m θέσεις, συνεπάγεται τον πολλαπλασιασμό αυτού επί 2 m, δηλαδή ο αριθμός που προκύπτει είναι ο Ν2 m. Εξυπακούεται φυσικά, ότι με κάθε μία αριστερή ολίσθηση το LSB του αριθμού "γεμίζει" με το δυαδικό ψηφίο 0. Αντίστοιχα, ολίσθηση ενός δυαδικού αριθμού Ν κατά m θέσεις δεξιά, συνεπάγεται την διαίρεση του αριθμού με το 2 m, δηλαδή ο αριθμός που προκύπτει είναι ο N2 m. Εξυπακούεται και πάλι ότι με κάθε δεξιά ολίσθηση το MSB του αριθμού "γεμίζει" με το δυαδικό ψηφίο 0. Αυτού του είδους η αριστερή ή δεξιά ολίσθηση ονομάζεται και αριθμητική ολίσθηση (arithmetic shift), σε αντιδιαστολή με την λογική ολίσθηση (logical shift) κατά την οποία τη θέση του ψηφίου που "λείπει" την παίρνει το ψηφίο που "περισσεύει". Η λογική ολίσθηση ονομάζεται και κυκλική ολίσθηση (circular shift). Στις ενότητες που ακολουθούν θα μελετήσουμε όλους τους τύπους καταχωρητών. Συγκεκριμένα, ασχολούμαστε με τους καταχωρητές σειριακής εισόδου και συνεχίζουμε με εκείνους παράλληλης εισόδου. Όλοι οι τύποι καταχωρητών, με εξαίρεση εκείνον της παράλληλης-εισόδου-παράλληλης-εξόδου, είναι καταχωρητές ολίσθησης. 36
37 Σχήμα 4.1 Τύποι καταχωρητών: (α) Σειριακής εισόδου Σειριακής εξόδου (β) Σειριακής εισόδου Παράλληλης εξόδου (γ) Παράλληλης εισόδου Παράλληλης εξόδου (δ) Παράλληλης εισόδου Σειριακής εξόδου Τα FFs που χρησιμοποιούμε για την κατασκευή των καταχωρητών είναι συνήθως τύπου D θετικής ή αρνητικής ακμής πυροδότησης. Τα D FFs όμως προέρχονται από JK ή RS flip-flops στα οποία η μία είσοδος είναι συμπληρωματική της άλλης. Έτσι στην πράξη οι καταχωρητές κατασκευάζονται κυρίως με FF τύπου JK ή RS. Η απροσδιοριστία των RS FFs δεν είναι πρόβλημα στην προκειμένη περίπτωση, αφού αυτά χρησιμοποιούνται μόνο για αποθήκευση δεδομένων και είναι πάντοτε R = S. Μετά την ολοκλήρωση της μελέτης της ενότητας αυτής θα είμαστε σε θέση να αναγνωρίζουμε και να κατανοούμε τη λειτουργία των διαφόρων τύπων καταχωρητών σειριακής ή παράλληλης εισόδου και σειριακής ή παράλληλης εξόδου, να σχεδιάζουμε καταχωρητές με δυνατότητα ολίσθησης προς τα δεξιά ή προς τα αριστερά και τέλος, να σχεδιάζουμε καταχωρητές με δυνατότητα παράλληλης ή σειριακής φόρτωσης. 37
38 3.3.1 Καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου Ένας καταχωρητής ολίσθησης σειριακής-εισόδου-σειριακής-εξόδου αποτελείται από μία συστοιχία FFs τύπου D, όπου η είσοδος καθενός (πλην του πρώτου στη σειρά) τροφοδοτείται από την έξοδο του προηγουμένου του. Όλα τα FFs χρονίζονται με τον ίδιο ωρολογιακό παλμό. Ένα παράδειγμα καταχωρητή ολίσθησης σειριακής-εισόδου-σειριακής-εξόδου των 4 bits δείχνεται στο Σχήμα 3.6. Με κάθε ενεργό του ωρολογιακού παλμού (δηλαδή με την αρνητική ακμή κάθε παλμού στην προκειμένη περίπτωση) το κάθε FF διαβάζει την έξοδο του προηγουμένου του και την μεταφέρει στην έξοδό του, εκτός από το πρώτο αριστερά FF, το οποίο διαβάζει την σειριακή είσοδο. Για παράδειγμα, αν όλα τα FFs του Σχήματος 4.2(α) είχαν εκκαθαριστεί και στην είσοδο D0 (στη σειριακή είσοδο) εφαρμόζαμε το λογικό 1, τότε οι κυματομορφές των εξόδων όλων των FFs για τους 4 πρώτους ωρολογιακούς παλμούς θα ήταν όπως αυτές του Σχήματος 3.6 (δ). Στα Σχήματα 3.6(β) και 3.6(γ) δείχνεται ο ίδιος καταχωρητής ολίσθησης κατασκευασμένος, όμως, με FF τύπου JK και SR αντίστοιχα. Παρατηρούμε ότι η σειριακή είσοδος εφαρμόζεται στην μία είσοδο του πρώτου αριστερά FF, ενώ στην άλλη είσοδο εφαρμόζεται η συμπληρωματική της. Έτσι το δεδομένο εισόδου εισέρχεται στο πρώτο FF με την εμφάνιση της ενεργού ακμής του ωρολογιακού παλμού. Έστω ότι η σειριακή είσοδος ισούται με 1. Τότε J0=1 και K0=J0 =0 (S0=1 και R0=S0 αντίστοιχα για το SR FF), οπότε η έξοδος Q0=1 και Q 0 =0. Στην περίπτωση που η σειριακή είσοδος ισούται με 0, γίνεται φανερό ότι η έξοδος Q0 θα γίνει και αυτή 0 με την εμφάνιση της ενεργού ακμής του ωρολογιακού παλμού. 38
39 Σχήμα 3.6 Καταχωρητής ολίσθησης σειριακής-εισόδου-σειριακής-εξόδου των 4 bits τύπου: (α) D, (β) JK, (γ) SR και (δ) κυματομορφές εξόδου για τέσσερις ωρολογιακούς παλμούς. Σημειώνεται ότι ο καταχωρητής ολίσθησης του Σχήματος 4.2 εκτελεί την ολίσθηση ενός αριθμού προς τα δεξιά. Αν ο αριθμός που έχει αποθηκευτεί σ' αυτόν έχει το MSB στο FF0 και το LSB στο FF3, δεξιά ολίσθηση κατά μία θέση θα έχει ως αποτέλεσμα την διαίρεση του αριθμού δια 2 (με την προϋπόθεση ότι η σειριακή είσοδος κρατείται στο μηδέν). Αν ο αριθμός έχει αποθηκευτεί κατά την αντίθετη φορά, δηλαδή το MSB στο FF3 και το LSB στο FF0, τότε δεξιά ολίσθηση κατά μία θέση θα έχει ως αποτέλεσμα τον πολλαπλασιασμό αυτού επί Καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου Οι καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου είναι ακριβώς ίδιοι με τους καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου με μόνη διαφορά ότι μας είναι διαθέσιμες οι έξοδοι Q όλων των FFs και όχι μόνον η έξοδος του τελευταίου. Στο Σχήμα 3.7. δείχνεται ο αντίστοιχος του Σχήματος 3.6 (α) καταχωρητής ολίσθησης σειριακής-εισόδου παράλληλης-εξόδου των 4 bits. Σχήμα 3.7 Καταχωρητής ολίσθησης σειριακής-εισόδου-παράλληλης-εξόδου των 4 bit 39
40 Οι κυματομορφές εισόδου-εξόδου του Σχήματος 3.6 (δ) είναι επίσης ίδιες και στην περίπτωση του καταχωρητή ολίσθησης του Σχήματος 3.7. Συνήθως οι καταχωρητές ολίσθησης έχουν επιπλέον εισόδους (CLEAR) ή και (PRESET) οι οποίες συνδέονται στις αντίστοιχες εισόδους όλων των FFs για την άμεση (ασύγχρονη) εκκαθάριση (δηλαδή όλες οι έξοδοι γίνονται 0) ή καθορισμό της υψηλής στάθμης του καταχωρητή (δηλαδή όλες οι έξοδοι γίνονται 1) Καταχωρητές παράλληλης-εισόδου-παράλληλης-εξόδου Ένας καταχωρητής παράλληλης-εισόδου-παράλληλης-εξόδου προκύπτει εύκολα από FF τύπου D στα οποία ελέγχουμε ανεξάρτητα τις εισόδους και εξόδους τους, όπως δείχνεται για την περίπτωση ενός 4 bit καταχωρητή στο Σχήμα 3.8 (α). Φυσικά όλα τα FFs χρονίζονται με τους ίδιους ωρολογιακούς παλμούς. Σχήμα 3.8. Καταχωρητής παράλληλης-εισόδου-παράλληλης-εξόδου με FFs τύπου D. Κάθε φορά που ενεργοποιείται ο ωρολογιακός παλμός (κατά την αρνητική ακμή στην προκειμένη περίπτωση) οι είσοδοι Di θα "διαβάζονται" και θα περνούν στις εξόδους Qi, όπου i=0,1,2,... Παρατηρούμε, δηλαδή, ότι όλες οι είσοδοι φορτώνονται παράλληλα στον καταχωρητή μ' έναν μόνο ωρολογιακό παλμό. Υπάρχει όμως ένα σοβαρό μειονέκτημα στο κύκλωμα αυτό. Ότι δηλαδή με κάθε νέο ωρολογιακό παλμό, νέα δεδομένα θα φορτώνονται στον καταχωρητή. Με άλλα λόγια, αν εμείς θέλουμε να φυλάξουμε τα δεδομένα, θα πρέπει να σταματήσουμε τους ωρολογιακούς παλμούς. Αυτό γίνεται εύκολα με την βοήθεια μιας πύλης AND, όπως φαίνεται στο Σχήμα 3.8 (β). Όταν η είσοδος ελέγχου Ε=1, τότε CLK=clock και το κύκλωμα λειτουργεί όπως περιγράψαμε στα προηγούμενα. Όταν όμως Ε=0, τότε CLK=0 και οι ωρολογιακοί παλμοί παύουν. Αν και φαίνεται πως με την προσθήκη της πύλης AND έχουμε επιλύσει το πρόβλημα, στην πράξη αυτό δεν γίνεται. Το να παρεμβάλουμε μια πύλη στην πορεία των ωρολογιακών παλμών, σημαίνει ότι προσθέτουμε καθυστερήσεις ανάμεσα στο κύριο ρολόι του συστήματος και στα επιμέρους ρολόγια των FFs. Κάτι τέτοιο μπορεί να οδηγήσει σε αποσυγχρονισμό του ψηφιακού συστήματος και τελικά σε αδυναμία λειτουργίας αυτού. Γι'αυτόν το λόγο, αφήνουμε τους ωρολογιακούς παλμούς ως έχουν και παρεμβαίνουμε στις εισόδους των FFs, για τον έλεγχο της φόρτωσης των δεδομένων. 40
41 Σχήμα 3.9. Καταχωρητής παράλληλης-εισόδου-παράλληλης-εξόδου των 4 bits με FFs τύπου SR. Ένας τέτοιος καταχωρητής παράλληλης-εισόδου-παράλληλης-εξόδου των 4 bits κατασκευασμένος με FFs τύπου SR, δείχνεται στο Σχήμα 4.7. Παρατηρούμε ότι: 1. Σε όλα τα FFs τροφοδοτούμε τους ίδιους ωρολογιακούς παλμούς CLK. 2. Υπάρχει μία είσοδος (CLEAR) για την άμεση εκκαθάριση του καταχωρητή, δηλαδή όλων των FFs. 3. Ο έλεγχος της παράλληλης εισόδου (φόρτωσης) των δεδομένων γίνεται μέσω της εισόδου E. Όταν E=1, τότε επιτρέπεται η φόρτωση των δεδομένων εισόδου Ιi, i=0,1,2,3. Για να γίνει αυτό κατανοητό, μπορούμε να δούμε τι συμβαίνει με τις πύλες AND που οδηγούν τις εισόδους S0, R0 του FF0. Βλέπουμε ότι για E=1 η πύλη επιτρέπει την διέλευση του δεδομένου Ι0 (δηλαδή S0=I0), και η πύλη επιτρέπει την διέλευση από αυτή του Ι0 (δηλαδή R0=I0 ). Έτσι αν Ι0=1, τότε στο FF0 καταχωρείται το λογικό 1 (αφού S0=1 και R0=0), ενώ για Ι0=0, τότε στο FF0 καταχωρείται το λογικό 0 (S0=0 και R0=1). Για E=0, οι έξοδοι όλων των πυλών AND είναι 0, ανεξάρτητα από τις τιμές των εισόδων Ii. Συνεπώς, Si=Ri=0 και άρα το FF δεν αλλάζει κατάσταση. Διευκρινίζεται ότι οι είσοδοι δεδομένων Ii και η είσοδος ελέγχου E μπορούν να αλλάζουν οποτεδήποτε, αρκεί να λαμβάνονται υπόψη οι χρόνοι προετοιμασίας και παραμονής σε σχέση με την ενεργό ακμή του ρολογιού. Η φόρτωση των δεδομένων γίνεται κατά την άφιξη της πρώτης ενεργού ακμής των ωρολογιακών παλμών. 41
42 Καταχωρητές παράλληλης-εισόδου-σειριακής-εξόδου Τα κυκλώματα αυτά έχουν την δυνατότητα να φορτώνουν τα δεδομένα παράλληλα και να τα αποστέλουν στην έξοδο σειριακά. Η φόρτωση n δυαδικών ψηφίων, όπως είναι φυσικό, γίνεται σε ένα κύκλο ρολογιού, ενώ η σειριακή έξοδος αυτών γίνεται σε n κύκλους του ρολογιού. Πρόκειται ουσιαστικά για έναν καταχωρητή ολίσθησης, ο οποίος όμως έχει επιπλέον την δυνατότητα παράλληλης φόρτωσης των δεδομένων. Το κύκλωμα ενός τέτοιου καταχωρητή των 4 bits δίνεται στο Σχήμα Σχήμα Καταχωρητής παράλληλης-εισόδου-σειριακής-εξόδου των 4 bits. Αυτό αποτελείται από 4 FFs τύπου SR αρνητικής ακμής πυροδότησης. Οι είσοδοι Si, Ri (i=0,1,2,3) του κάθε FF είναι συμπληρωματικές μεταξύ τους και τροφοδοτούνται από ένα συνδυασμό πυλών AND - OR. Ο συνδυασμός των πυλών εισόδου αποτελεί ένα απλό κύκλωμα πολύπλεξης 2 γραμμών σε 1. Συγκεκριμένα, όταν Ε=1, τότε μόνον η δεξιά AND επιτρέπει την είσοδο της Di να περάσει από αυτή, οπότε Si=Di και Ri=Di. Έτσι το δεδομένο Di καταχωρείται στο αντίστοιχο FFi. Όταν E=0, τότε μόνον η αριστερή AND επιτρέπει στην άλλη είσοδό της να περάσει από αυτή, οπότε Si=Qi-1 και Ri=Qi-1'. Δηλαδή η έξοδος Qi-1 του FFi-1 τροφοδοτείται στις εισόδους του FFi. Με τον τρόπο αυτό επιτυγχάνεται η ολίσθηση των δεδομένων προς τα δεξιά, και κατά συνέπεια η σειριακή τους έξοδος. Άρα, για Ε=1 έχουμε παράλληλη φόρτωση, ενώ για Ε=0 έχουμε ολίσθηση προς τα δεξιά. Εννοείται ότι η φόρτωση ή η ολίσθηση συμβαίνουν πάντοτε κατά την στιγμή της αρνητικής ακμής των ωρολογιακών παλμών για το συγκεκριμένο κύκλωμα. Παρατηρείστε ότι το κύκλωμα που μόλις περιγράψαμε διαθέτει και μια σειριακή είσοδο. Θα μπορούσε επομένως να χρησιμοποιηθεί και ως ένας καταχωρητής ολίσθησης σειριακής-εισόδου-σειριακήςεξόδου. Επίσης, μπορούμε να δούμε ότι αν είχαμε διαθέσιμες τις εξόδους Qi 42
43 (διακεκομμένες γραμμές του Σχήματος 3.10), τότε το ίδιο κύκλωμα θα μπορούσε να έχει επιπρόσθετα την δυνατότητα παράλληλης εξόδου των δεδομένων. Ένα τέτοιο κύκλωμα έχει στην πράξη όλες τις δυνατότητες των διαφορετικών καταχωρητών που περιγράψαμε μέχρι τώρα, δηλαδή σειριακής-εισόδου-σειριακήςεξόδου, σειριακής-εισόδου-παράλληλης-εξόδου, παράλληλης-εισόδου-παράλληληςεξόδου, παράλληλης- εισόδου-σειριακής-εξόδου. Στο εμπόριο διατίθενται σήμερα ολοκληρωμένα κυκλώματα καταχωρητών αυτού του είδους. Ένα άλλο στοιχείο που πρέπει να σημειωθεί για τον καταχωρητή που εξετάζουμε, αλλά και για όλους τους τύπους των καταχωρητών που μελετήσαμε μέχρι τώρα, είναι η δυνατότητά τους να συνδέονται ο ένας μετά τον άλλον για την καταχώρηση και ολίσθηση λέξεων πολλαπλάσιου μήκους. Έτσι, συνδέοντας δύο καταχωρητές των 4 bits ο καθένας, όπως αυτός του Σχήματος 3.10, μπορούμε να κατασκευάζουμε έναν καταχωρητή των 8 bits (βλ. Σχήμα 3.11). Εξυπακούεται ότι οι δύο καταχωρητές θα πρέπει να συγχρονίσουν την λειτουργία τους τροφοδοτούμενοι με τους ίδιους ωρολογιακούς παλμούς (CLK) και την ίδια είσοδο επιλογής Ε. Η σειριακή έξοδος του πρώτου συνδέεται στην σειριακή είσοδο του δεύτερου καταχωρητή. Σχήμα Καταχωρητής των 8 bits κατασκευασμένος από δύο καταχωρητές των 4 bits. Οι καταχωρητές παράλληλης-εισόδου-σειριακής-εξόδου και σειριακήςεισόδου-παράλληλης-εξόδου βρίσκουν ευρεία εφαρμογή στη σειριακή επικοινωνία ψηφιακών συστημάτων. Συγκεκριμένα, τα ψηφιακά συστήματα είναι συνήθως σχεδιασμένα ώστε να λειτουργούν παράλληλα, επιτυγχάνοντας έτσι μεγαλύτερες ταχύτητες επεξεργασίας. Η επικοινωνία δύο τέτοιων συστημάτων τα οποία βρίσκονται σε μεγάλη απόσταση το ένα από το άλλο γίνεται σειριακά. Για την σειριακή λοιπόν μετάδοση, απαιτείται ένας καταχωρητής παράλληλης-εισόδουσειριακής-εξόδου, ενώ για την σειριακή λήψη δεδομένων απαιτείται ένας καταχωρητής σειριακής-εισόδου-παράλληλης-εξόδου. 43
44 4. VHDL 4.1 Γενικά για την VHDL Η VHDL είναι µια γλώσσα περιγραφής υλικού για την ανάπτυξη ολοκληρωμένων ψηφιακών ηλεκτρονικών κυκλωμάτων. Ως λέξη αποτελεί συντόµευση των λέξεων: VHSIC Hardware Description Language. Τα δε αρχικά VHSIC είναι µε τη σειρά τους συντόµευση για Very High-Speed Integrated Circuit (Ολοκληρωµένα Κυκλώµατα Υψηλής Ταχύτητας). Περιγράφει τη συμπεριφορά ενός ηλεκτρονικού κυκλώματος ή συστήματος, με βάση την οποία μπορεί στη συνέχεια να υλοποιηθεί το κύκλωμα ή το σύστημα. Οι κύριες εφαρμογές της VHDL είναι στον τομέα των προγραμματιζόμενων λογικών στοιχείων (PLA) που περιλαμβάνει τα CPLD (complex programmable logic devices) και τα FPGA (field programmable gate arrays). 4.2 Δομή της VHDL Σχήμα 4.1 Δομή της VHDL 44
45 Η δομή ενός αυτόνομου τμήματος του κώδικα της VHDL (σχήμα 4.1), αποτελείται από τρείς βασικές ενότητες: Από την ενότητα δήλωσης των βιβλιοθηκών στην οποία δηλώνουμε τις βιβλιοθήκες που πρόκειται να χρησιμοποιηθούν στον σχεδιασμό. Από την ενότητα Entity η οποία καθορίζει του ακροδέκτες εισόδου/εξόδου του κυκλώματος. Από την Architecture, δηλαδή την ουσία του προγραμματισμού, αφού σε αυτό το τμήμα περιγράφεται η συμπεριφορά του κυκλώματος. 4.3 FPGA Το FPGA ή αλλιώς συστοιχία επιτόπια προγραμματιζόμενων πυλών, είναι ένας τύπος προγραμματιζόμενου ολοκληρωμένου κυκλώματος το οποίο διαθέτει πολύ μεγάλο αριθμό τυποποιημένων πυλών και άλλων ψηφιακών λειτουργιών όπως καταχωρητές μνήμης και απαριθμητές. Οι συσκευές FPGA μπορεί να είναι πολύπλοκες. Σήμερα είναι διαθέσιμα τσιπ που κατασκευάζονται με τεχνολογία αιχμής 0,09μm CMOS και με περισσότερους από 1000 ακροδέκτες εισόδου/εξόδου. Κατά τον προγραμματισμό του FPGA, ο οποίος γίνεται πάντοτε ενώ αυτό είναι τοποθετημένο στο τυπωμένο κύκλωμα, ενεργοποιούνται οι επιθυμητές λειτουργίες και διασυνδέονται μεταξύ τους έτσι ώστε το FPGA να συμπεριφέρεται ως ολοκληρωμένο κύκλωμα. Το FPGA έχει τα εξής χαρακτηριστικά: Το FPGA χάνει τον προγραμματισμό του κάθε φορά που διακόπτεται η τάση τροφοδοσίας του. Επομένως απαιτεί εξωτερικό μικροεπεξεργαστή ή μνήμη με μόνιμη συγκράτηση δεδομένων (non-volatile memory) από τα οποία θα προγραμματίζεται, κάθε φορά που επανέρχεται η τάση τροφοδοσίας. Ο προγραμματισμός του FPGA μπορεί να αλλάζει κάθε φορά που τροποποιείται το λογισμικό του μικροεπεξεργαστή ή τα δεδομένα της μνήμης που το ελέγχει. Δεν υπάρχει όριο στο πόσες φορές μπορεί να επαναπρογραμματιστεί. 45
46 4.4 Βασικά τμήματα κώδικα VHDL Ο κώδικας VHDL είναι από την φύση του συντρέχων, δηλαδή παράλληλος. Μοναδική εξαίρεση αποτελούν τα τμήματα που βρίσκονται μέσα σε μια διεργασία (Process), συνάρτηση (Function) ή διαδικασία (Procedure) και είναι ακολουθιακά, δηλαδή σειριακά. Σε αυτήν την περίπτωση όμως το τμήμα του κώδικα που εκτελείται ακολουθιακά, θα είναι συντρέχων ως προς τον υπόλοιπο κώδικα. Ο συντρέχων κώδικας ονομάζεται και κώδικας ροής δεδομένων (dataflow code) ενώ ο ακολουθιακός ονομάζεται και κώδικας συμπεριφοράς (behavioral). Με την χρήση συντρέχοντα κώδικα μπορούμε να περιγράψουμε μόνο συνδυαστικά λογικά κυκλώματα ενώ με την χρήση ακολουθιακού κώδικα μπορούμε κατά κύριο λόγο να περιγράψουμε ακολουθιακά λογικά κυκλώματα αλλά και συνδυαστικά λογικά κυκλώματα. Συνδυαστική λογική: Συνδυαστική λογική έχουμε όταν η έξοδος του κυκλώματος εξαρτάται αποκλειστικά από τις τρέχουσες εισόδους. Για αυτόν τον λόγο δεν απαιτείται χρήση μνήμης και μπορεί να υλοποιηθεί με χρήση συμβατικών λογικών πυλών. Ακολουθιακή λογική: Ακολουθιακή λογική έχουμε όταν η έξοδος εξαρτάται από προηγούμενες εισόδους. Για αυτόν τον λόγο αυτό απαιτείται η χρήση στοιχείων μνήμης τα οποία και θα είναι συνδεδεμένα με έναν βρόγχο ανάδρασης με το μπλοκ της συνδυαστικής λογικής έτσι ώστε οι αποθηκευμένες καταστάσεις να επηρεάζουν την έξοδο του κυκλώματος. Σχήμα 4.2 (α) Συνδυαστική λογική (β) Ακολουθιακή λογική 46
47 4.4.1 Διεργασίες ακολουθιακού κώδικα Όπως είπαμε και παραπάνω ένα τμήμα κώδικα της VHDL εκτελείται ακολουθιακά μονάχα αν αποτελεί διεργασία, συνάρτηση ή διαδικασία. Αυτό που θα μας χρειαστεί για την εκπόνηση της εργασίας, μιας και χρησιμοποιήσαμε ακολουθιακά τμήματα κώδικα, είναι η διεργασία (process). Η διεργασία (process) χαρακτηρίζεται κυρίως από την ύπαρξη εντολών που προορίζονται για ακολουθιακό κώδικα, όπως η IF, WAIT, CASE ή LOOP καθώς και από την ύπαρξη μιας λίστας ευαισθησίας. Η διεργασία πρέπει να βρίσκεται στον κύριο κώδικα και εκτελείται κάθε φορά που αλλάζει τιμή κάποιο σήμα από την λίστα ευαισθησίας. Μια διεργασία έχει την παρακάτω σύνταξη: Στην παραπάνω σύνταξη χρησιμοποιήσαμε μεταβλητές (VARIABLES) και πρέπει να δηλώνονται στο δηλωτικό μέρος της διεργασίας. Οι αρχικές τιμές λαμβάνονται υπόψιν μόνο στις προσομοιώσεις. Η ετικέτα, όπως και οι μεταβλητές και οι διεργασίες, είναι προαιρετικές και μπορούμε να της δώσουμε οποιαδήποτε λέξη μη-δεσμευμένη από την VHDL. VHDL. Φυσικά ένα ακολουθιακό κύκλωμα πρέπει να είναι και σύγχρονο για να λειτουργήσει σωστά. Για αυτόν τον λόγο απαιτείται και η χρήση ενός σήματος χρονισμού (clock).συνηθισμένο είναι να χρησιμοποιούμε την ιδιότητα EVENT για να ανιχνεύουμε την αλλαγή του σήματος του ρολογιού. Για παράδειγμα, αν το clock είναι σήμα στην λίστα ευαισθησίας τότε η εντολή clock'event επιστρέφει τιμή TRUE όταν συμβαίνει αλλαγή στο clock. Η αλλαγή του clock μπορεί να είναι ακμοπυρόδοτη (είτε στην ανερχόμενη είτε στην κατερχόμενη ακμή). 47
48 4.4.2 Συχνά χρησιμοποιούμενες ακολουθιακές εντολές Σε αυτήν την εργασία χρησιμοποιήθηκαν κατά κόρον κάποιες συγκεκριμένες εντολές. Οι κυριότερες περιγράφονται παρακάτω: Εντολή IF : Η εντολή IF προορίζεται για ακολουθιακό κώδικα και χρησιμοποιείται μέσα σε μια διεργασία, συνάρτηση ή διαδικασία. Αν και η ύπαρξη της εντολής IF μπορεί να οδηγήσει στην δημιουργία μη απαραίτητου κωδικοποιητή προτεραιότητας, το εργαλείο σύνθεσης θα βελτιστοποιήσει το κύκλωμα και θα αποφύγει το επιπλέον υλικό. Η σύνταξη της εντολής IF είναι η ακόλουθη: Παράδειγμα εντολής IF: 48
49 Εντολή LOOP: Η εντολή LOOP είναι πολύ χρήσιμη όταν ένα τμήμα του κώδικα θα πρέπει να χρησιμοποιηθεί πολλές φορές. Όπως και η εντολή IF χρησιμοποιείται αποκλειστικά και μόνο μέσα σε μια διεργασία, συνάρτηση ή διαδικασία δηλαδή αποκλειστικά και μόνο σε ακολουθιακό κώδικα. Η σύνταξη της εντολής LOOP εξαρτάται από το αν θέλουμε να εισάγουμε κάποια συνθήκη ή να βάλουμε τον βρόγχο να επαναληφθεί για κάποιο συγκεκριμένο αριθμό φορών. Θα έχουμε λοιπόν: Εντολή LOOP/FOR : θα επαναληφθεί ο βρόγχος ανάλογα με το εύρος Εντολή WHILE/LOOP : Ο βρόγχος θα επαναλαμβάνεται όσο ισχύει η συνθήκη που θα ορίσουμε Παράδειγμα της εντολής LOOP: 49
50 4.4.3 Καταχωρητής, πακέτο και συστατική επιστολή Καταχωρητής (register): Ο καταχωρητής είναι ακουλουθιακό λογικό κύκλωμα και αποτελείται από μια ομάδα flip-flop. Το κάθε flip-flop έχει την δυνατότητα να αποθηκεύσει ένα μπιτ πληροφορίας. Ένας καταχωρητής με n μπιτ αποτελείται από μια ομάδα n flip-flop ικανά να αποθηκεύσουνε n bits. Εκτός από τα flip-flop ένας καταχωρητής μπορεί να έχει και συνδυαστικές πύλες, οι οποίες εκτελούν ορισμένες λειτουργίες επεξεργασίας δεδομένων. O καταχωρητής έχει και ένα σήμα χρονισμού (α) το οποίο παρέχει σταθερό ρυθμό λειτουργίας σε όλα τα μέρη του κυκλώματος. Τέλος υπάρχει και ένα σήμα μηδενισμού (rst) το οποίο οδηγεί το κύκλωμα στην αρχική του κατάσταση. Στο παρακάτω σχήμα φαίνεται ένας καταχωρητής αποτελούμενος από τέσσερις D-μανταλωτής. Σχήμα bit καταχωρητής Πακέτο: Τα συχνά χρησιμοποιούμενα τμήματα κώδικα γράφονται συχνά με την μορφή συστατικών στοιχείων, συναρτήσεων ή διαδικασιών. Ο κώδικας αυτός τοποθετείτε σε ένα πακέτο (PACKAGE) και μεταγλωτίζεται στη βιβλιοθήκη προορισμού(σχήμα 4.4). Με την τεχνική αυτή καταφέρνουμε να διαμερίσουμε, και να επαναχρησιμοποιήσουμε τον κώδικα. Η δομή του πακέτου θα είναι η ακόλουθη: 50
51 Όπως μπορούμε να διαπιστώσουμε η σύνταξη χωρίζετε σε δύο μέρη, το πακέτο (PACKAGE) και το σώμα του πακέτου(package BODY). Στο πρώτο μέρος περιέχονται όλες οι δηλώσεις ενώ το δεύτερο μέρος χρησιμοποιείται μονάχα όταν στο πρώτο μέρος δηλώνονται ένα ή περισσότερα υποπρογράμματα(συναρτήσεις και διαδικασίες), όπου στην περίπτωση αυτή πρέπει να περιέχονται οι περιγραφές των υποπρογραμμάτων. Σχήμα 4.4 Θεμελιώδης μονάδες κώδικα VHDL 51
52 5. Αλγόριθμος Σε αυτό το σημείο θα γράψουμε τον κώδικα του 3 bit απαριθμητή σε γλώσσα VHDL είτε αυτός μετράει προσθετικά, είτε αφαιρετικά. Ας δούμε βήμα βήμα την κατασκευή του κώδικα. Δηλώνουμε πρώτα την βιβλιοθήκη που θα χρειαστούμε. Αυτή είναι η IEEE.STD_LOGIC_1164. Στην ενότητα ENTITY δηλώνουμε το 3bit σήμα εξόδου Count και ως σήματα εισόδου τα Dir, RstB και Clk. Στην ενότητα ARCHITECTURE δηλώνουμε μια διεργασία process βάζοντας στη λίστα τα σήματα Dir, RstB και Clk και θέτοντας ως αρχική κατάσταση του σήματος εξόδου ίσο με 0. Έπειτα αναγκάζουμε το κύκλωμα να λειτουργεί κάθε φορά που η τιμή του RstB είναι 1. Ύστερα προχαράμε σε μαθηματικές πράξεις σε περιπτώσεις κάθε φορά οι οποίες απαρτίζουν τον κώδικά μας. Το RstB λειτουργεί σαν ασφάλεια, όσο η τιμή το είναι 1 ο αλγόριθμος τρέχει κανονικά, όταν γίνει 0 σταματάει ακαριαία. Ανάλυση των εντολών για κάθε μια ξεχωριστά θα δούμε στο επόμενο κεφάλαιο. Ας δούμε τώρα τον κώδικά μας: library IEEE; use IEEE.std_logic_1164.all; entity UpDown3BitCounter is port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic end entity UpDown3BitCounter; ); 52
53 architecture structural of UpDown3BitCounter is signal Q: std_logic_vector(2 downto 0):= "000"; signal D: std_logic_vector(2 downto 0):= "000"; begin process(dir,rstb,clk) begin if (RstB='0') then Q<="000"; else if(dir='0') then D(0)<= not Q(0); if(q(0)='1') then D(1)<= not Q(1); end if; if(q(1)='1' and Q(0)='1') then D(2)<= not Q(2); end if; else D(0)<= not Q(0); if(q(0)='0') then D(1)<= not Q(1); end if; if(q(1)='0' and Q(0)='0') then D(2)<= not Q(2); end if; end if; 53
54 if (rising_edge(clk)) then end if; Q<=D; end if; end process; Count<=Q; end architecture; Για να μετράει ο καταχωρητής προς τα αριστερά ή προς τα δεξιά χρειαζόμαστε δυο βιβλιοθήκες, η μια μετράει προσθετικά και η άλλη αφαιρετικά αντίστοιχα. Περεταίρω ανάλυση συναντάμε στις παρακάτω βιβλιοθήκες. library ieee; use IEEE.std_logic_1164.all; entity testbench is end entity; architecture testb_up of testbench is component UpDown3BitCounter port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic ); end component; 54
55 signal reset: std_logic := '1'; signal clk: std_logic := '0'; signal dir: std_logic := '0'; signal count: std_logic_vector(2 downto 0); signal per: time := 20 ns; begin mycnt : UpDown3BitCounter port map( Count=>count, Dir=>dir, RstB=>Reset, Clk=>clk ); Reset<= '0', '1' after 50 ns; dir<='0'; clockprocess: process begin clk<='0'; wait for per/2; clk<='1'; wait for per/2; end process clockprocess; end; 55
56 architecture testb_down of testbench is component UpDown3BitCounter port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic ); end component; signal reset: std_logic := '1'; signal clk: std_logic := '0'; signal dir: std_logic := '0'; signal count: std_logic_vector(2 downto 0); signal per: time := 20 ns; begin mycnt : UpDown3BitCounter port map( Count=>count, Dir=>dir, RstB=>Reset, Clk=>clk ); Reset<= '0', '1' after 50 ns; dir<='1'; clockprocess: process 56
57 begin clk<='0'; wait for per/2; clk<='1'; wait for per/2; end process clockprocess; end; Για να εξετάσουμε τον κώδικά μας δημιουργήσαμε ένα testbench όπου όταν ο διακόπτης reset είναι 0 δεν έχουμε καμία μεταβολή, όταν γίνει 1, σε κάθε θετικό παλμό του ρολογιού (clk) έχουμε μεταβολές στις τιμές των 3 bit. Όσο η τιμή του dir είναι 0, ο καταχωρητής θα μετράει προσθετικά. Η κυματομορφή του παρακάτω σχήματος είναι η ίδια με αυτήν που περιγράψαμε στο κεφάλαιο και το σχήμα που εμφανίζεται είναι ακριβώς ίδιο με αυτό του σχήματος 3.4 της σελίδας 32. Βλέπουμε την αρχική τιμή του count να είναι 0 και όταν η τιμή του reset γίνει 1, αρχίζει να μετράει προσθετικά με δυαδική μορφή σε κάθε παλμό του ρολογιού. Ο χρόνος από την μία θετική ακμή του ενός ωρολογιακού παλμού μέχρι και του επόμενου, διαρκεί 20 nsec. Στο ακριβώς από κάτω σχήμα βλέπουμε όταν ο καταχωρητής μας μετράει αφαιρετικά, οι τιμές των εισόδων είναι οι ίδιες με τις από πάνω, μόνο που εδώ η τιμή τoυ dir είναι 1. H κυματομορφή θα είναι όπως αυτή του σχήματος 3.2 της σελίδας 30 και οι τιμές του count θα μετράνε αφαιρετικά. 57
58 6. Ανάλυση εντολών αλγορίθμου Σε αυτό το κεφάλαιο θα δούμε ποιες είναι οι εντολές του αλγορίθμου και ποια ακριβώς είναι η σημασία της κάθε μιας. Στον UpDown3bitCounter. library IEEE; use IEEE.std_logic_1164.all; ---Δηλώνουμε ποια βιβλιοθήκη θα χρησιμοποιήσουμε entity UpDown3BitCounter is port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic ); end entity UpDown3BitCounter; --- Στην ενότητα δηλώνουμε τις εισόδους και τις εξόδους. Όπου είσοδοι οι Dir, RstB και Clk και έξοδος ο out std_logic_vector. Dir η διεύθυνση της μέτρησης (0 για Up και 1 για Down) RstB o διακόπτης (κάνει reset όταν είναι 0) και Clk η θετική ακμή του ρολογιού (positive edge) 58
59 architecture structural of UpDown3BitCounter is --- H αρχιτεκτονική του UpDown3BitCounter signal Q: std_logic_vector(2 downto 0):= "000"; signal D: std_logic_vector(2 downto 0):= "000"; --- Σήματα Q και D τα οποία περιέχουν τιμές σε πίνακες από Bit process(dir,rstb,clk) begin if (RstB='0') then Q<="000"; --- Εδώ δηλώνουμε το process μας. Αυτό τρέχει στο dt χρόνο και έχει λίστα ευαισθησίας με τα σήματα που μας ενδιαφέρουν και επηρεάζουν άμεσα το σύστημα --- Από εδώ και πέρα όλα τρέχουν ταυτόχρονα --- Εδώ ελέγχουμε αν το Reset είναι Αν ναι, τότε η έξοδος των τριών flip-flop μας γίνεται μηδέν. else if(dir='0') then --- Εδώ το reset είναι 1, οπότε βλέπουμε αν η διεύθυνση μέτρησης είναι ίση με 0 (δηλαδή με up) D(0)<= not Q(0); --- Αν ναι τότε το D(0) θα γίνει ίσο με το αντίστροφο το Q(0) 59
60 if(q(0)='1') then --- Αν το Q(0) είναι 1 τότε D(1)<= not Q(1); --- αντιστρέφουμε και το επόμενο flip-flip, δηλαδή παίρνουμε την έξοδο Q(1) και την κάνουμε not και την τροφοδοτούμε στην είσοδο D(1) του flip-flop end if; if(q(1)='1' and Q(0)='1') then D(2)<= not Q(2); --- Αν τα Q(0) και Q(1) είναι 1 τότε --- αντιστρέφουμε και το τρίτο και τελευταίο flipflop end if; else --- Εδώ η διεύθυνση είναι 1 οπότε μετράμε προς τα κάτω (down) D(0)<= not Q(0); if(q(0)='0') then --- Αν ναι τότε το D(0) θα γίνει ίσο με το αντίστροφο το Q(0). Αυτό δεν αλλάζει οπότε αν θέλουμε το βγάζουμε ουσιαστικά και εκτός του if (Dir='0') --- Τώρα όμως βλέπουμε αν το Q(0) είναι 0 για να αναστρέψουμε το επόμενο flip-flop D(1)<= not Q(1); --- το D(1) θα γίνει ίσο με το αντίστροφο το Q(1) end if; 60
61 if(q(1)='0' and Q(0)='0') then D(2)<= not Q(2); --- Επίσης κι εδώ κοιτάμε αν τα Q(0) και Q(1) είναι ίσα με μηδέν για να αναστρέψουμε και το τρίτο flip-flop. --- αντιστρέφουμε και το τρίτο και τελευταίο flipflop end if; end if; if (rising_edge(clk)) then --- Εδώ ελέγχουμε αν έχουμε θετική ακμή στο ρολόι μας, οπότε και περνάμε τις εισόδους D στις εξόδους Q. Q<=D; end if; end if; end process; --- Τέλος διαδικασίας Count<=Q; end architecture; --- Εδώ ουσιαστικά περνάμε τις εξόδους των flip-flop στην έξοδο του counter. Αυτή είναι μόνιμη σύνδεση και δεν σχετίζεται με το ρολόι. Θα ήταν σαν να συνδέαμε τα Q των ff με καλώδια σε κάποια pad. --- Τέλος αρχιτεκτονικής 61
62 Στον Testbench. library ieee; use IEEE.std_logic_1164.all; --- H βιβλιοθήκη είναι η ίδια με το UpDown3bitCounter entity testbench is end entity; --- Τestbench για τον 3 bit Up/Down απαριθμητή architecture testb_up of testbench is component UpDown3BitCounter --- Αρχιτεκτονική του testbench για τον up απαριθμητή --- Το component στο testbench ουσιαστικά δηλώνει την οντότητα του απαριθμητή ώστε να ξέρει ο compiler ότι θα το χρειαστεί. port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic ); --- Ισχύει ότι ισχύει και στον Down3bitCounter end component; 62
63 signal reset: std_logic := '1'; signal clk: std_logic := '0'; signal dir: std_logic := '0'; signal count: std_logic_vector(2 downto 0); signal per: time := 20 ns; --- Δίνουμε τις λογικές τιμές 1 και 0 ως αρχική τιμή στα σήματα εισόδων και εξόδων --- Θέτουμε ως αρχική τιμή περιόδου τα 20 nsec begin mycnt : UpDown3BitCounter port map( Count=>count, Dir=>dir, RstB=>Reset, Clk=>clk ); --- O απαριθμητής με το όνομα mycnt, χρησιμεύει στο να συνδέω τοπικά τα σήματα του testbench. Reset<= '0', '1' after 50 ns; --- Στον διακόπτη αρχική τιμή το λογικό 0 και μετά από 50 nsec το λογικό 1 dir<='0'; --- Η τιμή του dir είναι 0 γιατί χρησιμοποιούμε την αρχιτεκτονική για τον up απαριθμητή 63
64 clockprocess: process --- Το process του ρολογιού (clock) begin clk<='0'; wait for per/2; clk<='1'; wait for per/2; end process clockprocess; --- Τετραγωνικός παλμός στο ρολόι, το πρώτο με περίοδο χωρισμένη σε δυο ίσα χρονικά διαστήματα, το πρώτο μισό λογικό 0 και το άλλο λογικό 1. Οι αλλαγές στις τιμές εξόδου γίνονται στο λογικό 1 (θετική ακμή ρολογιού) end; 64
65 architecture testb_down of testbench is --- Αρχιτεκτονική του testbench για τον down απαριθμητή component UpDown3BitCounter port (Count: out std_logic_vector(2 downto 0); Dir: in std_logic; RstB: in std_logic; Clk: in std_logic ); end component; --- Ότι ακριβώς περιγράψαμε στον up απαριθμητή signal reset: std_logic := '1'; signal clk: std_logic := '0'; signal dir: std_logic := '0'; signal count: std_logic_vector(2 downto 0); signal per: time := 20 ns; begin mycnt : UpDown3BitCounter port map( Count=>count, Dir=>dir, RstB=>Reset, Clk=>clk ); 65
66 Reset<= '0', '1' after 50 ns; dir<='1'; --- Η τιμή του dir είναι 1 γιατί χρησιμοποιούμε την αρχιτεκτονική για τον down απαριθμητή clockprocess: process begin clk<='0'; wait for per/2; clk<='1'; wait for per/2; end process clockprocess; end; 66
67 7. Ανάλυση χρονισμών Όταν τα σχέδια γίνονται πιο πολύπλοκα, η ανάγκη για προηγμένη ανάλυση ολοένα και αυξάνεται. Το χρονοδιάγραμμα στατικής ανάλυσης (static timing analysis) είναι μια μέθοδος ανάλυσης εντοπισμού σφαλμάτων (debugging) και πιστοποίησης (validating) στην απόδοση του χρονοδιαγράμματος. Το χρονοδιάγραμμα ανάλυσης μετρά την καθυστέρηση της κάθε διαδρομής του σχεδιασμού και μας αναφέρει την απόδοση του σχεδιασμού από άποψη μέγιστης συχνότητας των ρολογιών. Το χρονοδιάγραμμα στατικής ανάλυσης δεν ελέγχει την λειτουργικότητα του σχεδίου και πρέπει να το χρησιμοποιήσουμε μαζί με την προσομοίωση (simulation) για να επαληθεύσει την συνολική λειτουργία του σχεδίου μας. Βασικά στοιχεία ανάλυσης χρονισμών (Timing Analysis Basics) Ένα ολοκληρωμένο χρονοδιάγραμμα ανάλυσης περιλαμβάνει το setup time (tsu), το hold time (th), το clock to output delays (tco), τα maximum clock frequencies (fmax) και τα slack times of the design. Αναλύοντας αυτές τις τιμές που έχουμε πάρει από κάθε FPGA, μας δίνεται η δυνατότητα να βρούμε απόδοση του κυκλώματος. Λήψη λανθασμένων τιμών θα μπορούσε να οδηγήσει σε εσφαλμένη λειτουργία του κυκλώματος. Αυτή η ενότητα περιγράφει την βασική ανάλυση των μετρήσεων του χρονοδιαγράμματος. 7.1 Clock setup time (tsu) Είναι το μικρότερο χρονικό διάστημα που χρειάζονται να υπάρχουν στις εισόδους των καταχωρητών τα δεδομένα από την θετική ακμή του παλμού του ρολογιού. Το σχήμα 7.1 δείχνει το σχεδιάγραμμα του tsu. 67
68 To Micro tsu είναι το εσωτερικό setup time (internal setup time), δηλαδή είναι το χαρακτηριστικό του καταχωρητή και δεν επηρεάζεται από τα σήματα που τροφοδοτούν τον καταχωρητή. Η ακόλουθη εξίσωση υπολογίζει το tsu του κυκλώματος. Tsu = Data delay Clock Delay + Micro tsu Clock Delay είναι ο χρόνος καθυστέρησης του ρολογιού καθότι τα δίκτυα των ρολογιών παρουσιάζουν εγγενείς καθυστερήσεις. Data Delay είναι ο χρόνος καθυστέρησης μεταφοράς των δεδομένων κατά τον ίδιο τρόπο με το clock delay. 7.2 Clock hold time (th) Είναι το μικρότερο χρονικό διάστημα που πρέπει να παραμείνουν τα δεδομένα σταθερά στις εισόδους των καταχωρητών μετά την θετική ακμή του ρολογιού ώστε να μην υπάρχει πρόβλημα στην μαντάλωση (latching) των δεδομένων. Στο σχήμα 7.2 φαίνεται το σχεδιάγραμμα του th. To Micro th είναι το εσωτερικό Ηold time του καταχωρητή. Η ακόλουθη εξίσωση υπολογίζει το th σύμφωνα με το κύκλωμα του σχήματος 7.2. th = Clock Delay Data Delay + Micro th 68
69 7.3 Clock to Output Delay (tco) Είναι η χρονική διάρκεια που χρειάζεται το κύκλωμα να αποκτήσει μια έγκυρη τιμή εξόδου μετά από μια εμφάνιση ενός παλμού του ρολογιού που πουροδοτεί έναν καταχωρητή. Micro tco είναι η εσωτερική χρονική καθυστέρηση μέσα στο εσωτερικό του καταχωρητή. Tco = Clock Delay + Data Delay + Micro tco 7.4 Clock Maximum Clock Frequency (Fmax) Είναι η γρηγορότερη ταχύτητα με την οποία μπορεί να τρέξει το ρολόι χωρίς να μας καθυστερούν οι εσωτερικοί χρόνοι. Το Quartuw μπορεί να τρέξει την χρονική ανάλυση σε σχέδια με πολλαπλά ή με ένα μόνο ρολόι και αναγράφοντας την εσωτερική μέγιστη συχνότητα (Fmax) του συστήματος υπολογίζει τις εξωτερικές καθυστερήσεις από ή προς τη συσκευή συμπεριλαμβανομένων των tsu και tco. Restricted Fmax είναι η μέγιστη συχνότητα στην οποία είναι πιο κοντά η πραγματική συχνότητα λειτουργίας του σχεδίου. Δηλαδή εμπεριέχει και τυχόν καθυστερήσεις που υπάρχουν της συσκευής FPGA. 7.5 Slack Είναι το περιθώριο στο οποίο οι χρονικές απαιτήσεις (π.χ. του Fmax) πληρούνται ή δεν πληρούνται. Positive Slack υποδεικνύει ότι το κύκλωμα πληροί τις απαιτήσεις του χρονοδιαγράμματος. Το Negative Slack σηματοδοτεί ακριβώς το αντίθετο. Το Quartus καθορίζει την τιμή του slack με τις δυο ακόλουθες εξισώσεις. 69
70 Slack = Required Clock Period Actual Clock Period Slack = Slack Clock Period (Micro tco + Data Delay + Micro tsu) Διάγραμμα υπολογισμού των Slack 7.6 Ανάλυση του χρονισμού (setup the timing analyzer) Η ανάλυση του χρονοδιαγράμματος μπορεί να διευκρινιστεί μέσα από το Quartus. Για να εκτελεστεί σωστά η ανάλυση χρονισμού πρέπει πρώτα το σχέδιο να έχει μετταγλωτιστεί με επιτυχία (successfully compilation). Aν χρησιμοποιούμε παραπάνω από ένα αναλύσεις χρονισμών ταυτόχρονα, εδώ χρειάζεται να κάνουμε διαφορετικές ρυθμίσεις χωρίς να χρειαστεί να ξαναμετταγλωτίσουμε (re-compile). 70
71 7.7 Τρόπος εύρεσης μέγιστης συχνότητας FPGA Στη συνέχεια της υποενότητας θα δούμε πως ακριβώς βρίσκουμε τη μέγιστη συχνότητα ενός FPGA βήμα βήμα. Πρώτα ανοίγουμε το Quartus και ύστερα πάνω αριστερά στην ενότητα entity, κάνουμε δεξί κλικ με το ποντίκι και επιλέγουμε και επιλέγουμε device. 71
72 Επιλέγουμε την οικογένεια των FPGA, πόσα ποδαράκια θέλουμε να έχει το FPGA (pin count) και τέλος στο speed grade επιλέγουμε το fastest. Ακριβώς από κάτω μας βγάζει μια λίστα από FPGA και εμείς επιλέγουμε ένα από αυτά και πατάμε ΟΚ. 72
73 Στην αρχική σελίδα, πάνω πάνω πατάμε processing και start compilation για να αρχίσει η μετταγλώτιση. Η διαδικασία θα διαρκέσει αρκετή ώρα. 73
74 Μόλις τελειώσει η μετταγλώτιση θα μας εμφανιστεί το ακόλουθο μήνυμα. Πατάμε ΟΚ. 74
75 Επιλέγουμε το Time Quest Time Analyzer, πατάμε πάνω στο Slow.. Model και ύστερα πάνω στο Fmax Summary. Διπλό κλικ πάνω στο ΤimeQuest Timing Analyzer (μέση και αριστερά) ώστε να εμφανίσει σε νέο παράθυρο τον time analyzer. Πάνω πάνω σε μια οριζόντια σειρά εμφανίζεται η μέγιστη συχνότητα του FPGA που επιλέξαμε. 75
76 Στο νέο παράθυρο που μας άνοιξε πατάμε το Custom Reports και Report timing Και στη συνέχεια μας εμφανίζεται το ακόλουθο παράθυρο 76
77 Και στα δυο επιλέγουμε το clk και πατάμε Report Timing. Μας εμφανίζεται το παραπάνω παράθυρο και επιλέγουμε το path summary. Ο data arrival time είναι ο χρόνος που χρειάζεται για να περάσουν τα δεδομένα από το Q ενός καταχωρητή στο D ενός άλλου που ακολουθεί από την στιγμή της ακμής στον πρώτο, δηλαδή όσο ακόμα τα δεδομένα είναι στο D του πρώτου καταχωρητή. Είναι ο χρόνος που χρειάζεται ώστε τα δεδομένα να περάσουν από την είσοδο ενός καταχωρητή, από εκεί στην έξοδό του και να εμφανιστούν τελικά στη είσοδο ενός άλλου καταχωρητή που ακολουθεί. 77
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
ΑΣΚΗΣΗ 9. Tα Flip-Flop
 ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
Α. ΣΚΟΔΡΑΣ ΠΛΗ21 ΟΣΣ#2. 14 Δεκ 2008 ΠΑΤΡΑ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ 2008 Α. ΣΚΟΔΡΑΣ ΧΡΟΝΟΔΙΑΓΡΑΜΜΑ ΜΕΛΕΤΗΣ
 ΠΛΗ21 ΟΣΣ#2 14 Δεκ 2008 ΠΑΤΡΑ ΧΡΟΝΟΔΙΑΓΡΑΜΜΑ ΜΕΛΕΤΗΣ 7-segment display 7-segment display 7-segment display Αποκωδικοποιητής των 7 στοιχείων (τμημάτων) (7-segment decoder) Κύκλωμα αποκωδικοποίησης του στοιχείου
ΠΛΗ21 ΟΣΣ#2 14 Δεκ 2008 ΠΑΤΡΑ ΧΡΟΝΟΔΙΑΓΡΑΜΜΑ ΜΕΛΕΤΗΣ 7-segment display 7-segment display 7-segment display Αποκωδικοποιητής των 7 στοιχείων (τμημάτων) (7-segment decoder) Κύκλωμα αποκωδικοποίησης του στοιχείου
Κεφάλαιο 6. Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα
 Κεφάλαιο 6 Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα 6.1 Εισαγωγή Η εκτέλεση διαδοχικών λειτουργιών απαιτεί τη δημιουργία κυκλωμάτων που μπορούν να αποθηκεύουν πληροφορίες, στα ενδιάμεσα στάδια των
Κεφάλαιο 6 Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα 6.1 Εισαγωγή Η εκτέλεση διαδοχικών λειτουργιών απαιτεί τη δημιουργία κυκλωμάτων που μπορούν να αποθηκεύουν πληροφορίες, στα ενδιάμεσα στάδια των
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι απαριθμητές ή μετρητές (counters) είναι κυκλώματα που
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι απαριθμητές ή μετρητές (counters) είναι κυκλώματα που
ΚΕΦΑΛΑΙΟ 6 ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ. 6.1 Εισαγωγή
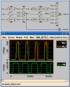 ΚΕΦΑΛΑΙΟ 6 ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 6. Εισαγωγή Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά και ακολουθιακά. Τα κυκλώματα που εξετάσαμε στα προηγούμενα κεφάλαια ήταν συνδυαστικά. Οι τιμές των
ΚΕΦΑΛΑΙΟ 6 ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 6. Εισαγωγή Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά και ακολουθιακά. Τα κυκλώματα που εξετάσαμε στα προηγούμενα κεφάλαια ήταν συνδυαστικά. Οι τιμές των
K24 Ψηφιακά Ηλεκτρονικά 9: Flip-Flops
 K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS)
 ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS) Αντικείμενο της άσκησης: H σχεδίαση και η χρήση ασύγχρονων απαριθμητών γεγονότων. Με τον όρο απαριθμητές ή μετρητές εννοούμε ένα ακολουθιακό κύκλωμα με FF, οι καταστάσεις
ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS) Αντικείμενο της άσκησης: H σχεδίαση και η χρήση ασύγχρονων απαριθμητών γεγονότων. Με τον όρο απαριθμητές ή μετρητές εννοούμε ένα ακολουθιακό κύκλωμα με FF, οι καταστάσεις
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Ακολουθιακή Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Εισαγωγή στην πληροφορική
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 4: Ψηφιακή Λογική, Άλγεβρα Boole, Πίνακες Αλήθειας (Μέρος B) Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 4: Ψηφιακή Λογική, Άλγεβρα Boole, Πίνακες Αλήθειας (Μέρος B) Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ
 ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
ΑΣΚΗΣΗ 10 ΣΧΕΔΙΑΣΗ ΑΚΟΛΟΥΘΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΑΣΚΗΣΗ ΣΧΕΔΙΑΣΗ ΑΚΟΛΟΥΘΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ.. ΣΚΟΠΟΣ Η σχεδίαση ακολουθιακών κυκλωμάτων..2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ.2.. ΑΛΓΟΡΙΘΜΟΣ ΣΧΕΔΙΑΣΗΣ ΑΚΟΛΟΥΘΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Τα ψηφιακά κυκλώματα με μνήμη ονομάζονται ακολουθιακά.
ΑΣΚΗΣΗ ΣΧΕΔΙΑΣΗ ΑΚΟΛΟΥΘΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ.. ΣΚΟΠΟΣ Η σχεδίαση ακολουθιακών κυκλωμάτων..2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ.2.. ΑΛΓΟΡΙΘΜΟΣ ΣΧΕΔΙΑΣΗΣ ΑΚΟΛΟΥΘΙΑΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Τα ψηφιακά κυκλώματα με μνήμη ονομάζονται ακολουθιακά.
Η συχνότητα f των παλµών 0 και 1 στην έξοδο Q n είναι. f Qn = 1/(T cl x 2 n+1 )
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των απαριθµητών. Υλοποίηση ασύγχρονου απαριθµητή 4-bit µε χρήση JK Flip-Flop. Κατανόηση της αλλαγής του υπολοίπου
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των απαριθµητών. Υλοποίηση ασύγχρονου απαριθµητή 4-bit µε χρήση JK Flip-Flop. Κατανόηση της αλλαγής του υπολοίπου
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
6.1 Καταχωρητές. Ένας καταχωρητής είναι μια ομάδα από f/f αλλά μπορεί να περιέχει και πύλες. Καταχωρητής των n ψηφίων αποτελείται από n f/f.
 6. Καταχωρητές Ένας καταχωρητής είναι μια ομάδα από f/f αλλά μπορεί να περιέχει και πύλες. Καταχωρητής των n ψηφίων αποτελείται από n f/f. Καταχωρητής 4 ψηφίων Καταχωρητής με παράλληλη φόρτωση Η εισαγωγή
6. Καταχωρητές Ένας καταχωρητής είναι μια ομάδα από f/f αλλά μπορεί να περιέχει και πύλες. Καταχωρητής των n ψηφίων αποτελείται από n f/f. Καταχωρητής 4 ψηφίων Καταχωρητής με παράλληλη φόρτωση Η εισαγωγή
7.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΑΝ ΑΛΩΤΕΣ FLIP FLOP Σκοπός: Η κατανόηση της λειτουργίας των βασικών ακολουθιακών κυκλωµάτων. Θα µελετηθούν συγκεκριµένα: ο µανδαλωτής (latch)
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΑΝ ΑΛΩΤΕΣ FLIP FLOP Σκοπός: Η κατανόηση της λειτουργίας των βασικών ακολουθιακών κυκλωµάτων. Θα µελετηθούν συγκεκριµένα: ο µανδαλωτής (latch)
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2006
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2006 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ, Θεωρητικής Κατεύθυνσης Ημερομηνία
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2006 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ, Θεωρητικής Κατεύθυνσης Ημερομηνία
ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΕΧΟΜΕΝΑ.3 ΑΣΥΓΧΡΟΝΟΣ ΔYΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.5 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.7 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ ΜΕ LATCH.
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ ΠΑΤΡΑ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων
 Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Με τον όρο ανάλυση ενός κυκλώματος εννοούμε τον προσδιορισμό της συμπεριφοράς του κάτω από συγκεκριμένες συνθήκες λειτουργίας. Έτσι, για ένα συνδυαστικό κύκλωμα,
Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Με τον όρο ανάλυση ενός κυκλώματος εννοούμε τον προσδιορισμό της συμπεριφοράς του κάτω από συγκεκριμένες συνθήκες λειτουργίας. Έτσι, για ένα συνδυαστικό κύκλωμα,
K24 Ψηφιακά Ηλεκτρονικά 10: Ακολουθιακά Κυκλώματα
 K24 Ψηφιακά Ηλεκτρονικά : TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 2 3 Γενικά Όπως είδαμε και σε προηγούμενα μαθήματα, ένα ψηφιακό κύκλωμα ονομάζεται
K24 Ψηφιακά Ηλεκτρονικά : TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 2 3 Γενικά Όπως είδαμε και σε προηγούμενα μαθήματα, ένα ψηφιακό κύκλωμα ονομάζεται
Ασύγχρονοι Απαριθμητές. Διάλεξη 7
 Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Καταχωρητές και Μετρητές 2. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Καταχωρητές και Μετρητές Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Καταχωρητής: είναι μία ομάδα από δυαδικά κύτταρα αποθήκευσης
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Καταχωρητές και Μετρητές Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Καταχωρητής: είναι μία ομάδα από δυαδικά κύτταρα αποθήκευσης
Ψηφιακά Συστήματα. 7. Κυκλώματα Μνήμης
 Ψηφιακά Συστήματα 7. Κυκλώματα Μνήμης Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L., Ψηφιακά
Ψηφιακά Συστήματα 7. Κυκλώματα Μνήμης Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L., Ψηφιακά
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL
 Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL 3.1 Εισαγωγή στα FLIP FLOP 3.1.1 Θεωρητικό Υπόβαθρο Τα σύγχρονα ακολουθιακά κυκλώματα με τα οποία θα ασχοληθούμε στο εργαστήριο των Ψηφιακών συστημάτων
Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL 3.1 Εισαγωγή στα FLIP FLOP 3.1.1 Θεωρητικό Υπόβαθρο Τα σύγχρονα ακολουθιακά κυκλώματα με τα οποία θα ασχοληθούμε στο εργαστήριο των Ψηφιακών συστημάτων
ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
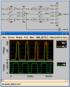 ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ FLIP-FLOP ΤΟ ΒΑΣΙΚΟ FLIP-FLOP ΧΡΟΝΙΖΟΜΕΝΑ FF ΤΥΠΟΥ FF ΤΥΠΟΥ D FLIP-FLOP Τ FLIP-FLOP ΠΥΡΟΔΟΤΗΣΗ ΤΩΝ FLIP-FLOP ΚΥΡΙΟ - ΕΞΑΡΤΗΜΕΝΟ FLIP-FLOP ΑΚΜΟΠΥΡΟΔΟΤΟΥΜΕΝΑ FLIP-FLOP ΚΥΚΛΩΜΑΤΑ
ΒΑΣΙΚΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ FLIP-FLOP ΤΟ ΒΑΣΙΚΟ FLIP-FLOP ΧΡΟΝΙΖΟΜΕΝΑ FF ΤΥΠΟΥ FF ΤΥΠΟΥ D FLIP-FLOP Τ FLIP-FLOP ΠΥΡΟΔΟΤΗΣΗ ΤΩΝ FLIP-FLOP ΚΥΡΙΟ - ΕΞΑΡΤΗΜΕΝΟ FLIP-FLOP ΑΚΜΟΠΥΡΟΔΟΤΟΥΜΕΝΑ FLIP-FLOP ΚΥΚΛΩΜΑΤΑ
Ακολουθιακό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται από τις τιμές εισόδου ΚΑΙ από την προηγούμενη κατάσταση του κυκλώματος
 1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης 2017
 Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης 2017 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το κατωτέρω διάγραμμα καταστάσεων,
Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης 2017 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το κατωτέρω διάγραμμα καταστάσεων,
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
 100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ. Καταχωρητές παράλληλης-εισόδου-παράλληληςεξόδου. Καταχωρητές παράλληλης-εισόδου-σειριακής-εξόδου
 ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ Καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου Καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου Καταχωρητές παράλληλης-εισόδου-παράλληληςεξόδου Καταχωρητές
ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ Καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου Καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου Καταχωρητές παράλληλης-εισόδου-παράλληληςεξόδου Καταχωρητές
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
 Θεµατική Ενότητα ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Ακαδηµαϊκό Έτος 2006 2007 Γραπτή Εργασία #2 Ηµεροµηνία Παράδοσης 28-0 - 2007 ΠΛΗ 2: Ψηφιακά Συστήµατα ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ Άσκηση : [5 µονάδες] Έχετε στη
Θεµατική Ενότητα ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Ακαδηµαϊκό Έτος 2006 2007 Γραπτή Εργασία #2 Ηµεροµηνία Παράδοσης 28-0 - 2007 ΠΛΗ 2: Ψηφιακά Συστήµατα ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ Άσκηση : [5 µονάδες] Έχετε στη
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Τεχνολογία και
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Τεχνολογία και
ΗΜΥ 210: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 2008
 ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops και Μετρητές Ριπής Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops και Μετρητές Ριπής Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΣΥΓΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
 ΣΥΓΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ Σύγχρονο ακολουθιακό κύκλωμα είναι εκείνο του οποίου όλα τα FFs χρονίζονταιμετοίδιο ρολόι (clock). Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Σχεδίαση Σύγχρονων Ακολουθιακών
ΣΥΓΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ Σύγχρονο ακολουθιακό κύκλωμα είναι εκείνο του οποίου όλα τα FFs χρονίζονταιμετοίδιο ρολόι (clock). Ανάλυση Σύγχρονων Ακολουθιακών Κυκλωμάτων Σχεδίαση Σύγχρονων Ακολουθιακών
Σχεδίαση Ψηφιακών Συστηµάτων
 Σχεδίαση Ψηφιακών Συστηµάτων Πανεπιστήμιο Δυτικής Αττικής Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών Γιάννης Βογιατζής Πάνος Καρκαζής 27-28 Παρουσίαση 4 η : Ψηφιακή Σχεδίαση Μέρος 3 Ανάλυση και Σχεδίαση
Σχεδίαση Ψηφιακών Συστηµάτων Πανεπιστήμιο Δυτικής Αττικής Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών Γιάννης Βογιατζής Πάνος Καρκαζής 27-28 Παρουσίαση 4 η : Ψηφιακή Σχεδίαση Μέρος 3 Ανάλυση και Σχεδίαση
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Μετρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Μετρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Μετρητής Ριπής Σύγχρονος υαδικός Μετρητής
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Μετρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Μετρητής Ριπής Σύγχρονος υαδικός Μετρητής
5. Σύγχρονα Ακολουθιακά Κυκλώματα
 5. Σύγχρονα Ακολουθιακά Κυκλώματα Ακολουθιακό (sequential) λέμε το σύστημα που περιέχει στοιχεία μνήμης, δηλ. κυκλώματα αποθήκευσης δυαδικής πληροφορίας Γενικό διάγραμμα ακολουθιακού κυκλώματος - Αποτελείται
5. Σύγχρονα Ακολουθιακά Κυκλώματα Ακολουθιακό (sequential) λέμε το σύστημα που περιέχει στοιχεία μνήμης, δηλ. κυκλώματα αποθήκευσης δυαδικής πληροφορίας Γενικό διάγραμμα ακολουθιακού κυκλώματος - Αποτελείται
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
Άσκηση 3 Ένα νέο είδος flip flop έχει τον ακόλουθο πίνακα αληθείας : I 1 I 0 Q (t+1) Q (t) 1 0 ~Q (t) Κατασκευάστε τον πίνακα
 Άσκηση Δίδονται οι ακόλουθες κυματομορφές ρολογιού και εισόδου D που είναι κοινή σε ένα D latch και ένα D flip flop. Το latch είναι θετικά ενεργό, ενώ το ff θετικά ακμοπυροδοτούμενο. Σχεδιάστε τις κυματομορφές
Άσκηση Δίδονται οι ακόλουθες κυματομορφές ρολογιού και εισόδου D που είναι κοινή σε ένα D latch και ένα D flip flop. Το latch είναι θετικά ενεργό, ενώ το ff θετικά ακμοπυροδοτούμενο. Σχεδιάστε τις κυματομορφές
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Μετρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Μετρητής Ριπής Σύγχρονος υαδικός
ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Μετρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Μετρητής Ριπής Σύγχρονος υαδικός
ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Γ ΕΠΑΛ 14 / 04 / 2019
 Γ ΕΠΑΛ 14 / 04 / 2019 ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι λανθασμένη.
Γ ΕΠΑΛ 14 / 04 / 2019 ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι λανθασμένη.
Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης Θέμα 1ο (3 μονάδες)
 Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης 2016 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το ανωτέρω διάγραμμα καταστάσεων,
Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα κανονικής εξέτασης 2016 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το ανωτέρω διάγραμμα καταστάσεων,
ΑΠΟ ΤΑ ΘΕΜΑΤΑ ΤΩΝ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΚΕΦΑΛΑΙΟ 7-8 (ΚΑΤΑΧΩΡΗΤΕΣ & ΑΠΑΡΙΘΜΗΤΕΣ)
 ΑΠΟ ΤΑ ΘΕΜΑΤΑ ΤΩΝ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2009 205 ΚΕΦΑΛΑΙΟ 7-8 (ΚΑΤΑΧΩΡΗΤΕΣ & ΑΠΑΡΙΘΜΗΤΕΣ) ΑΠΟ ΘΕΜΑ Α Ερωτήσεις. Γιατί στους ασύγχρονους απαριθμητές τα flip-flops δεν αλλάζουν ταυτόχρονα κατάσταση; 2. Να
ΑΠΟ ΤΑ ΘΕΜΑΤΑ ΤΩΝ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2009 205 ΚΕΦΑΛΑΙΟ 7-8 (ΚΑΤΑΧΩΡΗΤΕΣ & ΑΠΑΡΙΘΜΗΤΕΣ) ΑΠΟ ΘΕΜΑ Α Ερωτήσεις. Γιατί στους ασύγχρονους απαριθμητές τα flip-flops δεν αλλάζουν ταυτόχρονα κατάσταση; 2. Να
8. Στοιχεία μνήμης. Οι δυο έξοδοι του FF είναι συμπληρωματικές σημειώνονται δε σαν. Όταν αναφερόμαστε στο FF εννοούμε πάντα την κανονική έξοδο Q.
 8. ΣΟΙΧΕΙΑ ΜΝΗΜΗΣ 8. Εισαγωγή Στα συνδυαστικά κυκλώματα, που μελετήσαμε έως τώρα, δεν υπήρχε κάποια διαδικασία ανάδρασης (Feed Back) -δηλαδή οδήγηση της εξόδου των στοιχείων στην είσοδό τους- επομένως
8. ΣΟΙΧΕΙΑ ΜΝΗΜΗΣ 8. Εισαγωγή Στα συνδυαστικά κυκλώματα, που μελετήσαμε έως τώρα, δεν υπήρχε κάποια διαδικασία ανάδρασης (Feed Back) -δηλαδή οδήγηση της εξόδου των στοιχείων στην είσοδό τους- επομένως
ΑΣΚΗΣΗ 10 ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ
 ΑΣΚΗΣΗ ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Στόχος της άσκησης: Η διαδικασία σχεδίασης σύγχρονων ακολουθιακών κυκλωμάτων. Χαρακτηριστικό παράδειγμα σύγχρονων ακολουθιακών κυκλωμάτων είναι οι σύγχρονοι μετρητές. Τις αδυναμίες
ΑΣΚΗΣΗ ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Στόχος της άσκησης: Η διαδικασία σχεδίασης σύγχρονων ακολουθιακών κυκλωμάτων. Χαρακτηριστικό παράδειγμα σύγχρονων ακολουθιακών κυκλωμάτων είναι οι σύγχρονοι μετρητές. Τις αδυναμίες
8.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή
 6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
ΑΣΚΗΣΗ 7 FLIP - FLOP
 ΑΣΚΗΣΗ 7 FLIP - FLOP Αντικείμενο της άσκησης: Η κατανόηση της δομής και λειτουργίας των Flip Flop. Flip - Flop Τα Flip Flop είναι δισταθή λογικά κυκλώματα με χαρακτηριστικά μνήμης και είναι τα πλέον βασικά
ΑΣΚΗΣΗ 7 FLIP - FLOP Αντικείμενο της άσκησης: Η κατανόηση της δομής και λειτουργίας των Flip Flop. Flip - Flop Τα Flip Flop είναι δισταθή λογικά κυκλώματα με χαρακτηριστικά μνήμης και είναι τα πλέον βασικά
ε. Ένα κύκλωμα το οποίο παράγει τετραγωνικούς παλμούς και απαιτείται εξωτερική διέγερση ονομάζεται ασταθής πολυδονητής Λ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 16/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ (ΣΥΣΤΗΜΑΤΑ ΨΗΦΙΑΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΕΝΔΕΙΚΤΙΚΕΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 16/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ (ΣΥΣΤΗΜΑΤΑ ΨΗΦΙΑΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΕΝΔΕΙΚΤΙΚΕΣ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
Flip-Flop: D Control Systems Laboratory
 Flip-Flop: Control Systems Laboratory Είναι ένας τύπος συγχρονιζόμενου flip- flop, δηλαδή ενός flip- flop όπου οι έξοδοί του δεν αλλάζουν μόνο με αλλαγή των εισόδων R, S αλλά χρειάζεται ένας ωρολογιακός
Flip-Flop: Control Systems Laboratory Είναι ένας τύπος συγχρονιζόμενου flip- flop, δηλαδή ενός flip- flop όπου οι έξοδοί του δεν αλλάζουν μόνο με αλλαγή των εισόδων R, S αλλά χρειάζεται ένας ωρολογιακός
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Μετρητής Ριπής (Ripple Counter) Μετρητές (Counters) Μετρητής Ριπής (συν.
 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 ii: Μετρητές Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Μετρητής Ριπής Περίληψη Σύγχρονος υαδικός Μετρητής Σχεδιασµός µε Flip-Flops
ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 ii: Μετρητές Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Μετρητής Ριπής Περίληψη Σύγχρονος υαδικός Μετρητής Σχεδιασµός µε Flip-Flops
Περιεχόμενα. Πρώτο Κεφάλαιο. Εισαγωγή στα Ψηφιακά Συστήματα. Δεύτερο Κεφάλαιο. Αριθμητικά Συστήματα Κώδικες
 Πρώτο Κεφάλαιο Εισαγωγή στα Ψηφιακά Συστήματα 1.1 Αναλογικά και Ψηφιακά Σήματα και Συστήματα... 1 1.2 Βασικά Ψηφιακά Κυκλώματα... 3 1.3 Ολοκληρωμένα κυκλώματα... 4 1.4 Τυπωμένα κυκλώματα... 7 1.5 Εργαλεία
Πρώτο Κεφάλαιο Εισαγωγή στα Ψηφιακά Συστήματα 1.1 Αναλογικά και Ψηφιακά Σήματα και Συστήματα... 1 1.2 Βασικά Ψηφιακά Κυκλώματα... 3 1.3 Ολοκληρωμένα κυκλώματα... 4 1.4 Τυπωμένα κυκλώματα... 7 1.5 Εργαλεία
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 7 Καταχωρητές Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Καταχωρητές ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ ς-εισόδου-σειριακής-εξόδου
Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 7 Καταχωρητές Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Καταχωρητές ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ ς-εισόδου-σειριακής-εξόδου
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Τεχνολογία και
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Τεχνολογία και
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Ακολουθιακά Κυκλώματα: Μανδαλωτές και Flip-Flops 1
 ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Ακολουθιακά Κυκλώματα (συν.) Κυκλώματα που Κυκλώματα που αποθηκεύουν εξετάσαμε μέχρι τώρα πληροφορίες Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops
ΗΜΥ-211: Εργαστήριο Σχεδιασμού Ψηφιακών Συστημάτων Ακολουθιακά Κυκλώματα (συν.) Κυκλώματα που Κυκλώματα που αποθηκεύουν εξετάσαμε μέχρι τώρα πληροφορίες Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches), Flip-FlopsFlops
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 5. ΑΛΓΕΒΡΑ BOOLE ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ ΜΕΡΟΣ Β 2 Επαναληπτική
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 5. ΑΛΓΕΒΡΑ BOOLE ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ ΜΕΡΟΣ Β 2 Επαναληπτική
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το κατωτέρω διάγραμμα
 Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα επαναληπτικής εξέτασης 2016 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το κατωτέρω διάγραμμα καταστάσεων,
Ηλεκτρολόγοι Μηχανικοί ΕΜΠ Λογική Σχεδίαση Ψηφιακών Συστημάτων Διαγώνισμα επαναληπτικής εξέτασης 2016 Θέμα 1ο (3 μονάδες) Υλοποιήστε το ακoλουθιακό κύκλωμα που περιγράφεται από το κατωτέρω διάγραμμα καταστάσεων,
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 16: Μετρητές (Counters)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 16: Μετρητές (Counters) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Μετρητής Ριπής q Σύγχρονος
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 16: Μετρητές (Counters) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Μετρητής Ριπής q Σύγχρονος
7. Ψηφιακά Ηλεκτρονικά
 1 7. Ψηφιακά Ηλεκτρονικά 7.1 Εισαγωγή Στα προηγούμενα μελετήσαμε τη λειτουργία του τρανζίστορ στην ενεργό περιοχή, χαρακτηριστικό της οποίας είναι ότι τα σήματα εισόδου και εξόδου μπορούν να λάβουν συνεχείς
1 7. Ψηφιακά Ηλεκτρονικά 7.1 Εισαγωγή Στα προηγούμενα μελετήσαμε τη λειτουργία του τρανζίστορ στην ενεργό περιοχή, χαρακτηριστικό της οποίας είναι ότι τα σήματα εισόδου και εξόδου μπορούν να λάβουν συνεχείς
Κυκλώµατα. Εισαγωγή. Συνδυαστικό Κύκλωµα
 6 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων µνήµης Η έξοδος εξαρτάται από
6 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων µνήµης Η έξοδος εξαρτάται από
Υπάρχουν δύο τύποι μνήμης, η μνήμη τυχαίας προσπέλασης (Random Access Memory RAM) και η μνήμη ανάγνωσης-μόνο (Read-Only Memory ROM).
 Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2009
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2009 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2009 ΤΕΧΝΟΛΟΓΙΑ (ΙΙ) ΤΕΧΝΙΚΩΝ ΣΧΟΛΩΝ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα : Ψηφιακά Ηλεκτρονικά
f(x, y, z) = y z + xz
 Λύσεις θεμάτων Εξεταστικής Περιόδου Ιανουαρίου Φεβρουαρίου 27 ΘΕΜΑ Ο (2, μονάδες) Δίνεται η λογική συνάρτηση : f (, y, z ) = ( + y )(y + z ) + y z. Να συμπληρωθεί ο πίνακας αλήθειας της συνάρτησης. (,
Λύσεις θεμάτων Εξεταστικής Περιόδου Ιανουαρίου Φεβρουαρίου 27 ΘΕΜΑ Ο (2, μονάδες) Δίνεται η λογική συνάρτηση : f (, y, z ) = ( + y )(y + z ) + y z. Να συμπληρωθεί ο πίνακας αλήθειας της συνάρτησης. (,
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο Διάλεξη 8 η : Μηχανές Πεπερασμένων Κaταστάσεων σε FPGAs
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ. Τύποι καταχωρητών: (α) σειριακής-εισόδου-σειριακής-εξόδου, (β) σειριακήςεισόδου-παράλληλης-εξόδου,
 ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ Καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου Καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου Καταχωρητές παράλληλης-εισόδου-παράλληλης-εξόδου Καταχωρητές
ΚΑΤΑΧΩΡΗΤΕΣ ΣΕΙΡΙΑΚΟΙ ΚΑΙ ΠΑΡΑΛΛΗΛΟΙ ΚΑΤΑΧΩΡΗΤΕΣ Καταχωρητές σειριακής-εισόδου-σειριακής-εξόδου Καταχωρητές σειριακής-εισόδου-παράλληλης-εξόδου Καταχωρητές παράλληλης-εισόδου-παράλληλης-εξόδου Καταχωρητές
Αρχιτεκτονικές Υπολογιστών
 ΑΡΧΙΤΕΚΤΟΝΙΚΕΣ ΥΠΟΛΟΓΙΣΤΩΝ Μάθηµα: Αρχιτεκτονικές Υπολογιστών FLIP-FLOPS ΣΥΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΙΑ ΙΚΑΣΙΑ ΑΝΑΛΥΣΗΣ ΚΑΙ ΣΧΕ ΙΑΣΗ ΣΑΚ ιδάσκων: Αναπλ. Καθ. Κ. Λαµπρινουδάκης clam@uipi.gr Αρχιτεκτονικές
ΑΡΧΙΤΕΚΤΟΝΙΚΕΣ ΥΠΟΛΟΓΙΣΤΩΝ Μάθηµα: Αρχιτεκτονικές Υπολογιστών FLIP-FLOPS ΣΥΧΡΟΝΑ ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΙΑ ΙΚΑΣΙΑ ΑΝΑΛΥΣΗΣ ΚΑΙ ΣΧΕ ΙΑΣΗ ΣΑΚ ιδάσκων: Αναπλ. Καθ. Κ. Λαµπρινουδάκης clam@uipi.gr Αρχιτεκτονικές
ΕΙΣΑΓΩΓΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ... 3
 ΚΕΦΑΛΑΙΟ 3 ΑΠΑΡΙΘΜΗΤΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ... 3 ΕΝΟΤΗΤΑ 3.. ΑΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 4 3... ΑΣΥΓΧΡΟΝΟΙ ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 4 3..2. ΑΣΥΓΧΡΟΝΟΙ ΜΗ- ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 9 ΕΝΟΤΗΤΑ 3.2. ΣΥΓΧΡΟΝΟΙ
ΚΕΦΑΛΑΙΟ 3 ΑΠΑΡΙΘΜΗΤΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ... 3 ΕΝΟΤΗΤΑ 3.. ΑΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 4 3... ΑΣΥΓΧΡΟΝΟΙ ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 4 3..2. ΑΣΥΓΧΡΟΝΟΙ ΜΗ- ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ... 9 ΕΝΟΤΗΤΑ 3.2. ΣΥΓΧΡΟΝΟΙ
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία
Μετρητής Ριπής ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ. Αναφορά 9 ης. εργαστηριακής άσκησης: ΑΦΡΟΔΙΤΗ ΤΟΥΦΑ Α.Μ.:2024201100032
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 9 ης εργαστηριακής άσκησης: Μετρητής Ριπής ΑΦΡΟΔΙΤΗ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 9 ης εργαστηριακής άσκησης: Μετρητής Ριπής ΑΦΡΟΔΙΤΗ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ Τεχνικών Σχολών, Θεωρητικής Κατεύθυνσης
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ Τεχνικών Σχολών, Θεωρητικής Κατεύθυνσης
Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A].
![Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A]. Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A].](/thumbs/88/114625669.jpg) Κανονική μορφή συνάρτησης λογικής 5. Η κανονική μορφή μιας λογικής συνάρτησης (ΛΣ) ως άθροισμα ελαχιστόρων, από τον πίνακα αληθείας προκύπτει ως εξής: ) Παράγουμε ένα [A] όρων από την κάθε σειρά για την
Κανονική μορφή συνάρτησης λογικής 5. Η κανονική μορφή μιας λογικής συνάρτησης (ΛΣ) ως άθροισμα ελαχιστόρων, από τον πίνακα αληθείας προκύπτει ως εξής: ) Παράγουμε ένα [A] όρων από την κάθε σειρά για την
Εργαστήριο Ψηφιακής Σχεδίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Εργαστήριο Ψηφιακής Σχεδίασης 8 Εργαστηριακές Ασκήσεις Χρ. Καβουσιανός Επίκουρος Καθηγητής 2014 Εργαστηριακές Ασκήσεις Ψηφιακής Σχεδίασης 2 Εργαστηριακές Ασκήσεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Εργαστήριο Ψηφιακής Σχεδίασης 8 Εργαστηριακές Ασκήσεις Χρ. Καβουσιανός Επίκουρος Καθηγητής 2014 Εργαστηριακές Ασκήσεις Ψηφιακής Σχεδίασης 2 Εργαστηριακές Ασκήσεις
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ Τεχνικών Σχολών, Θεωρητικής Κατεύθυνσης
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα : Ψηφιακά Ηλεκτρονικά Τεχνολογία ΙΙ Τεχνικών Σχολών, Θεωρητικής Κατεύθυνσης
βαθµίδων µε D FLIP-FLOP. Μονάδες 5
 Κεφάλαιιο: 6 ο Τίίτλος Κεφαλαίίου:: Μανταλωτές & Flip Flop (Ιούνιος 2004 ΤΕΕ Ηµερήσιο) Να σχεδιάσετε καταχωρητή δεξιάς ολίσθησης τεσσάρων βαθµίδων µε D FLIP-FLOP. Μονάδες 5 (Ιούνιος 2005 ΤΕΕ Ηµερήσιο)
Κεφάλαιιο: 6 ο Τίίτλος Κεφαλαίίου:: Μανταλωτές & Flip Flop (Ιούνιος 2004 ΤΕΕ Ηµερήσιο) Να σχεδιάσετε καταχωρητή δεξιάς ολίσθησης τεσσάρων βαθµίδων µε D FLIP-FLOP. Μονάδες 5 (Ιούνιος 2005 ΤΕΕ Ηµερήσιο)
Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS
 Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS Γενικές Γραμμές Ακολουθιακή Λογική Μεταστάθεια S-R RLatch h( (active high h&l low) S-R Latch with Enable Latch Flip-Flop Ασύγχρονοι είσοδοι PRESET
Ενότητα ΑΡΧΕΣ ΑΚΟΛΟΥΘΙΑΚΗΣ ΛΟΓΙΚΗΣ LATCHES & FLIP-FLOPS Γενικές Γραμμές Ακολουθιακή Λογική Μεταστάθεια S-R RLatch h( (active high h&l low) S-R Latch with Enable Latch Flip-Flop Ασύγχρονοι είσοδοι PRESET
7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Μονάδες Μνήµης
 7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Εισαγωγή Καταχωρητής: είναι µία οµάδα από δυαδικά κύτταρα αποθήκευσης και από λογικές πύλες που διεκπεραιώνουν την µεταφορά πληροφοριών. Οι µετρητές είναι
7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Εισαγωγή Καταχωρητής: είναι µία οµάδα από δυαδικά κύτταρα αποθήκευσης και από λογικές πύλες που διεκπεραιώνουν την µεταφορά πληροφοριών. Οι µετρητές είναι
Ψηφιακά Συστήματα. 8. Καταχωρητές
 Ψηφιακά Συστήματα 8. Καταχωρητές Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L., Ψηφιακά
Ψηφιακά Συστήματα 8. Καταχωρητές Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L., Ψηφιακά
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων
 Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η λειτουργία RESET R IN OUT Εάν το σήμα R είναι λογικό «1» στην έξοδο
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η λειτουργία RESET R IN OUT Εάν το σήμα R είναι λογικό «1» στην έξοδο
Ακολουθιακό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται από τις τιμές εισόδου ΚΑΙ από την προηγούμενη κατάσταση του κυκλώματος
 1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
1 Συνδυαστικό κύκλωμα Η έξοδος του κυκλώματος εξαρτάται ΜΟΝΟ από τις εισόδους του Εάν γνωρίζουμε τις τιμές των εισόδων του κυκλώματος, τότε μπορούμε να προβλέψουμε ακριβώς τις εξόδους του Ακολουθιακό κύκλωμα
15 ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 18 ΙΟΥΝΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 18 ΙΟΥΝΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
Αυγ-13 Ακολουθιακά Κυκλώματα: Μανδαλωτές και Flip-Flops. ΗΜΥ 210: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 2009.
 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία Κ. Μιχαήλ Ακολουθιακά Κυκλώματα Συνδυαστική Λογική: Η τιμή σε μία έξοδο εξαρτάται
ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα: Μαρία Κ. Μιχαήλ Ακολουθιακά Κυκλώματα Συνδυαστική Λογική: Η τιμή σε μία έξοδο εξαρτάται
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ασύγχρονοι Απαριθμητές. Διάλεξη 7
 Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ. Κεφάλαιο 3
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Κεφάλαιο 3 Δυαδική λογική Με τον όρο λογική πρόταση ή απλά πρόταση καλούμε κάθε φράση η οποία μπορεί να χαρακτηριστεί αληθής ή ψευδής με βάση το νόημα της. π.χ. Σήμερα
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Κεφάλαιο 3 Δυαδική λογική Με τον όρο λογική πρόταση ή απλά πρόταση καλούμε κάθε φράση η οποία μπορεί να χαρακτηριστεί αληθής ή ψευδής με βάση το νόημα της. π.χ. Σήμερα
Κυκλώµατα. Εισαγωγή. Συνδυαστικό Κύκλωµα
 6 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων µνήµης Η έξοδος εξαρτάται από
6 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων µνήµης Η έξοδος εξαρτάται από
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ 1) Το παρακάτω κύκλωμα του σχήματος 1 είναι ένας καταχωρητής-ολισθητής
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΚΑΤΑΧΩΡΗΤΕΣ ΟΛΙΣΘΗΤΕΣ 1) Το παρακάτω κύκλωμα του σχήματος 1 είναι ένας καταχωρητής-ολισθητής
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
7. ΚΑΤΑΧΩΡΗΤΕΣ ΕΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ
 7. ΚΑΤΑΧΩΡΗΤΕΣ ΕΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ. Τι είναι ένας καταχωρητής; O καταχωρητής είναι μια ομάδα από flip-flop που μπορεί να αποθηκεύσει προσωρινά ψηφιακή πληροφορία. Μπορεί να διατηρήσει τα δεδομένα του αμετάβλητα
7. ΚΑΤΑΧΩΡΗΤΕΣ ΕΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ. Τι είναι ένας καταχωρητής; O καταχωρητής είναι μια ομάδα από flip-flop που μπορεί να αποθηκεύσει προσωρινά ψηφιακή πληροφορία. Μπορεί να διατηρήσει τα δεδομένα του αμετάβλητα
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων
 K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
Σύγχρονοι Απαριθμητές. Διάλεξη 8
 Σύγχρονοι Απαριθμητές Διάλεξη 8 Δομή της διάλεξης Εισαγωγή Σύγχρονος Δυαδικός Απαριθμητής Σύγχρονος Δεκαδικός Απαριθμητής Προγραμματιζόμενοι Απαριθμητές Ασκήσεις 2 Σύγχρονοι Απαριθμητές Εισαγωγή 3 Εισαγωγή
Σύγχρονοι Απαριθμητές Διάλεξη 8 Δομή της διάλεξης Εισαγωγή Σύγχρονος Δυαδικός Απαριθμητής Σύγχρονος Δεκαδικός Απαριθμητής Προγραμματιζόμενοι Απαριθμητές Ασκήσεις 2 Σύγχρονοι Απαριθμητές Εισαγωγή 3 Εισαγωγή
