Pulse Amplitude (PAM) Pulse Code (PCM) Pulse Width (PWM) Delta (DM) Pulse Position (PPM) Adaptive Delta (ADM)
|
|
|
- Νύξ Αλεξόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Εισαγωγή στις Τηλεπικοινωνίες ιαµόρφωση Παλµών Αναλογική/Ψηφιακή PCM/DPCM DM/ADM ρ. Αθανάσιος. Παναγόπουλος Λέκτορας ΕΜΠ 1 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
2 Πλεονεκτήµατα Χρήσης Ψηφιακών Σηµάτων Αντοχή στο θόρυβο µετάδοσης και στην παρεµβολή. Αποτελεσµατική αναγέννηση του σήµατος κατά µήκος της διαδροµής. υνατότητα οµοιόµορφου σχήµατος µετάδοσης για διαφορετικά είδη σήµατος βασικής ζώνης. 2 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
3 ιαµόρφωση Παλµών Αναλογική ιαµόρφωση Παλµών Pulse Amplitude (PAM) Pulse Width (PWM) Pulse Position (PPM) Ψηφιακή ιαµόρφωση Παλµών Pulse Code (PCM) Delta (DM) Adaptive Delta (ADM) 3 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
4 ιαµόρφωση Πλάτους Παλµών (PAM) Pulse Amplitude Modulation Στη διαµόρφωση πλάτους, τα πλάτη ορθογώνιων παλµών µεταβάλλονται σύµφωνα µε τις στιγµιαίες τιµές των δειγµάτων ενός συνεχούς σήµατος πληροφορίας. O σκοπός του διαµορφωτή είναι να µετατρέψει διακριτά σειριακά σύµβολά δεδοµένου πλάτους σε µια αναλογική έξοδο παλµών οι οποίοι µεταδίδονται πάνω από το δίαυλο. Ο αποδιαµόρφωτης πραγµατοποιεί την αντίστροφη διαδικασία. 4 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
5 ιαµόρφωση Πλάτους Παλµών (PAM) Pulse Amplitude Modulation Έστω s( t) η ακολουθία από παλµούς επίπεδης κορυφής: 1, 0 < t < T s( t) = m( nts ) h( t nts ) h( t) = n= 0, otherwise Το στιγµιαία δειγµατοληπτούµενο σήµα είναι is : m ( t) = m( nt ) δ ( t nt ) δ n= m ( t) h( t) = m ( τ ) h( t τ ) dτ = m( nts) δ ( τ nts) h( t τ ) dτ δ = m( nts) δ ( τ nts) h( t τ ) dτ Χρησιµοποιώντας την ιδίοτητα της ολίσθησης : mδ ( t) h( t) = m( nts) h( t nts) s n= n= δ s n = 5 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
6 ιαµόρφωση Πλάτους Παλµών (PAM) Pulse Amplitude Modulation To PAM σήµα s( t) s( t) = m ( t) h( t) δ M / Σ Fourier S( f ) = M ( f ) H ( f ) ( ) Ως γνωστό g ( t) f G f mf δ s m= M ( f ) = f M ( f k f ) δ s k= S( f ) = f M ( f k f ) H ( f ) s k= s s s δ 6 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες 9
7 ιαµόρφωση Πλάτους Παλµών (PAM) Pulse Amplitude Modulation Το εύρος ζώνης του φίλτρου είναι W. Η έξοδος του φίλτρου είναι f M ( f ) H ( f ). s Ο Μ/Σ Fourier του of h( t) δίνεται: H ( f ) = T sinc( f T )exp j 2 π f Παραµόρφωση T 2 Πλάτους Καθυστέρηση amplitude distortion delay = T 2 Φαινόµενο Ανοίγµατος aparture effect ( ) Συνάρτηση Μεταφοράς (Εξισωτή) 1 1 π f = = H ( f ) T sinc( f T ) sin( π f T ) Τότε ιδανικά το αρχικό σήµα m( t) µπορεί πλήρως να ανακατασκευαστεί. 7 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες 10
8 ιαµόρφωση Εύρους Παλµών (PWM) ιαµόρφωση Θέσης Παλµών (PPM) Στη διαµόρφωση εύρους παλµού (PWM), το εύρος κάθε παλµού είναι κατευθείαν ανάλογο του πλάτους του σήµατος πληροφορίας. Στη διαµόρφωση θέσης παλµών, σταθερή διάρκειας παλµοί χρησιµοποιούνται και η θέση ή ο χρόνος εµφάνισης κάθε παλµού από κάποιο χρόνο αναφοράς είναι ανάλογη µε το πλάτος του σήµατος πληροφορίας. 8 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
9 ιαµόρφωση Εύρους Παλµών 9 Εργαστήριο ECE6331 Κινητών Spring 2009 Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
10 ιαµόρφωση Θέσης Παλµών 10 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
11 Σήµα PAM ιαµόρφωση Πλάτους Παλµών (PAM) Pulse Amplitude Modulation s( t) 1 k m( nt ) h( t nt ) h( t) [ ] = + a s s = n= 1, 0 < t < T 0, otherwise k a : Ευαισθησία Πλάτους 1+k a m(nt s )>0 για όλα τα n 11 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
12 Παλµοκωδική ιαµόρφωση (PCM) Η παλµοκωδική διαµόρφωση (PCM) θεωρείται µια διαδικασία µετατροπής αναλογικού σήµατος σε ψηφιακό. Κβαντισµένη PAM. Όπως και σε κάθε άλλη τεχνική διαµόρφωσης παλµών ο ρυθµός της δειγµατοληψίας πρέπει να είναι σύµφωνος µε το ρυθµό Nyquist. Ο ρυθµός δειγµατοληψίας πρέπει να είναι µεγαλύτερος από τη διπλάσια µέγιστη συχνότητα του αναλογικού σήµατος. f s > 2f A (max) Telegraph time-division multiplex (TDM) µεταδόθηκε το 1853, by ένα Αµερικάνο Εφευρέτη και από έναν Ηλ/γο Μηχανικό W.M. Miner το Το PCM εφευρέθηκε από ένα Βρετανό Μηχανικό τον Alec Reeves το 1937 στη Γαλλία. Το 1943 οι µηχανικοί των Bell Labs χρησιµοποίησαν την PCM δυαδική κωδικοποίηση όπως αυτό προτάθηκε από τον Alec Reeves. 12 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
13 PCM Αριθµοί που πέρασαν από τον µετατροπέα ADC ώστε να παριστάνουν αναλογική τάση. 13 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
14 Βασικά Στοιχεία Συστήµατος PCM 14 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
15 Πλεονεκτήµατα PCM 1. Ευρωστία στο θόρυβο και στην παρεµβολή 2. Αποδοτικήαναγέννηση 3. Απόδοση σε επίπεδο SNR και εύρος ζώνης συµψηφισµός 4. Οµοιοµορφία στη µετάδοση 5. Ασφαλές (κρυπτογραφία) 15 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
16 Κβαντισµός (Quantization) Η µετατροπή ενός αναλογικού/συνεχούς δείγµατος του σήµατος σε µια ψηφιακή διακριτή µορφή καλείται διαδικασία κβαντοποίησης/κβάντισης. Αυτό σηµαίνει ότι µια ευθεία γραµµή που παριστάνει τη σχέση µεταξύ της εισόδου και εξόδου γίνεται µια κλιµακωτή συνάρτηση. Η διαφορά µεταξύ δύο γειτονικών τιµών ονοµάζεται quantum ή µέγεθος βήµατος. Υπάρχουν δύο είδη κβάντισης: Βαθµωτή Κβάντιση: κάθε σύµβολο εισόδου (δειγµατοληπτούµενο σήµα) το µεταχειριζόµαστε ξεχωριστά ώστε να προκύψει η έξοδος. (Scalar Quantization) ιανυσµατική Κβάντιση: τα σύµβολα εισόδου οµαδοποιούνται και τα µεταχειριζόµαστε ως διανύσµατα για να προκύψει η έξοδος. (Vector Quantization) Η οµαδοποίηση των δεδοµένων και η µεταχείριση τους ως µια µονάδα βελτιώνει τη βελτιστοποίηση του κβαντιστή αλλά ταυτόχρονα αυξάνει τη πολυπλοκότητα υπολογισµού. 16 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
17 { } Αν ορίσουµε το διάστηµα: : m < m m, k= 1,2,..., L k+ 1 όπου m είναι το επίπεδο απόφασης ή το κατώφλι απόφασης. k Κβαντισµός (Quantization) J k k Πλάτος Κβάντισης: Η διαδικασία µετατροπής ενός δείγµατος πλάτους m nt k+ 1 ( ) s σε ένα διακριτό πλάτος Εάν m( t) J τότε η έξοδος του κβαντιστή είναι νk όπου νk, k = 1,2,...,L k τα οπόια αποτελούν την επίπεδα αναπαράστασης και m m είναι το µέγεθος του βήµατος. k ( ) v nt s Η σχέση εισόδου-εξόδου v= g( m) ονοµάζεται χαρακτηριστική συνάρτηση κβαντιστή που είναι µια κλιµακωτή συνάρτηση. 17 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
18 Κβαντιστής Μid-Tread Η έξοδος του κβαντιστή µπορεί να εκφραστεί στη µορφή g( ) = H i όπου ± H = 0,1, 2,3... i : Μέγεθος κβάντουµ/βήµατος Το είναι κανονικοποιηµένο στην τιµή 1. Κβαντιστής τύπου µέσου πατήµατος (mid-tread) H αρχή των αξόνων βρίσκεται στο µέσο ενός οριζόντιου τµήµατος στο κλιµακωτό γράφηµα. 18 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
19 Κβαντιστής Μid-Riser Η έξοδος του κβαντιστή µπορεί να εκφραστεί στη µορφή ( ) g( ) = H / 2 i όπου ± H = 1,3,5... i : Μέγεθος κβάντουµ/βήµατος Το είναι κανονικοποιηµένο στην τιµή 1. Κβαντιστής τύπου µέσης ανύψωσης (mid-riser) H αρχή των αξόνων βρίσκεται στο µέσο ενός κατακόρυφου τµήµατος στο κλιµακωτό γράφηµα. 19 Εργαστήριο ECE6331 Κινητών Spring 2009 Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
20 Σφάλµα Κβαντισµού Το σφάλµα κβαντισµού υπολογίζεται από τη διαφορά µεταξύ των σηµάτων εισόδου και εξόδου του κβαντιστή. Η µέγιστη στιγµιαία τιµή αυτού του σφάλµατος είναι το µισό ενός quantum και το συνολικό εύρος της µεταβολής είναι από /2 έως και /2. 20 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
21 Παράδειγµα Κβάντισης x(t) Επίπεδο κβάντισης Όρια περιοχών Επίπεδο κβάντισης PCM Κωδική λέξη x q (nts): κβαντισµένες τιµές x(nts):δείγµατα Ts: χρόνοςδειγµατοληψίας t PCM ακολουθία 21 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
22 Σφάλµα Κβαντισµού Έστω το σφάλµα κβάντισης συµβολίζεται από την τυχαία µεταβλητή τηςτιµήςτου σφάλµατος q = m ν Q= M V q Έστω ένας οµοιόµορφος κβαντιστής Mid-Riser τύπου: 2mmax Το µέγεθος βήµατος είναι = L m < m< m, L: o συνολικός αριθµός των επιπέδων. max max Συνάρτηση πυκνότητας πιθανότητας οµοιόµορφης κατανοµής στο διάστηµα. σ f Q 1, < q ( q) = 2 2 E(Q)=0 0, otherwise Q [ ] Q ( ) 2 2 = E Q = q f q dq= q dq= 2 12 Q 22 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
23 SNR Κβάντισης Έαν το κβαντισµένο δείγµα εκφράζεται σε δυαδική µορφή: R L= 2 όπου Rείναι ο αριθµός των bits ανά δείγµα R= log L 2 2m max = R R σ Q = mmax 2 3 Αν Pείναι η µέση ισχύς του m( t) P 3P 2R ( SNR) q = = σ Q m max (SNR) αυξάνει εκθετικά µε αύξηση του R (αριθµός των bits). q 23 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
24 SNR Κβάντισης Αν f ( m) είναι η συνάρτηση πυκνότητας πιθανότητας του δείγµατος m τουσήµατος. Τότε η µέση ισχύς του είναι ίδια µε την απόκλιση της τυχαίας µεταβλητής m. mmax 2 2 m P= σ = m f ( m) dm m max m Τότε το SNR γίνεται : 2 3σ m 2R ( SNR) q = 2 2 m max 3 2 ( SNR) = µέγιστη τιµή του σήµατος m F max Αν ορίσουµε F = = RMS τιµή του σήµατος σ m mmax 10 log( SNR) q = 6.02R+ 10 log +4.77= σ m = 6.02R 20log F q 2 2R 6dB Rule για κάθε ένα έχτρα bit. 24 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
25 Ορισµός Παραµόρφωσης Έστω m(t) το µήνυµα προερχόµενο από µια στάσιµη στοχαστική διαδικασία M(t) -A m A m 1 = -A m L+1 =A m k m k+1 for k=1,2,., L Το kth τµήµα ορίζεται ως J k : m k < m m k+1 για k=1,2,., L d(m,v k ): είναι το µέτρο παραµόρφωσης για χρήσηv k για να παριστάνει τιµές µέσα στοj k. 25 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
26 Συνθήκες για Βέλτιστο Κβαντιστή L { ν } { J } k= 1 L k= 1 k k= 1 Βρείτε δύο σύνολα και, που ελαχιστοποιούν τη µέση παραµόρφωση D d( m, ν ) f ( m) dm όπου f ( m) είναι γνωστή συνάρτηση pdf M k L = J m k Η µέση τετραγωνική παραµόρφωση που χρησιµοποιείται είναι : d( m, ν ) = ( m ν ) k 2 H βελτιστοποίηση είναι µια µη-γραµµική διαδικασία που ίσως να µην έχει κλειστή λύση. Ο κβαντιστής αποτελείται από δύο στοιχεία : έναν κωδικοποιητή που χαρακτηρίζεται από το σύνολο J k και έναν αποκωδικοποιητή που χαρακτηρίζεται από το σύνολο k M k ν k 26 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
27 ιανυσµατικός Κβαντιστής Συµπίεση εικόνας και φωνής, Αναγνώριση Φωνής Στατιστική Αναγνώριση Προτύπων Απεικόνισηόγκουσεδιαστατήεικόνα. 27 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
28 Καµπύλες Παραµόρφωσης vs. Ρυθµός Ρυθµός: Πόσες κώδικες λέξεις (bits) χρησιµοποιούνται? π.χ.16-bit audio vs. 8-bit PCM φωνής Παραµόρφωση: Πόση παραµόρφωση εισάγεται? π.χ.: µέση απόλυτη διαφορά ( νόρµα L1), µέσο τετραγωνικό σφάλµα (νόρµα L2) VQ ιανυσµατικός Κβαντιστης συνήθως έχει καλύτερη επίδοση από τον SQ Βαθµωτό Κβαντιστή µε κόστος της πολυπλοκότητα. 28 Εργαστήριο ECE6331 Κινητών Spring 2009 Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
29 Κβάντιση Οµοιόµορφη Κβάντιση : Οµοιόµορφη απόσταση µεταξύ των επίπεδων κβαντισµού. Μη οµοιόµορφη Κβάντιση: Μεταβλητή απόσταση µεταξύ των επίπεδων κβαντισµού. Η περιοχή των τάσεων που καλύπτονται από σήµατα φωνής από τα ασθενή σήµατα µέχρι τα δυνατά είναι από 1 έως Αν χρησιµοποιήσουµε µη-οµοιόµορφο κβαντιστή µε το χαρακτηριστικό ότι το µέγεθος του βήµατος να αυξάνει καθώς η απόσταση από την αρχή των αξόνων της χαρακτηριστικής αυξάνει. Το τελευταίο βήµα του κβαντιστή µπορεί να συµπεριλάβει όλες τις πιθανές µεταβολές του πλάτους του σήµατος φωνής. Άρα τα ασθενή σήµατα προτιµώνται σε βάρος των ισχυρών. Με αυτό τον τρόπο απαιτούνται λιγότερα βήµατα από ότι στην περίπτωση που θα είχαµε οµοιόµορφο κβαντιστή. 29 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
30 Μη οµοιόµορφη Κβάντιση Κίνητρο Σήµατα Φωνής έχουν το εξής χαρακτηριστικό: ασθενή σήµατα (µικρού πλάτους τάσεις) συµβαίνουν πιο συχνά από τα ισχυρά σήµατα. Το σύστηµα ακοής του ανθρώπου επιδεικνύει λογαριθµική ευαισθησία χαρακτηριστική εισόδου εξόδου. Πιο ευαίσθητο στα ασθενή σήµατα (π.χ. το 0.1 ακούγεται διαφορετικά από το 0.2) Λιγότερο ευαίσθητο σε σήµατα ισχυρά µε µεγάλα πλάτη (π.χ. 0.8 δεν ακούγεται πολύ διαφορετικά από το 0.9) Συνάρτηση Πυκνότητας Πιθανότητας Κανονικοποιηµένο σήµα φωνής 30 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
31 Μη οµοιόµορφος Κβαντιστής Η χρήση µη οµοιόµορφου κβαντιστή είναι ισοδύναµη µε τη διέλευση ενός σήµατος βασικής ζώνης µέσω ενός συµπιεστή (compressor) και στη συνέχεια µε την εφαρµογή του συµπιεσµένου σήµατος σε ένα οµοιόµορφο κβαντιστή. Η αντίθετη διάταξη του συµπιεστή είναι ο αποσυµπιεστής (expander) F: µη γραµµική συνάρτηση συµπίεσης F -1 : µη γραµµική συνάρτηση αποσυµπίεσης y y^ x Q x^ Παράδειγµα : F F -1 F: y=log(x) F -1 : x=exp(x) Η µεθοδολογία συµπίεσης και αποσυµπίεσης ενός σήµατος βασικής ζώνης για την αντιµετώπιση καταστροφικών φαινοµένων ονοµάζεται Compansion (Com pression Ex-pansion). Compressing+Expanding = Companding 31 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
32 Ποµπός/ έκτης µε Κβαντιστή y= C(x) xˆ x (t) y(t) y ˆ( t) xˆ ( t) Compress x Ποµπός Qauntize ίαυλος Expand έκτης ŷ 32 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
33 Νόµος -µ / Νόµος -A A PCM O νόµος-µ αλγόριθµος (µ-law) είναι ένας αλγόριθµος συµπίεσης και αποσυµπίεσης που χρησιµοποιήθηκε για πρώτη φορά σε ψηφιακά τηλεπικοινωνιακά συστήµατα στη Β. Αµερική και στην Ιαπωνία. Ο στόχος του είναι να περιορίσει τη δυναµική κλίµακα ενός σήµατος µουσικής audio. Στο πεδίο των αναλογικών σηµάτων µπορεί να αυξήσει το σηµατοθορυβικό λόγο SNR κατά τη διάρκεια της µετάδοσης και στο πεδίο των ψηφιακών σηµάτων µειώνει το σφάλµα κβάντισης δηλαδή αυξάνει το λόγο σήµατος προς το θόρυβο κβάντισης. Ο νόµος-α χρησιµοποιείται στον υπόλοιπο κόσµο. Προσφέρει λίγο µεγαλύτερη δυναµική κλίµακα από το νόµο-µ µε το κόστος της χειρότερης παραµόρφωσης για µικρά σήµατα. Ο νόµος A χρησιµοποιείται διεθνώς εάν µια χώρα το χρησιµοποιεί. 33 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
34 Νόµος - µ df( x) = dx µ log 1 1 ( + µ ) ( + µ x ) 34 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
35 Νόµος - A Α=1 Οµοιόµορφη κβάντιση A 1 + log A df( x) = dx 1 (1+ log A) x 35 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
36 Κωδικοποίηση Μετά τις διαδικασίες δειγµατοληψίας και κβάντισης ακολουθεί η διαδικασία κωδικοποίησης. Η αναπαράσταση καθενός από αυτά τα διακριτά σύνολα τιµών σα µια ιδιαίτερη διάταξη διακριτών γεγονότων ονοµάζεται κώδικα. Ένα από τα διακριτά γεγονότα σε ένα κώδικα ονοµάζεται στοιχείο του κώδικα ή σύµβολο. Σε ένα δυαδικό κώδικα (binary code), κάθε σύµβολο µπορεί να πάρει δύο τιµές 0, 1. Αν υποθέσουµε ότι σε ένα δυαδικό κώδικα κάθε κωδική λέξη αποτελείται από n bits δυαδικά ψηφία. Ένα δείγµα κβαντισµένο σε µία από τις 128 στάθµες µπορεί να παρασταθεί µια κωδική λέξη των 7bits. Υπάρχουν πολλοί τρόποι αντιστοίχησης ένα προς ένα µεταξύ των κβαντισµένων σταθµών και των κωδικών λέξεων. Συνήθως εκφράζουµε τον αριθµό της κβαντισµένης στάθµης σαν ένα δυαδικό αριθµό Συνεπώς το Pulse code modulation (PCM): είναι η κωδικοποίηση των κβαντισµένων σηµάτων σε µια ψηφιακή λέξη. Ένα κβαντισµένο σήµα κωδικοποιείται ψηφιακά σε µια κωδική λέξη των l bits που σχετίζονται µε τα L επίπεδα κβάντισης: 36 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
37 T A Σ PCM ειγµατοληψία Κβάντιση Κωδικοποίηση H Σ Τ Α Θ Μ Ε Σ Τ Α Σ Η Time Χρόνος Υ Α Ι Κ Ο Ι Κ Ω Ι Κ Ε Σ ΟΝ-ΟFF Σηµατοδότηση Χρόνος 37 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
38 Kωδικοποίηση PCM NBC (Natural Binary Coding) FBC (Foldover Binary Coding) 38 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
39 Εύρος Ζώνης Μετάδοσης για Συστήµατα (PCM) Το απαιτούµενο εύρος ζώνης για τη µετάδοση ενός ψηφιακού σήµατος που έχει προέρθει από ένα αναλογικό µε δειγµατοληψία το οποίου το εύρος καθορίζεται από µια µέγιστη συχνότητα. Ρυθµός Μετάδοσης = Εύρος Ζώνης= ρυθµός δειγµατοληψίας * αριθµός των bits / δείγµα Το ακουστικό σήµα έχει περίπου µέγιστη συχνότητα αποκοπής 3.4kHz. Ο ρυθµός Nyquist είναι 6.8kHz. a) Αν έχουµε ρυθµό δειγµατοληψίας 8000 δείγµατα/sec, f s =8kHz b) Αν κβαντιστεί το σήµα σε µία από τις 128 στάθµες δηλαδή χρησιµοποιούµε 7bits/ανά δείγµα. Απαιτούµενος Ρυθµός= Εύρος ζώνης >= 56kHz 39 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
40 Μετάδοση Βασικής Ζώνης Η µετάδοση πληροφορίας µέσω φυσικών καναλιών, οι ακολουθίες PCM (κώδικες λέξεις) µετατρέπονται σε παλµούς κυµατοµορφές (waveforms). Κάθε κυµατοµορφή µεταφέρει ένα σύµβολο από ένα σύνολο συµβόλων µεγέθους M. Κάθε µεταδιδόµενο σύµβολο παριστάνει κωδικών λέξεων του PCM. k = log2 bits των Οι κυµατοµορφές PCM (κώδικες γραµµής) χρησιµοποιούνται για δυαδικά σύµβολα (M=2). M-ary διαµόρφωση παλµών χρησιµοποιούνται για µη δυαδικά σύµβολά (M>2). Σε ένα τριαδικό κώδικα (tenary code), κάθε σύµβολο µπορεί να είναι µία από τις 3 διακριτές τιµές ή είδη. M 40 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
41 Ηλεκτρική Αναπαράσταση υαδικών εδοµένων ΟΝ- ΟFF Το σύµβολο 1 παριστάνεται µε την µετάδοση ενός σταθερού παλµού κατά τη διάρκεια του συµβόλου. Το σύµβολο 0 παριστάνεται από τη διακοπή του παλµού. 41 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
42 Ηλεκτρική Αναπαράσταση υαδικών εδοµένων Polar NRZ Bit V 0 V 5 V Τα σύµβολα 1 και 0 παριστάνονται από παλµούς ίσου θετικού και αρνητικού πλάτους. Αυτός ο τύπος σήµατος είναι γνωστός ως πολικό σήµα (polar signal), ή σήµα µη επιστροφής στο µηδέν (Non Return to Zero - NRZ). To πλεονέκτηµα αυτού του τύπου του σήµατος σε σχέση µε τον On Off (NRZ) είναι ότι έχει µηδενική DC συνιστώσα. Η µηδενική DC συνιστώσα είναι επιθυµητή σε κάποιες εφαρµογές. 42 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
43 Ηλεκτρική Αναπαράσταση υαδικών εδοµένων RZ (ON/OFF) Bit V 0 V Για το σύµβολο 1 χρησιµοποιείται ένας ορθογώνιος παλµός διάρκειας µισού συµβόλου. Ενώ το σύµβολο 0 παριστάνεται µε απουσία παλµού. Αυτός ο τύπος σήµατος συµβολίζεται RZ-Return to Zero σήµα. Το πλεονέκτηµα αυτού του τύπου σε σχέση µε τα προηγούµενα είναι µια µεγάλη ακολουθία από 1 επειδή οι µεταβάσεις γίνονται στο κέντρο του συµβόλου ο συγχρονισµός των ψηφίων είναι πιο εύκολος. Μεγάλη ακολουθία από 0 είναι δύσκολο να συγχρονιστούν. 43 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
44 Ηλεκτρική Αναπαράσταση υαδικών εδοµένων RZ (POLAR) Bit V 0 V 5 V Για το σύµβολο 1 χρησιµοποιείται ένας θετικός ορθογώνιος παλµός διάρκειας µισού συµβόλου. Ενώ το σύµβολο 0 χρησιµοποιείται ένας αρνητικός ορθογώνιος παλµός διάρκειας µισού συµβόλου. Αυτός ο τύπος σήµατος συµβολίζεται RZ Polar Return to Zero Signal Πλεονεκτήµατα: Εύκολος συγχρονισµός και έχει και µηδενική DC 44 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
45 Ηλεκτρική Αναπαράσταση υαδικών εδοµένων BIPOLAR RZ Bit V 0 V 5 V Θετικοί και αρνητικοί παλµοί ίσου πλάτους χρησιµοποιούνται σε εναλλαγή για το σύµβολο 1 και απουσία παλµού για το σύµβολο 0. Αυτός ο τύπος σήµατος ονοµάζεται διπολικό σήµα επιστροφής στο 0 (Bipolar RZ). Μια χρήσιµη ιδιότητα αυτής της µεθόδου είναι ότι το φάσµα ισχύος του µεταδιδόµενου σήµατος δεν έχει συνιστώσα DC και έχει σχετικά αµελητέες συνιστώσες χαµηλής συχνότητας στην περίπτωση όπου τα σύµβολα 1 και 0 εµφανίζονται µε ίση πιθανότητα. 45 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
46 BI-PHASE (MANCESTER) Ηλεκτρική Αναπαράσταση υαδικών εδοµένων Bit V 0V or -5V To σύµβολο 1 παριστάνεται µε ένα θετικό παλµό, ο οποίος ακολουθείται από έναν αρνητικό παλµό. Οι δύο παλµοί έχουν ίσο πλάτος και εύρος µισού συµβόλου. Το σύµβολο 0 παριστάνεται µε αντιστραµµένη πολικότητα. Αυτός ο τύπος ονοµάζεται Κώδικας Manchester, Bi-Phase, Χωρισµού φάσης (Split-Phase) Πλεονεκτήµατα: δεν υπάρχει συνιστώσα DC και έχει σχετικά αµελητέες συνιστώσες χαµηλής συχνότητας ανεξάρτητα από τη στατιστική του σήµατος. 46 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
47 PCM Κυµατοµορφές Κριτήρια για τη σύγκριση και επιλογή των PCM κυµατοµορφών: Φασµατικό Περιεχόµενο των Κυµατοµορφών) Φασµατικές Χαρακτηριστικές (πυκνότητα ισχύος και αποδοτικότητας εύρους ζώνης) Ικανότητα Συγχρονισµού των Bits υνατότητα Ανίχνευση Λάθους Ατρωσία στις παρεµβολές και στο θόρυβο. Υλοποίηση, Κόστος και Πολυπλοκότητα 47 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
48 M-ary ιαµόρφωση Παλµών M-ary ιαµορφώσεις Παλµών: M-ary pulse-amplitude modulation (Μ-PAM) M-ary pulse-position modulation (Μ-PPM) M-ary pulse-duration modulation (Μ-PDM) M- PAM είναι µια πολύ επίπεδη σηµατοδοσία όπου κάθε σύµβολο λαµβάνει ένα από τα M διαθέσιµα επίπεδα πλάτους, και το καθένα αναπαρίσταται bits των κωδικών λέξεων PCM. k = log2 M Για ένα δεδοµένο ρυθµό δεδοµένων, η M-PAM (M>2) απαιτεί λιγότερο εύρος ζώνης σε σχέση µε το δυαδικό PCM. Για µια δεδοµένη µέση ισχύ παλµού, το δυαδικό PCM ανιχνεύεται πιο εύκολα από το M-PAM (M>2). 48 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
49 Παράδειγµα Μ-PAM 49 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
50 ιαφορική Παλµοκωδική ιαµόρφωση Differential PCM (DPCM) Όταν λαµβάνονται δείγµατα από σήµα φωνής ή video µε ρυθµό υψηλότερο από το ρυθµό Nyquist το σήµα που θα προκύψει εµφανίζει υψηλή συσχέτιση µεταξύ των δειγµάτων. Κατάµέσοόρο, τοσήµαδεµεταβάλλεταιαπότοµααπότοένα δείγµα στο επόµενο. Η διαφορά µεταξύ γειτονικών δειγµάτων έχει µεταβλητότητα µικρότερη από αυτή του σήµατος. Όταν αυτά τα δείγµατα κωδικοποιούνται µε PCM το κωδικοποιηµένο σήµα που θα προκύψει περιέχει πλεονάζουσα πληροφορία. (Redundant Information) 50 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
51 ιαφορική Παλµοκωδική ιαµόρφωση Differential PCM (DPCM) Πρόβλεψη-Εκτίµηση Σήµατος Εάν γνωρίζουµε ένα επαρκές τµήµα του πλεονάζοντος σήµατος µπορούµε να συµπεράνουµεγιατουπόλοιποήνακάνουµεµιαπιθανήεκτίµηση. Έστω ένα σήµα βασικής ζώνης m(t) και έστω ότι λαµβάνονται δείγµατα µε ρυθµό 1/Τ s. Στη διαφορική παλµοκωδική διαµόρφωση η είσοδος του κβαντιστή είναι ένα σήµα: e nt = m nt m nt ( ) ( ) ( ) s s s ιαφορά του σήµατος εισόδου και της πρόβλεψης του. 51 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
52 ιαφορική Παλµοκωδική ιαµόρφωση Differential PCM (DPCM) H τιµή m nt ( ) ( ) ( ) s παράγεται από το φίλτρο πρόβλεψης. Η είσοδος του φίλτρου πρόβλεψης είναι µια κβαντισµένη µορφή του σήµατος m nt m nt s q s Ποµπός DPCM 52 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
53 ιαφορική Παλµοκωδική ιαµόρφωση Differential PCM (DPCM) H εξοδος της πρόβλεψης από τον κβαντιστή: ( ) = ( ) + ( ) e nt e nt q nt q s s e s Είσοδο στοφίλτροπρόβλεψης: m nt = m nt + e nt ( ) ( ) ( ) ( ) ( ) ( ) q s s q s ( ) m nt = m nt + e nt + q nt m( nt ) q s s s e s Άρα : ( ) = ( ) + ( ) m nt m nt q nt q s s e s Κβαντισµένη µορφή του σήµατος s ( ) m nt s Αν η πρόβλεψη του σήµατος είναι καλή η µεταβλητότητα του σφάλµατος θα είναι µικρότερη ( ) από τη µεταβλητότητα του m nt s. Οκβαντιστής µπορεί να προσαρµοστεί και να παράγει σφάλµα κβαντισµού µικρότερο από το κλασικό PCM. 53 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
54 ιαφορική Παλµοκωδική ιαµόρφωση Differential PCM (DPCM) Σε ένα περιβάλλον ελεύθερο θορύβου τα φίλτρα πρόβλεψης στο ποµπό και στο δέκτη είναι ίδια. Προσαρµοστικό (Adaptive) DPCM (ADPCM) είναιέναµεταβαλλόµενο DPCM που µεταβάλλει το µέγεθος του βήµατος κβάντισης ώστε να επιτραπεί µεγαλύτερη µείωση του απαιτούµενουεύρουςζώνηςγιαέναδεδοµένο SNR. 54 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
55 ιαµόρφωση έλτα (Delta Modulation) H εκµετάλλευση των συσχετίσεων των σηµάτων στην DPCM υποδεικνύει την επιπλέον δυνατότητα του oversampling ώστε να έχουµε σκόπιµη αύξηση της συσχέτισης µεταξύ γειτονικών δειγµάτων και µε αυτό τον τρόπο να είναι δυνατή µια απλή στρατηγική κβάντισης. Η διαµόρφωση δέλτα DM είναι η εκδοχή ενός ψηφίου (ή δύο επιπέδων) της DPCM. H DM είναι µια κλιµακωτή προσέγγιση της υπερδειγµατοληφθείσας µορφής ενός σήµατος βασικής ζώνης. Στην πραγµατικότητα προσεγγίζεται η παράγωγος της εισόδου. Η διαφορά µεταξύ της εισόδου και της προσέγγισης κβαντοποιείται µόνο σε δύο στάθµες +/- που είναι οι θετικές και οι αρνητικές διαφορές αντίστοιχα. Αν υποθέσουµε τα δείγµατα δε µεταβάλλονται πολύ απότοµα, η κλιµακωτή προσέγγισηπαραµένεισεπεριοχή +/-. Η ακρίβεια της µεθόδου εξαρτάται από: το βήµα κβάντισης και το ρυθµό δειγµατοληψίας 55 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
56 ιαµόρφωση έλτα (Delta Modulation) 56 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
57 ιαµόρφωση έλτα (Delta Modulation) ιαµόρφωση έλτα ( s) ( s) q( s s) ( ) = sgn ( ) e nt = m nt m nt T eq nts e nts ( ) = ( ) + ( ) m nt m nt T e nt q s q s s q s Η έξοδος του ολοκληρωτή ακολουθεί τη µεταβολή του σήµατος. Αν είναι θετική η διαφορά τότε θα έχουµε ένα θετικό βήµα πλάτους, ενώ αν είναι αρνητική θα έχουµε ένα αρνητικό βήµα πλάτους. 57 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
58 ιαµόρφωση έλτα (Delta Modulation) Στη διαµόρφωση έλτα εκπέµπεται µια παλµοσειρά όχι του πλάτους του σήµατος αλλά της διαφοράς του σήµατος και της προσέγγισης. 58 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
59 ιαµόρφωση έλτα (Delta Modulation) Παραµόρφωση / Θόρυβος Κβαντισµού Παραµόρφωση λόγω υπερφόρτωση κλίσης. Κοκκώδης θόρυβος. q( s) = ( s) + e( s) ( s) = ( s) q( s s) e( nt ) = m( nt ) m( nt T ) q ( nt T ) m nt m nt q nt e nt m nt m nt T s s s s e s s αντίστροφη διαφορά/ ψηφιακή προσέγγιση της παραγώγισης Για να µπορέσει να ακολουθήσει η κλιµακωτή συνάρτηση τη µεταβολή του σήµατος τότε πρέπει: dm( t) max Τ dt s δηλαδή πρέπει να αυξάνει η ακολουθία των δειγµάτων m q (nt s ) ώστε να ακολουθεί το δείγµα m(nt s ) H µέγιστη κλίση της κλιµακωτής συνάρτησης είναι. Κλίση Υπερφόρτωσης Slope Overload Ένας ιαµορφωτής µε σταθερό βήµα λέγεται Γραµµικός ιαµορφωτής έλτα. 59 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
60 ιαµόρφωση έλτα (Delta Modulation) 60 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
61 ιαµόρφωση έλτα (Delta Modulation) ( ) = ( π m ) ( ) Αν m t Acos 2 f t dm t max = A 2π f dt Σφάλµα υπερφόρτωσης: A 2π f f A Κοκκώδης Θόρυβος (granular noise) m m s m f 2π f s m Tο βήµα είναι πολύ µεγάλο σε σχέση µε την κλίση. Έτσι η κλιµακωτή συνάρτηση στην ουσία παρακολουθεί ένα επίπεδο τµήµα της κυµατοµορφής εισόδου. Προσαρµοστική ιαµόρφωση έλτα Μικρές µεταβολές του σήµατος Μικρό Μεγάλες µεταβολές του σήµατος Μεγάλο 61 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
62 Q&A Ευχαριστώ για την προσοχήσας!!! Ε-mail: Παλ. Κτίρια Ηλ/γων Γρ Τηλ.: Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Τηλεπικοινωνίες. Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων. Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση σήματος PCM
 Μετάδοση σήματος PCM Συγχρονισμός ΌπωςσεόλατασυστήματαTDM, απαιτείται συγχρονισμός μεταξύ πομπού και δέκτη Εάν τα ρολόγια στον πομπό και τον δέκτη διαφέρουν, αυτό θα οδηγήσει σε παραμορφώσεις του σήματος
Μετάδοση σήματος PCM Συγχρονισμός ΌπωςσεόλατασυστήματαTDM, απαιτείται συγχρονισμός μεταξύ πομπού και δέκτη Εάν τα ρολόγια στον πομπό και τον δέκτη διαφέρουν, αυτό θα οδηγήσει σε παραμορφώσεις του σήματος
Μετάδοση πληροφορίας - Διαμόρφωση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Μορφοποίηση και ιαµόρφωση Σηµάτων Βασικής Ζώνης
 Μορφοποίηση και ιαµόρφωση Σηµάτων Βασικής Ζώνης Μορφοποίηση - Κωδικοποίηση πηγής Μορφοποίηση παλµών βασικής ζώνης Μορφοποίηση & µετάδοση βασικής ζώνης Mορφοποίηση-κωδικοποίηση πηγής Mορφοποίηση παλµών
Μορφοποίηση και ιαµόρφωση Σηµάτων Βασικής Ζώνης Μορφοποίηση - Κωδικοποίηση πηγής Μορφοποίηση παλµών βασικής ζώνης Μορφοποίηση & µετάδοση βασικής ζώνης Mορφοποίηση-κωδικοποίηση πηγής Mορφοποίηση παλµών
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 10: Παλμοκωδική Διαμόρφωση, Διαμόρφωση Δέλτα και Πολύπλεξη Διαίρεσης Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Παλμοκωδική Διαμόρφωση (PCM) Παλμοκωδική Διαμόρφωση
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 10: Παλμοκωδική Διαμόρφωση, Διαμόρφωση Δέλτα και Πολύπλεξη Διαίρεσης Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Παλμοκωδική Διαμόρφωση (PCM) Παλμοκωδική Διαμόρφωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst33
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst33
Ψηφιακές Τηλεπικοινωνίες. Κωδικοποίηση Κυματομορφής
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 8 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 8 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Διαδικασία Ψηφιοποίησης (1/2)
 Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ. Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Z
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 9 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 9 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 3: Εισαγωγή στην Έννοια της Διαμόρφωσης Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Η ανάγκη για διαμόρφωση 2. Είδη διαμόρφωσης 3. Διαμόρφωση με ημιτονοειδές
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 3: Εισαγωγή στην Έννοια της Διαμόρφωσης Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Η ανάγκη για διαμόρφωση 2. Είδη διαμόρφωσης 3. Διαμόρφωση με ημιτονοειδές
Σεραφείµ Καραµπογιάς ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Ψηφιακή μετάδοση στη βασική ζώνη + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Ψηφιακή μετάδοση στη βασική ζώνη + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
SOURCE. Transmitter. Channel Receiver
 Εισαγωγή στις Τηλεπικοινωνίες Εισαγωγή στα Σήµατα Ψηφιακές Επικοινωνίες - ειγµατοληψία ρ. Αθανάσιος. Παναγόπουλος Λέκτορας ΕΜΠ 1 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
Εισαγωγή στις Τηλεπικοινωνίες Εισαγωγή στα Σήµατα Ψηφιακές Επικοινωνίες - ειγµατοληψία ρ. Αθανάσιος. Παναγόπουλος Λέκτορας ΕΜΠ 1 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
Κεφάλαιο 7. Ψηφιακή Διαμόρφωση
 Κεφάλαιο 7 Ψηφιακή Διαμόρφωση Ψηφιακή Διαμόρφωση 2 Διαμόρφωση βασικής ζώνης H ψηφιακή πληροφορία μεταδίδεται απ ευθείας με τεχνικές διαμόρφωσης παλμών βασικής ζώνης, οι οποίες δεν απαιτούν τη χρήση ημιτονοειδούς
Κεφάλαιο 7 Ψηφιακή Διαμόρφωση Ψηφιακή Διαμόρφωση 2 Διαμόρφωση βασικής ζώνης H ψηφιακή πληροφορία μεταδίδεται απ ευθείας με τεχνικές διαμόρφωσης παλμών βασικής ζώνης, οι οποίες δεν απαιτούν τη χρήση ημιτονοειδούς
Ψηφιακή μετάδοση στη βασική ζώνη. Baseband digital transmission
 Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Το ψηφιακό σήμα δεν είναι τίποτε άλλο από μια διατεταγμένη σειρά συμβόλων παραγόμενη από μια διακριτή πηγή πληροφορίας Η πηγή
Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Το ψηφιακό σήμα δεν είναι τίποτε άλλο από μια διατεταγμένη σειρά συμβόλων παραγόμενη από μια διακριτή πηγή πληροφορίας Η πηγή
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΜΕΤΑΤΡΟΠΗ ΑΝΑΛΟΓΙΚΟΥ ΣΗΜΑΤΟΣ ΣΕ ΨΗΦΙΑΚΟ
 ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΜΕΤΑΤΡΟΠΗ ΑΝΑΛΟΓΙΚΟΥ ΣΗΜΑΤΟΣ ΣΕ ΨΗΦΙΑΚΟ 5.1 Tο θεώρημα δειγματοληψίας. Χαμηλοπερατά σήματα 5.2 Διαμόρφωση πλάτους παλμού 5.3 Εύρος ζώνης καναλιού για ένα PAM σήμα 5.4 Φυσική δειγματοληψία
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΜΕΤΑΤΡΟΠΗ ΑΝΑΛΟΓΙΚΟΥ ΣΗΜΑΤΟΣ ΣΕ ΨΗΦΙΑΚΟ 5.1 Tο θεώρημα δειγματοληψίας. Χαμηλοπερατά σήματα 5.2 Διαμόρφωση πλάτους παλμού 5.3 Εύρος ζώνης καναλιού για ένα PAM σήμα 5.4 Φυσική δειγματοληψία
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α)
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
Διαμόρφωση Παλμών. Pulse Modulation
 Διαμόρφωση Παλμών Pulse Modulation Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις
Διαμόρφωση Παλμών Pulse Modulation Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις
ΕΠΙΚΟΙΝΩΝΙΕΣ, ΔΙΚΤΥΑ & ΤΕΧΝΟΛΟΓΙΑ ΥΠΟΛΟΓΙΣΤΩΝ
 ΕΠΙΚΟΙΝΩΝΙΕΣ, ΔΙΚΤΥΑ & ΤΕΧΝΟΛΟΓΙΑ ΥΠΟΛΟΓΙΣΤΩΝ ΚΕΦΑΛΑΙΟ 2ο ΑΝΑΛΟΓΙΚΑ - ΨΗΦΙΑΚΑ ΣΗΜΑΤΑ & ΑΡΧΕΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Πληροφορία Επικοινωνία συντελείται με τη μεταβίβαση μηνυμάτων από ένα πομπό σε ένα δέκτη. Μήνυμα
ΕΠΙΚΟΙΝΩΝΙΕΣ, ΔΙΚΤΥΑ & ΤΕΧΝΟΛΟΓΙΑ ΥΠΟΛΟΓΙΣΤΩΝ ΚΕΦΑΛΑΙΟ 2ο ΑΝΑΛΟΓΙΚΑ - ΨΗΦΙΑΚΑ ΣΗΜΑΤΑ & ΑΡΧΕΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Πληροφορία Επικοινωνία συντελείται με τη μεταβίβαση μηνυμάτων από ένα πομπό σε ένα δέκτη. Μήνυμα
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Εισαγωγή Δειγματοληψία + Περιεχόμενα n Εισαγωγή n αναλογικό η ψηφιακό σήμα; n ψηφιακά συστήματα επικοινωνιών n Δειγματοληψία
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Εισαγωγή Δειγματοληψία + Περιεχόμενα n Εισαγωγή n αναλογικό η ψηφιακό σήμα; n ψηφιακά συστήματα επικοινωνιών n Δειγματοληψία
Ψηφιακή μετάδοση στη βασική ζώνη. Baseband digital transmission
 Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Ένα ψηφιακό σήμα δεν είναι τίποτα άλλο από μια διατεταγμένη ακολουθία συμβόλων Η πηγή πληροφορίας παράγει σύμβολα από ένα αλφάβητο
Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Ένα ψηφιακό σήμα δεν είναι τίποτα άλλο από μια διατεταγμένη ακολουθία συμβόλων Η πηγή πληροφορίας παράγει σύμβολα από ένα αλφάβητο
0, αλλιώς. Σεραφείµ Καραµπογιάς. Παράδειγµα 1 Η πηγή X(t) είναι στατική Gaussian µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος.
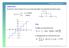 Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Διαμόρφωση Παλμών. Pulse Modulation
 Διαμόρφωση Παλμών Pulse Modulation Συστήματα διαμόρφωσης παλμών Είδη διαμόρφωσης παλμών Pulse Amplitude Modulation (PAM): A m(t) Pulse Position Modulation (PPM): T d m(t) Pulse Duration Modulation (PDM)
Διαμόρφωση Παλμών Pulse Modulation Συστήματα διαμόρφωσης παλμών Είδη διαμόρφωσης παλμών Pulse Amplitude Modulation (PAM): A m(t) Pulse Position Modulation (PPM): T d m(t) Pulse Duration Modulation (PDM)
Μετάδοση σήματος PCM
 Μετάδοση σήματος PCM Θόρυβος κατά τη μετάδοση Εύρος ζώνης μετάδοσης Το (διαμορφωμένο) σήμα PCM όταν μεταδίδεται μέσω του διαύλου είναι ένα σήμα συνεχούς χρόνου και έχει το δικό του εύρος ζώνης Το εύρος
Μετάδοση σήματος PCM Θόρυβος κατά τη μετάδοση Εύρος ζώνης μετάδοσης Το (διαμορφωμένο) σήμα PCM όταν μεταδίδεται μέσω του διαύλου είναι ένα σήμα συνεχούς χρόνου και έχει το δικό του εύρος ζώνης Το εύρος
Ψηφιακή Επεξεργασία Σηµμάτων
 Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio ΚΩΔΙΚΟΠΟΙΗΣΗ ΚΑΙ ΣΥΜΠΙΕΣΗ ΗΧΗΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΤΟ ΠΡΟΤΥΠΟ ISO/IEC 11172-3 MPEG-1 Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα:
Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio ΚΩΔΙΚΟΠΟΙΗΣΗ ΚΑΙ ΣΥΜΠΙΕΣΗ ΗΧΗΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΤΟ ΠΡΟΤΥΠΟ ISO/IEC 11172-3 MPEG-1 Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 6 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 6 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 6 ο : Διαμόρφωση Θέσης Παλμών Βασική Θεωρία Μ-αδική Διαμόρφωση Παλμών Κατά την μετατροπή
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 6 ο : Διαμόρφωση Θέσης Παλμών Βασική Θεωρία Μ-αδική Διαμόρφωση Παλμών Κατά την μετατροπή
Ημιτονοειδή σήματα Σ.Χ.
 Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Ήχος. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 04-1
 Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος και φωνή. Τεχνολογία Πολυµέσων 04-1
 Ήχος και φωνή Φύση του ήχου Ψηφιοποίηση µε µετασχηµατισµό Ψηφιοποίηση µε δειγµατοληψία Παλµοκωδική διαµόρφωση Αναπαράσταση µουσικής Ανάλυση και σύνθεση φωνής Μετάδοση φωνής Τεχνολογία Πολυµέσων 4-1 Φύση
Ήχος και φωνή Φύση του ήχου Ψηφιοποίηση µε µετασχηµατισµό Ψηφιοποίηση µε δειγµατοληψία Παλµοκωδική διαµόρφωση Αναπαράσταση µουσικής Ανάλυση και σύνθεση φωνής Μετάδοση φωνής Τεχνολογία Πολυµέσων 4-1 Φύση
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Wepage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Wepage: http://eclass.uop.gr/courses/tst233
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 5 ο : Διαμόρφωση Παλμών Βασική Θεωρία Μ-αδική Διαμόρφωση Παλμών Κατά την μετατροπή
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 5 ο : Διαμόρφωση Παλμών Βασική Θεωρία Μ-αδική Διαμόρφωση Παλμών Κατά την μετατροπή
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 7 ο : Διαμόρφωση Θέσης Παλμών
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 7 ο : Διαμόρφωση Θέσης Παλμών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 14 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: hp://ecla.uop.gr/coure/s15 e-mail:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 14 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: hp://ecla.uop.gr/coure/s15 e-mail:
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως:
 ΨΗΦΙΑΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ Πλεονεκτήματα: Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως: Αύξηση απαίτησης εύρους
ΨΗΦΙΑΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ Πλεονεκτήματα: Αντοχή (ruggedness) στο θόρυβο μετάδοσης Αποτελεσματική αναγέννηση (regeneration) Δυνατότητα ομοιόμορφου σχήματος (uniform format) μετάδοσης Όμως: Αύξηση απαίτησης εύρους
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 4 ο : Διαμόρφωση Παλμών Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 4 ο : Διαμόρφωση Παλμών Βασική
Παράδειγµα ενός ηλεκτρικού συστήµατος
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός aplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος A R B i( ) i
Σταθερή περιβάλλουσα (Constant Envelope)
 Διαμόρφωση ολίσθησης φάσης (Phase Shift Keying-PSK) Σταθερή περιβάλλουσα (Constant Envelope) Ίση Ενέργεια συμβόλων 1 Binary Phase Shift keying (BPSK) BPSK 2 Quaternary Phase Shift Keying (QPSK) 3 Αστερισμός-Διαγράμματα
Διαμόρφωση ολίσθησης φάσης (Phase Shift Keying-PSK) Σταθερή περιβάλλουσα (Constant Envelope) Ίση Ενέργεια συμβόλων 1 Binary Phase Shift keying (BPSK) BPSK 2 Quaternary Phase Shift Keying (QPSK) 3 Αστερισμός-Διαγράμματα
Ψηφιακές Επικοινωνίες
 Ψηφιακές Επικοινωνίες Ενότητα 3: Μαθιόπουλος Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέρος Α 3 Διαμόρφωση βασικής ζώνης (1) H ψηφιακή πληροφορία μεταδίδεται απ ευθείας με τεχνικές
Ψηφιακές Επικοινωνίες Ενότητα 3: Μαθιόπουλος Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέρος Α 3 Διαμόρφωση βασικής ζώνης (1) H ψηφιακή πληροφορία μεταδίδεται απ ευθείας με τεχνικές
Ψηφιακές Τηλεπικοινωνίες. Διαμόρφωση Παλμών κατά Πλάτος
 Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Συστήματα διαμόρφωσης παλμών Πολυπλεξία + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Συστήματα διαμόρφωσης παλμών Πολυπλεξία + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Baseband Transmission
 Ψηφιακές Επικοινωνίες Baseband ransmission Antipodal Signalling - Binary Orthogonal Signalling Probability of Error M-ary Orthogonal Signalling Waveforms Detection M-PAM detection Probability of error
Ψηφιακές Επικοινωνίες Baseband ransmission Antipodal Signalling - Binary Orthogonal Signalling Probability of Error M-ary Orthogonal Signalling Waveforms Detection M-PAM detection Probability of error
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
EΦΑΡΜΟΓΕΣ ΤΗΣ ΨΗΦΙΑΚΗΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ. Μετατροπείς A/D-Διαµόρφωση Δ Μετατροπείς Σ-Δ
 EΦΑΡΜΟΓΕΣ ΤΗΣ ΨΗΦΙΑΚΗΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ Μετατροπείς A/D-Διαµόρφση Δ Μετατροπείς Σ-Δ Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Μετατροπή A/D Μοντέλο Μετατροπέα Α/D xat
EΦΑΡΜΟΓΕΣ ΤΗΣ ΨΗΦΙΑΚΗΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ Μετατροπείς A/D-Διαµόρφση Δ Μετατροπείς Σ-Δ Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Μετατροπή A/D Μοντέλο Μετατροπέα Α/D xat
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
Εισαγωγή. Προχωρημένα Θέματα Τηλεπικοινωνιών. Ανάκτηση Χρονισμού. Τρόποι Συγχρονισμού Συμβόλων. Συγχρονισμός Συμβόλων. t mt
 Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 4: Μετατροπή Αναλογικών Σημάτων σε Ψηφιακά Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Δειγματοληψία: Ιδανική
Συστήματα Επικοινωνιών Ενότητα 4: Μετατροπή Αναλογικών Σημάτων σε Ψηφιακά Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Δειγματοληψία: Ιδανική
Περιεχόµενα διαλέξεων 2ης εβδοµάδας
 Εισαγωγή οµή και πόροι τηλεπικοινωνιακού συστήµατος Σήµατα Περιεχόµενα διαλέξεων 1ης εβδοµάδας Εισαγωγή Η έννοια της επικοινωνιας Ιστορική αναδροµή οµή και πόροι τηλεπικοινωνιακού συστήµατος οµή τηλεπικοινωνιακού
Εισαγωγή οµή και πόροι τηλεπικοινωνιακού συστήµατος Σήµατα Περιεχόµενα διαλέξεων 1ης εβδοµάδας Εισαγωγή Η έννοια της επικοινωνιας Ιστορική αναδροµή οµή και πόροι τηλεπικοινωνιακού συστήµατος οµή τηλεπικοινωνιακού
ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ /2/ :09:46 µµ
 ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ 013-14 18//014 1:09:46 µµ PULSE CODE MODULATION (PCM) 18//014 Το PCM είναι ένα σύστηµα, µε το οποίο µπορούµε να διαβιβάσουµε ένα αναλογικό (συνεχές) σήµα x(t) µέσω διακριτού καναλιού.
ΕΙΣ. ΣΥΣΤ. ΕΠΙΚΟΙΝΩΝΙΩΝ 013-14 18//014 1:09:46 µµ PULSE CODE MODULATION (PCM) 18//014 Το PCM είναι ένα σύστηµα, µε το οποίο µπορούµε να διαβιβάσουµε ένα αναλογικό (συνεχές) σήµα x(t) µέσω διακριτού καναλιού.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΉΜΑ ΕΠΙΣΤΉΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 7 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: hp://ecla.uop.gr/coure/tst25 e-ail:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΉΜΑ ΕΠΙΣΤΉΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 7 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: hp://ecla.uop.gr/coure/tst25 e-ail:
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 8: Δειγματοληψία - Διαμόρφωση παλμών Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της διαδικασίας
Συστήματα Επικοινωνιών Ενότητα 8: Δειγματοληψία - Διαμόρφωση παλμών Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της διαδικασίας
Γενική εικόνα τι είναι σήµα - Ορισµός. Ταξινόµηση σηµάτων. Βασικές ιδιότητες σηµάτων. Μετατροπές σήµατος ως προς το χρόνο. Στοιχειώδη σήµατα.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο Εργαστηριακή Άσκηση 7: Κβάντιση και Κωδικοποίηση Σημάτων Προσομοίωση σε Η/Υ Δρ. Ηρακλής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο Εργαστηριακή Άσκηση 7: Κβάντιση και Κωδικοποίηση Σημάτων Προσομοίωση σε Η/Υ Δρ. Ηρακλής
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Ψηφιακές Τηλεπικοινωνίες. Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση
 Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
Τι είναι σήµα; Σεραφείµ Καραµπογιάς
 Τι είναι σήµα; Σεραφείµ Καραµπογιάς Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές Παραδείγµατα: Σήµα οµιλίας Σήµα εικόνας
Τι είναι σήµα; Σεραφείµ Καραµπογιάς Ωςσήµαορίζεταιέναφυσικόµέγεθοςτοοποίοµεταβάλλεταισεσχέσηµετοχρόνοή το χώρο ή µε οποιαδήποτε άλλη ανεξάρτητη µεταβλητή ή µεταβλητές Παραδείγµατα: Σήµα οµιλίας Σήµα εικόνας
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI M-κά συστήματα διαμόρφωσης: Μ-PSK, M-FSK, M-QAM, DPSK + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI M-κά συστήματα διαμόρφωσης: Μ-PSK, M-FSK, M-QAM, DPSK + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
Δίκτυα Απευθείας Ζεύξης
 Δίκτυα Απευθείας Ζεύξης Επικοινωνία μεταξύ δύο υπολογιστώνοιοποίοιείναι απευθείας συνδεδεμένοι Φυσικό Επίπεδο. Περίληψη Ζεύξεις σημείου προς σημείο (point-to-point links) Ανάλυση σημάτων Μέγιστη χωρητικότητα
Δίκτυα Απευθείας Ζεύξης Επικοινωνία μεταξύ δύο υπολογιστώνοιοποίοιείναι απευθείας συνδεδεμένοι Φυσικό Επίπεδο. Περίληψη Ζεύξεις σημείου προς σημείο (point-to-point links) Ανάλυση σημάτων Μέγιστη χωρητικότητα
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε.
 ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ι 5 Ο ΕΞΑΜΗΝΟ ΔΙΔΑΣΚΩΝ: Δρ ΒΑΣΙΛΕΙΟΣ ΜΠΟΖΑΝΤΖΗΣ ΨΗΦΙΑΚΗ ΔΙΑΜΟΡΦΩΣΗ ΒΑΣΙΚΗΣ ΖΩΝΗΣ Τα είδη ψηφιακής
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ι 5 Ο ΕΞΑΜΗΝΟ ΔΙΔΑΣΚΩΝ: Δρ ΒΑΣΙΛΕΙΟΣ ΜΠΟΖΑΝΤΖΗΣ ΨΗΦΙΑΚΗ ΔΙΑΜΟΡΦΩΣΗ ΒΑΣΙΚΗΣ ΖΩΝΗΣ Τα είδη ψηφιακής
ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΤΩΝ ΕΦΑΡΜΟΓΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Ιωάννης Γ. Τίγκελης και Δημήτριος Ι. Φραντζεσκάκης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΤΩΝ ΕΦΑΡΜΟΓΩΝ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΥΣΤΗΜΑΤΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Ιωάννης Γ. Τίγκελης και Δημήτριος Ι. Φραντζεσκάκης
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Ψηφιακές Τηλεπικοινωνίες. Θεωρία Ρυθμού Παραμόρφωσης
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών)
 Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών) Κύριοι παράμετροι στη σχεδίαση παλμών είναι (στο πεδίο συχνοτήτων): Η Συχνότητα του 1ου μηδενισμού (θέλουμε μικρό BW). H ελάχιστη απόσβεση των πλαγίων λοβών
Παράμετροι σχεδίασης παλμών (Μορφοποίηση παλμών) Κύριοι παράμετροι στη σχεδίαση παλμών είναι (στο πεδίο συχνοτήτων): Η Συχνότητα του 1ου μηδενισμού (θέλουμε μικρό BW). H ελάχιστη απόσβεση των πλαγίων λοβών
Περιεχόµενα ΕΠΛ 422: στα Συστήµατα Πολυµέσων. Βιβλιογραφία. ειγµατοληψία. ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
Θόρυβος και λάθη στη μετάδοση PCM
 Θόρυβος και λάθη στη μετάδοση PCM Πότε συμβαίνουν λάθη Για μονοπολική (on-off) σηματοδότηση το σήμα στην έξοδο είναι, όπου α k =0 όταν y( kts) ak n( kts) μεταδίδεται το bit 0 και α k =Α όταν μεταδίδεται
Θόρυβος και λάθη στη μετάδοση PCM Πότε συμβαίνουν λάθη Για μονοπολική (on-off) σηματοδότηση το σήμα στην έξοδο είναι, όπου α k =0 όταν y( kts) ak n( kts) μεταδίδεται το bit 0 και α k =Α όταν μεταδίδεται
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 9 ο : Διαμόρφωση BPSK & QPSK Βασική Θεωρία Εισαγωγή Κατά την μετάδοση ψηφιακών δεδομένων
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 9 ο : Διαμόρφωση BPSK & QPSK Βασική Θεωρία Εισαγωγή Κατά την μετάδοση ψηφιακών δεδομένων
