ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ. Βιοστατική ΙΙ
|
|
|
- Σάββας Ανδρεάδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 3 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ Βιοστατική ΙΙ Ενότητα 3 είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Ιωάννης Ντζούφρας Τµήµα Στατιστικής Οικονοµικό Πανεπιστήµιο Αθηνών Πιο απλά : (στιγµιαίος) επιπολασµός πιθανότητα να έχουµε την υπό εξέταση νόσο d τη συγκεκριµένη χρονική στιγµή t. ίνεται από τον τύπο Prevalence d t N d t N t, Nt d είναι ο αριθµός των ατόµων του πληθυσµού µε την ασθένεια d τη χρονική στιγµή t και N t είναι το µέγεθος του συνολικού πληθυσµού τη χρονική στιγµή t. Αθήνα, 4 Νοεµβρίου 2006 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 2 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 4 Θεωρείται µέτρο συγχρονικών-διατµηµατικών µελετών (cross-sectional measure) 3.1 Μέτρα Νοσηρότητας - Εµφάνισης µιας Νόσου Επιπολασµός : Στιγµιαίος Επιπολασµός Ως στιγµιαίο επιπολασµό (prevalence) µιας ασθένειας ονοµάζουµε το ποσοστό (ή αναλογία) του πληθυσµού που έχει την νόσο τη χρονική στιγµή t. : Επιπολασµός Περιόδου Ως επιπολασµό περιόδου [t 0,t 1 ) µιας ασθένειας ονοµάζουµε το ποσοστό (ή αναλογία) του πληθυσµού που έχει την νόσο σε µία οποιαδήποτε χρονική στιγµή t µέσα στο διάστηµα [t 0,t 1 ) (δηλαδή t 0 t<t 1 ). ε λαµβάνει υπόψη του το χρόνο Εκτιµάται µόνο από µελέτες όπου η δειγµατοληψία είναι τυχαία και αντιπροσωπευτική του γενικού πληθυσµού. Η εκτίµηση του επιπολασµού γίνεται µε τον τύπο : Prevalence d 1 n n i1 Y d i nd n, όπου Yi d είναι µια δίτιµη-δείκτρια µεταβλητή που παίρνει τιµές ένα (1) και µηδέν (0) αν το i άτοµο έχει ή όχι τη νόσο d αντίστοιχα και n d είναι ο συνολικός αριθµός των ατόµων στο δείγµα που έχουν τη νόσο d. Οι παραπάνω τύποι αναφέρονται στο στιγµιαίο επιπολασµό. Για λεπτοµέρειες ϐλ. Daly et al. (1991, σελ ) και Pereira-Maxwell (1998, σελ. 62).
2 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 5 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Αθροιστική Επίπτωση Επιπολασµός στιγµιαίος δείκτης της έκτασης µιας νόσου στον πληθυσµό. Εδώ ϑα ορίσουµε δείκτες που λαµβάνουν υπόψη τους και το χρόνο. : Επεισόδιο ή περιστατικό µίας νόσου Μια περίπτωση (case) ονοµάζεται «επεισόδιο» ή «περιστατικό» (incident) τη στιγµή ακριβώς που εµφανίζει για πρώτη ϕορά τα συµπτώµατα της νόσου. : Αθροιστική επίπτωση «Αθροιστική επίπτωση» (cummulative incidence) µίας νόσου για το χρονικό διάστηµα [t 0,t 1 ) είναι η πιθανότητα ένα άτοµο που δεν έχει εκδηλώσει προηγουµένως την ίδια νόσο να εµφανίσει για πρώτη ϕορά τα συµπτώµατα της νόσου µέσα σε αυτό το διάστηµα (Rosner, 1994, σελ. 61). Εκτιµάται από προοπτικές µελέτες (σε αντίθεση µε τον επιπολασµό) από το τύπο : Î d t 0,t 1 n i1 Y Id(t 0,t 1 ) i n i1 Y Id(t0) i nid t 0,t 1 ni d t 0 ni d t 0,t 1 και ni d t 0 είναι οι αντίστοιχες δειγµατικές ποσότητες των NI d t 0,t 1 και NI(t 0 ) Y Id(t0,t1) i είναι δίτιµη-δείκτρια (0 1) µεταβλητή µε τιµή ένα αν το i άτοµο εµφανίσει επεισόδιο µίας νόσου στο χρονικό διάστηµα [t 0,t 1 ) Y Id(t0) i είναι δίτιµη-δείκτρια (0 1) µεταβλητή µε τιµή ένα αν το i άτοµο δεν έχει προϊστορία της νόσου µέχρι το χρόνο t 0 αντίστοιχα). Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 6 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 8 ίνεται από τη πιθανότητα I d t 0,t 1 P(t 0 <D d <t 1 D d >t 0 ) NI d t 0,t 1 NI d t 0 D d είναι ο χρόνος εµφάνισης της νόσου d, NIt d 0,t 1 είναι ο αριθµός των νέων επεισοδίων της νόσου d στο χρονικό διάστηµα [t 0,t 1 ) και NI(t 0 ) είναι αριθµός των ατόµων του πληθυσµού χωρίς να έχει εκδηλώσει τη νόσο d πρίν τον χρόνο t 0. : Συνάρτηση Επιβίωσης Συνάρτηση ή πιθανότητα αποφυγής της νόσου (ή επιβίωσης) µέχρι τον χρόνο t είναι η πιθανότητα να ένα άτοµο να µην εµφανίσει την νόσο πρίν τη χρονική στιγµή t (ή να επιβιώσει τουλάχιστον µέχρι τη χρονική στιγµή t). ίνεται από τον τύπο S(t) P(D d >t). Χρησιµοποιώντας τη συνάρτηση επιβίωσης µπορούµε να γράψουµε : I d t 0,t 1 S(t 0) S(t 1 ) S(t 0 ) 1 S(t 1) S(t 0 ).
3 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 9 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Ρυθµός Επίπτωσης Η αθροιστική επίπτωση... λαµβάνει υπόψη του το χρόνο ως πρός τα επεισόδια της νόσου που εµφανίζονται µέσα σε ένα χρονικό διάστηµα.... δε λαµβάνει υπόψη του το χρόνο διάρκειας µιας νόσου ο οποίος είναι σηµαντικός παράγοντας για τη κατανόηση της επίδρασης της νόσου στο πληθυσµό. Παράδειγµα µικρή πιθανότητα εµφάνισης Νόσος µε εµφανίζει υψηλό επιπολασµό. αλλά µεγάλη διάρκεια ηλαδή υπάρχουν πολλά άτοµα στο πληθυσµό που υποφέρουν από τη νόσο αυτή και για το λόγο αυτό να είναι σηµαντική η επίδρασή της στο σύνολο του πληθυσµού. Οσον αφορά το πληθυσµό, ο ϱυθµός επίπτωσης δίνεται από τον τύπο : IR d t 0,t 1 NI t d 0,t 1 T (t0,t1) NI d t 0,t 1 Nt 0 i1 T i,(t 0,t 1) N t0 είναι όλα τα άτοµα στο πληθυσµό το χρόνο t 0, T (t0,t 1) είναι ο συνολικός ανθρωποχρόνος παρακολούθησης και T i,(t0,t1) είναι ο χρόνος παρακολούθησης µέσα στο χρονικό διάστηµα [t 0,t 1 ) για το άτοµο i. Αν δεν υπάρχουν απώλειες στο χρόνο παρακολούθησης και ως συνέπεια όλα τα άτοµα παρακολουθούνται για χρόνο t 1 t 0 τότε ο ϱυθµός επίπτωσης δίνεται ως IR d t 0,t 1 NI d t 0,t 1 N t0 (t 1 t 0 ). Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 10 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου ιάρκεια Ασθένειας : Ρυθµός επίπτωσης Ετσι ορίζουµε το «ϱυθµό επίπτωσης» (incidence rate) ως το λόγο του αριθµού των νέων επεισοδίων µιας νόσου σε ένα χρονικό διάστηµα [t 0,t 1 ) προς «ανθρωποχρόνο κινδύνου» για την ίδια περίοδο (Pereira-Maxwell, 1998, σελ. 29). : Ανθρωποχρόνος κινδύνου Ο «ανθρωποχρόνος κινδύνου» δεν είναι τίποτα άλλο από το χρόνο παρακολούθησης αθροιστικά για όλα τα άτοµα του πληθυσµού. Ετσι, εδώ ο παρανοµαστής είναι χρόνος σε αντίθεση µε την αθροιστική επίπτωση όπου παρανοµαστής είναι ο αριθµός των ατόµων του πληθυσµού. Ως «διάρκεια ασθένειας» (duration) ορίζουµε το χρονικό διάστηµα από τη πρώτη εµφάνιση της νόσου ως την τελική ϑεραπεία και τη συµβολίζουµε ως D (ή D d ). Οταν µια ασθένεια είναι ϑανατηφόρα τότε ως διάρκεια ωής ονοµάζεται ο χρόνος µέχρι την κατάληξη του ασθενή. Οταν αναφερόµαστε σε ένα πληθυσµό ή ένα δείγµα τότε µας ενδιαφέρει η µέση διάρκεια της νόσου για τα άτοµα που έχουν εµφανίσει τη νόσο και τη συµβολίζουµε ως D (ή D d ). Η διάρκεια είναι σηµαντικό µέτρο της επίδρασης µίας ασθένειας σε ένα πληθυσµό : Ασθένειες µε µεγάλη µέση διάρκεια υψηλό επιπολασµό ακόµα και αν ο ϱυθµός επίπτωσης είναι µικρός.
4 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 13 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Εισαγωγικές Εννοιες για 2 2 Πίνακες Συνάφειας. 3.4 Μέτρα Κινδύνου για ίτιµα - Κατηγορικά εδοµένα. Στις Ιατρικές µελέτες η κύρια µεταβλητή απόκρισης είναι δίτιµη (η ασθένεια είναι παρούσα ή όχι). συνήθως και ο παράγοντας κινδύνου είναι επίσης κατηγορική µεταβλητή. Στην πιο απλή περίπτωση συγκρίνουµε τον κίνδυνο εµφάνισης µιας νόσου σε ένα άτοµο που έχει εκτεθεί στον παράγοντα κινδύνου 2. µε τον αντίστοιχο κίνδυνο ενός ατόµο που δεν έχει εκτεθεί στον ίδιο παράγοντα κινδύνου. Για το λόγο αυτό έµφαση ϑα δώσουµε στους δείκτες µέτρησης του κινδύνου εµφάνισης µίας νόσου όταν έχουµε δίτιµες κατηγορικές µεταβλητές Πίνακες Συνάφειας. Συνδιασµένη περιγραφή 2 κατηγορικών µεταβλητών Οµαδοποιηµένα ϱαβδοδιαγράµµατα (barchart) και Πίνακες συνάφειας διπλής εισόδου (two - way contingency tables). Οι πίνακες συνάφειας διπλής εισόδου είναι η κατανοµή συχνοτήτων του συνδιασµού των επιπέδων των 2 υπό εξέταση κατηγορικών µεταβλητών. Αν οι δύο µεταβλητές X και Y έχουν I και J επίπεδα τότε έχουµε I J συνδυασµούς. Εκτιµάει την από κοινού συνάρτηση πιθανότητας των δύο µεταβλητών που εξετάζουµε. Απεικόνιση µε ένα ορθογώνιο πίνακα µε I γραµµές και J στήλες. Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 14 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 16 Σύγκρισή οµάδων ως προς ποσοτικές µεταβλητές σύγκριση µέτρων κεντρικής ϑέσης (µέση τιµή και/ή διάµεσος). Σύγκρισή οµάδων ως προς κατηγορικές µεταβλητές σύγκριση των δεσµευµένων κατανοµών ή πιθανοτήτων. ηλαδή σύγκριση των ποσοστών (ή πιθανοτήτων ή αναλογιών) για κάθε διαφορετική οµάδα έκθεσης σε ένα παράγοντα κινδύνου. Στην ενότητα αυτή ϑα ασχοληθούµε µε την πιο απλή περίπτωση της σύγκρισης δίτιµων (Bernoulli) παραγόντων κινδύνου X σε δύο οµάδες µιας δεύτερης κατηγορικής µεταβλητής Y που συνήθως είναι η εµφάνιση της νόσου. ηλαδή ϑα επικεντρωθούµε στη σύγκριση κατηγορικών µεταβλητών που περιγράφονται από 2 2 πίνακες συνάφειας. Κάθε συνδυασµός εµφανίζεται στον πίνακα διπλής εισόδου ως ένα κουτί το οποίο ονοµάζεται κελί (cell). Ο αριθµός των εµφανίσεων κάθε συνδυασµού (X, Y )(i, j) στο δείγµα ονοµάζεται συχνότητα (count) και συµβολίζεται µε n ij. Το συνολικό µέγεθος του δείγµατος συµβολίζεται µε n και είναι ίσο µε n I i1 J j1 n ij. Η αντίστοιχη πιθανότητα P(X i, Y j) συµβολίζεται ως π ij και εκτιµάται από το p ij n ij /n.
5 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 17 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 19 Ενας I J πίνακα πίνακα συνάφειας διπλής εισόδου µε I γραµµές και J στήλες. Ενας 2 2 πίνακας διπλής εισόδου ϑα έχει την ακόλουθη µορφή : Y: Νόσος Περ.Κατ. X:Παρ. Κινδύνου 1 (Ασθενής) 2 (Υγιής) X 1(Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Περ.Κατ. Y n.1 n.2 n.. n Οι µονοµεταβλητές κατανοµές των X και Y δίνονται στην τελευταία στήλη και γραµµή του παραπάνω πίνακα και ονοµάζονται περιθωριακές κατανοµές (marginal distributions). Η περιθωριακή συχνότητα µιας κατηγορίας i της µεταβλητής X συµβολίζεται ως n i. (ή εναλλακτικά n i+ ): n i. J j1 n ij εσµευµένες Πιθανότητες. Σε κάθε πίνακα συνάφειας συνήθως ηµίαµεταβλητή(π.χ.y ) είναι το λογικό αποτέλεσµα - απόκριση (response) και η άλλη (π.χ. X) είναι η ανεξάρτητη ή επεξηγηµατική µεταβλητή (explanatory variable). Σε αυτή την περίπτωση η ανεξάρτητη µεταβλητή X µπορεί να είναι σταθερή ή προκαθορισµένη από το σχεδιασµό του πειράµατος και όχι τυχαία µεταβλητή. Τότε η πιθανότητα π ij P(X i, Y j) δεν έχει νόηµα (αφού η X δεν είναι τυχαία µεταβλητή). η περιθωριακή συχνότητα µιας κατηγορίας j της µεταβλητής Y συµβολίζεται ως n.j (ή εναλλακτικά n +j ):n.j I i1 n ij. Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 18 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 20 Μας ενδιαφέρει......ηκατανοµή της µεταβλητής Y για δεδοµένο (σταθερό) X. Η τελεία «.» ή εναλλακτικά το σύµβολο της πρόσθεσης «+» στους δείκτες υποδηλώνει άθροισµα. Με n.. ή n ++ πολύ συχνά συµβολίζεται το συνολικό άθροισµα του δείγµατος. Με παρόµοιο τρόπο ορίζονται και οι περιθωριακές πιθανότητες π i. και π.j των X και Y και οι αντίστοιχες δειγµατικές τους εκτιµήσεις p i. και p.j. Οι παραπάνω πίνακες διπλής εισόδου ονοµάζονται πίνακες συνάφειας (contingency tables) όταν τα κελιά περιέχουν συχνότητες (counts). Εναλλακτική ονοµασία είναι «πίνακες σταυρωτής καταχώρησης» (cross-classified tables). ηλαδή ϑέλουµε να εξετάσουµε πως η µεταβλητή Y αλλάζει για διαφορετικές τιµές του X. Ετσι έχει νόηµα η ανάλυση των υπό-συνθήκη πιθανοτήτων π j i P(Y j X i) µε J j1 π j i 1.Οιπιθανότητες(π 1 i,...,π J i ) δίνουν τη δεσµευµένη (ή υπό συνθήκη) κατανοµή (conditional distribution) της Y για το i επίπεδο της X. Σε 2 2 πίνακες : έλεγχος ανεξαρτησίας έλεγχος της ισότητας δύο και µόνο δεσµευµένων πιθανοτήτων Μπορούµε να ϕτιάξουµε διάφορα µέτρα ϐασισµένα στις πιθανοτήτες P(Ασθενής Κίνδυνος Παρόν) π j1 i1 & P(Ασθενής Κίνδυνος Απών) π j1 i2 και στην ουσία ϑα µετρούν την σχέση και απόκλιση των δύο αυτών πιθανοτήτων.
6 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 21 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Ανεξαρτησία ύο Κατηγορικών Μεταβλητών. Η ανεξαρτησία µεταξύ δύο µεταβλητών ορίζεται στατιστικά ως π ij P(X i, Y j) P(X i)p(y j) π i.π.j. Ανεξαρτησία των δύο µεταβλητών δεσµευµένες κατανοµές P(Y X i) είναι ίσες για όλα τα i εφόσον π j i P(Y j X i) P(Y j, X i) P(X i) P(Y j)p(x i) P(X i) P(Y j) π.j. Ολα τα µέτρα κινδύνου που ϑα περιγράψουµε πιο κάτω συγκρίνουν τον κίνδυνο, ο οποίος µετριέται µε την πιθανότητα εµφάνισης της νόσου, σε κάθε οµάδα έκθεσης σε ένα παράγοντα κινδύνου. Τα µέτρα κινδύνου στην ουσία µετράνε τις διαφορές στον κίνδυνο (πιθανότητα εµφάνισης της νόσου) και µας δίνουν ενα συνολικό δείκτη εξάρτησης µεταξύ του παράγοντα κινδύνου που εξετάζουµε και της νόσου. Ηεµφάνισητηςνόσου(Y ) παραµένει σταθερή ανεξάρτητα της έκθεσης ή όχι στον παράγοντα κινδύνου X. Με τον ίδιο τρόπο µπορούµε να ϐρούµε τα ίδια αποτελέσµατα για τις δεσµευµένες κατανοµές π i j P(X i Y j). Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 22 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 24 Συνεπώς ο έλεγχος της ανεξαρτησίας είναι ισοδύναµος µε τον έλεγχο H 0 : π j i π.j i 1,...,I και j 1,...,J. Ο περιορισµός J j1 π j i 1 οδείκτηςj µπορεί να πάρει τιµές µέχρι το J 1 εφόσον ισότητα των πιθανοτήτων των πρώτων J 1 επιπέδων ϑα συνεπάγεται αυτόµατα και ισότητα των πιθανοτήτων στο J επίπεδο. Για 2 2 πίνακες ο έλεγχος µπορεί να περιοριστεί στην απλή σχέση H 0 : π j1 i1 π j1 i2 έναντι της εναλλακτικής H 1 : π j1 i1 π j1 i2, (1) που για τη περίπτωση νόσου και παράγοντα κινδύνου µπορεί να γραφτεί ως H 0 : P(A E) P(A E) έναντι της εναλλακτικής H 1 : P(A E) P(A E), A είναι το ενδεχόµενο να είναι ένα άτοµο ασθενής, E και E είναι τα ενδεχόµενα ένα άτοµο να έχει εκτεθεί ή όχι στον παράγοντα κινδύνου αντιστοίχα Οφειλόµενος ή Αποδιδόµενος Κίνδυνος Ως αποδιδόµενο κίνδυνο ( αφνή, attributable risk) ή διαφορά κινδύνου (risk difference, Rosner, 1995, σελ ) ορίζουµε τη διαφορά µεταξύ των ϱυθµών επίπτωσης (ή των δεικτών ϑνησιµότητας) των οµάδων µε άτοµα εκτεθειµένα και µη εκτεθειµένα σε ένα παράγοντα κινδύνου. Εναλλακτικά ονοµάζεται και οφειλόµενος ή αποδοτέος κίνδυνος (Τριχόπουλος, 1982, σελ. 189).
7 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 25 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 27 ΣΤΑΤΙΣΤΙΚΟΣ : Πληθυσµός Σε 2 2 πίνακα αποδιδόµενος κίνδυνος διαφορά των δεσµευµένων πιθανοτήτων π j1 i1 και π j1 i2 : AR π E π E P(A E) P(A E) π j1 i1 π j1 i2 π j2 i2 π j2 i1 π E P(A E): πιθανότητα εµφάνισης της νόσου των εκτεθηµένων στον κίνδυνο (E) π E P(A E): πιθανότητα εµφάνισης της νόσου των µη εκτεθηµένων στον κίνδυνο (E). ΣΤΑΤΙΣΤΙΚΟΣ : Εκτίµηση από δείγµα ÂR p E p E p j1 i1 p j1 i2 n 11 n 1. n 21 n 2. n 11 n 11 + n 12 n 21 n 21 + n 22, p E και p E αντιστοιχούν στις δειγµατικές αναλογίες εµφάνισης της νόσου ανάλογα αν κάποιος έχει εκτεθεί στον κίνδυνο ή όχι. ΕΡΜΗΝΕΙΑ : Αποδιδόµενος Κίνδυνος Εστω AR a>0 Από το σύνολο των ατόµων που έχουν εκτεθεί σε κίνδυνο, το 100a% οφείλεται (ϑα µπορούσε να αποφευχθεί) στην έκθεση στον παράγοντα κινδύνου. 100a% των εκτεθειµένων σε κίνδυνο ατόµων ϑα είχε αποφύγει την υπό εξέταση νόσο εάν δεν είχε εκτεθεί στον παράγοντα κινδύνου (ή a n E άτοµα σε απόλυτους αριθµούς). Π.χ. Εστω AR % των εκτεθειµένων σε κίνδυνο ατόµων ϑα είχε αποφύγει την υπό εξέταση νόσο αν δεν είχε εκτεθεί στον παράγοντα κινδύνου. Αν n E 143 τότε σηµαίνει ότι ϑα απέφευγαν τη νόσο ( ) κατά µέσο όρο 14 άτοµα. Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 26 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 28 Ο έλεγχος ανεξαρτησίας (1) H 0 : AR 0versus H 1 : AR 0. Πρόβληµα : AR µετράει απόλυτες διαφορές. Π.χ. :Πιθανότητες(0.1, 0.2) & (0.6, 0.7) ίδιο AR 0.1. Γιατί πρόβληµα ; : Αγνοεί το γεγονός ότι στην 1η περίπτωση η πιθανότητα της µίας οµάδας είναι 2πλάσια από την άλλη. : Ποσοστιαίος Αποδιδόµενος Κίνδυνος Αυτό διορθώνεται µε τον ποσοστιαίο αποδιδόµενο κίνδυνο (Τριχόπουλος, 1982, σελ. 190): P(A E) P(A E) AR. P(A E) π E p AR π E π E π E π j1 i1 π j1 i2 π j1 i1 ΕΡΜΗΝΕΙΑ : Ποσοστιαίος Αποδιδόµενος Κίνδυνος Εστω PAR a>0 Από το σύνολο νοσούντων που έχουν εκτεθεί σε κίνδυνο, το 100a% οφείλεται (ϑα µπορούσε να αποφευχθεί) στην έκθεση στον παράγοντα κινδύνου. 100a% των νοσούντων από την εκτεθειµένη σε κίνδυνο οµάδα ατόµων, ϑα είχε αποφύγει την υπό εξέταση νόσο εάν δεν είχε εκτεθεί στον παράγοντα κινδύνου (ή a r E άτοµα σε απόλυτους αριθµούς). Π.χ. Εστω PAR 0.1/ % των νοσούντων στην οµάδα που έχει εκτεθεί στον παράγοντα κινδύνου, ϑα είχε αποφύγει την υπό εξέταση νόσο αν δεν είχε εκτεθεί στον παράγοντα κινδύνου. Αν r E τότε σηµαίνει ότι ϑα απέφευγαν τη νόσο (0.5 29) κατά µέσο όρο 14 άτοµα.
8 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 29 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Σχετικός Κίνδυνος (Relative Risk, RR) Ως «σχετικός κίνδυνος» (relative risk) ορίζεται ο λόγος της επίπτωσης ή της ϑνησιµότητας δύο οµάδων µε διαφορετική έκθεση στον παράγοντα κινδύνου. ΣΤΑΤΙΣΤΙΚΟΣ : Πληθυσµός Σε 2 2 πίνακες λόγος των πιθανοτήτων π j1 i1 προς π j1 i2 : RR π E π E P(A E) P(A E) π j1 i1 π j1 i2 1 π j2 i1 1 π j2 i2. ΣΤΑΤΙΣΤΙΚΟΣ : Εκτίµηση από δείγµα RR p E p E p j1 i1 p j1 i2 n 11/n 1. n 21 /n 2.. ΕΡΜΗΝΕΙΑ RR 2 Αν RR a, τότε η ερµηνεία του σχετικού κινδύνου µπορεί να γίνει µε οποιαδήποτε από τις παρακάτω προτάσεις : 1. Αν a>1 τότε : Η πιθανότητα εµφάνισης της νόσου (Y 1) όταν ένα άτοµο εκτεθεί στον παράγοντα κινδύνου (X 1) είναι ίση µε a 1 ϕορές µεγαλύτερη (ή (a 1)100% ϕορές µεγαλύτερη) από την ίδια πιθανότητα όταν δεν εκτεθεί στον κίνδυνο (X 2). 2. Αν a<1 τότε : Η πιθανότητα εµφάνισης της νόσου (Y 1) όταν ένα άτοµο εκτεθεί στον παράγοντα κινδύνου (X 1) είναι ίση µε 1 a ϕορές µικρότερη (ή (1 a)100% ϕορές µικρότερη) από την ίδια πιθανότητα όταν εκτεθεί στον κίνδυνο (X 2) (η µεταβλητή µας εδώ λέγεται προστατευτικός παράγοντας). 3. Αν a 1τότε : Η πιθανότητα εµφάνισης της νόσου (Y 1) όταν ένα άτοµο εκτεθεί στον παράγοντα κινδύνου (X 1) είναι ίση µε την ίδια πιθανότητα όταν δεν εκτεθεί έκθεση στον κίνδυνο (X 2) (δηλαδή η µεταβλητή X δεν επηρεάζει την εµφάνιση της νόσου συνεπώς δεν αποτελεί παράγοντα κινδύνου). Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 30 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου Λόγος Σχετικών Πιθανοτήτων (Odds Ratio, OR) Ο έλεγχος ανεξαρτησίας (1) H 0 : RR 1versus H 1 : RR 1. Συνεπώς, στην πράξη, αν ο σχετικός κίνδυνος είναι κοντά στο ένα ηπιθανότητα εµφάνισης της νόσου δεν επηρεάζεται από τη διαφορετική έκθεση στον παράγοντα κινδύνου X (ή δεν αλλάζει για τις διαφορετικές κατηγορίες της µεταβλητής X). ΕΡΜΗΝΕΙΑ RR 1 Αν RR a τότε Η πιθανότητα εµφάνισης της νόσου (Y 1)ότανέναάτοµοέχει εκτεθεί στον παράγοντα κινδύνου (X 1) είναι ίση µε a ϕορές την ίδια πιθανότητα όταν δεν εκτεθεί στον κίνδυνο (X 2) Σχετική Πιθανότητα (odds ) Ο όρος odds χρησιµοποιείται πολύ συχνά στην Αγγλική γλώσσα υποκαθιστώντας το όρο probability (πιθανότητα) και συνήθως δίνει µια εκτίµηση της τύχης που έχει κάποιος να κερδίσει σε ένα αγώνα ή στοίχηµα. ΣΤΑΤΙΣΤΙΚΟΣ Μαθηµατικά το odds ενός ενδεχοµένου A δίνεται από τον τύπο Odds(A) P(A) 1 P(A) και δεν είναι τίποτα άλλο από τον λόγο της πιθανότητας εµφάνισης ενός ενδεχοµένου έναντι της πιθανότητας µη εµφάνισης του (δηλαδή τη πιθανότητα του συµπληρωµατικού, ως προς το δειγµατικό χώρο, ενδεχοµένου).
9 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 33 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 35 Απόδοση στα Ελληνικά εν ήταν εύκολη υπόθεση. Στο λεξικό Αγγλικής γλώσσας του Longman (1987) ϐρίσκουµε τις ακόλουθες δύο ερµηνείες (σχετικές µε πιθανότητες): «Η πιθανότητα ότι κάτι ϑα συµβεί ή όχι» «Πιθανότητα εκφρασµένη σε αριθµούς για χρήση σε στοιχήµατα». Ο όρος χρησιµοποιείται κυρίως για στοιχήµατα : ίνει τις «ευκαιρίες» νίκης µιας οµάδας ή ενός διαγωνιζόµενου. Π.χ. : Η Ελληνική οµάδα ποδοσφαίρου πριν το Ευρωπαϊκό πρωτάθληµα ποδοσφαίρου του 2004 είχε, σύµφωνα µε τα διεθνή γραφεία στοιχηµάτων, πιθανότητα κατάκτησης (ή πιο σωστά αποτυχίας κατάκτησης) του πρωταθλήµατος 80 προς 1 (80 : 1) δηλαδή odds 1/80. Συνεπώς odds ο λόγος ή η αναλογία του αριθµού εµφάνισης ενός ενδεχοµένου (εκφρασµένο είτε σε απόλυτους αριθµούς είτε ως πιθανότητες) προς τον αριθµό µη εµφάνισης του ενδεχοµένου αυτού (Pereira-Maxwell, 1998, σελ. 49). Απόδοση στα Ελληνικά (3) Πρόβληµα µε τον όρο συµπληρωµατική πιθανότητα Οταν έχουµε πάνω από 2 ενδεχόµενα odds ονοµάζεται ο λόγος 2 ενδεχοµένων ακόµα και αν δεν είναι συµπληρωµατικά Συνεπώς odds 12 P(A 1 )/P(A 2 )π 1 /π 2 µε π 1 + π 2 1. Στην περίπτωση αυτή ο παραπάνω όρος δεν είναι σωστός. Για το λόγο αυτό ονοµάζουµε το odds «σχετική πιθανότητα» που µπορεί να ερµηνευτεί ως η πιθανότητα ενός ενδεχοµένου σε σχέση (αναλογικά) µε την πιθανότητα ενός άλλου ενδεχοµένου. Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 34 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 36 Απόδοση στα Ελληνικά (2) Αγγλο-ελληνικό λεξικό το odds «πιθανότητα» (δεν αποδίδει την ακριβή έννοια του όρου). Από τα παραπάνω odds το λόγο της πιθανότητας ενός ενδεχοµένου έναντι της πιθανότητας του συµπληρωµατικού ενδεχοµένου. Πληρέστερη και ακριβέστερη απόδοση του στα ελληνικά ϑα µπορούσε να γίνει µε τον όρο «Λόγος πιθανοτήτων συµπληρωµατικών ενδεχοµένων». Χρησιµοποιούµε τον πιο σύντοµο όρο «συµπληρωµατική πιθανότητα» πιο εύχρηστος αποδίδει τις δύο πιο σηµαντικές έννοιες του odds : την σχέση µε πιθανότητα και τη συµπληρωµατικότητα των ενδεχοµένων που συγκρίνουµε. Ο ελληνικός όρος «Συµπληρωµατική πιθανότητα» εµφανίστηκε στην Ελληνική ϐιβλιογραφία από τη συνάδελφο Ουρανία αφνή (ϐλέπε αφνή, 1997, σελ. 30). Πρακτικά η συµπληρωµατική πιθανότητα είναι 1 1 µετασχηµατισµός της αρχικής πιθανότητας. Οταν έχουµε δίτιµες µεταβλητές τότε odds π 1 π π odds 1+odds. που σηµαίνει ότι µεταφέρει ακριβώς την ίδια πληροφορία µε διαφορετικό τρόπο. Η ερµηνεία της ϑεωρείται πιο εύκολη από την απλή πιθανότητα διότι συγκρίνει την πιθανότητα εµφάνισης ενός ενδεχοµένου µε την πιθανότητα µη εµφάνισης. Π.χ. Οταν η Ελληνική οµάδα είχε σχετική πιθανότητα να µην κερδίσει το ευρωπαϊκό πρωτάθληµα του : 1 πιθανότητα να µην κερδίσει το πρωτάθληµα ήταν ίση µε 80 ϕορές την πιθανότητα να κερδίσει Πιο απλά η πιθανότητα να κερδίσει ήταν µόλις (1/(80 + 1) ) Στην Ιατρική µερικές ϕορές «Λόγος Συµπληρωµατικών Πιθανοτήτων».
10 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 37 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 39 Στην Ιατρική : Σχετική πιθανότητα πιθανότητα εµφάνισης της νόσου σε σχέση µε τη µη εµφάνιση της. ΕΡΜΗΝΕΙΑ (για δίτιµες µεταβλητές) 1. Αν odds 1 (ή 1:1) τότε οι πιθανότητες εµφάνισης ή µη εµφάνισης του ενδεχοµένου που εξεταζουµε είναι ίσες (δηλαδή 50%). 2. Αν odds a τότε η πιθανότητα εµφάνισης του ενδεχοµένου που εξετάζουµε είναι ίση µε a ϕορές την πιθανότητα µη εµφάνισης του. 3. Αν odds a και (α ) a > 1 τότε η πιθανότητα εµφάνισης του ενδεχοµένου που εξετάζουµε είναι a 1 (ή (a 1)100%) ϕορές µεγαλύτερη από την πιθανότητα µη εµφάνισης του. ΣΤΑΤΙΣΤΙΚΟΣ : odds σε 2 2 Πίνακες (Πληθυσµός) Ορίζουµε δύο σχετικές πιθανότητες ή odds (Χ) (ένα για κάθε επίπεδο της µεταβλητής X) από τις σχέσεις : odds(x 1) π 1 i1 π 2 i1 π 1 i1 1 π 1 i1 π11 π 12 & odds(x 2) π 1 i2 π 2 i2 ειγµατική Εκτίµηση odds από 2 2 Πίνακες π 1 i2 1 π 1 i2 π21 π 22. n11/n1. n21/n2. odds(x 1) p 1 i1 p 2 i1 n 12 /n 1. n11 & odds(x 2) p 1 i2 n 12 p 2 i2 n 22 /n 2. n21. n 22 (ϐ ) a<1 τότε η πιθανότητα εµφάνισης του ενδεχοµένου που εξετάζουµε είναι 1 a (ή (1 a)100%) ϕορές µικρότερη από την πιθανότητα µη εµφάνισης του. Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 38 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 40 ΕΡΜΗΝΕΙΑ 2 (για δίτιµες µεταβλητές) Συνεπώς όταν µιλάµε για την συµπληρωµατική πιθανότητα εµφάνισης της νόσου τότε : odds 1 συνεπάγεται ίση πιθανότητα εµφάνισης και µη εµφάνισης της νόσου. odds > 1 συνεπάγεται η εµφάνιση της νόσου είναι πιο πιθανή από τη πιθανότητα µη εµφάνισης της νόσου. odds < 1 συνεπάγεται η εµφάνιση της νόσου είναι λιγότερο πιθανή από τη πιθανότητα µη εµφάνισης της νόσου. Στην Ιατρική έρευνα µας ενδιαφέρουν οι σχετικές πιθανότητες εµφάνισης της νόσου όταν έχουµε έκθεση ή όχι στον παράγοντα κινδύνου. Συνεπώς µας ενδιαφέρουν οι συµπληρωµατικές πιθανότητες odds E P(A E) 1 P(A E) π E και odds 1 π E P(A E) E 1 P(A E) π E 1 π E οι οποίες εκτιµούνται από τους τύπους odds E p E 1 p E και odds E p E 1 p E.
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ. StatXact. ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ StatXact
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο StatXact ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 - συνέχεια ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ
Στόχος µαθήµατος: Παράδειγµα 1: µελέτη ασθενών-µαρτύρων ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 5 ΕΡΓΑΣΤΗΡΙΟ 1 ΜΕΤΡΑ ΚΙΝ ΥΝΟΥ & ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ. Βιοστατική ΙΙ
 Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 42 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ Βιοστατική ΙΙ Ενότητα 3 είκτες Νοσηρότητας, Μέτρα
Κεφάλαιο 3: είκτες Νοσηρότητας, Μέτρα Κινδύνου και ιαγνωστικού Ελέγχου 42 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ Βιοστατική ΙΙ Ενότητα 3 είκτες Νοσηρότητας, Μέτρα
Κλινική Επιδηµιολογία. Μέτρα κινδύνου Αιτιολογική συσχέτιση
 Κλινική Επιδηµιολογία Μέτρα κινδύνου Αιτιολογική συσχέτιση Μέτρα κινδύνου Αιτιολογική συσχέτιση Σύγκριση µεταξύ διαφορετικών πληθυσµών ως προς την έκθεση (exposure) Σύγκριση της κατανοµής της συχνότητας
Κλινική Επιδηµιολογία Μέτρα κινδύνου Αιτιολογική συσχέτιση Μέτρα κινδύνου Αιτιολογική συσχέτιση Σύγκριση µεταξύ διαφορετικών πληθυσµών ως προς την έκθεση (exposure) Σύγκριση της κατανοµής της συχνότητας
2.6 ΟΡΙΑ ΑΝΟΧΗΣ. πληθυσµού µε πιθανότητα τουλάχιστον ίση µε 100(1 α)%. Το. X ονοµάζεται κάτω όριο ανοχής ενώ το πάνω όριο ανοχής.
 2.6 ΟΡΙΑ ΑΝΟΧΗΣ Το διάστηµα εµπιστοσύνης παρέχει µία εκτίµηση µιας άγνωστης παραµέτρου µε την µορφή διαστήµατος και ένα συγκεκριµένο βαθµό εµπιστοσύνης ότι το διάστηµα αυτό, µε τον τρόπο που κατασκευάσθηκε,
2.6 ΟΡΙΑ ΑΝΟΧΗΣ Το διάστηµα εµπιστοσύνης παρέχει µία εκτίµηση µιας άγνωστης παραµέτρου µε την µορφή διαστήµατος και ένα συγκεκριµένο βαθµό εµπιστοσύνης ότι το διάστηµα αυτό, µε τον τρόπο που κατασκευάσθηκε,
Πινάκες συνάφειας. Βαρύτητα συμπτωμάτων. Φύλο Χαμηλή Υψηλή. Άνδρες. Γυναίκες
 Πινάκες συνάφειας εξερεύνηση σχέσεων μεταξύ τυχαίων μεταβλητών. Είναι λογικό λοιπόν, στην ανάλυση των κατηγορικών δεδομένων να μας ενδιαφέρει η σχέση μεταξύ δύο ή περισσότερων κατηγορικών μεταβλητών. Έστω
Πινάκες συνάφειας εξερεύνηση σχέσεων μεταξύ τυχαίων μεταβλητών. Είναι λογικό λοιπόν, στην ανάλυση των κατηγορικών δεδομένων να μας ενδιαφέρει η σχέση μεταξύ δύο ή περισσότερων κατηγορικών μεταβλητών. Έστω
Επιδημιολογία. Είδη υπό-μελέτη πληθυσμών. Ο ορισμός του υπό-μελέτη πληθυσμού ΜΕΤΡΗΣΗ ΚΑΙ ΣΥΓΚΡΙΣΗ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ ΤΩΝ ΝΟΣΗΜΑΤΩΝ
 Επιδημιολογία ΜΕΤΡΗΣΗ ΚΑΙ ΣΥΓΚΡΙΣΗ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ ΤΩΝ ΝΟΣΗΜΑΤΩΝ Ανδρονίκη Νάσκα, Αναπλ. Καθηγήτρια Εργαστήριο Υγιεινής, Επιδημιολογίας & Ιατρικής Στατιστικής anaska@med.uoa.gr Μελέτη της κατανομής και
Επιδημιολογία ΜΕΤΡΗΣΗ ΚΑΙ ΣΥΓΚΡΙΣΗ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ ΤΩΝ ΝΟΣΗΜΑΤΩΝ Ανδρονίκη Νάσκα, Αναπλ. Καθηγήτρια Εργαστήριο Υγιεινής, Επιδημιολογίας & Ιατρικής Στατιστικής anaska@med.uoa.gr Μελέτη της κατανομής και
ν ν = 6. όταν είναι πραγµατικός αριθµός.
 Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Σημασία παρονομαστών!!!
 Μέτρα συχνότητας νοσημάτων στην επιδημιολογική επιτήρηση και διερεύνηση επιδημιών Κρούσματα ιλαράς ανά νομό, Ελλάδα, Σεπτ. 005 - Απρ. 006 Νομός Αριθμός Κρουσμάτων Σύνολο Πληθυσμού Επίπτωση/ 100.000 Κεφαλληνίας
Μέτρα συχνότητας νοσημάτων στην επιδημιολογική επιτήρηση και διερεύνηση επιδημιών Κρούσματα ιλαράς ανά νομό, Ελλάδα, Σεπτ. 005 - Απρ. 006 Νομός Αριθμός Κρουσμάτων Σύνολο Πληθυσμού Επίπτωση/ 100.000 Κεφαλληνίας
ν ν = 6. όταν είναι πραγµατικός αριθµός.
 Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Α4. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράµµα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 7 ΑΠΡΙΛΙΟΥ 203 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α Α. Για δυο ασυµβίβαστα ενδεχόµενα
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 7 ΑΠΡΙΛΙΟΥ 203 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α Α. Για δυο ασυµβίβαστα ενδεχόµενα
X:S X(S) Έστω ότι στρίβουµε ένα αµερόληπτο νόµισµα δύο φορές και ενδιαφερόµαστε για τον αριθµό των Κ που θα εµφανιστούν.
 Στατιστική Ι: Ακαδηµαϊκό Έτος 6-7 Τυχαίες Μεταβλητές Έστω ότι εκτελούµε ένα πείραµα τύχης και ότι είµαστε σε θέση να µετρήσουµε όλα τα δυνατά αποτελέσµατα και να αντιστοιχούµε ένα πραγµατικό αριθµό σε
Στατιστική Ι: Ακαδηµαϊκό Έτος 6-7 Τυχαίες Μεταβλητές Έστω ότι εκτελούµε ένα πείραµα τύχης και ότι είµαστε σε θέση να µετρήσουµε όλα τα δυνατά αποτελέσµατα και να αντιστοιχούµε ένα πραγµατικό αριθµό σε
ΑΝΤΙΚΕΙΜΕΝΟ ΜΑΘΗΜΑΤΟΣ
 ΑΝΤΙΚΕΙΜΕΝΟ ΜΑΘΗΜΑΤΟΣ Γνωριµία και ερµηνεία των πιθανοτήτων Χρήση σε πρακτικά προβλήµατα και σε θέµατα στατιστικής συµπερασµατολογίας. Προσθετικός και πολλαπλασιαστικός κανόνας των πιθανοτήτων Έννοια της
ΑΝΤΙΚΕΙΜΕΝΟ ΜΑΘΗΜΑΤΟΣ Γνωριµία και ερµηνεία των πιθανοτήτων Χρήση σε πρακτικά προβλήµατα και σε θέµατα στατιστικής συµπερασµατολογίας. Προσθετικός και πολλαπλασιαστικός κανόνας των πιθανοτήτων Έννοια της
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2010 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Έστω t, t,..., t ν οι παρατηρήσεις µιας ποσοτικής µεταβλητής Χ ενός δείγµατος µεγέθους ν, που έχουν µέση τιµή x. Σχηµατίζουµε
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Έστω t, t,..., t ν οι παρατηρήσεις µιας ποσοτικής µεταβλητής Χ ενός δείγµατος µεγέθους ν, που έχουν µέση τιµή x. Σχηµατίζουµε
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι
Α. α) ίνεται η συνάρτηση F(x)=f(x)+g(x). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F (x)=f (x)+g (x).
 Νίκος Σούρµπης - - Γιώργος Βαρβαδούκας ΘΕΜΑ ο Α. α) ίνεται η συνάρτηση F()=f()+g(). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F ()=f ()+g (). β)να γράψετε στο τετράδιό σας τις παραγώγους
Νίκος Σούρµπης - - Γιώργος Βαρβαδούκας ΘΕΜΑ ο Α. α) ίνεται η συνάρτηση F()=f()+g(). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F ()=f ()+g (). β)να γράψετε στο τετράδιό σας τις παραγώγους
Κριτήρια επιλογής μέτρων συνάφειας
 Κριτήρια επιλογής μέτρων συνάφειας Ο όρος συνάφεια προέρχεται από τον Pearso (1904) όπου ορίζεται για ένα πίνακα IJ ως ένα μέτρο της συνολικής απόκλισης της ταξινόμησης από την ανεξάρτητη πιθανότητα. Από
Κριτήρια επιλογής μέτρων συνάφειας Ο όρος συνάφεια προέρχεται από τον Pearso (1904) όπου ορίζεται για ένα πίνακα IJ ως ένα μέτρο της συνολικής απόκλισης της ταξινόμησης από την ανεξάρτητη πιθανότητα. Από
Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου
 Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου Διαφορικός Λογισμός 1. Ισχύει f (g())) ) f ( = f (g())g () όπου f,g παραγωγίσιµες συναρτήσεις 2. Αν µια συνάρτηση f είναι παραγωγίσιµη σε ένα διάστηµα
Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου Διαφορικός Λογισμός 1. Ισχύει f (g())) ) f ( = f (g())g () όπου f,g παραγωγίσιµες συναρτήσεις 2. Αν µια συνάρτηση f είναι παραγωγίσιµη σε ένα διάστηµα
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Το σύνολο Α, που λέγεται πεδίο ορισµού της συνάρτησης,
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ - ΘΕΩΡΙΑ Γιάννης Ζαμπέλης ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Τι ονοµάζεται συνάρτηση Συνάρτηση (functon) είναι µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ - ΘΕΩΡΙΑ Γιάννης Ζαμπέλης ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Τι ονοµάζεται συνάρτηση Συνάρτηση (functon) είναι µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2004
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 004 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Α. Να αποδείξετε ότι η παράγωγος της σταθερής συνάρτησης fxc είναι ίση µε 0. Μονάδες 8 Β. Να δώσετε τον ορισµό της συνέχειας
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 004 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Α. Να αποδείξετε ότι η παράγωγος της σταθερής συνάρτησης fxc είναι ίση µε 0. Μονάδες 8 Β. Να δώσετε τον ορισµό της συνέχειας
Τεκµηριωµένη Ιατρική 2011-12 ΒΛΑΒΗ. Βασίλης Κ. Λιακόπουλος Λέκτορας Νεφρολογίας ΑΠΘ
 Τεκµηριωµένη Ιατρική 2011-12 ΒΛΑΒΗ Βασίλης Κ. Λιακόπουλος Λέκτορας Νεφρολογίας ΑΠΘ Αναλογία Λόγος Πηλίκο Αναλογία Proportion Αναλογία (Proportion) Ο αριθµητής ΣΥΜΠΕΡΙΛΑΜΒΑΝΕΤΑΙ ΑΠΑΡΑΙΤΗΤΩΣ στον παρανοµαστή
Τεκµηριωµένη Ιατρική 2011-12 ΒΛΑΒΗ Βασίλης Κ. Λιακόπουλος Λέκτορας Νεφρολογίας ΑΠΘ Αναλογία Λόγος Πηλίκο Αναλογία Proportion Αναλογία (Proportion) Ο αριθµητής ΣΥΜΠΕΡΙΛΑΜΒΑΝΕΤΑΙ ΑΠΑΡΑΙΤΗΤΩΣ στον παρανοµαστή
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΤΑΞΙΝΟΜΗΜΕΝΑ Ε ΟΜΕΝΑ
 ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΤΑΞΙΝΟΜΗΜΕΝΑ Ε ΟΜΕΝΑ Αριθµητικός Μέσος: όπου : αριθµός παρατηρήσεων ιάµεσος: εάν άρτιος εάν περιττός M + + M + Παράδειγµα: ηλ.: Εάν :,,, M + + 5 + +, 5 Εάν :,, M + Επικρατούσα Τιµή:
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΤΑΞΙΝΟΜΗΜΕΝΑ Ε ΟΜΕΝΑ Αριθµητικός Μέσος: όπου : αριθµός παρατηρήσεων ιάµεσος: εάν άρτιος εάν περιττός M + + M + Παράδειγµα: ηλ.: Εάν :,,, M + + 5 + +, 5 Εάν :,, M + Επικρατούσα Τιµή:
Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου
 Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου Θέµα Α A1. Για δυο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδείξετε ότι: Ρ( Α Β) = Ρ(Α) + Ρ(Β) Ρ( Α Β) Α. Πότε µια συνάρτηση f µε
Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου Θέµα Α A1. Για δυο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδείξετε ότι: Ρ( Α Β) = Ρ(Α) + Ρ(Β) Ρ( Α Β) Α. Πότε µια συνάρτηση f µε
Μάθηµα 11. Κεφάλαιο: Στατιστική
 Μάθηµα Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Παρουσίαση Στατιστικών εδοµένων (Στατιστικοί Πίνακες). Γενικά για στατιστικούς πίνακες. Τα στατιστικά δεδοµένα καταγράφονται σε στατιστικούς πίνακες (ή
Μάθηµα Κεφάλαιο: Στατιστική Θεµατικές Ενότητες:. Παρουσίαση Στατιστικών εδοµένων (Στατιστικοί Πίνακες). Γενικά για στατιστικούς πίνακες. Τα στατιστικά δεδοµένα καταγράφονται σε στατιστικούς πίνακες (ή
Είδη Μεταβλητών. κλίµακα µέτρησης
 ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρµοσµένες Επιστήµες Στατιστικός Πληθυσµός και Δείγµα Το στατιστικό
ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρµοσµένες Επιστήµες Στατιστικός Πληθυσµός και Δείγµα Το στατιστικό
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β )
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΚΥΡΙΑΚΗ /0/0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:ΕΝΝΕΑ (9) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΚΥΡΙΑΚΗ /0/0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:ΕΝΝΕΑ (9) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες
 Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ]
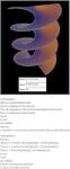
![cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ] cov(x, Y ) = E[(X E[X]) (Y E[Y ])] cov(x, Y ) = E[X Y ] E[X] E[Y ]](/thumbs/52/30692583.jpg) Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-317: Εφαρµοσµένες Στοχαστικές ιαδικασίες-εαρινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Συνδιασπορά - Συσχέτιση Τυχαίων Μεταβλητών Επιµέλεια : Κωνσταντίνα
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-317: Εφαρµοσµένες Στοχαστικές ιαδικασίες-εαρινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Συνδιασπορά - Συσχέτιση Τυχαίων Μεταβλητών Επιµέλεια : Κωνσταντίνα
Περίληψη ϐασικών εννοιών στην ϑεωρία πιθανοτήτων
 Περίληψη ϐασικών εννοιών στην ϑεωρία πιθανοτήτων 6 Απριλίου 2009 1 Συνδυαστική Η ϐασική αρχή µέτρησης µας λέει ότι αν σε ένα πείραµα που γίνεται σε δύο ϕάσεις και στο οποίο υπάρχουν n δυνατά αποτελέσµατα
Περίληψη ϐασικών εννοιών στην ϑεωρία πιθανοτήτων 6 Απριλίου 2009 1 Συνδυαστική Η ϐασική αρχή µέτρησης µας λέει ότι αν σε ένα πείραµα που γίνεται σε δύο ϕάσεις και στο οποίο υπάρχουν n δυνατά αποτελέσµατα
Εργαστήριο Μαθηµατικών & Στατιστικής. 1 η Πρόοδος στο Μάθηµα Στατιστική 5/12/08 Α ΣΕΙΡΑ ΘΕΜΑΤΩΝ. 3 ο Θέµα
 Εργαστήριο Μαθηµατικών & Στατιστικής Α ΣΕΙΡΑ ΘΕΜΑΤΩΝ η Πρόοδος στο Μάθηµα Στατιστική 5//8 ο Θέµα To % των ζώων µιας µεγάλης κτηνοτροφικής µονάδας έχει προσβληθεί από µια ασθένεια. Για τη διάγνωση της συγκεκριµένης
Εργαστήριο Μαθηµατικών & Στατιστικής Α ΣΕΙΡΑ ΘΕΜΑΤΩΝ η Πρόοδος στο Μάθηµα Στατιστική 5//8 ο Θέµα To % των ζώων µιας µεγάλης κτηνοτροφικής µονάδας έχει προσβληθεί από µια ασθένεια. Για τη διάγνωση της συγκεκριµένης
ΚΕΦΑΛΑΙΟ. 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής;
 Μαθηµατικά και Στοιχεία Στατιστικής ΚΕΦΑΛΑΙΟ ο 1 : ιαφορικός Λογισµός 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής; 2. Έστω µια
Μαθηµατικά και Στοιχεία Στατιστικής ΚΕΦΑΛΑΙΟ ο 1 : ιαφορικός Λογισµός 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής; 2. Έστω µια
Αναλυτική Στατιστική
 Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
Αναλυτική Στατιστική Συμπερασματολογία Στόχος: εξαγωγή συμπερασμάτων για το σύνολο ενός πληθυσμού, αντλώντας πληροφορίες από ένα μικρό υποσύνολο αυτού Ορισμοί Πληθυσμός: σύνολο όλων των υπό εξέταση μονάδων
Στατιστική Εισαγωγικές Έννοιες
 Στατιστική Εισαγωγικές Έννοιες Στατιστική: η επιστήµη που παρέχει µεθόδους και εργαλεία για την οργάνωση, συστηµατική περιγραφή και περιληπτική παρουσίαση δεδοµένων, καθώς και για την ανάλυση της πληροφορίας
Στατιστική Εισαγωγικές Έννοιες Στατιστική: η επιστήµη που παρέχει µεθόδους και εργαλεία για την οργάνωση, συστηµατική περιγραφή και περιληπτική παρουσίαση δεδοµένων, καθώς και για την ανάλυση της πληροφορίας
Μέτρα σχέσης. Ιωάννα Τζουλάκη Λέκτορας Επιδημιολογίας Υγιεινή και Επιδημιολογία
 Μέτρα σχέσης Ιωάννα Τζουλάκη Λέκτορας Επιδημιολογίας Υγιεινή και Επιδημιολογία Στο τέλος...(learning outcomes) Να γνωρίζετε τα κυριότερα μέτρα σχέσης που χρησιμοποιούνται για μετρήσουμε μια συσχέτηση μεταξύ
Μέτρα σχέσης Ιωάννα Τζουλάκη Λέκτορας Επιδημιολογίας Υγιεινή και Επιδημιολογία Στο τέλος...(learning outcomes) Να γνωρίζετε τα κυριότερα μέτρα σχέσης που χρησιμοποιούνται για μετρήσουμε μια συσχέτηση μεταξύ
Είδη Μεταβλητών Κλίμακα Μέτρησης Οι τεχνικές της Περιγραφικής στατιστικής ανάλογα με την κλίμακα μέτρησης Οι τελεστές Π και Σ
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρμοσμένες Επιστήμες Στατιστικός Πληθυσμός και Δείγμα Το στατιστικό
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 1 Εισαγωγικές Έννοιες 19 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Η Μεταβλητότητα Η Στατιστική Ανάλυση Η Στατιστική και οι Εφαρμοσμένες Επιστήμες Στατιστικός Πληθυσμός και Δείγμα Το στατιστικό
28/11/2016. Στατιστική Ι. 9 η Διάλεξη (Περιγραφική Στατιστική)
 Στατιστική Ι 9 η Διάλεξη (Περιγραφική Στατιστική) 1 2 Πληθυσμός ή στατιστικός πληθυσμός Ονομάζεται η κατανομή των τιμών μιας τ.μ., δηλαδή η κατανομή των τιμών που παίρνει ένα χαρακτηριστικό μιας ομάδας
Στατιστική Ι 9 η Διάλεξη (Περιγραφική Στατιστική) 1 2 Πληθυσμός ή στατιστικός πληθυσμός Ονομάζεται η κατανομή των τιμών μιας τ.μ., δηλαδή η κατανομή των τιμών που παίρνει ένα χαρακτηριστικό μιας ομάδας
ΕΞΕΤΑΣΗ ΤΗΣ ΣΧΕΣΗΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ
 ΕΞΕΤΑΣΗ ΤΗΣ ΣΧΕΣΗΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ ΔΥΟ ΠΟΙΟΤΙΚΕΣ ΠΙΝΑΚΕΣ ΣΥΝΑΦΕΙΑΣ ΕΞΕΤΑΣΗ ΤΗΣ ΥΠΑΡΞΗΣ Ή ΟΧΙ ΣΧΕΣΗΣ ΕΝΤΑΣΗ ΚΑΙ ΦΥΣΗ ΤΗΣ ΣΧΕΣΗΣ ΔΥΟ ΠΟΙΟΤΙΚΕΣ ΔΙΑΔΙΚΑΣΙΑ CROSSTABS ΠΙΝΑΚΑΣ ΣΥΝΑΦΕΙΑΣ Ο πίνακας συνάφειας είναι
ΕΞΕΤΑΣΗ ΤΗΣ ΣΧΕΣΗΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ ΔΥΟ ΠΟΙΟΤΙΚΕΣ ΠΙΝΑΚΕΣ ΣΥΝΑΦΕΙΑΣ ΕΞΕΤΑΣΗ ΤΗΣ ΥΠΑΡΞΗΣ Ή ΟΧΙ ΣΧΕΣΗΣ ΕΝΤΑΣΗ ΚΑΙ ΦΥΣΗ ΤΗΣ ΣΧΕΣΗΣ ΔΥΟ ΠΟΙΟΤΙΚΕΣ ΔΙΑΔΙΚΑΣΙΑ CROSSTABS ΠΙΝΑΚΑΣ ΣΥΝΑΦΕΙΑΣ Ο πίνακας συνάφειας είναι
Στόχος µαθήµατος: ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ. 1. Πολλαπλή γραµµική παλινδρόµηση. 1.2 Παράδειγµα 7 (συνέχεια)
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 12β ΕΡΓΑΣΤΗΡΙΟ 4β ΠΟΛΛΑΠΛΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝ ΡΟΜΗΣΗ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 2006-2007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 12β ΕΡΓΑΣΤΗΡΙΟ 4β ΠΟΛΛΑΠΛΗ ΓΡΑΜΜΙΚΗ ΠΑΛΙΝ ΡΟΜΗΣΗ ΜΕ ΤΗΝ ΧΡΗΣΗ SPSS
Έλεγχος Ανεξαρτησίας x2 του Pearson x2 του Pearson
 Έλεγχος Ανεξαρτησίας x του Parso Έστω ότι λαμβάνουμε δείγμα μεγέθους. Η πιθανότητα π εμφάνισης ενός χαρακτηριστικού να βρεθεί στο κελί (i,j) κάτω από την υπόθεση Η 0 της ανεξαρτησίας δίνεται από την σχέση
Έλεγχος Ανεξαρτησίας x του Parso Έστω ότι λαμβάνουμε δείγμα μεγέθους. Η πιθανότητα π εμφάνισης ενός χαρακτηριστικού να βρεθεί στο κελί (i,j) κάτω από την υπόθεση Η 0 της ανεξαρτησίας δίνεται από την σχέση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης. Λύσεις Τρίτης Σειράς Ασκήσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Λύσεις Τρίτης Σειράς Ασκήσεων Ασκηση 1. Σε κάθε περίπτωση πρέπει να χρησιµοποιήσουµε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2016 ιδάσκων : Π. Τσακαλίδης Λύσεις Τρίτης Σειράς Ασκήσεων Ασκηση 1. Σε κάθε περίπτωση πρέπει να χρησιµοποιήσουµε
ΤΕΣΤ ΣΤΑΤΙΣΤΙΚΗΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΩΡΓΙΚΟΥ ΠΕΙΡΑΜΑΤΙΣΜΟΥ. Τεστ 1 ο Κατανοµή Συχνοτήτων (50 βαθµοί)
 ΤΕΣΤ ΣΤΑΤΙΣΤΙΚΗΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΩΡΓΙΚΟΥ ΠΕΙΡΑΜΑΤΙΣΜΟΥ Τεστ 1 ο Κατανοµή Συχνοτήτων (50 βαθµοί) Α. Ερωτήσεις πολλαπλών επιλογών.(11 βαθµοί) (1:3 βαθµοί, 2-9:8 βαθµοί) 1. ίνεται ο πίνακας: Χ
ΤΕΣΤ ΣΤΑΤΙΣΤΙΚΗΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΩΡΓΙΚΟΥ ΠΕΙΡΑΜΑΤΙΣΜΟΥ Τεστ 1 ο Κατανοµή Συχνοτήτων (50 βαθµοί) Α. Ερωτήσεις πολλαπλών επιλογών.(11 βαθµοί) (1:3 βαθµοί, 2-9:8 βαθµοί) 1. ίνεται ο πίνακας: Χ
Στατιστική Επιχειρήσεων Ι. Περιγραφική Στατιστική 1
 Στατιστική Επιχειρήσεων Ι Περιγραφική Στατιστική 1 2 Πληθυσμός ή στατιστικός πληθυσμός Ονομάζεται η κατανομή των τιμών μιας τ.μ., δηλαδή η κατανομή των τιμών που παίρνει ένα χαρακτηριστικό μιας ομάδας
Στατιστική Επιχειρήσεων Ι Περιγραφική Στατιστική 1 2 Πληθυσμός ή στατιστικός πληθυσμός Ονομάζεται η κατανομή των τιμών μιας τ.μ., δηλαδή η κατανομή των τιμών που παίρνει ένα χαρακτηριστικό μιας ομάδας
Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου
 Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Πράξεις Γεγονότων Σχεδιάγραµµα της Υλης Βασικές Εννοιες της Θεωρίας Πιθανοτήτων
Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Πράξεις Γεγονότων Σχεδιάγραµµα της Υλης Βασικές Εννοιες της Θεωρίας Πιθανοτήτων
Βασικά στοιχεία της θεωρίας πιθανοτήτων
 Η έννοια του Πειράµατος Τύχης. 9 3 6 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ή δειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοωήsτου δειγµατικού χώρου
Η έννοια του Πειράµατος Τύχης. 9 3 6 Το σύνολο των πιθανών εκβάσεων ενός πειράµατος τύχης καλείται δειγµατοχώρος ή δειγµατικόςχώρος (sample space)καισυµβολίζεταιµεωήµε S.Έναστοιχείοωήsτου δειγµατικού χώρου
Θέμα 1 ο (ΜΑΪΟΣ 2004, ΜΑΪΟΣ 2008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Απόδειξη
 ΕΚΔΟΣΕΙΣ ΚΕΛΑΦΑ 59 Θέμα 1 ο (ΜΑΪΟΣ 004, ΜΑΪΟΣ 008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Έχουμε f (x+h) - f (x) = c - c = 0 και για h 0 είναι f (x + h) - f (x) 0 m
ΕΚΔΟΣΕΙΣ ΚΕΛΑΦΑ 59 Θέμα 1 ο (ΜΑΪΟΣ 004, ΜΑΪΟΣ 008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Έχουμε f (x+h) - f (x) = c - c = 0 και για h 0 είναι f (x + h) - f (x) 0 m
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 00 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΘΕΜΑ Α Α. Έστω t,t,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν,
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 00 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΘΕΜΑ Α Α. Έστω t,t,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν,
Δειγματοληψία. Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος n ij των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ ij συμβολίζουμε την μέση τιμή:
 Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΜΑΘΗΜΑ ΙΑΡΚΕΙΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 3 ΩΡΕΣ ΘΕΜΑ Ο Α ) Να αποδείξετε ότι για δυο ασυµβίβαστα ενδεχόµενα Α, Β ενός δειγµατικού χώρου Ω ισχύει P( A B) = P( A) + P( B) ( µονάδες 8 ) Β ) Να δώσετε τον
ΜΑΘΗΜΑ ΙΑΡΚΕΙΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 3 ΩΡΕΣ ΘΕΜΑ Ο Α ) Να αποδείξετε ότι για δυο ασυµβίβαστα ενδεχόµενα Α, Β ενός δειγµατικού χώρου Ω ισχύει P( A B) = P( A) + P( B) ( µονάδες 8 ) Β ) Να δώσετε τον
Δειγματοληψία. Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος n ij των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ ij συμβολίζουμε την μέση τιμή:
 Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
Δειγματοληψία Πρέπει να γνωρίζουμε πως πήραμε το δείγμα Το πλήθος των παρατηρήσεων σε κάθε κελί είναι τ.μ. με μ συμβολίζουμε την μέση τιμή: Επομένως στην δειγματοληψία πινάκων συνάφειας αναφερόμαστε στον
Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ. (Power of a Test) ΚΕΦΑΛΑΙΟ 21
 ΚΕΦΑΛΑΙΟ 21 Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ (Power of a Test) Όπως είδαμε προηγουμένως, στον Στατιστικό Έλεγχο Υποθέσεων, ορίζουμε δύο είδη πιθανών λαθών (κινδύνων) που μπορεί να συμβούν όταν παίρνουμε αποφάσεις
ΚΕΦΑΛΑΙΟ 21 Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ (Power of a Test) Όπως είδαμε προηγουμένως, στον Στατιστικό Έλεγχο Υποθέσεων, ορίζουμε δύο είδη πιθανών λαθών (κινδύνων) που μπορεί να συμβούν όταν παίρνουμε αποφάσεις
15, 11, 10, 10, 14, 16, 19, 18, 13, 17
 ΜΕΡΟΣ 1 0 Α Σ Κ Η Σ Ε Ι Σ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Σ 1. Σε ένα Λύκειο θέλουµε να εξετάσουµε την επίδοση 10 µαθητών στο µάθηµα της Στατιστικής στο τέλος του β τετραµήνου. Πήραµε τις ακόλουθες βαθµολογίες: 15,
ΜΕΡΟΣ 1 0 Α Σ Κ Η Σ Ε Ι Σ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Σ 1. Σε ένα Λύκειο θέλουµε να εξετάσουµε την επίδοση 10 µαθητών στο µάθηµα της Στατιστικής στο τέλος του β τετραµήνου. Πήραµε τις ακόλουθες βαθµολογίες: 15,
ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ Χ 2 test ανεξαρτησίας: σχέση 2 ποιοτικών μεταβλητών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΣΤΙΚΗΣ Χ 2 test ανεξαρτησίας: σχέση 2 ποιοτικών μεταβλητών
F είναι ίσος µε ν. i ÏÅÖÅ ( ) h 3,f 3.
 Επαναληπτικά Θέµατα ΟΕΦΕ 0 Γ' ΤΑΞΗ ΓΕΝ. ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ A ΕΚΦΩΝΗΣΕΙΣ Α. Για δύο συµπληρωµατικά ενδεχόµενα Α και A ενός δειγµατικού χώρου Ω να P A = P A.
Επαναληπτικά Θέµατα ΟΕΦΕ 0 Γ' ΤΑΞΗ ΓΕΝ. ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ A ΕΚΦΩΝΗΣΕΙΣ Α. Για δύο συµπληρωµατικά ενδεχόµενα Α και A ενός δειγµατικού χώρου Ω να P A = P A.
Εισαγωγή στη Στατιστική
 Εισαγωγή στη Στατιστική Μετεκπαιδευτικό Σεμινάριο στην ΨΥΧΟΚΟΙΝΩΝΙΚΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΨΥΧΟΚΟΙΝΩΝΙΚΕΣ ΘΕΡΑΠΕΥΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων
Εισαγωγή στη Στατιστική Μετεκπαιδευτικό Σεμινάριο στην ΨΥΧΟΚΟΙΝΩΝΙΚΗ ΑΠΟΚΑΤΑΣΤΑΣΗ ΨΥΧΟΚΟΙΝΩΝΙΚΕΣ ΘΕΡΑΠΕΥΤΙΚΕΣ ΠΡΟΣΕΓΓΙΣΕΙΣ Δημήτρης Φουσκάκης, Επίκουρος Καθηγητής, Τομέας Μαθηματικών, Σχολή Εφαρμοσμένων
ΣΥΛΛΟΓΗ ΚΑΙ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ
 ΤΕΤΑΡΤΟ ΠΑΚΕΤΟ ΣΗΜΕΙΩΣΕΩΝ ΣΥΛΛΟΓΗ ΚΑΙ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ ΓΕΝΙΚΑ Η συλλογή των στατιστικών δεδοµένων αποτελεί σηµαντικό στάδιο κάθε Στατιστικής έρευνας. Απαιτεί ιδιαίτερη προσοχή, διότι,
ΤΕΤΑΡΤΟ ΠΑΚΕΤΟ ΣΗΜΕΙΩΣΕΩΝ ΣΥΛΛΟΓΗ ΚΑΙ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ ΓΕΝΙΚΑ Η συλλογή των στατιστικών δεδοµένων αποτελεί σηµαντικό στάδιο κάθε Στατιστικής έρευνας. Απαιτεί ιδιαίτερη προσοχή, διότι,
ΑΝΑΛΥΣΗ ΚΑΤΗΓΟΡΙΚΩΝ ΔΕΔΟΜΕΝΩΝ. Σ. ΖΗΜΕΡΑΣ Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικών- Χρηματοοικονομικών Μαθηματικών Σάμος
 ΑΝΑΛΥΣΗ ΚΑΤΗΓΟΡΙΚΩΝ ΔΕΔΟΜΕΝΩΝ Σ. ΖΗΜΕΡΑΣ Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικών- Χρηματοοικονομικών Μαθηματικών Σάμος Εισαγωγή Αριθμητικά δεδομένα αντιστοιχούν σε πραγματοποιήσεις τυχαίων
ΑΝΑΛΥΣΗ ΚΑΤΗΓΟΡΙΚΩΝ ΔΕΔΟΜΕΝΩΝ Σ. ΖΗΜΕΡΑΣ Τμήμα Μαθηματικών Κατεύθυνση Στατιστικής και Αναλογιστικών- Χρηματοοικονομικών Μαθηματικών Σάμος Εισαγωγή Αριθμητικά δεδομένα αντιστοιχούν σε πραγματοποιήσεις τυχαίων
Ελλιπή δεδομένα. Εδώ έχουμε 1275. Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 1275 ατόμων
 Ελλιπή δεδομένα Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 75 ατόμων Εδώ έχουμε δ 75,0 75 5 Ηλικία Συχνότητες f 5-4 70 5-34 50 35-44 30 45-54 465 55-64 335 Δεν δήλωσαν 5 Σύνολο 75 Μπορεί
Ελλιπή δεδομένα Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 75 ατόμων Εδώ έχουμε δ 75,0 75 5 Ηλικία Συχνότητες f 5-4 70 5-34 50 35-44 30 45-54 465 55-64 335 Δεν δήλωσαν 5 Σύνολο 75 Μπορεί
Στόχος µαθήµατος: ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ. Α1.2 Παράδειγµα 1 (συνέχεια) Α1. ΙΤΙΜΕΣ ΚΑΤΗΓΟΡΙΚΕΣ ΜΕΤΑΒΛΗΤΕΣ ΣΕ ΕΞΑΡΤΗΜΕΝΑ ΕΙΓΜΑΤΑ Παράδειγµα 1: αρτηριακή πίεση
 ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 20062007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 9 ΕΡΓΑΣΤΗΡΙΟ 2 ΑΝΑΛΥΣΗ ΜΕΤΑΒΛΗΤΩΝ ΓΙΑ 2 ΕΞΑΡΤΗΜΕΝΑ ΕΙΓΜΑΤΑ & ΓΙΑ ΠΙΝΑΚΕΣ
ΠΜΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΥΓΕΙΑ, ΙΑΧΕΙΡΙΣΗ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΙΜΗΣΗ ΑΚ. ΕΤΟΣ 20062007, 3ο εξάµηνο ΒΙΟΣΤΑΤΙΣΤΙΚΗ ΙΙ ΜΑΘΗΜΑ 9 ΕΡΓΑΣΤΗΡΙΟ 2 ΑΝΑΛΥΣΗ ΜΕΤΑΒΛΗΤΩΝ ΓΙΑ 2 ΕΞΑΡΤΗΜΕΝΑ ΕΙΓΜΑΤΑ & ΓΙΑ ΠΙΝΑΚΕΣ
2 η ΕΚΑ Α ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ και. Έστω Α, Β ενδεχόµενα ενός δειγµατικού χώρου Ω µε Ρ(Α) = 8
 1 ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ η ΕΚΑ Α. Έστω Α, Β ενδεχόµενα ενός δειγµατικού χώρου Ω µε Ρ(Α) = 8 5 και Ρ(Β) = Ρ(Α ). Αν τα Α, Β είναι ασυµβίβαστα, να εξετάσετε αν είναι ασυµβίβαστα και τα Α, Β 5 i είξτε ότι Ρ(Α Β)=
1 ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ η ΕΚΑ Α. Έστω Α, Β ενδεχόµενα ενός δειγµατικού χώρου Ω µε Ρ(Α) = 8 5 και Ρ(Β) = Ρ(Α ). Αν τα Α, Β είναι ασυµβίβαστα, να εξετάσετε αν είναι ασυµβίβαστα και τα Α, Β 5 i είξτε ότι Ρ(Α Β)=
Μάθηµα 1 ο. Πιθανότητα-Έννοιες και Ορισµοί. Στο µάθηµα αυτό θα αναφερθούµε σε βασικές έννοιες και συµβολισµούς της θεωρίας πιθανοτήτων.
 Μάθηµα 1 ο Πιθανότητα-Έννοιες και Ορισµοί Στο µάθηµα αυτό θα αναφερθούµε σε βασικές έννοιες και συµβολισµούς της θεωρίας πιθανοτήτων. http://compus.uom.gr/inf267/index.php 1 Εισαγωγικά Βασικές Έννοιες
Μάθηµα 1 ο Πιθανότητα-Έννοιες και Ορισµοί Στο µάθηµα αυτό θα αναφερθούµε σε βασικές έννοιες και συµβολισµούς της θεωρίας πιθανοτήτων. http://compus.uom.gr/inf267/index.php 1 Εισαγωγικά Βασικές Έννοιες
2) Περιγραφή ιακριτών Ποσοτικών εδοµένων
 ) Περιγραφή ιακριτών Ποσοτικών εδοµένων Για να περιγράψουµε διακριτά ποσοτικά δεδοµένα µε λίγες τιµές ( σε περίπτωση πολλών τιµών τα θεωρούµε ως συνεχή) κάνουµε: Πίνακας συχνοτήτων Ραβδόγραµµα, Κυκλικό
) Περιγραφή ιακριτών Ποσοτικών εδοµένων Για να περιγράψουµε διακριτά ποσοτικά δεδοµένα µε λίγες τιµές ( σε περίπτωση πολλών τιµών τα θεωρούµε ως συνεχή) κάνουµε: Πίνακας συχνοτήτων Ραβδόγραµµα, Κυκλικό
Ορισµός. Παρατηρήσεις. Σχόλιο
 Ορισµός Έστω Α, Β δύο µη κενά σύνολα A Συνάρτηση από το σύνολο A στο σύνολο Β λέγεται µια διαδικασία, µε την οποία, κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του Β Τις συναρτήσεις
Ορισµός Έστω Α, Β δύο µη κενά σύνολα A Συνάρτηση από το σύνολο A στο σύνολο Β λέγεται µια διαδικασία, µε την οποία, κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο του Β Τις συναρτήσεις
P (A) = 1/2, P (B) = 1/2, P (C) = 1/9
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-1: Πιθανότητες - Χειµερινό Εξάµηνο 011 ιδάσκων : Π. Τσακαλίδης Λύσεις εύτερης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : /11/011 Ηµεροµηνία Παράδοσης : 1/11/011
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-1: Πιθανότητες - Χειµερινό Εξάµηνο 011 ιδάσκων : Π. Τσακαλίδης Λύσεις εύτερης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : /11/011 Ηµεροµηνία Παράδοσης : 1/11/011
Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 19/5/2017
 Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 2 Εισαγωγή Η ανάλυση παλινδρόμησης περιλαμβάνει το σύνολο των μεθόδων της στατιστικής που αναφέρονται σε ποσοτικές σχέσεις μεταξύ μεταβλητών Πρότυπα παλινδρόμησης
Απλή Γραμμική Παλινδρόμηση και Συσχέτιση 2 Εισαγωγή Η ανάλυση παλινδρόμησης περιλαμβάνει το σύνολο των μεθόδων της στατιστικής που αναφέρονται σε ποσοτικές σχέσεις μεταξύ μεταβλητών Πρότυπα παλινδρόμησης
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α.1. Να αποδείξετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α.1. Να αποδείξετε
Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ΤΟΠΙΚΟ ΕΛΑΧΙΣΤΟ
 1 Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ά ( ύ ) έ
1 Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ά ( ύ ) έ
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο, να αποδείξετε ότι (f() + g ()) f () + g (),. Μονάδες 7 Α. Σε ένα πείραµα µε ισοπίθανα
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο, να αποδείξετε ότι (f() + g ()) f () + g (),. Μονάδες 7 Α. Σε ένα πείραµα µε ισοπίθανα
3. Η µερική παράγωγος
 1 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 1 Μερική παραγώγιση παράγωγος µιας συνάρτησης µερική παράγωγος ( ( µιας µεταβλητής ορίζεται ως d d ( ( (1 Για συναρτήσεις δύο
1 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 1 Μερική παραγώγιση παράγωγος µιας συνάρτησης µερική παράγωγος ( ( µιας µεταβλητής ορίζεται ως d d ( ( (1 Για συναρτήσεις δύο
Μάθηµα 3 ο b. Από Κοινού Κατανοµή Τυχαίων Μεταβλητών
 Μάθηµα 3 ο b Από Κοινού Κατανοµή Τυχαίων Μεταβλητών Έχουµε δύο, ή περισσότερες, τυχαίες µεταβλητές έστω Χ και Υ. Η σκπ των ζευγών ( x, y ) λέγεται από κοινού κατανοµή του ζεύγους ή του διανύσµατος ( X,Y
Μάθηµα 3 ο b Από Κοινού Κατανοµή Τυχαίων Μεταβλητών Έχουµε δύο, ή περισσότερες, τυχαίες µεταβλητές έστω Χ και Υ. Η σκπ των ζευγών ( x, y ) λέγεται από κοινού κατανοµή του ζεύγους ή του διανύσµατος ( X,Y
Μελέτες ασθενών οµάδας ελέγχου
 Μελέτες ασθενών οµάδας ελέγχου Μελέτες ασθενών οµάδας ελέγχου ως µέθοδος αναπτύχθηκε στις αρχές του 50 διερεύνηση παραγόντων κινδύνου σε ασθένειες µε µακρά λανθάνουσα περίοδο, όπου οι µελέτες κοόρτης δεν
Μελέτες ασθενών οµάδας ελέγχου Μελέτες ασθενών οµάδας ελέγχου ως µέθοδος αναπτύχθηκε στις αρχές του 50 διερεύνηση παραγόντων κινδύνου σε ασθένειες µε µακρά λανθάνουσα περίοδο, όπου οι µελέτες κοόρτης δεν
Στατιστική ανάλυση αποτελεσμάτων
 HELLENIC OPEN UNIVERSITY School of Social Sciences ΜΒΑ Programme Στατιστική ανάλυση αποτελεσμάτων Βασίλης Αγγελής Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Πανεπιστήμιο Αιγαίου Κατερίνα Δημάκη Αν. Καθηγήτρια
HELLENIC OPEN UNIVERSITY School of Social Sciences ΜΒΑ Programme Στατιστική ανάλυση αποτελεσμάτων Βασίλης Αγγελής Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Πανεπιστήμιο Αιγαίου Κατερίνα Δημάκη Αν. Καθηγήτρια
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutra@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 20 ΜΑΪΟΥ 2013 ΑΠΑΝΤΗΣΕΙΣ. x x x 4
 ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 0 ΑΠΑΝΤΗΣΕΙΣ Α. Θεωρία, σχολικό βιβλίο σελ. 8 Α. Θεωρία, σχολικό βιβλίο σελ. 4 Α. Θεωρία, σχολικό βιβλίο σελ. 87 Α4.
ΘΕΜΑ Α ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 0 ΑΠΑΝΤΗΣΕΙΣ Α. Θεωρία, σχολικό βιβλίο σελ. 8 Α. Θεωρία, σχολικό βιβλίο σελ. 4 Α. Θεωρία, σχολικό βιβλίο σελ. 87 Α4.
Διμεταβλητές κατανομές πιθανοτήτων
 Διμεταβλητές κατανομές πιθανοτήτων Για να περιγράψουμε την σχέση ανάμεσα σε δύο τυχαίες μεταβλητές χρειαζόμαστε την κοινή κατανομή πιθανοτήτων τους. Η κοινή συνάρτηση πιθανότητ ικανοποιε ί τις συνθ ήκες
Διμεταβλητές κατανομές πιθανοτήτων Για να περιγράψουμε την σχέση ανάμεσα σε δύο τυχαίες μεταβλητές χρειαζόμαστε την κοινή κατανομή πιθανοτήτων τους. Η κοινή συνάρτηση πιθανότητ ικανοποιε ί τις συνθ ήκες
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος
 iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
A. Να δείξετε ότι για δύο συμπληρωματικά ενδεχόμενα Α και Α ενός δειγματικού χώρου, ισχύει
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 7 ΙΟΥΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 7 ΙΟΥΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση f () είναι παραγωγίσιμη στο R με f () Α Αν είναι οι τιμές μιας μεταβλητής Χ ενός δείγματος παρατηρήσεων μεγέθους ν ( ) να ορίσετε την
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση f () είναι παραγωγίσιμη στο R με f () Α Αν είναι οι τιμές μιας μεταβλητής Χ ενός δείγματος παρατηρήσεων μεγέθους ν ( ) να ορίσετε την
Βασικές έννοιες περιγραφικής επιδημιολογίας. Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας
 Βασικές έννοιες περιγραφικής επιδημιολογίας Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας Επιδημιολογία } Μελετά τη συχνότητα και των νόσων στους ανθρώπινους πληθυσμούς } Βασίζεται σε 2 υποθέσεις } Τα νοσήματα
Βασικές έννοιες περιγραφικής επιδημιολογίας Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας Επιδημιολογία } Μελετά τη συχνότητα και των νόσων στους ανθρώπινους πληθυσμούς } Βασίζεται σε 2 υποθέσεις } Τα νοσήματα
Τμήμα Λογιστικής και Χρηματοοικονομικής. Θεωρία Πιθανοτήτων. Δρ. Αγγελίδης Π. Βασίλειος
 Τμήμα Λογιστικής και Χρηματοοικονομικής 1 Θεωρία Πιθανοτήτων Δρ. Αγγελίδης Π. Βασίλειος 2 Περιεχόμενα Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους 3 Πείραμα
Τμήμα Λογιστικής και Χρηματοοικονομικής 1 Θεωρία Πιθανοτήτων Δρ. Αγγελίδης Π. Βασίλειος 2 Περιεχόμενα Έννοια πιθανότητας Ορισμοί πιθανότητας Τρόπος υπολογισμού Πράξεις πιθανοτήτων Χρησιμότητα τους 3 Πείραμα
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2012
 Ε_3.Μλ3Γ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή 1 Απριλίου 01 ΕΚΦΩΝΗΣΕΙΣ Α1. Για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου
Ε_3.Μλ3Γ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή 1 Απριλίου 01 ΕΚΦΩΝΗΣΕΙΣ Α1. Για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου
ΘΕΜΑ Α Α1. Έστω t 1,t 2,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν, που έχουν
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ 1ο Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ 1ο Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός
x 2 = x 2 1 + x 2 2. x 2 = u 2 + x 2 3 Χρησιµοποιώντας το συµβολισµό του ανάστροφου, αυτό γράφεται x 2 = x T x. = x T x.
 Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
2.5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test)
 .5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test) Ο διωνυμικός έλεγχος μπορεί να χρησιμοποιηθεί για τον έλεγχο υποθέσεων αναφερομένων στα ποσοστιαία σημεία μίας τυχαίας μεταβλητής. Στην
.5 ΕΛΕΓΧΟΣ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΚΑΤΑΝΟΜΗΣ (The Quantile Test) Ο διωνυμικός έλεγχος μπορεί να χρησιμοποιηθεί για τον έλεγχο υποθέσεων αναφερομένων στα ποσοστιαία σημεία μίας τυχαίας μεταβλητής. Στην
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2005
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Να αποδειχθεί ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει: P(A B) = P(A) + P(B) P(A B) Τα απλά ενδεχόµενα
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 005 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Να αποδειχθεί ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει: P(A B) = P(A) + P(B) P(A B) Τα απλά ενδεχόµενα
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014
 Ε_ΜλΓ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή Απριλίου 04 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Α Για δύο ενδεχόµενα Α και Β ενός
Ε_ΜλΓ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή Απριλίου 04 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Α Για δύο ενδεχόµενα Α και Β ενός
Μαθηµατικά & Στοιχεία Στατιστικής Γενικής Παιδείας Γ Λυκείου 2001
 Μαθηµατικά & Στοιχεία Στατιστικής Γενικής Παιδείας Γ Λυκείου 2001 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) = Ρ (Α) Ρ (Α Β). Μονάδες
Μαθηµατικά & Στοιχεία Στατιστικής Γενικής Παιδείας Γ Λυκείου 2001 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) = Ρ (Α) Ρ (Α Β). Μονάδες
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α.1. Να αποδείξετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 14 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α.1. Να αποδείξετε
Μέθοδος μέγιστης πιθανοφάνειας
 Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
Μέθοδος μέγιστης πιθανοφάνειας Αν x =,,, παρατηρήσεις των Χ =,,,, τότε έχουμε διαθέσιμο ένα δείγμα Χ={Χ, =,,,} της κατανομής F μεγέθους με από κοινού σ.κ. της Χ f x f x Ορισμός : Θεωρούμε ένα τυχαίο δείγμα
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟΥ ΕΠΑ.Λ. Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟΥ ΕΠΑ.Λ. 2013-2014 ΣΤΑΤΙΣΤΙΚΗ 1. Τι ονομάζουμε: i. πληθυσμό και μέγεθος πληθυσμού; (σελ. 59) ii. μεταβλητή; (σελ.59-60) 2. Ποιες μεταβλητές ονομάζονται ποσοτικές; (σελ.60)
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΟΥ ΕΠΑ.Λ. 2013-2014 ΣΤΑΤΙΣΤΙΚΗ 1. Τι ονομάζουμε: i. πληθυσμό και μέγεθος πληθυσμού; (σελ. 59) ii. μεταβλητή; (σελ.59-60) 2. Ποιες μεταβλητές ονομάζονται ποσοτικές; (σελ.60)
Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Εφαρμοσμένη Στατιστική Μάθημα 4 ο :Τυχαίες μεταβλητές Διδάσκουσα: Κοντογιάννη Αριστούλα
 Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Εφαρμοσμένη Στατιστική Μάθημα 4 ο :Τυχαίες μεταβλητές Διδάσκουσα: Κοντογιάννη Αριστούλα Ορισμός τυχαίας μεταβλητής Τυχαία μεταβλητή λέγεται η συνάρτηση
Τμήμα Τεχνολόγων Γεωπόνων-Κατεύθυνση Αγροτικής Οικονομίας Εφαρμοσμένη Στατιστική Μάθημα 4 ο :Τυχαίες μεταβλητές Διδάσκουσα: Κοντογιάννη Αριστούλα Ορισμός τυχαίας μεταβλητής Τυχαία μεταβλητή λέγεται η συνάρτηση
Μαθηµατικά & Στοιχεία Στατιστικης Γενικής Παιδείας Γ Λυκείου 2001 ÈÅÌÅËÉÏ
 Μαθηµατικά & Στοιχεία Στατιστικης Γενικής Παιδείας Γ Λυκείου 2001 Ζήτηµα 1ο Α.1. Α.2. Β.1. Β.2. Β.3. Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) = Ρ (Α)
Μαθηµατικά & Στοιχεία Στατιστικης Γενικής Παιδείας Γ Λυκείου 2001 Ζήτηµα 1ο Α.1. Α.2. Β.1. Β.2. Β.3. Α.1. Να αποδείξετε ότι για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω ισχύει ότι: Ρ (Α Β) = Ρ (Α)
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
Δισδιάστατη ανάλυση. Για παράδειγμα, έστω ότι 11 άτομα δήλωσαν ότι είναι άγαμοι (Α), 26 έγγαμοι (Ε), 12 χήροι (Χ) και 9 διαζευγμένοι (Δ).
 Δισδιάστατη ανάλυση Πίνακες διπλής εισόδου Σε πολλές περιπτώσεις μελετάμε περισσότερες από μία μεταβλητές ταυτόχρονα. Π.χ. μία έρευνα που έγινε σε ένα δείγμα 58 ατόμων περιείχε τις ερωτήσεις «ποια είναι
Δισδιάστατη ανάλυση Πίνακες διπλής εισόδου Σε πολλές περιπτώσεις μελετάμε περισσότερες από μία μεταβλητές ταυτόχρονα. Π.χ. μία έρευνα που έγινε σε ένα δείγμα 58 ατόμων περιείχε τις ερωτήσεις «ποια είναι
ΣΤΑΤΙΣΤΙΚΟΙ ΠΙΝΑΚΕΣ. ΓΕΝΙΚΟΙ (περιέχουν όλες τις πληροφορίες που προκύπτουν από μια στατιστική έρευνα) ΕΙΔΙΚΟΙ ( είναι συνοπτικοί και σαφείς )
 Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
