ΑΣΚΗΣΗ 6. Ηλικία και απόσταση Αστρικών Σµηνών
|
|
|
- Λητώ Βυζάντιος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΑΣΚΗΣΗ 6 Ηλικία και απόσταση Αστρικών Σµηνών Περιεχόµενα Διάγραµµα µεγέθους-χρώµατος o Κύρια Ακολουθία o Κύρια Ακολουθία Μηδενικής Ηλικίας o Ισόχρονες Μεσοαστρική Απόσβεση Εκτίµηση ηλικίας και απόστασης αστρικών σµηνών Στόχος της άσκησης Ενα από τα βασικά ερευνητικά αντικείµενα της Αστροφυσικής είναι η µελέτη της ηλικίας των αστρικών πληθυσµών που συνιστούν αστρικά σµήνη ή και ολόκληρους γαλαξίες. Ο πιό άµεσος τρόπος για την εκτίµηση της ηλικίας ενός αστρικού πληθυσµού είναι η µελέτη της κατανοµής του χρώµατος και της λαµπρότητας των αστεριών σε σχέση µε τις θεωρητικές κατανοµές πληθυσµών γνωστής ηλικίας. Σε αυτή την άσκηση θα χρησιµοποιήσουµε δεδοµένα από φωτοµετρικές παρατηρήσεις διαφορετικών αστρικών σµηνών µε σκοπό την εκτίµηση της ηλικίας τους και της απόστασής τους µε τη µέθοδο των Κυρίων Ακολουθιών. Δεδοµένα Φωτοµετρικά δεδοµένα σφαιρωτών και ανοικτών σµηνών στα φίλτρα B, V, Ι Ισόχρονες για διαφορετικές µεταλλικότητες και ηλικίες Δεδοµένα για τη µεσοαστρική απόσβεση στην κατεύθυνση του κάθε σµήνους
2 Διάγραµµα Μεγέθους-Χρώµατος, Ισόχρονες Το υπάρχον θεωρητικό πλαίσιο για την δοµή και εξέλιξη των άστρων περιγράφει µε επιτυχία τις παρατηρούµενες παραµέτρους των αστεριών, όπως η θερµοκρασία, η ακτίνα και η µάζα τους συναρτήσει της ηλικίας τους (αυτό είναι άλλωστε και βασικό προαπαιτούµενο για την επιτυχία µιας θεωρίας). Αυτό µας δίνει τη δυνατότητα να χρησιµοποιήσουµε τις θεωρητικές προβλέψεις προκειµένου να εκτιµήσουµε την ηλικία των αστρικών πληθυσµών. Όπως είναι γνωστό η λαµπρότητα και η θερµοκρασία των αστεριών σε διαφορετικά εξελικτικά στάδια ακολουθούν συγεκριµένες κατανοµές στο διάγραµµα Hertzsprung-Russell (Σχ. 1). Το ίδιο αποτέλεσµα παίρνουµε και εάν µελετήσουµε την κατανοµή των αστέρων σε ένα διάγραµµα µεγέθους-χρώµατος, καθώς το απόλυτο µέγεθος ενός αστέρα είναι άµεσα συνδεδεµένο µε τη λαµπρότητα του ενώ το χρώµα του είναι άµεσα εξαρτώµενο από τη θερµοκρασία του. Στο σχήµα 2 βλέπουµε τα διαγράµµατα µεγέθους-χρώµατος ανοικτών και σφαιρωτών σµηνών διαφορετικών ηλικιών. Τα διαγράµµατα αυτά έχουν κάποια κοινά χαρακτηριστικά (π.χ. την Κύρια Ακολουθία, τον κλάδο των γιγάντων), καθώς και χαρακτηριστικές διαφορές µε σηµαντικότερη τη διαφορετική έκταση της Κυρίας Ακολουθίας. Αυτή ακριβώς η διαφοροποίηση είναι που µας επιτρέπει την εκτίµηση της ηλικίας και της απόστασής τους. Σχήµα 1: Το διάγραµµα Hertzsprung-Russell του σφαιρωτού σµήνους Μ55. Στο διάγραµµα σηµειώνεται η θέση των διαφορετικών αστρικών εξελικτικών σταδίων ( Στο σχήµα 3 βλέπουµε την αναµενόµενη κατανοµή µεγέθους-χρώµατος για αστρικούς πληθυσµούς διαφορετικών ηλικιών. Κάθε µία από αυτές τις καµπύλες µας δίνει τη θέση σε αυτό το διάγραµµα αστέρων διαφορετικής αρχικής µάζας αλλά ίδιας ηλικίας. Γι αυτό το λόγο αυτές οι καµπύλες ονοµάζονται ισόχρονες. Η καµπύλη που βρίσκεται πιό αριστερά είναι η περιοχή του διαγράµµατος χρώµατος-µεγέθους που βρίσκονται αστέρια που µόλις έχουν εισέλθει στην Κύρια Ακολουθία. Γι αυτό το λόγο ονοµάζεται Κύρια Ακολουθία Μηδενικής Ηλικίας (Zero Age Main Sequence; ZAMS).
3 Σχήµα 2: Σύγκριση των διαγραµµάτων χρώµατος-µεγέθους (αριστερά) και των διαγραµµάτων HR (δεξιά) για διαφορετικά ανοικτά και σφαιρωτά σµήνη (Sandage 1958, Ricerche Astronomiche, 5, 41). Η ακριβής θέση της Κυριας Ακολουθίας Μηδενικής Ηλικίας εξαρτάται πρωτίστως από την ηλικία των αστρικών πληθυσµών, αλλά καί από τη µεταλλικότητα των αστέρων και το ακριβές µοντέλο αστρικής εξέλιξης που θεωρούµε. Εποµένως η σύγκριση των παρατηρησιακών διαγραµµάτων µε τις θεωρητικές κατανοµές για πληθυσµούς διαφορετικής ηλικίας µας δίνει τη δυνατότητα να εκτιµήσουµε την ηλικία τους. Σχήµα 3α (αριστερά): Σύγκριση των ισόχρονων για αστρικούς πληθυσµούς διαφορετικής ηλικίας (και ηλιακής µεταλλικότητας). Η Κύρια Ακολουθία Μηδενικής Ηλικίας αντιστοιχεί στην αριστερή κόκκινη καµπύλη. Οι ισόχρονες προέρχονται από την οµάδα της Geneva (Lejeune & Schaerer, 2001, Astronomy & Astrophysics, 366, 538). Σχήµα 3β (δεξιά): Σύγκριση των Κύριων Ακολουθιών Μηδενικής Ηλικίας για πληθυσµούς διαφορετικής µεταλλικότητας. Το διάνυσµα δείχνει τη µετατόπιση των ισόχρονων εαν υποστούν µεσοαστρική απόσβεση ίση µε Α V =1.0 mag.
4 Δεδοµένα Σε αυτή την άσκηση θα χρησιµοποιήσουµε φωτοµετρικά δεδοµένα από παρατηρήσεις των σφαιρωτών σµηνών 47 Tucanae (47 Tuc), Μ3, και του διπλού ανοικτού σµήνους h+χ Per που έχουν γίνει στα φίλτρα B, V και I. Επιπλέον χρησιµοποιούµε ισόχρονες από την οµάδα της Geneva (Σχ. 3). Ο πίνακας 1 περιγράφει τις παραµέτρους των σµηνών που θα µελετήσουµε και τα δεδοµένα που θα χρησιµοποιήσουµε. m-m (mag) Z Πίνακας 1 A v (mag) Δεδοµένα 47 Tuc NGC104.photometry_BV.dat 1 M NGC5272.photometry_BV.dat 2 h+χ Per hx_per.photometry_vi.dat 3 Μεσοαστρική Απόσβεση Το πρώτο βήµα είναι να εφαρµόσουµε διορθώσεις για τη µεσοαστρική απόσβεση στη κατεύθυνση του κάθε σµήνους. Η µεσοαστρική απόσβεση εξαρτάται σηµαντικά από το µήκος κύµατος, και εκφράζεται συνήθως ως την απόσβεση στο µήκος κύµατος που µας ενδιαφέρει σε σχέση µε την απόσβεση στο V φίλτρο (Σχ. 4). Η καµπύλη αυτή δίνει τους ακόλουθους συντελεστές απόσβεσης στα διαφορετικά φίλτρα της οπτικής περιοχής του φάσµατος: Πίνακας 2 Συντελεστές Μεσοαστρικής Απόσβεσης (Cardelli et al, 1989, Astrophysical Journal, 345, 245) Φίλτρο 1/λ (µm -1 ) Α(λ)/Α(V) U B V R Σ Σχήµα 4: Η καµπύλη µεσοαστρικής απόσβεσης (Cardelli et al, 1989). 1 Bergbusch and Stetson, 2009, Astronomical Journal, 138, 1455 ( ccda.hia- iha.nrc- cnrc.gc.ca/community/stetson/standards/) 2 ccda.hia- iha.nrc- cnrc.gc.ca/community/stetson/standards/ 3 Currie et al., 2010, Astrophysical Journal Supplement Series, 186, 191, ( bin/vizier?- source=j/apjs/186/191)
5 Εποµένως µε βάση τις παραπάνω σχέσεις µπορούµε να υπολογίσουµε την απόσβεση σε κάποιο φίλτρο δεδοµένης της απόσβεσης στο V φίλτρο. Ο πίνακας 1 δίνει τη µεσοαστρική απόσβεση στο V φίλτρο στην κατεύθυνση των 3 σµηνών που µελετούµε. Άσκηση: Με βάση τα δεδοµένα των Πινάκων 1 και 2, να υπολογίσετε τη µεσοαστρική απόσβεση για κάθε σµήνος στα φίλτρα Β, V, Ι. Να υπολογίσετε τα φαινόµενα µεγέθη για κάθε άστρο διορθωµένα για µεσοαστρική απόσβεση, καθώς και το χρώµα (Β- V). Υπολογισµός της απόστασης των σµηνών Πριν προχωρήσουµε στην εκτίµηση της ηλικίας των αστρικών σµηνών πρέπει να υπολογίσουµε την απόστασή τους. Αυτό µπορεί να γίνει µέσω της σύγκρισης της ZAMS µε το παρατηρούµενο διάγραµµα µεγέθους-χρώµατος. Η ZAMS µας δίνει το απόλυτο µεγέθος των αστέρων συναρτήσει του χρώµατός τους, ενώ τα παρατηρησιακά δεδοµένα µας δίνουν το φαινόµενο µέγεθος συναρτήσει του χρώµατός τους. Εποµένως η κατακόρυφη απόσταση των δύο κυρίων ακολουθιών θα ισούται µε µε τη διαφορά m-m, δηλαδή το µέτρο απόστασης του αστρικού πληθυσµού. Άσκηση: Να σχεδιάσετε τα διαγράµµατα µεγέθους-χρώµατος για τα τρία σµήνη και να αναγνωρίσετε τα αστέρια που ανήκουν σε διαφορετικές τάξεις λαµπρότητας. Στα ίδια διαγράµµατα να τοποθετήσετε την κατάλληλη ZAMS. Στη συνεχεια µε την παραπάνω µέθοδο να υπολογίσετε το µέτρο απόστασης για κάθε σµήνος. (Σηµείωση: να χρησιµοποιήσετε τη ZAMS µε τη σωστή µεταλλικότητα για κάθε σµήνος). Εκτίµηση της Ηλικίας Αστρικών Σµηνών Δεδοµένης της απόστασης του αστρικού πληθυσµού είµαστε έτοιµοι να κατασκευάσουµε το διάγραµµα λαµπρότητας (απόλυτου µεγέθους) χρώµατος. Όπως βλέπουµε από τις ισόχρονες στο Σχήµα 2, Κύριες Ακολουθίες πληθυσµών µικρότερης ηλικίας εκτείνονται σε άστρα µεγαλύτερης λαµπρότητας. Αυτό ακριβώς το χαρακτηριστικό µας βοηθάει ώστε να µετρήσουµε την ηλικία ενός σµήνους. Άσκηση: Να σχεδιάσετε τα διαγράµµατα απόλυτου µεγέθους χρώµατος για τα τρία σµήνη, µε βάση τις αποστάσεις που υπολογίσατε στο προηγούµενο µέρος. Να σχεδιάσετε ισόχρονες διαφορετικής ηλικίας για το κάθε σµήνος λαµβάνοντας υπ οψιν τη διαφορετική µεταλλικότητα των τριών σµηνών (Πίνακας 3). Με βάση τις ισόχρονες και τα διαγράµµατα χρώµατος-µεγέθους να εκτιµήσετε τις ηλικίες των τριών σµηνών. Ποιοί πιστεύετε ότι είναι οι βασικοί παράγοντες σφάλµατος;
ΑΣΚΗΣΗ 10. Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών
 ΑΣΚΗΣΗ 10 Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών Περιεχόµενα Κηφείδες Ερυθρά µετατόπιση Φάσµατα γαλαξιών Σκοπός της άσκησης Η µέτρηση της ερυθρής µετατόπισης των γαλαξιών είναι η βασική µέθοδος
ΑΣΚΗΣΗ 10 Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών Περιεχόµενα Κηφείδες Ερυθρά µετατόπιση Φάσµατα γαλαξιών Σκοπός της άσκησης Η µέτρηση της ερυθρής µετατόπισης των γαλαξιών είναι η βασική µέθοδος
ΑΣΚΗΣΗ 5. Χρώµα στην Αστρονοµία
 ΑΣΚΗΣΗ 5 Χρώµα στην Αστρονοµία Περιεχόµενα Χρώµα στην Αστρονοµία o Χρώµα άστρων o Χρώµα και θερµοκρασία Ο νόµος του Planck o Ακτινοβολία Μέλανος Σώµατος O νόµος της µετατόπισης του Wien Στόχος της άσκησης
ΑΣΚΗΣΗ 5 Χρώµα στην Αστρονοµία Περιεχόµενα Χρώµα στην Αστρονοµία o Χρώµα άστρων o Χρώµα και θερµοκρασία Ο νόµος του Planck o Ακτινοβολία Μέλανος Σώµατος O νόµος της µετατόπισης του Wien Στόχος της άσκησης
Αστρικά Συστήματα και Γαλαξίες
 Αστρικά Συστήματα και Γαλαξίες Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρικά Σμήνη Οι ομάδες των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρικά σμήνη Είναι
Αστρικά Συστήματα και Γαλαξίες Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρικά Σμήνη Οι ομάδες των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρικά σμήνη Είναι
ΑΣΚΗΣΗ 3. Φωτοµετρία εικόνων CCD µε το IRAF
 ΑΣΚΗΣΗ 3 Φωτοµετρία εικόνων CCD µε το IRAF Περιεχόµενα Απόλυτο και φαινόµενο µέγεθος Η κλίµακα του Pogson Το χρώµα των άστρων Ατµοσφαιρική απόσβεση Αέρια µάζα (airmass) και συντελεστές ατµοσφαιρικής απόσβεσης
ΑΣΚΗΣΗ 3 Φωτοµετρία εικόνων CCD µε το IRAF Περιεχόµενα Απόλυτο και φαινόµενο µέγεθος Η κλίµακα του Pogson Το χρώµα των άστρων Ατµοσφαιρική απόσβεση Αέρια µάζα (airmass) και συντελεστές ατµοσφαιρικής απόσβεσης
Αστρικά Σµήνη: Απόσταση του Σµήνους των Υάδων
 Αστρικά Σµήνη: Απόσταση του Σµήνους των Υάδων!1 Επειδή τα Αστρικά Σµήνη: (α) βρίσκονται στην ίδια απόσταση (άρα δm=δm) και διεύθυνση και εποµένως πάσχουν από την ίδια Γαλαξιακή και ατµοσφαιρική απορρόφηση,
Αστρικά Σµήνη: Απόσταση του Σµήνους των Υάδων!1 Επειδή τα Αστρικά Σµήνη: (α) βρίσκονται στην ίδια απόσταση (άρα δm=δm) και διεύθυνση και εποµένως πάσχουν από την ίδια Γαλαξιακή και ατµοσφαιρική απορρόφηση,
ΑΣΚΗΣΗ 4. Το διάγραµµα Hertszprung-Russell
 ΑΣΚΗΣΗ 4 Το διάγραµµα Hertzsprung-Russell Περιεχόµενα Το διάγραµµα Hertszprung-Russell o Ορισµός o Ερµηνεία o Κατασκευή Στόχος της άσκησης Ο στόχος αυτής της άσκησης είναι η εξοικείωση µε τις βασικές αρχές
ΑΣΚΗΣΗ 4 Το διάγραµµα Hertzsprung-Russell Περιεχόµενα Το διάγραµµα Hertszprung-Russell o Ορισµός o Ερµηνεία o Κατασκευή Στόχος της άσκησης Ο στόχος αυτής της άσκησης είναι η εξοικείωση µε τις βασικές αρχές
d = 10(m-M+5)/5 pc. (m-m distance modulus)
 Παρατηρησιακά χαρακτηριστικά αστέρων Α. Πόσο μακρυά βρίσκονται τα αστέρια; Μέση απόσταση Γης-'Ηλιου=1AU=149597870,7 km Απόσταση αστέρα: 206264 d= AU ή p'' d= 1 pc, p' ' όπου p είναι η παράλλαξη του αστέρα
Παρατηρησιακά χαρακτηριστικά αστέρων Α. Πόσο μακρυά βρίσκονται τα αστέρια; Μέση απόσταση Γης-'Ηλιου=1AU=149597870,7 km Απόσταση αστέρα: 206264 d= AU ή p'' d= 1 pc, p' ' όπου p είναι η παράλλαξη του αστέρα
Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών
 Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών Το φως που έρχεται από τα άστρα είναι σύνθετο και καλύπτει ολόκληρο το εύρος της ηλεκτρομαγνητικής ακτινοβολίας.
Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών Το φως που έρχεται από τα άστρα είναι σύνθετο και καλύπτει ολόκληρο το εύρος της ηλεκτρομαγνητικής ακτινοβολίας.
18 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2013. 4 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Ανάλυση Δεδομένων
 18 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2013 4 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Ανάλυση Δεδομένων Παρακαλούμε, διαβάστε προσεκτικά τα παρακάτω: 1. Μπορείτε να χρησιμοποιήσετε τον χάρακα και το κομπιουτεράκι
18 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2013 4 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Ανάλυση Δεδομένων Παρακαλούμε, διαβάστε προσεκτικά τα παρακάτω: 1. Μπορείτε να χρησιμοποιήσετε τον χάρακα και το κομπιουτεράκι
αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό
 αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό Αστερισμός του χαμαιλέοντα Φυσικά χαρακτηριστικά αστέρων Λαμπρότητα Μέγεθος Θερμοκρασία-χρώμα Φασματικός τύπος Λαμπρότητα
αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό Αστερισμός του χαμαιλέοντα Φυσικά χαρακτηριστικά αστέρων Λαμπρότητα Μέγεθος Θερμοκρασία-χρώμα Φασματικός τύπος Λαμπρότητα
ΑΣΤΡΙΚΑ ΣΜΗΝΗ Τα ρολόγια του σύμπαντος. Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Πανεπιστήμιο Αθηνών Τμήμα Φυσικής
 ΑΣΤΡΙΚΑ ΣΜΗΝΗ Τα ρολόγια του σύμπαντος Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Αστρικό σμήνος είναι 1 ομάδα από άστρα που Καταλαμβάνουν σχετικά μικρό χώρο στο
ΑΣΤΡΙΚΑ ΣΜΗΝΗ Τα ρολόγια του σύμπαντος Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Αστρικό σμήνος είναι 1 ομάδα από άστρα που Καταλαμβάνουν σχετικά μικρό χώρο στο
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος»
 Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
ΑΣΚΗΣΗ 1. Aνίχνευση ακτινοβολίας και η επίδραση των οργάνων παρατήρησης. Εισαγωγή
 ΑΣΚΗΣΗ 1 Aνίχνευση ακτινοβολίας και η επίδραση των οργάνων παρατήρησης Εισαγωγή Το βασικό εργαλείο που χρησιμοποιείται για τη μελέτη αστρονομικών αντικειμένων είναι η μέτρηση των χαρακτηριστικών της ακτινοβολίας
ΑΣΚΗΣΗ 1 Aνίχνευση ακτινοβολίας και η επίδραση των οργάνων παρατήρησης Εισαγωγή Το βασικό εργαλείο που χρησιμοποιείται για τη μελέτη αστρονομικών αντικειμένων είναι η μέτρηση των χαρακτηριστικών της ακτινοβολίας
Εισαγωγή στην Αστροφυσική
 Εισαγωγή στην Αστροφυσική Ενότητα: Ασκήσεις Ξενοφών Μουσάς Τμήμα: Φυσικής Σελίδα 2 1. Ασκήσεις... 4 Σελίδα 3 1. Ασκήσεις Άσκηση 1 α. Τι είναι οι κηλίδες; β. Πώς δημιουργούνται; Αναπτύξτε την σχετική θεωρία
Εισαγωγή στην Αστροφυσική Ενότητα: Ασκήσεις Ξενοφών Μουσάς Τμήμα: Φυσικής Σελίδα 2 1. Ασκήσεις... 4 Σελίδα 3 1. Ασκήσεις Άσκηση 1 α. Τι είναι οι κηλίδες; β. Πώς δημιουργούνται; Αναπτύξτε την σχετική θεωρία
Αστρική Εξέλιξη. Η ζωή και ο θάνατος των αστέρων. Κοσμάς Γαζέας. Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
 Αστρική Εξέλιξη Η ζωή και ο θάνατος των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρική εξέλιξη Η εξέλιξη ενός αστέρα καθορίζεται από την κατανάλωση διαδοχικών «κύκλων» πυρηνικών
Αστρική Εξέλιξη Η ζωή και ο θάνατος των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρική εξέλιξη Η εξέλιξη ενός αστέρα καθορίζεται από την κατανάλωση διαδοχικών «κύκλων» πυρηνικών
Αστρονομία. Ενότητα # 6: Φασματική Ταξινόμηση Αστέρων. Νικόλαος Στεργιούλας Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 6: Φασματική Ταξινόμηση Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 6: Φασματική Ταξινόμηση Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Άδειες
dλ (7) l A = l B = l = λk B T
 Αριστοτελειο Πανεπιστημιο Θεσσαλονικης ΤΜΗΜΑ ΦΥΣΙΚΗΣ 2ο Σετ Ασκήσεων Αστρονομίας Author: Σταμάτης Βρετινάρης Supervisor: Νικόλαος Στεργιούλας Λουκάς Βλάχος November 0, 205 Άσκηση (α) Αν η μέση αριθμητική
Αριστοτελειο Πανεπιστημιο Θεσσαλονικης ΤΜΗΜΑ ΦΥΣΙΚΗΣ 2ο Σετ Ασκήσεων Αστρονομίας Author: Σταμάτης Βρετινάρης Supervisor: Νικόλαος Στεργιούλας Λουκάς Βλάχος November 0, 205 Άσκηση (α) Αν η μέση αριθμητική
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Η γέννηση της Αστροφυσικής Οι αστρονόμοι μελετούν τα ουράνια σώματα βασισμένοι στο φως, που λαμβάνουν από αυτά. Στα πρώτα χρόνια των παρατηρήσεων,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Η γέννηση της Αστροφυσικής Οι αστρονόμοι μελετούν τα ουράνια σώματα βασισμένοι στο φως, που λαμβάνουν από αυτά. Στα πρώτα χρόνια των παρατηρήσεων,
ΜΕΤΡΗΣΗ ΚΟΣΜΙΚΩΝ ΑΠΟΣΤΑΣΕΩΝ
 ΜΕΤΡΗΣΗ ΚΟΣΜΙΚΩΝ ΑΠΟΣΤΑΣΕΩΝ Για να µπορέσουµε να ξεκινήσουµε στο ταξίδι µας στην κατανόηση του Σύµπαντος και των φυσικών διεργασιών που συνετλούνται είναι απαραίτητη προϋπόθεση να γνωρίζουµε να µετράµε
ΜΕΤΡΗΣΗ ΚΟΣΜΙΚΩΝ ΑΠΟΣΤΑΣΕΩΝ Για να µπορέσουµε να ξεκινήσουµε στο ταξίδι µας στην κατανόηση του Σύµπαντος και των φυσικών διεργασιών που συνετλούνται είναι απαραίτητη προϋπόθεση να γνωρίζουµε να µετράµε
Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ
 Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας.
 Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας. Παρ' όλα αυτά, πρώτος ο γάλλος µαθηµατικός Λαπλάςτο 1796 ανέφερε
Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας. Παρ' όλα αυτά, πρώτος ο γάλλος µαθηµατικός Λαπλάςτο 1796 ανέφερε
Τα παρατηρήσιμα μεγέθη των αστεριών (λαμπρότητα, L, επιφανειακή θερμοκρασία, T eff
 ΚΥΡΙΑ ΑΚΟΛΟΥΘΙΑ: oνομάζουμε το σύνολο των θέσεων που καταλαμβάνουν τα αστέρια σε διάγραμμα Λαμπρότητας Θερμοκρασίας όταν καίνε Η στο εσωτερικό τους και παράγουν He. Τα παρατηρήσιμα μεγέθη των αστεριών
ΚΥΡΙΑ ΑΚΟΛΟΥΘΙΑ: oνομάζουμε το σύνολο των θέσεων που καταλαμβάνουν τα αστέρια σε διάγραμμα Λαμπρότητας Θερμοκρασίας όταν καίνε Η στο εσωτερικό τους και παράγουν He. Τα παρατηρήσιμα μεγέθη των αστεριών
ΕΡΓΑΛΕΙΑ ΜΕΤΡΗΣΗΣ ΑΠΟΣΤΑΣΕΩΝ ΣΤΟ ΣΥΜΠΑΝ
 ΕΛΛΗΝΙΚΗ ΑΣΤΡΟΝΟΜΙΚΗ ΕΝΩΣΗ ΕΡΓΑΛΕΙΑ ΜΕΤΡΗΣΗΣ ΑΠΟΣΤΑΣΕΩΝ ΣΤΟ ΣΥΜΠΑΝ Οι αποστάσεις στο γνωστό σύμπαν είναι πολύ μεγαλύτερες από ό,τι μπορεί να συλλάβει ο ανθρώπινος νους. Δε μετριούνται σε μέτρα ή χιλιόμετρα.
ΕΛΛΗΝΙΚΗ ΑΣΤΡΟΝΟΜΙΚΗ ΕΝΩΣΗ ΕΡΓΑΛΕΙΑ ΜΕΤΡΗΣΗΣ ΑΠΟΣΤΑΣΕΩΝ ΣΤΟ ΣΥΜΠΑΝ Οι αποστάσεις στο γνωστό σύμπαν είναι πολύ μεγαλύτερες από ό,τι μπορεί να συλλάβει ο ανθρώπινος νους. Δε μετριούνται σε μέτρα ή χιλιόμετρα.
ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς
 ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το φυσικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την ταλάντωση
ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το φυσικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την ταλάντωση
Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015
 Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
Data Analysis Examination
 Data Analysis Examination Page 1 of (D1) Διπλός Πάλσαρ Κάνοντας συστηµατικές έρευνες τις τελευταίες δεκαετίες, οι αστρονόµοι κατάφεραν να εντοπίσουν ένα µεγάλο πλήθος από πάλσαρς µε περίοδο περιστροφής
Data Analysis Examination Page 1 of (D1) Διπλός Πάλσαρ Κάνοντας συστηµατικές έρευνες τις τελευταίες δεκαετίες, οι αστρονόµοι κατάφεραν να εντοπίσουν ένα µεγάλο πλήθος από πάλσαρς µε περίοδο περιστροφής
Πρακτική µε στοιχεία στατιστικής ανάλυσης
 Πρακτική µε στοιχεία στατιστικής ανάλυσης 1. Για να υπολογίσουµε µια ποσότητα q = x 2 y xy 2, µετρήσαµε τα µεγέθη x και y και βρήκαµε x = 3.0 ± 0.1και y = 2.0 ± 0.1. Να βρεθεί η ποσότητα q και η αβεβαιότητά
Πρακτική µε στοιχεία στατιστικής ανάλυσης 1. Για να υπολογίσουµε µια ποσότητα q = x 2 y xy 2, µετρήσαµε τα µεγέθη x και y και βρήκαµε x = 3.0 ± 0.1και y = 2.0 ± 0.1. Να βρεθεί η ποσότητα q και η αβεβαιότητά
Καθορισµός του γαλαξία του Τριγώνου (Μ33) ως σηµείο αναφοράς για τη µέτρηση της απόστασης των γαλαξιών
 ΠΡΟΓΡΑΜΜΑ ΕΠΙΣΤΗΜΟΝΙΚΩΝ ΜΕΛΕΤΩΝ 2011 Καθορισµός του γαλαξία του Τριγώνου (Μ33) ως σηµείο αναφοράς για τη µέτρηση της απόστασης των γαλαξιών Άλκηστις Μπονάνου (Εθνικό Αστεροσκοπείο Αθηνών) Norberto Castro
ΠΡΟΓΡΑΜΜΑ ΕΠΙΣΤΗΜΟΝΙΚΩΝ ΜΕΛΕΤΩΝ 2011 Καθορισµός του γαλαξία του Τριγώνου (Μ33) ως σηµείο αναφοράς για τη µέτρηση της απόστασης των γαλαξιών Άλκηστις Μπονάνου (Εθνικό Αστεροσκοπείο Αθηνών) Norberto Castro
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Π.Σ.Α.Π.Θ. ΤΟΜΕΑΣ Υ ΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ Υ ΡΟΛΟΓΙΑΣ 7ου εξαµήνου Αν.Καθηγητής Μ.
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Π.Σ.Α.Π.Θ. ΤΟΜΕΑΣ Υ ΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ Υ ΡΟΛΟΓΙΑΣ 7ου εξαµήνου Αν.Καθηγητής Μ.Βαφειάδης Ασκηση: ΙΟ ΕΥΣΗ ΠΛΗΜΜΥΡΑΣ ΣΕ ΤΑΜΙΕΥΤΗΡΑ (Από την Υδρολογία, Wilson)
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Π.Σ.Α.Π.Θ. ΤΟΜΕΑΣ Υ ΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ Υ ΡΟΛΟΓΙΑΣ 7ου εξαµήνου Αν.Καθηγητής Μ.Βαφειάδης Ασκηση: ΙΟ ΕΥΣΗ ΠΛΗΜΜΥΡΑΣ ΣΕ ΤΑΜΙΕΥΤΗΡΑ (Από την Υδρολογία, Wilson)
βαρυτικά συστήματα αστέρων, γαλαξιακών αερίων, αστρικής σκοτεινής ύλης. Η ετυμολογία της λέξης αναφέρεται στον δικό μας
 Οι γαλαξίες αποτελούν τεράστια βαρυτικά συστήματα αστέρων, γαλαξιακών αερίων, αστρικής σκόνης και (πιθανώς) αόρατης σκοτεινής ύλης. Η ετυμολογία της λέξης προέρχεται από τα ελληνικά και σημαίνει άξονας
Οι γαλαξίες αποτελούν τεράστια βαρυτικά συστήματα αστέρων, γαλαξιακών αερίων, αστρικής σκόνης και (πιθανώς) αόρατης σκοτεινής ύλης. Η ετυμολογία της λέξης προέρχεται από τα ελληνικά και σημαίνει άξονας
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 http://www.economics.edu.gr 1 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΕΦΑΛΑΙΟ 1 ο : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΣΚΗΣΕΙΣ ΥΠΟ ΕΙΓΜΑΤΑ ( τρόποι επίλυσης παρατηρήσεις σχόλια ) ΑΣΚΗΣΗ 1 Έστω ο πίνακας παραγωγικών δυνατοτήτων µιας
http://www.economics.edu.gr 1 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΕΦΑΛΑΙΟ 1 ο : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΣΚΗΣΕΙΣ ΥΠΟ ΕΙΓΜΑΤΑ ( τρόποι επίλυσης παρατηρήσεις σχόλια ) ΑΣΚΗΣΗ 1 Έστω ο πίνακας παραγωγικών δυνατοτήτων µιας
Θεωρητική Εξέταση. 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής η φάση: «ΠΤΟΛΕΜΑΙΟΣ»
 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2019 3 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2019 3 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2019 3 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2019 3 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΦΥΣΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΦΥΣΙΚΗ Μέρος Ι (Σημειώσεις από Πανεπιστημιακές παραδόσεις) Κ. Ε. ΑΛΥΣΣΑΝΔΡΑΚΗΣ Τομέας Αστρογεωφυσικής Τμήμα Φυσικής Πανεπιστήμιο Ιωαννίνων Ιωάννινα, 2010 Περιεχόμενα 1 Βασικές έννοιες,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΦΥΣΙΚΗ Μέρος Ι (Σημειώσεις από Πανεπιστημιακές παραδόσεις) Κ. Ε. ΑΛΥΣΣΑΝΔΡΑΚΗΣ Τομέας Αστρογεωφυσικής Τμήμα Φυσικής Πανεπιστήμιο Ιωαννίνων Ιωάννινα, 2010 Περιεχόμενα 1 Βασικές έννοιες,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 8. Συνεχείς Κατανομές Πιθανοτήτων Η Κανονική Κατανομή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΔΙΠΛΑ ΣΥΣΤΗΜΑΤΑ ΑΣΤΕΡΩΝ
 ΔΙΠΛΑ ΣΥΣΤΗΜΑΤΑ ΑΣΤΕΡΩΝ Οι διπλοί αστέρες διακρίνονται ως τέτοιοι αν η γωνιώδης απόσταση τους, ω, είναι µεγαλύτερη από την διακριτική ικανότητα του τηλεσκοπίου: ω min =1.22 λ/d λ=µήκος κύµατος παρατήρησης
ΔΙΠΛΑ ΣΥΣΤΗΜΑΤΑ ΑΣΤΕΡΩΝ Οι διπλοί αστέρες διακρίνονται ως τέτοιοι αν η γωνιώδης απόσταση τους, ω, είναι µεγαλύτερη από την διακριτική ικανότητα του τηλεσκοπίου: ω min =1.22 λ/d λ=µήκος κύµατος παρατήρησης
Αστρονομία. Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων. Νικόλαος Στεργιούλας Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
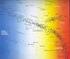 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης
Αστροφυσική. Ενότητα # 2: Αστρική Δομή - Εφαρμογές Ρευστοδυναμικής. Λουκάς Βλάχος Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 2: Αστρική Δομή - Εφαρμογές Ρευστοδυναμικής Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 2: Αστρική Δομή - Εφαρμογές Ρευστοδυναμικής Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
A2. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ
 A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
A. ΠΑΡΑΓΩΓΟΣ-ΚΛΙΣΗ-ΜΟΝΟΤΟΝΙΑ d df() = f() = f (), = d d.κλίση ευθείας.μεταβολές 3.(Οριακός) ρυθµός µεταβολής ή παράγωγος 4.Παράγωγοι βασικών συναρτήσεων 5. Κανόνες παραγώγισης 6.Αλυσωτή παράγωγος 7.Μονοτονία
ΤΕΙ ΧΑΛΚΙΔΑΣ ΣΤΕΦ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ. Βικτωρία Σγαρδώνη Ηλ/γος Μηχ/κος, ΜSc, DIC
 ΤΕΙ ΧΑΛΚΙΔΑΣ ΣΤΕΦ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ Βικτωρία Σγαρδώνη Ηλ/γος Μηχ/κος, ΜSc, DIC ΣΕΠΤΕΜΒΡΙΟΣ 2007 Οδηγίες για την σύνταξη τεχνικής έκθεσης Η δοµή της τεχνικής
ΤΕΙ ΧΑΛΚΙΔΑΣ ΣΤΕΦ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ Βικτωρία Σγαρδώνη Ηλ/γος Μηχ/κος, ΜSc, DIC ΣΕΠΤΕΜΒΡΙΟΣ 2007 Οδηγίες για την σύνταξη τεχνικής έκθεσης Η δοµή της τεχνικής
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
ΣΚΟΠΟΙ Η αισθητοποίηση του φαινοµένου του ηχητικού συντονισµού Η κατανόηση της αρχής λειτουργίας των πνευστών οργάνων ΥΛΙΚΑ-ΟΡΓΑΝΑ
 ΜΕΛΕΤΗ ΣΤΑΣΙΜΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΩΛΗΝΑ ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΤΑΧΥΤΗΤΑΣ ΤΟΥ ΗΧΟΥ ΣΤΟΝ ΑΕΡΑ ΣΚΟΠΟΙ Η αισθητοποίηση του φαινοµένου του ηχητικού συντονισµού Η κατανόηση της αρχής λειτουργίας των πνευστών οργάνων ΥΛΙΚΑ-ΟΡΓΑΝΑ
ΜΕΛΕΤΗ ΣΤΑΣΙΜΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΩΛΗΝΑ ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΤΑΧΥΤΗΤΑΣ ΤΟΥ ΗΧΟΥ ΣΤΟΝ ΑΕΡΑ ΣΚΟΠΟΙ Η αισθητοποίηση του φαινοµένου του ηχητικού συντονισµού Η κατανόηση της αρχής λειτουργίας των πνευστών οργάνων ΥΛΙΚΑ-ΟΡΓΑΝΑ
ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης
 ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε τις
ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε τις
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Μονάδες ΟΜΑ Α Α Στις προτάσεις από Α µέχρι και Α, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Μονάδες ΟΜΑ Α Α Στις προτάσεις από Α µέχρι και Α, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και
Θεωρητική Εξέταση - Σύντοµες Ερωτήσεις
 1. Στο Εθνικό Αστεροσκοπείο της Βραζιλίας, που βρίσκεται στη πόλη Ρίο ντε Τζανέιρο ( 22 54ʹ S, 43 12ʹ W), υπάρχει ένα ηλιακό ρολόι πάνω από την πόρτα του θόλου που είναι εγκατεστηµένο το τηλεσκόπιο των
1. Στο Εθνικό Αστεροσκοπείο της Βραζιλίας, που βρίσκεται στη πόλη Ρίο ντε Τζανέιρο ( 22 54ʹ S, 43 12ʹ W), υπάρχει ένα ηλιακό ρολόι πάνω από την πόρτα του θόλου που είναι εγκατεστηµένο το τηλεσκόπιο των
ΣΗΜΑΣΙΑ ΤΗΣ ΕΛΑΣΤΙΚΟΤΗΤΑΣ
 ΕΛΑΣΤΙΚΟΤΗΤΑ ΣΗΜΑΣΙΑ ΤΗΣ ΕΛΑΣΤΙΚΟΤΗΤΑΣ Οι οικονοµολόγοι ενδιαφέρονται να µετρήσουν ορισµένες µεταβλητές για να µπορέσουν να κάνουν προβλέψεις και για να εκτιµήσουν µε σχετική ακρίβεια τι αποτέλεσµα θα
ΕΛΑΣΤΙΚΟΤΗΤΑ ΣΗΜΑΣΙΑ ΤΗΣ ΕΛΑΣΤΙΚΟΤΗΤΑΣ Οι οικονοµολόγοι ενδιαφέρονται να µετρήσουν ορισµένες µεταβλητές για να µπορέσουν να κάνουν προβλέψεις και για να εκτιµήσουν µε σχετική ακρίβεια τι αποτέλεσµα θα
Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ
 ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ
 ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
ΠΕΙΡΑΜΑ III Μελέτη Ελευθερης Πτώσης
 ΠΕΙΡΑΜΑ III Μελέτη Ελευθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε τις
ΠΕΙΡΑΜΑ III Μελέτη Ελευθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε τις
Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής ΕΚΠΑ www/manowdanezis.gr. Εξέλιξη των Αστέρων
 Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής ΕΚΠΑ www/manowdanezis.gr Εξέλιξη των Αστέρων Φασματική Ταξινόμηση του Harvard Σύμφωνα με την ταξινόμηση του Harvard, όπως ονομάστηκε, τα
Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής ΕΚΠΑ www/manowdanezis.gr Εξέλιξη των Αστέρων Φασματική Ταξινόμηση του Harvard Σύμφωνα με την ταξινόμηση του Harvard, όπως ονομάστηκε, τα
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER
 ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΑΣΚΗΣΗ ΝΟ6 ΜΕΛΕΤΗ ΦΩΤΟΗΛΕΚΤΡΙΚΟΥ ΦΑΙΝΟΜΕ- ΝΟΥ ΜΕ ΧΡΗΣΗ ΦΩΤΟΕΚΠΕΜΠΟΥΣΩΝ ΙΟ ΩΝ (LEDS) Γ. Μήτσου Α. Θεωρία 1. Εισαγωγή
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΑΣΚΗΣΗ ΝΟ6 ΜΕΛΕΤΗ ΦΩΤΟΗΛΕΚΤΡΙΚΟΥ ΦΑΙΝΟΜΕ- ΝΟΥ ΜΕ ΧΡΗΣΗ ΦΩΤΟΕΚΠΕΜΠΟΥΣΩΝ ΙΟ ΩΝ (LEDS) Γ. Μήτσου Α. Θεωρία 1. Εισαγωγή
Μεθοδολογίες παρεµβολής σε DTM.
 Μάθηµα : Αλγοριθµικές Βάσεις στη Γεωπληροφορική ιδάσκων : Συµεών Κατσουγιαννόπουλος Μεθοδολογίες παρεµβολής σε DTM.. Μέθοδοι παρεµβολής. Η παρεµβολή σε ψηφιακό µοντέλο εδάφους (DTM) είναι η διαδικασία
Μάθηµα : Αλγοριθµικές Βάσεις στη Γεωπληροφορική ιδάσκων : Συµεών Κατσουγιαννόπουλος Μεθοδολογίες παρεµβολής σε DTM.. Μέθοδοι παρεµβολής. Η παρεµβολή σε ψηφιακό µοντέλο εδάφους (DTM) είναι η διαδικασία
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002 ΟΜΑ Α Α
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΟΜΑ Α Α Στις προτάσεις από Α1 µέχρι και Α5, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΟΜΑ Α Α Στις προτάσεις από Α1 µέχρι και Α5, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό
PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ ΜΕΡΟΣ ΤΡΙΤΟ Πολίτη Όλγα Α.Μ. 4528 Εξάµηνο 8ο Υπεύθυνος Καθηγητής Λυκοθανάσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ PROJECT ΣΤΟ ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΕΥΡΕΤΙΚΕΣ ΜΕΘΟ ΟΥΣ ΜΕΡΟΣ ΤΡΙΤΟ Πολίτη Όλγα Α.Μ. 4528 Εξάµηνο 8ο Υπεύθυνος Καθηγητής Λυκοθανάσης
δ) Αν ένα σηµείο του θετικού ηµιάξονα ταλαντώνεται µε πλάτος, να υπολογίσετε την απόσταση του σηµείου αυτού από τον πλησιέστερο δεσµό. ΑΣΚΗΣΗ 4 Μονοχρ
 ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
Περίθλαση από µία σχισµή.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
1. ** α) Αν η f είναι δυο φορές παραγωγίσιµη συνάρτηση, να αποδείξετε ότι. β α. = [f (x) ηµx] - [f (x) συνx] β α. ( )
![1. ** α) Αν η f είναι δυο φορές παραγωγίσιµη συνάρτηση, να αποδείξετε ότι. β α. = [f (x) ηµx] - [f (x) συνx] β α. ( ) 1. ** α) Αν η f είναι δυο φορές παραγωγίσιµη συνάρτηση, να αποδείξετε ότι. β α. = [f (x) ηµx] - [f (x) συνx] β α. ( )](/thumbs/52/29634211.jpg) Ερωτήσεις ανάπτυξης. ** α) Αν η f είναι δυο φορές παραγωγίσιµη συνάρτηση, να αποδείξετε ότι β ( f () f () ) + α ηµ d β α = [f () ηµ] - [f () συν] β α. ( ) β) Αν f () = ηµ, να αποδείξετε ότι f () + f ()
Ερωτήσεις ανάπτυξης. ** α) Αν η f είναι δυο φορές παραγωγίσιµη συνάρτηση, να αποδείξετε ότι β ( f () f () ) + α ηµ d β α = [f () ηµ] - [f () συν] β α. ( ) β) Αν f () = ηµ, να αποδείξετε ότι f () + f ()
[ ], σχηµατίζουµε το άθροισµα. Το άθροισµα αυτό είναι µια δυαδική πράξη η οποία αντιστοιχεί στις ακολουθίες f [ 1
![[ ], σχηµατίζουµε το άθροισµα. Το άθροισµα αυτό είναι µια δυαδική πράξη η οποία αντιστοιχεί στις ακολουθίες f [ 1 [ ], σχηµατίζουµε το άθροισµα. Το άθροισµα αυτό είναι µια δυαδική πράξη η οποία αντιστοιχεί στις ακολουθίες f [ 1](/thumbs/62/47162790.jpg) ΚΕΦΑΛΑΙΟ 4 ΣΥΝΕΛΙΞΗ 4.. ΣΥΝΕΛΙΞΗ Στην προηγούµενη παράγραφο εισαγάγαµε την ιδέα της συνέλιξης από τα συµφραζόµενα των γραµµικών συστηµάτων. Σ' αυτήν την παράγραφο ορίζουµε τη συνέλιξη σαν µια πράξη η οποία
ΚΕΦΑΛΑΙΟ 4 ΣΥΝΕΛΙΞΗ 4.. ΣΥΝΕΛΙΞΗ Στην προηγούµενη παράγραφο εισαγάγαµε την ιδέα της συνέλιξης από τα συµφραζόµενα των γραµµικών συστηµάτων. Σ' αυτήν την παράγραφο ορίζουµε τη συνέλιξη σαν µια πράξη η οποία
ΠΕΙΡΑΜΑ IV Απλή κυκλική κίνηση. Κεντροµόλος Δύναµη
 ΠΕΙΡΑΜΑ IV Απλή κυκλική κίνηση. Κεντροµόλος Δύναµη Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κυκλική κίνηση µίας σηµειακής µάζας και ιδιαίτερα την εξάρτηση της κεντροµόλου δύναµης από τη µάζα,
ΠΕΙΡΑΜΑ IV Απλή κυκλική κίνηση. Κεντροµόλος Δύναµη Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κυκλική κίνηση µίας σηµειακής µάζας και ιδιαίτερα την εξάρτηση της κεντροµόλου δύναµης από τη µάζα,
ΚΕΦΑΛΑΙΟ ΕΥΤΕΡΟ ΘΕΡΜΟ ΥΝΑΜΙΚΗ
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΚΕΦΑΛΑΙΟ ΕΥΤΕΡΟ ΘΕΡΜΟ ΥΝΑΜΙΚΗ 1. Τι εννοούµε λέγοντας θερµοδυναµικό σύστηµα; Είναι ένα κοµµάτι ύλης που αποµονώνουµε νοητά από το περιβάλλον. Περιβάλλον του συστήµατος είναι το σύνολο των
ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΚΕΦΑΛΑΙΟ ΕΥΤΕΡΟ ΘΕΡΜΟ ΥΝΑΜΙΚΗ 1. Τι εννοούµε λέγοντας θερµοδυναµικό σύστηµα; Είναι ένα κοµµάτι ύλης που αποµονώνουµε νοητά από το περιβάλλον. Περιβάλλον του συστήµατος είναι το σύνολο των
ΠΕΙΡΑΜΑ I Απλές Μετρήσεις και Σφάλµατα
 ΠΕΙΡΑΜΑ I Απλές Μετρήσεις και Σφάλµατα Σκοπός πειράµατος Στο πείραµα αυτό θα χρησιµοποιήσουµε βασικά όργανα του εργαστηρίου (διαστηµόµετρο, µικρόµετρο, χρονόµετρο) προκειµένου να: Να µετρήσουµε την πυκνότητα
ΠΕΙΡΑΜΑ I Απλές Μετρήσεις και Σφάλµατα Σκοπός πειράµατος Στο πείραµα αυτό θα χρησιµοποιήσουµε βασικά όργανα του εργαστηρίου (διαστηµόµετρο, µικρόµετρο, χρονόµετρο) προκειµένου να: Να µετρήσουµε την πυκνότητα
8. ΠΑΡΑΤΗΡΗΣΕΙΣ ΟΥ ΕΤΕΡΟΥ Υ ΡΟΓΟΝΟΥ ΣΤΗ ΓΡΑΜΜΗ ΤΩΝ 21 cm.
 8. ΠΑΡΑΤΗΡΗΣΕΙΣ ΟΥ ΕΤΕΡΟΥ Υ ΡΟΓΟΝΟΥ ΣΤΗ ΓΡΑΜΜΗ ΤΩΝ 21 cm. 8.1 Γενικά Η ανακάλυψη φασµατικών γραµµών στο ραδιοφωνικό τµήµα του ηλεκτροµαγνητικού φάσµατος το Σεπτέµβριο 1951 από τους H.I. Ewen και E.M. Purcell
8. ΠΑΡΑΤΗΡΗΣΕΙΣ ΟΥ ΕΤΕΡΟΥ Υ ΡΟΓΟΝΟΥ ΣΤΗ ΓΡΑΜΜΗ ΤΩΝ 21 cm. 8.1 Γενικά Η ανακάλυψη φασµατικών γραµµών στο ραδιοφωνικό τµήµα του ηλεκτροµαγνητικού φάσµατος το Σεπτέµβριο 1951 από τους H.I. Ewen και E.M. Purcell
Κεφάλαιο 1: ΕΙΣΑΓΩΓΗ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 130 Κεφάλαιο 1: ΕΙΣΑΓΩΓΗ Α. Απαντήσεις στις ερωτήσεις πολλαπλής επιλογής 1. α, β 2. γ 3. ε 4. β, δ 5. γ 6. α, β, γ, ε Β. Απαντήσεις στις ερωτήσεις συµπλήρωσης κενού 1. η αρχαιότερη
ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 130 Κεφάλαιο 1: ΕΙΣΑΓΩΓΗ Α. Απαντήσεις στις ερωτήσεις πολλαπλής επιλογής 1. α, β 2. γ 3. ε 4. β, δ 5. γ 6. α, β, γ, ε Β. Απαντήσεις στις ερωτήσεις συµπλήρωσης κενού 1. η αρχαιότερη
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση της ζήτησης και της προσφοράς.
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση της ζήτησης και της προσφοράς.
Ο είκτης Συσχέτισης. Υπάρχουν πολλές οι έρευνες στις οποίες µας ενδιαφέρει να µελετήσουµε αν υπάρχει ΑΛΛΗΛΕΞΑΡΤΗΣΗ µεταξύ δύο µεταβλητών
 Κεφάλαιο 8 Ο είκτης Συσχέτισης 1 Η έννοια της Αλληλεξάρτησης Υπάρχουν πολλές οι έρευνες στις οποίες µας ενδιαφέρει να µελετήσουµε αν υπάρχει ΑΛΛΗΛΕΞΑΡΤΗΣΗ µεταξύ δύο µεταβλητών ηλαδή, µας ενδιαφέρει να
Κεφάλαιο 8 Ο είκτης Συσχέτισης 1 Η έννοια της Αλληλεξάρτησης Υπάρχουν πολλές οι έρευνες στις οποίες µας ενδιαφέρει να µελετήσουµε αν υπάρχει ΑΛΛΗΛΕΞΑΡΤΗΣΗ µεταξύ δύο µεταβλητών ηλαδή, µας ενδιαφέρει να
ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης
 - &. ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε
- &. ΠΕΙΡΑΜΑ ΙΙ Μελέτη Ελεύθερης Πτώσης Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος καθώς πέφτει ελεύθερα υπό την επίδραση του βάρους του. Πιο συγκεκριµένα θα επαληθεύσουµε
T (K) m 2 /m
 Ορθοί και λανθασµένοι τρόποι απεικονίσεως δεδοµένων σε διάγραµµα Από µετρήσεις σηµείου ζέσεως σειράς διαλυµάτων προκύπτουν τα εξής δεδοµένα: m /m.5..5..5.55.. Σύµφωνα µε την θεωρία τα δεδοµένα πρέπει να
Ορθοί και λανθασµένοι τρόποι απεικονίσεως δεδοµένων σε διάγραµµα Από µετρήσεις σηµείου ζέσεως σειράς διαλυµάτων προκύπτουν τα εξής δεδοµένα: m /m.5..5..5.55.. Σύµφωνα µε την θεωρία τα δεδοµένα πρέπει να
Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009
 Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009 1. Μία περιοχή στο μεσοαστρικό χώρο με ερυθρωπή απόχρωση είναι a. Ο ψυχρός πυρήνας ενός μοριακού νέφους b. Μία περιοχή θερμού ιονισμένου αερίου c. Μία περιοχή
Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009 1. Μία περιοχή στο μεσοαστρικό χώρο με ερυθρωπή απόχρωση είναι a. Ο ψυχρός πυρήνας ενός μοριακού νέφους b. Μία περιοχή θερμού ιονισμένου αερίου c. Μία περιοχή
ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση
 ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος και θα διερευνήσουµε τους δυο πρώτους νόµους του Newton. Επιπλέον θα µετρήσουµε την επιτάχυνση
ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος και θα διερευνήσουµε τους δυο πρώτους νόµους του Newton. Επιπλέον θα µετρήσουµε την επιτάχυνση
----------Εισαγωγή στη Χρήση του SPSS for Windows ------------- Σελίδα: 0------------
 ----------Εισαγωγή στη Χρήση του SPSS for Windows ------------- Σελίδα: 0------------ ΚΕΦΑΛΑΙΟ 9 ο 9.1 ηµιουργία µοντέλων πρόβλεψης 9.2 Απλή Γραµµική Παλινδρόµηση 9.3 Αναλυτικά για το ιάγραµµα ιασποράς
----------Εισαγωγή στη Χρήση του SPSS for Windows ------------- Σελίδα: 0------------ ΚΕΦΑΛΑΙΟ 9 ο 9.1 ηµιουργία µοντέλων πρόβλεψης 9.2 Απλή Γραµµική Παλινδρόµηση 9.3 Αναλυτικά για το ιάγραµµα ιασποράς
Εξαμηνιαία Εργασία Β. Κανονική Κατανομή - Επαγωγική Στατιστική
 1 ΕΞΑΜΗΝΙΑΙΑ Β ΤΟ ΦΩΤΟΒΟΛΤΑΙΚΟ ΠΑΡΚΟ ΑΣΠΑΙΤΕ Τμήμα Εκπαιδευτικών Ηλεκτρολογίας Εργαστήριο Συλλογής και Επεξεργασίας Δεδομένων Διδάσκοντες: Σπύρος Αδάμ, Λουκάς Μιχάλης, Παναγιώτης Καράμπελας Εξαμηνιαία
1 ΕΞΑΜΗΝΙΑΙΑ Β ΤΟ ΦΩΤΟΒΟΛΤΑΙΚΟ ΠΑΡΚΟ ΑΣΠΑΙΤΕ Τμήμα Εκπαιδευτικών Ηλεκτρολογίας Εργαστήριο Συλλογής και Επεξεργασίας Δεδομένων Διδάσκοντες: Σπύρος Αδάμ, Λουκάς Μιχάλης, Παναγιώτης Καράμπελας Εξαμηνιαία
ΠΕΙΡΑΜΑ II-α Aπλό εκκρεµές
 ΠΕΙΡΑΜΑ II-α Aπλό εκκρεµές Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το απλό ή µαθηµατικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την
ΠΕΙΡΑΜΑ II-α Aπλό εκκρεµές Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το απλό ή µαθηµατικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ.
 ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΔΙΠΛΟΙ ΕΚΛΕΙΠΤΙΚΟΙ. Το διπλό σύστηµα Algol. Φαίνεται η διαφορά στο φαινόµενο µέγεθος που προκαλείται από τις κύριες και δευτερεύουσες εκλείψεις
 ΔΙΠΛΟΙ ΕΚΛΕΙΠΤΙΚΟΙ Διπλά εκλειπτικά συστήµατα φαίνονται ως µεταβλητός αστέρας, π.χ. ο µεταβλητός Algol που ανακαλύφθηκε το 1669 και ερµηνεύτηκε αργότερα ως διπλό σύστηµα. Το διπλό σύστηµα Algol. Φαίνεται
ΔΙΠΛΟΙ ΕΚΛΕΙΠΤΙΚΟΙ Διπλά εκλειπτικά συστήµατα φαίνονται ως µεταβλητός αστέρας, π.χ. ο µεταβλητός Algol που ανακαλύφθηκε το 1669 και ερµηνεύτηκε αργότερα ως διπλό σύστηµα. Το διπλό σύστηµα Algol. Φαίνεται
Εργαστηριακή άσκηση 1: ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ & ΓΡΑΜΜΙΚΩΝ ΦΑΣΜΑΤΩΝ Τροποποίηση του εργαστηριακού οδηγού (Βαγγέλης ηµητριάδης, 4 ο ΓΕΛ Ζωγράφου)
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΣΤΟΧΟΙ Εργαστηριακή άσκηση 1: ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ & ΓΡΑΜΜΙΚΩΝ ΦΑΣΜΑΤΩΝ Τροποποίηση του εργαστηριακού οδηγού (Βαγγέλης ηµητριάδης, 4 ο ΓΕΛ Ζωγράφου) Στόχοι αυτής της εργαστηριακής άσκησης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΣΤΟΧΟΙ Εργαστηριακή άσκηση 1: ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ & ΓΡΑΜΜΙΚΩΝ ΦΑΣΜΑΤΩΝ Τροποποίηση του εργαστηριακού οδηγού (Βαγγέλης ηµητριάδης, 4 ο ΓΕΛ Ζωγράφου) Στόχοι αυτής της εργαστηριακής άσκησης
8. Η ζήτηση ενός αγαθού µεταβάλλεται προς την αντίθετη κατεύθυνση µε τη µεταβολή της τιµής του υποκατάστατου αγαθού.
 ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σηµειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Η επιδίωξη της µέγιστης χρησιµότητας αποτελεί βασικό χαρακτηριστικό της συµπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σηµειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Η επιδίωξη της µέγιστης χρησιµότητας αποτελεί βασικό χαρακτηριστικό της συµπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση.
 ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση ph pk A pk B Τότε α 0 (διπρωτικού) = α 0 (µονοπρωτικού) α
ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση ph pk A pk B Τότε α 0 (διπρωτικού) = α 0 (µονοπρωτικού) α
ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση
 - &. ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος και θα διερευνήσουµε τους δυο πρώτους νόµους του Newton. Επιπλέον θα µετρήσουµε την επιτάχυνση
- &. ΠΕΙΡΑΜΑ V Ταχύτητα και Επιτάχυνση Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε την κίνηση ενός σώµατος και θα διερευνήσουµε τους δυο πρώτους νόµους του Newton. Επιπλέον θα µετρήσουµε την επιτάχυνση
Aναλαµπές ακτίνων -γ
 Aναλαµπές ακτίνων -γ Gamma Ray Bursts (GRB) Λουκάς Βλάχος 18/5/2004 1 Γενική παρατήρηση Η αστροφυσική διανύει αυτήν την εποχή τη δηµιουργικότερη περίοδο της ιστορίας της. Η πληθώρα των επίγειων αλλά και
Aναλαµπές ακτίνων -γ Gamma Ray Bursts (GRB) Λουκάς Βλάχος 18/5/2004 1 Γενική παρατήρηση Η αστροφυσική διανύει αυτήν την εποχή τη δηµιουργικότερη περίοδο της ιστορίας της. Η πληθώρα των επίγειων αλλά και
Zentrum für Astronomie, Universität Heidelberg, Germany
 1,2 1 Astronomisches Rechen-Institut Zentrum für Astronomie, Universität Heidelberg, Germany 2 Εργαστήριο Αστρονομίας, Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Τμήμα Φυσικής, Αριστοτέλειο Πανεπιστήμιο
1,2 1 Astronomisches Rechen-Institut Zentrum für Astronomie, Universität Heidelberg, Germany 2 Εργαστήριο Αστρονομίας, Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Τμήμα Φυσικής, Αριστοτέλειο Πανεπιστήμιο
ΑΣΚΗΣΕΙΣ ΠΡΟΣΤΑΣΙΑΣ ΣΗΕ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχανικών Υπολογιστών Τοµέας Ηλεκτρικής Ισχύος ΑΣΚΗΣΕΙΣ ΠΡΟΣΤΑΣΙΑΣ ΣΗΕ Γ. Κορρές, Αναπλ. Καθηγητής Ασκηση 1: Για το ακτινικό δίκτυο διανοµής του
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχανικών Υπολογιστών Τοµέας Ηλεκτρικής Ισχύος ΑΣΚΗΣΕΙΣ ΠΡΟΣΤΑΣΙΑΣ ΣΗΕ Γ. Κορρές, Αναπλ. Καθηγητής Ασκηση 1: Για το ακτινικό δίκτυο διανοµής του
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Επαναληπτικό ιαγώνισµα Β Ενιαίου Λυκείου ευτέρα 26 Γενάρη 2015 Στατικός Ηλεκτρισµός/Συνεχές Ρεύµα. Συνοπτικές Λύσεις. Θέµα Α.
 Επαναληπτικό ιαγώνισµα Β Ενιαίου Λυκείου ευτέρα 26 Γενάρη 2015 Στατικός Ηλεκτρισµός/Συνεχές Ρεύµα Συνοπτικές Λύσεις Θέµα Α Α.1. Ενα ϕορτίο q 1 = 4µC και ένα ϕορτίο q 2 = 8µC απέχουν µεταξύ τους απόσταση
Επαναληπτικό ιαγώνισµα Β Ενιαίου Λυκείου ευτέρα 26 Γενάρη 2015 Στατικός Ηλεκτρισµός/Συνεχές Ρεύµα Συνοπτικές Λύσεις Θέµα Α Α.1. Ενα ϕορτίο q 1 = 4µC και ένα ϕορτίο q 2 = 8µC απέχουν µεταξύ τους απόσταση
1. Εισαγωγή Ο έλεγχος υποθέσεων αναφέρεται στις ιδιότητες µιας άγνωστης παραµέτρους του πληθυσµού: Ο κατηγορούµενος είναι αθώος
 Έλεγχοι Υποθέσεων 1. Εισαγωγή Ο έλεγχος υποθέσεων αναφέρεται στις ιδιότητες µιας άγνωστης παραµέτρους του πληθυσµού: Ο κατηγορούµενος είναι αθώος µ = 100 Κάθε υπόθεση συνοδεύεται από µια εναλλακτική: Ο
Έλεγχοι Υποθέσεων 1. Εισαγωγή Ο έλεγχος υποθέσεων αναφέρεται στις ιδιότητες µιας άγνωστης παραµέτρους του πληθυσµού: Ο κατηγορούµενος είναι αθώος µ = 100 Κάθε υπόθεση συνοδεύεται από µια εναλλακτική: Ο
Κεφάλαιο 10 Περιστροφική Κίνηση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
L = T V = 1 2 (ṙ2 + r 2 φ2 + ż 2 ) U (3)
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
Εργαστηριακή Άσκηση 8 Εξάρτηση της αντίστασης αγωγού από τη θερμοκρασία.
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 9144 Εργαστηριακή Άσκηση 8 Εξάρτηση της αντίστασης αγωγού από τη θερμοκρασία. Συνεργάτες: Ιντζέογλου
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 9144 Εργαστηριακή Άσκηση 8 Εξάρτηση της αντίστασης αγωγού από τη θερμοκρασία. Συνεργάτες: Ιντζέογλου
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΤΙΚΗ FOURIER. Γ. Μήτσου
 ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
ΕΡΓΑΣΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΙΚΗΣ - ΟΠΟΗΛΕΚΡΟΝΙΚΗΣ & LASER ΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & /Υ ΑΣΚΗΣΗ ΝΟ7 ΟΠΙΚΗ FOURIER Γ. Μήτσου Μάρτιος 8 Α. Θεωρία. Εισαγωγή Η επεξεργασία οπτικών δεδοµένων, το φιλτράρισµα χωρικών συχνοτήτων
ΑΣΤΡΟΝΟΜΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΚΑΙ ΟΡΓΑΝΑ Sfaelos Ioannis
 ΑΣΤΡΟΝΟΜΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΚΑΙ ΟΡΓΑΝΑ Sfaelos Ioannis α) Πώς προβλέπονται και ερµηνεύονται τα αποτελέσµατα των αστρονοµικώνπαρατηρήσεων µε τη βοήθεια ενός θεωρητικού µοντέλου; β) Τι παρατηρούµε και πώς;
ΑΣΤΡΟΝΟΜΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΚΑΙ ΟΡΓΑΝΑ Sfaelos Ioannis α) Πώς προβλέπονται και ερµηνεύονται τα αποτελέσµατα των αστρονοµικώνπαρατηρήσεων µε τη βοήθεια ενός θεωρητικού µοντέλου; β) Τι παρατηρούµε και πώς;
ÔÏÕËÁ ÓÁÑÑÇ ÊÏÌÏÔÇÍÇ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 04 Ε_3.Φλ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Μαΐου 04 ιάρκεια Εξέτασης: ώρες A δ Α δ Α3 α Α4 γ Α5 (α)λ, (β)σ, (γ)λ, (δ)λ, (ε)σ ΘΕΜΑ Β Β. () α ΑΠΑΝΤΗΣΕΙΣ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 04 Ε_3.Φλ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Μαΐου 04 ιάρκεια Εξέτασης: ώρες A δ Α δ Α3 α Α4 γ Α5 (α)λ, (β)σ, (γ)λ, (δ)λ, (ε)σ ΘΕΜΑ Β Β. () α ΑΠΑΝΤΗΣΕΙΣ
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ
 ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ Πολυχρόνης Καραγκιοζίδης Mcs χημικός www.polkarag.gr Μετά τη δημιουργία του Σύμπαντος 380.000 έτη 6000 ο C Τα ηλεκτρόνια μπορούν να συνδεθούν με τα πρωτόνια ή τους άλλους
ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ Πολυχρόνης Καραγκιοζίδης Mcs χημικός www.polkarag.gr Μετά τη δημιουργία του Σύμπαντος 380.000 έτη 6000 ο C Τα ηλεκτρόνια μπορούν να συνδεθούν με τα πρωτόνια ή τους άλλους
ΜΗΧΑΝΙΚΗ ΠΕΤΡΕΛΑΙΩΝ ΚΕΦΑΛΑΙΟ 9 Μελέτες Περίπτωσης
 ΜΗΧΑΝΙΚΗ ΠΕΤΡΕΛΑΙΩΝ ΚΕΦΑΛΑΙΟ 9 Μελέτες Περίπτωσης Μελέτη Περίπτωσης - Εφαρµογή Μεθόδου Buckley-Leverett στη ευτερογενή Παραγωγή Πετρέλαιο εκτοπίζεται από νερό σε µια παραγωγική ζώνη η οποία είναι οριζόντια.
ΜΗΧΑΝΙΚΗ ΠΕΤΡΕΛΑΙΩΝ ΚΕΦΑΛΑΙΟ 9 Μελέτες Περίπτωσης Μελέτη Περίπτωσης - Εφαρµογή Μεθόδου Buckley-Leverett στη ευτερογενή Παραγωγή Πετρέλαιο εκτοπίζεται από νερό σε µια παραγωγική ζώνη η οποία είναι οριζόντια.
Εξέταση Φεβρουαρίου (2011/12) στο Μάθηµα: Γεωργικός Πειραµατισµός. Ζήτηµα 1 ο (2 µονάδες) Για κάθε λανθασµένη απάντηση δεν λαµβάνεται υπόψη µία σωστή
 Σειρά Β Εξέταση Φεβρουαρίου (0/) στο Μάθηµα: Γεωργικός Πειραµατισµός Θεσσαλονίκη: 4/0/0 Επώνυµο Όνοµα Αρ. Μητρώου Κατεύθυνση Ζήτηµα ο ( µονάδες) Για κάθε λανθασµένη απάντηση δεν λαµβάνεται υπόψη µία σωστή
Σειρά Β Εξέταση Φεβρουαρίου (0/) στο Μάθηµα: Γεωργικός Πειραµατισµός Θεσσαλονίκη: 4/0/0 Επώνυµο Όνοµα Αρ. Μητρώου Κατεύθυνση Ζήτηµα ο ( µονάδες) Για κάθε λανθασµένη απάντηση δεν λαµβάνεται υπόψη µία σωστή
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ 148
 ΚΥΜΤΙΚΗ - ΟΠΤΙΚΗ 48 3 ΦΙΝΟΜΕΝΟ DOPPLER Το φαινόµενο Doppler αναφέρεται γενικά στη µεταβολή της συχνότητας των κυµάτων που αντιλαµβάνεται ένας παρατηρητής ως προς τη συχνότητα που εκπέµπει µια πηγή όταν
ΚΥΜΤΙΚΗ - ΟΠΤΙΚΗ 48 3 ΦΙΝΟΜΕΝΟ DOPPLER Το φαινόµενο Doppler αναφέρεται γενικά στη µεταβολή της συχνότητας των κυµάτων που αντιλαµβάνεται ένας παρατηρητής ως προς τη συχνότητα που εκπέµπει µια πηγή όταν
Σύγχρονη Φυσική : Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων 11/04/16
 Σύγχρονη Φυσική - 06: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων /04/6 Διάλεξη 0: Πυρηνοσύνθεση Εισαγωγή Ένας από τους πλέον ενδιαφέροντες κλάδους της πυρηνικής φυσικής είναι ο τομέας της πυρηνικής
Σύγχρονη Φυσική - 06: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων /04/6 Διάλεξη 0: Πυρηνοσύνθεση Εισαγωγή Ένας από τους πλέον ενδιαφέροντες κλάδους της πυρηνικής φυσικής είναι ο τομέας της πυρηνικής
12ο ΓΕΛ ΠΕΙΡΑΙΑ Οµάδα Α. Στις παρακάτω ερωτήσεις να επιλέξετε το γράµµα που αντιστοιχεί στη σωστή απάντηση:
 12ο ΓΕΛ ΠΕΙΡΑΙΑ Οµάδα Α ΔΙΑΓΩΝΙΣΜΑ Α ΤΕΤΡ/ΝΟΥ ΣΤΗ ΦΥΣΙΚΗ Ονοµατεπώνυµο: Τµήµα: Ηµεροµηνία: 17/12/2010 Ζήτηµα 1ο Στις παρακάτω ερωτήσεις να επιλέξετε το γράµµα που αντιστοιχεί στη σωστή απάντηση: 1) Μια
12ο ΓΕΛ ΠΕΙΡΑΙΑ Οµάδα Α ΔΙΑΓΩΝΙΣΜΑ Α ΤΕΤΡ/ΝΟΥ ΣΤΗ ΦΥΣΙΚΗ Ονοµατεπώνυµο: Τµήµα: Ηµεροµηνία: 17/12/2010 Ζήτηµα 1ο Στις παρακάτω ερωτήσεις να επιλέξετε το γράµµα που αντιστοιχεί στη σωστή απάντηση: 1) Μια
Κεφάλαιο 2 ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Κεφάλαιο ο ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της συνάρτησης και μελετήσαμε ορισμένες βασικές συναρτήσεις. Στο κεφάλαιο αυτό θα μελετήσουμε στη γενική τους μορφή ιδιότητες
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
