Χρήση του προγράμματος Gambit για την επίλυση προβλημάτων θεωρίας παιγνίων
|
|
|
- Διάβολος Καψής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Χρήση του προγράμματος Gambit για την επίλυση προβλημάτων θεωρίας παιγνίων ΔΗΜΟΠΟΥΛΟΥ ΦΩΤΕΙΝΗ-ΓΕΩΡΓΙΑ Α.Μ.9627 ΣΑΒΕΤΑ ΙΝΤΡΙΖΙ Α.Μ ΕΠΟΠΤΕΥΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ: ΒΑΣΙΟΥ ΓΕΩΡΓΙΑ Πάτρα,
2 ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΛΗΨΗ... 4 ABSTRACT... 5 ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ... 6 ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Ιστορική Αναδρομή Σκοπός Θεωρίας Παιγνίων Βασικές Έννοιες Θεωρίας Παιγνίων... 7 ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΡΟΓΡΑΜΜΑ GAMBIT Ιστορική Αναδρομή Τι είναι το Gambit Βασικά Χαρακτηριστικά του Gambit Γραφικό περιβάλλον Μειονεκτήματα του Gambit Μορφές αρχείων Εγκατάσταση του προγράμματος ΚΕΦΑΛΑΙΟ ΤΡΙΤΟ ΑΝΑΛΥΣΗ ΠΡΟΓΡΑΜΜΑΤΟΣ Γενική διάταξη κύριου παραθύρου Αποδόσεις και πιθανότητες στο Gambit Παιχνίδια παιγνίου εκτεταμένης μορφής Δημιουργία ενός νέου παιχνιδιού εκτεταμένης μορφής Προσθήκη κινήσεων Αντιγραφή και μετακίνηση υποδένδρων Αφαίρεση μερών από παιχνίδι μορφής δέντρου Διαχείριση πληροφοριών Αποτελέσματα και αποδόσεις Έλεγχος διάταξης ενός δέντρου Παιχνίδια στρατηγικής Πλοήγηση σε ένα στρατηγικό παιχνίδι παιγνίου
3 3.7.2 Προσθήκη παικτών και στρατηγικών Επεξεργασία αποδόσεων Μελέτη κυριαρχούμενων στρατηγικών και δράσεων Κυριαρχούμενες δράσεις σε παιχνίδι εκτεταμένης μορφής Κυριαρχούμενες στρατηγικές σε παιχνίδι στρατηγικής μορφής Υπολογισμός ισορροπίας Nash Επιλογή των μεθόδων για την εύρεση των ισορροπιών Προβολή προφίλ υπολογιζόμενων ισορροπιών στο παιχνίδι ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα : Δίλημμα των κρατουμένων Παράδειγμα: Διακοπές (Δυναμικό παίγνιο) Παράδειγμα Ποδόσφαιρο( παίγνιο μηδενικού αθροίσματος) Παράδειγμα Αεροπορικές εταιρίες (παίγνιο πλήρους πληροφόρησης) Παράδειγμα επίλυσης παιγνίου με τη μέθοδο της οπισθογενής επαγωγής Παράδειγμα επίλυσης παιγνίου με τη μέθοδο Minimax Παράδειγμα αυτοκινητοβιομηχανίες (Μεικτές στρατηγικές ) ΒΙΒΛΙΟΓΡΑΦΙΑ
4 ΠΕΡΙΛΗΨΗ Το θεματικό αντικείμενο της παρούσας πτυχιακής εργασίας είναι η επίλυση προβλημάτων παιγνίων με τη χρήση του προγράμματος Gambit (έκδοση ),αλλά και η κατανόηση όσον αφορά τις λειτουργίες του προγράμματος. Το πρώτο στάδιο της πτυχιακής είναι η ανάλυση της θεωρίας παιγνίων όπου περιλαμβάνονται μια ιστορική αναδρομή σχετικά με την εξέλιξη της θεωρίας αυτής καθώς επίσης διατυπώνονται ορισμένες από τις βασικότερες έννοιες της. Στη συνέχεια, γίνεται μια εισαγωγή στο πρόγραμμα Gambit, όπου δίνονται πληροφορίες σχετικά με τα βασικά χαρακτηριστικά του το λογισμικού του προγράμματος και το γραφικό περιβάλλον του. Στο επόμενο στάδιο, αναφέρονται αναλυτικά όλες εκείνες οι ενέργειες που «περιστρέφονται» γύρω από την εισαγωγή και την επίλυση τον προβλημάτων παιγνίων. Τέλος, η πτυχιακή αυτή εργασία ολοκληρώνεται με την παρουσίαση και επίλυση ορισμένων παραδειγμάτων στο πρόγραμμα Gambit. 4
5 ABSTRACT The topic of this degree thesis is to solve gambling problems using Gambit program (version) , but also the understanding of the functions of the program. The first part of this degree thesis is the analysis of game theory including a historical overview on the development of this theory. Moreover, there are contained certain basic concepts of gambling theory. Subsequently, there is an introduction to Gambit program, where there are given some information about the main features of the software and the user interface on Gambit program. In the next part includes all these actions that resolve around the inputting and solving the problems of gambling. Finally, this degree thesis concludes with the presentation and resolution of examples in Gambit program. 5
6 ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ 1.1 Ιστορική Αναδρομή Η θεωρία παιγνίων ξεκίνησε ως ένα μαθηματικό υπόδειγμα με στόχο τη διαφώτιση της συμπεριφοράς των ορθολογικών παικτών μέσα σε ένα παίγνιο. Το πρώτο σύγγραμμα «Theory of Games and Economic Behavior» εκδόθηκε από τους John von Neumann και Oscar Morgenstem. Η μεγαλύτερη αδυναμία κατά την αρχή της θεωρίας ήταν απόδοση της βέλτιστης συμπεριφοράς δίχως τον υπολογισμό της αντίδρασης των υπόλοιπων παικτών. Με το πέρας του χρόνου όμως η θεωρία παιγνίων χρησιμοποιείται σε πολλούς τομείς της κοινωνίας. Σημαντικοί θεμελιωτές της είναι οι: John Forbes Nash : επινόησε την λύση ισορροπίας Nash που αφορούσε προβλήματα μη μηδενικού αθροίσματος. Reinhard Selten : δημιούργησε το εναρκτήριο λάκτισμα για την ικανοποιητική λύση προβλημάτων που αφορούσαν δυναμικά παιχνίδια. John Harsanyi : επικεντρώθηκε στα παιχνίδια με μερική πληροφόρηση. Πλέον η θεωρία παιγνίων είναι ένας κλάδος της Μικροοικονομικής που ασχολείται με την ανάλυση της άριστης λήψης αποφάσεων σε ανταγωνιστικές καταστάσεις μέσα στο οικονομικό και κοινωνικό περιβάλλον. 6
7 1.2 Σκοπός Θεωρίας Παιγνίων. Η θεωρία παιγνίων μπορεί να χρησιμοποιηθεί σε διάφορες καταστάσεις και περιπτώσεις όπως η συνεργασία ή η σύγκρουση σε θέματα που αφορούν την πολιτική, τη ψυχολογία, την οικονομία και την κοινωνιολογία.κύριο χαρακτηριστικό των παιγνίων είναι η αλληλεπίδραση των αποφάσεων που λαμβάνονται μεταξύ των παικτών, οι ενέργειες ενός παίκτη καθορίζουν κατά μεγάλο ποσοστό την τύχη των αποφάσεων των υπόλοιπων παικτών. 1.3 Βασικές Έννοιες Θεωρίας Παιγνίων Ορισμός έννοιας παιγνίου. Πρόκειται για μια κατάσταση όπου: α) Ν (>1) άτομα, επιχειρήσεις, κυβερνήσεις, συνδικάτα κλπ.( οι αποκαλούμενοι «παίκτες») κάνουν κάποιες επιλογές με στόχο ο καθένας την ικανοποίηση του συμφέροντος του και β) το αποτέλεσμα για κάθε παίκτη δεν εξαρτάται μόνο από την δική του επιλογή αλλά και από τις επιλογές των υπολοίπων Ν-1 παικτών. 1 Απαραίτητη προϋπόθεση για τη χρήση της θεωρίας παιγνίων είναι το πλήθος των παικτών να είναι περισσότερο από δύο. Ως «παίκτης» ενός παιγνίου μπορεί να είναι ένα φυσικό πρόσωπο μία οργάνωση ή ένα κράτος. Στόχος κάθε παίκτη μέσα σε ένα πρόβλημα παιγνίου είναι μετά την αξιολόγηση της κατάστασης στην οποία βρίσκεται να χρησιμοποιήσει όλα εκείνα τα μέσα που θα παρεμποδίσουν τον αντίπαλο παίκτη να βρεθεί σε πλεονεκτική θέση. Η έκβαση κάθε προβλήματος παιγνίου εξαρτάται από την ικανότητα-προσόντα του κάθε 1 Γιάνης Βαρουφάκης,2007 «Θεωρία Παιγνίων» - Η θεωρία που φιλοδοξεί να ενοποιήσει τις κοινωνικές επιστήμες Εκδόσεις Gutenberg Γιώργος & Κώστας Δάρδανος. 7
8 παίκτη, την εναλλακτική στρατηγική και την τύχη και είναι πάντα κέρδος ή απώλεια. Η αναπαράσταση των παιγνίων γίνεται με δύο τρόπους: 1. Κανονική μορφή μήτρας. 2. Αναλυτική μορφή μέσω δέντρου. Κανονική μορφή μήτρας: Η συνηθέστερη μορφή απεικόνισής παιγνίων γίνεται με την μορφή μήτρας. Σε κάθε γραμμή της μήτρας τοποθετείται η στρατηγική του πρώτου παίκτη ενώ σε κάθε στήλη η στρατηγική του δεύτερου παίκτη. Σε περίπτωση όπου οι παίκτες είναι περισσότεροι από δύο τότε αυξάνονται και οι διστάσει της μήτρας. Αναλυτική μορφή μέσω δέντρου: Η αναλυτική απεικόνισή μέσω δέντρο δίνει μια επιπλέον δυνατότητα για εμφάνιση όλων των λεπτομερειών που έχουν να κάνουν με τις αλληλεπιδράσεις των παικτών. Ενέργειες ορίζονται όλες οι πιθανές κινήσεις που κάνει ένας παίκτης κατά τη διάρκεια ενός παιγνίου. Ισορροπία κατά Nash Ο βραβευμένος με Νόμπελ Οικονομικών John Forbes Nash ήταν αυτός ο οποίος πρόσθεσέ στη θεωρία παιγνίων την σπουδαία ισορροπία κατά Nash. Στην ισορροπία κατά Nash κάθε παίκτης επιλέγει μια στρατηγική που του δίνει την υψηλότερη απόδοση, με δεδομένες τις στρατηγικές των άλλων παικτών που συμμετέχουν στο παίγνιο. 2 Ο ρόλος της στρατηγικής στα παίγνια. 2 D.Besanko R.Braeutigam, 2008, Μικροοικονομική, Εκδόσεις Gutenberg 8
9 Με τον όρο στρατηγική νοείται το σχέδιο που δημιουργείται από έναν παίκτη ώστε να υπερισχύσει ενάντια στους υπόλοιπους ανταγωνιστές-αντιπάλους. Με τον όρο στρατηγικές κινήσεις νοούνται όλες εκείνες οι ενέργειες που κάνει ένας παίκτης κατά την αρχή του παιγνίου με τις οποίες αλλάζει η δικιά του συμπεριφορά αλλά και των αντιπάλων του. Οι κατηγορίες των στρατηγικών είναι: 1. Αμιγής και μικτές 2. Αυστηρά Κυρίαρχες και Ασθενώς κυρίαρχες. 3. Κυριαρχούμενες Αμιγής και μικτές Στρατηγικές: Οι αμιγής στρατηγικές αφορούν τις κινήσεις εκείνες όπου επιλέγονται δίχως τη χρήση κανόνων πιθανοτήτων. Οι μικτές στρατηγικές βασίζονται σε έναν κανόνα επιλογής βάσει της αποτίμησης της πιθανότητας που θα επιφέρει τη νίκη. Ορισμένα παίγνια δεν έχουν ισορροπία κατά Nash στις αμιγής στρατηγικές, αυτό δεν συμβαίνει όμως και στις μικτές στρατηγικές όπου υπάρχει τουλάχιστον μια ισορροπία κατά Nash. Αυστηρά Κυρίαρχες Στρατηγικές: Μια στρατηγική ονομάζεται αυστηρά κυρίαρχη όταν είναι καλύτερη από οποιαδήποτε άλλη που θα μπορούσε να επιλέξει ο παίκτης, ανεξάρτητα από τη στρατηγική που θα επιλέξει ο αντίπαλος παίκτης. Η επιλογή της κυρίαρχης στρατηγικής σε ένα ταυτόχρονο παίγνιο επιφέρει πάντα κέρδος. Επίσης η κατοχή μιας κυρίαρχης στρατηγικής σημαίνει ότι είναι παράλληλα και ισορροπία κατά Nash.Πολλά είναι τα παίγνια όπου δεν προσφέρουν κυρίαρχες στρατηγικές. 9
10 Ασθενώς Κυρίαρχες Στρατηγικές: Ασθενώς κυρίαρχη στρατηγική είναι η στρατηγική, η οποία δίνει σε κάθε παίκτη τουλάχιστον εξίσου καλή απόδοση με κάθε άλλη διαθέσιμη στρατηγική. Κυριαρχούμενες Στρατηγικές: Μια κυριαρχούμενη στρατηγική είναι το αντίθετο μιας κυρίαρχης στρατηγικής. Δηλαδή μια στρατηγική ονομάζεται κυριαρχούμενη όταν ο παίκτης έχει στην διάθεση του μια άλλη στρατηγική με υψηλότερη απόδοση, ανεξάρτητα από τις κινήσεις του αντιπάλου. Στην περίπτωση όπου ο παίκτης έχει περισσότερες από δύο στρατηγικές τότε μπορεί ένας παίκτης να έχει μόνο κυριαρχούμενες στρατηγικές και καμία κυρίαρχη. Σε αντίθετη περίπτωση όπου υπάρχουν μόνο δύο στρατηγικές, τότε μια εκ των οποίον θα είναι κυρίαρχη και η άλλη κυριαρχούμενη. Σε ένα παίγνιο όπου κανένας παίκτης δεν έχει μια κυρίαρχη στρατηγική, η εύρεση των κυριαρχούμενων στρατηγικών ορισμένες φορές βοηθάει στον εντοπισμό της ισορροπίας κατά Nash. Ορισμένοι βασικοί τύποι παιγνίων είναι: 1. Μηδενικού αθροίσματος 2. Διαδοχικά ή ταυτόχρονα παίγνια. 3. Επαναλαμβανόμενα παίγνια. 4. Παίγνια Συνεργασίας ή μη Συνεργασίας. Παίγνια Μηδενικού αθροίσματος: Τα παίγνια μηδενικού αθροίσματος είναι ο πιο απλός τύπος παιγνίων, όπου ο ένας παίκτης κερδίζει ενώ ο αντίπαλος παίκτης χάνει. Για αυτό το λόγο το άθροισμα των αποτελεσμάτων είναι μηδέν διότι το κέρδος του ενός είναι η απώλεια του άλλου. Παίγνια διαδοχικών κινήσεων: Αφορούν τα παίγνια εκείνα όπου περιλαμβάνουν στρατηγικές που διεξάγονται μέσα από διαδοχικές και 10
11 εναλλασσόμενες κινήσεις των παικτών. Διαδοχικές κινήσεις θα μπορούσε να είναι οι κινήσεις σε ένα παιχνίδι σκάκι. Επιπλέον, οι επιλογές ενός παίκτη επηρεάζουν τόσο τις μελλοντικές εναλλακτικές του ίδιου του παίκτη όσο και των αντιπάλων του. Τέλος, σημαντική είναι πρώτη και η τελευταία κίνηση. Η απεικόνιση αυτών των παιγνίων επιτυγχάνεται με την προσομοίωση τους με ένα δέντρο (game tree), στο οποίο απεικονίζονται οι διαφορετικές στρατηγικές που μπορεί να εφαρμόσει κάθε παίκτης σε ένα παίγνιο, καθώς επίσης και η σειρά με την οποία γίνεται η επιλογή αυτών των στρατηγικών. Το δέντρο αποτελείται από τα παρακάτω δομικά μέρη: Κόμβος αφετηρίας-έναρξης Κόμβοι απόφασης Τερματικός κόμβος Κλάδους Μια μέθοδος επίλυσης παιγνίων μέσα από ένα δέντρο είναι η αντίστροφη εισαγωγή. Με τον όρο αντίστροφή εισαγωγή νοείται η διαδικασία εκείνη όπου η επίλυση ξεκινάει από το τέλος του δέντρου του παιγνίου και εντοπίζεται η βέλτιστη απόφαση που θα λάβει ο παίκτης σε κάθε ένα σημείο λήψης απόφασης. Παίγνια ταυτόχρονων κινήσεων: Σε αυτού του τύπου παίγνιων λόγο της ταυτόχρονης δράσης δεν υπάρχει δυνατότητα αναμονής της κίνησης του αντιπάλου. Σε αυτές τις περιπτώσεις ο παίκτης παίρνει αποφάσεις δίχως να γνωρίζει τις αποφάσεις του αντιπάλου αλλά δεν σταματά να υπολογίζει τις επιλογές που έχεις την διάθεση του ο αντίπαλος. Ο τρόπος επίλυσης τέτοιων προβλημάτων είναι η διαγραμματική περιγραφή, η οποία περιλαμβάνει πίνακα με τις ενδεχόμενες αποδόσεις. 11
12 Για παράδειγμα ταυτόχρονες κινήσεις είναι οι προσφορές που γίνονται για παράδειγμα σε ένα διαγωνισμό για την αγορά κάποιου εκθέματος. Επαναλαμβανόμενα παίγνια :Επαναλαμβανόμενα ονομάζονται τα παίγνια εκείνα που παίζονται περισσότερες από μια φορές. Υπάρχουν δύο υποκατηγορίες τέτοιων παιγνίων, αυτά που ολοκληρώνονται μετρά από έναν πεπερασμένο αριθμό γύρων και τα παίγνια που άπειρων γύρων.ως γύρος ορίζεται η κάθε επανάληψη του παιγνίου. Η συμπεριφορά των παικτών σε κάθε παίγνιο είναι τελείως διαφορετική. Επίσης μετά το πέρας κάθε γύρου οι παίκτες ενημερώνονται για τις κινήσεις των αντιπάλων παικτών. Ένα παίγνιο μπορεί να εμπείρως επαναλαμβανόμενο για λόγους όπως η υπομονή των παικτών, η συχνή επικοινωνία μεταξύ τους, ο εύκολος εντοπισμός της εξαπάτησης και το όφελος το οποίο μπορεί να είναι σχετικά μικρό. Παίγνια Συνεργασίας ή μη Συνεργασίας: Με τον όρο συνεργατικά παίγνια νοείται η συνεργασία μεταξύ των παικτών. Η συνεργασία αυτή δεν είναι άτυπη που σημαίνει ότι υπάρχουν δεσμεύσεις για την αποτροπή των παραβιάσεων. Σε αντίθετη περίπτωση σε παίγνια μη συνεργασίας δεν υπάρχει δέσμευση μεταξύ των παικτών, οι οποίο αγωνίζονται για προσωπικό όφελος και μόνο. Ο ρόλος της πληροφορίας στα παίγνια. Πληροφορία είναι κάθε γνωστικό στοιχείο που προέρχεται από την επεξεργασία δεδομένων. Οι πληροφορίες είναι ιδιαίτερα σημαντικές σε ένα παίγνιο διότι καθορίζουν κατά μεγάλο ποσοστό τις κινήσεις του κάθε παίκτη. Το είδος της πληροφόρησης σε ένα παίγνιο μπορεί να είναι: 1. Τέλεια ή ατελής. 12
13 2. Πλήρης ή ελλιπής. Τέλεια ή ατελής Πληροφόρηση: Στα παίγνια τέλειας πληροφόρησης ο παίκτης κατέχει τέλεια πληροφόρηση για τις κινήσεις του αντιπάλου κατά τη διάρκεια όλου του παιγνίου από την αρχή έως και το τέλος. Σε αντίθετη περίπτωση στην ατελή πληροφόρηση ο παίκτης δεν γνωρίζει καμία κίνηση του αντιπάλου που έχει γίνει στο παρελθόν του παιγνίου. Πλήρης ή ελλιπής Πληροφόρηση: Στην περίπτωση της πλήρης πληροφόρησης ο παίκτης γνωρίζει τα πλήρη χαρακτηριστικά του αντιπάλου του. Ενώ στην περίπτωση της ελλιπής πληροφόρησης ο παίκτης δεν γνωρίζει με απόλυτη ακρίβεια τα χαρακτηριστικά του αντιπάλου του. Το μόνο που είναι γνωστό είναι ή ιστορία των παικτών αλλά όχι περαιτέρω χαρακτηριστικά όπως για παράδειγμα η τεχνογνωσία της αντίπαλης επιχείρησης. Θεωρία: Οπισθογενής Επαγωγή. Η μέθοδος της οπισθογενής επαγωγής χρησιμοποιείται για την επίλυση παιγνίων διαδοχικών κινήσεων με πλήρη πληροφόρηση. Λόγω του ότι υπάρχει πλήρης πληροφόρηση, κάθε παίκτης προσαρμόζει την στρατηγική του βάσει των επιλογών του αντιπάλου του. Η εύρεση της ισορροπίας κατά Nash μέσω της οπισθογενής επαγωγής ξεκινάει πάντα από το τελευταίο στάδιο του δενδρογράμματος. 3 Λύση Minimax-Maximin Ο όρος Minimax προστέθηκε στη θεωρία παιγνίων από της John von Neumann. Ο John von Neumann ο οποίος ήταν ένας από τους ιδρυτές της θεωρίας παιγνίων παρουσίασε το 1928 τη λύση Minimax που αφορά μια ευρεία τάξη παιγνίων. Η λύση αυτή αποσκοπεί στη διευκόλυνση λήψης αποφάσεων όπου οι παίκτες λαμβάνουν αποφάσεις ώστε να 3 Robert Gibbons, 2009, Εισαγωγή στη Θεωρία Παιγνίων, Εκδόσεις Gutenberg. 13
14 μειωθεί το πιθανό κέρδος των αντιπάλων τους. Αντίθετα, ο όρος Maximin σημαίνει μεγιστοποίηση της ελάχιστης απόδοσης, ο όρος αυτός χρησιμοποιείται σε παίγνια μη μηδενικού αθροίσματος. 4 ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΡΟΓΡΑΜΜΑ GAMBIT 2.1 Ιστορική Αναδρομή Το πρόγραμμα Gambit δημιουργήθηκε στα μέσα του 1980 από τον Richard McKelvey στο ινστιτούτο τεχνολογίας της California. Ο αρχικός προγραμματισμός έγινε σε γλώσσα Basic ενώ το γραφικό περιβάλλον ήταν ιδιαίτερα απλό. Με τη βοήθεια του Bruce Bell tο 1990 ο αρχικός κώδικας του προγράμματος μετατράπηκε σε γλώσσα C και δόθηκε στο κοινό το έτος 1991 και 1992 με έκδοση Ένα σημαντικό βήμα στην εξέλιξη του Gambit ήταν η βράβευση του από το Εθνικό Ίδρυμα Επιστημών (NSF) της Αμερικής το 1994, με τους McKelvey και McLennan ως κύριους ερευνητές και κύριο προγραμματιστή τον Theodore Turocy. Η δωρεά επιχορήγησε εξολοκλήρου τον επανασχεδιασμό του κώδικα του Gambit σε Αντικειμενοστραφή γλώσσα προγραμματισμού C++. Το γραφικό περιβάλλον έγινε συμβατό με πλατφόρμες με την χρήση των wxwidgets. Η έκδοση 0.94 του Gambit κυκλοφόρησε στα τέλη του καλοκαιριού του 1994, ακολούθησε η έκδοση 0.96 το 1999 και η έκδοση 0.97 το Πλεον από το 2011 μέχρι και το 2014 έχουν κυκλοφορήσει και άλλες εκδόσεις του προγράμματος με τελευταία την έκδοση Αρκετοί όμως ήταν και οι φοιτητές που συνέβαλλαν 4 Γιάνης Βαρουφάκης,2007 «Θεωρία Παιγνίων» - Η θεωρία που φιλοδοξεί να ενοποιήσει τις κοινωνικές επιστήμες Εκδόσεις Gutenberg Γιώργος & Κώστας Δάρδανος. 14
15 στην προσπάθεια του προγραμματισμού, της δοκιμής της λειτουργίας του προγράμματος ακόμα και στην προσθήκη νέων λειτουργιών. Την ίδια περίοδο, ο Bernhard von Strengel από το London School of Economics, έκανε μια σημαντική συμβολή στην εφαρμογή της μεθόδου ακολουθίας που αφορούσε εκτεταμένα παιχνίδια παιγνίων δύο παικτών, καθώς επίσης και στην προσθήκη του κώδικα όπου εντοπίζει τις ισορροπίες σε στρατηγικά παιχνίδια δύο ατόμων καθώς και άλλες συμβουλές σχετικά με την εφαρμογή και την αρχιτεκτονική του δομή. Η ανάπτυξη από τα μέσα του 2000 επικεντρώθηκε σε δύο αντικείμενα. Πρώτον, το γραφικό περιβάλλον υλοποιήθηκε ξανά και εκσυγχρονιστικέ, με στόχο την τήρηση των άριστων αρχών σχεδιασμού αλληλεπίδρασης, ιδιαίτερα σε ότι ό,τι αφορά στη διευκόλυνση της καμπύλης μάθησης των νέων χρηστών του Gambit, οι οποίοι χρησιμοποιούν για πρώτη φορά την θεωρία παιγνίων. Δεύτερον, η εσωτερική αρχιτεκτονική του Gambit ανανεώθηκε ώστε να αυξηθεί η συμβατότητα μεταξύ εκείνων των εργαλείων που παρέχονται από το Gambit και εκείνων που έχουν συνταχθεί ανεξάρτητα. Το Gambit έχει συμμετάσχει στο πρόγραμμα Google Summer of Code τα καλοκαίρια του 2011 και 2012 ως οργανισμός καθοδήγησης. Η Python API, η οποία έγινε μέλος του Gambit 13, αναπτύχθηκε κατά τη διάρκεια εκείνων των καλοκαιριών, χάρη κυρίως στο έργο των Stephen Kunath και Alessandro Andrioni. 2.2 Τι είναι το Gambit Το Gambit είναι ένα σύνολο εργαλείων λογισμικού που έχουν ως σκοπό την επίλυση μη συνεργατικών παιχνιδιών παιγνίου. Περιλαμβάνει ένα γραφικό περιβάλλον αλληλεπίδρασης για τη δημιουργία και ανάλυση γενικών παιχνιδιών σε εκτεταμένη ή στρατηγική μορφή. Η 15
16 γραμμή εντολών στο μενού του προγράμματος περιλαμβάνει τον υπολογισμό της ισορροπίας κατά Nash και άλλες έννοιες -λύσεις στα παιχνίδια. Επίσης υπάρχει μια σειρά από μορφές αρχείων για την αποθήκευση και την επικοινωνία των παιχνιδιών με άλλα εξωτερικά εργαλεία. 2.3 Βασικά Χαρακτηριστικά του Gambit Το πρόγραμμα Gambit προσφέρει μια σειρά από χρήσιμες λειτουργίες, τόσο στον ερευνητή όσο και στον εκπαιδευτή. Διαδραστικό γραφικό περιβάλλον Ανεξάρτητης Πλατφόρμας: Όλα τα χαρακτηριστικά του Gambit είναι διαθέσιμα μέσα από το γραφικό περιβάλλον, το οποίο λειτουργεί με πολλαπλά λειτουργικά συστήματα όπως Windows,Linux και Mac OS X. Το λογισμικό προσφέρει ευέλικτες μεθόδους για τη δημιουργία παιχνιδιών παιγνίου εκτεταμένης και στρατηγικής μορφής. Προσφέρει επίσης μια διεπαφή για την εκτέλεση αλγορίθμων για τον υπολογισμό της ισορροπίας κατά Nash, καθώς και για την απεικόνιση των αποτελεσμάτων σε μορφή κανονική μορφή μήτρας ή σε αναλυτική μορφή μέσω δέντρου. Σημαντική είναι και η ανάλυση της δομής της κυριαρχίας των ενεργειών ή των στρατηγικών στο παιχνίδι παιγνίου μέσω ενός διαδραστικού εργαλείου.to Λογισμικό είναι εξίσου χρήσιμο και εξειδικευμένους ερευνητές, αλλά δίνει περισσότερη έμφαση στον να γίνεται κατανοητό και εύκολα προσβάσιμο σε μαθητές που πραγματοποιούν τα πρώτα μαθήματα πάνω στη θεωρία των παιγνίων. 16
17 Εργαλεία στη γραμμή εντολών για τον υπολογισμό των ισορροπιών. Πιο προηγμένες εφαρμογές συχνά απαιτούν εκτεταμένο υπολογιστικό χρόνο. Όλοι οι αλγόριθμοι στο Gambit είναι κατηγοριοποιημένοι ως ατομικά προγράμματα στη γραμμής εντολών, η λειτουργία των οποίων και η παραγωγή μπορεί να παραμετροποιηθεί. Αυτή η δυνατότητα δίνεται από τη χρήση της γλώσσας προγραμματισμού C++. Επεκτασιμότητα και διαλειτουργικότητα. Τα εργαλεία του Gambit διαβάζουν και επεξεργάζονται μορφές αρχείων κειμένου που είναι τεκμηριωμένα, καθιστώντας τα φορητά μεταξύ των διαφόρων συστημάτων και είναι σε θέση να αλληλοεπιδρούν με εξωτερικά εργαλεία. Επομένως, είναι εύκολο να επεκτείνουν τις δυνατότητες του προγράμματος, για παράδειγμα, την εφαρμογή μιας νέας μεθόδου για τον υπολογισμό της ισορροπίας, την εφαρμογή ενός υπάρχοντος πιο αποτελεσματικά, ή δημιουργώντας νέα εργαλεία για προγραμματισμό, δημιουργία, χειρισμό, και μετατροπή παιχνιδιών παιγνίου, είτε για οικονομετρική ανάλυση. 2.4 Γραφικό περιβάλλον. Το γραφικό περιβάλλον του προγράμματος παρέχει στους χρήστες ένα ολοκληρωμένο περιβάλλον ανάπτυξης με σκοπό τη διευκόλυνση δημιουργίας οπτικών παιχνιδιών παιγνίου και διερεύνησης των βασικών στρατηγικών τους χαρακτηριστικών. Η διαδραστική κατασκευή και ανάλυση των μικρομεσαίων παιχνιδιών είναι ένας κύριος σκοπός του 17
18 γραφικού περιβάλλοντος. Αυτό συμβαίνει διότι ο χρόνος υπολογισμού που απαιτείται για την ανάλυση της ισορροπίας των παιχνιδιών αυξάνεται ραγδαία όσο μεγαλύτερο είναι το παιχνίδι.το γραφικό περιβάλλον είναι ιδανικό για φοιτητές που μαθαίνουν τις βασικές αρχές της θεωρίας των παιγνίων, ή για τους επαγγελματίες που επιθυμούν να αναλύσουν πιο περίπλοκα παιχνίδια παιγνίου. 2.5 Μειονεκτήματα του Gambit. Πάρα τα πλεονεκτήματα το Gambit όπως όλα τα προγράμματα έχει και ορισμένα μειονεκτήματα-περιορισμούς όσον αφορά την εκτέλεση ορισμένων εφαρμογών. Παρακάτω ακολουθεί μια περιγραφή των περιορισμών αυτών. Αφορά παιχνίδια πεπερασμένου χρόνου μόνο. Λόγω της μαθηματικής δομής των πεπερασμένων παιχνιδιών παιγνίου, είναι δυνατόν να γράψει πολλές ρουτίνες γενικής χρήσης για την ανάλυση αυτών των παιχνιδιών. Έτσι, το Gambit μπορεί να χρησιμοποιηθεί σε μία ευρεία ποικιλία εφαρμογών της θεωρίας παιγνίων. Ωστόσο, τα παιχνίδια που δεν είναι πεπερασμένης μορφής, δηλαδή, παιχνίδια στα οποία οι παίκτες μπορούν να επιλέξουν από μια συνέχεια δράσεων, ή στο οποίο οι παίκτες μπορούν να έχουν μια συνέχεια των τύπων, δεν παραδέχονται τις ίδιες μεθόδους γενικής χρήσης. Αφορά μη συνεργατικά παιχνίδια παίγνιου. Το Gambit επικεντρώνεται στην κατηγορία της θεωρίας παιγνίων στα οποία οι κανόνες του παιχνιδιού αναγράφονται ρητά, και στο οποίο οι παίκτες επιλέγουν τις δράσεις τους ανεξάρτητα από τις 18
19 επιλογές των αντίπαλων παικτών. Τα αναλυτικά εργαλεία του προγράμματος επικεντρώνονται κατά κύριο λόγο γύρω στην ισορροπία κατά Nash, και των συναφών εννοιών του περιορισμένου ορθολογισμού, όπως η απάντηση κβαντικής ισορροπίας. Αυτή τη στιγμή το πρόγραμμα Gambit δεν παρέχει καμία αναπαράσταση, ή μέθοδο για ανάλυση παιχνιδιών γραμμένα σε μορφή συνεργασίας. (Θα πρέπει να σημειωθεί ότι ορισμένα προβλήματα σε συνεταιριστική μορφή δεν πάσχουν από υπολογιστική πολυπλοκότητα που επιφέρει η ισορροπία κατά Nash, και έτσι θα μπορούσε οι έννοιες αυτές θα μπορούσε να είναι μια ενδιαφέρουσα μελλοντική κατεύθυνση της ανάπτυξης.) Η ανάλυση μεγάλων παιχνιδιών παιγνίου μπορεί να καταστεί ανέφικτη ιδιαίτερα γρήγορα. Ενώ οι ειδικές κατηγορίες πολυπλοκότητας υπολογισμού ισορροπιών κατά Nash και παρόμοιες έννοιες είναι ένας τομές που βρίσκεται σε συνεχή έρευνα, είναι σαφές ότι, στην τυπική περίπτωση, η ποσότητα του χρόνου που απαιτείται για τον υπολογισμό της ισορροπίας αυξάνεται ταχέως ανάλογα με το μέγεθος του παιχνιδιού. Με άλλα λόγια, είναι αρκετά εύκολο να διατυπωθούν παιχνίδια που θα λάβει το Gambit ιδιαίτερα μεγάλο χρονικό διάστημα για τον υπολογισμό της ισορροπίας του. Υπάρχουν δύο τρόποι για να αντιμετωπιστεί αυτό το πρόβλημα στην πράξη. Ένας τρόπος είναι να προσδιοριστεί η καλύτερη προσέγγιση για την καθοδήγηση της διαδικασίας υπολογισμού της ισορροπίας. Ένας άλλος τρόπος είναι να ωφελιμότητα από γνωστά χαρακτηριστικά του παιχνιδιού για να υπάρξει μια καθοδήγηση της διαδικασία. Και οι δύο αυτές προσεγγίσεις αποτελούν ιδιαίτερο ενδιαφέρον και εμπεριέχονται στην περιοχή της ερευνάς. Αν και σίγουρα δεν θα είναι δυνατό να αναλυθεί κάθε παιχνίδι που κάποιος θα 19
20 ήθελε, υπάρχει η ελπίδα ότι θα το πρόγραμμα Gambit να συνεισφέρει τόσο σε αυτούς τους δύο τομείς της έρευνας, τόσο και στην διάθεση των αποτελεσμάτων από τις μεθόδους που προκύπτουν στους μαθητές και τους επαγγελματίες. 2.6 Μορφές αρχείων. Το λογισμικό του Gambit χειρίζεται πολλές διαφορετικές μορφές αρχείων για την αναπαράσταση των παιχνιδιών. Σε αυτή την υποενότητα περιλαμβάνεται μια σύντομη επισκόπηση των εν λόγω μορφών. Το Gambit έχει για πολλά χρόνια υποστηρίξει δύο μορφές αρχείων για την εμφάνιση των παιχνιδιών, μια για εκτεταμένης μορφής παιχνίδια (συνήθως χρησιμοποιώντας το όνομα του αρχείου με επέκταση.efg) και μια για παιχνίδια στρατηγικής (συνήθως χρησιμοποιώντας το όνομα του αρχείου με επέκταση.nfg). Αυτές οι μορφές αρχείων αναγνωρίζεται από όλες τις εκδόσεις του. Με την έκδοση xx, το λογισμικό διαβάζει και γράφει τώρα μια νέα μορφή αρχείου, το οποίο αναφέρεται ως "βιβλίο εργασίας Gambit." Αυτή η εκτεταμένη μορφή αρχείου περιλαμβάνει όχι μόνο την αναπαράσταση του παιχνιδιού, αλλά και πρόσθετες πληροφορίες, συμπεριλαμβανομένων των παραμέτρων σε παιχνίδια μορφής δέντρου,την ανάθεση χρωμάτων στους παίκτες, κάθε ισορροπία ή άλλη ανάλυση γίνεται στο παιχνίδι, και ούτω καθεξής. Έτσι, για παράδειγμα, το αρχείο βιβλίου εργασίας μπορεί να χρησιμοποιηθεί για την αποθήκευση της ανάλυση του παιχνιδιού. Τα αρχεία αυτά έχουν επέκταση.gbt Το λογισμικό αναγνωρίζει αρχεία σε όλες τις τρεις μορφές:.gbt,.efg, και.nfg. Οι εντολές "Αποθήκευση" και "Αποθήκευση ως", όμως, αποθηκεύουν πάντα σε μορφή (.gbt). Για να γίνει αποθήκευση του παιχνιδιού σε εκτεταμένη (.efg) ή στρατηγική μορφή (.nfg), θα πρέπει να 20
21 επιλεγεί «Export» από την επιλογή «File» στο κεντρικό μενού του προγράμματος. Αυτό είναι χρήσιμο στη διασύνδεση με τις παλαιότερες εκδόσεις του Gambit, με άλλα εργαλεία που διαβάζουν και να γράφουν τα έντυπα αυτά. Οι χρήστες που ενδιαφέρονται κυρίως για τη χρήση του Gambit μόνο μέσω του γραφικού περιβάλλοντος ενθαρρύνονται να χρησιμοποιούν αρχεία με επέκταση (.gbt). Δεδομένου ότι είναι μια νέα μορφή, η μορφή βιβλίου εργασίας Gambit είναι ακόμα υπό ανάπτυξη και μπορεί να αλλάξει σε λεπτομέρειες. Εννοείται ότι οι νεότερες εκδόσεις του γραφικού περιβάλλοντος θα εξακολουθούν να είναι σε θέση να διαβάζουν τα αρχεία από το βιβλίο εργασίας γραμμένο σε παλαιότερες μορφές. 2.7 Εγκατάσταση του προγράμματος. To πρόγραμμα Gambit λειτουργεί σε ετήσιο κύκλο, συγκεκριμένα μια νέα έκδοση κυκλοφορεί κάθε Αύγουστο. Ο μεγαλύτερος αριθμός έκδοσης είναι ίσος με τα δύο τελευταία ψηφία του έτους κατά το οποίο η έκδοση είναι σταθερή. Η τρέχουσα σταθερή έκδοση του προγράμματος είναι η , η οποία έγινε διαθέσιμη τον Αύγουστο του Η λήψη του μπορεί να γίνει από το Sourceforge. Ο πλήρης πηγαίος κώδικας είναι διαθέσιμος, ο οποίος είναι μεταγλωττισμένος ώστε να λειτουργεί και σε συστήματα Microsoft Windows και Mac OS X Η σταθερή έκδοση είναι κατάλληλη για τη διδασκαλία και την χρήση από τους σπουδαστές καθώς επίσης και για τους επαγγελματίες που απαιτούν μια έκδοση με API( Διεπαφή προγραμματισμού εφαρμογών). Επιπλέον εκδόσεις του Gambit 13 θα κυκλοφορήσουν για τη συντήρηση και τη διόρθωση σφαλμάτων. 21
22 Η νέα σειρά ανάπτυξης/έρευνας Gambit 14 που κυκλοφορεί απευθύνεται σε προγραμματιστές, ερευνητές που εργάζονται σε αλγορίθμους που έχουν να κάνουν με τη θεωρία παιγνίων, γενικότερα σε εκείνους που απαιτούν τις τελευταίες εφαρμογές για το ερευνητικό τους έργο. Δίνεται επίσης δυνατότητα εγκατάστασης παλαιότερων εκδόσεων του προγράμματος μέσα από την ιστοσελίδα : ΚΕΦΑΛΑΙΟ ΤΡΙΤΟ ΑΝΑΛΥΣΗ ΠΡΟΓΡΑΜΜΑΤΟΣ Το γραφικό περιβάλλον του Gambit παρέχει ένα "ολοκληρωμένο περιβάλλον ανάπτυξης" με σκοπό τη διευκόλυνση της οπτικής δημιουργίας παιχνιδιών παιγνίου και τη διερεύνηση των τα βασικών στρατηγικών χαρακτηριστικών τους. Κύριος στόχος του γραφικού περιβάλλοντος είναι η διαδραστική κατασκευή και η ανάλυση των μικρομεσαίων παιχνιδιών, διότι όπως ο χρόνος υπολογισμού που απαιτείται για την ανάλυση της ισορροπίας των παιχνιδιών αυξάνεται ραγδαία ανάλογα με το μέγεθος του παιχνιδιού. Το γραφικό περιβάλλον είναι ιδανικό για φοιτητές μαθαίνουν τις βασικές αρχές της θεωρίας των παιγνίων, ή για τους επαγγελματίες που επιθυμούν να επιλύσουν πιο εξειδικευμένα παιχνίδια. 3.1 Γενική διάταξη κύριου παραθύρου. 22
23 Το πλαίσιο που παρουσιάζει ένα παιχνίδι αποτελείται από δύο κύρια τμήματα, τον κύριο πίνακα και στη δεξιά μεριά τη γραφική παρουσίαση του παιχνιδιού. Όπως φαίνεται και στην παρακάτω εικόνα στην περίπτωση αυτή η απεικόνιση γίνεται με τη μορφή δέντρου. Στην αριστερή μεριά του παραθύρου εμφανίζονται οι δύο παίκτες Player 1 και Player 2, όπου ο καθένας έχει και από ένα διαφορετικό χρώμα για τον συμβολισμό των κινήσεων και των απολαβών. Το χρώμα καθώς και το όνομα κάθε παίκτη μπορούν να αλλάξουν κάνοντας διπλό κλικ στο χρώμα και στο όνομα αντίστοιχα. Η γραμμή εντολών περιλαμβάνει τις παρακάτω επιλογές: File: περιλαμβάνονται λειτουργίες όπως η δημιουργία νέου παιχνιδιού εκτεταμένης ή στρατηγικής μορφής, άνοιγα ήδη 23
24 υπάρχοντος παιχνιδιού, αποθήκευση, μετατροπή του αποθηκευμένου αρχείου σε διαφορετικές εκδόσεις :(Bmp, Jpeg,Png,PostScript Svg) εκτύπωση, κλείσιμο και έξοδος από το πρόγραμμα. Edit: περιλαμβάνονται λειτουργίες όπως αναίρεση κάποιας κίνησης, προσθήκη νέου παίκτη, προσθήκη κίνησης, προσθήκη δράσης, επαναφορά, διαγραφή υπόδεντρου, διαγραφή γονέα όσον αφορά τους κόμβους, διαγραφή απόδοσης, κόμβος, κίνηση και τέλος υπάρχει μια επιλογή Game (παιχνίδι) όπου γίνεται επεξεργασία στην ονομασία και το περιεχόμενο του παιχνιδιού. View : περιλαμβάνονται λειτουργίες όπως εμφάνιση προφίλ στρατηγικών του παιχνιδιού και εναλλαγές στην μορφή του παιχνιδιού σε δέντρο και προβολή στρατηγικού παιχνιδιού. Format : περιλαμβάνονται λειτουργίες όπως η προβολή διάταξης ενός παιχνιδιού σε μορφή δέντρου, η επεξεργασία των κόμβων του καθώς και επιλογές όσον αφορά την προβολή των διαγραμμάτων στο πρόγραμμα. Tools: περιλαμβάνονται λειτουργίες όπως η εμφάνιση νέας γραμμής εργαλείων για τον υπολογισμό των κυρίαρχων στρατηγικών καθώς επίσης και δυνατότητα εύρεσης ισορροπιών και κβαντικών ισορροπιών. Help: εμπεριέχονται γενικές πληροφορίες για το πρόγραμμα Gambit. Δύο επιπλέον πάνελ είναι διαθέσιμα στο πρόγραμμα: 1. Επιλέγοντας από το κεντρικό μενού Tools ->Dominance, εναλλάσσεται η εμφάνιση και εμφανίζεται μια νέα γραμμή εργαλείων σε όλη τη κορυφή του παραθύρου. Αυτή η γραμμή εργαλείων ελέγχει την ένδειξη και την εξάλειψη των δράσεων ή των κυρίαρχων 24
25 στρατηγικών. Αυτή η νέα γραμμή εργαλείων χρησιμοποιείται στη διερεύνηση των κυριαρχούμενων στρατηγικών και δράσεων. 2. Επιλέγοντας View-> Profiles ή κάνοντας κλικ στο εικονίδιο View the List of Computed strategy profiles, εναλλάσσεται η λίστα της εμφάνισης των υπολογιζόμενων προφίλ στρατηγικής για το παιχνίδι. 3.2 Αποδόσεις και πιθανότητες στο Gambit. Οι αποδόσεις κάθε παιχνιδιού μπορούν να αναγραφούν ως δεκαδικοί αριθμοί. Το Gambit υποστηρίζει την εκπροσώπηση των εξοφλήσεων μέσω ορθολογικών αριθμών. Για παράδειγμα σε οποιαδήποτε θέση στην οποία μπορεί να εμφανιστεί μια απόδοση ή το αποτέλεσμα ενός εκτεταμένου παιχνιδιού ή μια κατοχύρωση απόδοσης σε ένα στρατηγικό παιχνίδι, το αποτέλεσμα ένα δέκατο μπορεί να αναγραφεί είτε ως.1 ή 1/0. 25
26 Το πλεονέκτημα αυτής της μορφής είναι ότι σε ορισμένες περιπτώσεις το Gambit μπορεί να είναι σε θέση να υπολογίζει ακριβώς τις ισορροπίες. Επιπλέον, ορισμένες μέθοδοι εύρεσης ισορροπιών δημιουργούν καλές αριθμητικές προσέγγισες για τα σημεία ισορροπίας. Για τις μεθόδους αυτές οι υπολογισμένες ισορροπίες αποθηκεύονται σε μορφή κινητής υποδιαστολής. Για να γίνει του αριθμού των δεκαδικών ψηφίων που εμφανίζεται για αυτά τα προφίλ, πρέπει να γίνει κλικ αύξησης δεκαδικών ψηφίων. Για να γίνει αντίστοιχα μείωση των δεκαδικών ψηφίων θα πρέπει να γίνει κλικ στο εικονίδιο μείωσης δεκαδικών ψηφίων. Η αύξηση ή η μείωση των δεκαδικών ψηφίων που εμφανίζονται στο προφίλ στρατηγικού υπολογισμού δεν θα έχει κανένα αποτέλεσμα στο τελικό αποτέλεσμα του παιχνιδιού. 3.3 Παιχνίδια παιγνίου εκτεταμένης μορφής. Το γραφικό περιβάλλον του προγράμματος προσφέρει ένα ευέλικτο σύνολο εργασιών για τη δημιουργία και επεξεργασία γενικών παιχνιδιών παιγνίου εκτεταμένης μορφής Δημιουργία ενός νέου παιχνιδιού εκτεταμένης μορφής. Η δημιουργία ενός νέου παιχνιδιού εκτεταμένης μορφής γίνεται μέσα από τις εντολές File -> New-> Extensive game ή κάνοντας κλικ στο εικονίδιο «new extensive game». 26
27 Το εκτεταμένο παιχνίδι που δημιουργείται είναι ένα απλής μορφής παιχνίδι με δύο παίκτες, που ονομάζονται από προεπιλογή του προγράμματος Player 1 και Player 2. Επιπλέον, τα εκτεταμένα παιχνίδια έχουν μια επιλογή Chance, η οποία χρησιμοποιείται για την αναπαράσταση τυχαίων γεγονότων που δεν ελέγχονται από τις στρατηγικές των παικτών στο παιχνίδι όπως για παράδειγμα η ρίψη ενός ζαριού Προσθήκη κινήσεων. 27
28 Υπάρχουν δύο επιλογές για την προσθήκη κινήσεων σε μια γραφική απεικόνιση τύπου δέντρου: Drag and drop και Insert move dialog. Η προσθήκη των κινήσεων που γίνεται με τη χρήση του drag and drop, γίνεται από το παράθυρο της λίστας των παικτών, σέρνοντας το εικονίδιο που βρίσκεται στα αριστερά του παίκτη,το οποίο θα μπορεί να μετακινηθεί σε κάθε τερματικό κόμβο του δέντρου. Το δέντρο θα επεκταθεί με μια κίνηση για αυτόν τον παίκτη, με δύο δράσεις σε μία κίνηση. Η προσθήκη μια κίνησης για τον «παίκτη» Chance (πιθανότητα), γίνεται με τον ίδιο τρόπο σύροντας το εικονίδιο Dice (ζάρια) που εμφανίζεται στα αριστερά του παίκτη Chance στη λίστα των παικτών. Για τον «παίκτη» πιθανότητα Chance Player οι δύο δράσεις που δημιουργούνται θα πρέπει να δοθεί σε κάθε μία ξεχωριστά μια πιθανότητα με μισή βαρύτητα, όπως φαίνεται και στην παρακάτω εικόνα. Εάν η επιθυμητή κίνηση έχει περισσότερες από δύο δράσεις, μπορούν να προστεθούν συμπληρωματικές ενέργειες σέρνοντας το εικονίδιο του ίδιου παίκτη στον κόμβο της κίνησης. 28
29 1. Κάνοντας κλικ σε κάθε τερματικό κόμβο στο δέντρο και επιλέγοντας Edit ->Insert move, εμφανίζεται το παράθυρο εισαγωγής κίνησης. a) Ο πρώτος έλεγχος καθορίζει τον παίκτη που θα κάνει την κίνηση. Η κίνηση αυτή μπορεί να ανατεθεί σε έναν νέο παίκτη. b) Ο δεύτερος παίκτης επιλέγει τις πληροφορίες με τις οποίες θα προστεθεί η νέα κίνηση. c) Ο τρίτος έλεγχος ορίζει τον αριθμό των δράσεων. Αυτός ο έλεγχος είναι απενεργοποιημένος εκτός αν ο δεύτερος έλεγχος έχει οριστεί σε ένα νέο σύνολο πληροφοριών Αλλιώς, ρυθμίζεται αυτόματα με τον αριθμό των ενεργειών στο επιλεγμένο σύνολο πληροφοριών. Οι δύο παραπάνω μέθοδοι προσθήκης κινήσεων μπορούν να είναι χρήσιμοι σε διαφορετικά πλαίσια. Η προσέγγιση drag and drop είναι λίγο πιο γρήγορη στη χρήση, ειδικά κατά τη δημιουργία δέντρων που έχουν λίγες δράσεις σε κάθε κίνηση. Η προσέγγιση εισαγωγής κίνησης μέσω των εντολών Edit ->Insert move, είναι λίγο πιο ευέλικτη δίνοντας τη δυνατότητα εισαγωγής μιας κίνηση σε ένα απροσδιόριστο παίκτη, μια κίνηση μπορεί να μπορεί να προστεθεί σε ένα υπάρχον σύνολο πληροφοριών και μία κίνηση μπορεί να δοθεί άμεσα σε περσότερες από δύο δράσεις. 29
30 3.3.3 Αντιγραφή και μετακίνηση υποδένδρων. Πολλά παιχνίδια παιγνίου έχουν εκτεταμένες δομές που εμφανίζονται σε πολλά μέρη του δέντρου. Συχνά είναι αποτελεσματικό να δημιουργείται μια φορά η δομή και στη συνέχεια να γίνεται αντιγραφή του όπου αλλού απαιτείται. Το Gambit παρέχει μια ιδιαίτερα βολική δυνατότητα για αυτή τη λειτουργία. Κάνοντας κλικ σε κάθε μη τερματικό κόμβο και σύροντας το σε κάθε τερματικό κόμβο υλοποιείται μια λειτουργία μετακίνησης, η οποία μετακινεί ολόκληρο το υπόδενδρο στο αρχικό μη τερματικό κόμβο στο τερματικό. Όταν η ίδια λειτουργία γίνεται κρατώντας πατημένο του πλήκτρο Ctrl του πληκτρολόγιου, τότε μετατρέπεται σε λειτουργία αντιγραφής. Ολόκληρο το υπόδενδρο στον αρχικό κόμβο αντιγράφεται ξεκινώντας από τον τερματικό κόμβο. Υποστηρίζεται επίσης και η δυνατότητα αντιγραφής υπόδενδρου σε ένα τερματικό κόμβο του υπόδενρου. Σε αυτή την περίπτωση, η λειτουργία της αντιγραφής διακόπτεται όταν φθάσει στο τερματικό κόμβο, για να αποφευχθεί ένας άπειρος βρόγχος. Έτσι αυτό το χαρακτηριστικό μπορεί επίσης να είναι χρήσιμο για τη δημιουργία παιχνιδιών πολλαπλών σταδίων Αφαίρεση μερών από παιχνίδι μορφής δέντρου. Στα παιχνίδια εκτεταμένης μορφής υποστηρίζονται δύο λειτουργίες διαγραφής. Για να γίνει διαγραφή ολόκληρου υπόδενδρου σε ένα κόμβο, θα πρέπει να γίνει κλικ στο κόμβο αυτό και συνέχεια Edit -> Delete subtree. 30
31 Για να γίνει διαγραφή μεμονωμένης κίνησης στο παιχνίδι, θα πρέπει να γίνει κλικ σε ένα από τα «παιδία» του κόμβου και στη συνέχεια Edit -> Delete Parent. Αυτή η λειτουργία διαγράφει το μητρικό κόμβο, καθώς και όλα τα παιδία του εκτός από τον επιλεγμένο κόμβο. Ο επιλεγμένος κόμβος παιδί παίρνει τώρα τη θέση του μητρικού κόμβου στο δέντρο. 3.3 Διαχείριση πληροφοριών ΤΟ Gambit παρέχει διάφορες μεθόδους για τη βοήθεια της διαχείρισης της δομής των πληροφοριών σε ένα παιχνίδι εκτεταμένης μορφής. Κατά τη δημιουργία ενός δέντρου, μπορούν να εισαχθούν νέες πληροφορίες σε μια δεδομένη στιγμή, χρησιμοποιώντας την επιλογή Insert Move (εισαγωγή κίνησης). Επιπλέον, νέες κινήσεις μπορούν να εισαχθούν με την επιλογή drag and drop, κρατώντας πατημένο το πλήκτρο Shift και σέρνοντας έναν κόμβο στο δέντρο. Κατά τη διάρκεια της λειτουργίας της μεταφοράς, ο κέρσορας μετατρέπεται σε εικονίδιο κίνησης. Ρίχνοντας το εικονίδιο αυτό της κίνησης σε έναν άλλο κόμβο τοποθετεί τον κόμβο τοποθετείται ο κόμβος-στόχος στις ίδιες πληροφορίες που έχουν οριστεί σαν κόμβος όπου ξεκίνησε η λειτουργία μεταφοράς. Οι πληροφορίες που ανήκουν σε έναν κόμβο μπορούν επίσης να επεξεργαστούν μέσα από την επιλογή Edit-> Node. Έτσι εμφανίζεται το παράθυρο ιδιοτήτων κόμβου. Οι πληροφορίες θέτουν προκαθορισμένες επιλογές στις τρέχουσες πληροφορίες όπου ανήκει ο κόμβος επίσης εμπεριέχεται μια λίστα από όλες τις άλλες πληροφορίες του παιχνιδιού, οι οποίες είναι συμβατές με τον κόμβο. Επιπλέον, ο κόμβος μπορεί να μετακινηθεί σε ένα νέο σύνολο πληροφοριών που 31
32 καθορίζονται από τη ρύθμιση της αναπτυσσόμενης λίστα για το νέο σύνολο των πληροφοριών εισόδου. Κατά τη δημιουργία παιχνιδιού τύπου δέντρου, χρησιμοποιώντας την προσέγγιση Dart-and-drop για την αντιγραφή τμημάτων του δέντρου, οι κόμβοι που δημιουργούνται στο αντίγραφο του υποδένδρου παραμένουν στις ίδιες πληροφορίες που με τις αντίστοιχες των κόμβων του αρχικού υπόδενρου. Σε πολλές περιπτώσεις, όμως, τα δέντρα αυτά διαφέρουν ως προς τις διαθέσιμες πληροφορίες για μερικούς ή όλους τους παίκτες. Για να συμβάλει στην επιτάχυνση της διαδικασίας προσαρμογής της πληροφορίας το Gambit προσφέρει μια λειτουργία «αποκάλυψη», η οποία σπάει σύνολα δεδομένων με βάση τη δράση τους σε ένα συγκεκριμένο κόμβο. Κάνοντας κλικ σε έναν κόμβο στον οποίο τα μέτρα που ελήφθησαν πρόκειται να γίνουν γνωστά στη συνέχεια σε άλλους παίκτες, και επιλέγοντας Edit-> Reveal, εμφανίζεται ένα παράθυρο με τη λίστα των παικτών στο παιχνίδι. Επιλέγοντας τα πλαίσια δίπλα στους παίκτες που τηρούν το αποτέλεσμα της κίνησης στον κόμβο, και κάνοντας κλικ στο OK, οι πληροφορίες στους κόμβους κάτω από τον επιλεγμένο ρυθμίζονται με βάση την επιλεγμένη ενέργεια σε αυτόν τον κόμβο. 3.5 Αποτελέσματα και αποδόσεις. ΤΟ Gambit υποστηρίζει την προδιαγραφή των αποδόσεων σε κάθε κόμβο σε ένα παιχνίδι μορφής δέντρου, είτε είναι τερματικός είτε όχι. Στην περίπτωση αυτή, το αποτέλεσμα σε κάθε κόμβο είναι μηδέν σε όλους τους παίκτες. Στην περίπτωση όπου κάθε κόμβος που δημιουργείται δεν περιέχει κάποια απόδοση, τότε αποτέλεσμα τους είναι μηδέν για όλους τους παίκτες. Οι περιπτώσεις αυτές αναφέρονται 32
33 παιχνίδια μορφής δέντρου με την παρουσία ενός (υ) χρώματος ανοιχτό γκρι στην αριστερή μεριά κάθε κόμβου. Για τη ρύθμιση των αποδόσεων σε έναν κόμβο, θα πρέπει να γίνει διπλό κλικ στην ένδειξη (u) στα δεξιά του κόμβου. Έτσι δημιουργείται μια νέα έκβαση στον κόμβο, με απόδοση μηδέν για όλους τους παίκτες, και εμφανίζεται ένας συντάκτης για τη ρύθμιση της απόδοσης του πρώτου παίκτη. Η απολαβή σε έναν παίκτη για ένα αποτέλεσμα μπορεί να επεξεργαστεί με διπλό κλικ στην καταχώρηση πληρωμής. Η ενέργεια αυτή δημιουργεί ένα στοιχείο ελέγχου επεξεργασίας κειμένου στο οποίο η πληρωμή για τον εν λόγω παίκτης μπορεί να τροποποιηθεί. Η επεξεργασία της πληρωμής μπορεί να γίνει αποδεκτή πατώντας το πλήκτρο Εnter. Επιπλέον, η αποδοχή της πληρωμή γίνεται πατώντας το πλήκτρο Tab και οι δύο αλλαγές κατοχυρώνονται στην πληρωμή του παίκτη. Τα αποτελέσματα μπορούν επίσης να μετακινηθούν ή να αντιγραφούν χρησιμοποιώντας τη λειτουργία drag-and-drop. Κάνοντας αριστερό κλικ και σέρνοντας ένα αποτέλεσμα σε έναν άλλο κόμβο, τότε κινείται το αποτέλεσμα από τον αρχικό κόμβο στον κόμβο-στόχο. Η αντιγραφή του αποτελέσματος μπορεί να επιτευχθεί με τον ίδιο τρόπο, ενώ κρατώντας πατημένο το πλήκτρο Control (Ctrl) στο πληκτρολόγιο. Όταν γίνεται χρήση της λειτουργίας της αντιγραφής που περιγράφεται παραπάνω, γίνεται εκχώρηση των ίδιων αποτελεσμάτων στους εμπλεκόμενων κόμβους. Ως εκ τούτου, εάν στη συνέχεια οι αποδόσεις για το αποτέλεσμα έχουν εισαχθεί, τότε οι αποδόσεις και στους δύο κόμβους θα τροποποιηθούν. Για να γίνει αντιγραφή του αποτελέσματος με τέτοιο τρόπο ώστε το αποτέλεσμα στον κόμβο-στόχος να είναι διαφορετικό αποτέλεσμα από αυτό της πηγής, αλλά με τις ίδιες απολαβές, θα πρέπει να είναι πατημένο το πλήκτρο Shift, αντί του 33
34 πλήκτρου Control (Ctrl) κατά τη μετακίνηση. Για να γίνει αφαίρεση ενός αποτελέσματος από έναν κόμβο,θα πρέπει να γίνει κλικ στον κόμβο και επιλογή Edit -> Remove Outcome. 3.6 Έλεγχος διάταξης ενός δέντρου. Το Gambit εφαρμόζει ένα αυτόματο σύστημα διάταξης παιχνιδιών παιγνίου σε μορφή δέντρου, το οποίο παρέχει γενικά αξιόπιστα αποτελέσματα για τα περισσότερα παιχνίδια. Η ρύθμιση τους μπορεί να γίνει μέσα από τις επιλογές Format -> Layout. Οι παράμετροι διάταξης οργανώνονται σε τρείς καρτέλες. Η πρώτη καρτέλα με τίτλο Nodes (κόμβοι), ελέγχει το μέγεθος, την τοποθεσία και την απόδοση των κόμβων στο δέντρο. Οι κόμβοι μπορεί να δηλώνονται με πέντε διαφορετικά σχήματα: μία οριζόντια γραμμή, κουτί, διαμάντι, άδειος κύκλος και γεμάτος κύκλος. Τα σχήματα αυτά μπορούν να ρυθμιστούν ανεξάρτητα για να διακρίνουν την πιθανότητα και τους τερματικούς κόμβους από τους κόμβους των παικτών. 34
35 Η δεύτερη καρτέλα με τίτλο Branches (κλαδιά ),ελέγχει την εμφάνιση των κλαδιών του δέντρου. Ο παραδοσιακός τρόπος του Gambit για την κατάρτιση των κλαδιών είναι μια προσέγγιση fork-tine από το στην οποία υπάρχει ένα επίπεδο μέρος στο τέλος κάθε κλαδιού στο οποίο εμφανίζονται ετικέτες. Εναλλακτικά τα κλαδιά μπορούν να ενσωματωθούν σχεδιάζοντας ευθείες γραμμές μεταξύ των κόμβων. 35
36 Τέλος, η τρίτη καρτέλα με τίτλο Information Sets (Σύνολο πληροφοριών) απεικονίζει το σύνολο των πληροφοριών. Οι πληροφορίες μπορούν να τροποποιηθούν χρησιμοποιώντας μια ενιαία γραμμή για τη σύνδεση των κόμβων. Η χρήση των γραμμών για τη σύνδεση των κόμβων μπορεί να οδηγήσει σε μια πιο συμπαγή αναπαράσταση του δέντρου όπου υπάρχουν πολλά σύνολα πληροφοριών σε μια ίδια οριζόντια θέση. Η διάταξη του δέντρου μπορεί να είναι τέτοια ώστε τα μέλη της ίδιας ομάδας να εμφανίζονται σε διαφορετικές οριζόντιες θέσεις στο δέντρο. Σε μια τέτοια περίπτωση, από προεπιλογή του προγράμματος σχεδιάζεται ένα οριζόντιο βέλος που δείχνει από την δεξιά ή την αριστερή μεριά, τη συνέχιση του συνόλου των πληροφοριών. Αυτού του τύπου οι συνδέσεις μπορούν να απενεργοποιηθούν θέτοντας πληροφορίες στους παίκτες μόνο όταν βρίσκονται σε ίδιο επίπεδο. 36
37 3.7 Παιχνίδια στρατηγικής To Gambit προσφέρει πλήρη υποστήριξη στην κατασκευή και το χειρισμό παιχνιδιών στρατηγική μορφής. Για τα παιχνίδια εκτεταμένης μορφής, το Gambit υπολογίζει αυτόματα το αντίστοιχο μειωμένο στρατηγικό παιχνίδι. Για να εμφανιστεί το μειωμένο στρατηγικό παιχνίδι που αντιστοιχεί σε ένα εκτεταμένο παιχνίδι, θα πρέπει να επιλεγεί View -> Strategic game ή να γίνει κλικ στο εικονίδιο στο εικονίδιο Strategic game (στρατηγικό παιχνίδι) στην κεντρική γραμμή του μενού όπου βρίσκονται τα εργαλεία του προγράμματος. Τα παιχνίδια στρατηγικής μορφής υπολογίζονται από το Gambit ως ένα μειωμένο στρατηγικό παιχνίδι ενός εκτεταμένου παιχνιδιού και 37
38 δεν μπορεί να τροποποιηθεί άμεσα. Αντί να γίνεται επεξεργασία του αρχικού εκτεταμένου παιχνιδιού, το Gambit υπολογίζει αυτόματα το στρατηγικό παιχνίδι μετά τις όποιες αλλαγές γίνονται στο εκτεταμένο παιχνίδι. Στρατηγικά παιχνίδια μπορεί επίσης να εισάγονται άμεσα. Για να δημιουργηθεί ένα νέο στρατηγικό παιχνίδι, θα πρέπει να επιλεγεί File - >New -> Strategic game, ή να γίνει κλικ στο εικονίδιο νέου στρατηγικού παιχνιδιού στη γραμμή εργαλείων Πλοήγηση σε ένα στρατηγικό παιχνίδι παιγνίου. Το Gambit εμφανίζει τα στρατηγικά παιχνίδια σε μορφή πίνακα. Όλοι οι παίκτες που έχουν ανατεθεί είναι είτε παίκτες σειράς είτε παίκτες στήλης, και οι αποδόσεις για κάθε καταχώρηση στο στρατηγικό πίνακα του παιχνιδιού αντιστοιχούν στις εξοφλήσεις που αντιστοιχεί στην κατάσταση κατά την οποία όλοι οι παίκτες παίζουν στη σειρά της στρατηγικής που βρίσκονται, και όλοι οι παίκτες στήλης παίζουν τη στρατηγική που καθορίζεται στην εν λόγω στήλη όπου ανήκουν. Η προεπιλεγμένη παρουσίαση των παιχνιδιών στρατηγικής είναι ένας πίνακας που έχει ένα παίκτη γραμμής και έναν παίκτη στήλης. Ωστόσο, το Gambit επιτρέπει μια πιο ευέλικτη εκχώρηση, στην οποία πολλοί παίκτες μπορούν να αποδοθούν στις σειρές και πολλαπλοί παίκτες σε στήλες. Αυτή η δυνατότητα είναι ιδιαίτερα χρήσιμη για παιχνίδια με περισσότερους από δύο παίκτες. Σε έντυπη μορφή, ένα στρατηγικό παιχνίδι τριών παικτών παρουσιάζεται συνήθως ως μια 38
39 συλλογή από πίνακες, με έναν παίκτη να επιλέγει τη γραμμή, τον δεύτερο να επιλέγει τη στήλη, και τον τρίτο να επιλέγει τον πίνακα. Το Gambit παρουσιάζει τέτοια παιχνίδια ιεραρχικά παραθέτοντας τις στρατηγικές ενός ή περισσότερους παικτών και στις γραμμές και στις στήλες. Στο παρακάτω αυτό, ο πρώτος παίκτης Player 1 με κόκκινο χρώμα, έχει τις στρατηγικές που αναφέρονται στις σειρές του πίνακα, και ο δεύτερος παίκτης Player2, ο οποίος εμφανίζεται σε μπλε χρώμα, έχει τις στρατηγικές που αναφέρονται στις στήλες του πίνακα. Η ανάθεση των παικτών σε σειρές και στήλης είναι πλήρως παραμετροποίηση. Η αλλαγή στην αντιστοίχιση του παίκτη, μπορεί να επιτευχθεί σύροντας το εικονίδιο του προσώπου που εμφανίζεται στα αριστερά του ονόματος του παίκτη στη γραμμή εργαλείων του μενού σε οποιαδήποτε από τις περιοχές του πίνακα Προσθήκη παικτών και στρατηγικών. Για να γίνει προσθήκη ενός επιπλέον παίκτη σε ένα παιχνίδι στρατηγικής, θα πρέπει να επιλεγεί Edit-> Add Player ή να γίνει κλικ στο εικονίδιο προσθήκης νέου παίκτη,το οποίο βρίσκεται στην γραμμή εργαλείων του μενού. 39
40 Για να γίνει αντίστοιχα προσθήκη μιας νέας στρατηγικής για έναν παίκτη, θα πρέπει να γίνει κλικ στο εικονίδιο προσθήκης νέας στρατηγικής, το οποίο βρίσκεται στην αριστερή μεριά του ονόματος του παίκτη. Η επεξεργασία του ονόματος κάθε στρατηγικής γίνεται κάνοντας κλικ σε οποιοδήποτε κελί πάνω στο στρατηγικό πίνακα του παιχνιδιού όπου εμφανίζεται μια ετικέτα της στρατηγικής όπως φαίνεται και στην παρακάτω εικόνα. 40
41 3.7.3 Επεξεργασία αποδόσεων. Για να γίνει επεξεργασία των αποδόσεων στον στρατηγικό πίνακα του παιχνιδιού, θα πρέπει να γίνει κλικ στα κελιά του πίνακα. Η ακύρωση οποιασδήποτε επεξεργασίας γίνεται πατώντας από το πληκτρολόγιο το πλήκτρο Escape (Esc), έτσι γίνεται επαναφορά της αρχικής τιμής. Για να επιτευχθεί η επιτάχυνση της εισόδου πολλαπλών αποδόσεων, όπως είναι τυπικό όταν δημιουργείται ένα νέο παιχνίδι παιγνίου, κάνοντας αποδοχή μιας εισόδου αποδοχής μέσου του πλήκτρου Tab, αυτόματα κινείται το στοιχείο που επεξεργάζεται στο επόμενο κελί προς την αριστερή μεριά του πίνακα.αν η απόδοση βρίσκεται στο τελευταίο κελί μιας σειράς τότε η διαδικασία συνεχίζει στην επόμενη σειρά του πίνακα. Εστί η εισαγωγή των αποδόσεων σε ένα παιχνίδι παιγνίου στρατηγικής μορφής, γίνεται γρηγορότερα. 3.8 Μελέτη κυριαρχούμενων στρατηγικών και δράσεων. Επιλέγοντας Tools-> Dominance, εναλλάσσεται η εμφάνιση της γραμμής εργαλείων, η οποία μπορεί να χρησιμοποιηθεί για τη διερεύνηση της δομής των κυριαρχούμενων στρατηγικών και δράσεων. 41
42 3.8.1 Κυριαρχούμενες δράσεις σε παιχνίδι εκτεταμένης μορφής. Στα παιχνίδια εκτεταμένης μορφής, η νέα γραμμή εργαλείων κυριαρχίας, ελέγχει την εξάλειψη των δράσεων που κυριαρχούν υπό ορισμένους ρους. Οι δράσεις μπορούν να εξαλειφθούν με βάση δύο κριτήρια: Αυστηρή κυριαρχία: Η δράση είναι πάντα πιο ασήμαντη από τις υπόλοιπες, ανεξάρτητα από τις πεποιθήσεις στο σύνολο των πληροφοριών. Αυστηρή ή αδύναμη κυριαρχία: Όταν υπάρχει και μια άλλη δράση στο σύνολο των πληροφοριών που είναι πάντα τουλάχιστον τόσο καλή όσο η δράση, και αυστηρά καλύτερα σε ορισμένες περιπτώσεις. Σε γενικές γραμμές, περαιτέρω στάδια στην εξάλειψη δράσεων μπορούν να γίνουν με εκ νέου κάνοντας κλικ στο εικονίδιο επόμενο επίπεδο. Η γραμμή εργαλείων παρακολουθεί τον αριθμό των επιπέδων της εξάλειψης που εμφανίζονται. Το εικονίδιο προηγούμενο επίπεδο κινείται μέχρι ένα επίπεδο εξάλειψης. Η εξάλειψη των πολλαπλών επιπέδων μπορεί να αυτοματοποιηθεί με τη χρήση του fast forward εικονίδιο, το οποίο εξαλείφει επαναληπτικά κυριαρχούμενες ενέργειες μέχρι να μη μπορεί να γίνει καμία περαιτέρω εξάλειψη ενεργειών. Το εικονίδιο προς τα πίσω αποκαθιστά την εμφάνιση στο πλήρες παιχνίδι Κυριαρχούμενες στρατηγικές σε παιχνίδι στρατηγικής μορφής 42
43 Η νέα γραμμή εργαλείων κυριαρχίας λειτουργεί στα παιχνίδια στρατηγικής μορφής με τον ίδιο τρόπο όπως και στα παιχνίδια εκτεταμένης μορφής. Οι στρατηγικές μπορούν να εξαλειφθούν επαναληπτικά με βάση το αν αυτά είναι αυστηρά ή ασθενώς κυριαρχούμενες. Όταν η γραμμή εργαλείων κυριαρχίας φαίνεται, τότε ο στρατηγικός πίνακας περιέχει δείκτες των στρατηγικών που κυριαρχούνται. Επιπλέον, οι αποδόσεις που αντιστοιχούν στις κυριαρχούμενες στρατηγικές εξαλείφονται εμφανίζοντας σε κάθε κελί το σχήμα "Χ". Οι στρατηγικές που κυριαρχούνται ασθενώς,παρουσιάζονται με τον ίδιο τρόπο, εκτός του ότι το σχήμα "Χ" σχηματίζεται με πιο λεπτές γραμμές. Τέλος, κάνοντας κλικ στο εικονίδιο επόμενο επίπεδο, εξαλείφονται οι αυστηρά κυριαρχούμενες στρατηγικές από την οθόνη. Εικόνα: Εξάλειψη κυριαρχούμενων στρατηγικών. 3.9 Υπολογισμός ισορροπίας Nash. Το Gambit προσφέρει ευρεία υποστήριξη για τον υπολογισμό της ισορροπίας κατά Nash τόσο σε εκτεταμένης μορφής παιχνίδια αλλά και στρατηγικής μορφής. Για να ενεργοποιηθούν οι λειτουργίες αυτές τις 43
44 εύρεσης των ισορροπιών θα πρέπει να επιλεγεί Tools-> Equilibrium ή κλικ στο εικονίδιο στη γραμμή εργαλείων., το οποίο αποτελεί συντόμευση και βρίσκεται Επιλογή των μεθόδων για την εύρεση των ισορροπιών. Η διαδικασία του υπολογισμού των σημείων ισορροπίας Nash στα παιχνίδια εκτεταμένης και στρατηγικής μορφής είναι παρόμοια. Αυτή η υποενότητα εστιάζει στην περίπτωση των παιχνιδιών εκτεταμένης μορφής. Η διαδικασία για τα παιχνίδια στρατηγικής είναι ανάλογη, εκτός από τα παιχνίδια εκτεταμένης μορφής με ειδικά χαρακτηριστικά, όπως η εμφάνιση των προφίλ στο δέντρο του παιχνιδιού, η οποία δεν ισχύει. Το Gambit παρέχει καθοδήγηση σχετικά με τις επιλογές για τον υπολογισμό της ισορροπίας Nash σε μια καρτέλα. Οι μέθοδοι που εφαρμόζονται σε ένα συγκεκριμένο παιχνίδι εξαρτώνται από τρία κριτήρια: τον αριθμό των ισορροπιών που πρέπει να υπολογιστούν, ασχέτως αν ο υπολογισμός πρέπει να γίνει σε παιχνίδια εκτεταμένης ή στρατηγικής μορφής, καθώς και στις λεπτομέρειες του παιχνιδιού, όπως για παράδειγμα αν το παιχνίδι έχει δύο ή περισσότερους παίκτες, και αν το παιχνίδι είναι σταθερού ποσού. 44
45 Το πρώτο βήμα για την εύρεση ισορροπίας είναι o καθορισμός του αριθμού των ισορροπιών προς εύρεση. Ορισμένοι αλγόριθμοι υπολογισμού ισορροπιών είναι προσαρμοσμένοι στην εύρεση μιας ενιαίας ισορροπία, ενώ άλλοι προσπαθούν να υπολογίσουν όλο το σύνολο των ισορροπιών. Η πρώτη επιλογή στην καρτέλα υπολογισμού ισορροπιών καθορίζει πόσες ισορροπίες θα πρέπει να υπολογιστούν. Οι επιλογές που διατίθενται είναι ο υπολογισμός μια ισορροπίας Nash, η εύρεση όσο το δυνατόν περισσότερων ισορροπιών και ο υπολογισμός όλων των ισορροπιών. Για ορισμένα παιχνίδια, υπάρχουν αλγόριθμοι που υπολογίζουν πολλές ισορροπίες (σχετικά) αποτελεσματικά, αλλά δεν είναι εγγυούνται την εύρεση όλων των ισορροπιών. Για να απλοποιηθεί η διαδικασία της επιλογής της μεθόδου για τον υπολογισμό των ισορροπιών στην δεύτερη επιλογή, το Gambit παρέχει για κάθε παιχνίδι μεθόδους για τον υπολογισμό ενός, μερικών, και όλων των ισορροπιών Nash, αντίστοιχα. Αυτές οι μέθοδοι επιλέγονται με βάση την εμπειρία ως προς την αποτελεσματικότητα και την αξιοπιστία των μεθόδων, και γενικότερα λειτουργούν αξιόπιστα για 45
46 τα περισσότερα παιχνίδια. Για περισσότερο έλεγχο επί της διαδικασίας, ο χρήστης μπορεί να επιλέξει από το δεύτερη αναπτυσσόμενη λίστα μία από τις κατάλληλες μεθόδους για τον υπολογισμό ισορροπιών. Αυτή η λίστα εμφανίζει μόνο τις μεθόδους που είναι κατάλληλες για το παιχνίδι, με δεδομένη την επιλογή του αριθμού των ισορροπιών που πρέπει να υπολογιστούν. Τέλος, για τα παιχνίδια εκτεταμένης μορφής, υπάρχει η επιλογή του αν θα χρησιμοποιήσει εκτεταμένο ή στρατηγικό παιχνίδι για τον υπολογισμό. Σε γενικές γραμμές, ο υπολογισμός με τη χρήση εκτεταμένου παιχνιδιού προτιμάται, δεδομένου υπάρχει πιο συχνά μια πολύ πιο συμπαγή αναπαράσταση των στρατηγικών χαρακτηριστικών του παιχνιδιού. Ακόμα και για τα παιχνίδια μετρίου μεγέθους, ο υπολογισμός της ισορροπίας μπορεί να είναι μια χρονοβόρα διαδικασία. Το Gambit εκτελεί όλους τους υπολογισμούς στο παρασκήνιο, και εμφανίζει ένα παράθυρο που δείχνει όλα τα σημεία ισορροπίας που έχουν υπολογιστεί μέχρι στιγμής. 46
47 Ο υπολογισμός μπορεί να ακυρωθεί οποιαδήποτε στιγμή κάνοντας κλικ στο εικονίδιο ακυρώσει, η οποία τερματίζει τον υπολογισμό αλλά διατηρεί οποιαδήποτε ισορροπία έχει υπολογιστεί Προβολή προφίλ υπολογιζόμενων ισορροπιών στο παιχνίδι. Μετά τον υπολογισμό των ισορροπιών, εμφανίζεται αυτόματα ένας πίνακας, ο οποίος παρουσιάζει μια λίστα με τις ισορροπίες που έχουν υπολογισθεί. Ο πίνακας αυτός μπορεί να ενεργοποιηθεί επιλέγοντας View->Profiles ή κάνοντας κλικ στο εικονίδιο γραμμή εργαλείων. στη Εάν βρεθούν περισσότερες από μια ισορροπίες, τότε καταγράφονται όλες τις ισορροπίες που βρέθηκαν και ομαδοποιούνται σε με ξεχωριστή λίστα προφίλ, η οποία εμφανίζεται στο επάνω αριστερό μέρος του πίνακα. Στην παραπάνω εικόνα έχει επιλεγεί να εμφανίζεται η πρώτη στήλη προφίλ Ενώ στην κορυφή του πίνακα, αναγράφεται μια σύντομη 47
48 περιγραφή της μεθόδου που χρησιμοποιήθηκε για τον υπολογισμό της ισορροπίας. ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ ΠΑΡΑΔΕΙΓΜΑΤΑ 4.1 Παράδειγμα : Δίλημμα των κρατουμένων Ένα από τα δημοφιλέστερα προβλήματα στη θεωρία παιγνίων είναι αυτό του διλλήματος των κρατουμένων. Συγκεκριμένα, αφορά δύο κρατούμενους, οι οποίοι έχουν συλληφθεί για κάποιο αδίκημα. Οι αστυνομικοί που τους συνέλαβαν δεν έχουν όλα τα απαραίτητα στοιχεία ώστε να φυλακίσουν άμεσα τους κρατούμενους, πράγμα που γνωρίζουν και οι ίδιοι οι κρατούμενοι. Η ανάκριση των κρατούμενων γίνεται σε χωριστά δωμάτια ώστε να μην υπάρχει καμία επικοινωνία μεταξύ τους. Ο κάθε κρατούμενος έχει δύο επιλογές, είτε να ομολογήσει για το αδίκημα και να προδώσει τον συνεργό του, είτε να μην ομολογήσει για το αδίκημα. 48
49 Παρακάτω εμφανίζεται ο πίνακας με τις αποδόσεις κάθε επιλογήςκίνησης για κάθε κρατούμενο. ΚΡΑΤΟΥΜΕΝΟΣ 1 ΚΡΑΤΟΎΜΕΝΟΣ 2 Ομολογία Άρνηση Ομολογία Άρνηση Ανάλυση των αποδόσεων του πίνακα. Αν ομολογήσουν και οι δύο κρατούμενοι τότε η ποινή φυλάκισης θα είναι 5 χρόνια για τον καθένα. Αν δεν ομολογήσει κανένας από τους δύο κρατούμενους τότε η ποινή φυλάκισης θα είναι 1 χρόνος για τον καθένα. Αν ομολογήσει μόνος ένας από τους δύο κρατούμενους τότε ο ίδιος θα αφεθεί ελεύθερος ενώ ο συνεργός του θα λάβει ποινή φυλάκισης 10 ετών. Λύση του προβλήματος με τη χρήση του Gambit. Εφόσον γίνει επιλογή της εκκίνησης του προγράμματος εμφανίζεται το παρακάτω προκαθορισμένο παράθυρο του προγράμματος. 49
50 Στη συνέχεια, μέσα από τις επιλογές Files->New Strategic Game, γίνεται η δημιουργία ενός νέου παιγνίου στρατηγικής μορφής όπως στην παρακάτω εικόνα. 50
51 Επόμενο βήμα είναι η ονομασία του παιχνιδιού που μόλις δημιουργήθηκε μέσα από τις επιλογές Edit -> Game. Στο πλαίσιο Title που εμφανίζεται στο παρακάτω παράθυρο, αναγράφεται η ονομασία του παιχνιδιού,όπου στην προκειμένη περίπτωση είναι το «Δίλλημα Κρατουμένων». Στη συνέχεια, θα πρέπει να δοθούν ονομασίες στα ονόματα των παικτών, στις επιλογές τους καθώς επίσης να εισαχθούν μέσα στον πίνακα τα δεδομένα. Αυτό επιτυγχάνεται κάνοντας κλικ σε κάθε πεδίο που χρειάζεται. 51
52 Υπολογισμός Ισορροπίας κατά Nash. Εφόσον έχουν γίνει οι παραπάνω λειτουργίες για την εισαγωγή του προβλήματος στο Gambit, μπορεί να επιτευχθεί η επίλυση του υπολογίζοντας την ισορροπία κατά Nash. Η ισορροπία Nash υπολογίζεται μέσα από τις επιλογές Tools-> Εquilibrium ή κάνοντας κλικ στο εικονίδιο στην γραμμή εργαλείων του προγράμματος., το οποίο βρίσκεται Μέσα από αυτή την επιλογή εμφανίζεται το παρακάτω παράθυρο. Όπου επιλέγεται Compute all Nash equilibria και with Gambit s recommended method. Οι επιλογές αυτές αφορούν τον υπολογισμό όλων των πιθανών ισορροπιών του παιχνιδιού στην πρώτη περίπτωση και τον υπολογισμό μέσω της προκαθορισμένης μεθόδου του Gambit. 52
53 Επιλέγοντας OK στο παραπάνω παράθυρο γίνεται ο υπολογισμός της ισορροπίας και εμφανίζεται η λύση σε ένα νέο παράθυρο, το οποίο απεικονίζεται στην παρακάτω εικόνα. Υπενθυμίζουμε ότι με κόκκινο χρώμα απεικονίζονται οι επιλογές για τον Κρατούμενο 1 ενώ με μπλε χρώμα οι επιλογές για τον Κρατούμενου 2.Το αποτέλεσμα της αναζήτησης των ισορροπιών είναι η εύρεση μιας μόνο ισορροπίας Nash πράγμα που φαίνεται στο πάνω δεξιά μέρος του παραπάνω παραθύρου. 53
54 Όσον αφορά τις κυρίαρχες στρατηγικές του κάθε κρατούμενου, αυτές συμβολίζονται με τον αριθμό 1 στη δεύτερη γραμμή του νέου πίνακα που εμφανίστηκε. Συγκεκριμένα, κυρίαρχη στρατηγική και για τους δύο κρατούμενους είναι η Άρνηση δηλαδή να μην ομολογήσει κανείς τους για το αδίκημα. 4.2 Παράδειγμα: Διακοπές (Δυναμικό παίγνιο) Το παράδειγμα που θα αναλυθεί και θα επιλυθεί στη συνέχεια, είναι ένα δυναμικό παίγνιο το οποίο περιγράφεται υπό την μορφή δέντρου. Συγκεκριμένα, αφορά ένα ζευγάρι τον Κώστα και την Μαρία, οι οποίοι επιθυμούν να πάνε ένα ταξίδι. Το ταξίδι θα γίνει είτε στο εξωτερικό είτε στο εσωτερικό της Ελλάδας. Ο Κώστας θα είναι αυτός που θα επιλέξει αν το ταξίδι θα γίνει στην Ελλάδα ή στο Εξωτερικό,ενώ η Μαρία θα επιλέξει βάση της επιλογής του συντρόφου της την πόλη ή το νησί όπου θα επισκεφθούν. Εάν ο Κώστας επιλέξει να πάνε στο εξωτερικό τότε η Μαρία θα προτείνει δύο πόλεις, το Παρίσι και το Λονδίνο. Εάν ο Κώστας επιλέξει το ταξίδι να γίνει στην Ελλάδα τότε η Μαρία θα προτείνει να πάνε Στη Σαντορίνη ή στη Μύκονο. Παρακάτω φαίνεται ο πίνακας των αποδόσεων για την ευχαρίστηση που θα εκλάβει ο καθένας από κάθε επιλογή.(όσο μεγάλος είναι ο αριθμός τόσο μεγαλύτερη είναι και η ευχαρίστηση) 54
55 ΚΩΣΤΑΣ ΜΑΡΙΑ Λονδίνο Παρίσι Εξωτερικό Εσωτερικό Να βρεθεί ο προορισμός του ταξιδιού που θα δώσει την μεγαλύτερη ευχαρίστηση στο ζευγάρι. Λύση του προβλήματος με τη χρήση του Gambit. Εφόσον γίνει εκκίνηση του προγράμματος θα πρέπει να δημιουργηθεί ένα νέο παιχνίδι παιγνίου Δυναμικής μορφής μέσα από τις επιλογές File- >New->Extensive Game. Στη συνέχεια εμφανίζεται το παρακάτω παράθυρο όπου μπορεί να γίνει η διαμόρφωση του δενδροδιαγράμματος. 55
56 Προτού γίνουν όμως γίνει η εισαγωγή του προβλήματος στο πρόγραμμα θα πρέπει να δοθεί μια ονομασία στο πρόβλημα μέσα από τις Επιλογές Edit-> Game 56
57 Δημιουργία δενδροδιαγράμματος. Κάνοντας δεξί κλικ στην μαύρη κουκίδα δηλαδή τον πρώτο κόμβο και στη συνέχεια επιλογή Insert move,εμφανίζεται ένα νέο μικρότερο παράθυρο όπου υπάρχουν ορισμένες επιλογές για την εισαγωγή της κίνησης. Το νέο παράθυρο που εμφανίζεται περιλαμβάνει επιλογές όπως επιλογή του παίκτη που θα κάνει την κίνηση καθώς επίσης και την επιλογή του αριθμού των παρακλαδιών που θα εμφανιστούν. Στη συγκεκριμένη περίπτωση την πρώτη κίνηση την κάνει ο Κώστας. Κάνοντας κλικ στη επιλογή ΟΚ εμφανίζεται η κίνηση που δημιουργήθηκε για τον παίκτη Κώστα. 57
58 Στη συνέχεια, ακολουθώντας την ίδια διαδικασία μόνο που αυτή τη φορά οι δύο νέες κινήσεις αφορούν την Μαρία, δημιουργείται ολόκληρο το δενδροδιάγραμμα. Επόμενο βήμα είναι η εισαγωγή των τιμών και η ονομασία κάθε επιλογής, αυτό επιτυγχάνεται κάνοντας κλικ σε κάθε πεδίο που χρειάζεται πάνω στο δενδροδιάγραμμα. 58
59 Υπολογισμός Ισορροπίας κατά Nash. Εφόσον γίνουν οι παραπάνω λειτουργίες για την εισαγωγή του προβλήματος στο Gambit, μπορεί να επιτευχθεί η επίλυση του υπολογίζοντας την ισορροπία κατά Nash. Η ισορροπία Nash υπολογίζεται μέσα από τις επιλογές Tools-> Εquilibrium ή κάνοντας κλικ στο εικονίδιο εργαλείων του προγράμματος., το οποίο βρίσκεται στην γραμμή 59
60 Εφόσον γίνει η επιλογή της εύρεσης της ισορροπίας κατά Nash, εμφανίζεται ένα νέο παράθυρο το οποίο περιλαμβάνει επιλογές όπως ο αριθμός των ισορροπιών που επιθυμούμε να υπολογιστούν. Στην προκείμενη περίπτωση οι επιλογές που θα γίνουν είναι οι εξής: Compute all Nash equilibria (εύρεση όλων των ισορροπιών) With Gambit s recommended method (χρήση προκαθορισμένης μεθόδου υπολογισμού του Gambit) Using the extensive game (χρήση του δυναμικού παιχνιδιού) Εφόσον γίνει κλικ στην επιλογή OK, εμφανίζεται στο κάτω μέρος της ίδιας οθόνης το αποτέλεσμα του προβλήματος. 60
61 Όπως διαπιστώνεται και από την παραπάνω εικόνα, το σημείο ισορροπίας του προβλήματος είναι η επιλογή της Σαντορίνης που δίνει Payoff (απόδοση) δηλαδή ευχαρίστηση 3 μονάδες για τον Κώστα και 4 μονάδες για την Μαρία. 4.3 Παράδειγμα Ποδόσφαιρο( παίγνιο μηδενικού αθροίσματος) Στο παρακάτω παίγνιο αναλύεται η διαφορά που υπάρχει μεταξύ μιας αμιγής και μιας μεικτής στρατηγικής. Το παράδειγμα έχει ως εξής: Σε έναν τελικό ποδοσφαίρου ο αγώνας κρίνεται στον τελευταίο πέναλτι όπου ο παίκτης 1 είναι ο τερματοφύλακας και ο παίκτης 2 αυτός που θα εκτελέσει το πέναλτι. 61
62 Παρακάτω εμφανίζεται ο πίνακας με τις αποδόσεις για κάθε κίνηση: Παίκτης 1 Παίκτης 2 Δεξί σουτ Αριστερό σουτ Εκτίναξη δεξιά Εκτίναξη αριστερά Ανάλυση των αποδόσεων: Αν αποκρούσει ο Παίκτης 1, τότε η απόδοση για την ομάδα του θα είναι πέντε πόντοι. Σε αυτή την περίπτωση η ομάδα του Παίκτη 2 θα αποκομίσει μηδέν βαθμούς. Αν δεν αποκρούσει ο Παίκτης 1 το σουτ,τότε η απόδοση για την αμάδα του θα είναι μηδέν. Σε αυτή τη ν περίπτωση η ομάδα του Παίκτη 2 θα αποκομίσει τους πέντε βαθμούς. Λύση προβλήματος στο Gambit Εφόσον γίνει εκκίνηση του Gambit, επιλέγεται δημιουργία ενός νέου παιγνίου στρατηγικής μορφής μέσα από τις επιλογές Files->New - >Strategic Game 62
63 Στη συνέχεια γίνεται η συμπλήρωση του πίνακα επιλέγοντας κάθε φορά το πεδίο που θα γίνει η εισαγωγή των δεδομένων. Επόμενο βήμα είναι η εύρεση της ισορροπίας κατά Nash μέσα από τις επιλογές Tools-> Εquilibrium ή κάνοντας κλικ στο εικονίδιο οποίο βρίσκεται στην γραμμή εργαλείων του προγράμματος., το 63
64 Μέσα από αυτή την επιλογή εμφανίζεται το παρακάτω παράθυρο. Όπου επιλέγεται Compute all Nash equilibria και with Gambit s recommended method. Οι επιλογές αυτές αφορούν τον υπολογισμό όλων των πιθανών ισορροπιών του παιχνιδιού στην πρώτη περίπτωση και τον υπολογισμό μέσω της προκαθορισμένης μεθόδου του Gambit. Το αποτέλεσμα του παίγνιου αυτού εμφανίζεται στο κάτω μέρος του αρχικού παραθύρου. 64
65 Συμπέρασμα: Το συγκεκριμένο παίγνιο με μια πρώτη ματιά δεν παρουσιάζει καμία ισορροπία κατά Nash. Αυτό συμβαίνει διότι αν ο παίκτης 2 αποφασίσει να κάνει σουτ αριστερά τότε ο παίκτης 1 έχει ως καλύτερη στρατηγική την εκτίναξη στην αριστερή μεριά ενώ εάν ο παίκτης 2 αποφασίσει να κάνει σουτ δεξιά τότε ο παίκτης 1 έχει ως καλύτερη στρατηγική την εκτίναξη δεξιά. Υπενθυμίζοντας ότι: με τον όρο αμιγείς στρατηγική νοείται μια ειδική επιλογή ανάμεσα στις πιθανές κινήσεις σε ένα παίγνιο. Αντίθετα σε μια μεικτή στρατηγική ο παίκτης επιλέγει ανάμεσα σε δύο ή περισσότερες αμιγείς επιλογές σύμφωνα με προκαθορισμένες πιθανότητες. Παρόλο που μερικά παίγνια δεν έχουν ισορροπία κατά Nash στις αμιγείς στρατηγικές, κάθε παίγνιο έχει μια τουλάχιστον ισορροπία κατά Nash στις μεικτές στρατηγικές 5 Έτσι και το παράδειγμα αυτό σύμφωνα με τα αποτελέσματα του Gambit, παρουσιάζει ένα σημείο ισορροπίας στις μεικτές στρατηγικές. Συγκεκριμένα, ο παίκτης 1 θα πρέπει να κάνει σουτ αριστερά με πιθανότητα ½ ή να κάνει σουτ δεξιά με πιθανότητα ½. Αντίστοιχα, ο παίκτης 2 θα πρέπει να εκτιναχθεί αριστερά με πιθανότητα ½ ή δεξιά με πιθανότητα πάλι ½.Συνεπώς, όταν οι παίκτες κάνουν επιλογή των παραπάνω μεικτών στρατηγικών, ο καθένας προσπαθεί να κάνει ό,τι καλύτερο μπορεί με δεδομένες τις ενέργειες του αντιπάλου. Τέλος, αυτό που επισημαίνεται με τις μεικτές στρατηγικές είναι ότι υπάρχει ιδιαίτερη σημασία στο να είναι κάποιος παίκτης μη προβλέψιμος. 5 D.Besanko R.Braeutigam, 2008, Μικροοικονομική, Εκδόσεις Gutenberg 65
66 4.4 Παράδειγμα Αεροπορικές εταιρίες (παίγνιο πλήρους πληροφόρησης) Το παράδειγμα αυτό αγορά δύο ανταγωνιστικές εταιρίες την Aegean και την Ryanair.Οι εταιρίες αυτές ανταγωνίζονται στην αγορά των αεροπορικών εισιτηρίων. Παρακάτω παρουσιάζεται ο πίνακας με τα κέρδη κάθε εταιρίας (σε εκατομμύρια ) για διάφορους συνδυασμούς τιμών που θα μπορούσαν οι δύο εταιρίες να χρεώσουν την τιμή για το δρομολόγιο Αθήνα-Λονδίνο. Ryanair Aegean Λύση του προβλήματος στο Gambit. Εφόσον γίνει εκκίνηση του Gambit, επιλέγεται δημιουργία ενός νέου παιγνίου στρατηγικής μορφής μέσα από τις επιλογές Files->New - >Strategic Game 66
67 Η μετατροπή του αρχικού πίνακα 2Χ2 γίνεται 4Χ4 με τη χρήση του εικονιδίου, το οποίο βρίσκεται στις επιλογές του κάθε παίκτη και έχει ως λειτουργία την προσθήκη στρατηγικής. Στη συγκεκριμένη περίπτωση θα γίνει η χρήση του δύο φορές για κάθε παίκτη. Στη συνέχεια, γίνεται η συμπλήρωση του πίνακα επιλέγοντας κάθε φορά το πεδίο που θα γίνει η εισαγωγή των δεδομένων. Σημείωση: σε τέτοιου είδους προβλήματα που ο πίνακας είναι 4Χ4, τα δεδομένα εισάγονται γρηγορότερα πατώντας κάθε φορά μετά από κάποια εισαγωγή δεδομένου το πλήκτρο Tab ώστε να γίνεται η μεταφορά στο αμέσως επόμενο πεδίο. 67
68 Εφόσον γίνει η κατοχύρωση των δεδομένων στον πίνακα, θα εξετασθεί το ενδεχόμενο αν υπάρχει κυρίαρχη στρατηγική για τις δύο αεροπορικές εταιρίες. Αυτό γίνεται εφικτό μέσα από τις επιλογές Tools - >Dominance. Μετά από την παραπάνω επιλογή εμφανίζεται ο παρακάτω πίνακας, από τον οποίο συμπεραίνεται ότι η αεροπορική εταιρία Ryanair είναι η μονή που έχει κυρίαρχη στρατηγική. Συγκεκριμένα να κοστολογήσει το εισιτήριο για το δρομολόγιο Αθήνα-Λονδίνο στην τιμή των 350. Όσον αφορά την Aegean, η εταιρεία αυτή έχει μια κυριαρχούμενη στρατηγική αυτή της κοστολόγησης στην τιμή των
69 Στη συνέχεια μέσω της επιλογής, η οποία βρίσκεται στη νέα γραμμή εργαλείων που εμφανίζεται, γίνεται η απαλοιφή των κυριαρχούμενων στρατηγικών. Το συμπέρασμα από τον παραπάνω πίνακα είναι ότι η αεροπορική εταιρία Aegean έχει κυρίαρχη στρατηγική την κοστολόγηση του 69
70 εισιτήριο στην τιμή των 255 ενώ οι υπόλοιπες στρατηγικές της, είναι κυριαρχούμενες. Κάνοντας πάλι την ίδια διαδικασία δηλαδή την απαλοιφή των κυριαρχούμενων στρατηγικών μέσω της επιλογής, εμφανίζεται ο παρακάτω τελικός πίνακας με τις δύο κυρίαρχες στρατηγικές της κάθε αεροπορικής εταιρίας. Σημείωση: Η παραπάνω διαδικασία εύρεσης των κυρίαρχων και των κυριαρχούμενων στρατηγικών μπορεί να επιτευχθεί συντομότερα με τη χρήση της επιλογής, η οποία παρουσιάζει κατευθείαν τον τελικό πίνακα δίχως να παρουσιάζει όλους τους προηγούμενους πίνακες. 70
71 Υπολογισμός ισορροπίας κατά Nash. Η επαλήθευση του παραπάνω αποτελέσματος από τη εύρεση των κυρίαρχων στρατηγικών μπορεί να γίνει με τον υπολογισμό της ισορροπίας κατά Nash μέσα από τις επιλογές Tools-> Εquilibrium ή κάνοντας κλικ στο εικονίδιο εργαλείων του προγράμματος., το οποίο βρίσκεται στην γραμμή Μέσα από αυτή την επιλογή εμφανίζεται το παρακάτω παράθυρο. Όπου επιλέγεται Compute all Nash equilibria και with Gambit s recommended method. Οι επιλογές αυτές αφορούν τον υπολογισμό όλων των πιθανών ισορροπιών του παιχνιδιού στην πρώτη περίπτωση και τον υπολογισμό μέσω της προκαθορισμένης μεθόδου του Gambit. Το αποτέλεσμα του παίγνιου αυτού εμφανίζεται στο κάτω μέρος του αρχικού παραθύρου. 71
72 Όπως διαπιστώνεται το σημείο ισορροπίας βρίσκεται όντως στις στρατηγικές 340 για την αεροπορική εταιρία Ryanair και 255 για την αεροπορική εταιρία Aegean. 4.5 Παράδειγμα επίλυσης παιγνίου με τη μέθοδο της οπισθογενής επαγωγής. Οι παίκτες του παιγνίου αυτού είναι οι παίκτης 1 και παίκτης 2, οι οποίοι κατέχουν τις επιλογές Α,Β,Α1,Β1,Α2 και Β2. Το παίγνιο είναι διαδοχικό και πλήρους πληροφόρησης. Ο παίκτης 1 ξεκινώντας έχει τις επιλογές Α και Β, επιλέγοντας Α μπορεί να τερματίσει το παίγνιο αποκομίζοντας όφελος 4 μονάδες και όφελος 0 για τον παίκτη 2. Ο παίκτης 2 λόγω του ότι το παίγνιο είναι πλήρους πληροφόρησης παρατηρεί την επιλογή του παίκτη 1 και πράττει αναλόγως. Συγκεκριμένα, αν ο παίκτης 1 επιλέξει Β τότε επιλέγει Α1 ή Β1, με την επιλογή Α1 προσφέρει όφελος και στους δύο παίκτες 2 μονάδες. 72
73 Στη συνέχεια, ο παίκτης 1 επιλέγει Α2 ή Β2 με την προϋπόθεση ότι οι προηγούμενες επιλογές ήταν οι Β και ή Β1. Οι επιλογές του παίκτη 1 σε αυτό το στάδιο τερματίζουν το παίγνιο. Η επιλογή Α2 προσφέρει στον παίκτη 1 6 μονάδες και 0 μονάδες στον παίκτη 2, ενώ η επιλογή Β2 προσφέρει αντίστοιχα 0 και 4 μονάδες. Οι παραπάνω πληροφορίες σχετικά με τα οφέλη και τις επιλογές των δύο παικτών παρουσιάζονται στο παρακάτω δενδρόγραμμα. Εικόνα: Δενδρόγραμμα παραδείγματος οπισθογενής επίλυσης. Λύση του παιγνίου Όπως είναι ήδη γνωστό από τη θεωρία της οπισθογενής επαγωγής, η επίλυση τέτοιων παιγνίων ξεκινάει από το τελευταίο στάδιο. Στην προκείμενη περίπτωση το τελευταίο στάδιο είναι το τρίτο δηλαδή η δεύτερη κίνηση του παίκτη 1. 73
74 Στο τρίτο στάδιο ο παίκτης 1 έχει να επιλέξει μεταξύ των επιλογών Α2 και Β2, οι οποίες του αποφέρουν όφελος 6 και 0 αντίστοιχα όπου επιλέγει την άριστη επιλογή Α2. Στο δεύτερο στάδιο ο παίκτης 2 προβλέπει ότι εάν το παίγνιο φτάσει στο τρίτο στάδιο τότε ο παίκτης 1 θα επιλέξει την επιλογή Α2, η οποία θα αποφέρει όφελος 0 μονάδες στον παίκτη 2 διότι ο παίκτης 1 έχει το άριστο όφελος των 6 μονάδων. Για αυτό το λόγο,ο παίκτης 2 θα προτιμήσει να επιλέξει την επιλογή Α1, η οποία θα του αποφέρει όφελος 1 μονάδα και θα τερματίσει το παίγνιο παρά να επιλέξει την επιλογή Β2, η οποία θα το αποφέρει όφελος 0 μονάδες. Στο πρώτο στάδιο ο παίκτης 1 διαπιστώνει ότι ένα επιλέξει την επιλογή Β τότε ο παίκτης 2 με τη σειρά του θα επιλέξει την επιλογή Α1, η οποία θα αποφέρει και στους δύο όφελος 2 μονάδων. Εστί, η προτιμότερη δηλαδή η άριστη επιλογή του είναι να τερματίσει το παίγνιο επιλέγοντας της επιλογή Α αποκομίζοντας όφελος 4 μονάδων. Σημείωση: με την οπισθογενής επαγωγή η λύση σε ένα παίγνιο όπως και το παραπάνω μπορεί βρίσκεται και σε ένα ενδιάμεσο στάδιο και όχι απαραίτητα στο πρώτο όπως στην προκείμενη περίπτωση. 4.6 Παράδειγμα επίλυσης παιγνίου με τη μέθοδο Minimax. Το συγκεκριμένο παράδειγμα είναι ένα παίγνιο μηδενικού αθροίσματος όπου δύο παίκτες κατέχουν τις στρατηγικές A1, A2, A3 και B1, B2, B3 αντίστοιχα. Σύμφωνα με το θεώρημα του John von Neumann ισχύει ότι στα παίγνια μηδενικού αθροίσματος «το άθροισμα των αποδόσεων των δύο αντιπάλων για κάθε αποτέλεσμα είναι ίσο με μηδέν.» 74
75 Παρακάτω παρουσιάζεται ο πίνακας των αποδόσεων των στρατηγικών για κάθε παίκτη: Παίκτης 1 Παίκτης 2 Β1 Β2 Β3 Α Α Α Πίνακας αποδόσεων στρατηγικών Λύση παιγνίου Η επίλυση του παραπάνω παιγνίου γίνεται με τη μέθοδο Minimax όπου κάθε παίκτης προσπαθεί να ελαχιστοποιήσει το μέγιστο κέρδος του αντιπάλου του. Συγκεκριμένα, ο παίκτης 1 κάνει τις εξής υποθέσεις: εάν επιλέξει τη στρατηγική Α1 τότε ο παίκτης 2 θα επιλέξει τη στρατηγική Β1, η οποία προκαλεί απώλεια 4 μονάδων στον παίκτη 1. Άρα Min (A1)= -4 εάν επιλέξει τη στρατηγική Α2 τότε ο παίκτης 2 θα επιλέξει πάλι τη στρατηγική Β1, η οποία προκαλεί απώλεια 2 μονάδων στον παίκτη 1. Άρα Min (A2)= -2 εάν επιλέξει τη στρατηγική Α3 τότε ο παίκτης 2 θα επιλέξει τη στρατηγική Β3, η οποία προκαλεί απώλεια 12 μονάδων στον παίκτη 1. Άρα Min (A3)= -12 Άρα, από τα παραπάνω σενάρια ο παίκτης 1 καλείται να διαλέξει εκείνη τη στρατηγική, η οποία θα του αποφέρει την ελάχιστη απώλεια δηλαδή τη στρατηγική Α2=-2 μονάδες. 75
76 Σημείωση: η επιλογή της στρατηγικής Α2 γίνεται μόνο στην περίπτωση όπου ο παίκτης 1 είναι ιδιαίτερα απαισιόδοξος ή αρκετά ρεαλιστής. Αντίθετα, ο παίκτης 2 κάνει και αυτός τις παρακάτω υποθέσεις: εάν επιλέξει τη στρατηγική Β1 τότε ο παίκτης 1 θα επιλέξει τη στρατηγική Α2, η οποία προσφέρει μόνο 2 μονάδες στον παίκτη 2. Άρα Min (B1)= 2 εάν επιλέξει τη στρατηγική Β2 τότε ο παίκτης 1 θα επιλέξει πάλι τη στρατηγική Α2, η οποία προκαλεί απώλεια 4 μονάδων στον παίκτη 2. Άρα Min (B2)= -4 εάν επιλέξει τη στρατηγική Β3 τότε ο παίκτης 1 θα επιλέξει τη στρατηγική Α1, η οποία προκαλεί απώλεια 7 μονάδων στον παίκτη 2. Άρα Min (B3)= -17 Άρα, από τα παραπάνω σενάρια ο παίκτης 2 καλείται να διαλέξει εκείνη τη στρατηγική, η οποία θα του αποφέρει την ελάχιστη απώλεια δηλαδή τη στρατηγική Β1=2 μονάδες. Σίφωνα με τον John von Neumann στα παίγνια μηδενικού αθροίσματος ισχύει ότι το άθροισμα των τιμών maximin των παικτών είναι ίσο με μηδέν, όπως και στο παράδειγμα αυτό το maximin του παίκτη 1 είναι -2 και του παίκτη 2 είναι Παράδειγμα αυτοκινητοβιομηχανίες (Μεικτές στρατηγικές ) Το παράδειγμα αυτό αναφέρεται σε δύο αυτοκινητοβιομηχανίες, την FORD και την BMW. Οι αυτοκινητοβιομηχανίες αυτές ανταγωνίζονται στην προσθήκη δύο νέων τεχνολογιών σχετικά τους κινητήρες των αυτοκινήτων. 76
77 Παρακάτω εμφανίζεται ο πίνακας με τις αποδόσεις της κάθε στρατηγικής για τις δύο αυτοκινητοβιομηχανίες. FORD ΒMW Τεχνολογία Α Τεχνολογία Β Τεχνολογία Α Τεχνολογία Β Λύση Παιγνίου Για την εύρεση ισορροπιών του παραπάνω παιγνίου θα πρέπει να γίνουν τα εξής παρακάτω βήματα. Εφόσον γίνει εκκίνηση του προγράμματος θα πρέπει να δημιουργηθεί ένα νέο παιχνίδι παιγνίου Δυναμικής μορφής μέσα από τις επιλογές File- >New->Extensive Game. Στη συνέχεια συμπληρώνονται τα στοιχεία των παικτών και δίνεται ονομασία στο παιχνίδι. 77
78 Επόμενο βήμα είναι η δημιουργία του δενδροδιαγράμματος. Ο πρώτος παίκτης δηλαδή η αυτοκινητοβιομηχανία FORD είναι εκείνη που επιλέγει πρώτη την στρατηγική της. Κάνοντας δεξί κλικ στην μαύρη κουκίδα δηλαδή τον πρώτο κόμβο και στη συνέχεια επιλογή Insert move,εμφανίζεται ένα νέο μικρότερο παράθυρο όπου υπάρχουν ορισμένες επιλογές για την εισαγωγή της κίνησης. 78
79 Στο νέο αυτό παράθυρο γίνεται η επιλογή του παίκτη FORD καθώς επίσης και αριθμός των διαθέσιμων κινήσεων του, όπου στην προκείμενη περίπτωση είναι η τεχνολογία Α και Β. Με τον τρόπο αυτό εμφανίζονται όπως φαίνεται και στην παρακάτω εικόνα, οι δύο στρατηγικές του πρώτου παίκτη. Ακολουθώντας την ίδια διαδικασία, γίνεται η εισαγωγή των στρατηγικών του δεύτερου παίκτη δηλαδή της αυτοκινητοβιομηχανίας BMW. 79
80 Στη συνέχεια δίνεται ονομασία στις στρατηγικές και γίνεται εισαγωγή των δεδομένων στο δενδροδιάγραμμα. Με τον παραπάνω τρόπο ολοκληρώνεται η διαδικασία εισαγωγής του παιγνίου στο πρόγραμμα Gambit. Επόμενο βήμα είναι η επίλυση του βρίσκοντας τις ισορροπίες κατά Nash. Οι ισορροπίες ή η ισορροπία κατά Nash υπολογίζεται μέσα από τις επιλογές Tools-> Εquilibrium ή κάνοντας κλικ στο εικονίδιο εργαλείων του προγράμματος., το οποίο βρίσκεται στην γραμμή 80
81 Εφόσον γίνει η επιλογή της εύρεσης της ισορροπίας κατά Nash, εμφανίζεται ένα νέο παράθυρο το οποίο περιλαμβάνει επιλογές όπως ο αριθμός των ισορροπιών που επιθυμούμε να υπολογιστούν. Επιλέγοντας OK εμφανίζεται στο κάτω μέρος του ίδιου παραθύρου ο πίνακας με τις ισορροπίες δηλαδή τη λύση του παιγνίου. 81
ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΕΙ ΠΑΤΡΑΣ ΤΕΙ ΠΑΤΡΑΣ ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΏΝ ΠΑΙΓΝΙΩΝ- ΠΡΟΓΡΑΜΜΑ GAMBIT
 ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Α Κ Α Η Μ Α Ι Κ Ο Ε Τ Ο Σ 2 0 1 1-2 0 1 2 ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΏΝ ΠΑΙΓΝΙΩΝ- ΠΡΟΓΡΑΜΜΑ GAMBIT Ο συγκεκριµένος οδηγός για το πρόγραµµα
ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Α Κ Α Η Μ Α Ι Κ Ο Ε Τ Ο Σ 2 0 1 1-2 0 1 2 ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΏΝ ΠΑΙΓΝΙΩΝ- ΠΡΟΓΡΑΜΜΑ GAMBIT Ο συγκεκριµένος οδηγός για το πρόγραµµα
Αλλαγή της εμφάνισης κειμένου: μέγεθος γραμματοσειράς, είδος γραμματοσειράς
 3.3.1.1 Αλλαγή της εμφάνισης κειμένου: μέγεθος γραμματοσειράς, είδος γραμματοσειράς Γραμματοσειρές Η λέξη γραμματοσειρά αναφέρεται στο στυλ που εμφανίζονται τα γράμματα. Παρακάτω ακολουθούν κάποια παραδείγματα,
3.3.1.1 Αλλαγή της εμφάνισης κειμένου: μέγεθος γραμματοσειράς, είδος γραμματοσειράς Γραμματοσειρές Η λέξη γραμματοσειρά αναφέρεται στο στυλ που εμφανίζονται τα γράμματα. Παρακάτω ακολουθούν κάποια παραδείγματα,
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
Field Service Management ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ
 Field Service Management ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ 1 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΑΝΑΛΥΣΗ ΜΕΝΟΥ ΕΦΑΡΜΟΓΗΣ... 4 2. ΕΠΕΞΗΓΗΣΗ ΚΕΝΤΡΙΚΟΥ ΜΕΝΟΥ ΚΑΡΤΕΛΑΣ... 5 3. ΔΗΜΙΟΥΡΓΙΑ ΠΕΛΑΤΗ... 6 4. ΑΝΑΖΗΤΗΣΗ ΠΕΛΑΤΗ... 6 5. ΕΠΕΞΕΡΓΑΣΙΑ/ΔΙΑΓΡΑΦΗ
Field Service Management ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ 1 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΑΝΑΛΥΣΗ ΜΕΝΟΥ ΕΦΑΡΜΟΓΗΣ... 4 2. ΕΠΕΞΗΓΗΣΗ ΚΕΝΤΡΙΚΟΥ ΜΕΝΟΥ ΚΑΡΤΕΛΑΣ... 5 3. ΔΗΜΙΟΥΡΓΙΑ ΠΕΛΑΤΗ... 6 4. ΑΝΑΖΗΤΗΣΗ ΠΕΛΑΤΗ... 6 5. ΕΠΕΞΕΡΓΑΣΙΑ/ΔΙΑΓΡΑΦΗ
Κεφάλαιο 2.3: Ρυθμίσεις των Windows
 Κεφάλαιο 2.3: Ρυθμίσεις των Windows 2.3.1 Βασικές πληροφορίες συστήματος Για να δούμε βασικές πληροφορίες για τον υπολογιστή μας, πατάμε το κουμπί «Έναρξη» και επιλέγουμε διαδοχικά «Πίνακας Ελέγχου», «Σύστημα
Κεφάλαιο 2.3: Ρυθμίσεις των Windows 2.3.1 Βασικές πληροφορίες συστήματος Για να δούμε βασικές πληροφορίες για τον υπολογιστή μας, πατάμε το κουμπί «Έναρξη» και επιλέγουμε διαδοχικά «Πίνακας Ελέγχου», «Σύστημα
Κεφάλαιο 29 Θεωρία παιγνίων
 HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 29 Θεωρία παιγνίων Ύλη για τη Μίκρο ΙΙ: κεφάλαιο 29.1, 29.2, 29.4, 29.7, 29.8 Κεφάλαιο 29 Θεωρία παιγνίων Ταυτόχρονα
HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 29 Θεωρία παιγνίων Ύλη για τη Μίκρο ΙΙ: κεφάλαιο 29.1, 29.2, 29.4, 29.7, 29.8 Κεφάλαιο 29 Θεωρία παιγνίων Ταυτόχρονα
Εργαστήριο «Τεχνολογία Πολιτισμικού Λογισμικού» Ενότητα. Επεξεργασία πινάκων
 Ενότητα 4 Επεξεργασία πινάκων 36 37 4.1 Προσθήκη πεδίων Για να εισάγετε ένα πεδίο σε ένα πίνακα που υπάρχει ήδη στη βάση δεδομένων σας, βάζετε τον κέρσορα του ποντικιού στο πεδίο πάνω από το οποίο θέλετε
Ενότητα 4 Επεξεργασία πινάκων 36 37 4.1 Προσθήκη πεδίων Για να εισάγετε ένα πεδίο σε ένα πίνακα που υπάρχει ήδη στη βάση δεδομένων σας, βάζετε τον κέρσορα του ποντικιού στο πεδίο πάνω από το οποίο θέλετε
Browsers. Λειτουργικότητα και Παραμετροποίηση
 Browsers Λειτουργικότητα και Παραμετροποίηση 1 Πίνακας περιεχομένων Γενική περιγραφή... 3 Γενικά... 3 Ποιο αναλυτικά τα μέρη ενός browser... 4 Φίλτρα αναζήτησης... 4 Σενάρια αναζήτησης... 4 Όψεις εμφάνισης
Browsers Λειτουργικότητα και Παραμετροποίηση 1 Πίνακας περιεχομένων Γενική περιγραφή... 3 Γενικά... 3 Ποιο αναλυτικά τα μέρη ενός browser... 4 Φίλτρα αναζήτησης... 4 Σενάρια αναζήτησης... 4 Όψεις εμφάνισης
Εισαγωγή/ απομάκρυνση συμβόλων παραγράφου
 3.3.2.1 Εισαγωγή/ απομάκρυνση συμβόλων παραγράφου Υπάρχει μία μικρή διαφορά μεταξύ της λέξης παράγραφος, όπως τη χρησιμοποιούμε εδώ και όπως κοινώς χρησιμοποιείται. Τεχνικά, μία παράγραφος είναι ένα μπλοκ,
3.3.2.1 Εισαγωγή/ απομάκρυνση συμβόλων παραγράφου Υπάρχει μία μικρή διαφορά μεταξύ της λέξης παράγραφος, όπως τη χρησιμοποιούμε εδώ και όπως κοινώς χρησιμοποιείται. Τεχνικά, μία παράγραφος είναι ένα μπλοκ,
Microsoft PowerPoint 2010 Πανεπιστήμιο Κύπρου
 Microsoft PowerPoint 2010 Πανεπιστήμιο Κύπρου Ιούλιος 2017 Copyright 2017 Πανεπιστήμιο Κύπρου. Όλα τα πνευματικά δικαιώματα κατοχυρωμένα. Δημιουργός: Λευτέρης Γ. Ζαχαρία Πίνακας Περιεχομένων 1. Εισαγωγή....
Microsoft PowerPoint 2010 Πανεπιστήμιο Κύπρου Ιούλιος 2017 Copyright 2017 Πανεπιστήμιο Κύπρου. Όλα τα πνευματικά δικαιώματα κατοχυρωμένα. Δημιουργός: Λευτέρης Γ. Ζαχαρία Πίνακας Περιεχομένων 1. Εισαγωγή....
Περιεχόμενα. Κεφάλαιο 1 Γνωριμία με το Excel...9
 Περιεχόμενα Κεφάλαιο 1 Γνωριμία με το Excel...9 Τα στοιχεία του παραθύρου του Excel... 10 Κελιά και διευθύνσεις... 13 Σε ποιο κελί θα τοποθετηθούν τα δεδομένα;... 14 Καταχώριση δεδομένων... 15 Τι καταλαβαίνει
Περιεχόμενα Κεφάλαιο 1 Γνωριμία με το Excel...9 Τα στοιχεία του παραθύρου του Excel... 10 Κελιά και διευθύνσεις... 13 Σε ποιο κελί θα τοποθετηθούν τα δεδομένα;... 14 Καταχώριση δεδομένων... 15 Τι καταλαβαίνει
ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ "PROΩΘΗΣΗ" PROώθηση
 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ "PROΩΘΗΣΗ" PROώθηση Περιεχόμενα Εγκατάσταση ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΚΕΥΑΣΙΑΣ... 3 ΣΥΝΔΕΣΗ ΕΞΟΠΛΙΣΜΟΥ... 3 ΡΥΘΜΙΣΗ Wi-Fi... 4 ΕΙΣΟΔΟΣ ΧΡΗΣΤΗ... 6 ΠΡΟΣΘΗΚΗ ΝΕΑΣ ΣΥΣΚΕΥΗΣ... 6 ΚΑΤΑΣΤΑΣΗ ΣΥΣΚΕΥΗΣ...
ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ "PROΩΘΗΣΗ" PROώθηση Περιεχόμενα Εγκατάσταση ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΚΕΥΑΣΙΑΣ... 3 ΣΥΝΔΕΣΗ ΕΞΟΠΛΙΣΜΟΥ... 3 ΡΥΘΜΙΣΗ Wi-Fi... 4 ΕΙΣΟΔΟΣ ΧΡΗΣΤΗ... 6 ΠΡΟΣΘΗΚΗ ΝΕΑΣ ΣΥΣΚΕΥΗΣ... 6 ΚΑΤΑΣΤΑΣΗ ΣΥΣΚΕΥΗΣ...
Microsoft PowerPoint 2007
 Information Technology Services and Solutions Σύμβουλοι Μηχανογράφησης και Εκπαίδευσης Στεφ. Σκουλούδη 27, Καλλίπολη, Πειραιάς 210 45 38 177 http://www.itss.gr/ Microsoft PowerPoint 2007 Κωνσταντίνος Κωβαίος
Information Technology Services and Solutions Σύμβουλοι Μηχανογράφησης και Εκπαίδευσης Στεφ. Σκουλούδη 27, Καλλίπολη, Πειραιάς 210 45 38 177 http://www.itss.gr/ Microsoft PowerPoint 2007 Κωνσταντίνος Κωβαίος
Κάθε ένα κελί θα πρέπει να περιέχει ένα μόνο στοιχείο δεδομένων, για παράδειγμα το όνομα σε ένα κελί, το επίθετο σε άλλο κελί.
 ΜΑΘΗΜΑ 2 ΣΤΟΧΟΙ: 1. Εισαγωγή Δεδομένων Σε Κελιά 2. Αλλαγή Προβολής Φύλλου Εργασίας 3. Επιλογή Κελιών 4. Επιλογή Όλου Του Φύλλου Εργασίας 5. Μετακίνηση Στο Φύλλο Εργασίας 6. Επεξεργασία Δεδομένων Σε Ένα
ΜΑΘΗΜΑ 2 ΣΤΟΧΟΙ: 1. Εισαγωγή Δεδομένων Σε Κελιά 2. Αλλαγή Προβολής Φύλλου Εργασίας 3. Επιλογή Κελιών 4. Επιλογή Όλου Του Φύλλου Εργασίας 5. Μετακίνηση Στο Φύλλο Εργασίας 6. Επεξεργασία Δεδομένων Σε Ένα
Πληροφορική. Εργαστηριακή Ενότητα 2 η : Το βιβλίο εργασίας του MS Excel. Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Εργαστηριακή Ενότητα 2 η : Το βιβλίο εργασίας του MS Excel Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Εργαστηριακή Ενότητα 2 η : Το βιβλίο εργασίας του MS Excel Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες
Atlantis - Νέο user interface
 New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE... 2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ... 3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ... 4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)... 5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ... 6 Κεντρικό
New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE... 2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ... 3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ... 4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)... 5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ... 6 Κεντρικό
Εισαγωγή στο πρόγραμμα Microsoft word 2003
 Εισαγωγή στο πρόγραμμα Microsoft word 2003 Έναρξη 1. Εκκίνηση του προγράμματος Για να ξεκινήσουμε το Word, πατάμε στο κουμπί Εναρξη και από το μενού που εμφανίζεται επιλέγουμε Προγράμματα και Microsoft
Εισαγωγή στο πρόγραμμα Microsoft word 2003 Έναρξη 1. Εκκίνηση του προγράμματος Για να ξεκινήσουμε το Word, πατάμε στο κουμπί Εναρξη και από το μενού που εμφανίζεται επιλέγουμε Προγράμματα και Microsoft
Copyright 2017 HP Development Company, L.P.
 Οδηγός χρήσης Copyright 2017 HP Development Company, L.P. Οι πληροφορίες στο παρόν έγγραφο μπορεί να αλλάξουν χωρίς προειδοποίηση. Οι μοναδικές εγγυήσεις για τα προϊόντα και τις υπηρεσίες της HP είναι
Οδηγός χρήσης Copyright 2017 HP Development Company, L.P. Οι πληροφορίες στο παρόν έγγραφο μπορεί να αλλάξουν χωρίς προειδοποίηση. Οι μοναδικές εγγυήσεις για τα προϊόντα και τις υπηρεσίες της HP είναι
Microsoft Excel Κεφάλαιο 1. Εισαγωγή. Βιβλίο εργασίας
 Περιεχόμενα Κεφάλαιο 1 Microsoft Excel 2010... 7 Κεφάλαιο 2 Η δομή ενός φύλλου εργασίας... 19 Κεφάλαιο 3 ημιουργία νέου βιβλίου εργασίας και καταχώριση δεδομένων... 24 Κεφάλαιο 4 Συμβουλές για την καταχώριση
Περιεχόμενα Κεφάλαιο 1 Microsoft Excel 2010... 7 Κεφάλαιο 2 Η δομή ενός φύλλου εργασίας... 19 Κεφάλαιο 3 ημιουργία νέου βιβλίου εργασίας και καταχώριση δεδομένων... 24 Κεφάλαιο 4 Συμβουλές για την καταχώριση
PowerPoint Ένα εργαλείο παρουσίασης
 Εργασία 7η 2 Αρκετοί πιστεύουν πως η επιτυχία μιας παρουσίασης είναι δεδομένη εάν ο παρουσιαστής κατέχει το θέμα που πρόκειται να παρουσιάσει και είναι σε θέση να χειρίζεται ί ά άνετα έ ένα πρόγραμμα ό
Εργασία 7η 2 Αρκετοί πιστεύουν πως η επιτυχία μιας παρουσίασης είναι δεδομένη εάν ο παρουσιαστής κατέχει το θέμα που πρόκειται να παρουσιάσει και είναι σε θέση να χειρίζεται ί ά άνετα έ ένα πρόγραμμα ό
1. Τα τμήματα της επιφάνειας εργασίας των Windows
 1. Τα τμήματα της επιφάνειας εργασίας των Windows Εικονίδια συντομεύσεων (αρχείου-φακέλου) Εικονίδια Ανενεργά Ενεργό Επιφάνεια (αρχείου-φακέλου) παράθυρα παράθυρο εργασίας Γραμμή μενού Γραμμή εργαλείων
1. Τα τμήματα της επιφάνειας εργασίας των Windows Εικονίδια συντομεύσεων (αρχείου-φακέλου) Εικονίδια Ανενεργά Ενεργό Επιφάνεια (αρχείου-φακέλου) παράθυρα παράθυρο εργασίας Γραμμή μενού Γραμμή εργαλείων
Επιλογή ενός στοιχείου γραφήματος από μια λίστα στοιχείων γραφήματος
 - 217 - Το στοιχείο που θέλετε να επιλέξετε επισημαίνεται ξεκάθαρα με λαβές επιλογής. Συμβουλή: Για να σας βοηθήσει να εντοπίσετε το στοιχείο γραφήματος που θέλετε να επιλέξετε, το Microsoft Office Excel
- 217 - Το στοιχείο που θέλετε να επιλέξετε επισημαίνεται ξεκάθαρα με λαβές επιλογής. Συμβουλή: Για να σας βοηθήσει να εντοπίσετε το στοιχείο γραφήματος που θέλετε να επιλέξετε, το Microsoft Office Excel
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Περιεχόμενα. Κεφάλαιο 1 Γνωριμία με το Excel... 9
 Περιεχόμενα Κεφάλαιο 1 Γνωριμία με το Excel... 9 Τα στοιχεία του παραθύρου του Excel... 10 Κελιά και διευθύνσεις... 13 Σε ποιο κελί θα τοποθετηθούν τα δεδομένα;... 14 Καταχώριση δεδομένων... 15 Τι καταλαβαίνει
Περιεχόμενα Κεφάλαιο 1 Γνωριμία με το Excel... 9 Τα στοιχεία του παραθύρου του Excel... 10 Κελιά και διευθύνσεις... 13 Σε ποιο κελί θα τοποθετηθούν τα δεδομένα;... 14 Καταχώριση δεδομένων... 15 Τι καταλαβαίνει
Θεωρία Λήψης Αποφάσεων
 Θεωρία Λήψης Αποφάσεων Ενότητα 8: Αναζήτηση με Αντιπαλότητα Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Αναζήτηση
Θεωρία Λήψης Αποφάσεων Ενότητα 8: Αναζήτηση με Αντιπαλότητα Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Αναζήτηση
Stellarium Εγχειρίδιο Οδηγιών
 Προϋποθέσεις συστήματος: Windows (XP, Vista, 7) με DirectX 9.x και τελευταίες ServicePack ή MacOS X 10.3.x (ή υψηλότερη), κάρτα γραφικών 3D με υποστήριξη OpenGL, ελάχ. 512 MB RAM, 1 GB διαθέσιμος χώρος
Προϋποθέσεις συστήματος: Windows (XP, Vista, 7) με DirectX 9.x και τελευταίες ServicePack ή MacOS X 10.3.x (ή υψηλότερη), κάρτα γραφικών 3D με υποστήριξη OpenGL, ελάχ. 512 MB RAM, 1 GB διαθέσιμος χώρος
ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΣΕ ΔΙΣΚΕΤΑ ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΑΠΟ ΔΙΣΚΕΤΑ. Από τον κατάλογο που εμφανίζεται επιλέγω: Αποστολή προς Δισκέτα (3,5)
 ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΣΕ ΔΙΣΚΕΤΑ ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΑΠΟ ΔΙΣΚΕΤΑ Τοποθετώ μια δισκέτα στον οδηγό τη δισκέτας του υπολογιστή. Τοποθετώ τη δισκέτα που έχει το αρχείο μου στον οδηγό τη δισκέτας του υπολογιστή.
ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΣΕ ΔΙΣΚΕΤΑ ΑΝΤΙΓΡΑΦΗ ΑΡΧΕΙΟΥ ΑΠΟ ΔΙΣΚΕΤΑ Τοποθετώ μια δισκέτα στον οδηγό τη δισκέτας του υπολογιστή. Τοποθετώ τη δισκέτα που έχει το αρχείο μου στον οδηγό τη δισκέτας του υπολογιστή.
Οδηγός γρήγορης εκκίνησης
 Οδηγός γρήγορης εκκίνησης Το Microsoft Excel 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης. Προσθήκη
Οδηγός γρήγορης εκκίνησης Το Microsoft Excel 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης. Προσθήκη
Κεφάλαιο 1 Χρήση προτύπου 2. Κεφάλαιο 2 Τροποποίηση μιας παρουσίασης 9. Κεφάλαιο 4 Προσθήκη αντικειμένων 26. Κεφάλαιο 5 Ειδικά εφέ 35
 Περιεχόμενα Κεφάλαιο 1 Χρήση προτύπου 2 Κεφάλαιο 2 Τροποποίηση μιας παρουσίασης 9 Κεφάλαιο 3 Εφαρμογή σχεδίων 19 Κεφάλαιο 4 Προσθήκη αντικειμένων 26 Κεφάλαιο 5 Ειδικά εφέ 35 Κεφάλαιο 6 Κουμπιά ενεργειών
Περιεχόμενα Κεφάλαιο 1 Χρήση προτύπου 2 Κεφάλαιο 2 Τροποποίηση μιας παρουσίασης 9 Κεφάλαιο 3 Εφαρμογή σχεδίων 19 Κεφάλαιο 4 Προσθήκη αντικειμένων 26 Κεφάλαιο 5 Ειδικά εφέ 35 Κεφάλαιο 6 Κουμπιά ενεργειών
Αλλαγή προσανατολισμού εγγράφου σε κατακόρυφο ή οριζόντιο, αλλαγή μεγέθους σελίδας
 3.3.3.1 Αλλαγή προσανατολισμού εγγράφου σε κατακόρυφο ή οριζόντιο, αλλαγή μεγέθους σελίδας Συνήθως εκτυπώνουμε κατά τη μακρόστενη μεριά της σελίδας. Αυτού του είδους ο προσανατολισμός ονομάζεται κατακόρυφος.
3.3.3.1 Αλλαγή προσανατολισμού εγγράφου σε κατακόρυφο ή οριζόντιο, αλλαγή μεγέθους σελίδας Συνήθως εκτυπώνουμε κατά τη μακρόστενη μεριά της σελίδας. Αυτού του είδους ο προσανατολισμός ονομάζεται κατακόρυφος.
Visual Flowchart Γενικά
 Visual Flowchart 3.020 -Γενικά Το Visual Flowchart ή «Data-Flow Visual Programming Language 3.020» (http://www. emu8086.com/fp) είναι ένα περιβάλλον ανάπτυξης και εκτέλεσης αλγορίθμων απευθείας σε μορφή
Visual Flowchart 3.020 -Γενικά Το Visual Flowchart ή «Data-Flow Visual Programming Language 3.020» (http://www. emu8086.com/fp) είναι ένα περιβάλλον ανάπτυξης και εκτέλεσης αλγορίθμων απευθείας σε μορφή
Η προέλευση του Sketchpad 1
 Η προέλευση του Sketchpad 1 Το The Geometer s Sketchpad αναπτύχθηκε ως μέρος του Προγράμματος Οπτικής Γεωμετρίας, ενός προγράμματος χρηματοδοτούμενου από το Εθνικό Ίδρυμα Ερευνών (ΝSF) υπό τη διεύθυνση
Η προέλευση του Sketchpad 1 Το The Geometer s Sketchpad αναπτύχθηκε ως μέρος του Προγράμματος Οπτικής Γεωμετρίας, ενός προγράμματος χρηματοδοτούμενου από το Εθνικό Ίδρυμα Ερευνών (ΝSF) υπό τη διεύθυνση
Γεωργάκης Αριστείδης ΠΕ20
 1 Εκκίνηση για πρώτη φορά Όπως συμβαίνει και με τις υπόλοιπες εφαρμογές του OpenOffice, έτσι και το Impress μπορούμε να το εκκινήσουμε μέσω της συντόμευσης που εγκαθίσταται αυτόματα στην επιφάνεια εργασίας
1 Εκκίνηση για πρώτη φορά Όπως συμβαίνει και με τις υπόλοιπες εφαρμογές του OpenOffice, έτσι και το Impress μπορούμε να το εκκινήσουμε μέσω της συντόμευσης που εγκαθίσταται αυτόματα στην επιφάνεια εργασίας
Εννοιολογικός Χάρτης Cmap Tools
 Εννοιολογικός Χάρτης Cmap Tools Angelos Giannoulas http://cmap.ihmc.us/ http://cmap.ihmc.us/download/ Εγκατάσταση του λογισμικού Κάντε διπλό κλικ στο εικονίδιο εγκατάστασης της εφαρμογής Εγκατάσταση του
Εννοιολογικός Χάρτης Cmap Tools Angelos Giannoulas http://cmap.ihmc.us/ http://cmap.ihmc.us/download/ Εγκατάσταση του λογισμικού Κάντε διπλό κλικ στο εικονίδιο εγκατάστασης της εφαρμογής Εγκατάσταση του
ΕΡΩΤΗΣΕΙΣ στην επεξεργασία κειμένου (Word)
 1. Πώς δημιουργούμε ένα νέο έγγραφο; 2. Πώς αποθηκεύουμε ένα έγγραφο στη δισκέτα μας; 3. Μπορείτε να περιγράψετε τη βασική οθόνη του Word;. 4. Τι ακριβώς κάνει το εργαλείο ζουμ; 5. Ποιους κανόνες ακολουθεί
1. Πώς δημιουργούμε ένα νέο έγγραφο; 2. Πώς αποθηκεύουμε ένα έγγραφο στη δισκέτα μας; 3. Μπορείτε να περιγράψετε τη βασική οθόνη του Word;. 4. Τι ακριβώς κάνει το εργαλείο ζουμ; 5. Ποιους κανόνες ακολουθεί
Ο Οδηγός γρήγορης εκκίνησης
 Ο Οδηγός γρήγορης εκκίνησης του Microsoft PowerPoint 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης.
Ο Οδηγός γρήγορης εκκίνησης του Microsoft PowerPoint 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης.
Atlantis - Νέο user interface
 New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE...2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ...3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ...4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)...5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ...6 Κεντρικό μενού
New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE...2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ...3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ...4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)...5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ...6 Κεντρικό μενού
A7.2 Δημιουργία Απλής Γραφικής Εφαρμογής σε Περιβάλλον Scratch
 A7.2 Δημιουργία Απλής Γραφικής Εφαρμογής σε Περιβάλλον Scratch Τι θα μάθουμε σήμερα: Να ενεργοποιούμε το λογισμικό Scratch Να αναγνωρίζουμε τα κύρια μέρη του περιβάλλοντος του Scratch Να δημιουργούμε/εισάγουμε/τροποποιούμε
A7.2 Δημιουργία Απλής Γραφικής Εφαρμογής σε Περιβάλλον Scratch Τι θα μάθουμε σήμερα: Να ενεργοποιούμε το λογισμικό Scratch Να αναγνωρίζουμε τα κύρια μέρη του περιβάλλοντος του Scratch Να δημιουργούμε/εισάγουμε/τροποποιούμε
Μορφοποίηση εικόνων. Εισαγωγή. Στόχος κεφαλαίου
 Περιεχόμενα Κεφάλαιο 1: Προετοιμασία παρουσίασης...1 Κεφάλαιο 2: Διαχείριση διαφανειών...18 Κεφάλαιο 3: Διαχείριση γραφικών...31 Κεφάλαιο 4: Επεξεργασία εικόνων με το Adobe Photoshop...56 Κεφάλαιο 5: Μορφοποίηση
Περιεχόμενα Κεφάλαιο 1: Προετοιμασία παρουσίασης...1 Κεφάλαιο 2: Διαχείριση διαφανειών...18 Κεφάλαιο 3: Διαχείριση γραφικών...31 Κεφάλαιο 4: Επεξεργασία εικόνων με το Adobe Photoshop...56 Κεφάλαιο 5: Μορφοποίηση
Δημιουργία ενός κενού πίνακα
 3.4.1.1 Δημιουργία ενός κενού πίνακα Ένας πίνακας αποτελείται από έναν αριθμό γραμμών και στηλών που δημιουργούν ένα πλέγμα. Σε αυτό το πλέγμα είναι πιθανή η ύπαρξη ή μη περιθωρίων. Κάθε κελί του πίνακα
3.4.1.1 Δημιουργία ενός κενού πίνακα Ένας πίνακας αποτελείται από έναν αριθμό γραμμών και στηλών που δημιουργούν ένα πλέγμα. Σε αυτό το πλέγμα είναι πιθανή η ύπαρξη ή μη περιθωρίων. Κάθε κελί του πίνακα
ΤΕΙ Ηρακλείου. Τμήμα Λογιστικής Πληροφορική I 6 η Εργαστηριακή άσκηση (Excel)
 ΤΕΙ Ηρακλείου Τμήμα Λογιστικής Πληροφορική I 6 η Εργαστηριακή άσκηση (Excel) Ανοίγοντας το Excel (Έναρξη /Προγράμματα /Microsoft Office / Microsoft Office Excel 2003), ανοίγει μπροστά μας ένα βιβλίο εργασίας
ΤΕΙ Ηρακλείου Τμήμα Λογιστικής Πληροφορική I 6 η Εργαστηριακή άσκηση (Excel) Ανοίγοντας το Excel (Έναρξη /Προγράμματα /Microsoft Office / Microsoft Office Excel 2003), ανοίγει μπροστά μας ένα βιβλίο εργασίας
Εργασία-3: Παρουσίαση Εργασίας. Ομάδα Α. Προετοιμασία Αναφοράς
 Εργασία-3: Παρουσίαση Εργασίας Ομάδα Α. Προετοιμασία Αναφοράς Αρκετοί πιστεύουν πως η επιτυχία μιας παρουσίασης είναι δεδομένη εάν ο παρουσιαστής κατέχει το θέμα που πρόκειται να παρουσιάσει και είναι
Εργασία-3: Παρουσίαση Εργασίας Ομάδα Α. Προετοιμασία Αναφοράς Αρκετοί πιστεύουν πως η επιτυχία μιας παρουσίασης είναι δεδομένη εάν ο παρουσιαστής κατέχει το θέμα που πρόκειται να παρουσιάσει και είναι
Σημείωση για το προϊόν
 Έναρξη από εδώ Copyright 2013 Hewlett-Packard Development Company, L.P. Η ονομασία Windows είναι σήμα κατατεθέν της Microsoft Corporation στις ΗΠΑ. Οι πληροφορίες στο παρόν έγγραφο μπορεί να αλλάξουν χωρίς
Έναρξη από εδώ Copyright 2013 Hewlett-Packard Development Company, L.P. Η ονομασία Windows είναι σήμα κατατεθέν της Microsoft Corporation στις ΗΠΑ. Οι πληροφορίες στο παρόν έγγραφο μπορεί να αλλάξουν χωρίς
GreekLUG Ελεύθερο Λογισμικό & Λογισμικό Ανοικτού Κώδικα
 GreekLUG Ελεύθερο Λογισμικό & Λογισμικό Ανοικτού Κώδικα Μάθημα 6ο Σουίτα Γραφείου LibreOffice 2 Ύλη Μαθημάτων V Μαθ. 5/6 : Σουίτα Γραφείου LibreOffice LibreOffice Γενικά, Κειμενογράφος - LibreOffice Writer,
GreekLUG Ελεύθερο Λογισμικό & Λογισμικό Ανοικτού Κώδικα Μάθημα 6ο Σουίτα Γραφείου LibreOffice 2 Ύλη Μαθημάτων V Μαθ. 5/6 : Σουίτα Γραφείου LibreOffice LibreOffice Γενικά, Κειμενογράφος - LibreOffice Writer,
να ακολουθήσουμε Έναρξη Όλα τα Προγράμματα και να ενεργοποιήσουμε την επιλογή Microsoft Word.
 ΕΠΕΞΕΡΓΑΣΙΑ ΚΕΙΜΕΝΟΥ ΜΕ ΤΟ WORD Περιεχόμενα Εκκίνηση του Microsoft Word... 3 Το παράθυρο του Word... 3 Η Κορδέλα με τις καρτέλες... 4 Κεντρική... 4 Εισαγωγή... 4 Διάταξη Σελίδας... 5 Αναφορές... 5 Στοιχεία
ΕΠΕΞΕΡΓΑΣΙΑ ΚΕΙΜΕΝΟΥ ΜΕ ΤΟ WORD Περιεχόμενα Εκκίνηση του Microsoft Word... 3 Το παράθυρο του Word... 3 Η Κορδέλα με τις καρτέλες... 4 Κεντρική... 4 Εισαγωγή... 4 Διάταξη Σελίδας... 5 Αναφορές... 5 Στοιχεία
Πρακτικές οδηγίες για την Επεξεργασία Κειμένου
 11 Εργαλεία έκφρασης και δημιουργίας Επεξεργασία Κειμένου Α Γυμνασίου Πρακτικές οδηγίες για την Επεξεργασία Κειμένου Ένα πρόγραμμα επεξεργασίας κειμένου μας προσφέρει τη δυνατότητα να: προσθέτουμε, να
11 Εργαλεία έκφρασης και δημιουργίας Επεξεργασία Κειμένου Α Γυμνασίου Πρακτικές οδηγίες για την Επεξεργασία Κειμένου Ένα πρόγραμμα επεξεργασίας κειμένου μας προσφέρει τη δυνατότητα να: προσθέτουμε, να
Σ η μ ε ι ώ σ ε ι ς γ ι α τ ο υ π ο λ ο γ ι σ τ ι κ ό φ ύ λ λ ο
 Σ η μ ε ι ώ σ ε ι ς γ ι α τ ο υ π ο λ ο γ ι σ τ ι κ ό φ ύ λ λ ο Το λογισμικό αυτό μας διευκολύνει να κατηγοριοποιήσουμε τα δεδομένα μας, να τα ταξινομήσουμε με όποιον τρόπο θέλουμε και να κάνουμε σύνθετους
Σ η μ ε ι ώ σ ε ι ς γ ι α τ ο υ π ο λ ο γ ι σ τ ι κ ό φ ύ λ λ ο Το λογισμικό αυτό μας διευκολύνει να κατηγοριοποιήσουμε τα δεδομένα μας, να τα ταξινομήσουμε με όποιον τρόπο θέλουμε και να κάνουμε σύνθετους
του προγράμματος diagrama_rohs.zip )
 έκδοση 3.20 ( κατέβασμα του προγράμματος diagrama_rohs.zip ) Το πρόγραμμα αυτό γράφτηκε όχι να γίνει μια γλώσσα προγραμματισμού, αλλά να γίνει ένα εργαλείο για την εισαγωγή των μαθητών στον προγραμματισμό.
έκδοση 3.20 ( κατέβασμα του προγράμματος diagrama_rohs.zip ) Το πρόγραμμα αυτό γράφτηκε όχι να γίνει μια γλώσσα προγραμματισμού, αλλά να γίνει ένα εργαλείο για την εισαγωγή των μαθητών στον προγραμματισμό.
5.1.1 Περιγραφή των συστατικών τμημάτων ενός γραφήματος
 5. Γραφήματα 5.1 Εισαγωγή 5.1.1 Περιγραφή των συστατικών τμημάτων ενός γραφήματος Το Discoverer παρέχει μεγάλες δυνατότητες στη δημιουργία γραφημάτων, καθιστώντας δυνατή τη διαμόρφωση κάθε συστατικού μέρους
5. Γραφήματα 5.1 Εισαγωγή 5.1.1 Περιγραφή των συστατικών τμημάτων ενός γραφήματος Το Discoverer παρέχει μεγάλες δυνατότητες στη δημιουργία γραφημάτων, καθιστώντας δυνατή τη διαμόρφωση κάθε συστατικού μέρους
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 ΚΟΙΝΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ Players-Παίκτες Rules- Κανόνες. Τιµωρείσαι εάν τους παραβιάσεις.
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 ΚΟΙΝΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ Players-Παίκτες Rules- Κανόνες. Τιµωρείσαι εάν τους παραβιάσεις.
Εκπαιδευτικό Εργαλείο Κανονικοποίησης
 Εκπαιδευτικό Εργαλείο Κανονικοποίησης Σύντομες οδηγίες χρήσης Εισαγωγή Το πρόγραμμα Εκπαιδευτικό Εργαλείο Κανονικοποίησης αυτοματοποιεί τη διαδικασία της κανονικοποίησης πινάκων σε BCNF μορφή. Ο χρήστης
Εκπαιδευτικό Εργαλείο Κανονικοποίησης Σύντομες οδηγίες χρήσης Εισαγωγή Το πρόγραμμα Εκπαιδευτικό Εργαλείο Κανονικοποίησης αυτοματοποιεί τη διαδικασία της κανονικοποίησης πινάκων σε BCNF μορφή. Ο χρήστης
Παρακάτω προτείνεται μια αλληλουχία ενεργειών την οποία ο χρήστης πρέπει να ακολουθήσει για να αξιοποιήσει τις δυνατότητες της εφαρμογής.
 Έκδοση Επιταγών Το συγκεκριμένο εγχειρίδιο δημιουργήθηκε για να βοηθήσει την κατανόηση της διαδικασίας Έκδοσης Επιταγών στην εφαρμογή Λογιστική Διαχείριση της σειράς HyperΛογιστική. Παρακάτω προτείνεται
Έκδοση Επιταγών Το συγκεκριμένο εγχειρίδιο δημιουργήθηκε για να βοηθήσει την κατανόηση της διαδικασίας Έκδοσης Επιταγών στην εφαρμογή Λογιστική Διαχείριση της σειράς HyperΛογιστική. Παρακάτω προτείνεται
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 2 η Διάλεξη Παίγνια ελλιπούς πληροφόρησης Πληροφοριακά σύνολα Κανονική μορφή παιγνίου Ισοδύναμες στρατηγικές Παίγνια συνεργασίας και μη συνεργασίας Πεπερασμένα και
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 2 η Διάλεξη Παίγνια ελλιπούς πληροφόρησης Πληροφοριακά σύνολα Κανονική μορφή παιγνίου Ισοδύναμες στρατηγικές Παίγνια συνεργασίας και μη συνεργασίας Πεπερασμένα και
Διαχείριση Βάσης Δεδομένων (dbadmin)
 Published on PRISMA Win Help - Megasoft (http://docs.megasoft.gr) Home > Εμπορική Διαχείριση > Διαχείριση Βάσης Δεδομένων (dbadmin) Διαχείριση Βάσης Δεδομένων (dbadmin) Μέσα από τη διαχείριση βάσης δεδομένων
Published on PRISMA Win Help - Megasoft (http://docs.megasoft.gr) Home > Εμπορική Διαχείριση > Διαχείριση Βάσης Δεδομένων (dbadmin) Διαχείριση Βάσης Δεδομένων (dbadmin) Μέσα από τη διαχείριση βάσης δεδομένων
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
ΑΣΚΗΣΗ 1 ΑΣΚΗΣΗ 2 ΑΣΚΗΣΗ 3
 ΑΣΚΗΣΗ 1 Δύο επιχειρήσεις Α και Β, μοιράζονται το μεγαλύτερο μερίδιο της αγοράς για ένα συγκεκριμένο προϊόν. Καθεμία σχεδιάζει τη νέα της στρατηγική για τον επόμενο χρόνο, προκειμένου να αποσπάσει πωλήσεις
ΑΣΚΗΣΗ 1 Δύο επιχειρήσεις Α και Β, μοιράζονται το μεγαλύτερο μερίδιο της αγοράς για ένα συγκεκριμένο προϊόν. Καθεμία σχεδιάζει τη νέα της στρατηγική για τον επόμενο χρόνο, προκειμένου να αποσπάσει πωλήσεις
Επεξεργασία πολλαπλών φύλλων εργασίας - Γραφημάτων Excel
 Επεξεργασία πολλαπλών φύλλων εργασίας - Γραφημάτων Excel 11.1. Πολλαπλά φύλλα εργασίας Στο προηγούμενο κεφάλαιο δημιουργήσαμε ένα φύλλο εργασίας με τον προϋπολογισμό δαπανών του προσωπικού που θα συμμετάσχει
Επεξεργασία πολλαπλών φύλλων εργασίας - Γραφημάτων Excel 11.1. Πολλαπλά φύλλα εργασίας Στο προηγούμενο κεφάλαιο δημιουργήσαμε ένα φύλλο εργασίας με τον προϋπολογισμό δαπανών του προσωπικού που θα συμμετάσχει
Εγχειρίδιο του Accerciser, έκδοση 0.2.0
 i Εγχειρίδιο του Accerciser, ii Copyright 2006, 2007, 2008 IBM Corporation Ανάδραση Για να αναφέρετε ένα σφάλμα ή να κάνετε μια εισήγηση σχετικά με την εφαρμογή Accerciser ή με αυτό τον εγχειρίδιο, ακολουθήστε
i Εγχειρίδιο του Accerciser, ii Copyright 2006, 2007, 2008 IBM Corporation Ανάδραση Για να αναφέρετε ένα σφάλμα ή να κάνετε μια εισήγηση σχετικά με την εφαρμογή Accerciser ή με αυτό τον εγχειρίδιο, ακολουθήστε
Εργαστήριο «Τεχνολογία Πολιτισμικού Λογισμικού» Ενότητα. Σχεδίαση Βάσεων Δεδομένων
 Ενότητα 3 Σχεδίαση Βάσεων Δεδομένων 17 18 3.1 Εισαγωγή Μία βάση δεδομένων αποτελείται από δεδομένα για διάφορα θέματα τα οποία όμως σχετίζονται μεταξύ τους και είναι καταχωρημένα με συγκεκριμένο τρόπο.
Ενότητα 3 Σχεδίαση Βάσεων Δεδομένων 17 18 3.1 Εισαγωγή Μία βάση δεδομένων αποτελείται από δεδομένα για διάφορα θέματα τα οποία όμως σχετίζονται μεταξύ τους και είναι καταχωρημένα με συγκεκριμένο τρόπο.
4.1 Άνοιγμα υπάρχοντος βιβλίου εργασίας
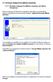 4.1 Άνοιγμα υπάρχοντος βιβλίου εργασίας 4.1.1 Άνοιγμα υπάρχοντος βιβλίου εργασίας από βάση δεδομένων Όταν εκκινήσουμε τον Discoverer εμφανίζεται στην οθόνη μας το παράθυρο διαλόγου του βοηθητικού προγράμματος
4.1 Άνοιγμα υπάρχοντος βιβλίου εργασίας 4.1.1 Άνοιγμα υπάρχοντος βιβλίου εργασίας από βάση δεδομένων Όταν εκκινήσουμε τον Discoverer εμφανίζεται στην οθόνη μας το παράθυρο διαλόγου του βοηθητικού προγράμματος
Kεφάλαιο 11 Λίστες και Ανάλυση Δεδομένων Kεφάλαιο 12 Εργαλεία ανάλυσης πιθανοτήτων Kεφάλαιο 13 Ανάλυση δεδομένων...
 Μέρος 2 Kεφάλαιο 11 Λίστες και Ανάλυση Δεδομένων... 211 Kεφάλαιο 12 Εργαλεία ανάλυσης πιθανοτήτων... 241 Kεφάλαιο 13 Ανάλυση δεδομένων... 257 Kεφάλαιο 14 Συναρτήσεις Μέρος Β... 285 Kεφάλαιο 15 Ευρετήριο
Μέρος 2 Kεφάλαιο 11 Λίστες και Ανάλυση Δεδομένων... 211 Kεφάλαιο 12 Εργαλεία ανάλυσης πιθανοτήτων... 241 Kεφάλαιο 13 Ανάλυση δεδομένων... 257 Kεφάλαιο 14 Συναρτήσεις Μέρος Β... 285 Kεφάλαιο 15 Ευρετήριο
Σημειώσεις στο PowerPoint
 Σημειώσεις στο PowerPoint Τι είναι το PowerPoint; Το PowerPoint 2010 είναι μια οπτική και γραφική εφαρμογή που χρησιμοποιείται κυρίως για τη δημιουργία παρουσιάσεων. Με το PowerPoint, μπορείτε να δημιουργήσετε
Σημειώσεις στο PowerPoint Τι είναι το PowerPoint; Το PowerPoint 2010 είναι μια οπτική και γραφική εφαρμογή που χρησιμοποιείται κυρίως για τη δημιουργία παρουσιάσεων. Με το PowerPoint, μπορείτε να δημιουργήσετε
7.Α.1 Παρουσιάσεις. 7.Α.2 Περιγραφή περιεχομένων της εφαρμογής
 Μάθημα 7ο Πολυμέσα 7.Α.1 Παρουσιάσεις Οι παρουσιάσεις είναι μια εφαρμογή που χρησιμεύει στην παρουσίαση των εργασιών μας. Αποτελούν μια συνοπτική μορφή των εργασιών μας. Μέσω δημιουργίας διαφανειών, μορφοποιήσεων
Μάθημα 7ο Πολυμέσα 7.Α.1 Παρουσιάσεις Οι παρουσιάσεις είναι μια εφαρμογή που χρησιμεύει στην παρουσίαση των εργασιών μας. Αποτελούν μια συνοπτική μορφή των εργασιών μας. Μέσω δημιουργίας διαφανειών, μορφοποιήσεων
1. Κατανόηση Και Αλλαγή Μεταξύ Προβολών Εμφάνισης Της Παρουσίασης. 1. Κατανόηση Και Αλλαγή Μεταξύ Προβολών Εμφάνισης Της Παρουσίασης
 ΜΑΘΗΜΑ 2 ΣΤΟΧΟΙ: 1. Κατανόηση Και Αλλαγή Μεταξύ Προβολών Εμφάνισης Της Παρουσίασης 2. Καρτέλα Διάρθρωσης (Outline Tab) 3. Προσθήκη Νέας Διαφάνειας 4. Αλλαγή Διάταξης Διαφάνειας 5. Προσθήκη Κειμένου Και
ΜΑΘΗΜΑ 2 ΣΤΟΧΟΙ: 1. Κατανόηση Και Αλλαγή Μεταξύ Προβολών Εμφάνισης Της Παρουσίασης 2. Καρτέλα Διάρθρωσης (Outline Tab) 3. Προσθήκη Νέας Διαφάνειας 4. Αλλαγή Διάταξης Διαφάνειας 5. Προσθήκη Κειμένου Και
ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΤΗ. της Πλατφόρμας Τηλεκατάρτισης
 ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΤΗ της Πλατφόρμας Τηλεκατάρτισης ΠΕΡΙΕΧΟΜΕΝΑ 1. Εισαγωγή...2 2. Αρχική σελίδα, Εισαγωγή & Περιβάλλον Συστήματος...3 2.1. Αρχική σελίδα εισαγωγής...3 2.2. Εισαγωγή στην Πλατφόρμα Τηλε-κατάρτισης...4
ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΤΗ της Πλατφόρμας Τηλεκατάρτισης ΠΕΡΙΕΧΟΜΕΝΑ 1. Εισαγωγή...2 2. Αρχική σελίδα, Εισαγωγή & Περιβάλλον Συστήματος...3 2.1. Αρχική σελίδα εισαγωγής...3 2.2. Εισαγωγή στην Πλατφόρμα Τηλε-κατάρτισης...4
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενα Μαθήµατα: Παίχτες: είναι αυτοί που λαµβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενα Μαθήµατα: Παίχτες: είναι αυτοί που λαµβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
GET SDI PORTAL v1. Οδηγός Βοήθειας
 GET SDI PORTAL v1 Οδηγός Βοήθειας Μεταδεδομένα εγγράφου Στοιχείο/Element Τιμή/value Ημερομηνία/Date 2011-06-16 Τίτλος/Title GETSDIPortal_v1_Help_v1.0 Θέμα/Subject Οδηγός Βοήθειας Έκδοση/Version 1.0 Σελίδα
GET SDI PORTAL v1 Οδηγός Βοήθειας Μεταδεδομένα εγγράφου Στοιχείο/Element Τιμή/value Ημερομηνία/Date 2011-06-16 Τίτλος/Title GETSDIPortal_v1_Help_v1.0 Θέμα/Subject Οδηγός Βοήθειας Έκδοση/Version 1.0 Σελίδα
Λίγα λόγια από το συγγραφέα Κεφάλαιο 1: Microsoft Excel Κεφάλαιο 2: Η δομή ενός φύλλου εργασίας... 26
 Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: Microsoft Excel 2002... 9 Κεφάλαιο 2: Η δομή ενός φύλλου εργασίας... 26 Κεφάλαιο 3: Δημιουργία νέου βιβλίου εργασίας και καταχώριση δεδομένων...
Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: Microsoft Excel 2002... 9 Κεφάλαιο 2: Η δομή ενός φύλλου εργασίας... 26 Κεφάλαιο 3: Δημιουργία νέου βιβλίου εργασίας και καταχώριση δεδομένων...
Σχεδιασμός εκτυπώσεων ERG
 Σχεδιασμός εκτυπώσεων ERG Περιεχόμενα Δημιουργία εκτυπώσεων ERG... 3 Επιλογή πεδίων... 4 Λεπτομέρειες... 6 Καθορισμός φίλτρων... 6 Ταξινόμηση και ομαδοποίηση... 7 Εξαγόμενο εκτύπωσης... 7 Δικαιώματα πρόσβασης...
Σχεδιασμός εκτυπώσεων ERG Περιεχόμενα Δημιουργία εκτυπώσεων ERG... 3 Επιλογή πεδίων... 4 Λεπτομέρειες... 6 Καθορισμός φίλτρων... 6 Ταξινόμηση και ομαδοποίηση... 7 Εξαγόμενο εκτύπωσης... 7 Δικαιώματα πρόσβασης...
Οδηγός γρήγορης εκκίνησης
 Οδηγός γρήγορης εκκίνησης Το Microsoft Word 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης. Γραμμή
Οδηγός γρήγορης εκκίνησης Το Microsoft Word 2013 έχει διαφορετική εμφάνιση από προηγούμενες εκδόσεις. Γι αυτό το λόγο, δημιουργήσαμε αυτόν τον οδηγό για να ελαχιστοποιήσουμε την καμπύλη εκμάθησης. Γραμμή
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων
 Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων Σε αυτό το εγχειρίδιο περιγράφεται η παραμετροποίηση και η χρήση της γρήγορης καταχώρησης πωλήσεων, καθώς και της κατηγορίας λιανικής των ειδών. Περιεχόμενα Παραμετροποίηση
Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων Σε αυτό το εγχειρίδιο περιγράφεται η παραμετροποίηση και η χρήση της γρήγορης καταχώρησης πωλήσεων, καθώς και της κατηγορίας λιανικής των ειδών. Περιεχόμενα Παραμετροποίηση
ΑΠΟΤΙΜΗΣΗ ΤΟΥ ΕΡΓΟΥ ΤΟΥ ΤΜΗΜΑΤΟΣ ΣΤΟΧΟΙ ΓΙΑ ΤΗΝ ΠΕΡΙΟΔΟ ΠΑΡΑΡΤΗΜΑ ΧΙ
 ΕΘΝΙΚΟΝ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟΝ ΠΑΝΕΠΙΣΤΗΜΙΟΝ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΠΟΤΙΜΗΣΗ ΤΟΥ ΕΡΓΟΥ ΤΟΥ ΤΜΗΜΑΤΟΣ ΣΤΟΧΟΙ ΓΙΑ ΤΗΝ ΠΕΡΙΟΔΟ 2008-2013 ΠΑΡΑΡΤΗΜΑ ΧΙ ΕΦΑΡΜΟΓΗ ΔΙΑΧΕΙΡΙΣΗΣ
ΕΘΝΙΚΟΝ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟΝ ΠΑΝΕΠΙΣΤΗΜΙΟΝ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΠΟΤΙΜΗΣΗ ΤΟΥ ΕΡΓΟΥ ΤΟΥ ΤΜΗΜΑΤΟΣ ΣΤΟΧΟΙ ΓΙΑ ΤΗΝ ΠΕΡΙΟΔΟ 2008-2013 ΠΑΡΑΡΤΗΜΑ ΧΙ ΕΦΑΡΜΟΓΗ ΔΙΑΧΕΙΡΙΣΗΣ
Λίγα λόγια από το συγγραφέα Κεφάλαιο 1: PowerPoint Κεφάλαιο 2: Εκκίνηση του PowerPoint... 13
 Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: PowerPoint... 9 Κεφάλαιο 2: Εκκίνηση του PowerPoint... 13 Κεφάλαιο 3: Δημιουργία νέας παρουσίασης... 27 Κεφάλαιο 4: Μορφοποίηση κειμένου παρουσίασης...
Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: PowerPoint... 9 Κεφάλαιο 2: Εκκίνηση του PowerPoint... 13 Κεφάλαιο 3: Δημιουργία νέας παρουσίασης... 27 Κεφάλαιο 4: Μορφοποίηση κειμένου παρουσίασης...
Περιεχόμενα. 1 Προετοιμασία βιβλίου εργασίας 47. 2 Εργασία με δεδομένα και πίνακες Excel 75. Ευχαριστίες...11. Εισαγωγή στο Microsoft Excel 2010...
 Περιεχόμενα Ευχαριστίες...11 Εισαγωγή στο Microsoft Excel 2010...13 Τροποποίηση της εμφάνισης της Κορδέλας...29 Χαρακτηριστικά και συμβάσεις του βιβλίου...35 Χρήση των αρχείων εξάσκησης...37 Βοήθεια...41
Περιεχόμενα Ευχαριστίες...11 Εισαγωγή στο Microsoft Excel 2010...13 Τροποποίηση της εμφάνισης της Κορδέλας...29 Χαρακτηριστικά και συμβάσεις του βιβλίου...35 Χρήση των αρχείων εξάσκησης...37 Βοήθεια...41
Περιεχόμενα. Κεφάλαιο 1 Εισαγωγή στο PowerPoint...9. Κεφάλαιο 2 Εργασία με κείμενο... 39
 Περιεχόμενα Κεφάλαιο 1 Εισαγωγή στο PowerPoint...9 Βασικές έννοιες... 10 Το παράθυρο του PowerPoint... 13 Δημιουργία νέας παρουσίασης... 15 Βασικές εργασίες με διαφάνειες... 22 Προβολές παρουσίασης...
Περιεχόμενα Κεφάλαιο 1 Εισαγωγή στο PowerPoint...9 Βασικές έννοιες... 10 Το παράθυρο του PowerPoint... 13 Δημιουργία νέας παρουσίασης... 15 Βασικές εργασίες με διαφάνειες... 22 Προβολές παρουσίασης...
Εφαρμογή Ηλεκτρονικής Υποβολής Δηλώσεων Ε9. Οδηγίες Χρήσης
 Εφαρμογή Ηλεκτρονικής Υποβολής Δηλώσεων Ε9 Οδηγίες Χρήσης Πίνακας Περιεχομένων 1. Αρχική οθόνη... 3 2. Αρχική Οθόνη Πιστοποιημένου Χρήστη... 4 2.1. Οριστικοποίηση της Περιουσιακής Εικόνας... 5 2.2. Καρτέλες
Εφαρμογή Ηλεκτρονικής Υποβολής Δηλώσεων Ε9 Οδηγίες Χρήσης Πίνακας Περιεχομένων 1. Αρχική οθόνη... 3 2. Αρχική Οθόνη Πιστοποιημένου Χρήστη... 4 2.1. Οριστικοποίηση της Περιουσιακής Εικόνας... 5 2.2. Καρτέλες
Μάθημα 4ο. Προγράμματα
 Μάθημα 4ο Προγράμματα Σελίδα 47 από 106 4.1 Εγκατάσταση προγραμμάτων Όπως έχουμε πει στο πρώτο μάθημα (Σημειώσεις 1ου Μαθήματος 1.3.3.Β σελ. 12) τα προγράμματα ή αλλιώς εφαρμογές αποτελούν μέρος του λογισμικού
Μάθημα 4ο Προγράμματα Σελίδα 47 από 106 4.1 Εγκατάσταση προγραμμάτων Όπως έχουμε πει στο πρώτο μάθημα (Σημειώσεις 1ου Μαθήματος 1.3.3.Β σελ. 12) τα προγράμματα ή αλλιώς εφαρμογές αποτελούν μέρος του λογισμικού
Περιεχόμενα. Κεφάλαιο 1 Εισαγωγή στην Access...9. Κεφάλαιο 2 Χειρισμός πινάκων... 25
 Περιεχόμενα Κεφάλαιο 1 Εισαγωγή στην Access...9 Γνωριμία με την Access... 12 Δημιουργία βάσης δεδομένων... 18 Άνοιγμα και κλείσιμο βάσης δεδομένων... 21 Ερωτήσεις ανακεφαλαίωσης... 22 Πρακτική εξάσκηση...
Περιεχόμενα Κεφάλαιο 1 Εισαγωγή στην Access...9 Γνωριμία με την Access... 12 Δημιουργία βάσης δεδομένων... 18 Άνοιγμα και κλείσιμο βάσης δεδομένων... 21 Ερωτήσεις ανακεφαλαίωσης... 22 Πρακτική εξάσκηση...
Ενότητα. Σχεδίαση Βάσεων Δεδομένων
 Ενότητα 3 Σχεδίαση Βάσεων Δεδομένων 2 3 3.1 Εισαγωγή Μία βάση δεδομένων αποτελείται από δεδομένα για διάφορα θέματα τα οποία όμως σχετίζονται μεταξύ τους και είναι καταχωρημένα με συγκεκριμένο τρόπο. Όλα
Ενότητα 3 Σχεδίαση Βάσεων Δεδομένων 2 3 3.1 Εισαγωγή Μία βάση δεδομένων αποτελείται από δεδομένα για διάφορα θέματα τα οποία όμως σχετίζονται μεταξύ τους και είναι καταχωρημένα με συγκεκριμένο τρόπο. Όλα
Μάθημα 6ο. Υπολογιστικό Φύλλο
 Μάθημα 6ο Υπολογιστικό Φύλλο Σελίδα 81 από 105 6.1 Εισαγωγή Ένα υπολογιστικό φύλλο, είναι μια πολύ χρήσιμη εφαρμογή, χωρισμένη σε γραμμές και στήλες για την ευκολότερη καταγραφή διάφορων δεδομένων. Με
Μάθημα 6ο Υπολογιστικό Φύλλο Σελίδα 81 από 105 6.1 Εισαγωγή Ένα υπολογιστικό φύλλο, είναι μια πολύ χρήσιμη εφαρμογή, χωρισμένη σε γραμμές και στήλες για την ευκολότερη καταγραφή διάφορων δεδομένων. Με
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑ : Η/Υ I (ενότητα WINDOWS) ΥΠΕΥΘΥΝΟΣ : ΑΝΑΣΤΑΣΙΟΣ ΟΙΚΟΝΟΜΙΔΗΣ, Καθηγητής ΕΡΓΑΣΤΗΡΙΑ : ΘΕΑΝΩ ΧΑΤΖΙΔΑΚΗ, Εργαστηριακό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑ : Η/Υ I (ενότητα WINDOWS) ΥΠΕΥΘΥΝΟΣ : ΑΝΑΣΤΑΣΙΟΣ ΟΙΚΟΝΟΜΙΔΗΣ, Καθηγητής ΕΡΓΑΣΤΗΡΙΑ : ΘΕΑΝΩ ΧΑΤΖΙΔΑΚΗ, Εργαστηριακό
Κυριαρχία και μεικτές στρατηγικές Μεικτές στρατηγικές και κυριαρχία Είδαμε ότι μια στρατηγική του παίκτη i είναι κυριαρχούμενη, αν υπάρχει κάποια άλλη
 Θεωρία παιγνίων: Μεικτές στρατηγικές και Ισορροπία Nash Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 18 Μαρτίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Μεικτές στρατηγικές 18 Μαρτίου 2012 1 / 9 Κυριαρχία και μεικτές
Θεωρία παιγνίων: Μεικτές στρατηγικές και Ισορροπία Nash Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 18 Μαρτίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Μεικτές στρατηγικές 18 Μαρτίου 2012 1 / 9 Κυριαρχία και μεικτές
Word 3: Δημιουργία πίνακα
 Word 3: Δημιουργία πίνακα Θα ολοκληρώσουμε την πρακτική μας άσκηση πάνω στο περιβάλλον του Microsoft Word 2013 πειραματιζόμενοι με την καταχώρηση ενός πίνακα στο εσωτερικό ενός εγγράφου. Πολλές φορές απαιτείται
Word 3: Δημιουργία πίνακα Θα ολοκληρώσουμε την πρακτική μας άσκηση πάνω στο περιβάλλον του Microsoft Word 2013 πειραματιζόμενοι με την καταχώρηση ενός πίνακα στο εσωτερικό ενός εγγράφου. Πολλές φορές απαιτείται
Τα Windows Πολύ Απλά και Πολύ Σύντομα
 Σαχπατζίδης Αβραάμ Καθηγητής Πληροφορικής Π.Ε 20 Master of Arts (M.A) in "Gender, New Forms of Education, New Forms of Employment and New Technologies in the Information Age". Τα Windows Πολύ Απλά και
Σαχπατζίδης Αβραάμ Καθηγητής Πληροφορικής Π.Ε 20 Master of Arts (M.A) in "Gender, New Forms of Education, New Forms of Employment and New Technologies in the Information Age". Τα Windows Πολύ Απλά και
ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΟΛΟΚΛΗΡΩΜΕΝΟΥ ΠΛΗΡΟΦΟΡΙΑΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (ΟΠΣ) ΓΙΑ ΤΗΝ ΠΡΟΓΡΑΜΜΑΤΙΚΗ ΠΕΡΙΟΔΟ ΣΕΣ
 ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΟΛΟΚΛΗΡΩΜΕΝΟΥ ΠΛΗΡΟΦΟΡΙΑΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (ΟΠΣ) ΓΙΑ ΤΗΝ ΠΡΟΓΡΑΜΜΑΤΙΚΗ ΠΕΡΙΟΔΟ ΣΕΣ 2014-2020 ΕΝΟΤΗΤΑ «ΔΙΑΧΕΙΡΙΣΗ ΠΡΟΣΚΛΗΣΕΩΝ ΕΡΓΩΝ ΣΧΕΔΙΩΝ ΧΟΡΗΓΙΩΝ» 1η Έκδοση: 2015 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΗ...3
ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΟΛΟΚΛΗΡΩΜΕΝΟΥ ΠΛΗΡΟΦΟΡΙΑΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (ΟΠΣ) ΓΙΑ ΤΗΝ ΠΡΟΓΡΑΜΜΑΤΙΚΗ ΠΕΡΙΟΔΟ ΣΕΣ 2014-2020 ΕΝΟΤΗΤΑ «ΔΙΑΧΕΙΡΙΣΗ ΠΡΟΣΚΛΗΣΕΩΝ ΕΡΓΩΝ ΣΧΕΔΙΩΝ ΧΟΡΗΓΙΩΝ» 1η Έκδοση: 2015 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΗ...3
Σχεδόν όλες οι ιστοσελίδες βασίζονται σε μεγάλο βαθμό σε πίνακες. Για να εισάγουμε έναν πίνακα επιλέγουμε από το μενού Insert->Table.
 DreamWeaver - Άσκηση 4η Πίνακες Παρακάτω θα δούμε πως μπορούμε να δημιουργούμε και να επεξεργαζόμαστε πίνακες, μια πολύ βασική δομή. Θα δούμε πως γίνεται εισαγωγή πίνακα, ένωση κελιών του πίνακα, προσθήκη
DreamWeaver - Άσκηση 4η Πίνακες Παρακάτω θα δούμε πως μπορούμε να δημιουργούμε και να επεξεργαζόμαστε πίνακες, μια πολύ βασική δομή. Θα δούμε πως γίνεται εισαγωγή πίνακα, ένωση κελιών του πίνακα, προσθήκη
Λίγα λόγια από το συγγραφέα Κεφάλαιο 1: Βάσεις δεδομένων και Microsoft Access Κεφάλαιο 2: Microsoft Access
 Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: Βάσεις δεδομένων και Microsoft Access... 9 Κεφάλαιο 2: Microsoft Access 2002... 20 Κεφάλαιο 3: Το σύστημα Βοήθειας του Microsoft Office ΧΡ... 36
Περιεχόμενα Λίγα λόγια από το συγγραφέα... 7 Κεφάλαιο 1: Βάσεις δεδομένων και Microsoft Access... 9 Κεφάλαιο 2: Microsoft Access 2002... 20 Κεφάλαιο 3: Το σύστημα Βοήθειας του Microsoft Office ΧΡ... 36
Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων
 Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων Περιεχόμενα Παραμετροποίηση Γρήγορης Καταχώρησης... 3 Γρήγορη Καταχώρηση... 4 Κατηγορία Λιανικής & Μαζική Ανάθεση Κατηγορίας στα είδη... 9 Γρήγορη Καταχώρηση Πωλήσεων
Διαχείριση Γρήγορης Καταχώρησης Πωλήσεων Περιεχόμενα Παραμετροποίηση Γρήγορης Καταχώρησης... 3 Γρήγορη Καταχώρηση... 4 Κατηγορία Λιανικής & Μαζική Ανάθεση Κατηγορίας στα είδη... 9 Γρήγορη Καταχώρηση Πωλήσεων
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ACCESS
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ACCESS Μια βάση δεδομένων είναι μια οργανωμένη συλλογή πληροφοριών, οι οποίες είναι αποθηκευμένες σε κάποιο αποθηκευτικό μέσο (π.χ σκληρό δίσκο). Οι πληροφορίες τις οποίες καταχωρούμε και
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ACCESS Μια βάση δεδομένων είναι μια οργανωμένη συλλογή πληροφοριών, οι οποίες είναι αποθηκευμένες σε κάποιο αποθηκευτικό μέσο (π.χ σκληρό δίσκο). Οι πληροφορίες τις οποίες καταχωρούμε και
MEDIWARE L.I.S ΟΔΗΓΙΕΣ ΥΠΟΠΡΟΓΡΑΜΜΑΤΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΠΙΣΚΕΨΕΩΝ
 MEDIWARE L.I.S. 2006 ΟΔΗΓΙΕΣ ΥΠΟΠΡΟΓΡΑΜΜΑΤΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΠΙΣΚΕΨΕΩΝ -1 -2 Προγραμματισμός Επισκέψεων. Με την επιλογή Προγραμματισμός Επισκέψεων ο χειριστής έχει τη δυνατότητα να καταχωρίσει τις μελλοντικές
MEDIWARE L.I.S. 2006 ΟΔΗΓΙΕΣ ΥΠΟΠΡΟΓΡΑΜΜΑΤΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΠΙΣΚΕΨΕΩΝ -1 -2 Προγραμματισμός Επισκέψεων. Με την επιλογή Προγραμματισμός Επισκέψεων ο χειριστής έχει τη δυνατότητα να καταχωρίσει τις μελλοντικές
Oικονομικές και Mαθηματικές Eφαρμογές
 Το πακέτο ΕXCEL: Oικονομικές και Mαθηματικές Eφαρμογές Eπιμέλεια των σημειώσεων και διδασκαλία: Ευαγγελία Χαλιώτη* Θέματα ανάλυσης: - Συναρτήσεις / Γραφικές απεικονίσεις - Πράξεις πινάκων - Συστήματα εξισώσεων
Το πακέτο ΕXCEL: Oικονομικές και Mαθηματικές Eφαρμογές Eπιμέλεια των σημειώσεων και διδασκαλία: Ευαγγελία Χαλιώτη* Θέματα ανάλυσης: - Συναρτήσεις / Γραφικές απεικονίσεις - Πράξεις πινάκων - Συστήματα εξισώσεων
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ Π ΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ Π ΕΡΙΒΑΛΛΟΝ Κ Υ Κ Λ Ο Υ Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ Κ Α Ι Υ Π Η Ρ Ε Σ Ι Ω Ν Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η
Διαγραφή Επιλέγετε Διαγραφή για να διαγράψετε μία ήδη υπάρχουσα διαδικασία εισαγωγής ASCII
 Published on PRISMA Win Help - Megasoft (http://docs.megasoft.gr) Home > Διαχείριση Βάσης Δεδομένων (dbadmin) > Αρχεία Αρχεία Εισαγωγή από αρχείο ASCII Με την εργασία αυτή έχετε την δυνατότητα να εισάγετε
Published on PRISMA Win Help - Megasoft (http://docs.megasoft.gr) Home > Διαχείριση Βάσης Δεδομένων (dbadmin) > Αρχεία Αρχεία Εισαγωγή από αρχείο ASCII Με την εργασία αυτή έχετε την δυνατότητα να εισάγετε
Γνωρίστε το χώρο εργασίας του PowerPoint
 Γνωρίστε το χώρο εργασίας του PowerPoint Για να εκκινήσουμε το Office PowerPoint 2007 ακολουθούμε τα εξής βήματα: Έναρξη à Όλα τα προγράμματα PowerPoint 2007. à Microsoft Office à Microsoft Office Όταν
Γνωρίστε το χώρο εργασίας του PowerPoint Για να εκκινήσουμε το Office PowerPoint 2007 ακολουθούμε τα εξής βήματα: Έναρξη à Όλα τα προγράμματα PowerPoint 2007. à Microsoft Office à Microsoft Office Όταν
Γρήγορη Εκκίνηση. Όταν ξεκινήσετε το GeoGebra, εμφανίζεται το παρακάτω παράθυρο:
 Τι είναι το GeoGebra; Γρήγορη Εκκίνηση Λογισμικό Δυναμικών Μαθηματικών σε ένα - απλό στη χρήση - πακέτο Για την εκμάθηση και τη διδασκαλία σε όλα τα επίπεδα της εκπαίδευσης Συνδυάζει διαδραστικά γεωμετρία,
Τι είναι το GeoGebra; Γρήγορη Εκκίνηση Λογισμικό Δυναμικών Μαθηματικών σε ένα - απλό στη χρήση - πακέτο Για την εκμάθηση και τη διδασκαλία σε όλα τα επίπεδα της εκπαίδευσης Συνδυάζει διαδραστικά γεωμετρία,
Οι νεότερες εξελίξεις στον GM EPC
 Οι νεότερες εξελίξεις στον GM EPC Πλοήγηση με χρήση γραφικών στοιχείων Ο κατάλογος επόμενης γενιάς GM Next Gen EPC διαθέτει διάφορες λειτουργίες που έχουν σχεδιαστεί για ταχύτερη και ευκολότερη εύρεση
Οι νεότερες εξελίξεις στον GM EPC Πλοήγηση με χρήση γραφικών στοιχείων Ο κατάλογος επόμενης γενιάς GM Next Gen EPC διαθέτει διάφορες λειτουργίες που έχουν σχεδιαστεί για ταχύτερη και ευκολότερη εύρεση
Γνωρίστε το Excel 2007
 Εισαγωγή τύπων Γνωρίστε το Excel 2007 Πληκτρολογήστε το σύμβολο της ισότητας (=), χρησιμοποιήστε ένα μαθηματικό τελεστή (+,-,*,/) και πατήστε το πλήκτρο ENTER. Πρόσθεση, διαίρεση, πολλαπλασιασμός και αφαίρεση
Εισαγωγή τύπων Γνωρίστε το Excel 2007 Πληκτρολογήστε το σύμβολο της ισότητας (=), χρησιμοποιήστε ένα μαθηματικό τελεστή (+,-,*,/) και πατήστε το πλήκτρο ENTER. Πρόσθεση, διαίρεση, πολλαπλασιασμός και αφαίρεση
Geogebra. Μακρή Βαρβάρα. Λογισµικό Geogebra
 Λογισµικό Geogebra 1 Τι είναι το πρόγραµµα Geogebra; Το πρόγραµµα GeoGebra, είναι ένα δυναµικό µαθηµατικό λογισµικό που συνδυάζει Γεωµετρία, Άλγεβρα και λογισµό. Αναπτύσσεται από τον Markus Hohenwarter
Λογισµικό Geogebra 1 Τι είναι το πρόγραµµα Geogebra; Το πρόγραµµα GeoGebra, είναι ένα δυναµικό µαθηµατικό λογισµικό που συνδυάζει Γεωµετρία, Άλγεβρα και λογισµό. Αναπτύσσεται από τον Markus Hohenwarter
ΚΕΦΑΛΑΙΟ ΙΙ. OpenOffice 3.x Calc
 ΚΕΦΑΛΑΙΟ ΙΙ OpenOffice 3.x Calc Στόχοι: Με τη βοήθεια του οδηγού αυτού ο εκπαιδευόμενος θα μπορεί να: χρησιμοποιεί τα βασικά εργαλεία του Calc κατασκευάζει πίνακες δημιουργεί φόρμουλες υπολογισμού κατασκευάζει
ΚΕΦΑΛΑΙΟ ΙΙ OpenOffice 3.x Calc Στόχοι: Με τη βοήθεια του οδηγού αυτού ο εκπαιδευόμενος θα μπορεί να: χρησιμοποιεί τα βασικά εργαλεία του Calc κατασκευάζει πίνακες δημιουργεί φόρμουλες υπολογισμού κατασκευάζει
