Διπλωματική Εργασία της φοιτήτριας του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών
|
|
|
- Βαρβάρα Παπακώστας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΡΓΑΣΤΗΡΙΟ ΑΥΤΟΜΑΤΙΣΜΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ Διπλωματική Εργασία της φοιτήτριας του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών ΚΥΡΙΤΟΠΟΥΛΟΥ ΜΑΡΙΑΣ του ΜΙΧΑΗΛ Αριθμός Μητρώου: 68 Θέμα «Δυναμική και Έλεγχος Ρομποτικής Πλατφόρμας Οστεογένεσης» Επιβλέπων Αντώνιος Τζες, Καθηγητής Αριθμός Διπλωματικής Εργασίας: Πάτρα, Οκτώβριος
2 ΠΙΣΤΟΠΟΙΗΣΗ Πιστοποιείται ότι η Διπλωματική Εργασία με θέμα «Δυναμική και Έλεγχος Ρομποτικής Πλατφόρμας Οστεογένεσης» Της φοιτήτριας του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΚΥΡΙΤΟΠΟΥΛΟΥ ΜΑΡΙΑΣ του ΜΙΧΑΗΛ Αριθμός Μητρώου: 68 Παρουσιάστηκε δημόσια και εξετάστηκε στο Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών στις.../../ Ο Επιβλέπων Αντώνιος Τζες Καθηγητής Ο Διευθυντής του Τομέα Νικόλαος Κούσουλας Καθηγητής
3 Αριθμός Διπλωματικής Εργασίας: Θέμα: «Δυναμική και Έλεγχος Ρομποτικής Πλατφόρμας Οστεογένεσης» Φοιτήτρια: Κυριτοπούλου Μαρία Επιβλέπων: Αντώνιος Τζες Περίληψη Σκοπός της διπλωματικής αυτής εργασίας είναι η μελέτη ρομποτικής διάταξης οστεογένεσης και πιο συγκεκριμένα η μελέτη της δυναμικής και ο έλεγχος αυτής. Πιο αναλυτικά τα κεφάλαια που ακολουθούν πραγματεύονται τα παρακάτω: Θα παρουσιαστεί γενικά ο μηχανισμός της οστεογένεσης από ιατρικής πλευράς καθώς επίσης θα παρουσιάσουμε τις διάφορες διατάξεις με τις οποίες πραγματοποιείται η διατατική οστεογένεση. Στη συνέχεια θα παρουσιάσουμε τις κινηματικές και δυναμικές εξισώσεις της πλατφόρμας Stewart με την οποία θα ασχοληθούμε στη συγκεκριμένη εργασία. Το τελευταίο μέρος αποτελεί και το πειραματικό μέρος της παρούσας εργασίας δηλαδή τον έλεγχο της συγκεκριμένης διάταξης μέσω του SiMechanics toolbox του πακέτου MatLab. Στο παράρτημα της εργασίας παρουσιάζονται τα αποτελέσματα των πειραμάτων με μορφή διαγραμμάτων.
4 Περιεχόμενα ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή...5. Διατατική Οστεογένεση...7. Μακροσκοπική δομή των οστών...7. Κυτταρική δομή των οστών...8. Ιστορική αναδρομή διατατικής οστεογένεσης Αρχές εφαρμογής....5 Προβλήματα και επιπλοκές....6 Περίοδος ωρίμανσης του πώρου Απεικόνιση της οστικής επιμήκυνσης Συστήματα υποστήριξης Πλατφόρμα Stewart- Κινηματικές Εξισώσεις Γενικά χαρακτηριστικά της διάταξης Ορθή κινηματική ανάλυση.... Αντίστροφη κινηματική ανάλυση Γεωμετρικοί περιορισμοί Χαμηλότερη θέση Υψηλότερη θέση Θέση με τη μεγαλύτερη κλίση Θέση με τη μεγαλύτερη περιστροφή....5 Η μήτρα Jacobian....6 Singularities Εισαγωγή Singularity ροπής Singularity θέσης Πλατφόρμα Stewart- Δυναμική Ανάλυση Προσομοίωση και Έλεγχος της Πλατφόρμας Stewart Σχεδιασμός του μοντέλου στο Siulink Προσομοίωση κίνησης Έλεγχος Δυνάμεων Επεκτάσεις... 6 Βιβλιογραφία... 8 Παράρτημα
5 Εισαγωγή ΕΙΣΑΓΩΓΗ Η διατατική οστεογένεση (μέθοδος Ilizarov) αποτελεί μια επαναστατική μέθοδο επιμήκυνσης των οστών και βασίζεται στις αρχές που εφάρμοσε ο Ρώσος καθηγητής και ακαδημαϊκός Gavriil Abraovich Ilizarov, εμπνευστής και δημιουργός της μεθόδου και της συσκευής που φέρει το όνομά του και διαμόρφωσε μια νέα εποχή στην ορθοπαιδική χειρουργική. Το 95 ο Ilizarov κατασκεύασε μια εξειδικευμένη συσκευή εξωτερικής οστεογένεσης, που αποτελείται από κυκλοτερείς δακτυλίους συγκρατούμενους μεταξύ τους με σπειροειδείς ράβδους. Συνδέονται με το οστούν με λεπτές διοστικές βελόνες υπό τάση, ούτως ώστε να σταθεροποιούνται τα κατεαγότα οστικά άκρα και να επιτρέπεται παράλληλα, η σταδιακή και ελεγχόμενη συμπίεση και διάταση (αναίμακτη μέθοδος). Η διατατική οστεογένεση είναι μια διαδικασία παραγωγής νέου οστού μεταξύ δύο αγγειούμενων οστικών επιφανειών που απομακρύνονται σταδιακά. Το κενό που δημιουργείται συμπληρώνεται από νέο οστούν (οστεογένεση), ενώ διατηρείται η σταθερότητα μεταξύ των οστικών τμημάτων με τη βοήθεια αυτής της συσκευής. 5
6 Εισαγωγή Χρησιμοποιώντας κανείς αυτή τη συσκευή μπορεί να πραγματοποιεί επεμβάσεις για την αντιμετώπιση ανισοσκελιών, καταγμάτων, ψευδαρθρώσεων, αλλά και για την αντιμετώπιση των οστικών λοιμώξεων, επιτυγχάνοντας την επιμήκυνση οστών και μαλακών μορίων. Για την αύξηση μήκους ενός εκατοστού απαιτούνται περίπου -4 ημέρες, γεγονός που σημαίνει ότι για την αύξηση περίπου εκατοστών απαιτείται ένας χρόνος. Αυτό ισχύει και για τις αμφοτερόπλευρες επιμηκύνσεις των μακρών οστών (π.χ. μηριαίου, κνήμης ή και βραχιονίου οστού), όπως και στις βραχυσωμίες. Η διατατική οστεογένεση αποτελεί επαναστατική και εντυπωσιακή ως προς την αποτελεσματικότητά της μέθοδο αντιμετώπισης δυσεπίλυτων ορθοπαιδικών προβλημάτων. Η μέθοδος της διατατικής οστεογένεσης δίνει νέες δυνατότητες στον ορθοπαιδικό χειρουργό για την αντιμετώπιση των προβλημάτων που είναι δύσκολο να αντιμετωπιστούν με παραδοσιακές μεθόδους. Η κλινική εφαρμογή της μεθόδου δίνει λύσεις και στην τραυματολογία στην αντιμετώπιση συντριπτικών καταγμάτων, ανοιχτών καταγμάτων, ενδαρθρικών καταγμάτων, άσηπτων και σηπτικών ψευδαρθρώσεων αλλά και σε ορθοπαιδικές παθήσεις που στο παρελθόν ήταν δύσκολη ή και αδύνατη η αντιμετώπισή τους. Σήμερα με τη δυνατότητα της ταυτόχρονης επιμήκυνσης και διόρθωσης των παραμορφώσεων οι ασθενείς βρίσκουν ικανοποιητική θεραπεία όπως σε περιπτώσεις ανισοσκελιών, συγγενών ανωμαλιών των οστών, παραμορφώσεων, οστικών ελλειμμάτων, βραχυσωμιών (αχονδροπλασία, άλλοι τύποι νανισμού), δυσκαμψιών των αρθρώσεων. Στην Ελλάδα προς το τέλος της ετίας του 98 άρχισε δειλά δειλά να εφαρμόζεται η μέθοδος Ilizarov για την αντιμετώπιση των δυσεπίλυτων προβλημάτων της ορθοπαιδικής και τραυματολογίας. Στους πρωτοπόρους ανήκει η ομάδα της Ορθοπαιδικής Κλινικής του Πανεπιστημίου Πατρών. Σήμερα η μέθοδος έχει επεκταθεί σε αρκετές νοσηλευτικές μονάδες της χώρας και πάρα πολλοί ασθενείς αντιμετωπίζονται με την παραπάνω τεχνική. Η μέθοδος Ilizarov ήρθε να συμπληρώσει άλλες τεχνικές και όχι να τις καταργήσει. 6
7 Κεφάλαιο : Διατατική Οστεογένεση ΚΕΦΑΛΑΙΟ : ΔΙΑΤΑΤΙΚΗ ΟΣΤΕΟΓΕΝΕΣΗ. Μακροσκοπική δομή των οστών Τα οστά αποτελούν τα μοναδικά «ζωντανά» κατασκευαστικά υλικά. Με τις μηχανικές ιδιότητες που διαθέτουν και με την συμμετοχή τους στις μεταβολικές διαδικασίες του οργανισμού, προσφέρουν στο ανθρώπινο σώμα προστασία, κινητικότητα, ευελιξία και αντοχή, ενώ αποτελούν μια ανεξάντλητη μεταβολική αποθήκη αλάτων. Είναι ενεργά μέλη με πολύπλοκη αιμάτωση, θεμέλιο ουσία που αποτιτανώνεται και εξειδικευμένους κυτταρικούς πληθυσμούς που είναι υπεύθυνοι για την συνεχή συντήρηση και ανακατασκευή τους. Η μορφή και το σχήμα των οστών ποικίλει ανάλογα με την περιοχή που ευρίσκονται και την μηχανική λειτουργία που επιτελούν. Διακρίνονται σε μακρά (π.χ. μηριαίο) και σε βραχέα οστά (π.χ. σπόνδυλος). Παρόλο που το σχήμα των ανθρωπίνων οστών ποικίλει, 7
8 Κεφάλαιο : Διατατική Οστεογένεση συγκρίσεις με αντίστοιχα ζώων δείχνουν ότι η αρχιτεκτονική των σπονδυλωτών ειδών είναι αρκετά συντηρητική και στερεότυπη. Από αρχιτεκτονικής πλευράς υπάρχουν δύο μορφές οστίτου ιστού: το εξωτερικό, φλοιώδες (cortical bone) και το εσωτερικό, σπογγώδες και δοκιδώδες οστούν (trabecular/cancellous bone) (Εικόνα.). Εικόνα.: Δομή οστού Παρόλο που φλοιώδες και σπογγώδες οστό αποτελούνται από τον ίδιο ιστό και μακροσκοπικά έχουν κατά προσέγγιση παρόμοια αρχιτεκτονική, παρουσιάζουν διαφορετική οστική πυκνότητα και μηχανική συμπεριφορά, καθώς σε μικροσκοπική κλίμακα φαίνεται ότι είναι ενεργοί ιστοί που συνεχώς προσαρμόζονται στο μηχανικό περιβάλλον τροποποιώντας τη σύνθεση και την αρχιτεκτονική τους.. Κυτταρική δομή των οστών Υπάρχουν τέσσερα είδη κυττάρων που είναι υπεύθυνα για τον σχηματισμό, για την συντήρηση-επιδιόρθωση και για την προσαρμογή του οστίτου ιστού: τα οστεοκύτταρα, οι οστεοβλάστες, οι οστεοκλάστες και τα αδιαφοροποίητα κύτταρα. Τα οστεοκύτταρα παίζουν σημαντικό ρόλο στη λειτουργία της προσαρμογής των οστών στο μηχανικό τους περιβάλλον και θεωρείται ότι έχουν τη δυνατότητα να μεταφέρουν το ερέθισμα μιας ενδεχόμενης αλλαγής των καταπονήσεων που δέχονται τα οστά. Οι οστεοβλάστες με την δράση τους παράγουν οστούν, ενώ οι οστεοκλάστες απορροφούν οστούν. Οι δύο αυτοί κυτταρικοί πληθυσμοί ευρίσκονται σε διαρκή συνεργασία και ισορροπία αλλά σε περιπτώσεις που ο οργανισμός έχει ανάγκη από πιο ισχυρή αρχιτεκτονική δομή, η οστεοβλαστική δραστηριότητα υπερισχύει της οστεοκλαστικής. Αυτή η κυτταρική συνεργασία περιγράφεται με το φαινόμενο της οστικής ανακατασκευής. Τα αδιαφοροποίητα κύτταρα, τέλος, ή, αλλιώς, πρώιμες μορφές οστεοκυττάρων αν δεχθούν κατάλληλο ερέθισμα διαφοροποιούνται σε οστεοβλάστες. Η οστική θεμέλιος ουσία αποτελείται από οργανικά μακρομόρια (κολλαγόνο) κατά %, ανόργανα άλατα (κυρίως υδροξυαπατίτης) κατά 7% και τα υγρά της θεμέλιας ουσίας. Το οργανικό τμήμα δίδει το σχήμα του οστού και συμβάλλει στην αντοχή σε εφελκυσμό και απουσία της τα καθιστά εύθρυπτα. Το ανόργανο τμήμα συμβάλλει στην αντοχή σε 8
9 Κεφάλαιο : Διατατική Οστεογένεση συμπίεση και ακαμψία. Η αποτιτάνωση (μετάλλωση) της θεμελίου ουσίας είναι υπεύθυνη για τις μηχανικές ιδιότητες του ώριμου οστίτη ιστού. Οστική Ανακατασκευή Ο οστίτης ιστός παρουσιάζει από την έβδομη εμβρυϊκή εβδομάδα και μέχρι τον θάνατο μια σημαντική λειτουργία που ονομάζεται οστική ανακατασκευή (Bone Reodeling), η οποία αναφέρθηκε παραπάνω ως κυτταρική συνεργασία οστεοκλαστών και οστεοβλαστών. Αποτέλεσμα αυτής της διαδικασίας είναι η συνεχής απορρόφηση και παραγωγή του οστίτη ιστού, με σκοπό την σωστή ανάπτυξη των οστών, την επιδιόρθωση μικρών ζημιών που προκύπτουν από την καθημερινή καταπόνηση του σκελετού και την διατήρηση της λειτουργικότητας του σώματος. Μια σχηματική εικόνα της οστικής ανακατασκευής φαίνεται στο Εικόνα. Εικόνα.: Σχηματικό διάγραμμα οστικής ανακατασκευής. Ιστορική Αναδρομή Διατατικής Οστεογένεσης Ο Alessandro Codivilla πρώην διευθυντής του Ινστιτούτου Rizzoli της Μπολόνια, θεωρείται ο πατέρας της επιμήκυνσης άκρου. Το 95 ανακοίνωσε περίπτωση επιμήκυνσης άκρων με την εφαρμογή τμηματικής σκελετικής έλξης μέσω βελόνας πτέρνης, μετά από οστεοτομία μηριαίου και περιέγραψε την αντίσταση των μαλακών μορίων στην έλξη καθώς και την αναγκαιότητα για σταδιακή επιμήκυνση (Εικόνα.). Το 9, ο Vittorio Putti, μαθητής του Codivilla, δημιούργησε μια συσκευή, τη λεγόμενη osteoton, η οποία εμπεριείχε ένα μηχανισμό ελατηρίου, προσαρμοζόταν με βελόνες στο εγγύς και το άπω τμήμα του μηριαίου, και επέτρεπε σταδιακή επιμήκυνση μετά από οστεοτομία. Ακολούθησαν πολλές παραλλαγές του συστήματος εξωτερικής οστεογένεσης. Το 9 οι Dickson και Diveley καθώς και οι Haboush και Finkelstein πρότειναν την χρήση λεπτών βελονών Kirshner αντί των κλασσικών βελονών ή καρφίδων, θέτοντας την βάση για την 9
10 Κεφάλαιο : Διατατική Οστεογένεση μετέπειτα χρησιμοποίηση λεπτών συρμάτων στα κυκλικά συστήματα εξωτερικής οστεογένεσης. Το 98, ο Bosworth ήταν ο πρώτος που συνέστησε περίοδο αναμονής ημερών μεταξύ της οστεοτομίας και της έναρξης της επιμήκυνσης. Εικόνα.: A. Codivilla, 95. Έλξη στην πτέρνα, οστεοτομία μηριαίου και προοδευτική επιμήκυνση Το 96, ήταν η χρονιά που ήρθε στην δημοσιότητα η μέθοδος του Wagner (Εικόνα.4) η οποία περιελάμβανε μια σειρά από διαδοχικές επεμβάσεις. Στην πρώτη γινόταν η οστεοτομία στην περιοχή της διάφυσης και τοποθετούταν ένα μονόπλευρο σύστημα εξωτερικής οστεογένεσης για την πραγματοποίηση της επιμήκυνσης. Στην συνέχεια γινόταν άμεση επιμήκυνση,5 c χωρίς παρεμβολή περιόδου αναμονής, ενώ το ζητούμενο μήκος του σκέλους επιτυγχανόταν το ταχύτερο δυνατόν με ρυθμό επιμήκυνσης,5- την ημέρα. Μετά την ολοκλήρωση της επιμήκυνσης, και καθώς η ποιότητα του αναγεννώμενου οστού ήταν πολύ πτωχή, ακολουθούσε η δεύτερη επέμβαση για την τοποθέτηση μοσχευμάτων στο οστικό κενό, η οποία συνοδευόταν από αφαίρεση της εξωτερικής οστεογένεσης και γεφύρωση του κενού με πλάκα. Η τρίτη επέμβαση περιλάμβανε την αφαίρεση της πλάκας. Η μέθοδος Wagner είχε υψηλά ποσοστά επιπλοκών όπως οξεία συστηματική υπέρταση την στιγμή της διάτασης, φλεγμονές καθώς και πρώιμα ή όψιμα κατάγματα στην περιοχή της επιμήκυνσης. Εικόνα.4: Σύστημα τύπου Wagner Ο Ilizarov (9-99) θεωρείται από πολλούς αυτός που διαμόρφωσε ουσιαστικά το θεωρητικό υπόβαθρο της διατατικής οστεογένεσης και ιστογένεσης (εικόνα.5). To 95, στο Kurgan της Σιβηρίας, ανέπτυξε τις αρχές τις διατατικής οστεογένεσης για την
11 Κεφάλαιο : Διατατική Οστεογένεση αντιμετώπιση καταγμάτων. Αρχικά η συσκευή του αποτελούνταν από λεπτές βελόνες Kirshner που συνδέονταν με κοχλιωτές ράβδους που χρησιμοποιούσε για διόρθωση συγκάμψεων γόνατος. Κατόπιν πρόσθεσε μεταλλικούς δακτυλίους ενώ παράλληλα μελέτησε την όλη διαδικασία την οποία ονόμασε διοστική οστεογένεση (transosseous Εικόνα.5: Συσκευή Ilizarov osteosynthesis). Οι βασικές αρχές της μεθόδου όπως διατυπώθηκαν από τον Ilizarov ήταν: α) η σταδιακή διάταση, β) η συμμετρική κατανομή της διάτασης μέσω της σταθερής κυκλοτερούς εξωτερικής οστεογένεσης που φέρει το όνομά του, (συσκευή Ilizarov) και γ) η διατήρηση του περιοστέου και των ενδαυλικών αγγείων δια της πραγματοποίησης της φλοιοτομής. Η δημιουργία του κατάλληλου εμβιομηχανικού περιβάλλοντος μετατρέπει το ερέθισμα της σταδιακής διάτασης σε βιολογική αντίδραση που εκφράζεται ως αύξηση της αιμάτωσης του σκέλους, ανάπτυξη ενδομεμβρανώδους οστέωσης, καθώς και δημιουργία συζευτικού χόνδρου στο κέντρο της επιμήκυνσης που παραπέμπει στην εμβριονική κατάσταση δραστηριοποίησης του οστού..4 Αρχές Εφαρμογής Τα βασικά στοιχεία που απαιτούνται για την διενέργεια της διατατικής οστεογένεσης περιλαμβάνουν: α) Την τοποθέτηση ενός συστήματος εξωτερικής οστεογένεσης που παρέχει σταθερότητα και εφαρμόζει δυνάμεις διάτασης ή συμπίεσης για την επίτευξη επιμήκυνσης, οστεομεταφοράς ή τη διόρθωση παραμόρφωσης. Το σύστημα αυτό μπορεί να είναι είτε κυκλικό, αποτελούμενο από δακτυλίους και λεπτές βελόνες (π.χ. συσκευή Ilizarov) είτε
12 Κεφάλαιο : Διατατική Οστεογένεση μονόπλευρο, αποτελούμενο από ένα κεντρικό σώμα επιμήκυνσης και κοχλιωτές βελόνες μισού σπειράματος, είτε υβριδικό αποτελούμενο από επιμέρους στοιχεία των πρώτων δύο. Ένα σταθερό σύστημα, που τοποθετείται ιδανικά έτσι ώστε να μην περιορίζει σημαντικά την λειτουργικότητα των δορυφορικών αρθρώσεων, επιτρέπει την εφαρμογή πλήρους φόρτισης στο σκέλος και διασφαλίζει την παρουσία μηχανικών και βιολογικών συνθηκών για την ανάπτυξη της νέο-οστεογένεσης. β) Την διενέργεια κορτικοτομής (Εικόνα.6) ή χαμηλής ενέργειας οστεοτομίας, με στόχο τη διαφύλαξη του περιοστέου κατά πρώτο λόγο αλλά και του ενδοστέου και των ενδομυελικών αγγείων όσο αυτό είναι δυνατό. γ) Την μετεγχειρητική περίοδο που περιλαμβάνει τις φάσεις της αναμονής, της διάτασης και της σταθεροποίησης του πώρου. Η φάση της αναμονής (latency period) αποτελεί την χρονική περίοδο μεταξύ κορτικοτομής και έναρξης διάτασης. Η φάση της διάτασης περιλαμβάνει το χρονικό διάστημα κατά το οποίο επιτελείται η σταδιακή επιμήκυνση ή η οστεομεταφορά ή η γωνιακή διόρθωση και που αναπτύσσεται καινούργιο οστό μέσα από την διαδικασία της οστικής αναγέννησης. Στη φάση της σταθεροποίησης του πώρου, συντελείται η ωρίμανση και ασβεστοποίηση του πώρου και ο σχηματισμός φλοιώδους οστού, γεγονός που επιτρέπει την αφαίρεση της εξωτερικής συσκευής και την πλήρη φόρτιση του πώρου. Εικόνα.6: Κορτικοτομή Η ποιότητα του νεοσχηματισμένου πώρου μπορεί να επηρεαστεί από διάφορους παράγοντες. Ένας από αυτούς είναι η ταχύτητα και ο ρυθμός της διάτασης. Μετά από
13 Κεφάλαιο : Διατατική Οστεογένεση πειράματα σε κνήμες κουνελιών, ο Ilizarov βρήκε ότι ταχύτητα διάτασης,5 / μέρα ή μικρότερη μπορεί να οδηγήσει σε πρώιμη σταθεροποίηση του πώρου, ενώ ταχύτητα διάτασης /μέρα ή μεγαλύτερη μπορεί προκαλέσει ενδιάμεση ανάπτυξη ινώδους ιστού και πτωχή οστική αναγέννηση. Η καλύτερη ποιότητα αναγεννώμενου οστού προέκυπτε όταν η διάταση γινόταν με ταχύτητα /μέρα και με ρυθμό,5/6 ώρες. Περαιτέρω μελέτες έδειξαν ότι η ποιότητα του πώρου επιμήκυνσης μπορεί να βελτιωθεί ακόμα περισσότερο, όταν χρησιμοποιηθεί αυτόματο σύστημα επιμήκυνσης που προκαλεί διάταση /μέρα, χωρισμένη όμως σε 6 ίσα βήματα. Μετά από κλινικές και πειραματικές μελέτες διαπιστώθηκε ότι η ανάπτυξη ενός υγιούς αναγεννώμενου οστικού πώρου σε συνάρτηση με ένα καλό κλινικό αποτέλεσμα προάγονται από τις παρακάτω πρακτικές: α) Προστασία της περιοστικής αιμάτωσης με την διενέργεια κορτικοτομής ή χαμηλής ενέργειας οστεοτομίας. β) Σταθερή εξωτερική οστεογένεση ικανή να αποτρέπει στροφικές και καμπτικές κινήσεις στην περιοχή της οστεοτομίας αλλά να επιτρέπει μικροκινήσεις παράλληλες στον διαφυσιακό οστικό άξονα. γ) Περίοδος καθυστέρησης της επιμήκυνσης 5-7 ημέρες. δ) Ταχύτητα επιμήκυνσης /μέρα, που εξατομικεύεται όπου χρειάζεται ε) Ρυθμός επιμήκυνσης σε ίσα χρονικά βήματα τουλάχιστον 4/μέρα. στ) Περίοδος σταθεροποίησης του πώρου μετά την επιμήκυνση όπου απαιτείται η παραμονή της εξωτερικής οστεογένεσης. ζ) Φυσιολογική χρήση του μέλους, που προάγει την διαδικασία πώρωσης και εξασφαλίζει φυσιολογικό εύρος κινήσεων..5 Προβλήματα και Επιπλοκές Η διαδικασία της διατατικής οστεογένεσης παρουσιάζει επιπλοκές, μερικές από τις συχνότερες παρατίθενται παρακάτω: Μυϊκές συσπάσεις Συνήθως είναι το αποτέλεσμα της τάσης που εφαρμόζεται σ ένα μυ κατά την διάρκεια της διάτασης. Η τάση αυτή αποτελεί αρχικά ερέθισμα για ενεργοποίηση αναγεννητικών μηχανισμών που οδηγούν στην επιμήκυνση των μυϊκών ινών. Όταν όμως ο ρυθμός επιμήκυνσης υπερβαίνει τον κριτικό ρυθμό επιμήκυνσης για κάποιες μυϊκές ίνες, αυτές χάνουν την ελαστικότητά τους και γίνονται μη λειτουργικές οδηγώντας σε συγκάμψεις. Η κατάσταση αυτή επιβαρύνεται στις περιοχές όπου οι βελόνες της συσκευής εξωτερικής οστεογένεσης διαπερνούν τους μύες και τους καθηλώνουν πάνω στο οστό εμποδίζοντας την διάτασή τους. Διαταραχή άξονα Κατά την διάρκεια της επιμήκυνσης, εξαιτίας της άσκησης διαφορετικών δυνάμεων από τις μυϊκές ομάδες πάνω στο οστό, υπάρχει η τάση να διαταραχθεί ο άξονας της επιμήκυνσης. Η κατεύθυνση αυτής της διαταραχής εξαρτάται από το οστό που επιμηκύνεται και από το επίπεδο της οστεοτομίας. Τη διαταραχή του άξονα επιτρέπει η αστάθεια της συσκευής εξαιτίας απώλειας της τάσης ή χαλάρωσης των βελονών.
14 Κεφάλαιο : Διατατική Οστεογένεση Καθυστέρηση ωρίμανσης του πώρου Η ωρίμανση του πώρου επιμήκυνσης μπορεί να επιβραδυνθεί εξαιτίας πολλαπλών παραγόντων όπως τραυματική φλοιοτομή, αρχική διάσταση στην φλοιοτομή, αστάθεια της συσκευής, υψηλός ρυθμός διάτασης, λοίμωξη. Διαγιγνώσκεται από την καθυστέρηση εμφάνισης οστού στις ακτινογραφίες. Το υπερηχογράφημα στην περιοχή του πώρου έχει υψηλή διαγνωστική αξία καθώς μπορεί να ανιχνεύσει οστική ανάπτυξη μόλις εβδομάδες μετά την έναρξη της επιμήκυνσης και συνεπώς να διαγνώσει εγκαίρως καθυστέρηση στην ωρίμανση. Για την αντιμετώπιση του προβλήματος γίνεται καθυστέρηση στον ρυθμό διάτασης ή τοποθέτηση οστικών μοσχευμάτων (ειδικότερα εάν ανευρίσκονται υπερηχογραφικά οστικές κύστεις μέσα στην περιοχή του πώρου). Η καθυστέρηση ωρίμανσης του πώρου μπορεί να οδηγήσει στην καθυστέρηση αφαίρεσης της συσκευής και την παράταση της εφαρμογής της για μεγάλο χρονικό διάστημα (τριπλάσιο ή τετραπλάσιο του χρόνου επιμήκυνσης). Ο παρατεταμένος χρόνος εφαρμογής μιας συσκευής εξωτερικής οστεογένεσης, προδιαθέτει σε φλεγμονές στα σημεία εισόδου των βελονών και χαλάρωση της σύνδεσης των βελονών με το οστό, γεγονός που επιβάλλει την αλλαγή τους. Προβλήματα στα σημεία εισόδου των βελονών Σχετίζονται άμεσα με την κίνηση του δέρματος στην περιοχή των βελονών, το ποσό μαλακών μορίων που παρεμβάλλεται μεταξύ οστού και δέρματος, καθώς και με την διάμετρο των βελονών που χρησιμοποιούνται. Η εξασφάλιση ικανοποιητικής τάσης στις βελόνες αποτελεί σημαντικό προστατευτικό παράγοντα καθώς ελαχιστοποιεί τις κινήσεις μεταξύ βελόνας-δέρματος και βελόνας-οστού. Επανακάταγμα Πρόκειται για μείζονα επιπλοκή που μπορεί να συμβεί μετά την αφαίρεση της συσκευής, σε ποσοστό που φτάνει ως το 5% των επιμηκύνσεων. Μπορεί να εμφανιστεί ως προοδευτική διαταραχή του άξονα σε περιπτώσεις ανωριμότητας του πώρου (πλαστική παραμόρφωση), ως τέλειο κάταγμα ή ως καθίζηση στην περιοχή του πώρου και απώλεια ύψους. Χρειάζεται προσεκτική εκτίμηση της ποιότητας και του βαθμού ωρίμανσης και σταθεροποίησης του πώρου επιμήκυνσης, πριν αποφασισθεί η αφαίρεση της συσκευής. Το νεοσχηματισθέν οστό πρέπει να εμφανίζεται στις ακτινογραφίες ομοιογενές, με συνοχή και εμφάνιση πυκνότητας φλοιού παρόμοιας με το γειτονικό οστικό τμήμα. Τα επανακατάγματα και οι παραμορφώσεις αντιμετωπίζονται ανάλογα με το είδος τους, είτε συντηρητικά με τοποθέτηση νάρθηκα είτε χειρουργικά με επανατοποθέτηση της συσκευής. Δυσκαμψία αρθρώσεων Πρόκειται για καθυστερημένη επιπλοκή που οφείλεται είτε στις παρατεταμένες μυϊκές συσπάσεις και την καθήλωση μυών και τενόντων από τις βελόνες της συσκευής είτε στις αυξημένες πιέσεις που αναπτύσσονται στην άρθρωση κατά την διάρκεια της επιμήκυνσης. Η συχνότητά της αυξάνεται δραματικά όταν η επιμήκυνση υπερβαίνει το 5% του οστού. Πόνος Αποτελεί το συχνότερο ενόχλημα για το οποίο παραπονείται ο ασθενής κατά την διάρκεια της περιόδου της επιμήκυνσης. Τις πρώτες ημέρες μετεγχειρητικά μπορεί να είναι αρκετά έντονος και οφείλεται στην δυσκολία κίνησης των μυών που είναι καθηλωμένοι από τις 4
15 Κεφάλαιο : Διατατική Οστεογένεση βελόνες και την οστεοτομία. Κατά την διάρκεια της φάσης επιμήκυνσης, πολλοί ασθενείς παραπονούνται για έναν βύθιο πόνο ο οποίος παρατείνεται και γίνεται ιδιαίτερα έντονος κατά την διάρκεια της νύκτας καθώς και κατά την διάρκεια της φυσιοθεραπείας ή της βάδισης. Το αίσθημα αυτό ποικίλει ανάλογα με τον ασθενή και είναι πιο συχνό σε μεγάλες επιμηκύνσεις. Ψυχολογικές επιπτώσεις Σημαντικές είναι και οι ψυχολογικές επιπτώσεις κατά τη διάρκεια της θεραπείας οι οποίες κυρίως οφείλονται στον πόνο, αλλά και στην έλλειψη λειτουργικότητας εξαιτίας της συσκευής. Οι επιπτώσεις αυτές εκδηλώνονται συνήθως με ανορεξία, απώλεια βάρους ή κατάθλιψη..6 Περίοδος Ωρίμανσης του Πώρου Η διαδικασία της οστικής επιμήκυνσης μέσω της μεθόδου της διατατικής οστεογένεσης περιλαμβάνει το στάδιο της ωρίμανσης και σταθεροποίησης του πώρου επιμήκυνσης χωρίς την χρήση εξωγενών οστικών μοσχευμάτων. Βασική προϋπόθεση για την επίτευξη οστικής ωριμότητας αποτελεί η παραμονή της εξωτερικής οστεογένεσης καθ όλο το διάστημα της διαδικασίας ωρίμανσης. Η φάση της ωρίμανσης του πώρου μετά το πέρας της επιμήκυνσης αποτελεί την τελευταία αλλά και μεγαλύτερη χρονικά περίοδο της διατατικής οστεογένεσης. Στο χρονικό αυτό διάστημα, το σχηματιζόμενο οστό στην περιοχή της διάτασης γεφυρώνει το διάστημα ανάμεσα στα οστικά τμήματα και σταδιακά λαμβάνει χαρακτήρες οστικού φλοιού. Όταν το νέο οστό κριθεί αρκετά ισχυρό, η συσκευή της εξωτερικής οστεογένεσης μπορεί να αφαιρεθεί χωρίς τον κίνδυνο βράχυνσης, πλαστικής παραμόρφωσης ή κατάγματος στην περιοχή της νέο-οστεογένεσης. Για την αξιολόγηση της οστικής ωριμότητας χρησιμοποιούνται κατά βάση οι κλασσικές ακτινογραφίες, καθώς και νεώτερες μέθοδοι, όπως η ποσοτική αξονική τομογραφία (qct) και το υπερηχογράφημα..7 Απεικόνιση της Οστικής Επιμήκυνσης Η οστική επιμήκυνση, μέσω της μεθόδου της διατατικής οστεογένεσης, χρειάζεται τόσο ακριβή προεγχειρητικό σχεδιασμό όσο και λεπτομερή παρακολούθηση κατά την διάρκεια της περιόδου επιμήκυνσης. Η συχνή απεικόνιση του οστού κατά την διάρκεια της επιμήκυνσης αποσκοπεί στην έγκαιρη διάγνωση μιας πιθανής οστεομυελίτιδας εξαιτίας επέκτασης φλεγμονής από την περιοχή εξόδου των βελονών, στην διόρθωση πιθανών διαταραχών στον άξονα του οστού καθώς και στην αξιολόγηση της διαδικασίας ωρίμανσης του πώρου. Η πιο κοινή μέθοδος που χρησιμοποιείται για την απεικόνιση του επιμηκυνθέντος πώρου είναι η απλή ακτινογραφία. Ιδιαίτερη σημασία έχει ο προσδιορισμός, μέσω της απεικόνισης του πώρου, της χρονικής στιγμής για την αφαίρεση της συσκευής. Δεν υπάρχει κάποια αναγνωρισμένη εμβιομηχανική μέθοδος για την μέτρηση της αντοχής του πώρου και έτσι η αφαίρεση της συσκευής βασίζεται σε ακτινολογικά και κλινικά κριτήρια. 5
16 Κεφάλαιο : Διατατική Οστεογένεση Απλή ακτινογραφία Η απλή ακτινογραφία σε άξονες (προσθιοπίσθια και πλάγια) αποτελεί την πλέον συνηθισμένη μέθοδο παρακολούθησης της προόδου της οστικής επιμήκυνσης ενώ τις περισσότερες φορές, μόνο με την χρήση της, καθορίζεται η περαιτέρω αντιμετώπιση των ασθενών. Όμως, στα αρχικά στάδια της επιμήκυνσης, δεν μπορεί να ανιχνεύσει ευκρινώς την οστική αναπαραγωγή παρά μόνο εφόσον έχει ήδη σχηματιστεί επαρκής ποσότητα οστού. Έτσι δεν είναι ιδιαίτερα αξιόπιστη μέθοδος για την εκτίμηση του ρυθμού της επιμήκυνσης ιδιαίτερα στα αρχικά στάδια όπου απεικονίζεται μόνο μια περιοχή οστικού κενού. Το οστικό αυτό κενό σταδιακά γεμίζει με οστεογενετικό υλικό αυξανόμενης πυκνότητας που συνήθως γίνεται ακτινολογικά ορατή μετά τις 6-8 εβδομάδες. Παρόλα αυτά είναι απλή, γρήγορη και φθηνή μέθοδος και δίνει σημαντικές πληροφορίες για την ποιότητα του πώρου στην φάση της ωρίμανσης, για τον οστικό άξονα και το μήκος του πώρου. Για να αφαιρεθεί η συσκευή της επιμήκυνσης, χρειάζεται ακτινολογικά ορατός σχηματισμός φλοιού γύρω από την περιοχή της επιμήκυνσης. Ποσοτική αξονική τομογραφία (Quantified CT) Το QCT παρέχει μια ποσοτική αξιολόγηση της οστικής ανάπτυξης κατά την διάρκεια της επιμήκυνσης. Πειραματικές εργασίες έχουν αποδείξει την ύπαρξη συγκεκριμένης πολικότητας στην ασβεστοποίηση εντός της οστεογενετικής περιοχής. Συγκεκριμένα, αυτή η ασβεστοποίηση συμβαίνει τόσο κατά τον επιμήκη όσο και κατά τον εγκάρσιο άξονα. Η εναπόθεση ασβεστίου στην περιοχή της επιμήκυνσης, αναδεικνύεται περίπου εβδομάδα νωρίτερα από ότι με την απλή ακτινογραφία. Η οστική πυκνότητα στο κέντρο της περιοχής επιμήκυνσης εμφανίζεται χαμηλότερη από ότι στα άκρα. Η συνολική οστική πυκνότητα στην επιμηκυνθείσα περιοχή αυξάνει σε μικρό χρονικό διάστημα μετά το τέλος της επιμήκυνσης, για να μειωθεί στη συνέχεια μέχρις ότου φτάσει σε μια σταθερή τιμή. Ωστόσο στην κλινική πράξη, πολλές διαταραχές εμφανίζονται από την παρουσία του μεταλλικού δακτυλίου. Η αξονική τομογραφία αποτελεί ίσως την πιο αξιόπιστη μέθοδο για την προεγχειρητική μέτρηση των ανισοσκελιών και την αξιολόγηση του αποτελέσματος μετά το τέλος της μεθόδου. Υπερηχογράφημα (U/S) Αποτελεί μια πολύ αξιόπιστη μέθοδο ανάδειξης της οστικής δημιουργίας στα επίπεδα. Μπορεί να χρησιμοποιηθεί συχνότατα κατά την διάρκεια της οστικής επιμήκυνσης, καθώς είναι γρήγορη, εύκολα διαθέσιμη και φθηνή μέθοδος, ενώ δεν επιβαρύνει τον ασθενή με ακτινοβολία. Μπορεί να ανιχνεύσει, τόσο την δημιουργία του πώρου σε πολύ πρώιμα στάδια (7-4 μέρες μετά την αρχή της επιμήκυνσης), όσο και πιθανές επιπλοκές της επιμήκυνσης. Δίνει σαφείς πληροφορίες για την ποιότητα του νεοσχηματιζόμενου πώρου, την ακεραιότητα, ευθυγράμμιση και παραλληλότητα των οστικών δεσμίδων, καθώς και για τον ρυθμό με τον οποίο πραγματοποιείται η διάταση. Εάν οι οστικές δεσμίδες δεν είναι ορατές ή διακόπτονται, σημαίνει ότι η διάταση γίνεται με πολύ γρήγορο ρυθμό. Επίσης, μπορεί να ανιχνεύσει ελλείμματα οστεοποίησης ή οστικές κύστεις μέσα στο νεοσχηματιζόμενο οστό, που υποδηλώνουν ότι ο ρυθμός της οστεογένεσης είναι βραδύτερος από τον ρυθμό της διάτασης. Επιπλέον, παρέχει ακριβείς μετρήσεις για το μήκος της επιμηκυνθείσας περιοχής. Αντίθετα, οι διαταραχές του άξονα, αν και μπορούν να εντοπισθούν, δεν μπορούν να αναδειχθούν λεπτομερώς. 6
17 Κεφάλαιο : Διατατική Οστεογένεση.8 Συστήματα Υποστήριξης Τα συστήματα εξωτερικής οστεογένεσης που χρησιμοποιούνται τελευταία για την συγκράτηση της οστεοτομίας και την σταδιακή επιμήκυνση των οστών μπορούν να ταξινομηθούν σε δύο ομάδες : ΜΟΝΟΕΠΙΠΕΔΕΣ ΣΥΣΚΕΥΕΣ Οι μονοεπίπεδες συσκευές χρησιμοποιούν ισχυρές βελόνες με σπείραμα, που συγκρατούνται με σφιγκτήρες και συνδέονται με την επιμήκη ράβδο με άρθρωση που σε μερικές μπορεί να είναι πολυαξονική. Αυτές οι συσκευές που έχουν πολυαξονική άρθρωση επιτρέπουν κάποιες διορθώσεις και μετά την τοποθέτησή τους στον πάσχοντα. Η μηχανική σταθερότητα του συστήματος βασίζεται σε μία άκαμπτη ράβδο, και σε μεγάλες διαμέτρου βελόνες που λειτουργούν σαν προτεταμένες δοκοί. Οι μονοεπίπεδες συσκευές έχουν μεγάλη σταθερότητα σε δυνάμεις αξονικής συμπίεσης, ιδίως όταν υπάρχει ανάταξη του κατάγματος. Έχουν επίσης μεγάλη σταθερότητα σε δυνάμεις που ασκούνται στο επίπεδο τοποθέτησης των βελονών, ενώ σε δυνάμεις γωνίωσης στο προσθιοπίσθιο επίπεδο είναι λιγότερο σταθερές (ειδικά αυτές που έχουν πολυαξονικές αρθρώσεις). Η σταθερότητα του συστήματος είναι μικρότερη σε δυνάμεις στροφικής παραμόρφωσης και ελαττώνεται ακόμη περισσότερο αν υπάρχουν χαλαρωμένες βελόνες. Η σταθερότητα των μονοεπίπεδων συστημάτων αυξάνεται όταν )Χρησιμοποιηθούν περισσότερες βελόνες στο σύστημα, π.χ. 6 αντί 4. )Ελαττωθεί η απόσταση μεταξύ της επιμήκους ράβδου και του οστού. )Αυξηθεί η απόσταση μεταξύ των βελονών. 4)Όταν αυξηθεί η διάμετρος των βελονών, και 5)Όταν χρησιμοποιηθεί δεύτερη ράβδος στο σύστημα. Σε πειράματα διαπιστώθηκε ότι σε φόρτιση kg προκαλείται αξονική κίνηση από,5 έως όταν τα άκρα του οστού δεν είναι σε επαφή. Σε σύγκριση συστήματος 4 βελονών με συστήματα 6 βελονών διαπιστώθηκε ότι αυτό με τις λιγότερες βελόνες είχε το 7% της ακαμψίας σε σχέση με το άλλο, σε δυνάμεις αξονικής και στροφικής παραμόρφωσης και σε δυνάμεις που ασκούνται στο επίπεδο των βελονών. Σε δυνάμεις όμως που ασκούνται στον προσθιοπίσθιο άξονα η σταθερότητα ήταν μόνο στο 5% σε σχέση με το σύστημα των 6 βελονών. ΠΛΕΟΝΕΚΤΗΜΑΤΑ Οι μονοεπίπεδες συσκευές έχουν τα μεγάλα πλεονεκτήματα της εύκολης και γρήγορης τοποθέτησης τους στον άρρωστο. Οι βελόνες τους περνούν από ασφαλή σημεία και δεν προκαλούν μεγάλη βλάβη στους ιστούς. Γι αυτό το λόγο η δυσκαμψία που μπορεί να παρατηρηθεί σε παρακείμενες αρθρώσεις μετά την τοποθέτηση τους δεν είναι μεγάλη. Επίσης είναι καλύτερα ανεκτές από τον άρρωστο και λόγω του μικρού όγκου τους επιτρέπουν ευκολότερη προσπέλαση στην περιοχή της βλάβης. 7
18 Κεφάλαιο : Διατατική Οστεογένεση ΜΕΙΟΝΕΚΤΗΜΑΤΑ Τα μειονεκτήματα τους είναι: ) Το περιορισμένο πεδίο εισόδου των βελονών που καθορίζεται από το μέγεθος του σφιγκτήρα. ) Αν χρειασθεί να αφαιρεθεί βελόνα λόγω χαλάρωσης ή φλεγμονής αυτό μπορεί να οδηγήσει σε απώλεια της ανάταξης. ) Επίσης, οι πολυαξονικές αρθρώσεις μπορεί να χαλαρώσουν στη διάρκεια της επιμήκυνσης. ΔΑΚΤΥΛΙΟΕΙΔΕΙΣ ΣΥΣΚΕΥΕΣ Στις συσκευές με δακτυλίους τα οστά συγκρατούνται με διοστικά σύρματα υπό τάση ή από ισχυρές βελόνες. Στην εμβιομηχανική του συστήματος αυτά που παίζουν καθοριστικό ρόλο είναι : )Η τάση των συρμάτων. ) Η γωνία τοποθέτησης των βελόνων ) Η θέση του οστού σε σχέση με το δακτύλιο και το μέγεθος του δακτυλίου. Μεγαλύτερη αξονική σταθερότητα επιτυγχάνεται με την αύξηση της τάσης των συρμάτων και την ελάττωση της διαμέτρου του δακτυλίου. Η γωνία τοποθέτησης των συρμάτων παίζει καθοριστικό ρόλο στη σταθερότητα του συστήματος σε διατμητικές δυνάμεις. Οι δακτυλιοειδείς συσκευές έχουν μικρότερη σταθερότητα στη γωνιακή παραμόρφωση. Έχουν επίσης ίδια η μεγαλύτερη σταθερότητα από τα μονοεπίπεδα στην προσθιοπίσθια γωνίωση και στη στροφική παραμόρφωση. Εκεί όμως που υπάρχει μεγάλη διαφορά είναι στην αξονική φόρτιση όπου παρουσιάζουν 75% μικρότερη σταθερότητα. Τη σταθερότητα του συστήματος αυξάνουν: ) Η χρήση βελονών με ελαία. ) Ο αριθμός των βελονών (όσο περισσότερες βελόνες τοποθετηθούν, τόσο σταθερότερο γίνεται το σύστημα). ) Η διάμετρος των βελονών (μεγαλύτερη διάμετρος αυξάνει τη σταθερότητα). 4) Ο αριθμός των δακτυλίων σε κάθε οστικό τμήμα. 5) Η ελάττωση της διαμέτρου των δακτυλίων. 6) Και η τοποθέτηση κεντρικών δακτυλίων κοντά στην εστία του κατάγματος. Το μεγάλο πλεονέκτημα των δακτυλιοειδών συστημάτων είναι η δυνατότητα τους να επιτρέπουν σταδιακές διορθώσεις μήκους, γωνίωσης, στροφικής παραμόρφωσης και πλάγιας μετατόπισης του οστού. ΜΕΙΟΝΕΚΤΗΜΑΤΑ Τα μειονεκτήματα των συστημάτων αυτών είναι : ) Η χρονοβόρος εφαρμογή τους που απαιτεί -6 ώρες. ) Συχνά τα σύρματα περνούν από επικίνδυνα ή ανασφαλή σημεία, δηλαδή σημεία όπου βρίσκονται αγγεία, νεύρα, τένοντες και μεγάλες μυϊκές μάζες. Για το λόγο αυτό προκαλούν μεγαλύτερη δυσκαμψία στις παρακείμενες αρθρώσεις. ) Επίσης, ο πόνος μετά την εφαρμογή του συστήματος είναι μεγαλύτερος σε σύγκριση με τις μονοεπίπεδες συσκευές. 4) Είναι ογκώδη και δυσκολεύουν την προσπέλαση στην περιοχή της βλάβης. 8
19 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις ΚΕΦΑΛΑΙΟ : ΠΛΑΤΦΟΡΜΑ STEWART ΚΙΝΗΜΑΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ. Γενικά Χαρακτηριστικά της Διάταξης Η πλατφόρμα Stewart είναι μια κλασσική διάταξη ελέγχου κίνησης και θέσης, που αρχικά προτάθηκε το 965 ως προσομοιωτής πτήσης, και ακόμα πολύ συχνά χρησιμοποιείται γι αυτο το σκοπό. Από τότε αρκετές εφαρμογές έχουν επωφεληθεί από αυτή τη διάταξη. Η πλατφόρμα έχει χρησιμοποιηθεί, ανάμεσα σε άλλα, για προσομοίωση πτήσης, κατασκευή γεφυρών, για βοήθεια σε συντήρηση οχημάτων, τοποθέτηση δορυφόρων. Η πλατφόρμα Stewart μπορεί να πραγματοποιήσει μια πληθώρα κινήσεων και μπορούμε πολύ εύκολα και με ακρίβεια να της καθορίσουμε τη θέση και τον προσανατολισμό. Οι πλατφόρμες αποτελούνται από μια σταθερή (κάτω) βάση και μια κινητή (πάνω). Επίσης έχουν έξι πόδια, τα οποία μπορούν να κινηθούν γραμμικά, με πληθώρα συνδυασμών όσον αφορά τη σύνδεσή τους με τις βάσεις. Επιλεκτικά παρουσιάζουμε μερικούς από αυτούς τους συνδυασμούς (Εικόνα.). 9
20 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Εικόνα.: Διάφοροι τύποι γεωμετρίας της πλατφόρμας Stewart Η πλατφόρμα με την οποία ασχοληθήκαμε ανήκει στον τύπο -6. Το κάθε πόδι συνδέεται στην κάτω βάση με universal joint. Επίσης κάθε πόδι αποτελείται από δύο μέρη, το πάνω και το κάτω, τα οποία συνδέονται με έναν κυλινδρικό σύνδεσμο. Το πάνω μέρος του κάθε ποδιού συνδέεται στην πάνω βάση με επίσης ένα universal joint. Επομένως η πλατφόρμα έχει 6*+= κινητά μέρη και 6*=8 συνδέσμους που τα ενώνουν. Εικόνα.: Μηχανικό διάγραμμα πλατφόρμας Stewart
21 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Εικόνα.: Μηχανικό διάγραμμα ποδιού Η πλατφόρμα Stewart έχει έξι βαθμούς ελευθερίας τους οποίους μπορούμε να χρησιμοποιήσουμε για να μεταβάλλουμε το μήκος των ποδιών και συνεπώς τη θέση και τον προσανατολισμό της πάνω βάσης.. Ορθή Κινηματική Ανάλυση H πλατφόρμα που μελετάμε είναι ένα πλήρως παράλληλο κινηματικό σύστημα συνδέσμων που έχει σημαντικές μηχανικές διαφορές από τα χαρακτηριστικά ρομπότ συνδέσμων. Η κλειστή κινηματική του, που του παρέχει τη μηχανική ακαμψία, δημιουργεί ένα εξαιρετικά δύσκολο πρόβλημα για την ευθεία κινηματική και δυναμική ανάλυση. Η κλειστή μηχανική αλυσίδα το καθιστά αδύνατο να παραγάγει κανείς τις σαφείς κινηματικές εξισώσεις. Δεδομένου ότι δεν υπάρχει καμία σαφής έκφραση διαθέσιμη για την ευθεία κινηματική, η παραγωγή των δυναμικών εξισώσεων άμεσα στο πεδίο συνδέσμων είναι αδύνατη. Θα χρησιμοποιήσουμε λοιπόν έναν απλό αλγόριθμο που περιλαμβάνει την επίλυση μόνο τριών μη γραμμικών αλγεβρικών εξισώσεων. Αυτός ο αλγόριθμος παρέχει όχι μόνο μια απλούστερη προσέγγιση κινηματικής ανάλυσης, αλλά και μια σχετικά απλούστερη προσέγγιση για να βρεθεί η μήτρα Jacobian και να εξεταστούν τα singularities της διάταξης.
22 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Η πλατφόρμα Stewart είναι μια διάταξη η οποία αποτελείται από μια κάτω βάση, η οποία έχει τη γεωμετρία ημικανονικού εξαγώνου, μια τριγωνική πάνω βάση και έξι πανομοιότυπους γραμμικούς ενεργοποιητές όπως φαίνεται στην Εικόνα.4. Εικόνα.4: Γεωμετρία πλατφόρμας Stewart Θεωρούμε αδρανειακό σύστημα αξόνων (X,Y,Z) στο κέντρο της κάτω βάσης, με τον Z άξονα να δείχνει κάθετα προς τα πάνω. Θεωρούμε ακόμα ένα σύστημα αξόνων (x,y,z) στο κέντρο βάρους της άνω βάσης, με τον z άξονα να είναι κάθετος στην πλατφόρμα δείχνοντας προς τα πάνω. Στη συνέχεια αυτά τα δύο συστήματα αξόνων θα τα αποκαλούμε σύστημα βάσης και κορυφής αντίστοιχα. Οι διαστάσεις της κάτω και άνω βάσης σε σχέση με το σύστημα της βάσης φαίνονται στην Εικόνα.5. Εικόνα.5: Φυσικές διαστάσεις της κάτω και άνω βάσης Για τη διαμόρφωση της πλατφόρμας χρησιμοποιούνται έξι διαφορετικές μεταβλητές θέσης και προσανατολισμού. Συμβολίζουμε τη θέση της άνω βάσης σε σχέση με το σύστημα βάσης με [p x, p y, p z ] T. Επίσης συμβολίζουμε με (α, β, γ) τις γωνίες περιστροφής του συστήματος κορυφής ως προς τους τρεις άξονες. Επομένως η θέση και ο προσανατολισμός της άνω βάσης καθορίζεται από το X p-o =[p x, p y, p z, α, β, γ] T.
23 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Αφού ο προσανατολισμός του συστήματος κορυφής σε σχέση με το σύστημα βάσης καθορίζεται περιστρέφοντας την άνω βάση με τη σειρά ως προς τους τρεις άξονες, αν σε κάποια φάση, δυο από τους άξονες περιστροφής συμπέσουν τότε δυο από τις γωνίες περιστροφής εξαρτώνται η μια από την άλλη. Τότε υπάρχουν μόνο πέντε ανεξάρτητες μεταβλητές. Σε αυτή την περίπτωση υπάρχει πρόβλημα γιατί η μήτρα Jacobian θα χάσει την τάξη της ακόμα και αν το σύστημα δεν έχει πέσει σε singurarity. Για να το αποφύγουμε αυτό μπορούμε είτε να επιλέξουμε τρεις σταθερούς άξονες ή τρεις κινούμενους ως άξονες περιστροφής. Αφού οι τρεις σταθεροί άξονες (ή οι κινούμενοι) δεν συμπίπτουν ποτέ, οι γωνίες περιστροφής είναι πάντα ανεξάρτητες μεταξύ τους. Ένα μειονέκτημα αυτής της επιλογής είναι ότι οι τιμές (α, β, γ) δεν μπορούν να υπολογιστούν. Οι γωνίες Euler καθορίζονται αν περιστρέψουμε το κινούμενο σύστημα πρώτα ως προς τον σταθερό Z-άξονα και στη συνέχεια ως προς τους κινούμενους y,z άξονες. Στην περίπτωσή μας αν η άνω βάση είναι παράλληλη ως προς την κάτω βάση, τότε ο Z-άξονας και ο z-άξονας συμπίπτουν. Σε αυτή την περίπτωση οι γωνίες περιστροφής (α, β, γ) καθορίζονται περιστρέφοντας το σύστημα κορυφής πρώτα ως προς τον σταθερό X-άξονα α μοίρες, μετά ως προς τον σταθερό Y-άξονα β μοίρες και τέλος ως προς τον κινητό z- άξονα γ μοίρες. Όλες οι γωνίες μετρώνται δεξιόστροφα. Οι γωνίες περιστροφής που καθορίζονται έχουν ένα πολύ ξεκάθαρο φυσικό νόημα. Οι α,β χρησιμοποιούνται για να καθορίσουν ένα διάνυσμα προσέγγισης της άνω βάσης. Η γ χρησιμοποιείται στη συνέχεια για να καθορίσει τη γωνία περιστροφής ως προς το διάνυσμα προσέγγισης. Δοθείσας οποιασδήποτε διαμόρφωσης οι αντίστοιχες τιμές για τις μεταβλητές (α, β, γ) υπολογίζονται εύκολα (Εικόνα.6). Παρόλα αυτά το πρόβλημα που παρουσιάστηκε πιο πάνω πιθανότατα θα παρουσιαστεί όταν α= 9 ο, που θεωρητικά στην περίπτωση αυτή ο σταθερός Y-άξονας και ο κινούμενος z-άξονας θα συμπέσουν, στην πράξη όμως δεν φτάνουμε ποτέ σε αυτή την περίπτωση λόγω μηχανικών περιορισμών της πλατφόρμας Stewart. Εικόνα.6: Γωνίες περιστροφής Στη συνέχεια ορίζουμε ένα διάνυσμα που περιέχει τα μήκη των έξι ποδιών L=[L, L, L, L 4, L 5, L 6 ] Τ. Η κινηματική είναι η αντιστοίχιση των έξι μηκών στη θέση και τον προσανατολισμό
24 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις της άνω βάσης X p-o. Θεωρούμε T [ X, Y, Z ] T (i=,,) που συμβολίζει τις i Ti Ti Ti συντεταγμένες των κορυφών της άνω βάσης σε σχέση με το σύστημα βάσης. Με βάση τις Εικόνες.4,.5, η άνω βάση είναι ένα ισόπλευρο τρίγωνο με πλευρά α. Η κάτω βάση είναι ένα ημι-κανονικό εξάγωνο με μήκη πλευρών b,d όπως φαίνεται στις εικόνες. Θα μελετήσουμε την ορθή κινηματική σε δύο στάδια. Βήμα. Βρίσκω τις συντεταγμένες του T i Δεδομένων των μηκών L -L 6 σχηματίζονται τρία τρίγωνα, T { L, B B, L }, i=,, RIAi i i i i όπου B j, j=,,..,6, είναι οι κορυφές της κάτω βάσης των οποίων οι συντεταγμένες, σύμφωνα με την Εικόνα.5, είναι: X B ( b d ) X B ( b d ) 6 6 () YB d YB ( b d ) () Z Z () B X B ( b d ) X B4 ( b d ) 6 6 (4) b YB 4 b (5) Z Z 4 (6) YB B X B5 ( b d ) X B6 ( b d ) 6 6 (7) YB 5 ( b d ) YB 6 d (8) Z Z 6 (9) B5 B B B Συμβολίζουμε το ύψος των τριγώνων με h, h, h. Επίσης συμβολίζουμε τις προβολές των L, L, L 5 στα B B, B B 4, B5 B6 με P, P, P. Τέλος συμβολίζω τις συντεταγμένες του σημείου τομής των h i και Bi Bi με ( X Pi, Y Pi ) (βλέπε Εικόνα.7). Είναι εύκολο να υπολογίσουμε τα h i και ( X, Y ) χρησιμοποιώντας τις παρακάτω εξισώσεις: Pi Pi P ( b L L ) i b i i=,, () i h L P i=,, () i i i X P ( b d P ) YP ( d P ) 6 () X P ( b d ) YP ( b P ) 6 () 4
25 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις X P ( b d P ) YP ( b d P ) (4) 6 Εικόνα.7: Γεωμετρικός υπολογισμός Αν δεν υπάρχει κανένας περιορισμός στην θέση των κορυφών T i, τότε τα τρίγωνα μπορούν να περιστραφούν ελεύθερα ως προς τις πλευρές τους B B. Κατά την περιστροφή οι i i κορυφές T i θα κινούνται σε ένα κύκλο με κέντρο ( X, Y ) με ακτίνα h i. Ο σκοπός του βήματος είναι να βρεθούν τα ( XTi, YTi, Z Ti). Παρόλο που είναι άγνωστα μέχρι τώρα, είναι εύκολο να αποδείξουμε ότι οι προβολές των τριών κορυφών της άνω βάσης στο επίπεδο X-Y μπορούν να κινηθούν μόνο κατά μήκος ευθειών που περνούν από τα σημεία ( X P, Y P) ή ( X P, Y P) ή ( X P, Y P) και είναι κάθετες στις μεγάλες πλευρές της κάτω εξαγωνικής βάσης, αντίστοιχα (Εικόνα.8). Pi Pi Εικόνα.8: Κάτοψη της κάτω βάσης 5
26 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις 6 Αυτό σημαίνει ότι οποιεσδήποτε τιμές και να πάρουν οι συντεταγμένες (, ) Ti Ti X Y, οι σχέσεις που τις συνδέουν είναι οι παρακάτω: ( ) ( ) T T P P T Y X X Y X L L b (5) 4 ( ) T P Y Y L L b (6) 5 6 ( ) ( ) T T P P T Y X X Y X L L b (7) Η προβολή του h i στο επίπεδο X-Y μπορεί να εκφραστεί ως: ( ) ( ) i Ti Pi Ti Pi H X X Y Y και η προβολή του h i στον Z-άξονα που στην ουσία ισοδυναμεί με τη συντεταγμένη Ti Z μπορεί να εκφραστεί με τη σχέση: Ti i i Z h H Συνδυάζοντας τις εξισώσεις (5)-(9) έχω: 4( ) T T P Z h X X () 4( ) T T P Z h X X () 4( ) T T P Z h X X () Καθώς οι αποστάσεις μεταξύ των κορυφών της άνω βάσης πρέπει να είναι ίσες με α, τρεις επιπλέον περιορισμοί πρέπει να προστεθούν. Λαμβάνοντας υπ όψιν τις σχέσεις (5)-(7) και ()-() προκύπτουν τρεις μη-γραμμικές εξισώσεις με τρεις αγνώστους Ti X i=,,. ] ) ( [ ] ) ( 4 [ ] 4 ) ( ) [( )] ( [ P T P T P P P P P T P P P P T T T X X h X X h X X h h Y Y X X X Y Y X X X X a () ] ) ( 4 [ ] ) ( 4 [ ] 4 ) ( ) ) ( [( )] ( [ )] ( [ 4 P T P T P P P P P P P P P P T P P P P T T T X X h X X h X X h h Y Y X X Y Y X X X Y Y X X X X X a (4) ] ) (4 [ ] ) ( 4 [ ] 4 ) ( ) [( )] ( [ P T P T P P P P P T P P P P T T T X X h X X h X X h h Y Y X X X Y Y X X X X a (5)
27 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Αφού οι εξισώσεις ()-(5) είναι μη-γραμμικές είναι αδύνατο να τις λύσουμε. Ο μόνος τρόπος να λυθούν είναι μέσω αριθμητικών μεθόδων. Μια καλή μέθοδος για την επίλυση είναι η Newton-Raphson. Όταν λοιπόν βρεθούν τα X T, X T, X T οι συντεταγμένες Y Ti, Z των κορυφών της άνω βάσης μπορούν να υπολογιστούν χρησιμοποιώντας τις σχέσεις Ti (5)-(7) και ()-(). Βήμα. Βρίσκω τη θέση και τον προσανατολισμό του κέντρου της άνω βάσης Δοθέντων των συντεταγμένων των T -T η θέση και ο προσανατολισμός του κέντρου της άνω βάσης μπορούν εύκολα να υπολογιστούν ως εξής: p x X Ti p Y Y Ti p z Z Ti (6) i i i και ο προσανατολισμός είναι ( Y T YT YT ) γ=arctan (7) ( YT YT ) [ X T( Z T Z T ) X T ( Z T Z T ) X T ( Z T Z T )] α=arctan (8) a ( YT YT YT ) sin ( YT YT ) cos ( Z β=arctan ( T T Z T T Z T T ) cos ) cos ( Z T ( X T Z T X T ) sin ) sin (9). Αντίστροφη Κινηματική Ανάλυση Η αντίστροφη κινηματική είναι η αντιστοίχιση από το X p-o στο L i. Σε αντίθεση με την ορθή κινηματική της πλατφόρμας Stewart, η αντίστροφη είναι αρκετά εύκολη και δίνει μοναδική λύση. Βήμα. Βρίσκω τις συντεταγμένες του T i. Δοθείσας της θέσης και του προσανατολισμού του κέντρου της άνω βάσης p x, p y, p z, α, β, γ, αφού οι συντεταγμένες ων κορυφών της άνω βάσης σε σχέση με το σύστημα κορυφής είναι (βλέπε Εικόνα.5) x T x T a x T a a 6 y T T a 6 y a z T z T z T και χρησιμοποιώντας ομογενείς μετασχηματισμούς, οι συντεταγμένες των κορυφών της άνω βάσης σε σχέση με το σύστημα βάσης μπορούν εύκολα να υπολογιστούν ως εξής: a X T px [sin sin sin( 6 ) cos cos( 6 )] y T 7
28 T p a cos sin( 6 ) ZT pz a [sin cos sin( 6 ) sin cos( 6 )] X T p x a [sin sin sin cos cos ] T p Y a cos sin ZT pz a [sin cos sin sin cos ] a X T px [sin sin sin( 6 ) cos cos( 6 )] T p Y a cos sin( 6 ) ZT pz a [sin cos sin( 6 ) sin cos( 6 )] Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Βήμα. Βρίσκω τα μήκη των πρισματικών αρθρώσεων Δοθέντων των ( XTi, YTi, Z Ti), i=,, σε σχέση με το σύστημα βάσης, αν οι συντεταγμένες των κορυφών της κάτω βάσης εκφράζονται ως προς το ίδιο σύστημα αξόνων, τα μήκη των ποδιών προκύπτουν ως εξής: L L L L L L ( X T d / d b / ) ( YT d / ) ZT ( X T d / b / ) ( YT d / b / ) ZT ( X T d / b / ) ( YT b / ) ZT 4 ( X T d / b / ) ( YT b / ) ZT 5 ( X T d / b / ) ( YT b / d / ) ZT 6 ( X T d / b / ) ( YT d / ) ZT Οι έξι αυτές εξισώσεις αποτελούν τη λύση του προβλήματος της αντίστροφης κινηματικής..4 Γεωμετρικοί Περιορισμοί Η πλατφόρμα Stewart είναι μια κλειστή κινηματική αλυσίδα που είναι αρκετά διαφορετική από έναν απλό ρομποτικό βραχίονα. Δεν υπάρχει μια μοναδική έκφραση που να περιγράφει την κινηματική της όπως φάνηκε στις προηγούμενες ενότητες. Επομένως είναι δύσκολο να ορίσουμε πλήρως το workspace της. Στη συνέχεια θα παρουσιάσουμε μερικές οριακές καταστάσεις. 8
29 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις.4. Χαμηλότερη θέση Η χαμηλότερη θέση της πλατφόρμας Stewart αντιστοιχεί στην περίπτωση που τα μήκη όλων των ποδιών έχουν τη μικρότερη δυνατή τιμή. Σε αυτή την περίπτωση οι συντεταγμένες των T, T, T είναι: a XT T a X XT a a a YT YT YT b ( a.5 b d) ZT ZT ZT LMIN 4 ενώ η θέση και ο προσανατολισμός του συστήματος κορυφής σε σχέση με το σύστημα βάσης είναι Ας σημειώσουμε ότι L X MIN θέση (θέση ισορροπίας)..4. Υψηλότερη θέση po( MIN ) T LMIN b ( a.5 b d) 4 b ( a.5 b d) το οποίο αντιστοιχεί στην αρχική 4 Η υψηλότερη θέση της πλατφόρμας Stewart αντιστοιχεί στην περίπτωση που τα μήκη όλων των ποδιών έχουν πάρει το μέγιστο δυνατό μήκος. Σε αυτή την περίπτωση η θέση και ο προσανατολισμός του συστήματος κορυφής σε σχέση με το σύστημα βάσης είναι: X po( MAX ) T LMAX b ( a.5 b d) 4.4. Θέση με τη μεγαλύτερη κλίση Οι έξι πρισματικοί σύνδεσμοι μπορούν να χωριστούν σε τρία ζευγάρια (L, L ), (L, L 4 ), (L 5, L 6 ). Η θέση με τη μεγαλύτερη κλίση αντιστοιχεί σε δύο περιπτώσεις. Στην πρώτη το ένα ζευγάρι έχει το μεγαλύτερο μήκος και τα άλλα δύο το μικρότερο, ενώ στη δεύτερη το ένα ζευγάρι έχει το μικρότερο μήκος και τα άλλα δύο το μεγαλύτερο. Για την πρώτη περίπτωση θεωρούμε χωρίς βλάβη της γενικότητας ότι L =L =. L MAX και L =L 4 =L 5 =L 6 = L MIN. Ο υπολογισμός των συντεταγμένων του Τ είναι περίπλοκος. Τελικά μετά από πολλές πράξεις προκύπτει:. 9
30 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις ( b d) ( b bd d ) ( b d) XT cc c ( c 4 c ) c c( LMAX cc c /( c 4 c ) όπου ( MAX MIN.5 ) c L L a b d ab ad bd c ( a b d) b ( a.5 b d) c LMIN 4 Η θέση του κέντρου της άνω βάσης είναι τότε: p a X 6 X ( TILTED) T p a X 6 Y ( TILTED ) T b pz ( TILTED ) c LMAX 4 XT ( b d) 4 Παρόμοια αποτελέσματα προκύπτουν και για τη δεύτερη περίπτωση..4.4 Θέση με τη μεγαλύτερη περιστροφή Στην περίπτωση αυτή θεωρούμε ότι η άνω βάση είναι πάντα παράλληλη ως προς την κάτω βάση και περιστρέφεται ως προς τον z-άξονα. Για να πραγματοποιηθεί αυτό πρέπει L =L =L =L MIN και L 4 =L 5 =L 6 =L MAX. Οι συντεταγμένες του κέντρου της άνω βάσης μετά από υπολογισμούς προκύπτουν οι εξής: p X py ( b d) p ( L L ) ( a b bd d ) a ( L L ) 4b Z MAX MIN MAX MIN o ( LMAX LMIN ) Arc tan 4a b ( LMAX LMIN ) /
31 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις.5 Η Μήτρα Jacobian Από την προηγούμενη ενότητα φαίνεται ότι το πρόβλημα της ορθής κινηματικής είναι αρκετά πολύπλοκο. Για την ακρίβεια δεν μπορούμε να καταλήξουμε σε μια ακριβή λύση των κινηματικών εξισώσεων. Επομένως είναι αδύνατο να μελετήσουμε τη δυναμική χρησιμοποιώντας τις κινηματικές εξισώσεις. Αντίθετα το αντίστροφο πρόβλημα είναι αρκετά πιο εύκολο. Χρησιμοποιώντας τα αποτελέσματα από την προηγούμενη ενότητα προκύπτει εύκολα η σχέση που συνδέει την ταχύτητα των ποδιών L και την ταχύτητα στον T καρτεσιανό χώρο X po p x p y p z a. Διαφορίζω τις εξισώσεις της αντίστροφης κινηματικής ως προς το χρόνο και έχω: L J ( ) X po X T () X ( ) T J X po X po () Όπου X X Y Z X Y Z X Y Z J X p o είναι:. Ο (6x9) πίνακας T T T T T T T T T T T L L L X T YT Z T L L L X T YT Z T L L L X T YT ZT J( X po) L4 L4 L 4 X T YT ZT L5 L5 L 5 X T YT ZT L6 L6 L 6 X T YT ZT () όπου L X T d / b / X L T L YT d / Y L T L Z Z L T T () L X T d / b / X L T L YT d / b / Y L T L Z Z L T T (4) L X T d / b / X L T L YT b / Y L T L Z Z L T T (5)
32 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις L4 X T d / b / X L T 4 L4 YT b / Y L T 4 L Z Z L 4 T T 4 (6) L5 X T d / b / X L T 5 L5 YT d / b / Y L T 5 L Z Z L 5 T T 5 (7) L6 X T d / b / X L T 6 και ο (9x6) πίνακας J X p o είναι: L6 YT d / Y L T 6 L Z Z L 6 T T 6 (8) X X ( YT py )sin ( ZT pz ) a Y Y sin asin( 6 ) Z Z ( YT py )cos ( XT px) X X ( YT py )sin ( ZT pz ) a Y Y J ( X po ) sin asin Z Z ( YT py ) cos ( XT px) X X ( Y )sin a o YT YT sin asin( 6 ) ZT ZT ( YT py ) cos ( X T px) T T o T T T T T T T T T T T T T py ( ZT pz ) (9) Συνδυάζοντας τις σχέσεις (), () έχω L J( X p o) J( X p o) X po J( X po) X (4) po από όπου προκύπτει η Jacobian μήτρα: L / X L / Y L / Z j j j L / X L / Y L / Z j j j L / X L / Y L / Z j j j J ( X po ) L / X L / Y L / Z j j j L / X L / Y L / Z j j j T T T,4,5,6 T T T,4,5,6 T T T,4,5,6 4 T 4 T 4 T 4,4 4,5 4,6 5 T 5 T 5 T 5,4 5,5 5,6 L6 / X T L6 / YT L6 / ZT j6,4 j6,5 j6,6 (4)
33 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις όπου αν i=,: Li Li Li a o ji,4 ( YT py )( sin cos ) sin asin( 6 ) X T ZT YT Li Li ji,5 ( T p ) ( T px ) X T ZT L,6 [ i L ( ) i L ( ) i ji ( Z Z )] X Y Z T T T αν i=,4: Li Li Li a ji,4 ( YT py )( sin cos ) sin a sin X T ZT T Li Li ji,5 ( T p) ( T px ) X T ZT L,6 [ i L ( ) i L ( ) i ji ( )] X Z T T T αν i=5,6: Li Li Li a o ji,4 ( YT py )( sin cos ) sin asin( 6 ) X T ZT T Li Li ji,5 ( T p ) ( T px ) X T ZT L,6 [ i L ( ) i L ( ) i ji ( )] X Z T T T.6 Singularities.6. Εισαγωγή Η σχέση (4) μας δίνει το μετασχηματισμό από το X p o στο L χρησιμοποιώντας τη Jacobian μήτρα. Επίσης δείχνει ότι εάν ο J ( X p o ) δεν είναι ιδιάζων, τότε οποιαδήποτε αλλαγή της ταχύτητας στο χώρο συνδέσμων μπορεί να μετασχηματιστεί με μοναδικό τρόπο στην αντίστοιχη μεταβολή της ταχύτητας στον καρτεσιανό χώρο. Επομένως η Jacobian είναι ο τρόπος να μετασχηματίζουμε από το χώρο συνδέσμων στον καρτεσιανό και αντίστροφα. Για παράδειγμα αν στο χώρο συνδέσμων δεν υπάρχει κίνηση, που σημαίνει L, τότε και στον καρτεσιανό χώρο δεν υπάρχει κίνηση, και η πλατφόρμα Stewart παραμένει ακίνητη. Εντούτοις, αν σε μερικές περιπτώσεις η μήτρα J ( X p o ) είναι ιδιάζουσα, τότε ο μετασχηματισμός από τον ένα χώρο στον άλλο είναι αδύνατος. Σε αυτή την
34 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις περίπτωση, ακόμα και αν δεν υπάρχει κίνηση στο πεδίο των συνδέσμων δηλαδή ισχύει L, η άνω βάση μπορεί πιθανότατα να κινείται. Με άλλα λόγια όταν η πλατφόρμα Stewart πέφτει σε singularity μπορεί να έχει περισσότερους βαθμούς ελευθερίας από έξι. Το πρόβλημα γίνεται ακόμα χειρότερο δεδομένου ότι καμία δύναμη ή ροπή του καρτεσιανού χώρου δεν μπορεί να μετασχηματιστεί στο χώρο συνδέσμων, που σημαίνει ότι η πλατφόρμα βρίσκεται εντελώς εκτός ελέγχου. Η γραμμική άλγεβρα μας λέει ότι εάν είτε ο πίνακας J είτε ο J χάνει τάξη, τότε η ορίζουσα του J πρέπει να είναι ίση με μηδέν. Επομένως ελέγχουμε ξεχωριστά την τάξη των J και J. Ο J είναι ένας (6x9) πίνακας. Μπορεί να χάσει τάξη αν και μόνο αν οι πρώτες δυο γραμμές του, ή οι μεσαίες δυο γραμμές του, ή οι τελευταίες δυο γραμμές του εξαρτώνται η μια από την άλλη. Όμως οι σχέσεις ()- (8) δείχνουν ότι αυτό δεν γίνεται ποτέ. Επομένως ο πίνακας J δεν χάνει ποτέ τάξη. Από την άλλη μεριά ο πίνακας J είναι ένας (9x6) πίνακας. Οι πρώτες τρεις στήλες του είναι προφανώς ανεξάρτητες μεταξύ τους. Οι τελευταίες τρεις στήλες εξαρτώνται μόνο από τις τιμές των (α,β,γ). Είναι εύκολο να αποδείξουμε ότι οποιεσδήποτε τιμές και αν πάρουν τα (α,β,γ) οι τελευταίες τρεις στήλες είναι ανεξάρτητες από τις τρεις πρώτες. Όταν όμως a 9 o, που αντιστοιχεί στην περίπτωση που η άνω βάση είναι κάθετη στην κάτω και ο z-άξονας είναι παράλληλος στον Y-άξονα, η πέμπτη και έκτη στήλη της J εξαρτώνται η μια από την άλλη και ο πίνακας που προκύπτει είναι ο εξής: a a o sin( 6) sin( 6 ) a o sin( 6 ) a o a o cos( 6 ) cos( 6 ) a a sin( ) sin( ) a J ( X po ) sin a a cos( ) cos( ) a o a o sin( 6 ) sin( 6 ) a o sin( 6 ) a o a o cos( 6 ) cos( 6 ) του οποίου η τάξη είναι μικρότερη από 6. Από τις ιδιότητες των οριζουσών, η ορίζουσα της Jacobian J JJ είναι ίση με μηδέν, το οποίο δείχνει ότι το σύστημα βρίσκεται σε singularity. Παρολ αυτά, στην πράξη η πλατφόρμα ούτε χάνει ούτε κερδίζει βαθμούς ελευθερίας σ αυτές τις περιπτώσεις. Όπως αναφέραμε προηγουμένως, το πρόβλημα αυτό οφείλεται σε κακώς ορισμένες 4
35 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις γωνίες περιστροφής. Αυτή η λάθος επιλογή μπορεί να οδηγήσει σε περαιτέρω δυσκολίες αφού το σύστημα όπως αναφέραμε και προηγουμένως βρίσκεται εκτός ελέγχου. Ευτυχώς το σύστημα δε φτάνει ποτέ σε αυτά τα σημεία λόγω μηχανικών περιορισμών. Από τα παραπάνω συμπεραίνουμε ότι ούτε ο J ούτε ο J χάνουν τάξη, οπότε προχωράμε στον έλεγχο ολόκληρης της Jacobian..6. Singularity ροπής Εάν η άνω βάση είναι παράλληλη στην κάτω τότε ισχύει: ZT ZT ZT pz Σε αυτή την περίπτωση η μήτρα Jacobian γίνεται L L pz pz pz L L ( YT py ) ( XT px ) [( X T X T ) ( YT YT ) ] XT YT L L L X T Y T L L pz pz pz L L ( YT py ) ( XT px ) [( X T X T ) ( YT YT ) ] XT YT L L L X T Y T L L pz pz pz L L ( YT py ) ( X T px ) [( X T XT ) ( YT YT ) ] X T YT L L L X T YT L4 L4 pz pz pz L4 L 4 ( YT py ) ( X T px ) [( X T XT ) ( YT YT ) ] X T YT L4 L4 L4 X T YT L5 L5 pz pz pz L5 L 5 ( YT py ) ( X T px ) [( X T XT ) ( YT YT ) ] X T X T L5 L5 L5 XT YT L6 L pz pz pz L6 L 6 ( YT py ) ( X T px ) [( X T XT ) ( YT YT ) ] X T YT L6 L6 L6 X T YT (4) Οι πρώτες πέντε στήλες δεν εξαρτώνται ποτέ η μια από την άλλη. Όμως αν η άνω βάση δεν είναι μόνο παράλληλη στην κάτω βάση, αλλά επιπλέον περιστρέφεται ως προς τον z-άξονα κατά Εικόνα.9α: Singularity ροπής, η περίπτωση 9 o (βλέπε Εικόνα.9α), τότε η τελευταία στήλη γίνεται: 5
36 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις a a a a L X ( ) L X T T ( ) T T a L X a L X L X T 4 T L Y L Y L Y 5 5 ( ) L X T T L Y 6 6 ( ) T T αφού σε αυτή την περίπτωση έχω: XT XT a X T ( X Y X T ) a YT YT YT YT Αυτή η στήλη είναι ακόμα ανεξάρτητη από τις υπόλοιπες πέντε. Αν επιπλέον ισχύει p p τότε η άνω βάση όχι μόνο είναι παράλληλη και έχει περιστραφεί ως X Y προς τον z-άξονα κατά 9 o αλλά επιπλέον ο z-άξονας συμπίπτει με τον Z-άξονα, όπως φαίνεται στην Εικόνα.9β. Εικόνα.9β: Singularity ροπής, η περίπτωση Σε αυτή την περίπτωση η τελευταία στήλη γίνεται και εξαρτάται από την τρίτη στήλη p Z... L L L6 Καταλήγουμε λοιπόν στο εξής συμπέρασμα: a ( d b)... 6 L L L6 T. T 6
37 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Αν η θέση και ο προσανατολισμός της άνω βάσης είναι o o o o o o X p o pz 9 ή X p o pz 9 τότε η θέση αυτή αντιστοιχεί σε singularity. Αυτό το είδος singularity προκύπτει μόνο όταν ικανοποιούνται οι τρεις παρακάτω συνθήκες.. Η άνω βάση είναι παράλληλη στην κάτω. Η άνω βάση περιστρέφεται ως προς τον z-άξονα κατά 9 o. Η άνω βάση έχει το ίδιο κέντρο με την κάτω Εάν οποιαδήποτε από τις παραπάνω συνθήκες δεν ισχύει, τότε το σύστημα δεν είναι σε singularity..6. Singularity θέσης Πριν ελέγξουμε την περίπτωση αυτή παρουσιάζουμε ένα θεώρημα. Θεώρημα Αν ένας πίνακας Μ (n x n) έχει την εξής δομή: A B M ka C (4) όπου A, B, C είναι (n x n) πίνακες, k είναι μια αυθαίρετη σταθερά τότε: det M det A det C kb ή Το παραπάνω θεώρημα μας επιτρέπει να ελέγξουμε τα singularities ενός πίνακα χωρισμένου σε μέρη, απλά ελέγχοντας ένα μέρος του για να δούμε αν ο αρχικός πίνακας έχει δομή σαν αυτή της σχέσης (4). Υποθέτουμε ότι η πλευρά T T της άνω βάσης είναι παράλληλη στον Y-άξονα, και η άνω βάση περιστρέφεται ως προς τον T T. Θα βρούμε τη συνθήκη για την οποία το σύστημα έχει πέσει σε singularity. Στην περίπτωση αυτή έχουμε: a Li L7 i (i=,,) a XT XT YT YT YT ZT ZT (44) Με αντικατάσταση των παραπάνω προκύπτει η Jacobian μήτρα j j j j j j j j j j j j j j j j j j J ( X po) j j j j j j j j j j j j j j j j j j,,,,4,5,6,,,,4,5,6,,,,4,5,6,,,,4,5,6,,,,4,5,6,,,,4,5,6 (45) και πραγματοποιώντας μετασχηματισμούς προκύπτει: 7
38 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις J new j, j, j,5 j, j,4 j,6 j, j, j,5 j, j,4 j,6 j, j, j,5 j, j,4 j,6 A B ( X po ) j, j, j,5 j, j,4 j,6 A B j, j, j,5 j, j,4 j,6 j, j, j,5 j, j,4 j,6 (46) που στην περίπτωση αυτή έχει τη δομή της σχέσης (4) με k= και C=-B. Σύμφωνα με το θεώρημα ο πίνακας J είναι ιδιάζων αν και μόνο αν οι υποπίνακες Α ή Β είναι ιδιάζοντες. Ελέγχω πρώτα την ορίζουσα του υποπίνακα Α. new L L a L L sin cos X T ZT X T ZT L L a L L X T ZT X T ZT L L a L L sin cos XT ZT XT Z T det sin cos a L L L L L L sin cos X T ZT ZT X T X T ZT (47) Ο πρώτος όρος της (47) είναι πάντα μη-μηδενικός, επομένως η μήτρα Jacobian είναι ιδιάζουσα αν ο τελευταίος όρος της (47) είναι μηδέν. Πριν εξετάσουμε αυτό τον όρο πρέπει να εκφράσουμε τα sin και cos συναρτήσει των συντεταγμένων της άνω βάσης. Από τον ορισμό των γωνιών περιστροφής, μπορεί να αποδειχθεί ότι σε αυτή την περίπτωση ( a ) η γωνία δεν είναι τίποτε άλλο από τη γωνία ανάμεσα στην άνω και την κάτω βάση. 8
39 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Εικόνα.: Singularity θέσης Αφού η πλευρά T T είναι παράλληλη στον Y-άξονα, σύμφωνα με την Εικόνα. ισχύει sin ( ) cos ( X X ) (48) Αντικαθιστώντας τα L / LXT, L / LZT και την (48) στο δεύτερο όρο της (47) προκύπτει L X L sin Z T T cos X d / b / Z ( Z Z ) ( X X ) (49) T T T T T T L L X ( d b) Z X ( d b) Z L T T T T και αν Z Z T T A J X p o X T ( b d ) X T ( b d ) det det ( ). (5) τότε η (49) είναι μηδέν και συνεπώς 9
40 Κεφάλαιο : Πλατφόρμα Stewart- Κινηματικές εξισώσεις Θα μελετήσουμε τώρα τη σχέση (5). Υποθέτουμε ότι τα XT( X T ) και ZT( Z T ) είναι σταθερά. Εάν τα μήκη L, L 4 διαφέρουν (στη συγκεκριμένη περίπτωση ισχύει πάντα L = L 4 ), τότε η άνω βάση θα περιστραφεί ως προς την πλευρά TT όπως φαίνεται στην Εικόνα.. Κάθε στιγμή η απόσταση από το Χ Τ μέχρι την πλευρά B B 4 είναι ( XT ( b d)/ ) και από το Χ Τ μέχρι την B B4 είναι ( X ( b d)/ ). Όταν και μόνο όταν η άνω βάση περιστρέφεται γύρω από T μία συγκεκριμένη θέση στην οποία το κέντρο της T T, το κέντρο της B B4 και η κορυφή Τ είναι πάνω στην ίδια ευθεία τότε ισχύει η σχέση (5) η οποία δίνει το εξής συμπέρασμα: Αν η πλευρά TT της άνω βάσης είναι παράλληλη με τον Υ-άξονα και το επίπεδο που ορίζεται από τα L, B B 4, L 4 είναι στο ίδιο επίπεδο με την άνω βάση τότε η κατάσταση αυτή αντιστοιχεί σε singularity. Εξαιτίας της συμμετρίας της πλατφόρμας προκύπτουν δυο ακόμα singularities. Αν η πλευρά TT ( T T ) της άνω βάσης είναι παράλληλη με την πλευρά B5 B 6 ( B B ) της κάτω βάσης και το επίπεδο που σχηματίζεται από τα L 5, B5 B 6, L 6 (L, B B, L ) είναι συνεπίπεδο με αυτό της άνω βάσης, τότε η κατάσταση αντιστοιχεί σε singularity. αυτή 4
41 Κεφάλαιο : Πλατφόρμα Stewart- Δυναμική ανάλυση ΚΕΦΑΛΑΙΟ : ΠΛΑΤΦΟΡΜΑ STEWART ΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ Σε αυτή την ενότητα θα ασχοληθούμε με τη μελέτη της δυναμικής της πλατφόρμας Stewart. Υπάρχουν γενικά δύο μέθοδοι για τη μελέτη της δυναμικής ενός κλασσικού ρομπότ. Η Newton-Euler και η Lagrange. Αφού αυτές οι μέθοδοι προέρχονται από τη γενική θεωρία της μηχανικής, θα μπορούν να εφαρμοστούν και στα παράλληλα ρομπότ. Στο παρελθόν έχει γίνει μελέτη των δυναμικών εξισώσεων της πλατφόρμας Stewart χρησιμοποιώντας τη μέθοδο Newton-Euler και μη λαμβάνοντας υπ όψιν τους όρους Coriolis-Centrifual. Στην περίπτωση όμως αυτή η γεωμετρία της πλατφόρμας μας είναι διαφορετική οπότε πρέπει να μελετήσουμε σε βάθος τους όρους Coriolis-Centrifual οι οποίοι δεν είναι αμελητέοι. Σε αυτό θα μας βοηθήσει η μέθοδος Lagrange. Θα δείξουμε ότι η δυναμική της πλατφόρμας Stewart μπορεί να εκφραστεί στη μορφή: M( X ) X N( X, X ) X G( X ) J T ( X ) F () po po po po po po po 4
42 Κεφάλαιο : Πλατφόρμα Stewart- Δυναμική ανάλυση Πρέπει να σημειώσουμε ότι ο πίνακας Jacobian που υπολογίσαμε στην προηγούμενη T ενότητα είναι για την ακρίβεια ο αντίστροφος Jacobian. Γι αυτο στη σχέση () έχουμε J T και όχι J, όπως ισχύει για ένα κλασσικό σειριακό ρομπότ. Είναι γνωστό ότι οι κλασσικές εξισώσεις της κίνησης μπορούν να προκύψουν τη μέθοδο Lagrange d K ( q, q ) K ( q, q ) P( q) ( ) dt q q q () n n όπου q R και R είναι οι γενικευμένες συντεταγμένες και γενικευμένες δυνάμεις αντίστοιχα. K ( q, q ) είναι η κινητική ενέργεια, P(q) είναι η δυναμική ενέργεια. Τα βήματα που θα ακολουθήσουμε είναι τα εξής: Υπολογισμός των τ, P(q) και K ( q, q ) Υπολογισμός των συντελεστών Μ(q), N ( q, q ) και G(q) χρησιμοποιώντας τις σχέσεις: P( q) G( q) q () T K( q, q ) q M ( q) q (4) T N( q, q ) ( M U M U M ), όπου T M M T U M ( In q )[... ] (5) q q n που το σύμβολο παριστάνει το γινόμενο Kronecker, το οποίο προκύπτει ως έξης: ab a B n αν A R r s, B R τότε A B an B anb Ο λόγος για τον οποίο χρησιμοποιούμε αυτή την πολύπλοκη σχέση για το N ( q, q ) είναι επειδή από αυτή τη σχέση είναι προφανές ότι ο πίνακας M N είναι αντι-συμμετρικός. T Με άλλα λόγια με αυτό το N ( q, q ) έχουμε ότι q ( M N) q. Αυτή η σχέση είναι πολύ βασική για τον προσαρμοστικό ή σθεναρό έλεγχο κλασσικών σειριακών ρομπότ. Για να υπολογίσουμε την κινητική και δυναμική ενέργεια, θα χωρίσουμε θεωρητικά την πλατφόρμα μας σε δύο μέρη: την άνω βάση (με μάζα u ) και τα έξι πόδια (το καθένα με μάζα l ). Μια απόλυτα σωστή προσέγγιση θα ήταν ο διαχωρισμός του κάθε ποδιού σε δύο μέρη (το πάνω και κάτω μέρος). Αυτό θα έδινε ακριβή έκφραση για τις ενέργειες. Επειδή όμως οι σχέσεις αυτές είναι εξαιρετικά περίπλοκες και δύσκολες στη χρήση, θα κάνουμε την υπόθεση ότι το κάθε πόδι μπορεί να μοντελοποιηθεί από το κέντρο βάρους του (G i ) και ότι η μάζα του είναι συγκεντρωμένη σε εκείνο το σημείο. Εδώ πρέπει να σημειώσουμε ότι το κέντρο βάρους του κάθε ποδιού αλλάζει με την πάροδο του χρόνου λόγω της επιμήκυνσης που παθαίνει το πόδι κατά τη διάρκεια της κίνησης. Για να καθορίσουμε το κινούμενο κέντρο βάρους G i λαμβάνουμε υπ όψιν τα εξής: 4
43 Κεφάλαιο : Πλατφόρμα Stewart- Δυναμική ανάλυση Το κέντρο βάρους G i του κάτω τμήματος του ποδιού δεν είναι το μέσο αυτού του μέρους, εξαιτίας της μεγάλης μάζας του dc κινητήρα. Ας θεωρήσουμε l το μήκος, τη μάζα αυτού του μέρους και δ την απόσταση BiG i Αντίθετα το πάνω μέρος κάθε γραμμικού ενεργοποιητή είναι ομοιόμορφο. Επομένως το κέντρο βάρους G είναι στο μέσο του τμήματος αυτού. Ας θεωρήσουμε l το μήκος, τη μάζα αυτού του μέρους. Τέλος ορίζω u i το μοναδιαίο διάνυσμα ( είναι περιττό και j=i/ εάν το i είναι άρτιο. Εύκολα προκύπτει i B T / B T ) όπου j=(i+)/ εάν το i i j i j ˆ B G l l L u l L u i i [(.5 ) i] i [ i ] i (6) l ˆ ( l.5 l )/( ) όπου Θεωρώ f i τη δύναμη που εφαρμόζεται στη διεύθυνση u i από τον ενεργοποιητή του ποδιού i και ορίζω F [ f, f,..., f6] T. Το στοιχειώδες έργο που παράγεται από κάθε πόδι είναι: T T dw d( BT ) f d( L u ) f i i j i i i i Αφού T T dl JdX poj F T T dw dx poj F τότε το στοιχειώδες έργο που σχετίζεται με τα έξι πόδια είναι το οποίο δίνει τη γενικευμένη δύναμη T J F (7) Η δυναμική ενέργεια της πλατφόρμας stewart εύκολα εκφράζεται ως εξής: P P P upper legs gp ( ) ( B G ) u Z i i 6 ˆ u g X po ( ) l ( ) ZTi Li L (8) i Η κινητική ενέργεια αποτελείται από δύο μέρη. Για την άνω βάση η κινητική ενέργεια είναι το άθροισμα της ενέργειας από μεταφορά και της ενέργειας από περιστροφή του σώματος ως προς το κέντρο βάρους. Από αυτό προκύπτει T Kupper u ( p X p Y p Z ) upiup (9) όπου το διάνυσμα ροπής αδράνειας Ι είναι της μορφής I diag{ I x, I y, I z}. up ορίζεται ως: 4
44 Κεφάλαιο : Πλατφόρμα Stewart- Δυναμική ανάλυση T ( ) T ( ) T ( ) T ( ) T ( ) T up ar R R R R R ( ) όπου Rx ( a ), Ry ( ), Rz ( ) είναι οι πίνακες περιστροφής γύρω από τους άξονες Χ-Υ-Ζ. Τελικά προκύπτει ( T upper X p om up ( X p o ) X po ) με M up u u u ( X po ) I X cos I sin ( I X IY ) cos a cos sin ( I X IY ) cos a cos sin cos a( I X sin I cos ) I Z sin a IZ sin a IZ () Για τα πόδια θα ορίσουμε Τότε V Gi την ταχύτητα του G i και V Tj την ταχύτητα του σημείου T j. lˆ V ( V L u ) V Gi Tj i i Tj Li και η κινητική ενέργεια του ενός ποδιού είναι ( )( T T T Ki hi VTj VTj ki VTj ui ui VTj ) όπου h i lˆ lˆ lˆ ( ) ( ), ki Li Li Li Εφόσον T Li Li L i ui X Tj YTj ZTj T οι ορισμοί για τα J, J δίνουν (( T Klegs X p om legs ( X p o ) X po ) με ( h h ) I O O k k T k T 4 k4 O O ( h5 h6 ) I k5 M legs ( ) J O ( h h ) I O J J J k 6 () 44
45 Κεφάλαιο : Πλατφόρμα Stewart- Δυναμική ανάλυση Στη σχέση () οι πίνακες O και I παριστάνουν έναν (x) μηδενικό και μοναδιαίο πίνακα αντίστοιχα. Δεν είναι δύσκολο να αποδειχθεί ότι η κινητική ενέργεια των ποδιών είναι συνάρτηση μόνο του X. p o Με τις εκφράσεις αυτές της κινητικής και δυναμικής ενέργειας T J F, K Kupper Klegs, P Pupper Plegs οι εξισώσεις της δυναμικής προκύπτουν πολύ εύκολα από τον τύπο (). 45
46 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart ΚΕΦΑΛΑΙΟ 4: ΠΡΟΣΟΜΟΙΩΣΗ ΚΑΙ ΕΛΕΓΧΟΣ ΤΗΣ ΠΛΑΤΦΟΡΜΑΣ STEWART 4. Σχεδιασμός του Μοντέλου στο Siulink Για να κάνουμε έλεγχο της πλατφόρμας Stewart χρησιμοποιήσαμε το SiMechanics toolbox του πακέτου MatLab το οποίο έχει ένα αρχικό deo της πλατφόρμας Stewart το οποίο όμως δεν παρουσιάζει την πλατφόρμα με τη γεωμετρία με την οποία τη μελετήσαμε εμείς πιο πάνω. Γι αυτο το λόγο θα διατηρήσουμε το ίδιο μοντέλο κάνοντας όμως τις απαραίτητες αλλαγές έτσι ώστε να το φέρουμε στη μορφή που έχουμε μελετήσει. Στην ενότητα αυτή θα ασχοληθούμε με τη γεωμετρία της πλατφόρμας και το πως θα ορίσουμε τις παραμέτρους στο Siulink. Στο Κεφάλαιο που έγινε η μελέτη της κινηματικής παρουσιάστηκαν οι συντεταγμένες των κορυφών της άνω και κάτω βάσης. Να θυμίσουμε ότι η κάτω βάση έχει τη μορφή ημικανονικού εξαγώνου, ενώ η πάνω βάση τη μορφή τριγώνου που σημαίνει ότι σε κάθε σημείο της καταλήγουν δύο πόδια της πλατφόρμας. Εμείς θα θεωρήσουμε για λόγους ευκολίας ότι η άνω βάση έχει και αυτή έξι κορυφές οι οποίες ανά δυο συμπίπτουν. 46
47 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Ξεκινώντας από την κάτω βάση ορίζουμε τις έξι κορυφές της με τις σχέσεις που δόθηκαν στο Κεφάλαιο : X B ( b d ) X B ( b d ) 6 6 YB d YB ( b d ) Z Z B B X B ( b d ) X B4 ( b d ) 6 6 b YB 4 b Z Z 4 YB B B X B5 ( b d ) X B6 ( b d ) 6 6 YB 5 ( b d ) YB 6 d Z Z 6 B5 B Στην περίπτωση μας έχουμε ως δεδομένα ότι το αρχικό μήκος των 6 ποδιών είναι c, b= 5 c, d= c, όπου b,d είναι η μεγάλη και η μικρή πλευρά αντίστοιχα της κάτω βάσης και a= c που είναι η πλευρά της τριγωνικής άνω βάσης. Επομένως προκύπτει ο εξής κώδικας: % base points b=.5; d=.; Xb=sqrt()*(*b+d)/6; Xb=-sqrt()*(b-d)/6; Xb=-sqrt()*(b+*d)/6; Xb4=Xb; Xb5=Xb; Xb6=Xb; Xb=[Xb;Xb;Xb;Xb4;Xb5;Xb6]; Yb=.5*d; Yb=.5*(b+d); Yb=.5*b; Yb4=-Yb; Yb5=-Yb; Yb6=-Yb; Yb=[Yb;Yb;Yb;Yb4;Yb5;Yb6]; Zb=[;;;;;]; pos_base=[xb Yb Zb]; 47
48 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Από όπου προκύπτει το εξής διάνυσμα που περιέχει τις κορυφές pos_base = Οι συντεταγμένες των κορυφών της άνω βάσης όπως έχουμε δει δεν προκύπτουν από συγκεκριμένες εξισώσεις, αλλά προκύπτουν από την επίλυση τριών μη-γραμμικών εξισώσεων. Με τη βοήθεια του Matlab θα βρούμε μια λύση αυτού του συστήματος και θα προχωρήσουμε στον ακριβή προσδιορισμό των κορυφών. Παρατίθεται ο κώδικας: % top points a=.; L=.; L=.; L=.; L4=.; L5=.; L6=.; %voithitikes etavlhtes P=(/(*b))*(b^+L^-L^); P=(/(*b))*(b^+L^-L4^); P=(/(*b))*(b^+L5^-L6^); xp=(sqrt())*(*b+d-*p)/6; xp=-(sqrt())*(b+*d)/6; yp=.5*(d+p); yp=.5*(b-*p); xp=-(sqrt())*(b-d-*p)/6; yp=-.5*(b+d-p); h=sqrt(l^-p^); h=sqrt(l^-p^); h=sqrt(l5^-p^); x = [xp; xp; xp]; % Make a starting guess at the solution options=optiset('display','iter'); % Option to display output [x,fval] = fsolve(@yfun,x,options); % Call optiizer xt=x(); xt=x(); xt=x(); yt=(sqrt())*xt-((sqrt())*xp-yp); yt=yp; yt=-(sqrt())*xt+((sqrt())*xp+yp); zt=sqrt(h^-4*(xt-xp)^); zt=sqrt((h^-(xt-xp)^)); zt=sqrt((h^-4*(xt-xp)^)); height=zt; %height in hoe configuration pos_top=[xt yt zt;xt yt zt;xt yt zt;xt yt zt;xt yt zt;xt yt zt]; 48
49 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart και η συνάρτηση yfun που περιέχει τις τρεις εξισώσεις και από τις οποίες προκύπτουν οι τρεις μεταβλητές x Τ, x Τ,x Τ είναι: function F = yfun(x) a=.; b=.5; d=.; L=.; L=.; L=.; L4=.; L5=.; L6=.; P=(/(*b))*(b^+L^-L^); P=(/(*b))*(b^+L^-L4^); P=(/(*b))*(b^+L5^-L6^); xp=(sqrt())*(*b+d-*p)/6; xp=-(sqrt())*(b+*d)/6; yp=.5*(d+p); yp=.5*(b-*p); xp=-(sqrt())*(b-d-*p)/6; yp=-.5*(b+d-p); h=sqrt(l^-p^); h=sqrt(l^-p^); h=sqrt(l5^-p^); %oi treis h graikes eksiswseis gia na vroue tis syntetagenes x F = [ a^+*x()*x()-*x()*(xp+sqrt()*(yp-yp))-*xp*x()-... ((sqrt()*xp-yp+yp)^+(h^+h^)-4*xp^-xp^)+... *sqrt((h^-4*(x()-xp)^)*(h^-(x()-xp)^)); a^-4*x()*x()-*x()*(xp-*xp+sqrt()*(yp-yp))-... *x()*(-*xp+xp+sqrt()*(yp-yp))-... ((sqrt()*(xp+xp)-yp+yp)^+(h^+h^)-4*xp^-4*xp^)+... *sqrt((h^-4*(x()-xp)^)*(h^-4*(x()-xp)^)); a^+*x()*x()-*x()*(xp+sqrt()*(yp-yp))-*xp*x()-... ((sqrt()*xp-yp+yp)^+(h^+h^)-xp^-4*xp^)+... *sqrt((h^-(x()-xp)^)*(h^-4*(x()-xp)^))]; Από όπου προκύπτει το διάνυσμα με τις έξι κορυφές: pos_top = Παρατηρούμε ότι ανά δύο τα σημεία συμπίπτουν. Πρέπει ακόμα να ορίσουμε το πάχος της πλατφόρμας. Καταρχήν το υλικό από το οποίο αποτελείται όλη η διάταξη είναι το αλουμίνιο 66 το οποίο έχει πυκνότητα,7e kg/. 49
50 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Το κάθε πόδι το θεωρούμε συμπαγές με ακτίνα,. Οι βάσεις έχουν πάχος,5 και έχουν δακτυλιοειδές σχήμα (δεν είναι συμπαγείς) με πάχος του δακτυλίου ίσο με. Όλα τα παραπάνω χαρακτηριστικά ορίζονται με τον παρακάτω κώδικα ο οποίος υπολογίζει τη μάζα και τη ροπή αδράνειας της άνω και κάτω πλάκας αλλά και των έξι ποδιών. % Inertia and ass calculation top_thickness =.5; base_thickness =.5; inner_radius = ; outer_radius =.; density =.7e; % 66 aluiniu density in Kg/^ %leg inertia and ass [lower_leg_ass, lower_leg_inertia] = inertiacylinder(density,.75*leg_length(),outer_radius, inner_radius); [upper_leg_ass, upper_leg_inertia] = inertiacylinder(density,.75*leg_length(),outer_radius, inner_radius); % top and base plate ass and inertia radius_t = sqrt((pos_top(,))^+(pos_top(,))^); radius_b = sqrt((pos_base(,))^+(pos_base(,))^); [top_ass, top_inertia] = inertiacylinder(density,top_thickness,.5*radius_t,.5*radius_t-.); [base_ass, base_inertia] = inertiacylinder(density,base_thickness,.5*radius_b,.5*radius_b-.); Επιπρόσθετο βάρος Για την προσομοίωση του συστήματος μας και για να αντιπροσωπεύει περισσότερο την πραγματικότητα το σύστημά μας, θα θεωρήσουμε ένα σώμα σε μορφή ημισφαιρίου στην άνω βάση. Επειδή θεωρούμε ότι η διάταξη της οστεογένεσης (πλατφόρμα Stewart) είναι τοποθετημένη στο ένα πόδι ενός ανθρώπου, και επειδή είναι δύσκολο να μοντελοποιήσουμε το ανθρώπινο σώμα, θεωρούμε προσεγγιστικά ότι το ανθρώπινο σώμα έχει τη μορφή ημισφαιρίου. Επομένως στο μοντέλο μας προσθέτουμε ένα βάρος πάνω από την άνω βάση για το οποίο όμως πρέπει να ορίσουμε τη μάζα και τον πίνακα ροπών αδράνειας. Θεωρούμε ότι ο άνθρωπος έχει μάζα 8 kg. Πρέπει όμως να διαχωρίσουμε τις εξής τρεις υποπεριπτώσεις: Στην περίπτωση που ο άνθρωπος στέκεται όρθιος το βάρος μοιράζεται στα δυο πόδια οπότε η πλατφόρμα δέχεται βάρος 4 kg. Όταν ο άνθρωπος περπατάει τότε το βάρος πέφτει σε κάθε πόδι εναλλάξ. Οπότε κατά τη διάρκεια της βάδισης το βάρος που δέχεται η πλατφόρμα είναι 8 kg και περίπου μηδέν, διαδοχικά. Οπότε τα πειράματα που πραγματοποιήσαμε, έγιναν για τρεις διαφορετικές μάζες: 8 kg, 4 kg, 5 kg. Το επόμενο βήμα είναι ο προσδιορισμός του πίνακα ροπών αδράνειας. Να σημειώσουμε εδώ ότι το κέντρο βάρους του ημισφαιρίου είναι R. Παρακάτω παρατίθεται ο 8 θεωρητικός υπολογισμός του πίνακα ροπών αδράνειας. 5
51 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart ( ) y z d xyd xzd I xyd ( x z ) d yzd xzd yzd ( x y ) d ( ) ( sin sin cos ) y z d r r dv r ( sin sin cos ) dv / R r (sin sin cos ) r sin drdd / 5 R (sin sin cos ) sin d d 5 5 / 5 / R R sin sin dd cos sin d d 5 5 / 5 / 5 R R cos (sin sin sin d ) d d / 5 R R (sin ( cos )sin d ) d d / / 5 R R ( sin ( sind cos sin d )) d 5 5 / 5 R / cos 5 sin ( cos ) d R R 5 sin d R R cos 5 d R 5 5 5
52 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 5 R d cos d R sin 5 R R R R 4 R 5 5 ( ) ( sin cos cos ) sin x z d r r r drd d / R 4 r cos sin (sin ) drd d / 5 R cos sin (sin ) dd 5 5 / R cos ( sin (sin ) d ) d 5 5 / / R cos ( sin d sin d ) d 5 5 / / R cos ( sin sind sin d ) d 5 5 / / / R cos sin d cos sin d sin d d 5 / 5 R / cos cos cos d 5 5
53 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 cos R d R cos d 5 5 R cos d sin R 5 R 5 ( ) ( sin cos sin sin ) x y d r r dv V / R r sin r sin drdd / R 4 d sin d r dr / 5 R sin sin d 5 / 5 ( cos )sin 5 R d / / 5 sin cos sin 5 R d d / 5 / cos R ( cos ) 5 5
54 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart R ( ) R 4 R 5 5 / R xzd r sin cos r cos r sin drd d / 5 R sin cos cos d d 5 / 5 R sin cos d 5 5 R cos ( ) d 5 sin 5 5 R / R yzd r sin sin r cos r sin drd d / 5 R sin cos sin d d 5 / 5 R sin sin d 5 5 R sin ( ) d 5 cos 5 5 R 54
55 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart / R xzd r sin cos r sin sin r sin drd d 5 / sin cos sin R d d 5 5 / R cos sin ( cos ) sind d 5 5 / / R cos sin sind cos sin d d 5 / 5 R / cos cos sin cos d 5 5 R cos sin d 5 5 cos R R Ο κώδικας που υπολογίζει τον παραπάνω πίνακα είναι ο εξής: %weight inertia weight_ass=8; weight_inertia=inertiaheisphere(weight_ass,radius_t); function [inertia]= inertiaheisphere (ass,radius) % calculates the inertia tensor of a solid heisphere Ixx=.4*ass*(radius^); Iyy=.*ass*(radius^); Izz=.4*ass*(radius^); inertia=[ixx ; Iyy ; Izz]; 55
56 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Η προσομοίωσή μας για να τρέξει χρειάζεται όλα αυτά τα δεδομένα, τα οποία βρίσκονται αποθηκευμένα σε ένα αρχείο, το οποίο τρέχει στην αρχή πριν από την προσομοίωση. Το αρχείο αυτό παρατίθεται παρακάτω. % Geoetry and dynaics inforation for Stewart platfor in the hoe configuration % Stewart platfor consists of a top plate, a botto plate, and six legs % connecting the top plate to the botto plate. The overall syste has six % of freedo. Each leg has six of freedo and is coposed of % two bodies, two u-joints, and one cylindrical joint degrad = pi/8; x_axis = [ ]; y_axis = [ ]; z_axis = [ ]; % base points %oi syntetagenes opws dinontai sto arthro b=.5; d=.; Xb=sqrt()*(*b+d)/6; Xb=-sqrt()*(b-d)/6; Xb=-sqrt()*(b+*d)/6; Xb4=Xb; Xb5=Xb; Xb6=Xb; Xb=[Xb;Xb;Xb;Xb4;Xb5;Xb6]; Yb=.5*d; Yb=.5*(b+d); Yb=.5*b; Yb4=-Yb; Yb5=-Yb; Yb6=-Yb; Yb=[Yb;Yb;Yb;Yb4;Yb5;Yb6]; Zb=[;;;;;]; pos_base=[xb Yb Zb]; % top points a=.; L=.; L=.; L=.; L4=.; L5=.; L6=.; %voithitikes etavlhtes P=(/(*b))*(b^+L^-L^); P=(/(*b))*(b^+L^-L4^); P=(/(*b))*(b^+L5^-L6^); 56
57 xp=(sqrt())*(*b+d-*p)/6; xp=-(sqrt())*(b+*d)/6; yp=.5*(d+p); yp=.5*(b-*p); xp=-(sqrt())*(b-d-*p)/6; yp=-.5*(b+d-p); h=sqrt(l^-p^); h=sqrt(l^-p^); h=sqrt(l5^-p^); % Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x = [xp; xp; xp]; % Make a starting guess at the solution options=optiset('display','iter'); % Option to display output [x,fval] = fsolve(@yfun,x,options); % Call optiizer xt=x(); xt=x(); xt=x(); yt=(sqrt())*xt-((sqrt())*xp-yp); yt=yp; yt=-(sqrt())*xt+((sqrt())*xp+yp); zt=sqrt(h^-4*(xt-xp)^); zt=sqrt((h^-(xt-xp)^)); zt=sqrt((h^-4*(xt-xp)^)); height=zt; %height in hoe configuration pos_top=[xt yt zt;xt yt zt;xt yt zt;xt yt zt;xt yt zt;xt yt zt]; %% % Copute points w.r.t. to the body frae in a x6 atrix [xi yi ] i=,...,6 %in hoe configuration body_pts = pos_top' - [zeros(,6);zt zt zt zt zt zt]; % leg vectors legs = pos_top - pos_base; for i = :6, leg_length(i) = nor(legs(i,:)); leg_vectors(i,:) = legs(i,:) / leg_length(i); end % Calculate revolute and cylindrical axes rev=[ ]; rev=[ ]; rev=[ ]; rev4=[ ]; cyl=[ ]; for i = :6, rev(i,:) = cross(leg_vectors(i,:), z_axis); rev(i,:) = rev(i,:) / nor(rev(i,:)); rev(i,:) = - cross(rev(i,:), leg_vectors(i,:)); rev(i,:) = rev(i,:) / nor(rev(i,:)); cyl(i,:) = leg_vectors(i,:); rev(i,:) = rev(i,:); 57
58 rev4(i,:) = rev(i,:); end Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart % Coordinate systes lower_leg = struct('origin', [ ], 'rotation', eye(), 'end_point', [ ]); upper_leg = struct('origin', [ ], 'rotation', eye(), 'end_point', [ ]); for i = :6, lower_leg(i).origin = pos_base(i,:) + (/8)*legs(i,:); lower_leg(i).end_point = pos_base(i,:) + (/4)*legs(i,:); lower_leg(i).rotation = [rev(i,:)', rev(i,:)', cyl(i,:)']; upper_leg(i).origin = pos_base(i,:) + (-/8)*legs(i,:); upper_leg(i).end_point = pos_base(i,:) + (/4)*legs(i,:); upper_leg(i).rotation = [rev(i,:)', rev(i,:)', cyl(i,:)']; end % Inertia and ass calculation top_thickness =.5; base_thickness =.5; inner_radius = ; outer_radius =.; density =.7e; % 66 aluiniu density in Kg/^ %leg inertia and ass [lower_leg_ass, lower_leg_inertia] = inertiacylinder(density,.75*leg_length(),outer_radius, inner_radius); [upper_leg_ass, upper_leg_inertia] = inertiacylinder(density,.75*leg_length(),outer_radius, inner_radius); % top and base plate ass and inertia radius_t = sqrt((pos_top(,))^+(pos_top(,))^); radius_b = sqrt((pos_base(,))^+(pos_base(,))^); [top_ass, top_inertia] = inertiacylinder(density,top_thickness,.5*radius_t,.5*radius_t-.); [base_ass, base_inertia] = inertiacylinder(density,base_thickness,.5*radius_b,.5*radius_b-.); %weight inertia weight_ass=5; weight_inertia=inertiaheisphere(weight_ass,radius_t); % plate_top=[ ]; plate_top_vectors=[ ]; plate_top_length=[ ]; for i=:6, top_o=[ height]; plate_top_vectors(i,:)=pos_top(i,:)-top_o; plate_top_length(i)=nor(pos_top(i,:)); plate_top_vectors(i,:)= plate_top_vectors(i,:) / plate_top_length(i); 58
59 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart end plate_top(i,:)=radius_t*plate_top_vectors(i,:); plate_base=[ ]; plate_base_vectors=[ ]; plate_base_length=[ ]; for i=:6, base_o=[ ]; plate_base_vectors(i,:)=pos_base(i,:)-top_o; plate_base_length(i)=nor(pos_base(i,:)); plate_base_vectors(i,:)= plate_base_vectors(i,:) / plate_base_length(i); plate_base(i,:)=radius_b*plate_base_vectors(i,:); end % Controller Gains Kp = e6; Ki = e4; Kd = 4.5e4; 59
60 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Το μοντέλο φαίνεται στην Εικόνα 4.. Επειδή το σύστημα αποτελείται από πολλά υποσυστήματα, παρατίθενται εικόνες για το καθένα ξεχωριστά. Εικόνα 4.: Απεικόνιση του μοντέλου προσομοίωσης της πλατφόρμας Stewart 6
61 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Όπως φαίνεται από την εικόνα το σύστημα αποτελείται από τρία μέρη. Το πρώτο μέρος αφορά την τροχιά που ζητάμε από το σύστημα να κάνει, το δεύτερο είναι ο ελεγκτής και το τελευταίο η πλατφόρμα. -C- pos_base Xang Yang Zang Xpos Ypos Zpos Desired Rotation Matrix EulerXYZ -C- -Cbody _pts Matrix Multiply Product noinal leg length leg vec no len Copute vector of leg lengths leg len len Create desired position atrix Control error for each leg length : (R*p_t + p) - p_b - l_n, where R is the rotation atrix for the top plate, p is the position of the origin of the top plate, p_t is the leg attachent point at the top plate, p_b is the leg attachent point at the base, and l _n is the noinal (reference ) distance between the top and base attachent points. Εικόνα 4.: Προσδιορισμός της τροχιάς που θέλουμε να ακολουθήσει το σύστημα Όπως φαίνεται από το σχήμα, εμείς αυτό που προσδιορίζουμε είναι οι συντεταγμένες του κέντρου βάρους της άνω βάσης, καθώς και οι γωνίες περιστροφής του. Με τα δεδομένα αυτά και με τη βοήθεια μετασχηματισμών προκύπτουν τα μήκη των ποδιών, δηλαδή η τροχιά που πρέπει να ακολουθήσει το καθένα για να φτάσει στην τελική τιμή. pos r_pos Kp P s Integrator Ki I Force vel - Gain Kd D Εικόνα 4.: Ελεγκτής Στην Εικόνα 4. δίνεται ο ελεγκτής του συστήματος ο οποίος είναι ένας απλός PID ελεγκτής. Οι τιμές των παραμέτρων του βρίσκονται στο αρχείο που τρέχει στην αρχή της προσομοίωσης (αυτό που αναφέραμε πιο πάνω) και βρέθηκαν μετά από δοκιμές και όχι με κάποια μέθοδο tuning του PID. 6
62 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Force Deux [F] [F] [F] [F4] [F5] [F6] Body CG CS B F Weld Top Plate CS CG CS CS CS7 CS4 CS5 CS8 CS6 [F] [F] [F] [F4] [F5] [F6] Force Top Force Top Force Top Force Top Force Top Force Top Leg Leg Leg Leg 4 Leg 5 Leg 6 Pos Vel Base Pos Vel Base Pos Vel Base Pos Vel Base Pos Vel Base Pos Vel Base [P] [P] [P] [P4] [P5] [P6] [V] [V] [V] [V4] [V5] [V6] Env [P] [P] [P] [P4] [P5] [P6] [V] [V] [V] [V4] [V5] [V6] Pos Vel Εικόνα 4.4: Κυρίως Σύστημα 6
63 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Όπως φαίνεται καθαρά το σύστημα αποτελείται από την άνω βάση, τα έξι επιμέρους πόδια και το επιπρόσθετο βάρος. Η κάτω βάση θεωρείται το περιβάλλον και δεν σχεδιάζεται ξεχωριστά, παρά μόνο ορίζονται οι συντεταγμένες των κορυφών της ως η βάση του κάθε ποδιού. Παρακάτω παρατίθεται το επιμέρους σύστημα ενός από τα έξι πόδια: Top Upper Leg Universal B F Upper Leg CS CS Joint Actuator Force Leg Cylindrical B F p Pos Lower Leg CS CS v Joint Sensor Vel Lower Leg Universal B F Base Εικόνα 4.5: Μοντέλο του κάθε ποδιού 6
64 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 4. Προσομοίωση Κίνησης Στην πραγματικότητα μια διάταξη οστεογένεσης θέλουμε συνήθως να πραγματοποιεί μια παράλληλη κίνηση με την κάτω βάση. Οι περιστροφές ή οι μετατοπίσεις ως προς τους άξονες x,y είναι σχετικά μικρές. Το κύριο πρόβλημά μας δηλαδή είναι η μετατόπιση ως προς τον z άξονα γιατί εκεί γίνεται η συνολική μεγαλύτερη μετατόπιση και γιατί εκεί χρειάζεται να δοθεί και η μεγαλύτερη δύναμη από τους κινητήρες. Η μετατόπιση που θέλουμε να πραγματοποιεί η πλατφόρμα είναι,6 /ημέρα. Επειδή η προσομοίωση μιας τέτοιας κίνησης είναι πολύ χρονοβόρα, εμείς επιλέξαμε να πραγματοποιήσουμε μια παρόμοια κίνηση αλλά σε πολύ μικρότερο χρονικό διάστημα. Επομένως αν τα αποτελέσματα είναι ικανοποιητικά σε αυτή την περίπτωση θα είναι ικανοποιητικά και στην παραπάνω απαίτηση. Πιο συγκεκριμένα πραγματοποιήσαμε το πείραμα αρχικά μεταβάλλοντας μια από τις έξι εισόδους μας (x pos, y pos, z pos, x ang, y ang, z ang ) διατηρώντας όλες τις άλλες σταθερές. Η κίνηση που θέλαμε να πραγματοποιήσουν ήταν προσέγγιση της βηματικής, η υπερβολική εφαπτομένη. Πιο κάτω φαίνεται διάγραμμα με τη μορφή της τροχιάς Εικόνα 4.6: Επιθυμητή τροχιά Η συνάρτηση είναι παρόμοια με μια βηματική αλλά με πιο ομαλές μεταβάσεις, αφού στην πραγματικότητα οι μεταβάσεις που ζητάει μια βηματική είναι αδύνατες. Παρακάτω θα παρουσιάσουμε μερικά από τα αποτελέσματα αυτού του πειράματος. Πιο συγκεκριμένα θα παρουσιάσουμε και για τις τρεις περιπτώσεις του επιπρόσθετου βάρους (8 kg, 4 kg, 5 kg) την είσοδο z pos που μας ενδιαφέρει περισσότερο καθώς και μια περιστροφή, πχ. την y ang. 64
65 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Σημείωση: Σε κάθε περίπτωση παρουσιάζονται οι τροχιές και των έξι εισόδων. z pos, 8 kg.5 x - x pos Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της z pos και βάρος 8 kg 8 x y pos Εικόνα 4.8: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της z pos και βάρος 8 kg 65
66 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.9: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της z pos και βάρος 8 kg 9 x x ang Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της z pos και βάρος 8 kg 66
67 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 6 x -8 y ang Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της z pos και βάρος 8 kg.5 x z ang -6.5 Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της z pos και βάρος 8 kg 67
68 z pos, 4 kg 8 x - Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της z pos και βάρος 4 kg.5 x y pos Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της z pos και βάρος 4 kg 68
69 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της z pos και βάρος 4 kg 9 x x ang Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της z pos και βάρος 4 kg 69
70 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x -8 y ang Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της z pos και βάρος 4 kg.4 x z ang Εικόνα 4.8: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της z pos και βάρος 4 kg 7
71 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos, 5 kg x - x pos Εικόνα 4.9: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της z pos και βάρος 5 kg x y pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της z pos και βάρος 5 kg 7
72 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της z pos και βάρος 5 kg 9 x x ang Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της z pos και βάρος 5 kg 7
73 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x -9 y ang Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της z pos και βάρος 5 kg.5 x z ang -6.5 Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της z pos και βάρος 5 kg Σε όλα τα διαγράμματα που θα παρουσιάσουμε και παρακάτω με πράσινο χρώμα παρουσιάζεται η επιθυμητή τροχιά που θέλουμε να ακολουθήσει η εκάστοτε είσοδος, ενώ με ροζ η πραγματική. Όπως παρατηρούμε στα προηγούμενα διαγράμματα τα 7
74 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart αποτελέσματα είναι εξαιρετικά αφού και η μεταβαλλόμενη είσοδος ακολουθεί πλήρως την επιθυμητή, αλλά και οι υπόλοιπες παραμένουν προσεγγιστικά μηδέν. y ang, 8 kg 6 x -6 x pos Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της y ang και βάρος 8 kg.5 x y pos Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της y ang και βάρος 8 kg 74
75 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.8 z pos Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της y ang και βάρος 8 kg x -6 x ang Εικόνα 4.8: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της y ang και βάρος 8 kg 75
76 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 y ang 5 5 Εικόνα 4.9: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της y ang και βάρος 8 kg.8 x z ang Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της y ang και βάρος 8 kg 76
77 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart y ang, 4 kg 8 x -6 x pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της y ang και βάρος 4 kg x y pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της y ang και βάρος 4 kg 77
78 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos Εικόνα 4.: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της y ang και βάρος 4 kg x x ang Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της y ang και βάρος 4 kg 78
79 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 y ang 5 5 Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της y ang και βάρος 4 kg.8 x z ang Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της y ang και βάρος 4 kg 79
80 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart y ang, 5 kg x -7 x pos Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή της y ang και βάρος 5 kg 4 x y pos Εικόνα 4.8: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή της y ang και βάρος 5 kg 8
81 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos.8 Εικόνα 4.9: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή της y ang και βάρος 5 kg.8 x -6 x ang Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή της y ang και βάρος 5 kg 8
82 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 y ang 5 5 Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή της y ang και βάρος 5 kg.8 x z ang Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή της y ang και βάρος 5 kg Ο ελεγκτής που έχουμε επιλέξει μας δίνει ικανοποιητικά αποτελέσματα, αφού τα αποτελέσματα όπως θα φανεί και στα παρακάτω πειράματα έχουν αμελητέα σφάλματα. 8
83 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Στη συνέχεια μεταβάλλαμε ανά δύο τις εισόδους διατηρώντας τις υπόλοιπες σταθερές. Στη συνέχεια θα παρουσιάσουμε μερικά από τα αποτελέσματα. Όλα τα αποτελέσματα των πειραμάτων παρουσιάζονται συγκεντρωμένα στο Παράρτημα. x pos, z pos, 8 kg.5 x pos Εικόνα 4.4: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των x pos, z pos και βάρος 8 kg 8 x y pos Εικόνα 4.44: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των x pos, z pos και βάρος 8kg 8
84 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.45: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των x pos, z pos και βάρος 8 kg.5 x x ang Εικόνα 4.46: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των x pos, z pos και βάρος 8kg 84
85 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 x - y ang Εικόνα 4.47: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των x pos, z pos και βάρος 8kg.8 x z ang Εικόνα 4.48: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των x pos, z pos και βάρος 8 kg 85
86 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x pos, z pos, 4 kg.5 x pos Εικόνα 4.49: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των x pos, z pos και βάρος 4 kg x y pos Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των x pos, z pos και βάρος 4kg 86
87 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των x pos, z pos και βάρος 4 kg.8 x x ang Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των x pos, z pos και βάρος 4kg 87
88 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x -4 y ang Εικόνα 4.5: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των x pos, z pos και βάρος 4kg.8 x z ang Εικόνα 4.54: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των x pos, z pos και βάρος 4 kg 88
89 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x pos, z pos, 5 kg.5 x pos Εικόνα 4.55: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των x pos, z pos και βάρος 5 kg x y pos Εικόνα 4.56: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των x pos, z pos και βάρος 5 kg 89
90 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos Εικόνα 4.57: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των x pos, z pos και βάρος 5 kg x -6 x ang Εικόνα 4.58: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των x pos, z pos και βάρος 5 kg 9
91 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 6 x -5 y ang Εικόνα 4.59: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των x pos, z pos και βάρος 5 kg.8 x -6 z ang Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των x pos, z pos και βάρος 5 kg 9
92 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos, x ang, 8 kg x -6 x pos Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των z pos, x ang και βάρος 8kg x y pos Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των z pos, x ang και βάρος 8kg 9
93 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.6: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των z pos, x ang και βάρος 8kg x ang Εικόνα 4.64: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των z pos, x ang και βάρος 8kg 9
94 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 4 x -4 y ang Εικόνα 4.65: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των z pos, x ang και βάρος 8kg x -4 z ang Εικόνα 4.66: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των z pos, x ang και βάρος 8kg 94
95 z pos, x ang, 4 kg.5 x -6 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart x pos Εικόνα 4.67: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των z pos, x ang και βάρος 4kg.5 x y pos Εικόνα 4.68: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των z pos, x ang και βάρος 4kg 95
96 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.69: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των z pos, x ang και βάρος 4kg x ang Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των z pos, x ang και βάρος 4kg 96
97 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 8 x -4 y ang Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των z pos, x ang και βάρος 4kg x z ang Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των z pos, x ang και βάρος 4kg 97
98 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos, x ang, 5 kg x -7 x pos Εικόνα 4.7: Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των z pos, x ang και βάρος 5kg.5 x y pos Εικόνα 4.74: Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των z pos, x ang και βάρος 5kg 98
99 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart.5 z pos Εικόνα 4.75: Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των z pos, x ang και βάρος 5kg 5 x ang 5 5 Εικόνα 4.76: Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των z pos, x ang και βάρος 5kg 99
100 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 8 x -5 y ang Εικόνα 4.77: Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των z pos, x ang και βάρος 5kg.5 x -5 z ang.5.5 Εικόνα 4.78: Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των z pos, x ang και βάρος 5kg
101 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Τέλος μπορούμε να παρουσιάσουμε τα αποτελέσματα που προκύπτουν αν ζητήσουμε και από τις έξι εισόδους να κινηθούν σε μια τροχιά στην περίπτωση που το επιπρόσθετο βάρος είναι 8 kg, όπου λογικά μπορεί να υπάρχει και το μεγαλύτερο σφάλμα..5 x pos Εικόνα 4.79:Πραγματική και επιθυμητή τροχιά της x pos για μεταβολή των εισόδων και βάρος 8kg y pos Εικόνα 4.8:Πραγματική και επιθυμητή τροχιά της y pos για μεταβολή των εισόδων και βάρος 8kg
102 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos Εικόνα 4.8:Πραγματική και επιθυμητή τροχιά της z pos για μεταβολή των εισόδων και βάρος 8kg x ang Εικόνα 4.8:Πραγματική και επιθυμητή τροχιά της x ang για μεταβολή των εισόδων και βάρος 8kg
103 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 5 y ang 5 5 Εικόνα 4.8:Πραγματική και επιθυμητή τροχιά της y ang για μεταβολή των εισόδων και βάρος 8kg z ang Εικόνα 4.84:Πραγματική και επιθυμητή τροχιά της z ang για μεταβολή των εισόδων και βάρος 8kg
104 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Από όλα τα παραπάνω διαγράμματα παρατηρούμε ότι οι είσοδοι που επιλέγουμε εμείς να εκτελέσουν μια κίνηση ακολουθούν εξαιρετικά καλά την επιθυμητή τροχιά. Αντίθετα οι υπόλοιπες είσοδοι μπορεί να μην μένουν ακριβώς αμετάβλητες αλλά η μεταβολή τους κυμαίνεται μέσα σε συγκεκριμένα όρια και το σφάλμα τελικά είναι αμελητέο. Επίσης παρατηρούμε στα διαγράμματα ότι το σφάλμα μειώνεται όσο μειώνεται και το βάρος που έχουμε τοποθετήσει στην άνω βάση. 4. Έλεγχος των δυνάμεων Μια ακόμα παράμετρος με την οποία πρέπει να ασχοληθούμε είναι οι δυνάμεις που πρέπει να δώσουν οι κινητήρες. Είναι απολύτως κατανοητό ότι δεν μπορούμε να ζητήσουμε από τη διάταξή μας να κάνει οποιαδήποτε κίνηση, επειδή η κινητήρες δεν μπορούν να μας δώσουν ανά πάσα στιγμή όση δύναμη και αν τους ζητήσουμε. Η μέγιστη δύναμη που πρέπει να δώσουν οι κινητήρες απαιτείται σε μια παράλληλη κίνηση της πλατφόρμας. Επομένως θα παρουσιάσουμε τα διαγράμματα των δυνάμεων σε παράλληλη μετατόπιση και για τις τρεις τιμές του βάρους. z pos, 8 kg N Εικόνα 4.85: Δύναμη των κινητήρων για παράλληλη μετατόπιση και βάρος 8kg 4
105 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart z pos, 4 kg N Εικόνα 4.86: Δύναμη των κινητήρων για παράλληλη μετατόπιση και βάρος 4kg z pos, 5 kg.6.4. N Εικόνα 4.87: Δύναμη των κινητήρων για παράλληλη μετατόπιση και βάρος 5kg 5
106 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart Αρχικά σημειώνουμε ότι οι έξι ενεργοποιητές χρειάζεται να δώσουν την ίδια δύναμη οπότε παρουσιάζουμε τα διαγράμματα για τον ένα από αυτούς. Από τα διαγράμματα των δυνάμεων βλέπουμε αρχικά ότι όσο μεγαλύτερο είναι το βάρος που πρέπει να σηκώσει η διάταξή μας τόσο μεγαλύτερη η δύναμη που πρέπει να δώσουν οι ενεργοποιητές, το οποίο είναι απολύτως λογικό. Ένα ακόμα πράγμα που πρέπει να παρατηρήσουμε είναι ότι οι τιμές της δύναμης που ζητάμε από τους ενεργοποιητές δεν είναι απαγορευτικές παρόλο που η κίνηση που πρέπει να κάνει το σώμα είναι σχετικά απότομη. Στη συνέχεια θα πραγματοποιήσουμε ένα ακόμα πείραμα για να παρατηρήσουμε τις δυνάμεις που δίνουν οι κινητήρες. Αυτή τη φορά θα πραγματοποιήσουμε πάλι παράλληλη μετατόπιση της άνω βάσης αλλά με περιστροφή ως προς τον z-άξονα. z pos, z ang, 8 kg 85 force N Εικόνα 4.88: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 8 kg 6
107 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 86 force N Εικόνα 4.89: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 8 kg 85 force N Εικόνα 4.9: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 8 kg 7
108 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 86 force N Εικόνα 4.9: Δύναμη του κινητήρα 4 για μεταβολή των z pos, z ang και βάρος 8 kg 85 force N Εικόνα 4.9: Δύναμη του κινητήρα 5 για μεταβολή των z pos, z ang και βάρος 8 kg 8
109 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 86 force N Εικόνα 4.9: Δύναμη του κινητήρα 6 για μεταβολή των z pos, z ang και βάρος 8 kg z pos, z ang, 4 kg 9 force 85 8 N Εικόνα 4.94: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 4 kg 9
110 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 9 force N Εικόνα 4.95: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 4 kg 9 force 85 8 N Εικόνα 4.96: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 4 kg
111 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 9 force N Εικόνα 4.97: Δύναμη του κινητήρα 4 για μεταβολή των z pos, z ang και βάρος 4 kg 9 force N Εικόνα 4.98: Δύναμη του κινητήρα 5 για μεταβολή των z pos, z ang και βάρος 4 kg
112 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart 9 force N Εικόνα 4.99: Δύναμη του κινητήρα 6 για μεταβολή των z pos, z ang και βάρος 4 kg z pos, z ang, 5 kg.5 force.5 N Εικόνα 4.: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 5 kg
113 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart force N Εικόνα 4.: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 5 kg.5 force.5 N Εικόνα 4.: Δύναμη του κινητήρα για μεταβολή των z pos, z ang και βάρος 5 kg
114 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart force N Εικόνα 4.: Δύναμη του κινητήρα 4 για μεταβολή των z pos, z ang και βάρος 5 kg.5 force5.5 N Εικόνα 4.4: Δύναμη του κινητήρα 5 για μεταβολή των z pos, z ang και βάρος 5 kg 4
115 Κεφάλαιο 4: Προσομοίωση και Έλεγχος της πλατφόρμας Stewart force N Εικόνα 4.5: Δύναμη του κινητήρα 6 για μεταβολή των z pos, z ang και βάρος 5 kg Συμπεράσματα Από τα πειράματα που πραγματοποιήσαμε έχουμε να συνοψίσουμε τις εξής παρατηρήσεις. Ο ελεγκτής που έχουμε επιλέξει για το σύστημα δίνει ικανοποιητικά αποτελέσματα αφού οι πραγματικές τροχιές που ακολουθούν οι είσοδοι σχεδόν συμπίπτουν με τις επιθυμητές, οπότε τα σφάλματα είναι πολύ μικρά. Πιο συγκεκριμένα το τελικό σφάλμα βρίσκεται μέσα σε συγκεκριμένα επιτρεπτά όρια. Αυτό φαίνεται καλύτερα στα διαγράμματα των εισόδων από τις οποίες έχουμε ζητήσει να παραμείνουν σταθερές. Επίσης από τα διαγράμματα παρατηρούμε ότι όσο μικρότερο είναι το βάρος που έχουμε τοποθετήσει στην άνω βάση της πλατφόρμας τόσο μικρότερο είναι και το σφάλμα της τροχιάς των εισόδων. Κατόπιν πραγματοποιήσαμε πειράματα για την παρατήρηση των δυνάμεων που πρέπει να δώσουν οι κινητήρες. Σε ένα τέτοιο σύστημα δεν μπορούμε να ζητήσουμε μια απότομη κίνηση, για παράδειγμα μια βηματική, αφού οι κινητήρες λόγω αδράνειας δεν θα μπορούν να δώσουν την απαραίτητη δύναμη. Τα αποτελέσματα που πρόεκυψαν δε δίνουν απαγορευτικές τιμές και για μια σχετικά απότομη κίνηση, αφού οι τιμές των κινητήρων είναι μικρότερες από N. Το μοναδικό κομμάτι που πιθανόν να υπάρχει πρόβλημα θα είναι τη χρονική στιγμή που υποτίθεται ότι οι κινητήρες είναι σε αδράνεια και πρέπει ακαριαία να δώσουν μια συκεκριμένη δύναμη. Τέλος παρατηρούμε και σε αυτή την περίπτωση ότι όσο μικρότερο είναι το βάρος που έχουμε τοποθετήσει στην άνω βάση, τόσο μικρότερη είναι και η δύναμη που απαιτείται από τους κινητήρες. 5
116 Κεφάλαιο 5: Συμπεράσματα- Επεκτάσεις ΚΕΦΑΛΑΙΟ 5: ΕΠΕΚΤΑΣΕΙΣ Όπως είδαμε στα προηγούμενα Κεφάλαια η πλατφόρμα Stewart είναι ένα πλήρες σύστημα εξωτερικής διατατικής οστεογένεσης το οποίο μπορεί να πραγματοποιήσει κάθε επιθυμητή κίνηση και με ευκολία αφού δεν απαιτούνται μεγάλες δυνάμεις από τους κινητήρες. Υπάρχει όμως μια μεγάλη ομάδα ασθενών που απαιτούν επιμήκυνση χωρίς να έχουν άλλη παραμόρφωση, πχ γωνιακή παραμόρφωση. Σε αυτές τις περιπτώσεις δεν είναι απαραίτητη η χρήση μιας τόσο πολύπλοκης συσκευής, αφού οι επιπλοκές που προκύπτουν κατά τη διάρκεια της επιμήκυνσης οφείλονται κυρίως στη συσκευή παρά στην ίδια τη διαδικασία. Σε τέτοιες περιπτώσεις χρησιμοποιούνται λιγότερο πολύπλοκες συσκευές. 6
Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ. Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών
 Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών 1951 Gavril Abramovich Ilizarov Μέθοδος Ilizarov «συνδυασμός φλοιοτομής και σταδιακής, ελεγχόμενης
Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών 1951 Gavril Abramovich Ilizarov Μέθοδος Ilizarov «συνδυασμός φλοιοτομής και σταδιακής, ελεγχόμενης
Γράφει: Τσαπακίδης Ιωάννης, Χειρουργός Ορθοπαιδικός
 Γράφει: Τσαπακίδης Ιωάννης, Χειρουργός Ορθοπαιδικός Η οστεοτομία είναι μια επέμβαση με την οποία ο χειρουργός διαχωρίζει το οστό (προκαλεί δηλαδή, τεχνικά κάταγμα). Στη συνέχεια επανατοποθετεί τα κομμάτια
Γράφει: Τσαπακίδης Ιωάννης, Χειρουργός Ορθοπαιδικός Η οστεοτομία είναι μια επέμβαση με την οποία ο χειρουργός διαχωρίζει το οστό (προκαλεί δηλαδή, τεχνικά κάταγμα). Στη συνέχεια επανατοποθετεί τα κομμάτια
ΔΙΑΣΩΣΗ Η ΑΚΡΩΤΗΡΙΑΣΜΟΣ ΣΕ ΣΟΒΑΡΕΣ ΛΟΙΜΩΞΕΙΣ
 ΔΙΑΣΩΣΗ Η ΑΚΡΩΤΗΡΙΑΣΜΟΣ ΣΕ ΣΟΒΑΡΕΣ ΛΟΙΜΩΞΕΙΣ Χατζώκος Γ. Ιπποκράτης Οι ακρωτηριασμοί στην Ορθοπαιδική αποτελούν την έσχατη λύση για την αντιμετώπιση σοβαρών προβλημάτων ενός άκρου το οποίο είναι αδύνατον
ΔΙΑΣΩΣΗ Η ΑΚΡΩΤΗΡΙΑΣΜΟΣ ΣΕ ΣΟΒΑΡΕΣ ΛΟΙΜΩΞΕΙΣ Χατζώκος Γ. Ιπποκράτης Οι ακρωτηριασμοί στην Ορθοπαιδική αποτελούν την έσχατη λύση για την αντιμετώπιση σοβαρών προβλημάτων ενός άκρου το οποίο είναι αδύνατον
ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ
 ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ Του Δρ. Κωνσταντίνου Δ. Στρατηγού Δ/ντού Ορθοπαιδικής Επανορθωτικής Χειρουργικής
ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ Του Δρ. Κωνσταντίνου Δ. Στρατηγού Δ/ντού Ορθοπαιδικής Επανορθωτικής Χειρουργικής
ΧΕΙΡΟΥΡΓΙΚΗ ΘΕΡΑΠΕΙΑ ΤΩΝ ΚΑΤΑΓΜΑΤΑΤΩΝ
 ΧΕΙΡΟΥΡΓΙΚΗ ΘΕΡΑΠΕΙΑ ΤΩΝ ΚΑΤΑΓΜΑΤΑΤΩΝ Κλειστά (χωρίς λύση της συνέχειας του δέρματος) Ανοικτά (λύση της συνέχειας του δέρματος) επείγουσα χειρουργική επέμβαση Grade I: Grade II: Grade III
ΧΕΙΡΟΥΡΓΙΚΗ ΘΕΡΑΠΕΙΑ ΤΩΝ ΚΑΤΑΓΜΑΤΑΤΩΝ Κλειστά (χωρίς λύση της συνέχειας του δέρματος) Ανοικτά (λύση της συνέχειας του δέρματος) επείγουσα χειρουργική επέμβαση Grade I: Grade II: Grade III
ΜΑΘΗΜΑ ΟΣΤΕΟΣΥΝΘΕΣΗ - ΔΙΑΤΑΤΙΚΗ ΙΣΤΟΓΕΝΕΣΗ Χατζώκος Γ. Ιπποκράτης
 ΜΑΘΗΜΑ ΟΣΤΕΟΣΥΝΘΕΣΗ - ΔΙΑΤΑΤΙΚΗ ΙΣΤΟΓΕΝΕΣΗ Χατζώκος Γ. Ιπποκράτης 3 Α. ΟΣΤΕΟΣΥΝΘΕΣΗ Οστεοσύνθεση καλείται η συγκράτηση των τµηµάτων ενός οστού µετά από κάταγµα ή άλλη αιτία, µε τα κατάλληλα υλικά που καλούνται
ΜΑΘΗΜΑ ΟΣΤΕΟΣΥΝΘΕΣΗ - ΔΙΑΤΑΤΙΚΗ ΙΣΤΟΓΕΝΕΣΗ Χατζώκος Γ. Ιπποκράτης 3 Α. ΟΣΤΕΟΣΥΝΘΕΣΗ Οστεοσύνθεση καλείται η συγκράτηση των τµηµάτων ενός οστού µετά από κάταγµα ή άλλη αιτία, µε τα κατάλληλα υλικά που καλούνται
ΔΙΑΓΝΩΣΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗΝ ΟΡΘΟΠΑΙΔΙΚΗ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ
 ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΙΣΤΟΡΙΚΟ + ΚΛΙΝΙΚΗ ΕΞΕΤΑΣΗ = Α & Ω ΣΤΗΝ! ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική απεικονιστική μέθοδος) ΠΡΟΣΘΙΟΠΙΣΘΙΑ ΠΛΑΓΙΑ ΛΟΞΗ ΕΙΔΙΚΗ ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική
ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΙΣΤΟΡΙΚΟ + ΚΛΙΝΙΚΗ ΕΞΕΤΑΣΗ = Α & Ω ΣΤΗΝ! ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική απεικονιστική μέθοδος) ΠΡΟΣΘΙΟΠΙΣΘΙΑ ΠΛΑΓΙΑ ΛΟΞΗ ΕΙΔΙΚΗ ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική
ΑΝΔΡΕΑΣ Χ. ΠΑΠΑΔΟΠΟΥΛΟΣ
 Πανεπιστήμιο Πατρών Σχολή Επιστημών Υγείας Τμήμα Ιατρικής Ορθοπαιδική Κλινική Διευθ.: Καθηγητής Ηλίας Λαμπίρης ΑΝΤΙΚΑΤΑΣΤΑΣΗ ΕΞΩΤΕΡΙΚΗΣ ΟΣΤΕΟΣΥΝΘΕΣΗΣ ΑΠΟ ΕΝΔΟΜΥΕΛΙΚΟ ΗΛΟ ΣΤΗ ΦΑΣΗ ΣΤΑΘΕΡΟΠΟΙΗΣΗΣ ΤΗΣ ΟΣΤΙΚΗΣ
Πανεπιστήμιο Πατρών Σχολή Επιστημών Υγείας Τμήμα Ιατρικής Ορθοπαιδική Κλινική Διευθ.: Καθηγητής Ηλίας Λαμπίρης ΑΝΤΙΚΑΤΑΣΤΑΣΗ ΕΞΩΤΕΡΙΚΗΣ ΟΣΤΕΟΣΥΝΘΕΣΗΣ ΑΠΟ ΕΝΔΟΜΥΕΛΙΚΟ ΗΛΟ ΣΤΗ ΦΑΣΗ ΣΤΑΘΕΡΟΠΟΙΗΣΗΣ ΤΗΣ ΟΣΤΙΚΗΣ
YΠΟΤΡΟΧΑΝΤΗΡΙΑ ΚΑΤΑΓΜΑΤΑ ΤΟΠΟΓΡΑΦΙΑ. Από τον ελάσσονα τροχαντήρα έως το όριο άνω προς μέσο τριτημόριο του μηριαίου
 YΠΟΤΡΟΧΑΝΤΗΡΙΑ ΚΑΤΑΓΜΑΤΑ ΤΟΠΟΓΡΑΦΙΑ Από τον ελάσσονα τροχαντήρα έως το όριο άνω προς μέσο τριτημόριο του μηριαίου ΚΛΙΝΙΚΗ ΕΙΚΩΝ Το κεντρικό τμήμα ευρίσκεται σε κάμψη απαγωγή έξω στροφή (λαγονοψοϊτης- απαγωγείς,
YΠΟΤΡΟΧΑΝΤΗΡΙΑ ΚΑΤΑΓΜΑΤΑ ΤΟΠΟΓΡΑΦΙΑ Από τον ελάσσονα τροχαντήρα έως το όριο άνω προς μέσο τριτημόριο του μηριαίου ΚΛΙΝΙΚΗ ΕΙΚΩΝ Το κεντρικό τμήμα ευρίσκεται σε κάμψη απαγωγή έξω στροφή (λαγονοψοϊτης- απαγωγείς,
ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - ΣΥΝΟΨΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - Π. ΑΣΒΕΣΤΑΣ E MAIL: pasv@uniwa.gr Εφαρμογές ρομποτικής στην Ιατρική Κλασσική χειρουργική Ορθοπεδικές επεμβάσεις Νευροχειρουργική Ακτινοθεραπεία Αποκατάσταση φυσιοθεραπεία 2 Βασικοί
ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - Π. ΑΣΒΕΣΤΑΣ E MAIL: pasv@uniwa.gr Εφαρμογές ρομποτικής στην Ιατρική Κλασσική χειρουργική Ορθοπεδικές επεμβάσεις Νευροχειρουργική Ακτινοθεραπεία Αποκατάσταση φυσιοθεραπεία 2 Βασικοί
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Σύνδροµο Μηροκοτυλιαίας Πρόσκρουσης Femoroacetabular Impingement Syndrome (FAI)
 Σύνδροµο Μηροκοτυλιαίας Πρόσκρουσης Femoroacetabular Impingement Syndrome (FAI) Τι είναι το σύνδροµο µηροκοτυλιαίας πρόσκρουσης; Φυσιολογικά, η κεφαλή του ισχίου δεν προσκρούει στο χείλος της κοτύλης κατά
Σύνδροµο Μηροκοτυλιαίας Πρόσκρουσης Femoroacetabular Impingement Syndrome (FAI) Τι είναι το σύνδροµο µηροκοτυλιαίας πρόσκρουσης; Φυσιολογικά, η κεφαλή του ισχίου δεν προσκρούει στο χείλος της κοτύλης κατά
Εργαστήριο Ιατρικής Φυσικής. Φυσική του Σκελετού
 Εργαστήριο Ιατρικής Φυσικής Φυσική του Σκελετού Τα οστά πραγματοποιούν τουλάχιστον έξι λειτουργίες στο ανθρώπινο σώμα: 1. Υποστήριξη 2. Κίνηση 3. Προστασία διαφόρων οργάνων 4. Αποθήκευση χημικών ουσιών
Εργαστήριο Ιατρικής Φυσικής Φυσική του Σκελετού Τα οστά πραγματοποιούν τουλάχιστον έξι λειτουργίες στο ανθρώπινο σώμα: 1. Υποστήριξη 2. Κίνηση 3. Προστασία διαφόρων οργάνων 4. Αποθήκευση χημικών ουσιών
Μηχανικές ιδιότητες των οστών
 Τα οστά δρουν σαν κατασκευές υποστήριξης και μεταφέρουν φορτία: h Απλή συμπίεση h Λυγισμός (φόρτιση του ενός φλοιού ελκυσμός του άλλου) h Στρέψη Μηχανικές ιδιότητες των οστών h Ισχυρότερα στη συμπίεση
Τα οστά δρουν σαν κατασκευές υποστήριξης και μεταφέρουν φορτία: h Απλή συμπίεση h Λυγισμός (φόρτιση του ενός φλοιού ελκυσμός του άλλου) h Στρέψη Μηχανικές ιδιότητες των οστών h Ισχυρότερα στη συμπίεση
ΣΤΑΘΕΡΟΠΟΙΗΣΗ ΚΑΤΑΓΜΑΤΩΝ ΕΠΔΕΣΜΟΛΟΓΙΑ
 ΣΤΑΘΕΡΟΠΟΙΗΣΗ ΚΑΤΑΓΜΑΤΩΝ ΕΠΔΕΣΜΟΛΟΓΙΑ ΘΕΡΑΠΕΙΑ ΚΑΤΑΓΜΑΤΟΣ Ανάταξη (κλειστή) Ακινητοποίηση Άσκηση ΜΕΘΟΔΟΙ ΣΤΑΘΕΡΟΠΟΙΗΣΗΣ Συνεχής έλξη Ακινητοποίηση σε νάρθηκα Λειτουργικός νάρθηκας Εφαρμογή επίδεσης 1)Ακινητοποίηση
ΣΤΑΘΕΡΟΠΟΙΗΣΗ ΚΑΤΑΓΜΑΤΩΝ ΕΠΔΕΣΜΟΛΟΓΙΑ ΘΕΡΑΠΕΙΑ ΚΑΤΑΓΜΑΤΟΣ Ανάταξη (κλειστή) Ακινητοποίηση Άσκηση ΜΕΘΟΔΟΙ ΣΤΑΘΕΡΟΠΟΙΗΣΗΣ Συνεχής έλξη Ακινητοποίηση σε νάρθηκα Λειτουργικός νάρθηκας Εφαρμογή επίδεσης 1)Ακινητοποίηση
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΦΥΣΙΟ 4 ΠΥΕΛΟΣ - ΙΣΧΙΑ
 ΦΥΣΙΟ 4 ΠΥΕΛΟΣ - ΙΣΧΙΑ ΠΥΕΛΟΣ 1. Πρόσθια κάτω λαγόνια άκανθα, 2. Ιερό οστό, 3. Πρόσθια άνω λαγόνια άκανθα, 4. Ηβική σύμφυση, 5. Λαγόνιο οστό, 6. Κόκκυγας, 7. 5ος οσφυϊκός σπόνδυλος, 8. Ιερολαγόνια άρθρωση,
ΦΥΣΙΟ 4 ΠΥΕΛΟΣ - ΙΣΧΙΑ ΠΥΕΛΟΣ 1. Πρόσθια κάτω λαγόνια άκανθα, 2. Ιερό οστό, 3. Πρόσθια άνω λαγόνια άκανθα, 4. Ηβική σύμφυση, 5. Λαγόνιο οστό, 6. Κόκκυγας, 7. 5ος οσφυϊκός σπόνδυλος, 8. Ιερολαγόνια άρθρωση,
Χειρουργική Θεραπεία της Οστεοαρθρίτιδας
 Χειρουργική Θεραπεία της Οστεοαρθρίτιδας Η οστεοαρθρίτιδα αντιμετωπίζεται χειρουργικά όταν: α) η καταστροφή του αρθρικού χόνδρου είναι ολοκληρωτική, β) όταν υπάρχουν σημαντικά συμπτώματα, όπως πόνος ή
Χειρουργική Θεραπεία της Οστεοαρθρίτιδας Η οστεοαρθρίτιδα αντιμετωπίζεται χειρουργικά όταν: α) η καταστροφή του αρθρικού χόνδρου είναι ολοκληρωτική, β) όταν υπάρχουν σημαντικά συμπτώματα, όπως πόνος ή
Η Αρθροσκόπηση της Ποδοκνημικής Άρθρωσης
 Η Αρθροσκόπηση της Ποδοκνημικής Άρθρωσης Ανατομική της Ποδοκνημικής Άρθρωσης Η ποδοκνημική άρθρωση είναι η άρθρωση που σχηματίζεται στη θέση σύνδεσης τριών οστών: του κάτω άκρου της περόνης προς τα έξω
Η Αρθροσκόπηση της Ποδοκνημικής Άρθρωσης Ανατομική της Ποδοκνημικής Άρθρωσης Η ποδοκνημική άρθρωση είναι η άρθρωση που σχηματίζεται στη θέση σύνδεσης τριών οστών: του κάτω άκρου της περόνης προς τα έξω
Χειρουργική Θεραπεία των Οστεοπορωτικών Καταγμάτων
 Χειρουργική Θεραπεία των Οστεοπορωτικών Καταγμάτων Η εμφάνιση καταγμάτων αποτελεί την κυριότερη επιπλοκή της οστεοπόρωσης. Τα περισσότερα κατάγματα επουλώνονται χωρίς να υπάρχει ανάγκη χειρουργικής επέμβασης,
Χειρουργική Θεραπεία των Οστεοπορωτικών Καταγμάτων Η εμφάνιση καταγμάτων αποτελεί την κυριότερη επιπλοκή της οστεοπόρωσης. Τα περισσότερα κατάγματα επουλώνονται χωρίς να υπάρχει ανάγκη χειρουργικής επέμβασης,
Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση
 Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση Τι είναι ο αρθρικός χόνδρος; Ο αρθρικός χόνδρος είναι ένας στιλπνός, ομαλός, λείος και ανάγγειος ιστός που καλύπτει τις αρθρικές επιφάνειες
Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση Τι είναι ο αρθρικός χόνδρος; Ο αρθρικός χόνδρος είναι ένας στιλπνός, ομαλός, λείος και ανάγγειος ιστός που καλύπτει τις αρθρικές επιφάνειες
ΠΛΑΤΥΠΟΔΙΑ ΒΛΑΙΣΟΠΛΑΤΥΠΟΔΙΑ. 06/Φεβ/2013 ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΑΚΡΟΥ ΠΟΔΟΣ ΒΛΑΙΣΟΠΛΑΤΥΠΟΔΙΑ ΔΡ. ΝΙΚΟΣ ΠΑΠΑΛΟΥΚΑΣ ΠΟΛΥΚΛΙΝΙΚΗ ΛΕΥΚΩΣΙΑΣ I.
 ΒΛΑΙΣΟ ΔΡ. ΝΙΚΟΣ ΠΑΠΑΛΟΥΚΑΣ ΠΟΛΥΚΛΙΝΙΚΗ ΛΕΥΚΩΣΙΑΣ 1 2 ΒΛΑΙΣΟ I. ΜΟΝΑΔΙΚΗ ΟΝΤΟΤΗΤΑ ΒΛΑΙΣΟ II. ΜΕΡΟΣ ΑΛΛΟΥ ΠΙΟ ΠΟΛΥΠΛΟΚΟΥ ΠΡΟΒΛΗΜΑΤΟΣ Γενικευμένης Χαλάρωσης Συνδέσμων Νευρολογικής ή Μυϊκής Πάθησης Γενετικής
ΒΛΑΙΣΟ ΔΡ. ΝΙΚΟΣ ΠΑΠΑΛΟΥΚΑΣ ΠΟΛΥΚΛΙΝΙΚΗ ΛΕΥΚΩΣΙΑΣ 1 2 ΒΛΑΙΣΟ I. ΜΟΝΑΔΙΚΗ ΟΝΤΟΤΗΤΑ ΒΛΑΙΣΟ II. ΜΕΡΟΣ ΑΛΛΟΥ ΠΙΟ ΠΟΛΥΠΛΟΚΟΥ ΠΡΟΒΛΗΜΑΤΟΣ Γενικευμένης Χαλάρωσης Συνδέσμων Νευρολογικής ή Μυϊκής Πάθησης Γενετικής
Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική
 Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική Ποιά είναι η ανατομική κατασκευή του γόνατος; Η άρθρωση του γόνατος σχηματίζεται από το μηριαίο οστό και από την κνήμη. Τα άκρα των οστών
Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική Ποιά είναι η ανατομική κατασκευή του γόνατος; Η άρθρωση του γόνατος σχηματίζεται από το μηριαίο οστό και από την κνήμη. Τα άκρα των οστών
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
Παθητικά στοιχεία. Οστά. Αρθρ. χόνδροι. Πολύπλοκη κατασκευή. Σύνδεσμοι τένοντες. Ενεργητικά στοιχεία. Ανομοιογενή βιολογικά υλικά.
 Κινησιοθεραπεία Ιδιότητες Υλικών 1 ΣΤΟΙΧΕΙΑ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Ανθρώπινο σώμα Παθητικά στοιχεία Οστά Αρθρ. χόνδροι Πολύπλοκη κατασκευή Σύνδεσμοι τένοντες Ανομοιογενή βιολογικά υλικά Ενεργητικά στοιχεία Μύες
Κινησιοθεραπεία Ιδιότητες Υλικών 1 ΣΤΟΙΧΕΙΑ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Ανθρώπινο σώμα Παθητικά στοιχεία Οστά Αρθρ. χόνδροι Πολύπλοκη κατασκευή Σύνδεσμοι τένοντες Ανομοιογενή βιολογικά υλικά Ενεργητικά στοιχεία Μύες
Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών Ακαδηµαϊκό έτος: Ε.Μ.Π. Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 3.
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ - 3.1 - Cpright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 2012. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ - 3.1 - Cpright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο υναµικής και Κατασκευών - 2012. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
Μιχαήλ Νικ. Πατσίκας
 Ακτινολογική εκτίμηση της πώρωσης των καταγμάτων Μιχαήλ Νικ. Πατσίκας Πτυχιούχος Κτηνιατρικής Α.Π.Θ. Πτυχιούχος Ιατρικής Α.Π.Θ Αναπληρωτής Καθηγητής Ακτινολογίας Κτηνιατρική Σχολή Α.Π.Θ. Διπλωματούχος
Ακτινολογική εκτίμηση της πώρωσης των καταγμάτων Μιχαήλ Νικ. Πατσίκας Πτυχιούχος Κτηνιατρικής Α.Π.Θ. Πτυχιούχος Ιατρικής Α.Π.Θ Αναπληρωτής Καθηγητής Ακτινολογίας Κτηνιατρική Σχολή Α.Π.Θ. Διπλωματούχος
ΓΕΝΙΚΑ ΚΑΤΑΓΜΑΤΑ ΚΑΙ ΚΑΤΑΓΜΑΤΑ ΑΝΩ ΚΑΙ ΚΑΤΩ ΑΚΡΟΥ ΤΟΥ ΒΡΑΧΙΟΝΙΟΥ Τ.Ε.Ι. ΛΑΡΙΣΑΣ ΣΧΟΛΗ: Σ.Ε.Υ.Π ΤΜΗΜΑ: ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΓΕΝΙΚΑ ΚΑΤΑΓΜΑΤΑ ΚΑΙ ΚΑΤΑΓΜΑΤΑ ΑΝΩ ΚΑΙ ΚΑΤΩ ΑΚΡΟΥ ΤΟΥ ΒΡΑΧΙΟΝΙΟΥ Τ.Ε.Ι. ΛΑΡΙΣΑΣ ΣΧΟΛΗ: Σ.Ε.Υ.Π ΤΜΗΜΑ: ΝΟΣΗΛΕΥΤΙΚΗΣ Σπουδαστής :Τσιούκας ηµήτριος ΛΑΡΙΣΑ 2009 Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α - ΙΑΙΡΕΣΗ ΚΑΤΑΓΜΑΤΩΝ -
ΓΕΝΙΚΑ ΚΑΤΑΓΜΑΤΑ ΚΑΙ ΚΑΤΑΓΜΑΤΑ ΑΝΩ ΚΑΙ ΚΑΤΩ ΑΚΡΟΥ ΤΟΥ ΒΡΑΧΙΟΝΙΟΥ Τ.Ε.Ι. ΛΑΡΙΣΑΣ ΣΧΟΛΗ: Σ.Ε.Υ.Π ΤΜΗΜΑ: ΝΟΣΗΛΕΥΤΙΚΗΣ Σπουδαστής :Τσιούκας ηµήτριος ΛΑΡΙΣΑ 2009 Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α - ΙΑΙΡΕΣΗ ΚΑΤΑΓΜΑΤΩΝ -
Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής κ. Σ. Νατσιάβας Αριθμητικές μέθοδοι σε ταλαντώσεις μηχανολογικών συστημάτων Στοιχεία Φοιτητή Ονοματεπώνυμο: Νατσάκης Αναστάσιος Αριθμός Ειδικού Μητρώου:
ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - ΑΣΚΗΣΕΙΣ. Π. Ασβεστάς Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Βιοϊατρικής Πανεπιστήμιο Δυτικής Αττικής
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - ΑΣΚΗΣΕΙΣ Π. Ασβεστάς Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Βιοϊατρικής Πανεπιστήμιο Δυτικής Αττικής E-mail: pasv@uniwa.gr ΑΣΚΗΣΗ 1 1. Έστω δύο 3Δ καρτεσιανά συστήματα συντεταγμένων,
ΕΙΣΑΓΩΓΗ ΣΤΗ ΡΟΜΠΟΤΙΚΗ - ΑΣΚΗΣΕΙΣ Π. Ασβεστάς Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Βιοϊατρικής Πανεπιστήμιο Δυτικής Αττικής E-mail: pasv@uniwa.gr ΑΣΚΗΣΗ 1 1. Έστω δύο 3Δ καρτεσιανά συστήματα συντεταγμένων,
Ελάχιστα επεμβατικές μέθοδοι για την αρθροπλαστική του ισχίου και του γόνατος
 Ελάχιστα επεμβατικές μέθοδοι για την αρθροπλαστική του ισχίου και του γόνατος 1. Τι είναι οι ελάχιστα επεμβατικές μέθοδοι για την αντικατάσταση ισχίου και γόνατος; Ο όρος ελάχιστα επεμβατικές μέθοδοι (ΕΕΜ)
Ελάχιστα επεμβατικές μέθοδοι για την αρθροπλαστική του ισχίου και του γόνατος 1. Τι είναι οι ελάχιστα επεμβατικές μέθοδοι για την αντικατάσταση ισχίου και γόνατος; Ο όρος ελάχιστα επεμβατικές μέθοδοι (ΕΕΜ)
Σύμφωνα με το Ινστιτούτο Ρομποτικής της Αμερικής
 ΡΟΜΠΟΤΙΚΗ: ΟΡΙΣΜΟΣ: Σύμφωνα με το Ινστιτούτο Ρομποτικής της Αμερικής, ρομπότ είναι ένας αναπρογραμματιζόμενος και πολυλειτουργικός χωρικός μηχανισμός σχεδιασμένος να μετακινεί υλικά, αντικείμενα, εργαλεία
ΡΟΜΠΟΤΙΚΗ: ΟΡΙΣΜΟΣ: Σύμφωνα με το Ινστιτούτο Ρομποτικής της Αμερικής, ρομπότ είναι ένας αναπρογραμματιζόμενος και πολυλειτουργικός χωρικός μηχανισμός σχεδιασμένος να μετακινεί υλικά, αντικείμενα, εργαλεία
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
EKΠΑΙΔΕΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011-2012
 EKΠΑΙΔΕΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011-2012 ΣEΠTEMBPIOΣ 2011 22/9/2011 U/S: γενικά (εφαρμογές, διάγνωση, βιοψίες) A. Ρηγοπούλου Βασικές αρχές οργάνωσης
EKΠΑΙΔΕΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011-2012 ΣEΠTEMBPIOΣ 2011 22/9/2011 U/S: γενικά (εφαρμογές, διάγνωση, βιοψίες) A. Ρηγοπούλου Βασικές αρχές οργάνωσης
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής. Διδάσκων: Γιάννης Χουλιάρας
 ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής Διδάσκων: Γιάννης Χουλιάρας Ισοστατικά πλαίσια με συνδέσμους (α) (β) Στατική επίλυση ισοστατικών πλαισίων
ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής Διδάσκων: Γιάννης Χουλιάρας Ισοστατικά πλαίσια με συνδέσμους (α) (β) Στατική επίλυση ισοστατικών πλαισίων
Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη
 Εισαγωγη στην Ορθοπαιδικη Κωνσταντινος Ν. ΜΑΛΙΖΟΣ Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη Εισαγωγη στην Ορθοπαιδικη Ορθοπαιδικη ή Ορθοπεδικη «παιδο-ορθωτικη» (Γ. Μπαμπινιωτης) Πανεπιστημιο Θεσσαλιας Ιατρικη
Εισαγωγη στην Ορθοπαιδικη Κωνσταντινος Ν. ΜΑΛΙΖΟΣ Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη Εισαγωγη στην Ορθοπαιδικη Ορθοπαιδικη ή Ορθοπεδικη «παιδο-ορθωτικη» (Γ. Μπαμπινιωτης) Πανεπιστημιο Θεσσαλιας Ιατρικη
Το παρακάτω διάγραμμα παριστάνει την απομάκρυνση y ενός σημείου Μ (x Μ =1,2 m) του μέσου σε συνάρτηση με το χρόνο.
 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 04-05 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 5. - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 04-05 opyight ΕΜΠ - Σχολή
Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 04-05 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 5. - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 04-05 opyight ΕΜΠ - Σχολή
6. Κάμψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών
 6. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας Ακτίνα καμπυλότητας 2 Εισαγωγή (1/2) Μελετήσαμε
6. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας Ακτίνα καμπυλότητας 2 Εισαγωγή (1/2) Μελετήσαμε
ΤΙ ΕΙΝΑΙ ΤΟ ΟΠΙΣΘΙΟ ΠΟΔΙ?
 ΕΙΔΗ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΠΑΡΑΜΕΛΗΜΜΕΝΕΣ ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΟΠΙΣΘΙΟΥ ΠΟΔΙΟΥ Υπάρχει λύση; Δρ. Νικόλαος Γκουγκουλιάς ΡΑΙΒΟΤΗΤΑ ΒΛΑΙΣΟΤΗΤΑ ΡΑΙΒΟΤΗΤΑ ΒΡΑΧΥΝΣΗ ΙΠΠΟΠΟΔΙΑ ΚΟΙΛΟΠΟΔΙΑ Ορθοπαιδικός Χειρουργός Θεσσαλονίκη
ΕΙΔΗ ΠΑΡΑΜΟΡΦΩΣΕΩΝ ΠΑΡΑΜΕΛΗΜΜΕΝΕΣ ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΟΠΙΣΘΙΟΥ ΠΟΔΙΟΥ Υπάρχει λύση; Δρ. Νικόλαος Γκουγκουλιάς ΡΑΙΒΟΤΗΤΑ ΒΛΑΙΣΟΤΗΤΑ ΡΑΙΒΟΤΗΤΑ ΒΡΑΧΥΝΣΗ ΙΠΠΟΠΟΔΙΑ ΚΟΙΛΟΠΟΔΙΑ Ορθοπαιδικός Χειρουργός Θεσσαλονίκη
Συγγενές Εξάρθρηµα του Ισχίου. Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός
 Συγγενές Εξάρθρηµα του Ισχίου Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός ΣΥΓΓΕΝΕΣ ΕΞΑΡΘΡΗΜΑ ΙΣΧΙΟΥ ΟΡΙΣΜΟΣ Συγγενής διαταραχή του ισχίου που προκαλείται από την ανώµαλη ανάπτυξη ενός ή όλων των
Συγγενές Εξάρθρηµα του Ισχίου Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός ΣΥΓΓΕΝΕΣ ΕΞΑΡΘΡΗΜΑ ΙΣΧΙΟΥ ΟΡΙΣΜΟΣ Συγγενής διαταραχή του ισχίου που προκαλείται από την ανώµαλη ανάπτυξη ενός ή όλων των
Αυτόματη προσγείωση τετρακόπτερου με χρήση κάμερας
 Διπλωματική εργασία Αυτόματη προσγείωση τετρακόπτερου με χρήση κάμερας Τζιβάρας Βασίλης Επιβλέπων: Κ. Κωνσταντίνος Βλάχος Τμήμα Μηχανικών Η/Υ και Πληροφορικής Ιωάννινα Φεβρουάριος 2018 Περιεχόμενα Εισαγωγή
Διπλωματική εργασία Αυτόματη προσγείωση τετρακόπτερου με χρήση κάμερας Τζιβάρας Βασίλης Επιβλέπων: Κ. Κωνσταντίνος Βλάχος Τμήμα Μηχανικών Η/Υ και Πληροφορικής Ιωάννινα Φεβρουάριος 2018 Περιεχόμενα Εισαγωγή
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
Ρήξη του Τενοντίου Πετάλου του Ώμου: Γενικές Πληροφορίες
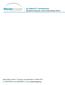 Ρήξη του Τενοντίου Πετάλου του Ώμου: Γενικές Πληροφορίες Ποιά είναι η ανατομική κατασκευή του ώμου; Η άρθρωση του ώμου σχηματίζεται από την σύνδεση τριών οστών: του βραχιονίου, της ωμοπλάτης και της κλείδας.
Ρήξη του Τενοντίου Πετάλου του Ώμου: Γενικές Πληροφορίες Ποιά είναι η ανατομική κατασκευή του ώμου; Η άρθρωση του ώμου σχηματίζεται από την σύνδεση τριών οστών: του βραχιονίου, της ωμοπλάτης και της κλείδας.
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Β5. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Β5. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΕΡΕΟ ΣΩΜΑ. Ταυτόχρονη διατήρηση της ορμής και της στροφορμής σε κρούση
 N B P Y T ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΕΡΕΟ ΣΩΜΑ 9 5 Ταυτόχρονη διατήρηση της ορμής και της στροφορμής σε κρούση - y y h + O x Ω + O V x υ a Σχήμα : Το σύστημα με τους δύο παρατηρητές του φαινομένου
N B P Y T ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΤΕΡΕΟ ΣΩΜΑ 9 5 Ταυτόχρονη διατήρηση της ορμής και της στροφορμής σε κρούση - y y h + O x Ω + O V x υ a Σχήμα : Το σύστημα με τους δύο παρατηρητές του φαινομένου
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι πολύ
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 6 Ιανουαρίου, Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε οποιαδήποτε ερώτηση Γενικές Οδηγίες: ) Είναι πολύ
2. ΚΑΤΑΓΜΑΤΑ ΥΠΟΚΕΦΑΛΙΚΑ 3. ΚΑΤΑΓΜΑΤΑ ΔΙΑΤΡΟΧΑΝΤΗΡΙΑ
 ΚΑΤΑΓΜΑΤΑ ΑΝΩ ΠΕΡΑΤΟΣ ΜΗΡΙΑΙΟΥ 1. ΚΑΤΑΓΜΑΤΑ ΚΕΦΑΛΗΣ 2. ΚΑΤΑΓΜΑΤΑ ΥΠΟΚΕΦΑΛΙΚΑ 3. ΚΑΤΑΓΜΑΤΑ ΔΙΑΤΡΟΧΑΝΤΗΡΙΑ ΚΑΤΑΓΜΑΤΑ ΚΑΦΑΛΗΣ ΜΗΡΙΑΙΟΥ Μηχανισμός κάκωσης Όταν το ισχίο είναι σε κάμψη 60 μοιρών η μεταφερόμενη
ΚΑΤΑΓΜΑΤΑ ΑΝΩ ΠΕΡΑΤΟΣ ΜΗΡΙΑΙΟΥ 1. ΚΑΤΑΓΜΑΤΑ ΚΕΦΑΛΗΣ 2. ΚΑΤΑΓΜΑΤΑ ΥΠΟΚΕΦΑΛΙΚΑ 3. ΚΑΤΑΓΜΑΤΑ ΔΙΑΤΡΟΧΑΝΤΗΡΙΑ ΚΑΤΑΓΜΑΤΑ ΚΑΦΑΛΗΣ ΜΗΡΙΑΙΟΥ Μηχανισμός κάκωσης Όταν το ισχίο είναι σε κάμψη 60 μοιρών η μεταφερόμενη
Κεφάλαιο 6β. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
Κεφάλαιο 6β Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Ροπή Ροπή ( ) είναι η τάση που έχει μια δύναμη να περιστρέψει ένα σώμα γύρω από κάποιον άξονα. d είναι η κάθετη απόσταση του άξονα περιστροφής
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
Ανατομική του Γόνατος Παθολογία και Χειρουργική των Συνδέσμων. Δρ. Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός
 Ανατομική του Γόνατος Παθολογία και Χειρουργική των Συνδέσμων Δρ. Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός Προσαγωγή (ραιβότητα) Απαγωγή (βλαισότητα) Έσω στροφή Έξω στροφή Περιαγωγή Κάμψη Έκταση
Ανατομική του Γόνατος Παθολογία και Χειρουργική των Συνδέσμων Δρ. Χρήστος Κ. Γιαννακόπουλος Ορθοπαιδικός Χειρουργός Προσαγωγή (ραιβότητα) Απαγωγή (βλαισότητα) Έσω στροφή Έξω στροφή Περιαγωγή Κάμψη Έκταση
Είναι γνωστό πόσο μεγάλο ρόλο παίζει το ισοκινητικό δυναμόμετρο στην φάση της
 - ΠΡΟΛΗΨΗ - ΓΡΗΓΟΡΗ ΑΠΟΚΑΤΑΣΤΑΣΗ - ΒΕΛΤΙΩΣΗ ΑΘΛΗΤΙΚΩΝ ΕΠΙΔΟΣΕΩΝ Το ισοκινητικό δυναμόμετρο είναι μονάδα υψηλής τεχνολογίας, συνδεδεμένη με ηλεκτρονικό υπολογιστή, ο οποίος αξιολογεί και συγκρίνει τις αρθρώσεις
- ΠΡΟΛΗΨΗ - ΓΡΗΓΟΡΗ ΑΠΟΚΑΤΑΣΤΑΣΗ - ΒΕΛΤΙΩΣΗ ΑΘΛΗΤΙΚΩΝ ΕΠΙΔΟΣΕΩΝ Το ισοκινητικό δυναμόμετρο είναι μονάδα υψηλής τεχνολογίας, συνδεδεμένη με ηλεκτρονικό υπολογιστή, ο οποίος αξιολογεί και συγκρίνει τις αρθρώσεις
% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου
![% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου % ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου](/thumbs/53/30956495.jpg) 1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου
 A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
A A N A B P Y A 9 5 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Η ενέργεια ταλάντωσης ενός κυλιόμενου κυλίνδρου Στερεό σώμα με κυλινδρική συμμετρία (κύλινδρος, σφαίρα, σφαιρικό κέλυφος, κυκλική στεφάνη κλπ) μπορεί να
ΤΕΧΝΙΚΕΣ ΠΡΟΔΙΑΓΡΑΦΕΣ ΟΡΘΟΠΕΔΙΚΟΥ Posted by OPTIMUM ORTHOPEDICS A.E - 13 Dec :42
 ΤΕΧΝΙΚΕΣ ΠΡΟΔΙΑΓΡΑΦΕΣ ΟΡΘΟΠΕΔΙΚΟΥ Posted by OPTIMUM ORTHOPEDICS A.E - 13 Dec 2016 13:42 A/A 1. Λάμες πριονιών σε διάφορες διαστάσεις, σχήματα και μεγέθη, αποστειρωμένες, με διαβάθμιση μήκους, για πριόνια
ΤΕΧΝΙΚΕΣ ΠΡΟΔΙΑΓΡΑΦΕΣ ΟΡΘΟΠΕΔΙΚΟΥ Posted by OPTIMUM ORTHOPEDICS A.E - 13 Dec 2016 13:42 A/A 1. Λάμες πριονιών σε διάφορες διαστάσεις, σχήματα και μεγέθη, αποστειρωμένες, με διαβάθμιση μήκους, για πριόνια
Bλάβες αρθρικού χόνδρου και σύγχρονες θεραπείες - Ο Δρόμος για την Θεραπεία Δευτέρα, 02 Ιούλιος :04
 Γράφει: Δρ. Νικόλαος Πισκοπάκης MD, PhD, Ορθοπεδικός Χειρουργός, Δ/ντής Ορθοπεδικής Κλινικής Αθλητικών Κακώσεων Ιατρικού Κέντρου Αθηνών, Πρόεδρος Ελληνικής Αρθροσκοπικής Εταιρείας (ΕΑΕ) Τι είναι ο αρθρικός
Γράφει: Δρ. Νικόλαος Πισκοπάκης MD, PhD, Ορθοπεδικός Χειρουργός, Δ/ντής Ορθοπεδικής Κλινικής Αθλητικών Κακώσεων Ιατρικού Κέντρου Αθηνών, Πρόεδρος Ελληνικής Αρθροσκοπικής Εταιρείας (ΕΑΕ) Τι είναι ο αρθρικός
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΚΦΥΛΙΣΤΙΚΕΣ ΠΑΘΗΣΕΙΣ ΤΗΣ ΑΥΧΕΝΙΚΗΣ ΜΟΙΡΑΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ (ΑΜΣΣ)
 ΕΚΦΥΛΙΣΤΙΚΕΣ ΠΑΘΗΣΕΙΣ ΤΗΣ ΑΥΧΕΝΙΚΗΣ ΜΟΙΡΑΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ (ΑΜΣΣ) Εκφυλιστική νόσος της ΑΜΣΣ Η διαδικασία εκφύλισης με την πάροδο της ηλικίας είναι συνάρτηση γενετικών και περιβαλλοντικών παραγόντων
ΕΚΦΥΛΙΣΤΙΚΕΣ ΠΑΘΗΣΕΙΣ ΤΗΣ ΑΥΧΕΝΙΚΗΣ ΜΟΙΡΑΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ (ΑΜΣΣ) Εκφυλιστική νόσος της ΑΜΣΣ Η διαδικασία εκφύλισης με την πάροδο της ηλικίας είναι συνάρτηση γενετικών και περιβαλλοντικών παραγόντων
Τα οστα αποτελούνται από το φλοιό και σπογγώδες οστό. Μεταξύ των δοκίδων του σπογγώδους οστού υπάρχει ο μυελός των οστών
 Οστεοπόρωση Τα οστα αποτελούνται από το φλοιό και σπογγώδες οστό Μεταξύ των δοκίδων του σπογγώδους οστού υπάρχει ο μυελός των οστών Φυσιολογικό οστό Οστεπορωτικό Οστεοπόρωση - Ορισμός Αύξηση του χώρου
Οστεοπόρωση Τα οστα αποτελούνται από το φλοιό και σπογγώδες οστό Μεταξύ των δοκίδων του σπογγώδους οστού υπάρχει ο μυελός των οστών Φυσιολογικό οστό Οστεπορωτικό Οστεοπόρωση - Ορισμός Αύξηση του χώρου
Ερειστικό Σύστημα. Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία.
 Ερειστικό Σύστημα Μια εργασία στο μάθημα της Βιολογίας από της μαθήτριες Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία. Υπεύθυνη Καθηγήτρια: Ζαρφτζιάν Μαριλένα Περιεχόμενα: Εισαγωγή Οστά Σύσταση του οστίτη
Ερειστικό Σύστημα Μια εργασία στο μάθημα της Βιολογίας από της μαθήτριες Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία. Υπεύθυνη Καθηγήτρια: Ζαρφτζιάν Μαριλένα Περιεχόμενα: Εισαγωγή Οστά Σύσταση του οστίτη
Theory Greek (Greece) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό.
 Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
Q1-1 Δύο προβλήματα Μηχανικής (10 Μονάδες) Παρακαλώ διαβάστε τις Γενικές Οδηγίες που θα βρείτε σε ξεχωριστό φάκελο πριν ξεκινήσετε να εργάζεστε στο πρόβλημα αυτό. Μέρος A. Ο Κρυμμένος Δίσκος (3.5 Μονάδες)
ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι
 Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
Ορολογία. Κάταγμα οστού( #) : Διακοπή της συνέχειάς του, η οποία μπορεί να είναι πλήρης ή ατελής.
 ΣΚΕΛΕΤΙΚΟ ΤΡΑΥΜΑ Ορολογία Κάταγμα οστού( #) : Διακοπή της συνέχειάς του, η οποία μπορεί να είναι πλήρης ή ατελής. Ορολογία Ανοιχτό ή κλειστό # Ακτινολογικά σημεία ανοικτού # Εμφανής προβολή των οστικών
ΣΚΕΛΕΤΙΚΟ ΤΡΑΥΜΑ Ορολογία Κάταγμα οστού( #) : Διακοπή της συνέχειάς του, η οποία μπορεί να είναι πλήρης ή ατελής. Ορολογία Ανοιχτό ή κλειστό # Ακτινολογικά σημεία ανοικτού # Εμφανής προβολή των οστικών
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 8. - opyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 202. Με επιφύλαξη παντός δικαιώµατος. ll rights reserved. Απαγορεύεται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 8. - opyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 202. Με επιφύλαξη παντός δικαιώµατος. ll rights reserved. Απαγορεύεται
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Πρόχειρες Σημειώσεις
 Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
ΕΠΙΛΥΣΗ ΥΠΕΡΣΤΑΤΙΚΩΝ ΦΟΡΕΩΝ Μέθοδος Cross. Διδάσκων: Γιάννης Χουλιάρας
 ΕΠΙΛΥΣΗ ΥΠΕΡΣΤΑΤΙΚΩΝ ΦΟΡΕΩΝ Μέθοδος Cross Διδάσκων: Γιάννης Χουλιάρας Μέθοδος Cross Η μέθοδος Cross ή μέθοδος κατανομής των ροπών, χρησιμοποιείται για την επίλυση συνεχών δοκών και πλαισίων. Είναι παραλλαγή
ΕΠΙΛΥΣΗ ΥΠΕΡΣΤΑΤΙΚΩΝ ΦΟΡΕΩΝ Μέθοδος Cross Διδάσκων: Γιάννης Χουλιάρας Μέθοδος Cross Η μέθοδος Cross ή μέθοδος κατανομής των ροπών, χρησιμοποιείται για την επίλυση συνεχών δοκών και πλαισίων. Είναι παραλλαγή
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
ΕΛΛΗΝΙΚΗ ΑΓΓΕΙΟΧΕΙΡΟΥΡΓΙΚΗ ΕΤΑΙΡΕΙΑ ΕΝΗΜΕΡΩΤΙΚΟ ΦΥΛΛΑΔΙΟ ΑΝΕΥΡΥΣΜΑ ΤΗΣ ΚΟΙΛΙΑΚΗΣ ΑΟΡΤΗΣ
 ΑΝΕΥΡΥΣΜΑ ΚΟΙΛΙΑΚΗΣ ΑΟΡΤΗΣ Κάθε χρόνο περίπου 200.000 νέοι ασθενείς διαγιγνώσκονται με Ανεύρυσμα Κοιλιακής Αορτής. Είναι γνωστό επίσης, ότι η ρήξη του Ανευρύσματος Κοιλιακής Αορτής οδηγεί σε ποσοστό τουλάχιστον
ΑΝΕΥΡΥΣΜΑ ΚΟΙΛΙΑΚΗΣ ΑΟΡΤΗΣ Κάθε χρόνο περίπου 200.000 νέοι ασθενείς διαγιγνώσκονται με Ανεύρυσμα Κοιλιακής Αορτής. Είναι γνωστό επίσης, ότι η ρήξη του Ανευρύσματος Κοιλιακής Αορτής οδηγεί σε ποσοστό τουλάχιστον
«διάστρεμμα» - «Ro ΠΔΚ F+Pr» ΕΠΩΔΥΝΗ ΠΟΔΟΚΝΗΜΙΚΗ ΣΤΟΝ ΑΘΛΗΤΗ ΔΙΑΣΤΡΕΜΜΑ 30/11/2013 6/52
 ΠΑΘΗΣΕΙΣ ΠΟΔΟΚΝΗΜΙΚΗΣ - ΑΚΡΟΥ ΠΟΔΟΣ ΗΜΕΡΙΔΑ ΝΟΣΟΚΟΜΕΙΟ ΠΑΠΑΓΕΩΡΓΙΟΥ 31 ΜΑΡΤΙΟΥ 2012 «διάστρεμμα» - «Ro ΠΔΚ F+Pr» ΕΠΩΔΥΝΗ ΠΟΔΟΚΝΗΜΙΚΗ ΣΤΟΝ ΑΘΛΗΤΗ Δρ. Νικόλαος Γκουγκουλιάς Ορθοπαιδικός Χειρουργός Consultant
ΠΑΘΗΣΕΙΣ ΠΟΔΟΚΝΗΜΙΚΗΣ - ΑΚΡΟΥ ΠΟΔΟΣ ΗΜΕΡΙΔΑ ΝΟΣΟΚΟΜΕΙΟ ΠΑΠΑΓΕΩΡΓΙΟΥ 31 ΜΑΡΤΙΟΥ 2012 «διάστρεμμα» - «Ro ΠΔΚ F+Pr» ΕΠΩΔΥΝΗ ΠΟΔΟΚΝΗΜΙΚΗ ΣΤΟΝ ΑΘΛΗΤΗ Δρ. Νικόλαος Γκουγκουλιάς Ορθοπαιδικός Χειρουργός Consultant
ΒΕΛΗΒΑΣΑΚΗΣ ΜΑΝΟΛΗΣ ΔΙΕΥΘ. Ε. Σ. Υ. ΠΑΝ/ΚΗΣ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΓΝΗ
 ΒΕΛΗΒΑΣΑΚΗΣ ΜΑΝΟΛΗΣ ΧΕΙΡΟΥΡΓΟΣ ΟΡΘΟΠΑΙΔΙΚΟΣ ΔΙΕΥΘ. Ε. Σ. Υ. ΠΑΝ/ΚΗΣ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΓΝΗ ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΕΚΤΙΜΗΣΗΣ ΚΑΙ ΑΝΤΙΜΕΤΩΠΙΣΗΣ ΚΑΤΑΓΜΑΤΩΝ ΣΕ ΑΣΘΕΝΕΙΣ ΜΕ ΑΝΩΡΙΜΟ ΣΚΕΛΕΤΟ ΑΝΑΤΟΜΙΑ ΑΝΩΡΙΜΟΥ ΟΣΤΟΥ
ΒΕΛΗΒΑΣΑΚΗΣ ΜΑΝΟΛΗΣ ΧΕΙΡΟΥΡΓΟΣ ΟΡΘΟΠΑΙΔΙΚΟΣ ΔΙΕΥΘ. Ε. Σ. Υ. ΠΑΝ/ΚΗΣ ΟΡΘΟΠΑΙΔΙΚΗΣ ΚΛΙΝΙΚΗΣ ΠΑΓΝΗ ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΕΚΤΙΜΗΣΗΣ ΚΑΙ ΑΝΤΙΜΕΤΩΠΙΣΗΣ ΚΑΤΑΓΜΑΤΩΝ ΣΕ ΑΣΘΕΝΕΙΣ ΜΕ ΑΝΩΡΙΜΟ ΣΚΕΛΕΤΟ ΑΝΑΤΟΜΙΑ ΑΝΩΡΙΜΟΥ ΟΣΤΟΥ
Συνδρομα Επωδυνων Ακρων
 www.printo.it/pediatric-rheumatology/cy/intro Συνδρομα Επωδυνων Ακρων Έκδοση από 2016 10. Οστεοχόνδρωση (Συνώνυμα: Οστεονέκρωση, Άσηπτη νέκρωση). 10.1 Τι είναι; Η λέξη «οστεοχόνδρωση» σημαίνει «οστικό
www.printo.it/pediatric-rheumatology/cy/intro Συνδρομα Επωδυνων Ακρων Έκδοση από 2016 10. Οστεοχόνδρωση (Συνώνυμα: Οστεονέκρωση, Άσηπτη νέκρωση). 10.1 Τι είναι; Η λέξη «οστεοχόνδρωση» σημαίνει «οστικό
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
Γενικευμένα Mονοβάθμια Συστήματα
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003
 1 EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003 1. Από την ίδια γραµµή αφετηρίας(από το ίδιο ύψος) ενός κεκλιµένου επιπέδου αφήστε να κυλήσουν, ταυτόχρονα προς τα κάτω, δύο κυλίνδροι της
1 EΡΓΑΣΙΑ 5 η Καταληκτική ηµεροµηνία παράδοσης: 20 Ιουλίου 2003 1. Από την ίδια γραµµή αφετηρίας(από το ίδιο ύψος) ενός κεκλιµένου επιπέδου αφήστε να κυλήσουν, ταυτόχρονα προς τα κάτω, δύο κυλίνδροι της
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 22 ΜΑΪΟΥ 2013 ΕΚΦΩΝΗΣΕΙΣ ÓÕÃ ÑÏÍÏ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β ΜΑΪΟΥ 03 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α-Α να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία συµπληρώνει
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β ΜΑΪΟΥ 03 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α-Α να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία συµπληρώνει
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ. Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ. 1.
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
3. ΥΝΑΜΙΚΗ ΡΟΜΠΟΤΙΚΩΝ ΒΡΑΧΙΟΝΩΝ
 3. ΥΝΑΜΙΚΗ ΡΟΜΠΟΤΙΚΩΝ ΒΡΑΧΙΟΝΩΝ Η δυναµική ασχολείται µε την εξαγωγή και τη µελέτη του δυναµικού µοντέλου ενός ροµποτικού βραχίονα. Το δυναµικό µοντέλο συνίσταται στις διαφορικές εξισώσεις που περιγράφουν
3. ΥΝΑΜΙΚΗ ΡΟΜΠΟΤΙΚΩΝ ΒΡΑΧΙΟΝΩΝ Η δυναµική ασχολείται µε την εξαγωγή και τη µελέτη του δυναµικού µοντέλου ενός ροµποτικού βραχίονα. Το δυναµικό µοντέλο συνίσταται στις διαφορικές εξισώσεις που περιγράφουν
Physics by Chris Simopoulos
 ΕΠΩΗ 1. Ευθύγραμμος αγωγός μήκους L = 1 m κινείται με σταθερή ταχύτητα υ = 2 m/s μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,8 Τ. Η κίνηση γίνεται έτσι ώστε η ταχύτητα του αγωγού να σχηματίζει γωνία
ΕΠΩΗ 1. Ευθύγραμμος αγωγός μήκους L = 1 m κινείται με σταθερή ταχύτητα υ = 2 m/s μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,8 Τ. Η κίνηση γίνεται έτσι ώστε η ταχύτητα του αγωγού να σχηματίζει γωνία
