Πιθανότητες ΙΙ 1 o Μέρος. Οικονομικό Πανεπιστήμιο Αθηνών
|
|
|
- Ζεβεδαῖος Αργυριάδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πιθανότητες ΙΙ o Μέρος Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών 4 Απριλίου 7
2
3 Κεφάλαιο Συνεχείς Τυχαίες Μεταβλητές. Η εκθετική κατανομή Η πυκνότητα πιθανότητας της εκθετικής κατανομής δίδεται από την σχέση f(x λe λx αν x, αν x <. (. Η παράμετρος λ της κατανομής είναι ϑετικός αριθμός. Η συνάρτηση κατανομής δίδεται από την σχέση F(x : x f(tdt, που δίνει F(x e λx αν x, αν x <. (. Σχήμα.: Εκθετική κατανομή, λ 3
4 Λήμμα.. Ισχύει ότι I n (x : n! n k x k k! e x x n e x dx, n,,,.... (.3 Απόδειξη. Αρκεί να δείξουμε ότι I n(x x n e x. Πράγματι, I n(x d dx ( n! ( + x! + x x n! ( + + x!! + + xn (n! x n e x, και επομένως η (.3 ισχύει.! + + xn (n! + xn e x n! e x + n! ( + x + x!! + + xn (n! + xn e x n! Οι ροπές της κατανομής δίδονται από την σχέση EX n x n λe λx dx λ n (λx n e λx λdx λ n u n e u du (.4 όπου u λx. Λαμβάνοντας υπ όψιν μας το Λήμμα. u n e u du I n (u ( n! n!. (.5 (Χρησιμοποιήσαμε το γεγονός ότι lim u n! n ( k uk k! e u καθώς και ότι I n ( n! +! +! + + n (n! + n n! n!. Επομένως, από την (.4 προκύπτει ότι EX n n!, n,,,.... (.6 λn Συγκεκριμένα, η μέση τιμή της εκθετικής είναι EX λ, η δεύτερη ροπή είναι EX λ, και η διασπορά δίδεται από την σχέση Var(X EX (EX λ. Ο συντελεστής μεταβλητότητας μιας κατανομής ορίζεται ως c v Var(X EX Για την εκθετική κατανομή έχουμε c v. Μια από τις σημαντικότερες ιδιότητες της εκ- ϑετικής κατανομής, η οποία και την χαρακτηρίζει, είναι η αμνήμων ιδιότητα (ή ιδιότητα έλλειψης μνήμης: Μια μή αρνητική τ.μ. X έχει την αμνήμονα ιδιότητα αν, s, t >, P(X > t + s X > t P(X > s. (.7 4
5 Είναι στοιχειώδες να ελέγξουμε ότι η έκθετική κατανομή ικανοποιεί την (.7. Πράγματι, P(X > t + s X > t P(X > t + s, X > t P(X > t P(X > s. P(X > t + s P(X > t e λ(t+s e λt e λs Πολύ πιό ενδιαφέρον όμως είναι το γεγονός ότι η εκθετική κατανομή είναι η μοναδική η οποία έχει αυτή την ιδιότητα. Εστω λοιπόν κάποια τ.μ. X που ικανοποιεί την (.7 και ας ϑέσουμε g(t P(X > t. Οπως είδαμε, η (.7 μπορεί να γραφτεί και ως P(X > t + s P(X > tp(x > s ή g(t + s g(tg(s. (.8 Εφαρμόζοντας την παραπάνω σχέση με s t έχουμε g( g( και επαγωγικά, Ομοια, g( g( n + + n g( n n ή g(n g( n. g(/n g( /n. Από τις δύο παραπάνω σχέσεις προκύπτει ότι, για κάθε ρητό, έστω r p/q g(p/q g( p/q ή g(r g( r. Απομένει να δείξουμε ότι η σχέση αυτή ισχύει για κάθε πραγματικό αριθμό t. Αφού < g( <, υπάρχει λ (, τέτοιο ώστε g( e λ, Συνεπώς, αν r, s είναι ρητοί τέτοιοι ώστε r < t < s, εφόσον η g(t είναι φθίνουσα συνάρτηση ισχύει ότι e λr g(r g(t g(s e λs Αφήνοντας r t, s t προκύπτει το ζητούμενο.. Η συνάρτηση Γάμμα Η συνάρτηση Γάμμα του Euler αποτελεί γενίκευση του παραγοντικού για μή ακέραια ορίσματα. Για κάθε α > ορίζουμε την συνάρτηση Γ(α : t α e t dt. (.9 (Παρατηρείστε ότι το παραπάνω είναι ένα γενικευμένο ολοκλήρωμα. Ισχύει ότι Γ( e t dt. (. 5
6 Χρησιμοποιώντας παραγοντική ολοκλήρωση βλέπουμε ότι Γ(α + + α t α e t dt t α e t dt t α ( e t dt t α e t + αt α e t dt και συνεπώς έχουμε Γ(α + α Γ(α, α >. (. Οταν το α είναι φυσικός αριθμός η παραπάνω σχέση δίνει Γ(n + nγ(n n(n Γ(n n(n (n Γ( και λαμβάνοντας υπ όψιν μας την (. έχουμε Γ(n + n!, n,,,.... (. Παρατηρείστε ότι η (. συμφωνεί με την (.5. Εφαρμόζοντας την σχέση (. επαγωγικά βλέπουμε ότι, για κάθε n N και α > Γ(α + n (α + n Γ(α + n (α + n (α + n Γ((α + n (α + n (α + n Γ(α + n (α + α Γ(α. (.3.3 Η κατανομή Γάμμα Εμείς ϑα συναντήσουμε την συνάρτηση Γ στα πλαίσια της κατανομής Γάμμα που έχει πυκνότητα πιθανότητας λ (λxα Γ(α e λx αν x > f(x (.4 αν x. Η παράμετρος λ ονομάζεται παράμετρος κλίμακος ενώ η α παράμετρος σχήματος. Η περίπτωση που η παράμετρος σχήματος είναι ακέραιος αριθμός έχει ιδιαίτερο ενδιαφέρον και ϑα την εξετάσουμε λεπτομερέστερα στη συνέχεια. (Παρατηρείστε ότι για α παίρνουμε την εκθετική πυκνότητα πιθανότητας. Η συνάρτηση κατανομής δεν μπορεί να εκφραστεί μέσω στοιχειωδών συναρτήσεων (εκτός από την περίπτωση που το α είναι φυσικός αριθμός. Εκφράζεται μέσω της μη πλήρους συνάρτησης Γάμμα (incomplete Gamma function που ορίζεται ως Γ(x; α : x t α e t dt, x. 6
7 Σχήμα.: Πυκνότητα Γάμμα για διάφορες τιμές της παραμέτρου σχήματος α και λ. Η συνάρτηση αυτή συμπεριλαμβάνεται σε όλα τα προγράμματα στατιστικής ανάλυσης όπως π.χ. η R. Παρατηρείστε ότι Γ( ; α : lim x Γ(x; α lim x tα e t dt Γ(α. Χρησιμοποιώντας την μη πλήρη συνάρτηση Γάμμα έχουμε x λ(λt α e λt dt λx και επομένως η συνάρτηση κατανομής εκφράζεται ως F(x Γ(λx; α Γ(α u α e u du Γ(λx; α αν x > αν x. Οι ροπές της κατανομής Γάμμα υπολογίζονται εύκολα: EX n x n f(xdx x n λ(λx α e λx dx Γ(α λ n λ n x n λ(λx α e λx dx Γ(α λ n Γ(α t n+α e t dt Γ(n + α λ n. Γ(α Λαμβάνοντας υπ όψιν μας την (.3 βλέπουμε ότι EX n α(α + (α + n, n,,.... (.5 λn 7
8 Συγκεκριμένα, οι δύο πρώτες ροπές είναι EX α λ, EX α(α + λ και η διασπορά είναι Var(X α λ..4 Η κατανομή Erlang Η κατανομή Erlang είναι μια ειδική περίπτωση της κατανομής Γάμμα όταν η παράμετρος σχήματος είναι ακέραια. Η πυκνότητα πιθανότητας της Erlang δίδεται από τον τύπο f(x { λ (λxk (k! e λx αν x αν x <. Η παράμετρος k είναι ϑετικός ακέραιος (όταν k παίρνουμε την εκθετική κατανομή και η λ > είναι παράμετρος κλίμακας. προκύπτει ολοκληρώνοντας την f(x δίδεται από τον τύπο k (λx m e λx αν x F(x m!. m αν x < Η αντίστοιχη συνάρτηση κατανομής που Παραδείγματος χάριν, όταν k, έχουμε F(x ( + λxe λx, (x. Εστω X τ.μ. με κατανομή Erlang(k, λ. Η ροπή τάξης r ϑα είναι EX r x r (λxk (k! e λx λdx (k!λ r y r+k e y dy (k + r! λ r. (k! Οι δύο πρώτες ροπές της Erlang(k, λ είναι EX k λ και EX k(k+, και συνεπώς η λ διασπορά είναι Var(X k(k+ k k. Ο συντελεστής διακύμανσης που προκύπτει λ λ λ είναι k/λ c V. k/λ k Βλέπουμε δηλαδή ότι η Erlang έχει πάντα συντελεστή μεταβλητότητας μικρότερο της μονάδας (η ισότητα ισχύει όταν k οπότε παίρνουμε την εκθετική. Οσο μεγαλύτερη είναι η παράμετρος k τόσο μικρότερος γίνεται ο συντελεστής μεταβλητότητας. 8
9 Σχήμα.3: Πυκνότητα Erlang για διάφορες τιμές της παραμέτρου σχήματος k και λ. 9
10 .5 Η συνάρτηση Βήτα Μια άλλη συνάρτηση η οποία σχετίζεται με την συνάρτηση Γάμμα και διαδραματίζει σημαντικό ρόλο είναι η συνάρτηση Βήτα η οποία έχει δύο μη αρνητικά ορίσματα, και η οποία ορίζεται ως B(α, β : t α ( t β dt, α >, β >. (.6 Οπως ϑα δούμε στη συνέχεια η συνάρτηση Βήτα συνδέεται με την Γάμμα μέσω της σχέσης B(α, β Γ(αΓ(β Γ(α + β. (.7 Παρατηρούμε ότι η συνάρτηση Βήτα είναι συμμετρική ως προς τα ορίσματά της. Πράγματι B(α, β t α ( t β dt ( s α s β ds s β ( s α ds B(β, α όπου στην παραπάνω σχέση κάναμε την αλλαγή μεταβλητής s t. Στην γενική περίπτωση ϑα δούμε την απόδειξη της (.7 λίγο αργότερα. Προς το παρόν ϑα δώσουμε μια απόδειξη στην περίπτωση που ο α είναι φυσικός αριθμός, έστω α m N. B(m, β t m ( t β dt ( t m ( t β dt β ( t m ( t β (m t m ( t β dt m B(m, β + β β Εφαρμόζοντας την παραπάνω σχέση επαγωγικά έχουμε B(m, β m (m (m B(m, β + B(m, β + (.8 β β(β + (m (m B(, β + m. (.9 β(β + (β + m Ομως και επομένως B(, β + m t ( t β+m dt β + m B(m, β (m (m β(β + (β + m (β + m Γ(mΓ(β Γ(β + m (m!γ(β Γ(β β(β + (β + m (β + m όπου χρησιμοποιήσαμε το γεγονός ότι Γ(β + m (β + m (β + m (β + β Γ(β (.3.
11 Από την (.7 παίρνουμε και το εξής ενδιαφέρον αποτέλεσμα: Αν α β / ϑα έχουμε B(/, / Γ(/ Γ( (. Ομως Γ( και B(/, / t / ( t / dt. Με την αλλαγή μεταβλητής t sin u, dt sin u cos u du έχουμε B(/, / π/ π/ (sinu ( sin u / sin u cos udu (sinu (cos u sin u cos udu du π Από την σχέση αυτή και την (. παίρνουμε Γ(/ π ή Γ(/ π. (..6 Η κατανομή Βήτα Η κατανομή Βήτα έχει πυκνότητα πιθανότητας f(x B(α, β xα ( x β αν < x < διαφορετικά. (. Οπως βλέπουμε και από το σχήμα (.4 η μορφή των πυκνοτήτων ποικίλει ανάλογα με τις τιμές των παραμέτρων α > και β >. Είναι εύκολο να δούμε ότι αν α β τότε η πυκνότητα πιθανότητας γίνεται f(x { αν < x < διαφορετικά δηλαδή ομοιόμορφη στο [, ]. Το σχήμα (.5 δίνει τις αντίστοιχες συναρτήσεις κατανομής. Οι ροπές της κατανομής Βήτα υπολογίζονται εύκολα ως εξής: EX n B(α, β Γ(α + nγ(β Γ(α + β Γ(α + β + n Γ(αΓ(β x n x α ( x β dx Γ(α + n Γ(α B(α + n, β B(α, β Γ(α + β Γ(α + β + n.
12 Σχήμα.4: Πυκνότητες Βήτα για διάφορες τιμές των παραμέτρων α και β.
13 Σχήμα.5: Συναρτήσεις κατανομής Βήτα για διάφορες τιμές των παραμέτρων α και β. 3
14 Από την τελευταία αυτή έκφραση, χρησιμοποιώντας την (.3, παίρνουμε EX n α (α + (α + n (α + β (α + β + (α + β + n,. (.3 Συγκεκριμένα οι δύο πρώτες ροπές είναι EX α α + β, EX α(α + (α + β(α + β +, και η δισπορά είναι Var(X αβ (α + β (α + β +..7 Ροπογεννήτριες συναρτήσεις Εστω X τ.μ. με συνάρτηση πυκνότητας πιθανότητας f. Η ροπογεννήτρια της X ορίζεται ως η συνάρτηση M X (θ : E[e θx ] e θx f(xdx (.4 για κάθε θ R για το οποίο το παραπάνω ολοκλήρωμα συγκλίνει. Ακολουθούν παραδείγματα ροπογεννητριών: Η ροπογεννήτρια συνάρτηση μιας κανονικής τ.μ. Εστω X κανονική τ.μ. με μέση τιμή και διασπορά. Η ροπογεννήτρια της X ορίζεται ως M X (θ : Ee θx Ο εκθέτης μέσα στο ολοκλήρωμα γράφεται ως έχουμε M X (θ e θ e θx e x x dx θx e dx. π π αφού το τελευταίο ολοκλήρωμα ισούται με την μονάδα. ( x θx + t + θ και επομένως e (x θ dx e θ (.5 π Τώρα ας υποθέσουμε ότι η Y είναι κανονική τ.μ. με μέση τιμή µ και διασπορά σ. Τότε έχουμε Y µ + σx και επομένως η ροπογεννήτρια σ αυτή την περίπτωση είναι M Y (θ Ee θy Ee θµ+θσx e tθµ M X (σθ e µθ+ σ θ. Η ροπογεννήτρια συνάρτηση μιας εκθετικής τ.μ. Εστω X εκθετική τ.μ. με πυκνότητα πιθανότητας f(x λe λx για x, και f(x όταν x <. Η ροπογεννήτριά της δίνεται από την σχέση M X (θ e θx λe xλ dx λ 4 e x(λ θ dx λ λ θ. (.6
15 Παρατηρείστε ότι ο παραπάνω υπολογισμός έχει νόημα μόνον όταν θ < λ. Αν το θ λ το ολοκλήρωμα απειρίζεται και η ροπογεννήτρια δεν ορίζεται. Η ροπογεννήτρια συνάρτηση μιας ομοιόμορφης τ.μ. Ας υποθέσουμε τώρα ότι η X είναι ομοιόμορφα κατανεμημένη στο διάστημα [a, b] με πυκνότητα πιθανότητας f(x b a όταν x [a, b] και αλλού. Η αντίστοιχη ροπογεννήτρια δίδεται από τη σχέση M X (θ b a e θx b a dx eθb e θa θ(b a. (.7 Η ροπογεννήτρια συνάρτηση μιας τ.μ. Γάμμα Εστω X μια τυχαία μεταβλητή με κατανομή Γαμμα(α, λ δηλαδή με πυκνότητα f(x λ (λxα Γ(α e λx όταν x > (και διαφορετικά. Η ροπογεννήτρια δίνεται από την έκφραση M(θ e θx λ (λxα e λx dx λα x α e x(λ θ dx Γ(α Γ(α ( λ α y α e y dy y x(λ θ λ θ Γ(α ( λ α υπό την προϋπόθεση ότι θ < λ. (.8 λ θ (Αν θ λ το ολοκλήρωμα αποκλίνει και η πιθανογεννήτρια δεν υπάρχει. Η ροπογεννήτριες συναρτήσεις παίρνουν το όνομά τους από το την ακόλουθη ιδιότητα: Παραγωγίζοντας την ροπογεννήτρια n φορές έχουμε d n dθ n M X(θ dn dθ n e θx d n f(xdx dθ n eθx f(xdx x n e θx f(xdx, (Στην παραπάνω εξίσωση υποθέσαμε ότι η εναλλαγή ολοκλήρωσης και παραγώγισης είναι ϑεμιτή. Δεν ϑα επεκταθούμε σ αυτό το ζήτημα. Θέτοντας στην παραπάνω εξίσωση θ, και συμβολίζοντας με M (n X (θ την n-οστή παράγωγο της M X έχουμε M (n X ( x n f(xdx µ n δηλαδή παρατηρούμε ότι η n-οστή παράγωγος της ροπογεννήτριας υπολογισμένη στο συμπίπτει με την n-οστή ροπή της κατανομής. Συνεπώς γνώση της ροπογεννήτριας συνεπάγεται γνώση όλων των ροπών της κατανομής. Ισχύει και το αντίστροφο, δηλαδή ότι οι ροπές προσδιορίζουν την ροπογεννήτρια: Πράγματι, από το ϑεώρημα του Taylor γνωρίζουμε ότι κάθε συνάρτηση που είναι αναλυτική σε μια περιοχή του μηδενός μπορεί να εκφραστεί ως μια δυναμοσειρά: M X (θ θ n n! M(n X n 5 ( n θ n n! µ n.
16 Για την τυποποιημένη κανονική κατανομή έχουμε M(θ e θ + θ! + θ4! + θ6 3 3! + + θn n n! + Παρατηρούμε ότι οι περιττές δυνάμεις του θ απουσιάζουν πράγμα που σημαίνει ότι οι ροπές περιττής τάξης είναι. Για τις ροπές άρτιας τάξης έχουμε µ n (n! n n! ( n n! 3 5 (n. (.9 n n Για παράδειγμα µ, µ 4 3, µ 6 3 5, µ Είναι ενδιαφέρον να παρατηρήσουμε ότι η έκφραση για την ροπή τάξης n που δίδεται στην (.9 είναι η λύση του ακόλουθου προβλήμτος συνδιαστικής ανάλυσης: Με πόσους διαφορετικούς τρόπους μπορούμε να χωρίσουμε n διαφορετικά αντικείμενα σε n ζευγάρια; Το πρώτο ζεύγος μπορούμε να το επιλέξουμε με ( ( n. Το δεύτερο ζευγάρι με n (επειδή μετά την επιλογή του πρώτου ζεύγους έχουν μείνει n αντικείμενα. Το τρίτο ζευγάρι με ( n 4 τρόπους και ούτω καθ εξής. Το προτελευταίο (n -οστό ζευγάρι με ( ( 4 τρόπους και το τελευταίο με τρόπους. Συνεπώς μπορούμε να φτιάξουμε n αριθμημένα (πρώτο, δεύτερο, τρίτο κ.ο.κ. ζευγάρια από n αντικείμενα με ( n ( n n(n ( n 4 ( 4 (n (n 3 ( (n 4(n (n! n. Δεδομένου όμως ότι δεν μας ενδιαφέρει η σειρά των ζευγαριών και ότι μπορούμε να διατάξουμε n ζευγάρια με n! τρόπους, ο συνολικός αριθμός των τρόπων με τους οποίους μπορούμε να φτιάξουμε n ζευγάρια από n διαφορετικά αντικείμενα είναι (n! n n!. Αυτό το αποτέλεσμα συμφωνεί με τον τύπο (.9..8 Παράμετροι ϑέσης και κλίμακας Θεώρημα.. Εστω X και Y τυχαίες μεταβλητές με συναρτήσεις κατανομής F και G αντίστοιχα. Αν Y µ + σx όπου µ R, σ > τότε ( x µ G(x F. (.3 σ 6
17 Αν επιπλέον η κατανομή F είναι συνεχής με πυκνότητα πιθανότητας f τότε και η κατανομή G είναι συνεχής με πυκνότητα πιθανότητας g(x ( x µ σ f. (.3 σ Απόδειξη Πράγματι ( G(x P(Y x P (µ + σx x P X x µ ( x µ F σ σ Παραγωγίζοντας την (.3 ως προς x παίρνουμε την (.3. Αν η συνάρτηση κατανομής μιας τ.μ. X μπορεί να γραφτεί υπό την μορφή ( x µ F(x G σ όπου µ R, σ >, και G είναι κάποια άλλη συνάρτηση τότε το µ ονομάζεται παράμετρος ϑέσης και το σ παράμετρος κλίμακας. Η συνάρτηση G είναι τότε G(x F(µ + σx και κατά συνέπεια είναι επίσης μια συνάρτηση κατανομής..9 Συναρτήσεις τυχαίων μεταβλητών Εστω X πραγματική τυχαία μεταβλητή με συνάρτηση κατανομής F X (x P(X x και πυκνότητα πιθανότητας f X (x F (x, x R. Εστω επίσης g : R R μια πραγματική συνάρτηση. Τότε η Y : g(x είναι τυχαία μεταβλητή. Η συνάρτηση κατανομής της Y, δίδεται από την σχέση F Y (y : P(Y y P(g(X y. (.3 Δεν ϑα εξετάσουμε το πρόβλημα στην πλήρη γενικότητά του εδώ. Θα περιοριστούμε στις εξής δύο σημαντικές περιπτώσεις..9. Η g είναι γνησίως μονοτονική, παραγωγίσιμη συνάρτηση Εστω g : I J όπου I, J ανοικτά υποσύνολα του R. Εφ όσον η g είναι γνησίως μονοτονική, η αντίστροφη συνάρτηση g : J I υπάρχει και είναι παραγωγίσιμη με (g (y g (g (y για κάθε y J. Αν η g είναι γνησίως αύξουσα, τότε και η g είναι γνησίως αύξουσα και επομένως η (.3 δίδει F Y (y P(X g (y F X (g (y. (g γνησίως αύξουσα 7
18 Συνεπώς, η πυκνότητα πιθανότητας της Y δίνεται από την σχέση f Y (y d dy F Y(y f X (g (y g (g (y. (.33 Στην περίπτωση που η g είναι γνησίως φθίνουσα το ίδιο ισχύει και για την g και επομένως F Y (y P(X g (y F X (g (y. (g γνησίως φθίνουσα Παραγωγίζοντας παίρνουμε σ αυτή την περίπτωση f Y (y d dy F Y(y f X (g (y g (g (y. (.34 Παρατηρούμε όμως ότι g (g (y < στην περίπτωση αυτή. Συνδιάζοντας τις (.33, (.34 έχουμε, ανεξαρτήτως αν η g είναι αύξουσα ή φθίνουσα, f Y (y f X (g (y g (g (y. (.35 Παράδειγμα. Εστω ότι η τυχαία μεταβλητή X είναι ομοιόμορφα κατανεμημένη στο διάστημα (,, δηλαδή f X (x ( < x < και g : (, (, είναι η συνάρτηση g(x log( x. (Παρατηρούμε ότι η g είναι αύξουσα. Αν y log( x τότε x e y δηλαδή g (y e y. Επίσης g (x x και g (g (y ( e y ey. Συνεπώς από την (.35 έχουμε f y (y f X ( e y e y ( < e y e y e y για y > δηλαδή η Y είναι εκθετικά κατανεμημένη τυχαία μεταβλητή με ρυθμό. Παράδειγμα. Οπως ϑα δούμε είναι απλούστερο να ακολουθούμε την διαδικασία α- πό την αρχή αντί να εφαρμόζουμε τον τύπο (.35. Είναι όμως σημαντικό να κατανούμε ποιοτικά την συμπεριφορά της συνάρτησης g (πεδίο ορισμου, πεδίο τιμών και μονοτονικότητα. Εστω και πάλι ότι η X είναι ομοιόμορφη στο (, και g(x tan(π(x. g(x arctan(π(x, x R. Στο σχήμα.6 βλέπουμε το γράφημα της arctan. Η συνάρτηση είναι γνησίως αύξουσα και το πεδίο τιμών είναι το σύνολο ( π, π. Επίσης γνωρίζουμε ότι d dx arctan(x. Αν Y arctan(x τότε +x F y (y P(tan(π(X y P(π(X arctan(y P(X + π arctan(y + π arctan(y (αφού η συνάρτηση κατανομής της X είναι F X (x x όταν x (,. Παραγωγίζοντας την παραπάνω σχέση f Y (y d ( dy + π arctan(y π + y, y R. 8
19 Σχήμα.6: Η συνάρτηση arctan. Σχήμα.7: Πυκνότητα και συνάρτηση κατανομής Cauchy. 9
20 Σχήμα.8: Λογαριθμοκανονική πυκνότητα και συνάρτηση κατανομής. Η κατανομή Cauchy δεν έχει ροπές, ούτε καν μέση τιμή. Ο λόγος είναι ότι το ολοκλήρωμα που ορίζει την μέση τιμή δεν συγκλίνει! Παράδειγμα 3. Η λογαριθμοκανονική κατανομή. Αν η X είναι τυποποιημένη κανονική τυχαία μεταβλητή η Y : e X ονομάζεται τυποποιημένη λογαριθμοκανονική τυχαία μεταβλητή. Η συνάρτηση κατανομής της X είναι βεβαίως η Φ(x : x π e t dt. Η συνάρτηση κατανομής της Y είναι F Y (y P(Y y P(e X y P(X log(y log y e t dt. π Παραγωγίζοντας την παραπάνω σχέση παίρνουμε f Y (y y π e (log y, y >. Οι ροπές της λογαριμθμοκανονικής κατανομής μπορούν να υπολογισθούν εύκολα από την σχέση που την ορίζει. E[Y n ] E[(e X n ] E[e nx ] e n Στην παραπάνω σχέση χρησιμοποιήσαμε την ροπογεννήτρια της τυποποιημένης κανονικής κατανομής. Συνεπώς E[Y] e, E[Y ] e, Var(Y e e e(e. Παράδειγμα 4. Εστω X τυποποιημένη κανονική τυχαία μεταβλητή με κατανομή Φ(x : P(X x x π e u du και πυκνότητα πιθανότητας ϕ(x : Φ (x π e x. Εστω Y X. Θέλουμε να βρούμε την συνάρτηση κατανομής και την πυκνότητα πι- ϑανότητας της Y. Παρατηρείστε ότι Y g(x όπου η συνάρτηση g(x x δεν είναι
21 μονοτονική. Εστω F(y : P(Y y P(X y. Αν y τότε F(y. Αν y > τότε F(y P( y X y Φ( y Φ( y. Η πυκνότητα της τυχαίας μεταβλητής Y για y > ϑα είναι επομένως f(y F (y (Φ( y Φ( y e ( y + y π e ( y y π π y e y π (y/ e (y/ (y/ Γ(/ e (y/ Στην παραπάνω σχέση χρησιμοποιήσαμε την (.. Παρατηρείστε ότι η Y έχει κατανομή Γαμμα(/, /. Παράδειγμα 5. Εστω X ομοιόμορφη τυχαία μεταβλητή στο [, ] και Y g(x όπου g(x x( x. Παρατηρούμε ότι η g δεν είναι μονοτονική και στο διάστημα [, ], όπου παίρνει τιμές η X, για κάθε τιμή y [, 4 ] η εξίσωση y x( x έχει δύο λύσεις, x + 4y και x 4y. Παρατηρούμε επίσης ότι το μέγιστο της συνάρτησης g βρίσκεται στο σημείο x / και είναι g(/ /4. Συνεπώς P(Y y P(X( X y όταν y /4. Επίσης, δεδομένου ότι η X παίρνει τιμές στο [, ], P(Y y P(X( X y όταν y αφού η x( x είναι μη αρντητική για x [, ]. Μένει να υπολογίσουμε την πιθανότητα P(Y y όταν y (, 4. ( 4y F Y (y : P(Y > y P(X( X > y P < X < + 4y + 4y 4y. 4y Συνεπώς η συνάρτηση κατανομής της Y είναι F Y (y και η πυκνότητα πιθανότητας επειδή η X είναι ομοιόμορφη στο [, ] αν y 4y αν < y 4 αν y > 4. f Y (y { 4y αν < y 4 διαφορετικά.
22 Σχήμα.9: Η συνάρτηση g(x x( x. Σχήμα.: Η συνάρτηση κατανομής και η πυκνότητα πιθανότητας της Y.
23 Κεφάλαιο Από κοινού κατανομή τυχαίων μεταβλητών. Από κοινού κατανομή δύο τυχαίων μεταβλητών Εστω δυο τυχαίες μεταβλητές X, Y, με τιμές στο N πιθανοτήτων (Ω, A, P. Το σύνολο των πιθανοτήτων ορισμένες πάνω στο ίδιο χώρο p X,Y (i, j : P(X i, Y j, i, j N, ονομάζεται από κοινού κατανομή των X, Y. Ισχύει ασφαλώς ότι i j p XY(i, j. Οι p X (i : P(X i p Y (j : P(Y j p X,Y (i, j j p X,Y (i, j ονομάζονται περιθώριες κατανομές των X και Y αντίστοιχα. Τα παραπάνω αθροίσματα γράφονται ως άπειρα αθροίσματα μη αρνητικών αριθμών, σε πολλές περιπτώσεις όμως είναι πεπερασμένα αθροίσματα αφού όλοι οι όροι πλην πεπερασμένων μπορεί να είναι μηδέν. Παράδειγμα.. Θεωρούμε τις τυχαίες μεταβλητές X με τιμές {,, 3, 4} και Y με τιμές {, }. Εστω ότι η από κοινού κατανομή τους δίνεται από τον πίνακα. i Y/X 3 4 / / / /6 /6 / /6 3
24 Οι περιθώριες πιθανότητες δίνονται από τις p X ( /4, p X ( /6, p X (3 /, p X (4 /, p Y ( 5/, p Y ( 7/. Ορισμός.. Δύο τυχαίες μεταβλητές, X, Y, ονομάζονται ανεξάρτητες αν, P(X i, Y j P(X ip(y j, για κάθε i, j. Ο παραπάνω ορισμός μπορεί επίσης να διατυπωθεί λέγοντας ότι η από κοινού κατανομή είναι το γινόμενο των περιθωρίων. Αυτό σημαίνει ότι, για να είναι οι δύο τυχαίες μεταβλητές ανεξάρτητες, ϑα πρέπει όλα τα ενδεχόμενα της μορφής {X i}, {Y j}, να είναι ανεξάρτητα. Οταν οι τυχαίες μεταβλητές X, Y, δεν είναι ανεξάρτητες τότε ϑα ονομάζονται εξαρτημένες. Για παράδειγμα οι τυχαίες μεταβλητές με την από κοινού κατανομή που δίνεται στον πίνακα. δεν είναι ανεξάρτητες αφού P(X, Y /6 ενώ P(X P(Y /3 5/ 5/36. Ορισμός.. Η δεσμευμένη κατανομή της τυχαίας μεταβλητής X, δεδομένης της Y δίδεται από την σχέση P(X i, Y j P(X i Y j. P(Y j Εστω f : N N R, μία συνάρτηση δύο μεταβλητών στους πραγματικούς αριθμούς. Τότε η μέση τιμή Ef(X, Y δίδεται από την σχέση E[f(X, Y] f(i, jp X,Y (i, j. (. i j Το επόμενο ϑεώρημα εκφράζει την ϑεμελιώδη ιδιότητα της γραμμικότητας της μέσης τιμής. Θεώρημα.. Αν X, Y δύο οποιεσδήποτε τυχαίες μεταβλητές και a, b, πραγματικοί αριθμοί, τότε E[aX + by] aex + bey. Απόδειξη. Χρησιμοποιώντας τον τύπο (., όπου f(i, j a i + b j, E[aX + by] (ai + bjp X,Y (i, j a i p X,Y (i, j + b j p X,Y (i, j i j i j j i j a i p X,Y (i, j + b j p X,Y (i, j i i a ip(x i + b jp(y j aex + bey. j i j 4
25 Θεώρημα.. Εστω f i, i,, δύο συναρτήσεις από τους φυσικούς στους πραγματικούς και X, X, δύο ανεξάρτητες τ.μ. Τότε E[f (X f (X ] E[f (X ] E[f (X ]. (. Το αποτέλεσμα αυτό επεκτείνεται επαγωγικά για οποιοδήποτε αριθμό τ.μ. Απόδειξη. Χρησιμοποιώντας τον τύπο (. έχουμε E[f (X f (X ] f (n f (n P(X n P(X n n n f (n P(X n f (n P(X n n n E[f (X ] E[f (X ]. Η συνδιακύμανση δύο τυχαίων μεταβλητών, X, X, ορίζεται ως Cov(X, X E [(X EX (X EX ] E[X X ] (EX (EX. Δυο τ.μ. των οποίων η συνδιακύμανση είναι ονομάζονται ασυσχέτιστες. Από την (. προκύπτει ότι όταν δύο τ.μ. είναι ανεξάρτητες τότε είναι και ασυσχέτιστες αφού σ αυτή την περίπτωση E[X X ] (EX (EX. Το αντίθετο όμως δεν ισχύει, δηλαδή δύο ασυσχέτιστες τ.μ. δεν είναι υποχρεωτικά ανεξάρτητητες. Ας δούμε το ακόλουθο χαρακτηριστικό αντιπαράδειγμα. Εστω X, Y τυχαίες μεταβλητές, ορισμένες στον ίδιο χώρο με τιμές στο σύνολο {,, } και από κοινού κατανομή που δίνεται από τον ακόλουθο πίνακα. Y/X /8 /8 / /8 /8 Η περιθώρια κατανομή της X είναι p X ( /4, p X ( /, p X ( /4. Η περιθώρια κατανομή της Y είναι ίδια με αυτή της X. Εχουμε συνεπώς ότι EX EY Η μέση τιμή του γινομένου των X και Y, γράφοντας μόνο τους μη μηδενικούς όρους, είναι EXY + 8 και επομένως η συνδιακύμανση είναι Cov(X, Y E[XY] EX EY. Άρα οι X και Y είναι ασυσχέτιστες. Δεν είναι όμως ανεξάρτητες. Για παράδειγμα P(X, Y 4 P(X P(Y, και επομένως η από κοινού κατανομή δεν είναι το γινόμενο των περιθωρίων. 5
26 Θεώρημα.3. Για δύο οποιεσδήποτε τ.μ. X, X, Var(X + X Var(X + Var(X + Cov(X, X. (.3 Όταν οι X, X είναι ασυσχέτιστες, Var(X + X Var(X + Var(X. Απόδειξη. Χρησιμοποιούμε την ακόλουθη έκφραση για την διασπορά Var(X + X E[(X + X ] (E[X + X ] E[X + X X + X ] ( (EX + EX EX + (EX E[X ] + E[X X ] + E[X ] (EX (EX EX EX όπου χρησιμοποιήσαμε κατ επανάληψη τη γραμμικότητα της μέσης τιμής. Συλλέγοντας όρους στο τελευταίο μέλος των παραπάνω εξισώσεων και λαμβάνοντας υπ όψιν ότι Var(X i EX i (EX i, i,, Cov(X, X E[X X ] EX EX, προκύπτει η (.3.. Η ανισότητα του Chebyshev Θεώρημα.4. Αν X είναι τυχαία μεταβλητή με μέσο µ και διασπορά σ τότε, για κάθε ɛ >, P( X µ > ɛ σ ɛ. (.4 Απόδειξη. σ (k µ p k k (k µ p k {k: k µ >ɛ} ɛ {k: k µ >ɛ} p k ɛ P( X µ > ɛ. (k µ p k + {k: k µ >ɛ} {k: k µ ɛ} (k µ p k Πόρισμα.. Αν για μια τυχαία μεταβλητή με μέσο µ και διασπορά σ ισχύει ότι σ τότε P(X µ. Απόδειξη. Από το δεξί μέλος της ανισότητας του Chebyshev ισχύει ότι P( X µ > ɛ για κάθε ɛ >. 6
27 Η παραπάνω ανισότητα μας δίνει ένα άνω όριο για την πιθανότητα μια τυχαία μεταβλητή να απέχει περισσότερο από ɛ από τη μέση της τιμή. Το άνω όριο δεν είναι εν γένει ικανοποιητικό για τις περισσότερες πρακτικές εφαρμογές, έχει όμως μεγάλη ϑεωρητική σημασία. Εδώ ϑα το χρησιμοποιήσουμε στην απόδειξη του Νόμου των Μεγάλων Αριθμών. Ως ένα παράδειγμα εφαρμογής της ανισότητας του Chebyshev, ας πάρουμε την X ομοιόμορφη στο σύνολο {,,..., }. Εχουμε EX 5, 5 και Var(X 833, 5. Με ɛ 4 η ανισότητα μας λέει ότι P( X 5, 5 > 4 833, 5 6, 5. Είναι όμως P( X 5, 5 > 4 P(X 9 + P(X,. Για μικρές τιμές του ɛ το δεξί μέλος της (.4 γίνεται μεγαλύτερο από την μονάδα κι έτσι η ανισότητα δεν μας δίνει καμία χρήσιμη πληροφορία. Οπως ϑα δούμε όμως, σαν ϑεωρητικό εργαλείο μπορεί να είναι εξαιρετικά χρήσιμη..3 Η ανισότητα Cauchy Schwarz Θεώρημα.5. Για δύο οποιεσδήποτε τυχαίες μεταβλητές X, Y, με πεπερασμένες διασπορές ισχύει ότι Cov(X, Y Var(XVar(Y. (.5 Αν η (.5 ισχύει ως ισότητα, τότε υπάρχουν a, b R τέτοια ώστε Y ax + b. Απόδειξη. Θεωρούμε την συνάρτηση f(t : Var(Y tx Var(Y + t Var(X tcov(x, Y με t R. Εφ όσον η f(t είναι διασπορά ϑα είναι υποχρεωτικά f(t για κάθε t R. Συνεπώς η διακρίνουσα του τριωνύμου ϑα είναι αρνητική ή μηδέν, πράγμα που σημαίνει ότι (Cov(X, Y Var(XVar(Y. Από την σχέση αυτή προκύπτει άμεσα η (.5. Αν η (.5 ισχύει ως ισότητα τότε η διακρίνουσα του τριωνύμου είναι και υπάρχει ακριβώς μια τιμή του t, έστω t a τέτοια ώστε f(a. Αυτό όμως σημαίνει ότι Var(Y ax και συνεπώς ότι P(Y ax b με b E[Y ax] από το πόρισμα της ανισότητας του Chebyshev. Η τιμή του a είναι Cov(X,Y Var(X. Ορισμός.3. Η ποσότητα Cov(X, Y ρ : Var(XVar(Y ονομάζεται συντελεστής συσχέτισης και παίρνει τιμές στο διάστημα [, ]. (.6 Το γεγονός ότι ο συντελεστής συσχέτισης ανήκει πάντα στο διάστημα [, ] είναι απόρροια της ανισότητας Cauchy Schwarz. 7
28 .4 Ο Νόμος των Μεγάλων Αριθμών Θεώρημα.6. Αν X, X, X 3,... είναι μια ακολουθία από ανεξάρτητες, ισόνομες τυχαίες μεταβλητές με μέσο µ και διασπορά σ τότε ο αριθμητικός μέσος X +X + +X n n πιθανότητα στην μέση τιμή όταν το n δηλαδή ( X + X + + X n P n τείνει κατά µ > ɛ ɛ > όταν n. (.7 Απόδειξη. Ας ϑέσουμε Y n : n (X + + X n. Θα έχουμε EY n n (µ + + µ µ από την γραμμικότητα της μέσης τιμής και αφού οι X i, i,,..., n, είναι ανεξάρτητες ϑα έχουμε επίσης ότι Var(Y n n (σ + + σ σ n. Το αριστερό μέλος της (.7 γράφεται ως P( Y n µ ɛ και από την ανισότητα του Chebyshev έχουμε ότι P( Y n µ > ɛ Var(Y n ɛ σ nɛ. Για ɛ > οσοδήποτε μικρό αλλά σταθερό, καθώς το n τείνει στο άπειρο το δεξί μέλος της παραπάνω σχέσης τείνει στο μηδέν! Αυτό αποδεικνύει την (.7. (Ισόνομες τυχαίες μεταβλητές είναι τυχαίες μεταβλητές που έχουν τον ίδιο «νόμο πιθανοτήτων» δηλαδή την ίδια κατανομή. Η υπόθεση αυτή δεν ήταν πραγματικά α- παραίτητη εδώ. Αρκεί οι τυχαίες μεταβλητές να είναι ανεξάρτητες (ή ακόμα και απλά ασυσχέτιστες και να έχουν την ίδια μέση τιμή και διασπορά..5 Κατανομή του αθροίσματος ανεξαρτήτων τ.μ. Εστω X, Y, ανεξάρτητες τ.μ. με δεδομένες κατανομές P(X n, P(Y m, n, m,,,.... Εστω Z X + Y, το άθροισμα των δύο τ.μ. Η κατανομή της Z υπολογίζεται ως εξής P(Z k P(X + Y k k P(X n, Y k n n k P(X np(y k n. (.8 n Η τελευταία σχέση οφείλεται στην ανεξαρτησία των X και Y το δε άθροισμα ονομάζεται συνέλιξη των δύο κατανομών. 8
29 Παράδειγμα.. Εστω X διωνυμική τ.μ. με παραμέτρους n και p δηλαδή P(X i ( n i p i q n i, για i,,,..., n, όπου q p. Η τ.μ. Y είναι επίσης διωνυμική με παραμέτρους m και p και ανεξάρτητη από την X. Η κατανομή της Z : X + Y δίνεται τότε από την συνέλιξη των δύο διωνυμικών κατανομών δηλαδή P(Z k k P(X ip(y k i i k ( ( n m p k q m+n k i k i i ( m + n p k q m+n k. k k i ( ( n m p i q n i p k i q m k+i i k i Στην τελευταία εξίσωση της παραπάνω σχέσης χρησιμοποιήσαμε την συνδυαστική ταυτότητα k ( n i i ( m k i ( m + n k. (.9 Παράδειγμα.3. Εστω X, Y ανεξάρτητες γεωμετρικές τ.μ. με παράμετρο p. Η κατανομή της Z : X + Y δίνεται από την συνέλιξη P(Z k k k P(X ip(y k i pq i pq k i i (k q k p. i (Η κατανομή αυτή όπως ϑα δούμε αργότερα είναι μια ειδική περίπτωση της αρνητικής διωνυμικής κατανομής ή κατανομής Pascal. Παράδειγμα.4. Εστω X τ.μ. Poisson με παράμετρο α, δηλαδή P(X k αk k! e α, k,,,.... Η τ.μ. Y είναι επίσης Poisson με παράμετρο α και ανεξάρτητη της X. Η κατανομή της Z : X + Y δίνεται τότε από την συνέλιξη των δύο κατανομών Poisson δηλαδή P(Z k k P(X np(y k n n e (α +α k n (α + α k e (α +α. k! k α n n! e α n α n α k n n! (k n! k! e (α +α α k n (k n! e α k n ( k α n n αk n Επομένως το άθροισμα δύο ανεξαρτήτων τ.μ. Poisson είναι πάλι Poisson με παράμετρο το άθροισμα των παραμέτρων. 9
30 .6 Παραδείγματα. Ας υποθέσουμε ότι ρίχνουμε δύο ζάρια διακριτά μεταξύ τους, π.χ. ένα κόκκινο και ένα πράσινο. Εστω X το αποτέλεσμα της ρίψης του κόκκινου ζαριού και Y το αποτέλεσμα της ρίψης του πράσινου. Η από κοινού κατανομή των X, Y, δίνεται από τον πίνακα Y/X /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 3 /36 /36 /36 /36 /36 /36 4 /36 /36 /36 /36 /36 /36 5 /36 /36 /36 /36 /36 /36 6 /36 /36 /36 /36 /36 /36 Εστω Z : min(x, Y και W : max(x, Y το μικρότερο και το μεγαλύτερο από τα δύο αποτελέσματα των δύο ζαριών. Οι Z και W είναι βεβαίως τυχαίες μεταβλητές. Η από κοινού κατανομή της X και της Z είναι Z/X /36 /36 /36 /36 /36 /36 5/36 /36 /36 /36 /36 3 4/36 /36 /36 /36 4 3/36 /36 /36 5 /36 /36 6 /36 (Κενές τιμές στον πίνακα είναι μηδέν. Δεν είναι δύσκολο να καταλάβουμε πώς συμπληρώνεται αυτός ο πίνακας. Για παράδειγμα P(X, Z 3 αφού είναι αδύνατον το μικρότερο από τα αποτελέσματα να είναι μεγαλύτερο από τό ελάχιστο των δύο. P(X 3, Z P(X 3, Y /36 αφού σ αυτή την περίπτωση η τιμή του Z αποκαλύπτει και την τιμή του Y. Τέλος P(X 3, Z 3 P(X 3, Y + P(X 3, Y + P(X 3, Y 3 3/36. Οι υπόλοιπες τιμές συμπληρώνονται με παρόμοιο τρόπο. Εντελώς ανάλογα μπορούμε να δούμε ότι W/X /36 /36 /36 3 /36 /36 3/36 4 /36 /36 /36 4/36 5 /36 /36 /36 /36 5/36 6 /36 /36 /36 /36 /36 6/36 3
31 Τέλος η από κοινού κατανομή του maximum και του minimum είναι W/Z /36 /36 /36 3 /36 /36 /36 4 /36 /36 /36 /36 5 /36 /36 /36 /36 /36 6 /36 /36 /36 /36 /36 /36 Για να καταλάβουμε πώς συμπληρώνεται ο τελευταίος πίνακας παρατηρούμε ότι P(W, Z P(X, Y /36. Τό ίδιο ισχύει βέβαια και για τα άλλα διαγώνια στοιχεία. Παρόμοια, P(W, Z 4 αφού το maximum δεν μπορεί να είναι μικρότερο από το minimum. Τέλος P(W 4, Z P(X, Y 4 + P(X 4, Y /36. Ας υπολογίσουμε τώρα τις περιθώριες κατανομές των Z και W. Θα χρησιμοποιήσουμε τον τρίτο πίνακα αλλά ϑα μπορούσαμε εναλλακτικά να χρησιμοποιήσουμε και τους δύο πρώτους. Εχουμε W /36 3/36 5/36 7/36 9/36 /36 Z /36 9/36 7/36 5/36 3/36 /36 Η μέση τιμή της W είναι EW 36 ( , 47. Δεν πρέπει να μας εκπλήσσει το γεγονός ότι η μέση τιμή της W είναι μεγαλύτερη από την EX 3, 5. Την μέση τιμή της Z ϑα μπορούσαμε να την υπολογίσουμε από τον ορισμό. Ομως είναι απλούστερο (και πιο διδακτικό να παρατηρήσουμε ότι X + Y min(x, Y + max(x, Y Z + W. Από την γραμμικότητα της μέσης τιμής ϑα έχουμε EX + EY EZ + EW και συνεπώς EZ 7 4, 47, 578. Οι διασπορές υπολογίζονται επίσης από τον ορισμό: Var(X, 967, Var(W Var(Z, 975. Παρατηρείστε ότι λόγω συμμετρίας οι διασπορές των Z και W είναι ίσες. Οι συνδιακυμάνσεις που υπολογίζονται από τον ορισμό είναι Cov(X, Z, 4583, Cov(X, W, 4583, Cov(Z, W, 945. Τέλος οι συντελεστές συσχέτισης είναι ρ XZ, 68, ρ XW, 68, ρ ZW, Παρατηρείστε ότι όλοι οι συντελεστές συσχέτισης είναι ϑετικοί. Αυτό είναι αναμενόμενο. Αν ξέρουμε ότι το X είναι μεγάλο τότε το minimum των X και Y επίσης ϑα τείνει 3
32 να είναι μεγαλύτερο από τη μέση του τιμή, όπως και το maximum. Αν ξέρουμε ότι το minimum είναι μεγαλύτερο από την μέση του τιμή τότε και το maximum ϑα τείνει να είναι μεγαλύτερο από τη δική του μέση τιμή. Ομως η γνώση του X μας δίνει μεγαλύτερη πληροφορία για το maximum απ ότι η γνώση του minimum και γι αυτό ρ XZ > ρ WZ..7 Ασκήσεις Πρόβλημα.. Εστω X, X ανεξάρτητες τυχαίες μεταβλητές Poisson με παραμέτρους α, α αντίστοιχα. Αν S X + X είναι το άθροισμά τους να ευρεθεί η πιθανότητα P(X k S n, k,,,..., n. Πρόβλημα.. X i, i,, 3, είναι ανεξάρτητες τυχαίες μεταβλητές με κατανομή Poisson με παραμέτρους α i αντίστοιχα. Αν W X + X 3 και V X + X 3 να υπολογίσετε τους μέσους των W, V, τις διακυμάνσεις, την συνδιακύμανση και τον συντελεστή συσχέτισης. Να υπολογίσετε επίσης και την από κοινού κατανομή των W και V. Πρόβλημα.3. Η από κοινού κατανομή των τυχαίων μεταβλητών X, Y, που παίρνουν τιμές στο σύνολο {,, } δίδεται από τον πίνακα /6 /6 /6 /6 /6 /6 Y/X Να ευρεθούν οι μέσοι, οι διακυμάνσεις και η συνδιακύμανση των X, Y. Είναι οι X, Y ανεξάρτητες;.8 Πιθανογεννήτριες Εστω X μια διακριτή τυχαία μεταβλητή με κατανομή P(X k p k, k,,,.... Η πιθανογεννήτρια της X είναι η συνάρτηση G(z : p k z k (. Η μεταβλητή z παίρνει πραγματικές τιμές (στις εφαρμογές που ϑα συζητήσουμε και κυμαίνεται στο διάστημα στο οποίο η σειρά (. συγκλίνει. Παρατηρείστε ότι η (. σημαίνει ότι G(z : E[z X ]. k 3
33 Η σειρά (. που ορίζει την πιθανογεννήτρια συγκλίνει τουλάχιστον όταν z [, ]. Συμβολίζουμε με G (k (z την παράγωγο τάξης k υπολογισμένη στην τιμή z. Τότε p k k! G(k (, k,,,..., (. Παρατηρούμε ότι η κατανομή {p k } προφανώς προσδιορίζει με μοναδικό τρόπο την πι- ϑανογεννήτρια G(z αλλά και η πιθανογεννήτρια G(z προσδιορίζει με μοναδικά την κατανομή {p k } μέσω της (.. Οι πιθανογεννήτριες είναι ιδιαίτερα χρήσιμες για τον προσδιορισμό της κατανομής αθροισμάτων ανεξάρτητων διακριτών τυχαίων μεταβλητών. Αν οι X, Y, είναι α- νεξάρτητες τυχαίες μεταβλητές με πιθανογεννήτριες G X (z, G Y (z αντίστοιχα, η πι- ϑανογεννήτρια του αθροίσματος Z X + Y είναι G Z (z G X (zg Y (z. Πράγματι, G Z (z E[z X+Y ] E[z X z Y ] Ez X Ez Y, όπου, η τελευταία ισότητα ισχύει λόγω της ανεξαρτησίας των X, Y. Η σχέση αυτή επεκτείνεται επαγωγικά για οποιοδήποτε πεπερασμένο πλήθος ανεξάρτητων τ.μ.. Αν X i, i,,..., n είναι ανεξάρτητες, ισόνομες τ.μ. με (κοινή πιθανογεννήτρια G X (z, τότε το άθροισμά τους S n : X + + X n έχει πιθανογεννήτρια G Sn (z (G X (z n. Παρ ότι η πιθανογεννήτρια του αθροίσματος S n προκύπτει εύκολα ως το γινόμενο των πιθανογεννητριών των X i, η κατανομή της S n είναι δυσκολότερο να υπολογιστεί. Βάσει των ανωτέρω, P(S n k d k k! dz k (G X(z n, z μια ποσότητα η οποία, εν γένει, δεν είναι εύκολο να υπολογιστεί..8. Παραδείγματα πιθανογεννητριών.8. Η κατανομή Bernoulli Η τυχαία μεταβλητή X { με πιθανότητα q με πιθανότητα p όπου p [, ] και q p ονομάζεται Bernoulli. Η κατανομή Bernouli ειναι η πλέον στοιχειώδης και αποτελεί δομικό λίθο για πιο περίπλοκες κατανομές. Η πιθανογεννήτρια της κατανομής αυτής είναι G(z z P(X + z P(X + z P(X + q + pz. Η μέση τιμή της X είναι E[X] G ( p. Η δεύτερη παραγοντική ροπή είναι E[X(X ] G (. Συνεπώς E[X X] και E[X ] E[X], δηλαδή E[X ] p. Συνεπώς Var(X E[X ] (E[X] p p p( p pq. 33
34 .8.3 Η Διωνυμική κατανομή Μια τυχαία μεταβλητή X με κατανομή ( n P(X k p k q n k, k αν k,,,..., n και διαφορετικά ονομάζεται διωνυμική. Περιγράφει την πιθανότητα να έχουμε k επιτυχίες σε n ανεξάρτητες δοκιμές, κάθε μια από τις οποίες έχει πιθανότητα επιτυχίας p [, ] (και πιθανότητα αποτυχίας q p. Η πιθανογεννήτρια της διωνυμικής κατανομής είναι G(z n k ( n p k q n k z k (q + pz n k όπου στην τελευταία σχέση χρησιμοποιήσαμε το διωνυμικό ϑεώρημα. Ο μέσος και η διασπορά μπορούν να υπολογισθούν από την πιθανογεννήτρια ως εξής: G (z np(q+ pz n και G (z n(n p (q + pz n (υποθέτουμε ότι n. E[X] G ( np (χρησιμοποιήσαμε το γεγονός ότι p + q. E[X(X ] n(n p. Συνεπώς E[X ] n(n p + E[X] n(n p + np και κατά συνέπεια Var(X E[X ] (E[X] n(n p + np n p np np np( p npq..8.4 Η κατανομή Poisson Η τυχαία μεταβλητή X έχει κατανομή Poisson με παράμετρο α > αν Η πιθανογεννήτριά της δίδεται από την G(z k P(X k k! αk e α, k,,,.... z k k! αk e α e α k! (αzk e α e zα e α( z. k Η μέση τιμή και η διασπορά της κατανομής Poisson υπολογίζεται εύκολα ως EX Var(X α. Μια από τις σημαντικότερες ιδιότητες της κατανομής Poisson είναι ότι προκύπτει ως το όριο της διωνυμικής κατανομής Binom(n, α/n όταν n (δηλαδή στην περίπτωση που έχουμε ένα μεγάλο αριθμό ανεξάρτητων δοκιμών, n, η κάθε μια από τις οποίες έχει μικρή πιθανότητα επιτυχίας, α/n. Αυτό είναι εύκολο να διαπιστωθεί εξετάζοντας την πιθανογεννήτρια της διωνυμικής κατανομής (n, α/n και παίρνοντας το όριο n. Πράγματι, ( lim α ( n n n n + zα lim n 34 α( z n e α( z n
35 το οποίο δείχνει ότι Binom(α/n, n Poi(α όταν n. Ισχύει επίσης ότι, αν X, X είναι ανεξέαρτητες τυχαίες μεταβλητές Poisson με παραμέτρους α, α αντίστοιχα, τότε X + X Poi(α + α. Ο απλούστερος τρόπος να το διαπιστώσουμε είναι να εξετάσουμε την πιθανογεννήτρια Ez X +X Ez X Ez X e α ( z e α ( z e (α +α ( z..8.5 Η Γεωμετρική Κατανόμή Η τυχαία μεταβλητή X είναι γεωμετρική με παράμετρο p όταν η κατανομή της δίδεται από την P(X k q k p, k,, 3,..., (. όπου p (, και q p. δίδεται από την σχέση G(z Η πιθανογεννήτρια συνάρτηση της κατανομής αυτής q k pz k k ( qz qz. (.3 Η παράμετρος p ονομάζεται συνήθως πιθανότητα επιτυχίας και η τιμή της X είναι ο αριθμός των ανεξάρτητων δοκιμών που απαιτούνται μέχρι την πρώτη επιτυχία αν κάθε δοκιμή έχει πιθανότητα επιτυχίας p. Εναλλακτικά, μπορούμε να εξετάσουμε τον αριθμό των αποτυχιών, Y, μέχρι την πρώτη επιτυχία. Στην περίπτωση αυτή Y X και με πιθανογεννήτρια P(Y k q k p, k,,,..., (.4 Ez Y q qz. (.5 Μπορούμε να δούμε εύκολα ότι EY q/p και Var(Y q/p. Επίσης, EX +EY /p και Var(X Var(Y q/p..8.6 Η Αρνητική Διωνυμική Κατανομή (Κατανομή Pascal Ξεκινάμε με τον ορισμό του διωνυμικού συντελεστή στην περίπτωση που a R και n N ως ( a a(a... (a n + :. n n! Αν ο a είναι φυσικός αριθμός τότε ( a n για κάθε n > a. Αν ο a είναι αρνητικός ακέραιος ή μη ακέραιος πραγματικός αριθμός, τότε ( a n για κάθε n N. Σύμφωνα με το διωνυμικό ϑεώρημα, για κάθε x < και α R: ( + x α k 35 ( α x k. (.6 k
36 (Αν ο α είναι ϑετικός ακέραιος τότε ( α k για κάθε k α +, α +, και συνεπώς η άπειρη σειρά (.6 γίνεται ένα άθροισμα με πεπερασμένο πλήθος όρων: ( + x α x k. α ( α k k Ο διωνυμικός συντελεστής ( α n γράφεται ως ( α n ( α( α ( α n + ( α n + n! n (α + n (α + n (α + α ( n! Συνεπώς, για κάθε x < ισχύει η ταυτότητα ( x α k ( α + n ( n. n ( α ( α + k ( x k x k. (.7 k k k Αν p (, και q p τότε η αρνητική διωνυμική κατανομή με παραμέτρους p και α > ορίζεται ως ( α + k P(X k p α q k, k,,,.... (.8 k Η παραπάνω έκφραση ορίζει πράγματι μια κατανομή πιθανότητας στους μη αρνητικούς ακεραίους δεδομένου ότι ( α+k k > όταν α > για κάθε k N και ( α+k k k p α q k p α ( q α, λόγω της σχέσης (.7. Η πιθανογεννήτρια της αρνητικής διωνυμικής κατανομής δίδεται από την G(z ( α + k k k p α q k z k ( p α. qz Η μέση τιμή της αρνητικής διωνυμικής τυχαίας μεταβλητής X είναι EX G ( αq pα ή ( q α+ EX α q p. ( Ομοίως, EX(X G ( α(α + q pα α(α + q. ( q p Τηυς ωε ηαε EX ( α+ ( ( α(α + q p + α q p ανδ τηυς Var(X α(α + q p + α q p (α q p α q p + q p ή Var(X α q p. Οταν α m N η αρνητική διωνυμική κατανομή είναι η κατανομή του αθροίσματος m ανεξάρτητων τυχαίων μεταβλητών γεωμετρικά κατανεμημένων (του τύπου (.4», η κάθε μια με πιθανότητα επιτυχίας p. Αυτό αποδεικνύεται εύκολα με την βοήθεια των πιθανογεννητριών. 36
37 Επίσης E[X(X (X k + ] G (k (. (.9 Η έκφραση (.9 ονομάζεται κατιούσα παραγοντική ροπή τάξης k. Οι συνήθεις ροπές μπορούν να υπολογιστούν από αυτές. 37
38 38
39 Κεφάλαιο 3 Πολυμεταβλητές Κατανομές 3. Πολυωνυμική Κατανομή Εστω ένα πείραμα που μπορεί να έχει m διαφορετικά αποτελέσματα, τα οποία ονομάζουμε a, a,..., a m. Η πιθανότητα το αποτέλεσμα του πειράματος να είναι το a i είναι p i και m i p i. Ενα τέτοιο παράδειγμα είναι η η ρίψη ενός τίμιου ζαριού όπου υπάρχουν έξι διαφορετικά ισοπίθανα αποτελέσματα. Εκτελούμε το πείραμα n φορές και υποθέτουμε ότι κάθε επανάληψη είναι ανεξάρτητη από όλες τις άλλες. Εστω X ο αριθμός των πειραμάτων στα οποία το αποτέλεσμα ήταν a, X ο αριθμός των πειραμάτων στα οποία το αποτέλεσμα ήταν a και X n ο αριθμός των πειραμάτων στα οποία το αποτέλεσμα ήταν a m. Τα X, X,..., X m είναι τυχαίες μεταβλητές οι οποίες βεβαίως δεν είναι ανεξάρτητες μεταξύ τους. Ισχύει μάλιστα, αναγκαστικά, ότι X + X + + X m n. Η από κοινού κατανομή των τυχαίων αυτών μεταβλητών ονομάζεται πολυωνυμική. Αν n, n,..., n m είναι μη αρνητικοί ακέραιοι, τέτοιοι ώστε m i n i n, τότε ( n P(X n, X n,..., X m n m p n n, n,..., n pn pnm m. (3. m Ας δούμε πρώτα ένα παράδειγμα. Εστω ένα πείραμα που έχει τρία δυνατά αποτελέσματα, τα a, a, και a 3 τα οποία συμβαίνουν με πιθανότητες p, p και p 3 αντίστοιχα, όπου βεβαίως p + p + p 3 εφόσον ένα από τα τρία αποτελέσματα ϑα συμβεί κάθε φορά. Ας υποθέσουμε ότι το εκτελούμε φορές και κάθε επανάληψη είναι ανεξάρτητη από όλες τις άλλες. X i, i,, 3, είναι ο αριθμός των πειραμάτων των οποίων το αποτέλεσμα ήταν a i. Ας υπολογίσουμε την πιθανότητα P(X 3, X 5, X 3. Η πιθανότητα να έχουμε τα αποτελέσματα a a a a a a a a a 3 a 3 είναι p 3 p5 p 3 λόγω της ανεξαρτησίας των πειραμάτων. Η πιθανότητα μιας οποιασδήποτε άλλης πραγματοποίησης με 3 a, 5 a και a 3 είναι η ίδια. Το μόνο ϑέμα που υπάρχει 39
40 είναι να δούμε πόσες διαφορετικές πραγματοποιήσεις υπάρχουν με τον συγκεκριμένο αριθμό των τριών αποτελεσμάτων, με πόσους διαφορετικούς τρόπους δηλαδή μπορούμε να βάλουμε στη σειρά 3 a, 5 a και a 3. Αυτός ο αριθμός όμως είναι ο αριθμός των επαναληπτικών μεταθέσεων που είναι ( 3,5, 5. Συνεπώς P(X 3, X 5, X 3 ( 3,5, p 3 p 5 p 3. Ως ένα δεύτερο παράδειγμα επιβεβαιώστε ότι η πιθανότητα σε 6 ρίψεις ενός τιμίου ζαριού να έχουμε δυάρια, τεσσάρια και εξάρια είναι ( 6 (,,,,, 6 ( 6 ( 6 ( 6 ( 6 ( 6 6!, 9.!!!!!! 66 Η από κοινού κατανομή του αριθμού των διαφορετικών αποτελεσμάτων, (X, X,..., X m, ονομάζεται πολυωνυμική κατανομή. Το αθροισμα των πολυωνυμικών πιθανοτήτων (3. για όλα τα n, n,..., n m τέτοια ώστε m i n i n είναι μονάδα λόγω του πολυωνυμικού ϑεωρήματος: {(n,...,n m: m i n in} ( n n, n,..., n m p n pn pnm m (p + + p m n n. Η περιθώρια κατανομή της X i μπορεί να υπολογισθεί αθροίζοντας τις πολυωνυμικές πιθανότητες. Ας δούμε ξανά το πείραμα που έχει τρία διαφορετικά αποτελέσματα, a, a, και a 3 τα οποία συμβαίνουν με πιθανότητες p, p και p 3 αντίστοιχα, όπου p + p + p 3, και το οποίο επαναλαμβάνουμε ανεξάρτητα n φορές. Εστω X, X, X 3, ο αριθμός των αποτελεσμάτων τύπου a, a, και a 3 στις n επαναλήψεις. Η από κοινού κατανομή των (X, X, X 3 ϑα είναι, σύμφωνα με τον τύπο (3. για m 3, P(X i, X j, X 3 k ( n p i i, j, k pj pk 3. (3. Για να βρούμε την περιθώρια κατανομή του X αρκεί να αθροίσουμε ως εξής: P(X i {(j,k:j+kn i, j,k N } ( n p i i, j, k pj pk 3 i,,,..., n. Λαμβάνοντας υπ όψιν ότι i + j + k n και ( n i, j, k n! (n i! (n i!i! (n i j!j! 4 ( ( n n i i j
41 η παραπάνω έκφραση γράφεται ισοδύναμα ως P(X i n i ( ( n n i i j j ( n i p i (p + p 3 n i p i pj pn i j 3 ( n n i ( n i p i p j i j pn i j 3 j ( n p i i ( p n i (3.3 όπου, στην προτελευταία ισότητα χρησιμοποιήσαμε το διωνυμικό ϑεώρημα και στην τελευταία το γεγονός ότι p + p 3 p. Από την (3.3 είναι σαφές ότι η X έχει Διωνυμική κατανομή με πιθανότητα επιτυχίας p και αριθμό δοκιμών n. Αυτό μπορεί να το καταλάβει κανείς άμεσα ϑεωρόντας ότι το πείραμα δεν έχει τρία αποτελέσματα αλλά μόνο δύο: το αποτέλεσμα a που συμβαίνει με πιθανότητα p και το αποτέλεσμα «όχι a» (δηλαδή a ή a 3 που συμβαίνει με πιθανότητα p + p 3 p. Με τον ίδιο ακριβώς τρόπο μπορούμε να αποδείξουμε γενικά (και οι δείκτες δεν πρέπει να μας αποθαρρύνουν ότι η περιθώριος κατανομή του X i για την γενική πολυωνυμική κατανομή (3. είναι διωνυμική: ( n P(X i n i p n i i ( p i n n i, n i,,..., n. (3.4 n i Από τις ιδιότητες της διωνυμικής κατανομής συμπεραίνουμε ότι EX i np i και Var(X i np i ( p i. Στη συνέχεια μπορούμε να υπολογίσουμε την από κοινού κατανομή των (X, X για την πολυωνυμική κατανομή (3. με τρία διαφορετικά αποτελέσματα. Αν i, j είναι δύο μη αρνητικοί ακέραιοι τέτοιοι ώστε i+j n τότε, λαμβάνοντας υπ όψιν ότι i+j+k n έχουμε P(X i, X j ( n p i i, j, k pj pk 3 ( n p i i, j, n i j pj ( p p n i j, i + j n. Προκειμένου να υπολογίσουμε την συνδιακύμανση των X, X, υπολογίζουμε πρώτα την μέση τιμή του γινομένου ( n E[X X ] ij p i i, j, n i j pj ( p p n i j {(i,j: i+j n, i, j } {(i,j: i+j n, i, j } n(n p p n! (i!(j!(n i j! pi pj ( p p n i j {(i,j: i +j n, i, j } 4 (n! (i!(j!(n (i (j! p i p j ( p p n (i (j.
42 Αν ϑέσουμε i i, j j, το τελευταίο σκέλος της παραπάνω εξίσωσης γράφεται ως n(n p p {(i,j : i +j n, i, j } (n! i!j!(n i j! pi pj ( p p n i j Ας ϑέσουμε k n i j. Παρατηρείστε ότι όταν προσδιορίζονται τα i, j, προσδιορίζεται ταυτόχρονα και το k. Το παραπάνω άθροισμα μπορεί να γραφτεί ισοδύναμα ως n(n p p {(i,j,k : i +j +k n, i,j,k } (n! i!j!k! pi pj ( p p k n(n p p (p + p + p p n n(n p p (3.5 όπου χρησιμοποιήσαμε το πολυωνυμικό ϑεώρημα. Συνεπώς Cov(X, X E[X X ] EX EX n(n p p np np np p. (3.6 Ο συντελεστής συσχέτισης ανάμεσα στο X και X είναι np p ρ np ( p np ( p p p ( p ( p. (3.7 Παρατηρήστε ότι ο συντελεστής συσχέτισης είναι αρνητικός. Αυτό είναι λογικό. Δεδομένου ότι ο αριθμός των πειραμάτων είναι σταθερός, αν έχουμε μεγάλο αριθμό αποτελεσμάτων a τότε αναγκαστικά ϑα τείνουμε να έχουμε μικρότερο αριθμό αποτελεσμάτων a. Πρόβλημα 3.. Ρίχνουμε ένα ζάρι φορές. Ποιά είναι η πιθανότητα να πάρουμε 4 εξάρια, 3 πεντάρια, τεσσάρια και ένα τριάρι (με οποιαδήποτε σειρά; ( (Απ. 4,3,, Η πολυμεταβλητή υπεργεωμετρική κατανομή Ας υποθέσουμε ότι σε μια κάλπη έχουμε K μπάλες χρώματος, K μπάλες χρώματος, κλπ. και K m μπάλες χρώματος m. Συνολικά δηλαδή στην κάλπη υπάρχουν N : K + K + + K m μπάλες, ασχέτως χρώματος. Από αυτές παίρνουμε, χωρίς ε- πανατοποθέτηση, n μπάλες με n N. Εστω X i ο αριθμός των μπαλών χρώματος i, i,,..., m στο δείγμα μεγέθους n που πήραμε. Τότε P(X n, X n,..., X m n m ( K ( K ( n n Km ( N, n i N, n nm m n i n. (3.8 Επισημαίνουμε πάλι ότι μπορούμε να χρησιμοποιήσουμε την παραπάνω έκφραση α- κόμα και στην περίπτωση που n i > K i μια και ο αντίστοιχος διωνυμικός συντελεστής 4 i
43 μηδενίζεται. Συνεπώς μπορούμε να χρησιμοποιήσουμε την έκφραση (3.8 για κάθε διάνυσμα μη αρνητικών ακεραίων (n,..., n m. Ο λόγος που ισχύει η (3.8 είναι ότι μπορούμε να διαλέξουμε n i μπάλες χρώματος i από K i που υπάρχουν στην κάλπη με ( K n i τρόπους ενώ μπορούμε να διαλέξουμε n μπάλες ασχέτως χρώματος από τις N που υπάρχουν στην κάλπη με ( N n τρόπους. Ας επαληθεύσουμε τώρα ότι {(n,...,n m} : m i n in P(X n,..., X m n m. (3.9 Προκειμένου να το δείξουμε αρκεί να δούμε ότι Ας εξετάσουμε το γινόμενο {(n,...,n m} : m i n in ( ( K K n n ( Km n m ( N. (3. n Ο συντελεστής του όρου x n xn xnm m ( + x K ( + x K ( + x m Km. ( ( K K n ϑα είναι n Αν ϑέσουμε τώρα x x x m x τότε ( Km n m. ( + x K ( + x K ( + x Km ( + x N (3. Με βάση τις παραπάνω παρατηρήσεις, ο συντελεστής του x n (n N m i K i στο αριστερό μέλος της (3. δίνεται από το αριστερό μέλος της (3. ενώ ο συντελεστής του x n στο δεξί μέλος της (3. δίνεται από το δεξί μέλος της (3.. Η περιθώρια κατανομή του X i είναι εύκολο να διαπιστώσουμε ότι είναι υπεργεωμετρική. Αρκεί να ϑεωρήσουμε ότι όλες οι μπάλες που δεν είναι χρώματος i είναι κάποιου άλλου χρώματος που δεν μας ενδιαφέρει και να διαπιστώσουμε ότι P(X i n i ( Ki ( N Ki n i n n i ( N n, n i,,..., n. (3. Με τον ίδιο τρόπο μπορούμε να δούμε ότι η από κοινού κατανομή των X i, X j είναι P(X i n i, X n j ( Ki ( Kj ( N Ki K j n i n j n n i n j ( N, n i + n j n. (3.3 n 43
44 Η μέση τιμή και η διασπορά των X i, X j δίνεται από τις γνωστές εκφράσεις για την υπεργεωμετρική κατανομή. EX i n K i N, Var(X i n K i N N K i N N n N. (3.4 Για να προσδιορίσουμε την συνδιακύμανση αρκεί να δούμε ότι EX X (n,n : n i,n j,{n +n n} K ik j ( N n {(n,n : n i,n, n +n n} ( Ki ( Kj n n n i ( N n ( N Ki K j n j n n i n j ( ( ( Ki Kj N Ki K j n i n j n n i n j Αν ϑέσουμε l i n i, l j n j η παραπάνω σχέση μπορεί να γραφεί ως EX X K ik j ( ( ( Ki Kj N (Ki (K j ( N n l i l j n l i l j {(l,l : l i,l, l +l n } ( N n K K K K ( N n(n n N(N. Συνεπώς η συνδιακύμανση των X, X είναι K K Cov(X, X E[X X ] EX EX n(n N(N nk N nk N n(n n K K N N N. (3.5 Τέλος ο συντελεστής συσχέτισης προσδιορίζεται εύκολα από την (3.5 και την (3.4 και μετά από εύκολες απλοποιήσεις προκύπτει ότι K i K j ρ (N K i (N K j. (3.6 Πρόβλημα 3.. Ενα κιβώτιο περιέχει χίλιους λαμπτήρες, από τους οποίους δεν λειτουργούν. Οι χίλιοι αυτοί λαμπτήρες τοποθετούνται τυχαία σε κουτιά. Ποιά είναι η πιθανότητα και οι χαλασμένοι λαμπτήρες να βρεθούν στο ίδιο κουτί; Αν X i, i,,...,, είναι ο αριθμός των χαλασμένων δοχείων στο κουτί i, ποιά είναι η από κοινού κατανομή των τυχαίων μεταβλητών αυτών; Πρόβλημα 3.3. Μια κάλπη έχει N σφαιρίδια που γράφουν τον αριθμό, N που γράφουν τον αριθμό και N 3 που γράφουν τον αριθμό 3. Διαλέγω (χωρίς επανατοποθέτηση n σφαιρίδια. Αν X i ο αριθμός των σφαιριδίων, μεταξύ αυτών που επέλεξα, που γράφουν τον αριθμό i, i,, 3, να βρείτε την από κοινού κατανομή των X, X, X 3. Επίσης να ευρεθούν οι μέσοι, διακυμάνσεις και συνδιακυμάνσεις. 44
45 Κεφάλαιο 4 Από κοινού κατανομή δύο συνεχών τυχαίων μεταβλητών 4. Από κοινού συνάρτηση κατανομής δύο συνεχών τυχαίων μεταβλητών Εστω X, Y, δύο τυχαίες μεταβλητές. Η από κοινού συνάρτηση κατανομής είναι η συνάρτηση F(x, y : P(X x, Y y, x, y R. (4. Η από κοινού συνάρτηση κατανομής έχει τις εξής ιδιότητες:. Είναι αύξουσα ως προς κάθε ένα από τα δύο ορίσματα, δηλαδή αν x x και y y τότε F(x, y F(x, y και F(x, y F(x, y. (4.. Ισχύει ότι lim Y(y x (Η περιθώρια συνάρτηση κατανομής της Y lim X(x y (Η περιθώρια συνάρτηση κατανομής της X lim F(x, y x y lim F(x, y x για κάθε y και lim F(x, y y για κάθε x. 3. Για κάθε x < x και y < y ισχύει ότι P(x < X x, y < Y y F(x, y F(x, y F(x, y + F(x, y. (4.3 Η ϑεμελιώδης σχέση (4.3 αποδεικνύεται ως εξής: Ορίζουμε τα σύνολα A {X x, Y y }, A {X x, Y y }, A {X x, Y y }, A {X x, Y y }, R {x < X x, y < Y y }. 45
46 Παρατηρείστε ότι R (A A και ότι A R (A A. Συνεπώς Επίσης A A A και συνεπώς Από τις παραπάνω σχέσεις προκύπτει ότι P(A P(R + P(A A P(A A P(A + P(A P(A. P(R P(A P(A P(A + P(A. Η απόδειξη είναι πλήρης δεδομένου ότι P(A ij F(x i, y j για i, j {, } και ότι P(R είναι το αριστερό μέρος της ( Μερικές παράγωγοι και διπλά ολοκληρώματα - Μια πρακτική εισαγωγή Θεωρούμε μια συνάρτηση δύο μεταβλητών φ(x, y. Η μερική παράγωγος της φ ως προς την μεταβλητή x συμβολίζεται με xφ και ορίζεται ως το όριο φ(x, y lim x δ Αντίστοιχα ορίζουμε την μερική παράγωγο της φ ως προς y ως φ(x, y lim y δ φ(x + δ, y φ(x, y. (4.4 δ φ(x, y + δ φ(x, y. δ Οπως βλέπουμε από τον ορισμό η μερική παράγωγος ως προς x υπολογίζεται κρατώντας το y σταθερό και παραγωγίζοντας ως προς x. Για παράδειγμα x (x y xy, (e xy + xy x + y ye xy + y, (e xy + xy y + y xe xy x y +, x + y x y x y x + x + y (y x. Η μερικές παράγωγοι φ y, ϑα είναι εν γένει συναρτήσεις των x και y και επομένως (αν είναι παραγωγίσιμες ϑα μπορούμε να τις παραγωγίσουμε εκ νέου. Αποδεικνύεται ότι, ύπο ορισμένες συνθήκες που πάντοτε ικανοποιούνται στις περιπτώσεις που ϑα ( ( εξετάσουμε, οι δεύτερες μερικές παράγωγοι y x φ και x y φ είναι πάντα ίσες. Η κοινή τιμή τους ονομάζεται δεύτερη μεικτή μερική παράγωγος ως προς x και y και συμβολίζεται ως x y φ ή y xφ αφού η σειρά με την οποία εκτελούνται οι παραγωγήσεις δεν επηρρεάζει το τελικό αποτέλεσμα. Δείτε τα ακόλουθα παραδείγματα: ( y x (x y ( (xy x, y x y (x y ( x x y x, φ 46
47 ( (e xy + xy y x + y ( ye xy + (xy e xy y y y ( (e xy + xy x y + y ( xe xy xy x + (xy e xy y 4.. Διπλά ολοκληρώματα Εστω g μια συνάρτηση δύο μεταβλητών ορισμένη σε ένα παραλληλόγραμμο χωρίο του R, g : [a, b] [c, d] R +. Η συνάρτηση αυτή ορίζει μια επιφάνεια αν ϑεωρήσουμε το σύνολο των σημείων του R 3 {(x, y, z : x [a, b], y [c, d], z g(x, y} καθώς επίσης και ένα στερεό, το υποσύνολο του R 3 που απαρτίζεται από τα σημεία S {(x, y, z : x [a, b], y [c, d], z g(x, y}. ( Εχουμε υποθέσει ότι η g παίρνει μη αρνητικές τιμές στο πεδίο ορισμού της. Εστω P x : {x i } i,,...,m μια διαμέριση του [a, b] δηλαδή a x < x < x <... < x m b και παρομοίως P y : {y j } j,,...,n μια διαμέριση του [c, d] με c y < y <... < y n d. Κατ αυτό τον τρόπο διαμερίσουμε το ορθογώνιο [a, b] [c, d] σε m n ορθογώνια, [x i, x i + x i ] [y j, y j + y j ] όπου x i x i+ x i και y j y j+ y j. Συμβολίζουμε την διαμέριση ως P : {(x i, y j } i,,...,m και ως μέγεθός της ορίζουμε την ποσότητα P : j,,...,n max( P x, P y όπου P x max i,,...,m x i και P y : max j,,...,n y j. Αν V είναι ο όγκος του στερεού S τότε η ποσότητα g(x i, y j x i y j (4.5 m n i j αποτελεί μια προσέγγιση του όγκου από ορθογώνια παραλληλεπίπεδα. Αποδεικνύεται ότι, για ομαλές συναρτήσεις g (πρακτικά μιλώντας, σε κάθε περίπτωση που πρόκειται να μας απασχολήσει ο όγκος του στερεού S είναι το όριο του αθροίσματος της (4.5 όταν το μέγεθος της διαμέρισης P τείνει στο (πράγμα που σημαίνει ότι τόσο το m όσο και το n τείνουν στο άπειρο δηλαδή V m lim P i n g(x i, y j x i y j. (4.6 j Στον μαθηματικό λογισμό αποδεικνύεται ότι, κάτω από συνθήκες που πάντα ισχύουν στην πράξη, μπορούμε να υπολογίσουμε το όριο στην (4.6 ως ένα διπλό όριο V lim V lim lim g(x i, y j x i y j, ή ως (4.7 m n P x P y i j lim P y P x j i n m g(x i, y j x i y j. (4.8 47
Κεφάλαιο Η εκθετική κατανομή. Η πυκνότητα πιθανότητας της εκθετικής κατανομής δίδεται από την σχέση (1.1) f(x) = 0 αν x < 0.
 Κεφάλαιο Συνεχείς Τυχαίες Μεταβλητές. Η εκθετική κατανομή Η πυκνότητα πιθανότητας της εκθετικής κατανομής δίδεται από την σχέση f(x) = λe λx αν x, αν x
Κεφάλαιο Συνεχείς Τυχαίες Μεταβλητές. Η εκθετική κατανομή Η πυκνότητα πιθανότητας της εκθετικής κατανομής δίδεται από την σχέση f(x) = λe λx αν x, αν x
Αποδεικτικές Διαδικασίες και Μαθηματική Επαγωγή.
 Αποδεικτικές Διαδικασίες και Μαθηματική Επαγωγή. Mαθηματικό σύστημα Ένα μαθηματικό σύστημα αποτελείται από αξιώματα, ορισμούς, μη καθορισμένες έννοιες και θεωρήματα. Η Ευκλείδειος γεωμετρία αποτελεί ένα
Αποδεικτικές Διαδικασίες και Μαθηματική Επαγωγή. Mαθηματικό σύστημα Ένα μαθηματικό σύστημα αποτελείται από αξιώματα, ορισμούς, μη καθορισμένες έννοιες και θεωρήματα. Η Ευκλείδειος γεωμετρία αποτελεί ένα
Επίλυση ειδικών μορφών ΣΔΕ
 15 Επίλυση ειδικών μορφών ΣΔΕ Σε αυτό το κεφάλαιο θα δούμε κάποιες ειδικές μορφές ΣΔΕ για τις οποίες υπάρχει μέθοδος επίλυσης. Περισσότερες μπορεί να δει κανείς στο Kloeden and Plaen (199), 4.-4.4. Θα
15 Επίλυση ειδικών μορφών ΣΔΕ Σε αυτό το κεφάλαιο θα δούμε κάποιες ειδικές μορφές ΣΔΕ για τις οποίες υπάρχει μέθοδος επίλυσης. Περισσότερες μπορεί να δει κανείς στο Kloeden and Plaen (199), 4.-4.4. Θα
Ας υποθέσουμε ότι ο παίκτης Ι διαλέγει πρώτος την τυχαιοποιημένη στρατηγική (x 1, x 2 ), x 1, x2 0,
 Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Στατιστικής Εισαγωγή στην Επιχειρησιακή Ερευνα Εαρινό Εξάμηνο 2015 Μ. Ζαζάνης Πρόβλημα 1. Να διατυπώσετε το παρακάτω παίγνιο μηδενικού αθροίσματος ως πρόβλημα γραμμικού
Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Στατιστικής Εισαγωγή στην Επιχειρησιακή Ερευνα Εαρινό Εξάμηνο 2015 Μ. Ζαζάνης Πρόβλημα 1. Να διατυπώσετε το παρακάτω παίγνιο μηδενικού αθροίσματος ως πρόβλημα γραμμικού
Ο Ισχυρός Νόμος των Μεγάλων Αριθμών
 1 Ο Ισχυρός Νόμος των Μεγάλων Αριθμών Στο κεφάλαιο αυτό παρουσιάζουμε ένα από τα σημαντικότερα αποτελέσματα της Θεωρίας Πιθανοτήτων, τον ισχυρό νόμο των μεγάλων αριθμών. Η διατύπωση που θα αποδείξουμε
1 Ο Ισχυρός Νόμος των Μεγάλων Αριθμών Στο κεφάλαιο αυτό παρουσιάζουμε ένα από τα σημαντικότερα αποτελέσματα της Θεωρίας Πιθανοτήτων, τον ισχυρό νόμο των μεγάλων αριθμών. Η διατύπωση που θα αποδείξουμε
Εισαγωγικά. 1.1 Η σ-αλγεβρα ως πληροφορία
 1 Εισαγωγικά 1.1 Η σ-αλγεβρα ως πληροφορία Στη θεωρία μέτρου, όταν δουλεύει κανείς σε έναν χώρο X, συνήθως έχει διαλέξει μια αρκετά μεγάλη σ-άλγεβρα στον X έτσι ώστε όλα τα σύνολα που εμφανίζονται να ανήκουν
1 Εισαγωγικά 1.1 Η σ-αλγεβρα ως πληροφορία Στη θεωρία μέτρου, όταν δουλεύει κανείς σε έναν χώρο X, συνήθως έχει διαλέξει μια αρκετά μεγάλη σ-άλγεβρα στον X έτσι ώστε όλα τα σύνολα που εμφανίζονται να ανήκουν
Ανεξαρτησία Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές
 10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
5.1 Μετρήσιμες συναρτήσεις
 5 Μετρήσιμες συναρτήσεις 5.1 Μετρήσιμες συναρτήσεις Ορισμός 5.1. Εστω (Ω, F ), (E, E) μετρήσιμοι χώροι. Μια συνάρτηση f : Ω E λέγεται F /Eμετρήσιμη αν f 1 (A) F για κάθε A E. (5.1) Συμβολίζουμε το σύνολο
5 Μετρήσιμες συναρτήσεις 5.1 Μετρήσιμες συναρτήσεις Ορισμός 5.1. Εστω (Ω, F ), (E, E) μετρήσιμοι χώροι. Μια συνάρτηση f : Ω E λέγεται F /Eμετρήσιμη αν f 1 (A) F για κάθε A E. (5.1) Συμβολίζουμε το σύνολο
Ανεξαρτησία Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές
 10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
Παντού σε αυτό το κεφάλαιο, αν δεν αναφέρεται κάτι διαφορετικό, δουλεύουμε σε ένα χώρο πιθανότητας (Ω, F, P) και η G F είναι μια σ-άλγεβρα.
 2 Δεσμευμένη μέση τιμή 2.1 Ορισμός Παντού σε αυτό το κεφάλαιο, αν δεν αναφέρεται κάτι διαφορετικό, δουλεύουμε σε ένα χώρο πιθανότητας (Ω, F, P) και η G F είναι μια σ-άλγεβρα. Ορισμός 2.1. Για X : Ω R τυχαία
2 Δεσμευμένη μέση τιμή 2.1 Ορισμός Παντού σε αυτό το κεφάλαιο, αν δεν αναφέρεται κάτι διαφορετικό, δουλεύουμε σε ένα χώρο πιθανότητας (Ω, F, P) και η G F είναι μια σ-άλγεβρα. Ορισμός 2.1. Για X : Ω R τυχαία
Εξαναγκασμένες ταλαντώσεις, Ιδιοτιμές με πολλαπλότητα, Εκθετικά πινάκων. 9 Απριλίου 2013, Βόλος
 ιαφορικές Εξισώσεις Εξαναγκασμένες ταλαντώσεις, Ιδιοτιμές με πολλαπλότητα, Ατελείς ιδιοτιμές Εκθετικά πινάκων Μανόλης Βάβαλης Τμήμα Μηχανικών Η/Υ Τηλεπικοινωνιών και ικτύων Πανεπιστήμιο Θεσσαλίας 9 Απριλίου
ιαφορικές Εξισώσεις Εξαναγκασμένες ταλαντώσεις, Ιδιοτιμές με πολλαπλότητα, Ατελείς ιδιοτιμές Εκθετικά πινάκων Μανόλης Βάβαλης Τμήμα Μηχανικών Η/Υ Τηλεπικοινωνιών και ικτύων Πανεπιστήμιο Θεσσαλίας 9 Απριλίου
Αναλυτικές ιδιότητες
 8 Αναλυτικές ιδιότητες 8. Βαθμός συνέχειας* Ξέρουμε ότι η κίνηση Brown είναι συνεχής και θα δείξουμε αργότερα ότι είναι πουθενά διαφορίσιμη. Πόσο ομαλή είναι λοιπόν; Μια ασθενέστερη μορφή ομαλότητας είναι
8 Αναλυτικές ιδιότητες 8. Βαθμός συνέχειας* Ξέρουμε ότι η κίνηση Brown είναι συνεχής και θα δείξουμε αργότερα ότι είναι πουθενά διαφορίσιμη. Πόσο ομαλή είναι λοιπόν; Μια ασθενέστερη μορφή ομαλότητας είναι
Εφαρμογές στην κίνηση Brown
 13 Εφαρμογές στην κίνηση Brown Σε αυτό το κεφάλαιο θέλουμε να κάνουμε για την πολυδιάστατη κίνηση Brown κάτι ανάλογο με αυτό που κάναμε στην Παράγραφο 7.2 για τη μονοδιάστατη κίνηση Brown. Δηλαδή να μελετήσουμε
13 Εφαρμογές στην κίνηση Brown Σε αυτό το κεφάλαιο θέλουμε να κάνουμε για την πολυδιάστατη κίνηση Brown κάτι ανάλογο με αυτό που κάναμε στην Παράγραφο 7.2 για τη μονοδιάστατη κίνηση Brown. Δηλαδή να μελετήσουμε
Αναγνώριση Προτύπων. Σημερινό Μάθημα
 Αναγνώριση Προτύπων Σημερινό Μάθημα Μη Παραμετρικός Υπολογισμός πυκνότητας με εκτίμηση Ιστόγραμμα Παράθυρα Parzen Εξομαλυμένη Kernel Ασκήσεις 1 Μη Παραμετρικός Υπολογισμός πυκνότητας με εκτίμηση Κατά τη
Αναγνώριση Προτύπων Σημερινό Μάθημα Μη Παραμετρικός Υπολογισμός πυκνότητας με εκτίμηση Ιστόγραμμα Παράθυρα Parzen Εξομαλυμένη Kernel Ασκήσεις 1 Μη Παραμετρικός Υπολογισμός πυκνότητας με εκτίμηση Κατά τη
Αναγνώριση Προτύπων. Σήμερα! Λόγος Πιθανοφάνειας Πιθανότητα Λάθους Κόστος Ρίσκο Bayes Ελάχιστη πιθανότητα λάθους για πολλές κλάσεις
 Αναγνώριση Προτύπων Σήμερα! Λόγος Πιθανοφάνειας Πιθανότητα Λάθους Πιθανότητα Λάθους Κόστος Ρίσκο Bayes Ελάχιστη πιθανότητα λάθους για πολλές κλάσεις 1 Λόγος Πιθανοφάνειας Ας υποθέσουμε ότι θέλουμε να ταξινομήσουμε
Αναγνώριση Προτύπων Σήμερα! Λόγος Πιθανοφάνειας Πιθανότητα Λάθους Πιθανότητα Λάθους Κόστος Ρίσκο Bayes Ελάχιστη πιθανότητα λάθους για πολλές κλάσεις 1 Λόγος Πιθανοφάνειας Ας υποθέσουμε ότι θέλουμε να ταξινομήσουμε
Martingales. 3.1 Ορισμός και παραδείγματα
 3 Martingales 3.1 Ορισμός και παραδείγματα Εστω χώρος πιθανότητας (Ω, F, P). Διήθηση σε αυτό τον χώρο λέμε μια αύξουσα ακολουθία (F n ) n 0 σ-αλγεβρών, η καθεμία από τις οποίες είναι υποσύνολο της F. Δηλαδή,
3 Martingales 3.1 Ορισμός και παραδείγματα Εστω χώρος πιθανότητας (Ω, F, P). Διήθηση σε αυτό τον χώρο λέμε μια αύξουσα ακολουθία (F n ) n 0 σ-αλγεβρών, η καθεμία από τις οποίες είναι υποσύνολο της F. Δηλαδή,
Εισαγωγή στις Διακριτές Πιθανότηες. Οικονομικό Πανεπιστήμιο Αθηνών
 Εισαγωγή στις Διακριτές Πιθανότηες Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών 27 Δεκεμβρίου 2010 2 Κεφάλαιο 1 Συνδιαστική Ανάλυση και Μαθηματικές Τεχνικές Η απαρίθμηση των στοιχείων
Εισαγωγή στις Διακριτές Πιθανότηες Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών 27 Δεκεμβρίου 2010 2 Κεφάλαιο 1 Συνδιαστική Ανάλυση και Μαθηματικές Τεχνικές Η απαρίθμηση των στοιχείων
Ανεξαρτησία Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές
 10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
10 Ανεξαρτησία 10.1 Ανεξαρτησία για οικογένειες συνόλων και τυχαίες μεταβλητές Στην παράγραφο αυτή δουλεύουμε σε χώρο πιθανότητας (Ω, F, P). Δίνουμε καταρχάς τον ορισμό της ανεξαρτησίας για ενδεχόμενα,
Εστω X σύνολο και A μια σ-άλγεβρα στο X. Ονομάζουμε το ζεύγος (X, A) μετρήσιμο χώρο.
 2 Μέτρα 2.1 Μέτρα σε μετρήσιμο χώρο Εστω X σύνολο και A μια σ-άλγεβρα στο X. Ονομάζουμε το ζεύγος (X, A) μετρήσιμο χώρο. Ορισμός 2.1. Μέτρο στον (X, A) λέμε κάθε συνάρτηση µ : A [0, ] που ικανοποιεί τις
2 Μέτρα 2.1 Μέτρα σε μετρήσιμο χώρο Εστω X σύνολο και A μια σ-άλγεβρα στο X. Ονομάζουμε το ζεύγος (X, A) μετρήσιμο χώρο. Ορισμός 2.1. Μέτρο στον (X, A) λέμε κάθε συνάρτηση µ : A [0, ] που ικανοποιεί τις
Ανελίξεις σε συνεχή χρόνο
 4 Ανελίξεις σε συνεχή χρόνο Σε αυτό το κεφάλαιο είναι συγκεντρωμένοι ορισμοί και αποτελέσματα από τη θεωρία των στοχαστικών ανελιξεων συνεχούς χρόνου. Με εξαίρεση την Παράγραφο 4.1, η οποία είναι εντελώς
4 Ανελίξεις σε συνεχή χρόνο Σε αυτό το κεφάλαιο είναι συγκεντρωμένοι ορισμοί και αποτελέσματα από τη θεωρία των στοχαστικών ανελιξεων συνεχούς χρόνου. Με εξαίρεση την Παράγραφο 4.1, η οποία είναι εντελώς
Επιχειρησιακή Ερευνα Ι
 Επιχειρησιακή Ερευνα Ι Μ. Ζαζάνης Κεφάλαιο 1 Τετραγωνικές μορφές στον R n και το ϑεώρημα του Taylor Ορισμός 1. Εστω a 11 a 1n A =.. a n1 a nn συμμετρικός πίνακας n n με στοιχεία στους πραγματικούς αριθμούς.
Επιχειρησιακή Ερευνα Ι Μ. Ζαζάνης Κεφάλαιο 1 Τετραγωνικές μορφές στον R n και το ϑεώρημα του Taylor Ορισμός 1. Εστω a 11 a 1n A =.. a n1 a nn συμμετρικός πίνακας n n με στοιχεία στους πραγματικούς αριθμούς.
Χαρακτηριστικές συναρτήσεις
 13 Χαρακτηριστικές συναρτήσεις 13.1 Μετασχηματισμός Fourier μέτρου πιθανότητας στο R Εστω (Ω, F, µ) χώρος μέτρου και f : Ω C Borel-μετρήσιμη συνάρτηση. Το πραγματικό και φανταστικό μέρος της f, που τα
13 Χαρακτηριστικές συναρτήσεις 13.1 Μετασχηματισμός Fourier μέτρου πιθανότητας στο R Εστω (Ω, F, µ) χώρος μέτρου και f : Ω C Borel-μετρήσιμη συνάρτηση. Το πραγματικό και φανταστικό μέρος της f, που τα
Γραμμική Ανεξαρτησία. Τμήμα Μηχανικών Η/Υ Τηλεπικοινωνιών και ικτύων Πανεπιστήμιο Θεσσαλίας. 17 Μαρτίου 2013, Βόλος
 Γραμμικές Συνήθεις ιαφορικές Εξισώσεις Ανώτερης Τάξης Γραμμικές Σ Ε 2ης τάξης Σ Ε 2ης τάξης με σταθερούς συντελεστές Μιγαδικές ρίζες Γραμμικές Σ Ε υψηλότερης τάξης Γραμμική Ανεξαρτησία Μανόλης Βάβαλης
Γραμμικές Συνήθεις ιαφορικές Εξισώσεις Ανώτερης Τάξης Γραμμικές Σ Ε 2ης τάξης Σ Ε 2ης τάξης με σταθερούς συντελεστές Μιγαδικές ρίζες Γραμμικές Σ Ε υψηλότερης τάξης Γραμμική Ανεξαρτησία Μανόλης Βάβαλης
Αναγνώριση Προτύπων. Σημερινό Μάθημα
 Αναγνώριση Προτύπων Σημερινό Μάθημα Bias (απόκλιση) και variance (διακύμανση) Ελεύθεροι Παράμετροι Ελεύθεροι Παράμετροι Διαίρεση dataset Μέθοδος holdout Cross Validation Bootstrap Bias (απόκλιση) και variance
Αναγνώριση Προτύπων Σημερινό Μάθημα Bias (απόκλιση) και variance (διακύμανση) Ελεύθεροι Παράμετροι Ελεύθεροι Παράμετροι Διαίρεση dataset Μέθοδος holdout Cross Validation Bootstrap Bias (απόκλιση) και variance
Η εξίσωση Black-Scholes
 8 Η εξίσωση Black-Scholes 8. Μια απλή αγορά Θεωρούμε ότι έχουμε μια αγορά που έχει μόνο δύο προϊόντα. Το ένα είναι η δυνατότητα κατάθεσης σε μια τράπεζα (ισοδύναμα, αγορά ομολόγων της τράπεζας) και το
8 Η εξίσωση Black-Scholes 8. Μια απλή αγορά Θεωρούμε ότι έχουμε μια αγορά που έχει μόνο δύο προϊόντα. Το ένα είναι η δυνατότητα κατάθεσης σε μια τράπεζα (ισοδύναμα, αγορά ομολόγων της τράπεζας) και το
{ i f i == 0 and p > 0
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Σχεδίαση και Ανάλυση Αλγορίθμων Διδάσκων: Ε. Μαρκάκης, Φθινοπωρινό εξάμηνο 014-015 Λύσεις 1ης Σειράς Ασκήσεων
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Σχεδίαση και Ανάλυση Αλγορίθμων Διδάσκων: Ε. Μαρκάκης, Φθινοπωρινό εξάμηνο 014-015 Λύσεις 1ης Σειράς Ασκήσεων
Ο τύπος του Itô. f (s) ds (12.1) f (g(s)) dg(s). (12.2) t f (B s ) db s + 1 2
 12 Ο τύπος του Itô Για συνάρτηση f : R R με συνεχή παράγωγο, έχουμε d f (s) = f (s) ds που σε ολοκληρωτική μορφή σημαίνει f (b) f (a) = b a f (s) ds (12.1) για κάθε a < b. Αν επιπλέον και η g : R R έχει
12 Ο τύπος του Itô Για συνάρτηση f : R R με συνεχή παράγωγο, έχουμε d f (s) = f (s) ds που σε ολοκληρωτική μορφή σημαίνει f (b) f (a) = b a f (s) ds (12.1) για κάθε a < b. Αν επιπλέον και η g : R R έχει
«ΔΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ»
 HY 118α «ΔΙΚΡΙΤ ΜΘΗΜΤΙΚ» ΣΚΗΣΕΙΣ ΠΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΙΣΤΩΝ εώργιος Φρ. εωργακόπουλος ΜΕΡΟΣ (1) ασικά στοιχεία της θεωρίας συνόλων. Π. ΚΡΗΤΗΣ ΤΜ. ΕΠ. ΥΠΟΛΟΙΣΤΩΝ «ΔΙΚΡΙΤ ΜΘΗΜΤΙΚ». Φ. εωργακόπουλος
HY 118α «ΔΙΚΡΙΤ ΜΘΗΜΤΙΚ» ΣΚΗΣΕΙΣ ΠΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΙΣΤΩΝ εώργιος Φρ. εωργακόπουλος ΜΕΡΟΣ (1) ασικά στοιχεία της θεωρίας συνόλων. Π. ΚΡΗΤΗΣ ΤΜ. ΕΠ. ΥΠΟΛΟΙΣΤΩΝ «ΔΙΚΡΙΤ ΜΘΗΜΤΙΚ». Φ. εωργακόπουλος
Μεγάλες αποκλίσεις* 17.1 Η έννοια της μεγάλης απόκλισης
 7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε (X = = (X = = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων αριθμών
7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε (X = = (X = = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων αριθμών
Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων. Οικονομικό Πανεπιστήμιο Αθηνών
 Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Κεφάλαιο Αλυσίδες Markov σε Συνεχή Χρόνο. Αλυσίδες
Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Κεφάλαιο Αλυσίδες Markov σε Συνεχή Χρόνο. Αλυσίδες
Μεγάλες αποκλίσεις* 17.1 Η έννοια της μεγάλης απόκλισης
 7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ) ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε P(X = ) = P(X = ) = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων
7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ) ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε P(X = ) = P(X = ) = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων
602. Συναρτησιακή Ανάλυση. Υποδείξεις για τις Ασκήσεις
 602. Συναρτησιακή Ανάλυση Υποδείξεις για τις Ασκήσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα 2018 Περιεχόμενα 1 Χώροι με νόρμα 1 2 Χώροι πεπερασμένης διάστασης 23 3 Γραμμικοί τελεστές και γραμμικά
602. Συναρτησιακή Ανάλυση Υποδείξεις για τις Ασκήσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα 2018 Περιεχόμενα 1 Χώροι με νόρμα 1 2 Χώροι πεπερασμένης διάστασης 23 3 Γραμμικοί τελεστές και γραμμικά
Μεγάλες αποκλίσεις* 17.1 Η έννοια της μεγάλης απόκλισης
 7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε P(X = = P(X = = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων
7 Μεγάλες αποκλίσεις* 7. Η έννοια της μεγάλης απόκλισης Εστω (X ανεξάρτητες και ισόνομες τυχαίες μεταβλητές ώστε P(X = = P(X = = /2 και S = k= X k το άθροισμα των πρώτων από αυτές. Ο νόμος των μεγάλων
Οι γέφυρες του ποταμού... Pregel (Konigsberg)
 Οι γέφυρες του ποταμού... Pregel (Konigsberg) Β Δ Β Δ Γ Γ Κύκλος του Euler (Euler cycle) είναι κύκλος σε γράφημα Γ που περιέχει κάθε κορυφή του γραφήματος, και κάθε ακμή αυτού ακριβώς μία φορά. Για γράφημα
Οι γέφυρες του ποταμού... Pregel (Konigsberg) Β Δ Β Δ Γ Γ Κύκλος του Euler (Euler cycle) είναι κύκλος σε γράφημα Γ που περιέχει κάθε κορυφή του γραφήματος, και κάθε ακμή αυτού ακριβώς μία φορά. Για γράφημα
HY 280. θεμελιακές έννοιες της επιστήμης του υπολογισμού ΑΣΚΗΣΕΙΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Γεώργιος Φρ.
 HY 280 «ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΟΥ» θεμελικές έννοιες της επιστήμης του υπολογισμού ΑΣΚΗΣΕΙΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Γεώργιος Φρ. Γεωργκόπουλος μέρος Α Εισγωγή, κι η σική θεωρί των πεπερσμένων
HY 280 «ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΟΥ» θεμελικές έννοιες της επιστήμης του υπολογισμού ΑΣΚΗΣΕΙΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Γεώργιος Φρ. Γεωργκόπουλος μέρος Α Εισγωγή, κι η σική θεωρί των πεπερσμένων
Κατασκευή της κίνησης Brown και απλές ιδιότητες
 5 Κατασκευή της κίνησης Brown και απλές ιδιότητες 51 Ορισμός, ύπαρξη, και μοναδικότητα Ορισμός 51 Μια στοχαστική ανέλιξη { : t } ορισμένη σε έναν χώρο πιθανότητας (Ω, F, P) και με τιμές στο R λέγεται (μονοδιάστατη)
5 Κατασκευή της κίνησης Brown και απλές ιδιότητες 51 Ορισμός, ύπαρξη, και μοναδικότητα Ορισμός 51 Μια στοχαστική ανέλιξη { : t } ορισμένη σε έναν χώρο πιθανότητας (Ω, F, P) και με τιμές στο R λέγεται (μονοδιάστατη)
Εκφωνήσεις και Λύσεις των Θεμάτων
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Δευτέρα 8 Μαΐου 0 Εκφωνήσεις και Λύσεις των Θεμάτων
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Δευτέρα 8 Μαΐου 0 Εκφωνήσεις και Λύσεις των Θεμάτων
Η ανισότητα α β α±β α + β με α, β C και η χρήση της στην εύρεση ακροτάτων.
 A A N A B P Y T A Άρθρο στους Μιγαδικούς Αριθμούς 9 5 0 Η ανισότητα α β α±β α + β με α, β C και η χρήση της στην εύρεση ακροτάτων. Δρ. Νίκος Σωτηρόπουλος, Μαθηματικός Εισαγωγή Το άρθρο αυτό γράφεται με
A A N A B P Y T A Άρθρο στους Μιγαδικούς Αριθμούς 9 5 0 Η ανισότητα α β α±β α + β με α, β C και η χρήση της στην εύρεση ακροτάτων. Δρ. Νίκος Σωτηρόπουλος, Μαθηματικός Εισαγωγή Το άρθρο αυτό γράφεται με
21/11/2005 Διακριτά Μαθηματικά. Γραφήματα ΒΑΣΙΚΗ ΟΡΟΛΟΓΙΑ : ΜΟΝΟΠΑΤΙΑ ΚΑΙ ΚΥΚΛΟΙ Δ Ι. Γεώργιος Βούρος Πανεπιστήμιο Αιγαίου
 Γραφήματα ΒΑΣΙΚΗ ΟΡΟΛΟΓΙΑ : ΜΟΝΟΠΑΤΙΑ ΚΑΙ ΚΥΚΛΟΙ A Ε B Ζ Η Γ K Θ Δ Ι Ορισμός Ένα (μη κατευθυνόμενο) γράφημα (non directed graph) Γ, είναι μία δυάδα από σύνολα Ε και V και συμβολίζεται με Γ=(Ε,V). Το σύνολο
Γραφήματα ΒΑΣΙΚΗ ΟΡΟΛΟΓΙΑ : ΜΟΝΟΠΑΤΙΑ ΚΑΙ ΚΥΚΛΟΙ A Ε B Ζ Η Γ K Θ Δ Ι Ορισμός Ένα (μη κατευθυνόμενο) γράφημα (non directed graph) Γ, είναι μία δυάδα από σύνολα Ε και V και συμβολίζεται με Γ=(Ε,V). Το σύνολο
17 Μαρτίου 2013, Βόλος
 Συνήθεις ιαφορικές Εξισώσεις 1ης Τάξης Σ Ε 1ης τάξης, Πεδία κατευθύνσεων, Υπαρξη και μοναδικότητα, ιαχωρίσιμες εξισώσεις, Ολοκληρωτικοί παράγοντες, Αντικαταστάσεις, Αυτόνομες εξισώσεις Μανόλης Βάβαλης
Συνήθεις ιαφορικές Εξισώσεις 1ης Τάξης Σ Ε 1ης τάξης, Πεδία κατευθύνσεων, Υπαρξη και μοναδικότητα, ιαχωρίσιμες εξισώσεις, Ολοκληρωτικοί παράγοντες, Αντικαταστάσεις, Αυτόνομες εξισώσεις Μανόλης Βάβαλης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. Εαρινό Εξάμηνο
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ231: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 2017-2018 Φροντιστήριο 3 - Λύσεις 1. Εστω ο πίνακας Α = [12, 23, 1, 5, 7, 19, 2, 14]. i. Να δώσετε την κατάσταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ231: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 2017-2018 Φροντιστήριο 3 - Λύσεις 1. Εστω ο πίνακας Α = [12, 23, 1, 5, 7, 19, 2, 14]. i. Να δώσετε την κατάσταση
Αναγνώριση Προτύπων. Σημερινό Μάθημα
 Αναγνώριση Προτύπων Σημερινό Μάθημα Εκτίμηση Πυκνότητας με k NN k NN vs Bayes classifier k NN vs Bayes classifier Ο κανόνας ταξινόμησης του πλησιέστερου γείτονα (k NN) lazy αλγόριθμοι O k NN ως χαλαρός
Αναγνώριση Προτύπων Σημερινό Μάθημα Εκτίμηση Πυκνότητας με k NN k NN vs Bayes classifier k NN vs Bayes classifier Ο κανόνας ταξινόμησης του πλησιέστερου γείτονα (k NN) lazy αλγόριθμοι O k NN ως χαλαρός
Γενικό Λύκειο Μαραθοκάμπου Σάμου. Άλγεβρα Β λυκείου. 13 Οκτώβρη 2016
 Γενικό Λύκειο Μαραθοκάμπου Σάμου Άλγεβρα Β λυκείου Εργασία2 η : «Συναρτήσεις» 13 Οκτώβρη 2016 Ερωτήσεις Θεωρίας 1.Πότελέμεότιμιασυνάρτησηfείναιγνησίωςάυξουσασεέναδιάστημα του πεδίου ορισμού της; 2.Πότελέμεότιμιασυνάρτησηfείναιγνησίωςφθίνουσασεέναδιάστημα
Γενικό Λύκειο Μαραθοκάμπου Σάμου Άλγεβρα Β λυκείου Εργασία2 η : «Συναρτήσεις» 13 Οκτώβρη 2016 Ερωτήσεις Θεωρίας 1.Πότελέμεότιμιασυνάρτησηfείναιγνησίωςάυξουσασεέναδιάστημα του πεδίου ορισμού της; 2.Πότελέμεότιμιασυνάρτησηfείναιγνησίωςφθίνουσασεέναδιάστημα
Εκφωνήσεις και Λύσεις των Θεμάτων
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Τετάρτη 23 Μαΐου 2012 Εκφωήσεις και Λύσεις
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Τετάρτη 23 Μαΐου 2012 Εκφωήσεις και Λύσεις
Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων. Οικονομικό Πανεπιστήμιο Αθηνών
 Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Κεφάλαιο Αλυσίδες Markov σε Συνεχή Χρόνο Αλυσίδες Markov
Εισαγωγικές Διαλέξεις στην Θεωρία των Αλυσίδων Markov και των Στοχαστικών Ανελίξεων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Κεφάλαιο Αλυσίδες Markov σε Συνεχή Χρόνο Αλυσίδες Markov
ιάσταση του Krull Α.Π.Θ. Θεσσαλονίκη Χ. Χαραλαμπους (ΑΠΘ) ιάσταση του Krull Ιανουάριος, / 27
 ιάσταση του Krull Χ. Χαραλάμπους Α.Π.Θ. Θεσσαλονίκη Ιανουάριος, 2017 Χ. Χαραλαμπους (ΑΠΘ) ιάσταση του Krull Ιανουάριος, 2017 1 / 27 Ορισμοί Εστω R (αντιμεταθετικός) δακτύλιος. Ορισμός Η διάσταση του Krull
ιάσταση του Krull Χ. Χαραλάμπους Α.Π.Θ. Θεσσαλονίκη Ιανουάριος, 2017 Χ. Χαραλαμπους (ΑΠΘ) ιάσταση του Krull Ιανουάριος, 2017 1 / 27 Ορισμοί Εστω R (αντιμεταθετικός) δακτύλιος. Ορισμός Η διάσταση του Krull
Στοχαστικές διαφορικές εξισώσεις
 14 Στοχαστικές διαφορικές εξισώσεις 14.1 Γενικά Στοχαστική διαφορική εξίσωση λέμε μια εξίσωση της μορφής dx = µ(, X ) d + σ(, X ) db, X = x, (14.1) με µ, σ : [, ) R R μετρήσιμες συναρτήσεις, x R, και B
14 Στοχαστικές διαφορικές εξισώσεις 14.1 Γενικά Στοχαστική διαφορική εξίσωση λέμε μια εξίσωση της μορφής dx = µ(, X ) d + σ(, X ) db, X = x, (14.1) με µ, σ : [, ) R R μετρήσιμες συναρτήσεις, x R, και B
ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ
 Δημήτρης Χελιώτης ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ B τ u(x):=e x {f(b τ ) u(x) = } x ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Εισαγωγή στον
Δημήτρης Χελιώτης ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ B τ u(x):=e x {f(b τ ) u(x) = } x ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Εισαγωγή στον
ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ
 Δημήτρης Χελιώτης ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ B τ u(x):=e x {f(b τ ) u(x) = } x ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Εισαγωγή στον
Δημήτρης Χελιώτης ΕΙΣΑΓΩΓΗ ΣΤΟN ΣΤΟΧΑΣΤΙΚΟ ΛΟΓΙΣΜΟ B τ u(x):=e x {f(b τ ) u(x) = } x ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Εισαγωγή στον
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 12 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ): ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 12 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΥΚΛΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΗΡΕΣΙΩΝ): ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ
Σχέσεις και ιδιότητές τους
 Σχέσεις και ιδιότητές τους Διμελής (binary) σχέση Σ από σύνολο Χ σε σύνολο Υ είναι ένα υποσύνολο του καρτεσιανού γινομένου Χ Υ. Αν (χ,ψ) Σ, λέμε ότι το χ σχετίζεται με το ψ και σημειώνουμε χσψ. Στην περίπτωση
Σχέσεις και ιδιότητές τους Διμελής (binary) σχέση Σ από σύνολο Χ σε σύνολο Υ είναι ένα υποσύνολο του καρτεσιανού γινομένου Χ Υ. Αν (χ,ψ) Σ, λέμε ότι το χ σχετίζεται με το ψ και σημειώνουμε χσψ. Στην περίπτωση
Δημήτρης Χελιώτης ΕΝΑ ΔΕΥΤΕΡΟ ΜΑΘΗΜΑ ΣΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ
 Δημήτρης Χελιώτης ΕΝΑ ΔΕΥΤΕΡΟ ΜΑΘΗΜΑ ΣΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Ενα δεύτερο μάθημα στις πιθανότητες Ενα δεύτερο
Δημήτρης Χελιώτης ΕΝΑ ΔΕΥΤΕΡΟ ΜΑΘΗΜΑ ΣΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ ii ΔΗΜΗΤΡΗΣ ΧΕΛΙΩΤΗΣ Επίκουρος καθηγητής Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Ενα δεύτερο μάθημα στις πιθανότητες Ενα δεύτερο
Εισαγωγή στη Μιγαδική Ανάλυση. (Πρώτη Ολοκληρωμένη Γραφή)
 Εισαωή στη Μιαδική Ανάλυση Σημειώσεις (Πρώτη Ολοκληρωμένη Γραφή) Ε. Στεφανόπουλος Τμήμα Μαθηματικών Πανεπιστήμιο Αιαίου Καρλόβασι Καλοκαίρι 26 Πρόλοος Οι σημειώσεις αυτές είναι αποτέλεσμα επεξερασίας
Εισαωή στη Μιαδική Ανάλυση Σημειώσεις (Πρώτη Ολοκληρωμένη Γραφή) Ε. Στεφανόπουλος Τμήμα Μαθηματικών Πανεπιστήμιο Αιαίου Καρλόβασι Καλοκαίρι 26 Πρόλοος Οι σημειώσεις αυτές είναι αποτέλεσμα επεξερασίας
ΣΥΝΟΛΑ (προσέξτε τα κοινά χαρακτηριστικά των παρακάτω προτάσεων) Οι άνθρωποι που σπουδάζουν ΤΠ&ΕΣ και βρίσκονται στην αίθουσα
 ΣΥΝΟΛΑ (προσέξτε τα κοινά χαρακτηριστικά των παρακάτω προτάσεων) Οι άνθρωποι που σπουδάζουν ΤΠ&ΕΣ και βρίσκονται στην αίθουσα Τα βιβλία διακριτών μαθηματικών του Γ.Β. Η/Υ με επεξεργαστή Pentium και χωρητικότητα
ΣΥΝΟΛΑ (προσέξτε τα κοινά χαρακτηριστικά των παρακάτω προτάσεων) Οι άνθρωποι που σπουδάζουν ΤΠ&ΕΣ και βρίσκονται στην αίθουσα Τα βιβλία διακριτών μαθηματικών του Γ.Β. Η/Υ με επεξεργαστή Pentium και χωρητικότητα
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ ΜΑΘΗΜΑ: ΕΡΩΤΗΣΕΙΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΜΑΘΗΜΑ: ΕΡΩΤΗΣΕΙΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Tα Πανεπιστημιακά Φροντιστήρια «ΚΟΛΛΙΝΤΖΑ» προετοιμάζοντας σε ολιγομελείς ομίλους τους υποψήφιους για τον επικείμενο διαγωνισμό του Υπουργείου Οικονομικών, με κορυφαίο
ΜΑΘΗΜΑ: ΕΡΩΤΗΣΕΙΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Tα Πανεπιστημιακά Φροντιστήρια «ΚΟΛΛΙΝΤΖΑ» προετοιμάζοντας σε ολιγομελείς ομίλους τους υποψήφιους για τον επικείμενο διαγωνισμό του Υπουργείου Οικονομικών, με κορυφαίο
Το κράτος είναι φτιαγμένο για τον άνθρωπο και όχι ο άνθρωπος για το κράτος. A. Einstein Πηγή:
 Ας πούμε και κάτι για τις δύσκολες μέρες που έρχονται Το κράτος είναι φτιαγμένο για τον άνθρωπο και όχι ο άνθρωπος για το κράτος. A. Einstein 1879-1955 Πηγή: http://www.cognosco.gr/gnwmika/ 1 ΚΥΚΛΙΚΟΣ
Ας πούμε και κάτι για τις δύσκολες μέρες που έρχονται Το κράτος είναι φτιαγμένο για τον άνθρωπο και όχι ο άνθρωπος για το κράτος. A. Einstein 1879-1955 Πηγή: http://www.cognosco.gr/gnwmika/ 1 ΚΥΚΛΙΚΟΣ
Κεφάλαιο 1. Πίνακες και απαλοιφή Gauss
 Κεφάλαιο 1 Πίνακες και απαλοιφή Gauss Γύρω απ το γινομένου πινάκων Κάτι σαν τυπολόγιο Αν AB = C, τότε: 1 (C) i j = (i-γραμμή A) ( j-στήλη B) Το συμβολίζει εσωτερικό γινόμενο 2 (i-γραμμή C) = k(a) ik (k-γραμμή
Κεφάλαιο 1 Πίνακες και απαλοιφή Gauss Γύρω απ το γινομένου πινάκων Κάτι σαν τυπολόγιο Αν AB = C, τότε: 1 (C) i j = (i-γραμμή A) ( j-στήλη B) Το συμβολίζει εσωτερικό γινόμενο 2 (i-γραμμή C) = k(a) ik (k-γραμμή
Δ Ι Α Κ Ρ Ι Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α. 1η σειρά ασκήσεων
 Δ Ι Α Κ Ρ Ι Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α 1η σειρά ασκήσεων Ονοματεπώνυμο: Αριθμός μητρώου: Ημερομηνία παράδοσης: Μέχρι την Τρίτη 2 Απριλίου 2019 Σημειώστε τις ασκήσεις για τις οποίες έχετε παραδώσει λύση: 1
Δ Ι Α Κ Ρ Ι Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α 1η σειρά ασκήσεων Ονοματεπώνυμο: Αριθμός μητρώου: Ημερομηνία παράδοσης: Μέχρι την Τρίτη 2 Απριλίου 2019 Σημειώστε τις ασκήσεις για τις οποίες έχετε παραδώσει λύση: 1
Ταξινόμηση των μοντέλων διασποράς ατμοσφαιρικών ρύπων βασισμένη σε μαθηματικά κριτήρια.
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ Ταξινόμηη των μοντέλων διαποράς ατμοφαιρικών ρύπων βαιμένη ε μαθηματικά κριτήρια. Μοντέλο Ελεριανά μοντέλα (Elerian) Λαγκρατζιανά μοντέλα (Lagrangian) Επιπρόθετος διαχωριμός Μοντέλα
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ Ταξινόμηη των μοντέλων διαποράς ατμοφαιρικών ρύπων βαιμένη ε μαθηματικά κριτήρια. Μοντέλο Ελεριανά μοντέλα (Elerian) Λαγκρατζιανά μοντέλα (Lagrangian) Επιπρόθετος διαχωριμός Μοντέλα
1. Εστω ότι A, B, C είναι γενικοί 2 2 πίνακες, δηλαδή, a 21 a, και ανάλογα για τους B, C. Υπολογίστε τους πίνακες (A B) C και A (B C) και
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Εαρινό Εξάμηνο 0 Ασκήσεις για προσωπική μελέτη Είναι απολύτως απαραίτητο να μπορείτε να τις λύνετε, τουλάχιστον τις υπολογιστικές! Εστω ότι A, B, C είναι γενικοί πίνακες,
ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Εαρινό Εξάμηνο 0 Ασκήσεις για προσωπική μελέτη Είναι απολύτως απαραίτητο να μπορείτε να τις λύνετε, τουλάχιστον τις υπολογιστικές! Εστω ότι A, B, C είναι γενικοί πίνακες,
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ ΜΑΘΗΜΑ: ΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ
 ΜΑΘΗΜΑ: ΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Την ευθύνη του εκπαιδευτικού υλικού έχει ο επιστημονικός συνεργάτης των Πανεπιστημιακών Φροντιστηρίων «ΚOΛΛΙΝΤΖΑ», οικονομολόγος συγγραφέας θεμάτων ΑΣΕΠ, Παναγιώτης Βεργούρος.
ΜΑΘΗΜΑ: ΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Την ευθύνη του εκπαιδευτικού υλικού έχει ο επιστημονικός συνεργάτης των Πανεπιστημιακών Φροντιστηρίων «ΚOΛΛΙΝΤΖΑ», οικονομολόγος συγγραφέας θεμάτων ΑΣΕΠ, Παναγιώτης Βεργούρος.
Ευρωπαϊκά παράγωγα Ευρωπαϊκά δικαιώματα
 17 Ευρωπαϊκά παράγωγα 17.1 Ευρωπαϊκά δικαιώματα Ορισμός 17.1. 1) Ευρωπαϊκό δικαίωμα αγοράς σε μία μετοχή είναι ένα συμβόλαιο που δίνει στον κάτοχό του το δικαίωμα να αγοράσει μία μετοχή από τον εκδότη
17 Ευρωπαϊκά παράγωγα 17.1 Ευρωπαϊκά δικαιώματα Ορισμός 17.1. 1) Ευρωπαϊκό δικαίωμα αγοράς σε μία μετοχή είναι ένα συμβόλαιο που δίνει στον κάτοχό του το δικαίωμα να αγοράσει μία μετοχή από τον εκδότη
Μαθηματικά Πληροφορικής
 Πανεπιστήμιο Αθηνών Μαθηματικά Πληροφορικής Ηλίας Κουτσουπιάς Αθήνα, Οκτώβριος 2009 Περιεχόμενα Περιεχόμενα 1 Σύνολα... 5 ΆλλαΣύμβολα... 6 1 Υποθέσεις και Θεωρήματα 9 1.1 Παρατήρηση-Υπόθεση-Απόδειξη...
Πανεπιστήμιο Αθηνών Μαθηματικά Πληροφορικής Ηλίας Κουτσουπιάς Αθήνα, Οκτώβριος 2009 Περιεχόμενα Περιεχόμενα 1 Σύνολα... 5 ΆλλαΣύμβολα... 6 1 Υποθέσεις και Θεωρήματα 9 1.1 Παρατήρηση-Υπόθεση-Απόδειξη...
α 0. α ν x ν +α ν 1 x ν α 1 x+α 0 α ν x ν,α ν 1 x ν 1,...,α 1 x,α 0, ...,α 1,α 0,
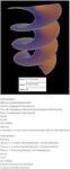 Άλγεβρα Β Λυκείου - Πολυώνυμα: Θεωρία, Μεθοδολογία και Λυμένες ασκήσεις Κώστας Ράπτης Μάιος 2011 Μέρος I Πολυώνυμα 1 Πολυώνυμα 1.1 Στοιχεία ϑεωρίας Καλούμε μονώνυμο του x κάθε παράσταση της μορφήςαx ν,
Άλγεβρα Β Λυκείου - Πολυώνυμα: Θεωρία, Μεθοδολογία και Λυμένες ασκήσεις Κώστας Ράπτης Μάιος 2011 Μέρος I Πολυώνυμα 1 Πολυώνυμα 1.1 Στοιχεία ϑεωρίας Καλούμε μονώνυμο του x κάθε παράσταση της μορφήςαx ν,
Σημειώσεις Μαθηματικών Μεθόδων. Οικονομικό Πανεπιστήμιο Αθηνών
 Σημειώσεις Μαθηματικών Μεθόδων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Φεβρουαρίου 08 Κεφάλαιο Το Μιγαδικό Εκθετικό Είναι γνωστό ότι η εκθετική συνάρτηση e x έχει το ανάπτυγμα
Σημειώσεις Μαθηματικών Μεθόδων Μιχάλης Ζαζάνης Τμήμα Στατιστικής Οικονομικό Πανεπιστήμιο Αθηνών Φεβρουαρίου 08 Κεφάλαιο Το Μιγαδικό Εκθετικό Είναι γνωστό ότι η εκθετική συνάρτηση e x έχει το ανάπτυγμα
Αναγνώριση Προτύπων. Σημερινό Μάθημα
 Αναγνώριση Προτύπων Σημερινό Μάθημα Η κατάρα της διαστατικότητας Μείωση διαστάσεων εξαγωγή χαρακτηριστικών επιλογή χαρακτηριστικών Αναπαράσταση έναντι Κατηγοριοποίησης Ανάλυση Κυρίων Συνιστωσών PCA Γραμμική
Αναγνώριση Προτύπων Σημερινό Μάθημα Η κατάρα της διαστατικότητας Μείωση διαστάσεων εξαγωγή χαρακτηριστικών επιλογή χαρακτηριστικών Αναπαράσταση έναντι Κατηγοριοποίησης Ανάλυση Κυρίων Συνιστωσών PCA Γραμμική
ΣΧΟΛΙΚΟ ΕΤΟΣ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ. Ονοματεπώνυμο Τμήμα
 Σελίδα 1 ΣΧΟΛΙΚΟ ΕΤΟΣ 2014 2015 ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ Ονοματεπώνυμο Τμήμα ΘΕΜΑ Α Οδηγία: Να γράψετε στην κόλλα σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Σελίδα 1 ΣΧΟΛΙΚΟ ΕΤΟΣ 2014 2015 ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ ΤΡΙΩΡΗ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ Ονοματεπώνυμο Τμήμα ΘΕΜΑ Α Οδηγία: Να γράψετε στην κόλλα σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Η έκδοση αυτή είναι υπό προετοιμασία. Γιάννης Α. Αντωνιάδης, Αριστείδης Κοντογεώργης
 Θεωρία Αριθμών και Εφαρμογές Η έκδοση αυτή είναι υπό προετοιμασία Γιάννης Α. Αντωνιάδης, Αριστείδης Κοντογεώργης 9 Φεβρουαρίου 2015 2 Περιεχόμενα I ΑΡΙΘΜΟΘΕΩΡΙΑ ΤΩΝ ΡΗΤΩΝ ΑΡΙΘΜΩΝ 7 1 ΔΙΑΙΡΕΤΟΤΗΤΑ ΚΑΙ ΠΡΩΤΟΙ
Θεωρία Αριθμών και Εφαρμογές Η έκδοση αυτή είναι υπό προετοιμασία Γιάννης Α. Αντωνιάδης, Αριστείδης Κοντογεώργης 9 Φεβρουαρίου 2015 2 Περιεχόμενα I ΑΡΙΘΜΟΘΕΩΡΙΑ ΤΩΝ ΡΗΤΩΝ ΑΡΙΘΜΩΝ 7 1 ΔΙΑΙΡΕΤΟΤΗΤΑ ΚΑΙ ΠΡΩΤΟΙ
Η Θεωρια Αριθμων στην Εκπαιδευση
 Η Θεωρια Αριθμων στην Εκπαιδευση Καθηγητὴς Ν.Γ. Τζανάκης Εφαρμογὲς τῶν συνεχῶν κλασμάτων 1 1. Η τιμὴ τοῦ π μὲ σωστὰ τὰ 50 πρῶτα δεκαδικὰ ψηφία μετὰ τὴν ὑποδιαστολή, εἶναι 3.14159265358979323846264338327950288419716939937511.
Η Θεωρια Αριθμων στην Εκπαιδευση Καθηγητὴς Ν.Γ. Τζανάκης Εφαρμογὲς τῶν συνεχῶν κλασμάτων 1 1. Η τιμὴ τοῦ π μὲ σωστὰ τὰ 50 πρῶτα δεκαδικὰ ψηφία μετὰ τὴν ὑποδιαστολή, εἶναι 3.14159265358979323846264338327950288419716939937511.
Αρτιες και περιττές συναρτήσεις
 Μελέτη Συναρτήσεων: άρτιες, περιττές συναρτήσεις - μονοτονία - ακρότατα Κωνσταντίνος Α. Ράπτης Άρτιες και περιττές συναρτήσεις Ὁι ψυχολόγοι κάνουν λόγο για δύο επίπεδα συλλογιστικής και μνήμης: το αρχαϊκό
Μελέτη Συναρτήσεων: άρτιες, περιττές συναρτήσεις - μονοτονία - ακρότατα Κωνσταντίνος Α. Ράπτης Άρτιες και περιττές συναρτήσεις Ὁι ψυχολόγοι κάνουν λόγο για δύο επίπεδα συλλογιστικής και μνήμης: το αρχαϊκό
Συναρτήσεις. Σημερινό μάθημα
 Συναρτήσεις Σημερινό μάθημα C++ Συναρτήσεις Δήλωση συνάρτησης Σύνταξη συνάρτησης Πρότυπο συνάρτησης & συνάρτηση Αλληλο καλούμενες συναρτήσεις συναρτήσεις μαθηματικών Παράμετροι συναρτήσεων Τοπικές μεταβλητές
Συναρτήσεις Σημερινό μάθημα C++ Συναρτήσεις Δήλωση συνάρτησης Σύνταξη συνάρτησης Πρότυπο συνάρτησης & συνάρτηση Αλληλο καλούμενες συναρτήσεις συναρτήσεις μαθηματικών Παράμετροι συναρτήσεων Τοπικές μεταβλητές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. Εαρινό Εξάμηνο
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ231: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 2017-2018 Φροντιστήριο 3 1. Εστω η στοίβα S και ο παρακάτω αλγόριθμος επεξεργασίας της. Να καταγράψετε την κατάσταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ231: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 2017-2018 Φροντιστήριο 3 1. Εστω η στοίβα S και ο παρακάτω αλγόριθμος επεξεργασίας της. Να καταγράψετε την κατάσταση
Διανυσματικές Συναρτήσεις
 Κεφάλαιο 5 Διανυσματικές Συναρτήσεις 51 Διανυσματατικές συναρτήσεις Μια συνάρτηση με τιμές στοr n, n>1 λέγεται διανυσματική συνάρτηση Τις διανυσματικές συναρτήσεις ϑα τις συμβολίζουμε με παχειά γράμματα,
Κεφάλαιο 5 Διανυσματικές Συναρτήσεις 51 Διανυσματατικές συναρτήσεις Μια συνάρτηση με τιμές στοr n, n>1 λέγεται διανυσματική συνάρτηση Τις διανυσματικές συναρτήσεις ϑα τις συμβολίζουμε με παχειά γράμματα,
Pointers. Σημερινό Μάθημα! Χρήση pointer Τελεστής * Τελεστής & Γενικοί δείκτες Ανάκληση Δέσμευση μνήμης new / delete Pointer σε αντικείμενο 2
 Pointers 1 Σημερινό Μάθημα! Χρήση pointer Τελεστής * Τελεστής & Γενικοί δείκτες Ανάκληση Δέσμευση μνήμης new / delete Pointer σε αντικείμενο 2 1 Μνήμη μεταβλητών Κάθε μεταβλητή έχει διεύθυνση Δεν χρειάζεται
Pointers 1 Σημερινό Μάθημα! Χρήση pointer Τελεστής * Τελεστής & Γενικοί δείκτες Ανάκληση Δέσμευση μνήμης new / delete Pointer σε αντικείμενο 2 1 Μνήμη μεταβλητών Κάθε μεταβλητή έχει διεύθυνση Δεν χρειάζεται
ΣΤΑΤΙΣΤΙΚΗ ΠΟΣΟΤΙΚΗ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ
 Σημειώσεις για το μάθημα ΣΤΑΤΙΣΤΙΚΗ ΠΟΣΟΤΙΚΗ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Παπάνα Αγγελική http://users.auth.gr/~agpapana/statlogistics E mail: papanagel@yahoo.gr, agpapana@gen.auth.gr Α.Τ.Ε.Ι. Θεσσαλονίκης ΠΑΡΑΡΤΗΜΑ
Σημειώσεις για το μάθημα ΣΤΑΤΙΣΤΙΚΗ ΠΟΣΟΤΙΚΗ ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Παπάνα Αγγελική http://users.auth.gr/~agpapana/statlogistics E mail: papanagel@yahoo.gr, agpapana@gen.auth.gr Α.Τ.Ε.Ι. Θεσσαλονίκης ΠΑΡΑΡΤΗΜΑ
Παραβολή ψ=αχ 2 +βχ+γ, α 0. Η παραβολή ψ = αχ 2. Γενικά : Κάθε συνάρτηση της μορφής ψ=αχ 2 + βχ +γ, α 0 λέγεται τετραγωνική συνάρτηση.
 Η παραβολή ψ=αχ 2 +βχ+γ Σελίδα 1 από 10 Παραβολή ψ=αχ 2 +βχ+γ, α0 Γενικά : Κάθε συνάρτηση της μορφής ψ=αχ 2 + βχ +γ, α0 λέγεται τετραγωνική συνάρτηση. Η παραβολή ψ = αχ 2 Η γραφική παράσταση της συνάρτησης
Η παραβολή ψ=αχ 2 +βχ+γ Σελίδα 1 από 10 Παραβολή ψ=αχ 2 +βχ+γ, α0 Γενικά : Κάθε συνάρτηση της μορφής ψ=αχ 2 + βχ +γ, α0 λέγεται τετραγωνική συνάρτηση. Η παραβολή ψ = αχ 2 Η γραφική παράσταση της συνάρτησης
Αρτιες και περιττές συναρτήσεις
 Μελέτη Συναρτήσεων: άρτιες, περιττές συναρτήσεις - μονοτονία - ακρότατα Κώστας Ράπτης Άρτιες και περιττές συναρτήσεις Ὁι ψυχολόγοι κάνουν λόγο για δύο επίπεδα συλλογιστικής και μνήμης: το αρχαϊκό και το
Μελέτη Συναρτήσεων: άρτιες, περιττές συναρτήσεις - μονοτονία - ακρότατα Κώστας Ράπτης Άρτιες και περιττές συναρτήσεις Ὁι ψυχολόγοι κάνουν λόγο για δύο επίπεδα συλλογιστικής και μνήμης: το αρχαϊκό και το
Ισοπεριμετρικές ανισότητες για το
 Ισοπεριμετρικές ανισότητες για το μέτρο του Gauss Διπλωματική Εργασία Μαρία Μαστροθεοδώρου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα 018 Περιεχόμενα 1 Εισαγωγή 1 1.1 Το ισοπεριμετρικό πρόβλημα................................
Ισοπεριμετρικές ανισότητες για το μέτρο του Gauss Διπλωματική Εργασία Μαρία Μαστροθεοδώρου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα 018 Περιεχόμενα 1 Εισαγωγή 1 1.1 Το ισοπεριμετρικό πρόβλημα................................
Αλγόριθμοι & Βελτιστοποίηση
 Αλγόριθμοι & Βελτιστοποίηση ΠΜΣ/ΕΤΥ: Μεταπτυχιακό Μάθημα 8η Ενότητα: Γραμμικός Προγραμματισμός ως Υπορουτίνα για Επίλυση Προβλημάτων Χρήστος Ζαρολιάγκης (zaro@ceid.upatras.gr) Σπύρος Κοντογιάννης (kontog@cs.uoi.gr)
Αλγόριθμοι & Βελτιστοποίηση ΠΜΣ/ΕΤΥ: Μεταπτυχιακό Μάθημα 8η Ενότητα: Γραμμικός Προγραμματισμός ως Υπορουτίνα για Επίλυση Προβλημάτων Χρήστος Ζαρολιάγκης (zaro@ceid.upatras.gr) Σπύρος Κοντογιάννης (kontog@cs.uoi.gr)
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ Γ ΛΥΚΕΙΟΥ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: ΕΠΩΝΥΜΟ: ΟΝΟΜΑ: ΟΜΑΔΑ Α Για τις προτάσεις Α1 μέχρι και Α6 να
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: ΕΠΩΝΥΜΟ: ΟΝΟΜΑ: ΟΜΑΔΑ Α Για τις προτάσεις Α1 μέχρι και Α6 να
τους στην Κρυπτογραφία και τα
 Οι Ομάδες των Πλεξίδων και Εφαρμογές τους στην Κρυπτογραφία και τα Πολυμερή Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών ΕΜΠ Επιβλέπουσα Καθηγήτρια: Λαμπροπούλου Σοφία Ιούλιος, 2013 Περιεχόμενα
Οι Ομάδες των Πλεξίδων και Εφαρμογές τους στην Κρυπτογραφία και τα Πολυμερή Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών ΕΜΠ Επιβλέπουσα Καθηγήτρια: Λαμπροπούλου Σοφία Ιούλιος, 2013 Περιεχόμενα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. Εαρινό Εξάμηνο
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ31: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 017-018 Φροντιστήριο 5 1. Δικαιολογήστε όλες τις απαντήσεις σας. i. Δώστε τις 3 βασικές ιδιότητες ενός AVL δένδρου.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ31: Δομές Δεδομένων και Αλγόριθμοι Εαρινό Εξάμηνο 017-018 Φροντιστήριο 5 1. Δικαιολογήστε όλες τις απαντήσεις σας. i. Δώστε τις 3 βασικές ιδιότητες ενός AVL δένδρου.
( ιμερείς) ΙΜΕΛΕΙΣ ΣΧΕΣΕΙΣ Α Β «απεικονίσεις»
 ( ιμερείς) ΙΜΕΛΕΙΣ ΣΧΕΣΕΙΣ Α Β «πεικονίσεις» 1. ΣΧΕΣΕΙΣ: το σκεπτικό κι ο ορισμός. Τ σύνολ νπριστούν ιδιότητες μεμονωμένων στοιχείων: δεδομένου συνόλου S, κι ενός στοιχείου σ, είνι δυντόν είτε σ S είτε
( ιμερείς) ΙΜΕΛΕΙΣ ΣΧΕΣΕΙΣ Α Β «πεικονίσεις» 1. ΣΧΕΣΕΙΣ: το σκεπτικό κι ο ορισμός. Τ σύνολ νπριστούν ιδιότητες μεμονωμένων στοιχείων: δεδομένου συνόλου S, κι ενός στοιχείου σ, είνι δυντόν είτε σ S είτε
Η κατανομή του Euler επί των αυτοαντίστροφων στοιχείων της
 Ε Κ Π Α Τ Μ Η κατανομή του Euler επί των αυτοαντίστροφων στοιχείων της υπεροκταεδρικής ομάδας Μ Ε Μουστάκας Βασίλης - Διονύσης : Χ Α. Α Αθήνα Ιούνιος 07 Στον πρώτο μου δάσκαλο, μαθηματικό Γιάννη Καρρά.
Ε Κ Π Α Τ Μ Η κατανομή του Euler επί των αυτοαντίστροφων στοιχείων της υπεροκταεδρικής ομάδας Μ Ε Μουστάκας Βασίλης - Διονύσης : Χ Α. Α Αθήνα Ιούνιος 07 Στον πρώτο μου δάσκαλο, μαθηματικό Γιάννη Καρρά.
Πανεπιστήμιο Πειραιώς. Πρόγραμμα Μεταπτυχιακών Σπουδών Αναλογιστική Επιστήμη και Διοικητική Κινδύνου
 Πανεπιστήμιο Πειραιώς Τμήμα Στατιστικής και Ασφαλιστικής Επιστήμης Πρόγραμμα Μεταπτυχιακών Σπουδών Αναλογιστική Επιστήμη και Διοικητική Κινδύνου Παραμετρικά Μοντέλα Επιβίωσης που προκύπτουν από μεταβολές
Πανεπιστήμιο Πειραιώς Τμήμα Στατιστικής και Ασφαλιστικής Επιστήμης Πρόγραμμα Μεταπτυχιακών Σπουδών Αναλογιστική Επιστήμη και Διοικητική Κινδύνου Παραμετρικά Μοντέλα Επιβίωσης που προκύπτουν από μεταβολές
CSE.UOI : Μεταπτυχιακό Μάθημα
 Θέματα Αλγορίθμων Αλγόριθμοι και Εφαρμογές στον Πραγματικό Κόσμο CSE.UOI : Μεταπτυχιακό Μάθημα 10η Ενότητα: Χρονικά Εξελισσόμενες ικτυακές Ροές Σπύρος Κοντογιάννης kntg@cse.ui.gr Τμήμα Μηχανικών Η/Υ &
Θέματα Αλγορίθμων Αλγόριθμοι και Εφαρμογές στον Πραγματικό Κόσμο CSE.UOI : Μεταπτυχιακό Μάθημα 10η Ενότητα: Χρονικά Εξελισσόμενες ικτυακές Ροές Σπύρος Κοντογιάννης kntg@cse.ui.gr Τμήμα Μηχανικών Η/Υ &
Τρίτη, 05 Ιουνίου 2001 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 Τρίτη, 05 Ιουνίου 2001 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 Α. Να µεταφέρετε στο τετράδιό σας και να συµπληρώσετε τον παρακάτω πίνακα αλήθειας δύο προτάσεων
Τρίτη, 05 Ιουνίου 2001 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1 Α. Να µεταφέρετε στο τετράδιό σας και να συµπληρώσετε τον παρακάτω πίνακα αλήθειας δύο προτάσεων
ΤΑΞΙΝΟΜΗΣΗ ΟΡΓΑΝΙΣΜΩΝ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1α ΤΑΞΙΝΟΜΗΣΗ ΟΡΓΑΝΙΣΜΩΝ Οι επιστήμονες ταξινομούν τους οργανισμούς σε ομάδες ανάλογα με τα κοινά τους χαρακτηριστικά. Τα πρώτα συστήματα ταξινόμησης βασιζόταν αποκλειστικά στα μορφολογικά
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1α ΤΑΞΙΝΟΜΗΣΗ ΟΡΓΑΝΙΣΜΩΝ Οι επιστήμονες ταξινομούν τους οργανισμούς σε ομάδες ανάλογα με τα κοινά τους χαρακτηριστικά. Τα πρώτα συστήματα ταξινόμησης βασιζόταν αποκλειστικά στα μορφολογικά
Επίλυση δικτύων διανομής
 ΑστικάΥδραυλικάΈργα Υδρεύσεις Επίλυση δικτύων διανομής Δημήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Διατύπωση του προβλήματος Δεδομένου ενός δικτύου αγωγών
ΑστικάΥδραυλικάΈργα Υδρεύσεις Επίλυση δικτύων διανομής Δημήτρης Κουτσογιάννης & Ανδρέας Ευστρατιάδης Τομέας Υδατικών Πόρων Εθνικό Μετσόβιο Πολυτεχνείο Διατύπωση του προβλήματος Δεδομένου ενός δικτύου αγωγών
ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Σχεδίαση Λογικών Κυκλωμάτων
 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Σχεδίαση Λογικών Κυκλωμάτων Γιάννης Λιαπέρδος [gliaperd@teikal.gr] Μάρτιος 2012 1 Ηλεκτρονικά Ελεγχόμενοι ιακόπτες Για την υλοποίηση των λογικών κυκλωμάτων χρησιμοποιούνται ηλεκτρονικά
ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Σχεδίαση Λογικών Κυκλωμάτων Γιάννης Λιαπέρδος [gliaperd@teikal.gr] Μάρτιος 2012 1 Ηλεκτρονικά Ελεγχόμενοι ιακόπτες Για την υλοποίηση των λογικών κυκλωμάτων χρησιμοποιούνται ηλεκτρονικά
ΕΙΣΑΓΩΓΗ. H λογική ασχολείται με δύο έννοιες, την αλήθεια και την απόδειξη. Oι έννοιες αυτές έχουν γίνει
 ΕΙΣΑΓΩΓΗ ------------------------------------------------------------------------------------- H λογική ασχολείται με δύο έννοιες, την αλήθεια και την απόδειξη. Oι έννοιες αυτές έχουν γίνει αντικείμενο
ΕΙΣΑΓΩΓΗ ------------------------------------------------------------------------------------- H λογική ασχολείται με δύο έννοιες, την αλήθεια και την απόδειξη. Oι έννοιες αυτές έχουν γίνει αντικείμενο
Περίληψη. του Frostman 4.1. Τέλος, η ϑεωρία του μέτρου Hausdorff αναπτύσσεται περαιτέρω στην τελευταία παράγραφο. Εισαγωγή 2
 Το Μέτρο και η Διάσταση Hausdorff Γεωργακόπουλος Νίκος Τερεζάκης Αλέξης Περίληψη Αναπτύσσουμε τη ϑεωρία του μέτρου και της διάστασης Hausdorff με εφαρμογές στον υπολογισμό διαστάσεων συνόλων fractal (Θεώρημα
Το Μέτρο και η Διάσταση Hausdorff Γεωργακόπουλος Νίκος Τερεζάκης Αλέξης Περίληψη Αναπτύσσουμε τη ϑεωρία του μέτρου και της διάστασης Hausdorff με εφαρμογές στον υπολογισμό διαστάσεων συνόλων fractal (Θεώρημα
Ψηφιακή Εικόνα. Σημερινό μάθημα!
 Ψηφιακή Εικόνα Σημερινό μάθημα! Ψηφιακή Εικόνα Αναλογική εικόνα Ψηφιοποίηση (digitalization) Δειγματοληψία Κβαντισμός Δυαδικές δ έ (Binary) εικόνες Ψηφιακή εικόνα & οθόνη Η/Υ 1 Ψηφιακή Εικόνα Μια ακίνητη
Ψηφιακή Εικόνα Σημερινό μάθημα! Ψηφιακή Εικόνα Αναλογική εικόνα Ψηφιοποίηση (digitalization) Δειγματοληψία Κβαντισμός Δυαδικές δ έ (Binary) εικόνες Ψηφιακή εικόνα & οθόνη Η/Υ 1 Ψηφιακή Εικόνα Μια ακίνητη
Εξέταση Ηλεκτρομαγνητισμού Ι 2 Φεβρουαρίου 2018
 ΕΚΠΑ, Τμήμα Φυσικής Εξέταση Ηλεκτρομαγνητισμού Ι 2 Φεβρουαρίου 2018 ΘΕΜΑ 1 Γραμμική κατανομή φορτίου εκτείνεται από h έως +h κατά μήκος του άξονα z με ετερογενή πυκνότητα λ 0 < 0 για h z < 0 και λ 0 >
ΕΚΠΑ, Τμήμα Φυσικής Εξέταση Ηλεκτρομαγνητισμού Ι 2 Φεβρουαρίου 2018 ΘΕΜΑ 1 Γραμμική κατανομή φορτίου εκτείνεται από h έως +h κατά μήκος του άξονα z με ετερογενή πυκνότητα λ 0 < 0 για h z < 0 και λ 0 >
(3 ο ) Εξαντλητική αναζήτηση I: μεταθέσεις & υποσύνολα (4 o ) Εξαντλητική αναζήτηση II: συνδυασμοί, διατάξεις & διαμερίσεις
 (3 ο ) Εξαντλητική αναζήτηση I: μεταθέσεις & υποσύνολα (4 o ) Εξαντλητική αναζήτηση II: συνδυασμοί, διατάξεις & διαμερίσεις Είναι πράγματι τα «προβλήματα» τόσο δύσκολα; Είδαμε (σύντομα) στα προηγούμενα
(3 ο ) Εξαντλητική αναζήτηση I: μεταθέσεις & υποσύνολα (4 o ) Εξαντλητική αναζήτηση II: συνδυασμοί, διατάξεις & διαμερίσεις Είναι πράγματι τα «προβλήματα» τόσο δύσκολα; Είδαμε (σύντομα) στα προηγούμενα
Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 01: ΕΞΑΝΤΛΗΤΙΚΗ ΑΝΑΖΗΤΗΣΗ
 Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 01: ΕΞΑΝΤΛΗΤΙΚΗ ΑΝΑΖΗΤΗΣΗ Δεδομένου ενός προβλήματος Q, ο πρώτος σκοπός μιας εξαντλητικής αναζήτησης είναι να μας εφασφαλίσει
Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 01: ΕΞΑΝΤΛΗΤΙΚΗ ΑΝΑΖΗΤΗΣΗ Δεδομένου ενός προβλήματος Q, ο πρώτος σκοπός μιας εξαντλητικής αναζήτησης είναι να μας εφασφαλίσει
Εκφωνήσεις και Λύσεις των Θεμάτων
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΚΑΤΕΥΘΥΝΣΗΣ) Τετάρτη 8 Μαΐου 26 Εκφωνήσεις και Λύσεις των Θεμάτων η LaT E X-έκδοση ( 22/5/26)
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΚΑΤΕΥΘΥΝΣΗΣ) Τετάρτη 8 Μαΐου 26 Εκφωνήσεις και Λύσεις των Θεμάτων η LaT E X-έκδοση ( 22/5/26)
14 Φεβρουαρίου 2014, Βόλος
 ιαφορικές Εξισώσεις Εισαγωγή Μανόλης Βάβαλης Τμήμα Μηχανικών Η/Υ Τηλεπικοινωνιών και ικτύων Πανεπιστήμιο Θεσσαλίας 14 Φεβρουαρίου 2014, Βόλος ιαδικαστικά Θέματα Ο τελικός βαθμός προτείνω να υπολογισθεί
ιαφορικές Εξισώσεις Εισαγωγή Μανόλης Βάβαλης Τμήμα Μηχανικών Η/Υ Τηλεπικοινωνιών και ικτύων Πανεπιστήμιο Θεσσαλίας 14 Φεβρουαρίου 2014, Βόλος ιαδικαστικά Θέματα Ο τελικός βαθμός προτείνω να υπολογισθεί
( ) Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 03: ΑΣΥΜΠΤΩΤΙΚΕΣ ΕΚΦΡΑΣΕΙΣ
 Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 03: ΑΣΥΜΠΤΩΤΙΚΕΣ ΕΚΦΡΑΣΕΙΣ Ενδιαφερόμαστε μεν για τους αλγορίθμους αλλά εντός ενός συγκεκριμμένου πλαισίου: (α) ως λύσεις προβλημάτων,
Π. ΚΡΗΤΗΣ, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΗΥ 380, «ΑΛΓΟΡΙΘΜΟΙ & ΠΟΛΥΠΛΟΚΟΤΗΤΑ» Φ 03: ΑΣΥΜΠΤΩΤΙΚΕΣ ΕΚΦΡΑΣΕΙΣ Ενδιαφερόμαστε μεν για τους αλγορίθμους αλλά εντός ενός συγκεκριμμένου πλαισίου: (α) ως λύσεις προβλημάτων,
ΠΙΘΑΝΟΤΗΤΕΣ 2. Σάμης Τρέβεζας
 ΠΙΘΑΝΟΤΗΤΕΣ 2 Σάμης Τρέβεζας ii ΣΑΜΗΣ ΤΡΕΒΕΖΑΣ Λέκτορας Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Πιθανότητες ΙΙ Σημειώσεις σε εξέλιξη... (02/03) Περιεχόμενα 1 Δομές σε Οικογένειες
ΠΙΘΑΝΟΤΗΤΕΣ 2 Σάμης Τρέβεζας ii ΣΑΜΗΣ ΤΡΕΒΕΖΑΣ Λέκτορας Τμήμα Μαθηματικών Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνων Πιθανότητες ΙΙ Σημειώσεις σε εξέλιξη... (02/03) Περιεχόμενα 1 Δομές σε Οικογένειες
