ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΣΕ ΥΛΙΚΑ Λ. ΠΕΡΙΒΟΛΑΡΟΠΟΥΛΟΣ. Poynting
|
|
|
- Άκανθα Βουγιουκλάκης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΣΗΜΕΙΩΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΣΕ ΥΛΙΚΑ Λ. ΠΕΡΙΒΟΛΑΡΟΠΟΥΛΟΣ Σκοπός Σκοπός του κεφαλαίου είναι η µελέτη της συµπεριφοράς ηλεκτροµαγνητικών κυµάτν στο εστερικό υλικών (διηλεκτρικών και αγγών και η επεξήγηση τν φαινοµένν της ανάκλασης και της διάθλασης. Προσδοκώµενα αποτελέσµατα Με την ολοκλήρση της µελέτης του κεφαλαίου, θα µπορείτε να: προσδιορίσετε πώς σχετίζεται η ένταση ηλεκτροµαγνητικού κύµατος µε το διάνυσµα Poynting προσδιορίσετε σε τι διαφέρει η ταχύτητα φάσης από την ταχύτητα οµάδας ηλεκτροµαγνητικού κύµατος αναφέρετε τον ορισµό της σχέσης διασποράς αποδείξετε το νόµο του Snell και να προσδιορίσετε αν ισχύει ο νόµος όταν υπάρχουν πηγές στις διαχριστικές επιφάνειες αναφέρετε τη συνθήκη που απαιτείται για το µηδενισµό του συντελεστή ανάκλασης ή διάδοσης στην κάθετη πρόσπτση εξηγήσετε τη µεγάλη ανακλαστικότητα τν µεταλλικών επιφανειών αναφέρετε τον ορισµό της γνίας Brewster. Έννοιες κλειδιά µετασχηµατισµός Lorentz χώρος Minowsi τετραδιάνυσµα τανυστής
2 σύστηµα αναφοράς δύναµη Minowsi ηλεκτροµαγνητικός τανυστής συναλλοίτη µορφή ταχύτητα φάσης ταχύτητα οµάδας κυµατάνυσµα πόλση ανάκλαση διάθλαση πρόσπτση ΕΝΟΤΗΤΑ.: Πόλση, ανάκλαση και διάθλαση ηλεκτροµαγνητικών κυµάτν Οι εξισώσεις του Maxwell σε διηλεκτρικά χρίς πηγές ( ρ, J : ε, B B, B ε t µ t f f (. (. ταυτίζονται µε τις εξισώσεις του Maxwell στο κενό (9.63-(9.66 µε αντικατάσταση ε ε και µ µ. Άρα οδηγούν σε παρόµοιες εξισώσεις ηλεκτροµαγνητικού κύµατος όπς στο κενό [(9.7 και (9.73], µε τη διαφορά ότι η ταχύτητα διάδοσης ηλεκτροµαγνητικού κύµατος σε διηλεκτρικό είναι µικρότερη και ισούται µε: v < c (.3 εµ ε µ Ο δείκτης διάθλασης ηλεκτροµαγνητικού κύµατος σε διηλεκτρικό ορίζεται ς ο λόγος ταχυτήτν κυµάτν: c εµ n > (.4 v ε µ
3 Τα πεδία επίπεδου πολµένου κύµατος σε διηλεκτρικά περιγράφονται από το πραγµατικό µέρος τν σχέσεν: ( x, t B( x, t B i( x vt e i( x vt e (.5 (.6 Αντικαθιστώντας τις (.5, (.6 στις εξισώσεις Maxwell (., βρίσκουµε εύκολα ότι, B (.7 Άρα, τα ηλεκτροµαγνητικά κύµατα έχουν πόλση κάθετη στη διεύθυνση διάδοσης και λέγονται εγκάρσια. Όµοια, αντικαθιστώντας τις (.5, (.6 στις (., βρίσκουµε: B, B (.8 µε Από τις (.8 είναι προφανές ότι B, και εποµένς τα, B, αποτελούν ορθογώνια τριάδα. Ακόµα, αντικαθιστώντας τις (.5, (.6 στις εξισώσεις κύµατος, προκύπτει ότι η ταχύτητα διάδοσης του κύµατος ισούται µε, δηλαδή: εµ v εµ (.9 που είναι η σχέση διασποράς του κύµατος. Σε διηλεκτρικά η ηλεκτρική διαπερατότητα ε εξαρτάται από τη γνιακή συχνότητα ( ε ε για µεγάλα, λόγ υστέρησης αλλαγής προσανατολισµού τν στοιχειδών διπόλν. Όταν ε ε ( [οπότε και v v( ], η ταχύτητα φάσης v ά φ σης (ταχύτητα µετακίνησης ενός σηµείου µε σταθερή φάση στο κύµα διαφέρει από την ταχύτητα d οµάδας vοµ. (ταχύτητα µετακίνησης της περιβάλλουσας ενός κυµατικού παλµού. d Η ένταση ηλεκτροµαγνητικού κύµατος Ι ταυτίζεται µε τη µέση ενεργειακή ροή, δηλαδή τη µέση τιµή της προβολής του ρεύµατος ενέργειας στη διεύθυνση διάδοσης, που είναι το διάνυσµα Poynting S επί Άρα: Η ταχύτητα οµάδας είναι η ταχύτητα µεταφοράς της πληροφορίας σε ένα κυµατικό σήµα.
4 I S B µ cos ( x t (. Χρησιµοποιώντας την καθετότητα µεταξύ ˆ, B, και τη σχέση B, που προκύπτει από το νόµο του Faraday, η (. γράφεται: I εv (. µ όπου το προέκυψε από τη µέση τιµή του cos ( x t. Άσκηση αυτοαξιολόγησης. Ως ένα παράδειγµα της ταχύτητας οµάδας θερήστε ένα Γκαουσιανό κυµατοπακέτο µιας συνάρτησης ( x, t φ που διαδίδεται ς κύµα και δίνεται από τη σχέση: όπου φ (, + i ( x t d ( x t e f ( f f e ( a π Το εύρος του είναι (, +, αλλά η ποσότητα στο ολοκλήρµα εµφανίζει µέγιστο για µε εύρος της τάξης του / a. Υποθέστε ότι στην περιοχή του µεγίστου το ( προσεγγίζεται από τη σχέση ( ( ( ( +. α Υπολογίστε το ολοκλήρµα και βρείτε τη συνάρτηση ( x, t φ. β είξτε ότι η ταχύτητα φάσης είναι ( / και η ταχύτητα οµάδας (. Άσκηση αυτοαξιολόγησης. Για ένα ηλεκτροµαγνητικό κύµα σε αραιό πλάσµα βρείτε την ταχύτητα φάσης και την ταχύτητα οµάδας ς συνάρτηση του. Άσκηση αυτοαξιολόγησης.3 Αποδείξτε ότι σε πλάσµα µικής αγγιµότητας σ και µαγνητικής διαπερατότητας µ το µαγνητικό πεδίο B ικανοποιεί την εξίσση
5 t B D B όπου D c / 4πσ. Άσκηση αυτοαξιολόγησης.4 Θερήστε ένα µοντέλο αγγιµότητας πλάσµατος στο οποίο η αγγιµότητα είναι φανταστική, δηλαδή J iσ στη µιγαδική αναπαράσταση του κύµατος. α Από τις εξισώσεις του Maxwell βρείτε τη σχέση µεταξύ και για ηλεκτροµαγνητικό κύµα που διαδίδεται στο πλάσµα µε πεδία που δίνονται ς: j e i( x t, B B e i( x t β είξτε ότι το J υπολείπεται σε φάση του κατά 9 µοίρες. ΕΝΟΤΗΤΑ.: Ανάκλαση και διάθλαση σε διαχριστική επιφάνεια διηλεκτρικών Έστ ότι το επίπεδο yz ( x αποτελεί διαχριστική επιφάνεια µεταξύ δύο γραµµικών διηλεκτρικών µε παραµέτρους ε µ, n ( x καιε, µ, n ( x >. Έστ ότι επίπεδο κύµα, µε κυµατάνυσµα ˆ προσπίπτει από την πλευρά x. Λόγ του προσπίπτοντος κύµατος, εµφανίζεται ένα ανακλώµενο επίπεδο κύµα µε κυµατάνυσµα στην περιοχή x και ένα διαθλώµενο επίπεδο κύµα µε κυµατάνυσµα στην περιοχή x >. Το ηλεκτρικό πεδίο, λόγ τν κυµάτν αυτών, γράφεται ς: i( x t( x t i( x t x ( x, t e + e i( x t x e (. και αντίστοιχα για το µαγνητικό πεδίο. Οι συνοριακές συνθήκες για τα πεδία στη διαχριστική επιφάνεια προκύπτουν εύκολα από τις (9.46-(9.49 µε µηδενισµό τν πηγών: ε ε, B B (.3 B B // // // //, (.4 µ µ
6 Οι συνοριακές αυτές συνθήκες θα πρέπει να ισχύουν για κάθε χρονική στιγµή t και για κάθε τιµή τν y και z πάν στη διαχριστική επιφάνεια. Η παρατήρηση αυτή σε συνδυασµό µε την (. οδηγεί στις συνθήκες: (.5 (.6 y y y (.7 z z z Η (.5 σε συνδυασµό µε τη σχέση διασποράς v οδηγεί στις σχέσεις για τους κυµατάριθµους (µέτρα κυµατανυσµάτν στις δύο πλευρές της διαχριστικής επιφάνειας: n (.8 v c n (.9 v c Μπορούµε να επιλέξουµε το επίπεδο xy έτσι ώστε το προσπίπτον κυµατάνυσµα να έχει. Τότε, λόγ της (.7, θα έχουµε, και εποµένς, λόγ τν (.8 z και (.9, τα κυµατανύσµατα, και µπορεί να γραφτούν ς: z z n ˆ ˆ ( i cosθ + j sin θ (. c n ˆ ˆ ( i cosθ + j sin θ (. c n ˆ ˆ 3 ( i cosθ + j sin θ (. c όπου θ η γνία πρόσπτσης, θ η γνία ανάκλασης και θ η γνία διάθλασης (δείτε Σχήµα 3. τν PS. Χρησιµοποιώντας τώρα την (.6 σε συνδυασµό µε τις (.-(., προκύπτουν οι παρακάτ σχέσεις µεταξύ τν γνιών θ, θ και θ : sin θ sinθ (.3 n sinθ n sinθ (.4
7 Η σχέση (.3, που εκφράζει την ισότητα µεταξύ γνιών πρόσπτσης και ανάκλασης, είναι ο γνστός νόµος της ανάκλασης. Η σχέση (.4 µεταξύ γνιών πρόσπτσης και διάθλασης είναι γνστή ς νόµος της διάθλασης ή νόµος του Snell. Όταν n > n, δηλαδή το διηλεκτρικό διάθλασης (υλικό είναι οπτικώς αραιότερο από το διηλεκτρικό πρόσπτσης (υλικό, οπότε και v > v, τότε θ > θ και υπάρχει µια κρίσιµη γνία π θ θc <, για την οποία διάθλαση αλλά ολική ανάκλαση. Για θ θc έχουµε: και εποµένς: π θ, και για γνίες θ > θc δεν υπάρχει π n sinθ c n,sin n n θ arcsin c (.5 n ΕΝΟΤΗΤΑ.3: Συντελεστές ανάκλασης και διάδοσης σε κάθετη πρόσπτση Σε κάθετη πρόσπτση έχουµε θ θ θ. Χρίς βλάβη της γενικότητας, µπορούµε να υποθέσουµε πόλση του ηλεκτρικού πεδίου στη διεύθυνση ĵ : x t (, ˆ i( x t ˆ i( x t je + je x ˆ i( x t je x > Από τον νόµο του Faraday και την (.6 έχουµε: B x t (, i( x t i( x t ze ˆ ze ˆ x i( x t ze ˆ x > (.6 (.7 Εφαρµόζοντας τώρα τις συνοριακές συνθήκες (.4 για τις παράλληλες συνιστώσες του ηλεκτρικού και του µαγνητικού πεδίου στις (.6 και (.7, έχουµε: + (.8
8 όπου v και v. (.9 µ v µ v Λύνοντας τώρα τις (.8, (.9 ς προς τα διαθλώµενα ( Ε και ανακλώµενα ( Ε πλάτη πεδίν, βρίσκουµε: Ε µ n µ n + µ n Ε (.3 µ n µ n Ε µ n + µ n Ε (.3 Στα περισσότερα διηλεκτρικά ισχύει µ µ, οπότε, αν το κύµα περνάει από οπτικά αραιότερο σε οπτικά πυκνότερο υλικό ( n n <, τότε, λόγ της (.3, τα Ε και Ε έχουν αντίθετο πρόσηµο. Κατά την ανάκλαση αυτή, το παλλόµενο ηλεκτρικό πεδίο παίρνει µια επιπλέον φάση κατά 8. Το ανακλώµενο όµς µαγνητικό πεδίο ˆ Β z έχει ένα επιπλέον πρόσηµο (, όπς φαίνεται στην (.7, άρα η φάση του δεν αλλάζει σε σχέση µε το προσπίπτον πεδίο. Το αντίθετο συµβαίνει αν n > n. Ο συντελεστής ανάκλασης του κύµατος ορίζεται ς: S I < > R (.3 I < S > και εποµένς από τις (. και (.3 έχουµε: µ n µ n R µ n + µ n (.33 Όµοια, για το συντελεστή διάδοσης Τ έχουµε: T I ε µ µ I ε v µ n µ n v 4 nn ( + (.34
9 όπου χρησιµοποιήσαµε τις (., (.3 και τον ορισµό του δείκτη διάθλασης c µε n. Προφανώς ισχύει T + R, όπς αναµένεται, λόγ διατήρησης της v µ ε ενέργειας. Άσκηση αυτοαξιολόγησης.5 Βρείτε τους συντελεστές ανάκλασης R και διέλευσης Τ για ΑΜ ραδιοκύµατα συχνότητας MHz που πέφτουν σε επιφάνεια λίµνης (για το νερό υποθέστε ε ε 8. ΕΝΟΤΗΤΑ.4: Πρόσπτση υπό αυθαίρετη γνία: ξισώσεις Fresnel Θα βρούµε τα πλάτη ανάκλασης και διάδοσης ηλεκτρικού πεδίου για αυθαίρετη γνία πρόσπτσης θ. Θα διακρίνουµε δύο περιπτώσεις: α του ηλεκτρικού πεδίου κάθετου στο επίπεδο πρόσπτσης (TΕ: Transverse lectric β πόλση του µαγνητικού πεδίου κάθετου στο επίπεδο πρόσπτσης (ΤΜ: Transverse Magnetic..4. Πόλση ΤΕ Στην περίπτση αυτή, αν το επίπεδο πρόσπτσης είναι το x, y, το ηλεκτρικό πεδίο είναι: i( x t ˆ i( x t ze + z ˆ e x ( x, t i ˆ ( x t z e x > (.35 Aπό τη σχέση διασποράς τα πλάτη τν κυµατανυσµάτν είναι:, v v Η µοναδική συνιστώσα του ηλεκτρικού πεδίου είναι παράλληλη µε τη διαχριστική επιφάνεια και, εποµένς, η σχετική συνοριακή συνθήκη είναι η, που δίνει, λόγ της (.35: + (.36
10 Για να βρούµε τα πεδία και συναρτήσει του, χρειαζόµαστε άλλη µια σχέση. Θα χρησιµοποιήσουµε τις συνοριακές συνθήκες για το µαγνητικό πεδίο. Σε αντιστοιχία µε τη (.34, το µαγνητικό πεδίο είναι: B x t (, i( x t i( x t Be + B e x i( x t B e x > (.37 Θα εκφράσουµε το πλάτος του µαγνητικού πεδίου συναρτήσει του πλάτους του ηλεκτρικού πεδίου χρησιµοποιώντας το νόµο του Faraday: B t Το προσπίπτον κυµατάνυσµα γράφεται ς: iˆ cosθ + ˆj sinθ v Άρα, το πλάτος του προσπίπτοντος κύµατος µαγνητικού πεδίου γράφεται: B ˆ ˆ j cosθ + i sinθ v (.38 (.39 όπου χρησιµοποιήσαµε και την (.35 για το προσπίπτον κύµα ηλεκτρικού πεδίου και το νόµο του Faraday. Για να βρούµε το πλάτος του ανακλώµενου κύµατος µαγνητικού πεδίου µέσ του νόµου του Faraday, πρώτα γράφουµε το κυµατάνυσµα του ανακλώµενου κύµατος ς: iˆ cosθ + ˆj sinθ v (.4 όπου χρησιµοποιήσαµε το νόµο της ανάκλασης, σύµφνα µε τον οποίο απλώς αντιστρέφουµε τη x συνιστώσα του προσπίπτοντος για να βρούµε το ανακλώµενο. Χρησιµοποιώντας τώρα το νόµο του Faraday, την (.39 και την (.35 για το ανακλώµενο ηλεκτρικό κύµα, βρίσκουµε το ανακλώµενο µαγνητικό κύµα ς: B ˆ ˆ j cosθ + i sinθ v (.4 Τέλος, για το διαθλώµενο µαγνητικό κύµα έχουµε: iˆ cosθ + ˆj sinθ v (.4
11 από την οποία προκύπτει: ˆ ˆsinθ B j cosθ i υ + Οι συνοριακές συνθήκες για το µαγνητικό πεδίο είναι: B B B B x B B x, µ µ (.43 (.44 Χρησιµοποιώντας τη συνέχεια της κάθετης συνιστώσας του µαγνητικού πεδίου και την (.37 [µε αντικατάσταση από τις (.39, (.4 και (.43], παίρνουµε: Η (.45 µε χρήση της (.36 γίνεται: που είναι ο νόµος του Snell. sinθ + sinθ sinθ (.45 v v v n sinθ n sinθ (.46 Χρησιµοποιώντας τη συνέχεια της παράλληλης συνιστώσας του B H µ και την (.37, παίρνουµε: θ θ θ µ v µ v µ v cos + cos cos (.47 Οι (.47 και (.36 αποτελούν τις ζητούµενες δύο εξισώσεις από τις οποίες µπορούµε να βρούµε το διαθλώµενο πλάτος και το ανακλώµενο πλάτος συναρτήσει του προσπίπτοντος πλάτους. Η λύση του συστήµατος (.47 και (.36 προκύπτει εύκολα ς: µ n cosθ µ n cosθ + µ n cosθ n cos n cos µ θ µ θ µ n cosθ + µ n cosθ (.48 (.49 Στην προσέγγιση µ µ µ, που ισχύει στα περισσότερα διηλεκτρικά, η (.49 γίνεται µε τη χρήση του νόµου του Snell:
12 sin sin ( θ θ ( θ + θ που είναι η εξίσση του Fresnel για πόλση ΤΕ. (.5.4. Πόλση ΤΜ Στην περίπτση πόλσης ΤΜ, το µαγνητικό πεδίο γράφεται ς: B x t (, i( x t i ˆ ˆ ( x t z e + z e x v v i ˆ ( x t z e x > v (.5 όπου χρησιµοποιήσαµε το νόµο του Faraday για τη συσχέτιση του πλάτους B µε το. Από τη συνθήκη Β Β µ µ έχουµε: ( + (.5 µ µ v v B Από τις σχέσεις (.38, (.4, (.4 και το νόµο του Faraday (π.χ. zˆ προκύπτουν τα πλάτη τν ηλεκτρικών κυµάτν (προσπίπτον, διαθλώµενο και ανακλώµενο ς: + j ( ˆsin ι θ ˆ cosθ i + j και το ηλεκτρικό πεδίο έχει τη µορφή: x t (, ( ˆsinθ ˆ cosθ j ( ˆsin ι θ ˆ cosθ i( x t i( x t e + e x i( x t e x > (.53 (.54 (.55 (.56 Από τη συνέχεια της παράλληλης συνιστώσας ĵ του ηλεκτρικού πεδίου έχουµε, λόγ τν (.53-(.56:
13 ( cosθ cosθ (.57 v n Οι (.57 και (.5 µε αποτελούν τις δύο βασικές σχέσεις από τις οποίες v n βρίσκουµε τα και συναρτήσει του. Το αποτέλεσµα είναι: µ n cosθ µ n cosθ + µ n cosθ µ n cosθ µ n cosθ µ n cosθ + µ n cosθ (.58 (.59 Στην προσέγγιση µ µ µ η (.59 γίνεται (µε χρήση του νόµου του Snell: tan tan που είναι η εξίσση Fresnel για πόλση ΤΜ. ( θ θ ( θ + θ (.6 π Όταν θ θ +, έχουµε από την (.6 και όλο το ΤΜ κύµα διαθλάται χρίς π καθόλου ανάκλαση. Θέτοντας στο νόµο του Snell θ + θ, έχουµε: ή n sinθ n sinθ n cosθ (.6 n tanθ tanθ B (.6 n Η γνία θ B, για την οποία έχουµε ολική διάθλαση του κύµατος ΤΜ, λέγεται γνία Brewster. Για θ θ B, το µόνο ανακλώµενο κύµα είναι πόλσης ΤΕ και είναι % πολµένο.
14 ΕΝΟΤΗΤΑ.5: Ηλεκτροµαγνητικά κύµατα σε αγγούς Θα θερήσουµε αγγούς ς γραµµικά υλικά µε αγγιµότητα σ και ελεύθερα ρεύµατα: J x, t σ ( x, t (.63 χρίς ελεύθερα φορτία ( f f ( ρ (τυχόν ελεύθερα φορτία απθούνται προς την επιφάνεια του αγγού και µε γραµµικές διηλεκτρικές και µαγνητικές ιδιότητες. Λόγ της (.63, οι εξισώσεις Maxwell στο εστερικό αγγού γράφονται ς:, B B, B t µσ µε + t (.64 (.65 Ο νέος όρος µελετήσουµε. µσ προκαλεί αλλαγές στη µορφή της κυµατικής εξίσσης, τις οποίες θα Για να βρούµε τη µορφή της κυµατικής εξίσσης, παίρνουµε την περιστροφή και στα δύο ισούται µε, αφού µέλη του νόµου του Faraday (.65. Η ( (λόγ.64. Η περιστροφή του δεξιού µέλους του νόµου του Faraday οδηγεί σε B, που µπορεί να εκφραστεί συναρτήσει του µε χρήση του νόµου Ampere- t Maxwell (.65. Έτσι, προκύπτει η γενικευµένη κυµατική εξίσση για το ηλεκτρικό πεδίο στο εστερικό αγγού ς: µσ µε t t + (.66 Η αντίστοιχη εξίσση για το B προκύπτει αν πάρουµε την περιστροφή και στα δύο µέλη της εξίσσης Ampere-Maxwell και µετά χρησιµοποιήσουµε το νόµο του Faraday και το νόµο του Gauss B. Βρίσκουµε: B B B µσ + µε (.67 t t Θερούµε τώρα δοκιµαστική λύση για την (.66 της µορφής: i x t x, t e ( ( (.68 όπου υποθέσαµε, χρίς βλάβη της γενικότητας, ότι το επίπεδο κύµα διαδίδεται στη διεύθυνση x.
15 Επειδή B, έχουµε i, και εποµένς το κύµα είναι αναγκαστικά εγκάρσιο. Για να βρούµε τη σχέση διασποράς, αντικαθιστούµε την (.68 στην (.66 και βρίσκουµε: iµσ + µε (.69 Για σ, βρίσκουµε τη γνστή σχέση διασποράς που ισχύει σε διηλεκτρικά. Για σ όµς, ο κυµατάριθµος είναι µιγαδικός και γράφεται ς: + i (.7 Με αντικατάσταση της (.7 στην (.69, εύκολα βρίσκουµε τα, ς: εµ σ + ± ε και εποµένς το ηλεκτρικό πεδίο είναι το πραγµατικό µέρος του: x i( x t x, t e e ( (.7 (.7 Η εκθετική πτώση του πλάτους του κύµατος µε το x οφείλεται στην απορρόφηση ενέργειας από την ηλεκτρική αντίσταση του αγγού. Η ταχύτητα φάσης του κύµατος είναι: v ph (.73 ( και εξαρτάται από τη συχνότητα. Σε υλικά που συµβαίνει αυτό, οι διαφορετικές συνιστώσες µε καθορισµένο που συνθέτουν παλµό κύµατος έχουν διαφορετική ταχύτητα φάσης κι ο παλµός αλλάζει µορφή κατά τη διάδοσή του. Η ταχύτητα διάδοσης του παλµού είναι η ταχύτητα οµάδας: v gr d d Το µαγνητικό πεδίο που αντιστοιχεί στην (.7 βρίσκεται από την (.68 και το νόµο του Faraday ς: ib i i (.74 ή B i e i( x ϖ t (.75
16 Η µιγαδική µορφή του εισάγει µια διαφορά φάσης µεταξύ και B που ισούται µε τη φάση του. Ο συντελεστής ανάκλασης ηλεκτροµαγνητικού κύµατος που προσπίπτει κάθετα από το κενό σε αγγό µπορεί να βρεθεί µε χρήση της (.3, θέτοντας µ µ µ, n και n c [το n στην (.3 προέκυψε ς c, όπου το προέκυψε µετά από χρική / παραγώγιση. Η ίδια χρική παραγώγιση οδηγεί στο µιγαδικό στην περίπτση του c c αγγού, αν και για τον αγγό έχουµε κανονικά n ]. v ph Με τις αντικαταστάσεις αυτές, η (.3 γίνεται: n c + n + c και εποµένς: I ( c + c R c I + c + c ( (.76 (.77 Για καλό αγγό, όµς, έχουµε σ >> ε, που, λόγ της (.7, οδηγεί σε c >>. Με τη συνθήκη αυτή η (.77 δίνει R και, εποµένς, αναµένουµε µεγάλη ανακλαστικότητα του φτός από καλούς αγγούς. Έτσι εξηγείται η µεγάλη ανακλαστικότητα (λάµψη τν µεταλλικών επιφανειών. Άσκηση αυτοαξιολόγησης.6 Βρείτε την πίεση ακτινοβολίας που ασκείται στην επιφάνεια αγγού λόγ κάθετης πρόσπτσης φτός δεδοµένης έντασης. Λύσεις Ασκήσεν αυτοαξιολόγησης Λύση. α Υπολογίζουµε το µετασχηµατισµό Fourier: φ (, + i ( x t d ( x t e f π
17 f e e e dq π ( ( i x t + i qx q ' t q a Θέτουµε q : f ( ( x ' e e π a i x t 4 a όπου είναι το υπολογισµένο στο και σηµαίνει d υπολογισµένο στο d. Παραπάν προσεγγίσαµε το ( ς: ( + ( ' και αλλάξαµε τη µεταβλητή ολοκλήρσης σε q. Έπειτα εφαρµόσαµε το γενικό τύπο ολοκλήρσης: + αq βq e e dq π exp α β 4 β φ έχει β Φασική ταχύτητα: Ένα σηµείο µε σταθερή φάση ( x, t x t ct δηλαδή: dx dt και έτσι dx dt η οποία εκφράζει τη φασική ταχύτητα. Ταχύτητα οµάδας: Το κέντρο του κυµατοπακέτου είναι στο x ' t. Εποµένς: dx d dt ' d η οποία εκφράζει την ταχύτητα της οµάδας. Λύση. Η διασπορά για ένα ηλεκτροµαγνητικό κύµα σε πλήρς ιονισµένο αέριο πολύ υψηλής θερµοκρασίας (δηλαδή κατάσταση πλάσµατος είναι: p + c
18 όπου ph είναι η συχνότητα του πλάσµατος (γνιακή συχνότητα. Η φασική ταχύτητα είναι: υ ph c p µε τον περιορισµό ότι > p, για να έχουµε διάδοση του κύµατος. Η ταχύτητα της οµάδας είναι: υ gr d c c d υ ph c p Λύση.3 Το ηλεκτροµαγνητικό πεδίο µέσα στο πλάσµα ικανοποιεί τις ακόλουθες εξισώσεις του Maxwell (σε Γκαουσιανές µονάδες: B D 4πρ f c t 4π B B j f σ και αν το πλάσµα είναι µικό, εµείς έχουµε επίσης: j σ f Άρα: 4π B σ c ή B D B ( c µε D. 4πσ Η εξίσση ( είναι εξίσση διάχυσης.
19 Λύση.4 Στο πλάσµα που ισχύει J iσ, το ηλεκτρικό και το µαγνητικό πεδίο είναι j e i( x t και B B e i( x t αντίστοιχα. α Από το νόµο του Faraday, B t B (, έχουµε ότι Από το νόµο του Ampere, B µ J + µ ε t, έχουµε ότι ib µ iσ µ ε i ( µ σ µ ε B ( Συνδυάζοντας τις ( και (, καταλήγουµε στην ισότητα B µ ε µ σ Εποµένς, η σχέση διασποράς είναι: µ ε µ σ β Η πυκνότητα του ηλεκτρικού ρεύµατος στο πλάσµα είναι: J iσ j e i x t π + σ Παρατηρούµε ότι υπάρχει µια διαφορά φάσης κατά π και το προηγείται του J. Για ένα τυχαίο σταθερό σηµείο x, το είναι µέγιστο για x t, δηλαδή για χρόνο t x. Το J είναι µέγιστο για x t + π, δηλαδή τη µεταγενέστερη χρονική +. στιγµή t x π ( Λύση.5 Η ανακλαστικότητα από ένα διηλεκτρικό υλικό για κάθετη πρόσπτση δίνεται από τη σχέση: µ n µ n n n R µ n + µ n n + n όπου η δεύτερη ισότητα είναι για την περίπτση όπου ισχύει µ µ. Για ραδιοκύµατα τα οποία προσκρούουν στην επιφάνεια µιας λίµνης, R.64, λαµβάνοντας υπόψη ότι ο
20 δείκτης διάθλασης για τον αέρα είναι n, ενώ ο αντίστοιχος για το νερό είναι n 8 9. Από τη διατήρηση της ενέργειας, ο συντελεστής διέλευσης είναι T.36. Λύση.6 Θερούµε µια δέσµη φτός που προσπίπτει κάθετα πάν σε µια µεταλλική επιφάνεια. Η ορµή της ροής του προσπίπτοντος ηλεκτροµαγνητικού κύµατος είναι: du dp c Ι Adt Adt c όπου I η ένταση (ροή της ενέργειας. Επιπλέον, θα πρέπει να διευκρινίσουµε ότι, για την παραπάν εξίσση, dp είναι η ορµή στον όγκο όπου διαδίδεται το κύµα που διέρχεται από µια µικρή περιοχή A κατά τη διάρκεια χρόνου dt, du είναι η ενέργεια στον ίδιο όγκο, που είναι ίση µε ( dp c. Από το ο Νόµο του Νεύτνα, η δύναµη στην περιοχή A είναι: F dp dt µε τον παράγοντα να εκφράζει την τέλεια ανάκλαση. Επιπλέον, η τάση είναι: F Ι A c Η παραπάν πίεση µπορεί να θερηθεί ότι προκύπτει και από τη δύναµη Lorentz ς εξής: Θερήστε ένα οδεύον κύµα κατά τη διεύθυνση του άξονα τν x, πολµένο κατά τον y άξονα και το οποίο προσπίπτει κανονικά πάν σε µεταλλική επιφάνεια. Το ηλεκτρικό πεδίο ταλαντώνεται κατά τη διεύθυνση ± j, ενώ το µαγνητικό πεδίο ταλαντώνεται κατά τη διεύθυνση ±. Θερήστε τη στιγµή στην οποία έχουµε j και B στην επιφάνεια. Η δύναµη Lorentz για ένα ελεύθερο φορτίο q σε µέταλλο είναι F qv B, όπου B είναι κατά τη διεύθυνση και qv είναι κατά τη διεύθυνση του, δηλαδή κατά τη διεύθυνση του µοναδιαίου j, επειδή J σ. Επιπλέον, η δύναµη που
21 i ασκείται στο φορτίο q είναι κατά τη διεύθυνση του j, το οποίο είναι κάθετο στην επιφάνεια. Ερτήσεις. Πώς σχετίζεται η ένταση ηλεκτροµαγνητικού κύµατος µε το διάνυσµα Poynting;. Σε τι διαφέρει η ταχύτητα φάσης από την ταχύτητα οµάδας ηλεκτροµαγνητικού κύµατος; 3. Πώς ορίζεται η σχέση διασποράς; 4. Περιγράψτε την απόδειξη του νόµου του Snell. Ισχύει ο νόµος αν υπάρχουν πηγές στις διαχριστικές επιφάνειες; 5. Ποια συνθήκη απαιτείται για το µηδενισµό του συντελεστή ανάκλασης στην κάθετη πρόσπτση; Για το µηδενισµό του συντελεστή διάδοσης; 6. Πώς εξηγείται η µεγάλη ανακλαστικότητα τν µεταλλικών επιφανειών; 7. Τι είναι η γνία Brewster; Άλυτες ασκήσεις είτε PS, τις άλυτες ασκήσεις του Κεφαλαίου 3, µε έµφαση στις: 3., 3.5, 3.7, 3.8, 3., 3.3, 3.9.
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
(ΚΕΦ 32) f( x x f( x) x z y
 (ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
(ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Ηλίας Γλύτσης, Τηλ. 21-7722479, e-mail:
Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34. Ιούλιος 2008 KYMATIKH. ιάρκεια: 210 λεπτά
 Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ)
 ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ Θέµα. Ένας αρµονικός ταλανττής µε ασθενή απόσβεση, (µάζα=, σταθερά ελατηρίου= s, συντελεστής τριβής= r διεγείρεται
ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ Θέµα. Ένας αρµονικός ταλανττής µε ασθενή απόσβεση, (µάζα=, σταθερά ελατηρίου= s, συντελεστής τριβής= r διεγείρεται
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ. H γραφική αναπαράσταση ενός κύματος φωτός δίνεται στο Σχήμα 1(α) που ακολουθεί: ΣΧΗΜΑ 1
 ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34
 Κυματική ΦΥΕ34 0/07/0 Ελληνικό Ανοικτό Πανεπιστήμιο Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34 KYMATIKH Διάρκεια: 80 λεπτά Ονοματεπώνυμο: Τμήμα: Θέμα ο (Μονάδες:.5) Α) Θεωρούμε
Κυματική ΦΥΕ34 0/07/0 Ελληνικό Ανοικτό Πανεπιστήμιο Ενδεικτικές Λύσεις Θεμάτων Τελικών Εξετάσεων στη Θεματική Ενότητα ΦΥΕ34 KYMATIKH Διάρκεια: 80 λεπτά Ονοματεπώνυμο: Τμήμα: Θέμα ο (Μονάδες:.5) Α) Θεωρούμε
ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα ΠεριεχόµεναΚεφαλαίου 31 Τα µεταβαλλόµενα ηλεκτρικά πεδία παράγουν µαγνητικά πεδία. Ο Νόµος του Ampère-Ρεύµα µετατόπισης Νόµος του Gauss s στο µαγνητισµό
Κεφάλαιο31 Εξισώσεις Maxwellκαι ΗλεκτροµαγνητικάΚύµατα ΠεριεχόµεναΚεφαλαίου 31 Τα µεταβαλλόµενα ηλεκτρικά πεδία παράγουν µαγνητικά πεδία. Ο Νόµος του Ampère-Ρεύµα µετατόπισης Νόµος του Gauss s στο µαγνητισµό
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
β) Για ένα μέσο, όπου το Η/Μ κύμα έχει ταχύτητα υ
 Ασκ. 5 (σελ 354) Το πλάτος του μαγνητικού πεδίου ενός ηλεκτρομαγνητικού κύματος ειναι 5.4 * 10 7 Τ. Υπολογίστε το πλάτος του ηλεκτρικού πεδίου, αν το κύμα διαδίδεται (a) στο κενό και (b) σε ένα μέσο στο
Ασκ. 5 (σελ 354) Το πλάτος του μαγνητικού πεδίου ενός ηλεκτρομαγνητικού κύματος ειναι 5.4 * 10 7 Τ. Υπολογίστε το πλάτος του ηλεκτρικού πεδίου, αν το κύμα διαδίδεται (a) στο κενό και (b) σε ένα μέσο στο
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ
 ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση
 11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
ιάδοση κυµάτων σε διηλεκτρικά. Απορρόφυση ακτινοβολίας. Μέρος 1ον : ιάδοση κυµάτων σε διηλεκτρικά.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 53 ιάδοση κυµάτων σε διηλεκτρικά. Απορρόφυση ακτινοβολίας. 5. Άσκηση 5 5.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 53 ιάδοση κυµάτων σε διηλεκτρικά. Απορρόφυση ακτινοβολίας. 5. Άσκηση 5 5.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την
4ο ιαγώνισµα - Κύµατα. Θέµα 1ο
 4ο ιαγώνισµα - Κύµατα Ηµεροµηνία : εκέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1. Οταν ένα κύµα συχνότητας
4ο ιαγώνισµα - Κύµατα Ηµεροµηνία : εκέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1. Οταν ένα κύµα συχνότητας
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ. Προθεσµία παράδοσης 11/11/08
 //8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
//8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
Η αριστερή μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι δυο πρέπει να είναι σταθερές. Καλούμε την σταθερά
 Πρόβλημα 8.3 Πρόβλημα 8.4 Η κυματικ εξίσωση δίνει Ψάχνουμε για λύσεις του τύπου Το τοποθετούμε αυτό και: Διαιρούμε με ZT: Η αριστερ μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι
Πρόβλημα 8.3 Πρόβλημα 8.4 Η κυματικ εξίσωση δίνει Ψάχνουμε για λύσεις του τύπου Το τοποθετούμε αυτό και: Διαιρούμε με ZT: Η αριστερ μεριά εξαρτάται μόνο από το z και η δεξιά μόνο από το t, έτσι και οι
KYMATA Ανάκλαση - Μετάδοση
 ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
m i r i z i Αν είναι x, y, z τα µοναδιαία διανύσµατα των τριών αξόνων, τότε τα διανύσµατα ω r και r i µπορούν αντίστοιχα να γραφούν: r r x i y i ω x
 ΓΕΝΙΚΗ ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΤΡΟΦΟΡΜΗ, ΤΑΝΥΣΤΗΣ Α ΡΑΝΕΙΑΣ, ΚΥΡΙΟΙ ΑΞΟΝΕΣ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ Έστ ότι το στερεό του σχήµατος στρέφεται µε γνιακή ταχύτητα (,, γύρ από άξονα που διέρχεται από σταθερό σηµείο Ο. Αν
ΓΕΝΙΚΗ ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΤΡΟΦΟΡΜΗ, ΤΑΝΥΣΤΗΣ Α ΡΑΝΕΙΑΣ, ΚΥΡΙΟΙ ΑΞΟΝΕΣ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ Έστ ότι το στερεό του σχήµατος στρέφεται µε γνιακή ταχύτητα (,, γύρ από άξονα που διέρχεται από σταθερό σηµείο Ο. Αν
ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ
 ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Οποτε ακούτε ραδιόφωνο, βλέπετε τηλεόραση, στέλνετε SMS χρησιµοποιείτε ηλεκτροµαγνητική ακτινοβολία (ΗΜΑ). Η ΗΜΑ ταξιδεύει µε
ΜΕΤΡΗΣΗ ΚΑΙ ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΜΗ ΙΟΝΙΖΟΥΣΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Οποτε ακούτε ραδιόφωνο, βλέπετε τηλεόραση, στέλνετε SMS χρησιµοποιείτε ηλεκτροµαγνητική ακτινοβολία (ΗΜΑ). Η ΗΜΑ ταξιδεύει µε
HMY 333 -Φωτονική Διάλεξη 10 Οι εξισώσεις του Fresnel
 HMY 333 -Φτονική Διάλεξη Οι εξισώσεις του Fesel Wdows look lke mos a h (whe you e a bhly l oom). Idoos Oudoos I I I I ou I ou I ou I >> I ou 4% 96% Oe-way mos (used by pole o eoae bad uys) ae us paal eleos
HMY 333 -Φτονική Διάλεξη Οι εξισώσεις του Fesel Wdows look lke mos a h (whe you e a bhly l oom). Idoos Oudoos I I I I ou I ou I ou I >> I ou 4% 96% Oe-way mos (used by pole o eoae bad uys) ae us paal eleos
ΑΣΚΗΣΕΙΣ ΣΤΑ ΦΙΛΤΡΑ. E T Τ E in. coupler
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΦΙΛΤΡΑ Άσκηση (α) Θερείστε την διάταξη του σχήµατος (συµβολόµετρο Mh- Zhndr-ΜΖΙ). είξτε ότι η διάταξη δρα σα φίλτρο όταν µία είσοδος είναι ενεργή. Βρείτε την συνάρτηση µεταφοράς του φίτρου
ΑΣΚΗΣΕΙΣ ΣΤΑ ΦΙΛΤΡΑ Άσκηση (α) Θερείστε την διάταξη του σχήµατος (συµβολόµετρο Mh- Zhndr-ΜΖΙ). είξτε ότι η διάταξη δρα σα φίλτρο όταν µία είσοδος είναι ενεργή. Βρείτε την συνάρτηση µεταφοράς του φίτρου
Πηγές μαγνητικού πεδίου Νόμος Ampere. Ιωάννης Γκιάλας 21 Μαίου 2014
 Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη ο Κεφάλαιο - Κύµατα
 4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 2ο Κεφάλαιο - Κύµατα Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 2ο Κεφάλαιο - Κύµατα Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΦΥΕ34 Λύσεις 5 ης Εργασίας
 ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 17/12/24 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 24-5 3 η ΕΡΓΑΣΙΑ Προθεσμία παράδοσης 31/1/25 Άσκηση 1 α) Το ηλεκτρικό πεδίο ενός επιπέδου ηλεκτρομαγνητικού κύματος έχει 2 1 πλάτος 1 Vm. Βρείτε (i) το μέτρο
17/12/24 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 24-5 3 η ΕΡΓΑΣΙΑ Προθεσμία παράδοσης 31/1/25 Άσκηση 1 α) Το ηλεκτρικό πεδίο ενός επιπέδου ηλεκτρομαγνητικού κύματος έχει 2 1 πλάτος 1 Vm. Βρείτε (i) το μέτρο
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 2013
 ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Φεβρουάριος 0 ΘΕΜΑ α) Να βρεθούν οι επιτρεπτές περιοχές της κίνησης στον άξονα x Ox για την απωστική δύναµη F x, > 0 και για ενέργεια Ε. β) Υλικό σηµείο µάζας m µπορεί να κινείται
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
= 2 3. Σε κάθε σηµείο του υγρού θα έχουµε συµβολή, έτσι η ενέργεια ταλάντωσης
 ΘΕΜΑ 1 1. Σηµειώστε στα παρακάτω σωστό λάθος 1. στο στάσιµο κύµα όλες οι κοιλίες ταλαντώνονται σύµφωνα µε την σχέση ψα ηµ(ωt). στο στάσιµο κύµα όλα τα σηµεία του µέσου έχουν την ίδια συχνότητα ταλάντωσης.
ΘΕΜΑ 1 1. Σηµειώστε στα παρακάτω σωστό λάθος 1. στο στάσιµο κύµα όλες οι κοιλίες ταλαντώνονται σύµφωνα µε την σχέση ψα ηµ(ωt). στο στάσιµο κύµα όλα τα σηµεία του µέσου έχουν την ίδια συχνότητα ταλάντωσης.
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
( )U 1 ( θ )U 3 ( ) = U 3. ( ) όπου U j περιγράφει περιστροφή ως προς! e j. Γωνίες Euler. ω i. ω = ϕ ( ) = ei = U ij ej j
 Γωνίες Euler ΦΥΣ 11 - Διαλ.3 1 q Όλοι σχεδόν οι υπολογισµοί που έχουµε κάνει για την κίνηση ενός στερεού στο σύστηµα συντεταγµένων του στερεού σώµατος Ø Για παράδειγµα η γωνιακή ταχύτητα είναι: ω = i ω
Γωνίες Euler ΦΥΣ 11 - Διαλ.3 1 q Όλοι σχεδόν οι υπολογισµοί που έχουµε κάνει για την κίνηση ενός στερεού στο σύστηµα συντεταγµένων του στερεού σώµατος Ø Για παράδειγµα η γωνιακή ταχύτητα είναι: ω = i ω
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
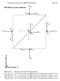 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
HMY 333 Φωτονική Διάλεξη 06. Εισαγωγή στις ταλαντώσεις και κύματα. Απλοί αρμονικοί ταλαντωτές. Γιατί εξετάζουμε την απλή αρμονική κίνηση;
 HMY 333 Φτονική Διάλεξη 6 Εισαγγή στις ταλαντώσεις και κύματα Απλοί αρμονικοί ταλανττές Μάζα-ελατήριο Mss-spring H. Chrisin, K.U.Ln(Wikipdi Εκκρεμές Pndlm U. o Monn LC κύκλμα hp://www.grnndwhi.n/~chb/lc_oscillor.hm
HMY 333 Φτονική Διάλεξη 6 Εισαγγή στις ταλαντώσεις και κύματα Απλοί αρμονικοί ταλανττές Μάζα-ελατήριο Mss-spring H. Chrisin, K.U.Ln(Wikipdi Εκκρεμές Pndlm U. o Monn LC κύκλμα hp://www.grnndwhi.n/~chb/lc_oscillor.hm
Είδη κυµάτων. Ηλεκτροµαγνητικά κύµατα. Σε κάποιο φυσικό µέσο προκαλείται µια διαταραχή. Το κύµα είναι η διάδοση της διαταραχής µέσα στο µέσο.
 Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/02/12 ΛΥΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
sin 2 n = sin A 2 sin 2 2 n = sin A = sin = cos
 1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
ΤΥΠΟΛΟΓΙΟ. q e = C Φορτίο Ηλεκτρονίου 1.1. Ηλεκτρικό Πεδίο 2.1. Ηλεκτρικό Πεδίο Σημειακού Φορτίου Q Ηλεκτρικό Πεδίο Σημειακού
 ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ
 ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ 11 -- ΠΕΙΡΑΙΑΣ -- 1853 -- ΤΗΛ. 10-4475, 43687 Θέμα 1: Α. γ Β. β Γ. α Δ. δ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ Ε. α. λάθος β. λάθος γ. σωστό δ. σωστό ε. λάθος Θέμα: Α. Ι. Σωστή απάντηση είναι
ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ 11 -- ΠΕΙΡΑΙΑΣ -- 1853 -- ΤΗΛ. 10-4475, 43687 Θέμα 1: Α. γ Β. β Γ. α Δ. δ ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ Ε. α. λάθος β. λάθος γ. σωστό δ. σωστό ε. λάθος Θέμα: Α. Ι. Σωστή απάντηση είναι
6.10 Ηλεκτροµαγνητικά Κύµατα
 Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Φυσική ΘΕΜΑ 1 ΘΕΜΑ 2 ΘΕΜΑ 3
 Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων
 Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
Μικροκυματικές Επικοινωνίες & Τεχνολογίες Χιλιοστομετρικών Κυμάτων ΕΙΣΑΓΩΓΗ - Το μάθημα αυτό πραγματεύεται θεμελιώδεις έννοιες των γραμμών μεταφοράς στην επιστημονική περιοχή των ηλεκτρονικών συστημάτων
Φίλιππος Φαρμάκης Επ. Καθηγητής. Δείκτης διάθλασης. Διάδοση του Η/Μ κύματος μέσα σε μέσο
 9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ
 ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
x(t) 2 = e 2 t = e 2t, t > 0
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 216-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Σήµατα και Συστήµατα Ασκηση
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη ο Κεφάλαιο - Κύµατα. Ενδεικτικές Λύσεις. Θέµα Α
 4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 Α.1. Τα ηλεκτροµαγνητικά κύµατα : 2ο Κεφάλαιο - Κύµατα Ενδεικτικές Λύσεις Θέµα Α (ϐ) υπακούουν στην αρχή της επαλληλίας. Α.2. υο σύγχρονες πηγές
4ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 21 εκέµβρη 2014 Α.1. Τα ηλεκτροµαγνητικά κύµατα : 2ο Κεφάλαιο - Κύµατα Ενδεικτικές Λύσεις Θέµα Α (ϐ) υπακούουν στην αρχή της επαλληλίας. Α.2. υο σύγχρονες πηγές
Kεφ. 6 ΔΙΑMOΡΦΩΣΗ ΚΥΜΑΤΟΣ, ΚΥΜΑΤΟΠΑΚΕΤΑ,
 Kεφ. 6 ΔΙΑMOΡΦΩΣΗ ΚΥΜΑΤΟΣ, ΚΥΜΑΤΟΠΑΚΕΤΑ, (part, pages -) Η μέχρι τώρα μελέτη μας αφορούσε κύματα ή ταλαντώσεις με μία μόνο συχνότητα. Στη συνέχεια θα μελετήσουμε την υπέρθεση πολλών κυμάτν που συνίστανται
Kεφ. 6 ΔΙΑMOΡΦΩΣΗ ΚΥΜΑΤΟΣ, ΚΥΜΑΤΟΠΑΚΕΤΑ, (part, pages -) Η μέχρι τώρα μελέτη μας αφορούσε κύματα ή ταλαντώσεις με μία μόνο συχνότητα. Στη συνέχεια θα μελετήσουμε την υπέρθεση πολλών κυμάτν που συνίστανται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ. Διδάσκων : Επίκ. Καθ. Μ.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική των Laser ΔΙΑΔΟΣΗ ΗΜ ΚΥΜΑΤΩΝ ΣΕ ΟΠΤΙΚΑ ΜΕΣΑ Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
Κλασική Ηλεκτροδυναμική Ενότητα 22: Κυματοπακέτα-Κυματοδηγοί Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την έννοια του κυματοπακέτου,
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
( ) ( ) ( )z. HMY Φωτονική. Διάλεξη 08 Οι εξισώσεις του Maxwell. r = A r. B r. ˆ det = Βαθμωτά και διανυσματικά μεγέθη
 HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
Ακουστικό Ανάλογο Μελανών Οπών
 Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Μέτρηση Γωνίας Brewster Νόμοι του Fresnel
 Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά?
 Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά? (Μη-μαγνητικά, μη-αγώγιμα, διαφανή στερεά ή υγρά με πυκνή, σχετικά κανονική διάταξη δομικών λίθων). Γραμμικά πολωμένο κύμα προσπίπτει σε ηλεκτρόνιο
Πως διαδίδονται τα Η/Μ κύματα σε διαφανή διηλεκτρικά? (Μη-μαγνητικά, μη-αγώγιμα, διαφανή στερεά ή υγρά με πυκνή, σχετικά κανονική διάταξη δομικών λίθων). Γραμμικά πολωμένο κύμα προσπίπτει σε ηλεκτρόνιο
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ. Προθεσµία παράδοσης 16/11/10
 9// ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 3 - η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης 6// Άσκηση A) Θεωρούµε x την απόσταση της µάζας m από το σηµείο ισορροπίας της και x, x3 τις αποστάσεις των µαζών m και m3 από το
9// ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 3 - η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης 6// Άσκηση A) Θεωρούµε x την απόσταση της µάζας m από το σηµείο ισορροπίας της και x, x3 τις αποστάσεις των µαζών m και m3 από το
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Γενικές εξετάσεις Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης
 Γενικές εξετάσεις 0 Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Γενικές εξετάσεις 0 Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
ΑΣΚΗΣΗ ΧΧ ΑΝΑΚΛΑΣΗ ΠΟΛΩΜΕΝΟΥ ΦΩΤΟΣ - ΕΞΙΣΩΣΕΙΣ FRESNEL
 ΑΣΚΗΣΗ ΧΧ ΑΝΑΚΛΑΣΗ ΠΟΛΩΜΕΝΟΥ ΦΩΤΟΣ - ΕΞΙΣΩΣΕΙΣ FRESNEL ΧΧ.1 Σκοπός Σκοπός αυτής της άσκησης είναι η μελέτη της συμπεριφοράς του γραμμικά πολωμένου φωτός, όταν ανακλάται σε επίπεδη επιφάνεια διηλεκτρικού
ΑΣΚΗΣΗ ΧΧ ΑΝΑΚΛΑΣΗ ΠΟΛΩΜΕΝΟΥ ΦΩΤΟΣ - ΕΞΙΣΩΣΕΙΣ FRESNEL ΧΧ.1 Σκοπός Σκοπός αυτής της άσκησης είναι η μελέτη της συμπεριφοράς του γραμμικά πολωμένου φωτός, όταν ανακλάται σε επίπεδη επιφάνεια διηλεκτρικού
συνίστανται από πολωτή που επιτρέπει να περνούν µόνο τα κατακόρυφα πολωµένα κύµατα.
 Γραµµικά πολωµένο ηλεκτροµαγνητικό κύµα. Νόµος του Malus Η κλασσική κυµατική θεωρία του φωτός µοντελοποιεί το φως (ή ένα τυχόν ηλεκτροµαγνητικό κύµα κατ επέκταση), στον ελεύθερο χώρο, ως ένα εγκάρσιο ηλεκτροµαγνητικό
Γραµµικά πολωµένο ηλεκτροµαγνητικό κύµα. Νόµος του Malus Η κλασσική κυµατική θεωρία του φωτός µοντελοποιεί το φως (ή ένα τυχόν ηλεκτροµαγνητικό κύµα κατ επέκταση), στον ελεύθερο χώρο, ως ένα εγκάρσιο ηλεκτροµαγνητικό
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΛΥΣΕΙΣ ΕΞΙΣΩΣΗΣ ΚΥΜΑΤΟΣ ΣΤΟΥΣ ΚΥΜΑΤΟΔΗΓΟΥΣ ΔΙΑΦΟΡΩΝ ΔΙΑΤΟΜΩΝ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ : Φυσικής και Εφαρμοσμένων Μαθηματικών Μάθημα : Εφαρμοσμένα Μαθηματικά Διδάσκων: Αν. καθηγητής Χρ. Σχοινάς Προαιρετική
ΦΥΣ Διαλ.33 1 KYMATA
 ΦΥΣ 131 - Διαλ.33 1 KYMATA q Κύµατα εµφανίζονται σε συστήµατα µε καταστάσεις ισορροπίας. Τα κύµατα είναι διαταραχές από τη θέση ισορροπίας. q Τα κύµατα προκαλούν κίνηση σε πολλά διαφορετικά σηµεία σε ένα
ΦΥΣ 131 - Διαλ.33 1 KYMATA q Κύµατα εµφανίζονται σε συστήµατα µε καταστάσεις ισορροπίας. Τα κύµατα είναι διαταραχές από τη θέση ισορροπίας. q Τα κύµατα προκαλούν κίνηση σε πολλά διαφορετικά σηµεία σε ένα
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός.
 1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
ΗΜ & Διάδοση ΗΜ Κυμάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
Παραμαγνητικός συντονισμός
 Παραμαγνητικός συντονισμός B B teˆ teˆ B eˆ, όπου Έστω ηλεκτρόνιο σε μαγνητικό πεδίο cos sin x y z B, B. Θεωρούμε ότι η σταθερή συνιστώσα του μαγνητικού πεδίου, Be, ˆz είναι ισχυρότερη από τη χρονοεξαρτώμενη
Παραμαγνητικός συντονισμός B B teˆ teˆ B eˆ, όπου Έστω ηλεκτρόνιο σε μαγνητικό πεδίο cos sin x y z B, B. Θεωρούμε ότι η σταθερή συνιστώσα του μαγνητικού πεδίου, Be, ˆz είναι ισχυρότερη από τη χρονοεξαρτώμενη
ΚΥΜΑΤΑ, ΦΩΣ ΚΑΙ ΔΙΑΔΟΣΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ, ΦΩΣ ΚΑΙ ΔΙΑΔΟΣΗ y f( x) x x z ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~86) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. q EdA Edl Νόμος Gauss
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ, ΦΩΣ ΚΑΙ ΔΙΑΔΟΣΗ y f( x) x x z ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~86) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. q EdA Edl Νόμος Gauss
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση Η/Μ ΚΥΜΑΤΑ. Ερωτήσεις Πολλαπλής επιλογής
 Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ΠΑΡΑΔΕΙΓΜΑΤΑ Διανύσματα - Διανυσματικές Συναρτήσεις
 ΜΑΘΗΜΑΤΙΚΑ ΙΙ ΠΑΡΑΔΕΙΓΜΑΤΑ Διανύσματα - Διανυσματικές Συναρτήσεις Επιμέλεια: Ι. Λυχναρόπουλος a) Να βρεθεί η ευθεία που διέρχεται από το σημείο P (5,,3) και είναι παράλληλη προς το διάνυσμα iˆ+ 4ˆj kˆ
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ΠΑΡΑΔΕΙΓΜΑΤΑ Διανύσματα - Διανυσματικές Συναρτήσεις Επιμέλεια: Ι. Λυχναρόπουλος a) Να βρεθεί η ευθεία που διέρχεται από το σημείο P (5,,3) και είναι παράλληλη προς το διάνυσμα iˆ+ 4ˆj kˆ
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 2012 ΘΕΜΑΤΑ Α
 ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2011 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 0 ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Σε
ΘΕΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 0 ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Σε
2. Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης
 Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
Κατά την φόρτιση πυκνωτή (Εξ. 37 στις σημειώσεις Ηλεκτρομαγνητισμού)
 1α Σε ένα κύκλωμα RC συνεχούς με διακόπτη, αντίσταση R = 650 Ω και πηγή 1 V όλα σε σειρά, ο διακόπτης κλείνει στο t = 0 και ο πυκνωτής είναι αρχικά αφόρτιστος. Η διαφορά δυναμικού στον πυκνωτή φτάνει στο
1α Σε ένα κύκλωμα RC συνεχούς με διακόπτη, αντίσταση R = 650 Ω και πηγή 1 V όλα σε σειρά, ο διακόπτης κλείνει στο t = 0 και ο πυκνωτής είναι αρχικά αφόρτιστος. Η διαφορά δυναμικού στον πυκνωτή φτάνει στο
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013
 ΘΕΜΑ 1: ( 3 µονάδες ) Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013 Ηλεκτρόνιο κινείται επάνω από µία αδιαπέραστη και αγώγιµη γειωµένη επιφάνεια που
ΘΕΜΑ 1: ( 3 µονάδες ) Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013 Ηλεκτρόνιο κινείται επάνω από µία αδιαπέραστη και αγώγιµη γειωµένη επιφάνεια που
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Τ Ο Μ Ε Α Σ Φ Υ Σ Ι Κ Η Σ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Σ Χ Ο Λ Η Ε Φ Α Ρ Μ Ο Σ Μ Ε Ν Ω Ν Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Κ Α Ι Φ Υ Σ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Τ Ο Μ Ε Α Σ Φ Υ Σ Ι Κ Η Σ Κανονική εξέταση στο µάθηµα ΕΙ
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Σ Χ Ο Λ Η Ε Φ Α Ρ Μ Ο Σ Μ Ε Ν Ω Ν Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Κ Α Ι Φ Υ Σ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Τ Ο Μ Ε Α Σ Φ Υ Σ Ι Κ Η Σ Κανονική εξέταση στο µάθηµα ΕΙ
Φ Υ ΣΙΚ Η ΚΑ ΤΕ ΥΘ ΥΝ ΣΗ Σ
 ΔΙΩΝΙΣΜ: Μ Θ Η Μ : www.paideia-agrinio.gr ΤΞΗΣ ΛΥΕΙΟΥ Φ Υ ΣΙ Η ΤΕ ΥΘ ΥΝ ΣΗ Σ Ε Π Ω Ν Τ Μ Ο :..... Ο Ν Ο Μ :...... Σ Μ Η Μ :..... Η Μ Ε Ρ Ο Μ Η Ν Ι : 23 / 0 3 / 2 0 1 4 Ε Π Ι Μ Ε Λ ΕΙ Θ ΕΜ Σ Ω Ν : ΥΡΜΗ
ΔΙΩΝΙΣΜ: Μ Θ Η Μ : www.paideia-agrinio.gr ΤΞΗΣ ΛΥΕΙΟΥ Φ Υ ΣΙ Η ΤΕ ΥΘ ΥΝ ΣΗ Σ Ε Π Ω Ν Τ Μ Ο :..... Ο Ν Ο Μ :...... Σ Μ Η Μ :..... Η Μ Ε Ρ Ο Μ Η Ν Ι : 23 / 0 3 / 2 0 1 4 Ε Π Ι Μ Ε Λ ΕΙ Θ ΕΜ Σ Ω Ν : ΥΡΜΗ
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
Κλασικη ιαφορικη Γεωµετρια
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Πρώτη Εργασία, 2018-19 1 Προαπαιτούµενες γνώσεις και ϐασική προετοιµασία
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Πρώτη Εργασία, 2018-19 1 Προαπαιτούµενες γνώσεις και ϐασική προετοιµασία
ενώ θεωρήσαμε το διάνυσμα R στην κατεύθυνση του άξονα z. + = + (172) Έτσι οι συναρτήσεις Green παίρνουν την τελική τους μορφή :
 Σε τρεις χρικές διαστάσεις θα έχουμε K( r, r ; t t dpp si( pτ dθ siθ exp( ip os θ π dp si( pτ si( p (171 Όπς και στο προηγούμενο κεφάλαιο (εξ. (8 έτσι και εδώ μεταγράψαμε την ολοκλήρση σε σφαιρικές συντεταγμένες,
Σε τρεις χρικές διαστάσεις θα έχουμε K( r, r ; t t dpp si( pτ dθ siθ exp( ip os θ π dp si( pτ si( p (171 Όπς και στο προηγούμενο κεφάλαιο (εξ. (8 έτσι και εδώ μεταγράψαμε την ολοκλήρση σε σφαιρικές συντεταγμένες,
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourir µιας συνάρτησης χρίς να καταφεύγουµε στην εξίσση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση συχνότητας
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourir µιας συνάρτησης χρίς να καταφεύγουµε στην εξίσση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση συχνότητας
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
1ο Κριτήριο Αξιολόγησης ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ-ΑΝΑΚΛΑΣΗ, ΙΑΘΛΑΣΗ- ΕΙΚΤΗΣ ΙΑΘΛΑΣΗΣ
 1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
