ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΟ ΤΟ ΚΕΦΑΛΑΙΟ 2
|
|
|
- Πελαγία Βουγιουκλάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΜΑΘΗΜΑΤΙΚΑ Β ΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΟ ΤΟ ΚΕΦΑΛΑΙΟ 2 ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΤΡΙΩΝΟΜΕΤΡΙΚΟΥΣ ΑΡΙΘΜΟΥΣ 1. Από το διπλανό σχήμα να βρείτε τα: 2. Σε ένα ορθογώνιοι τρίγωνο (Α = 90 ) είναι και Α = 9cm. Nα υπολογίσετε τις άλλες δύο πλευρές του τριγώνου 3. Εάν Α = 35 m και συν = 5, υπολογίστε: 6 i) την ΑΒ, ii ) τη Β και iii) τη γωνία Β. 4. Χρησιμοποιώντας το διπλανό σχήμα συνδέστε κάθε τριγωνομετρικό αριθμό της στήλης Α με B τον αντίστοιχο λόγο της στήλης Β. 5. ΣΤΗΛΗ Α α. β. ˆ γ. δ. ˆ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΣΤΗΛΗ Β ω A Δ φ α β γ δ 19
2 6. Να υπολογίσετε το ύψος του δέντρου στο διπλανό σχήμα 7. Στο παρακάτω τρίγωνο ΑΒ είναι Α = 16cm α) Να βρείτε την υποτείνουσα Β του τριγώνου ΑΒ. β) Να υπολογίσετε το εμβαδόν του τετραγώνου ΑΒΚΛ γ) Να υπολογίσετε το εμβαδόν του τραπεζίου ΚΛΒ 8. Να υπολογίσετε το χ στα παρακάτω σχήματα 9. Στο παρακάτω σχήμα είναι ΟΑ = 13 cm, AB = 7cm, ΑΔ = 5cm. Δ O θ 5 13 A 7 Β ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 20
3 Α) Να υπολογίσετε τα ημθ, συν θ, εφθ. Β) Nα υπολογίσετε τα ΟΔ, Ο, Δ, Β 10. Δίνεται ισόπλευρο τρίγωνο ΑΒ με ΑΒ = Β =Α = 4cm. α) Να υπολογίσετε το ύψος ΑΔ. β) Να υπολογίσετε το εμβαδόν του 11. Δίνεται ισόπλευρο τρίγωνο ΑΒ με ΑΒ = Β =Α = 3cm. α) Να υπολογίσετε το ύψος ΑΔ. β) Να υπολογίσετε το εμβαδόν του 12. Δίνεται το διπλανό σχήμα: α) να υπολογίσετε την πλευρά Α β) να υπολογίσετε τους αριθμούς ημ και εφ γ) να δείξετε ότι Δ=4 cm Ε Δ 3 cm 10 cm δ) να υπολογίσετε το τμήμα ΑΕ. 13. Δίνεται οξυγώνιο τρίγωνο ΑΒ με ΑΒ = 15cm, Β =20cm και φέρνουμε το ύψος του ΑΔ. Αν γνωρίζουμε ότι ΒΔ = 7 cm να υπολογίσετε: α) Την ωνία Β β) Το ύψος ΑΔ. γ) Την γωνία δ) Την γωνία ΒΑΔ ε) την γωνία ΔΑ (Χρησιμοποιήστε τον πίνακα τριγωνομετρικών αριθμών στο τέλος του βιβλίου) Α 6cm Β 14. Στο παρακάτω σχήμα το τρίγωνα ΑΒ και ΔΕΒ είναι ορθογώνια με Â=90 και Ê=90. Επιπλέον είναι: ΑΒ=6cm,A= 8cm, ΑΔ=1 cm, Β Ε=7 cm Ε α) Να υπολογίσετε τα μήκη των τμημάτων: Β, ΒΕ και ΒΔ ΑΒ =6 E= 7 β) Να υπολογίσετε τα : εφβ, ημ(βδε),εφ(αδ),συν ΑΔ=1 Α 8 ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 21
4 15. Στο διπλανό σχήμα να υπολογίσετε: α) Τις πλευρές του τριγώνου β) Το εμβαδόν του τριγώνου 16. Στο διπλανό ισοσκελές τρίγωνο να υπολογίσετε α) Το ύψος ΑΔ του τριγώνου β) Το εμβαδόν του 17. Στο παρακάτω σχήμα να υπολογίσετε τα x, y, ω, Δ και κατόπιν να εξετάσετε εάν το ΑΒ είναι ορθογώνιο 18. Στο διπλανό τρίγωνο να υπολογίσετε το εμβαδόν του 19. Στο διπλανό σχήμα, το τετράγωνο ΖΕΔ έχει εμβαδόν 36cm 2 και ΒΖ =2 cm α) Να βρείτε το μήκος της πλευράς Ζ β) Να υπολογίσετε το μήκος ΑΖ γ) Να βρείτε το εμβαδόν του τριγώνου ΑΒ δ) Να βρείτε το εμβαδόν του τραπεζίου ΑΔΕ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 22
5 20. Στο διπλανό τρίγωνο να υπολογίσετε α) την γωνία ω β) την γωνία γ) την πλευρά Α δ) Το εμβαδόν του τριγώνου ε) Το ύψος ΑΔ 21. Στο διπλανό σχήμα γνωρίζουμε ότι Δ=4, και ΑΒ = 60 μοίρες, ΒΔ= 30 μοίρες. Να υπολογίσετε τις γωνίες φ, θ καθώς και τα μήκη των πλευρών Β, ΑΒ και Α. Στη συνέχεια να προσδιορίσετε το εμβαδόν του τριγώνου ΒΔ. 22. Δίνεται ορθογώνιο ΑΒΔ και η διαγώνιός του Α. Αν ΒΕ κάθετο στο Α, Β=2 και Β Α=30 0. Να προσδιορίσετε: α) την διαγώνιο Α β) την πλευρά ΑΒ γ) το τμήμα ΒΕ δ) το εμβαδόν του τριγώνου ΑΒΕ. 23. Να υπολογίσετε το εμβαδόν του παραλληλογράμμου 24. Να υπολογίσετε το εμβαδόν του τραπεζίου ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 23
6 25. Να υπολογίσετε το εμβαδόν του τραπεζίου 26. Να εξετάσετε εάν το ΑΒΔ είναι ορθογώνιο 27. Να υπολογίσετε την παράσταση : Α = ημ45 - ημ Να δειχθεί ότι: συν45 + συν60 = ια να ανέβουμε μια ανηφόρα πιο εύκολα χτίζουμε σκαλοπάτια ύψους 20cm και πλάτους 40 cm. α) Να βρεθεί η κλίση ω της ανηφόρας από το έδαφος. β) Αν η ανηφόρα έχει μήκος 15 m πόσα σκαλοπάτια ω πρέπει να φτιάξουμε για να την ανεβούμε ; γ) Αν ανέβουμε 11 σκαλοπάτια πόσο μήκος της ανηφόρας έχομε διανύσει 30. Στο σχήμα δίνεται η τομή μιας σκάλας. Το σημείο Λ είναι μέσο της απόστασης ΚΜ. Υπολογίστε: α) Το μήκος ενός βήματος (Β = ΔΕ = ΖΗ = ΘΙ = ΚΛ). β) το πλάτος της σκάλας ΑΡ. ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 24
Γ Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 2
 Ε Ω Μ Ε Τ Ρ Ι - Κ Ε Φ Λ Ι Ο 2 Τριγωνομετρία ΛΟΟΣ ΕΥΘΥΡΜΜΩΝ ΤΜΗΜΤΩΝ α α β α β α β 1. ν 2, να υπολογίσετε τους λόγους :,, β β β α β 2. Σε ένα ισόπλευρο τρίγωνο με πλευρά 6 cm και ύψος, να υπολογίσετε τους
Ε Ω Μ Ε Τ Ρ Ι - Κ Ε Φ Λ Ι Ο 2 Τριγωνομετρία ΛΟΟΣ ΕΥΘΥΡΜΜΩΝ ΤΜΗΜΤΩΝ α α β α β α β 1. ν 2, να υπολογίσετε τους λόγους :,, β β β α β 2. Σε ένα ισόπλευρο τρίγωνο με πλευρά 6 cm και ύψος, να υπολογίσετε τους
Γ Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1
 Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1 Εμβαδά Επίπεδων Σχημάτων & Πυθαγόρειο Θεώρημα Η συλλογή των ασκήσεων προέρχεται από μια ποικιλία πηγών, σημαντικότερες από τις οποίες είναι το Mathematica.gr, παλιότερα
Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1 Εμβαδά Επίπεδων Σχημάτων & Πυθαγόρειο Θεώρημα Η συλλογή των ασκήσεων προέρχεται από μια ποικιλία πηγών, σημαντικότερες από τις οποίες είναι το Mathematica.gr, παλιότερα
ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΠΑΡΑΓΡΑΦΟΣ Β.1.4 ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΑΣΚΗΣΕΙΣ
 ΠΑΡΑΓΡΑΦΟΣ Β.1.4 ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΑΣΚΗΣΕΙΣ 1) Στον παρακάτω πίνακα τα ευθύγραμμα τμήματα ΑΒ, ΑΓ και ΒΓ είναι οι πλευρές ενός o ορθογωνίου τριγώνου ΑΒΓ με Â 90. Να συμπληρώσετε τον πίνακα αυτό. ΑΒ 6 3
ΠΑΡΑΓΡΑΦΟΣ Β.1.4 ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΑΣΚΗΣΕΙΣ 1) Στον παρακάτω πίνακα τα ευθύγραμμα τμήματα ΑΒ, ΑΓ και ΒΓ είναι οι πλευρές ενός o ορθογωνίου τριγώνου ΑΒΓ με Â 90. Να συμπληρώσετε τον πίνακα αυτό. ΑΒ 6 3
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ Α. ΕΦΑΠΤΟΜΕΝΗ ΟΞΕΙΑΣ ΓΩΝΙΑΣ 1. Στο τρίγωνο ΑΒΓ είναι ΑΒ = 8cm και η γωνία Β = 64 0. Να υπολογίσετε το μήκος της πλευράς ΑΓ. 2. Στο ορθογώνιο τρίγωνο ΑΒΓ είναι ΑΒ = 9cm και εφγ
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ Α. ΕΦΑΠΤΟΜΕΝΗ ΟΞΕΙΑΣ ΓΩΝΙΑΣ 1. Στο τρίγωνο ΑΒΓ είναι ΑΒ = 8cm και η γωνία Β = 64 0. Να υπολογίσετε το μήκος της πλευράς ΑΓ. 2. Στο ορθογώνιο τρίγωνο ΑΒΓ είναι ΑΒ = 9cm και εφγ
5. Τα μήκη των βάσεων ενός τραπεζίου είναι 8 cm και 12 cm και το ύψος του είναι 7. Να βρείτε το εμβαδό του.
 1 ΑΣΚΗΣΕΙΣ 1. Ένα παραλληλόγραμμο ΑΒΓΔ έχει μια πλευρά ίση με 48 και το αντίστοιχο σε αυτή την πλευρά ύψος είναι 4,5 dm. Να βρείτε το εμβαδό του παραλληλογράμμου 2. Ένα παραλληλόγραμμο έχει εμβαδό 72 2
1 ΑΣΚΗΣΕΙΣ 1. Ένα παραλληλόγραμμο ΑΒΓΔ έχει μια πλευρά ίση με 48 και το αντίστοιχο σε αυτή την πλευρά ύψος είναι 4,5 dm. Να βρείτε το εμβαδό του παραλληλογράμμου 2. Ένα παραλληλόγραμμο έχει εμβαδό 72 2
Αναλογίες. ΘΕΜΑ 2ο. (Μονάδες 5) β) Να υπολογίσετε το ΓΒ συναρτήσει του κ. (Μονάδες 5) ΑΒ από το σημείο Γ ; (Μονάδες 15)
 Αναλογίες 2_20863. Στο παρακάτω σχήμα είναι 12 και 8. α) Να υπολογίσετε τους λόγους και. (Μονάδες 6) β) Να υπολογίσετε το ΑΓ συναρτήσει του κ. (Μονάδες 5) γ) Να υπολογίσετε τον λόγο. Σε τι λόγο λ διαιρείται
Αναλογίες 2_20863. Στο παρακάτω σχήμα είναι 12 και 8. α) Να υπολογίσετε τους λόγους και. (Μονάδες 6) β) Να υπολογίσετε το ΑΓ συναρτήσει του κ. (Μονάδες 5) γ) Να υπολογίσετε τον λόγο. Σε τι λόγο λ διαιρείται
ΑΣΚΗΣΕΙΣ ΣΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
 ΑΣΚΗΣΕΙΣ ΣΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΑΣΚΗΣΗ. 1 Να υπολογίσετε την περίμετρο και το εμβαδόν του παρακάτω τρίγωνο ΑΒΓ που έχει ΑΒ = 17cm, ΑΓ = 25cm και ΑΔ = 15cm. ΑΣΚΗΣΗ. 2 Στο ορθογώνιο τραπέζιο είναι ΑΒ= 9cm,
ΑΣΚΗΣΕΙΣ ΣΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΑΣΚΗΣΗ. 1 Να υπολογίσετε την περίμετρο και το εμβαδόν του παρακάτω τρίγωνο ΑΒΓ που έχει ΑΒ = 17cm, ΑΓ = 25cm και ΑΔ = 15cm. ΑΣΚΗΣΗ. 2 Στο ορθογώνιο τραπέζιο είναι ΑΒ= 9cm,
Συνοπτική θεωρία. Οι σημαντικότερες αποδείξεις. Ερωτήσεις αντικειμενικού τύπου. Ασκήσεις. Διαγωνίσματα
 Γ Ε Ω Μ Ε Τ Ρ Ι Α Β Λ Υ Κ Ε Ι Ο Υ Συνοπτική θεωρία Οι σημαντικότερες αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα Μαθηματικός Περιηγητής 1 ΚΕΦΑΙΑΟ 9 ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
Γ Ε Ω Μ Ε Τ Ρ Ι Α Β Λ Υ Κ Ε Ι Ο Υ Συνοπτική θεωρία Οι σημαντικότερες αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα Μαθηματικός Περιηγητής 1 ΚΕΦΑΙΑΟ 9 ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
Επαναληπτικές Ασκήσεις
 Β' Γυμν. - Επαναληπτικές Ασκήσεις 1 Άσκηση 1 Απλοποίησε τις αλγεβρικές παραστάσεις (α) 2y 2z 8ω 8ω 2y 2z (β) 1x 2y 3z 3 3 z 2z z 2 x y Επαναληπτικές Ασκήσεις Άλγεβρα - Γεωμετρία Άσκηση 2 Υπολόγισε την
Β' Γυμν. - Επαναληπτικές Ασκήσεις 1 Άσκηση 1 Απλοποίησε τις αλγεβρικές παραστάσεις (α) 2y 2z 8ω 8ω 2y 2z (β) 1x 2y 3z 3 3 z 2z z 2 x y Επαναληπτικές Ασκήσεις Άλγεβρα - Γεωμετρία Άσκηση 2 Υπολόγισε την
Εφαπτομένη Οξείας Γωνίας - Φύλλο Εργασίας Απέναντι και προσκείμενη πλευρά σε γωνία ορθογωνίου τριγώνου. Εφαπτομένη Οξείας Γωνίας
 Εφαπτομένη Οξείας Γωνίας - Φύλλο Εργασίας Απέναντι και προσκείμενη πλευρά σε γωνία ορθογωνίου τριγώνου 1. Στο ορθογώνιο τρίγωνο ΑΒΓ του διπλανού σχήματος η πλευρά ΒΓ που βρίσκεται απέναντι από την ορθή
Εφαπτομένη Οξείας Γωνίας - Φύλλο Εργασίας Απέναντι και προσκείμενη πλευρά σε γωνία ορθογωνίου τριγώνου 1. Στο ορθογώνιο τρίγωνο ΑΒΓ του διπλανού σχήματος η πλευρά ΒΓ που βρίσκεται απέναντι από την ορθή
Τριγωνομετρικοί αριθμοί παραπληρωματικών γωνιών
 ΜΕΡΟΣ Β. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΠΛΗΡΩΜΑΤΙΚΩΝ ΓΩΝΙΩΝ 491. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΠΛΗΡΩΜΑΤΙΚΩΝ ΓΩΝΙΩΝ Τριγωνομετρικοί αριθμοί παραπληρωματικών γωνιών 8 Μ(x,y) 6 ρ 4 180-ω -10-5 5 Ο ω - -4 Οι παραπληρωματικές
ΜΕΡΟΣ Β. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΠΛΗΡΩΜΑΤΙΚΩΝ ΓΩΝΙΩΝ 491. ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΠΑΡΑΠΛΗΡΩΜΑΤΙΚΩΝ ΓΩΝΙΩΝ Τριγωνομετρικοί αριθμοί παραπληρωματικών γωνιών 8 Μ(x,y) 6 ρ 4 180-ω -10-5 5 Ο ω - -4 Οι παραπληρωματικές
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του
 ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ΤΩΝ ΕΠΑΛ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ΤΩΝ ΕΠΑΛ Για τις λύσεις συνεργάστηκαν οι μαθηματικοί: Κολλινιάτη Γιωργία Μιχαήλογλου Στέλιος Παπαθανάση Κέλλυ Πατσιμάς Ανδρέας Πατσιμάς Δημήτρης Ραμαντάνης Βαγγέλης
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ΤΩΝ ΕΠΑΛ Για τις λύσεις συνεργάστηκαν οι μαθηματικοί: Κολλινιάτη Γιωργία Μιχαήλογλου Στέλιος Παπαθανάση Κέλλυ Πατσιμάς Ανδρέας Πατσιμάς Δημήτρης Ραμαντάνης Βαγγέλης
ΜΕΡΟΣ Α. 1 ο ΚΕΦΑΛΑΙΟ
 ΜΕΡΟΣ Α ο ΚΕΦΑΛΑΙΟ. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών. Ονομάζεται αλγεβρική παράσταση μια παράσταση
ΜΕΡΟΣ Α ο ΚΕΦΑΛΑΙΟ. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών. Ονομάζεται αλγεβρική παράσταση μια παράσταση
1.4 ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
 1 1.4 ΠΥΘΑΟΡΕΙΟ ΘΕΩΡΗΜΑ ΘΕΩΡΙΑ 1. Πυθαγόρειο θεώρηµα : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο µε το άθροισµα των τετραγώνων των καθέτων πλευρών. γ α α = β + γ β. Αντίστροφο Πυθαγορείου
1 1.4 ΠΥΘΑΟΡΕΙΟ ΘΕΩΡΗΜΑ ΘΕΩΡΙΑ 1. Πυθαγόρειο θεώρηµα : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο µε το άθροισµα των τετραγώνων των καθέτων πλευρών. γ α α = β + γ β. Αντίστροφο Πυθαγορείου
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΓΡΑΠΤΗ ΔΟΚΙΜΑΣΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ
 μιας οξείας γωνίας; 0,5, 5 2,, 2 5 Σε ορθογώνιο τρίγωνο ΑΒΓ (Α=90 ο ) δίνεται ότι Β=5 ο και 8 τις πλευρές ΑΓ και ΒΓ με προσέγγιση ενός δεκαδικού ψηφίου. (Δίνονται οι τιμές: ημ5 ο =0,57, συν5 ο =0,82, εφ5
μιας οξείας γωνίας; 0,5, 5 2,, 2 5 Σε ορθογώνιο τρίγωνο ΑΒΓ (Α=90 ο ) δίνεται ότι Β=5 ο και 8 τις πλευρές ΑΓ και ΒΓ με προσέγγιση ενός δεκαδικού ψηφίου. (Δίνονται οι τιμές: ημ5 ο =0,57, συν5 ο =0,82, εφ5
Μαθηματικά Β' Γυμνασίου - Ασκήσεις επανάληψης στη Γεωμετρία Σελίδα 1. (απ.: Ε ΕΒΓΔΗΖ = 44 cm 2 ) (απ.: ΒΗ = 8 cm, (BHΝ) = 12 cm 2 )
 Μαθηματικά Β' Γυμνασίου - Ασκήσεις επανάληψης στη Γεωμετρία Σελίδα 1 1) Στο διπλανό ορθογώνιο ΑΒΓΔ, να υπολογίσετε το εμβαδόν του σκιασμένου χωρίου ΕΒΓΔΗΖ, όταν ΓΔ = 10 cm, ΒΓ = 6 cm, ΗΔ = 2 cm, ενώ ΗΖ
Μαθηματικά Β' Γυμνασίου - Ασκήσεις επανάληψης στη Γεωμετρία Σελίδα 1 1) Στο διπλανό ορθογώνιο ΑΒΓΔ, να υπολογίσετε το εμβαδόν του σκιασμένου χωρίου ΕΒΓΔΗΖ, όταν ΓΔ = 10 cm, ΒΓ = 6 cm, ΗΔ = 2 cm, ενώ ΗΖ
Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών
 Μαθηματικά Β Γυμνασίου Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών 1. Να χρησιμοποιήσετε μεταβλητές για να εκφράσετε με μια αλγεβρική παράσταση τις παρακάτω φράσεις: a. Η διαφορά δυο
Μαθηματικά Β Γυμνασίου Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών 1. Να χρησιμοποιήσετε μεταβλητές για να εκφράσετε με μια αλγεβρική παράσταση τις παρακάτω φράσεις: a. Η διαφορά δυο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΓΥΜΝΑΣΙΟΥ
 ΠΝΗΠΤΙ ΘΜΤ ΜΘΗΜΤΙΩΝ ΥΜΝΣΙΟΥ ΘΜ 1 ίνονται οι αλγεβρικές παραστάσεις x 1 3 x x 1 10x 19 και B x x 5 x 4. α) Να κάνετε τις πράξεις και να δείξετε ότι A x 3x 9x 7 και B 3x 6x 7x 54. β) Να παραγοντοποιήσετε
ΠΝΗΠΤΙ ΘΜΤ ΜΘΗΜΤΙΩΝ ΥΜΝΣΙΟΥ ΘΜ 1 ίνονται οι αλγεβρικές παραστάσεις x 1 3 x x 1 10x 19 και B x x 5 x 4. α) Να κάνετε τις πράξεις και να δείξετε ότι A x 3x 9x 7 και B 3x 6x 7x 54. β) Να παραγοντοποιήσετε
ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ
 ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ 1) Από εξωτερικό σημείο Ρ ενός κύκλου (Ο,ρ) φέρνουμε τα εφαπτόμενα τμήματα ΡΑ και ΡΒ. Αν Μ είναι ένα τυχαίο εσωτερικό σημείο του ευθύγραμμου τμήματος ΟΡ, να αποδείξετε ότι: α) τα
ΑΣΚΗΣΕΙΣ 3 Ο ΚΕΦΑΛΑΙΟ 1) Από εξωτερικό σημείο Ρ ενός κύκλου (Ο,ρ) φέρνουμε τα εφαπτόμενα τμήματα ΡΑ και ΡΒ. Αν Μ είναι ένα τυχαίο εσωτερικό σημείο του ευθύγραμμου τμήματος ΟΡ, να αποδείξετε ότι: α) τα
ΚΕΦΑΛΑΙΟ 9 ο ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ
 ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ Θεώρημα οξείας γωνίας Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από οξεία γωνία, είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, ελαττωμένο
ΓΕΝΙΚΕΥΣΗ ΠΥΘΑΓΟΡΕΙΟΥ ΘΕΩΡΗΜΑΤΟΣ Θεώρημα οξείας γωνίας Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από οξεία γωνία, είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, ελαττωμένο
ΑΣΚΗΣΕΙΣ (1) Να ανάγετε τους πιο κάτω τριγωνομετρικούς αριθμούς σε τριγωνομετρικούς αριθμούς οξειών γωνιών: α) 160 β) 135 γ) 150 δ) ( 120
 ΤΡΙΓΩΝΟΜΕΤΡΙΑ ΑΝΑΓΩΓΗ ΣΤΟ 1 ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΜΝΗΜΟΝΙΚΟΣ ΚΑΝΟΝΑΣ 1. Χωρίς να λάβουμε υπόψη το πρόσημο: Αν οι δυο γωνιές έουν άθροισμα ή διαφορά, 18, 6 μοίρες τότε ο τριγωνομετρικός αριθμός δεν αλλάζει: ημ
ΤΡΙΓΩΝΟΜΕΤΡΙΑ ΑΝΑΓΩΓΗ ΣΤΟ 1 ο ΤΕΤΑΡΤΗΜΟΡΙΟ ΜΝΗΜΟΝΙΚΟΣ ΚΑΝΟΝΑΣ 1. Χωρίς να λάβουμε υπόψη το πρόσημο: Αν οι δυο γωνιές έουν άθροισμα ή διαφορά, 18, 6 μοίρες τότε ο τριγωνομετρικός αριθμός δεν αλλάζει: ημ
στ) συν30 0 ΑΠΑΝΤΗΣΗ Εύκολα αντιστοιχίζουμε σύμφωνα με τον παραπάνω πίνακα α) i, β) iii, γ) i, δ) v,ε) iii,στ) v
 ΜΕΡΟΣ Β. ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΤΩΝ ΩΝΙΩΝ,5 ΚΙ 79. ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΤΩΝ ΩΝΙΩΝ,5 ΚΙ Πίνακας τριγωνομετρικών αριθμών των γωνιών,5 και ημίτονο συνημίτονο εφαπτομένη 5 ΕΡΩΤΗΣΕΙΣ ΚΤΝΟΗΣΗΣ. Σε κάθε αριθμό
ΜΕΡΟΣ Β. ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΤΩΝ ΩΝΙΩΝ,5 ΚΙ 79. ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ ΤΩΝ ΩΝΙΩΝ,5 ΚΙ Πίνακας τριγωνομετρικών αριθμών των γωνιών,5 και ημίτονο συνημίτονο εφαπτομένη 5 ΕΡΩΤΗΣΕΙΣ ΚΤΝΟΗΣΗΣ. Σε κάθε αριθμό
Επαναληπτικές ασκήσεις για το Πάσχα.
 Μαθηματικά B Γυμνασίου Επαναληπτικές ασκήσεις για το Πάσχα. Άλγεβρα. Κεφάλαιο 1 ο. 1. Να υπολογιστούν οι παρακάτω αριθμητικές παραστάσεις : 1 7 1 7 1 1 ) - 1 4 : ) -1 1 : 1 4 10 9 6. Να λυθούν οι εξισώσεις:
Μαθηματικά B Γυμνασίου Επαναληπτικές ασκήσεις για το Πάσχα. Άλγεβρα. Κεφάλαιο 1 ο. 1. Να υπολογιστούν οι παρακάτω αριθμητικές παραστάσεις : 1 7 1 7 1 1 ) - 1 4 : ) -1 1 : 1 4 10 9 6. Να λυθούν οι εξισώσεις:
Γεωμετρία. Κεφ 1 ο : Γεωμετρια.
 Μαθηματικά Γ Γυμνασίου Γεωμετρία. Κεφ 1 ο : Γεωμετρια. Μέρος Α Θεωρία. 1. Με τι είναι ίσο το άθροισμα των γωνιών ενός τριγώνου; 2. Ποιο τρίγωνο λέγετε οξυγώνιο αμβλυγώνιο ορθογώνιο. 3. Ποιο τρίγωνο λέγετε
Μαθηματικά Γ Γυμνασίου Γεωμετρία. Κεφ 1 ο : Γεωμετρια. Μέρος Α Θεωρία. 1. Με τι είναι ίσο το άθροισμα των γωνιών ενός τριγώνου; 2. Ποιο τρίγωνο λέγετε οξυγώνιο αμβλυγώνιο ορθογώνιο. 3. Ποιο τρίγωνο λέγετε
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ. Τριγωνομετρικοι αριθμοι οξειων γωνιων
 Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ Τριγωνομετρικοι αριθμοι οξειων γωνιων 9 ΑΥΓΟΥΣΤΟΥ 016 Κλίση ευθείας Όλοι έχουμε στο δρόμο τα παρακάτω σήματα, που από την εμπειρία μας καταλαβαίνουμε ότι πλησιάζουμε σε ανηφόρα.
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ Τριγωνομετρικοι αριθμοι οξειων γωνιων 9 ΑΥΓΟΥΣΤΟΥ 016 Κλίση ευθείας Όλοι έχουμε στο δρόμο τα παρακάτω σήματα, που από την εμπειρία μας καταλαβαίνουμε ότι πλησιάζουμε σε ανηφόρα.
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α Α1. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο η διάμεσος που αντιστοιχεί στην υποτείνουσα ισούται με το μισό της.
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΩΜΕΤΡΙΑ ΘΕΜΑ Α Α1. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο η διάμεσος που αντιστοιχεί στην υποτείνουσα ισούται με το μισό της.
β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι όμοια και στη συνέχεια να συμπληρώσετε
 ΘΕΜΑ 4 Στο διπλανό τραπέζιο ΑΒΓΔ η ευθεία ΜΛ είναι παράλληλη στις βάσεις ΑΒ και ΔΓ του τραπεζίου και ισχύει ότι = α) Να αποδείξετε ότι = και = (Μονάδες 8) β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι
ΘΕΜΑ 4 Στο διπλανό τραπέζιο ΑΒΓΔ η ευθεία ΜΛ είναι παράλληλη στις βάσεις ΑΒ και ΔΓ του τραπεζίου και ισχύει ότι = α) Να αποδείξετε ότι = και = (Μονάδες 8) β) Να αποδείξετε ότι τα τρίγωνα ΑΒΓ και ΚΛΓ είναι
ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Αμυραδάκη 20, Νίκαια (210-4903576) ΝΟΕΜΒΡΙΟΣ 2013 ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΓΕΩΜΕΤΡΙΑΣ...
 Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΘΕΜΑ 1 ΝΟΕΜΒΡΙΟΣ 013 Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα του ισούται με το γινόμενο
Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΘΕΜΑ 1 ΝΟΕΜΒΡΙΟΣ 013 Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο του ύψους που αντιστοιχεί στην υποτείνουσα του ισούται με το γινόμενο
ΤΡΙΓΩΝΟΜΕΤΡΙΑ Α. Τριγωνοµ ετρικοί αριθµ οί οξείας γωνίας ορθογωνίου τριγώνου
 ΤΡΙΓΩΝΟΜΕΤΡΙΑ Α Τριγωνοµ ετρικοί αριθµ οί οξείας γωνίας ορθογωνίου τριγώνου 18 Τριγωνοµετρικοί αριθµοί που συνδέονται µε τις οξείες γωνίες ενός ορθογωνίου τριγώνου 1. α) Με βάση το διπλανό σχήµα να χαρακτηρίσετε
ΤΡΙΓΩΝΟΜΕΤΡΙΑ Α Τριγωνοµ ετρικοί αριθµ οί οξείας γωνίας ορθογωνίου τριγώνου 18 Τριγωνοµετρικοί αριθµοί που συνδέονται µε τις οξείες γωνίες ενός ορθογωνίου τριγώνου 1. α) Με βάση το διπλανό σχήµα να χαρακτηρίσετε
2.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ 30 Ο 45 Ο 60 Ο
 .4 ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ 0 Ο 45 Ο 60 Ο ΘΕΩΡΙ. Τριγωνοµετρικοί αριθµοί 0 ο, 45 ο, 60 ο : ηµίτονο συνηµίτονο εφαπτοµένη 0 ο 45 ο 60 ο ΣΚΗΣΕΙΣ. Στο διπλανό πίνακα, σε κάθε πληροφορία της στήλης, να επιλέξετε
.4 ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ 0 Ο 45 Ο 60 Ο ΘΕΩΡΙ. Τριγωνοµετρικοί αριθµοί 0 ο, 45 ο, 60 ο : ηµίτονο συνηµίτονο εφαπτοµένη 0 ο 45 ο 60 ο ΣΚΗΣΕΙΣ. Στο διπλανό πίνακα, σε κάθε πληροφορία της στήλης, να επιλέξετε
ΚΕΦΑΛΑΙΟ 8 ο ΟΜΟΙΟΤΗΤΑ
 ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Οι ασκήσεις του φυλλαδίου δεν είναι ανά κεφάλαιο, αλλά τυχαία με σκοπό την τελική επανάληψη, και είναι θέματα εξετάσεων από διάφορα σχολεία του νομού Σερρών Σέρρες
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Οι ασκήσεις του φυλλαδίου δεν είναι ανά κεφάλαιο, αλλά τυχαία με σκοπό την τελική επανάληψη, και είναι θέματα εξετάσεων από διάφορα σχολεία του νομού Σερρών Σέρρες
ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ
 ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Βασικά θεωρήματα Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της
ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ Βασικά θεωρήματα Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της
ΑΣΚΗΣΕΙΣ ΓΥΜΝΑΣΙΟ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ Β
 ΥΜΝΑΣΙΟ - 010 48 Α. Τι λέγεται τετραγωνική ρίζα ενός θετικού αριθμού α και πώς συμβολίζεται αυτή; Β. Ποιος αριθμός ονομάζεται άρρητος;. Πώς ορίζονται οι πραγματικοί αριθμοί; Α. Τι λέγεται ημίτονο μιας
ΥΜΝΑΣΙΟ - 010 48 Α. Τι λέγεται τετραγωνική ρίζα ενός θετικού αριθμού α και πώς συμβολίζεται αυτή; Β. Ποιος αριθμός ονομάζεται άρρητος;. Πώς ορίζονται οι πραγματικοί αριθμοί; Α. Τι λέγεται ημίτονο μιας
ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ
 Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
Θέματα Εξετάσεων ΕΠΑ.Λ. Ορισμένα από τα θέματα συντάχθηκαν πριν την αναδιάταξη της διδακτέας ύλης μεταξύ Α και Β Λυκείου
 Θέματα Εξετάσεων ΕΠΑ.Λ. Ορισμένα από τα θέματα συντάχθηκαν πριν την αναδιάταξη της διδακτέας ύλης μεταξύ Α και Β Λυκείου Συλλογή-Επιμέλεια: Γ. Κοντογιάννης, Μαθηματικός ΜPhil Α Λυκείου Άλγεβρα Θέματα Εξετάσεων
Θέματα Εξετάσεων ΕΠΑ.Λ. Ορισμένα από τα θέματα συντάχθηκαν πριν την αναδιάταξη της διδακτέας ύλης μεταξύ Α και Β Λυκείου Συλλογή-Επιμέλεια: Γ. Κοντογιάννης, Μαθηματικός ΜPhil Α Λυκείου Άλγεβρα Θέματα Εξετάσεων
ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ. ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ Κεφάλαιο 9ο: Ερωτήσεις του τύπου «Σωστό-Λάθος»
 ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Α Σ.
 Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Θέματα ενδοσχολικών εξετάσεων Γεωμετρίας Β Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
Παράλληλες ευθείες που τέμνονται από μια άλλη ευθεία. είναι «επί τα αυτά».
 Παράλληλες ευθείες που τέμνονται από μια άλλη ευθεία Οι γωνίες που βρίσκονται ανάμεσα στις ευθείες ε 1 και ε ονομάζονται «εντός» (των ευθειών)και όλες οι άλλες «εκτός». Οι γωνίες B 4, B 3, 1, είναι εντός
Παράλληλες ευθείες που τέμνονται από μια άλλη ευθεία Οι γωνίες που βρίσκονται ανάμεσα στις ευθείες ε 1 και ε ονομάζονται «εντός» (των ευθειών)και όλες οι άλλες «εκτός». Οι γωνίες B 4, B 3, 1, είναι εντός
Από την αρχική σχέση έχουµε: ΑΒ + ΑΓ = ή ΑΓ = ΑΒ Άρα ΑΓ = ΑΓ = 2
 Ερωτήσεις ανάπτυξης 1. i. Από το ορθογώνιο τρίγωνο ΑΗ, µε εφαρµογή του Πυθαγορείου Θεωρήµατος, έχουµε: ΑΗ Α - Η 7-49 - 4 45. Άρα ΑΗ 45 3 5cm. K ii. ια το τρίγωνο ΑΒ έχουµε: (ΑΒ) ΒΚ Β ΑΗ Β ΑΗ Α Α ΒK, άρα
Ερωτήσεις ανάπτυξης 1. i. Από το ορθογώνιο τρίγωνο ΑΗ, µε εφαρµογή του Πυθαγορείου Θεωρήµατος, έχουµε: ΑΗ Α - Η 7-49 - 4 45. Άρα ΑΗ 45 3 5cm. K ii. ια το τρίγωνο ΑΒ έχουµε: (ΑΒ) ΒΚ Β ΑΗ Β ΑΗ Α Α ΒK, άρα
Άλγεβρα ( ) = ( 1)( 3 2) ( 1) 2. i) Να αποδείξετε ότι ( ) ii) Να υπολογίσετε την αριθμητική τιμή του ( ) iii) Να λύσετε την εξίσωση P( x ) = 0
 ΤΑΞΗ Γ ΓΥΜΝΑΣΙΟΥ MAΘΗΜΑΤΙΚΑ 016 ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Άλγεβρα 1) Δίνεται το πολυώνυμο ( ) = ( + 1)( 1) ( + 1)( 5 + 7) P x x x x x i) Να αποδείξετε ότι ( ) P x = 7x x 8 Να υπολογίσετε την αριθμητική τιμή
ΤΑΞΗ Γ ΓΥΜΝΑΣΙΟΥ MAΘΗΜΑΤΙΚΑ 016 ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Άλγεβρα 1) Δίνεται το πολυώνυμο ( ) = ( + 1)( 1) ( + 1)( 5 + 7) P x x x x x i) Να αποδείξετε ότι ( ) P x = 7x x 8 Να υπολογίσετε την αριθμητική τιμή
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ. Τριγωνομετρικοι αριθμοι οξειων γωνιων
 Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ Τριγωνομετρικοι αριθμοι οξειων γωνιων 22 ΙΑΝΟΥΑΡΙΟΥ 2014 Κλίση ευθείας Όλοι έχουμε στο δρόμο τα παρακάτω σήματα, που από την εμπειρία μας καταλαβαίνουμε ότι πλησιάζουμε σε
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΜΑΘΗΜΑΤΙΚΟΣ Τριγωνομετρικοι αριθμοι οξειων γωνιων 22 ΙΑΝΟΥΑΡΙΟΥ 2014 Κλίση ευθείας Όλοι έχουμε στο δρόμο τα παρακάτω σήματα, που από την εμπειρία μας καταλαβαίνουμε ότι πλησιάζουμε σε
ΓΕΩΜΕΤΡΙΑ Β ΓΥΜΝΑΣΙΟΥ
 ΕΩΜΕΤΡΙΑ ΥΜΝΑΣΙΟΥ Χρήστος Π. Μουρατίδης 2014 2015 ΤΑΞΗ ΦΥΛΛΟ ΕΡΑΣΙΑΣ Κ 1.1 ΕΝΟΤΗΤΑ : Εμβαδόν επίπεδης επιφάνειας Τάξη : υμνασίου. Καθ. Χρήστος Μουρατίδης Όνομα Μαθητή :.. Ημ/νία :. 1. Να βρείτε το εμβαδόν
ΕΩΜΕΤΡΙΑ ΥΜΝΑΣΙΟΥ Χρήστος Π. Μουρατίδης 2014 2015 ΤΑΞΗ ΦΥΛΛΟ ΕΡΑΣΙΑΣ Κ 1.1 ΕΝΟΤΗΤΑ : Εμβαδόν επίπεδης επιφάνειας Τάξη : υμνασίου. Καθ. Χρήστος Μουρατίδης Όνομα Μαθητή :.. Ημ/νία :. 1. Να βρείτε το εμβαδόν
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ. 3 2 x. β)
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου
 Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου Θέµα 1 Α. Να υπολογίσετε την πλευρά λ και το απόστηµα α τετραγώνου εγγεγραµµένου σε κύκλο (Ο, R) συναρτήσει της ακτίνας R (10 Μονάδες) Β. Να χαρακτηρίσετε τις
Επαναληπτικό Διαγώνισµα Γεωµετρίας Β Λυκείου Θέµα 1 Α. Να υπολογίσετε την πλευρά λ και το απόστηµα α τετραγώνου εγγεγραµµένου σε κύκλο (Ο, R) συναρτήσει της ακτίνας R (10 Μονάδες) Β. Να χαρακτηρίσετε τις
Μαθηματικά Γ Γυμνασίου, Κεφάλαιο 1ο
 1 Ερωτήσεις θεωρίας Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ 1. Τι ονομάζουμε μονώνυμο;. Τι ονομάζουμε ρητή αλγεβρική παράσταση; 3. Ποιες τιμές δεν μπορούν να πάρουν οι μεταβλητές
1 Ερωτήσεις θεωρίας Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ 1. Τι ονομάζουμε μονώνυμο;. Τι ονομάζουμε ρητή αλγεβρική παράσταση; 3. Ποιες τιμές δεν μπορούν να πάρουν οι μεταβλητές
ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο
 ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο τέλος της πρότασης αν αυτή είναι Σωστή και Λ αν αυτή είναι Λάθος: ύο τρίγωνα είναι ίσα αν έχουν ίσες
ΙΣΟΤΗΤΑ ΤΡΙΓΩΝΩΝ. 1. Καθεμιά από τις παρακάτω προτάσεις μπορεί να είναι σωστή ή λάθος Να γράψετε Σ στο τέλος της πρότασης αν αυτή είναι Σωστή και Λ αν αυτή είναι Λάθος: ύο τρίγωνα είναι ίσα αν έχουν ίσες
ΘΕΩΡΙΑ ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΣΑΞΗ: ΘΕΜΑ 1 ο. A. Τι ονομάζουμε τετραγωνική ρίζα θετικού αριθμού α ;
 ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΣΑΞΗ: B ΘΕΩΡΙΑ ΘΕΜΑ 1 ο A. Τι ονομάζουμε τετραγωνική ρίζα θετικού αριθμού α ; B. Να αντιγράψετε και να συμπληρώσετε τις παρακάτω σχέσεις: i. Αν α 0,
ΓΡΑΠΣΕ ΑΝΑΚΕΥΑΛΑΙΩΣΙΚΕ ΕΞΕΣΑΕΙ ΠΕΡΙΟΔΟΤ ΜΑΪΟΤ ΙΟΤΝΙΟΤ ΣΑΞΗ: B ΘΕΩΡΙΑ ΘΕΜΑ 1 ο A. Τι ονομάζουμε τετραγωνική ρίζα θετικού αριθμού α ; B. Να αντιγράψετε και να συμπληρώσετε τις παρακάτω σχέσεις: i. Αν α 0,
5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια
 5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια 7 η διδακτική ενότητα : Παραλληλόγραμμα-Είδη παραλληλογράμμων 1. Να εξετάσετε αν είναι σωστή ή λανθασμένη καθεμιά από τις επόμενες προτάσεις: α) Οι διαγώνιοι κάθε
5o ΚΕΦΑΛΑΙΟ : Παραλληλόγραμμα - Τραπέζια 7 η διδακτική ενότητα : Παραλληλόγραμμα-Είδη παραλληλογράμμων 1. Να εξετάσετε αν είναι σωστή ή λανθασμένη καθεμιά από τις επόμενες προτάσεις: α) Οι διαγώνιοι κάθε
ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ 0 ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ α α (ii)
 ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ 1-13 1 Ποιοι αριθμοί ονομάζονται ομόσημοι και ποιοι ετερόσημοι; 1 Δίνονται οι αριθμοί: 1,,.1,,, 9, + 3, 3 3.1 Ποιοι από αυτούς είναι θετικοί και ποιοι αρνητικοί;.
ΤΑΞΗ Β ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΟ ΟΔΗΓΟΣ ΕΠΑΝΑΛΗΨΗΣ 1-13 1 Ποιοι αριθμοί ονομάζονται ομόσημοι και ποιοι ετερόσημοι; 1 Δίνονται οι αριθμοί: 1,,.1,,, 9, + 3, 3 3.1 Ποιοι από αυτούς είναι θετικοί και ποιοι αρνητικοί;.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ Γ ΓΥΜΝΑΣΙΟΥ 4) Να κάνετε τις πράξεις και μετά να βρείτε την αριθμητική τιμή του
 ΕΠΑΝΑΗΠΤΙΚΕ ΑΚΗΕΙ Γ ΓΥΜΝΑΙΟΥ ΕΝΟΤΗΤΑ : Αξιοσημείωτες Ταυτότητες 1. Να βρείτε τα αναπτύγματα: 1) 3 ) 3) 5 3 3 5 3 5) 5 4) 3 5 6) ( α 3 + 3β ) 7) (7 + )(7 ) 8) (β 4 + 1)(β + 1)(β + 1)(β 1). Να κάνετε τις
ΕΠΑΝΑΗΠΤΙΚΕ ΑΚΗΕΙ Γ ΓΥΜΝΑΙΟΥ ΕΝΟΤΗΤΑ : Αξιοσημείωτες Ταυτότητες 1. Να βρείτε τα αναπτύγματα: 1) 3 ) 3) 5 3 3 5 3 5) 5 4) 3 5 6) ( α 3 + 3β ) 7) (7 + )(7 ) 8) (β 4 + 1)(β + 1)(β + 1)(β 1). Να κάνετε τις
ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ 1. Να αναπτύξετε τις ταυτότητες: α. (α+8) β. (-) γ. (γ+k) δ. (+γ) ε. (3k-5λ) ζ. (5/κ - 4/λ) η. (/3-χ/4) θ. (χ - 3/χ) ι. (χ/3+3ψ/4) κ. (3χ+χ/) λ. (χ+8)(χ-8)
ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ 1. Να αναπτύξετε τις ταυτότητες: α. (α+8) β. (-) γ. (γ+k) δ. (+γ) ε. (3k-5λ) ζ. (5/κ - 4/λ) η. (/3-χ/4) θ. (χ - 3/χ) ι. (χ/3+3ψ/4) κ. (3χ+χ/) λ. (χ+8)(χ-8)
Ασκήσεις για τις εξετάσεις Μάη Ιούνη στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ
 Ασκήσεις για τις εξετάσεις Μάη Ιούνη 014 στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ Άσκηση 1 η Δίνεται παραλληλόγραμμο ΑΒΓΔ και. Με διάμετρο τη διαγώνιο ΑΓ γράφουμε κύκλο με κέντρο Ο που τέμνει τη ΓΔ στο
Ασκήσεις για τις εξετάσεις Μάη Ιούνη 014 στη Γεωμετρία Β Λυκείου του ΜΑΝΩΛΗ ΨΑΡΡΑ Άσκηση 1 η Δίνεται παραλληλόγραμμο ΑΒΓΔ και. Με διάμετρο τη διαγώνιο ΑΓ γράφουμε κύκλο με κέντρο Ο που τέμνει τη ΓΔ στο
ΘΕΜΑΤΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ
 Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
Μ Α Θ Η Μ Α Τ Ι Κ Α Β Γ Υ Μ Ν Α Σ Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Ι Κ Α Β Γ Υ Μ Ν Α Σ Ι Ο Υ 1 Ερωτήσεις θεωρίας Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα 2 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Δώστε ένα παράδειγμα σχετικό με την έννοια της μεταβλητής 2. Να αναφέρετε
Μ Α Θ Η Μ Α Τ Ι Κ Α Β Γ Υ Μ Ν Α Σ Ι Ο Υ 1 Ερωτήσεις θεωρίας Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα 2 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Δώστε ένα παράδειγμα σχετικό με την έννοια της μεταβλητής 2. Να αναφέρετε
2 Ο ΓΥΜΝΑΣΙΟ ΚΕΡΚΥΡΑΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ 2010 ΤΑΞΗ: Β ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ
 Ο ΓΥΜΝΑΣΙΟ ΚΕΡΚΥΡΑΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ 00 ΤΑΞΗ: Β ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΩΡΙΑ Α. Να αντιστοιχίσετε κάθε στοιχείο της πρώτης στήλης με το αντίστοιχο στοιχείο
Ο ΓΥΜΝΑΣΙΟ ΚΕΡΚΥΡΑΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ 00 ΤΑΞΗ: Β ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΩΡΙΑ Α. Να αντιστοιχίσετε κάθε στοιχείο της πρώτης στήλης με το αντίστοιχο στοιχείο
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 Θέματα απολυτήριων εξετάσεων Γ Γυμνασίου σχολικού έτους 013-014 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών
Θέματα απολυτήριων εξετάσεων Γ Γυμνασίου σχολικού έτους 013-014 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών
ΓΥΜΝΑΣΙΟ ΑΓΛΑΝΤΖΙΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ 2018 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ
 ΓΥΜΝΑΣΙΟ ΑΓΛΑΝΤΖΙΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 017-018 ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ 018 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ Γυμνασίου ΗΜΕΡΟΜΗΝΙΑ: Δευτέρα, 4 Ιουνίου 018 ΧΡΟΝΟΣ: ώρες ΒΑΘΜΟΣ:. ΥΠΟΓΡΑΦΗ ΚΑΘΗΓΗΤΗ/ΤΡΙΑΣ
ΓΥΜΝΑΣΙΟ ΑΓΛΑΝΤΖΙΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 017-018 ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ 018 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ Γυμνασίου ΗΜΕΡΟΜΗΝΙΑ: Δευτέρα, 4 Ιουνίου 018 ΧΡΟΝΟΣ: ώρες ΒΑΘΜΟΣ:. ΥΠΟΓΡΑΦΗ ΚΑΘΗΓΗΤΗ/ΤΡΙΑΣ
ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ. 1. Τι ονομάζουμε εφαπτομένη μια οξείας γωνίας ενός ορθογωνίου τριγώνου; Να κάνετε σχήμα.
 ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ 1. Τι ονομάζουμε εφαπτομένη μια οξείας γωνίας ενός ορθογωνίου τριγώνου; Να κάνετε σχήμα. 2. Τι ονομάζουμε ημίτονο μια οξείας γωνίας ενός ορθογωνίου τριγώνου;
ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΤΡΙΓΩΝΟΜΕΤΡΙΑ 1. Τι ονομάζουμε εφαπτομένη μια οξείας γωνίας ενός ορθογωνίου τριγώνου; Να κάνετε σχήμα. 2. Τι ονομάζουμε ημίτονο μια οξείας γωνίας ενός ορθογωνίου τριγώνου;
Β Γενική Τριγωνομετρία
 Β Γενική Τριγωνομετρία 40 Γενικευμένη γωνία - Γενικευμένα τόξα - Το ακτίνιο Τριγωνομετρικός κύκλος - Τριγωνομετρικοί αριθμοί γενικευμένης γωνίας 1. Η γωνία ω του παρακάτω σχήματος είναι θετική. α) Συνδέστε
Β Γενική Τριγωνομετρία 40 Γενικευμένη γωνία - Γενικευμένα τόξα - Το ακτίνιο Τριγωνομετρικός κύκλος - Τριγωνομετρικοί αριθμοί γενικευμένης γωνίας 1. Η γωνία ω του παρακάτω σχήματος είναι θετική. α) Συνδέστε
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 73 ος ΠΑΝΕΛΛΗΝΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ο ΘΑΛΗΣ 20 Οκτωβρίου 2012 Β ΓΥΜΝΑΣΙΟΥ
 06 79 ΑΘΗΝΑ Τηλ. 36653-367784 - Fax: 36405 GR. 06 79 - Athens - HELLAS Tel. 36653-367784 - Fax: 36405 0 Οκτωβρίου 0 Β ΓΥΜΝΑΣΙΟΥ Πρόβλημα Να υπολογίσετε την τιμή της παράστασης: 5 44 39 8 : Α= 5 5 5 6 3+
06 79 ΑΘΗΝΑ Τηλ. 36653-367784 - Fax: 36405 GR. 06 79 - Athens - HELLAS Tel. 36653-367784 - Fax: 36405 0 Οκτωβρίου 0 Β ΓΥΜΝΑΣΙΟΥ Πρόβλημα Να υπολογίσετε την τιμή της παράστασης: 5 44 39 8 : Α= 5 5 5 6 3+
1. Οµόλογες πλευρές : Στα όµοια τρίγωνα οι οµόλογες πλευρές βρίσκονται απέναντι από τις ίσες γωνίες και αντίστροφα.
 1 1.5. ΟΜΟΙ ΤΡΙΩΝ ΘΩΡΙ 1. Όµοια τρίγωνα : ια τα όµοια τρίγωνα ισχύουν όλα όσα αναφέραµε στα όµοια πολύγωνα. 2. ποκλειστικά για τα τρίγωνα : ύο τρίγωνα είναι όµοια όταν έχουν δύο γωνίες ίσες ΣΧΟΛΙ 1. Οµόλογες
1 1.5. ΟΜΟΙ ΤΡΙΩΝ ΘΩΡΙ 1. Όµοια τρίγωνα : ια τα όµοια τρίγωνα ισχύουν όλα όσα αναφέραµε στα όµοια πολύγωνα. 2. ποκλειστικά για τα τρίγωνα : ύο τρίγωνα είναι όµοια όταν έχουν δύο γωνίες ίσες ΣΧΟΛΙ 1. Οµόλογες
2.7 ΑΝΑΛΥΣΗ ΔΙΑΝΥΣΜΑΤΟΣ ΣΕ ΔΥΟ ΚΑΘΕΤΕΣ ΣΥΝΙΣΤΩΣΕΣ
 ΜΕΡΟΣ Β.7 ΑΝΑ ΔΙΑΝΥΣΜΑΤΟΣ ΣΕ ΔΥΟ ΚΑΘΕΤΕΣ ΣΥΝΙΣΤΩΣΕΣ 33.7 ΑΝΑ ΔΙΑΝΥΣΜΑΤΟΣ ΣΕ ΔΥΟ ΚΑΘΕΤΕΣ ΣΥΝΙΣΤΩΣΕΣ Ανάλυση διανύσματος σε δυο κάθετες συνιστώσες y x Α Γ x Δ Β y Όπως φαίνεται στο παραπάνω σχήμα κατασκευάζουμε
ΜΕΡΟΣ Β.7 ΑΝΑ ΔΙΑΝΥΣΜΑΤΟΣ ΣΕ ΔΥΟ ΚΑΘΕΤΕΣ ΣΥΝΙΣΤΩΣΕΣ 33.7 ΑΝΑ ΔΙΑΝΥΣΜΑΤΟΣ ΣΕ ΔΥΟ ΚΑΘΕΤΕΣ ΣΥΝΙΣΤΩΣΕΣ Ανάλυση διανύσματος σε δυο κάθετες συνιστώσες y x Α Γ x Δ Β y Όπως φαίνεται στο παραπάνω σχήμα κατασκευάζουμε
Θέματα απολυτήριων εξετάσεων ΑΣΚΗΣΕΙΣ
 Α. Να συμπληρωθούν οι ισότητες: (α + β) =.., (α β) 3 = και (α + β)(α β) =.. Β. Να αποδείξετε τη δεύτερη. Θέμα ο Να γράψετε τα τρία (3) κριτήρια ισότητας τριγώνων. Να λυθεί η εξίσωση: 3 + 4 = 7 + 1 Άσκηση
Α. Να συμπληρωθούν οι ισότητες: (α + β) =.., (α β) 3 = και (α + β)(α β) =.. Β. Να αποδείξετε τη δεύτερη. Θέμα ο Να γράψετε τα τρία (3) κριτήρια ισότητας τριγώνων. Να λυθεί η εξίσωση: 3 + 4 = 7 + 1 Άσκηση
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων των απολυτήριων εξετάσεων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων των απολυτήριων εξετάσεων
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ ΘΕΩΡΙΑ : Μήκος κύκλου: L = Εμβαδόν κύκλου: Ε = ( όπου π = 3,14) Γνωρίζοντας ότι σε γωνία 360 0 αντιστοιχεί κύκλος με μήκος L και εμβαδόν Ε έχουμε : α) ημικύκλιο
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΜΗΚΟΣ ΚΥΚΛΟΥ ΕΜΒΑΔΟΝ ΚΥΚΛΟΥ ΘΕΩΡΙΑ : Μήκος κύκλου: L = Εμβαδόν κύκλου: Ε = ( όπου π = 3,14) Γνωρίζοντας ότι σε γωνία 360 0 αντιστοιχεί κύκλος με μήκος L και εμβαδόν Ε έχουμε : α) ημικύκλιο
ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017
 ΓΥΜΝΑΣΙΟ ΑΓΙΟΥ ΒΑΣΙΛΕΙΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 06 07 Βαθμός αριθμητικά:..... / 00 =.... / 0 Ολογράφως:...... / 0 Υπογραφή Καθηγητή/τριας:..... ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 07 Μάθημα: ΜΑΘΗΜΑΤΙΚΑ
ΓΥΜΝΑΣΙΟ ΑΓΙΟΥ ΒΑΣΙΛΕΙΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 06 07 Βαθμός αριθμητικά:..... / 00 =.... / 0 Ολογράφως:...... / 0 Υπογραφή Καθηγητή/τριας:..... ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 07 Μάθημα: ΜΑΘΗΜΑΤΙΚΑ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΓΥΜΝΑΣΙΟΥ ΣΤΥΡΩΝ 11/6/2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΓΥΜΝΑΣΙΟΥ ΣΤΥΡΩΝ 11/6/014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΝΑ ΑΠΑΝΤΗΣΕΤΕ ΕΝΑ ΑΠΟ ΤΑ ΔΥΟ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΚΑΙ ΔΥΟ ΑΠΟ ΤΙΣ ΤΡΕΙΣ ΑΣΚΗΣΕΙΣ ΟΙ ΑΣΚΗΣΕΙΣ ΚΑΙ ΤΑ ΘΕΜΑΤΑ ΤΗΣ ΘΕΩΡΙΑΣ ΕΙΝΑΙ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΓΥΜΝΑΣΙΟΥ ΣΤΥΡΩΝ 11/6/014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΝΑ ΑΠΑΝΤΗΣΕΤΕ ΕΝΑ ΑΠΟ ΤΑ ΔΥΟ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΚΑΙ ΔΥΟ ΑΠΟ ΤΙΣ ΤΡΕΙΣ ΑΣΚΗΣΕΙΣ ΟΙ ΑΣΚΗΣΕΙΣ ΚΑΙ ΤΑ ΘΕΜΑΤΑ ΤΗΣ ΘΕΩΡΙΑΣ ΕΙΝΑΙ
ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ
 ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ 1) Ο λόγος των μηκών δύο κύκλων ( Ο, ρ ) και ( Ο, ρ ) είναι 1 3. Αν ρ = 1,15 cm να βρείτε : Την ακτίνα ρ. Το μήκος του ( Ο, ρ ) Το λόγο των διαμέτρων τους. 2) Οι περίμετροι
ΜΕΤΡΗΣΗ ΚΥΚΛΟΥ ΘΕΜΑΤΑ ΓΙΑ ΕΡΓΑΣΙΑ 1) Ο λόγος των μηκών δύο κύκλων ( Ο, ρ ) και ( Ο, ρ ) είναι 1 3. Αν ρ = 1,15 cm να βρείτε : Την ακτίνα ρ. Το μήκος του ( Ο, ρ ) Το λόγο των διαμέτρων τους. 2) Οι περίμετροι
Καλή Επιτυχία!!! ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια ( ) ΤΑΞΗ... Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΓΕΩΜΕΤΡΙΑΣ...
 Αµυραδάκη 0, Νίκαια (10-4903576) ΝΟΕΜΒΡΙΟΣ 011 ΘΕΜΑ 1 Ο Να αποδείξετε ότι, σε ένα ορθογώνιο τρίγωνο, το τετράγωνο µιας κάθετης πλευράς του ισούται µε το γινόµενο της υποτείνουσας επί την προβολή της στην
Αµυραδάκη 0, Νίκαια (10-4903576) ΝΟΕΜΒΡΙΟΣ 011 ΘΕΜΑ 1 Ο Να αποδείξετε ότι, σε ένα ορθογώνιο τρίγωνο, το τετράγωνο µιας κάθετης πλευράς του ισούται µε το γινόµενο της υποτείνουσας επί την προβολή της στην
1. 3 3cm 2. E( ) 24 3cm 3. E( ) 12 3cm ) 1. 8cm 2. 18cm 3. E 56 3 cm 4. E 20 3 cm. 6cm, cm, 3 6 cm, E cm )
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( 1) 3( ) 5( 3). 4 ( 3) 6 3. 3(4 ) 5( 1) 1 3(1 ) 3( ) 4 3 4. 1 5. 4 6 3 1 1 4( ) 1 1 3 6. 1 7. 1 3 6 3 4 3 3 1
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( 1) 3( ) 5( 3). 4 ( 3) 6 3. 3(4 ) 5( 1) 1 3(1 ) 3( ) 4 3 4. 1 5. 4 6 3 1 1 4( ) 1 1 3 6. 1 7. 1 3 6 3 4 3 3 1
ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΠΑΡΑΓΡΑΦΟΣ Β.1.3 ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ ΑΣΚΗΣΕΙΣ. 2 cm
 ΠΑΡΑΡΑΦΟΣ Β.1.3 ΕΜΒΑΑ ΕΠΙΠΕΩΝ ΣΧΗΜΑΤΩΝ Τετράγωνο -Ορθογώνιο ΑΣΚΗΣΕΙΣ 1) Ένα τετράγωνο έχει εμβαδό 81 cm 2. Με πόσο ισούται η πλευρά του; (Απάντηση: 9 cm) 2) Ένα τετράγωνο έχει περίμετρο 32 m. Nα υπολογίσετε
ΠΑΡΑΡΑΦΟΣ Β.1.3 ΕΜΒΑΑ ΕΠΙΠΕΩΝ ΣΧΗΜΑΤΩΝ Τετράγωνο -Ορθογώνιο ΑΣΚΗΣΕΙΣ 1) Ένα τετράγωνο έχει εμβαδό 81 cm 2. Με πόσο ισούται η πλευρά του; (Απάντηση: 9 cm) 2) Ένα τετράγωνο έχει περίμετρο 32 m. Nα υπολογίσετε
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ Μαθηματικό Περιηγητή 97 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ 1. Τα θέματα και στι 3 τάξει του Γυμνασίου χωρίζονται σε δύο κατηγορίε. Στα θέματα τη θεωρία
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΑΞΗ: Γ ΓΥΜΝΑΣΙΟΥ Μαθηματικό Περιηγητή 97 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ 1. Τα θέματα και στι 3 τάξει του Γυμνασίου χωρίζονται σε δύο κατηγορίε. Στα θέματα τη θεωρία
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ 1 ΚΕΦΑΛΑΙΟ 3 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ B ΓΥΝΜΑΣΙΟΥ. 1. Να λυθούν οι εξισώσεις και οι ανισώσεις :
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x 4x 3 x 6x 7. Να λυθεί στο Q, η ανίσωση :. 5 8 8 3. Να λυθούν
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x 4x 3 x 6x 7. Να λυθεί στο Q, η ανίσωση :. 5 8 8 3. Να λυθούν
Προσομοίωση προαγωγικών εξετάσεων Β Γυμνασίου ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΑΝΣΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ Α.
 Προσομοίωση προαγωγικών εξετάσεων Β Γυμνασίου ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 014-015 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΑΝΣΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ Α. ΘΕΩΡΙΑ ΘΕΜΑ 1 ο Α. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν
Προσομοίωση προαγωγικών εξετάσεων Β Γυμνασίου ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 014-015 ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΑΝΣΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ Α. ΘΕΩΡΙΑ ΘΕΜΑ 1 ο Α. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν
ΜΑΝΟΣ ΔΟΥΚΑΣ ΓΙΩΡΓΟΣ ΚΟΥΡΕΜΠΑΝΑΣ
 ΜΑΝΟΣ ΔΟΥΚΑΣ ΓΙΩΡΓΟΣ ΚΟΥΡΕΜΠΑΝΑΣ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Α Σ.. Να συμπληρώσετε τα κενά : i) (α μ ) ν = ii) (κ.λ) ν = iii) α μ.α ν = iv) α μ : α ν =. v) (α : β) ν =.. vi) α -ν = a vii)... viii) a...
ΜΑΝΟΣ ΔΟΥΚΑΣ ΓΙΩΡΓΟΣ ΚΟΥΡΕΜΠΑΝΑΣ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Α Σ.. Να συμπληρώσετε τα κενά : i) (α μ ) ν = ii) (κ.λ) ν = iii) α μ.α ν = iv) α μ : α ν =. v) (α : β) ν =.. vi) α -ν = a vii)... viii) a...
ΙΑΓΩΝΙΣΜΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ 19/ 04/ 2012
 ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 12 - Κ. ΤΟΥΜΠΑ THΛ: 919113 949422 www.syghrono.gr ΗΜΕΡΟΜΗΝΙΑ:... ΙΑΓΩΝΙΣΜΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ 19/ 04/ 2012 ΘΕΜΑ
ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΤΣΙΜΙΣΚΗ &ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ: 270727 222594 ΑΡΤΑΚΗΣ 12 - Κ. ΤΟΥΜΠΑ THΛ: 919113 949422 www.syghrono.gr ΗΜΕΡΟΜΗΝΙΑ:... ΙΑΓΩΝΙΣΜΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ 19/ 04/ 2012 ΘΕΜΑ
ΘΕΜΑΤΑ. Μονάδες 8. Δίνεται κύκλος (Ο, R) και σημείο Ρ εκτός αυτού. Φέρουμε την εφαπτομένη ΡΑ ώστε
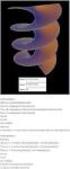 ΕΛ ΕΩΜΕΤΡΙΑ Β 1 ΕΛ ΕΩΜΕΤΡΙΑ Β 93 Α. Να αποδείξετε ότι: Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της πλευράς αυτής στην
ΕΛ ΕΩΜΕΤΡΙΑ Β 1 ΕΛ ΕΩΜΕΤΡΙΑ Β 93 Α. Να αποδείξετε ότι: Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο της υποτείνουσας επί την προβολή της πλευράς αυτής στην
Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]
![Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ] Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]](/thumbs/64/51524102.jpg) ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
ΕΝΟΤΗΤΑ Β.3.1. Στοιχεία τριγώνου - Είδη τριγώνων
 ΕΝΟΤΗΤΑ Β.3.1. Στοιχεία τριγώνου - Είδη τριγώνων ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Σελίδα 37 Στο παρακάτω σχήμα σχεδιάστε την διάμεσο ΑΜ, την διάμεσο ΒΛ και την διάμεσο ΓΝ. Τι παρατηρείτε; Να κατασκευάσετε
ΕΝΟΤΗΤΑ Β.3.1. Στοιχεία τριγώνου - Είδη τριγώνων ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Σελίδα 37 Στο παρακάτω σχήμα σχεδιάστε την διάμεσο ΑΜ, την διάμεσο ΒΛ και την διάμεσο ΓΝ. Τι παρατηρείτε; Να κατασκευάσετε
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ. Κεφάλαια επαναληπτικό 7. Ενότητα 5. β τεύχος
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ Κεφάλαια 36-44 επαναληπτικό 7 Ενότητα 5 β τεύχος επαναληπτικό 7 Κεφάλαια 36-44 1η Άσκηση Παρατηρούμε τα παρακάτω τρίγωνα και συμπληρώνουμε τον πίνακα, όπως στο
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ Κεφάλαια 36-44 επαναληπτικό 7 Ενότητα 5 β τεύχος επαναληπτικό 7 Κεφάλαια 36-44 1η Άσκηση Παρατηρούμε τα παρακάτω τρίγωνα και συμπληρώνουμε τον πίνακα, όπως στο
Ενότητα: Τετράπλευρα (Ιδιότητες Ταξινόμηση) Keywords: parallelogram, rectangular, rhombus, square, diagonals, height.
 Νέο Αναλυτικό Πρόγραμμα Σπουδών Σχολικό έτος 2016-17 Σπύρος Γ. Γλένης spyrosglenis@gmail.com Ενότητα: Τετράπλευρα (Ιδιότητες Ταξινόμηση) Keywords: parallelogram, rectangular, rhombus, square, diagonals,
Νέο Αναλυτικό Πρόγραμμα Σπουδών Σχολικό έτος 2016-17 Σπύρος Γ. Γλένης spyrosglenis@gmail.com Ενότητα: Τετράπλευρα (Ιδιότητες Ταξινόμηση) Keywords: parallelogram, rectangular, rhombus, square, diagonals,
1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: ii. Το ύψος ΒΚ
 Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
Οδηγίες & Ενδεικτικά θέματα προαγωγικών & απολυτηρίων εξετάσεων Γυμνασίου Σελίδα 1
 ΟΔΗΓIEΣ ΓΙΑ ΤΙΣ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΥΜΝΑΣΙΟΥ Α. ΘΕΩΡΙΑ Οι μαθητές υποχρεούνται σε διαπραγμάτευση ενός απλού από δύο τιθέμενα θέματα θεωρίας της διδαγμένης ύλης. Ένα θέμα από την Άλγεβρα και
ΟΔΗΓIEΣ ΓΙΑ ΤΙΣ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΥΜΝΑΣΙΟΥ Α. ΘΕΩΡΙΑ Οι μαθητές υποχρεούνται σε διαπραγμάτευση ενός απλού από δύο τιθέμενα θέματα θεωρίας της διδαγμένης ύλης. Ένα θέμα από την Άλγεβρα και
ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ ΧΡΟΝΟΣ : 2 Ώρες Υπογραφή :
 ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018 2019 ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ : Μαθηματικά ΤΑΞΗ : Γ ΗΜΕΡΟΜΗΝΙΑ : 5 / 6 / 2019 ΧΡΟΝΟΣ : 2 Ώρες Βαθμός : Ολογράφως
ΓΥΜΝΑΣΙΟ ΑΠΟΣΤΟΛΟΥ ΑΝΔΡΕΑ ΕΜΠΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2018 2019 ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΙΟΥΝΙΟΥ 2019 ΜΑΘΗΜΑ : Μαθηματικά ΤΑΞΗ : Γ ΗΜΕΡΟΜΗΝΙΑ : 5 / 6 / 2019 ΧΡΟΝΟΣ : 2 Ώρες Βαθμός : Ολογράφως
Οι γωνίες και που ονομάζονται «εντός εναλλάξ γωνίες» και είναι ίσες. «εντός-εκτός και επί τα αυτά μέρη γωνίες» και είναι ίσες.
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΓΥΜΝΑΣΙΟ ΤΑΞΗ Β 59 ΑΣΚΗΣΕΙΣ. Θέμα 1 ο. Θέμα 2 ο : Άσκηση 1 η. Άσκηση 2 η. Άσκηση 3 η
 ΥΜΝΑΣΙΟ ΤΑΞΗ ΥΜΝΑΣΙΟ ΤΑΞΗ Β 59 α. Να διατυπώσετε το Πυθαγόρειο Θεώρημα. β. Να διατυπώσετε το αντίστροφο του Πυθαγορείου Θεωρήματος. γ. Στο διπλανό σχήμα, το τρίγωνο ΔΕΖ είναι ορθογώνιο ( Δ = 90º) και ΔΑ
ΥΜΝΑΣΙΟ ΤΑΞΗ ΥΜΝΑΣΙΟ ΤΑΞΗ Β 59 α. Να διατυπώσετε το Πυθαγόρειο Θεώρημα. β. Να διατυπώσετε το αντίστροφο του Πυθαγορείου Θεωρήματος. γ. Στο διπλανό σχήμα, το τρίγωνο ΔΕΖ είναι ορθογώνιο ( Δ = 90º) και ΔΑ
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ 07-1-014 Ονοματεπώνυμο: Θέμα 1ο Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του ισούται με το γινόμενο της υποτείνουσας
ΠΡΟΓΡΑΜΜΑΤΙΣΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ 07-1-014 Ονοματεπώνυμο: Θέμα 1ο Α. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του ισούται με το γινόμενο της υποτείνουσας
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΧ. ΧΡ Ενότητα 2: Αξιοσημείωτες Ταυτότητες 1. Να βρείτε τα αναπτύγματα: (α) 2
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΧ. ΧΡ. 015-016 Ενότητα : Αξιοσημείωτες Ταυτότητες 1. Να βρείτε τα αναπτύγματα: (α) χ - 4 = (β) 3χ + = (γ) 3 χ + = (δ) 3 χ - 3 = (ε) χ - ψχ + ψ = (στ) 4χ - 3ψ = (ζ) αβ-γαβ+γ = (η) (x-3ω
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΧ. ΧΡ. 015-016 Ενότητα : Αξιοσημείωτες Ταυτότητες 1. Να βρείτε τα αναπτύγματα: (α) χ - 4 = (β) 3χ + = (γ) 3 χ + = (δ) 3 χ - 3 = (ε) χ - ψχ + ψ = (στ) 4χ - 3ψ = (ζ) αβ-γαβ+γ = (η) (x-3ω
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης. Διανύσματα ΚΑΤΗΓΟΡΙΑ 8. Εσωτερικό γινόµενο διανυσµάτων. Ασκήσεις προς λύση 1-50
 Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ' ΓΥΜΝΑΣΙΟΥ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ -ΙΟΥΝΙΟΥ ΘΕΩΡΙΑ :
 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ' ΓΥΜΝΑΣΙΟΥ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ -ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Θέμα 1 ον ΘΕΩΡΙΑ : α) Τι καλείται αριθμητική παράσταση και τι καλείται αλγεβρική παράσταση ; β) Να συμπληρώσετε
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ' ΓΥΜΝΑΣΙΟΥ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ -ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ Θέμα 1 ον ΘΕΩΡΙΑ : α) Τι καλείται αριθμητική παράσταση και τι καλείται αλγεβρική παράσταση ; β) Να συμπληρώσετε
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου
 ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο 1 ο ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α1.1 Ισότητα τριγώνων Στο διπλανό σχήμα το τρίγωνο ΑΒΓ είναι ισοσκελές με ΑΒ=ΑΓ. Προεκτείνουμε τη βάση ΒΓ κατά ίσα τμήματα
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο 1 ο ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α1.1 Ισότητα τριγώνων Στο διπλανό σχήμα το τρίγωνο ΑΒΓ είναι ισοσκελές με ΑΒ=ΑΓ. Προεκτείνουμε τη βάση ΒΓ κατά ίσα τμήματα
ΑΣΚHΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ
 ΣΚHΣΙΣ ΠΝΛΗΨΗΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΦΥΛΧΤΟΣ Π. ΣΜΪΛΗ. ΜYΡΙΙΝΝΗΣ. 1. Να λύσετε τις εξισώσεις : α) χ (χ 1) 3 = (1+5χ) β) x (3 3 x) 1 3(1 x) γ ) χ 3(χ ) +7 =( 3)( 5) 3χ δ) 5χ 19 3-(4χ-5) =χ (6χ 5) ε) 4 x 5 x
ΣΚHΣΙΣ ΠΝΛΗΨΗΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΦΥΛΧΤΟΣ Π. ΣΜΪΛΗ. ΜYΡΙΙΝΝΗΣ. 1. Να λύσετε τις εξισώσεις : α) χ (χ 1) 3 = (1+5χ) β) x (3 3 x) 1 3(1 x) γ ) χ 3(χ ) +7 =( 3)( 5) 3χ δ) 5χ 19 3-(4χ-5) =χ (6χ 5) ε) 4 x 5 x
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ
 ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΑΣΚΗΣΗ 1 η Να αποδείξετε ότι στις ομόλογες πλευρές δύο ίσων τριγώνων αντιστοιχούν ίσες διάμεσοι. Α Α ΑΠΟΔΕΙΞΗ Β Γ Β Γ Θα δείξουμε ότι ΑΜ=Α
Δ. Ε. ΚΟΝΤΟΚΩΣΤΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΑΣΚΗΣΗ 1 η Να αποδείξετε ότι στις ομόλογες πλευρές δύο ίσων τριγώνων αντιστοιχούν ίσες διάμεσοι. Α Α ΑΠΟΔΕΙΞΗ Β Γ Β Γ Θα δείξουμε ότι ΑΜ=Α
24 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 1ο Α. Nα αποδείξετε ότι το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Β. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί
1ο Α. Nα αποδείξετε ότι το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Β. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας τη λέξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί
2. Να κατασκευάσετε µια γωνία α τέτοια ώστε: εφ (90 - α) = 7. 3. Να κατασκευάσετε ένα τρίγωνο ΑΒΓ µε ύψος ΑΗ έτσι ώστε: 1 και εφγ = 3
 Προβλήµατα 1. Να κατασκευάσετε µια γωνία xαy, γνωρίζοντας ότι: 3 α) εφ xay = 5 β) συν xay = 0,8 γ) ηµ xay = 0,4 2. Να κατασκευάσετε µια γωνία α τέτοια ώστε: εφ (90 - α) = 7 4. 3. Να κατασκευάσετε ένα τρίγωνο
Προβλήµατα 1. Να κατασκευάσετε µια γωνία xαy, γνωρίζοντας ότι: 3 α) εφ xay = 5 β) συν xay = 0,8 γ) ηµ xay = 0,4 2. Να κατασκευάσετε µια γωνία α τέτοια ώστε: εφ (90 - α) = 7 4. 3. Να κατασκευάσετε ένα τρίγωνο
