Άλλος ένας χάρτης- µάθηµα, που χειρίζεται δύο βασικά θέµατα: - Το θέµα των υποδοχών, αµοιβαίων ή µεικτών, και - Το θέµα του χρονικού προσδιορισµού.
|
|
|
- Ευτέρπη Κουντουριώτης
- 9 χρόνια πριν
- Προβολές:
Transcript
1
2 Άλλος ένας χάρτης- µάθηµα, που χειρίζεται δύο βασικά θέµατα: - Το θέµα των υποδοχών, αµοιβαίων ή µεικτών, και - Το θέµα του χρονικού προσδιορισµού. Με αυτόν τον ωριαίο χάρτη επιβεβαιώνεται, ακόµα µια φορά, πόσο καλά λειτουργούν και δίνουν άµεση απάντηση οι υποδοχές µεταξύ των δύο σηµειοδοτών, ιδιαίτερα, όταν έχουµε να κάνουµε µε ερωτήσεις που αφορούν σε αισθηµατικά θέµατα. Πριν περάσουµε στην περιγραφή της υπόθεσης και την ερµηνεία του χάρτη, κρίνεται απαραίτητο να θυµηθούµε µερικά πράγµατα για τον τρόπο, µε τον οποίο οι υποδοχές δίνουν άµεσες απαντήσεις, είτε θετικές είτε αρνητικές, ανάλογα µε τη φύση της ερώτησης. Κάθε υποδοχή είναι µια σηµαντική κατάσταση που συµβαίνει µεταξύ δύο πλανητών. Αν και οι υποδοχές δεν αναφέρονται συχνά στα ελληνικά διασωθέντα κείµενα, εντούτοις, υπάρχουν κείµενα της αραβικής εποχής που καλύπτουν το θέµα µε ικανοποιητικό τρόπο. Συγκεκριµένα, ο Masha Allah στο έργο του On Reception αναφέρεται εκτενώς στις υποδοχές. Αργότερα, ο Abu Mashar διατυπώνει έναν ορισµό για τις υποδοχές, και, λίγους αιώνες µετά, ο William Lilly δίνει κι αυτός µε τη σειρά του τον ορισµό των υποδοχών. Γενικά, από την έρευνα στη βιβλιογραφία διαπιστώθηκε ότι όλοι οι κανόνες που έχουν διατυπωθεί για τις υποδοχές είναι πανοµοιότυποι. Ας δούµε τώρα την υπόθεση του χάρτη Η Ελένη περνούσε τις διακοπές της σε ένα θέρετρο µαζί µε πολλούς φίλους. Κάποια στιγµή, καθώς περπατούσε σε ένα πολύβουο µέρος µε την παρέα της, αναγνώρισε στο πρόσωπο κάποιου περαστικού, τον Γεράσιµο. Ο Γεράσιµος ήταν ένας µεγάλος έρωτας της ζωής της που είχε λήξει πριν 3,5 χρόνια, αφήνοντας, όµως, µόνο καλές αναµνήσεις. Προφανώς αναστατώθηκε και, έπειτα από ολιγόωρο, αλλά άκαρπο ψάξιµο, τριγύρω στο χώρο που νόµισε ότι τον είδε, διατύπωσε την ανωτέρω ερώτηση. Η Ελένη, που έκανε την ερώτηση, αντιπροσωπεύεται από τον 1ο οίκο και τον κυβερνήτη του, την Αφροδίτη, αφού ο 1ος οίκος έχει ακµή στις 9 Ζυγού. Βλέπουµε την Αφροδίτη να είναι ανάδροµη, τοποθετηµένη στον διάδοχο 11ο οίκο των φίλων και των οµάδων, στις Αυτή η Αφροδίτη δεν θα µπορούσε να περιγράψει καλύτερα την Ελένη, που είναι ένας αυθεντικά ροµαντικός χαρακτήρας µε µια αίσθηση δράµατος στη ζωή της ( ). Το 2
3 ντύσιµό της είναι πάντα καλαίσθητο ( ) και της αρέσει να ανήκει σε οµάδες και να καλλιεργεί φιλίες (11ος). Ο Γεράσιµος πάλι περιγράφεται πολύ σωστά από τον Άρη, αφού η ακµή του 7ου οίκου είναι στις 9 Κριού. Ο Άρης βρίσκεται στο ζώδιο των ιδύµων και περιγράφει πολύ καλά τον γρήγορο και ετοιµόλογο ( ) Γεράσιµο. Σύµφωνα µε τον κανόνα των 5 του Πτολεµαίου, ο Άρης είναι τοποθετηµένος στην ακµή του κατιόντα 9ου οίκου. Καµµία έκπληξη δεν µας προξενεί το γεγονός, ότι, για άλλη µια φορά, ο άξονας 1ου - 7ου οίκου κυβερνάται από τον Άρη και την Αφροδίτη, αφού πρόκειται για πολύ συχνό φαινόµενο σε χάρτες αισθηµατικών υποθέσεων. Ας δούµε τι περιγράφει ο χάρτης, για την κατάσταση που ίσχυε την ώρα που η Ελένη διατύπωσε την ερώτηση. Έχουµε: - Ελένη - Γεράσιµος Εκείνο που πρέπει αρχικά να ελεγχθεί είναι η σχέση που έχουν οι δύο σηµειοδότες (, ). ηλαδή: - Αν έχουν όψη µεταξύ τους - Τι είδους όψη είναι αυτή; Θετική ή αρνητική; - Συγκλίνουσα ή αποκλίνουσα; - Υπάρχουν υποδοχές µεταξύ των δύο σηµειοδοτών; - Τι είδους υποδοχές είναι; Αµοιβαίες ή µεικτές; - Συνδέονται οι αντισκιές τους; - Υπάρχει το φαινόµενο της µεταφοράς φωτός; Πράγµατι υπάρχει όψη µεταξύ της Αφροδίτης (Ελένη) και του Άρη (Γεράσιµος), µόνο που αυτή είναι αποκλίνουσα. Αν συµβουλετούµε τις εφηµερίδες, θα δούµε ότι η ακριβής όψη, που πραγµατοποιήθηκε µε την ανάδροµη κίνηση της Αφροδίτης, έγινε λίγες µέρες πριν, µε την Αφροδίτη στις και τον Άρη στις Μετά αποχωρίζονται. Τι σηµαίνει αυτό; Επιβεβαιώνει ότι πράγµατι υπήρχε στο παρελθόν δεσµός µεταξύ της Ελένης και του Γεράσιµου, ο οποίος όµως έχει λήξει. 3
4 Την απάντηση στο ερώτηµα της Ελένης, θα τη δώσει η Σελήνη, η οποία είναι κενή πορείας. Εδώ εφαρµόζεται το ίδιο σκεπτικό που ισχύει για κάθε χάρτη στον οποίο παρουσιάζεται το φαινόµενο της κενόδροµης Σελήνης. Τη στιγµή που ρώτησε η Ελένη είχε δεσµό µε το Γεράσιµο; Όχι... Είχαν χωρίσει προ πολλού". Άρα, εφόσον η κενή πορείας Σελήνη δεν ενεργοποιείται µε µελλοντική όψη, οι καταστάσεις δεν αλλάζουν. Παραµένουν όπως είχαν την ώρα της ερώτησης. Η απάντηση είναι σαφής: «Όχι, ο Γεράσιµος δεν ενδιαφέρεται. Τα πράγµατα παραµένουν ως έχουν». Όµως, η απάντηση στην Ελένη, µπορεί να δοθεί και από την εξέταση των υποδοχών, δηλαδή από την ανταλλαγή θεµελιώδων δυνάµεων µεταξύ των δύο σηµειοδοτών. Εκείνη ( - Ελένη) "βλέπει" τον, έστω και µε ασθενείς θεµελιώδεις δυνάµεις από όρια και πρόσωπο, που σηµαίνει ότι έχει κάποιο µικρό ενδιαφέρον ακόµα γι αυτόν, κάτι σαν αµυδρή νοσταλγία των παλιών καλών ηµερών. Ο Γεράσιµος ( ), όµως, δεν υποδέχεται, δεν "βλέπει" σε καµµία θεµελιώδη δύναµη την Αφροδίτη, που σηµαίνει ότι γι αυτόν ο κύκλος της σχέσης του µε την Ελένη έχει κλείσει οριστικά. Βλέπουµε λοιπόν ότι δύο δυνατές ενδείξεις µέσα στο χάρτη, η έλλειψη υποδοχών και η Σελήνη κενή πορείας, συνηγορούν στην ίδια απάντηση. «Όχι, ο Γεράσιµος δεν ενδιαφέρεται» Η αµοιβαία συγκλίνουσα όψη που πραγµατοποιείται µεταξύ της και του ανάδροµου δεν έχει κάτι άλλο να προσθέσει πάνω στο θέµα, πέραν του ότι ο Κρόνος είναι κυβερνήτης του 4ου οίκου, ο οποίος αντιπροσωπεύει το τέλος της υπόθεσης και συνεπώς η όψη αυτή επιβεβαιώνει όσα έχουν ήδη προαναφερθεί. Μια παρατήρηση για τους ερευνητές-µελετητές, που ίσως να είναι άσχετη µε το θέµα του χάρτη, αλλά χρήσιµη από άποψης µελέτης. Όλοι οι ωριαίοι χάρτες, που θα καταστρώνονταν εκείνες τις ηµέρες κατά τις πρωινές ώρες, θα είχαν τους,, σε κατάσταση Hayz. Ο κυριότερος λόγος που αυτός ο ωριαίος χάρτης αξίζει µιας εκτενέστερης ανάλυσης είναι επειδή µας βοηθάει να βρούµε τα κλειδιά για να αποκωδικοποιήσουµε τις πληροφορίες που αφορούν στα θέµατα µέτρησης του χρόνου. Εδώ, θα ακολουθήσουµε την κλασσική µέθοδο για την ανεύρεση χρόνου, που είναι η διαφορά µοιρών µεταξύ δύο σηµειοδοτών. 4
5 Η διαφορά των µοιρών µεταξύ της ανάδροµης Αφροδίτης (28 51 ) και του Άρη (2 38) είναι σχεδόν 3, 5. Αυτή η διαφορά 3,5 µοιρών είναι που κρύβει την πληροφορία για τον τρόπο που θα µετρηθεί και θα αξιολογηθεί ο χρόνος στο συγκεκριµένο χάρτη. Πώς γίνεται αυτό; Απ όσα γνωρίζουµε µέχρι στιγµής στα θέµατα χρονικού προσδιορισµού ισχύουν τα εξής: - Οι οίκοι στους οποίους είναι τοποθετηµένοι οι σηµειοδότες µάς υποδεικνύουν ποια είναι η καταλληλότερη µονάδα µέτρησης του χρόνου. Κατά κανόνα ισχύουν τα εξής: γωνιακοί οίκοι: δίνουν γρήγορους χρόνους διάδοχοι οίκοι: δίνουν µεσαίους χρόνους κατιόντες οίκοι: αντιπροσωπεύουν τα µεγάλα χρονικά διαστήµατα. Αλλά και τα ζώδια στα οποία είναι τοποθετηµένοι οι σηµειοδότες υποδεικνύουν τον τρόπο µέτρησης του χρόνου. Συνοπτικά έχουµε: Παρορµητικά ζώδια: η συντοµότερη µονάδα χρόνου Μεταβλητά ζώδια: ενδιάµεση µονάδα µέτρησης χρόνου Σταθερά ζώδια: η µεγαλύτερη µονάδα µέτρησης χρόνου Έτσι λοιπόν έχουµε = σε διάδοχο οίκο και σταθερό ζώδιο = σε κατιόντα οίκο και µεταβλητό ζώδιο Με την κοινή λογική συµπεραίνουµε, ότι ο συνδυασµός των θέσεων της Αφροδίτης και του Άρη µας δίνει µέτρηση σε χρόνια και όχι σε µήνες ή εβδοµάδες. Καταλήγουµε, λοιπόν, στο συµπέρασµα ότι οι 3,5 µοίρες αντιστοιχούν σε χρονικό διάστηµα 3,5 ετών και έτσι επιβεβαιώνεται το χρονικό διάστηµα που είχε µεσολαβήσει από τον χωρισµό της Ελένης µε το Γεράσιµο που ήταν όντως 3,5 χρόνια Σηµειώσεις 1) Ο χάρτης έχει ερµηνευθεί εξετάζοντας τους 7 παραδοσιακούς πλανήτες που χρησιµοποιούνται στην παραδοσιακή αστρολογία. Υπενθυµίζουµε εδώ, ότι ο Άρης κυβερνάει τα ζώδια του Κριού και του Σκορπιού, ο ίας τα ζώδια του Τοξότη και των Ιχθύων και ο Κρόνος τα ζώδια του Αιγόκερω και του Υδροχόου. 5
6 Αν όµως βρεθεί στο χάρτη κάποιος από τους εξωκρόνιους (,, À) να είναι πολύ κοντα ή σε σύνοδο ακριβείας µε την ακµή ενός γωνιακού οίκου, τότε λαµβάνονται υπόψη στην ερµηνεία του χάρτη µόνον οι ιδιότητές του ως πλανήτη και όχι ως κυβερνήτη ζωδίου (, œ, ). 2) Ο χάρτης έχει µελετηθεί σύµφωνα µε τις θεµελιώδεις δυνάµεις του ωρόθεου της Σιδώνας. 6
Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που
 Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που αφορούν στην εύρεση αντικειµένων και τον χρόνο στον οποίο το αντικείµενο θα ευρεθεί. Είναι το είδος της ερώτησης που
Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που αφορούν στην εύρεση αντικειµένων και τον χρόνο στον οποίο το αντικείµενο θα ευρεθεί. Είναι το είδος της ερώτησης που
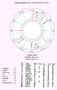
Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ;
 Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ; HORARY CHART 31/7/2007 03:09:11 μ.μ. 23Ε43, 37Ν58 (ΕΕD -3) Κυριαρχία +5 Έξαρση +4 Τριπλότητα +3 Όρια +2 εκανός +1 Αδυναμία -5 Πτώση -4 Περιπλανώμενος -5
Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ; HORARY CHART 31/7/2007 03:09:11 μ.μ. 23Ε43, 37Ν58 (ΕΕD -3) Κυριαρχία +5 Έξαρση +4 Τριπλότητα +3 Όρια +2 εκανός +1 Αδυναμία -5 Πτώση -4 Περιπλανώμενος -5
Η ερώτηση είχε ως εξής: «Θα αγοράσω το σπίτι που είδα σήµερα στη εξοχή; Θα είναι προς όφελός
 Η κυρία που διατύπωσε την ερώτηση είναι προσωπική φίλη και έψαχνε πολύ καιρό για ένα σπίτι µεγαλύτερο και µε περισσότερες ανέσεις, δίχως να µένει ικανοποιηµένη µε τις διάφορες προτάσεις που της έκαναν.
Η κυρία που διατύπωσε την ερώτηση είναι προσωπική φίλη και έψαχνε πολύ καιρό για ένα σπίτι µεγαλύτερο και µε περισσότερες ανέσεις, δίχως να µένει ικανοποιηµένη µε τις διάφορες προτάσεις που της έκαναν.
Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα
 Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα Ανεύρεση χαμένων ή παραπεταμένων αντικειμένων Σε ωριαίους χάρτες που αναφέρονται στην ανεύρεση χαμένων ή παραπεταμένων αντικειμένων πρέπει να ελεγχθούν
Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα Ανεύρεση χαμένων ή παραπεταμένων αντικειμένων Σε ωριαίους χάρτες που αναφέρονται στην ανεύρεση χαμένων ή παραπεταμένων αντικειμένων πρέπει να ελεγχθούν
ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη
 ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη Κατά τη διάρκεια των αιώνων, πολλοί αξιόλογοι μελετητές της αστρολογίας παρατήρησαν ότι ορισμένα αποτελέσματα επαναλαμβάνονταν κάτω
ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη Κατά τη διάρκεια των αιώνων, πολλοί αξιόλογοι μελετητές της αστρολογίας παρατήρησαν ότι ορισμένα αποτελέσματα επαναλαμβάνονταν κάτω
ΕΚΛΕΙΨΕΙΣ. Οι εκλείψεις στην Ωριαία αστρολογία
 ΕΚΛΕΙΨΕΙΣ Οι εκλείψεις στην Ωριαία αστρολογία Οι εκλείψεις παίζουν σημαντικό ρόλο στην Ωριαία αστρολογία. Από τα βάθη των αιώνων μέχρι σήμερα πολλοί αστρονόμοι και αστρολόγοι έχουν μελετήσει το φαινόμενο
ΕΚΛΕΙΨΕΙΣ Οι εκλείψεις στην Ωριαία αστρολογία Οι εκλείψεις παίζουν σημαντικό ρόλο στην Ωριαία αστρολογία. Από τα βάθη των αιώνων μέχρι σήμερα πολλοί αστρονόμοι και αστρολόγοι έχουν μελετήσει το φαινόμενο
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ).
 ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ). Οι ομάδες των πλανητών (Sects) και η σπουδαιότητά τους σε ένα χάρτη Η πρωταρχική ενέργεια που
ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ). Οι ομάδες των πλανητών (Sects) και η σπουδαιότητά τους σε ένα χάρτη Η πρωταρχική ενέργεια που
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Γ Λ Ω Σ Σ Α Ρ Ι. Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος.
 Γ Λ Ω Σ Σ Α Ρ Ι Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος. Αδυναμία: Ένας πλανήτης βρίσκεται σε αδυναμία όταν είναι τοποθετημένος στο απέναντι ζώδιο από αυτό που κυβερνά, π.χ. η αδυναμία της Σελήνης είναι στον
Γ Λ Ω Σ Σ Α Ρ Ι Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος. Αδυναμία: Ένας πλανήτης βρίσκεται σε αδυναμία όταν είναι τοποθετημένος στο απέναντι ζώδιο από αυτό που κυβερνά, π.χ. η αδυναμία της Σελήνης είναι στον
Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ;
 Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ; Μέχρι στιγμής έχουν αναφερθεί όλοι οι παράγοντες που πρέπει να εξεταστούν για να μπορέσει κανείς να εκτιμήσει σωστά το όποιο αποτέλεσμα σε ένα χάρτη ωριαίας ερώτησης,
Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ; Μέχρι στιγμής έχουν αναφερθεί όλοι οι παράγοντες που πρέπει να εξεταστούν για να μπορέσει κανείς να εκτιμήσει σωστά το όποιο αποτέλεσμα σε ένα χάρτη ωριαίας ερώτησης,
Ένατο µέρος. ... Συνέχεια από το προηγούµενο
 Ένατο µέρος... Συνέχεια από το προηγούµενο Στη συνέχεια θα ήθελα να αναλύσω ορισµένες ενδιαφέρουσες ελληνιστικές τεχνικές που είναι γενικής σηµασίας, µε την έννοια που περιέγραψα προηγουµένως, δηλαδή τεχνικές
Ένατο µέρος... Συνέχεια από το προηγούµενο Στη συνέχεια θα ήθελα να αναλύσω ορισµένες ενδιαφέρουσες ελληνιστικές τεχνικές που είναι γενικής σηµασίας, µε την έννοια που περιέγραψα προηγουµένως, δηλαδή τεχνικές
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος Άρης
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος Άρης
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΔΕΚΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΔΕΚΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΝΟΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΝΟΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΦΕΒΡΟΥΑΡΙΟΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΕΙΣΟΔΟΣ ΠΛΑΝΗΤΗ ΣΕ ΖΩΔΙΟ ΑΣΤΡΟΛΟΓΙΚΑ
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΕΙΣΟΔΟΣ ΠΛΑΝΗΤΗ ΣΕ ΖΩΔΙΟ ΑΣΤΡΟΛΟΓΙΚΑ
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΙΑΝΟΥΑΡΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΙΑΝΟΥΑΡΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΜΑΡΤΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΜΑΡΤΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
έκατο µέρος Συνέχεια από το προηγούµενο Τρόπος εύρεσης του Κυρίου του ωροσκοπίου
 έκατο µέρος Συνέχεια από το προηγούµενο Ο προσδιορισµός τώρα του Κυρίου του ωροσκοπίου είναι πολύ περίπλοκος. Στην πραγµατικότητα, είναι πολύ πιο δύσκολος από τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου,
έκατο µέρος Συνέχεια από το προηγούµενο Ο προσδιορισµός τώρα του Κυρίου του ωροσκοπίου είναι πολύ περίπλοκος. Στην πραγµατικότητα, είναι πολύ πιο δύσκολος από τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου,
ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ
 22 ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ H έρευνα του πρώτου μέρους αυτού του βιβλίου αναφέρεται αποκλειστικά στο αμερικανικό χρηματιστήριο. Κατά συνέπεια, η μελέτη των ωροσκοπίων των μετοχών που παρατίθενται στα
22 ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ H έρευνα του πρώτου μέρους αυτού του βιβλίου αναφέρεται αποκλειστικά στο αμερικανικό χρηματιστήριο. Κατά συνέπεια, η μελέτη των ωροσκοπίων των μετοχών που παρατίθενται στα
Έκτο µέρος. ... Συνέχεια από το προηγούµενο
 Έκτο µέρος 1... Συνέχεια από το προηγούµενο Προηγουµένως µίλησα για τις πολλαπλές απτές σηµασίες των ελληνιστικών πλανητών µε τις οποίες θα πρέπει να επανεξοικειωθούµε για να αποκοµίσουµε πλήρες όφελος
Έκτο µέρος 1... Συνέχεια από το προηγούµενο Προηγουµένως µίλησα για τις πολλαπλές απτές σηµασίες των ελληνιστικών πλανητών µε τις οποίες θα πρέπει να επανεξοικειωθούµε για να αποκοµίσουµε πλήρες όφελος
ΠΕΡΙ ΟΙΚΩΝ. Τεταρτημόρια
 ΠΕΡΙ ΟΙΚΩΝ Οι οίκοι είναι ένα από τα κυριότερα ερμηνευτικά μέσα που χρησιμοποιεί η αστρολογία. Μαζί με τους πλανήτες, τα ζώδια και τις όψεις αποτελούν τις βασικές αρχές στις οποίες στηρίζεται η ερμηνεία
ΠΕΡΙ ΟΙΚΩΝ Οι οίκοι είναι ένα από τα κυριότερα ερμηνευτικά μέσα που χρησιμοποιεί η αστρολογία. Μαζί με τους πλανήτες, τα ζώδια και τις όψεις αποτελούν τις βασικές αρχές στις οποίες στηρίζεται η ερμηνεία
Προειδοποιητικοί κανόνες (Considerations before judgment)
 Προειδοποιητικοί κανόνες (Considerations before judgment) της έσποινας Γιαννακοπούλου Ένα ευαίσθητο κεφάλαιο, που φαίνεται ότι δεν έχει κατανοηθεί πλήρως από τους ασκούντες την Ωριαία, είναι οι προειδοποιητικοί
Προειδοποιητικοί κανόνες (Considerations before judgment) της έσποινας Γιαννακοπούλου Ένα ευαίσθητο κεφάλαιο, που φαίνεται ότι δεν έχει κατανοηθεί πλήρως από τους ασκούντες την Ωριαία, είναι οι προειδοποιητικοί
Άρθρο :Ευδοκία Πεπονούλα
 Άρθρο :Ευδοκία Πεπονούλα Ο γενέθλιος χάρτης της Ιαπωνίας έχει Ήλιο στις 22 ο 37 του Υδροχόου. Ενεργοποιεί δηλαδή την κλείδα Ουρανού Σελήνης στις 23 ο του Σκορπιού. Μας μιλά λοιπόν για ένα κράτος με παλιές
Άρθρο :Ευδοκία Πεπονούλα Ο γενέθλιος χάρτης της Ιαπωνίας έχει Ήλιο στις 22 ο 37 του Υδροχόου. Ενεργοποιεί δηλαδή την κλείδα Ουρανού Σελήνης στις 23 ο του Σκορπιού. Μας μιλά λοιπόν για ένα κράτος με παλιές
Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ.
 Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ. Η Βαβυλωνιακή αστρολογία λέγεται ότι είχε επηρεάσει τους Έλληνες ήδη από τα μέσα του 4ου π.χ. αιώνα. Ακόμη και αν η προέλευση της αστρολογίας των
Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ. Η Βαβυλωνιακή αστρολογία λέγεται ότι είχε επηρεάσει τους Έλληνες ήδη από τα μέσα του 4ου π.χ. αιώνα. Ακόμη και αν η προέλευση της αστρολογίας των
Γλωσσάρι ελληνικής αστρολογίας. Γλωσσάρι ελληνικών αστρολογικών όρων
 285 Γλωσσάρι ελληνικών αστρολογικών όρων 287 ΓΛΩΣΣΑΡΙ Ἀγαθοδαιμονῶ: Η παρουσία ενός πλανήτη ή άλλου αστρολογικού σημείου στον 11o τόπο-οίκο, που ήταν γνωστός και ως Ἀγαθὸς Δαίμων. Ἀγαθοποιός: Η λέξη αναφέρεται
285 Γλωσσάρι ελληνικών αστρολογικών όρων 287 ΓΛΩΣΣΑΡΙ Ἀγαθοδαιμονῶ: Η παρουσία ενός πλανήτη ή άλλου αστρολογικού σημείου στον 11o τόπο-οίκο, που ήταν γνωστός και ως Ἀγαθὸς Δαίμων. Ἀγαθοποιός: Η λέξη αναφέρεται
μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16
 περιεχόμενα μάθημα πρώτο: αστρολογία & σχέσεις 6 μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16 ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ: με ποιον τρόπο αγαπάμε 42 ΜΑΘΗΜΑ ΠΕΜΠΤΟ: με
περιεχόμενα μάθημα πρώτο: αστρολογία & σχέσεις 6 μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16 ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ: με ποιον τρόπο αγαπάμε 42 ΜΑΘΗΜΑ ΠΕΜΠΤΟ: με
Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει. από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών
 Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών ταλαντώσεων Υλικό σηµείο Σ ενός ελαστικού µέσου εκτελεί περιοδική κίνηση (ιδιόµορφη ταλάντωση)
Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών ταλαντώσεων Υλικό σηµείο Σ ενός ελαστικού µέσου εκτελεί περιοδική κίνηση (ιδιόµορφη ταλάντωση)
Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις
 ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση
 8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Μία αστρολογική άποψη του τι συμβαίνει, σε αυτόν τον πλανήτη Γη εδώ για την 24 η Αυγούστου.
 Η Έκθεση Πέλε 24 Αυγούστου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Μία αστρολογική άποψη του τι συμβαίνει, σε αυτόν τον πλανήτη Γη εδώ για την 24 η Αυγούστου. Είμαι εδώ πάνω στα
Η Έκθεση Πέλε 24 Αυγούστου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Μία αστρολογική άποψη του τι συμβαίνει, σε αυτόν τον πλανήτη Γη εδώ για την 24 η Αυγούστου. Είμαι εδώ πάνω στα
Θεωρητικά Θέµατα. Ι. Θεωρία Οµάδων. x R y ή x R y ή x y(r) [x] R = { y X y R x } X. Μέρος Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις
![Θεωρητικά Θέµατα. Ι. Θεωρία Οµάδων. x R y ή x R y ή x y(r) [x] R = { y X y R x } X. Μέρος Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις Θεωρητικά Θέµατα. Ι. Θεωρία Οµάδων. x R y ή x R y ή x y(r) [x] R = { y X y R x } X. Μέρος Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις](/thumbs/93/111928837.jpg) 202 Μέρος 4. Θεωρητικά Θέµατα Ι. Θεωρία Οµάδων 1. Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις 1.1. Σχέσεις ισοδυναµίας. Εστω X ένα µη-κενό σύνολο. Ορισµός 1.1. Μια σχέση ισοδυναµίας επί του X είναι ένα
202 Μέρος 4. Θεωρητικά Θέµατα Ι. Θεωρία Οµάδων 1. Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις 1.1. Σχέσεις ισοδυναµίας. Εστω X ένα µη-κενό σύνολο. Ορισµός 1.1. Μια σχέση ισοδυναµίας επί του X είναι ένα
Ανοικτά και κλειστά σύνολα
 5 Ανοικτά και κλειστά σύνολα Στην παράγραφο αυτή αναπτύσσεται ο µηχανισµός που θα µας επιτρέψει να µελετήσουµε τις αναλυτικές ιδιότητες των συναρτήσεων πολλών µεταβλητών. Θα χρειαστούµε τις έννοιες της
5 Ανοικτά και κλειστά σύνολα Στην παράγραφο αυτή αναπτύσσεται ο µηχανισµός που θα µας επιτρέψει να µελετήσουµε τις αναλυτικές ιδιότητες των συναρτήσεων πολλών µεταβλητών. Θα χρειαστούµε τις έννοιες της
ΚΕΦΑΛΑΙΟ 9 ο ΤΟ ΠΕΡΙΒΑΛΛΟΝ. 9.1 Εισαγωγή
 ΚΕΦΑΛΑΙΟ 9 ο ΤΟ ΠΕΡΙΒΑΛΛΟΝ 9.1 Εισαγωγή Η βιώσιµη ανάπτυξη είναι µία πολυδιάστατη έννοια, η οποία αποτελεί µία εναλλακτική αντίληψη της ανάπτυξης, µε κύριο γνώµονα το καθαρότερο περιβάλλον και επιδρά στην
ΚΕΦΑΛΑΙΟ 9 ο ΤΟ ΠΕΡΙΒΑΛΛΟΝ 9.1 Εισαγωγή Η βιώσιµη ανάπτυξη είναι µία πολυδιάστατη έννοια, η οποία αποτελεί µία εναλλακτική αντίληψη της ανάπτυξης, µε κύριο γνώµονα το καθαρότερο περιβάλλον και επιδρά στην
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
ΖΩΔΙΑ ΚΑΙ ΣΥΜΒΟΥΛΕΣ ΓΙΑ ΤΗΝ ΕΒΔΟΜΑΔΑ ΑΠΟ 9 15 ΙΑΝΟΥΑΡΙΟΥ 2017 ΜΕ ΤΗΝ ΒΑΛΕΝΤΙΝΗ ΒΑΣΙΛΕΙΑΔΟΥ
 ΖΩΔΙΑ ΚΑΙ ΣΥΜΒΟΥΛΕΣ ΓΙΑ ΤΗΝ ΕΒΔΟΜΑΔΑ ΑΠΟ 9 15 ΙΑΝΟΥΑΡΙΟΥ 2017 ΜΕ ΤΗΝ ΒΑΛΕΝΤΙΝΗ ΒΑΣΙΛΕΙΑΔΟΥ Κριός Αυτή την εβδομάδα θα μπεις σε σκέψεις αγαπητέ Κριέ και θα αλλάξεις το σκεπτικό σου για το πως βλέπεις κάποια
ΖΩΔΙΑ ΚΑΙ ΣΥΜΒΟΥΛΕΣ ΓΙΑ ΤΗΝ ΕΒΔΟΜΑΔΑ ΑΠΟ 9 15 ΙΑΝΟΥΑΡΙΟΥ 2017 ΜΕ ΤΗΝ ΒΑΛΕΝΤΙΝΗ ΒΑΣΙΛΕΙΑΔΟΥ Κριός Αυτή την εβδομάδα θα μπεις σε σκέψεις αγαπητέ Κριέ και θα αλλάξεις το σκεπτικό σου για το πως βλέπεις κάποια
Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES
 Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES Σεμνός δημιουργός ή ευφυής κροίσος; Θα ήταν μεγάλη παράλειψη για ένα βιβλίο που εξετάζει τη σχέση χρήματος και αστρολογίας να μην αναφερθεί στους παράγοντες εκείνους
Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES Σεμνός δημιουργός ή ευφυής κροίσος; Θα ήταν μεγάλη παράλειψη για ένα βιβλίο που εξετάζει τη σχέση χρήματος και αστρολογίας να μην αναφερθεί στους παράγοντες εκείνους
Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ
 ΜΑΘΗΜΑ 17 Κεφάλαιο 4o : Περιγραφική Στατιστική Υποενότητα 4.5: Μέση Τιµή - ιάµεσος Θεµατικές Ενότητες: 1. Μέση Τιµή - ιάµεσος. Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ ΟΡΙΣΜΟΙ Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση
ΜΑΘΗΜΑ 17 Κεφάλαιο 4o : Περιγραφική Στατιστική Υποενότητα 4.5: Μέση Τιµή - ιάµεσος Θεµατικές Ενότητες: 1. Μέση Τιµή - ιάµεσος. Α. ΜΕΣΗ ΤΙΜΗ - ΙΑΜΕΣΟΣ ΟΡΙΣΜΟΙ Για πιο σύντοµη, αποδοτική και συγκρίσιµη θεώρηση
Η Έκθεση Πέλε 17 Φεβρουαρίου, Γεια σας ~ Καλημέρα ~
 Η Έκθεση Πέλε 17 Φεβρουαρίου, 2016 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, έναν αστρολογικό στοχασμό. Είναι για την εβδομάδα της 17ης Φεβρουαρίου του 2016, και αυτή είναι
Η Έκθεση Πέλε 17 Φεβρουαρίου, 2016 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, έναν αστρολογικό στοχασμό. Είναι για την εβδομάδα της 17ης Φεβρουαρίου του 2016, και αυτή είναι
Άσκηση 1 (α) ============================================================== Έχουµε L = π, εποµένως η σειρά Fourier είναι: 1 2 a. cos. a n. b n.
 http://elear.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις 6ης Γραπτής Εργασίας ΠΛΗ 7-8: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elear.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις 6ης Γραπτής Εργασίας ΠΛΗ 7-8: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
KΕΦΑΛΑΙΟ 6 ΥΝΑΜΟΣΕΙΡΕΣ-ΣΕΙΡΕΣ TAYLOR
 KΕΦΑΛΑΙΟ 6 ΥΝΑΜΟΣΕΙΡΕΣ-ΣΕΙΡΕΣ TAYLOR 6 Ορισµοί Ορισµός 6 Εστω α είναι µία πραγµατική ακολουθία και είναι πραγµατικοί αριθµοί Ένα άπειρο πολυώνυµο της µορφής: a ( ) () = καλείται δυναµοσειρά µε κέντρο το
KΕΦΑΛΑΙΟ 6 ΥΝΑΜΟΣΕΙΡΕΣ-ΣΕΙΡΕΣ TAYLOR 6 Ορισµοί Ορισµός 6 Εστω α είναι µία πραγµατική ακολουθία και είναι πραγµατικοί αριθµοί Ένα άπειρο πολυώνυµο της µορφής: a ( ) () = καλείται δυναµοσειρά µε κέντρο το
μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76
 περιεχόμενα μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76 μάθημα έβδομο: δίας 82 μάθημα ογδοο: κρονοσ
περιεχόμενα μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76 μάθημα έβδομο: δίας 82 μάθημα ογδοο: κρονοσ
Η έκθεση Πέλε 19 Αυγούστου, Γεια σας! ~ Καλημέρα! ~
 Η έκθεση Πέλε 19 Αυγούστου, 2015 Γεια σας! ~ Καλημέρα! ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε και η έκθεση αυτή είναι για τις 19 Αυγούστου του 2015. Θέλω να το ενώσουμε λίγο. Κάνω το ίδιο πράγμα
Η έκθεση Πέλε 19 Αυγούστου, 2015 Γεια σας! ~ Καλημέρα! ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε και η έκθεση αυτή είναι για τις 19 Αυγούστου του 2015. Θέλω να το ενώσουμε λίγο. Κάνω το ίδιο πράγμα
Η γέννηση της Αφροδίτης
 Η γέννηση της Αφροδίτης Ανάδρομη Αφροδίτη Κάθε 18 μήνες η Αφροδίτη φαινομενικά για τους Γήινους παρατηρητές κινείται με ανάδρομη πορεία στον ουράνιο θόλο. Και κάθε 8 χρόνια επαναλαμβάνει αυτή την ανάδρομη
Η γέννηση της Αφροδίτης Ανάδρομη Αφροδίτη Κάθε 18 μήνες η Αφροδίτη φαινομενικά για τους Γήινους παρατηρητές κινείται με ανάδρομη πορεία στον ουράνιο θόλο. Και κάθε 8 χρόνια επαναλαμβάνει αυτή την ανάδρομη
< 1 για κάθε k N, τότε η σειρά a k συγκλίνει. +, τότε η η σειρά a k αποκλίνει.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 3: Σειρές πραγµατικών αριθµών Α Οµάδα. Εστω ( ) µια ακολουθία πραγµατικών αριθµών. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 3: Σειρές πραγµατικών αριθµών Α Οµάδα. Εστω ( ) µια ακολουθία πραγµατικών αριθµών. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε
Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση
 8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα. Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα. Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
Η έκθεση Πέλε - 7η Οκτωβρίου του Γεια σας!
 Η έκθεση Πέλε - 7η Οκτωβρίου του 2015 Γεια σας! * ο Kaypacha δείχνει στην οθόνη την εφαρμογή Solar System Scope (Πεδίο του Ηλιακού Συστήματος) για το πρώτο μισό της Έκθεσης Πέλε ( καλό είναι να βλέπει
Η έκθεση Πέλε - 7η Οκτωβρίου του 2015 Γεια σας! * ο Kaypacha δείχνει στην οθόνη την εφαρμογή Solar System Scope (Πεδίο του Ηλιακού Συστήματος) για το πρώτο μισό της Έκθεσης Πέλε ( καλό είναι να βλέπει
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον
 Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Λύσεις µε κατάλληλο σχολιασµό και παρατηρήσεις σε θέµατα από παλαιότερες πανελλαδικές εξετάσεις. Γενικές οδηγίες και παρατηρήσεις κατά την αντιµετώπιση
Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Λύσεις µε κατάλληλο σχολιασµό και παρατηρήσεις σε θέµατα από παλαιότερες πανελλαδικές εξετάσεις. Γενικές οδηγίες και παρατηρήσεις κατά την αντιµετώπιση
3. Η παρακάτω συνάρτηση παραγωγής παρουσιάζει φθίνουσες, σταθερές, ή αύξουσες οικονοµίες κλίµακας; παραγωγής παρουσιάζει σταθερές αποδόσεις κλίµακας.
 1. Μια επιχείρηση έχει συνάρτηση παραγωγής την f(k,l), όπου Κ είναι οι µονάδες κεφαλαίου και L είναι οι µονάδες εργασίας που χρησιµοποιεί. Αν ξέρουµε ότι το οριακό προϊόν της εργασίας είναι θετικό, αλλά
1. Μια επιχείρηση έχει συνάρτηση παραγωγής την f(k,l), όπου Κ είναι οι µονάδες κεφαλαίου και L είναι οι µονάδες εργασίας που χρησιµοποιεί. Αν ξέρουµε ότι το οριακό προϊόν της εργασίας είναι θετικό, αλλά
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 202 Μέρος 4. Θεωρητικά
Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Σχέσεις Ισοδυναµίας, ιαµερίσεις, και Πράξεις Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 202 Μέρος 4. Θεωρητικά
Η Έκθεση Πέλε 29 Ιουλίου, 2015
 Η Έκθεση Πέλε 29 Ιουλίου, 2015 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 29 Ιουλίου 2015. Πρόκειται για κάτι σαν «Δελτίο Αστρολογίας». Σήμερα, ο Ήλιος είναι σε σύνοδο με τον Ερμή
Η Έκθεση Πέλε 29 Ιουλίου, 2015 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 29 Ιουλίου 2015. Πρόκειται για κάτι σαν «Δελτίο Αστρολογίας». Σήμερα, ο Ήλιος είναι σε σύνοδο με τον Ερμή
Πέµπτο µέρος. Η συνέχεια από το προηγούµενο
 1 Πέµπτο µέρος Η συνέχεια από το προηγούµενο Στην αρχική αραβική περίοδο, τώρα, οι αστρολόγοι έµοιαζαν όντως να προσκολλώνται σ αυτήν τη διάκριση, αλλά σε κάποιο σηµείο στην πορεία, κατά το τέλος της αραβικής
1 Πέµπτο µέρος Η συνέχεια από το προηγούµενο Στην αρχική αραβική περίοδο, τώρα, οι αστρολόγοι έµοιαζαν όντως να προσκολλώνται σ αυτήν τη διάκριση, αλλά σε κάποιο σηµείο στην πορεία, κατά το τέλος της αραβικής
ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ΚΕΦΑΛΑΙΟ 1 ο Η ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΣΗΜΕΡΑ. 1.1 Εισαγωγή
 ΚΕΦΑΛΑΙΟ 1 ο Η ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΣΗΜΕΡΑ 1.1 Εισαγωγή Η Ευρωπαϊκή Ένωση διευρύνεται και αλλάζει. Τον Μάιο του 2004, δέκα νέες χώρες εντάχθηκαν στην Ευρωπαϊκή Ένωση. Η διεύρυνση αποτελεί µια ζωτικής σηµασίας
ΚΕΦΑΛΑΙΟ 1 ο Η ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΣΗΜΕΡΑ 1.1 Εισαγωγή Η Ευρωπαϊκή Ένωση διευρύνεται και αλλάζει. Τον Μάιο του 2004, δέκα νέες χώρες εντάχθηκαν στην Ευρωπαϊκή Ένωση. Η διεύρυνση αποτελεί µια ζωτικής σηµασίας
Η Έκθεση Πέλε - 29 Σεπτεμβρίου, Γεια σας!
 Η Έκθεση Πέλε - 29 Σεπτεμβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 29 Σεπτεμβρίου 2016. Ξέρω ότι είναι με μια μέρα καθυστέρηση και συνήθως κάνω αυτά τα πράγματα την
Η Έκθεση Πέλε - 29 Σεπτεμβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 29 Σεπτεμβρίου 2016. Ξέρω ότι είναι με μια μέρα καθυστέρηση και συνήθως κάνω αυτά τα πράγματα την
Μάθηµα ευτέρας 20 / 11 / 17
 90 Μάθηµα ευτέρας 20 / / 7 5) ιανυσµατικά διαγράµµατα στην Η.Μ.Κ. Κατά την µελέτη ηλεκτρικών δικτύων στην Η.Μ.Κ. χρησιµοποιούνται πολύ συχνά τα λεγόµενα διανυσµατικά διαγράµµατα. Οι στρεφόµενοι µε την
90 Μάθηµα ευτέρας 20 / / 7 5) ιανυσµατικά διαγράµµατα στην Η.Μ.Κ. Κατά την µελέτη ηλεκτρικών δικτύων στην Η.Μ.Κ. χρησιµοποιούνται πολύ συχνά τα λεγόµενα διανυσµατικά διαγράµµατα. Οι στρεφόµενοι µε την
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 29 Νοεμβρίου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 29 Νοεμβρίου, 2017 Γεια σας! Είμαι ο Kaypacha με την Έκθεση Πέλε για τις 29 Νοεμβρίου του 2017. * O Kaypacha μιλάει δείχνοντας στην οθόνη το Solar Fire Software. Σκέφτηκα
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 29 Νοεμβρίου, 2017 Γεια σας! Είμαι ο Kaypacha με την Έκθεση Πέλε για τις 29 Νοεμβρίου του 2017. * O Kaypacha μιλάει δείχνοντας στην οθόνη το Solar Fire Software. Σκέφτηκα
Σχολικός Σύµβουλος ΠΕ03
 Ασκήσεις Μαθηµατικών Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις
Ασκήσεις Μαθηµατικών Θετικής & Τεχνολογικής Κατεύθυνσης Γ Λυκείου ρ. Παναγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Στην εργασία αυτή ξεχωρίζουµε και µελετάµε µερικές περιπτώσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ 12) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ 3
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Άσκηση. ( µον.). Έστω z ο µιγαδικός αριθµός z i, µε, R. (α) ίνεται η εξίσωση: z
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Άσκηση. ( µον.). Έστω z ο µιγαδικός αριθµός z i, µε, R. (α) ίνεται η εξίσωση: z
α) Πως ερµηνεύεται η φράση: «µε γωνιακές συχνότητες που διαφέρουν πολύ λίγο»; γ) Να βρεθούν η γωνιακή συχνότητα ω, η συχνότητα f και η περίοδος Τ των
 Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
Κεφάλαιο 4. Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία
 Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018 Γεια σας, κάτοικοι της Γης! Είμαι ο Kaypacha με άλλη μια εβδομαδιαία Έκθεση Πέλε, για την 17η Ιανουαρίου 2018. Και φυσικά, -είμαι κάτω δίπλα στο
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018 Γεια σας, κάτοικοι της Γης! Είμαι ο Kaypacha με άλλη μια εβδομαδιαία Έκθεση Πέλε, για την 17η Ιανουαρίου 2018. Και φυσικά, -είμαι κάτω δίπλα στο
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΠΑΙ ΑΓΩΓΙΚΟ ΤΜΗΜΑ. Ε. ΜΑΡΑΣΛΕΙΟ Ι ΑΣΚΑΛΕΙΟ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΠΑΙ ΑΓΩΓΙΚΟ ΤΜΗΜΑ. Ε. ΜΑΡΑΣΛΕΙΟ Ι ΑΣΚΑΛΕΙΟ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΧΟΙΝΑΣ ΗΜΗΤΡΙΟΣ Β ΕΤΟΣ ΕΙ ΙΚΗ ΑΓΩΓΗ ΑΜ:022038 ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ: «Ι ΑΣΚΑΛΙΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΠΑΙ ΑΓΩΓΙΚΟ ΤΜΗΜΑ. Ε. ΜΑΡΑΣΛΕΙΟ Ι ΑΣΚΑΛΕΙΟ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΧΟΙΝΑΣ ΗΜΗΤΡΙΟΣ Β ΕΤΟΣ ΕΙ ΙΚΗ ΑΓΩΓΗ ΑΜ:022038 ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ: «Ι ΑΣΚΑΛΙΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Ιανουαρίου, 2018
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Ιανουαρίου, 2018 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, τι άλλο είναι καινούριο? (* γελώντας) για τις 10 Ιανουαρίου 2018. Πρέπει να πάρω μια
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Ιανουαρίου, 2018 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, τι άλλο είναι καινούριο? (* γελώντας) για τις 10 Ιανουαρίου 2018. Πρέπει να πάρω μια
Ενδέκατο µέρος. ... Συνέχεια από το προηγούµενο
 Ενδέκατο µέρος... Συνέχεια από το προηγούµενο Έτσι, ο κυβερνήτης του Kλήρου της Τύχης παίζει κι αυτός κάποιο ρόλο σ αυτήν τη ναυτική µεταφορά. Αυτή η τρίτη τεχνική, που συνδυάζεται µε τη µελέτη του Ωροσκόπου
Ενδέκατο µέρος... Συνέχεια από το προηγούµενο Έτσι, ο κυβερνήτης του Kλήρου της Τύχης παίζει κι αυτός κάποιο ρόλο σ αυτήν τη ναυτική µεταφορά. Αυτή η τρίτη τεχνική, που συνδυάζεται µε τη µελέτη του Ωροσκόπου
 Λύνοντας ασκήσεις µε αντίστροφες συναρτήσεις ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Εισαγωγή Η αντίστροφη συνάρτηση µιας αντιστρέψιµης συνάρτησης είναι
Λύνοντας ασκήσεις µε αντίστροφες συναρτήσεις ρ. Παναγιώτης Λ. Θεοδωρόπουλος πρώην Σχολικός Σύµβουλος ΠΕ03 e-mail@p-theodoropoulos.gr Εισαγωγή Η αντίστροφη συνάρτηση µιας αντιστρέψιµης συνάρτησης είναι
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 6 Σεπτεμβρίου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 6 Σεπτεμβρίου, 2017 Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 6 Σεπτεμβρίου του 2017. Είναι η Έκθεση της Μπανάνας, φίλοι μου (δείχνει τις μπανάνες
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 6 Σεπτεμβρίου, 2017 Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 6 Σεπτεμβρίου του 2017. Είναι η Έκθεση της Μπανάνας, φίλοι μου (δείχνει τις μπανάνες
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, εδώ στο Flamingo Beach, (Κόστα Ρίκα) στις 10 Μαΐου 2017! Το νιώθετε; Νιώθετε ότι
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, εδώ στο Flamingo Beach, (Κόστα Ρίκα) στις 10 Μαΐου 2017! Το νιώθετε; Νιώθετε ότι
Η Έκθεση Πέλε - 13 Απριλίου, Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software.
 Η Έκθεση Πέλε - 13 Απριλίου, 2016 Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software. * Είμαι o Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι στην πραγματικότητα για
Η Έκθεση Πέλε - 13 Απριλίου, 2016 Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software. * Είμαι o Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι στην πραγματικότητα για
Ιδιότητες των Ζωδίων και των Πλανητών Διέλευση Πλανητών σε Ζώδια και Οίκους Επίδραση Πλανητών & Ζωδίων στην Υγεία Ανάδρομοι Πλανήτες Ερωτική Συναστρία
 Ιδιότητες των Ζωδίων και των Πλανητών Διέλευση Πλανητών σε Ζώδια και Οίκους Επίδραση Πλανητών & Ζωδίων στην Υγεία Ανάδρομοι Πλανήτες Ερωτική Συναστρία 2007 by Takis Karagiannopoulos Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν
Ιδιότητες των Ζωδίων και των Πλανητών Διέλευση Πλανητών σε Ζώδια και Οίκους Επίδραση Πλανητών & Ζωδίων στην Υγεία Ανάδρομοι Πλανήτες Ερωτική Συναστρία 2007 by Takis Karagiannopoulos Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν
Η Έκθεση Πέλε για τις 4 Νοεμβρίου, Γεια σας! Καλημέρα!
 Η Έκθεση Πέλε για τις 4 Νοεμβρίου, 2015 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 4 Νοεμβρίου του 2015. Αστρολογία για την Ψυχή. Είναι μια άποψη για το τι συμβαίνει με
Η Έκθεση Πέλε για τις 4 Νοεμβρίου, 2015 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 4 Νοεμβρίου του 2015. Αστρολογία για την Ψυχή. Είναι μια άποψη για το τι συμβαίνει με
f (x) = l R, τότε f (x 0 ) = l. = lim (0) = lim f(x) = f(x) f(0) = xf (ξ x ). = l. Εστω ε > 0. Αφού lim f (x) = l R, υπάρχει δ > 0
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο 5: Παράγωγος Α Οµάδα. Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς (αιτιολογήστε πλήρως την απάντησή σας). (α) Αν η f είναι παραγωγίσιµη
όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 10: Η γραφική παράσταση της συνάρτησης f (x) = 1/x.
 3 Ορια συναρτήσεων 3. Εισαγωγικές έννοιες. Ας ϑεωρήσουµε την συνάρτηση f () = όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 0: Η γραφική παράσταση της συνάρτησης f () = /. ϕυσικό να αναζητήσουµε την
3 Ορια συναρτήσεων 3. Εισαγωγικές έννοιες. Ας ϑεωρήσουµε την συνάρτηση f () = όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 0: Η γραφική παράσταση της συνάρτησης f () = /. ϕυσικό να αναζητήσουµε την
Σηµειώσεις στις σειρές
 . ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
. ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ
 ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 22 Φεβρουαρίου του 2017.
 Η Έκθεση Πέλε 22 Φεβρουαρίου 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 22 Φεβρουαρίου του 2017. * O Kaypacha μοιράζεται την οθόνη του υπολογιστή του που τρέχει το λογισμικό
Η Έκθεση Πέλε 22 Φεβρουαρίου 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 22 Φεβρουαρίου του 2017. * O Kaypacha μοιράζεται την οθόνη του υπολογιστή του που τρέχει το λογισμικό
Αρµονική Ανάλυση. Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young. Απόστολος Γιαννόπουλος.
 Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ενότητα: Το ϑεώρηµα παρεµβολής του Riesz και η ανισότητα Hausdorff-Young Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Η Έκθεση Πέλε - 5 Οκτωβρίου, 2016
 Η Έκθεση Πέλε - 5 Οκτωβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Σήμερα, δεν ξέρω, απλά νιώθω σαν να θέλω να καθίσω βλέποντας τα σύννεφα. (*γέλια) Ο Άρης είναι σε τετράγωνο
Η Έκθεση Πέλε - 5 Οκτωβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Σήμερα, δεν ξέρω, απλά νιώθω σαν να θέλω να καθίσω βλέποντας τα σύννεφα. (*γέλια) Ο Άρης είναι σε τετράγωνο
Ρετσινάς Σωτήριος ΠΕ 1703 Ηλεκτρολόγων ΑΣΕΤΕΜ
 Ρετσινάς Σωτήριος ΠΕ 1703 Ηλεκτρολόγων ΑΣΕΤΕΜ Τι είναι η ερευνητική εργασία Η ερευνητική εργασία στο σχολείο είναι μια δυναμική διαδικασία, ανοιχτή στην αναζήτηση για την κατανόηση του πραγματικού κόσμου.
Ρετσινάς Σωτήριος ΠΕ 1703 Ηλεκτρολόγων ΑΣΕΤΕΜ Τι είναι η ερευνητική εργασία Η ερευνητική εργασία στο σχολείο είναι μια δυναμική διαδικασία, ανοιχτή στην αναζήτηση για την κατανόηση του πραγματικού κόσμου.
h(x, y) = card ({ 1 i n : x i y i
 Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
ΑΣΚΗΣΕΙΣ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Β ΛΥΚ. ΕΞΙΣΩΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Β ΛΥΚ. ΕΞΙΣΩΣΕΙΣ Λυγάτσικας Ζήνων Πειραµατικό Γενικό Λύκειο Βαρβακείου Σχολής 6 Ιανουαρίου 013 1 Ασκήσεις 1.1 Ασκήσεις Επανάληψης 1. είξτε ότι : ηµ x + 3συν y 5.. Να αποδείξτε ότι
ΑΣΚΗΣΕΙΣ ΤΡΙΓΩΝΟΜΕΤΡΙΑΣ Β ΛΥΚ. ΕΞΙΣΩΣΕΙΣ Λυγάτσικας Ζήνων Πειραµατικό Γενικό Λύκειο Βαρβακείου Σχολής 6 Ιανουαρίου 013 1 Ασκήσεις 1.1 Ασκήσεις Επανάληψης 1. είξτε ότι : ηµ x + 3συν y 5.. Να αποδείξτε ότι
Πώς και γιατί μετακινούμαστε;
 Πώς και γιατί μετακινούμαστε; Διδακτική πρόταση 1: Συνοπτικό πλαίσιο μετακίνησης και εγκατάστασης Ερωτήματα-κλειδιά Γιατί και πώς μετακινούμαστε από τα πολύ παλιά χρόνια μέχρι σήμερα; Πού μένουμε από τα
Πώς και γιατί μετακινούμαστε; Διδακτική πρόταση 1: Συνοπτικό πλαίσιο μετακίνησης και εγκατάστασης Ερωτήματα-κλειδιά Γιατί και πώς μετακινούμαστε από τα πολύ παλιά χρόνια μέχρι σήμερα; Πού μένουμε από τα
Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών
 1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
1.1.3 t. t = t2 - t1 1.1.4 x2 - x1. x = x2 x1 . . 1
 1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
Εισαγωγή στην Τοπολογία
 Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
ΠΟΛΥΩΝΥΜΙΚΕΣ - ΡΗΤΕΣ ΑΝΙΣΩΣΕΙΣ P x = x+ 2 4 x x 3x x x x 3x
 o ΛΥΚΕΙΟ ΠΕΤΡΟΥΠΟΛΗΣ ΠΟΛΥΩΝΥΜΙΚΕΣ - Α ΠΡΟΣΗΜΟ ΠΟΛΥΩΝΥΜΟΥ Μέχρι τώρα ξέρουµε να βρίσκουµε το πρόσηµο ενός πολυωνύµου βαθµού ή δεύτερου βαθµού Για να βρούµε το πρόσηµο ενός πολυωνύµου f πρώτου f βαθµού µεγαλύτερου
o ΛΥΚΕΙΟ ΠΕΤΡΟΥΠΟΛΗΣ ΠΟΛΥΩΝΥΜΙΚΕΣ - Α ΠΡΟΣΗΜΟ ΠΟΛΥΩΝΥΜΟΥ Μέχρι τώρα ξέρουµε να βρίσκουµε το πρόσηµο ενός πολυωνύµου βαθµού ή δεύτερου βαθµού Για να βρούµε το πρόσηµο ενός πολυωνύµου f πρώτου f βαθµού µεγαλύτερου
3 Αναδροµή και Επαγωγή
 3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
4.3 Παραδείγµατα στην συνέχεια συναρτήσεων
 5. Η συνάρτηση είναι συνεχής στο R. 6. Η συνάρτηση sin είναι συνεχής στο R. 7. Η συνάρτηση cos είναι συνεχής στο R. 8. Η συνάρτηση tan είναι συνεχής σε κάθε R µε k π + π/2, k Z. 9. Η συνάρτηση cotan είναι
5. Η συνάρτηση είναι συνεχής στο R. 6. Η συνάρτηση sin είναι συνεχής στο R. 7. Η συνάρτηση cos είναι συνεχής στο R. 8. Η συνάρτηση tan είναι συνεχής σε κάθε R µε k π + π/2, k Z. 9. Η συνάρτηση cotan είναι
Α. ΠΡΟΣΘΕΣΗ - ΑΦΑΙΡΕΣΗ ΡΗΤΩΝ ΠΑΡΑΣΤΑΣΕΩΝ ΜΕ ΚΟΙΝΟ ΠΑΡΟΝΟΜΑΣΤΗ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποενότητα.: Πράξεις Ρητών Παραστάσεων. Θεµατικές Ενότητες:. Πρόσθεση - Αφαίρεση Ρητών Παραστάσεων µε Κοινό Παρονοµαστή.. Πρόσθεση - Αφαίρεση Ρητών Παραστάσεων
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποενότητα.: Πράξεις Ρητών Παραστάσεων. Θεµατικές Ενότητες:. Πρόσθεση - Αφαίρεση Ρητών Παραστάσεων µε Κοινό Παρονοµαστή.. Πρόσθεση - Αφαίρεση Ρητών Παραστάσεων
Κεφάλαιο 2ο (α) Αµιγείς Στρατηγικές (β) Μεικτές Στρατηγικές (α) Αµιγείς Στρατηγικές. Επαναλαµβάνουµε:
 Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 7
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 7 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 7 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Η έκθεση Πέλε 12Mαΐου 2015
 Η έκθεση Πέλε 12Mαΐου 2015 Hola ~ Μπουένος Dias ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Αρκετά με την καταπάτηση άλλων ιδιοκτησιών, αυτή τη φορά το κάνω στην αυλή μου. (* Γέλια) Η περασμένη
Η έκθεση Πέλε 12Mαΐου 2015 Hola ~ Μπουένος Dias ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Αρκετά με την καταπάτηση άλλων ιδιοκτησιών, αυτή τη φορά το κάνω στην αυλή μου. (* Γέλια) Η περασμένη
επ. Κωνσταντίνος Π. Χρήστου
 1 2 3 1 2 2 0 3 3 4 6 5 10 6 11 7 7 8 6 9 3 10 2 4 Εάν έχουµε οµαδοποιηµένη µεταβλητή τότε είναι το σηµείο τοµής των ευθυγράµµων τµηµάτων τα οποία ορίζονται από α) ΑΒ, όπου Α το άνω δεξί άκρο της κλάσης
1 2 3 1 2 2 0 3 3 4 6 5 10 6 11 7 7 8 6 9 3 10 2 4 Εάν έχουµε οµαδοποιηµένη µεταβλητή τότε είναι το σηµείο τοµής των ευθυγράµµων τµηµάτων τα οποία ορίζονται από α) ΑΒ, όπου Α το άνω δεξί άκρο της κλάσης
ΜΑΘΗΜΑ ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ xο
 ΜΑΘΗΜΑ 9.6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ ο R Θεωρία Σχόλια - Ασκήσεις ΘΕΩΡΙΑ. Ορισµός f ( ) ο σηµαίνει ότι οι τιµές f ( ) της συνάρτησης f γίνονται µεγαλύτερες από κάθε θετικό αριθµό Μ, καθώς.. Ορισµός f ( )
ΜΑΘΗΜΑ 9.6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ ο R Θεωρία Σχόλια - Ασκήσεις ΘΕΩΡΙΑ. Ορισµός f ( ) ο σηµαίνει ότι οι τιµές f ( ) της συνάρτησης f γίνονται µεγαλύτερες από κάθε θετικό αριθµό Μ, καθώς.. Ορισµός f ( )
ΠΡΟΣΟΧΗ: Διαβάστε προσεκτικά τις κάτωθι Οδηγίες για την συμμετοχή σας στην 1 η φάση «Εύδοξος»
 ΠΡΟΣΟΧΗ: Διαβάστε προσεκτικά τις κάτωθι Οδηγίες για την συμμετοχή σας στην 1 η φάση «Εύδοξος» Για να θεωρηθεί έγκυρη η συμμετοχή σας στην 1 η φάση, θα πρέπει απαραίτητα να έχετε συμπληρώσει τον πίνακα
ΠΡΟΣΟΧΗ: Διαβάστε προσεκτικά τις κάτωθι Οδηγίες για την συμμετοχή σας στην 1 η φάση «Εύδοξος» Για να θεωρηθεί έγκυρη η συμμετοχή σας στην 1 η φάση, θα πρέπει απαραίτητα να έχετε συμπληρώσει τον πίνακα
