ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ. Διπλωματική Εργασία ΜΗΧΑΝΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΟΣΤΙΚΗΣ ΑΝΑΓΕΝΝΗΣΗΣ ΖΙΑΚΑΣ ΠΑΝΑΓΙΩΤΗΣ
|
|
|
- Σαπφειρη Ζέρβας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Διπλωματική Εργασία ΜΗΧΑΝΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΟΣΤΙΚΗΣ ΑΝΑΓΕΝΝΗΣΗΣ ΖΙΑΚΑΣ ΠΑΝΑΓΙΩΤΗΣ
2 Ζιάκας Παναγιώτης Η έγκριση της διπλωματικής εργασίας από το Τμήμα Μηχανολόγων Μηχανικών της Πολυτεχνικής Σχολής του Πανεπιστημίου Θεσσαλίας δεν υποδηλώνει αποδοχή των απόψεων του συγγραφέα (Ν. 5343/32 αρ. 202 παρ. 2).
3 3 Εγκρίθηκε από τα Μέλη της Τριμελούς Εξεταστικής Επιτροπής: Πρώτος Εξεταστής (Επιβλέπων) Δρ. Λεωνίδας Σπύρου Ερευνητής Δ, Τομέας Μηχανοτρονικής, Ινστιτούτο Έρευνας και Τεχνολογίας Θεσσαλίας/ΕΚΕΤΑ Δεύτερος Εξεταστής (Συν-Επιβλέπων) Δρ. Νικόλαος Αράβας Καθηγητής, Τμήμα Μηχανολόγων Μηχανικών, Πανεπιστήμιο Θεσσαλίας Τρίτος Εξεταστής Δρ. Αλέξης Κερμανίδης Επίκουρος Καθηγητής, Τμήμα Μηχανολόγων Μηχανικών, Πανεπιστήμιο Θεσσαλίας Τέταρτος Εξεταστής Δρ. Μιχάλης Αγόρας Λέκτορας, Τμήμα Μηχανολόγων Μηχανικών, Πανεπιστήμιο Θεσσαλίας
4 4 Ευχαριστίες Αρχικά θα ήθελα να ευχαριστήσω τον κ.λεωνίδα Σπύρου για την καθοδήγησή του κατά τη διάρκεια της εργασίας. Επίσης οφείλω ευχαριστίες στα μέλη της εξεταστικής επιτροπής της διπλωματικής εργασίας μου κ. Νικόλαο Αράβα, κ.αλέξη Κερμανίδη και κ.μιχάλη Αγόρα για την προσεκτική ανάγνωση της εργασίας μου. Είμαι ευγνώμων στους συναδέλφους μου για την πολύτιμη βοήθειά τους. Τέλος ευχαριστώ θερμά την οικογένειά μου και τους συγγενείς μου για την υποστήριξή τους όλα αυτά τα χρόνια. Παναγιώτης Ζιάκας
5 5 ΜΗΧΑΝΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΟΣΤΙΚΗΣ ΑΝΑΓΕΝΝΗΣΗΣ ΖΙΑΚΑΣ ΠΑΝΑΓΙΩΤΗΣ Περίληψη Η μελέτη της οστεϊκής αναγέννησης είναι ένα πολύ βαθύ και σημαντικό κομμάτι της εμβιομηχανικής. Ερευνά εκτός των άλλων τους παράγοντες που επιδρούν στην ανάπλαση του οστού μετά από τραυματιμό του, ώστε να επιταχυνθεί κατά το δυνατόν το στάδιο της ανάρρωσης. Στην παρούσα εργασία προσομοιώνεται η οστεογένεση με τη βοήθεια μοντέλων που έχουν αναπτυχθεί στη βιβλιογραφία και εξετάζεται η επίδραση ορισμένων παραμέτρων της διαδικασίας.
6 6 Περιεχόμενα Κεφάλαιο 1 Θεωρητικό Μέρος Ο Ανθρώπινος Σκελετός Κατηγοριοποίηση οστών Σύνθεση οστού Μορφές οστίτη ιστού Δομή οστίτη ιστού Μικροσκοπική κατασκευή χόνδρου Σύνθεση χόνδρου Αύξηση χόνδρου Είδη χόνδρου Μακροσκοπική κατασκευή των οστών Η διαδικασία της οστεϊκής αναγέννησης Κεφάλαιο 2 Βιβλιογραφική Ανασκόπηση Κεφάλαιο 3 Περιγραφή Πλαισίου Ilizarov Πειραματική διάταξη Μοντέλο πεπερασμένων στοιχείων Κινηματικοί Περιορισμοί Υλικά πλαισίου Κεφάλαιο 4 Μοντέλο οστικής αναγέννησης Μοντελοποίηση πόρου Υλικό πόρου Αλγόριθμος Κεφάλαιο 5 Υπολογιστικές δοκιμές Αποτελέσματα Δοκιμή ελέγχου Επίδραση παραμέτρων σε πραγματικό σενάριο φόρτισης Εύρεση «οριακών» δυνάμεων και εξέταση παραμέτρων Επίδραση διαμέτρου δακτυλίων Εξάρτηση του μέτρου ελαστικότητας με την ακτίνα Παράρτημα Α Παράρτημα Β Παράρτημα Γ Βιβλιογραφία Κατάλογος Eικόνων... 83
7 7 Κατάλογος Πινάκων... 87
8 8
9 9 Κεφάλαιο 1 Θεωρητικό Μέρος 1.1. Ο Ανθρώπινος Σκελετός Ο σκελετός ενός ενήλικα ανθρώπου αποτελείται από 206 οστά. Διακρίνεται σε: σκελετό της κεφαλής (κρανίο και πρόσωπο) σκελετό του κορμού (θώρακας και σπονδυλική στήλη) σκελετό των άκρων (άνω άκρα δηλαδή χέρια, ωμοπλάτες, κλείδες και κάτω άκρα, δηλαδή πόδια, λεκάνη). Εικόνα 1: Ο σκελετός ενός ενήλικα (πηγή: Οι λειτουργίες που επιτελεί ο ανθρώπινος σκελετός διακρίνονται σε: 1. Στήριξη: Το σκελετικό σύστημα παρέχει τη δομική στήριξη των οργάνων του σώματος.
10 10 2. Αποθήκευση ιχνοστοιχείων: Τα κόκκαλα διατηρούν ένα μεγάλο απόθεμα ιόντων ασβεστίου, φωσφόρου και μαγνησίου. 3. Παραγωγή κυττάρων αίματος: Το εσωτερικό ορισμένων οστών περιέχει ερυθρό μυελό, όπου παράγονται τα κύτταρα του αίματος (ερυθρά αιμοσφαίρια,ορισμένα λεμφοκύτταρα, λευκά αιμοσφαίρια και αιμοπετάλια) 4. Προστασία: Ο σκελετός προστατεύει τους μαλακούς ιστούς και τα ευπαθή όργανα 5. Μηχανική βάση της κίνησης: Η διάρθρωση των οστών δημιουργεί μοχλούς που κατευθύνουν τις δυνάμεις που παράγονται από τους μύες Κατηγοριοποίηση οστών Με κριτήριο το σχήμα τους τα οστά διακρίνονται σε: Επιμήκη οστά, στα οποία το μήκος υπερέχει του πλάτους. Όλα τα κόκκαλα των άκρων εκτός του καρπού και του αγκώνα είναι μακριά οστά. Βραχέα οστά, έχουν κυβικό σχήμα και εμφανίζονται στους καρπούς και στους αστραγάλους. Πλατιά οστά, είναι λεπτά πλατιά και συνήθως καμπύλα. Τέτοια οστά περιλαμβάνονται στο κρανίο, τα πλευρά και το στέρνο. Ακανόνιστα οστά, δεν έχουν συγκεκριμένο σχήμα. Εικόνα 2: Κατάταξη οστών (πηγή Σύνθεση οστού Τα οστά αποτελούνται από οργανικό και ανόργανο μέρος. Το οργανικό μέρος συνιστά το 35% περίπου και το 65% είναι τα ανόργανα συστατικά.το οργανικό μέρος περιλαμβάνει: Τα κύτταρα του οστίτη ιστού Τα κολλαγόνα ινίδια (πρωτεΐνες με μεγάλη περιεκτικότητα σε γλυκίνη, προζίνη, οξυπροζίνη) Τη θεμέλια ουσία (πρωτεΐνες: κυρίως πολυσακχαρίδες). Τα κολλαγόνα ινίδια και η θεμέλια ουσία συνιστούν τη μεσοκυττάρια ουσία του οστίτη ιστού. Τα κύτταρα του οστίτη ιστού χωρίζονται σε οστεοβλάστες, οστεοκλάστες, κύτταρα υπεύθυνα για την αποδόμηση των οστών, οστεοκύτταρα, είναι οστεοβλάστες που εγκλείσθησαν μέσα στην οστέινη ουσία. Το οστό συντίθεται από τους οστεοβλάστες, συντηρείται από τα οστεοκύτταρα και αποδομείται από τους οστεοκλάστες.
11 11 Οι οστεοβλάστες αποτελούν τα οστεοπαραγωγικά κύτταρα που παράγουν και τη μεσοκυττάρια ουσία. Η τελευταία μετά την οστεοποίησή της περικλείει τους οστεοβλάστες που μετατρέπονται στη φάση αυτή σε οστεοκύτταρα. Τα οστεοκύτταρα δημιουργούν αποφυάδες που φέρονται μέσα στα οστικά σωληνάρια και έτσι επικοινωνούν μεταξύ τους. Τα κύτταρα αυτά συμμετέχουν στο μεταβολισμό και την ομοιόσταση του ασβεστίου. Οι οστεοκλάστες είναι πολυπύρηνα γιγαντοκύτταρα (με 2-60 πυρήνες) ειδικευμένα στην απορρόφηση οστίτη ιστού. Βρίσκονται σε θέσεις, όπου γίνεται αποδόμηση του οστίτη ιστού και ενεργοποιούνται ύστερα από δράση της παραθορμόνης. Τα κολλαγόνα ινίδια παράγονται από τους οστεοβλάστες και έχουν διαφορετική σύνθεση από τα ινίδια άλλων ιστών, γεγονός που κάνει δυνατή την εναπόθεση σε αυτά αλάτων ασβεστίου. Η µεσοκυττάρια ουσία του οστίτη ιστού αποτελείται από οργανική και ανόργανη φάση. Η οργανική φάση ή οστεοειδές αποτελείται από θεµέλια ουσία και κολλαγόνες ίνες οι οποίες σχηµατίζουν δεσµίδες από οστέινη ουσία, ενώ η ανόργανη κυρίως από άλατα κυρίως ασβεστίου. Τα άλατα προσδίδουν σκληρότητα και ανθεκτικότητα στα οστά.τα ινίδια κολλαγόνου τους προσδίδουν ελαστικότητα και ενισχύουν την αντοχή του οστού Μορφές οστίτη ιστού Ανάλογα με το τρόπο που διατάσσεται το οστεοειδές, το οστό χαρακτηρίζεται ως: δικτυωτό πεταλιώδες Στον υγιή ενήλικα, ουσιαστικά ολόκληρος ο οστίτης ιστός είναι στη πεταλιώδη μορφή, στην οποία το κολλαγόνο είναι διατεταγμένο σε πέταλα (λαμελοειδής μορφή) και έτσι έχει μεγαλύτερη ισχύ. Το δικτυωτό οστό αποτελεί το πρώτο είδος οστίτη ιστού που φτιάχνει ο οργανισμός είτε κατά την εμβρυική ανάπτυξη, είτε στην αποκατάσταση καταγμάτων. Χαρακτηρίζεται από άτακτες ίνες κολλαγόνου και έχει μειωμένη μηχανική ισχύ. Αντικαθίσταται σταδιακά από πεταλιώδες. Εικόνα 3: Δικτυωτή και Πεταλιώδης μορφή (πηγή:
12 Δομή οστίτη ιστού Ο οστίτης ιστός εμφανίζεται με δύο δομές: Τον συμπαγή ή φλοιώδη οστίτη ιστό (80% περίπου του σκελετού) Τον σπογγώδη ή δοκιδωτό οστίτη ιστό (20% περίπου του σκελετού) Εικόνα 4: Συμπαγής και Σπογγώδης οστίτης ιστός (πηγή: και Στον συµπαγή οστίτη ιστό η βασική του ουσία είναι ιδιαίτερα πυκνή και οι οστικές του δοκίδες έχουν τέτοια στενή επαφή µεταξύ τους, ώστε να σχηµατίζουν ένα οστό παχύ, οµοιογενές και στέρεο. Τα οστεοκύτταρα μαζί με τη μεσοκυττάρια ουσία διατάσσονται σε ομόκεντρα στρώματα γύρω από έναν αγωγό (σωλήνας του Havers) σχηματίζοντας έτσι μια μονάδα με κυλινδρικό σχήμα, τον οστεώνα ή σύστημα του Havers. Στους σωλήνες του Havers περιέχονται αιμοφόρα αγγεία, για τη θρέψη του οστού, και νεύρα. Ο πεταλιώδης συµπαγής οστίτης ιστός είναι ο κανονικός ή ώριµος ιστός. Σε περίπτωση που ο οργανιςµός βιάζεται να εναποθέσει νέο οστίτη ιστό (όπως π.χ. στον πώρο ενός κατάγµατος) ο νεοσχηµατιςµένος συµπαγής ιστός δεν έχει την πεταλιώδη ώριµη υφή, αλλά παρουσιάζεται άµορφος και είναι µηχανικά κατώτερος. Ο άµορφος οστίτης ιστός, όταν επικρατήσουν φυσιολογικές συνθήκες, θα αντικατασταθεί από πεταλιώδη ιστό. Ο συµπαγής ιστός παρουσιάζει τριών ειδών επιφάνειες: την περιοστική, η οποία χωρίζει την εξωτερική επιφάνεια του οστού από τα όργανα που το περιβάλλουν και η οποία καλύπτεται από το περιόστεο, την ενδοστική, που χωρίζει τον οστίτη ιστό από το περιεχόµενο του αυλού του µακρού οστού, το οποίο συνήθως αποτελείται από λίπος και ερυθρό µυελό, και τέλος, τις επιφάνειες των πόρων του HAVERS, οι οποίες βρίσκονται µέσα στο φλοιό του οστού. Εικόνα 5: Εσωτερικό του συμπαγούς οστίτη ιστού (πηγη:
13 13 Ο σπογγώδης οστίτης ιστός είναι λιγότερο πυκνός και εποµένως πιο ελαφρύς. εν έχει σωλήνες του HAVERS. Οι οστικές δοκίδες είναι τοποθετηµένες κατά τέτοιο τρόπο, ώστε µεταξύ τους σχηµατίζονται κοιλότητες, στο εσωτερικό των οποίων υπάρχει ο ερυθρός µυελός, ο οποίος σχηµατίζει τα ερυθρά αιµοσφαίρια του αίµατος. Η µορφή του σπογγώδη οστίτη ιστού θυµίζει σπόγγο και από αυτό ακριβώς παίρνει και το όνοµά του. Οι οστικές του δοκίδες έχουν µια συγκεκριµένη διάταξη, είναι δηλαδή προσανατολιςµένες έτσι, ώστε να δέχονται το βάρος και τις µηχανικές πιέσεις κατά τον καλύτερο τρόπο και είναι διατεταγµένες προς διάφορες κατευθύνσεις ανάλογα µε τις µηχανικές ανάγκες κάθε οστού Μικροσκοπική κατασκευή χόνδρου Σύνθεση χόνδρου Ο χόνδρος είναι ένας συμπαγής αλλά εύκαμπτος συνδετικός ιστός, που συμβάλλει στην απορρόφηση κραδασμών και στην εξασφάλιση ολισθηρής επιφάνειας για τις αρθρώσεις. Αποτελείται από: κύτταρα μεσοκυττάρια θεμέλια ουσία Τα κύτταρα του χόνδρου χωρίζονται σε χονδροβλάστες και χονδροκύτταρα. Οι χονδροβλάστες είναι τα πρόδρομα κύτταρα του χόνδρου, που διαφοροποιούνται σε χονδροκύτταρα. Συνθέτουν την εξωκυττάρια θεμέλια ουσία. Τα χονδροκύτταρα προέρχονται από τους χονδροβλάστες και συνθέτουν και συντηρούν την εξωκυττάρια θεμέλια ουσία. Το περιχόνδριο είναι συνδετικός ιστός που περιβάλλει τον χόνδρο και περιέχει αγγεία και νεύρα για τη θρέψη του χόνδρου καθώς και χονδροβλάστες, με δυνατότητα σχηματισμού νέου χόνδρου. (α) Εικόνα 6: (α) Χονδροβλάστες (β)χονδροκύτταρα (πηγή: (β)
14 Αύξηση χόνδρου Η αύξηση του χόνδρου γίνεται με δύο διεργασίες : την αποθετική αύξηση, διαφοροποίηση ινοβλαστών που βρίσκονται στο περιχόνδριο σε χονδροβλάστες τη διάμεση αύξηση, που προκύπτει από μιτωτικές διαιρέσεις των προυπαρχόντων χονδροβλαστών Είδη χόνδρου Υαλοειδής χόνδρος Ελαστικός χόνδρος Ινώδης χόνδρος Οι διαφορές τους οφείλονται στο είδος και στην αναλογία των συστατικών της εξωκυττάριας ουσίας. Ο υαλοειδής χόνδρος στο έμβρυο σχηματίζει ένα προσωρινό σκελετο, ο οποίος αντικαθίσταται από οστίτη ιστό κατά τη διάρκεια της ενδοχόνδριας οστεοποίησης. Λίγο μετά τη γέννηση και μέχρι την εφηβεία, ο υαλοειδής χόνδρος αποτελεί ιδανικό συστατικό των επιφυσιακών δίσκων ανάπτυξης οι οποίοι ρυθμίζουν την ανάπτυξη και το σχηματισμό των μακρών οστών. Επιπλέον, ο υαλοειδής χόνδρος περιβάλλει τις αρθρικές επιφάνειες των αρθρώσεων όπου λειτουργεί ως ένας αυτολειαντικός απορροφητήρας δονήσεων με ιδιότητες χαμηλής τριβής. Ο υαλοειδής χόνδρος παρέχει επίσης ημιάκαμπτη υποστήριξη στα τοιχώματα μερικών αεραγωγών του αναπνευστικού συστήματος.ο κατεστραμμένος υαλοειδής χόνδρος δεν μπορεί να επιδιορθωθεί, επειδή στον ενήλικα τα κύτταρά του, τα χονδροκύτταρα δεν εμφανίζουν μιτώσεις (διαδικασία διχoτόμησης του κυτταρικού πυρήνα στα ευκαρυωτικά κύτταρα). Ο ελαστικός χόνδρος παρατηρείται στο πτερύγιο του ωτός, στο τοίχωμα του έξω ακουστικού πόρου, στην επιγλωτίδα, σε μέρη των λαρυγγικών χόνδρων και στα τοιχώματα της ευσταχιανής σάλπιγγας. Η ιστολογική δομή του ελαστικού χόνδρου είναι πορόμοια με εκείνη του υαλοειδούς χόνδρου, αλλά πάντως η ελαστικότητα του προέρχεται από την παρουσία πολυάριθμων δεσμίδων διακλαδιζόμενων ελαστικών ινών μέσα στη χόνδρινη θεμέλια ουσία. Αυτό το δίκτυο των ελαστικών ινών είναι ιδιαίτερα πυκνό στην περιοχή γύρω από τα χονδροκύτταρα. Επίσης το κολλαγόνο αποτελεί το μείζον συστατικό της χόνδρινης θεμέλιας ουσίας και συνιστά τον κυτταρικό όγκο του περιχόνδριου, αναμιγμένο με μερικές ελαστικές ίνες. Η ανάπτυξη του ελαστικού χόνδρου πραγματοποιείται τόσο με διάμεση όσο και με αποθετική αύξηση κατά τον ίδιο τρόπο όπως και στον υαλοειδή χόνδρο. Ο ινώδης χόνδρος αποτελείται από εναλλασόμενες στιβάδες υαλοειδούς χόνδρινης θεμέλιας ουσίας και παχιές στιβάδες πυκνών κολλαγόνων ινών προσανατολισμένες προς τη κατεύθυνση των λειτουργικών καταπονήσεων. Προσκολλά το οστό στον τένοντα και επειδή έχει την ικανότητα να κατανέμει το φορτίο, βρίσκεται στους μηνίσκους των αρθρώσεων και στους μεσοσπονδύλιους δίσκους. Πυκνός ινώδης συνδετικός ιστός αντικαθιστά τον κατεστραμένο ινώδη χόνδρο.
15 15 (α) (β) (γ) Εικόνα 7: (α) Στον υαλοειδή χόνδρο, διακρίνονται οστεοβλάστες [Ο] που συχνά σχηματίζουν ομάδες και προέρχονται από τα αρχέγονα κύτταρα που βρίσκονται στο περιχόνδριο [Π] (β) Οι χρώσεις αργύρου κάνουν ορατές τις ελαστικές ίνες του ελαστικού χόνδρου (γ) Στον ινώδη χόνδρο είναι ορατές οι ίνες κολλαγόνου [Κ] (πηγή: (δ)αρθρωση γόνατος (πηγή: (δ) 1.4. Μακροσκοπική κατασκευή των οστών Τα επιμήκη οστά έχουν δύο άκρα που λέγονται επιφύσεις, ενώ το μεταξύ τους κυλινδρικό τμήμα είναι η διάφυση. Μία επιμήκης τομή σε ένα μακρύ οστό αποκαλύπτει ότι στο εσωτερικό του, κατά μήκος της διάφυσης, υπάρχει μία κοιλότητα, ο μυελώδης αυλός. Μέσα στην κοιλότητα αυτή υπάρχει ο μυελός των οστών. Η διάφυση επενδύεται, τόσο στην εξωτερική όσο και στην εσωτερική της επιφάνεια, με πυκνό συνδετικό ιστό, που ονομάζεται περιόστεο και ενδόστεο αντίστοιχα. Το περιόστεο και το ενδόστεο περιέχουν μεγάλο αριθμό οστεοβλαστών, που παίζουν ρόλο στην κατά πάχος αύξηση του οστού και στην αναγέννησή του στην περίπτωση που σπάσει (κάταγμα). Το περιόστεο, που έχει πολλά αγγεία και νεύρα, χρησιμεύει ακόμα για τη θρέψη του οστού, καθώς και για την πρόσφυση μυών και συνδέσμων. Η αποκόλλησή του σε μεγάλη έκταση προκαλεί νέκρωση του οστού. Από έξω προς τα μέσα, η διάφυση ενός μακρού οστού αποτελείται από το περιόστεο, συμπαγή οστίτη ιστό, και από το μυελώδη αυλό, που επενδύεται με ενδόστεο. Οι επιφύσεις Εικόνα 8: Δομή ενός μακρού οστού (πηγή:
16 16 του αποτελούνται εξωτερικά από ένα λεπτό στρώμα συμπαγούς οστίτη ιστού και εσωτερικά από σπογγώδη οστίτη ιστό. Οι επιφύσεις δεν περιβάλλονται από περιόστεο αλλά από ένα στρώμα χόνδρου, τον αρθρικό χόνδρο. Τα βραχέα οστά καλύπτονται από περιόστεο και έχουν κεντρικό τμήμα με σπογγώδη οστίτη ιστό, που περιβάλλεται από συμπαγή οστίτη ιστό. Τα πλατιά οστά καλύπτονται από περιόστεο και αποτελούνται από δύο πλάκες συμπαγούς οστίτη ιστού, μεταξύ των οποίων υπάρχει σπογγώδης ιστός Η διαδικασία της οστεϊκής αναγέννησης Η οστεϊκή αναγέννηση είναι η διαδικασία κατά την οποία το οστό επανακτά τη μορφή και τις ιδιότητές του μετά από οποιοδήποτε περιστατικό τραυματισμού, όπως ένα κάταγμα ή μια τοποθέτηση εμφυτεύματος. Η αναγεννητική απόκριση χωρίζεται σε πρωτογενή και δευτερογενή [1]. Η πρωτογενής αναγέννηση προϋποθέτει ιδανικές συνθήκες όπως απόλυτη μηχανική σταθερότητα και απουσία μικρορογμών και περιλαμβάνει μια ευθεία ανάπλαση του οστού χωρίς την παρουσία φλεγμονής και δημιουργίας χόνδρου. Η δευτερογενής αναγέννηση είναι η συνηθέστερη, πραγματοποιείται όταν οι ιδανικές συνθήκες απουσιάζουν, χαρακτηρίζεται από το σχηματισμό χόνδρου και χωρίζεται σε δύο είδη: ενδομεμβρανώδης οστεοποίηση ενδοχόνδρια οστεοποίηση Κατά την ενδομεμβρανώδη οστεοποίηση το οστό αναπτύσσεται από μια μεμβράνη συνδετικού ιστού μεσεγχυματικών κυττάρων. Τα «μεσεγχυματικά πολυδύναμα προγονικά κύτταρα» είναι πολυδύναμα μη-αιμοποιητικά κύτταρα, τα οποία έχουν τη δυνατότητα να διαφοροποιούνται σε άλλους τύπους κυττάρων όπως οστεοκύτταρα, χονδροκύτταρα και λιποκύτταρα. Αυτά αφού διαφοροποιηθούν σε οστεοβλάστες εκκρίνουν οστεοειδές στη μεμβράνη. Με αυτόν τον τρόπο καθίσταται δυνατός ο σχηματισμός σπογγόδους και συμπαγούς ιστού. Στη συνέχεια σχηματίζεται το περιόστεο και ο ερυθρός μυελός. Στην ενδοχόνδρια οστεοποίηση εμπλέκονται τόσο οστεοκύτταρα όσο και χονδροκύτταρα. Το οστό δημιουργείται από προσχηματισμένο υαλοειδή χόνδρο, με εναπόθεση οστικής θεμέλιας ουσίας σε προϋπάρχουσα θεμέλια ουσία χόνδρου. Συγκεκριμένα από τα πρωτογενή κέντρα οστεοποίησης ο χόνδρος αρχίζει να ασβεστοποιείται και σχηματίζεται το οστεοειδές. Γύρω από τη διάφυση σχηματίζεται το περιόστεο από οστεοβλάστες που βρίσκονται στην περιοχή. Στη συνέχεια στο εσωτερικό της διάφυσης αναπτύσσεται δοκιδωτός οστίτης ιστός που αποδομείται εν μέρη από τους οστεοκλάστες για να σχηματιστεί η ενδομυελική κοιλότητα. Το περιχόνδριο με τη μορφή συμπαγούς οστίτη ιστού προσφέρει σταθερότητα καθώς ο χόνδρος σε άλλες περιοχές συνεχίζει να αυξάνεται.
17 17 Η οστεϊκή δευτερογενής αναγέννηση διακρίνεται σε τέσσερα στάδια: φλεγμονή δημιουργία μαλακού χόνδρου δημιουργία δικτυωτού οστού δημιουργία πεταλιώδους οστού και ανάπλαση Παρά το γεγονός ότι τα ανωτέρω στάδια έχουν διακριτά χαρακτηριστικά η μετάβαση από τον ένα στο άλλο είναι απρόσκοπτη. Φλεγμονή Μετά την κάκωση, η διαδικασία της φλεγμονής ξεκινά άμεσα και διαρκεί μέχρι να αρχίσει η δημιουργία ινώδους ιστού, χόνδρου και οστού (1 έως 7 ημέρες μετά τον τραυματισμό). Το οστό διαθέτει ένα σύστημα καναλιών αιμοφόρων αγγείων στη δομή του και όταν προκύπτει το κάταγμα υπάρχει μια μαζική διακοπή αυτών των αγγείων με συνέπεια την άμεση αιμάτωση του σημείου. Αυτό προκαλεί πρήξιμο και μελάνιασμα. Η κατάσταση αυτή είναι γνωστή ως αιμάτωμα (Haematoma) δηλαδή εσωτερική αιμορραγία. Εικόνα 9: Κάταγμα οστού. Φάση φλεγμονής (πηγή: Ο κατεστραμένος ιστός αποδομείται από τους οστεοκλάστες, σε μια διαδικασία που απελευθερώνει κυτοκίνες, ουσιές που εκκινούν τη διαδικασία επούλωσης. Ωστόσο, οι οστεοβλάστες δεν είναι σε θέση σε αυτό το στάδιο να λειτουργήσουν για την ανάπλαση του οστού εξαιτίας των συνθηκών αστάθειας στην περιοχή που εμποδίζει τη δράση τους. Η βασικότερη αρχή της θεραπείας σε αυτήν την αρχική φάση είναι η διασφάλιση της επαναφοράς των οστεϊκών τμημάτων όσο το δυνατόν πλησιέστερα στην αρχική τους θέση. Αυτό έχει σαν αποτέλεσμα τη μείωση του πόνου και το περιορισμό της αιμορραγίας. Μέσα σε λίγες ώρες από τη στιγμή του τραυματισμού, το αίμα που έχει πήξει δημιουργεί ένα πλέγμα που αποτελεί και τον πρώτο τρόπο σύνδεσης των δύο μερών του οστού. Μέσα σε αυτό περιέχονται κύτταρα που ονομάζονται ινοβλάστες και δημιουργούν μια αρχική μορφή ινώδους ιστού (Granulation tissue) σε διάστημα 4 εως 10 ημερών. Ο ιστός αυτός αποτελεί ένα ικρίωμα από το οποίο θα ξεκινήσει η δημιουργία μαλακού χόνδρου.
18 18 Εικόνα 10: Φάση φλεγμονής. Μετασχηματισμός αιματώματος σε ινώδη ιστό (Granulation tissue) (πηγή: www2.aofoundation.org) Δημιουργία μαλακού χόνδρου Οι χημικές και μεταβολικές αντιδράσεις που παράγουν το μαλακό χόνδρο ξεκινούν λίγες μέρες μετά το περιστατικό του τραυματισμού. Σε αυτό το στάδιο αιμοφόρα αγγεία αναπτύσσονται στο εσωτερικό του ιστού (Granulation tissue) και τα μεσεγχυματικά κύτταρα διαφοροποιούνται καθοδηγούμενα από παράγοντες του περιβάλλοντός τους δηλαδή βιολογικά ερεθίσματα [2] και μηχανικά ερεθίσματα (Carter et al. 1998)[7]. Έτσι οστεοβλάστες εμφανίζονται στο περιόστεο και χονδροβλάστες στην κεντρική περιοχή του κατάγματος. Οι χονδροβλάστες που βρίσκονται στον ιστό αρχίζουν να δημιουργούν χόνδρο. Ο χόνδρος, που γεμίζει το διάκενο μεταξύ των δύο οστών, δεν είναι σε θέση να παραλάβει ικανά φορτία ακόμα. Για αυτόν τον λόγο σε αυτό το στάδιο είναι θεμιτή η περιορισμένη φόρτιση της περιοχής. Μετά το πέρας λίγων εβδομάδων, ο χόνδρος παρέχει μια μερική σταθερότητα στην περιοχή, τέτοια ώστε οι οστεοβλάστες στο περιόστεο να είναι σε θέση πλέον να δημιουργήσουν φλοιώδη και δοκιδωτό οστίτη ιστό σε δικτυωτή μορφή. Πρόκειται για μία διαδικασία ενδομεμβρανώδους οστεοποίησης όπου ο οστίτης ιστός δημιουργείται περιφερειακά σε αυτήν τη φάση και είναι μαλακός και δομικά ανοργάνωτος αλλά αποτελεί τον πρώτο οστεϊκό ιστό που ενώνει τα δύο μέρη του κατάγματος. Εικόνα 11: Φάση δημιουργίας μαλακού χόνδρου. Αντικατάσταση του ιστού (Granulation tissue) από χόνδρο και ανάπτυξη αιμοφόρων αγγείων. Ενδομεμβρανώδης οστεοποίηση δημιουργεί σταδιακά οστό ξεκινώντας από την περιφέρεια(πηγή: www2.aofoundation.org).
19 19 Δημιουργία δικτυωτού οστού Με το πέρασμα 2-3 εβδομάδων παράλληλα με την ενδομεμβρανώδη οστεοποίηση ξεκινάει και η διαδικασία της ενδοχόνδριας οστεοποίησης, κατά την οποία το εύθραυστο υλικό του μαλακού χόνδρου μετατρέπεται εξόλοκλήρου σε δικτυωτό οστό. Η διαδικασία αυτή που ξεκινάει από την περιφέρεια του οστού και προχωράει προς το κέντρο, συνεχίζεται μέχρι τις 5-12 εβδομάδες και εξαρτάται από το σημείο και τη μορφή του κατάγματος. Η δημιουργία δικτυωτού οστού είναι μια σύνθετη διεργασία που καθοδηγείται από τη μηχανική διέγερση και πραγματοποιείται με την απελευθέρωση μεταλλικών ενώσεων όπως ασβέστιο και φωσφορικό άλας μέσα στον χονδρικό ιστό (ασβεστοποίηση). Όταν ολοκληρωθεί ο σχηματισμός δικτυωτού οστού έχει επέλθει η ένωση των δύο μερών του κατάγματος. Ένας σημαντκός παράγοντας που επιταχύνει την οστεογένεση σε αυτό το στάδιο είναι η άσκηση επαναλαμβανόμενων ελεγχόμενων φορτίων επειδή το οστό αντιδράει φτιάχνοντας περισσότερο ιστό. Εικόνα 12: Φάση δημιουργίας δικτυωτού οστού. Πλήρης μετατροπή του χόνδρου σε οστεϊκό ιστό μέσω ενδομεμβρανώδους και ενδοχόνδριας οστεοποίησης (πηγή: www2.aofoundation.org) Ανάπλαση οστού (Remodeling) Το στάδιο της ανάπλασης εκκινείται όταν το διάκενο έχει καλυφθεί πλήρως με δικτυωτό οστό. Το ανοργάνωτο δικτυωτό οστό σταδιακά αντικαθίσταται από πεταλιώδες, που είναι
20 20 πυκνότερο και πιο ανθεκτικό. Ο φλοιώδης οστίτης ιστός δημιουργείται τόσο με ενδομεμβρανώδη όσο και με ενδοχόνδρια οστεογένεση ενώ ο δοκιδωτός κυρίως με ενδομεμβρανώδη. Υπό φυσιολογικές συνθήκες το τμήμα οστού που θα δημιουργηθεί στην περιοχή του κατάγματος θα είναι παχύτερο από το υπόλοιπο οστό. Με το πέρασμα του χρόνου το ομοιόμορφο σχήμα αποκαθίσταται καθώς οι οστεοβλάστες εναποθέτουν οστό και οι οστεοκλάστες το αφαιρούν, όπου χρειάζεται έτσι ώστε να είναι σε θέση το οστό να παραλάβει τα φορτία που του ασκούνται καθημερινά. Τελικά με την ολοκλήρωση της διαδικασίας επούλωσης το οστό θα πρέπει να έχει την αρχική του μορφή και είναι τουλάχιστον όσο ανθεκτικό ήταν αρχικά. Εικόνα 13: Φάση ανάπλασης. Μετατροπή του δικτυωτού οστού σε πεταλειώδες (πηγή: www2.aofoundation.org)
21 21 Κεφάλαιο 2 Βιβλιογραφική Ανασκόπηση Την τελευταία δεκαετία διάφορα μαθηματικά μοντέλα έχουν αναπτυχθεί με στόχο να διερευνηθεί η οστεϊκή αναγέννηση υπολογιστικά. Τα πρώτα μοντέλα θεωρούσαν ως μοναδικό παράγοντα που ρυθμίζει τη διαδικασία επούλωσης το μηχανικό φορτίο. Στη συνέχεια αναπτύχθηκαν τα βιορρυθμιστικά μοντέλα που αγνοούσαν το μηχανικό περιβάλλον και επικεντρώνονταν στην επιρροή των βιολογικών παραμέτρων κατά την οστεογένεση. Τα πιο πρόσφατα μαθηματικά μοντέλα συνδυάζουν τις δύο προσεγγίσεις. Παρακάτω παρουσιάζεταιη προϊστορία μόνο της πρώτης κατηγορίας με το μηχανικό φορτίο ως ρυθμιστή, που αφορά άμεσα το παρόν θέμα. Τα πρώτα μοντέλα που θεωρούσαν ως μοναδικό ρυθμιστή της αναγέννησης του οστού τα μηχανικά φορτία αναπτύχθηκαν από τον Pauwels (1960) [3]. Ο Pauwels κατέληξε στη θεωρία αυτή εξετάζοντας την ανάπτυξη του ιστού σε περιπτώσεις πλάγιας ψευδάρθρωσης (oblique pseudarthroses) και γωνιωδών καταγμάτων. Σύμφωνα με τη θεωρία του η τάση και η παραμόρφωση που υφίστανται τα μεσεγχυματικά κύτταρα (κύτταρα που χρησιμοποιούνται στην Αναγεννητική Ιατρική λόγω της ικανότητάς τους να διαφοροποιούνται σε πολλούς άλλους τύπους κυττάρων) καθορίζουν τη διαδικασία διαφοροποίησής τους. Η οκταεδρική τάση που ασκείται στον δημιουργούμενο ιστό περιλαμβάνει μία υδροστατική συνιστώσα (που οδηγεί σε μεταβολή όγκου) και μία διατμητική συνιστώσα (που οδηγεί σε μεταβολή του σχήματος). Υπέθεσε ότι λόγω διατμητικής παραμόρφωσης δημιουργείται ινώδης συνδετικός ιστός ενώ λόγω υδροστατικής συμπίεσης μορφοποιείται υαλοειδής χονδρώδης ιστός. Η ταυτόχρονη συνεισφορά και των δύο προκαλεί την ανάπτυξη ινώδους χόνδρου. Ωστόσο η θεωρία του Pauwels στερείται ενός συγκεκριμένου τρόπου διέγερσης με σκοπό τον σχηματισμό οστού.
22 22 Εικόνα 14: Θεωρία του Pauwels για την διαφοροποίηση των μεσεγχυματικών κυττάρων λόγω μηχανικής διέγερσης. Αρκετά χρόνια αργότερα αναπτύχθηκε η ιδέα της ανάλυσης με βάση τη διακαταγματική παραμόρφωση (interfragmentary strain) από τον Perren (1979) [4] τους Perren & Cordey (1980) [5]. Πρότειναν ότι ιστός με ένα συγκεκριμένο όριο παραμόρφωσης δεν μπορεί να μορφοποιηθεί σε περιοχές που η παραμόρφωση ξεπερνάει το όριο αυτό. Αυτό σημαίνει ότι η περιοχή ενός κατάγματος είναι σε θέση να συμπληρωθεί μόνο με ιστό ικανό να παραλάβει τοπική παραμόρφωση. Η θεωρία που στηρίζεται στην IFS παρέχει τη βάση για την ανάπτυξη στρατηγικών επούλωσης, αλλά δεν είναι κατάλληλη για την προσέγγιση της οστεϊκής αναγέννησης γενικότερα αφού αγνοεί τη δομική και μηχανική ανομοιογένεια του ιστού που σχηματίζεται στο κάταγμα. Με υπόβαθρο τις θεωρίες των Pauwels (1960), Perren (1979) και Perren & Cordey (1980) αρκετές ερευνητικές ομάδες ανέπτυξαν μοντέλα που σχετίζουν τα μηχανικά φορτία με τη διαφοροποίηση του ιστού. Οι Carter (1987) [6] και Carter et al. (1998) [7] τόνισαν τη σημασία υποβολής του ιστού σε κυκλική φόρτιση και πρότειναν μια μηχανική διέγερση που εξαρτάται από το εύρος της τάσης και της παραμόρφωσης στην περιοχή. Στην εργασία τους διαπραγματεύονται τον τρόπο με τον οποίο το μηχανικό φορτίο καθοδηγεί τη διαφοροποίηση των μεσεγχυματικών κυττάρων έτσι ώστε να δημιουργηθεί οστό, χόνδρος και ινώδης ιστός. Υποστήριξαν ότι η κυκλική φόρτιση και οι διατμητικές τάσεις που προκαλούνται επιφέρουν κυτταρικό πολλαπλασιασμό. Με την εφαρμογή αυτού του περιοδικού φορτίου προέκυψαν τα εξής συμπεράσματα: πρωτογενής αναγέννηση με ευθεία ανάπλαση οστού προκύπτει σε περιοχές με χαμηλή υδροστατική τάση και μικρές παραμορφώσεις ενδομεμβρανώδη οστεοποίηση προκύπτει σε περιοχές με μέτριες κύριες παραμορφώσεις και μέτρια εφελκυστική υδροστατική τάση θλιπτική υδροστατική πίεση επιφέρει τη δημιουργία χόνδρου κύριες παραμορφώσεις με παράλληλη εφαρμογή θλιπτικής υδροστατικής τάσης έχουν σαν αποτέλεσμα τη δημιουργία ινώδους χόνδρου. Δεν καθόρισαν όμως με ακρίβεια τις τιμές της διέγερσης που θα ευνοούσε την οστεοσύνθεση.
23 23 Εικόνα 15: Θεωρία των Carter et al. σχετικά με την επίδραση της μηχανικής διέγερσης πάνω στην ανάπτυξη των ιστών. Οι Claes & Heigele (1999) [8] συνδύασαν την ανάλυση πεπερασμένων στοιχείων πάνω στη μηχανική διέγερση επιφανειών του οστού που αναγεννώνται κατά την επούλωση με πειραματικές αναλύσεις πάνω σε πραγματικές γεωμετρίες οστών. Μοντελοποίησαν ένα κάταγμα 3mm με 1mm διακαταγματική κίνηση και χρησιμοποίησαν κατά την πορεία της επούλωσης πέντε ειδών ιστούς που διέφεραν ως προς το μέτρο ελαστικότητας. Στο μοντέλο τους κατά την αρχική φάση της επούλωσης έχει δημιουργηθεί μόνο συνδετικός ιστός (ICT). Στη συνέχεια δημιουργείται χόνδρος μέτριας στιβαρότητας σε μια περιοχή κοντά στο περιόστεο (MSC), στον οποίο εφάπτεται εξωτερικά μαλακός χόνδρος (SOC) ενώ παραμένει και ο αρχικός συνδετικός ιστός. Στην τρίτη φάση έχουν δημιουργηθεί πέντε είδη ιστών: ο αρχικός συνδετικός ιστός, ο μαλακός χόνδρος,ο χόνδρος μέτριας σκληρότητας, ο σκληρός χόνδρος (SC) και η ζώνη ενδοχόνδριας οστεοποίησης (COZ). Για να ελεχθεί η εγκυρότητα των υπολογιστικών αποτελεσμάτων τους διεξήγαγαν τρεις μελέτες μεταβάλλοντας τον αριθμό των στοιχείων του μοντέλου (5000 και 9000 στοιχεία) και τον τύπο των στοιχείων (4- κομβικά ή 8-κομβικά). Αξιολόγησαν τις τιμές της υδροστατικής τάσης και της παραμόρφωσης στην περιοχή του κατάγματος και βρήκαν πολύ μικρές διαφορές. (α)
24 24 (β) (γ) (δ)
25 25 (ε) Εικόνα 16: (α) Ιδιότητες υλικών για τους διαφορετικούς ιστούς στο μοντέλο των Claes & Heigele (1999) (β) Γεωμετρικές διαστάσεις του μοντέλου πεπερασμένων στοιχείων (γ) Πλεγματοποίηση, φόρτιση και συνοριακές συνθήκες (δ) Ζώνες της περιοχής του κατάγματος (ε) Πορεία οστειοποίησης 1,4 και 8 εβδομάδες αντίστοιχα από την στιγμή του τραυματισμού. Με αυτόν τον τρόπο κατέληξαν σε ένα μηχανικό μοντέλο που συσχετίζει τις τιμές της υδροστατικής πίεσης και των παραμορφώσεων με την πορεία της οστεοσύνθεσης. Πρότειναν ότι η ενδομεμβρανώδης οστεοσύνθεση εξελίσσεται σε επιφάνειες όπου η υδροστατική πίεση είναι μικρότερη από 0.15 Mpa και οι παραμορφώσεις μικρότερες από 5 τοις εκατό, ενώ η ενδοχόνδρια οστεοποίηση σε περιοχές όπου η θλιπτική υδροστατική πίεση ξεπερνά το όριο των 0.15 Mpa αλλά οι παραμορφώσεις είναι μικρότερες από 15 τοις εκατό. Όλες οι άλλες συνθήκες φόρτισης οδηγούν στη δημιουργία ινώδους ιστού ή ινώδους χόνδρου.
26 26 Εικόνα 17: Σχέση μεταξύ μηχανικών συνθηκών και μορφοποιούμενου ιστού στο μοντέλο των Claes & Heigele (1999). Όλες οι παραπάνω θεωρίες θεωρούν τους ιστούς ως συμπαγή ελαστικά υλικά. Οι Prendergast et al. (1997) [9] πρότειναν ένα μηχανικό μοντέλο πάνω στη διαφοροποίηση των ιστών, που βασίζεται στην ποροελαστική συμπεριφορά τους. Η μέγιστη διατμητική παραμόρφωση και η σχετική ταχύτητα ρευστού συνιστούν τις διεγέρσεις που ρυθμίζουν τη διαδικασία της κυτταρικής διαφοροποίησης. Στην περίπτωση που οι τιμές που παίρνουν είναι υψηλές ευνοείται η δημιουργία ινώδους ιστού, για ενδιάμεσες τιμές η δημιουργία χόνδρου ενώ μόνο για χαμηλές τιμές τους είναι δυνατή η δημιουργία οστού. Οι Huiskes et al. (1997) [10] ποσοτικοποίησαν τα άνω και κάτω όρια της μηχανικής διέγερσης που απαιτείται για την δημιουργία του εκάστοτε ιστού. Εικόνα 18: Θεωρία των Prendergast et al. πάνω στην κυτταρική διαφοροποίηση λόγω μηχανικής διέγερσης. Για να ποσοτικοποιηθεί η μηχανική διέγερση χρησιμοποίηθηκε ο τύπος:
27 27 όπου S η διέγερση, MDS η μέγιστη διατμητική παραμόρφωση (maximum distortional strain) και RFV η σχετική ταχύτητα ρευστού (relative fluid velocity). Θεωρήθηκε ότι για υψηλή μηχανική διέγερση (S>3) ευνοείται η διαφοροποίηση των μεσεγχυματικών κυττάρων σε ινοβλάστες, για ενδιάμεσες τιμές (S<3, S>1) σε χονδροβλάστες και για χαμηλές τιμές σε οστεοβλάστες (S<1). Επίσης συμπεριλήφθηκε η διάκριση ανάμεσα σε δικτυωτό και πεταλιώδες οστό με το δεύτερο να μορφοποιείται μόνο για πολύ χαμηλές τιμές της διέγερσης (S<0.2667). Το μοντέλο επεκτάθηκε από τους Lacroix & Prendergast (2002) [11] και Lacroix et al. (2002) [12] στο να συμπεριλάβει η μετακίνηση των μεσεγχυματικών κυττάρων στην περιοχή του κατάγματος μέσω μιας διαφορικής εξίσωσης και αυτό αποτέλεσε την πρώτη προσπάθεια ενσωμάτωσης κυτταρικών διεργασιών. Υποστήριξαν ότι η προέλευση των μεσεγχυματικών κυττάρων είναι: ο ερυθρός μυελός, το περιόστεο και ο εσωτερικός μαλακός ιστός. Τα κύτταρα αυτά είτε μεταναστεύουν είτε πολλαπλασιάζονται (μίτωση) και η κινητήριος δύναμη αυτών των διεργασιών είναι η διαφορά πυκνότητας σε κύτταρα στις διάφορες περιοχές του κατάγματος. Συνεπώς η διάχυση των κυττάρων μπορεί να περιγραφεί από την εξίσωση: όπου n η κυτταρική πυκνότητα t ο χρόνος και D ο συντελεστής διάχυσης σε m 2 ανά ημέρα τέτοιος ώστε μια ομοιόρφη κατανομή να επιτυγχάνεται σε διάστημα 4 ημερών. Κατέληξαν στο συμπέρασμα ότι το σημείο προέλευσης έχει καθοριστική επίδραση στο ρυθμό επούλωσης. Εικόνα 19: Θεωρία των Lacroix & Prendergast στην οποία συνυπολογίζεται η διάχυση των μεσεγχυματικών κυττάρων.
28 28 Παρόμοιο με το μοντέλο των Prendergast et al. (1997) ήταν αυτό των Kuiper et al. (2000) [13] στο οποίο οι διατμητικές τάσεις και παραμορφώσεις ρύθμιζαν το ρυθμό ανάπλασης του οστού. Η δημιουργία χόνδρου ενσωματώθηκε μέσω της ανάπτυξης πρόδρομου ιστού (granulation tissue) και υιοθετήθηκαν ρεαλιστικά μοτίβα επούλωσης. Μία διαφορετική προσσέγγιση πραγματοποιήθηκε από τους Ament & Hofer (2000) [14] οι οποίοι χρησιμοποίησαν τη μηχανική ενέργεια παραμόρφωσης για να καθορίσουν την κυτταρική διαφοροποίηση. Παρακάτω συνοψίζονατι τα σημαντικότερα μοντέλα πάνω στην κυτταρική διαφοροποίηση με τα κυριότερα χαρακτηριστικά τους. Τα μηχανικά μοντέλα που περιγράφηκαν, εφαρμόστηκαν σε πειραματικές δοκιμές ώστε να ελεγχθεί η αξιοπιστία τους. Το μοντέλο του Carter (Carter et. al 1988, 1998) χρησιμοποιήθηκε σε υπολογιστικές μελέτες πάνω στην έκτοπη οστεοποίηση (Blenman et. Εικόνα 20: Περίληψη μαθηματικών μοντέλων πάνω στην οστική αναγέννηση. (SED: strain energy density; GF: growth factor; MSC: mesenchymal stem cell; FB: fibroblast; CC: chondrocyte; OB: osteoblast; CGGF: chondrogenic growth factor; OGGF: osteogenic growth factor; VGF: vascular growth factor; EC: endothelial cell.)
29 29 al. 1989) [15], στον σχηματισμό ψευδάρθρωσης (Loboa et al. 2000) [16], σε μη συμμετρικά κλινικά κατάγματα (Gardner et al. 2006) [17] και στη διατατική οστεογένεση (Morgan et al. 2006) [18]. Ωστόσο καμία από τις μελέτες δεν προέβλεπε την διαφοροποίηση των κυττάρων σταδιακά με την πάροδο του χρόνου.οι Lacroix & Prendergast (2002) [19] εφάρμοσαν επιτυχώς το μοντέλο των Prendergast et al. (1997) [9] το οποίο αρχικώς είχε δημιουργηθεί με τη βοήθεια μιας συσκευής που εμφυτεύτηκε σε μηριαίους κονδύλους σκυλιών Labrador (Søballe 1993) [20], σε πραγματική επούλωση κατάγματος. Οι Andreykiv et al. (2005) [21] χρησιμοποίησαν το ίδιο μοντέλο για να ερευνήσουν τη γληνοειδή χαλάρωση σε εμφυτεύματα ώμου. Αυτό τους επέτρεψε να καταλήξουν σε συμπεράσματα σχετικά με τη σταθερότητα και τη δυσκαμψία των γλενοειδών εμφυτευμάτων. Οι Geris et al. (2003, 2004, 2008) βασίστηκαν σε διάφορετικά μηχανικά μοντέλα για να μελετήσουν την οστεοενσωμάτωση εμφυτευμάτων κάνοντας δειγματοληψίες σε πραγματικές συνθήκες. Τα μοντέλα που χρησιμοποίησαν ήταν των Lacroix & Prendergast και Claes et al. και τα πειραματικά δεδομένα με τα οποία έγιναν οι συγκρίσεις αφορούσαν την οστεογένεση σε οστό κνήμης ενήλικων κουνελιών. Αρκετά αποτελέσματα των υπολογιστικών δοκιμών επιβεβαιώθηκαν πειραματικά, όπως η ποσότητα οστού που μορφοποιείται κάτω από συγκεκριμένους τρόπους φόρτισης στο σημείο του εμφυτεύματος. Αντιθέτως, άλλα σημεία των υπολογιστικών αποτελεσμάτων, όπως οι προβλέψεις για το ποσοστό παρουσίας χόνδρου ήταν αντικρουόμενα με τα αντίστοιχα πειραματικά. Αμφότερα τα μοντέλα ήταν σε θέση να προσομοιώσουν την πορεία μια ομαλής επούλωσης κατάγματος με σχετική ακρίβεια. Εικόνα 21: Προσομοίωση του αλγορίθμου που χρησιμοποίησαν οι Geris et al. με βάση τη θεωρία των Lacroix & Prendergast. Αρχικά ολόκληρη η περιοχή του κατάγματος καλύπτεται από συνδετικό ιστό. Για κάθε κύκλο φόρτισης εφαρμόζεται το φορτίο, εξετάζεται η διάχυση των μεσεγχυματικών κυττάρων και η συγκέντρωσή τους σε κάθε σημείο και υπολογίζεται η βιοφυσική απόκριση. Στη συνέχεια ανανεώνονται οι ιδιότητες κάθε στοιχείου με βάση τον τύπο του ιστού που παράγεται, μετά απο μια διαδικασία εξομάλυνσης (Smoothening).
30 30 Εικόνα 22: Προσομοίωση του αλγορίθμου που χρησιμοποίησαν οι Geris et al. με βάση τη θεωρία των Claes et al. Αρχικά ολόκληρη η περιοχή του κατάγματος καλύπτεται από συνδετικό ιστό. Η δραστηριότητα των μεσεγχυματικών κυττάρων δεν συνυπολογίζεται. Μετά την εφαρμογή του φορτίου, για κάθε κύκλο, υπολογίζεται η βιοφυσική απόκριση και ανανεώνονται οι ιδιότητες κάθε στοιχείου. Ακολουθεί μια διαδικασία εξομάλυνσης (Smoothening). Παρά ταύτα κάτω από στρεπτικά φορτία, δηλαδή διαφορετικές μηχανικές συνθήκες από αυτές που χρησιμοποιήθηκαν για την ανάπτυξη αυτών των μοντέλων μόνο το αντίστοιχο των Prendergast et al. (1997) [9] ήταν ικανό να προβλέψει επιτυχώς την οστεϊκή ανάπλαση. Εφαρμόζοντας το τελευταίο σε μια περίπτωση οστού κνήμης (Isaksson et al. 2007) [22] σημειώθηκαν χωρικές και χρονικές μεταβολές στους ιστούς καθώς και διαφοροποιήσεις στην κατανομή των ιστών εξαιτίας διακυμάνσεων στο εύρος και στη συχνότητα φόρτισης, που επιβεβαιώθηκαν πειραματικά. Συγκεκριμένα, το μοντέλο των Prendergast et al. συμφωνούσε με τα αποτελέσματα πειραματικών δοκιμών σε οστά κνήμης κατά τις οποίες παρατηρήθηκε ότι: (α) η μείωση του εύρους φόρτισης (0.5 mm/day vs mm/day) είχε ως αποτέλεσμα την αύξηση του απαιτούμενου χρόνου για την ολοκλήρωση της οστεϊκής ανάπλασης και (β) η αύξηση της συχνότητας φόρτισης (0.5 mm/12 h vs mm/6 h) είχε ως αποτέλεσμα γρηγορότερη ανάπλαση. Εικόνα 23: Προσομοίωση του αλγορίθμου που χρησιμοποίησαν οι Geris et al. με βάση τη θεωρία των Lacroix & Prendergast. Αρχικά ολόκληρη η περιοχή του κατάγματος καλύπτεται από
31 31 συνδετικό ιστό. Για κάθε κύκλο φόρτισης εξετάζεται η διάχυση των μεσεγχυματικών κυττάρων, εφαρμόζεται το φορτίο και υπολογίζεται η βιοφυσική απόκριση με βάση την οκταεδρική διατμητική τάση και τη σχετική ταχύτητα του ρευστού. Στη συνέχεια καθορίζεται το είδος του ιστού για κάθε στοιχείο και ανανεώνεται η μορφή του πλέγματος καθώς και η συγκέντρωση των κυττάρων σε κάθε σημείο. Ένα παρόμοιο μοντέλο με των Prendergast et al. (1997) χρησιμοποιήθηκε από τους Idelsohn et al. (2006) [23] με σκοπό τη διερεύνηση της οστεογένεσης στην κάτω γνάθο. Οι Kelly & Prendergast (2005) [24] μέσω του ίδιου μοντέλου προσομοίωσαν ενδοχόνδρια οστική αναγέννηση και πέτυχαν την προσέγγιση μοτίβων κυτταρικής διαφοροποίησης που είχαν παρατηρηθεί πειραματικά στην αντίστοιχη διαδικασία επούλωσης. Οι Chang et al. (2011) [25] βασιζόμενοι στο μοντέλο του Perren μελέτησαν μια μέθοδο ευέλικτης στήριξης με μαλακά υλικά (άνθρακας/εποξικά πολυμερή και γυαλί/πολυπροπυλένιο) για την πρόληψη φαινομένων όπως οστεοπόρωση και ελλειπής αιμάτωση στην περιοχή του κατάγματος. Εικόνα 24: Η θεωρία του Perren που χρησιμοποίησαν οι Chang et al. στις δοκιμές τους. Το βέλτιστο εύρος παραμόρφωσης 0-2% εγγυάται τον υψηλότερο ρυθμό επούλωσης με ευθεία ανάπλαση οστού (πρωτογεννής αναγέννηση). Το εύρος παραμορφώσεων 2-10% προκαλεί δευτερογενή ανάπλαση ενώ όταν οι παραμορφώσεις υπερβαίνουν το όριο του 30% το οστό αποδομείται. Εικόνα 25: Μέθοδος στήριξης στο μοντέλο των Chang et al.
32 32 Εικόνα 26: Προσομοίωση του αλγορίθμου που χρησιμοποίησαν οι Chang et al. με βάση τη θεωρία του Perren. Η χρήση των μηχανικών μοντέλων έχει αυξήσει την κατανόηση πάνω στον τρόπο με τον οποίο η οστεϊκή αναγέννηση επηρεάζεται από τα μηχανικά φορτία. Μπορούν να χρησιμοποιηθούν για να προκύψουν κατευθυντήριες γραμμές πάνω στο μέγεθος των φορτίων σε πραγματικές συνθήκες που μπορούν να παραλάβουν οι ιστοί. Ένα μεγάλο μειονέκτημα αυτών των μοντέλων είναι η σχεδόν πλήρης απουσία βιολογικών μηχανισμών και ο τρόπος που αυτοί επηρεάζονται από τα μηχανικά φορτία. Αντιθέτως οι αλγόριθμοι περιγράφουν τη σύνδεση μεταξύ της μηχανικής διέγερσης και της μεταβολής των ιδιοτήτων των ιστών με έναν φαινομενολογικό τρόπο.
33 33 Κεφάλαιο 3 Περιγραφή Πλαισίου Ilizarov Εικόνα 27: Σύστημα εξωτερικής οστεοσύνθεσης Ilizarov (πηγή: Πειραματική διάταξη Το πλαίσιο Ilizarov είναι μια μορφή εξωτερικής οστεοσύνθεσης με κυκλικά πλαίσια (δακτυλίους). Αποτελείται από: 4 δακτυλίους εσωτερικής διαμέτρου 180mm και πάχους 5mm 8 ιατρικές βελόνες (τύπου Kirschner) διαμέτρου 1.8mm 12 συνδετικές ράβδους Τα τμήματα του οστού τοποθετούνται στο κέντρο των δακτυλίων, ενώ με κάθε τμήμα συνδέονται δύο δακτύλιοι μέσω των ιατρικών βελόνων. Οι ιατρικές αυτές βελόνες, αφού υποβληθούν σε προένταση, διέρχονται μέσω του οστού. Οι δακτύλιοι συνδέονται μεταξύ τους με τη βοήθεια μεταλλικών ράβδων. Το πλαίσιο μεταφέρει τις δυνάμεις μέσω των δακτυλίων και των κάθετων συνδετικών ράβδων από το άνω τμήμα του οστού στο κάτω. Με αυτόν τον τρόπο επιτρέπεται η κίνηση ολόκληρου του άκρου με την ελεγχόμενη φόρτισή του, ενώ περιορίζονται οι κινήσεις της διακαταγματικής περιοχής.
34 Μοντέλο πεπερασμένων στοιχείων Εικόνα 28: Προσομοίωση του παλισίου Ilizarov μέσω του προγράμματος πεπερασμένων στοιχείων ABAQUS CAE. Οι διαστάσεις της γεωμετρίας του πλαισίου στο πρόγραμμα πεπερασμένων στοιχείων αντιστοιχούν με τις πραγματικές που αναφέρθηκαν παραπάνω. Συγκεκριμένα: Οι δακτύλιοι Οι 4 δακτύλιοι είναι παράλληλοι μεταξύ τους, έχουν εσωτερική διάμετρο ίση με 180mm, πάχος ίσο με 5mm και 48 οπές συμμετρικά κατανεμημένες στην περιφέρειά τους διαμέτρου 7mm. Οι δακτύλιοι που τοποθετούνται σε κάθε τμήμα οστού έχουν απόσταση 40mm μεταξύ τους. Οι δύο ομόκεντροι δακτύλιοι που τοποθετούνται πιο κοντά στο κάταγμα έχουν απόσταση 140mm μεταξύ τους. Το πλέγμα τους δημιουργήθηκε χρησιμοποιώντας γραμμικής παρεμβολής εξαεδρικά στοιχεία μειωμένης ολοκλήρωσης (C3D8R). Εικόνα 29: Πλέγμα δακτυλίου. Οι ιατρικές βελόνες Kirschner Οι βελόνες Kirschner έχουν λείο κυλινδρικό σχήμα και διάμετρο 1.8mm. Τα τμήματα των βελόνων που εισέρχονται στο οστό μοντελοποιήθηκαν ως στέρεες κατασκευές, προκειμένου να συμπεριληφθούν στην ανάλυση οι παραμορφώσεις λόγω της
35 35 αλληλεπίδρασης επαφής μεταξύ του οστού και των προεντεταμένων βελόνων και για τη δημιουργία του πλέγματός τους χρησιμοποιήθηκαν τόσο εξαεδρικά στοιχεία γραμμικής παρεμβολής (C3D8R) εξωτερικά όσο και στοιχεία τύπου wedge (C3D6) εσωτερικά. Εικόνα 30: Πλέγμα βελόνας Kirschner. Το υπόλοιπο τμήμα της βελόνας μοντελοποιήθηκε με τετραγωνικής παρεμβολής στοιχεία τύπου δοκού Timoshenko (B32). Οι συνδετικές ράβδοι Οι 12 συνδετικές κάθετες ράβδοι που συνδέουν τους δακτυλίους μοντελοποιήθηκαν με τετραγωνικής παρεμβολής στοιχεία τύπου δοκού Timoshenko (B32). Οι ράβδοι που συνδέουν τους δακτυλίους του ίδιου τμήματος οστού έχουν μήκος 50mm ενώ αυτές που συνδέουν τους δακτυλίους εκατέρωθεν της διακαταγματικής περιοχής έχουν μήκος 150mm. Το οστό Τα τμήματα του οστού κνήμης προσομοιώθηκαν ως κυλινδρικές ράβδοι διαμέτρου 30mm και μήκους 167.5mm το κάθε ένα. Σε κατάλληλες θέσεις έχουν κυλινδρικές οπές, ώστε να μπορούν οι ιατρικές βελόνες να τα διαπεράσουν. Για τη δημιουργία του πλέγματος χρησιμοποιήθηκαν γραμμικής παρεμβολής τετραεδρικά στοιχεία (C3D4) με επιπλέον πύκνωση του πλέγματος στις περιοχές των οπών για ακριβέστερη αποτύπωση των επιφανειών τους. Εικόνα 31: Πλέγμα τμημάτων οστού. Το κάθε τμήμα έχει χωριστεί σε εξωτερικό και εσωτερικό μέρος προσομοιώνοντας το περιόστεο και τον μυελό των οστών.
36 Κινηματικοί Περιορισμοί Η επαφή μεταξύ της εσωτερικής επιφάνειας του οστού και της εξωτερικής επιφάνειας των βελόνων πραγματοποιήθηκε με συνθήκη απλής επαφής χωρίς τριβή. Η μετάβαση από τα στερεά στοιχεία στα στοιχεία τύπου δοκού στη βελόνα μοντελοποιήθηκε επιβάλλοντας περιορισμούς σύζευξης (coupling constraints) μεταξύ των κόμβων στις ακραίες διατομές της στερεής δοκού και των αντίστοιχων ακραίων κόμβων των τμημάτων των δοκών Timoshenko, οι οποίοι τοποθετούνται στα κέντρα των διατομών της στέρεης δοκού. Ο περιορισμός επιβάλλεται κατανέμοντας τα φορτία έτσι ώστε οι συνισταμένες των δυνάμεων στους κόμβους σύζευξης να είναι ισοδύναμες με τις δυνάμεις στον κόμβο αναφοράς και να διατηρείται ισορροπία δυνάμεων και ροπών των κατανεμημένων δυνάμεων ως προς τον κόμβο αναφοράς. Εικόνα 32: Επαφή χωρίς τριβή μεταξύ βελόνων και οστού. Εικόνα 33: Περιορισμοί σύζευξης μεταξύ των στερεών τμημάτων των δοκών και των δοκών Timoshenko. Αντίστοιχα πραγματοποιείται η σύνδεση μεταξύ των των ακραίων κόμβων των δοκών Timoshenko με τις οπές των δακτυλίων (kinematic coupling).
37 37 Εικόνα 34: Σύνδεση μεταξύ των δοκών Timoshenko και των οπών των δακτυλίων. Επίσης η ανώτερη διατομή του άνω οστού έρχεται σε επαφή με μια άκαμπτη πλάκα (rigit surface) με συντελεστή τριβής 0.2 με σκοπό την επιβολή κατακόρυφης δύναμης, ενώ οι ιατρικές βελόνες προεντείνονται με 930Ν. Εικόνα 35: Τρόπος επιβολής της δύναμης Υλικά πλαισίου Τα υλικά που χρησιμοποιήθηκαν κατά την μοντελοποίηση του πλαισίου είναι γραμμικώς ελαστικά και οι ιδιότητές τους φαίνονται στον πίνακα παρακάτω: Πίνακας 1: Ιδιότητες υλικών κατά την μοντελοποίηση. Μηχανικό Μέρος Ιατρικές βελόνες και συνδετικές ράβδοι Υλικό Μέτρο ελαστικότητας (Gpa) Λόγος Poisson (ν) Χάλυβας
38 38 Δακτύλιοι Αλουμίνιο Εξωτερικό μέρος οστού Εσωτερικό μέρος οστού Οστό Μυελός των Οστών
39 39 Κεφάλαιο 4 Μοντέλο οστικής αναγέννησης Εικόνα 36: Προσομοίωση πόρου Μοντελοποίηση πόρου Με σκοπό την προσομοίωση και ανάλυση του φαινομένου της οστικής αναγέννησης στην διακαταγματική περιοχή που αντιστοιχεί στον κενό χώρο ανάμεσα στα δύο τμήματα του οστού δημιουργείται ο κυκλικός δίσκος που αποτελεί τον πόρο. Η ακτίνα του πόρου είναι ίση με την ακτίνα των τμημάτων του οστού (R=15mm) και το πάχος του ίσο με πάχος του διακένου (h=5mm). Συνεπώς ο πόρος εφαρμόζει ακριβώς στα όρια του διακένου. Εικόνα 37: Οι διαστάσεις του πόρου: R=15mm, h=5mm. Για τη δημιουργία του πλέγματος του πόρου χρησιμοποιήθηκαν τετραεδρικά στοιχεία γραμμικής παρεμβολής (C3D4) και αποτελείται συνολικά από περίπου 1100 κόμβους. Το πλέγμα του πόρου αποτελεί συνέχεια του πλέγματος των δύο τμημάτων του οστού Υλικό πόρου Αλγόριθμος Το υλικό του πόρου είναι γραμμικώς ελαστικό με αρχικό μέτρο ελαστικότητας E a =0.2 MPa και λόγο του Poisson ν=0.2. Η χαμηλή αυτή αρχική τιμή του μέτρου ελαστικότητας επιλέχθηκε έτσι ώστε να συμπίπτει με την ύπαρξη συνδετικού ιστού (Granulation tissue) στη διακαταγματική περιοχή, κατά το στάδιο της φλεγμονής, που αποτελεί το ικρίωμα από το οποίο θα ξεκινήσει η οστική αναγέννηση. Η διαδικασία της οστικής αναγέννησης προσομοιώνεται από έναν αλγόριθμο που μεταβάλλει μέτρο ελαστικότητας του πόρου
40 40 καθόλη τη διάρκεια της φόρτισης και αποφόρτισης του. Αυτό πραγματοποιείται μέσω κατάλληλης υπορουτίνας UMAT που εισήχθη στο πρόγραμμα ABAQUS. Ο Αλγόριθμος Ο παρών αλγόριθμος βασίζεται στο πρόσφατο μοντέλο οστικής αναγέννησης των Garcia- Aznar et al. [26]. Συγκεκριμένα χρησιμοποιείται ως κύρια μεταβλητή μέτρησης του βαθμού επούλωσης η μεταβλητή α. Η μεταβλητή αυτή είναι κανονικοποιημένη αντιστοιχίζοντας το α=1 με επιτυχή πλήρη επούλωση του κατάγματος και το α=0 με μηδενική επούλωση. Υποθέτονται υλικά με γραμμικώς ελαστική συμπεριφορά, έτσι ώστε το μέτρο ελαστικότητας σε κάθε σημείο του πόρου να δίνεται από τη σχέση: tot 1 0 E a E a E όπου Ε 0 το αρχικό μέτρο ελαστικότητας του πόρου και E f το μέτρο ελαστικότητας ενός πλήρως επουλωμένου κατάγματος. Ο λόγος του Poisson διατηρείται σταθερός. Επιπλέον, το μοντέλο συνυπολογίζει την πιθανότητα μείωσης της μεταβλητής α, που αντιπροσωπεύει τη μηχανική αστοχία του ιστού που έχει δημιουργηθεί στο διάκενο, λόγω αδυναμίας να ανταποκριθεί στις τοπικές μηχανικές συνθήκες. f 1) Αύξηση της μεταβλητής επούλωσης α Η μεταβλητή επούλωσης α αυξάνεται εξαιτίας ανάπλασης του ιστού του κατάγματος και γι αυτό το λόγο υπολογιζεται ως το άθροισμα δύο επιμέρους συνιστωσών: a a a c όπου το α c αντικατοπτρίζει την αποκατάσταση των μηχανικών ιδιοτήτων του ιστού εξαιτίας της δημιουργίας χόνδρου, ενώ το α b αντικατοπτρίζει την αποκατάσταση των μηχανικών ιδοτήτων του ιστού εξαιτίας της δημιουργίας οστού. Με σκοπό να υπολογιστεί η στιγμιαία μεταβολή του α a ac ab σε κάθε στοιχείο, χρησιμοποιείται μια ρυθμιστική συνθήκη που βασίζεται σε τρεις διαφορετικές ζώνες επούλωσης (Claes & Heigele [8]). Αυτές καθορίζονται από τη συμπίεση (ε zz : ορθή παραμόρφωση στον κατακόρυφο άξονα) που απεικονίζεται στον άξονα x και τις διατμητικές 2 1 dev dev dev παραμορφώσεις shear mises :, tr 3 ε ε ε ε 3 ε δ, που απεικονείζονται στον άξονα y του διαγράμματος που ακολουθεί. b
41 41 Εικόνα 38: Ζώνες επούλωσης (πηγή: -Aznar et al. [26]) Ζώνη 1 Mηδενική επούλωση: Η παραμόρφωση στον κατακορυφο άξονα ε zz και οι διατμητικές παραμορφώσεις ε shear =ε mises καθώς και η συνεπαγόμενη διακαταγματική μετατόπιση (IFM) είναι τόσο υψηλές που αποτρέπουν μια επιτυχή επούλωση. Στην περιοχή του κατάγματος ενυπάρχει μόνο ινώδης συνδετικός ιστός και δεν προκαλείται καμία μεταβολή τόσο στην α c όσο και στην α b a a 0. c Ζώνη 2 Δημιουργία χόνδρου: Θεωρείται ότι στα στοιχεία εκείνα των οποίων οι παραμορφώσεις βρίσκονται σε αυτήν την ζώνη, δημιουργείται χόνδρος και γι αυτό αυξάνεται η μεταβλητή α c. Ωστόσο οι παραμορφώσεις σε αυτά τα στοιχεία θα πρέπει να βρίσκονται στη συγκεκριμένη ζώνη για μια καθορισμένη χρονική περίοδο M c προτού αρχίσει η α c να αυξάνεται και αυτό αντιπροσωπεύει το χρόνο ωρίμανσης του βιολογικού περιβάλλοντος που απαιτείται για να εκκινήσει η χονδρογένεση. Έχει καθοριστεί ότι η α c θα έχει μια εκθετική αύξηση με το χρόνο (Garcia-Aznar et al. [26]) και ως εκ τούτου όταν ο χρόνος ωρίμανσης M c παρέλθει η τιμή της α c θα αυξηθεί εκθετικά. Με την προϋπόθεση ότι οι παραμορφώσεις παραμένουν στα όρια της Ζώνης 2 για ένα ορισμένο χρονικό διάστημα t c (cartilage formation time) θα φτάσει τη μέγιστη τιμή της, α c,max. Εάν κατά τη διάρκεια της διαδικασίας επούλωσης και καθώς αυξάνεται η α c, οι παραμορφώσεις εισέλθουν στα όρια της Ζώνης 3 η α c θα συνεχίσει να αυξάνεται με τον ίδιο ρυθμό μέχρι να φτάσει τη μέγιστη τιμή της, α c,max. Για την χρονική περιγραφή της α c χρησιμοποιείται η ακόλουθη συνάρτηση: 0 if t M c A a e if M t M t 16 ac,max if t M c tc 1 2.6A1 t M c c 1 c c c όπου t είναι ο χρόνος που ξεκινά να μετρά από τη στιγμή που οι παραμορφώσεις ικανοποιούν τις συνθήκες για δημιουργία χόνδρου και A είναι μία αδιάστατη μεταβλητή. b
42 42 Εικόνα 39: Χρονική μεταβολή της α c (πηγή: -Aznar et al. [26]) Ζώνη 3 Δημιουργία οστού: Σε αυτή τη ζώνη οι παραμορφώσεις και η IFM είναι μικρότερες από την Ζώνη 2 και σαν αποτέλεσμα μορφοποιείται οστό και άρα αυξάνεται η α b. Επιπλέον ορίζεται ως M b ο χρόνος ωρίμανσης του βιολογικού περιβάλλοντος που απαιτείται για την οστεογένεση. Έχει καθοριστεί ότι η α b θα έχει μια γραμμική αύξηση με το χρόνο (Garcia- Aznar et al. [26]) και συνεπώς όταν ο χρόνος ωρίμανσης M b παρέλθει η α b θα αυξηθεί γραμμικά, δεδομένου ότι οι παραμορφώσεις παραμένουν καθόλη τη διάρκεια εντός των ορίων της Ζώνης 3, μέχρι να πάρει τη μέγιστη τιμή της α b,max στον χρόνο επούλωσης t b. Εάν η α b αρχίσει να αυξάνεται γιατί πληρούνται οι προϋποθέσεις για τον σχηματισμό οστού και η α c εξακολουθεί να αυξάνεται πραγματοποιείται μια ταυτόχρονη αύξηση των δύο μεταβλητών. 0 if t M b t M a a if M t M t ab,max if t M b tb b b b,max b b b tb όπου t είναι ο χρόνος που ξεκινά να μετρά από τη στιγμή που οι παραμορφώσεις ικανοποιούν τις συνθήκες για δημιουργία οστού. Εικόνα 40: Χρονική μταβολή της α b (πηγή: -Aznar et al. [26])
43 43 Σημειώνεται ότι αρκεί μία εκ των παραμορφώσεων να υπερβεί τα όρια κάποιας Ζώνης για να θεωρηθεί ότι οι συνθήκες για τη Ζώνη αυτή δεν ικανοποιούνται. Σύμφωνα με τον ορισμό του α η μέγιστη τιμή του είναι 1, που αντιστοιχεί σε μια επιτυχή πλήρη επούλωση και συνεπώς τ όρια της α c (α c,max ) και της α b (α b,max ) θα πρέπει να ικανοποιούν την ακόλουθη εξίσωση: a a a 1 a 1 a max c,max b,max c,max b,max Aκoλουθείο πίνακας με τις τιμές των παραμέτρων που χρησιμοποιούνται στην ανάλυση: Πίνακας 2: Οι τιμές των παραμέτρων όπως προκύπτουν από την εργασία των Garcia-Aznar et al. [26]. Model Parameters Value M c - Maturation time for cartilage (days) 4 M b - Maturation time for bone (days) 10 a b,max - Maximum value of a b 0.7 tc - Cartilage formation time (days) 36 tb - Bone healing time (days) 60 comp Lc - Compression strain limit for cartilage formation 0.6 comp Lb - Compression strain limit for bone formation 0.25 shear Lc - Shear strain limit for cartilage formation 0.25 shear Lb - Shear strain limit for bone formation 0.15 E 0 - Initial elastic modulus (MPa) 0.2 E f - Elastic modulus of healed bone (MPa) 50 - Poisson s ratio 0.2 2) Μηχανική αστοχία: Μείωση της μεταβλητής επούλωσης α. Κατά τη διάρκεια της διαδικασίας επούλωσης όπου α c >0 και α b >0 η μεταβλητή επούλωσης α ενδέχεται να μειωθεί εξαιτίας μίας πιθανής υπερφόρτισης που προκαλεί υψηλές τοπικές παραμορφώσεις. Στο παρόν μοντέλο έχει γίνει η θεώρηση ότι τόσο η α c όσο και η α b μηδενίζονται ακαριαία όταν οι παραμορφώσεις υπερβούν τα όρια της Ζώνης 2 και της Ζώνης 3 αντίστοιχα. Δηλαδή όταν οι παραμορφώσεις πάρουν μεγαλύτερες τιμές από αυτές που αντιστοιχούν στα όρια της Ζώνης 3 τότε ισχύει αυτομάτως α b =0 (καταστροφή του
44 44 οστού) ενώ όταν πάρουν μεγαλύτερες τιμές από αυτές που αντιστοιχούν στη Ζώνη 2 τότε ισχύει αυτομάτως α c =0 (καταστροφή του χόνδρου) και α b =0 (καταστροφή του οστού) καθώς όταν οι παραμορφώσεις βρίσκονται εκτός ορίων της Ζώνης 2 βρίσκονται ταυτόχρονα και εκτός ορίων της Ζώνης 3. Έρευνα των Garcia-Aznar et al. [26] Οι τιμές των παραμέτρων που χρησιμοποιούνται προέρχονται από την έρευνα των Garcia- Aznar et al. [26]. Αυτοί, χρησιμοποιώντας έναν παρόμοιο αλγόριθμο με αυτόν που περιγράφηκε παραπάνω, συνέκριναν τα αποτελέσματα της διακαταγματικής μετατόπισης (IFM) που προέκυπταν από το υπολογιστικό μοντέλο με πραγματικές μετρήσεις και κάτω από διαφορετικές μηχανικές συνθήκες. Συγκεκριμένα προσομοίωσαν δύο πειραματικές διαδικασίες, μία θλίψη και μία διάτμηση που υπήρχαν στη βιβλιογραφία. Με σκοπό να εκτιμηθούν οι τιμές των παραμέτρων L c comp, L b comp, α c,max, α b,max, M c, M b, t c και t h προσομοιώθηκαν τα πειράματα συμπίεσης που πραγματοποιήθηκαν από τους Claes et al. (1997) [27]. Αυτοί προσδιόρισαν την επιροή που έχει το μέγεθος του διακένου στην περιοχή του κατάγματος καθώς και η διακαταγματική παραμόρφωση (IFS) πάνω στη δημιουργία χόνδρου κατά την επούλωση ενός μετατάρσιου οστού προβάτου. Ακολούθως, με στόχο να ανταποκρίνονται οι τιμές των παραμέτρων και στην προσέγγιση της πορείας επούλωσης κάτω από συνθήκες διάτμησης προσομοιώθηκαν πειράματα που είχαν πραγματοποιηθεί από τους Bishop et al. (2006) [28] πάνω στην ανάπλαση οστού κνήμης προβάτου όπου εφαρμόστηκαν διατμητικά φορτία και έτσι προσδιορίστηκαν οι τιμές των μεταβλητών L c shear και L b shear. Οι τιμές των παραμέτρων E 0 και E f προέρχονται από μελέτες της βιβλιογραφίας. Στη συνέχεια, για να προσδιοριστεί η ακρίβεια στις προβλέψεις του μοντέλου, πραγματοποιήθηκαν τρία επιπλέον πειράματα (συμπίεσης, συνδυασμένης φόρτισης και θρυμματισμένου κατάγματος) με τη χρήση των παραμέτρων που υπολογίστηκαν. Εικόνα 41: Πίνακας πειραμάτων που προσομοίωσαν οι Garcia-Aznar et al. [26]. Η σύγκληση των πειραματικών και των υπολογιστικών αποτελεσμάτων είναι αρκετά ικανοποιητική. Παρακάτω παρατίθενται ενδεικτικά τα αποτελέσματα για την περίπτωση των δοκιμών εκτίμησης της πορείας επούλωσης του οστού κάτω από συμπίεση.
45 45 Εικόνα 42: Πορεία εξέλιξης της διακαταγματικής μετατόπισης (IFM) κατά την υπολογιστική προσομοίωση των Garcia-Aznar et al. [26] σε σύγκριση με τα υπολογιστικά δεδομένα (πηγή: - Aznar et al. [26])
46 46
47 47 Κεφάλαιο 5 Υπολογιστικές δοκιμές Αποτελέσματα Στο παρόν κεφάλαιο παρουσιάζονται οι υπολογιστικές δικιμές που πραγματοποιήθηκαν ούτως ώστε να προσομοιωθεί η οστική ανανγένηση σε διάφορες παραλλαγές του μοντέλου που περιγράφηκε. Σε όλες τις περιπτώσεις το οστό υποβάλλεται σε κυκλική φόρτιση, όπου μία ημέρα αντιστοιχεί σε έναν κύκλο φόρτισης-αποφόρτισης. Εικόνα 43: Η μεταβολή το αδιάστατου φορτίου συναρτήσει του χρόνου για έναν κύκλος φόρτισης που αντιστοιχεί σε μία ημέρα Δοκιμή ελέγχου Με σκοπό να ελεγχθεί η λειτουργικότητα του μοντέλου και η ορθότητα των αποτελεσμάτων που προκύπτουν πραγματοποιήθηκε ένα δοκιμαστικό σενάριο φόρτισης κατά το οποίο το οστό υποβάλλεται σε κυκλική φόρτιση για 60 ημέρες. Το σενάριο παρουσιάζεται αναλυτικά στον παρακάτω πίνακα. Πίνακας 3: Σενάριο φόρτισης δοκιμής ελέγχου. Ημέρες Δύναμη [N] 0 έως έως Το σενάριο φόρτισης αυτό είναι δοκιμαστικό αλλά είναι κοντά στην πραγματικότητα, δηλαδή στις προτεινόμενες από τους ιατρούς δυνάμεις που είναι θεμιτό να ασκούνται στην περιοχή του κατάγματος κατά την περίοδο της επούλωσης. Τα αποτελέσματα αφορούν τις παραμορφώσεις ε zz και ε shear =ε mises και τις τιμές που παίρνουν καθόλη τη διάρκεια της εφαρμογής του σεναρίου φόρτισης. Χρησιμοποιώντας σαν κριτήριο τις τιμές αυτές ο αλγόριθμος ανανεώνει το μέτρο ελαστικότητας του πόρου, προσομοιώνοντας τη διαδικασία επούλωσης. Επίσης, σαν αποτέλεσμα εξάγεται η κατακόρυφη μετατόπιση των κόμβων της άνω επιφάνειας του πόρου καθόλη τη διάρκεια της φόρτισης ούτως ώστε να μετουσιωθεί σε διάγραμμα διακαταγματικής μετατόπισης
48 48 (IFM) που αποτελεί την τελική μορφή διαγράμματος από την οποία παρακολουθείται και κρίνεται η πορεία επούλωσης. Τα αποτελέσματα που αφορούν τις παραμορφώσεις και αντιστοιχούν στην πλειοψηφία των στοιχείων του πόρου εξάγονται ενδεικτικά από ένα κεντρικό στοιχείο της επιφάνειας του πόρου, ενώ τα αποτελέσματα που αφορούν την IFM από έναν κεντρικό κόμβο της επιφάνειας του πόρου. (α) Εικόνα 44: Κεντρικό στοιχείο και κόμβος που χρησιμοποιούνται για την εξαγωγή των αποτελεσμάτων. Σημειώνεται ότι οι τιμές των παραμορφώσεων είναι σχεδόν ίδιες στην πλειοψηφία των στοιχείων του πόρου και το ίδιο ισχύει και για τις τιμές της κάθετης μετατόπισης στους κόμβους του πόρου. Επίσης στο πρόγραμμα τοποθετείται την ημέρα 0 έως 1 η προένταση των βελόνων και η ανάλυση ξεκινάει από την ημέρα 1 και συνεπώς οι ημέρες των διαγραμμάτων αντιστοιχούν στις πραγματικές ημέρες συν μία ημέρα. Ακόμα, όλες οι μετατοπίσεις των διαγραμμάτων μετρώνται σε mm. Συνεπώς με την εφαρμογή του σεναρίου τα αποτελέσματα που προκύπτουν είναι: (β) (α) (β)
49 49 (γ) Εικόνα 45: (α) Διάγραμμα ισοδύναμης παραμόρφωσης ε mises με τον χρόνο. (β) Διάγραμμα της παραμόρφωσης στον κατακόρυφο άξονα ε zz με τον χρόνο. (γ) Διάγραμμα της κατακόρυφης μετατόπισης με τον χρόνο. (δ) Διάγραμμα της μεταβολής επούλωσης α με τον χρόνο. (δ) Παρατηρείται από τα διαγράμματα των παραμορφώσεων ε zz και ε mises ότι σε κανένα σημείο οι τιμές τους δεν ξεπερνούν τα όρια της Ζώνης 3. Κατά συνέπεια προκύπτει το συμπέρασμα ότι καθόλη τη διάρκεια της φόρτισης υπάρχει μια ταυτόχρονη συνεισφορά τόσο της μεταβλήτης α c όσο και της μεταβλητής α b στην αύξηση του μέτρου ελαστικότητας. Αυτό αντιπροσωπεύει στο μοντέλο τη βέλτιστη πορεία επούλωσης, δηλαδή την ταχύτερη δυνατή ανάρρωση. Η ταυτόχρονη αυτή συνεισφορά γίνεται φανερή στην Εικόνα 48 όπου αρχικά μέχρι την ημέρα 10 η αύξηση της α είναι πολύ μικρή λόγω των χρόνων ωρίμανσης Μ c και M b, στη συνέχεια η αύξηση οφείλεται τόσο στην εκθετική μορφή της α c όσο και στη γραμμική μορφή της α b και μετά την ημέρα 40, όπου έχει παρέλθει ο χρόνος t c + Μ c και η α c έχει πάρει τη μέγιστη τιμή της α c,max (ολοκληρώνοντας τη δημιουργία χόνδρου), η αύξηση είναι γραμμική γιατί οφείλεται μόνο στην α b. Το τελικό διάγραμμα της διακαταγματικής μετατόπισης (IFM) εξάγεται από το διάγραμμα της Εικόνας 47 παίρνοντας για κάθε κύκλο φόρτισης το εύρος της κατακόρυφης μετατόπισης.
50 50 Εικόνα 46: Εύρος κατακόρυφης μετατόπισης για έναν κύκλο φόρτισης. Συνεπώς το διάγραμμα IFM που προκύπτει είναι: 1 0,9 0,8 0,7 0,6 IFM [mm] 0,5 0,4 0,3 0,2 0, DAY Εικόνα 47: Διάγραμμα διακαταγματικής μετατόπισης IFM. Η καμπύλη του διαγράμματος είναι σιγμοειδής και αποτελείται από δύο μέρη εκατέροθεν της ημέρας 20. Την ημέρα αυτή σύμφωνα με το σενάριο πραγματοποιείται η αλλαγή του επιβαλλόμενου φορτίου από τα 80N στα 300N και αυτό εξηγεί και την παρατηρούμενη αύξηση στη διακαταγματική μετατόπιση τη δεδομένη χρονική στιγμή. Αυτή κατά βάση αποτελεί και την τελική μορφή διαγράμματος, από την οποία εξετάζεται η πορεία επούλωσης στα μηχανικά μοντέλα.
51 51 Σε αυτό το σημείο είναι σκόπιμο να σχολιαστεί ότι κάθε χρονική στιγμή οι τιμές των παραμορφώσεων είναι σχεδόν ίδιες στην πλειοψηφία των στοιχείων του πόρου κάνοντας έτσι ανεξάρτητη την επιλογή του στοιχείου με τα αποτελέσματα. Παρακάτω φαίνονται οι τιμές των παραμορφώσεων στο σύνολο του πόρου σε μία τυχαία χρονική στιγμή. (α) (β) (γ)
52 52 (δ) Εικόνα 48: Κατανομή των τιμών των παραμορφώσεων μια τυχαία χρονική στιγμή στην επιφάνεια αλλά και στο εσωτερικό του πόρου. (α) και (β) παραμόρφωση εmises (γ) και (δ) παραμόρφωση εzz Επίδραση παραμέτρων σε πραγματικό σενάριο φόρτισης Με σκοπό να διερευνηθεί η επίδραση των παραμέτρων του μοντέλου στην πορεία επούλωσης σχεδιάστηκε ένα πλάνο αλλαγής μεταβλητών, σύμφωνα με το οποίο αλλάζει η τιμή μίας μόνο μεταβλητής κάθε φορά για να διαπιστωθεί η επίδρασή της στο τελικό αποτέλεσμα. Εικόνα 49: Πλάνο αλλαγής μεταβλητών. Φαίνεται η αρχική τιμή της κάθε μεταβλητής και οι δύο παραλλαγές για την κάθε μία. Σε κάθε μεταβλητή που εξετάζεται δίνονται δύο παραλλαγές, δηλαδή μία αυξημένη και μία μειωμένη τιμή. Η αλλαγή της τιμής του χρόνου tc (cartilage formation time) από 36 ημέρες στο αρχικό μοντέλο σε 26 και 46 ημέρες συνοδεύτηκε από μία παράλληλη αλλαγή στην τιμή της αδιάστατης μεταβλητής Α1 από στο αρχικό μοντέλο σε και αντίστοιχα. Αυτό έγινε για να παραμείνει η μέγιστη τιμή αc,max που λαμβάνεται στο τέλος της περιόδου
53 53 δημιουργίας χόνδρου (t c +M c ) ίση με 0.3. Η αλλαγή αυτή της μεταβλητής t c προσομοιώνει μία μεγαλύτερη και μία μικρότερη οργανική ικανότητα δημιουργίας χόνδρου αντίστοιχα. Η αλλαγή του χρόνου ωρίμανσης του βιολογικού περιβάλλοντος M c από 4 σε 2 και 6 ημέρες συνεπάγεται μια οριζόντια μετακίνηση της καμπύλης α c και προσομοιώνει μια μεγαλύτερη και μία μικρότερη οργανική ικανότητα εκκίνησης της διαδικασίας επούλωσης αντίστοιχα. α c , , , t c =26 A 1 =0.064 t c =36 A 1 =0.049 t c =46 A 1 = DAY Εικόνα 50: Επίδραση αλλαγής της τιμής της t c στο διάγραμμα της α c με ταυτόχρονη αλλαγή της Α 1 έτσι ώστε η μέγιστη τιμή α c,max στον αντίστοιχο χρόνο t c +M c να παραμείνει 0.3. Εικόνα 51: Η αλλαγή της τιμής της μεταβλητής M c συνεπάγεται μια οριζόντια μετακίνηση της καμπύλης α c και συνεπώς της ημέρας που λαμβάνεται η μέγιστη τιμή α c,max =0.3. Η αλλαγή της μέγιστης τιμής α b,max συνεπάγεται της αλλαγή της κλίσης της καμπύλης α b κια προσομοιώνει μια μεγαλύτερη και μία μικρότερη συμβολή του οστού αντίστοιχα στο συνολικο μέτρο ελαστικότητας της διακαταγματικής περιοχής.
54 54 Εικόνα 52: Η αλλαγή της τιμής της α b,max που επιφέρει μεταβολή στην κλίση της καμπύλης της α b. Επίσης μεταβλήθηκε η τιμή του αρχικού μέτρου ελαστικότητας E a και του τελικού μέτρου ελαστικότητας E f και πραγματοποιήθηκε ακόμα, μια δοκιμή του αρχικού μοντέλου με τα όρια των παραμορφώσεων να μειώνονται στο μισό. Ταυτοχρόνως με σκοπό να γίνει η προσομοίωση της οστικής αναγέννησης πιο ρεαλιστική ζητήθηκε η ιατρική καθοδήγηση σχετικά με τα συνιστόμενα ασκούμενα φορτία στην διακαταγματική περιοχή κατά τη διάρκεια της επούλωσης. Έτσι προέκυψε ένα καινούριο σενάριο φόρτισης που φαίνεται παρακάτω: Πίνακας 4: Συνιστόμενο από τους ιατρούς σενάριο φόρτισης. Ημέρες Δύναμη [Ν] 0 έως έως έως έως Αυτό το σενάριο φόρτισης εφαρμόστηκε για το αρχικό μοντέλο και για τις 4 παραλλαγές του που προκύπτουν από την αλλαγή των μέτρων ελαστικότητας E a και E f αλλάζοντας μία μόνο μεταβλητή κάθε φορά. Οι περιπτώσεις που εξετάστηκαν δηλαδή με το καινούριο σενάριο είναι: E a =0.2MPa και E f =50MPa (αρχικό μοντέλο) E a =0.2MPa και E f =25MPa E a =0.2MPa και E f =100MPa E a =0.02MPa και E f =50MPa E a =2MPa και E f =50MPa Τονίζεται ότι σε όλες τις περιπτώσεις οι υπόλοιπες μεταβλητές του μοντέλου έμειναν σταθερές.
55 55 Με την πραγματοποίηση αυτών των δοκιμών πάνω στο πραγματικό σενάριο φόρτισης προέκυψε ότι σε όλες τις περιπτώσεις με εξαίρεση την τελευταία οι παραμορφώσεις ξεπερνούν τα όρια της Ζώνης 3 όπου μορφοποιείται τόσο οστό όσο και χόνδρος καθιστώντας έτσι αδύνατη την βέλτιστη πορεία επούλωσης. Στην περίπτωση με E a =0.2MPa και E f =100MPa οι παραμορφώσεις κρατήθηκαν εντός των ορίων της Ζώνης 2 (και εκτός της Ζώνης 3) οδηγώντας έτσι στην αύξηση της α c χωρίς να αυξάνεται η α b. Σε όλες τις υπόλοιπες περιπτώσεις οι παραμορφώσεις ξεπέρασαν και τα όρια της Ζώνης 2 οδηγώντας στο μηδενισμό τόσο της α c όσο και της α b και συνεπώς σε μηδενική επούλωση με μόνη εξαίρεση την περίπτωση με E a =2MPa και E f =50MPa η οποία κατέληξε σε επιτυχή πλήρη επούλωση. Παρακάτω παρουσιάζονται τα γραφήματα των παραμορφώσεων και της μεταβλητής α για αυτήν την περίπτωση καθώς και το τελικό διάγραμμα IFM που προκύπτει. (α) (β) (γ) Εικόνα 53: Διαγράμματα παραμορφώσεων (α),(β) κατακόρυφης μετατόπισης (γ) και μεταβλητής α (δ) με το χρόνο για την περίπτωση E a =2MPa και E f =50MPa με την εφαρμογή του πραγματικού σεναρίου. (δ)
56 56 0,5 0,45 0,4 E a =2 E f =50 MPa IFM [mm] 0,35 0,3 0,25 0,2 0,15 0,1 0, DAY Εικόνα 54: Διάγραμμα διακαταγματικής μετατόπισης IFM για την περίπτωση E a =2MPa και E f =50MPa με την εφαρμογή του πραγματικού σεναρίου. Στο διάγραμμα της IFM είναι εμφανείς οι κατακόρυφες αυξήσεις των τιμών που οφείλονται στην αύξηση του φορτίου τις καθορισμένες ημέρες σύμφωνα με το πραγματικό σενάριο. Στις υπόλοιπες περιπτώσεις οι παραμορφώσεις βγήκαν εκτός ορίων της Ζώνης 3, όπως προαναφέρθηκε. Παρουσιάζονται παρακάτω ενδεικτικά τα αποτελέσματα για την περίπτωση E a =0.2MPa και E f =50MPa. (α) (β)
57 57 Εικόνα 55: Υποβολή της περίπτωσης E a =0.2MPa και E f =50MPa στο πραγματικό σενάριο φόρτισης (α) Διάγραμμα της παραμόρφωσης ε mises με τον χρόνο. (β) Διάγραμμα της παραμόρφωσης ε zz με τον χρόνο. (γ) Διάγραμμα της μεταβλητής α με το χρόνο. Όπως γίνεται φανερό τόσο η παραμόρφωση ε mises όσο και η παραμόρφωση ε zz με την επιβολή των 200N ξεπερνούν τα όρια της Ζώνης 3. Η μεταβλητή α μετά την εφαρμογή των 200N μηδενίζεται λόγω του ότι η παραμόρφωση ε mises έχει ξεπεράσει και τα όρια της Ζώνης 2. Αυτό συνεπάγεται μηδενική επούλωση. (γ) 5.3. Εύρεση «οριακών» δυνάμεων και εξέταση παραμέτρων Η αδυναμία του αρχικού μοντέλου και των περιπτώσεων που εξετάστηκαν να ανταποκριθούν στο πραγματικό σενάριο φόρτισης προκάλεσε την ανάγκη να βρεθούν εκείνες οι δυνάμεις για την κάθε περίπτωση του πλάνου αλλαγής μεταβλητών που να προκαλούν παραμορφώσεις εντός των ορίων της Ζώνης 3 με στόχο μία επιτυχή πλήρη επούλωση χωρίς όμως να καθιστούν τις δυνάμεις αμελητέες. Η αναζήτηση δηλαδή επικεντρώθηκε στην εύρεση εκείνων των «οριακών» δυνάμεων που για την κάθε περίπτωση του σεναρίου φόρτισης αν εφαρμοστούν τις αντίστοιχες ημέρες που προτείνονται στο πραγματικό σενάριο οι παραμορφώσεις που προκύπτουν θα βρίσκονται εντός της Ζώνης 3 αλλά κοντά στα όριά της χωρίς ποτέ όμως να τα ξεπερνούν. Αυτό σημαίνει ότι η παραμόρφωση ε mises θα παίρνει τιμές περίπου μέσα στο εύρος ~ ενώ η ε zz θα παίρνει τιμές περίπου μέσα στο εύρος 0.17~0.23. Οι δυνάμεις που προέκυψαν για την κάθε περίπτωση του πλάνου αλλαγής μεταβλητών παρουσιάζονται παρακάτω:
58 58 E a =0.2MPa E f =50MPa Ημέρες Δύναμη [N] 0 έως έως έως έως E a =0.2MPa E f =100MPa Ημέρες Δύναμη [N] 0 έως έως έως έως E a =0.2MPa E f =25MPa Ημέρες Δύναμη [N] 0 έως έως έως έως E a =2MPa E f =50MPa Ημέρες Δύναμη [N] 0 έως έως έως έως E a =0.02MPa E f =50MPa Ημέρες Δύναμη [N] 0 έως έως έως έως t c =26 days Ημέρες Δύναμη [N] 0 έως έως έως έως t c =46 days Ημέρες Δύναμη [N] 0 έως έως έως έως M c =2 days Ημέρες Δύναμη [N] 0 έως έως έως έως M c =6 days Ημέρες Δύναμη [N] 0 έως έως έως έως α b,max =0.8 Ημέρες Δύναμη [N] 0 έως έως έως έως α b,max =0.6 Ημέρες Δύναμη [N] 0 έως έως έως έως Limits 50% Ημέρες Δύναμη [N] 0 έως έως έως έως Μέσω παρατήρησης στα αποτελέσματα των δοκιμών εξήχθη το εμπειρικό συμπέρασμα ότι όταν η παραμόρφωση ε mises βρίσκεται εντός του ορίου που της αντιστοιχεί για τη Ζώνης 3 τότε και η ε zz βρίσκεται εντός του αντίστοιχου ορίου της Ζώνης 3. Αυτό σημαίνει ότι σε όλες τις αναλύσεις που πραγματοποιήθηκαν η ε mises ήταν αυτή που πρώτη ξεπερνούσε το όριό της για τη συγκεκριμένη Ζώνη και στη συνέχεια η ε zz είτε ακολουθούσε είτε παρέμενε εντός των ορίων. Συνεπώς διασφαλίζοντας ότι η πρώτη βρίσκεται εντός ορίων διασφαλίζεται ότι και η δεύτερη βρίσκεται εντός ορίων για τη Ζώνη 3 στις αναλύσεις που πραγματοποιήθηκαν.
59 59 Ενδεικτικά παρουσιάζονται κάποια αποτελέσματα της εφαρμογή αυτών των δυνάμεων για την περίπτωση E a =0.2MPa E f =50MPa. Οι δυνάμεις έχουν υπολογιστεί έτσι ώστε τα αποτελέσματα των παραμορφώσεων σε όλες τις περιπτώσεις να είναι παρόμοια. Όλες οι περιπτώσεις με την εφαρμογή των παραπάνω δυνάμεων οδηγούν σε επιτυχή πλήρη επούλωση. (α) (β) (γ) (δ) Εικόνα 56: Αποτελέσματα της εφαρμογής των «οριακών» δυνάμεων για την περίπτωση E a =0.2MPa E f =50MPa. (α) παραμόρφωση ε mises (β) παραμόρφωση ε zz (γ) κατακόρυφης μετατόπισης (δ) μεταβλητή α. Η μεταβλητή α αυξάνεται με το βέλτιστο τρόπο μέχρι την τιμή 1 οδηγώντας σε επιτυχή πλήρη επούλωση. Παρακάτω παρουσιάζονται σε συγκριτικά διαγράμματα οι τιμές των «οριακών» δυνάμεων, ούτως ώστε να γίνει φανερή η επίδραση της αλλαγής της τιμής της κάθε μεταβλητής σε κάθε περίπτωση.
60 F [N] E a =0.2 E f =100 MPa E a =0.2 E f =50 MPa E a =0.2 E f =25 MPa DAY Εικόνα 57: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις αλλαγής της μεταβλητής E f. Από το διάγραμμα φαίνεται ότι όσο αυξάνεται η μεταβλητή Ef τόσο αυξάνεται η τιμή του μέτρου ελαστικότητας κάθε στιγμή και συνεπώς οι δυνάμεις που παραλαμβάνονται χωρίς να υπερβούν οι παραμορφώσεις τα όρια της Ζώνης F [N] E a =2 E f =50 MPa E a =0.2 E f =50 MPa E a =0.02 E f =50 MPa DAY Εικόνα 58: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις αλλαγής της μεταβλητής E a.
61 61 Από το διάγραμμα επιβεβαιώνεται ότι με την αύξηση της E a αυξάνεται η τιμή του μέτρου ελαστικότητας κάθε στιγμή και συνεπώς οι δυνάμεις που παραλαμβάνονται χωρίς να υπερβούν οι παραμορφώσεις τα όρια της Ζώνης F [N] t c =26 t c =36 t c = DAY Εικόνα 59: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις αλλαγής της μεταβλητής t c. Όπως γίνεται εμφανές όσο μειώνεται η tc αυξάνεται ο ρυθμός δημιουργίας χόνδρου και συνεπώς οι τιμές του Ε κάθε στιγμή άρα και οι δυνάμεις που παραλαμβάνονται χωρίς να υπερβούν οι παραμορφώσεις τα όρια της Ζώνης 3.
62 F [N] M c =2 M c =4 M c = DAY Εικόνα 60: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις αλλαγής της μεταβλητής M c. Η μείωση της μεταβλητής Mc αντιστοιχεί σε ταχύτερη ωρίμανση του βιολογικού περιβάλλοντος για τη δημιουργία χόνδρου και συνεπώς επιταχύνεται η χονδρογένεση άρα και οι δυνάμεις που παραλαμβάνονται χωρίς να υπερβούν οι παραμορφώσεις τα όρια της Ζώνης F [N] a bmax =0.8 a bmax =0.7 a bmax = Εικόνα 61: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις αλλαγής της μεταβλητής α b,max. DAY
63 63 Παρά το ότι η αύξηση της α b,max συνοδεύεται υποχρεωτικά από μείωση της α c,max η συνολική επίδραση προκαλεί αύξηση του Ε κάθε στιγμή και συνεπώς αυξάνονται οι δυνάμεις που παραλαμβάνονται χωρίς να υπερβούν οι παραμορφώσεις τα όρια της Ζώνης 3. Από τις διάφορες περιπτώσεις αλλαγής των μεταβλητών αυτές που προκαλούν αύξηση του μέτρου ελαστικότητας και συνεπώς οδηγούν σε αυξημένες «οριακές» δυνάμεις σε σχέση με το αρχικό μοντέλο παρουσιάζονται παρακάτω F [N] E a =0.2 E f =100 MPa t c =26 M c =2 a bmax =0.8 E a =2 E f =50 MPa E a =0.2 E f =50 MPa DAY Εικόνα 62: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις που αυτές αυξήθηκαν σε σχέση με το αρχικό μοντέλο. Όπως γίνεται φανερό, τις μεγαλύτερες δυνάμεις χωρίς να ξεπεράσουν οι παραμορφώσεις τα όρια της Ζώνης 3, ήταν σε θέση να παραλάβει το μοντέλο με E a =0.2 και E f =100 MPa. Αυτό σημαίνει ότι στο μοντέλο αυτό οι τιμές του Ε κάθε στιγμή είναι οι πιό αυξημένες. Αντίστοιχα παρουσιάζεται το διάγραμμα με τις υπόλοιπες περιπτώσεις που προκαλούν μείωση του μέτρου ελαστικότητας και συνεπώς οδηγούν σε μειωμένες «οριακές» δυνάμεις σε σχέση με το αρχικό μοντέλο.
64 F [N] E a =0.2 E f =50 MPa E a =0.2 E f =25 MPa Limits 50% DAY Εικόνα 63: Διάγραμμα «οριακών» δυνάμεων για τις περιπτώσεις που αυτές μειώθηκαν σε σχέση με το αρχικό μοντέλο. Όπως δείχνεται απο το διάγραμμα με εξαίρεση το διάγραμμα που τα όρια των παραμορφώσεων μειώθηκαν στο μισό, η περίπτωση που απαιτεί τα μικρότερα φορτία ώστε οι παραμορφώσεις να παραμείνουν εντός της Ζώνης 3 είναι εκείνη με E a =0.2 και E f =25 MPa. Αυτό σημαίνει ότι στο μοντέλο αυτό οι τιμές του Ε κάθε στιγμή είναι οι πιό μειωμένες. Σε αυτό το σημείο τονίζεται ότι οι δυνάμεις για κάθε περίπτωση δεν είναι απόλυτες αλλά κυμαίνονται σε ένα εύρος τιμών όπως και οι θεμιτές παραμορφώσεις που προκαλούν. Συνεπώς και η κλίση των καμπυλών που παρουσιάζονται στα διαγράμματα παραπάνω δεν είναι απόλυτη. Με το κλείσιμο αυτής της ενότητας παρατίθεται ένα συνοπτικό διάγραμμα IFM με ορισμένες από τις περιπτώσεις με τις αλλαγμένες μεταβλητές στις οποίες έχουν εφαρμοστεί οι αντίστοιχες «οριακές» δυνάμεις:
65 65 1 0,9 0,8 IFM [mm] 0,7 0,6 0,5 0,4 0,3 E a =0.2 E f =50 MPa t c =26 a bmax =0.8 0,2 0, DAY Εικόνα 64: Συνοπτικό διάγραμμα IFM με κάποιες από τις περιπτώσεις στις οποίες εφαρμόστηκαν οι αντίστοιχες «οριακές» δυνάμεις. Από το διάγραμμα φαίνεται ότι ενώ τα φορτία διαφέρουν για κάθε περίπτωση υπάρχει μια σύγκλιση στην διακαταγματική μετατόπιση που προκαλείται πράγμα που αποτέλεσε και τον αρχικό στόχο της εύρεσης αυτών των δυνάμεων. Επίσης η κλίση των καμπυλών σε κάθε σημείο δηλώνει το ρυθμό αύξησης του α σε κάθε περίπτωση. Για παράδειγμα η περίπτωση με t c =26 παρουσιάζει την μεγαλύτερη κλίση για το χρονικό διάστημα 17 έως 30 ημέρες καθώς σε αυτήν μόνο το α c αυξάνεται γρηγορότερα σε σχέση με τις άλλες περιπτώσεις ενώ το α b διατηρεί τον ίδιο ρυθμό, με αποτέλεσμα συνολικά ο ρυθμός αύξησης του α να είναι μεγαλύτερος Επίδραση διαμέτρου δακτυλίων Η διάμετρος των δακτυλίων είναι ένας από τους παράγοντες που επιδρά στη στιβαρότητα της κατασκευής. Συγκεκριμένα μείωση της διαμέτρου των δακτυλίων έχει δειχθεί ότι επιφέρει αύξηση της στιβαρότητας. Με σκοπό να αποτυπωθεί πώς επιδρά η αλλαγή της διαμέτρου των δακτυλίων στα αποτελέσματα πραγματοποιήθηκαν δύο δοκιμές στις οποίες η αρχική διάμετρος 180mm έγινε 150mm και 230mm. Σε αυτές τις περιπτώσεις εφαρμόστηκε το σενάριο φόρτισης των «οριακών» δυνάμεων που ανιστοιχούν στο αρχικό μοντέλο με E a =0.2 E f =50 MPa με τελικό σκοπό να συγκριθούν τα διαγράμματα IFM.
66 66 (α) (β) (γ) Εικόνα 65: Το πλάισιο Ilizarov με τρείς διαφορετικές διαμέτρους δακτυλίων (α) 150mm (β) 180mm (αρχικό) και (γ) 230mm. Περίπτωση με D=150mm Η σύκριση των αποτελεσμάτων των δύο μοντέλων με D=150mm και D=180mm ακολουθεί παρακάτω:
67 67 (α) (β) Εικόνα 66: (α) Αποτελέσματα για το μοντέλο με D=150mm (β) Αποτελέσματα για το μοντέλο με D=180mm. Παρατηρείται μέσω σύγκρισης των αποτελεσμάτων ότι τοσο οι παραμορφώσεις όσο και η κατακόρυφη μετατόπιση μειώθηκαν στην περίπτωση με D=150mm. Αυτό ήταν αναμενόμενο λόγω της αύξησης της δυσκαμψίας της κατασκευής. Συνεπώς η επούλωση είναι επιτυχής. Περίπτωση με D=230mm Σε αυτήν την περίπτωση τα αποτελέσματα που προέκυψαν είναι:
68 68 Εικόνα 67: Αποτελέσματα εφαρμογής «οριακών» δυνάμεων για το μοντέλο με D=230mm. Σε αυτήν την περίπτωση η αναμενόμενη μείωση της στιβαρότητας της κατασκευής οδήγησε στο να υπερβεί η παραμόρφωση ε mises τα όρια της Ζώνης 3 και συνεπώς η επούλωση να μην είναι επιτυχής. Παρακάτω παρουσιάζεται το συγκριτικό διάγραμμα IFM για το αρχικό μοντέλο με D=180mm και την περίπτωση με D=150mm. 1 0,9 0,8 0,7 IFM [mm] 0,6 0,5 0,4 0,3 0,2 0, DAY D=180mm D=150mm Εικόνα 68: Διάγραμμα IFM των περιπτώσεων D=180mm και D=150mm.
69 69 Είναι εμφανές ότι η αύξηση τη στιβαρότητας της κατασκευής παρά το ότι μείωσε την κατακόρυφη μετατόπιση, δεν επέδρασε σημαντικά στη διακαταγματική μετατόπιση IFM που κατά το μεγαλύτερο μέρος έμεινε σταθερή Εξάρτηση του μέτρου ελαστικότητας με την ακτίνα Όπως παρουσιάστηκε παραπάνω η δομή του οστού από το εσωτερικό προς το εξωτερικό είναι: μυελώδης αυλός, συμπαγές οστό, περιόστεο (Εικόνα 8). Συνεπώς είναι εμφανές ότι το μέτρο ελαστικότητας στο εσωτερικό του πόρου δεν είναι σε κάθε σημείο το ίδιο αλλά παρουσιάζει μια κατανομή που εξαρτάται από την ακτίνα. Πιο συγκεκριμένα το μέτρο ελαστικότητας αυξάνεται από το εσωτερικό προς το εξωτερικό ξεκινώντας δηλαδή από τον μαλακότερο μυελό των οστών και φτάνοντας στο σκληρότερο περιόστεο. Με σκοπό να προσεγγιστεί αυτή η εξάρτηση έγινε μια υπόθεση παραβολικής αύξησης του μέτρου ελαστικότητας Ε με την ακτίνα r και τροποιήθηκε ο αλγόριθμος ώστε να εσωματωθεί η σχέση: όπου, Ε: Το μέτρο ελαστικότητας ενός στοιχείου του πόρου Ε tot : Το μέγιστο μέτρο ελαστικότητας που συναντάται στόν πόρο τη δεομένη χρονική στιγμή. Είναι αυτό που εξαρτάται άμεσα από τη μεταβλητή επούλωσης α όπως περιγράφηκε στην ανάλυση του αλγορίθμου. r: η απόσταση ενός στοιχείου του πόρου από το κέντρο R: η ακτίνα του πόρου Συνεπώς με την προσθήκη αυτής της παραβολικής σχέσης πραγματοποιήθηκε μια δοκιμή πάνω στο δοκιμαστικό σενάριο φόρτισης του Πίνακα 3. Πίνακας 5: Σενάριο φόρτισης δοκιμής ελέγχου. Ημέρες Δύναμη [N] 0 έως έως Ορισμένα ενδεικτικά αποτελέσματα ακολουθούν παρακάτω.
70 70 (α) (β) Εικόνα 69: (α),(β) Η κατανομή του μέτρου ελαστικότητας στον πόρο μία τυχαία χρονική στιγμή κατά τη διάρκεια εφαρμογής του δοκιμαστικού σεναρίου. (γ) Οι τιμές του μέτρου ελαστικότητας την ίδια στιγμή κατά μήκος της ακτίνας, που ακολουθούν την παραβολική σχέση. (γ) Για τη σύγκριση του αποτελέσματος της παρούσας δοκιμής με την αρχική παρατίθεται το διάγραμμα της κατακόρυφης μετατόπισης και το συνολικό συγκριτικό διάγραμμα IFM των δύο περιπτώσεων.
71 71 (α) Εικόνα 70: Η κατακόρυφη μετατόπιση που προκύπτει με τη χρήση της παραβολικής σχέσης πάνω στο δοκιμαστικό σενάριο (α) για την παρούσα περίπτωση (β) για την αρχική. Η σύκριση των δύο διαγραμμάτων δείχνει ότι η μετατόπιση στον κατακόρυφο άξονα στην παρούσα περίπτωση παίρνει μεγαλύτερες τιμές. 1,2 (β) 1 0,8 IFM [mm] 0,6 0,4 Αρχικό μοντέλο Μοντέλο με E(r) 0, DAY Εικόνα 71: Συγκριτικό διάγραμμα IFM του αρχικού μοντέλου και του μοντέλου με την προσθήκη της σχέσης E(r). Είναι εμφανές ότι στην τελευταία ρεαλιστικότερη περίπτωση η διακαταγματική μετατόπιση παίρνει μεγαλύτερες τιμές.
72 72
73 73 Παράρτημα Α Έλεγχος επίδρασης πλέγματος Προκειμένου να ελεγχθεί κατά πόσο η πυκνότητα του πλέγματος επηρεάζει τα αποτελέσματα πραγματοποιήθηκε μια δοκιμή μετά από πύκνωση του πλέγματος του πόρου. Ο αριθμός των κόμβων του πόρου μετά την πύκνωση τριπλασιάστηκε φτάνοντας περίπου τους 3300 κόμβους. (α) (β) Εικόνα 72: Ο πόρος πρίν (α) και μετά (β) την πύκνωση. Η δοκιμή προβλέπει την κάθετη μετατόπιση του άνω οστού κατά 3mm. Στο υλικό του πόρου έχει δοθεί μέτρο ελαστικότητας Ε=10 MPa και λόγος του Poisson ν=0.4. Για τις δύο περιπτώσεις συγκρίνονται οι τιμές ορισμένων ενδεικτικών παραμέτρων που αντιστοιχούν στους κόμβους μίας τυχαίας διαμέτρου στην επιφάνεια του πόρου κάθε περίπτωσης μία τυχαία χρονική στιγμή. Ezz 0-0,1-0,2-0,3-0,4-0,5-0,6-0, ,8 Distance along diameter (α)
74 74 SMISES [MPa] Distance along diameter (β) Szz [MPa] Distance along diameter Εικόνα 73: Διάγραμμα των τιμών της (α) παραμόρφωσης στον κατακόρυφο άξονα (β) ισοδύναμης τάσης (γ) τάσης στον κατακόρυφο άξονα για τους κόμβους μιας τυχαίας διαμέτρου πάνω στην επιφάνεια του πόρου για το πυκνό και για το αραιό πλέγμα. Όπως προκύπτει από την παρατήρηση των διαγραμμάτων οι τιμές στους κόμβους των πλεγμάτων του πόρου ταυτίζονται, με εξαίρεση τους πολύ ακριανούς κόμβους, όπου συμβάλλουν άλλοι υπολογιστικοί παράγοντες. (γ)
75 75 Παράρτημα Β Έλεγχος αποτελεσμάτων δοκιμαστικού σεναρίου φόρτισης Σε μία περίπτωση όπως του δοκιμαστικού σεναρίου όπου το μέτρο ελαστικότητας αυξάνει συνεχώς η ελάχιστη τιμή που λαμβάνει κατά τη διάρκεια μίας ημέρας είναι αυτή που αντιστοιχεί στην αρχή της ημέρας. Στο γεγονός αυτό στηρίχθηκε ένας αριθμός ελέγχων που πραγματοποιήθηκαν με σκοπό να ελεγχθεί η εγκυρότητα των τιμών του τελικού διαγράμματος. Συγκεκριμένα, χρησιμοποιήθηκε σε μία δοκιμή ενός μονού κύκλου φόρτισης-αποφόρτισης η τιμή του μέτρου ελαστικότητας που αντιστοιχεί στην αρχή μια τυχαίας ημέρας και αυτή η τιμή κρατήθηκε σταθερή καθόλη τη διάρκεια του κύκλου. Αυτό πραγματοποιήθηκε για ένα εύρος ημερών. Το αναμενόμενο αποτέλεσμα είναι για κάθε ημέρα στη δοκιμή του μονού κύκλου η μια διακαταγματική μετατόπιση που προκύπτει να είναι λίγο μεγαλύτερη από αυτήν του διαγράμματος IFM για την ημέρα αυτή. 1 0,9 0,8 IFM [mm] 0,7 0,6 0,5 0,4 0,3 IFM 1 CYCLE RUN 0,2 0, DAY Εικόνα 74: Τιμές διακαταγματικής μετατόπισης των ημερών για τις οποίες πραγματοποιήθηκαν έλεγχοι μονών κύκλων φόρτισης-αποφόρτισης. Για το σύνολο των μονών κύκλων ελέγχου το αναμενόμενο αποτέλεσμα επιβεβαιώθηκε.
76 76
77 77 Παράρτημα Γ To πλαίσιο Taylor Spatial Frame Εικόνα 75: Πλαίσιο Taylor Spatial Frame (πηγή: Το πλαίσιο Taylor Spatial Frame είναι ένα πλαίσιο εξωτερικής οστεοσύνθεσης παρόμοιο με το πλαίσιο Ilizarov. Μία βασική διαφορά τους είναι ότι στο σύστημα TSF χρησιμοποιούνται ρυθμιζόμενες μεταλλικές τηλεσκοπικές ράβδοι, οι οποίες συγκρατούνται με τους δακτυλίους μέσω ειδικών συνδέσμων και μπορεί ανεξάρτητα η κάθε μία να συσπειρώνεται και να επιμηκύνεται. Αυτή η δυνατότητα καθιστά το σύστημα ικανό να προσαρμόζεται στην εκάστοτε κλινική περίπτωση. Το πλαίσιο TSF απαρτίζεται από τα ακόλουθα στοιχεία: Άνω δακτύλιος εσωτερικής διαμέτρου 180mm και πάχους 8mm Κάτω δακτύλιος εσωτερικής διαμέτρου 155mm και πάχους 8mm 2 half pins διαμέτρου 6mm 3 half pins διαμέτρου 5mm 1 ιατρική βελόνα τύπου Kirshner διαμέτρου 1.8mm 6 τηλεσκοπικές ράβδοι (struts) διαμέτρου 12mm Ο άνω δακτύλιος του παλισίου είναι ανοιχτού τύπου ενώ ο κάτω κλειστού τύπου. Οι δακτύλιοι συνδέονται μεταξύ τους μέσω των τηλεσκοπικών ράβδων οι οποίοι στα άκρα τους έχουν την ευχέρεια να περιστρέφονται μέσω ελεύθερων αρθρώσεων. Στο σημείο επαφής των ράβδων με τους δακτυλίους εντοπίζεται η δυνατότητα μικροκίνησης (τζόγος) η
78 78 οποία συνεπάγεται ενδοτικότητα στη μηχανική συμπεριφορά του πλαισίου κατά το αρχικό στάδιο επιβολής θλιπτικής φόρτισης. Ο δακτύλιος μοντελοποιήθηκε υπολογιστικά χρησιμοποιώτας για τους δακτυλίους γραμμικής παρεμβολής εξαεδρικά στοιχεία μειωμένης ολοκλήρωσης (C3D8R), για την βελόνα Kirshner όπως και για τα half pins συνδυασμός στοιχείων C3D8R και στοιχείων τύπου wedge (C3D6) καθώς και στοιχεία τύπου δοκού Timoshenko (B2), για τα εξαρτήματα συγκράτησης των half pins στους δακτυλίους (Rancho Cubes) όπως και για το οστό χρησιμοποιήθηκαν γραμμικής παρεμβολής τετραεδρικά στοιχεία (C3D4) και για τις τηλεσκοπικές ράβδους (struts) στοιχεία τύπου δοκού Timoshenko (B2). Τα υλικά που χρησιμοποιήθηκαν κατά την μοντελοποίηση του πλαισίου είναι γραμμικώς ελαστικά και οι ιδιότητές τους φαίνονται στον πίνακα παρακάτω: Πίνακας 6: Ιδιότητες υλικών κατά την μοντελοποίηση. Μηχανικό Μέρος Ιατρικές βελόνες, συνδετικές ράβδοι και συνδετικά μέρη Υλικό Μέτρο ελαστικότητας (GPa) Λόγος Poisson (ν) Χάλυβας Δακτύλιοι Αλουμίνιο Εξωτερικό μέρος οστού Οστό Half pins Τιτάνιο Οι κινηματικοί περιορισμοί είναι παρόμοιοι με αυτούς που περιγράφηκαν στο πλαίσιο Ilizarov. Η βελόνα προεντείνεται με δύναμη 930N. Σε παλιότερη εργασία πραγματοποιήθηκε τόσο υπολογιστικά όσο και πειραματικά η δοκιμή κατακόρυφης μετατόπισης του άνω οστού κατά 3.5mm και παρατηρήθηκε απόκλιση των αποτελεσμάτων όταν οι συνδέσεις των τηλεσκοπικών ράβδων στους δακτυλίους θεωρηθούν άκαμπτες (stiff). Για να συνυπολογιστεί η ενδοτικότητα των συνδέσεων στην ανάλυση και να υπάρξει σύγκλιση των πειραματικών και των υπολογιστικών αποτελεσμάτων χρειάστηκε να θεωρηθεί ότι τα κατακόρυφα τμήματα των τηλεσκοπικών ράβδων έχουν χαμηλοτερη ελαστικότητα.
79 79 Εικόνα 76: Διάγραμμα δύναμης-μετατόπισης κατά την αξονική φόρτιση του πλαισίου TSF. Στην ανάλυση θεωρείται ότι τα κατακόρυφα τμήματα των τηλεσκοπικών ράβδων έχουν χαμηλότερη ελαστικότητα έτσι ώστε η συμπεριφορά που προκύπτει από την ανάλυση και την πειραματική διερεύνηση να συμφωνούν μεταξύ τους. Στο πλαίσιο της παρούσας εργασίας πραγματοποιήθηκε μια προσπάθεια ακριβέστερης μοντελοποίησης της σύνδεσης των τηλεσκοπικών ράβρων με τους δακτυλίους. Με αυτόν τον σκοπό προσομοιώθηκαν τα συνδετικά μέρη με τα οποία πραγματοποιείται η σύνδεση όπως φαίνεται παρακάτω: Εικόνα 77: Προσομοίωση των τμημάτων των τηλεσκοπικών ράβδων μέσω των οποίων πραγματοποιείται η σύνδεση με τους δακτυλίους. Για την μοντελοποίηση τους χρησιμοποιήθηκαν γραμμικής παρεμβολής τετραεδρικά στοιχεία (C3D4). Ταυτόχρονα κατά την μοντελοποίση συνυπολογίστηκε η δυνατότητα μικροκίνησης του συνδετικού τμήματος (τζόγος). Εικόνα 78: Τα συνδετικά μέρη δεν εφαρμόζουν πλήρως στον δακτύλιο αλλά υπάρχει δυνατότητα μικροκίνησης (τζόγος).
80 80 Εικόνα 79: Μοντέλο TSF με την τοποθέτηση των μοντελοποιημένων συνδετικών μερών. Μετά την τοποθέτηση των συνδετικών μερών στο υπολογιστικό πλαίσιο προσομοιώθηκε η ίδια δοκιμή κατακόρυφης μετατόπισης του άνω οστού κατά 3.5mm. Εικόνα 80: Υπολογιστική δοκιμή χωρίς συνδετικά μέρη για στοιβαρή σύνδεση και με συνδετικά μέρη για στοιβαρή σύνδεση. Η προσομοίωση πραγματοποιήθηκε με τα συνδετικά μέρη για κανονικό μέτρο ελαστικότητας των κατακόρυφων τηλεσκοπικών ράβδων. Η προσθήκη των συνδετικών μερών δεν φαίνεται να μειώνει τη δυσκαμψία του συστήματος.
Ερειστικό Σύστημα. Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία.
 Ερειστικό Σύστημα Μια εργασία στο μάθημα της Βιολογίας από της μαθήτριες Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία. Υπεύθυνη Καθηγήτρια: Ζαρφτζιάν Μαριλένα Περιεχόμενα: Εισαγωγή Οστά Σύσταση του οστίτη
Ερειστικό Σύστημα Μια εργασία στο μάθημα της Βιολογίας από της μαθήτριες Γεωργιάδου Ελευθερία και Μηλιάδου Αθανασία. Υπεύθυνη Καθηγήτρια: Ζαρφτζιάν Μαριλένα Περιεχόμενα: Εισαγωγή Οστά Σύσταση του οστίτη
Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας
 Οστίτης Ιστός Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας λ ί Οστά εξειδικευμένος στηρικτικός-συνδετικός ιστός χαρακτηριστικά: σκληρή σύσταση και ακαμψία, λόγω παρουσίας αλάτων ασβεστίου στην
Οστίτης Ιστός Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας λ ί Οστά εξειδικευμένος στηρικτικός-συνδετικός ιστός χαρακτηριστικά: σκληρή σύσταση και ακαμψία, λόγω παρουσίας αλάτων ασβεστίου στην
 Οστίτης Ιστός Dr. med. Λουκάς Κωνσταντίνου Ορθοπεδικός Χειρουργός Στήριξη Κίνηση Οστά εξειδικευµένος στηρικτικός-συνδετικός ιστός χαρακτηριστικά: σκληρήσύστασηκαι ακαµψία, λόγω παρουσίαςαλάτων ασβεστίουστην
Οστίτης Ιστός Dr. med. Λουκάς Κωνσταντίνου Ορθοπεδικός Χειρουργός Στήριξη Κίνηση Οστά εξειδικευµένος στηρικτικός-συνδετικός ιστός χαρακτηριστικά: σκληρήσύστασηκαι ακαµψία, λόγω παρουσίαςαλάτων ασβεστίουστην
ΜΕΡΟΣ ΠΡΩΤΟ: ΑΝΑΦΟΡΑ ΣΤΑ ΟΣΤΑ ΚΑΙ ΓΕΝΙΚΑ ΣΤΟΙΧΕΙΑ
 ΜΕΡΟΣ ΠΡΩΤΟ: ΑΝΑΦΟΡΑ ΣΤΑ ΟΣΤΑ ΚΑΙ ΓΕΝΙΚΑ ΣΤΟΙΧΕΙΑ - 7 - Αναφορά στα οστά και γενικά στοιχεία 1.1 Οστεολογία Οστεολογία ονοµάζουµε τον ειδικό εκείνο κλάδο της ανατοµίας που ασχολείται αποκλειστικά µε την
ΜΕΡΟΣ ΠΡΩΤΟ: ΑΝΑΦΟΡΑ ΣΤΑ ΟΣΤΑ ΚΑΙ ΓΕΝΙΚΑ ΣΤΟΙΧΕΙΑ - 7 - Αναφορά στα οστά και γενικά στοιχεία 1.1 Οστεολογία Οστεολογία ονοµάζουµε τον ειδικό εκείνο κλάδο της ανατοµίας που ασχολείται αποκλειστικά µε την
Χόνδρος Αρθρώσεις. Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας
 Χόνδρος Αρθρώσεις Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ς ιστός συμπαγής αλλά εύκαμπτος Λειτουργίες Χόνδρου υποστήριξη μαλακών ιστών απορρόφηση κραδασμών
Χόνδρος Αρθρώσεις Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ς ιστός συμπαγής αλλά εύκαμπτος Λειτουργίες Χόνδρου υποστήριξη μαλακών ιστών απορρόφηση κραδασμών
ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ
 ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ Θέμα: ΜΙΚΡΟΣΚΟΠΙΚΗ ΠΑΡΑΤΗΡΗΣΗ ΜΟΝΙΜΩΝ ΠΑΡΑΣΚΕΥΑΣΜΑΤΩΝ ΚΥΤΤΑΡΩΝ ΚΑΙ ΙΣΤΩΝ Μέσος χρόνος πειράματος: 45 λεπτά Α. ΑΝΑΛΩΣΙΜΑ
ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ Θέμα: ΜΙΚΡΟΣΚΟΠΙΚΗ ΠΑΡΑΤΗΡΗΣΗ ΜΟΝΙΜΩΝ ΠΑΡΑΣΚΕΥΑΣΜΑΤΩΝ ΚΥΤΤΑΡΩΝ ΚΑΙ ΙΣΤΩΝ Μέσος χρόνος πειράματος: 45 λεπτά Α. ΑΝΑΛΩΣΙΜΑ
ΚΥΤΤΑΡΑ. Καρβουντζή Ηλιάνα (Βιολόγος) 1
 ΚΥΤΤΑΡΑ ΖΥΓΩΤΟ: Το πρώτο κύτταρο του οργανισμού από το οποίο με συνεχείς κυτταρικές διαιρέσεις προκύπτουν όλα. ΔΙΑΦΟΡΟΠΟΙΗΣΗ: Διαδικασία με την οποία τα κύτταρα αποκτούν διαφορετικά μορφολογικά και λειτουργικά
ΚΥΤΤΑΡΑ ΖΥΓΩΤΟ: Το πρώτο κύτταρο του οργανισμού από το οποίο με συνεχείς κυτταρικές διαιρέσεις προκύπτουν όλα. ΔΙΑΦΟΡΟΠΟΙΗΣΗ: Διαδικασία με την οποία τα κύτταρα αποκτούν διαφορετικά μορφολογικά και λειτουργικά
ΕΠΑΝΑΛΗΨΗ ΚΕΦΑΛΑΙΩΝ 1-7-8
 ΕΠΑΝΑΛΗΨΗ ΚΕΦΑΛΑΙΩΝ 1-7-8 Α. ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Στον ανθρώπινο οργανισµό a) όλα τα κύτταρα έχουν το ίδιο σχήµα και την ίδια λειτουργία b) υπάρχουν κύτταρα µε το ίδιο σχήµα και την ίδια λειτουργία
ΕΠΑΝΑΛΗΨΗ ΚΕΦΑΛΑΙΩΝ 1-7-8 Α. ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Στον ανθρώπινο οργανισµό a) όλα τα κύτταρα έχουν το ίδιο σχήµα και την ίδια λειτουργία b) υπάρχουν κύτταρα µε το ίδιο σχήµα και την ίδια λειτουργία
5. Στήριξη και κίνηση
 5. Στήριξη και κίνηση 5.4 Το µυοσκελετικό σ ύ σ τ η µ α του ανθρώπου κεφαλή ΤΟ ΕΡΕΙΣΤΙΚΟ ΣYΣΤΗΜΑ (ΣΚΕΛΕΤΟΣ) ΤΟY ΑΝΘΡΩΠΟY άνω άκρα Ο σκελετός των άκρων κάτω άκρα Ο σκελετός του κορµού θώρακας σ π ο ν δ
5. Στήριξη και κίνηση 5.4 Το µυοσκελετικό σ ύ σ τ η µ α του ανθρώπου κεφαλή ΤΟ ΕΡΕΙΣΤΙΚΟ ΣYΣΤΗΜΑ (ΣΚΕΛΕΤΟΣ) ΤΟY ΑΝΘΡΩΠΟY άνω άκρα Ο σκελετός των άκρων κάτω άκρα Ο σκελετός του κορµού θώρακας σ π ο ν δ
ΕΡΓΑΣΤΗΡΙΟ ΙΣΤΟΛΟΓΙΑΣ Μ. ΠΑΥΛΙ ΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΙΣΤΟΛΟΓΙΑΣ Μ. ΠΑΥΛΙ ΗΣ Hράκλειο, εκέμβριος 2011 ΤΥΠΟΙ ΙΣΤΩΝ 1. Eπιθηλιακός Πολυεδρικά κύτταρα που είναι πάρα πολύ στενά συνδεδεμένα και φέρουν ελάχιστη μεσοκυττάρια ουσία 2. Συνδετικός Κύτταρα
ΕΡΓΑΣΤΗΡΙΟ ΙΣΤΟΛΟΓΙΑΣ Μ. ΠΑΥΛΙ ΗΣ Hράκλειο, εκέμβριος 2011 ΤΥΠΟΙ ΙΣΤΩΝ 1. Eπιθηλιακός Πολυεδρικά κύτταρα που είναι πάρα πολύ στενά συνδεδεμένα και φέρουν ελάχιστη μεσοκυττάρια ουσία 2. Συνδετικός Κύτταρα
Χόνδρος Αρθρώσεις. Σοφία Χαβάκη Επικ. Καθηγήτρια Εργαστήριο Ιστολογίας-Εμβρυολογίας
 Χόνδρος Αρθρώσεις Σοφία Χαβάκη Επικ. Καθηγήτρια Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ιστός συμπαγής αλλά εύκαμπτος Λειτουργίες Χόνδρου υποστήριξη μαλακών ιστών απορρόφηση κραδασμών
Χόνδρος Αρθρώσεις Σοφία Χαβάκη Επικ. Καθηγήτρια Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ιστός συμπαγής αλλά εύκαμπτος Λειτουργίες Χόνδρου υποστήριξη μαλακών ιστών απορρόφηση κραδασμών
Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη
 Εισαγωγη στην Ορθοπαιδικη Κωνσταντινος Ν. ΜΑΛΙΖΟΣ Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη Εισαγωγη στην Ορθοπαιδικη Ορθοπαιδικη ή Ορθοπεδικη «παιδο-ορθωτικη» (Γ. Μπαμπινιωτης) Πανεπιστημιο Θεσσαλιας Ιατρικη
Εισαγωγη στην Ορθοπαιδικη Κωνσταντινος Ν. ΜΑΛΙΖΟΣ Πανεπιστημιο Θεσσαλιας Ιατρικη Σχολη Εισαγωγη στην Ορθοπαιδικη Ορθοπαιδικη ή Ορθοπεδικη «παιδο-ορθωτικη» (Γ. Μπαμπινιωτης) Πανεπιστημιο Θεσσαλιας Ιατρικη
Εργαστήριο Ιατρικής Φυσικής. Φυσική του Σκελετού
 Εργαστήριο Ιατρικής Φυσικής Φυσική του Σκελετού Τα οστά πραγματοποιούν τουλάχιστον έξι λειτουργίες στο ανθρώπινο σώμα: 1. Υποστήριξη 2. Κίνηση 3. Προστασία διαφόρων οργάνων 4. Αποθήκευση χημικών ουσιών
Εργαστήριο Ιατρικής Φυσικής Φυσική του Σκελετού Τα οστά πραγματοποιούν τουλάχιστον έξι λειτουργίες στο ανθρώπινο σώμα: 1. Υποστήριξη 2. Κίνηση 3. Προστασία διαφόρων οργάνων 4. Αποθήκευση χημικών ουσιών
Παθητικά στοιχεία. Οστά. Αρθρ. χόνδροι. Πολύπλοκη κατασκευή. Σύνδεσμοι τένοντες. Ενεργητικά στοιχεία. Ανομοιογενή βιολογικά υλικά.
 Κινησιοθεραπεία Ιδιότητες Υλικών 1 ΣΤΟΙΧΕΙΑ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Ανθρώπινο σώμα Παθητικά στοιχεία Οστά Αρθρ. χόνδροι Πολύπλοκη κατασκευή Σύνδεσμοι τένοντες Ανομοιογενή βιολογικά υλικά Ενεργητικά στοιχεία Μύες
Κινησιοθεραπεία Ιδιότητες Υλικών 1 ΣΤΟΙΧΕΙΑ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Ανθρώπινο σώμα Παθητικά στοιχεία Οστά Αρθρ. χόνδροι Πολύπλοκη κατασκευή Σύνδεσμοι τένοντες Ανομοιογενή βιολογικά υλικά Ενεργητικά στοιχεία Μύες
Χόνδρος Οστίτης Ιστός. Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας
 Χόνδρος Οστίτης Ιστός Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ιστός συμπαγής αλλά εύκαμπτος υποστήριξη μαλακών ιστών εξασφάλιση oλισθηρής επιφάνειας για
Χόνδρος Οστίτης Ιστός Σοφία Χαβάκη Λέκτορας Εργαστήριο Ιστολογίας-Εμβρυολογίας Χόνδρος συνδετικός-στηρικτικός ιστός συμπαγής αλλά εύκαμπτος υποστήριξη μαλακών ιστών εξασφάλιση oλισθηρής επιφάνειας για
1. ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ
 ΚΕΦΑΛΑΙΟ 1 1. ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ ΚΥΤΤΑΡΑ ΚΑΙ ΙΣΤΟΙ Ο ανθρώπινος οργανισμός συνίσταται α- πό τρισεκατομμύρια κύτταρα. Τα κύτταρα αυτά εμφανίζουν σημαντική ποικιλομορφία, που αφορά το μέγεθος,
ΚΕΦΑΛΑΙΟ 1 1. ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ ΚΥΤΤΑΡΑ ΚΑΙ ΙΣΤΟΙ Ο ανθρώπινος οργανισμός συνίσταται α- πό τρισεκατομμύρια κύτταρα. Τα κύτταρα αυτά εμφανίζουν σημαντική ποικιλομορφία, που αφορά το μέγεθος,
5.4 Το μυοσκελετικό σύστημα του ανθρώπου ΜΙΚΡΕΣ ΕΡΕΥΝΕΣ ΚΑΙ ΕΡΓΑΣΙΕΣ
 3. Να βάλετε σε κύκλο το γράμμα που αντιστοιχεί στη φράση που συμπληρώνει σωστά την πρόταση: Α. Η μέλισσα είναι έντομο που: α. έχει σπονδυλική στήλη β. μπορεί να κολυμπάει γ. πετάει με τη βοήθεια μεμβρανωδών
3. Να βάλετε σε κύκλο το γράμμα που αντιστοιχεί στη φράση που συμπληρώνει σωστά την πρόταση: Α. Η μέλισσα είναι έντομο που: α. έχει σπονδυλική στήλη β. μπορεί να κολυμπάει γ. πετάει με τη βοήθεια μεμβρανωδών
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ. Κεφάλαιο 5 «Στήριξη και Κίνηση»
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Κεφάλαιο 5 «Στήριξη και Κίνηση» Ποια είναι η διαφορά ανάμεσα στις λέξεις κίνηση και μετακίνηση; Μετακινούνται όλοι οι οργανισμοί; Άσκηση σελ. 98 ΣΒ Α. Η Κίνηση στους μονοκύτταρους οργανισμούς
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Κεφάλαιο 5 «Στήριξη και Κίνηση» Ποια είναι η διαφορά ανάμεσα στις λέξεις κίνηση και μετακίνηση; Μετακινούνται όλοι οι οργανισμοί; Άσκηση σελ. 98 ΣΒ Α. Η Κίνηση στους μονοκύτταρους οργανισμούς
ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ. Ένα ταξίδι στις βασικές έννοιες βιολογίας...
 ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ Ένα ταξίδι στις βασικές έννοιες βιολογίας... Κύτταρο Η βασική δομική και λειτουργική μονάδα που εκδηλώνει το φαινόμενο της ζωής. Πρώτος ο Βρετανός Robert Hooke το 1665 παρατηρώντας
ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ Ένα ταξίδι στις βασικές έννοιες βιολογίας... Κύτταρο Η βασική δομική και λειτουργική μονάδα που εκδηλώνει το φαινόμενο της ζωής. Πρώτος ο Βρετανός Robert Hooke το 1665 παρατηρώντας
ΕΞΕΙΔΙΚΕΥΜΕΝΟΣ ΣΥΝΔΕΤΙΚΟΣ ΙΣΤΟΣ
 Κεφάλαιο 4 ΕΞΕΙΔΙΚΕΥΜΕΝΟΣ ΣΥΝΔΕΤΙΚΟΣ ΙΣΤΟΣ Στόχοι κεφαλαίου Αυτό το κεφάλαιο θα φανεί χρήσιμο στη(ν): 1. Διάκριση μεταξύ των τριών τύπων χόνδρου. 2. Διάκριση μεταξύ των διαφόρων κυτταρικών τύπων που φυσιολογικά
Κεφάλαιο 4 ΕΞΕΙΔΙΚΕΥΜΕΝΟΣ ΣΥΝΔΕΤΙΚΟΣ ΙΣΤΟΣ Στόχοι κεφαλαίου Αυτό το κεφάλαιο θα φανεί χρήσιμο στη(ν): 1. Διάκριση μεταξύ των τριών τύπων χόνδρου. 2. Διάκριση μεταξύ των διαφόρων κυτταρικών τύπων που φυσιολογικά
Κινητικό σύστημα του ανθρώπου Μέρος Ι: Ερειστικό, μυϊκό και συνδεσμικό σύστημα. Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια
 Κινητικό σύστημα του ανθρώπου Μέρος Ι: Ερειστικό, μυϊκό και συνδεσμικό σύστημα Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Τα συστήματα του ανθρώπινου σώματος Αναπνευστικό σύστημα (αποτελείται
Κινητικό σύστημα του ανθρώπου Μέρος Ι: Ερειστικό, μυϊκό και συνδεσμικό σύστημα Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Τα συστήματα του ανθρώπινου σώματος Αναπνευστικό σύστημα (αποτελείται
ΕΡΑΣΜΕΙΟΣ ΕΛΛΗΝΟΓΕΡΜΑΝΙΚΗ ΣΧΟΛΗ
 ΕΡΑΣΜΕΙΟΣ ΕΛΛΗΝΟΓΕΡΜΑΝΙΚΗ ΣΧΟΛΗ Ιδιωτικό Γενικό Λύκειο Όνομα: Ημερομηνία:././2014 ΤΑΞΗ : A Λυκείου ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΡΩΤΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 1: Από το κύτταρο στον οργανισμό ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΤΟ
ΕΡΑΣΜΕΙΟΣ ΕΛΛΗΝΟΓΕΡΜΑΝΙΚΗ ΣΧΟΛΗ Ιδιωτικό Γενικό Λύκειο Όνομα: Ημερομηνία:././2014 ΤΑΞΗ : A Λυκείου ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΡΩΤΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 1: Από το κύτταρο στον οργανισμό ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΤΟ
7. ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ. Αποτελεί αποθήκη αλάτων, κυρίως ασβεστίου και φωσφόρου. Στηρίζει το σώμα και καθορίζει τη μορφή του.
 7. ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ Το ερειστικό σύστημα περιλαμβάνει τα οστά, τα οποία συνδεόμενα στις αρθρώσεις σχηματίζουν το σκελετό (εικ. 7.1). Η λέξη σκελετός μας φέρνει συνήθως στο νου μία δομή σκληρή και ξερή.
7. ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ Το ερειστικό σύστημα περιλαμβάνει τα οστά, τα οποία συνδεόμενα στις αρθρώσεις σχηματίζουν το σκελετό (εικ. 7.1). Η λέξη σκελετός μας φέρνει συνήθως στο νου μία δομή σκληρή και ξερή.
ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ 15/9/2014. ΚΕΦΑΛΑΙΟ 1 ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ Κύτταρα και ιστοί Όργανα και συστήματα οργάνων
 Κύτταρα και ιστοί: Πλήθος κυττάρων ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ Ο ανθρώπινος οργανισμός αποτελείται από τρισεκατομμύρια κύτταρα. ΚΕΦΑΛΑΙΟ 1 ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ Κύτταρα και ιστοί Όργανα και συστήματα οργάνων
Κύτταρα και ιστοί: Πλήθος κυττάρων ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ Ο ανθρώπινος οργανισμός αποτελείται από τρισεκατομμύρια κύτταρα. ΚΕΦΑΛΑΙΟ 1 ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ Κύτταρα και ιστοί Όργανα και συστήματα οργάνων
ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΨΗ
 ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΜΑ 1ο 1. Κυτταρική διαφοροποίηση ονομάζουμε: α. Την δομική κυρίως εξειδίκευση των συστημάτων β. Την δομική και λειτουργική εξειδίκευση των κυττάρων γ. Την λειτουργική εξειδίκευση
ΒΙΟΛΟΓΙΑ Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΜΑ 1ο 1. Κυτταρική διαφοροποίηση ονομάζουμε: α. Την δομική κυρίως εξειδίκευση των συστημάτων β. Την δομική και λειτουργική εξειδίκευση των κυττάρων γ. Την λειτουργική εξειδίκευση
ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ
 ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΜΚ 0903 «Κινησιολογία» 1η Διάλεξη: «Οστά
ΕΠΕΑΕΚ ΑΝΑΜΟΡΦΩΣΗ ΤΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥΔΩΝ ΤΟΥ Τ.Ε.Φ.Α.Α. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΘΕΣΣΑΛΙΑΣ - ΑΥΤΕΠΙΣΤΑΣΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΜΚ 0903 «Κινησιολογία» 1η Διάλεξη: «Οστά
ΔΙΑΓΝΩΣΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗΝ ΟΡΘΟΠΑΙΔΙΚΗ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ
 ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΙΣΤΟΡΙΚΟ + ΚΛΙΝΙΚΗ ΕΞΕΤΑΣΗ = Α & Ω ΣΤΗΝ! ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική απεικονιστική μέθοδος) ΠΡΟΣΘΙΟΠΙΣΘΙΑ ΠΛΑΓΙΑ ΛΟΞΗ ΕΙΔΙΚΗ ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική
ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΙΣΤΟΡΙΚΟ + ΚΛΙΝΙΚΗ ΕΞΕΤΑΣΗ = Α & Ω ΣΤΗΝ! ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική απεικονιστική μέθοδος) ΠΡΟΣΘΙΟΠΙΣΘΙΑ ΠΛΑΓΙΑ ΛΟΞΗ ΕΙΔΙΚΗ ΑΠΛΕΣ ΑΚΤΙΝΟΓΡΑΦΙΕΣ (Βασική
Από το βιβλίο του Δρ. Πέτρου Α. Πουλμέντη
 Από το βιβλίο του Δρ. Πέτρου Α. Πουλμέντη Κεφάλαιο 1 Εισαγωγή στη βιολογική μηχανική Κεφάλαιο 2 Εκβιομηχανική των οστών Οι διαφάνειες που ακολουθούν Η ΑΝΑΤΟΜΙΚΗ ΘΕΣΗ ΤΟΥ ΑΝΘΡΩΠΟΥ Για να περιγράψουμε τα
Από το βιβλίο του Δρ. Πέτρου Α. Πουλμέντη Κεφάλαιο 1 Εισαγωγή στη βιολογική μηχανική Κεφάλαιο 2 Εκβιομηχανική των οστών Οι διαφάνειες που ακολουθούν Η ΑΝΑΤΟΜΙΚΗ ΘΕΣΗ ΤΟΥ ΑΝΘΡΩΠΟΥ Για να περιγράψουμε τα
Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ. Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών
 Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών 1951 Gavril Abramovich Ilizarov Μέθοδος Ilizarov «συνδυασμός φλοιοτομής και σταδιακής, ελεγχόμενης
Η ΑΝΤΙΜΕΤΩΠΙΣΗ ΤΩΝ ΟΣΤΙΚΩΝ ΕΛΛΕΙΜΜΑΤΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΟΣΤΕΟΜΕΤΑΦΟΡΑΣ Ορθοπαιδική Κλινική Πανεπιστημίου Πατρών 1951 Gavril Abramovich Ilizarov Μέθοδος Ilizarov «συνδυασμός φλοιοτομής και σταδιακής, ελεγχόμενης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Κινησιολογία Ενότητα 1: Οστά οστίτης ιστός Αθανάσιος Τσιόκανος Τμήμα Επιστήμης Φυσικής Αγωγής και Αθλητισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Κινησιολογία Ενότητα 1: Οστά οστίτης ιστός Αθανάσιος Τσιόκανος Τμήμα Επιστήμης Φυσικής Αγωγής και Αθλητισμού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ
 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ Από τι αποτελείται ο ανθρώπινος οργανισμός; Ο ανθρώπινος οργανισμός αποτελείται από περίπου 10 τρισεκατομμύρια κύτταρα, που οργανώνονται σε ιστούς, οι ιστοί σε όργανα και τα όργανα
2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΘΕΩΡΙΑΣ Από τι αποτελείται ο ανθρώπινος οργανισμός; Ο ανθρώπινος οργανισμός αποτελείται από περίπου 10 τρισεκατομμύρια κύτταρα, που οργανώνονται σε ιστούς, οι ιστοί σε όργανα και τα όργανα
ΙΣΤΟΙ Ως προς τη µορφή και τη λειτουργία τους. Κυτταρική διαφοροποίηση.
 ΙΣΤΟΙ 1. Τα κύτταρα που αποτελούν τον οργανισµό µας, διακρίνονται σε διάφορους τύπους, παρά το γεγονός ότι όλα, τελικώς, προέρχονται από το ζυγωτό, δηλαδή το πρώτο κύτταρο µε το οποίο ξεκίνησε η ζωή µας.
ΙΣΤΟΙ 1. Τα κύτταρα που αποτελούν τον οργανισµό µας, διακρίνονται σε διάφορους τύπους, παρά το γεγονός ότι όλα, τελικώς, προέρχονται από το ζυγωτό, δηλαδή το πρώτο κύτταρο µε το οποίο ξεκίνησε η ζωή µας.
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
Ανθρώπινος Σκελετός. ñ Ανθεκτικότητα στην αποικοδόµηση. ñ Ιδανική πηγή πληροφοριών: προϊστορικά, ιστορικά, σύγχρονα
 Ανθρώπινος Σκελετός ñ Ανθεκτικότητα στην αποικοδόµηση ñ Ιδανική πηγή πληροφοριών: προϊστορικά, ιστορικά, σύγχρονα ñ Σκελετική ανατοµία: γονίδια + περιβάλλον ñ Ποικιλοµορφία: οντογένεση, φύλο, πληθυσµός,
Ανθρώπινος Σκελετός ñ Ανθεκτικότητα στην αποικοδόµηση ñ Ιδανική πηγή πληροφοριών: προϊστορικά, ιστορικά, σύγχρονα ñ Σκελετική ανατοµία: γονίδια + περιβάλλον ñ Ποικιλοµορφία: οντογένεση, φύλο, πληθυσµός,
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες)
 Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Πυρήνες οστέωσης παιδικου σκελετου. Χρόνοι εμφάνισης.
 Πυρήνες οστέωσης παιδικου σκελετου. Χρόνοι εμφάνισης. Κωτούλα Αγορίτσα, Ιατρος ακτινολόγος, Επιμελήτρια Β Ακτινολογικό Εργαστήριο Νοσοκομείου Α.Ν.Θ. ΘΕΑΓΕΝΕΙΟ, Θεσ/νίκης Τα οστά σχηματίζονται με δύο τρόπους:
Πυρήνες οστέωσης παιδικου σκελετου. Χρόνοι εμφάνισης. Κωτούλα Αγορίτσα, Ιατρος ακτινολόγος, Επιμελήτρια Β Ακτινολογικό Εργαστήριο Νοσοκομείου Α.Ν.Θ. ΘΕΑΓΕΝΕΙΟ, Θεσ/νίκης Τα οστά σχηματίζονται με δύο τρόπους:
ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ
 ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ Του Δρ. Κωνσταντίνου Δ. Στρατηγού Δ/ντού Ορθοπαιδικής Επανορθωτικής Χειρουργικής
ΟΛΙΚΗ ΑΡΘΡΟΠΛΑΣΤΙΚΗ ΙΣΧΊΟΥ ΤΥΠΟΥ ΑΝΤΙΚΑΤΑΣΤΑΣΕΩΣ ΕΠΙΦΑΝΕΙΑΣ ΜΙΑ ΝΕΑ ΠΡΟΣΕΓΓΙΣΗ ΣΤΗΝ ΑΠΟΚΑΤΑΣΤΑΣΗ ΤΗΣ ΑΡΘΡΩΣΕΩΣ ΤΟΥ ΙΣΧΙΟΥ Του Δρ. Κωνσταντίνου Δ. Στρατηγού Δ/ντού Ορθοπαιδικής Επανορθωτικής Χειρουργικής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Αλληλεπίδραση μηχανικών και βιολογικών παραγόντων κατά την πώρωση των οστών ΜΕΤΑΠΤΥΧΙΑΚΗ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΠΜΣ ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΗΧΑΝΙΚΗ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Αλληλεπίδραση μηχανικών και βιολογικών παραγόντων κατά την πώρωση των οστών ΜΕΤΑΠΤΥΧΙΑΚΗ
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΟΙ ΙΣΤΟΙ ΤΩΝ ΖΩΙΚΩΝ ΟΡΓΑΝΙΣΜΩΝ
 75 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΟΙ ΙΣΤΟΙ ΤΩΝ ΖΩΙΚΩΝ ΟΡΓΑΝΙΣΜΩΝ 76 ΟΙ ΙΣΤΟΙ Όλα τα ευκαρυωτικά κύτταρα εμφανίζουν την ίδια βασική αρχιτεκτονική: εξωτερικά βρίσκεται η πλασματική μεμβράνη, η οποία περιβάλλει το
75 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΟΙ ΙΣΤΟΙ ΤΩΝ ΖΩΙΚΩΝ ΟΡΓΑΝΙΣΜΩΝ 76 ΟΙ ΙΣΤΟΙ Όλα τα ευκαρυωτικά κύτταρα εμφανίζουν την ίδια βασική αρχιτεκτονική: εξωτερικά βρίσκεται η πλασματική μεμβράνη, η οποία περιβάλλει το
Κινητικό σύστημα του ανθρώπου Σπονδυλική Στήλη
 Κινητικό σύστημα του ανθρώπου Σπονδυλική Στήλη Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Μπενέκα Νατάσσα Αναπλ. Καθηγήτρια ΤΕΦΑΑ ΔΠΘ . Σπονδυλική στήλη-περιγραφή οστών θωρακικού κλωβού και
Κινητικό σύστημα του ανθρώπου Σπονδυλική Στήλη Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Μπενέκα Νατάσσα Αναπλ. Καθηγήτρια ΤΕΦΑΑ ΔΠΘ . Σπονδυλική στήλη-περιγραφή οστών θωρακικού κλωβού και
ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ. Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας
 ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας Αντοχή και Δυσκαμψία (Strength and Stiffness) Η τάση (stress) εφαρμόζεται σ ένα υλικό μέσω της φόρτισής του Παραμόρφωση
ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας Αντοχή και Δυσκαμψία (Strength and Stiffness) Η τάση (stress) εφαρμόζεται σ ένα υλικό μέσω της φόρτισής του Παραμόρφωση
Είναι η σύνδεση δύο ή περισσότερων οστών με τη συμμετοχή ενός μαλακότερου ιστού
 Αρθρώσεις Είναι η σύνδεση δύο ή περισσότερων οστών με τη συμμετοχή ενός μαλακότερου ιστού Ανάλογα με το είδος αυτού του ιστού και τον τρόπο συμμετοχής του, καθορίζεται η κινητικότητα των οστών που συνδέονται.
Αρθρώσεις Είναι η σύνδεση δύο ή περισσότερων οστών με τη συμμετοχή ενός μαλακότερου ιστού Ανάλογα με το είδος αυτού του ιστού και τον τρόπο συμμετοχής του, καθορίζεται η κινητικότητα των οστών που συνδέονται.
Αφού παρακολουθήσετε τα βίντεο με τα σαρκοφάγα φυτά και τις ναστίες συμπληρώστε την παραπάνω ερώτηση. Με ποιους τρόπους στηρίζονται τα φυτά;
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Κεφάλαιο 5 «Στήριξη και Κίνηση» Ποια είναι η διαφορά ανάμεσα στις λέξεις κίνηση και μετακίνηση; Μετακινούνται όλοι οι ζωικοί οργανισμοί; Άσκηση σελ. 98 ΣΒ Α. Η Κίνηση στους μονοκύτταρους
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Κεφάλαιο 5 «Στήριξη και Κίνηση» Ποια είναι η διαφορά ανάμεσα στις λέξεις κίνηση και μετακίνηση; Μετακινούνται όλοι οι ζωικοί οργανισμοί; Άσκηση σελ. 98 ΣΒ Α. Η Κίνηση στους μονοκύτταρους
ΡΑΧΗ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ
 ΡΑΧΗ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΡΑΧΗ Αποτελεί τον μυοσκελετικό άξονα στήριξης του κορμού με κύριο οστικό στοιχείο τους σπονδύλους και την παράλληλη συμβολή
ΡΑΧΗ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΡΑΧΗ Αποτελεί τον μυοσκελετικό άξονα στήριξης του κορμού με κύριο οστικό στοιχείο τους σπονδύλους και την παράλληλη συμβολή
Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών
 Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
Στοιχεία Μηχανών. Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά
 Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΚΕΦΑΛΑΙΟ 1 Από το κύτταρο στον οργανισμό
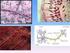 ΚΕΦΑΛΑΙΟ 1 Από το κύτταρο στον οργανισμό 1o ΔΙΑΓΩΝΙΣΜΑ - ΓΗ_Α_ΒΙΟ_0_11207, 2o ΔΙΑΓΩΝΙΣΜΑ - ΓΗ_Α_ΒΙΟ_0_11208 ΘΕΜΑ Δ Το ανθρώπινο σώμα, όπως και το σώμα κάθε πολυκύτταρου οργανισμού αποτελείται από πολλά
ΚΕΦΑΛΑΙΟ 1 Από το κύτταρο στον οργανισμό 1o ΔΙΑΓΩΝΙΣΜΑ - ΓΗ_Α_ΒΙΟ_0_11207, 2o ΔΙΑΓΩΝΙΣΜΑ - ΓΗ_Α_ΒΙΟ_0_11208 ΘΕΜΑ Δ Το ανθρώπινο σώμα, όπως και το σώμα κάθε πολυκύτταρου οργανισμού αποτελείται από πολλά
ΙΣΤΟΙ. Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια. Μπενέκα Νατάσσα Αναπλ. Καθηγήτρια ΤΕΦΑΑ ΔΠΘ
 ΙΣΤΟΙ Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Μπενέκα Νατάσσα Αναπλ. Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Ιστοί Οι ιστοί είναι σύνολο κυττάρων με την ίδια κατασκευή, μορφολογία και λειτουργία. Κάθε ιστός
ΙΣΤΟΙ Μάλλιου Βίβιαν Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Φυσικοθεραπεύτρια Μπενέκα Νατάσσα Αναπλ. Καθηγήτρια ΤΕΦΑΑ ΔΠΘ Ιστοί Οι ιστοί είναι σύνολο κυττάρων με την ίδια κατασκευή, μορφολογία και λειτουργία. Κάθε ιστός
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ» Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ» Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Το παρακάτω παράδειγμα είναι ένα παράδειγμα κυτταρικής διαφοροποίησης που αφορά στην παραγωγή των ερυθροκυττάρων
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «ΑΠΟ ΤΟ ΚΥΤΤΑΡΟ ΣΤΟΝ ΟΡΓΑΝΙΣΜΟ» Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Το παρακάτω παράδειγμα είναι ένα παράδειγμα κυτταρικής διαφοροποίησης που αφορά στην παραγωγή των ερυθροκυττάρων
4.1 ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ. 4.1.1 Εισαγωγή. 4.1.2 Μορφολογία των οστών.
 4. ΣΤΗΡΙΞΗ 4.1 ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ 4.1.1 Εισαγωγή Το ερειστικό σύστημα αποτελείται από τα οστά, που συνδέονται μεταξύ τους με διάφορα είδη κινητών αρθρώσεων, που επιτρέπουν την εκτέλεση ποικίλων κινήσεων
4. ΣΤΗΡΙΞΗ 4.1 ΕΡΕΙΣΤΙΚΟ ΣΥΣΤΗΜΑ 4.1.1 Εισαγωγή Το ερειστικό σύστημα αποτελείται από τα οστά, που συνδέονται μεταξύ τους με διάφορα είδη κινητών αρθρώσεων, που επιτρέπουν την εκτέλεση ποικίλων κινήσεων
Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική
 Μύες Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική κινητικότητα, την σπλαχνική κινητικότητα και τη κυκλοφορία
Μύες Το μυϊκό σύστημα αποτελείται από τους μύες. Ο αριθμός των μυών του μυϊκού συστήματος ανέρχεται στους 637. Οι μύες είναι όργανα για τη σωματική κινητικότητα, την σπλαχνική κινητικότητα και τη κυκλοφορία
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Μιχαήλ Νικ. Πατσίκας
 Ακτινολογική εκτίμηση της πώρωσης των καταγμάτων Μιχαήλ Νικ. Πατσίκας Πτυχιούχος Κτηνιατρικής Α.Π.Θ. Πτυχιούχος Ιατρικής Α.Π.Θ Αναπληρωτής Καθηγητής Ακτινολογίας Κτηνιατρική Σχολή Α.Π.Θ. Διπλωματούχος
Ακτινολογική εκτίμηση της πώρωσης των καταγμάτων Μιχαήλ Νικ. Πατσίκας Πτυχιούχος Κτηνιατρικής Α.Π.Θ. Πτυχιούχος Ιατρικής Α.Π.Θ Αναπληρωτής Καθηγητής Ακτινολογίας Κτηνιατρική Σχολή Α.Π.Θ. Διπλωματούχος
Στέφανος Πατεράκης (Φυσικ/τής)
 ΜΥΣ Οι μύες είναι όργανα του ανθρωπίνου σώματος. Σχηματίζονται από μυϊκό ιστό. Μαζί με τους τένοντες συμβάλουν στην κίνηση των οστών. Είδη των μυών Ο μυς της καρδιάς, Οι λείοι, και Οι γραμμωτοί. Ο μυς
ΜΥΣ Οι μύες είναι όργανα του ανθρωπίνου σώματος. Σχηματίζονται από μυϊκό ιστό. Μαζί με τους τένοντες συμβάλουν στην κίνηση των οστών. Είδη των μυών Ο μυς της καρδιάς, Οι λείοι, και Οι γραμμωτοί. Ο μυς
ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ. Ευάγγελος Καστής. Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου
 ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου Ευάγγελος Καστής Πολυτεχνείο Κρήτης-Χανιά 016 Παρουσίαση διπλωματικής
ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου Ευάγγελος Καστής Πολυτεχνείο Κρήτης-Χανιά 016 Παρουσίαση διπλωματικής
Σχήμα 1: Διάταξη δοκιμίου και όργανα μέτρησης 1 BUILDNET
 Παραμετρική ανάλυση κοχλιωτών συνδέσεων με μετωπική πλάκα χρησιμοποιώντας πεπερασμένα στοιχεία Χριστόφορος Δημόπουλος, Πολιτικός Μηχανικός, Υποψήφιος Διδάκτωρ ΕΜΠ Περίληψη Η εν λόγω εργασία παρουσιάζει
Παραμετρική ανάλυση κοχλιωτών συνδέσεων με μετωπική πλάκα χρησιμοποιώντας πεπερασμένα στοιχεία Χριστόφορος Δημόπουλος, Πολιτικός Μηχανικός, Υποψήφιος Διδάκτωρ ΕΜΠ Περίληψη Η εν λόγω εργασία παρουσιάζει
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
Μελέτη προβλημάτων ΠΗΙ λόγω λειτουργίας βοηθητικών προωστήριων μηχανισμών
 «ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
«ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
ΜΥΟΣΚΕΛΕΤΙΚΟ ΣΥΣΤΗΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ
 ΜΥΟΣΚΕΛΕΤΙΚΟ ΣΥΣΤΗΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΟΣΤΑ ΚΑΙ ΣΚΕΛΕΤΙΚΟ ΣΥΣΤΗΜΑ Τα οστά είναι μια στερεά μορφή συνδετικού ιστού, σχηματίζουν το μεγαλύτερο μέρος
ΜΥΟΣΚΕΛΕΤΙΚΟ ΣΥΣΤΗΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΗΣ ΙΑΤΡΙΚΗΣ ΣΧΟΛΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΟΣΤΑ ΚΑΙ ΣΚΕΛΕΤΙΚΟ ΣΥΣΤΗΜΑ Τα οστά είναι μια στερεά μορφή συνδετικού ιστού, σχηματίζουν το μεγαλύτερο μέρος
ΒΙΟΛΟΓΙΑ Β ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ - ΑΠΑΝΤΗΣΕΙΣ
 ΒΙΟΛΟΓΙΑ Β ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ - ΑΠΑΝΤΗΣΕΙΣ 1 ΠΕΡΙΕΧΟΜΕΝΑ (Από το βιβλίο της Α Γυμνασίου) ΚΕΦΑΛΑΙΟ 5: ΣΤΗΡΙΞΗ ΚΑΙ ΚΙΝΗΣΗ Στήριξη και κίνηση 5.1 Η στήριξη και
ΒΙΟΛΟΓΙΑ Β ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ - ΑΠΑΝΤΗΣΕΙΣ 1 ΠΕΡΙΕΧΟΜΕΝΑ (Από το βιβλίο της Α Γυμνασίου) ΚΕΦΑΛΑΙΟ 5: ΣΤΗΡΙΞΗ ΚΑΙ ΚΙΝΗΣΗ Στήριξη και κίνηση 5.1 Η στήριξη και
Βιολογία Εμφυτευμάτων
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Οστική Επούλωση Γεώργιος Μακρής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Οστική Επούλωση Γεώργιος Μακρής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Bλάβες αρθρικού χόνδρου και σύγχρονες θεραπείες - Ο Δρόμος για την Θεραπεία Δευτέρα, 02 Ιούλιος :04
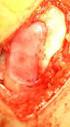 Γράφει: Δρ. Νικόλαος Πισκοπάκης MD, PhD, Ορθοπεδικός Χειρουργός, Δ/ντής Ορθοπεδικής Κλινικής Αθλητικών Κακώσεων Ιατρικού Κέντρου Αθηνών, Πρόεδρος Ελληνικής Αρθροσκοπικής Εταιρείας (ΕΑΕ) Τι είναι ο αρθρικός
Γράφει: Δρ. Νικόλαος Πισκοπάκης MD, PhD, Ορθοπεδικός Χειρουργός, Δ/ντής Ορθοπεδικής Κλινικής Αθλητικών Κακώσεων Ιατρικού Κέντρου Αθηνών, Πρόεδρος Ελληνικής Αρθροσκοπικής Εταιρείας (ΕΑΕ) Τι είναι ο αρθρικός
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 5 ο : Το οριακό
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 5 ο : Το οριακό
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Στηρικτικά Κύτταρα και Εξωκυττάρια Ουσία. Κοτσίνας Αθανάσιος Επικ. Καθηγητής Εργ. Ιστολογίας-Εμβρυολογίας Ιατρική Σχολή - ΕΚΠΑ
 Στηρικτικά Κύτταρα και Εξωκυττάρια Ουσία Κοτσίνας Αθανάσιος Επικ. Καθηγητής Εργ. Ιστολογίας-Εμβρυολογίας Ιατρική Σχολή - ΕΚΠΑ Συνδετικός Ιστός - Ορισμός Παρέχει το: Υποστηρικτικό και Συνδετικό πλαίσιο
Στηρικτικά Κύτταρα και Εξωκυττάρια Ουσία Κοτσίνας Αθανάσιος Επικ. Καθηγητής Εργ. Ιστολογίας-Εμβρυολογίας Ιατρική Σχολή - ΕΚΠΑ Συνδετικός Ιστός - Ορισμός Παρέχει το: Υποστηρικτικό και Συνδετικό πλαίσιο
MYOΣKEΛETIKO ΣYΣTHMA. Oι σκελετικοί µύες συµµετέχουν µε την σύσπαση τους > στη κίνηση των οστών
 MYOΣKEΛETIKO ΣYΣTHMA Παρέχει > µηχανική στήριξη στο σώµα & µετέχει στη λειτουργία της κίνησης > αποτελείται από σκελετικούς µύς τένοντες οστά αρθρώσεις & συνδέσµους Oι σκελετικοί µύες συµµετέχουν µε την
MYOΣKEΛETIKO ΣYΣTHMA Παρέχει > µηχανική στήριξη στο σώµα & µετέχει στη λειτουργία της κίνησης > αποτελείται από σκελετικούς µύς τένοντες οστά αρθρώσεις & συνδέσµους Oι σκελετικοί µύες συµµετέχουν µε την
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ. Ασκήσεις προηγούμενων εξετάσεων ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΥΠΟΓΕΙΑ ΑΝΑΠΤΥΞΗ. Μέθοδος θαλάμων και στύλων
 ΥΠΟΓΕΙΑ ΑΝΑΠΤΥΞΗ και A. Μπενάρδος Λέκτορας ΕΜΠ Δ. Καλιαμπάκος Καθηγητής ΕΜΠ και - Hunt Midwest (Subtroolis) και - Hunt Midwest (Subtroolis) Εφαρμογής - Η μέθοδος και (rooms and illars) ανήκει στην κατηγορία
ΥΠΟΓΕΙΑ ΑΝΑΠΤΥΞΗ και A. Μπενάρδος Λέκτορας ΕΜΠ Δ. Καλιαμπάκος Καθηγητής ΕΜΠ και - Hunt Midwest (Subtroolis) και - Hunt Midwest (Subtroolis) Εφαρμογής - Η μέθοδος και (rooms and illars) ανήκει στην κατηγορία
Μέθοδοι μέτρησης μηχανικών ιδιοτήτων κυττάρων και μοντέλα κυτταρικής μηχανικής συμπεριφοράς
 ΕΜΒΙΟΜΗΧΑΝΙΚΗ ΒΙΟΪΑΤΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μέθοδοι μέτρησης μηχανικών ιδιοτήτων κυττάρων και μοντέλα κυτταρικής μηχανικής συμπεριφοράς Πετρόπουλος Ηλίας Σωτηρόπουλος Εμμανουήλ Μέθοδοι μέτρησης των μηχανικών ιδιοτήτων
ΕΜΒΙΟΜΗΧΑΝΙΚΗ ΒΙΟΪΑΤΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μέθοδοι μέτρησης μηχανικών ιδιοτήτων κυττάρων και μοντέλα κυτταρικής μηχανικής συμπεριφοράς Πετρόπουλος Ηλίας Σωτηρόπουλος Εμμανουήλ Μέθοδοι μέτρησης των μηχανικών ιδιοτήτων
ΚΕΦΑΛΑΙΟ. Οι γραμμικοί φορείς. 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων
 ΚΕΦΑΛΑΙΟ 1 Οι γραμμικοί φορείς 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων 2 1. Οι γραμμικοί φορείς 1.1 Εισαγωγή 3 1.1 Εισαγωγή Για να γίνει ο υπολογισμός μιας κατασκευής, θα πρέπει ο μελετητής μηχανικός
ΚΕΦΑΛΑΙΟ 1 Οι γραμμικοί φορείς 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων 2 1. Οι γραμμικοί φορείς 1.1 Εισαγωγή 3 1.1 Εισαγωγή Για να γίνει ο υπολογισμός μιας κατασκευής, θα πρέπει ο μελετητής μηχανικός
«Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής»
 ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση
 Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση Τι είναι ο αρθρικός χόνδρος; Ο αρθρικός χόνδρος είναι ένας στιλπνός, ομαλός, λείος και ανάγγειος ιστός που καλύπτει τις αρθρικές επιφάνειες
Βλάβες του Αρθρικού Χόνδρου του Γόνατος: Διάγνωση και Αντιμετώπιση Τι είναι ο αρθρικός χόνδρος; Ο αρθρικός χόνδρος είναι ένας στιλπνός, ομαλός, λείος και ανάγγειος ιστός που καλύπτει τις αρθρικές επιφάνειες
Γεώργιος Τρανταλής. Επιμελητής Καρδιολογίας Κ. Υ. Καπανδριτίου Α Πανεπιστημιακή Καρδιολογική Κλινική
 Γεώργιος Τρανταλής Επιμελητής Καρδιολογίας Κ. Υ. Καπανδριτίου Α Πανεπιστημιακή Καρδιολογική Κλινική Ανατομία Φυσιοπαθολογία Μελλοντικές προεκτάσεις Ανατομία Φυσιοπαθολογία Μελλοντικές προεκτάσεις Η αορτική
Γεώργιος Τρανταλής Επιμελητής Καρδιολογίας Κ. Υ. Καπανδριτίου Α Πανεπιστημιακή Καρδιολογική Κλινική Ανατομία Φυσιοπαθολογία Μελλοντικές προεκτάσεις Ανατομία Φυσιοπαθολογία Μελλοντικές προεκτάσεις Η αορτική
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I
 ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I 1. ΕΙΣΑΓΩΓΗ Μηχανική συμπεριφορά αντανακλά την σχέση παραμόρφωση ασκούμενο φορτίο/δύναμη Να γνωρίζουμε τα χαρακτηριστικά του υλικού - να αποφευχθεί υπερβολική παραμόρφωση,
ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I 1. ΕΙΣΑΓΩΓΗ Μηχανική συμπεριφορά αντανακλά την σχέση παραμόρφωση ασκούμενο φορτίο/δύναμη Να γνωρίζουμε τα χαρακτηριστικά του υλικού - να αποφευχθεί υπερβολική παραμόρφωση,
Κεφάλαιο 1 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΕΥΡΟΦΥΣΙΟΛΟΓΙΑΣ
 Κεφάλαιο 1 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΕΥΡΟΦΥΣΙΟΛΟΓΙΑΣ 1.1. Εισαγωγή Ο ζωντανός οργανισµός έχει την ικανότητα να αντιδρά σε µεταβολές που συµβαίνουν στο περιβάλλον και στο εσωτερικό του. Οι µεταβολές αυτές ονοµάζονται
Κεφάλαιο 1 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΝΕΥΡΟΦΥΣΙΟΛΟΓΙΑΣ 1.1. Εισαγωγή Ο ζωντανός οργανισµός έχει την ικανότητα να αντιδρά σε µεταβολές που συµβαίνουν στο περιβάλλον και στο εσωτερικό του. Οι µεταβολές αυτές ονοµάζονται
ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής. Διδάσκων: Γιάννης Χουλιάρας
 ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής Διδάσκων: Γιάννης Χουλιάρας Ισοστατικά πλαίσια με συνδέσμους (α) (β) Στατική επίλυση ισοστατικών πλαισίων
ΙΣΟΣΤΑΤΙΚΑ ΠΛΑΙΣΙΑ ΜΕ ΣΥΝΔΕΣΜΟΥΣ Υπολογισμός αντιδράσεων και κατασκευή Μ,Ν, Q Γραμμές επιρροής Διδάσκων: Γιάννης Χουλιάρας Ισοστατικά πλαίσια με συνδέσμους (α) (β) Στατική επίλυση ισοστατικών πλαισίων
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Πρόχειρες Σημειώσεις
 Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
Ο ΣΚΕΛΕΤΟΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ
 Ο ΣΚΕΛΕΤΟΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ Αυχενικοί σπόνδυλοι 7 Θωρακικοί σπόνδυλοι 12 Οσφυϊκοί σπόνδυλοι 5 Ιερό οστό 5 συνοστεομένοι σπόνδυλοι Κόκκυγας Φυσιολογικά Κυρτώματα Σ.Σ. Η σπονδυλική στήλη δεν είναι
Ο ΣΚΕΛΕΤΟΣ ΤΗΣ ΣΠΟΝΔΥΛΙΚΗΣ ΣΤΗΛΗΣ Αυχενικοί σπόνδυλοι 7 Θωρακικοί σπόνδυλοι 12 Οσφυϊκοί σπόνδυλοι 5 Ιερό οστό 5 συνοστεομένοι σπόνδυλοι Κόκκυγας Φυσιολογικά Κυρτώματα Σ.Σ. Η σπονδυλική στήλη δεν είναι
ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΣΩΤΕΡΙΚΕΣ ΕΛΕΥΘΕΡΩΣΕΙΣ ΜΕΘΟΔΟΣ ΣΥΝΔΥΑΣΜΕΝΩΝ ΚΟΜΒΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ
 Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΥΑΓΓΕΛΙΑΣ Π. ΛΟΥΚΟΓΕΩΡΓΑΚΗ Διπλωματούχου Πολιτικού Μηχανικού ΟΛΟΚΛΗΡΩΜΕΝΟ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΥΑΓΓΕΛΙΑΣ Π. ΛΟΥΚΟΓΕΩΡΓΑΚΗ Διπλωματούχου Πολιτικού Μηχανικού ΟΛΟΚΛΗΡΩΜΕΝΟ
ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΣΤΡΕΨΗ ΕΠΙΜΕΛΕΙΑ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Μηχανικές ιδιότητες Στρέψη κυλινδρικών ράβδων Ελαστική περιοχή Πλαστική
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΣΤΡΕΨΗ ΕΠΙΜΕΛΕΙΑ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Μηχανικές ιδιότητες Στρέψη κυλινδρικών ράβδων Ελαστική περιοχή Πλαστική
AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών
 ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών Ασκήσεις για λύση Η ράβδος του σχήματος είναι ομοιόμορφα μεταβαλλόμενης κυκλικής 1 διατομής εφελκύεται αξονικά με δύναμη Ρ. Αν D d είναι οι διάμετροι των ακραίων
ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών Ασκήσεις για λύση Η ράβδος του σχήματος είναι ομοιόμορφα μεταβαλλόμενης κυκλικής 1 διατομής εφελκύεται αξονικά με δύναμη Ρ. Αν D d είναι οι διάμετροι των ακραίων
ΜΥΪΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (Β ΜΕΡΟΣ)
 ΑΝΑΤΟΜΙΑ και ΦΥΣΙΟΛΟΓΙΑ ΜΥΪΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (Β ΜΕΡΟΣ) ΦΥΣΙΟΛΟΓΙΑ ΜΥΪΚΟΥ ΣΥΣΤΗΜΑΤΟΣ Οι µύες είναι συσταλτά όργανα που χρησιµεύουν για να επιτελούνται οι ενεργητικές κινήσεις του οργανισµού. Οι µύες αποτελούνται
ΑΝΑΤΟΜΙΑ και ΦΥΣΙΟΛΟΓΙΑ ΜΥΪΚΟΥ ΣΥΣΤΗΜΑΤΟΣ (Β ΜΕΡΟΣ) ΦΥΣΙΟΛΟΓΙΑ ΜΥΪΚΟΥ ΣΥΣΤΗΜΑΤΟΣ Οι µύες είναι συσταλτά όργανα που χρησιµεύουν για να επιτελούνται οι ενεργητικές κινήσεις του οργανισµού. Οι µύες αποτελούνται
Μιχάλης Η. Χαντές. Αθλητικές κακώσεις: Κακώσεις μυών οστών Θεραπευτικές δυνατότητες Προστατευτικός εξοπλισμός.
 Αθλητικές κακώσεις: Κακώσεις μυών οστών Θεραπευτικές δυνατότητες Προστατευτικός εξοπλισμός. Μιχάλης Η. Χαντές Πανεπιστήμιο Θεσσαλίας Ορθοπαιδική Κλινική Διευθυντής: Καθηγητής Κ.Ν.Μαλίζος Μύες-Μυοτενόντια
Αθλητικές κακώσεις: Κακώσεις μυών οστών Θεραπευτικές δυνατότητες Προστατευτικός εξοπλισμός. Μιχάλης Η. Χαντές Πανεπιστήμιο Θεσσαλίας Ορθοπαιδική Κλινική Διευθυντής: Καθηγητής Κ.Ν.Μαλίζος Μύες-Μυοτενόντια
ΕΠΙΣΚΕΥΕΣ ΚΑΙ ΕΝΙΣΧΥΣΕΙΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ. Διδάσκων Καθηγητής Γιάννακας Νικόλαος Δρ. Πολιτικός Μηχανικός
 ΕΠΙΣΚΕΥΕΣ ΚΑΙ ΕΝΙΣΧΥΣΕΙΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Διδάσκων Καθηγητής Γιάννακας Νικόλαος Δρ. Πολιτικός Μηχανικός Κεφαλαιο 2 Μηχανισμοί μεταφοράς δυνάμεων Τα τελευταία χρόνια έχει γίνει συστηματική προσπάθεια για
ΕΠΙΣΚΕΥΕΣ ΚΑΙ ΕΝΙΣΧΥΣΕΙΣ ΤΩΝ ΚΑΤΑΣΚΕΥΩΝ Διδάσκων Καθηγητής Γιάννακας Νικόλαος Δρ. Πολιτικός Μηχανικός Κεφαλαιο 2 Μηχανισμοί μεταφοράς δυνάμεων Τα τελευταία χρόνια έχει γίνει συστηματική προσπάθεια για
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΠείραμαΚάμψης(ΕλαστικήΓραμμή) ΕργαστηριακήΆσκηση 7 η
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΠείραμαΚάμψης(ΕλαστικήΓραμμή) ΕργαστηριακήΆσκηση 7 η Σκοπός Σκοπός του πειράµατος είναι ο προσδιορισµός των χαρακτηριστικών τιµών αντοχής του υλικού που ορίζονταιστηκάµψη, όπωςτοόριοδιαρροήςσεκάµψηκαιτοόριοαντοχής
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΠείραμαΚάμψης(ΕλαστικήΓραμμή) ΕργαστηριακήΆσκηση 7 η Σκοπός Σκοπός του πειράµατος είναι ο προσδιορισµός των χαρακτηριστικών τιµών αντοχής του υλικού που ορίζονταιστηκάµψη, όπωςτοόριοδιαρροήςσεκάµψηκαιτοόριοαντοχής
Μηχανικές ιδιότητες των οστών
 Τα οστά δρουν σαν κατασκευές υποστήριξης και μεταφέρουν φορτία: h Απλή συμπίεση h Λυγισμός (φόρτιση του ενός φλοιού ελκυσμός του άλλου) h Στρέψη Μηχανικές ιδιότητες των οστών h Ισχυρότερα στη συμπίεση
Τα οστά δρουν σαν κατασκευές υποστήριξης και μεταφέρουν φορτία: h Απλή συμπίεση h Λυγισμός (φόρτιση του ενός φλοιού ελκυσμός του άλλου) h Στρέψη Μηχανικές ιδιότητες των οστών h Ισχυρότερα στη συμπίεση
Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές
 Παράρτηµα Γ Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές 1. Εισαγωγή Το σύνολο των προγραµµάτων ALGOR είναι ένα εργαλείο µελέτης (σχεδιασµού και ανάλυσης) κατασκευών και βασίζεται στη µέθοδο
Παράρτηµα Γ Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές 1. Εισαγωγή Το σύνολο των προγραµµάτων ALGOR είναι ένα εργαλείο µελέτης (σχεδιασµού και ανάλυσης) κατασκευών και βασίζεται στη µέθοδο
Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική
 Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική Ποιά είναι η ανατομική κατασκευή του γόνατος; Η άρθρωση του γόνατος σχηματίζεται από το μηριαίο οστό και από την κνήμη. Τα άκρα των οστών
Ο Πρόσθιος Χιαστός Σύνδεσμος του Γόνατος και η Συνδεσμοπλαστική Ποιά είναι η ανατομική κατασκευή του γόνατος; Η άρθρωση του γόνατος σχηματίζεται από το μηριαίο οστό και από την κνήμη. Τα άκρα των οστών
Η ΠΟΡΕΙΑ ΤΗΣ ΠΩΡΩΣΗΣ ΤΟΥ ΚΑΤΑΓΜΑΤΟΣ ΤΗΣ ΚΝΗΜΗΣ ΜΕΤΑ ΑΠΟ ΕΝΔΟΜΥΕΛΙΚΗ ΗΛΩΣΗ. ΠΥΚΝΟΜΕΤΡΙΚΗ ΜΕΛΕΤΗ ΣΕ ΕΠΙΜΥΕΣ
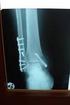 Η ΠΟΡΕΙΑ ΤΗΣ ΠΩΡΩΣΗΣ ΤΟΥ ΚΑΤΑΓΜΑΤΟΣ ΤΗΣ ΚΝΗΜΗΣ ΜΕΤΑ ΑΠΟ ΕΝΔΟΜΥΕΛΙΚΗ ΗΛΩΣΗ. ΠΥΚΝΟΜΕΤΡΙΚΗ ΜΕΛΕΤΗ ΣΕ ΕΠΙΜΥΕΣ Χ.Κ.Γιαννακόπουλος, Ε.Σταμάτης, Π.Καλογερά,Ι.Χατζηκομνηνός,Μ.Κατσίρη, Γ.Λυρίτης Εργαστήριο Έρευνας
Η ΠΟΡΕΙΑ ΤΗΣ ΠΩΡΩΣΗΣ ΤΟΥ ΚΑΤΑΓΜΑΤΟΣ ΤΗΣ ΚΝΗΜΗΣ ΜΕΤΑ ΑΠΟ ΕΝΔΟΜΥΕΛΙΚΗ ΗΛΩΣΗ. ΠΥΚΝΟΜΕΤΡΙΚΗ ΜΕΛΕΤΗ ΣΕ ΕΠΙΜΥΕΣ Χ.Κ.Γιαννακόπουλος, Ε.Σταμάτης, Π.Καλογερά,Ι.Χατζηκομνηνός,Μ.Κατσίρη, Γ.Λυρίτης Εργαστήριο Έρευνας
