Generalizations of the Inverse Weibull and Related Distributions with Applications
|
|
|
- Ευπραξία Σαμαράς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Georgia Souther Uiversity From the SelectedWors of Broderic O Oluyede April 26, 214 Geeralizatios of the Iverse Weibull ad Related Distributios with Applicatios Broderic O Oluyede, Georgia Souther Uiversity Tao Yag, Clemso Uiversity Available at: broderic_oluyede/33/
2 Electroic Joural of Applied Statistical Aalysis EJASA, Electro J App Stat Aal e-issn: DOI: 11285/i275948v71p94 Geeralizatios of the iverse Weibull ad related distributios with applicatio By Oluyede, Yag April 26, 214 This wor is copyrighted by Uiversità del Saleto, ad is licesed uder a Creative Commos Attribuzioe - No commerciale - No opere derivate 3 Italia Licese For more iformatio see:
3 Electroic Joural of Applied Statistical Aalysis Vol 7, Issue 1, 214, DOI: 11285/i275948v71p94 Geeralizatios of the iverse Weibull ad related distributios with applicatio Broderic O Oluyede a ad Tao Yag b a Departmet of Mathematical Scieces, Georgia Souther Uiversity, Georgia, Uited States b Departmet of Mathematical Scieces, Clemso Uiversity,Clemso, Uited States April 26, 214 I this paper, the geeralized iverse Weibull distributio icludig the expoetiated or proportioal reverse hazard ad Kumaraswamy geeralized iverse Weibull distributios are preseted Properties of these distributios icludig the behavior of the hazard ad reverse hazard fuctios, momets, coefficiets of variatio, sewess, ad urtosis, etropy, Fisher iformatio matrix are studied Estimates of the model parameters via method of maximum lielihood (ML, ad method of momets (MOM are preseted for complete ad cesored data Numerical examples are also preseted eywords: Iverse Weibull Distributio, Proportioal Iverse Weibull Distributio, Geeralized Distributio 1 Itroductio The iverse Weibull distributio ca be readily applied to a wide rage of situatios icludig applicatios i medicie, reliability ad ecology Keller et al (1985 obtaied the iverse Weibull model by ivestigatig failures of mechaical compoets subject to degradatio Calabria ad Pulcii (199 computed the maximum lielihood ad least squares estimates of the parameters of the iverse Weibull distributio They also obtaied the Bayes estimator of the model parameters as well as cofidece limits for reliability ad tolerace limits See Calabria ad Pulcii (1989, 1994, ad Johso et al (1984 for additioal details Kha et al (28 preseted some importat theoretical properties of the iverse Weibull distributio Samata ad Correspodig author: boluyede@georgiasoutheredu c Uiversità del Saleto ISSN:
4 Electroic Joural of Applied Statistical Aalysis 95 Bhowmic (21 preseted a determiistic ivetory system with Weibull distributio deterioratio ad ramp type demad rate The iverse Weibull (IW cumulative distributio fuctio (cdf is give by [ F(x;α, exp (α(x x, x x, α >, >, (1 where α, x ad are the scale, locatio ad shape parameters, respectively Ofte the parameter x is called the miimum life or guaratee time Whe α 1 ad x x + α, the F(α + x ;1; F(α + x ;1 e This value is i fact the characteristic life of the distributio I what follows, we assume that x, ad the iverse Weibull cdf becomes F(x;α, exp[ (αx, x, α >, > (2 Note that whe α 1, we have the Fréchet distributio fuctio The iverse Weibull probability desity fuctio (pdf is give by f (x;α, α x 1 exp[ (αx, x, α >, > (3 Whe 1 ad 2, the iverse Weibull distributio pdfs are referred to as the iverse expoetial ad iverse Raleigh pdfs, respectively The th raw or o cetral momets are give by E(X Γ(1 / α, for > (4 Note that E(X does ot exist whe See Johso et al (1984 This paper is orgaized as follows Sectio 2 cotais some basic utility otios I sectio 3, the expoetiated or proportioal iverse Weibull (PIW ad Kumaraswamy geeralized iverse Weibull distributios are preseted The mode, hazard fuctio ad reverse hazard fuctio are also preseted i sectio 3 Glaser s Lemma is applied to the PIW distributio to determie the behavior of the hazard fuctio I sectio 4, the momets, etropy measures ad Fisher iformatio are preseted Estimatio of the parameters of the PIW distributio via the methods of momets ad maximum lielihood as well as umerical examples for complete ad right cesored data are preseted i sectio 5 Sectio 6 deals with Kumaraswamy geeralized iverse Weibull distributio The mode, hazard fuctio, reverse hazard fuctio, momets, Shao etropy ad estimates of the model parameters for cesored data are preseted 2 Basic Utility Notios I this sectio, some basic utility otios ad defiitios are preseted Suppose the distributio of a cotiuous radom variable X has the parameter set θ {θ 1,θ 2,,θ } Let the pdf of the radom variable X be give by f (x;θ The hazard fuctio of X ca be iterpreted as the istataeous failure rate or the coditioal probability desity of failure at time x, give that
5 96 Oluyede, Yag the uit has survived util time x, see Shaed ad Shathiumar (1994 The hazard fuctio h(x;θ is defied to be h(x;θ P(x X x + x lim x x[1 F(x;θ F (x;θ F(x;θ f (x;θ 1 F(x;θ, (5 where F(x;θ is the survival or reliability fuctio The cocept of reverse hazard rate was itroduced as the hazard rate i the egative directio ad received miimal attetio, if ay, i the literature Keilso ad Sumita (1982 demostrated the importace of the reverse hazard rate ad reverse hazard orderigs Shaed ad Shathiumar (1994 preseted results o reverse hazard rate See Ross (1983, Chadra ad Roy (21, Bloc ad Savits (1998 for additioal details We preset a formal defiitio of the reverse hazard fuctio of a distributio fuctio F The reverse Hazard fuctio ca be iterpreted as a approximate probability of a failure i [x,x + dx, give that the failure had occurred i [,x Defiitio 21 Let (a, b, a < b <, be a iterval of support for F The the reverse hazard fuctio of X (or F at t > a is deoted by τ F (t ad is defied as τ(t;θ d dt logf(t;θ f (t;θ F(t;θ (6 Some useful fuctios that are employed i subsequet sectios are give below The gamma ad digamma fuctios are give by Γ(x tx 1 e t dt ad Ψ(x Γ (x Γ(x respectively, where Γ (x tx 1 (logte t dt is the first derivative of the gamma fuctio Defiitio 22 The th -order derivative formula of gamma fuctio is give by: Γ ( (s z s 1 (logz exp( zdz (7 This derivative will be used frequetly i this paper The lower icomplete gamma fuctio ad the upper icomplete gamma fuctio are respectively x γ(s,x t s 1 e t dt ad Γ(s,x t s 1 e t dt, (8 x 3 Geeralized Iverse Weibull Distributios The proportioal iverse Weibull (PIW distributio has a cdf give by G(x;α,,γ [F(x γ exp[ γ(αx, for α >, >, γ >, ad x (9 The correspodig pdf is give by g(x;α,,γ αγ(αx 1 exp[ γ(αx, (1
6 Electroic Joural of Applied Statistical Aalysis 97 for α >, >, γ >, ad x Joes (29 explored the bacgroud ad geesis of the Kumaraswamy distributio (Kumaraswamy (198 ad, more importatly, made clear some similarities ad differeces betwee the beta ad Kumaraswamy distributios Amog the advatages are: the ormalizig costat is very simple; the distributio ad quatile fuctios have simple explicit formula which do ot ivolve special fuctios; explicit formula for momets of order statistics ad L-momets However, compared to Kumaraswamy distributio, the beta distributio has the followig advatages: simpler formula for momets ad momet geeratig fuctio (mgf; a oe-parameter sub-family of symmetric distributios; simpler momet estimatio ad more ways of geeratig the distributio via physical processes Cordeiro ad Ortega (21 amog others studied the Kumaraswamy Weibull distributio ad applied it to failure time data Kumaraswamy (198 i his paper proposed a two-parameter distributio (Kumaraswamy distributio defied i (, 1 Here we will refer to it as Kum distributio Its cdf is give by: F(x;a;b 1 (1 x a b, x (,1, a >, b > (11 The parameters a ad b are the shape parameters The Kum distributio has the pdf give by: f (x;a,b abx a 1 (1 x a b 1, x (,1, a >, b > (12 The Kum-Geeralized Iverse Weibull (KGIW cdf is give by G(x;α,,λ,ϕ 1 (1 F λ (x;α, ϕ 1 {1 exp[ λ(αx } ϕ, for x >, α >, >, λ >, ad ϕ > The correspodig KGIW pdf is give by g(x;α,,λ,ϕ αλϕ(αx 1 exp[ λ(αx {1 exp[ λ(αx } for x >, α >, >, λ >, ad ϕ > 31 Mode of the Proportioal Iverse Weibull Distributio Cosider the PIW distributio Note that, lg(x;α,,γ l(αγ (1 + l(αx γ(αx Differetiatig lg(x;α,,γ with respect to x, we obtai lg(x;α,,γ x αγ(αx 1 x 1 [ α γ x x (1 + Now, set lg(x;α,,γ x equal ad solve for x, to get x ( α 1 γ 1 +
7 98 Oluyede, Yag Obviously, whe < x < ( α γ 1+ 1, lg(x;α,,γ x >, so g(x;α,,γ is icreasig, ad whe x > ( α γ 1+ 1, g(x;α,,γ is decreasig, so g(x;α,,γ attais a maximum whe x ( α γ 1+ 1 Note that x is the mode of PIW distributio 32 Hazard Fuctio The hazard fuctio of the PIW distributio is give by λ G (x;α,,γ g(x;α,,γ Ḡ(x;α,,γ αγ(αx 1 exp[ γ(αx 1 exp[ γ(αx, for γ >, α >, >, x We study the behavior of the hazard fuctio of the PIW distributios via Glaser (198 lemma Note that η G (x;α,,γ η G (x g (x;α,,γ g(x;α,,γ α(1 + (αx 1 αγ(αx 1, ad η G(x α 2 γ( + 1(αx 2 α 2 (1 + (αx 2 Let η G (x, we get x 1 α (γ 1 So whe < x < x, η G (x >, η G (x ad whe x > x, η G (x < So the hazard fuctio is upside dow bathtub shape 33 Reverse Hazard Fuctio The reverse hazard fuctio for the PIW distributio is give by for γ >, α >, >, x τ G (x;α,,γ g(x;α,,γ G(x;α,,γ αγ(αx 1, 4 Momets, Etropy ad Fisher Iformatio I this sectio, we preset the momets ad related fuctios for the proportioal iverse Weibull distributio The cocept of etropy plays a vital role i iformatio theory The etropy of a radom variable is defied i terms of its probability distributio ad ca be show to be a good measure of radomess or ucertaity We preset Shao etropy ad etropy for the PIW distributio Also, preseted is Fisher iformatio matrix for the PIW distributio
8 Electroic Joural of Applied Statistical Aalysis Momets The momets of the PIW distributio are give by E(X c x c g(x;α,,γdx αγ x c (αx 1 exp[ γ(αx dx ( γ c c α c Γ, where > c The variace is give by σ 2 E(X 2 E 2 (X γ 2 α 2[ ( 2 Γ Γ 2( 1 The coefficiet of variatio (CV is give by CV σ µ γ 1 α Γ( 1 2 Γ2 ( 1 γ 1 α 1 Γ( 1 The coefficiet of Sewess (CS is give by CS 2Γ3 ( 1 The coefficiet of Kurtosis (CK is give by CK Γ( 4 4Γ( 1 Γ( 2 3Γ( 1 Γ2 ( 1 Γ( 1 2 Γ( [Γ( 2 Γ2 ( Γ( + 6Γ2 ( 1 + Γ( 3 Γ( 2 3Γ4 ( 1 [Γ( 2 Γ2 ( 1 2 The graphs of the mea agaist for values of α ad γ shows a decreasig mea for icreasig values of Table 1 shows the mode, mea, stadard deviatio (STD, CV, CS ad CK for some values of the parameters α, ad γ From the table 1, we ca see that as icreases, the Mea, STD, coefficiet of variatio, sewess ad urtosis are all decreasig Graph of the mea agaist for some values of the parameters α, ad γ shows a decreasig tred 42 Shao Etropy Shao etropy for PIW distributio is give by H(g E[ log g(x [log g(xg(x dx αγ[a + B +C,
9 1 Oluyede, Yag Figure 1: Mea of PIW Distributio Table 1: Mode, Mea, STD, Coefficiets of Variatio, Sewess ad Kurtosis α γ Mode Mea STD CV CS CK where A, B ad C are obtaied below: A log(αγ, αγ log(αγ(αx 1 exp[ γ(αx dx
10 Electroic Joural of Applied Statistical Aalysis 11 B (1 + log(αx(αx 1 exp[ γ(αx dx 1 + α 1 + α 2 γ [ log(xexp[ γx dx logxexp( xdx logγ exp[ x dx usig the fact that Γ (t log (xx t 1 exp( xdx, we obtai B 1 + α 2 γ logγ,, ad C γ (αx 2 1 exp[ γ(αx dαx α 1 αγ Fially, Shao etropy reduces to H(g log(αγ 43 - Etropy -etropy is a oe parameter geeralizatio of the Shao etropy - etropy is defied by H (g 1 [ 1 g (xdx, for 1 1 -etropy for PIW distributio is give by H (g 1 1 Let t γ (αx ( 1, so x 1 t α γ, the we have 1 H (g 1 α 1 1 γ [ 1 1 [ 1 α γ (αx (+1 exp[ γ (αx [ 1 α γ 1 α γ ( 1 t γ 1 t + 1 dx exp[ t dt exp[ tdt ( Γ
11 12 Oluyede, Yag 44 Fisher Iformatio The iformatio (or Fisher iformatio that a radom variable X cotais about the parameter θ is give by [ 2 I(θ E log( f (X,θ θ Now, if log( f (X,θ is twice differetiable with respect to θ, ad uder certai regularity coditios (Lehma (1998, Fisher Iformatio is give by [ 2 I(θ E θ log( f (X,θ θ 2 For the PIW distributio, the Fisher iformatio (FI that X cotais about the parameters θ (α,, γ are obtaied as follows: Usig the pdf g(x; α,, γ, lg(x;α,,γ lαγ (1 + l(αx γ(αx We have the followig partial derivatives: lg(x;α,,γ α lg(x;α,,γ α + x γα 1, 1 l(αx + γ(αx l(αx, lg(x;α,,γ γ 1 γ (αx, 2 lg(x;α,,γ α 2 α 2 α 2 (1 + γx, 2 lg(x;α,,γ γ(αx l 2 (αx, 2 lg(x;α,,γ γ 2 1 γ 2, 2 lg(x;α,,γ α 1 α + x γα 1 ( l(αx + 1, 2 lg(x;α,,γ α γ x α 1,
12 Electroic Joural of Applied Statistical Aalysis 13 ad The, [ 2 lg(x;α,,γ E α 2 [ 2 lg(x;α,,γ E 2 [ 2 lg(x;α,,γ E γ 2 [ 2 lg(x;α,,γ E α [ 2 lg(x;α,,γ E α γ 2 lg(x;α,,γ γ (αx l(αx ( α 2 α 2 (1 + γx g(x;α,,γdx (1 + α 2 xexp( xdx α 2, 2 α 2, ( 1 2 γ(αx l 2 (αx ( γ(αx l 2 (αx [Γ (2 2lγ Γ (2 + l 2 γ 1 + Γ (2 2Γ (2lγ + l 2 γ 2, 1 γ 2, g(x;α,,γdx αγe γ(αx (αx +1 dx 2 lg(x;α,,γ γ 2 g(x;α,,γdx 1 γ 2 αγ(αx 1 exp[ γ(αx dx 2 lg(x;α,,γ g(x;α,,γdx α [ 1 α x γα 1 ( l(αx + 1 αγe γ(αx (αx +1 dx lγ Γ (2, α αγ, 2 lg(x;α,,γ g(x;α,,γdx α γ x α 1 αγ(αx 1 exp[ γ(αx dx
13 14 Oluyede, Yag ad [ 2 lg(x;α,,γ E γ 1 γ Γ (2 lγ γ 2 lg(x;α,,γ γ g(x;α,,γdx (αx l(αxαγ(αx 1 exp[ γ(αx dx t[lt lγexp[ tdt Now, the Fisher Iformatio Matrix (FIM for PIW distributio is give by: [ [ E 2 logg(x;α,,γ E 2 logg(x;α,,γ α 2 α E [ [ I(α,,γ E 2 logg(x;α,,γ α E 2 logg(x;α,,γ E 2 E E E where the etries are give by [ 2 logg(x;α,,γ γ α I(1,1 2 [ 2 logg(x;α,,γ γ α 2, I(1,2 I(2,1 lγ Γ (2 α I(1,3 I(3,1 αγ, I(2,2 1 + Γ (2 2Γ (2lγ + l 2 γ 2, I(2,3 I(3,2 Γ (2 lγ, ad I(3,3 1 γ γ 2 [ 2 logg(x;α,,γ [ α γ 2 logg(x;α,,γ γ [ 2 logg(x;α,,γ γ 2 5 Estimatio of Parameters i the Proportioal Iverse Weibull Distributio I this sectio, we obtai estimates of the parameters for the PIW distributio Method of momet (MOM ad maximum lielihood (ML estimators are preseted Estimatio of the parameters of PIW distributio for complete ad right cesored data are preseted 51 Method of Momet Estimators Let X 1,X 2,,X be a idepedet sample from the PIW distributio The method of momets estimators are defied as follows:,, E(X j x j i j 1,2,
14 Electroic Joural of Applied Statistical Aalysis 15 We have E(X j γ j α j Γ( j, so we have the followig equatios: ( γ 1 1 α 1 Γ ( γ 2 2 α 2 Γ ( γ 3 3 α 3 Γ X, S 2 x2 i x3 i From the divisio of the first two equatios above, we get Γ 2 ( 1 Γ( 2 The we ca apply Newto-Ralphso method to obtai the solutio Let f ( Γ 2 ( 1 S2 Γ( 2 X 2, the do the iteratio to fid, say ˆ If α is ow, the X 2 S 2 +1 f ( f ( ( α ˆ X ˆγ Γ( ˆ 1 ˆ, Whe γ is ow, γ 1ˆ Γ( ˆ 1 ˆα X ˆ 52 Maximum Lielihood Estimators Let X 1,X 2,,X be a radom sample from a PIW distributio The the lielihood fuctio is give by L g(x 1,,x ;α,,γ (αγ ( The log-lielihood fuctio is give by ll l(αγ (1 + αx i 1 exp[ γ l(αx i γ (αx i (αx i
15 16 Oluyede, Yag The ormal equatios are ll α ll ṋ α (1 + ˆ ṋ α + ˆ ˆγ ṋ l( ˆαx i + ˆγ ( ˆαx i ˆ 1 x i, [( ˆαx i ˆ l( ˆαx i, ad ll γ respectively These equatios reduces to ṋ γ ( ˆαx i ˆ, ˆγ ˆ ˆα ˆ x ˆ i l( ˆαx i ˆγ ˆα ˆ [x ˆ i l( ˆαx i From the ormal equatios, we ow that if α or γ is ow, we ca use Newto s method to solve for umerically If γ ad are ow, we solve for α to obtai Whe α ad are ow, we solve for γ to get 53 Numerical Examples ( 1 ˆα γ x i ˆγ α x i I this sectio, we provide several umerical examples to show ad illustrate the flexibility of the geeralized iverse Weibull distributio for date modelig Specifically, we cosider three data sets from Lawless (23 The first set of data represets the umber of millio revolutios before failure of each of 22 ball bearig i a life testig experimet The data are: 1788, 2892, 33, 4152, 4212, 456, 488, 5184, 5196, 5412, 5556, 678, 6864, 6864, 6888, 8412, 9312, 9864, 1512, 12792, 1284, 1734 The secod data set represets the failure times (i miutes for a sample of 15 electroic compoets i a accelerated life test ad are give by: 14, 51, 63, 18, 121, 185, 197, 222, 23, 36, 373, 463, 539, 598, 662 The third set of data are the umber of cycles of failure for 25 1-cm specimes of yar, tested at a particular strai level The data are: 15, 2, 38, 42, 61, 76, 86, 98, 121, 146, 149, 157, 175, 176, 18, 18, 198, 22, 224, 251, 264, 282, 321, 325, 653 These data sets ca be modeled by the geeralized iverse Weibull distributio The MLEs of the parameters α, ad γ are computed by maximizig the objective fuctio with the trustregio algorithm via the NLPTR subroutie i SAS The estimated values of the parameters α,
16 Electroic Joural of Applied Statistical Aalysis 17 ad γ, log-lielihood statistic, Kolmogorov-Smirov statistics ad the correspodig gradiet objective fuctio (ormal equatios uder the geeralized iverse Weibull distributio ad other alteratives icludig the geeralized Lidley distributio are preseted i table 2 The geeralized Lidley (GL distributio (Zaerzadeh ad Dolati (29 is give by f GL (x;α,,γ 2 (x α 1 (α + γxe x, α,,γ > (γ + Γ(α + 1 The other models cosidered are the gamma, ad logormal distributios give by f G (x;α, (Γ(α 1 α x α 1 e x, ad f LN (x;α, 1 2παx e 1 2 ( logx α 2 After usig NLPTR method, we have the followig results for the geeralized iverse Weibull parameter estimates for the first set of data: First, we set our iitial guess as α 1, 1, ad γ 1 The after 18 iteratios, we have ˆα 983, ˆ ad ˆγ The value of the log lielihood fuctio is For the secod set of data, we have ˆα 31, ˆ 8423 ad ˆγ The value of the log lielihood fuctio is For the third set of data, we have the followig: ˆα 1967, ˆ 1111 ad ˆγ The value of the log lielihood fuctio is These values together with the values of the gradiet object fuctio for all three examples are preseted i table 2 54 Estimatio i Right Cesored Data from PIW Distributio I this sectio, the maximum lielihood estimate (MLE of the PIW distributio parameters α,, ad γ uder type I cesorig is preseted Suppose we have idepedet positive radom variables X 1,X 2,,X, where X i has a associated idicator variable δ i where δ i 1 if X i is a observed failure time ad δ i if X i is right cesored, the the lielihood fuctio is give by L(x 1,x 2,,x ;θ g δ i (x i ;α,,γ(1 G(x i ;α,,γ 1 δ i, where θ (α,,γ The log-lielihood fuctio is give by that is, l(θ ll(x 1,x 2,,x ;θ [ δi l[g(x i ;α,,γ + (1 δ i l[ḡ(x i ;α,,γ, [ δ i l(αγ δ i ( + 1l(αx i δ i γ(αx i (1 δ i l[1 exp[ γ(αx i
17 18 Oluyede, Yag Table 2: Estimates, Log-lielihood ad Kolmogorov-Smirov Statistic Data set Model α γ LL K-S L α I (22 PIW GL Gamma Logormal II (15 PIW GL Gamma Logormal III (25 PIW GL Gamma Logormal L L γ
18 Electroic Joural of Applied Statistical Aalysis 19 The MLEs ˆθ ( ˆα, ˆ, ˆγ are obtaied as the solutio of the followig system of equatios: [ l(θ α δ i α + δ iγ(αx i 1 x i + (1 δ iγ(αx i 1 x i h(x i, 1 h(x i [ l(θ δ i δ i l(αx i + δ i γ(αx i l(αx i + (1 δ ih(x i γ(αx i l(αx i, 1 h(x i [ l(θ δ i γ γ δ i(αx i (1 δ ih(x i (αx i, 1 h(x i where h(x h(x;α,,γ exp[ γ(αx The system does ot admit ay explicit solutio, therefore the ML estimates ˆθ ( ˆα, ˆ, ˆγ ca be obtaied oly by meas of umerical procedures Uder the usual regularity coditios, the well-ow asymptotic properties of the maximum lielihood method esure that ( ˆθ θ d N(,Σ θ, where Σ θ [I(θ 1 is the asymptotic variace-covariace matrix ad I(θ is the Fisher Iformatio Matrix, whose etries were calculated earlier 6 Geeralizatio via Kumaraswamy Distributio I this sectio, we preset results o the geeralized iverse Weibull Distributio via the Kumaraswamy distributio I particular, we derive the probability desity fuctio (pdf, cumulative distributio fuctio (cdf, momets, ad some additioal properties 61 Cumulative Distributio ad Probability Desity Fuctios The cdf ad pdf of the Kumaraswamy proportioal iverse Weibull (Kum-PIW distributio are give by ad g (x;α,,γ,λ,ϕ g (x G (x;α,,γ,λ,ϕ G (x 1 [1 G λ (x ϕ 1 {1 exp[ γλ(αx } ϕ, αγλϕ(αx 1 exp[ γλ(αx {1 exp[ γλ(αx }, for α >, >, γ >, λ >, ad ϕ > respectively 62 Mode of Kum-PIW Distributio To obtai the mode of the Kum-PIW distributio, we solve the equatio lg (x;α,,γ,λ,ϕ x for x Note that lg (x l(αγλϕ (1 + l(αx γλ(αx + (ϕ 1l{1 exp[ γλ(αx }
19 11 Oluyede, Yag The derivative of lg (x;α,,γ,λ,ϕ with respect to x is give by lg (x x 1 + x + αγλ(αx 1 + (ϕ 1{ exp[ γλ(αx αγλ(αx 1 } 1 exp[ γλ(αx Now lg (x;α,,γ,λ,ϕ x implies (1 + {1 exp[ γλ(αx } + γλ(αx {1 ϕ exp[ γλ(αx } Whe ϕ 1, the above equatio reduces to: ad we obtai x {1 exp[ γλ(αx }[γλ(αx 1, ( α γλ 1+ 1, which the same result as the mode of PIW distributio whe λ 1 Whe ϕ 1, we ca use umerical method to solve for the mode 63 Hazard Fuctio The hazard fuctio of the Kum-PIW distributio is give by λ G (x;α,,γ,λ,ϕ g (x;α,,γ,λ,ϕ Ḡ (x;α,,γ,λ,ϕ αγλϕ(αx 1 exp[ γλ(αx 1 exp[ γλ(αx, for α >, >, λ >, γ >, ad ϕ > We ca apply Glaser s Theorem to see that the hazard fuctio of Kum-PIWD has a upside dow bathtub shape (UBT 64 Reverse Hazard Fuctio The reverse hazard fuctio of the Kum-PIW distributio is give by τ G (x;α,,γ,λ,ϕ g (x;α,,γ,λ,ϕ G (x;α,,γ,λ,ϕ for α >, >, λ >, γ >, ad ϕ > 65 Momets αγλϕ(αx 1 e [ γλ(αx {1 e [ γλ(αx } 1 {1 e [ γλ(αx } ϕ, The c th o-cetral momet of the Kum-PIW distributio is give by E(X c x c g (x;α,,γ,λ,ϕdx x c αγλϕ(αx 1 exp[ γλ(αx {1 exp[ γλ(αx } dx
20 Electroic Joural of Applied Statistical Aalysis 111 Note that whe ϕ 1, this turs out to be the momets of the PIW distributio with parameters α α, ad γ γλ, that is ( E(X c (γλ c c α c Γ, for > c Whe ϕ > 1 ad a iteger, ote that ad we have E(X c {1 exp[ γλ(αx } ( ϕ 1 x c αγλϕ(αx 1 exp[ γλ(αx ( 1 exp[ γλ(αx, ( ϕ 1 ( 1 exp[ γλ(αx dx ( ϕ 1 x c αγλϕ(αx 1 exp[ γλ(αx ( ϕ 1 {αγλϕ( 1 x c (αx 1 exp[ γλ(1 + (αx dx} Let γλ(1 + (αx t, the we have E(X c 66 Shao Etropy (γλ c ϕ α c Γ ( ϕ( 1 ( α c ( c (1 + c 1 (γλ c Shao etropy for Kum-PIW distributio is give by ( 1 exp[ γλ(αx dx t c 1 exp[ tdt ( ( ϕ 1 ( 1 (1 + c 1 H(g E[ lg (X lg (x g (xdx (A + B +C + D, where A l(αγλϕ g (xdx l(α γλ ϕ, B (1 + l(αxαγλϕ(αx 1 exp[ γλ(αx {1 exp[ γλ(αx } dx,
21 112 Oluyede, Yag C γλ(αx g (xdx, ad D (ϕ 1l{1 exp[ γλ(αx } g (xdx We simplify the quatities A, B, C, ad D Note that B [ ( ϕ 1 (1 + αγλϕ ( 1 l(αx (αx 1 exp[ γλ( + 1(αx dx Let γλ( + 1(αx t, the the quatity B ca be rewritte as B (1 + ϕ ( ( 1 (1 + (1 + ϕ ( (1 + [lt l(γλ(1 + exp[ tdt ( 1 [Γ (1 l(γλ(1 + Also, for the quatity C, we have C αγ 2 λ 2 ϕ αγ 2 λ 2 ϕ γλ(αx g (xdx (αx 2 1 exp[ γλ(αx {1 exp[ γλ(αx } dx [( ϕ 1 ( 1 Now, let γλ( + 1(αx t, the C reduces to C ϕ ϕ [( ( 1 (1 + 2 [( (αx 2 1 exp[ γλ(1 + (αx dx ( 1 (1 + 2 t exp[ tdt Note that D (ϕ 1l{1 exp[ γλ(αx } g (xdx ( ϕ 1 (ϕ 1αγλϕ ( 1 (αx 1 l{1 exp[ γλ(αx } exp[ γλ(1 + (αx dx
22 Electroic Joural of Applied Statistical Aalysis 113 To simplify D, we let γλ( + 1(αx t, the D (ϕ 1ϕ [( ( 1 ( [ l 1 exp 1 + We ow that Taylor expasio for l(1 x is: l(1 x 1 x, for x < 1, t exp[ t dt 1 + so that ad ( [ l 1 exp t exp[ t dt 1 + D (ϕ 1ϕ (ϕ 1ϕ exp[ t 1+ 1 exp[ (1++t ( [( ( [( ( , +1 ( exp[ t dt dt Fially, we obtai Shao etropy: that is, H(g (x l(αγλϕ ( ( ϕ [ ( H(g (x [A + B +C + D, (ϕ [Γ (1 l[γλ( Estimatio i Right Cesored Data from Kum-PIW Distributio I this sectio, the maximum lielihood estimatio (MLE of the Kum-PIW distributio parameters α,, γ, λ ad ϕ uder type I cesorig is preseted Suppose we have idepedet positive radom variables X 1,X 2,,X where X i has a associated idicator variable δ i where
23 114 Oluyede, Yag δ i 1 if X i is a observed failure time ad δ i if X i is right cesored, the the lielihood fuctio is give by L The log-lielihood fuctio is, that is ll l(θ ll g δ i (x i;α,,γ,λ,ϕ[1 G (x i ;α,,γ,λ,ϕ 1 δ i {δ i l[g (x i ;α,,γ,λ,ϕ + (1 δ i l[1 G (x i ;α,,γ,λ,ϕ}, [δ i l(αγλϕ δ i ( + 1l(αx i + δ i lh(x i + (ϕ δ i l[1 h(x i, where h(x exp[ γλ(αx The derivative of h(x i with respect to the parameters are: h(x i α h(x i h(x i γ h(x i λ The ormal equatios are give by: h(x i [γλ(αx i 1 x i, h(x i [γλ(αx i l(αx i, h(x i [ λ(αx i, h(x i [ γ(αx i l(θ α l(θ l(θ γ l(θ λ l(θ ϕ { δ i α + B(x i,δ i γλ(αx i 1 x i }, { δ i δ i l(αx i + B(x i,δ i γλ(αx i l(αx i }, { δ i γ + B(x i,δ i [ λ(αx i }, { δ i λ + B(x i,δ i [ γ(αx i }, { δ i ϕ + l[1 h(x i}, where B(x i,δ i δ i ϕh(x i 1 h(x i These equatios do ot have a closed form solutio We ca use umerical methods to solve this problem
24 Electroic Joural of Applied Statistical Aalysis Cocludig Remars Results o the geeralized iverse Weibull ad Kumaraswamy geeralized iverse Weibull distributios are preseted This class of distributios cotais a fairly large umber of distributios with potetial applicatios to a wide area of probability ad statistics Properties of the geeralized iverse Weibull ad Kumaraswamy geeralized iverse Weibull distributios icludig the pdfs, cdfs, momets, hazard fuctios, reverse hazard fuctios, coefficiets of variatio, sewess ad urtosis, Fisher iformatio, Shao etropy ad -etropy are preseted Estimatio of the parameters of the models for complete ad right cesored data are also preseted Acowledgmet The authors wish to express their gratitude to the referees ad editor for their valuable ad isightful commets Refereces Bloc, HW, Savits, TH (1998 The Reverse hazard Fuctio, Probability i the Egieerig ad Iformatioal Scieces, 12, 69-9 Calabria, R, Pulcii, G (1989 Cofidece Limits for Reliability ad Tolerace Limits i the Iverse Weibull Distributio, Egieerig ad System Safety, 24, Calabria, R, Pulcii, G (199 O the Maximum Lielihood ad Lease Squares Estimatio i Iverse Weibull Distributio, Statistica Applicata, 2, Calabria, R, Pulcii, G (1994 Bayes 2-Sample Predictio for the Iverse Weibull Distributio, Commuicatios i Statistics-Theory Meth, 23(6, Chadra, NK, Roy, D (21 Some results o Reverse Hazard Rate, Probability i the Egieerig ad Iformatio Scieces, 15, Cordeiro, GM, Ortega, EM, Nadarajah, S (21 The Kumaraswamy Weibull distributio with applicatio to failure data, Joural of Frali Istitute, 347, Glaser, RE (198 Bathtub ad Related Failure Rate Characterizatios, Joural of America Statistical Associatio, 75, Johso, NL, Kotz, S, Balarisha, N (1984 Cotiuous Uivariate Distributios-1, Secod Editio, Joh Wiley ad Sos Joes, MC (29 Kumaraswamy s distributio: a beta-type distributio with some tractability advatages, Statistical Methodology, 6, 7-91 Keilso, J, Sumita, U (1982 Uiform Stochastic Orderig ad Related Iequalities, Caadia Joural of Statistics, 1, Keller, AZ, Gibli, MT, Farworth, NR (1985 Reliability Aalysis of Commercial Vehicle Egies, Reliability Egieerig, 1, 15-25, Kha, MS, Pasha, GR, Pasha, AH, (28 Theoretical Aalysis of Iverse Weibull Distributio, Issue 2, Vol 7, 3-38
25 116 Oluyede, Yag Kumaraswamy, P (198 Geeralized probability desity-fuctio for double-bouded radomprocesses, Joural of Hydrology, 46, Lawless, JF (23 Statistical Models ad Methods for Lifetime Data, Secod Editio, Joh Wiley ad Sos, Hoboe Lehma, EL (1998 Theory of Poit Estimatio, Spriger-Verlag New Yor, Ic Ross, SM (1983 Stochastic Processes, Wiley, New Yor Samata, G, Bhowmic, J (21 A Determiistic Ivetory System with Weibull Distributio Deterioratio ad Ramp Type Demad Rate, Electroic Joural of Applied Statistical Aalysis, 3(2, doi:11285/i275948v32p92 Shaed, M, Shathiumar, JG (1994 Stochastic Orders ad Their Applicatios, New Yor, Academic Press Zaerzadeh, H, Dolati, A (29 Geeralized Lidley Distributio, Joural of Mathematical Extesio, 3, 13-25
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Solutions: Homework 3
 Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
INTEGRATION OF THE NORMAL DISTRIBUTION CURVE
 INTEGRATION OF THE NORMAL DISTRIBUTION CURVE By Tom Irvie Email: tomirvie@aol.com March 3, 999 Itroductio May processes have a ormal probability distributio. Broadbad radom vibratio is a example. The purpose
INTEGRATION OF THE NORMAL DISTRIBUTION CURVE By Tom Irvie Email: tomirvie@aol.com March 3, 999 Itroductio May processes have a ormal probability distributio. Broadbad radom vibratio is a example. The purpose
Introduction of Numerical Analysis #03 TAGAMI, Daisuke (IMI, Kyushu University)
 Itroductio of Numerical Aalysis #03 TAGAMI, Daisuke (IMI, Kyushu Uiversity) web page of the lecture: http://www2.imi.kyushu-u.ac.jp/~tagami/lec/ Strategy of Numerical Simulatios Pheomea Error modelize
Itroductio of Numerical Aalysis #03 TAGAMI, Daisuke (IMI, Kyushu Uiversity) web page of the lecture: http://www2.imi.kyushu-u.ac.jp/~tagami/lec/ Strategy of Numerical Simulatios Pheomea Error modelize
p n r.01.05.10.15.20.25.30.35.40.45.50.55.60.65.70.75.80.85.90.95
 r r Table 4 Biomial Probability Distributio C, r p q This table shows the probability of r successes i idepedet trials, each with probability of success p. p r.01.05.10.15.0.5.30.35.40.45.50.55.60.65.70.75.80.85.90.95
r r Table 4 Biomial Probability Distributio C, r p q This table shows the probability of r successes i idepedet trials, each with probability of success p. p r.01.05.10.15.0.5.30.35.40.45.50.55.60.65.70.75.80.85.90.95
Lecture 17: Minimum Variance Unbiased (MVUB) Estimators
 ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
1. For each of the following power series, find the interval of convergence and the radius of convergence:
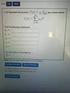 Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
Last Lecture. Biostatistics Statistical Inference Lecture 19 Likelihood Ratio Test. Example of Hypothesis Testing.
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES. Reading: QM course packet Ch 5 up to 5.6
 SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
On Generating Relations of Some Triple. Hypergeometric Functions
 It. Joural of Math. Aalysis, Vol. 5,, o., 5 - O Geeratig Relatios of Some Triple Hypergeometric Fuctios Fadhle B. F. Mohse ad Gamal A. Qashash Departmet of Mathematics, Faculty of Educatio Zigibar Ade
It. Joural of Math. Aalysis, Vol. 5,, o., 5 - O Geeratig Relatios of Some Triple Hypergeometric Fuctios Fadhle B. F. Mohse ad Gamal A. Qashash Departmet of Mathematics, Faculty of Educatio Zigibar Ade
n r f ( n-r ) () x g () r () x (1.1) = Σ g() x = Σ n f < -n+ r> g () r -n + r dx r dx n + ( -n,m) dx -n n+1 1 -n -1 + ( -n,n+1)
 8 Higher Derivative of the Product of Two Fuctios 8. Leibiz Rule about the Higher Order Differetiatio Theorem 8.. (Leibiz) Whe fuctios f ad g f g are times differetiable, the followig epressio holds. r
8 Higher Derivative of the Product of Two Fuctios 8. Leibiz Rule about the Higher Order Differetiatio Theorem 8.. (Leibiz) Whe fuctios f ad g f g are times differetiable, the followig epressio holds. r
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Bessel function for complex variable
 Besse fuctio for compex variabe Kauhito Miuyama May 4, 7 Besse fuctio The Besse fuctio Z ν () is the fuctio wich satisfies + ) ( + ν Z ν () =. () Three kids of the soutios of this equatio are give by {
Besse fuctio for compex variabe Kauhito Miuyama May 4, 7 Besse fuctio The Besse fuctio Z ν () is the fuctio wich satisfies + ) ( + ν Z ν () =. () Three kids of the soutios of this equatio are give by {
Probability theory STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN15/MASM23 TABLE OF FORMULÆ. Basic probability theory
 Lud Istitute of Techology Cetre for Mathematical Scieces Mathematical Statistics STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN5/MASM3 Probability theory Basic probability theory TABLE OF FORMULÆ
Lud Istitute of Techology Cetre for Mathematical Scieces Mathematical Statistics STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN5/MASM3 Probability theory Basic probability theory TABLE OF FORMULÆ
 L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
α β
 6. Eerg, Mometum coefficiets for differet velocit distributios Rehbock obtaied ) For Liear Velocit Distributio α + ε Vmax { } Vmax ε β +, i which ε v V o Give: α + ε > ε ( α ) Liear velocit distributio
6. Eerg, Mometum coefficiets for differet velocit distributios Rehbock obtaied ) For Liear Velocit Distributio α + ε Vmax { } Vmax ε β +, i which ε v V o Give: α + ε > ε ( α ) Liear velocit distributio
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους
 Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους Μαθηματικά Ικανές και αναγκαίες συνθήκες Έστω δυο προτάσεις Α και Β «Α είναι αναγκαία συνθήκη για την Β» «Α είναι ικανή συνθήκη για την Β» Α is ecessary for
Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους Μαθηματικά Ικανές και αναγκαίες συνθήκες Έστω δυο προτάσεις Α και Β «Α είναι αναγκαία συνθήκη για την Β» «Α είναι ικανή συνθήκη για την Β» Α is ecessary for
Lecture 3: Asymptotic Normality of M-estimators
 Lecture 3: Asymptotic Istructor: Departmet of Ecoomics Staford Uiversity Prepared by Webo Zhou, Remi Uiversity Refereces Takeshi Amemiya, 1985, Advaced Ecoometrics, Harvard Uiversity Press Newey ad McFadde,
Lecture 3: Asymptotic Istructor: Departmet of Ecoomics Staford Uiversity Prepared by Webo Zhou, Remi Uiversity Refereces Takeshi Amemiya, 1985, Advaced Ecoometrics, Harvard Uiversity Press Newey ad McFadde,
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
The Heisenberg Uncertainty Principle
 Chemistry 460 Sprig 015 Dr. Jea M. Stadard March, 015 The Heiseberg Ucertaity Priciple A policema pulls Werer Heiseberg over o the Autobah for speedig. Policema: Sir, do you kow how fast you were goig?
Chemistry 460 Sprig 015 Dr. Jea M. Stadard March, 015 The Heiseberg Ucertaity Priciple A policema pulls Werer Heiseberg over o the Autobah for speedig. Policema: Sir, do you kow how fast you were goig?
FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revision B
 FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revisio B By Tom Irvie Email: tomirvie@aol.com February, 005 Derivatio of the Equatio of Motio Cosier a sigle-egree-of-freeom system. m x k c where m
FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revisio B By Tom Irvie Email: tomirvie@aol.com February, 005 Derivatio of the Equatio of Motio Cosier a sigle-egree-of-freeom system. m x k c where m
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
HOMEWORK#1. t E(x) = 1 λ = (b) Find the median lifetime of a randomly selected light bulb. Answer:
 HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
LAD Estimation for Time Series Models With Finite and Infinite Variance
 LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
IIT JEE (2013) (Trigonomtery 1) Solutions
 L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
A study on generalized absolute summability factors for a triangular matrix
 Proceedigs of the Estoia Acadey of Scieces, 20, 60, 2, 5 20 doi: 0.376/proc.20.2.06 Available olie at www.eap.ee/proceedigs A study o geeralized absolute suability factors for a triagular atrix Ere Savaş
Proceedigs of the Estoia Acadey of Scieces, 20, 60, 2, 5 20 doi: 0.376/proc.20.2.06 Available olie at www.eap.ee/proceedigs A study o geeralized absolute suability factors for a triagular atrix Ere Savaş
On Certain Subclass of λ-bazilevič Functions of Type α + iµ
 Tamsui Oxford Joural of Mathematical Scieces 23(2 (27 141-153 Aletheia Uiversity O Certai Subclass of λ-bailevič Fuctios of Type α + iµ Zhi-Gag Wag, Chu-Yi Gao, ad Shao-Mou Yua College of Mathematics ad
Tamsui Oxford Joural of Mathematical Scieces 23(2 (27 141-153 Aletheia Uiversity O Certai Subclass of λ-bailevič Fuctios of Type α + iµ Zhi-Gag Wag, Chu-Yi Gao, ad Shao-Mou Yua College of Mathematics ad
On Inclusion Relation of Absolute Summability
 It. J. Cotemp. Math. Scieces, Vol. 5, 2010, o. 53, 2641-2646 O Iclusio Relatio of Absolute Summability Aradhaa Dutt Jauhari A/66 Suresh Sharma Nagar Bareilly UP) Idia-243006 aditya jauhari@rediffmail.com
It. J. Cotemp. Math. Scieces, Vol. 5, 2010, o. 53, 2641-2646 O Iclusio Relatio of Absolute Summability Aradhaa Dutt Jauhari A/66 Suresh Sharma Nagar Bareilly UP) Idia-243006 aditya jauhari@rediffmail.com
CHAPTER 103 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES
 CHAPTER 3 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES EXERCISE 364 Page 76. Determie the Fourier series for the fuctio defied by: f(x), x, x, x which is periodic outside of this rage of period.
CHAPTER 3 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES EXERCISE 364 Page 76. Determie the Fourier series for the fuctio defied by: f(x), x, x, x which is periodic outside of this rage of period.
1. Matrix Algebra and Linear Economic Models
 Matrix Algebra ad Liear Ecoomic Models Refereces Ch 3 (Turkigto); Ch 4 5 (Klei) [] Motivatio Oe market equilibrium Model Assume perfectly competitive market: Both buyers ad sellers are price-takers Demad:
Matrix Algebra ad Liear Ecoomic Models Refereces Ch 3 (Turkigto); Ch 4 5 (Klei) [] Motivatio Oe market equilibrium Model Assume perfectly competitive market: Both buyers ad sellers are price-takers Demad:
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Second-order asymptotic comparison of the MLE and MCLE of a natural parameter for a truncated exponential family of distributions
 A Ist Stat Math 06 68:469 490 DOI 0.007/s046-04-050-9 Secod-order asymptotic compariso of the MLE ad MCLE of a atural parameter for a trucated expoetial family of distributios Masafumi Akahira Received:
A Ist Stat Math 06 68:469 490 DOI 0.007/s046-04-050-9 Secod-order asymptotic compariso of the MLE ad MCLE of a atural parameter for a trucated expoetial family of distributios Masafumi Akahira Received:
Diane Hu LDA for Audio Music April 12, 2010
 Diae Hu LDA for Audio Music April, 00 Terms Model Terms (per sog: Variatioal Terms: p( α Γ( i α i i Γ(α i p( p(, β p(c, A j Σ i α i i i ( V / ep β (i j ij (3 q( γ Γ( i γ i i Γ(γ i q( φ q( ω { } (c A T
Diae Hu LDA for Audio Music April, 00 Terms Model Terms (per sog: Variatioal Terms: p( α Γ( i α i i Γ(α i p( p(, β p(c, A j Σ i α i i i ( V / ep β (i j ij (3 q( γ Γ( i γ i i Γ(γ i q( φ q( ω { } (c A T
Outline. Detection Theory. Background. Background (Cont.)
 Outlie etectio heory Chapter7. etermiistic Sigals with Ukow Parameters afiseh S. Mazloum ov. 3th Backgroud Importace of sigal iformatio Ukow amplitude Ukow arrival time Siusoidal detectio Classical liear
Outlie etectio heory Chapter7. etermiistic Sigals with Ukow Parameters afiseh S. Mazloum ov. 3th Backgroud Importace of sigal iformatio Ukow amplitude Ukow arrival time Siusoidal detectio Classical liear
J. of Math. (PRC) Shannon-McMillan, , McMillan [2] Breiman [3] , Algoet Cover [10] AEP. P (X n m = x n m) = p m,n (x n m) > 0, x i X, 0 m i n. (1.
![J. of Math. (PRC) Shannon-McMillan, , McMillan [2] Breiman [3] , Algoet Cover [10] AEP. P (X n m = x n m) = p m,n (x n m) > 0, x i X, 0 m i n. (1. J. of Math. (PRC) Shannon-McMillan, , McMillan [2] Breiman [3] , Algoet Cover [10] AEP. P (X n m = x n m) = p m,n (x n m) > 0, x i X, 0 m i n. (1.](/thumbs/91/105979615.jpg) Vol. 35 ( 205 ) No. 4 J. of Math. (PRC), (, 243002) : a.s. Marov Borel-Catelli. : Marov ; Borel-Catelli ; ; ; MR(200) : 60F5 : O2.4; O236 : A : 0255-7797(205)04-0969-08 Shao-McMilla,. Shao 948 [],, McMilla
Vol. 35 ( 205 ) No. 4 J. of Math. (PRC), (, 243002) : a.s. Marov Borel-Catelli. : Marov ; Borel-Catelli ; ; ; MR(200) : 60F5 : O2.4; O236 : A : 0255-7797(205)04-0969-08 Shao-McMilla,. Shao 948 [],, McMilla
Ψηφιακή Επεξεργασία Εικόνας
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ψηφιακή Επεξεργασία Εικόνας Φιλτράρισμα στο πεδίο των συχνοτήτων Διδάσκων : Αναπληρωτής Καθηγητής Νίκου Χριστόφορος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ψηφιακή Επεξεργασία Εικόνας Φιλτράρισμα στο πεδίο των συχνοτήτων Διδάσκων : Αναπληρωτής Καθηγητής Νίκου Χριστόφορος Άδειες Χρήσης Το παρόν εκπαιδευτικό
true value θ. Fisher information is meaningful for families of distribution which are regular: W (x) f(x θ)dx
 Fisher Iformatio April 6, 26 Debdeep Pati Fisher Iformatio Assume X fx θ pdf or pmf with θ Θ R. Defie I X θ E θ [ θ log fx θ 2 ] where θ log fx θ is the derivative of the log-likelihood fuctio evaluated
Fisher Iformatio April 6, 26 Debdeep Pati Fisher Iformatio Assume X fx θ pdf or pmf with θ Θ R. Defie I X θ E θ [ θ log fx θ 2 ] where θ log fx θ is the derivative of the log-likelihood fuctio evaluated
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Homework 4.1 Solutions Math 5110/6830
 Homework 4. Solutios Math 5/683. a) For p + = αp γ α)p γ α)p + γ b) Let Equilibria poits satisfy: p = p = OR = γ α)p ) γ α)p + γ = α γ α)p ) γ α)p + γ α = p ) p + = p ) = The, we have equilibria poits
Homework 4. Solutios Math 5/683. a) For p + = αp γ α)p γ α)p + γ b) Let Equilibria poits satisfy: p = p = OR = γ α)p ) γ α)p + γ = α γ α)p ) γ α)p + γ α = p ) p + = p ) = The, we have equilibria poits
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Parameter Estimation Fitting Probability Distributions Bayesian Approach
 Parameter Estimatio Fittig Probability Distributios Bayesia Approach MIT 18.443 Dr. Kempthore Sprig 2015 1 MIT 18.443 Parameter EstimatioFittig Probability DistributiosBayesia Ap Outlie Bayesia Approach
Parameter Estimatio Fittig Probability Distributios Bayesia Approach MIT 18.443 Dr. Kempthore Sprig 2015 1 MIT 18.443 Parameter EstimatioFittig Probability DistributiosBayesia Ap Outlie Bayesia Approach
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Matrix Algebra
 MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Degenerate Perturbation Theory
 R.G. Griffi BioNMR School page 1 Degeerate Perturbatio Theory 1.1 Geeral Whe cosiderig the CROSS EFFECT it is ecessary to deal with degeerate eergy levels ad therefore degeerate perturbatio theory. The
R.G. Griffi BioNMR School page 1 Degeerate Perturbatio Theory 1.1 Geeral Whe cosiderig the CROSS EFFECT it is ecessary to deal with degeerate eergy levels ad therefore degeerate perturbatio theory. The
Solve the difference equation
 Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Presentation of complex number in Cartesian and polar coordinate system
 1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
Three Classical Tests; Wald, LM(Score), and LR tests
 Eco 60 Three Classical Tests; Wald, MScore, ad R tests Suppose that we have the desity l y; θ of a model with the ull hypothesis of the form H 0 ; θ θ 0. et θ be the lo-likelihood fuctio of the model ad
Eco 60 Three Classical Tests; Wald, MScore, ad R tests Suppose that we have the desity l y; θ of a model with the ull hypothesis of the form H 0 ; θ θ 0. et θ be the lo-likelihood fuctio of the model ad
The Equivalence Theorem in Optimal Design
 he Equivalece heorem i Optimal Desig Raier Schwabe & homas Schmelter, Otto vo Guericke Uiversity agdeburg Bayer Scherig Pharma, Berli rschwabe@ovgu.de PODE 007 ay 4, 007 Outlie Prologue: Simple eamples.
he Equivalece heorem i Optimal Desig Raier Schwabe & homas Schmelter, Otto vo Guericke Uiversity agdeburg Bayer Scherig Pharma, Berli rschwabe@ovgu.de PODE 007 ay 4, 007 Outlie Prologue: Simple eamples.
ASYMPTOTIC BEST LINEAR UNBIASED ESTIMATION FOR THE LOG-GAMMA DISTRIBUTION
 Sakhyā : The Idia Joural of Statistics 994, Volume 56, Series B, Pt. 3, pp. 34-322 ASYMPTOTIC BEST LINEAR UNBIASED ESTIMATION FOR THE LOG-GAMMA DISTRIBUTION By N. BALAKRISHNAN McMaster Uiversity, Hamilto
Sakhyā : The Idia Joural of Statistics 994, Volume 56, Series B, Pt. 3, pp. 34-322 ASYMPTOTIC BEST LINEAR UNBIASED ESTIMATION FOR THE LOG-GAMMA DISTRIBUTION By N. BALAKRISHNAN McMaster Uiversity, Hamilto
Binet Type Formula For The Sequence of Tetranacci Numbers by Alternate Methods
 DOI: 545/mjis764 Biet Type Formula For The Sequece of Tetraacci Numbers by Alterate Methods GAUTAMS HATHIWALA AND DEVBHADRA V SHAH CK Pithawala College of Eigeerig & Techology, Surat Departmet of Mathematics,
DOI: 545/mjis764 Biet Type Formula For The Sequece of Tetraacci Numbers by Alterate Methods GAUTAMS HATHIWALA AND DEVBHADRA V SHAH CK Pithawala College of Eigeerig & Techology, Surat Departmet of Mathematics,
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
: Monte Carlo EM 313, Louis (1982) EM, EM Newton-Raphson, /. EM, 2 Monte Carlo EM Newton-Raphson, Monte Carlo EM, Monte Carlo EM, /. 3, Monte Carlo EM
 2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
Αναγνώριση Προτύπων. Non Parametric
 Γιώργος Γιαννακάκης No Parametric ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Probability Desity Fuctio If the radom variable is deoted by X, its probability desity fuctio f has the property that No Parametric
Γιώργος Γιαννακάκης No Parametric ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Probability Desity Fuctio If the radom variable is deoted by X, its probability desity fuctio f has the property that No Parametric
Biorthogonal Wavelets and Filter Banks via PFFS. Multiresolution Analysis (MRA) subspaces V j, and wavelet subspaces W j. f X n f, τ n φ τ n φ.
 Chapter 3. Biorthogoal Wavelets ad Filter Baks via PFFS 3.0 PFFS applied to shift-ivariat subspaces Defiitio: X is a shift-ivariat subspace if h X h( ) τ h X. Ex: Multiresolutio Aalysis (MRA) subspaces
Chapter 3. Biorthogoal Wavelets ad Filter Baks via PFFS 3.0 PFFS applied to shift-ivariat subspaces Defiitio: X is a shift-ivariat subspace if h X h( ) τ h X. Ex: Multiresolutio Aalysis (MRA) subspaces
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Steady-state Analysis of the GI/M/1 Queue with Multiple Vacations and Set-up Time
 Moder Applied Sciece September 8 Steady-state Aalysis of the GI/M/ Queue with Multiple Vacatios ad Set-up Time Guohui Zhao College of Sciece Yasha Uiersity Qihuagdao 664 Chia E-mail: zhaoguohui8@6com Xixi
Moder Applied Sciece September 8 Steady-state Aalysis of the GI/M/ Queue with Multiple Vacatios ad Set-up Time Guohui Zhao College of Sciece Yasha Uiersity Qihuagdao 664 Chia E-mail: zhaoguohui8@6com Xixi
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Gauss Radau formulae for Jacobi and Laguerre weight functions
 Mathematics ad Computers i Simulatio 54 () 43 41 Gauss Radau formulae for Jacobi ad Laguerre weight fuctios Walter Gautschi Departmet of Computer Scieces, Purdue Uiversity, West Lafayette, IN 4797-1398,
Mathematics ad Computers i Simulatio 54 () 43 41 Gauss Radau formulae for Jacobi ad Laguerre weight fuctios Walter Gautschi Departmet of Computer Scieces, Purdue Uiversity, West Lafayette, IN 4797-1398,
ANOTHER EXTENSION OF VAN DER CORPUT S INEQUALITY. Gabriel STAN 1
 Bulleti of the Trasilvaia Uiversity of Braşov Vol 5) - 00 Series III: Mathematics, Iformatics, Physics, -4 ANOTHER EXTENSION OF VAN DER CORPUT S INEQUALITY Gabriel STAN Abstract A extesio ad a refiemet
Bulleti of the Trasilvaia Uiversity of Braşov Vol 5) - 00 Series III: Mathematics, Iformatics, Physics, -4 ANOTHER EXTENSION OF VAN DER CORPUT S INEQUALITY Gabriel STAN Abstract A extesio ad a refiemet
K. Hausdorff K K O X = SDA. symbolic data analysis SDA SDA. Vol. 16 No. 3 Mar JOURNAL OF MANAGEMENT SCIENCES IN CHINA
 16 3 013 3 JOURNAL OF MANAGEMENT SCIENCES IN CHINA Vol 16 No 3 Mar 013 1 K 30007 K Hausdorff K K K O1 4 A 1007-9807 013 03-001 - 08 0 3 X = 5 36 K SDA 1 symbolic data aalysis SDA 3 5 SDA 1 011-06 - 15
16 3 013 3 JOURNAL OF MANAGEMENT SCIENCES IN CHINA Vol 16 No 3 Mar 013 1 K 30007 K Hausdorff K K K O1 4 A 1007-9807 013 03-001 - 08 0 3 X = 5 36 K SDA 1 symbolic data aalysis SDA 3 5 SDA 1 011-06 - 15
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
A Decomposition Algorithm for the Solution of Fractional Quadratic Riccati Differential Equations with Caputo Derivatives
 America Joural of Computatioal ad Applied Mathematics 01, (3): 83-91 DOI: 10.593/j.ajcam.01003.03 A Decompositio Algorithm for the Solutio of Fractioal Quadratic Riccati Differetial Equatios with Caputo
America Joural of Computatioal ad Applied Mathematics 01, (3): 83-91 DOI: 10.593/j.ajcam.01003.03 A Decompositio Algorithm for the Solutio of Fractioal Quadratic Riccati Differetial Equatios with Caputo
Proof of Lemmas Lemma 1 Consider ξ nt = r
 Supplemetary Material to "GMM Estimatio of Spatial Pael Data Models with Commo Factors ad Geeral Space-Time Filter" (Not for publicatio) Wei Wag & Lug-fei Lee April 207 Proof of Lemmas Lemma Cosider =
Supplemetary Material to "GMM Estimatio of Spatial Pael Data Models with Commo Factors ad Geeral Space-Time Filter" (Not for publicatio) Wei Wag & Lug-fei Lee April 207 Proof of Lemmas Lemma Cosider =
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Uniform Estimates for Distributions of the Sum of i.i.d. Random Variables with Fat Tail in the Threshold Case
 J. Math. Sci. Uiv. Tokyo 8 (2, 397 427. Uiform Estimates for Distributios of the Sum of i.i.d. om Variables with Fat Tail i the Threshold Case By Keji Nakahara Abstract. We show uiform estimates for distributios
J. Math. Sci. Uiv. Tokyo 8 (2, 397 427. Uiform Estimates for Distributios of the Sum of i.i.d. om Variables with Fat Tail i the Threshold Case By Keji Nakahara Abstract. We show uiform estimates for distributios
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Tired Waiting in Queues? Then get in line now to learn more about Queuing!
 Tired Waitig i Queues? The get i lie ow to lear more about Queuig! Some Begiig Notatio Let = the umber of objects i the system s = the umber of servers = mea arrival rate (arrivals per uit of time with
Tired Waitig i Queues? The get i lie ow to lear more about Queuig! Some Begiig Notatio Let = the umber of objects i the system s = the umber of servers = mea arrival rate (arrivals per uit of time with
EN40: Dynamics and Vibrations
 EN40: Dyamics a Vibratios School of Egieerig Brow Uiversity Solutios to Differetial Equatios of Motio for Vibratig Systems Here, we summarize the solutios to the most importat ifferetial equatios of motio
EN40: Dyamics a Vibratios School of Egieerig Brow Uiversity Solutios to Differetial Equatios of Motio for Vibratig Systems Here, we summarize the solutios to the most importat ifferetial equatios of motio
Outline. M/M/1 Queue (infinite buffer) M/M/1/N (finite buffer) Networks of M/M/1 Queues M/G/1 Priority Queue
 Queueig Aalysis Outlie M/M/ Queue (ifiite buffer M/M//N (fiite buffer M/M// (Erlag s B forula M/M/ (Erlag s C forula Networks of M/M/ Queues M/G/ Priority Queue M/M/ M: Markovia/Meoryless Arrival process
Queueig Aalysis Outlie M/M/ Queue (ifiite buffer M/M//N (fiite buffer M/M// (Erlag s B forula M/M/ (Erlag s C forula Networks of M/M/ Queues M/G/ Priority Queue M/M/ M: Markovia/Meoryless Arrival process
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Inertial Navigation Mechanization and Error Equations
 Iertial Navigatio Mechaizatio ad Error Equatios 1 Navigatio i Earth-cetered coordiates Coordiate systems: i iertial coordiate system; ECI. e earth fixed coordiate system; ECEF. avigatio coordiate system;
Iertial Navigatio Mechaizatio ad Error Equatios 1 Navigatio i Earth-cetered coordiates Coordiate systems: i iertial coordiate system; ECI. e earth fixed coordiate system; ECEF. avigatio coordiate system;
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
EE 570: Location and Navigation
 EE 570: Locatio ad Navigatio INS Iitializatio Aly El-Osery Electrical Egieerig Departmet, New Mexico Tech Socorro, New Mexico, USA April 25, 2013 Aly El-Osery (NMT) EE 570: Locatio ad Navigatio April 25,
EE 570: Locatio ad Navigatio INS Iitializatio Aly El-Osery Electrical Egieerig Departmet, New Mexico Tech Socorro, New Mexico, USA April 25, 2013 Aly El-Osery (NMT) EE 570: Locatio ad Navigatio April 25,
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
