Bazele Chimiei Organice
|
|
|
- reek Γεννάδιος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Bazele Chimiei Organice An universitar Lector dr. Adriana Urdă Partea a 3-a. Clase de compuși organici; polaritatea legăturilor covalente; aciditate bazicitate; corelații între proprietățile fizice și tipul forțelor de atracție între molecule. Obiectivele acestui curs: În această parte a cursului vor fi prezentate alte noțiuni fundamentale ale chimiei organice: clasele de compuși organici, polaritatea acestora, aciditatea sau bazicitatea lor și influența naturii forțelor de atracție dintre molecule asupra proprietăților lor fizice. Cuprins 1. Reprezentarea structurilor chimice 2. Consecințe ale legăturilor chimice clase de compuși organici, izomerie 3. Polaritatea legăturilor covalente 4. Sarcini formale 5. Acizi și baze 6. Legătura dintre proprietățile fizice (p.t, p.f., solubilitate) și tipul forțelor de atracție dintre molecule 1. Reprezentarea structurilor chimice În structurile compușilor organici discutați anterior, cei doi electroni ai legăturii covalente au fost reprezentați prin două puncte (reprezentări Lewis) sau printr-o o linie între doi atomi (reprezentări Kekulé). Deoarece reprezentarea tuturor legăturilor dintre atomi este greoaie, chimiștii au realizat căi mai rapide pentru scrierea structurilor. În structurile condensate legăturile C H nu sunt prezentate, uneori nici cele C C, ci sunt subînțelese [McMurry, p. 22; Hendrickson, p. 54]. Dacă un atom de carbon este legat de trei atomi de hidrogen, vom scrie CH 3. De ex., 2-metilbutanul (o hidrocarbură din clasa alcanilor) poate fi scris astfel: Structuri condensate sau sau 2-Metilbutan O reprezentare și mai simplificată este cea a structurilor de schelet, care poate fi realizată urmând câteva reguli simple: 1. Atomii de carbon nu sunt reprezentați, ci se subînțelege că există la intersecția a două linii (legături) sau la capătul fiecărei linii. Pentru a diferenția o legătură C C de următoarea, liniuțele sunt așezate la aprox. 120 (unghiul unui hexagon),
2 reprezentând cu aproximație unghiul real al legăturii. Ocazional, atomii de carbon sunt reprezentați pentru claritate sau pentru a fi evidențiați. 2. Atomii de hidrogen nu sunt reprezentați. Știind că atomul de carbon are valența 4, subînțelegem numărul corect de atomi de hidrogen pentru fiecare atom de carbon. 3. Alte tipuri de atomi (în afara celor de carbon și hidrogen) sunt întotdeauna reprezentate. Exemple de reprezentări de schelet: Izopren, C 5 H 8 Metilciclohexan, C 7 H 14 Fenol, C 6 H 6 O Deși grupările CH 3, OH, NH 2 etc. sunt scrise în mod obișnuit cu atomii C, O sau N în fața atomului de hidrogen, ordinea poate fi uneori inversată pentru a face mai clare conexiunile legăturilor din moleculă. Nu facem acest lucru și pentru grupele mai mari, ca de ex. CH 2 CH 3 (care inversată ar fi scrisă 3 HC 2 HC ) pentru a nu introduce confuzii. Ordine inversată pentru a evidenția legătura C C Ordine ne-inversată Ordine inversată pentru a evidenția legătura C O Ordine inversată pentru a evidenția legătura C N 2. Consecințe ale legăturilor chimice: clase de compuși organici, izomerie Există mai mult de 30 milioane de substanțe organice cunoscute, care au fost grupate, în funcție de caracteristicile structurale și reactivitatea chimică, în câteva zeci de familii de compuși. 2
3 Caracteristicile structurale care fac posibilă clasificarea compușilor organici în familii sunt denumite grupe funcționale [McMurry, p. 73]. O grupă funcțională este o grupare de atomi care prezintă aceeași comportare chimică în fiecare moleculă în care apare. Reactivitatea fiecărei molecule organice, indiferent de mărime și complexitate, este determinată de grupele sale funcționale. O moleculă formată doar din carbon și hidrogen se numește hidrocarbură. Grupările funcționale ale unei hidrocarburi sunt doar legăturile duble și triple (π), legăturile σ fiind mult mai puțin reactive. O moleculă sau o grupare fără legături π este numită saturată, în timp ce legăturile multiple constituie nesaturarea. Ceilalți atomi (în afară de C și H) sunt numiți heteroatomi (O, N, S, P, halogeni) și stau la baza majorității grupărilor funcționale. Cele mai importante clase de compuși organici sunt: - alchene: conțin legături C = C - alchine: conțin legături C C - aromate (arene): conțin inele aromatice - compuși halogenați: R X - compuși cu oxigen: R OH alcooli, fenoli; R O R eteri - compuși cu sulf: R SH tioli; R S R tioeteri (sulfuri); R S S R' (disulfuri) - compuși cu azot: R NH 2 amine (amină primară în exemplul alăturat); R NO 2 nitroderivați; imine conțin grupări C = N; R C N nitrili - compuși carbonilici: C = O ( R = H pentru aldehide; R = alchil pentru cetone) R - compuși carboxilici: C = O Z (Z = OH pentru acizi carboxilici, Z = X pentru halogenuri acide, Z = NH 2 pentru amide, Z = OR pentru esteri) Compușii organici care au aceeași formulă chimică dar prezintă structuri diferite se numesc izomeri. Izomeria este de două tipuri [McMurry, p. 310]: - izomerie de constituție (de structură), reprezentând compuși ai căror atomi sunt conectați diferit, și care la rândul ei poate fi împărțită în: - izomerie de catenă - izomerie de poziție - izomerie de funcțiune (funcțională) - tautomerie - stereoizomerie (sau izomerie spațială), reprezentând compuși ai căror atomi sunt conectați în aceeași ordine dar cu geometrie diferită, și care poate fi împărțită în: - izomerie de conformație: izomerii pot trece unul în celălalt prin rotirea în jurul unei legături simple din moleculă - izomerie de configurație, care poate fi la rândul ei împărțită în: enantiomerie (izomerie optică) diastereoizomerie izomerie cis-trans (izomerie geometrică, sau E Z) izomeri polichirali. Toate aceste categorii de izomeri vor fi discutate în partea a 4-a a cursului. 3
4 3. Polaritatea legăturilor covalente În moleculele compuse din atomi sau grupări de atomi identici (ex. H H, CH 3 CH 3 etc.), perechea de electroni a covalenței este repartizată uniform între cele două nuclee (în cazul etanului, între cei doi carboni) [Avram, p. 27; McMurry, p. 35]. În acest caz legătura covalentă este nepolarizată, iar molecula în ansamblu este nepolară. Cele mai multe dintre legături nu sunt, însă, nici complet ionice, nici complet covalente, ci între cele două extreme, fiind denumite legături covalente polare [McMurry, p. 35]. Aceste legături apar în moleculele formate din atomi diferiți, iar cei doi electroni ai legăturii covalente sunt atrași spre unul din nuclee datorită electronegativității diferite a celor doi atomi care formează legătura: distribuția electronilor între atomi nu este simetrică. Caracter ionic Legătură covalentă Legătură covalentă Legătură ionică nepolară polară Fig. 1. Distribuția electronilor în legăturile covalente nepolare, covalente polare și ionice [McMurry, p. 36]. Electronegativitatea reprezintă capacitatea unui atom de a atrage electronii puși în comun într-o legătură covalentă. Valorile electronegativității variază de la cesiu (EN = 0,7 cel mai puțin electronegativ element) la fluor (EN = 4,0 cel mai electronegativ). Carbonul are electronegativitatea 2,5, iar hidrogenul 2,1. În principiu, dacă diferența de electronegativitate dintre doi atomi este mai mică de 0,5 legătura este considerată covalentă nepolară; pentru o diferență de electronegativitate între 0,5 și 2 legătura este covalentă polară, iar pentru diferențe mai mari de 2 legătura este ionică [McMurry, p. 36]. Ca urmare, legăturile C H sunt relativ nepolare, în timp ce legăturile C O sau C N sunt covalente polare, electronii acestor legături fiind atrași spre O sau N. Acești atomi capătă o sarcină parțial negativă (notată δ ), în timp ce atomul de carbon, mai puțin electronegativ, va avea o sarcină parțială pozitivă (notată δ +), ca în exemplul clorurii de metil: CH 3 δ+ Cl δ- Săgeata tăiată este utilizată pentru a indica direcția de polaritate a legăturii (electronii se deplasează în direcția săgeții), de la δ+ către δ. Moleculele care conțin legături covalente polare pot fi, la rândul lor, polare. Polaritatea moleculei rezultă din însumarea vectorială a tuturor polarităților legăturilor și a contribuțiilor perechilor de electroni neparticipanți [McMurry, p. 38]. Polaritatea moleculelor este importantă, deoarece moleculele polare se dizolvă mai ales în solvenți polari (cum este apa), în timp ce moleculele nepolare sunt insolubile în apă. Polaritatea unei molecule este măsurată printr-o mărime denumită moment de dipol (μ). Dacă centrul de masă al tuturor sarcinilor pozitive din H Cl δ C δ+ H H 4
5 moleculă (nuclee) și centrul de masă al tuturor sarcinilor negative (electroni) nu coincid, atunci molecula are moment de dipol. Momentul de dipol al moleculei depinde de mărimea sarcinii electrice (δ + și δ ), de distanța ce separă sarcinile, de prezența perechilor de electroni neparticipanți, ca și de factori geometrici. În molecule ca tetraclorura de carbon, datorită simetriei, momentul de dipol molecular devine μ = Sarcini formale În strânsă legătură cu ideile de polaritate a legăturii și moment de dipol este conceptul de atribuire a sarcinilor formale anumitor atomi dintr-o moleculă, în special celor care au un număr aparent anormal de legături. Sarcinile formale sunt un formalism și nu implică prezența unor sarcini ionice reale într-o moleculă. Ele sunt doar un mod de numărare a electronilor: chiar dacă într-o legătură covalentă cei doi atomi participanți pun în comun câte un electron, fiecare atom poate fi considerat că deține electronul. De exemplu, în metan, carbonul are câte un electron din fiecare legătură C H, deci 4 electroni. Deoarece atomul neutru (izolat) de carbon are tot patru electroni de valență, sarcina formală a carbonului din metan va fi zero [McMurry, p. 41]: C H H C H Atom de C izolat, ce deține 4 e Atom de C din metan, deține tot 4 e Același lucru este valabil pentru atomul de azot din amoniac: el are trei legături covalente N H și o pereche de electroni neparticipanți. Azotul atomic are cinci electroni pe stratul de valență, iar azotul din amoniac tot cinci electroni (câte unul în fiecare din cele trei legături N H și doi în perechea neparticipantă), deci atomul de azot din amoniac are sarcina formală tot zero. În multe situații sarcina formală nu este zero. De exemplu, în dimetilsulfoxid (CH 3 SOCH 3, un solvent utilizat pentru păstrarea celulelor biologice la temperaturi scăzute), atomii de sulf și de oxigen au sarcini formale diferite de zero. Atomul de sulf are șase electroni de valență, dar sulful din dimetilsulfoxid are doar cinci (câte unul în legăturile simple C S, unul în legătura simplă S O și doi în perechea de electroni neparticipanți). Astfel, atomul de sulf a pierdut în mod formal un electron și are o sarcină pozitivă. Oxigenul are șase electroni de valență, dar atomul de oxigen din dimetilsulfoxid are șapte (unul în legătura simplă S O și șase în cele trei perechi neparticipante), deci a câștigat în mod formal un electron și are sarcină negativă. Sarcina totală a moleculei este, însă, zero: sarcina negativă a oxigenului este compensată de cea pozitivă a sulfului. H 5
6 În general, sarcina formală a unui atom se calculează ca diferență între numărul de electroni de valență dintr-un atom neutru, izolat, și numărul de electroni pe care îi posedă atomul într-o moleculă. Acesta din urmă este egal cu jumătate din numărul de electroni de legătură plus numărul de electroni din perechile neparticipante. Sarcinile formale dau deseori informații despre reactivitatea chimică, deci este util să le putem identifica și calcula corect. 5. Acizi și baze Un alt concept legat de electronegativitate și polaritate este cel de aciditate și bazicitate. O mare parte din chimia moleculelor organice poate fi explicată prin comportamentul lor acidobazic [McMurry, p. 49]. Acizii (și bazele) pot fi clasificați în două categorii mari: acizi și baze Brönsted, respectiv Lewis. Acizii Brönsted sunt acei acizi care pot ceda un proton (mai sunt denumiți acizi protonici), iar bazele Brönsted pot accepta un proton. Exemple de acizi Brönsted: HCl, H 2 SO 4 etc. Exemple de baze Brönsted: NaOH, NH 3 etc. Acizii Lewis sunt molecule cu deficit de electroni (care acceptă o pereche de electroni), în timp ce bazele Lewis pot ceda o pereche de electroni. Exemple de acizi Lewis: H +, AlCl 3, BF 3 etc. Exemple de baze Lewis: NH 3, HO. Este evident că o bază Lewis este și bază Brönsted, ceea ce nu este întotdeauna adevărat pentru acizii Lewis (ex. Ag +, CH 3 +, BF 3 etc.). Un acid și o bază care se formează reciproc prin donarea sau acceptarea unui proton se numesc pereche acid-bază conjugată; acidului HA îi corespunde baza conjugată A : H A + :B :A + H B + Acid Bază Bază Acid conjugată conjugat Cu cât acidul este mai tare, cu atât baza conjugată este mai slabă. Echilibrul în reacțiile de transfer de protoni favorizează formarea acizilor mai slabi și a bazelor mai slabe din acizii și bazele mai tari. Perechile acid bază conjugată (B: și H B + ; H A și A: ) pot fi exemplificate prin acizii carboxilici și anionii lor carboxilat (RCOOH și RCOO ) sau baze de tipul aminelor (RNH 2 ) și sărurile lor (RNH 3 + ). Aceste două grupări funcționale sunt cei mai importanți acizi și baze din chimia organică. Tăria exactă a unui acid HA în soluție apoasă este descrisă cu ajutorul constantei de echilibru (K) pentru echilibrul de disociere a acidului: HA + H 2 O A + H 3 O + în care concentrațiile speciilor din parantezele pătrate sunt exprimate în moli/l (concentrație molară, M). În soluțiile apoase diluate utilizate pentru măsurarea acidității, concentrația apei rămâne aproape constantă la aprox. 55,5 M în urma acestei reacții. De aceea putem rescrie expresia echilibrului folosind constanta de aciditate, K a, care reprezintă produsul dintre constanta de echilibru și concentrația molară a apei: 6
7 Acizii mai tari au echilibrele deplasate spre dreapta și, deci, au constante de aciditate mai mari, în timp ce acizii mai slabi au echilibrele deplasate spre stânga și constante mai mici de aciditate. Valorile K a variază de la pentru acizii cei mai tari până la pentru cei mai slabi. Disocierea acizilor și bazelor în alți solvenți decât apa implică transferul de proton la, sau de la, solvent. Ex.: ionizarea unui acid în acetonitril sau a unei baze în etanol: HA + CH 3 C N: CH 3 C N + H + A:.. B: + C 2 H 5 OH + BH + C 2 H 5.. O: De multe ori este convenabil să se exprime constantele de disociere în unități logaritmice. Pentru a putea compara numere pozitive (și nu negative), se folosește logaritmul negativ (pk a ) al constantei de aciditate. Pentru acidul acetic în apă, K a = 1, , iar pk a = lg (1, ) = 4,76. Un acid mai tare (K a mai mare) are pk a mai mic, iar un acid mai slab (K a mai mic) are pk a mai mare. Atunci când se folosesc valorile pk a trebuie să ținem cont că ele reprezintă puteri ale lui 10 ale constantelor de aciditate, iar o diferență de o unitate de pk a între doi acizi înseamnă că unul dintre ei este de zece ori mai acid ca celălalt. Putem prevedea dacă o anumită reacție acido-bazică are loc, deoarece H + va trece întotdeauna de la acidul mai tare la baza mai tare. Astfel, acidul va dona un proton către baza conjugată a unui acid slab, sau baza conjugată a acidului slab va îndepărta protonul de la acidul tare: Acid acetic Ion hidroxid Ion acetat Apă (pk a = 4,76) (pk a = 15,74) În ex. de mai sus, deoarece apa (pk a = 15,74) este un acid mai slab decât acidul acetic (pk a = 4,76), ionul hidroxid va reține protonul mai puternic decât ionul acetat. De aceea, ionul hidroxid reacționează cu acidul acetic, CH 3 COOH, pentru a forma ionul acetat și apă (acidul tare scoate acidul slab din sărurile lui). Un alt mod de a prezice reactivitatea acido-bazică este faptul că acidul conjugat produs în reacție (H 2 O) trebuie să fie mai slab și mai puțin reactiv decât acidul inițial (CH 3 COOH), iar baza conjugată produsă (CH 3 COO ) trebuie să fie mai slabă și mai puțin reactivă decât baza inițială (HO ). Legătura covalentă formată între un acid Lewis și o bază Lewis se numește legătură coordinativă. Ea nu se deosebește fizic de alte legături covalente, ci doar prin modul unilateral de donare a perechii de electroni la formarea covalenței. Legăturile coordinative au caracter dipolar: 7
8 H 2 O + HCl H 3 O + + Cl Direcția donării de electroni dinspre bază (H 2 O:) către acid (HCl) poate fi arătată folosind săgeți curbe, care arată direcția deplasării electronilor [McMurry, p. 59]: Acid Bază Acid Bază conjugat conjugată 6. Legătura dintre proprietățile fizice (p.f, p.t. etc.) și tipul forțelor de atracție dintre molecule Tipul forțelor de atracție dintre moleculele individuale determină multe dintre proprietățile compușilor organici [Bruice, p ]. Vom discuta, din acest punct de vedere, influențele asupra punctelor de fierbere, punctelor de topire și solubilității în diverși solvenți. Punctul de fierbere (p.f.) al unui compus este temperatura la care forma lichidă a compusului trece în fază de vapori (se vaporizează). Pentru a se vaporiza, forțele care mențin moleculele apropiate în faza lichidă trebuie depășite: cu cât aceste forțe sunt mai puternice, cu atât punctul de fierbere va fi mai ridicat, și va trebui să furnizăm mai multă energie pentru a vaporiza acel compus. De ex., moleculele alcanilor sunt menținute împreună de forțe slabe. Deoarece sunt alcătuiți doar din carbon și hidrogen, ale căror electronegativități sunt apropiate, legăturile din alcani sunt nepolare, deci nu există sarcini parțiale semnificative. Cu toate acestea, electronii se mișcă în atomii moleculelor continuu, deci în orice moment densitatea de electroni într-o parte a moleculei poate fi puțin mai mare decât în altă parte, ceea ce dă naștere unui dipol temporar. Acest dipol poate induce un dipol temporar într-o moleculă vecină, și se produc atracții slabe între părțile cu dipol de semn contrar ale moleculelor vecine. Interacțiile de acest tip, între dipoli temporari, se numesc forțe van der Waals și sunt cele mai slabe dintre toate atracțiile moleculare. Intensitatea forțelor van der Waals depinde direct de aria de contact dintre molecule. Dacă urmărim variația punctelor de fierbere ale alcanilor, vom constata că acestea cresc cu creșterea mărimii moleculei: - metan - 161,5 C - etan - 89 C - propan - 42,1 C - butan - 0,5 C - pentan + 36,1 C Această creștere este normală, pentru că o moleculă mai mare va avea o arie de contact mai mare cu moleculele vecine. Alcanii ramificați au, însă, puncte de fierbere mai scăzute decât cei neramificați, deoarece molecula ramificată este mai compactă și are o arie de contact mai scăzută decât una neramificată. Ex., următoarele puncte de fierbere: - pentan 36,1 C - i-pentan 27,9 C - neopentan 9,5 C Aceste observații sunt valabile pentru orice serie omoloagă de compuși organici (serie omoloagă = serie în care fiecare termen este urmat de unul mai mare cu o unitate). 8
9 Punct de topire ( C) Moleculele polare, care conțin legături polare în care unul dintre atomi este mai electronegativ, au un moment de dipol, iar părți diferite ale moleculei au sarcini parțiale diferite. Aceste molecule se pot alinia astfel încât capătul pozitiv al unui dipol este vecin cu cel negativ al altui dipol. Aceste interacțiuni, denumite interacțiuni dipol dipol, sunt mai puternice decât forțele van der Waals, dar nu la fel de puternice precum legăturile chimice. Ex.: ciclopentanul (p.f. = 49,3 C) și tetrahidrofuranul (C 4 H 8 O, eter ciclic, p.f. = 65 C). Alcoolii au puncte de fierbere mai ridicate decât alcanii corespunzători deoarece, pe lângă forțele van der Waals și interacțiunile dipol-dipol, alcoolii pot forma legături de hidrogen. Legătura de hidrogen este un caz special al interacțiunilor dipol-dipol, care se produce între un atom de hidrogen legat de un atom de oxigen, azot sau fluor, și perechea de electroni neparticipanți a unui alt atom de oxigen, azot sau fluor dintr-o altă moleculă. Legătura de hidrogen nu este la fel de puternică precum o legătură covalentă, dar este mai puternică decât o legătură dipol-dipol. Ex.: influența legăturilor de hidrogen asupra punctului de fierbere al apei. Tăria legăturilor de hidrogen depinde de electronegativitatea atomilor implicați. Oxigenul este mai electronegativ decât azotul, deci legăturile de hidrogen în molecule ce contin oxigen (ex. alcooli) sunt mai puternice decât în moleculele care conțin azot (ex. amine). În cazul aminelor, cele primare formează mai multe legături decât cele secundare, deci vor avea puncte de fierbere mai ridicate. Aminele terțiare nu formează legături de hidrogen (de ce?). Punctul de topire (p.t.) este temperatura la care un solid este transformat în lichid. Punctele de topire cresc în seria omoloagă a alcanilor, dar creșterea este mai puțin regulată decât în cazul punctului de fierbere, deoarece temperatura de topire este influențată de împachetarea moleculelor în solid. Cu cât împachetarea este mai compactă, cu atât mai multă energie este necesară pentru topire. Alcanii cu număr impar de atomi de carbon sunt împachetați mai puțin compact decât cei cu număr par, deoarece grupările metil de la capete conduc la o împachetare mai slabă, deci o temperatură de topire mai mică. Număr par de atomi de carbon Număr impar de atomi de carbon Număr de atomi de carbon Fig. 2. Creșterea punctelor de topire ale alcanilor [Bruice, p. 86]. Solubilitatea poate fi explicată pe baza regulii că substanțele care se aseamănă se dizolvă unele în altele: compușii polari se dizolvă în solvenți polari, iar compușii nepolari în solvenți nepolari. Acest lucru se întâmplă pentru că un solvent polar (cum este apa) are sarcini parțiale care pot interacționa cu sarcinile parțiale ale unui compus polar. Polii negativi ai moleculelor de solvent înconjoară polul pozitiv al compusului polar (și invers), iar aglomerarea de molecule de 9
10 solvent în jurul moleculei de compus polar îndepărtează această moleculă de altele similare, ceea ce produce dizolvarea. Interacțiunea dintre solvent și molecula dizolvată se numește solvatare: Fig. 3. Solvatarea unei molecule polare de către moleculele de apă [Bruice, p. 86]. Deoarece compușii nepolari nu au sarcini nete, solvenții polari nu sunt atrași de aceste molecule. Dimpotrivă, acești compuși se dizolvă în solvenți nepolari, deoarece interacțiunile de tip van der Waals sunt similare. Pentru moleculele care au atât grupări polare cât și grupări nepolare, solubilitatea într-un anumit solvent depinde de mărimea celor două tipuri de grupări. Pe măsură ce mărimea grupărilor nepolare crește, compusul devine din ce în ce mai puțin solubil în solvenți polari. De ex., alcoolii cu mai puțin de patru atomi de carbon sunt solubili în apă, în timp ce alcoolii cu mai mult de patru atomi de carbon sunt insolubili în apă (solubilitatea depinde și de forma grupării nepolare; alcoolul terț-butilic este mai solubil în apă decât cel n-butilic). Rezumatul cursului Moleculele organice sunt reprezentate în mod obișnuit folosind fie structuri condensate, fie structuri de schelet. În structurile condensate, legăturile C H (și uneori și cele C C) nu sunt prezentate. În structurile de schelet reprezentăm doar legăturile, nu și atomii. Atomul de carbon se presupune că se află la capetele și intersecțiile liniilor, iar numărul de atomi de hidrogen se subînțelege. Moleculele organice au deseori legături covalente polare datorită distribuției nesimetrice a electronilor în legăturile covalente, ca urmare a electronegativității diferite a atomilor. Multe molecule sunt, la rândul lor, polare datorită legăturilor polare pe care le conțin și prezenței electronilor neparticipanți. Polaritatea moleculei se măsoară prin momentul de dipol (μ). Ca urmare a prezenței legăturilor polare, se utilizează semnele + și pentru a indica prezența sarcinilor formale la atomii unei molecule. Sarcina formală a unui atom se calculează ca diferență între numărul de electroni de valență dintr-un atom neutru, izolat, și numărul de electroni pe care îi posedă atomul într-o moleculă. Acesta din urmă este egal cu jumătate din numărul de electroni de legătură plus numărul de electroni din perechile neparticipante. Acizii Brönsted (acizi protonici) sunt acei acizi care pot ceda un proton, iar bazele Brönsted pot accepta un proton. Acizii Lewis sunt molecule cu deficit de electroni (care acceptă o pereche de electroni), iar bazele Lewis pot ceda o pereche de electroni. Un acid și o bază care se formează una din cealaltă prin donarea sau acceptarea unui proton se numesc pereche acidbază conjugată. 10
11 Tăria unui acid HA în soluție apoasă este descrisă cu ajutorul constantei de echilibru (K) pentru disocierea acidului sau a constantei de aciditate K a = K [H 2 O]. Deseori se utilizează pk a = - lgk a. Legătura covalentă formată între un acid Lewis și o bază Lewis se numește legătură coordinativă. Ea nu se deosebește fizic de alte legături covalente, ci doar prin modul unilateral de donare a perechii de electroni la formarea covalenței. Punctul de fierbere (p.f.) al unui compus este temperatura la care forma lichidă a compusului trece în fază de vapori (se vaporizează). Pentru a se vaporiza, forțele care mențin moleculele apropiate în faza lichidă trebuie depășite: cu cât aceste forțe sunt mai puternice, cu atât punctul de fierbere va fi mai ridicat. Moleculele alcanilor sunt menținute împreună de forțe slabe, numite forțe van der Waals, a căror intensitate depinde de aria de contact dintre molecule. Punctele de fierbere ale alcanilor cresc cu creșterea mărimii moleculei. Alcanii ramificați au puncte de fierbere mai scăzute decât cei neramificați, deoarece molecula lor este mai compactă. Moleculele polare au un moment de dipol, și se pot alinia astfel încât capătul pozitiv al unui dipol este vecin cu cel negativ al altui dipol. Aceste interacțiuni, denumite interacțiuni dipol dipol, sunt mai puternice decât forțele van der Waals, dar nu la fel de puternice precum legăturile chimice. Alcoolii au puncte de fierbere mai ridicate decât alcanii corespunzători deoarece, pe lângă forțele van der Waals și interacțiunile dipol-dipol, alcoolii pot forma legături de hidrogen. Legătura de hidrogen se produce între un atom de hidrogen legat de un atom de oxigen, azot sau fluor, și perechea de electroni neparticipanți a unui alt atom de oxigen, azot sau fluor dintr-o altă moleculă. Legătura de hidrogen nu este la fel de puternică precum o legătură covalentă, dar este mai puternică decât o legătură dipol-dipol. Punctul de topire (p.t.) este temperatura la care un solid este transformat în lichid. Temperatura de topire este influențată de împachetarea moleculelor în solid: cu cât împachetarea este mai compactă, cu atât mai multă energie este necesară pentru topire. Alcanii cu număr impar de atomi de carbon sunt împachetați mai puțin compact decât cei cu număr par, deoarece grupările metil de la capete conduc la o împachetare mai slabă. Solubilitatea poate fi explicată pe baza regulii că substanțele care se aseamănă se dizolvă unele în altele: compușii polari se dizolvă în solvenți polari, iar compușii nepolari în solvenți nepolari. Interacțiunea dintre solvent și molecula dizolvată se numește solvatare: Bibliografie 1. Avram, M. (1983). Chimie Organică, vol. 1, Editura Academiei RSR, București 2. Bruice, P. (2003). Organic Chemistry, 4 th edition, Pearson Education 3. Hendrickson, J. B., Cram, D. J., Hammond, G. S., Chimie Organică (1976). Editura Științifică și Enciclopedică, București 4. McMurry, J., Organic Chemistry (2008). 7th ed., Thomson Brooks/Cole 11
I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare.
 Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
Capitolul 3 COMPUŞI ORGANICI MONOFUNCŢIONALI 3.2.ACIZI CARBOXILICI TEST 3.2.3. I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Reacţia dintre
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Activitatea A5. Introducerea unor module specifice de pregătire a studenţilor în vederea asigurării de şanse egale
 POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
POSDRU/156/1.2/G/138821 Investeşte în oameni! FONDUL SOCIAL EUROPEAN Programul Operaţional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educaţiaşiformareaprofesionalăînsprijinulcreşteriieconomiceşidezvoltăriisocietăţiibazatepecunoaştere
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Sulfonarea benzenului este o reacţie ireversibilă.
REACŢII DE ADIŢIE NUCLEOFILĂ (AN-REACŢII) (ALDEHIDE ŞI CETONE)
 EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
T e m a PROPRIETĂŢILE ACIDE ŞI BAZICE ALE COMPUŞILOR ORGANICI.
 T e m a PROPRIETĂŢILE ACIDE ŞI BAZICE ALE COMPUŞILOR ORGANICI. Cele mai importante grupe funcţionale, care se întâlnesc în componenţa compuşilor naturali biologic activi sunt: -ОН, -SH, NH 2, -COH, -COOH
T e m a PROPRIETĂŢILE ACIDE ŞI BAZICE ALE COMPUŞILOR ORGANICI. Cele mai importante grupe funcţionale, care se întâlnesc în componenţa compuşilor naturali biologic activi sunt: -ОН, -SH, NH 2, -COH, -COOH
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Bazele Teoretice ale Chimiei Organice. Hidrocarburi
 Bazele Teoretice ale Chimiei Organice. Hidrocarburi Tema 1. Hibridizare.Legătura chimică localizată.polaritate.efect inductiv Scurt istoric Despărțirea chimiei în două mari ramuri, anorganică și organică,
Bazele Teoretice ale Chimiei Organice. Hidrocarburi Tema 1. Hibridizare.Legătura chimică localizată.polaritate.efect inductiv Scurt istoric Despărțirea chimiei în două mari ramuri, anorganică și organică,
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling.
 Cursul 8 3.5.4. Electronegativitatea Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling. Cantitativ, ea se exprimă prin coeficienţii de electronegativitate
Cursul 8 3.5.4. Electronegativitatea Electronegativitatea = capacitatea unui atom legat de a atrage electronii comuni = concept introdus de Pauling. Cantitativ, ea se exprimă prin coeficienţii de electronegativitate
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Bazele Teoretice ale Chimiei Organice. Hidrocarburi
 Bazele Teoretice ale Chimiei Organice. Hidrocarburi An universitar 2013-2014 Lector dr. Adriana Urdă Cursul 1. Formarea legăturilor chimice. Hibridizare. Polaritatea legăturilor covalente. Obiectivele
Bazele Teoretice ale Chimiei Organice. Hidrocarburi An universitar 2013-2014 Lector dr. Adriana Urdă Cursul 1. Formarea legăturilor chimice. Hibridizare. Polaritatea legăturilor covalente. Obiectivele
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Teoria mecanic-cuantică a legăturii chimice - continuare. Hibridizarea orbitalilor
 Cursul 10 Teoria mecanic-cuantică a legăturii chimice - continuare Hibridizarea orbitalilor Orbital atomic = regiunea din jurul nucleului în care poate fi localizat 1 e - izolat, aflat într-o anumită stare
Cursul 10 Teoria mecanic-cuantică a legăturii chimice - continuare Hibridizarea orbitalilor Orbital atomic = regiunea din jurul nucleului în care poate fi localizat 1 e - izolat, aflat într-o anumită stare
Capitolul 1-INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme
 Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
Capitolul 1- INTRODUCERE ÎN STUDIUL CHIMIEI ORGANICE Exerciţii şi probleme ***************************************************************************** 1.1. Care este prima substanţă organică obţinută
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Activitatea A5. Introducerea unor module specifice de pregătire a studenților în vederea asigurării de șanse egale
 Investește în oameni! FONDUL SOCIAL EUROPEAN Programul Operațional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educația și formarea profesională în sprijinul creșterii
Investește în oameni! FONDUL SOCIAL EUROPEAN Programul Operațional Sectorial pentru Dezvoltarea Resurselor Umane 2007 2013 Axa prioritară nr. 1 Educația și formarea profesională în sprijinul creșterii
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE Exerciţii şi probleme E.P.2.4. 1. Scrie formulele de structură ale următoarele hidrocarburi şi precizează care dintre ele sunt izomeri: Rezolvare: a) 1,2-butadiena;
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
a. 0,1; 0,1; 0,1; b. 1, ; 5, ; 8, ; c. 4,87; 6,15; 8,04; d. 7; 7; 7; e. 9,74; 12,30;1 6,08.
 1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
1. În argentometrie, metoda Mohr: a. foloseşte ca indicator cromatul de potasiu, care formeazǎ la punctul de echivalenţă un precipitat colorat roşu-cărămiziu; b. foloseşte ca indicator fluoresceina, care
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
UNITĂŢI Ţ DE MĂSURĂ. Măsurarea mărimilor fizice. Exprimare în unităţile de măsură potrivite (mărimi adimensionale)
 PARTEA I BIOFIZICA MOLECULARĂ 2 CURSUL 1 Sisteme de unităţiţ de măsură. Atomi şi molecule. UNITĂŢI Ţ DE MĂSURĂ Măsurarea mărimilor fizice Exprimare în unităţile de măsură potrivite (mărimi adimensionale)
PARTEA I BIOFIZICA MOLECULARĂ 2 CURSUL 1 Sisteme de unităţiţ de măsură. Atomi şi molecule. UNITĂŢI Ţ DE MĂSURĂ Măsurarea mărimilor fizice Exprimare în unităţile de măsură potrivite (mărimi adimensionale)
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
2. LEGĂTURA CHIMICĂ. 2.1 Legătura ionică. Chimie Anorganică
 2. LEGĂTURA CIMICĂ 2.1 Legătura ionică Substanţele chimice sunt în marea lor majoritate compuşi chimici formaţi din atomi, molecule sau ioni. Numai gazele nobile pot fi considerate substanţe formate doar
2. LEGĂTURA CIMICĂ 2.1 Legătura ionică Substanţele chimice sunt în marea lor majoritate compuşi chimici formaţi din atomi, molecule sau ioni. Numai gazele nobile pot fi considerate substanţe formate doar
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Explicarea legăturii metalice cu ajutorul M.L.V. şi M.O.M.
 Cursul 1 Explicarea legăturii metalice cu ajutorul M.L.V. şi M.O.M. Legătura metalică se stabileşte numai în stările condensate ale materiei, între un număr N foarte mare de atomi (N ~ N A ) cu electronegativităţi
Cursul 1 Explicarea legăturii metalice cu ajutorul M.L.V. şi M.O.M. Legătura metalică se stabileşte numai în stările condensate ale materiei, între un număr N foarte mare de atomi (N ~ N A ) cu electronegativităţi
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Seria Balmer. Determinarea constantei lui Rydberg
 Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
ECHILIBRE ACIDO BAZICE - 1
 ECHILIBRE ACIDO-BAZICE 1 DISOCIEREA APEI 2 H 2 O H 3 O + + OH - H 3 O + H + PRODUS IONIC AL APEI: + c P H K = [ H ] [ OH ] = 2 O P H O = 2 = 10 14 M 2 (25 o C ) ÎN APA PURĂ + [ H ] = [ OH ] = PH 2 O =
ECHILIBRE ACIDO-BAZICE 1 DISOCIEREA APEI 2 H 2 O H 3 O + + OH - H 3 O + H + PRODUS IONIC AL APEI: + c P H K = [ H ] [ OH ] = 2 O P H O = 2 = 10 14 M 2 (25 o C ) ÎN APA PURĂ + [ H ] = [ OH ] = PH 2 O =
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
ŞTIINŢA ŞI INGINERIA. conf.dr.ing. Liana Balteş curs 7
 ŞTIINŢA ŞI INGINERIA MATERIALELOR conf.dr.ing. Liana Balteş baltes@unitbv.ro curs 7 DIAGRAMA Fe-Fe 3 C Utilizarea oţelului în rândul majorităţii aplicaţiilor a determinat studiul intens al sistemului metalic
ŞTIINŢA ŞI INGINERIA MATERIALELOR conf.dr.ing. Liana Balteş baltes@unitbv.ro curs 7 DIAGRAMA Fe-Fe 3 C Utilizarea oţelului în rândul majorităţii aplicaţiilor a determinat studiul intens al sistemului metalic
7. RETELE ELECTRICE TRIFAZATE 7.1. RETELE ELECTRICE TRIFAZATE IN REGIM PERMANENT SINUSOIDAL
 7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
7. RETEE EECTRICE TRIFAZATE 7.. RETEE EECTRICE TRIFAZATE IN REGIM PERMANENT SINSOIDA 7... Retea trifazata. Sistem trifazat de tensiuni si curenti Ansamblul format din m circuite electrice monofazate in
STRUCTURA MOLECULELOR
 STRUCTURA MOLECULELOR Legătura chimică - ansamblu de interacţiuni care se exercită între atomi, ioni sau molecule care conduce la formarea unor specii moleculare independente. Legături chimice: - tari
STRUCTURA MOLECULELOR Legătura chimică - ansamblu de interacţiuni care se exercită între atomi, ioni sau molecule care conduce la formarea unor specii moleculare independente. Legături chimice: - tari
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
a. Caracteristicile mecanice a motorului de c.c. cu excitaţie independentă (sau derivaţie)
 Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Acizi carboxilici heterofuncționali.
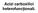 Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
Acizi carboxilici heterofuncționali. 1. Acizi carboxilici halogenați. R R 2 l l R 2 R l Acizi α-halogenați Acizi β-halogenați l R 2 2 l Acizi γ-halogenați Metode de obținere. 1. alogenarea directă a acizilor
Tema 5 (S N -REACŢII) REACŢII DE SUBSTITUŢIE NUCLEOFILĂ. ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON HIBRIDIZAT sp 3
 Tema 5 REACŢII DE SUBSTITUŢIE NUCLEOFILĂ (S N -REACŢII) ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON IBRIDIZAT sp 3 1. Reacții de substituție nucleofilă (SN reacții) Reacţiile de substituţie nucleofilă
Tema 5 REACŢII DE SUBSTITUŢIE NUCLEOFILĂ (S N -REACŢII) ŞI DE ELIMINARE (E - REACŢII) LA ATOMULDE CARBON IBRIDIZAT sp 3 1. Reacții de substituție nucleofilă (SN reacții) Reacţiile de substituţie nucleofilă
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener
 Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
EDITURA PARALELA 45 MATEMATICĂ DE EXCELENŢĂ. Clasa a X-a Ediţia a II-a, revizuită. pentru concursuri, olimpiade şi centre de excelenţă
 Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Unitatea atomică de masă (u.a.m.) = a 12-a parte din masa izotopului de carbon
 ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
Seminar electricitate. Seminar electricitate (AP)
 Seminar electricitate Structura atomului Particulele elementare sarcini elementare Protonii sarcini elementare pozitive Electronii sarcini elementare negative Atomii neutri dpdv electric nr. protoni =
Seminar electricitate Structura atomului Particulele elementare sarcini elementare Protonii sarcini elementare pozitive Electronii sarcini elementare negative Atomii neutri dpdv electric nr. protoni =
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
Lucrul mecanic. Puterea mecanică.
 1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
