ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης 3 Ιουλίου 2005)
|
|
|
- Ἀλεξανδρεύς Κουρμούλης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Άσκηση 1. (1 μονάδες) ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης Ιουλίου 5) Α) Δοκιμαστικό φορτίο q αφήνεται σε κάποιο σημείο μέσα σε ομογενές ηλεκτρικό πεδίο εντάσεως Ε. Να εξετάσετε πώς θα κινηθεί το φορτίο: α) Από σημείο υψηλότερης ηλεκτρικής δυναμικής ενέργειας σε σημείο χαμηλότερης ή αντίστροφα; β) Από σημείο υψηλότερου δυναμικού σε σημείο χαμηλότερου δυναμικού ή αντίστροφα; γ) Απαντήστε στα α) και β) υποθέτοντας τώρα αρνητικό φορτίο. Β) Δίνονται δύο φορτία Q1= 1 C, Q = 1 C που απέχουν μεταξύ τους απόσταση r=1 m. Να βρείτε την ηλεκτρική ροή που διαπερνά μια σφαιρική επιφάνεια με κέντρο το Q1 και ακτίνα: α) r=.5 m β) r=.7 m γ) r= 1. m. Ε Α F Β A) (α) Το ηλεκτρικό φορτίο αφήνεται σε ένα σημείο Α μέσα σε ομογενές ηλεκτρικό πεδίο. Θα αρχίσει να κινείται υπό την επίδραση της δύναμης του πεδίου και μετά από λίγο θα βρίσκεται στη θέση Β. Υπολογίζουμε το έργο W που παράγεται από τη δύναμη F του πεδίου που εξασκείται B B B πάνω στο φορτίο W = A B F dl = qe dl = qe dl = qe(αβ) > A A A Όπου dl είναι το στοιχειώδες διάνυσμα μετατόπισης με φορά από το Α προς το Β και (ΑΒ) η απόσταση των δύο σημείων. Άλλά W = A B U U A Bόπου UA Και U B η ηλεκτρική δυναμική ενέργεια του φορτίου q στις θέσεις Α και Β αντίστοιχα. WA B A B Επομένως: = U U = qe(αβ) > UA UB > UA > UB Άρα το φορτίο κινείται από σημεία υψηλότερης σε σημεία χαμηλότερης ηλεκτρικής δυναμικής ενέργειας ( Όπως και κάθε υπόθεμα μέσα στο αντίστοιχο πεδίο). (β) Ισχύει επίσης ότι: 1
2 WA B UA UB WA B qe(ab) = VA VB = VA VB = q q q q V V = E(AB) > V > V A B A B Άρα το θετικό ηλεκτρικό φορτίο q κινείται επίσης από σημεία υψηλότερου σε σημεία χαμηλότερου ηλεκτρικού δυναμικού. Β) Εάν αφήσουμε στη θέση Α ένα αρνητικό ηλεκτρικό φορτίο q τότε αυτό θα κινηθεί αντίθετα από την φορά των δυναμικών γραμμών. Ε Β F Α Προσέξτε ότι το διάνυσμα dl και το διάνυσμα Ε της έντασης του ηλεκτρικού πεδίου σχηματίζουν γωνία 18 ο. B B B B W = A B F dl = qe dl = qe dlcs(18 ) = qe dl = qe(αβ) > A A A A Όμως και το φορτίο q είναι αρνητικό, επομένως το έργο προκύπτει και πάλι θετικό. W = A B U A U = B qe(αβ) > U A U > B U > A UB Άρα και το αρνητικό φορτίο κινείται από θέσεις υψηλότερης σε θέσεις χαμηλότερης ηλεκτρικής δυναμικής ενέργειας. UA UB Αλλά: UA > UB < VA < V B q q γιατί διαιρούμε με το ηλεκτρικό φορτίο το οποίο είναι αρνητικό. Επομένως το αρνητικό φορτίο κινείται από θέσεις χαμηλότερου σε θέσεις υψηλότερου ηλεκτρικού δυναμικού. Β) r Q 1 Q Σύμφωνα με τον νόμο του Gauss έχουμε:
3 Q enclsed E ds= Άρα η ηλεκτρική ροή που διαπερνά την σφαιρική επιφάνεια ε ακτίνας r=.5m ισούται με το φορτίο που περικλείεται από την επιφάνεια προς την ηλεκτρική σταθερά του κενού ε ο. Q1 11 Επομένως: E ds= = W ε Εάν η σφαιρική επιφάνεια έχει ακτίνα r=.7m τότε πάλι το φορτίο που περικλείεται από αυτήν είναι το Q 1 και η ηλεκτρική ροή παραμένει η ίδια. Τέλος όταν r=1.m τότε έχουμε: Q Q Q = = = ε ε enclsed 1 E ds. Επομένως η ηλεκτρική ροή είναι μηδέν διότι η σφαιρική επιφάνεια περικλείει δύο ίσα και αντίθετα ηλεκτρικά φορτία. Το συνολικό «καθαρό» ηλεκτρικό φορτίο είναι μηδέν. Άσκηση. (1 μονάδες) Α) Μικρή σφαίρα μάζας gr κρεμιέται από ακλόνητο σημείο με αβαρές μη αγώγιμο νήμα μεταξύ δύο κατακόρυφων παραλλήλων πλακών απείρων διαστάσεων που απέχουν 5 cm μεταξύ τους. Η σφαίρα φέρει φορτίο 6 μc. Πόση διαφορά δυναμικού μεταξύ των πλακών θα αναγκάσει το νήμα να σχηματίσει γωνία με την κατακόρυφο; Β) Σημειακό φορτίο q1 = 6 μc κρατείται ακίνητο στην αρχή των αξόνων. Δεύτερο σημειακό φορτίο q =.5 μc βάλλεται προς το q1 κινούμενο πάνω στην ευθεία που ενώνει τα δύο φορτία. Όταν τα φορτία είναι σε απόσταση.8 m το q κινείται προς το q1 με ταχύτητα m/s. α) Ποια είναι η ταχύτητα του q όταν τα φορτία είναι σε απόσταση.5 m; β) Πόσο κοντά πλησιάζουν τα δύο φορτία; (Τα φορτία έχουν ίσες μάζες m=1 gr, αγνοήστε τη βαρύτητα). Για να ισορροπεί το φορτίο q πρέπει να ισχύει: Α) T B F q = όπου Τ η τάση του νήματος, Β το βάρος της σφαίρας και F q η ηλεκτρική δύναμη. Για ισορροπία στους άξονες x,y, από το σχήμα προκύπτει: T Tsinφ = F F φ F q q οπότε: εφφ = Tcsφ = B B Εάν V είναι η διαφορά δυναμικού και l η απόσταση μεταξύ των Β πλακών τότε έχουμε: V = =. Επομένως: Fq qe q l Fq qv mgl εφφ = = V = εφφ = 14V B mgl q
4 Β) α) u 1.8m q 1 q Το ηλεκτρικό φορτίο q κινείται μέσα στο συντηρητικό ηλεκτροστατικό ηλεκτρικό πεδίο με πηγή παραγωγής το q 1. Επομένως εάν εφαρμόσουμε την αρχή διατήρησης της μηχανικής ενέργειας ανάμεσα στην θέση Α όπου η απόσταση των δύο φορτίων είναι.8m και στη θέση Β όπου η απόσταση των φορτίων είναι.5m έχουμε: 1 1 q q 1 1 q q K U K U mu mu = 1 = 4πε r1 4πε r όπου u 1 =m/s, r 1 =.8m και r =.5m. Οπότε βρίσκουμε την ταχύτητα u. 1 1 u = u q q ( 1 ) =16.85 m/s r 1 1 πεm r1 β) Η μικρότερη απόσταση μεταξύ τους είναι η απόσταση r στην οποία η ταχύτητα u μηδενίζεται. Οπότε: mπεu 1 u = u1 q1q ( ) = r = πε m r r =.9 m r q q Άσκηση. (1 μονάδες) Το ηλεκτρικό δυναμικό V σε κάποια περιοχή του χώρου δίνεται από τη σχέση: V = ax ay az όπου a σταθερά. α) Να βρείτε μια έκφραση για την ένταση του ηλεκτρικού πεδίου Ε στην περιοχή αυτή. Υπόδειξη: Το ηλεκτρικό πεδίο και το δυναμικό συνδέονται με τη διανυσματική σχέση: V ˆ E V i V ˆ j V kˆ = =, όπου ο τελεστής όταν δράσει σε μια x y z x συνάρτηση πολλών μεταβλητών f(x,y,z, ) επιστρέφει την παράγωγο της συνάρτησης ως προς x θεωρώντας τις υπόλοιπες μεταβλητές σταθερές. (Όμοια για τους τελεστές y και παίρνουμε την παράγωγο ως προς y και z αντίστοιχα) z β) Να υπολογίσετε την σταθερά a αν είναι γνωστό ότι για τη μετακίνηση δοκιμαστικού φορτίου μc από το σημείο ( x,y,z)= (,,.1)m μέχρι την αρχή των 5 αξόνων, παράγεται από το πεδίο έργο 5 1 J. γ) Να δείξετε ότι σε κάθε επίπεδο παράλληλο προς το επίπεδο xy οι ισοδυναμικές γραμμές είναι κύκλοι. δ) Ποια είναι η ακτίνα της ισοδυναμικής γραμμής πάνω σε επίπεδο παράλληλο προς το επίπεδο xy με που αντιστοιχεί σε δυναμικό V=5 V. 4
5 (α) Σύμφωνα με την υπόδειξη, το ηλεκτρικό πεδίο και το δυναμικό συνδέονται με τη διανυσματική σχέση: V ˆ E V i V ˆ j V kˆ = =, x y z όπου iˆ, ˆj, kˆ είναι τα μοναδιαία διανύσματα στις διευθύνσεις Οx, Oy και Οz. Από τη συνάρτηση του δυναμικού έχουμε: V V V = ax, = ay, = 4az, και το πεδίο είναι: x y z E = ( ax iˆ ay ˆj 4 az k ˆ). (1) (β) Η δύναμη που ασκείται στο φορτίο q είναι F = qe, και το έργο που παράγει η δύναμη για στοιχειώδη μετατόπιση dr, είναι dw = F dr. Το φορτίο κινείται από το (,,.1) (,,) άρα κατά τη διεύθυνση Οz, συνεπώς το dr = kˆ dz. Ολοκληρώνοντας κατά μήκος του δρόμου βρίσκουμε το έργο: dw = F dr = qe kˆdz = q ax iˆ ay ˆj 4 az kˆ kˆ dz = 4qazdz και z ( ) ( 1 ) W 1 1 = 4 qazdz = qaz = qa z z z z z, όπου z =.1 m και z 1 = m. Λύνοντας την εξίσωση αυτή ως προς α έχουμε: 5 W 5, 1 J V a = = = 1, q( z1 z) (, 1 C)(, 1m ) m. (γ) Σε κάθε επίπεδο παράλληλο προς το επίπεδο x, y το z παραμένει σταθερό. Έστω λοιπόν ότι για τυχαίο επίπεδο είναι z = β και ότι V= σταθερό. Τότε: V = ax ay aβ ή ax ay = V aβ. Άρα, V x y =, όπου = β. () a Επομένως, η καμπύλη σταθερού δυναμικού, V, είναι κύκλος ακτίνας. (δ) Από τη () λύνοντας ως προς βρίσκουμε: V = β και αντικαθιστώντας =,8 m. a Άσκηση 4. (1 μονάδες) Δύο φορτισμένες επίπεδες πλάκες βρίσκονται σε διαφορά δυναμικού 1 V και απέχουν μεταξύ τους 4 cm. Ένα ηλεκτρόνιο αποσπάται από την αρνητική πλάκα ταυτόχρονα με πρωτόνιο που αποσπάται από τη θετική πλάκα. α) Σε πόση απόσταση από τη θετική πλάκα θα συναντηθούν; β) Ποιος είναι ο λόγος των ταχυτήτων τους πριν χτυπήσουν τις αντίθετες πλάκες; 5
6 γ) Ποιος είναι ο λόγος των κινητικών ενεργειών ακριβώς πριν χτυπήσουν τις αντίθετες πλάκες; (Αγνοήστε την αλληλεπίδραση μεταξύ των φορτίων και το πεδίο της βαρύτητας). Δίνονται: μάζα ηλεκτρονίου και μάζα πρωτονίου m = Kg, 7 m = Kg p e α) d F p F e ld Το ηλεκτρικό πεδίο μεταξύ των πλακών είναι V ομογενές και το μέτρο του είναι: E = όπου l l είναι η απόσταση μεταξύ των δύο πλακών και V είναι η διαφορά δυναμικού μεταξύ τους. Το ηλεκτρόνιο και το πρωτόνιο δέχονται τη δύναμη από το ηλεκτρικό πεδίο: V V Fe = qee= qe (1) και Fp = qpe= qp () l l Έστω ότι θα συναντηθούν στη θέση της διακεκομμένης γραμμής. Τότε το πρωτόνιο έχει διατρέξει απόσταση d και το ηλεκτρόνιο απόσταση ld. Η κίνηση την οποία εκτελούν είναι ευθύγραμμη ομαλά επιταχυνόμενη οπότε: 1 Fp d= t () και m p 1 F = (4) m e l d t e Διαιρούμε τις () και (4) κατά μέλη και έχουμε: υπόψη τις (1) και () έχουμε: d Fm p = l d Fm e p p e e e p και λαμβάνοντας d qm p e 1 5 = d = l =.18 1 m l d q m 1 m m β) Το έργο που παράγει η ηλεκτρική δύναμη ισούται με την κινητική ενέργεια κάθε ενός σωματίου ελάχιστα πριν κτυπήσει την πλάκα. Οπότε; 1 mu e e = qel e (5) και 1 mu p p = qel p (6) Διαιρώντας τις (5) και (6) έχουμε: ue m q m u m q m p e p = = = p e p e 4.9 6
7 γ) Από τις (5) και (6)μ έχουμε: 1 mu e e qe Ke = = 1 = 1 1 mu qp Kp p p Άσκηση 5. (1 μονάδες) Αγώγιμος μονωμένος σφαιρικός φλοιός με εσωτερική ακτίνα α και εξωτερική ακτίνα b έχει θετικό φορτίο Q τοποθετημένο στο κέντρο του. Το ολικό φορτίο πάνω στο φλοιό είναι, συνολικά, Q. (α) Πως κατανέμονται τα φορτία στην εσωτερική και εξωτερική επιφάνεια του αγώγιμου φλοιού; (β) Βρείτε εκφράσεις για το ηλεκτρικό πεδίο συναρτήσει της απόστασης r από το κέντρο της σφαίρας για τις περιοχές r<a, a<r<b και r>b. (α) Στο κέντρο του σφαιρικού φλοιού βρίσκεται φορτίο Q. Επομένως θα πρέπει εμφανίζεται εξ επαγωγής φορτίο Q Q στην εσωτερική επιφάνεια του φλοιού. Για να υπολογίσουμε το Q θεωρούμε μια b σφαιρική γκαουσιανή επιφάνεια στο εσωτερικό του a φλοιού, η οποία παριστάνεται με τη διακεκομμένη γραμμή του διπλανού σχήματος: Επειδή η ένταση Ε στο εσωτερικό του φλοιού είναι μηδέν η γκαουσιανή αυτή επιφάνεια πρέπει να περικλείει επίσης συνολικό φορτίο ίσο με το μηδέν. Περικλείει όμως ήδη το φορτίο Q. Επομένως στην εσωτερική επιφάνεια του φλοιού εμφανίζεται φορτίο Q. Το συνολικό φορτίο του φλοιού είναι Q. Άρα στην εξωτερική επιφάνεια του φλοιού εμφανίζεται φορτίο Q ώστε το άθροισμα των ηλεκτρικών φορτίων εσωτερικής και εξωτερικής επιφάνειας να ισούται με το συνολικό φορτίο του φλοιού. β) r<a: Θεωρούμε μια σφαιρική γκαουσιανή επιφάνεια όπως φαίνεται στο παρακάτω σχήμα με διακεκομμένη γραμμή και εφαρμόζουμε το νόμο του Gauss σε αυτή. Q Φ= E da= E( 4 πr ) =, ε Q E =, r < α 4πεr με κατεύθυνση ˆr. a<r<b: Επειδή ο σφαιρικός φλοιός είναι αγώγιμος το ηλεκτρικό πεδίο στο εσωτερικό του είναι μηδέν. r>b: Θεωρώντας μια γκαουσιανή σφαιρική ομόκεντρη επιφάνεια είναι εύκολο να δείξουμε, όπως στην περίπτωση r<a ότι το ηλεκτρικό πεδίο έχει μέτρο: Q a b 7
8 Q E =, r >b 4πε r με κατεύθυνση ˆr. Άσκηση 6. (1 μονάδες) Μία ηλεκτρική αντίσταση 1 = 5Ω, συνδέεται με δύο μεταλλικούς αγωγούς μηδενικής αντίστασης πολύ μεγάλου μήκους. Μεταλλική ράβδος μήκους l=1 m, μάζας m= 1 Kg και αντίστασης = 1Ω τοποθετείται κάθετα στους μεταλλικούς αγωγούς, όπως δείχνει το σχήμα. Το κύκλωμα τοποθετείται μέσα σε ομογενές μαγνητικό πεδίο Β =.5Τ με u διεύθυνση της μαγνητικής επαγωγής Β κάθετα στο επίπεδο που σχηματίζουν οι παράλληλοι αγωγοί και φορά πο υ εμφανίζεται στο σχήμα. Προσδίδουμε στη ράβδο αρχική ταχύτητα u = 1 m/s και την αφήνουμε να κινηθεί ελεύθερα μέσα στο μαγνητικό πεδίο ευρισκόμενη πάντα σε επαφή με τους μεταλλικούς αγωγούς. Αν ανάμεσα στη ράβδο και τους αγωγούς δεν υπάρχουν τριβές να βρεθούν: α) Η έκφραση της ταχύτητας u συναρτήσει του χρόνου. β) Η ταχύτητα τη χρονική στιγμή t= sec. γ) Ποια χρονική στιγμή θα σταματήσει η ράβδος; Α) Εφόσον η μεταλλική ράβδος κινείται μέσα σε μαγνητικό πεδίο καθίσταται, σύμφωνα με το φαινόμενο της μαγνητικής επαγωγής έδρα ηλεκτρεργετικής δύναμης. Η ηλεκτρεργετική δύναμη έχει τιμή: V= Bul όπου Β η μαγνητική επαγωγή, u η ταχύτητα του αγωγού και l το μήκος της μεταλλικής ράβδου. u F L I Τ ώρα το κύκλωμα που αποτελείται από τη μεταλλική ράβδο, τους δύο μεταλλικούς αγωγούς και την αντίσταση αρχίζει να διαρρέεται από ηλεκτρικό ρεύμα Ι. Η ένταση του ηλεκτρικού ρεύματος Ι είναι: 8
9 Bul I = ολ όπου ολ είναι το άθροισμα της αντίστασης της ράβδου και της εξωτερικής αντίστασης. Αλλά τώρα η μεταλλική ράβδος διαρρέεται από ηλεκτρικό ρεύμα εντάσεως Ι και βρίσκεται μέσα στο μαγνητικό πεδίο. Επομένως πάνω της εξασκείται δύναμη Laplace η οποία αντιτίθεται στην κίνηση της ράβδου. Επομένως Blu F = Il B ή, επειδή l και Β κάθετα F= B I l= ολ du B l u du du B l Άρα: F= m = m = dt dt ολ dt u ολm Λύνουμε την διαφορική εξίσωση με την μέθοδο των χωριζόμενων μεταβλητών οπότε: u t Bl t du B l u B l ολm = dt ln = t u = ue u u ολm u ολm (1) Β) Βρίσκουμε την ταχύτητα τη χρονική στιγμή t=s θέτοντας τα μεγέθη στην προηγούμενη σχέση. Προκύπτει u=9.5m/s. Γ) Από την σχέση (1) προκύπτει ότι πρέπει να περάσει άπειρος χρόνος μέχρι να σταματήσει η μεταλλική ράβδος. Άσκηση 7. (1 μονάδες) Το σύρμα του σχήματος διαρρέεται από ρεύμα I. Το σύρμα αποτελείται από ένα κατακόρυφο τμήμα πολύ μεγάλου μήκους, ένα τεταρτημόριο περιφέρειας κύκλου ακτίνας και από ένα δεύτερο οριζόντιο ευθύγραμμο τμήμα μεγάλου μήκους. Να υπολογίσετε το ολικό μαγνητικό πεδίο στο κέντρο καμπυλότητας του τεταρτημορίου (σημείο P στο σχήμα). Για να υπολογίσουμε το μαγνητικό πεδίο στο σημείο P αρκεί να υπολογίσουμε το μαγνητικό πεδίο που δημιουργούν τα δύο ευθύγραμμα μέρη του αγωγού καθώς και το κυκλικό μέρος του. Υπολογίζουμε το Β κάθε τμήματος με τον νόμο BitSavart. dl r P Β μ Idlxr db= 4π r Όπου dl είναι το διάνυσμα που περιγράφει ένα στοιχειώδες τμήμα του αγωγού και ˆr είναι το μοναδιαίο διάνυσμα στην ευθεία που ενώνει το στοιχειώδες τμήμα dl του αγωγού με το σημείο στο οποίο θέλουμε να υπολογίσουμε το Β. 9
10 Είναι φανερό ότι τα δύο ευθύγραμμα τμήματα του αγωγού δεν παράγουν μαγνητικό πεδίο στο Ρ διότι η γωνία που σχηματίζουν τα διανύσματα dl και r είναι μηδέν μοίρες. Επομένως το εξωτερικό γινόμενο του νόμου BitSavart είναι μηδέν. Άρα μόνο το τεταρτοκύκλιο παράγει μαγνητικό πεδίο. Έχουμε: μ Idlxr db db μ Idl = = 4π r 4π Γιατί τα διανύσματα dl και ˆr σχηματίζουν γωνία 9 ο και r=. Η διεύθυνση και η φορά του Β καθορίζεται από τη φορά του εξωτερικού γινομένου και εμφανίζεται στο σχήμα. μ Idl μ Idl μ I db = db B dl 4π = = 4π 4π Επομένως: μ I π μi B= B= 4π 8 Άσκηση 8. (1 μονάδες) Σε μία σφαιρική κατανομή φορτίου, η πυκνότητα φορτίου δίνεται από τις σχέσεις: ρ= ρ 1 r r ( ) ρ = r> όπου ρ = Q π και Q και είναι σταθερές. Να δείξετε ότι: α) Το ολικό φορτίο που περιέχεται σ αυτή την κατανομή φορτίου είναι Q. β) Στην περιοχή r>, το ηλεκτρικό πεδίο είναι το ίδιο με αυτό που παράγεται από ένα σημειακό φορτίο Q τοποθετημένο στη θέση r= (αρχή των αξόνων). γ) Να βρείτε μια έκφραση για την ένταση του ηλεκτρικού πεδίου στην περιοχή r. δ) Να συγκρίνετε τα αποτελέσματα στα οποία καταλήξατε στα υποερωτήματα β) και γ) για την ειδική θέση r=. (α) Το ολικό φορτίο που περιέχεται στην κατανομή φορτίου υπολογίζεται από τη σχέση: ολικό φορτίο = ρdv, δηλαδή ολοκληρώνοντας την πυκνότητα φορτίου σε όλο τον όγκο της σφαίρας. Επειδή η κατανομή φορτίου παρουσιάζει σφαιρική συμμετρία, μπορούμε να χρησιμοποιήσουμε ως στοιχείο όγκου dv το στοιχειώδη όγκο μεταξύ δύο σφαιρικών επιφανειών ακτίνων r και r dr. Ο όγκος αυτός ισούται με το εμβαδόν 4πr της μίας σφαιρικής επιφάνειας επί το πάχος dr του φλοιού, δηλαδή: dv = 4πr dr (Αυτή η έκφραση προκύπτει και αν διαφορίσουμε τον όγκο της σφαίρας, V = 4πr /). Έτσι προκύπτει ότι: V 1
11 r= r ολικό φορτίο = ρ 1 4 r= πrdr 4 4πρ r 4πρ r 4. = 4πρ rdr rdr= 4πρ πρ = 4πρ πρ = Αντικαθιστώντας την τιμή του ρ, βρίσκουμε ότι: ολικό φορτίο = Q. (β) Το μέτρο του ηλεκτρικού πεδίου στην περιοχή θα υπολογιστεί εφαρμόζοντας το νόμο του Gauss για μια ομόκεντρη σφαιρική επιφάνεια ακτίνας r : Q Φ= E da= E( 4 πr ) =, ε. Q E =, r 4πεr Η έκφραση αυτή είναι όπως για το ηλεκτρικό πεδίο που δημιουργείται από σημειακό φορτίο Q που βρίσκεται στο κέντρο της κατανομής. (γ) Το μέτρο του ηλεκτρικού πεδίου στην περιοχή r θα υπολογιστεί εφαρμόζοντας το νόμο του Gauss για μια ομόκεντρη σφαιρική επιφάνεια S ακτίνας r : Q Φ= E da= E( 4πr ) =, ε όπου Q είναι ίσο προς Q = ρdv, V = όγκος που περικλύεται από την S. V Χρησιμοποιούμε ως στοιχείο όγκου dv = 4πr dr. r r r r πq r πq r Q = ρ πr dr = r dr = r dr dr π π. 4 1πQ r r r = Q 4 = π 4 Επομένως, r r 4 Q Qr r E = = 4, r 4πε r 4πε και τελικά Qr r E = 4, r. 4πε (δ) Αντικαθιστώντας r= στις τελικές εκφράσεις του μέτρου του ηλεκτρικού πεδίου των υπο ερωτημάτων (β) και (γ) προκύπτει το ίδιο μέτρο του ηλεκτρικού πεδίου για Q την επιφάνεια της σφαίρας : E =, r = 4πε 11
12 Άσκηση 9. (1 μονάδες) Α) Ο χώρος μεταξύ των οπλισμών επίπεδου πυκνωτή γεμίζεται με δύο πλάκες διηλεκτρικού, μία με σχετική διηλεκτρική σταθερά Κ 1 και μία με διηλεκτρική σταθερά Κ. Κάθε πλάκα έχει πάχος d/, όπου d η απόσταση μεταξύ των οπλισμών του πυκνωτή. Να δείξετε ότι η χωρητικότητα είναι: εa KK 1 C = d K1 K d/ K 1 K d/ Β)Δίδονται δύο ευθύγραμμοι ρευματοφόροι αγωγοί πολύ μεγάλου μήκους και αμελητέου πάχους. Οι αγωγοί βρίσκονται πολύ κοντά ο ένας με τον άλλο και διαρρέονται από ηλεκτρικά ρεύματα εντάσεων Ι 1 =Α και Ι =1Α αντίστοιχα, όπως στο σχήμα. Να ευρεθεί το μαγνητικό πεδίο Β σε σημείο το οποίο απέχει απόσταση r=1m 7 από τους αγωγούς. Δίδεται το μ = 4π 1 W / A m Ι 1 x Ι Α) Υποθέτουμε ότι υπάρχει επιφανειακό φορτίο πυκνότητας σ στην επάνω πλάκα του πυκνωτή και σ στην κάτω. Θεωρούμε σαν γκαουσιανές επιφάνειες τις ΑΒΔΓ και ΑΒΖΕ (ορθογώνια παραλληλεπίπεδα με βάσεις εμβαδού Α 1 ) όπως στο σχήμα. Εφαρμόζοντας το νόμο του Gauss βρίσκουμε: σ A1 σ A1 KEA = και KEA 1 = ε ε σ σ Επομένως E1 = και E = K1ε Kε Η διαφορά δυναμικού μεταξύ των οπλισμών είναι: d d E dl = E dl E dl = E1 E = V αβγ αβ βγ αντικαθιστώντας: σ d σ d = V. Το φορτίο του πυκνωτή K ε K ε 1 θα είναι: Q = σ A και επομένως K 1 K Q ε σa εa KK 1 C = = = V 1 1 d K K σ d K 1 K γ α β Α Γ Ε 1 Ε 1 Ε Β Δ Ζ 1
13 Παρατήρηση: Το αποτέλεσμα αυτό συμπίπτει με τη θεώρηση δύο πυκνωτών συνδεδεμένων σε σειρά. Β) Ι 1 x r Ι B dl Το μαγνητικό πεδίο που παράγεται στο χώρο έχει κυλινδρική συμμετρία επομένως θεωρούμε κλειστή διαδρομή έναν κύκλο με κέντρο ένα σημείο των αγωγών και ακτίνα r σε επίπεδο κάθετο στους αγωγούς. Εφαρμόζουμε τον νόμο του Ampere για αυτή την κλειστή διαδρομή. Bdl = μi Έστω ότι κινούμαστε στην κλειστή διαδρομή με φορά αυτή που σημειώνεται στο σχήμα. Τότε τα διανύσματα dl και B είναι συγγραμικά και ομόρροπα. Οπότε από τον νόμο του Ampere έχουμε: Bdl = μ I B dl= μ I I B dl= μ I I 1 1 ( ) ( ) ( ) μ I1 I Bπr = μ( I1 I) B= πr 7 4π 1 ( 1) Wb 7 Αντικαθιστώντας, B = = 1 Τ π 1 m Άσκηση 1. (1 μονάδες) A) Υπολογίστε τα τρία ρεύματα που σημειώνονται στο διάγραμμα του κυκλώματος στο παρακάτω σχήμα: B) Η μαγνητική επαγωγή Β μαγνητικού πεδίου μέσα σε μακρύ ευθύγραμμο πηνίο ακτίνας, αυξάνει με ρυθμό db σταθ. dt = Να βρείτε: α) Το ρυθμό μεταβολής της μαγνητικής ροής μέσα σε κύκλο ακτίνας < τοποθετημένου εντός του πηνίου, κάθετα στον άξονά του και με το κέντρο του πάνω στον άξονα του πηνίου. β) Το επαγόμενο ηλεκτρικό πεδίο στο εσωτερικό του πηνίου σε απόσταση r1 < από τον άξονά του. γ) Το επαγόμενο ηλεκτρικό πεδίο στο εξωτερικό του πηνίου σε απόσταση r > από τον άξονά του. r1 1
14 δ) Να παραστήσετε γραφικά το μέτρο του επαγόμενου ηλεκτρικού πεδίου συναρτήσει της απόστασης από τον άξονά του από r= έως r=. Α) Ι 1 Ι 1 Έχει γίνει χρήση του κανόνα των ρευμάτων του Kirchhff και έχουν σημειωθεί τα ρεύματα των κλάδων συναρτήσει των Ι 1, Ι, Ι. Στους ενδιάμεσους υπολογισμούς τα σύμβολα και οι αριθμοί παριστάνουν αριθμητικές τιμές στο SI. Από τον κανόνα των βρόχων για το βρόχο 1 βρίσκουμε: 1, Ι 1 x 1, (Ι 1 Ι ) 5,= ή 6, x Ι 1 5, x Ι =1, (1) Από το βρόχο έχουμε: Ι x 1, 9, (Ι Ι ) x 8,= ή 9, x Ι 8, x Ι =9, () Από το βρόχο βρίσκουμε, Ι x 1, 9, Ι x 1, Ι 1 x 1, 1,= ή 1, x Ι 1, x Ι 1 1, x Ι =, () Από την εξίσωση (1) έχουμε: 5 I1 =, I 6 Από την εξίσωση () έχουμε: 8 I = 1, I 9 Αντικαθιστώντας στην εξίσωση () 1, 8 I 5 1,, I 1, 1, I =, 9 6 Άρα I 11 =, ή I =, Άρα Ι =,171 Α. 14
15 5 5 Επίσης I1 =, I =,,171 =,14Α Όμως I = 1, I = 1,,171 =,848Α. 9 9 Β) Θεωρούμε τον άξονα του πηνίου παράλληλο στον άξονα z. Το μαγνητικό πεδίο μέσα στο μακρύ και ευθύγραμμο πηνίο είναι παράλληλο στον άξονά του. Υποθέτουμε ότι το ηλεκτρικό ρεύμα που το διαπερνά είναι αριστερόστροφο. Τότε το μαγνητικό πεδίο μέσα στο πηνίο είναι B = Bzˆ. Η επιφάνεια της διατομής του πηνίου δίνεται από το διάνυσμα A = π zˆ. (α) Ο κύκλος με ακτίνα r, σε επίπεδο κάθετο στον άξονα με κέντρο σημείο του άξονα έχει επιφάνεια που δίνεται από το διάνυσμα a = πr zˆ 1. Η ροή του B μέσα από αυτό τον κύκλο είναι Φ B = B a = Ba. Ο ρυθμός μεταβολής της Φ B είναι: d Φ B d db ( Ba) a πr db = = = 1 dt dt dt dt (1) (β) Η ΗΕΔ που επάγεται στον κύκλο με ακτίνα r είναι : dφb db ε = = πr1 () dt dt Το db είναι θετικό και άρα ε <. Η ΗΕΔ δίνεται επίσης από το επικαμπύλιο dt ολοκλήρωμα: ε = Το ( ) E r1 d () E( r 1 ) έχει το ίδιο μέτρο σε κάθε σημείο της περιφέρειας του κύκλου λόγω αξονικής συμμετρίας. Η φορά του d επιλέγεται να είναι αριστερόστροφη σύμφωνα με τη σύμβαση για θετική ροή. Τότε: ε = = ( ) ( ) E r d E r πr (4) E r Εξισώνοντας τις () και (4) προκύπτει ( ) 1 Το αρνητικό πρόσημο δείχνει ότι η φορά του ( ) d. Άρα το ( ) είναι δεξιόστροφο. 1 r db =. dt E r 1 είναι αντίστροφη εκείνης του E r 1 (γ) Στο εξωτερικό του πηνίου, r >. Το μαγνητικό πεδίο όμως είναι μηδενικό για <r<r και άρα η ροή του μαγνητικού πεδίου από κύκλο με ακτίνα r > είναι: Φ B = Bπ. Τότε η ΗΕΔ δίνεται από τις σχέσεις: dφb db ε = = π (7) dt dt και = E r d = E r πr (8) ε ( ) ( ) 15
16 Εξισώνοντας τις (7) και (8) προκύπτει E( r ) δείχνει και πάλι ότι E( r ) είναι δεξιόστροφο. (γ) Η γραφική παράσταση δίνεται παρακάτω: db =. Το αρνητικό πρόσημο r dt E r 16
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Λύση Α. Σωστή η επιλογή α. Β.
 1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
 ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΘΕΜΑ 1. Ονοματεπώνυμο. Τμήμα
 Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ
 Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
Α) Η επιφάνεια Gauss έχει ακτίνα r μεγαλύτερη ή ίση της ακτίνας του κελύφους, r α.
 1. Ένα σφαιρικό κέλυφος που θεωρούμε ότι έχει αμελητέο πάχος έχει ακτίνα α και φέρει φορτίο Q, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Βρείτε την ένταση του ηλεκτρικού πεδίου στο εξωτερικό και στο
1. Ένα σφαιρικό κέλυφος που θεωρούμε ότι έχει αμελητέο πάχος έχει ακτίνα α και φέρει φορτίο Q, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Βρείτε την ένταση του ηλεκτρικού πεδίου στο εξωτερικό και στο
ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006
 ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006 Άσκηση 1 Δύο σφαίρες με ίσες μάζες m είναι δεμένες με νήματα μήκους l από το ίδιο σημείο της οροφής Σ. Αν η κάθε σφαίρα φέρει φορτίο q να βρεθεί η γωνία
ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006 Άσκηση 1 Δύο σφαίρες με ίσες μάζες m είναι δεμένες με νήματα μήκους l από το ίδιο σημείο της οροφής Σ. Αν η κάθε σφαίρα φέρει φορτίο q να βρεθεί η γωνία
ΦΥΕ14, 2009-2010-Εργασιά 6 η Ημερομηνία παράδοσης 28/6/2010
 ΦΥΕ4, 9--Εργασιά 6 η Ημερομηνία παράδοσης 8/6/ Άσκηση A) Μια ράβδος μήκους είναι ομοιόμορφα φορτισμένη θετικά με συνολικό ηλεκτρικό φορτίο Q και βρίσκεται κατά μήκος του θετικού άξονα x από το σημείο x
ΦΥΕ4, 9--Εργασιά 6 η Ημερομηνία παράδοσης 8/6/ Άσκηση A) Μια ράβδος μήκους είναι ομοιόμορφα φορτισμένη θετικά με συνολικό ηλεκτρικό φορτίο Q και βρίσκεται κατά μήκος του θετικού άξονα x από το σημείο x
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Γ ΚΥΚΛΟΣ ΠΡΟΣΟΜΟΙΩΤΙΚΩΝ ΔΙΑΓΩΝΙΣΜΑΤΩΝ ΣΥΓΧΡΟΝΟ Προτεινόμενα Θέματα Β Λυκείου Μάρτιος Φυσική ΘΕΜΑ A
 Φυσική ΘΕΜΑ 1. Οι δυναμικές γραμμές ενός ηλεκτροστατικού πεδίου: α) τέμνονται. β) απομακρύνονται από τα αρνητικά φορτία και κατευθύνονται στα θετικά. γ) είναι πάντα παράλληλες μεταξύ τους. γενικής παιδείας
Φυσική ΘΕΜΑ 1. Οι δυναμικές γραμμές ενός ηλεκτροστατικού πεδίου: α) τέμνονται. β) απομακρύνονται από τα αρνητικά φορτία και κατευθύνονται στα θετικά. γ) είναι πάντα παράλληλες μεταξύ τους. γενικής παιδείας
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ
 ΘΕΜΑ Δ (15732) Δύο ακίνητα σημειακά ηλεκτρικά φορτία 2 μc και 3 μc, βρίσκονται αντίστοιχα στις θέσεις 3 m και 6 m ενός άξονα, όπως φαίνεται στο παρακάτω σχήμα. Δ1) Να υπολογίσετε το δυναμικό του ηλεκτρικού
ΘΕΜΑ Δ (15732) Δύο ακίνητα σημειακά ηλεκτρικά φορτία 2 μc και 3 μc, βρίσκονται αντίστοιχα στις θέσεις 3 m και 6 m ενός άξονα, όπως φαίνεται στο παρακάτω σχήμα. Δ1) Να υπολογίσετε το δυναμικό του ηλεκτρικού
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΚΕΦΑΛΑΙΟ 1 ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ ΕΡΩΤΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 1 ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ ΕΡΩΤΗΣΕΙΣ 1. Κατά την ηλέκτριση με τριβή μεταφέρονται από το ένα σώμα στο άλλο i. πρωτόνια. ii. ηλεκτρόνια iii iν. νετρόνια ιόντα. 2. Το σχήμα απεικονίζει
ΚΕΦΑΛΑΙΟ 1 ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ ΕΡΩΤΗΣΕΙΣ 1. Κατά την ηλέκτριση με τριβή μεταφέρονται από το ένα σώμα στο άλλο i. πρωτόνια. ii. ηλεκτρόνια iii iν. νετρόνια ιόντα. 2. Το σχήμα απεικονίζει
ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ
 15 Α. ΝΟΜΟΣ ΤΟΥ COULOMB ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Στο χλωριούχο νάτριο (NaCl) η ελάχιστη απόσταση μεταξύ του ιόντος Να + και του ιόντος του Cl - είναι 2,3.10-10 m. Πόση είναι η
15 Α. ΝΟΜΟΣ ΤΟΥ COULOMB ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Στο χλωριούχο νάτριο (NaCl) η ελάχιστη απόσταση μεταξύ του ιόντος Να + και του ιόντος του Cl - είναι 2,3.10-10 m. Πόση είναι η
Physics by Chris Simopoulos
 ΕΠΩΗ 1. Ευθύγραμμος αγωγός μήκους L = 1 m κινείται με σταθερή ταχύτητα υ = 2 m/s μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,8 Τ. Η κίνηση γίνεται έτσι ώστε η ταχύτητα του αγωγού να σχηματίζει γωνία
ΕΠΩΗ 1. Ευθύγραμμος αγωγός μήκους L = 1 m κινείται με σταθερή ταχύτητα υ = 2 m/s μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,8 Τ. Η κίνηση γίνεται έτσι ώστε η ταχύτητα του αγωγού να σχηματίζει γωνία
Το βαρυτικό πεδίο της Γης.
 Το βαρυτικό πεδίο της Γης. Θα μελετήσουμε το βαρυτικό πεδίο της Γης, τόσο στο εξωτερικό της όσο και στο εσωτερικό της, χρησιμοποιώντας τη λογική μελέτης του ηλεκτροστατικού πεδίου, με την βοήθεια της ροής.
Το βαρυτικό πεδίο της Γης. Θα μελετήσουμε το βαρυτικό πεδίο της Γης, τόσο στο εξωτερικό της όσο και στο εσωτερικό της, χρησιμοποιώντας τη λογική μελέτης του ηλεκτροστατικού πεδίου, με την βοήθεια της ροής.
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα στις θέσεις x 1 = - 3 m και x 2 = + 6 m ενός άξονα x'x, όπως φαίνεται στο παρακάτω
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα στις θέσεις x 1 = - 3 m και x 2 = + 6 m ενός άξονα x'x, όπως φαίνεται στο παρακάτω
Δ2) Να υπολογίσετε την απόσταση ra του σημείου Α από το σημειακό φορτίο Q καθώς και τη τιμή του ηλεκτρικού φορτίου Q. Μονάδες 9
 14345 Ακίνητο σημειακό ηλεκτρικό φορτίο Q δημιουργεί γύρω του ηλεκτροστατικό πεδίο. Σε σημείο Α του πεδίου αυτού, το μέτρο της έντασης είναι N/ και η τιμή του δυναμικού είναι - 6 V. Δ1) Να παραστήσετε
14345 Ακίνητο σημειακό ηλεκτρικό φορτίο Q δημιουργεί γύρω του ηλεκτροστατικό πεδίο. Σε σημείο Α του πεδίου αυτού, το μέτρο της έντασης είναι N/ και η τιμή του δυναμικού είναι - 6 V. Δ1) Να παραστήσετε
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
B 2Tk. Παράδειγμα 1.2.1
 Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
ΤΥΠΟΛΟΓΙΟ Ο Ρ Ο Σ Η Μ Ο. Για το κενό ή αέρα στο SI: N m. , Μονάδα στο S.I. 1. Πως βρίσκουμε τη συνισταμένη δύο ή περισσοτέρων δυνάμεων:
 ΤΥΠΟΛΟΓΙΟ Φυσική της Λυκείου Γενικής Παιδείας Στατικός Ηλεκτρισμός Τύποι που ισχύουν Νόμος του Coulomb Πως βρίσκουμε τη συνισταμένη δύο ή περισσοτέρων δυνάμεων: α. Χρησιμοποιούμε τη μέθοδο του παραλλογράμμου
ΤΥΠΟΛΟΓΙΟ Φυσική της Λυκείου Γενικής Παιδείας Στατικός Ηλεκτρισμός Τύποι που ισχύουν Νόμος του Coulomb Πως βρίσκουμε τη συνισταμένη δύο ή περισσοτέρων δυνάμεων: α. Χρησιμοποιούμε τη μέθοδο του παραλλογράμμου
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Gauss
 Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
ΔΙΑΓΩΝΙΣΜΑ Β. Θέµα 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ Β Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Ένα πρωτόνιο και ένας πυρήνας ηλίου εισέρχονται σε οµογενές
ΔΙΑΓΩΝΙΣΜΑ Β Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Ένα πρωτόνιο και ένας πυρήνας ηλίου εισέρχονται σε οµογενές
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
 8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Ν. Τράκας, Ι. Ράπτης 2/4/2018
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΣΚΗΣΕΙΣ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΣΚΗΣΕΙΣ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ Ο νόμος του Coulomb Ηλεκτρικό πεδίο Δυναμικό Διαφορά Δυναμικού Πυκνωτές ΕΠΙΜΕΛΕΙΑ: ΑΘΑΝΑΣΙΟΣ Ι. ΜΠΑΛΑΣΚΑΣ ΦΥΣΙΚΟΣ
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΣΚΗΣΕΙΣ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ Ο νόμος του Coulomb Ηλεκτρικό πεδίο Δυναμικό Διαφορά Δυναμικού Πυκνωτές ΕΠΙΜΕΛΕΙΑ: ΑΘΑΝΑΣΙΟΣ Ι. ΜΠΑΛΑΣΚΑΣ ΦΥΣΙΚΟΣ
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ. Στατικός Ηλεκτρισµός
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ Στατικός Ηλεκτρισµός 1) Όταν η απόσταση µεταξύ δύο ηλεκτρικών φορτίων υποδιπλασιαστεί, τότε η δύναµη Coulomb µεταξύ τους: α) υποδιπλασιάζεται β) διπλασιάζεται γ) δεν αλλάζει δ) τετραπλασιάζεται
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ Στατικός Ηλεκτρισµός 1) Όταν η απόσταση µεταξύ δύο ηλεκτρικών φορτίων υποδιπλασιαστεί, τότε η δύναµη Coulomb µεταξύ τους: α) υποδιπλασιάζεται β) διπλασιάζεται γ) δεν αλλάζει δ) τετραπλασιάζεται
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΘEMA A: ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Αντιστάτης με αντίσταση R συνδέεται με ηλεκτρική πηγή, συνεχούς τάσης V
ΘEMA A: ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Αντιστάτης με αντίσταση R συνδέεται με ηλεκτρική πηγή, συνεχούς τάσης V
7.1 Τα πρώτα πειράματα της χρονιάς.
 7.1 Τα πρώτα πειράματα της χρονιάς. 7.Β. Μπορείτε να ερμηνεύσετε τις παρακάτω πειραματικές παρατηρήσεις; i) Μια αφόρτιστη μεταλλική ράβδος κρέμεται όπως στο σχήμα από μονωτικό νήμα και ηρεμεί. Όταν πλησιάσουμε
7.1 Τα πρώτα πειράματα της χρονιάς. 7.Β. Μπορείτε να ερμηνεύσετε τις παρακάτω πειραματικές παρατηρήσεις; i) Μια αφόρτιστη μεταλλική ράβδος κρέμεται όπως στο σχήμα από μονωτικό νήμα και ηρεμεί. Όταν πλησιάσουμε
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 Φυσική Κατεύθυνσης Β Λυκείου ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ κ ΙΑΓΩΝΙΣΜΑ Α Θέµα ο Να επιλέξετε τη σωστή απάντηση σε κάθε µία από τις παρακάτω ερωτήσεις: Σύµφωνα µε την κινητική θεωρία των ιδανικών αερίων
Φυσική Κατεύθυνσης Β Λυκείου ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ κ ΙΑΓΩΝΙΣΜΑ Α Θέµα ο Να επιλέξετε τη σωστή απάντηση σε κάθε µία από τις παρακάτω ερωτήσεις: Σύµφωνα µε την κινητική θεωρία των ιδανικών αερίων
Κίνηση σε Ηλεκτρικό Πεδίο.
 Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Ηλεκτρική δυναμική ενέργεια
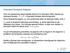 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics for scientists and engineers YOUNG H.D., University
Ηλεκτρικό φορτίο Ηλεκτρικό Πεδίο
 Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Προσοχή : στον τύπο της δυναμικής ενέργειας τα φορτία μπαίνουν με το
 ΜΕΘΟΔΟΛΟΓΙΑ 1. ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΔΥΟ ΦΟΡΤΙΩΝ Βήμα 1: σχεδιάζουμε τα δυο φορτία που δημιουργούν το πεδίο Coulomb την μεταξύ τους απόσταση Βήμα 2: γράφουμε την σχέση ου δίνει την δυναμική ενέργεια στο σημείο
ΜΕΘΟΔΟΛΟΓΙΑ 1. ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΔΥΟ ΦΟΡΤΙΩΝ Βήμα 1: σχεδιάζουμε τα δυο φορτία που δημιουργούν το πεδίο Coulomb την μεταξύ τους απόσταση Βήμα 2: γράφουμε την σχέση ου δίνει την δυναμική ενέργεια στο σημείο
Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας
 Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Δύο σώματα Α και Β ( ) εκτοξεύονται ταυτόχρονα οριζόντια
Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Δύο σώματα Α και Β ( ) εκτοξεύονται ταυτόχρονα οριζόντια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΘΕΜΑ 1 ο : Α. Να σημειώσετε ποιες από τις ακόλουθες σχέσεις, που αναφέρονται
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο : Α. Να σημειώσετε ποιες από τις ακόλουθες σχέσεις, που αναφέρονται στο διπλανό κύκλωμα είναι σωστές, αν R 1 > R 2. i. Ι 1 = Ι 2 ii. V = V 1 + V 2 iii. I = I
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο : Α. Να σημειώσετε ποιες από τις ακόλουθες σχέσεις, που αναφέρονται στο διπλανό κύκλωμα είναι σωστές, αν R 1 > R 2. i. Ι 1 = Ι 2 ii. V = V 1 + V 2 iii. I = I
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ TMHMA ΧΗΜΕΙΑΣ ΙΟΥΝΙΟΣ 2014
 ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ TMHMA ΧΗΜΕΙΑΣ ΙΟΥΝΙΟΣ 2014 Κυκλώνουμε τις σωστές απαντήσεις στο παρών φυλλάδιο το άλλο φυλλάδιο είναι πρόχειρο παραδίδουμε και τα δυο φυλλάδια. Κάθε σωστή απάντηση μετρά 0.5 μονάδες
ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ TMHMA ΧΗΜΕΙΑΣ ΙΟΥΝΙΟΣ 2014 Κυκλώνουμε τις σωστές απαντήσεις στο παρών φυλλάδιο το άλλο φυλλάδιο είναι πρόχειρο παραδίδουμε και τα δυο φυλλάδια. Κάθε σωστή απάντηση μετρά 0.5 μονάδες
ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ-ΙΟΥΝΙΟΣ 2011
 ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ-ΙΟΥΝΙΟΣ 2011 Κυκλώνουμε τις σωστές απαντήσεις στο παρών φυλλάδιο το άλλο φυλλάδιο είναι πρόχειρο. Κάθε σωστή απάντηση μετρά 0.5 μονάδες ενώ κάθε λάθος -0.1 μονάδες. Δίδεται k=1/(4πε
ΠΕΙΡΑΜΑΤΙΚΗ ΦΥΣΙΚΗ ΙΙ-ΙΟΥΝΙΟΣ 2011 Κυκλώνουμε τις σωστές απαντήσεις στο παρών φυλλάδιο το άλλο φυλλάδιο είναι πρόχειρο. Κάθε σωστή απάντηση μετρά 0.5 μονάδες ενώ κάθε λάθος -0.1 μονάδες. Δίδεται k=1/(4πε
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 22 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο 1.1 Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 22 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο 1.1 Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 05-06 ΑΛΛΗΛΕΠΙΔΡΑΣΗ
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 05-06 ΑΛΛΗΛΕΠΙΔΡΑΣΗ
d E dt Σχήμα 3.4. (α) Σχηματικό διάγραμμα απλού εναλλάκτη, όπου ένας αγώγιμος βρόχος περιστρέφεται μέσα
 Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1999
 Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1999 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΣΕΠΤΕΜΒΡΙΟΥ 1999 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις ερωτήσεις 1-4, να γράψετε στο τετράδιό
Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1999 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΣΕΠΤΕΜΒΡΙΟΥ 1999 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις ερωτήσεις 1-4, να γράψετε στο τετράδιό
5 σειρά ασκήσεων. 1. Να υπολογισθεί το μαγνητικό πεδίο που δημιουργεί ευθύγραμμος αγωγός με άπειρο μήκος, που διαρρέεται από ρεύμα σταθερής έντασης.
 η 5 σειρά ασκήσεων Σε όλα τα πιο κάτω προβλήματα δίνεται ότι μ o = 4πx10-7 Τm/Α 1. Να υπολογισθεί το μαγνητικό πεδίο που δημιουργεί ευθύγραμμος αγωγός με άπειρο μήκος, που διαρρέεται από ρεύμα σταθερής
η 5 σειρά ασκήσεων Σε όλα τα πιο κάτω προβλήματα δίνεται ότι μ o = 4πx10-7 Τm/Α 1. Να υπολογισθεί το μαγνητικό πεδίο που δημιουργεί ευθύγραμμος αγωγός με άπειρο μήκος, που διαρρέεται από ρεύμα σταθερής
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Α3. Να αντιστοιχίσετε τα φυσικά µεγέθη µε τις µονάδες τους. Ένταση ηλεκτρικού πεδίου. υναµική ενέργεια
 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΤΜΗΜΑ Β1 ΘΕΜΑ (ΟΜΑΔΑ Α) Για τις ερωτήσεις Α1 και Α2 να γράψετε στο φύλλο απαντήσεων τον αριθµό της ερώτησης και δεξιά απ αυτόν το γράµµα που αντιστοιχεί στη σωστή απάντηση. Α1. Σε κάποιο
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΤΜΗΜΑ Β1 ΘΕΜΑ (ΟΜΑΔΑ Α) Για τις ερωτήσεις Α1 και Α2 να γράψετε στο φύλλο απαντήσεων τον αριθµό της ερώτησης και δεξιά απ αυτόν το γράµµα που αντιστοιχεί στη σωστή απάντηση. Α1. Σε κάποιο
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ 25/12/2016. Νόμος του Coulomb q1 q2 F K. C 8,85 10 N m Ένταση πεδίου Coulomb σε σημείο του Α
 ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ 5/1/16 Τυπολόγιο 1ου Κεφαλαίου Στατικός Ηλεκτρισμός Τύποι που ισχύουν Νόμος του Coulomb 1 F K Για το κενό ή αέρα στο S: 9 k 91 N m / C Απόλυτη διηλεκτρική
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ 5/1/16 Τυπολόγιο 1ου Κεφαλαίου Στατικός Ηλεκτρισμός Τύποι που ισχύουν Νόμος του Coulomb 1 F K Για το κενό ή αέρα στο S: 9 k 91 N m / C Απόλυτη διηλεκτρική
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
 Δυνάμεις Μεταξύ Ηλεκτρικών Φορτίων σελ. 1 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Ο νόμος του Coulomb. Ηλεκτρικό πεδίο 3. Ηλεκτρική δυναμική ενέργεια 4. Δυναμικό
Δυνάμεις Μεταξύ Ηλεκτρικών Φορτίων σελ. 1 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Ο νόμος του Coulomb. Ηλεκτρικό πεδίο 3. Ηλεκτρική δυναμική ενέργεια 4. Δυναμικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
Κίνηση σε Ηλεκτρικό Πεδίο.
 Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενόςισοπλεύρου τριγώνου ΑΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σηµειακά ηλεκτρικά φορτία q 1 =2µC και q 2 αντίστοιχα.
Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενόςισοπλεύρου τριγώνου ΑΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σηµειακά ηλεκτρικά φορτία q 1 =2µC και q 2 αντίστοιχα.
ΘΕΜΑ 1 2 Ι =Ι. ομοιόμορφα στη διατομή του αγωγού θα ισχύει: = 2. Επομένως Β = μbοb r / 2παP P, για r α. I π r r
 I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΠΑΝΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 3 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ
 EΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 1999 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 3ο Ακίνητο σημειακό φορτίο Q=10-6 δημιουργεί ηλεκτροστατικό πεδίο. Ένα σημείο Α απέχει από το παραπάνω φορτίο απόσταση r A =
EΠΑΝΑΛΗΠΤΙΚΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 1999 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 3ο Ακίνητο σημειακό φορτίο Q=10-6 δημιουργεί ηλεκτροστατικό πεδίο. Ένα σημείο Α απέχει από το παραπάνω φορτίο απόσταση r A =
Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης περιγράφεται σωστά από το νόμο Coulomb
 Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Λυμένες ασκήσεις. Ηλεκτρική δυναμική ενέργεια
 Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
φορτισμένου πυκνωτή με διεύθυνση κάθετη στις δυναμικές γραμμές του πεδίου, όπως
 Ημερομηνία: 26/04/15 Διάρκεια διαγωνίσματος: 150 Εξεταζόμενο μάθημα: Φυσική Κατ. Β Λυκείου Υπεύθυνος καθηγητής: Μήτρου Ιωάννης ΘΕΜΑ 1 Ο Σωστό Λάθος A)1. Η κεντρομόλος δύναμη είναι η συνισταμένη των δυνάμεων
Ημερομηνία: 26/04/15 Διάρκεια διαγωνίσματος: 150 Εξεταζόμενο μάθημα: Φυσική Κατ. Β Λυκείου Υπεύθυνος καθηγητής: Μήτρου Ιωάννης ΘΕΜΑ 1 Ο Σωστό Λάθος A)1. Η κεντρομόλος δύναμη είναι η συνισταμένη των δυνάμεων
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1 ο :Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Η διαφορά δυναμικού μεταξύ δύο σημείων μιας δυναμικής γραμμής, ομογενούς ηλεκτρικού
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1 ο :Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Η διαφορά δυναμικού μεταξύ δύο σημείων μιας δυναμικής γραμμής, ομογενούς ηλεκτρικού
1. Νόμος του Faraday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας:
 1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
Ασκήσεις 7 ου Κεφαλαίου
 7η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 7 ου Κεφαλαίου 1. Κάτω από έναν οριζόντιο αγώγιμο δακτύλιο ακτίνας r που διαρρέεται από ρεύμα Ι τοποθετείται ένας ισχυρός μαγνήτης. Αν το μαγνητικό
7η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 7 ου Κεφαλαίου 1. Κάτω από έναν οριζόντιο αγώγιμο δακτύλιο ακτίνας r που διαρρέεται από ρεύμα Ι τοποθετείται ένας ισχυρός μαγνήτης. Αν το μαγνητικό
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος
 ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος παίρνει καθορισμένη τιμή. Ηλεκτρικό πεδίο Ηλεκτρικό πεδίο ονομάζεται ο χώρος, που σε κάθε σημείο
ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος παίρνει καθορισμένη τιμή. Ηλεκτρικό πεδίο Ηλεκτρικό πεδίο ονομάζεται ο χώρος, που σε κάθε σημείο
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
Physics by Chris Simopoulos
 ΘΕΜΑ 1 ο 1 ΘΕΜΑ 1 ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΘΕΜΑ 1 ο 1 ΘΕΜΑ 1 ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ. Παράδειγµα: Κίνηση φορτισµένου σωµατιδίου µέσα σε µαγνητικό πεδίο. z B. m υ MAΓΝΗTIKΟ ΠΕ ΙΟ
 1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
ΕΚΦΩΝΗΣΕΙΣ. Για τις παρακάτω ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα που αντιστοιχεί στην σωστή απάντηση
 B' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΖΗΤΗΜΑ 1 ΕΚΦΩΝΗΣΕΙΣ Για τις παρακάτω ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα που αντιστοιχεί στην σωστή απάντηση
B' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΖΗΤΗΜΑ 1 ΕΚΦΩΝΗΣΕΙΣ Για τις παρακάτω ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα που αντιστοιχεί στην σωστή απάντηση
