Παραλλαγές και επεκτάσεις αυτομάτων I
|
|
|
- Φορτουνάτος Βιτάλης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως προηγουμένως και δ είναι μία απεικόνιση από το Q ˆ Σ στο Q ˆ tl, Ru, δηλαδή δ : Q ˆ Σ Ñ Q ˆ tl, Ru. Εάν δ(q, a) = (p, L), τότε στην κατάσταση q, διαβάζοντας το σύμβολο a, το 2DFA πάει στην κατάσταση p και μετακινεί την κεφαλή προς τα αριστερά κατά μία θέση. Εάν δ(q, a) = (p, R), τότε το 2DFA πάει στην κατάσταση p και μετακινεί την κεφαλή προς τα δεξιά κατά μία θέση. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
2 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων II Configuration ή instantaneous description (ID) ενός 2DFA: περιγράφει το string εισόδου, την τρέχουσα κατάσταση και την τρέχουσα θέση της κεφαλής εισόδου. Ένα ID του M είναι ένα string στο Σ QΣ. Το ΙD wqx, όπου w, x P Σ, αντιπροσωπεύει τα εξής: 1 wx είναι το string εισόδου, 2 q είναι η τρέχουσα κατάσταση και 3 η κεφαλή εισόδου διαβάζει το πρώτο σύμβολο του x. Εάν το x = ε, τότε η κεφαλή εισόδου έχει μετακινηθεί στο δεξί άκρο της ταινίας εισόδου. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
3 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων III Στη συνέχεια εισάγουμε την σχέση $ M στα ID s, έτσι ώστε I 1 $ M I 2, αν και μόνο αν το M μπορεί να πάει από την instantaneous description I 1 στην I 2 με μία κίνηση. Ορίζουμε τη σχέση $ M, ή απλά $, αν το M εννοείται, ως εξής: 1 a 1 a 2... a i 1 qa i... a n $ a 1 a 2... a i 1 a i pa i+1... a n, όταν δ(q, a i ) = (p, R) και 2 a 1 a 2... a i 2 a i 1 qa i... a n $ a 1 a 2... a i 2 pa i 1 a i... a n, όταν δ(q, a i ) = (p, L) και i ą 1. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
4 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων IV Στα διαγράμματα, μία ακμή εκτός από το σύμβολο εισόδου έχει επίσης επιγραφή L ή R. Το ανακλαστικό, μεταβατικό κλείσιμο της σχέσης $ είναι το $. Computation is a legal finite sequence of configurations. Ορισμός L(M) = tw q 0 w $ wp για κάποιο p στο Fu. Θεώρημα Έστ M ένα 2DFA.Τότε L(M) είναι κανονική. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
5 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP FA με έξοδο I Μηχανή Moore Ορισμός Μία μηχανή Moore είναι μία εξάδα M = (Q, Σ,, δ, λ, q 0 ), όπου τα Q, Σ, δ και q 0 είναι όπως στα DFA, με δ : Q ˆ Σ Ñ Q. Επιπλέον: : αλφάβητο εξόδου λ: απεικόνιση από το Q στο, που δίνει την έξοδο που σχετίζεται με κάθε κατάσταση, δηλαδή λ: Q Ñ. input a 1 a 2 a n states q 0 q 1 q 2 q n 1 q n μήκος n + 1 output λ(q 0 ) λ(q 1 ) λ(q 2 ) λ(q n 1 ) λ(q n ) μήκος n + 1 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
6 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP FA με έξοδο II Μηχανή Moore Παρατηρήσεις: Κάθε μηχανή Moore δίνει έξοδο λ(q 0 ) = 5 για είσοδο ε. Το DFA μπορεί να θεωρηθεί ως μία ειδική περίπτωση μίας μηχανής Moore όπου το αλφάβητο είναι {0,1} και η κατάσταση q αποδέχεται αν και μόνο αν λ(q) = 1. Μία μηχανή Moore δεν έχει τελικές καταστάσεις και έχει μήκος εξόδου n + 1. Τα διαγράμματα μηχανών Moore είναι όπως αυτά των FA, αλλά επιπλέον σημειώνουμε μαζί με την κατάσταση το αντίστοιχο σύμβολο εξόδου ως εξής q i /(q i ), π.χ.: a q/b p/c Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
7 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP FA με έξοδο I Μηχανή Mealy Ορισμός Μία μηχανή Mealy είναι μια εξάδα M = (Q, Σ,, δ, λ, q 0 ), όπου όλα είναι όπως στη μηχανή Moore, με δ : Q ˆ Σ Ñ Q, εκτός από το λ που είναι απεικόνιση από το Q ˆ Σ στο, δηλαδή λ: Q ˆ Σ Ñ. Η έξοδος του M με είσοδο το a 1 a 2... a n είναι λ(q 0, a 1 )λ(q 1, a 2 )... λ(q n 1, a n ), όπου q 0, q 1,..., q n είναι η ακολουθία των καταστάσεων έτσι ώστε δ(q i 1, a i ) = q i, για 1 ď i ď n. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
8 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP FA με έξοδο II Μηχανή Mealy Παρατηρήσεις: Η ακολουθία εξόδου έχει μήκος n και όχι n + 1 όπως η μηχανή Moore και με είσοδο ε μία μηχανή Mealy δίνει έξοδο ε. Τα διαγράμματα μηχανών Mealy είναι όπως αυτά των FA, αλλά επιπλέον σημειώνουμε στις μεταβάσεις την αντίστοιχη έξοδο, π.χ.: a/b b/c q p r Μία γενίκευση των μηχανών Mealy είναι το Finite Transducer (ή finite state machine, FSM) με συνάρτηση: λ: Q ˆ Σ Ñ. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
9 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Ισοδυναμία μηχανών Moore και Mealy I Ορισμός Έστω M μία μηχανή Moore ή Mealy. Ορίζουμε T M (w), για είσοδο w να είναι η έξοδος που παράγεται από την M με είσοδο w. Παρατήρηση Δεν είναι δυνατόν ποτέ να είναι ίδιες οι συναρτήσεις T M (w), T M 1 (w), αν M είναι μία μηχανή Moore και M 1 μία μηχανή Mealy, επειδή T M (w) είναι ένα περισσότερο από T M 1 (w), για κάθε w. Ωστόσο, μπορούμε να δώσουμε τον παρακάτω ορισμό ισοδυναμίας: Ορισμός Μία μηχανή Mealy M και μία μηχανή Moore M 1 είναι 5T M (w) = T M 1 (w), όπου λ 1 (q 0 ) = 5 και T M 1 (ε) = 5, T M (w) = η έξοδος μετά την επεξεργασία του w. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
10 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Ισοδυναμία μηχανών Moore και Mealy II Μπορούμε να αποδείξουμε το ακόλουθο θεώρημα για την ισοδυναμία μεταξύ μηχανών Moore και Mealy: Moore ñ DM 1 Mealy Mealy ñ DM 1 Moore ισοδύναμη. Απόδειξη. 1 Έστω μία μηχανή Moore M 1. Κατασκευάζουμε μία ισοδύναμη μηχανή Mealy M 2 : ορίζουμε λ 1 (q, a) = λ(δ(q, a)) για όλες τις καταστάσεις q και για όλα τα σύμβολα εισόδου a. 2 Έστω M 1 μηχανή Mealy. Τότε M 2 = tq ˆ, Σ,, δ 1, λ 1, [q 0, b 0 ]u, όπου b 0 είναι τυχαίο στοιχείο του. Αυτό σημαίνει ότι οι καταστάσεις του M 2 είναι ζευγάρια της μορφής [q, b], αποτελούμενα από μία κατάσταση της M 1 και ένα σύμβολο εξόδου. Ορίζουμε δ 1 ([q, b], a) = [δ(q, a), λ(q, a)] και λ 1 ([q, b]) = b. Το δεύτερο στοιχείο μίας κατάστασης [q, b] της M 2 είναι η έξοδος που παράγεται από την M 1 σε κάποια μετάβαση στην κατάσταση q. Μόνο τα πρώτα στοιχεία των καταστάσεων της M 2 καθορίζουν τις κινήσεις της M 2. Εύκολα με επαγωγή στο n δείχνεται ότι αν η M 1 πηγαίνει στις καταστάσεις q 0, q 1,..., q n με είσοδο a 1 a 2... a n και δίνει έξοδο b 1, b 2,..., b n, τότε η M 2 πηγαίνει στις καταστάσεις [q 0, b 0 ], [q 1, b 1 ],..., [q n, b n ] και δίνει έξοδο b 0, b 1,..., b n. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
11 Ιδιότητες κανονικών συνόλων Pumping lemma για κανονικά σύνολα I Λήμμα (Pumping lemma) Εάν L είναι regular τότε: Dn P P L με z ě n, Du, v, w P Σ : [z = uvw ^ uv ď n ^ v ě 1 P N (uv i w P L)] Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
12 Ιδιότητες κανονικών συνόλων Pumping lemma για κανονικά σύνολα II Χρησιμοποιώντας το λήμμα δείχνουμε ότι ένα δοσμένο σύνολο δεν είναι regular. Η μέθοδος είναι η ακόλουθη: 1 Διαλέγεις τη γλώσσα που θέλεις να αποδείξεις πως δεν είναι regular. 2 Ο αντίπαλος (PL) επιλέγει ένα n. Θα πρέπει να μπορείς για οποιοδήποτε πεπερασμένο ακέραιο n διαλέξει, να αποδείξεις ότι η L δεν είναι regular, αλλά από τη στιγμή που ο αντίπαλος έχει διαλέξει ένα n αυτό είναι σταθερό στην απόδειξη. 3 Διαλέγεις ένα string z της L έτσι ώστε z ě n. 4 Ο αντίπαλος (PL) σπάει το z σε u, v και w που ικανοποιούν τους περιορισμούς uv ď n και v ě 1. 5 Φτάνεις σε αντίφαση δείχνοντας ότι για κάθε u, v, w που καθορίζονται από τον αντίπαλο, υπάρχει ένα i για το οποίο uv i w δεν ανήκει στην L. Τότε μπορούμε να συμπεράνουμε ότι η L δεν είναι regular. Η επιλογή του i μπορεί να εξαρτάται από τα n, u, v, w. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
13 Ιδιότητες κανονικών συνόλων Pumping lemma για κανονικά σύνολα III Παράδειγμα L = ta k b k k P Nu = tε, ab, aabb, aaabbb,...u 1 Υποθέτουμε ότι L είναι regular και χρησιμοποιούμε το pumping lemma. 2 PL: Dn P N 3 Διαλέγουμε z = a n b n. Εντάξει επιλογή, διότι z P L, z = 2n ě n. 4 PL: z μπορεί να γραφεί: z = uvw με uv ď n ^ v ě 1, ώστε v = a l με l ě 1. 5 Διαλέγουμε i = 2: uvvw = a n+l b n P L. Άτοπο Παράδειγμα Το σύνολο L = t0 k2 k ě 1u = t0, 0000, ,...u, δεν είναι regular. 1 Υποθέτουμε ότι L είναι regular και χρησιμοποιούμε το pumping lemma. 2 PL: Dn P N. 3 Διαλέγουμε z = 0 n2. Εντάξει επιλογή, διότι z = n 2 ě n. 4 PL: z μπορεί να γραφεί: z = uvw με uv ď n ^ v ě 1, ώστε v = 0 l με 1 ď l ď n. 5 Διαλέγουμε i = 2: uvvw = 0 n2 +l P L, αλλά n 2 + l δεν είναι τέλειο τετράγωνο, διότι: n 2 ă n ď n 2 + l ď n 2 + n = n(n + 1) ă (n + 1) 2. Άτοπο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
14 Ιδιότητες κανονικών συνόλων Ιδιότητες κλειστότητας για κανονικά σύνολα Λογικές (boolean) πράξεις Υπενθύμιση: Οι boolean (λογικές) πράξεις είναι η έν ση, η τομή και το συμπ ήρ μα. Θεώρημα Η κ άση τ ν regular sets είναι μηχανιστικά κ ειστή (effectively closed) ς προς τις ο ικές πράξεις, την παράθεση (concatenation) και το Kleene *. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
15 Ιδιότητες κανονικών συνόλων Ιδιότητες κλειστότητας για κανονικά σύνολα I Αντικαταστάσεις και ομομορφισμοί Αντικατάσταση: f: Σ Ñ Pow( ) Ειδική περίπτωση: Ομομορφισμός: h: Σ Ñ Αντίστροφος ομομορφισμός: h 1 (w) = tx h(x) = wu για string και h 1 (L) = tx h(x) P Lu για γλώσσα. Ιδιότητες: h(h 1 (L)) Ď L ενώ h 1 (h(l)) Ě L, για κάθε γλώσσα L. Η απεικόνιση f μπορεί να επεκταθεί και σε strings ως εξής: " f(ε) = ε f(wa) = f(w)f(a) Η f επεκτείνεται και σε γλώσσες: fˆ(l) = Ť xpl f(x). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
16 Ιδιότητες κανονικών συνόλων Ιδιότητες κλειστότητας για κανονικά σύνολα II Αντικαταστάσεις και ομομορφισμοί Ορισμός Κανονική αντικατάσταση (regular substitution): αντικατάσταση (substitution) τέτοια P Σ: f(a) είναι regular. Θεώρημα Η κ άση τ ν regular sets είναι μηχανιστικά κ ειστή (effectively closed) ς προς τις πράξεις της κανονικής αντικατάστασης, ομομορφισμού και αντίστροφου ομομορφισμού. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
17 Ιδιότητες κανονικών συνόλων Ιδιότητες κλειστότητας για κανονικά σύνολα Πηλίκα Γλωσσών (quotients of languages) Πηλίκο γλωσσών: L 1 /L 2 = tw Dv P L 2 : wv P L 1 u Παράδειγμα L 1 = ab c και L 2 = b c τότε L 1 /L 2 = ab. Θεώρημα Η κ άση τ ν regular sets είναι κ ειστή ς προς πη ίκο με τυχαίο σύνο ο. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
18 Ιδιότητες κανονικών συνόλων Αλγόριθμοι απόφασης για κανονικά σύνολα I Θεώρημα Έστ M ένα DFA με Q = n. Τότε 1 L(M) H ô Dz P L(M) με z ă n. 2 L(M) = 8 ô Dz P L(M) με n ď z ă 2n. Θεώρημα Υπάρχει μηχανιστικός α όριθμος που αποφασίζει αν δύο πεπερασμένα αυτόματα αποδέχονται το ίδιο σύνο ο, δη αδή αν είναι ισοδύναμα. Απόδειξη. Έστω M 1, M 2 τα αυτόματα που αποδέχονται την L 1, L 2 αντίστοιχα. Γνωρίζουμε από θεώρημα ότι υπάρχει αυτόματο M που αποδέχεται το L = (L 1 X L 2 ) Y (L 1 X L 2 ). Ισχύει L = H ô L 1 = L 2. Έτσι από το προηγούμενο θεώρημα υπάρχει αλγόριθμος που αποφασίζει αν L 1 = L 2. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
19 Ιδιότητες κανονικών συνόλων Αλγόριθμοι απόφασης για κανονικά σύνολα II L 1 L Σχήμα: Ισοδυναμία πεπερασμένων αυτομάτων Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
20 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode I Για κάθε γλώσσα L θα ορίσουμε μία αντίστοιχη σχέση ισοδυναμίας R L ως εξής: Ορισμός Ορίζουμε για x, y P Σ, x R L y, αν και μόνον αν για κάθε z P Σ, xz P L ακριβώς όταν yz P L (δηλαδή για κάθε z P Σ είτε αμφότερα τα xz, yz ανήκουν στην γλώσσα είτε κανένα από τα δύο δεν ανήκει στην γλώσσα). Ο δείκτης μίας σχέσης ισοδυναμίας είναι το πλήθος των κλάσεων ισοδυναμίας αυτής. Έτσι, λέμε ότι μία ισοδυναμία είναι πεπερασμένου δείκτη αν το πλήθος των κλάσεων ισοδυναμίας της είναι πεπερασμένο. Παρατήρηση: Όπως θα δείξουμε παρακάτω, κάτι που χαρακτηρίζει κάθε κανονική γλώσσα L είναι ότι η R L είναι πεπερασμένου δείκτη. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
21 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode II Επίσης, για κάθε πεπερασμένο αυτόματο M με αλφάβητο Σ ορίζουμε μία αντίστοιχη σχέση R M στο Σ ως εξής: Ορισμός x R M y αν και μόνον αν δ(q 0, x) = δ(q 0, y). Πρόταση Η R M είναι δεξιά αναλλοίωτη (right invariant), ς προς την παράθεση, δη αδή ια κάθε x, y P Σ με x R M y έχουμε ότι ια κάθε z P Σ ισχύει xz R M yz. Απόδειξη. δ(q 0, xz) = δ(δ(q 0, x), z) = δ(δ(q 0, y), z) = δ(q 0, yz). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
22 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode III Θεώρημα (Myhill-Nerode) Τα παρακάτ είναι ισοδύναμα ια μία ώσσα L: (i) η L είναι κανονική (ii) η L είναι έν ση κάποι ν από τις κ άσεις ισοδυναμίας μίας δεξιά ανα οί της σχέσης ισοδυναμίας πεπερασμένου δείκτη (iii) η σχέση R L είναι πεπερασμένου δείκτη. Απόδειξη: Θα δείξουμε τις εξής κατευθύνσεις: (i) Ñ (ii) Ñ (iii) Ñ (i). (i) ùñ (ii). Έστω DFA M = (Q, Σ, δ, q 0, F) που αποδέχεται την L. Όπως είδαμε, η R M είναι δεξιά αναλλοίωτη. Οι κλάσεις ισοδυναμίας της R M είναι όσες και οι καταστάσεις του αυτομάτου M, δηλαδή η R M είναι επιπλέον πεπερασμένου δείκτη. Προφανώς, η γλώσσα που γίνεται αποδεκτή από το αυτόματο M είναι ένωση των κλάσεων ισοδυναμίας που αντιστοιχούν σε τελικές καταστάσεις του αυτομάτου. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
23 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode IV (ii) ùñ (iii). Έστω ισοδυναμία E που ικανοποιεί την ιδιότητα που δίνεται στο (ii). Θα δείξουμε την συνεπαγωγή: Αν για x, y P Σ ισχύει x E y, τότε x R L y. Πράγματι έστω x E y. Αφού η E είναι δεξιά αναλλοίωτη, έχουμε ότι για κάθε z P Σ ισχύει xz E yz, δηλαδή είτε αμφότερα τα xz, yz ανήκουν στην γλώσσα L, είτε κανένα από τα δύο δεν ανήκει στην γλώσσα L, δηλαδή (από τον ορισμό της R L ) x R L y. Επομένως, κάθε κλάση ισοδυναμίας της E περιέχεται σε μία κλάση ισοδυναμίας της R L. Αυτό σημαίνει ότι η σχέση E αποτελεί εκ έπτυνση (refinement, βλέπε σχήμα) της σχέσης R L και αφού η E είναι πεπερασμένου δείκτη, δεν μπορεί παρά και η R L να είναι πεπερασμένου δείκτη. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
24 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode V Σ /R L Σ /E Σχήμα: Εκλέπτυνση (refinement) σχέσης ισοδυναμίας (fine-coarse=λεπτή-αδρή) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
25 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Το θεώρημα Myhill-Nerode VI (iii) ùñ (i). Αποδεικνύουμε πρώτα τον εξής ισχυρισμό: Η R L είναι δεξιά αναλλοίωτη. Πράγματι, αν x R L y τότε για κάθε u P Σ έχουμε xu R L yu αφού από τον ορισμό της R L για κάθε v P Σ έχουμε xuv P L ðñ yuv P L (αρκεί να θέσουμε z = uv). Τελικά, θα κατασκευάσουμε αυτόματο M = (Q, Σ, δ, q 0, F) που αποδέχεται την γλώσσα L, δεδομένης της σχέσης R L. Την κλάση ισοδυναμίας στην R L του τυχόντος στοιχείου x P Σ συμβολίζουμε με [x]. Το σύνολο των καταστάσεων Q είναι οι κλάσεις ισοδυναμίας της R L, δηλαδή Q = t[x] x P Σ u. Αρχική κατάσταση είναι η [ε] (η κλάση ισοδυναμίας στην οποία ανήκει η κενή συμβολοσειρά). Το σύνολο των τελικών καταστάσεων είναι F = t[x] x P Lu. Η συνάρτηση μετάβασης ορίζεται δ([x], a) = [xa] (ο ορισμός δεν εξαρτάται από το x και είναι συνεπής δεδομένου ότι η R L είναι δεξιά αναλλοίωτη). Το αυτόματο αποδέχεται την L αφού δ(q 0, x) = [x] κι επομένως x P L(M) αν και μόνον αν [x] P F. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
26 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα I Myhill-Nerode ñ μοναδικό DFA ελάχιστων καταστάσεων. Παράδειγμα: Έστω το αυτόματο M που φαίνεται στο σχήμα, το οποίο αποδέχεται την γλώσσα L = b 1 d 1 f a 1 c 0 e 0, 1 0 Στην L(M) υπάρχουν 6 κλάσεις ισοδυναμίας, οι ακόλουθες: C a = (00), C b = (00) 0, C c = (00) 1, C d = (00) 01, C e = 0 100, C f = (0 + 1), οπότε και L = C c Y C d Y C e. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
27 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα II Τα C a, C b είναι το C 1 (χωρίς 1) = 0. Τα C c, C d, C e είναι το C 2 (με ένα 1) = 0 10 και το C f είναι το C 3 (περισσότερα του ενός 1) = (0 + 1). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
28 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα III Το ελάχιστο αυτόματο φαίνεται στο παρακάτω σχήμα , 1 Ñ a, b 1 c, d, e 1 f Η ίδια μέθοδος συστηματικά με πίνακα: 1 Εξαλείφουμε όλες τις απρόσιτες καταστάσεις. 2 Συγχωνεύουμε ισοδύναμες καταστάσεις που δεν διακρίνονται με κανένα επόμενο string. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
29 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα IV Μέθοδος για το δεύτερο: Tο p είναι διακρίσιμο από το q εάν υπάρχει ένα x τέτοιο ώστε δ(p, x) είναι στο F και δ(q, x) δεν είναι ή αντίστροφα. Φτιάχνουμε ένα πίνακα για να συγκρίνουμε κάθε ζεύγος καταστάσεων. Βάζουμε ένα X σε κάθε θέση του πίνακα κάθε φορά που ανακαλύπτουμε ότι δύο καταστάσεις δεν είναι ισοδύναμες. Αρχικά εγγράφουμε X σε όλα τα ζεύγη που προφανώς διακρίνονται γιατί η μία είναι τελική και η άλλη δεν είναι. Μετά προσπαθούμε να δούμε αν διακρίνονται δύο καταστάσεις, διότι από αυτές με ένα σύμβολο a οδηγούμαστε σε διακρίσιμες καταστάσεις. Επαναλαμβάνουμε την πιο πάνω προσπάθεια ώσπου να μην προστίθεται κανένα X πια στον πίνακα. Τα υπόλοιπα ζευγάρια είναι μη διακρίσιμα και συνεπώς συγχωνεύσιμα. Στο πίνακα οι δείκτες 1 και 2 του X δείχνουν σε ποια επανάληψη εγγράφουμε το X. b c X 1 X 1 d X 1 X 1 e X 1 X 1 f X 2 X 2 X 1 X 1 X 1 a b c d e Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
30 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα V Τελικά οι ισοδύναμες καταστάσεις είναι a b, c d e. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
31 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα I Μέθοδος Beckmann Άλλη μέθοδος για την κατασκευή ενός ελάχιστου DFA είναι η μέθοδος Beckmann. 1 Κατασκεύασε το καθρέφτισμα του FA: δηλαδή ανάστρεψε τη φορά των τόξων. Αντάλλαξε τελικές με αρχικές καταστάσεις. 2 Κατασκεύασε DFA ισοδύναμο με το προκύπτον , 1 Ñ cde 1 ab 1 j Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
32 Αλγεβρική περιγραφή κανονικών συνόλων. Ελαχιστοποίηση DFA Ελαχιστοποιώντας πεπερασμένα αυτόματα II Μέθοδος Beckmann 3 Ξανακατασκεύασε το καθρέφτισμα. 0 0 Ñ ab 1 cde 4 Ξανακατασκεύασε ισοδύναμο DFA. Αυτό τώρα είναι το ελάχιστο DFA που βρήκαμε και παραπάνω, δηλ , 1 Ñ a, b 1 c, d, e 1 f Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
33 Τυπικές Γραμματικές Τυπικές Γραμματικές I Μια τυπική γραμματική (formal grammar) G = (V, T, P, S) αποτελείται από: ένα πεπερασμένο αλφάβητο V από μη τερματικά σύμβολα (non terminals) ή μεταβλητές (variables), ένα πεπερασμένο αλφάβητο T από τερματικά σύμβολα (terminals) ή σταθερές (constants), τ.ώ. V X T = H, ένα πεπερασμένο σύνολο P από κανόνες παραγωγής (production rules) ή απλούστερα παραγωγές (productions), δηλαδή διατεταγμένα ζεύγη (α, β) όπου α, β P (V Y T) και α ε (Σύμβαση: γράφουμε α Ñ β αντί για (α, β)), ένα αρχικό σύμβολο (start symbol) ή αξίωμα S P V. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
34 Τυπικές Γραμματικές Τυπικές Γραμματικές II Θα χρησιμοποιήσουμε την εξής σύμβαση για τη χρήση γραμμάτων: a, b, c, d,... P T A, B, C, D,... P V z, y, x, w, v, u,... P T α, β, γ, δ,... P (V Y T) Θα γράφουμε α Ñ β γ δ ως ένα κανόνα στο P αντί για τους τρεις κανόνες α Ñ β, α Ñ γ, α Ñ δ στο P. Για μια γραμματική G λέμε ότι το γ 1 βγ 2 προκύπτει (is derived from) από το γ 1 αγ 2 και γράφουμε γ 1 αγ 2 ñ γ 1 βγ 2, αν ο α Ñ β είναι κανόνας παραγωγής (δηλαδή (α, β) P P). G Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
35 Τυπικές Γραμματικές Τυπικές Γραμματικές III Συμβολίζουμε με ñ το ανακλαστικό, μεταβατικό κλείσιμο του ñ, δηλαδή α ñ β σημαίνει ότι υπάρχει μια ακολουθία παραγωγών (derivation): α ñ α 1 ñ α 2 ñ α k ñ β. Μια συμβολοκολουθία α P (V Y T) ονομάζεται προτασιακή μορφή (sentential form) αν ισxύει S ñ α. Ως γλώσσα που παράγεται από τη γραμματική G ορίζουμε την L(G) := tw P T S ñ wu. Δύο γραμματικές G 1, G 2 θα ονομάζονται ισοδύναμες αν L(G 1 ) = L(G 2 ). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
36 Τυπικές Γραμματικές Ιεραρχία Chomsky I Ο Noam Chomsky (1956) ταξινόμησε τις τυπικές γραμματικές σε μια ιεραρχία σύμφωνα με τη μορφή των κανόνων παραγωγής τους. Noam Chomsky Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Μάρτιος / 320
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2019 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2019 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA)
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών 6
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών. Προδιαγραφές
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αλγόριθμοι για αυτόματα
 Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α.
 Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α. Δύο Π.Α. Μ 1 και Μ 2 είναι ισοδύναμα ανν L(M 1 ) = L(M 2 ). Έστω Μ = (Q, Σ, q 0, Δ, F) μη Αιτ. Π.Α. Για κάθε κατάσταση q Q, ορίζουμε ως Ε(q) Q το σύνολο των καταστάσεων
Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α. Δύο Π.Α. Μ 1 και Μ 2 είναι ισοδύναμα ανν L(M 1 ) = L(M 2 ). Έστω Μ = (Q, Σ, q 0, Δ, F) μη Αιτ. Π.Α. Για κάθε κατάσταση q Q, ορίζουμε ως Ε(q) Q το σύνολο των καταστάσεων
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων Λύσεις Άσκηση Ορίζουμε τη συναρμογή δύο γλωσσών Α και Β ως ΑΒ = { uv u A, v B }. (α) Έστω Α = {α,β,γ} και Β =. Να περιγράψετε τη γλώσσα ΑΒ. (β) Θεωρήστε τις γλώσσες L, M και N. Να δείξετε
Σειρά Προβλημάτων Λύσεις Άσκηση Ορίζουμε τη συναρμογή δύο γλωσσών Α και Β ως ΑΒ = { uv u A, v B }. (α) Έστω Α = {α,β,γ} και Β =. Να περιγράψετε τη γλώσσα ΑΒ. (β) Θεωρήστε τις γλώσσες L, M και N. Να δείξετε
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών
 Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνοσεμφε 4η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Διδάσκοντες Θεωρία: Στάθης Ζάχος, Άρης Παγουρτζής Εργαστήριο: Δώρα Σούλιου Βοηθός διδασκαλίας:
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνοσεμφε 4η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Διδάσκοντες Θεωρία: Στάθης Ζάχος, Άρης Παγουρτζής Εργαστήριο: Δώρα Σούλιου Βοηθός διδασκαλίας:
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
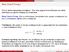 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Αυτόματα Στοίβας (2.2) Τυπικός Ορισμός Παραδείγματα Ισοδυναμία με Ασυμφραστικές
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Αυτόματα Στοίβας (2.2) Τυπικός Ορισμός Παραδείγματα Ισοδυναμία με Ασυμφραστικές
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Κανονικές Γλώσσες. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
Κανονικές Γλώσσες. Κανονικές Γλώσσες. Κανονικές Γλώσσες και Αυτόματα. Κανονικές Γλώσσες και Αυτόματα
 Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Το 10ο πρόβλημα του Hilbert I
 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
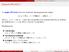 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Περιεχόμενα. 1 Υπολογισιμότητα. Ιστορία - Εισαγωγή. Μαθηματικό Υπόβαθρο. LOOP: Μια απλή γλώσσα προγραμματισμού
 Αυτόματα και Τυπικές Γλώσσες Περιεχόμενα 1 Υπολογισιμότητα Ιστορία - Εισαγωγή Μαθηματικό Υπόβαθρο LOOP: Μια απλή γλώσσα προγραμματισμού LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σταθερά
Αυτόματα και Τυπικές Γλώσσες Περιεχόμενα 1 Υπολογισιμότητα Ιστορία - Εισαγωγή Μαθηματικό Υπόβαθρο LOOP: Μια απλή γλώσσα προγραμματισμού LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σταθερά
p (R 1 (R 2 R 3 )) q pr 1 r 1, r 1 R 2 r 2, r 2 R 3 q p (R 1 R 2 ) r 2 και r 2 R 3 q p ((R 1 R 2 ) R 3 ) q άρα R 1 (R 2 R 3 ) (R 1 R 2 ) R 3
 Τμήμα Μαθηματικών Σχολή Θετικών Επιστημών Α.Π.Θ. Το Συντακτικό Μονοειδές Μιας Γλώσσας Ελένη Ζαβρακλή Σημειώσεις από το βιβλιο: Αυτόματα, Γλώσσες, Γραμματικές Σ.Μποζαπαλίδη Θεσσαλονίκη 2016 Βασικές Εννοιες
Τμήμα Μαθηματικών Σχολή Θετικών Επιστημών Α.Π.Θ. Το Συντακτικό Μονοειδές Μιας Γλώσσας Ελένη Ζαβρακλή Σημειώσεις από το βιβλιο: Αυτόματα, Γλώσσες, Γραμματικές Σ.Μποζαπαλίδη Θεσσαλονίκη 2016 Βασικές Εννοιες
HEAD INPUT. q0 q1 CONTROL UNIT
 Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Η δυαδική σχέση M ( «παράγει σε ένα βήμα» ) ορίζεται ως εξής: (q, w) M (q, w ), αν και μόνο αν w = σw, για κάποιο σ Σ
 Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {1010 2 10 3 10 n 1 10 n 1 n 1}. (β) Να διατυπώσετε
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {1010 2 10 3 10 n 1 10 n 1 n 1}. (β) Να διατυπώσετε
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 10: Αυτόματα Στοίβας II
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 10: Αυτόματα Στοίβας II Τι θα κάνουμε σήμερα Ισοδυναμία αυτομάτων στοίβας με ασυμφραστικές γραμματικές (2.2.3) 1 Ισοδυναμία PDA με CFG Θεώρημα: Μια
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 10: Αυτόματα Στοίβας II Τι θα κάνουμε σήμερα Ισοδυναμία αυτομάτων στοίβας με ασυμφραστικές γραμματικές (2.2.3) 1 Ισοδυναμία PDA με CFG Θεώρημα: Μια
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w w = (ab) 2m b m (ba) m, m 0 } (β) Να διατυπώσετε
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w w = (ab) 2m b m (ba) m, m 0 } (β) Να διατυπώσετε
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {w 1w 2 w 1 {0,1} * και w 2 = 0 k 1 m όπου k και m
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {w 1w 2 w 1 {0,1} * και w 2 = 0 k 1 m όπου k και m
Μεταγλωττιστές. Ενότητα 2: Τυπικές γλώσσες (Μέρος 1 ο ) Αγγελική Σγώρα Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Μεταγλωττιστές Ενότητα 2: Τυπικές γλώσσες (Μέρος 1 ο ) Αγγελική Σγώρα Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μεταγλωττιστές Ενότητα 2: Τυπικές γλώσσες (Μέρος 1 ο ) Αγγελική Σγώρα Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { a 2n b n c 3n n 2 } : H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { a 2n b n c 3n n 2 } : H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την
Τα Θεμέλια της Πληροφορικής
 Τα Θεμέλια της Πληροφορικής Στάθης Ζάχος Άρης Παγουρτζής . Περιεχόμενα Περιεχόμενα i 1 Εισαγωγή 1 1.1 Κλάδοι Επιστήμης των Υπολογιστών............... 2 1.2 Επανάληψη, επαγωγή, αναδρομή..................
Τα Θεμέλια της Πληροφορικής Στάθης Ζάχος Άρης Παγουρτζής . Περιεχόμενα Περιεχόμενα i 1 Εισαγωγή 1 1.1 Κλάδοι Επιστήμης των Υπολογιστών............... 2 1.2 Επανάληψη, επαγωγή, αναδρομή..................
Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές
 Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού 1 /
Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού 1 /
Ποιές οι θεµελιώδεις δυνατότητες και ποιοί οι εγγενείς περιορισµοί των υπολογιστών ; Τί µπορούµε και τί δε µπορούµε να υπολογίσουµε (και γιατί);
 Μοντελοποίηση του Υπολογισµού Στοιχεία Θεωρίας Υπολογισµού (): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ποιές οι θεµελιώδεις δυνατότητες
Μοντελοποίηση του Υπολογισµού Στοιχεία Θεωρίας Υπολογισµού (): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ποιές οι θεµελιώδεις δυνατότητες
Πεπερασμένα Αυτόματα και Κανονικές Παραστάσεις
 Κεφάλαιο 7 Πεπερασμένα Αυτόματα και Κανονικές Παραστάσεις 7.1 Εισαγωγή Στο κεφάλαιο αυτό θα ασχοληθούμε με τυπικές γλώσσες που μπορούν να περιγράψουν υπολογιστικά προβλήματα και επίσης χρησιμεύουν στον
Κεφάλαιο 7 Πεπερασμένα Αυτόματα και Κανονικές Παραστάσεις 7.1 Εισαγωγή Στο κεφάλαιο αυτό θα ασχοληθούμε με τυπικές γλώσσες που μπορούν να περιγράψουν υπολογιστικά προβλήματα και επίσης χρησιμεύουν στον
Γενικές Παρατηρήσεις. Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα (1) Το Λήµµα της Αντλησης. Χρήση του Λήµµατος Αντλησης.
 Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει την ακόλουθη γλώσσα. { a n b n+2 c n 2 n 2 } Λύση: H ζητούμενη μηχανή Turing μπορεί να
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει την ακόλουθη γλώσσα. { a n b n+2 c n 2 n 2 } Λύση: H ζητούμενη μηχανή Turing μπορεί να
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 13: Ελαχιστοποίηση αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Θεωρία Υπολογισμού Ενότητα 13: Ελαχιστοποίηση αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { n 3 } (α) H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την επτάδα Q,
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { n 3 } (α) H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την επτάδα Q,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Παρασκευή, 17 Μαρτίου 2017 Διάρκεια : 9.00 10.30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Παρασκευή, 17 Μαρτίου 2017 Διάρκεια : 9.00 10.30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Επανάληψη Μαθήματος
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών
 Θεμελιώδη Θέματα Επιστήμης Υπολογιστών ΣΗΜΜΥ ΣΕΜΦΕ ΕΜΠ 1η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής 1 Μηχανές πεπερασμένων καταστάσεων (FSM) Τρόπος
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών ΣΗΜΜΥ ΣΕΜΦΕ ΕΜΠ 1η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής 1 Μηχανές πεπερασμένων καταστάσεων (FSM) Τρόπος
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 3η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 3η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών
 Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνο ΣΕΜΦΕ 4η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/focs
Θεμελιώδη Θέματα Επιστήμης Υπολογιστών 5ο εξάμηνο ΣΕΜΦΕ 4η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/focs
Τυχαιότητα (Randomness) I
 I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
num(m(w 1 ;... ; w k )) = f(num(w 1 ),..., num(w k ))
 Υπολογισμοί με Μ.Τ. Εστω M = (K, Σ, δ, s, {y, n}) μια Μ.Τ. Κάθε συνολική κατάσταση τερματισμού της οποίας η κατάσταση τερματισμού είναι το y, θα ονομάζεται συνολική κατάσταση αποδοχής, ενώ αν η κατάσταση
Υπολογισμοί με Μ.Τ. Εστω M = (K, Σ, δ, s, {y, n}) μια Μ.Τ. Κάθε συνολική κατάσταση τερματισμού της οποίας η κατάσταση τερματισμού είναι το y, θα ονομάζεται συνολική κατάσταση αποδοχής, ενώ αν η κατάσταση
Σημειώσεις Λογικής I. Εαρινό Εξάμηνο Καθηγητής: Λ. Κυρούσης
 Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σχεδίαση Γλωσσών Προγραμματισμού Συντακτική Ανάλυση Ι. Εαρινό Εξάμηνο Lec /03/2019 Διδάσκων: Γεώργιος Χρ. Μακρής
 Σχεδίαση Γλωσσών Προγραμματισμού Συντακτική Ανάλυση Ι Εαρινό Εξάμηνο 2018-2019 Lec 09 18 /03/2019 Διδάσκων: Γεώργιος Χρ. Μακρής Φάσεις μεταγλώττισης Αρχικό Πρόγραμμα Λεκτική Ανάλυση λεκτικές μονάδες Πίνακας
Σχεδίαση Γλωσσών Προγραμματισμού Συντακτική Ανάλυση Ι Εαρινό Εξάμηνο 2018-2019 Lec 09 18 /03/2019 Διδάσκων: Γεώργιος Χρ. Μακρής Φάσεις μεταγλώττισης Αρχικό Πρόγραμμα Λεκτική Ανάλυση λεκτικές μονάδες Πίνακας
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Μεταγλωττιστές. Γιώργος Δημητρίου. Μάθημα 2 ο. Πανεπιστήμιο Θεσσαλίας - Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
 Γιώργος Δημητρίου Μάθημα 2 ο Αλφάβητα και Γλώσσες Αλφάβητο: Ένα μη κενό και πεπερασμένο σύνολο συμβόλων Γλώσσα: Ένα οποιοδήποτε υποσύνολο των συμβολοσειρών ενός αλφαβήτου (οι προτάσεις της γλώσσας, πχ.
Γιώργος Δημητρίου Μάθημα 2 ο Αλφάβητα και Γλώσσες Αλφάβητο: Ένα μη κενό και πεπερασμένο σύνολο συμβόλων Γλώσσα: Ένα οποιοδήποτε υποσύνολο των συμβολοσειρών ενός αλφαβήτου (οι προτάσεις της γλώσσας, πχ.
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 7: Ασυμφραστικές Γλώσσες (Γλώσσες Ελεύθερες Συμφραζομένων)
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 7: Ασυμφραστικές Γλώσσες (Γλώσσες Ελεύθερες Συμφραζομένων) Τι θα κάνουμε σήμερα Εισαγωγικά Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Της Ασυμφραστικής
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 7: Ασυμφραστικές Γλώσσες (Γλώσσες Ελεύθερες Συμφραζομένων) Τι θα κάνουμε σήμερα Εισαγωγικά Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Της Ασυμφραστικής
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Σχεδίαση Γλωσσών Προγραμματισμού Λεξική Ανάλυση Ι. Εαρινό Εξάμηνο Lec 05 & & 26 /02/2019 Διδάσκων: Γεώργιος Χρ.
 Σχεδίαση Γλωσσών Προγραμματισμού Λεξική Ανάλυση Ι Εαρινό Εξάμηνο 2018-2019 Lec 05 & 06 25 & 26 /02/2019 Διδάσκων: Γεώργιος Χρ. Μακρής Φάσεις μεταγλώττισης Αρχικό Πρόγραμμα Λεκτική Ανάλυση λεκτικές μονάδες
Σχεδίαση Γλωσσών Προγραμματισμού Λεξική Ανάλυση Ι Εαρινό Εξάμηνο 2018-2019 Lec 05 & 06 25 & 26 /02/2019 Διδάσκων: Γεώργιος Χρ. Μακρής Φάσεις μεταγλώττισης Αρχικό Πρόγραμμα Λεκτική Ανάλυση λεκτικές μονάδες
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να το αποδείξετε,
Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να το αποδείξετε,
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 5: Κανονικές Εκφράσεις
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 5: Κανονικές Εκφράσεις Τι θα κάνουμε σήμερα Κλειστότητα Κανονικών Πράξεων (1.2.3) Εισαγωγή στις Κανονικές Εκφράσεις Τυπικός ορισμός της κανονικής
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 5: Κανονικές Εκφράσεις Τι θα κάνουμε σήμερα Κλειστότητα Κανονικών Πράξεων (1.2.3) Εισαγωγή στις Κανονικές Εκφράσεις Τυπικός ορισμός της κανονικής
Αναδρομικές Συναρτήσεις και Σχέσεις I
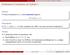 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w#z w, z {a,b}* και η z είναι υπολέξη της w}. Συγκεκριμένα,
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w#z w, z {a,b}* και η z είναι υπολέξη της w}. Συγκεκριμένα,
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 10. Μηχανές Turing 20,23 Μαρτίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μηχανές Turing: Ένα Γενικό Μοντέλο Υπολογισμού Ποια μοντέλα υπολογισμού μπορούν να δεχθούν γλώσσες
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 10. Μηχανές Turing 20,23 Μαρτίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μηχανές Turing: Ένα Γενικό Μοντέλο Υπολογισμού Ποια μοντέλα υπολογισμού μπορούν να δεχθούν γλώσσες
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Πιο κάτω υπάρχει ένα σχεδιάγραμμα που τοποθετεί τις κλάσεις των κανονικών, ασυμφραστικών, διαγνώσιμων και αναγνωρίσιμων γλωσσών μέσα στο σύνολο όλων των γλωσσών. Ακολουθούν
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Πιο κάτω υπάρχει ένα σχεδιάγραμμα που τοποθετεί τις κλάσεις των κανονικών, ασυμφραστικών, διαγνώσιμων και αναγνωρίσιμων γλωσσών μέσα στο σύνολο όλων των γλωσσών. Ακολουθούν
Σύνοψη Προηγούµενου. Κανονικές Γλώσσες (3) Παραδείγµατα µε Κανονικές Εκφράσεις. Σε αυτό το µάθηµα.
 Σύνοψη Προηγούµενου Κανονικές Γλώσσες (3) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς (Ντετερµινιστική) Κλειστότητα Κανονικών Γλωσσών ως προς Ενωση. Κατασκευή: DFA
Σύνοψη Προηγούµενου Κανονικές Γλώσσες (3) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς (Ντετερµινιστική) Κλειστότητα Κανονικών Γλωσσών ως προς Ενωση. Κατασκευή: DFA
Περιεχόμενα 1 Πρωτοβάθμια Λογική Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων ) / 60
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων
 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
Φροντιστήριο 10 Λύσεις
 Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Σχεδιασμός Ασυμφραστικών Γραμματικών
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Σχεδιασμός Ασυμφραστικών Γραμματικών
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Να βρείτε το σφάλμα στην πιο κάτω απόδειξη. Ισχυρισμός: Όλα τα βιβλία που έχουν γραφτεί στη Θεωρία Υπολογισμού έχουν τον ίδιο
ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Να βρείτε το σφάλμα στην πιο κάτω απόδειξη. Ισχυρισμός: Όλα τα βιβλία που έχουν γραφτεί στη Θεωρία Υπολογισμού έχουν τον ίδιο
Γλώσσες Χωρίς Συμφραζόμενα
 Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Γλώσσα χωρίς
Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Γλώσσα χωρίς
Υπολογίσιμες Συναρτήσεις
 Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
Σύνοψη Προηγούµενου. Γλώσσες χωρίς Συµφραζόµενα (2): Αυτόµατα Στοίβας. Παραδείγµατα Σχεδιασµού CFG. Παράδειγµα 1.
 Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα 2): Αυτόµατα Στοίβας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Μη Κανονικές Γλώσσες Το Λήµµα της Αντλησης για τις
Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα 2): Αυτόµατα Στοίβας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Μη Κανονικές Γλώσσες Το Λήµµα της Αντλησης για τις
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Θεωρία Υπολογισμού. Ενότητα 11 : Γραμματικές χωρίς συμφραζόμενα. Αλέξανδρος Τζάλλας
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Θεωρία Υπολογισμού Ενότητα 11 : Γραμματικές χωρίς συμφραζόμενα Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Τμήμα Μηχανικών Πληροφορικής
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Θεωρία Υπολογισμού Ενότητα 11 : Γραμματικές χωρίς συμφραζόμενα Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Τμήμα Μηχανικών Πληροφορικής
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (3)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (3) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Μη Ασυμφραστικές Γλώσσες (2.3) Λήμμα Άντλησης για Ασυμφραστικές Γλώσσες Παραδείγματα
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (3) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Μη Ασυμφραστικές Γλώσσες (2.3) Λήμμα Άντλησης για Ασυμφραστικές Γλώσσες Παραδείγματα
ή κανονικός ( regular ), αν για κάθε x και κάθε κλειστό αντιπαραδείγματα με τα οποία αποδεικνύεται ότι οι αντίστροφες συνεπαγωγές δεν ισχύουν.
 93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων
 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπ
 Θεωρία Υπολογισμού Ενότητα 11: Κλειστότητα, ΠΑ & καν. εκφράσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 11: Κλειστότητα, ΠΑ & καν. εκφράσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
m + s + q r + n + q p + s + n, P Q R P Q P R Q R F G
 Λύσεις Θεμάτων Θεμελίων των Μαθηματικών 1. Εστω A, B, C τυχόντα σύνολα. Να δειχθεί ότι A (B C) (A B) (A C). Απόδειξη. Εστω x τυχαίο στοιχείο του A (B C). Εξ ορισμού, το x ανήκει σε ακριβώς ένα από τα A,
Λύσεις Θεμάτων Θεμελίων των Μαθηματικών 1. Εστω A, B, C τυχόντα σύνολα. Να δειχθεί ότι A (B C) (A B) (A C). Απόδειξη. Εστω x τυχαίο στοιχείο του A (B C). Εξ ορισμού, το x ανήκει σε ακριβώς ένα από τα A,
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
Κεφάλαιο 2: Τυπικές γλώσσες. Νίκος Παπασπύρου, Κωστής Σαγώνας Μεταγλωττιστές Μάρτιος / 216
 Κεφάλαιο 2: Τυπικές γλώσσες Νίκος Παπασπύρου, Κωστής Σαγώνας Μεταγλωττιστές Μάρτιος 2017 13 / 216 Τυπικές γλώσσες (i) Βασικές έννοιες Αλφάβητο Σύμβολο Συμβολοσειρά Μήκος συμβολοσειράς Σύνολο συμβολοσειρών
Κεφάλαιο 2: Τυπικές γλώσσες Νίκος Παπασπύρου, Κωστής Σαγώνας Μεταγλωττιστές Μάρτιος 2017 13 / 216 Τυπικές γλώσσες (i) Βασικές έννοιες Αλφάβητο Σύμβολο Συμβολοσειρά Μήκος συμβολοσειράς Σύνολο συμβολοσειρών
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { xyxy rev x {a, b}, y {a, b} * } (α) Μια γραμματική για τη γλώσσα έχει ως εξής: S as a
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { xyxy rev x {a, b}, y {a, b} * } (α) Μια γραμματική για τη γλώσσα έχει ως εξής: S as a
Φροντιστήριο 9 Λύσεις
 Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
q 0 q 0.2 q 0.1 q 0.05 q 0.05 q 0.25 q 0.15 q 0.1 q 0.2 q 0.25 q 0.25 q 0.25
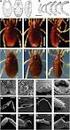 Κεφάλαιο 2 Κανονικές Γλώσσες & Πεπερασμένα Αυτόματα Σύνοψη Τα Πεπερασμένα Αυτόματα (ΠΑ) είναι το απλούστερο και το πιο ευρέως διαδεδομένο μοντέλο υπολογισμού από αυτά που θα εξετάσουμε. Είναι επίσης γνωστά
Κεφάλαιο 2 Κανονικές Γλώσσες & Πεπερασμένα Αυτόματα Σύνοψη Τα Πεπερασμένα Αυτόματα (ΠΑ) είναι το απλούστερο και το πιο ευρέως διαδεδομένο μοντέλο υπολογισμού από αυτά που θα εξετάσουμε. Είναι επίσης γνωστά
Απαρίθμηση ζευγών φυσικών αριθμών I. C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση
 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
Γλώσσες Χωρίς Συμφραζόμενα
 Γλώσσα χωρίς Συμφραζόμενα Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Γλώσσα χωρίς Συμφραζόμενα Γλώσσες Χωρίς Συμφραζόμενα Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
Ασκήσεις από παλιές εξετάσεις
 Άσκηση 2 - Τελική εξέταση 2012 Ασκήσεις από παλιές εξετάσεις (α) [10 μονάδες] Να μετατρέψετε το πιο κάτω NFA σε ένα ισοδύναμο DFA χρησιμοποιώντας την κατασκευή που μελετήσαμε στο μάθημα. a a q 0 a, ε q
Άσκηση 2 - Τελική εξέταση 2012 Ασκήσεις από παλιές εξετάσεις (α) [10 μονάδες] Να μετατρέψετε το πιο κάτω NFA σε ένα ισοδύναμο DFA χρησιμοποιώντας την κατασκευή που μελετήσαμε στο μάθημα. a a q 0 a, ε q
Θεωρία Υπολογισμού και Πολυπλοκότητα Διαγνωσιμότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Διαγνωσιμότητα Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Διαγνώσιμες Γλώσσες (4.1) Επιλύσιμα Προβλήματα σχετικά με Κανονικές Γλώσσες Επιλύσιμα Προβλήματα
Θεωρία Υπολογισμού και Πολυπλοκότητα Διαγνωσιμότητα Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Διαγνώσιμες Γλώσσες (4.1) Επιλύσιμα Προβλήματα σχετικά με Κανονικές Γλώσσες Επιλύσιμα Προβλήματα
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { ww rev w {a, b} * και w αποτελεί καρκινική λέξη } (α) H ζητούμενη μηχανή
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { ww rev w {a, b} * και w αποτελεί καρκινική λέξη } (α) H ζητούμενη μηχανή
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 4. Μη Ντετερμινιστικά Πεπερασμένα Αυτόματα 9,19 Φεβρουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μοντέλα Υπολογισμού Μη Ντετερμινιστικό Πεπερασμένα Αυτόματα: Διαφορά
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 4. Μη Ντετερμινιστικά Πεπερασμένα Αυτόματα 9,19 Φεβρουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μοντέλα Υπολογισμού Μη Ντετερμινιστικό Πεπερασμένα Αυτόματα: Διαφορά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a m b n c p m,n,p 0 και είτε m + n = p είτε m = n + p } (β) { xx rev yy rev x, y {a,b}
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a m b n c p m,n,p 0 και είτε m + n = p είτε m = n + p } (β) { xx rev yy rev x, y {a,b}
