Τεχνολογία Α! Τάξης. Καθηγητής : ΗΡΑΚΛΗΣ ΝΤΟΥΣΗΣ
|
|
|
- Νάρκισσος Οικονόμου
- 10 χρόνια πριν
- Προβολές:
Transcript
1 Τεχνολογία Α! Τάξης Καθηγητής : ΗΡΑΚΛΗΣ ΝΤΟΥΣΗΣ
2 Μελέτη Πριν από κάθε κατασκευή προηγούνται : 1. Μελέτη 2. Σχεδίαση *Τι σχήμα να τις δώσω; *Τι μέγεθος θα έχει (διαστάσεις); Σχεδίαση * Ποιοι είναι οι κανόνες σχεδίασης; *Τι μας δείχνει το χαρτί του σχεδίου; Κατασκευή *Τι υλικό να χρησιμοποιήσω; *Τι εργαλεία θα χρειαστώ; *Ποια είναι η σειρά των εργασιών;
3 Τι προσπαθούμε να κάνουμε με το σχέδιο ; Στην καθημερινή του ζωή ο άνθρωπος, χρησιμοποιεί τον προφορικό και τον γραπτό λόγο σαν μέσο επικοινωνίας με τους ανθρώπους. Οι τεχνικοί έχουν τον δικό τους τρόπο επικοινωνίας μεταξύ τους, το σχέδιο. Από τους τεχνικούς άλλοι μελετούν τα τεχνικά έργα και άλλοι τα κατασκευάζουν. Για να μπορέσουν λοιπόν να συνεννοηθούν ο μελετητής ενός έργου με τον κατασκευαστή χρησιμοποιούν το σχέδιο. Με το σχέδιο λοιπόν προσπαθούμε να παρουσιάσουμε με μια γραφική παράσταση - που μας δείχνει με σαφήνεια και με λεπτομέρειες- την μορφή που θέλουμε να δώσουμε σε κάτι που πρόκειται να κατασκευάσουμε.
4 Μελέτησα το θέμα που διάλεξα και παρατηρώ ότι έχει μεγάλη ομοιότητα με το ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕΔΟ
5 Από τις τάξεις του Δημοτικού σχολείου θυμάμαι, ότι το ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕΔΟ είναι ένα στερεό σχήμα, που αποτελείται από 6 διαφορετικές επιφάνειες (έδρες) που όπως φαίνεται πιο κάτω είναι ανά 2 όμοιες. 4 εκ. 6 εκ. 3 εκ. 1 η έδρα 6εκ. Χ 4εκ. (μπροστινή έδρα) 2 η έδρα / 6εκ.Χ 3εκ (πάνω έδρα) 3εκ. Χ 4 εκ. Αριστερή { 3 η } έδρα 4 η έδρα 6εκ. Χ 4εκ. (πίσω έδρα) 5 η έδρα / 6εκ.Χ 3εκ (κάτω έδρα) 3εκ. Χ 4 εκ. Δεξιά { 6 η } έδρα
6 Παρατήρησα ότι, αν αυτές τις έδρες τις δημιουργήσω μ ένα οποιοδήποτε υλικό και τις συνδέσω μεταξύ τους, σύμφωνα με το παρακάτω σχήμα τότε θα έχω κατασκευάσει ένα ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕΔΟ. 4 η έδρα 6εκ. Χ 4εκ. (πίσω έδρα) 2 η έδρα / 6εκ.Χ 3εκ (πάνω έδρα) 3εκ. Χ 4 εκ. Δεξιά { 6 η } έδρα 5 η έδρα / 6εκ.Χ 3εκ (κάτω έδρα) 3εκ. Χ 4 εκ. Αριστερή { 3 η } έδρα 1 η έδρα 6εκ. Χ 4εκ. (μπροστινή έδρα)
7 Πρακτικά όμως σε τεχνικές κατασκευές οι ονομασίες των 6 εδρών αλλάζουν και χαρακτηρίζονται από την θέση που βλέπω το αντικείμενο π.χ. αν θεωρήσω ότι στέκομαι στην μπροστινή έδρα αυτή θεωρείται ως πρόοψη, η πάνω πλευρά ως κάτοψη και αντίστοιχα οι υπόλοιπες 4 αριστερή πλάγια όψη,άνοψη, πίσω όψη και δεξιά πλάγια όψη. Κάτοψη Δεξιά Πλάγια όψη Πίσω όψη Πρόοψη Αριστερή Πλάγια όψη Άνοψη
8 Για να το καταλάβουμε καλύτερα ας δούμε ένα σχήμα λίγο δυσκολότερο
9 Για να κατανοήσουμε ακόμη καλύτερα τις 6 διαφορετικές θέσεις ας δούμε ένα παράδειγμα μ ένα σταθερό τηλέφωνο.
10 Εδώ φαίνεται το σχέδιο κάθε 1 όψης του σταθερού τηλεφώνου
11 Όπως παρατηρούμε οι όψεις ανά ζεύγη έχουν τις ίδιες διαστάσεις και έτσι έχει αποφασιστεί ότι αρκεί να σχεδιάζουμε τις 3 αντί των 6.Συγκεκριμμένα τις Πρόοψη κάτοψη και αριστερή πλάγια όψη, στις θέσεις που φαίνονται πιο κάτω. Πρόοψη Αριστερή πλάγια όψη Κάτοψη
12 Παράδειγμα τοποθέτησης όψεων αυτοκινήτου
13 Παράδειγμα τοποθέτησης όψεων αεροπλάνου
14 4,5 εκ. Αν έχω επιλέξει ένα θέμα με κυλινδρική μορφή (φάρος-ανεμόμυλος-πύραυλος) αλλάζει κάτι με την σχεδίαση των όψεων; Η πρόοψη με την αριστερή πλάγια όψη είναι κοινές. Πρέπει όμως να σχεδιάσουμε απαραίτητα στοιχεία όπως ο μύλος-η πόρτα εισόδου παράθυρα κ.ά. 6 εκ. 4,5 εκ. 6 εκ. 4,5 εκ.
15 Υπάρχουν και κάποιες κατασκευές που παραλείπεται ή κάτοψη γιατί είναι σημαντικότερες οι άλλες 2 όψεις. Σχεδίαση όψεων ανεμογεννήτριας
16 Το συμπέρασμα που έβγαλα είναι ότι αν μάθω να σχεδιάζω ικανοποιητικά τις όψεις-τις μεταφέρω σε κάποιο υλικό - και τις συνδέσω κατάλληλα μεταξύ τους μάλλον θα καταφέρω να φτιάξω αυτά που έχω σκεφτεί. Ας ξεκινήσω Με κατάλληλα εργαλεία δηλ. ένα μολύβι ΗΒ και αρκετά φύλλα χαρτιού τετραγωνισμένο καλύτερα θα σχεδιάζω αρχικά διάφορα απλά αντικείμενα π.χ. τις όψεις μιας τηλεόρασης ενός κινητού και σταδιακά θα προχωρήσω σε πιο σύνθετες σχεδιάσεις. Η σχεδίαση αρχικά θα γίνεται μα ελεύθερο χέρι και σταδιακά θα χρησιμοποιώ και τα κατάλληλα γεωμετρικά όργανα. Με λίγη εξάσκηση θα τα καταφέρω σίγουρα.
17 Παράδειγμα πρόχειρης σχεδίασης ((ΣΚΑΡΙΦΗΜΑ) των όψεων μίας τηλεόρασης σε χαρτί μιλιμετρέ (ή σε χαρτί με τετραγωνάκια καρέ ).
18 Πότε και πως θα χρησιμοποιήσω κλίμακα σχεδίασης ; Ο σχεδιασμός με κλίμακα μας επιτρέπει να αναπαραστήσουμε ένα αντικείμενο μεγάλο σε χαρτί μικρών διαστάσεων. Στα σχέδια πάντα αναγράφονται οι διαστάσεις που έχει το αντικείμενο στην πραγματικότητα. Στην πράξη, όταν λέμε σχεδιασμό υπό κλίμακα, εννοούμε τη σμίκρυνση ενός αντικειμένου ή τη διαίρεση όλων των διαστάσεών του με ένα συγκεκριμένο αριθμό. Αν θέλουμε π.χ. να σχεδιάσουμε μία καρέκλα, αρκεί να τη μικρύνουμε δύο φορές ή πέντε, δηλαδή να τη σχεδιάσουμε στην 1:2 ή στην 1:5 κλίμακα( η κλίμακα 1:1 είναι όταν ένα αντικείμενο σχεδιάζεται στις πραγματικές του διαστάσεις). Το 1:Χ κλίμακα σημαίνει ότι θα πρέπει να ξέρουμε όλες τις διαστάσεις του αντικειμένου και αυτές να τις διαιρέσουμε με το Χ (ο παρανομαστής στο κλάσμα της κλίμακας ). Όταν λοιπόν σχεδιάζουμε ένα αντικείμενο σε μία συγκεκριμένη κλίμακα, θα πρέπει να διαιρέσουμε όλες τις διαστάσεις του αντικειμένου με τον παρονομαστή της κλίμακας που διαλέξαμε σαν την πιο κατάλληλη για το χαρτί που εργαζόμαστε.
19 Παράδειγμα μετατροπής διαστάσεων αντικειμένου με κλίμακα 1:2 Οι διαστάσεις στο χαρτί σχεδίασης γράφουν τα πραγματικά μεγέθη, όμως οι διαστάσεις στο χαρτί έχουν τα μεγέθη που υπολογίζονται με την κλίμακα δηλ. στο παραπάνω παράδειγμα έχουν διαιρεθεί με το 2.
20 Ελπίζω οι λίγες αυτές πληροφορίες να σας βοηθήσουν να ανέβετε κάποια σκαλοπάτια στη γνώση της σχεδίασης. Με την δική σας προσπάθεια, είναι σίγουρο ότι θα ανέβετε όλη την σκάλα. ΚΑΛΗ ΕΠΙΤΥΧΙΑ!!!
1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα)
 20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου
 Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου Περιεχόμενα 1. Στόχος του εργαστηρίου... 3 2. ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ... 3 2.1 Εξοπλισμός σχεδίασης... 3 2.1.1 Μολύβια... 3 2.1.2. Επιφάνεια
Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου Περιεχόμενα 1. Στόχος του εργαστηρίου... 3 2. ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ... 3 2.1 Εξοπλισμός σχεδίασης... 3 2.1.1 Μολύβια... 3 2.1.2. Επιφάνεια
Σ ΣΤ Σ Η Τ Μ Η ΑΤ Α Α Τ ΠΑΡΑ Ρ ΓΩΓ Ω ΗΣ Η Σ ΜΕ Η/Υ (CAD-CAM-CAE) Ι
 ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΤΕΧΝΙΚΟ / ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Σύμβολα R: Radius-ακτίνα, Ø (Φι): Διάμετρος, κύκλου ή τόξου ΟΨΕΙΣ ΟΡΘΟΓΩΝΙΕΣ ΠΡΟΒΟΛΕΣ Βασικές όψεις: Ορθογώνιες προβολές στις έξι
ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΤΕΧΝΙΚΟ / ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Σύμβολα R: Radius-ακτίνα, Ø (Φι): Διάμετρος, κύκλου ή τόξου ΟΨΕΙΣ ΟΡΘΟΓΩΝΙΕΣ ΠΡΟΒΟΛΕΣ Βασικές όψεις: Ορθογώνιες προβολές στις έξι
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων
 1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
Αρχιτεκτονική σχεδίαση με ηλεκτρονικό υπολογιστή
 Γ Αρχιτεκτονική σχεδίαση με ηλεκτρονικό υπολογιστή Η χρήση των ηλεκτρονικών υπολογιστών στο τεχνικό σχέδιο, και ιδιαίτερα στο αρχιτεκτονικό, αποτελεί πλέον μία πραγματικότητα σε διαρκή εξέλιξη, που επηρεάζει
Γ Αρχιτεκτονική σχεδίαση με ηλεκτρονικό υπολογιστή Η χρήση των ηλεκτρονικών υπολογιστών στο τεχνικό σχέδιο, και ιδιαίτερα στο αρχιτεκτονικό, αποτελεί πλέον μία πραγματικότητα σε διαρκή εξέλιξη, που επηρεάζει
Τεχνικό Σχέδιο. Ενότητα 2: Μηχανολογικό Σχέδιο - Σχεδίαση όψεων
 Τεχνικό Σχέδιο Ενότητα 2: Μηχανολογικό Σχέδιο - Σχεδίαση όψεων Διάλεξη 2η Παναγής Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΤΕΧΝΙΚΟ ΣΧΕΔΙΟ ΣΧΕΔΙΑΣΗ ΤΡΙΣΔΙΑΣΤΑΤΩΝ
Τεχνικό Σχέδιο Ενότητα 2: Μηχανολογικό Σχέδιο - Σχεδίαση όψεων Διάλεξη 2η Παναγής Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΤΕΧΝΙΚΟ ΣΧΕΔΙΟ ΣΧΕΔΙΑΣΗ ΤΡΙΣΔΙΑΣΤΑΤΩΝ
1.2 Στοιχεία Μηχανολογικού Σχεδίου
 1.2 Στοιχεία Μηχανολογικού Σχεδίου Τα µηχανολογικά σχέδια, ανάλογα µε τον τρόπο σχεδίασης διακρίνονται στις παρακάτω κατηγορίες: Σκαριφήµατα Κανονικά µηχανολογικά σχέδια Προοπτικά σχέδια Σχηµατικές παραστάσεις.
1.2 Στοιχεία Μηχανολογικού Σχεδίου Τα µηχανολογικά σχέδια, ανάλογα µε τον τρόπο σχεδίασης διακρίνονται στις παρακάτω κατηγορίες: Σκαριφήµατα Κανονικά µηχανολογικά σχέδια Προοπτικά σχέδια Σχηµατικές παραστάσεις.
ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι
 ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΤΕΧΝΙΚΟ / ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Σύμβολα R: ακτίνα κύκλου ή τόξου Ø (Φ): Διάμετρος κύκλου ή τόξου 1 ΟΨΕΙΣ ΟΡΘΟΓΩΝΙΕΣ ΠΡΟΒΟΛΕΣ Βασικές όψεις: Ορθογώνιες προβολές
ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΤΕΧΝΙΚΟ / ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Σύμβολα R: ακτίνα κύκλου ή τόξου Ø (Φ): Διάμετρος κύκλου ή τόξου 1 ΟΨΕΙΣ ΟΡΘΟΓΩΝΙΕΣ ΠΡΟΒΟΛΕΣ Βασικές όψεις: Ορθογώνιες προβολές
Προγράμματα παρέμβασης στα Μαθηματικά, Μαρία Θ. Παπαδοπούλου, PhD, Σχολική Σύμβουλος 6ης Περιφέρειας Π.Ε. ν. Λάρισας
 ΠΡΟΓΡΑΜΜΑ ΠΑΡΕΜΒΑΣΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ-Α Φ.Α. ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΣΧΟΛΕΙΟ: ΗΜΕΡΟΜΗΝΙΑ ΓΕΝΝΗΣΗΣ:... ΤΑΞΗ: ΗΜΕΡΟΜΗΝΙΑ ΑΞΙΟΛΟΓΗΣΗΣ: ΗΜΕΡΟΜΗΝΙΑ ΕΝΑΡΞΗΣ ΠΑΡΕΜΒΑΣΗΣ: ΔΙΑΡΚΕΙΑ: ΑΝΑΛΥΣΗ ΕΡΓΟΥ Κατανοεί βασικές χωρικές
ΠΡΟΓΡΑΜΜΑ ΠΑΡΕΜΒΑΣΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ-Α Φ.Α. ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΣΧΟΛΕΙΟ: ΗΜΕΡΟΜΗΝΙΑ ΓΕΝΝΗΣΗΣ:... ΤΑΞΗ: ΗΜΕΡΟΜΗΝΙΑ ΑΞΙΟΛΟΓΗΣΗΣ: ΗΜΕΡΟΜΗΝΙΑ ΕΝΑΡΞΗΣ ΠΑΡΕΜΒΑΣΗΣ: ΔΙΑΡΚΕΙΑ: ΑΝΑΛΥΣΗ ΕΡΓΟΥ Κατανοεί βασικές χωρικές
1 ο Εξάμηνο. αποτύπωση. Εισαγωγικές έννοιες στην και τεκμηρίωση αντικειμένων
 1 ο Εξάμηνο 2015-2016 Εισαγωγικές έννοιες στην αποτύπωση και τεκμηρίωση αντικειμένων Μάθημα 2ο Τζώρτζια Πλατυπόδη Αρχιτέκτων Μηχανικός Ε.Μ.Π. MSc Διαχείριση Μνημείων Ε.Κ.Π.Α. Κλίμακες σχεδίασης Οι Κλίμακες
1 ο Εξάμηνο 2015-2016 Εισαγωγικές έννοιες στην αποτύπωση και τεκμηρίωση αντικειμένων Μάθημα 2ο Τζώρτζια Πλατυπόδη Αρχιτέκτων Μηχανικός Ε.Μ.Π. MSc Διαχείριση Μνημείων Ε.Κ.Π.Α. Κλίμακες σχεδίασης Οι Κλίμακες
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Κεφάλαιο 5 Καταρχήν, όταν ορίζουμε την παράγωγο μιας συνάρτησης δεν την ορίζουμε έτσι γενικά, αλλά σε κάποιο συγκεκριμένο
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Κεφάλαιο 5 Καταρχήν, όταν ορίζουμε την παράγωγο μιας συνάρτησης δεν την ορίζουμε έτσι γενικά, αλλά σε κάποιο συγκεκριμένο
Μηχανολογικό Σχέδιο Ι
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 2: Όψεις Όνομα Καθηγητή: Παρασκευοπούλου Ροδούλα Α.Π.Θ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 2: Όψεις Όνομα Καθηγητή: Παρασκευοπούλου Ροδούλα Α.Π.Θ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΝΟΤΗΤΑ 5 ΚΕΦΑΛΑΙΟ 25. Δεκαδικά Κλάσματα - Δεκαδικοί Αριθμοί ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ
 ΕΝΟΤΗΤΑ 5 ΚΕΦΑΛΑΙΟ 25 Δεκαδικά Κλάσματα - Δεκαδικοί Αριθμοί ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Πως μπορούμε να χωρίσουμε Η ακέραια μονάδα μπορεί να χωριστεί σε 10, 100, 1.000 κλπ. ίσα μέρη. 1 = 10
ΕΝΟΤΗΤΑ 5 ΚΕΦΑΛΑΙΟ 25 Δεκαδικά Κλάσματα - Δεκαδικοί Αριθμοί ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Πως μπορούμε να χωρίσουμε Η ακέραια μονάδα μπορεί να χωριστεί σε 10, 100, 1.000 κλπ. ίσα μέρη. 1 = 10
Η Δραστηριότητα 1 του Φύλλου Εργασίας 1 έχει ως στόχο την εξοικείωση με το περιβάλλον του scratch και πιο συγκεκριμένα με τις μορφές και τα σκηνικά.
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 Δραστηριότητα 1 Η Δραστηριότητα 1 του Φύλλου Εργασίας 1 έχει ως στόχο την εξοικείωση με το περιβάλλον του scratch και πιο συγκεκριμένα με τις μορφές και τα σκηνικά. Αρχικά θα μάθουμε να
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 Δραστηριότητα 1 Η Δραστηριότητα 1 του Φύλλου Εργασίας 1 έχει ως στόχο την εξοικείωση με το περιβάλλον του scratch και πιο συγκεκριμένα με τις μορφές και τα σκηνικά. Αρχικά θα μάθουμε να
13ο Μάθημα ΠΙΕΣΗ ΠΟΥ ΑΣΚΟΥΝ ΤΑ ΣΤΕΡΕΑ
 13ο Μάθημα ΠΙΕΣΗ ΠΟΥ ΑΣΚΟΥΝ ΤΑ ΣΤΕΡΕΑ Η δύναμη μπορεί να είναι μεγάλη, αλλά η πίεση μικρή Με το μάθημα αυτό, αρχίζουμε τη μελέτη μιας σημαντικής έννοιας, της πίεσης, που υπεισέρχεται σε πάρα πολλές περιπτώσεις
13ο Μάθημα ΠΙΕΣΗ ΠΟΥ ΑΣΚΟΥΝ ΤΑ ΣΤΕΡΕΑ Η δύναμη μπορεί να είναι μεγάλη, αλλά η πίεση μικρή Με το μάθημα αυτό, αρχίζουμε τη μελέτη μιας σημαντικής έννοιας, της πίεσης, που υπεισέρχεται σε πάρα πολλές περιπτώσεις
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΗ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ
ΕΝΟΤΗΤΑ 7. Σημείωση: Για τη διδασκαλία της ενότητας είναι πολύ σημαντική η χρήση των εποπτικών μέσων (στερεών και αναπτυγμάτων των στερεών).
 ΣΤΕΡΕΟΜΕΤΡΙΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΓΕΩΜΕΤΡΙΑ Διερεύνηση σχημάτων και χώρου Γ2.6 Ονομάζουν, περιγράφουν και ταξινομούν τρισδιάστατα σχήματα (κύβο, ορθογώνιο παραλληλεπίπεδο, πυραμίδα, σφαίρα, κύλινδρο, κώνο),
ΣΤΕΡΕΟΜΕΤΡΙΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΓΕΩΜΕΤΡΙΑ Διερεύνηση σχημάτων και χώρου Γ2.6 Ονομάζουν, περιγράφουν και ταξινομούν τρισδιάστατα σχήματα (κύβο, ορθογώνιο παραλληλεπίπεδο, πυραμίδα, σφαίρα, κύλινδρο, κώνο),
Σχεδίαση τομών Συνήθη σφάλματα και Παραδείγματα. Πότε;
 Σχεδίαση τομών... Πότε;...Συνήθη σφάλματα και Παραδείγματα Οταν 5 η Διάλεξη οι οψεις Τομές δημιουργουν συγχυση και δεν εμφανιζουν αμεσα το εσωτερικο των αντικειμένων Ι.Ν. ΑΓ. ΔΗΜΗΤΡΙΟΥ, ΗΠΕΙΡΟΣ Διαδικασία
Σχεδίαση τομών... Πότε;...Συνήθη σφάλματα και Παραδείγματα Οταν 5 η Διάλεξη οι οψεις Τομές δημιουργουν συγχυση και δεν εμφανιζουν αμεσα το εσωτερικο των αντικειμένων Ι.Ν. ΑΓ. ΔΗΜΗΤΡΙΟΥ, ΗΠΕΙΡΟΣ Διαδικασία
ΣΧΕΔΙΑΣΜΟΣ ΠΡΟΙΟΝΤΩΝ ΜΕ Η/Υ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι
 ΣΧΕΔΙΑΣΜΟΣ ΠΡΟΙΟΝΤΩΝ ΜΕ Η/Υ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΣΧΕΤΙΚΑ ΜΕ ΤΟ ΜΑΘΗΜΑ Βαθμολόγηση μαθήματος Βαθμός Γραπτής Εξέτασης: 70% του τελικού βαθμού Βαθμός Εργαστηρίου: 30% του τελικού βαθμού
ΣΧΕΔΙΑΣΜΟΣ ΠΡΟΙΟΝΤΩΝ ΜΕ Η/Υ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΜΕ Η/Υ (CAD-CAM-CAE) Ι ΣΧΕΤΙΚΑ ΜΕ ΤΟ ΜΑΘΗΜΑ Βαθμολόγηση μαθήματος Βαθμός Γραπτής Εξέτασης: 70% του τελικού βαθμού Βαθμός Εργαστηρίου: 30% του τελικού βαθμού
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2008 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : ΑΡΧΙΤΕΚΤΟΝΙΚΟ ΚΑΙ ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2008 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : ΑΡΧΙΤΕΚΤΟΝΙΚΟ ΚΑΙ ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ
Ο μαθητής (σχεδιαστής) πρέπει να αναπτύξει την ικανότητα επικοινωνίας, με τη βοήθεια σχεδίων ή σκίτσων.
 ΓΡΑΦΙΚΗ ΕΠΙΚΟΙΝΩΝΙΑ Η Γραφική Επικοινωνία αναφέρεται στις γραφικές δεξιότητες και τεχνικές που χρησιμοποιούνται στην Τεχνολογία. Περιλαμβάνει σχέδιο, χρήση χρωμάτων, καταχώρηση πληροφοριών και παρουσίαση
ΓΡΑΦΙΚΗ ΕΠΙΚΟΙΝΩΝΙΑ Η Γραφική Επικοινωνία αναφέρεται στις γραφικές δεξιότητες και τεχνικές που χρησιμοποιούνται στην Τεχνολογία. Περιλαμβάνει σχέδιο, χρήση χρωμάτων, καταχώρηση πληροφοριών και παρουσίαση
3.2 ιαγραµµικά σχέδια αµαξωµάτων
 3.2 ιαγραµµικά σχέδια αµαξωµάτων Τα διαγραµµικά σχέδια των αµαξωµάτων χρησιµοποιούνται για την απεικόνιση των γεωµετρικών στοιχείων των διαφόρων µερών τους, αλλά και την κατάδειξη των σηµείων όπου γίνονται
3.2 ιαγραµµικά σχέδια αµαξωµάτων Τα διαγραµµικά σχέδια των αµαξωµάτων χρησιµοποιούνται για την απεικόνιση των γεωµετρικών στοιχείων των διαφόρων µερών τους, αλλά και την κατάδειξη των σηµείων όπου γίνονται
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ. ΕΝΟΤΗΤΑ 1: Κεφάλαιο 6. 1η Άσκηση. Εκπαιδευτικός Οργανισμός Ν. Ξυδάς 1. Πως θα σκεφτώ για να λύσω την άσκηση;
 ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΕΝΟΤΗΤΑ 1: Κεφάλαιο 6 1η Άσκηση Πως θα σκεφτώ για να λύσω την άσκηση; Τι μας ζητάει να βρούμε αυτό το παράδειγμα; Θα πρέπει να βρούμε ποιο είναι το χρωματισμένο μέρος σε σχέση με όλο
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΕΝΟΤΗΤΑ 1: Κεφάλαιο 6 1η Άσκηση Πως θα σκεφτώ για να λύσω την άσκηση; Τι μας ζητάει να βρούμε αυτό το παράδειγμα; Θα πρέπει να βρούμε ποιο είναι το χρωματισμένο μέρος σε σχέση με όλο
ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών. Αναπληρωτής Καθηγητής ΤΕΧΝΙΚΟ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟ ΣΧΕΔΙΟ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΓΕΩΜΕΤΡΙΑ. Θέματα: - Έννοιες χώρου και καρτεσιανές συντεταγμένες - ισδιάστατη γεωμετρία - Γωνίες - Στερεομετρία - Συμμετρία/ μετασχηματισμοί
 ΓΕΩΜΕΤΡΙΑ Θέματα: - Έννοιες χώρου και καρτεσιανές συντεταγμένες - ισδιάστατη γεωμετρία - Γωνίες - Στερεομετρία - Συμμετρία/ μετασχηματισμοί 1 Έννοιες χώρου και καρτεσιανές συντεταγμένες 1. Ο χάρτης δείχνει
ΓΕΩΜΕΤΡΙΑ Θέματα: - Έννοιες χώρου και καρτεσιανές συντεταγμένες - ισδιάστατη γεωμετρία - Γωνίες - Στερεομετρία - Συμμετρία/ μετασχηματισμοί 1 Έννοιες χώρου και καρτεσιανές συντεταγμένες 1. Ο χάρτης δείχνει
1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων?
 ΣΧΕΔΙΑΣΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ - Εξεταστέα ύλη Β εξαμήνου 2011 1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων? Τρεις μέθοδοι προβολών
ΣΧΕΔΙΑΣΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ - Εξεταστέα ύλη Β εξαμήνου 2011 1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων? Τρεις μέθοδοι προβολών
ΤΕΛΟΣ 1ης ΑΠΟ 6 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΣΑΒΒΑΤΟ 28 ΙΟΥΝΙΟΥ 2014 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΕΞΙ (6) ΘΕΜΑ: «ΜΙΚΡΗ ΕΞΟΧΙΚΗ ΚΑΤΟΙΚΙΑ» ΠΕΡΙΓΡΑΦΗ: Το κτήριο
ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΣΑΒΒΑΤΟ 28 ΙΟΥΝΙΟΥ 2014 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΕΞΙ (6) ΘΕΜΑ: «ΜΙΚΡΗ ΕΞΟΧΙΚΗ ΚΑΤΟΙΚΙΑ» ΠΕΡΙΓΡΑΦΗ: Το κτήριο
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 20 ΔΕΚΕΜΒΡΙΟΣ 20 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ Οι ασκήσεις να λυθούν σε χαρτί Α4 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό
ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 20 ΔΕΚΕΜΒΡΙΟΣ 20 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ Οι ασκήσεις να λυθούν σε χαρτί Α4 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό
ΜΑΘΗΜΑΤΙΚΑ A ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 2016 14 ΙΑΝΟΥΑΡΙΟΥ 2017 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ 1 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό στάδιο, για τρέξιμο. Λόγω
ΕΠΑΝΑΛΗΠΤΙΚΟ ΦΥΛΛΑΔΙΟ ΧΡΙΣΤΟΥΓΕΝΝΩΝ 2016 14 ΙΑΝΟΥΑΡΙΟΥ 2017 Δ.Ε. ΚΟΝΤΟΚΩΣΤΑΣ 1 η ΑΣΚΗΣΗ Τρεις φίλοι, ο Γιώργος, ο Κώστας και ο Δημήτρης συνεννοήθηκαν να πηγαίνουν στο Δημοτικό στάδιο, για τρέξιμο. Λόγω
ΤΜΗΜΑ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑ: ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ ΚΑΙ ΕΙΣΑΓΩΓΗ ΣΤΟ MCAD
 ΤΜΗΜΑ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑ: ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ ΚΑΙ ΕΙΣΑΓΩΓΗ ΣΤΟ MCAD ΜΕΘΟΔΟΙ ΠΡΟΒΟΛΗΣ Προοπτική Προβολή Στο προοπτικό σχέδιο η εικόνα του αντικειμένου παρουσιάζεται, όπως προβάλλεται στο χαρτί σχεδιάσεως
ΤΜΗΜΑ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑ: ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ ΚΑΙ ΕΙΣΑΓΩΓΗ ΣΤΟ MCAD ΜΕΘΟΔΟΙ ΠΡΟΒΟΛΗΣ Προοπτική Προβολή Στο προοπτικό σχέδιο η εικόνα του αντικειμένου παρουσιάζεται, όπως προβάλλεται στο χαρτί σχεδιάσεως
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ: Σύνθεση με τέσσερα (4) αντικείμενα
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα (4)
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα (4)
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2)
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ:
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ:
2. τα ρωμαϊκά, που το λούκι έχει μετασχηματιστεί σε επίπεδο και έχει ενσωματωθεί στο καπάκι
 Οι αριθμοί αντιμετωπίζονται με τον ίδιο τρόπο, αλλά είναι σημαντικό να μελετήσουμε τον τρόπο που σημειώνονται οι αριθμοί που αποδίδουν στα σχέδια τις διαστάσεις του αντικειμένου. Οι γραμμές διαστάσεων
Οι αριθμοί αντιμετωπίζονται με τον ίδιο τρόπο, αλλά είναι σημαντικό να μελετήσουμε τον τρόπο που σημειώνονται οι αριθμοί που αποδίδουν στα σχέδια τις διαστάσεις του αντικειμένου. Οι γραμμές διαστάσεων
ΔΙΑΣΤΑΣΕΙΣ ΣΧΕΔΙΟΥ. Αναγκαιότητα τοποθέτησης διαστάσεων. 29/10/2015 Πολύζος Θωμάς
 Αναγκαιότητα τοποθέτησης διαστάσεων 29/10/2015 Πολύζος Θωμάς 1 Αναγκαιότητα τοποθέτησης διαστάσεων Σφάλμα μέτρησης που οφείλεται: Σε υποκειμενικό λάθος εκείνου που κάνει την μέτρηση. Σε σφάλμα του οργάνου
Αναγκαιότητα τοποθέτησης διαστάσεων 29/10/2015 Πολύζος Θωμάς 1 Αναγκαιότητα τοποθέτησης διαστάσεων Σφάλμα μέτρησης που οφείλεται: Σε υποκειμενικό λάθος εκείνου που κάνει την μέτρηση. Σε σφάλμα του οργάνου
Τεχνικό Σχέδιο. Ενότητα 4: Μηχανολογικό Σχέδιο - Διαστάσεις
 Τεχνικό Σχέδιο Ενότητα 4: Μηχανολογικό Σχέδιο - Διαστάσεις Διάλεξη 4η Παναγής Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΤΕΧΝΙΚΟ ΣΧΕΔΙΟ ΔΙΑΣΤΑΣΕΙΣ Τμήμα Ηλεκτρολόγων
Τεχνικό Σχέδιο Ενότητα 4: Μηχανολογικό Σχέδιο - Διαστάσεις Διάλεξη 4η Παναγής Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών ΤΕΧΝΙΚΟ ΣΧΕΔΙΟ ΔΙΑΣΤΑΣΕΙΣ Τμήμα Ηλεκτρολόγων
ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου
 Η ΜΕΤΑΤΡΟΠΉ ΜΙΑΣ ΑΣΚΗΣΗΣ ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΊΟΥ ΣΕ ΕΡΓΑΛΕΙΟ ΔΙΕΡΕΥΝΗΤΙΚΉΣ Στο σχολικό βιβλίο της Β τάξης γυμνασίου υπάρχει η διπλανή άσκηση. Στόχος της άσκησης είναι να εφαρμόζουν
Η ΜΕΤΑΤΡΟΠΉ ΜΙΑΣ ΑΣΚΗΣΗΣ ΜΑΘΗΣΗΣ Αλεξάνδρα Κούκιου ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΊΟΥ ΣΕ ΕΡΓΑΛΕΙΟ ΔΙΕΡΕΥΝΗΤΙΚΉΣ Στο σχολικό βιβλίο της Β τάξης γυμνασίου υπάρχει η διπλανή άσκηση. Στόχος της άσκησης είναι να εφαρμόζουν
Πώς να λύσετε τον κύβο του Rubik
 Πώς να λύσετε τον κύβο του Rubik από τον Έλτον 1 Σκόντι, Β Λυκείου 1 ο ΓΕ.Λ. Ελευσίνας σχολικό έτος 2008-9 ΒΗΜΑ 1 Ο : Φτιάχνουμε έναν σταυρό σε όποιο χρώμα θέλουμε. Δηλαδή: Αν π.χ. θέλουμε να φτιάξουμε
Πώς να λύσετε τον κύβο του Rubik από τον Έλτον 1 Σκόντι, Β Λυκείου 1 ο ΓΕ.Λ. Ελευσίνας σχολικό έτος 2008-9 ΒΗΜΑ 1 Ο : Φτιάχνουμε έναν σταυρό σε όποιο χρώμα θέλουμε. Δηλαδή: Αν π.χ. θέλουμε να φτιάξουμε
Σχεδιασμός αρχιτεκτονικών σχεδίων
 4. Σχεδιασμός αρχιτεκτονικών σχεδίων ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΕΙΣ Σαμίρ Μπαγιούκ Για να κάνουμε αντιληπτό ένα αντικείμενο στον χώρο, μπορούμε να χρησιμοποιήσουμε τη φωτογράφιση με πολλαπλές λήψεις από διάφορες
4. Σχεδιασμός αρχιτεκτονικών σχεδίων ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΕΙΣ Σαμίρ Μπαγιούκ Για να κάνουμε αντιληπτό ένα αντικείμενο στον χώρο, μπορούμε να χρησιμοποιήσουμε τη φωτογράφιση με πολλαπλές λήψεις από διάφορες
Σενάριο 13: Προγραμματίζοντας ένα Ρομπότ
 Σενάριο 13: Προγραμματίζοντας ένα Ρομπότ Φύλλο Εργασίας Τίτλος: Προγραμματίζοντας ένα Ρομπότ Γνωστικό Αντικείμενο: Πληροφορική Διδακτική Ενότητα: Ελέγχω-Προγραμματίζω τον Υπολογιστή Τάξη: Γ Γυμνασίου Διάρκεια:
Σενάριο 13: Προγραμματίζοντας ένα Ρομπότ Φύλλο Εργασίας Τίτλος: Προγραμματίζοντας ένα Ρομπότ Γνωστικό Αντικείμενο: Πληροφορική Διδακτική Ενότητα: Ελέγχω-Προγραμματίζω τον Υπολογιστή Τάξη: Γ Γυμνασίου Διάρκεια:
1 ο Εξάμηνο. αποτύπωση. Εισαγωγικές έννοιες στην και τεκμηρίωση αντικειμένων. Αποτυπώσεις Τεκμηρίωση Αντικειμένων
 1 ο Εξάμηνο 2015-2016 Εισαγωγικές έννοιες στην αποτύπωση και τεκμηρίωση αντικειμένων Αποτυπώσεις Τεκμηρίωση Αντικειμένων Μάθημα 1ο Τζώρτζια Πλατυπόδη Αρχιτέκτων Μηχανικός Ε.Μ.Π. MSc Διαχείριση Μνημείων
1 ο Εξάμηνο 2015-2016 Εισαγωγικές έννοιες στην αποτύπωση και τεκμηρίωση αντικειμένων Αποτυπώσεις Τεκμηρίωση Αντικειμένων Μάθημα 1ο Τζώρτζια Πλατυπόδη Αρχιτέκτων Μηχανικός Ε.Μ.Π. MSc Διαχείριση Μνημείων
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2010
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2010 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : ΑΡΧΙΤΕΚΤΟΝΙΚΟ ΚΑΙ ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2010 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑ : ΑΡΧΙΤΕΚΤΟΝΙΚΟ ΚΑΙ ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ
Ποια αντικείμενα υπάρχουν στην αίθουσά μας; Τα καταγράφουμε εδώ:
 Το σχέδιο της αίθουσάς μας Τι σχήμα έχει η αίθουσά μας; Επιλέγουμε το σωστό σχήμα και γράφουμε το όνομά του στο κάτω μέρος. Ποια αντικείμενα υπάρχουν στην αίθουσά μας; Τα καταγράφουμε εδώ: Πώς είναι τοποθετημένα
Το σχέδιο της αίθουσάς μας Τι σχήμα έχει η αίθουσά μας; Επιλέγουμε το σωστό σχήμα και γράφουμε το όνομά του στο κάτω μέρος. Ποια αντικείμενα υπάρχουν στην αίθουσά μας; Τα καταγράφουμε εδώ: Πώς είναι τοποθετημένα
4. Να βρείτε την εξίσωση της ευθείας που διέρχεται από την αρχή των αξόνων και το σημείο Α(,.
 1. Τι ξέρετε για τη γραφική παράσταση των συναρτήσεων της μορφής ; Πώς ονομάζεται το ; Η γραφική παράσταση των συναρτήσεων της μορφής, είναι ευθεία γραμμή που διέρχεται από την αρχή των αξόνων. Το ονομάζεται
1. Τι ξέρετε για τη γραφική παράσταση των συναρτήσεων της μορφής ; Πώς ονομάζεται το ; Η γραφική παράσταση των συναρτήσεων της μορφής, είναι ευθεία γραμμή που διέρχεται από την αρχή των αξόνων. Το ονομάζεται
ΣΧΕ ΙΑΣΜΟΥ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ
 ΚΛΙΜΑΚΙΟ ΣΧΕ ΙΑΣΜΟΥ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ στο Σχεδιασμό και Τεχνολογία Α Β ΠΕΡΙΕΡΓΑ...... ΜΑΤΑΚΙΑ Εισαγωγή: Αφόρμηση Πρόβλημα Στόχοι Πορεία ραστηριότητες Ιδέες Λύσεις Επέκταση Φύλλα εργασίας
ΚΛΙΜΑΚΙΟ ΣΧΕ ΙΑΣΜΟΥ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΗΜΟΤΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ στο Σχεδιασμό και Τεχνολογία Α Β ΠΕΡΙΕΡΓΑ...... ΜΑΤΑΚΙΑ Εισαγωγή: Αφόρμηση Πρόβλημα Στόχοι Πορεία ραστηριότητες Ιδέες Λύσεις Επέκταση Φύλλα εργασίας
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το
 Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
Παράδειγμα 1 Γράψε ένα δεκαδικό αριθμό μεταξύ του 2 και του 3 που δεν περιέχει το 5 που περιέχει το 7 και που βρίσκεται όσο πιο κοντά γίνεται με το 5/2 1 Παράδειγμα 2: Γράψε ένα κλάσμα που χρησιμοποιεί
Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο
 Κ Ε Φ Α Λ Α Ι Ο Α Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο Σκοπός Σκοπός του κεφαλαίου αυτού είναι να γνωρίσουν οι μαθητές τα υλικά που χρειάζονται για το ελεύθερο σχέδιο και τον τρόπο που θα τα
Κ Ε Φ Α Λ Α Ι Ο Α Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο Σκοπός Σκοπός του κεφαλαίου αυτού είναι να γνωρίσουν οι μαθητές τα υλικά που χρειάζονται για το ελεύθερο σχέδιο και τον τρόπο που θα τα
ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών. Αναπληρωτής Καθηγητής ΤΕΧΝΙΚΟ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟ ΣΧΕΔΙΟ Ι ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO
 1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας
 Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: α. Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών. Αναπληρωτής Καθηγητής ΤΕΧΝΙΚΟ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟ ΣΧΕΔΙΟ Ι ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΠΑΡΕΜΒΑΣΕΙΣ ΣΤΗ ΘΕΑΤΡΙΚΗ ΕΚΠΑΙΔΕΥΣΗ
 ΠΑΡΕΜΒΑΣΕΙΣ ΣΤΗ ΘΕΑΤΡΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: «ΕΠΙΔΑΠΕΔΙΟ ΠΑΙΧΝΙΔΙ» Δράσεις που υλοποιήθηκαν με τη Β Τάξη του 3 ου Διαπολιτισμικού Δημοτικού Σχολείου Μενεμένης. Σχολικό έτος 2011-2012 Συντελεστές
ΠΑΡΕΜΒΑΣΕΙΣ ΣΤΗ ΘΕΑΤΡΙΚΗ ΕΚΠΑΙΔΕΥΣΗ ΘΕΜΑ ΕΡΓΑΣΙΑΣ: «ΕΠΙΔΑΠΕΔΙΟ ΠΑΙΧΝΙΔΙ» Δράσεις που υλοποιήθηκαν με τη Β Τάξη του 3 ου Διαπολιτισμικού Δημοτικού Σχολείου Μενεμένης. Σχολικό έτος 2011-2012 Συντελεστές
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τρία αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τρία αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2)
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
1. Σχεδιασμός - Γραφική Επικοινωνία
 1. Σχεδιασμός - Γραφική Επικοινωνία 1.1 Εισαγωγή Πολλές φορές, όταν μιλάμε για την τεχνολογία, το μυαλό μας πηγαίνει στα τελευταία και πιο εντυπωσιακά της επιτεύγματα, όπως αυτά της μικροηλεκτρονικής και
1. Σχεδιασμός - Γραφική Επικοινωνία 1.1 Εισαγωγή Πολλές φορές, όταν μιλάμε για την τεχνολογία, το μυαλό μας πηγαίνει στα τελευταία και πιο εντυπωσιακά της επιτεύγματα, όπως αυτά της μικροηλεκτρονικής και
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΖΗΤΟΥΝΤΑΙ:
 AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 11 ΣΕΠΤΕΜΒΡΙΟΥ 2012 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ ΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Αρμονική απεικόνιση του θέματος στον
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 11 ΣΕΠΤΕΜΒΡΙΟΥ 2012 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ ΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Αρμονική απεικόνιση του θέματος στον
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
β. Πιο κάτω από τη βάση τοποθετούμε το εστιακό σημείο του παρατηρητή, σε κάτοψη.
 Προβολές σε άλλα επίπεδα - Προοπτικές απεικονίσεις Μπορεί να γίνει προβολή ως προς σημείο το οποίο μπορεί να είναι το ανθρώπινο μάτι, ή ακριβέστερα το εστιακό σημείο του ανθρώπινου ματιού: Η απεικόνιση
Προβολές σε άλλα επίπεδα - Προοπτικές απεικονίσεις Μπορεί να γίνει προβολή ως προς σημείο το οποίο μπορεί να είναι το ανθρώπινο μάτι, ή ακριβέστερα το εστιακό σημείο του ανθρώπινου ματιού: Η απεικόνιση
ΓΥΜΝΑΣΙΟ ΨΥΧΙΚΟΥ «ΚΩΝΣΤΑΝΤΙΝΟΣ ΚΑΡΑΘΕΟΔΩΡΗ» Μάζα- Βάρος
 Μάζα Σύμβολο: (ass) Μάζα- Βάρος Η μάζα ενός σώματος εκφράζει την ποσότητα της ύλης που περιέχει το σώμα. Η μάζα συνδέεται με το πόσο εύκολα ή δύσκολα μπορεί να κινηθεί ένα σώμα. Όσο μεγαλύτερη μάζα έχει
Μάζα Σύμβολο: (ass) Μάζα- Βάρος Η μάζα ενός σώματος εκφράζει την ποσότητα της ύλης που περιέχει το σώμα. Η μάζα συνδέεται με το πόσο εύκολα ή δύσκολα μπορεί να κινηθεί ένα σώμα. Όσο μεγαλύτερη μάζα έχει
ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΩΝ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
Πώς μπορούμε να δημιουργούμε γεωμετρικά σχέδια με τη Logo;
 Κεφάλαιο 2 Εισαγωγή Πώς μπορούμε να δημιουργούμε γεωμετρικά σχέδια με τη Logo; Η Logo είναι μία από τις πολλές γλώσσες προγραμματισμού. Κάθε γλώσσα προγραμματισμού έχει σκοπό τη δημιουργία προγραμμάτων
Κεφάλαιο 2 Εισαγωγή Πώς μπορούμε να δημιουργούμε γεωμετρικά σχέδια με τη Logo; Η Logo είναι μία από τις πολλές γλώσσες προγραμματισμού. Κάθε γλώσσα προγραμματισμού έχει σκοπό τη δημιουργία προγραμμάτων
Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων Τάξεις Ε+ΣΤ Δημοτικού
 Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων 2016-2017 Τάξεις Ε+ΣΤ Δημοτικού Περιεχόμενα Στόχοι Πηγή Υλικού 3.1 Αριθμοί Οι μαθητές πρέπει: Σχολικά βιβλία Ε και ΣΤ Φυσικοί, Δεκαδικοί, μετρήσεις Να μπορούν
Πρόγραμμα Σπουδών Εκπαίδευσης Παιδιών-Προφύγων 2016-2017 Τάξεις Ε+ΣΤ Δημοτικού Περιεχόμενα Στόχοι Πηγή Υλικού 3.1 Αριθμοί Οι μαθητές πρέπει: Σχολικά βιβλία Ε και ΣΤ Φυσικοί, Δεκαδικοί, μετρήσεις Να μπορούν
Περιληπτικά, τα βήματα που ακολουθούμε γενικά είναι τα εξής:
 Αυτό που πρέπει να θυμόμαστε, για να μη στεναχωριόμαστε, είναι πως τόσο στις εξισώσεις, όσο και στις ανισώσεις 1ου βαθμού, που θέλουμε να λύσουμε, ακολουθούμε ακριβώς τα ίδια βήματα! Εκεί που πρεπει να
Αυτό που πρέπει να θυμόμαστε, για να μη στεναχωριόμαστε, είναι πως τόσο στις εξισώσεις, όσο και στις ανισώσεις 1ου βαθμού, που θέλουμε να λύσουμε, ακολουθούμε ακριβώς τα ίδια βήματα! Εκεί που πρεπει να
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
Τεχνικό Τοπογραφικό Σχέδιο
 Τεχνικό Τοπογραφικό Σχέδιο Γ. Καριώτου ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ & ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τεχνικό Τοπογραφικό Σχέδιο Γ. Καριώτου ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ & ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Επαγγελματικές κάρτες
 Επαγγελματικές κάρτες Αφροδίτη Οικονόμου Νηπιαγωγός afoikon@uth.gr Η παρουσίαση αναπτύχθηκε για την πλατφόρμα Ταξίδι στον γραμματισμό Θεματική: Τα επαγγέλματα των γονιών της τάξης μας ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ:
Επαγγελματικές κάρτες Αφροδίτη Οικονόμου Νηπιαγωγός afoikon@uth.gr Η παρουσίαση αναπτύχθηκε για την πλατφόρμα Ταξίδι στον γραμματισμό Θεματική: Τα επαγγέλματα των γονιών της τάξης μας ΤΙΤΛΟΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ:
Ορθογωνούλης Αμβλυγωνούλης Οξυγωνούλης
 Ορθογωνούλης Αμβλυγωνούλης Οξυγωνούλης Μια φορά και έναν καιρό στην τριγωνογειτονιά ζούσαν 3 φίλοι: ο Αµβλυγωνούλης, ο Oξυγωνούλης και ο Oρθογωνούλης. Κάθε ένας ζούσε σε ένα σπιτάκι ανάλογο µε το σχήµα
Ορθογωνούλης Αμβλυγωνούλης Οξυγωνούλης Μια φορά και έναν καιρό στην τριγωνογειτονιά ζούσαν 3 φίλοι: ο Αµβλυγωνούλης, ο Oξυγωνούλης και ο Oρθογωνούλης. Κάθε ένας ζούσε σε ένα σπιτάκι ανάλογο µε το σχήµα
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Μηχανική Στερεού Σώματος. Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
Ανακτήθηκε από την Εκπαιδευτική Κλίμακα. ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ
 ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΠΕΝΤΕ (5) 15 Σεπτεμβρίου
ΑΡΧΗ 1ης ΣΕΛΙ ΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΓΡΑΜΜΙΚΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΠΕΝΤΕ (5) 15 Σεπτεμβρίου
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΔΟΜΕΣ. Γενική μορφή της επανάληψης επανάλαβε φορές [... ενέργειες...]
![ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΔΟΜΕΣ. Γενική μορφή της επανάληψης επανάλαβε φορές [... ενέργειες...] ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΔΟΜΕΣ. Γενική μορφή της επανάληψης επανάλαβε φορές [... ενέργειες...]](/thumbs/64/52169959.jpg) ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΔΟΜΕΣ Γενική μορφή της επανάληψης επανάλαβε φορές [... ενέργειες...] βρείτε στα παρακάτω σχήματα γράψτε με λόγια τι επαναλαμβάνεται (μονάδα επανάληψης) και πόσες φορές (πλήθος επανάληψης).....
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΔΟΜΕΣ Γενική μορφή της επανάληψης επανάλαβε φορές [... ενέργειες...] βρείτε στα παρακάτω σχήματα γράψτε με λόγια τι επαναλαμβάνεται (μονάδα επανάληψης) και πόσες φορές (πλήθος επανάληψης).....
ΑΣΚΗΣΗ 1 Ποιο από τα δύο σχήματα Α, Β έχει το μεγαλύτερο εμβαδόν;
 ΜΕΡΟΣ Β. ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ-ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ 05. ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΗΣ ΕΠΙΦΑΝΕΙΑΣ Ορισμός Το εμβαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, που εκφράζει την έκταση που καταλαμβάνει η επιφάνεια
ΜΕΡΟΣ Β. ΕΜΒΑΔΑ ΕΠΙΠΕΔΩΝ ΣΧΗΜΑΤΩΝ-ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ 05. ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΗΣ ΕΠΙΦΑΝΕΙΑΣ Ορισμός Το εμβαδόν μιας επίπεδης επιφάνειας είναι ένας θετικός αριθμός, που εκφράζει την έκταση που καταλαμβάνει η επιφάνεια
ΣΧΗΜΑΤΑ-ΓΡΑΜΜΕΣ-ΜΕΤΡΗΣΗ Μιχάλης Χριστοφορίδης Ανδρέας Σάββα Σύμβουλοι Μαθηματικών
 ΕΦΑΡΜΟΓΙΔΙΟ: Σχήματα-Γραμμές-Μέτρηση Είναι ένα εργαλείο που μας βοηθά στην κατασκευή και μέτρηση σχημάτων, γωνιών και γραμμών. Μας παρέχει ένα χάρακα, μοιρογνωμόνιο και υπολογιστική μηχανή για να μας βοηθάει
ΕΦΑΡΜΟΓΙΔΙΟ: Σχήματα-Γραμμές-Μέτρηση Είναι ένα εργαλείο που μας βοηθά στην κατασκευή και μέτρηση σχημάτων, γωνιών και γραμμών. Μας παρέχει ένα χάρακα, μοιρογνωμόνιο και υπολογιστική μηχανή για να μας βοηθάει
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14. Μιχαηλίδου Αγγελική Λάλας Γεώργιος
 ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14 Μιχαηλίδου Αγγελική Λάλας Γεώργιος Περιγραφή Πλαισίου Σχολείο: 2 ο Πρότυπο Πειραματικό Γυμνάσιο Αθηνών Τμήμα: Β 3 Υπεύθυνος καθηγητής: Δημήτριος Διαμαντίδης Συνοδός: Δημήτριος Πρωτοπαπάς
ΠΡΑΚΤΙΚΗ ΑΣΚΗΣΗ 2013/14 Μιχαηλίδου Αγγελική Λάλας Γεώργιος Περιγραφή Πλαισίου Σχολείο: 2 ο Πρότυπο Πειραματικό Γυμνάσιο Αθηνών Τμήμα: Β 3 Υπεύθυνος καθηγητής: Δημήτριος Διαμαντίδης Συνοδός: Δημήτριος Πρωτοπαπάς
1.6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ x
 6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ 5 Να γράψετε τις ιδιότητες του άπειρου ορίου στο o Απάντηση : Όπως στην περίπτωση των πεπερασμένων ορίων έτσι και για τα άπειρα όρια συναρτήσεων, που ορίζονται σε ένα σύνολο της
6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ 5 Να γράψετε τις ιδιότητες του άπειρου ορίου στο o Απάντηση : Όπως στην περίπτωση των πεπερασμένων ορίων έτσι και για τα άπειρα όρια συναρτήσεων, που ορίζονται σε ένα σύνολο της
ΕΝΤΟΛΕΣ. 7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα
 7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα ΕΝΤΟΛΕΣ χρησιμοποιηθούν παρακάτω στα παραδείγματα Βάζοντας την εντολή αυτή σε οποιοδήποτε χαρακτήρα μπορούμε να αλλάζουμε όψεις
7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα ΕΝΤΟΛΕΣ χρησιμοποιηθούν παρακάτω στα παραδείγματα Βάζοντας την εντολή αυτή σε οποιοδήποτε χαρακτήρα μπορούμε να αλλάζουμε όψεις
ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ 1. α. Τι γνωρίζετε για την Ευκλείδεια διαίρεση; Πότε λέγεται τέλεια; β. Αν σε μια διαίρεση είναι Δ=δ, πόσο είναι το πηλίκο και
1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Α ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ 1. α. Τι γνωρίζετε για την Ευκλείδεια διαίρεση; Πότε λέγεται τέλεια; β. Αν σε μια διαίρεση είναι Δ=δ, πόσο είναι το πηλίκο και
1.6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ x
 6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ 5 Να γράψετε τις ιδιότητες του άπειρου ορίου στο o Απάντηση : Όπως στην περίπτωση των πεπερασμένων ορίων έτσι και για τα άπειρα όρια συναρτήσεων, που ορίζονται σε ένα σύνολο της
6 ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ 5 Να γράψετε τις ιδιότητες του άπειρου ορίου στο o Απάντηση : Όπως στην περίπτωση των πεπερασμένων ορίων έτσι και για τα άπειρα όρια συναρτήσεων, που ορίζονται σε ένα σύνολο της
ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ 1. Τι ονομάζουμε συνάρτηση; Συνάρτηση ονομάζεται η αλληλεξάρτηση (ή η σχέση) δυο μεταβλητών εις τρόπον ώστε για κάθε τιμή της μιας
ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ 1. Τι ονομάζουμε συνάρτηση; Συνάρτηση ονομάζεται η αλληλεξάρτηση (ή η σχέση) δυο μεταβλητών εις τρόπον ώστε για κάθε τιμή της μιας
Δημοτικό Υπαίθριο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : 1).. 2).. 3).. 1 ΔΙΔΑΣΚΩΝ: Σούφαρη Αθανασία εκπ/κός ΠΕ03
 Φύλλο Εργασίας Δημοτικό Υπαίθριο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : 1).. 2).. 3).. 1 ΔΙΔΑΣΚΩΝ: Σούφαρη Αθανασία εκπ/κός ΠΕ03 2 ΔΙΔΑΣΚΩΝ: Σούφαρη Αθανασία εκπ/κός ΠΕ03 ΤΟ ΠΡΟΒΛΗΜΑ Είσαι πολιτικός μηχανικός
Φύλλο Εργασίας Δημοτικό Υπαίθριο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : 1).. 2).. 3).. 1 ΔΙΔΑΣΚΩΝ: Σούφαρη Αθανασία εκπ/κός ΠΕ03 2 ΔΙΔΑΣΚΩΝ: Σούφαρη Αθανασία εκπ/κός ΠΕ03 ΤΟ ΠΡΟΒΛΗΜΑ Είσαι πολιτικός μηχανικός
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 11 ο, Τμήμα Α. Γεωμετρία
 Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Σχέδιο Ειδικότητας Αµαξωµάτων
 65 ιδακτικοί στόχοι: Στο τέλος αυτής της διδακτικής ενότητας θα είσαι σε θέση: Να γνωρίζεις τα µέρη του αµαξώµατος και την ονοµατολογία τους. Να µπορείς να διαβάζεις, από τα διαγραµµατικά σχέδια των αµαξωµάτων,
65 ιδακτικοί στόχοι: Στο τέλος αυτής της διδακτικής ενότητας θα είσαι σε θέση: Να γνωρίζεις τα µέρη του αµαξώµατος και την ονοµατολογία τους. Να µπορείς να διαβάζεις, από τα διαγραµµατικά σχέδια των αµαξωµάτων,
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2015
 ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΒΑΘΜΟΣ : ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Αριθμητικά.. ΗΜΕΡΟΜΗΝΙΑ: 1/6/015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Α Ολογράφως:... ΧΡΟΝΟΣ: ώρες
ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 015 ΒΑΘΜΟΣ : ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Αριθμητικά.. ΗΜΕΡΟΜΗΝΙΑ: 1/6/015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Α Ολογράφως:... ΧΡΟΝΟΣ: ώρες
Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει:
 ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να αναγνωρίζει και να κατονομάζει τα διάφορα είδη προβολών. 2. Να αναγνωρίζει και να κατονομάζει
ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να αναγνωρίζει και να κατονομάζει τα διάφορα είδη προβολών. 2. Να αναγνωρίζει και να κατονομάζει
Α.2.1 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ
 ΚΕΦΑΛΑΙΟ Ο ΚΛΑΣΜΑΤΑ Α.. Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΟΣ ΜΕ ΤΟ Αν ο αριθμητής ενός κλάσματος είναι μεγαλύτερος από τον παρανομαστή, τότε το κλάσμα είναι μεγαλύτερο από το. Αν ο αριθμητής
ΚΕΦΑΛΑΙΟ Ο ΚΛΑΣΜΑΤΑ Α.. Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΜΕΘΟΔΟΛΟΓΙΑ ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΟΣ ΜΕ ΤΟ Αν ο αριθμητής ενός κλάσματος είναι μεγαλύτερος από τον παρανομαστή, τότε το κλάσμα είναι μεγαλύτερο από το. Αν ο αριθμητής
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Λεπτομέριες τοιχοποιίας Σχεδίαση κάτοψης
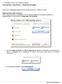 1 Λεπτομέριες τοιχοποιϊας Σχεδίαση κάτοψης Λεπτομέριες τοιχοποιίας Σχεδίαση κάτοψης Ξεκινώντας το πρόγραμμα εμφανίζονται οι επιλογές σχετικά με το τι θέλετε να κάνετε. Δημιουργώντας Νέο Δωμάτιο Όταν ο
1 Λεπτομέριες τοιχοποιϊας Σχεδίαση κάτοψης Λεπτομέριες τοιχοποιίας Σχεδίαση κάτοψης Ξεκινώντας το πρόγραμμα εμφανίζονται οι επιλογές σχετικά με το τι θέλετε να κάνετε. Δημιουργώντας Νέο Δωμάτιο Όταν ο
Διδακτική των Μαθηματικών
 Διδακτική των Μαθηματικών Ονοματεπώνυμο : Μαμτζέλλη Χρυσούλα Τάξη : Γ Δημοτικού Κεφάλαιο 43 : Η συμμετρία Πρόκειται για ένα εισαγωγικό μάθημα στην αξονική συμμετρία. Οι μαθητές θα μάθουν πότε δύο σχήματα
Διδακτική των Μαθηματικών Ονοματεπώνυμο : Μαμτζέλλη Χρυσούλα Τάξη : Γ Δημοτικού Κεφάλαιο 43 : Η συμμετρία Πρόκειται για ένα εισαγωγικό μάθημα στην αξονική συμμετρία. Οι μαθητές θα μάθουν πότε δύο σχήματα
Σύμβολα και σχεδιαστικά στοιχεία. Μάθημα 3
 Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ Δευτέρα, 24 Ιουνίου 2019 ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ Δευτέρα, 24 Ιουνίου 2019 ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση
ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018
 ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Β ΗΜΕΡΟΜΗΝΙΑ: 04/06/2018 ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ: 1,5 ώρα ΩΡΑ: 10:30-12:00 ΒΑΘΜΟΣ Αριθμητικώς:...
ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Β ΗΜΕΡΟΜΗΝΙΑ: 04/06/2018 ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ: 1,5 ώρα ΩΡΑ: 10:30-12:00 ΒΑΘΜΟΣ Αριθμητικώς:...
ΤΕΧΝΙΚΟΥ ΣΧΕΔΙΟΥ. (Μέρος πρώτο)
 ΤΕΙ ΛΑΡΙΣΑΣ - Παράρτημα Καρδίτσας ΤΜΗΜΑ ΣΧΕΔΙΑΣΜΟΥ & ΤΕΧΝΟΛΟΓΙΑΣ ΞΥΛΟΥ ΕΠΙΠΛΟΥ ΣΗΜΕΙΩΣΕΙΣ ΤΕΧΝΙΚΟΥ ΣΧΕΔΙΟΥ ΙΙ (Μέρος πρώτο) - ΠΛΑΓΙΑ ΠΡΟΒΟΛΗ - ΑΞΟΝΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ - ΑΝΟΧΕΣ - ΣΥΝΑΡΜΟΓΕΣ ΚΟΛΛΑΤΟΣ ΓΕΩΡΓΙΟΣ
ΤΕΙ ΛΑΡΙΣΑΣ - Παράρτημα Καρδίτσας ΤΜΗΜΑ ΣΧΕΔΙΑΣΜΟΥ & ΤΕΧΝΟΛΟΓΙΑΣ ΞΥΛΟΥ ΕΠΙΠΛΟΥ ΣΗΜΕΙΩΣΕΙΣ ΤΕΧΝΙΚΟΥ ΣΧΕΔΙΟΥ ΙΙ (Μέρος πρώτο) - ΠΛΑΓΙΑ ΠΡΟΒΟΛΗ - ΑΞΟΝΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ - ΑΝΟΧΕΣ - ΣΥΝΑΡΜΟΓΕΣ ΚΟΛΛΑΤΟΣ ΓΕΩΡΓΙΟΣ
Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]
![Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ] Άσκηση 1 η ( x 2) 2. i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0. ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 2 [ 3 8 ( 3) ]](/thumbs/64/51524102.jpg) ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
ά ς w w w.e - m at hs.g r ά έ ί ς ά ά έ ά ς ί ά Άσκηση 1 η i) Να βρείτε την τιμή της παράστασης Α, αν χ = 0 4 2 3 3 6 3 ( x 2) 2 x 1 x x 1 x 2 ii) Να βρείτε την τιμή της παράστασης Β, αν χ = 2 3 27 3 2
ΕΝΟΤΗΤΑ 1 ΚΕΦΑΛΑΙΟ 2. Υπενθύμιση Β μέρος ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ. Παράλληλες: Τι θα πρέπει να. Ποιες είναι οι παράλληλες ευθείες;
 ΕΝΟΤΗΤΑ 1 ΚΕΦΑΛΑΙΟ 2 Υπενθύμιση Β μέρος ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Παράλληλες: Τι θα πρέπει να θυμόμαστε από την γεωμετρία; Ποιες είναι οι παράλληλες ευθείες; Ποιες είναι οι κάθετες ευθείες;
ΕΝΟΤΗΤΑ 1 ΚΕΦΑΛΑΙΟ 2 Υπενθύμιση Β μέρος ΟΛΑ ΟΣΑ ΠΡΕΠΕΙ ΝΑ ΞΕΡΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ Παράλληλες: Τι θα πρέπει να θυμόμαστε από την γεωμετρία; Ποιες είναι οι παράλληλες ευθείες; Ποιες είναι οι κάθετες ευθείες;
ΝΙΚΟΣ ΤΟΥΝΤΑΣ ΠΡΟΛΟΓΟΣ:
 ΠΡΟΛΟΓΟΣ: Συνεχίζοντας το ταξίδι στον κόσμο των μαθηματικών αναρτώ την 3 η μου άσκηση η οποία καλύπτει την ύλη μέχρι και τα όρια. Δεν βασίζεται αυτήν την φορά σε άσκηση του σχολικού άλλα σε καθαρά δικιά
ΠΡΟΛΟΓΟΣ: Συνεχίζοντας το ταξίδι στον κόσμο των μαθηματικών αναρτώ την 3 η μου άσκηση η οποία καλύπτει την ύλη μέχρι και τα όρια. Δεν βασίζεται αυτήν την φορά σε άσκηση του σχολικού άλλα σε καθαρά δικιά
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ. ΔΙΑΡΚΕΙΑ: 1 περιόδους. 28/9/2008 12:48 Όνομα: Λεκάκης Κωνσταντίνος καθ.
 ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
Γράμματα και αριθμοί
 5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
Ερωτηματολόγιο Προγράμματος "Ασφαλώς Κυκλοφορώ" (αρχικό ερωτηματολόγιο) Για μαθητές Δ - Ε - ΣΤ Δημοτικού
 Ερωτηματολόγιο Προγράμματος "Ασφαλώς Κυκλοφορώ" (αρχικό ερωτηματολόγιο) Για μαθητές Δ - Ε - ΣΤ Δημοτικού Tάξη & Τμήμα:... Σχολείο:... Ημερομηνία:.../.../200... Όνομα:... Ερωτηματολόγιο Προγράμματος "Ασφαλώς
Ερωτηματολόγιο Προγράμματος "Ασφαλώς Κυκλοφορώ" (αρχικό ερωτηματολόγιο) Για μαθητές Δ - Ε - ΣΤ Δημοτικού Tάξη & Τμήμα:... Σχολείο:... Ημερομηνία:.../.../200... Όνομα:... Ερωτηματολόγιο Προγράμματος "Ασφαλώς
Κεφάλαιο 7 Γεωμετρικές Κατασκευές
 Κεφάλαιο 7 Γεωμετρικές Κατασκευές Συντομεύσεις Ακρωνύμια... 2 Σύνοψη... 3 Προαπαιτούμενη γνώση... 3 7.1. Κατασκευή ευθύγραμμων τμημάτων... 3 7.2. Κατασκευή γωνιών... 8 7.3. Κατασκευή πολυγώνων... 11 7.4.
Κεφάλαιο 7 Γεωμετρικές Κατασκευές Συντομεύσεις Ακρωνύμια... 2 Σύνοψη... 3 Προαπαιτούμενη γνώση... 3 7.1. Κατασκευή ευθύγραμμων τμημάτων... 3 7.2. Κατασκευή γωνιών... 8 7.3. Κατασκευή πολυγώνων... 11 7.4.
