Kεφ. 6 ΔΙΑMOΡΦΩΣΗ ΚΥΜΑΤΟΣ, ΚΥΜΑΤΟΠΑΚΕΤΑ,
|
|
|
- Ὑμέναιος Λύκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Kεφ. 6 ΔΙΑMOΡΦΩΣΗ ΚΥΜΑΤΟΣ, ΚΥΜΑΤΟΠΑΚΕΤΑ, (part, pages -) Η μέχρι τώρα μελέτη μας αφορούσε κύματα ή ταλαντώσεις με μία μόνο συχνότητα. Στη συνέχεια θα μελετήσουμε την υπέρθεση πολλών κυμάτν που συνίστανται από πολλές συχνότητες. Το συνιστάμενο κύμα είναι ένα οδεύον κύμα που θα αναφέρεται σαν κυματοπακέτο ή κυματοομάδα (wave packet) (το κύμα αυτό, αν και μεταφέρει ενέργεια και ορμή, δεν διατηρεί το σχήμα του καθώς διαδίδεται). Παράδειγμα, 5-μελής ομάδα μπάσκετ που κινείται (παίζοντας) κατά μήκος ενός δρόμου. Φασική ταχύτητα: η ταχύτητα με την οποία κινούνται οι διάφοροι διακυμάνσεις μέσα στην ομάδα (δεν μεταφέρεται ενέργεια ή πληροφορία και μπορεί να είναι μεγαλύτερη του c). Ταχύτητα ομάδος (group velocity): η ταχύτητα με τη οποία κινείται η ομάδα σαν σύνολο. Διαμόρφση σήματος: Το αρμονικό (οδεύον) κύμα δεν μεταφέρει πληροφορία, ενώ το διαμορφμένο κύμα μεταφέρει (Διαμόρφση πλάτους ή διαμόρφση συχνότητος). Το διαμορφμένο (οδεύον) κύμα γενικά αναπαρίσταται από μιά πολύπλοκη κυματοσυνάρτηση ψ(t). Για παράδειγμα, η ψ(t) μπορεί να σχηματιστεί από
2 υπέρθεση (άθροισμα) αρμονικών συναρτήσεν της μορφής Α()cos(t+φ()) Για παράδειγμα, η υπέρθεση τν 7 αρμονικών κυμάτν της επόμενης εικόνας, έχει παράγει το κυματοπακέτο που είδαμε προηγουμένς. Πράγματι, δεδομένης της συνάρτησης ψ(t), μπορούμε να υπολογίσουμε τα πλάτη Α() και τις σταθερές φάσης φ() με μεθόδους της ανάλυσης Fourier. Παράδειγμα: Υπέρθεση αρμονικών ταλαντώσεν Eχουμε δει από το Κεφ. ότι η υπέρθεση τν αρμονικών ταλαντώσεν με συχνότητες και, αντίστοιχα, ψ(t) A cos( t+φ ) + A cos( t+φ ) () (για ευκολία μας πήραμε A A A) δίδει την συνιστάμενη διαταραχή, ψ(t) A mod (t) cos(t+φ) ()
3 3 όπου ( + )/ είναι η μέση συχνότητα (καλείται φέρουσα συχνότητα), φ(φ +φ )/ και Α mod (t) είναι το διαμορφμένο πλάτος, Α mod (t)αcos( mod t+δ) (3) Με mod ( - )/ (καλείται συχνότητα διαμόρφσης) και δ(φ -φ )/. Η ταλάντση () παριστάνει μια σχεδόν αρμονική ταλάντση με (αρμονικά) διαμορφμένο πλάτος με συχνότητα mod. Γενικά, τα πλάτος (3) θα μπορούσε να έχει πιό σύνθετη μορφή. Παράδειγμα: Υπέρθεση οδευόντν κυμάτν Εστ ότι ένας πομπός παράγει κύματα της μορφής () στη θέση x0, δηλ. A cos( t+φ ), A cos( t+φ ) Επειδή καθένα κύμα δίδει ένα οδεύον κύμα στη θέση x, της μορφής A cos(k x- t+φ ), A cos(k x- t+φ ) η υπέρθεση τν κυμάτν στη θέση x δίδει το συνιστάμενο κύμα, ψ(x,t) A cos(k x- t+φ ) + A cos(k x- t+φ ) (4)
4 4 απ όπου λαμβάνουμε το διαμορφμένο (κατά πλάτος) οδεύον κύμα ψ(t) A mod (x,t) cos(kx-t+φ) (5) όπου ( + )/, k(k +k )/, φ(φ +φ )/ και Α mod (x,t) είναι το διαμορφμένο πλάτος, Α mod (x,t)αcos(k mod x- mod t+δ) (6) με mod ( - )/, k mod (k -k )/ και δ(φ -φ )/. Ταχύτητα διαμόρφσης Από την (6), για να παρακολουθήσουμε μια συγκεκριμένη τιμή του πλάτους διαμόρφσης, θα πρέπει η φάση της συνάρτησης να είναι σταθερή, (k mod x- mod t+δ)σταθ. την οποίαν διαφορίζοντας έχουμε, k mod dx- mod dt 0, απ όπου έπεται η ταχύτητα διαμόρφσης, υ mod dx mod (7) dt kmod k k Είναι η ταχύτητα μιας συγκεκριμένης τιμής του πλάτους διαμόρφσης. Λόγ όμς τν σχέσεν διασποράς, (k ) και (k ), οι οποίες μπορούν να αναπτυχθούν κατά Taylor γύρ από τη μέση τιμή k όπου k(k +k )/, ή
5 5 συνεπώς, d ( k) + (k d ( k) + (k + d (k k) + d (k k) + k) + d (k k )... + k) d Αντικαθιστώντας στην (7) προκύπτει, υ mod ,... d Ταχύτητα ομάδας: υ g δηλ. η ομάδα δεν διαδίδεται με τη μέση ταχύτητα υ( + )/(k +k ), όπς θα περίμενε κανείς, αλλά με τη ταχύτητα υ g d/. (Εχομε δεί στο Κεφ.4 ότι η ταχύτητα υ/k καλείται φασική ταχύτητα). Παράδειγμα: Ραδιοφνικά κύματα ΑΜ H φέρουσα συχνότης [ ]KHz H διεγείρουσα τάση που εφαρμόζεται στη κεραία του στο πομπό έχει διαμορφμένο πλάτος της μορφής, Α mod (t)α ο + mod Α( mod ) cos( mod t+δ) όπου η διαφορά (Α mod (t)-α ο ) είναι ανάλογη της πίεσης ενός ηχητικού κύματος (λειτουργία μικροφώνου). Οι συχνότητες διαμόρφσης mod για ηχητικά κύματα βρίσκονται μέσα στην ακουστική περιοχή, [0-0000]Ηz.
6 6 Εύρος ζώνης Αν είναι η φέρουσα συχνότητα, τότε οι συχνότητες που ακτινοβολούνται ανήκουν στη ζώνη συχνοτήτν, [- mod, + mod ] ή [ν -ν mod, ν +ν mod ] Η διαφορά της ελαχίστης συχνότητος από την μεγίστη συχνότητα καλείται εύρος ζώνης. Το εύρος ζώνης για τους εμπορικούς ραδιοφνικούς σταθμούς ΑΜ είναι ίσο με 0ΚΗz. Παλμοί Παλμός είναι η υπέρθεση πολλών αρμονικών ταλαντώσεν με ίδιο πλάτος και με γειτονικές συχνότητες στη ζώνη [, ]. Εστ ότι οι συχνότητες ισοκατανέμονται στη ζώνη [, ] εύρους Δ( - ). Αν ( - )/(Ν-), η υπέρθεση γράφεται ψ(t) A cos t + A cos ( +)t + A cos ( +)t + + A cos t sin[n t] Αcos[ t + (Ν ) t] sin( t) Αcos( + sin(n t) t) sin( t)
7 7 Bλέπουμε λοιπόν ότι ο παλμός διατηρεί την αρχική μορφή της απλής ταλάντσης, ψ(t)a(t) cos(t) όπου ( + )/ είναι η μέση συχνότητα, όμς το πλάτος της συνισταμένης ταλάντσης Α (t) sin(n t) Α sin( t) έχει τη σύνθετη διαμόρφση τν διακροτημάτν. Για Ν, το πλάτος τείνει στο όριο: Α(t) NΑ (την οποία θα καλέσουμε Α(0), ς η τιμή για t0). Στο όριο Ν, με τη προϋπόθεση ότι το γινόμενο Ν Δ παραμένει σταθερό (που σημαίνει ότι 0), το πλάτος γράφεται Α(t) sin(n t) Α sin( t) sin(n t) Α(0) (Ν t) t Α(0) 0 Θα μελετήσουμε τη κυματοσυνάρτηση ψ(t) στο όριο Α(0) Α(0) 0. Αν λάβουμε υπόψιν ότι Α, Ν Δ η αρχική υπέρθεση γράφεται, ψ(t) Acos t+acos ( +)t +Acos ( +)t +
8 8 Α(0) [cos t + cos( + )t + cos( + )t +...] Δ ή Α(0) Δ cost d, ψ(t) Α(0) Δ cost d Η μορφή αυτή αποτελεί μιά συνεχή αναπαράσταση κατά Fourier της κυματοσυνάρτησης ψ(t). Γενικά, κάθε συνεχής περιοδική συνάρτηση ψ(t) μπορεί να αναπαρασταθεί κατά Fourier ς εξής, ψ(t) Α()sin t d + Β() cost d 0 όπου οι συναρτήσεις Α() και Β() καλούνται συνεχείς συντελεστές Fourier (ή μετασχηματισμοί Fourier) και προκύπτει από τον παραπάν ορισμό ότι Α() Β() π π + 0 ψ(t)sin t dt + ψ(t)cost dt Η κυματοσυνάρτηση ψ(t) είναι σημαντική μόνο μέσα στο χρονικό διάστημα Δt (λέγεται διάρκεια του παλμού), που ορίζεται από τη σχέση ΔΔtπ ή ΔνΔt
9 9 Στο παρακάτ σχήμα φαίνεται ένας παλμός ψ(t) Στο επόμενο σχήμα φαίνεται ο συντελεστής Fourier Β(). Παρατηρούμε ότι ο συντελεστής Β()Α(0)/Δ για [, ] και είναι μηδέν εκτός του διάστηματος.
10 0 Οδεύον κυματοπακέτο Εστ ότι ένας πομπός (στη θέση x0) εκπέμπει ένα παλμό ψ(t) της μορφής του παραπάν σχήματος. Το σήμα αυτό διαδίδεται στο χώρο σαν οδεύον κύμα, περιορισμένο σε έκταση στο χώρο (είναι δηλ. εντοπισμένο) και καλείται οδεύον κυματοπακέτο. Η ταχύτητα διάδοσης του είναι ίση με τη ταχύτητα της ομάδος υ g. Εφόσον μεταξύ -k υφίσταται η σχέση διασποράς, (k) ή kk(), η ύπαρξη ζώνης Δ στις συχνότητες συνεπάγεται την ύπαρξη αντίστοιχης ζώνης Δk και στους κυματαριθμούς, δηλ. Δ k k k k( ) k( ) ( ) d (ενδιάμεσα έχει γίνει ανάπτυξη κατά Taylor). ο Δ υ Από το παραπάν σχήμα παρατηρούμε ότι το μήκος του παλμού (ή το ανάπτυγμα του παλμού στο χώρο) ισούται χονδρικά με Δxυ g Δt, όπου Δt η διάρκειά του. Έπεται επομένς ΔxΔkΔΔtπ (στη πραγματικότητα το γινόμενο τν αβεβαιοτήτν είναι π, κατά την αρχή του Heisenberg). Το μήκος Δx του κυματοπακέτου μεγαλώνει (λέμε ότι απλώνει) καθώς διαδίδεται στο χώρο. g
11 Αυτό αιτιολογείται ς εξής: η ταχύτητα ομάδος υ g d/ εξαρτάται από το k, και για κάθε k που ανήκει στη ζώνη [k,k ] αντιστοιχεί και μια τιμή της ταχύτητας υ g, επομένς προκύπτει και μιά αντίστοιχη ζώνη Δυ g για τις ταχύτητες, Δυ g dυ g ο Δk d ο Δk Οπότε το μήκος (Δx) o του κυματοπακέτου μετά από χρόνο t θα έχει γίνει, (Δx)(Δx) o +(Δυ g )t
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
H ΥΠΕΝΘΥΜΙΖΕΤΑΙ ΟΤΙ Η ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΟΝΤΟΤΗΤΑ
 θ cot T H ΥΠΕΝΘΥΜΙΖΕΤΑΙ ΟΤΙ Η ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΟΝΤΟΤΗΤΑ Η ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΑΝΑΦΕΡΕΤΑΙ ΣΤΟ ΤΟ ΑΡΜΟΝΙΚΟ ΚΥΜΑ ΠΟΥ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΟΝΤΟΤΗΤΑ! x t TO AΡMONIKO KYMA ΕΧΕΙ ΑΠΕΙΡΗ ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ
θ cot T H ΥΠΕΝΘΥΜΙΖΕΤΑΙ ΟΤΙ Η ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΟΝΤΟΤΗΤΑ Η ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΑΝΑΦΕΡΕΤΑΙ ΣΤΟ ΤΟ ΑΡΜΟΝΙΚΟ ΚΥΜΑ ΠΟΥ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΟΝΤΟΤΗΤΑ! x t TO AΡMONIKO KYMA ΕΧΕΙ ΑΠΕΙΡΗ ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΑΠΛΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΑΠΛΩΝ ΣΥΣΤΗΜΑΤΩΝ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΑΠΛΩΝ ΣΥΣΤΗΜΑΤΩΝ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη users.auth.gr/~katsiki
 ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
Σήματα και Συστήματα. Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
HMY 333 Φωτονική Διάλεξη 06. Εισαγωγή στις ταλαντώσεις και κύματα. Απλοί αρμονικοί ταλαντωτές. Γιατί εξετάζουμε την απλή αρμονική κίνηση;
 HMY 333 Φτονική Διάλεξη 6 Εισαγγή στις ταλαντώσεις και κύματα Απλοί αρμονικοί ταλανττές Μάζα-ελατήριο Mss-spring H. Chrisin, K.U.Ln(Wikipdi Εκκρεμές Pndlm U. o Monn LC κύκλμα hp://www.grnndwhi.n/~chb/lc_oscillor.hm
HMY 333 Φτονική Διάλεξη 6 Εισαγγή στις ταλαντώσεις και κύματα Απλοί αρμονικοί ταλανττές Μάζα-ελατήριο Mss-spring H. Chrisin, K.U.Ln(Wikipdi Εκκρεμές Pndlm U. o Monn LC κύκλμα hp://www.grnndwhi.n/~chb/lc_oscillor.hm
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά κύματα που απομακρύνονται
Φυσική για Μηχανικούς Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά κύματα που απομακρύνονται
KYMATA Ανάκλαση - Μετάδοση
 ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
4. Εισαγωγή στην Κυματική
 4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
ΟΡΟΣΗΜΟ. 1ο Κριτήριο αξιολόγησης στα κεφ Θέμα 1. Κριτήρια αξιολόγησης Ταλαντώσεις - Κύματα.
 1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
Είδη κυµάτων. Ηλεκτροµαγνητικά κύµατα. Σε κάποιο φυσικό µέσο προκαλείται µια διαταραχή. Το κύµα είναι η διάδοση της διαταραχής µέσα στο µέσο.
 Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΥΖΕΥΓΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
δ. Ο χρόνος ανάμεσα σε δυο διαδοχικούς μηδενισμούς του πλάτους είναι Τ =
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 01/11/2015 ΘΕΜΑ 1 Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 01/11/2015 ΘΕΜΑ 1 Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
. Σήματα και Συστήματα
 Σήματα και Συστήματα Βασίλειος Δαλάκας & Παναγιώτης Ριζομυλιώτης Τμήμα Πληροφορικής & Τηλεματικής Χαροκόπειο Πανεπιστήμιο Σήματα και Συστήματα 1/17 Πρόβλημα 1 (βιβλίο σελίδα 93) Να αποδειχθεί ότι: α) Κάθε
Σήματα και Συστήματα Βασίλειος Δαλάκας & Παναγιώτης Ριζομυλιώτης Τμήμα Πληροφορικής & Τηλεματικής Χαροκόπειο Πανεπιστήμιο Σήματα και Συστήματα 1/17 Πρόβλημα 1 (βιβλίο σελίδα 93) Να αποδειχθεί ότι: α) Κάθε
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min
 ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
1 ον ΜΕΡΟΣ ΑΠΟ ΤΗ ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΣΤΗΝ ΤΑΧΥΤΗΤΑ ΟΜΑΔΟΣ 2 ον ΜΕΡΟΣ ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΠΟ ΔΙΑΦΟΡΕΣ ΠΕΡΙΟΧΕΣ ΤΗΣ ΦΥΣΙΚΗΣ. Η ΑΝΤΑΓΩΝΙΣΜΟΣ ΜΕ ΤΑ ΜΗ ΓΡΑΜΜΙΚΑ
 ΜΕΡΟΣ 1 Κ. ΕΥΤΑΞΙΑΣ H TAXYTHTA OMAΔΟΣ! 1 ον ΜΕΡΟΣ ΑΠΟ ΤΗ ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΣΤΗΝ ΤΑΧΥΤΗΤΑ ΟΜΑΔΟΣ 2 ον ΜΕΡΟΣ ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΠΟ ΔΙΑΦΟΡΕΣ ΠΕΡΙΟΧΕΣ ΤΗΣ ΦΥΣΙΚΗΣ. Η ΑΝΤΑΓΩΝΙΣΜΟΣ ΜΕ ΤΑ ΜΗ ΓΡΑΜΜΙΚΑ ΦΑΙΝΟΜΕΝΑ SOLITONS
ΜΕΡΟΣ 1 Κ. ΕΥΤΑΞΙΑΣ H TAXYTHTA OMAΔΟΣ! 1 ον ΜΕΡΟΣ ΑΠΟ ΤΗ ΦΑΣΙΚΗ ΤΑΧΥΤΗΤΑ ΣΤΗΝ ΤΑΧΥΤΗΤΑ ΟΜΑΔΟΣ 2 ον ΜΕΡΟΣ ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΠΟ ΔΙΑΦΟΡΕΣ ΠΕΡΙΟΧΕΣ ΤΗΣ ΦΥΣΙΚΗΣ. Η ΑΝΤΑΓΩΝΙΣΜΟΣ ΜΕ ΤΑ ΜΗ ΓΡΑΜΜΙΚΑ ΦΑΙΝΟΜΕΝΑ SOLITONS
1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το
 Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου Αρχή της επαλληλίας Όταν σε ένα μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση ενός σημείου του ελαστικού μέσου είναι ίση με τη συνισταμένη
Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου Αρχή της επαλληλίας Όταν σε ένα μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση ενός σημείου του ελαστικού μέσου είναι ίση με τη συνισταμένη
Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα.
 ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
1. [Απ.: [Απ.: 3. [Απ.: [Απ.:
 1. Η εξίσωση ενός αρμονικού κύματος, το οποίο διαδίδεται κατά μήκος ενός γραμμικού ελαστικού μέσου, που έχει τη διεύθυνση του άξονα x'x, είναι: γ=0,04ημπ(200t - 8x) (τα x και y είναι σε m και το t σε s).
1. Η εξίσωση ενός αρμονικού κύματος, το οποίο διαδίδεται κατά μήκος ενός γραμμικού ελαστικού μέσου, που έχει τη διεύθυνση του άξονα x'x, είναι: γ=0,04ημπ(200t - 8x) (τα x και y είναι σε m και το t σε s).
2.1 Τρέχοντα Κύματα. Ομάδα Ε.
 2.1 Τρέχοντα Κύματα. Ομάδα Ε. 2.1.61. Δύο κύματα χωρίς εξισώσεις. Κατά μήκος ενός ελαστικού μέσου διαδίδονται αντίθετα δύο κύματα, του ίδιου πλάτους και τη στιγμή t 0 έχουμε την εικόνα του σχήματος. (
2.1 Τρέχοντα Κύματα. Ομάδα Ε. 2.1.61. Δύο κύματα χωρίς εξισώσεις. Κατά μήκος ενός ελαστικού μέσου διαδίδονται αντίθετα δύο κύματα, του ίδιου πλάτους και τη στιγμή t 0 έχουμε την εικόνα του σχήματος. (
Exουμε βρεί την εξίσωση κύματος: λν = υ, όπου υ = Τ /μ στη περίπτωση της χορδής. Οπότε. υ ν = = λ
 Kεφ. (part, pages - Σχέση διασπράς Exυμε βρεί την εξίσωση κύματς: λν = υ, όπυ υ = Τ /μ στη περίπτωση της χρδς. Οπότε υ ν = = λ ω = Τ /μ Τ /μ λ k H σχέση αυτ πυ συνδέει την γωνιακ συχνότητα ω με τν κυματαριθμό
Kεφ. (part, pages - Σχέση διασπράς Exυμε βρεί την εξίσωση κύματς: λν = υ, όπυ υ = Τ /μ στη περίπτωση της χρδς. Οπότε υ ν = = λ ω = Τ /μ Τ /μ λ k H σχέση αυτ πυ συνδέει την γωνιακ συχνότητα ω με τν κυματαριθμό
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σχήμα 1 Μορφές κυμάτων (α) Μονοδιάστατο, (β) Διδιάστατο, (γ) και (δ) Τρισδιάστατα. [1]
![Σχήμα 1 Μορφές κυμάτων (α) Μονοδιάστατο, (β) Διδιάστατο, (γ) και (δ) Τρισδιάστατα. [1] Σχήμα 1 Μορφές κυμάτων (α) Μονοδιάστατο, (β) Διδιάστατο, (γ) και (δ) Τρισδιάστατα. [1]](/thumbs/66/55074045.jpg) Άσκηση 3 - Κύματα Η δημιουργία κυμάτων είναι το αποτέλεσμα πολλών φυσικών διεργασιών. Κύματα εμφανίζονται στην επιφάνεια της θάλασσας, τα ηχητικά κύματα οφείλονται στις διαταραχές της πίεσης του αέρα,
Άσκηση 3 - Κύματα Η δημιουργία κυμάτων είναι το αποτέλεσμα πολλών φυσικών διεργασιών. Κύματα εμφανίζονται στην επιφάνεια της θάλασσας, τα ηχητικά κύματα οφείλονται στις διαταραχές της πίεσης του αέρα,
Τρέχοντα κύματα. Ερωτήσεις με δικαιολόγηση.
 Τρέχοντα κύματα. Ερωτήσεις με δικαιολόγηση. Η φάση ενός σημείου κατά τη διάδοση κύματος Κατά μήκος ενός ελαστικού μέσου διαδίδεται ένα κύμα προς τα δεξιά του θετικού ημιάξονα, με μήκος κύματος λ=2m. Ένα
Τρέχοντα κύματα. Ερωτήσεις με δικαιολόγηση. Η φάση ενός σημείου κατά τη διάδοση κύματος Κατά μήκος ενός ελαστικού μέσου διαδίδεται ένα κύμα προς τα δεξιά του θετικού ημιάξονα, με μήκος κύματος λ=2m. Ένα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
β. Το πλάτος της σύνθετης ταλάντωσης είναι : Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν φ) (φ = π rad) Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν π) Α = [Α 1 ² + Α 2
 1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
ΚΕΦΑΛΑΙΟ 2 Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ 2: ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ
 ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
Επαλληλία-Υπέρθεση Κυμάτων. Επαλληλία (υπέρθεση) Κυμάτων. Επαλληλία (Υπέρθεση) Κυμάτων. Επαλληλία: Συμβολή κυμάτων. Συμβολή αρμονικών κυμάτων
 Γραμμικά φαινόμενα μηχανικών κυμάτων Επαηία-Υπέρθεση Κυμάτων Υπέρθεση (επαηία) κυμάτων (superpositio) Συμβοή (χωρική) κυμάτων (iterferece) (stadig waves) Κανονικοί τρόποι ταάντωσης (ormal modes) Διακροτήματα
Γραμμικά φαινόμενα μηχανικών κυμάτων Επαηία-Υπέρθεση Κυμάτων Υπέρθεση (επαηία) κυμάτων (superpositio) Συμβοή (χωρική) κυμάτων (iterferece) (stadig waves) Κανονικοί τρόποι ταάντωσης (ormal modes) Διακροτήματα
2-1 ΕΙΣΑΓΩΓΗ 2-2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΔΟΥΑΡΔΟΥ ΛΑΓΑΝΑ Ph.D. Κεντρικό : Λεωφ. Κηφισίας 56, Αμπελόκηποι Αθήνα Τηλ.: ,
 ΕΔΟΥΑΡΔΟΥ ΛΑΓΑΝΑ Ph.D., Αμπελόκηποι Αθήνα Τηλ.: 0 69 97 985, www.edlag.gr ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ ΚΕΝΤΡΟ ΘΕΩΡΗΤΙΚΗΣ ΦΥΣΙΚΗΣ & ΧΗΜΕΙΑΣ Τηλ.: 0 69 97 985, e-mail: edlag@otenet.gr, www.edlag.gr
ΕΔΟΥΑΡΔΟΥ ΛΑΓΑΝΑ Ph.D., Αμπελόκηποι Αθήνα Τηλ.: 0 69 97 985, www.edlag.gr ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ ΚΕΝΤΡΟ ΘΕΩΡΗΤΙΚΗΣ ΦΥΣΙΚΗΣ & ΧΗΜΕΙΑΣ Τηλ.: 0 69 97 985, e-mail: edlag@otenet.gr, www.edlag.gr
Εξαναγκασμένη Ταλάντωση. Αρμονική Φόρτιση
 Εξαναγκασμένη Ταλάντωση Αρμονική Φόρτιση Αρμονική Ταλάντωση Εξαναγκασμένη Ταλάντωση: Αρμονική Φόρτιση: Δ8- Η αρμονική διέγερση αποτελεί θεμελιώδη μορφή διέγερσης στη Δυναμική των Κατασκευών λόγω της μαθηματικής
Εξαναγκασμένη Ταλάντωση Αρμονική Φόρτιση Αρμονική Ταλάντωση Εξαναγκασμένη Ταλάντωση: Αρμονική Φόρτιση: Δ8- Η αρμονική διέγερση αποτελεί θεμελιώδη μορφή διέγερσης στη Δυναμική των Κατασκευών λόγω της μαθηματικής
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ. Προθεσµία παράδοσης 11/11/08
 //8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
//8 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 8-9 η ΕΡΓΑΣΙΑ Προθεσµία παράδοσης //8 Άσκηση Α) Έστω, οι µετατοπίσεις των µαζών από τη θέση ισορροπίας όπως στο Σχήµα. Στη µάζα ενεργούν µόνο οι δυνάµεις από τα
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 4 ο και 5 ο
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 4 ο και 5 ο Φυσικά μεγέθη από προηγούμενες τάξεις Θέση: x Μονάδα (στο SI) m Μετατόπιση: Δx Μονάδα (στο SI) m Τύπος Δx=x 2 -x 1 Ύψος: h Μονάδα (στο SI) m Μήκος: l Μονάδα (στο
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ ΚΕΦΑΛΑΙΟ 4 ο και 5 ο Φυσικά μεγέθη από προηγούμενες τάξεις Θέση: x Μονάδα (στο SI) m Μετατόπιση: Δx Μονάδα (στο SI) m Τύπος Δx=x 2 -x 1 Ύψος: h Μονάδα (στο SI) m Μήκος: l Μονάδα (στο
ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ)
 ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ Θέµα. Ένας αρµονικός ταλανττής µε ασθενή απόσβεση, (µάζα=, σταθερά ελατηρίου= s, συντελεστής τριβής= r διεγείρεται
ΣΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΗΣ: ΦΥΣΙΚΗ-ΙΙΙ (ΚΥΜΑΤΙΚΗ Θέµα. Ένας αρµονικός ταλανττής µε ασθενή απόσβεση, (µάζα=, σταθερά ελατηρίου= s, συντελεστής τριβής= r διεγείρεται
Ε.Μ.Π. Σχολή Πολιτικών Μηχανικών Μάθημα «Φυσική (Ταλαντώσεις και Κύματα)», ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ (Διάρκεια 2 h 30 min)
 Ε.Μ.Π. Σχολή Πολιτικών Μηχανικών Μάθημα «Φυσική (Ταλαντώσεις και Κύματα)», 4-5 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ (Διάρκεια h 3 min) Η. Σ. Ζουμπούλης, Γ. Σ. Ράπτης Αθήνα, /9/5 Θέμα. Το ελατήριο του καθίσματος αυτοκινήτου
Ε.Μ.Π. Σχολή Πολιτικών Μηχανικών Μάθημα «Φυσική (Ταλαντώσεις και Κύματα)», 4-5 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ (Διάρκεια h 3 min) Η. Σ. Ζουμπούλης, Γ. Σ. Ράπτης Αθήνα, /9/5 Θέμα. Το ελατήριο του καθίσματος αυτοκινήτου
ΔΙΑΔΟΣΗ ΥΠΕΡΗΧΩΝ ΣΤΟΝ ΑΕΡΑ. Εξοικείωση με πειραματικές συσκευές υπερήχων και μελέτη της διάδοσης του ήχου:
 ΔΙΑΔΟΣΗ ΥΠΕΡΗΧΩΝ ΣΤΟΝ ΑΕΡΑ [1] ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Εξοικείωση με πειραματικές συσκευές υπερήχων και μελέτη της διάδοσης του ήχου: Σύστημα πομπού-δέκτη Διάδοση υπερήχων στον αέρα Ανάκλαση σε στερεά σώματα
ΔΙΑΔΟΣΗ ΥΠΕΡΗΧΩΝ ΣΤΟΝ ΑΕΡΑ [1] ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Εξοικείωση με πειραματικές συσκευές υπερήχων και μελέτη της διάδοσης του ήχου: Σύστημα πομπού-δέκτη Διάδοση υπερήχων στον αέρα Ανάκλαση σε στερεά σώματα
Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ. 31 Εκκρεµή - Απλό εκκρεµές θ l T mg r F Αυτή η εξίσωση είναι δύσκολο να λυθεί. Δεν µοιάζει µε τη γνωστή εξίσωση Για µικρές γωνίες θ µπορούµε όµως να γράψουµε Εποµένως
Αρµονικοί ταλαντωτές ΦΥΣ 131 - Διαλ. 31 Εκκρεµή - Απλό εκκρεµές θ l T mg r F Αυτή η εξίσωση είναι δύσκολο να λυθεί. Δεν µοιάζει µε τη γνωστή εξίσωση Για µικρές γωνίες θ µπορούµε όµως να γράψουµε Εποµένως
Μάθημα Ακουστικής. Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ
 Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ
 ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
ΚΕΦΑΛΑΙΟ 4: ΚΕΝΤΡΙΚΕΣ ΥΝΑΜΕΙΣ Οι σηµαντικότερες αντιπρόσποι της κατηγορίας αυτής τν δυνάµεν είναι οι δυνάµεις βαρύτητος και οι ηλεκτροστατικές δυνάµεις, που είναι ανάλογες του αντιστρόφου τετραγώνου της
Προτεινόμενα θέματα για τις εξετάσεις 2011
 Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ Άσκηση 1 Προσδιορίστε τη Σειρά Fourier (δηλαδή τους συντελεστές πλάτους A n και φάσης φ n ) του παρακάτω
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ Άσκηση 1 Προσδιορίστε τη Σειρά Fourier (δηλαδή τους συντελεστές πλάτους A n και φάσης φ n ) του παρακάτω
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β
 ΕΠΑΝΑΛΗΨΗ ΚΥΜΑΤΑ 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι
ΕΠΑΝΑΛΗΨΗ ΚΥΜΑΤΑ 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηχητικά Κύματα Εικόνα: Τα αυτιά του ανθρώπου έχουν εξελιχθεί να ακούν και να ερμηνεύουν ηχητικά κύματα ως φωνή ή ως ήχους. Κάποια ζώα, όπως το είδος αλεπούς με τα αυτιά νυχτερίδας,
Φυσική για Μηχανικούς Ηχητικά Κύματα Εικόνα: Τα αυτιά του ανθρώπου έχουν εξελιχθεί να ακούν και να ερμηνεύουν ηχητικά κύματα ως φωνή ή ως ήχους. Κάποια ζώα, όπως το είδος αλεπούς με τα αυτιά νυχτερίδας,
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s.
 1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
Κλινική χρήση των ήχων
 Κλινική χρήση των ήχων Ήχοι και ακουστότητα Κύματα υπερήχων Ακουστικά κύματα, Ήχοι, Είδη ήχων Ήχους υπό την ευρεία έννοια καλούμε κάθε κύμα πίεσης που υπάρχει και διαδίδεται στο εσωτερικό των σωμάτων.
Κλινική χρήση των ήχων Ήχοι και ακουστότητα Κύματα υπερήχων Ακουστικά κύματα, Ήχοι, Είδη ήχων Ήχους υπό την ευρεία έννοια καλούμε κάθε κύμα πίεσης που υπάρχει και διαδίδεται στο εσωτερικό των σωμάτων.
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΑ ΚΕΦΑΛΑΙΑ: ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΤΑΛΑΝΤΩΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ
 Σελίδα 1 από 6 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΑ ΚΕΦΑΛΑΙΑ: ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΤΑΛΑΝΤΩΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... ΘΕΜΑ Α Στις παρακάτω προτάσεις 1-5 να γράψετε στο τετράδιο
Σελίδα 1 από 6 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΑ ΚΕΦΑΛΑΙΑ: ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΤΑΛΑΝΤΩΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... ΘΕΜΑ Α Στις παρακάτω προτάσεις 1-5 να γράψετε στο τετράδιο
Το φαινόμενο Doppler
 Το φαινόμενο Doppler Η προσωπική μου άποψη είναι ότι και οι δύο αποδείξεις του σχολικού βιβλίου που αφορούν το φαινόμενο Doppler είναι λάθος. Ο κύριος λόγος για την ανωτέρω θέση μου είναι η χρήση της θεμελιώδους
Το φαινόμενο Doppler Η προσωπική μου άποψη είναι ότι και οι δύο αποδείξεις του σχολικού βιβλίου που αφορούν το φαινόμενο Doppler είναι λάθος. Ο κύριος λόγος για την ανωτέρω θέση μου είναι η χρήση της θεμελιώδους
2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier
 2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια του μετασχηματισμού Fourier συνίσταται στο ότι μία κυματομορφή
2 ο κεφάλαιο: Ανάλυση και Σύνθεση κυματομορφών με τον Μετασχηματισμό Fourier Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια του μετασχηματισμού Fourier συνίσταται στο ότι μία κυματομορφή
Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες:
 ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΩΝ (1) ΘΕΜΑ 1 ο Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες: 1) Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια και ορμή, αλλά όχι ύλη. 2) Σε
ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΩΝ (1) ΘΕΜΑ 1 ο Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες: 1) Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια και ορμή, αλλά όχι ύλη. 2) Σε
ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA -ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
EΞΑΝΑΓΚΑΣΜΕΝΕΣ TAΛANTΩΣEIΣ
 Kεφ. 3 EΞΑΝΑΓΚΑΣΕΝΕΣ TAΛANTΩΣEIΣ Θα εξετάσυμε τη περίπτση εφαρμγής σ ένα σύστημα μιάς δεδμένης εξτερικής δύναμης η πία να εξαρτάται από τ χρόν (δηλ. τ σύστημα υπβάλλεται σε εξτερική διέγερση. η περίπτση:
Kεφ. 3 EΞΑΝΑΓΚΑΣΕΝΕΣ TAΛANTΩΣEIΣ Θα εξετάσυμε τη περίπτση εφαρμγής σ ένα σύστημα μιάς δεδμένης εξτερικής δύναμης η πία να εξαρτάται από τ χρόν (δηλ. τ σύστημα υπβάλλεται σε εξτερική διέγερση. η περίπτση:
2.1. Τρέχοντα Κύματα.
 2.1. Τρέχοντα Κύματα. 2.1.1. Στιγμιότυπο κύματος Στη θέση x=0 ενός γραμμικού ομογενούς ελαστικού μέσου υπάρχει πηγή κύματος η οποία αρχίζει να ταλαντώνεται σύμφωνα με την εξίσωση y= 0,2ημπt (μονάδες στο
2.1. Τρέχοντα Κύματα. 2.1.1. Στιγμιότυπο κύματος Στη θέση x=0 ενός γραμμικού ομογενούς ελαστικού μέσου υπάρχει πηγή κύματος η οποία αρχίζει να ταλαντώνεται σύμφωνα με την εξίσωση y= 0,2ημπt (μονάδες στο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
Τεστ Αρμονικό κύμα Φάση κύματος
 Τεστ Αρμονικό κύμα Φάση κύματος ~Διάρκεια 90 min~ Θέμα Α 1) Όταν ένα κύμα αλλάζει μέσο διάδοσης, αλλάζουν i) η ταχύτητα διάδοσης του κύματος και η συχνότητά του ii) το μήκος κύματος και η συχνότητά του
Τεστ Αρμονικό κύμα Φάση κύματος ~Διάρκεια 90 min~ Θέμα Α 1) Όταν ένα κύμα αλλάζει μέσο διάδοσης, αλλάζουν i) η ταχύτητα διάδοσης του κύματος και η συχνότητά του ii) το μήκος κύματος και η συχνότητά του
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ενέργεια Συστήματος Εικόνα: Στη φυσική, η ενέργεια είναι μια ιδιότητα των αντικειμένων που μπορεί να μεταφερθεί σε άλλα αντικείμενα ή να μετατραπεί σε διάφορες μορφές, αλλά δεν μπορεί
Φυσική για Μηχανικούς Ενέργεια Συστήματος Εικόνα: Στη φυσική, η ενέργεια είναι μια ιδιότητα των αντικειμένων που μπορεί να μεταφερθεί σε άλλα αντικείμενα ή να μετατραπεί σε διάφορες μορφές, αλλά δεν μπορεί
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
2.6 Κύματα που παράγονται από δύο σύγχρονες. 2.7 Κύματα που παράγονται από δύο σύγχρονες. 2.8 Κύματα παράγονται από δύο σύγχρονες
 ΚΕΦΑΛΑΙΟ 2 Συμβολή κυμάτων 2.1 Το φαινόμενο της συμβολής των κυμάτων, ισχύει: α. μόνο στα μηχανικά κύματα, β. σε όλα τα είδη των κυμάτων, γ. μόνο στα ηλεκτρομαγνητικά. 2.2 Δύο σημεία Π, Π της ήρεμης επιφάνειας
ΚΕΦΑΛΑΙΟ 2 Συμβολή κυμάτων 2.1 Το φαινόμενο της συμβολής των κυμάτων, ισχύει: α. μόνο στα μηχανικά κύματα, β. σε όλα τα είδη των κυμάτων, γ. μόνο στα ηλεκτρομαγνητικά. 2.2 Δύο σημεία Π, Π της ήρεμης επιφάνειας
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 5.4 Η ταχύτητα υ διάδοσης του κύματος, η περίοδός του Τ και το μήκος κύματος λ, συνδέονται με τη σχέση:
 Αρμονικό κύμα ΚΕΦΑΛΑΙΟ 2 51 Κατά τη διάδοση ενός κύματος σε ένα ελαστικό μέσο: α μεταφέρεται ύλη, β μεταφέρεται ενέργεια και ύλη, γ όλα τα σημεία του ελαστικού μέσου έχουν την ίδια φάση την ίδια χρονική
Αρμονικό κύμα ΚΕΦΑΛΑΙΟ 2 51 Κατά τη διάδοση ενός κύματος σε ένα ελαστικό μέσο: α μεταφέρεται ύλη, β μεταφέρεται ενέργεια και ύλη, γ όλα τα σημεία του ελαστικού μέσου έχουν την ίδια φάση την ίδια χρονική
Θεωρία Κεφάλαιο 4 ο Γ Λυκείου Doppler
 Θεωρία Κεφάλαιο 4 ο Γ Λυκείου Doppler Φαινόμενο Doppler Η συχνότητα που αντιλαμβάνεται ο παρατηρητής δεν είναι ίδια με αυτήν που εκπέμπει μία πηγή όταν ο παρατηρητής και η πηγή βρίσκονται σε σχετική κίνηση
Θεωρία Κεφάλαιο 4 ο Γ Λυκείου Doppler Φαινόμενο Doppler Η συχνότητα που αντιλαμβάνεται ο παρατηρητής δεν είναι ίδια με αυτήν που εκπέμπει μία πηγή όταν ο παρατηρητής και η πηγή βρίσκονται σε σχετική κίνηση
Κβαντική Φυσική Ι. Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική. Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την εφαρμογή της
Κβαντική Φυσική Ι Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την εφαρμογή της
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
E = 1 2 k. V (x) = Kx e αx, dv dx = K (1 αx) e αx, dv dx = 0 (1 αx) = 0 x = 1 α,
 Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : ΗΜΕΡΟΜΗΝΙΑ :.
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : ΗΜΕΡΟΜΗΝΙΑ :. ΘΕΜΑ Α Α.1 Σε μια ελαστική χορδή ΟΓ, μήκους L δημιουργείται στάσιμο κύμα με 7 δεσμούς ως αποτέλεσμα της συμβολής δυο αρμονικών κυμάτων. Το
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ : ΗΜΕΡΟΜΗΝΙΑ :. ΘΕΜΑ Α Α.1 Σε μια ελαστική χορδή ΟΓ, μήκους L δημιουργείται στάσιμο κύμα με 7 δεσμούς ως αποτέλεσμα της συμβολής δυο αρμονικών κυμάτων. Το
Παραδείγµατα σχέσεων διασποράς Παραπάνω, φαίνεται η απόκριση ενός διηλεκτρικού µέσου σε
 Παραδείγµατα σχέσεων διασποράς Παραπάνω, φαίνεται η απόκριση ενός διηλεκτρικού µέσου σε ηλεκτροµαγνητικό κύµα κυκλ. Συχνότητας ω. Παρατηρούµε ότι η πολωσιµότητα του µέσου εξαρτάται µε την εκφραση 2.42
Παραδείγµατα σχέσεων διασποράς Παραπάνω, φαίνεται η απόκριση ενός διηλεκτρικού µέσου σε ηλεκτροµαγνητικό κύµα κυκλ. Συχνότητας ω. Παρατηρούµε ότι η πολωσιµότητα του µέσου εξαρτάται µε την εκφραση 2.42
H ENNOIA TΗΣ ΕΜΠΕΔΗΣΗΣ ΑΝΑΚΛΑΣΗ - ΔΙΑΘΛΑΣΗ ΜΕΡΟΣ I. Κωνσταντίνος Ευταξίας
 H ENNOI TΗΣ ΕΜΠΕΔΗΣΗΣ ΑΝΑΚΛΑΣΗ - ΔΙΑΘΛΑΣΗ ΜΕΡΟΣ I Κωνσταντίνος Ευταξίας H ΕΜΠΕΔΗΣΗ ΣΤΗΝ ΕΙΣΟΔΟ ΙΔΕΑΤΗΣ ΤΕΝΤΩΜΕΝΗΣ ΕΛΑΣΤΙΚΗΣ ΧΟΡΔΗΣ ΑΠΕΙΡΟΥ ΜΗΚΟΥΣ dm ή F dm έ F dm 0 0 0, y dm F F dm έ dm ή 0 dm έ y dm
H ENNOI TΗΣ ΕΜΠΕΔΗΣΗΣ ΑΝΑΚΛΑΣΗ - ΔΙΑΘΛΑΣΗ ΜΕΡΟΣ I Κωνσταντίνος Ευταξίας H ΕΜΠΕΔΗΣΗ ΣΤΗΝ ΕΙΣΟΔΟ ΙΔΕΑΤΗΣ ΤΕΝΤΩΜΕΝΗΣ ΕΛΑΣΤΙΚΗΣ ΧΟΡΔΗΣ ΑΠΕΙΡΟΥ ΜΗΚΟΥΣ dm ή F dm έ F dm 0 0 0, y dm F F dm έ dm ή 0 dm έ y dm
1. Κατά μήκος μιας χορδής μεγάλου μήκους, η οποία ταυτίζεται με τον άξονα x Ox, διαδίδονται ταυτόχρονα
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ 1. Κατά μήκος μιας χορδής μεγάλου μήκους, η οποία ταυτίζεται με τον άξονα x Ox, διαδίδονται ταυτόχρονα δύο αρμονικά κύματα που έχουν εξισώσεις y 1 = 0,1ημπ(5t,5x) (S.I.) και y = 0,1ημπ(5t
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ 1. Κατά μήκος μιας χορδής μεγάλου μήκους, η οποία ταυτίζεται με τον άξονα x Ox, διαδίδονται ταυτόχρονα δύο αρμονικά κύματα που έχουν εξισώσεις y 1 = 0,1ημπ(5t,5x) (S.I.) και y = 0,1ημπ(5t
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Διατήρηση της Ενέργειας Εικόνα: Η μετατροπή της δυναμικής ενέργειας σε κινητική κατά την ολίσθηση ενός παιχνιδιού σε μια πλατφόρμα. Μπορούμε να αναλύσουμε τέτοιες καταστάσεις με τις
Φυσική για Μηχανικούς Διατήρηση της Ενέργειας Εικόνα: Η μετατροπή της δυναμικής ενέργειας σε κινητική κατά την ολίσθηση ενός παιχνιδιού σε μια πλατφόρμα. Μπορούμε να αναλύσουμε τέτοιες καταστάσεις με τις
HMY 220: Σήματα και Συστήματα Ι
 HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου t (α) Αν το παραπάνω σύστηµα, ( m, s,
 Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου 9-1 ιάρκεια εξέτασης :3 5//1 Ι. Σ. Ράπτης Ε. Φωκίτης Θέµα 1. Ένας αρµονικός ταλαντωτής µε ασθενή απόσβεση (µάζα m σταθερά ελατηρίου
Σχολή E.Μ.Φ.Ε ΦΥΣΙΚΗ ΙΙΙ (ΚΥΜΑΤΙΚΗ) Κανονικές Εξετάσεις Χειµερινού εξαµήνου 9-1 ιάρκεια εξέτασης :3 5//1 Ι. Σ. Ράπτης Ε. Φωκίτης Θέµα 1. Ένας αρµονικός ταλαντωτής µε ασθενή απόσβεση (µάζα m σταθερά ελατηρίου
Παρατηρήσεις σε Θέματα Α. Επιλεγμένα θέματα από το study4exams, για τα οποία δίδονται επεξηγήσεις
 Παρατηρήσεις σε Θέματα Α Επιλεγμένα θέματα από το study4exams, για τα οποία δίδονται επεξηγήσεις 1. Αν μεταβληθεί η σταθερά αυτεπαγωγής του πηνίου σε ένα κύκλωμα L με αντιστάτη και πηγή εναλλασσόμενης
Παρατηρήσεις σε Θέματα Α Επιλεγμένα θέματα από το study4exams, για τα οποία δίδονται επεξηγήσεις 1. Αν μεταβληθεί η σταθερά αυτεπαγωγής του πηνίου σε ένα κύκλωμα L με αντιστάτη και πηγή εναλλασσόμενης
Δυναμική Μηχανών I. Απόκριση Γραμμικών Συστημάτων στο. Πεδίο της Συχνότητας
 Δυναμική Μηχανών I Απόκριση Γραμμικών Συστημάτων στο 7 4 Πεδίο της Συχνότητας 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς
Δυναμική Μηχανών I Απόκριση Γραμμικών Συστημάτων στο 7 4 Πεδίο της Συχνότητας 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς
ΔΙΑΓΩΝΙΣΜΑ. Ονοματεπώνυμο: Τμήμα: Γ ΘΕΜΑΤΑ:
 ΔΙΑΓΩΝΙΣΜΑ Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: 3 ΩΡΕΣ Ονοματεπώνυμο: Τμήμα: Γ ΘΕΜΑ Α ΘΕΜΑΤΑ: 1. Στα εγκάρσια κύματα, το μήκος κύματος λ είναι ίσο με την απόσταση: α) μεταξύ δύο
ΔΙΑΓΩΝΙΣΜΑ Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: 3 ΩΡΕΣ Ονοματεπώνυμο: Τμήμα: Γ ΘΕΜΑ Α ΘΕΜΑΤΑ: 1. Στα εγκάρσια κύματα, το μήκος κύματος λ είναι ίσο με την απόσταση: α) μεταξύ δύο
Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Ηλεκτρομαγνητικά Διαδίδονται στο κενό
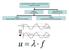 Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
ΣΤΑΣΙΜΟ ΚΥΜΑ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΥΤΑΞΙΑΣ
 ΣΤΑΣΙΜΟ ΚΥΜΑ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΥΤΑΞΙΑΣ TO ΣTAΣIMO KYMA: AΠΟΤΕΛΕΣΜΑ ΜΙΑΣ ΙΔΙΑΖΟΥΣΑΣ ΑΡΧΙΚΗΣ ΠΑΡΑΜΟΡΦΩΣΗΣ y y =0 = φ. T Σε χορδή έχει δοθεί το περίγραμμα y =0 = φ. O μηχανισμός που δίνει το περίγραμμα αποσύρεται
ΣΤΑΣΙΜΟ ΚΥΜΑ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΥΤΑΞΙΑΣ TO ΣTAΣIMO KYMA: AΠΟΤΕΛΕΣΜΑ ΜΙΑΣ ΙΔΙΑΖΟΥΣΑΣ ΑΡΧΙΚΗΣ ΠΑΡΑΜΟΡΦΩΣΗΣ y y =0 = φ. T Σε χορδή έχει δοθεί το περίγραμμα y =0 = φ. O μηχανισμός που δίνει το περίγραμμα αποσύρεται
3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α-Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α-Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
