ΠΛΗΡΕΣ ΒΟΗΘΗΜΑ ΣΤΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
|
|
|
- Ευδώρα Κλωθώ Κούνδουρος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΛΗΡΕΣ ΒΟΗΘΗΜΑ ΣΤΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ένα βοήθημα στο μάθημα για σίγουρη επιτυχία σε επτά βήματα Μουρατίδης Μάριος Μοσχονησιώτης Στέλιος Τερζόγλου Κυριάκος ISBN : ΔΡΑΠΕΤΣΩΝΑ 2015
2 ΠΛΗΡΕΣ ΒΟΗΘΗΜΑ ΣΤΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ένα βοήθημα στο μάθημα για σίγουρη επιτυχία σε επτά βήματα Μ. Μουρατίδης Σ. Μοσχονησιώτης Κ. Τερζόγλου ΠΕΡΙΕΧΕΙ : 145 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ 228 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 51 ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΣΤΟΙΧΙΣΗΣ ΠΛΗΡΕΣ ΤΥΠΟΛΟΓΙΟ ΑΣΚΗΣΕΩΝ 71 ΠΛΗΡΩΣ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 100 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ( ΔΙΝΟΝΤΑΙ ΟΙ ΑΠΑΝΤΗΣΕΙΣ ) ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΗΝΙΩΝ ( ΔΙΝΟΝΤΑΙ ΟΙ ΑΠΑΝΤΗΣΕΙΣ ISBN: Copyright Μ. Μουρατίδης Σ. Μοσχονησιώτης Κ. Τερζόγλου, Με επιφύλαξη παντός δικαιώματος. All rights reserved. Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή της παρούσας εργασίας, εξ ολοκλήρου ή τμήματος αυτής, για εμπορικό σκοπό. Επιτρέπεται η ανατύπωση, αποθήκευση και διανομή για σκοπό μη κερδοσκοπικό, εκπαιδευτικής φύσης, υπό την προϋπόθεση να αναφέρεται η πηγή προέλευσης και να διατηρείται το παρόν μήνυμα.
3 ΑΦΙΕΡΩΣΕΙΣ ΣΥΓΓΡΑΦΕΩΝ ΜΟΥΡΑΤΙΔΗΣ ΜΑΡΙΟΣ : Αφιερώνεται στην βαφτιστήρα μου Μαρία ΜΟΣΧΟΝΗΣΙΩΤΗΣ ΣΤΕΛΙΟΣ : Αφιερώνεται στην γυναίκα μου Ελένη και στα παιδιά μου Ευαγγελιάκι και Γιαννάκο ΤΕΡΖΟΓΛΟΥ ΚΥΡΙΑΚΟΣ : Αφιερώνεται στους μαθητές μου Νίκο και Δημήτρη καθώς και στους συναδέλφους που δουλέψαμε μαζί
4 ΕΙΣΑΓΩΓΗ Μέσα από τη συνεχή ενασχόλησή μας με το πανελλαδικά εξεταζόμενο μάθημα «Στοιχεία Μηχανών» ανακαλύψαμε την ολοένα και μεγαλύτερη αναγκαιότητα ενός βοηθήματος που θα κάλυπτε το μαθητικό δυναμικό στον τομέα όπου κατά τεκμήριο κρίνεται η εισαγωγή τους στην τριτοβάθμια εκπαίδευση: στην επίλυση των ασκήσεων. Με αυτό το σκεπτικό προσπαθήσαμε να δώσουμε με απλό τρόπο την στρατηγική επίλυσης των ασκήσεων μέσα από μια σειρά από καθορισμένα βήματα τα οποία προτείνουμε στο μαθητή να ακολουθήσει: ΒΗΜΑ 1 Ο : Πριν ξεκινήσεις την προσπάθεια σου για τις ασκήσεις σιγουρέψου ότι κατέχεις σε υψηλό επίπεδο τη θεωρία του αντίστοιχου κεφαλαίου. ΒΗΜΑ 2 Ο : Διάβασε προσεκτικά την πρώτη σελίδα απο κάθε ενότητα που δίνει το σύμβολο και τις μονάδες απο κάθε χρησιμοποιούμενο μέγεθος της ενότητας. Δεν μπορείς να επεξεργαστείς ασκήσεις αν δεν γνωρίζεις ποιών μεγεθών η τιμή ζητείται και σε ποιες μονάδες. ΒΗΜΑ 3 Ο : Διάβασε συστηματικά το τυπολόγιο που σου δίνεται ακολούθως. Όλες οι ασκήσεις στα «Στοιχεία Μηχανών» όπως διδάσκονται είναι ασκήσεις αντικατάστασης και άρα οι τύποι που εμπλέκονται τα μεγέθη πρέπει να γίνουν κτήμα σου. Θα προχωρήσεις στο επόμενο βήμα μόνο όταν εισαι σε θέση μόνος σου να αναπαράγεις το τυπολόγιο. ΒΗΜΑ 4 Ο : Ακολουθεί μια σειρά από ασκήσεις συμπλήρωσης πινάκων. Ο στόχος αυτών των ασκήσεων είναι η απλή εφαρμογή των τύπων. Όσο και αν σου φανεί βαρετή η διαδικασία συμπλήρωσης τους μη την προσπεράσεις. Θα σε βοηθήσει να αυτοματοποιήσεις και να εμπεδώσεις τη χρήση του τυπολόγιου. ΒΗΜΑ 5 Ο : Παρακάτω ακολουθεί μια σειρά από λυμένες ασκήσεις. Προσπάθησε να τις λύσεις με τις υπάρχουσες γνώσεις σου. Αν δεν το καταφέρεις μην απογοητευτείς. Οι ασκήσεις αυτές καλύπτουν ένα ευρύ φάσμα στη μηχανολογία, απαιτούν κριτική σκέψη και εμπειρία. Γιαυτό το λόγο δίνονται και λυμένες. Σημασία όμως έχει να κοπιάσεις πριν καταφύγεις στην «έτοιμη» λύση. Η ενασχόλησή σου με αυτές θα σε εισάγει στην πραγματική φύση του μαθήματος, θα σου αποκαλύψει γνώση. ΒΗΜΑ 6 Ο : Η σειρά από άλυτες ασκήσεις που έπεται θα πρέπει εύκολα ή δύσκολά πλέον να λύνονται. Το αποτέλεσμα σε κάθε άσκηση δίνεται ώστε να ελέξεις την λύση που έδωσες. Είναι το τελευταίο και πιο επίπονο βήμα πριν το τελικό. ΒΗΜΑ 7 Ο : Το τελευταίο βήμα αναφέρεται στα ως τώρα θέματα των πανελληνίων εξετάσεων. Προφανώς δίνονται άλυτα με τις απαντήσεις τους. Θεώρησε σίγουρο πως αν έχεις ακολουθήσει πιστά τα προηγούμενα βήματα θα χρειαστείς 8 έως 10 λεπτά το πολύ για την επίλυση κάθε θέματος. Εκεί θα συνειδητοποιήσεις και πόσο έτοιμος και σίγουρος θα είσαι για την τελική εξέταση.
5 Το βοήθημα συμπληρώνεται με ερωτήσεις κλειστού τύπου (σωστό λάθος, αντιστοίχησης, πολλαπλής επιλογής) καθώς και με ερωτήσεις ανοικτού τύπου σύμφωνα με τα προβλεπόμενα για επανάληψη της εξεταστέας ύλης. Ευχόμαστε η προσπάθεια να τύχει ανταπόκρισης τόσο στον μαθητικό όσο και στον εκπαιδευτικό κόσμο του μηχανολογικού τομέα. Τέλος δίνονται σε ένα παράρτημα το οποίο χωρίζεται σε τρία μέρη τα εξής : α) Οι απαντήσεις των ερωτήσεων αντιστοίχησης και Σωστού Λάθους, β) Οι ερωτήσεις που αποτέλεσαν θέματα Πανελλαδικών εξετάσεων και γ) οι απαραίτητες διορθώσεις που πρέπει να γίνουν στο άμεσο μέλλον στο σχολικό εγχειρίδιο σύμφωνα με έγγραφο με τις παρατηρήσεις μας που έχει αποσταλλεί από το Φεβρουάριο του 2015, στους σχολικούς συμβούλους. Το παράρτημα 3 δεν αφορά το μαθητή επι του παρόντος αλλά το διδάσκων του μαθήματος. Δεχόμενοι κάθε καλόπιστη κριτική κλείνουμε με τις θερμότερες ευχές μας για καλή επιτυχία στις εξετάσεις. Η συγγραφική ομάδα
6 1 [ΕΙΣΑΓΩΓΗ] Υπενθύμιση εισαγωγικών εννοιών για την καλύτερη κατανόηση της θεωρίας και των ασκήσεων
7 ΕΙΣΑΓΩΓΗ Μ.Μ.Τ ΣΥΜΒΟΛΙΣΜΟΙ : F ορθή δύναμη (κάθετη στην επιφάνεια N, ddd, KK Q διατμητική δύναμη (πάνω στην επιφάνεια) N, ddd, KK A επιφάνεια καταπόνησης m 2, cc 2. mm 2 M b ροπή κάμψης N m, ddd m, ddd cc M t ροπή στρέψης N m, ddd m, ddd cc W b ροπή αντίστασης έναντι κάμψης m 3, cc 3. mm 3 W t ροπή αντίστασης έναντι στρέψης m 3, cc 3. mm 3 σ τ ορθή τάση διατμητική τάση Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 ν συντελεστής ασφαλείας σ επ. τ επ. σ θρ. τ θρ. ορθή επιτρεπόμενη τάση διατμητική επιτρεπομένη τάση όριο θραύσης ορθής τάσης όριο θραύσης διατμητικής τάσης Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 Ν m 2, ddd m 2, ddd cc 2, ddd mm 2 2
8 ΕΙΣΑΓΩΓΗ Μ.Μ.Τ ΚΑΤΑΠΟΝΗΣΕΙΣ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΤΟΧΗΣ : ΚΑΤΑΠΟΝΗΣΗ ΑΙΤΙΟ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΔΙΑΤΟΜΗΣ Εφελκυσμός-θλίψη Αξονική δύναμη F Επιφάνεια Α ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΑΝΤΟΧΗΣ ΥΛΙΚΟΥ Επιτρεπόμενη ορθή τάση σ επ σ = F A σ εε ΚΑΤΑΠΟΝΗΣΗ ΑΙΤΙΟ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΔΙΑΤΟΜΗΣ Διάτμηση Εγκάρσια δύναμη Q Επιφάνεια Α ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΑΝΤΟΧΗΣ ΥΛΙΚΟΥ Επιτρεπόμενη διατμητική τάση τ επ τ = Q A τ εε 3
9 ΕΙΣΑΓΩΓΗ Μ.Μ.Τ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΚΑΤΑΠΟΝΗΣΗ ΑΙΤΙΟ ΔΙΑΤΟΜΗΣ Ροπή αντίστασης σε Κάμψη Ροπή κάμψης M b κάμψη W b ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΑΝΤΟΧΗΣ ΥΛΙΚΟΥ Επιτρεπόμενη ορθή τάση σ επ σ b = M b W b σ εε ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΚΑΤΑΠΟΝΗΣΗ ΑΙΤΙΟ ΔΙΑΤΟΜΗΣ Ροπή αντίστασης σε Στρέψη Ροπή στρέψης M t στρέψηw t ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΑΝΤΟΧΗΣ ΥΛΙΚΟΥ Επιτρεπόμενη διατμητική τάση τ επ τ t = M t W t τ εε ΣΥΝΤΕΛΕΣΤΗΣ ΑΣΦΑΛΕΙΑΣ : ν = σ θθ. σ εε., ν = τ θθ. τ εε. 4
10 2 [ΗΛΩΣΕΙΣ] Περιλαμβάνει ερωτήσεις ανάπτυξης, ερωτήσεις σωστού- λάθους, ερωτήσεις αντιστοιχισης, τυπολόγιο ασκήσεων ηλώσεων,εφαρμογές επι του τυπολογίου,λυμένες ασκήσεις, Αλυτες ασκήσεις με απάντησεις και θέματα Πανελλαδικών Εξετάσεων με τις απαντήσεις
11 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΗΛΟΙ-ΗΛΩΣΕΙΣ ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΧΤΟΥ ΤΥΠΟΥ 1. Ποιος είναι ο σκοπός της χρήσης των μέσων σύνδεσης; (σ.131) 2. Ποια είναι τα βασικά μέσα σύνδεσης; (σ.131) 3. Σε τι διακρίνονται οι συνδέσεις ανάλογα με τα χαρακτηριστικά που παρουσιάζουν; (σ.132) 4. Από πόσα και ποια μέρη αποτελείται ο ήλος; (σ.133) 5. Πως κατασκευάζεται ένας ήλος; (σ.133) 6. Ποιες είναι οι κατηγορίες των ήλων ανάλογα με τη μορφή της κεφαλής τους; (σ.133) 7. Ποιες είναι οι κατηγορίες των ήλων ανάλογα με τη διάμετρο του κορμού τους; (σ.134) 8. Από τι υλικά κατασκευάζονται οι ήλοι; (σ.134) 9. Ποιες είναι οι κύριες διαστάσεις ενός ήλου; (σ.135) 10. Ποια στοιχεία δίνουμε για την προμήθεια ενός ήλου; (σ.135) 11. Τι είναι ήλωση; (σ.136) 12. Ποια είναι τα μειονεκτήματα των ηλώσεων; (σ.136) 13. Σε ποιες περιπτώσεις οι ηλώσεις θεωρούνται αναντικατάστατες; (σ.136) 14. Ποιοι είναι οι τύποι των ηλώσεων ανάλογα με το σκοπό και τις απαιτήσεις που προορίζονται; (σ ) 15. Ποιοι είναι οι τύποι των ηλώσεων ανάλογα με τον τρόπο κατασκευής; (σ.137) 16. Ποιοι είναι οι τύποι των ηλώσεων ανάλογα με τις σειρές των ήλων; (σ.137) 17. Ποιοι είναι οι τύποι των ηλώσεων ανάλογα με τον αριθμό των διατομών των ήλων; (σ.139) 18. Τι συμβολίζουν στην ήλωση τα: 1) t, 2) e, 3) e 1 και 4) e 2 ; (σ.140) 19. Ποιες είναι οι μέθοδοι κατασκευής των ηλώσεων; (σ.140) 20. Τι προσέχουμε για να είναι επιτυχημένη μια ήλωση; (σ.141) 6
12 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ Να βρείτε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος 1. Υπάρχουν περιπτώσεις που οι συνδέσεις γίνονται χωρίς μέσο σύνδεσης π.χ (η σύνδεση άξονατρύματος), με θέρμανση ή ψύξη του ενός από τα δύο. 2. Λυόμενες συνδέσεις ονομάζονται αυτές που τα συνδεόμενα κομμάτια αποσυναρμολογούνται μόνο με καταστροφή του μέσου σύνδεσης. 3. Με τις συνδέσεις επιτυγχάνεται η μεταβίβαση δυνάμεων ή ροπών από το ένα κομμάτι στο άλλο. 4. Η ήλωση είναι λυόμενη σύνδεση. 5. Η κεφαλή των ημιστρόγγυλων ήλων μπορεί να είναι βυθισμένη στα κομμάτια που συνδέει ή ημιβυθισμένη. 6. Στους βυθισμένους ήλους, σαν μήκος (l) του ήλου λαμβάνεται το μήκος του κορμού συν το ύψος της κεφαλής (k). 7. Η επιλογή του υλικού του ήλου γίνεται με βάση την αντοχή του. 8. Οι ηλώσεις που χρησιμοποιούνται για την κατασκευή γερανών είναι ηλώσεις προσκολλήσεως. 9. Σταθερές και στεγανές (στερεοστεγανές ηλώσεις) χρησιμοποιούνται εκεί που επιθυμούμε στεγανότητα και μεταφορά δυνάμεων. 10. Στην ήλωση με αρμοκαλύπτρες τα συνδεόμενα ελάσματα τοποθετούνται μετωπικά. 11. Όταν οι άξονες των ήλων συμπίπτουν, η ήλωση ονομάζεται ρομβοειδής ή ζικ-ζακ. 12. Η απόσταση μεταξύ δύο γειτονικών ήλων της ίδιας σειράς ονομάζεται βήμα της ήλωσης. 13. Στη μηχανική μέθοδο κατασκευής ηλώσεων η σύσφιξη των ελασμάτων γίνεται αυτόματα με τη μηχανή. 14. Στην ήλωση πρέπει η οπή να ανοίγεται ταυτόχρονα και στα δύο ελάσματα. 15. Πριν το τρύπημα δε χρειάζεται να γίνει σύσφιξη των ελασμάτων. 7
13 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΣΤΟΙΧΙΣΗΣ ΑΝΤΙΣΤΟΙΧΙΣΗ 1 1. d = 1 ως 3mm Α. Επιπεδοκαμπύλος 2. d = 1 ως 9mm Β. Φακοειδής 3. d > 10mm Γ. Ημιστρόγγυλος 4. Μεγάλη και καμπυλωτή κεφαλή Δ. Σωληνωτός 5. Βυθισμένος ή ημιβυθισμένος Ε. Λεβητόκαρφο ΣΤ. Πριτσίνι ΑΝΤΙΣΤΟΙΧΙΣΗ 2 1. Ήλωση Α. Λυόμενη σύνδεση με μπουζόνια 2. Κοχλιοσύνδεση Β. Μόνιμη σύνδεση με διαμόρφωση 3. Σύνδεση με σφήνα Γ. Μόνιμη σύνδεση που απαιτεί θερμότητα 4. Συγκόλληση Δ. Λυόμενη σύνδεση απόσβεσης κραδασμών 5. Σύνδεση με ελατήρια Ε. Λυόμενη σύνδεση που συνδέει άξονα με τρύμα ΣΤ. Μόνιμη σύνδεση με κοχλίες κεφαλής 8
14 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 3 1. Σταθερή ήλωση Α. Επένδυση σκελετού σε ελικόπτερο 2. Στεγανή ήλωση Β. Τα συνδεόμενα ελάσματα τοποθετούνται μετωπικά 3. Στερεοστεγανή ήλωση Γ. Δοχείο νερού 4. Ήλωση προσκολλήσεως Δ. Μεταλλικό κτίριο 5. Ήλωση με αρμοκαλύπτρα Ε. Τα συνδεόμενα ελάσματα τοποθετούνται το ένα πάνω στο άλλο ΣΤ. Λέβητας ατμού ΑΝΤΙΣΤΟΙΧΙΣΗ 4 1. t Α. Μήκος κορμού ήλου 2. d Β. Βήμα ήλωσης 3. k Γ. Απόσταση ακραίας σειράς ήλων από άκρη ελάσματος 4. l Δ. Απόσταση μεταξύ δύο παράλληλων σειρών ήλων 5. e Ε. Διάμετρος κορμού ήλου ΣΤ. Ύψος κεφαλής ήλου 9
15 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ 1. ΑΝΤΙΣΤΟΙΧΙΣΗ 5 Α. ΗΜΙΣΤΡΟΓΓΥΛΟΣ ΗΛΟΣ 2. Β. ΗΜΙΣΤΡΟΓΓΥΛΟΣ ΒΥΘΙΣΜΕΝΟΣ ΗΛΟΣ 3. Γ. ΦΑΚΟΕΙΔΗΣ ΗΜΙΒΥΘΙΣΜΕΝΟΣ ΗΛΟΣ 4. Δ. ΠΛΑΤΥΚΕΦΑΛΟΣ ΗΛΟΣ 5. Ε. ΣΩΛΗΝΩΤΟΣ ΗΛΟΣ ΣΤ. ΦΑΚΟΕΙΔΗΣ ΒΥΘΙΣΜΕΝΟΣ ΗΛΟΣ 10
16 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 6 Α. ΜΗΚΟΣ ΗΛΟΥ (l) Β. ΚΕΦΑΛΗ ΗΛΟΥ Γ. ΔΙΑΜΕΤΡΟΣ ΚΟΡΜΟΥ (d) Δ. ΚΟΡΜΟΣ ΗΛΟΥ Ε. ΔΙΑΜΕΤΡΟΣ ΚΕΦΑΛΗΣ (D) ΣΤ. ΥΨΟΣ ΚΕΦΑΛΗΣ (K) ΑΝΤΙΣΟΙΧΙΣΗ 7 Α. e 1 Β. t Γ. d 1 Δ. e Ε. e 2 ΣΤ. d 11
17 ΘΕΩΡΙΑ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 8 1. ΗΛΩΣΗ ΜΕ ΕΠΙΚΑΛΥΨΗ, ΔΙΠΛΗΣ ΣΕΙΡΑΣ ΖΙΚ-ΖΑΚ Α. 2. ΗΛΩΣΗ ΜΕ ΔΙΠΛΗ ΑΡΜΟΚΑΛΥΠΤΡΑ, ΔΙΠΛΗΣ ΣΕΙΡΑΣ Β. 3. ΗΛΩΣΗ ΜΕ ΕΠΙΚΑΛΥΨΗ, ΔΙΠΛΗΣ ΣΕΙΡΑΣ ΠΑΡΑΛΛΗΛΗ Γ. 4. ΗΛΩΣΗ ΜΕ ΔΙΠΛΗ ΑΡΜΟΚΑΛΥΠΤΡΑ, ΑΠΛΗΣ ΣΕΙΡΑΣ Δ. 5. ΗΛΩΣΗ ΜΕ ΕΠΙΚΑΛΥΨΗ ΤΡΙΠΛΗΣ ΣΕΙΡΑΣ ΖΙΚ-ΖΑΚ Ε. ΣΤ 12
18 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΣΥΜΒΟΛΙΣΜΟΙ : ΣΥΜΒΟΛΟ ΕΠΕΞΗΓΗΣΗ ΜΟΝΑΔΕΣ τ Διατμητική τάση του ήλου dan/cm 2 Q Διατμητικη δύναμη στον ήλο dan n Αριθμός σειρών ήλωσης m Αριθμός τομών της ήλωσης z Συνολικός Αριθμός ήλων A Εμβαδόν διατομής του ήλου cm 2 z κ Αριμός ήλων στην κρίσιμη διατομή Ακ Εμβαδόν ελάσματος στην κρίσιμη διατομή cm 2 d Διάμετρος ήλου mm,cm d 1 Διάμετρος καρφότρυπας mm,cm t Βήμα ήλωσης mm,cm s Πάχος ελάσματος mm,cm s1,s2 Πάχη αρμοκαλύπτρας mm,cm F Εφελκυστική δύναμη ελάσματος dan e Απόσταση μεταξύ δύο παράλληλων σειρών ήλων mm,cm e 1 Απόσταση της ακραίας σειράς ήλων από την άκρη του ελάσματος mm,cm e 2 Απόσταση του άξονα των ήλων από τον αρμό ( σε αρμοκαλύπτρες ) mm,cm μ Συντελεστής τριβής ελασμάτων σ L Πίεση συνθλιψης dan/cm 2 F τρ Δύναμη τριβής των ελασμάτων dan σ επ Επιτρεπόμενη εφελκυστική τάση dan/cm 2 τ επ Επιτρεπόμενη διατμητική τάση dan/cm 2 13
19 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ Α) ΚΑΤΗΓΟΡΙΕΣ ΗΛΩΣΕΩΝ ΤΥΠΟΛΟΓΙΟ ΗΛΩΣΕΩΝ Ηλωση επικάλυψης (n=1) Ηλωση μονής αρμοκαλύπτρας (n=2) Ηλωση διπλής αρμοκαλύπτρας (n=2) Α) Διατμητική καταπόνηση στους ήλους ττ = m =1 για ήλωση επικάλυψης και μονής αρμοκαλύπτρας m =2 για ήλωση με διπλή αρμοκαλύπτρα z : Συνολικός αριθμός ήλων στην ήλωση QQ zz AA mm (σε ηλώσεις με αρμοκαλύπτρα ο συνολικός zθεωρείται δεξιά ή αριστερά του αρμού ) Q : Δύναμη καταπόνησης των ήλων Εμβαδό διατομής ήλου ππ dd2 ΑΑ = 4 Διάμετρος καρφοτρύπας dd 1 = (dd + 1)mmmm Ελεγχος διατμητικής αντοχής των ήλων ττ ττ εεεε 14
20 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ Β) Εφελκυστική καταπόνηση των ελασμάτων σσ = FF AA κκ F : Δύναμη εφελκυσμού του ελάσματος ( ίδια με την διατμητική δύναμη Q του ήλου ) Ακ : Εμβαδό ελάσματος στην κρίσιμη διατομή ΑΑ κκ = (bb zz kk dd 1 ) ss b : Πλάτος ελάσματος s : Πάχος ελάσματος z κ : Αριθμός ήλων στην κρίσιμη διατομή Ελεγχος εφελκυστικής αντοχής των ελασμάτων σσ σσ εεεε Γ) Πίεση σύνθλιψης της εσωτερικής επιφάνειας της οπής Σχέση πίεσης σύνθλιψης με την επιτρεπόμενη τάση Δ) Δύναμη τριβής FF ττττ = FF aaaa μμ μ : Συντελεστής τριβής των ελασμάτων FF aaaa : Αξονική δύναμη που καταπονεί τον ήλο σσ LL = QQ zz dd ss σσ LL < 2.5 σσ εεεε σσ = FF AA 15
21 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ Ε) Διαστάσεις ηλωσεων t βήμα ήλωσης : απόσταση δύο διαδοχικών ήλων της ίδιας σειράς e1 : απόσταση ακραίας σειράς ήλων από τον αρμό e : Απόσταση σειράς των ήλων Για στεγανές ηλώσεις dd 1 = 5 SS 0.4 cccc tt = (3 dd + 0.5)cccc ee 1 = 1.5 dd Για σταθερές dd 1 = 5 ss 0.2 cccc tt = (3 dd)cccc 16
22 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΣΤ) Εμπέδωση για την σωστή χρήση των τύπων σε ασκήσεις Σε ήλωση επικάλυψης ή μονής αρμοκαλύπτρας n=1, m=1, z=3,z k =3 n=2, m=1, z=3, z k =2 n=1, m=1, z=4,z k =4 n=2, m=1, z=4, z k =2 n=1, m=1, z=4, z k =4 n=2, m=1, z=4,z k =2 17
23 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ Σε ήλωση διπλής αρμοκαλύπτρας n=1, m=2, z=3,z k =3 n=2, m=1, z=3, z k =2 n=1, m=2, z=4,z k =4 n=2, m=2, z=4, z k =2 n=3, m=2, z=5,z k =2 n=2, m=2, z=5, z k =3 18
24 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ Εφαρμογές επί του τυπολογίου τ ( kp/cm 2 ) Q ( kp) A ( cm 2 ) z m d ( mm ) A (cm 2 ) A ( cm 2 ) b ( cm ) z κ d 1 ( cm ) S ( cm ) σ ( kp/cm 2 ) F ( kp ) A ( cm 2 ) σ ( kp/cm 2 ) F ( kp ) A ( cm 2 ) d ( cm ) d 1 ( cm ) z κ b ( cm ) S ( cm ) σ L ( dan/cm 2 ) Q (dan ) z d ( cm ) s ( cm )
25 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΗΛΩΣΕΙΣ 1/Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,φορτίο Q=9420daN,τεπ= 1000 dan cm 2.Ζητούνται : α/η διάμετρος των ήλων d, β/η διάμετρος οπών των ελασμάτων d 1 α) Χρησιμοποιώντας την σχέση διατμητικής αντοχής του ήλου θα έχουμε : τ τ επ και στην ακραία περίπτωση τ = τ επ Για την διάμετρο του ήλου βρίσκουμε αρχικά το εμβαδόν του ήλου Α από τον τύπο: τ επ = Q m z k A Α = Q m z k τ επ Αντικαθιστώντας τις τιμές από την εκφώνηση και θέτωντας m=1 διότι έχουμε ηλωση επικάλυψης θα έχουμε : Α = Q m z k τ επ Α = 9420daN dan cm 2 A = cm2 A = 3.14cm 2 Η διάμετρος του ήλου θα βρεθεί από τον τύπο : Α = π d2 4 d 2 = 4 A π d2 = cm d 2 = 4cm 2 Και αποτετραγωνίζοντας θα έχουμε : d 2 = 4cm 2 d = 4cm 2 d = 4 cm 2 d = 2cm ή d = 20mm β) Η διάμετρος οπών των ελασμάτων θα βρεθεί από τον τύπο : d 1 = (d + 1)mm d 1 = (20 + 1)mm d 1 = 21mm 20
26 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 2/Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,φορτίο Q=9420daN,τεπ= 1000 dan cm 2. Ζητούνται : α/η διάμετρος των ήλων d, β/η διάμετρος οπών των ελασμάτων d 1 ( Δίνεται ότι 2 = 1,41 ) α) Χρησιμοποιώντας την σχέση διατμητικής αντοχής του ήλου θα έχουμε : τ τ επ και στην ακραία περίπτωση τ = τ επ Για την διάμετρο του ήλου βρίσκουμε αρχικά το εμβαδόν του ήλου Α από τον τύπο: τ επ = Q m zz A Α = Q m z τ επ Αντικαθιστώντας τις τιμές από την εκφώνηση και θέτωντας m=2 (ήλωση με διπλή αρμοκαλύπτρα )θα έχουμε : Α = Q m z τ επ Α = 9420daN dan cm 2 A = cm2 A = 1,57cm 2 Η διάμετρος του ήλου θα βρεθεί από τον τύπο : Α = π d2 4 d 2 = 4 A π d2 = 4 1,57cm d 2 = 2cm 2 Και αποτετραγωνίζοντας θα έχουμε : d 2 = 2cm 2 d = 2cm 2 d = 2 cm 2 d = 1,41cm ή d = 14,1mm Επιλέγεται ήλος με διάμετρό d =15mm β) Η διάμετρος οπών των ελασμάτων θα βρεθεί από τον τύπο : d 1 = (d + 1)mm d 1 = (15 + 1)mm d 1 = 16mm 21
27 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 3/Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,τ θρ = 2500 dan cm 2, συντελεστής ασφαλείας ν=5 και διάμετρος καρφότρυπας d 1 =11mm. Ζητήται η δύναμη Q των ήλων Χρησιμοποιώντας την σχέση διατμητικής αντοχής του ήλου θα έχουμε : τ τ επ και στην ακραία περίπτωση τ = τ επ Για την διάμετρο του ήλου έχουμε d 1 = (d + 1)mm dd = (d 1 1)mm d = (11 1)mm d = 10mm Το εμβαδό του ήλου θα είναι : Α = π d2 4 Α = 3,14 12 cccc 2 4 A = 0.785cccc 2 Για το τ επ θα έχουμε : ν = τ θρ τ τ επ = τ θρ επ ν τ επ = 2500 dan cm 2 5 τ επ = 500 dan cm 2 Τέλος η επιτρεπόμενη διατμητική δύναμη Q του ήλου θα προκύψει από τον τύπο : τ επ = Q m zz A QQ = τ επ m z A Q = 500 dan cm cccc 2 Q = daN 4/Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,φορτίο F=2000 dan,διάμετρος ήλων d=10mm,τ επ =200 dan cm 2. Να ελεγχθούν οι ήλοι σε διάτμηση Αρχικά βρίσκουμε το εμβαδόν του κάθε ήλου σε cm από τον τύπο : Α = π d2 4 A = cm 2 4 A = 3.14cm 2 Η διατμητική τάση για την ήλωση επικάλυψης θα βρεθεί από τον τύπο : τ = Και θέτωντας m=1 ( ήλωση επικάλυψης ) θα έχουμε : τ = Q m zz A 2000daN cm 2 τ = 2000daN 12,56cm 2 τ = 159,23 dan cm 2 Για να ελεγχθούν οι ήλοι σε διάτμηση θα πρέπει : τ τ επ Και επειδή το τ = 159,23 dan cm 2 είναι μικρότερο από το τ επ =200 dan cm 2 οι ήλοι αντέχουν σε διάτμηση 22
28 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 5/Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,φορτίο Q=9420daN,σ επ = 2300 dan cm 2, διάμετρος καρφότρυπας d 1 =21mm, πλάτος ελασμάτων b=144 mm,πάχος ελασμάτων s=5mm.ζητούνται : α/η επιφάνεια του ελάσματος μετά το τρύπημα Α κ και β/να γίνει έλεγχος αντοχής των ελασμάτων σε εφελκυσμό. α) Η επιφάνεια του ελάσματος μετά το τρύπημα θα βρεθεί από τον τύπο : Α κκ = (b z k d 1 ) s Θα είναι καλύτερο το εμβαδόν του ελάσματος να βρεθεί σε cm 2 οπότε : Α κ = (b z k d 1 ) s Α κ = (14.4cm 3 2.1cm) 0.5cm Α κ = 4.05cm 2 β)από την σχέση αντοχής των ελασμάτων θα πρέπει : σ σ επ Η εφελκυστική τάση του ελάσματος θα βρεθεί από τον τύπο : σ = F Α κ Τονίζουμε ότι η δύναμη Q=9420daN είναι διατμητική για τους ήλους ενώ είναι εφελκυστική για το έλασμα οπότε θα είναι F=9420daN και αντικαθιστώντας θα έχουμε : σ = F σ = 9420daN Α κ 4.05cm 2 σ = dan cm 2 Και επειδή το σ = dan cm 2 είναι μεγαλύτερο από το σ επ = 2300 dan cm 2 τα ελάσματα δεν αντέχουν στον εφελκυσμό Σκέψη : Τι θα μπορούσαμε να αλλάξουμε ετσι ώστε τα ελάσματα να αντέχουν τελικά σε εφελκυσμό ; Διαφορετικό ύλικό με σ επ μεγαλύτερο Μεγαλύτερο πλάτος ή πάχος ή και τα δύο για το έλασμα Μεγαλύτερη διάμετρος ήλων οπότε και καρφοτρύπας εφόσον τηρούνται οι αποστάσεις ( t=3d ) 23
29 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 6/ Για μια ήλωση γνωρίζουμε ότι τ επ = 1500 dan cm 2, το τ θρ = 3000 dan cm 2 ενώ το σ επ = 1000 dan cm 2 και το σ θρ = 3000 dan cm 2. Να υπολογισθεί ο συνολικός συντελεστής ασφαλείας v Από τον τύπο του συντελεστή ασφαλείας θα έχουμε για την διάτμηση : ν = τ θρ ν = 3000 dan cm 2 τ επ 1500 dan cm 2 ν = 2 Από τον τύπο του συντελεστή ασφαλείας θα έχουμε για τον εφελκυσμό : ν = σ θρ ν = 3000 dan cm 2 σ επ 1000 dan cm 2 ν = 3 Παρατηρούμε ότι έχουμε διαφορετικό συντελεστή για την διάτμηση και διαφορετικό συντελεστή για τα ελάσματα. Σε αυτήν την περίπτωση εκλέγουμε συνολικό συντελεστή για την ήλωση τον μεγαλύτερό δηλαδή ν=3 7/ Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,φορτίο Q=9420daN,σ επ = 1200 dan cm 2, διάμετρος καρφότρυπας d 1 =21mm, και πάχος ελασμάτων s=10mm. Να βρεθεί το απαιτούμενο πλάτος των ελασμάτων Από την συνθήκη εφελκυστικής αντοχής των ελασμάτων θα πρέπει : σ σ επ και στην ακραία περίπτωση σ = σ επ Γνωρίζοντας το σ επ και το φορτίο F=9420daN θα βρούμε το εμβαδό των ελασμάτων από τον τύπο : σ επ = F Α κ Α κ = F σ επ Α κ = 9420daN 1200 dan cm 2 Α κ = 7.85cm 2 Και τελικά το απαιτούμενο πλάτος στην κρίσιμη διατομή θα βρεθεί από τον τύπο : Και έπειτα : Α κ = (b z k d 1 ) s (b z k d 1 ) = Α κ s (b z k d 1 ) = 7.85cm2 1cm (b z k d 1 ) = 7.85cm (b z k d 1 ) = 7.85cm b = 7.85cm + z k d 1 b = 7.85cm cm b = 14.15cm 24
30 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 8/ Δυο ελάσματα πρόκειται να συνδεθούν με ήλωση επικάλυψης με 3 ήλους σε διπλή σειρά, αρχικής διαμέτρου (πριν τη τοποθέτηση) d= 19mm ο καθένας. Η επιτρεπόμενη εφελκυστική τάση είναι 150 dan cm 2 και το πάχος κάθε ελάσματος 10mm, το δε πλάτος τους είναι 540 mm. α )αν η δύναμη που αναλαμβάνει ο κάθε ήλος είναι 2500 dan να ελεγχθούν τα ελάσματα σε εφελκυσμό β) αν οι ήλοι τοποθετηθούν σε μια σειρά να επαναλάβετε τον έλεγχο.τι παρατηρείτε; α) Από την εκφώνηση γνωρίζουμε ότι έχουμε 3 ήλους σε 2 σειρές οπότε το z k =2 Για την διάμετρο της καρφότρυπας θα έχουμε : dd 1 = (dd + 1)mmmm dd 1 = (19 + 1)mmmm dd 1 = 20mmmm Οπότε θα έχουμε για το εμβαδόν Α ( αφού μετατρέψουμε τα mm σε cm): Α κ = (bb zz kk dd 1 ) ss Α κ = (54cccc 2 2cccc) 1cccc Α κ = 50cccc 2 Η δύναμη F θα είναι : FF = 2500dddddd zz kk FF = 2500dddddd 2 FF = 5000dddddd Η τάση εφελκυσμού των ελασμάτων θα είναι : σσ = FF σσ = 5000dddddd Α κ 50cccc 2 σσ = 100 dan cm 2 Και αφού το σσ = 100 dan cm 2 <σσ εεεε = 150 dan cm 2 τα ελάσματα αντέχουν β) Από την εκφώνηση γνωρίζουμε ότι έχουμε 3 ήλους σε 1 σειρά οπότε το z k =3 25
31 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ To εμβαδόν Α θα είναι : Η δύναμη F θα είναι : Α κ = (bb zz kk dd 1 ) ss Α κ = (54cccc 3 2cccc) 1cccc Α κ = 48cccc 2 Η τάση εφελκυσμού των ελασμάτων θα είναι : FF = 2500dddddd zz kk FF = 2500dddddd 3 FF = 7500dddddd σσ = FF σσ = 7500dddddd Α κ 48cccc 2 σσ = dan cm 2 Και αφού το σσ = dan cm 2 >σσ εεεε = 150 dan cm 2 τα ελάσματα δεν αντέχουν Παρατήρηση : Μεγάλη προσοχή θα πρέπει να δοθεί στην κατανομή των ήλων στις σειρές δίοτι όπως φάνηκε και από την άσκηση οι 3 ήλοι σε μια σειρά έχουν διαφορετική συμπεριφόρα από τους 3 ήλους σε δύο σειρές. Εδώ φαίνεται ακριβώς η σημασία του z k στην χρήση των τύπων. 9/Σε μια στεγανή ήλωση επικάλυψης με n=1 και z=3 ήλους το πάχος του ελάσματος είναι S=5cm. Να βρεθούν α) η διάμετρος της οπής β) το βήμα t της ήλωσης και γ) η απόσταση μεταξύ της ακραίας σειράς των ήλών από την άκρη του ελάσματος e 1 α) Η διάμετρος της οπής της ήλωσης δίνεται από τον τύπο : και με απλή αντικατάσταση θα έχουμε d 1 = 5 S 0.4 cm d 1 = 5 S 0.4 cm d 1 = cm d 1 = cm d 1 = (5 0.4)cm d 1 = 4.6cm β) Για τον υπολογισμό του βήματος θα χρησιμοποιήσουμε τον τύπο : t = (3 d + 0.5)cm Το d η διάμετρος του ήλου δηλαδή θα βρεθεί από τον τύπο Οπότε θα έχουμε d 1 = (d + 1)mm d = (d 1 1)mm d = (46 1)mm d = 45mm ή d = 4.5cm Ετσι για το βήμα θα έχουμε : t = ( )cm t = ( )cm t = 14cm γ)ηαπόσταση e 1 δίνεται από τον τύπο Καιαντικαθιστώντας θα έχουμε e 1 = 1.5 d e 1 = 1.5 4,5 = 6.75cm 26
32 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 10/Σε μια σταθερή ήλωση επικάλυψης με n=1 και z=3 ήλους το πάχος του ελάσματος είναι S=5cm. Να βρεθούν α) η διάμετρος της οπής β) το βήμα t της ήλωσης α) Η διάμετρος της οπής της ήλωσης δίνεται από τον τύπο : και με απλή αντικατάσταση θα έχουμε d 1 = 5 s 0.2 cm d 1 = 5 s 0.4 cm d 1 = cm d 1 = cm d 1 = (5 0.4)cm d 1 = 4.8cm β) Για τον υπολογισμό του βήματος θα χρησιμοποιήσουμε τον τύπο : t = (3 d)cm Το d η διάμετρος του ήλου δηλαδή θα βρεθεί από τον τύπο d 1 = (d + 1)mm Οπότε θα έχουμε: d = (d 1 1)mm d = (48 1)cm d = 47mm ή d = 4.7cm Ετσι το βήμα θα γίνει t = (3 4.7)cm = 14,1cm 11/ Να υπολογιστεί α) η πίεση σύνθλιψης της εσωτερικής επιφάνειας της οπής σε μια ήλωση όταν το φορτίο Q=2000 dan, αριθμός ήλων z=4, διάμετρος ήλων d=1cm και πάχος ελάσματος s=5mm και β) Ποια η μέγιστη τιμή της επιτρεπόμενης τάσης εφελκυσμού α)η πίεση σύνθλιψης της εσωτερικής επιφάνειας της οπής δίνεται από τον τύπο σ L = Q z d s οπότε με απλή αντικατάσταση καθώς και μετατροπή του πάχους ελάσματος σε cm θα έχουμε : σ L = Q z d s σ L = 2000daN 4 1cm 0.5cm σ L = 1000 dan cm 2 β) Η πίεση σύνθλιψης και η επιτρεπόμενη ταση εφελκυσμού συνδέονται με τον τύπο σ L < 2.5 σ επ Οπότε η μέγιστη τιμή της επιτρεπόμενης τάσης εφελκυσμού θα έιναι σ L < 2.5 σ επ σ επ = σ L 2.5 σ επ < 1000 dan cm 2 2,5 σ επ < 400 dan cm 2 27
33 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ 12/ Ήλος συνδέει με επικάλυψη δυο ελάσματα που έχουν συντελεστή τριβής μεταξύ τους μ = 0,4. Αν η διάμετρος του τοποθετημένου ήλου είναι 20 mm, και η επιτρεπόμενη τάση για το υλικό του είναι σ επ =1000 dan cm 2 να βρεθεί : α/ η αξονική δύναμη που καταπονεί τον ήλο και β/ η συνολική δύναμη (φορτίο) που αναλαμβάνει η ήλωση. α) Η αξονική δύναμη που καταπονεί τον ήλο θα βρεθεί από τον τύπο : Για το εμβαδό του ήλου σε cm θα έχουμε : σ επ = F A Οπότε η αξονική δύναμη θα είναι : Α = π d2 4 Α = cm 2 2 A = 1.57cm 2 σ επ = F A F = σ επ A F = 1000 dan cm cm 2 F = 1570daN β) Η συνολική δύναμη που αναλαμβάνει η ήλωση ή αλλίως η δύναμη τριβής θα είναι : F τρ = F μ F τρ = daN F τρ = 628daN 13/ Σε ήλωση επικάλυψης με παράλληλη σύνδεση δίνονται : αριθμός σειρών n=2,αριθμός ήλων : z=10, φορτίο F=8000 dan, διάμετρος ήλων d=19mm,πλάτος ελασμάτων b=500mm, επιτρεπόμενη τάση εφελκυσμού σεπ=1000 dan /cm 2. Ζητούνται :α) η διάμετρος της καρφότρυπας d1 β) το απαιτούμενο πάχος των ελασμάτων που επιλέγετε μετά τον έλεγχο της σύνδεσης σε εφελκυσμό και πίεση σύνθλιψης. α) Η διάμετρος της καρφότρυπας θα βρεθεί από τον τύπο : d 1 = (d + 1)mm d 1 = (19 + 1)mm d 1 = 20mm β) Το απαιτούμενο πάχος των ελασμάτων θα βρεθεί θεωρώντας ότι τα ελάσματα αντέχουν και σε εφελκυσμό αλλά και σε πίεση σύνθλιψης Για την αντοχή σε εφελκυσμό θα έχουμε τα εξής : Και κατά συνέπεια : Αφού τα ελάσματα αντέχουν τότε σ σ επ F F σ Α επ κ (b z k d 1 ) s σ F επ s (b z k d 1 ) σ επ Αντικαθιστώντας και μετατρέποντας τα mm σε cm θα έχουμε διαδοχικά : 28
34 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ s F (b z k d 1 ) σ επ s 8000daN (50cm 5 2cm) 1000 dan cm 2 s 8 cm s 0.2cm 40 Για την αντοχή σε πίεση σύνθλιψης θα έχουμε : Και κατά συνέπεια : σ L < 2.5 σ επ σ L < 2, dan cm 2 σ L < 2500 dan cm 2 F( οοοοοοή δδδδδδδδδδδδή ) z d s < 2500 dan cm 2 Αντικαθιστώντας και μετατρέποντας τα mm σε cm θα έχουμε διαδοχικά : 8000daN cm s 2500 dan cm 2 s 8000daN 47500daN/cm s 0.168cccc Οπότε το ελάχιστο απαιτούμενο πάχος των ελασμάτων που θα εξυπηρετεί και τις δύο περιπτώσεις θα είναι το s = 0.2cm 29
35 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 1 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=2,φορτίο Q=1570daN,τ επ = 1000 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=10mm, β) d 1 =11mm ΑΣΚΗΣΗ 2 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=2,φορτίο Q=1570daN, τ επ = 500 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=10mm, β) d 1 =11mm ΑΣΚΗΣΗ 3 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=5,φορτίο Q=105975daN,τ επ = 1500 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=30mm, β) d 1 =31mm 30
36 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 4 Σε ήλωση με μονή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=5,φορτίο Q=52987,5daN,τ επ = 1500 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=30mm, β) d 1 =31mm ΑΣΚΗΣΗ 5 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=2,αριθμός ήλων z=4,φορτίο Q=15072 dan,τεπ= 1200 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=20mm, β) d 1 =21mm ΑΣΚΗΣΗ 6 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=2,αριθμός ήλων z=4,φορτίο Q=30144daN,τεπ= 1200 dan cm 2. Ζητούνται : α) η διάμετρος των ήλων d, β) η διάμετρος οπών των ελασμάτων d Απ. : α) d=20mm, β) d 1 =21mm 31
37 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 7 Σε ήλωση μονής αρμοκαλύπτρας δίνονται : αριθμός σειρών n=2,αριθμός ήλων z=4, φορτίο Q=30144daN, τεπ= 500 dan cm 2, και διάμετρος καρφότρυπας d1=51mm. Ζητούνται : α) η διάμετρος των ήλων d, β) Ο έλεγχος των ήλων σε διάτμηση Απ. : α) d=50mm, β) τ=384 dan cm 2 <τεπ= 2000 dan cm 2 οι ήλοι αντέχουν ΑΣΚΗΣΗ 8 Σε ήλωση διπλής αρμοκαλύπτρας δίνονται : αριθμός σειρών n=2,αριθμός ήλων z=2, φορτίο Q=9420daN, τ θρ = 3000 dan cm 2, με συντελεστή ασφαλείας ν=3 και διάμετρος καρφότρυπας d 1 =11mm. Ζητούνται : α) η διάμετρος των ήλων d, β) Ο έλεγχος των ήλων σε διάτμηση Απ. : α) d=10mm, β) τ=3000 dan cm 2, > τεπ= 1000 dan cm 2 οι ήλοι δεν αντέχουν ΑΣΚΗΣΗ 9 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,τεπ= 600 dan cm 2, και διάμετρος καρφότρυπας d 1 =41mm. Ζητήται η δύναμη Q των ήλων Απ. : Q= 22608daN 32
38 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 10 Σε ήλωση διπλής αρμοκαλύπτρας δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,τεπ= 500 dan cm 2, και διάμετρος καρφότρυπας d 1 =41mm. Ζητήται η δύναμη Q των ήλων Απ. : Q= dan ΑΣΚΗΣΗ 11 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=5,φορτίο Q=3925daN,σ επ = 1200 dan cm 2, διάμετρος καρφότρυπας d 1 =11mm, πλάτος ελασμάτων b=120 mm, πάχος ελασμάτων s=5mm. Ζητούνται : α/η επιφάνεια του ελάσματος στην κρίσιμη διατομή, β/να γίνει έλεγχος αντοχής των ελασμάτων σε εφελκυσμό Απ. : α) Ακ=3,25cm 2, β) σ=1207,7 dan cm 2, > σεπ= 1200 dan cm 2 τα ελάσματα δεν αντέχουν ΑΣΚΗΣΗ 12 Σε ήλωση διπλής αρμοκαλύπτρας δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,φορτίο Q=18840daN,σ επ = 1200 dan cm 2, διάμετρος καρφότρυπας d 1 =21mm, πλάτος ελασμάτων b=200 mm, πάχος ελασμάτων s=20mm. Ζητούνται : α/η επιφάνεια του ελάσματος μετά το τρύπημα, β/να γίνει έλεγχος αντοχής των ελασμάτων σε εφελκυσμό Απ. : α) Α=23,2cm 2, β) σ=812,07 dan cm 2, < σεπ= 1200 dan cm 2 τα ελάσματα αντέχουν 33
39 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 13 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=3,φορτίο Q=4070daN,σ επ = 1100 dan cm 2, διάμετρος καρφότρυπας d 1 =31mm, και πλάτος ελασμάτων b=130mm. Να βρεθεί το απαιτούμενο πάχος των ελασμάτων Απ. : s = 10mm ΑΣΚΗΣΗ 14 Σε ήλωση με μονή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=8,φορτίο Q=4050daN,σ θρ = 2000 dan cm 2, συντελεστής ασφαλείας ν=4, διάμετρος καρφότρυπας d 1 =11mm και πάχος ελασμάτων s=5mm. Να βρεθεί το απαιτούμενο πλάτος των ελασμάτων Απ. : b = 250mm ΑΣΚΗΣΗ 15 Σε ήλωση με επικάλυψη δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=6,σεπ= 800 dan cm 2, διάμετρος καρφότρυπας d 1 =11mm πλάτος ελασμάτων b=150mmκαι πάχος ελασμάτων s=5mm. Να βρεθεί η ελάχιστη δύναμη F που απαιτείται ετσι ώστε τα ελάσματα να αντέχουν σε εφελκυσμό Απ. : F=3360daN 34
40 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 16 Σε ήλωση με πίεση σύνθλιψης της εσωτερικής επιφάνειας της οπήςσ L =1500daN/cm 2, με φορτίο F=6000 dan, πάχος ελάσματος s=1cm και αριθμό ήλων z=4 να βρεθεί η διάμετρος των ήλων d. ( Απ. d= 1cm) ΑΣΚΗΣΗ 17 Σε μια στεγανή ήλωση η διάμετρος της οπής d 1 =1,6cm Να βρεθούν α) το πάχος του ελάσματος S, β) το βήμα t και γ) η απόσταση e 1.. (Απ. α) s= 0,8cm, β) t=5cm, γ) e 1 =2,25cm) ΑΣΚΗΣΗ 18 Σε μια σταθερή ήλωση η διάμετρος της οπής d 1 =1,8cm Να βρεθούν α) το πάχος του ελάσματος s και β) το βήμα t.... (Απ. α) s= 0,8cm, β) t=5,7cm) ΑΣΚΗΣΗ 19 Ήλος συνδέει με επικάλυψη δυο ελάσματα που έχουν συντελεστή τριβής μεταξύ τους μ = 0,3. Αν η διάμετρος του τοποθετημένου ήλου είναι 10 mm, και η επιτρεπόμενη τάση για το υλικό του είναι σ επ =500 dan cm 2 να βρεθεί : α/ η αξονική δύναμη που καταπονεί τον ήλο F αξ και β/ η συνολική δύναμη F τρ που αναλαμβάνει η ήλωση (Απ. α) F αξ =392.5daN, β) F τρ =117,75cm) 35
41 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 20 Σε στεγανή ήλωση με μονή αρμοκαλύπτρα διπλής σειράς με αριθμό ήλων z=4, που αναλαμβάνει φορτίο Q= dan ζητούνται : α) να βρεθεί το βήμα και η απόσταση των σειρώνe 1 και β) αν μετατρέψουμε την ήλωση σε διπλή αρμοκαλύπτρα ποια δύναμη αναλαμβάνει ο κάθε ήλος; Ποια θα ήταν η διάμετρος του κάθε ήλου;δίνεται επιτρεπόμενη τάση διάτμησης τ επ =500 dan /cm2 και 2 = 1, (Απ. α) t = 12.5cm, e 1 =18.75cm, β) F=785daN,d=2.8cm) ΑΣΚΗΣΗ 21 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=8,φορτίο Q=4050daN, διάμετρος καρφότρυπας d 1 =11mm,πλάτος ελασμάτων b=250mm και πάχος ελασμάτων s=5mm. Να βρεθεί το σ επ ( Απ. : σ επ =500 dan cm 2 ) 36
42 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 1 ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,φορτίο F=3140 dan,τ επ = 1000 dan /cm 2,σ επ = 1200 dan /cm 2,πλάτος ελασμάτων b=144 mm,πάχος ελασμάτων s=5mm.ζητούνται : α/η διάμετρος των ήλων d, β/η διάμετρος οπών των ελασμάτων d1 και γ/να γίνει έλεγχος αντοχής των ελασμάτων σε εφελκυσμό. (ΤΕΕ 2005) ( Απ. : d=10mm, d 1 =11mm, σ=628dan/cm 2 <σ επ άρα αντέχουν σε εφελκυσμό ) ΑΣΚΗΣΗ 2 Σε ήλωση με διπλή αρμοκαλύπτρα δίνονται : αριθμός σειρών n=1,αριθμός ήλων:z=4, φορτίο Q=25120 dan,τ επ =1000 dan /cm 2. Ζητούνται :α/η διάμετρος των ήλων d,β/ η διάμετρος οπών των ελασμάτων d 1 και γ/αν η τάση θραύσης είναι τ θρ = 2000 dan /cm 2, να βρεθεί ο συντελεστής ασφαλείας ν των ήλων. (ΤΕΕ 2006) ( Απ. : d=10mm, d 1 =11mm, v=2 ) ΑΣΚΗΣΗ 3 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,φορτίο Q=6280 dan,τ επ =500 dan /cm 2. Ζητούνται : α/η διάμετρος των ήλων d, β/ η διάμετρος οπών των ελασμάτων d 1. (ΤΕΕ 2009) ( Απ. : d=10mm, d 1 =11mm ) 37
43 ΑΣΚΗΣΕΙΣ ΗΛΩΣΕΩΝ Μ.Μ.Τ ΑΣΚΗΣΗ 4 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4,φορτίο F=6000 dan,διάμετρος ήλων d=9mm,πλάτος ελασμάτων b=140mm,επιτρεπόμενη τάση εφελκυσμού σ επ =1200 dan /cm 2. Ζητούνται : α/η διάμετρος της καρφότρυπας d 1 β/το απαιτούμενο πάχος των ελασμάτων s. (ΕΠΑΛ 2009) ( Απ. : d 1 =10mm, s=0.5cm ) ΑΣΚΗΣΗ 5 Σε ήλωση επικάλυψης δίνονται : αριθμός σειρών n=1,αριθμός ήλων z=4, διάμετρος ήλων d=10 mm,τ επ = 1000 dan /cm 2. Να βρεθεί το συνολικό φορτίο Q που έχουν τη δυνατότητα να παραλάβουν οι ήλοι. (ΕΠΑΛ 2011) ( Απ. : Q=3140daN ) ΑΣΚΗΣΗ 6 Σε ήλωση διπλής αρμοκαλύπτρας δίνονται : αριθμός σειρών n=1,διάμετρος ήλων d=10 mm,τ επ = 1000 kp /cm 2, Φορτίο Q=6280kp. Να υπολογιστεί ο αριθμός z των ήλων (ΕΠΑΛ 2015) ( Απ. : z=4 ) 38
44 3 [ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ] Περιλαμβάνει ερωτήσεις ανάπτυξης, ερωτήσεις σωστού- λάθους, ερωτήσεις αντιστοιχισης, τυπολόγιο ασκήσεων κοχλιώσεων,εφαρμογές επι του τυπολογίου,λυμένες ασκήσεις, Αλυτες ασκήσεις με απάντησεις και θέματα Πανελλαδικών Εξετάσεων με τις απαντήσεις
45 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΚΟΧΛΙΕΣ - ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΧΤΟΥ ΤΥΠΟΥ 1. Να αναφέρετε τις χρήσεις του κοχλία στις κατασκευές. (σ.142) 2. Από ποια μέρη αποτελείται ο κοχλίας; (σ.142) 3. Ποια είναι η βάση για τη δημιουργία του σπειρώματος; (σ.143) 4. Ποια είναι τα είδη των σπειρωμάτων ανάλογα με την κατατομή τους; (σ.144) 5. Τι είδους σπειρώματα είναι τα παρακάτω; (σ.144) Α) Β) 6. Σε τι κοχλίες χρησιμοποιούνται τριγωνικά σπειρώματα, ποια είναι τα πιο συνηθισμένα και ποιες είναι οι κύριες διαφορές τους; (σ.146) 7. Σε τι κοχλίες χρησιμοποιούνται τα τραπεζοειδή σπειρώματα; (σ.146) 8. Ποιο είναι το κύριο χαρακτηριστικό του πριονοειδούς σπειρώματος; (σ.146) 9. Που χρησιμοποιούνται τα ειδικά σπειρώματα; (σ.146) 10. Που χρησιμοποιείται το λεπτό μετρικό σπείρωμα (f); (σ.146) 11. Τι σημαίνει σπείρωμα «Μ20Χ1,5» ; (σ.146) 12. Ποια στοιχεία εκτός από τον κοχλία περιλαμβάνει η κοχλίωση; (σ147) 13. Τι είναι το περικόχλιο και ποιες είναι διαστάσεις του (εκτός από αυτές του σπειρώματος); (σ.148) 14. Ποιοι είναι οι δύο τρόποι ασφάλισης των περικοχλίων; (σ.149) 15. Ποια είναι τα είδη των κοχλιών σύνδεσης ή σύσφιξης; (σ.150) 41
46 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ Να βρείτε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος 1. Το σπείρωμα του περικοχλίου είναι εξωτερικό σπείρωμα. 2. Στον κοχλία ονομαστική διάμετρος είναι η διάμετρος του πυρήνα του (d 1 ). 3. Το σπείρωμα Whitworth έχει γωνία κορυφής α=55 ο. 4. Το τραπεζοειδές σπείρωμα είναι κατάλληλο για τη μεταφορά μεγάλων φορτίων. 5. Οι κοχλίες κεφαλής χρησιμοποιούνται χωρίς περικόχλιο. 6. Οι φυτευτοί κοχλίες (μπουζόνια) περνούν ελεύθερα και στα δύο κομμάτια που συνδέουν. 7. Στους κοχλίες σύνδεσης χρησιμοποιούνται μόνο τριγωνικής μορφής σπειρώματα. 8. Κατά τη σύσφιξη ο κοχλίας καταπονείται σε εφελκυσμό ενώ τα συνδεόμενα κομμάτια σε θλίψη. 9. Το περικόχλιο καταπονείται σε εφελκυσμό. 10. Το σπείρωμα καταπονείται σε κάμψη. 11. Τα τραπεζοειδή σπειρώματα έχουν μεγαλύτερο βήμα από τα τριγωνικά γι αυτό και χρησιμοποιούνται στους κοχλίες κίνησης. 12. Οι κοχλίες κίνησης καταπονούνται από αξονική δύναμη Ρ και ροπή στρέψης M t. ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΣΤΟΙΧΙΣΗΣ ΑΝΤΙΣΤΟΙΧΙΣΗ 1 1. Χρησιμοποιείται ως μέσο λυόμενης σύνδεσης Α. Ρυθμιστικός κοχλίας 2. Χρησιμοποιείται για τη δημιουργία προέντασης Β. Κοχλίας κίνησης 3. Χρησιμοποιείται για τη ρύθμιση διακένου Γ. Κοχλίας μέτρησης 4. Χρησιμοποιείται στο μικρόμετρο Δ. Κοχλίας τάσης 5. Χρησιμοποιείται για τη μετατροπή της περιστροφικής κίνησης σε γραμμική ή αντίστροφα Ε. Διαφορικός κοχλίας ΣΤ. Κοχλίας σύσφιξης 42
47 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 2 1. Ονομαστική διάμετρος Α. h 2. Εσωτερική διάμετρος του πυρήνα Β. d 2 3. Βήμα σπειρώματος Γ. α 4. Γωνία κορυφής σπειρώματος Δ. h 3 5. Μέση διάμετρος σπειρώματος Ε. d 1 ΣΤ. d ΑΝΤΙΣΤΟΙΧΙΣΗ 3 1. Μετρικό σπείρωμα (Μ) Α. Χρησιμοποιείται για γενική χρήση 2. Σπείρωμα Whitworth (W, R) Β. Χρησιμοποιείται αν δεν υπάρχουν προδιαγραφές για την ακρίβεια 3. Τραπεζοειδές σπείρωμα Γ. Χρησιμοποιείται σε κοχλίες κίνησης 4. Λεπτό σπείρωμα (f) Δ. Έχει γωνία κορυφής α=60 ο 5. Μέσο σπείρωμα (m) Ε. Έχει γωνία κορυφής α=55 ο ΣΤ. Χρησιμοποιείται για σπείρωμα μεγάλης ακρίβειας 43
48 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 4 Α. ΤΡΑΠΕΖΟΕΙΔΕΣ ΣΠΕΙΡΩΜΑ 1. Β. ΠΡΙΟΝΩΤΟ ΣΠΕΙΡΩΜΑ 2. Γ. ΤΡΙΓΩΝΙΚΟ ΣΠΕΙΡΩΜΑ Δ. ΕΛΛΕΙΠΤΙΚΟ ΣΠΕΙΡΩΜΑ 5. Ε. ΟΡΘΟΓΩΝΙΚΟ ΣΠΕΙΡΩΜΑ ΣΤ. ΣΤΡΟΓΓΥΛΟ ΣΠΕΙΡΩΜΑ 44
49 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 5 Α. ΟΝΟΜΑΣΤΙΚΗ ΔΙΑΜΕΤΡΟΣ ΣΠΕΙΡΩΜΑΤΟΣ Β. ΓΩΝΙΑ ΚΟΡΥΦΗΣ ΣΠΕΙΡΩΜΑΤΟΣ Γ. ΒΑΘΟΣ ΣΠΕΙΡΩΜΑΤΟΣ Δ. ΔΙΑΜΕΤΡΟΣ ΠΥΡΗΝΑ ΣΠΕΙΡΩΜΑΤΟΣ Ε. ΒΗΜΑ ΣΠΕΙΡΩΜΑΤΟΣ ΣΤ. ΜΕΣΗ ΔΙΑΜΕΤΡΟΣ ΣΠΕΙΡΩΜΑΤΟΣ ΑΝΤΙΣΤΟΙΧΙΣΗ 6 1. Α. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕ ΑΝΤΙΠΕΡΙΚΟΧΛΙΟ 2. Β. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕ ΑΣΦΑΛΙΣΤΙΚΗ ΠΕΡΟΝΗ 3. Γ. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕ ΕΛΑΣΜΑ Δ. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕΑΥΤΟΑΣΦΑΛΙΖΟΜΕΝΟ ΠΕΡΙΚΟΧΛΙΟ 4. Ε. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕ ΣΥΡΜΑΤΑ 5. ΣΤ. ΑΣΦΑΛΙΣΗ ΚΟΧΛΙΑ ΜΕ ΚΩΝΙΚΗ ΕΠΑΦΗ 45
50 ΘΕΩΡΙΑ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΑΝΤΙΣΤΟΙΧΙΣΗ 7 A. ΦΥΤΕΥΤΟΣ ΚΟΧΛΙΑΣ (ΜΠΟΥΖΟΝΙ) 1. Β. ΠΕΡΑΣΤΟΣ ΚΟΧΛΙΑΣ 2. Γ. ΚΟΧΛΙΑΣ ΚΙΝΗΣΗΣ 3. Δ. ΚΟΧΛΙΑΣ ΤΑΣΗΣ 4. Ε. ΚΟΧΛΙΑΣ ΑΓΚΥΡΩΣΕΩΣ 5. ΣΤ. ΚΟΧΛΙΑΣ ΚΕΦΑΛΗΣ 46
51 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΣΥΜΒΟΛΙΣΜΟΙ : ΣΥΜΒΟΛΟ ΕΠΕΞΗΓΗΣΗ ΜΟΝΑΔΕΣ P Φορτίο σε αξονική καταπόνηση του κοχλία N,daN,kp,kg,tn F Φορτίο σε σύνθετη καταπόνηση του κοχλία N,daN,kp,kg,tn Q Φορτίο σε διάτμηση του κοχλία N,daN,kp,kg,tn d 1 Διάμετρος πυρήνα κοχλία cm, mm d Ονομαστική διάμετρος βίδας mm d 2 Μέση διάμετρος κοχλία mm t Βάθος σπειρώματος mm h Βήμα σπειρώματος του κοχλία mm z Αριθμός σπειρωμάτων σε επαφή μεταξύ κοχλία και περικόχλιου - m Αριθμός τομών κοχλίωσης - A Διατομή του πυρήνα του κοχλία cm 2, mm 2 ν Συντελεστής ασφαλείας - σ Αναπτυσσόμενη ορθή τάση στον κοχλία Επιτρεπόμενη ορθήτάση σ επ σ θρ τ τ επ τ θρ p p επ Ορθή Τάση θραύσης Διατμητική τάση στον κοχλία Επιτρεπόμενη διατμητική τάση ΔιατμητικήΤάση θραύσης Ανηγμένη πίεση σπειρώματος κοχλια και περικοχλίου Επιτρεπόμενη ανηγμένη πίεση 1) Βασικες διαστάσεις σπειρώματος Τυπολόγιο N/cm 2, dan/cm 2, kp/cm 2, N/mm 2, dan/mm 2, kp/mm 2 2) Εμβαδό διατομής πυρήνα του κοχλία Α : ΑΑ = ππ dd
52 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ 3) Κοχλίας σε εφελκυσμό - θλίψη - Αναπτυσσόμενη τάση στον κοχλία σ : σσ = PP AA - Ελεγχος αντοχής του κοχλία σε εφελκυσμό θλίψη : σσ σσ εεεε 4) Κοχλίας σε διάτμηση - Αναπτυσσόμενη τάση στον κοχλία τ : ττ = QQ AA - Ελεγχος αντοχής του κοχλία σε διάτμηση : ττ ττ εεεε 5) Κοχλίας σε σύνθετη καταπόνηση ( εφελκυσμός θλίψη και στρέψη ) - Αναπτυσσόμενη δύναμη στον κοχλία F : FF = 0.6 dd 1 2 σσ εεεε - Ανηγμένη πίεση μεταξύ σπειρωμάτων κοχλία και περικόχλιου p : FF pp = ππ 4 (dd2 dd 2 1 ) zz Για κοχλίες σύνδεσης από χάλυβα p επ =200daN/cm 2 Για κοχλίες κίνησης p επ =75-100daN/cm 2 για κοινό χάλυβα η χυτοσίδηρο ή μπρουντζο Ενώ p επ =150daN/cm 2 για βελτιωμένο χάλυβα ή βελτιωμένο μπρούντζο - Ελεγχος αντοχής του κοχλία σε ανηγμένη πίεση : pp pp εεεε 48
53 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ Συμπλήρωση πινάκων ( εξοικοίωση με τους τύπους ) Με την βοήθεια του τυπολογίου συμπληρώστε τους παρακάτω πίνακες d 1 ( cm ) A (cm 2 ) d 1 ( mm ) A (cm 2 ) σ ( kp/cm 2 ) P ( kp ) A ( cm 2 ) τ ( kp/cm 2 ) Q ( kp ) A ( cm 2 ) F ( dan ) d 1 ( cm ) σ επ (dan/cm 2 ) p (dan/cm 2 ) F ( dan ) d ( cm ) d 1 ( cm ) z
54 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ 1/Δίνεται κοχλίας με διάμετρο πυρήνα d 1 =10mm και υλικό με σ επ = 1600daN/cm 2. Ζητείται η μέγιστη επιτρεπόμενη φόρτιση P του κοχλία σε εφελκυσμό Από την συνθήκη αντοχής του κοχλία σε εφελκυσμό έχουμε : Η διατομή του πυρήνα του κοχλία θα είναι : σσ σσ εεεε κκκκκκ σσσσσσσσ ααααααααίαα ππππππίππππππππππ σσ = σσ εεεε ΑΑ = ππ dd ΑΑ = cccc 2 4 AA = cccc2 AA = 0.785cccc 2 Η μέγιστη επιτρεπόμενη φόρτιση του κοχλία σε εφελκυσμό θα είναι : PP εεεε = σσ εεεε ΑΑ PP εεεε = 1500 dddddd cccc cccc 2 PP εεεε = 1256dddddd 2/Κοχλίας καταπονείται σε εφελκυσμό με φορτίο P=9420 dan. Υλικό κοχλία με σ επ = 3000 dan/cm 2. Ζητούνται: α/ η διάμετρος πυρήνα d 1 Από την συνθήκη αντοχής του κοχλία σε εφελκυσμό έχουμε : σσ σσ εεεε κκκκκκ σσσσσσσσ ααααααααίαα ππππππίππππππππππ σσ = σσ εεεε Η διατομή του πυρηνά του κοχλία θα βρεθεί από τον τύπο : ΑΑ = FF σσ εεεε ΑΑ = 9420dddddd 3000 dddddd cccc 2 AA = 3.14cccc 2 Ενώ η διάμετρος του πυρήνα του κοχλία θα είναι : ΑΑ = ππ dd dd 1 2 = 4 AA ππ dd 1 2 = cccc2 3,14 dd 1 2 = 4cccc 2 Και αποτετραγωνίζοντας θα έχουμε dd 1 2 = 4cccc 2 dd 1 = 4 cccc 2 dd 1 = 2ccccήdd 1 = 20mmmm 50
55 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ 3/ Για τη σύνδεση δύο ελασμάτων χρησιμοποιούνται 5 ίδιοι κοχλίες, οι οποίοι καταπονούνται ομοιόμορφα μόνο σε εφελκυσμό. Η συνολικά εξασκούμενη δύναμη εφελκυσμού των κοχλιών είναι P=15700daN ενώ η διάμετρος του κάθε κοχλία είναι 30mm. Για το υλικό των κοχλιών δίνεται σ θρ =3000 dan/cm 2 και συντελεστής ασφαλείας ν=3. Να ελεγχθούν οι κοχλίες ως προς την αντοχή τους Βρίσκουμε αρχίκά την δύναμη εφελκυσμού του κάθε κοχλία : Η διατομή του πυρήνα του ήλου θα είναι : PP = 15700dddddd 5 PP = 3140dddddd ΑΑ = ππ dd ΑΑ = cccc 2 4 AA = cccc2 AA = 7,065cccc 2 Η έφελκυστική τάση που ασκείται σε κάθε κοχλία θα είναι : σσ = PP AA 3140dddddd σσ = 7,065cccc 2 σσ = 444,44 dddddd cccc 2 Η επιτρεπόμενη εφελκυστική τάση θα είναι : νν = σσ θθθθ σσ σσ εεεε = σσ θθθθ εεεε νν σσ εεεε = 3000 dddddd cccc 2 3 σσ εεεε = 1000 dddddd cccc 2 Για τον έλεγχο θα συγκρίνουμε το σ του κοχλία με το σ επ οπότε : Οπότε οι κοχλίες αντέχουν. σσ = 444,44 dddddd cccc 2 < σσ εεεε = 1000 dddddd cccc 2 4/Κοχλίας με διάμετρο πυρήνα d 1 = 15mm από υλικό με σ επ = 2000 dan / cm 2 καταπονείται σε εφελκυσμό και στρέψη. Να υπολογίσετε τη μέγιστη επιτρεπόμενη φόρτιση F. Η μέγιστη επιτρεπόμενη φόρτιση θα βρεθεί από τον τύπο : FF = 0.6 dd 2 1 σσ εεεε FF = cccc dddddd cccc 2 FF = 2700dddddd 51
56 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ 5/ Κοχλίας πρέσας τετραγωνικού σπειρώματος με ονομαστική διάμετρο d=30mm και διάμετρο πυρήνα d 1 =20mm,είναι κατασκευασμένος από χάλυβα με επιτρεπόμενη τάση σ επ = 500 dan/cm 2. Να υπολογιστεί η μέγιστη επιτρεπόμενη φόρτιση του κοχλία και η επιφανειακή πίεση των σπειρωμάτων του οδηγού περικοχλίου αν ο αριθμός συνεργαζομένων σπειρωμάτων είναι z=8. Η μέγιστη επιτρεπόμενη φόρτιση θα βρεθεί από τον τύπο : FF = 0.6 dd 2 1 σσ εεεε FF = cccc dddddd cccc 2 FF = 1200dddddd Η επιφανειακή πίεση των σπειρωμάτων του οδηγού περικόχλιου θα είναι : pp = FF ππ 4 (dd2 dd 2 1 ) zz pp = 1200dddddd ( )cccc 2 8 pp = 1200dddddd 31.4cccc 2 pp = dddddd cccc 2 6/Δίνεται κοχλίας που καταπονείται σε σύνθετη καταπόνηση, με φορτίο F=8000daN. Δίνεται επιτρεπόμενη πίεση επιφανείας ρ επ =200 dan/cm 2,ονομαστική διάμετρος d=40mm, διάμετρος πυρήνα d 1 =30mm, αριθμός των συνεργαζόμενων σπειρωμάτων κοχλία-περικοχλίου z=10. Να ελεγχθεί η επιφανειακή πίεση p των σπειρωμάτων. Η επιφανειακή πίεση των σπειρωμάτων του οδηγού περικόχλιου θα είναι : pp = FF ππ 4 (dd2 dd 2 1 ) zz pp = 8000dddddd ( )cccc 2 10 pp = 8000dddddd 54.95cccc 2 pp = dddddd cccc 2 Συγκρίνουμε την επιφανειακή πίεση που βρέθηκε με την επιτρεπόμενη πίεση επιφανείας : Οπότε οι κοχλίες αντέχουν στην πίεση επιφανείας pp = dddddd cccc 2 < pp εεεε = 200 dddddd cccc 2 7) Κοχλίας καταπονείται σε διάτμηση. Δίνονται φορτίο Q=6280daN, επιτρεπόμενη τάση τ επ =500daN/cm 2. Να υπολογιστεί η διάμετρος πυρήνα d 1. Από την συνθήκη αντοχής του κοχλία σε διάτμηση έχουμε : ττ ττ εεεε κκκκκκ σσσσσσσσ ααααααααίαα ππππππίππππππππππ ττ = ττ εεεε Η διατομή του πυρηνά του κοχλία θα βρεθεί από τον τύπο : ΑΑ = QQ ττ εεεε ΑΑ = 6280dddddd 500 dddddd cccc 2 AA = 12.56cccc 2 52
57 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ Ενώ η διάμετρος του πυρήνα του κοχλία θα είναι : ΑΑ = ππ dd dd 1 2 = 4 AA ππ dd 1 2 = cccc2 3,14 dd 1 2 = 16cccc 2 Και αποτετραγωνίζοντας θα έχουμε dd 1 2 = 16cccc 2 dd 1 = 16 cccc 2 dd 1 = 4ccccήdd 1 = 40mmmm 8/Δίνεται κοχλίας με διάμετρο πυρήνα d 1 =10mm και υλικό με τ επ = 1200 dan/cm 2. Ζητείται η μέγιστη επιτρεπόμενη φόρτιση Q του κοχλία σε διάτμηση Από την συνθήκη αντοχής του κοχλία σε διάτμηση έχουμε : Η διατομή του πυρήνα του κοχλία θα είναι : ττ ττ εεεε κκκκκκ σσσσσσσσ ααααααααίαα ππππππίππππππππππ ττ = ττ εεεε ΑΑ = ππ dd ΑΑ = cccc 2 4 AA = cccc2 AA = 0.785cccc 2 Η μέγιστη επιτρεπόμενη φόρτιση του κοχλία σε διάτμηση θα είναι : QQ εεεε = ττ εεεε ΑΑ QQ εεεε = 1200 dddddd cccc cccc 2 FF εεεε = 942dddddd 9/ Τυποποιημένος κοχλίας Μ8x1.25 καταπονείται σε εφελκυσμό και στρέψη. Ποίο είναι το μέγιστο εφελκυστικό φορτίο αν σ επ = 500 dan/cm 2 Για την περίπτωση ενός τυποποιημένου κοχλία η διάμετρός του d 1 θα βρεθεί από πίνακες που περιέχουν στοιχεία τυποποιημένων κοχλιών. Από τον πίνακα του σχολικού βιβλίου!!! Θα έχουμε για τον τυποποιημένο κοχλία Μ8x1.25 την διάμετρό του d 1 =6.466mm Το μέγιστό εφελκυστικό φορτίο θα είναι τότε : FF = 0.6 dd 2 1 σσ εεεε FF = 0.6 0, cccc dddddd cccc 2 FF = 125,42dddddd 53
58 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ 10/ Τυποποιημένος κοχλίας καταπονείται σε διάτμηση. Αν το φορτίο είναι Q=1600daN και το τ επ = 1600 dan/cm 2 να επιλέξετε τον τυποποιημένο κοχλία. Το εμβαδό του τυποποιημένου κοχλία θα είναι : ΑΑ = QQ ττ εεεε ΑΑ = Η διάμετρος d 1 του τυποποιημένου κοχλία θα είναι : 1600dddddd 1600 dddddd cccc 2 AA = 1cccc 2 dd 1 = 4 AA ππ dd 1 = 4 1cccc2 3,14 dd 1 = 1.27cccc dd 1 = 1.126ccccήdd 1 = 11,26mmmm Με την βοήθεια του πίνακα του σχολικού βιβλίου εκλέγουμε τυποποιημένο κοχλία Μ12x2 11/ Κοχλίας κίνησης από βελτιωμένο χάλυβα καταπονείται σε στρέψη και θλίψη και συνεργάζεται με οκτώ σπείρες περικοχλίου. Ο τετραγωνικός κοχλίας έχει εξωτερική διάμετρο d=60 mm και διάμετρο πυρήναd 1 =50 mm. Αν το όριο θραύσης του υλικού είναι daN /cm 2 να βρεθεί ο συντελεστής ασφαλείας της διάταξης. Για κοχλία κίνησης από βελτιωμένο χάλυβα γνωρίζουμε ότι p επ =150 dddddd cccc 2 Η μέγιστη επιτρεπόμενη φόρτιση θα βρεθεί από τον τύπο : pp εεεε = FF ππ 4 (dd2 dd 2 1 ) zz FF = pp ππ εεεε 4 (dd2 dd 2 1 ) zz FF = 150 dddddd cccc 2 ( )cccc 2 8 To σ επ θα βρεθεί από τον τύπο : FF = 10362dddddd FF = 0.6 dd 1 2 σσ εεεε σσ εεεε = Ο συντελεστής ασφαλείας θα είναι : FF dd σσ εεεε = 10362dddddd cccc 2 σσ εεεε = dddddd cccc 2 νν = σσ θθθθ νν = dddddd cccc 2 σσ εεεε 690,8 dddddd νν = 4 cccc 2 54
59 ΑΣΚΗΣΕΙΣ ΚΟΧΛΙΩΝ Μ.Μ.Τ 12/Δυο κοχλίες χρησιμοποιούνται για να συνδέσουν γωνιακό έλασμα που θα αναλάβει φορτίο Ρ όπως φαίνεται στο σχήμα. Αν η επιτρεπόμενη τάση διάτμησης είναι τ επ =500 dan/cm 2 και η εσωτερική διάμετρος των όμοιων κοχλιών είναι d 1 =20mm να βρεθεί το μέγιστο φορτίο που μπορούν να αναλάβουν. Από την συνθήκη αντοχής του κοχλία σε διάτμηση έχουμε : Η διατμητική τάση στον κάθε κοχλία θα είναι : ττ ττ εεεε κκκκκκ σσσσσσσσ ααααααααίαα ππππππίππππππππππ ττ = ττ εεεε ττ = QQ AA Στην περίπτωση της άσκησης όμως το διατμητικό φορτίο Q είναι το φορτίο P Το οποίο μοιράζεται εξίσου στους δύο κοχλίες. Οπότε ο παραπάνω τύπος θα γίνει ττ εεεε = PP εεεε 2 AA Το εμβαδό του κοχλία θα είναι : ΑΑ = ππ dd ΑΑ = cccc 2 4 Και το μέγιστο φορτίο που μπορεί να αναλάβει ο κοχλίας θα είναι : AA = 3.14cccc 2 ττ εεεε = PP εεεε 2 AA PP εεεε = 2 AA ττ εεεε PP εεεε = cccc dddddd cccc 2 PP εεεε = 3140dddddd 13/Καπάκι κυκλικής διατομής αεροφιάλης συγκρατείται από 16 όμοιους κοχλίες. Η πίεση (η ασκούμενη δύναμη σε μια επιφάνεια προς την επιφάνεια) μέσα στην αεροφιάλη είναι 4 dddddd cccc 2 και η επιτρεπόμενη τάση είναι για το καπάκι και τους κοχλίες σ επ =400 dddddd cccc 2. Αν η διάμετρος του πυρήνα των κοχλιών είναι 20mm, να βρεθεί η ελάχιστη διάμετρος που πρέπει να έχει το καπάκι της αεροφιάλης. Οι κοχλίες καταπονούνται σε εφελκυσμό και η μέγιστη επιτρεπόμενη φόρτιση για τον κάθε κοχλία θα είναι σσ σσ εεεε FF εεεε 16 AA σσ εεεε FF εεεε σσ εεεε ΑΑ 16 Το εμβαδό του κοχλία θα είναι : ΑΑ = ππ dd ΑΑ = cccc 2 4 AA = 3.14cccc 2 Και τελικά μέγιστη επιτρεπόμενη φόρτιση για τον κάθε κοχλία θα είναι : FF εεεε σσ εεεε ΑΑ 16 FF εεεε 400 dddddd cccc cccc 2 16 FF εεεε,κκκκκκκκκκκκκκ ύ 20096dddddd 55
ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΕΠΑΛ
 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΕΠΑΛ Προτεινόμενα θέματα 2017-2018 ΕΚΠΑΙΔΕΥΤΙΚΟΣ: ΒΑΝΤΣΗΣ Β. ΓΕΩΡΓΙΟΣ ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΕ17 1 ο Θ Ε Μ Α Α. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις
ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΕΠΑΛ Προτεινόμενα θέματα 2017-2018 ΕΚΠΑΙΔΕΥΤΙΚΟΣ: ΒΑΝΤΣΗΣ Β. ΓΕΩΡΓΙΟΣ ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΕ17 1 ο Θ Ε Μ Α Α. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 3-1 ΚΑΡΦΙΑ ΚΑΡΦΟΣΥΝΔΕΣΕΙΣ,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 3-1 ΚΑΡΦΙΑ ΚΑΡΦΟΣΥΝΔΕΣΕΙΣ,
«ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» προορίζονται για αυτούς που
 Οι σύντομες αυτές σημειώσεις θέματα στο μάθημα «ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» προορίζονται για αυτούς που υπηρετούν τη δημόσια και δωρεάν παιδεία, και τα αγαπητά «παιδιά μου». ΔΡΑΠΕΤΣΩΝΑ 10/2013 ΜΑΡΙΟΣ ΜΟΥΡΑΤΙΔΗΣ
Οι σύντομες αυτές σημειώσεις θέματα στο μάθημα «ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» προορίζονται για αυτούς που υπηρετούν τη δημόσια και δωρεάν παιδεία, και τα αγαπητά «παιδιά μου». ΔΡΑΠΕΤΣΩΝΑ 10/2013 ΜΑΡΙΟΣ ΜΟΥΡΑΤΙΔΗΣ
2 β. ιάμετρος κεφαλών (ή κορυφών) 3 γ. Βήμα οδόντωσης 4 δ. ιάμετρος ποδιών 5 ε. Πάχος δοντιού Αρχική διάμετρος
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΤΡΙΤΗ 11 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΤΡΙΤΗ 11 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
 1 ΕΠΑΛ ΔΡΑΠΕΤΣΩΝΑΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΜΟΥΡΑΤΙΔΗΣ Μ. ΜΑΡΙΟΣ 2014/15 Περιέχονται όλα τα θέματα των πανελλαδικών εξετάσεων στο μάθημα, από το 1997 έως σήμερα ταξινομημένα σε κεφάλαια.
1 ΕΠΑΛ ΔΡΑΠΕΤΣΩΝΑΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΜΟΥΡΑΤΙΔΗΣ Μ. ΜΑΡΙΟΣ 2014/15 Περιέχονται όλα τα θέματα των πανελλαδικών εξετάσεων στο μάθημα, από το 1997 έως σήμερα ταξινομημένα σε κεφάλαια.
ΘΕΜΑ 1 ο Α. Ποια είναι τα μορφολογικά χαρακτηριστικά και ποια τα υλικά κατασκευής των δισκοειδών συνδέσμων; Μονάδες 12
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Α ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 30 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Α ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 30 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
Ερωτήσεις, λυμένες ασκήσεις και τυπολόγια
 Ερωτήσεις, λυμένες ασκήσεις και τυπολόγια Κ. ΝΤΑΒΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Α. ΗΛΩΣΕΙΣ. Να αναφέρετε τα μέσα σύνδεσης.. Σε ποιες κατηγορίες διακρίνονται οι συνδέσεις;. Ποιες συνδέσεις ονομάζονται
Ερωτήσεις, λυμένες ασκήσεις και τυπολόγια Κ. ΝΤΑΒΟΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Α. ΗΛΩΣΕΙΣ. Να αναφέρετε τα μέσα σύνδεσης.. Σε ποιες κατηγορίες διακρίνονται οι συνδέσεις;. Ποιες συνδέσεις ονομάζονται
TEXNIKH MHXANIKH 7. ΚΑΜΨΗ, ΔΙΑΤΜΗΣΗ, ΣΤΡΕΨΗ, ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ
 TEXNIKH MHXANIKH 7. ΚΑΜΨΗ, ΔΙΑΤΜΗΣΗ, ΣΤΡΕΨΗ, ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΓΚΛΩΤΣΟΣ ΔΗΜΗΤΡΗΣ dimglo@uniwa.gr Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Πανεπιστήμιο Δυτικής Αττικής Ιανουάριος 2018 1 ΠΕΡΙΕΧΟΜΕΝΑ 1.
TEXNIKH MHXANIKH 7. ΚΑΜΨΗ, ΔΙΑΤΜΗΣΗ, ΣΤΡΕΨΗ, ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΓΚΛΩΤΣΟΣ ΔΗΜΗΤΡΗΣ dimglo@uniwa.gr Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Πανεπιστήμιο Δυτικής Αττικής Ιανουάριος 2018 1 ΠΕΡΙΕΧΟΜΕΝΑ 1.
Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης
![Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης](/thumbs/64/50942463.jpg) Ηλοσυνδέσεις Ελάχιστη επιτρεπόμενη διάμετρος ήλου που καταπονείται σε διάτμηση 4Q = [cm] zxπτ επ : διάμετρος ήλου σε [cm] Q : Μέγιστη διατμητική δύναμη σε [an] τ επ : επιτρεπόμενη διατμητική τάση σε [an/cm
Ηλοσυνδέσεις Ελάχιστη επιτρεπόμενη διάμετρος ήλου που καταπονείται σε διάτμηση 4Q = [cm] zxπτ επ : διάμετρος ήλου σε [cm] Q : Μέγιστη διατμητική δύναμη σε [an] τ επ : επιτρεπόμενη διατμητική τάση σε [an/cm
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΙΣΗΓΗΤΗΣ : ΜΑΡΚΟΥ ΑΘΑΝΑΣΙΟΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΙΣΗΓΗΤΗΣ : ΜΑΡΚΟΥ ΑΘΑΝΑΣΙΟΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕΛΕΤΗ ΥΠΟΛΟΓΙΣΜΟΣ ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ TREYLOR ΜΕΓΙΣΤΗΣ ΙΚΑΝΟΤΗΤΑΣ ΜΕΤΑΦΟΡΑΣ ΦΟΡΤΙΟΥ 500Kp ΣΠΟΥΔΑΣΤΕΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΙΣΗΓΗΤΗΣ : ΜΑΡΚΟΥ ΑΘΑΝΑΣΙΟΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕΛΕΤΗ ΥΠΟΛΟΓΙΣΜΟΣ ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ TREYLOR ΜΕΓΙΣΤΗΣ ΙΚΑΝΟΤΗΤΑΣ ΜΕΤΑΦΟΡΑΣ ΦΟΡΤΙΟΥ 500Kp ΣΠΟΥΔΑΣΤΕΣ
α. Άτρακτος ονομάζεται κάθε ράβδος που περιστρέφεται μεταφέροντας ροπή. Σ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 08/04/05 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 08/04/05 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 4
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 4
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ. Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι.
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΔΙΑΤΜΗΣΗ 1. Γενικά Όλοι γνωρίζουμε ότι σε μια διατομή ενός καταπονούμενου φορέα
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΔΙΑΤΜΗΣΗ 1. Γενικά Όλοι γνωρίζουμε ότι σε μια διατομή ενός καταπονούμενου φορέα
Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων
 1 Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων Πρόβλημα 3.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές.
1 Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων Πρόβλημα 3.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές.
4/26/2016. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3)
 ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3) Η εξεταστέα ύλη για τις περιγραφικές ερωτήσεις (στο πρώτο μέρος της γραπτής εξέτασης) θα είναι η παρακάτω: - Κεφ. 1: Ποια είναι τα δύο πλεονεκτήματα
ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3) Η εξεταστέα ύλη για τις περιγραφικές ερωτήσεις (στο πρώτο μέρος της γραπτής εξέτασης) θα είναι η παρακάτω: - Κεφ. 1: Ποια είναι τα δύο πλεονεκτήματα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ Τμήμα Μηχανολόγων Μηχανικών ΤΕ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι ΚΑΘΗΓΗΤΗΣ κ. ΜΟΣΧΙΔΗΣ ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ Τμήμα Μηχανολόγων Μηχανικών ΤΕ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι ΚΑΘΗΓΗΤΗΣ κ. ΜΟΣΧΙΔΗΣ ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ
 ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ ΕΠΙΜΟΡΥΩΜΕΝΟ ΣΟ ART DESIGN AND TECHNOLOGY IN THE UNIVERSITY OF MIDDLESEX ΦΙΟ 16 ΕΠΣΕΜΒΡΙΟΤ 2004
ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ ΕΠΙΜΟΡΥΩΜΕΝΟ ΣΟ ART DESIGN AND TECHNOLOGY IN THE UNIVERSITY OF MIDDLESEX ΦΙΟ 16 ΕΠΣΕΜΒΡΙΟΤ 2004
4/11/2017. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ Διαμόρφωση Σπειρώματος Το σπείρωμα δημιουργείται από την κίνηση ενός παράγοντος σχήματος (τρίγωνο, ορθογώνιο κλπ) πάνω σε έλικα που
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ Διαμόρφωση Σπειρώματος Το σπείρωμα δημιουργείται από την κίνηση ενός παράγοντος σχήματος (τρίγωνο, ορθογώνιο κλπ) πάνω σε έλικα που
5/14/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80)
 Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
Σπειρώματα. Περιεχόμενα. Είδη σύνδεσης. Τύποι σύνδεσης. 1. Μόνιμες συνδέσεις. 2. Λυόμενες συνδέσεις. Εισαγωγή. Σπειρώματα - ονοματολογία
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή Σπειρώματα Κοχλίες Σχεδίαση και διαστασιολόγηση σπειρωμάτων Κοχλίες Τύποι σύνδεσης 1. Μόνιμες συνδέσεις Συγκόλληση
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή Σπειρώματα Κοχλίες Σχεδίαση και διαστασιολόγηση σπειρωμάτων Κοχλίες Τύποι σύνδεσης 1. Μόνιμες συνδέσεις Συγκόλληση
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ Διαμόρφωση Σπειρώματος Το σπείρωμα δημιουργείται από την κίνηση ενός παράγοντος σχήματος (τρίγωνο, ορθογώνιο κλπ) πάνω σε έλικα που
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΠΕΙΡΩΜΑΤΑ - ΚΟΧΛΙΕΣ Διαμόρφωση Σπειρώματος Το σπείρωμα δημιουργείται από την κίνηση ενός παράγοντος σχήματος (τρίγωνο, ορθογώνιο κλπ) πάνω σε έλικα που
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» ΕΠΑ.Λ.
 ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» ΕΠΑ.Λ. ΖΗΤΗΜΑ 1 ο ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ ΤΜΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ Τ.Ε.Λ. ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΕΙ ΙΚΟΤΗΤΑΣ ΜΟΝΟ ΓΙΑ ΤΟΥΣ ΑΠΟΦΟΙΤΟΥΣ
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ» ΕΠΑ.Λ. ΖΗΤΗΜΑ 1 ο ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ ΤΜΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ Τ.Ε.Λ. ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΕΙ ΙΚΟΤΗΤΑΣ ΜΟΝΟ ΓΙΑ ΤΟΥΣ ΑΠΟΦΟΙΤΟΥΣ
Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων
 Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων Πρόβλημα Ε.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές. Η
Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων Πρόβλημα Ε.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές. Η
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΟΧΗΜΑΤΩΝ
 2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ
 ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ ΕΠΙΜΟΡΥΩΜΕΝΟ ΣΟ ART DESIGN AND TECHNOLOGY IN THE UNIVERSITY OF MIDDLESEX ΦΙΟ 20 ΕΠΣΕΜΒΡΙΟΤ 2004
ΣΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΚΑΘΗΓΗΣΗ ΜΑΘΗΜΑΣΟ ΚΩΝΣΑΝΣΙΝΟ-ΒΙΚΣΩΡ ΧΑΣΖΗΣΑΜΑΣΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΣΕΦΝΟΛΟΓΟ ΜΗΦΑΝΟΛΟΓΟ ΜΗΦΑΝΙΚΟ ΕΠΙΜΟΡΥΩΜΕΝΟ ΣΟ ART DESIGN AND TECHNOLOGY IN THE UNIVERSITY OF MIDDLESEX ΦΙΟ 20 ΕΠΣΕΜΒΡΙΟΤ 2004
Στοιχεία Μηχανών. Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά
 Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ
 Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ Δ1. Η φέρουσα διατομή και ο ρόλος της στον υπολογισμό αντοχής Όπως ξέρουμε, το αν θα αντέξει ένα σώμα καθορίζεται όχι μόνο από το φορτίο που επιβάλλουμε αλλά και
Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ Δ1. Η φέρουσα διατομή και ο ρόλος της στον υπολογισμό αντοχής Όπως ξέρουμε, το αν θα αντέξει ένα σώμα καθορίζεται όχι μόνο από το φορτίο που επιβάλλουμε αλλά και
Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους.
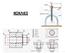 ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑΤΑ
 ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑ Α ΘΕΜΑΤΑ Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης
ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑ Α ΘΕΜΑΤΑ Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
Οδοντωτοί τροχοί. Εισαγωγή. Είδη οδοντωτών τροχών. Σκοπός : Μετωπικοί τροχοί με ευθύγραμμους οδόντες
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Διδάσκοντες : X. Παπαδόπουλος Λ. Καικτσής Οδοντωτοί τροχοί Εισαγωγή Σκοπός : Μετάδοση περιστροφικής κίνησης, ισχύος και ροπής από έναν άξονα
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Διδάσκοντες : X. Παπαδόπουλος Λ. Καικτσής Οδοντωτοί τροχοί Εισαγωγή Σκοπός : Μετάδοση περιστροφικής κίνησης, ισχύος και ροπής από έναν άξονα
ΥΛΗ ΓΙΑ ΤΟ 2ο ΤΕΣΤ ΕΡΓΑΣΤΗΡΙΟΥ ΣΤΟΙΧΕΙΩΝ ΜΗΧΑΝΩΝ Ι
 ΥΛΗ ΓΙΑ ΤΟ 2ο ΤΕΣΤ ΕΡΓΑΣΤΗΡΙΟΥ ΣΤΟΙΧΕΙΩΝ ΜΗΧΑΝΩΝ Ι Το τεστ θα περιλαμβάνει ασκήσεις στα παρακάτω κεφάλαια: Υπολογισμός ελέγχου συγκόλλησης Υπολογισμός μελέτης δοκού που φορτίζεται σε κάμψη Υπολογισμός
ΥΛΗ ΓΙΑ ΤΟ 2ο ΤΕΣΤ ΕΡΓΑΣΤΗΡΙΟΥ ΣΤΟΙΧΕΙΩΝ ΜΗΧΑΝΩΝ Ι Το τεστ θα περιλαμβάνει ασκήσεις στα παρακάτω κεφάλαια: Υπολογισμός ελέγχου συγκόλλησης Υπολογισμός μελέτης δοκού που φορτίζεται σε κάμψη Υπολογισμός
Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους.
 ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 2008
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 008 ΘΕΜΑ Ο α. Οι ήλοι, ανάλογα µε την µορφή της κεφαλής τους διακρίνονται σε Ηµιστρόγγυλους. Φακοειδείς. Η κεφαλή είναι λιγότερο καµπυλωτή από αυτή των ηµιστρόγγυλων και µοιάζει
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 008 ΘΕΜΑ Ο α. Οι ήλοι, ανάλογα µε την µορφή της κεφαλής τους διακρίνονται σε Ηµιστρόγγυλους. Φακοειδείς. Η κεφαλή είναι λιγότερο καµπυλωτή από αυτή των ηµιστρόγγυλων και µοιάζει
TEXNIKH MHXANIKH 6. ΕΦΕΛΚΥΣΜΟΣ-ΘΛΙΨΗ
 TEXNIKH MHXANIKH 6. ΓΚΛΩΤΣΟΣ ΔΗΜΗΤΡΗΣ dimglo@uniwa.gr Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Πανεπιστήμιο Δυτικής Αττικής Δεκέμβριος 018 1 ΚΑΤΑΠΟΝΗΣΕΙΣ Είδη καταπονήσεων Εφελκυσμός: προκαλείται από την
TEXNIKH MHXANIKH 6. ΓΚΛΩΤΣΟΣ ΔΗΜΗΤΡΗΣ dimglo@uniwa.gr Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας Πανεπιστήμιο Δυτικής Αττικής Δεκέμβριος 018 1 ΚΑΤΑΠΟΝΗΣΕΙΣ Είδη καταπονήσεων Εφελκυσμός: προκαλείται από την
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 2007
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 007 ΘΕΜΑ Ο α. Κατά την σύσφιξη ο κοχλίας καταπονείται σε εφελκυσµό και τα κοµµάτια σε θλίψη. Το περικόχλιο ίσης θλίβεται. Οι δυνάµεις που καταπονούν τον κοχλία είναι θλιπτικές
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 007 ΘΕΜΑ Ο α. Κατά την σύσφιξη ο κοχλίας καταπονείται σε εφελκυσµό και τα κοµµάτια σε θλίψη. Το περικόχλιο ίσης θλίβεται. Οι δυνάµεις που καταπονούν τον κοχλία είναι θλιπτικές
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
ΑΡΧΗ ΜΑ: ΘΕΜΑ Α1. Να. στ. σης. εγκοπή. Πείρος με
 Γ ΤΑΞΗΣ ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΑΡΑΣΚΕΥΗ ΣΕΠΤΕΜΒΡΙΟΥ 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ ΣΥΝΟΛΟ
Γ ΤΑΞΗΣ ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΑΡΑΣΚΕΥΗ ΣΕΠΤΕΜΒΡΙΟΥ 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ ΣΥΝΟΛΟ
Γενικές αρχές στοιχείων μηχανών και αντοχής υλικών
 Γενικές αρχές στοιχείων μηχανών και αντοχής υλικών Στοιχεία Μηχανών Τα στοιχεία μηχανών είναι τεμάχια που χρησιμοποιούνται κατ' επανάληψη, στην ίδια ή παραπλήσια μορφή, για τη συγκρότηση μηχανών, συσκευών
Γενικές αρχές στοιχείων μηχανών και αντοχής υλικών Στοιχεία Μηχανών Τα στοιχεία μηχανών είναι τεμάχια που χρησιμοποιούνται κατ' επανάληψη, στην ίδια ή παραπλήσια μορφή, για τη συγκρότηση μηχανών, συσκευών
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΕΤΑΔΟΣΗ ΚΙΝΗΣΗΣ - ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΕΤΑΔΟΣΗ ΚΙΝΗΣΗΣ - ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ
Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ ΤΕΤΑΡΤΗ 9/04/07 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ ΤΕΤΑΡΤΗ 9/04/07 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις που
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-2 ΑΤΡΑΚΤΟΙ ΑΞΟΝΕΣ - ΣΤΡΟΦΕΙΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-2 ΑΤΡΑΚΤΟΙ ΑΞΟΝΕΣ - ΣΤΡΟΦΕΙΣ
ΜΗΧΑΝΙΚΕΣ ΚΑΤΕΡΓΑΣΙΕΣ. Υπολογισμοί συγκολλήσεων
 Σχήμα 1 Δυο ελάσματα πάχους h, συγκολλημένα σε μήκος L, με υλικό συγκόλλησης ορίου ροής S y, που εφελκύονται με δύναμη P. Αν το πάχος της συγκόλλησης είναι h, τότε η αναπτυσσόμενη στο υλικό της συγκόλλησης
Σχήμα 1 Δυο ελάσματα πάχους h, συγκολλημένα σε μήκος L, με υλικό συγκόλλησης ορίου ροής S y, που εφελκύονται με δύναμη P. Αν το πάχος της συγκόλλησης είναι h, τότε η αναπτυσσόμενη στο υλικό της συγκόλλησης
Τ.Ε.Ι.Θ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 1. Ονοματεπώνυμο : Αναγνωστάκης Γιάννης Τμήμα : Οχημάτων Ημερομηνία : 25/5/00 Άσκηση : Ν 4
 Τ.Ε.Ι.Θ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 1 Ονοματεπώνυμο : Αναγνωστάκης Γιάννης Τμήμα : Οχημάτων Ημερομηνία : 25/5/00 Άσκηση : Ν 4 1 Δεδομένα : 1 3000 2 2000 3 12000 4 15000 d 1 12 d 2 15 Ζητούμενα : Να γίνει ο έλεγχος
Τ.Ε.Ι.Θ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 1 Ονοματεπώνυμο : Αναγνωστάκης Γιάννης Τμήμα : Οχημάτων Ημερομηνία : 25/5/00 Άσκηση : Ν 4 1 Δεδομένα : 1 3000 2 2000 3 12000 4 15000 d 1 12 d 2 15 Ζητούμενα : Να γίνει ο έλεγχος
Αναλυτικά Λυμένα Παραδείγματα. Στοιχεία Θεωρίας. Άλυτες Ασκήσεις. Ερωτήσεις Θεωρίας
 ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Αναλυτικά Λυμένα Παραδείγματα Στοιχεία Θεωρίας Άλυτες Ασκήσεις Ερωτήσεις Θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης ( chon nik o@g ma il.co
ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Αναλυτικά Λυμένα Παραδείγματα Στοιχεία Θεωρίας Άλυτες Ασκήσεις Ερωτήσεις Θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης ( chon nik o@g ma il.co
Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μη μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους.
 ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μη μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΚΟΧΛΙΕΣ 1 Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μη μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν κατά κανόνα την
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ. Αντοχή Υλικού
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ Αντοχή Υλικού Ερρίκος Μουρατίδης (BSc, MSc) Σεπτέμβριος 015 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ Αντοχή Υλικού Ερρίκος Μουρατίδης (BSc, MSc) Σεπτέμβριος 015 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΣΧΕΔΙΑΣΗ ΑΤΡΑΚΤΩΝ. Λειτουργικές Παράμετροι
 Άτρακτος: περιστρεφόμενο στοιχείο κυκλικής (συνήθως) διατομής (πλήρους ή σωληνωτής) που χρησιμοποιείται για να μεταφέρει ισχύ ή κίνηση Άξονας: μη περιστρεφόμενο στοιχείο που δεν μεταφέρει ροπή και χρησιμοποιείται
Άτρακτος: περιστρεφόμενο στοιχείο κυκλικής (συνήθως) διατομής (πλήρους ή σωληνωτής) που χρησιμοποιείται για να μεταφέρει ισχύ ή κίνηση Άξονας: μη περιστρεφόμενο στοιχείο που δεν μεταφέρει ροπή και χρησιμοποιείται
Στοιχεία Μηχανών ΙΙ. Α. Ασκήσεις άλυτες. Άσκηση Α.1: Πλήρης υπολογισμός οδοντοτροχών με ευθεία οδόντωση
 Στοιχεία Μηχανών ΙΙ Α. Ασκήσεις άλυτες Άσκηση Α.1: Πλήρης υπολογισμός οδοντοτροχών με ευθεία οδόντωση Περιγραφή της κατασκευής: Σε μία αποθήκη υλικών σιδήρου χρησιμοποιείται μία γερανογέφυρα ανυψωτικής
Στοιχεία Μηχανών ΙΙ Α. Ασκήσεις άλυτες Άσκηση Α.1: Πλήρης υπολογισμός οδοντοτροχών με ευθεία οδόντωση Περιγραφή της κατασκευής: Σε μία αποθήκη υλικών σιδήρου χρησιμοποιείται μία γερανογέφυρα ανυψωτικής
ΜΗΧΑΝΙΚΕΣ ΚΑΤΕΡΓΑΣΙΕΣ. Διαμορφώσεις
 Διαμορφώσεις Σχήμα 1 Στην κατεργασία μετάλλου υπάρχουν δύο κατηγορίες διαμορφώσεων, κατεργασίες με αφαίρεση υλικού και μηχανικής διαμόρφωσης χωρίς αφαίρεση υλικού 1. Ποια η διαφορά των μηχανικών διαμορφώσεων/κατεργασιών
Διαμορφώσεις Σχήμα 1 Στην κατεργασία μετάλλου υπάρχουν δύο κατηγορίες διαμορφώσεων, κατεργασίες με αφαίρεση υλικού και μηχανικής διαμόρφωσης χωρίς αφαίρεση υλικού 1. Ποια η διαφορά των μηχανικών διαμορφώσεων/κατεργασιών
Δυναμική Αντοχή. Σύνδεση με προηγούμενο μάθημα. Περιεχόμενα F = A V = M r = J. Δυναμική καταπόνηση κόπωση. Καμπύλη Woehler.
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Δυναμική Αντοχή Σύνδεση με προηγούμενο μάθημα Καμπύλη τάσης παραμόρφωσης Βασικές φορτίσεις A V y A M y M x M I
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Δυναμική Αντοχή Σύνδεση με προηγούμενο μάθημα Καμπύλη τάσης παραμόρφωσης Βασικές φορτίσεις A V y A M y M x M I
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΤΥΠΟΛΟΓΙΟ ΙΜΑΝΤΟΚΙΝΗΣΕΩΝ
 ΤΥΠΟΛΟΓΙΟ ΙΜΑΝΤΟΚΙΝΗΣΕΩΝ β ελκόμενος κλάδος β n 2 n 1 α 1 d d 2 α 1 2 (α) κινητήρια τροχαλία έλκων κλάδος a β κινούμενη τροχαλία F 2 n 1 α 1 F 2 FA κινητήρια τροχαλία F 1 (β) F 1 Σχήμα 1 (α) Γεωμετρικά
ΤΥΠΟΛΟΓΙΟ ΙΜΑΝΤΟΚΙΝΗΣΕΩΝ β ελκόμενος κλάδος β n 2 n 1 α 1 d d 2 α 1 2 (α) κινητήρια τροχαλία έλκων κλάδος a β κινούμενη τροχαλία F 2 n 1 α 1 F 2 FA κινητήρια τροχαλία F 1 (β) F 1 Σχήμα 1 (α) Γεωμετρικά
Ανοξείδωτοι Χάλυβες - Μέρος 1.4 του Ευρωκώδικα 3 Ιωάννη Ραυτογιάννη Γιώργου Ιωαννίδη
 Ανοξείδωτοι Χάλυβες - Μέρος 1.4 του Ευρωκώδικα 3 Ιωάννη Ραυτογιάννη Γιώργου Ιωαννίδη 1. Εισαγωγή Οι ανοξείδωτοι χάλυβες ως υλικό κατασκευής φερόντων στοιχείων στα δομικά έργα παρουσιάζει διαφορές ως προ
Ανοξείδωτοι Χάλυβες - Μέρος 1.4 του Ευρωκώδικα 3 Ιωάννη Ραυτογιάννη Γιώργου Ιωαννίδη 1. Εισαγωγή Οι ανοξείδωτοι χάλυβες ως υλικό κατασκευής φερόντων στοιχείων στα δομικά έργα παρουσιάζει διαφορές ως προ
Πανεπιστήμιο Θεσσαλίας Τμήμα Μηχανολόγων Μηχ/κων Στοιχεία Μηχανών Διδάσκων: Αλ. Κερμανίδης. Κοχλίες
 Κοχλίες Γενικά-Ορισμοί- Προδιαγραφές Ανάλογα με τον σκοπό οι κοχλίες διακρίνονται σε (α) κοχλίες σύσφιγξης (σύνδεση με κοχλίες) και σε () κοχλίες κινήσεως ή μεταφοράς ισχύος Οι κοχλίες σύσφιγξης χρησιμοποιούνται
Κοχλίες Γενικά-Ορισμοί- Προδιαγραφές Ανάλογα με τον σκοπό οι κοχλίες διακρίνονται σε (α) κοχλίες σύσφιγξης (σύνδεση με κοχλίες) και σε () κοχλίες κινήσεως ή μεταφοράς ισχύος Οι κοχλίες σύσφιγξης χρησιμοποιούνται
ΒΑΘΜΟΣ : /100, /20 ΥΠΟΓΡΑΦΗ:..
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /20 ΥΠΟΓΡΑΦΗ:.. Μάθημα: ΜΗΧΑΝΙΚΗ
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2018 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΤΡΙΑΣ:.... ΒΑΘΜΟΣ : /100, /20 ΥΠΟΓΡΑΦΗ:.. Μάθημα: ΜΗΧΑΝΙΚΗ
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 2014
 ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 03-04 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 04 Κατεύθυνση: Θεωρητική Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Τάξη: Β' Αριθμός Μαθητών: 0 Κλάδος: Μηχανολογίας
ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 03-04 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 04 Κατεύθυνση: Θεωρητική Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Τάξη: Β' Αριθμός Μαθητών: 0 Κλάδος: Μηχανολογίας
( ) L v. δ Τύμπανο. κίνησης. Αντίβαρο τάνυσης. 600m. 6000Ν ανά cm πλάτους ιµάντα και ανά ενίσχυση 0.065
 Ανυψωτικές & Μεταφορικές Μηχανές Ακαδημαϊκό έτος: 010-011 Άσκηση (Θέμα Επαναληπτικής Γραπτής Εξέτασης Σεπ010 / Βαρύτητα: 50%) Έστω η εγκατάσταση της ευθύγραµµης µεταφορικής ταινίας του Σχήµατος 1, η οποία
Ανυψωτικές & Μεταφορικές Μηχανές Ακαδημαϊκό έτος: 010-011 Άσκηση (Θέμα Επαναληπτικής Γραπτής Εξέτασης Σεπ010 / Βαρύτητα: 50%) Έστω η εγκατάσταση της ευθύγραµµης µεταφορικής ταινίας του Σχήµατος 1, η οποία
ΑΡΧΗ ΣΕΙΣ ΣΑΒΒΑΤΟ ΜΑ: ΘΕΜΑ Α1. Να ΣΤΗΛΗ. α. β. γ. δ. ε. στ. Κεφαλής. Γρύλος
 Γ ΤΑΞΗΣ HMEΡΗΣΙΩΝ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣ ΣΕΙΣ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 10 ΙΟΥΝΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ ΣΥΝΟΛΟ ΣΕΛΙ
Γ ΤΑΞΗΣ HMEΡΗΣΙΩΝ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣ ΣΕΙΣ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 10 ΙΟΥΝΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ ΣΥΝΟΛΟ ΣΕΛΙ
ΑΡΧΗ ΣΕΙΣ ΣΑΒΒΑΤΟ ΜΑ: ΘΕΜΑ Α1. Να. Foititikanea.gr ΣΤΗΛΗ. α. β. γ. δ. ε. στ. Κεφαλής. Γρύλος
 Γ ΤΑΞΗΣ HMEΡΗΣΙΩΝ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης Β που δίνει τη σωστή αντιστοίχιση. Σημειώνεται
Γ ΤΑΞΗΣ HMEΡΗΣΙΩΝ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης Β που δίνει τη σωστή αντιστοίχιση. Σημειώνεται
ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι. Δρ. Στέργιος Μαρόπουλος
 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι Δρ. Στέργιος Μαρόπουλος ΠΕΡΙΕΧΟΜΕΝΑ 1. ΓΕΝΙΚΑ...1 2. ΤΥΠΟΠΟΙΗΣΗ - ΣΥΝΑΡΜΟΓΕΣ...1 3. ΑΡΧΕΣ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ...25 4. ΗΛΟΙ...47 5. ΚΟΧΛΙΕΣ...61 6. ΣΥΓΚΟΛΛΗΣΕΙΣ...92 7. ΕΛΑΤΗΡΙΑ...124 8. ΑΤΡΑΚΤΟΙ
ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι Δρ. Στέργιος Μαρόπουλος ΠΕΡΙΕΧΟΜΕΝΑ 1. ΓΕΝΙΚΑ...1 2. ΤΥΠΟΠΟΙΗΣΗ - ΣΥΝΑΡΜΟΓΕΣ...1 3. ΑΡΧΕΣ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ...25 4. ΗΛΟΙ...47 5. ΚΟΧΛΙΕΣ...61 6. ΣΥΓΚΟΛΛΗΣΕΙΣ...92 7. ΕΛΑΤΗΡΙΑ...124 8. ΑΤΡΑΚΤΟΙ
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ. Ασκήσεις προηγούμενων εξετάσεων ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
α. Οι ήλοι κατασκευάζονται από ανθρακούχο χάλυβα, χαλκό ή αλουμίνιο. Σ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 6/04/206 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΑΒΒΑΤΟ 6/04/206 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ ο ) Να χαρακτηρίσετε τις προτάσεις
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών
 ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών Ασκήσεις για λύση Η ράβδος του σχήματος είναι ομοιόμορφα μεταβαλλόμενης κυκλικής 1 διατομής εφελκύεται αξονικά με δύναμη Ρ. Αν D d είναι οι διάμετροι των ακραίων
ΛΥΣΕΙΣ άλυτων ΑΣΚΗΣΕΩΝ στην Αντοχή των Υλικών Ασκήσεις για λύση Η ράβδος του σχήματος είναι ομοιόμορφα μεταβαλλόμενης κυκλικής 1 διατομής εφελκύεται αξονικά με δύναμη Ρ. Αν D d είναι οι διάμετροι των ακραίων
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης. ΕργαστηριακήΆσκηση 3 η
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης ΕργαστηριακήΆσκηση 3 η Σκοπός Σκοπός του πειράµατος είναι ηκατανόησητωνδιαδικασιώνκατάτηκαταπόνησηστρέψης, η κατανόηση του διαγράµµατος διατµητικής τάσης παραµόρφωσης η ικανότητα
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης ΕργαστηριακήΆσκηση 3 η Σκοπός Σκοπός του πειράµατος είναι ηκατανόησητωνδιαδικασιώνκατάτηκαταπόνησηστρέψης, η κατανόηση του διαγράµµατος διατµητικής τάσης παραµόρφωσης η ικανότητα
Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 3 η
 Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 3 η Δομή παρουσίασης 1. ΕΙΣΑΓΩΓΗ ΙΣΤΟΡΙΚΑ ΣΤΟΙΧΕΙΑ 2. ΕΙΔΗ
Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 3 η Δομή παρουσίασης 1. ΕΙΣΑΓΩΓΗ ΙΣΤΟΡΙΚΑ ΣΤΟΙΧΕΙΑ 2. ΕΙΔΗ
ΑΡΧΗ ΜΑ: ΘΕΜΑ Α1. Να
 Γ ΤΑΞΗΣ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 21 ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ
Γ ΤΑΞΗΣ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 21 ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜ ΜΑ: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝΝ
ΒΙΔΕΣ ΚΑΤΑ DIN 933. d 6 8 10 12 14 16 18 20 22 24 27 30 s 10 13 17 19 22 24 27 30 32 36 41 46 k 4 5,3 6,4 7,5 8,8 10 11,5 12,5 14 15 17 18,7
 ΒΙΔΕΣ ΚΑΤΑ DIN 933 ΠΟΙΟΤ: 8.8 d 6 8 10 12 14 16 18 20 22 24 27 30 s 10 13 17 19 22 24 27 30 32 36 41 46 k 4 5,3 6,4 7,5 8,8 10 11,5 12,5 14 15 17 18,7 BHMA (P) 1 1,25 1,5 1,75 2 2 2,5 2,5 2,5 3 3 3,5 ΜΗΚΟΣ
ΒΙΔΕΣ ΚΑΤΑ DIN 933 ΠΟΙΟΤ: 8.8 d 6 8 10 12 14 16 18 20 22 24 27 30 s 10 13 17 19 22 24 27 30 32 36 41 46 k 4 5,3 6,4 7,5 8,8 10 11,5 12,5 14 15 17 18,7 BHMA (P) 1 1,25 1,5 1,75 2 2 2,5 2,5 2,5 3 3 3,5 ΜΗΚΟΣ
Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η
 Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η ΓΕΩΜΕΤΡΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ d - Εξωτερική διάμετρος d
Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η ΓΕΩΜΕΤΡΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ d - Εξωτερική διάμετρος d
Διοίκηση Εργοταξίου (Construction Management) Διδάσκων: Γιάννης Χουλιάρας
 ΤΕΙ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Διοίκηση Εργοταξίου (Construction Management) Διδάσκων: Γιάννης Χουλιάρας Εισαγωγή. Αρχές υπολογισμού στοιχείων μηχανών, στοιχείων μη λυομένων συνδέσεων (ηλώσεις,
ΤΕΙ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Διοίκηση Εργοταξίου (Construction Management) Διδάσκων: Γιάννης Χουλιάρας Εισαγωγή. Αρχές υπολογισμού στοιχείων μηχανών, στοιχείων μη λυομένων συνδέσεων (ηλώσεις,
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σχήμα 12-7: Σκαρίφημα άξονα με τις φορτίσεις του
 1.6.1 ΑΣΚΗΣΗ Ζητείται να υπολογιστεί ένας άξονας μετάδοσης κίνησης και ισχύος με είσοδο από την τρίτη τροχαλία του σχήματος, όπου φαίνονται οι με βασικές προδιαγραφές του προβλήματος. Ο άξονας περιστρέφεται
1.6.1 ΑΣΚΗΣΗ Ζητείται να υπολογιστεί ένας άξονας μετάδοσης κίνησης και ισχύος με είσοδο από την τρίτη τροχαλία του σχήματος, όπου φαίνονται οι με βασικές προδιαγραφές του προβλήματος. Ο άξονας περιστρέφεται
8. ΔΙΚΤΥΩΜΑΤΑ. 8.1 Ορισμοί:
 8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
Ρόλος συνδέσεων στις μεταλλικές κατασκευές
 Ρόλος συνδέσεων στις μεταλλικές κατασκευές Σύνδεση μελών κατασκευής μεταξύ τους Ασφαλής μεταφορά εντατικών μεγεθών από μέλος σε μέλος Απαιτήσεις: Ασφάλεια Κατασκευασιμότητα Συνέπεια με υπολογιστικό προσομοίωμα
Ρόλος συνδέσεων στις μεταλλικές κατασκευές Σύνδεση μελών κατασκευής μεταξύ τους Ασφαλής μεταφορά εντατικών μεγεθών από μέλος σε μέλος Απαιτήσεις: Ασφάλεια Κατασκευασιμότητα Συνέπεια με υπολογιστικό προσομοίωμα
Παράδειγμα 1 P 1 P 4 P 2 P 3 A B Γ Δ. Παράδειγμα 2
 Παράδειγμα 1 Μία ράβδος ομογενής σταθερής διατομής Α = 5 cm 2 καταπονείται όπως στο σχήμα. Να βρείτε την συνολική επιμήκυνση της ράβδου. Δίνεται το μέτρο ελαστικότητας Ε = 2*10 7 Ν/cm 2 και ακόμη : 1 =
Παράδειγμα 1 Μία ράβδος ομογενής σταθερής διατομής Α = 5 cm 2 καταπονείται όπως στο σχήμα. Να βρείτε την συνολική επιμήκυνση της ράβδου. Δίνεται το μέτρο ελαστικότητας Ε = 2*10 7 Ν/cm 2 και ακόμη : 1 =
ΚΕΦΑΛΑΙΟ ΣΥΓΚΟΛΛΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 8 ΣΥΓΚΟΛΛΗΣΕΙΣ - 2 / 22 - Παπαδόπουλος Α. Χρήστος 8 Συγκολλήσεις είναι η διαδικασία της μόνιμης τοπικής ένωσης μεταλλικών μερών σε ημιτετηγμένη μορφή με εφαρμογή πίεσης ή την ένωση των μερών σε
ΚΕΦΑΛΑΙΟ 8 ΣΥΓΚΟΛΛΗΣΕΙΣ - 2 / 22 - Παπαδόπουλος Α. Χρήστος 8 Συγκολλήσεις είναι η διαδικασία της μόνιμης τοπικής ένωσης μεταλλικών μερών σε ημιτετηγμένη μορφή με εφαρμογή πίεσης ή την ένωση των μερών σε
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2010
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 010 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα: Βασικά Στοιχεία Εφαρμοσμένης Μηχανικής
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 010 ΤΕΧΝΟΛΟΓΙΑ (Ι) ΠΡΑΚΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Μάθημα: Βασικά Στοιχεία Εφαρμοσμένης Μηχανικής
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης ΘΕΜΑ: ΣΧΕΔΙΑΣΜΟΣ, ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΔΥΟ ΒΑΣΕΩΝ ΣΤΗΡΙΞΗΣ ΚΙΝΗΤΗΡΩΝ ΓΙΑ ΤΟ ΕΡΓΑΣΤΗΡΙΟ Μ.Ε.Κ.
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης ΘΕΜΑ: ΣΧΕΔΙΑΣΜΟΣ, ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΔΥΟ ΒΑΣΕΩΝ ΣΤΗΡΙΞΗΣ ΚΙΝΗΤΗΡΩΝ ΓΙΑ ΤΟ ΕΡΓΑΣΤΗΡΙΟ Μ.Ε.Κ. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Του Σταύρου Μηλιαρά Επιβλέπων καθηγητής Κουδουμάς Γεώργιος
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης ΘΕΜΑ: ΣΧΕΔΙΑΣΜΟΣ, ΜΕΛΕΤΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΔΥΟ ΒΑΣΕΩΝ ΣΤΗΡΙΞΗΣ ΚΙΝΗΤΗΡΩΝ ΓΙΑ ΤΟ ΕΡΓΑΣΤΗΡΙΟ Μ.Ε.Κ. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Του Σταύρου Μηλιαρά Επιβλέπων καθηγητής Κουδουμάς Γεώργιος
Μάθημα: Πειραματική αντοχή των υλικών Πείραμα Στρέψης
 Μάθημα: Πειραματική αντοχή των υλικών Πείραμα Στρέψης Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχήμα 1 Στρέψη κυκλικής διατομής
Μάθημα: Πειραματική αντοχή των υλικών Πείραμα Στρέψης Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχήμα 1 Στρέψη κυκλικής διατομής
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ. Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ. 1.
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η
 Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η ΓΕΩΜΕΤΡΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ d - Εξωτερική διάμετρος d
Μετροτεχνικό Εργαστήριο Τομέας Βιομηχανικής Διοίκησης & Επιχειρησιακής Έρευνας Σχολή Μηχανολόγων Μηχανικών Έλεγχος Μηχανουργικού Προϊόντος Άσκηση 4 η ΓΕΩΜΕΤΡΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ d - Εξωτερική διάμετρος d
ΙΜΑΝΤΟΚΙΝΗΣΗ (ΤΡΟΧΑΛΙΕΣ - ΙΜΑΝΤΕΣ)
 ΙΜΑΝΤΟΚΙΝΗΣΗ (ΤΡΟΧΑΛΙΕΣ - ΙΜΑΝΤΕΣ) Για να παραλάβει μία άτρακτος περιστροφική κίνηση από μία άλλη, η οποία βρίσκεται σε αρκετή απόσταση, χρησιμοποιείται ως μέσο μετάδοσης κίνησης ο ιμάντας (λουρί) Θα πρέπει
ΙΜΑΝΤΟΚΙΝΗΣΗ (ΤΡΟΧΑΛΙΕΣ - ΙΜΑΝΤΕΣ) Για να παραλάβει μία άτρακτος περιστροφική κίνηση από μία άλλη, η οποία βρίσκεται σε αρκετή απόσταση, χρησιμοποιείται ως μέσο μετάδοσης κίνησης ο ιμάντας (λουρί) Θα πρέπει
Παράδειγμα υπολογισμού μελέτης και ελέγχου ζεύγους ατέρμονα-κορώνας
 Παράδειγμα υπολογισμού μελέτης και ελέγχου ζεύγους ατέρμονα-κορώνας Δεδομένα: Στρεπτική ροπή στον ατέρμονα: Τ1 = Μ t1 = 10 Νm Περιστροφική ταχύτητα του ατέρμονα: n1 = 600 Σ/min Σχέση μετάδοσης: i = 40
Παράδειγμα υπολογισμού μελέτης και ελέγχου ζεύγους ατέρμονα-κορώνας Δεδομένα: Στρεπτική ροπή στον ατέρμονα: Τ1 = Μ t1 = 10 Νm Περιστροφική ταχύτητα του ατέρμονα: n1 = 600 Σ/min Σχέση μετάδοσης: i = 40
ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ. ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc)
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc) ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΠΣΕ60 Ακαδημαϊκό Έτος: 207-208 η Γραπτή Εργασία Επιβλέπων
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ (MSc) ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΠΣΕ60 Ακαδημαϊκό Έτος: 207-208 η Γραπτή Εργασία Επιβλέπων
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2016-2017 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Επιτρεπόμενη διάρκεια γραπτού 2,5ώρες (150 λεπτά). Μάθημα: ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΕΦΑΡΜΟΣΜΕΝΗΣ
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2016-2017 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Επιτρεπόμενη διάρκεια γραπτού 2,5ώρες (150 λεπτά). Μάθημα: ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΕΦΑΡΜΟΣΜΕΝΗΣ
ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ ΠΑΡΑΔΕΙΓΜΑ 1: Ο κύλινδρος που φαίνεται στο σχήμα είναι από χάλυβα που έχει ένα ειδικό βάρος 80.000 N/m 3. Υπολογίστε την θλιπτική τάση που ενεργεί στα σημεία Α και
ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ ΠΑΡΑΔΕΙΓΜΑ 1: Ο κύλινδρος που φαίνεται στο σχήμα είναι από χάλυβα που έχει ένα ειδικό βάρος 80.000 N/m 3. Υπολογίστε την θλιπτική τάση που ενεργεί στα σημεία Α και
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 017 3. Διαγράμματα NQM Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Α3. Διαγράμματα NQΜ/ Μηχανική Υλικών 1 Σκοποί ενότητας Να εξοικειωθεί ο φοιτητής
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 017 3. Διαγράμματα NQM Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Α3. Διαγράμματα NQΜ/ Μηχανική Υλικών 1 Σκοποί ενότητας Να εξοικειωθεί ο φοιτητής
Σιδηρές Κατασκευές ΙΙ Άσκηση 7 Σύνδεση με κοχλίες τύπου D και E. Σχολή Πολιτικών Μηχανικών Εργαστήριο Μεταλλικών Κατασκευών
 ιδηρές ατασκευές Άσκηση 7 ύνδεση με κοχλίες τύπου D και E χολή Πολιτικών ηχανικών ργαστήριο εταλλικών ατασκευών Άδεια Χρήσης ο παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. ια εκπαιδευτικό
ιδηρές ατασκευές Άσκηση 7 ύνδεση με κοχλίες τύπου D και E χολή Πολιτικών ηχανικών ργαστήριο εταλλικών ατασκευών Άδεια Χρήσης ο παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. ια εκπαιδευτικό
Εισαγωγή. Σύνδεση με μαθήματα Σχολής ΝΜΜ. Μειωτήρας Στροφών Βασική λειτουργία
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ιδάσκων: Χ. Παπαδόπουλος Σύνδεση με μαθήματα Σχολής ΝΜΜ Μηχανική Φορτίσεις, Είδη φορτίσεων (εφελκυσμός, θλίψη,
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ιδάσκων: Χ. Παπαδόπουλος Σύνδεση με μαθήματα Σχολής ΝΜΜ Μηχανική Φορτίσεις, Είδη φορτίσεων (εφελκυσμός, θλίψη,
ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2016 ΗΜΕΡΟΜΗΝΙΑ 07 ΣΕΠΤΕΜΒΡΙΟΥ 2016
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΚΑΘΗΓΗΤΗΣ Μ. ΣΑΜΟΥΗΛΙΔΗΣ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 016
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΚΑΘΗΓΗΤΗΣ Μ. ΣΑΜΟΥΗΛΙΔΗΣ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ ΑΝΤΟΧΗ ΠΛΟΙΟΥ 5 ου ΕΞΑΜΗΝΟΥ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 016
Κεφ. 3. ΕΙΔΗ ΦΟΡΤΙΣΕΩΝ
 Κεφ. 3. ΕΙΔΗ ΦΟΡΤΙΣΕΩΝ 3.1. Εφελκυσμός Τάση λόγω εφελκυσμού: Ν σz = ----(3-1) Α όπου Ν = η εφελκυστική δύναμη Α = το εμβαδό της διατομής του σώματος («διατομή» είναι το σχήμα που έχει το σώμα σε μία κάθετη
Κεφ. 3. ΕΙΔΗ ΦΟΡΤΙΣΕΩΝ 3.1. Εφελκυσμός Τάση λόγω εφελκυσμού: Ν σz = ----(3-1) Α όπου Ν = η εφελκυστική δύναμη Α = το εμβαδό της διατομής του σώματος («διατομή» είναι το σχήμα που έχει το σώμα σε μία κάθετη
ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι
 Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Ε.202-2: ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΜΑΤΟΣ (ΘΕΩΡΙΑ, ΑΣΚΗΣΕΙΣ ΠΡΑΞΕΙΣ, ΕΡΓΑΣΤΗΡΙΟ)
 ΚΩΔΙΚΟΣ: Ε.202-2 ΕΝΤΥΠΑ ΣΥΣΤΗΜΑΤΟΣ ΠΟΙΟΤΗΤΑΣ ΕΝΤΥΠΟ: ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΜΑΤΟΣ ΕΚΔΟΤΗΣ: ΥΠΕΥΘΥΝΟΣ ΣΥΝΤΑΞΗΣ ΕΓΧΕΙΡΙΔΙΟΥ Ε.202-2: ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΜΑΤΟΣ (ΘΕΩΡΙΑ, ΑΣΚΗΣΕΙΣ ΠΡΑΞΕΙΣ, ΕΡΓΑΣΤΗΡΙΟ) A ΜΕΡΟΣ 1. ΓΕΝΙΚΑ
ΚΩΔΙΚΟΣ: Ε.202-2 ΕΝΤΥΠΑ ΣΥΣΤΗΜΑΤΟΣ ΠΟΙΟΤΗΤΑΣ ΕΝΤΥΠΟ: ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΜΑΤΟΣ ΕΚΔΟΤΗΣ: ΥΠΕΥΘΥΝΟΣ ΣΥΝΤΑΞΗΣ ΕΓΧΕΙΡΙΔΙΟΥ Ε.202-2: ΕΓΧΕΙΡΙΔΙΟ ΜΑΘΗΜΑΤΟΣ (ΘΕΩΡΙΑ, ΑΣΚΗΣΕΙΣ ΠΡΑΞΕΙΣ, ΕΡΓΑΣΤΗΡΙΟ) A ΜΕΡΟΣ 1. ΓΕΝΙΚΑ
Σχήμα 22: Αλυσίδες κυλίνδρων
 Αλυσοκινήσεις Πλεονεκτήματα ακριβής σχέση μετάδοση λόγω μη ύπαρξης διολίσθησης, η συναρμολόγηση χωρίς αρχική πρόταση επειδή η μετάδοση δεν βασίζεται στην τριβή καθώς επίσης και ο υψηλός βαθμός απόδοσης
Αλυσοκινήσεις Πλεονεκτήματα ακριβής σχέση μετάδοση λόγω μη ύπαρξης διολίσθησης, η συναρμολόγηση χωρίς αρχική πρόταση επειδή η μετάδοση δεν βασίζεται στην τριβή καθώς επίσης και ο υψηλός βαθμός απόδοσης
