Αναλυτικά Λυμένα Παραδείγματα. Στοιχεία Θεωρίας. Άλυτες Ασκήσεις. Ερωτήσεις Θεωρίας
|
|
|
- Διώνη Διαμαντόπουλος
- 10 χρόνια πριν
- Προβολές:
Transcript
1 ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Αναλυτικά Λυμένα Παραδείγματα Στοιχεία Θεωρίας Άλυτες Ασκήσεις Ερωτήσεις Θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός)
2 ... Νικόλαος Γ. Χονδράκης ( chon nik o@g ma il.co m) Διπλωματούχος Μηχανολόγος Μηχανικός ISBN Copyright Νικόλαος Γ. Χονδράκης, Με επιφύλαξη παντός δικαιώματος. All rights reserved. Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή της παρούσας εργασίας, εξ ολοκλήρου ή τμήματος αυτής, για εμπορικό σκοπό. Επιτρέπεται η ανατύπωση, αποθήκευση και διανομή για σκοπό μη κερδοσκοπικό, εκπαιδευτικής φύσης, υπό την προϋπόθεση να αναφέρεται η πηγή προέλευσης και να διατηρείται το παρόν μήνυμα. Ερωτήματα που αφορούν τη χρήση της εργασίας για κερδοσκοπικό σκοπό πρέπει να απευθύνονται προς τον συγγραφέα.
3 ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Αναλυτικά Λυμένα Παραδείγματα - Στοιχεία Θεωρίας Ασκήσεις - Ερωτήσεις Θεωρίας Για τους μαθητές των ΕΠΑΛ και τους υποψήφιους που εξετάζονται στο μάθημα: Στοιχεία Μηχανών. Νικόλαος Χονδράκης (chonniko@gmail.com)
4
5 Πρόλογος Αιτία για τη συγγραφή του παρόντος βοηθήματος, για τη λύση των ασκήσεων του μαθήματος των Στοιχείων Μηχανών, στάθηκε η διαπίστωση ότι πολλοί μαθητές, ενώ έχουν διάθεση να μελετήσουν το μάθημα, αντιμετωπίζουν προβλήματα στην κατανόηση της επίλυσης των ασκήσεων. Το αποτέλεσμα είναι να αποτυγχάνουν λιγότερο ή περισσότερο στις εξετάσεις τους. Σκοπός μας επομένως ήταν να απλοποιήσουμε τον τρόπο λύσης των ασκήσεων. Με την αναλυτική παρουσίαση πολλών λυμένων παραδειγμάτων υποδείχνουμε τον τρόπο που πρέπει να σκέφτεται ένας μαθητής που λύνει μια άσκηση. Το περιεχόμενο της συγγραφής απευθύνεται στους υποψήφιους των Πανελλαδικών εξετάσεων, είτε αυτοί θεωρούνται καλοί μαθητές, είτε έχουν κενά και με τη μελέτη του παρόντος θα τα καλύψουν. Οι ασκήσεις εδώ λύνονται πολύ αναλυτικά, στην ουσία γράφουμε τις σκέψεις μας προχωρώντας στη λύση. Με την λεπτομερή καταγραφή της λύσης, ο μαθητής θα μάθει να σκέφτεται πώς να αντιμετωπίζει όλες τις ασκήσεις, αρκεί να γνωρίζει τους μαθηματικούς τύπους που απαιτούνται. Ο τρόπος αυτός της παρουσίασης, επίσης, εξυπηρετεί τους μαθητές που είναι αδύνατοι στα μαθηματικά και γενικότερα δεν έχουν εμπειρία στη λύση ασκήσεων οποιουδήποτε μαθήματος. Δεν αρέσει στο συγγραφέα να δίνει με «τυφλοσούρτη» τον τρόπο που λύνεται η άσκηση. Αν γινόταν αυτό κινδυνεύει ο μαθητής να παγιδευτεί σε μια απλή άσκηση, που όμως είναι λίγο διαφορετική από τις αναμενόμενες. Εδώ θέλουμε να επιστήσουμε την προσοχή, των αδύνατων ιδιαίτερα μαθητών, στο εξής: αν κατά την προετοιμασία σας δεν λύσετε πολλές ασκήσεις, θα απομακρυνθεί η πιθανότητα επιτυχίας σας. Αυτό ισχύει σε κάθε μάθημα που έχει ασκήσεις. Λύσετε όσο πιο πολλές ασκήσεις μπορείτε. Έτσι θα πετύχετε τρία πράγματα: Θα μάθετε τους τύπους που χρειάζεστε Θα μάθετε να αντιμετωπίζετε κάθε είδους άσκηση Θα λύσετε εύκολα, και κυρίως γρήγορα, τις ασκήσεις και θα σας μείνει αρκετός χρόνος για να σκεφτείτε στις εξετάσεις ένα δύσκολο θέμα που απαιτεί πολύ χρόνο. Από την εμπειρία πολλών ετών στις εξετάσεις των Επαγγελματικών Λυκείων, έχουμε αντιληφτεί ότι οι καλύτερα προετοιμασμένοι μαθητές λύνουν όλα τα θέματα των Πανελλαδικών στο μισό χρόνο από εκείνον που έχουν στη διάθεσή τους. Στο πρώτο κεφάλαιο παρουσιάζονται οι απαραίτητες πληροφορίες όσον αφορά στις αναγκαίες γνώσεις μαθηματικών και μηχανικής-αντοχής. Αναφέρονται όλες οι μονάδες των μεγεθών που εμφανίζονται στο μάθημα, καθώς και οι σχέσεις μεταξύ τους. Δίνονται όλες οι πληροφορίες που χρειάζονται για τη λύση των ασκήσεων και σχετίζονται με τον κύκλο, που είναι το πιο συνηθισμένο γεωμετρικό σχήμα του μαθήματος. Ακολούθως δίνονται όλες εκείνες οι πληροφορίες από το μάθημα «μηχανική και αντοχή των υλικών» της Δευτέρας τάξης. Η παρουσίαση είναι αναλυτική ώστε και εκείνοι που δεν τα θυμούνται επαρκώς να μπορέσουν να παρακολουθήσουν τη συνέχεια του μαθήματος. Αν νομίζετε ότι δεν είναι αρκετά για σας, πρέπει να ανατρέξετε στο αντίστοιχο βιβλίο, τουλάχιστον όταν θα φτάσετε στο κεφάλαιο όπου νομίζετε ότι σας χρειάζεται. Στα κεφάλαια που ακολουθούν δίνονται λυμένες ασκήσεις ανά κεφάλαιο του σχολικού βιβλίου, αφού πρώτα δοθούν με αναλυτικές εξηγήσεις οι τύποι που θα χρησιμοποιηθούν. Ίσως οι καλύτεροι μαθητές βρουν κουραστική την αναλυτική παρουσίαση της λύσης που δίνεται. Εκείνοι ας δουν μόνο τις εξισώσεις ή ό,τι άλλο χρειάζονται. Στο βιβλίο του σχολείου οι λύσεις των εξισώσεων δεν περιλαμβάνουν τις αντίστοιχες μονάδες των μεγεθών αλλά εμείς εδώ, σχεδόν σε όλες τις ασκήσεις, βάζαμε τις αντίστοιχες μονάδες κατά τη λύση. Όπως σημειώνεται συχνά και κατά τη λύση των ασκήσεων, εσείς πρέπει να μαθαίνετε τους τύπους με τις αντίστοιχες μονάδες, διότι δεν ακολουθούν όλοι οι τύποι του σχολικού βιβλίου το Διεθνές Σύστημα Μονάδων (SI). Στις υποδειγματικά λυμένες ασκήσεις περιέχονται και μερικές που δεν είναι πολύ πιθανό να βρίσκονται ποτέ μεταξύ των θεμάτων στις Πανελλαδικές εξετάσεις. Και δεν είναι πιθανόν είτε επειδή δεν υπάρχουν αντίστοιχες ασκήσεις στο σχολικό βιβλίο, είτε επειδή ενώ υπάρχουν όμοιες ασκήσεις, δεν είναι πιθανές επειδή πρέπει να σας δοθούν και αρκετοί πίνακες με διάφορα στοιχεία μαζί με την εκφώνηση. Πίνακες μπορεί να δοθούν μαζί με τα
6 θέματα, όμως όχι πάνω από ένας για κάθε άσκηση. Τουλάχιστον, αυτό δείχνει η εμπειρία από τα παλιότερα θέματα. Επειδή όμως υπάρχουν στο βιβλίο αντίστοιχες ασκήσεις, δώσαμε κι εμείς ορισμένα παραδείγματα. Όπου υπάρχουν τέτοιες (απίθανο να δοθούν στις εξετάσεις) ασκήσεις το αναφέρουμε και σε πρώτη ανάγνωση μπορείτε να μην τις κοιτάξετε, αλλά καλό είναι, αν θέλετε να είστε άριστα προετοιμασμένοι, να τις δείτε κάποια στιγμή. Στα τελευταία κεφάλαια δίνονται κατά σειράν: οι άλυτες ασκήσεις του βιβλίου λυμένες, ασκήσεις προς λύση από εσάς, ερωτήσεις σωστού λάθους (με τις απαντήσεις τους), ερωτήσεις θεωρίας για να απαντήσετε και στο τέλος ένα μικρό τυπολόγιο με όλους τους τύπους που πρέπει να θυμόσαστε. Στο τυπολόγιο δεν αναφέρονται οι μονάδες των τύπων και θα πρέπει να ανατρέξετε στα προηγούμενα για να τις βρείτε. Πιστεύουμε ότι αν μελετήσετε το παρόν βιβλίο με την δέουσα προσοχή, δεν θα αντιμετωπίσετε κανένα πρόβλημα στη λύση των ασκήσεων στις εξετάσεις. Είναι απίθανο να δοθεί μεταξύ των θεμάτων άσκηση πιο δύσκολη ή διαφορετική από τις λυμένες ασκήσεις που έχουμε δώσει εδώ. Ως τώρα στις εξετάσεις δεν υπήρξε ποτέ κανένα θέμα που να έχει αμφισβητήσιμη λύση. Αυτό σημαίνει ότι η επιτροπή των θεμάτων ανέκαθεν ήταν προσεκτική στην επιλογή των θεμάτων που έκανε ώστε να μη δημιουργείται πρόβλημα. Το παρόν βιβλίο διατίθεται σε ελεύθερη χρήση προς τους υποψήφιους μέσω του διαδικτύου. Ο συγγραφέας με χαρά θα δεχτεί ερωτήσεις για διευκρινίσεις ή υποδείξεις, είτε από μαθητές είτε από εκπαιδευτικούς Αθήνα, Απρίλιος 2014
7 Περιεχόμενα 1. Βασικές γνώσεις Μεγέθη Μονάδες Μετατροπή Μονάδων Εμβαδόν και Διάμετρος κύκλου Λύση εξισώσεων πρώτου βαθμού Τάση Καταπόνηση Επιτρεπόμενη Τάση Εφελκυσμός Διάτμηση Παραδείγματα Αντιδράσεις στήριξης Ροπή Παραδείγματα Περιστροφική κίνηση Έργο - Ισχύς Υποδείξεις για τη λύση ασκήσεων Συντελεστής Ασφαλείας Ηλώσεις Κοχλιοσυνδέσεις Άτρακτοι - Άξονες Έδρανα Κύλισης (ρουλεμάν) Οδοντώσεις Λειτουργικές σχέσεις οδοντωτών τροχών Διαστασιολόγηση και αντοχή παράλληλων οδοντωτών τροχών Διαστασιολόγηση άλλων τύπων οδοντωτών τροχών Ιμάντες Αλυσίδες Λύση των άλυτων ασκήσεων του σχολικού βιβλίου Προτεινόμενες άλυτες ασκήσεις Εφελκυσμός Ηλώσεις Κοχλιοσυνδέσεις Περιστροφική κίνηση Άξονες - Άτρακτοι Έδρανα κύλισης Οδοντωτοί τροχοί Ιμάντες - Αλυσίδες Ερωτήσεις Σωστού - Λάθους Ερωτήσεις θεωρίας Μέσα σύνδεσης - Ηλώσεις Κοχλιωτές συνδέσεις Συγκολλήσεις 170
8 13.4. Σφήνες Περιστροφική κίνηση Άξονες Άτρακτοι - Στροφείς Έδρανα Σύνδεσμοι Οδοντώσεις Ιμάντες Αλυσίδες Μηχανισμός στροφάλου Ερωτήσεις θεωρίας από το 14ο κεφάλαιο Τυπολόγιο 175
9 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 1. Βασικές γνώσεις Στο πρώτο κεφάλαιο θα ασχοληθούμε με εκείνες τις γνώσεις που απαιτείται να γνωρίζετε για να προχωρήσετε χωρίς ιδιαίτερες δυσκολίες στη μελέτη του μαθήματος. Περιλαμβάνονται γενικές γνώσεις από τη φυσική και τα μαθηματικά καθώς και από το μάθημα «Μηχανική Αντοχή των Υλικών» που διδάσκεται στη Δευτέρα τάξη των ΕΠΑ.Λ. Ορισμένα από τα θέματα που διαπραγματεύεται το κεφάλαιο αυτό υπάρχουν και στο σχολικό βιβλίο του μαθήματος «Στοιχεία Μηχανών». Όμως επειδή αφορούν ουσιαστικά βασικές γνώσεις, αναφέρονται σε αυτό το τμήμα του παρόντος βιβλίου Μεγέθη Μονάδες Μετατροπή Μονάδων Εάν θέλουμε να έχουμε επιτυχία στην επίλυση των ασκήσεων του μαθήματος, πρέπει πρώτα από όλα να γνωρίζουμε τα διάφορα μεγέθη, τις μονάδες τους, καθώς και τη μετατροπή των μονάδων για κάθε μέγεθος. Στο κεφάλαιο αυτό θα ασχοληθούμε μόνο με τα μεγέθη εκείνα και τις μονάδες που έχουν σχέση με το μάθημα των Στοιχείων Μηχανών, όπως αυτά δίνονται στο σχολικό βιβλίο. Τα μεγέθη και οι μονάδες θεωρείται ότι είναι γνωστά από μαθήματα όπως η μηχανική, η αντοχή και η φυσική, περασμένων ετών. Στο μάθημα των Στοιχείων Μηχανών, και γενικότερα στα τεχνικά μαθήματα, όταν λέμε μέγεθος εννοούμε οτιδήποτε σχετικό που μπορεί να μετρηθεί. Μέγεθος είναι το μήκος και μετριέται με μέτρα, χιλιόμετρα, έτη φωτός και άλλα πολλά, τα οποία ονομάζονται μονάδες μέτρησης του μήκους. Ένα άλλο μέγεθος είναι ο χρόνος που έχει ως μονάδες μέτρησης την ώρα, το δευτερόλεπτο, το έτος και άλλα πολλά. Άλλα μεγέθη είναι ο όγκος, η δύναμη, η πίεση, η ισχύς, η θερμότητα. Υπάρχουν και εκείνα που χρησιμοποιούνται στο μάθημα, τα οποία είναι πιο τεχνικά, όπως η τάση, η ροπή, η σχέση μετάδοσης, η γωνιακή ταχύτητα και ορισμένα άλλα ακόμη. Το καθένα μέγεθος έχει τις δικές του μονάδες μέτρησης, οι οποίες συνήθως είναι περισσότερες από μία. Υπάρχουν και μεγέθη τα οποία ενώ μετρώνται με κάποιους αριθμούς, δεν έχουν μονάδα μέτρησης μετρώνται με καθαρούς αριθμούς, όπως λέγεται. Οι μονάδες κάθε μεγέθους είναι πολλές γιατί δεν βολεύει κάθε μονάδα σε όλες τις χρήσεις. Για παράδειγμα, όταν μετράμε αποστάσεις πόλεων, είναι βολικό να έχουμε ως μονάδα μέτρησης του μήκους (δηλαδή της απόστασης ανάμεσα στις πόλεις) το χιλιόμετρο. Δεν είναι καθόλου άνετο να χρησιμοποιείται το εκατοστό, ούτε καν το μέτρο, για να πούμε την απόσταση από τη Λαμία στην Αθήνα. Αν θάλαμε να πούμε για τις αποστάσεις των αστεριών δεν βολεύει ούτε το χιλιόμετρο και γι αυτό χρησιμοποιείται μια ακόμα μεγαλύτερη μονάδα μέτρησης της απόστασης, που είναι το έτος φωτός. Αν θέλουμε να μετρήσουμε το μήκος ενός μολυβιού το πιο κατάλληλο μέγεθος είναι το εκατοστό. Παράδειγμα άλλου συνηθισμένου μεγέθους είναι το βάρος, με μονάδες μέτρησης το κιλό, τον τόνο, το γραμμάριο και άλλα. Συγκεκριμένα για το βάρος, πρέπει να γίνει μια διευκρίνιση για τις μονάδες του, οι οποίες συχνά συγχέονται από τους μαθητές με τις μονάδες της μάζας. Ευτυχώς η μάζα δεν χρησιμοποιείται καθόλου στο μάθημά μας και δεν θα χρειαστούν οι μονάδες της (που είναι τα γραμμάρια, τα χιλιόγραμμα κλπ.). Όμως το βάρος είναι ένα είδος δύναμης και έχει τις μονάδες μέτρησης της δύναμης, όπως θα τις περιγράψουμε παρακάτω. Ένα άλλο πολύ σημαντικό θέμα που πρέπει να γνωρίζετε είναι η μετατροπή των μονάδων και η σχέση που έχουν μεταξύ τους. Μετατροπή σημαίνει να μπορείτε να αλλάζετε τη μονάδα ενός μεγέθους σε μια άλλη, εννοείται του ίδιου μεγέθους. Για παράδειγμα, αν σας δώσουν τη διάμετρο ενός σωλήνα ίση με 2 εκατοστά, θα χρειαστεί να την μετατρέψετε σε χιλιοστά και να πείτε ότι είναι ίση με 20 χιλιοστά. Δηλαδή πρέπει να ξέρετε ότι ένα εκατοστό έχει 10 χιλιοστά. Και αν αυτό σας φαίνεται εύκολο, και είναι, πολλοί θα δυσκολευτούν να μετατρέψουν τα 2 τετραγωνικά μέτρα σε τετραγωνικά εκατοστά. Όλα αυτά θα τα δούμε παρακάτω. Οι μονάδες μέτρησης (εκατοστό, δευτερόλεπτο, κιλό, κλπ.) πάντα γράφονται με συντομογραφία, διεθνώς αναγνωρισμένη με λατινικούς χαρακτήρες (cm, s, kp, κλπ.). Υπάρχουν διάφορα συστήματα μονάδων, που σημαίνει ότι σε κάθε σύστημα κάθε μέγεθος έχει μία και μόνο μονάδα μέτρησης. Το σύστημα που έχει επικρατήσει είναι το Διεθνές Σύστημα Μονάδων (SI). Σε αυτό, το μήκος έχει μονάδα το μέτρο (m), ο χρόνος το ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 9
10 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ δευτερόλεπτο (s) και η μάζα το χιλιόγραμμο (kg). Αυτά είναι τρία από τα θεμελιώδη (βασικά) μεγέθη που περιλαμβάνει. Έχει και άλλα θεμελιώδη μεγέθη (με αντίστοιχες θεμελιώδεις μονάδες), αλλά δεν αφορούν το μάθημα. Μεγέθη όπως η επιφάνεια, η δύναμη, η ενέργεια, η τάση, η ροπή κλπ. δεν θεωρούνται θεμελιώδη και έχουν μονάδες που παράγονται από τις τρεις θεμελιώδεις. Οι μονάδες αυτών των μεγεθών ονομάζονται παράγωγες και προέρχονται από συνδυασμό των θεμελιωδών. Για παράδειγμα η επιφάνεια έχει ως μονάδα το m 2 που παράγεται προφανώς από το m. Η δύναμη έχει μονάδα το Ν (Newton) και παράγεται με συνδυασμό όλων των θεμελιωδών που προαναφέρθηκαν ως εξής: kg m s -2. Δεν θα χρειαστεί να γνωρίζετε αυτή τη λεπτομέρεια για το Newton, απλά εδώ την αναφέρουμε. Υπάρχουν σε όλα τα μαθήματα διάφοροι μαθηματικοί τύποι (π.χ. F=m a ή σ= F/Α), στους οποίους όταν κάνουμε αντικατάσταση των τιμών των μεγεθών, πρέπει να είναι αυτές οι τιμές στο Διεθνές Σύστημα Μονάδων. Επομένως χρειάζονται μετατροπή όσες από αυτές δεν είναι σε αυτό το σύστημα. Υπάρχουν όμως και άλλοι τύποι που δεν είναι προσαρμοσμένοι στο SI. Σε αυτούς, για το κάθε μέγεθος που περιέχει ο τύπος, πρέπει να μας δώσουν τις μονάδες του ξεχωριστά. Τέτοιους τύπους θα συναντήσουμε πολλούς στο μάθημα. Γι αυτό πρέπει να προσέχουμε πάντα τις μονάδες που έχουν τα μεγέθη κάθε τύπου. Θα δούμε τώρα τα μεγέθη εκείνα που χρησιμοποιούνται στο μάθημα και τις μονάδες τους. Ακολούθως θα δούμε τη σχέση μεταξύ των διαφόρων μονάδων κάθε μεγέθους, που απαιτούνται για τις ασκήσεις. Στον πίνακα φαίνονται όλα τα μεγέθη που χρησιμοποιούνται στο σχολικό βιβλίο και οι αντίστοιχες μονάδες. Μέγεθος Μονάδα στο SI Άλλη μονάδα Μήκος m mm cm Επιφάνεια m 2 mm 2 cm 2 Χρόνος s min h Άλλη μονάδα Kp Δύναμη N dan ή kp Τάση N/m 2 dan/cm2 dan/mm 2 ή kp/cm 2 ή kp/mm 2 Ροπή Ροπή Αντίστασης N m dan m ή kp m dan cm ή kp cm m 3 cm 3 mm 3 Στροφές Hz ή στρ/s RPM ή rpm Ισχύς Ταχύτητα W m/s PS ή HP (είναι σχεδόν ίσα) Υπάρχουν λίγα ακόμα μεγέθη που αναφέρονται στο βιβλίο αλλά δεν χρησιμοποιούνται σε ασκήσεις. Τέτοια είναι η γωνιακή ταχύτητα, η συχνότητα, η ενέργεια κλπ. Ας δούμε τώρα τη σχέση μεταξύ των μονάδων του ίδιου μεγέθους (μετατροπή μονάδων), για τα μεγέθη εκείνα που έχει ο προηγούμενος πίνακας. Θα αναφερθούν κυρίως εκείνες οι σχέσεις που είναι πιθανό να συναντήσετε στις ασκήσεις. Μήκος 1 m = 100 cm = 1000 mm 1 cm = 10 mm 1 cm = 0,01 m 1 mm = 0,1 cm = 0,001 m kw 10 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
11 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Επιφάνεια 1 m 2 = cm 2 = mm 2 1 cm 2 = 100 mm 2 1 cm 2 = 0,0001 m 2 1 mm 2 = 0,01 cm 2 1 mm 2 = 0, m 2 Χρόνος 1 min = 60 s 1 min = 1/60 h 1 s = 1/60 min 1 s = 1/3600 h 1 h = 60 min = 3600 s Δύναμη 1 N = 0,1 dan ~ 0,1 kp 1 kp 1 dan = 10 N (για την ακρίβεια 1 kp είναι ίσο με 9,81 Ν) 1 dan = 10 N Τάση 1 N/m 2 = 0,0001 N/cm 2 = 0,00001 dan/cm 2 1 dan/cm 2 1 kp/cm 2 1 dan/cm 2 = 0,01 dan/mm 2, 1 kp/cm 2 = 0,01 kp/mm 2 1 dan/mm 2 = 100 dan/cm 2, 1 kp/mm 2 = 100 kp/cm 2 Ροπή 1 N m = 100 N cm = 0,1 dan m 1 dan m 1kp m 1 dan m = 10 N m = 100 dan cm ~ 100 kp cm Ροπή Αντίστασης 1 m 3 = cm 3 1 cm 3 = 1000 mm 3 1 mm 3 = 0,001 cm 3 Στροφές 1 στρ/min = 1RPM = 60 στρ/s 1 RPM = 1/60 στρ/h Ισχύς 1 W = 0,001 kw 1 kw = 1000 W 1 HP = 746 W 1 PS = 736 W Το σχολικό βιβλίο θεωρεί τις μονάδες HP και PS ίσες, αλλά δεν ζητά την μετατροπή τους σε W ή το αντίστροφο, επομένως δε θα υπάρξει περίπτωση σύγχυσης Εμβαδόν και Διάμετρος κύκλου Σε πολλές ασκήσεις του μαθήματος χρειάζεται να βρούμε το εμβαδόν ενός κύκλου (σε κυκλική διατομή) όταν γνωρίζουμε την διάμετρο του κύκλου ή το αντίστροφο, δηλαδή να βρούμε την διάμετρο όταν είναι γνωστό το εμβαδόν του κύκλου. Εδώ είναι καλά να πούμε τι εννοούμε λέγοντας διατομή, γιατί είναι μια έννοια που συναντούμε συχνά στο μάθημα και στις ασκήσεις. Ας πούμε ότι έχουμε μια ράβδο (π.χ. σιδερένια βέργα) και με ένα σιδεροπρίονο την κόβουμε. Το μέρος της ράβδου που κόψαμε είναι η διατομή της ράβδου και είναι ένας κύκλος (κυκλική διατομή). Αν δεν ήταν ράβδος αλλά ένας σωλήνας και τον κόβαμε, η διατομή θα είχε σχήμα δαχτυλιδιού. Γενικά, διατομή ονομάζουμε το σχήμα που έχει η τομή (το κόψιμο) ενός αντικειμένου όταν φανταστούμε ότι το κόβουμε με ένα φανταστικό επίπεδο (το πριόνι). Τα σχήματα διατομών που θα χρειαστεί να γνωρίζουμε στο ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 11
12 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ μάθημα είναι ο κύκλος, το δαχτυλίδι και το ορθογώνιο παραλληλόγραμμο. σχήμα φαίνονται αυτές οι τρεις διατομές. Στο επόμενο Αν η διατομή είναι τετράγωνο και μας δώσουν την πλευρά του α, το εμβαδόν της διατομής θα είναι α 2. Αν είναι ορθογώνιο με πλευρές α και β το εμβαδόν θα είναι α β και αν είναι κύκλος με ακτίνα r το εμβαδόν θα είναι π r 2 = 3,14 r 2. Και επειδή στην πράξη οι μηχανικοί δεν χρησιμοποιούν την ακτίνα του κύκλου αλλά τη διάμετρο D ή d, ο τύπος για το εμβαδόν της διατομής γίνεται π d 2 /4. Επομένως για το εμβαδόν της διατομής που συμβολίζεται με Α θα έχουμε: Τετράγωνο: (1.1) Ορθογώνιο: (1.2) Κύκλος: (1.3) Στην αντίθετη περίπτωση, που γνωρίζουμε το εμβαδόν της διατομής και ζητούμε τις διαστάσεις, τότε εφαρμόζουμε τους προηγούμενους τύπους αντίθετα. Τετράγωνο με πλευρά α: (1.4) Κύκλος με διάμετρο D: (1.5) Τους τύπους αυτούς, ειδικά για τον κύκλο, θα πρέπει να τους γνωρίζετε και να τους χρησιμοποιείτε πολύ άνετα, ώστε να μη χάνετε χρόνο όταν λύνετε μια άσκηση. Για να βρούμε μια πλευρά ενός ορθογωνίου όταν γνωρίζουμε την άλλη και το εμβαδόν θα το δούμε στο αντίστοιχο κεφάλαιο με την ανάλογη άσκηση. Παρακάτω θα δούμε και το εμβαδόν ενός δαχτυλιδιού. Θα δώσουμε τώρα ορισμένα παραδείγματα εφαρμόζοντας τους παραπάνω τύπους και τις προαναφερθείσες μετατροπές μονάδων. Η μεθοδολογία που θα ακολουθηθεί είναι εκείνη του σχολικού βιβλίου, αλλά με λίγο πιο αναλυτικό τρόπο, για καλύτερη κατανόηση των λύσεων. Μια άλλη παρατήρηση που έχουμε να κάνουμε, είναι ότι το βιβλίο για τη λύση εφαρμόζει τον κατάλληλο τύπο, λύνει τον τύπο ως προς τον άγνωστο και μετά αντικαθιστά τα νούμερα. Κατά την αντικατάσταση συνήθως δεν βάζει τις μονάδες των μεγεθών αλλά μόνο τις αριθμητικές τιμές τους. Τις μονάδες τις βάζει μόνο στο τελικό αποτέλεσμα (συνήθως). Άσκηση 1.1 Η διατομή μιας ράβδου έχει σχήμα τετραγώνου με πλευρά 12 mm. Να βρεθεί το εμβαδόν της διατομής της ράβδου. Απάντηση Συμβολίζουμε το μήκος της πλευράς α=12 mm. Θα εφαρμόσουμε τον τύπο 1.1 και έχουμε: Εάν βάζαμε τις μονάδες θα κάναμε τη λύση ως εξής: 12 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
13 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Επομένως η διατομή έχει εμβαδόν 144 mm 2 ή αν λάβουμε υπ όψιν ότι 1 mm 2 = 0,01 cm 2, τότε Α=1,44 cm 2 Άσκηση 1.2 Η διατομή μιας ράβδου είναι κυκλική με διάμετρο ίση με 1,5 cm. Να βρεθεί το εμβαδόν της διατομής της ράβδου. Απάντηση Συμβολίζουμε τη διάμετρο με D=1,5 cm. Θα εφαρμόσουμε τον τύπο 1.3 και έχουμε: Επομένως η διατομή έχει εμβαδόν 1,77 cm 2, ή αν λάβουμε υπ όψιν ότι 1 cm 2 = 100 mm 2, τότε Α=177 mm 2. Θα μπορούσαμε στον τύπο να αντικαταστήσουμε μαζί με την τιμή της διαμέτρου και τις μονάδες της, οπότε θα είχαμε: Όπως βλέπετε, διαφορά στο αποτέλεσμα δεν υπάρχει. Άσκηση 1.3 Ένας σωλήνας έχει εσωτερική διάμετρο ίση με 14 mm και εξωτερική ίση με 16 mm. Να βρεθεί το εμβαδόν της διατομής του. Απάντηση Η διατομή θα έχει σχήμα δαχτυλιδιού με εσωτερική διάμετρο D εσ =14 mm και εξωτερική ίση με D εξ =16 mm. Μπορούμε εύκολα να καταλάβουμε ότι το πάχος του σωλήνα είναι 1 mm. Το εμβαδόν της διατομής θα βρεθεί αν από το εμβαδόν του εξωτερικού κύκλου (διαμέτρου D εξ ) αφαιρεθεί το εμβαδόν του εσωτερικού κύκλου (διαμέτρου D εσ ). Άρα θα ισχύει: Επομένως η ζητούμενη διατομή, που στο σχήμα είναι η χρωματισμένη, θα είναι 47,1 mm 2. Άσκηση 1.4 Η διατομή μιας ράβδου έχει σχήμα τετραγώνου και το εμβαδόν της είναι 625 mm 2. Να βρεθεί το μήκος της κάθε πλευράς της διατομής της ράβδου (του τετραγώνου). Απάντηση Συμβολίζουμε με α το μήκος της πλευράς και με Α το εμβαδόν της διατομής. Σύμφωνα με τον τύπο 1.4 έχουμε: Επομένως η πλευρά της διατομής έχει μήκος 25 mm. Σημείωση: Η άσκηση θα μπορούσε να λυθεί λίγο πιο αναλυτικά, παίρνοντας τον βασικότερο τύπο για το εμβαδόν του τετραγώνου 1.1 και να λύσουμε ως προς την πλευρά α: Άσκηση 1.5 Μια διατομή είναι κυκλική και έχει εμβαδόν ίσο με 2 cm 2. Να βρεθεί η διάμετρος της διατομής. Απάντηση Συμβολίζουμε με Α το εμβαδόν (Α=2 cm 2 ) και με D την ζητούμενη διάμετρο. Από τον γνωστό τύπο 1.3 (εναλλακτικά μπορούσαμε να πάρουμε κατευθείαν τον τύπο 1.5) θα λύσουμε ως προς τη διάμετρο, θα αντικαταστήσουμε και θα βρούμε το αποτέλεσμα. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 13
14 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Βρήκαμε ότι η διάμετρος της διατομής είναι 1,6 cm ή 16 mm Λύση εξισώσεων πρώτου βαθμού Στις ασκήσεις που θα συναντήσετε θα χρειαστεί πολλές φορές να λύσετε μια εξίσωση πρώτου βαθμού. Παρακάτω δίνονται μερικές συμβουλές για λύση απλών περιπτώσεων. Για καλύτερη αντιμετώπιση του θέματος πρέπει να δείτε τα βιβλία μαθηματικών των πρώτων τάξεων του Γυμνασίου. Πρέπει να προσέξετε τη λύση των εξισώσεων όταν ο άγνωστος δεν δίνεται κατευθείαν από τον τύπο του βιβλίου. Για τις ασκήσεις που θα αντιμετωπίσουμε στο μάθημα οι περισσότερες περιπτώσεις έχουν μια από τις μορφές που δίνονται παρακάτω. Σε αυτές x είναι ο ζητούμενος άγνωστος και με κεφαλαία γράμματα συμβολίζονται εκείνα τα μεγέθη που είναι γνωστά, για τα οποία δηλαδή έχουμε μια τιμή. Εμείς θα πρέπει να λύσουμε ως προς τον x. Οι μορφές που θα αντιμετωπίσουμε, μαζί με τον τρόπο που λύνονται, είναι οι εξής: 1. Το γράμμα Α στην αρχική εξίσωση ονομάζεται συντελεστής του αγνώστου. Για να λύσουμε την εξίσωση αυτής της μορφής διαιρούμε με τον συντελεστή του αγνώστου και τα δύο μέλη (μέλος= πλευρά ή μέρος) της εξίσωσης και μετά απλοποιούμε το επάνω με το κάτω Α και ο άγνωστος μένει μόνος του. 2. Εδώ για να βρούμε τον x, πολλαπλασιάζουμε και τα δυο μέλη της εξίσωσης με το Α. Μετά απλοποιείται το Α στο πρώτο μέλος στον αριθμητή και στον παρονομαστή και μένει το χ μόνο του. 3. Θα μπορούσαμε εναλλακτικά να πούμε ότι κάνουμε χιαστί και μετά λύνουμε κατά τον πρώτο τρόπο, που περιγράψαμε πριν. Όμως αυτό που έγινε εδώ είναι ο πολλαπλασιασμός με το x και των δύο μελών, οπότε το x απλοποιήθηκε στο πρώτο μέλος και έμεινε το x μόνο στο δεύτερο και έτσι καταλήξαμε στην πρώτη περίπτωση που είδαμε πριν. Αν έχουμε τη μορφή: Α Β = x Γ, αυτή είναι ίδια με την αναφερθείσα 1, αφού μπορούμε να πούμε ότι: Α Β = Δ, οπότε γίνεται: Δ = x Γ που είναι ίδια με την x Γ = Δ, και αυτή είναι η περίπτωση 1. Δηλαδή δεν έχει σημασία αν ο άγνωστος x είναι στο δεύτερο μέλος (δηλαδή μετά το =), αφού μεταθέτουμε τα δυο μέλη και πηγαίνει στο πρώτο μέλος. Επίσης αν ο τύπος έχει γινόμενο δυο ή τριών μεγεθών που τα γνωρίζουμε είναι σα να είναι ένα το μέγεθος, αφού μπορούμε να κάνουμε τον πολλαπλασιασμό. Στο μάθημα των Στοιχείων Μηχανών θα συναντήσουμε και λίγο πιο δύσκολες περιπτώσεις, με δυνάμεις και ρίζες μεγεθών, τις οποίες θα αντιμετωπίσουμε όπως πρέπει, όταν φτάσουμε στις συγκεκριμένες ασκήσεις και μαθηματικούς τύπους. 14 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
15 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ Τάση Ένα πολύ σημαντικό μέγεθος στο μάθημα που εξετάζουμε είναι η τάση, που είναι γνωστή από το μάθημα της Αντοχής. Θα θυμηθούμε τώρα εκείνα που πρέπει να γνωρίζετε για το μάθημα των Στοιχείων Μηχανών, όσον αφορά και στη θεωρία αλλά και στις ασκήσεις. Τάση είναι ένα άλλο όνομα της πίεσης, που χρησιμοποιείται από τους μηχανικούς. Είναι γνωστό ότι πίεση ονομάζεται το πηλίκο της δύναμης που ασκείται σε μια επιφάνεια προς το εμβαδόν αυτής της επιφάνειας. Το ίδιο ακριβώς είναι και η τάση που είναι όρος που χρησιμοποιείται περισσότερο στη Μηχανική, στην Αντοχή και στα Στοιχεία Μηχανών. Για παράδειγμα, ένας άνθρωπος με βάρος 80 kp πατώντας στα δυο του πόδια, που το καθένα (ας πούμε) έχει εμβαδόν επιφάνειας που ακουμπά στο έδαφος 200 cm 2, θα ασκεί στο έδαφος μια πίεση ίση με 80kp/400cm 2 =0,2 και οι μονάδες θα είναι kp/ cm 2 (τάση ίση με 0,2 kp/ cm 2 ). Δηλαδή βρήκαμε ότι αφού τα 80 kp κατανέμονται σε 400 cm 2, σημαίνει ότι σε κάθε cm 2 αναλογούν 0,2 kp. Αυτό το γράφουμε 0,2 kp/ cm 2 και διαβάζουμε ότι η τάση είναι 0,2 kp ανά cm 2. Το ενδιαφέρον είναι ότι και το κάθε πόδι χωριστά ασκεί στο έδαφος την ίδια τάση (πίεση). Πράγματι αφού είναι ο άνθρωπος 80 kp το κάθε πόδι ασκεί 40 kp σε επιφάνεια ενός ποδιού, δηλαδή σε 200 cm 2, επομένως η τάση θα είναι τώρα 40kp/200cm 2 =0,2 kp/ cm 2, ίδια με την προηγούμενη. Ενώ η πίεση συμβολίζεται με p η τάση συμβολίζεται διεθνώς με το ελληνικό γράμμα σ. Επειδή τη δύναμη τη συμβολίζουμε με F ή Q και το εμβαδόν με Α, θα ισχύει ο τύπος: Μονάδες της τάσης που χρησιμοποιούνται συχνότερα, εκτός από το kp/cm 2 είναι το dan/cm 2 και το dan/mm 2, όπου το dan είναι περίπου ίσο με το kp, όπως έχουμε πει. Τελικά τάση σε μια επιφάνεια μπορούμε να πούμε ότι είναι η δύναμη που ασκείται στη μονάδα αυτής της επιφάνειας. Δηλαδή θα είναι η δύναμη που ασκείται σε κάθε τετραγωνικό εκατοστό της ή σε κάθε τετραγωνικό χιλιοστό της κλπ. Προφανώς επειδή η επιφάνεια θα έχει εμβαδόν όχι ακριβώς ίσο με τη μονάδα επιφανείας θα πρέπει να διαιρέσουμε τη δύναμη με αυτό το εμβαδόν και έτσι θα προκύψει η δύναμη που αντιστοιχεί στη μονάδα επιφανείας. Για παράδειγμα αν δύναμη 1000 dan ασκείται σε μια επιφάνεια 4 cm 2 τότε θα κάνουμε: 1000/4=250 και θα βρω ότι σε κάθε cm 2 ασκούνται 250 dan. Άρα η τάση είναι 250 dan/cm 2. Παρατηρούμε ότι σε μια τέτοια περίπτωση η δύναμη που ασκείται σε κάθε επιφάνεια εξαρτάται από το εμβαδόν της επιφάνειας ενώ η τάση όχι, δηλαδή είναι ίδια παντού. Παραδείγματος χάριν σε 2 cm 2 η δύναμη που αντιστοιχεί θα είναι 500 dan, αφού θα είναι στη μισή επιφάνεια, ενώ η τάση θα είναι 500/2=250 dan/cm 2, δηλαδή η ίδια με πριν. Το σημαντικό συμπέρασμα που έχουμε από όλα αυτά είναι ότι αν θα αντέξει ένα δοκίμιο (ράβδος, μεταλλικό φύλλο, έλασμα, βίδα, κλπ.) εξαρτάται όχι μόνο από το μέγεθος της δύναμης αλλά και από την επιφάνεια που ασκείται αυτή η δύναμη, δηλαδή από την τάση. Έτσι, αν θέλουμε να ελέγξουμε την ικανότητα σε αντοχή ενός δοκιμίου, θα ελέγξουμε την τάση που ασκείται σε αυτό και όχι μόνο τη δύναμη Καταπόνηση Επιτρεπόμενη Τάση Όταν σε ένα σώμα ασκούνται κάποιες δυνάμεις ή ροπές, τότε λέμε ότι το σώμα καταπονείται ή με άλλα λόγια ότι υφίσταται καταπόνηση. Σε ένα σώμα που καταπονείται δημιουργούνται τάσεις ή παραμορφώσεις. Όταν λέμε ότι δημιουργούνται τάσεις εννοούμε ότι το σώμα (π.χ. ένα κομμάτι σίδερο) μπορεί να ισορροπεί αλλά μέσα τα μόριά του δεν είναι ήρεμα, αλλά λόγω της καταπόνησης υπάρχει μικρός ή μεγάλος κίνδυνος να αποχωριστούν μεταξύ τους και το κομμάτι να λυγίσει ή να σπάσει. Είναι όπως όταν είμαστε εμείς όρθιοι, τα πόδια μας ενώ φαίνονται μια χαρά, επειδή σηκώνουν το βάρος του σώματός μας κουράζονται. Αυτό οφείλεται στις τάσεις που δημιουργεί σ αυτά η καταπόνησή τους, δηλαδή η επίδραση του βάρους μας. Οι βασικές καταπονήσεις είναι οι εξής: 1. Εφελκυσμός (όταν σε ένα κομμάτι ασκούνται δυνάμεις που βρίσκονται στην ίδια ευθεία, οπότε το κομμάτι «τραβιέται» ώστε να τεντώσει) ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 15
16 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 2. Θλίψη (το αντίθετο του εφελκυσμού) 3. Διάτμηση και τμήση (όταν πάει μια δύναμη να κόψει το κομμάτι) 4. Κάμψη (όταν οι δυνάμεις δημιουργούν ροπή που πάει να σπάσει το κομμάτι, για παράδειγμα όταν έχουμε απλωμένο το χέρι μας και κρατάμε ένα βάρος) 5. Στρέψη (όταν έχουμε ένα κομμάτι και είναι σταθερό από τη μια μεριά και από την άλλη μια ροπή πάει να το περιστρέψει γύρω από τον διαμήκη άξονά του, για παράδειγμα όταν με το κατσαβίδι περιστρέφουμε μια βίδα) Ένας από τους βασικούς σκοπούς της αντοχής των υλικών είναι να μπορεί να υπολογίσει για κάθε περίπτωση καταπόνησης, τις τάσεις που δημιουργούνται σε ένα μέταλλο. Όταν γίνει αυτό θα μπορέσουμε να ελέγξουμε αν το μεταλλικό κομμάτι κινδυνεύει να σπάσει. Ένα άλλο τμήμα της αντοχής των υλικών είναι αυτό που μας λέει μέχρι ποια τάση (επιτρεπόμενη τάση) πρέπει να φτάνει η καταπόνηση σε ένα μέταλλο για να μην υπάρχει κίνδυνος να λυγίσει υπερβολικά ή και να σπάσει. Ο συνδυασμός αυτών των δυο, μας επιτρέπει να βρίσκουμε το μέγεθος (πάχος) που πρέπει να έχει ένα κομμάτι για να μην υπερβεί την επιτρεπόμενη τάση και έτσι δε θα υπάρχει κίνδυνος να σπάσει. Αν δηλαδή, η καταπόνηση που δέχεται είναι τέτοια που οι τάσεις ξεπερνούν την επιτρεπόμενη τιμή, θα πρέπει να το κάνουμε μεγαλύτερο (να επιλέξουμε πιο χοντρό) ώστε να αντέξει. Τώρα μπορούμε να καταλάβουμε γιατί στην αντοχή, στους υπολογισμούς, δεν αρκεί να βρούμε τις δυνάμεις αλλά πρέπει να υπολογίσουμε τις τάσεις. Διότι αν η δύναμη ασκείται σε ένα χονδρό κομμάτι αυτό δεν έχει πρόβλημα, ενώ η ίδια δύναμη σε ένα πιο λεπτό ίσως το σπάσει. Η τάση όμως επειδή λαμβάνει υπ όψιν της και τη διατομή, μας λέει καλύτερα αν το κομμάτι θα αντέξει ή όχι. Ας πούμε λίγα λόγια για την επιτρεπόμενη τάση. Κατ αρχάς είναι ένα νούμερο που έχει σχέση με δυο πράγματα: Το υλικό από το οποίο είναι φτιαγμένο το κομμάτι Την καταπόνηση. Επειδή για κάθε είδος καταπόνησης έχουμε και τη δράση διαφορετικών τάσεων, για κάθε καταπόνηση έχουμε και μια διαφορετική επιτρεπόμενη τάση. Επίσης για διαφορετικά υλικά έχουμε και διαφορετικές επιτρεπόμενες τάσεις, όχι όμως και για διαφορετικές διαστάσεις. Οι διαστάσεις δεν παίζουν κανένα ρόλο στην επιτρεπόμενη τάση, διότι είπαμε ότι η τάση είναι ίδια σε όλα τα σημεία μιας διατομής του κομματιού. Και στο κάτω-κάτω η επιτρεπόμενη τάση μας λέει πόση δύναμη αντέχει κάθε cm 2 της διατομής. Στην πράξη λοιπόν αν θέλουμε να δούμε αν ένα κομμάτι αντέχει σε μια καταπόνηση, βρίσκουμε την τάση που αυτή η καταπόνηση δημιουργεί και κοιτάμε να είναι μικρότερη από την επιτρεπόμενη. Αν σε ένα κομμάτι δημιουργηθεί τάση ίση ή λίγο μεγαλύτερη από την επιτρεπόμενη αυτό δεν σημαίνει ότι το κομμάτι θα σπάσει. Η επιτρεπόμενη τάση έχει μια τιμή που δεν πρέπει να ξεπερνάμε διότι αν αυτό γίνεται συχνά, κάποια στιγμή αργά ή γρήγορα, το κομμάτι είτε θα λυγίσει υπερβολικά είτε θα σπάσει. Είναι αυτό που λέμε: ότι έχουμε ένα συντελεστή ασφαλείας, που σημαίνει ότι για λόγους ασφαλείας η επιτρεπόμενη τάση είναι τέτοια που το κομμάτι ουσιαστικά αντέχει για λίγο μια μικρή παραπάνω δύναμη. Ο συντελεστής ασφαλείας μας δείχνει πόσες φορές μεγαλύτερη τάση πρέπει να ασκηθεί στο κομμάτι ώστε αυτό να σπάσει. Συνήθως στα στοιχεία των μηχανών ο συντελεστής ασφαλείας είναι μεγαλύτερος από 2, αλλά η τιμή του μπορεί να ξεπεράσει και το 10. Γι αυτόν θα αναφέρουμε περισσότερα σε άλλο σημείο. Τις επιτρεπόμενες τάσεις για κάθε υλικό και για κάθε καταπόνηση, τις βρίσκουμε σε πίνακες. Οι υπολογισμοί που μας ζητούν να κάνουμε στις απλές ασκήσεις, είναι τριών ειδών και οι τύποι που χρησιμοποιούμε προκύπτουν από τη σχέση 1.6: 1. Μας ζητούν να υπολογίσουμε το εμβαδόν της διατομής ενός κομματιού για να αντέχει. Πρέπει να μας δίνουν τις δυνάμεις καταπόνησης και την επιτρεπόμενη τάση του υλικού. Το εμβαδόν το βρίσκουμε από τον τύπο:. 16 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
17 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 2. Μας ζητούν να υπολογίσουμε τη δύναμη μέχρι την οποία αντέχει ένα κομμάτι. Πρέπει να μας δίνουν τη διατομή και την επιτρεπόμενη τάση του υλικού. Χρησιμοποιούμε τη σχέση:. 3. Μας ζητούν να ελέγξουμε αν ένα κομμάτι αντέχει. Μας δίνουν τις διαστάσεις και τις δυνάμεις που το καταπονούν και εμείς ελέγχουμε αν η τάση που δημιουργείται στο κομμάτι είναι μικρότερη ή όχι από την επιτρεπόμενη. Δηλαδή ελέγχουμε αν ή, αφού πρώτα βρούμε το σ από τη σχέση:. Εννοείται ότι σ όλες τις ασκήσεις μας δίνουν την επιτρεπόμενη τάση ή την βρίσκουμε από πίνακες με τις επιτρεπόμενες τάσεις των διαφόρων υλικών, σε συνδυασμό με τη χρήση τους. Υπάρχει και μια άλλη περίπτωση που δε μας δίνουν το υλικό κατασκευής του κομματιού, οπότε μας το ζητάνε (το υλικό), ώστε να κατασκευαστεί το κομμάτι και να αντέχει. Αυτή η περίπτωση είναι ίδια με την τρίτη από τις προηγούμενες, αφού όταν ξέρουμε τις διαστάσεις και τις δυνάμεις, υπολογίζουμε την τάση. Κατόπιν από τους πίνακες με τις επιτρεπόμενες τάσεις βρίσκουμε το υλικό με επιτρεπόμενη τάση λίγο μεγαλύτερη (για λόγους ασφαλείας και οικονομίας) από αυτή που βρήκαμε και το επιλέγουμε Εφελκυσμός Διάτμηση Παραδείγματα Ως εφελκυσμό ορίζουμε την καταπόνηση που έχει ένα δοκίμιο ή μια διατομή όταν ασκούνται σ αυτό δυνάμεις συνευθειακές που έχουν αντίθετες κατευθύνσεις και την τάση να το διασπάσουν και όχι να το συνθλίψουν. Γενικά και μια δύναμη να ασκείται σε ένα σώμα με φορά έξω από τη μάζα του αν αυτό το σώμα το κρατάει κάτι ώστε να μην μετακινείται, πάλι θα εφελκύεται, αφού θα υπάρχει η αντίδραση της πρώτης δύναμης. Στον εφελκυσμό θα ισχύει η γνωστή σχέση 1.6:. Σε αυτήν F είναι η δύναμη που ασκείται στο κομμάτι, Α είναι η επιφάνεια πάνω στην οποία κατανέμεται η δύναμη (το εμβαδόν της διατομής) και σ είναι η τάση που λέμε ότι θα ασκείται στην επιφάνεια Α της διατομής. Έχουμε πει ότι οι μονάδες που πιο συχνά χρησιμοποιούνται είναι για την τάση: dan/cm 2, για τη δύναμη: dan και για την επιφάνεια Α: cm 2. Πολύ συχνά το εμβαδόν της επιφάνειας το ονομάζουμε απλά διατομή και συνήθως στις ασκήσεις δεν μας δίνουν το εμβαδόν της, αλλά τις διαστάσεις για να το υπολογίσουμε. Όταν έχουμε μια ράβδο που δεν εφελκύεται μόνο αλλά δέχεται και δυνάμεις κάθετες στον άξονά της (δηλαδή κάθετες στο μήκος της, που λέγονται εγκάρσιες), τότε λέμε ότι δέχεται και διατμητικές δυνάμεις ή και καμπτικές, άρα δέχεται και τα δυο είδη των δυνάμεων. Προς το παρόν θα ασχοληθούμε μόνο με τις διατμητικές δυνάμεις. Επειδή οι διατμητικές δυνάμεις έχουν άλλο τρόπο καταπόνησης ελέγχονται χωριστά από τις εφελκυστικές. Ισχύει ο ίδιος τύπος (1.6) με πριν, μόνο που στη θέση της δύναμης βάζουμε το σύμβολο Q αντί για το F που βάζαμε. Σαν διατομή Α χρησιμοποιούμε την ίδια ακριβώς με πριν. Το μόνο που αλλάζει είναι η τάση που πλέον συμβολίζεται με το γράμμα τ. έτσι έχουμε τον τύπο για τη διάτμηση: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 17
18 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Μια ακόμη αλλαγή που πρέπει να προσέξουμε είναι ότι στη διάτμηση δεν χρησιμοποιούμε ως επιτρεπόμενη τάση την σ επ αλλά μίαν άλλη που συμβολίζεται με τ επ και παίρνουμε επίσης από πίνακες όπως και την σ επ. Πρακτικά στις ασκήσεις, εμείς από το είδος της καταπόνησης πρέπει να καταλαβαίνουμε αν έχουμε διάτμηση οπότε χρησιμοποιώντας το νέο τύπο και το τ επ δουλεύουμε όπως και στον εφελκυσμό. Άσκηση 1.6 Έστω μια ράβδος που θα εφελκύεται με μέγιστη δύναμη 4800 dan (το πολύ δηλαδή η δύναμη να φτάσει αυτή την τιμή) και είναι φτιαγμένη από ένα υλικό με επιτρεπόμενη τάση ίση με 1200 dan/cm 2 (δηλαδή σ επ =1200 dan/cm 2 ). Αν η ράβδος έχει διατομή που είναι τετράγωνη να βρείτε την πλευρά της και αν είναι κύκλος να βρείτε την διάμετρό του. Απάντηση Πρώτα θα βρούμε το εμβαδόν. Η άσκηση μας δίνει ότι η μέγιστη τάση που μπορεί να ασκηθεί στη ράβδο είναι 1200 dan/cm 2 και προφανώς αυτή θα υπάρχει στην περίπτωση που ασκείται η μέγιστη δύναμη, δηλαδή τα 4800 dan. Όταν συμβαίνει αυτό, θα βρούμε το εμβαδόν της διατομής από τον τύπο της τάσης: σ=f/a. Άρα θα λύσουμε τον τύπο αυτό ως προς Α και θα βρούμε το εμβαδόν: Άρα το εμβαδόν είναι 4 cm 2. Αν η ράβδος είναι τετράγωνη, η πλευρά της θα υπολογιστεί από τον τύπο 1.1: Αν η ράβδος είναι κυκλική, η διάμετρός της θα είναι (τύπος 1.5): Άρα η πλευρά του τετραγώνου θα είναι τουλάχιστον 2 cm και η διάμετρος του κύκλου θα είναι τουλάχιστον 2,26 cm. Άσκηση 1.7 Έχουμε μια ράβδο από σίδερο με διάμετρο 16 χιλιοστά η οποία είναι από υλικό που έχει σ επ =1600 dan/cm 2. Να βρείτε πόσο είναι το μέγιστο φορτίο (δύναμη) που μπορούμε να του κρεμάσουμε. Απάντηση Προφανώς η ράβδος καταπονείται σε εφελκυσμό. Κάθε φορτίο δημιουργεί τάση στη ράβδο, έτσι θα κάνει και το φορτίο που θα βάλουμε στη ράβδο μας. Εμείς θέλουμε αυτή η τάση που δημιουργείται να μην ξεπερνά το σ επ που έχει το υλικό. Άρα αν η δύναμη που ψάχνουμε είναι η F, τότε η τάση που δημιουργεί είναι σ= F/Α, όπου Α είναι το εμβαδόν της διατομής. Για να βρούμε την F θα πρέπει στην προηγούμενη εξίσωση να αντικαταστήσουμε το σ με το σ επ και να λύσουμε ως προς τη δύναμη: Το Α πρέπει να το βρούμε. Επειδή η διάμετρος είναι 16mm το εμβαδόν του κύκλου θα είναι: Τώρα μπορούμε να βρούμε τη δύναμη: 18 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
19 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Επομένως το μέγιστο φορτίο που μπορεί να δεχτεί η ράβδος είναι 3216 dan. Άσκηση 1.8 Θέλουμε να χρησιμοποιήσουμε μια ράβδο από σίδερο με διάμετρο 16 χιλιοστά και υλικό με σ επ =1200 dan/cm 2. Θα κρεμάσουμε από αυτήν βάρος 5000 dan. Να βρείτε αν θα αντέξει η ράβδος. Απάντηση Πρώτα πρέπει να βρούμε το εμβαδόν της διατομής. Επειδή η διάμετρος είναι D=16 mm το εμβαδόν του κύκλου: Θα υπολογίσουμε την τάση σ που δημιουργεί αυτή η δύναμη F στη ράβδο που έχουμε. Επειδή σημαίνει ότι σ > σ επ και η ράβδος αυτή δεν θα αντέξει. Η άσκηση εδώ έχει τελειώσει, αλλά εμείς θα κάνουμε μια μικρή διερεύνηση. Αφού δεν αντέχει θα πρέπει να βάλουμε άλλο υλικό με σ επ μεγαλύτερο ή ίσο με 2500 dan/cm 2 ή να μεγαλώσουμε τη διατομή της ράβδου. Άρα ή θα ανατρέξουμε στους πίνακες με τις επιτρεπόμενες τάσεις ή θα διαλέξουμε μεγαλύτερη διάμετρο. Ας πούμε ότι θα κάνουμε το δεύτερο. Μπορούμε να εργαστούμε όπως στην άσκηση 1.6 και θα βρούμε το αντίστοιχο αποτέλεσμα. Ας υποθέσουμε όμως ότι παίρνουμε μια άλλη ράβδο με διάμετρο 24 mm. Θα ελέγξουμε αν αντέχει με αυτή τη μεγαλύτερη διάμετρο. Το εμβαδόν της θα είναι: Η τάση θα είναι Η τάση των που βρήκαμε είναι μικρότερη από την επιτρεπόμενη άρα τη δεχόμαστε. Σημείωση: Μερικές φορές δεν θα έχουμε στις ασκήσεις ράβδους, που είναι απλό να βρούμε την διατομή που εφελκύεται. Είναι πιθανό να έχουμε σύνθετα σχήματα και πρέπει εμείς να υπολογίσουμε ποια ακριβώς διατομή είναι εκείνη που εφελκύεται (αφαιρώντας ίσως κάποια τμήματα που υπάρχουν τρύπες κλπ.) για να βάλουμε το εμβαδόν της στον τύπο. Άσκηση 1.9 Μια ράβδος θα υφίσταται μόνο διάτμηση με μέγιστη δύναμη 5000 dan και είναι φτιαγμένη από υλικό με επιτρεπόμενη διατμητική τάση ίση με 700 dan/cm 2 (τ επ =700 dan/cm 2 ). Αν η ράβδος είναι κυκλικής διατομής, να βρείτε την διάμετρό της. Απάντηση Πρώτα θα βρούμε το εμβαδόν. Μας δίνε τε ότι η μέγιστη διατμητική τάση που μπορεί να ασκηθεί στη ράβδο είναι 700 dan/cm 2 και αυτή θα υπάρχει όταν ασκείται η μέγιστη δύναμη, δηλαδή τα F =5000 dan. Όταν συμβαίνει αυτό, θα βρούμε το εμβαδόν της διατομής Α από τον τύπο της τάσης (1.7): τ=f/a. Άρα θα λύσουμε τον τύπο αυτό ως προς Α και θα βρούμε το εμβαδόν. Άρα το εμβαδόν είναι 7,14 cm 2. Η ράβδος είναι κυκλική και η διάμετρός της θα είναι: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 19
20 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Άρα η διάμετρος θα πρέπει να είναι τουλάχιστον 3,02 cm=30,2 mm. Σημείωση: Η άσκηση αυτή μοιάζει με την 1.6, μόνο που αντί για εφελκυσμό η ράβδος δέχεται διάτμηση. Η λύση είναι ίδια. Η διαφορά είναι ότι η επιτρεπόμενη τάση για διάτμηση είναι διαφορετική από την επιτρεπόμενη τάση για εφελκυσμό. Άσκηση 1.10 Ένα φύλλο μετάλλου (παχύ έλασμα ή μεταλλική πλάκα) με πάχος 1 cm και πλάτος 20 cm εφελκύεται με δύναμη F= dan. Όπως φαίνεται στο σχήμα το φύλλο έχει στο μέσον μια οπή διαμέτρου 2 cm. Να βρεθεί η μεγαλύτερη τάση που καταπονεί το έλασμα, και η θέση που εμφανίζεται αυτή. Απάντηση Κατ αρχήν, πρέπει να κατανοήσουμε την άσκηση. Δεν πρέπει να προχωράμε στη λύση μιας άσκησης αν δεν έχουμε καταλάβει πλήρως και τα δεδομένα και τα ζητούμενα. Δηλαδή να έχουμε νιώσει γιατί μας δίνει στην εκφώνηση όλα εκείνα που δίνονται. Είναι πολύ απίθανο να έχει η άσκηση κάποια στοιχεία που να μη χρειάζονται για τη λύση της. Αφού κατανοήσουμε τα δεδομένα πρέπει να καταλάβουμε το νόημα των ερωτήσεων. Ας δούμε αυτά τα θέματα στην άσκηση που έχουμε. Κατ αρχάς έχουμε το σχήμα: βλέπουμε το έλασμα και τις δύο δυνάμεις F και -F. Μία δύναμη ασκείται στο μεταλλικό φύλλο, η F, και η -F είναι η αντίδρασή της. Αυτό σημαίνει ότι το έλασμα είναι κάπου δεμένο (ας πούμε στην αριστερή πλευρά του) κι εμείς το τραβάμε από την δεξιά πλευρά με την F. Αναγκαστικά θα εμφανιστεί και η αντίδραση της F (η -F δηλαδή) στα αριστερά για να μην μετακινηθεί το κομμάτι, να είναι δηλαδή σε ισορροπία. Ακολούθως βλέπουμε τις διαστάσεις που είναι σημειωμένες στο σχήμα: το πλάτος, το πάχος και τη θέση της οπής με τη διάμετρο d των 2 cm. Κατανοώ ότι αφού το πλάτος είναι 20 cm και οπή έχει διάμετρο 2 cm μένουν μετά την οπή 9 cm προς κάθε πλευρά της οπής. Στο σχήμα βλέπουμε και τα διπλά βέλη ΚΛ και ΜΝ, τα οποία δεν είναι στα δεδομένα αλλά θα δούμε το νόημά τους στη λύση της άσκησης παρακάτω. Μετά το σχήμα πρέπει να δούμε τα αριθμητικά δεδομένα που είναι οι διαστάσεις και η δύναμη που ασκείται. Αν η δύναμη είναι πολύ μεγάλη το έλασμα θα κοπεί στα δύο. Το αν θα κοπεί η όχι, εξαρτάται από την τιμή της τάσης, όπως έχουμε πει στα εισαγωγικά της θεωρίας. Η τάση είναι τόσο μεγαλύτερη όσο μεγαλύτερη είναι η δύναμη και μικρότερη η διατομή, στην οποία κινδυνεύει να κοπεί το δοκίμιο. Εδώ η δύναμη μας δίνεται από την εκφώνηση και την θεωρούμε σταθερή. Και η διατομή είναι σταθερή αλλά να προσέξουμε ότι εκεί που βρίσκεται η οπή είναι λίγο μικρότερη. Εξασθενεί λόγω της τρύπας. Στα σημεία ΚΛ και ΜΝ το εμβαδόν της διατομής είναι ακέραιο: 1cm 20cm = 20cm 2, διότι εκεί δεν υπάρχει μείωσή της εξ αιτίας της οπής. Στη διατομή όμως ΑΒ το εμβαδόν μειώνεται. Στο επόμενο σχήμα φαίνεται πόσο είναι αυτό. Σύμφωνα με το σχήμα, το εμβαδόν της διατομής στην τομή ΑΒ αποτελείται από το άθροισμα των εμβαδών των ορθογωνίων ΑΓΔΕ και ΒΖΗΘ. Επομένως η διατομή (λέγεται επικίνδυνη διατομή, επειδή εκεί θα κοπεί το κομμάτι αν σπάσει) που καταπονείται από τη 20 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
21 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 δύναμη F έχει εμβαδόν: 2x(1cm 9cm = 9cm 2 ) δηλαδή θα είναι 18 cm 2, αντί για 20 cm 2 που θα ήταν αν δεν υπήρχε η οπή. Σύμφωνα με την τελευταία παρατήρηση, η μεγαλύτερη τάση θα είναι στη διατομή ΑΒ που είναι και η μικρότερη. Με όλα αυτά έχει ολοκληρωθεί η κατανόηση της άσκησης και η ανάλυση που ήταν απαραίτητη για τη λύση της. Εφαρμόζουμε τώρα τα γνωστά για την τάση στη διατομή ΑΒ: Άρα η ζητούμενη τάση είναι. Αν δεν υπήρχε η οπή (στη διατομή ΚΛ ή ΜΝ) θα είχαμε: Η τάση θα ήταν μικρότερη:. Αυτό είναι προφανές αφού η διατομή σε αυτή την περίπτωση θα είναι μεγαλύτερη. Διαφορετικά θα λέγαμε ότι η δύναμη F κατανέμεται σε μικρότερη επιφάνεια, άρα προκαλεί μεγαλύτερη τάση. Άσκηση 1.11 Μια σωληνωτή ράβδος (ένας ευθύγραμμος σωλήνας δηλαδή) εφελκύεται με δύναμη F ίση με 1000 dan. Το υλικό του σωλήνα έχει επιτρεπόμενη τάση ίση με σ επ =800 dan/cm 2. Γνωρίζουμε ότι ο σωλήνας έχει εσωτερική διάμετρο ίση με 15 mm και εξωτερική 17 mm. (Αντί των προηγούμενων διαστάσεων θα μπορούσε να δοθεί μόνο η μία από τις δυο διαμέτρους και ότι το πάχος του σωλήνα είναι 1 mm.) Να ελεγχθεί εάν η ράβδος θα αντέξει την καταπόνηση. Απάντηση Κατ αρχάς να διευκρινίσουμε ότι το όλο θέμα δεν έχει καμιά σχέση με το μήκος του σωλήνα. Συνεχίζουμε υπολογίζοντας τη διατομή του σωλήνα, η οποία έχει τη μορφή δακτυλίου. Επομένως θα πρέπει να αντιμετωπίσουμε μια άσκηση ίδια με την άσκηση 1.3, από την οποία θα μεταφέρουμε και το σχήμα. Σύμφωνα με την εκφώνηση θα έχουμε: D εσ =15 mm και D εξ =17 mm. Για να βρεθεί το εμβαδόν της διατομής θα κάνουμε ό,τι ακριβώς και στην άσκηση 1.3: Επομένως η διατομή που καταπονείται έχει εμβαδόν 50,3 mm 2. Σε αυτή τη διατομή θα ελέγξουμε την τάση αν υπερβαίνει την επιτρεπόμενη. Θα εφαρμόσουμε τον γνωστό τύπο για ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 21
22 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ τον υπολογισμό της τάσης. Όμως επειδή η επιτρεπόμενη τάση είναι σε μονάδες dan/cm 2, θα πρέπει να μετατρέψουμε και τις μονάδες της διατομής σε cm 2. Αυτό θα γίνει με διαίρεση της τιμής του εμβαδού με το 100, αφού είναι γνωστό ότι ένα cm 2 έχει 100 mm 2. Άρα το εμβαδόν Α της διατομής θα είναι 50,3 /100=0,503 cm 2. Έτσι θα έχουμε: Βρήκαμε ότι σ=1988 dan/cm 2 που είναι πολύ μεγαλύτερο από την σ επ, επομένως μπορούμε να απαντήσουμε ότι ο σωλήνας δεν θα αντέξει αυτή τη δύναμη. Σημείωση: Για να άντεχε, αφού η τάση που βρέθηκε είναι σχεδόν διπλάσια από την επιτρεπόμενη, θα έπρεπε να είχε σχεδόν διπλάσιο εμβαδόν η διατομή. Αν διπλασιάζαμε το πάχος, για παράδειγμα, τότε θα άντεχε. Ας δούμε τι έχουμε αν αντί για D εξ =17 mm πάρουμε D εξ =19 mm Το εμβαδόν θα είναι: Και η αναπτυσσόμενη τάση: Βρήκαμε λοιπόν ότι η τάση θα είναι μικρότερη από την επιτρεπόμενη και το δοκίμιο θα αντέξει Αντιδράσεις στήριξης Ροπή Παραδείγματα Στο μάθημα των Στοιχείων Μηχανών θα χρειαστεί ορισμένες φορές να υπολογίσουμε εμείς κάποιες από τις δυνάμεις που ασκούνται σε ένα δοκίμιο. Ο υπολογισμός ενδέχεται να προκύπτει από την εφαρμογή ενός μαθηματικού τύπου (πχ. F=σ Α, κλπ.) αλλά υπάρχουν και περιπτώσεις που εμείς θα πρέπει να προχωρήσουμε σε μια ανάλυση και επεξεργασία των δεδομένων για τον υπολογισμό της ή των δυνάμεων. Μια εφαρμογή που θα μας είναι χρήσιμη στην επίλυση ασκήσεων του μαθήματος είναι ο υπολογισμός των αντιδράσεων στήριξης μιας δοκού (ράβδου, δοκιμίου, κλπ.). Για παράδειγμα ας δούμε το επόμενο σχήμα: Έχουμε μια δοκό που στηρίζεται στα δυο άκρα Α και Β, και στο μέσον της, στο επάνω μέρος, ασκείται μια δύναμη F. Θεωρούμε ότι αυτό το δοκάρι δεν έχει βάρος. Μας είναι προφανές ότι σε κάθε άκρη της ράβδου, εκεί που στηρίζεται, θα ασκείται μια δύναμη ίση με F/2. Είναι σαν να κουβαλούν δυο εργαζόμενοι ένα μεγάλο δοκάρι και ο ένας το έχει στον ώμο του από μπροστά και ο άλλος στον δικό του ώμο στο πίσω μέρος. Αν το δοκάρι ζυγίζει 100 κιλά (100 kp ή 100 dan), κάθε ένας θα σηκώνει από 50 κιλά. Αυτά τα 50 κιλά είναι η αντίδραση που προκύπτει από την δύναμη (βάρος) του δοκαριού που επιδρά στους εργαζόμενους. Κάθε ένας από αυτούς θα πρέπει να ασκήσει δύναμη ίση με 50 κιλά ώστε να ισορροπήσει η ράβδος και να μην πέσει κάτω. Θα πρέπει δηλαδή οι δύο αντιδράσεις να είναι 22 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
23 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 ίσες και αντίθετες με το βάρος του δοκαριού. (Στο παράδειγμα με το δοκάρι που σηκώνουν οι δύο άνθρωποι, το ρόλο της F παίζει το βάρος του δοκαριού.) Στο παράδειγμα που δώσαμε με το σχήμα, επειδή η δύναμη ήταν στο μέσον του δοκιμίου ήταν εύκολο να βρούμε την τιμή της κάθε αντίδρασης στα άκρα Α και Β. Αν όμως η δύναμη δεν είναι στο μέσον το πράγμα γίνεται λίγο πιο δύσκολο. Ας δούμε το παράδειγμα του επόμενου σχήματος, που η δύναμη είναι πιο κοντά στο Α και μάλιστα η απόστασή της από το Β είναι διπλάσια από εκείνη από το Α (ΑF=L και FΒ=2 L). Καταλαβαίνουμε ότι αν έχουμε πάλι τους δυο εργαζόμενους που σηκώνουν ένα φορτίο αντίστοιχο με εκείνο του σχήματος, εκείνος που είναι στη θέση Α θα επωμίζεται μεγαλύτερο βάρος από τον άλλο. Όμως, πόσο είναι αυτό; Για να το βρούμε θα πρέπει να αντιληφτούμε δυο πράγματα: 1. Οι δυνάμεις των δυο εργαζομένων (F A και F B ) όταν προστεθούν πρέπει να μας κάνουν την δύναμη F. Δηλαδή θα ισχύει: F = F A + F B. Αυτή η σχέση ονομάζεται σχέση ισορροπίας των δυνάμεων και είναι γνωστή από το μάθημα της Μηχανικής. Λέει με απλά λόγια ότι όταν ένα σώμα ισορροπεί (το δοκάρι που έχουμε δηλαδή) το άθροισμα των δυνάμεων που ασκούνται σε αυτό θα είναι μηδέν. Αυτό συμβολίζεται μαθηματικά με την σχέση: ΣF=0. Στο δοκάρι του σχήματος ασκούνται τρεις δυνάμεις: το βάρος F του δοκαριού, κατακόρυφα προς τα κάτω, και οι αντιδράσεις F A και F B κατακόρυφα προς τα επάνω. Το ότι το άθροισμά τους θα είναι μηδέν, σημαίνει πολύ απλά ότι οι δυνάμεις που ασκούνται από πάνω προς τα κάτω (F) θα είναι ίσες με εκείνες που ασκούνται από κάτω προς τα επάνω (F A και F B ). Δηλαδή:. Αυτό συμβαίνει γιατί και οι τρεις δυνάμεις είναι κατακόρυφες. Μόνο τέτοιες περιπτώσεις θα συναντήσουμε στο μάθημα. Θα μπορούσαμε να θεωρήσουμε τις προς τα επάνω δυνάμεις ως θετικές και τις προς τα κάτω αρνητικές. Θα είχαμε την ίδια τελική εξίσωση. 2. Θεωρούμε (θεωρούμε σημαίνει «ας υποθέσουμε ότι έχουμε») το δοκίμιο (ράβδος, δοκάρι) και τα σημεία στήριξης. Αυτά ισορροπούν προφανώς. Αυτό σημαίνει ότι αφενός το δοκάρι δεν μετακινείται πάνω ή κάτω αλλά και ότι δεν περιστρέφεται γύρω από οποιοδήποτε σημείο, που αν υπήρχε θα ονομαζόταν άξονας περιστροφής. Το ότι δεν έχουμε περιστροφή, στη μηχανική λέμε ότι έχουμε ισορροπία των ροπών. Αυτός είναι ο δεύτερος κανόνας που χρησιμοποιούμε για τη λύση τέτοιων ασκήσεων ο οποίος λέει: όταν ένα σώμα ισορροπεί, το άθροισμα των ροπών που ασκούν όλες οι δυνάμεις πάνω του είναι μηδέν: ΣΜ=0. Το νόημα αυτής της πρότασης είναι ότι, επειδή το δοκίμιο δεν περιστρέφεται σημαίνει ότι αν πάρουμε τη ροπή που δημιουργεί κάθε δύναμη στο σώμα, ως προς το ίδιο σημείο περιστροφής, και τις προσθέσουμε το άθροισμα τους θα είναι μηδέν. Αυτό ονομάζεται θεώρημα των ροπών. Για να κατανοήσουμε την τελευταία πρόταση πρέπει να θυμηθούμε από το μάθημα της μηχανικής τι είναι η ροπή. Ροπή είναι η αιτία της περιστροφής ενός σώματος και οφείλεται στην ενέργεια μιας ή περισσότερων δυνάμεων στο σώμα. Αν το σώμα τελικά περιστρέφεται σημαίνει ότι η συνολική ροπή σε αυτό δεν είναι μηδενική. Ας δούμε τη ράβδο ΑΒ του ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 23
24 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ επόμενου σχήματος στα αριστερά. Στηρίζεται στον τοίχο, στο άκρο της Α. Θεωρούμε ότι δεν έχει βάρος (είναι αμελητέο) και ασκούνται σε αυτήν οι δύο δυνάμεις F 1 και F 2 στα σημεία Γ και Β αντιστοίχως. Θα πούμε τώρα μερικά πράγματα για τις ροπές στηριζόμενοι σε αυτό το σχήμα. Υποθέτουμε ότι με την επενέργεια των δύο δυνάμεων η ράβδος ισορροπεί. Ας φανταστούμε τώρα ότι υπάρχει μόνο η δύναμη F 1 και όχι η F 2. Καταλαβαίνουμε ότι η F 1 σπρώχνει τη ράβδο προς τα κάτω, την λυγίζει ίσως, αφού δεν υπάρχει η F 2. Μπορούμε δηλαδή να πούμε ότι η F 1 πάει να περιστρέψει προς τα δεξιά τη ράβδο, αφού το σημείο περιστροφής είναι προφανώς το Α, στο οποίο στηρίζεται. Λέμε τότε ότι η F 1 ασκεί μια ροπή Μ 1 στη ράβδο ίση με το γινόμενο F 1 β, δηλαδή το γινόμενο της δύναμης επί την απόσταση της δύναμης από το σημείο περιστροφής το οποίο εξετάζουμε. Δηλαδή θα ισχύει: Μ 1 =F 1 β. Αυτό μας οδηγεί στον ορισμό της ροπής: Ροπή ως προς ένα σημείο ή ένα άξονα είναι το γινόμενο της δύναμης επί την (κάθετη) απόσταση της δύναμης από το σημείο ή τον άξονα. Το αν θα περιστραφεί ή όχι το δοκίμιο, προς το παρόν, δε μας απασχολεί. Προφανώς οι μονάδες της ροπής θα είναι οι μονάδες της δύναμης επί τις μονάδες του μήκους, δηλαδή: dan m, dan cm, N m, N cm, kp m, kp cm, οι πιο συνηθισμένες μονάδες. Αυτές που χρησιμοποιούνται πιο πολύ στο μάθημά μας είναι οι δυο πρώτες. Όταν μας ζητάνε μια ροπή, πρέπει να προσδιορίσουμε τρία πράγματα: Το σημείο που θα θεωρήσουμε ως σημείο περιστροφής, άσχετα αν το δοκίμιο είναι σταθερό. Το μέγεθος της δύναμης ή των δυνάμεων και την κατεύθυνση που έχουν. Η κατεύθυνση χρειάζεται για να βρούμε την απόστασή της από το σημείο περιστροφής. Την απόσταση της δύναμης από το σημείο περιστροφής. Να προσέξουμε ότι απόσταση της δύναμης από ένα σημείο θα είναι η κάθετη απόσταση του σημείου από την ευθεία που ανήκει η δύναμη. Για παράδειγμα ας δούμε το προηγούμενο σχήμα στα δεξιά. Έχουμε την F που παριστάνεται από το διάνυσμα ΑΒ. Αν θεωρήσουμε το σημείο Ο, η απόσταση της F από αυτό θα είναι το τμήμα ΟΜ (όπου το ΟΜ είναι κάθετο στην ευθεία ΓΒ) και όχι το ΟΑ ή κάποιο άλλο. Η ροπή της F ως προς το σημείο Ο θα είναι Μ Ο = F (ΟΜ). Συνεχίζουμε τώρα με το προηγούμενο σχήμα στα αριστερά. Υποθέτουμε ότι δεν υπάρχει η F 1 αλλά μόνο η F 2 και ζητάμε τη ροπή της ως προς το σημείο στήριξης Α. θα εφαρμόσουμε τον τύπο και θα βρούμε Μ 2 = F 2 α. Στη ράβδο ΑΒ εκτός από τις F 1 και F 2 υπάρχει και άλλη μια δύναμη που δεν έχει σχεδιαστεί στο σχήμα (δεν χρειάζεται) και είναι η αντίδραση του τοίχου στο σημείο στήριξης Α. Αν μας ζητήσουν τη συνολική ροπή στη ράβδο ως προς το σημείο Α (πάντα θα μας λένε και ως προς ποιο σημείο θέλουν τη ροπή, αφού αλλιώς δεν θα μπορούσαμε να βρούμε τις αποστάσεις των δυνάμεων) θα πάρουμε μόνο τη ροπή της F 1 και της F 2. Η ροπή της άλλης δύναμης, που είναι ως αντίδραση στο Α, θα είναι μηδέν αφού η απόσταση της δύναμης αυτής από το Α θα είναι μηδέν. Είναι μηδέν διότι περνά από αυτό. Επομένως η συνολική 24 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
25 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 ροπή των δυνάμεων που ασκούνται στη ράβδο ως προς το σημείο Α θα είναι μόνο το άθροισμα των ροπών Μ 1 =F 1 β και η Μ 2 = F 2 α. Ας δούμε τώρα πως γίνεται το άθροισμά τους να είναι μηδενικό, ως προς το σημείο Α. Μια ροπή δεν είναι πάντα θετική. Θα είναι αρνητική αν πάει να περιστρέψει το δοκίμιο προς τα αριστερά, δηλαδή αντίθετα από την κίνηση των δεικτών του ρολογιού, (όπως εδώ η δύναμη F 2 ) και θετική αν πάει να το περιστρέψει προς τα δεξιά, δηλαδή σύμφωνα με την κίνηση των δεικτών του ρολογιού (όπως η δύναμη F 1 ). Σημειώνουμε ότι δεν θα άλλαζε τίποτα αν τα πρόσημα έμπαιναν αντίθετα. Επομένως στο παράδειγμά μας η συνολική ροπή ως προς το Α, θα είναι η ροπή της F 1 που είναι θετική και η ροπή της F 2 που είναι αρνητική. Έτσι μπορούμε να γράψουμε: Στο επόμενο σχήμα φαίνεται πιο παραστατικά ό,τι έχει σχέση με τα πρόσημα των ροπών. Συνοψίζουμε: Όταν έχουμε άσκηση και θέλουμε να υπολογίσουμε τις αντιδράσεις στήριξης, εφαρμόζουμε τις δυο εξισώσεις για την ισορροπία των δυνάμεων και των ροπών. Με τις εξισώσεις που θα προκύψουν μπορούμε να υπολογίσουμε τις ζητούμενες αντιδράσεις. Θα τα δούμε αυτά πως γίνονται με συγκεκριμένα παραδείγματα. Πρέπει να σημειώσουμε ότι η ροπή μιας δύναμης μπορεί να έχει θετικό πρόσημο ως προς ένα σημείο και αρνητικό ως προς ένα άλλο, ή να είναι και μηδενική. Όταν παίρνουμε την εξίσωση ΣF=0 για τις δυνάμεις θα ισχύει για ένα άξονα, όπως θα ισχύει και για κάθε άλλον. Αυτό δε θα σας απασχολήσει στις ασκήσεις του μαθήματος αφού πάντα ο άξονας θα είναι ο κατακόρυφος, γι αυτό θα γράφουμε την εξίσωση με τη μορφή ΣF ψ =0 για να δείξουμε ότι παίρνουμε τις δυνάμεις (τις προβολές τους όπως λέγεται) στον κατακόρυφο άξονα. Αντίστοιχα για τη ροπή η εξίσωση ΣΜ=0 εννοείται ότι εφαρμόζεται κάθε φορά ως προς ένα σημείο. Γι αυτό είναι καλύτερα να γράφουμε ΣΜ Α =0 όταν παίρνουμε τις ροπές ως προς το Α. Άσκηση 1.12 Δίνεται το δίπλα σχήμα, όπου μια ράβδος σε οριζόντια θέση δέχεται τις δύο δυνάμεις που φαίνονται στις αποστάσεις που είναι σημειωμένες σε αυτό. Η ράβδος έχει συνολικό μήκος 100 cm και στηρίζεται χαλαρά στο Α σε ένα τοίχο. Η δύναμη F 1 είναι ίση με 200 dan και δρα κατακόρυφα σε απόσταση 60 cm από το σημείο στήριξης. Η δύναμη F 2 δεν δίνεται από την άσκηση, αλλά είναι εκείνο που ζητείται για να έχουμε ισορροπία. Απάντηση Για να λυθεί η άσκηση θα χρησιμοποιηθεί ο νόμος για την ισορροπία των ροπών. Μάλιστα θα πάρουμε την ισορροπία ως προς το σημείο Α διότι μας συμφέρει να πάρουμε το σημείο στο οποίο υπάρχει μια δύναμη την οποία δεν γνωρίζουμε. Η δύναμη που υπάρχει στο σημείο στήριξης Α (που περνά από αυτό) έχει ροπή μηδέν ως προς αυτό, αφού η απόστασή της από το Α είναι μηδέν. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 25
26 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Η δύναμη F 2 τείνει να περιστρέψει τη ράβδο προς τα αριστερά (σε σχέση με το σημείο περιστροφής που θεωρήσαμε ότι είναι το Α) ενώ η F 1 προς τα δεξιά, ενώ όπως είπαμε η ροπή της τρίτης δύναμης που υπάρχει στο Α έχει ροπή μηδέν. Επομένως η ροπή της F 1 πρέπει να είναι ίση με τη ροπή της F 2. Θα γράψουμε και θα λύσουμε την εξίσωση: Υπολογίστηκε λοιπόν με την επίλυση μόνο μιας εξίσωσης η δύναμη F 2. Σημείωση: Θα μπορούσαμε να κάνουμε πιο αναλυτική επίλυση εφαρμόζοντας το θεώρημα των ροπών: επειδή η ράβδος ισορροπεί θα ισχύει ότι ΣΜ Α =0. Θα καταλήξουμε στην ίδια εξίσωση λαμβάνοντας υπόψιν ότι η F 2 δημιουργεί αρνητική ροπή ενώ η F 1 θετική: Και φυσικά θα καταλήξουμε στο ίδιο αποτέλεσμα. Άσκηση 1.13 Δίνεται η ράβδος του επόμενου σχήματος που στηρίζεται στα σημεία Α και Β ενώ δέχεται τις δυνάμεις F 1 και F 2 στις θέσεις και με τις τιμές στο μέγεθός τους όπως φαίνονται στο σχήμα. Οι αντιδράσεις στα Α και Β είναι αντιστοίχως F Α και F Β. Πριν προχωρήσετε στο επόμενο ερώτημα να γράψετε το θεώρημα για την ισορροπία των ροπών χωριστά αν θεωρήσετε ως σημεία περιστροφής τα Α και Β. Κατόπιν να υπολογίσετε τις αντιδράσεις F Α και F Β. Απάντηση Αφού η ράβδος ισορροπεί το θεώρημα των ροπών μας λέει ότι ως προς οποιοδήποτε σημείο της ράβδου το άθροισμα των ροπών των δυνάμεων που ασκούνται στη ράβδο (οι οποίες είναι τέσσερις: F 1, F 2, F A, F B ) θα είναι μηδέν. Άρα θα ισχύει: ΣΜΑ=0 και ΣΜΒ=0. Ως προς Α: F 1, F 2 θετική ροπή (δεξιόστροφη) F B αρνητική ροπή (αριστερόστροφη) F Α μηδενική ροπή Εξίσωση: Ως προς Β: F 1, F 2 αρνητική ροπή (αριστερόστροφη) F Α θετική ροπή (δεξιόστροφη) F Β μηδενική ροπή Εξίσωση: (Α) (Β) 26 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
27 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Για καλύτερη κατανόηση στο πρόσημο των ροπών δείτε τα επόμενα σχήματα. Με βέλη φαίνονται η περιστροφή που θα προκαλούσε στη ράβδο η κάθε δύναμη ανάλογα με το εκάστοτε σημείο που θεωρούμε ως σημείο περιστροφής. Σε κάθε βέλος έχει σημειωθεί από ποια δύναμη προκαλείται η ροπή και το πρόσημό της. Θα υπολογίσουμε τώρα την αντίδραση στο σημείο στήριξης Α, την δύναμη F Α. Σε τέτοιες ασκήσεις για τον υπολογισμό της αντίδρασης σε ένα σημείο στήριξης, βολεύει πολύ να εφαρμόζουμε το θεώρημα των ροπών ως προς το άλλο σημείο. Αυτό το κάνουμε γιατί η αντίδραση στο άλλο σημείο στήριξης θα έχει μηδενική ροπή, ως προς το σημείο που εφαρμόζουμε το θεώρημα ισορροπίας των ροπών. Επομένως θα πάρουμε την τελική εξίσωση (Β) που βρήκαμε πριν για τις ροπές με σημείο περιστροφής το Β. Έτσι θα μηδενίζεται η ροπή της F B και η δύναμη αυτή δεν θα υπάρχει ως άγνωστος στην εξίσωση. Υπολογίζουμε: Επομένως η αντίδραση στήριξης στο Α θα είναι 200 dan. Ακολούθως θα υπολογίσουμε την αντίδραση στο σημείο στήριξης Β, την δύναμη F Β. Θα πάρουμε τώρα την τελική εξίσωση (Α) που βρήκαμε με σημείο περιστροφής το Α. Έτσι θα μηδενίζεται η ροπή της F Α και η δύναμη αυτή δεν θα υπάρχει ως άγνωστος στην εξίσωση. Υπολογίζουμε: Βρήκαμε ότι η αντίδραση στο σημείο Β είναι 300 dan. Σημείωση: Δεν εφαρμόσαμε την ισορροπία των δυνάμεων, αφού βρέθηκε η F Α, αν και θα μας διευκόλυνε, για να δείτε πως δουλεύουμε με τις ροπές. Όμως θα μπορούσαμε να πούμε ότι το άθροισμα των δυνάμεων πρέπει να είναι μηδέν, ως προς τον κατακόρυφο άξονα. Δηλαδή οι δυνάμεις που ασκούνται προς τα κάτω θα έχουν άθροισμα όσο και οι δυνάμεις που ασκούνται προς τα πάνω. Δηλαδή θα ισχύει η σχέση: (Γ) Επομένως αφού βρούμε την μια αντίδραση διευκολύνει να εφαρμόσουμε την εξίσωση για την ισορροπία των δυνάμεων και από αυτό που θα βρούμε να υπολογίσουμε την άλλη αντίδραση. Δηλαδή αφού βρήκαμε ότι F Α = 200 dan να χρησιμοποιήσουμε την εξίσωση (Γ), οπότε θα έχουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 27
28 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Και έτσι βρήκαμε πιο εύκολα την F Β. Και τώρα που βρήκαμε τις δύο αντιδράσεις ας κάνουμε μια μικρή διερεύνηση. Ας υπολογίσουμε τη συνολική ροπή ως προς το σημείο Γ. Σύμφωνα με τη θεωρία, αφού η ράβδος ισορροπεί η ΣΜ Γ πρέπει να είναι μηδέν. Για να δούμε τι βγάζει η εξίσωση: Πράγματι λοιπόν η συνολική ροπή ως προς το σημείο Γ είναι μηδέν. Το ίδιο θα βρίσκαμε και για το σημείο Δ, αλλά και για οποιοδήποτε άλλο σημείο. Άσκηση 1.14 Δίνεται η ράβδος του επόμενου σχήματος, που στηρίζεται στα σημεία Α και Β ενώ δέχεται την δύναμη F=300 dan σε απόσταση 50 cm από το Α. Το μήκος της ράβδου είναι 200 cm. Να βρεθούν οι αντιδράσεις στα άκρα της ράβδου. Σε αυτές τις ασκήσεις πάντα εφαρμόζουμε τις εξισώσεις για την ισορροπία της ράβδου: την εξίσωση για την ισορροπία α) των δυνάμεων και β) των ροπών. Τις εξισώσεις αυτές μπορούμε να τις γράψουμε με δυο μορφές. Είτε: (Α1) (Β1) Είτε: (Α2) Ροπές ως προς το σημείο Α: (Β2) Το σχολικό βιβλίο γράφει πρώτα την πρώτη μορφή (Α1 και Β1) των δυο εξισώσεων, που είναι πιο γενική, και μετά γράφει την επόμενη μορφή (Α2 και Β2). Για τη λύση της άσκησης ξεκινάμε με την εξίσωση για τις ροπές (Β2) που έχει ένα άγνωστο (την δύναμη F Β ). Δεν έχει νόημα να αρχίσουμε να επεξεργαζόμαστε την εξίσωση με τις δύο αντιδράσεις (Α2), αφού δεν μπορούμε να την επιλύσουμε επειδή έχει δυο αγνώστους (τις δυνάμεις F Α και F Β ). Προσέξτε ότι η εξίσωση για τις ροπές είναι πάντα ως προς ένα σημείο στήριξης ώστε να μην έχει και αυτή δυο αγνώστους. Λύνουμε λοιπόν πρώτα την εξίσωση Β2 ως προς την άγνωστη δύναμη F Β : Βρέθηκε λοιπόν η μία από τις αντιδράσεις, η F Β. Τώρα, από την εξίσωση Α2 θα βρούμε και την άλλη αντίδραση F Α : Βρέθηκε και η άλλη αντίδραση F Α =225 dan. 28 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
29 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ Περιστροφική κίνηση Σε ορισμένα κεφάλαια της ύλης του μαθήματος θα χρειαστεί να γνωρίζουμε στοιχεία από την περιστροφική κίνηση των σωμάτων. Γι αυτό θα αναφέρουμε ορισμένα θέματα για την γραμμική και τη γωνιακή ταχύτητα στην περιστροφική κίνηση. Φανταστείτε ένα τροχό ο οποίος περιστρέφεται με σταθερή ταχύτητα. Αυτό σημαίνει ότι κάνει κάθε κύκλο στον ίδιο χρόνο κάθε φορά. Αυτό με άλλα λόγια λέγεται ότι «γράφει (δηλαδή αφήνει το ίχνος του) το ίδιο τόξο του κύκλου στη μονάδα του χρόνου» ή «γράφει ίσα τόξα σε ίσους χρόνους». Η ουσία είναι ότι περιστρέφεται με σταθερή ταχύτητα. Μόνο που υπάρχουν στην περιστροφική κίνηση δύο ειδών ταχύτητες: η γραμμική και η γωνιακή. Ας δούμε την κάθε μία. Βλέπουμε τον κύκλο στο διπλανό σχήμα και υποθέτουμε ότι αυτό είναι ένας δρόμος που ένα σώμα κινείται με σταθερή ταχύτητα. Ας πούμε ότι πηγαίνει από το Α στο Β σε χρόνο t, προχωρεί δηλαδή για απόσταση «α» πάνω στον κύκλο σε αυτό το χρόνο t. Σύμφωνα με τη φυσική, ταχύτητα ενός κινητού (ενός σώματος δηλαδή που κινείται) ορίζεται το πηλίκο της απόστασης προς το χρόνο. Για παράδειγμα, αν το κινητό ήταν ένα αυτοκίνητο και πήγαινε με σταθερή ταχύτητα για 120 χιλιόμετρα σε δύο ώρες θα λέγαμε ότι η ταχύτητά του είναι 60 χιλιόμετρα την ώρα. Θα το βρίσκαμε διαιρώντας την απόσταση των 120 χιλιομέτρων με το χρόνο των δύο ωρών, που κάνει 60. Επανερχόμενοι στον κύκλο του σχήματος, θα λέγαμε ότι η ταχύτητα του κινητού είναι:. Αυτή η ταχύτητα ονομάζεται γραμμική ταχύτητα και οι μονάδες της στο Διεθνές Σύστημα είναι m/s. Γραμμική ταχύτητα είναι η γνωστή σε όλους ταχύτητα που μετράμε στα αυτοκίνητα, στους ανθρώπους, στα αεροπλάνα, κλπ. Υπάρχει και γωνιακή ταχύτητα, η οποία δεν μετρά σε κάποιο χρόνο την απόσταση που κάνει το κινητό, αλλά την γωνία κατά την οποία περιστρέφεται σε αυτό το χρόνο. Στον αριθμητή της γωνιακής ταχύτητας αντί για την απόσταση που διανύει το κινητό είναι η γωνία που σχηματίζει η αρχή και το τέλος της κίνησης με το κέντρο του κύκλου. Στο παράδειγμα του σχήματος η γωνία αυτή είναι η ΑΟΒ ή. Οι μονάδες που μετριέται η γωνία στο Διεθνές Σύστημα Μονάδων είναι τα ακτίνια. Δεν θα αναφέρομε περισσότερα εδώ για τα ακτίνια και τη γωνιακή ταχύτητα, διότι δεν θα χρειαστούν στις ασκήσεις του μαθήματος. Παρόμοια έννοια είναι οι στροφές ενός κινητού, που συμβολίζονται με n και δείχνουν πόσες στροφές θα κάνει το κινητό που περιστρέφεται, στη μονάδα του χρόνου, που θα είναι είτε το δευτερόλεπτο είτε το λεπτό. Δηλαδή μονάδα του n είναι οι στροφές ανά δευτερόλεπτο (στο SI) ή το πιο συνηθισμένο: στροφές ανά λεπτό, που συμβολίζεται rpm ή και RPM. Όταν ένα σώμα κάνει περιστροφική κίνηση η γραμμική ταχύτητά του συνδέεται με τις στροφές του και με τη διάμετρο d του κύκλου με τη σχέση: Δηλαδή όταν γνωρίζουμε την διάμετρο του κύκλου και τον αριθμό των στροφών που εκτελεί στη μονάδα του χρόνου, τότε μπορούμε να βρούμε την ταχύτητα του κινητού. Η προηγούμενη σχέση ισχύει στο SI, άρα η ταχύτητα είναι σε m/s, η διάμετρος σε m και οι στροφές σε στρ/s. Αν οι στροφές δίνονται σε στρ/λεπτό (RPM) (και η ταχύτητα και η διάμετρος στις ίδιες με πριν μονάδες) τότε ο τύπος γίνεται: Παράδειγμα: Ένα αυτοκίνητο κάνει κύκλους σε μια πίστα με διάμετρο 200 μέτρα και έχει κάνει 60 στροφές σε μισή ώρα. Με τι ταχύτητα έτρεχε; Η διάμετρος του κύκλου είναι 200 μέτρα δηλαδή 0,2 χιλιόμετρα. Οι στροφές αφού είναι 60 στη μισή ώρα θα είναι 120 στη μία ώρα. Άρα από τον τύπο βρίσκουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 29
30 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ Έτσι βρήκαμε την (γραμμική) ταχύτητα του αυτοκινήτου. Στην εξίσωση αυτή βάλαμε τις μονάδες που είχαμε χωρίς να τις αλλάξουμε. Αν δουλεύαμε στο SI θα λέγαμε ότι αφού κάνει 120 στροφές την ώρα θα κάνει 120/3600=0,03333 στροφές το δευτερόλεπτο. Τότε βάσει του τύπου θα βρίσκαμε: Και αν θέλαμε να χρησιμοποιήσουμε τον τύπο θα βάζαμε τις στροφές σε RPM και οι 120 στροφές την ώρα θα ήταν120/60 δηλαδή 2 στροφές το λεπτό ή 2 RPM. Και θα είχαμε: Φυσικά βρέθηκε το ίδιο αποτέλεσμα αφού οι μονάδες είναι ίδιες. Να προσέξουμε ότι δεν ισχύουν όλα αυτά, και άλλα, μόνο για την περίπτωση που ένα σώμα κινείται κυκλικά, αλλά και στην περίπτωση που έχουμε, ας πούμε, μια ρόδα που περιστρέφεται. Τότε, κάθε σημείο της ρόδας κάνει περιστροφική κίνηση και ισχύουν τα προηγούμενα, σαν να ήταν το κάθε σημείο της ρόδας ένα χωριστό αντικείμενο που περιστρεφόταν. Θα μπορούσε δηλαδή στο προηγούμενο σχήμα να είχαμε μία ρόδα και τα σημεία Α και Β να ήταν στα άκρα της. Θα λέγαμε ότι κάθε σημείο της περιφέρειας της ρόδας έχει γραμμική ταχύτητα. Πρέπει να προσέξουμε όμως το εξής: ας πούμε ότι το προηγούμενο σχήμα παριστάνει ένα δίσκο που περιστρέφεται. Ας δούμε τα σημεία Κ και Λ, όπου το Κ είναι πιο έξω από το Λ. Το Λ είναι πιο κοντά στο κέντρο του δίσκου. Αν κάνει ένα κύκλο το Κ θα κάνει το ίδιο και το Λ. Αυτό σημαίνει ότι τα σημεία Κ και Λ έχουν την ίδια γωνιακή ταχύτητα, όπως και κάθε σημείο του δίσκου, αφού όσους κύκλους κάνει το ένα κάνουν και όλα τα άλλα. Αλλά ίδια γωνιακή ταχύτητα σημαίνει ότι έχουν και τον ίδιο αριθμό στροφών. Όμως δεν έχουν την ίδια γραμμική ταχύτητα, γιατί αυτή εξαρτάται από την απόσταση και όχι τη γωνία που έκαναν τα δύο σημεία Κ και Λ. Το σημείο Κ που βρίσκεται πιο μακριά από το Λ, όταν κάνει ένα κύκλο κάνει μεγαλύτερη απόσταση από το Λ, που κάνει πιο μικρό κύκλο. Δηλαδή το Κ στον ίδιο χρόνο με το Λ, κάνει πιο μεγάλη απόσταση, άρα τρέχει πιο γρήγορα. Το συμπέρασμα λοιπόν είναι ότι όσο πιο μακριά από το κέντρο περιστροφής βρίσκεται ένα σημείο, τόσο μεγαλύτερη γραμμική ταχύτητα έχει. Ας δούμε τώρα τι ισχύει όταν έχουμε δυο συνεργαζόμενους τροχούς. Εδώ έχουμε δυο περιπτώσεις: α) οι τροχοί να είναι σε επαφή και β) οι τροχοί να είναι σε απόσταση και να συνδέονται με κάποιο μέσο (ιμάντα ή αλυσίδα). Στο επόμενο σχήμα φαίνονται οι δυο περιπτώσεις. Οι δυο πρώτοι τροχοί με κέντρα τα Ο 1 και Ο 2 έχουν σημείο επαφής το Α. Για να μεταδίδει ο ένας την κίνηση στον άλλο μέσω του σημείου επαφής, στην περιφέρεια των τροχών υπάρχει η λεγόμενη οδόντωση, ώστε να παρασύρει ο τροχός που έχει κίνηση (ονομάζεται 30 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
31 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 κινητήριος) τον άλλο (που ονομάζεται κινούμενος). Ο ένας από τους δύο περιστρέφεται παίρνοντας κίνηση με κάποιο μηχανικό ή ηλεκτρικό μέσο (πχ. κινητήρα) και ο άλλος παίρνει κίνηση από τον πρώτο. Στο σχήμα φαίνεται η φορά περιστροφής (κατεύθυνση) των δυο τροχών όταν κινούνται. Οι δύο άλλοι τροχοί με κέντρα Ο 3 και Ο 4 βρίσκονται σε απόσταση και γι αυτό χρησιμοποιείται ένας ιμάντας ή μια αλυσίδα για να μεταδώσει την κίνηση. Πάλι υπάρχει ο κινητήριος, που δίνει την κίνηση στον κινούμενο. Εδώ η φορά της περιστροφής είναι λίγο διαφορετική από πριν στους δυο τροχούς σε επαφή και φαίνεται στο προηγούμενο σχήμα. Η κίνηση μεταδίδεται από τον κινητήριο στον κινούμενο μέσω της τριβής που δημιουργεί ο ιμάντας ή με την αλυσίδα και τα δόντια που έχουν σε αυτή την περίπτωση οι δυο τροχοί. Άσχετα από το αν οι δυο τροχοί είναι σε επαφή ή σε απόσταση, υπάρχουν ορισμένες σχέσεις κοινές, που ισχύουν μεταξύ των μεγεθών που περιγράφουν τις κινήσεις τους. Για παράδειγμα η σχέση μετάδοσης, η οποία ορίζεται ως το πηλίκο των στροφών του κινούμενου τροχού προς τον αριθμό των στροφών που έχει ο κινητήριος. Αν συμβολίσουμε με i τη σχέση μετάδοσης, n 1 τον αριθμό των στροφών του κινητήριου τροχού και n 2 τις στροφές του κινούμενου τροχού, τότε σύμφωνα με τον ορισμό θα ισχύει: Αυτός είναι ένας απλός ορισμός, αλλά η σχέση αυτή είναι πολύ χρήσιμη. Κατ αρχάς αποδεικνύεται ότι οι στροφές ενός τροχού είναι αντιστρόφως ανάλογες της διαμέτρου του τροχού. Δηλαδή όταν έχουμε δυο συνεργαζόμενους οδοντωτούς τροχούς ή δυο τροχούς που περιστρέφονται με ιμάντα ή αλυσίδα, όσες φορές μεγαλύτερος είναι ο ένας από τον άλλον τόσες φορές πιο αργά θα περιστρέφεται. Για παράδειγμα, αν ο ένας έχει διπλάσια διάμετρο από τον άλλο, θα περιστρέφεται με τις μισές στροφές από εκείνον. Δηλαδή ισχύει η σχέση: Η σχέση αυτή συνάγεται (προέρχεται) από το ότι οι δυο τροχοί έχουν τις ίδιες περιφερειακές γραμμικές ταχύτητες. Δηλαδή οι περιφέρειές τους έχουν την ίδια γραμμική ταχύτητα. Στην περίπτωση των οδοντωτών τροχών οι περιφέρειες είναι σε επαφή και η μία κυλίεται στην άλλη, άρα οι ταχύτητές τους είναι ίσες. Στην περίπτωση του ιμάντα ή της αλυσίδας οι περιφέρειες των δυο τροχών έχουν την ίδια ταχύτητα γιατί έχουν την ταχύτητα του ιμάντα ή της αλυσίδας. Στο ακριβώς πιο πάνω σχήμα βλέπουμε πάλι τους δύο τροχούς όπου ο Ο 1 κινεί τον Ο 2 με τη φορά περιστροφής όπως φαίνεται στο σχήμα. Φαίνεται και η δύναμη F που ασκεί ο τροχός Ο 1 ώστε να περιστρέψει τον Ο 2. Αυτή η δύναμη μεταφέρεται από την οδόντωση του πρώτου τροχού στην οδόντωση του δεύτερου και ασκείται στο σημείο επαφής Α των δύο τροχών. Πρέπει να καταλάβετε ότι η F μεταφέρεται στον δεύτερο τροχό για να τον περιστρέψει, δηλαδή υπάρχει και στους δύο τροχούς. Θα μπορούσαμε να είχαμε ζωγραφίσει δύο δυνάμεις: F 1 και F 2 αντί για την F και ίσες με την F. Αυτές οι δυνάμεις προκαλούν μία ροπή στον κάθε τροχό, την Μ 1 στον πρώτο και την Μ 2 στο δεύτερο. Ενώ οι δυνάμεις F 1 και F 2 είναι ίσες, οι δύο ροπές δεν είναι, αφού η κάθε μία προκύπτει από τον ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 31
32 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ πολλαπλασιασμό της F με την απόστασή της από το κέντρο περιστροφής του κάθε τροχού. Άρα η δύναμη F 1 που πάει να περιστρέψει τον πρώτο τροχό (ουσιαστικά προέρχεται από την περιστροφή του, αφού αυτός είναι ο κινητήριος) θα έχει ροπή Μ 1 που θα είναι ίση με το γινόμενο της F 1 επί την απόσταση Ο 1 Α, που είναι η ακτίνα του τροχού, άρα είναι ίση με το μισό της διαμέτρου d 1 /2. Αντιστοίχως θα ισχύει και για τη ροπή Μ 2 του δεύτερου τροχού. Επομένως θα ισχύουν οι σχέσεις: Με συνδυασμό αυτών των σχέσεων και της προηγούμενης προκύπτει: Το συμπέρασμα είναι ότι η ροπή για κάθε τροχό είναι ανάλογη της διαμέτρου του τροχού, ενώ οι στροφές του αντιστρόφως ανάλογες της διαμέτρου Έργο - Ισχύς Άλλα χρήσιμα στοιχεία, από το κεφάλαιο του βιβλίου για την περιστροφική κίνηση, είναι τα σχετικά με την ισχύ και την ενέργεια-έργο. Ας πούμε μερικά λόγια για να κατανοήσουμε τις έννοιες αυτές. Όταν χρησιμοποιούμε το αυτοκίνητο για να μας μεταφέρει κάπου, εκείνο καταναλώνει ενέργεια καίγοντας καύσιμο, την οποία ενέργεια εκμεταλλευόμαστε εμείς. Αυτό που γίνεται, είναι η μετατροπή της ενέργειας που περιέχει το καύσιμο σε μηχανική. Καταλαβαίνουμε από το παράδειγμα ότι ενέργεια είναι το να μπορούμε εμείς να μετακινηθούμε. Αντιστοίχως, ενέργεια παίρνουμε όταν χρησιμοποιούμε ένα βενζινοκίνητο αλυσοπρίονο για να κόψουμε ξύλα. Χωρίς δηλαδή να μας μεταφέρει κάπου. Ακόμα λέμε ότι πρέπει να καταναλώσουμε ενέργεια για να κουβαλήσουμε μια ποσότητα με ξύλα από το δρόμο στην αποθήκη. Άλλο παράδειγμα είναι το ηλεκτρικό φως. Παίρνουν οι ηλεκτρικοί λαμπτήρες ρεύμα και φωτίζουν. Ακόμα δηλαδή και το φως είναι ενέργεια, όπως και η φωτιά που ζεσταίνει ή μαγειρεύει, μια ανεμογεννήτρια που λέμε ότι παράγει ενέργεια, το νερό που είναι στο υδροηλεκτρικό φράγμα και άλλα πολλά. Γενικά σήμερα, ό,τι τεχνολογικά εξελιγμένο μέσον και να χρησιμοποιήσουμε, έχει σχέση με ηλεκτρικό ρεύμα και επομένως με ενέργεια. Όταν ένα μηχάνημα αναγράφει σε μια ταμπέλα την ιπποδύναμή του, σημαίνει ότι μας δίνει πληροφορία για την ενέργεια που μπορεί να παραγάγει. Σημειώνουμε εδώ ότι η ιπποδύναμη δεν είναι ακριβώς ενέργεια, αλλά ισχύς, που παρακάτω θα την πούμε αναλυτικά. Όταν ένα μηχάνημα ή άνθρωπος μπορεί και δίνει ενέργεια λέμε ότι παράγει έργο. Δηλαδή έργο λέμε ότι παράγεται από μια δύναμη όταν μπορεί και μετακινεί ένα σώμα. Και είναι τόσο περισσότερο όσο μεγαλύτερη η δύναμη και όσο πιο μακριά γίνεται η μετακίνηση. Γι αυτό και ο ορισμός για το έργο μας λέει ότι έργο είναι το γινόμενο της δύναμης επί την απόσταση που μετακινείται το σώμα. Ο τύπος που ισχύει είναι: Όπου W είναι το έργο, F είναι η δύναμη και είναι η απόσταση της μετατόπισης. Αν δηλαδή δεν υπάρξει μετακίνηση δεν έχουμε και κατανάλωση ή παραγωγή έργου. Οι μονάδες για το έργο είναι εκείνες της ενέργειας και είναι στο Διεθνές Σύστημα Μονάδων το Joule (J) που ισοδυναμεί με N m. Θα δώσουμε τώρα δυο παραδείγματα για καλύτερη κατανόηση. Δείτε το παρακάτω σχήμα. Έχουμε ένα κιβώτιο πάνω σε ένα οριζόντιο επίπεδο και το τραβάμε με δύναμη F=100 Ν. Λόγω της τριβής υπάρχει η δύναμη Τ=100 Ν που αντιστέκεται στη μετακίνηση. Το σώμα έχει βάρος Β και μετακινείται κατά 5 m. Η F και η Τ είναι ίσες, διότι για να μετακινηθεί το κιβώτιο, εμείς το τραβάμε με όση δύναμη χρειάζεται για να υπερνικήσει την τριβή Τ. Η μετακίνηση πάντως θεωρείται ότι γίνεται με σταθερή ταχύτητα. Δεν θα μπούμε σε άλλες λεπτομέρειες, γιατί δεν απαιτούνται για το μάθημά μας. 32 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
33 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Μπορούμε να πούμε τα εξής: Η δύναμη F καταναλώνει (και το δίνει για τη μετακίνηση του κιβωτίου) έργο ίσο με: Η δύναμη Τ της τριβής καταναλώνει έργο ίσο με: Για να μετακινηθεί το κιβώτιο κατά 5 μέτρα πρέπει να καταναλωθεί έργο ίσο με το έργο της δύναμης F. Επειδή η κίνηση είναι οριζόντια το έργο της F στην ουσία δίνεται για την υπερνίκηση της τριβής. Βλέπουμε ότι για τη μετακίνηση του κιβωτίου απαιτούνται 500J, διότι ως δύναμη που ενεργεί σε αυτό λαμβάνεται η F. Αν το κιβώτιο είχε στο κάτω μέρος ρόδες, τότε η τριβή θα ήταν λιγότερη και το απαιτούμενο έργο θα ήταν αντιστοίχως μικρότερο, αφού η F θα ήταν πιο μικρή, ίση πάλι με την νέα μικρότερη τριβή. Μια άλλη παρατήρηση σε αυτή τη λύση είναι ότι το έργο κάθε δύναμης είναι χωριστό από το έργο των άλλων δυνάμεων. Βλέπουμε επίσης ότι το βάρος του κιβωτίου δεν παίζει κανένα ρόλο στην ποσότητα του έργου που απαιτείται. Αυτό οφείλεται στο ότι η δύναμη του βάρους είναι κάθετη στη μετακίνηση και είναι γνωστό ότι οι κάθετες στη μετακίνηση δυνάμεις δεν προκαλούν έργο, αφού άλλωστε δεν προκαλούν κατακόρυφη μετακίνηση. Ένα άλλο σημαντικό στοιχείο που μπορούμε να προσθέσουμε είναι ότι το έργο δεν έχει σχέση με το χρόνο που θα χρειαστούμε να μετακινήσουμε το κιβώτιο. Αυτό είναι πολύ σπουδαίο γιατί όταν σε λίγο μιλήσουμε για την ισχύ, θα δούμε ότι ο χρόνος είναι πολύ σημαντικός γι αυτήν. Ας δούμε ένα ακόμα παράδειγμα, όπου ένα κιβώτιο που με ένα γερανό θέλουμε να το ανεβάσουμε σε ένα ύψος 10 m. Το βάρος του κιβωτίου είναι Β=1000 N (περίπου 100 κιλά), επομένως ο γερανός χρειάζεται να ασκήσει δύναμη F ίση με Β για να το υψώσει. Η μετακίνηση είναι κατακόρυφη, κατά την φορά (κατεύθυνση) των δυνάμεων F και Β άρα το έργο που απαιτείται για την ανύψωση είναι: Άρα το έργο είναι J. Αυτό το έργο θα καταναλώσει το βάρος Β και είναι το έργο που πρέπει να δώσει η F άρα και το έργο που θα καταναλώσει ο γερανός (σε ηλεκτρική ενέργεια) για να κάνουμε τη δουλειά μας. Γενικά οποιαδήποτε δύναμη μετακινεί ένα σώμα παράγει (ή καταναλώνει) έργο. Για την ύπαρξη έργου δεν είναι αναγκαίο να έχουμε μετακίνηση ενός σώματος από ένα σημείο σε ένα άλλο, αλλά μπορεί το σώμα να περιστρέφεται. Η περιστροφή ενός σώματος, όπως έχουμε πει, συνεπάγεται την ύπαρξη μιας ροπής, η οποία με τη σειρά της προκαλείται από μια δύναμη. Αυτή η δύναμη καταναλώνει ενέργεια αφού περιστρέφει το σώμα, στο οποίο μπορεί να μην έχουμε μετακίνηση του κέντρου βάρους του, αλλά τα διάφορα επί μέρους μικρά τμήματά του μετακινούνται περιστρεφόμενα, άρα απαιτούν την κατανάλωση ενέργειας. Στην περίπτωση αυτή δεν εφαρμόζουμε τον τύπο:, αφού το δεν υπάρχει για όλο ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 33
34 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ το περιστρεφόμενο σώμα. Για τον υπολογισμό του έργου πρέπει να προχωρήσουμε στην έννοια της ισχύος, η οποία συμβολίζεται με το γράμμα Ρ. Ισχύς ορίζεται το πηλίκο της ενέργειας προς το χρόνο, ή διαφορετικά, είναι η ενέργεια που καταναλώνεται ή παράγεται στη μονάδα του χρόνου. Επομένως ισχύει ο τύπος: Η ισχύς έχει ως μονάδα το Watt (W) το οποίο ισούται με ένα Joule/s στο Διεθνές Σύστημα Μονάδων. Αυτό σημαίνει ότι αν εφαρμόσουμε τον παραπάνω τύπο και η ενέργεια είναι σε Joule και ο χρόνος σε δευτερόλεπτα η ισχύς θα είναι σε W. Να δούμε τώρα λίγο πιο αναλυτικά την έννοια της ισχύος, που τη συναντάμε στην καθημερινή μας ζωή συνεχώς και οφείλουμε να τη γνωρίζουμε. Ας επανέλθουμε στο παράδειγμα που είχαμε πριν με το κιβώτιο που ανεβάσαμε σε ύψος 10 μέτρων. Η ενέργεια που χρειάζεται γι αυτό είναι J, ανεξάρτητα από το χρόνο που θα γίνει αυτό (και ανεξάρτητα από τον δρόμο που θα ακολουθήσουμε, αλλά αυτό δεν μας αφορά τώρα). Δηλαδή, είτε χρησιμοποιήσουμε ένα μικρό γερανό και η ανύψωση γίνει σε 20 δευτερόλεπτα είτε ένα μεγαλύτερο και η ανύψωση γίνει σε 10 δευτερόλεπτα το έργο δεν αλλάζει. Κάτι όμως φαίνεται να είναι διαφορετικό, και χαρακτηρίζει την ικανότητα του γερανού, και αυτό είναι η ισχύς. Λέμε ότι ο γερανός που κάνει την ανύψωση πιο γρήγορα έχει μεγαλύτερη ισχύ. Σύμφωνα με τον τύπο της ισχύος για κάθε μια περίπτωση θα έχουμε: Με Ρ 10 συμβολίσαμε την ισχύ του γερανού που ανεβάζει το κιβώτιο σε 10 δευτερόλεπτα και με Ρ 20 την ισχύ του άλλου γερανού που ανεβάζει το κιβώτιο σε 20 δευτερόλεπτα. Βλέπουμε ότι ο γρήγορος γερανός έχει μεγαλύτερη ισχύ από τον πιο αργό. Αυτή η ταχύτητα είναι που χαρακτηρίζει τα μηχανήματα που έχουν μεγάλη ισχύ. Το έργο έτσι κι αλλιώς που θα αποδώσουν είναι το ίδιο, αλλά σημασία έχει ο χρόνος που θα το κάνουν. Αυτό σημαίνει ότι αν έχουμε τους δύο προηγούμενους γερανούς, όπου ο ένας έχει διπλάσια ισχύ από τον άλλο, και τους βάλουμε να εργάζονται, τον γρήγορο για πέντε ώρες και τον πιο αργό για δέκα ώρες θα έχουν αποδώσει το ίδιο έργο. Με όλα τα παραπάνω θέλουμε να πούμε ότι η ισχύς είναι ένα μέγεθος που χαρακτηρίζει ένα μηχάνημα και δείχνει την γρηγοράδα του για την παραγωγή έργου, ενώ η ενέργεια είναι ένα μέγεθος που δεν χαρακτηρίζει το μηχάνημα, αλλά τη δουλειά που κάνει. Αν δουλεύει επί πολύ χρόνο, η ενέργεια που θα παράγει θα είναι πολλή, αλλά η ισχύς του δε θα αλλάξει. Όταν δούμε στην ταμπέλα ενός μηχανήματος να αναγράφεται ότι η ισχύς είναι W εννοεί ότι η καταναλισκόμενη (ηλεκτρική) ισχύς είναι W, που είναι ίση με 10 kw. (Ο όρος καταναλισκόμενη ισχύς δεν είναι σωστός, αλλά το γράψαμε εδώ για να το κατανοήσετε καλύτερα.) Αυτό σημαίνει ότι αν δουλέψει επί μία ώρα συνεχώς το μηχάνημα, η ενέργεια που θα ξοδέψει θα είναι: Βρήκαμε ότι η ενέργεια που θα καταναλώσει θα είναι 10. Το είναι η γνωστή κιλοβατώρα που πληρώνουμε στη ΔΕΗ και είναι μονάδα ενέργειας. Είναι λάθος να πούμε ότι ένα μηχάνημα ξοδεύει 2 kw την ώρα. Τα kw δεν καταναλώνονται διότι είναι ισχύς. Η ενέργεια καταναλώνεται, άρα μπορούμε να πούμε ότι μια συσκευή καταναλώνει 2 την ώρα. Η ισχύς είναι κάτι σαν το όνομα της συσκευής, που δεν αλλάζει. Ας δούμε όμως ένα παράδειγμα με την έννοια της ισχύος. Ένας προβολέας είναι ισχύος 500 W. Να βρείτε πόση ενέργεια θα ξοδέψει ένα βράδυ που είναι αναμμένος για 14 ώρες. Από τον τύπο της ισχύος θα έχουμε για την ισχύ και το χρόνο που δίνεται: 34 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
35 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 Άρα η ενέργεια που θα ξοδέψει θα είναι 7 κιλοβατώρες. Ένα άλλο παράδειγμα είναι το εξής: ένας γερανός ανεβάζει βάρος 1000 κιλών σε ύψος 20 μέτρων σε 40 δευτερόλεπτα. Να βρείτε την ισχύ του. Ξεκινάμε βάζοντας σωστά την μονάδα του βάρους. Συχνά λέμε κιλό για το βάρος, αλλά αυτό σημαίνει μάζα. Όμως μάζα ενός κιλού έχει βάρος ενός kp, δηλαδή περίπου 10 Ν = 1 dan. Άρα το βάρος εδώ θα είναι 1000 dan 10= N. Η ανύψωση χρειάζεται ενέργεια που θα βρούμε εφαρμόζοντας τον τύπο: Η ενέργεια για την ανύψωση είναι Τώρα από το γνωστό τύπο της ισχύος θα βρούμε την ισχύ: Επομένως η ισχύς του μηχανήματος είναι 5. Παρατηρούμε εδώ ότι η ενέργεια των δεν έχει καμία σχέση με το χρόνο που χρειάζεται για την ανύψωση. Οι μονάδες της ισχύος είναι κυρίως τα W, τα kw και οι ίπποι που συμβολίζονται με PS ή HP. Έχουμε ήδη πει ότι ένας HP ισούται με 746 W και ένας PS με 736 W. Στο βιβλίο αυτοί οι δύο συμβολισμοί δεν διαχωρίζονται και μάλιστα δεν χρειάζεται να γίνει και μετατροπή μονάδων στις ασκήσεις, γιατί οι τύποι δεν είναι συνήθως στο SI, αλλά για κάθε τύπο που θα χρησιμοποιήσετε πρέπει να γνωρίζετε τις μονάδες των μεγεθών. Ας επανέλθουμε τώρα στον περιστρεφόμενο τροχό για να δούμε πως υπολογίζεται η ισχύς και η ενέργεια που αποδίδονται σε αυτόν. Υπάρχει η σχέση: Αυτή η σχέση μας λέει ότι σε ένα περιστρεφόμενο σώμα η ροπή Μ που το περιστρέφει, η ισχύς Ρ που μεταδίδεται ή που δέχεται το σώμα και ο αριθμός των στροφών n, συνδέονται με την παραπάνω σχέση. Όταν χρησιμοποιούμε τον τύπο αυτό πρέπει να θυμόμαστε τις μονάδες των μεγεθών, οι οποίες είναι οι εξής: ροπή: dan m, ισχύς: PS ή HP (έχουμε πει ότι στο σχολικό βιβλίο αυτές οι δύο μονάδες της ισχύος, αν και δεν είναι ακριβώς ίσες, χρησιμοποιούνται αδιακρίτως) και στροφές σε στροφές ανά λεπτό δηλαδή RPM (στο βιβλίο γράφονται και με τα μικρά τους γράμματα: rpm). Αν η ροπή δίνεται ή βρίσκεται σε dan cm (και όχι σε dan m) τότε ο προηγούμενος τύπος παίρνει τη μορφή: Και είναι λογικό να αυξάνεται κατά τον παράγοντα 100 ο συντελεστής, αφού η ροπή βρίσκεται σε dan cm που είναι κατά 100 φορές μικρότερη μονάδα από την dan m. Αυτός ο τύπος έχει το εξής νόημα: όταν ένα σώμα περιστρέφεται, η ισχύς που υπάρχει ή μεταδίδεται μέσω αυτού, εξαρτάται από τις στροφές και την ροπή σε αυτό. Όσο μεγαλύτερη η ροπή και περισσότερες οι στροφές τόσο περισσότερη η μεταδιδόμενη ισχύς. Αντιστοίχως μπορούμε να πούμε ότι όσο μεγαλύτερη η ισχύς που μεταδίδεται τόσο μεγαλύτερη η ροπή που θα ασκείται, ενώ όσο περισσότερες οι στροφές τόσο μικρότερη η ροπή (για την ίδια μεταφερόμενη ισχύ). Θα επανέλθουμε τώρα στο θέμα του υπολογισμού του έργου (αν και δεν χρειάζεται συχνά σε ασκήσεις) σε ένα περιστρεφόμενο τροχό. Αν χρειαστεί να το υπολογίσουμε (το έργο) θα το βρούμε μέσω της ισχύος. Αφού βρούμε την ισχύ με τον παραπάνω τύπο, θα χρησιμοποιήσουμε τον τύπο ορισμού της ισχύος για να υπολογίσουμε το έργο:. Ένα άλλο χρήσιμο μέγεθος είναι ο βαθμός απόδοσης, τον οποίο πρέπει να γνωρίζετε και άσχετα από το μάθημα. Συνήθως αφορά μηχανήματα και συσκευές. Ο βαθμός απόδοσης ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 35
36 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ είναι ένα μέγεθος που μας δείχνει αν μια μηχανή εκμεταλλεύεται αρκετά την ενέργεια (συνήθως ηλεκτρική ή καύσιμο) που χρησιμοποιεί για να μας αποδώσει κάποιο έργο. Για παράδειγμα έχουμε δυο ίδιες αντλίες νερού, μια παλιά και μια καινούρια. Καταλαβαίνουμε όλοι ότι η παλιά δεν θα έχει την ίδια απόδοση με την καινούρια. Δηλαδή, η παλιά, ενώ ξοδεύει το ίδιο ρεύμα (ηλεκτρική ενέργεια) σε μια ώρα, μεταφέρει λιγότερο νερό από την καινούρια. Και δεν φταίει ότι χάνει νερό διότι δεν έχει καλή στεγανότητα. Απλά, έχει πιο πολλές τριβές και οι περιστροφές στα διάφορα εξαρτήματα δεν είναι τόσο καλές όσο της καινούριας, οπότε το νερό που μεταφέρει είναι λιγότερο. Αυτό σημαίνει ότι η παλιά αντλία μας δίνει λιγότερο έργο από αυτό που μας δίνει η καινούρια, ενώ ξοδεύουν το ίδιο έργο στη μονάδα του χρόνου. Και η παλιά και η καινούρια όμως αντλία μας δίνουν λιγότερη ενέργεια από εκείνη που καταναλώνουν. Με άλλα λόγια: η ισχύς που παίρνουμε (άρα αποδίδει το μηχάνημα) είναι πάντα λιγότερη από την ολική ισχύ που δέχεται το μηχάνημα. Ο λόγος (πηλίκο) της ισχύος που ωφελούμαστε από ένα μηχάνημα ή μια συσκευή, προς την ολική καταναλισκόμενη ισχύ του μηχανήματος ονομάζεται βαθμός απόδοσης αυτού. Έτσι έχουμε τον τύπο: Αυτός ο ορισμός ισχύει για όλες τις συσκευές και η στην ουσία είναι η ισχύς που αναγράφει η συσκευή στην ταμπέλα της. Η τιμή του βαθμού απόδοσης είναι πάντα μικρότερη από τη μονάδα διότι, οι μηχανές δεν μπορούν να αποδώσουν όλη την ενέργεια που απορροφούν από το ηλεκτρικό ρεύμα ή το καύσιμο. Υπάρχει μια μικρή διαφοροποίηση σε συνεργαζόμενους άξονες, όταν μεταδίδεται κίνηση από τον ένα στον άλλο. Μπορεί λόγω τριβών και άλλων ατελειών του συστήματος μετάδοσης να μην μεταβιβάζεται όλη η ισχύς στον κινούμενο άξονα, αλλά να μετατρέπεται ένα μικρό ή μεγάλο ποσοστό σε θερμότητα (πάντα θα γίνεται αυτό). Αυτό μειώνει το βαθμό απόδοσης, ο οποίος στην περίπτωση των αξόνων, ορίζεται ως ο λόγος της ισχύος του κινητήριου άξονα προς την ισχύ του κινούμενου. Αυτό που πρέπει να κρατήσουμε από αυτό το σημείο του μαθήματος είναι ότι όταν γνωρίζουμε το βαθμό απόδοσης, μπορούμε να υπολογίσουμε την μεταφερόμενη ισχύ στον κινούμενο άξονα Υποδείξεις για τη λύση ασκήσεων Θα πούμε τώρα μερικά βασικά που θα σας βοηθήσουν, αν τα ακολουθήσετε, να λύνετε πιο εύκολα τις ασκήσεις. Κανόνας πρώτος: Μαθαίνουμε καλά τους τύπους που έχει το σχολικό βιβλίο. Χωρίς να τους γνωρίζετε δεν έχει νόημα να προσπαθείτε να λύνετε ασκήσεις. Όμως, ισχύει και ότι για να τους μάθετε πρέπει να λύσετε πολλές ασκήσεις. Όσο και να νομίζετε ότι γνωρίζετε κάποιες μαθηματικές σχέσεις απ έξω, αν δεν τις εφαρμόσετε σε ασκήσεις μόνοι σας χωρίς τη βοήθεια του βιβλίου ή των σημειώσεών σας, δεν θα τις έχετε μάθει σωστά και καλά. Άρα, για να μάθουμε τις μαθηματικές σχέσεις του βιβλίου, τις γράφουμε μερικές φορές για να τις θυμόμαστε καλύτερα και μετά λύνουμε ασκήσεις προσπαθώντας να τις θυμηθούμε και όχι να τις αντιγράψουμε. Θυμόμαστε τις μονάδες που έχει κάθε τύπος που έχουμε μάθει. Πολλοί τύποι είναι στο Διεθνές Σύστημα Μονάδων (SI) αλλά πολλοί δεν ανήκουν σε αυτό και πρέπει να θυμάστε τις μονάδες κάθε μεγέθους του τύπου. Για παράδειγμα υπάρχει ο τύπος:. Σε αυτόν πρέπει υποχρεωτικά η δύναμη αν μπει σε μονάδες N, η ταχύτητα σε m/s και η ισχύς σε W. Αν βάλουμε άλλες μονάδες σε αυτόν τον τύπο θα κάνουμε σίγουρα λάθος. Για τις ίδιες ασκήσεις χρησιμοποιείται και ο τύπος:. Σε αυτόν οι μονάδες είναι διαφορετικές. Η δύναμη είναι σε dan, η ταχύτητα πάλι σε m/s και η ισχύς σε PS. Καταλαβαίνουμε πόσο σημαντικό είναι να θυμόμαστε αν ο τύπος είναι στο SI ή αν δεν είναι να θυμόμαστε όλες τις μονάδες των μεγεθών. Πριν αρχίσουμε να λύνουμε την άσκηση να σιγουρευτούμε ότι κατανοήσαμε την εκφώνηση και τα ζητούμενα. Μη σας φαίνεται τόσο απλό αυτό. Μερικές φορές οι μαθητές προσπαθούν να λύσουν μια άσκηση τελείως μηχανικά, με τον λεγόμενο 36 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
37 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 1 τυφλοσούρτη. Αυτό βολεύει στις εύκολες και απλές ασκήσεις, αλλά σε μια πιο σύνθετη άσκηση δεν θα «δουλέψει» και θα έχετε πρόβλημα. Διαβάζοντας την άσκηση να βάλετε στο μυαλό σας τη μηχανή ή το εξάρτημα που περιγράφει και να σκεφτείτε αν είναι λογικά αυτά που δίνει και που ζητά. Να προσέξετε, ας πούμε, αν ο ιμάντας είναι τραπεζοειδής ή ορθογωνικός. Αν μιλά η άσκηση για εφελκυσμό ή για στρέψη ή κάμψη. Να συνειδητοποιήσετε ότι τα δεδομένα της άσκησης είναι αρκετά για να τη λύσετε. Αν σας φαίνονται λίγα, σημαίνει ότι δεν έχετε καταλάβει καλά τι συμβαίνει, γιατί είναι απίθανο να έχει γίνει λάθος στην εκφώνηση. Προσέχουμε να μην μπερδέψουμε κάποιο από τα δεδομένα της άσκησης με άλλο παρόμοιο. Για παράδειγμα, να μην αλλάξουμε στους τύπους το κινητήριο με το κινούμενο γρανάζι ή κάτι άλλο. Η άσκηση μπορεί να έχει μία ή περισσότερες ερωτήσεις. Αν έχει πάνω από μία, τις απαντάμε με τη σειρά, και συνήθως αυτό που θα βρούμε σε μια ερώτηση θα χρειαστεί να το χρησιμοποιήσουμε και στις επόμενες. Μην το ξεχνάτε αυτό, γιατί τις περισσότερες φορές ισχύει. Όταν είστε έτοιμοι να απαντήσετε μια ερώτηση της άσκησης, προσπαθείτε να ανακαλύψετε τον τύπο που είναι κατάλληλος για να βρείτε το ζητούμενο. Προφανώς ο τύπος που ζητάμε θα περιέχει τον άγνωστο. Αν είμαστε τυχεροί θα τον δίνει κατ ευθείαν και δεν θα χρειαστεί να λύσουμε ως προς αυτόν. Για παράδειγμα αν ζητά την ροπή ενός άξονα ο τύπος την δίνει αμέσως. Αν όμως ζητά την ισχύ Ρ πρέπει να λύσουμε τη σχέση αυτή ως προς την ισχύ. Όμως ένα άλλο ζήτημα είναι να ελέγξουμε αν ο τύπος που έχουμε στο νου είναι εκείνος που θα πρέπει να χρησιμοποιηθεί. Στο παράδειγμα που δώσαμε πριν θα μπορούσε να χρησιμοποιηθεί και ο τύπος. Πρέπει να δούμε ποιος είναι ο κατάλληλος. Κατάλληλος είναι εκείνος που μας δίνονται τα μεγέθη που έχει ή μπορούμε να τα βρούμε. Γι αυτό χρειάζεται εμπειρία και να λύσετε πολλές ασκήσεις. Διαφορετικά θα πρέπει να δοκιμάσετε και να δεχτείτε ή να απορρίψετε έναν τύπο. Όταν θα έχουμε βρει τον σωστό τύπο πρέπει να θυμηθούμε τις μονάδες κάθε μεγέθους σε αυτόν. Μπορεί να χρειαστεί να αλλάξουμε κάποιες από αυτές που δίνει η εκφώνηση ώστε να μετατραπούν σε εκείνες που απαιτεί ο τύπος. Πρέπει να κάνουμε αντικατάσταση των μεγεθών με τις σωστές τιμές, όσον αφορά στις μονάδες. Την αντικατάσταση αυτή είναι καλύτερα να την κάνουμε αφού λύσουμε τον τύπο ως προς τον άγνωστο που ζητούμε. Για παράδειγμα, αν ζητάνε την ροπή Μ 2 και εμείς θα χρησιμοποιήσουμε τον τύπο πρώτα να λύσουμε ως προς Μ 2 και μετά να αντικαταστήσουμε. Δηλαδή να φτάσουμε στην σχέση: και μετά να βάλουμε σε αυτόν τις τιμές στα μεγέθη Μ 1, n 1 και n 2. Τις μονάδες των μεγεθών δεν είναι απαραίτητο να τις βάζετε κατά την αντικατάσταση των τιμών τους, αφού και το σχολικό βιβλίο του μαθήματος δεν το κάνει. Πρέπει όμως να λέτε ποιες είναι αυτές. Ποτέ μην ξεχνάτε στο τέλος και στην απάντησή σας, να βάζετε τις μονάδες στο ζητούμενο μέγεθος που έχετε βρει. Αν, ας πούμε, βρείτε τη ροπή 15 και δεν γράψετε ότι είναι 15 dan m, θα χάσετε σίγουρα κάποια μόρια. Όταν βρείτε το ζητούμενο, καλό είναι να ελέγχετε αν η τιμή που βρήκατε γι αυτό, είναι φυσιολογική. Για παράδειγμα, αν βρείτε ότι ένας άξονας περιστρέφεται με 4 rpm, οι στροφές αυτές είναι πολύ λίγες και αποκλείεται να είναι σωστή η λύση που κάνατε. Να ψάξετε να βρείτε το λάθος σας. Μπορεί να κάνατε λάθος στις πράξεις ή ξεχάσατε να μετατρέψετε κάποιες μονάδες. Τα θέματα στις πανελλαδικές είναι τέσσερα και πρέπει να απαντήσετε σε όλα για να πάρετε το άριστα. Ενώ συνηθίζεται σε άλλα μαθήματα τα δύο πρώτα θέματα να είναι θεωρίας και τα δύο τελευταία ασκήσεων, επειδή αυτό δεν είναι υποχρεωτικό, στα Στοιχεία Μηχανών υπάρχει ποικιλία περιπτώσεων. Έχει τύχει να μπει στο πρώτο θέμα μία ερώτηση θεωρίας και μία άσκηση. Γι αυτό πρέπει να είστε προετοιμασμένοι για κάθε περίπτωση. Εκείνο που ισχύει είναι ότι πρέπει κάθε θέμα να έχει δύο ερωτήσεις. Η εφημερίδα της ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 37
38 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ κυβέρνησης (Τεύχος Δεύτερο, Αρ. Φύλλου 373, 3 Μαρτίου 2009, άρθρο 5 για τον τρόπο εξέτασης των μαθημάτων) αναφέρει για τα Στοιχεία Μηχανών: Δίνονται για εξέταση τέσσερα (4) θέματα κλιμακούμενης δυσκολίας, μεταξύ των οποίων και ασκήσεις. Κάθε θέμα μπορεί να περιέχει έως δύο ερωτήματα. Μην είστε σίγουροι ότι θα ισχύσει αυτό και σε σας. μπορεί η επιτροπή εξετάσεων να κάνει διαφορετική ερμηνεία και να βάλει δύο ερωτήματα σε κάθε ερώτηση του θέματος. Κανονικά, όπως αναφέρεται πιο πάνω στο φύλλο της κυβέρνησης, τα θέματα πρέπει να είναι αυξανόμενης δυσκολίας, αλλά η δυσκολία δεν μετριέται πολύ εύκολα πάντα. Γι αυτό μην θεωρήσετε δεδομένο ότι το τέταρτο θα είναι το δυσκολότερο θέμα. Άλλωστε, για πολλούς μαθητές τα εύκολα ανήκουν στην θεωρία, αλλά αρκετοί είναι πιο δυνατοί στις ασκήσεις. Ένα άλλο ζήτημα είναι πόσα μόρια παίρνει η θεωρία και πόσα οι ασκήσεις. Τα τελευταία χρόνια είναι μοιρασμένα, αλλά αυτό δεν είναι υποχρεωτικό για εκείνους που βάζουν τα θέματα. Δεν είναι απίθανο μια χρονιά να είναι περισσότερα τα μόρια στις ασκήσεις. Το να είναι περισσότερα της θεωρίας είναι μάλλον απίθανο. Εσείς καλό είναι να ξεκινάτε πρώτα από το θέμα που γνωρίζετε καλύτερα, ώστε να πάρετε θάρρος και να σας φύγει όσο γίνεται το άγχος. 38 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
39 ΣΥΝΤΕΛΕΣΤΗΣ ΑΣΦΑΛΕΙΑΣ ΚΕΦΑΛΑΙΟ 2 2. Συντελεστής Ασφαλείας Πριν αναφερθούμε στις ηλώσεις θα δώσουμε μερικά παραδείγματα για να εξοικειωθείτε με τον συντελεστή ασφαλείας, τον οποίο ήδη έχουμε αναφέρει. Έχουμε πει ότι είναι ένας αριθμός που μας λέει πόσο μεγαλύτερη τάση πρέπει να ασκηθεί από την επιτρεπόμενη για να σπάσει ένα δοκίμιο, να υπερβεί δηλαδή την τάση θραύσης του. Επομένως για τις ορθές τάσεις (που γενικά συμβολίζονται με το γράμμα σ) θα ισχύουν οι σχέσεις: Αντιστοίχως για τις διατμητικές τάσεις (που γενικά συμβολίζονται με το γράμμα τ) θα ισχύουν οι σχέσεις: Ας δούμε μερικά παραδείγματα. Άσκηση 2.1 Ένα (καινούριο) συρματόσχοινο έχει συντελεστή ασφαλείας ίσο με 5. Το χρησιμοποιήσαμε για να ανυψώσουμε ένα μεγάλο φορτίο που είχε σαν αποτέλεσμα να σπάσει το συρματόσχοινο. Η τάση στο συρματόσχοινο τη στιγμή που αυτό έσπασε υπολογίστηκε σε Να υπολογίσετε ποια ήταν η επιτρεπόμενη τάση του συρματόσχοινου ( ). Από τα δεδομένα της άσκησης έχουμε ότι: και επομένως από τον τύπο 2.1 υπολογίζουμε: (2.1) (2.2) Επομένως η ζητούμενη επιτρεπόμενη τάση είναι. Άσκηση 2.2 Ένα (καινούριο) συρματόσχοινο έχει συντελεστή ασφαλείας ίσο με 10 και αποτελείται από 100 σύρματα με διάμετρο 1 mm το κάθε σύρμα. Αν η επιτρεπόμενη τάση του υλικού των συρμάτων για εφελκυσμό είναι να βρείτε με πόσο βάρος θα σπάσει το συρματόσχοινο και με πόσο βάρος επιτρέπεται να το φορτίσουμε. Για να λυθεί η άσκηση σκεφτόμαστε ως εξής: κατ αρχάς ζητείται το βάρος θραύσης (το βάρος που σπα το συρματόσχοινο), άρα ζητείται η τάση θραύσης. Για την τάση θραύσης γνωρίζουμε τον τύπο 2.1 από τον οποίο για να τη βρούμε πρέπει να γνωρίζουμε την επιτρεπόμενη τάση και το συντελεστή ασφαλείας. Τα δύο τελευταία μεγέθη όντως δίνονται από την εκφώνηση της άσκησης. Εφαρμόζουμε λοιπόν τον τύπο 2.1: Το βάρος θα βρεθεί από τον τύπο της τάσης:, αν τον εφαρμόσουμε για την, ενώ Β είναι το βάρος υπό το οποίο θα σπάσει το συρματόσχοινο. Το εμβαδόν της διατομής Α είναι η διατομή των 100 συρμάτων. Το κάθε σύρμα έχει εμβαδόν διατομής που δίνεται από τον τύπο: όπου είναι η διάμετρος 1 mm που δίνει η εκφώνηση. Άρα θα υπολογίσουμε: Επομένως η συνολική διάμετρος του συρματόσχοινου θα είναι: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 39
40 ΚΕΦΑΛΑΙΟ 2 ΣΥΝΤΕΛΕΣΤΗΣ ΑΣΦΑΛΕΙΑΣ Το ζητούμενο βάρος Β θα το βρούμε επιλύοντας τον τύπο: Άρα το βάρος που θα σπάσει το συρματόσχοινο είναι 3140 dan, ενώ το επιτρεπόμενο βάρος είναι μόλις 314 dan, δηλαδή 10 φορές λιγότερο, αφού τόσο είναι και ο συντελεστής ασφαλείας. Καταλαβαίνουμε επομένως ότι ο συντελεστής ασφαλείας μπαίνει στα διάφορα υλικά, εξαρτήματα ή μηχανές για να τα προστατεύσει όχι από σπάσιμο, αλλά από μερική φθορά που θα επιφέρει μείωση της αντοχής τους και ελάττωση των ιδιοτήτων τους και τελικά σπάσιμο μετά από αρκετές καταπονήσεις. Πάντως οφείλουμε να γνωρίζουμε ως τεχνικοί ότι το μεγάλο πρόβλημα στις μηχανές δεν είναι τόσο το σπάσιμο όσο η μεταβολή προς το χειρότερο των ιδιοτήτων των εξαρτημάτων τους. Ο συντελεστής ασφαλείας για το ίδιο εξάρτημα, είναι τόσο μεγαλύτερος όσο πιο επώδυνα είναι τα αποτελέσματα που θα επιφέρει μια βλάβη του. Για παράδειγμα, το ίδιο συρματόσχοινο αν χρησιμοποιηθεί σε ένα γερανό ανύψωσης φορτίων στο λιμάνι θα έχει συντελεστή ασφαλείας, ας πούμε, 7, ενώ αν χρησιμοποιηθεί σε ένα ανελκυστήρα προσώπων ο συντελεστής θα είναι 14. Αυτό σημαίνει ότι το στην πρώτη περίπτωση θα είναι διπλάσιο από το στη δεύτερη περίπτωση. Επομένως όσο μεγαλύτερος ο συντελεστής ασφαλείας για το ίδιο υλικό και εξάρτημα τόσο μικρότερη η επιτρεπόμενη τάση του εξαρτήματος. Ας δούμε μια άσκηση πάνω σε αυτό το θέμα. Άσκηση 2.3 Ένα συρματόσχοινο έχει εμβαδόν διατομής ίσο με Α σ και χρησιμοποιείται σε δύο διαφορετικές περιπτώσεις, όπου στη μία απαιτείται συντελεστής ασφαλείας ίσος με 10 ) και στη δεύτερη ίσος με 5 ( ). Αν στη δεύτερη περίπτωση το μέγιστο βάρος που επιτρέπεται αν σηκώσει (εφελκυσμός) είναι να βρείτε πόσο βάρος ( ) επιτρέπεται να σηκώσει στη πρώτη περίπτωση. Μετά να βρείτε με πόσο βάρος θα σπάσει στις δύο περιπτώσεις το συρματόσχοινο. Υπενθυμίζουμε ότι οι δυνάμεις (βάρη) και είναι οι μέγιστες επιτρεπτές όχι για να μη σπάσουν τα συρματόσχοινα, αλλά για να μην μειωθούν οι ιδιότητές τους και γίνει επικίνδυνη η χρήση τους. Σημείωση: αυτή η άσκηση θεωρείται δύσκολη όσον αφορά στα μαθηματικά της. Αφού πρόκειται για ακριβώς το ίδιο συρματόσχοινο, η τάση θραύσης ( ) θα είναι ίδια και στις δύο χρήσεις. Αυτά που αλλάζουν είναι ο συντελεστής ασφαλείας ( και ) και η επιτρεπόμενη τάση ( ). Τις δύο επιτρεπόμενες τάσεις δεν τις γνωρίζουμε. Ας ονομάσουμε την πρώτη, με συντελεστή ασφαλείας 10, και τη δεύτερη. Εφαρμόζουμε την εξίσωση 2.1 για τα δύο συρματόσχοινα: Αφού τα πρώτα μέλη των εξισώσεων είναι ίδια ( ισχύει: ) θα είναι και τα δεύτερα, άρα θα Βρήκαμε ότι η δεύτερη επιτρεπόμενη τάση είναι διπλάσια από την πρώτη. Είναι λογικό αφού είχαμε αναφέρει πριν ότι, όσο μεγαλύτερος ο συντελεστής ασφαλείας για το ίδιο υλικό τόσο μικρότερη η επιτρεπόμενη τάση του εξαρτήματος. 40 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
41 ΣΥΝΤΕΛΕΣΤΗΣ ΑΣΦΑΛΕΙΑΣ ΚΕΦΑΛΑΙΟ 2 Θέλουμε τώρα να υπολογίσουμε πόσο βάρος θα μπορεί (επιτρέπεται) να σηκώσει το εξάρτημα με την αφού γνωρίζουμε ότι το συρματόσχοινο με μπορεί να δεχτεί φορτίο ίσο με Υπενθυμίζουμε ότι τα δύο συρματόσχοινα έχουν την ίδια διατομή Α σ και από τον τύπο της τάσης θα έχουμε στις δύο περιπτώσεις: Στις δύο αυτές εξισώσεις τα πρώτα μέλη είναι ίσα ( ) άρα και τα δεύτερα. Επομένως θα έχουμε: Βρήκαμε λοιπόν ότι το πρώτο συρματόσχοινο με τον μεγάλο συντελεστή ασφαλείας (10) επιτρέπεται να δεχτεί μέχρι φορτίο. Αυτό είναι λογικό, αφού έχοντας μεγάλο συντελεστή ασφαλείας, το φορτίο που θα πρέπει να δεχτεί δεν πρέπει να είναι πολύ μεγάλο, σε σχέση με εκείνο που θα δεχόταν αν είχε μικρότερο συντελεστή ασφαλείας. Η δεύτερη ερώτηση της άσκησης έχει προφανή απάντηση, που είπαμε ευθύς εξ αρχής: Αφού τα δύο συρματόσχοινα είναι ίδια θα έχουν ίδια δύναμη θραύσης, άσχετα από το είδος της καταπόνησης και τη χρήση τους. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 41
42
43 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 3. Ηλώσεις Όταν σαν μέσον σύνδεσης χρησιμοποιείται ο ήλος, λέμε ότι έχουμε μια ήλωση. Οι ήλοι τοποθετούνται σε οπές που γίνονται στα ελάσματα που θέλουμε να συνδέσουμε. Τα ελάσματα είναι χονδρές λαμαρίνες που χρησιμοποιούνται συχνά για να κατασκευαστούν μεταλλικά βαρέλια στα οποία τοποθετούνται ρευστά υπό πίεση, με αποτέλεσμα οι ηλώσεις να δέχονται ισχυρές καταπονήσεις. Ηλώσεις χρησιμοποιούνται και σε μεταλλικές κατασκευές, όπως γερανογέφυρες, όπου και εκεί δέχονται εφελκυστικές και διατμητικές δυνάμεις κυρίως. Στο επόμενο σχήμα βλέπουμε δυο ελάσματα τα οποία συνδέονται με επικάλυψη και χρησιμοποιείται μια σειρά ήλων. Ο ήλος είναι ο ΑΒ με τις δύο κεφαλές και τον κορμό του. Τώρα ο ήλος έχει συμμετρική μορφή, με το κάθε τμήμα να περιλαμβάνει τον μισό κορμό και τη μια κεφαλή. Κάθε ένα από τα τμήματα αυτά είναι προσκολλημένο στο ένα έλασμα. Όταν τα ελάσματα εφελκύονται με δύο ίσες και αντίθετες δυνάμεις, F και F, το επάνω έλασμα τραβά προς τα αριστερά το επάνω μισό του ήλου και το κάτω έλασμα τραβά προς τα δεξιά το κάτω μισό του ήλου μέσω του κορμού του. Έτσι όπως τραβούν τον κορμό του ήλου τα δυο ελάσματα, φαίνεται ότι ο ήλος πάει να κοπεί στην τομή ΓΔ, σαν να τον κόβει ένα ψαλίδι. Αυτού του είδους η καταπόνηση ονομάζεται διάτμηση και όπως σε κάθε υλικό υπάρχει η επιτρεπόμενη τάση εφελκυσμού, παρομοίως υπάρχει και η επιτρεπόμενη τάση διάτμησης για να συγκριθεί με αυτήν η ασκούμενη τάση διάτμησης. Η τάση διάτμησης (ή αλλιώς: διατμητική τάση) ενός δοκιμίου δίνεται από τον τύπο 1.7 τον οποίο μεταφέρουμε εδώ. Για τη λύση ασκήσεων όπου ασκείται τάση διάτμησης, εργαζόμαστε το ίδιο με την τάση εφελκυσμού, απλά η επιτρεπόμενη τάση δεν είναι η σ επ αλλά η τ επ, την οποία παίρνουμε από πίνακες και στις ασκήσεις συνήθως δίνεται στην εκφώνηση. Πρέπει να ισχύει: Η επιφάνεια εμβαδού Α είναι το άθροισμα όλων των διατομών του ήλου που κινδυνεύουν από τη διάτμηση. Έχουμε δύο περιπτώσεις: αν η ήλωση είναι με επικάλυψη σε κάθε ήλο υπάρχει μία διατομή που καταπονείται, αλλά αν έχουμε δυο αρμοκαλύπτρες κάθε ήλος έχει δύο διατομές. Και φυσικά στην διατομή συνυπολογίζουμε όλους τους ήλους, δηλαδή αθροίζουμε όλες τις διατομές στις οποίες έχουμε διάτμηση. Στο επόμενο σχήμα φαίνεται μια ήλωση απλής σειράς με αρμοκαλύπτρες. Η δύναμη Q τραβά τον ήλο με τάση να τον κόψει στις τομές Α και Β, ενώ το ίδιο κάνει και η αντίδραση της Q, δηλαδή η Q, στη σειρά (ή στις σειρές αν έχουμε πολλές) των ήλων στην απέναντι πλευρά του ελάσματος. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 43
44 ΚΕΦΑΛΑΙΟ 3 ΗΛΩΣΕΙΣ Επομένως η επιφάνεια Α στον τύπο 3.1 θα είναι: Όπου είναι ο αριθμός των ήλων (θα ληφθούν μόνο οι ήλοι που βρίσκονται στη μία πλευρά του ελάσματος), είναι ο αριθμός των καταπονούμενων διατομών (θα είναι ή ), θα είναι η επιφάνεια της διατομής του ήλου. Ένας ήλος που είναι τοποθετημένος σε δύο ελάσματα κινδυνεύει να καταστραφεί και από άλλο είδος καταπόνησης, την σύνθλιψη. Σε αυτή την περίπτωση υπάρχει πιθανότητα ο κορμός του ήλου να είναι ικανός να αντέξει στο κόψιμο, αλλά όχι και στην πίεση που του ασκεί στο τοίχωμα το έλασμα. Στο επόμενο σχήμα βλέπουμε σχηματικά την πίεση που ασκεί το ένα έλασμα στον κορμό του ήλου. Στο σχήμα αυτό σχεδιάστηκε μόνο το τμήμα από τον κορμό του ήλου που συνθλίβεται από το ένα έλασμα. Αν η πίεση αυτή είναι ισχυρή, είναι δυνατόν το υλικό του ήλου να συνθλιβεί και να παραμορφωθεί ο ήλος με αποτέλεσμα την καταστροφή του άμεσα ή αργότερα. Δεν υπάρχουν πίνακες να δίνουν επιτρεπόμενη τάση σύνθλιψης ( ), αλλά την τιμή της την παίρνουμε ίση με 2,5 φορές την σ επ. Η τάση σύνθλιψης συμβολίζεται με σ L και θα ισχύει ο γνωστός τύπος για την κάθε τάση: Ας υποθέσουμε ότι η ήλωση έχει ένα μόνο ήλο. Στους τύπους το σύμβολο Α είναι η επιφάνεια που καταπονείται σε σύνθλιψη. Αυτή η επιφάνεια δεν είναι η διατομή του κορμού του ήλου, αλλά το πλευρικό τοίχωμα που δέχεται την πίεση από το έλασμα. Το πλευρικό αυτό τοίχωμα έχει μορφή ορθογωνίου με ύψος το πάχος του ελάσματος και πλάτος τη διάμετρο του κορμού του ήλου, όπως φαίνεται στο επόμενο σχήμα. Επομένως το εμβαδόν Α 1 του ενός ήλου που συνθλίβεται θα είναι ίσο με: A 1 =d s. Όταν τα δυο ελάσματα εφελκύονται τείνουν να συνθλίψουν όλους τους ήλους μαζί. Αν ο αριθμός των ήλων είναι z τότε η συνολική επιφάνεια που συνθλίβεται είναι η επιφάνεια των z ήλων, επομένως η συνολική επιφάνεια θα είναι: Α=z d s. Ο τελικός τύπος ελέγχου για την τάση σύνθλιψης θα είναι ο τύπος: Όταν μας δίνεται μια άσκηση σχετική με το θέμα αυτό θα μας ζητείται συγκεκριμένα ο έλεγχος που πρέπει να κάνουμε. Αν η άσκηση λέει να γίνει έλεγχος μόνο για την αντοχή του ήλου σε διάτμηση θα ελεγχθεί μόνο βάσει του τύπου 2.1 και ως διατομή θα πάρουμε το εμβαδόν της διατομής του κορμού. Αν όμως ζητηθεί να γίνει και έλεγχος σε σύνθλιψη θα γίνει έλεγχος και με τη σχέση 2.3. Δηλαδή μπορεί να ζητηθεί έλεγχος της μίας ή και των δύο καταπονήσεων. Εκτός όμως από τον έλεγχο του ήλου σε μια ήλωση, πρέπει να γίνεται έλεγχος και στο έλασμα, συνήθως μόνο σε εφελκυσμό και εφόσον βέβαια αυτό ζητηθεί από την άσκηση. Αυτό γίνεται γιατί μπορεί το έλασμα να είναι σχετικά λεπτό (μικρό πάχος ελάσματος s) οπότε δεν αντέχει την εφελκυστική δύναμη. Στην περίπτωση αυτή ο ήλος αντέχει αλλά το έλασμα όχι. Όμως η διατομή του ελάσματος ελαττώνεται και λόγω των οπών για τους ήλους. Στην άσκηση 1.10 αναλύσαμε την περίπτωση αυτή. Σύμφωνα με τη λύση της άσκησης εκείνης, για 44 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
45 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 να ελεγχθεί η αντοχή σε εφελκυσμό παίρνουμε την μικρότερη διατομή, που είναι εκεί που βρίσκονται οι περισσότερες οπές με τους ήλους. Οι οπές στο έλασμα αφαιρούν μέρος της διατομής που θα αναλάμβανε και αυτό μέρος της καταπόνησης. Επομένως η διατομή Α για εφαρμογή του τύπου σ=f/a στο έλασμα θα είναι όσο η συνολική διατομή του ελάσματος μείον την επιφάνεια που κόβεται από τις οπές. Ας δούμε το παραπάνω σχήμα που περιγράφει μια τέτοια περίπτωση. Βλέπουμε το έλασμα σε τομή, να εφελκύεται με τη δύναμη F και να έχει δυο οπές για τους δύο ήλους που θα τοποθετηθούν. Αν δε υπήρχαν οι οπές η διατομή του ελάσματος που καταπονείται θα ήταν ίση με το μήκος του L επί το πάχος του s. Άρα θα είχαμε Α 1 =L s. Στην περίπτωση όμως που υπάρχουν οι οπές, πρέπει να αφαιρεθεί για κάθε οπή η μετωπική επιφάνειά της (όχι το εσωτερικό καμπύλο τμήμα που είναι μεγαλύτερο), που είναι ίση με το πάχος του ελάσματος s επί τη διάμετρο d της οπής, δηλαδή A οπής =s d. Άρα το πραγματικό εμβαδόν διατομής Α συν που θα χρησιμοποιηθεί για τον έλεγχο σε εφελκυσμό θα είναι: Σημειώνουμε ότι αν ένα έλασμα έχει δύο σειρές από ήλους, θα ελεγχθεί μόνο η μία από αυτές και θα είναι εκείνη με το μικρότερο εμβαδόν, αφού θα έχει τη δυσμενέστερη καταπόνηση. Θα είναι δηλαδή αυτή με τις περισσότερες οπές για ήλους. Η διάμετρος d που θα παίρνουμε για τον υπολογισμό της μετωπικής επιφάνειας που αφαιρείται θα είναι η διάμετρος της οπής και όχι του ήλου. Ως γνωστόν η διάμετρος της οπής είναι κατά ένα χιλιοστό (1 mm) μεγαλύτερη από τη διάμετρο του ήλου. Στο σχολικό βιβλίο υπάρχουν και κάποιες ακόμα πληροφορίες για τις ηλώσεις που μπορούν να χρησιμοποιηθούν σε ασκήσεις, αλλά στο βιβλίο δεν υπάρχουν πάνω σε αυτά ούτε λυμένες ούτε άλυτες ασκήσεις. Αυτό σημαίνει ότι είναι λίγο δύσκολο να δοθεί σχετική άσκηση, αλλά δεν είναι και απίθανο. Εμείς θα τα αναφέρουμε εδώ και θα δώσουμε και τα απαραίτητα παραδείγματα. Υπάρχουν οι στεγανές ηλώσεις που χρησιμοποιούνται για την κατασκευή δοχείων και η διάμετρος της οπής d 1 πρέπει να είναι ίση με: Όπου s είναι το πάχος του ελάσματος σε cm και η διάμετρος d 1 θα βρεθεί επίσης σε cm. Το βήμα της ήλωσης t, δηλαδή η απόσταση μεταξύ των κέντρων δύο διαδοχικών ήλων, θα δίνεται από τον τύπο 3.6 στον οποίο το βήμα και η διάμετρος του ήλου d δίνονται σε cm: Τέλος, αν η ήλωση έχει δύο σειρές ήλων, η απόστασή τους e θα δίνεται από τον τύπο 3.7, όπου φαίνεται ότι η απόσταση e θα είναι μιάμιση φορά μεγαλύτερη από τη διάμετρο του ήλου. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 45
46 ΚΕΦΑΛΑΙΟ 3 ΗΛΩΣΕΙΣ Για τις σταθερές ηλώσεις οι διαστάσεις της ήλωσης διαφοροποιούνται μερικώς. Η διάμετρος της οπής d 1 δίνεται από τη σχέση: Πάλι οι διαστάσεις πρέπει να τοποθετούνται σε εκατοστά. Αν στη σταθερή ήλωση έχουμε αρμοκαλύπτρα, τότε το άθροισμα των παχών των ελασμάτων δεν πρέπει να ξεπερνά το τετραπλάσιο της διαμέτρου του ήλου, άρα: Στη σταθερή ήλωση το βήμα πρέπει να είναι 3 έως 3,5 φορές την διάμετρο του ήλου, δηλαδή: Το σχολικό βιβλίο στο τελευταίο κεφάλαιο που έχει συγκεντρώσει όλες τις ασκήσεις, για τις ηλώσεις δίνει μόνο δύο λυμένες και καμία άλυτη. Όμως οι ασκήσεις επί των ηλώσεων είναι ουσιαστικές και αν τις κατανοήσετε θα έχετε κατανοήσει αρκετά από εκείνα που χρειάζονται για τις ασκήσεις και των άλλων κεφαλαίων. Γι αυτό θα λύσουμε αναλυτικά αρκετές από αυτές. Άσκηση 3.1 Για την κατασκευή ενός στεγανού βαρελιού θα χρησιμοποιηθεί έλασμα πάχους 5 mm. Η σύνδεση των ελασμάτων θα γίνει με ήλωση επικάλυψης διπλής σειράς. Να βρείτε α) την διάμετρο των ήλων που θα χρησιμοποιηθούν, β) το βήμα της ήλωσης και γ) την απόσταση των δύο σειρών από ήλους. α) Αφού στην εκφώνηση δίνεται ότι το βαρέλι θα είναι στεγανό, στεγανή θα είναι και η ήλωση, άρα για να βρούμε την διάμετρο της οπής θα χρησιμοποιήσουμε τον τύπο 3.5. Πρώτα μετατρέπουμε τα 5 mm που είναι το πάχος του ελάσματος σε εκατοστά και θα είναι 0,5 cm. Τώρα υπολογίζουμε την διάμετρο της οπής : Άρα η διάμετρος των οπών θα είναι, αλλά η άσκηση ζητά τη διάμετρο των ήλων. Αυτή θα είναι κατά ένα χιλιοστό μικρότερη από τη διάμετρο των οπών, άρα θα είναι. Αν συμβολίσουμε τη διάμετρο των ήλων με d θα είναι:. Σημείωση: Κάτω από το σύμβολο της τετραγωνικής ρίζας δεν βάλαμε τις μονάδες του πάχους του ελάσματος για να μην υπάρχει πρόβλημα με τη συμφωνία των μονάδων. β) Το βήμα της ήλωσης δίνεται από τον τύπο 3.6 και οι διαστάσεις μπαίνουν σε εκατοστά. Θα έχουμε: Άρα το βήμα της ήλωσης θα είναι. γ) Η απόσταση e των δύο σειρών των ήλων δίνεται από τον τύπο 3.7 και θα έχουμε: Επομένως η ζητούμενη απόσταση των σειρών των ήλων σε αυτή τη στεγανή ήλωση είναι. Άσκηση 3.2 Θα εξετάσουμε τώρα την προηγούμενη άσκηση για μια ήλωση σταθερή αλλά όχι στεγανή. Επομένως, έχουμε έλασμα πάχους 5 mm και τη σύνδεση των ελασμάτων με ήλωση επικάλυψης διπλής σειράς. Ζητάμε α) την διάμετρο των ήλων που θα χρησιμοποιηθούν, β) να εξετάσετε αν το πάχος του ελάσματος είναι συμβατό με την διάμετρο του ήλου και γ) το βήμα της ήλωσης. 46 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
47 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 α) Για να βρούμε την διάμετρο της οπής θα χρησιμοποιήσουμε τον τύπο 3.8, λαμβάνοντας υπ όψιν ότι τα 5 mm που είναι το πάχος του ελάσματος είναι ίσα με 0,5 cm. Τώρα υπολογίζουμε την διάμετρο της οπής : Άρα η διάμετρος των οπών θα είναι. Η διάμετρος των ήλων θα είναι κατά ένα χιλιοστό μικρότερη από τη διάμετρο των οπών, άρα θα είναι. Αν συμβολίσουμε τη διάμετρο των ήλων με d θα είναι:. β) Το πάχος των ελασμάτων στη θέση της ήλωσης θα είναι δύο φορές το πάχος του ενός, άρα θα είναι 0,5+0,5 cm = 1 cm. Σύμφωνα με την σχέση 3.9 που πρέπει να ικανοποιείται θα είναι: Βλέπουμε ότι η τελευταία ανίσωση ικανοποιείται, άρα το πάχος του ελάσματος είναι μικρότερο από το μέγιστο όριο που απαιτείται. γ) Το βήμα της ήλωσης δίνεται από τον τύπο 3.10 και οι διαστάσεις μπαίνουν σε εκατοστά. Θα έχουμε: Άρα το βήμα της ήλωσης θα έχει διαστάσεις από Σημείωση: Συγκρίνοντας τα αποτελέσματα των δύο ασκήσεων παρατηρούμε ότι ουσιαστικά η μόνη διαφορά που έχουν οι ηλώσεις είναι το πάχος (διάμετρος) των ήλων, όπου στη στεγανή θα είναι κατά δύο χιλιοστά πιο μεγάλο. Άσκηση 3.3 Έχουμε μια σταθερή ήλωση με διπλή αρμοκαλύπτρα, και το πάχος της αρμοκαλύπτρας είναι 12 mm ενώ το πάχος του ελάσματος είναι 14 mm. Να εξετάσετε αν μπορούν οι ήλοι που θα χρησιμοποιηθούν να έχουν διάμετρο ίση με 8 mm. Αν όχι, να βρείτε την επιτρεπτή διάμετρο των ήλων. Σε σταθερές ηλώσεις θα πρέπει για τα πάχη των ελασμάτων να ισχύει η σχέση 3.9, σύμφωνα με την οποία τα ελάσματα που θα συνενωθούν δεν πρέπει να έχουν συνολικό πάχος μεγαλύτερο από το τετραπλάσιο της διαμέτρου του ήλου. Εδώ τα ελάσματα που συνδέει ο ήλος είναι οι δύο αρμοκαλύπτρες και το προς ένωση έλασμα. Αν συμβολίσουμε το πάχος του ελάσματος της αρμοκαλύπτρας με s α, το πάχος του ελάσματος που θα γίνει η ήλωση με s και τη διάμετρο του ήλου με d, θα πρέπει να ισχύει: Βλέπουμε ότι η τελευταία σχέση δεν ισχύει, άρα η διάμετρος των 8 mm (=0,8 cm) δεν μπορεί αν γίνει δεκτή. Για να βρούμε την αποδεκτή διάμετρο του ήλου πρέπει να λύσουμε την πιο πάνω ανίσωση με άγνωστο τη διάμετρο d. Θα έχουμε παραλείποντας τις μονάδες, οι οποίες θα είναι τα χιλιοστά τώρα: Επομένως βρήκαμε ότι η διάμετρος των ήλων πρέπει να είναι μεγαλύτερη από 9,5 mm. Άσκηση 3.4 Έχουμε κατασκευάσει ένα μεταλλικό βαρέλι με έλασμα και σύνδεση των άκρων των ελασμάτων με τη μέθοδο της στεγανής ήλωσης. Στο επόμενο σχήμα φαίνεται η φανταστική ευθεία ΑΒ πάνω στην οποία έχει γίνει η ήλωση με επικάλυψη. Φαίνονται οι κεφαλές των τοποθετημένων ήλων. Το δοχείο είναι γεμάτο με ένα ρευστό υπό πίεση. Α) Να πείτε με τι είδους καταπόνηση καταπονείται το έλασμα στις πλευρές του δοχείου, και ειδικά στην ευθεία της ήλωσης (παντού η καταπόνηση είναι ίδιου είδους, αλλά να επικεντρωθείτε στην ήλωση). Β) Σε ποια από τις δύο ευθείες ΑΒ και ΓΔ κινδυνεύει να κοπεί το έλασμα, αν υποθέσουμε ότι οι ήλοι είναι αρκετά ικανοί και δεν παρουσιάζουν πρόβλημα διάτμησης ή σύνθλιψης; ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 47
48 ΚΕΦΑΛΑΙΟ 3 ΗΛΩΣΕΙΣ Α) Η εσωτερική πίεση, τείνει να αυξήσει τον όγκο του δοχείου. Αυτό έχει σαν αποτέλεσμα το πλευρικό τοίχωμα του βαρελιού να έχει τάση να επεκταθεί προς όλες τις κατευθύνσεις. Έτσι αν εξετάζουμε την τομή ΑΒ η δυνάμεις που ασκούνται από το εσωτερικό του βαρελιού θα έχουν την κατεύθυνση των βελών του κατωτέρω σχήματος. Πάντως θα υπάρχουν και διαμήκεις δυνάμεις, κατά μήκος δηλαδή της ΑΒ, που θα έχουν τάση αν αυξήσουν το μήκος του βαρελιού, εκτός από τη διάμετρο. Β) Το έλασμα θα κοπεί εκεί που η τάση είναι μεγαλύτερη. Από τον τύπο της τάσης εφελκυσμού: γνωρίζουμε ότι η τάση είναι μεγαλύτερη όσο μεγαλύτερη είναι η δύναμη F και όσο μικρότερο είναι το εμβαδόν της επιφάνειας Α. Η δύναμη που καταπονεί τα πλευρικά τοιχώματα του δοχείου είναι ίδια παντού, άρα δεν υπάρχει διαφορά μεταξύ της δύναμης στις ευθείες ΑΒ και ΓΔ. Επομένως στρεφόμαστε στην επιφάνεια της διατομής Α. Στην τομή ΓΔ το εμβαδόν είναι ίσο με το γινόμενο του μήκους του βαρελιού επί το πάχος του ελάσματος. Στην τομή ΑΒ είναι όσο το προηγούμενο μειωμένο όμως κατά την επιφάνεια που κόβουμε από την τομή για να κάνουμε τις οπές των ήλων (βλέπε σχέση 3.4). Άρα η διατομή Α θα είναι μικρότερη, επομένως η τάση θα είναι μεγαλύτερη στην τομή ΑΒ. Άρα σε αυτή την τομή κινδυνεύει πιο πολύ να κοπεί το έλασμα. Άσκηση 3.5 Έχουμε μια ήλωση με επικάλυψη στην οποία χρησιμοποιείται μία σειρά τεσσάρων ήλων με διάμετρο d 1 =12 mm. Το μήκος του ελάσματος κατά μήκος της ήλωσης είναι L=200 mm και το πάχος του είναι s=8 mm. Το υλικό από το οποίο είναι το έλασμα έχει επιτρεπόμενη τάση εφελκυσμού ίση με σ επ =1200 kp/cm 2. Η επιτρεπόμενη τάση διάτμησης του υλικού του ήλου είναι ίση με τ επ =1400 kp/cm 2 και η επιτρεπόμενη τάση εφελκυσμού του ήλου ίση με σ επη =1000 kp/cm 2. Η εφελκυστική δύναμη που καταπονεί έλασμα και ήλωση είναι Q=6000 kp. Α) Να βρεθεί αν θα αντέξει στον εφελκυσμό το έλασμα. Β) Να βρεθεί αν θα αντέξουν στη διάτμηση οι κοχλίες. Γ) να βρεθεί αν θα αντέξουν σε σύνθλιψη οι κοχλίες. Το επόμενο σχήμα δείχνει την κατάσταση την οποία έχουμε. Α) Η δυσμενέστερα καταπονούμενη διατομή του ελάσματος είναι εκείνη που περιέχει τους άξονες όλων των ήλων, διότι εκεί έχει αφαιρεθεί η επιφάνεια των οπών για την τοποθέτηση 48 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
49 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 των ήλων. Η κάθε οπή έχει διάμετρο κατά ένα χιλιοστό μεγαλύτερη από τη διάμετρο του κορμού των ήλων d 1, άρα θα είναι d=13 mm. Η επιφάνεια (διατομή) του ελάσματος πριν την αφαίρεση των οπών θα είναι ίση με: Η μετωπική επιφάνεια κάθε οπής θα είναι ίση με τη διάμετρο της οπής επί το ύψος της που είναι ίσο με το πάχος του ενός ελάσματος. Παίρνουμε μόνο το ένα έλασμα αφού το ένα από τα δύο θα σπάσει πρώτο. Άρα θα είναι: Επειδή έχουμε 4 οπές η επιφάνεια θα αφαιρεθεί 4 φορές από την επιφάνεια. Μπορούμε να χρησιμοποιήσουμε κατ ευθείαν τον τύπο 3.4 και θα έχουμε: Άρα η δυσμενέστερα καταπονούμενη σε εφελκυσμό επιφάνεια του ελάσματος έχει εμβαδόν. Θα υπολογίσουμε τώρα την τάση είναι μικρότερη από την επιτρεπόμενη. που δέχεται αυτή η επιφάνεια και θα ελέγξουμε αν Επομένως το έλασμα αντέχει σε εφελκυσμό. Β) Για να ελεγχθεί αν αντέχει σε διάτμηση ο ήλος εφαρμόζουμε τον τύπο 3.1:. Εδώ βέβαια στη δύναμη F του τύπου έχει δοθεί το σύμβολο Q. Αυτό δεν πρέπει να μας ενοχλεί, αφού δεν αλλάζει σε τίποτα η λύση της άσκησης. Όμως εδώ το εμβαδόν Α του τύπου δεν έχει σχέση με τις προηγούμενες επιφάνειες με τις οποίες εργαστήκαμε. Τώρα το Α είναι το εμβαδόν της διατομής του πυρήνα του ήλου. Προφανώς θα το υπολογίσουμε από τον τύπο που δίνει το εμβαδόν του κύκλου και είναι ο τύπος 1.3: Αυτό είναι το Α αλλά η δύναμη Q μοιράζεται στους 4 ήλους άρα κάθε ένας (κάθε επιφάνεια Α) καταπονείται με δύναμη ίση με : Με αυτή τη δύναμη θα γίνει ο έλεγχος για τη διάτμηση: Επομένως οι ήλοι δεν κινδυνεύουν από τη διάτμηση. Γ) Θα κάνουμε τώρα τον έλεγχο για τη σύνθλιψη των ήλων με βάση τον τύπο 3.3 για 4 ήλους (z=4). Η δύναμη θα είναι η και η τάση σύνθλιψης θα υπολογισθεί: Επομένως οι ήλοι αντέχουν και σε σύνθλιψη. Προσέξετε ότι για τον έλεγχο σε σύνθλιψη χρησιμοποιείται η επιτρεπόμενη τάση εφελκυσμού του ήλου. Σημείωση: Στο σχολικό βιβλίο στην εφαρμογή των μαθηματικών τύπων στις ασκήσεις, δεν τοποθετούνται μονάδες στα διάφορα μεγέθη όταν γίνεται αριθμητική αντικατάστασή τους. Οι ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 49
50 ΚΕΦΑΛΑΙΟ 3 ΗΛΩΣΕΙΣ μονάδες δηλώνονται στην αρχή της άσκησης ή στην εκφώνηση και στο τελικό αποτέλεσμα. Εμείς εδώ ακολουθούμε και αυτό τον τρόπο αλλά συνήθως οι μονάδες συνοδεύουν την αριθμητική τιμή του μεγέθους κατά την αντικατάσταση. Άσκηση 3.6 Σε μια ήλωση με επικάλυψη έχουμε μία σειρά οκτώ ήλων. Η επιτρεπόμενη τάση διάτμησης του υλικού του ήλου ίση με τ επ =1000 kp/cm 2 και η επιτρεπόμενη τάση εφελκυσμού του ίση με σ επ =1200 kp/cm 2. Η εφελκυστική δύναμη που καταπονεί έλασμα και ήλωση είναι Q= kp. Να υπολογίσετε τη διάμετρο των ήλων που θα χρησιμοποιηθούν κάνοντας έλεγχο σε Α) διάτμηση και Β) σύνθλιψη αν το πάχος του ελάσματος είναι s = 10 mm = 1 cm. Α) Όταν γίνεται έλεγχος σε διάτμηση στους ήλους πρέπει αρχικά να προσδιορίσουμε σε κάθε ήλο πόσες διατομές υφίστανται διάτμηση. Όταν έχουμε επικάλυψη υπάρχει μόνο μία τέτοια διατομή, ενώ όταν έχουμε διπλή αρμοκαλύπτρα οι διατομές είναι δύο. Εδώ επομένως σε κάθε ήλο υπάρχει μόνο μια διατομή και επειδή έχουμε 8 ήλους οι διατομές που κινδυνεύουν είναι οκτώ. Κάθε διατομή έχει εμβαδόν Α και διάμετρο d. Αν Α συν είναι η συνολική διατομή όλων των ήλων που καταπονείται θα έχουμε: Α συν =8 Α. Θα ελέγξουμε τώρα την διατμητική τάση που καταπονεί τον ήλο. Γίνεται με τον τύπο 3.1 στον οποίο αντί της τοποθετούμε την : Άρα η διατομή κάθε ήλου θα είναι ίση ή μεγαλύτερη από χρησιμοποιήσουμε τώρα τον τύπο 1.5 για την εύρεση της διαμέτρου του κύκλου.. Θα Βρήκαμε ότι η διάμετρος των ήλων θα πρέπει είναι μεγαλύτερη από. Θεωρούμε ότι θα έχουν αυτή τη διάμετρο. Β) Για τον έλεγχο σε σύνθλιψη θα χρησιμοποιηθεί ο τύπος 3.3 για οκτώ ήλους. Άρα οι ήλοι αντέχουν στην καταπόνηση της σύνθλιψης. Εδώ λύσαμε την άσκηση με τον τρόπο του βιβλίου όσον αφορά στις μονάδες, οι οποίες δεν τοποθετήθηκαν κατά την επίλυση των εξισώσεων, αλλά μόνο στο τέλος. Άσκηση 3.7 Θέλουμε να κατασκευάσουμε μια ήλωση με επικάλυψη και μία σειρά ήλων σε μήκος ελάσματος L = 92 cm. Το πάχος του ελάσματος είναι s = 8 mm = 0,8 cm και καταπονείται με εφελκυστική δύναμη Q = 8000 kp. Η επιτρεπόμενη τάση διάτμησης του υλικού του ήλου είναι ίση με τ επ =1100 kp/cm 2 και η επιτρεπόμενη τάση εφελκυσμού του ίση με σ επ = ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
51 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 kp/cm 2. α) Να υπολογίσετε τον ελάχιστο αριθμό των ήλων που απαιτούνται αν η διάμετρός τους είναι. Να κάνετε έλεγχο των ήλων μόνο σε διάτμηση. β) Πόσο νομίζετε ότι θα είναι το βήμα της ήλωσης; Να υποθέσετε ότι τα κέντρα των ακραίων ήλων απέχουν από το άκρο του ελάσματος 1 cm. γ) Κατόπιν να ελέγξετε την αντοχή του ελάσματος σε καταπόνηση εφελκυσμού. α) Οι ήλοι πρέπει να είναι αρκετοί ώστε να αντέξουν και να μην σπάσουν καταπονούμενοι σε διάτμηση. Θα σπάσουν εάν η τάση που θα αναλογεί στον καθένα από αυτούς είναι πέραν της επιτρεπόμενης σε διάτμηση. Η τάση δίνεται από τον τύπο: Όπου είναι η συνολικά καταπονούμενη επιφάνεια, δηλαδή αν ένας ήλος έχει επιφάνεια διατομής ίση με Α και ο αριθμός των ήλων είναι z, τότε:. Έτσι ο προηγούμενος τύπος γίνεται: Από αυτή τη σχέση θα βρεθεί το z αφού αντικατασταθεί η τιμή του Α. Προχωράμε στον υπολογισμό του Α, ως το εμβαδόν του κυκλικού κορμού του ήλου: Αφού βρήκαμε το εμβαδόν Α υπολογίζουμε τον αριθμό των ήλων: Βρέθηκε οπότε θα πάρουμε, δηλαδή 10 ήλους (τουλάχιστον). β) Στο επόμενο σχήμα φαίνεται το σχήμα τοποθέτησης των 10 ήλων στο έλασμα. Φαίνεται σαφώς ότι οι ήλοι θα έχουν εννέα διαστήματα μεταξύ τους και το μήκος όλων των διαστημάτων θα είναι 90 cm, επομένως η απόσταση των ήλων θα είναι 90:10=9 cm. Άρα το βήμα της ήλωσης θα είναι. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 51
52 ΚΕΦΑΛΑΙΟ 3 ΗΛΩΣΕΙΣ γ) Για τον έλεγχο σε καταπόνηση εφελκυσμού του ελάσματος θα εφαρμόσουμε τον τύπο 3.4. Και επειδή ο τύπος αυτός δεν δίνεται από το σχολικό βιβλίο πρέπει να τον εξηγήσετε: Το έλασμα έχει διατομή. Από αυτήν θα αφαιρεθεί το εμβαδόν των δέκα οπών των ήλων, οι οποίες θα έχουν διάμετρο 1 mm επί πλέον της διαμέτρου των ήλων δηλαδή 10+1=11 mm. Επομένως θα έχουμε για το καταπονούμενο εμβαδόν Α κατ : Αυτή η επιφάνεια θα ελεγχθεί για την αντοχή της στον εφελκυσμό. Θα δούμε αν η τάση που δέχεται είναι μικρότερη ή όχι από την επιτρεπόμενη. Επομένως δεν έχει πρόβλημα το έλασμα. Σημείωση: Σε αυτή την άσκηση δεν ελέγχουμε την ήλωση κατά τα άλλα, δηλαδή αν είναι στεγανή ή σταθερή και είναι μέσα στα επιτρεπόμενα όρια τα αποτελέσματά μας. Αυτό το κάνουμε μόνο όταν μας το ζητά η άσκηση. Άσκηση 3.8 Μια ήλωση με αρμοκαλύπτρες (βλέπε επόμενο σχήμα με όψη σε τομή και κάτοψη) και απλή σειρά ήλων με πέντε ήλους, έχει πλάτος 300 mm (το έλασμα και οι αρμοκαλύπτρες). Το πάχος του ελάσματος είναι 12 mm και το πάχος κάθε αρμοκαλύπτρας είναι 8 mm. Το εφελκυστικό φορτίο που καταπονεί την ήλωση είναι Q=15.000kp. Η επιτρεπόμενη τάση διάτμησης του ήλου είναι ίση με τ επ =800 kp/cm 2 και η επιτρεπόμενη τάση εφελκυσμού του ίση με σ επη =1000 kp/cm 2. α) Να υπολογιστεί η απαιτούμενη διάμετρος των ήλων (να ελεγχθούν οι ήλοι σε διάτμηση και σύνθλιψη). β) να γίνει έλεγχος του ελάσματος σε εφελκυσμό, αν γνωρίζουμε ότι γι αυτό σ επε =800 kp/cm 2. γ) Το υλικό της αρμοκαλύπτρας είναι ίδιο με το υλικό του ελάσματος. Να κάνετε έλεγχο εφελκυσμού γι αυτές. Σε αυτή την άσκηση, όπως και σε όλες του κεφαλαίου των ηλώσεων τις διαστάσεις μήκους και επιφανείας τις μετατρέπουμε σε cm ή cm 2, αφού στους τύπους η τάση πάντα δίνεται kp/cm 2, οπότε είναι βολική η χρήση του μήκους σε cm. 52 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
53 ΗΛΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 3 α) Για τον έλεγχο του ήλου σε διάτμηση βρίσκουμε, από την τάση που τον καταπονεί, την επιφάνεια που πρέπει να έχει η διατομή του κορμού του Α ηλ. Γι αυτό στον τύπο για την τάση χρησιμοποιούμε την τ επ. Πρέπει κατ αρχάς να υπολογίσουμε τον αριθμό των διατομών που καταπονούνται σε διάτμηση. Οι ήλοι που είναι σε κάθε σειρά είναι 5. Να προσέξετε ότι ενώ καταπονούνται και οι δέκα, οι πέντε καταπονούνται από την δράση της Q και οι άλλοι πέντε από την αντίδρασή της Q. Σε κάθε ήλο είναι δύο οι διατομές που κινδυνεύουν να κοπούν (διάτμηση), οπότε συνολικά οι επικίνδυνες διατομές είναι 10. Αυτό τον αριθμό θα χρησιμοποιήσουμε στον τύπο για την τάση. Μπορούμε να σκεφτούμε με δυο τρόπους: είτε ότι σε κάθε διατομή από τις δέκα αναλογούν είτε ότι έχουμε 10 διατομές Α ηλ, οπότε εργαζόμαστε ως εξής: Αφού βρήκαμε τη διατομή κάθε ήλου θα προχωρήσουμε στον υπολογισμό της διαμέτρου: Επομένως οι ήλοι πρέπει να έχουν διάμετρο κορμού ίση τουλάχιστον με 16 mm. Θα ελέγξουμε και σε σύνθλιψη τους ήλους με τον τύπο 3.3. Θα λάβουμε υπ όψιν ότι έχουμε 5 ήλους (z=5), ότι η διάμετρος είναι d=1,6cm και το πάχος του ελάσματος s=1,2cm. Επομένως οι ήλοι γίνονται δεκτοί αφού αντέχουν και σε σύνθλιψη. β) Για τον έλεγχο σε καταπόνηση εφελκυσμού του ελάσματος θα υπολογίσουμε την καθαρή επιφάνειά του που καταπονείται Α κατ. Η οπή θα έχει διάμετρο 1,7 cm, δηλαδή ένα χιλιοστό περισσότερο από τη διάμετρο των ήλων. Θα έχουμε (Διαστάσεις σε cm): Αυτή η επιφάνεια του ελάσματος θα ελεγχθεί για την αντοχή της σε εφελκυσμό. Θα δούμε αν η τάση που δέχεται είναι μικρότερη ή όχι από την επιτρεπόμενη. Επομένως το έλασμα αντέχει σε εφελκυσμό. γ) Η δύναμη Q καταπονεί ταυτόχρονα και τις δύο αρμοκαλύπτρες και θα ελέγξουμε αν οι επιφάνειές τους αντέχουν σε εφελκυσμό. Η επικίνδυνη διατομή τους είναι εκεί που έχουμε τις οπές για τους ήλους. Άρα θα υπολογίσουμε το εμβαδόν αυτής της διατομής, όπως γίνεται και στην περίπτωση του ελάσματος. την δύναμη παραλαμβάνουν και οι δύο αρμοκαλύπτρες, επομένως από τη γεωμετρία του σχήματος η συνολικά καταπονούμενη επιφάνεια γι αυτές Α αρμ θα είναι: Θα εφαρμόσουμε τη γνωστή σχέση για την τάση: Επομένως οι αρμοκαλύπτρες δεν κινδυνεύουν. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 53
54
55 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 4. Κοχλιοσυνδέσεις Με τους κοχλίες (βίδες) συνδέουμε διάφορα στοιχεία μηχανών ή άλλα μεταλλικά και άλλων υλικών αντικείμενα. Το πλεονέκτημα που έχουν σε σχέση με τους ήλους, είναι ότι λύονται, δηλαδή μπορούμε να τους αφαιρέσουμε, να κάνουμε μια εργασία, και να τους επανατοποθετήσουμε ή να κάνουμε ό, τι άλλο θέλουμε. Τα αντικείμενα τα οποία συνδέουν οι κοχλίες ασφαλώς θα δέχονται ορισμένες δυνάμεις που μεταφέρονται σε αυτούς. Επομένως οι κοχλίες δέχονται πολλών ειδών καταπονήσεις και κινδυνεύουν να χάσουν τις ιδιότητες που έχουν και τελικά να σπάσουν. Γι αυτό το λόγο γίνονται έλεγχοι ώστε να διαπιστωθεί αν η σύνδεση που κάνουν θα έχει πρόβλημα αντοχής. Παρακάτω θα δούμε τις πιθανές καταπονήσεις των κοχλιών και τον τρόπο ελέγχου. 1) Αξονική φόρτιση. Οι κοχλίες σύνδεσης όταν έχουν σφιχτεί καταπονούνται σε εφελκυσμό διότι ενώ η κεφαλή μένει σταθερή το περικόχλιο όπως περιστρέφεται (βιδώνει) εφελκύει (τραβά) τον πυρήνα του κοχλία με αποτέλεσμα την καταπόνηση του πυρήνα σε εφελκυσμό. Για τον έλεγχο σε εφελκυσμό χρησιμοποιούμε τον γνωστό τύπο 1.6, σύμφωνα με τον οποίο υπολογίζουμε την τάση και πρέπει να είναι μικρότερη από την επιτρεπόμενη : Όπου Ρ είναι το φορτίο εφελκυσμού και Α είναι το εμβαδόν της διατομής του πυρήνα. Στο επόμενο σχήμα φαίνεται ένας κοχλίας και πρέπει να προσέξετε ότι για τον υπολογισμό της διατομής Α παίρνουμε την διάμετρο d 1 του πυρήνα και όχι την ονομαστική διάμετρο d. Αυτό γίνεται γιατί ο κοχλίας κινδυνεύει να κοπεί στη διατομή ΑΒ (επικίνδυνη διατομή), όπου η διάμετρος είναι μικρότερη από την ονομαστική. Όπως γνωρίζουμε οι υπολογισμοί αντοχής των στοιχείων μηχανών γίνονται στη δυσμενέστερη διατομή. Επομένως θα υπολογίσουμε το εμβαδόν Α από τη σχέση: Εάν γνωρίζουμε την διατομή και θέλουμε να υπολογίσουμε την διάμετρο του πυρήνα θα το κάνουμε από τη σχέση: Στους τύπους που αναφέρθηκαν μπορούν να χρησιμοποιηθούν ως μονάδες εκείνες του SI, αλλά συνήθως για το μήκος χρησιμοποιείται το cm, για τη δύναμη το kp ή το dan και για την τάση το kp/cm 2 ή το dan/cm 2. Γενικά για τις μονάδες που θα χρησιμοποιήσουμε ισχύουν όσα είπαμε στο προηγούμενο κεφάλαιο. 2) Επιφανειακή πίεση. Οι κοχλίες ενδέχεται να καταστραφούν λόγω θραύσης του σπειρώματός τους και η καταπόνηση ονομάζεται επιφανειακή πίεση ή πίεση επιφανείας. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 55
56 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ Αυτό σημαίνει το εξής: υποθέστε ότι ο κοχλίας εφελκύεται αλλά δεν έχει πρόβλημα αντοχής ο πυρήνας του. Όμως αν το περικόχλιο είναι μικρό ή δεν έχουν βιδωθεί αρκετές σπείρες ή το υλικό δεν αντέχει, υπάρχει περίπτωση να καταστραφεί μόνο το σπείρωμα που δένει με το περικόχλιο. Αυτό θα συμβεί αν δεν αντέξουν οι σπείρες του κοχλία στην πίεση που ασκούν οι σπείρες του περικοχλίου. Την πίεση θα την παραλάβουν φυσικά μόνο οι σπείρες που βιδώνουν στο περικόχλιο και μόνο η επιφάνεια μεταξύ των διαμέτρων d και d 1. Δείτε το επόμενο σχήμα στα αριστερά, που παρουσιάζει τον προηγούμενο κοχλία να συνδέει δύο μεταλλικά κομμάτια και να έχει τοποθετηθεί το περικόχλιο. Ο κοχλίας έχει συνολικά εννέα σπείρες. Το περικόχλιο έχει συσφίξει τις τέσσερις από αυτές. Αν θεωρήσουμε τον κοχλία σταθερό και μια δύναμη να τραβά το περικόχλιο προς τα δεξιά, αυτό κρατιέται από αυτές μόνο τις 4 σπείρες. Στο δεξιά σχήμα βλέπουμε τις 4 σπείρες να ωθούνται από τη δύναμη, η οποία κατανέμεται στις 4 σπείρες. Η επιφάνεια στην οποία ασκείται η δύναμη περιορίζεται ανάμεσα στους κύκλους με διαμέτρους d και d 1. Άρα, αν γενικά έχουμε αριθμό καταπονούμενων σπειρών ίσο με z, και για κάθε σπείρα η επιφάνεια που καταπονείται είναι η Α σπείρα, η επιφάνεια που δέχεται την πίεση θα έχει εμβαδόν ίσο με: Το εμβαδόν της επιφάνειας αυτής θα πρέπει να ελεγχθεί εάν αντέχει την εφελκυστική δύναμη F. Ως επιτρεπόμενη τάση (p επ ) θα πάρουμε μία τιμή που δίνεται σε πίνακες για το υλικό του κοχλία. Αυτές οι επιτρεπόμενες τάσεις είναι σχετικά μικρές και εξαρτώνται από το είδος της καταπόνησης. Ο μαθηματικός τύπος με τον οποίο θα γίνει ο έλεγχος θα είναι: Επιφανειακή πίεση δέχονται όλοι οι κοχλίες, είτε καταπονούνται σε απλό εφελκυσμό είτε σε σύνθετη καταπόνηση (εφελκυσμό, θλίψη και στρέψη). Στο σχολικό βιβλίο αναφέρεται η σχέση 4.5 σαν να ισχύει μόνο σε σύνθετη καταπόνηση. Εμείς εδώ τη δεχόμαστε και για τον απλό εφελκυσμό. Το ζήτημα είναι αν το p επ αφορά σε απλό εφελκυσμό ή σύνθετη καταπόνηση. Και εδώ στους τύπους οι μονάδες είναι εκείνες του SI, αλλά πιο συχνά για το μήκος χρησιμοποιείται το cm, για τη δύναμη το kp ή το dan και για την τάση το kp/cm 2 ή το dan/cm 2. 3) Καταπόνηση σε διάτμηση. Οι κοχλίες συχνά καταπονούνται σε διάτμηση, με τρόπο παρόμοιο με τους ήλους. Ο τρόπος ελέγχου είναι ο ίδιος, δηλαδή ο γνωστός τύπος της τάσης 56 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
57 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 με εμβαδόν επιφάνειας να θεωρείται το εμβαδόν του πυρήνα και επιτρεπόμενη τάση η διατμητική τ επ για το υλικό του κοχλία. Άρα γίνεται έλεγχος με τον τύπο: Προφανώς στον τύπο 4.6 για τις μονάδες ισχύουν τα ίδια με πριν, δηλαδή μπορεί να γίνει χρήση των μονάδων του SI, αλλά πιο συχνά για το μήκος χρησιμοποιείται το cm, για τη δύναμη το kp ή το dan και για την τάση το kp/cm 2 ή το dan/cm 2. 4) Σύνθετη καταπόνηση. Οι κοχλίες πολύ συχνά χρησιμοποιούνται σε μηχανές που κάνουν εργασίες που έχουν ως αποτέλεσμα να καταπονούνται οι κοχλίες ταυτόχρονα σε ποικιλία καταπονήσεων. Οι πιο συχνές είναι ο εφελκυσμός, η θλίψη και η στρέψη. Τότε λέμε ότι ο κοχλίας υφίσταται σύνθετη καταπόνηση. Σε αυτή την περίπτωση η τάση που θα αναπτυχθεί στον κοχλία δεν επιτρέπεται να είναι πολύ μεγάλη, όπως σε ένα απλό εφελκυσμό. Γι αυτό η επιτρεπόμενη τάση είναι τα ¾ της επιτρεπόμενης στον εφελκυσμό. Αυτό σημαίνει ότι αν είχαμε απλό εφελκυσμό η μέγιστη επιτρεπτή δύναμη θα ήταν:. Αν όμως έχουμε σύνθετη καταπόνηση, η μέγιστη δύναμη θα είναι μικρότερη από την προηγούμενη κατά τα ¾ αυτής, διότι θα ισχύει: Αν λάβουμε υπ όψιν ότι ως Α είναι το εμβαδόν της διατομής του πυρήνα (διάμετρος d 1 ) έχουμε ότι: Ας διευκρινίσουμε το εξής: αν ένας κοχλίας καταπονείται σε απλό εφελκυσμό έχει, ας πούμε, διατομή Α, η οποία θα είναι ίση με:. Αν αντί για αυτόν θέλουμε να τοποθετήσουμε έναν άλλο κοχλία από το ίδιο υλικό, ο οποίος όμως θα δέχεται σύνθετη καταπόνηση ίσης μέγιστης δύναμης, θα πρέπει να έχει διατομή ίση με: Παρατηρούμε ότι σε αυτή την περίπτωση η διατομή θα είναι κατά μεγαλύτερη (από τη διατομή στον απλό εφελκυσμό) για να αντέξει την σύνθετη καταπόνηση. Και εδώ για τις μονάδες ισχύουν όσα αναφέρθηκαν προηγουμένως. Στις ασκήσεις ακολουθούμε το σκεπτικό που περιγράφτηκε στην παράγραφο 1.4 και χρησιμοποιούμε της αντίστοιχες σχέσεις που αναφέρθηκαν πριν. Όταν μας δοθεί μια άσκηση, είτε θα μας ζητά τις διαστάσεις του κοχλία (ουσιαστικά μόνο την διάμετρο του πυρήνα ή την ονομαστική), είτε να ελέγξουμε την αντοχή του. Στην πρώτη περίπτωση θα βρίσκουμε τη διατομή από τον έλεγχο αντοχής που είναι κατάλληλος για την περίπτωση και θα προχωράμε στον υπολογισμό της διαμέτρου. Στη δεύτερη θα υπολογίζουμε την αναπτυσσόμενη τάση και θα τη συγκρίνουμε με την επιτρεπόμενη. Φυσικά υπάρχει και το ενδεχόμενο να μας ζητά το μέγιστο φορτίο αντοχής του κοχλία, οπότε το κάνουμε με την σχέση ή από τη σχέση 4.8. Συχνά επίσης θα ζητείται και έλεγχος του κοχλία ή των κοχλιών σε συγκεκριμένη καταπόνηση, όπως ας πούμε σε επιφανειακή πίεση ή διάτμηση. Πολλές φορές κάνοντας έλεγχο της αντοχής ενός κοχλία υπολογίζουμε τη διάμετρό του, η οποία είναι αρκετή για την καταπόνηση από την οποία προέκυψε, όμως ίσως δεν είναι ικανή σε μια άλλη καταπόνηση. Για παράδειγμα στην άσκηση μπορεί να μας λέει ότι είναι σε επαφή πέντε σπείρες, αλλά αυτές να αποδειχτεί ότι είναι λίγες γιατί δεν αντέχουν σε πίεση επιφανείας. Ίσως μας ζητήσουν να υπολογίσουμε πόσες σπείρες είναι απαραίτητες για να αντέξει το σπείρωμα. Δηλαδή κατά πόσο πρέπει να αυξηθεί η επιφάνεια του σπειρώματος για να αντέξει στην καταπόνηση. Θα τα δούμε αυτά σε παραδείγματα που θα κάνουμε παρακάτω. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 57
58 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ Άσκηση Να υπολογιστεί ένας κοχλίας που καταπονείται σε εφελκυσμό με μέγιστη δύναμη F=2000 kp και το υλικό με το οποίο είναι κατασκευασμένος έχει σ επ =800 kp/cm Κατόπιν να τον υπολογίσετε αν η καταπόνηση ήταν σύνθετη. 1. Απλός εφελκυσμός: Χρησιμοποιείται η γνωστή σχέση 4.1, από την οποία υπολογίζεται η διατομή του πυρήνα του κοχλία: Τώρα από τη σχέση 4.2 ή την 4.3 θα υπολογιστεί η διάμετρος του πυρήνα d 1 : Η διάμετρος του πυρήνα θα είναι τουλάχιστον 17,8 mm. Αν δούμε τον πίνακα 14.4.α της σελίδας 316 του σχολικού βιβλίου καταλήγουμε σε κοχλία με ονομαστική διάμετρο Μ22, ο οποίος έχει διάμετρο d 1 =18,933 mm και βήμα 2,5 mm. Στον πίνακα αυτόν να προσέξουμε ότι για κάθε ονομαστική διάμετρο αντιστοιχεί ένας κοχλίας. Οι κοχλίες των οποίων οι ονομαστικές διάμετροι είναι σημειωμένες είναι οι πιο συχνά χρησιμοποιούμενοι. Εκεί που είναι οι κενές γραμμές αντιστοιχούν κοχλίες λιγότερο χρησιμοποιούμενοι. Για να βρούμε την ονομαστική τους διάμετρο υπολογίζουμε το άθροισμα της διαμέτρου του πυρήνα συν δύο βάθη σπειρώματος. 2. Σύνθετη καταπόνηση: Θα χρησιμοποιήσουμε τον τύπο 4.8 που δίνεται και από το βιβλίο, και θα λύσουμε ως προς d 1 : Βρέθηκε όπως ήταν φυσικό μεγαλύτερη διάμετρος πυρήνα. Από τον ίδιο πίνακα του βιβλίου βρίσκουμε κοχλία με ονομαστική διάμετρο Μ27 και βήμα 3 mm ο οποίος έχει d 1 =23,319 mm. Για λίγο δεν είναι αποδεκτός ο Μ24 με βήμα 3 mm. Άσκηση 4.2 Ένας κοχλίας καταπονείται σε απλό εφελκυσμό με μέγιστη δύναμη Q=3000kp και το υλικό του έχει σ επ =1000 kp/cm 2 και p επ =200 kp/cm 2. 1) Να υπολογίσετε την απαιτούμενη διάμετρό του ώστε να αντέχει την δύναμη Q. 2) Αν το περικόχλιο είναι σε επαφή με 4 σπείρες να γίνει έλεγχος σε επιφανειακή πίεση (να χρησιμοποιηθεί η σχέση 4.5). 3) Αν ο κοχλίας δεν αντέχει στην πίεση επιφανείας, να υπολογίσετε πόσες σπείρες θα έπρεπε να συνεργάζονται με το περικόχλιο. 1). Για τον απλό εφελκυσμό εφαρμόζουμε τον γνωστό τύπο ελέγχου και έχουμε: Από την διατομή του πυρήνα υπολογίζεται η διάμετρός του: 58 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
59 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 Από τον πίνακα 14.4.α της σελίδας 316 του σχολικού βιβλίου καταλήγουμε σε κοχλία με ονομαστική διάμετρο Μ24, ο οποίος έχει διάμετρο d 1 =20,319 mm και βήμα 3 mm. 2). Για τον έλεγχο σε επιφανειακή πίεση χρησιμοποιούμε τον τύπο 4.5. Βλέπουμε ότι στον τύπο αυτό πρέπει να γνωρίζουμε την ονομαστική διάμετρο του κοχλία η οποία είναι 24 mm =2,4 cm. Ως διάμετρο σπειρώματος βάζουμε στον τύπο όχι τα 19,54 mm που βρήκαμε αλλά τα 20,319 mm=2,0319 cm του κοχλία που θα χρησιμοποιηθεί: Επομένως δεν αντέχει σε πίεση επιφανείας ο κοχλίας. 3). Για να βρεθεί ο αριθμός των σπειρών που πρέπει να είναι σε επαφή με το περικόχλιο για να αντέξουν, πρέπει να λύσουμε την εξίσωση 4.5 ως προς z θέτοντας όπου η p την p επ. Αφού βρέθηκε z=11,72 σπείρες θα πρέπει οι σπείρες να είναι στον πλησιέστερο μεγαλύτερο ακέραιο, ο οποίος είναι το 12, άρα το περικόχλιο πρέπει να είναι ικανό να είναι σε επαφή με 12 σπείρες. Σημείωση: Σε αυτή την λύση δεν χρησιμοποιήσαμε τις μονάδες κατά την επίλυση των εξισώσεων, αλλά μόνο στα αποτελέσματα. Άσκηση 4.3 Πέντε κοχλίες συνδέουν δύο ελάσματα και καταπονούνται σε διάτμηση με δύναμη Q= kp και το υλικό τους έχει τ επ =1000 kp/cm 2. Να υπολογίσετε την απαιτούμενη διάμετρό τους ώστε να αντέχουν. Για τον υπολογισμό σε διάτμηση θα χρησιμοποιήσουμε τον τύπο 4.6, όπου ως φορτίο όμως θα πάρουμε το που αντιστοιχεί σε κάθε κοχλία και θα είναι ίσο με Q/5=3600 kp, ενώ βέβαια Α 1 θα είναι η διατομή του πυρήνα με διάμετρο d 1. Σύμφωνα με την σχέση 4.6 θα έχουμε: Επομένως η διάμετρος του πυρήνα των κοχλιών θα είναι 21,4 mm και σύμφωνα με τον πίνακα 14.4.α της σελίδας 316 του βιβλίου ο κοχλίας θα έχει ονομαστική διάμετρο Μ27 που έχει διάμετρο πυρήνα 23,319 mm. Άσκηση 4.4 Ένας σφιγκτήρας χρησιμοποιείται για να τεντώνει ένα συρματόσχοινο και το περικόχλιό του έχει 10 σπείρες. Η εφελκυστική δύναμη είναι Q=4000 kp και το υλικό του σφιγκτήρα αλλά και του κοχλία έχει σ επ =1100 kp/cm 2 και p επ =140 kp/cm 2. Να υπολογίσετε τον κοχλία ώστε να αντέχει σε εφελκυσμό και να ελέγξετε αν αντέχει τότε σε επιφανειακή πίεση το σπείρωμά του. Ο υπολογισμός του κοχλία θα γίνει από τον έλεγχο της αντοχής του σε εφελκυσμό. Αυτό γίνεται με χρήση του τύπου 4.1: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 59
60 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ Η διατομή του πυρήνα Α έχει εμβαδόν ίσο με 3,64 cm 2. Από αυτό βρίσκουμε τη διάμετρο που πρέπει αν έχει ο πυρήνας: Αυτή είναι η διάμετρος του πυρήνα. Από τον πίνακα 14.4.α της σελίδας 316 του σχολικού βιβλίου επιλέγουμε κοχλία με ονομαστική διάμετρο Μ27, ο οποίος έχει διάμετρο d 1 =23,319 mm και βήμα 3 mm. Αφού η ονομαστική διάμετρος του κοχλία είναι 27 mm σημαίνει ότι έχουμε d=27 mm, και θα χρησιμοποιήσουμε την σχέση 4.5 για τον έλεγχο της επιφανειακής πίεσης. Θα λάβουμε υπ όψιν ότι z=10 και p επ =140 kp/cm 2 και θα υπολογίσουμε: Επομένως ο κοχλίας αν και αντέχει σε εφελκυσμό δεν αντέχει σε επιφανειακή πίεση. Για να αντέχει ο κοχλίας σε επιφανειακή πίεση θα πρέπει ή να αυξηθούν οι σπείρες του σφιγκτήρα ή να μεγαλώσει ο κοχλίας ώστε το σπείρωμά του να έχει μεγαλύτερη επιφάνεια. Άσκηση 4.5 Έχει υπολογιστεί ότι το φορτίο που θα παραλάβει ένας κοχλίας μιας πρέσας είναι Q=2000 kp. Αν επιλεγεί κοχλίας από χάλυβα με σ επ =1200 kp/cm 2 να υπολογίσετε τη διάμετρο που πρέπει να έχει. Να θεωρήσετε ότι ο κοχλίας θα υφίσταται σύνθετη καταπόνηση. Ο υπολογισμός του κοχλία σε σύνθετη καταπόνηση γίνεται με βάση τον τύπο 4.8. Έχοντας γνωστό το φορτίο Q (στον τύπο 4.8 αντικαθιστούμε την F με Q) και την επιτρεπόμενη τάση, λύνουμε την εξίσωση ως προς τη διάμετρο του πυρήνα: Επομένως η διάμετρος του πυρήνα θα είναι d 1 =16,67mm. Από τον πίνακα 14.4.α του βιβλίου επιλέγεται κοχλίας Μ20. Άσκηση 4.6 Έχουμε κοχλία Μ24 από υλικό με σ επ =1000 kp/cm 2. Να προσδιορίσετε το μέγιστο φορτίο που μπορεί να δεχτεί: α) αν φορτιστεί σε εφελκυσμό και β) αν υφίσταται σύνθετη καταπόνηση. Για τον υπολογισμό τον κοχλιών λαμβάνεται στους τύπους η διάμετρος του πυρήνα d 1 την οποία θα βρούμε εδώ από τον πίνακα 14.4.α του βιβλίου, όπου για κοχλία Μ24 είναι d 1 =20,319 mm=2,0319 cm. Ο υπολογισμός των δύο δυνάμεων θα γίνει χωριστά για τις δύο καταπονήσεις. Δεν πρέπει να ξεχνάμε ότι οι υπολογισμοί γίνονται με μονάδα του μήκους το cm. α) Για τον εφελκυσμό θα χρησιμοποιήσουμε τη σχέση 4.1, από την οποία θα βρούμε την Ρ εφ που ζητείται. Πρώτα όμως πρέπει να υπολογίσουμε το εμβαδόν Α της διατομής του πυρήνα από τη σχέση 4.2: Τώρα από τον τύπο 4.1, αφού θέσουμε όπου σ το σ επ, θα βρούμε την δύναμη: 60 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
61 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 Επομένως η εφελκυστική δύναμη που επιτρέπεται στον κοχλία για εφελκυσμό είναι 3240 kp. Β) Στη σύνθετη καταπόνηση αφού η επιτρεπόμενη τάση είναι κατά τα ¾ μικρότερη, κατά τα ¾ θα είναι μικρότερο και το μέγιστο επιτρεπόμενο φορτίο Ρ συν. Επομένως θα είναι: Όμως μπορούμε να υπολογίσουμε την Ρ συν και πιο αναλυτικά από τη σχέση 4.8. Μπορούμε να χρησιμοποιήσουμε και το τελευταίο σκέλος της σχέσης 4.8, αλλά αυτό είναι προσεγγιστικό και το αποτέλεσμα θα έχει μια μικρή διαφορά από το προηγούμενο. Ας το δούμε όμως: Βλέπουμε ότι υπάρχει μια διαφορά περίπου 2%. Όμως, όποιον και από τους δύο τύπους και να χρησιμοποιήσετε για τη λύση σας, το αποτέλεσμα θα γίνει δεκτό. Σημείωση: Για να σας δοθεί μια τέτοια άσκηση θα πρέπει στην εκφώνηση να δοθεί και ο πίνακας με τις διαστάσεις των σπειρωμάτων, δηλαδή όλος ή ένα μέρος από τον πίνακα 14.4.α του βιβλίου. Δεν είναι καθόλου απίθανο. Άσκηση 4.7 Ένας κοχλίας Μ24 από υλικό με σ επ =1200 kp/cm 2 και τ επ =1000 kp/cm 2 συνδέει δύο ελάσματα όπως φαίνεται στο επόμενο σχήμα, στα οποία ασκείται η δύναμη F=5000 kp και η αντίδρασή της F. Να ελέγξετε την αντοχή του κοχλία, αφού προσδιορίσετε το είδος της καταπόνησης την οποία υφίσταται. Ο κοχλίας είναι προφανές ότι καταπονείται σε διάτμηση, αφού η δύναμη F και η αντίδρασή της με τον τρόπο που ασκούνται, τείνουν να κόψουν τον κοχλία στην διάμετρο του πυρήνα, εκεί που έρχονται σε επαφή τα δύο ελάσματα. Επομένως θα κάνουμε έλεγχο του κοχλία σε διάτμηση με τον τύπο 4.6. Προφανώς θα χρησιμοποιηθεί μόνο η επιτρεπόμενη τάση διάτμησης και όχι εφελκυσμού (το σ επ δόθηκε παραπλανητικά, κάτι που αποφεύγεται στις εξετάσεις). Η διάμετρος πυρήνα του κοχλία Μ24 δίνεται από τον πίνακα 14.4.α του βιβλίου και είναι d 1 =20,319 mm = 2,0319 cm. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 61
62 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ Επομένως ο κοχλίας δεν θα αντέξει. Αν θέλαμε να κάνουμε κάτι για να αντέξει η κοχλιοσύνδεση αυτή τη δύναμη είχαμε δυο επιλογές: α) να επιλέξουμε ένα κοχλία με μεγαλύτερη από 1543 kp/cm 2 επιτρεπόμενη τάση διάτμησης. β) να επιλέξουμε ένα κοχλία με μεγαλύτερη διάμετρο πυρήνα. Αυτή τη διάμετρο μπορούμε να υπολογίσουμε από τον τύπο 4.6, θέτοντας όπου τ το τ επ και λύνοντάς την ως προς d 1 : Με τη διάμετρο πυρήνα d 1 =25,24 mm που βρήκαμε ότι πρέπει να έχει ο κοχλίας, από τον πίνακα 14.4.α του βιβλίου επιλέγουμε κοχλία Μ30 με d 1 =25,706 mm Άσκηση 4.8 Θέλουμε να τοποθετήσουμε ένα κοχλία από υλικό με σ επ =1400 kp/cm 2 και p επ =200 kp/cm 2 σε εργαλειομηχανή ώστε να μεταφέρει μια ροπή. Το φορτίο που καταπονεί τον κοχλία είναι F=2000 kp. Να βρείτε πόσες σπείρες z πρέπει να έρθουν σε επαφή με το περικόχλιο ώστε να αντέξει ο κοχλίας σε επιφανειακή πίεση. Κατ αρχάς αναφέρουμε ότι αφού ο κοχλίας μεταφέρει ροπή, η καταπόνησή του θεωρείται σύνθετη. Για να βρεθεί ο αριθμός των σπειρών χρησιμοποιείται ο τύπος 4.5. Σε αυτόν όμως είναι άγνωστες οι διάμετροι d και d 1 τις οποίες πρέπει να υπολογίσουμε. Αυτό μπορεί να γίνει από τον έλεγχο σε σύνθετη καταπόνηση, με βάση τον τύπο 4.8. Από τον 4.8 θα βρούμε μία ελάχιστη απαιτούμενη διάμετρο. Αν θελήσουμε να τοποθετήσουμε κοχλία με μεγαλύτερη διάμετρο, μπορούμε, και οι σπείρες θα είναι λιγότερες. Επομένως από τη σχέση 4.8 μπορούμε να υπολογίσουμε την διάμετρο του πυρήνα του. Από τον πίνακα 14.4.α του βιβλίου επιλέγουμε κοχλία Μ20 με d 1 =16,933 mm=1,6933 cm και d=20 mm=2 cm. Τώρα από τον τύπο 4.5 για την επιφανειακή πίεση μπορούμε να επιλύσουμε ως προς z για να βρούμε τον αριθμό των σπειρών που απαιτούνται. Όπου p θα θέσουμε p επ. Επομένως απαιτείται η επαφή 12 σπειρών του κοχλία με το περικόχλιο. Επειδή οι σπείρες είναι σχετικά πολλές, μπορούμε να πάρουμε κοχλία Μ24 που είναι μεγαλύτερος και να υπολογίσουμε τον νέο αριθμό σπειρών. 62 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
63 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 Άσκηση 4.9 Θέλουμε να συνδέσουμε με τέσσερις κοχλίες δύο ελάσματα που καταπονούνται σε εφελκυσμό. Το φορτίο που καταπονεί τα ελάσματα είναι F= kp και το εφελκυστικό φορτίο στους κοχλίες είναι Q=8000 kp. Οι κοχλίες είναι από υλικό με σ επ =1400 kp/cm 2 και τ επ =1200 kp/cm 2. Να βρείτε την διάμετρο του πυρήνα των κοχλιών που θα επιλέξουμε. Κατ αρχάς κατανοούμε ότι οι κοχλίες πρέπει να ελεγχθούν και σε εφελκυσμό και σε διάτμηση. Η διάτμηση προέρχεται από τον εφελκυσμό των ελασμάτων, που μεταφέρεται ως διάτμηση στους κοχλίες. Ο εφελκυσμός δίνεται από την εκφώνηση της άσκησης. Επειδή οι κοχλίες είναι 4 τα φορτία που δίνονται στην εκφώνηση επιμερίζονται σε όλους, άρα διαιρούνται με το 4 και σε κάθε κοχλία αναλογεί: φορτίο εφελκυσμού: F 1 =3.000 kp και φορτίο διάτμησης: Q 1 =2000 kp. Θα κάνουμε δύο ξεχωριστούς ελέγχους και θα βρούμε τη διάμετρο του πυρήνα και στις δύο περιπτώσεις και θα επιλέξουμε τη μεγαλύτερη. Για τον εφελκυσμό επιλέγουμε στους συμβολισμούς τον δείκτη 1 και στη διάτμηση τον δείκτη 2. Έτσι Α 1 και d 11 είναι η διατομή και η διάμετρος πυρήνα αντιστοίχως που βρίσκουμε από τον έλεγχο του εφελκυσμού και Α 2 και d 12 είναι για την διάτμηση. Για τον εφελκυσμό έχουμε τη σχέση 4.1 και 4.2 και αφού θέσουμε όπου σ την σ επ θα έχουμε: Ανάλογα κάνουμε και στη διάτμηση: Επειδή η διάμετρος πυρήνα που βρέθηκε στον έλεγχο εφελκυσμού είναι μεγαλύτερη από την διάμετρο που βρέθηκε από το έλεγχο διάτμησης, επιλέγεται η διάμετρος του εφελκυσμού: d 1 =16,5mm. (Και αν ανατρέξουμε στον πίνακα 14.4.α του βιβλίου θα επιλέξουμε κοχλία Μ20.) Άσκηση 4.10 Θέλουμε να αγοράσουμε πολλούς κοχλίες της σειράς Μ24 (d 1 =20,319 mm). Αυτοί θα συνδέουν δύο ελάσματα και καταπονούνται (οι κοχλίες) σε εφελκυσμό με φορτίο Q=4000 kp. Οι κοχλίες που διατίθενται στην αγορά έχουν επιτρεπόμενες τάσεις εφελκυσμού όπως αυτές φαίνονται στον παρακάτω πίνακα. Οι κοχλίες με την μεγαλύτερη σ επ είναι και ακριβότεροι. Να επιλέξετε τον τύπο κοχλία που μας συμφέρει να αγοράσουμε. Τύπος κοχλία Α Β Γ Δ Ε σ επ (kp/cm 2 ) Προφανώς θα επιλέξουμε ένα κοχλία που να έχει τάση μικρότερη από κάποιαν από τις επιτρεπόμενες τάσεις που δίνει ο πίνακας. Και από τους τύπους των κοχλιών του πίνακα θα επιλέξουμε εκείνον με την ακριβώς μεγαλύτερη σ επ από την τάση που θα υπολογίσουμε ότι δέχονται οι κοχλίες. Αυτή την τάση θα την υπολογίσουμε από τον τύπο 4.1, αφού πρώτα βρούμε το εμβαδόν Α (με d 1 =2,0319 cm) της διατομής από τον τύπο 4.2. Θα έχουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 63
64 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ Υπολογίσαμε την ασκούμενη τάση ίση με 1235 kp/cm 2 επομένως πρέπει να επιλέξουμε τους κοχλίες τύπου Δ με σ επ =1400kp/cm 2. Άσκηση 4.11 Σε πρέσα χρησιμοποιούνται 4 κοχλίες τετραγωνικού σπειρώματος για να συνδέσουν δύο περιστρεφόμενες ατράκτους. Η ονομαστική διάμετρος των κοχλιών είναι 42 mm, ενώ η διάμετρος του πυρήνα είναι 34 mm. Το υλικό των κοχλιών έχει επιτρεπόμενη τάση εφελκυσμού σ επ =800 kp/cm 2 και επιτρεπόμενη επιφανειακή πίεση p επ =150 kp/cm 2. α) Να υπολογίσετε την μέγιστη αξονική φόρτιση που μπορεί να δεχτεί η άτρακτος όταν εργάζεται η πρέσα. β) Να ελέγξετε αν οι κοχλίες με τη μέγιστη αυτή φόρτιση αντέχουν σε πίεση επιφανείας, αν κάθε περικόχλιο συνεργάζεται με 10 σπείρες. α) Εφόσον οι κοχλίωση βρίσκεται σε ατράκτους πρέσας θα υφίσταται σύνθετη καταπόνηση. Όσον αφορά στο μέγιστο φορτίο (δύναμη) κάθε ενός κοχλία, θα υπολογιστεί από τη σχέση 4.8 όπου d 1 =34 mm=3,4 cm και θα έχουμε: Επομένως κάθε κοχλίας μπορεί να δεχτεί μέγιστο φορτίο ίσο με 5549 kp. Άρα η άτρακτος που έχει 4 κοχλίες μπορεί να δεχτεί τετραπλάσιο φορτίο:. β) Για τον έλεγχο των κοχλιών σε επιφανειακή πίεση χρησιμοποιείται ο τύπος 4.5, όπου για κάθε κοχλία έχουμε: d 1 =3,4 cm, d=4,2 cm, z=10 και F=5549 kp. Επομένως οι 10 σπείρες είναι αρκετές για την αντοχή των κοχλιών σε επιφανειακή πίεση. Άσκηση 4.12 Σε εργαλειομηχανή θέλουμε να χρησιμοποιήσουμε ένα κοχλία τετραγωνικού σπειρώματος, ο οποίος θα έχει διάμετρο πυρήνα d 1 =3 cm και θα είναι από υλικό με επιτρεπόμενες τάσης εφελκυσμού και επιφανειακής πίεσης αντίστοιχα σ επ =1000 kp/cm 2 και p επ =200 kp/cm 2. Εάν το περικόχλιο έχει 8 σπείρες να υπολογίσετε: α) το μέγιστο φορτίο που μπορεί να δεχτεί αυτός ο κοχλίας και β) το βάθος σπειρώματος του κοχλία για να αντέξει την επιφανειακή πίεση. 64 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
65 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 α) Το μέγιστο φορτίο που μπορεί να παραλάβει ο κοχλίας, θα υπολογιστεί από τη σχέση 4.8 όπου d 1 =3 cm και έχουμε: Επομένως ο κοχλίας μπορεί να δεχτεί μέγιστο φορτίο ίσο με 5400 kp. β) Για την επιφανειακή πίεση η μόνη σχέση που έχουμε είναι η 4.5, στην οποία αν θέσουμε όπου το το μόνο άγνωστο που μένει σε αυτόν είναι η διάμετρος d. Επομένως, αν λύσουμε ως προς αυτήν, το βάθος του σπειρώματος β θα προκύψει από το ότι, όπως φαίνεται και στο πιο πάνω σχήμα. Επομένως η εξωτερική διάμετρος του κοχλία θα είναι 3,64 cm. Το βάθος του σπειρώματος θα το βρούμε από τη σχέση: Επομένως το βάθος του σπειρώματος θα είναι 3,2 mm. Σημείωση: Την εξίσωση για την πίεση επιφανείας την λύσαμε αφού πρώτα επιλύσαμε ως προς τον άγνωστο d. Μπορούμε όμως (αν και δεν το συστήνουμε) να αντικαταστήσουμε τις τιμές των μεγεθών πριν τον τελικό τύπο, οπότε θα έχουμε τα εξής: Φυσικά βρήκαμε την ίδια διάμετρο d και θα βρεθεί το ίδιο βάθος σπειρώματος. Άσκηση 4.13 Θέλουμε να χρησιμοποιήσουμε κοχλίες Μ20 για να στερεώσουμε ένα φορτίο που υφίσταται καταπόνηση εφελκυσμού με μέγιστη συνολική δύναμη F=8400 dan. Οι κοχλίες έχουν σ επ =1200 daν/cm 2. Να υπολογίσετε πόσους τέτοιους κοχλίες πρέπει να χρησιμοποιήσουμε. Κατ αρχάς από την δύναμη και την επιτρεπόμενη τάση θα βρούμε το συνολικό εμβαδόν A που απαιτείται να έχουν όλοι οι κοχλίες για να αντέξουν στην καταπόνηση. Αυτό θα γίνει από τον τύπο 4.1 αν όπου σ θέσουμε σ επ, οπότε θα έχουμε: Την επιφάνεια Α θα έχουν όλοι μαζί οι κοχλίες. Επομένως πρέπει να βρούμε την επιφάνεια A 1 καθενός κοχλία Μ20. Από τον πίνακα14.4.α του βιβλίου θα βρούμε τη διάμετρο ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 65
66 ΚΕΦΑΛΑΙΟ 4 ΚΟΧΛΙΟΣΥΝΔΕΣΕΙΣ του πυρήνα, γιατί η διατομή του πυρήνα είναι που καταπονείται από την δύναμη. Βρίσκουμε ότι d 1 =16,933 mm= 1,6933 cm. Η επιφάνεια της διατομής του πυρήνα κάθε κοχλία θα δίνεται από τον τύπο 4.2 και έχουμε: Επομένως η διατομή του πυρήνα κάθε κοχλία είναι 2,25 cm 2. Για να βρούμε τον αριθμό των κοχλιών που απαιτούνται θα διαιρέσουμε αυτή την επιφάνεια με την συνολική Α και βρίσκουμε:. Επομένως απαιτούνται περισσότεροι από 3 κοχλίες, άρα θα πάρουμε τέσσερις. Άσκηση 4.14 Θα λύσουμε την προηγούμενη άσκηση όταν η καταπόνηση δεν είναι απλός εφελκυσμός αλλά σύνθετη καταπόνηση. Η εκφώνηση θα έχει ως εξής: Θέλουμε να χρησιμοποιήσουμε κοχλίες Μ20 για να στερεώσουμε ένα φορτίο που υφίσταται ΣΥΝΘΕΤΗ καταπόνηση με μέγιστη συνολική δύναμη F=8400 dan. Οι κοχλίες έχουν σ επ =1200 daν/cm 2. Να υπολογίσετε πόσους τέτοιους κοχλίες πρέπει να χρησιμοποιήσουμε. Η άσκηση θα λυθεί ακριβώς όπως η προηγούμενη, με τη μόνη διαφορά ότι θα αλλάξει η επιτρεπόμενη τάση σ επ και θα γίνει κατά τα ¾ μικρότερη, όπως μας λέει η θεωρία. Επομένως η νέα επιτρεπόμενη τάση θα είναι η σ επ1 =¾ 1200 daν/cm 2 =900 daν/cm 2. Θα κάνουμε τη λύση όπως και πριν, για να δούμε το αποτέλεσμα κατά πόσο θα αλλάξει. Η συνολική διατομή θα είναι: Η διατομή κάθε κοχλία θα είναι ίδια όπως και πριν Α 1 =2,25 cm 2. Θα βρούμε τώρα τον αριθμό των κοχλιών:. Επομένως απαιτούνται περισσότεροι από 4 κοχλίες, άρα θα πάρουμε πέντε, έναν παραπάνω από την περίπτωση του απλού εφελκυσμού. Το αποτέλεσμα είναι λογικό αφού η σύνθετη καταπόνηση είναι πιο επικίνδυνη. Σημείωση: Προφανώς δεν μπορούμε να χρησιμοποιήσουμε τον τύπο 4.8 (επιλύοντάς τον ως προς γιατί δεν έχει κανένα νόημα να βρούμε τη διάμετρο που θα είχε η χρήση ενός και μόνο κοχλία. Άσκηση 4.15 Έχουμε ένα κοχλία Μ16 που υφίσταται σύνθετη καταπόνηση και πρέπει να παραλάβει F=500 dan και έχει p επ = 100 daν/cm 2. Να βρείτε το μήκος που πρέπει να έχει το σπείρωμα που χρησιμοποιείται με το περικόχλιο. Σας δίνεται ότι το βήμα του σπειρώματος είναι h=2 mm. Προφανώς θα γίνει έλεγχος σε πίεση επιφανείας και θα χρησιμοποιήσουμε τον τύπο 4.5, από τον οποίο θα βρούμε τον αριθμό των σπειρών. Από τον πίνακα 14.4.α του βιβλίου για κοχλία Μ16 (d=16 mm=1,6 cm) βρίσκουμε ότι d 1 =13,546 mm=1,3546 cm. Τώρα θα έχουμε: Επομένως οι σπείρες θα είναι τουλάχιστον 9 και αφού το βήμα είναι h=2 mm το μήκος (ύψος) του περικοχλίου θα είναι τουλάχιστον 2 9=18 mm. 66 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
67 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ ΚΕΦΑΛΑΙΟ 5 5. Άτρακτοι - Άξονες Οι άτρακτοι και οι άξονες χρησιμοποιούνται όπου υπάρχει περιστροφή, είτε για να την διευκολύνουν (πχ. προεκτείνουν) είτε για να μεταφέρουν ροπή. Ενώ στη θεωρία υπάρχει διαχωρισμός μεταξύ των εννοιών της ατράκτου και του άξονα στις ασκήσεις συνήθως, όπως και στην καθομιλουμένη, δεν υπάρχει. Δηλαδή οι δύο όροι χρησιμοποιούνται άσχετα εάν μεταφέρεται ροπή (οπότε θα είχαμε άτρακτο) ή όχι (τότε θα λέγαμε για άξονα). Εμείς εδώ θα χρησιμοποιούμε πιο πολύ τον όρο άξονα, ανεξάρτητα αν μεταφέρεται ροπή ή όχι. Στις ασκήσεις συνήθως θα ζητείται ο υπολογισμός του άξονα για καταπόνηση σε στρέψη, που σημαίνει ότι πρέπει να υπολογίσουμε τη διάμετρο. Για να γίνει αυτό πρέπει να γνωρίζουμε ορισμένα μεγέθη που επηρεάζουν την τιμή που θα έχει η διάμετρος. Τα μεγέθη αυτά είναι: οι στροφές με τις οποίες περιστρέφεται ο άξονας (n) η ισχύς την οποία μεταφέρει (P) η ροπή στρέψης του άξονα (M t ) η επιτρεπόμενη διατμητική τάση του υλικού του άξονα (τ επ ) Οι ασκήσεις του βιβλίου περιορίζονται μόνο στις περιπτώσεις που οι άξονες καταπονούνται σε απλή στρέψη (και όχι σε κάμψη επί πλέον). Αν και στον πίνακα 14.6.α στη σελίδα 323 δίνονται οι τύποι και για την περίπτωση της κάμψης, δεν χρησιμοποιούνται σε καμία άσκηση του βιβλίου, επομένως θεωρείται απίθανο να ζητηθεί κάποιος από αυτούς. Επίσης δεν κρίνεται απαραίτητο να αναφερθούμε στην πολική ροπή αντίστασης, γιατί ούτε αυτό το μέγεθος εμφανίζεται σε κάποια άσκηση του βιβλίου. Σύμφωνα με το βιβλίο, στο κεφάλαιο αυτό χρησιμοποιούνται μόλις δύο μαθηματικοί τύποι, στους οποίους υπάρχουν αυτά τα μεγέθη. Ο ένας δίνει την ροπή στρέψης (M t ) του άξονα σε συνάρτηση της ισχύος (P) που μεταφέρεται και του αριθμού των στροφών (n). Είδαμε αυτές τις έννοιες στο πρώτο κεφάλαιο στην παράγραφο 1.8 για το έργο και την ισχύ. Η σχέση που δίνει την ροπή στρέψης είναι η: Στον τύπο αυτό (όπως είπαμε και στο πρώτο κεφάλαιο) οι μονάδες των μεγεθών είναι: ροπή στρέψης σε dan m, ισχύς σε HP και οι στροφές σε RPM. Ο ίδιος τύπος αλλάζει λίγο αν η ροπή έχει μονάδες dan cm και γίνεται: Η διάμετρος d δίνεται από τον τύπο: Στον τύπο 5.3 πρέπει επίσης να θυμόμαστε τις μονάδες των μεγεθών. Η ροπή στρέψης μπαίνει σε dan cm ή kp cm και η επιτρεπόμενη τάση τ επ σε kp/cm 2 ή dan/cm 2. Να θυμηθούμε ότι dan και kp είναι κατά προσέγγιση ίσα. Η διάμετρος θα προκύψει σε cm. Στους τύπους 5.3 χρησιμοποιήσαμε τους δύο συμβολισμούς για τις ρίζες που γνωρίζουμε από τα μαθηματικά. Πρόκειται για την «τρίτη ρίζα», όπως λέγεται, ενός αριθμού ή μιας μαθηματικής παράστασης. Οι δυο ισοδύναμοι συμβολισμοί για την τρίτη ρίζα είναι: Όταν θα επιλύουμε ασκήσεις θα πούμε περισσότερα για το πώς εργαζόμαστε σε αυτές τις περιπτώσεις. Θα εξηγήσουμε τώρα πως επιδρά κάθε μέγεθος από τα προηγούμενα στην καταπόνηση της ατράκτου και κατά συνέπεια στην διάμετρό της. Είναι προφανές ότι όσο περισσότερη ισχύς μεταφέρεται από την άτρακτο τόσο πιο μεγάλος (μεγαλύτερη διάμετρος) πρέπει να είναι ο άξονας για να αντέξει. Αντίστοιχα καταλαβαίνουμε ότι όσο μεγαλύτερη η ροπή που και ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 67
68 ΚΕΦΑΛΑΙΟ 5 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ μεταφέρει τόσο πιο μεγάλη η διάμετρος της ατράκτου. Επίσης, όσο πιο καλό είναι το υλικό του άξονα τόσο μικρότερη θα είναι η διάμετρός του, αφού θα αντέχει καλύτερα. Επομένως όσο μεγαλύτερο το τ επ, τόσο μικρότερο θα είναι το d. Εκεί που είναι λίγο δύσκολη η κατανόηση είναι το γιατί όταν οι στροφές είναι λιγότερες η διάμετρος θα είναι μεγαλύτερη. Θα περίμενε κανείς ότι όσο περισσότερες είναι οι στροφές, τόσο περισσότερο καταπονείται ο άξονας, επομένως θα πρέπει η διάμετρός του να είναι μεγαλύτερη. Και έτσι είναι, απλά στους τύπους αυτούς εμφανίζονται πάντα οι στροφές μαζί με την ισχύ στο πηλίκο: Ρ/n. Πρέπει να δούμε αυτό το πηλίκο σαν ένα αριθμό. Αυτός λοιπόν ο αριθμός όσο μεγαλύτερος είναι τόσο μεγαλύτερη είναι και η διάμετρος του άξονα. Αυτό γίνεται κατανοητό και από το ότι στους πίνακες (όπως ο 14.6.γ και ο 14.6.δ στις σελίδες 324 και 325 του σχολικού βιβλίου) δίνεται αυτός ο λόγος (ισχύος προς στροφές) και όχι κάθε μέγεθος από τα δύο χωριστά. Στους πίνακες αυτούς δίνεται κατά προσέγγιση η τιμή της διαμέτρου της ατράκτου όταν γνωρίζουμε τον λόγο Ρ/n ή την ροπή στρέψης για άξονες από μαλακό χάλυβα St37 και St42. Αυτό σημαίνει ότι δεν χρειάζεται να χρησιμοποιήσουμε τους τύπους για τους υπολογισμούς. Όμως το αποτέλεσμα δεν έχει την ακρίβεια των υπολογισμών. Οι επιτρεπόμενες ορθές και διατμητικές τάσεις διαφόρων υλικών δίνονται από τον πίνακα 14.6.β του βιβλίου για να χρησιμοποιηθούν στις ασκήσεις. Να σημειώσουμε ότι όταν υπολογίζεται ένας άξονας βρίσκουμε τη διάμετρο της επικίνδυνης διατομής. Αυτό σημαίνει ουσιαστικά ότι μας ενδιαφέρει το σημείο που αναπτύσσεται η μεγαλύτερη τάση και αυτό είναι εκεί που η διατομή είναι (για κατασκευαστικούς λόγους συνήθως) η μικρότερη. Στις ασκήσεις αυτό το σημείο υπολογίζεται αλλά δεν γίνεται λόγος κάθε φορά, απλά υπολογίζουμε τη διάμετρο του άξονα. Οι ασκήσεις που έχει το βιβλίο (λυμένες και άλυτες) περιορίζονται μόνο στον υπολογισμό της διαμέτρου του άξονα. Εμείς εδώ θα παρουσιάσουμε και άλλες ασκήσεις όπου θα ζητείται και ένα άλλο μέγεθος, το οποίο όμως θα προκύπτει από την επίλυση των ίδιων εξισώσεων. Εκτός από τη χρήση των τύπων για την επίλυση μιας άσκησης μπορεί να ζητηθεί να την λύσετε με τη χρήση των πινάκων14.6.γ ή 14.6.δ. Άσκηση 5.1 Μια άτρακτος μεταφέρει ισχύ 20 HP σε μια άλλη άτρακτο και περιστρέφεται με 4000 rpm. Να υπολογίσετε τη ροπή στρέψης της πρώτης ατράκτου. Είναι προφανές ότι θα χρησιμοποιήσουμε τον τύπο 5.1 (ή τον 5.2). Οι μονάδες δεν θέλουν καμία αλλαγή και θα έχουμε: Επομένως η ροπή στρέψης θα είναι 3,581 kp m. Οι μονάδες αυτές θα μπορούσαν να είναι και 3,581 dan m αφού kp και dan θεωρούνται ίσα. Αν χρησιμοποιούσαμε τον τύπο 5.2, επειδή η ροπή αντί για kp m θα είχε ως μονάδες τα kp cm και θα ήταν 100 φορές μεγαλύτερη (αφού τα cm είναι 100 φορές μικρότερη μονάδα από το m). Ας το δούμε όμως και στην πράξη: Βρήκαμε αυτό που περιμέναμε. Άσκηση 5.2 Ο στροφαλοφόρος άξονας ενός αυτοκινήτου με ισχύ κινητήρα στον στροφαλοφόρο ίση με 100 HP περιστρέφεται με 5000 rpm. Να υπολογίσετε τη ροπή στρέψης του στροφαλοφόρου, αν θεωρήσουμε ότι αυτός καταπονείται μόνο σε στρέψη. Η άσκηση είναι ίδια με την προηγούμενη, με διαφορετικά νούμερα. Επειδή στα αυτοκίνητα συνηθίζεται η ροπή να δίνεται σε kp m θα πάρουμε τον τύπο 5.1 και θα έχουμε. 68 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
69 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ ΚΕΦΑΛΑΙΟ 5 Υπολογίσαμε ότι η ροπή στον στροφαλοφόρο είναι 14,324 kp m. Η τιμή αυτή είναι ενδεικτική, αφού γνωρίζουμε ότι η ροπή στα αυτοκίνητα εξαρτάται και από άλλους παράγοντες και όχι μόνο από την ισχύ και τις στροφές. Άσκηση 5.3 Μια άτρακτος ηλεκτροκινητήρα περιστρέφεται με 1500 rpm και υπολογίστηκε ότι η μεταφερόμενη ροπή είναι 1074,3 kp cm. Να υπολογίσετε την ισχύ (ιπποδύναμη) του ηλεκτροκινητήρα. Θα χρησιμοποιήσουμε τον τύπο 5.2 (αφού μας δίνεται η ροπή σε kp cm και όχι σε kp m) για να βρούμε την ισχύ σε HP. Θα λύσουμε το τύπο αυτό ως προς τη ζητούμενη ισχύ και θα έχουμε: Επομένως η ισχύς του κινητήρα θα είναι 22,5 HP. Άσκηση 5.4 Να υπολογίσετε τις στροφές μιας ατράκτου που μεταφέρει ισχύ 20 HP και έχει ροπή ίση με 716,2 kp cm (είναι ίση με 7,162 kp m). Θα χρησιμοποιήσουμε τον τύπο 5.2 τον οποίο θα επιλύσουμε ως προς τον αριθμό των στροφών n: Επομένως η άτρακτος περιστρέφεται με 2000 στροφές το λεπτό. Θα προχωρήσουμε τώρα στη λύση ασκήσεων όπου ζητείται να βρεθεί η διάμετρος του άξονα με χρήση του τύπου 5.3. Πρέπει να γνωρίζουμε τι σημαίνει τρίτη ρίζα ενός αριθμού και γι αυτό θα δοθούν κάποια παραδείγματα. Ο ορισμός της τρίτης ρίζας είναι ο εξής: Τρίτη ρίζα ενός αριθμού είναι ένας άλλος αριθμός τον οποίο αν υψώσουμε στην Τρίτη δύναμη θα προκύψει ο πρώτος. Για παράδειγμα, η τρίτη ρίζα του 1000 είναι το 10 αφού αν το 10 υψωθεί στην τρίτη δύναμη (ή στον κύβο όπως λέγεται) μας δίνει Δηλαδή 10 3 =1000. Αυτό μπορεί να γραφεί και ως εξής: Πρέπει να καταλάβετε ότι το και το είναι σύμβολα και το Α είναι ένας αριθμός. Ας δούμε και άλλα παραδείγματα: Η τρίτη ρίζα του 8 είναι το 2 γιατί 2 3 =2 2 2=8 και θα μπορούσαμε να γράψουμε:. Μπορούμε να δούμε και το εξής: επειδή 5 3 =125 τότε η τρίτη ρίζα του 125 είναι το 5 και γράφουμε. Στις ασκήσεις με τους άξονες υπάρχει ο τύπος 5.3. Εμείς για να βρούμε τη διάμετρο d θα βρίσκουμε την παράσταση που είναι μέσα στην τρίτη ρίζα (υπόριζο) και μετά θα προσπαθούμε να βρούμε τον αριθμό που αν πολλαπλασιαστεί τρεις φορές (τρίτη δύναμη) με τον εαυτό του θα δώσει αυτό τον αριθμό. Η παράσταση που θα υπολογίζουμε είναι η: Ας δώσουμε ένα παράδειγμα: έστω M t =540 και τ επ =100 τότε θα έχουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 69
70 ΚΕΦΑΛΑΙΟ 5 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ Τώρα θα σκεφτούμε ως εξής: Ποιόν αριθμό αν υψώσουμε στην τρίτη δύναμη θα μας δώσει τον 27; Είναι ο 3 διότι 3 3 3=27. Άρα η διάμετρος, που είναι η τρίτη ρίζα του 27 θα είναι το 3. Συνήθως στις ασκήσεις που μπαίνουν στις εξετάσεις, ο αριθμός του οποίου πρέπει να βρούμε την τρίτη ρίζα είναι ακέραιος και η τρίτη ρίζα είναι επίσης ακέραιος. Παρακάτω φαίνονται οι πρώτοι ακέραιοι που μπορεί να σας τύχουν σε πιθανή άσκηση. Είναι δύσκολο να τύχει κάποιος άλλος αφού μετά η διάμετρος θα προκύψει μεγαλύτερη από 10 cm, που είναι λίγο απίθανη περίπτωση. Έχουμε λοιπόν τις περιπτώσεις: 1: 1 3 =1 2: 2 3 =8 3: 3 3 =27 4: 4 3 =64 5: 5 3 =125 6: 6 3 =216 7: 7 3 =343 8: 8 3 =512 9: 9 3 =729 10: 10 3 =1000 Δεν χρειάζεται να θυμάστε τους αριθμούς αυτούς, αλλά να έχετε μια ιδέα. Αν τύχει και προκύψει ένας άλλος αριθμός του οποίου πρέπει να βρείτε την τρίτη ρίζα πρέπει να πάτε ψαχτά, με δοκιμές. Για παράδειγμα αν προκύψει ο αριθμός 400 και ζητάτε την τρίτη ρίζα του να σκεφτείτε ως εξής: αν είναι ο 5 θα έπρεπε να είναι αντί για 400 ο αριθμός 5 3 που είναι ο 125. Πρέπει να είναι κάποιος μεγαλύτερος από τον 5. Ας πούμε ο 6. Τότε 6 3 =216. Και αυτός είναι μικρός. Πάμε σε μεγαλύτερο, στον 7. Έχουμε 7 3 =343. Και αυτός είναι μικρός, άρα πάω στον 8, όπου 8 3 =512. Το περάσαμε το 400, άρα ο ζητούμενος αριθμός είναι μεταξύ 7 και 8. Εδώ τώρα θα επιλέξουμε ένα δεκαδικό αριθμό ανάμεσα στο 7 και 8. Επειδή το 400 είναι πιο κοντά στο 343 από ότι στο 512 επιλέγουμε τον 7,3 ή θα μπορούσαμε και τον 7,4. Δε θα σας πάρουν λάθος όποιο και να πάρετε αφού είστε κοντά στην απάντηση και δεν μπορείτε να χρησιμοποιήσετε κομπιούτερ. Αυτός ο τρόπος χρησιμοποιεί ένα είδος παρεμβολής, στην οποία θα αναφερθούμε αμέσως μετά. Θα προχωρήσουμε τώρα στην επίλυση μερικών ασκήσεων υπολογισμού της διαμέτρου αξόνων. Οι ασκήσεις αυτές είναι ίδιες με τις προηγούμενες που ζητιόταν η ροπή στρέψης, μόνο που προστίθεται η ερώτηση για τον υπολογισμό του άξονα. Άσκηση 5.5 Να υπολογίσετε τη διάμετρο μιας ατράκτου που μεταφέρει ισχύ 43,1 HP περιστρεφόμενη με 300 rpm και το υλικό της είναι από St42. Με χρήση του τύπου 5.2 θα βρούμε αρχικά τη ροπή στρέψης που μεταφέρει η άτρακτος. Οι μονάδες είναι τέτοιες που θα βρεθεί σε kp cm. Θα έχουμε: Η ροπή βρέθηκε ίση με 10289,4 kp cm. Τώρα με χρήση του τύπου 5.3 θα βρούμε τη διάμετρο τα ατράκτου. Όμως δεν γνωρίζουμε την επιτρεπόμενη τάση στρέψης. Θα βρεθεί μέσω της πληροφορίας ότι η άτρακτος είναι από St42, οπότε από τον πίνακα της σελίδας 324 του βιβλίου βρίσκουμε ότι έτσι θα έχουμε: 70 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
71 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ ΚΕΦΑΛΑΙΟ 5 Επομένως η διάμετρος της ατράκτου είναι 7cm ή 70mm. Το σχολικό βιβλίο έχουμε ήδη αναφέρει ότι ορισμένες φορές χρησιμοποιεί την αντικατάσταση των μονάδων στους τύπους και άλλες όχι. Στην λυμένη άσκηση στη σελίδα 325 στην εφαρμογή του πρώτου τύπου χρησιμοποιεί τις μονάδες, αλλά όχι και στην εφαρμογή του τύπου για την εύρεση της διαμέτρου αμέσως μετά. Εσείς αν θέλετε τις βάζετε τις μονάδες, αν δεν θέλετε πρέπει να τις αναφέρετε. Προσέξετε πάντως όταν τις βάζετε να είστε σωστοί διότι υπάρχουν κάποιες δυσκολίες, όπως για παράδειγμα εδώ, όπου στο τέλος του υπολογισμού της διαμέτρου έχουμε την παράσταση που σε κάποιους μπορεί να φανεί περίεργη. Όμως έτσι πρέπει να γραφεί. Αν έχει δοθεί ένας από τους πίνακες (στην παρούσα άσκηση ο 14.6.γ) των σελίδων 324 ή 325 του σχολικού βιβλίου, μπορεί να ζητηθεί ο πρόχειρος υπολογισμός της διαμέτρου από αυτόν. Στην άσκηση που μόλις λύσαμε μπορούμε να κάνουμε το εξής: βρίσκουμε τον λόγο P/n και είναι: και με παρεμβολή μεταξύ 0,116 (για d=70mm) και 0,15 (για d=75mm) βρίσκουμε περίπου d=74mm, οπότε είμαστε πολύ κοντά στον αναλυτικό υπολογισμό. Να σημειώσουμε εδώ ότι η παρεμβολή είναι μια σχετικά πολύπλοκη μαθηματική μέθοδος, που δεν σας χρειάζεται για το μάθημα των Στοιχείων Μηχανών να τη μάθετε. Αρκεί να καταλάβετε ότι επειδή ο πίνακας δεν περιέχει τον αριθμό που έχετε (στη συγκεκριμένη περίπτωση τον 0,144) προσπαθούμε να προσεγγίσουμε την τιμή που θα είχε ο πίνακας για τη διάμετρο αν περιείχε όλους τους αριθμούς. Το 0,144 είναι πολύ κοντά στο 0,15 σε σχέση με το 0,116, άρα θα αντιστοιχεί διάμετρος πολύ κοντά στην d=75mm και παίρνουμε την d=74mm. Αν σας ζητηθεί να κάνετε υπολογισμό της διαμέτρου με αυτό τον τρόπο θα το κάνετε με τη λογική που μόλις περιγράψαμε. Άσκηση 5.6 Να υπολογιστεί η διάμετρος ατράκτου που περιστρέφεται με 1000 rpm και μεταφέρει ισχύ 69,81 HP και το υλικό της είναι από St60. Θα εργαστούμε ακριβώς όπως στην προηγούμενη άσκηση. Αρχικά θα βρούμε την ροπή στρέψης αφού γνωρίζουμε τις στροφές και την ισχύ. Οι μονάδες της ροπής θα βρεθούν σε kp cm. Για να βρούμε τη διάμετρο θα χρησιμοποιήσουμε τον τύπο 5.3, αλλά το δεύτερο μέρος του ώστε να εξοικειώνεστε και σε αυτή τη μορφή. Κατά τα άλλα δεν αλλάζει κάτι άλλο. Η επιτρεπόμενη τάση στρέψης βρίσκεται από τον πίνακα 14.6.β για το υλικό St60 ότι είναι Θα έχουμε: Επομένως βρέθηκε ότι η διάμετρος της ατράκτου θα πρέπει να είναι d=50 mm Ας δούμε με την χρήση του πίνακα 14.6.δ πόσο θα βρούμε. Πάμε σε αυτόν τον πίνακα γιατί περιέχει το υλικό St60. Υπολογίζουμε πρώτα τον λόγο P/n ο οποίος είναι:. Σύμφωνα με τον πίνακα πρέπει να κάνουμε παρεμβολή μεταξύ 0,044 (για d=55mm) και 0,082 (για d=60mm) και επειδή το 0,07 είναι πιο κοντά στο 0,082 από ότι στο ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 71
72 ΚΕΦΑΛΑΙΟ 5 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ 0,044 επιλέγουμε d=58mm. Παρατηρούμε ότι εδώ η διάμετρος βρέθηκε σχετικά πολύ μεγαλύτερη από την υπολογισθείσα. Αυτό όμως είναι φυσικό σε προσεγγιστικές (και όχι αναλυτικές-μαθηματικές) λύσεις. Με την ευκαιρία ας δούμε τι σημαίνουν οι ονομασίες St37, St42, St50 και St60 που υπάρχουν στον πίνακα 14.6.β του βιβλίου. Κατ αρχάς ότι πρόκειται για χάλυβα και μετά ο αριθμός δείχνει την αντοχή του σε εφελκυσμό, αρκεί να προσέξετε ότι ο St37 έχει σ επ =370, ο χάλυβας St42 έχει σ επ =420, ο χάλυβας St50 έχει σ επ =500 και ο χάλυβας St60 έχει σ επ =600. Καταλαβαίνουμε ότι το σύμβολο δείχνει και την αντοχή του χάλυβα. Άσκηση 5.7 Να υπολογίσετε την άτρακτο που περιστρέφεται με 715 rpm, μεταφέρει ισχύ ίση με 23HP και το υλικό από το οποίο θα κατασκευαστεί είναι χάλυβας St50 με Θα εργαστούμε όπως και στις προηγούμενες ασκήσεις υπολογίζοντας κατ αρχάς την ροπή στρέψης, της οποίας οι μονάδες θα είναι σε kp cm αφού οι στροφές είναι σε rpm και η ισχύς σε HP: Την τιμή 2303,9 kp cm της ροπής θα χρησιμοποιήσουμε στον τύπο 5.3 για τον υπολογισμό της διαμέτρου της ατράκτου: Επομένως η διάμετρος της ατράκτου θα είναι 40 mm. Μπορούμε να κάνουμε τον υπολογισμό με χρήση του πίνακα 14.6.δ όπου για St50 και. Σύμφωνα με τον πίνακα πρέπει να κάνουμε παρεμβολή μεταξύ 0,03 (για d=50mm) και 0,044 (για d=55mm) και επειδή το 0,032 είναι πιο κοντά στο 0,03 από ότι στο 0,044 επιλέγουμε d=51mm, που είναι πολύ κοντά στην υπολογισθείσα αναλυτικά. Άσκηση 5.8 Θέλουμε να κατασκευάσουμε μια άτρακτο με διάμετρο d=50mm η οποία να μεταφέρει ισχύ 40HP περιστρεφόμενη με n=600 rpm. Από τι υλικό πρέπει να κατασκευαστεί η άτρακτος; Αυτή η άσκηση είναι λίγο διαφορετική από εκείνες του βιβλίου, αλλά είναι μέσα στο πνεύμα των εξετάσεων. Εδώ ο άγνωστος είναι το υλικό της ατράκτου και αυτό προσδιορίζεται αν βρούμε την αντοχή που πρέπει να έχει σε στρέψη η άτρακτος. Αν δηλαδή υπολογίσουμε το τ επ της ατράκτου. Επομένως θα εργαστούμε λίγο αντίστροφα στον τύπο 5.3 που δίνει τη διάμετρο. Ας βρούμε όμως πρώτα την ροπή στρέψης: Αφού βρήκαμε την ροπή θα λύσουμε τον τύπο 5.3 ως προς την τ επ. Πρώτα θα μετατρέψουμε τις μονάδες της διαμέτρου από mm σε cm, αφού ο τύπος 5.3 δίνει τη διάμετρο σε cm. Άρα θα βάλουμε d=5 cm και θα έχουμε: Βρήκαμε ότι η επιτρεπόμενη τάση θα πρέπει να είναι ίση με. Για να επιλέξουμε το υλικό θα ψάξουμε στον πίνακα 14.6.β να βρούμε το υλικό με επιτρεπόμενη τάση μεγαλύτερη από την (αφού υλικό με ίσο με εκείνο που βρήκαμε είναι δύσκολο να υπάρχει) και αυτό είναι το St60 με 72 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
73 ΑΤΡΑΚΤΟΙ - ΑΞΟΝΕΣ ΚΕΦΑΛΑΙΟ 5 Στην άσκηση αυτή δεν βάλαμε μονάδες στην επίλυση του τύπου 5.3, όπως κάνει και το βιβλίο. Αν θέλουμε να βάλουμε τις μονάδες θα έχουμε τα εξής: Σημείωση: Για να λύσουμε την εξίσωση ως προς τ επ χρησιμοποιήσαμε λίγα μαθηματικά που μερικοί μαθητές δυσκολεύονται, γι αυτό θα τα κάνουμε πιο αναλυτικά. Πρώτα-πρώτα κάναμε την μετατροπή: των δύο μελών της εξίσωσης. Εφαρμόζεται τα θεωρήματα: Είχαμε δηλαδή την εξίσωση. Αυτό λέγεται ύψωση στην τρίτη δύναμη και και υψώσαμε και τα δύο μέλη της στον κύβο (τρίτη δύναμη). Χρησιμοποιήσαμε αυτό που θα κάναμε για να λύσουμε την εξής άσκηση: αν τότε, αλλά είναι γνωστό ότι, άρα αφού 2 3 =8. Άσκηση 5.9 Πόση πρέπει να είναι η διάμετρος μιας ατράκτου που μεταφέρει ροπή ίση με 1500 kp cm και είναι κατασκευασμένη από χάλυβα St50; Ο υπολογισμός να γίνει και α) με χρήση πινάκων του βιβλίου και β) αναλυτικά. α) Η εκτίμηση της διαμέτρου θα γίνει από τον πίνακα 14.6.δ ο οποίος δίνει τις διαμέτρους για χάλυβα St50. Για ροπή στρέψης M t =1500 kp cm, ο πίνακας δίνει διάμετρο μεταξύ 45 mm (για M t =1414 kp cm) και 50 mm (για M t =2153 kp cm). Με τη γραμμική παρεμβολή η διάμετρος θα είναι περίπου 46 mm. β) Γνωρίζοντας την ροπή στρέψης, θα υπολογίσουμε τη διάμετρο από τον τύπο 5.3. Από τον πίνακα 14.6.β για St50 βλέπουμε ότι Θα έχουμε: Υπολογίσαμε ότι η διάμετρος θα είναι 35 mm. Παρατηρούμε ότι στον αναλυτικό υπολογισμό η διάμετρος προκύπτει πάντα μικρότερη απ ό, τι με τη χρήση των πινάκων 14.6.γ ή 14.6.δ. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 73
74
75 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 6. Έδρανα Κύλισης (Ρουλεμάν) Τα έδρανα κύλισης είναι τα γνωστά μας ρουλεμάν. Ανήκουν στην κατηγορία των εδράνων μαζί με τα έδρανα ολίσθησης. Για την τελευταία κατηγορία δεν υπάρχουν ασκήσεις στο βιβλίο σας. Οι ασκήσεις εδράνων κύλισης που έχουν δοθεί ως τώρα στις εξετάσεις είναι παρόμοιες με εκείνες του βιβλίου. Σε αυτές πάντα ζητείται ο υπολογισμός δύο εδράνων στα άκρα μιας ατράκτου η οποία καταπονείται με μία ή δύο εγκάρσιες δυνάμεις. Κάθε άσκηση έχει δύο σκέλη για να φτάσουμε στη λύση της: α) να βρεθούν οι αντιδράσεις στα σημεία που τοποθετούνται τα ρουλεμάν και β) να γίνει ο υπολογισμός των συγκεκριμένων εδράνων κύλισης που θα πρέπει να τοποθετηθούν για να καλύψουν την καταπόνηση της ατράκτου, με χρήση πινάκων του βιβλίου. Το πρώτο σκέλος της άσκησης έχει καλυφθεί με παραδείγματα στο πρώτο κεφάλαιο, στην παράγραφο 1.6. Εκεί στα παραδείγματα μιλούσαμε για ράβδο ενώ εδώ θα μιλάμε για άξονα ή άτρακτο. Η άσκηση αντιμετωπίζεται με τον ίδιο τρόπο. Πρέπει να μπορείτε να βρίσκετε τις αντιδράσεις στα σημεία τοποθέτησης των εδράνων. Κατόπιν θα προχωράμε στην επιλογή των κατάλληλων εδράνων. Αυτό γίνεται με την ακόλουθη διαδικασία: Στην εκφώνηση της άσκησης πρέπει να δίνονται πληροφορίες για το που χρησιμοποιείται η άτρακτος, ώστε να γίνει η σωστή επιλογή του εδράνου. Για τη σωστή επιλογή από τους πίνακες πρέπει να γνωρίζουμε διάφορα στοιχεία που επηρεάζουν τη διάρκεια ζωής του εδράνου. Ένα είναι οι στροφές με τις οποίες αυτό θα περιστρέφεται. Καταλαβαίνουμε ότι όσο περισσότερες είναι τόσο πιο γρήγορα θα φθαρεί το έδρανο, άρα θα πρέπει να επιλέξουμε ένα πιο καλό. Ένας άλλος παράγοντας είναι πόσες ώρες προσδοκούμε να εργαστεί το έδρανο (θεωρητική διάρκεια λειτουργίας ή ζωής) μέχρι να το αντικαταστήσουμε. Αν έχουμε δυο ρουλεμάν που καταπονούνται με την ίδια δύναμη αλλά το ένα θέλουμε να εργαστεί (μέχρι την αντικατάστασή του) για 1000 ώρες ενώ το άλλο για ώρες, προφανώς το δεύτερο θα πρέπει να το επιλέξουμε καλύτερο. Με βάση αυτά και τη δύναμη που καταπονεί το έδρανο θα γίνει η επιλογή του από πίνακα του βιβλίου, που στις εξετάσεις θα σας δοθεί. Όταν έχουμε την εκφώνηση της άσκησης και έχουμε υπολογίσει και την δύναμη που καταπονεί το έδρανο κύλισης, κάνουμε τα εξής βήματα για τη σωστή επιλογή του ρουλεμάν: 1. Από τη μηχανή στην οποία μας λέει η εκφώνηση ότι βρίσκεται το έδρανο βρίσκουμε από τον πίνακα 14.7.γ της σελίδας 330 του βιβλίου την θεωρητική διάρκεια ζωής του σε ώρες. Για παράδειγμα αν η μηχανή είναι ένα μικρό αυτοκίνητο ο πίνακας δίνει στο Α/Α 8 δίνει θεωρητική διάρκεια λειτουργίας ίση με 1000 ως 2000 ώρες. Εμείς καλό είναι να παίρνουμε μια ενδιάμεση τιμή που να βρίσκεται και στον επόμενο πίνακα. Εδώ ας πούμε θα παίρναμε 1600 ώρες. Το βιβλίο σε ένα λυμένο παράδειγμα που έχει, αλλά και στις ασκήσεις που προτείνει προς λύση, παίρνει τη μέγιστη τιμή. Εμείς δεν είναι απαραίτητο να το ακολουθούμε. 2. Προχωράμε στον πίνακα 14.7.α της σελίδας 328 για να συνεχίσουμε. Εδώ εκτός από τον αριθμό των ωρών που έχουμε προσδιορίσει στο προηγούμενο βήμα, χρειαζόμαστε και τις στροφές με τις οποίες περιστρέφεται το ρουλεμάν. Αυτό πρέπει να δίνεται στην εκφώνηση. Ας πούμε ότι οι ώρες είναι οι 1600 που είπαμε πριν και μας δίνουν τις στροφές ότι είναι 2000 rpm. Θα πάμε στον πίνακα και θα βρούμε το νούμερο που αντιστοιχεί σε αυτά τα δύο. Οι 2000 rpm είναι στο δεύτερο μισό του πίνακα και οι 1600 ώρες δίνουν ένα αριθμό 5,75. Στο σχήμα της επόμενης σελίδας φαίνεται παραστατικά ο προσδιορισμός του αριθμού αυτού ο οποίος ονομάζεται λόγος φόρτισης C/P. Δηλαδή. 3. Στον λόγο φόρτισης, Ρ (ονομάζεται ισοδύναμο δυναμικό φορτίο) είναι η δύναμη που καταπονεί το έδρανο και οι μονάδες της είναι οπωσδήποτε σε Ν (Newton, μονάδες της δύναμης στο Διεθνές Σύστημα). C είναι το Δυναμικό φορτίο [στον πίνακα14.7.δ της σελίδας 331 ονομάζεται Βασικό Δυναμικό ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 75
76 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ Φορτίο (Basic Dynamic Load)]. Από την τιμή που βρήκαμε για τον λόγο φόρτισης C/P λύνουμε ως προς C και το βρίσκουμε σε μονάδες Ν. Για παράδειγμα αν έχουμε υπολογίσει Ρ=4000 Ν τότε θα έχουμε: Επομένως βρήκαμε ότι το C είναι Ν. Προχωράμε τώρα στην επιλογή του εδράνου. 4. Ο μόνος πίνακας για να επιλεγεί το έδρανο είναι ο 14.7.δ της σελίδας 331. Αφορά μονόσφαιρα έδρανα. Το κύριο στοιχείο για την επιλογή μας είναι ο C που θα τον βρούμε στην αντίστοιχη στήλη του πίνακα. Εμείς επιλέγουμε ένα ρουλεμάν που θα πρέπει να έχει λίγο μεγαλύτερη ή ίση τιμή για το C από την τιμή που βρήκαμε στο προηγούμενο βήμα. Ο τύπος του ρουλεμάν δίνεται στην τελευταία στήλη. Εμείς για το παράδειγμά μας όπου C=23.000Ν μπορούμε να επιλέξουμε όποιο ρουλεμάν θέλουμε με διάμετρο 45 mm έως 70 mm αρκεί να έχει έστω και λίγο μεγαλύτερο C από την τιμή Ν. Οι τύποι που μπορούμε να επιλέξουμε ανάλογα με τη διάμετρο φαίνονται στο σχήμα της επόμενης σελίδας. Έχουμε επιλέξει ένα τύπο από κάθε διάμετρο του πίνακα και αυτοί είναι: διάμετρος 45 mm τύπος 6209, διάμετρος 50 mm 76 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
77 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 τύπος 6210, διάμετρος 55 mm τύπος 6011, διάμετρος 60 mm τύπος 6012, διάμετρος 65 mm τύπος 6013, διάμετρος 70 mm τύπος Στις εξετάσεις εάν ζητηθεί να υπολογίσετε και να επιλέξετε ένα έδρανο κύλισης θα σας δίνονται και οι αντίστοιχοι πίνακες, φωτοτυπημένοι από το βιβλίο. Το πιο πιθανό επίσης είναι να σας δίνεται και η εσωτερική διάμετρος του εδράνου, ώστε να μπορείτε να επιλέξετε μόνο από τους τύπους αυτής της διαμέτρου τον έναν. Θα προχωρήσουμε τώρα στην επίλυση ορισμένων ασκήσεων στο πνεύμα του βιβλίου. Για να τις κατανοήσετε πιο εύκολα, πρέπει να έχετε υπ όψιν σας τις ασκήσεις της παραγράφου 1.6, όπου έχουν γίνει υπολογισμοί των αντιδράσεων αναλυτικότερα. Σε όλες θα έχουμε ως δεδομένο ότι 1 kp 10 N. Άσκηση 6.1 Να υπολογιστούν τα έδρανα κύλισης στα άκρα της ατράκτου του παρακάτω σχήματος, που έχει διάμετρο 50 mm. Η εγκάρσια δύναμη F=600 kp ασκείται στο μέσον της ατράκτου που έχει μήκος 80 cm. Η άτρακτος βρίσκεται σε βαγονέτο και περιστρέφεται με 500 rpm. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 77
78 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ Για τον υπολογισμό και την επιλογή των δύο εδράνων πρέπει να υπολογίσουμε τη δύναμη που ασκείται σε καθένα από αυτά. Αυτό σημαίνει ότι θα πρέπει να υπολογίσουμε τις αντιδράσεις στα σημεία που βρίσκονται τα έδρανα, στα άκρα της ατράκτου. Για τον υπολογισμό θα εφαρμόσουμε τις εξισώσεις ισορροπίας για την άτρακτο. Αυτές περιλαμβάνουν: α) Την εξίσωση για την ισορροπία των δυνάμεων και β) Την εξίσωση για την ισορροπία των ροπών. Αυτές οι δυο εξισώσεις ουσιαστικά αποτελούν ένα σύστημα δύο εξισώσεων με δύο αγνώστους, το οποίο επιλύουμε και τους βρίσκουμε. Βέβαια τα πράγματα είναι πιο απλά, όπως είδαμε και στην παράγραφο 1.6. Θα επιλέξουμε για την ισορροπία των ροπών ως σημείο περιστροφής το ένα άκρο της ατράκτου και από την εξίσωση που θα λύσουμε θα προκύψει η μία αντίδραση, οπότε από την ισορροπία των δυνάμεων (στον κατακόρυφο άξονα) θα προκύψει και η άλλη αντίδραση. Θα κάνουμε το επόμενο σχήμα με τα σημεία και τις αντιδράσεις για να έχουμε καλύτερη εποπτεία και κατανόηση των εξισώσεων. Οι αντιδράσεις στα σημεία Α και Β είναι η F A και η F B. Οι αποστάσεις των F A και η F B από την θέση της F είναι α και β που συμβαίνει εδώ να είναι ίσες με 40 cm κάθε μία. Παραθέτουμε λοιπόν τις δύο εξισώσεις ισορροπίας: Η πρώτη εξίσωση μας λέει ότι η δύναμη F που έχει φορά (κατεύθυνση) προς τα κάτω πρέπει να είναι ίση με τις F A και η F B που έχουν φορά προς τα επάνω. Η εξίσωση (2) λέει ότι αν θεωρήσουμε ακινητοποιημένη την άτρακτο στο άκρο Α (θεωρούμενο σημείο περιστροφής είναι δηλαδή το Α), τότε η ροπή της F B (που πάει να στρέψει την άτρακτο αριστερόστροφα) πρέπει να είναι ίση με τη ροπή της F (που πάει να στρέψει την άτρακτο δεξιόστροφα). Αυτές είναι οι δύο εξισώσεις που θα επιλύσουμε. Ξεκινάμε από την (2) διότι όπως είπαμε θα προκύψει η μία δύναμη, η F B. Θα έχουμε: Επομένως η μία αντίδραση είναι F B = 300 kp και η άλλη θα προκύψει από την εξίσωση (1): Βρήκαμε ότι οι δύο αντιδράσεις είναι ίσες με 300 kp. Αυτό είναι πολύ λογικό, αφού η F είναι 600 kp και ενεργεί στο μέσον της ατράκτου, άρα ισοκατανέμεται στα δύο άκρα. Θα 78 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
79 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 μπορούσαμε να το πούμε εξ αρχής και να μην κάνουμε τις πράξεις. Όμως το κάναμε αναλυτικά για δική σας εξάσκηση, στην γενική περίπτωση που η δύναμη ασκείται σε τυχαίο σημείο της ατράκτου. Έχοντας βρει τις αντιδράσεις μπορούμε να προχωρήσουμε στην επιλογή των κατάλληλων εδράνων. Ακολουθούμε τα βήματα που περιγράψαμε προηγουμένως. 1. Η εκφώνηση δίνει ότι το έδρανο βρίσκεται σε βαγονέτο και βρίσκουμε από τον πίνακα 14.7.γ της σελίδας 330 του βιβλίου την θεωρητική διάρκεια λειτουργίας του σε ώρες ότι είναι 5000 (είναι το νούμερο 11). 2. Από τον πίνακα 14.7.α της σελίδας 328 για 2000 rpm και 5000 ώρες βρίσκουμε από το πρώτο μέρος του πίνακα (επάνω υποπίνακα) το λόγο φόρτισης C/P ότι είναι 5, Υπολογίζουμε το C, αφού πρώτα βρούμε το P σε Ν. Το Ρ είναι στην περίπτωσή μας το F Α και το F B, δηλαδή τα 300 kp, που προσεγγιστικά είναι 3000Ν. Επομένως θα έχουμε: Με την τιμή του C=15.960Ν προχωράμε στην επιλογή του τύπου του εδράνου. 4. Επειδή το βιβλίο έχει μόνο μονόσφαιρα έδρανα θα κάνουμε την επιλογή από τον πίνακα 14.7.δ. Στην εκφώνηση δίνεται ότι η διάμετρος είναι 50 mm, οπότε γι αυτή τη διάμετρο και για C=15.960Ν η επιλογή είναι ο τύπος με C=16.300Ν. προφανώς και τα δύο έδρανα θα είναι ίδιου τύπου αφού δέχονται την ίδια καταπόνηση. Έτσι ολοκληρώνεται η άσκηση με την επιλογή των δύο εδράνων Ασφαλώς οι ασκήσεις αυτού του είδους δεν χρειάζονται τόσο αναλυτική λύση. Πρέπει να είστε πιο σύντομοι στη λύση σας. Εδώ δίνουμε πολλές διευκρινήσεις και γι αυτό παίρνει πολύ χώρο. Άσκηση 6.2 Να υπολογιστούν τα κατάλληλα έδρανα κύλισης στα άκρα Α και Β μιας ατράκτου που περιστρέφεται με 350 rpm. Η άτρακτος καταπονείται με τη δύναμη F=1200 kp που ασκείται στο σημείο όπως αυτό φαίνεται στο σχήμα πιο κάτω. Να λάβετε υπ όψιν σας ότι η άτρακτος ανήκει σε αγροτική μηχανή και έχει διάμετρο 55 mm. Πρέπει να υπολογίσουμε τις αντιδράσεις στις θέσεις των εδράνων τις οποίες συμβολίζουμε με F A και F B. Θα εφαρμόσουμε τις δύο σχέσεις για την ισορροπία των δυνάμεων και των ροπών. Αρχίζουμε με τις ροπές ως προς το σημείο Α: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 79
80 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ Αφού βρήκαμε την F B θα βρούμε την F Α με εφαρμογή της εξίσωσης για την ισορροπία των δυνάμεων: Αφού έχουμε βρει τις δύο αντιδράσεις που είναι οι δυνάμεις που καταπονούν τα έδρανα, θα προχωρήσουμε στην επιλογή των κατάλληλων εδράνων. Αρχικά σκεφτόμαστε ότι επειδή οι δυνάμεις F A και F B έχουν μεγάλη διαφορά ίσως είναι καλύτερα (για οικονομικούς λόγους) να επιλέξουμε ένα μικρό για τη θέση Α και ένα μεγαλύτερο ρουλεμάν για τη θέση Β. Επομένως θα γίνει δυο φορές η επιλογή. Σύμφωνα με την εκφώνηση τα έδρανα θα τοποθετηθούν σε αγροτική μηχανή και από τον πίνακα 14.7.γ του βιβλίου τα έδρανα σε αυτές έχουν διάρκεια λειτουργίας από 3000 ως 6000 ώρες (νούμερο 20 του πίνακα). Εμείς από τις τιμές που είναι μεταξύ των 3000 και των 6000 ωρών πρέπει να επιλέξουμε μία τιμή. Επιλέγουμε την τιμή 5000 ώρες η οποία υπάρχει και στον πίνακα για την επιλογή του λόγου φόρτισης. Οι στροφές που είναι 350 rpm βλέπουμε ότι δεν υπάρχουν στον πίνακα 14.7.α και για αυτό βρίσκουμε το λόγο φόρτισης που είναι πιο κοντά στις 350 rpm. Για 5000 ώρες και 320 rpm έχουμε C/P=4,56 ενώ για 5000 ώρες και 400 rpm έχουμε C/P=4,93. Με παρεμβολή μεταξύ των τιμών αυτών επιλέγουμε C/P=4,7 που θα είναι κοντά στην πραγματική τιμή για 350 rpm. Μετατρέπουμε τις F A και F B σε Ν και έχουμε: F A =8000 Ν και F B =4000 Ν. Από το λόγο φόρτισης C/P=4,7 βρίσκουμε το δυναμικό φορτίο C A και C B στις δύο περιπτώσεις. Τώρα από τον πίνακα 14.7.δ για τα μονόσφαιρα ρουλεμάν θα επιλέξουμε για διάμετρο 55 mm και για C Α = Ν το ρουλεμάν 6211 που θα τοποθετηθεί στη θέση Α της ατράκτου και για C Β = Ν το ρουλεμάν που θα τοποθετηθεί στη θέση Β της ατράκτου. 80 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
81 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 Στις παραπάνω εικόνες φαίνεται πως κάναμε την επιλογή του λόγου φόρτισης και των εδράνων. Θα μπορούσατε να επιλέξετε μόνο το έδρανο που δέχεται τη μεγαλύτερη ακτινική φόρτιση (το έδρανο που είναι στη θέση Α δηλαδή) αφού αυτό θα επαρκούσε και για τη θέση Β που δέχεται μικρότερο φορτίο. Άσκηση 6.3 Να υπολογιστούν τα κατάλληλα έδρανα κύλισης στα άκρα Α και Β μιας ατράκτου που καταπονείται με τη δύναμη F=200 kp και ασκείται στο σημείο όπως αυτό φαίνεται στο σχήμα πιο κάτω. Η άτρακτος περιστρέφεται με 1500 rpm και ανήκει σε μηχάνημα χαρτοποιίας με συνεχή λειτουργία, διαμέτρου 50 mm. Θα είμαστε τώρα περισσότερο σύντομοι στη λύση και λιγότερο αναλυτικοί. Από την ισορροπία των ροπών ως προς το σημείο Α θα έχουμε: Από την ισορροπία των δυνάμεων θα έχουμε: Μετατρέπουμε τις F A και F B σε Ν με την προσέγγιση 1 kp = 10 Ν και έχουμε: F A = 400 Ν και F B = 1600 Ν. Για μηχάνημα χαρτοποιίας με συνεχή λειτουργία έχουμε από τον πίνακα 14.7.γ διάρκεια λειτουργίας για τα έδρανα (νούμερο 31) ως ώρες. Επιλέγουμε μια ενδιάμεση τιμή που να βολεύει και αυτή είναι οι ώρες που υπάρχει και στον πίνακα για την επιλογή του λόγου φόρτισης. Ο λόγος φόρτισης βρίσκεται από τον πίνακα 14.7.α για ώρες και 1500 rpm. Οι στροφές δεν υπάρχουν ακριβώς και για το λόγο C/P με παρεμβολή μεταξύ του 16,8 για 1250 rpm και 18,2 για 1600 rpm επιλέγουμε την τιμή C/P = 17,8. Υπολογίζουμε το C για τις θέσεις Α και Β: Α: B: Από τον πίνακα 14.7.δ επιλέγουμε τα έδρανα για 50 mm σε κάθε θέση. Α: (C= N) Β: 6210 (C= N) Στην άσκηση αυτή παρατηρούμε ότι ενώ οι δυνάμεις F A και F B που ασκούνται στα ρουλεμάν δεν είναι πολύ μεγάλες, επιλέγονται ισχυρά έδρανα διότι το δυναμικό φορτίο ( C ) ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 81
82 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ είναι σχετικώς μεγάλο. Αυτό οφείλεται στις πολλές στροφές με τις οποίες περιστρέφονται και το αποτέλεσμα είναι να καταπονούνται πολύ. Άσκηση 6.4 Να λυθεί η ίδια με πριν άσκηση, μόνο που τώρα η δύναμη F θα ασκείται με ανάποδη φορά. Θα είναι δηλαδή από κάτω προς τα επάνω. Το σχήμα θα είναι το επόμενο. Η λύση δεν αλλάζει σε τίποτα από την προηγούμενη άσκηση, παρά μόνο στο ότι αλλάζει η φορά (κατεύθυνση) όλων των δυνάμεων. Οι εξισώσεις θα είναι ίδιες όπως και οι τιμές των μεγεθών. Οι αντιδράσεις στα έδρανα θα είναι πλέον όπως αυτές φαίνονται στο πιο πάνω σχήμα, αλλά οι τιμές τους θα είναι όσο βρέθηκαν στην προηγούμενη άσκηση. Επομένως τα έδρανα που επιλέχτηκαν πριν θα είναι τα ίδια. Τώρα θα κάνουμε μερικές ασκήσεις όπου δύο δυνάμεις καταπονούν τον άξονα. Στην παράγραφο 1.6 δόθηκε ένα παράδειγμα υπολογισμού των αντιδράσεων με δυο δυνάμεις και εξηγήθηκε αναλυτικά ο υπολογισμός τους. Εδώ θα είμαστε πιο σύντομοι. Σημειώνουμε ότι η διαδικασία δεν αλλάζει για τη λύση της άσκησης. Μόνο στις εξισώσεις ισορροπίας των δυνάμεων και των ροπών προστίθεται άλλη μία δύναμη. Άσκηση 6.5 Να υπολογιστούν τα έδρανα στα άκρα Α και Β μιας ατράκτου που καταπονείται με τις δυνάμεις F 1 και F 2 που ασκούνται στις θέσεις όπως αυτές φαίνονται στο σχήμα πιο κάτω. Η άτρακτος έχει διαμέτρου 50 mm και περιστρέφεται με 500 rpm. Ανήκει σε μικρό φορτηγό. Στο σχήμα φαίνονται οι αντιδράσεις F A και F B στις θέσεις Α και Β που πρέπει να υπολογιστούν. Για τις ροπές ως προς το σημείο Α έχουμε την ροπή της F A να είναι μηδέν, αφού η δύναμη περνά από το θεωρούμενο σημείο περιστροφής, η ροπή της F B είναι 82 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
83 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 αριστερόστροφη [και ίση με F B (α+β+γ)], η ροπή της F 1 που είναι δεξιόστροφη (και ίση με F 1 α) και η ροπή της F 2 που είναι δεξιόστροφη [και ίση με F 2 (α+β)]. Εφαρμόζοντας την εξίσωση ισορροπίας των ροπών ως προς το σημείο Α θα πρέπει η ροπή της F B να εξισορροπεί τις ροπές των F 1 και F 2 και θα έχουμε: Έχοντας βρει την F B, μπορούμε εύκολα να βρούμε την F Α εφαρμόζοντας την εξίσωση ισορροπίας των δυνάμεων: Έτσι υπολογίσαμε τις αντιδράσεις που είναι και οι δυνάμεις που καταπονούν τα έδρανα. Προχωράμε τώρα στην επιλογή των εδράνων, μετατρέποντας πρώτα τα kp σε Ν πολλαπλασιάζοντας με το 10 και έχουμε: F A =3500 Ν και F B =2500 Ν. Για τα μικρά φορτηγά η διάρκεια ζωής των ρουλεμάν είναι από 1500 ώρες μέχρι 2500 ώρες (νούμερο 9 του πίνακα 14.7.γ). Επιλέγουμε την ενδιάμεση τιμή 2000 ώρες, που περιλαμβάνεται και στους πίνακες για τον υπολογισμό του λόγου φόρτισης. Οι στροφές είναι 500 rpm και η τιμή αυτή βρίσκεται στον πίνακα 14.7.α, πράγμα που μας βολεύει. Συνδυάζοντας στροφές και ώρες βρίσκουμε λόγο φόρτισης C/P=3,91. Θέτοντας το Ρ διαδοχικά ίσο με F A =3500 Ν και F B =2500 Ν, βρίσκουμε τα δυναμικά φορτία C Α και C Β : Τώρα από τον πίνακα 14.7.δ και για τις τιμές αυτές του C και διάμετρο 50 mm επιλέγουμε και για τις δύο θέσεις Α και Β το έδρανο Σημείωση: Θα λύσουμε την ίδια ακριβώς άσκηση, αλλά σαν σημείο περιστροφής για τις ροπές θα πάρουμε αντί του Α το άλλο άκρο Β. Με εφαρμογή της εξίσωσης ισορροπίας των ροπών ως προς Β θα δούμε ότι υπολογίζεται η F A και όχι η F B όπως πριν. Ως προς το σημείο Β έχουμε την ροπή της F Β να είναι μηδέν, αφού η δύναμη περνά από το σημείο περιστροφής, η ροπή της F Α είναι δεξιόστροφη [και ίση με F Α (α+β+γ)], η ροπή της F 1 είναι αριστερόστροφη [και ίση με F 1 (β+γ)] και η ροπή της F 2 είναι αριστερόστροφη (και ίση με F 2 γ). Από την εξίσωση ισορροπίας των ροπών ως προς το σημείο Β θα πρέπει η ροπή της F Α να εξισορροπεί τις ροπές των F 1 και F 2 και θα έχουμε: Βλέπουμε ότι βρήκαμε ίδια τιμή με πριν για την F Α. Μπορούμε να βρούμε τώρα την F Β εφαρμόζοντας την εξίσωση ισορροπίας των δυνάμεων: Βλέπουμε ότι βρήκαμε τα ίδια αποτελέσματα. Θα μπορούσαμε να επιλέξουμε για την εφαρμογή της εξίσωσης για την ισορροπία των ροπών και άλλο σημείο της ατράκτου (και οποιοδήποτε άλλο σημείο του χώρου), απλά θα ήταν πιο δύσκολα τα μαθηματικά για την επίλυση των εξισώσεων (σύστημα εξισώσεων). Για τη δική σας εξάσκηση θα εφαρμόσουμε το θεώρημα των ροπών για το σημείο εφαρμογής Κ της δύναμης F 1. Ως προς αυτό έχουμε την ροπή της F 1 να είναι μηδέν, αφού η δύναμη περνά ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 83
84 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ από το σημείο περιστροφής, η ροπή της F Α είναι δεξιόστροφη (και ίση με F Α α), η ροπή της F Β που είναι αριστερόστροφη [και ίση με F Β (β+γ)] και η ροπή της F 2 που είναι δεξιόστροφη (και ίση με F 2 β). Η αριστερόστροφη ροπή της F Β θα είναι ίση με το άθροισμα των δεξιόστροφων ροπών των F Α και F 2. Δεν θα χρησιμοποιήσουμε μονάδες, γνωρίζοντας ότι οι δυνάμεις είναι σε kp και οι αποστάσεις σεm, οπότε το αποτέλεσμα θα είναι σε kp. Θα έχουμε: Βλέπουμε ότι εδώ δεν βρήκαμε κάποια από τις αντιδράσεις. Προχωράμε στην εξίσωση ισορροπίας των δυνάμεων: Αντικαθιστούμε από τη δεύτερη εξίσωση το F Α στην πρώτη και έχουμε: Βρήκαμε ότι η F B είναι ίση με 250 kp, τιμή που είχαμε βρει και στις άλλες περιπτώσεις. Ασφαλώς επιλύοντας την εξίσωση ισορροπίας των δυνάμεων θα βρούμε και την F Α : Όπως βλέπετε εδώ οι εξισώσεις είχαν λίγο περισσότερο κόπο, αλλά το αποτέλεσμα είναι το ίδιο. Άσκηση 6.6 Να υπολογιστούν τα έδρανα στα άκρα Α και Β μιας ατράκτου που καταπονείται με τις δυνάμεις F 1 και F 2 που ασκούνται στις θέσεις όπως αυτές φαίνονται στο σχήμα πιο κάτω. Η άτρακτος έχει διάμετρο 45 mm και περιστρέφεται με 800 rpm. Ανήκει σε αγροτική μηχανή. Προσέχουμε ότι εδώ μια δύναμη, η F 2 έχει αντίθετη φορά από την F 1. Αυτό δεν αλλάζει τα πράγματα, ως προς τη λύση. Εμείς θα εφαρμόσουμε τις γνωστές εξισώσεις για να βρούμε τις F A και F B και δεν μας ενοχλεί η φορά της F 2, αρκεί να προσέξουμε τις ροπές, ποιες είναι δεξιόστροφες και ποιες αριστερόστροφες ως προς το σημείο περιστροφής που θα επιλέξουμε. Μόνο μια παρατήρηση: ενδέχεται μία ή και οι δύο αντιδράσεις F A και F B να προκύψουν αρνητικές. Αυτό δε σημαίνει παρά μόνο ότι η φορά που έχουμε βάλει στο σχήμα είναι λάθος και έπρεπε να βάλουμε την αντίθετη. Δηλαδή όχι από κάτω προς τα επάνω, αλλά από πάνω προς τα κάτω. Ας δούμε την εξίσωση για την ισορροπία των ροπών με σημείο περιστροφής το Α. Η ροπή της F A θα είναι μηδέν, αφού η δύναμη περνά από το θεωρούμενο σημείο περιστροφής, η ροπή της F B είναι αριστερόστροφη [και ίση με F B (α+β+γ)], η ροπή της F 1 είναι δεξιόστροφη 84 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
85 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 (και ίση με F 1 α) και η ροπή της F 2 είναι αριστερόστροφη [και ίση με F 2 (α+β)]. Από την εξίσωση ισορροπίας των ροπών ως προς το σημείο Α θα πρέπει η ροπή της F 1 να εξισορροπεί τις ροπές των F 2 και F Β και θα έχουμε: Αφού βρήκαμε ότι η F B έχει αρνητική τιμή θα πρέπει η φορά της να είναι αντίθετη από εκείνη που σχεδιάσαμε, άρα είναι από πάνω προς τα κάτω. Αυτό πάντως δεν επηρεάζει την καταπόνηση που δέχεται το έδρανο. Έχοντας βρει την F B, θα βρούμε την F Α κάνοντας χρήση της εξίσωσης ισορροπίας των δυνάμεων. Αν αφήσουμε το αρνητικό πρόσημο στην F B θα γράψουμε την εξίσωση σύμφωνα με το σχήμα μας και θα έχουμε: Βρέθηκε ότι η F Α έχει θετική τιμή, άρα η σχεδιασμένη φορά της είναι σωστή. Υπολογίσαμε λοιπόν τις αντιδράσεις, που είναι και οι δυνάμεις που καταπονούν τα έδρανα. Στο επόμενο σχήμα φαίνονται οι δυνάμεις με τη σωστή φορά και τα μεγέθη τους. Για την επιλογή των εδράνων θα μετατρέψουμε πρώτα τα kp σε Ν πολλαπλασιάζοντας με το 10 και έχουμε: F A =400 Ν και F B =2400 Ν. Για τις αγροτικές μηχανές η διάρκεια ζωής των ρουλεμάν (νούμερο 20 του πίνακα 14.7.γ) είναι από 3000 ώρες μέχρι 6000 ώρες. Επιλέγουμε την ενδιάμεση τιμή 5000 ώρες, που περιλαμβάνεται και στους πίνακες για τον υπολογισμό του λόγου φόρτισης. Οι στροφές είναι 800 rpm και η τιμή αυτή ακριβώς βρίσκεται στον πίνακα 14.7.α, άρα δεν χρειάζεται παρεμβολή. Σύμφωνα με τις στροφές και τις ώρες βρίσκουμε λόγο φόρτισης C/P=6,20. Θέτοντας το Ρ διαδοχικά ίσο με F A =400 Ν και F B =2400 Ν, βρίσκουμε το δυναμικό φορτίο C: Από τον πίνακα 14.7.δ επιλέγουμε τα έδρανα για 45 mm σε κάθε θέση. Α: (C=6050 N) Β: (C= N) ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 85
86 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ Άσκηση 6.7 Να υπολογιστούν τα έδρανα στα άκρα Α και Β μιας ατράκτου που καταπονείται με τις δυνάμεις F 1 και F 2 που ασκούνται στις θέσεις όπως αυτές φαίνονται στο σχήμα πιο κάτω. Η άτρακτος έχει διάμετρο 70 mm και περιστρέφεται με 900 rpm. Ανήκει σε λεωφορείο. Εδώ το σχήμα φαίνεται λίγο περίεργο, αλλά η άσκηση δεν διαφέρει ιδιαίτερα από τις άλλες που έχουμε δει ως τώρα. Η δύναμη F 2 ασκείται έξω από την περιοχή της ατράκτου που βρίσκεται μεταξύ των δύο ρουλεμάν. Όμως εμείς θα δουλέψουμε τις εξισώσεις ισορροπίας δυνάμεων και ροπών όπως κάναμε και στις άλλες ασκήσεις. Ξεκινάμε με τις ροπές ως προς το σημείο περιστροφής Α και θα έχουμε για την ισορροπία τους: Η ροπή της F A θα είναι μηδέν, αφού η δύναμη περνά από το σημείο Α, η ροπή της F B είναι αριστερόστροφη [και ίση με F B (α+β)], η ροπή της F 1 είναι δεξιόστροφη (και ίση με F 1 α) και η ροπή της F 2 είναι δεξιόστροφη [και ίση με F 2 (α+β+γ)]. Από την εξίσωση ισορροπίας των ροπών ως προς το σημείο Α θα πρέπει η ροπή της F Β να εξισορροπεί τις ροπές των F 1 και F 2 και θα έχουμε: Έχουμε βρει την F B και μπορούμε εύκολα να βρούμε την F Α εφαρμόζοντας την εξίσωση ισορροπίας των δυνάμεων: Οι δυνάμεις αυτές (αντιδράσεις στα σημεία στήριξης) είναι εκείνες που καταπονούν τα έδρανα, και βάσει αυτών θα υπολογιστούν τα ρουλεμάν που πρέπει να τοποθετηθούν. Η επιλογή των εδράνων θα γίνει αφού μετατρέψουμε τα kp σε Ν πολλαπλασιάζοντας με το 10 και έχουμε: F A =8500 Ν και F B = Ν. Για τα μικρά λεωφορεία η διάρκεια ζωής των ρουλεμάν είναι από 2000 ώρες μέχρι 5000 ώρες (νούμερο 10 του πίνακα 14.7.γ). Επιλέγουμε την ενδιάμεση τιμή 4000 ώρες, που περιλαμβάνεται και στους πίνακες για τον υπολογισμό του λόγου φόρτισης. Οι στροφές είναι 900 rpm και η τιμή αυτή δεν βρίσκεται στον πίνακα 14.7.α. Για μονόσφαιρα έδρανα κύλισης από τον πίνακα, για 4000 ώρες και για 800 rpm έχουμε C/P=5,75 και για 1000 rpm έχουμε C/P=6,20. Με παρεμβολή ανάμεσα σε αυτές τις δύο τιμές του λόγου φόρτισης παίρνουμε C/P=5,98. Θέτοντας το Ρ ίσο με F A =8500 Ν και κατόπιν με F B = Ν, βρίσκουμε το δυναμικό φορτίο C: 86 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
87 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 Από τον πίνακα 14.7.δ επιλέγουμε τα έδρανα για 70 mm σε κάθε θέση. Α: 6214 (C= N) Β: 6414 (C= N) Στο θέμα των ασκήσεων το βιβλίο ασχολείται μόνο με το ζήτημα της επιλογής των κατάλληλων εδράνων σε ατράκτους που δίνει τα απαραίτητα στοιχεία για τον δέοντα υπολογισμό. Το λογικό είναι ότι μόνο τέτοιου είδους άσκηση θα μπει στις εξετάσεις. Όμως καλό είναι να δούμε και κάτι διαφορετικό, που όμως δεν ξεφεύγει από τα πιθανά θέματα. Δεν υπάρχει κάποια ιδιαίτερη δυσκολία στις επόμενες ασκήσεις που θα δούμε, απλά το σχολικό βιβλίο δεν έχει παρόμοια παραδείγματα. Άσκηση 6.8 Μια άτρακτος καταπονείται με τη δύναμη F που ασκείται στο μέσον της και περιστρέφεται με 800 rpm. Η άτρακτος έχει μήκος 2 m και ανήκει σε μικρό αυτοκίνητο. Αν υποθέσουμε ότι τα ρουλεμάν στα άκρα της ατράκτου έχουν υπολογιστεί για 2000 ώρες και είναι δύο ίδια μονόσφαιρα τύπου 6010, να βρείτε μέχρι πόσο (μέγιστη τιμή) μπορεί να είναι το μέγεθος της δύναμης F. Η άσκηση θα πρέπει να λυθεί ακολουθώντας μια αντίστροφη πορεία εκείνης που χρησιμοποιήσαμε ως τώρα. Ξεκινάμε από τον τύπο του ρουλεμάν, και με τη βοήθεια του πίνακα 14.7.δ θα βρούμε το δυναμικό φορτίο που μπορεί να δεχτεί το κάθε έδρανο. Ο τύπος 6010 είναι ένα ρουλεμάν διαμέτρου 50 mm και έχει C= N. Από τον πίνακα 14.7.α και για 2000 ώρες στις 800 rpm βρίσκουμε λόγο φόρτισης C/P=4,56. Αντικαθιστώντας στο λόγο φόρτισης την τιμή του C για τα ρουλεμάν που έχουμε θα βρούμε το φορτίο Ρ. Η τιμή του Ρ που βρήκαμε είναι η μέγιστη δύναμη που επιτρέπεται να ασκηθεί σε κάθε ρουλεμάν. Επειδή η μέγιστη δύναμη F που ζητά η άσκηση ασκείται στο μέσον της ατράκτου θα ισοκατανέμεται στα έδρανα. (Κανονικά αυτό πρέπει να το αποδείξουμε λύνοντας τις εξισώσεις ισορροπίας δυνάμεων και ροπών, όπως κάναμε στην άσκηση 6.1.) Αφού όμως κάθε έδρανο βρήκαμε ότι μπορεί να δεχθεί μέχρι 474 kp και τα δύο μαζί μπορούν να δεχτούν μέχρι 2 474=948 kp. Επομένως η ζητούμενη δύναμη είναι F=948 kp. Άσκηση 6.9 Έχουμε ένα έδρανο κύλισης τύπου 6310 και θέλουμε να το τοποθετήσουμε σε ένα μικρό ανυψωτικό μηχάνημα στο οποίο θα περιστρέφεται με 1200 rpm. Να βρείτε πόση ακτινική δύναμη μπορεί να δεχτεί αυτό το ρουλεμάν. Από τον πίνακα 14.7.δ του βιβλίου βρίσκουμε ότι το δυναμικό φορτίο που μπορεί να δεχτεί το έδρανο 6310 είναι C= N. Από τον πίνακα 14.7.γ για μικρό ανυψωτικό μηχάνημα βρίσκουμε ότι οι διάρκεια λειτουργίας του ρουλεμάν θα είναι μεταξύ 5000 και ώρες (νούμερο 21 στον πίνακα). Εμείς ας δεχτούμε τη διάρκεια ζωής 8000 ώρες. Από τον πίνακα 14.7.α θα βρούμε τον λόγο φόρτισης για 8000 ώρες και 1200 rpm. Με παρεμβολή, αφού η τιμή για τις 1200 rpm δεν υπάρχει στον πίνακα, βρίσκουμε ότι C/P=8,30. Με επίλυση της εξίσωσης αυτής ως προς τον άγνωστο Ρ βρίσκουμε το φορτίο που μπορεί να δεχτεί το ρουλεμάν: Επομένως η ακτινική φόρτιση που μπορεί να δεχτεί το έδρανο είναι 745 kp. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 87
88 ΚΕΦΑΛΑΙΟ 6 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ Άσκηση 6.10 Έχουμε ένα μονόσφαιρο έδρανο κύλισης τύπου 6010 το οποίο δίνεται για διάρκεια λειτουργίας (ζωής) 5000 ωρών. Αν η ακτινική δύναμη που το καταπονεί είναι 500 kp, να βρείτε με πόσες το πολύ στροφές πρέπει να περιστρέφεται η άτρακτος στην οποία θα τοποθετηθεί, ώστε να έχει τη διάρκεια ζωής για την οποία διατίθεται. Από τον πίνακα 14.7.δ του βιβλίου βρίσκουμε ότι το δυναμικό φορτίο που μπορεί να δεχτεί το έδρανο 6010 είναι C= N. Το φορτίο που δέχεται θα είναι Ρ=500 kp 5000 Ν, επομένως ο λόγος φόρτισης υπολογίζεται: Ο λόγος φόρτισης είναι 4,36 και εμείς πρέπει να βρούμε τον μέγιστο επιτρεπτό αριθμό στροφών για τη χρήση του. Από τον πίνακα 14.7.α βλέπουμε ότι για ένα δεδομένο αριθμό ωρών, όσο περισσότερες οι στροφές τόσο μεγαλύτερος ο λόγος φόρτισης. Αυτό σημαίνει ότι για ένα συγκεκριμένο ρουλεμάν, όσες πιο πολλές οι στροφές του τόσο μικρότερο το φορτίο που μπορεί να δεχτεί. Αυτό είναι λογικό αφού αν το ρουλεμάν περιστρέφεται πιο γρήγορα, για να αντέξει θα πρέπει να δέχεται μικρότερη δύναμη. Συμπερασματικά για τις 5000 ώρες θα μπορεί το ρουλεμάν να περιστρέφεται με στροφές λιγότερες από εκείνες που αντιστοιχούν σε λόγο φόρτισης μικρότερο του 4,36. Η τιμή αυτή δεν υπάρχει στον πίνακα 14.7.α για τις 5000 ώρες και το έδρανο θα μπορεί να περιστρέφεται με τις στροφές που αντιστοιχούν στις μικρότερες τιμές από την 4,36 του πίνακα. Για τις 5000 ώρες ο μεγαλύτερος λόγος φόρτισης (που είναι μικρότερος από 4,36) είναι ο 4,23 για 250 rpm. Επομένως το έδρανο κύλισης πρέπει να περιστρέφεται με λιγότερες από 250 στροφές το λεπτό. Καταλαβαίνουμε βέβαια ότι αν περιστρεφόταν με 320 στροφές το λεπτό ο λόγος φόρτισης είναι 4.56 που δεν επιτρέπεται τόσο μεγάλος. Άσκηση 6.11 Μία άτρακτος περιλαμβάνει ένα μονόσφαιρο έδρανο κύλισης τύπου 6011 και περιστρέφεται με 1000 rpm. Η ακτινική δύναμη που καταπονεί το ρουλεμάν είναι 300 kp και ζητείται να βρείτε τη διάρκεια λειτουργίας την οποία θα έχει. Θα υπολογίσουμε τον λόγο φόρτισης του εδράνου. Από τον πίνακα 14.7.δ για το έδρανο 6011 βρίσκουμε ότι C= N. Η δύναμη καταπόνησης είναι Ρ=300 kp 3000 Ν, επομένως ο λόγος φόρτισης υπολογίζεται: Στον πίνακα 14.7.α παρατηρούμε ότι ο λόγος φόρτισης αυξάνεται όσο αυξάνεται η διάρκεια ζωής του ρουλεμάν για σταθερές στροφές. Επομένως πρέπει να προσδιορίσουμε τη μέγιστη διάρκεια ζωής με λόγο φόρτισης ίσο ή μικρότερο του 9,37. Βλέπουμε ότι είναι οι ώρες με λόγο φόρτισης 9,11 9,37. Άρα ώρες είναι η διάρκεια ζωής του εδράνου. Σημείωση: Αν υποθέσουμε ότι οι στροφές ήταν λιγότερες από τις 1000 rpm καταλαβαίνουμε ότι το ρουλεμάν θα έπρεπε να έχει μεγαλύτερη διάρκεια ζωής, αφού θα καταπονείται λιγότερο. Πράγματι, αν οι στροφές ήταν οι μισές: 500 rpm βρίσκουμε διάρκεια ζωής μικρότερη από ώρες. Παρατηρούμε δηλαδή ότι η διάρκεια λειτουργίας του εδράνου είναι αντιστρόφως ανάλογη των στροφών του. Για να δούμε πόση θα ήταν η διάρκεια ζωής αν η δύναμη ήταν διπλάσια, δηλαδή 600 kp. Τότε: Ρ=600 kp 6000 Ν και ο λόγος φόρτισης: Βλέπουμε ότι ο λόγος φόρτισης είναι ο μισός από πριν. Για τις 1000 rpm με C/P=4,68 η διάρκεια λειτουργίας είναι μόλις 1600 ώρες. Δηλαδή ενώ διπλασιάστηκε η καταπόνηση με την ακτινική δύναμη, η διάρκεια λειτουργίας έγινε πολύ μικρότερη από την μισή. 88 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
89 ΕΔΡΑΝΑ ΚΥΛΙΣΗΣ ΚΕΦΑΛΑΙΟ 6 Τα έδρανα κύλισης έχουν κωδικοποιημένες ονομασίες και θα πρέπει να θυμόσαστε όχι τι σημαίνει κάθε αριθμός της ονομασίας, αλλά ποιο χαρακτηριστικό αντιπροσωπεύει. Αυτά αναφέρονται στη σελίδα 327 του βιβλίου, καθώς και στο σχήμα της σελίδας 199. Εκείνο που ως άσκηση είναι πιο σπουδαίο είναι ότι τα τελευταία δύο ψηφία δείχνουν την εσωτερική διάμετρο του ρουλεμάν, αφού έχει διαιρεθεί με το 5. Άρα αν πολλαπλασιάσουμε τα δύο τελευταία ψηφία του τύπου του ρουλεμάν με το 5 θα βρούμε την εσωτερική διάμετρο σε mm. Πχ. Το έδρανο 6210 έχει εσωτερική διάμετρο 10 5=50 mm, ενώ το έδρανο 6213 έχει εσωτερική διάμετρο ίση με 13 5=65 mm. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 89
90
91 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 7. Οδοντώσεις Το κεφάλαιο των ασκήσεων στις οδοντώσεις ασχολείται με τους οδοντωτούς τροχούς που είναι γνωστοί ως γρανάζια. Ως τροχοί που είναι, θα έχουν πολλά κοινά με τους άξονες στις ασκήσεις, αφού εκτελούν και εκείνοι περιστροφική κίνηση. Στην παράγραφο 1.7 είχαμε πει αρκετά σχετικά με την περιστροφική κίνηση που περιλαμβάνονται και στο κεφάλαιο των οδοντωτών τροχών. Έτσι θα πρέπει να ανατρέξετε μερικές φορές σε εκείνο το κεφάλαιο ώστε να έχετε αναλυτική ενημέρωση. Οι ασκήσεις τούτου του κεφαλαίου χωρίζονται σε ασκήσεις με τις λειτουργικές σχέσεις των οδοντωτών τροχών, με τη διαστασιολόγησή τους και με υπολογισμούς αντοχής Λειτουργικές σχέσεις οδοντωτών τροχών Πρώτα ας πούμε για την σχέση μετάδοσης, που συμβολίζεται με το γράμμα i και ορίζεται ως ο λόγος των στροφών του κινούμενου τροχού (n 2 ) προς τις στροφές του κινητήριου (n 1 ): Καταλαβαίνουμε ότι η σχέση μετάδοσης είναι ο αριθμός (καθαρός αριθμός, χωρίς μονάδες) που μας λέει πόσες φορές περισσότερες ή λιγότερες στροφές έχει ο κινούμενος τροχός από τον κινητήριο. Αν έχουμε για παράδειγμα i=2, τότε ο κινούμενος τροχός θα έχει διπλάσιες στροφές από τον κινητήριο. Άλλο παράδειγμα: αν i=0,5 τότε θα έχει τις μισές στροφές ο κινούμενος τροχός. Αν i=1,5 τότε ο κινούμενος τροχός θα έχει μιάμιση φορά περισσότερες στροφές από τον κινητήριο. Πχ. αν το κινητήριο γρανάζι περιστρέφεται με 100 rpm το κινούμενο γρανάζι θα περιστρέφεται με 150 rpm (αφού 1,5 100=150). Επομένως, αν η σχέση μετάδοσης είναι μεγαλύτερη από τη μονάδα τότε θα έχουμε αύξηση στροφών, ενώ αν είναι μικρότερη από τη μονάδα θα έχουμε μείωση (μειωτήρας στροφών). Πρέπει να σημειώσουμε ότι ο ορισμός μέσω της σχέσης 7.1 δεν είναι απόλυτος και πολλές φορές μπορεί να δείτε ότι η σχέση μετάδοσης είναι ο λόγος n 1 /n 2, δηλαδή ο αντίστροφος. Εσείς αν ερωτηθείτε στις εξετάσεις σε ερώτηση θεωρίας θα δώσετε τον πρώτο ορισμό, σύμφωνα με τον τύπο 7.1, ή σε μια άσκηση θα απαντήσετε βάσει αυτού. Ο αντίστροφος λόγος όταν χρησιμοποιείται γίνεται απολύτως κατανοητό σε τι αναφέρεται. Όπως ήδη γνωρίζουμε οι στροφές δύο αξόνων που συνεργάζονται, άρα και των οδοντωτών τροχών, είναι αντιστρόφως ανάλογες των διαμέτρων των τροχών. Πρέπει να προσέξουμε ότι στις οδοντώσεις η διάμετρος του τροχού που σχετίζεται με τις στροφές δεν είναι η εξωτερική (διάμετρος κεφαλών) αλλά η αρχική διάμετρος d 0. Έτσι θα ισχύει η σχέση: Υπενθυμίζουμε ότι όταν δύο γρανάζια συνεργάζονται, οι φανταστικές περιφέρειες (κύκλοι), που παριστάνουν τα γρανάζια και εφάπτονται καθώς φαίνονται να κυλίεται η μία στην επιφάνεια της άλλης, είναι οι αρχικές περιφέρειες των γραναζιών. Σε ένα οδοντωτό τροχό η αρχική περιφέρεια έχει διάμετρο την αρχική που συμβολίζεται με τον δείκτη μηδέν: d 0. Όταν έχουμε ένα ή περισσότερα ζεύγη συνεργαζόμενων γραναζιών οι αρχικές διάμετροί τους συμβολίζονται: d 01, d 02, d 03, d 04, κλπ. Η περιφέρεια (δηλαδή το μήκος) ενός κύκλου είναι γνωστό ότι είναι ανάλογο της διαμέτρου του κύκλου, αφού η περιφέρεια του κύκλου δίνεται από τον τύπο: Επομένως και ο αριθμός των δοντιών που είναι ανάλογος της περιφέρειας, θα είναι και ανάλογος της διαμέτρου. Άρα σε δύο συνεργαζόμενα γρανάζια που έχουν αρχικές διαμέτρους d 01 και d 02 και αριθμούς δοντιών z 1 και z 2 θα ισχύει η αναλογία: Οι σχέσεις 7.1, 7.2 και 7.3 συνδυαζόμενες δίνουν τη σχέση: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 91
92 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Η απόσταση των κέντρων των δύο γραναζιών (ή των αξόνων τους), που συμβολίζεται με α, θα είναι ίση με το άθροισμα των ακτινών τους, όπως φαίνεται και στο επόμενο σχήμα. Αλλά επειδή η ακτίνα είναι ίση με τη μισή διάμετρο, τότε η απόσταση α θα ισούται με το ημιάθροισμα των αρχικών διαμέτρων τους. Άρα θα ισχύει η σχέση: Αυτή η απόσταση είναι πολύ σημαντική γιατί καθορίζει την πραγματική απόσταση των αξόνων στους οποίους είναι τοποθετημένα τα γρανάζια. Για τη στρεπτική ροπή που μεταφέρει κάθε γρανάζι, ή μπορούμε να πούμε ο άξονας κάθε γραναζιού, ισχύουν αυτά που είπαμε στην παράγραφο για τις ατράκτους στο κεφάλαιο 5 και οι τύποι είναι ίδιοι με τους 5.1 και 5.2. Τους ξαναγράφουμε εδώ: Ο πρώτος από τους δύο δίνει τη ροπή στρέψης Μ σε μονάδες kp m και ο δεύτερος σε kp cm. Η ισχύς Ρ δίνεται σε HP ή PS και οι στροφές σε rpm. Στο κεφάλαιο αυτό το σχολικό βιβλίο χρησιμοποιεί τον πρώτο από τους δύο τύπους και οι μονάδες της ροπής είναι αντί του kp m το dan m, που έχουμε πει ότι είναι σχεδόν ίσα, αφού 1 kp 1 dan. Επίσης στο κεφάλαιο αυτό, για την ισχύ της ατράκτου, αντί του HP, που χρησιμοποιούσε στις ασκήσεις υπολογισμού ατράκτου, λύνει τις ασκήσεις εδώ με τη μονάδα PS, που είναι σχεδόν ίση με την HP. Οι τύποι 7.6 δείχνουν ότι η ροπή είναι αντιστρόφως ανάλογη των στροφών του άξονα με τον οποίο μεταφέρεται. Επομένως όταν δύο άξονες συνεργάζονται μέσω δύο γραναζιών, τότε οι στροφές των αξόνων n 1 και n 2 συνδέονται με τις ροπές στρέψης των αξόνων Μ 1 και Μ 2 με την ακόλουθη σχέση: Η ισχύς της σχέσης 7.7 προϋποθέτει ότι δεν έχουμε απώλεια ισχύος στο σύστημα των τροχών (λόγω τριβών) και η ισχύς του κινητήριου άξονα ισούται με την ισχύ του κινούμενου. 92 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
93 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Αν έχουμε απώλειες (δηλαδή ο βαθμός απόδοσης δεν είναι η μονάδα) τότε την ροπή ενός άξονα την υπολογίζουμε μόνο μέσω της σχέσης 7.6. Πολλές φορές έχουμε διαδοχικά πολλά ζεύγη οδοντωτών τροχών να συνεργάζονται, όπως στο κιβώτιο ταχυτήτων ενός αυτοκινήτου. Σε αυτή την περίπτωση το πρώτο ζεύγος γραναζιών περιλαμβάνει το πρώτο και το δεύτερο γρανάζι που συμβολίζουμε τις διαμέτρους τους με d 01 και d 02, όπου d 01 είναι το κινητήριο γρανάζι και d 02 το κινούμενο. Το δεύτερο ζεύγος γραναζιών περιλαμβάνει τα γρανάζια d 03 και d 04. Στα συνεργαζόμενα ζεύγη, το κινούμενο γρανάζι του πρώτου ζεύγους κινεί μία άτρακτο (την άτρακτο 1 στο επόμενο σχήμα) στην οποία είναι συνδεδεμένο το κινητήριο γρανάζι (το d 03 ) του δεύτερου ζεύγους, επομένως τα γρανάζια με διαμέτρους d 02 και d 03 κινούνται στην ίδια άτρακτο (την 2), άρα έχουν τις ίδιες στροφές n 2. Στο σχήμα που ακολουθεί φαίνονται τα δύο ζεύγη γραναζιών με τους τέσσερις τροχούς, οι διάμετροί τους, οι στροφές τους και οι άτρακτοι στις οποίες είναι συνδεδεμένοι. Όταν έχουμε να συνεργάζονται περισσότερα από ένα ζεύγη οδοντωτών τροχών, τότε έχουμε την σχέση μετάδοσης του συστήματος των γραναζιών (συμβολίζεται με i ολ ) και θα είναι ο λόγος των στροφών του τελευταίου τροχού προς τις στροφές του πρώτου. Επομένως στο παράδειγμα του σχήματος θα ισχύει: Η σχέση μετάδοσης του πρώτου ζεύγους θα είναι η i 1 και του δεύτερου η i 2. Από τον ορισμό της σχέσης μετάδοσης θα ισχύει: Αν πολλαπλασιάσουμε τις δύο σχέσεις μετάδοσης i 1 και i 2 μεταξύ τους (πολλαπλασιασμός κατά μέλη, λέγεται στα μαθηματικά) θα έχουμε: Παρατηρούμε ότι το γινόμενο των επί μέρους σχέσεων μετάδοσης, ισούται με τη συνολική σχέση μετάδοσης του συστήματος των οδοντωτών τροχών. Αυτό ισχύει όχι μόνο όταν έχουμε δύο ζεύγη γραναζιών αλλά και περισσότερα, εξ ου και η σχέση: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 93
94 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Στην παράγραφο 1.8 είχαμε δώσει τον ορισμό του βαθμού απόδοσης μιας μηχανής, ως το πηλίκο της ωφέλιμης ισχύος προς την καταναλισκόμενη. Σε ένα ζεύγος συνεργαζόμενων οδοντωτών τροχών ισχύει κάτι ανάλογο: βαθμός απόδοσης ενός ζεύγους γραναζιών είναι ο λόγος της ισχύος του κινούμενου γραναζιού (ωφέλιμη ισχύς, Ρ 2 ) προς την ισχύ του κινητήριου γραναζιού (καταναλισκόμενη ισχύς, Ρ 1 ). Είναι δηλαδή ένας αριθμός μικρότερος από τη μονάδα (χωρίς μονάδες-καθαρός αριθμός) που δείχνει πόση ισχύς μεταφέρεται με την οδόντωση στον κινούμενο άξονα από τον κινητήριο (άρα πόση χάνεται με τις τριβές των τροχών και των αξόνων). Ξαναγράφουμε τον τύπο ορισμού του βαθμού απόδοσης για τους οδοντωτούς τροχούς: Αν έχουμε ένα σύστημα πολλών ζευγών οδοντωτών τροχών με βαθμούς απόδοσης n 1, n 2, n 3 κλπ, τότε αποδεικνύεται ότι θα ισχύει η σχέση: Δηλαδή ο συνολικός βαθμός απόδοσης είναι ίσος με το γινόμενο των επί μέρους βαθμών απόδοσης των ζευγών των τροχών. Να προσέξετε λίγο τα σύμβολα γιατί στο σχολικό βιβλίο τον βαθμό απόδοσης και τις στροφές μπορεί να τις δείτε είτε με το ελληνικό «η» είτε με το αγγλικό «n». Εμείς στο βαθμό απόδοσης θα έχουμε το ελληνικό σύμβολο και στις στροφές το αγγλικό. Ας πούμε δυο λόγια για τις μονάδες που θα χρησιμοποιούμε στους προαναφερθέντες τύπους. Το καλύτερο είναι να βάζετε τις εξής μονάδες σε κάθε μέγεθος: στροφές- rpm, διάμετρος-mm, απόσταση αξόνων-mm, ισχύς-ps, ροπή-dan m, σχέση μετάδοσης και βαθμός απόδοσης καθαροί αριθμοί, χωρίς μονάδες. Αν χρησιμοποιήσετε διαφορετικές από αυτές τις μονάδες πρέπει να είστε πολύ προσεκτικοί. Για παράδειγμα στον τύπο 7.1 μπορεί οι στροφές να έχουν μονάδες στροφές το δευτερόλεπτο, αλλά θα πρέπει να τις έχουν και οι στροφές n 1 και οι n 2. Όμως στον τύπο 7.6 δεν μπορεί οι στροφές να έχουν μονάδες διαφορετικές από τις rpm. Τελικά το καλύτερο είναι αν η άσκηση δίνει τα μεγέθη αυτά σε άλλες μονάδες να τις μετατρέπετε στις αναφερθείσες πιο πάνω. Θα δούμε τώρα εφαρμογές των προαναφερθέντων σχέσεων σε συστήματα οδοντωτών τροχών. Άσκηση 7.1 Ο κινητήριος οδοντωτός τροχός σε ένα σύστημα δύο γραναζιών περιστρέφεται με 600 rpm και ο κινούμενος περιστρέφεται με 1500 rpm. Να βρείτε τη σχέση μετάδοσης του συστήματος. Κατ αρχήν πρέπει να αναγνωρίζουμε γνωστούς και αγνώστους της άσκησης και να βάζουμε τα κατάλληλα σύμβολα πριν ξεκινήσουμε τη λύση της άσκησης. Σύμφωνα με τον ορισμό και τον τύπο 7.1 η σχέση μετάδοσης i είναι ο λόγος των στροφών του κινούμενου τροχού n 2 (1500 rpm) προς τις στροφές του κινητήριου n 1 (600 rpm). Επομένως θα έχουμε: Άρα η ζητούμενη σχέση μετάδοσης είναι 2,5, που σημαίνει ότι οι στροφές του κινητήριου άξονα αυξάνονται κατά δυόμισι φορές με τη χρήση αυτών των γραναζιών. Άσκηση 7.2 Η σχέση μετάδοσης σε ένα σύστημα δύο γραναζιών είναι 2,4 και ο κινητήριος τροχός περιστρέφεται με 250 rpm. Να βρείτε με πόσες στροφές n 1 περιστρέφεται ο κινούμενος τροχός. Θα εφαρμόσουμε τον τύπο 7.1 τον οποίο θα λύσουμε ως προς n 2 που είναι ο άγνωστος. 94 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
95 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Επομένως ο κινούμενος τροχός θα περιστρέφεται με 600 rpm. Άσκηση 7.3 Η σχέση μετάδοσης σε ένα σύστημα δύο γραναζιών είναι 1,5 και ο κινούμενος τροχός περιστρέφεται με 750 rpm. Να βρείτε με πόσες στροφές περιστρέφεται ο κινητήριος τροχός. Σύμφωνα με την εκφώνηση έχουμε i=1,5 και n 2 =750 rpm. Θα εφαρμόσουμε τον τύπο 7.1 τον οποίο θα λύσουμε ως προς n 1 που είναι ο άγνωστος. Επομένως ο κινητήριος τροχός περιστρέφεται με 500 rpm. Άσκηση 7.4 Η σχέση μετάδοσης σε ένα σύστημα δύο γραναζιών είναι 3 και ο κινούμενος τροχός έχει αρχική διάμετρο 60 mm. Να βρείτε τη διάμετρο που έχει ο κινητήριος τροχός. Βάζουμε τα κατάλληλα σύμβολα στους γνωστούς και στον άγνωστο: i=3, d 02 =60 mm, d 01 : άγνωστος. Από τη σχέση 7.4 απομονώνουμε το τμήμα που μας ενδιαφέρει με τις διαμέτρους και τη σχέση μετάδοσης και λύνουμε ως προς τον άγνωστο: Επομένως η ζητούμενη διάμετρος του κινητήριου γραναζιού είναι d 01 =180 mm. Άσκηση 7.5 Ο κινητήριος οδοντωτός τροχός σε ένα σύστημα δύο γραναζιών περιστρέφεται με 1200 rpm και έχει αρχική διάμετρο 40 mm ενώ ο κινούμενος περιστρέφεται με 960 rpm. Α) Να βρείτε τη σχέση μετάδοσης του συστήματος. Β) Να υπολογίσετε την αρχική διάμετρο του άλλου τροχού Γ) Να βρείτε πόσα δόντια έχει ο κινούμενος αν ο κινητήριος έχει 45. Τοποθετούμε τα σωστά σύμβολα στα δεδομένα σύμφωνα με όσα γνωρίζουμε. Θα είναι: n 1 =1200 rpm, d 01 =40 mm, n 2 =960 rpm, z 2 =45. Επειδή έχει πολλές ερωτήσεις, τα σύμβολα των αγνώστων θα τα τοποθετήσουμε (ορίσουμε) όταν λύνουμε την αντίστοιχη ερώτηση. Μπορεί τα σύμβολα να είναι ίδια με εκείνα που χρησιμοποιεί το βιβλίο, όμως καλό είναι να τα λέμε και κατά τη λύση της άσκησης. Αν τα παραλείψετε δεν θα σας μειωθεί ο βαθμός, αρκεί να είναι ακριβώς ίδια με του σχολικού βιβλίου. Άλλωστε μπορούμε να τα αλλάξουμε, αν και πρέπει να το αποφεύγουμε, γιατί ίσως μας μπερδέψει. Αν παρ όλ αυτά αποφασίσετε να τα αλλάξετε, τότε πρέπει να ορίσετε σαφώς τα καινούρια σύμβολα. Α) Η σχέση μετάδοσης i θα βρεθεί με εφαρμογή της σχέσης 7.1 και θα έχουμε: Άρα η σχέση μετάδοσης είναι i=0,8 Β) Η αρχική διάμετρος του κινούμενου τροχού d 02 θα βρεθεί από τη σχέση 7.2 ή την 7.4. Θα το κάνουμε και με τις δύο. Ας πάρουμε πρώτα την 7.4 και από αυτήν θα επιλέξουμε μόνο αυτά που έχουν σχέση με τη σχέση μετάδοσης και τις διαμέτρους, οπότε θα έχουμε: Άρα ο κινούμενος τροχός θα έχει αρχική διάμετρο d 02 =50 mm. Η τιμή αυτή είναι λογική, αφού η σχέση μετάδοσης είναι μικρότερη από τη μονάδα, που σημαίνει ότι έχουμε μείωση στροφών, η οποία επιτυγχάνεται με μεγαλύτερο (από το κινητήριο) κινούμενο γρανάζι. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 95
96 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Ας υπολογίσουμε τώρα το d 02 μέσω της σχέσης 7.2. Θα έχουμε: Προφανώς βρήκαμε το ίδιο αποτέλεσμα, αλλά λύσαμε λίγο πιο δύσκολη εξίσωση. Γ) Εδώ ζητούμε τα δόντια z 1 που θα έχει ο κινητήριος τροχός. Πάλι μπορούμε να χρησιμοποιήσουμε δύο σχέσεις: την 7.3 ή την 7.4 με τη σχέση μετάδοσης. Θα πάρουμε την 7.4 που είναι πιο απλή και θα έχουμε: Επομένως ο κινητήριος τροχός θα έχει 36 δόντια, που είναι λογικό αφού είναι μικρότερος. Άσκηση 7.6 Δύο συνεργαζόμενα γρανάζια έχουν αρχικές διαμέτρους d 01 =60 mm και d 02 =100 mm. Να βρείτε την απόσταση των αξόνων που είναι τοποθετημένοι. Προφανώς θα χρησιμοποιηθεί ο τύπος 7.5 που δίνει τη ζητούμενη απόσταση α των αξόνων. Αντικαθιστώντας τις διαμέτρους θα έχουμε: Άρα η απόσταση των αξόνων είναι 80 mm. Άσκηση 7.7 Ένα γρανάζι έχει αρχική διάμετρο 120 mm και θα τοποθετηθεί για συνεργασία με άλλο γρανάζι σε άξονα που απέχει από τον άλλο απόσταση ίση με 180 mm. Α) Ποια θα είναι η διάμετρος του άλλου γραναζιού; Β) Ποια θα είναι η σχέση μετάδοσης μεταξύ των δύο γραναζιών; Α) Σύμφωνα με την εκφώνηση θα έχουμε τους συμβολισμούς α=180 mm και d 01 =120 mm. Το ότι θέσαμε το σύμβολο d 01 στην αρχική διάμετρο ήταν αυθαίρετο (αφού δεν γνωρίζουμε πιο γρανάζι είναι το κινητήριο) και θα μπορούσαμε να χρησιμοποιήσουμε και τον d 02. Δεν θα άλλαζε το αποτέλεσμα. Χρησιμοποιώντας τον τύπο 7.5 θα λύσουμε ως προς τον άγνωστο d 02 και θα έχουμε: Επομένως η αρχική διάμετρος του άλλου οδοντωτού τροχού θα είναι 240 mm. Β) Την σχέση μετάδοσης i θα βρούμε εφαρμόζοντας τον τύπο 7.4 για τη σχέση μετάδοσης και τις αρχικές διαμέτρους: Η σχέση μετάδοσης θα είναι 0,5. Άσκηση 7.8 Ένας κινητήρας έχει ισχύ ίση με 8 PS και ο άξονάς του περιστρέφεται με 1500 rpm. Στο άκρο του έχει γρανάζι αρχικής διαμέτρου 100 mm, το οποίο συνεργάζεται με γρανάζι άλλου άξονα στον οποίο θέλουμε να μεταφέρονται 600 rpm. Αν δεν έχουμε απώλεια ισχύος στο σύστημα των γραναζιών, να υπολογίσετε τα εξής: Α) Την ροπή του άξονα του κινητήρα. Β) τη ροπή του συνεργαζόμενου άξονα Γ) Πόση θα είναι η αρχική διάμετρος του γραναζιού του δεύτερου άξονα; Δ) Ποια είναι η σχέση μετάδοσης; Ε) Ποια η απόσταση των δύο αξόνων; 96 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
97 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Κατ αρχήν βάζουμε τα σύμβολα που θα χρησιμοποιηθούν στην άσκηση. Ορίζουμε ότι ο άξονας του κινητήρα και τα μεγέθη που σχετίζονται με αυτόν θα έχουν τον δείκτη 1, ενώ του συνεργαζόμενου άξονα τον δείκτη 2. Άρα η ροπή του άξονα του κινητήρα θα είναι Μ 1 και του συνεργαζόμενου Μ 2. Αυτές οι δύο ροπές ζητούνται. Θα είναι n 1 =1500 rpm, n 2 =600 rpm και d 01 =100 mm. Η διάμετρος d 02 ζητείται καθώς και η σχέση μετάδοσης i. Για την ισχύ των αξόνων θα έχουμε τους συμβολισμούς Ρ 1 και Ρ 2 και προφανώς ισχύει ότι Ρ 1 =Ρ 2 =8 PS. Η απόσταση των αξόνων συμβολίζεται κατά τα γνωστά με α. Προχωράμε στις απαντήσεις: Α) Η ροπή Μ 1 του πρώτου άξονα θα υπολογιστεί από τη σχέση 7.6: Επομένως η ροπή του κινητήριου άξονα είναι 3,82 dan m. Β) Η ροπή Μ 2 του κινούμενου άξονα θα υπολογιστεί και αυτή από τη σχέση 7.6: Επομένως η ροπή του κινούμενου άξονα είναι 9,55 dan m. Γ) Για τον υπολογισμό της αρχικής διαμέτρου d 02 του τροχού του κινούμενου άξονα θα χρησιμοποιήσουμε τον τύπο 7.2 λύνοντάς τον ως προς d 02 : Άρα ο κινούμενος τροχός θα έχει αρχική διάμετρο d 02 =250 mm. Δ) Η σχέση μετάδοσης θα υπολογιστεί από τον τύπο ορισμού της 7.1 και θα προκύψει: Άρα η ζητούμενη σχέση μετάδοσης είναι 0,4. Ε) Η απόσταση α των αξόνων υπολογίζεται από τη σχέση 7.5. Άρα η απόσταση των αξόνων είναι 175 mm. Άσκηση 7.9 Δύο οδοντωτοί τροχοί, με σχέση μετάδοσης ίση με 1,5 συνεργάζονται για να μεταδώσουν κίνηση σε ένα άξονα που περιστρέφεται με 800 rpm και έχει ένα γρανάζι που έχει αρχική διάμετρο 180 mm και 24 δόντια. Η μεταδιδόμενη ισχύς (δεν έχουμε απώλειες) είναι 16 PS. Ζητούνται: Α) Οι ροπές των δύο αξόνων. Β) Τα στοιχεία του πρώτου γραναζιού, δηλαδή: η αρχική διάμετρος, οι στροφές και ο αριθμός των δοντιών του. Γ) Η απόσταση των αξόνων Βάζουμε τα σύμβολα που θα χρησιμοποιηθούν στην άσκηση. Ορίζουμε ότι ο πρώτος άξονας και τα μεγέθη που σχετίζονται με αυτόν θα έχουν τον δείκτη 1, ενώ του συνεργαζόμενου άξονα τον δείκτη 2. Άρα η ροπή του πρώτου άξονα είναι Μ 1 και του συνεργαζόμενου Μ 2. Θα είναι σύμφωνα με την εκφώνηση: n 2 =800 rpm, d 02 =180 mm, i=1,5 και z 2 =24. Η διάμετρος d 01, οι στροφές n 1 και τα δόντια z 1 του πρώτου τροχού ζητούνται καθώς και η σχέση μετάδοσης i. Η απόσταση των αξόνων συμβολίζεται με α. Για την ισχύ των αξόνων θα έχουμε Ρ 1 και Ρ 2 και ισχύει ότι Ρ 1 =Ρ 2 =16 PS. Προχωράμε στις απαντήσεις: Α) Την ροπή Μ 2 στον δεύτερο άξονα την υπολογίζουμε από τη σχέση 7.6 και έχουμε: Επομένως υπολογίσαμε την ροπή στον δεύτερο άξονα Μ 2 =14,324 dan m. Για τον υπολογισμό της ροπής στον πρώτο άξονα θα χρησιμοποιήσουμε τον τύπο 7.7 με την σχέση μετάδοσης και θα έχουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 97
98 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Άρα η ροπή στον πρώτο και κινητήριο άξονα είναι Μ 1 =21,486 dan m. Β) Τα στοιχεία που ζητούνται θα υπολογιστούν από τη σχέση 7.4, παίρνοντας τη σχέση μετάδοσης χωριστά με κάθε κλάσμα, που περιέχει ένα άγνωστο. Υπολογίσαμε ότι η αρχική διάμετρος του γραναζιού στον πρώτο άξονα είναι d 01 =270 mm, έχει 36 δόντιά και περιστρέφεται με n 1 =533,333 rpm. Γ) Η απόσταση των αξόνων «α» θα βρεθεί με χρήση του τύπου 7.5: Η απόσταση των αξόνων θα είναι 225 mm. Άσκηση 7.10 Η ισχύς στον άξονα ενός κινητήρα είναι 20 PS και περιστρέφεται με 1000 rpm. Η ισχύς μεταφέρεται σε άλλο άξονα μέσω δύο γραναζιών με βαθμό απόδοσης 0,9. Αν τα γρανάζια έχουν σχέση μετάδοσης ίση με 0,5 να υπολογίσετε: Α) Την ισχύ που μεταφέρεται στον δεύτερο άξονα. Β) Τις στροφές του δεύτερου άξονα. Γ) Την ροπή στο πρώτο και στο δεύτερο άξονα. Τοποθετούμε τα κατάλληλα σύμβολα για τη λύση της άσκησης. Ορίζουμε ότι ο πρώτος άξονας έχει τον δείκτη «1» και ο δεύτερος τον δείκτη «2». Άρα θα είναι: ισχύς Ρ 1 =20 PS, στροφές n 1 =1000 rpm, σχέση μετάδοσης i=0,5, βαθμός απόδοσης η=0,9. Αυτά είναι τα γνωστά. Εκείνα που ζητούνται θα έχουν τα σύμβολα: Ρ 2, n 2, Μ 1, Μ 2. Προχωράμε στη λύση της άσκησης: Α) Από τον ορισμό του βαθμού απόδοσης, τον τύπο 7.9, θα βρούμε την ισχύ του κινούμενου άξονα: Άρα ο δεύτερος άξονας (κινούμενος) έχει ισχύ 18 PS. Β) Οι στροφές του δεύτερου άξονα θα υπολογιστούν από τη σχέση μετάδοσης, τύπος 7.1: Επομένως ο κινούμενος άξονας θα περιστρέφεται με 500 rpm. Γ) Για τις ροπές εφαρμόζουμε τον τύπο 7.6 μία φορά για κάθε άξονα με την ισχύ και τις στροφές του καθενός όπως αυτά δίνονται ή υπολογίστηκαν. Επομένως υπολογίσαμε ότι η ροπή του κινητήριου άξονα είναι 14,324 dan m, ενώ του κινούμενου είναι 25,783 dan m. Σημείωση: Παρατηρούμε ότι αν διαιρέσουμε τις δύο ροπές αυτές δεν θα βρούμε την σχέση μετάδοσης του συστήματος των οδοντωτών τροχών σύμφωνα με τον τύπο 7.7: 98 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
99 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Ούτε ισχύει η σχέση 7.7 με τις ροπές και τις στροφές: Αυτές οι «παρατυπίες» οφείλονται στο ότι υπάρχει απώλεια ισχύος, και όπως είπαμε όταν γράψαμε πρώτη φορά τη σχέση 7.7, για τον υπολογισμό της ροπής, όταν ο βαθμός απόδοσης δεν είναι μονάδα, εφαρμόζουμε τον τύπο 7.6. Αν δεν είχαμε απώλεια ισχύος η ροπή του κινούμενου άξονα θα ήταν διπλάσια από τη ροπή του κινητήριου: Η τιμή αυτή αν πολλαπλασιαστεί με τον βαθμό απόδοσης 0,9 θα μας δώσει την σωστή τιμή που βρήκαμε πριν. Πράγματι: Άσκηση 7.11 Θέλουμε να κατασκευάσουμε ένα μειωτήρα στροφών, ώστε οι στροφές του κινητήρα που είναι 1500 rpm να μειωθούν στις 250 rpm. Αν χρησιμοποιήσουμε δύο ζεύξη γραναζιών, να δώσετε δύο παραδείγματα σχέσεων μετάδοσης και τις αντίστοιχες στροφές, που θα ταίριαζαν για να κάνουμε την επιθυμητή μείωση στροφών. Θέτουμε τα κατάλληλα σύμβολα στις στροφές που δίνονται στην εκφώνηση: n 1 =1500 rpm και n 2 =250 rpm. Η σχέση μετάδοσης που θέλουμε να πραγματοποιήσουμε είναι σύμφωνα με τον τύπο 7.1: Τα δύο ζεύγη γραναζιών θα έχουν σχέσεις μετάδοσης i 1 και i 2 και σύμφωνα με τον τύπο 7.8 θα πρέπει να ισχύει: i = i 1 i 2. Πρέπει δηλαδή να βρούμε δύο αριθμούς i 1 και i 2 των οποίων το γινόμενο να δίνει αποτέλεσμα 1/6. Για να λύσουμε πιο απλά την άσκηση θα βρούμε δύο αριθμούς που το γινόμενό τους να δίνει 6 και μετά θα τους αντιστρέψουμε για να βρούμε τις σωστές σχέσεις μετάδοσης. Δύο τέτοιοι αριθμοί είναι το 2 και το 3 αφού: 2 3=6. Επομένως οι σχέσεις μετάδοσης που θα έχουμε τότε είναι οι και αφού Για να βρούμε τις στροφές του δεύτερου γραναζιού του πρώτου ζεύγους (τις οποίες στροφές θα συμβολίσουμε με n 12 ) με σχέση μετάδοσης i 1, εφαρμόζουμε τον τύπο 7.1 και λύνουμε ως προς το n 12. Προσέξτε ότι το κινητήριο γρανάζι είναι το γρανάζι με τις στροφές n 1 και θα μπουν οι στροφές αυτές στον παρονομαστή του κλάσματος. Άρα το δεύτερο γρανάζι στο πρώτο ζεύγος θα έχει 750 rpm και θα είναι τώρα αυτές οι στροφές που θα δίνουν κίνηση στο δεύτερο ζεύγος τροχών. Επομένως οι στροφές n 12 θα είναι οι στροφές του πρώτου γραναζιού στο δεύτερο ζεύγος. Ας εφαρμόσουμε τον τύπο για τη σχέση μετάδοσης να επαληθεύσουμε ότι το δεύτερο ζεύγος έχει σχέση μετάδοσης 1/3. Οι στροφές n 12 θα μπουν στον παρονομαστή του κλάσματος αφού είναι του κινητήριου γραναζιού. Άρα όντως η δεύτερη σχέση μετάδοσης είναι η αναμενόμενη. Θα μπορούσαμε να χρησιμοποιήσουμε τη σχέση μετάδοσης 1/3 και τις στροφές n 2 για να επαληθεύσουμε το ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 99
100 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ αποτέλεσμα που βρήκαμε για τις στροφές n 12. Κάνει το ίδιο. Το επόμενο σχήμα δείχνει το σύστημα των γραναζιών με τα αποτελέσματα. Το μέγεθος των γραναζιών στο σχήμα είναι το ανάλογο και κατάλληλο για τις στροφές που αντιστοιχούν σε αυτές. Αν θέλουμε να βρούμε τις στροφές για ένα άλλο ζεύγος γραναζιών με συνολική σχέση μετάδοσης 1/6, θα βρούμε δυο αριθμούς πάλι που το γινόμενό τους να δίνει 6. Αυτοί μπορεί να είναι το 4 και το 1,5. Πράγματι: 4 1,5=6. Αν η πρώτη σχέση μετάδοσης είναι 1/4 οι στροφές του δεύτερου γραναζιού θα είναι 4 φορές πιο λίγες άρα θα είναι1500:4=375 rpm. Και μετά αν διαιρεθεί το 375 με το 1,5 πρέπει να βρούμε τις στροφές του τελευταίου γραναζιού. Πράγματι: 375:1,5=250 rpm. Άρα ο ενδιάμεσος άξονας που έχει τα δύο γρανάζια θα περιστρέφεται με 375 rpm. Αν στο τελευταίο παράδειγμα το πρώτο ζεύγος τροχών είχε τη σχέση μετάδοσης 1/1,5, (αυτή η σχέση είναι ισοδύναμη με την 2/3) τότε για να βρούμε τις στροφές του ενδιάμεσου άξονα πρέπει να διαιρέσουμε τις αρχικές στροφές με το 1,5 και θα έχουμε: 1500:1,5=1000 rpm. Δηλαδή με αυτό το συνδυασμό οι στροφές του ενδιάμεσου άξονα είναι 1000 rpm. Και αν διαιρεθούν οι 1000 rpm με το 4 θα βρούμε τις στροφές του τελευταίου γραναζιού. Πράγματι: 1000:4=250 rpm. Η διαφορά από την προηγούμενη περίπτωση, εκτός από τη διαφορά των στροφών στο ενδιάμεσο γρανάζι, είναι φυσικά και η διαφορά στα μεγέθη των δύο γραναζιών του ενδιάμεσου άξονα. Τα επόμενα σχήματα δείχνουν τα αποτελέσματα σε αυτές τις δύο περιπτώσεις. Τα μεγέθη των διαμέτρων των τροχών στα σχήματα είναι εκείνα που αντιστοιχούν στις στροφές που πήραμε στις δύο περιπτώσεις. Άσκηση 7.12 Ένας άξονας περιστρέφεται με 3000 rpm και θέλουμε να μειώσουμε τις στροφές στις 250 rpm χρησιμοποιώντας τρία ζεύγη οδοντωτών τροχών με μικρότερες σχέσεις μετάδοσης. Θέλουμε και στα τρία ζεύγη ο μικρός τροχός να έχει την ίδια αρχική διάμετρο που είναι ίση με d 0 =60 mm. Από τις πολλές επιλογές που έχετε για τις αρχικές διαμέτρους των γραναζιών των τριών ζευγών, να επιλέξετε μία και να υπολογίσετε τις διαμέτρους των άλλων τροχών. 100 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
101 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Θέτουμε τα κατάλληλα σύμβολα στα δεδομένα και στα ζητούμενα της άσκησης: n 1 =3000 rpm, n τ =250 rpm (θέσαμε αυτό το συμβολισμό για να δείξουμε ότι οι τελικές στροφές του συστήματος των τροχών είναι οι 250 rpm). Στο επόμενο σχήμα φαίνεται το σύστημα των οδοντωτών τροχών με όλα τα χαρακτηριστικά στοιχεία τους. Οι σχέσεις μετάδοσης είναι αντίστοιχα i 1, i 2 και i 3. Οι τρεις ζητούμενες διάμετροι είναι d 01, d 02 και d 03. Οι στροφές των δύο ενδιάμεσων αξόνων είναι n 2 και n 3. Βλέπουμε στο σχήμα ότι και στα τρία ζεύγη ο μικρός τροχός έχει την ίδια διάμετρο. Η σχέση μετάδοσης του συστήματος i συν θα είναι ο λόγος των στροφών του τελευταίου άξονα n τ προς τις στροφές του πρώτου n 1. Θα υπολογιστεί από τη γνωστή σχέση 7.1: Αφού υπάρχουν τρία ζεύγη τροχών, θα πρέπει να κάνουμε τον αριθμό 12 γινόμενο τριών αριθμών, όχι απαραίτητα ακεραίων. Μια εύκολη επιλογή είναι η αφού 3 2 2=12 και οι σχέσεις μετάδοσης στα τρία ζεύγη θα είναι 1/3, 1/2 και 1/2. Μια άλλη επιλογή είναι το 4-2-1,5 αφού το γινόμενό τους είναι 4 2 1,5=12. Αυτές οι επιλογές θα μπορούσαν να είναι με τους ίδιους αριθμούς αλλά με άλλη σειρά. Πχ. Αντί να είναι ή Προφανώς οι αρχικές και τελικές στροφές δεν θα αλλάξουν σε αυτές τις εναλλακτικές περιπτώσεις. Μόνον οι στροφές των ενδιάμεσων αξόνων και η διάταξη των τροχών σε αυτούς. Στο σχήμα φαίνεται, με διακεκομμένης γραμμής βέλη, η διαδρομή της μετάδοσης της κίνησης μέσω των τροχών και των αξόνων. Για τη λύση της άσκησης επιλέγουμε τις σχέσεις μετάδοσης που διαλέξαμε στην αρχή, δηλαδή: 1/3, 1/2 και 1/2. Θα υπολογίσουμε τις αρχικές διαμέτρους d 01, d 02 και d 03 των τριών οδοντωτών τροχών που συνεργάζονται με τους τρεις τροχούς που έχουν όλοι αρχική διάμετρο d 0. Αυτό θα γίνει διαδοχικά μέσω των γνωστών σχέσεων μετάδοσης. Σύμφωνα και με το σχήμα του συστήματος και τον τύπο 7.4 για τις διαμέτρους και τη σχέση μετάδοσης, θα ισχύουν οι σχέσεις: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 101
102 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Επομένως οι ζητούμενες διάμετροι των τροχών θα είναι αντιστοίχως 180 mm, 120 mm και 120 mm. Σημείωση: Η λύση των προηγούμενων εξισώσεων για τον υπολογισμό των διαμέτρων μπορεί να γίνει και χωρίς να χρησιμοποιήσουμε γνώσεις από τα μαθηματικά για τα σύνθετα κλάσματα. Θα αντικαταστήσουμε την τιμή της σχέσης μετάδοσης από την αρχή και έτσι θα έχουμε: Ομοίως θα υπολογίζαμε και τις άλλες διαμέτρους Διαστασιολόγηση και αντοχή παράλληλων οδοντωτών τροχών Διαστασιολόγηση σημαίνει να βρούμε τις επί μέρους διαστάσεις ενός αντικειμένου και εδώ εννοείται ότι είναι οι διαστάσεις των οδοντωτών τροχών. Συγκεκριμένα θα λύσουμε ορισμένες ασκήσεις που θα χρησιμοποιούν τις σχέσεις για τις διαστάσεις του παρακάτω πίνακα, για ένα οδοντωτό τροχό. Δίνονται σε αυτόν τα σύμβολα και οι τύποι υπολογισμού για μια κανονική οδόντωση. Κανονικό δόντι είναι εκείνο για του οποίου τις διαστάσεις ισχύουν οι πιο κάτω σχέσεις. Είναι μια συμφωνία μεταξύ των κατασκευαστών για την ομοιομορφία των οδοντώσεων. Τα περισσότερα από τα μεγέθη του οδοντωτού τροχού φαίνονται και στο σχήμα που ακολουθεί με τα δύο δόντια. Βασικό χαρακτηριστικό των κανονικών οδοντώσεων είναι το τυποποιημένο modul, το οποίο στα ελληνικά ονομάζεται διαμετρικό βήμα. Το modul ορίζεται από τις σχέσεις που φαίνονται στον παραπάνω πίνακα και έχει συγκεκριμένες τιμές, και δεν μπορεί να έχει διαφορετικές από αυτές. Οι τιμές του δίνονται από ένα πίνακα (σελίδα 235 του σχολικού βιβλίου) και οι διαστάσεις του είναι σε mm. Εδώ ξαναγράφουμε τις τιμές αυτές με αύξουσα σειρά: 0,1 0,12 0,16 0,20 0,25 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,25 1,5 2 2, Modul m (7.11) Βήμα t (7.12) Ύψος κεφαλής h k (7.13) Ύψος ποδιού h f (7.14) Ύψος δοντιού h (7.15) Πάχος δοντιού s (περίπου) (7.16) Διάκενο δοντιού w (περίπου) (7.17) Μήκος δοντιού (πάχος γραναζιού) Διάμετρος κεφαλών b (7.18) d k (7.19) (7.20) (7.21) 102 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
103 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Εκτός από τις παραπάνω σχέσεις, σημειώνουμε ότι για χυτά ακατέργαστα δόντια το πάχος του δοντιού θα είναι: Και για κατεργασμένα σε εργαλειομηχανές το πάχος θα είναι: Εννοείται ότι το υπόλοιπο τμήμα από το βήμα θα είναι το διάκενο w. Για να έχουμε μέτρο σύγκρισης μεταξύ των δύο αυτών σχέσεων θα ξαναγράψουμε την 7.22 με παρονομαστή ίδιον με εκείνο της 7.23:. Δηλαδή από το βήμα τα είναι το δόντι, ενώ στα κατεργασμένα το δόντι είναι τα. Επομένως στα ακατέργαστα δόντια το πάχος του δοντιού είναι μικρότερο από το πάχος του στα κατεργασμένα. Αυτό οφείλεται στο ότι τα ακατέργαστα έχουν μικρότερη ακρίβεια και τα δόντια γίνονται πιο λεπτά για να μην υπάρχουν μεγάλες τριβές και φθορές. Σημειώνουμε ότι στον πίνακα δίνεται ότι το πάχος του δοντιού είναι περίπου όσο και το μισό βήμα, άρα περίπου ίσο με το διάκενο. Αν θέλουμε ακρίβεια υπολογισμών θα χρησιμοποιήσουμε τις σχέσεις 7.22 ή Πρέπει να προσέξουμε ότι το πάχος του δοντιού, το διάκενο και το βήμα μετρώνται πάνω στην αρχική περιφέρεια. Δεν είναι ευθείες γραμμές αλλά τόξα κύκλου. Κατά την επιλογή των οδοντωτών τροχών πρέπει να προσέξουμε τους περιορισμούς στον αριθμό των δοντιών. Αν γίνονται με ειδική χάραξη τότε ο ελάχιστος αριθμός τους είναι 12, ενώ αν μας δίνεται γενικά μια οδόντωση η επιλογή μας δεν πρέπει να δίνει στον τροχό περισσότερα από 18 δόντια. Όταν κατασκευάζονται οδοντώσεις καλής ποιότητας προσέχουμε ώστε οι σχέσεις μετάδοσης να είναι της μορφής κλάσματος με αριθμητή τη μονάδα:,,,,, κλπ. Όταν όμως κατασκευάζονται γρανάζια κακής ποιότητας τότε προτιμώνται οι σχέσεις μετάδοσης που ο αριθμητής και ο παρονομαστής του κλάσματος είναι πρώτοι αριθμοί μεταξύ τους, δηλαδή:, κλπ. Όταν η οδόντωση είναι καλής ποιότητας είναι καλύτερο κάθε δόντι του μεγάλου γραναζιού να συνεργάζεται σε κάθε περιστροφή του πάντα με το ίδιο διάκενο του μικρού γραναζιού και αυτό επιτυγχάνεται με τις προαναφερθείσες σχέσεις μετάδοσης. Αντιστρόφως, όταν τα γρανάζια είναι μέτριας ποιότητας, είναι προτιμότερο κάθε δόντι του μεγάλου γραναζιού να μπαίνει σε περισσότερα του ενός διάκενα του μικρού γραναζιού, ώστε να υφίσταται ομοιόμορφη φθορά. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 103
104 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Για να κατανοήσετε καλύτερα τα προηγούμενα με τους αριθμούς θα υποθέσουμε ότι έχουμε δυο συνεργαζόμενα γρανάζια με σχέση μετάδοσης. Για λόγους απλότητας υποθέτουμε ότι το μικρό γρανάζι έχει 3 δόντια και το μεγάλο θα έχει 9, αφού η σχέση μετάδοσης είναι. Ας αριθμήσουμε κάθε δόντι του μικρού τροχού με τα γράμματα α, β και γ και του μεγάλου τροχού με τους αριθμούς 1, 2, 3, 4, 5, 6, 7, 8, και 9. Κατά τη συνεργασία των δύο τροχών το δόντι α συνεργάζεται με το δόντι 1 του μεγάλου τροχού, το β με το 2, το γ με το 3 και ξανά το α με το 4 τώρα κλπ. Στον επόμενο πίνακα φαίνονται αυτές οι συνεργασίες των δοντιών. α β γ α β γ α β γ α β γ α β γ α β γ α β γ α β Φαίνεται ότι το δόντι 1 συνεργάζεται πάντα με το δόντι α, το 2 πάντα με το β, το 3 με το γ, το 4 με το α, κλπ. Στην επόμενη στροφή του μεγάλου τροχού πάλι το δόντι 1 θα συνεργαστεί με το α του μικρού τροχού, το 2 με το β, κλπ. Ώστε κάθε δόντι του μεγάλου συνεργάζεται πάντα με το ίδιο του μικρού. Βέβαια κάθε δόντι του μικρού συνεργάζεται με τρία του μεγάλου. Ας δούμε τώρα ένα παράδειγμα με δύο τροχούς που έχουν σχέση μετάδοσης. Αν ο μικρός τροχός έχει 4 δόντια (φανταστική περίπτωση μόνο για το παράδειγμα) ο μεγάλος θα έχει 6 δόντια. Αριθμούμε τα δόντια του μικρού τροχού με α, β, γ και δ και του μεγάλου με 1, 2, 3, 4, 5 και 6. Κάνουμε πάλι τον πίνακα για την συγκεκριμένη σχέση μετάδοσης: α β γ δ α β γ δ α β γ δ α β γ δ α β γ δ α β γ Βλέπουμε ότι το δόντι 1 συνεργάζεται εναλλάξ με τα δόντια α και γ, ενώ το 2 με τα β και δ κλπ. Επομένως τα δόντια του μεγάλου τροχού συνεργάζονται με διάφορα δόντια του μικρού, και έτσι έχουν όλα τα δόντια περίπου την ίδια φθορά. Κατά την συνεργασία δύο οδοντωτών τροχών, για να μεταφερθεί ροπή από ένα άξονα σε ένα άλλο, αναπτύσσονται διάφορες δυνάμεις, τάσεις και ροπές. Η ανάλυση όλων αυτών είναι πολύπλοκη και δεν εξυπηρετεί τους εκπαιδευτικούς σκοπούς του επιπέδου του λυκείου. Στο σχολικό βιβλίο αναφέρονται ορισμένα περί των δυνάμεων που αναπτύσσονται στα δόντια των τροχών κατά την εμπλοκή τους, καθώς και της καμπτικής και στρεπτικής ροπής. Ενώ όμως αναφέρονται αρκετοί ορισμοί και μαθηματικοί τύποι, στο ένα παράδειγμα που έχει στο μέρος των υπολογισμών, χρησιμοποιείται μόνο μία σχέση που αφορά στον υπολογισμό του βήματος της οδόντωσης. Θεωρούμε ότι είναι η μόνη πιθανή περίπτωση εξέτασής σας στο θέμα της αντοχής και των διαστάσεων, γι αυτό δεν θα επεκταθούμε στα υπόλοιπα, τα οποία άλλωστε απαιτούν και γνώσεις από άλλα μαθήματα, που δεν διδάσκονται στα ΕΠΑΛ. Για τον υπολογισμό του βήματος μιας οδόντωσης οι παράγοντες που επιδρούν είναι οι εξής: 1. Η μεταφερόμενη ισχύς Ρ. 2. Ο αριθμός των στροφών του άξονα n. 3. Ο αριθμός των δοντιών κάθε γραναζιού z. 4. Ο συντελεστής μορφής του δοντιού y, που εξαρτάται από την ποιότητα κατεργασίας των δοντιών. Ο συντελεστής μορφής y είναι τόσο μεγαλύτερος όσο καλύτερης ποιότητας είναι η κατεργασία των δοντιών. Παίρνει τιμές που δίνονται στον πίνακα 14.8.β της σελίδας 339 του σχολικού βιβλίου. 5. Το υλικό κατασκευής του γραναζιού. Κανονικά το υλικό κατασκευής ενός αντικειμένου το απεικονίζει η επιτρεπόμενη τάση σ επ, αλλά στην συγκεκριμένη περίπτωση αντ αυτής μπαίνει ο συντελεστής φόρτισης c που δίνεται στον πίνακα 14.8.γ της σελίδας 339 του σχολικού βιβλίου. Όσο καλύτερο το υλικό τόσο μεγαλύτερος ο συντελεστής. Κατασκευαστικά αναφέρουμε ότι όσο καλύτερα τα υλικά και η ποιότητά τους τόσο μικρότερα κατασκευάζονται τα στοιχεία των μηχανών. Έτσι, όσο μεγαλύτεροι είναι οι συντελεστές y και c, τόσο μικρότερο θα είναι το βήμα του γραναζιού (τα μεγέθη όμως δεν είναι αντιστρόφως ανάλογα). Ο μαθηματικός τύπος υπολογισμού του βήματος t είναι: 104 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
105 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Στον τύπο αυτό το βήμα έχει μονάδες mm, η ισχύς είναι σε ίππους PS, ο αριθμός των στροφών έχει μονάδες rpm και οι συντελεστές y και c είναι καθαροί αριθμοί. Βλέπουμε ότι για τον υπολογισμό υπάρχει μια παρένθεση που υψώνεται στην δύναμη. Στην ουσία είναι σαν να υπολογίζουμε την τρίτη ρίζα του αριθμού που υπάρχει στην παρένθεση μέσα. Πρέπει να ανατρέξετε στο κεφάλαιο 5 όπου αναφέρθηκαν εκτενώς τα σχετικά με την τρίτη ρίζα. Για ασκήσεις που χρησιμοποιούν τον τύπο 7.24 θα πρέπει να θυμηθείτε τις ασκήσεις του πέμπτου κεφαλαίου για τον υπολογισμό των διαμέτρων των ατράκτων. Εδώ για το βήμα της οδόντωσης θα κάνετε χρήση και των πινάκων 14.8.β και 14.8.γ του βιβλίου. Τονίζουμε ότι η σχέση αυτή είναι προσεγγιστική και για τον προσδιορισμό της ακριβούς τιμής του βήματος πρέπει να γίνει έλεγχος για την τιμή του modul, αν είναι μεταξύ των τυποποιημένων. Άσκηση 7.13 Ποιο είναι το βήμα μιας οδόντωσης με modul ίσο με 5 mm; Το βήμα της οδόντωσης συμβολίζεται με t και ισχύει ο τύπος 7.11 (ο δεύτερος), τον οποίο λύνουμε ως προς το άγνωστο και ζητούμενο βήμα: Επομένως το βήμα της οδόντωσης θα είναι 15,7 mm. Άσκηση 7.14 Πόσα δόντια έχει ένας οδοντωτός τροχός με modul ίσο με 6 mm και αρχική διάμετρο ίση με 132 mm. Θα χρησιμοποιήσουμε τη σχέση 7.11 και θα την επιλύσουμε ως προς τον αριθμό των δοντιών z. Γνωρίζουμε την αρχική διάμετρο d 0 =132 mm και το modul που είναι ίσο με m=6 mm. Θα έχουμε: Ο τροχός θα έχει 22 δόντια. Άσκηση 7.14 Ποιο είναι το βήμα μιας οδόντωσης με αρχική διάμετρο ίση με 120 mm και 40 δόντια;. Το βήμα της οδόντωσης θα υπολογιστεί από τύπους που περιέχουν τα μεγέθη που δίνονται στην εκφώνηση της άσκησης. Δεν υπάρχει λόγος να πηγαίνετε σε τύπους που περιέχουν την ισχύ ή άλλα άγνωστα στοιχεία. Μπορούμε να χρησιμοποιήσουμε κατ ευθείαν τον τύπο 7.12 για τον υπολογισμό του βήματος. Τα γνωστά μεγέθη είναι: αρχική διάμετρος d 0 =120 mm και αριθμός δοντιών z=40 δόντια. Άρα θα έχουμε: Το βήμα της οδόντωσης θα είναι 9,42 mm. Η σχέση υπάρχει στο βιβλίο (σελ.234) και μπορείτε να την χρησιμοποιείτε ελεύθερα. Όμως η σχέση δεν υπάρχει στη θεωρία, οπότε πρέπει να την αποδεικνύουμε κάθε φορά που μας χρειάζεται. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 105
106 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Σημείωση: Δίνουμε και μια άλλη λύση: Θα μπορούσαμε να βρούμε πρώτα από την εξίσωση το modul και μετά από την λύνοντας ως προς το βήμα να το υπολογίσουμε. Ασφαλώς βρήκαμε το ίδιο αποτέλεσμα. Άσκηση 7.15 Σε μια κανονική οδόντωση με κατεργασία σε εργαλειομηχανή το modul είναι 4 mm. Να βρεθούν οι χαρακτηριστικές διαστάσεις της οδόντωσης, δηλαδή: βήμα, ύψος κεφαλής, ύψος ποδιού, πάχος δοντιού και διάκενο. Οι διαστάσεις θα βρεθούν αν εφαρμόσουμε διαδοχικά τις σχέσεις 7.11 για το βήμα t, 7.13 για το ύψος κεφαλής h k, 7.14 για το ύψος ποδιού h f, 7.23 για το πάχος δοντιού s σε κατεργασμένα σε εργαλειομηχανή δόντια και το διάκενο w θα υπολογιστεί αν αφαιρέσουμε από το βήμα το πάχος του δοντιού. Έτσι θα έχουμε: Επομένως βρήκαμε ότι: βήμα t=12,56 mm, ύψος κεφαλής h k = 4 mm, ύψος ποδιού h f =4,68 mm, πάχος δοντιού s=6,123 mm και το διάκενο w=6,437 mm. Άσκηση 7.16 Ένας οδοντωτός τροχός έχει κανονικά δόντια, το modul είναι 1,25 mm και η αρχική διάμετρος ίση με 25 mm. Να υπολογίσετε: Α) τη διάμετρο κεφαλών Β) το βήμα της οδόντωσης Γ) τον αριθμό των δοντιών του γραναζιού. Συμβολίζουμε με τα γνωστά σύμβολα τα δεδομένα και τα ζητούμενα: modul: m=1,25 mm, αρχική διάμετρος: d 0 =25 mm, διάμετρος κεφαλών: dk, βήμα: t και αριθμός δοντιών: z. Α) Τη διάμετρο κεφαλών θα την υπολογίσουμε από τη σχέση 7.20: Β) Το βήμα θα υπολογιστεί από τη σχέση 7.11: Γ) Ο αριθμός των δοντιών θα υπολογιστεί από την εξίσωση 7.11: Άσκηση 7.17 Ο οδοντωτός τροχός σε μια οδόντωση έχει κανονικά δόντια (κανονική οδόντωση) και αρχική διάμετρο ίση με 50 mm. Αν το modul είναι 2 mm να υπολογίσετε: Α) το βήμα της οδόντωσης, Β) τον αριθμό των δοντιών του γραναζιού, Γ) το ύψος κεφαλής του δοντιού, Δ) το ύψος όλου του δοντιού, Ε) τη διάμετρο κεφαλών και Ζ) τη διάμετρο ποδιών. 106 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
107 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Τα ζητούμενα θα βρεθούν εφαρμόζοντας διαδοχικά τις σχέσεις που έχουν προαναφερθεί. Τα σύμβολα της αρχικής διαμέτρου και του modul είναι αντίστοιχα: d 0 =50mm και m=2 mm. Θα έχουμε: Α) Από τη σχέση 7.11 για το βήμα t: Β) Από τη σχέση 7.11 για τον αριθμό των δοντιών z: Γ) Από τη σχέση 7.13 για το ύψος κεφαλής h k : Δ) Από τη σχέση 7.15 για το ύψος δοντιού h: Ε) Από τη σχέση 7.19 θα υπολογιστεί η διάμετρος κεφαλών. Θα μπορούσε να υπολογιστεί και από τις σχέσεις 7.20 ή 7.21 αφού όλα τα στοιχεία τους είναι γνωστά: Ζ) Είναι προφανές από τη γεωμετρία του οδοντωτού τροχού (φαίνεται άλλωστε και από το επόμενο σχήμα) ότι αν αφαιρέσουμε από την διάμετρο κεφαλών την διάμετρο ποδιών θα έχουμε το διπλάσιο του ύψους του δοντιού. Άρα θα ισχύει: Σημείωση: Στο σχήμα σχεδιάστηκαν μόνο 11 δόντια και σε μεγέθυνση για λόγους απλότητας. Στην πραγματικότητα το γρανάζι έχει 25 δόντια, όπως βρήκαμε στο ερώτημα Β. Άσκηση 7.18 Ένας κινητήριος οδοντωτός τροχός έχει αρχική διάμετρο 320 mm και modul ίσο με 8 mm. Συνεργάζεται με άλλο τροχό με σχέση μετάδοσης ίση με 2 και ζητούνται για τον συνεργαζόμενο κινούμενο τροχό: α) το βήμα β) η αρχική διάμετρος γ) η διάμετρος κεφαλών δ) το διάκενο των δοντιών αν είναι χυτά ακατέργαστα δόντια. Πρέπει από την αρχή να πούμε ότι δύο συνεργαζόμενα γρανάζια έχουν πάντα το ίδιο modul. Αυτό είναι προφανές αν σκεφτούμε ότι ισχύει ο τύπος 7.11:, που σημαίνει ότι το modul εξαρτάται μόνο από το βήμα t, αφού το είναι σταθερός αριθμός. Αφού δύο γρανάζια συνεργάζονται θα έχουν το ίδιο βήμα επομένως και το ίδιο modul. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 107
108 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Θα εφαρμόσουμε διαδοχικά τις γνωστές σχέσεις από τη διαστασιολόγηση των γραναζιών. Τα δεδομένα είναι η αρχική διάμετρος του κινητήριου τροχού d 01 =320mm, το modul m=8 mm και η σχέση μετάδοσης i=2. α) Το βήμα t θα βρεθεί από τη σχέση 7.11: β) Η αρχική διάμετρος του κινούμενου τροχού d 02 θα βρεθεί με επίλυση της εξίσωσης 7.4 για τη σχέση μετάδοσης και τις αρχικές διαμέτρους: γ) Η διάμετρος κεφαλών d k2 του κινούμενου τροχού θα υπολογιστεί με μία από τις σχέσεις 7.19, 7.20 ή Όμως στις 7.19 και 7.21 δεν γνωρίζουμε και τα δύο μεγέθη του δεύτερου μέλους, ώστε να κάνουμε τον υπολογισμό. Και στις δύο γνωρίζουμε μόνο το ένα μέγεθος: το d 02 στην πρώτη και το m στην Βολεύει όμως να χρησιμοποιήσουμε την 7.20: δ) Το διάκενο w θα υπολογιστεί από τη σχέση 7.22 για ακατέργαστα χυτά δόντια: Ασφαλώς το διάκενο αυτό θα ισχύει και για τον κινητήριο τροχό. Άσκηση 7.19 Ένας οδοντωτός τροχός με κανονικά δόντια έχει διάμετρο κεφαλών ίση με 170 mm και 32 δόντια. Να βρείτε το modul του τροχού. Ψάχνοντας τις σχέσεις που περιέχουν στοιχεία για τις διαστάσεις των οδοντωτών τροχών, βλέπουμε ότι η σχέση 7.21 περιλαμβάνει ακριβώς τα δύο μεγέθη που μας δίνει η άσκηση και τον άγνωστο. Άρα θα χρησιμοποιήσουμε αυτή τη σχέση. Για τους συμβολισμούς έχουμε d k =170 mm και z=32 δόντια. Θα επιλύσουμε τον τύπο 7.21 ως προς τον άγνωστο m: Άρα το modul είναι 5 mm, που είναι τυποποιημένο και το δεχόμαστε. Άσκηση 7.20 Ένας οδοντωτός τροχός με κατεργασμένα κοινά δόντια (κανονική οδόντωση) από κοινό χάλυβα βρίσκεται σε άξονα που μεταφέρει ισχύ 12 PS και περιστρέφεται με 1000 rpm. Ο τροχός έχει 40 δόντια. Να υπολογίσετε: 1. Το βήμα και το modul του οδοντωτού τροχού. 2. Την αρχική διάμετρο του τροχού. 3. Τη διάμετρο κεφαλών του τροχού. 1) Για το βήμα του τροχού θα χρησιμοποιηθεί η σχέση 7.24, αφού μας δίνονται όλα τα στοιχεία που περιέχει. Το μυαλό μας μπορεί να πάει και σε άλλες σχέσεις που περιέχουν το βήμα, όπως η 7.11 και η 7.12, αλλά σε αυτές δεν είναι γνωστό το modul ή η διάμετρος. Έτσι αναγκαστικά θα πάμε στην Σε αυτήν έχουμε γνωστά ή βρίσκουμε από πίνακες τα μεγέθη: Ισχύς P=12 PS Στροφές n=1000 rpm Αριθμός δοντιών z=40 δόντια Αρχική διάμετρος d 0 Διάμετρος κεφαλών d k Συντελεστής μορφής y=3 κατεργασμένα κοινά δόντια από τον πίνακα 14.8.β 108 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
109 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Συντελεστής φόρτισης c=80. Παίρνουμε μια μέση τιμή του πίνακα 14.8.γ για δόντια από κοινό χάλυβα Τώρα είμαστε σε θέση να υπολογίσουμε το βήμα: Το βήμα βρέθηκε ίσο με 8,25 mm. Αυτή η τιμή δεν είναι η τελική διότι πρέπει να ελέγξουμε αν το modul είναι μέσα στον πίνακα με τα τυποποιημένα. Αυτός ο έλεγχος γίνεται με τη σχέση 7.11 από την οποία το modul προκύπτει: Το πιο κοντινό και μεγαλύτερο modul στην τιμή m=2,63 mm είναι το m=3 mm. Βάσει αυτής της τιμής θα υπολογίσουμε την τελική τιμή του βήματος από τη σχέση 7.11: Επομένως ο τροχός θα έχει modul 3 mm και βήμα 9,42 mm. Στη λύση αυτή χρησιμοποιήσαμε τις μονάδες των μεγεθών, αν και το σχολικό βιβλίο δεν το κάνει. 2) Η αρχική διάμετρος του οδοντωτού τροχού θα υπολογιστεί από τη σχέση 7.11 αφού γνωρίζουμε το modul και τον αριθμό των δοντιών: Επομένως η αρχική διάμετρος είναι 120 mm. 3) Η διάμετρος κεφαλών d k θα υπολογιστεί από τη σχέση 7.21 (θα μπορούσε να υπολογιστεί και από τη σχέση 7.20): Οπότε η διάμετρος κεφαλών είναι 126 mm. Άσκηση 7.21 Ο κινητήριος οδοντωτός τροχός μιας οδοντοκίνησης έχει z 1 =22 δόντια και περιστρέφεται με n 1 =1200 rpm. Αν η σχέση μετάδοσης είναι i=1/2 και το βήμα των τροχών πρέπει να είναι τουλάχιστον t=7 mm, να βρείτε: 1. Το modul και το ακριβές βήμα. 2. Το ύψος των δοντιών. 3. Τον αριθμό των δοντιών που έχει το κινούμενο γρανάζι. 4. Την αρχική διάμετρο του κάθε γραναζιού. 5. Την απόσταση των αξόνων. Εκτός από τους συμβολισμούς των μεγεθών που δόθηκαν στην εκφώνηση, θα δώσουμε και τους συμβολισμούς των ζητούμενων μεγεθών. Θα είναι: modul m, ύψος δοντιών h, αριθμός δοντιών του κινούμενου γραναζιού z 2, αρχική διάμετρος κινητήριου γραναζιού d 01, αρχική διάμετρος κινούμενου γραναζιού d 02 και απόσταση αξόνων α. Ακολουθούν οι απαντήσεις στα ερωτήματα της άσκησης: 1) Το modul θα βρεθεί από τη δεύτερη σχέση της Θα βάλουμε στη θέση του βήματος την ελάχιστη τιμή 7 mm και από το αποτέλεσμα θα τυποποιήσουμε το modul για να προκύψει η οριστική τιμή του βήματος. Θα έχουμε: Το modul τυποποιείται στην τιμή 2,5 mm, οπότε ο προηγούμενος τύπος δίνει για το βήμα την τελική τιμή: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 109
110 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Άρα το βήμα θα είναι 7,85 mm και το modul 2,5 mm. 2) Το ύψος των δοντιών δίνεται από τον τύπο 7.15: Επομένως το ύψος των δοντιών θα είναι 5,425 mm. 3) Ο αριθμός των δοντιών του κινούμενου γραναζιού θα βρεθεί από τη σχέση 7.4 και θα έχουμε: Άρα το κινούμενο γρανάζι θα έχει 44 δόντια. 4) Για τον υπολογισμό των αρχικών διαμέτρων θα χρησιμοποιήσουμε τον πρώτο από τους δύο τύπους της 7.11, αφού έχουμε πλέον υπολογίσει το modul και τον αριθμό των δοντιών. Έχουμε: Άρα οι αρχικές διάμετροι είναι 55 mm και 110 mm αντίστοιχα. 5) Η απόσταση των αξόνων των γραναζιών δίνεται από τον τύπο 7.5 και από αυτόν θα την υπολογίσουμε: Άρα οι άξονες που φέρουν τα γρανάζια θα έχουν απόσταση 82,5 mm. Άσκηση 7.22 Ένας οδοντωτός τροχός με γωνιώδη δόντια από κοινό χάλυβα περιστρέφεται με 800 rpm. Ο τροχός έχει 50 δόντια και το modul που έχει είναι ίσο με 5 mm. Να υπολογίσετε: 1. Το βήμα του οδοντωτού τροχού. 2. Την αρχική διάμετρο του τροχού. 3. Την ισχύ που μπορεί να μεταφέρει. Κατ αρχήν θα δώσουμε τα γνωστά σύμβολα στα διάφορα μεγέθη: Στροφές n=800 rpm Αριθμός δοντιών z=50 δόντια Modul m=5 mm Βήμα t Αρχική διάμετρος d 0 Ισχύς Ρ 1) Το βήμα του τροχού θα βρεθεί από τη δεύτερη σχέση της 7.11: 2) Η αρχική διάμετρος θα βρεθεί και αυτή από την πρώτη σχέση της 7.11: 3) Η ισχύς που ζητείται σε αυτό το ερώτημα θα βρεθεί από τη σχέση Μια άλλη σχέση που θα μπορούσε να χρησιμοποιηθεί είναι η 7.6, αλλά δεν έχουμε την ροπή, ούτε μπορούμε να την υπολογίσουμε από τα δεδομένα της άσκησης. Άρα εκείνο που μας μένει 110 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
111 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 είναι να λύσουμε την σχέση 7.24 ως προς την ισχύ Ρ. Η λύση δεν είναι δύσκολη, αρκεί να γνωρίζουμε την εξής μαθηματική ισότητα: Επίσης, γνωρίζουμε ότι αν έχουμε μια ισότητα μπορούμε να υψώσουμε και τα δύο μέρη της στην τρίτη δύναμη και παραμένει ισότητα. Για παράδειγμα: Δηλαδή είχαμε την ισότητα: και υψώσαμε το πρώτο μέλος στην τρίτη δύναμη και έγινε Α και υψώσαμε και το δεύτερο και έγινε. Άρα Α=125. Πρέπει να γνωρίζετε άλλη μία ιδιότητα των αριθμών, που θα χρησιμοποιηθεί, η οποία είναι η εξίσωση: Πριν προχωρήσουμε στη λύση της εξίσωσης 7.24, θα πρέπει να βρούμε από τους πίνακες 14.8.β και 14.8.γ τους συντελεστές y και c. Για γωνιώδη δόντια παίρνουμε y=4 και για κοινό χάλυβα c=80 που είναι μια μέση τιμή για κοινό χάλυβα. Αν θέλαμε να έχουμε περισσότερη σιγουριά στο αποτέλεσμα θα έπρεπε να πάρουμε τη μικρότερη τιμή c=55, οπότε θα λέγαμε ότι η ισχύς που θα βρούμε θα είναι η μικρότερη δυνατή. Μετά από όλα αυτά θα λύσουμε την εξίσωση 7.24 ως προς Ρ: Επομένως ο τροχός θα μπορεί να μεταφέρει ισχύ περίπου 110 PS Διαστασιολόγηση άλλων τύπων οδοντωτών τροχών Στο σχολικό βιβλίο περιλαμβάνονται ορισμένες σχέσεις που ισχύουν σε γρανάζια με όχι παράλληλες οδοντώσεις, όπως είναι ελικοειδείς και οι κωνικοί οδοντωτοί τροχοί και το σύστημα ατέρμονα-κορώνας. Στο τμήμα των ασκήσεων το βιβλίο δεν έχει κάποια παραδείγματα χρήσης αυτών των σχέσεων, όμως εμείς θα δώσουμε μερικά, ώστε να είστε εξοικειωμένοι με αυτό το αντικείμενο. Στους ελικοειδείς οδοντωτούς τροχούς έχουμε δύο βήματα ανάλογα με την κατεύθυνση που μετράμε την απόσταση μεταξύ δύο δοντιών: το μετωπικό βήμα (σύμβολο t s ) και το κάθετο βήμα (σύμβολο t π ). Το μετωπικό είναι το βήμα που βλέπουμε όταν κοιτάμε τον τροχό από τη μεριά που φαίνεται στο επόμενο αριστερό σχήμα. Το κάθετο είναι εκείνο που μετράμε όταν κοιτάμε τον τροχό από το πάνω μέρος και η μέτρηση είναι κάθετη στη χάραξη του δοντιού, όπως φαίνεται στο επόμενο σχήμα στα δεξιά. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 111
112 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ Προφανώς το κάθετο βήμα είναι μικρότερο από το μετωπικό. Αντιστοίχως υπάρχουν και δύο modul, το μετωπικό και το κάθετο. Επειδή το modul ισούται με τον λόγο t/π το μετωπικό θα είναι πιο μεγάλο από το κάθετο. Θα ισχύουν οι σχέσεις: Οι σχέσεις αυτές δεν δίνονται στο βιβλίο, αλλά εννοούνται από τα λεγόμενα, άρα θεωρούνται γνωστές. Κατά τα άλλα οι σχέσεις για τις διαστάσεις των γραναζιών είναι όμοιες με τις σχέσεις που αναφέραμε στα γρανάζια με παράλληλες οδοντώσεις όπου θα χρησιμοποιείται το μετωπικό modul. Το κάθετο modul χρησιμοποιείται για τη χάραξη (κατασκευή) των οδοντώσεων στα ελικοειδή γρανάζια. Στα κωνικά γρανάζια, λόγω της μορφής τους, έχουμε δύο αρχικές διαμέτρους: την μεγάλη ή εξωτερική (d a ), που αντιστοιχεί στην πλευρά της οδόντωσης που βρίσκεται στο εξωτερικό άνοιγμα του κώνου, και την μικρή ή εσωτερική (d ε ). Αντίστοιχα υπάρχουν και δύο modul αλλά και δύο βήματα. Αυτό το καταλαβαίνουμε από το ότι λόγω της σχέσης ορισμού του modul: και επειδή ο αριθμός των δοντιών z στο ίδιο κωνικό γρανάζι είναι ίδιος και αλλάζει μόνο το d 0, το modul μεταβάλλεται ανάλογα με την αρχική διάμετρο. Αν D 0 είναι η μεγάλη (αρχική) διάμετρος ενός κωνικού γραναζιού τότε προφανώς θα ισχύει: Στα συνεργαζόμενα κωνικά γρανάζια με εξωτερικές αρχικές διαμέτρους D 01 και D 02 και αριθμό δοντιών z 1 και z 2 αντίστοιχα, θα ισχύουν οι σχέσεις: Εφόσον έχουμε δύο διαφορετικά modul, θα έχουμε στα κωνικά γρανάζια και δύο διαφορετικά βήματα αφού ισχύει ο τύπος. Ένας άλλος τύπος οδοντωτών τροχών είναι ο ατέρμονας κοχλίας με κορώνα. Η σχέση μετάδοσης είναι λίγο ιδιότυπη αφού ο ατέρμονας δεν έχει δόντια, αλλά είναι σαν ένας κοχλίας, που θα έχει μία ή περισσότερες αρχές. Οι αρχές είναι σημαντικό στοιχείο του ατέρμονα γιατί παίζουν το ρόλο των δοντιών σε αυτόν. Έτσι αν ένας ατέρμονας έχει z 1 αρχές και περιστρέφεται με n 1 στροφές, ενώ η κορώνα έχει z 2 δόντια και περιστρέφεται με n 2 στροφές η σχέση μετάδοσης του συστήματος θα είναι: Για να καταλάβετε τι είναι οι λεγόμενες αρχές στους κοχλίες, πρέπει να φανταστείτε ότι φτιάχνουμε ένα κοχλία παίρνοντας μια κυλινδρική ράβδο και γύρω από αυτήν τυλίγουμε ένα ελαστικό τριγωνικό πρίσμα. Στο επόμενο σχήμα αριστερά φαίνεται ο κύλινδρος και το ένα πρίσμα. Τότε ο κοχλίας (ή ο ατέρμονας) θα έχει μία αρχή. Αν αντί για ένα πρίσμα τυλίξουμε δύο πρίσματα, το ένα κολλημένο στο άλλο, θα προκύψει ατέρμονας με δύο αρχές (επάνω δεξιό σχήμα). Αν τυλιγόταν τρία πρίσματα θα είχαμε τρεις αρχές. 112 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
113 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Άσκηση 7.23 Ένας οδοντωτός τροχός με ελικοειδή οδόντωση έχει μετωπικό βήμα ίσο με 4,71 mm και κάθετο ίσο με 3,925 mm. Να βρείτε το μετωπικό και κάθετο modul του τροχού. Μας δίνονται τα δύο βήματα: το μετωπικό t s =4,71 mm και το κάθετο t π =3,925 mm. Για την εύρεση των δύο modul θα εφαρμόσουμε τις σχέσεις Επειδή αυτές οι σχέσεις δεν δίνονται στο βιβλίο με αυτή τη μορφή αλλά μόνο περιγράφονται, θα πρέπει να αναφέρετε ότι το modul ισούται με τον λόγο οπότε το μετωπικό θα είναι και το κάθετο. Επομένως το μετωπικό και το κάθετο modul θα είναι: Υπολογίστηκαν τα δύο ζητούμενα modul, τα οποία μάλιστα είναι και στον πίνακα με τα συνιστώμενα. Άσκηση 7.24 Μια ελικοειδής οδόντωση ενός τροχού με 32 δόντια έχει μετωπικό βήμα ίσο με 7,85 mm και κάθετο ίσο με 6,28 mm. Να βρείτε Α) την αρχική διάμετρο του τροχού, Β) το ύψος των δοντιών. Μας δίνονται τα δύο βήματα, αλλά για τον υπολογισμό των διαστάσεων του τροχού είναι γνωστό ότι χρησιμοποιείται το μετωπικό βήμα. Στην άσκηση δώσαμε και τα δύο για να ελεγχθεί αν γνωρίζετε ποιο από τα δύο πρέπει να χρησιμοποιήσετε. Τα δεδομένα είναι z=32 δόντια και μετωπικό βήμα t s =7,85 mm. Α) Η αρχική διάμετρος d 0 θα υπολογιστεί από τη σχέση 7.11: αφού πρώτα υπολογίσουμε το μετωπικό modul m s από τη σχέση θα έχουμε: Άρα η αρχική διάμετρος του ελικοειδούς γραναζιού θα είναι 80 mm. Β) Το ύψος των δοντιών h θα υπολογιστεί από τη σχέση 7.15 και θα έχουμε: Επομένως το ύψος κάθε δοντιού θα είναι 5,425 mm. Άσκηση 7.25 Ένα κωνικό γρανάζι έχει μεγάλη αρχική διάμετρο ίση με 100 mm, μικρή 70 mm και το μεγάλο modul 5 mm. Να υπολογίσετε πόσα δόντια θα έχει. Δίνονται και η μικρή και η μεγάλη αρχική διάμετρος, αλλά για τον υπολογισμό των δοντιών του τροχού απαιτείται μόνο η μεγάλη (αφού έχουμε το μεγάλο modul) και θα χρησιμοποιηθεί η σχέση 7.26, όπου D 0 =100 mm m=5 mm. Θα έχουμε: Επομένως τα δόντια του κωνικού τροχού είναι 20. Άσκηση 7.26 Δυο κωνικοί τροχοί συνεργάζονται με σχέση μετάδοσης ίση με 2,5. Ο μεγάλος έχει εξωτερική αρχική διάμετρο ίση με 200 mm, περιστρέφεται με 600 rpm και έχει μεγάλο modul 5 mm. Να υπολογίσετε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 113
114 ΚΕΦΑΛΑΙΟ 7 ΟΔΟΝΤΩΣΕΙΣ 1. Την εξωτερική αρχική διάμετρο του μικρού τροχού. 2. Πόσα δόντια θα έχει ο μεγάλος και πόσα ο μικρός τροχός. 3. Τις στροφές του μικρού τροχού. Κατ αρχήν θα δώσουμε τους απαραίτητους συμβολισμούς: Σχέση μετάδοσης i=2,5 Εξωτερική (ή μεγάλη) αρχική διάμετρος του μεγάλου τροχού D 01 =200 mm Στροφές μεγάλου τροχού n 1 =600 rpm Modul συνεργαζόμενων τροχών m=5 mm Εξωτερική αρχική διάμετρος του μικρού τροχού D 02 Δόντια μεγάλου τροχού z 1 Δόντια μικρού τροχού z 2 Στροφές μικρού τροχού n 2 Ακολουθούν οι απαντήσεις: 1) Η εξωτερική αρχική διάμετρο του μικρού τροχού θα υπολογιστεί από τη σχέση 7.27 για τις διαμέτρους και τη σχέση μετάδοσης: 2) Τα δόντια των δύο τροχών θα υπολογιστούν από την εξίσωση 7.26, εφαρμόζοντάς την δυο φορές: Άρα ο μεγάλος έχει 40 δόντια και ο μικρός 16 δόντια. 3) Τις ζητούμενες στροφές θα τις υπολογίσουμε από τη σχέση 7.26: Επομένως ο μικρός τροχός θα περιστρέφεται με 1500 rpm. Άσκηση 7.27 Ένας ατέρμονας κοχλίας έχει δύο αρχές και περιστρέφεται με 1800 rpm. Αν η σχέση μετάδοσης που έχει με τη συνεργαζόμενη κορώνα είναι 1/20 και το modul της κορώνας είναι 10 mm να υπολογίσετε: 1. Τις στροφές της κορώνας. 2. Τον αριθμό των δοντιών που έχει η κορώνα. 3. Την διάμετρο κεφαλών της κορώνας. Θα δώσουμε τα σύμβολα γνωστών και αγνώστων: Αρχές ατέρμονα z 1 =2 Στροφές ατέρμονα n 1 =1800 rpm Modul m=10 mm Σχέση μετάδοσης i=1/20=0,05 Στροφές της κορώνας n 2 Αριθμός δοντιών της κορώνας z 2 Διάμετρος κεφαλών κορώνας d k Προχωρούμε τώρα στις απαντήσεις των ερωτημάτων της άσκησης: 1) Οι στροφές της κορώνας θα υπολογιστούν από τη σχέση 7.28: 114 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
115 ΟΔΟΝΤΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 7 Άρα η κορώνα θα έχει 90 rpm, θα περιστρέφεται δηλαδή 20 φορές πιο αργά από τον ατέρμονα. 2) Ο αριθμός των δοντιών της κορώνας θα υπολογιστεί από τη σχέση 7.28, συνδυάζοντας τον αριθμό των δοντιών είτε με τη σχέση μετάδοσης είτε με τις στροφές. Θα το κάνουμε και με τους δύο τρόπους: Και με τους δύο τρόπους βρήκαμε ότι η κορώνα θα έχει 40 δόντια. 3) Για τη διάμετρο κεφαλών της κορώνας θα χρησιμοποιήσουμε τη σχέση 7.21 και θα έχουμε: Επομένως η διάμετρος κεφαλών της κορώνας θα είναι 420 mm ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 115
116
117 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 8. Ιμάντες Η ιμαντοκίνηση είναι ένας τρόπος μετάδοσης της περιστροφικής κίνησης όταν οι άξονες δεν βρίσκονται πολύ κοντά μεταξύ τους. Γι αυτό παρεμβάλλεται ο ιμάντας, προσαρμοσμένος σε δύο τροχαλίες, που κάθε μία βρίσκεται στον ένα άξονα. Η μία από αυτές είναι η κινητήρια, και λόγω της μεγάλης τριβής που έχει με τον ιμάντα τον παρασύρει στην περιστροφική της κίνηση. Ουσιαστικά, μεταξύ ιμάντα και τροχαλίας δεν υπάρχει ολίσθηση, διότι ο συντελεστής τριβής μεταξύ τους και η κάθετη δύναμη από την τροχαλία στον ιμάντα (που από αυτήν εξαρτάται η δύναμη της τριβής) έχουν τιμές που κάνουν την τριβή μεγαλύτερη από την περιφερειακή δύναμη. Αν η περιφερειακή δύναμη γίνει πιο μεγάλη από την δύναμη της τριβής τότε ο ιμάντας θα ολισθήσει πάνω στην τροχαλία. Πρακτικά, κατά τη λειτουργία της ιμαντοκίνησης προκύπτει με την πάροδο του χρόνου και τις φθορές των υλικών μια ολίσθηση, που αν είναι μέχρι 3% είναι αποδεκτή, διαφορετικά πρέπει να γίνει διόρθωση του συστήματος. Η ολίσθηση του ιμάντα κατά 3% θα έχει σαν αποτέλεσμα η κινούμενη τροχαλία να έχει λιγότερες στροφές κατά το ίδιο ποσοστό, από τις αναμενόμενες. Με διαφορετικό τρόπο θα λέγαμε ότι έχει το 97% των στροφών που θα είχε αν δεν υπήρχε η ολίσθηση. Θα θυμηθούμε τώρα ορισμένα στοιχεία από την φυσική για την τριβή, όσα είναι απαραίτητα για να καταλάβετε τα θέματα που είναι σχετικά με τους ιμάντες. Έχουμε το σώμα που φαίνεται στο επόμενο σχήμα, το οποίο έχει βάρος Β και ασκείται σε αυτό η οριζόντια δύναμη F. Το σώμα πάνω στο δάπεδο είτε θα είναι ακίνητο είτε θα ολισθαίνει προς τα δεξιά. Επομένως στον κατακόρυφο άξονα και στις δύο περιπτώσεις δεν θα υπάρχει κίνηση του σώματος, άρα θα είναι F k =B, λόγω της ισορροπίας των δυνάμεων. Η F k είναι η αντίδραση του εδάφους στο βάρος του σώματος. Ας υποθέσουμε ότι η F είναι αρκετά μεγάλη και το σώμα ολισθαίνει. Τότε η συνολική δύναμη (συνισταμένη) στο σώμα θα είναι η F-Τ. Η δύναμη Τ είναι η δύναμη της τριβής και είναι πάντα αντίθετη στην κίνηση του σώματος και το μέτρο της (μέγεθος) είναι ίσο με: Τ=μ F k, όπου μ είναι ο συντελεστής τριβής μεταξύ του σώματος και του δαπέδου. Ο συντελεστής μ είναι ένας αριθμός που εξαρτάται από τις δύο επιφάνειες που βρίσκονται σε επαφή. Όσο μεγαλύτερος είναι τόσο πιο μεγάλη η τριβή. Στο συγκεκριμένο παράδειγμα η τριβή Τ δεν εξαρτάται από τη δύναμη F, (επειδή η F συμβαίνει να είναι παράλληλη στο δάπεδο). Το σώμα θα μετακινηθεί μόνο εφ όσον η δύναμη F είναι μεγαλύτερη από την τριβή μ F k. Όσο είναι μικρότερη, η τριβή θα είναι μικρότερη από την τιμή μ F k και μάλιστα θα είναι ίση με την F, με αποτέλεσμα το σώμα να μην ολισθαίνει. Επομένως, αν δεν θέλουμε ένα σώμα να ολισθαίνει πάνω σε ένα άλλο, θα πρέπει η δύναμη που ασκείται σε αυτό να είναι μικρότερη από τη δύναμη της τριβής μ F k. Αυτό επιδιώκουμε και στην ιμαντοκίνηση. Στους τραπεζοειδείς ιμάντες, ο ιμάντας σφηνώνει στην αυλάκωση της τροχαλίας, με αποτέλεσμα να είναι μεγάλη η δύναμη F k (μάλιστα είναι δύο, μία από κάθε πλευρά) οπότε μεγαλώνει η τριβή και ο ιμάντας δεν ολισθαίνει. Η δύναμη που θα μπορούσε να κάνει τον ιμάντα να ολισθήσει είναι η περιφερειακή, που είναι η διαφορά της δύναμης που ασκείται στον ιμάντα από τον κινητήριο τροχό από την έλκουσα πλευρά, μείον την δύναμη από την ελκυόμενη πλευρά. Σύμφωνα με το επόμενο σχήμα είναι η διαφορά Τ 1 - Τ 2. Δηλαδή για να δούμε τη δύναμη που ασκείται στον ιμάντα στη μεριά του κινούμενου τροχού 2, βλέπουμε ότι τον ιμάντα τραβά από τη μια πλευρά η Τ 1 και από την άλλη η Τ 2, άρα η συνισταμένη τους είναι η Τ 1 -Τ 2. Αυτή είναι η περιφερειακή δύναμη F. Ισχύει ο τύπος: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 117
118 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Και στον κινητήριο τροχό 1, οι ίδιες δυνάμεις ασκούνται λόγω δράσης-αντίδρασης. Είναι εκείνες που φαίνονται στο επόμενο σχήμα. Έχουν μπει αρνητικά πρόσημα για να δείξουν ότι έχουν αντίθετη φορά από τις αντίστοιχες του τροχού 2. Ο κινητήριος τροχός 1 περιστρέφεται δεξιόστροφα και γι αυτό τραβά με την δύναμη Τ 1 μέσω του ιμάντα τον άλλο τροχό 2. Έτσι ο τροχός 2 δέχεται από το κάτω μέρος του τη δύναμη που τον περιστρέφει. Και οι δύο τροχοί πρέπει να έχουν μεγάλη τριβή με τον ιμάντα, ώστε να υπερνικείται η περιφερειακή δύναμη. Για να γίνεται αυτό πρέπει το τόξο επαφής στους δύο τροχούς να είναι σχετικά μεγάλο. Το τόξο επαφής είναι η γωνία που σχηματίζεται από τις δύο ακτίνες του τροχού που καταλήγουν στα σημεία που τελειώνει η επαφή του ιμάντα με τον τροχό. Στον τροχό 2 είναι η γωνία α που φαίνεται στο σχήμα. Αποδεικνύεται ότι ο λόγος των δυνάμεων στις δύο πλευρές του ιμάντα στον κάθε τροχό, ο οποίος εξαρτάται από τον συντελεστή τριβής (μ) και από την γωνία επαφής (α), δίνεται από τον τύπο: Το e στον τύπο 8.2 είναι η λεγόμενη βάση των φυσικών λογαρίθμων. Η τιμή του είναι περίπου 2,72 και είναι άρρητος αριθμός. Στο μάθημά μας δεν μας αφορά κάτι περισσότερο από το να γνωρίζουμε ότι είναι ένας σταθερός αριθμός. Η γωνία α στον τύπο 8.2 έχει μονάδες τα ακτίνια (όχι τη συνηθισμένη μονάδα που είναι οι μοίρες). Το ακτίνιο είναι μια μονάδα για γωνίες και τα 3,14 ακτίνια (στην ουσία ο αριθμός π που γνωρίζουμε από τη γεωμετρία) είναι ίσα με 180 μοίρες. Οι άλλες γωνίες βγαίνουν αναλογικά με αυτή τη σχέση. Δηλαδή οι 60 μοίρες που είναι 180:3 θα είναι π:3=1,047 ακτίνια. Γενικά αν μια γωνία φ είναι χ ακτίνια θα ισχύει:. Πάντως θεωρούμε απίθανο να σας δοθεί θέμα που να χρειάζεται να κάνετε πράξεις με την εξίσωση 8.2 και με ακτίνια. Όμως μπορεί να σας δοθεί το αποτέλεσμα της πράξης αυτής και να σας ζητηθεί να υπολογίσετε τις Τ 1 και Τ 2 ή κάτι άλλο. Ένα θέμα που προκύπτει και το διαπραγματεύεται σύντομα το σχολικό βιβλίο στη σελίδα 349, είναι το μήκος του ιμάντα. Αρχικά λέμε ότι το μήκος του ιμάντα σπανίως χρειάζεται να το γνωρίζουμε με μεγάλη ακρίβεια. Εμείς εδώ θα δώσουμε μια προσεγγιστική σχέση που θα την αποδείξουμε εύκολα και ισχύει για τροχαλίες που έχουν διαφορετικές διαμέτρους. Η σχέση που δίνει το βιβλίο στη σελίδα 349 είναι δύσχρηστη και δεν δίνει την απόδειξη. Αν θέλετε να τη θυμόσαστε κάντε το, αλλά θα δείτε ότι η επόμενη σχέση που θα προτείνουμε είναι πιο εύκολη. Το μήκος του ιμάντα προφανώς θα υπολογιστεί σε συνάρτηση της απόστασης C των κέντρων των δύο τροχαλιών και των διαμέτρων τους. Ας δούμε το επόμενο σχήμα, που φαίνεται ο ιμάντας τεντωμένος γύρω από τις δύο τροχαλίες. Το μήκος του L θα είναι το άθροισμα των εξής τεσσάρων τμημάτων: Επειδή η απόσταση των δύο τροχαλιών συνήθως είναι μεγάλη, υποθέτουμε ότι η απόσταση (ΑΓ) του ιμάντα είναι ίση με τη διάκεντρο (Ο 1 Ο 2 )=C των δύο κύκλων των τροχαλιών. Αυτό φαίνεται στο σχήμα. Επομένως θα ισχύει: (ΑΓ)=(ΔΒ)= (Ο 1 Ο 2 )=C. 118 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
119 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 Μένει τώρα να υπολογιστούν τα τόξα (ΓΛΔ) και (ΒΚΑ). Με καλή προσέγγιση το καθένα τους είναι ίσο με τη μισή περιφέρεια στην οποία ανήκει. Η περιφέρεια ενός κύκλου διαμέτρου d δίνεται από τον τύπο: π d, άρα η μισή περιφέρεια θα είναι π d/2. Επομένως θα ισχύουν οι σχέσεις: Τελικά το μήκος του ιμάντα θα είναι: Ο τελευταίος τύπος που βρήκαμε είναι ένας απλός και με καλή προσέγγιση τύπος για την εκτίμηση του μήκους του ιμάντα. Σε περίπτωση που οι δύο τροχαλίες βρίσκονται πολύ κοντά και ταυτόχρονα έχουν και μεγάλη διαφορά στη διάμετρο, όπως ας πούμε στο δίπλα σχήμα, πρέπει να γίνεται αναλυτικός υπολογισμός του μήκους του ιμάντα. Ο τύπος του βιβλίου είναι: Η διαφορά του 8.4 από τον 8.3 είναι ότι ο πρώτος περιέχει τον προσθετέο οποίος είναι ελάχιστος, αλλά προσθέτει δυσκολία στο να τον θυμόμαστε. Στο βιβλίο για C=1400 mm, d 1 =280 mm και d 2 =500 mm βρίσκει L=4033 mm. Με τον τύπο 8.3 για τις ίδιες τιμές βρίσκουμε L=4025 mm. Δηλαδή η διαφορά είναι 8 mm (είναι ο όρος ο ), αλλά έτσι κι αλλιώς η επιλογή είναι ιμάντας με μήκος 4000 mm. Η ακριβής απόσταση των ιμάντων καθορίζεται μετά την επιλογή του ιμάντα ή τοποθετείται τανυστήρας. Οι ιμάντες πουλιούνται κλειστοί και έχουν συγκεκριμένα μεγέθη μήκους τα οποία είναι τυποποιημένα. Το σχολικό βιβλίο στη σελίδα 350 έχει πίνακα με τα τυποποιημένα μήκη συγκεκριμένων ιμάντων. Επίσης υπάρχουν και τυποποιημένες διάμετροι τροχαλιών στη σελίδα 348. Η περιφερειακή δύναμη F είναι εκείνη που προκαλεί την στρεπτική ροπή Μ που περιστρέφει τον τροχό. Και επειδή η F δρα περιφερειακά του τροχού με κέντρο περιστροφής το κέντρο του, η ροπή της θα ισούται με το γινόμενο της F επί την ακτίνα του τροχού (δηλαδή την διάμετρο δια 2). Επομένως αν d είναι η διάμετρος του τροχού, θα ισχύει η σχέση: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 119
120 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Αν θεωρήσουμε ότι δεν υπάρχει ολίσθηση του ιμάντα πάνω στην τροχαλία τότε η γραμμική ταχύτητα του ιμάντα θα είναι ίση με την περιφερειακή ταχύτητα της κάθε τροχαλίας και θα ισχύει η γνωστή από την περιστροφική κίνηση σχέση: Όπου d είναι η διάμετρος της τροχαλίας και ο αντίστοιχος αριθμός στροφών. Η πρώτη από τις δύο σχέσεις ισχύει για το σύστημα SI και η ταχύτητα έχει μονάδες m/s, η διάμετρος m και οι στροφές είναι ανά δευτερόλεπτο (rps). Στη δεύτερη σχέση η μόνη διαφορά είναι στις στροφές που είναι ανά λεπτό (rpm). Η δεύτερη είναι εκείνη που χρησιμοποιείται περισσότερο. Το σχολικό βιβλίο την αναφέρει στη σελίδα 264. Επίσης θα ισχύει ότι ο αριθμός των στροφών θα είναι αντιστρόφως ανάλογος της διαμέτρου της τροχαλίας (απούσης της ολίσθησης) και θα ισχύει η γνωστή σχέση: Στον τύπο 8.7 d 1 και d 2 είναι οι διάμετροι των τροχαλιών, n 1 και n 2 οι αντίστοιχες στροφές και i η σχέση μετάδοσης. Τέλος για τις ροπές των δύο τροχαλιών θα ισχύει η σχέση: Όλες οι σχέσεις που γράψαμε ως τώρα ισχύουν για το διεθνές σύστημα μονάδων (εκτός από τη δεύτερη σχέση στην 8.6). Σημειώνουμε όμως ότι στις σχέσεις που έχουν λόγους όμοιων μεγεθών (πχ. ) επειδή οι μονάδες απλοποιούνται με τις πράξεις, μπορούν να είναι οποιεσδήποτε, αρκεί να είναι ίδιες. Αυτό σημαίνει ότι στη σχέση μπορεί η διάμετροι d 1 και d 2 να είναι είτε σε mm ή cm ή τέλος σε m, αρκεί να είναι στην ίδια μονάδα αριθμητής και παρονομαστής. Επίσης οι στροφές μπορεί να είναι και οι δύο σε μονάδες στροφών ανά λεπτό ή ανά δευτερόλεπτο. Αυτό δεν μπορεί να γίνει στις σχέσεις 8.5 και 8.6. Εκεί θα χρησιμοποιείτε τις μονάδες του Διεθνούς Συστήματος Μονάδων (SI). Μόνο οι αρκετά εξοικειωμένοι με τα θέματα αυτά θα πρέπει να χρησιμοποιούν μονάδες διαφορετικές από εκείνες που αναφέρονται εδώ. Όταν αναφέρθηκε προηγουμένως η σχέση 8.6, είπαμε για την περιφερειακή ταχύτητα του ιμάντα και των τροχαλιών. Αυτή είναι πολύ σημαντική για τους ιμάντες, διότι εάν μεταφέρεται μια συγκεκριμένη ισχύς Ρ με τον ιμάντα, τότε η ταχύτητα του ιμάντα επηρεάζει την δύναμη που τον καταπονεί. Στο SI ισχύει η σχέση: F είναι η περιφερειακή δύναμη που καταπονεί τον ιμάντα. Είναι δηλαδή εκείνη από την οποία εξαρτάται αν ο ιμάντας θα αντέξει στις συνθήκες λειτουργίας του. Για να καταλάβουμε τη σχέση αυτή θα δώσουμε ένα παράδειγμα. Ας πούμε ότι θέλουμε να μεταφέρουμε ισχύ W με ένα ιμάντα. Αν χρησιμοποιήσουμε τροχαλίες ώστε ο ιμάντας να περιστρέφεται με ταχύτητα τότε η F θα είναι και προκύπτει F=1000 Ν. Αν όμως ο ιμάντας περιστρέφεται πιο αργά ώστε η ταχύτητα να είναι τότε για την ίδια ισχύ από τη σχέση 8.9 η δύναμη θα είναι 4000 Ν. Θα είναι δηλαδή 4 φορές μεγαλύτερη από πριν, άρα ο ιμάντας θα καταπονείται περισσότερο. Γι αυτό οι ιμάντες δεν πρέπει να εργάζονται σε πολύ χαμηλές στροφές, αν δεν είναι απαραίτητο. Ο λόγος είναι ότι αναπτύσσονται μεγάλες δυνάμεις και η αντοχή τους δεν είναι αντιστοίχως μεγάλη. Επειδή συνήθως την ισχύ των μηχανών που κινούν τους ιμάντες την μετράμε σε ίππους PS μπορούμε να χρησιμοποιούμε και τον τύπο του βιβλίου: Στον τύπο 8.10 η ισχύς έχει μονάδες PS, η δύναμη dan και η ταχύτητα m/s. 120 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
121 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 Η δύναμη που καταπονεί τον ιμάντα τον καταπονεί σε εφελκυσμό και για να ελέγξουμε την αντοχή του θα κάνουμε τον γνωστό έλεγχο σε εφελκυσμό. Θα εφαρμόσουμε τη γνωστή σχέση: Υπενθυμίζουμε ότι η σχέση αυτή σημαίνει ότι η τάση εφελκυσμού σ του ιμάντα, που είναι ίση με το πηλίκο της εφελκυστικής δύναμης F προς την διατομή του ιμάντα Α, πρέπει να είναι μικρότερη από την επιτρεπόμενη τάση του υλικού του ιμάντα σ επ. Το σχολικό βιβλίο εξετάζει μόνο την περίπτωση που ο ιμάντας είναι ορθογωνικής διατομής με πάχος s και πλάτος b. Τότε η διατομή Α θα είναι το γινόμενο του πάχους επί το πλάτος και θα ισχύει: Α=b s. Αν θέλουμε να υπολογίσουμε τη δύναμη που μπορεί αν αντέξει ένας ιμάντας, θα είναι εκείνη για την οποία η τάση γίνεται μέγιστη, δηλαδή ίση με την επιτρεπόμενη σ επ. Οπότε από τη σχέση της τάσης (για την ισότητα της σ με την σ επ ) προκύπτει η μέγιστη δύναμη αντοχής του ορθογωνικής διατομής ιμάντα: Η σχέση αυτή ισχύει στο σύστημα SI, αλλά επειδή τα F και σ επ δίνονται συνήθως σε μονάδες dan και dan/cm 2 αντίστοιχα, τα μήκη πρέπει να τα βάζουμε σε cm. Με τη χρήση των τύπων 8.10 και 8.11 γίνεται ο έλεγχος αντοχής για τους ιμάντες ορθογωνικής διατομής. Αν ο ιμάντας έχει τραπεζοειδή διατομή τότε το εμβαδόν Α δίνεται από άλλο τύπο. Σε ένα τραπέζιο το εμβαδόν δίνεται από τη σχέση: Οι διαστάσεις α και β είναι η μικρή και η μεγάλη βάση του τραπεζίου (όπως αυτές φαίνονται στο επόμενο σχήμα) και h είναι το ύψος του τραπεζίου. Άρα για τραπεζοειδή ιμάντα με z κλάδους η μέγιστη δύναμη εφελκυσμού θα είναι: Προφανώς αν ο ιμάντας έχει μόνο ένα κλάδο το z θα είναι μονάδα. Για τις μονάδες στον τύπο, ισχύουν τα ίδια με τον τύπο Στην περίπτωση του ιμάντα με ορθογώνια διατομή η τροχαλία γίνεται λίγο μεγαλύτερη από το πλάτος του ιμάντα. Συγκεκριμένα το πλάτος της τροχαλίας, που συμβολίζεται με b 1, θα είναι κατά 10% μεγαλύτερο από το πλάτος του ιμάντα συν 10 mm. (Στα μαθηματικά το 10% ενός αριθμού Α, δίνεται από το γινόμενο του 0,1 επί τον αριθμό, δηλαδή θα είναι: 0,1 Α. Για παράδειγμα το 10% του 30 είναι το 0,1 30=3. Και όταν θέλουμε ένα αριθμό κατά 10% μεγαλύτερο από τον αριθμό Α, αυτός θα είναι ο: Α+0,1 Α=1,1 Α.) Επομένως το πλάτος της τροχαλίας ενός επίπεδου ιμάντα θα δίνεται από τη σχέση: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 121
122 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Θα συνεχίσουμε τώρα με επίλυση ασκήσεων, πάνω στις σχέσεις που αναφέρθηκαν στο κεφάλαιο αυτό. Θα επικεντρωθούμε σε ασκήσεις παρόμοιες με εκείνες του βιβλίου, αλλά θα κάνουμε και άλλες, εφαρμόζοντας όλες τις σχέσεις. Άσκηση 8.1 Ένας ιμάντας συνεργάζεται με δύο τροχαλίες που έχουν διαμέτρους 400 mm και 1200 mm αντίστοιχα. Αν η δύναμη που τον καταπονεί είναι ίση με 1200 dan, να υπολογίσετε τη ροπή σε κάθε τροχαλία. Είναι γνωστό ότι ισχύει η σχέση 8.5, η οποία δίνει τη ροπή σε κάθε τροχαλία διαμέτρου d όταν η δύναμη που ασκείται στον ιμάντα είναι η F (η οποία είναι η συνισταμένη δύο αντίρροπων περιφερειακών δυνάμεων στην τροχαλία). Θα συμβολίσομε την διάμετρο της μικρής τροχαλίας με d 1 και της μεγάλης με d 2. Θα εργαστούμε στο Διεθνές Σύστημα Μονάδων και θα είναι d 1 =0,4 m και d 2 =1,2 m. Η ροπή της μικρής θα είναι Μ 1 και της μεγάλης τροχαλίας Μ 2. Θα επιλύσομε τη σχέση 8.5 δύο φορές, μία για τη διάμετρο κάθε τροχαλίας, ενώ η δύναμη, ως γνωστόν, είναι ίδια και στις δύο περιπτώσεις: Επομένως οι ροπές είναι 240 dan m και 720 dan m αντίστοιχα.. Άσκηση 8.2 Ένας ιμάντας σε μία τροχαλία έχει συντελεστή τριβής μ=0,5 και το τόξο τύλιξης είναι 180 μοίρες. Αν είναι γνωστό ότι η δύναμη που καταπονεί τον ιμάντα είναι 800 dan να βρείτε την δύναμη που ασκείται στον ελκυόμενο και στον έλκοντα κλάδο του ιμάντα. Είναι προφανές ότι θα χρησιμοποιήσουμε τις σχέσεις 8.1 και 8.2. Σε αυτές είναι γνωστοί όλοι οι όροι εκτός από τις ζητούμενες δυνάμεις Τ 1 και Τ 2. Σύμφωνα με την εκφώνηση θα έχουμε F=800 dan και το τόξο τύλιξης σε ακτίνια θα είναι π=3,14 ακτίνια, αφού είδαμε στις προηγούμενες σελίδες ότι οι 180 μοίρες είναι ίσες με π ακτίνια. Θα εργαστούμε στο SI. Μόνο οι δυνάμεις και η γωνία (με μονάδα τα ακτίνια) έχουν μονάδες στους τύπους αυτούς. Για τη λύση της άσκησης θα αρχίσουμε από την εξίσωση 8.2 και θα λύσουμε ως προς την δύναμη Τ 1. Θα μπορούσαμε να λύσουμε και ως προς την Τ 2 ή να ξεκινήσουμε από την εξίσωση 8.1. Απλά, πιο εύκολο είναι αυτό που κάνουμε εδώ. Μετά, αφού βρούμε την δύναμη Τ 1, με χρήση της 8.1 θα βρούμε την Τ 2. Παρακάτω φαίνεται η λύση του συστήματος: Επομένως η έλκουσα δύναμη είναι η Τ 1 =1010,5 dan και ο ελκυόμενος κλάδος δέχεται δύναμη Τ 2 =210,5 dan. Σημείωση: Οι δύο τύποι που χρησιμοποιήθηκαν έχουν μονάδες στο SI και η δύναμη θα έπρεπε να μπει σε μονάδες Ν. Όμως, επειδή η χρήση των τιμών της δύναμης έγινε από τον τύπο δεν έχει επίδραση αν μπουν οποιεσδήποτε μονάδες. Αν η αντικατάσταση γινόταν στο τύπο πάλι δεν θα υπήρχε πρόβλημα. Αυτό γίνεται γιατί δεν υπεισέρχονται άλλα μεγέθη εκτός από τις δυνάμεις στους τύπους. Πρέπει να είμαστε προσεκτικοί όταν δεν χρησιμοποιούμε το σύστημα μονάδων SI ή τις μονάδες που προτείνει 122 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
123 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 το βιβλίο για έναν τύπο. Αυτή η άσκηση δόθηκε για εξάσκηση και δε νομίζουμε ότι υπάρχει μεγάλη πιθανότητα να δοθεί ως θέμα εξετάσεων. Άσκηση 8.3 Μια τροχαλία με διάμετρο 500 mm κινεί άλλη τροχαλία διαμέτρου 1600 mm με ένα τραπεζοειδή ιμάντα τύπου SPC (σελίδα 350 του σχολικού βιβλίου). Τα κέντρα των δύο τροχαλιών απέχουν 3 μέτρα. Να εκλέξετε το τυποποιημένο μήκος του ιμάντα. Θα χρησιμοποιήσουμε τον τύπο 8.3 για τον υπολογισμό του μήκους L του ιμάντα. Κανονικά θα πρέπει να τον αποδείξετε ή να θυμόσαστε τον τύπο 8.4 που περιέχεται στο βιβλίο. Θα κάνουμε τον υπολογισμό του μήκους και με του δύο. Στους συμβολισμούς θα έχουμε: d 1 =1600 mm d 2 =500 mm C=3m=3000 mm Ο τύπος 8.3 δίνει: Ο τύπος 8.4 δίνει: Παρατηρούμε ότι τα δύο μήκη που υπολογίστηκαν διαφέρουν μόλις 101 mm, που είναι περίπου το 1% του μήκους του ιμάντα Από τα τυποποιημένα μήκη του πίνακα στη σελίδα 350 του σχολικού βιβλίου πρέπει να επιλέξουμε ανάμεσα στα μήκη 9000 mm και 9500 mm. Επιλέγουμε το δεύτερο μήκος 9500 mm και η ακριβής απόσταση των τροχαλιών θα καθοριστεί κατά τη συναρμολόγηση. Άσκηση 8.4 Ένας ιμάντας συνδέει δύο τροχαλίες με διαμέτρους 250 mm και 750 mm αντίστοιχα. Η ισχύς που πρέπει να μεταφέρεται είναι 70 PS. Η μικρή τροχαλία είναι η κινητήρια και περιστρέφεται με 270 rpm. Να υπολογίσετε: 1. Τις στροφές της κινούμενης τροχαλίας. 2. Τη σχέση μετάδοσης της ιμαντοκίνησης. 3. Την γραμμική ταχύτητα του ιμάντα. 4. Τη δύναμη που καταπονεί τον ιμάντα. Θα δώσουμε τους απαραίτητους συμβολισμούς στα μεγέθη που δίνονται και ζητούνται. Έχουμε κάνει και τις απαραίτητες μετατροπές εκεί που τα μεγέθη μπορεί αν χρειαστεί να είναι στο σύστημα SI. Διάμετρος μικρής τροχαλίας d 1 =250 mm=0,25 m Διάμετρος μεγάλης τροχαλίας d 2 =750 mm=0,75 m Στροφές μικρής τροχαλίας n 1 =270 rpm=270/60=4,5 rps στροφές το δευτερόλεπτο Ισχύς P=70 PS Στροφές μεγάλης τροχαλίας n 2 Σχέση μετάδοσης i Γραμμική ταχύτητα ιμάντα Δύναμη στον ιμάντα F Ακολουθούν οι απαντήσεις στα ερωτήματα της άσκησης: 1) Τις στροφές της μεγάλης τροχαλίας θα τις υπολογίσουμε από τη σχέση 8.7: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 123
124 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Άρα η μεγάλη τροχαλία περιστρέφεται με 90 rpm. 2) Η σχέση μετάδοσης θα υπολογιστεί και αυτή από τη σχέση 8.7: Επομένως η σχέση μετάδοσης είναι 1/3. 3) Η γραμμική ταχύτητα του ιμάντα υπολογίζεται από τη σχέση 8.6. η σχέση αυτή δίνει την περιφερειακή ταχύτητα της κάθε τροχαλίας, η οποία όμως είναι ίση με την ταχύτητα του ιμάντα, αν υποθέσουμε ότι δε υπάρχει ολίσθηση. Οι περιφερειακές ταχύτητες των τροχαλιών προφανώς είναι ίσες και γι αυτό στην πρώτη από τις σχέσεις 8.6 μπορούμε να χρησιμοποιήσουμε τα στοιχεία από όποιαν τροχαλία θέλουμε. Ας πάρουμε την μικρή. Υπενθυμίζουμε ότι η σχέση αυτή απαιτεί μονάδες του συστήματος SI: Για να δείτε ότι δεν υπάρχει διαφορά στο αποτέλεσμα αν χρησιμοποιήσουμε τη μεγάλη τροχαλία, θα το κάνουμε. Θα μετατρέψουμε τις στροφές n 2 στο SI διαιρώντας με το 60: n 2 =90 rpm=90/60=1,5 rps στροφές το δευτερόλεπτο Πράγματι, βρέθηκε το ίδιο αποτέλεσμα. Πιο εύκολο είναι να χρησιμοποιείτε την δεύτερη από τις σχέσεις 8.6, αν και τη διαίρεση με το 60 δεν την αποφεύγετε, απλά δεν γράφετε τη μετατροπή των μονάδων στις στροφές. 4) Για τον υπολογισμό της δύναμης θα εφαρμόσουμε τον τύπο 8.10 και θα βρεθεί η δύναμη σε dan: Άρα η δύναμη που καταπονεί τον ιμάντα είναι 1487 dan. Σημείωση: Η δύναμη αυτού του μεγέθους είναι μεγάλη για ιμάντα. Οι ιμάντες είναι από υλικό που συνήθως έχει επιτρεπόμενη τάση περίπου σ επ =20 dan/cm 2. Αυτό σημαίνει ότι η διατομή του ιμάντα θα πρέπει να είναι για να αντέξει: Η διατομή 74,35 cm 2 είναι σχετικά μεγάλη, διότι αν το πάχος είναι 2 cm = 20 mm τότε το πλάτος θα είναι 74,35/2 37 cm = 370 mm, που είναι μεγάλο. Αν θέλαμε να μειώσουμε τις διαστάσεις του ιμάντα θα έπρεπε να μειωθεί η καταπονούσα δύναμη. Για να γίνει αυτό, όπως φαίνεται στον τύπο 8.10 θα πρέπει να αυξηθεί η ταχύτητα του ιμάντα, άρα οι στροφές του. Αν, ας πούμε, θέλουμε να μειώσουμε τη διατομή τέσσερις φορές (και να την κάνουμε για παράδειγμα 10 mm 185 mm), θα μειώσουμε τη δύναμη 4 φορές. Αυτό σημαίνει ότι θα πρέπει να αυξήσουμε την ταχύτητα 4 φορές, δηλαδή τις στροφές. Άρα οι στροφές των δύο τροχαλιών θα ήταν 360 rpm και 1080 rpm. Το ότι η γραμμική ταχύτητα είναι ανάλογη των στροφών φαίνεται από τη σχέση 8.6. Μπορούμε βέβαια να τοποθετήσουμε και πολλούς μικρότερους ιμάντες με συνολική διατομή εκείνη που βρέθηκε. Άσκηση 8.5 Ένας ιμάντας μεταφέρει ισχύ 40 PS και η μικρή τροχαλία έχει διάμετρο 150 mm και περιστρέφεται με 500 rpm. Να υπολογίσετε τη δύναμη που καταπονεί τον ιμάντα. Θα κάνουμε λίγο πιο αναλυτική τη σκέψη μας στη λύση για να σας δείξουμε πως πρέπει να σκέφτεστε. Τη δύναμη που καταπονεί γενικά ένα ιμάντα, μπορούμε να την υπολογίσουμε από τους τύπους 8.1, 8.5, 8.10, 8.11 και Σε όλες αυτές τις σχέσεις υπεισέρχεται η 124 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
125 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 δύναμη F, αλλά δεν σημαίνει ότι όλες είναι και οι κατάλληλες για τον ζητούμενο υπολογισμό. Ας δούμε μία-μία γιατί δεν μπορούν να χρησιμοποιηθούν εκτός από την 8.10: Για να χρησιμοποιηθεί η 8.1 πρέπει αν γνωρίζουμε ή να δίνονται στοιχεία για τον υπολογισμό των δυνάμεων Τ 1 και Τ 2, πράγμα που δεν συμβαίνει, αφού δε δίνονται συντελεστής τριβής και τόξο τύλιξης. Για τον 8.5 χρειάζεται η ροπή Μ η οποία δεν δίνεται, αλλά ούτε και δίνονται στοιχεία για τον υπολογισμό της. Για τους τύπους 8.11 και 8.13 (για ορθογωνικό ή τραπεζοειδή ιμάντα αντίστοιχα) πρέπει να είναι γνωστές οι διαστάσεις του ιμάντα και η επιτρεπόμενη τάση. Επομένως μένει μόνο η σχέση 8.10 στην οποία δίνεται η ισχύς Ρ=40 PS και η ταχύτητα μπορεί να υπολογιστεί από τη σχέση 8.6 αφού δίνονται οι στροφές και η διάμετρος της τροχαλίας. Πρώτα λοιπόν θα υπολογιστεί η ταχύτητα από τη σχέση 8.6. Θα πάρουμε τη δεύτερη από τις δύο σχέσεις, όπου d=150 mm=0,15 m και n=500 rpm: Έχοντας βρει την ταχύτητα, από τη σχέση 8.10 θα υπολογίσουμε την δύναμη F: Επομένως η καταπονούσα δύναμη είναι 764,3 dan. Άσκηση 8.6 Ένας ιμάντας από υλικό με σ επ =20 dan/cm 2 ορθογωνικής διατομής, μεταφέρει ισχύ 80 PS μέσω μιας τροχαλίας που έχει διάμετρο 400 mm και περιστρέφεται με 1000 rpm. Να υπολογίσετε: 1. Την περιφερειακή ταχύτητα της τροχαλίας. 2. Την δύναμη που καταπονεί τον ιμάντα. 3. Το πλάτος του ιμάντα αν το πάχος του είναι 10 mm. 4. Το πλάτος της τροχαλίας. Εδώ θα μπορούσε να δοθεί κατ ευθείαν η τρίτη ή και η τέταρτη ερώτηση, χωρίς να έχετε τις προηγούμενες. Όμως θα έπρεπε από μόνοι σας να ακολουθήσετε τα βήματα ένα-ένα που τώρα ζητούνται από την εκφώνηση. Μπορούμε να δώσουμε από την αρχή τα σύμβολα για τα μεγέθη που δίνονται και που ζητούνται ή να τα δίνουμε σε κάθε ερώτηση με την απάντησή της χωριστά. Θα ακολουθήσουμε τη δεύτερη μέθοδο. 1) Η περιφερειακή ταχύτητα της τροχαλίας είναι ίδια με τη γραμμική ταχύτητα του ιμάντα και θα υπολογιστεί από τη σχέση 8.6 (τη δεύτερη καλύτερα, από τις δύο). Η διάμετρος θα είναι d =400 mm=0,4 m και οι στροφές n=1000 rpm: Άρα η ζητούμενη ταχύτητα είναι 20,93 m/s. 2) Η δύναμη F θα υπολογιστεί από τη σχέση 8.10 αφού γνωρίζουμε την ισχύ Ρ=80 PS και υπολογίσαμε την ταχύτητα: Η δύναμη που καταπονεί τον ιμάντα βρέθηκε ίση με 286,7 dan. Παρατηρούμε ότι είναι πολύ μικρότερη από την προηγούμενη άσκηση, παρ ότι η μεταφερόμενη ισχύς είναι διπλάσια. Αυτό οφείλεται στο ότι η τροχαλία είναι μεγαλύτερη και οι στροφές περισσότερες, με αποτέλεσμα η ταχύτητα του ιμάντα να είναι μεγαλύτερη από πριν. Αυτό, όπως είναι γνωστό μειώνει τη δύναμη. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 125
126 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ 3) Η διατομή του ιμάντα θα βρεθεί με χρήση της σχέσης 8.11 στην οποία δίνεται η επιτρεπόμενη τάση σ επ, το πάχος του ιμάντα s=10 mm=1 cm και η δύναμη F υπολογίστηκα πριν: Επομένως το πλάτος του ιμάντα πρέπει να είναι τουλάχιστον 144 mm. 4) Για το πλάτος (σύμβολο b 1 ) της τροχαλίας ισχύει η σχέση 8.14, όπου το πλάτος του ιμάντα b θα έχει μονάδες mm: Επομένως το πλάτος της τροχαλίας θα είναι 170 mm. Σημείωση: Αν μας δινόταν κατ ευθείαν η τέταρτη ερώτηση, θα σκεφτόμασταν ως εξής: το πλάτος της τροχαλίας θα το βρούμε από την εξίσωση Μας λείπει το πλάτος b το οποίο θα βρούμε από την 8.11 (δεν υπάρχει σε άλλο τύπο της θεωρίας το πλάτος του ιμάντα). Αλλά στην 8.11 ενώ ξέρομε όλα τα μεγέθη μας λείπει το F. Αυτό θα το βρούμε από την 8.10, αφού δεν υπάρχει άλλος τύπος προσφορότερος. Αλλά και στην 8.10 δεν γνωρίζομε την ταχύτητα του ιμάντα. Την ταχύτητα θα τη βρούμε από την 8.6, στην οποία γνωρίζουμε όλα τα μεγέθη. Από εδώ επομένως θα ξεκινήσουμε. Όταν κάνουμε αυτές τις σκέψεις, θα λύσουμε την άσκηση ακολουθώντας τα βήματα αντίστροφα. Άσκηση 8.7 Ένας τραπεζοειδής ιμάντας με τρεις κλάδους από υλικό με σ επ =25 dan/cm 2, έχει διαστάσεις: ύψος h=13 mm και μήκη βάσεων: β=16 mm και α=10 mm. Να υπολογίσετε την δύναμη που μπορεί να αντέξει ο ιμάντας. Επειδή πρόκειται για τραπεζοειδή ιμάντα, το εμβαδόν της διατομής του θα βρεθεί εφαρμόζοντας τη σχέση 8.12, αφού έχουμε όλες τις διαστάσεις. Αφού τα μήκη δίνονται σε mm το αποτέλεσμα θα βρεθεί σε mm 2. Επειδή όμως στις επιτρεπόμενες τάσεις χρησιμοποιούνται τα cm 2, έχουμε πει ότι είναι καλύτερα να χρησιμοποιούμε διαστάσεις στα μήκη τα cm. Γι αυτό κάνουμε τη μετατροπή των mm σε cm: h=1,3 cm, β=1,6 cm και α=1 cm. Από τη σχέση 8.12 θα έχουμε: Υπολογίσαμε τη διατομή ίση με 1,69 cm 2 και τώρα από τη γενική σχέση θέτοντας την σ επ στην θέση της τάσης σ, θα λύσουμε την εξίσωση : Επομένως κάθε κλάδος του ιμάντα μπορεί να δεχθεί δύναμη μέχρι 42,25 dan, άρα και οι τρεις κλάδοι δέχονται 3 42,25 dan=126,75 dan. Σημείωση 1: Την άσκηση μπορούσαμε να λύσουμε εφαρμόζοντας κατ ευθείαν τη σχέση 8.13, οπότε θα είχαμε: Προφανώς βρήκαμε το ίδιο αποτέλεσμα. Η σχέση αυτή δεν βρίσκεται στο βιβλίο και γι αυτό δεν μπορείτε να τη χρησιμοποιήσετε στις εξετάσεις ως γνωστή. Η πρώτη λύση που δώσαμε όμως είναι μέσα στο πλαίσιο του μαθήματος. Σημείωση 2: Η άσκηση αυτή δόθηκε καθαρά για να γίνει χρήση του τύπου υπολογισμού της δύναμης. Ο πραγματικός προσδιορισμός της δύναμης αντοχής απαιτεί και άλλα στοιχεία 126 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
127 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 της ιμαντοκίνησης. Αυτά τα στοιχεία δίνονται στις σελίδες 345 μέχρι 354. Όπως όμως αναφέρεται και στο σχολικό βιβλίο, οι υπολογισμοί με τη χρήση των πινάκων αυτών δεν μπορούν να αποτελούν πλήρεις ασκήσεις του μαθήματος. Ουσιαστικά γίνεται μόνο χρήση των πινάκων στην εκλογή ιμάντων. Αυτό στην πράξη είναι μια πολύ σημαντική εργασία για το μηχανικό, απαιτεί όμως εμπειρία και κατοχή στοιχείων για την επιλογή ιμάντα και από άλλες εταιρίες. Αν και δεν θεωρείται πιθανό ένα θέμα από την περιοχή αυτή του μαθήματος, θα δώσουμε ένα παράδειγμα στο πνεύμα της άσκησης του βιβλίου των σελίδων 345 ως 353. Οι τύποι που χρησιμοποιούνται στο τμήμα αυτό των ασκήσεων δεν έχουν δοθεί στην αρχή του κεφαλαίου αυτού, γιατί δεν είναι απαραίτητο να τους γνωρίζετε. Άσκηση 8.8 Ένας τραπεζοειδής ιμάντας συνδέει ηλεκτροκινητήρα με εκκίνηση αστέρα-τριγώνου, ισχύος 100 kw με εργαλειομηχανή (machine tools) ίδιας ισχύος. Οι στροφές του κινητήρα είναι n 1 =1500 rpm και η εργαλειομηχανή στρέφεται με n 2 =750 rpm. Δίνεται ότι η ημερήσια λειτουργία του μηχανήματος θα είναι 12 ώρες, η απόσταση των δύο τροχαλιών θα είναι περίπου 1,5 m (των κέντρων τους) και η τροχαλία του κινητήρα έχει διάμετρο d 1 κοντά στα 250 mm. Απαντήσετε στα επόμενα ερωτήματα: 1. Να επιλέξετε τύπο ιμάντα από την εικόνα 14.9.γ του βιβλίου. 2. Να προσδιορίσετε ακριβώς τις διαμέτρους των δύο τροχαλιών. 3. Ποιο είναι το απαιτούμενο μήκος του ιμάντα; 1) Για την επιλογή του τύπου του ιμάντα θα χρησιμοποιηθεί όχι η ισχύς των Ρ=100 kw, αλλά άλλη, προσαυξημένη λόγω των συνθηκών λειτουργίας κατά ένα παράγοντα που συμβολίζεται με c 2 και τον προσδιορίζουμε (με προσέγγιση) από τον πίνακα 14.9.β. Για κινητήρα εργαλειομηχανής (machine tools) με εκκίνηση αστέρα-τρίγωνο (AC star delta start) και για 12 ώρες λειτουργίας (Over 10 to 16, Hours per day duty) ο πίνακας δίνει c 2 =1,2. Άρα η ισχύς θα γίνει P b αντί Ρ, όπου P b =1,2 Ρ. Υπολογίζουμε: Τώρα από το διάγραμμα 14.9.γ θα επιλέξουμε τον κατάλληλο ιμάντα. Η επιλογή με βάση τα μεγέθη που είναι στον κάθετο και στον οριζόντιο άξονα, δηλαδή στις στροφές της μικρής τροχαλίας και την αυξημένη ισχύ P b. Σε μια μετάδοση περιστροφικής κίνησης τις περισσότερες στροφές τις έχει η μικρή τροχαλία, άρα οι στροφές της μικρής τροχαλίας είναι 1500 rpm. Η ισχύς P b υπολογίστηκε στα 120 kw. Θέτοντας αυτές τις τιμές στους άξονες προσδιορίζουμε ένα σημείο, το οποίο μας οδηγεί στην επιλογή ιμάντα τύπου SPB. 2) Για τον προσδιορισμό της διαμέτρου των τροχαλιών θα χρησιμοποιήσουμε τον πίνακα 14.9.δ. Για ιμάντα τύπου SPB βλέπουμε ότι μπορούμε να επιλέξουμε διάμετρο ακριβώς 250 mm. Με d 1 =250 mm από τη σχέση 8.7 θα υπολογίσουμε τη διάμετρο d 2 της μεγάλης τροχαλίας: Από τον ίδιο πίνακα 14.9.δ βλέπουμε ότι η διάμετρος d 2 =500 mm υπάρχει στις προτεινόμενες για τους ιμάντες τύπου SPB, άρα την επιλέγουμε. Για τις επιλογές που έγιναν δεν έχει αλλάξει καμιά διάμετρος ούτε και η σχέση μετάδοσης. Επομένως προχωράμε δεχόμενοι τις στροφές που έχουν δοθεί από την αρχή στην άσκηση. 3) Για τον υπολογισμό του μήκους του ιμάντα L θα χρησιμοποιήσουμε τον τύπο 8.4 του βιβλίου, με απόσταση τροχαλιών ίση με C=1,5 m=1500 mm που δίνετε στην εκφώνηση και θα έχουμε (στην αντικατάσταση των μεγεθών δεν θα βάλουμε μονάδες που όλες θα είναι τα mm): ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 127
128 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Μην σας ενοχλεί που στην παράσταση αφαιρείτε μεγάλος αριθμός από μικρό, γιατί μετά υψώνεται στο τετράγωνο και γίνεται θετικός αριθμός. Από τον πίνακα 14.9.ε για ιμάντα τύπου SPB επιλέγουμε τυποποιημένο μήκος κλειστού ιμάντα 4250 mm. Σημείωση: στην άσκηση-παράδειγμα του βιβλίου στις σελίδες 345 ως 353 δεν δίνονται αρκετές διευκρινήσεις και επί πλέον πίνακες ώστε να γίνει πιο σύνθετη η άσκηση αυτή. Άσκηση 8.9 Ένας ιμάντας βρίσκεται σε τροχαλία με διάμετρο 400 mm και περιστρέφεται με 1800 rpm. Ο ιμάντας μεταφέρει ισχύ ίση με 60 PS. 1. Να υπολογίσετε την δύναμη που ασκείται στον ιμάντα αυτόν κατά την περιστροφή του. 2. Ο ίδιος ιμάντας στην ίδια τροχαλία περιστρέφεται με 600 rpm. Πόση θα είναι η δύναμη που τον καταπονεί τώρα; 3. Να υπολογίσετε τη ροπή στις δύο περιπτώσεις με τις διαφορετικές στροφές της τροχαλίας. Κατ αρχήν θα δώσουμε τα σύμβολα στα γνωστά και ζητούμενα μεγέθη: Διάμετρος τροχαλίας d=400 mm =0,4 m. Ισχύς που μεταφέρει ο ιμάντας Ρ=60 PS. Στροφές τροχαλίας στην πρώτη περίπτωση n 1 =1800 rpm. Στροφές τροχαλίας στην δεύτερη περίπτωση n 2 =600 rpm. Ταχύτητα ιμάντα στην πρώτη περίπτωση. Ταχύτητα ιμάντα στην δεύτερη περίπτωση. Δύναμη στον ιμάντα στην πρώτη περίπτωση F 1. Δύναμη στον ιμάντα στην δεύτερη περίπτωση F 2. Ροπή τροχαλίας στην πρώτη περίπτωση Μ 1. Ροπή τροχαλίας στην δεύτερη περίπτωση Μ 2. 1) Η δύναμη στον ιμάντα θα υπολογιστεί από τη σχέση 8.10:, όμως σε αυτήν είναι άγνωστη η ταχύτητα του ιμάντα. Θα υπολογιστεί από τη σχέση 8.6 (την δεύτερη από τις δύο). Σε αυτήν όλα τα μεγέθη είναι γνωστά και οι μονάδες είναι εντάξει. Έχοντας βρει την ταχύτητα θα υπολογίσουμε την δύναμη από την 8.10: Επομένως η δύναμη που καταπονεί τον ιμάντα στην πρώτη περίπτωση είναι ίση με 119,4 dan. 2) Στην δεύτερη περίπτωση θα κάνουμε τα ίδια με πριν, αλλά με τις στροφές n 2 =600 rpm: Η δύναμη που καταπονεί τον ιμάντα στη δεύτερη περίπτωση είναι ίση με 358,2 dan, δηλαδή είναι τρεις φορές μεγαλύτερη από πριν. Αυτό δείχνει ότι όσο μικρότερη είναι η ταχύτητα του ιμάντα τόσο περισσότερο καταπονείται. 3) Η ροπή στις τροχαλίες των ιμάντων υπολογίζεται όπως και σε κάθε τροχό, δηλαδή από τη σχέση 8.5. Έχοντας βρει τις δυνάμεις F 1 και F 2 θα υπολογίσουμε τις ροπές στις δύο περιπτώσεις. 128 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
129 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 Αυτές είναι οι ροπές στις δύο περιπτώσεις. Βλέπουμε ότι στις λιγότερες στροφές η ροπή είναι μεγαλύτερη. Αυτό βέβαια είναι φυσικό αφού τότε η δύναμη είναι επίσης μεγαλύτερη ενώ η διάμετρος παραμένει ίδια. Άσκηση 8.10 Μία τροχαλία με διάμετρο 240 mm περιστρέφεται με 1600 rpm και κινεί με ιμάντα μια άλλη τροχαλία με σχέση μετάδοσης i=1:3,5. Αν η ισχύς που μεταφέρεται είναι 30 PS, να υπολογίσετε: 1. Την γραμμική ταχύτητα του ιμάντα. 2. Την δύναμη που καταπονεί τον ιμάντα. 3. Την ροπή στην κινητήρια τροχαλία. 4. Την ροπή στην κινούμενη τροχαλία. Θα δώσουμε τα σύμβολα στα διάφορα μεγέθη, θέτοντας τον δείκτη 1 στην πρώτη τροχαλία και τον δείκτη 2 στην κινούμενη: Διάμετρος τροχαλιών d 1 =240 mm =0,24 m και d 2. Ισχύς που μεταφέρει ο ιμάντας Ρ=30 PS. Στροφές τροχαλιών n 1 =1600 rpm και n 2. Σχέση μετάδοσης i=1/3,5. Ταχύτητα ιμάντα. Δύναμη στον ιμάντα F. Ροπή στην κάθε τροχαλία Μ 1 και Μ 2. 1) Η γραμμική ταχύτητα του ιμάντα θα υπολογιστεί από τη σχέση 8.6 (την δεύτερη) όπου διάμετρο και στροφές θα πάρουμε τις τιμές για την πρώτη τροχαλία (γιατί αυτής τα στοιχεία έχουμε): Άρα η ταχύτητα του ιμάντα είναι 20,1 m/s. 2) Τώρα που βρήκαμε την ταχύτητα, την δύναμη στον ιμάντα θα υπολογίσουμε από τη σχέση 8.10: Επομένως η δύναμη στον ιμάντα είναι 112 dan. 3) Έχοντας βρει τη δύναμη στον ιμάντα η ροπή που ασκείται από αυτόν στην τροχαλία θα υπολογιστεί από τη σχέση 8.5: Επομένως η ροπή στην πρώτη τροχαλία είναι 13,44 dan m. Σημείωση: Θα μπορούσε να ζητά τη ροπή κατ ευθείαν χωρίς να έχουν προηγηθεί τα δύο πρώτα ερωτήματα. Τότε θα σκεφτόμασταν ως εξής: Τη ροπή θα τη βρούμε από τη σχέση: αλλά δεν γνωρίζουμε τη δύναμη F. Θα τη βρούμε από τη σχέση: από την οποία μας λείπει η ταχύτητα που θα βρούμε από την σχέση: στην οποία όλα τα μεγέθη είναι γνωστά. Δηλαδή ψάχνουμε τον άγνωστο από μια σχέση και σκεφτόμαστε αντίστροφα, από ποιες σχέσεις θα υπολογίσουμε τους ενδιάμεσους αγνώστους, μέχρι να καταλήξουμε σε σχέση με όλα τα μεγέθη γνωστά. 4) Η ροπή στη δεύτερη τροχαλία θα υπολογιστεί από τη σχέση 8.8 που συνδέει τις ροπές των δύο τροχαλιών με τη σχέση μετάδοσης. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 129
130 ΚΕΦΑΛΑΙΟ 8 ΙΜΑΝΤΕΣ Άρα η ροπή στην τροχαλία 2 είναι 47,04 dan m. Σημείωση: Επειδή μπορεί να σας δυσκολεύει η πράξη με το σύνθετο κλάσμα στον υπολογισμό της Μ 2, μπορούμε την εξίσωση να την λύσουμε και ως εξής: Φαίνεται ότι είναι λίγο πιο απλή αυτή η λύση στο τέταρτο ερώτημα. Άσκηση 8.11 Η κίνηση μεταφέρεται από μια τροχαλία διαμέτρου d=300 mm με ορθογωνικής διατομής ιμάντα σε άλλη τροχαλία ίδιας διαμέτρου. Αν η απόσταση των κέντρων των τροχαλιών είναι C=1,2 m, να υπολογίσετε το μήκος του ιμάντα. Στο επόμενο σχήμα φαίνονται οι δύο τροχαλίες και ο ιμάντας που παριστάνεται από τη γραμμή (ΑΒΓΔΕΖΑ). Τα τμήματα του ιμάντα (ΑΒ) και (ΔΕ) είναι ίσα μεταξύ τους και ίσα με την απόσταση των κέντρων (Κ 1 Κ 2 )=C=1,2 m. Το τμήμα του ιμάντα (ΕΖΑ) είναι ίσο με μισό κύκλο. Το ίδιο και το τμήμα (ΒΓΔ) στην άλλη τροχαλία. Αυτά γίνονται γιατί οι δύο τροχαλίες είναι ίσες και θεωρούμε ότι τα τμήματα (ΑΒ) και (ΔΕ) είναι ευθείες, δηλαδή ο ιμάντας είναι τεντωμένος. Το μήκος της περιφέρειας Π κάθε τροχαλίας δίνεται από τη σχέση: Έχουμε μετατρέψει τη διάμετρο της τροχαλίας από mm σε m, δηλαδή d=300 mm=0,3 m. Έχουμε όλη την περιφέρεια της κάθε τροχαλίας, άρα η μισή, που αντιπροσωπεύει το κάθε τμήμα (ΕΖΑ) και (ΒΓΔ), θα είναι ίση με Π/2=0,471 m. Τελικά το συνολικό μήκος του ιμάντα προκύπτει: Ο υπολογισμός αυτός είναι προσεγγιστικός, αλλά θα δούμε ότι δίνει ακριβώς το ίδιο αποτέλεσμα με τον υπολογισμό που γίνεται με τη σχέση 8.4 του βιβλίου, όπου d 1 =d 2 =d: Το ότι έχουμε το ίδιο αποτέλεσμα οφείλεται στο ότι στην ουσία είναι ό ίδιος τύπος, μόνο που είναι για διαφορετικές διαμέτρους τροχαλιών και όχι ίδιες που έχει η άσκησή μας. 130 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
131 ΙΜΑΝΤΕΣ ΚΕΦΑΛΑΙΟ 8 Άσκηση 8.12 Ένας ιμάντας με ορθογωνική διατομή από υλικό με σ επ =12 dan/cm 2 καταπονείται με δύναμη F=120 dan. Αν ο ιμάντας έχει πάχος s=8 mm να υπολογίσετε το πλάτος που πρέπει να έχει για να αντέχει στην καταπόνηση αυτή. Μετά να υπολογίσετε το πλάτος και της τροχαλίας. Προφανώς θα χρησιμοποιήσουμε τη σχέση 8.11, την οποία θα επιλύσουμε ως προς το ζητούμενο πλάτος του ιμάντα. Θα μετατρέψουμε πρώτα το πάχος από mm σε cm: s=8 mm=0,8 cm. Έτσι το πλάτος θα προκύψει σε εκατοστά, αφού και η επιτρεπόμενη τάση είναι σε dan/cm 2. Άρα ο ιμάντας θα έχει πλάτος 125 mm. Το πλάτος της τροχαλίας θα προκύψει από τον τύπο 8.14: Επομένως το πλάτος της τροχαλίας θα είναι 147,5 mm. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 131
132
133 ΑΛΥΣΙΔΕΣ ΚΕΦΑΛΑΙΟ 9 9. Αλυσίδες Στο κεφάλαιο των αλυσίδων οι ασκήσεις έχουν πολλές ομοιότητες με εκείνες των ιμάντων. Οι σχέσεις λειτουργίας είναι ακριβώς ίδιες. Έτσι, οι ασκήσεις που έχουμε στους ιμάντες (για τις σχέσεις λειτουργίας) θα μπορούσαν να είναι και για τις αλυσίδες. Δεν θα επαναλάβουμε εδώ τις λεπτομέρειες για κάθε σχέση, αλλά θα τις αναφέρουμε απλώς. Το σχολικό βιβλίο δίνει μόνο ένα λυμένο παράδειγμα και αφορά στη μέθοδο επιλογής αλυσίδων, στο οποίο μάλιστα χρησιμοποιούνται πίνακες συγκεκριμένου κατασκευαστή. Οι σχέσεις για τις αλυσίδες που αναφέρει το σχολικό βιβλίο στις σελίδες 264 και 265 είναι οι εξής: Προφανώς τα σύμβολα και οι μονάδες στους ανωτέρω τύπους αναφέρονται στα γνωστά από τους ιμάντες μεγέθη. Στη σχέση 9.4 προσθέσαμε και τον λόγο του αριθμού των δοντιών των αλυσοτροχών. Ο αριθμός των δοντιών κάθε αλυσοτροχού είναι ανάλογος με τη διάμετρό του. Ασκήσεις στις αλυσίδες μπορεί να είναι ίδιες με εκείνες των ιμάντων ή συνδυασμός με τους περιορισμούς στα δόντια ή στη λίπανση. Ας δούμε μερικές τέτοιες ασκήσεις. Άσκηση 9.1 Η αλυσίδα σε ένα αλυσοτροχό με διάμετρο 200 mm μεταφέρει ισχύ 90 PS και περιστρέφεται με 1000 rpm. Να υπολογίσετε: 5. Την γραμμική ταχύτητα της αλυσίδας. 6. Την δύναμη που καταπονεί την αλυσίδα. 7. Την ροπή που ασκεί η αλυσίδα στον τροχό. 8. Με ποιο τρόπο θα πρέπει να λιπαίνεται η αλυσίδα αυτή; 1) Η γραμμική ταχύτητα της αλυσίδας θα υπολογιστεί από τη σχέση 9.1 (τη δεύτερη από τις δύο). Η διάμετρος είναι d =200 mm=0,2 m και οι στροφές n=1000 rpm: Άρα η ζητούμενη ταχύτητα είναι 10,47 m/s. 2) Η δύναμη F θα υπολογιστεί από τη σχέση 9.2 με γνωστή την ισχύ Ρ=90 PS και την ταχύτητα που βρέθηκε στο πρώτο ερώτημα: Η δύναμη που καταπονεί τον ιμάντα βρέθηκε ίση με 644,7 dan. 3) Για τον υπολογισμό της ροπής θα χρησιμοποιήσουμε τον τύπο 9.3: Άρα η ζητούμενη ροπή είναι 64,5 dan m. 4) Η λίπανση των αλυσίδων εξαρτάται από την ταχύτητά τους. Η ταχύτητα της αλυσίδας που έχουμε είναι μεγάλη και ο τρόπος είναι με εκτόξευση λιπαντικού με μπεκ. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 133
134 ΚΕΦΑΛΑΙΟ 9 ΑΛΥΣΙΔΕΣ Άσκηση 9.2 Η αλυσίδα σε μια μοτοσυκλέτα συνδέει τον μικρό τροχό που έχει 17 δόντια με τον μεγάλο που έχει 51 δόντια. 1. Να υπολογίσετε την σχέση μετάδοσης του συστήματος. 2. Αν θέλουμε να αυξήσουμε την τελική ταχύτητα της μοτοσυκλέτας αλλάζοντας ένα τροχό από τους δύο, να πείτε ποια αλλαγή πρέπει να κάνουμε στον μικρό ή στον μεγάλο τροχό (κάθε φορά χωριστά). 1) Η σχέση μετάδοσης θα βρεθεί από τον τύπο 9.4. Συμβολίζουμε με z 1 τον αριθμό των δοντιών του μικρού τροχού και με z 2 του μεγάλου. Δηλαδή z 1 =17 και z 2 =51. Θα έχουμε: Άρα η σχέση μετάδοσης είναι 1/3. 2) Αν θέλουμε να αυξήσουμε την τελική ταχύτητα της μοτοσυκλέτας, σημαίνει ότι πρέπει για τις ίδιες στροφές του μικρού αλυσοτροχού (που αντιστοιχούν στις στροφές του κινητήρα που δίνει την μέγιστη ταχύτητα), να έχουμε περισσότερες στροφές στον μεγάλο αλυσοτροχό. Όμως περισσότερες στροφές στον τροχό σημαίνει μικρότερη διάμετρο, άρα λιγότερα δόντια. Επομένως αν αλλάξουμε τον πίσω αλυσοτροχό πρέπει να βάλουμε ένα άλλο με λιγότερα δόντια. Από τη σχέση για τα δόντια που γράψαμε στο προηγούμενο ερώτημα, φαίνεται ότι η σχέση μετάδοσης πρέπει να «κοντύνει». Αν ο μεγάλος αλυσοτροχός δεν αλλάξει, για να κοντύνει η σχέση πρέπει να αυξηθεί ο αριθμητής (με σταθερό τον παρονομαστή). Άρα να αυξηθούν τα δόντια του μικρού τροχού, δηλαδή από 17 να γίνουν πχ. 18 ή 19. Άσκηση 9.3 Σε ένα αλυσοτροχό με διάμετρο 100 mm θέλουμε η ταχύτητα της αλυσίδας να μην υπερβεί τα 4 m/s. Να υπολογίσετε τον μέγιστο αριθμό στροφών που θα έχει ο τροχός. Για τον υπολογισμό των στροφών θα χρησιμοποιήσουμε τον τύπο 9.1, λύνοντάς τον ως προς τις στροφές n. Η διάμετρος θα είναι στο SI και οι στροφές θα προκύψουν σε rpm. Ο συμβολισμός των μεγεθών και οι τιμές τους θα είναι: Διάμετρος αλυσοτροχού d=100 mm=0,1 m Ταχύτητα αλυσίδας =4 m/s Από τον τύπο 9.1 θα έχουμε: Άρα ο αλυσοτροχός δεν πρέπει να υπερβεί τις 764,3 rpm. Άσκηση 9.4 Μια αλυσίδα θέλουμε να μεταφέρει, με ομαλή και χωρίς κραδασμούς λειτουργία, την ισχύ ενός μεγάλου αλυσοτροχού, ο οποίος έχει 44 δόντια. Αν η σχέση μετάδοσης είναι ίση με 4 να προτείνετε ένα τρόπο για τον τρόπο της μετάδοσης. Για τη λύση δεν θα αναφερθείτε στις διαμέτρους των αλυσοτροχών αλλά μόνο στα δόντια. Σύμφωνα με τη σχέση μετάδοσης, που είναι 4, θα εφαρμόσουμε τον τύπο 9.4 για να υπολογίσουμε πόσα δόντια θα έχει ο μικρός τροχός. Τα δόντια του μεγάλου συμβολίζονται με z 1 =44. Θα έχουμε: Κανονικά η απάντηση θα ήταν 11 δόντια, αλλά είναι γνωστό ότι δεν επιτρέπεται ένας αλυσοτροχός να έχει τόσο λίγα δόντια. Μάλιστα όταν ο τροχός είναι κινούμενος, όπως εδώ, ο ελάχιστος αριθμός δοντιών που επιτρέπεται να έχει είναι 21. Με λιγότερα δόντια η λειτουργία 134 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
135 ΑΛΥΣΙΔΕΣ ΚΕΦΑΛΑΙΟ 9 δεν θα είναι ομαλή και χωρίς κραδασμούς, όπως απαιτείται από την εκφώνηση. Όμως με τόσο πολλά δόντια στο μικρό τροχό η σχέση μετάδοσης δεν μπορεί να είναι 4. Επομένως θα πρέπει να επιλέξουμε δύο ζεύγη αλυσοτροχών με δύο χωριστές αλυσίδες, όπως κάναμε στους οδοντωτούς τροχούς. Προχωράμε σε αυτή τη λύση. Επειδή 4=2 2, επιλέγουμε δύο σχέσεις μετάδοσης ίσες κάθε μία με 2. Θα λύσουμε ξανά τη σχέση 9.4 με i 1 =2 και αριθμό δοντιών του μικρού τροχού z 3. Θα υπολογίσουμε το z 3 : Για τη συνέχεια και επειδή η σχέση μετάδοσης είναι ίδια με πριν μπορούμε να επιλέξουμε ζεύγος μεγάλου και μικρού τροχού ίδιο με πριν, δηλαδή με 44 και 22 δόντια και θα έχουμε λύσει το πρόβλημα. Το επόμενο σχήμα δείχνει παραστατικά την επιλογή που κάναμε. Φαίνονται οι τέσσερις αλυσοτροχοί με τον αντίστοιχο αριθμό δοντιών που έχει ο καθένας και οι άξονες με τις στροφές τους. Επειδή δεν έχουμε ακριβή αριθμό των στροφών, υποθέτουμε ότι ο κινητήριος άξονας έχει α στροφές (όπου α ένας αριθμός, ας πούμε 300 rpm). Τότε ο συνεργαζόμενος άξονας θα έχει διπλάσιες στροφές (δηλαδή 2 α) και ο τελικός θα έχει 4 α στροφές. Η τελική απάντηση στο ερώτημα της άσκησης είναι ότι επιλέγουμε δύο ίδιες αλυσίδες και δύο ίδια ζεύγη αλυσοτροχών με 44 και 22 δόντια αντίστοιχα. Άσκηση 9.5 Η άσκηση που ακολουθεί είναι ίδιου τύπου με το παράδειγμα του σχολικού βιβλίου. Υπενθυμίζουμε ότι τέτοιου είδους ασκήσεις δεν έχουν πολλές πιθανότητες να είναι μεταξύ των θεμάτων των εξετάσεων. Αν δεν έχετε πολύ χρόνο μπορείτε να την παραλείψετε, γιατί έχει αρκετές δυσκολίες, εκτός από την έλλειψη των απαραίτητων πινάκων για να είναι μία πλήρης άσκηση. Ένας ανεμιστήρας που περιστρέφεται με n 2 =100 rpm (και περιλαμβάνει τον μεγάλο τροχό του συστήματος των δύο αλυσοτροχών) κινείται με αλυσίδα από ηλεκτροκινητήρα ισχύος 20 kw και υπάρχει σχέση μετάδοσης 1:2,25 (θα μπορούσαμε να την πούμε και 2,25 σύμφωνα με το βιβλίο σας). Η ταχύτητα της αλυσίδας είναι 3. Να υπολογίσετε τα στοιχεία των δύο αλυσοτροχών. Συμβολίζουμε με δείκτη το 1 τα στοιχεία του μικρού αλυσοτροχού και με δείκτη 2 του μεγάλου. Ανάλογα με τις συνθήκες λειτουργίες της αλυσοκίνησης η επιλογή της αλυσίδας γίνεται για ισχύ συνήθως μεγαλύτερη από εκείνη που υπάρχει στην πραγματικότητα. Η διόρθωση αυτή γίνεται με χρήση του πίνακα β μέσω του συντελεστή y. Στην περίπτωσή μας για ηλεκτροκινητήρα που κινεί ανεμιστήρα, είμαστε στην πρώτη γραμμή και στη δεύτερη στήλη, οπότε βρίσκουμε y=1, άρα η ισχύς των Ρ=20 kw δεν αλλάζει. Σύμφωνα με τη σχέση μετάδοσης i και αφού ο τροχός του ανεμιστήρα είναι ο μεγάλος θα πρέπει ο μικρός κινητήριος τροχός να περιστρέφεται με n 1 στροφές και θα είναι: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 135
136 ΚΕΦΑΛΑΙΟ 9 ΑΛΥΣΙΔΕΣ Επομένως οι στροφές του μικρού τροχού είναι n 1 =225 rpm. Πηγαίνουμε τώρα στον πίνακα δ από όπου για ισχύ Ρ=20 kw και στροφές μικρού τροχού 225 rpm, επιλέγεται η αλυσίδα τύπου 20Β με βήμα 31,75 mm. Η άσκηση αυτή δόθηκε έτσι ώστε να προκύψει αλυσίδα ίδιου τύπου με εκείνη που έχει ή άσκηση του βιβλίου. Αυτό έγινε διότι ο επόμενος πίνακας που θα χρησιμοποιήσουμε αφορά αυτό τον τύπο αλυσίδας, και δεν υπάρχει άλλος στο βιβλίο. Από την ταχύτητα της αλυσίδας και τις 225 rpm του μικρού τροχού με χρήση του τύπου 9.1 προϋπολογίζουμε την διάμετρο d 1 του μικρού τροχού: Επομένως η διάμετρος του μικρού αλυσοτροχού πρέπει να είναι περίπου 255 mm. Από τον πίνακα ε για την επιλεγμένη αλυσίδα, για τις 225 rpm του μικρού αλυσοτροχού και για διάμετρο 253,30 mm (που είναι πολύ κοντά στην d 1 των 255 mm) επιλέγουμε τροχό με z 1 =25 δόντια και λίπανση με εμβάπτιση. Βλέπουμε από τον ίδιο πίνακα ότι η αλυσίδα αυτή μπορεί να χρησιμοποιηθεί για ισχύ μέχρι 27 kw (Υπολογισμός με γραμμική παρεμβολή στην ισχύ). Έχοντας προσδιορίσει επακριβώς τη διάμετρο d 1 μπορούμε να υπολογίσουμε την ακριβή σχέση μετάδοσης, και τις ακριβείς διαστάσεις του άλλου αλυσοτροχού (διάμετρο d 1 και αριθμό δοντιών) και την ταχύτητα της αλυσίδας. Αρχικά η ταχύτητα προκύπτει από τον τύπο 9.1 για d 1 =253,3 mm =0,2533 m: Από τη σχέση μετάδοσης που δίνεται θα προσδιοριστεί ο αριθμός των δοντιών του μεγάλου τροχού μέσω της σχέσης 9.4: Τώρα πηγαίνουμε στον πίνακα στ από όπου για αριθμό δοντιών 25 και 56 τυποποιούμε τη σχέση μετάδοσης στην i=2,28 (ή θα λέγαμε 1:2,28), οπότε τα δόντια του μεγάλου τροχού θα είναι: Και η οριστική διάμετρος του μεγάλου τροχού θα είναι: Εδώ δεν μπορούμε να κάνουμε χρήση του πίνακα 10.3.ιβ του σχολικού βιβλίου, αφού τον αριθμό των 25 δοντιών δεν τον περιλαμβάνει ο πίνακας αυτός. 136 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
137 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ Λύση των άλυτων ασκήσεων του σχολικού βιβλίου Ακολουθεί σε αυτό το κεφάλαιο η λύση των ασκήσεων που προτείνονται από το σχολικό βιβλίο (άλυτες ασκήσεις). Οι ασκήσεις που δίνονται είναι λίγες (ενώ η έκταση της θεωρίας πολύ περισσότερη), αλλά στις Πανελλαδικές εξετάσεις περιλαμβάνουν περίπου τα μισά θέματα. 1. Σελίδα 318. Άσκηση 1 Κοχλίας με διάμετρο πυρήνα d 1 =20 mm καταπονείται σε εφελκυσμό. Αν είναι από υλικό με σ επ =1000 dan/cm 2, ποιο το επιτρεπόμενο φορτίο; Το επιτρεπόμενο φορτίο θα το βρούμε από τη σχέση 4.1, αν τη λύσουμε ως προς το φορτίο Ρ. Αν Α είναι η διατομή του πυρήνα του κοχλία, η οποία δεν δίνεται από την εκφώνηση της άσκησης, πρέπει να υπολογιστεί από τη διάμετρο που δίνεται. Θα βρεθεί από τη σχέση 4.2, λαμβάνοντας υπ όψιν ότι d 1 =20 mm=2 cm: Τώρα που γνωρίζουμε τη διατομή Α μπορούμε να χρησιμοποιήσουμε την σχέση 4.1 για να βρούμε το ζητούμενο φορτίο. Η χρήση της σχέσης 4.1 γίνεται με τον τρόπο που περιγράψαμε στην παράγραφο 1.4 για την καταπόνηση (δεύτερη από τις τρεις περιπτώσεις): Επομένως η μέγιστη εφελκυστική δύναμη (φορτίο) που μπορεί να δεχτεί ο κοχλίας είναι 3140 dan. 2. Σελίδα 318. Άσκηση 2 Τυποποιημένος κοχλίας Μ24 καταπονείται σε εφελκυσμό και στρέψη. Ποιο είναι το μέγιστο επιτρεπόμενο εφελκυστικό φορτίο, αν σ επ =1000 dan/cm 2 ; Από τον πίνακα 14.4.α του σχολικού βιβλίου για κοχλία Μ24 έχουμε διάμετρο πυρήνα d 1 =20,319 mm=2,0319 cm. Τώρα συνεχίζουμε για τον υπολογισμό της διατομής Α του πυρήνα με τρόπο όμοιο με εκείνον της προηγούμενης άσκησης: Υπολογίσαμε τη διατομή Α και μπορούμε με τη σχέση 4.8 για σύνθετη καταπόνηση (εφελκυσμός και στρέψη), να βρούμε το ζητούμενο φορτίο. Επομένως το επιτρεπόμενο εφελκυστικό φορτίο είναι 2477 dan. 3. Σελίδα 318. Άσκηση 3 Να διαλέξετε τυποποιημένο κοχλία για διατμητικό φορτίο Q=1600 dan, όταν είναι τ επ =800 dan/cm 2. Για τη διάτμηση χρησιμοποιούμε τη σχέση 4.6 (ή την 1.7 αν θέλετε) με την οποία υπολογίζουμε την απαιτούμενη διατομή του κοχλία (και κατόπιν μέσω αυτής την διάμετρό του). Για διατμητική τάση θα χρησιμοποιήσουμε την τιμή της επιτρεπόμενης διατμητικής τάσης τ επ (σύμφωνα με τα αναφερθέντα στην παράγραφο 1.4 για την καταπόνηση, στην πρώτη από τις τρεις περιπτώσεις): ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 137
138 ΚΕΦΑΛΑΙΟ 10 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Από τη διατομή Α=2 cm 2 που βρήκαμε και με χρήση του τύπου 4.3 θα υπολογίσουμε την απαιτούμενη διάμετρο του πυρήνα: Η τιμή d 1 =1,596 cm=15,96 mm= είναι η απαιτούμενη ελάχιστη διάμετρος του πυρήνα του κοχλία. Τώρα από τον πίνακα 14.4.α επιλέγουμε τυποποιημένο κοχλία με διάμετρο πυρήνα λίγο μεγαλύτερη από την υπολογισθείσα. Επιλέγουμε τον κοχλία Μ20 με d 1 =16,933 mm. Ο προηγούμενος μικρότερος τυποποιημένος κοχλίας έχει διάμετρο πυρήνα d 1 =14,933 mm, που είναι μικρότερη από την ευρεθείσα, και δεν θα είναι αρκετή να αντέξει την καταπόνηση που δέχεται ο κοχλίας. 4. Σελίδα 326. Άσκηση 1 Να επιλέξετε από τον πίνακα 14.6.δ άτρακτο, που μεταφέρει κίνηση από ένα ηλεκτροκινητήρα με ισχύ 80 HP, ο οποίος στρέφεται με 1400 RPM (στροφές το λεπτό). Το υλικό της ατράκτου πρέπει να είναι St50. Αφού η άσκηση λέει να επιλέξουμε από τον πίνακα τη διάμετρο της ατράκτου, δεν χρειάζεται να κάνουμε υπολογισμό, αλλά να γίνει επιλογή με βάση τα δεδομένα. Θα βρούμε λοιπόν το λόγο P/n, και βάσει αυτού θα επιλεγεί η διάμετρος. Έχουμε ότι P=80 HP και n=1400 RPM (οι μονάδες της ισχύος και των στροφών είναι οι κατάλληλες για τον πίνακα), άρα: Με την τιμή αυτή του λόγου P/n προκύπτει από τον πίνακα 14.6.δ για τη διάμετρο της ατράκτου η τυποποιημένη τιμή d=60 mm. Με γραμμική παρεμβολή για διάμετρο 55 mm με P/n=0,044 και για διάμετρο 60 mm με P/n=0,082, προκύπτει διάμετρος d=57 mm. Σημειώνουμε ότι η τιμή αυτή για τη διάμετρο δεν είναι τυποποιημένη. Θα κάνουμε στα γρήγορα και μια αναλυτική λύση σύμφωνα με τα γνωστά. Η ροπή στρέψης M t θα είναι: Aν λάβουμε υπ όψιν ότι για το St50 ο πίνακας 14.6.β δίνει τ επ =180 kp/cm 2 η διάμετρος θα είναι: Με τον υπολογισμό βρήκαμε μικρότερη διάμετρο, και θα μπορούσαμε να πάρουμε την τυποποιημένη των 50 mm. 5. Σελίδα 326. Άσκηση 2 Μπορείτε να υπολογίσετε την άτρακτο που μεταφέρει κίνηση από ένα ηλεκτροκινητήρα με ισχύ 100 HP, ο οποίος στρέφεται με 300 RPM (στροφές το λεπτό); Το υλικό της ατράκτου πρέπει να είναι St60 Αφού μας ζητά να υπολογίσουμε τη διάμετρο της ατράκτου θα κάνουμε αναλυτικό υπολογισμό. Για το υλικό St60 ο πίνακας 14.6.β δίνει τ επ =200 kp/cm 2. Συμβολίζουμε την ισχύ P=100 HP και τις στροφές n=300 RPM. Θα υπολογίσουμε πρώτα την ροπή στρέψης M t : 138 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
139 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ 10 Με γνωστή τη ροπή, από τη σχέση 5.3 θα υπολογίσουμε τη διάμετρο της ατράκτου d: Σημείωση: Η απάντηση του βιβλίου είναι με βάση όχι υπολογισμό, αλλά εκτίμηση από τον πίνακα 14.6.δ, η οποία έγινε με βάση ή τον λόγο P/n=100/300=0,333 ή την υπολογισθείσα προηγουμένως ροπή στρέψης M t = kp cm. Με γραμμική παρεμβολή ανάμεσα στη διάμετρο 90 mm με P/n=0,318 και στη διάμετρο 95 mm με P/n=0,385, προκύπτει διάμετρος d=92 mm. 6. Σελίδα 333. Άσκηση 1 Να υπολογίσετε τα κατάλληλα έδρανα για την άτρακτο μιας αγροτικής μηχανής που φαίνεται στην επόμενη εικόνα. Τα γεωμετρικά χαρακτηριστικά της φόρτισης είναι: F 1 =500 kp, F 2 =850 kp, d=50 mm, n=400 RPM, l 1 =100 mm, l 2 =130 mm, l 3 =150 mm Θα ακολουθήσουμε την πορεία λύσης που χρησιμοποιήσαμε στο κεφάλαιο 6 για τα έδρανα. Είναι καλύτερα να μετατρέψουμε τα μήκη από mm σε m, οπότε θα έχουμε: l 1 =0,1 m, l 2 =0,13 m, l 3 =0,15 m. Οι αντιδράσεις στις θέσεις στήριξης Α και Β είναι F 3 και F 4 και πρέπει να υπολογιστούν. Θα πάρουμε τις ροπές ως προς το σημείο Α. Η ροπή της F 3 είναι μηδέν, αφού η δύναμη περνά από το θεωρούμενο σημείο περιστροφής, η ροπή της F 4 είναι αριστερόστροφη [και ίση με F B ( l 1 + l 2 + l 3 )], η ροπή της F 1 που είναι δεξιόστροφη (και ίση με F 1 l 1 ) και η ροπή της F 2 που είναι δεξιόστροφη [και ίση με F 2 ( l 1 + l 2 )]. Εφαρμόζοντας την εξίσωση ισορροπίας των ροπών ως προς το σημείο Α θα πρέπει η ροπή της F 4 να εξισορροπεί τις ροπές των F 1 και F 2 και θα έχουμε: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 139
140 ΚΕΦΑΛΑΙΟ 10 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Έχοντας βρει την F 4, μπορούμε να βρούμε την F 3 εφαρμόζοντας την εξίσωση ισορροπίας των δυνάμεων: Έτσι υπολογίσαμε τις αντιδράσεις στα έδρανα. Προχωράμε τώρα στην επιλογή των εδράνων, μετατρέποντας πρώτα τα kp σε Ν, πολλαπλασιάζοντας με το 10, και έχουμε: F 3 =7040 Ν και F 4 =6460 Ν. Για τις αγροτικές μηχανές η διάρκεια ζωής των ρουλεμάν είναι από 3000 ώρες μέχρι 6000 ώρες (νούμερο 20 του πίνακα 14.7.γ). Επιλέγουμε την ενδιάμεση τιμή 4000 ώρες, που περιλαμβάνεται και στους πίνακες για τον υπολογισμό του λόγου φόρτισης. Οι στροφές είναι 400 RPM και η τιμή αυτή βρίσκεται στον πίνακα 14.7.α. Συνδυάζοντας στροφές και ώρες βρίσκουμε λόγο φόρτισης C/P=4,56. Θέτοντας το Ρ διαδοχικά ίσο με F 3 =7040 Ν και F 4 =6460 Ν, βρίσκουμε τα δυναμικά φορτία C 3 και C 4 αντίστοιχα: Τώρα από τον πίνακα 14.7.δ και για τις τιμές αυτές του C και διάμετρο 50 mm επιλέγουμε και για τις δύο θέσεις Α και Β το έδρανο 6210, το οποίο έχει C= Ν. Η απάντηση που βρήκαμε είναι λίγο διαφορετική από εκείνη του βιβλίου διότι προφανώς η λύση του σχολικού βιβλίου έχει πάρει για τις ώρες λειτουργίας (θεωρητική διάρκεια λειτουργίας σε ώρες) διαφορετική τιμή από τις 4000 ώρες που πήραμε εμείς για τη λύση. Αυτό μη σας τρομάζει γιατί δεν θεωρείται λάθος αρκεί να έχετε επιλέξει μια τιμή εντός των τιμών του πίνακα. Το σχολικό βιβλίο για τη λύση μάλλον επέλεξε την μέγιστη τιμή των 6000 ωρών. Τότε προκύπτει C/P=5,2 (με γραμμική παρεμβολή) και τα δυναμικά φορτία υπολογίζονται: Εκ των αποτελεσμάτων φαίνεται ότι πρέπει να επιλεγούν δύο διαφορετικά ρουλεμάν, τα οποία είναι τα 6310 και 6210 αντίστοιχα. Όμως επειδή οι καταπονούσες δυνάμεις είναι σχεδόν ίσες, πρακτικά θα επιλέγαμε δύο ίδια έδρανα και όχι διαφορετικά. 7. Σελίδα 333. Άσκηση 2 Να υπολογίσετε τα κατάλληλα έδρανα για την άτρακτο μηχανής χαρτοποιίας που φαίνεται στην παρακάτω εικόνα. Τα γεωμετρικά χαρακτηριστικά φόρτισης είναι: F 2 =300 kp, F 4 =1150 kp, d=45 mm, n=600 RPM, l 1 =250 mm, l 2 =100 mm, l 3 =300 mm Η άσκηση 6.6 που λύσαμε στο κεφάλαιο των εδράνων είναι παρόμοια και θα ακολουθήσουμε την ίδια διαδικασία επίλυσης και εδώ. Θα εφαρμόσουμε τις γνωστές εξισώσεις για να βρούμε τις αντιδράσεις στήριξης F 1 και F 3. Η φορά της F 4 δεν μας ενοχλεί, αρκεί να προσέξουμε τη φορά στις ροπές. Εδώ θα μετατρέψουμε τα μήκη από mm σε m, οπότε θα έχουμε: l 1 =0,25 m, l 2 =0,1 m, l 3 =0,3 m. Θα δούμε την εξίσωση για την ισορροπία των ροπών με σημείο περιστροφής το Α. Η ροπή της F 1 θα είναι μηδέν, αφού η δύναμη περνά από το θεωρούμενο σημείο περιστροφής, η ροπή της F 3 είναι δεξιόστροφη [και ίση με F 3 (l 1 + l 2 + l 3 )], η ροπή της F 2 είναι δεξιόστροφη 140 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
141 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ 10 (και ίση με F 2 l 1 ) και η ροπή της F 4 είναι αριστερόστροφη [και ίση με F 4 (l 1 + l 2 )]. Από την εξίσωση ισορροπίας των ροπών ως προς το σημείο Α θα πρέπει η ροπή της F 4 να εξισορροπεί τις ροπές των F 2 και F 3 και θα έχουμε: Αφού βρήκαμε ότι η F 3 έχει θετική τιμή η φορά που σχεδιάστηκε είναι η σωστή. Η φορά αυτή δεν επηρεάζει την καταπόνηση που δέχεται το έδρανο. Έχοντας βρει την F 3, θα βρούμε την F 1 κάνοντας χρήση της εξίσωσης ισορροπίας των δυνάμεων. Σύμφωνα με το σχήμα μας και θα έχουμε: Βρέθηκε ότι και η F 1 έχει θετική τιμή, άρα η σχεδιασμένη φορά της είναι σωστή. Για την επιλογή των εδράνων θα μετατρέψουμε πρώτα τα kp σε Ν πολλαπλασιάζοντας με το 10 και έχουμε: F 1 =3460 Ν και F 3 =5040 Ν. Για τα μηχανήματα χαρτοποιίας η διάρκεια ζωής των ρουλεμάν (νούμερο 31 του πίνακα 14.7.γ) είναι από ώρες μέχρι ώρες. Επιλέγουμε την μέγιστη τιμή ώρες, που περιλαμβάνεται και στους πίνακες για τον υπολογισμό του λόγου φόρτισης. Οι στροφές είναι 600 RPM και η τιμή αυτή δεν βρίσκεται στον πίνακα 14.7.α, άρα χρειάζεται παρεμβολή. Σύμφωνα με τις στροφές, με την παρεμβολή για την επιλογή, και τις ώρες βρίσκουμε λόγο φόρτισης C/P=14,3. Θέτοντας το Ρ διαδοχικά ίσο με F 1 =3460 Ν και F 3 =5040 Ν, βρίσκουμε το δυναμικό φορτίο C: Από τον πίνακα 14.7.δ για διάμετρο 45 mm επιλέγουμε τα έδρανα σε κάθε θέση: Α: 6309 (C= N) Β: 6409 (C= N) ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 141
142 ΚΕΦΑΛΑΙΟ 10 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Σημειώνουμε ότι στην λυμένη αλλά και στις άλυτες ασκήσεις για τα έδρανα, το σχολικό βιβλίο παίρνει ως ώρες λειτουργίας τις μέγιστες του πίνακα 14.7.γ. Είπαμε και προηγουμένως ότι αν πάρετε μια ενδιάμεση τιμή δεν θα θεωρηθεί λάθος. 8. Σελίδα 337. Άσκηση 1 Σε μετάδοση κίνησης με παράλληλους οδοντωτούς τροχούς δίνονται: για το κινούμενο γρανάζι n 2 =250 rpm, d 02 =200 mm και z 2 =100 δόντια. Ποιες είναι οι αντίστοιχες τιμές για το κινητήριο ώστε η σχέση μετάδοσης να είναι και ποια η απόσταση των αξόνων; Για τον κινητήριο τροχό θα έχουμε τα ίδια σύμβολα, με τη διαφορά ότι ο δείκτης θα είναι το 1, αντί για 2. Από τη σχέση μετάδοσης 7.1 θα υπολογίσουμε τις στροφές του κινητήριου τροχού: Η αρχική διάμετρος του τροχού θα υπολογιστεί από τη σχέση 7.4: Τέλος, ο αριθμός των δοντιών θα υπολογιστεί πάλι από τη σχέση 7.4: Επομένως υπολογίστηκαν τα στοιχεία του κινητήριου τροχού: n 1 =1000 rpm, d 01 =50 mm και z 1 =25 δόντια. 9. Σελίδα 337. Άσκηση 2 Κινητήρια μηχανή έχει (στον άξονά της) ισχύ P 1 =40 PS και περιστρέφει, μέσω γραναζιών με βαθμό απόδοσης η=0,9, κινούμενο άξονα με n 2 =360 rpm. Ζητούνται η ισχύς και η ροπή του κινούμενου άξονα. Από τη σχέση 7.9 για το βαθμό απόδοσης θα υπολογίσουμε τη μεταφερόμενη ισχύ στον κινούμενο άξονα. Η ωφέλιμη ισχύς Ρ 2 είναι εκείνη που παίρνουμε στον κινούμενο άξονα και η καταναλισκόμενη P 1 είναι εκείνη που έχει ο κινητήριος άξονας. Άρα η ισχύς στον κινούμενο άξονα είναι 36 PS. Η ροπή του κινούμενου άξονα θα βρεθεί από την εξίσωση 7.6. Οι μονάδες της ισχύος και των στροφών είναι οι κατάλληλες ώστε η ροπή Μ 2 να βρεθεί σε dan m: Επομένως η ροπή στον άξονα είναι 71,62 dan m. Σημείωση: Ας κάνουμε ορισμένες διευκρινήσεις σχετικά με την ισχύ στους άξονες. Θα γίνει με παράδειγμα στην άσκηση που μόλις λύσαμε. Ας υποθέσουμε ότι η μετάδοση έχει σχέση μετάδοσης ίση με μονάδα: i=1, δηλαδή έχουμε στον κινητήριο άξονα ένα ίδιο γρανάζι με εκείνο του κινούμενου, το οποίο περιστρέφεται με τις ίδιες στροφές. Η ισχύς όμως Ρ 1 θα είναι διαφορετική, άρα διαφορετική θα είναι και η ροπή του Μ 1. Έχουμε δηλαδή δυο ίδια γρανάζια που συνεργάζονται αλλά έχουν διαφορική ροπή και ισχύ. Το πρώτο έχει την μεγαλύτερη ισχύ των 40 PS. Η ισχύς που χάνεται αλλά και η ροπή που μειώνεται στο δεύτερο γρανάζι, γίνονται θερμότητα στις τριβές των γραναζιών και των άλλων εξαρτημάτων. Λόγω αυτής της μείωσης ροπής και ισχύος και ο πρώτος άξονας περιστρέφεται με λιγότερες στροφές από εκείνες που θα είχε αν ο βαθμός απόδοσης ήταν μονάδα. Αυτό σημαίνει ότι αν με κάποιο 142 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
143 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ 10 τρόπο μειώναμε τις τριβές και ο βαθμός απόδοσης γινόταν πχ. 0,97 τότε τα γρανάζια θα περιστρεφόταν πιο γρήγορα ή θα μπορούσαν να ασκήσουν μεγαλύτερη ροπή. 10. Σελίδα 341. Άσκηση 1 Σε μια οδόντωση με παράλληλους τροχούς, οι στροφές των αξόνων θα είναι n 1 =1000 rpm και n 2 =500 rpm. Ο υπολογισμός των γραναζιών σε αντοχή έδωσε ελάχιστο απαιτούμενο βήμα t=6,2 mm. Ζητούνται: το modul, οι διάμετροι των τροχών και η απόσταση των αξόνων τους. Για τον κινητήριο τροχό επιλέγεται z 1 = 20 δόντια. Από τη σχέση 7.11 θα γίνει μια πρώτη εκτίμηση του modul, αφού θέσουμε ως βήμα την τιμή t=6,2 mm που δίνεται ως ελάχιστο: Η τιμή 1,97 mm για το modul είναι η ελάχιστη και γι αυτό επιλέγουμε την επόμενη μεγαλύτερη από τις τυποποιημένες τιμές, η οποία είναι m=2 mm. Αυτό είναι και το modul των τροχών, και για τον καθένα θα ισχύει η σχέση 7.11: Για τον πρώτο τροχό η αρχική διάμετρος είναι η d 01 και για τον δεύτερο η d 02. Από τη σχέση αυτή υπολογίζουμε την αρχική διάμετρο του πρώτου τροχού: Από τη σχέση 7.4 βρίσκουμε την αρχική διάμετρο του δεύτερου τροχού αν λύσουμε ως προς d 02 : Έχουμε βρει τις δύο αρχικές διαμέτρους και με χρήση της σχέσης 7.5 θα υπολογίσουμε την απόσταση των αξόνων: Επομένως η απόσταση των αξόνων είναι 60 mm. Για τις δύο διαμέτρους κεφαλών d k1 και d k2 δύο φορές τη σχέση 7.20: Επομένως οι διάμετροι κεφαλών των δύο οδοντωτών τροχών είναι 44 mm και 84 mm αντίστοιχα. Σημείωση: Εδώ ακολουθήσαμε μια πορεία για τη λύση, αλλά η σειρά εφαρμογής των τύπων θα μπορούσε να είναι διαφορετική. Επίσης θα μπορούσε να γίνει χρήση και διαφορετικών τύπων (ας πούμε με χρήση της σχέσης μετάδοσης) χωρίς να αλλάξει το αποτέλεσμα. 11. Σελίδα 341. Άσκηση 2 Για κινητήριο μετρήθηκαν d k1 =88 mm και z 1 = 20 δόντια. Ζητούνται το modul, οι διάμετροι και ο αριθμός δοντιών του κινούμενου τροχού, που πρόκειται να κατασκευαστεί, αν η σχέση μετάδοσης είναι i=1/3. Από τη σχέση 7.21 θα λύσουμε ως προς το modul για να το υπολογίσουμε: Από τη σχέση 7.4 θα υπολογιστεί ο αριθμός των δοντιών z 2 του κινούμενου τροχού: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 143
144 ΚΕΦΑΛΑΙΟ 10 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Τώρα από τη σχέση 7.21 θα υπολογιστεί η διάμετρος κεφαλών d k2 του κινούμενου τροχού: Και τέλος από τη σχέση 7.11 θα υπολογιστεί η αρχική διάμετρος d 02 : Επομένως η αρχική διάμετρος του κινούμενου τροχού είναι d 02 =240 mm. 12. Σελίδα 343. Άσκηση 1 Πόση ισχύ μπορεί να μεταφέρει ένας ιμάντας με επιτρεπόμενη περιφερειακή δύναμη F=130 dan σε κινούμενη τροχαλία με d 2 =1400 mm που περιστρέφεται με 80 rpm: Η ζητούμενη ισχύς μπορεί να βρεθεί είτε από τον τύπο 8.10: είτε από τον γενικότερο τύπο 5.1:. Και στους δύο όμως έχουμε έναν άγνωστο, που θα πρέπει να υπολογίσουμε από ένα άλλο τύπο. Στον πρώτο δε γνωρίζουμε την ταχύτητα και θα υπολογιστεί από τη σχέση 8.6: και στον δεύτερο είναι άγνωστη η ροπή στρέψης και θα υπολογιστεί από τη σχέση 8.5:. Θα κάνουμε τους υπολογισμούς και με τις δύο εξισώσεις και ασφαλώς θα βρούμε το ίδιο αποτέλεσμα. Ονομάζουμε τις στροφές: n 2 =80 rpm και μετατρέπουμε τις μονάδες της διαμέτρου σε μέτρα: d 2 =1400 mm=1,4 m. Τώρα υπολογίζουμε την ταχύτητα: Και τώρα θα υπολογίσουμε την ισχύ από τη σχέση 8.10, στον οποίο οι μονάδες της δύναμης και της ταχύτητας είναι οι κατάλληλες ώστε η ισχύς να προκύψει σε PS: Επομένως η ζητούμενη ισχύς είναι 10,16 PS. Θα λύσουμε τώρα και με τον άλλο τρόπο την άσκηση. Αρχικά υπολογίζουμε τη ροπή στον άξονα της τροχαλίας από τη σχέση 8.5: Τώρα θα επιλύσουμε τη σχέση 5.1 ως προς τη ζητούμενη ισχύ. Προσέχουμε ότι επειδή η σχέση αυτή έχει τον συντελεστή 716,2 (και όχι τον 71620) θα χρησιμοποιηθεί η ροπή με τις μονάδες που ήδη βρήκαμε, δηλαδή dan m: Όπως προείπαμε η ισχύς προέκυψε πάλι 10,16 PS. 13. Σελίδα 343. Άσκηση 2 Πόση πρέπει να είναι η ροπή του κινητήριου άξονα της προηγούμενης άσκησης, αν i=1/2; Η ροπή στον κινούμενο άξονα βρέθηκε στη λύση της προηγούμενης άσκησης. Επαναλαμβάνουμε την λύση της εξίσωσης 8.5 βάζοντας τον δείκτη 2 σε αυτήν: 144 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
145 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ 10 Γνωρίζοντας τη σχέση μετάδοσης θα χρησιμοποιήσουμε τη σχέση 8.8 για τον υπολογισμό της ροπής Μ 1 στον κινητήριο άξονα: Άρα η ροπή στον κινητήριο άξονα είναι η μισή από εκείνη στον κινούμενο, αφού η σχέση μετάδοσης είναι 1/ Σελίδα 344. Άσκηση Να επιλέξετε επίπεδο δερμάτινο ιμάντα για τροχαλία d=600 mm και n=300 rpm. Η ισχύς είναι 7,5 PS. Δεχθείτε σ επ =15 dan/cm 2. Επιλογή του ιμάντα σημαίνει να βρούμε τις διαστάσεις του, οι οποίες θα προκύψουν από τον έλεγχο σε αντοχή του ιμάντα, που γίνεται με τη σχέση 8.11:. Σε αυτή τη σχέση βλέπουμε ότι λείπει η δύναμη F, την οποία θα υπολογίσουμε από τη σχέση 8.10:. Στον τύπο αυτόν Ρ είναι η ισχύς Ρ=7,5 PS. Και σε αυτή τη σχέση έχουμε άγνωστη την ταχύτητα την οποία με τη σειρά της θα υπολογίσουμε από την σχέση 8.6:. Σε αυτήν όλα είναι γνωστά μόνο μένει να μετατρέψουμε τις μονάδες της διαμέτρου σε μέτρα: d=600 mm=0,6 m. Προχωράμε στον υπολογισμό με εφαρμογή των εξισώσεων που αναφέραμε πριν με την ανάστροφη σειρά. Βρήκαμε ότι η διατομή θα έχει εμβαδόν 398 mm 2 ενώ το βιβλίο στην απάντηση δίνει 400 mm 2. Δεν είναι πρόβλημα η μικρή αυτή διαφορά και εμείς δεχόμαστε αυτή την τιμή για ευκολία στην επιλογή των διαστάσεων του ιμάντα που θα πρέπει το γινόμενο του πλάτους επί το πάχος να δίνουν 400 mm 2. Έτσι μπορούμε να επιλέξουμε ιμάντα με πάχος 5 mm και πλάτος 80 mm. Μπορούμε εναλλακτικά να επιλέξουμε ιμάντα 10x40, δηλαδή πάχος 10 mm και πλάτος 40 mm. 15. Σελίδα 354. Άσκηση 1 Φυγοκεντρική αντλία ισχύος 35 kw και n 2 =1600 rpm κινείται από 4κύλινδρη ΜΕΚ με n 1 =800 rpm και εργάζεται 12 ώρες την ημέρα. Για ποια ισχύ πρέπει να υπολογιστεί η ιμαντοκίνηση; Η ιμαντοκίνηση θα υπολογιστεί σαν η μεταφερόμενη από τον ιμάντα ισχύς της αντλίας να είναι μεγαλύτερη από την ισχύ των 35 kw που έχει η αντλία. Η ισχύς αυτή υπολογισμού συμβολίζεται με P b και είναι ίση με την πραγματική ισχύ της αντλίας (35 kw) επί τον παράγοντα c 2 που τον παίρνουμε από τον πίνακα 14.9.β του σχολικού βιβλίου. Σύμφωνα με αυτόν για φυγοκεντρική αντλία (centrifugal compressors and pumps), 4κύλινδρη μηχανή (Internal combustion engines with 4 or more cylinders) με 10 ως 16 ώρες λειτουργίας (over 10 to 16 hours per day duty) ο παράγοντας c 2 είναι 1,1. (Στην απάντηση του σχολικού βιβλίου είναι λάθος η τιμή c 2 =1,2 που δίνει. Αν η αντλία ήταν περιστροφική (rotary pump) ή εργαζόταν πάνω από 16 ώρες ημερησίως τότε το c 2 θα ήταν 1,2.) Επομένως η ισχύς που θα υπολογιστεί ο ιμάντας υπολογίζεται ως ακολούθως: Άρα η ζητούμενη ισχύς είναι 38,5 kw. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 145
146 ΚΕΦΑΛΑΙΟ 10 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ 16. Σελίδα 354. Άσκηση 2 Αν για τη μικρή τροχαλία είναι d 1 =200 mm και n 1 =1600 rpm για πόση ισχύ μπορεί να χρησιμοποιηθεί ο κλάδος ιμάντα με τα χαρακτηριστικά του πίνακα 14.9.στ; Ο πίνακας αφορά σε ένα κλάδο ενός συγκεκριμένου ιμάντα και για τις τιμές της διαμέτρου της μικρής τροχαλίας και του αριθμού των στροφών παίρνουμε την τιμή για την ισχύ που μπορεί να μεταφέρει ο κλάδος αυτός: Ρ Ν =13,47 kw 17. Σελίδα 354. Άσκηση 3 Αν η ισχύς είναι 35 kw και οι διορθωτικοί συντελεστές είναι: λόγω μήκους c 3 =0,91 και λόγω τόξου περιέλιξης c 1 =1, πόσοι κλάδοι χρειάζονται από τον ιμάντα του προηγούμενου παραδείγματος; Ο αριθμός των κλάδων θα υπολογιστεί από τη σχέση που δίνεται στη σελίδα 350 του σχολικού βιβλίου:. Αν και η εκφώνηση της άσκησης δεν το διευκρινίζει θα πάρουμε P b =35 kw, ενώ η ισχύς κάθε κλάδου υπολογίστηκε στην προηγούμενη άσκηση Ρ Ν =13,47 kw. κάνοντας τους υπολογισμούς θα έχουμε: Αφού υπολογίσαμε ότι ο αριθμός των κλάδων είναι z=2,86 και είναι δεκαδικός αριθμός, πρέπει να επιλέξουμε τον επόμενο ακέραιο και επιλέγουμε 3 κλάδους. 18. Σελίδα 362. Άσκηση 1 Για ποια ισχύ πρέπει να υπολογιστεί η αλυσοκίνηση πετρελαιοκίνητης φυγοκεντρικής αντλίας 20 kw με μηχανική μετάδοση; Πρέπει να υπολογιστεί ο συντελεστής προσαύξησης y της αρχικής ισχύος Ρ 0 =20 kw από τον πίνακα β. Επειδή η μετάδοση είναι μηχανική θα πάμε στην τελευταία στήλη και επειδή η κινούμενη μηχανή είναι φυγοκεντρική αντλία θα επιλέξουμε την πρώτη γραμμή. Άρα ο συντελεστής είναι 1,2 και η ισχύς για τον υπολογισμό θα είναι: Επομένως η ζητούμενη ισχύς είναι 24 kw. 19. Σελίδα 362. Άσκηση 2 Ποιον τύπο θα διαλέγατε από τις αλυσίδες της εικόνας δ για ισχύ 10 kw και στροφές μικρού τροχού 400 rpm; Αν στον οριζόντιο άξονα του διαγράμματος πάμε στις 400 rpm και στον αριστερό κατακόρυφο στην ισχύ 10 kw, θα δούμε ότι οι δύο ευθείες τέμνονται ακριβώς στην γραμμή της αλυσίδας 12 Β με βήμα 19,05 mm. 20. Σελίδα 362. Άσκηση 3 Για πόση ισχύ είναι κατάλληλος ο τύπος 20 Β, αν ο μικρός τροχός έχει 19 δόντια και στρέφεται με 100 rpm; Από τα δεδομένα της άσκησης καταλαβαίνουμε ότι θα πάμε στον πίνακα ε του βιβλίου, από όπου για τις 100 rpm και τα 19 δόντια φαίνεται ότι η αλυσίδα μπορεί να μεταφέρει μέχρι 9,67 kw και προτείνεται η λίπανση με σταγόνες (Drip lubrication). Υπενθυμίζουμε ότι ο πίνακας ε (όπως και ο στ) αφορούν αποκλειστικά αλυσίδες τύπου 20 Β. Στην άσκηση αυτή δεν μπορούσαμε να πάμε στον πίνακα δ (από όπου θα βρίσκαμε ισχύ μέχρι 15 kw περίπου) γιατί αφορά όλους τους δυνατούς αριθμούς δοντιών. Τότε θα βλέπαμε ότι αν πηγαίναμε στην ισχύ των 15 kw από τον πίνακα ε, ο αλυσοτροχός θα έπρεπε να έχει 28 δόντια. 146 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
147 ΛΥΣΗ ΤΩΝ ΑΣΚΗΣΕΩΝ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΕΦΑΛΑΙΟ Σελίδα 362. Άσκηση 4 Ποια ισχύ μπορεί αν δώσει ο προηγούμενος τύπος στις ίδιες συνθήκες, αν έχει τρεις κλάδους. Από τον πίνακα γ βλέπουμε ότι για τρεις κλάδους πρέπει να χρησιμοποιηθεί συντελεστής ισχύος 2,5. Αυτό σημαίνει ότι αντί να πολλαπλασιαστεί η τιμή των 9,67 kw της ισχύος, που βρέθηκε στην προηγούμενη άσκηση για κάθε κλάδο, με το 3 (που είναι οι 3 κλάδοι της αλυσοκίνησης) θα πρέπει να πολλαπλασιαστεί με τον συντελεστή 2,5. Έτσι προκύπτει η ισχύς: 2,5 9,67 kw=24,175 kw, η οποία είναι η ζητούμενη. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 147
148
149 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Προτεινόμενες άλυτες ασκήσεις Παρακάτω δίνονται άλυτες ασκήσεις, για να εξασκηθείτε λύνοντάς τις. Σε κάθε κεφάλαιο οι πρώτες είναι σχετικά απλές και ακολουθούν πιο δύσκολες, ορισμένες από τις οποίες δεν είναι επιπέδου πανελληνίων, αλλά δυσκολότερες. Εσείς προσπαθήστε να τις λύσετε όλες, και αν το καταφέρετε σημαίνει ότι στις εξετάσεις τα θέματα με τις ασκήσεις θα σας φανούν εύκολα. Στις προτεινόμενες ασκήσεις δεν έχουν περιληφθεί εκείνες που κάνουν χρήση πολλών πινάκων του βιβλίου (ρουλεμάν, ιμάντες κλπ.). Αυτό έγινε γιατί πιστεύουμε ότι δεν έχουν μεγάλη πιθανότητα να είναι μεταξύ των θεμάτων στις πανελλήνιες. Άλλωστε, στα αντίστοιχα κεφάλαια με τις λυμένες ασκήσεις δόθηκαν αρκετά παραδείγματα, που θα σας καταστήσουν ικανούς να αντεπεξέλθετε σε παρόμοιες ασκήσεις Εφελκυσμός 1. Η ακτίνα μιας κυκλικής διατομής είναι 10 mm. Να βρείτε το εμβαδόν της διατομής. 2. Πόσα mm 2 έχει ένα cm 2 ; 3. Μια ράβδος έχει διατομή με διάμετρο 10 mm. Να βρείτε το εμβαδόν της σε mm 2 και σε cm Η διατομή μίας ράβδου είναι κυκλική και έχει εμβαδόν 314 mm 2. Να βρείτε την διάμετρο που έχει. 5. Μια ράβδος έχει διατομή με διάμετρο 2 cm. Να βρείτε το εμβαδόν της. 6. Η διατομή μίας ράβδου είναι κυκλική και έχει εμβαδόν 6,28 cm 2. Να βρείτε την ακτίνα που έχει. 7. Έστω μια ράβδος που θα εφελκύεται με δύναμη 4800 dan (το πολύ δηλαδή η δύναμη να φτάσει αυτή την τιμή) και είναι φτιαγμένη από ένα υλικό με επιτρεπόμενη τάση ίση με 1200 dan/cm 2 (δηλαδή σ επ =1200 dan/cm 2 ). Αν η ράβδος έχει τετραγωνική διατομή να βρείτε την πλευρά της και αν κυκλική να βρείτε την διάμετρό της. 8. Έχουμε μια ράβδο από σίδερο με διάμετρο 16 mm η οποία έχει σ επ =1600 dan/cm 2. Να βρείτε πόσο είναι το μέγιστο φορτίο (δύναμη) που μπορούμε να του κρεμάσουμε (εφελκυσμός). 9. Θέλουμε να χρησιμοποιήσουμε μια ράβδο από σίδερο με διάμετρο 16 mm και σ επ =1200 dan/cm 2. Θα κρεμάσουμε από αυτήν βάρος 4000 dan. Να βρείτε αν θα αντέξει η ράβδος. 10. Θέλουμε να χρησιμοποιήσουμε μια ράβδο από σίδερο με διατομή 314 mm 2 και σ επ =1000 dan/cm 2. Θα κρεμάσουμε από αυτήν βάρος 5000 dan. Να βρείτε αν θα αντέξει η ράβδος. Αν δεν αντέχει, να βρείτε πόση πρέπει να είναι η διάμετρος που πρέπει να έχει για να αντέξει. (Υπενθυμίζουμε ότι στις ασκήσεις λέγοντας ότι η ράβδος δεν θα αντέξει δεν εννοούμε ότι με αυτό το φορτίο θα σπάσει, αλλά ότι δεν επιτρέπεται να είναι τόσο το φορτίο γιατί είναι επικίνδυνο να έχει φθορά η ράβδος.) 11. Έχουμε μια ράβδο από σίδερο με διάμετρο 40 mm που έχει σ επ =800 dan/cm 2. Να βρείτε πόσο είναι το μέγιστο φορτίο (δύναμη) που μπορούμε να του κρεμάσουμε. Αν θέλαμε να κρεμάσουμε το διπλάσιο φορτίο από μια ίδιου μεγέθους (ίσης διατομής) ράβδο να βρείτε πόση τουλάχιστον πρέπει να είναι η επιτρεπόμενη τάση που πρέπει να έχει το νέο υλικό. 12. Έστω μια ράβδος που θα εφελκύεται με δύναμη 6000 dan και είναι φτιαγμένη από ένα υλικό με επιτρεπόμενη τάση ίση με 1000 dan/cm 2. Αν η ράβδος είναι τετράγωνη να βρείτε την πλευρά της και αν είναι κύκλος να βρείτε την διάμετρό του. 13. Έστω δύο ίδιες ράβδοι με κυκλική διατομή που θα εφελκύονται και οι δύο μαζί με δύναμη dan και είναι φτιαγμένες από ένα υλικό με επιτρεπόμενη τάση ίση με 1200 dan/cm 2. Να βρείτε τη διάμετρο της κάθε μίας. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 149
150 ΚΕΦΑΛΑΙΟ 11 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Ηλώσεις 14. Δύο ελάσματα συνδέονται με επικάλυψη και μία σειρά 4 ήλων, οι οποίοι έχουν επιτρεπόμενη διατμητική τάση ίση με 1600 dan/cm 2. Τα ελάσματα εφελκύονται με δύναμη dan. Πόση πρέπει να είναι η διάμετρος των ήλων ώστε να αντέξουν την διατμητική καταπόνηση; 15. Δύο ελάσματα συνδέονται με διπλή αρμοκαλύπτρα και μία σειρά 4 ήλων (σύνολο ήλων σύνδεσης 8), οι οποίοι έχουν επιτρεπόμενη διατμητική τάση ίση με 1600 dan/cm 2. Τα ελάσματα εφελκύονται με δύναμη dan. Πόση πρέπει να είναι η διάμετρος των ήλων ώστε να αντέξουν την διατμητική καταπόνηση; 16. Θέλουμε να κατασκευάσουμε μια ήλωση και έχουμε να επιλέξουμε μεταξύ της ήλωσης με επικάλυψη και της ήλωσης με διπλή αρμοκαλύπτρα. Και οι δύο τρόποι ήλωσης θα είναι με μονή σειρά 5 ήλων. Σε ποια από τις δύο περιπτώσεις θα πρέπει να έχουν οι ήλοι μεγαλύτερη διάμετρο και γιατί, αν θεωρήσετε ότι ελέγχονται μόνο σε διάτμηση και είναι από το ίδιο υλικό; 17. Δύο ελάσματα συνδέονται με επικάλυψη και μία σειρά 2 ήλων, οι οποίοι έχουν επιτρεπόμενη διατμητική τάση ίση με 2000 dan/cm 2. Τα ελάσματα εφελκύονται με δύναμη dan. Τα ελάσματα έχουν πλάτος 100 mm, πάχος 10 mm και επιτρεπόμενη εφελκυστική τάση ίση με 1500 dan/cm 2. A. Πόση πρέπει να είναι η διάμετρος των ήλων ώστε να αντέξουν την διατμητική καταπόνηση; B. Να γίνει ο έλεγχος του ελάσματος σε εφελκυσμό. 18. Μια ήλωση έχει γίνει με επικάλυψη των ελασμάτων που έχουν πάχος 10 mm και πλάτος 160 mm. Έχουν χρησιμοποιηθεί 6 ήλοι με διάμετρο 15 mm, που πρέπει να παραλάβουν δύναμη εφελκυσμού των ελασμάτων dan. Δίνονται οι επιτρεπόμενες τάσεις : Για διάτμηση των ήλων: 1400 daν/cm 2 Για εφελκυσμό των ελασμάτων: 1600 daν/cm 2 Να γίνει έλεγχος αντοχής των ήλων σε διάτμηση και των ελασμάτων σε εφελκυσμό. 19. Θέλουμε να ενώσουμε δυο ελάσματα πλάτους 40 cm και πάχους 8 mm με τη μέθοδο της επικάλυψης με μια σειρά 10 ήλων. Το υλικό που θα χρησιμοποιηθεί έχει για τους ήλους επιτρεπόμενη τάση διάτμησης τ επ = 1000 daν/cm 2 και για τα ελάσματα επιτρεπόμενη τάση εφελκυσμού σ επ = 1000 daν/cm 2. Υπολογίστηκε ότι τα ελάσματα θα καταπονούνται σε εφελκυσμό με δύναμη dan. Να υπολογιστούν οι ήλοι που θα χρησιμοποιηθούν σε διάτμηση και τα ελάσματα σε εφελκυσμό. Αν τα ελάσματα δεν αντέχουν να βρείτε το πάχος που πρέπει να έχουν για να αντέξουν. Να λυθεί η ίδια άσκηση και να κάνετε τους ίδιους ελέγχους αν αντί για 10 ήλους χρησιμοποιηθούν μόνο Ενώνουμε δυο ελάσματα πάχους 10 mm με την μέθοδο της διπλής αρμοκαλύπτρας πάχους 5 mm με μια σειρά τεσσάρων ήλων (z = 4). Το πλάτος των ελασμάτων είναι 200 mm και η δύναμη που τα εφελκύει είναι daν. Για τους ήλους δίνεται τ επ = 20 daν/mm 2 και για τα ελάσματα σ επ = 15 daν/mm 2. Να ευρεθούν: A. Η διάμετρος που πρέπει να έχει κάθε ήλος ώστε να αντέχει η κατασκευή B. Να ελεγχθεί αν τα ελάσματα αντέχουν σε καταπόνηση εφελκυσμού Κοχλιοσυνδέσεις 21. Από τον πίνακα της σελίδας 316 να βρείτε το βήμα, την διάμετρο πυρήνα και το βάθος του σπειρώματος για ένα κοχλία Μ20 και έναν Μ Αν η διάμετρος του πυρήνα σε ένα κοχλία Μ20 είναι 16,933 mm να βρείτε πόσο θα είναι το βάθος του σπειρώματος. (Υπόδειξη: Η εξωτερική διάμετρος θα είναι 20 mm, άρα το 150 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
151 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 11 βάθος σπειρώματος θα είναι: 14.4.α.). Τόσο δίνει και ο πίνακας 23. Η επιτρεπόμενη τάση ενός υλικού κοχλία είναι σ επ =1200 daν/cm 2. Αν χρησιμοποιηθεί σε σύνδεση με συντελεστή ασφαλείας ν ασφ = 4 να βρείτε την τάση θραύσης σ θρ του κοχλία. 24. Ένας κοχλίας σπάει όταν η τάση είναι σ θρ = daν/cm 2 και απαιτείται ο συντελεστής ασφαλείας εκεί που θα χρησιμοποιηθεί να είναι ν ασφ = 8. Να υπολογίσετε την επιτρεπόμενη τάση που πρέπει να δοθεί στο υλικό του κοχλία. 25. Ένας κοχλίας έχει διάμετρο πυρήνα 18 mm και έχει σ επ =1200 daν/cm 2. Ποιο είναι το επιτρεπόμενο φορτίο που μπορεί να αντέξει αν καταπονείται σε απλό εφελκυσμό και ποιο όταν υφίσταται σύνθετη καταπόνηση; 26. Ένας κοχλίας καταπονείται σε διάτμηση με φορτίο Q=2000 dan και έχει τ επ =1200 daν/cm 2. Από τον πίνακα της σελίδας 316 να βρείτε ένα κοχλία που να ταιριάζει στην περίπτωση αυτή. 27. Ένα φορτίο βάρους dan, που υφίσταται σύνθετη καταπόνηση (εφελκυσμό, κάμψη, στρέψη) δένεται με οκτώ κοχλίες Μ20 (d 1 =17 mm) που έχουν σ επ =1200 daν/cm 2. Το μήκος του σπειρώματος των κοχλιών που χρησιμοποιείται είναι 15 mm και το βήμα 2,5 mm. Δίνεται p επ = 200 daν/cm 2. Να ελέγξετε αν αντέχουν οι κοχλίες και σε σύνθετη καταπόνηση και σε πίεση επιφανείας. 28. Έχουμε ένα κοχλία Μ16 (d 1 =15 mm, βήμα σπειρώματος: h=2 mm) που πρέπει να παραλάβει 500 dan και έχει p επ = 200 daν/cm 2. Να βρείτε το μήκος που πρέπει να έχει το σπείρωμα που χρησιμοποιείται με το περικόχλιο. 29. Ένας κοχλίας με τετραγωνικό σπείρωμα, ονομαστική διάμετρο 56 mm και διάμετρο πυρήνα 44 mm υφίσταται απλό εφελκυσμό. Το υλικό από το οποίο είναι κατασκευασμένος έχει σ επ =800 daν/cm 2 και p επ =100 daν/cm 2. Με το περικόχλιο συνεργάζονται 10 σπειρώματα. Να βρεθεί το μέγιστο φορτίο που μπορεί να αντέξει ο πυρήνας του κοχλία και κατόπιν να ελεγχθεί αν αντέχει και σε πίεση επιφανείας. 30. Θέλουμε να χρησιμοποιήσουμε κοχλίες Μ20 (d 1 =17 mm) για να στερεώσουμε ένα φορτίο που υφίσταται σύνθετη καταπόνηση με μέγιστη συνολική δύναμη 8000 dan. Οι κοχλίες έχουν σ επ =1200 daν/cm 2. Να υπολογίσετε πόσους τέτοιους κοχλίες πρέπει να χρησιμοποιήσουμε. 31. Ένας κοχλίας Μ24 (d 1 =20 mm) υφίσταται μόνο αξονική φόρτιση με δύναμη 2000 daν. Να ελέγξετε αν αντέχει, γνωρίζοντας ότι σ επ =800 daν/cm 2. Κατόπιν να ελέγξετε αν ο ίδιος κοχλίας θα αντέξει σε σύνθετη καταπόνηση. 32. Ένας κοχλίας Μ20 (d 1 =17 mm) είναι από υλικό με σ επ =1200 daν/cm 2. Να βρείτε πόσο είναι το μέγιστο φορτίο που θα μπορεί να δεχτεί: α) όταν έχει απλό εφελκυσμό και β) όταν δέχεται σύνθετη καταπόνηση. 33. Τρεις κοχλίες συνδέουν δυο ελάσματα που καταπονούνται με συνολική δύναμη 9000 kp. Αν το υλικό από το οποίο είναι κατασκευασμένοι έχει σ επ =1000 kp/cm 2 να υπολογιστούν οι κοχλίες, δηλαδή να βρείτε την διάμετρο του πυρήνα, όταν δεχτούμε ότι οι κοχλίες καταπονούνται σε: A. Απλό εφελκυσμό B. Σύνθετη καταπόνηση Περιστροφική κίνηση Άξονες Άτρακτοι 34. Μία άτρακτος έχει διάμετρο 40 cm. Αν η δύναμη που την περιστρέφει είναι 120 kp να βρείτε τη ροπή που μεταφέρει. 35. Με μία άτρακτο διαμέτρου 20 cm θέλουμε να μεταφέρουμε ροπή ίση με 20 kp m. Πόση θα είναι η δύναμη που ασκείται σε αυτήν; ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 151
152 ΚΕΦΑΛΑΙΟ 11 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 36. Ένας κυκλικός δίσκος έχει διάμετρο 1 m και περιστρέφεται με 200 RPM. Ποια είναι η περιφερειακή ταχύτητα στο άκρο του δίσκου και ποια στο μέσον της ακτίνας του; 37. Μία άτρακτος μεταφέρει ισχύ ίση με 20 PS και περιστρέφεται με 200 RPM. Πόση είναι η ροπή που μεταφέρεται από αυτήν; 38. Μία άτρακτος μεταφέρει ροπή ίση με 400 kp m και περιστρέφεται με 200 RPM. Πόση είναι η ισχύς που μεταφέρεται από αυτήν; Με χρήση των πινάκων των σελίδων 324 και 325 να υπολογίσετε την διάμετρο που θα έχει η άτρακτος στις περιπτώσεις που είναι κατασκευασμένη από τα υλικά: 1. st37 2. st Μία περιστρεφόμενη άτρακτος με 500 RPM μεταφέρει ροπή 200 kp m σε μία άλλη άτρακτο που περιστρέφεται με 200 RPM. Πόση θα είναι η ροπή που μεταφέρει η δεύτερη άτρακτος; Ποια είναι η σχέση μετάδοσης; Πόση ισχύς μεταφέρεται από το σύστημα των ατράκτων; 40. Δύο συνεργαζόμενοι τροχοί (οδοντωτοί ή με ιμάντα ή με αλυσίδα) έχουν διαμέτρους d 1 =20 cm και d 2 =5 cm. Ο άξονας του τροχού 1 περιστρέφεται με 100 RPM. Με πόσες στροφές περιστρέφεται ο τροχός 2; Ποια είναι η σχέση μετάδοσης στη συνεργασία αυτή; 41. Σε δύο συνεργαζόμενους άξονες οι απώλειες ισχύος είναι 5%. Αν η ισχύς που έχει ο πρώτος άξονας είναι 50 PS πόση θα μεταφερθεί στον δεύτερο άξονα; 42. Ποιος είναι ο βαθμός απόδοσης μιας μηχανής που έχει ισχύ 20 PS αλλά ωφελούμαστε μόνο 18 PS; 43. Μία κινητήρια άτρακτος περιστρέφεται με 200 RPM και μεταφέρει ισχύ 20 PS σε μια άλλη με σχέση μετάδοσης ίση με: i=2. Ποια είναι η ροπή στη δεύτερη άτρακτο; (Δεν έχουμε απώλειες ισχύος) 44. Μία άτρακτος περιστρέφεται με 1000 RPM και μεταφέρει ισχύ 20 PS σε μία άλλη άτρακτο που περιστρέφεται με 400 RPM. Πόση είναι η ροπή στην πρώτη άτρακτο και πόση στην δεύτερη; Πόση είναι η μεταφερόμενη ισχύς στη δεύτερη άτρακτο όταν δεν υπάρχουν απώλειες ισχύος και πόση όταν οι απώλειες είναι 10%; 45. Έχουμε δυο άξονες με γρανάζια που συνεργάζονται και το κινητήριο έχει d 1 =30 mm το δε κινούμενο d 2 =60 mm. Το d 1 περιστρέφεται με 1500 RPM και μεταδίδει ισχύ 10 PS. 1. Αν οι απώλειες λόγω τριβών στα γρανάζια είναι αμελητέες να βρείτε την ισχύ και τη ροπή που παίρνει το δεύτερο γρανάζι. 2. Αν οι απώλειες ισχύος είναι 5% να βρείτε την ισχύ και τη ροπή που παίρνει τώρα το δεύτερο γρανάζι. 3. Να βρείτε την διάμετρο που πρέπει να έχει η άτρακτος του πρώτου γραναζιού αν είναι από υλικό με τ επ = 150 kp/cm Έχουμε δυο άξονες με γρανάζια που συνεργάζονται και το κινητήριο παίρνει κίνηση από ένα κινητήρα με ισχύ 40 PS, περιστρέφεται με 1000 RPM, και έχει διάμετρο d 1 =50 mm, ενώ το κινούμενο έχει διάμετρο d 2 =100 mm. Οι άξονες των δυο γραναζιών κατασκευάζονται από υλικό με σ επ = 500 kp/cm 2 και τ επ = 180 kp/cm 2. Ζητείται να υπολογιστούν οι δυο αυτοί άξονες. 47. Μια άτρακτος μεταφέρει την κίνηση ενός ηλεκτροκινητήρα ισχύος 50 ΗΡ με 1500 RPM. 1. Να βρείτε τη ροπή που μεταφέρεται από την άτρακτο. 2. Να υπολογιστεί η διάμετρος της ατράκτου αυτής αν έχει τ επ =180 dan/cm Να υπολογίσετε τη διάμετρο και με άλλο τρόπο: χρησιμοποιώντας τον πίνακα της σελίδας ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
153 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Έδρανα κύλισης 48. Να εξηγήσετε τι σημαίνουν οι αριθμοί στο έδρανο κύλισης (ρουλεμάν): Δίνεται η αμφιέριστη δοκός του επόμενου σχήματος με τη δύναμη F 1 να ασκείται στο σημείο που δείχνει το σχήμα. Να βρείτε τις αντιδράσεις των στηρίξεων Α και Β (μέτρο, διεύθυνση και φορά). (Τα σημεία Α και Β συμπίπτουν με τα άκρα της ράβδου) 50. Δίνεται η αμφιέριστη δοκός του επόμενου σχήματος με τις δυνάμεις F 1 και F 2 να ασκούνται στα σημεία που δείχνει το σχήμα. Να βρείτε την συνισταμένη των δυο παραλλήλων δυνάμεων F 1 και F 2 (μέτρο, διεύθυνση και φορά). Να βρείτε τις αντιδράσεις των στηρίξεων Α και Β (μέτρο, διεύθυνση και φορά). (Τα σημεία Α και Β συμπίπτουν με τα άκρα της ράβδου) 51. Να βρείτε τις αντιδράσεις στα σημεία στήριξης Α και Β. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 153
154 ΚΕΦΑΛΑΙΟ 11 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 52. Να βρείτε τις αντιδράσεις στο Α και στο Β. 53. Για το παρακάτω σχήμα μίας ατράκτου με δύο ρουλεμάν δίνεται ότι η δύναμη είναι F=2000 kp, η διάμετρος της ατράκτου d=60 mm και οι στροφές της n=400 RPM. Να υπολογίσετε τα έδρανα κύλισης που πρέπει να χρησιμοποιηθούν με βάση τον πίνακα της σελίδας 331. Να θεωρήσετε ότι η άτρακτος θα χρησιμοποιηθεί σε φορτηγό αυτοκίνητο. 54. Για το παρακάτω σχήμα μίας ατράκτου με δύο ρουλεμάν δίνονται ότι οι δυνάμεις είναι F 1 =1000 kp και F 2 =3000 kp, η διάμετρος d=55 mm και οι στροφές n=500 RPM. Να υπολογίσετε τα έδρανα κύλισης που πρέπει να χρησιμοποιηθούν με βάση τον πίνακα της σελίδας 331. Να θεωρήσετε ότι η άτρακτος θα χρησιμοποιηθεί σε ένα μειωτήρα στροφών. 55. Για την άτρακτο του σχήματος με δύο ρουλεμάν δίνεται ότι η δύναμη είναι F=1000 kp, η διάμετρος d=50 mm και οι στροφές n=320 RPM. Να υπολογίσετε τα έδρανα κύλισης που πρέπει να χρησιμοποιηθούν με βάση τον πίνακα της σελίδας 331. Να θεωρήσετε ότι η άτρακτος θα χρησιμοποιηθεί σε κιβώτιο ταχυτήτων εργαλειομηχανής. 56. Για το παρακάτω σχήμα μίας ατράκτου με δύο ρουλεμάν δίνονται ότι οι δυνάμεις είναι F 1 =1000 kp και F 2 =3000 kp, η διάμετρος d=55 mm και οι στροφές n=500 RPM. Να υπολογίσετε τα έδρανα κύλισης που πρέπει να χρησιμοποιηθούν με βάση τον πίνακα 154 ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ
155 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 11 της σελίδας 331. Να θεωρήσετε ότι η άτρακτος θα χρησιμοποιηθεί σε μειωτήρα στροφών Οδοντωτοί τροχοί 57. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι αρχικές διάμετροι των τροχών: d 01 =50 mm και d 02 =125 mm και οι στροφές του πρώτου: n 1 =500 rpm. Να βρείτε με πόσες στροφές θα περιστρέφεται ο δεύτερος τροχός και ποια είναι η σχέση μετάδοσης. 58. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι στροφές των τροχών: n 1 =500 rpm και n 2 =750 rpm και η αρχική διάμετρος του πρώτου: d 01 =150 mm. Να βρείτε την αρχική διάμετρο που θα έχει ο δεύτερος τροχός και ποια είναι η σχέση μετάδοσης. 59. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι αρχικές διάμετροι των τροχών: d 01 =50 mm και d 02 =125 mm και τα δόντια του πρώτου: z 1 =20. Να βρείτε πόσα δόντια θα έχει ο δεύτερος τροχός. Αφού βρείτε το modul των τροχών να βρείτε το βήμα τους. 60. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι στροφές των τροχών: n 1 =500 rpm και n 2 =750 rpm. Να βρείτε την σχέση μετάδοσης. 61. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι στροφές του πρώτου τροχού: n 1 =500 rpm και η σχέση μετάδοσης i=3,5. Να βρείτε με πόσες στροφές θα περιστρέφεται ο δεύτερος τροχός. 62. Σε ένα ζευγάρι οδοντωτών τροχών τα δόντια του πρώτου τροχού είναι: z 1 =18 και του δεύτερου: z 2 =36. Να βρείτε την σχέση μετάδοσης. 63. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι αρχικές διάμετροι των τροχών: d 01 =60 mm και d 02 =150 mm. Να βρείτε την σχέση μετάδοσης. 64. Σε ένα ζευγάρι οδοντωτών τροχών τα δόντια του πρώτου τροχού είναι: z 1 =18 και η σχέση μετάδοσης είναι i=1/2. Να βρείτε τον αριθμό των δοντιών του άλλου τροχού. Αν το modul είναι ίσο με 4 mm να υπολογίσετε τις αρχικές διαμέτρους των δύο τροχών. 65. Σε ένα τροχό η αρχική διάμετρος είναι d 0 =60 mm και τα δόντια που έχει είναι z=20. Να βρείτε το modul του τροχού. 66. Θα μπορούσε ένα γρανάζι κανονικής οδόντωσης να έχει αρχική διάμετρο 60 mm και 17 δόντια; Αν όχι να εξηγήσετε γιατί. (Απ. Διότι το modul δεν ανήκει στα τυποποιημένα) 67. Ένας οδοντωτός τροχός έχει οδόντωση με βήμα περίπου t=10 mm. Ποιο modul πρέπει να έχει ο τροχός αυτός; Αφού βρείτε το modul να υπολογίσετε το ακριβές βήμα που θα έχει ο τροχός. Αν ο τροχός έχει 20 δόντια πόση θα είναι η αρχική του διάμετρος; 68. Ένας οδοντωτός τροχός έχει modul ίσο με 5 mm και αρχική διάμετρο d 0 =90 mm. Πόσα δόντια θα έχει; Πόσο είναι το βήμα του τροχού; 69. Ένας οδοντωτός τροχός έχει modul ίσο με 10 mm. Να βρείτε πόσο θα είναι το βήμα του. 70. Σε ένα ζευγάρι οδοντωτών τροχών δίνονται οι αρχικές διάμετροι των τροχών: d 01 =100 mm και d 02 =175 mm. Να βρείτε την απόσταση των αξόνων των τροχών. ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ 155
Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ
 Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ Δ1. Η φέρουσα διατομή και ο ρόλος της στον υπολογισμό αντοχής Όπως ξέρουμε, το αν θα αντέξει ένα σώμα καθορίζεται όχι μόνο από το φορτίο που επιβάλλουμε αλλά και
Δ. ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΣΕΩΝ - ΕΛΕΓΧΟΣ ΑΝΤΟΧΗΣ Δ1. Η φέρουσα διατομή και ο ρόλος της στον υπολογισμό αντοχής Όπως ξέρουμε, το αν θα αντέξει ένα σώμα καθορίζεται όχι μόνο από το φορτίο που επιβάλλουμε αλλά και
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Μηχανική Στερεού Σώματος. Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
ΜΑΘΗΜΑΤΙΚΑ - Γ ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ Α': ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο: Αλγεβρικές παραστάσεις Παράγραφος A..: Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) Β: Πράξεις με μονώνυμα Τα σημαντικότερα σημεία
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Γ. ΥΠΟΛΟΓΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M)
 . ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
. ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ
 ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Ροπή Δύναμης Θα έχετε παρατηρήσει πως κλείνετε ευκολότερα μια πόρτα, αν την σπρώξετε σε μια θέση που βρίσκεται σχετικά μακρύτερα από τον άξονα περιστροφής της (τους μεντεσέδες
ΡΟΠΕΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ Ροπή Δύναμης Θα έχετε παρατηρήσει πως κλείνετε ευκολότερα μια πόρτα, αν την σπρώξετε σε μια θέση που βρίσκεται σχετικά μακρύτερα από τον άξονα περιστροφής της (τους μεντεσέδες
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
Ασκήσεις κέντρου μάζας και ροπής αδράνειας. αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας m i και θέσης r i
 Κέντρο μάζας Ασκήσεις κέντρου μάζας και ροπής αδράνειας Η θέση κέντρου μάζας ορίζεται ως r r i i αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας i και θέσης r i. Συμβολίζουμε
Κέντρο μάζας Ασκήσεις κέντρου μάζας και ροπής αδράνειας Η θέση κέντρου μάζας ορίζεται ως r r i i αν φανταστούμε ότι το χωρίζουμε το στερεό σώμα σε μικρά κομμάτια, μόρια, μάζας i και θέσης r i. Συμβολίζουμε
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων
 Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων Πρόβλημα Ε.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές. Η
Ε.3 Λυμένες ασκήσεις με υπολογισμό τάσεων Πρόβλημα Ε.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές. Η
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
2. Επίδραση των δυνάμεων στην περιστροφική κίνηση Ισοδύναμα συστήματα δυνάμεων
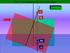 2. Επίδραση των δυνάμεων στην περιστροφική κίνηση Ισοδύναμα συστήματα δυνάμεων 2.1 Όπως είναι γνωστό, όταν σε κάποιο σώμα ενεργούν δυνάμεις, ένα από τα αποτελέσματά τους μπορεί να είναι να αλλάξει η κατάσταση
2. Επίδραση των δυνάμεων στην περιστροφική κίνηση Ισοδύναμα συστήματα δυνάμεων 2.1 Όπως είναι γνωστό, όταν σε κάποιο σώμα ενεργούν δυνάμεις, ένα από τα αποτελέσματά τους μπορεί να είναι να αλλάξει η κατάσταση
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 2 0 Κεφάλαιο
 Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ
 ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων
 1 Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων Πρόβλημα 3.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές.
1 Λυμένες ασκήσεις του κεφαλαίου 3: Είδη φορτίσεων Πρόβλημα 3.1 Να ελεγχθεί αν αντέχουν σε εφελκυσμό οι ράβδοι στα παρακάτω σχήματα. (Έχουν όλες την ίδια εφελκυστική δύναμη Ν=5000Ν αλλά διαφορετικές διατομές.
Περιληπτικά, τα βήματα που ακολουθούμε γενικά είναι τα εξής:
 Αυτό που πρέπει να θυμόμαστε, για να μη στεναχωριόμαστε, είναι πως τόσο στις εξισώσεις, όσο και στις ανισώσεις 1ου βαθμού, που θέλουμε να λύσουμε, ακολουθούμε ακριβώς τα ίδια βήματα! Εκεί που πρεπει να
Αυτό που πρέπει να θυμόμαστε, για να μη στεναχωριόμαστε, είναι πως τόσο στις εξισώσεις, όσο και στις ανισώσεις 1ου βαθμού, που θέλουμε να λύσουμε, ακολουθούμε ακριβώς τα ίδια βήματα! Εκεί που πρεπει να
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
ΕΝΟΤΗΤΑ 2: ΡΟΠΗ ΔΥΝΑΜΗΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Γ. γ) η στατική τριβή στον δίσκο καθώς και το μέτρο της δύναμης που ασκεί το κεκλιμένο επίπεδο στο δίσκο.
 ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΡΟΠΗ ΔΥΝΑΜΗΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Γ Άσκηση 1. Ο δίσκος ισορροπεί με τη βοήθεια ενός νήματος παράλληλου στο κεκλιμένο επίπεδο. Αν το βάρος του δίσκου είναι
ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΡΟΠΗ ΔΥΝΑΜΗΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Γ Άσκηση 1. Ο δίσκος ισορροπεί με τη βοήθεια ενός νήματος παράλληλου στο κεκλιμένο επίπεδο. Αν το βάρος του δίσκου είναι
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
ΓΕΝΙΚΗ ΜΗΧΑΝΟΛΟΓΙΑ - ΣΤΕΡΕΟΣΤΑΤΙΚΗ. 2. Στερεοστατική. 2.1 Ισοδύναμα συστήματα δυνάμεων Δύναμη
 2. Στερεοστατική 2.1 Ισοδύναμα συστήματα δυνάμεων 2.1.1 Δύναμη Στο πλαίσιο της καθημερινής ζωής κάνουμε διάφορες ενέργειες που προκαλούν διάφορα αποτελέσματα. Όταν για παράδειγμα λέμε ότι κάποιος σπρώχνει
2. Στερεοστατική 2.1 Ισοδύναμα συστήματα δυνάμεων 2.1.1 Δύναμη Στο πλαίσιο της καθημερινής ζωής κάνουμε διάφορες ενέργειες που προκαλούν διάφορα αποτελέσματα. Όταν για παράδειγμα λέμε ότι κάποιος σπρώχνει
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ Τμήμα Μηχανολόγων Μηχανικών ΤΕ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι ΚΑΘΗΓΗΤΗΣ κ. ΜΟΣΧΙΔΗΣ ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ Τμήμα Μηχανολόγων Μηχανικών ΤΕ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Ι ΚΑΘΗΓΗΤΗΣ κ. ΜΟΣΧΙΔΗΣ ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΓΥΜΝΑΣΙΟ ΚΑΣΤΕΛΛΑΝΩΝ ΜΕΣΗΣ ΑΛΓΕΒΡΑ
 ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
Σύστημα σωμάτων vs Στερεό σώμα
 Σύστημα σωμάτων vs Στερεό σώμα Μια σφαίρα μάζας Μ και ακτίνας R είναι συνδεμένη με ράβδο μήκους l και μάζας m μέσω ενός κατακόρυφου άξονα περιστροφής, έτσι ώστε να υπάρχει η δυνατότητα περιστροφής της
Σύστημα σωμάτων vs Στερεό σώμα Μια σφαίρα μάζας Μ και ακτίνας R είναι συνδεμένη με ράβδο μήκους l και μάζας m μέσω ενός κατακόρυφου άξονα περιστροφής, έτσι ώστε να υπάρχει η δυνατότητα περιστροφής της
Γ ΛΥΚΕΙΟΥ ΟΙ ΚΙΝΗΣΕΙΣ ΤΩΝ ΣΤΕΡΕΩΝ ΣΩΜΑΤΩΝ
 Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ. Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι.
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΔΙΑΤΜΗΣΗ 1. Γενικά Όλοι γνωρίζουμε ότι σε μια διατομή ενός καταπονούμενου φορέα
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΔΙΑΤΜΗΣΗ 1. Γενικά Όλοι γνωρίζουμε ότι σε μια διατομή ενός καταπονούμενου φορέα
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 2014
 ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 03-04 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 04 Κατεύθυνση: Θεωρητική Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Τάξη: Β' Αριθμός Μαθητών: 0 Κλάδος: Μηχανολογίας
ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 03-04 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 04 Κατεύθυνση: Θεωρητική Μάθημα: Εφαρμοσμένη Μηχανική Επιστήμη Τάξη: Β' Αριθμός Μαθητών: 0 Κλάδος: Μηχανολογίας
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α
5. ΚΕΝΤΡΟ ΒΑΡΟΥΣ 5.1 Η
 5. ΚΕΝΤΡΟ ΒΑΡΟΥΣ 5. Η έννοια του κέντρου βάρους Έστω ότι ένα σώμα αποτελείται από δύο ή περισσότερα μέρη,... με απλό σχήμα, και ότι τα βάρη των μερών του είναι Β, Β.... Οι δυνάμεις Β, Β... θα ενεργούν
5. ΚΕΝΤΡΟ ΒΑΡΟΥΣ 5. Η έννοια του κέντρου βάρους Έστω ότι ένα σώμα αποτελείται από δύο ή περισσότερα μέρη,... με απλό σχήμα, και ότι τα βάρη των μερών του είναι Β, Β.... Οι δυνάμεις Β, Β... θα ενεργούν
1.2 Εξισώσεις 1 ου Βαθμού
 1.2 Εξισώσεις 1 ου Βαθμού Διδακτικοί Στόχοι: Θα μάθουμε: Να κατανοούμε την έννοια της εξίσωσης και τη σχετική ορολογία. Να επιλύουμε εξισώσεις πρώτου βαθμού με έναν άγνωστο. Να διακρίνουμε πότε μια εξίσωση
1.2 Εξισώσεις 1 ου Βαθμού Διδακτικοί Στόχοι: Θα μάθουμε: Να κατανοούμε την έννοια της εξίσωσης και τη σχετική ορολογία. Να επιλύουμε εξισώσεις πρώτου βαθμού με έναν άγνωστο. Να διακρίνουμε πότε μια εξίσωση
Εσωτερικές Αλληλεπιδράσεις Νο 3.
 Το θέμα του 05, (επαναληπτικές) Εσωτερικές λληλεπιδράσεις Νο 3. Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους και σχηματίζουν σταθερή γωνία 60 ο μεταξύ τους, όπως φαίνεται στο Σχήμα. Οι ράβδοι είναι διαφορετικές
Το θέμα του 05, (επαναληπτικές) Εσωτερικές λληλεπιδράσεις Νο 3. Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους και σχηματίζουν σταθερή γωνία 60 ο μεταξύ τους, όπως φαίνεται στο Σχήμα. Οι ράβδοι είναι διαφορετικές
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ.
 Τίτλος Μαθήματος ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ
Τίτλος Μαθήματος ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ
ΔΥΝΑΜΗ, ΝΟΜΟΙ ΤΟΥ NEWTON
 1 ΔΥΝΑΜΗ, ΝΟΜΟΙ ΤΟΥ NEWTON Τι είναι «δύναμη»; Θα πρέπει να ξεκαθαρίσουμε ότι ο όρος «δύναμη» στη Φυσική έχει αρκετά διαφορετική σημασία από ότι στην καθημερινή γλώσσα. Εκφράσεις όπως «τον χτύπησε με δύναμη»,
1 ΔΥΝΑΜΗ, ΝΟΜΟΙ ΤΟΥ NEWTON Τι είναι «δύναμη»; Θα πρέπει να ξεκαθαρίσουμε ότι ο όρος «δύναμη» στη Φυσική έχει αρκετά διαφορετική σημασία από ότι στην καθημερινή γλώσσα. Εκφράσεις όπως «τον χτύπησε με δύναμη»,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ.
 Τίτλος Μαθήματος ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ
Τίτλος Μαθήματος ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΜΗΧΑΝΙΚΗ Ι ΕΡΓΑΣΤΗΡΙΟ Καθηγητής Δρ. Μοσχίδης Νικόλαος ΣΕΡΡΕΣ, ΣΕΠΤΕΜΒΡΙΟΣ
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ
 Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ Φαινόμενο, ονομάζεται οτιδήποτε συμβαίνει τριγύρω μας. Για παράδειγμα η αύξηση του ύψους του ανθρώπου, η έκρηξη ενός ηφαιστείου κλπ. Τις μεταβολές αυτές, που συμβαίνουν στην φύση
Κεφάλαιο 1 ο ΕΙΣΑΓΩΓΗ Φαινόμενο, ονομάζεται οτιδήποτε συμβαίνει τριγύρω μας. Για παράδειγμα η αύξηση του ύψους του ανθρώπου, η έκρηξη ενός ηφαιστείου κλπ. Τις μεταβολές αυτές, που συμβαίνουν στην φύση
ΕΙΔΗ ΔΥΝΑΜΕΩΝ ΔΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕΔΟ
 ΕΙΔΗ ΔΥΝΑΜΕΩΝ ΔΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕΔΟ ΕΙΔΗ ΔΥΝΑΜΕΩΝ 1 Οι δυνάμεις μπορούν να χωριστούν σε δυο κατηγορίες: Σε δυνάμεις επαφής, που ασκούνται μόνο ανάμεσα σε σώματα που βρίσκονται σε επαφή, και σε δυνάμεις
ΕΙΔΗ ΔΥΝΑΜΕΩΝ ΔΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕΔΟ ΕΙΔΗ ΔΥΝΑΜΕΩΝ 1 Οι δυνάμεις μπορούν να χωριστούν σε δυο κατηγορίες: Σε δυνάμεις επαφής, που ασκούνται μόνο ανάμεσα σε σώματα που βρίσκονται σε επαφή, και σε δυνάμεις
Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα
 Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα Μάθημα: Μαθηματικά Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών (1 ο, 2 ο, 3 ο Κεφάλαιο) 11-10-2017, 18-10-2017 Διδάσκουσα: Αριστούλα Κοντογιάννη ΩΡΕΣ ΔΙΔΑΣΚΑΛΙΑΣ
Τμήμα Τεχνολόγων Γεωπόνων - Φλώρινα Μάθημα: Μαθηματικά Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών (1 ο, 2 ο, 3 ο Κεφάλαιο) 11-10-2017, 18-10-2017 Διδάσκουσα: Αριστούλα Κοντογιάννη ΩΡΕΣ ΔΙΔΑΣΚΑΛΙΑΣ
Κεφάλαιο 1 Εισαγωγή. Φυσική Β Γυμνασίου
 Κεφάλαιο 1 Εισαγωγή Φυσική Β Γυμνασίου Απαντήσεις ερωτήσεων σχολικού βιβλίου σχ. βιβλίο (σ.σ. 18-19) Γυμνάσιο: 9.000 μαθήματα με βίντεο-διδασκαλία για όλο το σχολικό έτος μόνο με 150 ευρώ! Μελέτη όπου,
Κεφάλαιο 1 Εισαγωγή Φυσική Β Γυμνασίου Απαντήσεις ερωτήσεων σχολικού βιβλίου σχ. βιβλίο (σ.σ. 18-19) Γυμνάσιο: 9.000 μαθήματα με βίντεο-διδασκαλία για όλο το σχολικό έτος μόνο με 150 ευρώ! Μελέτη όπου,
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΟΧΗΜΑΤΩΝ
 2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑΤΑ
 ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑ Α ΘΕΜΑΤΑ Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης
ΠΑΝΕΛΛΗΝΙΕΣ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ ΘΕΜΑ Α ΘΕΜΑΤΑ Α1. Να γράψετε στο τετράδιό σας τους αριθμούς 1, 2, 3, 4, 5 από τη στήλη Α και δίπλα ένα από τα γράμματα α, β, γ, δ, ε, στ της στήλης
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 2014
 ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2013 2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 2014 Κατεύθυνση: ΠΡΑΚΤΙΚΗ Μάθημα: ΦΥΣΙΚΗ (2ωρο) Τάξη: Α Αρ. Μαθητών: 156 Κλάδος: ΟΛΟΙ Ημερομηνία: 03/06/14
ΤΕΧΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2013 2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ/ ΙΟΥΝΙΟΥ 2014 Κατεύθυνση: ΠΡΑΚΤΙΚΗ Μάθημα: ΦΥΣΙΚΗ (2ωρο) Τάξη: Α Αρ. Μαθητών: 156 Κλάδος: ΟΛΟΙ Ημερομηνία: 03/06/14
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
Όπου m είναι η μάζα του σώματος και υ η ταχύτητά του.
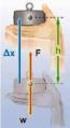 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
2ο video (επίλυση ανίσωσης 1 ου βαθμού)
 2ο video (επίλυση ανίσωσης 1 ου βαθμού) 1 Γεια σας και πάλι! Συγχαρητήρια για την επιτυχία σας στην πρώτη ενότητα! 2 Σε αυτό το video θα θυμηθούμε τη διαδικασία επίλυσης πρωτοβάθμιας ανίσωσης, δηλαδή όλα
2ο video (επίλυση ανίσωσης 1 ου βαθμού) 1 Γεια σας και πάλι! Συγχαρητήρια για την επιτυχία σας στην πρώτη ενότητα! 2 Σε αυτό το video θα θυμηθούμε τη διαδικασία επίλυσης πρωτοβάθμιας ανίσωσης, δηλαδή όλα
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου
 ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
Πρόχειρες Σημειώσεις
 Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
Πρόχειρες Σημειώσεις ΛΕΠΤΟΤΟΙΧΑ ΔΟΧΕΙΑ ΠΙΕΣΗΣ Τα λεπτότοιχα δοχεία πίεσης μπορεί να είναι κυλινδρικά, σφαιρικά ή κωνικά και υπόκεινται σε εσωτερική ή εξωτερική πίεση από αέριο ή υγρό. Θα ασχοληθούμε μόνο
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη
 Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
Από το Γυμνάσιο στο Λύκειο Δειγματικός χώρος Ενδεχόμενα Εύρεση δειγματικού χώρου... 46
 ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11 2. Σύνολα..............................................................
ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11 2. Σύνολα..............................................................
2.3 ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ
 ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ.ptetragono.gr Σελίδα. ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Να βρεθεί το μέτρο των μιγαδικών :..... 0 0. 5 5 6.. 0 0. 5. 5 5 0 0 0 0 0 0 0 0 ΜΕΘΟΔΟΛΟΓΙΑ : ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ Αν τότε. Αν χρειαστεί
ΕΠΙΜΕΛΕΙΑ : ΠΑΛΑΙΟΛΟΓΟΥ ΠΑΥΛΟΣ.ptetragono.gr Σελίδα. ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Να βρεθεί το μέτρο των μιγαδικών :..... 0 0. 5 5 6.. 0 0. 5. 5 5 0 0 0 0 0 0 0 0 ΜΕΘΟΔΟΛΟΓΙΑ : ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ Αν τότε. Αν χρειαστεί
ΤΕΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ANΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ Ειδικότητες: Όλες Ώρα εξέτασης: 07:30-09:30
 ΤΕΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ANΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2014 Κατεύθυνση: ΠΡΑΚΤΙΚΗ Μάθημα: ΦΥΣΙΚΗ (2ωρο) Τάξη: Α Αρ. Μαθητών: 7 Κλάδος: Όλοι Ημερομηνία: Ειδικότητες: Όλες Ώρα εξέτασης:
ΤΕΝΙΚΗ ΣΧΟΛΗ ΜΑΚΑΡΙΟΣ Γ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ANΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2014 Κατεύθυνση: ΠΡΑΚΤΙΚΗ Μάθημα: ΦΥΣΙΚΗ (2ωρο) Τάξη: Α Αρ. Μαθητών: 7 Κλάδος: Όλοι Ημερομηνία: Ειδικότητες: Όλες Ώρα εξέτασης:
Από το Γυμνάσιο στο Λύκειο... 7. 3. Δειγματικός χώρος Ενδεχόμενα... 42 Εύρεση δειγματικού χώρου... 46
 ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11. Σύνολα..............................................................
ΠEΡΙΕΧΟΜΕΝΑ Από το Γυμνάσιο στο Λύκειο................................................ 7 1. Το Λεξιλόγιο της Λογικής.............................................. 11. Σύνολα..............................................................
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ 16118 Δύο σφαιρίδια Σ 1 και Σ 2 βρίσκονται σε λείο οριζόντιο τραπέζι (κάτοψη του οποίου φαίνεται στο
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ 16118 Δύο σφαιρίδια Σ 1 και Σ 2 βρίσκονται σε λείο οριζόντιο τραπέζι (κάτοψη του οποίου φαίνεται στο
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα.
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ. Στοιχεία Θεωρίας - Λυμένα Παραδείγματα. Ασκήσεις - Ερωτήσεις Θεωρίας. Νικόλαος Χονδράκης (Εκπαιδευτικός)
 ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΨΥΞΗΣ Στοιχεία Θεωρίας - Λυμένα Παραδείγματα Ασκήσεις - Ερωτήσεις Θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης Διπλωματούχος Μηχανολόγος Μηχανικός
ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΨΥΞΗΣ Στοιχεία Θεωρίας - Λυμένα Παραδείγματα Ασκήσεις - Ερωτήσεις Θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης Διπλωματούχος Μηχανολόγος Μηχανικός
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα
 Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα Μαθηματικά Α Γυμνασίου Μέρο Α - Κεφάλαιο 2 Α. 2.1. Όταν ένα μέγεθο ή ένα σύνολο ομοειδών αντικειμένων χωρισθεί σε ν ίσα μέρη, το κάθε ένα
Α Γυμνασίου, Μέρο Α : Αριθμητική Άλγεβρα, Κεφάλαιο 2 - Κλάσματα Μαθηματικά Α Γυμνασίου Μέρο Α - Κεφάλαιο 2 Α. 2.1. Όταν ένα μέγεθο ή ένα σύνολο ομοειδών αντικειμένων χωρισθεί σε ν ίσα μέρη, το κάθε ένα
Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης
![Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης Ηλοσυνδέσεις. = [cm] Μαυρογένειο ΕΠΑΛ Σάμου. Στοιχεία Μηχανών - Τυπολόγιο. Χατζής Δημήτρης](/thumbs/64/50942463.jpg) Ηλοσυνδέσεις Ελάχιστη επιτρεπόμενη διάμετρος ήλου που καταπονείται σε διάτμηση 4Q = [cm] zxπτ επ : διάμετρος ήλου σε [cm] Q : Μέγιστη διατμητική δύναμη σε [an] τ επ : επιτρεπόμενη διατμητική τάση σε [an/cm
Ηλοσυνδέσεις Ελάχιστη επιτρεπόμενη διάμετρος ήλου που καταπονείται σε διάτμηση 4Q = [cm] zxπτ επ : διάμετρος ήλου σε [cm] Q : Μέγιστη διατμητική δύναμη σε [an] τ επ : επιτρεπόμενη διατμητική τάση σε [an/cm
εξισώσεις-ανισώσεις Μαθηματικά α λυκείου Φροντιστήρια Μ.Ε. ΠΑΙΔΕΙΑ σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες
 Με τον διεθνή όρο φράκταλ (fractal, ελλ. μορφόκλασμα ή μορφοκλασματικό σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο
Με τον διεθνή όρο φράκταλ (fractal, ελλ. μορφόκλασμα ή μορφοκλασματικό σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΜΣ «ΑΝΑΛΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΚΑΙ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ» Παραδείγματα Variation Μεταπτυχιακός Φοιτητής:
ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΠΜΣ «ΑΝΑΛΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΚΑΙ ΔΙΔΑΚΤΙΚΗ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ» Παραδείγματα Variation Μεταπτυχιακός Φοιτητής:
Ευθύγραμμες Κινήσεις
 Οι παρακάτω σημειώσεις διανέμονται υπό την άδεια: Creaive Commons Αναφορά Δημιουργού - Μη Εμπορική Χρήση - Παρόμοια Διανομή 4.0 Διεθνές. 1 Θέση και Σύστημα αναφοράς Στην καθημερινή μας ζωή για να περιγράψουμε
Οι παρακάτω σημειώσεις διανέμονται υπό την άδεια: Creaive Commons Αναφορά Δημιουργού - Μη Εμπορική Χρήση - Παρόμοια Διανομή 4.0 Διεθνές. 1 Θέση και Σύστημα αναφοράς Στην καθημερινή μας ζωή για να περιγράψουμε
Φυσική: Ασκήσεις. Β Γυμνασίου. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 0 Β Γυμνασίου Φυσική: Ασκήσεις Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 0 1 Ασκήσεις στο 1 ο Κεφάλαιο Ασκήσεις με κενά 1. Να συμπληρώσεις τα κενά στις παρακάτω προτάσεις:
0 Β Γυμνασίου Φυσική: Ασκήσεις Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 0 1 Ασκήσεις στο 1 ο Κεφάλαιο Ασκήσεις με κενά 1. Να συμπληρώσεις τα κενά στις παρακάτω προτάσεις:
ΑΛΓΕΒΡΑ Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η
 Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ. Στοιχεία Θεωρίας - Λυμένα παραδείγματα. Ασκήσεις - Ερωτήσεις θεωρίας. Νικόλαος Χονδράκης (Εκπαιδευτικός)
 ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΨΥΞΗΣ Στοιχεία Θεωρίας - Λυμένα παραδείγματα Ασκήσεις - Ερωτήσεις θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης Διπλωματούχος Μηχανολόγος Μηχανικός
ΒΟΗΘΗΜΑ ΣΤΟ ΜΑΘΗΜΑ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΨΥΞΗΣ Στοιχεία Θεωρίας - Λυμένα παραδείγματα Ασκήσεις - Ερωτήσεις θεωρίας Νικόλαος Χονδράκης (Εκπαιδευτικός) ... Νικόλαος Γ. Χονδράκης Διπλωματούχος Μηχανολόγος Μηχανικός
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
κατά την οποία το μέτρο της ταχύτητας του κέντρου μάζας του τροχού είναι ίσο με
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Ισχύουν οι αρχές διατήρησης; Πώς εφαρμόζονται;
 Ισχύουν οι αρχές διατήρησης; Πώς εφαρμόζονται; - Ένα βλήμα σφηνώνεται σε ένα ξύλο που είναι πακτωμένο στο έδαφος. Για την κρούση αυτή ισχύει η αρχή διατήρησης της ορμής (Α.Δ.Ο.), για το σύστημα βλήμα -
Ισχύουν οι αρχές διατήρησης; Πώς εφαρμόζονται; - Ένα βλήμα σφηνώνεται σε ένα ξύλο που είναι πακτωμένο στο έδαφος. Για την κρούση αυτή ισχύει η αρχή διατήρησης της ορμής (Α.Δ.Ο.), για το σύστημα βλήμα -
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
8. Σύνθεση και ανάλυση δυνάμεων
 8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό.
 Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό. Η ταχύτητα (υ), είναι το πηλίκο της μετατόπισης (Δx)
Μετατόπιση, είναι η αλλαγή (μεταβολή) της θέσης ενός κινητού. Η μετατόπιση εκφράζει την απόσταση των δύο θέσεων μεταξύ των οποίων κινήθηκε το κινητό. Η ταχύτητα (υ), είναι το πηλίκο της μετατόπισης (Δx)
Στοιχεία Μηχανών. Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά
 Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
8. ΔΙΚΤΥΩΜΑΤΑ. 8.1 Ορισμοί:
 8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
8. ΔΙΚΤΥΩΜΑΤΑ Σχ. 8.1 Παραδείγματα δικτυωμάτων 8.1 Ορισμοί: Δικτύωμα θα λέγεται ένας σύνθετος φορέας που όλα τα μέλη του είναι ράβδοι. Παραδείγματα δικτυωμάτων δίνονται στο σχήμα παραπάνω. Πλεονέκτημα
Προτεινόμενα θέματα Πανελλαδικών εξετάσεων. Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ
 Προτεινόμενα θέματα Πανελλαδικών εξετάσεων Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης 3o ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις
Προτεινόμενα θέματα Πανελλαδικών εξετάσεων Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης 3o ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις
Η ΚΙΝΗΣΗ ΣΩΜΑΤΙΟ Ή ΥΛΙΚΟ ΣΗΜΕΙΟ Ή ΣΗΜΕΙΑΚΟ ΑΝΤΙΚΕΙΜΕΝΟ
 «Μπορούμε να παρομοιάσουμε τις έννοιες που δεν έχουν καμιά θεμελίωση στη φύση, με τα δάση εκείνα του Βορρά όπου τα δένδρα δεν έχουν καθόλου ρίζες. Αρκεί ένα φύσημα του αγέρα, ένα ασήμαντο γεγονός για να
«Μπορούμε να παρομοιάσουμε τις έννοιες που δεν έχουν καμιά θεμελίωση στη φύση, με τα δάση εκείνα του Βορρά όπου τα δένδρα δεν έχουν καθόλου ρίζες. Αρκεί ένα φύσημα του αγέρα, ένα ασήμαντο γεγονός για να
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-2 ΑΤΡΑΚΤΟΙ ΑΞΟΝΕΣ - ΣΤΡΟΦΕΙΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-2 ΑΤΡΑΚΤΟΙ ΑΞΟΝΕΣ - ΣΤΡΟΦΕΙΣ
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 25/12/2016 ΘΕΜΑ
 ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 5//06 ΘΕΜΑ Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 5//06 ΘΕΜΑ Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη
ΣΤΑΤΙΚΗ 1 ΔΥΝΑΜΕΙΣ. Παράδειγμα 1.1
 ΣΤΤΙΚΗ 1 ΥΝΜΕΙΣ Στατική είναι ο κλάδος της μηχανικής που μελετά την ισορροπία των σωμάτων. Κατά την μελέτη δεχόμαστε ότι τα σώματα δεν παραμορφώνονται από τις δυνάμεις που ασκούνται σ αυτά. Οι παραμορφώσεις
ΣΤΤΙΚΗ 1 ΥΝΜΕΙΣ Στατική είναι ο κλάδος της μηχανικής που μελετά την ισορροπία των σωμάτων. Κατά την μελέτη δεχόμαστε ότι τα σώματα δεν παραμορφώνονται από τις δυνάμεις που ασκούνται σ αυτά. Οι παραμορφώσεις
3.3. Δυναμική στερεού.
 3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 11 ο, Τμήμα Α. Γεωμετρία
 Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μαθηματικά: ριθμητική και Άλγεβρα Μάθημα 11 ο, Τμήμα Γεωμετρία Η γεωμετρία σε σχέση με την άλγεβρα ή την αριθμητική έχει την εξής ιδιαιτερότητα: πρέπει να είμαστε πολύ ακριβείς στην περιγραφή μας (σκέψη
Μονάδα μέτρησης του ηλεκτρικού φορτίου στο Διεθνές Σύστημα (S.I.) είναι το προς τιμήν του Γάλλου φυσικού Charles Augustin de Coulomb.
 Βασικές έννοιες Τα σώματα μπορούν να αλληλεπιδράσουν ηλεκτρικά. Ο Θαλής ο Μιλήσιος παρατήρησε πρώτος την έλξη μικρών αντικειμένων από ήλεκτρο, αφού πρώτα τριφτεί σε ξηρό ύφασμα. Το φαινόμενο αυτό ονομάστηκε
Βασικές έννοιες Τα σώματα μπορούν να αλληλεπιδράσουν ηλεκτρικά. Ο Θαλής ο Μιλήσιος παρατήρησε πρώτος την έλξη μικρών αντικειμένων από ήλεκτρο, αφού πρώτα τριφτεί σε ξηρό ύφασμα. Το φαινόμενο αυτό ονομάστηκε
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2016-2017 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Επιτρεπόμενη διάρκεια γραπτού 2,5ώρες (150 λεπτά). Μάθημα: ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΕΦΑΡΜΟΣΜΕΝΗΣ
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2016-2017 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ ΙΟΥΝΙΟΥ 2017 ΜΕΣΗΣ ΤΕΧΝΙΚΗΣ ΚΑΙ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Επιτρεπόμενη διάρκεια γραπτού 2,5ώρες (150 λεπτά). Μάθημα: ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΕΦΑΡΜΟΣΜΕΝΗΣ
ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3)
 ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3) Η εξεταστέα ύλη για τις περιγραφικές ερωτήσεις (στο πρώτο μέρος της γραπτής εξέτασης) θα είναι η παρακάτω: - Κεφ. 1: Ποια είναι τα δύο πλεονεκτήματα
ΣΤΟΙΧΕΙA ΜΗΧΑΝΩΝ Ι - ΘΕΩΡΙΑ (για τις ασκήσεις βλ. σελ. 3) Η εξεταστέα ύλη για τις περιγραφικές ερωτήσεις (στο πρώτο μέρος της γραπτής εξέτασης) θα είναι η παρακάτω: - Κεφ. 1: Ποια είναι τα δύο πλεονεκτήματα
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
