( ) x. 1.1 Τριγωνομετρικές Συναρτήσεις. =. Να. 1. Δίνονται οι συναρτήσεις f ( x ) ( x 2
|
|
|
- Άνεμονη Μπότσαρης
- 10 χρόνια πριν
- Προβολές:
Transcript
1 11 Τριγωνομετρικές Συναρτήσεις 1 Δίνονται οι συναρτήσεις f ( ) ( ημ ) + σφ =, g( ) ημ ημ = και h( ) ημ( ) αποδειχθεί ότι η f είναι άρτια, η g περιττή και η h ούτε άρτια ούτε περιττή Να εξετασθεί αν είναι άρτια ή περιττή η συνάρτηση f με τύπο: i f ( ) = εφ + σφ συν συν ii f ( ) = + 1 ημ 1+ ημ ημ ημ iii f ( ) = + 1 συν 1+ συν Να αποδείξετε ότι οι παρακάτω συναρτήσεις είναι άρτιες α) f ημ + συν + β) f = συν ( ) = 1 ( ) + συν + συν + συν γ) f ( ) = δ) ( ) + ημ = 1+ συν f 4 Να αποδείξετε ότι οι παρακάτω συναρτήσεις είναι περιττές α) f ( ) ημ + β) f = ημ + εφ γ) f ημ5 + ημ δ) f = ημ εφ = ( ) ( ) = ( ) = Να 57
2 5 Να εξετάσετε αν οι παρακάτω συναρτήσεις είναι άρτιες ή περιττές i f ( ) = ημ συν ii f( ) = συν + συν + iii f ( ) = ημ iv f( ) = ημ + ημ 4 4 Να δείξετε ότι η συνάρ 6 τηση: i f ( ) = ημ( συν) είναι άρτια ii g ( ) = συν ( ημ) είναι περιττή 7 Να αποδείξετε ότι: α) Η συνάρτηση f ( ) = ημ συν + 1 έχει περίοδο τον αρι θμό T = π β) Η συνάρτηση f ( ) = εφ + σφ έχει περίοδο τον αριθμό T = π γ) Η συνάρτηση f ( ) συν = έχει περίοδο τον αριθμό T = π 4 δ ) Η συνάρτηση f ( ) = 1 ημ έχει περίοδο τον αριθμό T = π ( ) g ( ) συν ημ 8 Δίνονται οι συναρτήσεις f = ημ και = Να αποδειχθεί ότι είναι περιοδικές με περίοδο αντίστοιχα T = π (για την f) και T = π (για τη g) 9 Να αποδείξετε ότι η συνάρτηση: ( ) είναι σταθερή 1 1 f = 1+ σφ 1 + εφ + με ημ συν κπ, κ Ζ Να αποδειχθεί ότι οι παρακάτω συναρτήσ ις είναι σταθερές 10 ε 4 4 i f = ημ + συν + ημ συν ii g ( ) εφ ( ) = + ( συν + 1) 1+ εφ 11 Να βρείτε το μέγιστο και το ελάχιστο των σ υναρτήσεων: α) f ( ) 4ημ β) γ) f ημ δ) = f ( ) = συν ( ) = f ( ) = 5συν 1 Να βρείτε την περίοδο των συναρτήσεων: α) f ( ) ημ β) γ) f ( ) 5ημ = f ( ) = συν = δ) f ( ) = συν 58
3 1 Να σχεδιάσετε τις γραφικές παραστάσεις των συναρτήσεων, κάθε φορά στο ίδιο σύστημα αξόνων : i) f() = ημ, g() = 0,5ημ, h() = -ημ, 0 π ii) f() = συν, g() = 0,5συν, h() = -συν, 0 π 14 Σε ένα σύστημα αξόνων να σχεδιάσετε τη γραφική παράσταση της συνάρτησης f() = ημ και στην συνέχεια τις γραφικές παραστάσεις των συναρτήσεων: g() = 1+ημ και h() = -1+ημ 15 Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f( ) = ημ και g() = ημ, 0 π 16 Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f( ) = συν και g() = συν, 0 π 17 Έστω η συνάρτηση f() = ημ Ποια είναι η μέγιστη και ποια η ελάχιστη τιμή της συνάρτησης αυτής Ποια είναι η περίοδος της εν λόγω συνάρτησης; Να σχεδιάσετε την γραφική παράσταση της f σε διάστημα πλάτους μιας περιόδου 18 Έστω η συνάρτηση f() = συν Ποια είναι η μέγιστη και ποια η ελάχιστη τιμή της συνάρτησης αυτής Ποια είναι η περίοδος της εν λόγω συνάρτησης; Να σχεδιάσετε την γραφική παράσταση της f σε διάστημα πλάτους μιας περιόδου 19 Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: i) f() = εφ ii) g() = 1+εφ iii) h() = -1+εφ 0 Να μελετήσετε και να παραστήσετε γραφικά τη συνάρτηση f() = εφ Να βρείτε την περίοδο τιμή των συναρτήσεων 1, τη μέγιστη και την ελάχιστη i f( ) = συν ii f ( ) = ημ ( ) 5 Να σεδιάσετε τις γραφικές παραστάσεις των συναρτήσεων: α) f() = εφ β) f() = εφ γ) f() = -1+εφ δ) f() = εφ 4 59
4 Στο ίδιο σύστημα αξόνων να γίνουν οι γραφικές παραστάσεις των συναρτήσεων 1 f ( ) = ημ, g( ) = ημ και h ( ) = ημ (όλες με 0 4π ) 4 Στο ίδιο σύστημα αξόνων να σχεδιαστούν οι γραφικές παραστάσεις των συναρτήσεων f = συν g( ) = + συν και h( ) = συν ( ), 5 Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων ( ) = ημ g ( ) = συν + f και 4 6 Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων ( ) = εφ + g ( ) = σφ f και 4 7 Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων f ( ) h( ) = σφ ( ) 8 Δίνεται η συνάρτηση f = αημ, με α > 0 η οποία έχει μέγιστο το α) Να βρείτε το πεδίο ορισμού της f και την τιμή του α β) Να βρείτε την περίοδο της f g = f γ) Να χαράξετε τη γραφική παράσταση των f ( ) και ( ) ( ) δ) Να αποδείξετε ότι η εξίσωση f ( ) = 4 είναι αδύνατη = + σφ, g = + σφ και ( ) 9 Αν η γραφική παράσταση της συνάρτησης f ( ) M( π, ), να βρείτε: α) την περίοδο της f β) το μέγιστο και το ελάχιστο της f γ) Να χαράξετε τη γραφική παράσταση της f 0 Δίνεται η συνάρτηση f ( ) = ημ α) Να βρείτε το πεδίο ορισμού Α της f β) Να βρείτε τα ακρότατα της f γ) Να βρείτε την περίοδο της f = ασυν διέρχεται από το σημείο C g( ) f ( ) δ) Να κάνετε τη γραφική παράσταση της f καθώς και της συνάρτησης f στο ίδιο σύστημα αξόνων 60 =,
5 1 Δίνεται η συνάρτηση ( ) = ημ( π ) + συν f α) Να αποδείξετε ότι f ( ) = ημ και να βρείτε το πεδίο ορισμού Α της f β) Να βρείτε την περίοδο, το μέγιστο και το ελάχιστο της f γ) Να κάνετε τη γραφική παράσταση C f της f δ) Να εξετάσετε αν η εξίσωση f ( ) = 4 έχει λύση Δίνεται η συνάρτηση f ( ) συν ( π ) + συν ( π + ) α) Να αποδείξετε ότι f ( ) = συν = β) Να βρείτε το πεδίο ορισμού Α, την περίοδο και τα ακρότατα της f γ) Να χαράξετε τη γραφική παράσταση C f της f ( ) δ) Να χαράξετε τη γραφική παράσταση των συναρτήσεων: i g = f ii g ( ) = f ( ) + 1 ( ) ( ) iii g ( ) = f iv g ( ) = f + π Στο παρακάτω σχήμα βλέπετε τη γραφική παράσταση μιας τριγωνομετρικής περιοδικής συνάρτησης f ( ) α) Να βρείτε τον τύπο της f ( ) β) Στο ίδιο ή σε άλλο σύστημα αξόνων να σχεδιάσετε τις γραφικές παραστάσεις των συναρτήσεων: i 1 g ( ) = f ( ) ii h ( ) = f 4 iii φ( ) = f + 4 iv ω ( ) = f ( ) π ( ) 61
6 4 Δίνεται η γραφική παράσταση της συνάρτησης f ( ) β + ρ ημ ( α ) =, α) Να βρείτε τις τιμές των α, β και ρ β) Για ποιες τιμές του η f παρουσιάζει τη μέγιστη και την ελάχιστη τιμή; ) Να εξετάσετε αν η f, A, είναι περιοδική γ ( ) 5 Να βρείτε τις συναρτήσεις που έχουν γραφικές παραστάσεις τις γραμμές που φαίνονται στα σχή ματα α) 6
7 β) 6 Να βρείτε τις εξισώσεις των ημιτονοειδών καμπυλών: 7 Να βρείτε την περίοδο των συναρτήσεων των οποίων οι γραφικές παραστάσεις δίνονται στα παρακάτω σχήματα 6
8 y y y (α) (β) (γ) 8 Η παλίρ ροια σε μια θαλάσσια περιοχή περιγράφεται κατά προσέγγιση με την συνάρτηση y π = ημ t, όπου y το ύψος της στάθμης των υδάτων σε μέτρα και t ο χρόνος σε ώρες 6 i) Να βρείτε την χαμηλότερη άμπωτη υψομετρική διαφορά ανάμεσα στην ψηλότερη πλημμυρίδα και την ii) Nα κάνετε την γραφική παράσταση της συνάρτησης για 0 t 1 9 Ένα παιγνίδι κρέμεται με ένα ελατήριο από το ταβάνι και απέχει από το πάτωμα 1m Όταν 1 το παιγνίδι ανεβοκατεβαίνει, το ύψος του από το πάτωμα σε μέτρα είναι h = 1+ συνt, όπου t ο χρόνος σε δευτερόλεπτα i) Να υπολογίσετε την διαφορά ανάμεσα στο μέγιστο και στο ελάχιστο ύψος ii) Να βρείτε την περίοδο της ταλάντωσης iii) Να κάνετε τη γραφική παράσταση της συνάρτησης για 0 t π Αν 40 i ii π < < < π 1, να συγκριθούν οι αριθμοί: 1 συν και συν π σφ 1 και π σφ 64
9 41 Δ ίνεται η συνάρτηση f : R R για την οποία ισχύει η σχέση 4f ( ) f ( ) = ημ για κ άθε R Να αποδειχθεί ότι η f είναι περιττή 4 Να εξετάσετε αν η f είναι άρτια ή περιττή όταν: i f ( ) = + εφ ii f ( ) = ημ + συν 5 iii f ( ) = συν ( ημ) iv f ( ) = ημ v f ( ) = ημ( εφ) vi f( ) = ημ + vii f( ) = α + β + ημ α+ β, όπου α, β 1 ημ, > π viii f ( ) = ημ ( ημ) i f( ) = π, π π 1 + ημ, < π 1 4 Δίνεται η συνάρτηση f με τύπο: f ( ) ( ) ( ) ( π) συν( π ) 1+ συν π ημ π + = + ημ + α) Να βρείτε το πεδίο ορισμού Α της συνάρτησης f και να απλοποιήσετε τον τύπο της β ) Να αποδείξετε ότι ο αριθμός Τ = π είναι περίοδος της f π ημ ( ) 44 Δίνεται η συνάρτηση ( ) + + ημ π + 1 = + ημ( + π) + συν( π) f α) Να βρείτε το πεδίο ορισμού της f β) Να απλοποιήσετε τον τύπο της f γ ) Να αποδείξετε ότι ο αριθμός Τ = π είναι περίοδος της f 45 Να αποδειχθεί ό τι οι παρακάτω συναρτήσεις δεν είναι περιοδικές: f = + i ( ) ii g( ) = + 65
10 46 Αν η συνάρτηση ( ) f = ασυν με α, β > 0 έχει μέγιστο το και περίοδο τον αριθμό β Τ = 6π, να βρείτε: α) τον τύπο της συνάρτησης β) τις τιμές f ( π) και f 47 Αν η γραφική παράσταση της συνάρτησης f ( ) M( π, ), να βρείτε: α) την περίοδο της f β) το μέγιστο και το ελάχιστο της f γ) Να χαράξετε τη γραφική παράσταση της f 48 Δίνονται οι συναρτήσεις: ( ) ( λ +1) f = κ + + ημ και g( ) = ασυν διέρχεται από το σημείο ( ) κ = 6λ + 10 συν 4 Να βρείτε τις τιμές των κ και λ αν είναι γνωστό ότι έχουν την ίδια μέγιστη τιμή και η περίοδος της f είναι τριπλάσια από την περίοδο της g 49 Έστω η συνάρτηση f ( ) = γ + αημβ, α, β > 0 Αν η γραφική παράσταση της f διέρχεται από την αρχή των αξόνων, η f έχει περίοδο Τ = και ελάχιστη τιμή το α να βρείτε τα α, β, γ 50 Να μελετηθεί η συνάρτηση f ( ) = 1 συν 51 Να γίνει η γραφική παράσταση της συνάρτησης ( ) 1 5 Να χαράξετε τις γραφικές παραστάσεις των συναρτήσεων: f = ημ κα g = ημ α) ( ) ι ( ) β ) f ( ) = συν και f ( ) = συν 5 Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων: f 1+ συν συν 0 π i ( ) = ( ) ii g( ) = 1+ ημ + ημ ( 0 π) f = + ημ ημ όπου 0 π 66
11 π 54 Να χαράξετε τη γραφική παράσταση της συνάρτησης f( ) κημ = αν είναι γνωστό 4 π ότι διέρχεται από το σημείο Α, Να αποδεχθεί ότι είναι ημ 1 > ημ και εφ 1 < εφ όταν π < 4 1 < π < 56 Μια συνάρτηση : R R έχει την ιδιότητα f 1 + f 1+ = f, για κάθε R Να αποδεί ξετε ότι: α) Η f ( ) είναι άρτια συνάρτηση β) f ( + ) = f () και f ( + 6) = f ( ), για κάθε R γ ) Ο αριθμός 6 είναι περίοδος της f f ( ) ( ) ( ) T = ( ) 57 Αν η συνάρτηση f : R R είναι άρτια και υπάρχει α > 0, ώστε η συνάρτηση g : R R με = f α να, να αποδείξετε ότι η f είναι περιοδική με περίοδο T = 4α g( ) ( ) είναι περιττή ( ) 58 Δίνεται μια συνάρτηση f με πεδίο ορισμού το Αν υπάρχει να ισχύει f ( +Τ ) = f( ), να αποδείξετε ότι η f είναι περιοδική * Τ ώστε για κάθε 59 Αν ν, Α= ν + 1 ν ν ν + 1 και Β=, να αποδείξετε ότι: ν + ν 1 ν + ν + 1 i Ο αριθμός Α είναι μεγαλύτερος από το μέγιστο της συνάρτησης f ( ) = ημ ii Ο αριθμός Β είναι μικρότερος από το ελάχιστο της συνάρτησης g( ) = συν 60 Να αποδείξετε ότι το ελάχιστο της συνάρτησης f( ) = + 4 είναι ίσο με το μέγιστο π της συνάρτησης g ( ) = ημ και ότι οι C f και C g τέμνονται σε ένα σημείο με τετμημένη = 67
12 1 61 i) Να αποδείξετε ότι + για κάθε > 0 (πότε ισχύει το ίσον); 1 ii) Να αποδείξετε ότι το ελάχιστο της συνάρτησης f( ) = + είναι ίσο με το μέγιστο της συνάρτησης g ( ) = 1 + συν (4 π ) και ότι οι C f και C g τέμνονται σε σημείο με τετμημένη 0 = 1 π 6 Αν 0 < θ <, να αποδειχθεί ότι ημθ < συνθ Στη συνέχεια, με δεδομένο ότι ημθ + συνθ =, να αποδειχθεί ότι ημθ = και συνθ = 68
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα
 Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις
 2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
ΣΥΝΑΡΤΗΣΕΙΣ. H Εννοια του διανυσματος. Σ υ ν ο λ α - Ο ρ ι σ μ ο ι
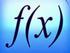 ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ
 ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
υναµική στο επίπεδο.
 στο επίπεδο. 1.3.1. Η τάση του νήµατος, πού και γιατί; Έστω ότι σε ένα λείο οριζόντιο επίπεδο ηρεµούν δύο σώµατα Α και Β µε µάζες Μ=3kg και m=2kg αντίστοιχα, τα οποία συνδέονται µε ένα νήµα. Σε µια στιγµή
στο επίπεδο. 1.3.1. Η τάση του νήµατος, πού και γιατί; Έστω ότι σε ένα λείο οριζόντιο επίπεδο ηρεµούν δύο σώµατα Α και Β µε µάζες Μ=3kg και m=2kg αντίστοιχα, τα οποία συνδέονται µε ένα νήµα. Σε µια στιγµή
Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο ΕΑΠ. Επιµέλεια Όµηρος Κορακιανίτης
 Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο ΕΑΠ Επιµέλεια Όµηρος Κορακιανίτης Άλγερα και πράξεις: (ή το µυστικό της επιτυχίας) - Όταν ένα γινόµενο
Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο ΕΑΠ Επιµέλεια Όµηρος Κορακιανίτης Άλγερα και πράξεις: (ή το µυστικό της επιτυχίας) - Όταν ένα γινόµενο
Τριγωνομετρία ΓΙΩΡΓΟΣ ΚΑΡΙΠΙΔΗΣ 2 ΑΝΘΟΥΛΑ ΣΟΦΙΑΝΟΠΟΥΛΟΥ
 ΕΥΚΛΕΙΔΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ ΤΟ ΒΑΣΙΚΟ ΘΕΩΡΗΜΑ: ημ χ+συν χ= ημ χ=-συν χ συν χ=- ημ χ εφχ + σφ χ = εφχ ημχ συνχ = σφχ = ημ χ εφχσφχ σφχ = = συνχ ημχ + εφ χ = συν χ Γωνία χ Τριγωνομετρικοί Αριθμοί
ΕΥΚΛΕΙΔΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ ΤΟ ΒΑΣΙΚΟ ΘΕΩΡΗΜΑ: ημ χ+συν χ= ημ χ=-συν χ συν χ=- ημ χ εφχ + σφ χ = εφχ ημχ συνχ = σφχ = ημ χ εφχσφχ σφχ = = συνχ ημχ + εφ χ = συν χ Γωνία χ Τριγωνομετρικοί Αριθμοί
Προσδιορισμός της σταθεράς ενός ελατηρίου.
 Μ3 Προσδιορισμός της σταθεράς ενός ελατηρίου. 1 Σκοπός Στην άσκηση αυτή θα προσδιοριστεί η σταθερά ενός ελατηρίου χρησιμοποιώντας στην ακολουθούμενη διαδικασία τον νόμο του Hooke και τη σχέση της περιόδου
Μ3 Προσδιορισμός της σταθεράς ενός ελατηρίου. 1 Σκοπός Στην άσκηση αυτή θα προσδιοριστεί η σταθερά ενός ελατηρίου χρησιμοποιώντας στην ακολουθούμενη διαδικασία τον νόμο του Hooke και τη σχέση της περιόδου
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))
![ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( )) ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))](/thumbs/17/113546.jpg) ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
Εξαιτίας της συμβολής δύο κυμάτων του ίδιου πλάτους και της ίδιας συχνότητας. που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό ελαστικό μέσο
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
1 Τράπεζα θεμάτων 2014-15 ΦΡΟΝΤΙΣΤΗΡΙΑ ΠΟΥΚΑΜΙΣΑΣ
 1 2 ΘΕΜΑ B Ένταση του ηλεκτρικού ρεύματος 1. ΘΕΜΑ Β 2-15438 B.1 Ένας αγωγός διαρρέεται από ηλεκτρικό ρεύμα έντασης i = 5 A. Το ηλεκτρικό φορτίο q που περνά από μια διατομή του αγωγού σε χρόνο t = 10 s
1 2 ΘΕΜΑ B Ένταση του ηλεκτρικού ρεύματος 1. ΘΕΜΑ Β 2-15438 B.1 Ένας αγωγός διαρρέεται από ηλεκτρικό ρεύμα έντασης i = 5 A. Το ηλεκτρικό φορτίο q που περνά από μια διατομή του αγωγού σε χρόνο t = 10 s
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
Πριν λύσεις την εργασία σου διάβασε τα ποιο κάτω για να θυμηθείς. Η ενέργεια ταλάντωσης δεν είναι πάντα ιση με τη μηχανική ενέργεια συστήματος.
 Πριν λύσεις την εργασία σου διάβασε τα ποιο κάτω για να θυμηθείς Η ενέργεια ταλάντωσης δεν είναι πάντα ιση με τη μηχανική ενέργεια συστήματος. Παράδειγμα : Έστω ένα σώμα αφήνεται από τη θέση φυσικού μήκους
Πριν λύσεις την εργασία σου διάβασε τα ποιο κάτω για να θυμηθείς Η ενέργεια ταλάντωσης δεν είναι πάντα ιση με τη μηχανική ενέργεια συστήματος. Παράδειγμα : Έστω ένα σώμα αφήνεται από τη θέση φυσικού μήκους
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟ ΟΙ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟ ΟΙ 1. ίνεται η αριθµητική πρόοδος µε α 2 =0 και α 4 =4. α) Να δείξετε ότι ω=2 και α 1 = 2. β) Να δείξετε ότι α ν =2ν 4 και να βρείτε ποιος όρος της είναι το 98. (51 ος ) 2. α) Να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟ ΟΙ 1. ίνεται η αριθµητική πρόοδος µε α 2 =0 και α 4 =4. α) Να δείξετε ότι ω=2 και α 1 = 2. β) Να δείξετε ότι α ν =2ν 4 και να βρείτε ποιος όρος της είναι το 98. (51 ος ) 2. α) Να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟΔΟΙ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟΔΟΙ 1. Δίνεται η αριθμητική πρόοδος με α 2 =0 και α 4 =4. α) Να δείξετε ότι ω=2 και α 1 = 2. β) Να δείξετε ότι α ν =2ν 4 και να βρείτε ποιος όρος της είναι το 98. (51 ος ) 2. α) Να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΠΡΟΟΔΟΙ 1. Δίνεται η αριθμητική πρόοδος με α 2 =0 και α 4 =4. α) Να δείξετε ότι ω=2 και α 1 = 2. β) Να δείξετε ότι α ν =2ν 4 και να βρείτε ποιος όρος της είναι το 98. (51 ος ) 2. α) Να
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου
 Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου 1 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΚΑΙ ΠΡΟΤΕΡΑΙΟΤΗΤΑ ΠΡΑΞΕΩΝ 1.1 Προτεραιότητα Πράξεων Η προτεραιότητα των πράξεων είναι: (Από τις πράξεις που πρέπει να γίνονται πρώτες,
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου 1 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΚΑΙ ΠΡΟΤΕΡΑΙΟΤΗΤΑ ΠΡΑΞΕΩΝ 1.1 Προτεραιότητα Πράξεων Η προτεραιότητα των πράξεων είναι: (Από τις πράξεις που πρέπει να γίνονται πρώτες,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που
ΝΕΚΤΑΡΙΟΣ ΤΣΙΛΙΒΙΓΚΟΣ
 ΝΕΚΤΑΡΙΟΣ ΤΣΙΛΙΒΙΓΚΟΣ ΦΥΣΙΚΗ Α Λυκείου Σαλαμίνα Φυσική Α Λυκείου 2 ΝΕΚΤΑΡΙΟΣ ΤΣΙΛΙΒΙΓΚΟΣ ΠΡΟΛΟΓΟΣ Με το μικρό αυτό βιβλίου θα ήθελα να βοηθήσω τους μαθητές της Α τάξης του Ενιαίου Λυκείου να οργανώσουν
ΝΕΚΤΑΡΙΟΣ ΤΣΙΛΙΒΙΓΚΟΣ ΦΥΣΙΚΗ Α Λυκείου Σαλαμίνα Φυσική Α Λυκείου 2 ΝΕΚΤΑΡΙΟΣ ΤΣΙΛΙΒΙΓΚΟΣ ΠΡΟΛΟΓΟΣ Με το μικρό αυτό βιβλίου θα ήθελα να βοηθήσω τους μαθητές της Α τάξης του Ενιαίου Λυκείου να οργανώσουν
, y 1. y y y y = x ( )
 ΚΕΦΑΛΑΙΟ Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕ Ο ΠΑΡΑΓΡΑΦΟΣ. ΕΞΙΣΩΣΗ ΓΡΑΜΜΗΣ Μία εξίσωση µε αγνώστους x, y λέγεται εξίσωση µίας γραµµής C, όταν οι συντεταγµένες των σηµείων της C και µόνο αυτές την επαληθεύουν. Αν έχουµε
ΚΕΦΑΛΑΙΟ Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕ Ο ΠΑΡΑΓΡΑΦΟΣ. ΕΞΙΣΩΣΗ ΓΡΑΜΜΗΣ Μία εξίσωση µε αγνώστους x, y λέγεται εξίσωση µίας γραµµής C, όταν οι συντεταγµένες των σηµείων της C και µόνο αυτές την επαληθεύουν. Αν έχουµε
0 0 30 π/6 45 π/4 60 π/3 90 π/2
 Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
Λυση. και επομένως. Αντικαθιστούμε στη σχέση. Λυση. y = f 3 και y = f 3
 Ø ÔØÓÑ Ò ½ Á ÒÓÙ ÖÓÙ ¾¼¼ Ασκηση Δίνεται η συνάρτηση f (x) =x +lnx. Να βρεθεί η εφαπτομένη της C f στοσημείομετετμημένηe. Η εξίσωση της τυχούσας εφαπτομένης της C f είναι y = f (x 0 ) x + f (x 0 ) f (x
Ø ÔØÓÑ Ò ½ Á ÒÓÙ ÖÓÙ ¾¼¼ Ασκηση Δίνεται η συνάρτηση f (x) =x +lnx. Να βρεθεί η εφαπτομένη της C f στοσημείομετετμημένηe. Η εξίσωση της τυχούσας εφαπτομένης της C f είναι y = f (x 0 ) x + f (x 0 ) f (x
Γ. ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΠΙΘΑΝΟΤΗΤΕΣ. Μαθηματικά Γενικής Παιδείας. Γ.Λυκείου
 Γ. ΛΥΚΕΙΟΥ ΜΘΗΜΤΙΚ ΓΕΝΙΚΗΣ ΠΙΔΕΙΣ ΠΙΘΝΟΤΗΤΕΣ Μαθηματικά Γενικής Παιδείας Γ.Λυκείου Π Ι Θ Ν Ο Τ Η Τ Ε Σ ΟΡΙΣΜΟΙ Πείραμα τύχης λέγεται το πείραμα το οποίο όσες φορές και αν επαναληφθεί (φαινομενικά τουλάχιστον
Γ. ΛΥΚΕΙΟΥ ΜΘΗΜΤΙΚ ΓΕΝΙΚΗΣ ΠΙΔΕΙΣ ΠΙΘΝΟΤΗΤΕΣ Μαθηματικά Γενικής Παιδείας Γ.Λυκείου Π Ι Θ Ν Ο Τ Η Τ Ε Σ ΟΡΙΣΜΟΙ Πείραμα τύχης λέγεται το πείραμα το οποίο όσες φορές και αν επαναληφθεί (φαινομενικά τουλάχιστον
ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ
 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ 9 40 4 ΒΑΣΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ 4 4 ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ. Να βρείτε την αριθµητική τιµή των παραστάσεων. i) α -α 6α, ii) 4α, για α iii) αβ α β (αβ),
ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ 9 40 4 ΒΑΣΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ 4 4 ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ. Να βρείτε την αριθµητική τιµή των παραστάσεων. i) α -α 6α, ii) 4α, για α iii) αβ α β (αβ),
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης
 Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Καρτεσιανές συντεταγμένες Γραφική παράσταση συνάρτησης Ορθοκανονικό σύστημα αξόνων ονομάζεται ένα σύστημα από δύο κάθετους άξονες με κοινή αρχή στους οποίους οι μονάδες έχουν το ίδιο μήκος. Υπάρχουν περιπτώσεις
Συνεπώς, προσπαθώντας να μην ξεχάσω κάποιον, οφείλω και χαίρομαι να αναφέρω τους εξής:
 Στο παρόν υλικό περιέχονται 490 Ασκήσεις και, κυρίως, Προβλήματα που αφορούν στο μάθημα της Φυσικής της Γ Λυκείου, για την Θετική και την Τεχνολογική Κατεύθυνση. Το επίπεδο δυσκολίας των θεμάτων είναι
Στο παρόν υλικό περιέχονται 490 Ασκήσεις και, κυρίως, Προβλήματα που αφορούν στο μάθημα της Φυσικής της Γ Λυκείου, για την Θετική και την Τεχνολογική Κατεύθυνση. Το επίπεδο δυσκολίας των θεμάτων είναι
Αθ.Κεχαγιας. Σηµειωσεις Αναλυτικης Γεωµετριας. Θ. Κεχαγιας. Σεπτεµβρης 2009, υ.0.95
 Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 2009, υ.0.95 Περιεχόµενα Εισαγωγη 1 Επιπεδα στον Τρισδιαστατο Χωρο 1 1.1 Θεωρια.................................... 1 1.2 Λυµενες Ασκησεις..............................
Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 2009, υ.0.95 Περιεχόµενα Εισαγωγη 1 Επιπεδα στον Τρισδιαστατο Χωρο 1 1.1 Θεωρια.................................... 1 1.2 Λυµενες Ασκησεις..............................
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Όταν το χ τότε το. στο,µπορούµε να θεωρήσουµε ότι το
 ΕΝΝΟΙΑ ΤΟΥ ΟΡΙΟΥ Όταν στα µαθηµατικά λέµε ότι το τείνει στο και συµβολίζεται, εννοούµε ότι οι τιµές προσεγγίζουν την τιµή, είτε µε από τιµές µικρότερες του δηλ από αριστερά του, είτε από τιµές µεγαλύτερες
ΕΝΝΟΙΑ ΤΟΥ ΟΡΙΟΥ Όταν στα µαθηµατικά λέµε ότι το τείνει στο και συµβολίζεται, εννοούµε ότι οι τιµές προσεγγίζουν την τιµή, είτε µε από τιµές µικρότερες του δηλ από αριστερά του, είτε από τιµές µεγαλύτερες
Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου
 ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 9 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 9 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ
Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1. Μιγαδικοί αριθμοί. ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
