Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο ΕΑΠ. Επιµέλεια Όµηρος Κορακιανίτης
|
|
|
- Φιλόθεος Βιλαέτης
- 10 χρόνια πριν
- Προβολές:
Transcript
1 Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο ΕΑΠ Επιµέλεια Όµηρος Κορακιανίτης
2 Άλγερα και πράξεις: (ή το µυστικό της επιτυχίας) - Όταν ένα γινόµενο παραγόντων είναι µηδέν τι συµπέρασµα µπορούµε να γάλουµε; Όταν ένα γινόµενο παραγόντων είναι µηδέν, τότε ένας τουλάχιστον από τους παράγοντες του πρέπει να είναι µηδέν. Για παράδειγµα, α γ = 0 α = 0 ή = 0 ή γ = 0. (-)(+) = 0 - = 0 ή + =0 - ή = - - Όταν ένα κλάσµα είναι µηδέν τι συµπεράσµατα µπορούµε να γάλουµε; Ότι ο αριθµητής είναι µηδέν (Προσοχή! Ο παρονοµαστής είναι πάντα διαφορετικός 3 + από το µηδέν). Για παράδειγµα, = = 0 και 0 ή =. - Τι µπορούµε να κάνουµε και στα δύο µέλη µιας ισότητας; α) Μπορούµε να προσθέσουµε και στα δύο µέλη µιας ισότητας τον ίδιο αριθµό. ηλαδή ισχύει: α = α + γ = + γ. ) Μπορούµε να πολλαπλασιάσουµε τα δύο µέλη µιας ισότητας µε τον ίδιο αριθµό. ηλαδή ισχύει: α = α γ = γ, γ 0. γ) Μπορούµε να διαιρέσουµε και τα µέλη µιάς ισότητας µε τον ίδιο µη µηδενικό αριθµό. Μην ξεχνάµε ότι διαίρεση είναι πολλαπλασιασµός µε τον αντίστροφο! - Τι ονοµάζουµε δύναµη α ν ; ύναµη α ν µε άση έναν πραγµατικό αριθµό α και εκθέτη ένα φυσικό αριθµό ν είναι ένα γινόµενο ν παραγόντων, που ο καθένας είναι ίσος µε τον α i) α ν = α α α.α (ν παράγοντες) δηλαδή ν φορές. ii) Aν ν =, τότε ισχύει α = α iii) Αν ν = 0, και α 0, τότε είναι: α 0 =. - Ποιες είναι οι ιδιότητες των δυνάµεων; α κ α λ = α κ+λ a κ κ α = κ, 0 (α κ ) λ = α κλ =(α λ ) κ α κ :α λ = α κ-λ, α 0 (α ) κ = α κ κ α -κ = κ, α 0 a - Βασικές ταυτότητες: α) (α +) = α + α + ) (α-) = α α + γ) (α+)(α-) = α δ) α 3 3 = (α-)(α + α+ ) ε) α = (α+)(α α + ) στ) (α+) 3 = α 3 +3α + 3α + 3 η) (α-) 3 = α 3 3α + 3α 3 θ) α ν ν = (α-)(α ν- + α ν- + +α ν- + ν- ) ι) α γ 3 3αγ = (α++γ)[ ( a ) + ( γ ) + ( γ α) ] κ) Αν α + + γ = 0, τότε α γ 3 = 3αγ
3 Προσοχή! Τις ταυτότητες πρέπει να τις λέπουµε και ως Άραες (δηλαδή από τα δεξιά προς τα αριστερά), για παράδειγµα, 9 = 3 = (-3)(+3) και έχουµε κάνει παραγοντοποίηση, δηλαδή γινόµενο παραγόντων. - Πότε λέµε ότι ένας αριθµός α είναι µεγαλύτερος από τον αριθµό ; Ένας αριθµός α λέµε ότι είναι µεγαλύτερος από τον, όταν η διαφορά α- είναι θετικός αριθµός: Ισχύει: α α 0 - Ποιες ιδιότητες ισχύουν στις ανισότητες; i) Αν α 0 και 0, τότε α + 0 (Το άθροισµα θετικών αριθµών είναι θετικό) ii) Αν α 0 και 0, τότε α + 0 (Το άθροισµα αρνητικών αριθµών είναι αρνητικό) a iii) α, οµόσηµοι α 0 και 0. a iv) α, ετερόσηµοι α 0 και 0 v) Για κάθε α R ισχύει: α 0 - Για τη διάταξη ισχύει: α και γ α γ (µεταατική ιδιότητα) - Τι µπορούµε να κάνουµε και στα δύο µέλη µιας ανισότητας; i) Μπορούµε να προσθέσουµε τον ίδιο αριθµό στα µέλη µιας ανισότητας. ηλαδή: Αν α, τότε ισχύει α + γ + γ ii) Μπορούµε να πολλαπλασιάσουµε τα µέλη µιας ανισότητας µε τον ίδιο θετικό αριθµό, οπότε προκύπτει ανισότητα µε την ίδια φορά. ηλαδή: Αν γ 0 και α, τότε α γ γ iii) Μπορούµε να πολλαπλασιάσουµε τα µέλη µιας ανισότητας µε τον ίδιο αρνητικό αριθµό, οπότε προκύπτει ανισότητα µε αντίθετη φορά. ηλαδή: Αν γ 0 και α, τότε ισχύει α γ γ ηλαδή πρέπει να ξέρουµε το πρόσηµο του αριθµού µε τον οποίο πολλαπλασιάζουµε και τα µέλη µιάς ανισότητας! (λέπε π.χ. σελίδα ) Παράδειγµα: Να λυθεί η ανίσωση + (κλασµατική ανίσωση γιατί ο άγνωστος είναι στον παρονοµαστή) Λύση: (τα κάνουµε οµώνυµα). ( + ) ( ) ( )( ) + + ( + ) 0 0 ( ) ( ) + 0 ( ) ( + ) 0 ( ) 3
4 (+) (-) (+)(-) ή 0 Περιορισµοί: 0 και. Άρα το σύνολο λύσεων είναι ή 0 < <. (, ] (0,) - Τι µπορούµε να κάνουµε µε δύο ανισότητες; α) Μπορούµε να τις προσθέσουµε κατά µέλη, όταν έχουν την ίδια φορά, οπότε προκύπτει ανισότητα µε την ίδια φορά. ηλαδή: α Αν, τότε α + γ + δ γ δ ) Μπορούµε να τις πολλαπλασιάζουµε κατά µέλη, όταν έχουν την ίδια φορά και θετικούς όρους, οπότε προκύπτει ανισότητα µε την ίδια φορά. ηλαδή: α Αν α,, γ, δ 0 και, τότε ισχύει α γ δ γ δ - Αν α, 0 και ν N, τότε ισχύουν: α) α α ν ν και ) α ν a ν. - Αν δύο αριθµοί α, είναι οµόσηµοι, τότε ο αντίστροφος του µεγαλύτερου είναι µικρότερος από τον αντίστροφο του µικρότερου, δηλαδή: Αν α, οµόσηµοι και α, τότε a - Τι ονοµάζουµε νιοστή ρίζα ενός µη αρνητικού αριθµού α; Είναι ο µη αρνητικός αριθµός, που όταν υψωθεί στη ν, δίνει α. ηλαδή: ν a = ν = α, 0 - Ιδιότητες των ριζών. Η ρίζα είναι δύναµη! Πράγµατι, α = α / ) Αν α 0 τότε ( ) ν ν α = α ) ν α ν = α, αν ν άρτιος και ν α ν = α, αν ν περιττός. πχ 3) Αν α, 0, τότε: ν a ν = ν α ν α α 4) Αν α, 0 µε 0, τότε: = ν ν 5) Αν α, 0 και κ, ν θετικοί ακέραιοι, τότε: ν κ α = ( ) κ ν α και ν ν α = α ν 6) Αν α 0 και µ,ν ρ θετικοί ακέραιοι, τότε: µ ν a = µ ν α 7) α = α, ν ρ α µ ρ 3 3 α = α = ν α µ 8) Αν α 0 και µ Ζ και ν θετικός ακέραιος, τότε: α µ/ν = ν a µ εν χρειάζεται να ξέρετε «απ έξω» αυτές τις ιδιότητες!! Είναι ίδιες µε αυτές των δυνάµεων, πχ µν a = µν a = α µ ν = ν µ a = ν α / µ = ν µ α 4
5 Προσοχή! Όταν έχουµε εξισώσεις µε ρίζες για να τις διώξουµε υψώνουµε στο τετράγωνο. Με τον τρόπο αυτόν άθελά µας εισάγουµε και νέες ανεπιθύµητες ρίζες. Για τον λόγο αυτόν ελέγχουµε µία-µία τις ρίζες που ρήκαµε αν επαναληθεύουν την αρχική εξίσωση, αν όχι τις απορρίπτουµε. Παράδειγµα: Να λύσετε την εξίσωση = 6 Περιορισµοί: Θα πρέπει ( 0. Άρα ( ) = = και η αρχική εξίσωση γράφεται: ) = (6 ) = = 0 = 4 ή =9. Επαναλήθευση: 4 = 6 4 ισχύει. Άρα δεκτή ρίζα = 4. 9 = δεν ισχύει. Απορρίπτεται! - Πως παραγοντοποιούµε το τριώνυµο α + + γ µε α 0; Προσοχή! Το τριώνυµο εµφανίζεται παντού! Είναι το αλάτι των µαθηµατικών! α) Αν 0, τότε το τριώνυµο έχει δύο ρίζες, έστω ρ ρ και τρέπεται σε γινόµενο: α + + γ = α(-ρ )( ρ ) ) Αν = 0, τότε το τριώνυµο έχει µια διπλή ρίζα, έστω την ρ και έχουµε: α + + γ = α( ρ) γ) Αν 0, τότε το τριώνυµο δεν έχει πραγµατικές ρίζες και δεν παραγοντοποιείται. - Ποιο το πρόσηµο του τριωνύµου α + + γ µε α 0 και R; Α) Αν 0, τότε έχει δύο ρίζες πραγµατικές και άνισες, τις και έχουµε: - + f() οµόσηµο ετερόσηµο οµόσηµο του α 0 του α 0 του α Εποµένως το τριώνυµο έχει το πρόσηµό του α (οµόσηµο του α) όταν το παίρνει τιµές εκτός του διαστήµατος των ριζών και αντίθετο πρόσηµο (ετερόσηµο του α) µόνο όταν το παίρνει τιµές ανάµεσα στις ρίζες του τριωνύµου. B) Αν = 0, τότε για το πρόσηµο του f() έχουµε τον παρακάτω πίνακα: - - α f() οµόσηµο οµόσηµο του α 0 του α + Εποµένως το f() είναι οµόσηµο του α σε όλο το R εκτός του -, όπου µηδενίζεται. α Γ) Αν 0, τότε το τριώνυµο είναι οµόσηµο του α για κάθε R. Συνοψίζοντας, η µόνη περίπτωση που το τριώνυµο είναι ετερόσηµο του α είναι όταν < < όπου, είναι οι ρίζες του τριωνύµου. Άθροισµα και γινόµενο ριζών τριωνύµου: Για κάθε τριώνυµο α + + γ = f() µε ρίζες, ισχύει + = -/α και = γ/α 5
6 - Κλασµατικές εξισώσεις: Όταν ο άγνωστος ρίσκεται στον παρονοµαστή. Προσοχή! Εδώ (όπως και στις εξισώσεις µε ρίζες) υπάρχουν περιορισµοί! Παράδειγµα: Να λύσετε την εξίσωση 0 0 = Λύση: Περιορισµοί: Πολλαπλασιάζουµε την αρχική εξίσωση µε το ΕΚΠ (ελάχιστο κοινό πολλαπλάσιο) των 0 0 ( + )( + 3) ( + )( + 3) = ( + )( + 3) παρονοµαστών, ( + 3) ( + )( + 3) = 0( + ) = 0 = ή = -7 και οι δύο δεν ανήκουν στους παραπάνω περιορισµούς, άρα είναι δεκτές. -Απόλυτη τιµή πραγµατικού αριθµού Ορισµός: a = α, αν α 0 -α, αν α 0 -Ιδιότητες των απόλυτων τιµών ) a 0 a α και a - α ενώ a = α ) Αν θ 0, τότε: = θ = θ ή = - θ = a = α ή = - α 3) Αν θ 0, τότε : θ - θ θ 4) Αν θ 0, τότε: θ - θ ή θ 5) α = α Προσοχή! η ρίζα και το τετράγωνο φεύγουν και αφήνουν πίσω τους την απόλυτη τιµή! Σε ορισµένες περιπτώσεις για να διώξουµε την απόλυτη τιµή «συµφέρει» να υψώσουµε στο τετράγωνο, για παράδειγµα η εξίσωση + = = = ( ) + = = 3 = 3 ενώ σε άλλες όχι, για παράδειγµα: Να λυθεί η εξίσωση + = Λύση: Εδώ φτιάχνουµε πινακάκι µε τις ρίζες κάθε παράγοντα ( και ) 6
7 Άρα έχουµε: Για < : = - = - = < δεκτή ρίζα Για : = αδύνατη. Για > : 5-3 = = 5 = > δεκτή ρίζα. Παραγοντοποίηση πολυωνύµου: Για να γράψουµε ένα πολυώνυµο ως γινόµενο πρωτοάθµιων παραγόντων (-ρ) θα χρησιµοποιήσουµε τα παρακάτω θεωρήµατα: Θεώρηµα 0 : Ένα πολυώνυµο P() έχει παράγοντα το -ρ αν και µόνο αν το ρ είναι ρίζα του P(), δηλαδή αν και µόνο αν P(ρ)=0 Θεώρηµα 0 : Αν ο ακέραιος ρ ( 0) είναι ρίζα της πολυωνυµικής εξίσωσης α ν ν + α ν- ν- + α +α 0 = 0 µε ακέραιους συντελεστές α 0, α,, α ν τότε ο ρ είναι διαιρέτης του σταθερού όρου α 0. Με άλλα λόγια πρώτα ψάχνουµε στους διαιρέτες του σταθερού όρου, ελπίζοντας να ρούµε κάποια ρίζα και µετά κάνουµε πολυωνυµική διαίρεση, όπως φαίνεται στο παρακάτω παράδειγµα: Παράδειγµα: Να πραγµατοποιήσετε το πολυώνυµο P() = και στη συνέχεια να λύσετε την εξίσωση P() = 0 Λύση: Οι πιθανές ακέραιες ρίζες είναι οι διαιρέτες του δηλαδή ±, ±.Με δοκιµές ρίσκουµε P() = 0 άρα το είναι παράγοντας (δηλαδή διαιρεί ακριώς) του P(). Στη συνέχεια κάνουµε πολυωνυµικές διαιρέσεις: ιαιρούµε το 3 µε το -> Πολλαπλασιάζουµε και αλλάζουµε πρόσηµο + Προσθέτουµε Υπόλοιπο 0 (τέλεια διαίρεση) Άρα P() = (-) ( --) To τριώνυµο - έχει ρίζες P() = (-) ( - )( - ) 5 και + 5 άρα τελικά 7
8 P () = 0 = ή = 5 ή = Συστήµατα Γραµµικών Εξισώσεων Έστω ένα γραµµικό σύστηµα (, δηλαδή εξισώσεων µε αγνώστους): α + y = γ α + y = γ (Σ ) µε α,,γ εr Η πιο απλή µέθοδος επίλυσης του είναι η αντικατάσταση, δηλαδή λύνουµε την πρώτη εξίσωση ως προς τον έναν άγνωστο (π.χ. το y) και αντικαθιστούµε στην δεύτερη. Μια άλλη µέθοδος επίλυσης είναι µε ορίζουσες (ενδείκνυται όταν έχουµε παραµετρικά συστήµατα) D = a a γ, D = γ α, Dy = α Τότε: α) αν D 0 το (Σ) έχει µοναδική λύση = D D, y = D Dy ) αν D = 0 και (D 0 ή Dy 0) τότε το (Σ) είναι αδύνατο γ) αν D = 0 και D = 0 και Dy = 0 τότε το (Σ) είναι αόριστο(απαιτείται επιπλέον διερεύνηση) γ γ Παράδειγµα: Να λυθεί το σύστηµα λ - y = λ - λ - y = λ Παρατηρούµε ότι οι συντελεστές και οι σταθεροί όροι δεν είναι όλοι συγκεκριµένοι αριθµοί αλλά εξαρτώνται από το λ (παράµετρος). Πρέπει εποµένως, για τις διάφορες τιµές του λ, να εξετάσουµε πότε προκύπτει σύστηµα που έχει µοναδική λύση την οποία και να ρούµε ή πότε προκύπτει σύστηµα αδύνατο ή µε άπειρες λύσεις: Η εργασία αυτή λέγεται διερεύνηση. Έχοντας υπόψη τον παρακάτω πίνακα, ακολουθούµε τα εξής ήµατα - Βήµα : Υπολογίζουµε τις ορίζουσες D, D, D y : λ Έχουµε: D = λ λ D = λ λ Dy = λ λ λ = - λ + λ = λ (λ-) = -(λ-) + λ = λ = λ λ (λ-) = λ (-λ +) = λ (-λ) - Βήµα : Βρίσκουµε τις τιµές της παραµέτρου, για τις οποίες είναι D = 0 Έχουµε: D = 0 λ (λ-) = 0 λ = 0 ή λ = - Βήµα 3: Εξετάζουµε περιπτώσεις ανάλογα µε τις τιµές της παραµέτρου λ. i) Αν λ 0 και λ, τότε είναι D 0 και εποµένως το σύστηµα έχει µια και µοναδική λύση, την : D λ ( λ ) = = = D λ( λ ) λ( λ ) = - λ 8
9 Dy λ ( λ) λ ( λ ) y = = = = -λ D λ( λ ) λ( λ ) ii) Αν λ = 0, τότε το σύστηµα γίνεται: 0 y = y = ή που είναι αδύνατο 0 y = 0 y = 0 iii) Αν λ =, τότε το σύστηµα γίνεται: y = y = ή 4 y = y = που έχει άπειρες λύσεις Επειδή y = y = -, λύσεις του συστήµατος στην περίπτωση αυτήν είναι όλα τα ζεύγη της µορφής (, -), όπου οποιοσδήποτε πραγµατικός αριθµός. - Πρόοδοι: - Αριθµητική πρόοδος (ΑΠ), είναι η ακολουθία των αριθµών (όρων) α, α, α 3,,α ν, όπου ο κάθε όρος προκύπτει από τον προηγούµενο συν κάποιον σταθερό µη µηδενικό αριθµό που λέγεται διαφορά ω, δηλαδή α ν = α + (ν-) ω (µε ω 0) είναι ο γενικός (ν- οστός) όρος ν α και S ν = = + αν [ a + ( ν )ω ] = ν είναι το άθροισµα των ν-πρώτων όρων της ΑΠ - Γεωµετρική Πρόοδος (ΓΠ) είναι η ακολουθία α, α, α 3,.α ν, όπου ο κάθε όρος προκύπτει από τον προηγούµενο επί κάποιον σταθερό ( 0 και ) αριθµό, δηλαδή α ν = α λ ν- a είναι ο γενικός (ν- οστός) όρος και S ( ) ν = είναι το άθροισµα των ν- λ a πρώτων όρων της ΓΠ και S = είναι το άθροισµα απείρων πρώτων όρων της ΓΠ µε λ - λ και λ 0. Εκθετική συνάρτηση Έστω α ένας θετικός αριθµός. Για κάθε εir ορίζεται η δύναµη α (λέπε σελ). Εποµένως αντιστοιχίζοντας κάθε εir στη δύναµη α, ορίζουµε τη συνάρτηση: f: IR IR µε f() = α, η οποία, στην περίπτωση που είναι α, λέγεται εκθετική συνάρτηση µε άση το α. (Αν είναι α =, τότε έχουµε τη σταθερή συνάρτηση f() =.) Η συνάρτηση αυτή, καθώς και κάθε συνάρτηση της µορφής f() = α µε α >, έχει τις εξής ιδιότητες: Έχει πεδίο ορισµού το IR. (λέπε σελ.6) Έχει σύνολο τιµών (λέπε σελ.6) το διάστηµα (0, + ) των θετικών πραγµατικών αριθµών. Είναι γνησίως αύξουσα στο IR. ηλαδή για κάθε, εir ισχύει : αν <, τότε α < α που χρησιµοποιείται στην επίλυση ανισώσεων Η γραφική της παράστασης τέµνει τον άξονα y y στο σηµείο Α(0,) και έχει ασύµπτωτη τον αρνητικό ηµιάξονα των. και επιπλέον ΟΛΕΣ τις ιδιότητες των δυνάµεων που παρουσιάσαµε παραπάνω (σελ.) λ ν 9
10 Παρόµοιες ιδιότητες έχει και η συνάρτηση f() = α R και έχει ασύµπτωτη τον θετικό ηµιάξονα των. µε 0<α<, µόνο που είναι γν. φθίνουσα στο Σχόλιο: Από τη µονοτονία της εκθετικής συνάρτησης f() = α µε 0<α, προκύπτει ότι: αν τότε a a οπότε, µε απαγωγή σε άτοπο, έχουµε ότι : αν a = a, τότε =. Εποµένως, ισχύει η ισοδυναµία: a = a = που εφαρµόζεται στην επίλυση εξισώσεων Παραδείγµατα: ο Να λυθούν οι εξισώσεις: i) 3 = ii) = 0 64 Λύση i) Η εξίσωση γράφεται διαδοχικά: = = 3 = 6 64 = [Επειδή η εκθετική συνάρτηση είναι -] ii) H εξίσωση γράφεται = 0 (3 ) = 0 επειδή 9=3 και (3 ) =3 Αν θέσουµε 3 = y, αυτή ισοδυναµεί µε το τριώνυµο y 8y 9 = 0 το οποίο έχει ρίζες τους αριθµούς - και 9. Εποµένως η αρχική εξίσωση έχει ως λύσεις τις λύσεις των εξισώσεων: 3 = - και 3 = 9. Απ αυτές η πρώτη είναι αδύνατη, αφού 3 > 0, ενώ η δεύτερη γράφεται 3 = 3 και έχει ρίζα το =, που είναι και µοναδική ρίζα της αρχικής εξίσωσης. ο Να λυθούν οι ανισώσεις: 3 i) 3 > ii) 9 Λύση i) Έχουµε ( ) + < > 3 > 3 3 > 9 διότι η συνάρτηση 3 είναι γν. αύξουσα σύµφωνα µε τα παραπάνω > 0 < ii) Έχουµε + + ( ) < ( ) < ( ) + > + > 0 < 4 διότι η συνάρτηση (/) είναι γν. φθίνουσα σύµφωνα µε τα παραπάνω. ή > ή > Λογάριθµοι: Έννοια λογάριθµου: Σε ποιόν αριθµό πρέπει να υψώσω το e ώστε να πάρω ; Η απάντηση είναι y. Οµοίως, και πιο εύκολα κατανοητό, όταν η άση είναι κάποιος άλλος θετικός αριθµός ( ) πχ, δηλαδή, σε ποιόν αριθµό πρέπει να υψώσω το ώστε να πάρω 8; Η απάντηση είναι log 8 = 3 γιατί 3 = =8! Γι αυτό η λογαριθµική είναι η αντίστροφη συνάρτηση της εκθετικής! 0
11 Ιδιότητες λογαρίθµων: ln( y) = ln + lny ln y = ln lny ln κ = κ ln ln = 0, lne = Σε όλες τις ιδιότητες, y 0. Οι ίδιες ιδιότητες ισχύουν και για log (δηλαδή λογάριθµο µε άση το 0). Ορισµός ασική έννοια λογαρίθµου: ln = y = e y (και log = y = 0 (το e είναι η άση του λογαρίθµου, δηλαδή log e = ln. Επίσης είναι η άση και της εκθετικής συνάρτησης. Οµοίως για το 0 όταν έχουµε log) Που χρησιµοποιούνται οι λογάριθµοι; Παντού, αλλά κυρίως στην ανάλυση. Για παράδειγµα στο 0 θέµα των Πανελλαδικών εξετάσεων 004 στα Μαθηµατικά κατεύθυνσης Γ Λυκείου έπρεπε να λύσει ο µαθητής την εξίσωση: ln + = 0 (ln + ) = 0. - Λογάριθµοι και εξισώσεις ανισώσεις. Επειδή οι συναρτήσεις y = ln και y = log είναι γνησίως αύξουσες ισχύει ln ln (οµοίως για log). Με την ιδιότητα αυτή λύνουµε λογαριθµικές ανισότητες. Επίσης ισχύει = ln = ln δηλαδή είναι συναρτήσεις «-». Με την ιδιότητα αυτή λύνουµε λογαριθµικές εξισώσεις όπως στα πιο κάτω παραδείγµατα. Για παράδειγµα στις Πανελλαδικές 004, Μαθηµατικά ΓΠ Β Λυκείου 4 0 Θέµα καταλήγαµε στην ανισότητα ( ) ln ln( ) ln 5 5 γιατί η συνάρτηση y = ln είναι γνησίως αύξουσα. Άρα ln ln 0 Όµως το ln < γιατί 5 < οπότε αν διαιρέσω παντού µε ln παίρνω 5 y ) ln 0 (αλλάζει η φορά!) ln 5 Επίσης στη Φυσική Γενικής Παιδείας στις Πανελλαδικές Εξετάσεις 004 στο Θέµα 4 που αναφερόταν στη διάσπαση ραδιενεργών πυρήνων καταλήγαµε στην εξίσωση N 0 N N = O N - = 0 N = = N 8 N 8 N 8 λ t N e 8 την οποία έπρεπε να λύσουµε ως προς t: e λt = λt = ln t = ln 8 8 λ 8 Άλλο παράδειγµα από Πανελλαδικές εξετάσεις είναι το ακόλουθο: 0
12 Για την µελέτη των ακροτάτων (τοπικό µέγιστο ή/και τ. ελάχιστο) µίας συνάρτησης καταλήγαµε στην επίλυση της εξίσωσης (ln+)=0 = 0 ή ln + = 0 = 0 ή ln = - = 0 ή = e -/. Η πρώτη ρίζα απορρίπτεται γιατί το πεδίο ορισµού της ln είναι το (0, + ). Άρα καταλήγουµε στη δεύτερη ρίζα = e -/ =. e Στη συνέχεια για να µελετήσουµε την συνάρτηση ως προς την µονοτονία (γν. αύξουσα ή φθίνουσα) έπρεπε να λύσουµε την ανίσωση: (ln +) 0. ln + 0 αφού ήδη ξέρουµε ότι (0, + ) δηλαδή 0. Άρα έχουµε ln + 0 ln - Eδώ πρέπει να θυµηθούµε ότι η συνάρτηση y = ln είναι γνησίως αύξουσα, δηλαδή ln α ln α. -/ ln - ln lne e -/ e (το νούµερο αυτό φάνηκε άσχηµο στους µαθητές και σε ορισµένους καθηγητές αλλά ο αριθµός e είναι από τους σηµαντικότερους στην ιστορία των Μαθηµατικών και εµφανίζεται σε µία από τις πιο όµορφες, σηµαντικές και πλήρεις εξισώσεις την e iπ + =0!). - Ευθεία και Κωνικές Τοµές: Γραµµή Εξίσωση Παρατηρήσεις Ευθεία y = λ + Έχει συντελεστή διεύθυνσης λ και κόει τον άξονα y y στο σηµείο (0,) Ευθεία y y o = λ (- o ) Έχει συντελεστή διεύθυνσης λ και περνά από το σηµείο ( o, y o ) Ευθεία = 0 Κατακόρυφη ευθεία για την οποία δεν ορίζεται συντελεστής διεύθυνσης Κύκλος (- o ) + (y y o ) = ρ Έχει κέντρο το σηµείο Κ( o,y o ) και ακτίνα ρ Παραολή y = p Έχει εστία στο σηµείο Ε( p,0) και διευθετούσα Έλλειψη Υπερολή a a y + y - = = p την ευθεία = Έχει εστίες τα σηµεία Ε (-γ, 0), Ε(γ, 0) µε γ = α Έχει εστίες τα σηµεία Ε (-γ, 0), Ε(γ, 0)µε γ = α +
13 y y - Συντελεστής διεύθυνσης ευθείας λ = όπου A(,y ) και B(,y ) είναι σηµεία της ευθείας. Ισχύει λ = εφθ όπου θ η γωνία που σχηµατίζει ο θετικός άξονας µε την ευθεία. Αν δύο ευθείες ε : y = λ + και ε : y = λ + είναι παράλληλες τότε έχουν τον ίδιο συντελεστή διεύθυνσης, δηλαδή ε //ε λ = λ Αν δύο ευθείες ε : y = λ + και ε : y = λ + είναι κάθετες τότε το γινόµενο των συντελεστών διεύθυνσής τους είναι -, δηλαδή ε ε λ λ = - Που χρησιµοποιούνται; Κυρίως στους µιγαδικούς (εύρεση γεωµετρικών τόπων) ενώ η ευθεία εµφανίζεται παντού! (γεωµετρικοί τόποι, εφαπτοµένη καµπύλης κλπ) Παράδειγµα 0 : Σε πολλές περιπτώσεις µας ζητάνε να ρούµε την εξίσωση της µεσοκαθέτου του ευθύγραµµου τµήµατος ΑΒ µε γνωστά άκρα Α( A,y A ) και Β( B,y B ). ε Α Μ Β A + B y A + y H (ε) περνάει από το Μ (το µέσο του ΑΒ) το οποίο έχει συντεταγµένες, έχει συντελεστή διεύθυνσης λ (ε), για τον οποίο ισχύει y λ (ε) λ ΑΒ = - αφού η (ε) ΑΒ. Άρα λ(ε) = και λ ΑΒ = Β y A B A λ (ε) = -. y y λ AB B A y A + y Άρα η (ε) έχει εξίσωση: y - B ( B A ) + = A B yb y A (προσοχή! µε συγκεκριµένα νούµερα τα πράγµατα είναι πιο απλά!) Πρέπει να παρατηρήσουµε ότι όλα τα σηµεία της ευθείας (ε) ισαπέχουν από το Α και Β. Άρα η ευθεία (ε) είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου που ισαπέχουν από συγκεκριµένα γνωστά σηµεία Α και Β, ή d(μ,α) = d(μ,β) όπου Μ(,y) ε (ε). Παράδειγµα 0 : Ο κύκλος είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου που απέχουν από ένα συγκεκριµένο και γνωστό σηµείο Κ( o,y o ) συγκεκριµένη και γνωστή απόσταση ρ. ηλαδή, η εξίσωση του κύκλου C, ( o ) + (y - y o ) = ρ είναι ισοδύναµη µε την πιο απλή d(m,k) = ρ, όπου Μ(,y) C ένα τυχαίο σηµείο του κύκλου, Κ το κέντρο του και ρ (>0) η ακτίνα του κύκλου. Πρέπει δηλαδή να κατανοήσουµε την ευθεία και τις κωνικές τοµές µε τον ορισµό τους, δηλαδή την πραγµατική τους υπόσταση ως γεωµετρικούς τόπους. B A B και - Τριγωνοµετρία (για όχι και τόσο γερές µνήµες) 3
14 - Πίνακας τριγωνοµετρικών αριθµών ορισµένων γωνιών. ω ηµω συνω εφω σφω 0 ο ή 0 rad 0 0 δεν ορίζεται 30 0 π ή π ή ή 3 π ή π 0 δεν ορίζεται (γιατί ο παρονοµαστής = 0) Προσοχή! 80 0 µοίρες αντιστοιχούν σε π rad, άρα µ (µοίρες) = 80 0 α (rad) / π Σχέσεις µεταξύ τριγωνοµετρικών αριθµών: α) Αντιθέτων τόξων Τα αντίθετα τόξα, - έχουν το ίδιο συνηµίτονο και αντίθετους όλους τους άλλους τριγωνοµετρικούς αριθµούς δηλαδή: ηµ(-) = -ηµ, συν(-) = συν, εφ(-) = -εφ, σφ(-) = - σφ ) Παραπληρωµατικών τόξων Τα παραπληρωµατικά τόξα, π- έχουν το ίδιο ηµίτονο και αντίθετους όλους τους άλλους τριγωνοµετρικούς αριθµούς, δηλαδή: ηµ(π-) = ηµ, συν(π-) = -συν, εφ(π-) = -εφ, σφ(π-)= -σφ γ) Συµπληρωµατικών τόξων Στα συµπληρωµατικά τόξα, π - το ηµίτονο του ενός τόξου είναι το συνηµίτονο του άλλου και η εφαπτοµένη του ενός είναι συνεφαπτοµένη του άλλου δηλαδή: ηµ( π -) = συν, συν( π -) = ηµ, εφ( π -) =σφ, σφ( π -)=εφ δ) Τόξων που διαφέρουν κατά π Τα τόξα που διαφέρουν κατά π, π+ έχουν αντίθετο ηµίτονο και συνηµίτονο και ίση εφαπτόµενη και συνεφαπτόµενη, δηλαδή: ηµ(π+) = -ηµ, συν(π+) = -συν, εφ(π+)=εφ, σφ(π+) = σφ - Άλλοι χρήσιµοι τύποι ηµ(α+) = ηµα συν + ηµ συνα συν(α+) = συνα συν ηµα ηµ εφα + εφ εφ(α+) = εφα εφ ηµ(α-) = ηµα συν - ηµ συνα συν(α-) = συνα συν + ηµα ηµ εφα εφ εφ(α-) = + εφα εφ ηµα = ηµα συνα συνα = συν α - συν + συν α α = () 4
15 συνα = συν α ηµ α εφα εφα = εφ α συνα = -ηµ α ηµ συν α α = () Οι τύποι () και () λέγονται τύποι αποτετραγωνισµού γιατί «φεύγουν» τα τετράγωνα. Προσοχή! Ο δεύτερος πίνακας γαίνει από τον πρώτο µε αντικατάσταση =α. Γενικά η τριγωνοµετρία θέλει περισσότερο κατανόηση του τριγωνοµετρικού κύκλου και κάποιων ασικών σχέσεων παρά αποµνηµόνευση. - Τριγωνοµετρικές εξισώσεις Για να λύσουµε µία τριγωνοµετρική εξίσωση προσπαθούµε µετά την εκτέλεση των πράξεων να φτάσουµε σε µία από τις παρακάτω µορφές.( ίπλα σε καθεµιά δίνεται η λύση της) = κπ + θ ή α) ηµ = ηµθ, κ Z. = κπ + π θ ) συν = συνθ = κπ ± θ, κ Z γ) εφ = εφθ = κπ + θ, κ Ζ δ) σφ = σφθ = κπ + θ, κ Ζ Προσοχή! Όταν µας ζητούν τις λύσεις µίας τριγωνοµετρικής εξίσωσης σε συγκεκριµένο διάστηµα, πχ στο [0,π), τότε χρησιµοποιούµε τους παραπάνω γενικούς τύπους και αντικαθιστούµε το κ µε 0, ±, ± κλπ µέχρι να «γούµε» έξω από το συγκεκριµένο διάστηµα, πχ [0,π). - Πώς ορίζουµε το ηµίτονο και το συνηµίτονο µιας γωνίας στον τριγωνοµετρικό κύκλο και ποιες είναι οι άµεσες συνέπειες του ορισµού; Αν η τελική πλευρά της γωνίας ω τέµνει τον τριγωνοµετρικό κύκλο στο σηµείο Μ(,y),τότε: i) ηµω = y (η τεταγµένη του Μ) ii) συνω= (η τετµηµένη του Μ) Άµεση συνέπεια των ορισµών αυτών είναι: Οι τιµές των ηµω και συνω δεν µπορούν να υπερούν κατ απόλυτη τιµή την ακτίνα του κύκλου, δηλαδή το. Όπότε: - ηµω και - συνω iii) Από το Πυθαγόρειο θεώρηµα +y = έχουµε τη ασική τριγωνοµετρική ταυτότητα ηµ ω + συν ω = για κάθε γωνία ω. Τα πρόσηµα των τριγωνοµετρικών αριθµών ανάλογα µε το τεταρτηµόριο στο οποίο ρίσκεται η τελική πλευρά φαίνονται στο παρακάτω σχήµα (για τους παπαγάλους, το ΟΗΕΣ) ηµ συν εφ σφ θετικοί Όλοι Ηµιτ Εφ Συν 5
16 ηµω M(,y) εφω ω συνω Ο τριγωνοµετρικός κύκλος: Ο άξονας αντιστοιχεί στο συνω και ο y y στο ηµω. Η ακτίνα του κύκλου είναι ίση µε. Συναρτήσεις (η πεµπτουσία των µαθηµατικών! ή όλα είναι συναρτήσεις) - Τι ονοµάζουµε πραγµατική συνάρτηση µε πεδίο ορισµού το Α; Έστω Α ένα µη κενό υποσύνολο του R. Ονοµάζουµε πραγµατική συνάρτηση µε πεδίο ορισµού το Α µια διαδικασία (function) f, µε την οποία κάθε στοιχείο A αντιστοιχίζεται σε ένα µόνο πραγµατικό αριθµό y. Το y ονοµάζεται τιµή της συνάρτησης f στο και συµολίζεται µε f(). Για να εκφράσουµε τη διαδικασία αυτή γράφουµε: f: Α R έτσι ώστε κάθε A f() = y R. Το, που παριστάνει οποιοδήποτε στοιχείο του Α λέγεται ανεξάρτητη µεταλητή, ενώ το γράµµα y που παριστάνει την τιµή της f στο, λέγεται εξαρτηµένη µεταλητή (γιατί εξαρτάται από το ). Το πεδίο ορισµού Α της f το παριστάνουµε και µε D f. - Τι ονοµάζουµε µαθηµατικό τύπο µιας συνάρτησης; Η εξίσωση που δίνει την τιµή µιας συνάρτησης στο λέγεται µαθηµατικός τύπος της συνάρτησης. π.χ για τη συνάρτηση f για την οποία έχουµε: ο µαθηµατικός τύπος της είναι f() = - Τι ονοµάζουµε σύνολο (ή πεδίο) τιµών της συνάρτησης f µε πεδίο ορισµού το Α; Είναι το σύνολο που έχει για στοιχεία του τις τιµές της f σε όλα τα A, συµολίζεται µε f(a). Είναι f(a) = {y R έτσι ώστε υπάρχει A µε y = f()} - Ποια στοιχεία πρέπει να δοθούν για να οριστεί µια συνάρτηση; Πρέπει να δοθούν α) Το πεδίο ορισµού της Α και ) Η τιµή της συνάρτησης f() σε κάθε A, δηλαδή ο µαθηµατικός τύπος της συνάρτησης. Προσοχή! Γενικά στην ανάλυση αν µας δώσουν µόνο τον µαθηµατικό τύπο της συνάρτησης θα πρέπει να ρούµε εµείς το πεδίο ορισµού της! - Όταν για µια συνάρτηση δίνεται µόνο ο τύπος της, τότε ποιο είναι το πεδίο ορισµού της; Είναι το σύνολο όλων των πραγµατικών αριθµών, για τους οποίους το f() έχει νόηµα, δηλαδή f() R. ιακρίνουµε τις εξής ασικές περιπτώσεις: 6
17 Αν η συνάρτηση είναι κλασµατική τότε ρίσκουµε τις ρίζες του παρανοµαστή και τις εξαιρούµε από το R. + πχ όταν δοθεί ο τύπος f() = της συνάρτησης f, ρίσκουµε τις ρίζες του παρονοµαστή - λύνοντας την εξίσωση - = 0 ( = ή = -) Οπότε το πεδίο ορισµού της f είναι Α = R {-,}. Αν η συνάρτηση είναι άρρητη, τότε εξαιρούµε από το R τις τιµές του που κάνουν το υπόρριζο αρνητικό, δηλαδή το υπόρριζο να είναι µη αρνητικό. πχ Αν f() = 4, τότε πρέπει: ή (το τριώνυµο πρέπει να είναι θετικό ή µηδέν, δηλαδή οµόσηµο του ). Άρα το πεδίο ορισµού της f είναι Α = (-, -] [, + ). Η συνάρτηση f() = α, α, α 0 έχει πεδίο ορισµού το R. H συνάρτηση f() = log α, α, α 0 έχει πεδίο ορισµού το Α = (0, + ) Αν η συνάρτηση περιέχει log α, ή ln τότε η ποσότητα που λογαριθµίζεται πρέπει να είναι θετική (αυστηρά, δηλαδή >0). πχ f() = ln( 5 +4) Πρέπει (τι σας έλεγα για το τριώνυµο;) Είναι = 5 6= 9 και = =, = = 4. Κάνουµε πίνακα προσήµων του Άρα το πεδίο ορισµού της συνάρτησης f είναι: D f = (-, ) (4, + ) Συνδυασµός των παραπάνω, για παράδειγµα f() = / ( 5 +4),όπου θα πρέπει ο παρονοµαστής να είναι διαφορετικός από µηδέν και η υπόριζη ποσότητα (το τριώνυµο) να είναι θετική, άρα -5+4>0 (-)(-4)>0 < ή >4, δηλαδή Α=(-,) (4, + ). - Τι ονοµάζουµε γραφική παράσταση συνάρτησης f που έχει πεδίο ορισµού Α; Είναι το σύνολο των σηµείων Μ(,y) για τα οποία ισχύει y = f(), δηλαδή το σύνολο των σηµείων Μ(,f()), A. Η γραφική παράσταση της συνάρτησης f συµολίζεται µε C f. Προσοχή! όλα τα σηµεία που ανήκουν στη C f ικανοποιούν την σχέση y = f() και αντιστρόφως, όλα τα ζεύγη αριθµών (,y) που ικανοποιούν τη σχέση y = f() είναι σηµεία της C f. - Τι ονοµάζουµε εξίσωση της γραφικής παράστασης της συνάρτησης f; Ονοµάζουµε την εξίσωση: y = f() πχ για τη συνάρτηση f() = η εξίσωση της γραφικής παράστασης είναι η ευθεία µε εξίσωση y = Πώς µπορούµε να καταλάουµε ότι µια γραµµή είναι γραφική παράσταση συνάρτησης; Όταν οποιαδήποτε κατακόρυφη ευθεία έχει µε τη γραµµή το πολύ ένα κοινό σηµείο. 7
18 y f ( 0 )?? 0 Ο κύκλος δεν είναι συνάρτηση! Η γραφική του παράσταση και η ευθεία = 0 τέµνονται σε σηµεία. - Πώς µπορούµε να ρούµε το πεδίο ορισµού και το σύνολο τιµών µιας συνάρτησης αν γνωρίζουµε τη γραφική της παράσταση; Ι) Το πεδίο ορισµού είναι το σύνολο όλων των τετµηµένων των σηµείων της C f Για το παρακάτω σχήµα είναι D f = [α, ] II) Το σύνολο τιµών της f, είναι το σύνολο f(a) των τεταγµένων των σηµείων της C f Για το παρακάτω σχήµα είναι: f (A) = [f(α), f()] f() α f(α) - Πώς ρίσκουµε την τιµή της συνάρτησης f στο o A από τη γραφική της παράσταση; Βρίσκουµε την τεταγµένη του σηµείου τοµής της ευθείας = 0 µε την γραφική παράσταση. ηλαδή, φέρνουµε κάθετη προς τον άξονα στο σηµείο του µε τετµηµένη o, η οποία τέµνει τη γραφική παράσταση στο σηµείο Α και από το Α φέρνουµε κάθετη προς τον άξονα y y που τον τέµνει στο σηµείο µε τεταγµένη f( o ) Άρα η τιµή της f στο o είναι το f( o ). -Πως κάνουµε την γραφική παράσταση µίας συνάρτησης;. Βρίσκουµε το πεδίο ορισµού 8
19 . Βρίσκουµε τα τοπικά ελάχιστα και τοπικά µέγιστα (ακρότατα) 3. Βρίσκουµε την µονοτονία (γν. αύξουσα, γν. φθίνουσα) 4. Φτιάχνουµε έναν πίνακα τιµών ((, f()) και ρίσκουµε τα σηµεία τοµής µε τους άξονες (οι λύσεις της εξίσωσης f()=y=0), y y (τα σηµεία (0,f(0)) εφόσον υπάρχουν. Στα και 3 θα µας οηθήσουν πολύ οι γνώσεις που θα µάθουµε φέτος για την παράγωγο της συνάρτησης. Στο παρακάτω σχήµα φαίνεται η γραφική παράσταση της συνάρτησης y=(-) (+) Y X Created with a trial version of Advanced Grapher - / agra Τι συµπεράσµατα γάζετε από το παραπάνω σχήµα για:. Το πεδίο ορισµού της f. Τα ακρότατα της f 3. Την µονοτονία της f 9
20 . Να λύσετε την εξίσωση: + 4 = 0 ΑΣΚΗΣΕΙΣ. Να λύσετε τις ανισώσεις: i) 5 ii) 4 iii) log(+) + log 5 < 3. Να λύσετε τo σύστηµα: y 3 + = y 3 = 7 4. Να λυθούν οι εξισώσεις: i) log(+) + log(-) = log ii) log( +) log = log iii) 5 = - iv) 3 - = + 5. Να λυθούν οι εξισώσεις: i) 3 = 8 ii) + 3 = 5 6. Να λυθούν οι ανισώσεις: i) + 3 ii) Να λυθεί η εξίσωση: - + = 8. Αν 3 7, να δείξετε ότι η παράσταση Α= είναι ανεξάρτητη του. 9. Να λυθούν οι εξισώσεις: i) ηµ = ii) ηµ = - iii) ηµ = 0 iv) συν = v) συν = - vi) συν = 0 0. Να λυθούν οι εξισώσεις: i) εφ = ii) σφ = - iii) εφ = 3 iv) ηµ = 3 v) ηµ 3 ηµ + = 0. Να κάνετε τις γραφικές παραστάσεις των παρακάτω συναρτήσεων: i) y = ηµ ii) y = συν iii) y = / iv) y= -3 + v) y= +3 + vi) y=e vii) y = ln viii) y = + i) y = + ) y=e - i) y=ln(-). Να παραγοντοποιήσετε το πολυώνυµο P() και στη συνέχεια να λύσετε την ανισότητα P()>0, όπου P() =
Σηµειώσεις στους πραγµατικούς και µιγαδικούς αριθµούς
 Σηµειώσεις στους πραγµατικούς και µιγαδικούς αριθµούς Τα βασικά αριθµητικά σύνολα Οι πρώτοι αριθµοί που διδάσκεται ο µαθητής στο δηµοτικό σχολείο είναι οι φυσικοί αριθµοί Αυτοί είναι οι 0,,,, 4, κτλ Το
Σηµειώσεις στους πραγµατικούς και µιγαδικούς αριθµούς Τα βασικά αριθµητικά σύνολα Οι πρώτοι αριθµοί που διδάσκεται ο µαθητής στο δηµοτικό σχολείο είναι οι φυσικοί αριθµοί Αυτοί είναι οι 0,,,, 4, κτλ Το
, y 1. y y y y = x ( )
 ΚΕΦΑΛΑΙΟ Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕ Ο ΠΑΡΑΓΡΑΦΟΣ. ΕΞΙΣΩΣΗ ΓΡΑΜΜΗΣ Μία εξίσωση µε αγνώστους x, y λέγεται εξίσωση µίας γραµµής C, όταν οι συντεταγµένες των σηµείων της C και µόνο αυτές την επαληθεύουν. Αν έχουµε
ΚΕΦΑΛΑΙΟ Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕ Ο ΠΑΡΑΓΡΑΦΟΣ. ΕΞΙΣΩΣΗ ΓΡΑΜΜΗΣ Μία εξίσωση µε αγνώστους x, y λέγεται εξίσωση µίας γραµµής C, όταν οι συντεταγµένες των σηµείων της C και µόνο αυτές την επαληθεύουν. Αν έχουµε
ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ
 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ 9 40 4 ΒΑΣΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ 4 4 ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ. Να βρείτε την αριθµητική τιµή των παραστάσεων. i) α -α 6α, ii) 4α, για α iii) αβ α β (αβ),
ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ-ΜΟΝΩΝΥΜΑ-ΠΟΛΥΩΝΥΜΑ- ΒΑΣΙΚΕΣΤΑΥΤΟΤΗΤΕΣ 9 40 4 ΒΑΣΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ 4 4 ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ. Να βρείτε την αριθµητική τιµή των παραστάσεων. i) α -α 6α, ii) 4α, για α iii) αβ α β (αβ),
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Όταν το χ τότε το. στο,µπορούµε να θεωρήσουµε ότι το
 ΕΝΝΟΙΑ ΤΟΥ ΟΡΙΟΥ Όταν στα µαθηµατικά λέµε ότι το τείνει στο και συµβολίζεται, εννοούµε ότι οι τιµές προσεγγίζουν την τιµή, είτε µε από τιµές µικρότερες του δηλ από αριστερά του, είτε από τιµές µεγαλύτερες
ΕΝΝΟΙΑ ΤΟΥ ΟΡΙΟΥ Όταν στα µαθηµατικά λέµε ότι το τείνει στο και συµβολίζεται, εννοούµε ότι οι τιµές προσεγγίζουν την τιµή, είτε µε από τιµές µικρότερες του δηλ από αριστερά του, είτε από τιµές µεγαλύτερες
Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις
 2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))
![ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( )) ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))](/thumbs/17/113546.jpg) ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1. Μιγαδικοί αριθμοί. ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
Σημειώσεις μαθήματος Μ1113 Επίπεδο και Χώρος Χρήσ τος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014
 Σημειώσεις μαθήματος Μ1113 Επίπεδο και Χώρος Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Εισαγωγή Θα συμπληρωθεί 1 Κεφάλαιο 1 Γεωμετρικά διανύσματα στο επίπεδο Ενα γεωμετρικό διάνυσμα
Σημειώσεις μαθήματος Μ1113 Επίπεδο και Χώρος Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Εισαγωγή Θα συμπληρωθεί 1 Κεφάλαιο 1 Γεωμετρικά διανύσματα στο επίπεδο Ενα γεωμετρικό διάνυσμα
Σηµειώσεις στις σειρές
 . ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
. ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ
 ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
ΣΥΝΑΡΤΗΣΕΙΣ I. ΣΥΝΟΛΑ 1.Τι ονοµάζεται σύνολο; Σύνολο ονοµάζεται κάθε συλλογή αντικειµένων, που προέρχονται από την εµπειρία µας ή την διανόηση µας, είναι καλά ορισµένα και διακρίνονται το ένα από το άλλο.
ΕΞΙΣΩΣΕΙΣ. 2.1 ΕΞΙΣΩΣΕΙΣ 1 ου ΒΑΘΜΟΥ. Η εξίσωση αx β 0
 ΕΞΙΣΩΣΕΙΣ.1 ΕΞΙΣΩΣΕΙΣ 1 ου ΒΑΘΜΟΥ Η εξίσωση α 0 Στο Γυμνάσιο μάθαμε τον τρόπο επίλυσης των εξισώσεων της μορφής α 0 για συγκεκριμένους αριθμούς α,,με α 0 Γενικότερα τώρα, θα δούμε πώς με την οήθεια των
ΕΞΙΣΩΣΕΙΣ.1 ΕΞΙΣΩΣΕΙΣ 1 ου ΒΑΘΜΟΥ Η εξίσωση α 0 Στο Γυμνάσιο μάθαμε τον τρόπο επίλυσης των εξισώσεων της μορφής α 0 για συγκεκριμένους αριθμούς α,,με α 0 Γενικότερα τώρα, θα δούμε πώς με την οήθεια των
Πρόλογος. Η νέα έκδοση των παρόντων σημειώσεων θα ολοκληρωθεί κατά το εαρινό εξάμηνο του ακαδημαϊκού έτους 2008-2009. Αύγουστος 2008.
 Πρόλογος Οι παρούσες σημειώσεις αποτελούν το μεγαλύτερο μέρος του υλικού που διδάχτηκε στις παραδόσεις του προπτυχιακού μαθήματος της Αριθμητικής Ανάλυσης, το εαρινό εξάμηνο 7-8, στο Μαθηματικό τμήμα του
Πρόλογος Οι παρούσες σημειώσεις αποτελούν το μεγαλύτερο μέρος του υλικού που διδάχτηκε στις παραδόσεις του προπτυχιακού μαθήματος της Αριθμητικής Ανάλυσης, το εαρινό εξάμηνο 7-8, στο Μαθηματικό τμήμα του
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου
 Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου 1 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΚΑΙ ΠΡΟΤΕΡΑΙΟΤΗΤΑ ΠΡΑΞΕΩΝ 1.1 Προτεραιότητα Πράξεων Η προτεραιότητα των πράξεων είναι: (Από τις πράξεις που πρέπει να γίνονται πρώτες,
Στοιχεία εισαγωγής για τη Φυσική Α Λυκείου 1 ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΚΑΙ ΠΡΟΤΕΡΑΙΟΤΗΤΑ ΠΡΑΞΕΩΝ 1.1 Προτεραιότητα Πράξεων Η προτεραιότητα των πράξεων είναι: (Από τις πράξεις που πρέπει να γίνονται πρώτες,
0 0 30 π/6 45 π/4 60 π/3 90 π/2
 Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
Βασικός Πίνακας Μοίρες (Degrees) Ακτίνια (Radians) ΓΩΝΙΕΣ 0 0 30 π/6 45 π/4 60 π/3 90 π/2 Έστω ότι θέλω να μετατρέψω μοίρες σε ακτίνια : Έχω μία γωνία σε φ μοίρες. Για να την κάνω σε ακτίνια, πολλαπλασιάζω
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
Αθ.Κεχαγιας. Σηµειωσεις Αναλυτικης Γεωµετριας. Θ. Κεχαγιας. Σεπτεµβρης 2009, υ.0.95
 Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 2009, υ.0.95 Περιεχόµενα Εισαγωγη 1 Επιπεδα στον Τρισδιαστατο Χωρο 1 1.1 Θεωρια.................................... 1 1.2 Λυµενες Ασκησεις..............................
Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 2009, υ.0.95 Περιεχόµενα Εισαγωγη 1 Επιπεδα στον Τρισδιαστατο Χωρο 1 1.1 Θεωρια.................................... 1 1.2 Λυµενες Ασκησεις..............................
Γ. ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΠΙΘΑΝΟΤΗΤΕΣ. Μαθηματικά Γενικής Παιδείας. Γ.Λυκείου
 Γ. ΛΥΚΕΙΟΥ ΜΘΗΜΤΙΚ ΓΕΝΙΚΗΣ ΠΙΔΕΙΣ ΠΙΘΝΟΤΗΤΕΣ Μαθηματικά Γενικής Παιδείας Γ.Λυκείου Π Ι Θ Ν Ο Τ Η Τ Ε Σ ΟΡΙΣΜΟΙ Πείραμα τύχης λέγεται το πείραμα το οποίο όσες φορές και αν επαναληφθεί (φαινομενικά τουλάχιστον
Γ. ΛΥΚΕΙΟΥ ΜΘΗΜΤΙΚ ΓΕΝΙΚΗΣ ΠΙΔΕΙΣ ΠΙΘΝΟΤΗΤΕΣ Μαθηματικά Γενικής Παιδείας Γ.Λυκείου Π Ι Θ Ν Ο Τ Η Τ Ε Σ ΟΡΙΣΜΟΙ Πείραμα τύχης λέγεται το πείραμα το οποίο όσες φορές και αν επαναληφθεί (φαινομενικά τουλάχιστον
Στην παράγραφο αυτή θα δούµε τις διάφορες µορφές εξισώσεων των κα- µπύλων του χώρου και των επιφανειών. ( )
 ΚΕΦΑΛΑΙ 6 ΕΥΘΕΙΑ-ΕΠΙΠΕ 6 Γεωµετρικοί τόποι και εξισώσεις στο χώρο Στην παράγραφο αυτή θα δούµε τις διάφορες µορφές εξισώσεων των κα- µπύλων του χώρου και των επιφανειών ρισµός 6 Θεωρούµε τη συνάρτηση F:Α,
ΚΕΦΑΛΑΙ 6 ΕΥΘΕΙΑ-ΕΠΙΠΕ 6 Γεωµετρικοί τόποι και εξισώσεις στο χώρο Στην παράγραφο αυτή θα δούµε τις διάφορες µορφές εξισώσεων των κα- µπύλων του χώρου και των επιφανειών ρισµός 6 Θεωρούµε τη συνάρτηση F:Α,
ΣΥΝΑΡΤΗΣΕΙΣ. H Εννοια του διανυσματος. Σ υ ν ο λ α - Ο ρ ι σ μ ο ι
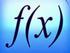 ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ΣΥΝΑΡΤΗΣΕΙΣ Σ υ ν ο λ α - Ο ρ ι σ μ ο ι Συνολο λεγεται καθε συλλογη 3. Να δειχτει αντικειμενων, οτι α + 0 που προερχονται 0α. Ποτε ισχυει απ την το εμπειρια ισον; μας η τη διανοηση 3 3. μας, Aν α, ειναι
ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ
 ÐÁÍÅÐÉÓÔÇÌÉÏ ÉÙÁÍÍÉÍÙÍ ÓïöïêëÞò Ä. ÃáëÜíçò ÁíáðëçñùôÞò ÊáèçãçôÞò ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ É Ù Á Í Í É Í Á 0 0 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ. Γενικά. Αλγόριθμος του Συμπληρώματος 6.3
ÐÁÍÅÐÉÓÔÇÌÉÏ ÉÙÁÍÍÉÍÙÍ ÓïöïêëÞò Ä. ÃáëÜíçò ÁíáðëçñùôÞò ÊáèçãçôÞò ÅÉÓÁÃÙÃÇ ÓÔÇÍ ÁÑÉÈÌÇÔÉÊÇ ÁÍÁËÕÓÇ É Ù Á Í Í É Í Á 0 0 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ. Γενικά. Αλγόριθμος του Συμπληρώματος 6.3
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ. Νώντας Κεχαγιάς Τµήµα Μαθηµατικών, Πανεπιστηµίου Ιωαννίνων
 ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Νώντας Κεχαγιάς Τµήµα Μαθηµατικών, Πανεπιστηµίου Ιωαννίνων Ιωάννινα, 2008 ii Περιεχόµενα 1 ΕΙΣΑΓΩΓΗ...................... vii 1.1 ΠΡΟΛΟΓΟΣ ΕΥΤΕΡΗΣ ΕΚ ΟΣΗΣ......... vii
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Νώντας Κεχαγιάς Τµήµα Μαθηµατικών, Πανεπιστηµίου Ιωαννίνων Ιωάννινα, 2008 ii Περιεχόµενα 1 ΕΙΣΑΓΩΓΗ...................... vii 1.1 ΠΡΟΛΟΓΟΣ ΕΥΤΕΡΗΣ ΕΚ ΟΣΗΣ......... vii
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα
 Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
ιανυσµατική ανάλυση Κεφάλαιο 1 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα
 Κεφάλαιο 1 ιανυσµατική ανάλυση 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα Αν περπατήσετε 4 µίλια προς τον βορρά και µετά 3 µίλια προς την ανατολή (Σχ. 1.1), θα έχετε διανύσει συνολικά 7 µίλια,
Κεφάλαιο 1 ιανυσµατική ανάλυση 1.1 ιανυσµατική άλγεβρα 1.1.1 Πράξεις µε διανύσµατα Αν περπατήσετε 4 µίλια προς τον βορρά και µετά 3 µίλια προς την ανατολή (Σχ. 1.1), θα έχετε διανύσει συνολικά 7 µίλια,
Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου
 Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου Θετικής & Τεχνολογικής Κατεύθυνσης Μιχάλης Ε. Καραδηµητριου MSc Φυσικός Ηράκλειο Κρήτης 2η Εκδοση - Ιούλης 2013 2 Μιχάλης Ε. Καραδηµητρίου Περιεχόµενα 1 Ταλαντώσεις
Πρόχειρες Σηµειώσεις Φυσικής Γ Λυκείου Θετικής & Τεχνολογικής Κατεύθυνσης Μιχάλης Ε. Καραδηµητριου MSc Φυσικός Ηράκλειο Κρήτης 2η Εκδοση - Ιούλης 2013 2 Μιχάλης Ε. Καραδηµητρίου Περιεχόµενα 1 Ταλαντώσεις
ΑΛΓΕΒΡΑ Α και Β ΛΥΚΕΙΟΥ για τις παν.εξετ. των ΕΠΑ.Λ.
 ΑΛΓΕΒΡΑ Α και Β ΛΥΚΕΙΟΥ για τις παν.εξετ. των ΕΠΑ.Λ. Μια συνοπτική παρουσίαση της Άλγεβρας, για όσους θέλουν να προετοιμαστούν για τις Πανελλαδικές Εξετάσεις των ΕΠΑ.Λ. Για απορίες στο www.commonmaths.weebly.com
ΑΛΓΕΒΡΑ Α και Β ΛΥΚΕΙΟΥ για τις παν.εξετ. των ΕΠΑ.Λ. Μια συνοπτική παρουσίαση της Άλγεβρας, για όσους θέλουν να προετοιμαστούν για τις Πανελλαδικές Εξετάσεις των ΕΠΑ.Λ. Για απορίες στο www.commonmaths.weebly.com
ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 ΔΗΜΗΤΡΗΣ ΣΟΥΡΛΑΣ ΑΝΑΠΛΗΡΩΤΗΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 3 ( ) ( ) ( ) = 4( ) d d ΕΚΔΟΣΕΙΣ ΣΥΜΜΕΤΡΙΑ ΑΘΗΝΑ 00 Email: dsourlas@phsics.upatras.gr www.phsics.upatras.gr
ΔΗΜΗΤΡΗΣ ΣΟΥΡΛΑΣ ΑΝΑΠΛΗΡΩΤΗΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 3 ( ) ( ) ( ) = 4( ) d d ΕΚΔΟΣΕΙΣ ΣΥΜΜΕΤΡΙΑ ΑΘΗΝΑ 00 Email: dsourlas@phsics.upatras.gr www.phsics.upatras.gr
ΤΟ ΟΛΟΚΛΗΡΩΜΑ ΕΙΣΑΓΩΓΗ
 ΤΟ ΟΛΟΚΛΗΡΩΜΑ ΕΙΣΑΓΩΓΗ Ο κύριος στόχος αυτού του κεφαλαίου είναι να δείξουµε ότι η ολοκλήρωση είναι η αντίστροφη πράξη της παραγώγισης και να δώσουµε τις βασικές µεθόδους υπολογισµού των ολοκληρωµάτων
ΤΟ ΟΛΟΚΛΗΡΩΜΑ ΕΙΣΑΓΩΓΗ Ο κύριος στόχος αυτού του κεφαλαίου είναι να δείξουµε ότι η ολοκλήρωση είναι η αντίστροφη πράξη της παραγώγισης και να δώσουµε τις βασικές µεθόδους υπολογισµού των ολοκληρωµάτων
1. στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι αβελιανή οµάδα, δηλαδή
 KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
Προτάσεις, Σύνολα, Απεικονίσεις
 Κεϕάλαιο 1 Προτάσεις, Σύνολα, Απεικονίσεις Το κεϕάλαιο αυτό είναι εισαγωγικό και έχει σκοπό να υπενθυµίσει και να γενικεύσει κάποιες εν µέρει γνωστές έννοιες καθώς και τη σχετική ορολογία και το συµβολισµό.
Κεϕάλαιο 1 Προτάσεις, Σύνολα, Απεικονίσεις Το κεϕάλαιο αυτό είναι εισαγωγικό και έχει σκοπό να υπενθυµίσει και να γενικεύσει κάποιες εν µέρει γνωστές έννοιες καθώς και τη σχετική ορολογία και το συµβολισµό.
