(Proper Orthogonal Decomposition, POD) POD POD Galerkin Projection PIV. Proper Orthogonal Decomposition in Fluid Flow Analysis: 1.

Transcript

1 115 連載 固有直交分解による流体解析 : 1. ( ) (Proper Orthogonal Decomposition, POD) POD POD Galerkin Projection PI Proper Orthogonal Decomposition in Fluid Flow Analysis: 1. Introduction Kunihiko TAIRA, Fundamental Technology Research Center, Honda R&D Co., Ltd. (Received 14 January, 2011; in revised form 4 March, 2011) With increasing capabilities of capturing the vector flow field from simulations and experiments, a systematic approach to extract physically important flow structures (modes) from the data is required. In addition, describing complex flow physics with a reduced-order model also calls for a low-dimensional basis that captures the flow field in a constructive manner. In this paper, we revisit the use of Proper Orthogonal Decomposition (POD), a technique that optimally extracts spatial modes from flow data. As Part 1 of a two-part series, the fundamentals of POD are summarized with emphasis for use in fluid mechanics. Reduced-order models based on Galerkin projection with POD modes are also discussed. In Part 2, applications of POD in fluid mechanics, aeroacoustics, flow control, PI, and aerodynamic design are reviewed. Finally, other methods related to POD are mentioned. (KEY WORDS): proper orthogonal decomposition (POD), principal component analysis (PCA), reduced order model, Galerkin projection, fluid mechanics 1 Particle Image elocimetry (PI) kunihiko taira@n.f.rd.honda.co.jp

2 116 (Proper Orthogonal Decomposition, POD) POD (Principal Component Analysis, PCA) Karhunen- Loève Compressive Sampling POD POD Jolliffe 1) Chatterjee 2) Lumley 3) 1967 POD POD POD Berkooz 4) Holmes 5) 90 POD POD POD 6) POD POD Snapshot POD Gappy POD POD POD POD PI POD Balanced POD 2 (POD, ) 2.1 POD (POD, ) POD 1 n r (r n) 1 1 1POD ( 1 ) POD 1 POD 2 x(t) R n, t min < t < t max. (1) x(t) r n (arg min) 3 {ϕ k } r k=1 P = r k=1 ϕ kϕ T k (arg max) tmax {ϕ k } r k=1 = arg min { ϕ k } r k=1 t min = arg max { ϕ k } r k=1 R = tmax tmax t min x(t) P x(t) P x(t) 2 dt 2 dt where P = ϕ k ϕ T k k=1 (2) t min x(t)x T (t)dt R n n (3) (ϕ k ) (λ k ) 5) Rϕ k = λ k ϕ k, λ 1... λ n 0. (4) 2 x(t) Holmes 5) x(t) 3 arg min f(x) {x y : f(x) f(y)} arg min (cos(x)) = x x (2n + 1)π, n Z

3 117 R ϕi, ϕ j = δij, i, j = 1,..., n. (5) 1 r tmax t min P x(t) 2 dt = λ k (6) k=1 / n λ k λ k 1 (7) k=1 k=1 r r POD POD R R R ˆR ˆR = P RP T = Λ. (8) P R (p k = ϕ k ) Λ R (4) POD 2.2 Snapshot POD POD n n n(e.g. CFD ) n = O(10 7 ) Snapshot POD 7) POD Snapshot POD t min = t 1,..., t m = t max (Snapshot) x(t j ) m m POD m R = ω j x(t j )x T (t j ) (9) j=1 ω j (e.g. ) X = [ ω 1 x(t 1 )... ω m x(t m )] R n m (10) R = XX T (11) (W ) R = XX T W. (12) (e.g. ) POD XX T R n n X T X R m m X T Xu k = λ k u k, u k R m, m n (13) ( X T W Xu k = λ k u k ) POD Snapshot POD r POD / ϕ k = Xu k λk (14) Φ = XUΛ 1/2 (15) ϕ k u k Φ = [ϕ 1... ϕ m ] R n m (16) U = [u 1... u m ] R m m (17) Λ R m m λ k POD Snapshot POD 1 ( ) Snapshot POD

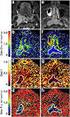
4 Gappy POD Gappy POD 8) X 0 if x ij is missing or incorrect n ij = (18) 1 if x ij is known. POD POD POD POD POD Bui-Thanh 9) Snapshot POD Immersed Boundary Projection 10, 11) Taira & Colonius 12) α = 30 Re = (Re = 100) (Re = 300, AR = 2) x = (u, v) T POD POD ( ) u-,v- curl x = (u, v, w) T POD x = Q (Q-Criterion, 2 ) POD 4 POD POD u-velocity v-velocity vorticity mode 5 mode 3 mode 2 mode 1 mean 2 α = 30 2 POD 1-5

5 POD POD % 6 100% 3.1 λ i POD ϕ i X L 2 13) r r k=1 λ k r ( ) (2) ( ) x (u 1, u 2, u 3 ) T x 2 ( = u u u 2 ) 3 d (19) x 2 = ( ω ω2 2 + ω3 2 ) d (20) POD ρ e [ x 2 = ρe + 1 ] 2 ρ(u2 1 + u u 2 3) d (21) x = ( ρe, ρu1, ρu 2, ρu 3 ) T Rowley 13) x 2 = [ ] 2a 2 γ 1 + (u2 1 + u u 2 3) d. (22) a γ α x 2 ( = α1 u α 2 u α 3 u α 4 a 2 + α 5 p 2) d (23) 14) 4 6) λ ( 3 ) 3.2 ( u = 0) (u D = 0) 2 POD 3.3 POD π/ Gappy POD n α

6 120 15) POD POD Fourier 7) 3.4 POD POD POD POD POD POD 4 POD 2 POD 2 POD 1 2 POD POD 4 POD (Reduced-Order Model, ROM) Navier Stokes POD POD Navier Stokes n 5 POD r Galerkin Projection 4.1 POD u(x, t) = a j (t)ϕ j (x) (24) j=0 a 0 = 1 ϕ 0 (x) = ū(x) Navier Stokes POD i POD ( f ϕ i ) f, ϕ i f ϕ i d (25) Navier Stokes n (i.e., x(t) R n ) 1 n = 2n x n y n r (r n) Navier Skotes u t + (u )u = p + 1 Re 2 u (26) (24) ϕ i j=0 da j dt ϕi, ϕ j + j=0 k=0 = ϕ i, p + 1 Re a j a k ϕi, (ϕ j )ϕ k a j ϕi, 2 ϕ j, j=0 i = 1, 2,..., r (27) POD p, ϕ i = [ (pϕ i ) p ϕ i ] d (28) = pϕ i ˆndS = 0 S ( ϕ i = 0) S(ˆn S ) ū Noack 16) POD 6 ϕi, ϕ j = δij (27) da i dt = j=0 k=0 F ijk a j a k + G ij a j, (29) j=0 F ijk = ϕ i, ϕ j ϕ k, (30) G ij = 1 ϕi, 2 ϕ Re j, i = 1,..., r. (31) Navier Stokes POD 17) POD a i (t 0 ) = u(x, t 0 ) ū(x), ϕ i (x), i = 1,..., r. (32) (24) POD n r a i F ijk G ij 6 i, j = 1, 2,..., r ϕ 0 = ū POD

7 121 u-velocity v-velocity w-velocity Q-criterion mode 2 mode 1 4 α = 30 (AR = 2) 3 POD POD (u,v,w-elocity) POD (Q-Criterion) q = [ρ, u 1, u 2, u 3, T ] T Navier Stokes 13) ρ t = (ρu j ) x j (33) ρ u i t = ρu u i j p + τ ij x j x i x j (34) ρ T t = ρu T j ρ(γ 1)T u k x j x k + γ Re Φ + γ 2 T ReP r x k x k (35) p = γ 1 ρt γ (36) τ ij = 1 ( 2S ij 2 ) u k Re 3 x k (37) Φ = 2S ij S ij 2 ( ) 2 uk 3 x k (38) S ij = 1 ( ui + u ) j. 2 x j x i (39) (A 0 + A 1 ) q = b 1 + b 2 + b 3 (40) A 0 = diag(1, 0, 0, 0, 0) (41) A 1 = diag(0, ρ, ρ, ρ, ρ) (42) b 1 (q) b 2 (q, q) b 3 (q, q, q) q b 1, b 2, b 3 q POD Navier Stokes Galerkin Projection q q(x, t) = a j (t)ϕ j (x) (43) j=0 (40) ϕ i M ij (a) a j = H i (a) (44) where M ij (a) = ϕ i, A 0 ϕ j + a k ϕi, A 1 (ϕ k )ϕ j (45) H i (a) = + + k=0 a k ϕi, b 1 (ϕ k ) k=0 k=0 m=0 a k a m ϕi, b 2 (ϕ k, ϕ m ) k=0 m=0 n=0 a k a m a n ϕi, b 3 (ϕ k, ϕ m, ϕ n ) (46) ϕ i, b 3 (ϕ k, ϕ m, ϕ n ) 4 Rowley 13) T 0 4 q = (u 1, u 2, u 3, a) T 3 (a ) Rowley 13) Navier Stokes Galerkin Projection q 5 CFD PI (POD)

8 122 POD POD (POD) POD Snapshot POD Gappy POD POD Navier Stokes 6) POD PI POD 1 POD X Snapshot POD POD u = (u, v) (x p, y q ), p = 1,..., n x, q = 1,..., n y (47) u pq = (u pq, v pq) = (u(x p, y q), v(x p, y q)) (48) ( 5 ) Snapshot POD t j stack 2 u u 3 n x u 1n y... u n xny v v n x v 1ny... v nxny t=t j stack unstack u 11 C. A u 1ny. 0 1 u n x1 C. A x(t j) u n 0 xny 1 v 11 R n C. A v 1ny. 0 1 v nx1 6 B C 7. A 5 v n xny t=t j (49) n (i.e., n = 2n xn y) x q = n y q = 2 q = 1 p = 1 p = 2 5 X v pq (x p, y q ) u pq p = n x X = [ ω 1 x(t 1 )... ω m x(t m )] R n m. (50) ω j (12) 2.2 Snapshot POD X T Xu k = λ k u k, u k R m, m n (51) ( )r (r m) POD ϕ k = Xu k.p λk R n, k = 1,..., r (52) (49) unstack ϕ k ( 2 4 ) 1) Jolliffe, I.T.: Principal Component Analysis, Springer Series in Statistics, 2nd ed, Springer (2002). 2) Chatterjee, A.: An introduction to the proper orthogonal decomposition, Current Science 78(7) (2000) ) Lumley, J. L.: The structure of inhomogeneous turbulent flows, In Atmospheric turbulence and wave propagation, eds. Yaglom, A. M. & Tatarski,. I., Moscow, Nauka (1967) ) Berkooz, G., Holmes, P. & Lumley, J. L.: The proper orthogonal decomposition in the analysis of turbulent flows, Ann. Rev. Fluid Mech. 25 (1993) ) Holmes, P., Lumley, J. L & Berkooz, G.: Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge Univ. Press (1996). 6) : : 2., 30(3) (2011) in press. 7) Sirovich, L.: Turbulence and the dynamics of coherent structures, Parts I III. Q. Appl. Math. XL (1987)

9 123 8) Everson, R. & Sirovich, L.: The Karhunen-Loève procedure for gappy data, J. Opt. Soc. Am. A 12(8) (1995) ) Bui-Thanh, T., Damodaran, M & Wilcox, K.: Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition, AIAA J. 42(8) (2004) ) Taira, K. & Colonius, T.: The immersed boundary method: A projection approach, J. Comp. Phys. 225 (2007) ) Colonius, T. & Taira, K.: A fast immersed boundary method using a nullspace approach and multi-domain far-field boundary conditions, Comput. Methods Appl. Mech. Engrg. 197 (2008) ) Taira, K. & Colonius, T.: Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers, J. Fluid Mech. 623 (2009) ) Rowley, C. W., Colonius, T. & Murray, R. M.: Model reduction for compressible flows using POD and Galerkin projection, Physica D 189 (2004) ) Freund, J. B. & Colonius, T.: Turbulence and soundfield POD analysis of a turbulent jet, Int l J. Aeroacoustics 8(7) (2009) ) Tadmor, G., Bissex, D., Noack, B. R., Morzyński, M., Colonius, T. & Taira, K.: Temporal-harmonic specific POD mode extraction, 4th Flow Control Conference, Paper , AIAA (2008). 16) Noack, B. R., Papas, P. & Monkewitz, P.: The need for pressure-term representation in empirical Galerkin models of incompressible shear flows, J. Fluid Mech. 523 (2005) ) Aubry, N., Holmes, P., Lumley, J. L. & Stone, E.: The dynamics of coherent structures in the wall region of a turbulent boundary layer, J. Fluid Mech. 192 (1988) (also see: Corrigendum 324 (1996) ).

10