Graded Refractive-Index

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "Graded Refractive-Index"

Γῆ Βλαστός
6 χρόνια πριν
Προβολές:

1 Graded Refractive-Index

2 Common Devices

3 Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x

4 Ray Optics for graded refractive index

5 Phase-change due to propagation k x T = tan 1 γ s k x + tan 1 γ c k x + m π k x x = ω c n x cos θ x = = ω c = ω c n 2 x n x sin θ x 2 = n 2 x N 2 k x x T N θ x i k x x i Δx i i n x i θ x i+1 n x i+1 ω c 0 x t n 2 x N 2 dx

6 Cladding-Film Interface k x T = tan 1 γ s k x + tan 1 γ c k x + m π N at x = 0 γ c = ω c N 2 n c 2 k x = ω c n 2 x = 0 N 2 = ω c n f 2 N 2 tan 1 γ c = tan 1 N2 2 n c π k x n 2 f N 2 2

7 Turning Point Interface k x T = tan 1 γ s k x + tan 1 γ c k x + m π N x t at x = x t k x = ω c n 2 x = x t + x N 2 γ s = ω c N 2 n 2 x = x t x n x = x t = N tan 1 γ c = tan 1 N 2 n 2 x=x t x tan 1 1 = π k x n 2 x=x t + x N 2 4

8 Bringing all the pieces together: k x T = tan 1 γ s k x + tan 1 γ c k x + m π ω c 0 x t n 2 x N 2 dx = π 4 + π 2 + m π x t N ω c 0 x t n 2 x N 2 dx = m π dispersion relation for a graded-refractive index waveguide

9 WKB Technique for graded refractive index

Solving for TE modes d 2 E y x dx 2 + ω2 c

10 Solving for TE modes d 2 E y x dx 2 + ω2 c 2 n2 x N 2 E y x = 0 k x x = ω c n 2 x N 2 If: n x = n f k x x = k x E y x = A e j k x x (constant) (constant) (constant) When: Δ n 2 x N 2 Δx/λ x 1 E y x = A x e j k x x x E y x = A x ej φ x where: k x x x φ x

11 Major steps in the derivation: E y x = A x ej φ x d 2 E y x dx 2 + ω2 c 2 n2 x N 2 E y x = 0 A A φ 2 = kx 2 A A + 2 j A φ + j A φ A φ 2 = kx 2 A 2 A φ + A φ = 0 A A φ 2 = kx 2 A A = φ 2 kx 2 A φ 2 kx 2 0 φ x = ± k x x dx 2 A φ + A φ = 0 A 2 φ = 0 A x = constant k x x

12 General Solution E y x = c 1 k x x e+j k x x dx + c 2 k x x e j k x x dx k x x = ω c n 2 x N 2

13 Cladding Region E y x = c 1 k x x e+j k x x dx + c 2 k x x e j k x x dx x k x x = ω c n 2 x N 2 for x < 0 k x x = ω c n 2 x N 2 = ω c n c 2 N 2 = j ω c N 2 n c 2 = j γc E y x = c 1 j γ c e 0 x γ c dx + c 2 j γ c e + 0 x γ c dx E y x = A γ c e γ c x

14 Guiding Region E y x = c 1 k x x e+j k x x dx + c 2 k x x e j k x x dx k x x = ω c n 2 x N 2 x for 0 < x < x t k x x = ω c n 2 x N 2 E y x = B k x x e+j x t x k x x dx + C k x x e j x t x k x x dx

15 Beyond Turning Point E y x = c 1 k x x e+j k x x dx + c 2 k x x e j k x x dx k x x = ω c n 2 x N 2 x for x > x t k x x = ω c n 2 x N 2 = j ω c N 2 n 2 x = j γ s x E y x = D γ s x e x x t γ s x dx

16 3D Waveguides Channel Waveguides Optical Fibers

17 Channel Waveguides x x y III T n 5 V I n 1 II n 3 n 2 IV n 4 y W typically: width(w) > thickness (T)

18 a) Marcatili s Method H y TM-like modes: H y & E x E x

19 Transverse confinement along x-axis, tangential H y Region I: H y x, y = H 1 cos k x x + φ 1 T < x < 0 Region II : x < T H y x, y = H 2 e γ x,2 x+t Region III: x > 0 H y x, y = H 3 e γ x,3 x k x T = tan 1 γ x,2 n 2 2 n 1 2 k x + tan 1 γ x,3 n 3 2 n 1 2 k x + p π

20 Lateral confinement along y-axis, tangential E x Region I: E x x, y = E 1 cos k y y + φ 2 W 2 < x < W 2 Region IV : E x x, y = E 4 e γ y,4 y W 2 y > W 2 Region V: E x x, y = E 5 e γ 5,y y+ W 2 y < W 2 k y W = tan 1 γ y,4 k y + tan 1 γ y,5 k y + q π

21 Finding the propagation constants: k x T = tan 1 γ 2 x,2 n 1 + tan 1 γ 2 x,3 n 1 n 2 2 k x n 2 3 k x + p π F 1 k x, γ x,2, γ x,3, β = 0 k y W = tan 1 γ y,4 k y + tan 1 γ y,5 k y + q π F 2 k y, γ x,4, γ x,5, β = 0 n 1 2 ω2 c 2 = k 1 2 = k x 2 + k y 2 + β 2 G 1 k x, k y, β = 0 n 2 2 ω2 c 2 = k 2 2 = γ x,2 2 + k y 2 + β 2 n 3 2 ω2 c 2 = k 3 2 = γ x,3 2 + k y 2 + β 2 n 4 2 ω2 c 2 = k 4 2 = k x 2 γ y,4 2 + β 2 n 5 2 ω2 c 2 = k 5 2 = k x 2 γ y,5 2 + β 2 G 2 γ x,2, k y, β = 0 G 3 γ x,3, k y, β = 0 G 4 k x, γ y,4, β = 0 G 5 k x, γ y,5, β = 0

22 b) Effective Index Method n f n s n c n f n s n s N I n s

23 TM-like modes I) n c, n f, T, n s (TM) F a M, b M N I, V I = 0 N I II) n s, N I, W, n s (TE) F a E, b E N II, V II = 0 N II

24 Criteria for Single-Mode Operation n f = n s + n with n n s Transverse confinement: I) Transverse confinement: cut-off condition for mode p : b I,p = 0 V I,p = tan 1 a I + p π Requirement for existence of only one mode in transverse direction: tan 1 a I < V I < tan 1 a I + π

25 Lateral confinement: II) Lateral confinement: cut-off condition for mode q : b II,q = 0 V II,q = tan 1 a II + q π it is a symmetric waveguide, so we have: a II = 0 Requirement for existence of only one mode in lateral direction: 0 < V II < π

26 A little bit of algebra leads to: V I = ω c T n f 2 n s 2 b I N I 2 n s 2 n f 2 n s 2 V II = ω c W N I 2 n s 2 = ω c W b I n f 2 n s 2 = W T V I b I 0 < V II < π 0 < W T < π V I b I and tan 1 a I < V I < tan 1 a I + π single-mode region a I

27 step-index multimode step-index singlemode GRIN Optical Fibers a cylindrical dielectric waveguide

28 Modes in Optical Fibers Cartesian coordinates 2 E x, y x E x, y y 2 + n2 ω 2 c 2 β2 E x, y = 0 E x, y, z, t = E x, y ej ω t β z Cylindrical coordinates 2 E r, φ r r E r, φ r + 1 r 2 2 E r, φ φ 2 + n2 ω 2 c 2 β2 E r, φ = 0 E r, φ, z, t = E r, φ ej ω t β z

29 Solutions E r, φ = u r e j l φ e d 2 u dr du r dr + n2 ω 2 c 2 β2 l2 r 2 u = 0 k T 2 n co 2 ω 2 c 2 β 2 γ 2 β 2 n cl 2 ω 2 c 2 Boundary conditions for E z, H z, E φ, H φ

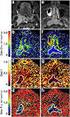
30 Graphical Representation

31 Power Confinement Fraction of the power propagating inside the core against the V-number. Right above the cut-off, very little power is inside the core. As the core diameter increases, the power of the mode becomes confined inside the core.

32 Optical Attenuation 0.16 db = (3.6 %) 1 db = 10 log T

33 Numerical Aperture NA = n 0 sin θ 0 = n co 2 n cl 2 V-number V = 2π a λ n co 2 n cl 2 = 2π a λ NA single-mode operation V < Number of Guided Modes in an Optical Fiber M = 4 π 2 V2

34 Coupled Mode Theory

35 A few examples:

36 Decomposition into the eigenmodes of the original structure E t x, y, z = a α z α E t,α x, y e j β α z + radiation modes H t x, y, z = a α z α H t,α x, y e j β α z + radiation modes

37 After a Careful (& Long) Analysis, Final Result: ± da μ dz = j α a α z e j β α β μ z Κ μ,α Κ μ,α Κ t μ,α + Κz μ,α 4 Κ t μ,α ω ε x, y, z E t,μ Et,α dx dy 4Κ z μ,α ω ε ε ε + ε E z,μ E z,α dx dy whenever ε is a real number, then Κ μ,α = Κ α,μ

38 Co-Directional Couplers: A z 2 = cos 2 β c z + 2 β 2 sin2 β c z = c 1 F sin 2 β c z B z 2 Κ 2 = = β 2 sin2 β c z c F sin 2 β c z F Κ2 β 2 = Κ 2 c Κ A z 2 when: β b = β a β b β a 2 = 0 F = 1 β c Κ = Κ L = π 2 β c = π 2 Κ π 2 F = 0.2 F = 0.8 B z 2 z βc z βc

39 Counter-Directional Couplers = 0 Κ c = 0.2 A z 2 L = 5 A z 2 = 1 + F sinh2 α z L 1 + F sinh 2 α L B z 2 B z 2 = F sinh2 α z L 1 + F sinh 2 α L A z 2 L = 9 F Κ c 2 Κ c 2 2 > 1 when: = 0 L π Κ c B z 2

Σχετικά έγγραφα

Homework 8 Model Solution Section

MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx