Συμπίεση Πολυμεσικών Δεδομένων
|
|
|
- Παύλος Ζαΐμης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Κώστας Μπερμπερίδης Εργαστήριο Σημάτων & Τηλεπικοινωνιών Τμήμα Μηχανικών Η/Υ & Πληροφορικής
2 Ψηφιακή Αναπαράσταση Συμπίεση για Αποθήκευση ή/και Μετάδοση Η ψηφιακή αναπαράσταση των δεδομένων έχει σαφή πλεονεκτήματα: μεγαλύτερη ανοσία σε «θόρυβο» ευελιξία στην ανταλλαγή εύρους ζώνης και ισχύος τεχνικές κρυπτογράφησης και προστασίας ευκολία υλοποίησης σε υλικό (VLSI) Αν τα δεδομένα είναι Αναλογικά, θα πρέπει να μετατραπούν σε Ψηφιακά (πώς ;) Ερώτηση: Χάνεται πληροφορία κατά τη μετατροπή A/D; Τα πολυμεσικά δεδομένα είναι κατά βάση αναλογικά. 2
3 Θεωρία Πληροφορίας Βασικός στόχος της Συμπίεσης: η αποδοτική αναπαράσταση των δεδομένων που παράγει μια πηγή πληροφορίας Το πρόβλημα της συμπίεσης είναι επίσης γνωστό ως κωδικοποίηση πηγής (source coding) Το αντικείμενο της συμπίεσης δεδομένων ανήκει στον ευρύτερο χώρο της θεωρίας πληροφορίας (information theory) 3
4 Κωδικοποίηση Πηγής Στόχος: η αποδοτική αναπαράσταση/κωδικοποίηση/συμπίεση της πληροφορίας/σήματος/εξόδου μιας πηγής Ερωτήματα που προκύπτουν: πώς ορίζεται η πληροφορία μιας πηγής; πότε μια πηγή εξάγει περισσότερη πληροφορία; μπορώ να τη μετρήσω μαθηματικά; τι παθαίνει η πληροφορία μιας πηγής όταν εφαρμόζω κάποια επεξεργασία (π.χ. μετατροπή A/D); πόσο πολύ μπορώ να συμπιέσω τα δεδομένα μιας πηγής; Απαντήσεις δίνονται μέσα από τη θεωρία πληροφορίας και τις τεχνικές κωδικοποίησης πηγής 4
5 Πηγές Πληροφορίας Η έξοδος της πηγής είναι κάτι τυχαίο και άγνωστο, μια τυχαία διαδικασία (αν είναι κάτι σταθερό ή γενικότερα ντετερμινιστικό, δεν υπάρχει λόγος να το μεταδώσουμε ή να το αποθηκεύσουμε) Παραδείγματα πηγών πληροφορίας: ακολουθία από bits χαρακτήρες ASCII ήχος (ομιλία) εικόνα video Διάκριση ως προς το χρόνο: συνεχούς χρόνου (π.χ. αναλογικό ηχητικό σήμα) διακριτού χρόνου (δειγματοληπτημένο σήμα ή σύμβολα) Διάκριση ως προς τις δυνατές τιμές (αλφάβητο): συνεχείς τιμές (π.χ. αναλογικό σήμα) διακριτές τιμές (π.χ. ASCII) 5
6 Πηγές Πληροφορίας (2) Αν η πηγή είναι αναλογική τότε απαιτείται: Μετατροπή της πηγής από συνεχούς σε διακριτού χρόνου δειγματοληψία το σήμα πρέπει να έχει πεπερασμένο εύρος ζώνης αν είναι κατωπερατό με μέγιστη συχνότητα f max, τότε η συνθήκη Nyquist μας λέει ότι αρκεί να το δειγματοληπτήσω με και μπορώ να ανακατασκευάσω το αναλογικό σήμα από τα δείγματα του χωρίς απώλειες Οι πηγές που μας ενδιαφέρουν, έχουν περιορισμένο εύρος ζώνης f s 2 f ή μπορούμε να το περιορίσουμε εμείς με φιλτράρισμα Περίπτωση στοχαστικών σημάτων: ανακατασκευή με μηδενικό MSE Συμπέρασμα: αρκεί να μελετήσω τις πηγές διακριτού χρόνου max 6
7 Πληροφορία Η θεωρητική ανάλυση παρουσιάζεται για πηγές πληροφορίας με διακριτό αλφάβητο λόγω ευκολίας (μπορεί να γενικευτεί σε πηγές με συνεχές αλφάβητο) Αλφάβητο Διακριτής Πηγής: Φ= s s 1, 2 sn { } Παράδειγμα: ο καιρός στην Ελλάδα κάθε 15 Αυγούστου s 1 : χιόνι s 2 : βροχή s 3 : λιακάδα Πότε δίνεται περισσότερη πληροφορία; όταν τυχαίνει το σύμβολο s 1 ή το s 3 ; με τι σχετίζεται η πληροφορία που φέρει κάθε σύμβολο; 7
8 Μέτρο Πληροφορίας (1) Ιδιότητες του μέτρου της πληροφορίας: ( ) = 0 ( ) = 1 I s for p s k ( ) 0 0 ( ) 1 I s for p s k ( ) > ( ) ( ) < ( ) I s I s for ps ps k l k l k k ( ) = ( ) + ( ), ά ά I s s I s I s s s k l k l εαν k l στατιστικ ανεξ ρτητα 5. Μικρή αλλαγή στην πιθανότητα μικρή αλλαγή στην πληροφορία (συνεχής συνάρτηση) 8
9 Μέτρο Πληροφορίας (2) Η Πληροφορία ενός συμβόλου (Information) s i με πιθανότητα εμφάνισης p(s i ) ορίζεται ως ( ) I s i 1 = log = log p s ( ) i ( ) p s i Βάση του λογαρίθμου συνήθως χρησιμοποιείται το 2 με μονάδα μέτρησης bit δεν ταυτίζεται με το bit που γνωρίζουμε ως δυαδικό ψηφίο Σύνθετη πηγή: (, ) = ( ) + ( ) I s a I s I a i j i j 9
10 Μέτρο Πληροφορίας (3) Παρατηρήσεις: 1. Φθίνουσα 2. Πεδίο ορισμού (που ορίζεται;) 3. Όρια (τι συμβαίνει στα άκρα;) 4. Είναι συνεχής; 10
11 Διακριτή Πηγή Χωρίς Μνήμη Discrete Memoryless Source (DMS): διακριτού χρόνου διακριτού αλφαβήτου τα σύμβολα στην έξοδό της είναι ανεξάρτητα ακολουθούν την ίδια κατανομή πιθανότητας Περιγράφεται πλήρως από: το αλφάβητο Φ= s,, 1 sn { } και τις πιθανότητες εμφάνισης p,, 1 pn { } Ειδικές Περιπτώσεις: Δυαδική Πηγή Χωρίς Μνήμη: Φ= { 0,1} { p,1 p} Για p=0.5, Δυαδική Συμμετρική Πηγή Χωρίς Μνήμη 11
12 Εντροπία Η εντροπία μιας DMS ορίζεται ως Φυσική Σημασία: N Φ = = H pi s p log p ( ) ( ) 2 i i i i i= 1 i= 1 εκφράζει τη μέση αβεβαιότητα που έχω για την πηγή είναι ο μέσος όρος της πληροφορίας των συμβόλων N Όσο μεγαλύτερη εντροπία έχει μια πηγή, τόσο περισσότερη πληροφορία φέρει, και τόσο περισσότερα bits χρειάζονται για την κωδικοποίησή της 12
13 Συνάρτηση Δυαδικής Εντροπίας Αν έχω δυαδική DMS Φ={0,1}, με πιθανότητες εμφάνισης {p,1-p}, τότε ορίζεται η συνάρτηση δυαδικής εντροπίας H p = plog p 1 p log 1 p b ( ) ( ) ( ) 2 2 Παρατηρήσεις: 1. ελαχιστοποιείται όταν p=0 ή 1, Η(0)=Η(1)=0 2. μεγιστοποιείται όταν τα σύμβολα είναι ισοπίθανα, Η(0.5)=1 13
14 Εντροπία Ομοιόμορφης Πηγής Είδαμε ότι η εντροπία της δυαδικής DMS μεγιστοποιείται για ισοπίθανα σύμβολα Γενίκευση: Η εντροπία μιας Ν-αδικής DMS μεγιστοποιείται όταν τα σύμβολά της ακολουθούν ομοιόμορφη κατανομή, δηλαδή p i =1/N για i=1,,n Συμπέρασμα: Η εντροπία φράσσεται ως 0 H Φ log ( ) 2 N όπου N το πλήθος του αλφαβήτου και το άνω όριο επιτυγχάνεται για ομοιόμορφη πηγή 14
15 Κωδικοποίηση Πηγής Στόχος: Η αποδοτική αναπαράσταση μιας Μιαδικής πηγής Κώδικες μεταβλητού μήκους: Αξιοποιεί τη γνώση των στατιστικών ιδιοτήτων της πηγής Λειτουργικές απαιτήσεις: Οι κωδικές λέξεις είναι δυαδικές Ο κώδικας είναι μοναδικά αποκωδικοποιήσιμος Μέσο μήκος κώδικα N i= 1 ( ) ( ) L= p si l s i 15
16 Θεώρημα Κωδικοποίησης Πηγής ή «Το Πρώτο Θεώρημα του Shannon» (1948) Χρησιμότητα: πόσο μπορούμε να συμπιέσουμε μια πηγή χωρίς να εισάγουμε σφάλματα; Θεώρημα: Έστω πηγή με εντροπία H που κωδικοποιείται ώστε να παρέχει ρυθμό R (bits/έξοδο πηγής). Αν R>H, η πηγή μπορεί να κωδικοποιηθεί με οσοδήποτε μικρή πιθανότητα σφάλματος Αν R<H, όσο πολύπλοκος κι αν είναι ο κωδικοποιητής πηγής, η πιθανότητα σφάλματος θα είναι μακριά από το 0 Σχόλια: Όπου R μπορείτε να θεωρήσετε το μέσο μήκος κώδικα (\bar{l}) ο Shannon δίνει την ικανή και αναγκαία συνθήκη όμως δεν προτείνει κάποιο αλγόριθμο/μεθοδολογία για να φτιάξουμε έναν κωδικοποιητή όταν R>H R<H : Data compression, Rate-Distortion Theory 16
17 Ομοιόμορφη Πηγή: H(X)=log 2 N Ειδικές Περιπτώσεις δε μπορεί να συμπιεστεί κάθε ακολουθία εξόδου είναι δυνατή (τυπική) και ισοπίθανη Πηγές με μνήμη: ο ρυθμός εντροπίας παίζει τον ίδιο ρόλο με την εντροπία για στατικές πηγές ο ρυθμός εντροπίας συγκλίνει γρήγορα στην τελική τιμή Παράδειγμα πηγής με μνήμη: αγγλικό κείμενο για n=1 (αγνοώντας τη μνήμη), H(X)=4.03 bits/letter για μπλοκ γραμμάτων (π.χ. n=10) συγκλίνει στην τιμή H(X)=1.3 bits/letter 17
18 Μη απωλεστική κωδικοποίηση δεδομένων - Προθεματικοί κώδικες - Αλγόριθμος Huffman
19 Προθεματικοί κώδικες Αλγόριθμοι κωδικοποίησης (συμπίεσης) πηγής Επιτυγχάνουν ρυθμούς κωδικοποίησης κοντά στην εντροπία (στο όριο συμπίεσης χωρίς απώλειες) Κωδικοποίηση από σταθερό σε μεταβλητό μήκος: είσοδος: μπλοκ συμβόλων σταθερού μήκους (μήκος μπλοκ 1 ) έξοδος: μπλοκ bits μεταβλητού μήκους (κωδική λέξη) Πρόβλημα: Συγχρονισμός πώς μπορώ να βρω τα όρια των μπλοκ στην έξοδο για να γίνει η αποκωδικοποίηση Λύση: Προθεματικός Καμμία κωδική λέξη δεν αποτελεί πρόθεμα κάποιας άλλης» μοναδικά αποκωδικοποιήσιμος (κάθε έξοδος αντιστοιχεί σε μοναδική είσοδο)» άμεσος (επιτρέπει απευθείας αποκωδικοποίηση) 19
20 Μέσο Μήκος Κώδικα Έστω DMS με πιθανότητες εμφάνισης p(s i ) και ένας κωδικοποιητής πηγής που αναθέτει l(s i ) bits στο σύμβολο s i Εάν ένας κώδικας είναι προθεματικός έχει τις εξής ιδιότητες: Kraft-McMillan inequality (αναγκαία και ικανή) i= 1 Φράγματα στο μέσο μήκος. N l( si ) 2 1 Μπορεί να κατασκευαστεί προθεματικός για τον οποίο: H( X) L< H( X)
21 Αποδοτικότητα Κώδικα Η αποδοτικότητα ενός κώδικα ορίζεται ως H( X) η = 1 L και δείχνει πόσο κοντά βρίσκεται ο κωδικοποιητής στο όριο συμπίεσης της πηγής (εντροπία) Ένας κώδικας είναι αποδοτικός, όσο το η πλησιάζει στο 1 21
22 Ν-οστής Τάξης Επέκταση Πηγής Ο προθεματικός κώδικας (π.χ. ο αλγόριθμος Huffman) θεωρεί ένα μπλοκ από σύμβολα ως επεκτεταμένη είσοδο και τα κωδικοποιεί ως ένα σύνθετο σύμβολο, δηλαδή έστω s i και s j θέτει σ κ =(s i,s j ) με πιθανότητα εμφάνισης p(σ κ )=p(s i )p(s j ) για πηγή χωρίς μνήμη Γενικεύεται σε n-οστή επέκταση της πηγής και ισχύει ( n) ( n ) n < + 1 H X L H X Μέσο μήκος κώδικα της επεκταμένης ακολουθίας πηγής L= Ln n 22
23 Ν-οστής Τάξης Επέκταση Πηγής (2) Για πηγή χωρίς μνήμη, αποδεικνύεται ( n ) = nh ( X ) H X Προκύπτει H X L< H X + ( ) ( ) 1 n Συμπέρασμα: Η n-οστής τάξης επέκταση μιας πηγής αποφέρει κώδικες που είναι ολοένα και πιο κοντά στο όριο συμπίεσης (εντροπία) της πηγής lim n L = H X ( ) Ερώτηση: Γιατί δε χρησιμοποιώ ένα πολύ μεγάλο n, ώστε να πετύχω συμπίεση κοντά στο όριο της εντροπίας; 23
24 Βήματα Αλγορίθμου Huffman (1) Δημιουργία Δυαδικού Δέντρου: 1. Διάταξε τις εισόδους κατά φθίνουσα σειρά πιθανοτήτων 2. Συγχώνευσε τα δύο σύμβολα με τις μικρότερες πιθανότητες και δημιούργησε νέο «σύμβολο» 3. Ανάθεσε στα δύο σύμβολα «0» και «1» 4. Ταξινόμησε εκ νέου τη λίστα των συμβόλων 5. Επανέλαβε τα παραπάνω μέχρι όλα τα σύμβολα συγχωνευτούν σε ένα τελικό σύμβολο Δημιουργήθηκε ένα δυαδικό δέντρο: ρίζα: το τελικό σύνθετο σύμβολο φύλλα: τα αρχικά σύμβολα ενδιάμεσοι κόμβοι: σύνθετα σύμβολα 24
25 Βήματα Αλγορίθμου (2) Ανάθεση Bits σε Σύμβολα Εισόδου 1. Ξεκίνα από τη ρίζα και κινήσου προς ένα φύλλο 2. Η ακολουθία των bits που συναντώνται είναι η ακολουθία κωδικοποίησης 3. Επανέλαβε για όλα τα σύμβολα (φύλλα) 25
26 Παράδειγμα Huffman Προθεματική αντιστοίχηση: s 0 : 1 s 1 : 00 s 2 : 01 Μονοσήμαντη και άμεση αποκωδικοποίηση s s s s s s
27 Χαρακτηριστικά Huffman Μειονέκτημα: απαιτεί να γνωρίζει εκ των προτέρων τις πιθανότητες εμφάνισης των συμβόλων της πηγής δε μπορεί να χρησιμοποιηθεί σε εφαρμογές πραγματικού χρόνου Βέλτιστος: ανάμεσα σε όλους τους προθεματικούς κώδικες (άρα μονοσήμαντα αποκωδικοποιήσιμους και άμεσους) πετυχαίνει το ελάχιστο μέσο μήκος κώδικα Συμβάσεις: Ο τρόπος ανάθεσης 0 και 1 Η ταξινόμηση σε φθίνουσα σειρά (σχετίζεται με τη διασπορά του κώδικα) 27
28 Απωλεστική Κωδικοποίηση Θεωρία Ρυθμού - Παραμόρφωσης
29 Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: > διακριτή πηγή: η πηγή να έχει πολύ μεγάλη εντροπία (πολλά bits/symbol) αλλά οι πόροι (αποθήκευσης, μετάδοσης) να είναι περιορισμένοι > αναλογική πηγή: - χάνεται πληροφορία κατά την κβάντιση - άπειρο πλήθος bits για ιδανική αναπαράσταση Συμπέρασμα: Πολλές φορές κατά την κωδικοποίηση πηγής δε μπορώ να φτάσω στην εντροπία Εισάγεται κάποια παραμόρφωση Πώς σχετίζεται η παραμόρφωση με τη συμπίεση; Η απάντηση προαπαιτεί να οριστούν κάποια μεγέθη 29
30 Ρυθμός vs Παραμόρφωση Αν δε μπορώ να διαθέσω H(X) bits/έξοδο, τα σφάλματα είναι αναπόφευκτα Ερώτηση: Για δεδομένο ρυθμό bits/έξοδο, ποιος είναι ο ελάχιστος ρυθμός σφαλμάτων; Αντίστροφο Ερώτημα: Για δεδομένη παραμόρφωση, ποιος είναι ο ελάχιστος ρυθμός bits/έξοδο; Αλλά, πώς ορίζεται η παραμόρφωση; 30
31 Παραμόρφωση Κατά την κωδικοποίηση/αποκωδικοποίηση μιας πηγής, πόσο «κοντά» είναι το αναπαραχθέν σήμα στο αρχικό; Επιθυμητές ιδιότητες μέτρου παραμόρφωσης αντιστρόφως ανάλογο της εγγύτητας/πιστότητας (μεγάλη εγγύτητα μικρή παραμόρφωση) απλό και μαθηματικά εύχρηστο να ενσωματώνει στοιχεία από τη διαδικασία αντίληψης Παράδειγμα αντίληψης: ηχητικό σήμα: το αυτί δεν αντιλαμβάνεται τη φάση σήμα εικόνας: το μάτι είναι ευαίσθητο στη φάση 31
32 Παραμόρφωση (2) Παραμόρφωση Hamming (πηγές με διακριτό αλφάβητο) d H xx, ˆ ( ) 1, x = 0, x= Παραμόρφωση Τετραγωνικού Σφάλματος (πηγές συνεχούς αλφαβήτου) (, ˆ) = ( ˆ) 2 d xx x x Αν έχω ένα μπλοκ από n δείγματα πηγής, ορίζω d n 1 = xˆ xˆ ( n n x, xˆ ) d( x, ˆ ) i xi n i = 1 είναι ο μέσος όρος των παραμορφώσεων ανεξάρτητο της θέσης του σφάλματος μέσα στο μπλοκ 32
33 Παραμόρφωση (3) Η έξοδος της πηγής είναι τυχαία διαδικασία Η απόσταση αρχικού σήματος και αναπαραγωγής είναι επίσης τυχαία διαδικασία Η μέση τιμή της είναι η παραμόρφωση του κωδικοποιητή ( n ˆ n X, X ) (, ˆ) D= E d = E d X X η δεύτερη ισότητα υποθέτει στασιμότητα της πηγής δηλαδή ότι τα δείγματα της τυχαίας διαδικασίας κάθε χρονική στιγμή ακολουθούν την ίδια κατανομή 33
34 Θεώρημα Ρυθμού-Παραμόρφωσης Θεώρημα: Ο ελάχιστος αριθμός bits/έξοδο που απαιτείται για να αναπαραχθεί μια πηγή χωρίς μνήμη με παραμόρφωση μικρότερη ή ίση του D ονομάζεται συνάρτηση ρυθμού-παραμόρφωσης, R(D), και είναι R D ( ) = min I( X; Xˆ ) ( ˆ ): (, ˆ ) D p xx E d X X Η ποσότητα I(X;Y) καλείται αμοιβαία πληροφορία Φυσική Σημασία: τι πληροφορία μαθαίνω για την τυχαία μεταβλητή Χ αν γνωρίζω την τυχαία μεταβλητή Υ I X Y H X H X Y ( ; ) = ( ) ( ) 34
35 Κβάντιση δειγμάτων αναλογικών πηγών
36 Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης: θεμελιώδης σχέση ανάμεσα σε ρυθμό bits/έξοδο του κωδικοποιητή παραμόρφωση που εισάγεται Διάκριση Κβαντιστών Βαθμωτός Κβαντιστής: κάθε δείγμα της πηγής κβαντίζεται (κωδικοποιείται) ξεχωριστά Διανυσματικός Κβαντιστής: τα δείγματα κβαντίζονται κατά μπλοκ 36
37 Βαθμωτή Κβάντιση Κάθε δείγμα (έξοδος της πηγής) κβαντίζεται χωριστά Γενικά x(n) πραγματικός αριθμός Απαιτεί άπειρο αριθμό bits για τέλεια αναπαράσταση Χωρίζω το σύνολο των πραγματικών σε N μη επικαλυπτόμενες περιοχές, R k, k=1,,n, με όρια α κ-1 και α κ Για κάθε περιοχή επιλέγεται μια αντιπροσωπευτική τιμή Αν η έξοδος x ανήκει στην R k, κβαντίζεται στο Στέλνουμε τη δυαδική αναπαράσταση της περιοχής k, Απαιτούνται R=log 2 N bits/έξοδο Παρατήρηση: τα bits αναπαράστασης μειώθηκαν από άπειρα σε log 2 N αλλά εισήχθηκε παραμόρφωση xˆk xˆk 37
38 Παράδειγμα Βαθμωτής Κβάντισης Περιοχές: R 1 =(-,α 1 ] R 2 =(α 1, α 2 ]... R 8 =(α 7, ) Τιμές κβάντισης: xˆ,, xˆ
39 Συνάρτηση Κβάντισης Συνάρτηση Κβάντισης ( ) = Q x x x R ˆi i Μη γραμμική Μη αναστρέψιμη όλα τα σημεία της R k απεικονίζονται στο ίδιο σημείο ένα ποσό πληροφορίας χάνεται ανεπιστρεπτί Μέτρο στιγμιαίας παραμόρφωσης: τετραγωνικό σφάλμα (, ˆ) ( ) ( ) 2 2 d xx = x Q x = x Παραμόρφωση ( ) 2 2 (, ˆ ) ( ) D= E d X X = E X Q X = E x 39
40 Θόρυβος Κβάντισης Το τελικό (κβαντισμένο) σήμα μπορεί να εκφραστεί ως xˆ = Q( x) = x x Η δεύτερη ποσότητα (\tilde{x}) καλείται θόρυβος κβάντισης Στόχος: ο θόρυβος κβάντισης να έχει μικρή ισχύ P X 2 = E X Πιο σημαντικός στόχος: η ισχύς του θορύβου να είναι μικρή σε σχέση με την ισχύ του αρχικού σήματος (κανονικοποίηση) Ορισμός: Λόγος Σήματος προς Θόρυβο Κβάντισης (Signal to Quantization Noise Ratio, SQNR) 2 E X PX SQNR = = 2 E X PX 40
41 Ομοιόμορφη και Μη Ομοιόμορφη Κβάντιση Ομοιόμορφη κβάντιση: Περιοχές ίδιου εύρους και τιμές εξόδου τα κέντρα των περιοχών Μη Ομοιόμορφη κβάντιση: Χαλαρώνουμε τις παραπάνω συνθήκες Αποτέλεσμα: αν η πηγή δεν είναι ομοιόμορφη, δεν υπάρχει λόγος για ομοιόμορφο κβαντιστή λιγότεροι περιορισμοί κατά την ελαχιστοποίηση ο κβαντιστής έχει καλύτερες επιδόσεις Σχεδιασμός Κβαντιστή: ελαχιστοποιώ την παραμόρφωση ως προς x i, α i, δηλαδή ως προς (2Ν-1) παραμέτρους 41
42 Συνθήκες Lloyd-Max Οι συνθήκες: 1. τα άκρα των περιοχών κβάντισης δίνονται από τον αριθμητικό μέσο των γειτονικών τιμών κβάντισης 2. οι τιμές κβάντισης είναι τα κέντρα μάζας των περιοχών κβάντισης είναι αναγκαίες για να είναι βέλτιστος ένας βαθμωτός κβαντιστής Ερώτημα: Αν ξέρω την pdf της πηγής και με βάση τις παραπάνω συνθήκες, μπορώ να σχεδιάσω το βέλτιστο κβαντιστή; 42
43 Αλγόριθμος Lloyd-Max Πρακτική λύση: ένας επαναληπτικός αλγόριθμος οι δύο συνθήκες ικανοποιούνται εναλλάξ Αλγόριθμος: 1. Επέλεξε τυχαία ή ομοιόμορφα τις περιοχές κβάντισης 2. Υπολόγισε τις τιμές κβάντισης ως τα κέντρα μάζας των περιοχών 3. Υπολόγισε τα άκρα των περιοχών ως το μέσο όρο των γειτονικών τιμών κβάντισης 4. Επανέλαβε τα βήματα 2 και 3 έως ότου συγκλίνει η διαδικασία Αποτέλεσμα: με αυτόν τον τρόπο μπορώ να σχεδιάσω το βέλτιστο μη ομοιόμορφο κβαντιστή για οποιαδήποτε πηγή 43
44 Βαθμωτός vs Διανυσματικός Βαθμωτή κβάντιση: κάθε έξοδος κβαντίζεται ξεχωριστά Παράδειγμα: κβάντιση με 2bits/έξοδο 44
45 Βαθμωτός vs Διανυσματικός Διανυσματική κβάντιση: μπλοκ εξόδων κβαντίζονται ταυτόχρονα Παράδειγμα: θεωρούμε δύο δείγματα εξόδου μαζί απεικονίζονται στο επίπεδο χωρίζω το επίπεδο σε 16 περιοχές απαιτούνται 4 bits/ζεύγος εξόδων δηλαδή 2bits/έξοδο ίδιος ρυθμός με τη βαθμωτή Ερώτηση: ποιο είναι το κέρδος; 45
46 Απάντηση: Διανυσματική Κβάντιση οι περιοχές μπορεί να μην είναι ορθογώνιες έτσι μπορώ να πετύχω μικρότερη παραμόρφωση κατά την κβάντιση με τον ίδιο ρυθμό R 46
47 Γενίκευση: Διανυσματική Κβάντιση (2) μπορώ να πάρω n δείγματα εξόδου ταυτόχρονα αυτά αναπαρίστανται στον n-διάστατο Ευκλείδιο χώρο ο βέλτιστος κβαντιστής σχεδιάζεται στο συγκεκριμένο χώρο Ρυθμός: Χωρίζω τον n-διάστατο χώρο σε K περιοχές απαιτούνται log 2 K bits για να τις δεικτοδοτήσω R = log 2 n K bits/έξοδο 47
48 Βέλτιστος Διανυσματικός Κβαντιστής Κριτήρια σχεδίασης Γενικεύσεις του βαθμωτού 1. Η περιοχή R i είναι το σύνολο των σημείων που ικανοποιεί { x n : x xˆ x xˆ, } R = < j i i i j 2. Οι τιμές κβάντιστης είναι τα κέντρα μάζας των περιοχών 1 xˆ = ( ) i xf d P R R X x x X i ( ) i Ο σχεδιασμός του κβαντιστή γίνεται με γενίκευση του επαναληπτικού αλγορίθμου που είδαμε 48
49 Σχόλια Η διανυσματική κβάντιση έχει πολλές εφαρμογές, π.χ. κωδικοποίηση ομιλίας κωδικοποίηση video Η διανυσματική κβάντιση για να είναι αποδοτική προϋποθέτει συσχέτιση μεταξύ των δειγμάτων εξόδου της πηγής (δηλαδή να έχουμε πηγή με μνήμη) γιατί; Αποδεικνύεται ότι για στατικές και εργοδικές πηγές, ο βέλτιστος διανυσματικός κβαντιστής προσεγγίζει τα όρια της συνάρτησης ρυθμού παραμόρφωσης για n 49
50 Παράδειγμα 1: Συμπίεση Φωνής
51 Τεχνικές Κωδικοποίησης Φωνής Κωδικοποίηση Φωνής: Ιδιαίτερα χρήσιμη διαδικασία αν αναλογιστούμε ότι μεγάλο μέρος της διακινούμενης πληροφορίας είναι φωνή και ότι μέσω της συμπίεσης της μπορεί να επιτευχθεί σημαντική μείωση του απαιτούμενου εύρους ζώνης (μέχρι και 4-5 φορές, χωρίς αισθητή υποβάθμιση της ποιότητας). Γενική κατηγοριοποίηση των τεχνικών 1) Waveform Coding - Temporal - Spectral (Transform) 2) Model-based Coding Παρόμοια κατηγοριοποίηση ισχύει και σε άλλου τύπου αναλογικές πηγές, π.χ. εικόνα ή video (η φυσική σκηνή είναι σχεδόν πάντα αναλογική)
52 Τεχνικές Κωδικοποίησης Φωνής
53 Τεχνικές Κωδικοποίησης Φωνής Ιεραρχική κατηγοριοποίηση των διαφόρων τεχνικών κωδικοποίησης
54 Τεχνικές Κωδικοποίησης Φωνής Ένα βασικό μοντέλο παραγωγής φωνής Απαιτείται η εκτίμηση των εξής: Οι παράμετροι της βασικής φωνητικής οδού Το αν το φώνημα είναι εύφωνο (voiced) ή άφωνο (unvoiced) Η θεμελιώδης συχνότητα (pitch) Η μέση ισχύς του φωνήματος
55 Τεχνικές Κωδικοποίησης Φωνής Κωδικοποιητές φωνής (Vocoders) τύπου LPC (Linear Predictive Coding) Ένας LPC Vocoder μοντελοποιεί τη φωνητική οδό ως ένα γραμμικό σύστημα τύπου all-pole με συνάρτηση μεταφοράς: Προσδιορισμός των συντελεστών του LPC Vocoder : To τρέχον δείγμα γράφεται ως γραμμικός συνδυασμός προηγουμένων δειγμάτων : min{σ e 2 n} w.r.t. α k R α = r (R = Toeplitz) (Levinson-Durbin Alg.)
56 Τεχνικές Κωδικοποίησης Φωνής Διάγραμμα βαθμίδων ενός κωδικοποιητή LPC Απαιτούμενη πληροφορία στον δέκτη: - Συντελεστές LPC (κβαντισμένοι) - Voiced/unvoiced decision - Pitch period - Gain
57 Τεχνικές Κωδικοποίησης Φωνής Διάφορες εναλλακτικές μέθοδοι δημιουργίας του σήματος διέγερσης στον αποκωδικοποιητή LPC LPC Vocoder MPE-LPC (Multipulse Excitation) Χρήση πολλών παλμών ανά περίοδο με μεταβαλλόμενα πλάτη και θέσεις CELP (Code Excited LP) Χρήση ενός προκαθορισμένου codebook με σήματα διέγερσης
58 Τεχνικές Κωδικοποίησης Φωνής Διάγραμμα βαθμίδων της διαδικασίας code book search του συστήματος κωδικοποίησης CELP (Code Excited Linear Predictive) Οι βασικές διαδικασίες στον κωδικοποιητή CELP: - Υπολογισμός των δύο προβλεπτών (LTP, STP) από το εκάστοτε τμήμα φωνής (Long Term & Short Term Prediction) - Εύρεση της βέλτιστης διέγερσης (από το codebook). Το αντικειμενικό σφάλμα ανακατασκευής (error) υφίσταται περαιτέρω μετασχηματισμό σύμφωνα με τον αντιληπτικό μηχανισμό μας (perceptual masking)
59 Τεχνικές Κωδικοποίησης Φωνής Τεχνικές κωδικοποίησης που χρησιμοποιούνται σε διάφορα συστήματα κινητών επικοινωνιών Πρότυπο Τύπος Υπηρεσίας Κωδικοποιητ ής Φωνής Bit Rate (kbps) GSM Cellular RPE-LTP 13 CD-900 Cellular SBC 16 USDC (IS-54) Cellular VSELP 8 IS-95 Cellular CELP 1.2, 2.4, 4.8, 9.6 IS-95 PCS PCS CELP 14.4 PDC Cellular VSELP 4.5, 6.7, 11.2 CT2 Cordless ADPCM 32 DECT Cordless ADPCM 32 PHS Cordless ADPCM 32 DCS-1800 PCS RPE-LTP 13 PACS PCS ADPCM 32 Συστήματα 3ης γενιάς: Adaptive Multirate (AMR) speech codec Το σύστημα επιτρέπει συμπίεση σε διαφορετικούς ρυθμούς ανάλογα με τις συνθήκες. Στον πυρήνα του συστήματος είναι η τεχνική ACELP (Algebraic CELP) που είναι κατά βάση η CELP με διαφορετικό coodbook design and search.
60 Τεχνικές Κωδικοποίησης Φωνής Αξιολόγηση της απόδοσης διαφόρων τεχνικών κωδικοποίησης με βάση τον δείκτη MOS (Mean Opinion Score)
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Κωδικοποίησης Πηγής Η Περίπτωση της Φωνής
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Κωδικοποίησης Πηγής Η Περίπτωση της Φωνής
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Αναλογικής Πηγής: Κβάντιση Εισαγωγή Αναλογική πηγή: μετά από δειγματοληψία γίνεται διακριτού χρόνου άπειρος αριθμός bits/έξοδο για τέλεια αναπαράσταση Θεωρία Ρυθμού-Παραμόρφωσης
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Κωδικοποίηση Πηγής Ψηφιακή Μετάδοση Υπάρχουν ιδιαίτερα εξελιγμένες τεχνικές αναλογικής μετάδοσης (που ακόμη χρησιμοποιούνται σε ορισμένες εφαρμογές) Επίσης,
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Ψηφιακές Τηλεπικοινωνίες. Θεωρία Ρυθμού Παραμόρφωσης
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Ψηφιακές Τηλεπικοινωνίες Θεωρία Ρυθμού Παραμόρφωσης Θεωρία Ρυθμού-Παραμόρφωσης Θεώρημα Κωδικοποίησης Πηγής: αν έχω αρκετά μεγάλο μπλοκ δεδομένων, μπορώ να φτάσω κοντά στην εντροπία Πιθανά Προβλήματα: >
Θεώρημα κωδικοποίησης πηγής
 Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Σημείωμα Αδειοδότησης
 Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Μελέτη Περιπτώσεων στη Λήψη Αποφάσεων Σημείωμα Αδειοδότησης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Εισαγωγή στη θεωρία πληροφορίας
 Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Ψηφιακές Τηλεπικοινωνίες
 Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
Ψηφιακές Τηλεπικοινωνίες Θεωρία Πληροφορίας: Χωρητικότητα Καναλιού Χωρητικότητα Καναλιού Η θεωρία πληροφορίας περιλαμβάνει μεταξύ άλλων: κωδικοποίηση πηγής κωδικοποίηση καναλιού Κωδικοποίηση πηγής: πόση
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o
 Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Διαδικασία Ψηφιοποίησης (1/2)
 Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
Διαδικασία Ψηφιοποίησης (1/2) Η διαδικασία ψηφιοποίησης περιλαμβάνει: Φιλτράρισμα και δειγματοληψία Κβαντισμό και κωδικοποίηση Φιλτράρισμα και δειγματοληψία Κβαντισμός και κωδικοποίηση Κβαντισμός Τα αναλογικά
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
( ) log 2 = E. Σεραφείµ Καραµπογιάς
 Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Άσκηση 5.1 Για ένα σήμα που έχει τη σ.π.π. του σχήματος να υπολογίσετε: μήκος του δυαδικού κώδικα για Ν επίπεδα κβάντισης για σταθερό μήκος λέξης;
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πληροφορία Μέτρο πληροφορίας Μέση πληροφορία ή Εντροπία Από κοινού εντροπία
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 2 : Πληροφορία και Εντροπία Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Πιθανότητες Πληροφορία Μέτρο
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ. Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Z
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές Παράδειγµα ενός ηλεκτρικού συστήµατος Σύστηµα Παράδειγµα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ Κβάντιση και Κωδικοποίηση ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Χειμερινό Εξάμηνο Τμήμα Πληροφορικής και Τηλεπικοινωνίων Νικόλαος Χ. Σαγιάς Αναπληρωτής Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 7: Μετατροπή Σήματος από Αναλογική Μορφή σε Ψηφιακή Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετατροπή Αναλογικού Σήματος σε Ψηφιακό Είδη Δειγματοληψίας: Ιδανική
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
0, αλλιώς. Σεραφείµ Καραµπογιάς. Παράδειγµα 1 Η πηγή X(t) είναι στατική Gaussian µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος.
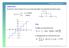 Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
Παράδειγµα Η πηγή X(t) είναι στατική Gussin µε µέση τιµή µηδέν και φασµατική πυκνότητα ισχύος S X ( f ) 70, f < 00Hz 0, αλλιώς S X ( f ) 00 00 f 50 Λύση: 60 40 0 30 0 0 30 0 40 60 Ο ρυθµός που απαιτείται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 7 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Ήχος. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 04-1
 Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Τεχνολογία Πολυμέσων. Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣΟΡ Κεφάλαιο 1 : Εισαγωγή στη Θεωρία ωία Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Έννοια της πληροφορίας Άλλες βασικές έννοιες Στόχος
Κωδικοποίηση ήχου. Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής
 Κωδικοποίηση ήχου Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής T. Painter and A. Spanias, Perceptual Coding of Digital Audio, Proceedings of the IEEE, pp. 451-513, April 2000. P. Noll, MPEG digital audio
Κωδικοποίηση ήχου Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής T. Painter and A. Spanias, Perceptual Coding of Digital Audio, Proceedings of the IEEE, pp. 451-513, April 2000. P. Noll, MPEG digital audio
Ημιτονοειδή σήματα Σ.Χ.
 Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
Ημιτονοειδή σήματα Σ.Χ. Αρμονική ταλάντωση και επειδή Ω=2πF Περιοδικό με βασική περίοδο Τ p =1/F Ημιτονοειδή σήματα Σ.Χ. 1 Ημιτονοειδή σήματα Σ.Χ. Σύμφωνα με την ταυτότητα του Euler Το ημιτονοειδές σήμα
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Θεωρία πληροφοριών. Τεχνολογία Πολυµέσων 07-1
 Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Ψηφιακές Τηλεπικοινωνίες. Κωδικοποίηση Κυματομορφής
 Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
Ψηφιακές Τηλεπικοινωνίες Κωδικοποίηση Κυματομορφής Σύνδεση με τα Προηγούμενα Οι τεχνικές κωδικοποίησης αναλογικής πηγής διακρίνονται σε τεχνικές κωδικοποίησης κυματομορφής τεχνικές ανάλυσης σύνθεσης Οι
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
ΚΩ ΙΚΟΠΟΙΗΣΗ ΟΜΙΛΙΑΣ. Μικρότερος ρυθµός µετάδοσης Μεγαλύτερη χωρητικότητα. Νοε-06 Γ.Ι.Στεφάνου 1
 ΚΩ ΙΚΟΠΟΙΗΣΗ ΟΜΙΛΙΑΣ Μικρότερος ρυθµός µετάδοσης Μεγαλύτερη χωρητικότητα Νοε-06 Γ.Ι.Στεφάνου 1 WAVEFORM CODERS Ανεξάρτητοι από το είδος της πηγής Ελάχιστα σύνθετοι Μεγάλοι ρυθµοί ΚΩ ΙΚΟΠΟΙΗΤΕΣ ΟΜΙΛΙΑΣ
ΚΩ ΙΚΟΠΟΙΗΣΗ ΟΜΙΛΙΑΣ Μικρότερος ρυθµός µετάδοσης Μεγαλύτερη χωρητικότητα Νοε-06 Γ.Ι.Στεφάνου 1 WAVEFORM CODERS Ανεξάρτητοι από το είδος της πηγής Ελάχιστα σύνθετοι Μεγάλοι ρυθµοί ΚΩ ΙΚΟΠΟΙΗΤΕΣ ΟΜΙΛΙΑΣ
Μοντέλο Επικοινωνίας Δεδομένων. Επικοινωνίες Δεδομένων Μάθημα 6 ο
 Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α)
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
Μετάδοση πληροφορίας - Διαμόρφωση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ψηφιακές Επικοινωνίες Εργαστήριο 4 ο : Κβάντιση-Κωδικοποίηση Βασική Θεωρία Κβάντιση Κατά την μετατροπή ενός αναλογικού
ΠΛΗ21 Κεφάλαιο 1. ΠΛΗ21 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή
 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι τα Αναλογικά κ τι τα Ψηφιακά Μεγέθη Τι είναι Σήμα, Αναλογικό Σήμα, Ψηφιακό Σήμα Τι είναι Δυαδικό Σήμα
Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι τα Αναλογικά κ τι τα Ψηφιακά Μεγέθη Τι είναι Σήμα, Αναλογικό Σήμα, Ψηφιακό Σήμα Τι είναι Δυαδικό Σήμα
Τηλεπικοινωνίες. Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων. Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ
 Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Τηλεπικοινωνίες Ενότητα 5: Ψηφιακή Μετάδοση Αναλογικών Σημάτων Μιχάλας Άγγελος Τμήμα Μηχανικών Πληροφορικής ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Κωδικοποίηση Πηγής. Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα):
 Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
Αρχές κωδικοποίησης. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θέματα Συστημάτων Πολυμέσων Ενότητα # 5: Βασική Θεωρία Πληροφορίας Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Κβάντιση-Κωδικοποίηση
Ήχος και φωνή. Τεχνολογία Πολυµέσων 04-1
 Ήχος και φωνή Φύση του ήχου Ψηφιοποίηση µε µετασχηµατισµό Ψηφιοποίηση µε δειγµατοληψία Παλµοκωδική διαµόρφωση Αναπαράσταση µουσικής Ανάλυση και σύνθεση φωνής Μετάδοση φωνής Τεχνολογία Πολυµέσων 4-1 Φύση
Ήχος και φωνή Φύση του ήχου Ψηφιοποίηση µε µετασχηµατισµό Ψηφιοποίηση µε δειγµατοληψία Παλµοκωδική διαµόρφωση Αναπαράσταση µουσικής Ανάλυση και σύνθεση φωνής Μετάδοση φωνής Τεχνολογία Πολυµέσων 4-1 Φύση
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Συμπίεση Δεδομένων 2014-2015 Στοιχεία Επεξεργασίας Σήματος Δρ. Ν. Π. Σγούρος 2 Εργοδικές Διαδικασίες Η μέση τιμή διαφόρων στιγμιότυπων της διαδικασίας (στατιστική μέση τιμή) ταυτίζεται με τη χρονική μέση
Μάθημα Επισκόπηση των Τηλεπικοινωνιών
 Μάθημα Επισκόπηση των Τηλεπικοινωνιών Κωδικοποίηση Πηγής & Καναλιού Μάθημα 8 ο 9 ο ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Επισκόπηση των Τηλεπικοινωνιών Κωδικοποίηση Πηγής & Καναλιού Μάθημα 8 ο 9 ο ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ
 ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
ΚΕΦΑΛΑΙΟ ΠΕΜΠΤΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ 5. Εισαγωγή Ο σκοπός κάθε συστήματος τηλεπικοινωνιών είναι η μεταφορά πληροφορίας από ένα σημείο (πηγή) σ ένα άλλο (δέκτης). Συνεπώς, κάθε μελέτη ενός τέτοιου συστήματος
Τεχνολογία Πολυμέσων. Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Θ.Ε. ΠΛΗ22 (2012-13) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #4. Έκδοση v2 με διόρθωση τυπογραφικού λάθους στο ερώτημα 6.3 Στόχος: Βασικό στόχο της 4 ης εργασίας αποτελεί η εξοικείωση με τα μέτρα ποσότητας πληροφορίας τυχαίων
Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο Εργαστηριακή Άσκηση 7: Κβάντιση και Κωδικοποίηση Σημάτων Προσομοίωση σε Η/Υ Δρ. Ηρακλής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες / Εργαστήριο Εργαστηριακή Άσκηση 7: Κβάντιση και Κωδικοποίηση Σημάτων Προσομοίωση σε Η/Υ Δρ. Ηρακλής
Συστήματα Πολυμέσων. Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 8 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 8 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
Συστήματα Επικοινωνιών Ενότητα 5: Pulse Code Modulation (PCM) Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Γνωριμία με την περισσότερο εφαρμοζόμενη
Τεχνολογία Πολυμέσων. Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Περιεχόμενα. 4.1 Χαρακτηριστικά του ήχου... 58 4.2 Ψηφιοποίηση με μετασχηματισμό... 59 4.3 Ψηφιοποίηση με δειγματοληψία... 60. Πρόλογος...
 Περιεχόμενα Πρόλογος...13 1 Εισαγωγή...17 1.1 Χαρακτηριστικά των μέσων... 18 1.2 Ιδιότητες των συστημάτων πολυμέσων... 19 1.3 Δομή των συστημάτων πολυμέσων... 20 1.4 Δικτυακά συστήματα πολυμέσων... 21
Περιεχόμενα Πρόλογος...13 1 Εισαγωγή...17 1.1 Χαρακτηριστικά των μέσων... 18 1.2 Ιδιότητες των συστημάτων πολυμέσων... 19 1.3 Δομή των συστημάτων πολυμέσων... 20 1.4 Δικτυακά συστήματα πολυμέσων... 21
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM
 ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM ΠΗΓΗ ΜΕ ΔΙΑΚΡΙΤΑ ΣΥΜΒΟΛΑ Τα στοιχεία της ακολουθίας των συμβόλων Διακριτή Πηγή Χωρίς Μνήμη-DMS Σύμβολα μεταξύ τους στατιστικά ανεξάρτητα: (X i =α k & X j =α l )=
ΣΤOIΧΕΙΑ ΑΠΟ ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ και PCM ΠΗΓΗ ΜΕ ΔΙΑΚΡΙΤΑ ΣΥΜΒΟΛΑ Τα στοιχεία της ακολουθίας των συμβόλων Διακριτή Πηγή Χωρίς Μνήμη-DMS Σύμβολα μεταξύ τους στατιστικά ανεξάρτητα: (X i =α k & X j =α l )=
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω:
 Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
Συστήματα Επικοινωνιών Ενότητα 9: Παλμοκωδική Διαμόρφωση (PCM) Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή της μεθόδου παλμοκωδικής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
Θεωρία της Πληροφορίας 3 ο Εξάμηνο
 Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Σμήμα Πληροφορικής & Επικοινωνιών Θεωρία της Πληροφορίας 3 ο Εξάμηνο Τομέας Τηλεπικοινωνιών και Δικτύων Δρ. Αναστάσιος Πολίτης Καθηγητής Εφαρμογών 1 Διεξαγωγή και Εξέταση του Μαθήματος Μάθημα Πώς? 13 Διαλέξεις.
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής. Εντροπία Shannon
 Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
Αθανάσιος Χρ. Τζέμος Τομέας Θεωρητικής Φυσικής Εντροπία Shannon Ένα από τα βασικά ερωτήματα της θεωρίας της πληροφορίας ήταν ανέκαθεν το πώς θα μπορούσε να ποσοτικοποιηθεί η πληροφορία, ώστε να μπορούμε
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Πρόλογος 1. 1 Μαθηµατικό υπόβαθρο 9
 Πρόλογος 1 Μαθηµατικό υπόβαθρο 7 1 Μαθηµατικό υπόβαθρο 9 1.1 Η αριθµητική υπολοίπων.............. 10 1.2 Η πολυωνυµική αριθµητική............ 14 1.3 Θεωρία πεπερασµένων οµάδων και σωµάτων.... 17 1.4 Πράξεις
Πρόλογος 1 Μαθηµατικό υπόβαθρο 7 1 Μαθηµατικό υπόβαθρο 9 1.1 Η αριθµητική υπολοίπων.............. 10 1.2 Η πολυωνυµική αριθµητική............ 14 1.3 Θεωρία πεπερασµένων οµάδων και σωµάτων.... 17 1.4 Πράξεις
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 4 : Δειγματοληψία και κβάντιση (Sampling and Quantization) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 4 : Δειγματοληψία και κβάντιση (Sampling and Quantization) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium iv
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Καναλιού. Καναλιού. Προχωρημένα Θέματα Τηλεπικοινωνιών. Κατηγορίες Κωδικών Καναλιού. Τι πετυχαίνει η Κωδ. Καναλιού. Κωδικοποίηση Καναλιού.
 Προχωρημένα Θέματα Τηλεπικοινωνιών Πηγή Δεδομένων Κωδικοποίηση Καναλιού Κώδικας Πηγής Κώδικας Καναλιού Διαμόρφωση Κανάλι Δέκτης Δεδομένων Αποκωδ/ση Πηγής Αποκωδ/ση Καναλιού Αποδιαμόρφωση Κωδικοποίηση Καναλιού
Προχωρημένα Θέματα Τηλεπικοινωνιών Πηγή Δεδομένων Κωδικοποίηση Καναλιού Κώδικας Πηγής Κώδικας Καναλιού Διαμόρφωση Κανάλι Δέκτης Δεδομένων Αποκωδ/ση Πηγής Αποκωδ/ση Καναλιού Αποδιαμόρφωση Κωδικοποίηση Καναλιού
Κωδικοποίηση Πηγής. Δρ. Α. Πολίτης
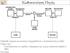 Κωδικοποίηση Πηγής Coder Decoder Μεταξύ πομπού και καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας της πηγής με εναλλακτικά σύμβολα ή λέξεις. Κωδικοποίηση
Κωδικοποίηση Πηγής Coder Decoder Μεταξύ πομπού και καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας της πηγής με εναλλακτικά σύμβολα ή λέξεις. Κωδικοποίηση
Συστήµατα Πολυµέσων Ενδιάµεση Εξέταση: Οκτώβριος 2004
 Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Τεχνικές Μείωσης Διαστάσεων. Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας
 Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Κωδικοποίηση ήχου. Κωδικοποίηση καναλιού φωνής Κωδικοποίηση πηγής φωνής Αντιληπτική κωδικοποίηση Κωδικοποίηση ήχου MPEG
 Κωδικοποίηση ήχου Κωδικοποίηση καναλιού φωνής Κωδικοποίηση πηγής φωνής Αντιληπτική κωδικοποίηση Κωδικοποίηση ήχου MPEG Τεχνολογία Πολυµέσων και Πολυµεσικές Επικοινωνίες 10-1 Κωδικοποίηση καναλιού φωνής
Κωδικοποίηση ήχου Κωδικοποίηση καναλιού φωνής Κωδικοποίηση πηγής φωνής Αντιληπτική κωδικοποίηση Κωδικοποίηση ήχου MPEG Τεχνολογία Πολυµέσων και Πολυµεσικές Επικοινωνίες 10-1 Κωδικοποίηση καναλιού φωνής
Αρχές κωδικοποίησης. Τεχνολογία Πολυµέσων 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
