Στοχαστικές Ανελίξεις
|
|
|
- Παναγιώτα Κυπραίος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες συναρτήσεις του χρόνου. Ένα τυχαίο σήμα μπορεί να θεωρηθεί ότι ανήκει σε μια συλλογή ή σύνολο σημάτων, όπου κάθε σήμα του συνόλου είναι διαφορετικό. Γ. Αθανασιάδου Σε ένα τηλεπικοινωνιακό σύστημα, το λαμβανόμενο σήμα συνήθως αποτελείται από: μια συνιστώσα σήματος πληροφορίας (ormato-bearg sgal μια συνιστώσα τυχαίας παρεμβολής (tererece και από θόρυβο (ose. Μια σημαντική πηγή θορύβου είναι ο θερμικός θόρυβος (thermal ose που προκαλείται από την τυχαία κίνηση των ηλεκτρονίων στους αγωγούς και στις διατάξεις στην είσοδο του δέκτη. Ο θόρυβος είναι ένα τυχαίο σήμα. Η περιγραφή ενός τυχαίου σήματος γίνεται χρησιμοποιώντας τις στατιστικές του ιδιότητες, όπως είναι η μέση ισχύς του τυχαίου σήματος ή η φασματική κατανομή αυτής της μέσης τιμής της ισχύος. Θεωρία Πιθανοτήτων 3 Τα τυχαία σήματα στις τηλεπικοινωνίες έχουν δύο ιδιότητες: / Τα σήματα είναι χρονικές συναρτήσεις που ορίζονται σε κάποιο διάστημα παρατήρησης. / Τα σήματα είναι τυχαία με την έννοια ότι πριν τη διενέργεια ενός πειράματος δεν είναι δυνατό να περιγράψουμε ακριβώς τις κυματομορφές που θα παρατηρηθούν. Ορίζουμε μια στοχαστική ανέλιξη σαν ένα σύνολο χρονικών συναρτήσεων μαζί με έναν πιθανοτικό κανόνα που αποδίδει μία πιθανότητα σε κάθε σημαντικό γεγονός συνδεόμενο με την παρατήρηση μίας από αυτές τις συναρτήσεις. Ένα σύνολο από συναρτήσεις δείγματα: Συνεπώς κάθε δείγμα στο χώρο δειγμάτων είναι μια χρονική συνάρτηση. Έστω στοχαστική ανέλιξη Χ(t που παριστάνεται από το σύνολο των συναρτήσεων δειγμάτων (sample uctos {x j (t}, j,,.,. Ο χώρος δειγμάτων ή το σύνολο που περιλαμβάνει τις χρονικές συναρτήσεις ονομάζεται τυχαία διαδικασία ή στοχαστική ανέλιξη (radom or stochastc process. 4 Η συνάρτηση δείγμα ή κυματομορφή x j (t με πιθανότητα εμφάνησης P(s j, αντιστοιχεί στο δείγμα s j του χώρου δειγμάτων. 5 6
2 Σε κάποια χρονική στιγμή tt, κάθε δείγμα s j του χώρου δειγμάτων έχει συνδεδεμένο με αυτό έναν αριθμό x j (t και μια πιθανότητα P(s j. Το προκύπτον σύνολο αριθμών (t {x j (t } αποτελεί μια τυχαία μεταβλητή (radom varable. Η διαφορά μεταξύ μιας τυχαίας μεταβλητής και μιας στοχαστικής ανέλιξης είναι ότι: για μια τυχαία μεταβλητή η έκβαση ενός πειράματος απεικονίζεται με έναν αριθμό, ενώ για μια στοχαστική ανέλιξη η έκβαση απεικονίζεται με μια κυματομορφή που είναι χρονική συνάρτηση. 7 F (t (x συνάρτηση κατανομής της τυχαίας μεταβλητής (t. Από κοινού συνάρτηση κατανομής (jot dsrtbuto ucto: F (t,(t, (t (x,x,...,x ή αλλιώς F (t (x P((t x,(t x,, (t x Από κοινού συνάρτηση πυκνότητας πιθανότητας του τυχαίου διανύσματος (t: r r x x... x ( ( x F ( ( x r r r t t (μη αρνητική, με συνολικό όγκο ένα r 8 Παράδειγμα: Εύρεση της πιθανότητας να λάβουμε μια συνάρ-τηση δείγμα ή κυματομορφή x(t της στοχαστικής ανέλιξης Χ(t που διέρχεται από ένα σύνολο παραθύρων. Θέλουμε δηλαδή να βρούμε την πιθανότητα του συνδυασμένου γεγονότος: P { a < ( t b },,,..., b b (... r ( ( x r t a a b 3 a 3 r dx dx... dx 9 - Στατικότητα Η στοχαστική ανέλιξη (t είναι αυστηρά στατική (strctly statoary ή στατική με την στενή έννοια (statoary the strct sese αν η από κοινού συνάρτηση πυκνότητας πιθανότητας παραμένει αμετάβλητη σε μετατοπίσεις της αρχής του χρόνου, δηλαδή αν ισχύει η ισότητα: (t (x (t+ (x για κάθε πεπερασμένο σύνολο χρονικών στιγμών {t j }, j,,, για κάθε χρονική μετατόπιση Τ και διάνυσμα x. μη στατικές (ostatoary στοχαστικές ανελίξεις. Παράδειγμα: Απεικόνιση της έννοιας της στατικότητας Έστω σ.α. Χ(t αυστηρά στατική. Μια επίπτωση της στατικότητας είναι ότι η πιθανότητα ένα σύνολο συναρτήσεων δειγμάτων αυτής της διαδικασίας να διέρχεται μέσα από τα παράθυρα του πάνω σχήματος είναι ίση με την πιθανότητα ένα σύνολο συναρτήσεων δειγμάτων να διέρχεται μέσα από τα αντίστοιχα χρονικά μετατοπισμένα παράθυρα του κάτω σχήματος. Σε πολλές πρακτικές περιπτώσεις δεν είναι δυνατό να καθορίσουμε τη συνάρτηση κατανομής μιας στοχαστικής ανέλιξης και περιοριζόμαστε σε μια μερική περιγραφή (partal descrpto της κατανομής, χρησιμοποιώντας τη μέση τιμή, τις συναρτήσεις συσχέτισης και συμμεταβλητότητας. Μέση τιμή: m ( t E[ ( t ] m ( t x ( ( x dx t
3 Συνάρτηση αυτοσυσχέτισης (autocorrelato ucto της στοχαστικής ανέλιξης (t, συναρτήσει δύο χρονικών μεταβλητών t και t : ( t, t E[ ( t ( t ] ( t, t xy ( t ( ( x y, t dxdy, Συνάρτηση αυτομεταβλητότητας (autocovarace ucto της στοχαστικής ανέλιξης (t: K ( t, t E[ ( ( t m ( t ( ( t m ( t ] K ( t, t ( t, t m ( t m ( t Η στοχαστική ανέλιξη (t είναι ευρείας έννοιας στατική (wdesese statoary ή στατική με την ευρεία έννοια (statoary the wde sese αν ικανοποιούνται οι συνθήκες: ( t m m για όλα τα t ( t, t ( t t ( τ ( t, t K ( t t K ( τ K 3 4 όπου τ t t 5 ( τ E[ ( t τ ( τ ] + Ιδιότητες της συνάρτησης αυτοσυσχέτισης μιας στατικής ανέλιξης (t: [ ] ( E ( t ( τ ( τ ( τ ( 6 Απεικόνιση των συναρτήσεων αυτοσυσχέτισης μιας αργά και μιας απότομα ταλαντούμενης στοχαστικής ανέλιξης: 7 Παράδειγμα: Ημιτονική κυματομορφή με τυχαία φάση Έστω ημιτονικό σήμα με τυχαία φάση: ( t cos ( π t + Θ όπου Α και c σταθερές, και Θ τυχαία μεταβλητή ομοιόμορφα κατανεμημένη στο διάστημα εως π, δηλ.:, θ π Θ ( θ π, αλλο ύ Η συνάρτηση αυτοσυσχέτισης της Χ(t είναι: ( τ Ε[ ( t + τ ( t ] Ε cos ( π ( t + τ + Θ cos ( π t + Θ [ ] { Ε[ cos ( 4π t + π τ + Θ ] + Ε[ cos ( π τ ]} π cos π ( 4π t + π τ + θ dθ + cos( π τ 8 3
4 Παράδειγμα: (συνέχεια ( τ cos ( π τ Συναρτήσεις συσχέτισης (crosscorrelato uctos των στοχαστικών ανελίξεων (t και Υ(t: ( t, u E[ ( t ( u ] ( t, u E[ ( t ( u ] Οι στοχαστικές ανελίξεις (t και Υ(t είναι από κοινού στατικές με την ευρεία έννοια όταν: ( t u ( t u, ( t u ( t u ( ( t u t u Η συνάρτηση αυτοσυσχέτισης ημιτονικής κυματομορφής με τυχαία φάση είναι μια άλλη ημιτονική κυματομορφή της ίδιας συχνότητας στο τ-πεδίο αντί στο πεδίο του χρόνου. 9 Πίνακας συσχέτισης (correlato matrx των (t και Υ(t: ( t, u ( t, u ( t, u ( ( t, u t, u Ισχύει: ( τ ( τ x Χρονικήμέσητιμή(tme-averaged mea value της συνάρτησης δείγματος x(t μιας στοχαστικής ανέλιξης (t: x ( t lm x( t Χρονικόμέσοτηςσυνάρτησηςαυτοσυσχέτισης(tme-averaged autocorrelato ucto της συνάρτησης δείγματος x(t μιας στοχαστικής ανέλιξης (t: ( t + τ x( t lm x( t + τ x( t dt lm x( t x( t τ dt dt - Εργοδικότητα Mια στοχαστική ανέλιξη (t λέγεται ότι είναι εργοδική (ergotc process, στην πιο γενική μορφή, αν όλες οι στατιστικές της ιδιότητες μπορούν να καθοριστούν από μία συνάρτηση δείγμα που παριστάνει μια δυνατή εμφάνιση της ανέλιξης. Είναι απαραίτητο για μια στοχαστική ανέλιξη να είναι στατική με τη στενή έννοια για να είναι εργοδική, αλλά το αντίθετο δεν είναι πάντα αληθές. 3 - Εργοδικότητα Μια στοχαστική ανέλιξη (t είναι εργοδική ως προς τη μέση τιμή (ergodc the mea αν, με πιθανότητα ένα, ισχύει: x ( t lm x( t dt m Μια στοχαστική ανέλιξη (t είναι εργοδική ως προς τη συνάρτηση αυτοσυσχέτισης (ergodc the autocorrelato ucto αν, με πιθανότητα ένα, ισχύει: x + ( t τ x( t lm x( t + τ x( t dt ( τ 4 4
5 - Εργοδικότητα Εκτός από συγκεκριμένες απλές περιπτώσεις, είναι συνήθως πολύ δύσκολο να αποδείξουμε αν μια στοχαστική ανέλιξη ικανοποιεί τα κριτήρια για την εργοδικότητα. Συχνά αναγκαζόμαστε να θεωρήσουμε τη φυσική προέλευση της στοχαστικής ανέλιξης και συνεπώς να κάνουμε μια κατά κάποιο τρόπο διαισθητική κρίση για το κατά πόσο είναι λογικό να εναλλάξουμε το χρονικό μέσο με το μέσο συνόλου. 5 Παράδειγμα: Ημιτονική κυματομορφή με τυχαία φάση (συνέχεια Έστω το ημιτονικό σήμα με τυχαία φάση:, ( t cos ( π t + Θ Θ ( θ π, Η μέση τιμή της σ.α. Χ(t είναι: π Α m Αcos Θ π θ π αλλο ύ ( π t + θ ( θ dθ cos( π t + θ dθ Η συνάρτηση αυτοσυσχέτισης της Χ(t: ( τ cos ( π τ Έστω x(t μια συνάρτηση δείγμα της σ.α. (t: x ( t ( t Παράδειγμα: (συνέχεια Η χρονική μέση τιμή της x(t είναι: x( t lm cos ( + π t θ dt O χρονικός μέσος της συνάρτησης αυτοσυσχέτισης είναι: x ( t + τ x( t lm lm cos ( π ( t + τ + θ cos ( π t + θ [ cos ( π τ + cos ( 4π t + π t + θ ] ( π τ 6 7 cos π + θ cos dt dt Η σ.α. είναι συνεπώς εργοδική τόσο ως προς τη μέση τιμή όσο και ως προς τη συνάρτηση αυτοσυσχέτισης. m Μετάδοση Στοχαστικής Ανελίξης Μέσω Γραμμικού Φίλτρου Έστω ότι στατική με την ευρεία έννοια στοχαστική ανέλιξη (t εφαρμόζεται σαν είσοδος σε ΓΧΑ φίλτρο με κρουστική απόκριση h(t, παράγοντας μια στοχαστική ανέλιξη (t στην έξοδο του φίλτρου. m ( t E[ ( t ] E h( τ Χ( t τ dτ Δεδομένου ότι η αναμενόμενη τιμή Ε[(t] είναι πεπερασμένη για όλα τα t και το σύστημα είναι σταθερό: ( t h( τ E[ Χ( t τ ] dτ h( τ m ( t τ dτ m h( τ dτ m Μετάδοση Στοχαστικής Ανελίξης Μέσω Γραμμικού Φίλτρου Συνάρτηση αυτοσυσχέτισης της στοχαστικής ανέλιξης εξόδου (t: ( t, u E[ ( t ( u ] E h( τ Χ( t τ dτ h( τ Χ( u τ dτ m H ( 8 9 Δεδομένου ότι το Ε[ (t] είναι πεπερασμένο για όλα τα t και το σύστημα είναι σταθερό: ( t, u h( τ dτ h( τ dτ E[ Χ( t τ Χ( u τ ] ( τ dτ h( τ dτ ( t τ u h, τ Μετάδοση Στοχαστικής Ανελίξης Μέσω Γραμμικού Φίλτρου Δεδομένου ότι η (t είναι στατική, η συνάρτηση αυτοσυσχέτισής της είναι συνάρτηση μόνο της διαφοράς μεταξύ των χρόνων παρατήρησης: dτ dτ ( τ h( τ h( τ ( τ τ + τ Άρα, αν η είσοδος σε ένα σταθερό γραμμικό χρονικά αμετάβλητο φίλτρο είναι μία στατική με την ευρεία έννοια στοχαστική ανέλιξη, τότε η έξοδος του φίλτρου είναι επίσης μία στατική με την ευρεία έννοια στοχαστική ανέλιξη. 3 5
6 E Μετάδοση Στοχαστικής Ανελίξης Μέσω Γραμμικού Φίλτρου dτ dτ ( τ h( τ h( τ ( τ τ + τ [ ( t ] ( τ h( τ h( τ ( τ + τ dτ dτ ct Η μέση τετραγωνική τιμή της στοχαστικής ανέλιξης εξόδου Υ(t είναι μία σταθερά. 3 Γ. Αθανασιάδου Πυκνότητα Φάσματος Ισχύος Χαρακτηρισμός των στοχαστικών ανελίξεων στο πεδίο της συχνότητας. E [ ( t ] ( τ h ( τ h( τ ( τ + τ d τ d τ H ( exp ( j π τ d h( τ ( τ + τ dτ d τ H ( d h( τ d τ ( τ + τ exp ( j π τ d τ H ( d h( τ exp ( j π τ d τ ( τ exp ( j π τ d τ H * ( [ ( t ] H ( d ( τ exp ( j π τ E d τ 3 Πυκνότητα Φάσματος Ισχύος ( ( τ exp( j πτ dτ x ( πυκνότητα φάσματος ισχύος (power spectral desty ή φάσμα ισχύος (power spectrum (Watt/Hertz E [ ( t ] H ( ( d Η μέση τετραγωνική τιμή της εξόδου ενός σταθερού, γραμμικού, χρονικά αμετάβλητου (ΓΧΑ φίλτρου σε απόκριση στατικής με την ευρεία έννοια στοχαστικής ανέλιξης είναι ίση με το ολοκλήρωμα πάνω από όλες τις συχνότητες της πυκνότητας φάσματος ισχύος της στοχαστικής ανέλιξης εισόδου πολλαπλασιασμένης με το τετράγωνο του μέτρου της 33 συνάρτησης μεταφοράς του φίλτρου. Πυκνότητα Φάσματος Ισχύος Ιδιότητες της πυκνότητας φάσματος ισχύος μιας στατικής με την ευρεία έννοια στοχαστικής ανέλιξης: Η πυκνότητα φάσματος ισχύος x ( και η συνάρτηση αυτοσυσχέτισης x (τ μιας στατικής με την ευρεία έννοια σ.α. αποτελούν ζευγάρι ΜΣ Fourer. ( ( τ ( ( τ dτ E ( t [ ] ( ( d ( ( ( 34 Παράδειγμα: Ημιτονική κυματομορφή με τυχαία φάση Έστω το ημιτονικό σήμα με τυχαία φάση: (συνέχεια, θ π ( t cos ( π t + Θ Θ ( θ π, αλλο ύ Η συνάρτηση αυτοσυσχέτισης της Χ(t: ( τ cos ( π τ Η πυκνότητα φάσματος ισχύος της σ.α Χ(t (ΜΣ Fourer της x (τ: + 4 ( [ δ ( + δ ( ] Επαλήθευσε τη σχέση: ( ( d 35 Παράδειγμα: Μίξη στοχαστικής ανέλιξης με ημιτονική κυματομορφή Θέλουμε να βρούμε την πυκνότητα φάσματος ισχύος της σ.α.: ( t ( t cos ( π t + Θ Η συνάρτηση αυτοσυσχέτισης της Υ(t: ( τ Ε ( t + τ ( t [ ] Ε[ ( t + τ cos ( π ( t + τ + Θ ( t cos ( π t + Θ ] Ε[ ( t + τ ( t ] Ε[ cos ( π ( t + τ + Θ cos ( π t + Θ ] ( ( τ Ε[ cos ( 4π t + π τ + Θ + cos ( π τ ] ( ( τ cos ( π τ Η πυκνότητα φάσματος ισχύος της σ.α Υ(t (ΜΣ Fourer της Υ (τ: ( [ ( ( ] 36 6
7 Πυκνότητα Φάσματος Ισχύος Σχέση μεταξύ των πυκνοτήτων φάσματος ισχύος των στοχαστικών ανελίξεων εισόδου και εξόδου: ( H ( ( Η πυκνότητα φάσματος ισχύος της εξόδου ισούται με την πυκνότητα φάσματος ισχύος της εισόδου πολλαπλασιασμένης με το τετράγωνο του μέτρου της συνάρτησης μεταφοράς του φίλτρου. 37 Πυκνότητα Φάσματος Ισχύος - Ετεροφασματικές πυκνότητες Οι ετεροφασματικές πυκνότητες παρέχουν ένα μέτρο της συσχέτισης συχνότητας μεταξύ δύο στοχαστικών ανελίξεων. Έστω Χ(t και Υ(t δύο από κοινού στατικές με την ευρεία έννοια στοχαστικές ανελίξεις, με συναρτήσεις συσχέτισης (τ και (τ. Οι ετεροφασματικές πυκνότητες (cross-spectral destes ( και ( είναι οι ΜΣ Fourer των αντιστοίχων συναρτήσεων συσχέτισης. * ( ( ( 38 Παράδειγμα: Άθροισμα στοχαστικών ανελίξεων Έστω οι σ.α. (t και Υ(t με μηδενικές μέσες τιμές και η καθεμία στατική με την ευρεία έννοια. Η σ.α. του αθροίσματος είναι: ( t ( t ( t Z + Η συνάρτηση αυτοσυσχέτισης της Ζ(t: ( t, u Ε[ Z ( t Z ( u ] ( t, u + ( t, u + ( t, u + ( t u Z, Ορίζοντας τ t-u: Z ( τ ( τ + ( τ + ( τ ( τ + Η πυκνότητα φάσματος ισχύος της σ.α Z(t (ΜΣ Fourer της Z (τ: Z ( τ ( τ + ( τ + ( τ ( τ + Όταν οι (t και Υ(t είναι ασυσχέτιστες: Z ( τ ( τ ( τ + 39 Στοχαστική Ανέλιξη Gauss g ( t ( t H ονομάζεται γραμμική συναρτησιακή (lear uctoal της Χ(t. H ανέλιξη (t είναι ανέλιξη Gauss αν κάθε γραμμική συναρτησιακή της (t είναι τυχαία μεταβλητή Gauss. H τιμή της τυχαίας μεταβλητής Υ εξαρτάται από τη συνάρτηση όρισμα g(t(t στο διάστημα παρατήρησης ως Τ. Το πεδίο τιμών μιας συναρτησιακής είναι ένα σύνολο ή χώρος επιτρεπτών συναρτήσεων παρά μια περιοχή ενός χώρου συντεταγμένων. dt 4 Στοχαστική Ανέλιξη Gauss Η τυχαία μεταβλητή Υ έχει κατανομή Gauss αν η συνάρτηση πυκνότητας πιθανότητας αυτής έχει τη μορφή: ( y m y ( y exp πσ Υ σ Υ Mια τυχαία μεταβλητή με κατανομή Gauss είναι πλήρως καθορισμένη αν καθορίσουμε το μέσο όρο της και τη μεταβλητότητά της. (θεώρημα κεντρικού ορίου Κανονικοποιημένη κατανομή Gauss: 4 Στοχαστική Ανέλιξη Gauss Iδιότητες μιας ανέλιξης Gauss: Ιδιότητα : Εάν μια ανέλιξη Gauss (t εφαρμόζεται σε γραμμικό, σταθερό φίλτρο, τότε η στοχαστική ανέλιξη Υ(t που εμφανίζεται στην έξοδο του φίλτρου, είναι επίσης Gauss. Ιδιότητα : Θεωρείστε ένα σύνολο τυχαίων μεταβλητών ή δειγμάτων Χ(t, Χ(t,, Χ(t, που λαμβάνονται παρατηρώντας μία στοχαστική ανέλιξη Χ(t τις χρονικές στιγμές t, t,, t. Εάν η ανέλιξη Χ(t είναι Gauss, τότε αυτό το σύνολο των τυχαίων μεταβλητών είναι από κοινού Gauss για κάθε, με τη -διάστατη από κοινού συνάρτηση πυκνότητας πιθανότητας να είναι πλήρως καθορισμένη από το σύνολο των μέσων τιμών m (t E[(t ],,,, και το σύνολο των συναρτήσεων αυτομεταβλητότητας Κ x (t, t E[((t -m (t ((t -m (t ],,,,. 4 7
8 Στοχαστική Ανέλιξη Gauss Ιδιότητα 3: Εάν η ανέλιξη Gauss είναι στατική με την ευρεία έννοια, τότε η ανέλιξη είναι επίσης στατική με τη στενή έννοια. Ιδιότητα 4: Εάν το σύνολο των τυχαίων μεταβλητών Χ(t, Χ(t,, Χ(t, που λαμβάνονται με δειγματοληψία της στοχαστικής ανέλιξης Gauss Χ(t τις χρονικές στιγμές t, t,, t, είναι ασυσχέτιστες, δηλαδή E[((t -m (t ((t -m (t ], τότε αυτές οι τυχαίες μεταβλητές είναι στατικά ανεξάρτητες. 43 Θόρυβος Ο όρος θόρυβος (ose χρησιμοποιείται για να προσδιορίσει τις ανεπιθύμητες κυματομορφές που τείνουν να ενοχλούν τη μετάδοση και την επεξεργασία των σημάτων στα τηλεπικοινωνιακά συστήματα και πάνω στις οποίες δεν έχουμε πλήρη έλεγχο. Θόρυβος βολής Ο θόρυβος βολής εμφανίζεται στις ηλεκτρονικές διατάξεις εξ αιτίας της διακριτής φύσης της ροής του ρεύματος στη διάταξη. Έχει κατανομή Gauss με μηδενική μέση τιμή. 44 Θερμικός θόρυβος Θόρυβος Ο θερμικός θόρυβος είναι το όνομα που δίνεται στον ηλεκτρικό θόρυβο που εμφανίζεται κατά την τυχαία κίνηση των ηλεκτρονίων σε ένα αγωγό. Η μέση τετραγωνική τιμή της τάσης/έντασης θερμικού θορύβου που εμφανίζεται στα άκρα αντίστασης, μετρούμενη σε εύρος ζώνης Δ hertz δίνεται από: [ V ] 4 volt E Δ [ I ] E[ ] E V σταθερά Boltzma.38x -3 joule ανά βαθμό Kelv Από το θεώρημα κεντρικού ορίου συνεπάγεται ότι ο θερμικός θόρυβος έχει κατανομή Gauss με μηδενική μέση τιμή. 45 Λευκός Θόρυβος Λευκός Θόρυβος Λευκός Θόρυβος Η ανάλυση θορύβου στα τηλεπικοινωνιακά συστήματα βασίζεται σε μια ιδανική μορφή του θορύβου που καλείται λευκός θόρυβος (whte ose, η πυκνότητα φάσματος ισχύος του οποίου είναι ανεξάρτητη της συχνότητας λειτουργίας. ( W Ο παράγοντας / έχει περιληφθεί για να δείξει ότι το μισό της ισχύος συνδέεται με θετική συχνότητα και το μισό με αρνητική. 46 Η παράμετρος Ν (Watt/Hertz μπορεί να εκφραστεί σαν: σταθερά Boltzma e e Ισοδύναμη θερμοκρασία θορύβου (equvalet ose temperature στο δέκτη, δηλαδή η θερμοκρασία στην οποία πρέπει να διατηρηθεί μια αντίσταση θορύβου έτσι ώστε, συνδέοντας την αντίσταση στην είσοδο μιας χωρίς θόρυβο μορφής του συστήματος, να παράγει την ίδια διαθέσιμη ισχύ θορύβου στην έξοδο του συστήματος με αυτήν που παράγεται από όλες τις πηγές θορύβου στο πραγματικό σύστημα. Συνάρτηση αυτοσυσχέτισης του λευκού θορύβου: ( τ δ ( τ W Επομένως, οποιοδήποτε δύο διαφορετικά δείγματα λευκού θορύβου, ανεξάρτητα από το πόσο κοντά στο χρόνο λαμβάνονται, είναι ασυσχέτιστα. Αν ο λευκός θόρυβος w(t είναι επίσης Gauss, τότε τα δύο δείγματα είναι στατιστικά ανεξάρτητα. Η 47 e εξαρτάται μόνο από τις παραμέτρους του συστήματος. 48 8
9 Λευκός Θόρυβος Λευκός Θόρυβος Παράδειγμα: Ιδανικός βαθυπερατός λευκός θόρυβος Χαρακτηριστικές λευκού θορύβου: Ο λευκός θόρυβος έχει άπειρη ισχύ, και σαν τέτοιος δεν είναι φυσικά πραγματοποιήσιμος. Όσο όμως το εύρος ζώνης μιας στοχαστικής ανέλιξης θορύβου στην είσοδο ενός συστήματος είναι αισθητά μεγαλύτερο από αυτό του ίδιου του συστήματος, τότε μπορούμε να θεωρήσουμε το λευκό θόρυβο σα μοντέλο της ανέλιξης θορύβου στην είσοδο. Έστω λευκός θόρυβος Gauss w(t μηδενικής μέσης τιμής και πυκνότητας φάσματος ισχύος Ν / εφαρμόζεται σε ιδανικό βαθυπερατό φίλτρο εύρους ζώνης Β και απόκρισης πλάτους στη ζώνη διέλευση ίση με ένα. Η θόρυβος (t στην έξοδο έχει τις εξής χαρακτηριστικές: Παράδειγμα: (συνέχεια Αφού η είσοδος είναι Gauss, και η έξοδος του φίλτρου είναι Gauss. Αν λαμβάνονται δείγματα του (t με ρυθμό Β φορές ανά δευτερόλεπτο, τα δείγματα είναι ασυσχέτιστα, και όντας Gauss είναι και στατιστικά ανεξάρτητα. Συνεπώς η από κοινού συνάρτηση πυκνότητας πιθανότητας του συνόλου αυτών των δειγμάτων είναι ίση με το γινόμενο των ξεχωριστών συναρτήσεων πυκνότητας πιθανότητας. (Σημειώστε ότι κάθε τέτοιο δείγμα θορύβου έχει μηδενική μέση τιμή και μεταβλητότητα Ν Β. Στην είσοδο του δέκτη πρακτικών τηλεπικοινωνιακών συστημάτων συνήθως υπάρχει ένα φίλτρο στενής ζώνης, δηλαδή η συχνότητα στο μέσο της ζώνης είναι μεγάλη συγκρινόμενη με το εύρος ζώνης του. Η στοχαστική ανέλιξη θορύβου που εμφανίζεται στην έξοδο ενός τέτοιου φίλτρου ονομάζεται θόρυβος στενής ζώνης. H συνάρτηση δείγμα (t μιας τέτοιας ανέλιξης εμφανίζεται περίπου παρόμοια με μια ημιτονική κυματομορφή συχνότητας c, που κυματώνεται αργά τόσο σε φάση όσο και σε πλάτος. Ν ( - c -Β - c - c +Β c -Β c c +Β Συνάρτηση δείγμα θορύβου στενής ζώνης: (t t 5 53 /Β / c 54 9
10 Έστω θόρυβος (t που παράγεται στην έξοδο ενός φίλτρου στενής ζώνης, σε απόκριση της συνάρτησης δείγματος w(t μιας ανέλιξης λευκού θορύβου Gauss με m w και w (. Θεωρούμε ότι το φάσμα ισχύος του (t είναι κεντραρισμένο γύρω από την c : ~ + ( t ( t + jˆ ( t ( t ( t exp( jπ t + Αναπαράσταση του θορύβου στενής ζώνης (t σε κανονική μορφή: ( t ( t cos( π t ( t s ( π t Ιδιότητα : Εάν ο θόρυβος στενής ζώνης (t, έχει μηδενική μέση τιμή, τότε η (t και η (t έχουν επίσης μηδενική μέση τιμή. ( H ( ~ ( t ( t j ( t c + s Ιδιότητα : Εάν ο θόρυβος στενής ζώνης (t είναι Gauss, τότε η (t και η (t είναι από κοινού Gauss. Οποιοσδήποτε θόρυβος στενής ζώνης που συναντιέται στην πράξη μπορεί να μοντελοποιηθεί εφαρμόζοντας λευκό θόρυβο σε κατάλληλο φίλτρο. 55 ( t ( t cos ( π t + ˆ ( t s ( π t ( t ˆ ( t cos( π t ( t s ( π t 56 Ιδιότητα 3: Εάν ο θόρυβος στενής ζώνης (t είναι στατικός με την ευρεία έννοια, τότε η (t και η (t είναι από κοινού στατικές με την ευρεία έννοια. 57 Ιδιότητα 4: Η (t και η (t έχουν την ίδια πυκνότητα φάσματος ισχύος: ( (, ( + ( +, αλλού B B Ιδιότητα 6: Οι ετεροφασματικές πυκνότητες των (t και (t είναι καθαρά φανταστικές: ( ( j, [ ( + ( ], αλλού B B Παράδειγμα: Ιδανικός ζωνοπερατός λευκός θόρυβος Έστω λευκός θόρυβος Gauss w(t μηδενικής μέσης τιμής και πυκνότητας φάσματος ισχύος Ν / εφαρμόζεται σε ιδανικό ζωνοπερατό φίλτρο εύρους ζώνης Β, κεντρική συχνότητα και απόκρισης πλάτους στη ζώνη διέλευση ίση με ένα. Ιδιότητα 5: Εάν ο θόρυβος στενής ζώνης (t, έχει μηδενική μέση τιμή, τότε η (t και η (t έχουν την ίδια μεταβλητότητα με αυτή του (t. 58 Ιδιότητα 7: Εάν θόρυβος στενής ζώνης (t είναι Gauss με μηδενική μέση τιμή και η πυκνότητα φάσματος ισχύος ( αυτού είναι τοπικά συμμετρική γύρω από την ± τότε η (t και η (t είναι στατιστικά ανεξάρτητες. 59 6
11 Παράδειγμα: (συνέχεια + B ( τ exp( jπτ d + exp( jπτ B Bs c ( Bτ cos( π τ + B B d Από την πυκνότητα φάσματος ισχύος της συμφασικής και της ορθογωνικής υπολογίζεται εύκολα ότι: ( τ ( τ Bsc( Bτ 6 Αναπαράσταση του θορύβου στενής ζώνης συναρτήσει της περιβάλλουσας και της φάσης: ( t r( t cos[ π t + ( t ] ψ r [ ] c + s ( t ( t ( t ψ ( t ta ( t ( s c t 6 Οι τυχαίες μεταβλητές και Ψ είναι στατιστικά ανεξάρτητες. Η Ψ είναι ομοιόμορφα κατανεμημένη μέσα στο διάστημα ως π: Ψ ( ψ, π, ψ π αλλο ύ Η συνάρτηση πυκνότητας πιθανότητας της είναι: ( r r r r σ exp, σ, αλλο ύ 63 Για ευκολία στη γραφική παράσταση, έστω: υr/σ και V (υσ ( Κανονικοποιημένη κατανομή aylegh: V υ υ exp, ( υ υ, αλλού 64
Στοχαστικές Ανελίξεις
 Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Ντετερμινιστικά Σήματα - Τυχαία Σήματα Ταξινόμηση των σημάτων ανάλογα με τη βεβαιότητα όσο αφορά την τιμή τους κάθε χρονική στιγμή. Τα ντετερμινιστικά σήματα μπορούν να αναπαρασταθούν σαν πλήρως καθορισμένες
Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου
 Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Στοχαστικές Διαδικασίες 2 Στοχαστική Διαδικασία Στοχαστικές Ανελίξεις Α. Αλεξίου 3 Στοχαστική Διαδικασία ως συλλογή από συναρτήσεις χρόνου
Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Στοχαστικές Διαδικασίες 2 Στοχαστική Διαδικασία Στοχαστικές Ανελίξεις Α. Αλεξίου 3 Στοχαστική Διαδικασία ως συλλογή από συναρτήσεις χρόνου
h(t τ k ) X (t) = X (t) = (shot noise). 3/28 4/28
 Θόρυβος Στοχαστικά συστήματα & επικοινωνίες 6 Δεκεμβρίου 2012 1/28 2/28 Ο θόρυβος βολής εμφανίζεται στις ηλεκτρονικές συσκευές, όπως οι δίοδοι και τα τρανζίστορ, εξαιτίας της διακριτής φύσης της ροής του
Θόρυβος Στοχαστικά συστήματα & επικοινωνίες 6 Δεκεμβρίου 2012 1/28 2/28 Ο θόρυβος βολής εμφανίζεται στις ηλεκτρονικές συσκευές, όπως οι δίοδοι και τα τρανζίστορ, εξαιτίας της διακριτής φύσης της ροής του
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις Άσκηση σε Στοχαστική Ανέλιξη Poisso Ασκήσεις 5.9, 5.1, 5.19 Άσκηση σε Στοχαστική
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις Άσκηση σε Στοχαστική Ανέλιξη Poisso Ασκήσεις 5.9, 5.1, 5.19 Άσκηση σε Στοχαστική
Δέκτες ΑΜ ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ CW
 ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ Στα συστήματα διαμόρφωσης (otiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (output igl-tooie rtio). λόγος σήματος προς
ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ Στα συστήματα διαμόρφωσης (otiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (output igl-tooie rtio). λόγος σήματος προς
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ. () t. Διαμόρφωση Γωνίας. Περιεχόμενα:
 ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ Περιεχόμενα: Διαμόρφωση Φάσης (PM) και Συχνότητας (FM) Διαμόρφωση FM από Απλό Τόνο - - Στενής Ζώνης - - Ευρείας Ζώνης - - από Πολλούς Τόνους Εύρος Ζώνης Μετάδοσης Κυματομορφών FM Απόκριση
ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ Περιεχόμενα: Διαμόρφωση Φάσης (PM) και Συχνότητας (FM) Διαμόρφωση FM από Απλό Τόνο - - Στενής Ζώνης - - Ευρείας Ζώνης - - από Πολλούς Τόνους Εύρος Ζώνης Μετάδοσης Κυματομορφών FM Απόκριση
MAJ. MONTELOPOIHSH II
 MAJ MONTELOPOIHSH II ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 009 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΙV Οι ασκήσεις είναι από το βιβλίο του Simon Haykin Θα ακολουθήσει ακόμη ένα φυλλάδιο τις επόμενες μέρες Άσκηση
MAJ MONTELOPOIHSH II ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 009 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΙV Οι ασκήσεις είναι από το βιβλίο του Simon Haykin Θα ακολουθήσει ακόμη ένα φυλλάδιο τις επόμενες μέρες Άσκηση
Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου
 Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου alexiou@unipi.gr 1 Ενότητες Μαθήματος Ενότητα 1 Εισαγωγή Ορισμός Στοχαστικών ανελίξεων Στατιστική Στοχαστικών Διαδικασιών Στασιμότητα Εργοδικότητα Ενότητα 2 Διαδικασίες
Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου alexiou@unipi.gr 1 Ενότητες Μαθήματος Ενότητα 1 Εισαγωγή Ορισμός Στοχαστικών ανελίξεων Στατιστική Στοχαστικών Διαδικασιών Στασιμότητα Εργοδικότητα Ενότητα 2 Διαδικασίες
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3 5.6: Μέση Τιμή, Συναρτήσεις Συσχέτισης & Συνδιασποράς 5.7: Μετάδοση Στοχαστικής
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3 5.6: Μέση Τιμή, Συναρτήσεις Συσχέτισης & Συνδιασποράς 5.7: Μετάδοση Στοχαστικής
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3 5.6: Μέση Τιμή, Συναρτήσεις Συσχέτισης (Correlation) & Συνδιασποράς (Covariance)
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 3 5.6: Μέση Τιμή, Συναρτήσεις Συσχέτισης (Correlation) & Συνδιασποράς (Covariance)
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5 5.10: Θόρυβος (Πηγές Θορύβου, Κατανομή Poisson, Λευκός Θόρυβος, Ισοδύναμο
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5 5.10: Θόρυβος (Πηγές Θορύβου, Κατανομή Poisson, Λευκός Θόρυβος, Ισοδύναμο
Δέκτες ΑΜ. Υπερετερόδυνος (superheterodyne) δέκτης
 ΘΟΡΥΒΟ Ε ΔΙΑΜΟΡΦΩΗ τα συστήματα διαμόρφωσης (oiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (oupu igl-ooie rio). λόγος σήματος προς θόρυβο στην
ΘΟΡΥΒΟ Ε ΔΙΑΜΟΡΦΩΗ τα συστήματα διαμόρφωσης (oiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (oupu igl-ooie rio). λόγος σήματος προς θόρυβο στην
Διαμόρφωση Γωνίας. Η διαμόρφωση γωνίας (angle modulation) είναι ένας. Έχει καλύτερη συμπεριφορά ως προς το θόρυβο και την
 ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ Περιεχόμενα: Διαμόρφωση Φάσης (PM) και Συχνότητας (FM) Διαμόρφωση FM από Απλό Τόνο - - Στενής Ζώνης - - Ευρείας Ζώνης - - από Πολλούς Τόνους Απόκριση Γραμμικών Φίλτρων σε Κυματομορφές
ΔΙΑΜΟΡΦΩΣΗ ΓΩΝΙΑΣ Περιεχόμενα: Διαμόρφωση Φάσης (PM) και Συχνότητας (FM) Διαμόρφωση FM από Απλό Τόνο - - Στενής Ζώνης - - Ευρείας Ζώνης - - από Πολλούς Τόνους Απόκριση Γραμμικών Φίλτρων σε Κυματομορφές
Αναλογικές και Ψηφιακές Επικοινωνίες
 Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5 5.10 Θόρυβος (Noise) καθ. Βασίλης Μάγκλαρης maglaris@etmode.tua.gr www.etmode.tua.gr
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5 5.10 Θόρυβος (Noise) καθ. Βασίλης Μάγκλαρης maglaris@etmode.tua.gr www.etmode.tua.gr
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η Έννοια της τυχαίας Διαδικασίας Η έννοια της τυχαίας διαδικασίας βασίζεται στην επέκταση
Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Η Έννοια της τυχαίας Διαδικασίας Η έννοια της τυχαίας διαδικασίας βασίζεται στην επέκταση
Σήματα και Συστήματα. Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
Σήματα και Συστήματα Διάλεξη 6: Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ανάλυση Σημάτων σε Ανάπτυγμα Σειράς Fourier 1. Ανάπτυγμα σήματος σε Σειρά Fourier
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. Χρόνου (Ι)
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourier µιας συνάρτησης χωρίς να καταφεύγουµε στην εξίσωση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουµε εύκολα τον αντίστροφο Μετασχηµατισµό Fourier µιας συνάρτησης χωρίς να καταφεύγουµε στην εξίσωση ανάλυσης. Υπολογίζουµε εύκολα την απόκριση
Άσκηση 1: Λύση: Για το άθροισμα ισχύει: κι επειδή οι μέσες τιμές των Χ και Υ είναι 0: Έτσι η διασπορά της Ζ=Χ+Υ είναι:
 Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier 2 Αθανάσιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier 2 Αθανάσιος
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου
 Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Πιθανότητες & Τυχαία Σήματα. Διγαλάκης Βασίλης
 Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Τυχαία Σήματα Γενίκευση τυχαίων διανυσμάτων Άπειρο σύνολο πιθανά αριθμήσιμο από τυχαίες μεταβλητές Παραδείγματα τυχαίων σημάτων: Τηλεπικοινωνίες: Σήμα πληροφορίας
Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Τυχαία Σήματα Γενίκευση τυχαίων διανυσμάτων Άπειρο σύνολο πιθανά αριθμήσιμο από τυχαίες μεταβλητές Παραδείγματα τυχαίων σημάτων: Τηλεπικοινωνίες: Σήμα πληροφορίας
Πιθανότητες & Τυχαία Σήματα. Διγαλάκης Βασίλης
 Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Στατικές (Στάσιμες) Διαδικασίες Στατική (Stationary) ορίζεται η διαδικασία της οποίας οι στατιστικές ιδιότητες δεν μεταβάλλονται με την πάροδο του χρόνου.
Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Στατικές (Στάσιμες) Διαδικασίες Στατική (Stationary) ορίζεται η διαδικασία της οποίας οι στατιστικές ιδιότητες δεν μεταβάλλονται με την πάροδο του χρόνου.
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 4
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 4 5.9 Η Στοχαστική Ανέλιξη Gauss (οι διαφάνειες ακολουθούν διαφορετική
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 4 5.9 Η Στοχαστική Ανέλιξη Gauss (οι διαφάνειες ακολουθούν διαφορετική
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 2: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Τυχαίες Διαδικασίες: Ορισμοί, Μέσες τιμές συνόλου (Ensemble averages),
Συστήματα Επικοινωνιών Ενότητα 2: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Τυχαίες Διαδικασίες: Ορισμοί, Μέσες τιμές συνόλου (Ensemble averages),
Επομένως το εύρος ζώνης του διαμορφωμένου σήματος είναι 2.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΠΛΗ ΓΙΑ ΤΙΣ ΕΞΕΤΑΣΕΙΣ ΘΕΜΑ Το φέρον σε ένα σύστημα DSB διαμόρφωσης είναι c t A t μηνύματος είναι το m( t) sin c( t) sin c ( t) ( ) cos 4 c και το σήμα. Το διαμορφωμένο σήμα διέρχεται
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Κεφάλαιο 1 ο. Βασικά στοιχεία των Κυκλωμάτων
 Κεφάλαιο 1 ο Βασικά στοιχεία των Κυκλωμάτων Ένα ηλεκτρικό/ηλεκτρονικό σύστημα μπορεί εν γένει να παρασταθεί από ένα κυκλωματικό διάγραμμα ή δικτύωμα, το οποίο αποτελείται από στοιχεία δύο ακροδεκτών συνδεδεμένα
Κεφάλαιο 1 ο Βασικά στοιχεία των Κυκλωμάτων Ένα ηλεκτρικό/ηλεκτρονικό σύστημα μπορεί εν γένει να παρασταθεί από ένα κυκλωματικό διάγραμμα ή δικτύωμα, το οποίο αποτελείται από στοιχεία δύο ακροδεκτών συνδεδεμένα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Θ.Ε. ΠΛΗ22 ( ) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ #1 ΑΠΑΝΤΗΣΕΙΣ
 Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Θ.Ε. ΠΛΗ (0-3) ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ # ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Στόχος της άσκησης είναι η εξοικείωση με γραφικές παραστάσεις βασικών σημάτων και πράξεις, καθώς και τον υπολογισμό ΜΣ Fourier βασικών σημάτων με τη χρήση
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 1 Oct 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 4 η Γεωμετρική Αναπαράσταση
1 Oct 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 4 η Γεωμετρική Αναπαράσταση
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 2
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5.4: Στατιστικοί Μέσοι Όροι 5.5 Στοχαστικές Ανελίξεις (Stochastic Processes)
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 5.4: Στατιστικοί Μέσοι Όροι 5.5 Στοχαστικές Ανελίξεις (Stochastic Processes)
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Εισαγωγή στη Σχεδίαση RF Κυκλωμάτων
 Εισαγωγή στη Σχεδίαση F Κυκλωμάτων Κεφάλαιο,.3 Βασικές έννοιες Σχεδίασης F Κυκλωμάτων Σωτήριος Ματακιάς, 0-3, Σχεδίαση Τηλεπικοινωνιακών LI Κυκλωμάτων, Κεφάλαιο /34 Φασματική πυκνότητα ισχύος Power pectral
Εισαγωγή στη Σχεδίαση F Κυκλωμάτων Κεφάλαιο,.3 Βασικές έννοιες Σχεδίασης F Κυκλωμάτων Σωτήριος Ματακιάς, 0-3, Σχεδίαση Τηλεπικοινωνιακών LI Κυκλωμάτων, Κεφάλαιο /34 Φασματική πυκνότητα ισχύος Power pectral
HY:433 Σχεδίαση Αναλογικών/Μεικτών και Υψισυχνών Κυκλωμάτων
 HY:433 Σχεδίαση Αναλογικών/Μεικτών και Υψισυχνών Κυκλωμάτων «Ηλεκτρικός Θόρυβος» Φώτης Πλέσσας fplessas@e-ce.uth.gr Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Δομή Παρουσίασης Εισαγωγή Στατιστικά Χαρακτηριστικά
HY:433 Σχεδίαση Αναλογικών/Μεικτών και Υψισυχνών Κυκλωμάτων «Ηλεκτρικός Θόρυβος» Φώτης Πλέσσας fplessas@e-ce.uth.gr Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Δομή Παρουσίασης Εισαγωγή Στατιστικά Χαρακτηριστικά
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourier μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης.
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourir μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης. Υπολογίζουμε εύκολα την απόκριση
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Υπολογίζουμε εύκολα τον αντίστροφο Μετασχηματισμό Fourir μιας συνάρτησης χωρίς να καταφεύγουμε στην εξίσωση ανάλυσης. Υπολογίζουμε εύκολα την απόκριση
Σήματα και Συστήματα. Διάλεξη 10: Γραμμικά Φίλτρα. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
Σήματα και Συστήματα Διάλεξη 10: Γραμμικά Φίλτρα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Γραμμικά Φίλτρα 1. Ιδανικά Γραμμικά Φίλτρα Ιδανικό Κατωδιαβατό Φίλτρο Ιδανικό Ανωδιαβατό Φίλτρο Ιδανικό Ζωνοδιαβατό
Πιθανότητες & Τυχαία Σήματα. Διγαλάκης Βασίλης
 Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Συνεχή/Διακριτά Γραμμικά/Μη Γραμμικά Αν Τότε Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Χρονικά
Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Συνεχή/Διακριτά Γραμμικά/Μη Γραμμικά Αν Τότε Γραμμικά Συστήματα Σύστημα: x(t) T y(t) Κατηγορίες: Χρονικά
Θ.Ε. ΠΛΗ22 ( ) 2η Γραπτή Εργασία
 Θ.Ε. ΠΛΗ22 (2012-13) 2η Γραπτή Εργασία Στόχος: Η 2 η εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Θ.Ε. ΠΛΗ22 (2012-13) 2η Γραπτή Εργασία Στόχος: Η 2 η εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 3: Δειγματοληψία και Ανακατασκευή Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
Επικοινωνίες στη Ναυτιλία
 Επικοινωνίες στη Ναυτιλία Εισαγωγή Α. Παπαδάκης, Αναπλ. Καθ. ΑΣΠΑΙΤΕ Δρ. ΗΜΜΥ Μηχ. ΕΜΠ Βασικά Αντικείμενα Μαθήματος Σήματα Κατηγοριοποίηση, ψηφιοποίηση, δειγματοληψία, κβαντισμός Βασικά σήματα ήχος, εικόνα,
Επικοινωνίες στη Ναυτιλία Εισαγωγή Α. Παπαδάκης, Αναπλ. Καθ. ΑΣΠΑΙΤΕ Δρ. ΗΜΜΥ Μηχ. ΕΜΠ Βασικά Αντικείμενα Μαθήματος Σήματα Κατηγοριοποίηση, ψηφιοποίηση, δειγματοληψία, κβαντισμός Βασικά σήματα ήχος, εικόνα,
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
Η Έννοια της τυχαίας ιαδικασίας Η έννοια της τυχαίας διαδικασίας, βασίζεται στην επέκταση της έννοιας της τυχαίας µεταβλητής, ώστε να συµπεριλάβει το χρόνο. Σεκάθεαποτέλεσµα s k ενόςπειράµατοςτύχης αντιστοιχούµε,
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
6 Nv 6 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέχρι τώρα η μελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (μέση τιμή, συναρτήσεις
Επεξεργασία Στοχαστικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Μέχρι τώρα η μελέτη των τυχαίων διαδικασιών έγινε στο πεδίο του χρόνου (μέση τιμή, συναρτήσεις
Αρχές Τηλεπικοινωνιών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
Συστήματα Επικοινωνιών Ι
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών Ι Συναρτήσεις συσχέτισης/αυτοσυσχέτισης Φίλτρα Μετασχηματισμός Hilbert + Περιεχόμενα n Συνάρτηση αυτοσυσχέτισης n Συνάρτηση
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών Ι Συναρτήσεις συσχέτισης/αυτοσυσχέτισης Φίλτρα Μετασχηματισμός Hilbert + Περιεχόμενα n Συνάρτηση αυτοσυσχέτισης n Συνάρτηση
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Ψηφιακή μετάδοση στη βασική ζώνη + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Ψηφιακή μετάδοση στη βασική ζώνη + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
Θεώρημα δειγματοληψίας
 Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις τιμές του σε χρονικές στιγμές ισαπέχουσες
Δειγματοληψία Θεώρημα δειγματοληψίας Ένα βαθυπερατό σήμα πεπερασμένης ενέργειας που δεν περιέχει συχνότητες μεγαλύτερες των W Hertz μπορεί να περιγραφθεί πλήρως από τις τιμές του σε χρονικές στιγμές ισαπέχουσες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
( x) Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ. Βασικά αξιώµατα και ιδιότητες της πιθανότητας. Σεραφείµ Καραµπογιάς
 Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ - ΠΙΘΑΝΟΤΗΤΑΣ Βασικά αξιώµατα και ιδιότητες της πιθανότητας Σεραφείµ Καραµπογιάς Η αθροιστική συνάρτηση κατανοµής cumulaive diribuio ucio CDF µίας τυχαίας µεταβλητής X ορίζεται
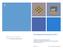
Συστήματα Επικοινωνιών Ι
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών Ι Διαμόρφωση Συχνότητας Ευρείας Ζώνης Εύρος ζώνης μετάδοσης διαμορφωμένων κατά γωνία σημάτων Παραγωγή σημάτων FM + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών Ι Διαμόρφωση Συχνότητας Ευρείας Ζώνης Εύρος ζώνης μετάδοσης διαμορφωμένων κατά γωνία σημάτων Παραγωγή σημάτων FM + Περιεχόμενα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ. Θ.Ε. ΠΛΗ22 ( ) 2η Γραπτή Εργασία
 Θ.Ε. ΠΛΗ 0-3 η Γραπτή Εργασία Στόχος: Η η ΑΠΑΝΤΗΣΕΙΣ εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
Θ.Ε. ΠΛΗ 0-3 η Γραπτή Εργασία Στόχος: Η η ΑΠΑΝΤΗΣΕΙΣ εργασία αποσκοπεί στην κατανόηση των συστατικών στοιχείων των αναλογικών διαμορφώσεων, της δειγματοληψίας, και της μετατροπής του αναλογικού σήματος
2.1 Έννοια του στοχαστικού σήµατος. Θεωρούµε ένα µονοδιάστατο γραµµικό δυναµικό σύστηµα που περιγράφεται από τις σχέσεις:
 Στοχαστικά σήµατα Έννοια του στοχαστικού σήµατος Θερούµε ένα µονοδιάστατο γραµµικό δυναµικό σύστηµα που περιγράφεται από τις σχέσεις: & α Γνρίζουµε µε απόλυτη βεβαιότητα (µε πιθανότητα ένα), ότι η αρχική
Στοχαστικά σήµατα Έννοια του στοχαστικού σήµατος Θερούµε ένα µονοδιάστατο γραµµικό δυναµικό σύστηµα που περιγράφεται από τις σχέσεις: & α Γνρίζουµε µε απόλυτη βεβαιότητα (µε πιθανότητα ένα), ότι η αρχική
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 1, Μέρος 2ο: ΠΕΡΙ ΣΗΜΑΤΩΝ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 1, Μέρος 2ο: ΠΕΡΙ ΣΗΜΑΤΩΝ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές
 Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές Εαρινό εξάμηνο 2018-2019 μήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό μήμα, Πανεπιστήμιο
Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές Εαρινό εξάμηνο 2018-2019 μήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό μήμα, Πανεπιστήμιο
HMY 799 1: Αναγνώριση Συστημάτων
 HMY 799 : Αναγνώριση Συστημάτων Διάλεξη Στοχαστικές Τυχαίες Μεταβλητές/ Στοχαστικά Σήματα Πειραματικά δεδομένα >Επιλογή τύπου μοντέλου >Επιλογή κριτηρίου >Υπολογισμός >Επικύρωση Προσαρμογή καμπύλης (Curve
HMY 799 : Αναγνώριση Συστημάτων Διάλεξη Στοχαστικές Τυχαίες Μεταβλητές/ Στοχαστικά Σήματα Πειραματικά δεδομένα >Επιλογή τύπου μοντέλου >Επιλογή κριτηρίου >Υπολογισμός >Επικύρωση Προσαρμογή καμπύλης (Curve
2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier
 2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
2.1 2. Ανάλυση και Σύνθεση κυματομορφών με την μέθοδο Fourier 2.1 Εισαγωγή Η βασική ιδέα στην ανάλυση των κυματομορφών με την βοήθεια της μεθόδου Fourier συνίσταται στο ότι μία κυματομορφή μιας οποιασδήποτε
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Τρεις ισοδύναμες μορφές: () = = = = Σειρές Fourier j( 2π ) t Τ.. x () t FS a jω0t xt () = ae =
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
Σήματα και Συστήματα. Διάλεξη 8: Ιδιότητες του Μετασχηματισμού Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
Σήματα και Συστήματα Διάλεξη 8: Ιδιότητες του Μετασχηματισμού ourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ιδιότητες του Μετασχηματισμού ourier 1. Ιδιότητες του Μετασχηματισμού ourier 2. Θεώρημα
Εισαγωγή στις Τηλεπικοινωνίες
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος Κανάτας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Ανάπτυξη σε Σειρές Furier Αθανάσιος Κανάτας
Εφαρμογή στις ψηφιακές επικοινωνίες
 Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
Δειγματοληψία Εφαρμογή στις ψηφιακές επικοινωνίες Γεννήτρια σήματος RF, (up converter Ενισχυτής) Προενισχυτής down-converter Ψηφιοποιητής σήματος RF Μονάδα ψηφ. επεξεργασίας Μονάδα ψηφ. επεξεργασίας 100
Σύνδεση με τα Προηγούμενα. Προχωρημένα Θέματα Τηλεπικοινωνιών. Εισαγωγή (2) Εισαγωγή. Βέλτιστος Δέκτης. παρουσία AWGN.
 Προχωρημένα Θέματα Τηλεπικοινωνιών Βέλτιστος Δέκτης για Ψηφιακά Διαμορφωμένα Σήματα παρουσία AWGN Σύνδεση με τα Προηγούμενα Στις «Ψηφιακές Τηλεπικοινωνίες», αναφερθήκαμε στο βέλτιστο δέκτη ψηφιακά διαμορφωμένων
Προχωρημένα Θέματα Τηλεπικοινωνιών Βέλτιστος Δέκτης για Ψηφιακά Διαμορφωμένα Σήματα παρουσία AWGN Σύνδεση με τα Προηγούμενα Στις «Ψηφιακές Τηλεπικοινωνίες», αναφερθήκαμε στο βέλτιστο δέκτη ψηφιακά διαμορφωμένων
x(t) = m(t) cos(2πf c t)
 Διαμόρφωση πλάτους (διπλής πλευρικής) Στοχαστικά συστήματα & επικοινωνίες 8 Νοεμβρίου 2012 1/27 2/27 Γιατί και πού χρειάζεται η διαμόρφωση Για τη χρήση πολυπλεξίας (διέλευση πολλών σημάτων μέσα από το
Διαμόρφωση πλάτους (διπλής πλευρικής) Στοχαστικά συστήματα & επικοινωνίες 8 Νοεμβρίου 2012 1/27 2/27 Γιατί και πού χρειάζεται η διαμόρφωση Για τη χρήση πολυπλεξίας (διέλευση πολλών σημάτων μέσα από το
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής
 ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
E[ (x- ) ]= trace[(x-x)(x- ) ]
![E[ (x- ) ]= trace[(x-x)(x- ) ] E[ (x- ) ]= trace[(x-x)(x- ) ]](/thumbs/55/36021260.jpg) 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Σήματα και Συστήματα. Διάλεξη 7: Μετασχηματισμός Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
Σήματα και Συστήματα Διάλεξη 7: Μετασχηματισμός Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier 1. Ορισμός του Μετασχηματισμού Fourier 2. Φυσική Σημασία του Μετασχηματισμού
HMY 220: Σήματα και Συστήματα Ι
 Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
Σύγκλιση Σειρών Fourier Ιδιότητες Σειρών Fourier Παραδείγματα HMY 0: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #10 Σειρές Fourier: Προσέγγιση Οι Σειρές Fourier μπορούν να αναπαραστήσουν μια πολύ μεγάλη κλάση περιοδικών
Συστήματα Επικοινωνιών Ι
 + Διδάσκων: Δρ. Κ. Δεμέστιχας Συστήματα Επικοινωνιών Ι Τηλεπικοινωνιακά Σήματα και Συστήματα + Περιεχόμενα 2 n Εισαγωγή n Εφαρμογές συστημάτων επικοινωνίας n Μοντέλο τηλεπικοινωνιακού συστήματος n Σήματα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας Συστήματα Επικοινωνιών Ι Τηλεπικοινωνιακά Σήματα και Συστήματα + Περιεχόμενα 2 n Εισαγωγή n Εφαρμογές συστημάτων επικοινωνίας n Μοντέλο τηλεπικοινωνιακού συστήματος n Σήματα
Ψηφιακή μετάδοση στη βασική ζώνη. Baseband digital transmission
 Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Το ψηφιακό σήμα δεν είναι τίποτε άλλο από μια διατεταγμένη σειρά συμβόλων παραγόμενη από μια διακριτή πηγή πληροφορίας Η πηγή
Ψηφιακή μετάδοση στη βασική ζώνη Baseband digital transmission Ψηφιακά σήματα Το ψηφιακό σήμα δεν είναι τίποτε άλλο από μια διατεταγμένη σειρά συμβόλων παραγόμενη από μια διακριτή πηγή πληροφορίας Η πηγή
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
A 1 y 1 (t) + A 2 y 2 (t)
 5. ΔΙΕΛΕΥΣΗ ΣΗΜΑΤΟΣ ΑΠΟ ΓΡΑΜΜΙΚΟ ΚΑΙ XΡONIKA AMETABΛHTO ΣΥΣΤΗΜΑ 5.. Γενικά περί γραμμικών και χρονικά αμετάβλητων συστημάτων 5... Ορισμός Γραμμικό είναι ένα σύστημα το οποίο, όταν στην είσοδό του εμφανιστεί
5. ΔΙΕΛΕΥΣΗ ΣΗΜΑΤΟΣ ΑΠΟ ΓΡΑΜΜΙΚΟ ΚΑΙ XΡONIKA AMETABΛHTO ΣΥΣΤΗΜΑ 5.. Γενικά περί γραμμικών και χρονικά αμετάβλητων συστημάτων 5... Ορισμός Γραμμικό είναι ένα σύστημα το οποίο, όταν στην είσοδό του εμφανιστεί
X(t) = A cos(2πf c t + Θ) (1) 0, αλλού. 2 cos(2πf cτ) (9)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
Ψηφιακές Τηλεπικοινωνίες. Διαμόρφωση Παλμών κατά Πλάτος
 Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
Ψηφιακές Τηλεπικοινωνίες Διαμόρφωση Παλμών κατά Πλάτος Διαμόρφωση Παλμών κατά Πλάτος Είπαμε ότι κατά την ψηφιακή μετάδοση μέσα από αναλογικό κανάλι κάθε σύμβολο αντιστοιχίζεται σε μια κυματομορφή σήματος
H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ. στις τηλεπικοινωνίες
 H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ στις τηλεπικοινωνίες Διάταξη συστήματος ψηφιακής επικοινωνίας Γεννήτρια σήματος RF, (up-coverter Ενισχυτής Προενισχυτής- dow-coverter- Ψηφιοποιητής σήματος RF Μονάδα ψηφ.
H ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΟΣ στις τηλεπικοινωνίες Διάταξη συστήματος ψηφιακής επικοινωνίας Γεννήτρια σήματος RF, (up-coverter Ενισχυτής Προενισχυτής- dow-coverter- Ψηφιοποιητής σήματος RF Μονάδα ψηφ.
Σήματα και Συστήματα. Διάλεξη 5: Γραφική Μέθοδος Υπολογισμού του Συνελικτικού Ολοκληρώματος. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 5: Γραφική Μέθοδος Υπολογισμού του Συνελικτικού Ολοκληρώματος Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής . Γραφική Μέθοδος Υπολογισμού του Συνελικτικού Ολοκληρώματος 2 Γραφικός
Σήματα και Συστήματα Διάλεξη 5: Γραφική Μέθοδος Υπολογισμού του Συνελικτικού Ολοκληρώματος Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής . Γραφική Μέθοδος Υπολογισμού του Συνελικτικού Ολοκληρώματος 2 Γραφικός
SOURCE. Transmitter. Channel Receiver
 Εισαγωγή στις Τηλεπικοινωνίες Εισαγωγή στα Σήµατα Ψηφιακές Επικοινωνίες - ειγµατοληψία ρ. Αθανάσιος. Παναγόπουλος Λέκτορας ΕΜΠ 1 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
Εισαγωγή στις Τηλεπικοινωνίες Εισαγωγή στα Σήµατα Ψηφιακές Επικοινωνίες - ειγµατοληψία ρ. Αθανάσιος. Παναγόπουλος Λέκτορας ΕΜΠ 1 Εργαστήριο Κινητών Ραδιοεπικοινωνιών, ΣΗΜΜΥ ΕΜΠ Εισαγωγή στις Τηλεπικοινωνίες
Ενότητα 4: Δειγματοληψία - Αναδίπλωση
 Ενότητα 4: Δειγματοληψία - Αναδίπλωση Σήματα και Συστήματα Τα συστήματα επεξεργάζονται ένα ή περισσότερα σήματα: Το παραπάνω σύστημα μετατρέπει το σήμα x(t) σε y(t). π.χ. Σε ένα σήμα ήχου μπορεί να ενισχύσει
Ενότητα 4: Δειγματοληψία - Αναδίπλωση Σήματα και Συστήματα Τα συστήματα επεξεργάζονται ένα ή περισσότερα σήματα: Το παραπάνω σύστημα μετατρέπει το σήμα x(t) σε y(t). π.χ. Σε ένα σήμα ήχου μπορεί να ενισχύσει
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 1
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 1 5.1: Εισαγωγή 5.2: Πιθανότητες 5.3: Τυχαίες Μεταβλητές καθ. Βασίλης Μάγκλαρης
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 3, Νέα Κτίρια ΣΗΜΜΥ Θεωρία Πιθανοτήτων & Στοχαστικές Ανελίξεις - 1 5.1: Εισαγωγή 5.2: Πιθανότητες 5.3: Τυχαίες Μεταβλητές καθ. Βασίλης Μάγκλαρης
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Βέλτιστα γραμμικά χρονικά αναλλοίωτα συστήματα
E(X(t)) = 1 k + k sin(2π) + k cos(2π) = 1 k + k 0 + k 1 = 1
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών ΤΗΛ 2: ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΤΥΧΑΙΑ ΣΗΜΑΤΑ 4ο Εξάμηνο 2009-200 4η ΕΡΓΑΣΙΑ ΑΣΚΗΣΗ Εστω τυχαία διαδικασία X(t) =
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών ΤΗΛ 2: ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΤΥΧΑΙΑ ΣΗΜΑΤΑ 4ο Εξάμηνο 2009-200 4η ΕΡΓΑΣΙΑ ΑΣΚΗΣΗ Εστω τυχαία διαδικασία X(t) =
17-Φεβ-2009 ΗΜΥ Ιδιότητες Συνέλιξης Συσχέτιση
 ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
3-Φεβ-2009 ΗΜΥ 429. 4. Σήματα
 3-Φεβ-2009 ΗΜΥ 429 4. Σήματα 1 Σήματα Σήματα είναι: σχήματα αλλαγών που αντιπροσωπεύουν ή κωδικοποιούν πληροφορίες σύνολο πληροφορίας ή δεδομένων σχήματα αλλαγών στο χρόνο, π.χ. ήχος, ηλεκτρικό σήμα εγκεφάλου
3-Φεβ-2009 ΗΜΥ 429 4. Σήματα 1 Σήματα Σήματα είναι: σχήματα αλλαγών που αντιπροσωπεύουν ή κωδικοποιούν πληροφορίες σύνολο πληροφορίας ή δεδομένων σχήματα αλλαγών στο χρόνο, π.χ. ήχος, ηλεκτρικό σήμα εγκεφάλου
Περιεχόµενα διαλέξεων 2ης εβδοµάδας
 Εισαγωγή οµή και πόροι τηλεπικοινωνιακού συστήµατος Σήµατα Περιεχόµενα διαλέξεων 1ης εβδοµάδας Εισαγωγή Η έννοια της επικοινωνιας Ιστορική αναδροµή οµή και πόροι τηλεπικοινωνιακού συστήµατος οµή τηλεπικοινωνιακού
Εισαγωγή οµή και πόροι τηλεπικοινωνιακού συστήµατος Σήµατα Περιεχόµενα διαλέξεων 1ης εβδοµάδας Εισαγωγή Η έννοια της επικοινωνιας Ιστορική αναδροµή οµή και πόροι τηλεπικοινωνιακού συστήµατος οµή τηλεπικοινωνιακού
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 3 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Παλμοκωδική Διαμόρφωση. Pulse Code Modulation (PCM)
 Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
Παλμοκωδική Διαμόρφωση Pulse Code Modulation (PCM) Pulse-code modulation (PCM) Η PCM είναι ένας στοιχειώδης τρόπος διαμόρφωσης που δεν χρησιμοποιεί φέρον! Το μεταδιδόμενο (διαμορφωμένο) σήμα PCM είναι
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
Εισαγωγή στη θεωρία πληροφορίας
 Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
Θεωρία πληροφορίας Εισαγωγή στη θεωρία πληροφορίας Τηλεπικοινωνιακά συστήματα Όλα τα τηλεπικοινωνιακά συστήματα σχεδιάζονται για να μεταφέρουν πληροφορία Σε κάθε τηλεπικοινωνιακό σύστημα υπάρχει μια πηγή
ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ ΘΟΡΥΒΟΣ
 ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ ΘΟΡΥΒΟΣ. Εισαγωγή Ο θόρυβος (se) ορίζεται σαν ένα ανεπιθύμητο σήμα, που υπάρχει πάντοτε στα συστήματα τηλεπικοινωνιών και δυσκολεύει την ανάκτηση της πληροφορίας στο δέκτη. Η μελέτη του
ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ ΘΟΡΥΒΟΣ. Εισαγωγή Ο θόρυβος (se) ορίζεται σαν ένα ανεπιθύμητο σήμα, που υπάρχει πάντοτε στα συστήματα τηλεπικοινωνιών και δυσκολεύει την ανάκτηση της πληροφορίας στο δέκτη. Η μελέτη του
