ΣΧΗΜΑΤΙΚΗ ΠΑΡΑΣΤΑΣΗ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
|
|
|
- Τρύφων Κοντόσταυλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 3Α ΣΧΗΜΑΤΙΚΗ ΠΑΡΑΣΤΑΣΗ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου δίνονται οι γραφικές παραστάσεις των ακτινικών και γωνιακών συναρτήσεων, καθώς και των συναρτήσεων πιθανότητας των ατομικών τροχιακών. Προσδιορίζεται ο αριθμός των σφαιρικών και γωνιακών κόμβων και συσχετίζεται αυτός με την ενέργεια του τροχιακού. Στο Β μέρος του κεφαλαίου δίνονται ερωτήσεις ανοικτού και κλειστού τύπου και στο Γ μέρος δίνονται οι απαντήσεις με αναλυτικές εξηγήσεις για την εμπέδωση της θεωρίας. Προαπαιτούμενη γνώση Προαπαιτούμενη γνώση, είναι αυτή του 1ου κεφαλαίου του βιβλίου Χημείας Λυκείου θετικής κατεύθυνσης Εισαγωγή Η επίλυση της εξίσωσης Schrödinger απαιτεί την εισαγωγή τριών κβαντικών αριθμών, ενώ λόγω της σφαιρικής συμμετρίας του ατόμου βολεύει η χρήση σφαιρικών, αντί των καρτεσιανών συντεταγμένων. Κατόπιν τούτων, η κυματική παράσταση Ψ μπορεί να εκφραστεί ως το γινόμενο τριών συναρτήσεων, δηλαδή: Ψ(ρ,θ,φ) = R(r) Θ(θ) Φ(φ) όπου, R(r): η ακτινική κυματοσυνάρτηση. Θ(θ): η γωνιακή ζενιθιακή κυματοσυνάρτηση. Φ(φ): η γωνιακή αζιμουθιακή κυματοσυνάρτηση. Η επίλυση της εξίσωσης Schrödinger συνιστά την επίλυση καθεμιάς από τις συνιστώσες κυματοσυναρτήσεις. Η επίλυση της εξίσωσης Schrödinger για ορισμένες τιμές κβαντικών αριθμών έχει δώσει τις τιμές ακτινικής R(r) και γωνιακής συνάρτησης Α(θ,φ) = Θ(θ) Φ(φ). Τα τροχιακά (Ψ) και τα ηλεκτρονιακά νέφη ( Ψ 2 ) εκφράζονται μαθηματικά υπό μορφή πολύπλοκων συναρτήσεων, που δύσκολα μπορεί κανείς να ανακαλέσει. Αντίθετα, οι γραφικές παραστάσεις των Ψ και Ψ 2 α- ποτελούν ένα πλέον αποδεκτό και εύχρηστο τρόπο παρουσίασης. Η γραφική παράσταση Ψ(r,θ,φ) προϋποθέτει τετραδιάστατο γράφημα. Για να παρακάμψουμε το πρόβλημα μπορούμε να δώσουμε δύο γραφικές παραστάσεις: τη γραφική παράσταση R(r) - r, της ακτινικής συνάρτησης R(r) σε σχέση με την απόσταση του ηλεκτρονίου από τον πυρήνα. Το διάγραμμα αυτό συσχετίζεται με το μέγεθος του τροχιακού. τη γραφική παράσταση Α(θ,φ) - θ-φ, της γωνιακής συνάρτησης Α(θ,φ) σε σχέση με τις σφαιρικές γωνιακές συντεταγμένες θ, φ. Το διάγραμμα αυτό συσχετίζεται με το σχήμα του τροχιακού. Με ανάλογο σκεπτικό η γραφική παράσταση των ηλεκτρονιακών νεφών (συναρτήσεων πυκνότητας πιθανότητας) Ψ 2 περιλαμβάνει: τη γραφική παράσταση του R 2 (r) -r. τη γραφική παράσταση της συνάρτησης Α 2 (θ,φ) - θ-φ Ακτινικές συναρτήσεις R(r) και συναρτήσεις πιθανότητας R 2 (r) Στην εικόνα 3.1, απεικονίζονται οι γραφικές παραστάσεις των ακτινικών συναρτήσεων R(r) και R 2 (r) με την απόσταση r από τον πυρήνα, για ορισμένα τροχιακά του ατόμου του υδρογόνου. 47
2 Μεγαλύτερη σημασία παρουσιάζουν οι γραφικές παραστάσεις R 2 -r, οι οποίες εκφράζουν την πιθανότητα εύρεσης του ηλεκτρονίου σε διάφορα σημεία του χώρου γύρω από τον πυρήνα (Εικόνα 3.1). Όπως βλέπουμε η ακτινική συνάρτηση R 2 (2s) διαπερνά τον πυρήνα, καθώς στον πυρήνα έχει τη μέγιστη πιθανότητα εύρεσης. Αντίθετα, η R 2 (2p) έχει μηδενική πιθανότητα να βρεθεί στον πυρήνα. Τα σημεία στα οποία η πιθανότητα εύρεσης του ηλεκτρονίου είναι μηδενική χαρακτηρίζονται ως κομβικά ή ακριβέστερα ακτινικοί κόμβοι. Εικόνα 3.1 Γραφική παράσταση ακτινικών συναρτήσεων R(r) και R 2 (r) για n=1, 2, Συναρτήσεις ακτινικής πιθανότητας 4πr 2 R 2 (r) Ένας πιο συνηθισμένος τρόπος εξέτασης της κατανομής του ηλεκτρονιακού νέφους είναι να θεωρήσουμε ότι το άτομο συγκροτείται από «φλοιούς». Με βάση το σκεπτικό αυτό, η πιθανότητα να βρεθεί το ηλεκτρόνιο στο φλοιό όγκου dv εσωτερικής ακτίνας r και εξωτερικής ακτίνας r+dr είναι: R 2 dv =R 2 d(4πr 3 /3) = R 2 4πr 2 dr Η συνάρτηση4πr 2 R 2 ονομάζεται συνάρτηση ακτινικής πιθανότητας. 48
3 Εικόνα 3.2 Ο όγκος φλοιού πάχους dr είναι: dv =d(4πr 3 /3) = 4πr 2 dr. Στην εικόνα 3.3 απεικονίζονται γραφικά οι συναρτήσεις ακτινικής πιθανότητας 4πr 2 R 2 για ορισμένα ατομικά τροχιακά του υδρογόνου. Εικόνα 3.3 Γραφική παράσταση της συνάρτησης ακτινικής πιθανότητας 4πr 2 R 2 για τα τροχιακά 1s, 2s, 2p, 3s και 3p και σχηματική παρουσίαση της αντίστοιχης κατανομής της ηλεκτρονιακής πυκνότητας (με τις λευκές περιοχές απεικονίζονται. οι κομβικές επιφάνειες). 49
4 Με βάση τις γραφικές παραστάσεις των συναρτήσεων ακτινικής πιθανότητας 4πr 2 R 2 (r)για τα τροχιακά 1s, 2s, 3s, 3p και 3d παρατηρούμε: Όταν r = 0, τότε 4πr 2 R 2 = 0. Δηλαδή, η πιθανότητα να βρεθεί το ηλεκτρόνιο στον πυρήνα είναι μηδενική. Όταν η απόσταση r από τον πυρήνα είναι μεγάλη, τότε 4πr 2 R 2 τείνει στο μηδέν. Δηλαδή, μακριά από τον πυρήνα έχει πολύ μικρή πιθανότητα να βρεθεί το ηλεκτρόνιο. Τα μέγιστα των γραφικών παραστάσεων, όπου η πιθανότητα εύρεσης του ηλεκτρονίου σε σφαιρική επιφάνεια ακτίνας r είναι μεγίστη, μπορούν να συσχετιστούν με τις ακτίνες των τροχιών του Bohr. Για παράδειγμα το ηλεκτρόνιο του τροχιακού 1s έχει μέγιστη πιθανότητα να βρεθεί σε σφαιρική επιφάνεια ακτίνας 0,53 Å, όση υπολογίζεται ότι είναι η ακτίνα της πρώτης τροχιάς (Κ) του Bohr. Μεταξύ του πυρήνα και των μεγίστων κορυφών υπάρχουν περιοχές μηδενικής πιθανότητας εύρεσης των ηλεκτρονίων (σφαιρικές κομβικές επιφάνειες). Σε ένα τροχιακό ο αριθμός των κόμβων της αντίστοιχης ακτινικής συνάρτησής του είναι: n-l-1. H παρουσία μεγάλου αριθμού κόμβων αυξάνει την ηλεκτρονιακή πυκνότητα κοντά στον πυρήνα, με αποτέλεσμα να αυξάνεται η διεισδυτικότητα του τροχιακού. Αυτή είναι η βασική αιτία για τη σειρά των ενεργειακών επιπέδων των τροχιακών, π.χ. E(3s) < E(3p) < E(3d). Δηλαδή ισχύει ότι: Όσο περισσότερες είναι οι κομβικές επιφάνειες τόσο χαμηλότερη είναι η ενέργεια του αντίστοιχου τροχιακού. Στην εικόνα 3.4 απεικονίζεται η συνάρτηση ακτινικής πιθανότητας 4πr 2 R 2 για το τροχιακό 3d. Για συγκριτικούς λόγους, στην ίδια εικόνα, παρατίθενται οι αντίστοιχες συναρτήσεις ακτινικής πιθανότητας των 3s και 3p. Εικόνα 3.4 Γραφική παράσταση της συνάρτησης ακτινικής πιθανότητας 4πr 2 R 2 σε συνάρτηση με την απόσταση r από τον πυρήνα, για τα τροχιακά 3s, 3p και 3d. 50
5 3.4. Γωνιακές συναρτήσεις Α(θ,φ) Η γωνιακή συνάρτηση Α(θ,φ) καθορίζει τη μορφή και τον προσανατολισμό του ηλεκτρονιακού νέφους στο χώρο. Για τα s τροχιακά η γωνιακή συνάρτηση Α(θ,φ) είναι ανεξάρτητη από τις γωνίες θ και φ. Αντίθετα, στα p τροχιακά, η γωνιακή συνάρτηση Α(θ,φ) εξαρτάται από τις γωνίες θ και φ. Στο τρισδιάστατο σύστημα, τα s τροχιακά παρίστανται ως σφαίρες. Η γραφική παράσταση Α(θ,φ) των τροχιακών p x, p y, p z είναι δύο εφαπτόμενες σφαίρες με σημείο επαφής τον πυρήνα, προσανατολισμένες κατά μήκος των αξόνων x, y και z, αντίστοιχα (Εικόνα 3.5). Από τις δύο αυτές σφαίρες, η μία αντιστοιχεί σε θετικές τιμές της γωνιακής συνάρτησης Α(θ,φ) και η άλλη σε αρνητικές τιμές. Μεταξύ των σφαιρών υπάρχει ένα κομβικό επίπεδο, όπου η γωνιακή συνάρτηση μηδενίζεται. Γενικότερα, ο αριθμός των γωνιακών κόμβων (κομβικών επιφανειών) σε ένα τροχιακό ισούται με τον αζιμουθιακό κβαντικό αριθμό l. Με την ίδια λογική προκύπτουν οι γραφικές παραστάσεις Α(θ,φ) των πέντε d ατομικών τροχιακών: d x2- y2, d z2, d xy, d xz, d yz. Κάθε d τροχιακό απεικονίζεται με τέσσερις κωδωνοειδείς λοβούς (εκτός από το dz 2 που έχει δύο λοβούς και ένα δακτύλιο). Οι δύο από τους λοβούς αυτούς είναι θετικοί και οι άλλοι δύο αρνητικοί (στο d z2 οι δύο λοβοί είναι θετικοί και ο δακτύλιος αρνητικός). Εικόνα 3.5 Γραφική παράσταση της γωνιακής συνάρτησης Α(θ, φ) για τα τροχιακά s, p και d. 51
6 Με βάση την παραπάνω εικόνα 3.5, τα τροχιακά ταξινομούνται σε δύο κατηγορίες: τα συμμετρικά ή άρτια στα οποία η κυματοσυνάρτηση Ψ έχει το ίδιο αλγεβρικό πρόσημο σε σημεία συμμετρικά ως προς το κέντρο (σημείο τομής των αξόνων x, y, z), όπως συμβαίνει στα τροχιακά s και d z2. τα ασύμμετρα ή περιττά στα οποία η κυματοσυνάρτηση Ψ έχει το αντίθετο πρόσημο σε σημεία συμμετρικά ως προς το κέντρο, όπως συμβαίνει στα τροχιακά p. Δηλαδή, στις περιπτώσεις αυτές η κυματοσυνάρτηση αλλάζει πρόσημο από τον ένα λοβό του ατομικού τροχιακού στον άλλο Συναρτήσεις γωνιακής πιθανότητας Α 2 (θ,φ) Όπως η συνάρτηση 4πr 2 R 2 εκφράζει την πιθανότητα εύρεσης του ηλεκτρονίου στο φλοιό r - r+dr, το ίδιο και η συνάρτηση Α 2 (θ,φ) καθορίζει την πιθανότητα εύρεσης του ηλεκτρονίου στο χώρο με βάση τις συντεταγμένες θ και φ. Για τα τροχιακά s η ύψωση στο τετράγωνο δεν προκαλεί καμιά μεταβολή. Έτσι, το Α 2 (θ,φ) παρίσταται και πάλι με σφαίρα. Για τα p τροχιακά η ύψωση στο τετράγωνο προκαλεί μια επιμήκυνση των σφαιρών (αποκτούν κωδωνοειδή μορφή), ενώ οι τιμές των Α 2 (θ,φ) είναι προφανώς μόνο θετικές. Στην εικόνα 3.6 απεικονίζονταιοι γραφικές παραστάσεις τωνα 2 (θ,φ) για τα s, p και d τροχιακά. Το θετικό πρόσημο της κυματοσυνάρτησης Α επισημαίνεται με μπλε γραμμοσκίαση της γραφικής παράστασης του τροχιακού. Εικόνα 3.6 Γραφική παράσταση της συνάρτησης γωνιακής πιθανότηταςα 2 (θ,φ) για τα τροχιακά s, p και d. 52
7 3.6. Γραφική παράσταση συναρτήσεων κατανομής πιθανότητας (ή πυκνότητας ηλεκτρονιακού νέφους) Ψ 2 Ένας πιο ακριβής τρόπος γραφικής παράστασης του Ψ 2 μπορεί να γίνει με τις ισόπυκνες καμπύλες, δηλαδή με διαγράμματα ίσης ηλεκτρονιακής πυκνότητας (Εικόνα 3.7). Τα διαγράμματα αυτά προκύπτουν με λεπτομερείς υπολογισμούς μέσω της εξίσωσης Schrodinger. Είναι τομές τροχιακών αποτελούμενες από καμπύλες ίσης πιθανότητας εύρεσης του ηλεκτρονίου, όπως είναι τα τοπογραφικά διαγράμματα με τις ισοϋψείς καμπύλες. Οι τιμές που αναγράφονται στις καμπύλες εκφράζουν το κλάσμα της μέγιστης πιθανότητας ή το κλάσμα της μέγιστης ηλεκτρονιακής πυκνότητας. Στην ίδια εικόνα αναγράφονται οι κομβικές επιφάνειες, το μέγεθος του ηλεκτρονιακού νέφους, καθώς και το πρόσημο που έχει η κυματοσυνάρτηση Ψ. Επίσης, να παρατηρήσουμε ότι οι ισόπυκνες του ίδιου τροχιακού έχουν περίπου την ίδια εμφάνιση. Εικόνα 3.7 Ισόπυκνες ηλεκτρονιακής κατανομής του τροχιακού 3p z για το άτομο του χλωρίου Ένας απλός τρόπος απεικόνισης των τροχιακών Πρακτικά τα τροχιακά (τα τετράγωνα των τροχιακών για την ακρίβεια Ψ 2 ) μπορούν να παρασταθούν με οριακές καμπύλες που περικλείουν το % της πυκνότητας του ηλεκτρονιακού νέφους. Το σχήμα των περιγραμμάτων αυτών καθορίζεται από τα διαγράμματα των συναρτήσεων γωνιακής πιθανότητας Α 2 (θ,φ), ενώ το σχετικό μέγεθος τους καθορίζεται από τα διαγράμματα των συναρτήσεων ακτινικής πιθανότητας 4πr 2 R 2. Ο πρόχειρος αυτός τρόπος παρουσίασης των τροχιακών στερείται θεωρητικής βάσης, έχει όμως το διπλό πλεονέκτημα ότι είναι εύκολο να σχεδιαστούν και ότι δείχνουν επίσης τον κομβικό τύπο του τροχιακού. Στην παρακάτω εικόνα δίνονται τα οριακά διαγράμματα 50% (που περικλείει το 50% του ηλεκτρονιακού νέφους) και 99% (που περικλείει το 99% του ηλεκτρονιακού νέφους) για τα τροχιακά sκαι 2p z. Εικόνα 3.8 Σχηματική παρουσίαση των τροχιακών 1s και 2p z με οριακές καμπύλες που περικλείουν το 50% ή το 99% του ηλεκτρονιακού νέφους. 53
8 Πίνακας αντιστοίχισης ελληνόγλωσσων - ξενόγλωσσων όρων Ακτινική κυματοσυνάρτηση Ασύμμετρα ή περιττά τροχιακά Γωνιακή κυματοσυνάρτηση Ηλεκτρονιακό νέφος Ισόπυκνες καμπύλες ηλεκτρονιακής κατανομής Κομβικά σημεία Κόμβοι ακτινικοί Κόμβοι γωνιακοί Συμμετρικά ή άρτια τροχιακά Συνάρτηση ακτινικής πιθανότητας Συνάρτηση γωνιακής πιθανότητας radial wave function ungerade orbitals angular wave function dot density diagrams electron density contour maps nodes radial nodes angular nodes gerade orbitals radial electron density angular electron density 54
9 Βιβλιογραφία/Αναφορές 1. Δ. Κατάκη, «Μαθήματα Ανοργάνου Χημείας», Αθήνα, M. Gerloch, Orbitals, Terms and States, Wiley, New York, Γ. Ε. Μανουσάκη, Γενική και Ανόργανη Χημεία», Β έκδοση, Αφοι Κυριακίδη, Θεσσαλονίκη, I. S. Butler, J. F. Harrod, «Ανόργανη Χημεία, Αρχές και Εφαρμογές», Μετάφραση, επιστημονική επιμέλεια: Α. Κουτσολέλος, εκδόσεις Π. Τραυλός-Ε. Κωσταράκη, Αθήνα, Κ.Τσίπης, «Χημεία Ι. Άτομα και Μόρια», Εκδόσεις Ζήτη, Θεσσαλονίκη, Ν. Δ. Κλούρα «Βασική Ανόργανη Χημεία», Εκδόσεις Π. Τραυλός- Ε. Κωσταράκη», 2 η έκδοση, Αθήνα, Ν. Δ. Κλούρα «441 λυμένες ασκήσεις στη Βασική Ανόργανη Χημεία», Πάτρα, Π. Π. Καραγιαννίδης, «Ανόργανη Χημεία», Εκδόσεις Ζήτη, Θεσσαλονίκη, J. E. Huheey, E. A. Keiter, R. L. Keiter, Inorganic Chemistry- Principles of Structure and Reactivity, 4 th Edition, Harper Collins College Publishers, New York, J. E. Huheey, «Ανόργανη Χημεία - Αρχές Δομής και Δραστικότητα», Μετάφραση: Ν. Χατζηλιάδης, Θ. Καμπανός, Σ. Περλεπές, 3 η έκδοση, εκδόσεις ΙΩΝ, Περιστέρι, F. A. Cotton, G. Wilkinson, P. L. Gaus, Basic Inorganic chemistry, 3 rd Edition, J. Wiley & sons, New York, P.A. Cox, Introduction to Quantum Theory and Atomic Structure, Oxford University Press, Oxford, S. S. Zumdahl, Chemical principles, 3 rd Edition, Houghton Mifflin, Boston, G. L. Miessler, D. A. Tarr, Inorganic Chemistry, 2 nd Ed., Prentice Hall, New Jersey, G. Wulfsberg, Inorganic Chemistry, University Science Books, California, K. W. Whitten, R. E. Davis, M. L. Peck, General Chemistry, 6 th edition, Prentice-Hall, New Jersey, V. M. Gil, Orbitals in Chemistry: A. Modern Guide for Students, Cambridge University Press, Cambridge, C. E. Housecroft, A. G. Sharpe Inorganic Chemistry, Prentice Hall (an imprint of Pearson Education, Essex, R. J. Gillespie, P. L. A. Popelier, Chemical Bonding and Molecular Geometry - from Lewis to Electron Density-, Oxford University Press, New York, Ε. A. Orgyzlo and G. B. Porter, Contour Surfaces for Atomic and Molecular Orbitals, J. Chem. Educ., 40 (1963) R. C. Johnson and R. R. Rettew, Shapes of Atoms, J. Chem. Educ., 42 (1965) R. S. Berry, Atomic Orbitals, J. Chem. Educ., 43 (1966) R.E. Powell, The Five Equivalent d Orbitals, J. Chem. Educ., 45 (1968) B. Perlmutter-Hayman, The Graphical Representation of Hydrogen-Like Functions, J. Chem. Educ., 46 (1969)
10 25. A. Szabo, Contour Diagrams for Relativistic Orbitals, J. Chem. Educ., 46 (1969) Q. Kikuchi and K. Suzuki, Orbitals Shape Representations, J. Chem. Educ., 62 (1985) T. C. W. Mak and W. Li, Probability of Locating the Electron in a Hydrogen Atom, J. Chem. Educ., 77 (2000) B. G. Moore, Orbital Plots Using Gnu plot, J. Chem. Educ., 77 (2000) M.G. Lagorio, Electron Densities: Pictorial Analogies for Apparent Ambiguities in Probability Calculations, J. Chem. Educ., 77 (2000) E. R. Scerri, Have Orbitals Really Been Observed?, J. Chem. Educ., 77 (2000) D. G. Miles Jr. and T. A. Francis, A Graphical Approach to the Angular Momentum Schrödinger Equation, J. Chem. Educ., 78 (2001) 405. Περίπατοι στο διαδίκτυο 32. Τρισδιάστατα Γραφικά Ατομικών Μοριακών 56
11 3Β ΣΧΗΜΑΤΙΚΗ ΠΑΡΑΣΤΑΣΗ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ ΑΣΚΗΣΕΙΣ Ερωτήσεις πολλαπλής επιλογής 3.1 Σε ένα τροχιακό ο αριθμός των κόμβων της ακτινικής συνάρτησής του είναι: Α. ίσος με n, Β. ίσος με l, Γ. ίσος με n-l-1, Δ. ίσος με n-l-m l. 3.2 Η επίλυση της εξίσωσης Schrödinger απαιτεί την εισαγωγή των κβαντικών αριθμών: Α. n, l Β. n, l και m l Γ. n, l, m l και m s Δ. μόνο του αζιμουθιακού l. 3.3 Ο αριθμός των σφαιρικών κομβικών επιφανειών του τροχιακού 3s είναι: Α. δύο, Β. τρία, Γ. μηδέν, Δ. ένας. 3.4 Ο αριθμός των γωνιακών κόμβων του τροχιακού 3d z 2 είναι: Α. ένας, Β. δύο, Γ. τρία, Δ. μηδέν. 3.5 Συμμετρικά ή άρτια τροχιακά είναι: Α. μόνο τα s τροχιακά, Β. τα s και p z, Γ. τα s και d z2, Δ. τα s, p z και d z Η γραφική παράσταση της γωνιακής συνάρτησης Α(θ,φ) που απεικονίζεται παρακάτω αφορά τα τροχιακά: 57
12 Α. p z Β. d z Γ. fz Δ. d z Η διεισδυτικότητα των τροχιακών με κύριο κβαντικό αριθμό n=3 μεταβάλλεται ως εξής: Α. 3s< 3p< 3d, Β. 3d< 3p< 3s, Γ. 3s = 3p = 3d, Δ. 3s = 3p< 3d. 3.8 Η οριακή επιφάνεια που καλύπτει το 99% του ηλεκτρονιακού νέφους για το 2s τροχιακό είναι μια σφαίρα με ακτίνα 500 pm. Η οριακή επιφάνεια που καλύπτει το 99% του ηλεκτρονιακού νέφους για το 1s τροχιακό είναι μια σφαίρα με ακτίνα: Α. 200 pm, Β. 500 pm, Γ. 600 pm, Δ. 800 pm. 3.9 Η οριακή επιφάνεια που καλύπτει το 99% του ηλεκτρονιακού νέφους για το 2s τροχιακό είναι μια σφαίρα με ακτίνα 500 ppm. Η σφαίρα που περικλείει το 90% του ηλεκτρονιακού νέφους για το 2s ατομικό τροχιακό μπορεί να έχει ακτίνα: Α. 400 pm, Β. 500 pm, Γ. 900 pm, Δ. οποιαδήποτε απ αυτές Σε μια περιοχή γύρω από ένα σημείο Α η πυκνότητα του ηλεκτρονιακού νέφους είναι μεγαλύτερη από αυτή που είναι γύρω από ένα σημείο Β. Τι σημαίνει αυτό; Α. Στην περιοχή Β κινούνται λιγότερα ηλεκτρόνια από ότι στην περιοχή Α. Β. Τα ηλεκτρόνια ξοδεύουν λιγότερο χρόνο στην περιοχή Β. Γ. Το σημείο Β βρίσκεται πιο μακριά από τον πυρήνα του ατόμου. Δ. Η τιμή της κυματοσυνάρτησης Ψ στο σημείο Α είναι μεγαλύτερη από ότι η αντίστοιχη τιμή στο σημείο Α Η παρακάτω γραφική παράσταση της συνάρτησης ακτινικής πιθανότητας 4πr 2 R 2 (r) αφορά το ατομικό τροχιακό: Α. 2s, Β. 2p, Γ. 3s, Δ. 3d. 58
13 3.12 Ποιο από τα παρακάτω διαγράμματα αποτελεί γραφική παράσταση της συνάρτησης ακτινικής πιθανότητας 4πr 2 R 2 ενός 2s ηλεκτρονίου; Α. α, Β. β, Γ. γ, Δ. δ Ποια από τις παρακάτω εκφράσεις αποδίδει τη συνάρτηση ακτινικής πιθανότητας; Α. 4πrR 2 dr, Β. 4πr 2 R 2 dr, Γ. 4πr 2 Rdr, Δ. 4πrRdr. Ερωτήσεις τύπου «σωστό - λάθος» με αιτιολόγηση 3.14 Το 2s τροχιακό έχει 2 σφαιρικές κομβικές επιφάνειες Το 3s τροχιακό έχει 1 γωνιακό κόμβο Όλα τα p τροχιακά είναι περιττά τροχιακά. Ερωτήσεις ανοικτού τύπου 3.17 Ποια τροχιακά χαρακτηρίζονται συμμετρικά ή άρτια τροχιακά και ποια ασύμμετρα ή περιττά τροχιακά; Ποια από τα παρακάτω τροχιακά είναι συμμετρικά και ποια ασύμμετρα s, d xy, d z2, p y ; 3.18 Δίνεται η παρακάτω γραφική παράσταση της συνάρτησης ακτινικής πιθανότητας ηλεκτρονιακής κατανομής πυκνότητας για το άτομο του υδρογόνου. Με βάση το διάγραμμα αυτό να απαντήσετε στα εξής: α. Πόσους κόμβους έχει η συνάρτηση αυτή; β. Ποιος τύπος τροχιακού εμπλέκεται στην περίπτωση αυτή; γ. Τι είδος τροχιακό θα είχαμε αν υπήρχε ένας ακόμα κόμβος; 59
14 3.19 Πώς τα ηλεκτρόνια διασχίζουν τις κομβικές επιφάνειες; Για παράδειγμα πως ένα p ηλεκτρόνιο περνά από τον ένα λοβό στον άλλο; 3.20 Πόσοι κόμβοι υπάρχουν στην ακτινική και πόσοι στην γωνιακή συνάρτηση ενός 3d τροχιακού; 3.21 Να κάνετε τις γραφικές παραστάσεις για τα τροχιακά 1s, 2s, 2p, 3s και 3p: α. της ακτινικής συνάρτησης R(r), β. της ακτινικής πιθανότητας 4πr 2 R 2 (r), γ. της γωνιακής συνάρτησης Α(θ,φ), δ. της συνάρτησης γωνιακής πιθανότητας Α 2 (θ,φ) Τι καθορίζει η θέση της μέγιστης κορυφής στα παρακάτω διαγράμματα 4πr 2 R 2 r; 3.23 Παρακάτω δίνονται σχηματικά, με περιγράμματα (οριακές καμπύλες) ηλεκτρονιακής πυκνότητας, τα τροχιακά 4f. Να εξηγήσετε τι εκφράζουν οι παραστάσεις αυτές και πως προκύπτουν; Γιατί υπάρχουν επτά διαφορετικά f τροχιακά; 3.24 Τι πληροφορίες μας δίνουν οι ισόπυκνες καμπύλες ηλεκτρονιακής κατανομής; 60
15 3Γ ΣΧΗΜΑΤΙΚΗ ΠΑΡΑΣΤΑΣΗ ΑΤΟΜΙΚΩΝ ΤΡΟΧΙΑΚΩΝ - ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Ερωτήσεις πολλαπλής επιλογής 3.1 Σωστή απάντηση: Γ Αιτιολόγηση: Σε ένα τροχιακό ο αριθμός των κόμβων της αντίστοιχης ακτινικής συνάρτησής του είναι: n-l-1 (βλέπε εικόνα 3.1 στην ενότητα 3.1 της συνοπτικής θεωρίας). 3.2 Σωστή απάντηση: Β Αιτιολόγηση: Η επίλυση της εξίσωσης Schrödinger μπορεί να χωριστεί σε τρεις διαφορετικές εξισώσεις: την ακτινική, τη ζενιθιακή και την αζιμουθιακή που δίνουν αντίστοιχα τις λύσεις R(r), Θ(θ) και Φ(φ).Η Φ(φ) περιέχει την παράμετρο m l, της οποίας οι τιμές (0, ±1, ±2, ±3 ) καθορίζονται από την απαίτηση της Φ(φ) να είναι μονότιμη συνάρτηση. Ανάλογα, η Θ(θ) περιέχει τις παραμέτρους l (0, 1, 2, ) και m l (0, ±1, ±2, ±3 ), ενώ η R(r) περιέχει τις παραμέτρους n (1, 2, 3,..) και l (0,1, 2, ). 3.3 Σωστή απάντηση: Α Αιτιολόγηση: Σε ένα τροχιακό ο αριθμός των σφαιρικών κόμβων είναι: n-l-1. Στην προκειμένη περίπτωση είναι 3-0-1= Σωστή απάντηση:b Αιτιολόγηση: Ο αριθμός των γωνιακών κόμβων (κομβικών επιφανειών) σε ένα τροχιακό ισούται με τον αζιμουθιακό κβαντικό αριθμό l. Στην προκειμένη περίπτωση είναι l= Σωστή απάντηση: Γ Αιτιολόγηση: Στα συμμετρικά ή άρτια τροχιακά η κυματοσυνάρτηση Ψ έχει το ίδιο αλγεβρικό πρόσημο σε σημεία συμμετρικά ως προς το κέντρο (σημείο τομής των αξόνων x, y, z), όπως συμβαίνει στα τροχιακά s και d z Σωστή απάντηση: Δ Αιτιολόγηση: Βλέπε συνοπτική θεωρία (ενότητα 3.4, εικόνα 3.5). 3.7 Σωστή απάντηση: Α Αιτιολόγηση: H παρουσία μεγάλου αριθμού κόμβων (ο αριθμός των σφαιρικών κόμβων είναι: n-l-1) αυξάνει την ηλεκτρονιακή πυκνότητα κοντά στον πυρήνα, με αποτέλεσμα να αυξάνεται η διεισδυτικότητα του τροχιακού. 3.8 Σωστή απάντηση: Α Αιτιολόγηση: Το1s τροχιακό έχει μικρότερο μέγεθος από το 2s τροχιακό. 61
16 3.9 Σωστή απάντηση: Α Αιτιολόγηση: Όσο μεγαλύτερο ποσοστό του ηλεκτρονιακού νέφους περικλείει η σφαίρα, τόσο μεγαλύτερη είναι η ακτίνα της (βλέπε εικόνα 3.8 συνοπτικής θεωρίας) Σωστή απάντηση: Β Αιτιολόγηση: Η πιθανότητα να βρεθεί το ηλεκτρόνιο στο σημείο Β είναι μικρότερη από αυτή του να βρίσκεται στο σημείο Α. Συνεπώς, το ηλεκτρόνιο ξοδεύει λιγότερο χρόνο στην περιοχή Β Σωστή απάντηση: Γ Αιτιολόγηση: Το διάγραμμα παρουσιάζει 2 κόμβους. Με δεδομένο ότι ο αριθμός των σφαιρικών κόμβων είναι n-l-1 έχουμε: Α =1, Β =0, Γ. =3-0-1=2, Δ = Σωστή απάντηση: Γ Αιτιολόγηση: Βλέπε εικόνα 3.3, ενότητα 3.3, συνοπτικής θεωρίας Σωστή απάντηση: B Αιτιολόγηση: Βλέπε ενότητα 3.3 συνοπτικής θεωρίας. Ερωτήσεις τύπου «σωστό - λάθος» με αιτιολόγηση 3.14 Λάθος Αιτιολόγηση: Σε ένα τροχιακό ο αριθμός των σφαιρικών κόμβων είναι: n-l-1. Στην προκειμένη περίπτωση 3-0-1= Λάθος Αιτιολόγηση: Σε ένα τροχιακό ο αριθμός των γωνιακών κόμβων είναι ίσος με τον αζιμουθιακό κβαντικό α- ριθμό, l. Στην προκειμένη περίπτωση l= Σωστό Αιτιολόγηση: Στα ασύμμετρα ή περιττά τροχιακά η κυματοσυνάρτηση Ψ έχει το αντίθετο πρόσημο σε σημεία συμμετρικά ως προς το κέντρο (σημείο τομής των αξόνων x, y, z). Αυτό συμβαίνει στα p τροχιακά, αφού η κυματοσυνάρτηση Ψ αλλάζει πρόσημο από τον ένα λοβό του ατομικού τροχιακού στον άλλο (βλέπε εικόνα 3.5, ενότητα 3.4 συνοπτικής θεωρίας). Ερωτήσεις ανοικτού τύπου 3.17 Απάντηση: Βλέπε συνοπτική θεωρία ενότητα 3.4. Συμμετρικά είναι τα τροχιακά s, d xy, d z 2 και ασύμμετρο είναι το p y. 62
17 3.18 Απάντηση: Με βάση τη θεωρία μεταξύ του πυρήνα και των μεγίστων κορυφών υπάρχουν περιοχές μηδενικής πιθανότητας εύρεσης των ηλεκτρονίων που ονομάζονται σφαιρικές κομβικές επιφάνειες. Στο γράφημα υπάρχει 1 κόμβος. Σε ένα τροχιακό ο αριθμός των κόμβων είναι: n-l-1. Κατόπιν τούτων, ο τύπος του τροχιακού που εμπλέκεται στην περίπτωση αυτή είναι το 2s. Το τροχιακό που έχει 2 κόμβους είναι το 3s Απάντηση: Ερμηνεία στο παραπάνω θέμα μπορεί να δοθεί εφόσον θεωρήσουμε το ηλεκτρόνιο κύμα και όχι σωματίδιο. Τα τροχιακά είναι κυματοσυναρτήσεις που περιγράφουν κύματα. Απλό παράδειγμα συνάρτησης που περιγράφει κύμα είναι η y = ημθ. Η συνάρτηση αυτή μηδενίζεται όταν θ = π ή θ =2π κλπ. Κατ αυτή την έννοια οι κυματοσυναρτήσεις μηδενίζονται για ορισμένες τιμές των μεταβλητών τους Απάντηση: Ο αριθμός των σφαιρικών κομβικών επιφανειών στην ακτινική συνάρτηση δίνεται από τη σχέση: αριθμός κόμβων = n - l-1 όπου, n ο κύριος κβαντικός αριθμός του τροχιακού, που στην προκειμένη περίπτωση είναι 3 και l αζιμουθιακός κβαντικός αριθμός, που στην προκειμένη περίπτωση είναι 2. Κατόπιν τούτων ο αριθμός των κόμβων στην ακτινική συνάρτηση είναι: = 0. Όσον αφορά τον αριθμό των κομβικών επιφανειών στη γωνιακή συνάρτηση, αυτός ισούται με τον αζιμουθιακό κβαντικό αριθμό l. Δηλαδή στην προκειμένη περίπτωση ισούται με Απάντηση: Βλέπε εικόνες 3.1, 3.3, 3.5 και 3.6 της συνοπτικής θεωρίας Απάντηση: Η θέση της μέγιστης κορυφής στα διαγράμματα 4πr 2 R 2 (r) r συσχετίζονται με τις κυκλικές τροχιές του Bohr. Συγκεκριμένα μας δίνουν την ακτίνα Bohr. Έτσι, προκύπτει α 0 για το 1s ηλεκτρόνιο, 4α 0 για το 2s και 9α 0 για το 3s Απάντηση: Οι οριακές καμπύλες περικλείουν το % της πυκνότητας του ηλεκτρονιακού νέφους. Το σχήμα των περιγραμμάτων αυτών καθορίζεται από τα διαγράμματα των συναρτήσεων γωνιακής πιθανότητας Α 2 (θ,φ), ενώ το σχετικό μέγεθος τους καθορίζεται από τα διαγράμματα των συναρτήσεων ακτινικής πιθανότητας 4πr 2 R 2. Τα τροχιακά f έχουν αζιμουθιακό κβαντικό αριθμό l=3. Συνεπώς ο μαγνητικός κβαντικός αριθμός μπορεί να λάβει τις τιμές m l = -3,-2,-1, 0, +1, +2, +3. Με αποτέλεσμα να προκύπτουν 7 τροχιακά Απάντηση: Είναι διαγράμματα ίσης ηλεκτρονιακής πυκνότητας, όπως είναι τα τοπογραφικά διαγράμματα με τις ισοϋψείς καμπύλες, που προκύπτουν με λεπτομερείς υπολογισμούς μέσω της εξίσωσης Schrödinger. Οι τιμές που αναγράφονται στις καμπύλες εκφράζουν το κλάσμα της μέγιστης πιθανότητας ή το κλάσμα της μέγιστης ηλεκτρονιακής πυκνότητας. 63
Η Ψ = Ε Ψ. Ψ = f(x, y, z, t, λ)
 Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
Κύριος κβαντικός αριθμός (n)
 Κύριος κβαντικός αριθμός (n) Επιτρεπτές τιμές: n = 1, 2, 3, Καθορίζει: το μέγεθος του ηλεκτρονιακού νέφους κατά μεγάλο μέρος, την ενέργεια του τροχιακού τη στιβάδα στην οποία κινείται το ηλεκτρόνιο Όσομεγαλύτερηείναιητιμήτουn
Κύριος κβαντικός αριθμός (n) Επιτρεπτές τιμές: n = 1, 2, 3, Καθορίζει: το μέγεθος του ηλεκτρονιακού νέφους κατά μεγάλο μέρος, την ενέργεια του τροχιακού τη στιβάδα στην οποία κινείται το ηλεκτρόνιο Όσομεγαλύτερηείναιητιμήτουn
Κβαντικοί αριθμοί τρεις κβαντικοί αριθμοί
 Κβαντικοί αριθμοί Στην κβαντομηχανική εισάγονται τρεις κβαντικοί αριθμοί για τον καθορισμό της κατανομής του ηλεκτρονιακού νέφους (ατομικού τροχιακού). Οι κβαντικοί αυτοί αριθμοί προκύπτουν από την επίλυση
Κβαντικοί αριθμοί Στην κβαντομηχανική εισάγονται τρεις κβαντικοί αριθμοί για τον καθορισμό της κατανομής του ηλεκτρονιακού νέφους (ατομικού τροχιακού). Οι κβαντικοί αυτοί αριθμοί προκύπτουν από την επίλυση
Η ΘΕΩΡΙΑ ΤΩΝ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
 9Α Η ΘΕΩΡΙΑ ΤΩΝ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου διατυπώνεται συνοπτικά η κβαντική θεωρία των μοριακών τροχιακών (MO) για την ερμηνεία της μοριακής δόμησης. Ορίζονται
9Α Η ΘΕΩΡΙΑ ΤΩΝ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου διατυπώνεται συνοπτικά η κβαντική θεωρία των μοριακών τροχιακών (MO) για την ερμηνεία της μοριακής δόμησης. Ορίζονται
Από τι αποτελείται το Φως (1873)
 Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
ΕΙΣΑΓΩΓΗ ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ
 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Στο ατομικό πρότυπο του Bohr ο κύριος κβαντικός αριθμός (n) εισάγεται αυθαίρετα, για τον καθορισμό
ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Στο ατομικό πρότυπο του Bohr ο κύριος κβαντικός αριθμός (n) εισάγεται αυθαίρετα, για τον καθορισμό
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 8 Ατομικά Τροχιακά Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 8 Ατομικά Τροχιακά Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 8 Ατομικά Τροχιακά Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία.
 Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία. Η κβαντική θεωρία αναπτύχθηκε με τις ιδέες των ακόλουθων επιστημόνων: Κβάντωση της ενέργειας (Max Planck, 1900). Κυματική θεωρία της ύλης (De Broglie,
Σύγχρονες αντιλήψεις γύρω από το άτομο. Κβαντική θεωρία. Η κβαντική θεωρία αναπτύχθηκε με τις ιδέες των ακόλουθων επιστημόνων: Κβάντωση της ενέργειας (Max Planck, 1900). Κυματική θεωρία της ύλης (De Broglie,
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης
 Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Κβαντομηχανική ή κυματομηχανική
 Κβαντομηχανική ή κυματομηχανική Ποια ήταν τα αναπάντητα ερωτήματα της θεωρίας του Bohr; 1. Φάσματα πολυηλεκτρονικών ατόμων 2. Κυκλικές τροχιές 3. Γιατί η ενέργεια του e είναι κβαντισμένη; Κβαντομηχανική
Κβαντομηχανική ή κυματομηχανική Ποια ήταν τα αναπάντητα ερωτήματα της θεωρίας του Bohr; 1. Φάσματα πολυηλεκτρονικών ατόμων 2. Κυκλικές τροχιές 3. Γιατί η ενέργεια του e είναι κβαντισμένη; Κβαντομηχανική
Κομβικές επιφάνειες. Από τη γνωστή σχέση: Ψ(r, θ, φ) = R(r).Θ(θ).Φ(φ) για Ψ = 0 θα πρέπει είτε R(r) = 0 ή Θ(θ).Φ(φ) = 0
 Κομβικές επιφάνειες Από τα σχήματα των ατομικών τροχιακών αλλά και από τις μαθηματικές εκφράσεις είναι φανερό ότι υπάρχουν επιφάνειες όπου το Ψ 2 μηδενίζεται, πάνω στις οποίες δηλαδή είναι αδύνατο να βρεθεί
Κομβικές επιφάνειες Από τα σχήματα των ατομικών τροχιακών αλλά και από τις μαθηματικές εκφράσεις είναι φανερό ότι υπάρχουν επιφάνειες όπου το Ψ 2 μηδενίζεται, πάνω στις οποίες δηλαδή είναι αδύνατο να βρεθεί
ΑΣΚΗΣΕΙΣ ΚΑΙ ΛΥΣΕΙΣ ΣΤΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗ ΧΗΜΕΙΑ. Ν. Μαραβελάκη Επίκουρος Καθηγήτρια Γενικού Τµήµατος Πολυτεχνείου Κρήτης
 ΑΣΚΗΣΕΙΣ ΚΑΙ ΛΥΣΕΙΣ ΣΤΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗ ΧΗΜΕΙΑ Ν. Μαραβελάκη Επίκουρος Καθηγήτρια Γενικού Τµήµατος Πολυτεχνείου Κρήτης Χανιά Απρίλιος 011 Ασκήσεις και Λύσεις στο µάθηµα Γενική & Ανόργανη Χηµεία 1. Εάν ο
ΑΣΚΗΣΕΙΣ ΚΑΙ ΛΥΣΕΙΣ ΣΤΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗ ΧΗΜΕΙΑ Ν. Μαραβελάκη Επίκουρος Καθηγήτρια Γενικού Τµήµατος Πολυτεχνείου Κρήτης Χανιά Απρίλιος 011 Ασκήσεις και Λύσεις στο µάθηµα Γενική & Ανόργανη Χηµεία 1. Εάν ο
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση:
 Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει το ατοµικό πρότυπο του Bohr καθώς και τα µειονεκτήµατά του. Να υπολογίζει την ενέργεια που εκπέµπεται ή απορροφάται
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει το ατοµικό πρότυπο του Bohr καθώς και τα µειονεκτήµατά του. Να υπολογίζει την ενέργεια που εκπέµπεται ή απορροφάται
Κβαντομηχανική εικόνα του ατομικού μοντέλου
 Κβαντομηχανική εικόνα του ατομικού μοντέλου 1. Ερώτηση: Τι είναι η κβαντομηχανική; H κβαντομηχανική, είναι η σύγχρονη αντίληψη μιας νέας μηχανικής που μπορεί να εφαρμοστεί στο μικρόκοσμο του ατόμου. Σήμερα
Κβαντομηχανική εικόνα του ατομικού μοντέλου 1. Ερώτηση: Τι είναι η κβαντομηχανική; H κβαντομηχανική, είναι η σύγχρονη αντίληψη μιας νέας μηχανικής που μπορεί να εφαρμοστεί στο μικρόκοσμο του ατόμου. Σήμερα
Κεφάλαιο 39 Κβαντική Μηχανική Ατόμων
 Κεφάλαιο 39 Κβαντική Μηχανική Ατόμων Περιεχόμενα Κεφαλαίου 39 Τα άτομα από την σκοπιά της κβαντικής μηχανικής Το άτομο του Υδρογόνου: Η εξίσωση του Schrödinger και οι κβαντικοί αριθμοί ΟΙ κυματοσυναρτήσεις
Κεφάλαιο 39 Κβαντική Μηχανική Ατόμων Περιεχόμενα Κεφαλαίου 39 Τα άτομα από την σκοπιά της κβαντικής μηχανικής Το άτομο του Υδρογόνου: Η εξίσωση του Schrödinger και οι κβαντικοί αριθμοί ΟΙ κυματοσυναρτήσεις
Μάθημα 7ο. Υλοκύματα Και Η Σύγχρονη Ατομική Θεωρία
 Μάθημα 7ο Υλοκύματα Και Η Σύγχρονη Ατομική Θεωρία h m U(x,y,z, t) ih t (x, y,z,t) (x, y,z)e iet / h H E Γενική & Ανόργανη Χημεία 06-7 Ewin Schöinge Η ανεξάρτητη από τον χρόνο εξίσωση Schöinge U m H E E
Μάθημα 7ο Υλοκύματα Και Η Σύγχρονη Ατομική Θεωρία h m U(x,y,z, t) ih t (x, y,z,t) (x, y,z)e iet / h H E Γενική & Ανόργανη Χημεία 06-7 Ewin Schöinge Η ανεξάρτητη από τον χρόνο εξίσωση Schöinge U m H E E
Κβαντομηχανική σε. τρεις διαστάσεις. Εξίσωση Schrödinger σε 3D. Τελεστές 2 )
 vs of Io vs of Io D of Ms Scc & gg Couo Ms Scc ική Θεωλης ική Θεωλης ιδάσκων: Λευτέρης Λοιδωρίκης Π 746 dok@cc.uo.g cs.s.uo.g/dok ομηχ ομηχ δ ά τρεις διαστ Εξίσωση Schödg σε D Σε μία διάσταση Σε τρείς
vs of Io vs of Io D of Ms Scc & gg Couo Ms Scc ική Θεωλης ική Θεωλης ιδάσκων: Λευτέρης Λοιδωρίκης Π 746 dok@cc.uo.g cs.s.uo.g/dok ομηχ ομηχ δ ά τρεις διαστ Εξίσωση Schödg σε D Σε μία διάσταση Σε τρείς
Κβαντικοί αριθμοί. l =0 υποφλοιός S σφαίρα m l =0 ένα τροχιακό με σφαιρική συμμετρία
 Κβαντικοί αριθμοί Η θεωρία του Bohr χρειάζεται μόνο τον κύριο κβαντικό αριθμό η, για να καθορίσει ενέργεια για το άτομο του υδρογόνου Ε η =-2,18.10-18 /η 2 κυκλική τροχιά. και επιτρεπτή Στην κβαντομηχανική
Κβαντικοί αριθμοί Η θεωρία του Bohr χρειάζεται μόνο τον κύριο κβαντικό αριθμό η, για να καθορίσει ενέργεια για το άτομο του υδρογόνου Ε η =-2,18.10-18 /η 2 κυκλική τροχιά. και επιτρεπτή Στην κβαντομηχανική
Πανεπιστήμιο Κύπρου Τμήμα Χημείας. ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΕΙΑ ΓΙΑ ΒΙΟΛΟΓΟΥΣ ΚΑΙ ΦΥΣΙΚΟΥΣ ΧΗΜ 021 Χειμερινό Εξάμηνο 2008
 Πανεπιστήμιο Κύπρου Τμήμα Χημείας ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΕΙΑ ΓΙΑ ΒΙΟΛΟΓΟΥΣ ΚΑΙ ΦΥΣΙΚΟΥΣ ΧΗΜ 021 Χειμερινό Εξάμηνο 2008 Κωνσταντίνος Ζεϊναλιπούρ Λευκωσία, Σεπτέμβριος 2008 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Στην κβαντομηχανική ο
Πανεπιστήμιο Κύπρου Τμήμα Χημείας ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΕΙΑ ΓΙΑ ΒΙΟΛΟΓΟΥΣ ΚΑΙ ΦΥΣΙΚΟΥΣ ΧΗΜ 021 Χειμερινό Εξάμηνο 2008 Κωνσταντίνος Ζεϊναλιπούρ Λευκωσία, Σεπτέμβριος 2008 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Στην κβαντομηχανική ο
ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # (2): Άτομο Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # (2): Άτομο Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ασκήσεις
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ασκήσεις Ενότητα 8 Ατομικά Τροχιακά Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Άσκηση 1 Να υπολογιστεί η πιθανότερη ακτίνα, *, στην οποία θα βρίσκεται
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ασκήσεις Ενότητα 8 Ατομικά Τροχιακά Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Άσκηση 1 Να υπολογιστεί η πιθανότερη ακτίνα, *, στην οποία θα βρίσκεται
Δομή Διάλεξης. Εύρεση ακτινικού μέρους εξίσωσης Schrödinger. Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους. Εφαρμογή σε άτομο υδρογόνου
 Κεντρικά Δυναμικά Δομή Διάλεξης Εύρεση ακτινικού μέρους εξίσωσης Schrödinger Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους Εφαρμογή σε άτομο υδρογόνου Ακτινική Συνιστώσα Ορμής Έστω Χαμιλτονιανή
Κεντρικά Δυναμικά Δομή Διάλεξης Εύρεση ακτινικού μέρους εξίσωσης Schrödinger Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους Εφαρμογή σε άτομο υδρογόνου Ακτινική Συνιστώσα Ορμής Έστω Χαμιλτονιανή
Πρωτόνια, νετρόνια και ηλεκτρόνια. πρωτόνιο 1 (1,67X10-24 g) +1 νετρόνιο 1 0 1,6X10-19 Cb ηλεκτρόνιο 1/1836 (9X10-28 g) -1
 Πρωτόνια, νετρόνια και ηλεκτρόνια. σχετική μάζα σχετικό φορτίο πρωτόνιο 1 (1,67X10-24 g) +1 νετρόνιο 1 0 1,6X10-19 Cb ηλεκτρόνιο 1/1836 (9X10-28 g) -1 Ο πυρήνας βρίσκεται στο κέντρο του ατόμου και περιέχει
Πρωτόνια, νετρόνια και ηλεκτρόνια. σχετική μάζα σχετικό φορτίο πρωτόνιο 1 (1,67X10-24 g) +1 νετρόνιο 1 0 1,6X10-19 Cb ηλεκτρόνιο 1/1836 (9X10-28 g) -1 Ο πυρήνας βρίσκεται στο κέντρο του ατόμου και περιέχει
Κβαντική θεωρία και ηλεκτρονιακή δομή των ατόμων
 Κβαντική θεωρία και ηλεκτρονιακή δομή των ατόμων Κβαντικοί αριθμοί Κύριος κβαντικός αριθμός (n) Αζιμουθιακός κβαντικός αριθμός (l) Μαγνητικός κβαντικός αριθμός (ml) Στροφορμή (Spin) ηλεκτρονίου κβαντικός
Κβαντική θεωρία και ηλεκτρονιακή δομή των ατόμων Κβαντικοί αριθμοί Κύριος κβαντικός αριθμός (n) Αζιμουθιακός κβαντικός αριθμός (l) Μαγνητικός κβαντικός αριθμός (ml) Στροφορμή (Spin) ηλεκτρονίου κβαντικός
Διάλεξη 3: Το άτομο του Υδρογόνου. Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schrödinger για το κεντρικό δυναμικό
 Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöding για το κεντρικό δυναμικό Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 3 k V ) Αποδεικνύεται ότι οι λύσεις της ακτινικής εξίσωσης
Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöding για το κεντρικό δυναμικό Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 3 k V ) Αποδεικνύεται ότι οι λύσεις της ακτινικής εξίσωσης
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Κίνηση σε κεντρικά δυναµικά 1.1.1 Κλασική περιγραφή Η Χαµιλτωνιανή κλασικού συστήµατος που κινείται
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Κίνηση σε κεντρικά δυναµικά 1.1.1 Κλασική περιγραφή Η Χαµιλτωνιανή κλασικού συστήµατος που κινείται
Διάλεξη 2: Κεντρικά Δυναμικά. Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schrödinger για κεντρικά δυναμικά
 Διάλεξη : Κεντρικά Δυναμικά Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöing για κεντρικά δυναμικά Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 03 Κεντρικά δυναμικά Εξάρτηση δυναμικού
Διάλεξη : Κεντρικά Δυναμικά Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöing για κεντρικά δυναμικά Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 03 Κεντρικά δυναμικά Εξάρτηση δυναμικού
ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΑ ΑΤΟΜΑ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
 4Α ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΑ ΑΤΟΜΑ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου καταγράφονται οι παράγοντες που καθορίζουν την ενέργεια των τροχιακών των πολυηλεκτρονιακών ατόμων. Δίνονται οι κανόνες που καθορίζουν
4Α ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΑ ΑΤΟΜΑ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου καταγράφονται οι παράγοντες που καθορίζουν την ενέργεια των τροχιακών των πολυηλεκτρονιακών ατόμων. Δίνονται οι κανόνες που καθορίζουν
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Κβαντική Θεωρία ΙΙ. Κεντρικά Δυναμικά Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κβαντική Θεωρία ΙΙ Κεντρικά Δυναμικά Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κβαντική Θεωρία ΙΙ Κεντρικά Δυναμικά Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
Δρ. Ιωάννης Καλαμαράς, Διδάκτωρ Χημικός. 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις
 1 ο Κεφάλαιο Χημείας Θετικής Κατεύθυνσης Γ Λυκείου 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις 1. Η εξίσωση E = h v μας δίνει την ενέργεια μιας ηλεκτρομαγνητικής ακτινοβολίας 2. H κβαντική
1 ο Κεφάλαιο Χημείας Θετικής Κατεύθυνσης Γ Λυκείου 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις 1. Η εξίσωση E = h v μας δίνει την ενέργεια μιας ηλεκτρομαγνητικής ακτινοβολίας 2. H κβαντική
ΑΤΟΜΙΚΑ ΤΟΜΙΚΑ ΠΡΟΤΥΠΑ
 ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Thomson (σταφιδόψωμο) Rutherford (πλανητικό μοντέλο) Bohr (επιτρεπόμενες τροχιές ενεργειακές στάθμες) Κβαντομηχανική β ή (τροχιακό) ρχ 24/9/2008 1 ΑΤΟΜΙΚΟ ΠΡΟΤΥΠΟ Bohr 1η Συνθήκη (Μηχανική
ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Thomson (σταφιδόψωμο) Rutherford (πλανητικό μοντέλο) Bohr (επιτρεπόμενες τροχιές ενεργειακές στάθμες) Κβαντομηχανική β ή (τροχιακό) ρχ 24/9/2008 1 ΑΤΟΜΙΚΟ ΠΡΟΤΥΠΟ Bohr 1η Συνθήκη (Μηχανική
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί
 1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
Μοριακή δομή Ο2 σύμφωνα με VB διαμαγνητικό
 Μοριακή δομή Ο 2 σύμφωνα με VB? διαμαγνητικό Θεωρία Μοριακών Τροχιακών Μolecular Orbital Theory (MO) Τα μοριακά τροχιακά (molecular orbital) είναι κυματοσυναρτήσεις οι οποίες προκύτπουναπότογραμμικόσυνδυασμότωνκυματοσυναρτήσεωντωναο.
Μοριακή δομή Ο 2 σύμφωνα με VB? διαμαγνητικό Θεωρία Μοριακών Τροχιακών Μolecular Orbital Theory (MO) Τα μοριακά τροχιακά (molecular orbital) είναι κυματοσυναρτήσεις οι οποίες προκύτπουναπότογραμμικόσυνδυασμότωνκυματοσυναρτήσεωντωναο.
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή. Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής
 Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
ΤΟ ΚΒΑΝΤΟΜΗΧΑΝΙΚΟ ΜΟΝΤΕΛΟ ΤΟΥ ΑΤΟΜΟΥ
 682 ΤΟ ΚΒΑΝΤΟΜΗΧΑΝΙΚΟ ΜΟΝΤΕΛΟ ΤΟΥ ΑΤΟΜΟΥ Παπαχρήστου Βασίλειος Χημικός, MSc στη διδακτική της Χημείας vasipa@in.gr ΠΕΡΙΛΗΨΗ Το παρόν CD-Rom αποτελείται από τέσσερις ενότητες: Η πρώτη ενότητα αναφέρεται
682 ΤΟ ΚΒΑΝΤΟΜΗΧΑΝΙΚΟ ΜΟΝΤΕΛΟ ΤΟΥ ΑΤΟΜΟΥ Παπαχρήστου Βασίλειος Χημικός, MSc στη διδακτική της Χημείας vasipa@in.gr ΠΕΡΙΛΗΨΗ Το παρόν CD-Rom αποτελείται από τέσσερις ενότητες: Η πρώτη ενότητα αναφέρεται
ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2017
 ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2017-2018 ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2017 Το μάθημα αυτό προσφέρεται στους πρωτοετείς φοιτητές του Τμήματος Μηχανολόγων Μηχανικών της Πολυτεχνικής Σχολής του Αριστοτέλειου Πανεπιστημίου
ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2017-2018 ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2017 Το μάθημα αυτό προσφέρεται στους πρωτοετείς φοιτητές του Τμήματος Μηχανολόγων Μηχανικών της Πολυτεχνικής Σχολής του Αριστοτέλειου Πανεπιστημίου
ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ
 ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ Ενότητα 9 Ηλεκτρονική Φασματοσκοπία Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins,
ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ Ενότητα 9 Ηλεκτρονική Φασματοσκοπία Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins,
ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5
 Κβαντική Μηχανική ΙΙ Ακ. Ετος 2013-14, Α. Λαχανάς 1/ 53 ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5 Α. Λαχανάς ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, Τµήµα Φυσικής Τοµέας Πυρηνικής Φυσικής & Στοιχειωδών Σωµατιδίων Ακαδηµαικό έτος
Κβαντική Μηχανική ΙΙ Ακ. Ετος 2013-14, Α. Λαχανάς 1/ 53 ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5 Α. Λαχανάς ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, Τµήµα Φυσικής Τοµέας Πυρηνικής Φυσικής & Στοιχειωδών Σωµατιδίων Ακαδηµαικό έτος
KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κυματική εξίσωση Schrödiger Η δυνατότητα ενός σωματιδίου να συμπεριφέρεται ταυτόχρονα και ως κύμα, δηλαδή να είναι εντοπισμένο
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κυματική εξίσωση Schrödiger Η δυνατότητα ενός σωματιδίου να συμπεριφέρεται ταυτόχρονα και ως κύμα, δηλαδή να είναι εντοπισμένο
ΕΙΣΑΓΩΓΗ ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ III. ΤΟ ΣΥΓΧΡΟΝΟ ΑΤΟΜΙΚΟ ΠΡΟΤΥΠΟ
 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Η εικόνα του ατόμου που είναι τόσο γνωστή, δηλαδή ο πυρήνας και γύρω του σε τροχιές τα ηλεκτρόνια σαν πλανήτες (το πρότυπο του Ruterford
ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Η εικόνα του ατόμου που είναι τόσο γνωστή, δηλαδή ο πυρήνας και γύρω του σε τροχιές τα ηλεκτρόνια σαν πλανήτες (το πρότυπο του Ruterford
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί
 1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
H εικόνα του ατόμου έχει αλλάξει δραστικά
 Δομή Ατόμου και Ατομικά Τροχιακά Α Τα κλασσικά πρότυπα Η ιστορία της δομής του ατόμου (1/2) ατομική θεωρία Δημόκριτου (άτομοι) ατομική θεωρία Dalton Πλανητικό πρότυπο Rutherford πρότυπο Schrodinger 460
Δομή Ατόμου και Ατομικά Τροχιακά Α Τα κλασσικά πρότυπα Η ιστορία της δομής του ατόμου (1/2) ατομική θεωρία Δημόκριτου (άτομοι) ατομική θεωρία Dalton Πλανητικό πρότυπο Rutherford πρότυπο Schrodinger 460
Η ΚΥΜΑΤΟΣΩΜΑΤΙΔΙΑΚΗ ΑΝΤΙΛΗΨΗ ΓΙΑ ΤΗΝ ΑΤΟΜΙΚΗ ΔΟΜΗΣΗ - ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
 2Α Η ΚΥΜΑΤΟΣΩΜΑΤΙΔΙΑΚΗ ΑΝΤΙΛΗΨΗ ΓΙΑ ΤΗΝ ΑΤΟΜΙΚΗ ΔΟΜΗΣΗ - ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου διατυπώνεται συνοπτικά η κβαντική θεώρηση της ατομικής δόμησης, με πυλώνες την κβαντική θεωρία
2Α Η ΚΥΜΑΤΟΣΩΜΑΤΙΔΙΑΚΗ ΑΝΤΙΛΗΨΗ ΓΙΑ ΤΗΝ ΑΤΟΜΙΚΗ ΔΟΜΗΣΗ - ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Σύνοψη Στο Α μέρος του κεφαλαίου διατυπώνεται συνοπτικά η κβαντική θεώρηση της ατομικής δόμησης, με πυλώνες την κβαντική θεωρία
Ατομική δομή. Το άτομο του υδρογόνου Σφαιρικά συμμετρικές λύσεις ψ = ψ(r) Εξίσωση Schrodinger (σφαιρικές συντεταγμένες) ħ2. Εξίσωση Schrodinger (1D)
 Ατομική δομή Το άτομο του υδρογόνου Σφαιρικά συμμετρικές λύσεις ψ = ψ(r) Εξίσωση Schrodinger (1D) Εξίσωση Schrodinger (σφαιρικές συντεταγμένες) ħ2 2m 2 ψ + V r ψ = Εψ Τελεστής Λαπλασιανής για σφαιρικές
Ατομική δομή Το άτομο του υδρογόνου Σφαιρικά συμμετρικές λύσεις ψ = ψ(r) Εξίσωση Schrodinger (1D) Εξίσωση Schrodinger (σφαιρικές συντεταγμένες) ħ2 2m 2 ψ + V r ψ = Εψ Τελεστής Λαπλασιανής για σφαιρικές
Γενική & Ανόργανη Χημεία Καλή (aκαδημαϊκή) Χρονιά!
 1 Καλή (aκαδημαϊκή) Χρονιά! Γενική και Ανόργανη Χημεία Ακ. Έτος 2016-17 ΚΑΛΩΣ ΗΛΘΑΤΕ!! Έχετε επιτύχει με τις μέχρι τώρα προσπάθειές σας να εισαχθείτε σε ένα δραστήριο Τμήμα Χημικής Μηχανικής το οποίο έχει
1 Καλή (aκαδημαϊκή) Χρονιά! Γενική και Ανόργανη Χημεία Ακ. Έτος 2016-17 ΚΑΛΩΣ ΗΛΘΑΤΕ!! Έχετε επιτύχει με τις μέχρι τώρα προσπάθειές σας να εισαχθείτε σε ένα δραστήριο Τμήμα Χημικής Μηχανικής το οποίο έχει
το ένα με ηλεκτρικό φορτίο Ζe και το άλλο με e. Η χαμιλτονιανή του συστήματος (στο πλαίσιο της προσέγγισης Coulomb) μπορεί να έλθει στη μορφή
 ΚΕΦΑΛΑΙΟ 9: ΑΤΟΜΑ, Σελ. 19 έως 14 του βιβλίου ΚΣ ENOTHTA 1 Η, 13 ο VIDEO, 15/11/013, Από 55λ έως 1ω,5λ (τέλος), Σελ. 19 έως 13 του βιβλίου ΚΣ: ΙΔΙΟΤΗΤΕΣ Της ΒΑΣΙΚΉΣ ΚΑΤΑΣΤΑΣΗΣ ΥΔΡΟΓΟΝΟΕΙΔΟΥΣ ΔΥΝΑΜΙΚΟΥ
ΚΕΦΑΛΑΙΟ 9: ΑΤΟΜΑ, Σελ. 19 έως 14 του βιβλίου ΚΣ ENOTHTA 1 Η, 13 ο VIDEO, 15/11/013, Από 55λ έως 1ω,5λ (τέλος), Σελ. 19 έως 13 του βιβλίου ΚΣ: ΙΔΙΟΤΗΤΕΣ Της ΒΑΣΙΚΉΣ ΚΑΤΑΣΤΑΣΗΣ ΥΔΡΟΓΟΝΟΕΙΔΟΥΣ ΔΥΝΑΜΙΚΟΥ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Σύγxρονη Φυσική II. Το άτομο του Υδρογόνου Διδάσκων : Επίκ. Καθ. Μ. Μπενής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Το άτομο του Υδρογόνου Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cetive
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Το άτομο του Υδρογόνου Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cetive
1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού
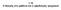 1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού Η δομή του Μεθανίου τετραεδρική γωνίες δεσμού = 109.5 Μήκη δεσμού = 110 pm αλλά η δομή εμφανίζεται ασυνεπής με την ηλεκτρονική διάταξη του άνθρακα Η
1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού Η δομή του Μεθανίου τετραεδρική γωνίες δεσμού = 109.5 Μήκη δεσμού = 110 pm αλλά η δομή εμφανίζεται ασυνεπής με την ηλεκτρονική διάταξη του άνθρακα Η
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not defined. Σκοποί Μαθήματος (Επικεφαλίδα
Ηλεκτρονική φασματοσκοπία ατόμων
 Ηλεκτρονική φασματοσκοπία ατόμων Εξίσωση του chrodger H H H µ µ m e e 4πε r Ζe 4πε r για το άτοµο του υδρογόνου για τα υδρογονοειδή άτοµα He Ζe 4πε r < j Ζe 4πε r j για πολυηλεκτρονικά άτοµα µ m m m e
Ηλεκτρονική φασματοσκοπία ατόμων Εξίσωση του chrodger H H H µ µ m e e 4πε r Ζe 4πε r για το άτοµο του υδρογόνου για τα υδρογονοειδή άτοµα He Ζe 4πε r < j Ζe 4πε r j για πολυηλεκτρονικά άτοµα µ m m m e
ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 1 ο ΚΕΦΑΛΑΙΟΥ (2000-2011) Χημεία Γ Λυκείου. Υπεύθυνη καθηγήτρια: Ε. Ατσαλάκη
 Υπεύθυνη καθηγήτρια: Ε. Ατσαλάκη ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 1 ο ΚΕΦΑΛΑΙΟΥ (2000-2011) Χημεία Γ Λυκείου Α) Να επιλέξετε σε κάθε μία από τις παρακάτω προτάσεις τη σωστή απάντηση: 1. To στοιχείο που περιέχει
Υπεύθυνη καθηγήτρια: Ε. Ατσαλάκη ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 1 ο ΚΕΦΑΛΑΙΟΥ (2000-2011) Χημεία Γ Λυκείου Α) Να επιλέξετε σε κάθε μία από τις παρακάτω προτάσεις τη σωστή απάντηση: 1. To στοιχείο που περιέχει
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Αρχές Κβαντικής Χημείας και Φασματοσκοπίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αρχές Κβαντικής Χημείας και Φασματοσκοπίας Ενότητα # (6): LCAO - Εξισώσεις Roothaan-Hartree-Fock - Αυτοσυνεπές πεδίο Καραφίλογλου Παντελεήμων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αρχές Κβαντικής Χημείας και Φασματοσκοπίας Ενότητα # (6): LCAO - Εξισώσεις Roothaan-Hartree-Fock - Αυτοσυνεπές πεδίο Καραφίλογλου Παντελεήμων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Σύγxρονη Φυσική II. Κεντρικά Δυναμικά Διδάσκων : Επίκ. Καθ. Μ. Μπενής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Κεντρικά Δυναμικά Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Coons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Κεντρικά Δυναμικά Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Coons.
ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2016
 ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2016-2017 ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2016 Το μάθημα αυτό προσφέρεται στους πρωτοετείς φοιτητές του Τμήματος Χημικών Μηχανικών της Πολυτεχνικής Σχολής του Αριστοτέλειου Πανεπιστημίου
ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2016-2017 ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2016 Το μάθημα αυτό προσφέρεται στους πρωτοετείς φοιτητές του Τμήματος Χημικών Μηχανικών της Πολυτεχνικής Σχολής του Αριστοτέλειου Πανεπιστημίου
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 3 η : Περιοδικότητα & Ατομική Δομή. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 3 η : Περιοδικότητα & Ατομική Δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Φως & Ηλεκτρομαγνητικό Φάσμα 2 Το ορατό φως, η υπεριώδης
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 3 η : Περιοδικότητα & Ατομική Δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Φως & Ηλεκτρομαγνητικό Φάσμα 2 Το ορατό φως, η υπεριώδης
Κεφάλαιο 38 Κβαντική Μηχανική
 Κεφάλαιο 38 Κβαντική Μηχανική Περιεχόμενα Κεφαλαίου 38 Κβαντική Μηχανική Μια καινούργια Θεωρία Η κυματοσυνάρτηση και η εξήγησή της. Το πείραμα της διπλής σχισμής. Η αρχή της αβεβαιότητας του Heisenberg.
Κεφάλαιο 38 Κβαντική Μηχανική Περιεχόμενα Κεφαλαίου 38 Κβαντική Μηχανική Μια καινούργια Θεωρία Η κυματοσυνάρτηση και η εξήγησή της. Το πείραμα της διπλής σχισμής. Η αρχή της αβεβαιότητας του Heisenberg.
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
0 είναι η παράγωγος v ( t 0
 ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ ΟΡΙΣΜΟΣ Τι λέμε ρυθμό μεταβολής του μεγέθους y ως προς το μέγεθος για, αν y f( είναι παραγωγίσιμη συνάρτηση ; Απάντηση : Αν δύο μεταβλητά μεγέθη, y συνδέονται με τη σχέση y f(, όταν f
ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ ΟΡΙΣΜΟΣ Τι λέμε ρυθμό μεταβολής του μεγέθους y ως προς το μέγεθος για, αν y f( είναι παραγωγίσιμη συνάρτηση ; Απάντηση : Αν δύο μεταβλητά μεγέθη, y συνδέονται με τη σχέση y f(, όταν f
Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις
 Ύλη μαθήματος «Σύγχρονη Φυσική» Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις Σ2-Σελίδες: 673-705, (όλο το κεφάλαιο από το βιβλίο) και η παρουσίαση Σ2 που έχει αναρτηθεί στο e-class
Ύλη μαθήματος «Σύγχρονη Φυσική» Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις Σ2-Σελίδες: 673-705, (όλο το κεφάλαιο από το βιβλίο) και η παρουσίαση Σ2 που έχει αναρτηθεί στο e-class
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Διάλεξη 1: Κβαντομηχανική σε τρεις διαστάσεις
 Διάλεξη : Κβαντομηχανική σε τρεις διαστάσεις Βασικές Αρχές της Κβαντομηχανικής H κατάσταση ενός φυσικού συστήματος περιγράφεται από την κυματοσυνάρτησή του και αποτελεί το πλάτος πιθανότητας να βρεθεί
Διάλεξη : Κβαντομηχανική σε τρεις διαστάσεις Βασικές Αρχές της Κβαντομηχανικής H κατάσταση ενός φυσικού συστήματος περιγράφεται από την κυματοσυνάρτησή του και αποτελεί το πλάτος πιθανότητας να βρεθεί
ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Εφαρμογές κβαντικής θεωρίας
 Εφαρμογές κβαντικής θεωρίας Στοιχειώδες μαθηματικό υπόβαθρο Σχέση Euler Χρησιμοποιώντας τη σχέση Euler, ένα αρμονικό κύμα της μορφής Acos(kx) (πραγματική συνάρτηση), μπορεί να γραφτεί ως Re[Ae ikx ] που
Εφαρμογές κβαντικής θεωρίας Στοιχειώδες μαθηματικό υπόβαθρο Σχέση Euler Χρησιμοποιώντας τη σχέση Euler, ένα αρμονικό κύμα της μορφής Acos(kx) (πραγματική συνάρτηση), μπορεί να γραφτεί ως Re[Ae ikx ] που
Μάθημα 6 α) β-διάσπαση β) Χαρακτηριστικά πυρήνων, πέρα από μέγεθος και μάζα
 Στοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων (5ου εξαμήνου, χειμερινό 2011-12) Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου Μάθημα 6 α) β-διάσπαση β) Χαρακτηριστικά πυρήνων, πέρα από μέγεθος και μάζα Κώστας
Στοιχεία Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων (5ου εξαμήνου, χειμερινό 2011-12) Τμήμα G3: Κ. Κορδάς & Χ. Πετρίδου Μάθημα 6 α) β-διάσπαση β) Χαρακτηριστικά πυρήνων, πέρα από μέγεθος και μάζα Κώστας
κυματικής συνάρτησης (Ψ) κυματική συνάρτηση
 Στην κβαντομηχανική ο χώρος μέσα στον οποίο κινείται το ηλεκτρόνιο γύρω από τον πυρήνα παύει να περιγράφεται από μια απλή τροχιά, χαρακτηριστικό του μοντέλου του Bohr, αλλά περιγράφεται ο χώρος μέσα στον
Στην κβαντομηχανική ο χώρος μέσα στον οποίο κινείται το ηλεκτρόνιο γύρω από τον πυρήνα παύει να περιγράφεται από μια απλή τροχιά, χαρακτηριστικό του μοντέλου του Bohr, αλλά περιγράφεται ο χώρος μέσα στον
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανολόγων Μηχανικών. Χημεία. Ενότητα 2: Κβαντομηχανική προσέγγιση του ατόμου
 Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 2: Κβαντομηχανική προσέγγιση του ατόμου Τόλης Ευάγγελος e-mail: etolis@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 2: Κβαντομηχανική προσέγγιση του ατόμου Τόλης Ευάγγελος e-mail: etolis@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΦΥΣ Διάλ Άλγεβρα. 1 a. Άσκηση για το σπίτι: Διαβάστε το παράρτημα Β του βιβλίου
 ΦΥΣ 131 - Διάλ. 4 1 Άλγεβρα a 1 a a ( ± y) a a ± y log a a 10 log a ± logb log( ab ± 1 ) log( a n ) n log( a) ln a a e ln a ± ln b ln( ab ± 1 ) ln( a n ) nln( a) Άσκηση για το σπίτι: Διαβάστε το παράρτημα
ΦΥΣ 131 - Διάλ. 4 1 Άλγεβρα a 1 a a ( ± y) a a ± y log a a 10 log a ± logb log( ab ± 1 ) log( a n ) n log( a) ln a a e ln a ± ln b ln( ab ± 1 ) ln( a n ) nln( a) Άσκηση για το σπίτι: Διαβάστε το παράρτημα
Αρχές Κβαντικής Χημείας και Φασματοσκοπίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αρχές Κβαντικής Χημείας και Φασματοσκοπίας Ενότητα # (4): Συμμετρία, Πολικότητα και Οπτική Ενεργότητα των μορίων Σιγάλας Μιχάλης Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αρχές Κβαντικής Χημείας και Φασματοσκοπίας Ενότητα # (4): Συμμετρία, Πολικότητα και Οπτική Ενεργότητα των μορίων Σιγάλας Μιχάλης Άδειες
3. Το πρότυπο του Bohr εξήγησε το ότι το φάσμα της ακτινοβολίας που εκπέμπει το αέριο υδρογόνο, είναι γραμμικό.
 ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 16 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ-ΠΡΟΤΥΠΟ BOHR ΟΜΑΔΑ Α Να χαρακτηρίσετε τις παρακάτω προτάσεις ως Σωστές ή Λάθος και να αιτιολογήσετε αυτές που είναι λάθος : 1.
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 16 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ-ΠΡΟΤΥΠΟ BOHR ΟΜΑΔΑ Α Να χαρακτηρίσετε τις παρακάτω προτάσεις ως Σωστές ή Λάθος και να αιτιολογήσετε αυτές που είναι λάθος : 1.
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ατομικός αριθμός = Αριθμός πρωτονίων. Μαζικός αριθμός = Αριθμός πρωτονίων + Αριθμός νετρονίων (nucleon number)
 Δομή Ατόμου και Ατομικά Τροχιακά Ατομικός και μαζικός αριθμός Ατομικός αριθμός = Αριθμός πρωτονίων (proton number) Μαζικός αριθμός = Αριθμός πρωτονίων + Αριθμός νετρονίων (nucleon number) 2 Ισότοπα Ισοβαρή
Δομή Ατόμου και Ατομικά Τροχιακά Ατομικός και μαζικός αριθμός Ατομικός αριθμός = Αριθμός πρωτονίων (proton number) Μαζικός αριθμός = Αριθμός πρωτονίων + Αριθμός νετρονίων (nucleon number) 2 Ισότοπα Ισοβαρή
Μαθηματικά Γενικής Παιδείας Κεφάλαιο 1ο Ανάλυση ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΝΑΛΥΣΗ
 Μαθηματικά Γενικής Παιδείας Κεφάλαιο ο Ανάλυση ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΝΑΛΥΣΗ Ερωτήσεις του τύπου «Σωστό - Λάθος». * Η διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α
Μαθηματικά Γενικής Παιδείας Κεφάλαιο ο Ανάλυση ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΝΑΛΥΣΗ Ερωτήσεις του τύπου «Σωστό - Λάθος». * Η διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α
Το άτομο του Υδρογόνου- Υδρογονοειδή άτομα
 Το άτομο του Υδρογόνου- Υδρογονοειδή άτομα Το πιο απλό κβαντομηχανικό ρεαλιστικό σύστημα, το οποίο λύνεται ακριβώς, είναι το άτομο του Υδρογόνου (1 πρωτόνιο και 1 ηλεκτρόνιο) Το δυναμικό στην περίπτωση
Το άτομο του Υδρογόνου- Υδρογονοειδή άτομα Το πιο απλό κβαντομηχανικό ρεαλιστικό σύστημα, το οποίο λύνεται ακριβώς, είναι το άτομο του Υδρογόνου (1 πρωτόνιο και 1 ηλεκτρόνιο) Το δυναμικό στην περίπτωση
Ομοιοπολικός Δεσμός. Ασκήσεις
 Ασκήσεις Ομοιοπολικός Δεσμός 1. Δίνεται η οργανική ένωση CH 3 -CH 2 -C CH της οποίας τα άτομα αριθμούνται από 1 έως 4, όπως φαίνεται παραπάνω. Πόσοι και τι είδους σ δεσμοί και π δεσμοί υπάρχουν στην ένωση;
Ασκήσεις Ομοιοπολικός Δεσμός 1. Δίνεται η οργανική ένωση CH 3 -CH 2 -C CH της οποίας τα άτομα αριθμούνται από 1 έως 4, όπως φαίνεται παραπάνω. Πόσοι και τι είδους σ δεσμοί και π δεσμοί υπάρχουν στην ένωση;
Χημεία είναι επιστήμη που ερευνά τις ιδιότητες της ύλης σε σχέση με τη μοριακή δομή της. Με άλλα λόγια: μοριακής δομής της ύλης με τις ιδιότητές της
 Τι είναι Χημεία; Χημεία είναι επιστήμη που ερευνά τις ιδιότητες της ύλης σε σχέση με τη μοριακή δομή της Με άλλα λόγια: Αντικείμενο της Χημείας είναι η συσχέτιση της μοριακής δομής της ύλης με τις ιδιότητές
Τι είναι Χημεία; Χημεία είναι επιστήμη που ερευνά τις ιδιότητες της ύλης σε σχέση με τη μοριακή δομή της Με άλλα λόγια: Αντικείμενο της Χημείας είναι η συσχέτιση της μοριακής δομής της ύλης με τις ιδιότητές
8 Βασικές Αρχές και Τεχνικές για την Εφαρμογή της Θεωρίας Ομάδων στη Χημεία
 8 Βασικές Αρχές και Τεχνικές για την Εφαρμογή της Θεωρίας Ομάδων στη Χημεία Διδακτικοί στόχοι Μετά την ολοκλήρωση της μελέτης του κεφαλαίου αυτού θα μπορείτε: - Na καταστρώνετε τις εκπροσωπήσεις χαρακτήρων
8 Βασικές Αρχές και Τεχνικές για την Εφαρμογή της Θεωρίας Ομάδων στη Χημεία Διδακτικοί στόχοι Μετά την ολοκλήρωση της μελέτης του κεφαλαίου αυτού θα μπορείτε: - Na καταστρώνετε τις εκπροσωπήσεις χαρακτήρων
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 6 Περιστροφική Κίνηση Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 6 Περιστροφική Κίνηση Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paua
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 6 Περιστροφική Κίνηση Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paua
ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ 1 ου ΚΕΦΑΛΑΙΟΥ
 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ο ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ-ΚΟΡΔΕΛΙΟΥ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ 1 ου ΚΕΦΑΛΑΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: 1 2 1. ΣΩΣΤΟ (Σ) ή ΛΑΘΟΣ (Λ); Αιτιολογήστε σύντομα. 1.1 Ένα ηλεκτρόνιο σθένους του ατόμου
ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ο ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ-ΚΟΡΔΕΛΙΟΥ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ 1 ου ΚΕΦΑΛΑΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: 1 2 1. ΣΩΣΤΟ (Σ) ή ΛΑΘΟΣ (Λ); Αιτιολογήστε σύντομα. 1.1 Ένα ηλεκτρόνιο σθένους του ατόμου
Η επιτάχυνση και ο ρόλος της.
 Η επιτάχυνση και ο ρόλος της. Το μέγεθος «επιτάχυνση» το συναντήσαμε κατά τη διδασκαλία στην Α Λυκείου, όπου και ορίσθηκε με βάση την εξίσωση: t Όπου η παραπάνω μαθηματική εξίσωση μας λέει ότι η επιτάχυνση:
Η επιτάχυνση και ο ρόλος της. Το μέγεθος «επιτάχυνση» το συναντήσαμε κατά τη διδασκαλία στην Α Λυκείου, όπου και ορίσθηκε με βάση την εξίσωση: t Όπου η παραπάνω μαθηματική εξίσωση μας λέει ότι η επιτάχυνση:
ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ
 ΕΡΜΗΝΕΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΧΗΜΙΚΩΝ ΕΣΜΩΝ ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΘΕΩΡΙΑ ΕΣΜΟΥ ΣΘΕΝΟΥΣ 1. Κατά την ανάπτυξη ομοιοπολικού δεσμού ανάμεσα σε δύο άτομα, τροχιακά της στιβάδας σθένους του
ΕΡΜΗΝΕΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΧΗΜΙΚΩΝ ΕΣΜΩΝ ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΘΕΩΡΙΑ ΕΣΜΟΥ ΣΘΕΝΟΥΣ 1. Κατά την ανάπτυξη ομοιοπολικού δεσμού ανάμεσα σε δύο άτομα, τροχιακά της στιβάδας σθένους του
Ατομική και Μοριακή Φυσική
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Το άτομο του Υδρογόνου Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Το άτομο του Υδρογόνου Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που
 ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών Βασικά σημεία της κβαντομηχανικής Διδάσκων : Επίκουρη Καθηγήτρια Χριστίνα Λέκκα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών Βασικά σημεία της κβαντομηχανικής Διδάσκων : Επίκουρη Καθηγήτρια Χριστίνα Λέκκα
Οι δομές, οι οποίες δεν περιέχουν τυπικά φορτία υψηλά (δηλαδή είναι 2) είναι:
 Answers to Homework Set 3 12162016 1. Πριν από μερικά χρόνια δημοσιεύθηκε η σύνθεση του ιόντος 5 +. Ποια είναι η πλέον πιθανή α) γεωμετρία ηλεκτρονικών ζευγών, και β) μοριακή γεωμετρική δομή του ιόντος
Answers to Homework Set 3 12162016 1. Πριν από μερικά χρόνια δημοσιεύθηκε η σύνθεση του ιόντος 5 +. Ποια είναι η πλέον πιθανή α) γεωμετρία ηλεκτρονικών ζευγών, και β) μοριακή γεωμετρική δομή του ιόντος
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης
 ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Τις προσεχείς ώρες θα συζητήσουμε τα πέντε πρώτα
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Τις προσεχείς ώρες θα συζητήσουμε τα πέντε πρώτα
1.1. Ιστορική Εξέλιξη των Αντιλήψεων για τα Άτομα
 Περιεχόμενα 1.1. Ιστορική εξέλιξη των αντιλήψεων για τα άτομα 1.2. Η φύση του φωτός. Τα φάσματα των στοιχείων 1.3. Κυματομηχανική θεώρηση 1.4. Η εξίσωση Schröedinger 1.5. Πολυηλεκτρονικά άτομα 1.6. Ηλεκτρονική
Περιεχόμενα 1.1. Ιστορική εξέλιξη των αντιλήψεων για τα άτομα 1.2. Η φύση του φωτός. Τα φάσματα των στοιχείων 1.3. Κυματομηχανική θεώρηση 1.4. Η εξίσωση Schröedinger 1.5. Πολυηλεκτρονικά άτομα 1.6. Ηλεκτρονική
 http://mathesis.cup.gr/courses/physics/phys1.1/2016_t3/about http://mathesis.cup.gr/courses/course-v1:physics+phys1.2+2016_t4/about f atomic orbitals http://www.orbitals.com/orb/orbtable.htm g atomic orbitals
http://mathesis.cup.gr/courses/physics/phys1.1/2016_t3/about http://mathesis.cup.gr/courses/course-v1:physics+phys1.2+2016_t4/about f atomic orbitals http://www.orbitals.com/orb/orbtable.htm g atomic orbitals
Κεφάλαιο 1 Χημικός δεσμός
 Κεφάλαιο 1 Χημικός δεσμός 1.1 Άτομα, Ηλεκτρόνια, και Τροχιακά Τα άτομα αποτελούνται από + Πρωτόνια φορτισμένα θετικά μάζα = 1.6726 X 10-27 kg Νετρόνια ουδέτερα μάζα = 1.6750 X 10-27 kg Ηλεκτρόνια φορτισμένα
Κεφάλαιο 1 Χημικός δεσμός 1.1 Άτομα, Ηλεκτρόνια, και Τροχιακά Τα άτομα αποτελούνται από + Πρωτόνια φορτισμένα θετικά μάζα = 1.6726 X 10-27 kg Νετρόνια ουδέτερα μάζα = 1.6750 X 10-27 kg Ηλεκτρόνια φορτισμένα
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
7 ο Κεφάλαιο Οργανική Χημεία. Δ. Παπαδόπουλος, χημικός
 7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός Βύρωνας, 2015 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός Βύρωνας, 2015 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
Μοντέρνα Φυσική. Κβαντική Θεωρία. Ατομική Φυσική. Μοριακή Φυσική. Πυρηνική Φυσική. Φασματοσκοπία
 Μοντέρνα Φυσική Κβαντική Θεωρία Ατομική Φυσική Μοριακή Φυσική Πυρηνική Φυσική Φασματοσκοπία ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ Φωτόνια: ενέργεια E = hf = hc/λ (όπου h = σταθερά Planck) Κυματική φύση των σωματιδίων της ύλης:
Μοντέρνα Φυσική Κβαντική Θεωρία Ατομική Φυσική Μοριακή Φυσική Πυρηνική Φυσική Φασματοσκοπία ΚΒΑΝΤΙΚΗ ΘΕΩΡΙΑ Φωτόνια: ενέργεια E = hf = hc/λ (όπου h = σταθερά Planck) Κυματική φύση των σωματιδίων της ύλης:
1. Η διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σ ένα ακριβώς στοιχείο ενός άλλου συνόλου Β είναι συνάρτηση.
 Μαθηματικά Γενικής Παιδείας Ανάλυση o Κεφάλαιο ΑΝΑΛΥΣΗ Ερωτήσεις του τύπου «Σωστό - Λάθος». Η διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σ ένα ακριβώς στοιχείο ενός άλλου συνόλου
Μαθηματικά Γενικής Παιδείας Ανάλυση o Κεφάλαιο ΑΝΑΛΥΣΗ Ερωτήσεις του τύπου «Σωστό - Λάθος». Η διαδικασία, με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σ ένα ακριβώς στοιχείο ενός άλλου συνόλου
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ. Κεφάλαιο 8. Συνεχείς Κατανομές Πιθανοτήτων Η Κανονική Κατανομή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΣΤΑΤΙΣΤΙΚΗ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
ΣΗΜΕΙΩΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 1 ΣΤΗ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟ ΚΕΦΑΙΛΑΙΟ 1. Α) Μηχανική συνθήκη ( βελάκι σελ 3) Β) Οπτική συνθήκη (1 ο βελάκι σελ 4 )
 ΣΗΜΕΙΩΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 1 ΣΤΗ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟ ΚΕΦΑΙΛΑΙΟ 1 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚOΣ ΠΙΝΑΚΑΣ 1)Ατομικό πρότυπο του Bohr ( πυρήνας,..., περιστρεφόμενα ηλεκτρόνια) περιγράφεται
ΣΗΜΕΙΩΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 1 ΣΤΗ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟ ΚΕΦΑΙΛΑΙΟ 1 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚOΣ ΠΙΝΑΚΑΣ 1)Ατομικό πρότυπο του Bohr ( πυρήνας,..., περιστρεφόμενα ηλεκτρόνια) περιγράφεται
