HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. 1 ΗΥ330 - Διάλεξη 11η - Κυκλώματα Δεδομένων

Transcript

1 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν 1 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 2 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 1

2 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 3 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κατηγορίες Αριθμητικές, Λογικές Μονάδες Παραδείγματα Αθροιστές, Πολλαπλασιαστές, Ολισθητές, Συγκριτές, κτλ. Μνήμη RM, ROM, ουρές, καταχωρητές Κυκλώματα Ελέγχου Μετρητές, Μηχανές Πεπερασμένων Καταστάσεων Κυκλώματα Διασυνδεσιμότητας Δρομολογητές (witches), Διαιτητές (rbiters), Κυκλώματα Διαύλων (Bus) 4 2

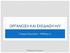
3 Παράδειγμα Επεξεργαστή 9-1 Mux 5-1 Mux a g64 CRRYGEN node1 ck1 UMEL REG sum sumb to Cache 9-1 Mux 2-1 Mux b UMGEN + LU s0 s1 LU : Logical Unit 1000um Μονάδες Εκτέλεσης Itanium (x6 στον επεξεργαστή) 5 Δομή κυκλώματος κατατετμημένου ανά ψηφίο (bit-sliced) Control Bit 3 Data-In Register dder hifter Multiplexer Bit 2 Bit 1 Bit 0 Data-Out Η μεθοδολογία κατάτμησης ανά bit χωροθετεί Οριζοντίως τα ψηφία των δρώμενων 6 Είσοδος και Tile Έξοδος identical οριζόντιαprocessing elements Καθέτως τα τμήματα των κυκλώματα επεξεργασίας τους Σήματα Ελέγχου κάθετα 3

4 Bit slice 63 Loopback Bus Loopback Bus Loopback Bus Bit slice 2 Bit slice 1 Bit slice 0 Δομή κυκλώματος κατατετμημένου ανά ψηφίο (bit-sliced) From register files / Cache / Bypass Multiplexers hifter dder stage 1 Wiring dder stage 2 Wiring dder stage 3 um elect To register files / Cache 7 Itanium Ακέραιο Τμήμα 8 4

5 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 9 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Πλήρης Αθροιστής (Full dder) a b ci co s κρατούμενο αναίρεση αναίρεση προώθηση προώθηση προώθηση προώθηση ανάθεση ανάθεση s = a b ci + a bci + ab ci + abci = ci (a b + ab) + ci (a b + ab ) = ci (a (+) b) + ci (a (+) b) = a (+) b (+) c co = a bci + ab ci + abci + abci = ab (ci + ci ) + ci (a b + ab ) = ab + ci(a (+) b) 10 5

6 Ιδιότητα Αντιστροφής B B C i F C o C i F C o BC i = BC i C BC = o i C BC o i 11 Ιδιότητα Αντιστροφής Even cell Odd cell 0 B 0 1 B 1 2 B 2 3 B 3 C i,0 C o,0 C o,1 C o,2 C o,3 F F F F Χρησιμοποιώντας την ιδιότητα Αντιστροφής 12 6

7 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 13 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Στατικός Πλήρης Αθροιστής CMO V DD V DD C i B B B C i X B C i V DD C i C i B B V DD B C i C o B 28 Transistors 14 7

8 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 15 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Έμμεση Υλοποίηση και Σήματα a b ci co s κρατούμενο αναίρεση αναίρεση προώθηση προώθηση προώθηση προώθηση ανάθεση ανάθεση Σε κάποιες υλοποιήσεις αθροιστών οι έξοδοι (s, co) προκύπτουν από έμμεσες εκφράσεις: G =.B D =.B P = + B ή P = (+) B Έτσι, οι εκφράσεις για co, s μετατρέπονται ως εξής: co = G + P ci και s = p (+) ci 16 8

9 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 17 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Σειριακό Κρατούμενο Η απλούστερη υλοποίηση ενός ν-bit αθροιστή Εν σειρά το κάθε ψηφίο ν παίρνει κρατούμενο από το (ν-1) Μειονεκτήματα Μεγάλης καθυστέρησης κρίσιμο μονοπάτι Από το co μέχρι το δεξιότερο κρατούμενο 18 9

10 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 19 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Αθροιστής Mirror «Καθρέφτης» V DD V DD V DD "0"-Propagate C i B B Kill C o B C i B C i "1"-Propagate B B Generate B C i C i B 24 transistors Βασίζεται στις: co = G + P ci, s = p (+) ci, d = a b, g = ab, p = a + b 20 10

11 Γράμμο-διάγραμμα Αθροιστή Mirror V DD B C i B C i C o C i B C o GND 21 Αθροιστής Mirror Μέχρι 2 τρανζίστορ σε σειρά στο κρατούμενο Τρανζίστορ Ci κοντά στην έξοδο Στην σχεδίαση της διάταξης ο σημαντικότερος περιορισμός είναι η μείωση της χωρητικότητας Co μείωση των 4 χωρητικοτήτων διάχυσης! Η χωρητικότητα στο Co αναλογεί σε 4 εσωτερικές διάχυσης 2 εσωτερικές πύλης-εξόδου 6 εξωτερικές Τρανζίστορ του ελάχιστο μέγεθος 22 11

12 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 23 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Αθροιστής Τρανζίστορ Διέλευσης P V DD V DD P C i C i P um Generation V DD B P B P P V DD C o Carry Generation C i C i etup C i P 24 τρανζίστορ 24 12

13 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 25 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Αλυσίδα Κρατουμένου Manchester (Manchester Carry Chain) - 1 Απλοποίηση του αθροιστή με τρανζίστορ διέλευσης: V DD P i P i V DD C o G i C i Ci C o G i P i D i (α) Στατική Υλοποίηση (β) Δυναμική Υλοποίηση 26 13

14 Αλυσίδα Κρατουμένου Manchester (Manchester Carry Chain) - 2 V DD P 0 P 1 P 2 P 3 C 3 C i,0 G 0 G 1 G 2 G 3 c1 = G0 + P0 c0, c2 = G1 + P1 c1 = G1 + P1(G0 + P0 c0), 27 C 0 C 1 C 2 C 3 Αλυσίδα Κρατουμένου Manchester (Manchester Carry Chain) Γράμμο-Διάγραμμα Propagate/Generate Row V DD P i G i P i + 1 G i + 1 C i C i - 1 C i + 1 GND Inverter/um Row 28 14

15 Αθροιστής Παράκαμψης (Carry- Bypass/kip) P 0 G 1 P 0 G 1 P 2 G 2 P 3 G 3 ή Carry-kip C i,0 C o,0 C o,1 C o,2 F F F F C o,3 P 0 G 1 P 0 G 1 P 2 G 2 P 3 G 3 BP=P o P 1 P 2 P 3 C i,0 C o,0 C o,1 C o,2 F F F F Multiplexer C o,3 If (P0P1P2P3) Idea: If (P0 and Co,3 P1 and = P2 1 and P3 = 1) then C o3 = else C 0, else Co,3 kill = or Ci,0 generate. else GENERTE or DELETE 29 Αθροιστής Παράκαμψης (Carry- Bypass/kip) Bit 0 3 etup t setup Bit 4 7 etup t bypass Bit 8 11 etup Bit etup Carry propagation Carry propagation Carry propagation Carry propagation um um um t sum um M bits t adder = t setup + M tcarry + (N/M-1)t bypass + (M-1)t carry + t sum 30 15

16 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 31 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Αθροιστής Παράκαμψης (Carry- Bypass/kip) t p ripple adder bypass adder 4..8 N 32 16

17 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 33 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Αθροιστής Επιλογής Κρατουμένου etup P,G "0" "0" Carry Propagation "1" "1" Carry Propagation C o,k-1 Multiplexer C o,k+3 um Generation Carry Vector 34 17

18 Αθροιστής Επιλογής Κρατουμένου - Γραμμικός Bit 0 3 Bit 4 7 Bit 8 11 Bit etup etup etup etup 0 0-Carry 0 0-Carry 0 0-Carry 0 0-Carry 1 1-Carry 1 1-Carry 1 1-Carry 1 1-Carry Multiplexer Multiplexer Multiplexer Multiplexer C i,0 C o,3 C o,7 C o,11 C o,15 um Generation um Generation um Generation um Generation Αθροιστής Επιλογής Κρατουμένου Ρίζας Bit 0-1 Bit 2-4 Bit 5-8 Bit 9-13 Bit etup etup etup etup (1) "0" "0" Carry "0" "0" Carry "0" "0" Carry "0" "0" Carry (1) "1" "1" Carry "1" "1" Carry "1" "1" Carry "1" "1" Carry (3) (3) (4) (5) (6) (4) (5) (6) (7) Multiplexer Multiplexer Multiplexer Multiplexer C i,0 um Generation um Generation um Generation um Generation (7) Mux (8) um (9) 36 18

19 t p (in unit delays) Αθροιστής Επιλογής Κρατουμένου Ρίζας Ripple adder Linear select 10 quare root select N Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 38 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 19

20 Πρόγνωση Κρατουμένου Ο βασικός στόχος είναι να μειωθεί η μεγάλη καθυστέρηση της αλυσίδας των κρατουμένων των ν-bit Βασική ιδέα Ακριβής πρόγνωση κρατουμένου πριν αυτό προκύψει από τις εξισώσεις Για ομάδες ν-bit (όπου συνήθως v ~ 4) Υπολογίζεται η πρόγνωση του κρατουμένου αυτή προωθείται στην επόμενη ομάδα Η καθυστέρηση της πρόγνωσης είναι σημαντικά μικρότερη από τον σειριακή προώθηση του κρατουμένου 39 Πρόγνωση Κρατουμένου - Γένεση, Προώθηση Στην πρόσθεση + Β παράγεται κρατούμενο μόνο όταν ΑΒ: G = B Ένα κρατούμενο προάγεται στο επόμενο ψηφίο όταν: P = + B Το κρατούμενο μπορεί να εκφραστεί ως: co = G + P ci Για ν=4-bits: c1 = G0 + P0 c0 c2 = G1 + P1 c1 = G1 + P1(G0 + P0 c0) = G1 + G0P1 + c0p0p1 c3 = G2 + G1P2 + G0P1P2 + C0P0P1P2 C4 = G3 + G2P3 + G1P2P3 + C0P0P1P2P

21 Πρόγνωση Κρατουμένου 4-bit Αθροιστής C4 = (G3 + G2P3 + G1P2P3 + G0P1P2P3) + C0(P0P1P2P3) PG = P0P1P2P3 GG = G3 + G2P3 + G1P2P3 + G0P1P2P3 C4 = GG + C0 PG 41 Πρόγνωση Κρατουμένου 16-bit Αθροιστής Ιεραρχικά η μονάδα LCU υπολογίζει τα: PG, GG c

22 Πρόγνωση Κρατουμένου 64-bit Αθροιστής Ίδια ιδέα με 2 ο επίπεδο ιεραρχίας 43 Αθροιστής Πρόγνωσης Κρατουμένου (Lookahead) 0, B 0 1, B 1 N-1, B N-1 C i,0 P 0 C i,1 P 1 C i, N-1 P N N-1 C ok = f k B k C G P ok 1 = + C k k o k

23 Πρόγνωση Κρατουμένου - επίπεδο τρανζίστορ Εξισώσεις Expanding Κρατουμένου Lookahead : equations: V DD C ok = G k + P k G k 1 + P k 1 C o k 2 G 3 ll Πλήρης the way: Ανάπτυξη: C ok = G k + P k G k 1 + P k 1 + P 1 G 0 + P 0 C i0 C i,0 G 2 G 1 G 0 C o,3 P 0 P 1 P 2 P 3 45 Πρόγνωση Κρατουμένου - Γραμμική ή Λογαριθμική Διάταξη 0 F t p N F t p log 2 (N) διάταξη δέντρου κατά τον υπολογισμό συνεπάγεται λογαριθμική καθυστέρηση! 46 23

24 Parallel Prefix dders Prefix um y 0 = x 0 y 1 = x 0 + x 1 y 2 = x 0 + x 1 + x 2 input numbers prefix sums Parallel Prefix ums Problem is defined as: Given: x 0 x 1 x 2 x 3 x k-1 Find: x 0 x 0 + x 1 x 0 + x 1 + x 2 x 0 + x 1 + x 2 + x 3 x 0 + x 1 + x 2 + x x k-1 47 Carry Operator for CL dders Define (g, p ) c (g, p ) = (g, p) g = g + g p, and p = p p Carry Operator Properties ssociative ((g0, p0) c (g1, p1)) c(g2, p2) = (g0, p0) c ((g1, p1) c(g2, p2)) NOT Commutative (g0, p0) c (g1, p1) (g1, p1) c (g0, p0) ssociative nature of Carry Operator can be used to Compute Prefix Carry Networks! 48 24

25 Parallel Prefix Carry Networks PPCN built using two k/2-input networks and k/2 adders PPCN built using one k/2-input networks and k - 1 adders D(k) = D(k/2) + 1 = log 2 k C(k) = 2C(k/2) + k/2 = (k/2) log 2 k D(k) = D(k/2) + 2 = 2log 2 k - 1 C(k) = C(k/2) + k - 1 = 2k 2 - log 2 k 49 Parallel Prefix Carry Networks Brent-Kung 16-input Parallel Prefix dder 50 25

26 Parallel Prefix Carry Networks Kogge-tone16-input Parallel Prefix dder 51 Parallel Prefix Carry Networks Kogge-tone16-input Parallel Prefix dder 52 26

27 Parallel Prefix Carry Networks Radix and parsity Radix how many carry results (from the previous level of computation) are used to generate the current carry level (all 2 so far) parsity Number of carry bits generated by tree parsity 4, 16-bit Kogge-tone dder 53 Parallel Prefix um Computation prefix sum can be calculated in parallel by the following steps. Compute the sums of consecutive pairs of items in which the first item of the pair has an even index: z 0 = x 0 + x 1, z 1 = x 2 + x 3, etc. Recursively compute the prefix sum w 0, w 1, w 2,... of the sequence z 0, z 1, z 2,... Express each term of the final sequence y 0, y 1, y 2,... as the sum of up to two terms of these intermediate sequences: y 0 = x 0, y 1 = z 0, y 2 = z 0 + x 2, y 3 = w 0, etc. fter the first value, each successive number y i is either copied from a position half as far through the w sequence, or is the previous value added to one value in the x sequence

28 Δέντρα Κρατουμένων C o2 C o1 C o0 = G 0 + P 0 C i0 = G 1 + P 1 G 0 + P 1 P 0 C i0 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 C i0 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 0 C i0 = G 2:1 + P 2:1 C o0 Ορίζουμε σύνθετα σήματα Gx:y και Px:y, όπως παραπάνω Ορίζουμε πράξη (υποκύκλωμα) : ( G, P) ( G', P') ( G PG', PP') η παραπάνω πράξη μας επιτρέπει να υλοποιήσουμε διαφορετικές αρχιτεκτονικές αθροιστών με πρόγνωση (C 3:0 ) = [(G 3,P 3 ) (G 2,P 2 ) (G 1,P 1 ) (G 0,P 0 )] (C i,0), και (G 3:0,P 3:0 ) = (G 3:2,P 3:2 ) (G 1:0,P 1:0 ) 55 Λογαριθμικός Αθροιστής Πρόγνωσης ( 0, B 0 ) ( 1, B 1 ) ( 2, B 2 ) ( 3, B 3 ) ( 4, B 4 ) ( 5, B 5 ) ( 6, B 6 ) ( 7, B 7 ) ( 8, B 8 ) ( 9, B 9 ) ( 10, B 10 ) ( 11, B 11 ) ( 12, B 12 ) ( 13, B 13 ) ( 14, B 14 ) ( 15, B 15 ) Δέντρο 16-bit, Βάσης-2 Kogge-tone 56 28

29 Δυναμικά Κυκλώματα Πρόγνωσης Κρατουμένου - 1 V DD V DD Clk G i = a i b i Clk P i = a i + b i a i a i b i b i Clk Clk Propagate Generate 57 Δυναμικά Κυκλώματα Πρόγνωσης Κρατουμένου - 2 V DD V DD Clk k P i:i-2k+1 Clk k G i:i-2k+1 P i:i-k+1 P i:i-k+1 G i:i-k+1 P i-k:i-2k+1 G i-k:i-2k+1 Propagate Generate 58 29

30 Δυναμικά Κυκλώματα Πρόγνωσης Κρατουμένου Έξοδος Αθροίσματος 59 Λογαριθμικός Αθροιστής Πρόγνωσης - 2 ( 0, B 0 ) ( 1, B 1 ) ( 2, B 2 ) ( 3, B 3 ) ( 4, B 4 ) ( 5, B 5 ) ( 6, B 6 ) ( 7, B 7 ) ( 8, B 8 ) ( 9, B 9 ) ( 10, B 10 ) ( 11, B 11 ) ( 12, B 12 ) ( 13, B 13 ) ( 14, B 14 ) ( 15, B 15 ) Δέντρο Brent-Kung 60 30

31 Λογαριθμικός Αθροιστής Πρόγνωσης - 3 (a 0, b 0 ) (a 1, b 1 ) (a 2, b 2 ) (a 3, b 3 ) (a 4, b 4 ) (a 5, b 5 ) (a 6, b 6 ) (a 7, b 7 ) (a 8, b 8 ) (a 9, b 9 ) (a 10, b 10 ) (a 11, b 11 ) (a 12, b 12 ) (a 13, b 13 ) (a 14, b 14 ) (a 15, b 15 ) Δέντρο 16-bit, Βάσης-4 Kogge-tone 61 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 62 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 31

32 Αλγόριθμος Πολλαπλασιασμού MULTIPLY(x, y, m) // Είσοδοι - x : πολλαπλασιαστέος, y : πολλαπλασιαστής, Έξοδος m : γινόμενο { n = LENGTH(y); m = 0; t = x; // ολισθητής // for i in 1 to n // για κάθε ψηφίο του y // { if (y[i] == 1) m = m + t; // πρόσθεση μερικού παράγοντα // t = t << 1; // ολίσθηση 1 ψηφίο δεξιά για κάθε ψηφίο του y // } return r; } 63 Πολλαπλασιασμός Μερικών Γινομένων 67 x 54 1 ο με 1 ο 2 ο με 1 ο 1 ο με 2 ο 2 ο με 2 ο 67 X X X X οι τέσσερις αυτοί συνδυασμοί μπορούν να γίνουν σε σύνολα από δυαδικά ψηφία 64 32

33 Πολλαπλασιασμός Μερικών Παραγόντων Multiplicand Πολλαπλασιαστέος x Multiplier Πολλαπλασιαστής Partial Μερικά products Γινόμενα Result Τελικό Αποτέλεσμα Μια πύλη ND αρκεί για κάθε ψηφίο του πολλαπλασια 65 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 66 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 33

34 Πολλαπλασιαστής Πίνακα (rray) X 3 X 2 X 1 X 0 Y 0 X 3 X 2 X 1 X 0 Y 1 Z 0 H F F H X3 X 2 X 1 X 0 Y 2 Z 1 F F F H X3 X 2 X 1 X 0 Y 3 Z 2 F F F H Z 7 Z 6 Z 5 Z 4 Z 3 67 Πολλαπλασιαστής Πίνακα (rray) - Κρίσιμη Οδός H F F H F F F H Critical Path 1 Critical Path 2 F F F H Critical Path 1 & 2 NxM πολλαπλασιασμός 68 34

35 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 69 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Πολλαπλασιαστής Αποθήκευσης Κρατουμένου (Carry ave) H H H H H F F F H F F F H F F H Vector Merging dder 70 35

36 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 71 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Χωροθέτηση Πολλαπλασιαστή X 3 X 2 X 1 X 0 Y 0 Y 1 C C C C Z 0 H Multiplier Cell F Multiplier Cell Y 2 C C C C Z 1 Vector Merging Cell Y 3 C C C C Z 2 X and Y signals are broadcasted through the complete array. ( ) C C C C Z 7 Z 6 Z 5 Z 4 Z

37 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 73 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές Πολλαπλασιαστής Δέντρου Wallace Partial Μερικά products Γινόμενα First Πρώτο stage Στάδιο Bit position (a) (b) econd Δεύτερο stage Στάδιο Final Τελικό adderστάδιο F (c) H (d) 74 37

38 Πολλαπλασιαστής Δέντρου Wallace Μερικά Γινόμενα Πρώτο Στάδιο Δεύτερο Στάδιο Τελικό Στάδιο 75 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 76 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 38

39 Διαίρεση (450) (17) 77 Διαίρεση (450) (17) (26) 5-bit διαιρέτης < διαιρετέο κατεβάζουμε ψηφίο ολίσθηση-αφαίρεση, 1 στο πηλίκο κατεβάζουμε ψηφίο ολίσθηση-αφαίρεση, 1 στο πηλίκο κατεβάζουμε ψηφίο, υπόλοιπο < διαιρέτη, 0 στο πηλίκο κατεβάζουμε ψηφίο Ολίσθηση-αφαίρεση, 1 στο πηλίκο κατεβάζουμε ψηφίο, υπόλοιπο < διαιρέτη, 0 στο πηλίκο Σε κάθε βήμα κάνουμε: Σύγκριση Ολίσθηση Αφαίρεση 78 39

40 Αλγόριθμος Διαίρεσης LONG_DIVIION(D, d, q, r) // Είσοδοι - D : Διαιρετέος, d : διαιρέτης, Έξοδοι q : πηλίκο, r : υπόλοιπο { n = MB(D); m = (n LENGTH(d)); x = 0; Dt = D; do { while (Dt[n:m] < d) // υπόλοιπο < διαιρέτη // q[x++] = 0; m = m 1; // 0 στο πηλίκο, κατεβάζουμε ψηφίο // q[x++] = 1; // 1 στο πηλίκο // r[n-m:0] = Dt[n:m] d; // νέο υπόλοιπο // m = m 1; // κατεβάζουμε ψηφίο // Dt[n:0] = {r, D[m-1:0]};// συνένωση υπολοίπου με διαιρετέο // } while (r > d); return (q[0:x], r[n-m:0]); } 79 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους Αθροιστή Ιδιότητα Αντιστροφής Στατικός Πλήρης Αθροιστής CMO Έμμεση Υλοποίηση Αθροιστή και Σήματα Σειριακό Κρατούμενο Αθροιστής «Καθρέφτης» (Mirror) Γράμμο-διάγραμμα Αθροιστής Τρανζίστορ Διέλευσης Δυναμικός Αθροιστής Διέλευσης Αλυσίδα Κρατουμένου Manchester Γράμμο-Διάγραμμα Αθροιστής Παράκαμψης (Carry Bypass) Αθροιστής Επιλογής Κρατουμένου (Carry elect) 80 Γραμμική Υλοποίηση Υλοποίηση Ρίζας Πρόγνωση Κρατουμένου (Carry Lookahead) γένεση, προώθηση, επίπεδο τρανζίστορ, λογαριθμική διάταξη δέντρα κρατουμένων, δυναμικά κυκλώματα πρόγνωσης Πολλαπλασιασμός αλγόριθμος, μερικά γινόμενα Πολλαπλασιαστής Πίνακα Πολλαπλασιαστής αποθήκευσης κρατουμένου Χωροθέτηση Πολλαπλασιαστή Πολλαπλασιαστής Δέντρου Wallace Διαίρεση Ολισθητές 40

41 Δυαδικός Ολισθητής Right nop Left i B i i-1 B i-1 Bit-lice i Περιστροφικός Ολισθητής (Barrel) 3 B 3 h1 2 B 2 h2 : Data Wire 1 B 1 : Control Wire h3 0 B 0 h0 h1 h2 h

42 Περιστροφικός Ολισθητής 4x h0 h1 h2 h3 Width barrel ~ 2 p m M Buffer 83 Λογαριθμικός Ολισθητής h1 h1 h2 h2 h4 h4 3 B 3 2 B 2 1 B 1 0 B

43 0-7 bit Λογαριθμικός Ολισθητής Out3 Out2 Out1 Out