HY422 Ειςαγωγό ςτα υςτόματα VLSI. 1 ΗΤ422 - Διάλεξθ 11θ Κυκλϊματα Δεδομζνων
|
|
|
- Πολυξένη Δάβης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 HY422 Ειςαγωγό ςτα υςτόματα VLI Διδϊςκων: Χ. ωτηρύου, Βοηθόσ: Π. Ματτθαιϊκησ 1 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 2 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 1
2 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 3 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Δομικού Λύθοι Ψηφιακών Κυκλωμϊτων Κατηγορίεσ Αρικμθτικζσ, Λογικζσ Μονάδεσ Παραδείγματα Ακροιςτζσ, Πολλαπλαςιαςτζσ, Ολιςκθτζσ, υγκριτζσ, κτλ. Μνιμθ RM, ROM, ουρζσ, καταχωρθτζσ Κυκλϊματα Ελζγχου Μετρθτζσ, Μθχανζσ Πεπεραςμζνων Καταςτάςεων Κυκλϊματα Διαςυνδεςιμότθτασ Δρομολογθτζσ (witches), Διαιτθτζσ (rbiters), Κυκλϊματα Διαφλων (us) 4 2
3 9-1 Mux 9-1 Mux 5-1 Mux 2-1 Mux UMEL REG 9/5/2011 Παρϊδειγμα Επεξεργαςτό a g64 CRRYGEN node1 ck1 sum sumb to Cache b UMGEN + LU s0 s1 LU : Logical Unit 1000um Μονάδεσ Εκτζλεςθσ Itanium (x6 ςτον επεξεργαςτι) 5 Δομό κυκλώματοσ κατατετμημϋνου ανϊ ψηφύο (bit-sliced) Control it 3 Data-In Register dder hifter Multiplexer it 2 it 1 it 0 Data-Out Η μεκοδολογία κατάτμθςθσ ανά bit χωροκετεί Οριηοντίωσ τα ψθφία των δρϊμενων Είςοδοσ και Tile Ζξοδοσ identical οριηόντια processing elements Κακζτωσ τα τμιματα των κυκλϊματα επεξεργαςίασ τουσ ιματα Ελζγχου κάκετα 6 3
4 it slice 63 Loopback us Loopback us Loopback us it slice 2 it slice 1 it slice 0 9/5/2011 Δομό κυκλώματοσ κατατετμημϋνου ανϊ ψηφύο (bit-sliced) From register files / Cache / ypass Multiplexers hifter dder stage 1 Wiring dder stage 2 Wiring dder stage 3 um elect To register files / Cache 7 Itanium Ακϋραιο Σμόμα Δεδομϋνων 8 4
5 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 9 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Πλόρησ Αθροιςτόσ (Full dder) a b ci co s κρατοφμενο αναίρεςθ αναίρεςθ προϊκθςθ προϊκθςθ προϊκθςθ προϊκθςθ ανάκεςθ ανάκεςθ s = a b ci + a bci + ab ci + abci = ci (a b + ab) + ci (a b + ab ) = ci (a (+) b) + ci (a (+) b) = a (+) b (+) c co = a bci + ab ci + abci + abci = ab (ci + ci ) + ci (a b + ab ) = ab + ci(a (+) b) 10 5
6 Ιδιότητα Αντιςτροφόσ F C o F C o = C C = o i C C o i 11 Ιδιότητα Αντιςτροφόσ Even cell Odd cell ,0 C o,0 C o,1 C o,2 C o,3 F F F F Χρησιμοποιώντας την ιδιότητα Αντιστρουής 12 6
7 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 13 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ τατικόσ Πλόρησ Αθροιςτόσ CMO X C o 28 Transistors 14 7
8 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 15 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Έμμεςη Τλοπούηςη και όματα a b ci co s κρατοφμενο αναίρεςθ αναίρεςθ προϊκθςθ προϊκθςθ προϊκθςθ προϊκθςθ ανάκεςθ ανάκεςθ ε κάποιεσ υλοποιιςεισ ακροιςτϊν οι ζξοδοι (s, co) προκφπτουν από ζμμεςεσ εκφράςεισ: G =. D =. P = + ι P = (+) Έτσι, οι εκυπάσειρ για co, s μετατπέπονται ωρ εξήρ: co = G + P ci και s = p (+) ci 16 8
9 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 17 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ ειριακό Κρατούμενο Η απλοφςτερθ υλοποίθςθ ενόσ ν-bit ακροιςτι Εν ςειρά το κάκε ψθφίο ν παίρνει κρατοφμενο από το (ν-1) Μειονεκτιματα Μεγάλθσ κακυςτζρθςθσ κρίςιμο μονοπάτι Από το co μζχρι το δεξιότερο κρατοφμενο 18 9
10 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 19 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Αθροιςτόσ Mirror «Καθρϋφτησ» "0"-Propagate Kill C o "1"-Propagate Generate 24 transistors Βαςίηεται ςτισ: co = G + P ci, s = p (+) ci, d = a b, g = ab, p = a + b 20 10
11 Γρϊμμο-διϊγραμμα Αθροιςτό Mirror C o C o GND 21 Αθροιςτόσ Mirror Μζχρι 2 τρανηίςτορ ςε ςειρά ςτο κρατοφμενο Σρανηίςτορ Ci κοντά ςτθν ζξοδο τθν ςχεδίαςθ τθσ διάταξθσ ο ςθμαντικότεροσ περιοριςμόσ είναι θ μείωςθ τθσ χωρθτικότθτασ Co μείωςθ των 4 χωρθτικοτιτων διάχυςθσ! Η χωρθτικότθτα ςτο Co αναλογεί ςε 4 εςωτερικζσ διάχυςθσ 2 εςωτερικζσ πφλθσ-εξόδου 6 εξωτερικζσ Σρανηίςτορ του ελάχιςτο μζγεκοσ 22 11
12 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 23 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Αθροιςτόσ Σρανζύςτορ Διϋλευςησ P P P um Generation P P P C o Carry Generation etup P 24 τρανηίςτορ 24 12
13 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 25 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Αλυςύδα Κρατουμϋνου Manchester (Manchester Carry Chain) - 1 Απλοποίθςθ του ακροιςτι με τρανηίςτορ διζλευςθσ: P i P i C o G i Ci C o G i P i D i (α) Στατική Υλοποίηση (β) Δςναμική Υλοποίηση 26 13
14 Αλυςύδα Κρατουμϋνου Manchester (Manchester Carry Chain) - 2 P 0 P 1 P 2 P 3 C 3,0 G 0 G 1 G 2 G 3 c1 = G0 + P0 c0, c2 = G1 + P1 c1 = G1 + P1(G0 + P0 c0), 27 C 0 C 1 C 2 C 3 Αλυςύδα Κρατουμϋνου Manchester (Manchester Carry Chain) Γρϊμμο-Διϊγραμμα Propagate/Generate Row P i G i P i + 1 G i GND Inverter/um Row 28 14
15 Αθροιςτόσ Παρϊκαμψησ (Carry- ypass/kip) P 0 G 1 P 0 G 1 P 2 G 2 P 3 G 3 ή Carry-kip,0 C o,0 C o,1 C o,2 F F F F C o,3 P 0 G 1 P 0 G 1 P 2 G 2 P 3 G 3 P=P o P 1 P 2 P 3,0 C o,0 C o,1 C o,2 F F F F Multiplexer C o,3 If (P0P1P2P3) Idea: If (P0 and Co,3 P1 and = P2 1 and P3 = 1) then C o3 = else C 0, else Co,3 kill = or Ci,0 generate. else GENERTE or DELETE 29 Αθροιςτόσ Παρϊκαμψησ (Carry- ypass/kip) it 0 3 etup t setup it 4 7 etup t bypass it 8 11 etup it etup Carry propagation Carry propagation Carry propagation Carry propagation um um um t sum um M bits t adder = t setup + M tcarry + (N/M-1)t bypass + (M-1)t carry + t sum 30 15
16 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 31 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Αθροιςτόσ Παρϊκαμψησ (Carry- ypass/kip) t p ripple adder bypass adder 4..8 N 32 16
17 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 33 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Αθροιςτόσ Επιλογόσ Κρατουμϋνου etup P,G "0" "0" Carry Propagation "1" "1" Carry Propagation C o,k-1 Multiplexer C o,k+3 um Generation Carry Vector 34 17
18 Αθροιςτόσ Επιλογόσ Κρατουμϋνου - Γραμμικόσ it 0 3 it 4 7 it 8 11 it etup etup etup etup 0 0-Carry 0 0-Carry 0 0-Carry 0 0-Carry 1 1-Carry 1 1-Carry 1 1-Carry 1 1-Carry Multiplexer Multiplexer Multiplexer Multiplexer,0 C o,3 C o,7 C o,11 C o,15 um Generation um Generation um Generation um Generation Αθροιςτόσ Επιλογόσ Κρατουμϋνου Ρύζασ it 0-1 it 2-4 it 5-8 it 9-13 it etup etup etup etup (1) "0" "0" Carry "0" "0" Carry "0" "0" Carry "0" "0" Carry (1) "1" "1" Carry "1" "1" Carry "1" "1" Carry "1" "1" Carry (3) (3) (4) (5) (6) (4) (5) (6) (7) Multiplexer Multiplexer Multiplexer Multiplexer,0 um Generation um Generation um Generation um Generation (7) Mux (8) um (9) 36 18
19 t p (in unit delays) 9/5/2011 Αθροιςτόσ Επιλογόσ Κρατουμϋνου Ρύζασ Ripple adder Linear select 10 quare root select N Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 38 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 19
20 Πρόγνωςη Κρατουμϋνου Ο βαςικόσ ςτόχοσ είναι να μειωκεί θ μεγάλθ κακυςτζρθςθ τθσ αλυςίδασ των κρατουμζνων των ν-bit Βαςικι ιδζα Ακριβισ πρόγνωςθ κρατουμζνου πριν αυτό προκφψει από τισ εξιςϊςεισ Για ομάδεσ ν-bit (όπου ςυνικωσ v ~ 4) Τπολογίηεται θ πρόγνωςθ του κρατουμζνου αυτι προωκείται ςτθν επόμενθ ομάδα Η κακυςτζρθςθ τθσ πρόγνωςθσ είναι ςθμαντικά μικρότερθ από τον ςειριακι προϊκθςθ του κρατουμζνου 39 Πρόγνωςη Κρατουμϋνου - Γϋνεςη, Προώθηςη τθν πρόςκεςθ + Β παράγεται κρατοφμενο μόνο όταν ΑΒ: G = Ζνα κρατοφμενο προάγεται ςτο επόμενο ψθφίο όταν: P = + Σο κρατοφμενο μπορεί να εκφραςτεί ωσ: co = G + P ci Για ν=4-bits: c1 = G0 + P0 c0 c2 = G1 + P1 c1 = G1 + P1(G0 + P0 c0) = G1 + G0P1 + c0p0p1 c3 = G2 + G1P2 + G0P1P2 + C0P0P1P2 C4 = G3 + G2P3 + G1P2P3 + C0P0P1P2P
21 Πρόγνωςη Κρατουμϋνου 4-bit Αθροιςτόσ C4 = (G3 + G2P3 + G1P2P3 + G0P1P2P3) + C0(P0P1P2P3) PG = P0P1P2P3 GG = G3 + G2P3 + G1P2P3 + G0P1P2P3 C4 = GG + C0 PG 41 Πρόγνωςη Κρατουμϋνου 16-bit Αθροιςτόσ Ιεραρχικά θ μονάδα LCU υπολογίηει τα: PG, GG c
22 Πρόγνωςη Κρατουμϋνου 64-bit Αθροιςτόσ Ίδια ιδζα με 2 ο επίπεδο ιεραρχίασ 43 Αθροιςτόσ Πρόγνωςησ Κρατουμϋνου (Lookahead) 0, 0 1, 1 N-1, N-1,0 P 0,1 P 1, N-1 P N N-1 C ok = f k k C G P ok 1 = + C k k o k
23 Πρόγνωςη Κρατουμϋνου - επύπεδο τρανζύςτορ Εξιςϊςεισ Expanding Κρατουμζνου Lookahead : equations: C ok = G k + P k G k 1 + P k 1 C o k 2 G 3 ll Πλιρθσ the way: Ανάπτυξθ: C ok = G k + P k G k 1 + P k 1 + P 1 G 0 + P 0 0,0 G 2 G 1 G 0 C o,3 P 0 P 1 P 2 P 3 45 Πρόγνωςη Κρατουμϋνου - Γραμμικό ό Λογαριθμικό Διϊταξη 0 F t p N F t p log 2 (N) διάταξθ δζντρου κατά τον υπολογιςμό ςυνεπάγεται λογαρικμικι κακυςτζρθςθ! 46 23
24 ( 0, 0 ) ( 1, 1 ) ( 2, 2 ) ( 3, 3 ) ( 4, 4 ) ( 5, 5 ) ( 6, 6 ) 9/5/2011 Δϋντρα Κρατουμϋνων C o2 C o1 C o0 = G 0 + P 0 0 = G 1 + P 1 G 0 + P 1 P 0 0 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 0 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 0 0 = G 2:1 + P 2:1 C o0 Ορίηουμε ςφνκετα ςιματα Gx:y και Px:y, όπωσ παραπάνω Ορίηουμε πράξθ (υποκφκλωμα) : ( G, P) ( G', P') ( G PG', PP') θ παραπάνω πράξθ μασ επιτρζπει να υλοποιιςουμε διαφορετικζσ αρχιτεκτονικζσ ακροιςτϊν με πρόγνωςθ (C 3:0 ) = [(G 3,P 3 ) (G 2,P 2 ) (G 1,P 1 ) (G 0,P 0 )] (,0), και (G 3:0,P 3:0 ) = (G 3:2,P 3:2 ) (G 1:0,P 1:0 ) 47 Λογαριθμικόσ Αθροιςτόσ Πρόγνωςησ ( 7, 7 ) ( 8, 8 ) ( 9, 9 ) ( 10, 10 ) ( 11, 11 ) ( 12, 12 ) ( 13, 13 ) ( 14, 14 ) ( 15, 15 ) Γέντρο 16-bit, Βάσης-2 Kogge-tone 48 24
25 Δυναμικϊ Κυκλώματα Πρόγνωςησ Κρατουμϋνου - 1 Clk G i = a i b i Clk P i = a i + b i a i a i b i b i Clk Clk Propagate Generate 49 Δυναμικϊ Κυκλώματα Πρόγνωςησ Κρατουμϋνου - 2 Clk k P i:i-2k+1 Clk k G i:i-2k+1 P i:i-k+1 P i:i-k+1 G i:i-k+1 P i-k:i-2k+1 G i-k:i-2k+1 Propagate Generate 50 25
26 Δυναμικϊ Κυκλώματα Πρόγνωςησ Κρατουμϋνου Έξοδοσ Αθρούςματοσ 51 Λογαριθμικόσ Αθροιςτόσ Πρόγνωςησ ( 0, 0 ) ( 1, 1 ) ( 2, 2 ) ( 3, 3 ) ( 4, 4 ) ( 5, 5 ) ( 6, 6 ) ( 7, 7 ) ( 8, 8 ) ( 9, 9 ) ( 10, 10 ) ( 11, 11 ) ( 12, 12 ) ( 13, 13 ) ( 14, 14 ) ( 15, 15 ) Γέντρο rent-kung 52 26
27 (a 0, b 0 ) (a 1, b 1 ) (a 2, b 2 ) (a 3, b 3 ) (a 4, b 4 ) (a 5, b 5 ) (a 6, b 6 ) (a 7, b 7 ) (a 8, b 8 ) (a 9, b 9 ) (a 10, b 10 ) (a 11, b 11 ) (a 12, b 12 ) (a 13, b 13 ) (a 14, b 14 ) (a 15, b 15 ) 9/5/2011 Λογαριθμικόσ Αθροιςτόσ Πρόγνωςησ Γέντρο 16-bit, Βάσης-4 Kogge-tone 53 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 54 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 27
28 Αλγόριθμοσ Πολλαπλαςιαςμού MULTIPLY(x, y, m) // Είςοδοι - x : πολλαπλαςιαςτζοσ, y : πολλαπλαςιαςτισ, Ζξοδοσ m : γινόμενο { n = LENGTH(y); m = 0; t = x; // ολιςκθτισ // for i in 1 to n // για κάκε ψθφίο του y // { if (y[i] == 1) m = m + t; // πρόςκεςθ μερικοφ παράγοντα // t = t << 1; // ολίςκθςθ 1 ψθφίο δεξιά για κάκε ψθφίο του y // } return r; } 55 Πολλαπλαςιαςμόσ Μερικών Γινομϋνων 67 x 54 1 ο με 1 ο 2 ο με 1 ο 1 ο με 2 ο 2 ο με 2 ο 67 X X X X οι τζςςερισ αυτοί ςυνδυαςμοί μποροφν να γίνουν ςε ςφνολα από δυαδικά ψηφία 56 28
29 Πολλαπλαςιαςμόσ Μερικών Παραγόντων Multiplicand Πολλαπλαςιαςτζοσ x Multiplier Πολλαπλαςιαςτισ Partial Μερικά products Γινόμενα Result Σελικό Αποτζλεςμα Μια πφλθ ND αρκεί για κάκε ψθφίο του πολλαπλαςια 57 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 58 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 29
30 Πολλαπλαςιαςτόσ Πύνακα (rray) X 3 X 2 X 1 X 0 Y 0 X 3 X 2 X 1 X 0 Y 1 Z 0 H F F H X3 X 2 X 1 X 0 Y 2 Z 1 F F F H X3 X 2 X 1 X 0 Y 3 Z 2 F F F H Z 7 Z 6 Z 5 Z 4 Z 3 59 Πολλαπλαςιαςτόσ Πύνακα (rray) - Κρύςιμη Οδόσ H F F H F F F H Critical Path 1 Critical Path 2 F F F H Critical Path 1 & 2 NxM πολλαπλαςιαςμόσ 60 30
31 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 61 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Πολλαπλαςιαςτόσ Αποθόκευςησ Κρατουμϋνου (Carry ave) H H H H H F F F H F F F H F F H Vector Merging dder 62 31
32 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 63 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Χωροθϋτηςη Πολλαπλαςιαςτό X 3 X 2 X 1 X 0 Y 0 Y 1 C C C C Z 0 H Multiplier Cell F Multiplier Cell Y 2 C C C C Z 1 Vector Merging Cell Y 3 C C C C Z 2 X and Y signals are broadcasted through the complete array. ( ) C C C C Z 7 Z 6 Z 5 Z 4 Z
33 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 65 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ Πολλαπλαςιαςτόσ Δϋντρου Wallace Partial Μερικά products Γινόμενα First Πρϊτο stage τάδιο it position (a) (b) econd Δεφτερο stage τάδιο Final Σελικό adderτάδιο F (c) H (d) 66 33
34 Πολλαπλαςιαςτόσ Δϋντρου Wallace Μερικά Γινόμενα Πρϊτο τάδιο Δεφτερο τάδιο Σελικό τάδιο 67 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 68 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 34
35 Διαύρεςη (450) (17) 69 Διαύρεςη (450) (17) (26) 5-bit διαιρζτθσ < διαιρετζο κατεβάηουμε ψθφίο ολίςκθςθ-αφαίρεςθ, 1 ςτο πθλίκο κατεβάηουμε ψθφίο ολίςκθςθ-αφαίρεςθ, 1 ςτο πθλίκο κατεβάηουμε ψθφίο, υπόλοιπο < διαιρζτθ, 0 ςτο πθλίκο κατεβάηουμε ψθφίο Ολίςκθςθ-αφαίρεςθ, 1 ςτο πθλίκο κατεβάηουμε ψθφίο, υπόλοιπο < διαιρζτθ, 0 ςτο πθλίκο ε κάκε βιμα κάνουμε: Σφγκριςη Ολίςθηςη Αφαίρεςη 70 35
36 Αλγόριθμοσ Διαύρεςησ LONG_DIVIION(D, d, q, r) // Είςοδοι - D : Διαιρετζοσ, d : διαιρζτθσ, Ζξοδοι q : πθλίκο, r : υπόλοιπο { n = M(D); m = (n LENGTH(d)); x = 0; Dt = D; do { while (Dt[n:m] < d) // υπόλοιπο < διαιρζτθ // q[x++] = 0; m = m 1; // 0 ςτο πθλίκο, κατεβάηουμε ψθφίο // q[x++] = 1; // 1 ςτο πθλίκο // r[n-m:0] = Dt[n:m] d; // νζο υπόλοιπο // m = m 1; // κατεβάηουμε ψθφίο // Dt[n:0] = {r, D[m-1:0]};// ςυνζνωςθ υπολοίπου με διαιρετζο // } while (r > d); return (q[0:x], r[n-m:0]); } 71 Περιεχόμενα Δομικοί Λίκοι Ψθφιακϊν Κυκλωμάτων Κφκλωμα Πλιρουσ Ακροιςτι Ιδιότθτα Αντιςτροφισ τατικόσ Πλιρθσ Ακροιςτισ CMO Ζμμεςθ Τλοποίθςθ Ακροιςτι και ιματα ειριακό Κρατοφμενο Ακροιςτισ «Κακρζφτθσ» (Mirror) Γράμμο-διάγραμμα Ακροιςτισ Σρανηίςτορ Διζλευςθσ Δυναμικόσ Ακροιςτισ Διζλευςθσ Αλυςίδα Κρατουμζνου Manchester Γράμμο-Διάγραμμα Ακροιςτισ Παράκαμψθσ (Carry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου (Carry elect) 72 Γραμμικι Τλοποίθςθ Τλοποίθςθ Ρίηασ Πρόγνωςθ Κρατουμζνου (Carry Lookahead) γζνεςθ, προϊκθςθ, επίπεδο τρανηίςτορ, λογαρικμικι διάταξθ δζντρα κρατουμζνων, δυναμικά κυκλϊματα πρόγνωςθσ Πολλαπλαςιαςμόσ αλγόρικμοσ, μερικά γινόμενα Πολλαπλαςιαςτισ Πίνακα Πολλαπλαςιαςτισ αποκικευςθσ κρατουμζνου Χωροκζτθςθ Πολλαπλαςιαςτι Πολλαπλαςιαςτισ Δζντρου Wallace Διαίρεςθ Ολιςκθτζσ 36
37 Δυαδικόσ Ολιςθητόσ Right nop Left i i i-1 i-1 it-lice i Περιςτροφικόσ Ολιςθητόσ (arrel) 3 3 h1 2 2 h2 : Data Wire 1 1 : Control Wire h3 0 0 h0 h1 h2 h
38 Περιςτροφικόσ Ολιςθητόσ 4x h0 h1 h2 h3 Width barrel ~ 2 p m M uffer 75 Λογαριθμικόσ Ολιςθητόσ h1 h1 h2 h2 h4 h
39 0-7 bit Λογαριθμικόσ Ολιςθητόσ Out3 Out2 Out1 Out
HY121 Ηλεκτρικϊ Κυκλώματα
 HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. ωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Στατικόσ Πλιρθσ Ακροιςτισ MO Ακροιςτισ Παράκαμψθσ (arry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου
HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. ωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Στατικόσ Πλιρθσ Ακροιςτισ MO Ακροιςτισ Παράκαμψθσ (arry ypass) Ακροιςτισ Επιλογισ Κρατουμζνου
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων.
 HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 ΗΥ220 - Διάλεξθ 7θ - Αρικμθτικά Κυκλϊματα Κυκλϊματα Πρόςκεςθσ Half-adder
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 ΗΥ220 - Διάλεξθ 7θ - Αρικμθτικά Κυκλϊματα Κυκλϊματα Πρόςκεςθσ Half-adder
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. 1 ΗΥ330 - Διάλεξη 11η - Κυκλώματα Δεδομένων
 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Περιεχόμενα Δομικοί Λίθοι Ψηφιακών Κυκλωμάτων Κύκλωμα Πλήρους
HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων.
 HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων Διδάσκων: Χ. Σωτηρίου, Βοηθός: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Κυκλώματα Πρόσθεσης Half-adder Full-Adder Σειριακό Κρατούμενο
HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων Διδάσκων: Χ. Σωτηρίου, Βοηθός: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Κυκλώματα Πρόσθεσης Half-adder Full-Adder Σειριακό Κρατούμενο
Παραπάνω παρουςιάηεται ο πιο ςυνικθσ χωροκζτθςθ αρικμθτικϊν, λογικϊν κυκλωμάτων. Η μονάδα επεξεργαςίασ είναι θ λζξθ (λ.χ. 32-bit ςε επεξεργαςτζσ,
 1 2 3 4 Παραπάνω παρουςιάηεται ο πιο ςυνικθσ χωροκζτθςθ αρικμθτικϊν, λογικϊν κυκλωμάτων. Η μονάδα επεξεργαςίασ είναι θ λζξθ (λ.χ. 32-bit ςε επεξεργαςτζσ, 8-bit ςε DSP) και αυτι κακορίηει και τθν δομι τθσ
1 2 3 4 Παραπάνω παρουςιάηεται ο πιο ςυνικθσ χωροκζτθςθ αρικμθτικϊν, λογικϊν κυκλωμάτων. Η μονάδα επεξεργαςίασ είναι θ λζξθ (λ.χ. 32-bit ςε επεξεργαςτζσ, 8-bit ςε DSP) και αυτι κακορίηει και τθν δομι τθσ
Λαμβάνοντασ υπόψη ότι κατά την πρόςθεςη δφο δυαδικϊν ψηφίων ιςχφει: Κρατοφμενο
 Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 Παραπάνω παρουσιάζεται ο πιο συνήθης χωροθέτηση αριθμητικών, λογικών κυκλωμάτων. Η μονάδα επεξεργασίας είναι η λέξη (λ.χ. 32-bit σε επεξεργαστές, 8-bit σε DSP)
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 Παραπάνω παρουσιάζεται ο πιο συνήθης χωροθέτηση αριθμητικών, λογικών κυκλωμάτων. Η μονάδα επεξεργασίας είναι η λέξη (λ.χ. 32-bit σε επεξεργαστές, 8-bit σε DSP)
Δυαδικοσ πολλαπλαςιαςμοσ και διαιρεςη ακεραιων
 Δυαδικοσ πολλαπλαςιαςμοσ και διαιρεςη ακεραιων Δρ. Χρήστος Ηλιούδης Πολλαπλαςιαςμόσ μη προςημαςμζνων ακεραίων βρίςκουμε ζνα άκροιςμα το οποίο αποτελείται από μετατοπιςμζνα γινόμενα, τα οποία προζκυψαν
Δυαδικοσ πολλαπλαςιαςμοσ και διαιρεςη ακεραιων Δρ. Χρήστος Ηλιούδης Πολλαπλαςιαςμόσ μη προςημαςμζνων ακεραίων βρίςκουμε ζνα άκροιςμα το οποίο αποτελείται από μετατοπιςμζνα γινόμενα, τα οποία προζκυψαν
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
x n D 2 ENCODER m - σε n (m 2 n ) x 1 Παραδείγματα κωδικοποιθτϊν είναι ο κωδικοποιθτισ οκταδικοφ ςε δυαδικό και ο κωδικοποιθτισ BCD ςε δυαδικό.
 Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
EE434 ASIC & Digital Systems Arithmetic Circuits
 EE434 ASIC & Digital Systems Arithmetic Circuits Spring 25 Dae Hyun Kim daehyun@eecs.wsu.edu Arithmetic Circuits What we will learn Adders Basic High-speed 2 Adder -bit adder SSSSSS = AA BB CCCC CCCC =
EE434 ASIC & Digital Systems Arithmetic Circuits Spring 25 Dae Hyun Kim daehyun@eecs.wsu.edu Arithmetic Circuits What we will learn Adders Basic High-speed 2 Adder -bit adder SSSSSS = AA BB CCCC CCCC =
HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού.
 HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού Διδϊςκων: Χ. ωτηρύου http://www.csd.uoc.gr/~hy523 1 Περιεχόμενα Ροι Φυςικισ χεδίαςθσ χεδίαςθ με Κακιερωμζνα
HY523 Εργαςτηριακό χεδύαςη Ψηφιακών Κυκλωμϊτων με εργαλεύα Ηλεκτρονικού χεδιαςτικού Αυτοματιςμού Διδϊςκων: Χ. ωτηρύου http://www.csd.uoc.gr/~hy523 1 Περιεχόμενα Ροι Φυςικισ χεδίαςθσ χεδίαςθ με Κακιερωμζνα
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 ΗΥ437 - Πολυεπίπεδθ Λογικι Απλοποίθςθ με Περιεχόμενα Είδθ Αδιάφορων Τιμϊν ςε Πολφ-επίπεδα Δυαδικά Δίκτυα Αδιάφορεσ
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 ΗΥ437 - Πολυεπίπεδθ Λογικι Απλοποίθςθ με Περιεχόμενα Είδθ Αδιάφορων Τιμϊν ςε Πολφ-επίπεδα Δυαδικά Δίκτυα Αδιάφορεσ
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
i Το τρανζίστορ αυτό είναι τύπου NMOS. Υπάρχει και το συμπληρωματικό PMOS. ; Τι συμβαίνει στο τρανζίστορ PMOS; Το τρανζίστορ MOS(FET)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ
 3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ 1 2 3 4 5 6 7 Παραπάνω φαίνεται θ χαρακτθριςτικι καμπφλθ μετάβαςθσ δυναμικοφ (voltage transfer characteristic) για ζναν αντιςτροφζα,
3 θ διάλεξθ Επανάλθψθ, Επιςκόπθςθ των βαςικϊν γνϊςεων τθσ Ψθφιακισ Σχεδίαςθσ 1 2 3 4 5 6 7 Παραπάνω φαίνεται θ χαρακτθριςτικι καμπφλθ μετάβαςθσ δυναμικοφ (voltage transfer characteristic) για ζναν αντιςτροφζα,
Ψηφιακή Λογική και Σχεδίαση
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
Ψηφιακά Συστήματα VLSI
 Ψηφιακά Συστήματα VLSI. ΑΡΙΘΜΗΤΙΚΑ ΚΥΚΛΩΜΑΤΑ VLSI Αθροιστές, Πολλαπλασιαστές (Σειριακοί- Παράλληλοι). ΠΡΑΞΕΙΣ ΜΕ ΠΡΟΣΗΜΑΣΜΕΝΟΥΣ ΑΡΙΘΜΟΥΣ Συμπλήρωμα ως προς, Αφαιρέτες, Booth, Modified Booth, αριθμητικά
Ψηφιακά Συστήματα VLSI. ΑΡΙΘΜΗΤΙΚΑ ΚΥΚΛΩΜΑΤΑ VLSI Αθροιστές, Πολλαπλασιαστές (Σειριακοί- Παράλληλοι). ΠΡΑΞΕΙΣ ΜΕ ΠΡΟΣΗΜΑΣΜΕΝΟΥΣ ΑΡΙΘΜΟΥΣ Συμπλήρωμα ως προς, Αφαιρέτες, Booth, Modified Booth, αριθμητικά
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Αριθμητικές Συναρτήσεις και Κυκλώματα Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πρόσθεση
ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Αριθμητικές Συναρτήσεις και Κυκλώματα Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πρόσθεση
Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ψηφιακά Κυκλώματα (1 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Κανονικζσ Μορφζσ Οριςμόσ των Δυαδικών Διαγραμμάτων Αποφάςεων (Binary Decision Diagrams BDDs) Αναπαράςταςθ
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Κανονικζσ Μορφζσ Οριςμόσ των Δυαδικών Διαγραμμάτων Αποφάςεων (Binary Decision Diagrams BDDs) Αναπαράςταςθ
HY121 Ηλεκτρικϊ Κυκλώματα
 HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
HY Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy Περιεχόμενα Στατικζσ Πφλεσ CMOS και Μεγζκθ Τρανηίςτορ Λογικι Λόγου Αντίςταςθσ/Μεγεκών (NMOS) Διαφορικι
ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ : Κ. ΠΕΚΜΕΣΤΖΗ
 ΠΡΑΞΕΙΣ ΜΕ ΠΡΟΣΗΜΑΣΜΕΝΟΥΣ ΑΡΙΘΜΟΥΣ ΚΥΚΛΩΜΑΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΠΑΡΑΣΤΑΣΗ ΑΡΙΘΜΩΝ Συμπλήρωμα ως προς 2 Booth, Modified Booth Reduntant αριθμητικά συστήματα Signed Digit αριθμητική Κανονική
ΠΡΑΞΕΙΣ ΜΕ ΠΡΟΣΗΜΑΣΜΕΝΟΥΣ ΑΡΙΘΜΟΥΣ ΚΥΚΛΩΜΑΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΠΑΡΑΣΤΑΣΗ ΑΡΙΘΜΩΝ Συμπλήρωμα ως προς 2 Booth, Modified Booth Reduntant αριθμητικά συστήματα Signed Digit αριθμητική Κανονική
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4
 Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Διάλεξθ 4 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Υποσυστήματα Χειρισμού Δεδομένων
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II VLSI ΙI 2011-2012 1 Κεφάλαιο 11 Υποσυστήματα Χειρισμού Δεδομένων VLSI ΙI 2011-2012 2 1 Περίγραμμα Διάλεξης Πρόσθεση / Αφαίρεση Ανιχνευτές 1/0 Συγκριτές Μετρητές
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II VLSI ΙI 2011-2012 1 Κεφάλαιο 11 Υποσυστήματα Χειρισμού Δεδομένων VLSI ΙI 2011-2012 2 1 Περίγραμμα Διάλεξης Πρόσθεση / Αφαίρεση Ανιχνευτές 1/0 Συγκριτές Μετρητές
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδϊςκων: Χ. Σωτηρύου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Στόχοι τθσ Τεχνολογικισ Απεικόνιςθσ Περιγραφι σ ωσ Βαςικοί Γράφοι Μεταςχθματιςμόσ Δυαδικοφ Κυκλϊματοσ
HY437 Αλγόριθμοι CAD Διδϊςκων: Χ. Σωτηρύου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Στόχοι τθσ Τεχνολογικισ Απεικόνιςθσ Περιγραφι σ ωσ Βαςικοί Γράφοι Μεταςχθματιςμόσ Δυαδικοφ Κυκλϊματοσ
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Άλλες Αριθμητικές Συναρτήσεις/Κυκλώματα
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Αριθμητικές Συναρτήσεις και Κυκλώματα Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πρόσθεση υαδική Πρόσθεση
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Αριθμητικές Συναρτήσεις και Κυκλώματα Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Πρόσθεση υαδική Πρόσθεση
Υποσυστήματα Χειρισμού Δεδομένων
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II VLSI ΙI 1 Υποσυστήματα Χειρισμού Δεδομένων VLSI ΙI 2 1 Περίγραμμα Διάλεξης Πρόσθεση / Αφαίρεση Ανιχνευτές 1/0 Συγκριτές Μετρητές Κωδικοποίηση Ολισθητές Πολλαπλασιασμός
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II VLSI ΙI 1 Υποσυστήματα Χειρισμού Δεδομένων VLSI ΙI 2 1 Περίγραμμα Διάλεξης Πρόσθεση / Αφαίρεση Ανιχνευτές 1/0 Συγκριτές Μετρητές Κωδικοποίηση Ολισθητές Πολλαπλασιασμός
! Εάν ο αριθμός διαθέτει περισσότερα bits, χρησιμοποιούμε μεγαλύτερες δυνάμεις του 2. ! Προσοχή στη θέση του περισσότερο σημαντικού bit!
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 9: Σχεδιασµός Συνδυαστικών Κυκλωµάτων ΙΙ (Κεφάλαιο 5) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 9: Σχεδιασµός Συνδυαστικών Κυκλωµάτων ΙΙ (Κεφάλαιο 5) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 6 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 6 η :
Ενότητα 9 ΑΡΙΘΜΗΤΙΚΑ & ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ
 Ενότητα 9 ΑΡΙΘΜΗΤΙΚΑ & ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Προσημασμένοι Ακέραιοι Δυαδικοί Αριθμοί Ημιαθροιστής - Ημιαφαιρέτης Πλήρης Αθροιστής - Πλήρης Αφαιρέτης Αθροιστής Διάδοσης Κρατούμενου Επαναληπτικές
Ενότητα 9 ΑΡΙΘΜΗΤΙΚΑ & ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Προσημασμένοι Ακέραιοι Δυαδικοί Αριθμοί Ημιαθροιστής - Ημιαφαιρέτης Πλήρης Αθροιστής - Πλήρης Αφαιρέτης Αθροιστής Διάδοσης Κρατούμενου Επαναληπτικές
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΕΙΡΙΑΚΗ ΠΡΟΣΘΕΣΗ
 ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ & ΗΛΕΚΤΡΟΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ & μ-υπολογιστων ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΕΙΡΙΑΚΗ ΠΡΟΣΘΕΣΗ Θεωρητικό Μέρος Οι σειριακές λειτουργίες είναι πιο
ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ & ΗΛΕΚΤΡΟΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ & μ-υπολογιστων ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΕΙΡΙΑΚΗ ΠΡΟΣΘΕΣΗ Θεωρητικό Μέρος Οι σειριακές λειτουργίες είναι πιο
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ. Κεφάλαιο 8 Η γλϊςςα Pascal
 ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Σχεδίαση Ψηφιακών Συστημάτων. Ενότητα: ΚΑΤΑΧΩΡΗΤΕΣ - ΑΠΑΡΙΘΜΗΤΕΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ᄃ Σχεδίαση Ψηφιακών Συστημάτων Ενότητα: ΚΑΤΑΧΩΡΗΤΕΣ - ΑΠΑΡΙΘΜΗΤΕΣ Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ᄃ Σχεδίαση Ψηφιακών Συστημάτων Ενότητα: ΚΑΤΑΧΩΡΗΤΕΣ - ΑΠΑΡΙΘΜΗΤΕΣ Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
Πανεπιστήμιο Ιωαννίνων Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Συστημάτων VLSI και Αρχιτεκτονικής Υπολογιστών. Γεώργιος Τσιατούχας
 Πανεπιστήμιο Ιωαννίνων ΚΥΚΛΩΜΑΤΑ VLI Εργαστηριακές Ασκήσεις Γεώργιος Τσιατούχας Ιωάννινα 2016 VLI ystems and Computer rchitecture Lab ΚΥΚΛΩΜΑΤΑ VLI ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΕΧΟΜΕΝΑ Χαρακτηριστικές MO
Πανεπιστήμιο Ιωαννίνων ΚΥΚΛΩΜΑΤΑ VLI Εργαστηριακές Ασκήσεις Γεώργιος Τσιατούχας Ιωάννινα 2016 VLI ystems and Computer rchitecture Lab ΚΥΚΛΩΜΑΤΑ VLI ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΕΧΟΜΕΝΑ Χαρακτηριστικές MO
HY437 Αλγόριθμοι CAD
 HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Ζλεγχοσ Σφαλμάτων μετά τθν Καταςκευι Μοντζλο Κολλθμζνο-ςτο-0, -1 Παραδείγματα Διαδικαςίασ Ελζγχου Λογικι
HY437 Αλγόριθμοι CAD Διδάςκων: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce437/ 1 Περιεχόμενα Ζλεγχοσ Σφαλμάτων μετά τθν Καταςκευι Μοντζλο Κολλθμζνο-ςτο-0, -1 Παραδείγματα Διαδικαςίασ Ελζγχου Λογικι
Οργάνωση Η/Υ. Γιώργος Δημητρίου. Μάθημα 2 ο Σύντομη Επανάληψη. Πανεπιστήμιο Θεσσαλίας - Τμήμα Πληροφορικής
 Γιώργος Δημητρίου Μάθημα 2 ο Σύντομη Επανάληψη Από την Εισαγωγή στους Η/Υ Γλώσσες Μηχανής Πεδία εντολής Μέθοδοι διευθυνσιοδότησης Αρχιτεκτονικές συνόλου εντολών Κύκλος εντολής Αλγόριθμοι/Υλικό Αριθμητικών
Γιώργος Δημητρίου Μάθημα 2 ο Σύντομη Επανάληψη Από την Εισαγωγή στους Η/Υ Γλώσσες Μηχανής Πεδία εντολής Μέθοδοι διευθυνσιοδότησης Αρχιτεκτονικές συνόλου εντολών Κύκλος εντολής Αλγόριθμοι/Υλικό Αριθμητικών
HY121 Ηλεκτρικϊ Κυκλώματα
 HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 HY121 - Τρανηίςτορ και Στατικζσ 3/11/2013 Περιεχόμενα Το Τρανηίςτορ ωσ Διακόπτθσ Δομι MOSFET
HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 HY121 - Τρανηίςτορ και Στατικζσ 3/11/2013 Περιεχόμενα Το Τρανηίςτορ ωσ Διακόπτθσ Δομι MOSFET
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 2013 Διάρκεια εξέτασης : 160 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών:
 Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΟΜΑ Α Α Αριθµητική Λογική Μονάδα των 8-bit 1. Εισαγωγή Γενικά µια αριθµητική λογική µονάδα (ALU, Arithmetic Logic Unit)
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΟΜΑ Α Α Αριθµητική Λογική Μονάδα των 8-bit 1. Εισαγωγή Γενικά µια αριθµητική λογική µονάδα (ALU, Arithmetic Logic Unit)
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΑΣΚΗΣΗ 4 ΣΧΕΔΙΑΣΗ ΑΡΙΘΜΗΤΙΚΩΝ ΛΟΓΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ
 ΑΣΚΗΣΗ 4 ΣΧΕΔΙΑΣΗ ΑΡΙΘΜΗΤΙΚΩΝ ΛΟΓΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Αντικείμενο της άσκησης: Λογική και μεθοδολογία σχεδίασης αριθμητικών λογικών κυκλωμάτων και λειτουργική εξομοίωση με το λογισμικό EWB.. Αθροιστές. Σχεδίαση
ΑΣΚΗΣΗ 4 ΣΧΕΔΙΑΣΗ ΑΡΙΘΜΗΤΙΚΩΝ ΛΟΓΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Αντικείμενο της άσκησης: Λογική και μεθοδολογία σχεδίασης αριθμητικών λογικών κυκλωμάτων και λειτουργική εξομοίωση με το λογισμικό EWB.. Αθροιστές. Σχεδίαση
Οργάνωση Η/Υ. Γιώργος ηµητρίου. Μάθηµα 3 ο. Πανεπιστήµιο Θεσσαλίας - Τµήµα Μηχανικών Η/Υ, Τηλεπικοινωνιών και ικτύων
 Γιώργος ηµητρίου Μάθηµα 3 ο Πανεπιστήµιο Θεσσαλίας - Τµήµα Μηχανικών Η/Υ, Τηλεπικοινωνιών και ικτύων Μονάδα Επεξεργασίας εδοµένων Υποµονάδες πράξεων n Αριθµητική/Λογική Μονάδα (ΑΛΜ - ALU): Βασικές αριθµητικές
Γιώργος ηµητρίου Μάθηµα 3 ο Πανεπιστήµιο Θεσσαλίας - Τµήµα Μηχανικών Η/Υ, Τηλεπικοινωνιών και ικτύων Μονάδα Επεξεργασίας εδοµένων Υποµονάδες πράξεων n Αριθµητική/Λογική Μονάδα (ΑΛΜ - ALU): Βασικές αριθµητικές
Προςζξτε ότι για τα A, B ςε ςειρά, θ πθγι του πάνω, όταν είναι ανοικτό φτάνει μόνο τα (Vdd Vtn)V.
 1 2 Όπωσ και ςτον αντιςτροφζα, ζτςι και ςτισ βαςικζσ ι πολφπλοκεσ ςτατικζσ διατάξεισ τρανηίςτορ μποροφμε να χρθςιμοποιιςουμε το μοντζλο τθσ ιςοδφναμθσ αντίςταςθσ. Με αυτό τον τρόπο προκφπτουν πιο πολφπλοκα
1 2 Όπωσ και ςτον αντιςτροφζα, ζτςι και ςτισ βαςικζσ ι πολφπλοκεσ ςτατικζσ διατάξεισ τρανηίςτορ μποροφμε να χρθςιμοποιιςουμε το μοντζλο τθσ ιςοδφναμθσ αντίςταςθσ. Με αυτό τον τρόπο προκφπτουν πιο πολφπλοκα
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 00 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Δυαδική λογική Πύλες AND, OR, NOT, NAND,
ΗΜΥ 00 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Δυαδική λογική Πύλες AND, OR, NOT, NAND,
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II 3 η Εργαστηριακή Άσκηση Σχεδίαση και Υλοποίηση μίας ALU δύο εισόδων VHDL Εργαστήριο_2 2012-2013 1 Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II 3 η Εργαστηριακή Άσκηση Σχεδίαση και Υλοποίηση μίας ALU δύο εισόδων VHDL Εργαστήριο_2 2012-2013 1 Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας
Ψηφιακά Συστήματα. 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων
 Ψηφιακά Συστήματα 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd
Ψηφιακά Συστήματα 6. Σχεδίαση Συνδυαστικών Κυκλωμάτων Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
HY121 Ηλεκτρικϊ Κυκλώματα
 HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Συςκευζσ ςτο Πυρίτιο Πυρίτιο n και p Δίοδοσ Θετικι, αρνθτικι πόλωςθ Εξίςωςθ
HY121 Ηλεκτρικϊ Κυκλώματα Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Βαςιλϊκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Συςκευζσ ςτο Πυρίτιο Πυρίτιο n και p Δίοδοσ Θετικι, αρνθτικι πόλωςθ Εξίςωςθ
Ψηφιακή Σχεδίαση Ενότητα 10:
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
ΣΕΙ ΕΡΡΩΝ ΜΑΙΟ 2013 ΠΣΤΧΙΑΚΗ ΕΡΓΑΙΑ ΣΙΜΕΝΙΔΗ ΣΕΦΑΝΟ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΣΗ : ΜΑΔΕΜΛΗ ΙΩΑΝΝΗ
 ΣΕΙ ΕΡΡΩΝ ΜΑΙΟ 2013 ΠΣΤΧΙΑΚΗ ΕΡΓΑΙΑ ΠΟΤΔΑΣΕ: ΛΑΔΑ ΧΡΙΣΙΝΑ ΣΙΜΕΝΙΔΗ ΣΕΦΑΝΟ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΣΗ : ΜΑΔΕΜΛΗ ΙΩΑΝΝΗ ΘΕΜΑ: ΧΕΔΙΑΗ ΚΑΙ ΤΛΟΠOΙΗΗ ΕΚΠΑΙΔΕΤΣΙΚΩΝ ΑΝΑΠΣΤΓΜΑΣΩΝ ΜΕΛΕΣΗ ΨΗΦΙΑΚΩΝ ΚΤΚΛΩΜΑΣΩΝ ΚΑΙ ΤΓΓΡΑΦΗ
ΣΕΙ ΕΡΡΩΝ ΜΑΙΟ 2013 ΠΣΤΧΙΑΚΗ ΕΡΓΑΙΑ ΠΟΤΔΑΣΕ: ΛΑΔΑ ΧΡΙΣΙΝΑ ΣΙΜΕΝΙΔΗ ΣΕΦΑΝΟ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΣΗ : ΜΑΔΕΜΛΗ ΙΩΑΝΝΗ ΘΕΜΑ: ΧΕΔΙΑΗ ΚΑΙ ΤΛΟΠOΙΗΗ ΕΚΠΑΙΔΕΤΣΙΚΩΝ ΑΝΑΠΣΤΓΜΑΣΩΝ ΜΕΛΕΣΗ ΨΗΦΙΑΚΩΝ ΚΤΚΛΩΜΑΣΩΝ ΚΑΙ ΤΓΓΡΑΦΗ
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων. 9/28/ ΗΥ220 - Διάλεξθ 3θ, Επανάλθψθ
 HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Συςτιματα Αρικμϊν και Δυαδικοί Αρικμοί Ψθφιακι Λογικι Ηλεκτρικά
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Συςτιματα Αρικμϊν και Δυαδικοί Αρικμοί Ψθφιακι Λογικι Ηλεκτρικά
ΚΥΚΛΩΜΑΤΑ VLSI. Ασκήσεις Ι. Γ. Τσιατούχας. Πανεπιςτιμιο Ιωαννίνων. Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18
 ΚΥΚΛΩΜΑΤΑ LSI Πανεπιςτιμιο Ιωαννίνων Ασκήσεις Ι Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18 Γ. Τσιατούχας Άσκηση 1 1) Σχεδιάςτε τισ ςφνκετεσ COS λογικζσ πφλεσ (ςε επίπεδο τρανηίςτορ) που υλοποιοφν τισ
ΚΥΚΛΩΜΑΤΑ LSI Πανεπιςτιμιο Ιωαννίνων Ασκήσεις Ι Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18 Γ. Τσιατούχας Άσκηση 1 1) Σχεδιάςτε τισ ςφνκετεσ COS λογικζσ πφλεσ (ςε επίπεδο τρανηίςτορ) που υλοποιοφν τισ
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
Παρουςίαςθ 2 θσ Άςκθςθσ:
 Εθνικό Μετςόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχανικών Υπολογιςτών Εργαςτήριο Υπολογιςτικών Συςτημάτων Παρουςίαςθ 2 θσ Άςκθςθσ: Ανάπτυξη παράλληλου κώδικα και μελζτη επίδοςησ του αλγόριθμου
Εθνικό Μετςόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχανικών Υπολογιςτών Εργαςτήριο Υπολογιςτικών Συςτημάτων Παρουςίαςθ 2 θσ Άςκθςθσ: Ανάπτυξη παράλληλου κώδικα και μελζτη επίδοςησ του αλγόριθμου
Επεξεργαστής Υλοποίηση ενός κύκλου μηχανής
 ΗΥ 232 Οργάνωση και Σχεδίαση Υπολογιστών Διάλεξη 9 Επεξεργαστής Υλοποίηση ενός κύκλου μηχανής Νίκος Μπέλλας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ 1 Ti είναι Αρχιτεκτονική και τι Μικροαρχιτεκτονική
ΗΥ 232 Οργάνωση και Σχεδίαση Υπολογιστών Διάλεξη 9 Επεξεργαστής Υλοποίηση ενός κύκλου μηχανής Νίκος Μπέλλας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ 1 Ti είναι Αρχιτεκτονική και τι Μικροαρχιτεκτονική
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Συνδυαστική Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Συνδυαστική Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ψηφιακά Κυκλώματα Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά (combinational)
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Συνδυαστική Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ψηφιακά Κυκλώματα Τα ψηφιακά κυκλώματα διακρίνονται σε συνδυαστικά (combinational)
Πανεπιστήμιο Θεσσαλίας - Τμήμα Πληροφορικής. Οργάνωση Η/Υ. Γιώργος ηµητρίου. Μάθηµα 2 ο Σύντοµη Επανάληψη
 Γιώργος ηµητρίου Μάθηµα 2 ο Σύντοµη Επανάληψη Από την Εισαγωγή στους Η/Υ Γλώσσες Μηχανής n Πεδία εντολής n Μέθοδοι διευθυνσιοδότησης n Αρχιτεκτονικές συνόλου εντολών n Κύκλος εντολής Αλγόριθµοι/Υλικό Αριθµητικών
Γιώργος ηµητρίου Μάθηµα 2 ο Σύντοµη Επανάληψη Από την Εισαγωγή στους Η/Υ Γλώσσες Μηχανής n Πεδία εντολής n Μέθοδοι διευθυνσιοδότησης n Αρχιτεκτονικές συνόλου εντολών n Κύκλος εντολής Αλγόριθµοι/Υλικό Αριθµητικών
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 8 Σχεδίαση στο Επίπεδο Μεταφοράς Περιεχομένων Καταχωρητών Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Περίγραμμα Κεφαλαίου
Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 8 Σχεδίαση στο Επίπεδο Μεταφοράς Περιεχομένων Καταχωρητών Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Περίγραμμα Κεφαλαίου
ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΙΣΟΤΣΟ ΚΤΠΡΟΤ Πρόγραμμα Επιμόρυωσης Τποψηυίων Καθηγητών Σεχνολογίας. Ηλεκτρονικά ΙΙ
 ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΙΣΟΤΣΟ ΚΤΠΡΟΤ Πρόγραμμα Επιμόρυωσης Τποψηυίων Καθηγητών Σεχνολογίας Ηλεκτρονικά ΙΙ Πέμπτη 3/3/2011 Διδάζκων: Γιώργος Χαηζηιωάννοσ Τηλέθωνο: 99653828 Ε-mail: georghios.h@cytanet.com.cy Ώρες
ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΙΣΟΤΣΟ ΚΤΠΡΟΤ Πρόγραμμα Επιμόρυωσης Τποψηυίων Καθηγητών Σεχνολογίας Ηλεκτρονικά ΙΙ Πέμπτη 3/3/2011 Διδάζκων: Γιώργος Χαηζηιωάννοσ Τηλέθωνο: 99653828 Ε-mail: georghios.h@cytanet.com.cy Ώρες
Εισαγωγή στους Υπολογιστές
 Εισαγωγή στους Υπολογιστές Ενότητα 10: Ψηφιακή Αριθμητική Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Εισαγωγικές έννοιες ψηφιακής λογικής
Εισαγωγή στους Υπολογιστές Ενότητα 10: Ψηφιακή Αριθμητική Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Εισαγωγικές έννοιες ψηφιακής λογικής
Δζντρα. Δομζσ Δεδομζνων
 Δζντρα Δομζσ Δεδομζνων Περιεχόμενα Δζντρα Γενικζσ ζννοιεσ Κόμβοσ ενόσ δζντρου Δυαδικά δζντρα αναηιτθςθσ Αναηιτθςθ Κόμβου Ειςαγωγι ι δθμιουργία κόμβου Δζντρα Γενικζσ ζννοιεσ Οι προθγοφμενεσ δομζσ που εξετάςτθκαν
Δζντρα Δομζσ Δεδομζνων Περιεχόμενα Δζντρα Γενικζσ ζννοιεσ Κόμβοσ ενόσ δζντρου Δυαδικά δζντρα αναηιτθςθσ Αναηιτθςθ Κόμβου Ειςαγωγι ι δθμιουργία κόμβου Δζντρα Γενικζσ ζννοιεσ Οι προθγοφμενεσ δομζσ που εξετάςτθκαν
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II Επιμέλεια: Βασίλης Παλιουράς, Αναπληρωτής Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας 1 Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II Επιμέλεια: Βασίλης Παλιουράς, Αναπληρωτής Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας 1 Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
 100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2017-2018 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2017-2018 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
HY225 Οργάνωςη Τπολογιςτών
 HY225 Οργάνωςη Τπολογιςτών Διδάςκοντεσ: Δ. Νικολόπουλοσ, Φ. ωτηρίου. http://www.csd.uoc.gr/~hy225 1 Περιεχόμενα Αναςκόπθςθ χεδίαςθ/τλοποίθςθ Επεξεργαςτι Διαδικαςία Εκτζλεςθσ Εντολισ Επιςκόπθςθ δομισ Επεξεργαςτι
HY225 Οργάνωςη Τπολογιςτών Διδάςκοντεσ: Δ. Νικολόπουλοσ, Φ. ωτηρίου. http://www.csd.uoc.gr/~hy225 1 Περιεχόμενα Αναςκόπθςθ χεδίαςθ/τλοποίθςθ Επεξεργαςτι Διαδικαςία Εκτζλεςθσ Εντολισ Επιςκόπθςθ δομισ Επεξεργαςτι
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων. Πολυπλζκτεσ Καμπφλθ Παρζτο. Κωδικοποιθτζσ/Από-κωδικοποιθτζσ D FF
 HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ Περιεχόμενα Περιγραφζσ και υνκζςιμεσ Δομζσ Πολυπλζκτεσ Καμπφλθ Παρζτο Κωδικοποιθτζσ/Από-κωδικοποιθτζσ
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ Περιεχόμενα Περιγραφζσ και υνκζςιμεσ Δομζσ Πολυπλζκτεσ Καμπφλθ Παρζτο Κωδικοποιθτζσ/Από-κωδικοποιθτζσ
ΟΡΓΑΝΩΣΗ ΚΑΙ ΣΧΕΔΙΑΣΗ Η/Υ
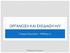 ΟΡΓΑΝΩΣΗ ΚΑΙ ΣΧΕΔΙΑΣΗ Η/Υ Γιώργος Δημητρίου Μάθημα 4 ο ΜΣ Εφαρμοσμένη ληροφορική ΜΟΝΑΔΑ ΕΕΞΕΡΓΑΣΙΑΣ ΔΕΔΟΜΕΝΩΝ Υπομονάδες πράξεων Αριθμητική/Λογική Μονάδα (ΑΛΜ - ALU): Βασικές αριθμητικές πράξεις Λογικές
ΟΡΓΑΝΩΣΗ ΚΑΙ ΣΧΕΔΙΑΣΗ Η/Υ Γιώργος Δημητρίου Μάθημα 4 ο ΜΣ Εφαρμοσμένη ληροφορική ΜΟΝΑΔΑ ΕΕΞΕΡΓΑΣΙΑΣ ΔΕΔΟΜΕΝΩΝ Υπομονάδες πράξεων Αριθμητική/Λογική Μονάδα (ΑΛΜ - ALU): Βασικές αριθμητικές πράξεις Λογικές
Λάμπρος Μπισδούνης. ρ. Ηλεκτρολόγος Μηχανικός
 ΑΝΑΛΥΣΗ ΚΑΤΑΝΑΛΩΣΗΣ ΕΝΕΡΓΕΙΑΣ & ΚΑΘΥΣΤΕΡΗΣΗΣ ΚΥΚΛΩΜΑΤΩΝ CMOS & ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΑΡΙΘΜΗΤΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΕ ΧΑΜΗΛΗ ΚΑΤΑΝΑΛΩΣΗ ΕΝΕΡΓΕΙΑΣ & ΥΨΗΛΗ ΤΑΧΥΤΗΤΑ Λάμπρος Μπισδούνης ρ. Ηλεκτρολόγος Μηχανικός Χανιά
ΑΝΑΛΥΣΗ ΚΑΤΑΝΑΛΩΣΗΣ ΕΝΕΡΓΕΙΑΣ & ΚΑΘΥΣΤΕΡΗΣΗΣ ΚΥΚΛΩΜΑΤΩΝ CMOS & ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΑΡΙΘΜΗΤΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΕ ΧΑΜΗΛΗ ΚΑΤΑΝΑΛΩΣΗ ΕΝΕΡΓΕΙΑΣ & ΥΨΗΛΗ ΤΑΧΥΤΗΤΑ Λάμπρος Μπισδούνης ρ. Ηλεκτρολόγος Μηχανικός Χανιά
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
Σχεδίαση Βασικών Κυκλωµάτων. Χρ. Καβουσιανός. Επίκουρος Καθηγητής
 Σχεδίαση Βασικών Κυκλωµάτων Χρ. Καβουσιανός Επίκουρος Καθηγητής Εισαγωγή Τα αριθµητικά κυκλώµατα χρησιµοποιούνται ευρέως στην σχεδίαση συστηµάτων. Data Paths Επεξεργαστές ASICs Κυρίαρχες Αριθµητικές Πράξεις:
Σχεδίαση Βασικών Κυκλωµάτων Χρ. Καβουσιανός Επίκουρος Καθηγητής Εισαγωγή Τα αριθµητικά κυκλώµατα χρησιµοποιούνται ευρέως στην σχεδίαση συστηµάτων. Data Paths Επεξεργαστές ASICs Κυρίαρχες Αριθµητικές Πράξεις:
Σχεδίαση Ψηφιακών Συστημάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 4: Σχεδιασμός Σειριακού Αθροιστή Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 4: Σχεδιασμός Σειριακού Αθροιστή Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
Μετατροπεσ Παραςταςεων
 Δρ. Χρήστος Ηλιούδης Μεηαηποπή 346 10 ζε δςαδικο 346 10 1) 346/2 = 173 με ςπόλοιπο 0 2) 173/2 = 86 με ςπόλοιπο 1 3) 86/2 = 43 με ςπόλοιπο 0 4) 43/2 = 21 με ςπόλοιπο 1 5) 21/2 = 10 με ςπόλοιπο 1 6) 10/2
Δρ. Χρήστος Ηλιούδης Μεηαηποπή 346 10 ζε δςαδικο 346 10 1) 346/2 = 173 με ςπόλοιπο 0 2) 173/2 = 86 με ςπόλοιπο 1 3) 86/2 = 43 με ςπόλοιπο 0 4) 43/2 = 21 με ςπόλοιπο 1 5) 21/2 = 10 με ςπόλοιπο 1 6) 10/2
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή
Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή (ως τρόπος οργάνωσης αρχείου) μέγεθος
Δυναμικός Κατακερματισμός 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή (ως τρόπος οργάνωσης αρχείου) μέγεθος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Αποδοτική σχεδίαση Multiplier-Adder/Accumulator για αριθμούς σε μορφή
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Αποδοτική σχεδίαση Multiplier-Adder/Accumulator για αριθμούς σε μορφή
Παράρτηµα Γ. Τα Βασικά της Λογικής Σχεδίασης. Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση
 Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Παράρτηµα Γ Τα Βασικά της Λογικής Σχεδίασης ιαφάνειες διδασκαλίας του πρωτότυπου βιβλίου µεταφρασµένες στα ελληνικά και εµπλουτισµένες
Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Παράρτηµα Γ Τα Βασικά της Λογικής Σχεδίασης ιαφάνειες διδασκαλίας του πρωτότυπου βιβλίου µεταφρασµένες στα ελληνικά και εµπλουτισµένες
ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ (Τμήματα Υπολογιστή) ΕΚΠΑΙΔΕΥΤΗΣ:ΠΟΖΟΥΚΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΟΥ ΥΠΟΛΟΓΙΣΤΗ Κάθε ηλεκτρονικός υπολογιστής αποτελείται
ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ (Τμήματα Υπολογιστή) ΕΚΠΑΙΔΕΥΤΗΣ:ΠΟΖΟΥΚΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΟΥ ΥΠΟΛΟΓΙΣΤΗ Κάθε ηλεκτρονικός υπολογιστής αποτελείται
Γράφοι. Δομζσ Δεδομζνων Διάλεξθ 9
 Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών πράξεων
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών πράξεων
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων.
 HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Συπικι Ροι χεδίαςθσ Ιεραρχία ςτθν χεδίαςθ Η Γλϊςςα Verilog
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Συπικι Ροι χεδίαςθσ Ιεραρχία ςτθν χεδίαςθ Η Γλϊςςα Verilog
HY121 Ηλεκτρικά Κυκλώματα
 HY121 Ηλεκτρικά Κυκλώματα Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Βαςιλάκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Μζτρα ποιότθτασ Κυκλϊματοσ Κόςτοσ Παραγωγισ Ψθφιακι Λογικι - Καμπφλθ Μετάβαςθσ
HY121 Ηλεκτρικά Κυκλώματα Διδάςκων: Χ. Σωτηρίου, Βοηθοί: Ε. Βαςιλάκησ, Δ. Πούλιοσ http://www.csd.uoc.gr/~hy121 1 Περιεχόμενα Μζτρα ποιότθτασ Κυκλϊματοσ Κόςτοσ Παραγωγισ Ψθφιακι Λογικι - Καμπφλθ Μετάβαςθσ
Ραραπάνω παρουςιάηεται ο πυρινασ των εντολϊν του επεξεργαςτι MIPS, με τισ οποίεσ, και τθν υλοποίθςθ τουσ ςε υλικό κα αςχολθκοφμε.
 1 2 3 Ραραπάνω παρουςιάηεται ο πυρινασ των εντολϊν του επεξεργαςτι MIPS, με τισ οποίεσ, και τθν υλοποίθςθ τουσ ςε υλικό κα αςχολθκοφμε. 4 5 Ραραπάνω φαίνονται τα απαιτοφμενα βιματα για τθν εκτζλεςθ κάθε
1 2 3 Ραραπάνω παρουςιάηεται ο πυρινασ των εντολϊν του επεξεργαςτι MIPS, με τισ οποίεσ, και τθν υλοποίθςθ τουσ ςε υλικό κα αςχολθκοφμε. 4 5 Ραραπάνω φαίνονται τα απαιτοφμενα βιματα για τθν εκτζλεςθ κάθε
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων. Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ.
 HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Κακυςτζρθςθ και παράγοντεσ που τθν επθρεάηουν
HY220 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθοί: Ε. Κουναλάκησ, Π. Ματτθαιάκησ, Δ. Σςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Κακυςτζρθςθ και παράγοντεσ που τθν επθρεάηουν
HY422 Ειςαγωγή ςτα Συςτήματα VLSI. HY422 - Διάλεξθ 4θ - Διαςυνδζςεισ
 HY422 Ειςαγωγή ςτα Συςτήματα VLSI Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy422 Περιεχόμενα Διαςυνδζςεισ Μοντελοποίθςθ των Παραςιτικών Διαςυνδζςεισ ςε ζνα Πραγματικό Κφκλωμα
HY422 Ειςαγωγή ςτα Συςτήματα VLSI Διδάςκων: Χ. Σωτηρίου, Βοηθόσ: Π. Ματτθαιάκησ http://www.csd.uoc.gr/~hy422 Περιεχόμενα Διαςυνδζςεισ Μοντελοποίθςθ των Παραςιτικών Διαςυνδζςεισ ςε ζνα Πραγματικό Κφκλωμα
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Δομζσ Δεδομζνων Πίνακεσ
 Δομζσ Δεδομζνων Πίνακεσ Διάλεξθ 2 Περιεχόμενα Πίνακεσ: Οριςμοί, Γενικζσ ζννοιεσ Αποκικευςθ πινάκων Ειδικζσ μορφζσ πινάκων Αλγόρικμοι Αναηιτθςθσ Σειριακι Αναηιτθςθ Δυαδικι Αναηιτθςθ Οριςμοί, Γενικζσ ζννοιεσ
Δομζσ Δεδομζνων Πίνακεσ Διάλεξθ 2 Περιεχόμενα Πίνακεσ: Οριςμοί, Γενικζσ ζννοιεσ Αποκικευςθ πινάκων Ειδικζσ μορφζσ πινάκων Αλγόρικμοι Αναηιτθςθσ Σειριακι Αναηιτθςθ Δυαδικι Αναηιτθςθ Οριςμοί, Γενικζσ ζννοιεσ
9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ
 ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 61 9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ I. Βασική Θεωρία Οι πύλες NAND και NOR ονομάζονται οικουμενικές πύλες (universal gates) γιατί κάθε συνδυαστικό κύκλωμα μπορεί να υλοποιηθεί
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 61 9. OIΚΟΥΜΕΝΙΚΕΣ ΠΥΛΕΣ ΠΟΛΛΑΠΛΩΝ ΕΙΣΟ ΩΝ I. Βασική Θεωρία Οι πύλες NAND και NOR ονομάζονται οικουμενικές πύλες (universal gates) γιατί κάθε συνδυαστικό κύκλωμα μπορεί να υλοποιηθεί
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 6: Δυαδικές Πράξεις, Συμπλήρωμα του 2, Δυαδικοί Αποκωδικοποιητές, Κωδικοποιητές, Πολυπλέκτες Δρ. Μηνάς Δασυγένης @ieee.ormdasygg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 6: Δυαδικές Πράξεις, Συμπλήρωμα του 2, Δυαδικοί Αποκωδικοποιητές, Κωδικοποιητές, Πολυπλέκτες Δρ. Μηνάς Δασυγένης @ieee.ormdasygg
Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A].
![Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A]. Η κανονική μορφή της συνάρτησης που υλοποιείται με τον προηγούμενο πίνακα αληθείας σε μορφή ελαχιστόρων είναι η Q = [A].](/thumbs/88/114625669.jpg) Κανονική μορφή συνάρτησης λογικής 5. Η κανονική μορφή μιας λογικής συνάρτησης (ΛΣ) ως άθροισμα ελαχιστόρων, από τον πίνακα αληθείας προκύπτει ως εξής: ) Παράγουμε ένα [A] όρων από την κάθε σειρά για την
Κανονική μορφή συνάρτησης λογικής 5. Η κανονική μορφή μιας λογικής συνάρτησης (ΛΣ) ως άθροισμα ελαχιστόρων, από τον πίνακα αληθείας προκύπτει ως εξής: ) Παράγουμε ένα [A] όρων από την κάθε σειρά για την
Εισαγωγή στους Υπολογιστές
 Εισαγωγή στους Υπολογιστές Ενότητα 11: Βασικές έννοιες ψηφιακής λογικής Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Γιατί χρησιμοποιούμε
Εισαγωγή στους Υπολογιστές Ενότητα 11: Βασικές έννοιες ψηφιακής λογικής Βασίλης Παλιουράς Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Γιατί χρησιμοποιούμε
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων
 Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
 HY422 Ειςαγωγό ςτα Συςτόματα VLSI Διδϊςκων: Χ. Σωτηρύου, Βοηθόσ: Π. Ματθαιϊκησ http://www.csd.uoc.gr/~hy422 1 Μανταλωτζσ κετικισ, αρνθτικισ πολικότθτασ χεδίαςθ με Μανταλωτζσ Κακυςτζρθςθ FF τφπου HLFF (AM
HY422 Ειςαγωγό ςτα Συςτόματα VLSI Διδϊςκων: Χ. Σωτηρύου, Βοηθόσ: Π. Ματθαιϊκησ http://www.csd.uoc.gr/~hy422 1 Μανταλωτζσ κετικισ, αρνθτικισ πολικότθτασ χεδίαςθ με Μανταλωτζσ Κακυςτζρθςθ FF τφπου HLFF (AM
