x 2 = x o2 ηµ(ωt + ϕ o +θ)
|
|
|
- Ἀπφία Αλεξάνδρου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ F 1 F F Όταν σε ένα σώµα ασκούνται δυο δυνάµεις τότε το σώµα κινείται στη διεύθυνση και φορά της συνισταµένης των δυο δυνάµεων Μπο ρούµε µάλιστα να " ξεχάσουµε" εντελώς την ύπαρξη των δυο συνιστωσών και να µελετήσουµε την κίνηση ωσάν να ασκείται στο σώµα µόνο µια δύναµη, η συνισταµένη F Πώς παράγεται ένα απλός αρµονικος ήχος; Από ποιούς παράγοες εξαρτάται το απολεσµα της σύνθεσης ταλαντώσεων; Το ίδιο συµβαίνει και στην περίπτωση που ένα σώµα οφείλει να εκτελέσει δυο ταλαντώσειςπχ η ακουστική µεµβράνη στο αυτί µας εκτελεί ταλάντωση που προκύπτει σαν η συνισταµένη των ταλαντώσεων που θα εκτελούσε λόγω κάθε απλού αρµονικού ήχου, χωριστά( Απλός αρµονικός ήχος: ήχος που παράγεται από σώµα - πηγή που εκτελεί γραµµική αρµονική ταλάντωση ) Η συνισταµένη κίνηση που προκύπτει από τη σύνθεση ταλαντώσεων εξαρτάται: α) Από τις διευθύνσεις των συνιστωσών ταλαντώσεων β) Από τις συχνότητές τους γ) Από τα πλάτη τους δ) Από τη σχέση των φάσεών τους ε) Από τη θέση ισορροπίας της κάθε ταλάντωσης Τί ονοµάζουµε διαφορά φάσης δυο ταλαντώσεων µε ίδια συχ- Θα ασχοληθούµε µε τη σύνθεση ταλαντώσεων που έχουν την ίδια διεύθυνση και ίδια θέση ισορροπίας ( Σε αντίθετη περίπτωση η κίνηση του σώµατος που εκτελεί τη συνισταµένη ταλάντωση γίνεται στο χώρο και είναι ιδιαίτερα πολύπλοκη) Έστω η αποµάκρυνση δυο ταλαντώσεων είναι: x 1 = x o1 ηµ(ωt + ϕ o) Η αποµάκρυνση λόγω µιας άλλης ταλάντωσης είναι: x = x o ηµ(ωt + ϕ o +θ) Πότε δυο ταλαντώσεις βρίσκονται σε συµφωνία φάσης; Οι δυο συναρτήσεις έχουν την ίδια συχνότητα και η διαφορά φάσης τους είναι θ Όταν η διαφορά φάσης είναι µηδέν ή γενικώτερα : θ=κπ, ( κ= 0,1,,), λέµε ότι οι δυο ταλαντώσεις βρίσκονται σε συµφωνία φάσης Αυτό σηµαίνει ότι τα µεγέθη των δυο ταλαντώσεων: αποµάκρυνση x, ταχύτητα U, επιτάχυνση γ, ταυτόχρονα παίρνουν τη µέγιστη τιµή τους και ταυτόχρονα επίσης µηδενίζονται
2 Ποιό το αποτέλεσµα της σύνθεσης δυο ταλαντώσεων µε ίδια συχνότητα ω, που βρίσκονται σε συµφωνία φάσης; ( Οι ταλαντώσεις έχουν την ίδια θέση ισορροπίας ) Έστω ένα υλικό σηµείο στο οποίο επιδρούν δυο αίτια Λόγω του κάθε αιτίου το υλικό σηµείο θα εκτελούσε γατ µε αποµάκρυνση από τη θέση ισορροπίας µε αποµάκρυνση x 1, λόγω του ενός αιτίου και x λόγω του δεύτερου αιτίου Οι ταλαντώσεις εξελίσσονται στην ίδια διεύθυνση και γύρω απ την ίδια θέση ισορροπίας Η συνολική αποµάκρυνση x θα βρεθεί ως εξής: x 1 = x o1 ηµ(ωt + ϕ o) x = x o ηµ(ωt + ϕ o) x oλ = x 1 + x x oλ = (x o1 + x o ) ηµ(ωt + ϕ o x oλ = X o ηµ(ωt + ϕ o) X o = x o1 + x o ηλαδή το αποτέλεσµα αυτής της σύνθεσης θα είναι ταλάντωση ίδιας συχνότητας και πλάτος το άθροισµα των πλατών της κάθε ταλάντωσης y + A x O ωt +φ o A Περιστρεφόµενο διάνυσµα και γραµµική αρµονική Η εξίσωση της στιγµιαίας αποµάκρυνσης y δίνεται από τη σχέση x=x o ηµ (ωt + φ) Μπορούµε να έχουµε πλήρη µελέτη της γατ και συγκεκριµένα του µεγέθους της, στιγµιαία αποµάκρυνση x, µε την εξής αντιστοιχία Θεωρούµε ένα περιστρεφόµενο διάνυσµα µε: 1 Μήκος ίσο µε το πλάτος ταλάντωσης x o Η γωνιακή ταχύτητα περιστροφής του, είναι ίση µε τη κυκλική συχνότητα ω της γατ 3 Η φάση, ωt+φ ο, είναι ίση µε την επίκεντρο γωνία ΑΟΑ' 4 Η αλγεβρική τιµή της προβολής του διανύσµατος πάνω στη διεύθυνση yy', είναι ίση µε τη στιγµιαία τιµή της αποµάκρυνσης x Παρατηρήσεις: α) Η µέτρηση των γωνιών αρχίζει από το Α OΑ κάθετος στη διεύθυνση yy' β) Εάν η αρχική φάση είναι µηδέν, φ ο =0, τότε τo περιστρεφόµενο διάνυσµα τη χρονική στιγµή t=0 θα ταυτίζεται µε την ακτίνα ΟΑ
3 Ποιό το αποτέλεσµα της σύνθεσης δυο ταλαντώσεων µε ίδια συχνότητα ω Οι ταλαντώσεις έχουν διαφορά φάσης φ( Οι ταλα- ντώσεις έχουν την ίδια θέση ισορροπίας και την ίδια διεύθυν- ση) Έστω ένα σώµα εκτελεί ταυτόχρονα δυο απλές αρµονικές ταλαντώσεις Οι επιµέρους ταλαντώσεις εξελίσσονται στην ίδια ευθεία µε την ίδια κυκλική συχνότητα ω και έχουν το ίδιο σηµείο ισορροπίας Η αποµάκρυνση λόγω της κάθε ταλάντωσης χωριστά δίνεται από τις x 1 =α ηµωt x =β ηµ(ωt + φ) Η στιγµιαία αποµάκρυνση που θα χαρακτηρίζει το σώµα θα βρεθεί από το αλγεβρικό άθροισµα, των αποµακρύνσεων x 1, x x oλ = x 1 + x =α ηµ(ωt) +β ηµ(ωt + φ) Η εύρεση της συνάρτησης της συνολικής αποµάκρυνσης x ολ µπορεί να προκύψει από την παραπάνω εξίωση, επιστρατεύοντας τις γνώσεις µας στην τριγωνοµέτρία αλλά κύρια την υποµονή µας αφού οι τριγωνοµετρικές πράξεις δεν θα είναι λίγες Ευτυχώς για µας η χρησιµοποίηση της έννοιας του περιστρεφόµενου διανύσµατος δίνει αποτέλεσµα µε λιγώτερο κόπο Έχουµε: N M Z O + M φ ωt θ Z A N φ OZ =α OZ = x 1 OM = β OM = x Το διάνυσµα που προκύπτει από τη διανυσµατική πρόσθεση των διανυσµάτων α, β, είναι το διάνυσµα γ, που εκφράζει το πλάτος της συνισταµένης ταλάντωσης ON =γ ON = x + x = x oλ Από τον κανόνα του παραλληλογράµµου: γ= α +β + α β συνφ Από το νόµο των ηµιτόνων για το τρίγωνο ΖΟΝ: ηµθ ZN = ηµ(π φ) ηµθ OZ β = ηµφ γ ηµθ= β γ ηµφ Η στιγµιαία αποµάκρυνση από τη θέση ισορροπίας θα δίνεται από τη σχέση: x oλ = γ ηµ(ωt +θ)
4 Ðïéü ôï áðïôýëåóìá ôçò óýíèåóçò äõï áñìïíêþí ôáëáíôþóåùí ðïõ åîåëßóóïíôáé ðüíù óôçí ßäéá åõèåßá ãýñù áðü ôçí ßäéá èýóç éóïññïðßáò êáé ìå óõ íüôçôåò ç ìéá íá åßíáé ðïëëáðëüóéï ôçò Τί γίνεται στην περίπτωση που οι δυο ταλαντώσεις που συντίθενται δεν έχουν την ίδια συχνότητα; Σ' αυτή την περίπτωση ενώ οι δυο ταλαντώσεις ενεργούν στην ίδια διεύθυνση γύρω από την ίδια θέση ισορροπίας η κίνηση που προκύπτει είναι ιδιαίτερα πολύπλοκη Στην περίπτωση όµως που έχουµε σύνθεση δυ αρµονικών ταλαντώσεων, που οι συχνότητές τους είναι η µια ακέραιο πολλαπλάσιο της άλλης τότε προκύπτει κίνηση περιοδική αλλά όχι αρµονική Η κυκλική συχνότητα της περιοδικής κίνησης, θα είναι ίση µε την µικρότερη κυκλική συχνότητα πχ Εάν x 1 =α ηµ(ω 1 t) x =β ηµ(ω t) και ω 1 =κ ω κ: ακέραιος µεγαλύτερος του 1 Η εξίσωση της αποµάκρυνσης της συνισταµένης κίνησης θα είναι συνάρτηση περιοδική αλλά όχι αρµονική Η συχνότητα της περιοδικής κίνησης θα είναι ίση µε τη συχνότητα της µικρότερης κυκλικής συχνότητας, την ω στην παραπάνω περίπτωση Ôé ãíùñßæåôå ãéá ôçí áíüëõóç ôùí ðåñéïäéêþí êéíþóåùí êáôü Fourier; Ôé åßíáé ç èåìåëéþäçò áñìïíéêþ; O Fourier έδειξε ότι: Κάθε περιοδική κίνηση συχνότητας ν ο µπορεί να αναλυθεί σε µεγάλο αριθµό απλών αρµονικών ταλαντώσεων που οι συχνότητές τους είναι ακέραια πολλαπλάσια της συχνότητας ν ο ηλαδή µια περιοδική κίνηση µε συχνότητα ν ο µπορεί να θεωρηθεί σαν συνισταµένη ταλάντωση αρµονικών ταλαντώσεων που ενεργούν στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, ταλαντώσεων που έχουν συχνότητες ακέραια πολλαπλάσια της συχνότητας ν ο Η συχνότητα ν ο της περιοδικής κίνησης ονοµάζεται θεµελιώδης ή πρώτη αρµονική Η συχνότητα ν=ν ο : δεύτερη αρµονική, ν'=3ν ο : τρίτη αρµονική κοκ x ν o 1η αρµονική x 3ν o 3η αρµονική Äåí åßìáé óßãïõñïò ãéá ôï ðüóï áíôýîáôå íá äéáâüæåôå ãéá áñìïíéêýò êáé äåí ìðþêáôå óôïí ðåéñáóìü íá áêïýóåôå áñìïíßåò Áí áõôü äåí Ý åé ãßíåé, áò ãßíåé ôþñá Êáéñüò ãéá äéüëëåéìá Áíïßîôå ôï ñáäéüöùíï x 5ν o x 5η αρµονική ν o περιοδική, όχι αρµονική, συχνότητας ν ο
5 ιακρότηµα Έστω ένα σώµα που εκτελεί ταυτόχρονα δυο αρµονικές ταλαντώσεις που εξελίσσονται πάνω στην ίδια ευθεία γώρω από την ίδια θέση ισορροπίας που έχουν επίσης το ίδιο πλάτος Εάν οι κυκλικές τους συχνότητες διαφέρουν ελάχιστα µεταξύ τους, ποιό το είδος της κίνησης που εκτελεί το σώµα; Έστω: x 1 = x o ηµ(ω 1 t) x = x o ηµ(ω t) x = x 1 + x x = x o [ηµ(ω 1 t) +ηµ(ω t)] ηµα + ηµβ = συν α β ηµα+β x = x o συν ω 1 ω ω 1 ω ω= ω1+ω Επειδή: t ηµ ω 1+ω t ω 1 ω, ν ν 1 ν ω 1 ω 0 ω 1 ω Άρα ο παράγοντας: συν ω 1 ω t 0 (1 µεταβάλλεται πάρα πολύ αργά, οπότε µπορούµε να επιλέξουµε τον παράγοντα: x o συν ω 1 ω t = X o σαν πλάτος της ταλάντωσης Τελικά: (1) x = X o ηµ(ω 1 t) () X o = x o συν ω 1 ω t Συµπεράσµατα: 1 Η συνισταµένη κίνηση είναι κίνηση περιοδική όχι αρµονική Η συχνότητα της περιοδικής κίνησης είναι η µέση τιµή των δυο συχνοτήτων σχεδόν ίση µε τις συχνότητες των συνιστωσών ταλαντώσεων, αφού ω 1 περίπου ίση µε την ω 3 Το πλάτος αυτής της κίνησης µεταβάλλεται µεταξύ των τιµών 0 και x o 4 H περιοδική αυτή κίνηση ονοµάζεται διακρότηµα και το χρονικό διάστηµα µεταξύ δυο µεγιστοποιήσεων, κατ' απόλυτο τιµή, του πλάτους ταλάντωσης, λέγεται περίοδος Τ δ του διακροτήµατος (3) x o
6 Ποιά η περίοδος του διακροτήµατος; Το χρονικό διάστηµα µεταξύ δυο µεγιστοποιήσεων, κατ' απόλυτο τιµή, του πλάτους ταλάντωσης, λέγεται περίοδος Τ δ, του διακροτήµατος Έστω τη χρονική στιγµή t 1 το πλάτος είναι µέγιστο x o, τότε: Αφού: X o = x o συν ω 1 ω t ω 1 ω t 1 = πκ (4) Έστω τη χρονική στιγµή (t 1 +Τ δ ), το πλάτος γίνεται -x o, πρώτη µεγιστοποίηση του πλάτους µετά από την κατάσταση µε πλάτος x o ( Εστω ότι το συνηµίτονο έχει κάποια στιγµή τιµή+1 Θα πάρει την τιµή -1 και µετά ξανά την τιµή +1) ω 1 ω (t 1 + T δ ) = (κ+1) π (5) (5) (4) ω 1 ω T δ =π π(ν 1 ν ) T δ =π T δ = T δ = 1 ν 1 ν 1 ν 1 ν x o T δ x o Όταν συµβάλουν δυο ήχοι που έχουν παραπλήσια συχνότητα τότε το φαινόµενο του διακροτήµατος γίνεται εύκολα αντιληπτό, αφού αυτό σηµαίνει ότι καταγράφουµε χρονικές στιγµές που: α) εν ακούµε τίποτα - συνολικό πλάτος ταλάντωσης 0 - καστρεπτική συµβολή β) Στιγµές που ακούµε τον ήχο σε µέγιστη ένταση, αυτό συµβαίνει όταν οι δυο ήχοι συµβάλλουν ενισχυτικά και το πλάτος ταλάντωσης είναι x o Το χρονικό διάστηµα που µεσολαβεί µεταξύ δυο διαδοχικών δυνατών ακουσµάτων είναι η περίοδος του διακροτήµατος
7 Παράδειγµα 7 ο Σε ένα σώµα ενεργούν δυο ταλαντώσεις που ενργούν στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας Οι εξισώσεις τους είναι: x 1 = 5 ηµ 10πt + π 6 cm x = 8 ηµ 10πt + π cm Nα βρεθούν: α) Το πλάτος της συνισταµένης ταλάντωσης β) Η µέγιστη ταχύτητα που αποκτά κατά την ταλάντωσή του το σώµα γ) Να γραφεί η εξίσωση της στιγµιαίας αποµάκρυνσης του σώµατος δ) Να γραφεί η εξίσωση της στιγµιαίας ταχύτητας του σώµατος Λύση Λ x o, x o K θ A π 3 Z O x o,1 ωt Ισχύουν: φ = 10πt + π 10πt + π 6 = π 3 x 0,1 = 5cm, x o, = 8cm x 0 = συν π 3 x 0 = 19 cm 11, 58cm Στο ορθογώνιο τρίγωνο ΟΖΚ (ΟΑ=5cm, AK=OΛ=8 cm,) εφθ = x 0, ηµ π 3 x 0,1 +x 0, συν π 3 = = Στιγµιαία αποµάκρυνση x = x o ηµ 10πt + π 3 +θ = 19 ηµ 10πt + π 3 +θ cm Στιγµιαία ταχύτητα Μέγιστη ταχύτητα U = U o συν 10πt + π 3 +θ = 10π 19 συν 10πt + π 3 +θ cm sec U o =ω x o = 10 π 19 cm sec
5 Σύνθεση Ταλαντώσεων
 Πρόχειρες Σηµειώσεις 011-01 5 Σύνθεση Ταλαντώσεων Ενα σώµα µπορει να εκτελεί ταυτόχρονα δυο αρµονικές ταλαντώσεις, οι οποίες µπορεί να έχουν οποιαδήποτε διεύθυνση. Το αποτέλεσµα είναι, γενικά, µια πολύπλοκη
Πρόχειρες Σηµειώσεις 011-01 5 Σύνθεση Ταλαντώσεων Ενα σώµα µπορει να εκτελεί ταυτόχρονα δυο αρµονικές ταλαντώσεις, οι οποίες µπορεί να έχουν οποιαδήποτε διεύθυνση. Το αποτέλεσµα είναι, γενικά, µια πολύπλοκη
Α. Σύνθεση δύο ΑΑΤ της ίδιας συχνότητας, που γίνονται γύρω από το ίδιο σηµείο στην ίδια διεύθυνση
 Σύνθεση Ταλαντώσεων Σύνθετη ταλάντωση Αρχή της επαλληλίας Το αποτέλεσµα αυτής της σύνθεσης εξαρτάται από τα χαρακτηριστικά των συνιστωσών αρµονικών ταλαντώσεων, δηλαδή τις διευθύνσεις τους τις συχνότητές
Σύνθεση Ταλαντώσεων Σύνθετη ταλάντωση Αρχή της επαλληλίας Το αποτέλεσµα αυτής της σύνθεσης εξαρτάται από τα χαρακτηριστικά των συνιστωσών αρµονικών ταλαντώσεων, δηλαδή τις διευθύνσεις τους τις συχνότητές
α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες
 ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ α. Σύνδεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιας διεύθυνσης, οι οποίες εξελίσσονται γύρω από την ίδια δέση ισορροπίας Έστω ότι ένα σώμα εκτελεί ταυτόχρονα δύο απλές
α) Πως ερµηνεύεται η φράση: «µε γωνιακές συχνότητες που διαφέρουν πολύ λίγο»; γ) Να βρεθούν η γωνιακή συχνότητα ω, η συχνότητα f και η περίοδος Τ των
 Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
Σύνθεση δύο ΑρµονικώνΤαλαντώσεων που εξελίσσονται στην ίδια ευθεία γύρω από την ίδια θέση µε ίδιο πλάτος και γωνιακές συχνότητες που διαφέρουν πολύ λίγο Έστω ότι υλικό σηµείο εκτελεί ταυτόχρονα τις ταλαντώσεις:
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΔΙΑΚΡΟΤΗΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.ΤΜΗΜΑ. δ. Α =
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΔΙΑΚΡΟΤΗΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.ΤΜΗΜΑ. 1. Δύο απλές αρμονικές ταλαντώσεις πραγματοποιούνται στο ίδιο σημείο, έχουν την ίδια διεύθυνση και συχνότητα, και πλάτη Α 1 και Α.
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΔΙΑΚΡΟΤΗΜΑΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.ΤΜΗΜΑ. 1. Δύο απλές αρμονικές ταλαντώσεις πραγματοποιούνται στο ίδιο σημείο, έχουν την ίδια διεύθυνση και συχνότητα, και πλάτη Α 1 και Α.
1.4. Σύνθεση Ταλαντώσεων. Ομάδα Β
 1.4. Σύνθεση Ταλαντώσεων. Ομάδα Β 1.4.1. Σύνθεση ταλαντώσεων ίδιας συχνότητας Ένα σώμα εκτελεί ταυτόχρονα δύο ταλαντώσεις της ίδιας διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις: y 1 =0,2
1.4. Σύνθεση Ταλαντώσεων. Ομάδα Β 1.4.1. Σύνθεση ταλαντώσεων ίδιας συχνότητας Ένα σώμα εκτελεί ταυτόχρονα δύο ταλαντώσεις της ίδιας διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις: y 1 =0,2
ΟΡΟΣΗΜΟ. 3.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων;
 ΚΕΦΑΛΑΙΟ 1 Σύνθεση ταλαντώσεων 3.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων; 3. Να γίνει η σύνθεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας, ίδ ιας διεύθυνσης, διαφοράς φάσης μεταξύ τους φ,
ΚΕΦΑΛΑΙΟ 1 Σύνθεση ταλαντώσεων 3.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων; 3. Να γίνει η σύνθεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας, ίδ ιας διεύθυνσης, διαφοράς φάσης μεταξύ τους φ,
α. φ Α < φ Β, u A < 0 και u Β < 0. β. φ Α > φ Β, u A > 0 και u Β > 0. γ. φ Α < φ Β, u A > 0 και u Β < 0. δ. φ Α > φ Β, u A < 0 και u Β > 0.
 ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΛΥΥΚΚΕΕΙΙΟΥΥ ΚΚυυρρι ιιαακκήή 1133 ΙΙααννοουυααρρί ίίοουυ 001133 Θέμα 1 ο (Μονάδες 5) 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος
ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΤΕΕΥΥΘΥΥΝΣΗΣ ΓΓ ΛΛΥΥΚΚΕΕΙΙΟΥΥ ΚΚυυρρι ιιαακκήή 1133 ΙΙααννοουυααρρί ίίοουυ 001133 Θέμα 1 ο (Μονάδες 5) 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος
Α = 0,6 m A = 0,3 m ω - ω t = 4π t ω ω = 8π rad/s () και ω + ω t = 500π t ω + ω = 000π rad/s () () + () ω = 008π ω = 504π rad/s και ω = 000π 504π = 49
 ΑΠΑΝΤΗΣΕΕΙΙΣ ΣΤΟ ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ Σ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ Θέµα ο. δ. γ 3. α 4. γ 5. β ΚΚυυρρι ιιαακκήή 33 ΙΙααννοουυααρρί ίίοουυ 0033 Θέµα ο. Α) Σωστή απάντηση: (β) Αφού ο τροχός κυλίεται
ΑΠΑΝΤΗΣΕΕΙΙΣ ΣΤΟ ΙΙΑΓΓΩΝΙΙΣΜΑ ΦΥΥΣΙΙΚΚΗΣ ΚΚΑΤΕΕΥΥΘΥΥΝΣΗΣ Σ ΓΓ ΛΥΥΚΚΕΕΙΙΟΥΥ Θέµα ο. δ. γ 3. α 4. γ 5. β ΚΚυυρρι ιιαακκήή 33 ΙΙααννοουυααρρί ίίοουυ 0033 Θέµα ο. Α) Σωστή απάντηση: (β) Αφού ο τροχός κυλίεται
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΜΕ ΠΑΡΑΠΛΗΣΙΕΣ ΚΥΚΛΙΚΕΣ ΣΥΧΝΟΤΗΤΕΣ (ΔΙΑΚΡΟΤΗΜΑ)
 ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΜΕ ΠΑΡΑΠΛΗΣΙΕΣ ΚΥΚΛΙΚΕΣ ΣΥΧΝΟΤΗΤΕΣ (ΔΙΑΚΡΟΤΗΜΑ). Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις () και () που εξελίσσονται στην ίδια διεύθυνση και γύρω από την ίδια θέση
ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΜΕ ΠΑΡΑΠΛΗΣΙΕΣ ΚΥΚΛΙΚΕΣ ΣΥΧΝΟΤΗΤΕΣ (ΔΙΑΚΡΟΤΗΜΑ). Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις () και () που εξελίσσονται στην ίδια διεύθυνση και γύρω από την ίδια θέση
0,4 2 t (όλα τα μεγέθη στο S.I.). Η σύνθετη ταλάντωση περιγράφεται (στο
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 5: ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί κίνηση που προέρχεται από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων, ίδιας
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 5: ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί κίνηση που προέρχεται από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων, ίδιας
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος http://users.uoa.gr/ papost/ papost@phys.uoa.gr, papost@teiion.gr ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 018-019 Υπάρχουν φυσικά φαινόμενα κατά τα οποία η κίνηση ενός σώματος προκύπτει
Δρ. Παντελής Σ. Αποστολόπουλος http://users.uoa.gr/ papost/ papost@phys.uoa.gr, papost@teiion.gr ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 018-019 Υπάρχουν φυσικά φαινόμενα κατά τα οποία η κίνηση ενός σώματος προκύπτει
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 3 18
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 3 18 Άσκηση 3. ταλαντώσεων, ίδιας διεύθυνσης, γύρω από το ίδιο σημείο, με εξισώσεις x 1 =0,7ημπt και x =0,4ημπt (όλα τα μεγέθη στο S.I.). Η σύνθετη ταλάντωση περιγράφεται (στο S.I.)
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 3 18 Άσκηση 3. ταλαντώσεων, ίδιας διεύθυνσης, γύρω από το ίδιο σημείο, με εξισώσεις x 1 =0,7ημπt και x =0,4ημπt (όλα τα μεγέθη στο S.I.). Η σύνθετη ταλάντωση περιγράφεται (στο S.I.)
Θέμα 1 ο (Μονάδες 25) προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες ταλάντωσης των σημείων Α και Β του μέσου ισχύει:
 ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΥ 99 11 -- 1111 Θέμα 1 ο 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος που διαδίδεται προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες
ΙΓΩΝΙΣΜ ΦΥΣΙΚΗΣ ΚΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΥ 99 11 -- 1111 Θέμα 1 ο 1. Στο σχήμα φαίνεται το στιγμιότυπο ενός εγκάρσιου αρμονικού κύματος που διαδίδεται προς τη θετική φορά του άξονα χ. Για τις φάσεις και τις ταχύτητες
NTÙÍÉÏÓ ÃÊÏÕÔÓÉÁÓ - ÖÕÓÉÊÏÓ www.geocities.com/gutsi1 -- www.gutsias.gr
 Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
1 ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια (20-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ... ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ. Στην απλή αρµονική ταλάντωση, το ταλαντούµενο
ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια (20-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ... ο ΤΕΣΤ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ. Στην απλή αρµονική ταλάντωση, το ταλαντούµενο
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α ΘΕΜΑ Β. 2 cm. = Q. Q 2 = q. I 1 = ω 1 Q =
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΗΡΙΩΝ ΕΞΕΑΣΕΩΝ Γ ΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 6 ΑΠΡΙΛΙΟΥ 05 ΕΞΕΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΙΚΗΣ - ΕΧΝΟΛΟΓΙΚΗΣ ΚΑΕΥΘΥΝΣΗΣ ΑΠΑΝΗΣΕΙΣ ΘΕΜΑ Α Α. δ Α. γ Α3. β Α4. α Α5. α) Λ β) Λ γ)
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΗΡΙΩΝ ΕΞΕΑΣΕΩΝ Γ ΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 6 ΑΠΡΙΛΙΟΥ 05 ΕΞΕΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΙΚΗΣ - ΕΧΝΟΛΟΓΙΚΗΣ ΚΑΕΥΘΥΝΣΗΣ ΑΠΑΝΗΣΕΙΣ ΘΕΜΑ Α Α. δ Α. γ Α3. β Α4. α Α5. α) Λ β) Λ γ)
ΟΠΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 4.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων;
 Σύνθεση ταλαντώσεων ΚΕΦΑΛΑΙΟ 1 4.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων; 4.2 Να γίνει η σύνθεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας, ίδιας διεύθυνσης, διαφοράς φάσης μεταξύ τους φ,
Σύνθεση ταλαντώσεων ΚΕΦΑΛΑΙΟ 1 4.1 Τι ονομάζουμε σύνθεση αρμονικών ταλαντώσεων; 4.2 Να γίνει η σύνθεση δύο απλών αρμονικών ταλαντώσεων ίδιας συχνότητας, ίδιας διεύθυνσης, διαφοράς φάσης μεταξύ τους φ,
ΘΕΜΑ Α Στις ερωτήσεις να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση χωρίς να αιτιολογήσετε την επιλογή σας.
 '' Περί Γνώσεως'' Φροντιστήριο Μ.Ε. Φυσική Προσανατολισμού Γ' Λ. ΜΑΘΗΜΑ /Ομάδα Προσανατολισμού Θ.Σπουδών / ΤΑΞΗ : ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΦΥΣΙΚΗ / Προσανατολισμού / Γ ΛΥΚΕΙΟΥ 2 o ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ
'' Περί Γνώσεως'' Φροντιστήριο Μ.Ε. Φυσική Προσανατολισμού Γ' Λ. ΜΑΘΗΜΑ /Ομάδα Προσανατολισμού Θ.Σπουδών / ΤΑΞΗ : ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΦΥΣΙΚΗ / Προσανατολισμού / Γ ΛΥΚΕΙΟΥ 2 o ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ
ΘΕΜΑ 1 ο Οδηγία: Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στην σωστή απάντηση.
 ΚΟΨΙΔΑΣ ΔΗΜΗΤΡΙΟΣ Καθηγητς Φυσικς ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΑΝΤΙΚΕΙΜΕΝΟ: ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ (ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Διάρκεια εξέτασης: ώρα ΘΕΜΑ ο Οδηγία: Στις ερωτσεις - να γράψετε στο τετράδιο σας τον
ΚΟΨΙΔΑΣ ΔΗΜΗΤΡΙΟΣ Καθηγητς Φυσικς ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΑΝΤΙΚΕΙΜΕΝΟ: ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ (ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Διάρκεια εξέτασης: ώρα ΘΕΜΑ ο Οδηγία: Στις ερωτσεις - να γράψετε στο τετράδιο σας τον
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 0 A] i. Η ράβδος ισορροπεί με τη δράση των δυνάμεων Β,Τ, Β και Ν, έτσι από τις συνθήκες ισορροπίας έχουμε : Σ το ( ) = 0 ττ + τ 0 Β + τβ = Τ l Β ( l) Β ( l)
ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 0 A] i. Η ράβδος ισορροπεί με τη δράση των δυνάμεων Β,Τ, Β και Ν, έτσι από τις συνθήκες ισορροπίας έχουμε : Σ το ( ) = 0 ττ + τ 0 Β + τβ = Τ l Β ( l) Β ( l)
Εναλλασσόμενο και μιγαδικοί
 (olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
(olts) Εναλλασσόμενο και μιγαδικοί Γενικά Σε κυκλώματα DC, οι ηλεκτρικές μεγέθη εξαρτώνται αποκλειστικά από τις ωμικές αντιστάσεις, φυσικά μετά την ολοκλήρωση πιθανών μεταβατικών φαινομένων λόγω παρουσίας
Θέμα 1 ο. Θέμα 2 ο. Η ιδιοσυχνότητα του συστήματος δίνεται από τη σχέση:
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) Θέμα 1 ο 1100 11 -- 001111 1. α. γ 3. β 4. γ 5. α) Λ β) Σ γ) Λ δ) Σ ε) Λ 1. Α. ΣΣωωσσττόό ττοο αα.. Θέμα ο Η ιδιοσυχνότητα του συστήματος
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) Θέμα 1 ο 1100 11 -- 001111 1. α. γ 3. β 4. γ 5. α) Λ β) Σ γ) Λ δ) Σ ε) Λ 1. Α. ΣΣωωσσττόό ττοο αα.. Θέμα ο Η ιδιοσυχνότητα του συστήματος
Θέμα 1 ο (Μονάδες 25)
 ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) 10 01-011 Θέμα 1 ο (Μονάδες 5) 1. Κατά τη σύνθεση δύο ΑΑΤ, που γίνονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, προκύπτει μια νέα
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) 10 01-011 Θέμα 1 ο (Μονάδες 5) 1. Κατά τη σύνθεση δύο ΑΑΤ, που γίνονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, προκύπτει μια νέα
ΕΞΙΣΩΣΕΙΣ ΤΑΛΑΝΤΩΣΗΣ Επιλέξτε τη σωστή απάντηση στη παρακάτω πρόταση :
 ΕΞΙΣΩΣΕΙΣ ΤΑΛΑΝΤΩΣΗΣ Επιλέξτε τη σωστή απάντηση στη παρακάτω πρόταση : Η απλή αρμονική κίνηση α. ευθύγραμμη ομαλή. β. ευθύγραμμη ομαλά μεταβαλλόμενη. γ. ομαλή κυκλική. δ. ευθύγραμμη περιοδική. Σημειακό
ΕΞΙΣΩΣΕΙΣ ΤΑΛΑΝΤΩΣΗΣ Επιλέξτε τη σωστή απάντηση στη παρακάτω πρόταση : Η απλή αρμονική κίνηση α. ευθύγραμμη ομαλή. β. ευθύγραμμη ομαλά μεταβαλλόμενη. γ. ομαλή κυκλική. δ. ευθύγραμμη περιοδική. Σημειακό
β. Το πλάτος της σύνθετης ταλάντωσης είναι : Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν φ) (φ = π rad) Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν π) Α = [Α 1 ² + Α 2
 1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
i) Σε κάθε πλήρη περιστροφή το κινητό Α διαγράφει τόξο ίσου µήκους µε το τόξο που διαγράφει το κινητό Β
 Φύλλο Εργασίας: ΚΙΝΗΜΑΤΙΚΗ ΟΜΑΛΗΣ ΚΥΚΛΙΚΗΣ ΚΙΝΗΣΗΣ Λίγη γεωµετρία πριν ξεκινήσουµε: Σε κύκλο ακτίνας, η επίκεντρη γωνία Δθ µετρηµένη σε ακτίνια (rad) και το µήκος του τόξου Δs στο οποίο βαίνει, συνδέονται
Φύλλο Εργασίας: ΚΙΝΗΜΑΤΙΚΗ ΟΜΑΛΗΣ ΚΥΚΛΙΚΗΣ ΚΙΝΗΣΗΣ Λίγη γεωµετρία πριν ξεκινήσουµε: Σε κύκλο ακτίνας, η επίκεντρη γωνία Δθ µετρηµένη σε ακτίνια (rad) και το µήκος του τόξου Δs στο οποίο βαίνει, συνδέονται
Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει. από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών
 Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών ταλαντώσεων Υλικό σηµείο Σ ενός ελαστικού µέσου εκτελεί περιοδική κίνηση (ιδιόµορφη ταλάντωση)
Μια ιδιόµορφη ταλάντωση µε εξίσωση αποµάκρυνσης που προκύπτει από την επαλληλία των εξισώσεων κίνησης δύο αρµονικών ταλαντώσεων Υλικό σηµείο Σ ενός ελαστικού µέσου εκτελεί περιοδική κίνηση (ιδιόµορφη ταλάντωση)
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
(1.1α) Η ταχύτητά του εκείνη την στιγμή αποδεικνύεται ότι ισούται με: υ=αωσυνωt. (1.2α) a=-αω 2 ημωt. (1.3α) 1 ο ΚΕΦΑΛΑΙΟ-ΟΙ ΤΑΛΑΝΤΩΣΕΙΣ 1.
 1.1 ΕΙΣΑΓΩΓΗ 1 ο ΚΕΦΑΛΑΙΟ-ΟΙ ΤΑΛΑΝΤΩΣΕΙΣ Η ταλάντωση είναι ένα είδος περιοδικής κινήσεως η οποία πραγματοποιείται μεταξύ δύο θέσεων και γύρω από μια άλλη θέση την οποία στην συνέχεια θα λέμε «Θέση Ισορροπίας
1.1 ΕΙΣΑΓΩΓΗ 1 ο ΚΕΦΑΛΑΙΟ-ΟΙ ΤΑΛΑΝΤΩΣΕΙΣ Η ταλάντωση είναι ένα είδος περιοδικής κινήσεως η οποία πραγματοποιείται μεταξύ δύο θέσεων και γύρω από μια άλλη θέση την οποία στην συνέχεια θα λέμε «Θέση Ισορροπίας
43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : 210/ /
 43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : /76..47 /76..79 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ (ΚΑΤΕΥΘΥΝΣΗΣ) Γ ΛΥΚΕΙΟΥ Θέµα ο Α. Στις παρακάτω προτάσεις απαντήστε µε Σωστό
43 Χρόνια Φροντιστήρια Μέσης Εκπαίδευσης ΣΑΒΒΑΪ Η ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσοστόµου Σµύρνης 3 : /76..47 /76..79 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ (ΚΑΤΕΥΘΥΝΣΗΣ) Γ ΛΥΚΕΙΟΥ Θέµα ο Α. Στις παρακάτω προτάσεις απαντήστε µε Σωστό
Ονοματεπώνυμο: Επιμέλεια διαγωνίσματος: Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
1 f. d F D x m a D x m D x dt. 2 t. Όλες οι αποδείξεις στην Φυσική Κατεύθυνσης Γ Λυκείου. Αποδείξεις. d t dt dt dt. 1. Απόδειξη της σχέσης.
 Αποδείξεις. Απόδειξη της σχέσης N t T N t T. Απόδειξη της σχέσης t t T T 3. Απόδειξη της σχέσης t Ικανή και αναγκαία συνθήκη για την Α.Α.Τ. είναι : d F D ma D m D Η εξίσωση αυτή είναι μια Ομογενής Διαφορική
Αποδείξεις. Απόδειξη της σχέσης N t T N t T. Απόδειξη της σχέσης t t T T 3. Απόδειξη της σχέσης t Ικανή και αναγκαία συνθήκη για την Α.Α.Τ. είναι : d F D ma D m D Η εξίσωση αυτή είναι μια Ομογενής Διαφορική
1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ
 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΗΣ ΘΕΤΙΗΣ-ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΕΙΟΥ Θέμα ο. ύλινδρος περιστρέφεται γύρω από άξονα που διέρχεται από το κέντρο μάζας του με γωνιακή ταχύτητα ω. Αν ο συγκεκριμένος κύλινδρος περιστρεφόταν
ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΗΣ ΘΕΤΙΗΣ-ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΕΙΟΥ Θέμα ο. ύλινδρος περιστρέφεται γύρω από άξονα που διέρχεται από το κέντρο μάζας του με γωνιακή ταχύτητα ω. Αν ο συγκεκριμένος κύλινδρος περιστρεφόταν
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 30/12/11 ΑΠΑΝΤΗΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 30// ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 30// ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
Β3. ΣΣωσσττήή ααππάάννττηησσηη εεί ίίννααι ιι ηη ββ.. Το πλάτος του (Σ) µετά τη συµβολή των κυµάτων ισούται µε: r 1 - r u t 1 - u t Α Σ = Α συνπ = Α σ
 ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥΓ ΛΥΚΕΙΟΥ Κυριακή 13 Νοεµβρίου 016 Θέµα Α Α1. δ Α. γ Α3. γ Α4. δ Α5. α) Σ β) Λ γ) Λ δ) Σ ε) Λ Θέµα Β Β1. Σωστή είναι η απάντηση (β). Εφόσον παρατηρούνται
ΑΠΑΝΤΗΣΕΙΣ ΣΤΟ ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥΓ ΛΥΚΕΙΟΥ Κυριακή 13 Νοεµβρίου 016 Θέµα Α Α1. δ Α. γ Α3. γ Α4. δ Α5. α) Σ β) Λ γ) Λ δ) Σ ε) Λ Θέµα Β Β1. Σωστή είναι η απάντηση (β). Εφόσον παρατηρούνται
5. Ένα σώµα ταλαντώνεται µεταξύ των σηµείων Α και Ε. Στο σχήµα φαίνονται πέντε θέσεις Α,Β,Γ, και Ε, οι οποίες ισαπέχουν µεταξύ 1
 1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002 ÈÅÌÅËÉÏ
 ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΤΑΛΑΝΤΩΣΕΙΣ Θέµα ο ) Ενώ ακούµε ένα ραδιοφωνικό σταθµό που εκπέµπει σε συχνότητα 00MHz, θέλουµε να ακούσουµε το σταθµό που εκπέµπει σε 00,4MHz.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΤΑΛΑΝΤΩΣΕΙΣ Θέµα ο ) Ενώ ακούµε ένα ραδιοφωνικό σταθµό που εκπέµπει σε συχνότητα 00MHz, θέλουµε να ακούσουµε το σταθµό που εκπέµπει σε 00,4MHz.
Ενδεικτικές Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
Physics by Chris Simopoulos. rad. rad. 10 β) Είναι Α=0,4 m και 0,4 10. Η χρονική εξίσωση της απομάκρυνσης είναι ) 3 U U 3
 . ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΛΥΣΕΙΣ 9. α) Από το κανόνα του παραλληλογράμμου έχουμε, (, ),,,,, π Οπότε θ, / sec και, sec β) Είναι Α=, και, / sec Η χρονική εξίσωση της απομάκρυνσης είναι A
. ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΛΥΣΕΙΣ 9. α) Από το κανόνα του παραλληλογράμμου έχουμε, (, ),,,,, π Οπότε θ, / sec και, sec β) Είναι Α=, και, / sec Η χρονική εξίσωση της απομάκρυνσης είναι A
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Μονάδες Ταλαντωτής εκτελεί ταυτόχρονα δύο αρμονικές ταλαντώσεις που έχουν ίσες συχνότητες, πλάτη Α1 = 1 m και A2
 Φυσική ΘΕΜΑ A κατεύθυνσης Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις -5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές
Φυσική ΘΕΜΑ A κατεύθυνσης Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις -5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές
1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση. Θέµα 2ο
 1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση Θέµα 1ο 1.1. Η εξίσωση της αποµάκρυνσης ενός υλικού σηµείου, που εκτελεί απλή αρµονική ταλάντωση πλάτους Α και γωνιακής συχνότητας ω, είναι της µορφής x =
1ο ιαγώνισµα - Λύσεις Απλή Αρµονική Ταλάντωση Θέµα 1ο 1.1. Η εξίσωση της αποµάκρυνσης ενός υλικού σηµείου, που εκτελεί απλή αρµονική ταλάντωση πλάτους Α και γωνιακής συχνότητας ω, είναι της µορφής x =
Κεφάλαιο 0 Μιγαδικοί Αριθμοί
 Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
Κεφάλαιο 0 Μιγαδικοί Αριθμοί 0 Βασικοί ορισμοί και πράξεις Είναι γνωστό ότι δεν υπάρχει πραγματικός αριθμός που επαληθεύει την εξίσωση x Η ανάγκη επίλυσης τέτοιων εξισώσεων οδηγεί στο σύνολο των μιγαδικών
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κρούσεις - Αρµονική Ταλάντωση Α.1. Σε µια κρούση δύο σφαιρών : Ενδεικτικές Λύσεις Θέµα Α (γ) το άθροισµα των ορµών των σφαιρών πριν από την κρούση είναι πάντα ίσο µε το
ÂÚÈ fiìâó ÏÂÎÙÚÈÎ ªË ÓÈÎ Ù Ï ÓÙÒÛÂÈ. Οι εξισώσεις της απλής αρμονικής ταλάντωσης... 9. Η δύναμη στην απλή αρμονική ταλάντωση...
 1.1 1. 1. 1.4 1.5 ÂÊ Ï ÈÔ 1 ÂÚÈ fiìâó ÏÂÎÙÚÈÎ ªË ÓÈÎ Ù Ï ÓÙÒÛÂÈ Οι εξισώσεις της απλής αρμονικής ταλάντωσης... 9 Η δύναμη στην απλή αρμονική ταλάντωση... 6 Η ενέργεια στην απλή αρμονική ταλάντωση... 80
1.1 1. 1. 1.4 1.5 ÂÊ Ï ÈÔ 1 ÂÚÈ fiìâó ÏÂÎÙÚÈÎ ªË ÓÈÎ Ù Ï ÓÙÒÛÂÈ Οι εξισώσεις της απλής αρμονικής ταλάντωσης... 9 Η δύναμη στην απλή αρμονική ταλάντωση... 6 Η ενέργεια στην απλή αρμονική ταλάντωση... 80
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Α.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 19/01/2014
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 19/01/2014 ΘΕΜΑ 1ο Α. Όταν αυξάνεται το πλάτος ενός μηχανικού κύματος που διαδίδεται σε ομογενές ελαστικό μέσο: α) αυξάνεται η ταχύτητά του. β) αυξάνεται η ενέργεια
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 19/01/2014 ΘΕΜΑ 1ο Α. Όταν αυξάνεται το πλάτος ενός μηχανικού κύματος που διαδίδεται σε ομογενές ελαστικό μέσο: α) αυξάνεται η ταχύτητά του. β) αυξάνεται η ενέργεια
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
ΙΑΓΩΝΙΣΜΑ Γ ΤΑΞΗΣ ΕΝΩΜΕΝΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΚΥΡΙΑΚΗ 9/1/2011
 ΙΑΓΩΝΙΣΜΑ Γ ΤΑΞΗΣ ΕΝΩΜΕΝΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΚΥΡΙΑΚΗ 9/1/011 ΘΕΜΑ 1o Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
ΙΑΓΩΝΙΣΜΑ Γ ΤΑΞΗΣ ΕΝΩΜΕΝΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΚΥΡΙΑΚΗ 9/1/011 ΘΕΜΑ 1o Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη
Φυσική Ο.Π. Γ Λυκείου
 Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
1. Κίνηση Υλικού Σημείου
 1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη 018 Θέµα Α Α.1. Ταλαντωτής εκτελεί ϕθίνουσα ταλάντωση µικρής απόσβεσης. Η αντιτιθέµενη δύναµη είναι
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη 018 Θέµα Α Α.1. Ταλαντωτής εκτελεί ϕθίνουσα ταλάντωση µικρής απόσβεσης. Η αντιτιθέµενη δύναµη είναι
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
ΑΠΑΝΤΗΣΕΙΣ. Η κινητική ενέργεια του κυλίνδρου λόγω της μεταφορικής του κίνησης δίνεται από την σχέση: Κ μετ = 1 m u 2 cm
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΟΥ ΛΥΕΙΟΥ Μ.ΤΕΤΑΡΤΗ 0 ΑΠΡΙΛΙΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΗ ΘΕΤΙΗΣ - ΤΕΧΝΟΛΟΓΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ Θέμα 1 ο 1. γ. γ 3. α 4. δ 5. α) Λ β) Σ γ)
ΚΑΛΗ ΧΡΟΝΙΑ. b. x = 5ημ10πt (S.I.). c. x = 5ημ(10πt+π) (S.I.). d. x = 15ημ10πt (S.I.). ( μονάδες 5)
 ΚΑΛΗ ΧΡΟΝΙΑ ΘΕΜΑ Α 1) Στο πρότυπο του απλού αρμονικού ταλαντωτή η δυναμική του ενέργεια: Επιλογή μίας απάντησης. Α) έχει τη μέγιστη τιμή της στη θέση ισορροπίας. Β) είναι ίση με την ολική του ενέργεια
ΚΑΛΗ ΧΡΟΝΙΑ ΘΕΜΑ Α 1) Στο πρότυπο του απλού αρμονικού ταλαντωτή η δυναμική του ενέργεια: Επιλογή μίας απάντησης. Α) έχει τη μέγιστη τιμή της στη θέση ισορροπίας. Β) είναι ίση με την ολική του ενέργεια
1 Απλή Αρµονική Ταλάντωση
 ,Θετικής & Τεχνολογικής Κατεύθυνσης Καραδηµητρίου Ε. Μιχάλης http://perifysikhs.wordpress.com mixalis.karadimitriou@gmail.com Πρόχειρες Σηµειώσεις 2011-2012 1 Απλή Αρµονική Ταλάντωση 1.1 Περιοδικά Φαινόµενα
,Θετικής & Τεχνολογικής Κατεύθυνσης Καραδηµητρίου Ε. Μιχάλης http://perifysikhs.wordpress.com mixalis.karadimitriou@gmail.com Πρόχειρες Σηµειώσεις 2011-2012 1 Απλή Αρµονική Ταλάντωση 1.1 Περιοδικά Φαινόµενα
U I = U I = Q D 1 C. m L
 Από την αντιστοιχία της µάζας που εκτελεί γ.α.τ. µε περίοδο Τ και της εκφόρτισης πυκνωτή µέσω πηνίου L, µπορούµε να ανακεφαλαιώσουµε τις αντιστοιχίες των µεγεθών τους. Έχουµε: ΜΑΖΑ ΠΟΥ ΕΚΤΕΛΕΙ γ.α.τ..
Από την αντιστοιχία της µάζας που εκτελεί γ.α.τ. µε περίοδο Τ και της εκφόρτισης πυκνωτή µέσω πηνίου L, µπορούµε να ανακεφαλαιώσουµε τις αντιστοιχίες των µεγεθών τους. Έχουµε: ΜΑΖΑ ΠΟΥ ΕΚΤΕΛΕΙ γ.α.τ..
. Αυτό σηµαίνει ότι το κέντρο µάζας κινείται ευθύγραµµα µε σταθερή επιτάχυνση a! = F!
 Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
Οµογενής κυκλικός δίσκος µάζας m και ακτίνας, βρίσκεται πάνω σε λείο οριζόντιο έδαφος µε τον άξονα συµµετρίας του κατα κόρυφο. Εάν σ ένα σηµείο της περιφέρειας του δίσκου εξασκείται συνεχώς µια σταθερή
1. Κατά τη σύνθεση δύο ΑΑΤ, που γίνονται στην ίδια διεύθυνση και γύρω από την ίδια
 ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) 9 0-0 Θέμα ο. Κατά τη σύνθεση δύο ΑΑΤ, που γίνονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, προκύπτει μια νέα ΑΑΤ σταθερού πλάτους,
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ((ΑΠΟΦΟΙΤΟΙ)) 9 0-0 Θέμα ο. Κατά τη σύνθεση δύο ΑΑΤ, που γίνονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας, προκύπτει μια νέα ΑΑΤ σταθερού πλάτους,
1.0 Βασικές Έννοιες στην Τριγωνομετρία
 .0 Βασικές Έννοιες στην Τριγωνομετρία Εύρεση τριγωνομετρικών αριθμών οξείας γωνίας σε ορθογώνιο τρίγωνο. ΑΠΑΝΤΗΣΗ Έστω ορθογώνιο τρίγωνο ΑΒΓ (Α= 90 0 ). Οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορίζονται
.0 Βασικές Έννοιες στην Τριγωνομετρία Εύρεση τριγωνομετρικών αριθμών οξείας γωνίας σε ορθογώνιο τρίγωνο. ΑΠΑΝΤΗΣΗ Έστω ορθογώνιο τρίγωνο ΑΒΓ (Α= 90 0 ). Οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορίζονται
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 1
 ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ ΠΕΡΙΟΔΙΚΑ ΦΑΙΝΟΜΕΝΑ Περίοδος (Τ) ενός περιοδικού φαινομένου είναι ο χρόνος που απαιτείται για μια πλήρη επανάληψη του φαινομένου. Αν σε χρόνο t γίνονται Ν επαναλήψεις
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ ΠΕΡΙΟΔΙΚΑ ΦΑΙΝΟΜΕΝΑ Περίοδος (Τ) ενός περιοδικού φαινομένου είναι ο χρόνος που απαιτείται για μια πλήρη επανάληψη του φαινομένου. Αν σε χρόνο t γίνονται Ν επαναλήψεις
2 ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 10 ΙΟΥΝΙΟΥ 2014 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε
Τηλ./Fax: , Τηλ: Λεωφόρος Μαραθώνος &Χρυσοστόµου Σµύρνης 3, 1
 . 1. Η απλή αρµονική ταλάντωση είναι κίνηση: α. ευθύγραµµη οµαλή β. ευθύγραµµη οµαλά µεταβαλλόµενη γ. οµαλή κυκλική δ. ευθύγραµµη περιοδική. Η φάση της αποµάκρυνσης στην απλή αρµονική ταλάντωση: α. αυξάνεται
. 1. Η απλή αρµονική ταλάντωση είναι κίνηση: α. ευθύγραµµη οµαλή β. ευθύγραµµη οµαλά µεταβαλλόµενη γ. οµαλή κυκλική δ. ευθύγραµµη περιοδική. Η φάση της αποµάκρυνσης στην απλή αρµονική ταλάντωση: α. αυξάνεται
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Α ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Α ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
A e (t σε sec). Το πλάτος των ταλαντώσεων
 ΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 Επιλέξτε την σωστή απάντηση. 1. Σηµειακό αντικείµενο εκτελεί φθίνουσες ταλαντώσεις µε πλάτος που µειώνεται εκθετικά µε το χρόνο σύµφωνα µε την 0,01t σχέση
ΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1 Επιλέξτε την σωστή απάντηση. 1. Σηµειακό αντικείµενο εκτελεί φθίνουσες ταλαντώσεις µε πλάτος που µειώνεται εκθετικά µε το χρόνο σύµφωνα µε την 0,01t σχέση
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό µέσο, διπλασιάζεται χωρίς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό µέσο, διπλασιάζεται χωρίς
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Β.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το
 Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
Η φάση του αρμονικού κύματος 1. Πηγή αρμονικών κυμάτων συχνότητας 5 Hz εξαναγκάζει το άκρο Ο ενός γραμμικού ελαστικού μέσου, το οποίο ταυτίζεται με τον οριζόντιο ημιάξονα O, να εκτελεί απλή αρμονική ταλάντωση
ΛΥΣΕΙΣ. Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΘΗΜ / ΤΞΗ: ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡ: η (ΘΕΡΙΝ) ΗΜΕΡΟΜΗΝΙ: /0/ ΘΕΜ ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί
ΜΘΗΜ / ΤΞΗ: ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡ: η (ΘΕΡΙΝ) ΗΜΕΡΟΜΗΝΙ: /0/ ΘΕΜ ο ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί
Physics by Chris Simopoulos
 ΝΟΜΟΣ COULOMB Πριν την ανάπτυξη της μεθοδογίας κρίνεται σκόπιμο να τονίσουμε τον τρόπο γραφής της δύναμης Coulomb που ασκείται μεταξύ δύο φορτίων. Συγκεκριμένα για αποφυγή των λαθών των μαθητών στις δυνάμεις
ΝΟΜΟΣ COULOMB Πριν την ανάπτυξη της μεθοδογίας κρίνεται σκόπιμο να τονίσουμε τον τρόπο γραφής της δύναμης Coulomb που ασκείται μεταξύ δύο φορτίων. Συγκεκριμένα για αποφυγή των λαθών των μαθητών στις δυνάμεις
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Α ΦΑΣΗ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 7 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ηµιτελείς προτάσεις Α Α4
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 7 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ηµιτελείς προτάσεις Α Α4
= = = = 2. max,1 = 2. max,2
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ ΑΠΡΙΛΙΟΥ 03 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ - ΤΕΧΝΟΛΟΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. α Α. β Α3. β Α. γ Α5. α) Σ β) Λ γ)
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ ΑΠΡΙΛΙΟΥ 03 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ - ΤΕΧΝΟΛΟΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. α Α. β Α3. β Α. γ Α5. α) Σ β) Λ γ)
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
Φθίνουσες - Εξαναγκασµένες - Σύνθεση 3ο Σετ Ασκήσεων - Φθινόπωρο 2012
 Φθίνουσες - Εξαναγκασµένες - Σύνθεση - Φθινόπωρο 2012 Επιµέλεια: Μιχάλης Ε. Καραδηµητριου, MSc Φυσικός http://perifysikhs.wordpress.com Α. Ερωτήσεις πολλαπλής επιλογής Α.1.Σε έναν ταλαντούµενο σύστηµα,
Φθίνουσες - Εξαναγκασµένες - Σύνθεση - Φθινόπωρο 2012 Επιµέλεια: Μιχάλης Ε. Καραδηµητριου, MSc Φυσικός http://perifysikhs.wordpress.com Α. Ερωτήσεις πολλαπλής επιλογής Α.1.Σε έναν ταλαντούµενο σύστηµα,
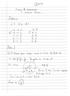 ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ o Α. Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων α, β. Μονάδες 4 Β. Να αποδείξετε ότι το εσωτερικό γινόµενο δύο διανυσµάτων
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ o Α. Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων α, β. Μονάδες 4 Β. Να αποδείξετε ότι το εσωτερικό γινόµενο δύο διανυσµάτων
Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου Αρχή της επαλληλίας Όταν σε ένα μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση ενός σημείου του ελαστικού μέσου είναι ίση με τη συνισταμένη
Κεφάλαιο 2 ο Ενότητα 2 η : Συμβολή κυμάτων Θεωρία Γ Λυκείου Αρχή της επαλληλίας Όταν σε ένα μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση ενός σημείου του ελαστικού μέσου είναι ίση με τη συνισταμένη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΑΠΑΝΤΗΣΕΙΣ. x = Aημ ( ωt + φ) Α= Aημφ ημφ = ημφ = ημ. φ = 2κπ + π + φ = rad
 Just Physics Σελίδα - 5 - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. α, Α. β, Α3. β, Α. α, Α5. α-σ, β-λ, γ-σ, δ-σ, ε-λ. ΘΕΜΑ Β Β. Σωστή η δ. Από τη διατήρηση της ενέργειας στον ταλαντωτή παίρνουμε. K= U A K+ U= E U= E Dx =
Just Physics Σελίδα - 5 - ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α. α, Α. β, Α3. β, Α. α, Α5. α-σ, β-λ, γ-σ, δ-σ, ε-λ. ΘΕΜΑ Β Β. Σωστή η δ. Από τη διατήρηση της ενέργειας στον ταλαντωτή παίρνουμε. K= U A K+ U= E U= E Dx =
1 ΦΕΠ 012 Φυσική και Εφαρμογές
 1 ΦΕΠ 012 Φυσική και Εφαρμογές Διάλεξη 10 η Ομαλή κυκλική κίνηση Δθ = ω = σταθερό Δt X = Rσυν (ωt) => X 2 +Υ 2 = R 2 Υ = Rημ(ωt) Οι προβολές της κίνησης στους άξονες των x και y είναι αρμονικές ταλαντώσεις
1 ΦΕΠ 012 Φυσική και Εφαρμογές Διάλεξη 10 η Ομαλή κυκλική κίνηση Δθ = ω = σταθερό Δt X = Rσυν (ωt) => X 2 +Υ 2 = R 2 Υ = Rημ(ωt) Οι προβολές της κίνησης στους άξονες των x και y είναι αρμονικές ταλαντώσεις
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 2011 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 0 ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Σε
ΘΕΜΑ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 0 ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία τη συµπληρώνει σωστά. Α. Σε
Η Επιτάχυνση. η τα- χύτητά του ( Σχήμα 1 ). Από τον ορισμό της ταχύτητας θα ισχύει (3)
 Η Επιτάχυνση η τα- Έστω r ( t ) ( t ) i ( t ) j z ( t ) k το διάνυσμα θέσης του κινητού Μ και ( t ) χύτητά του ( Σχήμα 1 ). Από τον ορισμό της ταχύτητας θα ισχύει r ( t ) r ( t ) ή πιο απλά (1) t t Άρα
Η Επιτάχυνση η τα- Έστω r ( t ) ( t ) i ( t ) j z ( t ) k το διάνυσμα θέσης του κινητού Μ και ( t ) χύτητά του ( Σχήμα 1 ). Από τον ορισμό της ταχύτητας θα ισχύει r ( t ) r ( t ) ή πιο απλά (1) t t Άρα
15 s. F= b υ+k x-mω 2 x F= b ω A συνωt+(k-mω 2 ) A ηµωt. F= b ω Α. b ω ( )
 1 48. ΕΞΝΓΚΣΜΕΝΗ ΤΛΝΤΩΣΗ. Στη διάταξη του σχήµατος δίνονται η σταθερά του ιδανικού ελατηρίου K1N/m και ότι η µάζα του σώµατος Σ είναι m4kg.η τροχαλία θεωρείται αβαρής. Το χέρι µας ασκεί περιοδική δύναµη,
1 48. ΕΞΝΓΚΣΜΕΝΗ ΤΛΝΤΩΣΗ. Στη διάταξη του σχήµατος δίνονται η σταθερά του ιδανικού ελατηρίου K1N/m και ότι η µάζα του σώµατος Σ είναι m4kg.η τροχαλία θεωρείται αβαρής. Το χέρι µας ασκεί περιοδική δύναµη,
Συμβολή Δύο Κυμάτων στην Επιφάνεια Υγρού
 Φυσική Γ Θετ. και Τεχν/κης Κατ/σης 017-18 ΕΠΑΛΛΗΛΙΑ-ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΥΓΡΟΥ (.-.4, μαθήματα) Αρχή επαλληλίας ή υπέρθεσης: όταν σε ένα ελαστικό μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση
Φυσική Γ Θετ. και Τεχν/κης Κατ/σης 017-18 ΕΠΑΛΛΗΛΙΑ-ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΥΓΡΟΥ (.-.4, μαθήματα) Αρχή επαλληλίας ή υπέρθεσης: όταν σε ένα ελαστικό μέσο διαδίδονται δύο ή περισσότερα κύματα η απομάκρυνση
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α:. Σωστό το B.. Σωστό το Γ. 3. Σωστό το Δ. 4. Σωστά τα Α, Β, Γ. 5. Σωστό το Δ. ΘΕΜΑ Β:. Σωστό το Β. Αιτιολόγηση: Έχουµε διαδοχικά:. Σωστό το Α. D D K E U =
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α:. Σωστό το B.. Σωστό το Γ. 3. Σωστό το Δ. 4. Σωστά τα Α, Β, Γ. 5. Σωστό το Δ. ΘΕΜΑ Β:. Σωστό το Β. Αιτιολόγηση: Έχουµε διαδοχικά:. Σωστό το Α. D D K E U =
Ασκήσεις στη συµβολή κυµάτων
 Ασκήσεις στη συµβολή κυµάτων. Οι δύο σύγχρονες πηγές Π και Π παράγουν την ίδια στιγµή κύµατα, συχνότητας f=0 Hz, τα οποία διαδίδονται στο ελαστικό µέσο µε ταχύτητα υ=30 m/s. Σε όλα τα σηµεία της µεσοκαθέτου
Ασκήσεις στη συµβολή κυµάτων. Οι δύο σύγχρονες πηγές Π και Π παράγουν την ίδια στιγµή κύµατα, συχνότητας f=0 Hz, τα οποία διαδίδονται στο ελαστικό µέσο µε ταχύτητα υ=30 m/s. Σε όλα τα σηµεία της µεσοκαθέτου
ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου
 ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου Ηµεροµηνία: / / 2011 Θ 1 Θ 2 Θ 3 Θ 4 Βαθµός Ονοµατεπώνυµο:. Τµήµα: Γ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-10
ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου Ηµεροµηνία: / / 2011 Θ 1 Θ 2 Θ 3 Θ 4 Βαθµός Ονοµατεπώνυµο:. Τµήµα: Γ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-10
Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα.
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
Κυλιόµενος κύλινδρος πέφτει πάνω σε οριζόντιο στερεωµένο ελατήριο. 3 m/sec. Να εξετάσετε στην περίπτωση αυτή αν, τη
 Κυλιόµενος κύλινδρος πέφτει πάνω σε οριζόντιο στερεωµένο ελατήριο m υ ο k R Α Ο οµογενής κύλινδρος του σχήµατος έχει µάζα m = 8 kg, ακτίνα R και κυλίεται χωρίς να ολισθαίνει στο οριζόντιο επίπεδο έτσι
Κυλιόµενος κύλινδρος πέφτει πάνω σε οριζόντιο στερεωµένο ελατήριο m υ ο k R Α Ο οµογενής κύλινδρος του σχήµατος έχει µάζα m = 8 kg, ακτίνα R και κυλίεται χωρίς να ολισθαίνει στο οριζόντιο επίπεδο έτσι
ΘΕΜΑ 2 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο.
 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. (Μονάδες 10) β) Να παραστήσετε γραφικά στο επίπεδο τις δυο εξισώσεις
α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. (Μονάδες 10) β) Να παραστήσετε γραφικά στο επίπεδο τις δυο εξισώσεις
με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4).
 Δίνεται το σύστημα: x 2y= 9 ax+ βy= γ με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4). (Μονάδες 13) β) Να επιλέξετε
Δίνεται το σύστημα: x 2y= 9 ax+ βy= γ με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4). (Μονάδες 13) β) Να επιλέξετε
Κεφάλαιο 1: Κινηματική των Ταλαντώσεων
 Κεφάλαιο : Κινηματική των Ταλαντώσεων Κεφάλαιο : Κινηματική των Ταλαντώσεων. Φαινομενολογικός ορισμός ταλαντώσεων Μεταβολές σε φυσικά φαινόμενα που χαρακτηρίζονται από μια κανονική επανάληψη κατά ορισμένα
Κεφάλαιο : Κινηματική των Ταλαντώσεων Κεφάλαιο : Κινηματική των Ταλαντώσεων. Φαινομενολογικός ορισμός ταλαντώσεων Μεταβολές σε φυσικά φαινόμενα που χαρακτηρίζονται από μια κανονική επανάληψη κατά ορισμένα
