343 Ειςαγωγι ςτον Προγραμματιςμό
|
|
|
- Άιμον Δημαράς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13
2 Θ: διάλεξη (θεωρία) Ε: Εργαστήριο Q: Σεστ quiz Επιπλζον Προαιρετικό Εργαςτιριο Οκτώβριος 2015 Δ Σ Σ Π Π Θ Θ Θ 24 Ε 25 Ε Νοέμβριος 2015 Δ Σ Σ Π Π Θ 7 Ε 8 Ε Θ 14 Ε Θ 21 Σ Θ 28 Ε 29 Ε 30 Δεκέμβριος 2015 Δ Σ Σ Π Π 1 2 Θ 5 E 6 Ε Θ 6 ο Εργαςτήριο: Προαιρετικό (χωρίσ παρουςία) Δευτζρα 19 Δεκεμβρίου Τρίτθ 20 Δεκεμβρίου ϊρεσ 14-15:30, Τμιματα Α1 & Α ϊρεσ 15:30-17, Τμιματα Α3 & Α ϊρεσ 17-18:30, Τμιματα Α5 & Β Q Θ Ε Ιανουάριος 2016 Δ Σ Σ Π Π Θ
3 Τελικι Βακμολογία Επιτυχήσ παρακολοφθηςη των υποχρεωτικϊν εργαςτθρίων μια (1) το πολφ απουςία ςτα 5 ή 6 εργαςτθριακά μακιματα Ζνα (1) τεςτ (Τ1) με βάροσ 15% του ςυνολικοφ βακμοφ. Ανάπτυξθ Κϊδικα ςτο Εργαςτιριο Ζνα (1) quiz (Q2) με βάροσ 15% του ςυνολικοφ βακμοφ. Ερωτιςεισ Πολλαπλϊν Επιλογϊν Όςοι απουςιάςουν ςε ζνα τεςτ ι quiz: μθδενίηεται το 15% Παλαιότεροι φοιτητζσ: μποροφν να λάβουν μζροσ ςτα τεςτ ι ςτα quiz Σελική βαθμολογία (με επιτυχι παρακολοφκθςθ εργαςτθρίων): TB = max 15% Τ1 + 15% Q2 + 70% ΓρΕξ ΓρΕξ
4 2 ο Quiz Το 2 ο quiz κα διεξαχκεί τθν Δευτζρα 12 Δεκεμβρίου Διάρκεια: 45 λεπτά 12 Ερωτιςεισ με απαντιςεισ πολλαπλϊν επιλογϊν + 2 Ερωτιςεισ: Ονοματεπϊνυμο & Α.Μ. Ώρεσ Α. Μ. 14:00-14:45 ΤΜΗΜΑ Α1 14:45-15:30 ΤΜΗΜΑ Α2 15:30-16:15 ΤΜΗΜΑ Α3 16:15-17:00 ΤΜΗΜΑ Α4 17:00-17:45 ΤΜΗΜΑ Α5 17:45-18:30 ΤΜΗΜΑ Β1 Αν λείψετε: Δεν μετράει ωσ απουςία Μθδενίηεται το 15% 18:30-19:15 ΤΜΗΜΑ που δεν ανικουν Α1-Α5,Β1 6-4
5 ecourse.uoi.gr 8-5
6 ecourse.uoi.gr 8-6
7 ecourse.uoi.gr 8-7
8 ecourse.uoi.gr Σθμειϊςτε: Username & Password 8-8
9 Θ: διάλεξη (θεωρία) Ε: Εργαστήριο Q: Σεστ quiz Οκτώβριος 2015 Δ Σ Σ Π Π Θ Θ Θ 24 Ε 25 Ε Νοέμβριος 2015 Δ Σ Σ Π Π Θ 7 Ε 8 Ε Θ 14 Ε Θ 21 Σ Θ 28 Ε 29 Ε 30 Δεκέμβριος 2015 Δ Σ Σ Π Π 1 2 Θ 5 E 6 Ε Θ 12 Q Θ Ε Ιανουάριος 2016 Δ Σ Σ Π Π Θ Ημερολόγιο Μακιματοσ Εβδομάδα Θζματα Υλη βιβλιογραφίασ Πα, 7 Οκτωβρίου Εισαγωγικά μαθήματος & Δυαδική *1+: 1.1, Παράρτθμα 3 αναπαράσταση *2+: Κεφ. 1, Β, Δ Πα, 14 Οκτωβρίου Είσοδος/Έξοδος δεδομένων, τύποι δεδομένων & *1+: 1.2, 1.3, 1.4, 1.5, Παράρτθμα 1 μεταβλητών *2+: Κεφ. 2, Γ Πα, 21 Οκτωβρίου Προεπεξεργαστής, αριθμητικοί και λογικοί *1+: 2.1, Παράρτθμα 2 τελεστές *2+: 4.11, 4.12, Α, ΣΤ Δε, Σρ, Οκτ 1 ο Εργαστήριο Πα, 4 Νοεμβρίου Ροή ελέγχου: if/else, switch, for, while, do-while [1]: 2.2, 2.3 και ροή ελέγχου if/else *2+: Κεφ. 4, Κεφ. 5 Δε, Σρ, 7-8 Νοε 2 ο Εργαστήριο Πα, 11 Νοεμβρίου υναρτήσεις, εμβέλεια μεταβλητών και [1]: 3.1, 3.2, 3.3, 4.1, 4.2, 13.1, 13.2 αναδρομή *2+: Κεφ. 6 Δε, Σρ, Νοε 3 ο Εργαστήριο Πα, 18 Νοεμβρίου Επανάληψη Εργαστηρίου [1]: 5.1, 5.2, 5.4 *2+: Κεφ. 7 Δε, 21 Νοε 1 ο Test (Ανάπτυξη κώδικα) Πα, 25 Νοεμβρίου Επανάληψη με Παραδείγματα [1]: 5.1, 5.2, 5.4 *2+: Κεφ. 7 Δε, Σρ, Νοε 4 ο Εργαστήριο Πα, 2 Δεκεμβρίου Πίνακες (μονοδιάστατοι και πολυδιάστατοι) *1+: Παράρτθμα 4, 9.1, 9.2, 9.3 *2+: 6.7, 6.8, Κεφ. 18 Δε, Σρ, 5-6 Δεκ 5 ο Εργαστήριο Πα, 9 Δεκεμβρίου Εφαρμογές σε ταξινομήσεις και αναζήτηση *1+: Παράρτθμα 4, 9.1, 9.2, 9.3 στοιχείων *2+: 6.7, 6.8, Κεφ. 18 Δε, 12 Δεκ 2 ο Quiz (Ερωτήσεις πολλαπλών επιλογών) Πα, 16 Δεκεμβρίου υμβολοσειρές, εγγραφές, δομές και χρήση [1]: 6.1, 5.3, 12.1, 12.2, 12.4, 13.3 αρχείων *2+: Κεφ. 21, 7.7, 7.8, , 19 Δε, 19 Δεκ 6 ο Εργαστήριο (Προαιρετικό) Πα, 13 Ιανουαρίου Επανάληψη
10 Θ: διάλεξη (θεωρία) Ε: Εργαστήριο Q: Σεστ quiz Οκτώβριος 2015 Δ Σ Σ Π Π Θ Θ Θ 24 Ε 25 Ε Νοέμβριος 2015 Δ Σ Σ Π Π Θ 7 Ε 8 Ε Θ 14 Ε Θ 21 Σ Θ 28 Ε 29 Ε 30 Δεκέμβριος 2015 Δ Σ Σ Π Π 1 2 Θ 5 E 6 Ε Θ 12 Q Θ Ε Ιανουάριος 2016 Δ Σ Σ Π Π Θ Ημερολόγιο Μακιματοσ Εβδομάδα Θζματα Υλη βιβλιογραφίασ Πα, 7 Οκτωβρίου Εισαγωγικά μαθήματος & Δυαδική *1+: 1.1, Παράρτθμα 3 αναπαράσταση *2+: Κεφ. 1, Β, Δ Πα, 14 Οκτωβρίου Είσοδος/Έξοδος δεδομένων, τύποι δεδομένων & *1+: 1.2, 1.3, 1.4, 1.5, Παράρτθμα 1 μεταβλητών *2+: Κεφ. 2, Γ Πα, 21 Οκτωβρίου Προεπεξεργαστής, αριθμητικοί και λογικοί *1+: 2.1, Παράρτθμα 2 τελεστές *2+: 4.11, 4.12, Α, ΣΤ Δε, Σρ, Οκτ 1 ο Εργαστήριο Πα, 4 Νοεμβρίου Ροή ελέγχου: if/else, switch, for, while, do-while [1]: 2.2, 2.3 και ροή ελέγχου if/else *2+: Κεφ. 4, Κεφ. 5 Δε, Σρ, 7-8 Νοε 2 ο Εργαστήριο Πα, 11 Νοεμβρίου υναρτήσεις, εμβέλεια μεταβλητών και [1]: 3.1, 3.2, 3.3, 4.1, 4.2, 13.1, 13.2 αναδρομή *2+: Κεφ. 6 Δε, Σρ, Νοε 3 ο Εργαστήριο Πα, 18 Νοεμβρίου Επανάληψη Εργαστηρίου [1]: 5.1, 5.2, 5.4 *2+: Κεφ. 7 Δε, 21 Νοε 1 ο Test (Ανάπτυξη κώδικα) Πα, 25 Νοεμβρίου Επανάληψη με Παραδείγματα [1]: 5.1, 5.2, 5.4 *2+: Κεφ. 7 Δε, Σρ, Νοε 4 ο Εργαστήριο Πα, 2 Δεκεμβρίου Πίνακες (μονοδιάστατοι και πολυδιάστατοι) *1+: Παράρτθμα 4, 9.1, 9.2, 9.3 *2+: 6.7, 6.8, Κεφ. 18 Δε, Σρ, 5-6 Δεκ 5 ο Εργαστήριο Πα, 9 Δεκεμβρίου Εφαρμογές σε ταξινομήσεις και αναζήτηση *1+: Παράρτθμα 4, 9.1, 9.2, 9.3 στοιχείων *2+: 6.7, 6.8, Κεφ. 18 Δε, 12 Δεκ 2 ο Quiz (Ερωτήσεις πολλαπλών επιλογών) Πα, 16 Δεκεμβρίου υμβολοσειρές, εγγραφές, δομές και χρήση [1]: 6.1, 5.3, 12.1, 12.2, 12.4, 13.3 αρχείων *2+: Κεφ. 21, 7.7, 7.8, , 19 Δε, 19 Δεκ 6 ο Εργαστήριο (Προαιρετικό) Πα, 13 Ιανουαρίου Επανάληψη
11 Ενότθτα 17 ΑΛΓΟΡΙΘΜΟΙ ΣΑΞΙΝΟΜΗΗ 8-11
12 Αποτελεςματικότθτα Αλγορίκμου Θα εξετάςουμε διάφορουσ αλγορίκμουσ που επιλφουν ίδια προβλιματα. Όταν ςχεδιάηουμε ζναν αλγόρικμο μασ ενδιαφζρει θ αποτελεςματικότητά του (ταχφτθτα) Ζνασ γνωςτόσ τρόποσ για να ποςοτικοποιοφμε τθν αποτελεςματικότθτα ενόσ αλγορίκμου (πρόγραμμα) γίνεται με τθν εφρεςθ του πλήθοσ των ςυγκρίςεων που χρηςιμοποιεί. Το πλικοσ των ςυγκρίςεων μπορεί να εξαρτάται από τθν είςοδο. Περιπτϊςεισ: χειρότερη, μέςη, καλφτερη 8-12
13 Παραδείγματα if ( i < 5) i++; if (( i < 5 ) && ( i >0 )) i++; Γίνονται 1 και 2 ςυγκρίςεισ, αντίςτοιχα. Στο ακόλουκο κομμάτι πόςεσ ςυγκρίςεισ γίνονται; for(i=0; i<n; i++) cout << " i = " << i << endl; Στο ακόλουκο (δοκιμάςτε με αρχικζσ τιμζσ i=0 και i=4): while(i<5){ cout << " i = " << i << endl; i+=2; } 8-13
14 Ταξινόμθςθ Πινάκων Ταξινόμθςθ ςε αφξουςα τάξθ: a[0] a*1+... a[99] Ταξινόμθςθ ςε φκίνουςα τάξθ: a[0] a[1]... a[99] Πολφ ςπουδαία εφαρμογι Σχεδόν κάκε οργανιςμόσ πρζπει να ταξινομεί κάποια δεδομζνα Συνικωσ οι επιχειριςεισ πρζπει να ταξινομοφν ι να κρατάνε ταξινομθμζνα μεγάλο όγκο δεδομζνων Ταξινομοφμε ζνα πίνακα με n (< 100) ςτοιχεία Θεωροφμε τον πίνακα ωσ μερικϊσ ςυμπλθρωμζνο πίνακα 8-14
15 Χριςθ ςυναρτιςεων Σε όλουσ τουσ αλγορίκμουσ κα χρθςιμοποιιςουμε τισ ακόλουκεσ ςυναρτιςεισ: Εναλλαγι ςτοιχείων void swapvalues(int& v1, int& v2) { int temp; temp = v1; v1 = v2; v2 = temp; } Θα μποροφςε και με αυτι τθν διλωςθ void swap(int a[], int i, int j) { int temp; temp = a[i]; a[i] = a[j]; a[j] = temp; } 8-15
16 Χριςθ ςυναρτιςεων Σε όλουσ τουσ αλγορίκμουσ κα χρθςιμοποιιςουμε τισ ακόλουκεσ ςυναρτιςεισ: Διάβαςμα void fillarray(int a[], int size, int& numberused) { cout << "Δώσε θετικούς αριθμούς (αρνητικό για τέλος).\n"; int next, index = 0; cin >> next; while ((next >= 0) && (index < size)) { a[index] = next; index++; cin >> next; } } numberused = index; 8-16
17 Χριςθ ςυναρτιςεων Σε όλουσ τουσ αλγορίκμουσ κα χρθςιμοποιιςουμε τισ ακόλουκεσ ςυναρτιςεισ: Εκτφπωςθ void printarray(int a[], int size) { for(int i = 0; i < size; i++) cout << a[i] << " "; cout << endl; }... printarray(a, numberused)
18 #include <iostream> using namespace std; const int MAX_SIZE = 100; void fillarray(int a[], int size, int& numberused); void printarray(int a[], int size); void swapvalues(int& v1, int& v2); void sort(int a[], int size); int main( ) { int a[max_size], numberused; fillarray(a, MAX_SIZE, numberused); sort(a, numberused); printarray(a, numberused); } return 0; 8-18
19 Ταξινόμθςθ Πινάκων - Bubble Sort Μζκοδοσ τθσ πζτρασ (παραλλαγι: μζκοδοσ φυςαλίδασ ) Κάνει n-1 περάςματα πάνω από τον πίνακα: p=1,2,,n-1 Κατά το p πζραςμα, διαδοχικά ηεφγθ ςτοιχείων ςτισ κζςεισ i=0,1,,n-p ςυγκρίνονται Εάν είναι ςε αφξουςα τάξθ (ι ίςα), τα αφινουμε ζτςι Εάν δεν είναι ςε αφξουςα τάξθ, τα ανταλλάςςουμε Σε κάκε πζραςμα το επόμενο μεγαλφτερο ςτοιχείο βυκίηεται ςτθν ςωςτι κζςθ Επαναλαμβάνουμε μζχρι πλιρουσ ταξινόμθςθσ Εφκολο πρόγραμμα αλλά αργό Αρχίηοντασ τισ ςυγκρίςεισ από το τζλοσ του πίνακα προσ τθν αρχι ζχουμε τον αλγόρικμο τθσ φυςαλίδασ, όπου ςε κάκε πζραςμα το επόμενο μικρότερο ςτοιχείο ανεβαίνει ςτθν ςωςτι κζςθ 8-19
20 Ταξινόμθςθ Πινάκων - Bubble Sort Παράδειγμα Αρχικόσ πίνακασ: Πζραςμα 1: Πζραςμα 2: Πζραςμα 3: Πζραςμα 4:
21 Ταξινόμθςθ Πινάκων - Bubble Sort Παράδειγμα Αρχικόσ πίνακασ: Πζραςμα 1: Πζραςμα 2: Πζραςμα 3: Πζραςμα 4: void sort(int a[], int size) { for(int pass = 1; pass < size; pass++) for(int i = 0; i < size pass; i++) if( a[i] > a[i+1]) swapvalues(a[i], a[i+1]); } 8-21
22 Ταξινόμθςθ Πινάκων Selection Sort Μζκοδοσ τθσ επιλογισ του επόμενου μικρότερου ςτοιχείου Κάνει n-1 περάςματα πάνω από τον πίνακα: p=0,1,2,3,,n-2 Στο p πζραςμα επιλζγουμε το μικρότερο ςτοιχείο μεταξφ των ςτοιχείων ςτισ κζςεισ i=p,,n-1 και το ανταλλάςςουμε με αυτό ςτθν p κζςθ του πίνακα Στο πρϊτο πζραςμα επιλζγουμε το μικρότερο ςτοιχείο και το βάηουμε ςτθν πρϊτθ κζςθ του πίνακα, μετά επιλζγουμε το επόμενο μικρότερο ςτοιχείο και το ανταλλάςςουμε με αυτό ςτθν δεφτερθ κζςθ, κ.ο.κ Επαναλαμβάνουμε μζχρι πλιρουσ ταξινόμθςθσ Εφκολο πρόγραμμα αλλά αργό 8-22
23 Ταξινόμθςθ Πινάκων Selection Sort Παράδειγμα Αρχικόσ πίνακασ: Πζραςμα 1: Πζραςμα 2: Πζραςμα 3: Πζραςμα 4: Δυο εκδοχζσ Μποροφμε να δουλζψουμε και με maximum 8-23
24 Ταξινόμθςθ Πινάκων Selection Sort void sort(int a[], int size) { int min; for(int pass = 0; pass < size-1; pass++) { min = pass; for(int i = pass+1; i < size; i++) if( a[i] < a[min]) min = i; } swapvalues(a[pass], a[min]); } 8-24
25 Ταξινόμθςθ Πινάκων Insertion Sort Μζκοδοσ τθσ ειςαγωγισ του επόμενου ςτοιχείου ςτθν κατάλλθλθ κζςθ Κάνει n-1 περάςματα πάνω από τον πίνακα p=1,2,3,,n-1 Στο p πζραςμα το p ςτοιχείο ειςάγεται ςτθν ςωςτι κζςθ ςυγκρινόμενο με τα ςτοιχεία ςτισ κζςεισ i=0,1,,p-1. Θεωροφμε ότι τα ςτοιχεία ςτισ κζςεισ i=0,1,,p-1 είναι ιδθ ταξινομθμζνα Σε κάκε πζραςμα ζνα ςτοιχείο ςυγκρίνεται με τα ςτοιχεία πριν από αυτό και ειςάγεται ςτθν ςωςτι κζςθ γίνονται ανταλλαγζσ με τα μεγαλφτερα από αυτό ςτοιχεία Επαναλαμβάνουμε μζχρι πλιρουσ ταξινόμθςθσ Εφκολο πρόγραμμα αλλά αργό 8-25
26 Ταξινόμθςθ Πινάκων Selection Sort Παράδειγμα Αρχικόσ πίνακασ: Πζραςμα 1: Πζραςμα 1: Πζραςμα 2: Πζραςμα 2: Πζραςμα 3: Πζραςμα 3: Πζραςμα 4: Πζραςμα 4:
27 Ταξινόμθςθ Πινάκων Selection Sort Παράδειγμα Αρχικόσ πίνακασ: Πζραςμα 1: Πζραςμα 1: Πζραςμα 2: Πζραςμα 2: Πζραςμα 3: Πζραςμα 3: Πζραςμα 4: Πζραςμα 4: temp = a[i]; j = i; while( temp < a[ j - 1 ] ) { a[ j ] = a[ j - 1 ]; j--; }
28 Ταξινόμθςθ Πινάκων Insertion Sort void sort(int a[], int size) { int i, j, temp; for( int i = 1; i < size; i++ ) { temp = a[ i ]; Δεν ζχει βρεκεί ακόμα θ ςωςτι κζςθ } for(j = i; j > 0 && temp < a[ j - 1 ]; j-- ) a[ j ] = a[ j - 1 ]; Μετακίνθςθ όλων των a[ j ] = temp; ςτοιχείων μια κζςθ δεξιά } 8-28
29 Ενότθτα 18 ΑΝΑΖΗΣΗΗ ΣΟΙΧΕΙΟΤ 8-29
30 Αναηιτθςθ ςτοιχείου ςε πίνακα Αναηιτθςθ κάποιασ τιμισ κλειδί ςε ζνα μονοδιάςτατο πίνακα. Υπάρχουν δφο βαςικζσ μζκοδοι. Γραμμικι αναηιτθςθ Απλι Συγκρίνουμε κάκε ςτοιχείο με τθν τιμι κλειδί που αναηθτάμε Χριςιμθ για μικροφσ μθ ταξινομθμζνουσ πίνακεσ Πολφ αργι, είναι δυνατόν να κάνει n ςυγκρίςεισ ςε ζνα πίνακα με n ςτοιχεία 8-30
31 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=0 8-31
32 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=1 8-32
33 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=2 8-33
34 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=3 8-34
35 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=4 8-35
36 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=5 8-36
37 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=6 8-37
38 Παράδειγμα γραμμικισ αναηιτθςθσ Κλειδί αναηιτθςθσ: key = 7 Ελζγχουμε A[i] == key Α*0+ Α*1] Α*2] Α*3] Α*4] Α*5] Α*6] Α = [ 1, 3, 3, 6, 8, 9, 4 ] i=6 Αν δεν βρζκθκε (δεν επιςτρζψαμε τθν κζςθ i του πίνακα) τότε επιςτρζφουμε -1 (θ κζςθ -1 ςε πίνακα δεν υπάρχει) 8-38
39 int search(int a[ ], int numberused, int target) { int index = 0; bool found = false; while ((!found) && (index < numberused)) { } if (target == a[index]) else found = true; index++; } if (found) return index; else return -1; return -1; 8-39
40 Δυαδικι Αναηιτθςθ Για ταξινομθμζνουσ πίνακεσ Δυαδικι Αναηιτθςθ Συγκρίνουμε το μεςαίο ςτοιχείο (middle) του πίνακα με το κλειδί (key) που αναηθτάμε If key = middle, τότε βρζκθκε If key < middle, τότε θ αναηιτθςθ γίνεται ςτο αριςτερό ιμιςυ του πίνακα If key > middle, τότε θ αναηιτθςθ γίνεται ςτο δεξιό ιμιςυ του πίνακα Επαναλαμβάνουμε τθν δυαδικι αναηιτθςθ ςτο ιμιςυ που επιλζξαμε Πολφ γριγορθ, κάνει το πολφ log(n) ςυγκρίςεισ ςε ζνα πίνακα με n ςτοιχεία Για n = 1024 κάνει το πολφ 10 ςυγκρίςεισ 8-40
41 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] low mid high 8-41
42 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] low mid high 8-42
43 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] low high mid 8-43
44 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] high low mid 8-44
45 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] high low mid 8-45
46 Παράδειγμα Κλειδί αναηιτθςθσ: key = 8 mid = (low+high)/2 Ελζγχουμε A[mid] == key return mid A[mid] < key low=mid+1 A[mid] > key high=mid-1 Α*0+ Α*1+ Α*2+ Α*3+ Α*4+ Α*5+ Α*6+ Α*7] Α = [ 1, 3, 3, 4, 6, 7, 7, 9 ] high < low: δεν βρέθηκε! high low mid 8-46
47 bool binarysearch(int a[ ], int low, int high, int key) { int mid; } if (low > high) else { } return false; mid = (low + high)/2; if (key == a[mid]) return true; else if (key < a[mid]) return binarysearch(a, low, mid - 1, key); else if (key > a[mid]) return binarysearch(a, mid + 1, high, key); 8-47
48 bool binarysearch(int a[ ], int low, int high, int key) { int mid; } if (low > high) else { } return false; mid = (low + high)/2; if (key == a[mid]) return true; else if (key < a[mid]) return binarysearch(a, low, mid - 1, key); else if (key > a[mid]) Αν κζλουμε και τθν κζςθ που βρίςκεται το key; return binarysearch(a, mid + 1, high, key); 8-48
49 Ενότθτα 19 ΕΛΑΧΙΣΑ & ΜΕΓΙΣΑ ΣΟΙΧΕΙΑ 8-49
50 Εφρεςθ Μεγίςτου Ελαχίςτου ταυτόχρονα Αν κζλουμε το μζγιςτο και το ελάχιςτο ςτοιχείο ενόσ πίνακα: void minmax1(int a[], int size, int& min, int& max) { max = 0; min = 0; for(int i=0; i < size; i++) { if(a[i] > a[max]) max = i; if(a[i] < a[min]) min = i; } } Κάνει 2n-2 ςυγκρίςεισ ςε ζνα πίνακα με n ςτοιχεία 8-50
51 Εφρεςθ Μεγίςτου Ελαχίςτου ταυτόχρονα Αν κζλουμε το μζγιςτο και το ελάχιςτο ςτοιχείο ενόσ πίνακα: void minmax2(int a[], int size, int& min, int& max) { max = 0; min = 0; for(int i=0; i < size; i++) { if(a[i] > a[max]) max = i; else if(a[i] < a[min]) min = i; } } Κάνει κατά μζςο όρο n-1 + n/2 ςυγκρίςεισ ςε ζνα πίνακα με n ςτοιχεία 8-51
52 Εφρεςθ Μεγίςτου Ελαχίςτου ταυτόχρονα Πιο γριγοροσ: διαιρεί τον πίνακα ςε δφο ιμιςυ και βρίςκει αναδρομικά μζγιςτο και ελάχιςτο ςε κάκε μιςό Το ολικό ελάχιςτο είναι το ελάχιςτο των δφο ελαχίςτων και αντίςτοιχα για το ολικό μζγιςτο MaxMin m=(f+l) / 2 Α F m m+1 L max1, min1 max2, min2 Α F m Α m+1 L Kάνει το πολφ 3n/2-2 ςυγκρίςεισ max=maximum(max1,max2) min=minimum(min1,min2) 8-52
53 void minmax3(int a[], int low, int high, int& min, int& max) { int min1, max1, min2, max2; int size; } size = high low + 1; if(size == 1) // high = low { min = a[low]; max = a[high]; } else if(size == 2) // a[] = {a[low], a[high]} { if(a[low] < a[high]) { min = a[low]; max = a[high]; } else { min = a[high]; max = a[low]; } } else { minmax3(a, low, (low + size/2-1), min1, max1); minmax3(a, (low + size/2), high, min2, max2); min = (min1 < min2)? min1 : min2 ; max = (max1 > max2)? max1 : max2 ; } 8-53
54 Πίνακεσ (ςφνοψθ) Είναι μια ςυλλογι από μεταβλθτζσ Βρόχοι for ταιριάηουν απόλυτα για τουσ πίνακεσ Είςτε υπεφκυνοι για να μθν βγείτε ζξω από τα όρια του πίνακα Η παράμετροσ Πίνακα είναι ζνα "νζοσ" τφποσ Παρόμοια με το παράμετρο με αναφορά Τα ςτοιχεία του πίνακα αποκθκεφονται ςειριακά "Συνεχόμενο" κομμάτι ςτθν μνιμθ Μόνο θ διεφκυνςθ του 1 ου ςτοιχείου περνάει ςε ςυν/ςεισ Μερικϊσ ςυμπλθρωμζνοι πίνακεσ περιςςότερεσ μεταβλθτζσ Πολυδιάςτατοι πίνακεσ "πίνακασ από πίνακεσ" 8-54
55 Βιβλιογραφία Καλι Μελζτθ [1] W. Savitch, Πλιρθσ C++, Εκδόςεισ Τηιόλα, 2011 [2+ Η. Deitel and P. Deitel, C++ Προγραμματιςμόσ 6θ Εκδοςθ, Εκδόςεισ Μ. Γκιοφρδασ, 2013 [1]: 5.3, 13.3 Υλη βιβλιογραφίασ *2+: 7.7, 7.8, 8.6, Κεφ
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Εφαρμογές σε ταξινομήσεις και αναζήτηση στοιχείων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Εφαρμογές σε ταξινομήσεις και αναζήτηση στοιχείων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό
Δομζσ Δεδομζνων. Αναηιτθςθ και Ταξινόμθςθ Διάλεξθ 3
 Δομζσ Δεδομζνων Αναηιτθςθ και Ταξινόμθςθ Διάλεξθ 3 Περιεχόμενα Αλγόρικμοι αναηιτθςθσ Σειριακι αναηιτθςθ Αναηιτθςθ κατά ομάδεσ Δυαδικι Αναηιτθςθ Ταξινόμθςθ Ταξινόμθςθ με παρεμβολι (insertion sort) Ταξινόμθςθ
Δομζσ Δεδομζνων Αναηιτθςθ και Ταξινόμθςθ Διάλεξθ 3 Περιεχόμενα Αλγόρικμοι αναηιτθςθσ Σειριακι αναηιτθςθ Αναηιτθςθ κατά ομάδεσ Δυαδικι Αναηιτθςθ Ταξινόμθςθ Ταξινόμθςθ με παρεμβολι (insertion sort) Ταξινόμθςθ
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2018-2019 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Σρίτθ 11-13 Ενότθτεσ 1-24 ΕΠΑΝΑΛΗΨΗ
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2018-2019 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Σρίτθ 11-13 Ενότθτεσ 1-24 ΕΠΑΝΑΛΗΨΗ
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Επανάληψη σε συναρτήσεις Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Επανάληψη σε συναρτήσεις Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Σμιματα Εργαςτθρίων
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Σμιματα Εργαςτθρίων
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
Δομές Δεδομένων & Αλγόριθμοι
 Δομές Δεδομένων & Αναζήτηση & Ταξινόμηση 1 Αναζήτηση Έχω έναν πίνακα Α με Ν στοιχεία. Πρόβλημα: Βρες αν το στοιχείο x ανήκει στον πίνακα Αν ο πίνακας είναι αταξινόμητος τότε μόνη λύση σειριακή αναζήτηση
Δομές Δεδομένων & Αναζήτηση & Ταξινόμηση 1 Αναζήτηση Έχω έναν πίνακα Α με Ν στοιχεία. Πρόβλημα: Βρες αν το στοιχείο x ανήκει στον πίνακα Αν ο πίνακας είναι αταξινόμητος τότε μόνη λύση σειριακή αναζήτηση
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Πίνακες (μονοδιάστατοι και πολυδιάστατοι) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Πίνακες (μονοδιάστατοι και πολυδιάστατοι) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν
Δομές Δεδομένων & Αλγόριθμοι
 Δομές Δεδομένων & Αναζήτηση & Ταξινόμηση 1 Αναζήτηση Έχω έναν πίνακα Α με Ν στοιχεία. Πρόβλημα: Βρες αν το στοιχείο x ανήκει στον πίνακα Αν ο πίνακας είναι αταξινόμητος τότε μόνη λύση σειριακή αναζήτηση
Δομές Δεδομένων & Αναζήτηση & Ταξινόμηση 1 Αναζήτηση Έχω έναν πίνακα Α με Ν στοιχεία. Πρόβλημα: Βρες αν το στοιχείο x ανήκει στον πίνακα Αν ο πίνακας είναι αταξινόμητος τότε μόνη λύση σειριακή αναζήτηση
17. Πολυδιάςτατοι πίνακεσ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 ελίδα Μακιματοσ:
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2017-2018 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 ελίδα Μακιματοσ:
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Τμιματα Εργαςτθρίων
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Τμιματα Εργαςτθρίων
242 -ΕισαγωγήστουςΗ/Υ
 1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) 2 ήλωση: Πίνακες στην ΕΑΓ δηλωση ( [1 : 1, 1 : 2,..., 1: ν ] ) παραταξη ; Π.χ.: δηλωση
1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) 2 ήλωση: Πίνακες στην ΕΑΓ δηλωση ( [1 : 1, 1 : 2,..., 1: ν ] ) παραταξη ; Π.χ.: δηλωση
Δομζσ Δεδομζνων Πίνακεσ
 Δομζσ Δεδομζνων Πίνακεσ Διάλεξθ 2 Περιεχόμενα Πίνακεσ: Οριςμοί, Γενικζσ ζννοιεσ Αποκικευςθ πινάκων Ειδικζσ μορφζσ πινάκων Αλγόρικμοι Αναηιτθςθσ Σειριακι Αναηιτθςθ Δυαδικι Αναηιτθςθ Οριςμοί, Γενικζσ ζννοιεσ
Δομζσ Δεδομζνων Πίνακεσ Διάλεξθ 2 Περιεχόμενα Πίνακεσ: Οριςμοί, Γενικζσ ζννοιεσ Αποκικευςθ πινάκων Ειδικζσ μορφζσ πινάκων Αλγόρικμοι Αναηιτθςθσ Σειριακι Αναηιτθςθ Δυαδικι Αναηιτθςθ Οριςμοί, Γενικζσ ζννοιεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων. 15. Πίνακεσ ΙI. Ιωάννθσ Κατάκθσ. ΕΠΛ 032: Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 15. Πίνακεσ ΙI Ιωάννθσ Κατάκθσ Σιμερα o Ειςαγωγι o Διλωςθ o Αρχικοποίθςθ o Πρόςβαςθ o Παραδείγματα Πίνακεσ - Επανάλθψθ o Στθν προθγοφμενθ διάλεξθ κάναμε μια
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 15. Πίνακεσ ΙI Ιωάννθσ Κατάκθσ Σιμερα o Ειςαγωγι o Διλωςθ o Αρχικοποίθςθ o Πρόςβαςθ o Παραδείγματα Πίνακεσ - Επανάλθψθ o Στθν προθγοφμενθ διάλεξθ κάναμε μια
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
Πληροφορική 2. Αλγόριθμοι
 Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Δομές Δεδομένων & Αλγόριθμοι
 - Πίνακες 1 Πίνακες Οι πίνακες έχουν σταθερό μέγεθος και τύπο δεδομένων. Βασικά πλεονεκτήματά τους είναι η απλότητα προγραμματισμού τους και η ταχύτητα. Ωστόσο δεν παρέχουν την ευελιξία η οποία απαιτείται
- Πίνακες 1 Πίνακες Οι πίνακες έχουν σταθερό μέγεθος και τύπο δεδομένων. Βασικά πλεονεκτήματά τους είναι η απλότητα προγραμματισμού τους και η ταχύτητα. Ωστόσο δεν παρέχουν την ευελιξία η οποία απαιτείται
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4.1
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Ροή ελέγχου: if/else, switch, for, while, do-while Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Ροή ελέγχου: if/else, switch, for, while, do-while Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα
Διάλεξη 17η: Ταξινόμηση και Αναζήτηση
 Διάλεξη 17η: Ταξινόμηση και Αναζήτηση Τμήμα Επιστήμης Υπολογιστών, Πανεπιστήμιο Κρήτης Εισαγωγή στην Επιστήμη Υπολογιστών Πρατικάκης (CSD) Ταξινόμηση CS100, 2016-2017 1 / 10 Το πρόβλημα της Αναζήτησης
Διάλεξη 17η: Ταξινόμηση και Αναζήτηση Τμήμα Επιστήμης Υπολογιστών, Πανεπιστήμιο Κρήτης Εισαγωγή στην Επιστήμη Υπολογιστών Πρατικάκης (CSD) Ταξινόμηση CS100, 2016-2017 1 / 10 Το πρόβλημα της Αναζήτησης
Στόχοι και αντικείμενο ενότητας. Πέρασμα Πίνακα σε Συνάρτηση (συν.) Πέρασμα Πίνακα σε Συνάρτηση. #8.. Ειδικά Θέματα Αλγορίθμων
 Στόχοι και αντικείμενο ενότητας Πέρασμα Πίνακα σε Συνάρτηση #8.. Ειδικά Θέματα Αλγορίθμων Προβλήματα Αναζήτησης Γραμμική Αναζήτηση (Linear Search) Ενημέρωση Μέτρηση Δυαδική Αναζήτηση (Binary Search) Προβλήματα
Στόχοι και αντικείμενο ενότητας Πέρασμα Πίνακα σε Συνάρτηση #8.. Ειδικά Θέματα Αλγορίθμων Προβλήματα Αναζήτησης Γραμμική Αναζήτηση (Linear Search) Ενημέρωση Μέτρηση Δυαδική Αναζήτηση (Binary Search) Προβλήματα
16. Πίνακεσ και Συναρτήςεισ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Εισαγωγή στον Προγραμματισμό
 Εισαγωγή στον Προγραμματισμό Ενότητα 6 Πίνακες Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Τύπος πίνακα (array) Σύνθετος τύπος δεδομένων Αναπαριστά ένα σύνολο ομοειδών
Εισαγωγή στον Προγραμματισμό Ενότητα 6 Πίνακες Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Τύπος πίνακα (array) Σύνθετος τύπος δεδομένων Αναπαριστά ένα σύνολο ομοειδών
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Εργαστηριακή Άσκηση 1
 Εργαστηριακή Άσκηση 1 Επανάληψη προγραμματισμού Βασικοί Αλγόριθμοι Είσοδος τιμών από το πληκτρολόγιο Σε όλα τα προγράμματα που θα γράψουμε στην συνέχεια του εξαμήνου θα χρειαστεί να εισάγουμε τιμές σε
Εργαστηριακή Άσκηση 1 Επανάληψη προγραμματισμού Βασικοί Αλγόριθμοι Είσοδος τιμών από το πληκτρολόγιο Σε όλα τα προγράμματα που θα γράψουμε στην συνέχεια του εξαμήνου θα χρειαστεί να εισάγουμε τιμές σε
Η εντολή if-else. Η απλή μορφή της εντολής if είναι η ακόλουθη: if (συνθήκη) { Η γενική μορφή της εντολής ifelse. εντολή_1; εντολή_2;..
 Επιλογή - Επανάληψη Η εντολή if-else Ο τελεστής παράστασης συνθήκης H εντολή switch Η εντολές for και while Η εντολή do-while Η εντολές break - continue - goto Μαθηματικές συναρτήσεις Λέξεις κλειδιά στη
Επιλογή - Επανάληψη Η εντολή if-else Ο τελεστής παράστασης συνθήκης H εντολή switch Η εντολές for και while Η εντολή do-while Η εντολές break - continue - goto Μαθηματικές συναρτήσεις Λέξεις κλειδιά στη
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Εργαστήριο 2: Πίνακες
 Εργαστήριο 2: Πίνακες Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Επεξεργασία Πινάκων - Υλοποίηση της Δυαδικής Αναζήτησης σε πίνακες - Υλοποίηση της Ταξινόμησης με Επιλογής σε πίνακες ΕΠΛ035
Εργαστήριο 2: Πίνακες Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Επεξεργασία Πινάκων - Υλοποίηση της Δυαδικής Αναζήτησης σε πίνακες - Υλοποίηση της Ταξινόμησης με Επιλογής σε πίνακες ΕΠΛ035
Οντοκεντρικόσ Προγραμματιςμόσ
 Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Templates Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικών Η/Τ & Πλθροφορικισ Templates Ειςαγωγι Templates o
Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Templates Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικών Η/Τ & Πλθροφορικισ Templates Ειςαγωγι Templates o
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Ιοφνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1.Εθνικό Τυπογραφείο... 3 1.1. Είςοδοσ... 3 1.2. Αρχική Οθόνη... 4 1.3. Διεκπεραίωςη αίτηςησ...
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Ιοφνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1.Εθνικό Τυπογραφείο... 3 1.1. Είςοδοσ... 3 1.2. Αρχική Οθόνη... 4 1.3. Διεκπεραίωςη αίτηςησ...
ΗΥ-150. Ταξινόµηση και Αναζήτηση
 ΗΥ-150 Ταξινόµηση και Αναζήτηση To πρόβληµα της Αναζήτησης οθέντος δεδοµένων, λ.χ. σε Πίνακα (P) Ψάχνω να βρω κάποιο συγκεκριµένο στοιχείο (key) Αν ο πίνακας δεν είναι ταξινοµηµένος Γραµµική Αναζήτηση
ΗΥ-150 Ταξινόµηση και Αναζήτηση To πρόβληµα της Αναζήτησης οθέντος δεδοµένων, λ.χ. σε Πίνακα (P) Ψάχνω να βρω κάποιο συγκεκριµένο στοιχείο (key) Αν ο πίνακας δεν είναι ταξινοµηµένος Γραµµική Αναζήτηση
Οντοκεντρικόσ Ρρογραμματιςμόσ
 Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΥΡΕΦΟΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΕΣΕΙΣ Υπερφόρτωςθ Τελεςτών Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Ρλθροφορικισ Υπερφόρτωςθ Τελεςτών
Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΥΡΕΦΟΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΕΣΕΙΣ Υπερφόρτωςθ Τελεςτών Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Ρλθροφορικισ Υπερφόρτωςθ Τελεςτών
Προγραμματισμός Η/Υ (ΤΛ2007 )
 Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε.Ι. Κρήτης Προγραμματισμός Η/Υ (ΤΛ00 ) Δρ. Μηχ. Νικόλαος Πετράκης (npet@chania.teicrete.gr) Ιστοσελίδα Μαθήματος: https://eclass.chania.teicrete.gr/ Εξάμηνο: Εαρινό 01-15
Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε.Ι. Κρήτης Προγραμματισμός Η/Υ (ΤΛ00 ) Δρ. Μηχ. Νικόλαος Πετράκης (npet@chania.teicrete.gr) Ιστοσελίδα Μαθήματος: https://eclass.chania.teicrete.gr/ Εξάμηνο: Εαρινό 01-15
Ιςοηυγιςμζνα δζντρα και Β- δζντρα. Δομζσ Δεδομζνων
 Ιςοηυγιςμζνα δζντρα και Β- δζντρα Δομζσ Δεδομζνων Περιεχόμενα Ιςοηυγιςμζνα δζντρα Μζκοδοι ιςοηφγιςθσ δζντρων Μονι Περιςτροφι Διπλι Περιςτροφι Β - δζντρα Ιςοηυγιςμζνα δζντρα Η μορφι ενόσ δυαδικοφ δζντρου
Ιςοηυγιςμζνα δζντρα και Β- δζντρα Δομζσ Δεδομζνων Περιεχόμενα Ιςοηυγιςμζνα δζντρα Μζκοδοι ιςοηφγιςθσ δζντρων Μονι Περιςτροφι Διπλι Περιςτροφι Β - δζντρα Ιςοηυγιςμζνα δζντρα Η μορφι ενόσ δυαδικοφ δζντρου
Δομθμζνοσ Προγραμματιςμόσ. Βαγγζλθσ Οικονόμου Εργαςτιριο 9
 Δομθμζνοσ Προγραμματιςμόσ Βαγγζλθσ Οικονόμου Εργαςτιριο 9 Συναρτιςεισ Αφαιρετικότθτα ςτισ διεργαςίεσ Συνάρτθςεισ Διλωςθ, Κλιςθ και Οριςμόσ Εμβζλεια Μεταβλθτών Μεταβίβαςθ παραμζτρων ςε ςυναρτιςεισ Συναρτιςεισ
Δομθμζνοσ Προγραμματιςμόσ Βαγγζλθσ Οικονόμου Εργαςτιριο 9 Συναρτιςεισ Αφαιρετικότθτα ςτισ διεργαςίεσ Συνάρτθςεισ Διλωςθ, Κλιςθ και Οριςμόσ Εμβζλεια Μεταβλθτών Μεταβίβαςθ παραμζτρων ςε ςυναρτιςεισ Συναρτιςεισ
Εργαςτιριο Βάςεων Δεδομζνων
 Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
Εισαγωγή στον δομημένο προγραμματισμό
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στον δομημένο προγραμματισμό Ενότητα 5 η : Πίνακες (Προχωρημένα Θέματα) Αν. καθηγητής Στεργίου Κώστας e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στον δομημένο προγραμματισμό Ενότητα 5 η : Πίνακες (Προχωρημένα Θέματα) Αν. καθηγητής Στεργίου Κώστας e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2015-2016 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 ελίδα Μακιματοσ:
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2015-2016 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 ελίδα Μακιματοσ:
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα
 Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Πάτρα, 2013 Περιεχόμενα: Ειςαγωγή... 4 1. Επιμελητήριο... Error! Bookmark not defined. 1.1 Διαχειριςτήσ Αιτήςεων Επιμελητηρίου...
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Πάτρα, 2013 Περιεχόμενα: Ειςαγωγή... 4 1. Επιμελητήριο... Error! Bookmark not defined. 1.1 Διαχειριςτήσ Αιτήςεων Επιμελητηρίου...
Διαδικασιακός Προγραμματισμός
 Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 12 η Αναζήτηση/Ταξινόμηση Πίνακα Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην
Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 12 η Αναζήτηση/Ταξινόμηση Πίνακα Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
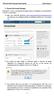 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον
 Γραπτι Εξζταςθ ςτο μάκθμα Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον Όνομα: Επϊνυμο: Τμιμα: Ημερομθνία: 20/02/11 Θζμα 1 ο Α. Να χαρακτθρίςετε κακεμιά από τισ παρακάτω προτάςεισ ωσ Σωςτι (Σ) ι Λάκοσ
Γραπτι Εξζταςθ ςτο μάκθμα Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον Όνομα: Επϊνυμο: Τμιμα: Ημερομθνία: 20/02/11 Θζμα 1 ο Α. Να χαρακτθρίςετε κακεμιά από τισ παρακάτω προτάςεισ ωσ Σωςτι (Σ) ι Λάκοσ
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2016-2017 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Πζμπτθ 11-13 Θ: διάλεξη (θεωρία)
Ειδικά Θζματα Βάςεων Δεδομζνων
 Ειδικά Θζματα Βάςεων Δεδομζνων Ενότθτα 12: Ευρετιρια Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικϊν Πλθροφορικισ ΤΕ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για
Ειδικά Θζματα Βάςεων Δεδομζνων Ενότθτα 12: Ευρετιρια Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικϊν Πλθροφορικισ ΤΕ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για
Δομές Επανάληψης. Εισαγωγή στη C++
 Δομές Επανάληψης Εισαγωγή στη C++ Επαναληπτικές δηλώσεις Οι βρόγχοι (loops) αναγκάζουν ένα τμήμα κώδικα να επαναλαμβάνεται. Η επανάληψη συνεχίζεται για όσο μία λογική συνθήκη είναι αληθής. Όταν η συνθήκη
Δομές Επανάληψης Εισαγωγή στη C++ Επαναληπτικές δηλώσεις Οι βρόγχοι (loops) αναγκάζουν ένα τμήμα κώδικα να επαναλαμβάνεται. Η επανάληψη συνεχίζεται για όσο μία λογική συνθήκη είναι αληθής. Όταν η συνθήκη
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Πληροφορική II. Ενότητα 2 : Αλγόριθμοι. Δρ. Γκόγκος Χρήστος
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 2 : Αλγόριθμοι Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 2 : Αλγόριθμοι Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Προγραμματισμός Η/Υ. Ενότητα 8: Ειδικά Θέματα Αλγορίθμων
 Προγραμματισμός Η/Υ Ενότητα 8: Ειδικά Θέματα Αλγορίθμων Νίκος Καρακαπιλίδης, Καθηγητής Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Κατανόηση
Προγραμματισμός Η/Υ Ενότητα 8: Ειδικά Θέματα Αλγορίθμων Νίκος Καρακαπιλίδης, Καθηγητής Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Κατανόηση
ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ
 ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ Ειςαγωγή Τπάρχουν τρία επίπεδα ςτα οποία καλείςτε να αξιολογιςετε το εργαςτιριο D-ID: Νζα κζματα Σεχνολογία Διδακτικι Νέα θέματα Σο εργαςτιριο κα ειςαγάγουν τουσ ςυμμετζχοντεσ
ΑΞΙΟΛΟΓΗΣΗ ΕΚΠΑΙΔΕΥΤΙΚΟΥ Ειςαγωγή Τπάρχουν τρία επίπεδα ςτα οποία καλείςτε να αξιολογιςετε το εργαςτιριο D-ID: Νζα κζματα Σεχνολογία Διδακτικι Νέα θέματα Σο εργαςτιριο κα ειςαγάγουν τουσ ςυμμετζχοντεσ
Προχωρημένες έννοιες προγραμματισμού σε C
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr)
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr)
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
Γράφοι. Δομζσ Δεδομζνων Διάλεξθ 9
 Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
x n D 2 ENCODER m - σε n (m 2 n ) x 1 Παραδείγματα κωδικοποιθτϊν είναι ο κωδικοποιθτισ οκταδικοφ ςε δυαδικό και ο κωδικοποιθτισ BCD ςε δυαδικό.
 Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Γ7.5 Αλγόριθμοι Αναζήτησης. Γ Λυκείου Κατεύθυνσης
 Γ7.5 Αλγόριθμοι Αναζήτησης Γ Λυκείου Κατεύθυνσης Εισαγωγή Αλγόριθμος αναζήτησης θεωρείται ένας αλγόριθμος, ο οποίος προσπαθεί να εντοπίσει ένα στοιχείο με συγκεκριμένες ιδιότητες, μέσα σε μία συλλογή από
Γ7.5 Αλγόριθμοι Αναζήτησης Γ Λυκείου Κατεύθυνσης Εισαγωγή Αλγόριθμος αναζήτησης θεωρείται ένας αλγόριθμος, ο οποίος προσπαθεί να εντοπίσει ένα στοιχείο με συγκεκριμένες ιδιότητες, μέσα σε μία συλλογή από
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ. ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι
 ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι Βοικεια (Help), Ευρετιριο, Κόμβοσ, Λζξθ κλειδί, Σφνδεςμόσ, Υπερκείμενο Τι είναι θ «Βοικεια» ςτουσ υπολογιςτζσ; Πώσ ενεργοποιοφμε
ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι Βοικεια (Help), Ευρετιριο, Κόμβοσ, Λζξθ κλειδί, Σφνδεςμόσ, Υπερκείμενο Τι είναι θ «Βοικεια» ςτουσ υπολογιςτζσ; Πώσ ενεργοποιοφμε
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ. Φιλιοποφλου Ειρινθ
 ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
Αλγόριθμοι Ταξινόμησης Μέρος 1
 Αλγόριθμοι Ταξινόμησης Μέρος 1 Μανόλης Κουμπαράκης 1 Το Πρόβλημα της Ταξινόμησης Το πρόβλημα της ταξινόμησης (sorting) μιας ακολουθίας στοιχείων με κλειδιά ενός γνωστού τύπου (π.χ., τους ακέραιους ή τις
Αλγόριθμοι Ταξινόμησης Μέρος 1 Μανόλης Κουμπαράκης 1 Το Πρόβλημα της Ταξινόμησης Το πρόβλημα της ταξινόμησης (sorting) μιας ακολουθίας στοιχείων με κλειδιά ενός γνωστού τύπου (π.χ., τους ακέραιους ή τις
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Αναζήτηση και ταξινόμηση
 ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Αναζήτηση και ταξινόμηση Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Αναζήτηση και ταξινόµηση 7 Αναζήτηση (search) Πρόβληµα: αναζήτηση της καταχώρησης key στη
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Αναζήτηση και ταξινόμηση Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Αναζήτηση και ταξινόµηση 7 Αναζήτηση (search) Πρόβληµα: αναζήτηση της καταχώρησης key στη
Δζντρα. Δομζσ Δεδομζνων
 Δζντρα Δομζσ Δεδομζνων Περιεχόμενα Δζντρα Γενικζσ ζννοιεσ Κόμβοσ ενόσ δζντρου Δυαδικά δζντρα αναηιτθςθσ Αναηιτθςθ Κόμβου Ειςαγωγι ι δθμιουργία κόμβου Δζντρα Γενικζσ ζννοιεσ Οι προθγοφμενεσ δομζσ που εξετάςτθκαν
Δζντρα Δομζσ Δεδομζνων Περιεχόμενα Δζντρα Γενικζσ ζννοιεσ Κόμβοσ ενόσ δζντρου Δυαδικά δζντρα αναηιτθςθσ Αναηιτθςθ Κόμβου Ειςαγωγι ι δθμιουργία κόμβου Δζντρα Γενικζσ ζννοιεσ Οι προθγοφμενεσ δομζσ που εξετάςτθκαν
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ
 5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
Αλγόριθμοι Αναζήτησης
 Αλγόριθμοι Αναζήτησης ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Αλγόριθμοι Αναζήτησης ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τίτλος Μαθήματος: Θεωρία Γραφημάτων. Ενότητα: Εισαγωγικά μαθήματος. Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Γραφημάτων Ενότητα: Εισαγωγικά μαθήματος Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεωρία Γραφθμάτων Χάρθσ Παπαδόπουλοσ Γενικά για το μάκθμα ΌΛΟΙ όςοι ενδιαφζρονται
Τίτλος Μαθήματος: Θεωρία Γραφημάτων Ενότητα: Εισαγωγικά μαθήματος Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεωρία Γραφθμάτων Χάρθσ Παπαδόπουλοσ Γενικά για το μάκθμα ΌΛΟΙ όςοι ενδιαφζρονται
Εργαστήριο 6: Αναζήτηση, Ανάλυση Πολυπλοκότητας
 Εργαστήριο 6: Αναζήτηση, Ανάλυση Πολυπλοκότητας Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Αναζήτηση με linearsearch, binarysearch, ternarysearch - Ανάλυση Πολυπλοκότητας ternarysearch
Εργαστήριο 6: Αναζήτηση, Ανάλυση Πολυπλοκότητας Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Αναζήτηση με linearsearch, binarysearch, ternarysearch - Ανάλυση Πολυπλοκότητας ternarysearch
Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων
 Πανελλόνιεσ εξετϊςεισ Γ Τϊξησ 2011 Ανϊπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβϊλλον ΘΕΜΑ Α Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων Α1. Σ/Λ 1. Σωςτι 2. Σωςτι 3. Λάκοσ 4. Λάκοσ 5. Λάκοσ Α2. Σ/Λ 1. Σωςτι 2.
Πανελλόνιεσ εξετϊςεισ Γ Τϊξησ 2011 Ανϊπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβϊλλον ΘΕΜΑ Α Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων Α1. Σ/Λ 1. Σωςτι 2. Σωςτι 3. Λάκοσ 4. Λάκοσ 5. Λάκοσ Α2. Σ/Λ 1. Σωςτι 2.
Joomla! - User Guide
 Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
343 Ειςαγωγι ςτον Προγραμματιςμό
 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο Ιωαννίνων Ακαδθμαϊκό Ζτοσ 2013-2014 Χάρθσ Παπαδόπουλοσ 207δ, B όροφοσ e-mail: charis@cs.uoi.gr Ωρεσ Γραφείου: Δευτζρα 11-13 & Παραςκευι 11-13
Δομημένος Προγραμματισμός (ΤΛ1006)
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Σχολή Εφαρμοσμένων Επιστημών Τμήμα Ηλεκτρονικών Μηχανικών Τομέας Αυτοματισμού και Πληροφορικής Δομημένος Προγραμματισμός (ΤΛ100) Δρ. Μηχ. Νικόλαος Πετράκης, Καθηγητής
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Κρήτης Σχολή Εφαρμοσμένων Επιστημών Τμήμα Ηλεκτρονικών Μηχανικών Τομέας Αυτοματισμού και Πληροφορικής Δομημένος Προγραμματισμός (ΤΛ100) Δρ. Μηχ. Νικόλαος Πετράκης, Καθηγητής
Η γλώςςα προγραμματιςμού C
 Η γλώςςα προγραμματιςμού C Οι εντολζσ επανάλθψθσ (while, do-while, for) Γενικά για τισ εντολζσ επανάλθψθσ Συχνά ςτο προγραμματιςμό είναι επικυμθτι θ πολλαπλι εκτζλεςθ μιασ ενότθτασ εντολϊν, είτε για ζνα
Η γλώςςα προγραμματιςμού C Οι εντολζσ επανάλθψθσ (while, do-while, for) Γενικά για τισ εντολζσ επανάλθψθσ Συχνά ςτο προγραμματιςμό είναι επικυμθτι θ πολλαπλι εκτζλεςθ μιασ ενότθτασ εντολϊν, είτε για ζνα
5. Απλή Ταξινόμηση. ομές εδομένων. Χρήστος ουλκερίδης. Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Απλή Ταξινόμηση 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 11/11/2016 Εισαγωγή Η
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Απλή Ταξινόμηση 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 11/11/2016 Εισαγωγή Η
ΜΥΥ105: Εισαγωγή στον Προγραμματισμό. Αναζήτηση και Ταξινόμηση Χειμερινό Εξάμηνο 2016
 ΜΥΥ105: Εισαγωγή στον Προγραμματισμό Αναζήτηση και Ταξινόμηση Χειμερινό Εξάμηνο 2016 Αναζήτηση και Ταξινόμηση Βασικές λειτουργίες σε προγράμματα Αναζήτηση (searching): Βρες ένα ζητούμενο στοιχείο σε μια
ΜΥΥ105: Εισαγωγή στον Προγραμματισμό Αναζήτηση και Ταξινόμηση Χειμερινό Εξάμηνο 2016 Αναζήτηση και Ταξινόμηση Βασικές λειτουργίες σε προγράμματα Αναζήτηση (searching): Βρες ένα ζητούμενο στοιχείο σε μια
Προγραμματιστικές Τεχνικές
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόμων Τοπογράφων Μηχανικών Προγραμματιστικές Τεχνικές Βασίλειος Βεσκούκης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωμύλος Κορακίτης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόμων Τοπογράφων Μηχανικών Προγραμματιστικές Τεχνικές Βασίλειος Βεσκούκης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωμύλος Κορακίτης
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες) Ιούνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1. Περιφζρεια... 3 1.1 Διαχειριςτήσ Αιτήςεων Περιφζρειασ... 3 1.1.1. Είςοδοσ... 3 1.1.2. Αρχική
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες) Ιούνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1. Περιφζρεια... 3 1.1 Διαχειριςτήσ Αιτήςεων Περιφζρειασ... 3 1.1.1. Είςοδοσ... 3 1.1.2. Αρχική
Διδάςκων: Κωνςταντίνοσ τεφανίδθσ
 ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΧΟΛΗ ΘΕΣΙΚΩΝ ΕΠΙΣΗΜΩΝ ΣΜΗΜΑ ΕΠΙΣΗΜΗ ΤΠΟΛΟΓΙΣΩΝ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗ ΗΤ-564 ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΣΑ ΕΠΙΚΟΙΝΩΝΙΑ ΑΝΘΡΩΠΟΤ - ΜΗΧΑΝΗ Διδάςκων: Κωνςταντίνοσ τεφανίδθσ τόχοσ τθσ ςυγκεκριμζνθσ εργαςίασ
ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΧΟΛΗ ΘΕΣΙΚΩΝ ΕΠΙΣΗΜΩΝ ΣΜΗΜΑ ΕΠΙΣΗΜΗ ΤΠΟΛΟΓΙΣΩΝ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗ ΗΤ-564 ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΣΑ ΕΠΙΚΟΙΝΩΝΙΑ ΑΝΘΡΩΠΟΤ - ΜΗΧΑΝΗ Διδάςκων: Κωνςταντίνοσ τεφανίδθσ τόχοσ τθσ ςυγκεκριμζνθσ εργαςίασ
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Αριθμητικοί και λογικοί τελεστές Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Αριθμητικοί και λογικοί τελεστές Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Τμιμα Μακθματικϊν Πανεπιςτιμιο
Προγραμματισμός Ι (ΗΥ120)
 Προγραμματισμός Ι (ΗΥ120) Διάλεξη 10: Ταξινόμηση Πίνακα Αναζήτηση σε Ταξινομημένο Πίνακα Πρόβλημα Δίνεται πίνακας t από Ν ακεραίους. Ζητούμενο: να ταξινομηθούν τα περιεχόμενα του πίνακα σε αύξουσα αριθμητική
Προγραμματισμός Ι (ΗΥ120) Διάλεξη 10: Ταξινόμηση Πίνακα Αναζήτηση σε Ταξινομημένο Πίνακα Πρόβλημα Δίνεται πίνακας t από Ν ακεραίους. Ζητούμενο: να ταξινομηθούν τα περιεχόμενα του πίνακα σε αύξουσα αριθμητική
Διάλεξη 04: Παραδείγματα Ανάλυσης
 Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ
 ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
242 -ΕισαγωγήστουςΗ/Υ
 1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) Πίνακες σαν παράµετροι 2 Πίνακες σαν παράµετροι 3 Πίνακες σαν παράµετροι Περνάµε ένα πίνακα σαν παράµετρο σε µια
1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) Πίνακες σαν παράµετροι 2 Πίνακες σαν παράµετροι 3 Πίνακες σαν παράµετροι Περνάµε ένα πίνακα σαν παράµετρο σε µια
Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Σεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνασ Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε) Ενδεικτική επίλυςη άςκηςησ 1 Δρ. Θωμάσ Π. Μαηαράκοσ Τμιμα Ναυπθγϊν Μθχανικϊν ΤΕ Το
Ανοικτά Ακαδημαϊκά Μαθήματα Σεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνασ Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε) Ενδεικτική επίλυςη άςκηςησ 1 Δρ. Θωμάσ Π. Μαηαράκοσ Τμιμα Ναυπθγϊν Μθχανικϊν ΤΕ Το
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων
 Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
ΕΠΛ231 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων
 ΕΠΛ31 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα
ΕΠΛ31 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα
ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_<όνομα παραμζτρου> (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων).
 ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_ (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων). Βαςικοί παράμετροι @EDT@_ @CHK@_ @CXD@_ @CXDC@_ @CMB@_ @CHKLB@_ Παράμετροσ που
ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_ (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων). Βαςικοί παράμετροι @EDT@_ @CHK@_ @CXD@_ @CXDC@_ @CMB@_ @CHKLB@_ Παράμετροσ που
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό
 Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Αλφαριθμητικά και Συμβολοσειρές Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο
Τίτλος Μαθήματος: Εισαγωγή στον Προγραμματισμό Ενότητα: Αλφαριθμητικά και Συμβολοσειρές Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 343 Ειςαγωγι ςτον Προγραμματιςμό Σμιμα Μακθματικϊν Πανεπιςτιμιο
ιαφάνειες παρουσίασης #4
 ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ http://www.softlab.ntua.gr/~nickie/courses/progtech/ ιδάσκοντες: Γιάννης Μαΐστρος (maistros@cs.ntua.gr) Στάθης Ζάχος (zachos@cs.ntua.gr) (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης
ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ http://www.softlab.ntua.gr/~nickie/courses/progtech/ ιδάσκοντες: Γιάννης Μαΐστρος (maistros@cs.ntua.gr) Στάθης Ζάχος (zachos@cs.ntua.gr) (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης
assessment.gr USER S MANUAL (users)
 assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ. Κεφάλαιο 8 Η γλϊςςα Pascal
 ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
