Ψθφιακι Επεξεργαςία ιματοσ
|
|
|
- Χρύσηίς Σπηλιωτόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 8 : Διακριτόσ Μεταςχθματιςμόσ Fourier Κωνςταντίνοσ Αγγζλθσ 1
2 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικών Πλθροφορικισ Σ.Ε. Ψθφιακι Επεξεργαςία ιματοσ Ενότητα 8: Διακριτόσ Μεταςχθματιςμόσ Fourier Κωνςταντίνοσ Αγγζλθσ Κακθγθτισ Άρτα,
3 Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό υλικό, όπωσ εικόνεσ, που υπόκειται ςε άλλου τφπου άδειασ χριςθσ, θ άδεια χριςθσ αναφζρεται ρθτώσ. 3
4 Σκοποί ενότητασ Να ειςάγει τον οριςμό του διακριτοφ μεταςχθματιςμοφ Fourier και του αντίςτροφου Μετατροπι βαςικών ςθμάτων ςε διακριτά με τθ χριςθ του μεταςχθματιςμοφ fourier. Παρουςίαςθ και χριςθ των ιδιοτιτων του μεταςχθματιςμοφ Fourier 4
5 Περιεχόμενα ενότητασ Οπιζμοί DFT-IDFT Σσέζη ηος DFT με DTFT 1ο παπάδειγμα Ιδιόηηηερ διακπιηού μεηαζσημαηιζμού Fourier Discrete Time Fourier Transform DTFT Ζεςγάπια Μεηαζσημαηιζμών DTFT Απόκπιζη Σςσνόηηηαρ 5
6 Περιεχόμενα ενότητασ Σςζηήμαηα ζςνδεδεμένα ζε ζειπά Σςζηήμαηα ζςνδεδεμένα παπάλληλα 6
7 Οριζμοί DFT-IDFT Ο εςθύρ διακπιηόρ μεηαζσημαηιζμόρ Fourier (Discrete Fourier Transform DFT) οπίζεηαι ωρ: X N N ( ) k n 1 0 x n ( k) W kn N, 0 k N 1 Όπος W N exp j 2 N O ανηίζηποθορ διακπιηόρ μεηαζσημαηιζμόρ Fourier (Inverse Discrete Fourier Transform N 1 IDFT) οπίζεηαι ωρ: 1 kn x( n) N k0 X ( k) N W N 7
8 Στέζη ηοσ DFT με DTFT Αν ηο ζήμα είναι πεπεπαζμένος σπόνος ζηο διάζηημα [0: N 1 τότε αν τότε N 1 X e jω = x(n) e jωn n=0 ω k = (2 π N) k, k [0: N 1 N 1 j(2 / N ) k j(2 / N ) kn X e x( n) e X ( k) n0 8
9 1ο παράδειγμα Δίνεηαι ηο ζήμα x( n) ( n) 2 ( n 5) Ο διακπιηόρ μεηαζσημαηιζμού Fourier N 10 ζημείων ηος ζήμαηορ είναι: 9 nk j X ( k) x( n) W, k [0:9] n0 Επομένωρ 9 n n0 W e e 10 2 /10 j/5 X ( k) ( n) 2 ( n 5) W, k [0:9] j/5 5k j 10 nk nk 0 k 5k X ( k) ( n) 2 ( n 5) W 1 W 2 W e 1 2 e, k [0:9] k 9
10 1ο παράδειγμα Χπηζιμοποιώνηαρ ηην ταυτότητα του Euler e j cos( ) jsin( ) k k k j X ( k) 1 2 e 1 2 cos( ) j sin( ) 1 2 cos( ) j sin( ) k j , k[0:9] k 10
11 Ιδιόηηηες διακριηού μεηαζτημαηιζμού Fourier Ιδιόηηηα διακπιηού μεηαζσημαηιζμού Fourier (DFT) Σήμα διακπιηού σπόνος xn ( ) Διακπιηόρ μεηαζσημαηιζμόρ Fourier (DFT) X( k ) Γπαμμικόηηηα c1 x1 ( n) c2 x2 ( n) c1 X1( k) c2 X 2( k) Σςμμεηπία xn ( ) * ππαγμαηικού X ( k) X (( N k)) N ζήμαηορ ππαγμαηικό ζήμα Σςμμεηπία θανηαζηικού ζήμαηορ xn ( ) θανηαζηικό ζήμα X k X N k * ( ) (( )) N Κςκλική nk 0 x(( n n0 )) μεηαηόπιζη N WN X ( k) Κςκλική x(( n)) * αναδίπλωζη N X ( k ) Κςκλική x1( n) # x2( n) X1( k) X 2( k) ζςνέλιξη 11
12 Discrete Time Fourier Transform - DTFT Ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος (DTFT) ενόρ ζήμαηορ x(n) οπίζεηαι ωρ ακολούθωρ: X ( e j ) x( n) e jn Ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος ηος ζήμαηορ x(n) ςπάπσει αν ιζσύει η ζσέζη: n n x( n) S 12
13 Discrete Time Fourier Transform - DTFT Ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος είναι πεπιοδικόρ ωρ ππορ ω με πεπίοδο 2π 13
14 Ζεσγάρια Μεηαζτημαηιζμών DTFT 14
15 Ιδιόηηηες DTFT 15
16 Απόκριζη Σστνόηηηας Ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος (DTFT) H(e jω ) ηηρ κποςζηικήρ απόκπιζηρ h(n) ονομάζεηαι απόκριζη ζστνόηηηας: H( e j ) n h( n) e jn Ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος (DTFT) X(ejω) ηηρ ειζόδος x(n) και ο μεηαζσημαηιζμόρ Fourier διακπιηού σπόνος (DTFT) Y(ejω) ηηρ εξόδος y(n) ηος θίληπος ζςνδέονηαι με ηη ζσέζη: Y(e jω )=H(e jω ) X(e jω ) 16
17 Σσζηήμαηα ζσνδεδεμένα ζε ζειρά Αν ένα ζύζηημα W(e jω )= H 1 (e jω ) X(e jω ) ζςνδεθεί ζε ζειρά με ένα ζύζηημα Y(e jω )= H 2 (e jω ) W(e jω ) ηόηε ηο ζςνολικό ζύζηημα έσει είζοδο x(n), έξοδο y(n) και απόκπιζη ζςσνόηηηαρ H(e jω )= H 1 (e jω ) H 2 (e jω ) όπος Y(e jω )= H(e jω ) X(e jω ) 17
18 Σσζηήμαηα ζσνδεδεμένα παράλληλα Αν ένα ζύζηημα W(e jω )= H 1 (e jω ) X(e jω ) ζςνδεθεί παπάλληλα με ένα ζύζηημα V(e jω )= H 2 (e jω ) X(e jω ) πποζθέηονηαρ ηιρ εξόδοςρ ηων θίληπων, δηλαδή: Y(e jω )= W(e jω ) + V(e jω ) ηόηε ηο ζςνολικό ζύζηημα έσει είζοδο x(n), έξοδο y(n) και απόκπιζη ζςσνόηηηαρ όπος Y(e jω )= H(e jω ) X(e jω ) H(e jω )= H 1 (e jω ) + H 2 (e jω ) 18
19 θμείωμα Αναφοράσ Copyright Σεχνολογικό Ίδρυμα Ηπείρου. Κωνςταντίνοσ Αγγζλθσ. Ψθφιακι Επεξεργαςία ιματοσ. Ζκδοςθ: 1.0 Άρτα, Διακζςιμο από τθ δικτυακι διεφκυνςθ: Ειςαγωγή, Διακριτόσ Ενότθτα Μεταςχηματιςμόσ 2, Σμιμα Μθχανικών Fourier- Ενότθτα Πλθροφορικισ 8, Σμιμα Σ.Ε., Μθχανικών ΣΕΙ ΗΠΕΙΡΟΤ Πλθροφορικισ - Ανοιχτά Ακαδημαϊκά Σ.Ε., ΣΕΙ ΗΠΕΙΡΟΤ - Ανοιχτά Ακαδημαϊκά Μαθήματα Μαθήματα ςτο ΤΕΙ Ηπείρου ςτο ΤΕΙ Ηπείρου 19
20 θμείωμα Αδειοδότθςθσ Σο παρόν υλικό διατίκεται με τουσ όρουσ τθσ άδειασ χριςθσ Creative Commons Αναφορά Δθμιουργοφ-Μθ Εμπορικι Χριςθ-Όχι Παράγωγα Ζργα 4.0 Διεκνζσ [1] ι μεταγενζςτερθ. Εξαιροφνται τα αυτοτελι ζργα τρίτων π.χ. φωτογραφίεσ, Διαγράμματα κ.λ.π., τα οποία εμπεριζχονται ςε αυτό και τα οποία αναφζρονται μαηί με τουσ όρουσ χριςθσ τουσ ςτο «θμείωμα Χριςθσ Ζργων Σρίτων». Ο δικαιοφχοσ μπορεί να παρζχει ςτον αδειοδόχο ξεχωριςτι άδεια να χρθςιμοποιεί το ζργο για εμπορικι χριςθ, εφόςον αυτό του ηθτθκεί. [1] 20
21 Τζλοσ Ενότητασ Επεξεργαςία: Κολοβοφ Ξανθή Άρτα,
22 Διατιρθςθ θμειωμάτων Οποιαδιποτε αναπαραγωγι ι διαςκευι του υλικοφ κα πρζπει να ςυμπεριλαμβάνει: το θμείωμα Αναφοράσ το θμείωμα Αδειοδότθςθσ τθ Διλωςθ Διατιρθςθσ θμειωμάτων το θμείωμα Χριςθσ Ζργων Σρίτων (εφόςον υπάρχει) μαηί με τουσ ςυνοδευόμενουσ υπερςυνδζςμουσ. Διακριτόσ Μεταςχηματιςμόσ Fourier- Ενότθτα 8, Σμιμα Μθχανικών Πλθροφορικισ Σ.Ε., ΣΕΙ ΗΠΕΙΡΟΤ - Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου 22
23 Σζλοσ Ενότθτασ Διακριτόσ Μεταςχθματιςμόσ Fourier 23
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 9 : Σαχφσ Μεταςχθματιςμόσ Fourier (FFT) Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 9 : Σαχφσ Μεταςχθματιςμόσ Fourier (FFT) Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 4 : Μετατροπι Αναλογικοφ ιματοσ ςε Ψθφιακό Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 4 : Μετατροπι Αναλογικοφ ιματοσ ςε Ψθφιακό Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 6 : Κβαντιςμόσ Καταςτάςεων Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικϊν
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 6 : Κβαντιςμόσ Καταςτάςεων Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικϊν
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 5 : Θεϊρθμα Shanon Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικϊν Πλθροφορικισ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 5 : Θεϊρθμα Shanon Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικϊν Πλθροφορικισ
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 3 : Παρακφρωςθ Δεδομζνων Κωνςταντίνοσ Αγγζλθσ Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικών
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 3 : Παρακφρωςθ Δεδομζνων Κωνςταντίνοσ Αγγζλθσ Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα Μθχανικών
Ψθφιακά Ηλεκτρονικά. Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 5 : Ανάλυςθ κυκλώματοσ με D και JK FLIP- FLOP Φώτιοσ Βαρτηιώτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 12 : Φίλτρα FIR με μζκοδο δειγματολθψίασ Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 12 : Φίλτρα FIR με μζκοδο δειγματολθψίασ Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου
Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 7 η : Το πρόβλημα τησ Μεταφοράσ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ Σχολι
Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 7 η : Το πρόβλημα τησ Μεταφοράσ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ Σχολι
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 9: Διαδικαςία φνκεςθσ Φϊτιοσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 9 : Διαδικαςία φνκεςθσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 9: Διαδικαςία φνκεςθσ Φϊτιοσ
Aντιπτζριςη (ΕΠ027) Ενότητα 10
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 10: Σακτικι Απλοφ τεπάν-αρκίσ Παρτεμιάν Σμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 10: Σακτικι Απλοφ τεπάν-αρκίσ Παρτεμιάν Σμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ
Aντιπτζριςθ (ΕΠ027) Ενότθτα 12
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςθ (ΕΠ027) Ενότθτα 12: Σακτικι διπλοφ μικτοφ τεπάν-αρκίσ Παρτεμιάν Σμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςθ (ΕΠ027) Ενότθτα 12: Σακτικι διπλοφ μικτοφ τεπάν-αρκίσ Παρτεμιάν Σμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 11: Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 11 : Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 11: Μετρθτζσ Ριπισ Φϊτιοσ Βαρτηιϊτθσ
Ειςαγωγή ςτη διδακτική των γλωςςών
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 2: Μζκοδοι διδαςκαλίασ I Άννα Μουτι, Α.Π.Θ & Πανεπιςτιμιο Θεςςαλίασ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 2: Μζκοδοι διδαςκαλίασ I Άννα Μουτι, Α.Π.Θ & Πανεπιςτιμιο Θεςςαλίασ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 7: Φιλολογικζσ και Λογοτεχνικζσ Εξαρτιςεισ / Το Παράδειγμα των Παραβολών Αικατερίνθ Τςαλαμποφνθ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 7: Φιλολογικζσ και Λογοτεχνικζσ Εξαρτιςεισ / Το Παράδειγμα των Παραβολών Αικατερίνθ Τςαλαμποφνθ
Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Σεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνασ Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε) Ενδεικτική επίλυςη άςκηςησ 1 Δρ. Θωμάσ Π. Μαηαράκοσ Τμιμα Ναυπθγϊν Μθχανικϊν ΤΕ Το
Ανοικτά Ακαδημαϊκά Μαθήματα Σεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνασ Ειδικζσ Ναυπηγικζσ Καταςκευζσ και Ιςτιοφόρα κάφη (Ε) Ενδεικτική επίλυςη άςκηςησ 1 Δρ. Θωμάσ Π. Μαηαράκοσ Τμιμα Ναυπθγϊν Μθχανικϊν ΤΕ Το
Οντοκεντρικόσ Προγραμματιςμόσ
 Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Templates Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικών Η/Τ & Πλθροφορικισ Templates Ειςαγωγι Templates o
Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Templates Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικών Η/Τ & Πλθροφορικισ Templates Ειςαγωγι Templates o
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 6: Παφλοσ. Ευαγγζλιο και Νόμοσ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 6: Παφλοσ. Ευαγγζλιο και Νόμοσ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αποτυπώςεισ & Τεκμηρίωςη Αντικειμζνων
 Ανοικτά Ακαδθμαϊκά Μακιματα ςτο ΤΕΙ Ιονίων Νιςων Αποτυπώςεισ & Τεκμηρίωςη Αντικειμζνων Ενότητα 3: Συγγραφι εργαςιών Το περιεχόμενο του μακιματοσ διατίκεται με άδεια Creative Commons εκτόσ και αν αναφζρεται
Ανοικτά Ακαδθμαϊκά Μακιματα ςτο ΤΕΙ Ιονίων Νιςων Αποτυπώςεισ & Τεκμηρίωςη Αντικειμζνων Ενότητα 3: Συγγραφι εργαςιών Το περιεχόμενο του μακιματοσ διατίκεται με άδεια Creative Commons εκτόσ και αν αναφζρεται
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 7: Χριςτολογία του κατά Λουκάν Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 7: Χριςτολογία του κατά Λουκάν Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 10 : χεδίαςθ Ψθφιακών Φίλτρων Γενικά Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 10 : χεδίαςθ Ψθφιακών Φίλτρων Γενικά Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότθτα 1: Οργάνωςθ μακιματοσ Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότθτα 1: Οργάνωςθ μακιματοσ Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
Διαγλωςςική Επικοινωνία
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Διαγλωςςική Επικοινωνία Ενότητα 6 : Μετάφραςθ και εκδόςεισ Ελζνθ Καςάπθ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Διαγλωςςική Επικοινωνία Ενότητα 6 : Μετάφραςθ και εκδόςεισ Ελζνθ Καςάπθ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ
Διδακτικι τθσ Γλϊςςασ Ι
 Διδακτικι τθσ Γλϊςςασ Ι Ενότθτα 1: Ειςαγωγικά Μαριάννα Κoνδφλθ Σχολι Ανκρωπιςτικϊν και Κοινωνικϊν Επιςτθμϊν Τ.Ε.Ε.Α.Π.Η. Σκοποί ενότθτασ Να καταρριφκοφν οι προεπιςτθμονικοί μφκοι για τθ γλϊςςα Να αναδειχκεί
Διδακτικι τθσ Γλϊςςασ Ι Ενότθτα 1: Ειςαγωγικά Μαριάννα Κoνδφλθ Σχολι Ανκρωπιςτικϊν και Κοινωνικϊν Επιςτθμϊν Τ.Ε.Ε.Α.Π.Η. Σκοποί ενότθτασ Να καταρριφκοφν οι προεπιςτθμονικοί μφκοι για τθ γλϊςςα Να αναδειχκεί
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότθτα 3: Κοινωνικζσ ικανότθτεσ και «ευ αγωνίηεςκαι» Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότθτα 3: Κοινωνικζσ ικανότθτεσ και «ευ αγωνίηεςκαι» Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ
Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 2: XML Δομθμζνα Ζγγραφα Ιςτοφ, Μζροσ 4 ο XPath
 Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 2: XML Δομθμζνα Ζγγραφα Ιςτοφ, Μζροσ 4 ο XPath Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχ/κών Η/Υπολογιςτών & Πλθροφορικισ Περιεχόμενα ενότθτασ
Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 2: XML Δομθμζνα Ζγγραφα Ιςτοφ, Μζροσ 4 ο XPath Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχ/κών Η/Υπολογιςτών & Πλθροφορικισ Περιεχόμενα ενότθτασ
Διαγλωςςική Επικοινωνία
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Διαγλωςςική Επικοινωνία Ενότητα 7 : Εγκυρότθτα κειμζνου πθγι και αξιολόγθςθ πολλαπλών μεταφράςεων Ελζνθ Καςάπθ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Διαγλωςςική Επικοινωνία Ενότητα 7 : Εγκυρότθτα κειμζνου πθγι και αξιολόγθςθ πολλαπλών μεταφράςεων Ελζνθ Καςάπθ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
Οντοκεντρικόσ Προγραμματιςμόσ
 Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 2: Η ΓΛΩΣΣΑ JAVA Βιβλιοκικεσ Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Πλθροφορικισ ΒΙΒΛΙΟΘΗΚΗ JAVA ΒΑΙΚΗ ΒΙΒΛΙΟΘΗΚΗ JAVA Ζνα ςφνολο κλάςεων
Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 2: Η ΓΛΩΣΣΑ JAVA Βιβλιοκικεσ Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Πλθροφορικισ ΒΙΒΛΙΟΘΗΚΗ JAVA ΒΑΙΚΗ ΒΙΒΛΙΟΘΗΚΗ JAVA Ζνα ςφνολο κλάςεων
Τεχνικό Σχζδιο - CAD
 Ανοικτά Ακαδθμαϊκά Μακιματα ςτο ΤΕΙ Ιονίων Νιςων Τεχνικό Σχζδιο - CAD Ενότητα 2: Τεχνικό Σχζδιο με τθ βοικεια Η/Υ Το περιεχόμενο του μακιματοσ διατίκεται με άδεια Creative Commons εκτόσ και αν αναφζρεται
Ανοικτά Ακαδθμαϊκά Μακιματα ςτο ΤΕΙ Ιονίων Νιςων Τεχνικό Σχζδιο - CAD Ενότητα 2: Τεχνικό Σχζδιο με τθ βοικεια Η/Υ Το περιεχόμενο του μακιματοσ διατίκεται με άδεια Creative Commons εκτόσ και αν αναφζρεται
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 9: Το ιδιαίτερο υλικό του Μτ και Λκ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 9: Το ιδιαίτερο υλικό του Μτ και Λκ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ. Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
ΘΕΡΜΟΔΤΝΑΜΙΚΗ IΙ Ενότθτα 4: Χθμικζσ αντιδράςεισ αερίων τακερά Χθμικισ Ιςορροπίασ Πρότυπθ Ελεφκερθ Ενζργεια ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 1: Ειςαγωγι - Ιςτορία ζρευνασ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 1: Ειςαγωγι - Ιςτορία ζρευνασ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 8: Διά βίου άκλθςθ για υγεία (ευκαμψία) Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 8: Διά βίου άκλθςθ για υγεία (ευκαμψία) Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ
Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ Ενότητα 6:
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ Ενότητα 6:
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 4: Στόχοι τθσ εκπαίδευςθσ Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 4: Στόχοι τθσ εκπαίδευςθσ Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 1: Περιγραφι και Λφςεισ που προτάκθκαν Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 1: Περιγραφι και Λφςεισ που προτάκθκαν Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
Aντιπτζριςη (ΕΠ027) Ενότητα 6
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 6: Backhand Overhead Clear Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 6: Backhand Overhead Clear Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων
 Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 3: υςτιματα ουρϊν αναμονισ Κακθγθτισ Γιάννθσ Γιαννίκοσ χολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Σμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ Μελζτθ ςυςτθμάτων
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 13: Πρόςλθψθ τθσ διδαςκαλίασ τθσ ΚΔ από τουσ Πατζρεσ Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 13: Πρόςλθψθ τθσ διδαςκαλίασ τθσ ΚΔ από τουσ Πατζρεσ Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό
ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 11: Το Γνωςτικό Ευαγγζλιο του Ιοφδα Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 11: Το Γνωςτικό Ευαγγζλιο του Ιοφδα Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΘΕΡΜΟΔΤΝΑΜΙΚΘ IΙ. Ενότθτα 11: Διαλυτότθτα Ιδανικά διαλφματα ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών
 ΘΕΡΜΟΔΤΝΑΜΙΚΘ IΙ Ενότθτα 11: Διαλυτότθτα Ιδανικά διαλφματα ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι o οριςμόσ του ιδανικοφ διαλφματοσ με βάςθ
ΘΕΡΜΟΔΤΝΑΜΙΚΘ IΙ Ενότθτα 11: Διαλυτότθτα Ιδανικά διαλφματα ογομών Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικών Μθχανικών κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι o οριςμόσ του ιδανικοφ διαλφματοσ με βάςθ
Ερωτήσεις επανάληψης. Ενδοκρινείς αδένες. Τμήμα Ιαηρικής Πανεπιζηήμιο Παηρών
 Ερωτήσεις επανάληψης Ενδοκρινείς αδένες Τμήμα Ιαηρικής Πανεπιζηήμιο Παηρών Υπόφυςη Ποια είδθ ορμονϊν γνωρίηετε με βάςθ τον τρόπο δράςθσ τουσ; Ποιοι είναι οι διαφορετικοί τρόποι μετάδοςθσ του ςιματοσ εντόσ
Ερωτήσεις επανάληψης Ενδοκρινείς αδένες Τμήμα Ιαηρικής Πανεπιζηήμιο Παηρών Υπόφυςη Ποια είδθ ορμονϊν γνωρίηετε με βάςθ τον τρόπο δράςθσ τουσ; Ποιοι είναι οι διαφορετικοί τρόποι μετάδοςθσ του ςιματοσ εντόσ
Ειςαγωγή ςτη διδακτική των γλωςςών
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 6: Μζκοδοι διδαςκαλίασ V Τψθλάντθσ Γεϊργιοσ, αναπλθρωτισ κακθγθτισ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 6: Μζκοδοι διδαςκαλίασ V Τψθλάντθσ Γεϊργιοσ, αναπλθρωτισ κακθγθτισ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
Κλαςικι Ηλεκτροδυναμικι
 Κλαςικι Ηλεκτροδυναμικι Ενότθτα 21: Διάδοςθ θλεκτρομαγνθτικών κυμάτων Ανδρζασ Τερηισ Σχολι Θετικών Επιςτθμών Τμιμα Φυςικισ Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ είναι να ςυνεχίςει τθν μελζτθ που αφορά τθν
Κλαςικι Ηλεκτροδυναμικι Ενότθτα 21: Διάδοςθ θλεκτρομαγνθτικών κυμάτων Ανδρζασ Τερηισ Σχολι Θετικών Επιςτθμών Τμιμα Φυςικισ Σκοποί ενότθτασ Σκοπόσ τθσ ενότθτασ είναι να ςυνεχίςει τθν μελζτθ που αφορά τθν
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 10: Θεολογία των Πράξεων των Αποςτόλων Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 10: Θεολογία των Πράξεων των Αποςτόλων Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 3 : τοιχεία Μνιμθσ flip-flop.
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 3 : τοιχεία Μνιμθσ flip-flop Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 3: τοιχεία
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 3 : τοιχεία Μνιμθσ flip-flop Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 3: τοιχεία
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 8: Θεολογία του κατά Ιωάννθν (πνευματολογία και χριςτολογία) Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 8: Θεολογία του κατά Ιωάννθν (πνευματολογία και χριςτολογία) Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 11: Ο Ματκαίοσ κι ο Λουκάσ ωσ αναγνώςτεσ του Μάρκου Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 11: Ο Ματκαίοσ κι ο Λουκάσ ωσ αναγνώςτεσ του Μάρκου Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν
Οντοκεντρικόσ Ρρογραμματιςμόσ
 Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΥΡΕΦΟΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΕΣΕΙΣ Υπερφόρτωςθ Τελεςτών Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Ρλθροφορικισ Υπερφόρτωςθ Τελεςτών
Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΥΡΕΦΟΤΩΣΗ ΤΕΛΕΣΤΩΝ, ΕΞΑΙΕΣΕΙΣ Υπερφόρτωςθ Τελεςτών Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικών Η/Υ & Ρλθροφορικισ Υπερφόρτωςθ Τελεςτών
Aντιπτζριςη (ΕΠ027) Ενότητα 5
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 5: Lift Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ Το παρόν
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 5: Lift Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ Το παρόν
Ψθφιακά Ηλεκτρονικά. Ενότθτα 7 : Ελαχιςτοποίθςθ και κωδικοποίθςθ καταςτάςεων Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 7 : Ελαχιςτοποίθςθ και κωδικοποίθςθ καταςτάςεων Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Τμιμα
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 7 : Ελαχιςτοποίθςθ και κωδικοποίθςθ καταςτάςεων Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Τμιμα
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 13: Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
Ελλθνικι Δθμοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 13 : Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Τμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 13: Άλλοι Μετρθτζσ Φϊτιοσ Βαρτηιϊτθσ
Εκκλθςιαςτικό Δίκαιο ΙΙΙ (Μεταπτυχιακό)
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Εκκλθςιαςτικό Δίκαιο ΙΙΙ (Μεταπτυχιακό) Ενότθτα 1θ: Συςτιματα χωριςμοφ κράτουσ - κρθςκευμάτων Κυριάκοσ Κυριαηόπουλοσ Άδειεσ Χριςθσ Το παρόν
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Εκκλθςιαςτικό Δίκαιο ΙΙΙ (Μεταπτυχιακό) Ενότθτα 1θ: Συςτιματα χωριςμοφ κράτουσ - κρθςκευμάτων Κυριάκοσ Κυριαηόπουλοσ Άδειεσ Χριςθσ Το παρόν
Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 5: Κανόνεσ Λογικι και Συμπεραςμόσ
 Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 5: Κανόνεσ Λογικι και Συμπεραςμόσ Ιωάννησ Χατζηλυγεροφδησ Πολυτεχνικι Σχολι Τμιμα Μθχ/κών Η/Υπολογιςτών & Πλθροφορικισ Περιεχόμενα ενότθτασ 1. Λογικι & Κανόνεσ
Αναπαράςταςθ Γνώςθσ ςτον Παγκόςμιο Ιςτό Ενότθτα 5: Κανόνεσ Λογικι και Συμπεραςμόσ Ιωάννησ Χατζηλυγεροφδησ Πολυτεχνικι Σχολι Τμιμα Μθχ/κών Η/Υπολογιςτών & Πλθροφορικισ Περιεχόμενα ενότθτασ 1. Λογικι & Κανόνεσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Ψθφιακά Ηλεκτρονικά. Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 10 : Καταχωρθτζσ Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Σμιμα Ψθφιακά Ηλεκτρονικά Ενότητα 10: Καταχωρθτζσ Φϊτιοσ
Ψθφιακι Επεξεργαςία ιματοσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 1 : Ειςαγωγι Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα Σμιμα Μθχανικϊν Πλθροφορικισ Σ.Ε. Ψθφιακι
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ψθφιακι Επεξεργαςία ιματοσ Ενότθτα 1 : Ειςαγωγι Κωνςταντίνοσ Αγγζλθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα Σμιμα Μθχανικϊν Πλθροφορικισ Σ.Ε. Ψθφιακι
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 2: Οι ςφγχρονεσ τάςεισ ςτθν ζρευνα Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 2: Οι ςφγχρονεσ τάςεισ ςτθν ζρευνα Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 9: Θεολογία του κατά Ιωάννθν (εκκλθςιολογία και εςχατολογία) Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΘΕΟΛΟΓΙΑ ΚΑΙΝΗΣ ΔΙΑΘΗΚΗΣ Ενότητα 9: Θεολογία του κατά Ιωάννθν (εκκλθςιολογία και εςχατολογία) Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 3: Μθδενικόσ Νόμοσ - Ζργο ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και των κεμελιωδϊν εννοιϊν
ΠΡΟΠΟΝΗΣΙΚΕ ΠΡΟΑΡΜΟΓΕ ΣΙ ΑΝΑΠΣΤΞΙΑΚΕ ΗΛΙΚΙΕ (555)
 ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΡΟΠΟΝΗΣΙΚΕ ΠΡΟΑΡΜΟΓΕ ΣΙ ΑΝΑΠΣΤΞΙΑΚΕ ΗΛΙΚΙΕ (555) Ενότητα 11: Παρουςιάςεισ φοιτθτών/τριών Χριςτοσ Κοτηαμανίδθσ Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΡΟΠΟΝΗΣΙΚΕ ΠΡΟΑΡΜΟΓΕ ΣΙ ΑΝΑΠΣΤΞΙΑΚΕ ΗΛΙΚΙΕ (555) Ενότητα 11: Παρουςιάςεισ φοιτθτών/τριών Χριςτοσ Κοτηαμανίδθσ Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 8: Κατά Μάρκον: Προτεραιότθτα και Πθγζσ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 8: Κατά Μάρκον: Προτεραιότθτα και Πθγζσ Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΗΡΙΟ ΠΑΙΔΟΚΑΡΔΙΟΛΟΓΙΑ Ενότητα: Φυςιολογία εμβρυϊκισ και περιγεννθτικισ κυκλοφορίασ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΗΡΙΟ ΠΑΙΔΟΚΑΡΔΙΟΛΟΓΙΑ Ενότητα: Φυςιολογία εμβρυϊκισ και περιγεννθτικισ κυκλοφορίασ Ιωάννθσ Γερμανάκθσ Επίκουροσ Κακθγθτισ Παιδιατρικισ, Πανεπιςτιμιο
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΗΡΙΟ ΠΑΙΔΟΚΑΡΔΙΟΛΟΓΙΑ Ενότητα: Φυςιολογία εμβρυϊκισ και περιγεννθτικισ κυκλοφορίασ Ιωάννθσ Γερμανάκθσ Επίκουροσ Κακθγθτισ Παιδιατρικισ, Πανεπιςτιμιο
Ειςαγωγή ςτη διδακτική των γλωςςών
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 5: Μζκοδοι διδαςκαλίασ IV Άννα Μουτι, Α.Π.Θ & Πανεπιςτιμιο Θεςςαλίασ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγή ςτη διδακτική των γλωςςών Ενότητα 5: Μζκοδοι διδαςκαλίασ IV Άννα Μουτι, Α.Π.Θ & Πανεπιςτιμιο Θεςςαλίασ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 10: Ιδιαίτερα Θεολογικά Θζματα και Μοτίβα Α : Το Μυςτικό του Μεςςία και Χριςτολογικοί Τίτλοι Αικατερίνθ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 10: Ιδιαίτερα Θεολογικά Θζματα και Μοτίβα Α : Το Μυςτικό του Μεςςία και Χριςτολογικοί Τίτλοι Αικατερίνθ
ΔΙΔΑΚΣΙΚΗ ΣΗ ΠΑΙΔΑΓΩΓΙΚΗ ΓΤΜΝΑΣΙΚΗ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΣΙΚΗ ΣΗ ΠΑΙΔΑΓΩΓΙΚΗ ΓΤΜΝΑΣΙΚΗ ΙΙ Ενότητα 9: Διδαςκαλία ακλοπαιδιϊν ςτο ςχολείο Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΣΙΚΗ ΣΗ ΠΑΙΔΑΓΩΓΙΚΗ ΓΤΜΝΑΣΙΚΗ ΙΙ Ενότητα 9: Διδαςκαλία ακλοπαιδιϊν ςτο ςχολείο Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και
Διεπαφζσ Φορητών Συςκευών
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Διεπαφζσ Φορητών Συςκευών Ενότητα: 2 θ Δ. Πολίτθσ Τμιμα Πλθροφορικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Διεπαφζσ Φορητών Συςκευών Ενότητα: 2 θ Δ. Πολίτθσ Τμιμα Πλθροφορικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 10 : Φυσιολογία φωνής (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 10 : Φυσιολογία φωνής (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
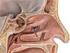 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 9 : Φυσιολογία φωνής (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 9 : Φυσιολογία φωνής (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι. Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ. ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν
 ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και και
ΘΕΡΜΟΔΤΝΑΜΙΚΗ Ι Ενότθτα 1: Βαςικά χαρακτθριςτικά τθσ Θερμοδυναμικισ ογομϊν Μπογοςιάν Πολυτεχνικι χολι Σμιμα Χθμικϊν Μθχανικϊν κοποί ενότθτασ κοπόσ τθσ ενότθτασ αυτισ είναι θ περιγραφι των οριςμϊν και και
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
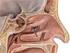 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 2 : Περιγραφή του ωτός Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 2 : Περιγραφή του ωτός Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 6 : Στοματική κοιλότητα - Φάρυγγας (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 6 : Στοματική κοιλότητα - Φάρυγγας (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα
Ψηφιακή Επεξεργασία Σημάτων
 Ψηφιακή Επεξεργασία Σημάτων Ενότητα 10: Διακριτός Μετασχηματισμός Fourier (DFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Διακριτός Μετασχηματισμός Fourier (DFT)
Ψηφιακή Επεξεργασία Σημάτων Ενότητα 10: Διακριτός Μετασχηματισμός Fourier (DFT) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μετασχηματισμός Fourier Διακριτού Χρόνου Διακριτός Μετασχηματισμός Fourier (DFT)
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 7 : Λάρυγγας (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 7 : Λάρυγγας (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 6: Συνοπτικά και θ ςχζςθ τουσ με το Ευαγγζλιο του Θωμά Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 6: Συνοπτικά και θ ςχζςθ τουσ με το Ευαγγζλιο του Θωμά Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ. DTFT και Περιοδική/Κυκλική Συνέλιξη
 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ DTFT και Περιοδική/Κυκλική Συνέλιξη Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ DTFT και Περιοδική/Κυκλική Συνέλιξη Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
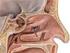 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 1 : Ακουστική οδός Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Λογοθεραπείας
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 1 : Ακουστική οδός Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Λογοθεραπείας
Γενικά Μαθηματικά Ι. Ενότητα 15: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 5 η : Η Μζθοδοσ Simplex Παρουςίαςη τησ μεθόδου Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 5 η : Η Μζθοδοσ Simplex Παρουςίαςη τησ μεθόδου Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Στερεών Αποβλιτων Ενότθτα 4: Μθχανικόσ Διαχωριςμόσ. Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών
 Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Στερεών Αποβλιτων Ενότθτα 4: Μθχανικόσ Διαχωριςμόσ Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών Mθχανικόσ Διαχωριςμόσ Διαχωριςμόσ των διαφόρων υλικών από
Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Στερεών Αποβλιτων Ενότθτα 4: Μθχανικόσ Διαχωριςμόσ Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών Mθχανικόσ Διαχωριςμόσ Διαχωριςμόσ των διαφόρων υλικών από
Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ Ενότητα 7:
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Παράγοντεσ υμμετοχήσ Ενηλίκων ςτην Εκπαίδευςη: Ζητήματα Κινητοποίηςησ και Πρόςβαςησ ςε Οργανωμζνεσ Εκπαιδευτικζσ Δραςτηριότητεσ Ενότητα 7:
Οντοκεντρικόσ Προγραμματιςμόσ
 Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Χειριςμόσ Εξαιρζςεων Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικϊν Η/Τ & Πλθροφορικισ Χειριςμόσ Εξαιρζςεων
Οντοκεντρικόσ Προγραμματιςμόσ Ενότθτα 7: C++ TEMPLATES, ΤΠΕΡΦΟΡΣΩΗ ΣΕΛΕΣΩΝ, ΕΞΑΙΡΕΕΙ Χειριςμόσ Εξαιρζςεων Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι χολι Σμιμα Μθχανικϊν Η/Τ & Πλθροφορικισ Χειριςμόσ Εξαιρζςεων
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ειςαγωγι ςτισ Μεταφραςτικζσ Σπουδζσ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγι ςτισ Μεταφραςτικζσ Σπουδζσ Ενότθτα 6 : Θεωρία τθσ μετάφραςθσ Ελζνθ Καςάπθ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Ειςαγωγι ςτισ Μεταφραςτικζσ Σπουδζσ Ενότθτα 6 : Θεωρία τθσ μετάφραςθσ Ελζνθ Καςάπθ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ
Ψθφιακά Ηλεκτρονικά. Ενότθτα 4 : Ανάλυςθ ακολουκιακϊν κυκλωμάτων με ρολόι Φϊτιοσ Βαρτηιϊτθσ
 Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 4 : Ανάλυςθ ακολουκιακϊν κυκλωμάτων με ρολόι Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
Ελλθνικι Δθμοκρατία Σεχνολογικό Εκπαιδευτικό Κδρυμα Ηπείρου Ψθφιακά Ηλεκτρονικά Ενότθτα 4 : Ανάλυςθ ακολουκιακϊν κυκλωμάτων με ρολόι Φϊτιοσ Βαρτηιϊτθσ 1 Ανοιχτά Ακαδημαϊκά Μαθήματα ςτο ΤΕΙ Ηπείρου Σμιμα
ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 10: Ψυχοκινθτικι Αγωγι Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΑΙΔΑΓΩΓΙΚΗΣ ΓΥΜΝΑΣΤΙΚΗΣ ΙΙ Ενότητα 10: Ψυχοκινθτικι Αγωγι Χατηόπουλοσ Δθμιτρθσ Σχολι Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ
Aντιπτζριςη (ΕΠ027) Ενότητα 2
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 2: Λαβι ρακζτασ Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Aντιπτζριςη (ΕΠ027) Ενότητα 2: Λαβι ρακζτασ Στεπάν-Σαρκίσ Παρτεμιάν Τμιμα Επιςτιμθσ Φυςικισ Αγωγισ και Ακλθτιςμοφ Θεςςαλονίκθσ Άδειεσ Χρήςησ
Τεχνθτι Νοθμοςφνθ. Ενότθτα 4: Στρατθγικζσ Ελζγχου Επίλυςθσ. Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχανικϊν Η/Υ & Πλθροφορικισ
 Τεχνθτι Νοθμοςφνθ Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχανικϊν Η/Υ & Πλθροφορικισ Στρατθγικζσ Ελζγχου Επίλυςθσ Στρατθγικζσ Ελζγχου Επίλυςθσ (1) Η μθ ελεγχόμενθ χριςθ τθσ αρχισ τθσ επίλυςθσ
Τεχνθτι Νοθμοςφνθ Ιωάννθσ Χατηθλυγεροφδθσ Πολυτεχνικι Σχολι Τμιμα Μθχανικϊν Η/Υ & Πλθροφορικισ Στρατθγικζσ Ελζγχου Επίλυςθσ Στρατθγικζσ Ελζγχου Επίλυςθσ (1) Η μθ ελεγχόμενθ χριςθ τθσ αρχισ τθσ επίλυςθσ
ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 9: Το Γνωςτικό Ευαγγζλιο του Φιλίππου Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 9: Το Γνωςτικό Ευαγγζλιο του Φιλίππου Αικατερίνθ Τςαλαμποφνθ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων
 Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 7: Ειςαγωγι ςτο Δυναμικό Προγραμματιςμό Κακθγθτισ Γιάννθσ Γιαννίκοσ Σχολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Τμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ
Τεχνικζσ Ανάλυςησ Διοικητικών Αποφάςεων Ενότητα 7: Ειςαγωγι ςτο Δυναμικό Προγραμματιςμό Κακθγθτισ Γιάννθσ Γιαννίκοσ Σχολι Οργάνωςθσ και Διοίκθςθσ Επιχειριςεων Τμιμα Διοίκθςθσ Επιχειριςεων Σκοποί ενότητασ
Μυκθτολογικζσ αςκζνειεσ δενδρωδϊν και αμπζλου
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Μυκθτολογικζσ αςκζνειεσ δενδρωδϊν και αμπζλου 2 θ Επανάλθψθ. Αδρομυκϊςεισ και ςιψεισ ξφλου. Αναςταςία Λαγοπόδθ Επίκ. Κακθγιτρια Φυτοπακολογίασ,
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ Μυκθτολογικζσ αςκζνειεσ δενδρωδϊν και αμπζλου 2 θ Επανάλθψθ. Αδρομυκϊςεισ και ςιψεισ ξφλου. Αναςταςία Λαγοπόδθ Επίκ. Κακθγιτρια Φυτοπακολογίασ,
ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 3: Το Ευαγγζλιο του Θωμά Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 3: Το Ευαγγζλιο του Θωμά Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ. Διακριτός Μετασχηματισμός Fourier DFT
 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ Διακριτός Μετασχηματισμός Fourier DFT Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΥΣΗ FOURIER ΔΙΑΚΡΙΤΩΝ ΣΗΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ Διακριτός Μετασχηματισμός Fourier DFT Διακριτός μετασχηματισμός συνημιτόνου DCT discrete cosine transform Η σχέση αποτελεί «πυρήνα»
ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 4: Το Πρωτευαγγζλιο του Ιακώβου Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΣΑ ΑΠΟΚΡΤΦΑ ΕΤΑΓΓΕΛΙΑ Ενότητα 4: Το Πρωτευαγγζλιο του Ιακώβου Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται ςε
Οντοκεντρικόσ Ρρογραμματιςμόσ
 Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 9: C++ ΕΙΣΟΔΟΣ - ΕΞΟΔΟΣ / ΑΛΦΑΙΘΜΗΤΙΚΑ / ΑΧΕΙΑ Διαχείριςθ Αρχείων Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικϊν Η/Υ & Ρλθροφορικισ Διαχείριςθ Αρχείων Ιεραρχία
Οντοκεντρικόσ Ρρογραμματιςμόσ Ενότθτα 9: C++ ΕΙΣΟΔΟΣ - ΕΞΟΔΟΣ / ΑΛΦΑΙΘΜΗΤΙΚΑ / ΑΧΕΙΑ Διαχείριςθ Αρχείων Ιωάννθσ Χατηθλυγεροφδθσ Ρολυτεχνικι Σχολι Τμιμα Μθχανικϊν Η/Υ & Ρλθροφορικισ Διαχείριςθ Αρχείων Ιεραρχία
Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία
 Ελληνική ημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία Ενότητα 13 : Γεωργία Ακριβείας, η Γεωργία του Μέλλοντος Επισκόπηση Μαθήματος Μελετίου Γεράσιμος 1
Ελληνική ημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία Ενότητα 13 : Γεωργία Ακριβείας, η Γεωργία του Μέλλοντος Επισκόπηση Μαθήματος Μελετίου Γεράσιμος 1
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 3: Προφορικότθτα (Ειςαγωγικά) Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΣΑ ΠΟΤΔΗ ΣΗ ΤΝΟΠΣΙΚΗ ΠΑΡΑΔΟΗ ΚΑΙ ΣΗΝ Q Ενότητα 3: Προφορικότθτα (Ειςαγωγικά) Αικατερίνθ Τςαλαμποφνθ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Σήματα και Συστήματα ΙΙ
 Σήματα και Συστήματα ΙΙ Ενότητα 2: Μετασχηματισμός Fourier Διακριτού Χρόνου (DTFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής Γεώργιος
Σήματα και Συστήματα ΙΙ Ενότητα 2: Μετασχηματισμός Fourier Διακριτού Χρόνου (DTFT) Α. Ν. Σκόδρας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Επιμέλεια: Αθανάσιος Ν. Σκόδρας, Καθηγητής Γεώργιος
Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Υγρών Αποβλιτων Ενότθτα 9: Απολφμανςθ. Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών
 Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Υγρών Αποβλιτων Ενότθτα 9: Απολφμανςθ Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών Απολφμανςθ Η εκροι που προζρχεται από πρωτοβάκμια, δευτεροβάκμια ι τριτοβάκμια
Τεχνολογία Περιβάλλοντοσ: Διαχείριςθ Υγρών Αποβλιτων Ενότθτα 9: Απολφμανςθ Κορνάροσ Μιχαιλ Πολυτεχνικι Σχολι Τμιμα Χθμικών Μθχανικών Απολφμανςθ Η εκροι που προζρχεται από πρωτοβάκμια, δευτεροβάκμια ι τριτοβάκμια
Φωνολογική Ανάπτυξη και Διαταραχές
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Φωνολογική Ανάπτυξη και Διαταραχές Ενότητα 16: Ασκήσεις Πράξης Ζακοπούλου Βικτωρία 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Λογοθεραπείας
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Φωνολογική Ανάπτυξη και Διαταραχές Ενότητα 16: Ασκήσεις Πράξης Ζακοπούλου Βικτωρία 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Λογοθεραπείας
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
