ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ
|
|
|
- Ευδοκία Σπανός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ Μεταπτυχιακό Πρόγραµµα «Ολοκληρωµένα Συστήµατα Υλικού & Λογισµικού» Μεταπτυχιακή Εργασία Θέµα: «Ανάπτυξη εξοµοιωτή σφαλµάτων για σφάλµατα µετάβασης σε ψηφιακά ολοκληρωµένα κυκλώµατα» Επιβλέπων καθηγητής: κ. Νικολός ηµήτρης Υπεύθυνος φοιτητής: Κασερίδης ηµήτρης ΑΜ: 96 Πάτρα 2006
2 - 1 -
3 Ευχαριστίες Καταρχήν οφείλω να ευχαριστήσω τον επιβλέποντα καθηγητή κ. ηµήτρη Νικολό για την συνεχή καθοδήγηση και την πολύτιµη βοήθεια του στην διεκπεραίωση της µεταπτυχιακή αυτής εργασίας. Επιπρόσθετα, ευχαριστώ τον ρ. Ε. Καλλίγερο για την καθοδήγηση, την πολύτιµη βοήθεια του και τις χρήσιµες συζητήσεις µας πάνω στα ευρύτερα θέµατα του ελέγχου ορθής λειτουργίας. Η συµβολή του ήταν καθοριστική για την πορεία και ολοκλήρωση της εργασίας αυτής. Παράλληλα µε τα προηγούµενα πρόσωπα, θέλω να ευχαριστήσω τους γονείς µου Βασίλη, έσποινα και την αδερφή µου Άννα, για την αµέριστη υποστήριξη και συµπαράσταση που µου προσφέρουν όλα αυτά τα χρόνια. Επιπλέον αυτών, ευχαριστώ όλους τους φίλους µου για την υποστήριξη και την συνεχή βοήθεια τους. Χωρίς αυτούς, η ολοκλήρωση της εργασίας αυτής θα ήταν αρκετά πιο δύσκολη και η καθηµερινότητα σίγουρα πιο βαρετή. Τέλος, ευχαριστώ τα υπόλοιπα µέλη της τριµελούς επιτροπής της εργασίας αυτής κ. X. Βέργο και κ. X. Καβουσιανό
4 Περίληψη Η µεταπτυχιακή αυτή εργασία µπορεί να χωριστεί σε δύο λογικά µέρη (Μέρος Α και Μέρος Β ). Το πρώτο µέρος αφορά τον έλεγχο ορθής λειτουργίας ψηφιακών κυκλωµάτων χρησιµοποιώντας το µοντέλο των Μεταβατικών (Transient) σφαλµάτων και πιο συγκεκριµένα περιλαµβάνει την µελέτη για το µοντέλο, τρόπο λειτουργίας και την υλοποίηση ενός Εξοµοιωτή Μεταβατικών Σφαλµάτων (Transition Faults Simulator). Ο εξοµοιωτής σφαλµάτων αποτελεί το πιο σηµαντικό µέρος της αλυσίδας εργαλείων που απαιτούνται για τον σχεδιασµό και εφαρµογή τεχνικών ελέγχου ορθής λειτουργίας και η ύπαρξη ενός τέτοιου εργαλείου επιτρέπει την µελέτη νέων τεχνικών ελέγχου κάνοντας χρήση του Μεταβατικού µοντέλου σφαλµάτων. Το δεύτερο µέρος της εργασίας συνοψίζει την µελέτη που πραγµατοποιήθηκε για την δηµιουργία ενός νέου αλγόριθµου επιλογής διανυσµάτων ελέγχου στην περίπτωση των Test Set Embedding τεχνικών ελέγχου. Ο αλγόριθµος επιτυγχάνει σηµαντικές µειώσεις τόσο στον όγκο των απαιτούµενων δεδοµένων που είναι απαραίτητο να αποθηκευτούν για την αναπαραγωγή του ελέγχου, σε σχέση µε τις κλασικές προσεγγίσεις ελέγχου, όσο και στο µήκος των απαιτούµενων ακολουθιών ελέγχου που εφαρµόζονται στο υπό-έλεγχο κύκλωµα σε σχέση µε προγενέστερους Test Set Embedding αλγορίθµους. Στο τέλος του µέρους Β προτείνεται µία αρχιτεκτονική για την υλοποίηση του αλγόριθµου σε Built-In Self-Test περιβάλλον ελέγχου ορθής λειτουργίας ακολουθούµενη από την εκτίµηση της απόδοσης αυτής και σύγκριση της µε την καλύτερη ως τώρα προτεινόµενη αρχιτεκτονική που υπάρχει στην βιβλιογραφία (Βλέπε Παράρτηµα Α)
5 Περιεχόµενα ΠΕΡΙΕΧΟΜΕΝΑ 4 1. ΜΕΡΟΣ A ΕΙΣΑΓΩΓΗ Μοντέλα σφαλµάτων Μοντέλο Μόνιµης Τιµής (Stuck-at) Μοντέλο Μεταβατικών Σφαλµάτων Μοντέλο Καθυστέρησης Μονοπατιού Μεθοδολογία Εφαρµογής ιανυσµάτων ΕΞΟΜΟΙΩΤΗΣ ΜΕΤΑΒΑΤΙΚΩΝ ΣΦΑΛΜΑΤΩΝ Σχετικές Μεθοδολογίες στην Βιβλιογραφία Μεταβατικά Σφάλµατα Stuck-open Σφάλµατα Σφάλµατα καθυστέρησης Έλεγχος για Συνδυαστικά Μεταβατικά Σφάλµατα Μεταβατικοί Έλεγχοι Ενεργά Μεταβατικά Μονοπάτια και Παθητικά Μεταβατικά Μονοπάτια Επαγωγικοί Κανόνες ιάδοσης Λιστών Σφαλµάτων Παραγωγή ιανυσµάτων Καθυστέρησης µε Χρήση Τ-Μονοπατιών ΧΡΗΣΗ ΚΑΙ ΥΛΟΠΟΙΗΣΗ ΕΞΟΜΟΙΩΤΗ υνατότητες του Εξοµοιωτή Τρόπος Χρήσης Εξοµοιωτή Βασικός Τρόπος Εκτέλεσης Συνοδευτικά Αρχεία Εισόδου 34 Απαραίτητα αρχεία Αρχείο διανυσµάτων ελέγχου 34 Προαιρετικά αρχεία Αρχείο δήλωσης υπό εξέταση σφαλµάτων Αρχείο Εξόδου Παράµετροι Εκτέλεσης Εξοµοιωτή t - καθορισµός αρχείου εισόδου διανυσµάτων ελέγχου f - επιλογή αρχείου καθορισµού των υπό εξέταση σφαλµάτων ο - επιλογή αρχείου αποθήκευσης ανιχνευµένων σφαλµάτων gf επιλογή αρχείου αποθήκευσης συνολικών ανιχνευµένων σφαλµάτων v - επιλογή φλύαρης λειτουργίας (verbose mode) h - επιλογή βοηθητικής λειτουργίας ΈΝΑ ΑΠΛΟ ΠΑΡΑ ΕΙΓΜΑ Αρχεία Εισόδου 42 Περιγραφή κυκλώµατος 42 Αρχείο διανυσµάτων ελέγχου
6 Αρχείο υπό εξέτασης λίστας µεταβατικών σφαλµάτων Εκτέλεση και Αποτελέσµατα 44 Παράδειγµα πλήρης εξοµοίωσης 44 Παράδειγµα επιλεκτικής-µερικής εξοµοίωσης ΜΕΡΟΣ Β Εισαγωγή Built-In Self-Test (BIST) Linear Feedback Shift Register (LFSR) Multiple Input Signature Register (MISR) Phase Shifter Scan Έλεγχος Ορθής Λειτουργίας Scan Αλυσίδα Πλεονεκτήµατα Μειονεκτήµατα Scan Αρχιτεκτονικής SEED-SELECTION ΑΛΓΟΡΙΘΜΟΣ Βασική Ιδέα Αλγορίθµου Ευρετικά Κριτήρια Επιλογής Επίλυσης Συστήµατος ΤΕΧΝΙΚΗ ΜΕΙΩΣΗΣ ΑΚΟΛΟΥΘΙΩΝ ΕΛΕΓΧΟΥ Αλγόριθµος Τµηµατοποίησης Παραθύρων Τεχνική Αναδιάταξης Παραθύρων Προτεινόµενη Αρχιτεκτονική ΕΚΤΙΜΗΣΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΣΥΓΚΡΙΣΕΙΣ Επιλογή Μεγέθους του κάθε Παραθύρου Απόδοση Προτεινόµενης Τεχνικής Αποτελέσµατα Σύγκρισης Προτεινόµενης Τεχνικής ΒΙΒΛΙΟΓΡΑΦΙΑ 84 Α. ΠΑΡΑΡΤΗΜΑ 87 Α.1 Εισαγωγή 87 Α.2 Περιγραφή Τεχνικής 88 Α.3 Αποσυγκρότηση των Care Bits 93 Α.5 Σύνοψη
7 Α Μέρος 1. Μέρος A 1.1 ΕΙΣΑΓΩΓΗ Ο κύριος στόχος του παραδοσιακού ελέγχου ορθής λειτουργίας εδώ και δεκαετίες είναι η παροχή υψηλού επιπέδου καλυψηµότητας σφαλµάτων ( Fault Coverage) χρησιµοποιώντας το µοντέλο µόνιµης τιµής (Stuck-at Fault). Παρόλα αυτά, η παρουσία τυχαίων ελαττωµάτων στα σύγχρονα κυκλώµατα, που επηρεάζουν παροδικά την ορθή λειτουργία τους ή τροποποιούν ελαφρά τις παραµέτρους λειτουργίας τους (π.χ. ταχύτητα διάδοσης λογικής τιµής, κατανάλωση ισχύος, ρεύµατα διαρροής), επηρεάζουν την ορθή λειτουργία των κυκλωµάτων µόνο κατά την χρήση τους σε υψηλές συχνότητες χρονισµού ενώ αντίθετα σε χαµηλότερες συχνότητες τα ελαττώµατα αυτά κρύβονται. Αυτό το είδος ελαττωµάτων καλούνται ελαττώµατα καθυστέρησης (Delay faults). Με την συνεχή τάση για χρήση µικρότερων διαστάσεων τρανζίστορ και µετάλλων και την παράλληλη αύξηση της συχνότητας λειτουργίας των ολοκληρωµένων η παρουσία αυτών των ελαττωµάτων γίνεται σταδιακά εντονότερη. Η υιοθέτηση τεχνικών και κατά επέκταση δηµιουργία µοντέλων για την αποτελεσµατική ανίχνευση τέτοιων σφαλµάτων είναι µονόδροµος για την βιοµηχανία έτσι ώστε να διατηρηθεί το απαιτούµενο από την αγορά, υψηλό επίπεδο ορθότητας των ολοκληρωµένο και τα επέκταση ποιότητας αυτών. Ο σκοπός του ελέγχου για σφάλµατα καθυστέρησης είναι η επιβεβαίωση ότι ο εκάστοτε σχεδιασµός υλοποιηµένος σε µία συγκεκριµένη τεχνολογία λειτουργεί σωστά στην επιθυµητή από τον σχεδιαστή συχνότητα χρονισµού. Ήδη στην βιβλιογραφία έχει αποδειχθεί ότι η χρήση του απλού stuck-at µοντέλου είναι ικανή να ανιχνεύσει µόνο ένα µικρό ποσοστό αυτών των σφαλµάτων και έτσι η υιοθέτηση ενός νέου εµπλουτισµένου µοντέλου είναι αναγκαία. Στο παρελθόν ο έλεγχος ορθής λειτουργίας στηριζόταν βασικά µόνο σε χρήση διανυσµάτων ελέγχου που είχαν σαν στόχο την επιβεβαίωση της λειτουργικής ορθότητας του σχεδιασµού. Η εφαρµογή όµως των διανυσµάτων αυτών σε
8 Κεφάλαιο 1 Εισαγωγή Μέρους Α 7 σύγχρονους σχεδιασµούς, υψηλών ταχυτήτων, για την ανίχνευση σφαλµάτων καθυστέρησης είναι δύσκολη έως αδύνατη διότι απαιτείται η εφαρµογή ενός τεράστιου όγκου δεδοµένων σε ρυθµό παραπλήσιο της συχνότητας λειτουργίας. Παράλληλα, η λογική χρήσης scan αλυσίδων επιδεινώνει το πρόβληµα αφού πρέπει η εισαγωγή των διανυσµάτων ελέγχου από ένα εξωτερικό µηχανισµό ελέγχου (Automatic Test Equipment ATE) να πραγµατοποιηθεί µε πολλαπλάσιο ρυθµό ώστε να γίνει at-seed έλεγχος ορθής λειτουργίας. Όλα τα παραπάνω θέτουν µία σηµαντική πολυπλοκότητα στις ΑΤΕ µηχανές και αυξάνουν υπέρογκα το κόστος τους επιδεικνύοντας παράλληλα την ανάγκη για υιοθέτηση ευριστικών τεχνικών και µεθοδολογιών που θα καταστήσουν την εφαρµογή διανυσµάτων ελέγχου για µεταβατικά σφάλµα εφικτή. 1.2 Μοντέλα σφαλµάτων Οι φυσικές αποτυχίες και τα κατασκευαστικά ελαττώµατα που µπορούν να υπάρξουν σε ένα ολοκληρωµένο µπορούν µόνο να µοντελοποιηθούν για λογικά σφάλµατααφού η µαθηµατική τους µοντελοποίηση είναι πάρα πολύ δύσκολη. Τα λογικά αυτά σφάλµατα µπορούν να χωριστούν σε δοµικά σφάλµατα (Structural Faults), που περιλαµβάνουν τα σφάλµατα σχετικά µε την κατασκευή του κάθε συστήµατος, και τα λειτουργικά σφάλµατα (Functional Faults) που είναι σχετικά µε την λειτουργία του συστήµατος. Ο έλεγχος για λειτουργικά σφάλµατα επιβεβαιώνει την σωστή λειτουργία του συστήµατος έχοντας όµως την έννοια της σωστή µετάφρασης / µετάβασης της περιγραφής του κυκλώµατος µέσω των διαφόρων βηµάτων ανάπτυξης του και επιπέδων αναπαράστασης ( φυσικό επίπεδο, τρανζιστορ, RTL κ.τ.λ). Αντίθετα, ο έλεγχος για δοµικά σφάλµατα στοχεύει καθαρά στα κατασκευαστικά ελαττώµατα του ολοκληρωµένου θεωρώντας ότι η τελική περιγραφή του συστήµατος είναι σύµφωνη µε τις αρχικές προδιαγραφές. Στην εργασία αυτή οι όροι λάθος, σφάλµα, ελάττωµα αναφέρονται καθαρά σε κατασκευαστικά λάθη και σε αυτά επικεντρώνεται η προσοχή Αναλύοντας προσεκτικότερα τις επιπτώσεις που µπορεί να έχουν όλα τα δυνατά κατασκευαστικά λάθη, κάποιος µπορεί να τα κατηγοριοποιήσει σε αυτά που επηρεάζουν µόνιµα την ορθή λειτουργία του συστήµατος, οδηγώντας σε λανθασµένες αποκρίσεις και σε αυτά που τα αποτελέσµατα τους έχουν µία χρονική / προσωρινή
9 Κεφάλαιο 1 Εισαγωγή Μέρους Α 8 επίπτωση στο σύστηµα. Σαν βασικός εκπρόσωπος της πρώτης κατηγορίας έχει καθιερωθεί το µοντέλο σφαλµάτων µόνιµης τιµής (Stuck-at fault model). Αντίθετα µε αυτό, τα φυσικά ελαττώµατα που µπορούν να προκαλέσουν την αύξηση της καθυστέρησης διάδοσης της τιµή ενός σήµατος µπορούν να µοντελοποιηθούν µε τα ονοµαζόµενα µοντέλα καθυστέρησης (Delay Faults). Αξίζει να σηµειωθεί ότι ο ορισµός και των δύο µοντέλων σφαλµάτων έχει λάβει µέρος σχετικά νωρίς στην ιστορία του ελέγχου ορθής λειτουργίας και γενικά της επιστήµης των υπολογιστών και περίπου την ίδια χρονική περίοδο αλλά για λόγους που θα επισηµανθούν στην συνέχεια το δε πρώτο έχει καθιερωθεί και χρησιµοποιείται εδώ και χρόνια από την βιοµηχανία ενώ το δεύτερο πρακτικά ακόµα δεν έχει εισαχθεί σε σηµαντικές γραµµές παραγωγής ολοκληρωµένων κυκλωµάτων. Υπάρχουν δύο γενικές κατηγορίες τέτοιων µοντέλων, το µοντέλο καθυστέρησης πύλης (Gate delay fault model) [1,2,3,4] και το µοντέλο καθυστέρησης µονοπατιού (Path delay fault model) [5,6]. Παρόλο που το path delay fault model θεωρείται γενικά πιο ρεαλιστικό και αποτελεσµατικό στην µοντελοποίηση των φυσικών ελαττωµάτων που προκαλούν καθυστέρηση στην διάδοση των σηµάτων, είναι επίσης και πιο δύσκολο να χρησιµοποιηθεί στην πράξη εξαιτίας κυρίως της µεγάλης πολυπλοκότητας που εισάγει στην ανάλυση των µεγάλων κυκλωµάτων, αφού σε αυτά περιλαµβάνεται ένας τεράστιος αριθµός από διαφορετικά µονοπάτια. Για τον λόγο αυτό, το gate delay fault model είναι κατά κόρων το fault model που προτιµάται στην βιοµηχανία αλλά και στην βιβλιογραφία. Το πιο κοινά αποδεκτό τέτοιο µοντέλο που χρησιµοποιείται είναι το µοντέλο µεταβατικών σφαλµάτων (transition fault mode) [1]. Στις επόµενες ενότητες αναλύεται τα κάθε µοντέλο σφαλµάτων ξεχωριστά, δίνοντας περισσότερη βαρύτητα στο Μοντέλο Μεταβατικών σφαλµάτων διότι είναι αυτό που θα χρησιµοποιηθεί στην συνέχεια της παρούσας εργασίας Μοντέλο Μόνιµης Τιµής (Stuck-at) To µοντέλο µόνιµης τιµής ή αλλιώς γνωστό στην βιβλιογραφία ως stuck-at µοντέλο σφαλµάτων [7] ακολουθεί την απλή παραδοχή ότι σε ένα κατασκευασµένο κύκλωµα, ελαττώµατα είναι δυνατόν να εµφανιστούν µόνο στην διασύνδεση των επιµέρους λειτουργικών κοµµατιών που το συνθέτουν, θεωρώντας τα λειτουργικά κοµµάτια αυτά απαλλαγµένα από κάθε φυσικό ελάττωµα µετά την κατασκευή τους
10 Κεφάλαιο 1 Εισαγωγή Μέρους Α 9 επάνω σε ένα ολοκληρωµένο. Στην απλούστερη περίπτωση, τα λειτουργικά κοµµάτια είναι οι πύλες και η διασύνδεση είναι τα κοµµάτια αγωγού που διασυνδέουν φυσικά τις πύλες αυτές. Παλαιότερα είχαν µελετηθεί στην βιβλιογραφία και µοντέλα µόνιµης τιµής που τα λειτουργικά κοµµάτια ήταν τα τρανζίστορ και η διασύνδεση περιλάµβανε ακόµα και τα κοµµάτια αγωγού που διασυνδέαν τα τρανζίστορ αυτά µέσα σε µία πύλη. Με την πάροδο του χρόνου κυριάρχησε η απλούστερη µορφή για την απλότητα της και εξαιτίας του γεγονότος ότι τα οφέλη αναλυτικότερη µορφή δεν Παρόλο που η παραδοχή αυτή φαίνεται ότι δεν είναι αρκετά ισχυρή ώστε το µοντέλο αυτό σφαλµάτων να προσεγγίζει την πραγµατική συµπεριφορά των κυκλωµάτων, µελέτες έχουν δείξει ότι το απλό, κατά τα άλλα µοντέλο, αυτό µοντέλο είναι ιδιαίτερα αποτελεσµατικό στο να συλλαµβάνει µία ευρεία περιοχή ελαττωµάτων κατασκευασµένων ολοκληρωµένων. Έτσι το µοντέλο µόνιµης τιµής µπορεί να αναπαραστήσει σφάλµατα που προκαλούνται από ανοικτούς αγωγούς,αγωγούς που είναι µόνιµα συνδεδεµένοι στην παροχή ή στην γείωση, τρανζίστορ που άγουν πάντα ή ποτέ, αλλά και γενικά οποιαδήποτε εσωτερικά σε µια πύλη ελαττώµατα που έχουν ως αποτέλεσµα κάποια σήµατα του ενός κυκλώµατος να παραµένουν σε µία µόνιµη τιµή ανεξαρτήτως των διεγέρσεων που εφαρµόζονται στις εισόδους του κυκλώµατος αυτού. Για την εφαρµογή του ελέγχου αυτού απαιτούνται δύο βασικά βήµατα. Το πρώτο βήµα είναι να δηµιουργηθεί ένα διάνυσµα ελέγχου που όταν εφαρµοστεί στις κατάλληλες κύριες εισόδους του κυκλώµατος αυτό θα διεγείρει το επιθυµητό σφάλµα µέσα στο κύκλωµα. Το δεύτερο βήµα είναι επιλεγούν οι κατάλληλες τιµές για τις εναποµείναντες κύριες εισόδους που να εξασφαλίζουν ότι η λανθασµένη απόκριση του κυκλώµατος θα διαδοθεί προς τις κύριες εξόδους του κυκλώµατος ή σε κάποιο scan flip flop στην περίπτωση ακολουθιακού κυκλώµατος. Εξαιτίας τις απλότητας του µοντέλου αλλά και της ευκολίας που υπάρχει, όπως θα φανεί και στις επόµενες παραγράφους, για την δηµιουργία και αποθήκευση των διανυσµάτων ελέγχου για αυτό, το µοντέλο µόνιµης τιµής είναι το πλέον διαδεδοµένο µοντέλο σφαλµάτων και χρησιµοποιείται σχεδόν παντού πλέον την βιοµηχανία για τον έλεγχο ορθής λειτουργίας,
11 Κεφάλαιο 1 Εισαγωγή Μέρους Α Μοντέλο Μεταβατικών Σφαλµάτων Η βασική ιδέα του µεταβατικού µοντέλου σφαλµάτων [1] είναι παρόµοια µε αυτή του µοντέλου µόνιµης τιµής. Η ύπαρξη ενός τέτοιου σφάλµατος σε κάποιο κόµβο του κυκλώµατος έχει σαν αποτέλεσµα µία νόµιµη µετάβαση της τιµή του σήµατος στον κόµβο αυτό να µην φτάνει σε κάποιο scan flip-flop ή σε µία κύρια έξοδο µέσα στον αναµενόµενο χρόνο, µε αποτέλεσµα η δειγµατοληπτειµένη τιµή µε βάση το ρολόι του συστήµατος να είναι λανθασµένη. Αξίζει να σηµειωθεί ότι µετά από κάποιο χρονικό διάστηµα η τιµή στον κόµβο εξόδου / παρατήρησης µπορεί να πάρει την σωστή αναµενόµενη τιµή αλλά αυτή η σωστή τιµή δεν µπορεί να επηρεάζει την λανθασµένη κατάσταση που δηµιουργήθηκε και έχει διαδοθεί στην υπόλοιπη λογική του σχεδιασµού. Παράλληλα µε τα παραπάνω, το µοντέλο αυτό περιλαµβάνει και τις περιπτώσεις που η τελική σωστή τιµή απαιτεί άπειρο χρόνο να φτάσει στον τελικό κόµβο (µε αποτέλεσµα να µην γίνεται πρακτικά ποτέ η µετάβαση) περιλαµβάνοντας κατά τον τρόπο αυτό και τα σφάλµατα µόνιµης τιµής. Σύµφωνα µε το µοντέλο αυτό [1] υπάρχουν δύο δυνατά σφάλµατα σε κάθε κόµβο του κυκλώµατος: το slow-to-rise σφάλµα (0 1) και το slow-to-fall σφάλµα (1 0). Η ύπαρξη ενός slow-to-rise σφάλµατος σε έναν κόµβο σηµαίνει ότι µία οποιαδήποτε µετάβαση από το 0 στο 1 στον κόµβο δεν παράγει το σωστό τελικό αποτέλεσµα όταν το κύκλωµα δουλεύει στην κανονική συχνότητα λειτουργίας του. Οµοίως ισχύει για το slow-to-fall κατά το οποίο µία οποιαδήποτε µετάβαση από το 1 στο 0 στον κόµβο αυτό οδηγεί σε λάθος αποτελέσµατα. Σε ένα κύκλωµα µπορούµε να ορίσουµε σαν χρονικό διάστηµα καθυστέρησης (slack) για ένα δεδοµένο µονοπάτι την διαφορά µεταξύ της περιόδου του ρολογιού λειτουργίας κατά την οποία οι έξοδοι του «κλειδώνονται» / δειγµατοληπτούνται,και την καθυστέρηση διάδοσης των τελικών σωστών / αναµενόµενων τιµών πάνω στο δεδοµένο αυτό µονοπάτι. Ένα σφάλµα µετάβασης για να προκαλέσει κάποιο παρατηρήσιµο σφάλµα που να οδηγεί σε λανθασµένο «κλείδωµα» / δειγµατοληψία θα πρέπει να είναι τέτοιου µεγέθους που ο χρόνος διάδοσης της σωστής τιµή να ξεπερνάει το slack αυτό χρονικό διάστηµα. Για να είναι εφικτή η µελέτη των κυκλωµάτων µε το µοντέλο αυτό, γίνεται η παραδοχή ότι για όλα τα µονοπάτια που περνάνε από τον κόµβο που παρουσιάζει ένα µεταβατικό σφάλµα, η καθυστέρηση διάδοσης τους ξεπερνάει το µέγιστο επιτρεπτό χρονικό διάστηµα slack. Η προσέγγιση αυτή είναι γνωστή στην βιβλιογραφία ως gross delay fault.
12 Κεφάλαιο 1 Εισαγωγή Μέρους Α 11 Κάνοντας χρήση αυτή της θεώρησης, είναι δυνατόν µε χρήση / εφαρµογή ενός ζεύγους διανυσµάτων ελέγχου {V 1, V 2 } να γίνει ο έλεγχος για την ύπαρξη ενός µεταβατικού σφάλµατος. Για να ισχύει κάτι τέτοιο θα πρέπει να λαµβάνουν χώρο τα παρακάτω: 1. Όταν οι είσοδοι του κυκλώµατος αλλάζουν από V 1 σε V 2 το slow-to-rise (slow-to-fall) σφάλµα ενεργοποιείται µε µία 1 0 (0 1) µετάβαση 2. Το V 2 είναι διάνυσµα δοκιµής για το stuck-at-0 (stuck-at-0) σφάλµα Για την παραγωγή ενός ζεύγους διανύσµατος δοκιµής απαιτούνται συνολικά δύο βήµατα. Στο πρώτο βήµα πρέπει να βρεθεί το ζεύγος διανυσµάτων που ενεργοποιεί το σφάλµα στόχο δηµιουργώντας την επιθυµητή µετάβαση στον συγκεκριµένο κόµβο στόχο για τον οποίο είναι επιθυµητό να γίνει ο έλεγχος. Το δεύτερο βήµα είναι να εξασφαλιστεί η διάδοση του αποτελέσµατος του σφάλµατος σε µία παρατηρήσιµη έξοδο µέσω της κατάλληλης ενεργοποίησης όλων των κόµβων του κυκλώµατος που µεσολαβούν από τον κόµβο µέχρι της έξοδο αυτή. Τα σφάλµατα αυτά αν τα συγκρίνουµε µε τα αντίστοιχα του stuck-at µοντέλου θα δούµε ότι η µόνη διαφορά είναι ότι χρειαζόµαστε ένα επιπλέον διάνυσµα για να θέσουµε τον κόµβο στην αρχική επιθυµητή τιµή πριν την εφαρµογή του δεύτερου διανύσµατος. Αξίζει να σηµειωθεί όµως ότι η καλυψηµότητα που επιτυγχάνεται από το µεταβατικό µοντέλο δεν είναι η ίδια µε την αντίστοιχη που επιτυγχάνεται αν εφαρµοστούν τα stuck-at απλά διανύσµατα δοκιµής. Για µία αναλυτική εξήγηση της διαφοράς αυτής και γιατί αυτή προκαλείται ο αναγνώστης µπορεί να ανατρέξει στην εργασία [8] Μοντέλο Καθυστέρησης Μονοπατιού Σε αντίθεση µε το µεταβατικό µοντέλο, το οποίο θεωρεί µόνο τοπικές καθυστερήσεις σε κάθε πύλη κατά την διάδοση των τιµών των σηµάτων από τις εισόδους της πύλης προς τις εξόδους αυτής, το µοντέλο καθυστέρησης µονοπατιού λαµβάνει υπόψιν την συνολική καθυστέρηση που λαµβάνει χώρο σε ένα µονοπάτι. Γενικά, είναι εύκολα αντιληπτό ότι οι µεµονωµένες καθυστερήσεις σε κάθε ξεχωριστή πύλη ενός µονοπατιού µπορεί να είναι τέτοιες που να βρίσκονται εντός των προδιαγραφών που έχουν τεθεί κατά την θέσπιση των προδιαγραφών του
13 Κεφάλαιο 1 Εισαγωγή Μέρους Α 12 σχεδιασµού ενώ αντίθετα η συνολική συσσωρευτική καθυστέρηση πάνω στο µονοπάτι, το οποίο αποτελείται από τις ίδιες πύλες, να είναι τέτοια που τελικά να οδηγεί σε λανθασµένη δειγµατοληψία των τιµών εξόδου, ξεπερνώντας την περίοδο του λειτουργικού χρονισµού. υστυχώς, αν και η µελέτη κάθε µονοπατιού ξεχωριστά οδηγεί σε ακριβέστερα και ρεαλιστικότερα αποτελέσµατα, η πολυπλοκότητα µελέτης κάθε µονοπατιού αυξάνεται σηµαντικά. Ενδεικτικά, αν ένα µονοπάτι έχει n κόµβους τότε µπορεί να έχει µόνο 2n µεταβατικά σφάλµατα αλλά µέχρι και n 2 σφάλµατα καθυστέρησης µονοπατιού [9]. Αυτό σηµαίνει ότι η πολυπλοκότητα αυξάνεται εκθετικά µε το µέγεθος του κυκλώµατος και έτσι είναι απαραίτητες αποδοτικές τεχνικές για την εύρεση των κρίσιµων µονοπατιών που περιορίζοντας την αναζήτηση µόνο σε αυτά τα µονοπάτια. Οι απαιτήσεις αυτές κάνουν την χρήση του µοντέλου καθυστέρησης µονοπατιού αρκετά πολύπλοκη και δαπανηρή για τις εταιρίες και για το λόγο αυτό το απλούστερο µεταβατικό µοντέλο σφαλµάτων έχει κυριαρχήσει [10][11] έναντι αυτού, για την ανίχνευση σφαλµάτων καθυστέρησης. 1.3 Μεθοδολογία Εφαρµογής ιανυσµάτων Στην βιβλιογραφία έχουν προταθεί τρεις διαφορετικοί τρόποι για την εφαρµογή των διανυσµάτων ελέγχου µεταβατικών σφαλµάτων. Οι τρεις αυτοί τρόποι είναι: Broad-side delay test [12], Skewed load transition testing και τέλος Enhancedscan transition testing κάνοντας χρήση του hold-scan κελιού για την scan αλυσίδα [13]. Η πρώτη µεθοδολογία είναι αλλιώς γνωστή ως launch-from-capture τεχνική κατά την οποία το πρώτο διάνυσµα από το απαραίτητο ζεύγος εισάγεται σειριακά στην στις αλυσίδα ενώ το δεύτερο διάνυσµα θεωρείται ότι είναι η απόκριση του συνδυαστικού κυκλώµατος µετά την εφαρµογή του πρώτου. Η απόκριση ενός ακολουθιακού κυκλώµατος ως γνωστόν αποθηκεύεται στην scan αλυσίδα ώστε αυτή να µπορεί να παρατηρηθεί εξάγοντας της σειριακά προς τον µηχανισµό εφαρµογής του ελέγχου. Είναι προφανές ότι σύµφωνα µε την τεχνική αυτή είναι δύσκολο να καλυφτούν όλα τα δυνατά ζεύγη διανυσµάτων ελέγχου αφού πρέπει η συνδυαστική λογική να είναι τέτοια που να δίνει την αντίστοιχες-επιθυµητές αποκρίσεις. Το σηµαντικό πλεονέκτηµα της µεθοδολογίας αυτής είναι ότι ο όγκος των δεδοµένων που εισάγονται στην σειριακή scan αλυσίδα και τελικά πρέπει να αποθηκευτούν είτε
14 Κεφάλαιο 1 Εισαγωγή Μέρους Α 13 τοπικά στο κύκλωµα (BIST) είτε στον µηχανισµό ελέγχου (πληρώνοντας όµως το κόστος και την πολυπλοκότητα για την µεταφορά τους προς το κύκλωµα) είναι ο ίδιος µε το stuck-at µοντέλο σφαλµάτων. Σύµφωνα µε την δεύτερη τεχνική που είναι αλλιώς γνωστή ως launch-from-shift technique. τα δύο διανύσµατα ελέγχου που απαρτίζουν το επιθυµητό ζεύγος πρέπει να εισάγονται και τα δύο σειριακά στην scan αλυσίδα. Εάν η scan αλυσίδα έχει µήκος Ν κελιά, τότε στους Ν πρώτους κύκλους εισάγεται το πρώτο διάνυσµα. Στο σηµείο αυτό πρέπει να επισηµανθεί ότι το κάθε διάνυσµα που εισάγεται σειριακά την scan αλυσίδα στην ουσία εφαρµόζεται και στο συνδυαστικό κύκλωµα υπό έλεγχο αφού συνήθως για οικονοµία υλικού, χώρου και πολυπλοκότητας η αλυσίδα δεν αποµονώνεται από το συνδυαστικό κύκλωµα. Για τον λόγο αυτό, στο τέλος του Ν-1 κύκλο ρολογιού σειριακής εισαγωγής του πρώτου διανύσµατος αυτό θεωρείται ότι εφαρµόζεται στο κύκλωµα. Με τον επόµενο κύκλο ρολογιού εφαρµόζεται το δεύτερο διάνυσµα του ζεύγους που στην ουσία είναι το πρώτο µετατοπισµένο κατά µία θέση και έχοντας εισάγει ένα νέο δυαδικό ψηφίο στο πρώτο κελί. Αµέσως ακολουθεί έναν κύκλος capture για γίνει να συλληφθεί η απόκριση του κυκλώµατος αµέσως µετά την εφαρµογή του ζεύγους διανυσµάτων. Τα πλεονεκτήµατα της µεθόδου αυτής είναι ότι, όπως και στην περίπτωση της προηγούµενης µεθόδου, έχει αρκετά µικρότερο απαιτούµενο όγκο δεδοµένων και ότι η εφαρµογή των δύο διανυσµάτων γίνεται σε δύο διαδοχικούς κύκλος ρολογιού ικανοποιώντας έτσι την απαίτηση για όσο το δυνατόν µικρότερη καθυστέρηση µεταξύ της εφαρµογής των δύο διανυσµάτων. Είναι προφανές όµως ότι ο χώρος αναζήτησης των διανυσµάτων ελέγχου περιορίζεται από την οργάνωση της αλυσίδας και τις εισόδους που συνδέεται το κάθε κελί της scan αλυσίδας. Συνεπώς, ορισµένα διανύσµατα ελέγχου είναι δυνατόν να µην µπορούν να εφαρµοστούν στο κύκλωµα για µία δεδοµένη οργάνωση αλυσίδας. Προφανώς, διαφορετικές οργανώσεις της αλυσίδας ίσως µπορεί να οδηγήσουν σε καλύτερα αποτελέσµατα, όµως και µόνο η ανάγκη για έλεγχο και αλλαγή της οργάνωσης εισάγει µία σηµαντική πολυπλοκότητα στον σχεδιασµό του ελέγχου ορθής λειτουργίας ενώ ευριστικά κριτήρια που να «οδηγούν» την αναζήτηση κρίνονται απαραίτητα για την αποφυγή χρήσης brute forge λογικής αναζήτησης. Η τελευταία τεχνική, Enhanced-scan transition testing, ακολουθεί µια διαφορετική λογική που προσφέρει µεγαλύτερη ευελιξία σε σχέση µε τις δύο προηγούµενες τεχνικές. Σύµφωνα µε αυτήν, το πρώτο διάνυσµα εισάγεται σειριακή στην αλυσίδα και τελικά, όταν τελειώσει η εισαγωγή, εφαρµόζεται στο κύκλωµα. Η
15 Κεφάλαιο 1 Εισαγωγή Μέρους Α 14 εισαγωγή και εφαρµογή αυτή στη ουσία πραγµατοποιεί την αρχικοποίηση του κυκλώµατος υπό έλεγχο σε µία δεδοµένη αρχική κατάσταση, όπως ακριβώς απαιτεί η λογική του µεταβατικού µοντέλο σφαλµάτων. Στην συνέχεια το δεύτερο διάνυσµα εισάγεται στην αλυσίδα κατά την ίδια λογική. Το σηµαντικό σηµείο για την σωστή λειτουργία της τεχνική είναι η αρχικοποίηση του κυκλώµατος µε το πρώτο διάνυσµα να µην χαθεί και την εισαγωγή του δεύτερου διανύσµατος αλλά να διατηρηθεί, κρατώντας µε τον τρόπο αυτό το κύκλωµα στην δεδοµένη αρχική κατάσταση. Για την επίτευξη αυτής της λειτουργίας είναι αναγκαία η τροποποίηση του κλασικού κελιού που χρησιµοποιείται στην scan αλυσίδα χρησιµοποιώντας τον Hold-scan σχεδιασµό που παρουσιάζεται στην εργασία [13]. Για την χρήση του κελιού αυτού απαιτείται περισσότερη λογική και επιπλέον διασύνδεση ενώ µπορεί να οδηγήσει και σε αύξηση της περιόδου του χρονισµού εφαρµογής του ελέγχου διότι η scan αλυσίδα αποτελεί συνήθως το κρίσιµο µονοπάτι τουλάχιστον για το κύκλωµα εφαρµογής του ελέγχου. Έτσι, παρόλο που το πλεονέκτηµα της ευελιξία που προσφέρει είναι σηµαντικό, η τεχνική πολλές φορές δεν είναι χρήσιµη σε πραγµατικές εφαρµογές που η πολυπλοκότητα και το κόστος αποτελούν τα σηµαντικότερα κριτήρια αξιολόγησης για την υιοθέτηση µία τεχνικής ελέγχου.
16 2 ο Εξοµοιωτής Μεταβατικών Σφαλµάτων 2. Εξοµοιωτής µεταβατικών σφαλµάτων Στο κεφάλαιο αυτό παρουσιάζεται η θεωρία πίσω από τον εξοµοιωτή µεταβατικών σφαλµάτων που αναπτύχθηκε. Πιο συγκεκριµένα, αναλύεται το µοντέλο µεταβατικών σφαλµάτων που τελικά χρησιµοποιήθηκε, η βασική ιδέα λειτουργίας του εξοµοιωτή καθώς και όλοι οι κανόνες που αυτός ακολουθεί. Για την καλύτερη κατανόηση της θεωρίας εισάγονται κάποιο ορισµοί και ένα τελικό θεώρηµα που συνοψίζει τον τρόπο λειτουργίας. 2.1 Σχετικές Μεθοδολογίες στην Βιβλιογραφία Γενικά έχουν προταθεί διάφορες τεχνικές στην βιβλιογραφία σχετικά µε την εξοµοίωση και την παραγωγή µεταβατικών διανυσµάτων ελέγχου για CMOS κυκλώµατα. Στην εργασία [14] είχε προταθεί αρχικά ένα τροποποιηµένο µοντέλο για την αναπαράσταση των ιδιοτήτων µνήµης που παρουσιάζουν οι πύλες κάτω από την επήρεια open transistor σφαλµάτων. Επιπλέον αυτής, δύο παραπλήσιες εργασίες [15,16] προτείνουν στην επέκταση του συνόλου των λογικών τιµών που µπορεί να έχει ο κάθε κόµβος του κυκλώµατος, εξαφανίζοντας έτσι την ανάγκη για εισαγωγή επιπλέον λογικής στα τελικά κυκλώµατα για την εξοµοίωση µεταβατικών σφαλµάτων των CMOS κυκλωµάτων όπως γινόταν στο παρελθόν. Το πρόβληµα της δηµιουργίας διανυσµάτων δοκιµής µεταβατικών σφαλµάτων αναπτύχθηκε πριν αρκετά χρόνια στην εργασία [17] όπου και προτάθηκαν δύο στρατηγικές. Κατά την πρώτη, γίνεται µία αναζήτηση στο σύνολο των διανυσµάτων για απλά stuck-at σφάλµατα µε σκοπό να βρεθεί µία κατάλληλη ακολουθία από διανύσµατα που να είναι ικανή να διεγείρει κάποια επιθυµητά µεταβατικά σφάλµατα στόχους και να διαδώσει την επήρεια αυτών προς µία παρατηρήσιµη έξοδο, σύµφωνα µε την ανάλυση που προηγήθηκε σχετικά µε τα χαρακτηριστικά που έχουν τα διανύσµατα ελέγχου µεταβατικών σφαλµάτων. Η δεύτερη στρατηγική, θέλει την δηµιουργία των ακολουθιών διανυσµάτων ελέγχου κάνοντας χρήση line-justification
17 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 16 και εξοµοίωσης για την επίτευξη της επιθυµητής ανίχνευσης ακολουθώντας µε τον τρόπο αυτό µία στρατηγική παραπλήσια µε αυτή που ακολουθείται για τα απλά stuckat σφάλµατα. Στην µεταπτυχιακή αυτή εργασία ακολουθείται η λογική της επιστηµονικής εργασίας [18] κατά την οποία τα CMOS transistor stuck-at open σφάλµατα τα χειριζόµαστε σαν απλά transistor σφάλµατα τα οποία όµως αποτρέπουν την εµφάνιση κάποιων µεταβάσεων. Ο σκοπός είναι να βρεθούν κάποιοι συνδυασµοί µεταβατικών συνόλων δοκιµή που να µπορούν να ανιχνεύσουν τις προβληµατικές αυτές µεταβάσεις. Τα διανύσµατα αυτά δοκιµής εξάγονται από µονοπάτια (transition path ή T-paths) που είναι ευαίσθητα σε µεταβατικά σφάλµατα και συνδέουν κύριες εισόδους µε κύριες εξόδους του κυκλώµατος υπό έλεγχο. Στην εργασία αυτή υλοποιήθηκε ένας εξοµοιωτής που κάνει χρήση της T-path µεθόδου παραγωγής διανυσµάτων ελέγχου µε τον περιορισµό ότι µπορεί να εφαρµοστεί µόνο σε συνδυαστικά κυκλώµατα. Η δηµιουργία εξοµοιωτή µεταβατικών σφαλµάτων που θα χειρίζεται ακολουθιακά κυκλώµατα αποτελεί µέρος της µελλοντικής δουλειάς / επέκτασης του εξοµοιωτή. Παρόλα αυτά, ο εξοµοιωτής για συνδυαστικά κυκλώµατα µπορεί εύκολα να χρησιµοποιηθεί σε ακολουθιακά κυκλώµατα εάν οι ψευδο-είσοδοι και ψευδο-έξοδοι της scan αλυσίδας µετατραπούν σε κύριες έξοδοι και είσοδοι αντίστοιχα του κυκλώµατος. Η τεχνική αυτή αν και είναι γνωστή στην βιβλιογραφία είναι προφανές ότι η εξοµοίωση που προσφέρει δεν είναι το ίδιο ρεαλιστική µε µία αντίστοιχη που λαµβάνει υπόψιν και την λειτουργία της scan αλυσίδας, µετά τα πλεονεκτήµατα αλλά και περιορισµούς που αυτή θέτει κατά την εφαρµογή του ελέγχου. 2.2 Μεταβατικά Σφάλµατα Ο γενικός ορισµός των µεταβατικών σφαλµάτων έχει γίνει σε προηγούµενη ενότητα. Στην υποενότητα αυτή δίνεται ένας πιο λεπτοµερείς ορισµός, εισάγοντας παράλληλα κάποιους συµβολισµούς που βοηθάνε τον αναγνώστη να κατανοήσει καλύτερα τον αλγόριθµο της µεθόδου που χρησιµοποιείται για την τελική εξοµοίωση. Ορισµος 1. Ένα σφάλµα που τροποποιεί την καθυστέρηση εµφάνισης µίας από 0 σε 1 (ή αλλιώς 0-1) µετάβασης σε έναν κόµβο x λέγεται 0-1 µεταβατικό σφάλµα και συµβολίζεται ως x 01. To συµπληρωµατικό αυτού, µεταβατικό σφάλµα, είναι η καθυστέρηση της µετάβασης 1 σε 0 ή αλλιώς 1-0, που συµβολίζεται ως x 01.
18 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 17 Ο παραπάνω ορισµός καλύπτει και την περίπτωση κατά την οποία το σφάλµα στο κόµβο στόχο αποτρέπει εντελώς την µετάβαση και µπορεί να θεωρηθεί σαν µία καθυστέρηση µε άπειρο χρόνο. Στην εργασία αυτή περιλαµβάνονται δύο είδη σφαλµάτων που επηρεάζουν την µετάβαση µίας λογικής τιµής: τα ανοικτά µεταβατικά σφάλµατα (open transistor faults) και τα σφάλµατα καθυστέρησης (delay faults). Τα πρώτα αποτρέπουν µία µετάβαση ενώ τα δεύτερα στην ουσία τροποποιούν τον χρόνο µετάβασης των σηµάτων στους κόµβους στόχους που τα σφάλµατα επηρεάζουν Stuck-open Σφάλµατα Στο σχήµα 2.1 παρουσιάζεται µία CMOS NOR2 πύλη σε επίπεδο αναπαράστασης transistor. Η πύλη εναλλακτικά µπορεί να συµβολιστεί µε ένα απλό pull-up / pull-down µοντέλο όπου το pull-up µέρος είναι υπεύθυνο για να θέτει την λογική τιµή 1 στην έξοδο και πρακτικά υλοποιεί την συνάρτηση a b ενώ το pulldown µέρος είναι υπεύθυνο για να θέτει την λογική τιµή 0 στην έξοδο υλοποιώντας την συνάρτηση α+b. Υπάρχουν συνολικά 4 transistors στον σχεδιασµό για τα οποία αντιστοιχεί και από ένα απλό open transistor σφάλµα. Από την στιγµή που η ύπαρξη ενός τέτοιου σφάλµατος προκαλεί κάποιο από τα pull-up ή pull-down transistors να παραµείνει κλειστό (δηλαδή να µην περνάει ρεύµα από αυτό), οποιοδήποτε διάνυσµα ελέγχου για ένα από αυτά τα σφάλµατα θα πρέπει να είναι τέτοιο που να θέτει το αντίστοιχο transistor σε ανοικτή κατάσταση (δηλαδή το transistor να επιτρέπει την ροή ρεύµατος µέσω αυτού) όταν το σφάλµα απουσιάζει. Κατά την CMOS λογική σχεδιασµού κυκλωµάτων τα pull-up και pull -down µέρη είναι συµπληρωµατικά µεταξύ τους και έτσι η υπάρξει ενός open transistor σφάλµατος οδηγεί στο να είναι και τα δύο µέρη σε κλειστή κατάσταση. Ο σκοπός του ελέγχου είναι να κάνει την κατάσταση αυτή παρατηρήσιµη. Η CMOS τεχνολογία χαρακτηρίζεται από πολύ υψηλή εµπέδηση εξόδου όταν τα pull-up και pull-down τµήµα µία πύλης δεν έχουν αγώγιµο µονοπάτι µε την έξοδο (δηλαδή είναι «κλειστά»). Ταυτόχρονα, η εµπέδηση εισόδου είναι επίσης υψηλή αφού το δυναµικό τις πύλης των transistors στην ουσία ελέγχει µόνο την δηµιουργία ή όχι αγώγιµου καναλιού µεταξύ της πηγής (Gate) και της καταβόθρας (Drain). εδοµένου ότι τα ρεύµατα διαρροής είναι πολύ µικρά (βασικό χαρακτηριστικό της τεχνολογίας αυτής), τα φορτία που είναι αποθηκευµένα στην χωρητικότητα εξόδου µπορούν να διατηρηθούν για σχετικά µεγάλα χρονικά διαστήµατα έως ότου τελικά να
19 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 18 αποφορτιστούν λόγο της ύπαρξης των ρευµάτων αυτών. Κάνοντας χρήση αυτής της ιδιότητας, για την ανίχνευση εάν το pull-up και το pull-down µέρος µίας πύλης είναι και ταυτόχρονα τα δύο «κλειστά» το µόνο που χρειάζεται να γίνει είναι να τεθεί η προηγούµενη χρονικά έξοδος της πύλης στην αντίθετη λογική τιµή από αυτή που πρέπει να έχει την στιγµή του ελέγχου. Είναι λογικό ότι ο έλεγχος αυτός έχει νόηµα µόνο όταν τα διανύσµατα δοκιµής εφαρµόζονται µε έναν αρκετά υψηλό ρυθµό έτσι ώστε να ρεύµατα διαρροής να µην προλαβαίνουν να αποφορτίσουν την χωρητικότητα εξόδου οδηγώντας κατά τον τρόπο αυτό σε λανθασµένα συµπεράσµατα. Pull-up Pull-down Σχήµα 2.1 CMOS NOR2 πύλη Ο παρακάτω πίνακας (Πίνακας 2.1) δείχνει ότι τα stuck-open σφάλµατα που σχετίζονται µε την είσοδο b της NOR πύλης µπορούν να ανιχνευτούν στην έξοδο της πύλης (χωρίς δηλαδή να είναι απαραίτητη η τροποποίηση της πύλης) εφαρµόζοντας την ακολουθία b=0-1-0 ενώ η είσοδος a=0. Επίσης, ο συνδυασµός b=1-0-1 ενώ a=0 είναι ικανός να ανιχνεύσει τα ίδια σφάλµατα που σχετίζονται µε την είσοδο b. Στο πίνακα οι άγνωστες τιµές συµβολίζονται µε το x ενώ ο αστερίσκος σηµαίνει ότι είναι δυνατή η ανίχνευση του σφάλµατος. Πίνακας 2.1 Συσχέτιση της καταστάσεις των τρανζίστορ µε την έξοδο της πύλης {a, b} Μ3 ανοικτό Μ4 ανοικτό Μ1 ανοικτό Μ2 ανοικτό Σωστή έξοδος χωρίς λάθη 0 0 x x * * 0* * * 0* 1 1 1
20 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων Σφάλµατα καθυστέρησης Τα σφάλµατα καθυστέρησης αλλάζουν τον χρονισµό κάποιον συγκεκριµένων µεταβάσεων στο κύκλωµα. Η µόνη διαφορά µεταξύ αυτών των σφαλµάτων και των σφαλµάτων που αποτρέπουν µία µετάβαση είναι ότι οι έξοδοι θα πρέπει να παρακολουθούνται µέσα σε ένα καθορισµένο χρονικό διάστηµα για να είναι δυνατή η ανίχνευση των σφαλµάτων αυτών. Τα αποτελέσµατα των σφαλµάτων καθυστέρησης είναι παρατηρήσιµα µόνο για ένα περιορισµένο χρονικό παράθυρο. 2.3 Έλεγχος για Συνδυαστικά Μεταβατικά Σφάλµατα Μεταβατικοί Έλεγχοι Ορισµός 2. Ένα διάνυσµα δοκιµής µεταβατικού σφάλµατος για ένα δοθέν σύνολο µεταβατικών σφαλµάτων είναι ένας έλεγχος που αποτελείται από δύο διανύσµατα που διαφέρουν τουλάχιστον σε µία είσοδο και έχει την δύναµη να ανιχνεύει τουλάχιστον ένα σφάλµα του συνόλου. Από εδώ και πέρα µία απλή µετάβαση της λογικής τιµής ενός κόµβου από 0 σε 1 (1 σε µηδέν) θα συµβολίζεται µε Α (Α ). Ένα απλό παράδειγµα φαίνεται στο παρακάτω κύκλωµα. Η µετάβαση 0-1 (Α) στον αρχικό κόµβο α διαδίδεται έως την έξοδο Ζ. Ο έλεγχος αυτός ανιχνεύει 0-1 µεταβατικά σφάλµατα στους κόµβους µε την τιµή Α και 1-0 µεταβατικά σφάλµατα στους κόµβους µε την λογική τιµή Α. Τα υπόλοιπα µεταβατικά σφάλµατα µπορούν να ανιχνευτούν θέτοντας την τιµή Α στον αρχικό κόµβο α. Στην περίπτωση αυτή ο έλεγχος είναι εύκολος διότι έχουµε ένα πλήρης µονοπάτι από την µία είσοδο σε µία έξοδο. Αντίθετα µπορεί να υπάρξουν περιπτώσεις που να µην είναι δυνατόν να σχηµατιστεί ένα τέτοιο µονοπάτι. Κάτι τέτοιο φαίνεται στο παρακάτω παράδειγµα. Σχήµα 2.2 Κύκλωµα για παράδειγµα ενός απλού διανύσµατος ελέγχου
21 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 20 Στο κύκλωµα στο επόµενου σχήµατος το διάνυσµα ελέγχου c=b=0 και z=1 0 δεν αντιστοιχεί σε ένα πλήρης µονοπάτι µετάβασης από τις εισόδους προς τις εξόδους του κυκλώµατος αλλά ανιχνεύει το µεταβατικό σφάλµα c 10, δηλαδή το CMOS stuckopen transistor fault στο pull-down µέρος του transistor του αντιστροφέα. Η λανθασµένη έξοδος z παρουσιάζει µία µετάβαση 1 0 αντί να παραµείνει σταθερή στην σωστή τιµή 0. Σχήµα 2.3 εύτερο κύκλωµα για παράδειγµα ενός απλού διανύσµατος ελέγχου Το παραπάνω παράδειγµα δείχνει την ανάγκη προσθήκης δύο επιπλέον συµβόλων τα P και P. Το σύµβολο P (P ) σηµαίνει ότι η fault-free τιµή ενός κόµβου πρέπει να είναι σταθερή στο 1 (0) ενώ η λανθασµένη (faulty) µπορεί να είναι Α (Α) Ενεργά Μεταβατικά Μονοπάτια και Παθητικά Μεταβατικά Μονοπάτια Στην ενότητα αυτή θα παρουσιαστεί ο τρόπος χειρισµού της διάδοσης των µεταβατικών σφαλµάτων κατά µήκος µονοπατιών. Καταρχήν, σε κάθε σηµείο-κόµβο του κυκλώµατος είναι δυνατόν να αντιστοιχεί µία λίστα µε µεταβατικά σφάλµατα. Οι λίστες αυτές είναι πανοµοιότυπες µε τις λίστες της Deductive τεχνικής εξοµοίωσης [19]. Σύµφωνα µε αυτήν, για την διάδοση των σφαλµάτων από τις εισόδους µία πύλης προς τις εξόδους αυτής, στις λίστες που αντιστοιχούν στις εισόδους εφαρµόζονται οι κατάλληλες λογικές πράξης ώστε η τελική λίστα στην έξοδο να περιλαµβάνει µόνο τα σφάλµατα από όλες τις λίστες των εισόδων που πραγµατικά µπορούν να διαδοθούν στην έξοδο θεωρώντας τις δεδοµένες κάθε φορά λογικές τιµές εισόδου. Ο αναγνώστης µπορεί να ανατρέξει στην εργασία [19] για µία πιο λεπτοµερή ανάλυση της τεχνικής αν και η ανάλυση που ακολουθεί χρησιµοποιεί τις ίδιες αρχές.
22 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 21 Ορισµός 3. Μία λίστα σφαλµάτων S ανατίθεται σε κάθε κόµβο s του κυκλώµατος του οποίου η λογική τιµή είναι Α, Α, P, P. Η λίστα αυτή αποτελείται από σφάλµατα που µπορούν να προκαλέσουν τον κόµβο s να βρίσκεται στην τιµή 0, 1, Α και Α εάν οι απαλλαγµένη από λάθη τιµή είναι Α, Α, P, P, αντίστοιχα. Απο εδώ και πέρα οι λίστες σφαλµάτων θα συµβολίζονται µε κεφαλαία γράµµατα για να τις ξεχωρίζουµε από του κόµβους του κυκλώµατος. Η τεχνική της µεθόδου διάδοσης των σφαλµάτων είναι αρχικά σε κάθε κόµβοείσοδο του κυκλώµατος να ανατίθεται µία λίστα σφαλµάτων εάν το διάνυσµα δοκιµής περιλαµβάνει µία από τις τιµές Α, Α, P, P, όπως ακριβώς ορίστηκε παραπάνω. Στην συνέχεια κατά την διάρκεια της διάδοσης των λιστών από πύλη σε πύλη, σύµφωνα µε την deductive λογική εξοµοίωσης, είναι δυνατόν νέα τοπικά µεταβατικά σφάλµατα να προστίθενται κατά µήκος των µονοπατιών. Ο κανόνας είναι ότι εάν η τιµή εξόδου µίας πύλης ή γενικά ένα κόµβος σε επόµενο επίπεδο, έχει τιµή Α (Α ) τότε το µεταβατικό σφάλµα s01 (s10) προστίθεται στην λίστα του κόµβου αυτού. Στην περίπτωση λογικής τιµής P ή P κανένα νέο σφάλµα δεν προστίθεται. Η διάδοση των λογικών τιµών και των λιστών γίνεται από πύλη σε πύλη ακολουθώντας µία σειρά από κανόνες που εξαρτάται από την λογική συνάρτηση που υλοποιεί η συγκεκριµένη πύλη. Η περίπτωση που η µία πύλη έχει περισσότερες από δύο εισόδους καλύπτεται από τους πίνακες αυτούς εάν γίνει αναδροµική χρήση των κανόνων για το πλήθος των εισόδων. Αυτό είναι δυνατών από την στιγµή που η δυαδική αριθµητική µας επιτρέπει να αντικαθιστούµε µία πύλη n εισόδων µε ένα δένδρο n(n-1)/2 πυλών και log2(n) επιπέδων. Ένα τέτοιο παράδειγµα φαίνεται το παρακάτω σχήµα. Σχήµα 2.4 Αντιστοιχία µίας πύλης AND4 σε ένα δίκτυο τριών AND Επαγωγικοί Κανόνες ιάδοσης Λιστών Σφαλµάτων Οι πίνακες 2.2 έως 2.7 περιέχουν τους κανόνες για κάθε λογική πύλη θεωρώντας ότι η κάθε πύλη έχει δύο εισόδους την x και y και µία έξοδο την z. Στην περίπτωση κατά την οποία οι τιµή εισόδου δεν είναι γνωστή τότε αυτή θεωρείται άγνωστη και ανατίθεται σε αυτήν η τιµή Χ. Η τιµή αυτή είναι απαραίτητη για να είναι δυνατή η χρήση test-cubes, δηλαδή διανυσµάτων ελέγχου που περιέχουν τιµές που είτε είναι άγνωστες είτε αδιάφορες. Με τον τρόπο αυτό βελτιώνεται ο χρόνος
23 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 22 εξοµοίωσης και δηµιουργίας διανυσµάτων ελέγχου, δεδοµένου ότι υπάρχει η απαραίτητη πληροφορία για το ποιες είσοδοι είναι αδιάφορες/άγνωστες. Ταυτόχρονα µε την σωστή έξοδο (Στήλη z) για κάθε συνδυασµό εισόδων, δίνεται και ο κανόνας διάδοσης των λιστών σφαλµάτων (Στήλη Ζ). Στους κανόνες αυτούς ο χαρακτήρας & είναι το η λογική πράξη της τοµής (AND) και ο χαρακτήρας αναφέρεται στην λογική πράξη της ένωσης (OR) ενώ στην περίπτωση που ο κανόνας δηλώνει ότι δεν πρέπει να χρησιµοποιηθεί η λίστα µίας από τις εισόδους τότε µπροστά από το όνοµα της λίστας υπάρχει η λέξη NOT. Για παράδειγµα, εάν ο κανόνας για την διάδοση των λιστών σφαλµάτων είναι Χ & ΝΟΤ_Υ τότε ο κανόνας δηλώνει ότι η λίστα σφαλµάτων της εξόδου της πύλης είναι όλα τα σφάλµα που υπάρχουν στην λίστα της εισόδου Χ και δεν υπάρχουν στην λίστα της εισόδου Υ. Τέλος, εάν η έξοδος µίας πύλης είναι 0 ή 1 τότε σε αυτήν δεν ανατίθεται µία λίστα σφαλµάτων και στον πίνακα υπάρχει η ένδειξη NO, δηλαδή ότι δεν υπάρχει κανόνας. Πίνακας 2.2 Κανόνες για την πύλη AND x y z Z x y z Z NO A P A X&NOT_Y NO A P P X&Y 0 A 0 NO A x X NO 0 A 0 NO P 0 0 NO 0 P 0 NO P 1 P X 0 P 0 NO P A A X Y 0 x 0 NO P A NOT_A NOT_X&Y NO P P P X Y NO P P NOT_P NOT_X&Y 1 A A Y P x X NO 1 A A Y P 0 0 NO 1 P P Y P 1 NOT_P X 1 P P Y P A NOT_P X&NOT_Y 1 x X NO P A NOT_P X&Y A 0 0 NO P P NOT_P X&NOT_Y A 1 A X P P NOT_P X&Y A A A X Y P x X NO A A P ΝΟΤ_X&Y X 0 0 NO A P A X Y X 1 X NO A P P NOT_X&Y X A X NO A x X NO X A 0 NO A 0 0 NO X P X NO A 1 A X X P X NO A A P X&ΝΟΤ_Y X x X NO A A A X&Y
24 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 23 Πίνακας 2.3 Κανόνες για την πύλη NAND x y z Z x y z Z NO A P A X&NOT_Y NO A P P X&Y 0 A 1 NO A x X NO 0 A 1 NO P 0 1 NO 0 P 1 NO P 1 NOT_P X 0 P 1 NO P A NOT_A X Y 0 x 1 NO P A A NOT_X&Y NO P P NOT_P X Y NO P P P NOT_X&Y 1 A NOT_A Y P x X NO 1 A A Y P 0 0 NO 1 P NOT_P Y P 1 P X 1 P P Y P A P X&NOT_Y 1 x X NO P A P X&Y A 0 1 NO P P P X&NOT_Y A 1 NOT_A X P P P X&Y A A NOT_A X Y P x X NO A A P NOT_X&Y X 0 1 NO A P NOT_A X Y X 1 X NO A P P NOT_X&Y X A X NO A x X NO X A 1 NO A 0 1 NO X P X NO A 1 A X X P X NO A A P X&NOT_Y X x X NO A A A X&Y
25 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 24 Πίνακας 2.4 Κανόνες για την πύλη NOR x y z Z x y z Z NO A P NOT_P NOT_X&Y NO A P A X Y 0 A NOT_A Y A x X NO 0 A A Y P 0 NOT_P X 0 P NOT_P Y P 1 0 NO 0 P P Y P A NOT_P X&Y 0 x X NO P A NOT_P X&NOT_Y NO P P NOT_P X&Y NO P P NOT_P X&NOT_Y 1 A 0 NO P x X NO 1 A 0 NO P 0 P X 1 P 0 NO P 1 0 NO 1 P 0 NO P A NOT_A NOT_X&Y 1 x 0 NO P A A X Y A 0 NOT_A X P P NOT_P NOT_X&Y A 1 0 NO P P P X Y A A NOT_A X&Y P x X NO A A NOT_P X&NOT_Y X 0 X NO A P NOT_P X&Y X 1 0 NO A P NOT_A X&NOT_Y X A 0 NO A x 0 NO X A X NO A 0 A X X P X NO A 1 0 NO X P X NO A A NOT_P NOT_X&Y X x X NO A A A X Y
26 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 25 Πίνακας 2.5 Κανόνες για την πύλη OR x y z Z x y z Z NO A P P NOT_X&Y NO A P NOT_A X Y 0 A A Y A x X NO 0 A NOT_A Y P 0 P X 0 P P Y P 1 1 NO 0 P NOT_P Y P A P X&Y 0 x X NO P A P X&NOT_Y NO P P P X&Y NO P P P X&NOT_Y 1 A 1 NO P x NOT_P X 1 A 1 NO P 0 1 NO 1 P 1 NO P 1 A NOT_X&Y 1 P 1 NO P A NOT_A X Y 1 x 1 NO P A P NOT_X&Y A 0 A X P P NOT_P X Y A 1 1 NO P P X NO A A A X&Y P x NOT_P X A A P X&NOT_Y X 0 X NO A P P X&Y X 1 1 NO A P A X&NOT_Y X A 1 NO A x 1 NO X A X NO A 0 NOT_A X X P X NO A 1 1 NO X P X NO A A P NOT_X&Y X X X NO A A NOT_A X Y
27 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 26 Πίνακας 2.6 Κανόνες για την πύλη XOR x y z Z x y z Z NO A P A X^Y NO A P A X^Y 0 A A Y A x X NO 0 A NOT_A Y P 0 P X 0 P P Y P 1 NOT_P X 0 P NOT_P Y P A NOT_A X^Y 0 x X NO P A A X^Y NO P P NOT_P X^Y NO P P P X^Y 1 A NOT_A Y P x X NO 1 A A Y P 0 NOT_P X 1 P NOT_P Y P 1 P X 1 P P Y P A A X^Y 1 x X NO P A NOT_A X^Y A 0 A X P P P X^Y A 1 NOT_A X P P NOT_P X^Y A A NOT_P X^Y P x X NO A A P X^Y X 0 X NO A P NOT_A X^Y X 1 X NO A P A X^Y X A X NO A x X NO X A X NO A 0 NOT_A X X P X NO A 1 A X X P X NO A A P X^Y X x X NO A A NOT_P X^Y Πίνακας 2.7 Κανόνες για την πύλη NOT x z Z 0 1 NO 1 0 NO A NOT_A X NOT_A A X P NOT_P X NOT_P P X X X NO
28 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 27 Στην περίπτωση fan-out διακλαδώσεων, οι λίστες σφαλµάτων που σχετίζονται µε την πηγή του Fan-out stem διαδίδονται σε όλες τις εξόδους της διακλάδωσης και τα αντίστοιχα µεταβατικά σφάλµατα προστίθενται στις λίστες των εξόδων εάν το µονοπάτι είναι ένα ενεργό µονοπάτι. ηλαδή, το σφάλµα x 01 (x 10 ) προστίθεται στην λίστα του X εάν x= A ( x= A ). Η όλη διαδικασία διάδοσης φαίνεται στο επόµενο παράδειγµα. Θεωρώντας το κύκλωµα του παρακάτω σχήµατος γίνεται χρήση των οι κανόνες που περιλαµβάνονται στους προηγούµενους πίνακες για τον υπολογισµό της εξόδου της τελικής XOR πύλης καθώς και της λίστα σφαλµάτων που η έξοδος αυτή περιλαµβάνει. Στο παράδειγµα θεωρείται ότι τα µεταβατικό διάνυσµα ελέγχου που εφαρµόζεται στο κυκλώµατα είναι το x=a και y=a. Τι τελικές τιµές κάθε κόµβου και η λίστα σφαλµάτων που αυτό περιέχει έχοντας διατρέξει το κύκλωµα πύλη-πύλη, είναι οι παρακάτω: x=a X =x 01 y=a Y =y 10 z=a Z =z 01 v=p V =y 10 w=a W =y 10 Σχήµα 2.5 Παράδειγµα διάδοσης τιµών και εφαρµογής κανόνων Σχήµα 2.6 Παράδειγµα διάδοσης µε µόνο µετάβαση εισόδου Ένα διαφορετικό παράδειγµα για το ίδιο κύκλωµα µε µόνο µία µετάβαση σε µία είσοδο θεωρώντας το διάνυσµα µεταβατικού ελέγχου x=a y=1 φαίνεται στο επόµενο σχήµα. Οι τιµές κάθε κόµβοι και οι λίστες σφαλµάτων είναι οι παρακάτω:
29 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 28 x=a X =x 01 z=a Z =z 01 v=α V =y 01, v 01 w=p W =y 01, v 01 Σύµφωνα µε όλα τα παραπάνω µπορούµε να καταλήξουµε στον παρακάτω ορισµό. Ορισµός 4. Ένα µεταβατικό µονοπάτι είναι ένα µονοπάτι διάδοσης (propagation path) που παράγεται χρησιµοποιώντας τους κανόνες που ορίσθηκαν παραπάνω και διαδίδεται από τις εισόδους προς τις εξόδους ενός κυκλώµατος. Το παρακάτω θεώρηµα συνοψίζει την λογική λειτουργίας του εξοµοιωτή: Θεώρηµα 1. Θεώρησε ένα κύκλωµα µε µία έξοδο f. Εάν για ένα µεταβατικό µονοπάτι του κυκλώµατος f=a, f=a, f=p ή f=p τότε τα σφάλµατα που υπάρχουν στην τελική λίστα F θα ανιχνεύονται από το µεταβατικό διάνυσµα ελέγχου που εφαρµόστηκε στην έξοδο για την δηµιουργία του µονοπατιού. Για την διάρκεια του πραγµατικού ελέγχου, εάν f=a ή f=a η παρουσία των σφαλµάτων της λίστας F θα ακυρώσουν µία µετάβαση στην έξοδο f ενώ εάν f=p ή f=p η παρουσία ενός από τα σφάλµατα της λίστας F θα προκαλέσει µία λανθασµένη µετάβαση στην έξοδο f Παραγωγή ιανυσµάτων Καθυστέρησης µε Χρήση Τ- Μονοπατιών Το προηγούµενο µοντέλο µπορεί εύκολα να επεκταθεί µε σκοπό την ανίχνευση σφαλµάτων καθυστέρησης. Αν θεωρήσουµε ότι σε µία κύρια έξοδο του κυκλώµατος, έστω f, µετά την εφαρµογή του προηγούµενου µοντέλου έχει ανατεθεί ένα σφάλµα Α δηλαδή µία καθυστερηµένη µετάβαση 0-1, τότε για την ανίχνευση του διανύσµατος καθυστέρησης το µόνο που πρέπει να γίνει είναι ο έλεγχος να πραγµατοποιηθεί σε ένα καθορισµένο χρονικό σηµείο.
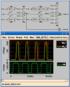
30 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 29 Θεώρηµα 2. Θεώρησε ένα κύκλωµα µε µία έξοδο f. Ένας Τ- έλεγχος δηµιουργείται και εφαρµόζεται στο κύκλωµα. Εάν f=a, f=not_a, f=p, f=not_p τότε η παρουσία ενός stuck σφάλµατος στην λίστα σφαλµάτων F υποδηλώνει την ανίχνευση του σφάλµατος καθυστέρησης κατά την εµφάνιση του σφάλµατος αυτού κατά την εφαρµογή της µετάβασης στην είσοδο Α ή ΝΟΤ_Α. Εάν κατά την διάρκεια του ελέγχου f=a ή f= NOT_A τότε η παρουσία του σφάλµατος καθυστέρησης θα έχει ως αποτέλεσµα την καθυστέρηση της µετάβασης στην έξοδο f ( συγκρινόµενη µε την τιµή της ίδιας εξόδους για την περίπτωση χωρίς την εµφάνιση του σφάλµατος). Εάν f= P ή f= NOT_Α τότε η παρουσία του σφάλµατος αυτού θα δηµιουργήσει έναν παροδικό παλµό στην έξοδο f αντί για µία απλή µετάβαση. Τα αποτελέσµατα του σφάλµατος καθυστέρησης είναι παροδικά και ορατά για ένα περιορισµένο χρονικό διάστηµα που σχετίζεται µε το σφάλµα καθαυτό. Αποτέλεσµα αυτού είναι, σε συνδυαστικά κυκλώµατα να απαιτείται η σύλληψη της τιµής της εξόδου την κατάλληλη στιγµή και όχι µετά το τέλος της παροδικής αυτής κατάστασης. Η περίπτωση αυτή είναι διαφορετική από την περίπτωση των ακουλουθιακών κυκλωµάτων όπου οι επιδράσεις των µεταβατικών σφαλµάτων είναι δυνατό να αποθηκευτούν στα στοιχεία µνήµης του σχεδιασµού και έτσι να είναι εύκολη η παρατήρηση της λανθασµένης απόκρισης του σχεδιασµού. Ένα παράδειγµα φαίνεται στο παρακάτω σχήµα (Σχήµα 2.7 ). Σχήµα 2.7 Παράδειγµα ανίχνευσης σφάλµατος καθυστέρησης Η εφαρµογή της µεθοδολογία που περιγράφτηκε στις προηγούµενες µεθόδους δίνει ως αποτέλεσµα τις παρακάτω λίστες σφαλµάτων: x = A X= { } z = A Z= { } v = A V= { z 01, v 01 } w = NOT_P W= { z 01,v 01 }
31 Κεφάλαιο 2 Εξοµοιωτής Μεταβατικών Σφαλµάτων 30 H παρουσία του σφάλµατος z=a στην λίστα του W που έχει τιµή NOT_P σηµαίνει ότι στην περίπτωση που προκληθεί ένα σφάλµα καθυστέρησης Α στην έξοδο z τότε στην κύρια έξοδο w θα παρατηρηθεί έναν παλµός. Θεωρώντας ότι η καθυστέρηση διάδοσης των λογικών τιµών µέσω των πυλών είναι πρακτικά ίση µε το µηδέν, οι λογικές µεταβάσεις που θα πραγµατοποιηθούν σε όλα του κόµβους του κυκλώµατος που θεωρήθηκε για το παράδειγµα, φαίνονται στο παρακάτω σχήµα (Σχήµα 2.8). Σχήµα 2.8 Λογικές Μεταβάσεις των τιµών σε κάθε κόµβο του κυκλώµατος στο σχήµα 2.7
32 3 ο Χρήση και Υλοποίηση Εξοµοιωτή 3. Χρήση και Υλοποίηση Εξοµοιωτή Στο κεφάλαιο αυτό παρουσιάζεται ο εξοµοιωτής µεταβατικών σφαλµάτων, του οποίου η θεωρία πίσω από τον τρόπο λειτουργίας του περιγράφτηκε στο προηγούµενο κεφάλαιο, αλλά αυτήν την φορά σαν ένα εργαλείο. Το κεφάλαιο χωρίζεται σε δύο µέρη: Κατά το πρώτο, δίνεται έµφαση στον τρόπο χρήσης του εξοµοιωτή παρουσιάζοντας τις δυνατότητες του, την µορφή των αρχείων που απαιτεί και τον τρόπο ερµηνείας των αρχείων εξόδου. Παράλληλα µε αυτό, υπάρχει και ένα δεύτερο µέρος που δίνει µερικές λεπτοµέρειες για τον τρόπο υλοποίησης του εξοµοιωτή. Η όλη υλοποίηση του αποδείχθηκε αρκετά απαιτητική για να επίτευξη ρεαλιστικών χρόνων απόκρισης και λογικών απαιτήσεων σε µνήµη οδηγώντας στην ανάγκη χρήσης µερικών προχωρηµένων αλγορίθµων χειρισµού δοµών δεδοµένων. Στο δεύτερο µέρος αυτό παρουσιάζονται συνοπτικά οι δοµές δεδοµένων, οι αλγόριθµοι αναζήτησης και τέλος το σχήµα χειρισµού µνήµης που υιοθετήθηκε. 3.1 υνατότητες του Εξοµοιωτή Ο εξοµοιωτής εν συντοµία παρέχει τις παρακάτω δυνατότητες: 1. Εισαγωγή της περιγραφής του κυκλώµατος σε Bench µορφή, δηλαδή την µορφή που περιγράφονται τα ISCAS 89 µετρό-κυκλώµατα. 2. Εξοµοίωση λαµβάνοντας υπόψιν όλα τα δυνατά µεταβατικά σφάλµατα που υπάρχουν σε ένα κύκλωµα (χωρίς να χρειάζεται αυτά να οριστούν από τον χρήστη) ή εξοµοίωση µόνο για τα µεταβατικά σφάλµατα που επιθυµεί ο χρήστης 3. Εξοµοίωση για οποιοδήποτε αριθµό διανυσµάτων ελέγχου που δίνονται σαν είσοδο σε αυτόν. Παράλληλα, κάνοντας χρήση ειδικών συµβόλων αντικαθιστάτε τα απαραίτητο ζεύγος διανυσµάτων ελέγχου µε ένα µόνο διάνυσµα που είναι ευκολότερο στο γράψιµο και έλεγχο της ορθότητας του.
33 Κεφάλαιο 3 Χρήση και Υλοποίηση Εξοµοιωτή υνατότητα παραµετροποίησης της λειτουργίας του εξοµοιωτή κάνοντας χρήση των κατάλληλων παραµέτρων κατά την εκτέλεση του. 5. Καταγραφεί όλων των συµβάντων σε log αρχεία για την σωστή ενηµέρωση του χρήστη. 3.2 Τρόπος Χρήσης Εξοµοιωτή Η ενότητα αυτή περιγράφει τον τρόπο εκτέλεσης και χρήσης του εξοµοιωτή. Έτσι αρχικά περιγράφεται ο βασικός τρόπος εκτέλεσης ενώ στην συνέχεια εξηγείται η χρήση και µορφολογία των αρχείων εισόδου και εξόδου που δέχεται και δίνει ο εξοµοιωτής, αντίστοιχα. Στο τέλος της ενότητας περιγράφονται αναλυτικά οι παράµετροι εκτέλεσης που υποστηρίζει ο εξοµοιωτής Βασικός Τρόπος Εκτέλεσης Για την εκτέλεση του εξοµοιωτή σαν ξεχωριστό εργαλείο αρκεί να εκτελεστεί το εκτελέσιµο αρχείο Transition_fault_simulator.exe. Ο βασικός τρόπος εκτέλεσης του είναι: Transition_fault_simulator [circuit file],µε το [circuit file] να είναι το όνοµα του αρχείου που περιέχει την περιγραφή του κυκλώµατος σε Bench µορφή χωρίς όµως να περιέχεται η κατάληξη.bench που έχουν όλα οι bench περιγραφές. Π.χ. για την εκτέλεση του εξοµοιωτή πάνω στο s9234.bench κύκλωµα αρκεί να δοθεί η εντολή c:\ > Transition_fault_simulator s9234 Τρέχοντας την παραπάνω εντολή ο εξοµοιωτής θα εκτελέσει µία πλήρη εξοµοίωση του κυκλώµατος θεωρώντας ότι αναζητεί όλα τα δυνατά transition faults που µπορεί το κάθε διάνυσµα ελέγχου να ανιχνεύσει. Τα διανύσµατα ελέγχου διαβάζονται από το αρχείο [circuit_file].patters ενώ τα τελικά αποτελέσµατα αποθηκεύονται στο αρχείο [circuit_file].output. Κάθε στιγµή όλα τα µηνύµατα (πληροφοριών ή σφαλµάτων) που τυπώνονται στην οθόνη, αποθηκεύονται παράλληλα και στο αρχείο [circuit_file].log έτσι ώστε ο χρήστης να µπορεί να ανατρέξει στο ιστορικό των ενεργειών που το πρόγραµµα πραγµατοποίησε. Πρέπει να σηµειωθεί ότι τα ονόµατα των παραπάνω αρχείων µπορούν να αλλάξουν κατά την
«Εγχειρίδιο Προγράμματος Hope (version 2)»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ «Εγχειρίδιο Προγράμματος Hope (version 2)» Μαργαρίτα Κουτσουπιά Μηχ. Η/Υ και Πληροφορικής ΠΑΤΡΑ 2009 Το Hope αποτελεί έναν Παράλληλο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ «Εγχειρίδιο Προγράμματος Hope (version 2)» Μαργαρίτα Κουτσουπιά Μηχ. Η/Υ και Πληροφορικής ΠΑΤΡΑ 2009 Το Hope αποτελεί έναν Παράλληλο
Σωστή απάντηση το: Γ. Απάντηση
 Ειδικά Θέματα Ελέγχου Ορθής Λειτουργίας VLSI Συστημάτων - Σχεδιασμός για Εύκολο Έλεγχο Εξετάσεις ΟΣΥΛ & ΕΤΥ 4-7- 2016 Ειδικά Θέματα Σχεδίασης Ψηφιακών Συστημάτων Εξετάσεις μαθήματος επιλογής Τμήματος Μηχανικών
Ειδικά Θέματα Ελέγχου Ορθής Λειτουργίας VLSI Συστημάτων - Σχεδιασμός για Εύκολο Έλεγχο Εξετάσεις ΟΣΥΛ & ΕΤΥ 4-7- 2016 Ειδικά Θέματα Σχεδίασης Ψηφιακών Συστημάτων Εξετάσεις μαθήματος επιλογής Τμήματος Μηχανικών
Bλάβες, ελαττώματα και. Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών
 Bλάβες, ελαττώματα και μοντέλα σφαλμάτων Περίγραμμα ργρ παρουσίασης Βλάβες (Failures) Ελαττώματα (Defects) Μοντέλα σφαλμάτων (Fault models) Μοντέλο σφαλμάτων μόνιμης μης τιμής (Stuck-at faults Βραχυκυκλώματα
Bλάβες, ελαττώματα και μοντέλα σφαλμάτων Περίγραμμα ργρ παρουσίασης Βλάβες (Failures) Ελαττώματα (Defects) Μοντέλα σφαλμάτων (Fault models) Μοντέλο σφαλμάτων μόνιμης μης τιμής (Stuck-at faults Βραχυκυκλώματα
«Εγχειρίδιο Προγράμματος Atalanta 2.0»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ «Εγχειρίδιο Προγράμματος Atalanta 2.0» Μαργαρίτα Κουτσουπιά Μηχ. Η/Υ και Πληροφορικής ΠΑΤΡΑ 2009 Το Atalanta αποτελεί μία Αυτόματη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ «Εγχειρίδιο Προγράμματος Atalanta 2.0» Μαργαρίτα Κουτσουπιά Μηχ. Η/Υ και Πληροφορικής ΠΑΤΡΑ 2009 Το Atalanta αποτελεί μία Αυτόματη
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
σφαλμάτων Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών
 Λογική εξομοίωση και εξομοίωση σφαλμάτων Περίγραμμα ργρ Επιβεβαίωση σχεδιασμού και εξομοίωση (Verification and Simulation) Είδη εξομοίωσης (Types of Simulation) Εξομοίωση σφαλμάτων (Fault Simulation) Σειριακή
Λογική εξομοίωση και εξομοίωση σφαλμάτων Περίγραμμα ργρ Επιβεβαίωση σχεδιασμού και εξομοίωση (Verification and Simulation) Είδη εξομοίωσης (Types of Simulation) Εξομοίωση σφαλμάτων (Fault Simulation) Σειριακή
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή
 6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
Καταστάσεων. Καταστάσεων
 8 η Θεµατική Ενότητα : Εισαγωγή Ησχεδίαση ενός ψηφιακού συστήµατος µπορεί να διαιρεθεί σε δύο µέρη: τα κυκλώµατα επεξεργασίας δεδοµένων και τα κυκλώµατα ελέγχου. Το κύκλωµα ελέγχου δηµιουργεί σήµατα για
8 η Θεµατική Ενότητα : Εισαγωγή Ησχεδίαση ενός ψηφιακού συστήµατος µπορεί να διαιρεθεί σε δύο µέρη: τα κυκλώµατα επεξεργασίας δεδοµένων και τα κυκλώµατα ελέγχου. Το κύκλωµα ελέγχου δηµιουργεί σήµατα για
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ ΠΑΤΡΑ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΕΡΙΕΧΟΜΕΝΑ ΠΕΡΙΕΧΟΜΕΝΑ.3 ΑΣΥΓΧΡΟΝΟΣ ΔYΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.5 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ.7 ΑΣΥΓΧΡΟΝΟΣ ΔΕΚΑΔΙΚΟΣ ΑΠΑΡΙΘΜΗΤΗΣ ΜΕ LATCH.
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΑΠΑΡΙΘΜΗΤΕΣ Κ. ΕΥΣΤΑΘΙΟΥ, Γ. ΠΑΠΑΔΟΠΟΥΛΟΣ
ΑΣΚΗΣΗ 9. Tα Flip-Flop
 ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
ΑΣΚΗΣΗ 9 Tα Flip-Flop 9.1. ΣΚΟΠΟΣ Η κατανόηση της λειτουργίας των στοιχείων μνήμης των ψηφιακών κυκλωμάτων. Τα δομικά στοιχεία μνήμης είναι οι μανδαλωτές (latches) και τα Flip-Flop. 9.2. ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL
 Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL 3.1 Εισαγωγή στα FLIP FLOP 3.1.1 Θεωρητικό Υπόβαθρο Τα σύγχρονα ακολουθιακά κυκλώματα με τα οποία θα ασχοληθούμε στο εργαστήριο των Ψηφιακών συστημάτων
Κεφάλαιο 3 ο Ακολουθιακά Κυκλώματα με ολοκληρωμένα ΤΤL 3.1 Εισαγωγή στα FLIP FLOP 3.1.1 Θεωρητικό Υπόβαθρο Τα σύγχρονα ακολουθιακά κυκλώματα με τα οποία θα ασχοληθούμε στο εργαστήριο των Ψηφιακών συστημάτων
Υλοποίηση λογικών πυλών µε τρανζίστορ MOS. Εισαγωγή στην Ηλεκτρονική
 Υλοποίηση λογικών πυλών µε τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Λογική MOS Η αναπαράσταση των λογικών µεταβλητών 0 και 1 στα ψηφιακά κυκλώµατα γίνεται µέσω κατάλληλων επιπέδων τάσης, όπου κατά σύµβαση
Υλοποίηση λογικών πυλών µε τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Λογική MOS Η αναπαράσταση των λογικών µεταβλητών 0 και 1 στα ψηφιακά κυκλώµατα γίνεται µέσω κατάλληλων επιπέδων τάσης, όπου κατά σύµβαση
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
 100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3 ΑΠΛΟΠΟΙΗΣΗ και ΥΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σκοπός: Η κατανόηση της σχέσης µιας λογικής συνάρτησης µε το αντίστοιχο κύκλωµα. Η απλοποίηση λογικών συναρτήσεων
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 3 ΑΠΛΟΠΟΙΗΣΗ και ΥΛΟΠΟΙΗΣΗ ΛΟΓΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Σκοπός: Η κατανόηση της σχέσης µιας λογικής συνάρτησης µε το αντίστοιχο κύκλωµα. Η απλοποίηση λογικών συναρτήσεων
8.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
Εξαγωγή Διανυσμάτων Δοκιμής. Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών
 Εξαγωγή Διανυσμάτων Δοκιμής Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών Περίγραμμα ργρ Παρουσίασης Είδη Συνόλων Δοκιμής Ντετερμινιστικά σύνολα δοκιμής Συμβολισμοί
Εξαγωγή Διανυσμάτων Δοκιμής Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν. Πατρών Περίγραμμα ργρ Παρουσίασης Είδη Συνόλων Δοκιμής Ντετερμινιστικά σύνολα δοκιμής Συμβολισμοί
Υπάρχουν δύο τύποι μνήμης, η μνήμη τυχαίας προσπέλασης (Random Access Memory RAM) και η μνήμη ανάγνωσης-μόνο (Read-Only Memory ROM).
 Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
Κεφάλαιο Τρία: Ψηφιακά Ηλεκτρονικά
 Κεφάλαιο Τρία: 3.1 Τι είναι αναλογικό και τι ψηφιακό µέγεθος Αναλογικό ονοµάζεται το µέγεθος που µπορεί να πάρει οποιαδήποτε τιµή σε µια συγκεκριµένη περιοχή τιµών π.χ. η ταχύτητα ενός αυτοκινήτου. Ψηφιακό
Κεφάλαιο Τρία: 3.1 Τι είναι αναλογικό και τι ψηφιακό µέγεθος Αναλογικό ονοµάζεται το µέγεθος που µπορεί να πάρει οποιαδήποτε τιµή σε µια συγκεκριµένη περιοχή τιµών π.χ. η ταχύτητα ενός αυτοκινήτου. Ψηφιακό
Συμπίεση Δεδομένων Δοκιμής (Test Data Compression) Νικολός Δημήτριος, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών & Πληροφορικής, Παν Πατρών
 Συμπίεση Δεδομένων Δοκιμής (Test Data Compression), Παν Πατρών Test resource partitioning techniques ΑΤΕ Automatic Test Equipment (ATE) based BIST based Έλεγχος παραγωγής γής βασισμένος σε ΑΤΕ Μεγάλος
Συμπίεση Δεδομένων Δοκιμής (Test Data Compression), Παν Πατρών Test resource partitioning techniques ΑΤΕ Automatic Test Equipment (ATE) based BIST based Έλεγχος παραγωγής γής βασισμένος σε ΑΤΕ Μεγάλος
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής
 Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
Μία μέθοδος προσομοίωσης ψηφιακών κυκλωμάτων Εξελικτικής Υπολογιστικής Βασισμένο σε μια εργασία των Καζαρλή, Καλόμοιρου, Μαστοροκώστα, Μπαλουκτσή, Καλαϊτζή, Βαλαή, Πετρίδη Εισαγωγή Η Εξελικτική Υπολογιστική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 121 ΕΡΓΑΣΤΗΡΙΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΝΗΜΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΖΟΜΕΝΗ ΛΟΓΙΚΗ ΥΠΕΥΘΥΝΟΣ ΕΡΓΑΣΤΗΡΙΩΝ: ΧΡΥΣΟΣΤΟΜΟΣ ΧΡΥΣΟΣΤΟΜΟΥ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2001 ΕΠΛ 121 ΕΡΓΑΣΤΗΡΙΑ ΨΗΦΙΑΚΩΝ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 121 ΕΡΓΑΣΤΗΡΙΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΜΝΗΜΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΖΟΜΕΝΗ ΛΟΓΙΚΗ ΥΠΕΥΘΥΝΟΣ ΕΡΓΑΣΤΗΡΙΩΝ: ΧΡΥΣΟΣΤΟΜΟΣ ΧΡΥΣΟΣΤΟΜΟΥ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2001 ΕΠΛ 121 ΕΡΓΑΣΤΗΡΙΑ ΨΗΦΙΑΚΩΝ
ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS)
 ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS) Αντικείμενο της άσκησης: H σχεδίαση και η χρήση ασύγχρονων απαριθμητών γεγονότων. Με τον όρο απαριθμητές ή μετρητές εννοούμε ένα ακολουθιακό κύκλωμα με FF, οι καταστάσεις
ΑΣΚΗΣΗ 9 ΑΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ (COUNTERS) Αντικείμενο της άσκησης: H σχεδίαση και η χρήση ασύγχρονων απαριθμητών γεγονότων. Με τον όρο απαριθμητές ή μετρητές εννοούμε ένα ακολουθιακό κύκλωμα με FF, οι καταστάσεις
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων. 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης
 Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
Εισαγωγή στα κυκλώµατα CMOS 2
 1 η Θεµατική Ενότητα : Εισαγωγή στα κυκλώµατα CMOS Επιµέλεια διαφανειών:. Μπακάλης Εισαγωγή Τεχνολογία CMOS = Complementary Metal Oxide Semiconductor Συµπληρωµατικού Ηµιαγωγού Μετάλλου Οξειδίου Αποτελείται
1 η Θεµατική Ενότητα : Εισαγωγή στα κυκλώµατα CMOS Επιµέλεια διαφανειών:. Μπακάλης Εισαγωγή Τεχνολογία CMOS = Complementary Metal Oxide Semiconductor Συµπληρωµατικού Ηµιαγωγού Μετάλλου Οξειδίου Αποτελείται
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ
 Τμήμα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρματης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Μάθημα 10: Ασύχρονα ακολουθιακά κυκλώµατα (µερος Α ) Διδάσκων: Καθηγητής Ν. Φακωτάκης Ασύγχρονα ακολουθιακά κυκλώµατα
Τμήμα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρματης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Μάθημα 10: Ασύχρονα ακολουθιακά κυκλώµατα (µερος Α ) Διδάσκων: Καθηγητής Ν. Φακωτάκης Ασύγχρονα ακολουθιακά κυκλώµατα
Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Εκτέλεση πράξεων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Εκτέλεση πράξεων
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Κεφάλαιο 15 o. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Έλεγχος Ορθής Λειτουργίας 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Έλεγχος Ορθής Λειτουργίας Κεφάλαιο 15 o Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Ελαττώματα, σφάλματα, λάθη 2. Ανίχνευση σφαλμάτων
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Έλεγχος Ορθής Λειτουργίας Κεφάλαιο 15 o Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Ελαττώματα, σφάλματα, λάθη 2. Ανίχνευση σφαλμάτων
Ακολουθιακά Κυκλώµατα. ΗΜΥ 210: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο Ακολουθιακά Κυκλώµατα (συν.) Ακολουθιακή Λογική: Έννοια
 ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 6-i: Ακολουθιακά Κυκλώµατα Μανδαλωτές (Latches) και Flip-Flops Ακολουθιακά Κυκλώµατα Συνδυαστική Λογική:
ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 6-i: Ακολουθιακά Κυκλώµατα Μανδαλωτές (Latches) και Flip-Flops Ακολουθιακά Κυκλώµατα Συνδυαστική Λογική:
σύνθεση και απλοποίησή τους θεωρήµατα της άλγεβρας Boole, αξιώµατα του Huntington, κλπ.
 Εισαγωγή Εργαστήριο 2 ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός του εργαστηρίου είναι να κατανοήσουµε τον τρόπο µε τον οποίο εκφράζεται η ψηφιακή λογική υλοποιώντας ασκήσεις απλά και σύνθετα λογικά κυκλώµατα (χρήση του
Εισαγωγή Εργαστήριο 2 ΛΟΓΙΚΑ ΚΥΚΛΩΜΑΤΑ Σκοπός του εργαστηρίου είναι να κατανοήσουµε τον τρόπο µε τον οποίο εκφράζεται η ψηφιακή λογική υλοποιώντας ασκήσεις απλά και σύνθετα λογικά κυκλώµατα (χρήση του
Εισαγωγή στον έλεγχο ορθής λειτουργίας ψηφιακών συστημάτων. Δημήτρης Νικολός, Τμήμα Μηχ. Ηλεκτρονικών Υπολογιστών και Πληροφορικής, Παν.
 Εισαγωγή στον έλεγχο ορθής λειτουργίας ψηφιακών συστημάτων 1 Περίγραμμα παρουσίασης Ανάγκη για έλεγχο ορθής λειτουργίας Επιβεβαίωση σχεδιασμού έναντι επιβεβαίωσης ορθής λειτουργίας μετά την κατασκευή και
Εισαγωγή στον έλεγχο ορθής λειτουργίας ψηφιακών συστημάτων 1 Περίγραμμα παρουσίασης Ανάγκη για έλεγχο ορθής λειτουργίας Επιβεβαίωση σχεδιασμού έναντι επιβεβαίωσης ορθής λειτουργίας μετά την κατασκευή και
Ψηφιακή Λογική και Σχεδίαση
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ. Κεφάλαιο 3
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Κεφάλαιο 3 Δυαδική λογική Με τον όρο λογική πρόταση ή απλά πρόταση καλούμε κάθε φράση η οποία μπορεί να χαρακτηριστεί αληθής ή ψευδής με βάση το νόημα της. π.χ. Σήμερα
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΨΗΦΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Κεφάλαιο 3 Δυαδική λογική Με τον όρο λογική πρόταση ή απλά πρόταση καλούμε κάθε φράση η οποία μπορεί να χαρακτηριστεί αληθής ή ψευδής με βάση το νόημα της. π.χ. Σήμερα
4/10/2008. Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης. Πραγματικά τρανζίστορ. Ψηφιακή λειτουργία. Κανόνες ψηφιακής λειτουργίας
 2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
Αλγόριθµοι Εκτίµησης Καθυστέρησης και
 Αλγόριθµοι Εκτίµησης Καθυστέρησης και Βελτιστοποίησης Εισαγωγή Το κύριο πρόβληµα στην σχεδίαση κυκλωµάτων είναι η επίτευξη της µέγιστης απόδοσης για την δεδοµένη τεχνολογία. Μεγιστοποίηση απόδοσης: (α)
Αλγόριθµοι Εκτίµησης Καθυστέρησης και Βελτιστοποίησης Εισαγωγή Το κύριο πρόβληµα στην σχεδίαση κυκλωµάτων είναι η επίτευξη της µέγιστης απόδοσης για την δεδοµένη τεχνολογία. Μεγιστοποίηση απόδοσης: (α)
7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Μονάδες Μνήµης
 7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Εισαγωγή Καταχωρητής: είναι µία οµάδα από δυαδικά κύτταρα αποθήκευσης και από λογικές πύλες που διεκπεραιώνουν την µεταφορά πληροφοριών. Οι µετρητές είναι
7 η Θεµατική Ενότητα : Καταχωρητές, Μετρητές και Εισαγωγή Καταχωρητής: είναι µία οµάδα από δυαδικά κύτταρα αποθήκευσης και από λογικές πύλες που διεκπεραιώνουν την µεταφορά πληροφοριών. Οι µετρητές είναι
Ψηφιακά Κυκλώματα (1 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
Κεφάλαιο 6. Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα
 Κεφάλαιο 6 Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα 6.1 Εισαγωγή Η εκτέλεση διαδοχικών λειτουργιών απαιτεί τη δημιουργία κυκλωμάτων που μπορούν να αποθηκεύουν πληροφορίες, στα ενδιάμεσα στάδια των
Κεφάλαιο 6 Σύγχρονα και ασύγχρονα ακολουθιακά κυκλώματα 6.1 Εισαγωγή Η εκτέλεση διαδοχικών λειτουργιών απαιτεί τη δημιουργία κυκλωμάτων που μπορούν να αποθηκεύουν πληροφορίες, στα ενδιάμεσα στάδια των
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές
 Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 12 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ E-mail: leo@mail.ntua.gr URL: http://users.ntua.gr/leo 1 GROUP I A Λ ΤΡΙΤΗ PC-Lab GROUP IΙ Μ Ω ΠΑΡΑΣΚΕΥΗ Central Κέντρο
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 12 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ E-mail: leo@mail.ntua.gr URL: http://users.ntua.gr/leo 1 GROUP I A Λ ΤΡΙΤΗ PC-Lab GROUP IΙ Μ Ω ΠΑΡΑΣΚΕΥΗ Central Κέντρο
7.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΑΝ ΑΛΩΤΕΣ FLIP FLOP Σκοπός: Η κατανόηση της λειτουργίας των βασικών ακολουθιακών κυκλωµάτων. Θα µελετηθούν συγκεκριµένα: ο µανδαλωτής (latch)
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΑΚΟΛΟΥΘΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΑΝ ΑΛΩΤΕΣ FLIP FLOP Σκοπός: Η κατανόηση της λειτουργίας των βασικών ακολουθιακών κυκλωµάτων. Θα µελετηθούν συγκεκριµένα: ο µανδαλωτής (latch)
Μνήμες RAM. Διάλεξη 12
 Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
Μοντέλα. χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες.
 Γλώσσες Περιγραφής Μοντέλα Ένα µοντέλο ενός κυκλώµατος είναι µία αναπαράσταση που παρουσιάζει χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες. Τα τυπικά µοντέλα έχουν καλά ορισµένη σύνταξη. Τα αυτόµατα
Γλώσσες Περιγραφής Μοντέλα Ένα µοντέλο ενός κυκλώµατος είναι µία αναπαράσταση που παρουσιάζει χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες. Τα τυπικά µοντέλα έχουν καλά ορισµένη σύνταξη. Τα αυτόµατα
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
Τα µπιτ και η σηµασία τους. Σχήµα bit. ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) 1.7 Αποθήκευση κλασµάτων 1.8 Συµπίεση δεδοµένων 1.9 Σφάλµατα επικοινωνίας
 ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (2/2) 1.1 Τα bits και ο τρόπος που αποθηκεύονται 1.2 Κύρια µνήµη 1.3 Αποθηκευτικά µέσα 1.4 Αναπαράσταση πληροφοριών ως σχηµάτων bits
ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (2/2) 1.1 Τα bits και ο τρόπος που αποθηκεύονται 1.2 Κύρια µνήµη 1.3 Αποθηκευτικά µέσα 1.4 Αναπαράσταση πληροφοριών ως σχηµάτων bits
ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ
 Τμήμα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρματης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Μάθημα 8: Σύγχρονα ακολουθιακά κυκλώµατα (µέρος Α ) Διδάσκων: Καθηγητής Ν. Φακωτάκης Κυκλώµατα οδηγούµενα από
Τμήμα Ηλεκτρολόγων Μηχανικών Εργαστήριο Ενσύρματης Τηλεπικοινωνίας ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Μάθημα 8: Σύγχρονα ακολουθιακά κυκλώµατα (µέρος Α ) Διδάσκων: Καθηγητής Ν. Φακωτάκης Κυκλώµατα οδηγούµενα από
C D C D C D C D A B
 Απλοποίηση µέσω Πίνακα Karnaugh: Παράδειγµα - 2 Στον παρακάτω πίνακα έχει ήδη γίνει το «βήμα- 1». Επομένως: Βήμα 2: Δεν υπάρχουν απομονωμένα κελιά. Βήμα 3: Στο ζεύγος (3,7) το κελί 3 γειτνιάζει μόνο με
Απλοποίηση µέσω Πίνακα Karnaugh: Παράδειγµα - 2 Στον παρακάτω πίνακα έχει ήδη γίνει το «βήμα- 1». Επομένως: Βήμα 2: Δεν υπάρχουν απομονωμένα κελιά. Βήμα 3: Στο ζεύγος (3,7) το κελί 3 γειτνιάζει μόνο με
Τεχνικές σχεδιασμού μονοπατιών ολίσθησης
 Τεχνικές σχεδιασμού μονοπατιών ολίσθησης (Scan Path Design Techniques) Περίγραμμα παρουσίασης Προβλήματα ελέγχου ορθής λειτουργίας ακολουθιακών κυκλωμάτων Μονοπάτι ολίσθησης (scan path) Στοιχεία μνήμης
Τεχνικές σχεδιασμού μονοπατιών ολίσθησης (Scan Path Design Techniques) Περίγραμμα παρουσίασης Προβλήματα ελέγχου ορθής λειτουργίας ακολουθιακών κυκλωμάτων Μονοπάτι ολίσθησης (scan path) Στοιχεία μνήμης
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Μετρητής Ριπής (Ripple Counter) Μετρητές (Counters) Μετρητής Ριπής (συν.
 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 ii: Μετρητές Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Μετρητής Ριπής Περίληψη Σύγχρονος υαδικός Μετρητής Σχεδιασµός µε Flip-Flops
ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 ii: Μετρητές Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Μετρητής Ριπής Περίληψη Σύγχρονος υαδικός Μετρητής Σχεδιασµός µε Flip-Flops
Καθυστέρηση στατικών πυλών CMOS
 Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
Οι Εξελικτικοί Αλγόριθμοι (ΕΑ) είναι καθολικοί στοχαστικοί αλγόριθμοι βελτιστοποίησης, εμπνευσμένοι από τις βασικές αρχές της φυσικής εξέλιξης.
 Οι Εξελικτικοί Αλγόριθμοι (ΕΑ) είναι καθολικοί στοχαστικοί αλγόριθμοι βελτιστοποίησης, εμπνευσμένοι από τις βασικές αρχές της φυσικής εξέλιξης. Ένα από τα γνωστότερα παραδείγματα των ΕΑ είναι ο Γενετικός
Οι Εξελικτικοί Αλγόριθμοι (ΕΑ) είναι καθολικοί στοχαστικοί αλγόριθμοι βελτιστοποίησης, εμπνευσμένοι από τις βασικές αρχές της φυσικής εξέλιξης. Ένα από τα γνωστότερα παραδείγματα των ΕΑ είναι ο Γενετικός
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη.
 4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
4.4 Μετατροπή από μία μορφή δομής επανάληψης σε μία άλλη. Η μετατροπή μιας εντολής επανάληψης σε μία άλλη ή στις άλλες δύο εντολές επανάληψης, αποτελεί ένα θέμα που αρκετές φορές έχει εξεταστεί σε πανελλαδικό
7 η Θεµατική Ενότητα : Εισαγωγή στις Γλώσσες Περιγραφής Υλικού
 7 η Θεµατική Ενότητα : Εισαγωγή στις Γλώσσες Περιγραφής Υλικού Εισαγωγή Η χειρονακτική σχεδίαση ενός ψηφιακού συστήµατος είναι εξαιρετικά δύσκολη και επιρρεπής σε λάθη Συστήµατα που ξεπερνούς τις µερικές
7 η Θεµατική Ενότητα : Εισαγωγή στις Γλώσσες Περιγραφής Υλικού Εισαγωγή Η χειρονακτική σχεδίαση ενός ψηφιακού συστήµατος είναι εξαιρετικά δύσκολη και επιρρεπής σε λάθη Συστήµατα που ξεπερνούς τις µερικές
5.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΟΜΑ Α ΑΣΚΗΣΕΩΝ ΑΣΚΗΣΗ Στην εικόνα παρακάτω φαίνεται ένα νευρωνικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΜΣΕ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ ΚΑΙ ΕΞΕΛΙΚΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ ΟΜΑ Α ΑΣΚΗΣΕΩΝ ΑΣΚΗΣΗ Στην εικόνα παρακάτω φαίνεται ένα νευρωνικό
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Ακολουθιακή Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Εισαγωγή στην επιστήµη των υπολογιστών. Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών
 Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος
Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
ΠΛΗ10 Κεφάλαιο 2. ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών
 ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.3 : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές αρχές αριθμητικής των Η/Υ. Ποια είναι τα κυκλώματα
ΠΛH10 Εισαγωγή στην Πληροφορική: Τόμος Α Κεφάλαιο: 2 2.3 : Αριθμητική περιοχή της ALU 2.5: Κυκλώματα Υπολογιστών Στόχοι Μαθήματος: Να γνωρίσετε τις βασικές αρχές αριθμητικής των Η/Υ. Ποια είναι τα κυκλώματα
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ
 ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΗΜΥ 210: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο Ένα συνδυαστικό κύκλωµα µπορεί να περιγραφεί από: Φεβ-05. n-είσοδοι
 ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 Φεβ-5 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 3 -i: Σχεδιασµός Συνδυαστικών Κυκλωµάτων Περίληψη Αρχές σχεδιασµού Ιεραρχία σχεδιασµού Σχεδιασµός
ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 Φεβ-5 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 3 -i: Σχεδιασµός Συνδυαστικών Κυκλωµάτων Περίληψη Αρχές σχεδιασµού Ιεραρχία σχεδιασµού Σχεδιασµός
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino)
 Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Εισαγωγή στην επιστήµη των υπολογιστών. Αναπαράσταση Αριθµών
 Εισαγωγή στην επιστήµη των υπολογιστών Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος είναι το 10 αναπτύχθηκε τον 8
Εισαγωγή στην επιστήµη των υπολογιστών Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος είναι το 10 αναπτύχθηκε τον 8
ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ
 ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
ΣΧΟΛΗ ΑΣΠΑΙΤΕ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΣΥΓΧΡΟΝΟΙ ΜΕΤΡΗΤΕΣ 1) Οι σύγχρονοι μετρητές υλοποιούνται με Flip-Flop τύπου T
i Το τρανζίστορ αυτό είναι τύπου NMOS. Υπάρχει και το συμπληρωματικό PMOS. ; Τι συμβαίνει στο τρανζίστορ PMOS; Το τρανζίστορ MOS(FET)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
Απλοποιεί τα γεγονότα έτσι ώστε να περιγράφει τι έχει γίνει και όχι πως έχει γίνει.
 οµηµένες τεχνικές Ο στόχος των δοµηµένων τεχνικών είναι: Υψηλής ποιότητας προγράµµατα Εύκολη τροποποίηση προγραµµάτων Απλοποιηµένα προγράµµατα Μείωση κόστους και χρόνου ανάπτυξης. Οι βασικές αρχές τους
οµηµένες τεχνικές Ο στόχος των δοµηµένων τεχνικών είναι: Υψηλής ποιότητας προγράµµατα Εύκολη τροποποίηση προγραµµάτων Απλοποιηµένα προγράµµατα Μείωση κόστους και χρόνου ανάπτυξης. Οι βασικές αρχές τους
ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ
 ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ, αν είναι
ΑΣΚΗΣΗ 10 ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ
 ΑΣΚΗΣΗ ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Στόχος της άσκησης: Η διαδικασία σχεδίασης σύγχρονων ακολουθιακών κυκλωμάτων. Χαρακτηριστικό παράδειγμα σύγχρονων ακολουθιακών κυκλωμάτων είναι οι σύγχρονοι μετρητές. Τις αδυναμίες
ΑΣΚΗΣΗ ΣΥΓΧΡΟΝΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Στόχος της άσκησης: Η διαδικασία σχεδίασης σύγχρονων ακολουθιακών κυκλωμάτων. Χαρακτηριστικό παράδειγμα σύγχρονων ακολουθιακών κυκλωμάτων είναι οι σύγχρονοι μετρητές. Τις αδυναμίες
Ψηφιακά Ηλεκτρονικά. Μάθηµα 5ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 27 Νοε-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Ακολουθιακά Κυκλώματα: Μανδαλωτές (Latches) και Flip-Flops Flops Διδάσκουσα:
K24 Ψηφιακά Ηλεκτρονικά 9: Flip-Flops
 K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
 Θεµατική Ενότητα ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Ακαδηµαϊκό Έτος 2006 2007 Γραπτή Εργασία #2 Ηµεροµηνία Παράδοσης 28-0 - 2007 ΠΛΗ 2: Ψηφιακά Συστήµατα ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ Άσκηση : [5 µονάδες] Έχετε στη
Θεµατική Ενότητα ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Ακαδηµαϊκό Έτος 2006 2007 Γραπτή Εργασία #2 Ηµεροµηνία Παράδοσης 28-0 - 2007 ΠΛΗ 2: Ψηφιακά Συστήµατα ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΛΥΣΕΙΣ Άσκηση : [5 µονάδες] Έχετε στη
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Εκτέλεση πράξεων. Ψηφιακά Ηλεκτρονικά και Δυαδική Λογική. Πράξεις με δυαδικούς αριθμούς. Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 24-5 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης ; Ποιες κατηγορίες
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 24-5 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης ; Ποιες κατηγορίες
ΑΣΚΗΣΗ 7 FLIP - FLOP
 ΑΣΚΗΣΗ 7 FLIP - FLOP Αντικείμενο της άσκησης: Η κατανόηση της δομής και λειτουργίας των Flip Flop. Flip - Flop Τα Flip Flop είναι δισταθή λογικά κυκλώματα με χαρακτηριστικά μνήμης και είναι τα πλέον βασικά
ΑΣΚΗΣΗ 7 FLIP - FLOP Αντικείμενο της άσκησης: Η κατανόηση της δομής και λειτουργίας των Flip Flop. Flip - Flop Τα Flip Flop είναι δισταθή λογικά κυκλώματα με χαρακτηριστικά μνήμης και είναι τα πλέον βασικά
Εισαγωγή στη Σχεδίαση Λογισμικού
 Εισαγωγή στη Σχεδίαση Λογισμικού περιεχόμενα παρουσίασης Τι είναι η σχεδίαση λογισμικού Έννοιες σχεδίασης Δραστηριότητες σχεδίασης Σχεδίαση και υποδείγματα ανάπτυξης λογισμικού σχεδίαση Η σχεδίαση του
Εισαγωγή στη Σχεδίαση Λογισμικού περιεχόμενα παρουσίασης Τι είναι η σχεδίαση λογισμικού Έννοιες σχεδίασης Δραστηριότητες σχεδίασης Σχεδίαση και υποδείγματα ανάπτυξης λογισμικού σχεδίαση Η σχεδίαση του
PLD. Εισαγωγή. 5 η Θεµατική Ενότητα : Συνδυαστικά. PLAs. PLDs FPGAs
 5 η Θεµατική Ενότητα : Συνδυαστικά Κυκλώµατα µε MSI και Εισαγωγή Οι προγραµµατιζόµενες διατάξεις είναι ολοκληρωµένα µε εσωτερικές πύλες οι οποίες µπορούν να υλοποιήσουν οποιαδήποτε συνάρτηση αν υποστούν
5 η Θεµατική Ενότητα : Συνδυαστικά Κυκλώµατα µε MSI και Εισαγωγή Οι προγραµµατιζόµενες διατάξεις είναι ολοκληρωµένα µε εσωτερικές πύλες οι οποίες µπορούν να υλοποιήσουν οποιαδήποτε συνάρτηση αν υποστούν
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗΣ
 Εισαγωγή στη Μικροηλεκτρονική (ΕΤΥ-482) 1 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗΣ A. Πίνακες αληθείας λογικών πυλών. Στη θετική λογική το λογικό 0 παριστάνεται µε ένα χαµηλό δυναµικό, V L, ενώ το λογικό 1
Εισαγωγή στη Μικροηλεκτρονική (ΕΤΥ-482) 1 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗΣ A. Πίνακες αληθείας λογικών πυλών. Στη θετική λογική το λογικό 0 παριστάνεται µε ένα χαµηλό δυναµικό, V L, ενώ το λογικό 1
Atlantis - Νέο user interface
 New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE...2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ...3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ...4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)...5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ...6 Κεντρικό μενού
New Desktop 1 Atlantis - Νέο user interface ATLANTIS - ΝΕΟ USER INTERFACE...2 ΓΕΝΙΚΗ ΠΑΡΟΥΣΙΑΣΗ...3 ΓΡΑΜΜΗ ΣΥΣΤΗΜΑΤΟΣ...4 ΜΠΑΡΑ ΧΡΗΣΤΗ (USER TOOLBAR)...5 ΚΕΝΤΡΙΚΟ ΜΕΝΟΥ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ...6 Κεντρικό μενού
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
Η συχνότητα f των παλµών 0 και 1 στην έξοδο Q n είναι. f Qn = 1/(T cl x 2 n+1 )
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των απαριθµητών. Υλοποίηση ασύγχρονου απαριθµητή 4-bit µε χρήση JK Flip-Flop. Κατανόηση της αλλαγής του υπολοίπου
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΥΑ ΙΚΟΙ ΑΠΑΡΙΘΜΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των απαριθµητών. Υλοποίηση ασύγχρονου απαριθµητή 4-bit µε χρήση JK Flip-Flop. Κατανόηση της αλλαγής του υπολοίπου
9. ΚΑΤΑΧΩΡΗΤΕΣ (REGISTERS)
 9. ΚΑΤΑΧΩΡΗΤΕΣ (REGISTERS) 9.. ΕΙΣΑΓΩΓΗ Όπως έχουμε ήδη αναφέρει για την αποθήκευση μιας πληροφορίας ενός ψηφίου ( bit) απαιτείται ένα στοιχείο μνήμης δηλαδή ένα FF. Επομένως για περισσότερα του ενός ψηφία
9. ΚΑΤΑΧΩΡΗΤΕΣ (REGISTERS) 9.. ΕΙΣΑΓΩΓΗ Όπως έχουμε ήδη αναφέρει για την αποθήκευση μιας πληροφορίας ενός ψηφίου ( bit) απαιτείται ένα στοιχείο μνήμης δηλαδή ένα FF. Επομένως για περισσότερα του ενός ψηφία
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 6 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 6 η :
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΟΜΑ Α Α Αριθµητική Λογική Μονάδα των 8-bit 1. Εισαγωγή Γενικά µια αριθµητική λογική µονάδα (ALU, Arithmetic Logic Unit)
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΟΜΑ Α Α Αριθµητική Λογική Μονάδα των 8-bit 1. Εισαγωγή Γενικά µια αριθµητική λογική µονάδα (ALU, Arithmetic Logic Unit)
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε αναστροφείς CMOS VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Τεχνικές βελτιστοποίησης µε σκοπό την επίτευξη χαµηλής κατανάλωσης ισχύος
 Low power techniques Τεχνικές βελτιστοποίησης µε σκοπό την επίτευξη χαµηλής κατανάλωσης ισχύος Γενικά Τεχνικές βιοµηχανίας Μείωση χωρητικοτήτων chip και package Μέσω process development πολύ αποτελεσµατική
Low power techniques Τεχνικές βελτιστοποίησης µε σκοπό την επίτευξη χαµηλής κατανάλωσης ισχύος Γενικά Τεχνικές βιοµηχανίας Μείωση χωρητικοτήτων chip και package Μέσω process development πολύ αποτελεσµατική
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. Σχεδίαση και αξιολόγηση ψευδοτυχαίων γεννητριών για μειωμένη κατανάλωση ισχύος κατά τον έλεγχο ορθής λειτουργίας
 ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Επιβλέπων: Σχεδίαση και αξιολόγηση ψευδοτυχαίων γεννητριών για μειωμένη κατανάλωση ισχύος κατά τον έλεγχο ορθής λειτουργίας Καθηγητής Δημήτριος Νικολός Λαουδιάς Χρήστος Α.Μ. 2142
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Επιβλέπων: Σχεδίαση και αξιολόγηση ψευδοτυχαίων γεννητριών για μειωμένη κατανάλωση ισχύος κατά τον έλεγχο ορθής λειτουργίας Καθηγητής Δημήτριος Νικολός Λαουδιάς Χρήστος Α.Μ. 2142
Σύγχρονοι Απαριθμητές. Διάλεξη 8
 Σύγχρονοι Απαριθμητές Διάλεξη 8 Δομή της διάλεξης Εισαγωγή Σύγχρονος Δυαδικός Απαριθμητής Σύγχρονος Δεκαδικός Απαριθμητής Προγραμματιζόμενοι Απαριθμητές Ασκήσεις 2 Σύγχρονοι Απαριθμητές Εισαγωγή 3 Εισαγωγή
Σύγχρονοι Απαριθμητές Διάλεξη 8 Δομή της διάλεξης Εισαγωγή Σύγχρονος Δυαδικός Απαριθμητής Σύγχρονος Δεκαδικός Απαριθμητής Προγραμματιζόμενοι Απαριθμητές Ασκήσεις 2 Σύγχρονοι Απαριθμητές Εισαγωγή 3 Εισαγωγή
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ
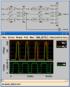 Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων
 K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
K15 Ψηφιακή Λογική Σχεδίαση 7-8: Ανάλυση και σύνθεση συνδυαστικών λογικών κυκλωμάτων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Η έννοια του συνδυαστικού
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
