Réamhrá CAIBIDIL AN FHISIC: FREAGRA AR MHÓRÁN CEISTEANNA AG DÉANAMH STAIDÉIR AR AN BHFISIC CÉARD ATÁ I GCEIST LEIS AN BHFISIC?
|
|
|
- Ζακχαῖος Δυοβουνιώτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Réamhrá AIBIDIL AN FHISI: FREAGRA AR MHÓRÁN EISTEANNA Daoine iosracha is ea eolaithe; teastaíonn uathu a háil amach cén chaoi agus cén áth a dtarlaíonn rudaí. Bíonn isiceoirí ag lorg eolais aoi na dlíthe a rialaíonn an domhan mar tugann na dlíthe sin tuiscint níos earr dúinn ar an domhan ina mairimid. Tabharar reagra sa chúrsa seo ar go leor de na ceisteanna a bheadh agat aoin gcaoi a bheidhmíonn an domhan. Mar shampla, ar chuir sé iontas ort riamh gur éidir le peann giota páipéir a phiocadh suas tar éis duit an peann a chuimilt de do chuid gruaige, nó aoin bháth a ndealraíonn sé go lúbann spúnóg a chuirtear in uisce ag an áit a dtéann sí isteach san uisce? Ar chuir tú aon cheann de na ceisteanna seo a leanas ort éin riamh: én áth a bheicim dathanna ar dhlúthdhiosca? én chaoi a bheicimid scáileanna i scáthán? én áth a mbíonn bogha báistí ann uaireanta nuair a bhíonn sé liuch? onas is éidir linn an taobh istigh de cholainn an duine a heiceáil le gléas X-ghathanna? én áth a n-aomann iarann maighnéad? onas a oibríonn luasghunnaí na ngardaí? éard is meabhalscáil ann, agus céard is cúis léi? Má tá tú sách iosrach aoi aon cheann de na rudaí sin, bainidh tú taitneamh as an bhisic. Is ábhar í a dtagann beocht inti nuair a théann tú i ngleic léi. Agus tú ag dul tríd an gcúrsa bainidh tú úsáid as trealamh eolaíoch speisialta agus cuiridh tú teoiricí i bheidhm éachaint cén chaoi agus cén áth a dtarlaíonn rudaí; reagróar gach ceann de na ceisteanna thuas, agus go leor eile. abhróidh Fisic don Ré Nua leat teacht ar an eolas aoin ngaol atá idir an Fhisic agus an gnáthshaol, agus aoin tionchar atá ag an bhfisic ar shochaí an lae inniu. AG DÉANAMH STAIDÉIR AR AN BHFISI Nuair a bhíonn tú ag déanamh staidéir ar an bhfisic: smaoinigh mar eolaí, bí iosrach agus lorg míniúchán ar gach rud, ná bíodh eagla ort ceisteanna a chur, agus lean leis na ceisteanna go dtí go dtuigeann tú go soiléir an earnáil den Fhisic atáthar a mhúineadh duit, bí ag smaoineamh go loighciúil, bain taitneamh as na turgnaimh a dhéanamh agus as na reagraí cearta a háil. ÉARD ATÁ I GEIST LEIS AN BHFISI? Brainse den eolaíocht atá san Fhisic ina ndéantar staidéar ar dhamhna agus uinneamh agus an coibhneas eatarthu.
2 Fisic don Ré Nua RÉIMSÍ STAIDÉIR SAN FHISI Sa húrsa Fisice don Ardteistiméireacht déanaidh tú staidéar ar thopaicí éagsúla sna réimsí seo a leanas: Meicnic agus Gluaisne Leictreachas agus Maighnéadas Teas Fisic Adamhach agus an Tonnta agus Fuaim Leictreonaic Solas agus an Optaic Fisic Núicléach agus áithníní TURGNAIMH SAN FHISI Tá dhá phríomhchineál turgnaimh san hisic: turgnaimh ina ndéantar breathnú ach nach ndéantar aon tomhas iontu, agus turgnaimh ina ndéantar tomhas. BREATHNÚ Má rinne tú staidéar ar an eolaíocht roimhe seo is dócha go ndearna tú turgnamh, nó go bhaca tú turgnamh á dhéanamh, chun a thaispeáint go bhorbraíonn solad nuair a théitear é. B héidir go bhaca tú turgnamh reisin a thaispeáin go n-oibríonn corna sreinge atá ag iompar srutha leictrigh mar a oibríonn barra-mhaighnéad. Breathnú a bhí i gceist sna turgnaimh sin cé nár thomhais tú aon rud. TOMHAS Abair go raibh innealltóir sibhialta ag iarraidh a oibriú amach cén horbairt a dhéanadh droichead an lá is teo sa samhradh. Níor mhór eolas a bheith aige/aici ar an méid a horbraíonn cruach agus coincréit nuair a théitear iad. Agus dá mbeadh innealltóir leictreach ag iarraidh leictreamhaighnéad a dhearadh a d ardódh dramhiarann chaitheadh cur amach a bheith aige/aici ar mhéid an tsrutha leictrigh agus an chorna a theastódh chun réimse maighnéadach a thabhairt a bheadh sách láidir chun an dramhiarann a ardú. Beidh tomhas le déanamh i gcuid de na turgnaimh a dhéanaidh tú sa tsaotharlann sa húrsa Fisice don Ardteistiméireacht. hun é sin a dhéanamh beidh ort leas a bhaint as cainníochtaí isiceacha. Mar seo a leanas a shainmhínítear cainníocht hisiceach: SAMPLAÍ DE HAINNÍOHTAÍ ad ama an luasghéarú an teocht an diríocht poitéinsil an ad an mhais an mhinicíocht an hriotaíocht an t-achar an móiminteam an huaimdhéine an losc maighnéadach an toirt an órsa an leibhéal uaimdhéine an loscdhlús maighnéadach ad slí móimint órsa lucht leictreach gníomhaíocht oinse an díláithriú an obair neart réimse leictrigh radaighníomhaí an luas an uinneamh an toilleas an treoluas an chumhacht sruth leictreach AD IS TOMHAS ANN? 2 Le tomhas a léirítear go bhuil giota sreinge 2 mhéadar ar ad. Is é sin, tá an píosa sreinge dhá oiread déag níos aide ná an méadar. Is é an méadar an t-aonad aid. Le tomhas a léirítear go bhuil dhá aimpéar de shruth leictreach ag sreabhadh i sreang. Is é sin, tá an sruth sa tsreang dhá oiread níos mó ná an t-aimpéar. Is é an t-aimpéar an t-aonad srutha leictrigh.
3 Réamhrá Uimhir iolraithe aoi aonad an toradh ar thomhas i gcónaí. Méid na cainníochta atá á tomhas a thugtar air seo (an uimhir agus an t-aonad). AONAID SI Sa bhliain 960 shocraigh na heolaithe ar chóras ar leith a úsáid do na haonaid: Le Système International d Unités (óras Idirnáisiúnta na naonad). Aonad SI a thugtar ar aonad ar bith sa chóras sin. Bainear úsáid as aonaid SI go orleathan i do chúrsa isice. Tá samplaí de chainníochtaí agus dá n-aonaid SI i bhfíor. ainníocht Fad ama An díláithriú An luas An Fórsa An hriotaíocht An mhinicíocht Aonad SI soicind méadar méadar sa soicind niútan óm heirts Fíor. BUNAONAID D héadaí aonad neamhspléach a roghnú don tomhas i gcás gach cainníochta ar leith. Ní bheadh bunghaol idir na haonaid éagsúla ansin áach. hun cúrsaí a shimpliú, roghnaíodh seacht gcainníocht ar a dtugtar na bunchainníochtaí, agus tugtar bunaonad ar an aonad a úsáidtear do gach cainníocht díobh. Tá sainmhíniú an-chruinn ar na seacht mbunaonad sin, agus tiocaimid suas leis na sainmhínithe sin ar ball. Tá ainmneacha agus siombailí na gcúig bhunchainníocht agus bunaonad ar an gcúrsa i bhfíor.2. Bunchainníocht Siombail Ainm an Aonaid SI Siombail ad l nó s méadar m am t soicind s mais m cileagram kg sruth leictreach I aimpéar A teocht T ceilvin K Fíor.2 AONAID DHÍORTHAITHE Aonad díorthaithe a thugtar ar an aonad a bhaineann le gach cainníocht eile óir is éidir é a scríobh mar iolrach nó líon ceann amháin nó níos mó de na bunaonaid. Tá samplaí de chainníochtaí agus dá n-aonaid dhíorthaithei bhfíor.3. ainníocht Fhisiceach Siombail Ainm an Aonaid SI Siombail Achar A méadar cearnach m 2 Toirt V méadar ciúbach m 3 Luas v nó u méadar sa soicind ms - nó m/s Dlús ρ cileagram sa mhéadar ciúbach kg m -3 nó kg/m 3 Fíor.3 HUN AONAD DÍORTHAITHE AINNÍOHTA A FHÁIL Fadhb : Réiteach: Fadhb 2: Faigh aonad SI na toirte Ó tá: Toirt ad leithead airde Aonad SI na toirte (aonad aid)(aonad leithid)(aonad airde) (m)(m)(m) m 3 an méadar ciúbach Faigh aonad SI an luais ad aonad aid m Réiteach: Luas am aonad SI an luais m s aonad ama s - An méadar sa soicind a thugtar air. (uimhnigh sa mhatamaitic go scríobhtar m x mar x -. Dá réir sin: s m s m s- ) 3
4 Fisic don Ré Nua Fadhb 3: Réiteach: Faigh aonad SI an dlúis mais Ó tá dlús toirt Aonad SI an dlúis aonad maise aonad toirte cileagram méadar ciúbach cileagram sa mhéadar ciúbach Fadhb 4: kg m -3 nó kg/m 3 Feicidh tú i gaibidil 9 nuair a oibríonn órsa F ar chorp dar mais m ionas go dtugann sé luasghéarú a don chorp sin, go bhuil: Fórsa mais luasghéarú i.e. F ma. Más é m s -2 aonad an luasghéaraithe, aigh aonad SI an hórsa i dtéarmaí bunaonad. Réiteach: F ma Aonad Forsa (aonad maise)(aonad luasghéaraithe) (kg)(m s -2 ) kg m s -2 Fadhb 5: Réiteach: An niútan (N) a thugtar ar an aonad órsa sin in ómós d Isaac Newton, eolaí agus matamaiticeoir mór le rá. Nuair a ghluaiseann órsa F trí had s in aontreo leis an bhórsa, tugtar an obair atá déanta W leis an bhoirmle: Obair Fórsa Fad, i.e. W Fs. Faigh: (a) aonad SI na hoibre i dtéarmaí an niútain. (b) aonad SI na hoibre i dtéarmaí bunaonad. (a) Obair Fórsa Fad Aonad SI na hoibre (aonad órsa)(aonad aid) méadar niútain. An giúl (J) a thugtar ar an aonad sin in ómós do James Joule, eolaí cáiliúil. Dá réir sin J N m (b) Ó hadhb 4: N kg m s -2 Aonad oibre N m (kg m s -2 )(m) kg m 2 s -2 Dá réir sin tá an t-aonad oibre, an giúl kg m 2 s -2 Fíor.4 Má scríobhtar aonad i dtéarmaí bunaonad bíonn cuma chasta air uaireanta, agus is minic a thugtar ainm eile ar a leithéid ainm eolaí, b héidir, a rinne ionnachtain thábhachtach sa réimse eolaíochta ina mbíonn an t-aonad sin in úsáid. I gcás mar sin scríobhtar siombail an aonaid le ceannlitir ach ní chuirtear ceannlitir le hainm an aonaid. Tá roinnt aonad den chineál sin i bhfíor.4. (Is iad Newton, Pascal, Joule, Watt, Hertz, Tesla, Weber agus Becquerel na heolaithe atá i gceist.) ainníocht Siombail Aonad Siombail Siombail eile Siombail i dtéarmaí bunaonad Fórsa F niútan N kg m s -2 kg m s -2 Brú P nó p pascal Pa N m -2 kg m - s -2 Obair W giúl J Nm kg m 2 s -2 Fuinneamh E giúl J N m kg m 2 s -2 umhacht P vata W J s - kg m 2 s -3 Minicíocht ƒ heirts Hz s - s - Floscdhlús Maighnéadach B teisle T Flosc Maighnéadach Φ weber Wb Gníomhaíocht hoinse radaighníomhaí A beicireil Bq 4
5 Réamhrá AONAID SI A ÚSÁID Nuair atá adhbanna uimhriúla á réiteach agat san hisic is iad na haonaid SI is ceart a úsáid, agus iad sin amháin. Bíodh luach gach cainníochta slonnta san aonad SI ceart sula dtosaíonn tú. Ní gá na haonaid a scríobh síos ag gach céim den argóint agus an t-áireamh á dhéanamh. Mar sin éin nuair atá an reagra oibrithe amach ní oláir é a scríobh agus an t-aonad ceart (nó siombail an aonaid) ina dhiaidh. aillidh tú marcanna sa scrúdú go cinnte mura ndéanann tú é sin! Agus méid chainníochta á scríobh lena siombail chuí aonaid, ágtar spás idir an uimhir agus siombail an aonaid. Mar shampla, is 5 m seachas 5m a scríobhtar le haghaidh cúig mhéadar. Agus aonad á scríobh i dtéarmaí bunaonad, ágtar spás idir na siombailí do gach bunaonad ar leith. Mar shampla, is é kg m -3, agus ní hé kgm -3 an giorrúchán don aonad dlúis; is é m s - agus ní hé ms - an giorrúchán don aonad luais. Fíor.5 IOLRAITHE AGUS ODÁIN NA NAONAD AIGHDEÁNAH Uaireanta bíonn na haonaid chaighdeánacha SI rómhór nó róbheag le húsáid go héasca, agus úsáidtear iolraithe nó codáin na n-aonad caighdeánach atá i bhfíor.6. Tabhair aoi deara an méid seo a leanas: Roimh ainm an aonaid a chuirtear an réimír, mar shampla 0 gciliméadar, 5 mhilliniútan Ní bhíonn spás idir an réimír agus siombail an aonaid, mar shampla is 60 mm a scríobhtar i gcás 60 milliméadar; agus 20 kw i gcás 20 cileavata. Iolraithe de 0 i gcumhacht a 3 a úsáidtear de ghnáth. Tá nós ann, gan an réimír ceinti- a úsáid ach leis an méadar amháin. Tá tábla cosúil le Fíor.6 ar leathanach 5 de do chuid táblaí matamaitice. Fadhb 6: Réiteach: Scríobh gach ceann díobh seo a leanas ina aonaid chaighdeánacha SI: (i) 2 mm (ii) 400 mj (iii) 7 MW (i) 2 mm m m (ii) 400 mj J 0.4 J (iii) 7 MW W Iolraí nó codáin Réimír Siombail 0 9 gigi- gigea- G 0 6 meigi- meigea - M 0 3 cili- cilea- k 0-2 ceinti- ceintea- c 0-3 milli- millea- m 0-6 micri- micrea- Ì 0-9 nanai- nana- Ë 0-2 pici picea- p Fíor.6 5
6 Fisic don Ré Nua LEAHTADH.. Taispeáin gurb é an méadar cearnach aonad SI an achair. 2. Má tá corp dar mais m cileagram ag gluaiseacht aoi threoluas v méadar sa soicind, is leis an gcothromóid seo a leanas a shainmhínítear P, an móiminteam: P mv. Faigh aonad SI an mhóimintim i dtéarmaí na mbunaonad. 3. Nuair a athraíonn treoluas coirp, tugtar a mheánluasghéarú a le: a athrú treoluais am a thógtar don athrú Faigh aonad SI an luasghéaraithe. 4. ad é aonad SI an dlúis? ruthaigh go bhuil an reagra i gceart agat. 5. Fórsa san aonad achair, sin an sainmhíniú ar bhrú P, i.e. P F/A. Más é an niútan (N) aonad SI an hórsa, aigh aonad SI an bhrú i dtéarmaí an niútain agus an mhéadair. 6. (a) é mhéad ceintiméadar cearnach atá i méadar cearnach amháin? (b) é mhéad ceintiméadar ciúbach atá i méadar ciúbach amháin? (c) é mhéad gram atá i gcileagram? 7. Sloinn gach ceann díobh seo a leanas ina aonaid chaighdeánacha SI: 8. Scríobh gach ceann de na tomhais seo a leanas ina aonaid chaighdeánacha SI: (i) 05 km (vi) 00 km h - (ii) 57 mm (iii) cm (iv) gram (vii) 5 nn (viii) 0 ÌW (ix) 5 Gm (v) 9 ngram sa cheintiméadar ciúbach. 9. An méadar sa soicind cearnach (m s -2 ), sin an t-aonad luasghéaraithe a. Mais iolraithe aoi luasghéarú, sin órsa, i.e. F m a. Is é an niútan an t-aonad órsa. Scríobh an niútan i dtéarmaí na mbunaonad. 0. Fórsa F iolraithe aoin bhad a taistealaíodh, sin an sainmhíniú ar obair W, i.e. W F s. Is é an giúl (J) an t-aonad oibre. Scríobh an giúl i dtéarmaí an niútain.. Bain úsáid as torthaí an dá cheist díreach roimhe seo chun an t-aonad oibre, an giúl, a scríobh i dtéarmaí na mbunaonad. 2. An obair a rinneadh roinnte ar an am a tógadh, sin an sainmhíniú ar chumhacht P, i.e. P W t. An vata (W) a thugtar ar an aonad cumhachta. Sloinn an vata i dtéarmaí an ghiúil agus an tsoicind. Ansin sloinn an vata i dtéarmaí na mbunaonad. (i) 5 cm 2 (iv) 456 cm 3 (ii) 40 cm 2 (v) cm 3 (iii) cm 3 00 ceintiméadar ciúbach atá sa tsraith seo Dá bhrí sin tá 00 x ceintiméadar ciúbach sa slisne uachtarach 00 ceintiméadar ciúbach atá sa tsraith seo 00 sraith atá ann ar ad. m m m Fíor.7 é mhéad cm 3 atá in m 3? tá (00)(0 000) cm 3 in aon m 3 i.e. m cm cm 3 cm m 3 6
7 An Optaic Gheoiméadrach 2 AIBIDIL NÍ HANN DON RADHAR GAN AN SOLAS Má tá tú i seomra agus má tá na soilse múchta agus na doirse agus na uinneoga dúnta agus clúdaithe sa chaoi nach éidir le haon solas teacht isteach sa seomra, ní bheidh tú in ann aon rud a heiceáil. hun rithne a heiceáil, caithidh an solas a thagann ón bhrithne sin dul isteach i do shúil. Ós rud é nach mbeadh rithní inheicthe gan an solas, is minic a thugtar solas inheicthe ar an solas. Ní hé go bheiceann tú an solas éin áach ní heiceann tú ach an hrithne óna dtagann an solas. Tá rithní ann a thugann a gcuid solais éin amach. Frithne héinlonrach a thugtar ar hrithne a thugann amach a chuid solais éin, mar shampla an Ghrian, na réaltaí, tine agus bolgán leictreach (atá ar lasadh agus ag obair). Frithne neamhlonrach a thugtar ar hrithne nach dtugann amach solas dá chuid éin. Ní heicidh tú rithne dá leithéid mura léimeann solas ó hoinse eile ar ais ón bhrithne sin agus isteach i do shúil. AD IS SOLAS ANN? Is cineál uinnimh é an solas a thaistealaíonn amach ón bhoinse a tháirgeann é aoi luas dochreidte méadar sa soicind, nó thart ar míle sa soicind (ní gá na igiúirí a chur de ghlanmheabhair). Fadhb : Tá an Ghrian.5 0 m ón Domhan. én ad ama a thógann sé ar an solas taisteal ón ngrian go dtí an Domhan. Fad.5 0 Réiteach: Am a thógtar s 8.33 nóim Luas 3 0 Mar sin, an solas a shroicheann an Domhan anois, d hág sé an Ghrian 8.33 nóiméad ó shin. ONAS ATÁ A FHIOS AGAINN GUR INEÁL FUINNIMH É AN SOLAS? Fuinneamh i bhoirm eile a bhíonn ag teastáil i gcónaí chun solas a tháirgeadh in aon hoinse solais: uinneamh leictreach a thiontaítear ina huinneamh solais i mbolgán, mar shampla; uinneamh ceimiceach a thiontaítear ina huinneamh solais i gcás tine. Is éidir leis an solas ótaichill a chur ag táirgeadh srutha leictrigh. Is é atá i ngrianphainéil ná líon mór ótaicheall le chéile agus méid mór solais á thiontú ina huinneamh leictreach acu (Fíor 2.). Fíor 2. Aschur cumhachta 000 vata a bheadh ag an ngrianphainéal seo aoi lánsolas ghrian an tsamhraidh. 7
8 Fisic don Ré Nua radaiméadar rookes (Fíor 2.2), rothlaíonn na heití. Dá réir sin tiontaíonn sé uinneamh an tsolais ina huinneamh cinéiteach. Fíor 2.2 Tiontaíonn radaiméadar rookes uinneamh an tsolais ina huinneamh cinéiteach. INA LÍNTE DÍREAHA A THAISTEALAÍONN AN SOLAS Ina línte díreacha a thaistealaíonn an solas de ghnáth. Is dócha go dtuigeann tú é sin cheana éin, má chonaic tú riamh léas solais ó léasar nó ó sholas cuardaigh nó ó cheannsolas cairr ag soilsiú trí dheannach nó trí cheo. Taispeánann an deannach nó an ceo conair an tsolais, agus gur línte díreacha atá ar thaobhanna an léis solais (Fíor 2.3). Giota snátha Bolgán Fíor 2.3 onair an tsolais á thaispeáint ag deannach agus taise san aer. Ina línte díreacha a thaistealaíonn an solas Fíor 2.4 An trealamh a úsáidtear i dturgnamh chun a léiriú go dtaistealaíonn an solas ina línte díreacha. Léas comhthreomhar Léas inréimneach Léas eisréimneach Fíor 2.5 Léasacha solais atá comhthreomhar, inréimneach agus eisréimneach. hun a thaispeáint gur ina línte díreacha a thaistealaíonn an solas, socraigh bolgán agus trí nó ceithre cinn de leatháin chairtchláir a bhuil poll beag i lár gach ceann acu. uir giota snátha trí na poill. Má thugann tú aoi bhreathnú ar an mbolgán atá ar lasadh ní bheidh tú in ann é a heiceáil mura mbíonn na poill in aon líne amháin, is é sin, nuair atá an snáth tarraingthe go teann. Taispeánann sé sin nach bhuil solas an bholgáin in ann é éin a lúbadh agus nach rachaidh sé trí na poill mura mbíonn siad in aon líne amháin. D héadadh léas solais a bheith ag scaipeadh amach mar a dhéanann solas tóirse: sin léas eisréimneach. D héadadh léas a bheith ag caolú reisin: sin léas inréimneach. Nó d héadadh léas anacht ar an leithead céanna: sin léas comhthreomhar. Taispeánann Fíor 2.5 léas comhthreomhar, léas inréimneach agus léas eisréimneach. Ga solais a thugtar ar líne dhíreach a léiríonn an treo ina mbíonn an solas ag taisteal. Líne dhíreach atá i léas comhthreomhar an-chaol, a léiríonn an treo ina bhuil an solas ag taisteal, agus is ga solais é. FRITHHAITHEAMH AN TSOLAIS Nuair a bhuaileann an solas dromchla rithne ionsúitear cuid den solas i gcónaí agus preabann cuid den solas ar ais ón dromchla i gcónaí. 8
9 An Optaic Gheoiméadrach FRITHHAITHEAMH IDIRLEATA Nuair is ar dhromchla garbh a shoilsíonn an solas, scaiptear an solas rithchaite ón dromchla i ngach treo (Fíor 2.6). Frithchaitheamh idirleata a thugtar air. Tá solas idirleata á hrithchaitheamh i ngach treo ón gcuid is mó de na rudaí sa seomra ina bhuil tú aoi láthair, ionas gur éidir leat iad a heiceáil ó áiteanna diriúla sa seomra agus tú ag siúl timpeall. FRITHHAITHEAMH RIALTA Maidir le rithne ar a mbíonn dromchla airgeadta mín snasta scáthán a thugtar ar dhromchla dá leithéid ní hé go scaiptear an solas i ngach treo ach rithchaitear den dromchla é mar atá léirithe i bhfíor 2.7. Fíor 2.6 Frithchaitheamh idirleata. Is éidir le gach duine an hrithne a heiceáil. An normal ag an bpointe ionsaithe Ga ionsaithe An pointe ionsaithe Scáthán plánach An uillinn An uillinn ionsaithe rithchaithimh i r Ga rithchaite Fíor 2.7 Frithchaitheamh rialta an tsolais de scáthán plánach. Fíor 2.8 Sin rithchaitheamh rialta. Scáthán plánach a thugtar ar scáthán réidh cothrom. Breathnaigh íor 2.8: An ga ionsaithe a thugtar ar an nga solais atá ag titim ar an scáthán, An normal ag an bpointe ionsaithe a thugtar ar an líne atá ingearach leis an scáthán áit a mbuaileann an ga an scáthán, An ga rithchaite a thugtar ar an nga atá ag imeacht ón scáthán, An uillinn ionsaithe a thugtar ar an uillinn idir an ga ionsaithe agus an normal. Is é i an tsiombail uirthi, Anuillinn rithchaithimh a thugtar ar an uillinn idir an ga rithchaite agus an normal. Is é r an tsiombail uirthi. Ga ionsaithe Ga rithchaite An normal i r DLÍTHE FHRITHHAITHEAMH AN TSOLAIS Seasann na dlíthe seo a leanas maidir le solas a hrithchaitear de scáthán plánach. Fíor 2.9 Dlí : Luíonn an ga ionsaithe, an normal agus an ga rithchaite ar an bplána céanna. Dlí 2: i r Scáthán Taispeánann Fíor 2.9 na dlíthe i bhoirm léaráide. Is é a deir Dlí ná go luíonn an ga rithchaite ar an bplána a dhéanann an ga ionsaithe agus an normal. Ní dhéantar sraonadh deisil ná tuathail ar an nga rithchaite. 9
10 Fisic don Ré Nua T URGNAMH HUN DLÍTHE FHRITHHAITHEAMH AN TSOLAIS A LÉIRIÚ. Socraigh an trealamh mar a léirítear i bhfíor 2.7 (lch. 9). oigeartaigh an bosca gathanna go dtí go dtáirgeann sé léas an-chaol, i.e. ga. Leag an scáthán ar an bpáipéar líníochta agus marcáil a shuíomh le peann luaidhe. Soilsigh an ga ar an scáthán. Marcáil (le peann luaidhe) treo an gha sula mbuaileann sé an scáthán, agus marcáil treo an gha a hrithchaitear amach ón scáthán ansin. Bain an scáthán.tarraing an normal ag an bpointe ionsaithe, an ga ionsaithe agus an ga rithchaite ar an bpáipéar. Tomhais an uillinn ionsaithe (i) agus an uillinn rithchaithimh (r) le huillinntomhas. Scríobh síos na luachanna sin. Déan an turgnamh arís le luachanna diriúla don uillinn ionsaithe. An Toradh Gheoar, taobh istigh de theorainneacha earráide turgnamhaí, go bhuil an uillinn ionsaithe cothrom leis an uillinn rithchaithimh, léiriú ar Dhlí 2. Beidh an ga rithchaite ag taisteal comhthreomhar leis an bpáipéar, i.e. ní bheidh sé ag éirí aníos ón bpáipéar ná ag dul isteach sa pháipéar. Beidh sé sa phlána céanna leis an nga ionsaithe agus an normal, léiriú ar Dhlí. MAR A HRUTHAÍTEAR ÍOMHÁ I SÁTHÁN PLÁNAH Taispeánann Fíor 2.0 cuid de na gathanna ó phonchrithne a bhuaileann scáthán plánach. Frithchaitear gach ga den scáthán de réir dhlíthe an hrithchaithimh. Don té atá ag éachaint ar an scáthán dealraíonn sé go bhuil an hrithne P ag an bpointe Q, taobh thiar den scáthán. Íomhá P a thugtar ar Q. Dealraíonn sé don tsúil gur ag teacht ó Q atá na gathanna solais atá ag teacht isteach sa tsúil, cé nach dtéann aon ghathanna solais trí Q dáiríre. Deirimid gurb é trasnú dealraitheach na ngathanna a chruthaíonn an íomhá ag Q. Íomhá híorúil a thugtar ar íomhá dá leithéid. Frithne P Q i r Íomhá híorúil de P i 2 r 2 i 3 r 3 i r i 2 r 2 i 3 r 3 Fíor 2.0 Mar a chruthaítear íomhá i scáthán plánach. Maidir leis an íomhá híorúil i scáthán plánach gheoar trí thurgnaimh: go bhuil sí ar an ingear ón bhrithne go dtí an scáthán. go bhuil sí an ad céanna taobh thiar den scáthán is atá an hrithne os comhair an scátháin amach. 0
11 An Optaic Gheoiméadrach ÍOMHÁ FRITHNE SÍNTE I SÁTHÁN PLÁNAH I bhfíor 2. tá íomhá sa scáthán de gach pointe ar an lámh. Is é an toradh atá air ná íomhá híorúil den lámh iomlán i gcúl an scátháin. Tá an íomhá ar cóimhéid leis an bhrithne. Tabhair aoi deara go bhuil de dhiríocht idir an íomhá agus an hrithne go ndealraíonn sé gur ciotóg atá san íomhá nuair is deasóg í an hrithne. Sin inbhéartú cliathánach. Sin an áth a mbreathnaíonn scríbhneoireacht aisteach i scáthán. RRAHRAHTO a chaitheadh a bheith scríoa ar thosach otharchairr i dtreo is go mbeadh tiománaí in ann OTHARHARR a léamh ina scáthán cúil agus ligean don otharcharr dul amach thairis. ÚSÁID A BHAINTEAR AS SÁTHÁIN PHLÁNAHA Is éidir tú éin a heiceáil i scáthán plánach. I bhfíor 2.2 rithchaitear cuid den solas ó ghruaig an bhuachalla den scáthán agus téann sé isteach ina shúil ionas go bhuil sé in ann a chuid gruaige a heiceáil sa scáthán. An peireascóp. Gaireas simplí atá sa pheireascóp atá bunaithe ar dhlíthe hrithchaitheamh an tsolais. Dhá scáthán phlánacha atá ann (Fíor 2.3 (A)). Frithchaitear an solas ón bhrithne ar a bhuil tú ag éachaint den dá scáthán agus ansin isteach i do shúil, rud a chuireann ar do chumas éachaint thar constaic nó timpeall ar chonstaic a bheadh sa tslí ort (Fíor 2.3 (B)). Fíor 2. Solas ón bhrithne onstaic Fíor 2.2 (A) Fíor 2.3 MODH NA heaspa SAOBHDHIALLAIS HUN ÍOMHÁ A AIMSIÚ oinnigh dhá pheann luaidhe amach os do chomhair mar atá léirithe i bhfíor 2.4(A), i dtreo is go ndealraíonn sé go bhuil na pinn luaidhe sa líne cheartingearach chéanna. Gan ceachtar den dá pheann luaidhe a chorraí, bog do chloigeann ar dheis. Tabhair aoi deara go ndealraíonn sé gur bhog ceann de na pinn luaidhe an ceann is aide uait ar dheis reisin, i gcomparáid leis an bpeann luaidhe eile. Bog do chloigeann ar chlé agus tabhair aoi deara go ndealraíonn sé gur bhog an peann luaidhe céanna ar chlé leat reisin. Saobhdhiallas a thugtar ar ghluaisne dhealraitheach sin an phinn luaidhe a tharlaíonn de bharr gluaisne an bhreathnóra. Má chuireann tú na pinn luaidhe anois mar atá siad i bhfíor 2.4 (B), an dá rinn ag comhthitim ar a chéile, ní thabharaidh tú aon ghluaisne choibhneasta aoi deara eatarthu de réir mar a bhogann tú do chloigeann ar dheis nó ar chlé. Deirtear go bhuil siad ar easpa saobhdhiallais. Mura mbíonn saobhdhiallas idir rudaí, is léir go gcaithidh go bhuil siad sa líne chéanna agus an ad céanna ón mbreathnóir. Is éidir linn an híric sin a úsáid chun íomhá rithne i scáthán plánach a aimsiú. (B) (A) Fíor 2.4 atá in uachtar níos aide uait (B) Mar a heiceann tú iad Mar a heiceann tú iad nuair a bhogann tú do chloigeann ar dheis
12 Fisic don Ré Nua T URGNAMH HUN ÍOMHÁ A AIMSIÚ I SÁTHÁN PLÁNAH TRÍ MHODH NA HEASPA SAOBHDHIALLAIS An Modh Socraigh an trealamh mar atá i bhfíor 2.5. Beidh íomhá híorúil le eiceáil sa scáthán. oigeartaigh airde an tóirbhioráin go dtí go mbíonn a rinn díreach os cionn bharr an scátháin. Ag breathnú duit i dtreo an scátháin agus gan aird agat ar an mbiorán rithne ba cheart go bheiceá: (i) An íomhá sa scáthán, (ii) An tóirbhiorán os cionn an scátháin, Fíor 2.5 oigeartaigh an tóirbhiorán go dtí go ndealraíonn sé go bhuil sé in aon líne leis an íomhá. Biorán rithne Breathnóir Tóirbhiorán (greamaithe sa teanntán) Bog an tóirbhiorán isteach nó amach ón scáthán go dtí nach mbíonn saobhdhiallas idir an íomhá agus an tóirbhiorán. Léiríonn an tóirbhiorán suíomh na híomhá ansin. Tomhais an ad (u) ón bhrithne go dtí airgead an scátháin le méadarshlat. Tomhais an ad (v) ón tóirbhiorán go dtí airgead an scátháin (ad atá cothrom leis an bhad ón bhrithne go dtí an scáthán). v v Íomhá híorúil sa scáthán lár líníochta Scáthán plánach Taobh istigh de theorainneacha earráide turgnamhaí beidh u cothrom le v, rud a híoraíonn go mbíonn an íomhá i scáthán plánach an ad céanna taobh thiar den scáthán is a bhíonn an hrithne amach os a chomhair. LEAHTADH 2.. Tá an Ghealach m ón Domhan. Is é ms - luas an tsolais. én ad ama a thógann sé ar an solas a hrithchaitear den Ghealach dul ad leis an Domhan? 2. I bhfíor 2.6 ainmnigh A, B,, D agus E. B 3. Taispeánann Fíor 2.7 trí gha solais ag ágáil na rithne O agus ag titim ar scáthán plánach. Déan cóip den léaráid agus tarraing gach ceann de na gathanna sin go cruinn tar éis rithchaitheamh dóibh. Taispeáin suíomh na híomhá atá ag O. ED A Fíor 2.6 Fíor 2.7 O 4. Tá buachaill ina sheasamh 4 m ó scáthán plánach. én ad agus cén treo ina gcaithidh sé bogadh chun go mbeidh sé: (i) 4 m óna íomhá, (ii) m óna íomhá? 5. Neach a tháinig ó réaltra i bhad uainn, tá sé 2 m ar airde, agus an t-aon súil bheag amháin atá aige is díreach ar bharr a chinn atá sí. ad é an airde is lú a chaitheadh a bheith i scáthán chun go mbeadh sé in ann é éin a heiceáil ina iomlán sa scáthán. Bain úsáid as ga-léaráid chun a thaispeáint nach mbraitheann sé ar had an scátháin ón neach km uainn atá an réalta is gaire dúinn. é mhéad bliain a thógann sé ar an solas an ad sin a thaisteal? (Luas an tsolais m s - ). 2
13 An Optaic Gheoiméadrach 7. Déanann ga solais uillinn ionsaithe 30 ar scáthán plánach (Fíor 2.8). Agus an ga ionsaithe osaithe, rothlaítear an scáthán deiseal 20 timpeall ar an bpointe p. (i) ad í an uillinn ionsaithe nua? (ii) ad í an uillinn rithchaithimh nua? (iii) én uillinn ar rothlaigh an ga rithchaite tríthi? 30 P 8. Duine atá ag gluaiseacht go díreach i dtreo scáthán plánach, druideann sé i dtreo a íomhá éin aoi luas 4 m s -. én luas aoina ngluaiseann sé? 9. Bean atá.8 m ar airde, tá a súile suite.2 m ón talamh agus í ina seasamh caoldíreach. Seasann sí os comhair scáthán plánach agus tá sí díreach in ann í éin a heiceáil ina hiomlán sa scáthán atá suite i bplána ceartingearach. ad é airde an scátháin 0. Sainmhínigh gach ceann díobh seo a leanas: Frithne héinlonrach; Frithne neamhlonrach; Léas inréimneach; Léas eisréimneach; Léas comhthreomhar; Frithchaitheamh an tsolais; Frithchaitheamh idirleata; Frithchaitheamh rialta; Ga ionsaithe; An normal ag an bpointe ionsaithe; An uillinn ionsaithe; An uillinn rithchaithimh.. Luaigh Dlíthe Fhrithchaitheamh an tsolais. 2. ad is Íomhá Fhíorúil ann? LIOSTA SEIEÁLA NA AIBIDLE uimhnigh arís ar na reagraí ar cheisteanna 0, agus 2 thuas. uir síos ar thurgnamh a léiríonn Dlíthe Fhrithchaitheamh an tsolais. Tarraing ga-léaráid chun a thaispeáint mar a chruthaítear íomhá i scáthán plánach. Bain úsáid as modh na heaspa saobhdhiallais chun suíomh íomhá a aimsiú. 3
14 AIBIDIL 3 Frithchaitheamh an tsolais de Scátháin Séaracha rithchaiteach Scáthán cuasach Scáthán dronnach Dromchla rithchaiteach SÁTHÁIN HUASAHA AGUS SÁTHÁIN DHRONNAHA Frithchaitheamh an tsolais de scátháin séaracha a bheidh i gceist sa chaibidil seo. Tá dhá chineál scáthán séarach ann; an scáthán cuasach agus an scáthán dronnach (Fíor 3.). Mar is léir ó Fhíor 3., titeann an dromchla rithchaiteach i scáthán cuasach isteach i dtreo a láir, ach bolgann an dromchla rithchaiteach amach ar scáthán dronnach. Tugtar scátháin séaracha ar na scátháin sin mar is cuid de dhromchla séir í an ghloine (nó ábhar eile) as a ndéantar iad. Fíor 3. Scátháin séarúla An phríomhais Dromchla rithchaiteach An pol An Phríomhais P Dromchla rithchaiteach An lár cuaire An ócas An pol F P TÉARMAÍ A ÚSÁIDTEAR HUN UR SÍOS AR SÁTHÁIN SFÉARAHA Tugtar pol an scátháin ar lár scátháin séaraigh. I bhfíor 3.2 is é P an pol. An ad ócasach An ócas F An ad ócasach An lár cuaire Tugtar lár cuaire an scátháin ar lár an séir as a bhuil an scáthán déanta. I bhfíor 3.2 is é an lár cuaire. Tugtar an phríomhais ar an líne dhíreach idir an lár cuaire agus pol an scátháin (tabharaimid an ais uirthi). Tugtar an ócas nó an pointe ócasach ar an bpointe atá leath slí idir an lár cuaire agus an pol. I bhfíor 3.2 is é F an ócas. Tugtar ad ócasach an scátháin ar an bhad idir an ócas agus an pol. An litir an tsiombail air. Fíor 3.2 FRITHHAITHEAMH AN TSOLAIS DE SÁTHÁN UASAH An ais Fíor 3.3 An lár cuaire An normal Ga ionsaithe Ga rithchaite i r P Baineann dlíthe hrithchaitheamh an tsolais le scátháin séaracha reisin. Ga solais a bhuaileann scáthán cuasach mar atá i bhfíor 3.3, cuir i gcás. á dtéann an ga nuair a hrithchaitear é? hun é sin a háil amach tarraing an normal ag an bpointe ionsaithe. Is é an normal i gcás scátháin mar sin an líne a cheanglaíonn an pointe ionsaithe le lár cuaire an scátháin. Is í an uillinn ionsaithe i an uillinn idir an ga ionsaithe agus an normal. Deir dlíthe hrithchaitheamh an tsolais go bhuil an uillinn rithchaithimh r cothrom leis an uillinn i. Dá bhrí sin rithchaitear an ga mar atá léirithe. Is éidir aon gha eile a bhuaileann an scáthán tar éis rithchaitheamh dó a aimsiú leis an modh céanna. 4
15 Frithchaitheamh an tsolais le Scátháin Séaracha Scáthán cuasach agus cuaire mhór ann Scáthán cuasach agus cuaire bheag ann 5 Fíor 3.4 Tógann sé i bhad an ga rithchaite a aimsiú. Ní úsáidimid ach na torthaí seo a leanas ar iarmhairtí Dlíthe Fhrithchaitheamh an tsolais iad. Ga a bhuaileann an pol, rithchaitear é ar uillinn leis an ais atá cothrom leis an uillinn ionsaithe. Ga a ghabhann tríd an lár cuaire agus a bhuaileann an scáthán, rithchaitear ar ais é ar a chonair éin. Ga ionsaithe An ais Ga rithchaite i r i r An pol An ais An lár cuaire P Fíor 3.5 Fíor 3.6 Má tá an scáthán ar bheagán cuaire (i.e. más uillinn níos lú ná 5 a iompraíonn an scáthán ag an lár cuaire (Fíor 3.4)), is éidir na íricí seo a leanas a chruthú: Ga a thagann isteach comthreomhar leis an ais, gabhann sé tríd an bhócas agus é rithchaite den scáthán. Ga a ghabhann tríd an bhócas agus a bhuaileann an scáthán ansin, rithchaitear é comhthreomhar leis an ais. Ga ionsaithe Ga rithchaite An ais An ócas P An Ais An ócas P Ga rithchaite Fíor 3.7 Fíor 3.8 Ní gá a bheith in ann na torthaí thuas a chruthú, ach meabhraigh iad. Is éidir iad a híorú sa tsaotharlann go urasta le bosca gathanna agus scáthán cuasach. 5
16 Fisic don Ré Nua MAR A HRUTHAÍTEAR ÍOMHÁ I SÁTHÁN UASAH Tá solas á chaitheamh amach i ngach treo ó gach pointe ar an bhrithne i bhfíor 3.9. Taispeántar cuid de na gathanna solais ó bharr na rithne ag bualadh an scátháin agus á bhrithchaitheamh de. Gabhann gach ga tríd an bpointe céanna X nuair a hrithchaitear iad. Is éidir a thaispeáint go rachadh aon gha eile ó bharr na rithne tríd an bpointe X nuair a hrithchaitear é chomh maith. Fágann sin go bheicidh an tsúil (i.e. an breathnóir) íomhá de bharr na rithne ag X mar a léirítear, ó tá gathanna a bhí ag eisréimniú ó P i dtosach ag eisréimniú anois ó X. Ach an próiseas a dhéanamh arís is arís eile i gcás pointí eile ar an bhrithne, bheadh íomhá den hrithne iomlán le eiceáil mar atá i bhfíor 3.9. Frithne shoilsithe Pointe P airtchlár Frithne Pointe Q Íomhá X F Bosca gathanna nó oinse solais ros-snáitheanna u v Scáileán Fíoríomhá ar scáileán Fíor 3.9 Fíor 3.0 Fíoríomhá a thugtar ar an íomhá sin de bhrí gur trasnú iarbhír gathanna is cúis léi. Tabhair aoi deara nach bhuil an íomhá agus an hrithne ar cóimhéid. Ní hionann méid na rithne agus méid na híomhá i gcás scáthán cuasach ach amháin nuair a luíonn an hrithne ar an lár cuaire (Fíor 3.(B)). AIRIÓNNA FÍORÍOMHÁ Is éidir íoríomhá a heiceáil ar scáileán an íomhá ar an scáileán sa phictiúrlann, mar shampla. Is éidir íoríomhá a theilgean ar scáileán go héasca leis an trealamh i bhfíor 3.0. Gearradh poll sa chairtchlár agus síneadh dhá ghiota snátha trasna ar an bpoll. Soilsíonn an bosca gathanna solas ar na cros-snáitheanna sin agus eidhmíonn siad mar hrithne shoilsithe. Má athraítear an ad idir an scáileán agus an scáthán aimseoar áit a mbeidh íomhá ghlan shoiléir de na cros-snáitheanna le eiceáil ar an scáileán. Mura éidir íomhá dá leithéid a aimsiú, tá an scáthán ró-ghar don bhosca gathanna agus ba cheart é a dhruidim siar uaidh. Is éidir íoríomhá a aimsiú le modh na heaspa saobhdhiallais - a léiríodh ar leathanach 2 - reisin. Ní gá na gathanna go léir a thaispeántar i bhfíor 3.9 a tharraingt chun an áit a aimsiú ina gcruthaítear íomhá i scáthán cuasach. Is leor dhá gha. Taispeánann na ga-léaráidí i bhfíor 3. conas íomhá rithne a aimsiú nuair atá an hrithne lasmuigh de ; ag ; idir agus F; ag F agus laistigh de F. Déan iarracht na léaráidí cuí a tharraingt tú éin sula bhéachann tú ar Fhíor 3.. Léiríonn na ga-léaráidí i bhfíor 3. na íricí seo a leanas: 6
17 Frithchaitheamh an tsolais le Scátháin Séaracha Frithne F Frithne F Íomhá laghdaithe Íomhá ar cóimhéid (A) (B) Íomhá hormhéadaithe Frithne F Frithne F Íomhá ag an éigríoch () (D) Frithne F Íomhá híorúil hormhéadaithe (E) Fíor 3. ÍOMHÁ FHÍORÚIL honaic tú ar lch. 0 gur le trasnú dealraitheach na ngathanna a chruthaítear íomhá híorúil. Íomhá ar bith a chruthaítear i scáthán plánach is íomhá híorúil í. An íomhá a chruthaítear i scáthán cuasach nuair atá an hrithne ag an bhócas nó laistigh de, is íomhá híorúil í. ÍOMHÁ FRITHNE I GÉIN I SÁTHÁN UASAH Má tá rithne i bhad i gcéin ó scáthán cuasach, is íoríomhá a bhíonn aici agus í suite ag ócas an scátháin. uir i gcás gur pointe é P ar hrithne i gcéin (Fíor 3.2). aitheann P solas amach i ngach treo. Ó tá P i bhad i gcéin is mar léas comhthreomhar a thagann an solas uaidh go dtí an scáthán. Agus is mar léas comhthreomhar a thagann gathanna ó Q, pointe eile ar an bhrithne chéanna. I bhíor 3.2 tugtar an léas ó P chun ócais mar atá léirithe. Tugtar an léas ó Q chun ócais ag pointe ócasach an scátháin. Dá réir sin, cruthaítear íoríomhá den hrithne i gcéin ag plána ócasach an scátháin. Tá sé éasca é sin a léiriú sa tsaotharlann mar atá déanta i bhfíor 3.3. Fíor 3.2 P Léas comhthreomhar ó P Q Frithne i gcéin Léas comhthreomhar ó Q Plána ócasach Fíor 3.3 Scáthán cuasach ag tabhairt íoríomhá d huinneog i gcéin ar scáileán cairtchláir sa tsaotharlann. 7
18 Fisic don Ré Nua AN FHOIRMLE DO SÁTHÁN UASAH Athraíonn ad na híomhá ó scáthán cuasach de réir mar a athraíonn ad na rithne ón scáthán, agus ní bhíonn na aid sin mar a chéile ach amháin nuair a bhíonn an hrithne ag an lár cuaire. Tá oirmle shimplí ann do na aid sin ní gá a bheith in ann é a chruthú. Abair gurb é u an ad ón bhrithne go dtí an scáthán Abair gurb é v an ad ón íomhá go dtí an scáthán Abair gurb é an ad ócasach. Ansin: Nuair is íoríomhá atá ann : u + Nuair is íomhá híorúil atá ann v u v FORMHÉADÚ Ní hionann airde na híomhá agus airde na rithne de ghnáth. Abair go raibh an hrithne 4 cm ar airde agus an íomhá 20 cm ar airde. Ansin bheadh an íomhá cúig huaire níos airde ná an hrithne. Sin ormhéadú aoi 5. An ormhéadú (m) a thugtar ar chóimheas airde na híomhá le hairde na rithne. Is éidir a chruthú go bhuil an ormhéadú a dhéantar le scáthán cuasach cothrom le ad na híomhá / ad na rithne. (Ní gá duit é sin a chruthú.) Formhéadú Airde na híomhá Airde na rithne Fad na híomhá i.e. Fad na rithne v m u Fadhb : Réiteach: Leagtar rithne 30 cm amach os comhair scáthán cuasach dar ad ócasach 20 cm. Faigh suíomh agus nádúr na rithne. Tá u 30 agus 20 anseo. Tá luach v le haimsiú. Ó tá an hrithne lasmuigh den hócas, is íoríomhá atá i gceist agus is é /u +/v / an hoirmle atá le húsáid. Agus is éidir an hoirmle sin a úsáid iú mura mbeimis cinnte cé acu íoríomhá nó íomhá híorúil í. Má tharlaíonn go bhuil v deimhneach, is íoríomhá í; má tharlaíonn go bhuil v diúltach, is íomhá híorúil í. + u v 30 + v 20 v v v 60 cm Mar sin, is ioríomhá í (a nádúr) agus tá sí suite 60 cm amach os comhair an scátháin. 8
19 Frithchaitheamh an tsolais le Scátháin Séaracha Fadhb 2: Réiteach: Leagtar rithne 2 cm amach os comhair scáthán cuasach dar ad ócasach 20 cm. Faigh suíomh, nádúr agus ormhéadú na híomhá. Tá an hrithne laistigh den hócas, dá bhrí sin is íomhá híorúil atá ann agus is é /u - /v / an hoirmle a úsáidtear. Ach, mura mbeadh a hios againn cé acu íoríomhá nó íomhá híorúil a bhí ann agus dá n-úsáidimis an hoirmle /u +/v / ansin: v u v 2 v 20 v 20 2 v cm Léiríonn an luach diúltach gur íomhá híorúil í. Tá sí suite 30 cm laistiar den scáthán. v 30 Formhéadú m 2. 5 u 2 Is é sin, tá an íomhá 2.5 uair níos airde ná an hrithne. Fadhb 3: Réiteach: Frithne atá suite 5 cm os comhair scáthán cuasach tugann sí íoríomhá atá 30 cm amach ón scáthán. Ríomh ad ócasach an scátháin. Má tá an hrithne 5 cm ar airde, cén airde atá san íomhá? Tá u 5, v 30 agus ní ios luach u v 5 30 (5)(30) cm 45 i.e. tá ad ócasach an scátháin 0 cm Formhéadú Airde na híomhá Airde na rithne v u Airde na híomhá Airde na híomhá (5) (30) 5 0cm Fadhb 4: Réiteach: ruthaítear íomhá i scáthán cuasach dar ad ócasach 20 cm. Tá an íomhá trí huaire níos mó ná an hrithne. én áit a chaithidh an hrithne a bheith suite: (i) más íoríomhá í (ii) más íomhá híorúil í? v Formhéadú: 3 v 3u u Fíoríomhá: u v u 3u 3u 20 4 u cm 3u 20 Íomhá Fhíorúil: u v u 3u 2 u 3.33 cm 3u u 20 aithear an hrithne a shuí cm ón scáthán chun íoríomhá a thabhairt agus 3.33 cm ón scáthán chun íomhá híorúil a thabhairt. 9
20 Fisic don Ré Nua ÚSÁIDÍ A BHAINTEAR AS SÁTHÁIN HUASAHA Má chuirtear bolgán ag pointe ócasach scátháin chuasaigh, rithchaitear solas an bholgáin a bhuaileann an scáthán amach comhthreomhar leis an ais (Fíor 3.4). Baintear úsáid phraiticiúil as an bhíric sin i dtóirshoilse agus i roinnt tuilshoilse. Más laistigh d hócas scátháin chuasaigh a shuítear rithne, ormhéadóar an íomhá agus beidh sí ina seasamh mar is ceart. Baintear úsáid as an bhíric sin i scáthán bearrtha agus i scáthán smididh (Fíor 3.5). Is éidir le iaclóir breathnú timpeall ar bhéal othair le scáthán cuasach. Úsáidtear scáthán cuasach i dteilgeoir sleamhnán reisin chun solas ón mbolgán a hrithchaitheamh, solas a rachadh amú gan tairbhe murach an scáthán. Frithchaitheann an scáthán an solas ar ais tríd an sleamhnán, ionas go mbíonn an íomhá níos gile. Fíor 3.4 Fíor 3.5 LEAHTADH cm os comhair scáthán cuasach atá rithne agus cruthaíonn sí íoríomhá atá 50 cm ón scáthán. Ríomh ad ócasach an scátháin cm os comhair scáthán cuasach atá rithne agus cruthaíonn sí íomhá híorúil atá 30 cm laistiar den scáthán. Ríomh ad ócasach an scátháin cm os comhair scáthán cuasach dar ad ócasach 0 cm atá rithne. én ad ón scáthán a chruthóar a híomhá? ad é nádúr agus ormhéadú na híomhá? Má tá an hrithne éin 2 cm ar airde cén airde a bheidh san íomhá? 4. 0 cm os comhair scáthán cuasach dar ad ócasach 20 cm atá rithne. Faigh suíomh, nádúr agus ormhéadú na híomhá. 5. ruthaíonn scáthán cuasach dar ad ócasach 40 cm íoríomhá atá ceithre huaire níos airde ná an hrithne. én ad ón scáthán atá an hrithne. 6. ruthaíonn scáthán cuasach dar ad ócasach 20 cm íomhá atá trí huaire níos airde ná an hrithne. Faigh ad na rithne ón scáthán: (i) más íoríomhá í. (ii) más íomhá híorúil í. 7. Faigh an dá shuíomh inar éidir rithne a shuí ionas go gcruthóaí íomhá atá dhá uair níos airde ná an hrithne i scáthán cuasach dar ad ócasach 50 cm. 8. én ad amach os comhair scáthán cuasach dar ad ócasach 00 cm is gá seasamh chun go mbeidh tú in ann íomhá de d aghaidh a heiceáil, í ina seasamh agus í ormhéadaithe aoi thrí? 9. I bhad i gcéin ó scáthán cuasach dar ad ócasach 40 cm atá rithne. Faigh an ad ón íomhá go dtí an scáthán. é acu íoríomhá nó íomhá híorúil a bheidh ann? 0. á gcaithear rithne a shuí chun íomhá nach bhuil inti ach an tríú cuid d airde na rithne éin a chruthú i scáthán cuasach dar ad ócasach 40 cm? 20
21 Frithchaitheamh an tsolais le Scátháin Séaracha T URGNAMH SOLAS FAD FÓASAH SÁTHÁIN HUASAIGH A THOMHAS Achoimre ar an Modh Sa turgnamh seo leagaidh tú cros-snáitheanna soilsithe mar hrithne os comhair scáthán cuasach agus aimseoidh tú íomhá na gcros-snáitheanna ar scáileán cairtchláir bháin. Déanaidh tú an ad u ó na cros-snáitheanna go dtí an scáthán agus an ad v ón scáileán go dtí an scáthán a thomhas. Is éidir ad ócasach an scátháin a aimsiú ach an hormle seo a úsáid: +. u v An Trealamh a theastaíonn Scáthán cuasach agus seastán Seastán reangáin agus teanntán Frithne shoilsithe. Is éidir í sin a dhéanamh ach poll beag ciorclach a ghearradh i leathán cairtchláir agus dhá ghiota snátha a ghreamú trasna ar an bpoll le téip ghreamaitheach. Soilsítear é le solas ó bhosca gathanna. Bosca gathanna, leathán cairtchláir bháin agus méadarshlat An Modh. Faigh garluach ar had ócasach an scátháin: déan íomhá rithne i gcéin a hócasú ar leathán cairtchláir (Fíor 3.3, Lch. 7). Is garluach ar an bhad ócasach é an ad ón íomhá go dtí an scáthán. Tomhais agus breac síos an ad sin. 2. Socraigh an trealamh mar atá i bhíor 3.0 ar leathanach 6. Ní oláir an ad ón bhrithne go dtí an scáthán a bheith níos mó ná an ad ócasach a uarthas i géim, nó ní íoríomhá a gheobhaidh tú. 3. uir an leathán cairtchláir ar an seastán reangáin. Sin an scáileán. 4. oigeartaigh suíomh an scáileáin go dtí go mbíonn íomhá na gcros-snáitheanna air san hócas is glinne is éidir. 5. Tomhais le méadarshlat: an ad u ó na cros-snáitheanna go dtí pol an scátháin, an ad v ón bhíoríomhá ar an scáileán go dtí pol an scátháin. Breac síos na luachanna sin. 6. Athraigh luach u agus athdhéan éimeanna 4 agus 5 ceithre huaire ar a laghad. Sonraí Turgnamhacha agus Torthaí Garluach ar an bhad ócasach a aimsíodh ach íomhá rithne i gcéin a hócasú ar scáileán u / cm v / cm u v + u v / cm Meánluach an haid hócasaigh 2
22 Fisic don Ré Nua Na sonraí a láimhseáil Modh omhlánaigh an tábla agus ríomh meánluach. Sin ad ócasach an scátháin. Nuair atá /u +/v á ríomh agat bíodh trí higiúir bhunúsacha ar a laghad agat i do chuid áirimh. Modh 2 Breac ar ghrapháipéar gra de /u i gcoinne na luachanna comhhreagracha de /v. Tarraing an líne dhíreach is earr a ghabhann leis na pointí agus lean ar an líne go dtrasnaíonn sí an dá ais. Léigh luach /u ón ngra ag an bpointe a dtrasnaíonn an gra ais /u, agus léigh luach /v ag an áit a dtrasnaíonn sé ais /v. Faigh meánluach an dá luach sin ( /). Faigh deilín an toraidh sin. Ba cheart go mbeadh sé an-chosúil leis an luach a uarthas i Modh don had ócasach. Foinsí Earráide Tarlaíonn earráidí: (i) agus tú ag iarraidh a chinntiú cathain a bhí an íomhá ar an scáileán san hócas is glinne, (ii) nuair atá ad u agus v á dtomhas agat leis an méadarshlat. D héadadh earráid níos mó a bheith ann i gcás v ná u, mar ní bhíonn i gceist le u ach earráid in úsáid na méadarslaite. eisteanna. Mura raibh tú in ann íomhá shoiléir de na cros-snáitheanna a háil ar an scáileán, cad ba chúis leis, an dóigh leat? onas a réiteoá an hadhb? 2. én áth a mbíonn an luach a haightear ar u níos cruinne ná an luach ar v? 3. Luaigh dhá réamhchúram ba chóir a ghlacadh agus u á thomhas. 4. Tarlaíonn earráidí nuair atá suíomh na híomhá á aimsiú agus a ad ón bpol á thomhas. Luaigh réamhchúram amháin a d héadá a ghlacadh i gcás gach ceann díobh chun na hearráidí sin a laghdú. Míniú ar an ngra /v Fíor 3.6 Gra de u i gcoinne v. /u Líne dhíreach atá sa ghra de u i gcoinne v (ar an y-ais) (Fíor 3.6). Tá a hios agat ón matamaitic (céimseata chomhordanáideach na líne dírí) go dtrasnaíonn líne dhíreach an x-ais nuair atá y 0. trasnaíonn an líne + ais nuair atá 0 u v u v Dá réir sin: + 0 tá áit a ngearrann an líne ais u u u Ar an gcuma chéanna, tá áit a ngearrann an líne ais v v 22
23 Frithchaitheamh an tsolais le Scátháin Séaracha FRITHHAITHEAMH AN TSOLAIS LE SÁTHÁIN DHRONNAHA Baineann dlíthe hrithchaitheamh an tsolais le scátháin dhronnacha reisin. uir i gcás go mbuaileann ga solais scáthán dronnach mar atá i bhfíor 3.7. Is é an normal ag an bpointe ionsaithe ná an líne ón bpointe ionsaithe go dtí lár cuaire an scátháin. Taispeántar an uillinn ionsaithe i sa léaráid reisin. Leanann as na dlíthe rithchaithimh go bhuil an uillinn rithchaithimh r cothrom le i, (i r). Mar sin rithchaitear an ga mar atá léirithe. i r An normal F Is éidir aon gha eile a thiteann ar an scáthán a aimsiú tar éis rithchaitheamh dó leis an modh sin reisin. (Dála an scátháin chuasaigh, tógann sé i bhad an ga rithchaite a aimsiú sa chás seo reisin.) Ní dhéanaimid ach na torthaí seo a leanas a úsáid, torthaí a leanann as Dlíthe Fhrithchaitheamh an tsolais. Ní gá a bheith in ann iad a chruthú, ach glac leo agus meabhraigh iad. Fíor 3.7 Ga a bhuaileann an pol, nuair a hrithchaitear é déanann sé uillinn chomhionann leis an ais. Ga atá ag taisteal i dtreo an láir chuaire rithchaitear é ar ais ar a chonair éin. An ais i r F An ais F i r Fíor 3.8 Mura bhuil an scáthán an-chuar: Ga a thagann isteach comhthreomhar leis an ais, rithchaitear é amhail is gur ag teacht ón bhócas a bhí sé. Fíor 3.9 Ga atá ag dul i dtreo an hócais agus a bhuaileann an scáthán, rithchaitear amach é comhthreomhar leis an ais. An ais F An ais F Fíor 3.20 Fíor 3.2 MAR A HRUTHAÍONN SÁTHÁN DRONNAH ÍOMHÁ Taispeánann Fíor 3.22 (lch 24) rithne os comhair scáthán dronnach. Tá solas ag teacht i ngach treo ó gach pointe ar an bhrithne. Tá cuid de na gathanna solais ó bharr na rithne curtha isteach sa léaráid agus taispeántar cá dtéann siad tar éis rithchaitheamh dóibh. ad a thugaimid aoi deara? Dealraíonn sé go bhuil gach ceann de na gathanna sin ag eisréimniú ón bpointe céanna (X) tar éis rithchaitheamh dóibh. Is éidir a chruthú go ndealródh sé go mbeadh aon gha eile ó bharr na rithne ag eisréimniú ó X tar éis rithchaitheamh dó chomh maith. 23
24 Fisic don Ré Nua íomhá de rinn na rithne ag X, mar go ndealraíonn sé go bhuil na gathanna a bhí ag eisréimniú ó P i dtosach ag eisréimniú ó X anois. Sa tslí chéanna, is éidir íomhá de phointe ar bith eile Q ar an bhrithne a aimsiú ach na gathanna ón bpointe sin a tharraingt. Bheadh íomhá den hrithne iomlán le eiceáil mar atá i bhfíor 3.22 ach an próiseas a dhéanamh arís i gcás pointí eile ar an bhrithne. Íomhá híorúil atá san íomhá sin ó tharla gur trasnú dealraitheach na ngathanna aoi deara í. P Q Pointe X Frithne Íomhá F Frithne Íomhá F Pointe Íomhá F Fíor 3.22 Fíor 3.23 Ní gá na gathanna go léir a léirítear i bhfíor 3.22 a tharraingt chun an áit ina gcruthaítear an íomhá i scáthán dronnach a aimsiú. Is leor dhá gha. Má aimsíonn tú an íomhá nuair atá an hrithne i suímh éagsúla (Fíor 3.23) eicidh tú gur mar seo atá: AN FHOIRMLE DO SÁTHÁN UASAH Tá an hoirmle maidir leis an scáthán dronnach an-chosúil leis an bhoirmle don scáthán cuasach. uir i gcás arís gurb é u an ad ón bhrithne go dtí an scáthán, agus v an ad ón íomhá go dtí an scáthán, agus gurb é ad ócasach an scátháin. Ansin: Maidir le scáthán dronnach: (Tabhair aoi deara go mbíonn agus diúltach i gcónaí.) u v v FORMHÉADÚ Airde na híomhá i gcóimheas le hairde na rithne éin, sin an ormhéadú. Is éidir a chruthú gurb é v /u an ormhéadú a thugann scáthán dronnach. Formhéadú Airde na híomhá Fad na híomhá v i.e. m Airde na rithne Fad na rithne u 24
25 Frithchaitheamh an tsolais le Scátháin Séaracha ÚSÁIDÍ A BHAINTEAR AS SÁTHÁIN DHRONNAHA Ós rud é gur íomhá laghdaithe a chruthaítear i scáthán dronnach i gcónaí bíonn réimse radhairc níos mó ag gabháil le scáthán dronnach ná le scáthán plánach (Fíor 3.24). Úsáidtear scátháin dhronnacha: (i) mar scáthán dorais ar ghluaisteáin, (ii) ag oscailtí ceilte chun radharc a thabhairt ar an trácht ar an mbóthar, (iii) i siopaí chun cosc a chur le gadaíocht (Fior 3.25), (iv) i stáisiúin traenach. + u v (A) (B) Fíor 3.24 Tugann an scáthán dronnach réimse radhairc níos mó ná an scáthán plánach. Fadhb 5: Réiteach: Fadhb 6: Frithne atá suite 40 cm os comhair scáthán dronnach dar ad ócasach 24 cm. én ad ón scáthán a ndéanar an íomhá? Faigh nádúr agus ormhéadú na híomhá. u v v v 24 8v 20 v v 5 cm Tá an íomhá 5 cm ón scáthán. Is íomhá híorúil í mar is íomhá híorúil a bhíonn i scáthán dronnach i gcónaí. Formhéadú v u 5 3 níl ach de mhéid na rithne san íomhá ruthaíonn scáthán dronnach dar ad ócasach 5 cm íomhá a bhuil an tríú cuid de mhéid na rithne inti. Faigh suíomh na rithne agus na híomhá. 40 Réiteach: Méid na híomhá ( ) Méid na rithne Formhéadú 3 3 v 3v u Ach é a ionadú in: aightear u 3 u v 3v v 5 3 3v 2 3v 30 v 0 cm 5 3v 5 u 3v u (3)(0) 30 cm. Mar sin tá an íomhá 0 cm ón scáthán agus tá an hrithne 30 cm ón scáthán. 25
26 Fisic don Ré Nua LEAHTADH cm os comhair scáthán dronnach dar ad ócasach 2 cm atá rithne. Faigh suíomh, nádúr agus ormhéadú na híomhá. Fíor cm os comhair scáthán dronnach dar ad ócasach 2 cm atá rithne. Faigh suíomh, nádúr agus ormhéadú na híomhá. 3. ruthaíonn scáthán dronnach dar ad ócasach 0 cm íomhá nach bhuil ach an ceathrú cuid de mhéid na rithne inti. Faigh suíomh na rithne agus na híomhá. 4. ruthaíonn scáthán dronnach íomhá atá 0 cm ón scáthán. Tá an hrithne 5 cm ar airde agus tá an íomhá 2 cm ar airde. Faigh ad ócasach an scátháin. 5. ruthaíonn scáthán dronnach íomhá atá 4 cm ón scáthán. Tá an íomhá 4 cm ar airde agus tá an hrithne 6 cm ar airde. ad é ad ócasach an scátháin? 6. á gcaithear rithne a shuí chun go gcruthóar íomhá nach bhuil ach an tríú cuid d airde na rithne inti i scáthán dronnach dar ad ócasach 20 cm? 7. á gcaithear rithne a shuí chun go mbeidh an íomhá a chruthaítear i scáthán dronnach dar ad ócasach 40 cm leath chomh hard leis an bhrithne? 8. á gcaithear rithne a shuí chun go mbeidh an íomhá a chruthaítear i scáthán dronnach leath chomh hard leis an bhrithne? LIOSTA SEIEÁLA NA AIBIDLE Abair cad is ciall le gach ceann díobh seo a leanas i gcomhthéacs scáthán séarach: an pol, an lár cuaire, an ais, an ócas, an ad ócasach. Sainmhínigh gach ceann díobh seo a leanas; Fíoríomhá, Íomhá híorúil, Formhéadú. Tarraing ga-léaráid chun suíomh íomhá a cruthaíodh i scáthán cuasach nó dronnach a aimsiú, cuma cén suíomh ina bhuil an hrithne. Meabhraigh na oirmlí adhbanna a réiteach. + agus u v v m u agus bain úsáid astu chun uir síos ar thurgnamh chun ad ócasach scátháin chuasaigh a thomhas agus déan an turgnamh. Déan liosta de na húsáidí a bhaintear as scátháin chuasacha agus as scátháin dhronnacha sa ghnáthshaol. 26
27 An tathraonadh 4 AIBIDIL ATHRAONADH AN TSOLAIS honaic tú ar leathanach 8 gur ina línte díreacha a thaistealaíonn an solas de ghnáth. Nuair a théann ga solais ó mheán áirithe agus isteach i meán eile, d héadadh a threo athrú ar dhul isteach sa dara meán dó, i.e. d héadadh an ga lúbadh (Fíor 4. (A)). Athraonadh an tsolais a thugtar ar an lúbadh sin (Feicidh tú i gaibidil 6 nach dtarlaíonn athraonadh ach amháin nuair a bhíonn luas an tsolais sa dara meán diriúil lena luas sa chéad mheán. Bíonn athraonadh i gceist reisin ar ndóigh nuair a théann solas isteach i bholús agus nuair a hágann sé olús (seachas nuair a bhíonn sé ingearach leis an bholús)). Tabhair aoi deara nach lúbann an ga (nach dtarlaíonn aon athraonadh), nuair is go hingearach a bhuaileann an ga an dara meán (Fíor 4. (B)) Bosca gathanna Bosca gathanna Ga solais Tarlaíonn athraonadh Ga solais Tarlaíonn athraonadh Bloc gloine Bloc gloine Fíor 4.(A) Fíor 4.(B) Ní tharlaíonn athraonadh nuair a bhuaileann ga solais an ghloine go hingearach An normal ag an bpointe ionsaithe An uillinn ionsaithe Baintear úsáid as na téarmaí seo a leanas maidir le ga solais a shoilsíonn ar bhloc gloine (Fíor 4.2) nó ar mheán trédhearcach eile: An ga ionsaithe a thugtar ar an nga atá ag titim ar an mbloc gloine. An ga ionsaithe Aer Gloine i r An pointe ionsaithe An uillinn athraonta An normal ag an bpointe ionsaithe a thugtar ar an líne a tharraingítear ingearach leis an mbloc gloine ag an bpointe a mbuaileann an ga an bloc. An An ga ga athraonta athraonta An ga athraonta a thugtar ar an nga sa bhloc gloine. An uillinn ionsaithe (i ) a thugtar ar an uillinn idir an ga ionsaithe agus an normal. Fíor 4.2 An uillinn athraonta (r) a thugtar ar an uillinn idir an ga athraonta agus an normal. 27
28 Fisic don Ré Nua T URGNAMH HUN AN TATHRAONADH A LÉIRIÚ Leis an trealamh atá léirithe i bhfíor 4.3, coigeartaigh an bosca gathanna go dtí go dtáirgeann sé léas an-chaol, i.e. ga. Soilsigh an ga ar thaobh amháin den bhloc gloine. Tabhair aoi deara mar a lúbann an ga ar dhul isteach sa ghloine dó, agus arís ar hágáil an bhloic dó. Tabhair aoi deara go bhuil an ga atá ag teacht amach as an mbloc gloine comhthreomhar leis an nga a bhuaileann an bloc. Soilsigh an ga ar an mbloc gloine i dtreo is go mbuailidh sé an bloc go hingearach. Tabhair aoi deara nach lúbann an ga nuair a théann sé isteach sa ghloine ach go dtéann sé díreach tríthi. Déan an turgnamh arís le luachanna diriúla don uillinn ionsaithe. Feicidh tú go méadaíonn an uillinn athraonta de réir mar a mhéadaíonn an uillinn ionsaithe (Fíor 4.4). Má thomhaiseann tú na huillinneacha eicidh tú nach méadú comhréireach a bhíonn i gceist. Fíor 4.3 Aer i i 2 i 3 i 4 Gloine r r2 r 2 r 3 r 4 Fíor 4.4 Méadaíonn an uillinn athraonta de réir mar a mhéadaíonn an uillinn ionsaithe ach ní mhéadaíonn siad i gcomhréir lena chéile. honaic tú sa turgnamh deireanach go n-athraontar (go lúbtar) ga solais i dtreo an normail nuair a théann sé ón aer isteach sa ghloine, ach go n-athraontar ón normal é nuair a imíonn sé ón ngloine isteach san aer. De ghnáth: An normal An normal Meán níos éadlúithe Meán níos dlúithe Meán níos dlúithe Meán níos éadlúithe Fíor 4.5 Fíor 4.6 IARMHAIRTÍ AN ATHRAONTA Nuair a thumtar spúnóg in umar uisce, dealraíonn sé go lúbann sí ag an bpointe a dtéann sí isteach san uisce. Tarlaíonn sé mar go mbíonn solas ag teacht ó na codanna sin den spúnóg atá aoin uisce, agus is amhlaidh a athraontar an solas sin ar hágáil an uisce dó. Dealraíonn sé don tsúil os cionn an uisce gur ag teacht ó phointe eile atá an solas sin (Fíor 4.7), an áit a bheiceann an tsúil an spúnóg agus dealraíonn sí a bheith lúbtha dá bharr. Fíor
29 An tathraonadh Ní héachann an t-uisce i linn snámha, in abhainn nó i loch chomh domhain is atá sé dáiríre. Dealraíonn sé reisin go bhuil iasc in uisce níos congaraí do bharr an uisce ná mar atá sé dáiríre. Beidh an iarmhairt chéanna le eiceáil má héachann tú ar ghiota scríbhneoireachta trí bhloc tiubh gloine (Fíor 4.8), agus bíonn sé níos soiléire ós más ar claon a bhíonn tú ag éachaint ar an ngloine. Dealraíonn sé go bhuil an scríbhneoireacht i bhad níos congaraí duit tríd an ngloine ná mar atá dáirire (éach lch 33 reisin). DLÍTHE ATHRAONTA AN TSOLAIS Tugann Dlíthe Athraonta an tsolais léiriú cruinn ar an gcoibhneas atá ag an uillinn ionsaithe leis an uillinn athraonta, agus is éidir na dlíthe sin a híorú go turgnamhach. An ga ionsaithe An normal ag an bpointe ionsaithe i An An ga ga athraonta athraonta r Gloine An chomhéieacht athraonta idir an dá mheán a thugtar ar n, agus braitheann a luach ar an dá mheán atá i gceist. DLÍ SNELL i.e. Sin i Sin r n nuair is tairiseach é n Tugtar Dlí Snell ar dhara dlí an athraonta uaireanta in onóir dowillebrord Snell (59-626), matamaiticeoir Dúitseach a tháinig air in 62. Níl ach diríocht híorbheag ann idir solas a bheith ag taisteal ón aer nó ó holús isteach i meán eile, agus is éidir neamhaird a thabhairt uirthi anseo. Dá réir sin is ionann comhéieacht athraonta meáin agus síneas na huillinne ionsaithe i gcóimheas le síneas na huillinne athraonta nuair a ghluaiseann solas ón AER isteach sa mheán sin reisin. Tá comhéieacht athraonta roinnt meán coitianta tugtha i bhfíor 4.0. Aer Fíor 4.9 Luíonn an ga ionsaithe, an normal ag an bpointe ionsaithe agus an ga athraonta ar an bplána céanna. Substaint Fíor 4.0 omhéieacht Athraonta Folús Aer.0003 Uisce.33 Gloine (chorónach).5 Gloine (bhreochloiche).6 Diamant 2.4 NÓTA Dá mhéad é comhéieacht athraonta meáin is ea is mó an méid a athraonann (a lúbann) an meán sin an solas maidir le huillinn ionsaithe ar leith Bíonn n (comhéieacht athraonta an mheáin) cothrom le nó níos mó ná, de bharr gur i dtreo an normail a lúbtar an solas a théann ó holús isteach i meán eile Sin i r < i Sín r < Sín i > Sin r 29
30 Fisic don Ré Nua Maidir le dhá mheán ar bith x agus y: xn y yn x Aer X Gloine i Y r Z Tá tábhacht leis an ord ina dtaistealaíonn an solas trí na meáin sin. Mar shampla, is é 0.9 an chomhéieacht athraonta nuair a théann an solas ón ngloine isteach in uisce, ach is é. an chomhéieacht athraonta nuair a théann solas ón uisce agus isteach sa ghloine. Is mar seo a scríobhtar é: g n u 0.9 nó u n g. oibhneas simplí atá ag an dá uimhir sin lena chéile: 0.9 nó Is íor an toradh sin de ghnáth, mar shampla an g 3 agus gn a 2 Is íric thurgnamhach é go bhillidh ga solais ar a chonair éin. Dá réir sin má shoilsítear ga eadh na líne ZY mar atá i bhfíor 4. tiocaidh sé amach san aer eadh na líne YX. Ón léaráid: an g Ach tá Sin i Sin r Sin i Sin r agus g n a Sin r / Sin i Sin r Sin i Dá réir sin, a n g gna 2 3 Fíor 4. Fadhb : Téann ga solais isteach i ngloine ón aer. 30 atá san uillinn ionsaithe agus 9 atá san uillinn athraonta. ad é comhéieacht athraonta na gloine? Sin i Sin Réiteach: omhéieacht athraonta na gloine an g.53 Sin r Sin Fadhb 2: Téann ga solais isteach in uisce ón aer (Fíor 4.2). Más é 40 atá san uillinn ionsaithe, aigh an uillinn athraonta. Is é.33 comhéieacht athraonta an uisce. Sin 40 Réiteach: I bhfíor 4.2: an u Sin r Fadhb 3: Sin r Sin an uillinn athraonta r Sin - (0.4833) 28.9 Fíor 4.2 Is é 0.9 an chomhéieacht athraonta idir gloine agus uisce. ad é an chomhéieacht athraonta idir uisce agus gloine? Aer Uisce r Réiteach: un g gnu 0.9. Fadhb 4: Réiteach: 9 un g 8. Téann solas isteach in uisce ón ngloine. Más 40 atá san uillinn ionsaithe, aigh an uillinn athraonta. Tarraing léaráid chun a bheith soiléir aoina bhuil á lorg (Fíor 4.3). 9 8 un g gn u 8 9 Fíor 4.3 Gloine Uisce 40 r Ag dul ón ngloine isteach in uisce gn u (9)(0.6428) an uillinn athraonta r Sin - (8) Sin 40 8 Sin r Sin r 9 Sin
31 An tathraonadh LEAHTADH 4.. Téann ga solais isteach i ngloine ón aer. 25 atá san uillinn ionsaithe agus 6.4 atá san uillinn athraonta. Ríomh comhéieacht athraonta na gloine. 2. Téann ga solais isteach i ndiamant ón aer. 60 atá san uillinn ionsaithe agus 2 atá san uillinn athraonta. Ríomh comhéieacht athraonta an diamaint. 3. Is é.33 comhéieacht athraonta an uisce. Déanann ga solais uillinn ionsaithe 30 agus é ag dul isteach san uisce ón aer. Faigh an uillinn athraonta. 4. Is é.5 comhéieacht athraonta na gloine. ad é an chomhéieacht athraonta idir an ghloine agus an t-aer? 5. Is é.3 an chomhéieacht athraonta idir an t-uisce agus an ghloine. ad é an chomhéieacht athraonta idir an ghloine agus an t-uisce? 6. Gluaiseann ga solais isteach in aer ón ngloine. 35 atá san uillinn ionsaithe agus 69 atá san uillinn athraonta. Faigh comhéieacht athraonta na gloine. 7. Fágann ga solais diamant dronuilleogach agus téann sé isteach san aer. 5 atá san uillinn athraonta a dhéanann sé. Más é 2.42 comhéieacht athraonta diamaint, aigh an uillinn ionsaithe. 8. Is é 2.42 comhéieacht athraonta an diamaint. 20 atá san uillinn ionsaithe a dhéanann ga solais atá ag taisteal ón taobh istigh de dhiamant isteach san aer. Faigh an uillinn athraonta. T URGNAMH SOLAS 2 HUN DLÍ SNELL A FHÍORÚ AGUS UAIDH SIN OMHÉIFEAHT ATHRAONTA NA GLOINE A THOMHAS. Sa turgnamh seo bainidh tú úsáid as dhá bhiorán chun treo an gha sholais a bhuaileann an bloc gloine a mharcáil. Úsáididh tú dhá bhiorán eile chun an ga céanna a mharcáil tar éis dó an bloc a hágáil (Fíor 4.4). Is éidir an uillinn ionsaithe i a dhéanann an ga ar an mbloc agus an uillinn athraonta r laistigh den bhloc a thomhas ansin. Déanaidh tú é sin arís le luachanna diriúla do i, agus íoróidh tú gur tairiseach is ea an cóimheas Sin i / Sin r. Sin íorú ar Dhlí Snell. An luach tairiseach, sin comhéieacht athraonta na gloine. Breacaidh tú gra de Sin i i gcoinne Sin r. Líne dhíreach tríd an mbunphointe an toradh, íorú eile ar Dhlí Snell. Fána an ghrai, sin an chomhéieacht athraonta. Fíor 4.4 An ga éiritheach An ga ionsaithe A B An Trealamh a theastaíonn Bloc dronuilleogach gloine Bileog pháipéir agus clár líníochta eithre bhiorán, peann luaidhe, rialóir agus uillinntomhas. An Modh. Leag an bhileog pháipéir ar an gclár líníochta agus cuir an bloc gloine ar an bpáipéar. 2. Tarraing imlíne an bhloic ghloine ar an bpáipéar le peann luaidhe géar. Déan deimhin de nach mbogann tú an bloc ón suíomh marcáilte trí thimpiste. 3. Greamaigh dhá bhiorán A agus B sa pháipéar agus sa chlár líníochta (Fíor 4.4) ionas go ndéanann an líne AB géaruillinn le ceann d aghaidheanna an bhloic. 4. Breathnaigh anonn trí aghaidh urchomhaireach an bhloic ghloine, agus bog do shúil go dtí nach éidir biorán A a heiceáil toisc biorán B a bheith sa tslí air. Déan an treo sin a mharcáil le dhá bhiorán eile agus D. D An ga athraonta Bioráin Páipéar Bioráin in Bloc gloine 3
32 5. Marcáil suíomh gach ceann de na bioráin ar an bpáipéar trí chiorcal beag a tharraingt timpeall orthu le peann luaidhe. Bain na bioráin agus an bloc gloine den chlár. 6. Tarraing an ga ionsaithe agus an ga éiritheach. Tarraing líne dhíreach chun an pointe ionsaithe a cheangal leis an bpointe éirithe sin an ga athraonta laistigh den bhloc. Tarraing an normal ag an bpointe ionsaithe le huillinntomhas (Fíor 4.5). Tomhais an uillinn ionsaithe i agus an uillinn athraonta r leis an uillinntomhas. Scríobh síos na luachanna sin. 7. uir an bloc in áit eile ar an bpáipéar nó aigh bileog eile, agus déan céimeanna 2 go 6 cúig huaire ar a laghad le luachanna diriúla don uillinn ionsaithe. Tabharaidh sé sin sraith d uillinneacha ionsaithe mar aon leis na huillinneacha athraonta a hreagraíonn dóibh. An uillinn ionsaithe i An normal ag an bpointe ionsaithe An pointe ionsaithe Fána an ghrai Sin i Sin r comhéieacht athraonta r An uillinn athraonta Imlíne an bhloic Sin i An ga athraonta An pointe éirithe An ga éiritheach Sin r Fíor 4.5 Fíor 4.6 Láimhseáil na Sonraí Modh omhlánaigh an Tábla le cuidiú d áireamháin An luach céanna, a bheag nó a mhór, a gheoar i gcolún 5 íorú ar Dhlí Snell. Sin i Ríomh meánluach (an colún deiridh sa tábla). Sin comhéieacht athraonta na gloine sa bhloc. Sin r i r Sin i Sin r Sin i / Sin r Sin i omhéieacht athraonta an ábhair sa bhloc Meánluach Sin r Modh 2 Breac gra de Sin i (ar an y-ais) i gcoinne Sin r (ar an x-ais) ar ghrapháipéar. Taobh istigh de theorainneacha na hearráide turgnamhaí, is ar líne dhíreach tríd an mbunphointe a luíidh na pointí sin ar ad (Fíor 4.6). Líne dhíreach tríd an mbunphointe atá sa ghra, sin íorú go bhuil Sin i Sin r é (i.e. íorú ar Dhlí Snell). Tomhais ána an ghrai. Sin comhéieacht athraonta na gloine sa bhloc. Foinsí Earráide hun earráidí a mhaolú déan deimhin de nach bhuil na bioráin A agus B róghar dá chéile agus an ga ionsaithe á mharcáil agat. Mar an gcéanna na bioráin agus D. Úsáid peann luaidhe géar. Ná bíodh luach an-íseal ar i, nó beidh sé an-deacair i agus r a thomhas. 32
33 An tathraonadh T URGNAMH SOLAS 2 MODH EILE HUN DLÍ SNELL A FHÍORÚ AGUS UAIDH SIN OMHÉIFEAHT ATHRAONTA NA GLOINE A THOMHAS. Sa turgnamh seo úsáididh tú bosca gathanna chun ga solais a tháirgeadh a bhuaileann bloc gloine (Fíor 4.7). Tarraingeoidh tú na gathanna agus imlíne an bhloic ar bhileog páipéir. Is éidir uillinn ionsaithe i an gha ar an mbloc agus an uillinn athraonta r laistigh den bhloc a thomhas ansin. Déanaidh tú é sin arís do luachanna diriúla de i agus íoróidh tú go mbíonn an cóimheas Sin i / Sin r mar a chéile i gconaí, íorú ar Dhlí Snell. Luach tairiseach an chóimheasa, sin comhéieacht athraonta na gloine. Breacaidh tú gra de Sin i i gcoinne Sin r. Líne dhíreach tríd an mbunphointe an toradh a bheidh air, íorú eile ar Dhlí Snell. Fána an ghrai, sin an chomhéieacht athraonta. An ga ionsaithe Bosca gathanna i r An normal ag an bpointe ionsaithe An ga athraonta An Trealamh a theastaíonn An ga éiritheach Bosca gathanna agus soláthar cumhachta Bileog de pháipéar líníochta Fíor 4.7 Bloc dronuilleogach gloine Peann luaidhe, rialóir agus uillinntomhas An Modh. Leag an páipear líníochta ar an mbinse agus leag an bloc gloine ar an bpáipéar. 2. Rianaigh imlíne an bhloic ghloine ar an bpáipéar le peann luaidhe géar. Déan deimhin de sa chuid eile den turgnamh nach mbogann tú an bloc trí thimpiste ón suíomh marcáilte. 3. Socraigh an bosca gathanna mar atá i bhfíor 4.7 agus soilsigh ga solais ar an mbloc. Marcáil an ga ionsaithe agus an ga éiritheach atá ag teacht as taobh eile an bhloic le peann luaidhe. Múch an bosca gathanna agus bain an bloc den pháipéar. 4. Tarraing an ga ionsaithe agus an ga éiritheach. 5. Le do pheann luaidhe tarraing líne dhíreach chun an pointe ag a mbuaileann an ga ionsaithe an bloc gloine a cheangal leis an bpointe ag a bhágann an ga éiritheach an bloc. Sin an ga athraonta laistigh den bhloc. Tarraing an normal ag an bpointe ionsaithe le huillinntomhas (Fíor 4.5). Tá an uillinn ionsaithe agus an uillinn athraonta a hreagraíonn di tarraingthe ar an bpáipéar anois. 6. Tomhais na huillinneacha sin leis an uillinntomhas. Scríobh síos na luachanna. 7. uir an bloc in áit eile ar an bpáipéar nó aigh bileog eile agus déan céimeanna 2 go 6 cúig huaire ar a laghad le luachanna diriúla den uillinn ionsaithe rud a thabharaidh sraith d uillinneacha ionsaithe i agus d uillinneacha athraonta comhhreagracha r. Láimhseáil na Sonraí Déileáil leis na sonraí mar a rinne tú sa turgnamh roimhe seo. Bloc gloine FÍORDHOIMHNEAHT AGUS DOIMHNEAHT DHEALRAITHEAH honaic tú ar leathanach 29 go ndealraíonn sé go bhuil rithne níos congaraí duit ná mar atá dáiríre nuair is trí bhloc gloine a bhreathnaíonn tú uirthi. Is íor reisin go ndealraíonn sé nach bhuil an t-uisce i linn snámha chomh domhain céanna is atá dáiríre. Athraonadh is cúis leis na hiarmhairtí sin agus is mar seo a leanas a mhínítear iad: Frithne bheag i mbun umair uisce atá i bhfíor 4.8 (lch 34). Léirítear roinnt gathanna solais ón bhrithne nuair a bhuaileann siad dromchla an uisce. Déantar athraonadh orthu ag an dromchla. Dealraíonn sé don té atá ag breathnú orthu ón aer go bhuil na gathanna ag eisréimniú ón bpointe Q, dá réir sin dealraíonn sé gur ag Q atá an pointe P, i.e. go bhuil sé níos congaraí don dromchla ná mar atá dáiríre. Íomhá híorúil de P is ea Q. Fíordhoimhneacht na rithne is ea SP agus doimhneacht dhealraitheach na rithne is ea SQ. 33
34 Fisic don Ré Nua Aer Fíordhoimhneacht Doimhneacht dhealraitheach Q P S Frithne Uisce Fíor 4.8 Fíor 4.9 Aer Q P Q P Frithne Mar a léirítear i bhfíor 4.9 is amhlaidh a laghdaíonn an doimhneacht dhealraitheach de réir mar bhogann d amharc ar an bhrithne cliathánach. Bíonn an doimhneacht dhealraitheach ar an méid is mó agus tú ag breathnú anuas ceartingearach ar an bhrithne. Bain triail as sa tsaotharlann nó sa bhaile. AN HOMHÉIFEAHT ATHRAONTA I DTÉARMAÍ FÍORDHOIMHNEAHTA AGUS DOIMHNEAHTA DEALRAITHÍ Tá cruthú ann (ní gá an cruthú a bheith ar eolas agat) go bhuil an chomhéieacht athraonta n íordhoimhneacht / doimhneacht dhealraitheach Q P Uisce Fadhb 5: Réiteach: Fadhb 6: Réiteach: Leagtar bloc gloine dar tiús 4 cm ar mharc ar an mbinse. Nuair a bhreathnaítear ar an marc go ceartingearach tríd an ngloine nochtann íomhá híorúil de atá 2.67 cm ó bharr an bhloic. Ríomh comhéieacht athraonta na gloine. An homhéieacht Athraonta n Fíordhoimhneacht Doimhneacht dhealraitheach 2 m ar doimhneacht atá linn uisce. Má bhreathnaítear go ceartingearach ón aer ar íochtar na linne cén doimhneacht a dhealraítear léi? omhéieacht athraonta an uisce.33 an u Fíordhoimhneacht Doimhneacht dhealraitheach Doimhneacht dhealraitheach m Doimhneacht dhealraitheach. Leagtar bloc gloine dar tiús 5 cm ar mharc ar an mbinse. Nuair a bhreathnaítear ar an marc go ceartingearach tríd an ngloine nochtann íomhá híorúil de agus í 3.33 cm ó bharr an bhloic. Faigh comhéieacht athraonta na gloine. 2. Linn uisce atá 0 m ar doimhneacht. Má bhreathnaítear go ceartingearach ón aer ar íochtar na linne, cén doimhneacht a dhealraítear léi? (omhéieacht athraonta an uisce.33) m ar doimhneacht a dhealraíonn linn uisce a bheith nuair a bhreathnaítear anuas uithi go ceartingearach. én híordhoimhneacht atá san linn? (omhéieacht athraonta an uisce 4 3). LEAHTADH Breathnaítear go ceartingearach ar thaobh amháin de bhloc dronuilleogach gloine dar toisí 5 cm 5 cm 6 cm agus dealraíonn sé gur ciúb atá ann. ad é comhéieacht athraonta ábhar an bhloic ghloine? 5. Leagtar bloc gloine dar comhéieacht athraonta.5 ar mharc ar bhileog pháipéir. Nuair a bhreathnaítear an marc go ceartingearach tríd an ngloine nochtann íomhá híorúil den mharc, agus í 3.33 cm ó bhun an bhloic. én tiús atá sa bhloc gloine? 34
35 An tathraonadh T URGNAMH SOLAS 3 OMHÉIFEAHT ATHRAONTA LEAHTA A AIMSIÚ AH FÍORDHOIMHNEAHT AGUS DOIMHNEAHT DHEALRAITHEAH FRITHNE SA LEAHT A THOMHAS. An dara biorán Achoimre ar an Modh Sa turgnamh seo breathnóidh tú ar bhiorán ag bun eascra uisce tríd an uisce éin (Fíor 4.20). Íomhá bhioráin eile i scáthán plánach a bheidh agat mar thóirbhiorán. Déanaidh tú airde an dara biorán a choigeartú go dtí go mbeidh an íomhá san uisce agus an íomhá sa scáthán plánach ar easpa saobhdhiallais. Mar is léir i bhfíor 4.20, tá an ad X an híordhoimhneacht agus an ad Y an doimhneacht dhealraitheach. An cóimheas idir an dá thomhas, sin cómhéieacht athraonta an uisce, i.e. omhéieacht athraonta uisce aer n uisce Fíordhoimhneacht Doimhneacht dhealraitheach Doimhneacht dhealraitheach Y Íomhá na rithne san uisce Biorán rithne Is í íomhá an dara biorán ag bun an eascra sa scáthán plánach an tóirbhiorán. Fíor 4.20 X Scáthán plánach Fíordhoimhneacht Roinnt eascraí ar doimhneachtaí éagsúla. Bí cinnte gur éidir na heascraí a líonadh go barr, tá eascraí ann nach éidir a líonadh go barr mar gheall ar an ngob atá orthu. Seastán reangáin, corc agus dhá bhiorán Scáthán plánach agus méadarshlat An Modh. Líon ceann de na heascraí le huisce agus leag biorán ar bhun an eascra ina lár (Fíor 4.20). Is é an biorán sin an hrithne. 2. uir an scáthán plánach thar bharr an eascra. Déan deimhin de go bhuil cúl an scátháin i dteagmháil leis an uisce. 3. Greamaigh an dara biorán sa chorc ar an seastán reangáin. oigeartaigh suíomh an dara biorán go mbíonn a íomhá sa scáthán plánach ar aon líne le híomhá an chéad bhiorán san uisce (Fíor 4.2). 4. oigeartaigh airde an dara biorán go dtí go bhuil an dá íomhá ar easpa saobhdhiallais. 5. Tomhais leis an méadarshlat: an ad ón mbiorán rithne go barr an eascra (X), an ad ón dara biorán go barr an uisce (Y). 6. láraigh na luachanna sin. Íomhá an dara biorán sa scáthán Íomhá an bhioráin rithne san uisce 7. Athdhéan an turgnamh ceithre huaire ar a laghad, agus eascraí ar doimhneachtaí éagsúla in úsáid agat. 8. omhlánaigh an Tábla agus ríomh meánluach don Fhíordhoimhneacht / Doimhneacht dhealraitheach. Sin comhéieacht athraonta an uisce. Amharc ón mbarr Fíor 4.2 Ag breathnú anuas ar an eascra agus an scáthán Fíordhoimhneacht X / cm Doimhneacht dhealraitheach Y/cm Fíordhoimhneacht Doimhneacht dhealraitheach Fíordhoimhneacht Meánluach omhéieacht Athraonta an leachta Doimhneacht dhealraitheach Foinsí Earráide Tarlaíonn earráidí nuair atá suíomh na heaspa saobhdhiallais á aimsiú, agus nuair atá na aid á dtomhas leis an méadarshlat. 35
36 Fisic don Ré Nua i Meán Luas an tsolais c r AN HOMHÉIFEAHT ATHRAONTA I DTÉARMAÍ LUASANNA OIBHNEASTA Meán 2 Luas an tsolais c 2 n 2 Athraíonn luas an tsolais, ar tonn é, de ghnáth agus é ag taisteal ó mheán áirithe agus isteach i meán eile (bíonn an luas is airde aoi agus é i bholús, sin ms - ). Is é an t-athrú luais sin aoi deara don solas a threo a athrú ar dhul isteach sa dara meán dó. Tá míniú níos iomláine ar leathanach 80. Más é c an luas i meán a haon agus más é c 2 an luas i meán a dó, is éidir a chruthú go bhuil: c c 2 i.e. Sin i Sin r c c 2 (Féach Fíor 4.22) Leanann uaidh sin d aon mheán x, go bhuil, aern x i.e. omhéieacht athraonta an mheáin c c aer x Luas an tsolais in aer Luas an tsolais sa mheán Leanann uaidh sin go bhuil luas an tsolais i meán An luas in aer omhéieacht athraonta an mheáin Dá mhéad é an chomhéieacht athraonta is ea is moille luas an tsolais. Fadhb 7: ad é comhéieacht athraonta meáin a dtaistealaíonn solas ann aoi luas m s -? Luas an tsolais in aer m s - Réiteach: aern x 8 c aer Luas in aer c x Luas sa mheán Fadhb 8: omhéieacht athraonta an uisce.33 agus luas an tsolais in aer m s -. Ríomh luas an tsolais in uisce. Réiteach: an u c c aer uisce Luas in uisce Luas in aer Luas in uisce Luas in aer m s - LEAHTADH 4.3 Glac le m s - do luas an tsolais in aer. ad é luas an tsolais i ngloine dar comhéieacht athraonta.5? 2. ad é luas an tsolais i ndiamant dar comhéieacht athraonta 2.42? 3. ad é comhéieacht athraonta meáin ina bhuil luas an tsolais m s -? 4. ad é comhéieacht athraonta meáin ina bhuil luas an tsolais m s -? FRITHHAITHEAMH INMHEÁNAH IOMLÁN Ga solais atá ag gluaiseacht ó mheán áirithe agus isteach i meán eile atá níos éadlúithe ná é athraontar amach ón normal é (lch 28). De réir mar a mhéadaítear an uillinn ionsaithe is amhlaidh a mhéadaítear an uillinn athraonta reisin (Fíor 4.23). 90 a bheidh san uillinn athraonta ag pointe áirithe. An uillinn ionsaithe ag a dtarlaíonn sé sin, sin an uillinn chriticiúil don dá mheán sin. An litir an ghnáthshiombail uirthi. 36
37 An tathraonadh An uillinn athraonta 90 r r 2 i i 2 Fíor 4.23 An uillinn chriticiúil Tarlaíonn rithchaitheamh inmheánach iomlán Má mhéadaítear an uillinn ionsaithe thar an uillinn chriticiúil, ní ghabhaidh an ga solais isteach sa dara meán in aon chor. Frithchaitear an ga ar ais sa chéad mheán arís de réir dlíthe hrithchaitheamh an tsolais. Frithchaitheamh inmheánach iomlán a thugtar ar a leithéid (is é atá i gceist leis sin ná go bhrithchaitear an solas ar ad, ní ionsúitear aon chuid de. Ionsúitear 4% den solas ionsaithe ar an ngnáthscáthán is earr atá ar áil agus rithchaitear an chuid eile). T URGNAMH HUN FRITHHAITHEAMH INMHEÁNAH IOMLÁN A LÉIRIÚ Socraigh bosca gathanna agus leac leathchiorclach gloine mar atá i bhfíor 4.24 (A). Tosaigh le huillinn ionsaithe bheag agus méadaigh ar an uillinn sin de réir a chéile. Ní ada go mbainidh tú an uillinn chriticiúil amach agus beidh an ga athraonta ag sciorradh eadh dhromchla cothrom na gloine. Má mhéadaíonn tú an uillinn ionsaithe a thuilleadh ansin, léimidh an ga athraonta go tobann agus in ionad an leagain atá léirithe i bhfíor 4.24 (B) is amhlaidh a gheobhaidh tú leagan ar nós Fíor 4.24 (), is é sin, an ga iomlán rithchaite go hinmheánach. r r 90 i i 2 r 2 Leac leathchiorclach gloine An uillinn chriticiúil i 2 r 2 Bosca gathanna (A) (B) () Fíor AN OIBHNEAS IDIR AN HOMHÉIFEAHT ATHRAONTA AGUS AN UILLINN HRITIIÚIL Meán y Níos éadlúithe Ga solais atá i bhfíor 4.25 agus é ag taisteal ó mheán áirithe agus isteach i meán eile atá níos éadlúithe ná é. Buaileann sé an meán atá níos éadlúithe ag an uillinn chriticiúil. Ach Dlí Snell a chur i bheidhm: Níos dlúithe Meán x xn y Sin Sin90 Sin Sin Fíor
38 Fisic don Ré Nua i.e. omhéieacht Athraonta meáin n Más aer (nó olús) atá sa dara meán (an meán is éadlúithe) is mar seo a leanas a bheidh an chothromóid: xn a Sin an x Sin Sin nuair is é an uillinn chriticiúil Fadhb 9: Réiteach: Fadhb 0: Réiteach: 50 an uillinn chriticiúil atá ag meán áirithe. Faigh comhéieacht athraonta an mheáin. omhéieacht athraonta n.3 Sin Sin50 Is é.5 comhéieacht athraonta na gloine. ad é uillinn chriticiúil na gloine? an g Sin Sin a n g i.e. Sin Sin Uillinn chriticiúil 4.8 Priosma a úsáid chun ga solais a chasadh trí (i) 90 (ii) 80 Má théann ga solais isteach i bpriosma mar atá léirithe i bhfíor 4.26(A), is 45 a bheidh san uillinn ionsaithe nuair a bhuaileann sé taobh deas an phriosma. Ós rud é go bhuil an uillinn sin níos mó ná an uillinn chriticiúil, beidh rithchaitheamh inmheánach iomlán ann ag O agus rithchaithear an ga mar atá léiríthe. Ós rud é gur 45 atá san uillinn rithchaithimh reisin, is 90 atá san uillinn idir an ga ionsaithe agus an ga rithchaite, i.e. casadh an ga solais trí uillinn 90. Agus is éidir ga a chasadh 80 reisin leis an bpriosma céanna (Féach Fíor 4.26(B)) i45 r45 O (A) Ga solais á chasadh trí 90 le priosma (B) Ga solais á chasadh trí 80 le priosma Fíor 4.26 Fadhb : Réiteach: Má tá priosma chun casadh 90 a bhaint as ga solais mar atá i bhfíor 4.26 (A), cad é an luach is lú a d héadadh a bheith ag comhéieacht athraonta an ábhair sa phriosma? 45 atá san uillinn ionsaithe a dhéanann an ga ar an dromchla gloine-aeir. Agus an ga ag dul ó ghloine go haer caithidh an uillinn ionsaithe a bheith níos mó ná an uillinn chriticiúil chun go mbeidh rithchaitheamh inmheánach iomlán ann. i.e. chun go mbeidh rithchaitheamh inmheánach iomlán ann 45 > i.e. < 45 Sin < Sin 45 Sin <0.707 Sin > Ach /Sin comhéieacht athraonta na gloine agus / aithidh go mbeadh an chomhéieacht athraonta níos mó ná.44 38
39 An tathraonadh Fadhb 2: Réiteach: 2 m aoi dhromchla an uisce i lochán socair atá P, ponchoinse solais. Faigh ga an chiorcail ar dhromchla an uisce trínar éidir leis an solas dul isteach san aer. omhéieacht athraonta an uisce 4. 3 Léiriú ar an suíomh atá i bhfíor Solas ón bhoinse a bhuaileann Aer an dromchla ag uillinn ionsaithe atá níos mó ná an uillinn chriticiúil, r ní hágaidh sé an t-uisce. 4 omhéieacht athraonta an uisce 3 3 Sin 2m (4/3) 4 An uillinn chriticiúil Uisce Ón léaráid: P r Tan 2 r 2Tan r 2 Tan m Fíor 4.27 Is éidir le ga solais illeadh ar ais ar a chonair éin. Dá réir sin maidir le solas a rachaidh isteach san uisce ón aer agus ad leis an bpointe P aoin dromchla, gheoar, mar a uarthas thuas nach sroichidh solas ar bith an Pointe P ach amháin an solas a bhuaileann an dromchla lastigh de chiorcal dar ga r. Dá réir sin sin, má tá tú aoin uisce agus ag breathnú suas uait, ní éidir le solas ón taobh amuigh teacht isteach san uisce ach amháin tríd an gciorcal dar ga r. Léiríonn Fíor 4.28 go soiléir é. Fuinneog Snell a thugann na tumadóirí air. uir i gcás go socraítear trí scátháin phlánacha ionas go bhuil siad ingearach dá chéile. Má shoilsítear ga solais ar cheann díobh ionas go bhrithchaitear é de gach scáthán eile díobh i ndiaidh a chéile, beidh an ga a hágann na scátháin ag illeadh ar ais sa treo as a dtáinig an chéad gha i dtosach. Baintear úsáid as an bhíric sin sna rithchaiteoirí sábháilteachta ar rothar nó ar ghluaisteán (Fíor 4.29). In ionad scáthán a bheith iontu, is amhlaidh a mhúnlaítear an plaisteach nó an t-ábhar eile as a ndéantar an rithchaiteoir ina lán priosmaí dronuilleacha. Le rithchaitheamh inmheánach iomlán a hrithchaitear an solas i ngach priosma díobh agus dá réir sin rithchaitear ar ais é sa treo as a dtáinig sé ar dtús. Ar an bprionsabal céanna a heidhmíonn cuid de na comharthaí rithchaiteacha ar na bóithre. Fíor 4.28 Fíor 4.29 LEAHTADH an uillinn chriticiúil atá ag meán áirithe. ad é comhéieacht athraonta an mheáin? an uillinn chriticiúil atá ag diamant. ad é comhéieacht athraonta an diamaint? 3. Is é.2 an chomhéieacht athraonta atá ag gloine de chineál áirithe. ad é an uillinn chriticiúil idir an ghloine agus an t-aer? 4. Is é.33 an chomhéieacht athraonta atá ag uisce. ad é an uillinn chriticiúil idir uisce agus aer? 5. Faigh an uillinn chriticiúil atá ag meán dar comhéieacht athraonta Frithne i mbloc ábhair darb uillinn chriticiúil 40, cén doimhneacht dhealraitheach atá aici? Go ceartingearach ón aer atáthar ag breathnú ar an bhrithne agus í ar híordhoimhneacht 2 cm. 7. Foinse solais ar ghrinneall locháin 4 m ar doimhneacht, astaíonn sí solas aníos i ngach treo. Trí dhiosca dar ga r ar dhromchla an uisce a ghabhann na gathanna a hágann an t-uisce agus a théann isteach san aer. Faigh ga an diosca sin. Is é.33 comhéieacht athraonta an uisce. 39
40 Fisic don Ré Nua 8. 2 m aoin dromchla i linn uisce atá ponchoinse solais. Is é 2.3 m ga an chiorcail trínar éidir le solas ón bhoinse dul isteach san aer. Ríomh comhéieacht athraonta an uisce. 9. An t-ábhar as a ndéantar priosma , cad é an chomhéieacht athraonta is lú a d héadadh a bheith aige chun go gcasadh sé ga solais trí 90, aoi mar atá léirithe i bhfíor 4.26 (A) (lch 38)? SNÁITHÍNÍ OPTÚLA Feidhm shuimiúil thábhachtach den hrithchaitheamh inmheánach iomlán is ea an snáithín optúil. Fíor 4.30 Snáithín optúil ag gabháil trí chró snáthaide i > i 2 > i Fíor 4.3 tarlaíonn rithchaitheamh inmheánach iomlán Fíor 4.32 Má bhuaileann dhá shnáithín optúla le chéile, d héadadh solas éalú as ceann amháin díobh agus a ghabháil isteach sa cheann eile. i 2 Feadáin solais a thugtar ar na snáithíní optúla uaireanta. Ní oireann an t-ainm sin áach ó tharla go mbíonn snáithíní optúla soladach seachas toll. Ó tá na snáithíní an-chaol, tá siad solúbtha agus dá réir sin is éidir leo solas a iompar timpeall coirnéal. TARHUR AN TSOLAIS TRÍ SHNÁITHÍN OPTÚIL Téann an solas isteach sa snáithín agus buaileann sé an taobh istigh ag uillinn atá níos mó ná an uillinn chriticiúil. Déantar rithchaitheamh inmheánach iomlán. Frithchaitear an ga solais go dtí an taobh eile den snáithín agus tarlaíonn rithchaitheamh inmheánach iomlán arís (Fíor 4.3). Leanann an próiseas ar aghaidh agus gluaiseann an solas tríd an snáithín. Éalaíonn solas as snáithíní optúla ar dhá shlí: Má lúbtar snáithín optúil trí uillinn atá rómhór d héadadh an ga solais atá ag taisteal laistigh de é a bhualadh ag uillinn atá níos lú ná an uillinn chriticiúil, ionas nach ndéanaí rithchaitheamh inmheánach iomlán ar an solas agus go n-éalódh sé as an snáithín. Má theagmhaíonn snáithín optúil le snáithín eile, (nó le cuid eile de éin) b héidir nach mbeadh an ga solais taobh istigh ag taisteal ó ghloine isteach in aer níos mó, ach ó ghloine agus isteach i ngloine. Sa chás sin ní tharlóidh rithchaitheamh inmheánach iomlán ach gluaisidh an ga solais ó shnáithín amháin agus isteach sa snáithín eile (Fíor 4.32). Bealach amháin chun é sin a chosc ná an snáithín a chlúdach le craiceann gloine a mbeadh comhéieacht athraonta níos lú aici ná gloine an tsnáithín. Tarlóidh rithchaitheamh inmheánach iomlán ansin iú má theagmhaíonn dhá shnáithín lena chéile mar beidh an solas ag taisteal ó ghloine áirithe isteach i ngloine atá níos éadlúithe ná í ag uillinn ionsaithe atá níos mó ná an uillinn chriticiúil (Fíor 4.33). raiceann dar comhéieacht athraonta n 2 2 <n Snáithín dar comhéieacht athraonta n Fíor 4.33 Ach an snáithín optúil a chlúdach le hábhar ar chomhéieacht athraonta níos lú, ní éalóidh an solas as iú má theagmhaíonn sé le snáithín eile. 40
41 An tathraonadh ÚSÁID A BHAINTEAR AS SNÁITHÍNÍ OPTÚLA Úsáidtear snáithíní optúla sa teileachumarsáid chun comharthaí teileaóin a tharchur i riocht bíog solais: cruthaíonn na comharthaí leictreacha teileaóin comharthaí solais comhhreagracha atá in ann taisteal trí shnáithíní optúla; cruthaíonn na comharthaí solais comharthaí leictreacha ag ceann eile an tsnáithín chun na teileaóin a chur ag obair. Seo a leanas na buntáistí atá leis: (i) Bíonn an caillteanas uinnimh i bhad níos lú i snáithíní optúla ná i gcáblaí leictreacha. (ii) Tá na snáithíní optúla a theastaíonn chun méid áirithe comharthaí a iompar i bhad níos lú ná na cáblaí leictreacha a bheadh ag teastáil chun an méid céanna comharthaí a iompar. (iii) Ní tharlaíonn an oiread céanna trasnaíochta sna snáithíní optúla. Úsáidtear snáithíní optúla i gcúrsaí leighis chun solas a thabhairt chuig agus ar ais as codanna dorochtana den cholainn an goile, mar shampla chun scrúdú a dhéanamh orthu. Bailiúchán snáithíní optúla atá san ionscóp (Fíor 4.34) agus úsáidtear le haghaidh a leithéide é. Tugann snáithíní optúla an solas anchóngarach do bhéalmhír druilire an hiaclóra, agus éadann an iaclóir an taobh istigh de bhéal an othair a heiceáil ad atá sé ag druileáil iacaile. Fíor 4.34 Íomhá ionscópach d héatas daonna. MEABHALSÁILEANNA Athraíonn comhéieacht athraonta an aeir beagán leis an teocht. Is é an t-athrú sin is cúis leis an meabhalscáil a heictear ar an mbóthar lá breá te samhraidh. Mar lochán lonrach uisce ar an mbóthar a heictear é agus íomhánna de rudaí atá in aice láimhe le eiceáil ann (Fíor 4.35). An ghrian agus í ag soilsiú ar bhóthar atá i bhfíor Ionsúnn an bóthar an teas agus déantar an t-aer díreach os a chionn a théamh go mór. Laghdaíonn an teocht de réir mar a théann sé in airde. Bíonn aer te níos éadlúithe ná aer ionnuar, agus comhéieacht athraonta beagán níos ísle aige dá réir. uir i gcás ga solais atá ag déanamh ar an mbóthar ón spéir. Ag taisteal ó mheán áirithe agus isteach i meán níos éadlúithe atá sé, agus dá réir sin déanar é a athraonadh amach ón normal agus a lúbadh mar atá léirithe. Má tharlaíonn go bhuil an uillinn ionsaithe níos mó ná an uillinn chriticiúil ag pointe éigin, déanar rithchaitheamh inmheánach iomlán ar an nga agus rithchaithear in airde é. Feicidh breathnóir íomhá den spéir sa talamh. Sin an lochán lonrach, i.e. an mheabhalscáil. D héadaí rithne atá in aice láimhe a heiceáil bun os cionn sa lochán ar an gcúis chéanna. Frithne AER ATÁ NÍOS FUAIRE (níos dlúithe) AER TE (atá níos éadlúithe) Feiceann an breathnóir lochán uisce ar crithlonrú anseo Fíor 4.35 Fíor
42 Fisic don Ré Nua LIOSTA SEIEÁLA NA AIBIDLE Sainmhínigh gach ceann díobh seo a leanas: An tathraonadh; An homhéieacht athraonta; An Uillinn hriticiúil; Frithchaitheamh Inmheánach Iomlán. Tabhair Dlíthe Athraonta an tsolais agus Dlí Snell. Mínigh: Fíordhoimhneacht; Doimhneacht Dhealraitheach; Snáithín Optúil. uir síos ar thurgnamh agus déan é chun: An tathraonadh a léiriú; Dlí Snell a híorú; An homhéieacht athraonta a thomhas; Frithchaitheamh inmheánach iomlán a léiriú. Meabhraigh na oirmlí seo a leanas agus bain úsáid astu: Sin i Fíordhoimhneacht n ; xn y ; n Sin r yn x Doimhneacht dhealraitheach ; n Sin ; n 2 c c 2 Déan liosta de roinnt iarmhairtí praiticiúla a ghabhann leis an athraonadh. Taispeáin conas is éidir priosma a úsáid chun ga solais a chasadh trí 90 agus 80. uimhnigh gur ar an bhrithchaitheamh inmheánach iomlán atá comharthaí rithchaiteacha bóthair, meabhalscáileanna, rithchaiteoirí priosmacha agus snáithíní optúla bunaithe. 42
43 Lionsaí 5 AIBIDIL LIONSAÍ Athraonadh an tsolais trí lionsaí a bheidh i gceist sa chaibidil seo. Beidh dhá chineál lionsa i gceist an lionsa dronnach agus an lionsa cuasach (Fíor 5.). Tá an lionsa dronnach níos tibhe ina lár ná ag na himill agus tá an lionsa cuasach níos tibhe ag na himill ná ina lár. Lionsa dronnach (lionsa inréimneach) Bíonn lionsaí in úsáid i ngnáthrudaí ar nós spéaclaí, lionsaí tadhaill, ceamaraí, Fíor 5. Fíor 5.2 teilgeoirí, teileascóip, déshúiligh agus micreascóip. Níl i ngloine ormhéadúcháin ach lionsa dronnach. An lár optúil a thugtar ar lár an lionsa (Fíor 5.2). Lionsa cuasach (lionsa eisréimneach) An phríomhais nó an ais a thugtar ar an líne dhíreach a ghabhann tríd an lár optúil agus í ingearach le héadan an lionsa (Fíor 5.2). An ócas An phríomhais An ócas An phríomhais An lár optúil An lár optúil An ócas An ócas An príomhhócas AIRÍ FÓASAITHE LIONSAÍ Maidir le lionsa dronnach atá tanaí, aightear go dtugtar léas solais a thiteann ar an lionsa chun ócais ag pointe ar leith (Fíor 5.3). Má tá an léas comhthreomhar le hais an lionsa, is é príomhhócas nó ócas an lionsa a thugtar ar an bpointe ar a mbíonn an léas ag inréimniú. Fad ócasach an lionsa a thugtar ar an bhad idir an lár optúil agus príomhhócas an lionsa. Tabhair aoi deara na nithe seo a leanas: Bíonn ócas ar an dá thaobh den lionsa. Bíonn an dá hócas an ad céanna amach ón lár optúil. Tugtar lionsa inréimneach ar lionsa dronnach reisin ós rud é go n-athraíonn sé léas comhthreomhar ina léas inréimneach. Léas comhthreomhar solais a thiteann ar lionsa cuasach tanaí, spréann an léas amach amhail is go raibh sé ag teacht ó phointe ar leith (Fíor 5.4). An príomhhócas nó ócas an lionsa a thugtar ar an bpointe sin má tá an léas comhthreomhar le hais an lionsa. Tá ócas ar dhá thaobh an lionsa agus iad araon an ad céanna amach ón lár optúil. Ó tharla go n-athraíonn lionsa cuasach léas comhthreomhar ina léas eisréimneach is amhlaidh a thugtar lionsa eisréimneach reisin ar lionsa cuasach. ATHRAONADH AN TSOLAIS LE LIONSA DRONNAH TANAÍ Agus íomhá á haimsiú i lionsa dronnach againn bainimid úsáid as na torthaí seo a leanas (Fíor 5.5). Ní gá a bheith in ann iad a chruthú. Glac leo agus meabhraigh iad. Léas comhthreomhar Léas comhthreomhar Fíor 5.3 Léas comhthreomhar An príomhhócas Fíor 5.4 Léas inréimneach An ad ócasach Léas inréimneach An príomhhócas An ad ócasach Léas eisréimneach An ócas 43
44 Fisic don Ré Nua Ga a bhuaileann an lár optúil gabhann sé díreach tríd an lionsa. Ga a bhuaileann an lionsa agus é ag taisteal comhthreomhar leis an ais, gabhann sé tríd an bhócas ar an taobh eile den lionsa. Ga a ghabhann tríd an bhócas agus a bhuaileann an lionsa ansin, tagann sé amach comhthreomhar leis an bpríomhais. An lár optúil An ócas An ócas An ócas An ócas Fíor 5.5 MAR A HRUTHAÍTEAR ÍOMHÁ I LIONSA DRONNAH Frithne agus í suite os comhair lionsa dronnach atá i bhfíor 5.6. Is cuma cé acu rithne héinlonrach atá ann nó rithne a dhéanann rithchaitheamh idirleata, tá solas á chaitheamh amach i ngach treo ó gach pointe ar an bhrithne. P An lár optúil An íomhá Bosca gathanna ros-snáitheanna soilsithe mar hrithne Lionsa dronnach Fíoríomhá na gcros-snáitheanna ar scáileán. X Fíor 5.6 Fíor 5.7 Léirítear gathanna solais ón bpointe P ag uachtar na rithne, an lionsa á bhualadh acu agus iad á n-athraonadh. ad atá le tabhairt aoi deara? Nuair a dhéantar athraonadh orthu ag an lionsa, gabhann gach ga díobh tríd an bpointe céanna, X. Is éidir a thaispeáint reisin go rachadh ga ar bith eile as P trí X i ndiaidh a athraonta. Mar a léirítear i bhfíor 5.6, leanann uaidh sin go bheicidh an tsúil (i.e. an breathnóir) íomhá d uachtar na rithne ag X ós rud é go bhuil na gathanna a bhí ag eisréimniú ó P i dtosach ag eisréimniú ó X anois. Ach an próiseas a dhéanamh arís is arís eile i gcás pointí eile ar an bhrithne d heicimis go gcruthaítear íomhá na rithne ina hiomláine mar atá i bhfíor 5.6. Fíoríomhá is ea í sin mar is le íorthrasnú gathanna a chruthaítear í. Is urasta an híoríomhá a chruthaítear le lionsa dronnach a theilgean ar scáileán nó ar bhalla, mar athaispeántar i bhfíor 5.7. MAR A ATHRAÍONN AN ÍOMHÁ DE RÉIR MAR A ATHRAÍONN SUÍOMH NA FRITHNE hun suíomh íomhá a aimsiú ní gá na trí gha a tharraingt, mar atá i bhfíor 5.6. Is leor dhá gha. Feicimid anois an áit a bhuil an íomhá nuair atá an hrithne: lasmuigh de 2 ag 2 ; idir agus 2 ; ag an bhócas; laistigh den hócas. 44
45 Lionsaí Déan iarracht na ga-léaráidí cuí a tharraingt tú éin sula bhéachann tú ar Fhíor 5.8. Feicimid an méid seo a leanas ó Fhíor 5.8: ÍOMHÁ FRITHNE I GÉIN I LIONSA Frithne DRONNAH Má tá rithne i bhad i gcéin ón lionsa (ag an éigríoch, a deirtear) is íoríomhá a chruthaítear agus í ag an bhócas (ag an bplána ócasach, i ndáiríre). uimhnigh gur mar léas comhthreomhar a thagann an solas ó phointe ar hrithne i bhad i gcéin, agus nach comhthreomhar lena chéile a bheidh na léasacha ó dhá phointe dhiriúla ar an bhrithne sin. I bhfíor 5.9 titeann solas ar lionsa dronnach ó bharr (P) agus ó bhun (Q) rithne atá i bhad ón lionsa. Tugtar an léas atá comhthreomhar leis an ais chun ócais ag príomhhócas an lionsa. Tugtar an léas eile chun ócais ag áit ar a dtugtar plána ócasach an lionsa, mar atá léirithe. Dá réir sin, cruthaítear íoríomhá den hrithne i gcéin ag plána ócasach an lionsa. Is éidir é sin a thaispeáint go héasca sa tsaotharlann mar atá i bhfíor 5.0. FÍORÍOMHÁ 2 2 Frithne 2 Frithne Íomhá laghdaithe An íomhá ar cóimhéid Íomhá hormhéadaithe P Achar ada Léas comhthreomhar ó P Fíoríomhá ar phlána ócasach an lionsa Q Léas comhthreomhar ó Q An íomhá ag an éigríoch Frithne Fíor ÍOMHÁ FHÍORÚIL Íomhá híorúil hormhéadaithe 2 Frithne 2 Fíor 5.8 Fíor 5.0 Lionsa dronnach agus íoríomhá á cruthú aige d hrithne atá i bhad i gcéin 45
Coimisiún na Scrúduithe Stáit
 2014. M 38T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hrdteistiméirecht, 2014 FISIC GUS CEIMIC RDLEIBHÉL DÉ LUIN, 16 MEITHEMH MIDIN, 9:30 go 12:30 Sé cheist le freagairt. Freagair trí cheist ar bith as Roinn
2014. M 38T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hrdteistiméirecht, 2014 FISIC GUS CEIMIC RDLEIBHÉL DÉ LUIN, 16 MEITHEMH MIDIN, 9:30 go 12:30 Sé cheist le freagairt. Freagair trí cheist ar bith as Roinn
Matamaitic (Tionscadal Mata Céim 2)
 2014. S235ST Coimisiún na Scrúduithe Stáit An Teastas Sóisearach, 2014 Matamaitic (Tionscadal Mata Céim 2) Páipéar 2 Ardleibhéal Am: 2 uair, 30 nóiméad 300 marc Iomlán reatha Scrúduimhir Stampa an Ionaid
2014. S235ST Coimisiún na Scrúduithe Stáit An Teastas Sóisearach, 2014 Matamaitic (Tionscadal Mata Céim 2) Páipéar 2 Ardleibhéal Am: 2 uair, 30 nóiméad 300 marc Iomlán reatha Scrúduimhir Stampa an Ionaid
Pre-Leaving Certificate Examination, 2012 Triailscrúdú na hardteistiméireachta, 2012
 *Pg16* Pre-Leaving Certificate Examination, 2012 Triailscrúdú na hardteistiméireachta, 2012 FISIC ARDLEIBHÉAL Am: 3 uair an chloig Freagair trí cheist as roinn A agus cúig cheist as roinn B. Lch 1 de 11
*Pg16* Pre-Leaving Certificate Examination, 2012 Triailscrúdú na hardteistiméireachta, 2012 FISIC ARDLEIBHÉAL Am: 3 uair an chloig Freagair trí cheist as roinn A agus cúig cheist as roinn B. Lch 1 de 11
An Luas, An Díláithriú agus An Treoluas
 CAIBIDIL 6 An Luas, An Díláithriú agus An Treoluas AN taonad AMA An soicind (s), sin an t-aonad ama. NÓTÁIL 1 milleasoicind (ms) = 10-3 s 1 micreasoicind (μs) = 10-6 s (Táblaí Matamaitice Lch. 5) AM Cainníocht
CAIBIDIL 6 An Luas, An Díláithriú agus An Treoluas AN taonad AMA An soicind (s), sin an t-aonad ama. NÓTÁIL 1 milleasoicind (ms) = 10-3 s 1 micreasoicind (μs) = 10-6 s (Táblaí Matamaitice Lch. 5) AM Cainníocht
Coimisiún na Scrúduithe Stáit
 2010. M35T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hardteistiméireachta, 2010 FISIC GNÁTHLEIBHÉAL DÉ LUAIN, 21 MEITHEAMH MAIDIN, 9:30 go 12:30 Freagair trí cheist as Roinn A agus cúig cheist as Roinn B.
2010. M35T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hardteistiméireachta, 2010 FISIC GNÁTHLEIBHÉAL DÉ LUAIN, 21 MEITHEAMH MAIDIN, 9:30 go 12:30 Freagair trí cheist as Roinn A agus cúig cheist as Roinn B.
BRÉAGSCRÚDÚ NA hardteistiméireachta, 2005 FISIC GNÁTHLEIBHÉAL. AM: 3 huair a chloig
 BRÉAGSCRÚDÚ NA hardteistiméireachta, 2005 FISIC GNÁTHLEIBHÉAL AM: 3 huair a chloig Freagair trí cheist as roinn A agus cúig cheist as roinn B. ROINN A (120 marc) Freagair trí cheist as an roinn seo. Tá
BRÉAGSCRÚDÚ NA hardteistiméireachta, 2005 FISIC GNÁTHLEIBHÉAL AM: 3 huair a chloig Freagair trí cheist as roinn A agus cúig cheist as roinn B. ROINN A (120 marc) Freagair trí cheist as an roinn seo. Tá
Tionscadal Mata Ceardlann 8
 Tionscadal Mata Ceardlann 8 Forbairt Tuiscint Scoláirí: Naisc a Dhéanamhs Name: Ainm: School: Scoil: Clár WS8.1 Réiteach Fadhbanna mar Mhodh seachas mar Sprioc... 2 WS8.2 Buneolas Neamhfhoirmiúil ar Theorainneacha
Tionscadal Mata Ceardlann 8 Forbairt Tuiscint Scoláirí: Naisc a Dhéanamhs Name: Ainm: School: Scoil: Clár WS8.1 Réiteach Fadhbanna mar Mhodh seachas mar Sprioc... 2 WS8.2 Buneolas Neamhfhoirmiúil ar Theorainneacha
Coimisiún na Scrúduithe Stáit
 2012. M34T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hardteistiméireachta, 2012 CEIMIC ARDLEIBHÉAL DÉ MÁIRT, 19 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 400 MARC Freagair ocht gceist ar fad Ní mór dhá cheist
2012. M34T Coimisiún na Scrúduithe Stáit SCRÚDÚ na hardteistiméireachta, 2012 CEIMIC ARDLEIBHÉAL DÉ MÁIRT, 19 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 400 MARC Freagair ocht gceist ar fad Ní mór dhá cheist
(Gan Áireamhán) Bonnsraith
 Uimhir Lárionaid 71 Uimhir Iarrthóra General Certificate of Secondary Education 2006 Matamaitic Modúl MF Páipéar 1 (Gan Áireamhán) Bonnsraith [GMM61] AM 1 uair an chloig. TREOIR D IARRTHÓIRÍ GMM61S6 2238.02
Uimhir Lárionaid 71 Uimhir Iarrthóra General Certificate of Secondary Education 2006 Matamaitic Modúl MF Páipéar 1 (Gan Áireamhán) Bonnsraith [GMM61] AM 1 uair an chloig. TREOIR D IARRTHÓIRÍ GMM61S6 2238.02
TÁBHACHTACH: Léigh na Treoracha Oibriúcháin agus Sábháilteachta seo roimh an Mini-Ductor II+ a Úsáid TREORACHA OIBRIÚCHÁIN AGUS SÁBHÁILTEACHTA
 TÁBHACHTACH: Léigh na Treoracha Oibriúcháin agus Sábháilteachta seo roimh an Mini-Ductor II+ a Úsáid MINI-DUCTOR II+ CE TREORACHA OIBRIÚCHÁIN AGUS SÁBHÁILTEACHTA Sainfheidhmiú i dtéamh Ionduchtaithe Árdfheidhmíochta
TÁBHACHTACH: Léigh na Treoracha Oibriúcháin agus Sábháilteachta seo roimh an Mini-Ductor II+ a Úsáid MINI-DUCTOR II+ CE TREORACHA OIBRIÚCHÁIN AGUS SÁBHÁILTEACHTA Sainfheidhmiú i dtéamh Ionduchtaithe Árdfheidhmíochta
Feidhmithe Matamaiticiúla (200 marc)
 2015. AP8ST Coimisiún na Scrúduithe Stáit An Ardteistiméireacht Fheidhmeach, 2015 Feidhmithe Matamaiticiúla (200 marc) Am: 2 uair an chloig Treoracha Ginearálta 1. Scríobh do SCRÚDUIMHIR sa spás seo: 2.
2015. AP8ST Coimisiún na Scrúduithe Stáit An Ardteistiméireacht Fheidhmeach, 2015 Feidhmithe Matamaiticiúla (200 marc) Am: 2 uair an chloig Treoracha Ginearálta 1. Scríobh do SCRÚDUIMHIR sa spás seo: 2.
Riachtanais chun tacú le Tionscnamh Eorpach ó na Saoránaigh
 Riachtanais chun tacú le Tinscnamh Erpach ó na Saránaigh RIACHTANAIS GHINEARÁLTA Chun tacú le tinscnamh Erpach ó na Saránaigh, ní mór d shínitheirí bheith ina saránaigh de chuid an AE (náisiúnaigh ballstáit
Riachtanais chun tacú le Tinscnamh Erpach ó na Saránaigh RIACHTANAIS GHINEARÁLTA Chun tacú le tinscnamh Erpach ó na Saránaigh, ní mór d shínitheirí bheith ina saránaigh de chuid an AE (náisiúnaigh ballstáit
Coimisiún na Scrúduithe Stáit
 Coimisiún na Scrúduithe Stáit An Ardteistiméireacht 2014 Scéim Mharcála GAEILGE Ardleibhéal Nóta do mhúinteoirí agus do scoláirí faoi úsáid na scéimeanna marcála foilsithe Níl na scéimeanna marcála a fhoilsíonn
Coimisiún na Scrúduithe Stáit An Ardteistiméireacht 2014 Scéim Mharcála GAEILGE Ardleibhéal Nóta do mhúinteoirí agus do scoláirí faoi úsáid na scéimeanna marcála foilsithe Níl na scéimeanna marcála a fhoilsíonn
Coimisiún na Scrúduithe Stáit GRÉIGIS ÁRSA GNÁTHLEIBHÉAL
 2007, M 1T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2007 GRÉIGIS ÁRSA GNÁTHLEIBHÉAL (400 marc) AM: 3 Uair Lch. 1 de 5 1. Cuir Gaeilge ar thrí cinn ar bith de na sleachta A, B, C, D.
2007, M 1T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2007 GRÉIGIS ÁRSA GNÁTHLEIBHÉAL (400 marc) AM: 3 Uair Lch. 1 de 5 1. Cuir Gaeilge ar thrí cinn ar bith de na sleachta A, B, C, D.
Teisteanais Nàiseanta
 Teisteanais Nàiseanta AH08 X774/77/ Matamataig DIARDAOIN, CÈITEAN 9:00 M :00 F Comharran gu lèir 00 Feuch na ceistean UILE. Faodaidh tu àireamhair a chleachdadh. Gus na comharran gu lèir fhaighinn, feumaidh
Teisteanais Nàiseanta AH08 X774/77/ Matamataig DIARDAOIN, CÈITEAN 9:00 M :00 F Comharran gu lèir 00 Feuch na ceistean UILE. Faodaidh tu àireamhair a chleachdadh. Gus na comharran gu lèir fhaighinn, feumaidh
Coimisiún na Scrúduithe Stáit State Examinations Commission. GRÉIGIS ÁRSA GNÁTHLEIBHÉAL (400 marc)
 M 1T Coimisiún na Scrúduithe Stáit State Examinations Commission SCRÚDÚ NA hardteistiméireachta, 2004 GRÉIGIS ÁRSA GNÁTHLEIBHÉAL (400 marc) DÉ haoine, 25 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 Lch. 1 de
M 1T Coimisiún na Scrúduithe Stáit State Examinations Commission SCRÚDÚ NA hardteistiméireachta, 2004 GRÉIGIS ÁRSA GNÁTHLEIBHÉAL (400 marc) DÉ haoine, 25 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 Lch. 1 de
Coimisiún na Scrúduithe Stáit GRÉIGIS ÁRSA ARDLEIBHÉAL
 2007, M 2T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2007 GRÉIGIS ÁRSA ARDLEIBHÉAL (400 marc) AM: 3 Uair Lch. 1 de 7 1. Freagair Roinn A nó Roinn B: [50] A. Cuir Gréigis air seo: Tar
2007, M 2T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2007 GRÉIGIS ÁRSA ARDLEIBHÉAL (400 marc) AM: 3 Uair Lch. 1 de 7 1. Freagair Roinn A nó Roinn B: [50] A. Cuir Gréigis air seo: Tar
AN ROINN OIDEACHAIS AGUS EOLAÍOCHTA SCRÚDÚ ARDTEISTIMÉIREACHTA, 2001 GRÉIGIS ARDLEIBHÉAL. (400 marc)
 M. 2 T AN ROINN OIDEACHAIS AGUS EOLAÍOCHTA SCRÚDÚ ARDTEISTIMÉIREACHTA, 2001 GRÉIGIS ARDLEIBHÉAL (400 marc) DÉ haoine, 22 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 Lch. 1 de 7 1. Freagair Roinn A nó Roinn B:
M. 2 T AN ROINN OIDEACHAIS AGUS EOLAÍOCHTA SCRÚDÚ ARDTEISTIMÉIREACHTA, 2001 GRÉIGIS ARDLEIBHÉAL (400 marc) DÉ haoine, 22 MEITHEAMH TRÁTHNÓNA 2.00 go dtí 5.00 Lch. 1 de 7 1. Freagair Roinn A nó Roinn B:
Coimisiún na Scrúduithe Stáit GRÉIGIS ÁRSA ÁRDLEIBHÉAL
 M 2T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2005 GRÉIGIS ÁRSA ÁRDLEIBHÉAL (400 marc) AM: 3 Uair Leathanach 1 de 7 1. Freagair Roinn A nó Roinn B: [50] A. Cuir Gréigis ar: Uair amháin
M 2T Coimisiún na Scrúduithe Stáit SCRÚDÚ NA hardteistiméireachta, 2005 GRÉIGIS ÁRSA ÁRDLEIBHÉAL (400 marc) AM: 3 Uair Leathanach 1 de 7 1. Freagair Roinn A nó Roinn B: [50] A. Cuir Gréigis ar: Uair amháin
TUARASCÁIL BHLIANTÚIL 2016 AN LIA-BHIÚRÓ UM SHÁBHÁILTEACHT AR BHÓITHRE
 TUARASCÁIL BHLIANTÚIL 2016 AN LIA-BHIÚRÓ UM SHÁBHÁILTEACHT AR BHÓITHRE CLÁR Réamhrá an Stiúrthóra 3 Misean 4 Feidhmeanna an Lia-Bhiúró um Shábháilteacht ar Bhóithre 4 Saincheisteanna Suntasacha 6 Samplaí
TUARASCÁIL BHLIANTÚIL 2016 AN LIA-BHIÚRÓ UM SHÁBHÁILTEACHT AR BHÓITHRE CLÁR Réamhrá an Stiúrthóra 3 Misean 4 Feidhmeanna an Lia-Bhiúró um Shábháilteacht ar Bhóithre 4 Saincheisteanna Suntasacha 6 Samplaí
Plean Scoile don Ghaeilge Scoil Íde
 Réamhráiteas Plean Scoile don Ghaeilge Scoil Íde (a) Cuireadh an plean seo le chéile i mí Feabhra 2015 i Scoil Íde. Bhí gach múinteoir i láthair. ( b) Ta gá leis an bplean seo: chun cabhrú linn an Curaclam
Réamhráiteas Plean Scoile don Ghaeilge Scoil Íde (a) Cuireadh an plean seo le chéile i mí Feabhra 2015 i Scoil Íde. Bhí gach múinteoir i láthair. ( b) Ta gá leis an bplean seo: chun cabhrú linn an Curaclam
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Αλληλεπίδραση ακτίνων-χ με την ύλη
 Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
 ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
 ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
Appendix B Table of Radionuclides Γ Container 1 Posting Level cm per (mci) mci
 3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής
 ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
(2), ,. 1).
 178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
 Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Answers to practice exercises
 Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS
 Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.
 Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
SIEMENS Squirrel Cage Induction Standard Three-phase Motors
 - SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
- SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
r t t r t t à ré ér t é r t st é é t r s s2stè s t rs ts t s
 r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
Από τις διαλέξεις του μαθήματος του Α εξαμήνου σπουδών του Τμήματος. Κ. Παπαθεοδώρου, Αναπληρωτής Καθηγητής Οκτώβριος Δεκέμβριος 2013
 Συγγραφή Τεχνικών Κειμένων Σχήματα, Πίνακες, Εικόνες, Αριθμοί Από τις διαλέξεις του μαθήματος του Α εξαμήνου σπουδών του Τμήματος Πολιτικών Μηχανικών και Μηχανικών Τοπογραφίας & Γεωπληροφορικής Κ. Παπαθεοδώρου,
Συγγραφή Τεχνικών Κειμένων Σχήματα, Πίνακες, Εικόνες, Αριθμοί Από τις διαλέξεις του μαθήματος του Α εξαμήνου σπουδών του Τμήματος Πολιτικών Μηχανικών και Μηχανικών Τοπογραφίας & Γεωπληροφορικής Κ. Παπαθεοδώρου,
τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n, l)
 ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
ΑΤΟΜΙΚΑ ΤΡΟΧΙΑΚΑ Σχέση κβαντικών αριθµών µε στιβάδες υποστιβάδες - τροχιακά Η στιβάδα καθορίζεται από τον κύριο κβαντικό αριθµό (n) Η υποστιβάδα καθορίζεται από τους δύο πρώτους κβαντικούς αριθµούς (n,
ΤΡΙΤΗ 10 ΙΟΥΛΙΟΥ 2007
 2-001 ΤΡΙΤΗ 10 ΙΟΥΛΙΟΥ 2007 2-002 ΠΡΟΕΔΡΙΑ ΤΟΥ κ. MARTÍNEZ MARTÍNEZ Αντιπροέδρου 2-003 Έναρξη της συνεδρίασης 2-004 (Η συνεδρίαση αρχίζει στις 9.00) 2-005 Κατάθεση εγγράφων: βλ. Συνοπτικά Πρακτικά 2-006
2-001 ΤΡΙΤΗ 10 ΙΟΥΛΙΟΥ 2007 2-002 ΠΡΟΕΔΡΙΑ ΤΟΥ κ. MARTÍNEZ MARTÍNEZ Αντιπροέδρου 2-003 Έναρξη της συνεδρίασης 2-004 (Η συνεδρίαση αρχίζει στις 9.00) 2-005 Κατάθεση εγγράφων: βλ. Συνοπτικά Πρακτικά 2-006
Sheet H d-2 3D Pythagoras - Answers
 1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
Α. ΚΑΝΑΠΙΤΣΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΤΕΙ ΛΑΜΙΑΣ ΛΑΜΙΑ, 2006
 ιαλέξεις στη ΦΥΣΙΚΗ Α. ΚΑΝΑΠΙΤΣΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΤΕΙ ΛΑΜΙΑΣ ΛΑΜΙΑ, 2006 Σηµειώσεις εποπτικό υλικό για το µάθηµα ΦΥΣΙΚΗ. Τα παρακάτω είναι βασισµένα στις διαλέξεις του διδάσκοντα. Το υλικό αποτελεί
ιαλέξεις στη ΦΥΣΙΚΗ Α. ΚΑΝΑΠΙΤΣΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΤΕΙ ΛΑΜΙΑΣ ΛΑΜΙΑ, 2006 Σηµειώσεις εποπτικό υλικό για το µάθηµα ΦΥΣΙΚΗ. Τα παρακάτω είναι βασισµένα στις διαλέξεις του διδάσκοντα. Το υλικό αποτελεί
Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής
 Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής Φυσικά Μεγέθη Φυσικά μεγέθη είναι έννοιες που μπορούν να μετρηθούν και χρησιμοποιούνται για την περιγραφή των φαινομένων. Διεθνές σύστημα μονάδων S. I Το διεθνές
Εισαγωγή Σε Βασικές Έννοιες Της Φυσικής Φυσικά Μεγέθη Φυσικά μεγέθη είναι έννοιες που μπορούν να μετρηθούν και χρησιμοποιούνται για την περιγραφή των φαινομένων. Διεθνές σύστημα μονάδων S. I Το διεθνές
Επιτραπέζια μίξερ C LINE 10 C LINE 20
 Επιτραπέζια μίξερ C LINE 10 Χωρητικότητα κάδου : 10 lt Ναί Βάρος: 100 Kg Ισχύς: 0,5 Kw C LINE 20 Χωρητικότητα κάδου : 20 lt Βάρος: 105 Kg Ισχύς: 0,7 Kw Ναί Επιδαπέδια μίξερ σειρά C LINE C LINE 10 Χωρητικότητα
Επιτραπέζια μίξερ C LINE 10 Χωρητικότητα κάδου : 10 lt Ναί Βάρος: 100 Kg Ισχύς: 0,5 Kw C LINE 20 Χωρητικότητα κάδου : 20 lt Βάρος: 105 Kg Ισχύς: 0,7 Kw Ναί Επιδαπέδια μίξερ σειρά C LINE C LINE 10 Χωρητικότητα
MICROMASTER Vector MIDIMASTER Vector
 s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
 r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
Alterazioni del sistema cardiovascolare nel volo spaziale
 POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
CÁC CÔNG THỨC CỰC TRỊ ĐIỆN XOAY CHIỀU
 Tà lệ kha test đầ xân 4 Á ÔNG THỨ Ự TỊ ĐỆN XOAY HỀ GÁO VÊN : ĐẶNG VỆT HÙNG. Đạn mạch có thay đổ: * Kh thì Max max ; P Max còn Mn ư ý: và mắc lên tếp nha * Kh thì Max * Vớ = hặc = thì có cùng gá trị thì
Tà lệ kha test đầ xân 4 Á ÔNG THỨ Ự TỊ ĐỆN XOAY HỀ GÁO VÊN : ĐẶNG VỆT HÙNG. Đạn mạch có thay đổ: * Kh thì Max max ; P Max còn Mn ư ý: và mắc lên tếp nha * Kh thì Max * Vớ = hặc = thì có cùng gá trị thì
➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I
 tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
STEAM TABLES. Mollier Diagram
 STEAM TABLES and Mollier Diagram (S.I. Units) dharm \M-therm\C-steam.pm5 CONTENTS Table No. Page No. 1. Saturated Water and Steam (Temperature) Tables I (ii) 2. Saturated Water and Steam (Pressure) Tables
STEAM TABLES and Mollier Diagram (S.I. Units) dharm \M-therm\C-steam.pm5 CONTENTS Table No. Page No. 1. Saturated Water and Steam (Temperature) Tables I (ii) 2. Saturated Water and Steam (Pressure) Tables
Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Πανεπιστήμιο Δυτικής Αττικής - ΣΑΕΤ
 Γενική και Ανόργανη Χημεία Περιοδικές ιδιότητες των στοιχείων. Σχηματισμός ιόντων. Στ. Μπογιατζής 1 Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Π Δ Χειμερινό εξάμηνο 2018-2019 Π
Γενική και Ανόργανη Χημεία Περιοδικές ιδιότητες των στοιχείων. Σχηματισμός ιόντων. Στ. Μπογιατζής 1 Αναπληρωτής Καθηγητής Τμήμα Συντήρησης Αρχαιοτήτων και Έργων Τέχνης Π Δ Χειμερινό εξάμηνο 2018-2019 Π
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Metal-free Oxidative Coupling of Amines with Sodium Sulfinates: A Mild Access to Sulfonamides
 Electronic Supplementary Material (ESI) for RSC Advances. This journal is The Royal Society of Chemistry 2014 Supporting information for Metal-free Oxidative Coupling of Amines with Sodium Sulfinates:
Electronic Supplementary Material (ESI) for RSC Advances. This journal is The Royal Society of Chemistry 2014 Supporting information for Metal-free Oxidative Coupling of Amines with Sodium Sulfinates:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΠΑΝΤΗΣΕΙΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Τζαγκαράκης Γιάννης, Δημοπούλου Ηρώ, Αδάμη Μαρία, Αγγελίδης Άγγελος, Παπαθανασίου Θάνος, Παπασταμάτης Στέφανος
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 03/05/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Τζαγκαράκης Γιάννης, Δημοπούλου Ηρώ, Αδάμη Μαρία, Αγγελίδης Άγγελος, Παπαθανασίου Θάνος, Παπασταμάτης Στέφανος
 ) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 3
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 3 12 Σεπτεµβρίου, 2005 Ηλίας Κυριακίδης Λέκτορας ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2005Ηλίας Κυριακίδης,
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 3 12 Σεπτεµβρίου, 2005 Ηλίας Κυριακίδης Λέκτορας ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2005Ηλίας Κυριακίδης,
Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 636 ˆ ˆ Šˆ Œ ˆŸ ˆŒˆ - Šˆ Œ Š ˆ ˆ 638 Š ˆ ˆ ˆ : ˆ ˆŸ 643 ˆ ˆ Šˆ Š 646 Œ ˆ Šˆ 652 Œ ˆ Šˆ Š ˆ -2 ˆ ˆ -2Œ 656 ˆ ˆ Šˆ Š œ Š ˆ Œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 636 ˆ ˆ Šˆ Œ ˆŸ ˆŒˆ - Šˆ Œ Š ˆ ˆ 638 Š ˆ ˆ ˆ : ˆ ˆŸ 643 ˆ ˆ Šˆ Š 646 Œ ˆ Šˆ 652 Œ ˆ Šˆ Š ˆ -2 ˆ ˆ -2Œ 656 ˆ ˆ Šˆ Š œ Š ˆ Œ
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
 728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Γενικής Παιδείας Βιολογία Γ Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΚΩΣΤΑΣ ΓΚΑΤΖΕΛΑΚΗΣ
 ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Βιολογία Γ Λυκείου Επιμέλεια: ΚΩΣΤΑΣ ΓΚΑΤΖΕΛΑΚΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr 1 2010 2011 µ..., µ..,... 2011. 1:, 19-21
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Βιολογία Γ Λυκείου Επιμέλεια: ΚΩΣΤΑΣ ΓΚΑΤΖΕΛΑΚΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr 1 2010 2011 µ..., µ..,... 2011. 1:, 19-21
ΤΡΙΤΗ 22 ΜΑΪΟΥ Παγκόσμια Ευρώπη - Εξωτερικές πτυχές της ανταγωνιστικότητας (συζήτηση) ΠΡΟΕΔΡΙΑ ΤΗΣ κ. MORGANTINI Αντιπροέδρου
 2-001 ΤΡΙΤΗ 22 ΜΑΪΟΥ 2007 2-002 2-003 ΠΡΟΕΔΡΙΑ ΤΗΣ κ. MORGANTINI Αντιπροέδρου Έναρξη της συνεδρίασης 2-004 (Η συνεδρίαση αρχίζει στις 9.00) 2-005 2-006 2-007 Χρονοδιάγραμμα των περιόδων συνόδου: βλ. Συνοπτικά
2-001 ΤΡΙΤΗ 22 ΜΑΪΟΥ 2007 2-002 2-003 ΠΡΟΕΔΡΙΑ ΤΗΣ κ. MORGANTINI Αντιπροέδρου Έναρξη της συνεδρίασης 2-004 (Η συνεδρίαση αρχίζει στις 9.00) 2-005 2-006 2-007 Χρονοδιάγραμμα των περιόδων συνόδου: βλ. Συνοπτικά
P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r
 r s s s t t P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r t t s st ä r t str t st t tt2 t s s t st
r s s s t t P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r t t s st ä r t str t st t tt2 t s s t st
Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en)
 Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) 7057/17 ADD 1 TRANS 97 ΔΙΑΒΙΒΑΣΤΙΚΟ ΣΗΜΕΙΩΜΑ Αποστολέας: Ημερομηνία Παραλαβής: Αποδέκτης: Για τον Γενικό Γραμματέα της Ευρωπαϊκής Επιτροπής,
Συμβούλιο της Ευρωπαϊκής Ένωσης Βρυξέλλες, 7 Μαρτίου 2017 (OR. en) 7057/17 ADD 1 TRANS 97 ΔΙΑΒΙΒΑΣΤΙΚΟ ΣΗΜΕΙΩΜΑ Αποστολέας: Ημερομηνία Παραλαβής: Αποδέκτης: Για τον Γενικό Γραμματέα της Ευρωπαϊκής Επιτροπής,
μ μ μ μ μ, μ ,.. μ : μ μ. μ μ 2003 μ μ μ 2004 μ μ μ μ 1 bar μ
 μ μ μ μ μ μ. μ μ,,.. μ μ μ μ μ μ. μ,,. μ : μ μ μ μ μ μ μ μ. μ μ μ μ. μ μ μ μ 2003 μ μ. μ μ μ μ, μ 2004 μ μ μ μ 1 bar μ 1 2003 μ μ μ μ μ μ. μ μ μ μ μ μ μ. μ μ μ μ :,,, μ,,. μ μ μ μ...... 1, μ, μ. 2 μ μ,,
μ μ μ μ μ μ. μ μ,,.. μ μ μ μ μ μ. μ,,. μ : μ μ μ μ μ μ μ μ. μ μ μ μ. μ μ μ μ 2003 μ μ. μ μ μ μ, μ 2004 μ μ μ μ 1 bar μ 1 2003 μ μ μ μ μ μ. μ μ μ μ μ μ μ. μ μ μ μ :,,, μ,,. μ μ μ μ...... 1, μ, μ. 2 μ μ,,
1 B0 C00. nly Difo. r II. on III t o. ly II II. Di XR. Di un 5.8. Di Dinly. Di F/ / Dint. mou. on.3 3 D. 3.5 ird Thi. oun F/2. s m F/3 /3.
 . F/ /3 3. I F/ 7 7 0 0 Mo ode del 0 00 0 00 A 6 A C00 00 0 S 0 C 0 008 06 007 07 09 A 0 00 0 00 0 009 09 A 7 I 7 7 0 0 F/.. 6 6 8 8 0 00 0 F/3 /3. fo I t o nt un D ou s ds 3. ird F/ /3 Thi ur T ou 0 Fo
. F/ /3 3. I F/ 7 7 0 0 Mo ode del 0 00 0 00 A 6 A C00 00 0 S 0 C 0 008 06 007 07 09 A 0 00 0 00 0 009 09 A 7 I 7 7 0 0 F/.. 6 6 8 8 0 00 0 F/3 /3. fo I t o nt un D ou s ds 3. ird F/ /3 Thi ur T ou 0 Fo
ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 2000-10 V1.4
 3 ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 000-0 V.4 4 Περιεχόμενα 5 Ειαγωγή...9 Ανοχή χαλύβων...9 3 Φόριη... 4 Υπολογιμός ε δυναμική θραύη... 4. Ονομαικές άεις (ημιεύρος δυναμικής
3 ΣΥΝΤΟΜΕΣ ΟΔΗΓΙΕΣ ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΑΤΡΑΚΤΩΝ ΑΞΟΝΩΝ ΚΑΤΑ DIN 743 : 000-0 V.4 4 Περιεχόμενα 5 Ειαγωγή...9 Ανοχή χαλύβων...9 3 Φόριη... 4 Υπολογιμός ε δυναμική θραύη... 4. Ονομαικές άεις (ημιεύρος δυναμικής
Meren virsi Eino Leino
 œ_ œ _ q = 72 Meren virsi Eino Leino Toivo Kuua o. 11/2 (1909) c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne rien nät, vie ri vä vir ta? Kun ne c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne
œ_ œ _ q = 72 Meren virsi Eino Leino Toivo Kuua o. 11/2 (1909) c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne rien nät, vie ri vä vir ta? Kun ne c c F c Kun ne F iu L? c œ J J J J œ_ œ_ nœ_ Min ne
ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ.
 ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ. Η σύσταση του φλοιού ουσιαστικά καθορίζεται από τα πυριγενή πετρώματα μια που τα ιζήματα και τα μεταμορφωμένα είναι σε ασήμαντες ποσότητες συγκριτικά. Η δημιουργία των βασαλτικών-γαββρικών
ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ. Η σύσταση του φλοιού ουσιαστικά καθορίζεται από τα πυριγενή πετρώματα μια που τα ιζήματα και τα μεταμορφωμένα είναι σε ασήμαντες ποσότητες συγκριτικά. Η δημιουργία των βασαλτικών-γαββρικών
-! " #!$ %& ' %( #! )! ' 2003
 -! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
-! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
SONATA D 295X245. caza
 SONATA D 295X245 caza 01 Γωνιακός καναπές προσαρμόζεται σε όλα τα μέτρα σε όλους τους χώρους με μηχανισμούς ανάκλησης στα κεφαλάρια για περισσότερή αναπαυτικότητα στην χρήση του-βγαίνει με κρεβάτι η χωρίς
SONATA D 295X245 caza 01 Γωνιακός καναπές προσαρμόζεται σε όλα τα μέτρα σε όλους τους χώρους με μηχανισμούς ανάκλησης στα κεφαλάρια για περισσότερή αναπαυτικότητα στην χρήση του-βγαίνει με κρεβάτι η χωρίς
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis
 Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
2 μ Gauss 1. Equation Chapter 1 Section 1 GAUSS GAUSS
 2 μ Gauss 1 Equation Chapter 1 Section 1 2 GAUSS GAUSS 2 2 μ Gauss μ μ μ μ μ μ μ. μ μ μ μ. μ μ μ μ Coulomb μ. μ 1: μ μ μ μ μ, μ. μ μ. μ μ. μ μ μ μ μμ. μμ μ μ μ. μ μ μμ μ. μ μ μ. μ μ μ μ μ. μ μ μ μ μ μ
2 μ Gauss 1 Equation Chapter 1 Section 1 2 GAUSS GAUSS 2 2 μ Gauss μ μ μ μ μ μ μ. μ μ μ μ. μ μ μ μ Coulomb μ. μ 1: μ μ μ μ μ, μ. μ μ. μ μ. μ μ μ μ μμ. μμ μ μ μ. μ μ μμ μ. μ μ μ. μ μ μ μ μ. μ μ μ μ μ μ
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Ασκήσεις. 5Β: 1s 2 2s 2 2p 2, β) 10 Νe: 1s 2 2s 2 2p 4 3s 2, γ) 19 Κ: 1s 2 2s 2 2p 6 3s 2 3p 6,
 Ασκήσεις 1. Να γίνει η ηλεκτρονιακή δόμηση για τα ακόλουθα άτομα στη θεμελιώδη τους κατάσταση: 29Cu, 33As, 38Sr, 42Mo, 55Cs. Πόσα ηλεκτρόνια έχει η εξωτερική τους στιβάδα και πόσα ασύζευκτα ηλεκτρόνια
Ασκήσεις 1. Να γίνει η ηλεκτρονιακή δόμηση για τα ακόλουθα άτομα στη θεμελιώδη τους κατάσταση: 29Cu, 33As, 38Sr, 42Mo, 55Cs. Πόσα ηλεκτρόνια έχει η εξωτερική τους στιβάδα και πόσα ασύζευκτα ηλεκτρόνια
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 6
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 6 25 επτεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΧΟΛΗ ΠΑΝΕΠΙΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 6 25 επτεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΧΟΛΗ ΠΑΝΕΠΙΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑ
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
ΜΕΛΕΤΗ ΤΗΣ ΥΝΑΤΟΤΗΤΑΣ ΑΞΙΟΠΟΙΗΣΗΣ ΤΟΥ ΓΕΩΘΕΡΜΙΚΟΥ ΠΕ ΙΟΥ ΘΕΡΜΩΝ ΝΙΓΡΙΤΑΣ (Ν. ΣΕΡΡΩΝ)
 ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
m 1, m 2 F 12, F 21 F12 = F 21
 m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
m 1, m 2 F 12, F 21 F12 = F 21 r 1, r 2 r = r 1 r 2 = r 1 r 2 ê r = rê r F 12 = f(r)ê r F 21 = f(r)ê r f(r) f(r) < 0 f(r) > 0 m 1 r1 = f(r)ê r m 2 r2 = f(r)ê r r = r 1 r 2 r 1 = 1 m 1 f(r)ê r r 2 = 1 m
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Westfalia Bedienungsanleitung. Nr
 Westfalia Bedienungsanleitung Nr. 108230 Erich Schäfer KG Tel. 02737/5010 Seite 1/8 RATED VALUES STARTING VALUES EFF 2 MOTOR OUTPUT SPEED CURRENT MOMENT CURRENT TORQUE TYPE I A / I N M A / M N Mk/ Mn %
Westfalia Bedienungsanleitung Nr. 108230 Erich Schäfer KG Tel. 02737/5010 Seite 1/8 RATED VALUES STARTING VALUES EFF 2 MOTOR OUTPUT SPEED CURRENT MOMENT CURRENT TORQUE TYPE I A / I N M A / M N Mk/ Mn %
Μάθημα 12ο. O Περιοδικός Πίνακας Και το περιεχόμενό του
 Μάθημα 12ο O Περιοδικός Πίνακας Και το περιεχόμενό του Γενική και Ανόργανη Χημεία 201-17 2 Η χημεία ΠΠΠ (= προ περιοδικού πίνακα) μαύρο χάλι από αταξία της πληροφορίας!!! Καμμία οργάνωση των στοιχείων.
Μάθημα 12ο O Περιοδικός Πίνακας Και το περιεχόμενό του Γενική και Ανόργανη Χημεία 201-17 2 Η χημεία ΠΠΠ (= προ περιοδικού πίνακα) μαύρο χάλι από αταξία της πληροφορίας!!! Καμμία οργάνωση των στοιχείων.
ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ Παραδόσεις μαθήματος, Ακ. Έτος 2018-19 1 ΒΑΣΙΚΕΣ ΔΙΑΣΤΑΣΕΙΣ ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ Διάσταση Μήκος
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΧΗΜΙΚΗ ΜΗΧΑΝΙΚΗ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ Παραδόσεις μαθήματος, Ακ. Έτος 2018-19 1 ΒΑΣΙΚΕΣ ΔΙΑΣΤΑΣΕΙΣ ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ Διάσταση Μήκος
..,..,.. ! " # $ % #! & %
 ..,..,.. - -, - 2008 378.146(075.8) -481.28 73 69 69.. - : /..,..,... : - -, 2008. 204. ISBN 5-98298-269-5. - -,, -.,,, -., -. - «- -»,. 378.146(075.8) -481.28 73 -,..,.. ISBN 5-98298-269-5..,..,.., 2008,
..,..,.. - -, - 2008 378.146(075.8) -481.28 73 69 69.. - : /..,..,... : - -, 2008. 204. ISBN 5-98298-269-5. - -,, -.,,, -., -. - «- -»,. 378.146(075.8) -481.28 73 -,..,.. ISBN 5-98298-269-5..,..,.., 2008,
( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.
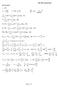 Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ( ) ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 25 o C. Ημιαντιδράσεις αναγωγής , V. Antimony. Bromine. Arsenic.
 ΠΑΡΑΡΤΗΜΑ V. ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C, V, V Auminum Bervium A ( H ) e A H. 0 Be e Be H. 1 ( ) [ ] e A F. 09 AF
ΠΑΡΑΡΤΗΜΑ V. ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C, V, V Auminum Bervium A ( H ) e A H. 0 Be e Be H. 1 ( ) [ ] e A F. 09 AF
6 720 645 304-00.1O. Λέβητας συμπύκνωσης αερίου. Condens 2000 W ZWB 24-1 AR. Υποδείξεις για την απαγωγή καυσαερίων 6 720 812 517 (2014/08) GR
 6 720 645 304-00.1O Λέβητας συμπύκνωσης αερίου ZWB 24-1 AR Υποδείξεις για την απαγωγή καυσαερίων GR 2 Πίνακας περιεχομένων Πίνακας περιεχομένων 1 Υποδείξεις ασφαλείας και επεξήγηση συμβόλων...........
6 720 645 304-00.1O Λέβητας συμπύκνωσης αερίου ZWB 24-1 AR Υποδείξεις για την απαγωγή καυσαερίων GR 2 Πίνακας περιεχομένων Πίνακας περιεχομένων 1 Υποδείξεις ασφαλείας και επεξήγηση συμβόλων...........
 φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Register your product and get support at PPX 4150 GR Ο
 Register your product and get support at www.philips.com/welcome PPX 4150 GR Ο μ Α π π...3 μ...3 μ π...3...4 Ε...4...4 Επ...5...6 μ...6...6 μ...6 μ...7 μ μ...7...8 Ε...8 / μπ...8...8 μ π...9 μ HDMI...9...9
Register your product and get support at www.philips.com/welcome PPX 4150 GR Ο μ Α π π...3 μ...3 μ π...3...4 Ε...4...4 Επ...5...6 μ...6...6 μ...6 μ...7 μ μ...7...8 Ε...8 / μπ...8...8 μ π...9 μ HDMI...9...9
A 1 A 2 A 3 B 1 B 2 B 3
 16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
Γενική Φυσική. Μεγέθη & μονάδες. Φυσικά φαινόμενα. Η παρατήρηση. Η παρατήρηση. Το πείραμα. Μεγέθη και μονάδες 24/9/2014. Κωνσταντίνος Χ.
 Γενική Φυσική Μεγέθη & μονάδες Κωνσταντίνος Χ. Παύλου Φυσικός Ραδιοηλεκτρολόγος (MSc) Καστοριά, Σεπτέμβριος 14 1. Φυσικό μέγεθος κατηγορίες μεγεθών 2. Αριθμητική τιμή σύστημα μονάδων 3. Το ιεθνές Σύστημα
Γενική Φυσική Μεγέθη & μονάδες Κωνσταντίνος Χ. Παύλου Φυσικός Ραδιοηλεκτρολόγος (MSc) Καστοριά, Σεπτέμβριος 14 1. Φυσικό μέγεθος κατηγορίες μεγεθών 2. Αριθμητική τιμή σύστημα μονάδων 3. Το ιεθνές Σύστημα
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t
 ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FichaCatalografica :: Fichacatalografica https://www3.dti.ufv.br/bbt/ficha/cadastrarficha/visua... Ficha catalográfica preparada
ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FichaCatalografica :: Fichacatalografica https://www3.dti.ufv.br/bbt/ficha/cadastrarficha/visua... Ficha catalográfica preparada
