Αλγόριθµοι και Πολυπλοκότητα
|
|
|
- Ελλάδιος Παπανικολάου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
2 Εισαγωγή Ο δυναµικός προγραµµατισµός (dynamic programming), αποτελεί ένα ισχυρό εργαλείο, για την επίλυση συνδυαστικών προβληµάτων ϐελτιστοποίησης. Στον δυναµικό προγραµµατισµό, η επίλυση ενός προβλήµατος, προκύπτει από την λύση µικρότερων υποπροβληµάτων τα οποία αλληλοεπικαλύπτονται (overlapping subproblems). Κάθε υποπρόβληµα λύνεται µια µόνο ϕορά και η ϐέλτιστη λύση αποθηκεύεται σ ένα πίνακα. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
3 Εισαγωγή Τέσσερα είναι τα ϐασικά ϐήµατα για την ανάπτυξη ενός αλγορίθµου δυναµικού προγραµµατισµού. 1 Χαρακτηρισµός της δοµής της ϐέλτιστης λύσης. 2 Αναδροµικός ορισµός της τιµής της ϐέλτιστης λύσης. 3 Υπολογισµός της τιµής της ϐέλτιστης λύσης από κάτω προς τα πάνω. 4 Κατασκευή της ϐέλτιστης λύσης µε χρήση πίνακα. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
4 Βασικά Στοιχεία υναµικού Προγραµµατισµού Βέλτιστα διασπώµενη δοµή (optimal substructure) Κάθε υποστρατηγική µιας ϐέλτιστης στρατηγικής είναι και η ίδια ϐέλτιστη. Η ϐέλτιστη λύση ενός προβλήµατος, εµπεριέχει ϐέλτιστες λύσεις υποπροβληµάτων του. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
5 Βέλτιστα διασπώµενη δοµή (optimal substructure) Μια µεθοδολογία για να ανακαλύψουµε την ϐέλτιστα διασπώµενη δοµή 1 Αποδεικνύουµε ότι µια οποιαδήποτε λύση στο πρόβληµα, συνίσταται στο να κάνουµε µια επιλογή. Η επιλογή αυτή οδηγεί σε ένα ή περισσότερα υποπροβλήµατα τα οποια πρέπει να επιλυθούν. 2 Θεωρούµε τώρα ότι έχουµε δεδοµένη την επιλογή η οποία οδηγεί στην ϐέλτιστη λύση, χωρίς να µας απασχολεί προς το παρόν, πως ορίζεται αυτή. 3 εδοµένης λοιπόν της επιλογής αυτής, ορίζουµε τα νέα υποπροβλήµατα. 4 Τέλος αποδεικνύουµε ότι όντως οι ϐέλτιστες λύσεις των υποπροβληµάτων αυτών οδηγούν στη ϐέλτιστη λύση του αρχικού προβλήµατος. Η απόδειξη γίνεται συνήθως µε εις άτοπον απαγωγή. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
6 Βέλτιστα διασπώµενη δοµή (optimal substructure) Η τεχνική του δυναµικού προγραµµατισµού χρησιµοποιεί τη ϐέλτιστα διασπώµενη δοµή, από κάτω προς τα πάνω (bottom-up). Στην ουσία χρησιµοποιούµε µια αναδροµική σχέση ώστε να υπολογίσουµε τη ϐέλτιστη λύση του αρχικού προβλήµατος. Κριτήριο ανεξαρτησίας (independency) των υποπροβληµάτων: διασφαλίζει τη ϐέλτιστα διασπώµενη δοµή, δηλ. ότι η λύση ενός προβλήµατος δεν επηρεάζει τα υπόλοιπα. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
7 Βέλτιστα διασπώµενη δοµή (optimal substructure) Εστω το µέγιστο απλό µονοπάτι q t, δυο µέγιστα απλά µονοπάτια p 1 : q r και p 2 : r t. Οµως το p 1 είναι το q s t r. Ο συνδυασµός των λύσεων δίνει µέγιστο µονοπάτι που δεν είναι απλό. εν υπάρχει λύση για το δεύτερο υποπρόβληµα άρα το αρχικό µας πρόβληµα δεν έχει λύση. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
8 Το γράφηµα του σχήµατος δείχνει ότι δεν υπάρχει ϐέλτιστα διασπώµενη δοµή για το πρόβληµα του µέγιστου απλού µονοπατιού q r t s Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
9 Επικαλυπτόµενα υποπροβλήµατα (Overlapping subproblems) Το δεύτερο κριτήριο είναι των επικαλυπτόµενων υποπροβληµάτων. Κάθε αλγόριθµος δυναµικού προγραµµατισµού, παράγει πολυωνυµικό, πλήθος διαφορετικών υποπροβληµάτων. Κάθε ένα από τα υποπροβλήµατα εµφανίζεται, πιθανόν, αρκετές ϕορές. Μόλις επιλυθεί ένα υποπρόβληµα, η τιµή της ϐέλτιστης λύσης του, αποθηκεύεται σ ένα πίνακα. Οταν απαιτηθεί να επιλυθεί ξανά, τότε απλά ανακαλείται η τιµή της ϐέλτισης λύσης του υποπροβλήµατος από τον πίνακα (σε σταθερό χρόνο). Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
10 Επικαλυπτόµενα υποπροβλήµατα (Overlapping subproblems) Παρατηρήσεις εν ϑα πρέπει να δηµιουργείται σύγχυση ανάµεσα στην ιδιότητα της επικάλυψης µε αυτή της ανεξαρτησίας. περίπτωση 1: Το ίδιο υποπρόβληµα που εµφανίζεται περισσότερες ϕορές κατά την διάρκεια της εκτέλεσης. περίπτωση 2: Ανεξαρτησία των δεδοµένων του υποπροβλήµατος. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
11 Εφαρµογές Χρονοδροµολόγηση γραµµής παραγωγής Ζητάµε να αποφασίσουµε από ποιούς σταθµούς ϑα περάσει το αυτοκίνητο έτσι ώστε να ελαχιστοποιήσουµε το χρόνο κατασκευής του. Εργοστάσιο κατασκευής αυτοκινήτων µε δύο γραµµές παραγωγής. e 1 S 1,1 S 1,2 S 1,3 S 1,n 1 S 1,n a 1,1 a 1,2 a 1,3 a a 1,n 1,n 1 t 1,1 t 1,2 t 1,3 t 1,n 1 x 1 Entrance e 2 t 2,1 t 2,2 t 2,3 t 2,n 1 a 2,1 a 2,2 a 2,3 a 2,n 1 a 2,n S 2,1 S 2,2 S 2,3 S 2,n 1 S 2,n x 2 Exit Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
12 Εφαρµογές Βήµα 1: Βέλτιστα διασπώµενη δοµή: Η ϐέλτιστη λύση του προβλήµατος της εύρεσης του συντοµότερου µονοπατίου µέχρι τον S 1j εµπεριέχει τις ϐέλτιστες λύσεις στα υποπροβλήµατα των συντοµότερων µονοπατιών προς τους σταθµούς S 1j 1 και S 2j 1. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
13 Εφαρµογές Βήµα 2: Αναδροµικός ορισµός της τιµής της ϐέλτιστης λύσης Ορίζουµε τον πίνακα f διάστασης 2 n, όπου στη ϑέση f ij (i = 1, 2 και j = 1, 2,..., n) αποθηκεύουµε τον ελάχιστο χρόνο µέχρι και τον σταθµό S ij. Η ϐέλτιστη λύση: f = min{f 1n + x 1, f 2n + x 2 } (1) ύο αναδροµικές σχέσεις που υπολογίζουν τις δύο γραµµές του πίνακα f. f 1j = { e1 + a 11 j = 1 min{f 1j 1 + a 1j, f 2j 1 + t 2j 1 + a 1j } j 2 (2) και όµοια: f 2j = { e2 + a 21 j = 1 min{f 2j 1 + a 2j, f 1j 1 + t 1j 1 + a 2j } j 2 (3) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
14 Εφαρµογές Βήµα 3: Υπολογισµός του ελάχιστου χρόνου από (1), (2) ή (3) T 1 (n) = T 2 (n) = T 1 (n 1)+T 2 (n 1). Αρα T 1 (n) = T 2 (n) = Ω(2 n ). Μπορούµε να κάνουµε καλύτερα από εκθετικό χρόνο Ναι. Αποθηκεύουµε κάθε τιµή f ij σε ένα πίνακα (διαστάσεων 2 n) Ανακαλούµε κάθε ϕορά την τιµή από κάποιο προηγούµενο ϐήµα. Βέλτιστη διαδροµή σε χρόνοθ(n). Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
15 1. f 11 e 1 + a 1,1 2. f 21 e 2 + a 2,1 3. for j = 2 to n do 4. if f 1,j 1 + a 1,j f 2,j 1 + t 2,j 1 + a 1,j then 5. f 1j = f 1,j 1 + a 1,j 6. l 1j = 1 7. else 8. f 1j = f 2,j 1 + t 2,j 1 + a 1,j 9. l 1j = end if 11. if f 2,j 1 + a 2,j f 1,j 1 + t 1,j 1 + a 2,j then 12. f 2j = f 2,j 1 + a 2,j 13. l 2j = else 15. f 2j = f 1,j 1 + t 1,j 1 + a 2,j 16. l 2j = end if 18. if f 1n + x 1 f 2n + x 2 then 19. f = f 1n + x l = else 22. f = f 2n + x l = end if Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
16 S 1,1 S 1,2 S 1,3 S 1,4 S 1,5 S 1,6 assembly line enter exit 2 assembly line S 2,1 S 2,2 S 2,3 S 2,4 S 2,5 S 2, f 1 [j] l 1 [j] f 2 [j] l 2 [j] f = 38 l = 1 Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
17 Αλυσιδωτός πολλαπλασιασµός πινάκων Ζητάµε να υπολογίσουµε το γινόµενο A 1 A 2...A n (4) όσο το δυνατόν πιο αποδοτικά (µε το λιγότερο δυνατό κόστος). Το κόστος πολλαπλασιασµού δύο πινάκων A, B µε διαστάσεις p q και q r αντίστοιχα, είναι p q r. Το κόστος του πολλαπλασιασµόυ µεταβαλλεται ανάλογα µε τη σειρά που ϑα εκτελέσουµε τους πολλαπλασιασµούς. Παράδειγµα: Εστω το γινόµενο A 1 A 2 A 3 A 4. (A 1 ((A 2 A 3 ) A 4 )) ή ((A 1 A 2 ) (A 3 A 4 )) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
18 Αλυσιδωτός πολλαπλασιασµός πινάκων Ασκηση: Να δειχθεί ότι ο υπολογισµός του αριθµού των παρενθετοποιήσεων δίδεται από την αναδροµή: T(n) = Επίσης να δειχθέι ότι η λύση είναιω(2 n ). { 1 αν, n = 1 n 1 k=1 T(k)T(n k), αν n 2 (5) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
19 Αλυσιδωτός πολλαπλασιασµός πινάκων Βήµα 1: Βέλτιστα διασπώµενη δοµή Βήµα 1: Βέλτιστα διασπώµενη δοµή ϑα χρησιµοποιήσουµε τον συµβολισµό A ij εννοώντας το γινόµενο A i A i+1...a j όπου i j. Συµβολικά έχουµε: cost(a ij ) = cost(a ik )+cost(a k+1,j )+cost(a ik A k+1,j ) (6) Η ϐέλτιστη παρενθετοποίηση του γινοµένου A ij είναι αυτή που προκύπτει από την ϐέλτιστη παρενθετοποίηση των γινοµένων A ik και A k+1,j. Η ϐέλτιστη λύση του προβλήµατος µας, έγκειται στον υπολογισµό του ελαχίστου κόστους της παρενθετοποίησης του γινοµένου A 1n. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
20 Αλυσιδωτός πολλαπλασιασµός πινάκων Βήµα 2: Αναδροµικός ορισµός της τιµής της ϐέλτιστης λύσης Ο πίνακας A ik έχει διαστάσεις p i 1 p k και αντίστοιχα ο A k+1,j, p k p j cost(a ik A k+1,j ) = p i 1 p k p j. 1 i k < j n Ορίζουµε τον πίνακα m διάστασης n n, όπου στη ϑέση m[i, j] αποθηκεύουµε το ελάχιστο κόστος που απαιτείται για τον υπολογισµό του γινοµένου A ij. Στη ϑέση m[1, n] αποθηκεύεται το ελάχιστο κόστος υπολογισµού του γινοµένου A 1n. m[i, j] = min i k<j {m[i, k]+m[k + 1, j]+p i 1 p k p j }. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
21 Αλυσιδωτός πολλαπλασιασµός πινάκων Βήµα 2: Αναδροµικός ορισµός της τιµής της ϐέλτιστης λύσης Συνοπτικά λοιπόν έχουµε: { 0, i = j m[i, j] = { min i k<j m[i, k]+m[k + 1, j]+p i 1 p k p j }, i < j (7) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
22 Αλυσιδωτός πολλαπλασιασµός πινάκων Η 7 υλοποιείται ως εξής: ΑΝΑ ΡΟΜΙΚΗ ΑΚΟΛΟΥΘΙΑ ΠΙΝΑΚΩΝ(p, i, j) 1. Αν i = j 2. τότε επιστροφή 0 3. m[i, j] = 4. Για k = i έως j 1 5. q =ΑΝΑ ΡΟΜΙΚΗ ΑΚΟΛΟΥΘΙΑ ΠΙΝΑΚΩΝ(p, i, k) 6. + ΑΝΑ ΡΟΜΙΚΗ ΑΚΟΛΟΥΘΙΑ ΠΙΝΑΚΩΝ(p, k + 1, n) 7. +p i 1 p k p j 8. αν q < m[i, j] 9. τότε m[i, j] = q 10. επιστροφή m[i, j] Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
23 Αλυσιδωτός πολλαπλασιασµός πινάκων T(1) 1 n 1 T(n) 1+ (T(k)+T(n k)+1), n > 1 k=1 n 1 T(n) 2 T(i)+ n k=1 Μέθοδος αντικατάστασης Θα δείξουµε ότι Βάση: n = 1 έχουµε T(n) 2 n 1 T(1) 2 0 = 1 το οποίο ισχύει. Βήµα: Για n 2 έχουµε Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
24 Αλυσιδωτός πολλαπλασιασµός πινάκων- Μέθοδος αντικατάστασης Εποµένως n 1 T(n) 2 2 i 1 + n i=1 n 2 = 2 2 i + n i=0 = 2( n 2 )+n ( ) 2 n = + n 2 1 = 2(2 n 1 1)+n = 2 n + n 2 2 n 1 T(n) = Ω(2 n ). Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
25 Υποµνηµατισµός Η ϐασική ιδέα είναι να υποµνηµατίσουµε τον ϕυσικό, αλλά ϐραδύ, αναδροµικό αλγόριθµο. Τηρούµε έναν πίνακα µε λύσεις υποπροβληµάτων Ενας υποµνηµατικός αναδροµικός αλγόριθµος τηρεί ένα στοιχείο πίνακα για τη λύση του κάθε υποπροβλήµατος. Το κάθε στοιχείο πίνακα αρχικά περιέχει µια ειδική τιµή η οποία υποδεικνύει ότι το στοιχείο δεν έχει ακόµα συµπληρωθεί. Οταν το αντίστοιχο υποπρόβληµα απαντάται για πρώτη ϕορά κατά την εκτέλεση του αναδροµικού αλγορίθµου, υπολογίζεται η λύση του και κατόπιν αποθηκεύεται στον πίνακα. Στη συνέχεια, κάθε ϕορά που απαντάται ξανά το συγκεκριµένο υποπρόβληµα, απλώς ανακαλείται και επιστρέφεται η τιµή που είναι αποθηκευµένη στον πίνακα. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
26 Υποµνηµατισµός ΥΠΟΜΝΗΜΑΤΙΚΗ ΑΚΟΛΟΥΘΙΑ ΠΙΝΑΚΩΝ(p) 1. n µήκος[p] 1 2. Για i 1 έως n 3. για j 1 έως n 4. m[i, j] 5. επιστροφή ΑΝΑΚΛΗΣΗ ΑΛΛΗΛΟΥΧΙΑΣ(p, 1, n) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
27 Υποµνηµατισµός ΑΝΑΚΛΗΣΗ ΑΛΛΗΛΟΥΧΙΑΣ(p, i, j) 1. αν m[i, j] < 2. τότε επιστροφή m[i, j] 3. αν i = j 4. m[i, j] 0 5. άλλως για k i έως j 1 6. q ΑΝΑΚΛΗΣΗ ΑΛΛΗΛΟΥΧΙΑΣ(p, i, k) 7. +ΑΝΑΚΛΗΣΗ ΑΛΛΗΛΟΥΧΙΑΣ(p, k + 1, j)+p i 1 p k p j 8. αν q < m[i, j] 9. τότε m[i, j] q 10. επιστροφή m[i, j] Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
28 Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
29 Αλυσιδωτός πολλαπλασιασµός πινάκων Βήµα 3: Υπολογισµός του ελαχίστου κόστους Matrix Chain Order(p) 1. n = length[p] 1 2. for i = 1 to n do 3. m[i, i] = 0 4. end for 5. for l = 2 to n do 6. for i = 1 to n l + 1 do 7. j = i + l 1 8. m[i, j] = 9. for k = i to j 1 do 10. q = m[i, k]+m[k + 1, j]+p i 1 p k p j Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
30 Αλυσιδωτός πολλαπλασιασµός πινάκων 11. if q < m[i, j] then 12. m[i, j] = q 13. s[i, j] = k 14. end if 15. end for 16. end for 17. end for 18. return m, s Βήµα 4: Κατασκευή της ϐέλτιστης λύσης Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
31 Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
32 Print Optimal Parents(s, i, j) 1. if i = j then 2. τύπωσε Α i 3. else 4. τύπωσε ( 5. Print Optimal Parents(s, i, s[i, j]) 6. Print Optimal Parents(s, s[i, j]+1, j) 7. τύπωσε ) 8. end if Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
33 Το πρόβληµα του σακιδίου Ενα σύνολο X = {x 1, x 2,...,x n } από n αντικείµενα το καθένα έχει ϐάρος a i και ένα κέρδος c i, i = 1, 2,...,n. ίνεται ένας ακέραιος W. Ζητάµε να επιλέξουµε ένα υποσύνολο Y X τέτοιο ώστε x i Y c i = max και επιπλέον x i Y a i W. Το πρόβληµα αυτό είναι N P hard. Θα δώσουµε αλγόριθµο δυναµικού προγραµµατισµού, που επιλύει το πρόβληµα αυτό σε ψευδοπολυωνυµικό χρόνο. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
34 Το πρόβληµα του σακιδίου Βήµα 1: Βέλτιστα διασπώµενη δοµή P k (y) = { max k c j x j, j=1 k j=1 } a j x j y, x j = 0 ή 1 (8) 0 y W, 1 k n Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
35 Το πρόβληµα του σακιδίου Βήµα 2: Αναδροµικός ορισµός της τιµής της ϐέλτιστης λύσης Εστω f k (y) η τιµή της ϐέλτιστης λύσης του υποπροβλήµατος P k (y). Τότε { fk (y) } αν a k+1 > y f k+1 (y) = max {f k (y), f k (y a k+1 )+c k+1, διαφορετικά (9) για 1 k n και 0 y W. Η ϐέλτιστη λύση του προβλήµατος P n (W) έχει την τιµή f n (W). Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
36 Αναδροµικός Αλγόριθµος ΚΟΣΤΟΣ(k, y) 1 αν k = 1 τότε 2 αν a 1 > y τότε 3 f(1, y) 0 4 άλλως 5 f(1, y) c 1 6 άλλως 7 αν a k+1 > y τότε 8 f(k, y) ΚΟΣΤΟΣ(k, y) 9 άλλως 10 f(k, y) max{κοστοσ(k, y), ΚΟΣΤΟΣ(k, y a k+1 )+c k+1 } 11 Επιστροφή f(k, y) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
37 Απόδειξη Ορθότητας Επαγωγή Βάση. Για k = 1 έχουµε, λόγω των 1-5 ΚΟΣΤΟΣ(1, y) = { 0, αν a1 > y c 1, διαφορετικά ή, λόγω της (9) ΚΟΣΤΟΣ(1, y) = f 1 (y), 0 y W. Επαγωγικό Βήµα Υποθέτουµε ότι ισχύει ΚΟΣΤΟΣ(k, y) = f k (y), 0 y W. (10) και ϑα δείξουµε ότι ΚΟΣΤΟΣ(k + 1, y) = f k+1 (y), 0 y W. (11) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
38 Ορθότητα Εχουµε, λόγω των 7-10, ότι { ΚΟΣΤΟΣ(k, y), αν a ΚΟΣΤΟΣ(k + 1, y) = k+1 > y max{κοστοσ(k, y), ΚΟΣΤΟΣ(k, y a k+1 )+c k+1 } (12) Λόγω της επαγωγικής υπόθεσης (10) έχουµε και ΚΟΣΤΟΣ(k, y) = f k (y) ΚΟΣΤΟΣ(k, y a k+1 ) = f k (y a k+1 ) (13) Η (12), λόγω της (13) δίνει την (11). Πολυπλοκότητα T(n) = Ω(2 n ) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
39 Το πρόβληµα του σακιδίου Βήµα 3: Υπολογισµός της ϐέλτιστης λύσης DYNAMIC KNAPSACK(A, C, W) n = length(c) for y = 0 to W do if a 1 > y then f 1(y) = 0 else f 1(y) = c 1 end if end for for k = 1 to n 1do Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
40 Το πρόβληµα του σακιδίου 10. for y = 0 to W do 11. if a k+1 > y then 12. f k+1(y) = f k(y) 13. x y k+1 = else if f k(y) > f k(y a k+1)+c k f k+1(y) = f k(y) 16. x y k+1 = else 18. f k+1(y) = f k(y a k+1)+c k x y k+1 = end if 21. end for 22. end for 23. return f, x Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
41 Το πρόβληµα του σακιδίου Πολυπλοκότητα T(n) = O(nW) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
42 Παράδειγµα Βήµα 4: Κατασκευή της ϐέλτιστης λύσης Αντικείµενα µε ϐάρη και αξίες (9, 20),(8, 16),(6, 11),(5, 9),(4, 7),(1, 1) (0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 20(1) 20(1) 20(1) 20(1) 2 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 16(1) 20(0) 20(0) 20(0) 20(0) 3 0(0) 0(0) 0(0) 0(0) 0(0) 11(1) 11(1) 16(0) 20(0) 20(0) 20(0) 20(0) 4 0(0) 0(0) 0(0) 0(0) 9(1) 11(0) 11(0) 16(0) 20(0) 20(0) 20(0) 20(0) 5 0(0) 0(0) 0(0) 7(1) 9(0) 11(0) 11(0) 16(0) 20(0) 20(0) 20(0) 23(1) 6 1(1) 1(1) 1(1) 7(0) 9(0) 11(0) 12(1) 16(0) 20(0) 21(1) 21(1) 23(0) Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
43 Το πρόβληµα του σακιδίου Βήµα 4: Κατασκευή της ϐέλτιστης λύσης Αλγόριθµος κατασκευής ϐέλτιστης λύσης από τον πίνακα Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
44 Το πρόβληµα του σακιδίου Construct Knapsack(x) 1. τύπωσε: αξία ϐέλτιστης λύσης: f n (W) 2. τύπωσε Αντικείµενα στην λύση: 3. while W > 0 do 4. if xk W = 1 then 5. τύπωσε: k 6. W = W a k 7. end if 8. k = k 1 9. end while Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
45 Το πρόβληµα του σακιδίου Βήµα 4: Κατασκευή της ϐέλτιστης λύσης (9, 20),(8, 16),(6, 11),(5, 9),(4, 7),(1, 1) (0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 20(1) 20(1) 20(1) 20(1) 2 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 0(0) 16(1) 20(0) 20(0) 20(0) 20(0) 3 0(0) 0(0) 0(0) 0(0) 0(0) 11(1) 11(1) 16(0) 20(0) 20(0) 20(0) 20(0) 4 0(0) 0(0) 0(0) 0(0) 9(1) 11(0) 11(0) 16(0) 20(0) 20(0) 20(0) 20(0) 5 0(0) 0(0) 0(0) 7(1) 9(0) 11(0) 11(0) 16(0) 20(0) 20(0) 20(0) 23(1) 6 1(1) 1(1) 1(1) 7(0) 9(0) 11(0) 12(1) 16(0) 20(0) 21(1) 21(1) 23(0) Πίνακασ: Παράδειγµα υπολογισµού της ϐέλτιστης λύσης. Με έντονα γράµµατα έχουν σηµειωθεί οι ϑέσεις του πίνακα που περνάει ο αλγόριθµος ώστε να τυπώσει την ϐέλτιστη λύση, που είναι η επιλογή των αντικειµένων 2, 5 µε συνολικό κέρδος 23. Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου / 45
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 5 υναµικός Προγραµµατισµός Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 5 1 / 49 Εισαγωγή
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 5 υναµικός Προγραµµατισµός Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 5 1 / 49 Εισαγωγή
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου 2015 1 / 17 Μέγιστη Κοινή Υπακολουθία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου 2015 1 / 17 Μέγιστη Κοινή Υπακολουθία
Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Δυναμικός Προγραμματισμός Δυναμικός Προγραμματισμός 1 Περίληψη
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Δυναμικός Προγραμματισμός Δυναμικός Προγραμματισμός 1 Περίληψη
Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα:
 υναµικός Προγραµµατισµός Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε υναµικό Προγραµµατισµό Το πρόβληµα του πολλαπλασιασµού πινάκων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα 3- υναµικός
υναµικός Προγραµµατισµός Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε υναµικό Προγραµµατισµό Το πρόβληµα του πολλαπλασιασµού πινάκων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα 3- υναµικός
Ν. Μ. Μισυρλής. Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών. Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου / 18
 Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου 2017 1 / 18 Βέλτιστα (στατικά) δυαδικά δένδρα αναζήτησης Παράδειγµα: Σχεδιασµός προγράµµατος
Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου 2017 1 / 18 Βέλτιστα (στατικά) δυαδικά δένδρα αναζήτησης Παράδειγµα: Σχεδιασµός προγράµµατος
Αλγόριθµοι. Παράδειγµα. ιαίρει και Βασίλευε. Παράδειγµα MergeSort. Τεχνικές Σχεδιασµού Αλγορίθµων
 Τεχνικές Σχεδιασµού Αλγορίθµων Αλγόριθµοι Παύλος Εφραιµίδης pefraimi@ee.duth.gr Ορισµένες γενικές αρχές για τον σχεδιασµό αλγορίθµων είναι: ιαίρει και Βασίλευε (Divide and Conquer) υναµικός Προγραµµατισµός
Τεχνικές Σχεδιασµού Αλγορίθµων Αλγόριθµοι Παύλος Εφραιµίδης pefraimi@ee.duth.gr Ορισµένες γενικές αρχές για τον σχεδιασµό αλγορίθµων είναι: ιαίρει και Βασίλευε (Divide and Conquer) υναµικός Προγραµµατισµός
Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα:
 υναµικός Προγραµµατισµός Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε υναµικό Προγραµµατισµό Το πρόβληµα του πολλαπλασιασµού πινάκων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα 3- υναµικός
υναµικός Προγραµµατισµός Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε υναµικό Προγραµµατισµό Το πρόβληµα του πολλαπλασιασµού πινάκων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα 3- υναµικός
Θέματα Εφαρμογών Βάσεων Δεδομένων: Ιδιωτικότητα Δεδομένων
 Θέματα Εφαρμογών Βάσεων Δεδομένων: Ιδιωτικότητα Δεδομένων 3. Δυναμικός Προγραμματισμός Ζαγορίσιος Παναγώτης Παπαοικονόμου Χριστίνα Δυναμικός Προγραμματισμός Μέθοδος επίλυσης σύνθετων προβλημάτων. Όπως
Θέματα Εφαρμογών Βάσεων Δεδομένων: Ιδιωτικότητα Δεδομένων 3. Δυναμικός Προγραμματισμός Ζαγορίσιος Παναγώτης Παπαοικονόμου Χριστίνα Δυναμικός Προγραμματισμός Μέθοδος επίλυσης σύνθετων προβλημάτων. Όπως
Άπληστοι Αλγόριθµοι (CLR, κεφάλαιο 17)
 Άπληστοι Αλγόριθµοι (CLR, κεφάλαιο 17) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε Άπληστους Αλγόριθµους Στοιχεία άπληστων αλγορίθµων Το πρόβληµα επιλογής εργασιών ΕΠΛ 232
Άπληστοι Αλγόριθµοι (CLR, κεφάλαιο 17) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Σχεδιασµός αλγορίθµων µε Άπληστους Αλγόριθµους Στοιχεία άπληστων αλγορίθµων Το πρόβληµα επιλογής εργασιών ΕΠΛ 232
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 31 Μαΐου 2019 1 / 10 Ελάχιστα τετράγωνα
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 31 Μαΐου 2019 1 / 10 Ελάχιστα τετράγωνα
Δυναµικός Προγραµµατισµός (ΔΠ)
 Δυναµικός Προγραµµατισµός (ΔΠ) Περίληψη Δυναµικός Προγραµµατισµός Αρχή του Βέλτιστου Παραδείγµατα Δυναµικός Προγραµµατισµός ΔΠ (Dynamic Programming DP) Μέθοδος σχεδιασµού αλγορίθµων Είναι µια γενική µεθοδολογία
Δυναµικός Προγραµµατισµός (ΔΠ) Περίληψη Δυναµικός Προγραµµατισµός Αρχή του Βέλτιστου Παραδείγµατα Δυναµικός Προγραµµατισµός ΔΠ (Dynamic Programming DP) Μέθοδος σχεδιασµού αλγορίθµων Είναι µια γενική µεθοδολογία
υναμικός Προγραμματισμός
 υναμικός Προγραμματισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιωνυμικοί Συντελεστές ιωνυμικοί
υναμικός Προγραμματισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιωνυμικοί Συντελεστές ιωνυμικοί
Δυναμικός Προγραμματισμός
 Τρίγωνο του Pascal Δυναμικός Προγραμματισμός Διωνυμικοί συντελεστές Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
Τρίγωνο του Pascal Δυναμικός Προγραμματισμός Διωνυμικοί συντελεστές Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο
ΕΠΛ 232 Αλγόριθµοι και Πολυπλοκότητα 2-1
 ιαίρει και Βασίλευε Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Η Μέθοδος Σχεδιασµού Αλγορίθµων ιαίρει και Βασίλευε Επίλυση Αναδροµικών Εξισώσεων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα - ιαίρει και Βασίλευε
ιαίρει και Βασίλευε Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Η Μέθοδος Σχεδιασµού Αλγορίθµων ιαίρει και Βασίλευε Επίλυση Αναδροµικών Εξισώσεων ΕΠΛ 3 Αλγόριθµοι και Πολυπλοκότητα - ιαίρει και Βασίλευε
Δυναμικός Προγραμματισμός
 Δυναμικός Προγραμματισμός Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διωνυμικοί Συντελεστές Διωνυμικοί
Δυναμικός Προγραμματισμός Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διωνυμικοί Συντελεστές Διωνυμικοί
Αλγοριθμικές Τεχνικές
 Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Αλγοριθμικές Τεχνικές 1 Τεχνικές Σχεδιασμού Αλγορίθμων Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και
Αλγοριθμικές Τεχνικές. Brute Force. Διαίρει και Βασίλευε. Παράδειγμα MergeSort. Παράδειγμα. Τεχνικές Σχεδιασμού Αλγορίθμων
 Τεχνικές Σχεδιασμού Αλγορίθμων Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και Βασίλευε (Divide and
Τεχνικές Σχεδιασμού Αλγορίθμων Αλγοριθμικές Τεχνικές Παύλος Εφραιμίδης, Λέκτορας http://pericles.ee.duth.gr Ορισμένες γενικές αρχές για τον σχεδιασμό αλγορίθμων είναι: Διαίρει και Βασίλευε (Divide and
υναμικός Προγραμματισμός
 υναμικός Προγραμματισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιωνυμικοί Συντελεστές ιωνυμικοί
υναμικός Προγραμματισμός ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιωνυμικοί Συντελεστές ιωνυμικοί
υναμικός Προγραμματισμός
 υναμικός Προγραμματισμός ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιακριτό Πρόβλημα Σακιδίου ίνονται n αντικείμενα και σακίδιο μεγέθους Β. Αντικείμενο
υναμικός Προγραμματισμός ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιακριτό Πρόβλημα Σακιδίου ίνονται n αντικείμενα και σακίδιο μεγέθους Β. Αντικείμενο
Τεχνικές Σχεδιασμού Αλγορίθμων
 Τεχνικές Σχεδιασμού Αλγορίθμων Διαίρει και Βασίλευε Δυναμικός Προγραμματισμός Απληστία Π. Μποζάνης ΤHMMY - Αλγόριθμοι 2014-2015 1 Διαίρει και Βασίλευε Βασικά Βήματα Διαίρει: Κατάτμηση του αρχικού προβλήματος
Τεχνικές Σχεδιασμού Αλγορίθμων Διαίρει και Βασίλευε Δυναμικός Προγραμματισμός Απληστία Π. Μποζάνης ΤHMMY - Αλγόριθμοι 2014-2015 1 Διαίρει και Βασίλευε Βασικά Βήματα Διαίρει: Κατάτμηση του αρχικού προβλήματος
Χαρακτηριστικά Δυναμικού Προγραμματισμού. Εισαγωγικά. 2 Δυναμικός Προγραμματισμός
 Δυναμικός Προγραμματισμός Τμήμα Ηλεκτρονικών Μηχ. & Μηχ. Υπολογιστών Φθινόπωρο 00 ΣΕΛ 40: Παράλληλοι Αλγόριθμοι και Software Διδάσκων: Τάσος Δημητρίου Δυναμικός Προγραμματισμός είχε υπολογιστεί προηγουμένως
Δυναμικός Προγραμματισμός Τμήμα Ηλεκτρονικών Μηχ. & Μηχ. Υπολογιστών Φθινόπωρο 00 ΣΕΛ 40: Παράλληλοι Αλγόριθμοι και Software Διδάσκων: Τάσος Δημητρίου Δυναμικός Προγραμματισμός είχε υπολογιστεί προηγουμένως
Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις
 Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική και τη συµµετρική ιδιότητα του Θ. Λύση Μεταβατική Ιδιότητα (ορισµός): Αν f(n) = Θ(g(n)) και g(n) = Θ(h(n)) τότε f(n)=θ(h(n)). Για
Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική και τη συµµετρική ιδιότητα του Θ. Λύση Μεταβατική Ιδιότητα (ορισµός): Αν f(n) = Θ(g(n)) και g(n) = Θ(h(n)) τότε f(n)=θ(h(n)). Για
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 23 Μαρτίου 2017 1 / 20 Επιλογή Το πρόβληµα
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 23 Μαρτίου 2017 1 / 20 Επιλογή Το πρόβληµα
Ενότητα 9 Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find)
 Ενότητα 9 Ξένα Σύνολα που υποστηρίζουν τη (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή
Ενότητα 9 Ξένα Σύνολα που υποστηρίζουν τη (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Διωνυµικοί Συντελεστές. Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Δυναµικός Προγραµµατισµός 1
 Διωνυµικοί Συντελεστές Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Δυναµικός Προγραµµατισµός 1 Διωνυµικοί Συντελεστές Διωνυµικοί συντελεστές Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Δυναµικός Προγραµµατισµός
Διωνυµικοί Συντελεστές Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Δυναµικός Προγραµµατισµός 1 Διωνυµικοί Συντελεστές Διωνυµικοί συντελεστές Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Δυναµικός Προγραµµατισµός
Μοντελοποίηση προβληµάτων
 Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Δυναμικός Προγραμματισμός
 Δυναμικός Προγραμματισμός Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις /προσθήκες: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διωνυμικοί Συντελεστές
Δυναμικός Προγραμματισμός Επιμέλεια διαφανειών: Δ. Φωτάκης Τροποποιήσεις /προσθήκες: Α. Παγουρτζής Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διωνυμικοί Συντελεστές
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 30 Απριλίου 2015 1 / 48 Εύρεση Ελάχιστου
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 30 Απριλίου 2015 1 / 48 Εύρεση Ελάχιστου
Ορισµός. Εστω συναρτήσεις: f : N R και g : N R. η f(n) είναι fi( g(n) ) αν υπάρχουν σταθερές C 1, C 2 και n 0, τέτοιες ώστε:
 Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα Φεβρουαρίου 0 / ένδρα Ενα δένδρο είναι
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα Φεβρουαρίου 0 / ένδρα Ενα δένδρο είναι
Σχεδίαση Αλγορίθμων - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1
 Σχεδίαση Αλγορίθμων Δυναμικός Προγραμματισμός http://delab.csd.auth.gr/~gounaris/courses/ad Σχεδίαση Αλγορίθμων - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1 Δυναμικός προγραμματισμός Ο Δυναμικός Προγραμματισμός
Σχεδίαση Αλγορίθμων Δυναμικός Προγραμματισμός http://delab.csd.auth.gr/~gounaris/courses/ad Σχεδίαση Αλγορίθμων - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1 Δυναμικός προγραμματισμός Ο Δυναμικός Προγραμματισμός
Αλγόριθμοι - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1
 Αλγόριθμοι Δυναμικός Προγραμματισμός http://delab.csd.auth.gr/courses/algorithms/ Αλγόριθμοι - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1 Δυναμικός προγραμματισμός Ο Δυναμικός Προγραμματισμός προτάθηκε από τον
Αλγόριθμοι Δυναμικός Προγραμματισμός http://delab.csd.auth.gr/courses/algorithms/ Αλγόριθμοι - Τμήμα Πληροφορικής ΑΠΘ -4ο εξάμηνο 1 Δυναμικός προγραμματισμός Ο Δυναμικός Προγραμματισμός προτάθηκε από τον
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 1 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 1 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική
Βραχύτερα Μονοπάτια σε Γράφους (CLR, κεφάλαιο 25)
 Βραχύτερα Μονοπάτια σε Γράφους (CLR, κεφάλαιο 5) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Βραχύτερα Μονοπάτια για όλα τα Ζεύγη Λύση υναµικού Προγραµµατισµού Ο αλγόριθµος των Floyd-Warshal ΕΠΛ 3
Βραχύτερα Μονοπάτια σε Γράφους (CLR, κεφάλαιο 5) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Βραχύτερα Μονοπάτια για όλα τα Ζεύγη Λύση υναµικού Προγραµµατισµού Ο αλγόριθµος των Floyd-Warshal ΕΠΛ 3
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 3 Αλγόριθµοι Γραφηµάτων Bellman Ford Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 3 Bellman
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 3 Αλγόριθµοι Γραφηµάτων Bellman Ford Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 3 Bellman
Διαίρει-και-Βασίλευε. Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2
 Διαίρει-και-Βασίλευε Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2 Διαίρει-και-Βασίλευε Γενική µέθοδος σχεδιασµού αλγορίθµων: Διαίρεση σε ( 2) υποπροβλήµατα (σηµαντικά) µικρότερου µεγέθους.
Διαίρει-και-Βασίλευε Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2 Διαίρει-και-Βασίλευε Γενική µέθοδος σχεδιασµού αλγορίθµων: Διαίρεση σε ( 2) υποπροβλήµατα (σηµαντικά) µικρότερου µεγέθους.
ΕΠΛ 232: Αλγόριθµοι και Πολυπλοκότητα. Κατ οίκον Εργασία 1 Σκελετοί Λύσεων
 ΕΠΛ 22: Αλγόριθµοι και Πολυπλοκότητα Κατ οίκον Εργασία Σκελετοί Λύσεων. (α) Έστω δροµολόγηση e, e 2,, e των εργασιών, 2,,. Τότε οι χρόνοι συµπλήρωσης των εργασιών είναι e d e e 2 d e + d e 2 e d e + d
ΕΠΛ 22: Αλγόριθµοι και Πολυπλοκότητα Κατ οίκον Εργασία Σκελετοί Λύσεων. (α) Έστω δροµολόγηση e, e 2,, e των εργασιών, 2,,. Τότε οι χρόνοι συµπλήρωσης των εργασιών είναι e d e e 2 d e + d e 2 e d e + d
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 2 ιαίρει και Βασίλευε Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 2 1 / 24 Επιλογή Το πρόβληµα
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 2 ιαίρει και Βασίλευε Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 2 1 / 24 Επιλογή Το πρόβληµα
Άπληστοι Αλγόριθµοι. Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Άπληστοι Αλγόριθµοι 1
 Άπληστοι Αλγόριθµοι Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Άπληστοι Αλγόριθµοι 1 Άπληστοι Αλγόριθµοι... για προβλήµατα βελτιστοποίησης: Λειτουργούν σε βήµατα. Κάθε βήµα κάνει µια αµετάκλητη επιλογή
Άπληστοι Αλγόριθµοι Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Άπληστοι Αλγόριθµοι 1 Άπληστοι Αλγόριθµοι... για προβλήµατα βελτιστοποίησης: Λειτουργούν σε βήµατα. Κάθε βήµα κάνει µια αµετάκλητη επιλογή
Εξαντλητική Απαρίθµηση
 Υπενθύµιση Χαράκτηρίζουµε τους αλγόριθµους ως προς το χρόνο εκτέλεσης συναρτήσει της εισόδου Υπενθύµιση Χαράκτηρίζουµε τους αλγόριθµους ως προς το χρόνο εκτέλεσης συναρτήσει της εισόδου Ως µέτρο ϑεωρούµε
Υπενθύµιση Χαράκτηρίζουµε τους αλγόριθµους ως προς το χρόνο εκτέλεσης συναρτήσει της εισόδου Υπενθύµιση Χαράκτηρίζουµε τους αλγόριθµους ως προς το χρόνο εκτέλεσης συναρτήσει της εισόδου Ως µέτρο ϑεωρούµε
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
Γενικό πλάνο. Μαθηµατικά για Πληροφορική. Παράδειγµα αναδροµικού ορισµού. οµική επαγωγή ΠΑΡΑ ΕΙΓΜΑ. 3ο Μάθηµα
 Γενικό πλάνο Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 1 Παράδειγµα δοµικής επαγωγής 2 Ορισµός δοµικής
Γενικό πλάνο Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 1 Παράδειγµα δοµικής επαγωγής 2 Ορισµός δοµικής
Μαθηµατικά για Πληροφορική
 Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 14/10/2008 1 / 24 Γενικό πλάνο 1 Παράδειγµα δοµικής επαγωγής
Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 14/10/2008 1 / 24 Γενικό πλάνο 1 Παράδειγµα δοµικής επαγωγής
Ενότητα 9 Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find)
 Ενότητα 9 (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή ισχύει ότι S i S j =, για κάθε i,j µε i j και S 1 S k = U. Λειτουργίες q MakeSet(X): επιστρέφει
Ενότητα 9 (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή ισχύει ότι S i S j =, για κάθε i,j µε i j και S 1 S k = U. Λειτουργίες q MakeSet(X): επιστρέφει
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 6 Μαΐου 2015 1 / 42 Εύρεση Ελάχιστου Μονοπατιού
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 6 Μαΐου 2015 1 / 42 Εύρεση Ελάχιστου Μονοπατιού
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές»
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
ΑΛΓΟΡΙΘΜΟΙ. Ενότητα 8: Δυναμικός Προγραμματισμός. Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Τμήμα Πληροφορικής ΑΠΘ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 8: Δυναμικός Προγραμματισμός Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 8: Δυναμικός Προγραμματισμός Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες Χρήσης
Δομές Δεδομένων & Αλγόριθμοι
 Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Πρόβληµα, Στιγµιότυπο, Αλγόριθµος Εργαλεία εκτίµησης πολυπλοκότητας: οι τάξεις Ο(n), Ω(n), Θ(n) Ανάλυση Πολυπλοκότητας Αλγορίθµων
Αλγόριθµοι και Πολυπλοκότητα Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Πρόβληµα, Στιγµιότυπο, Αλγόριθµος Εργαλεία εκτίµησης πολυπλοκότητας: οι τάξεις Ο(n), Ω(n), Θ(n) Ανάλυση Πολυπλοκότητας Αλγορίθµων
3 Αναδροµή και Επαγωγή
 3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
1 Ορισµός ακολουθίας πραγµατικών αριθµών
 ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
ΜΑΣ 02. Απειροστικός Λογισµός Ι Ορισµός ακολουθίας πραγµατικών αριθµών Ορισµός.. Ονοµάζουµε ακολουθία πραγµατικών αριθµών κάθε απεικόνιση του συνόλου N των ϕυσικών αριθµών, στο σύνολο R των πραγµατικών
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 25 Φεβρουαρίου 2015 1 / 53 Περιεχόµενα
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 25 Φεβρουαρίου 2015 1 / 53 Περιεχόµενα
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 3 Αλγόριθµοι Γραφηµάτων Dijkstra Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 3 Dijkstra
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 3 Αλγόριθµοι Γραφηµάτων Dijkstra Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 3 Dijkstra
Κατ οίκον Εργασία 1 Σκελετοί Λύσεων
 EΠΛ Αλγόριθµοι και Πολυπλοκότητα Φεβρουάριος 00 Κατ οίκον Εργασία Σκελετοί Λύσεων. Ο αλγόριθµος διαίρει και βασίλευε για το πρόβληµα έχει ως εξής: Μοίρασε τον πίνακα σε δύο µισά. Υπολόγισε αναδροµικά τα
EΠΛ Αλγόριθµοι και Πολυπλοκότητα Φεβρουάριος 00 Κατ οίκον Εργασία Σκελετοί Λύσεων. Ο αλγόριθµος διαίρει και βασίλευε για το πρόβληµα έχει ως εξής: Μοίρασε τον πίνακα σε δύο µισά. Υπολόγισε αναδροµικά τα
ΑΛΓΟΡΙΘΜΟΙ Άνοιξη I. ΜΗΛΗΣ
 ΑΛΓΟΡΙΘΜΟΙ http://eclass.aueb.gr/courses/inf161/ Άνοιξη 2017 - I. ΜΗΛΗΣ ΔΥΝΑΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Knapsack problems ΑΛΓΟΡΙΘΜΟΙ - ΑΝΟΙΞΗ 2017 - Ι. ΜΗΛΗΣ 10 DP III 1 Knapsack problems ΕΙΣΟΔΟΣ: Σακίδιο χωρητικότητας
ΑΛΓΟΡΙΘΜΟΙ http://eclass.aueb.gr/courses/inf161/ Άνοιξη 2017 - I. ΜΗΛΗΣ ΔΥΝΑΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Knapsack problems ΑΛΓΟΡΙΘΜΟΙ - ΑΝΟΙΞΗ 2017 - Ι. ΜΗΛΗΣ 10 DP III 1 Knapsack problems ΕΙΣΟΔΟΣ: Σακίδιο χωρητικότητας
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 4 Απληστοι Αλγόριθµοι Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 4 1 / 91 Απληστοι Αλγόριθµοι
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 4 Απληστοι Αλγόριθµοι Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 4 1 / 91 Απληστοι Αλγόριθµοι
Στοιχεία Αλγορίθµων και Πολυπλοκότητας
 Στοιχεία Αλγορίθµων και Πολυπλοκότητας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Πολυπλοκότητα 1 / 16 «Ζέσταµα» Να γράψετε τις συναρτήσεις
Στοιχεία Αλγορίθµων και Πολυπλοκότητας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Πολυπλοκότητα 1 / 16 «Ζέσταµα» Να γράψετε τις συναρτήσεις
ΣΗΜΕΙΩΣΕΙΣ ΥΝΑΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΥΝΑΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Επιµέλεια Σηµειώσεων : Βασιλειάδης Γεώργιος Θεσσαλονίκη 2012 2 Περιεχόµενα 1 υναµικός
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΥΝΑΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Επιµέλεια Σηµειώσεων : Βασιλειάδης Γεώργιος Θεσσαλονίκη 2012 2 Περιεχόµενα 1 υναµικός
a 1d L(A) = {m 1 a m d a d : m i Z} a 11 a A = M B, B = N A, k=1
 Α44 ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΗΜΕΙΩΣΕΙΣ #12 ΘΕΟ ΟΥΛΟΣ ΓΑΡΕΦΑΛΑΚΗΣ 1 Πλεγµατα Εστω ο διανυσµατικός χώρος R d διάστασης d Ο χώρος R d έρχεται µε ένα εσωτερικό γινόµενο x, y = d i=1 x iy i και τη σχετική νόρµα x = x,
Α44 ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΗΜΕΙΩΣΕΙΣ #12 ΘΕΟ ΟΥΛΟΣ ΓΑΡΕΦΑΛΑΚΗΣ 1 Πλεγµατα Εστω ο διανυσµατικός χώρος R d διάστασης d Ο χώρος R d έρχεται µε ένα εσωτερικό γινόµενο x, y = d i=1 x iy i και τη σχετική νόρµα x = x,
Κεφάλαιο 5ο: Εντολές Επανάληψης
 Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
Σχεδίαση & Ανάλυση Αλγορίθμων
 Σχεδίαση & Ανάλυση Αλγορίθμων Ενότητα 1 Αλγόριθμοι και Πολυπλοκότητα Σταύρος Δ. Νικολόπουλος Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros Εισαγωγή Ας ξεκινήσουμε
Σχεδίαση & Ανάλυση Αλγορίθμων Ενότητα 1 Αλγόριθμοι και Πολυπλοκότητα Σταύρος Δ. Νικολόπουλος Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros Εισαγωγή Ας ξεκινήσουμε
Αξιολόγηση Ευριστικών Αλγορίθµων
 Προσεγγιστικοί Αλγόριθµοι Πολλές ϕορές η εύρεση της ϐέλτιστων λύσεων προβληµάτων ακέραιου γραµµικού προγραµµατισµού είναι µια χρονοβόρα διαδικασία (εκθετική πολυπλοκότητα) Προσεγγιστικοί Αλγόριθµοι Πολλές
Προσεγγιστικοί Αλγόριθµοι Πολλές ϕορές η εύρεση της ϐέλτιστων λύσεων προβληµάτων ακέραιου γραµµικού προγραµµατισµού είναι µια χρονοβόρα διαδικασία (εκθετική πολυπλοκότητα) Προσεγγιστικοί Αλγόριθµοι Πολλές
Heapsort Using Multiple Heaps
 sort sort Using Multiple s. Λεβεντέας Χ. Ζαρολιάγκης Τµήµα Μηχανικών Η/Υ & Πληροφορικής 29 Αυγούστου 2008 sort 1 Ορισµός ify Build- 2 sort Πως δουλεύει Ιδιότητες 3 4 Προβλήµατα Προτάσεις Ανάλυση Κόστους
sort sort Using Multiple s. Λεβεντέας Χ. Ζαρολιάγκης Τµήµα Μηχανικών Η/Υ & Πληροφορικής 29 Αυγούστου 2008 sort 1 Ορισµός ify Build- 2 sort Πως δουλεύει Ιδιότητες 3 4 Προβλήµατα Προτάσεις Ανάλυση Κόστους
Σχεδίαση και Ανάλυση Αλγορίθμων
 Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 4.0 Επιλογή Αλγόριθμοι Επιλογής Select και Quick-Select Σταύρος Δ. Νικολόπουλος 2016-17 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 4.0 Επιλογή Αλγόριθμοι Επιλογής Select και Quick-Select Σταύρος Δ. Νικολόπουλος 2016-17 Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros
Εισαγωγή στους Αλγορίθμους Ενότητα 11η
 Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Δυναμικός Προγραμματισμός Σταθμισμένος Χρονοπρογραμματισμός
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Δυναμικός Προγραμματισμός Σταθμισμένος Χρονοπρογραμματισμός
2 Αποδείξεις. 2.1 Εξαντλητική µέθοδος. Εκδοση 2005/03/22. Υπάρχουν πολλών ειδών αποδείξεις. Εδώ ϑα δούµε τις πιο κοινές:
 2 Αποδείξεις Υπάρχουν πολλών ειδών αποδείξεις. Εδώ ϑα δούµε τις πιο κοινές: Εκδοση 2005/03/22 Εξαντλητική µέθοδος ή µέθοδος επισκόπησης. Οταν το πρόβληµα έχει πεπερασµένες αριθµό περιπτώσεων τις εξετάζουµε
2 Αποδείξεις Υπάρχουν πολλών ειδών αποδείξεις. Εδώ ϑα δούµε τις πιο κοινές: Εκδοση 2005/03/22 Εξαντλητική µέθοδος ή µέθοδος επισκόπησης. Οταν το πρόβληµα έχει πεπερασµένες αριθµό περιπτώσεων τις εξετάζουµε
Αναδροµή. Σε αυτήν την (βοηθητική) ενότητα θα µελετηθούν τα εξής : Η έννοια της αναδροµής Υλοποίηση και αποδοτικότητα Αφαίρεση της αναδροµής
 Αναδροµή Σε αυτήν την (βοηθητική) ενότητα θα µελετηθούν τα εξής : Η έννοια της αναδροµής Υλοποίηση και αποδοτικότητα Αφαίρεση της αναδροµής 1 Αναδροµή Βασική έννοια στα Μαθηµατικά και στην Πληροφορική.
Αναδροµή Σε αυτήν την (βοηθητική) ενότητα θα µελετηθούν τα εξής : Η έννοια της αναδροµής Υλοποίηση και αποδοτικότητα Αφαίρεση της αναδροµής 1 Αναδροµή Βασική έννοια στα Μαθηµατικά και στην Πληροφορική.
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 26 Ιουνίου 201 1 / Απληστοι (Greedy) Αλγόριθµοι
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 26 Ιουνίου 201 1 / Απληστοι (Greedy) Αλγόριθµοι
Σχεδίαση & Ανάλυση Αλγορίθμων
 Σχεδίαση & Ανάλυση Αλγορίθμων Ενότητα 3 Αλγόριθμοι Επιλογής Σταύρος Δ. Νικολόπουλος Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros Αλγόριθμοι Επιλογής Γνωρίζουμε
Σχεδίαση & Ανάλυση Αλγορίθμων Ενότητα 3 Αλγόριθμοι Επιλογής Σταύρος Δ. Νικολόπουλος Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Ιωαννίνων Webpage: www.cs.uoi.gr/~stavros Αλγόριθμοι Επιλογής Γνωρίζουμε
Κεφάλαιο 4. Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 4 Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Τεχνικές Σχεδίασης Αλγορίθµων Απληστία. Χτίζουµε µια λύση σταδιακά, βελτιστοποιώντας
Κεφάλαιο 4 Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Τεχνικές Σχεδίασης Αλγορίθµων Απληστία. Χτίζουµε µια λύση σταδιακά, βελτιστοποιώντας
Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 4)
 Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 4) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Δρ. Δημήτρης Βαρσάμης Αριθμητικές Μέθοδοι (E 4) Σεπτέμβριος 2015
Τμήμα Μηχανικών Πληροφορικής Αριθμητικές Μέθοδοι σε Προγραμματιστικό Περιβάλλον (Εργαστήριο 4) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Δρ. Δημήτρης Βαρσάμης Αριθμητικές Μέθοδοι (E 4) Σεπτέμβριος 2015
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα Μαΐου 201 1 / Απληστοι (Greedy) Αλγόριθµοι
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα Μαΐου 201 1 / Απληστοι (Greedy) Αλγόριθµοι
ιαίρει-και-βασίλευε ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
 ιαίρει-και-βασίλευε ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιαίρει-και-βασίλευε Γενική μέθοδος σχεδιασμού αλγορίθμων: ιαίρεση σε ( 2) υποπροβλήματα
ιαίρει-και-βασίλευε ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιαίρει-και-βασίλευε Γενική μέθοδος σχεδιασμού αλγορίθμων: ιαίρεση σε ( 2) υποπροβλήματα
Δυναμικός Προγραμματισμός
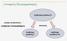 πρόβλημα μεγέθους Ν «Διαίρει και βασίλευε» : ανεξάρτητα υποπροβλήματα διάσπαση πρόβλημα μεγέθους k πρόβλημα μεγέθους Ν-k πρόβλημα μεγέθους Ν Σε κάποιες περιπτώσεις όμως τα υποπροβλήματα δεν είναι ανεξάρτητα
πρόβλημα μεγέθους Ν «Διαίρει και βασίλευε» : ανεξάρτητα υποπροβλήματα διάσπαση πρόβλημα μεγέθους k πρόβλημα μεγέθους Ν-k πρόβλημα μεγέθους Ν Σε κάποιες περιπτώσεις όμως τα υποπροβλήματα δεν είναι ανεξάρτητα
Branch and Bound. Branch and Bound
 Μέθοδος επίλυσης προβληµάτων ακέραιου γραµµικού προγραµµατισµού Μέθοδος επίλυσης προβληµάτων ακέραιου γραµµικού προγραµµατισµού Προσπαθούµε να αποφύγουµε την εξαντλητική αναζήτηση Μέθοδος επίλυσης προβληµάτων
Μέθοδος επίλυσης προβληµάτων ακέραιου γραµµικού προγραµµατισµού Μέθοδος επίλυσης προβληµάτων ακέραιου γραµµικού προγραµµατισµού Προσπαθούµε να αποφύγουµε την εξαντλητική αναζήτηση Μέθοδος επίλυσης προβληµάτων
οµές εδοµένων 3 ο Εξάµηνο Τµήµα Πανεπιστήµιο Πληροφορικής Ιωαννίνων ΟΜΕΣ Ε ΟΜΕΝΩΝ
 Τµήµα Πανεπιστήµιο Πληροφορικής Ιωαννίνων ΟΜΕΣ Ε ΟΜΕΝΩΝ ΕΝΟΤΗΤΑ 1 ΕΙΣΑΓΩΓΗ 1 εδοµένα Σύνολο από πληροφορίες που πρέπει να αποθηκευτούν σε έναν υπολογιστή Υπολογιστικό Μοντέλο ένας επεξεργαστής και µεγάλος
Τµήµα Πανεπιστήµιο Πληροφορικής Ιωαννίνων ΟΜΕΣ Ε ΟΜΕΝΩΝ ΕΝΟΤΗΤΑ 1 ΕΙΣΑΓΩΓΗ 1 εδοµένα Σύνολο από πληροφορίες που πρέπει να αποθηκευτούν σε έναν υπολογιστή Υπολογιστικό Μοντέλο ένας επεξεργαστής και µεγάλος
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Δυναμικός προγραμματισμός για δέντρα
 ΘΕ5 Ιδιότητες Δέντρων και Αναδρομή για Δέντρα Δυναμικός προγραμματισμός για δέντρα Έστω ότι, για k=1,..., m, το γράφημα Γ k = (V k, E k ) είναι δέντρο. Έστω w V 1... V m, z k V k, για k=1,..., m. Συμβολίζουμε
ΘΕ5 Ιδιότητες Δέντρων και Αναδρομή για Δέντρα Δυναμικός προγραμματισμός για δέντρα Έστω ότι, για k=1,..., m, το γράφημα Γ k = (V k, E k ) είναι δέντρο. Έστω w V 1... V m, z k V k, για k=1,..., m. Συμβολίζουμε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Επίλυση ενός τριδιαγώνιου γραµµικού συστήµατος Ax = d µε τη µέθοδο απαλοιφής του Gauss (µέθοδος του Thomas)
 Επίλυση ενός τριδιαγώνιου γραµµικού συστήµατος Ax = d µε τη µέθοδο απαλοιφής του Gauss (µέθοδος του Thomas) Εστω το ακόλουθο n n τριδιαγώνιο γραµµικό σύστηµα Ax = d A = b 1 c 1 a 2 b 2 c 2 0 a 3 b 3 c
Επίλυση ενός τριδιαγώνιου γραµµικού συστήµατος Ax = d µε τη µέθοδο απαλοιφής του Gauss (µέθοδος του Thomas) Εστω το ακόλουθο n n τριδιαγώνιο γραµµικό σύστηµα Ax = d A = b 1 c 1 a 2 b 2 c 2 0 a 3 b 3 c
Η ΤΕΧΝΗ ΤΟΥ ΙΑΒΑΣΜΑΤΟΣ ΜΕΤΑΞΥ ΤΩΝ ΑΡΙΘΜΩΝ (ΠΑΡΕΜΒΟΛΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΗ)
 Η ΤΕΧΝΗ ΤΟΥ ΙΑΒΑΣΜΑΤΟΣ ΜΕΤΑΞΥ ΤΩΝ ΑΡΙΘΜΩΝ (ΠΑΡΕΜΒΟΛΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΗ) ΜΙΧΑΛΗΣ ΤΖΟΥΜΑΣ ΕΣΠΟΤΑΤΟΥ 3 ΑΓΡΙΝΙΟ. ΠΕΡΙΛΗΨΗ Η έννοια της συνάρτησης είναι στενά συνυφασµένη µε τον πίνακα τιµών και τη γραφική παράσταση.
Η ΤΕΧΝΗ ΤΟΥ ΙΑΒΑΣΜΑΤΟΣ ΜΕΤΑΞΥ ΤΩΝ ΑΡΙΘΜΩΝ (ΠΑΡΕΜΒΟΛΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΗ) ΜΙΧΑΛΗΣ ΤΖΟΥΜΑΣ ΕΣΠΟΤΑΤΟΥ 3 ΑΓΡΙΝΙΟ. ΠΕΡΙΛΗΨΗ Η έννοια της συνάρτησης είναι στενά συνυφασµένη µε τον πίνακα τιµών και τη γραφική παράσταση.
Αναδροµή (Recursion) ύο παρεξηγήσεις. Σκέψου Αναδροµικά. Τρίγωνο Sierpinski Μη αναδροµικός ορισµός;
 Αναδροµή (Recursion) Πώς να λύσουµε ένα πρόβληµα κάνοντας λίγη δουλειά και ανάγοντας το υπόλοιπο να λυθεί µε τον ίδιο τρόπο. Πού χρειάζεται; Πολλές µαθηµατικές συναρτήσεις ορίζονται αναδροµικά. εν είναι
Αναδροµή (Recursion) Πώς να λύσουµε ένα πρόβληµα κάνοντας λίγη δουλειά και ανάγοντας το υπόλοιπο να λυθεί µε τον ίδιο τρόπο. Πού χρειάζεται; Πολλές µαθηµατικές συναρτήσεις ορίζονται αναδροµικά. εν είναι
Συναρτησιακές Εξαρτήσεις. Βάσεις εδοµένων Ευαγγελία Πιτουρά 1
 Συναρτησιακές Εξαρτήσεις Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Θεωρία για το πότε ένας σχεδιασµός είναι «καλός» Η θεωρία βασίζεται στις Συναρτησιακές Εξαρτήσεις (Functional Dependencies)
Συναρτησιακές Εξαρτήσεις Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Θεωρία για το πότε ένας σχεδιασµός είναι «καλός» Η θεωρία βασίζεται στις Συναρτησιακές Εξαρτήσεις (Functional Dependencies)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 23: οµές εδοµένων και Αλγόριθµοι Ενδιάµεση Εξέταση Ηµεροµηνία : ευτέρα, 3 Νοεµβρίου 2008 ιάρκεια : 2.00-4.00 ιδάσκουσα : Άννα Φιλίππου Ονοµατεπώνυµο: ΣΚΕΛΕΤΟΙ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 23: οµές εδοµένων και Αλγόριθµοι Ενδιάµεση Εξέταση Ηµεροµηνία : ευτέρα, 3 Νοεµβρίου 2008 ιάρκεια : 2.00-4.00 ιδάσκουσα : Άννα Φιλίππου Ονοµατεπώνυµο: ΣΚΕΛΕΤΟΙ
επιστρέφει το αμέσως μεγαλύτερο από το x στοιχείο του S επιστρέφει το αμέσως μικρότερο από το x στοιχείο του S
 Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών,, τα οποίo είναι υποσύνολο του. Υποστηριζόμενες λειτουργίες αναζήτηση(s,x): εισαγωγή(s,x): διαγραφή(s,x): διάδοχος(s,x): προκάτοχος(s,x):
Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών,, τα οποίo είναι υποσύνολο του. Υποστηριζόμενες λειτουργίες αναζήτηση(s,x): εισαγωγή(s,x): διαγραφή(s,x): διάδοχος(s,x): προκάτοχος(s,x):
HY118- ιακριτά Μαθηµατικά. Θεωρία γράφων / γραφήµατα. Τι έχουµε δει µέχρι τώρα. Υπογράφηµα Γράφοι
 HY118- ιακριτά Μαθηµατικά Θεωρία γράφων / γραφήµατα Πέµπτη, 19/05/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 5/22/2016 1 1 5/22/2016 2 2 Τι έχουµε δει µέχρι τώρα Κατευθυνόµενοι µη κατευθυνόµενοι
HY118- ιακριτά Μαθηµατικά Θεωρία γράφων / γραφήµατα Πέµπτη, 19/05/2016 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 5/22/2016 1 1 5/22/2016 2 2 Τι έχουµε δει µέχρι τώρα Κατευθυνόµενοι µη κατευθυνόµενοι
ΠΛΗ111. Ανοιξη Μάθηµα 2 ο. Αλγόριθµοι και Αφηρηµένοι Τύποι εδοµένων. Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνείο Κρήτης
 ΠΛΗ111 οµηµένος Προγραµµατισµός Ανοιξη 2005 Μάθηµα 2 ο Αλγόριθµοι και Αφηρηµένοι Τύποι εδοµένων Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνείο Κρήτης Αλγόριθµοι Ορισµός Παράδειγµα Ασυµπτωτική
ΠΛΗ111 οµηµένος Προγραµµατισµός Ανοιξη 2005 Μάθηµα 2 ο Αλγόριθµοι και Αφηρηµένοι Τύποι εδοµένων Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Πολυτεχνείο Κρήτης Αλγόριθµοι Ορισµός Παράδειγµα Ασυµπτωτική
Εισαγωγή στους Αλγόριθµους. Αλγόριθµοι. Ιστορικά Στοιχεία. Ο πρώτος Αλγόριθµος. Παραδείγµατα Αλγορίθµων. Τι είναι Αλγόριθµος
 Εισαγωγή στους Αλγόριθµους Αλγόριθµοι Τι είναι αλγόριθµος; Τι µπορεί να υπολογίσει ένας αλγόριθµος; Πως αξιολογείται ένας αλγόριθµος; Παύλος Εφραιµίδης pefraimi@ee.duth.gr Αλγόριθµοι Εισαγωγικές Έννοιες
Εισαγωγή στους Αλγόριθµους Αλγόριθµοι Τι είναι αλγόριθµος; Τι µπορεί να υπολογίσει ένας αλγόριθµος; Πως αξιολογείται ένας αλγόριθµος; Παύλος Εφραιµίδης pefraimi@ee.duth.gr Αλγόριθµοι Εισαγωγικές Έννοιες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii018/laii018html ευτέρα 3 Απριλίου 018 Αν C = x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 5 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii018/laii018html ευτέρα 3 Απριλίου 018 Αν C = x
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 23 Μαρτίου 2017 1 / 170 Αναδροµή ιαίρει
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 23 Μαρτίου 2017 1 / 170 Αναδροµή ιαίρει
Προσεγγιστικοί Αλγόριθμοι
 Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. http://xkcd.com/287/ Πολλά NP-πλήρη προβλήματα έχουν μεγάλο πρακτικό ενδιαφέρον. Πως μπορούμε να αντιμετωπίσουμε το γεγονός ότι είναι απίθανη(;)
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 4: Αναδρομικές σχέσεις και ανάλυση αλγορίθμων Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 4: Αναδρομικές σχέσεις και ανάλυση αλγορίθμων Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ανάλυση αλγορίθμων. Χρόνος εκτέλεσης: Αναμενόμενη περίπτωση. - απαιτεί γνώση της κατανομής εισόδου
 Ανάλυση αλγορίθμων Παράμετροι απόδοσης ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, επικοινωνία (π.χ. σε κατανεμημένα συστήματα) Προσπάθεια υλοποίησης Ανάλυση της απόδοσης Θεωρητική
Ανάλυση αλγορίθμων Παράμετροι απόδοσης ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, επικοινωνία (π.χ. σε κατανεμημένα συστήματα) Προσπάθεια υλοποίησης Ανάλυση της απόδοσης Θεωρητική
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 1 Εισαγωγικές έννοιες Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 1 1 / 57 Περιεχόµενα 1.
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 1 Εισαγωγικές έννοιες Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 1 1 / 57 Περιεχόµενα 1.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
Αριθµητική Ανάλυση 1 εκεµβρίου / 43
 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Εισαγωγή. Οπως είδαµε για την εκκίνηση της Simplex χρειαζόµαστε µια Αρχική Βασική Εφικτή Λύση. υϊσµός
 Εισαγωγή Οπως είδαµε για την εκκίνηση της Simplex χρειαζόµαστε µια Αρχική Βασική Εφικτή Λύση Εισαγωγή Οπως είδαµε για την εκκίνηση της Simplex χρειαζόµαστε µια Αρχική Βασική Εφικτή Λύση Σε περιπτώσεις
Εισαγωγή Οπως είδαµε για την εκκίνηση της Simplex χρειαζόµαστε µια Αρχική Βασική Εφικτή Λύση Εισαγωγή Οπως είδαµε για την εκκίνηση της Simplex χρειαζόµαστε µια Αρχική Βασική Εφικτή Λύση Σε περιπτώσεις
Θεωρία Αποφάσεων και Βελτιστοποίηση
 Θεωρία Αποφάσεων και Βελτιστοποίηση http://www.di.uoa.gr/ telelis/opt.html Ορέστης Τελέλης telelis@di.uoa.gr Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών Θεωρία Αποφάσεων και Βελτιστοποίηση
Θεωρία Αποφάσεων και Βελτιστοποίηση http://www.di.uoa.gr/ telelis/opt.html Ορέστης Τελέλης telelis@di.uoa.gr Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών Θεωρία Αποφάσεων και Βελτιστοποίηση
Παράλληλοι Αλγόριθµοι
 Παράλληλοι Αλγόριθµοι Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Το µοντέλο PRAΜ Πολλαπλασιασµός πινάκων Υπολογισµός αθροισµάτων προθέµατος ΕΠΛ 232 Αλγόριθµοι και Πολυπλοκότητα 13-1 Παράλληλοι Αλγόριθµοι
Παράλληλοι Αλγόριθµοι Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Το µοντέλο PRAΜ Πολλαπλασιασµός πινάκων Υπολογισµός αθροισµάτων προθέµατος ΕΠΛ 232 Αλγόριθµοι και Πολυπλοκότητα 13-1 Παράλληλοι Αλγόριθµοι
