3.2.2 Το CL file... 22
|
|
|
- Ζηνόβιος Γκόφας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΤΕΙ ΧΑΛΚΙ ΑΣ ΣΤΕΦ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΧΕ ΙΑΣΗ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ (CAD) ΚΑΙ ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ (CAM) ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ Μαρία Γεωργακάλου, Χριστόφορος Οικονοµάκος, Σταµατία Στεφανάτου Ψαχνά, Νοέµβριος 2010
2 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ... i ΚΕΦΑΛΑΙΟ 1: Εντολές του AutoCAD Εντολές σχεδίασης Η εντολή LINE Τρόποι εισαγωγής της εντολής POINT Παραδείγµατα εισαγωγής της εντολής LINE Η εντολή CIRCLE Τρόποι εισαγωγής Παραδείγµατα Η εντολή ARC Τρόποι εισαγωγής Βοηθητικές εντολές H εντολή GRID Η εντολή SNAP Η εντολή OSNAP Η εντολή PAN Η εντολή BREAK Η εντολή TRIM Η εντολή FILLET Η εντολή CHAMFER Η εντολή LAYER Η εντολή ISOPLANE Η εντολή MIRROR... 9 ΚΕΦΑΛΑΙΟ 2: CAM Συστήµατα Μ/Μ/ Ανασκόπηση θεωρίας Χρήση (Utilization) Εκτίµηση του χρόνου Αναµονής Ο υπολογισµός του χρόνου αναµονής µε τον τύπο του Little Κατανοµή του Χρόνου αναµονής των ουρών M/M/ Παραδείγµατα Παράδειγµα Παράδειγµα Η ουρά M/M/m/m Ανασκόπηση θεωρίας: Ο εύτερος τύπος του Erlang (Erlang-B formula) Παράδειγµα Γενικά περί CNC G-codes Προγραµµατισµός των µηχανών CNC Η γλώσσα APT Παράδειγµα : Παρατηρήσεις-Σχόλια: Παράδειγµα- Άσκηση: Το CL file Παράδειγµα Παρατηρήσεις-Σχόλια Η γλώσσα «Dumb APT» Η χρήση των γραµµάτων I, J και K i
3 4. Εισαγωγή στα Ευέλικτα Συστήµατα Παραγωγής [FMS (Flexible Manufacturing Systems)] Ανασκόπηση Θεωρίας Παράδειγµα Βιβλιογραφία ΠΑΡΑΡΤΗΜΑ 1: Παραδείγµατα των εντολών CIRCLE, ARC καθώς και των βοηθητικών εντολών µε χρήση της έκδοσης 2010 του AutoCAD ΠΑΡΑΡΤΗΜΑ 2: Παραδείγµατα χρήσης AutoCAD Παράδειγµα Παράδειγµα 2: (σταυρός της Μάλτας) ii
4 ΚΕΦΑΛΑΙΟ 1: Εντολές του AutoCAD 1.1. Εντολές σχεδίασης Η εντολή LINE Με την εντολή LINE, σχεδιάζουµε γραµµές. Υπάρχουν τέσσερις τρόποι για να γίνει η εισαγωγή των συντεταγµένων των ακραίων σηµείων ενός ευθύγραµµου τµήµατος Τρόποι εισαγωγής της εντολής POINT α) Απόλυτος µε εισαγωγή των απολύτων συντεταγµένων των σηµείου από την prompt περιοχή Παράδειγµα Command: Point <return> Point: 2,1 <return> Command: <return> POINT <return> β) Σχετικός, µε εισαγωγή των σχετικών συντεταγµένων του σηµείου, ως προς το προηγούµενο ορισµένο σηµείο, από την prompt περιοχή γ) Σχετικός, µε εισαγωγή της απόστασης και της γωνίας που σχηµατίζει αυτή µε τον οριζόντιο άξονα, µε θετική φορά την αντίθετη απ αυτήν των δεικτών του ρολογιού, από την prompt περιοχή Παράδειγµα Command:<return> POINT <return> δ) Με το σταυρόνηµα, παρατηρώντας τις τρέχουσες συντεταγµένες του κέντρου του στην Status Line Παραδείγµατα εισαγωγής της εντολής LINE Command: line <return> From point: 4, 2 <return> To point: 6, 5 <return> To point: <return> Απόλυτη εισαγωγή σηµείου αρχής Απόλυτη εισαγωγή Σηµείου πέρατος ιακοπή εντολής Command: LINE <return> From point: 6, 5 <return> To point: 6, 8 <return> To point: 8, 16.5 <return> 1
5 To <return> Σχετική εισαγωγή συντεταγµένων σηµείου πέρατος. Με το συγκεκριµένο παράδειγµα, ζητούµε το σηµείο πέρατος να είναι στο σηµείο: χ= (8+2)=10, ψ=( )=3. To <200 To point: c <return> Σχετική εισαγωγή συντεταγµένων του σηµείου πέρατος. Με το συγκεκριµένο παράδειγµα, ζητούµε τον σχεδιασµό ενός ευθυγράµµου τµήµατος που έχει µήκος 1 και σχηµατίζει µε τον οριζόντιο άξονα, γωνία 200 µοιρών. Το σηµείο αρχής είναι το σηµείο τέλους του προηγούµενου ευθύγραµµου τµήµατος (δηλαδή, το 10,3) και σαν θετική φορά, θεωρούµε αυτήν που είναι αντίθετη από την φορά των δεικτών του ρολογιού. Κλείσιµο της πολυγωνικής γραµµής µε εισαγωγή του χαρακτήρα c (close) Η εντολή CIRCLE Με την εντολή CIRCLE, σχεδιάζουµε έναν κύκλο. Υπάρχουν τέσσερις τρόποι ορισµού ενός κύκλου στο AutoCAD Τρόποι εισαγωγής α) Τρία σηµεία της περιφέρειας του κύκλου. β) ύο αντιδιαµετρικά σηµεία του γ) Το κέντρο και την ακτίνα δ) Το κέντρο και τη διάµετρο Παραδείγµατα Command: circle <return> 3P/2P/<Center point>: 3P <return> (Επιλογή των τριών σηµείων) First point: 3, 4 <return> Second point: 4, 5 <return> Third point: 5,5 <return> Command: <return> Command: CIRCLE <return> 3P/2P/ <Center point>: 2P <return> First point on diameter: 3, 8 <return> Second point on diameter: 5, 10 <return> Command: <return> (2 αντιδιαµετρικά σηµεία) Command: CIRCLE <return> 3P/2P/<Center point>: 9, 8 <return> (εισαγωγή του κέντρου του κύκλου) Diameter/<Radius>: 2 <return> (ορισµός µήκους ακτίνας 2) Command:<return> 2
6 Command: CIRCLE <return> 3P/2P/<Center point>: 9, 5 <return> (ορισµός κέντρου) Diameter/<Radius>: d <return> (d η διάµετρος) Diameter: 8 <return> Η εντολή ARC Με την εντολή ARC σχεδιάζουµε τόξα. Υπάρχουν οκτώ τρόποι σχεδίασης ενός τόξου στο AutoCAD. Επίσης, θετική είναι η φορά που είναι αντίθετη από αυτήν των δεικτών του ρολογιού Τρόποι εισαγωγής (ΠΡΟΣΟΧΗ: Αν κάποιο από τα σηµεία που εισάγουµε δεν είναι «συµβατό» µε τα προηγούµενα, το τόξο σταµατά στο σηµείο τοµής του µε την ευθεία: κέντροσηµείο τέλους, ανεξάρτητα από τον τρόπο εισαγωγής του τόξου) α) Τρία σηµεία: Αρχή, ενδιάµεσο σηµείο, τέλος. Παράδειγµα: Command: arc <return> Center/<Start point>: 3, 6.6 <return> Center/End/<Second point>: 2, 7.6 <return> End point: 2, 5.6 <return> β) Τρία σηµεία: Σηµείο αρχής, κέντρο κύκλου που περιέχει το τόξο, τέλος. Παράδειγµα: Command: ARC <return> Center/ <Start point>: 5, 6<return> Center/ End/<Second point>: c <return> Center: 4, 6 <return> Angle/Length of chord/<end point>: 4, 8 <return> (αν το σηµείο τέλους δεν είναι «συµβατό» µε τα προηγούµενα, το τόξο σταµατά στο σηµείο τοµής του µε την ευθεία: κέντρο-σηµείο τέλους) γ) Σηµείο αρχής, κέντρο κύκλου, επίκεντρη γωνία του τόξου. Παράδειγµα: Command: ARC <return> Center/<Start point>: 7, 6 <return> Center/ End/<Second point>: c <return> Center: 6, 6 <return> Angle/Length of chord/<end point>: a <return> Included angle: 50 or 50 <return> 3
7 δ) Σηµείο αρχής, κέντρο κύκλου, µήκος της αντίστοιχης χορδής. Παράδειγµα: Command: ARC <return> Center/<start point>: 9, 6 <return> Center/ End/ <Second point>: c <return> Center: 8, 6 <return> Angle/ Length of chord/ <End point>: l <return> Length of chord: 1.5 <return> ε) Σηµεία αρχής, τέλους και µήκος ακτίνας του κύκλου. Παράδειγµα: Command: ARC <return> Center/ <Start point>: 3, 2 <return> Center/ End/ <Second point>: e <return> End point: 2, 3 <return> Angle/ Direction/ Radius/ <Center point>: r <return> Radius: 1.5 <return> στ) Σηµεία αρχής, τέλους και επίκεντρη γωνία. Παράδειγµα: Command: ARC <return> Center/ <Start point>: 5.5, 2 <return> Center/ End/ <Second point>: e <return> End point: 4.5, 3 <return> Angle/ Direction/ Radius/ <Center point>: a <return> Included angle: 60 or -60 <return> ζ) Σηµεία αρχής, τέλους και τη γωνία που σχηµατίζει η εφαπτόµενη στο σηµείο αρχής, µε τον οριζόντιο άξονα ( ιεύθυνση). Παράδειγµα: Command: ARC <return> Center/ <Start point>: 8, 2 <return> Center/ End/ <Second point>: e <return> End point: 6, 3 <return> Angle/ Direction/ Radius/ <Center point>: d <return> Direction from start point: 42 <return> (Με τον όρο direction, εννοούµε τη διεύθυνση που εκφράζει τη γωνία που σχηµατίζει η εφαπτόµενη του τόξου στο σηµείο αρχής µε τον οριζόντιο άξονα.) 4
8 η) Κατασκευή τόξου σαν συνέχεια κάποιου άλλου, δίνοντας µόνο το σηµείο τέλους του νέου τόξου και όπου το πρόγραµµα θεωρεί σαν σηµείο αρχής το τέλος του προηγούµενου και µε την ίδια διεύθυνση. Παράδειγµα: Command: ARC <return> Center/ <Start point>: <return> End point: 7, 2 <return> (Με αυτόν τον τρόπο, η χάραξη τόξου γίνεται µε σηµείο αρχής το τέλος του προηγούµενου και µε την προηγούµενη διεύθυνση) Βοηθητικές εντολές H εντολή GRID Με την εντολή GRID δηµιουργούµε το σταυρόνηµα Η εντολή SNAP Με την εντολή SNAP επιτυγχάνουµε την µεθοδευµένη µετακίνηση του σταυρονήµατος. Επίσης, έχουµε τη δυνατότητα τροποποίησης της κλίσης των αξόνων του, ανάλογα µε τις σχεδιαστικές µας απαιτήσεις. Παραδείγµατα: Command: snap <return> SNAP On/Off/ Value/Aspect/Rotate/Style: 0.2 <return> (ορίζουµε το βήµα µετακίνησης του σταυρονήµατος σε 0.2, χρησιµοποιώντας απ ευθείας την εντολή value) Command: snap <return> SNAP On/Off/Value/Aspect/Rotate/Style: off <return> (απενεργοποίηση του snap) Command: snap <return> SNAP On/Off/Value/Aspect/Rotate/Style: On <return> (ενεργοποίηση) Η εντολή OSNAP Με την εντολή αυτή µας δίνεται η δυνατότητα να επιλέξουµε µία ή περισσότερες συνθήκες που στη συνέχεια θα χρησιµοποιούµε για την επιλογή σηµείων. Παράδειγµα Command: OSNAP <return> Object Snap Modes: END, MID <return> (Απαντούµε στην prompt περιοχή µε τις συνθήκες End, Mid για την επιλογή τελικών και µεσαίων σηµείων, αντίστοιχα) Command: OSNAP <return> Object Snap Modes: None <return> (Αναιρούµε τις προηγούµενες επιλογές.) Τέλος, υπάρχουν στην εντολή OSNAP και οι επιλογές On/Off. 5
9 1.2.4 Η εντολή PAN Η εντολή ΡΑΝ µας δίνει τη δυνατότητα να µετακινήσουµε το σχέδιο προς κάθε διεύθυνση. Παράδειγµα Command: pan <return> Displacement: 6,2 <return> (ορισµός πρώτου σηµείου µετακίνησης) Second point: 8,5 <return> (ορισµός σηµείου οθόνης στο οποίο επιθυµούµε να βρεθεί το πρώτο µετά την µετακίνηση) Η εντολή BREAK Σχεδιάζουµε µία απλή γραµµή και στη συνέχεια Command: break <return> Select object: (Με το σταυρόνηµα επιλέγουµε ένα σηµείο πάνω στην ευθεία. Επιλέγουµε το αντικείµενο του οποίου επιθυµούµε να διακόψουµε τη συνέχεια και παρατηρούµε ότι το αντικείµενο που επιλέξαµε µισοσβήνει) Enter second point or F: 5,2 <return> (επιλέγουµε ένα δεύτερο σηµείο) Παρατηρούµε ότι το κοµµάτι της γραµµής µεταξύ των δύο σηµείων δεν υπάρχει πλέον (έχει αποκοπεί µετά την εφαρµογή της εντολής «break») Θα µπορούσαµε εναλλακτικά να κάνουµε την επιλογή των δύο σηµείων µε χρήση του σταυρονήµατος, αν επιλέγαµε Command: break <return> Select object: (επιλέγουµε µε το σταυρόνηµα) Enter second point or F: F <return> Enter first point: 6,1<return> Enter second point: 6,2<return> Η εντολή TRIM (κάναµε εισαγωγή των δύο σηµείων µε χρήση του σταυρονήµατος) Με την εντολή TRIM, επιλέγουµε το όριο και στη συνέχεια κόβουµε αυτά που περισσεύουν. Παράδειγµα: Όριο είναι η επάνω πλευρά του παραλληλογράµµου και θέλουµε να κόψουµε τις δύο γραµµές που περισσεύουν προς τα κάτω. Εποµένως, µαρκάρουµε το όριο και κάνουµε ΤRIM πρώτα στην αριστερή γραµµή που περισσεύει 6
10 και µετά στη δεξιά Η εντολή FILLET Με την εντολή αυτή ενώνουµε δύο γραµµές χρησιµοποιώντας στην προσαρµογή τους κυκλικά τόξα Παράδειγµα Command: FILLET <return> Polyline/ Radius/<Select two lines>: R <return> Enter fillet radius: 1.5 <return> Command: FILLET <return> Polyline/ Radius/<Select two lines>: Command: <return> Η εντολή CHAMFER Με την χρήση της εντολής CHAMFER δηµιουργούµε αποτµήσεις σε κάποιες κορυφές Παράδειγµα Command: CHAMFER <return> Polyline/Distances/<Select first line>: D Enter first Chamfer Distance <0,0>: 1.5 <return> Enter second chamfer Distance <1,0>: 0.5 <return> Command: CHAMFER <return> Chamfer Polyline/Distances/<Select first line>: Select second line: (επιλέγουµε αποστάσεις) Η εντολή LAYER Η εντολή LAYER χρησιµοποιείται για να έχουµε τα διάφορα τµήµατα του σχεδίου σε διαφορετικά επίπεδα. Για παράδειγµα στην κάτοψη ενός σπιτιού, µπορούµε να φτιάξουµε διαφορετικά επίπεδα για το αρχιτεκτονικό σχέδιο, για το µηχανολογικό, το ηλεκτρολογικό, το υδραυλικό και το διακοσµητικό. Κάθε φορά ενεργοποιούµε το επίπεδο πάνω στο οποίο θέλουµε να δουλέψουµε, ενώ όποτε θέλουµε µπορούµε να δούµε όλα τα επίπεδα µαζί (δηλαδή το πλήρες σχέδιο). Παραδείγµατα: Command: LAYER <return>?/set/new/on/off/color/ltype/freeze/thaw:? <return> ( ώσαµε την επιλογή «?») Layer name(s) for listing<*>: <return> 7
11 Στο σηµείο αυτό µπορούµε να απαντήσουµε 1 (το όνοµα του νέου layer) Αν απαντήσουµε: New?/Set/New/On/Off/Color/Ltype/Freeze/Thaw: New <return> New Layer name(s): squares, circles, lines <return> (ορίσαµε 3 νέα layers µε αντίστοιχα ονόµατα «squares», «circles», «lines» <return>) Αν απαντήσουµε: Set?/Set/New/On/Off/Color/Ltype/Freeze/Thaw: Set <return> New current Layer <1>: Squares (ορίσαµε το «Square» ως το τρέχον σχεδιαστικό επίπεδο. Με άλλα λόγια, µόνο σε αυτό το επίπεδο µπορούµε να σχεδιάσουµε) Οι επιλογές: On/Off ορίζουν τι αν τα µη ενεργά επίπεδα θα είναι ορατά ή όχι. Αν απαντήσουµε: c (δηλαδή Color)?/Set/New/On/Off/Color/Ltype/Freeze/Thaw: c <return> Color: 4 <return> (χρώµα 3, δηλαδή πράσινο) Layer name(s) for color 4 (red) <0>: Squares <return> (ορίσαµε ότι θέλουµε κόκκινο να είναι το επίπεδο «Squares» Αν απαντήσουµε: Ltype?/Set/New/On/Off/Color/Ltype/Freeze/Thaw: ltype<return> Linetype (or?) <CONTINUOUS>: <return> (ορίσαµε ότι θέλουµε οι γραµµές να είναι συνεχείς) Αν απαντήσουµε: Freeze?/Set/New/On/Off/Color/Ltype/Freeze/Thaw: Freeze <return> Layer name(s) to Freeze: Circle <return> (ορίσαµε ότι θέλουµε το επίπεδο «Circle» να παγώσει) Αν απαντήσουµε: Thaw, «ξεπαγώνουµε» το αντίστοιχο επίπεδο, δηλαδή επαναφέρουµε κάποιο Layer, το οποίο προηγουµένως είχαµε κάνει «Freeze» Η εντολή ISOPLANE Αν θέλουµε να σχεδιάσουµε ένα αξονοµετρικό σχέδιο που αποτελείται από γραµµές µε κλίση 30, 90 και 150 µοιρών µε τις εξής κατευθύνσεις: - Γραµµές 30 µε δεξιά κατεύθυνση - Γραµµές 90 µε κάθετη κατεύθυνση - Γραµµές 150 µε αριστερή κατεύθυνση Command: snap <return> On/Off/ Value/Aspect/Rotate/Style: 0.2 <return> Command: <return> Snap On/Off/Value/Aspect/Style: s <return> Standard/Isometric: I <return> Vertical spacing <0.20>: <return> 8
12 (ορίσαµε Snap-On µε βήµα 0.20, επιλέξαµε την ισοµετρική µορφή του σταυρονήµατος) Command: isoplane <return> Left/Top/Right (toggle): <return> Current isometric plan is: Top Πατώντας µερικές φορές το <return>, παρατηρούµε ότι η εντολή επαναλαµβάνεται µεταβάλλοντας την ενεργό ισοµετρία (Current isometric plan) διαδοχικά, σε right, left, top κτλ. Η επιλογή γίνεται µε το αρχικό γράµµα και <return>. Επιλέγουµε τη δεξιά ισοµετρία και παρατηρούµε τη µεταβολή της κλίσης του οριζόντιου άξονα σε 30. Επανερχόµαστε στην αρχική (οριζόντια) θέση του σταυρονήµατος: Command: snap <return> On/Off/Value/Aspect/Rotate/Style: s <return> Standard/Isometric: s <return> Value/Aspect <0.20>: <return> Η εντολή MIRROR Με την εντολή MIRROR, σχεδιάζουµε κατοπτρικά (συµµετρικά) αντικείµενα. Command: mirror Select objects or Window or Last: (Επιλέγουµε το αντικείµενο του οποίου θέλουµε να κατασκευαστεί το κατοπτρικό) Select objects or Window or Last <return> (Στο σηµείο αυτό ζητείται ένα σηµείο στον άξονα συµµετρίας, µε βάση τον οποίο θα δηµιουργηθεί το κατοπτρικό του σχήµατος) Second point: (Στο σηµείο αυτό πρέπει να κάνουµε εισαγωγή ενός δεύτερου σηµείου, που µαζί µε το πρώτο θα ορίζουν τον άξονα συµµετρίας) Delete old objects? <N> <return> (το πρόγραµµα στο σηµείο αυτό ρωτάει αν θέλουµε να διαγραφεί το πρωτότυπο σχήµα, µετά την δηµιουργία του κατοπτρικού µε την επιλογή <Ν> να θεωρείται default) 9
13 ΚΕΦΑΛΑΙΟ 2: CAM 2.1 Συστήµατα Μ/Μ/ Ανασκόπηση θεωρίας Η ουρά Μ/Μ/1 είναι η πιο σηµαντική διαδικασία ουράς Άφιξη: ιαδικασία Poisson Εξυπηρέτηση: Ακολουθεί εκθετική κατανοµή Εξυπηρετητής: Ένας Χώρος αναµονής: Άπειρος Ας υποθέσουµε ότι N(t) είναι ο αριθµός των πελατών στο σύστηµα (συµπεριλαµβανοµένου και αυτού που εξυπηρετείται τώρα). Τότε N(t) είναι η διαδικασία γέννησης-θανάτου µε: λ k = λ µ k = µ P(Άφιξη ακριβώς ενός πελάτης στο χρονικό διάστηµα [t, t + t]) = λ t P( εδοµένου ότι υπάρχει τουλάχιστον ένας πελάτης στο σύστηµα, ακριβώς µία εξυπηρέτηση ολοκληρώνεται στο χρονικό διάστηµα [t, t + t]) = µ t Μία ουρά M/M/1 είναι η διαδικασία γέννησης-θανάτου µε σταθερό ρυθµό γέννησης (ρυθµό αφίξεων) και σταθερό ρυθµό θανάτου (ρυθµό εξυπηρέτησης). Όταν ρ< 1, τότε p k = P[N(t) = k] = (1- ρ) ρ k, όπου ρ= λ/ µ Χρήση (Utilization) Τότε, από το γεγονός ότι p k = 1, έχουµε: p k = (1- ρ) ρ k. Εύκολα προκύπτει ότι: E[N(t)] = ρ /(1- ρ). Η ποσότητα ρ αποκαλείται χρήση (utilization) του συστήµατος. Αφού p 0 είναι η πιθανότητα το σύστηµα να είναι άδειο, τότε ρ= 1- p 0 είναι η πιθανότητα ο m να είναι ο πελάτης υπό εξυπηρέτηση. Όταν ρ 1, τότε το σύστηµα είναι ασταθές (unstable). Πράγµατι, ο αριθµός των πελατών στο σύστηµα θα αρχίσει να τείνει στο Εκτίµηση του χρόνου Αναµονής Για τον πελάτη του συστήµατος, ο χρόνος αναµονής είναι πιο σηµαντικός από τον αριθµό των πελατών που βρίσκονται στο σύστηµα. Η πληροφορία σχετικά µε τον χρόνο αναµονής, µπορεί να εξαχθεί µε δύο τρόπους: Ο υπολογισµός του χρόνου αναµονής µε τον τύπο του Little Ας υποθέσουµε ότι Sn είναι ο χρόνος εξυπηρέτησης του n-ιοστού πελάτη και ότι Wn είναι ο χρόνος αναµονής του. Ο χρόνος παραµονής Yn προκύπτει από την σχέση: Yn =Wn+Sn. 10
14 E[W] = (ρ/ µ) /(1- ρ) Κατανοµή του Χρόνου αναµονής των ουρών M/M/1 Ο τύπος του Little δίνει µία εκτίµηση του µέσου χρόνου αναµονής. Η ίδια η κατανοµή, όµως προκύπτει από την παρακάτω σχέση, πού είναι η κατανοµή του Erlang (Erlang distribution). Αν {Si}i=1,...,m είναι µία ακολουθία ανεξάρτητων και ταυτόσηµων τυχαίων µεταβλητών που ακολουθούν την εκθετική κατανοµή και µέσο 1/ µ, και m X = Σ S i, i=1 τότε έχουµε ότι: dp{x t}/dt = [λ( λt) m-1 / (m-1)!] e -λt. Αν W είναι ο χρόνος αναµονής µίας ουράς M/M/1, τότε έχουµε ότι µ (1-ρ) w P [W w] = 1- ρ e 2.2 Παραδείγµατα Παράδειγµα 1 Ας θεωρήσουµε ένα σύστηµα γέννησης/ θανάτου Μ/Μ/1 µε τα εξής χαρακτηριστικά: Οι µηχανές συνδέονται σε σειρά εν υπάρχουν ενδιάµεσοι χώροι αποθήκευσης. Οι χρόνοι είναι εκθετικοί. Οι εξισώσεις που εκφράζουν αυτό το σύστηµα είναι της µορφής: P k (t), k =0,1 Είναι προφανές, ότι το σύστηµα µπορεί να έχει δύο καταστάσεις: Στην κατάσταση 0 το σύστηµα είναι άδειο Στην κατάσταση 1 το σύστηµα είναι γεµάτο. Ο ρυθµός εισαγωγής στο σύστηµα είναι λ, ενώ ο ρυθµός εξυπηρέτησης είναι µ. Το διάγραµµα ροής των πιθανοτήτων για το παραπάνω σύστηµα είναι το εξής: λ 0 1 µ 11
15 Οι διαφορικές εξισώσεις που εκφράζουν το συγκεκριµένο σύστηµα είναι οι εξής: dp 0 /dt = - λ P 0 (t) + µp 1 (t) (1) dp 1 /dt= - µ P 1 (t) + λ P 0 (t) (2) p 0 (t)+p 1 (t) = 1 (3) Από τις σχέσεις (1) και (3), συµπεραίνουµε ότι: dp 0 /dt= -(λ+µ) P 0 (t) + µ Επιλύοντας την διαφορική εξίσωση: P 0 (t)= [µ/ (λ+µ)] + {P 0 (0)- [λ/(λ+µ)]} e (λ+µ)t Προφανώς: P 1 (t) = 1 P 0 (t) Παράδειγµα 2 Θεωρήστε έναν εξυπηρετητή WWW. Οι χρήστες προσεγγίζουν τον εξυπηρετητή ακολουθώντας µία διαδικασία Poisson µε µέση τιµή 10 προσεγγίσεις/sec. Ο εξυπηρετητής επεξεργάζεται τη κάθε προσέγγιση ανάλογα µε τον χρόνο, που ακολουθεί εκθετική κατανοµή µε µέση τιµή 0.01 sec. λ= 10. 1/ µ= ρ= λ/ µ= = 0.1. Έτσι το σύστηµα έχει χρήση 0.1 και ο αριθµός των πελατών που είναι στην αναµονή έχουν την εξής κατανοµή: P[N(t) = n] = (1- ρ) ρ n = n E[N(t)] =ρ/(1- ρ) = 1/ Η ουρά M/M/m/m Ανασκόπηση θεωρίας: Ο εύτερος τύπος του Erlang (Erlang-B formula) Αφίξεις: ιαδικασία Poisson Εξυπηρέτηση: Εκθετική κατανοµή Εξυπηρετητές: m Χώρος αναµονής: 0 Όποιος πελάτης εισέρχεται σε µία ουρά M/M/m/m στο χρόνο που όλοι οι εξυπηρετητές είναι απασχοληµένοι θα µπλοκαριστεί και θα χαθεί. Η κατανοµή της σταθερής κατάστασης (steady-state distribution), προκύπτει από τη σχέση: p k = (λ/µ) k m k! Σ(λ/µ) i (1/i!) i=0 η πιθανότητα όλοι οι εξυπηρετητές να είναι απασχοληµένοι, ή αλλιώς η Erlang-B formula, δίνεται από τη σχέση: 12
16 p m = (λ/µ) m m m! Σ (λ/µ) i (1/i!) i=0 Η p m καλείται πιθανότητα µπλοκαρίσµατος (blocking probability) Παράδειγµα Εκτιµήστε την πιθανότητα µπλοκαρίσµατος (blocking probability) µίας γραµµής εισητηρίων µε 200 γραµµές. Ο µέσος αριθµός των πιθανών τηλεφωνικών κλήσεων από πελάτες είναι 50 κλήσεις/λεπτό και κάθε κλήση έχει µέσο χρόνο εξυπηρέτησης 3 λεπτά. Εποµένως: λ= 50 µ= 1/3 m = 200 Τότε η πιθανότητα µπλοκαρίσµατος µπορεί να υπολογιστεί από την σχέση: p m = (λ/µ) m m m! Σ (λ/µ) i (1/i!) i=0 13
17 3. Γενικά περί CNC CNC είναι τα αρχικά των λέξεων Computer Numerical Control και αναφέρεται στην λειτουργία µίας εργαλειοµηχανής µε χρήση µηχανισµών, διακοπτών, κτλ., µε έναν υπολογιστή ο οποίος έχει τον γενικό έλεγχο. DNC: Πρόκειται είτε για την συντοµογραφία του Direct Numerical Control, είτε για την συντοµογραφία του Distributed Numerical Control. Όλοι οι ορισµοί πάντως εµπεριέχουν την επικοινωνία του υπολογιστή µε την εργαλειοµηχανή. Αρχικά, επρόκειτο για µία φιλόδοξη προσέγγιση η οποία περιελάµβανε τον έλεγχο πολλαπλών εργαλειοµηχανών κατ ευθείαν από έναν κεντρικό υπολογιστή. Ο κεντρικός υπολογιστής ήταν απ ευθείας συνδεδεµένος µε τις σερβοµηχανές. Σταδιακά, ο όρος «DNC» υιοθετήθηκε, ιδιαίτερα από τη στιγµή που η προσέγγιση του κεντρικού υπολογιστή δεν ήταν και πολύ επιτυχηµένη. 3.1 G-codes Τα προγράµµατα CNC συνήθως φτιάχνονται από λεκτικές διευθύνσεις (word addresses). Αυτές ξεκινούν µε ένα γράµµα και συνήθως ακολουθούνται από µία αριθµητική τιµή. Συνήθως, η αναφορά σε µία λέξη γίνεται µε το γράµµα της, έτσι για παράδειγµα η λέξη X3.5 (η οποία καθορίζει µία συγκεκριµένη θέση πάνω στον άξονα X) αποκαλείται «λέξη-χ» («X-word») και η λέξη F15.0 -η οποία συµβολίζει µία ταχύτητα κοπής (feedrate)- αποκαλείται «λέξη- F» («F-word»). Η ταχύτητα κοπής αναφέρεται µε διάφορους τρόπους καθορίζοντας την ταχύτητα µε την οποία το εργαλείο κινείται κατά µήκος του υλικού. Συνήθως προσδιορίζεται σε ένα πρόγραµµα CNC µε µία «F-word», όπως για παράδειγµα F30.0. Για µία εργαλειοµηχανή, η οδήγηση του κοπτικού εργαλείου από το ένα σηµείο στο διάστηµα προς κάποιο άλλο και µε την προκαθορισµένη ταχύτητα, ο κάθε άξονας είναι πιθανόν να χρειάζεται να κινηθεί µε µία διαφορετική ταχύτητα. Σε µία καµπύλη, το άκρο του κοπτικού εργαλείου θα κόβει µε διαφορετική ταχύτητα από αυτήν µε την οποία κόβει το κέντρο. Οι «λέξεις- G» («G-words») παριστούν τους «Κώδικες Συναρτήσεων Προετοιµασίας» (Preparatory Function Codes). Οι G-codes συνήθως προκαλούν την κίνηση των µηχανών και για να είµαστε τεχνικά ακριβείς, συχνά προκαλούν την ολίσθηση ή την κίνηση των αξόνων. Μερικές φορές ωστόσο, χρησιµοποιούµενοι αντικανονικά, µπορεί να προκαλέσουν και κίνηση µηχανής. Πρόκειται µε άλλα λόγια για 26 µετρητές οι οποίοι αποκαλούνται µε τα γράµµατα A- Z µέσα στον CNC ελεγκτή. Το G0 χρησιµοποιείται γενικά για να καταδείξει µία ταχεία διάσχιση (rapid traverse). Για παράδειγµα, η εντολή G0 X5.0 Z3.5 θα έχει σαν αποτέλεσµα το εργαλείο να κινηθεί σε µία θέση στον άξονα των Χ στο 5.0 και στον άξονα των Ζ στο 3.5 όσο το δυνατό γρηγορότερα. Το G1 χρησιµοποιείται για να µετακινηθεί ένα εργαλείο σε µία ευθεία µε τον ρυθµό κοπής που έχει καθοριστεί. Αυτό είναι λίγο πιο περίπλοκο απ ό,τι µπορεί να φαίνεται εκ πρώτης όψεως από την στιγµή που η κίνηση από το σηµείο A στο σηµείο B µε µία συγκεκριµένη ταχύτητα πολύ συχνά σηµαίνει ταυτόγχρονη κίνηση 3 αξόνων της 14
18 µηχανής προς τρεις διαφορετικές κατευθύνσεις. Οι κώδικες G1 συχνά καλούνται γραµµική παρεµβολή (linear interpolation). Για παράδειγµα, η εντολή G1 X4.5 Y3.0 Z-2.5 F20.0 θα έχει σαν αποτέλεσµα το εργαλείο να κινηθεί στην καθορισµένη θέση XYZ position µε έναν ρυθµό της τάξης των 20 ιντσών ή millimetres ανά λεπτό. Το G2 είναι το σηµείο όπου τα πράγµατα ξεκινούν να γίνονται ακόµη πιο περίπλοκα. Χρησιµοποιείται πάντα για την κατασκευή ενός τόξου, κινούµενο µε την φορά των δεικτών του ρολογιού µε την ταχύτητα που καθορίζουµε. Το G2 format που περιγράφεται στη συνέχεια, φτιάχνει ένα τόξο στο επίπεδο XY και καθορίζει το κέντρο του τόξου αυξητικά. Για παράδειγµα η εντολή G2 X-0.26 Y1.14 I0.5 J0.0 σηµαίνει: Ξεκινώντας από το σηµείο όπου αυτή τη στιγµή βρίσκεται το εργαλείο, κινήσου µε την φορά των δεικτών του ρολογιού σχηµατίζοντας ένα τόξο. Το κέντρο του τόξου έχει µία τιµή X 0.5 µεγαλύτερη από αυτήν της τρέχουσας θέσης (από το I0.5) και την ίδια τιµή Y µε την τρέχουσα θέση (J0.0). Σταµάτησε όταν φθάσεις στο σηµείο X-0.26 και Y1.14. Προχώρα µε οποιαδήποτε ταχύτητα κοπής έχει οριστεί τελευταία. Τα πράγµατα γίνονται ακόµη πιο περίπλοκα αν χρειαζόµαστε ένα τόξο που δεν είναι παράλληλο µε το επίπεδο XY. Κάποιες µηχανές επιτρέπουν στο G2 εντολές τόσο στο επίπεδο YZ όσο και στο ZX. Στην περίπτωση αυτή, οι αναφορές στο κέντρο ως προς τον άξονα Z διευθετούνται µε την χρήση των K-word. Μερικές µηχανές φτιάχνουν έλικες µε την χρήση ενός G2. Κάποιες άλλες φτιάχνουν έναν κύκλο µε τη χρήση µίας εντολής G2, ενώ άλλες µπορεί να περιορίζονται σε λιγότερες από 90 µοίρες. Συνήθως, δεχόµαστε ότι η εντολή G2 ενός ελεγκτή κάνει ένα τόξο µε τη φορά των δεικτών του ρολογιού, αλλά όχι ότι αυτό θα ορίζεται µε τον προηγούµενο τρόπο. Μερικοί ελεγκτές χρειάζονται απόλυτες συντεταγµένες του κέντρου, ενώ κάποιοι άλλοι απαιτούν την ακτίνα του τόξου. Τέλος, κάποιοι άλλοι επιτρέπουν την χρήση όλων των προαναφερθέντων τρόπων και µεθόδων και διάφορους συνδυασµούς αυτών. Περισσότερες λεπτοµέρειες υπάρχουν στα EIA standards. Το G3 είναι όπως το G2, αλλά µε κίνηση µε φορά αντίθετη από αυτήν των δεικτών του ρολογιού. Το G4 δεν κάνει τίποτα για έναν προκαθορισµένο χρόνο. Μόνο βοηθά στην κανονική στιγµιαία διακοπή κινήσεως του µηχανήµατος (dwells). Κάποιοι ελεγκτές χρησιµοποιούν X, F, ή P words σε milliseconds, κάποιοι άλλοι επιτρέπουν σε S word τον καθορισµό της περιστροφικής κίνησης της ατράκτου, ενώ κάποιοι άλλοι δεν επιτρέπουν τίποτα και απλά καθυστερούν για περίπου µισό δευτερόλεπτο. Οι κωδικοί G5 µε G89 θα αντιµετωπιστούν ως άδειες χρόνου (time permits). Για τώρα, οι σηµαντικοί κωδικοί είναι οι G17, G18 και G19. Αυτοί οι κωδικοί έχουν δραµατική επίδραση στους G2 και G3. Επίσης, οι G53 µε G59 µπορούν να µετασχηµατίσουν ολόκληρο το πρόγραµµα και οι κωδικοί της σειράς του G80 µπορούν να κάνουν οπές. 15
19 Το G90 καθορίζει ότι οι προγραµµατισµένες τιµές πρέπει να θεωρούνται απόλυτες, ή πραγµατικές τιµές συντεταγµένων. Αν το πρόγραµµα εκδόσει µία εντολή G1 X5.0 Z 2.0, τότε το εργαλείο κινείται προς αυτήν την θέση. Το G91 καθορίζει ότι οι προγραµµατισµένες τιµές πρέπει να αντιµετωπισθούν ως προσθετικές ή τιµές σχετικών συντεταγµένων. Αν το πρόγραµµα εκδώσει την εντολή G1 X5.0 Z 2.0, τότε το εργαλείο κινείται πέντε µονάδες στην θετική κατεύθυνση του X και δύο µονάδες στην θετική κατεύθυνση του Z. Πιο συγκεκριµένα, έχουµε ότι 1 : G00-Ταχεία Μετακίνηση- Κίνηση επί του άξονα µε µέγιστη ταχύτητα Φρεζάρισµα και Τορνάρισµα G01-Γραµµική Παρεµβολή- Ευθεία γραµµική κίνηση άξονα µε ελεγχόµενη ταχύτητα κοπής Φρεζάρισµα και Τορνάρισµα G02-Κυκλική κίνηση µε χρήση δύο αξόνων µε τη φορά των δεικτών του ρολογιού.- Φρεζάρισµα και Τορνάρισµα G03- Κυκλική κίνηση µε χρήση δύο αξόνων µε φορά αντίθετη από αυτήν των δεικτών του ρολογιού.- Φρεζάρισµα και Τορνάρισµα G04- Στιγµιαία διακοπή (dwell), της κίνησης των αξόνων, για µία καθορισµένη χρονική περίοδο.- Φρεζάρισµα και Τορνάρισµα G17- Επιλογή επιπέδου X,Y.- Φρεζάρισµα G18- Επιλογή επιπέδου X,Z.- Φρεζάρισµα G19-Επιλογή επιπέδου Y,Z.-Φρεζάρισµα G20-G70- Μονάδες σε ίντσες- Φρεζάρισµα και Τορνάρισµα G21-G71- Μετρικές µονάδες- Φρεζάρισµα και Τορνάρισµα G28-Αυτόµατη επιστροφή σε κάποιο σηµείο αναφοράς.-φρεζάρισµα και Τορνάρισµα G29-Αυτόµατη επιστροφή από κάποιο σηµείο αναφοράς.- Φρεζάρισµα και Τορνάρισµα G40-Φρεζάρισµα- Ακύρωση της διαµέτρου αντιστάθµισης του κοπτικού εργαλείου G40-Τορνάρισµα- Ακύρωση της αντιστάθµισης του άκρου του κοπτικού εργαλείου. G41-Φρεζάρισµα- Ενεργοποίηση Αντιστάθµισης διαµέτρου κοπτικού εργαλείου, το κοπτικό εργαλείο προς τα αριστερά. G41-Τορνάρισµα-Αντιστάθµιση της ακτίνας του άκρου του κοπτικού εργαλείου προς τα αριστερά G42-Φρεζάρισµα- Ενεργοποίηση Αντιστάθµισης διαµέτρου κοπτικού εργαλείου, το κοπτικό εργαλείο προς τα δεξιά. G42-Τορνάρισµα- Τορνάρισµα-Αντιστάθµιση της ακτίνας του άκρου του κοπτικού εργαλείου προς τα δεξιά G70-Τορνάρισµα- Εγγεγραµµένος Κύκλος τελειώµατος (Canned Finishing Cycle) G71- Τορνάρισµα- Εγγεγραµµένος Κύκλος αρχικής κατεργασίας (Canned Roughing Cycle) G72-Τορνάρισµα- Εγγεγραµµένος κύκλος όψεων (Canned Facing Cycle) G74-Τορνάρισµα-Εγγεργαµµένος κύκλος γραµµικών αυλακώσεων G75-Τορνάρισµα-Εγγεγρµµάνος κύκλος αυλακώσεων G76-Τορνάρισµα- Εγγεγραµµένος κύκλος σπειρώµατος G80- Φρεζάρισµα- Ακύρωση εγγεγραµµένου κύκλου. G81- Τορνάρισµα- Ακύρωση κύκλου γραµµικών αυλακώσεων G82- Φρεζάρισµα 1 Πηγή (9) 16
20 G83- Φρεζάρισµα G90-Φρεζάρισµα- Απόλυτη τοποθέτηση G91-Φρεζάρισµα- Σχετική τοποθέτηση G92-Φρεζάρισµα- Επανατοποθέτηση ή επαναπροσδιορισµός του σηµείου αρχής. G98-Φρεζάρισµα- Το αρχικό σύστηµα τοποθέτησης της µηχανής G98-Τορνάρισµα-Γραµµική Ταχύτητα Κοπής ανά χρονική µονάδα. G99-Φρεζάρισµα- Ακύρωση των σηµείων που ορίστηκαν µε την χρήση του κωδικού G92. G99-Τορνάρισµα-Ταχύτητα κοπής ανά περιστροφή 3.2 Προγραµµατισµός των µηχανών CNC Για τον προγραµµατισµό των µηχανών CNC χρησιµοποιούνται διάφορες µέθοδοι. Η πιο απλή µέθοδος είναι να κάνει κάποιος απλά και µόνο τους απαραίτητους γεωµετρικούς υπολογισµούς µε µία αριθµοµηχανή και να γράψει το πρόγραµµα κατ ευθείαν χρησιµοποιώντας G-codes, M-codes κτλ. Το πρόγραµµα τότε πληκτρολογείται άµεσα στον ελεγκτή, ο οποίος συνήθως καλείται MDI (Manual Data Input) ή πληκτρολογείται στον υπολογιστή και µεταφέρεται από εκεί στον ελεγκτή. Μερικοί ελεγκτές µπορούν να προγραµµατιστούν µε χρήση µίας µεθόδου «συζήτησης» («conversational» method). Αυτό µπορεί να σηµαίνει την χρήση µιας πιο προηγµένης γλώσσας προγραµµατισµού ή την χρήση πλήκτρων µε σύµβολα. Εξειδικευµένες γλώσσες όπως είναι η APT και η COMPACT II χρησιµοποιούνται από την δεκαετία του Με αυτές τις γλώσσες δηµιουργείται ένα ανεξάρτητο από τον χρησιµοποιούµενο ελεγκτή µονοπάτι του εργαλείου (controller-neutral tool path), το οποίο συνήθως καλείται CL File [Cutter Location (θέση κοπτικού εργαλείου) ή Center Line (γραµµή κέντρου)], που στη συνέχεια µετατρέπεται σε πρόγραµµα CNC το οποίο και είναι αποδεκτό από έναν δεδοµένο ελεγκτή CNC. Ένας ξεχωριστός µεταεπεξεργαστής (postprocessor) χρησιµοποιείται γενικά για κάθε ελεγκτή CNC ή οικογένεια ελεγκτών. Πρόκειται για ένα πρόγραµµα το οποίο διαβάζει ένα CL file και παράγει ένα πρόγραµµα CNC για µία συγκεκριµένη εργαλειοµηχανή. Ένας µεταεπεξεργαστής πρέπει να µπορεί να παράγει σωστό έξοδο. Η έξοδος του µεταεπεξεργαστή πρέπει να µπορεί να χρησιµοποιηθεί από τον ελεγκτή χωρίς να χρειάζεται περαιτέρω τροποποίηση. Η COMPACT II χρησιµοποιεί διαφορετική ορολογία αλλά η βασική ιδέα είναι παρόµοια. Η APT κάνει περίπλοκους γεωµετρικούς υπολογισµούς και δηµιούργησε µοντέρνα στοιχεία όπως την διασυνδεσιµότητα των µονοπατιών των εργαλείων (tool path associativity). Γραφικά συστήµατα CAD/CAM για σχεδιασµό και προγραµµατισµό NC διατέθηκαν στα τέλη της δεκαετίας του Όπως η APT, συνήθως δηµιουργούν ένα ουδέτερο αρχείο που συνήθως αποκαλείται CL File παρόλο που το αντίστοιχο format είναι σε γενικές γραµµές πολύ διαφορετικό από το παραδοσιακό format των CL Files της APT. 17
p k = (1- ρ) ρ k. E[N(t)] = ρ /(1- ρ).
![p k = (1- ρ) ρ k. E[N(t)] = ρ /(1- ρ). p k = (1- ρ) ρ k. E[N(t)] = ρ /(1- ρ).](/thumbs/24/2872872.jpg) ΚΕΦΑΛΑΙΟ 2: CAM 2.1 Συστήµατα Μ/Μ/1 2.1.1 Ανασκόπηση θεωρίας Η ουρά Μ/Μ/1 είναι η πιο σηµαντική διαδικασία ουράς Άφιξη: ιαδικασία Poisson Εξυπηρέτηση: Ακολουθεί εκθετική κατανοµή Εξυπηρετητής: Ένας Χώρος
ΚΕΦΑΛΑΙΟ 2: CAM 2.1 Συστήµατα Μ/Μ/1 2.1.1 Ανασκόπηση θεωρίας Η ουρά Μ/Μ/1 είναι η πιο σηµαντική διαδικασία ουράς Άφιξη: ιαδικασία Poisson Εξυπηρέτηση: Ακολουθεί εκθετική κατανοµή Εξυπηρετητής: Ένας Χώρος
Κεφάλαιο 3 Βασική Σχεδίαση και Επεξεργασία
 Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Το μεσαίο πλήκτρο ενεργοποιεί τα Osnaps μόνο αν η μεταβλητή MBUTTONPAN έχει τιμή 1.
 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΗΜΕΙΑ ΕΛΞΗΣ Ο μηχανισμός OBJECT SNAP ή OSNAP (έλξη σε αντικείμενα) μας επιτρέπει να προσδιορίζουμε, όποτε χρειάζεται, σημεία σε χαρακτηριστικές θέσεις πάνω σε αντικείμενα του σχεδίου μας,
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΗΜΕΙΑ ΕΛΞΗΣ Ο μηχανισμός OBJECT SNAP ή OSNAP (έλξη σε αντικείμενα) μας επιτρέπει να προσδιορίζουμε, όποτε χρειάζεται, σημεία σε χαρακτηριστικές θέσεις πάνω σε αντικείμενα του σχεδίου μας,
Eur.Ing. Δρ. Φ. Σκιττίδης. xxi ΠΕΡΙΕΧΟΜΕΝΑ
 Eur.Ing. Δρ. Φ. Σκιττίδης ΠΕΡΙΕΧΟΜΕΝΑ xxi ΚΕΦΑΛΑΙΟ 1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΤΙΚΟΥ ΕΛΕΓΧΟΥ 1.1 Ορισμός του αριθμητικού ελέγχου. 1 1.2 Ιστορική εξέλιξη του αριθμητικού ελέγχου. 1 1.3 Η εξέλιξη της τεχνολογίας
Eur.Ing. Δρ. Φ. Σκιττίδης ΠΕΡΙΕΧΟΜΕΝΑ xxi ΚΕΦΑΛΑΙΟ 1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΤΙΚΟΥ ΕΛΕΓΧΟΥ 1.1 Ορισμός του αριθμητικού ελέγχου. 1 1.2 Ιστορική εξέλιξη του αριθμητικού ελέγχου. 1 1.3 Η εξέλιξη της τεχνολογίας
3.2.2 Το CL file... 23
 ΑΤΕΙ ΧΑΛΚΙ ΑΣ ΣΤΕΦ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΧΕ ΙΑΣΗ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ (CAD) ΚΑΙ ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ (CAM) ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ Μαρία Γεωργακάλου, Χριστόφορος Οικονοµάκος, Σταµατία Στεφανάτου Ψαχνά, Νοέµβριος
ΑΤΕΙ ΧΑΛΚΙ ΑΣ ΣΤΕΦ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ ΣΧΕ ΙΑΣΗ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ (CAD) ΚΑΙ ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ (CAM) ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ Μαρία Γεωργακάλου, Χριστόφορος Οικονοµάκος, Σταµατία Στεφανάτου Ψαχνά, Νοέµβριος
Ο ΣΚΟΠΟΣ ΤΟΥ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΠΑΡΑ ΕΙΓΜΑΤΟΣ ΕΙΝΑΙ Η ΣΧΕ ΙΑΣΗ ΤΟΥ ΠΑΡΑΚΑΤΩ ΣΧΗΜΑΤΟΣ
 Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Ι Εκπαιδευτικό παράδειγμα για την εκμάθηση σχεδίασης με την βοήθεια του σχεδιαστικού πακέτου Auto
Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Ι Εκπαιδευτικό παράδειγμα για την εκμάθηση σχεδίασης με την βοήθεια του σχεδιαστικού πακέτου Auto
Μπορούμε να χρησιμοποιήσουμε τις παρακάτω μορφές συντεταγμένων με οποιοδήποτε συνδυασμό θέλουμε.
 2. ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
2. ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
Εργασία 1 Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD.
 Εργασία 1 Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης
Εργασία 1 Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟΣ ΤΟΜΕΑΣ ΕΚΠΑΙΔΕΥΤΙΚΟ ΠΑΡΑΔΕΙΓΜΑ 2
 ΒΗΜΑ 1. Άνοιγμα προτύπου (template) οριζόντιου Α3 (που δίδεται με την εκφώνηση της άσκησης), εισαγωγή των στοιχείων μας στο υπάρχον υπόμνημα και αποθήκευση του προτύπου με τα προσωπικά μας δεδομένα (αυτό
ΒΗΜΑ 1. Άνοιγμα προτύπου (template) οριζόντιου Α3 (που δίδεται με την εκφώνηση της άσκησης), εισαγωγή των στοιχείων μας στο υπάρχον υπόμνημα και αποθήκευση του προτύπου με τα προσωπικά μας δεδομένα (αυτό
Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Ομοιόθετη αναπαραγωγή Η εντολή offset. Πανομοιότυπη αναπαραγωγή Η εντολή copy.
 Εργασία 1 Κάτοψη στο AutoCAD. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης στο AutoCAD. Ομοιόθετη αναπαραγωγή Η εντολή
Εργασία 1 Κάτοψη στο AutoCAD. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης στο AutoCAD. Ομοιόθετη αναπαραγωγή Η εντολή
03. Τροποποίηση σχεδιασμένων οντοτήτων
 03. Τροποποίηση σχεδιασμένων οντοτήτων Μηχανολογικό Σχέδιο ΙΙ Περιεχόμενα 1. Μετατόπιση Αντιγραφή 2. Παράλληλη αντιγραφή 3. Περιστροφή 4. Απότμηση 5. Προέκταση 6. Στρογγύλεμα γωνιών 7. Λοξοτομή γωνιών
03. Τροποποίηση σχεδιασμένων οντοτήτων Μηχανολογικό Σχέδιο ΙΙ Περιεχόμενα 1. Μετατόπιση Αντιγραφή 2. Παράλληλη αντιγραφή 3. Περιστροφή 4. Απότμηση 5. Προέκταση 6. Στρογγύλεμα γωνιών 7. Λοξοτομή γωνιών
Μηχανολογικό Σχέδιο. Εργαστηριακή Άσκηση 1 Σχέδιο 1 2. Σπύρος Ερμίδης. Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π
 Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π Μηχανολογικό Σχέδιο Εργαστηριακή Άσκηση 1 Σχέδιο 1 2 Σπύρος Ερμίδης Η παρουσίαση προετοιμάστηκε το ακ. έτος 2014 15 από τον Σερράο Απόστολο (nm11046@mail.ntua.gr)
Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π Μηχανολογικό Σχέδιο Εργαστηριακή Άσκηση 1 Σχέδιο 1 2 Σπύρος Ερμίδης Η παρουσίαση προετοιμάστηκε το ακ. έτος 2014 15 από τον Σερράο Απόστολο (nm11046@mail.ntua.gr)
ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΩΝ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Μηχανολογίας
 ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Μηχανολογίας Σχεδιασµός κατασκευών µε τη χρήση Ηλεκτρονικού Υπολογιστή (CAD) ρ. Κωνσταντίνος Στεργίου Αναπληρωτής Καθηγητής 2006 ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΡΟΓΡΑΜΜΑ AUTODESK INVENTOR Το INVENTOR είναι
ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Μηχανολογίας Σχεδιασµός κατασκευών µε τη χρήση Ηλεκτρονικού Υπολογιστή (CAD) ρ. Κωνσταντίνος Στεργίου Αναπληρωτής Καθηγητής 2006 ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΡΟΓΡΑΜΜΑ AUTODESK INVENTOR Το INVENTOR είναι
Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά των Υπόλοιπων Πλευρών & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD.
 Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά των Υπόλοιπων Πλευρών & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse.
Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD Μέρος Β : Ανοίγματα, Διαχωριστικά των Υπόλοιπων Πλευρών & Μπαλκόνια. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse.
Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Πανομοιότυπη αναπαραγωγή Η εντολή copy.
 Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης στο AutoCAD. Ομοιόθετη αναπαραγωγή
Εργασία 2 Δεύτερη Κάτοψη στο AutoCAD. Σχεδίαση μίας κάτοψης στο AutoCAD. Ρυθμίσεις σχεδίου στο AutoCAD. Σκοπός Οι εντολές Line και Ellipse. Βασικές τεχνικές σχεδίασης στο AutoCAD. Ομοιόθετη αναπαραγωγή
01. Σχεδίαση με ΗΥ. Dr. Ing. Β. Ιακωβάκης
 01. Σχεδίαση με ΗΥ Μηχανολογικό Σχέδιο ΙΙ Περιεχόμενα 1. Γενικά περί σχεδίασης με ΗΥ 2. Γνωριμία με το AutoCAD 3. Σχεδίαση απλών γεωμετρικών οντοτήτων (γραμμή, ή κύκλος) ) 4. Απαλοιφή σχεδιασμένων οντοτήτων
01. Σχεδίαση με ΗΥ Μηχανολογικό Σχέδιο ΙΙ Περιεχόμενα 1. Γενικά περί σχεδίασης με ΗΥ 2. Γνωριμία με το AutoCAD 3. Σχεδίαση απλών γεωμετρικών οντοτήτων (γραμμή, ή κύκλος) ) 4. Απαλοιφή σχεδιασμένων οντοτήτων
Σχεδίαση με το AutoCAD
 Σχεδίαση με το AutoCAD Δημιουργία Αποθήκευση Αρχείων, Σχεδίαση & Επεξεργασία Γεωμετρικών Σχημάτων. Το παράθυρο του AutoCAD Δημιουργία - Αποθήκευση Νέου Σχεδίου Από το menu εφαρμογής επιλέγετε New και εμφανίζεται
Σχεδίαση με το AutoCAD Δημιουργία Αποθήκευση Αρχείων, Σχεδίαση & Επεξεργασία Γεωμετρικών Σχημάτων. Το παράθυρο του AutoCAD Δημιουργία - Αποθήκευση Νέου Σχεδίου Από το menu εφαρμογής επιλέγετε New και εμφανίζεται
Κώδικας Προγραµµατισµού, Μορφή των Λέξεων
 Κώδικας Προγραµµατισµού, Μορφή των Λέξεων Οι κώδικες προγραµµατισµού και η ερµηνεία τους δίνονται αναλυτικά στους παρακάτω πίνακες. Ν0000 Αριθµός block Εισάγεται στην αρχή κάθε block και προσδιορίζει τα
Κώδικας Προγραµµατισµού, Μορφή των Λέξεων Οι κώδικες προγραµµατισµού και η ερµηνεία τους δίνονται αναλυτικά στους παρακάτω πίνακες. Ν0000 Αριθµός block Εισάγεται στην αρχή κάθε block και προσδιορίζει τα
α) Κύκλος από δύο δοσµένα σηµεία Α, Β. Το ένα από τα δύο σηµεία ορίζεται ως κέντρο αν το επιλέξουµε πρώτο. β) Κύκλος από δοσµένο σηµείο και δοσµένο ευ
 ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
Διαδραστικός προγραμματισμός CNC
 Διαδραστικός προγραμματισμός CNC Διαλογικός προγραμματισμός Προγραμματισμός CAM Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ γλώσσες προγραμματισμού CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης Creative Commons
Διαδραστικός προγραμματισμός CNC Διαλογικός προγραμματισμός Προγραμματισμός CAM Γ.Βοσνιάκος-ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ γλώσσες προγραμματισμού CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης Creative Commons
Τεχνικό Σχέδιο - CAD
 Τεχνικό Σχέδιο - CAD Σχεδίαση με Συντεταγμένες ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Καρτεσιανό Σύστημα Συντεταγμένων Αρχή συστήματος συντεταγμένων
Τεχνικό Σχέδιο - CAD Σχεδίαση με Συντεταγμένες ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Καρτεσιανό Σύστημα Συντεταγμένων Αρχή συστήματος συντεταγμένων
ΠΕΓΑ_ΤΕΧΝΟΛΟΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΣΥΓΧΡΟΝΩΝ ΥΛΙΚΩΝ (MIS: )
 Επιχειρησιακό Πρόγραμμα Εκπαίδευση και Δια Βίου Μάθηση «Επικαιροποίηση γνώσεων αποφοίτων Α.Ε.Ι.» ΠΕΓΑ_ΤΕΧΝΟΛΟΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΣΥΓΧΡΟΝΩΝ ΥΛΙΚΩΝ (MIS: 478889) ΔΙΔΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
Επιχειρησιακό Πρόγραμμα Εκπαίδευση και Δια Βίου Μάθηση «Επικαιροποίηση γνώσεων αποφοίτων Α.Ε.Ι.» ΠΕΓΑ_ΤΕΧΝΟΛΟΓΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΣΥΓΧΡΟΝΩΝ ΥΛΙΚΩΝ (MIS: 478889) ΔΙΔΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
Από το χαρτί στον Η/Υ - Περιήγηση στο Περιβάλλον Σχεδίασης ηµιουργία και αποθήκευση αρχείου - Χρήση συντεταγµένων
 Α/Α ΣΤΟΧΟΙ (επιθυµητές γνώσεις-δεξιότητεςικανότητες) ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (Τίτλοι) ΠΕΡΙΕΧΟΜΕΝΟ ΕΝΟΤΗΤΩΝ (περιγραφή) ΕΚΠΑΙ ΕΥΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΙΑΡΚΕΙΑ (ενδεικτικά σε ώρες) 1. Οι επιµορφωνόµενοι/ες θα είναι σε
Α/Α ΣΤΟΧΟΙ (επιθυµητές γνώσεις-δεξιότητεςικανότητες) ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ (Τίτλοι) ΠΕΡΙΕΧΟΜΕΝΟ ΕΝΟΤΗΤΩΝ (περιγραφή) ΕΚΠΑΙ ΕΥΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΙΑΡΚΕΙΑ (ενδεικτικά σε ώρες) 1. Οι επιµορφωνόµενοι/ες θα είναι σε
ΜΑΘΗΜΑ: ΣΧΕΔΙΟ ΣΤΟΝ Η/Υ
 ΜΑΘΗΜΑ: ΣΧΕΔΙΟ ΣΤΟΝ Η/Υ ΔΙΔΑΣΚΩΝ: Παπαδόπουλος Χρήστος ΤΜΗΜΑ: Διαχείρισης Εκκλησιαστικών Κειμηλίων 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΜΑΘΗΜΑ: ΣΧΕΔΙΟ ΣΤΟΝ Η/Υ ΔΙΔΑΣΚΩΝ: Παπαδόπουλος Χρήστος ΤΜΗΜΑ: Διαχείρισης Εκκλησιαστικών Κειμηλίων 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
1.1.1 Το περιβάλλον εργασίας. Περιοχές της οθόνης και λειτουργία τους
 1 ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΕΡΙΒΑΛΛΟΝ ΤΟΥ AutoCAD Δρ. Ευαγγελία Πέππα, ΑΜ, Διδάκτωρ Μηχανικός ΕΜΠ 1.1 Η επικοινωνία με το χρήστη 1.1.1 Το περιβάλλον εργασίας. Περιοχές της οθόνης και λειτουργία τους 1.1.1.1 Οθόνη
1 ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΕΡΙΒΑΛΛΟΝ ΤΟΥ AutoCAD Δρ. Ευαγγελία Πέππα, ΑΜ, Διδάκτωρ Μηχανικός ΕΜΠ 1.1 Η επικοινωνία με το χρήστη 1.1.1 Το περιβάλλον εργασίας. Περιοχές της οθόνης και λειτουργία τους 1.1.1.1 Οθόνη
Εφαρμογές Πληροφορικής στην Τοπογραφία 4η Ενότητα - Εντολές σχεδίασης παραλληλόγραμμου, κύκλου και τόξου
 Εφαρμογές Πληροφορικής στην Τοπογραφία 4η Ενότητα - Εντολές σχεδίασης παραλληλόγραμμου, κύκλου και τόξου Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών Θεσσαλονίκη, Φεβρουάριος
Εφαρμογές Πληροφορικής στην Τοπογραφία 4η Ενότητα - Εντολές σχεδίασης παραλληλόγραμμου, κύκλου και τόξου Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών Θεσσαλονίκη, Φεβρουάριος
Εισαγωγικά μαθήματα Autocad. Κατασκευή Σήραγγας. Κατασκευή Υπόγειου Χώρου
 Εισαγωγικά μαθήματα Autocad Κατασκευή Σήραγγας Κατασκευή Υπόγειου Χώρου Α. Μπενάρδος Λέκτορας ΕΜΠ Κατασκευή σήραγγας Δημιουργία της βασικής χάραξης (centerline) [polyline] Βελτίωση των χαρακτηριστικών
Εισαγωγικά μαθήματα Autocad Κατασκευή Σήραγγας Κατασκευή Υπόγειου Χώρου Α. Μπενάρδος Λέκτορας ΕΜΠ Κατασκευή σήραγγας Δημιουργία της βασικής χάραξης (centerline) [polyline] Βελτίωση των χαρακτηριστικών
04. Μορφοποίηση περιεχομένων σχεδίου & σύνθετα εργαλεία σχεδίασης
 04. Μορφοποίηση περιεχομένων σχεδίου & σύνθετα εργαλεία σχεδίασης Μηχανολογικό Σχέδιο ΙΙ Dr.-Ing. Β. Β. Ιακωβάκης Περιεχόμενα I. Μορφοποίηση οντοτήτων 1. Ιδιότητες οντοτήτων 2. Επιλογή χρώματος 3. Επιλογή
04. Μορφοποίηση περιεχομένων σχεδίου & σύνθετα εργαλεία σχεδίασης Μηχανολογικό Σχέδιο ΙΙ Dr.-Ing. Β. Β. Ιακωβάκης Περιεχόμενα I. Μορφοποίηση οντοτήτων 1. Ιδιότητες οντοτήτων 2. Επιλογή χρώματος 3. Επιλογή
Offset Link.
 Offset Link Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για
Offset Link Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων
 1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
Εφαρμογές Πληροφορικής στην Τοπογραφία 6η Ενότητα - Εντολές μεταβολής σχεδιαστικών αντικειμένων
 Εφαρμογές Πληροφορικής στην Τοπογραφία 6η Ενότητα - Εντολές μεταβολής σχεδιαστικών αντικειμένων Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών Θεσσαλονίκη, Φεβρουάριος 2014
Εφαρμογές Πληροφορικής στην Τοπογραφία 6η Ενότητα - Εντολές μεταβολής σχεδιαστικών αντικειμένων Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών Θεσσαλονίκη, Φεβρουάριος 2014
ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Ι
 Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Ι Εκπαιδευτικό παράδειγμα για την εκμάθηση σχεδίασης με την βοήθεια του σχεδιαστικού πακέτου Auto
Πανεπιστήμιο Πατρών - Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών ΜΗΧΑΝΟΛΟΓΙΚΟ ΣΧΕΔΙΟ Ι Εκπαιδευτικό παράδειγμα για την εκμάθηση σχεδίασης με την βοήθεια του σχεδιαστικού πακέτου Auto
ΔΙΑΣΤΑΣΕΙΣ. Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων
 ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
Σχεδίαση με Η/Υ. Το AutoCAD στην πράξη ΔΑΥΙΔ ΚΩΝΣΤΑΝΤΙΝΟΣ ΑΝΘΥΜΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ. Διδάκτορας Μηχανολόγος Μηχανικός
 Σχεδίαση με Η/Υ Το AutoCAD στην πράξη ΔΑΥΙΔ ΚΩΝΣΤΑΝΤΙΝΟΣ Διδάκτορας Μηχανολόγος Μηχανικός ΑΝΘΥΜΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ Διδάκτορας Μηχανολόγος Μηχανικός 0_CONT_ (AutoCAD).indd iii τίτλος: ΣΧΕΔΙΑΣΗ ΜΕ Η/Υ: ΤΟ
Σχεδίαση με Η/Υ Το AutoCAD στην πράξη ΔΑΥΙΔ ΚΩΝΣΤΑΝΤΙΝΟΣ Διδάκτορας Μηχανολόγος Μηχανικός ΑΝΘΥΜΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ Διδάκτορας Μηχανολόγος Μηχανικός 0_CONT_ (AutoCAD).indd iii τίτλος: ΣΧΕΔΙΑΣΗ ΜΕ Η/Υ: ΤΟ
ΕΞΕΤΑΣΤΕΑ ΥΛΗ (SYLLABUS) GLOBAL ADVANCED
 ΕΞΕΤΑΣΤΕΑ ΥΛΗ (SYLLABUS) GLOBAL ADVANCED AUTOCAD 2D AutoCAD 2D ΚΕΦΑΛΑΙΟ 1 Το περιβάλλον εργασίας του AutoCAD 2d Οι γραμμές εργαλείων Η περιοχή εντολών Η κορδέλα εργασιών Οι παλέτες εργαλείων ΚΕΦΑΛΑΙΟ 2
ΕΞΕΤΑΣΤΕΑ ΥΛΗ (SYLLABUS) GLOBAL ADVANCED AUTOCAD 2D AutoCAD 2D ΚΕΦΑΛΑΙΟ 1 Το περιβάλλον εργασίας του AutoCAD 2d Οι γραμμές εργαλείων Η περιοχή εντολών Η κορδέλα εργασιών Οι παλέτες εργαλείων ΚΕΦΑΛΑΙΟ 2
Μπορούμε να χρησιμοποιήσουμε τις παρακάτω μορφές συντεταγμένων με οποιοδήποτε συνδυασμό θέλουμε. Καρτεσιανές συντεταγμένες
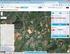 ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Βασικό Επίπεδο στο Modellus
 Βασικό Επίπεδο στο Modellus Το λογισµικό Modellus επιτρέπει στον χρήστη να οικοδοµήσει µαθηµατικά µοντέλα και να τα εξερευνήσει µε προσοµοιώσεις, γραφήµατα, πίνακες τιµών. Ο χρήστης πρέπει να γράψει τις
Βασικό Επίπεδο στο Modellus Το λογισµικό Modellus επιτρέπει στον χρήστη να οικοδοµήσει µαθηµατικά µοντέλα και να τα εξερευνήσει µε προσοµοιώσεις, γραφήµατα, πίνακες τιµών. Ο χρήστης πρέπει να γράψει τις
Συστήµατα Computer Aided Manufacturing - CAM
 Συστήµατα Computer Aided Manufacturing - CAM Σχεδιασµός της διαδικασίας παραγωγής τεµαχίων σε ψηφιακά καθοδηγούµενες εργαλειοµηχανές Στόχος του λογισµικού CAM: Η δηµιουργία του προγράµµατος ψηφιακής καθοδήγησης
Συστήµατα Computer Aided Manufacturing - CAM Σχεδιασµός της διαδικασίας παραγωγής τεµαχίων σε ψηφιακά καθοδηγούµενες εργαλειοµηχανές Στόχος του λογισµικού CAM: Η δηµιουργία του προγράµµατος ψηφιακής καθοδήγησης
 ΣΧΕ ΙΑΣΜΟΣ ΕΠΙΦΑΝΕΙΑΣ Με το σχεδιασµό επιφάνειας (Custom επιφάνεια) µπορούµε να σχεδιάσουµε επιφάνειες και αντικείµενα που δεν υπάρχουν στους καταλόγους του 1992. Τι µπορούµε να κάνουµε µε το σχεδιασµό
ΣΧΕ ΙΑΣΜΟΣ ΕΠΙΦΑΝΕΙΑΣ Με το σχεδιασµό επιφάνειας (Custom επιφάνεια) µπορούµε να σχεδιάσουµε επιφάνειες και αντικείµενα που δεν υπάρχουν στους καταλόγους του 1992. Τι µπορούµε να κάνουµε µε το σχεδιασµό
Σχεδίαση με χρήση Η/Υ
 Αστέριος Κ. Τολίδης Σχεδίαση με χρήση Η/Υ Σημειώσεις για το εργαστήριο του μαθήματος «Τεχνικές Σχεδίασης με χρήση Η/Υ» ΘΕΣΣΑΛΟΝΙΚΗ 2006 Περιεχόμενα 1. Εισαγωγή στο CAD...5 1.1 Συστήματα CAE...6 2. Εισαγωγή
Αστέριος Κ. Τολίδης Σχεδίαση με χρήση Η/Υ Σημειώσεις για το εργαστήριο του μαθήματος «Τεχνικές Σχεδίασης με χρήση Η/Υ» ΘΕΣΣΑΛΟΝΙΚΗ 2006 Περιεχόμενα 1. Εισαγωγή στο CAD...5 1.1 Συστήματα CAE...6 2. Εισαγωγή
Σχεδίαση με χρήση Η/Υ
 Αστέριος Κ. Τολίδης Σχεδίαση με χρήση Η/Υ Σημειώσεις για το εργαστήριο του μαθήματος «Τεχνικές Σχεδίασης με χρήση Η/Υ» ΘΕΣΣΑΛΟΝΙΚΗ 2006 Περιεχόμενα 1. Εισαγωγή στο CAD...5 1.1 Συστήματα CAE...6 2. Εισαγωγή
Αστέριος Κ. Τολίδης Σχεδίαση με χρήση Η/Υ Σημειώσεις για το εργαστήριο του μαθήματος «Τεχνικές Σχεδίασης με χρήση Η/Υ» ΘΕΣΣΑΛΟΝΙΚΗ 2006 Περιεχόμενα 1. Εισαγωγή στο CAD...5 1.1 Συστήματα CAE...6 2. Εισαγωγή
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΜΕ ΥΠΟΛΟΓΙΣΤΗ με χρήση της σχεδιαστικής εφαρμογής AutoCAD
 Τ.Ε.Ι. ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΤΟΠΟΓΡΑΦΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΜΕ ΥΠΟΛΟΓΙΣΤΗ με χρήση της σχεδιαστικής εφαρμογής AutoCAD ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΕΥΑΓΓΕΛΙΑ
Τ.Ε.Ι. ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΤΟΠΟΓΡΑΦΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΣΧΕΔΙΑΣΗΣ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΜΕ ΥΠΟΛΟΓΙΣΤΗ με χρήση της σχεδιαστικής εφαρμογής AutoCAD ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΕΥΑΓΓΕΛΙΑ
Stroke.
 Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για την καλύτερη
Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για την καλύτερη
AUTOCAD 2D ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΤΗ ΚΑΙ ΑΣΚΗΣΕΙΣ LABTECH
 ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΤΗ ΚΑΙ ΑΣΚΗΣΕΙΣ LABTECH 04_04_Inquiry... 21 04_04_01_Measure Distance (Μέτρηση απόστασης)... 21 04_04_02_Measure Radius (Μέτρηση ακτίνας)... 21 04_04_03_Measure Angle (Μέτρηση γωνίας)...
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΤΗ ΚΑΙ ΑΣΚΗΣΕΙΣ LABTECH 04_04_Inquiry... 21 04_04_01_Measure Distance (Μέτρηση απόστασης)... 21 04_04_02_Measure Radius (Μέτρηση ακτίνας)... 21 04_04_03_Measure Angle (Μέτρηση γωνίας)...
Μηχανουργικές κατεργασίες με χρήση Η/Υ για βιομηχανική παραγωγή
 Προγραμματισμός Εργαλειομηχανών CNC Ο προγραμματισμός για την κατεργασία ενός τεμαχίου σε εργαλειομηχανή, με ψηφιακή καθοδήγηση, γίνεται με τον κώδικα μηχανής. Πρόκειται για μια σειρά τυποποιημένων εντολών,
Προγραμματισμός Εργαλειομηχανών CNC Ο προγραμματισμός για την κατεργασία ενός τεμαχίου σε εργαλειομηχανή, με ψηφιακή καθοδήγηση, γίνεται με τον κώδικα μηχανής. Πρόκειται για μια σειρά τυποποιημένων εντολών,
ΘΕΜΑ ΠΤΥΧΙΑΚΗΣ ΕΡΓΑΣΙΑΣ
 ΑΝΩΤΑΤΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΤ. ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟΣ ΘΕΜΑ ΠΤΥΧΙΑΚΗΣ ΕΡΓΑΣΙΑΣ ΑΝΑΠΤΥΞΗ XLS ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΤΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΤΩΝ
ΑΝΩΤΑΤΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΤ. ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟΣ ΘΕΜΑ ΠΤΥΧΙΑΚΗΣ ΕΡΓΑΣΙΑΣ ΑΝΑΠΤΥΞΗ XLS ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΤΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΤΩΝ
Pivot Support.
 Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για την καλύτερη
Το φυλλάδιο οδηγιών που κρατάτε στα χέρια σας βρίσκεται και σε ηλεκτρονική μορφή (αρχείο Acrobatpdf) στον φάκελο PDF του υπολογιστή (υπάρχει η σχετική συντόμευση την επιφάνεια εργασίας). Για την καλύτερη
ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΟΥ ΜΕ ΧΡΗΣΗ Η/Υ CAD I. Λαμπούδης Δημήτρης
 ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΟΥ ΜΕ ΧΡΗΣΗ Η/Υ CAD I Καρδίτσα 2005 Περιεχόμενα Εισαγωγικό σημείωμα... 3 1. Βασικές Έννοιες... 4 2. Τα βασικά του AutoCAD... 7 2.1. Πώς εκκινούμε το πρόγραμμα AutoCAD... 7 2.2.
ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΟΥ ΜΕ ΧΡΗΣΗ Η/Υ CAD I Καρδίτσα 2005 Περιεχόμενα Εισαγωγικό σημείωμα... 3 1. Βασικές Έννοιες... 4 2. Τα βασικά του AutoCAD... 7 2.1. Πώς εκκινούμε το πρόγραμμα AutoCAD... 7 2.2.
ΕΘΝΙΚΟ!ΜΕΤΣΟΒΙΟ!ΠΟΛΥΤΕΧΝΕΙΟ! ΣΧΟΛΗ!ΧΗΜΙΚΩΝ!ΜΗΧΑΝΙΚΩΝ!!
 ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)4 Ο :) ΡΟΗ)ΣΕ)ΑΓΩΓΟ)ΜΕ)ΑΠΟΤΟΜΗ)ΑΥΞΗΣΗ) ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ
ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)4 Ο :) ΡΟΗ)ΣΕ)ΑΓΩΓΟ)ΜΕ)ΑΠΟΤΟΜΗ)ΑΥΞΗΣΗ) ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ
Εφαρμογές Πληροφορικής στην Τοπογραφία 7η Ενότητα Μονάδες, εντολές Text, List, μετρήσεις, μετασχηματισμοί και άσκηση χάραξης
 Εφαρμογές Πληροφορικής στην Τοπογραφία 7η Ενότητα Μονάδες, εντολές Text, List, μετρήσεις, μετασχηματισμοί και άσκηση χάραξης Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών
Εφαρμογές Πληροφορικής στην Τοπογραφία 7η Ενότητα Μονάδες, εντολές Text, List, μετρήσεις, μετασχηματισμοί και άσκηση χάραξης Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων Μηχανικών
ΠANEΠIΣTHMIO ΠATPΩN TMHMA MHXANOΛOΓΩN ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ MHXANIKΩN
 ΠANEΠIΣTHMIO ΠATPΩN TMHMA MHXANOΛOΓΩN ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ MHXANIKΩN Εργαστήριο Συστημάτων Παραγωγής και Αυτοματισμού Διδάσκων: Αναπλ. Καθηγητής Δ. Μούρτζης ΑΡΙΘΜΗΤΙΚΟΣ ΕΛΕΓΧΟΣ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ CNC Εργαστηριακή
ΠANEΠIΣTHMIO ΠATPΩN TMHMA MHXANOΛOΓΩN ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ MHXANIKΩN Εργαστήριο Συστημάτων Παραγωγής και Αυτοματισμού Διδάσκων: Αναπλ. Καθηγητής Δ. Μούρτζης ΑΡΙΘΜΗΤΙΚΟΣ ΕΛΕΓΧΟΣ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ CNC Εργαστηριακή
Αφού ολοκληρωθεί η εγκατάσταση, ανοίξτε το πρόγραμμα επιλέξτε το Enter a License.
 Πώς εγκαθιστούμε το Rhino (download). Το πρόγραμμα προσφέρεται δωρεάν (δοκιμαστική) χρήση για 90 ημέρες. Πηγαίνετε στην ηλεκτρονική διεύθυνση: https://www.rhino3d.com/download Επιλέξτε το Rhino 5 for Windows
Πώς εγκαθιστούμε το Rhino (download). Το πρόγραμμα προσφέρεται δωρεάν (δοκιμαστική) χρήση για 90 ημέρες. Πηγαίνετε στην ηλεκτρονική διεύθυνση: https://www.rhino3d.com/download Επιλέξτε το Rhino 5 for Windows
ΕΝΟΤΗΤΑ 2 η Μηχανολογικά Κατασκευαστικά Σχέδια
 ΕΝΟΤΗΤΑ 2 η Μηχανολογικά Κατασκευαστικά Σχέδια Μάθημα 2.6 Τρισδιάστατη στερεά μοντελοποίηση εξαρτημάτων ημιουργία ενός τρισδιάστατου μοντέλου από ένα σχέδιο δύο διαστάσεων. Ορθές προβολές (Top, Bottom,
ΕΝΟΤΗΤΑ 2 η Μηχανολογικά Κατασκευαστικά Σχέδια Μάθημα 2.6 Τρισδιάστατη στερεά μοντελοποίηση εξαρτημάτων ημιουργία ενός τρισδιάστατου μοντέλου από ένα σχέδιο δύο διαστάσεων. Ορθές προβολές (Top, Bottom,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ (ΑΡΤΑ) ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΤΗΛΕΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ (ΑΡΤΑ) ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΤΗΛΕΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ ΣΧΕΔΙΑΣΜΟΣ ΜΕ ΤΗ ΒΟΗΘΕΙΑ Η/Υ ΣΥΝΤΕΛΕΣΤΗΣ ΕΡΓΑΣΙΑΣ : ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ (ΑΡΤΑ) ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΤΗΛΕΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ ΣΧΕΔΙΑΣΜΟΣ ΜΕ ΤΗ ΒΟΗΘΕΙΑ Η/Υ ΣΥΝΤΕΛΕΣΤΗΣ ΕΡΓΑΣΙΑΣ : ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ
άσκηση 1 Χειροκίνητη Ψηφιοποίηση Χαρτογραφικων εδοµένων Ψηφιακή Χαρτογραφία ΣΑΤΜ ΕΜΠ -1-
 άσκηση 1 Χειροκίνητη Ψηφιοποίηση Χαρτογραφικων εδοµένων -1- ΛΟΓΙΣΜΙΚΟ ΕΙ ΟΣ ΧΡΗΣΗ AutoCAD Corel - CorelDRAW! - Corel PHOTO- PAINT - Corel TRACE DM Σχεδιαστικό πακέτο Λογισµικό Γραφικών Τεχνών - Περιβάλλον
άσκηση 1 Χειροκίνητη Ψηφιοποίηση Χαρτογραφικων εδοµένων -1- ΛΟΓΙΣΜΙΚΟ ΕΙ ΟΣ ΧΡΗΣΗ AutoCAD Corel - CorelDRAW! - Corel PHOTO- PAINT - Corel TRACE DM Σχεδιαστικό πακέτο Λογισµικό Γραφικών Τεχνών - Περιβάλλον
ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΩΝ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΕΘΝΙΚΟ!ΜΕΤΣΟΒΙΟ!ΠΟΛΥΤΕΧΝΕΙΟ! ΣΧΟΛΗ!ΧΗΜΙΚΩΝ!ΜΗΧΑΝΙΚΩΝ!!
 ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ) Ο :) ΜΕΤΑΦΟΡΑ)ΘΕΡΜΟΤΗΤΑΣ)ΣΕ)ΑΓΩΓΟ) ΚΥΚΛΙΚΗΣ)ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ
ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ) Ο :) ΜΕΤΑΦΟΡΑ)ΘΕΡΜΟΤΗΤΑΣ)ΣΕ)ΑΓΩΓΟ) ΚΥΚΛΙΚΗΣ)ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ
ΕΘΝΙΚΟ!ΜΕΤΣΟΒΙΟ!ΠΟΛΥΤΕΧΝΕΙΟ! ΣΧΟΛΗ!ΧΗΜΙΚΩΝ!ΜΗΧΑΝΙΚΩΝ!!
 ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)4 Ο :) ΡΟΗ)ΣΕ)ΑΓΩΓΟ)ΜΕ)ΑΠΟΤΟΜΗ)ΑΥΞΗΣΗ) ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ
ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)4 Ο :) ΡΟΗ)ΣΕ)ΑΓΩΓΟ)ΜΕ)ΑΠΟΤΟΜΗ)ΑΥΞΗΣΗ) ΔΙΑΤΟΜΗΣ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ
Εισαγωγή στην Αριθμητική Ανάλυση
 Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Άσκηση 5 Ανύψωση Σχηµάτων. Στόχος της άσκησης
 Άσκηση 5 Ανύψωση Σχηµάτων Στόχος της άσκησης Στην παρούσα άσκηση θα δούµε πώς µπορούµε να ανυψώσουµε µία διατοµή κατά µήκος µίας καµπύλης spline, η οποία παίζει το ρόλο της διαδροµής, µε σκοπό να δηµιουργήσουµε
Άσκηση 5 Ανύψωση Σχηµάτων Στόχος της άσκησης Στην παρούσα άσκηση θα δούµε πώς µπορούµε να ανυψώσουµε µία διατοµή κατά µήκος µίας καµπύλης spline, η οποία παίζει το ρόλο της διαδροµής, µε σκοπό να δηµιουργήσουµε
Ορισµός. (neighboring) καταστάσεων. ηλαδή στην περίπτωση αλυσίδας Markov. 1.2 ιαµόρφωση µοντέλου
 200-04-25. ιαδικασίες γεννήσεων-θανάτων. Ορισµός Οι διαδικασίες γεννήσεων-θανάτων (birth-death rocesses) αποτελούν µια σπουδαία κλάση αλυσίδων Markov (διακριτού ή συνεχούς χρόνου). Η ιδιαίτερη συνθήκη
200-04-25. ιαδικασίες γεννήσεων-θανάτων. Ορισµός Οι διαδικασίες γεννήσεων-θανάτων (birth-death rocesses) αποτελούν µια σπουδαία κλάση αλυσίδων Markov (διακριτού ή συνεχούς χρόνου). Η ιδιαίτερη συνθήκη
ΘΕΜΑ ΠΤΥΧΙΑΚΗΣ: ΗΜΙΟΥΡΓΙΑ ΑΣΚΗΣΕΩΝ ΦΡΕΖΑΣ ΚΑΙ ΤΟΡΝΟΥ ΓΙΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ CNC ΜΕ ΚΩ ΙΚΟΥΣ G, M ΓΙΑ ΕΚΠΑΙ ΕΥΤΙΚΟΥΣ ΣΚΟΠΟΥΣ.
 1 ΑΝΩΤΑΤΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΕΙΡΑΙΑ Τ.Τ. ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΣΠΟΥ ΑΣΤΕΣ : ΚΑΡΑΛΗΣ ΠΑΝΑΓΙΩΤΗΣ ΜΕ ΑΜ 30040 ΛΙΒΑΣΙ ΗΣ ΓΙΩΡΓΟΣ
1 ΑΝΩΤΑΤΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΕΙΡΑΙΑ Τ.Τ. ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΣΠΟΥ ΑΣΤΕΣ : ΚΑΡΑΛΗΣ ΠΑΝΑΓΙΩΤΗΣ ΜΕ ΑΜ 30040 ΛΙΒΑΣΙ ΗΣ ΓΙΩΡΓΟΣ
Σχεδίαση τροχιάς. (α) (β) (γ) (δ) Σχήµα 2.5
 Σχεδίαση τροχιάς Η πιο απλή κίνηση ενός βραχίονα είναι από σηµείο σε σηµείο. Με την µέθοδο αυτή το ροµπότ κινείται από µία αρχική θέση σε µία τελική θέση χωρίς να µας ενδιαφέρει η ενδιάµεση διαδροµή που
Σχεδίαση τροχιάς Η πιο απλή κίνηση ενός βραχίονα είναι από σηµείο σε σηµείο. Με την µέθοδο αυτή το ροµπότ κινείται από µία αρχική θέση σε µία τελική θέση χωρίς να µας ενδιαφέρει η ενδιάµεση διαδροµή που
Άσκηση 6 Ανύψωση Σχηµάτων. Στόχος της άσκησης
 Άσκηση 6 Ανύψωση Σχηµάτων Στόχος της άσκησης Στην παρούσα άσκηση θα δούµε πως µπορούµε να ανυψώσουµε µία διατοµή κατά µήκος µίας καµπύλης spline, η οποία παίζει το ρόλο της διαδροµής, µε σκοπό να δηµιουργήσουµε
Άσκηση 6 Ανύψωση Σχηµάτων Στόχος της άσκησης Στην παρούσα άσκηση θα δούµε πως µπορούµε να ανυψώσουµε µία διατοµή κατά µήκος µίας καµπύλης spline, η οποία παίζει το ρόλο της διαδροµής, µε σκοπό να δηµιουργήσουµε
Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC
 Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC Ιστορία Κύρια μέρη Εργαλειομηχανών Αρχές CNC Γ.Βοσνιάκος- ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Εισαγωγή στις εργαλειομηχανές CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC Ιστορία Κύρια μέρη Εργαλειομηχανών Αρχές CNC Γ.Βοσνιάκος- ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Εισαγωγή στις εργαλειομηχανές CNC Άδεια Χρήσης Το παρόν υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC
 Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC Ιστορία Κύρια μέρη Εργαλειομηχανών Αρχές CNC Γ.Βοσνιάκος- ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Εισαγωγή στις εργαλειομηχανές CNC 1 Ιστορία -1 1949-1952 από J. Parsons - ΜΙΤ εφεύρεση
Εισαγωγή στις σύγχρονες Εργαλειομηχανές CNC Ιστορία Κύρια μέρη Εργαλειομηχανών Αρχές CNC Γ.Βοσνιάκος- ΕΡΓΑΛΕΙΟΜΗΧΑΝΕΣ Εισαγωγή στις εργαλειομηχανές CNC 1 Ιστορία -1 1949-1952 από J. Parsons - ΜΙΤ εφεύρεση
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας. Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης:
 Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Στροφορµή. υο παρατηρήσεις: 1) Η στροφορµή ενός υλικού σηµείου, που υπολογίζουµε µε βάση τα προηγούµενα, αναφέρεται. σε µια ορισµένη χρονική στιγµή.
 Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
ΣΧΕΔΙΑΣΜΟΣ ΠΑΡΑΓΩΓΗΣ ΕΠΙΠΛΩΝ ΜΕ ΧΡΗΣΗ ΥΠΟΛΟΓΙΣΤΗ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΧΕΔΙΑΣΗΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ
 Σχεδίαση με τη χρήση Η/Υ ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΧΕΔΙΑΣΗΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Ορισμοί: Σχέδιο (sketch/schizzo): από την αρχαία
Σχεδίαση με τη χρήση Η/Υ ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΧΕΔΙΑΣΗΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Ορισμοί: Σχέδιο (sketch/schizzo): από την αρχαία
1.2 Στοιχεία Μηχανολογικού Σχεδίου
 1.2 Στοιχεία Μηχανολογικού Σχεδίου Τα µηχανολογικά σχέδια, ανάλογα µε τον τρόπο σχεδίασης διακρίνονται στις παρακάτω κατηγορίες: Σκαριφήµατα Κανονικά µηχανολογικά σχέδια Προοπτικά σχέδια Σχηµατικές παραστάσεις.
1.2 Στοιχεία Μηχανολογικού Σχεδίου Τα µηχανολογικά σχέδια, ανάλογα µε τον τρόπο σχεδίασης διακρίνονται στις παρακάτω κατηγορίες: Σκαριφήµατα Κανονικά µηχανολογικά σχέδια Προοπτικά σχέδια Σχηµατικές παραστάσεις.
Συμβατικός προγραμματισμός κέντρων κατεργασιών CNC
 Συμβατικός προγραμματισμός κέντρων κατεργασιών CNC Αρχές προγραμματισμού Τυποποιημένες εντολές Μη τυποποιημένες εντολές Φασεολόγια Εργαλεία Γ.Βοσνιάκος-2014 Προγραμματισμός κέντρων κατεργασιών Άδεια Χρήσης
Συμβατικός προγραμματισμός κέντρων κατεργασιών CNC Αρχές προγραμματισμού Τυποποιημένες εντολές Μη τυποποιημένες εντολές Φασεολόγια Εργαλεία Γ.Βοσνιάκος-2014 Προγραμματισμός κέντρων κατεργασιών Άδεια Χρήσης
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας
 Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
Εφαρμογές Πληροφορικής στην Τοπογραφία 5η Ενότητα - Δημιουργία διαφανειών (layers) και δημιουργία νέου είδους γραμμών (linetype) στο AutoCAD
 Εφαρμογές Πληροφορικής στην Τοπογραφία 5η Ενότητα - Δημιουργία διαφανειών (layers) και δημιουργία νέου είδους γραμμών (linetype) στο AutoCAD Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων
Εφαρμογές Πληροφορικής στην Τοπογραφία 5η Ενότητα - Δημιουργία διαφανειών (layers) και δημιουργία νέου είδους γραμμών (linetype) στο AutoCAD Τσιούκας Βασίλειος, Αναπληρωτής Καθηγητής Τμήμα Αγρονόμων Τοπογράφων
Σχήµα 4.1: Εισαγωγή βρόγχου while-loop.
 Ο βρόγχος While-loop 1. Ο βρόγχος while-loop εκτελείται έως ότου ικανοποιηθεί µία προκαθορισµένη συνθήκη. 2. Ο αριθµός των επαναλήψεων ενός βρόγχου while-loop δεν είναι εκ των προτέρων προκαθορισµένος,
Ο βρόγχος While-loop 1. Ο βρόγχος while-loop εκτελείται έως ότου ικανοποιηθεί µία προκαθορισµένη συνθήκη. 2. Ο αριθµός των επαναλήψεων ενός βρόγχου while-loop δεν είναι εκ των προτέρων προκαθορισµένος,
Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ
 ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα)
 20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
ιαστασιολόγηση Περιεχόμενα Ορισμός Μηχανολογικός Σχεδιασμός Εισαγωγή Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή ιαστασιολόγηση η Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων Πρακτική διαστασιολόγησης Μηχανολογικός
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή ιαστασιολόγηση η Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων Πρακτική διαστασιολόγησης Μηχανολογικός
Καµπύλες στον R. σ τελικό σηµείο της σ. Το σ. σ =. Η σ λέγεται διαφορίσιµη ( αντιστοίχως
 Καµπύλες στον R 9. Ορισµός Μια καµπύλη στον R είναι µια συνεχής συνάρτηση σ : Ι R R όπου Ι διάστηµα ( συνήθως κλειστό και φραγµένο ) στον R. Συνήθως φανταζόµαστε την µεταβλητή t Ι ως τον χρόνο και την
Καµπύλες στον R 9. Ορισµός Μια καµπύλη στον R είναι µια συνεχής συνάρτηση σ : Ι R R όπου Ι διάστηµα ( συνήθως κλειστό και φραγµένο ) στον R. Συνήθως φανταζόµαστε την µεταβλητή t Ι ως τον χρόνο και την
14 Εφαρµογές των ολοκληρωµάτων
 14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
2. Κάντε κλικ στο παράθυρο όψης Top για να το ενεργοποιήσετε, ώστε να σχεδιάσετε το πάτωµα του δωµατίου.
 Άσκηση 7 Σύνθετα Αντικείµενα Στόχος της άσκησης Στόχος της παρούσας άσκησης είναι η εξοικείωση µε τη δηµιουργία σύνθετων αντικειµένων που δηµιουργούνται από τον συνδυασµό δύο ή περισσότερων τρισδιάστατων
Άσκηση 7 Σύνθετα Αντικείµενα Στόχος της άσκησης Στόχος της παρούσας άσκησης είναι η εξοικείωση µε τη δηµιουργία σύνθετων αντικειµένων που δηµιουργούνται από τον συνδυασµό δύο ή περισσότερων τρισδιάστατων
Jewellery CAD. Εισαγωγή στο Περιβάλλομ του Jewellery CAD. Η αρχική οθόνη του Jewellery CAD είναι αυτή που φαίνεται στην Εικόνα 1:
 Jewellery CAD Εισαγωγή στο Περιβάλλομ του Jewellery CAD Σο εγχειρίδιο αυτό δομείται βασιζόμενο στη λογική εξέλιξη της κατασκευής ενός μοντέλου. Ξεκινάει με τη βάση δεδομένων, στη συνέχεια περνάει στο 2D
Jewellery CAD Εισαγωγή στο Περιβάλλομ του Jewellery CAD Σο εγχειρίδιο αυτό δομείται βασιζόμενο στη λογική εξέλιξη της κατασκευής ενός μοντέλου. Ξεκινάει με τη βάση δεδομένων, στη συνέχεια περνάει στο 2D
ΕΘΝΙΚΟ!ΜΕΤΣΟΒΙΟ!ΠΟΛΥΤΕΧΝΕΙΟ! ΣΧΟΛΗ!ΧΗΜΙΚΩΝ!ΜΗΧΑΝΙΚΩΝ!!
 ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ) Ο :) ΡΟΗ)HAGENPOISEUILLE) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ ΕΚΦΩΝΗΣΗ ii Α Ανοιγµα
ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ) Ο :) ΡΟΗ)HAGENPOISEUILLE) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ ΕΚΦΩΝΗΣΗ ii Α Ανοιγµα
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Εξαμηνιαία Εργασία 2015 Εμπορικό / Βιομηχανικό Κτίριο στο FINE. Σχεδίαση του δικτύου μίας ηλεκτρικής εγκατάστασης.
 Εξαμηνιαία Εργασία 2015 Εμπορικό / Βιομηχανικό Κτίριο στο FINE. Σχεδίαση του δικτύου μίας ηλεκτρικής εγκατάστασης. Σχεδίαση του κεντρικού οριζόντιου δικτύου. Σκοπός Τοποθέτηση Υποδοχέων (φορτίων) στο δίκτυο
Εξαμηνιαία Εργασία 2015 Εμπορικό / Βιομηχανικό Κτίριο στο FINE. Σχεδίαση του δικτύου μίας ηλεκτρικής εγκατάστασης. Σχεδίαση του κεντρικού οριζόντιου δικτύου. Σκοπός Τοποθέτηση Υποδοχέων (φορτίων) στο δίκτυο
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
11 Το ολοκλήρωµα Riemann
 Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
Άσκηση 2 η 2 Σχήµατα Καµπύλες Ι. Στόχος της άσκησης
 Άσκηση 2 η 2 Σχήµατα Καµπύλες Ι Στόχος της άσκησης Σην παρούσα άσκηση επιχηρείται η σχεδίαση ενός τρισδιάστατου αντικειµένου µε τη χρήση διδιάστατων καµπυλών. Στόχος της άσκησης είναι η εξοικείωση µε τη
Άσκηση 2 η 2 Σχήµατα Καµπύλες Ι Στόχος της άσκησης Σην παρούσα άσκηση επιχηρείται η σχεδίαση ενός τρισδιάστατου αντικειµένου µε τη χρήση διδιάστατων καµπυλών. Στόχος της άσκησης είναι η εξοικείωση µε τη
Μελέτη 1 Πρώτη Μελέτη Διαμερίσματος στο FINE. Εισαγωγή αρχιτεκτονικών σχεδίων σε μία μελέτη, στο FINE.
 Σκοπός Μελέτη 1 Πρώτη Μελέτη Διαμερίσματος στο FINE. Δημιουργία Νέας Μελέτης. Εισαγωγή αρχιτεκτονικών σχεδίων σε μία μελέτη, στο FINE. Διαδικασία wblock. Καθορισμός Κτιρίου. Σχεδίαση του δικτύου, μίας
Σκοπός Μελέτη 1 Πρώτη Μελέτη Διαμερίσματος στο FINE. Δημιουργία Νέας Μελέτης. Εισαγωγή αρχιτεκτονικών σχεδίων σε μία μελέτη, στο FINE. Διαδικασία wblock. Καθορισμός Κτιρίου. Σχεδίαση του δικτύου, μίας
οµή δικτύου ΣΧΗΜΑ 8.1
 8. ίκτυα Kohonen Το µοντέλο αυτό των δικτύων προτάθηκε το 1984 από τον Kοhonen, και αφορά διαδικασία εκµάθησης χωρίς επίβλεψη, δηλαδή δεν δίδεται καµία εξωτερική επέµβαση σχετικά µε τους στόχους που πρέπει
8. ίκτυα Kohonen Το µοντέλο αυτό των δικτύων προτάθηκε το 1984 από τον Kοhonen, και αφορά διαδικασία εκµάθησης χωρίς επίβλεψη, δηλαδή δεν δίδεται καµία εξωτερική επέµβαση σχετικά µε τους στόχους που πρέπει
Κεφάλαιο 6 Παράγωγος
 Σελίδα από 5 Κεφάλαιο 6 Παράγωγος Στο κεφάλαιο αυτό στόχος µας είναι να συνδέσουµε µία συγκεκριµένη συνάρτηση f ( ) µε µία δεύτερη συνάρτηση f ( ), την οποία και θα ονοµάζουµε παράγωγο της f. Η τιµή της
Σελίδα από 5 Κεφάλαιο 6 Παράγωγος Στο κεφάλαιο αυτό στόχος µας είναι να συνδέσουµε µία συγκεκριµένη συνάρτηση f ( ) µε µία δεύτερη συνάρτηση f ( ), την οποία και θα ονοµάζουµε παράγωγο της f. Η τιµή της
ΕΘΝΙΚΟ!ΜΕΤΣΟΒΙΟ!ΠΟΛΥΤΕΧΝΕΙΟ! ΣΧΟΛΗ!ΧΗΜΙΚΩΝ!ΜΗΧΑΝΙΚΩΝ!!
 ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)1 Ο :) ΜΕΤΑΦΟΡΑ)ΘΕΡΜΟΤΗΤΑΣ)ΣΕ)ΔΙΣΚΟ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ ΕΚΦΩΝΗΣΗ
ΕΘΝΙΚΟΜΕΤΣΟΒΙΟΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗΧΗΜΙΚΩΝΜΗΧΑΝΙΚΩΝ ΦΑΙΝΟΜΕΝΑΜΕΤΑΦΟΡΑΣΙ ΥΠΟΛΟΓΙΣΤΙΚΟΕΡΓΑΣΤΗΡΙΟ COMSOLMULTIPHYSICS ΠΑΡΑΔΕΙΓΜΑ)1 Ο :) ΜΕΤΑΦΟΡΑ)ΘΕΡΜΟΤΗΤΑΣ)ΣΕ)ΔΙΣΚΟ) ΕΠΙΜΕΛΕΙΑ: ΕΛΕΝΗΚΟΡΩΝΑΚΗ ΠΕΡΙΕΧΟΜΕΝΑ ΕΚΦΩΝΗΣΗ
sin ϕ = cos ϕ = tan ϕ =
 Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ ΜΕ ΤΗ ΒΟΗΘΕΙΑ Η/Υ (CAM)
 Α.Τ.Ε.Ι. ΠΑΤΡΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ ΜΕ ΤΗ ΒΟΗΘΕΙΑ Η/Υ (CAM) ΜΠΑΡΟΥΝΗ ΑΝΤΙΓΟΝΗ ΜΗΧΑΝΟΛΟΓΟΣ & ΑΕΡΟΝΑΥΠΗΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΑΤΡΑ
Α.Τ.Ε.Ι. ΠΑΤΡΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΣΗΜΕΙΩΣΕΙΣ ΕΡΓΑΣΤΗΡΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΡΓΑΛΕΙΟΜΗΧΑΝΩΝ ΜΕ ΤΗ ΒΟΗΘΕΙΑ Η/Υ (CAM) ΜΠΑΡΟΥΝΗ ΑΝΤΙΓΟΝΗ ΜΗΧΑΝΟΛΟΓΟΣ & ΑΕΡΟΝΑΥΠΗΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΑΤΡΑ
Πανεπιστήµιο Θεσσαλίας
 Πανεπιστήµιο Θεσσαλίας Τµήµα Πληροφορικής Ενότητα 8η: Συσκευές Ε/Ε - Αρτηρίες Άσκηση 1: Υπολογίστε το µέσο χρόνο ανάγνωσης ενός τµήµατος των 512 bytes σε µια µονάδα σκληρού δίσκου µε ταχύτητα περιστροφής
Πανεπιστήµιο Θεσσαλίας Τµήµα Πληροφορικής Ενότητα 8η: Συσκευές Ε/Ε - Αρτηρίες Άσκηση 1: Υπολογίστε το µέσο χρόνο ανάγνωσης ενός τµήµατος των 512 bytes σε µια µονάδα σκληρού δίσκου µε ταχύτητα περιστροφής
Ο ΗΓΙΕΣ DOCUMENT DESIGNER
 Ο ΗΓΙΕΣ DOCUMENT DESIGNER ΕΙΣΑΓΩΓΗ Εάν δεν επιθυµείτε να χρησιµοποιείτε τις προσχεδιασµένες φόρµες εντύπων της Singular, η εργασία αυτή σας δίνει τη δυνατότητα να σχεδιάζετε φόρµες µε βάση τις οποίες επιθυµείτε
Ο ΗΓΙΕΣ DOCUMENT DESIGNER ΕΙΣΑΓΩΓΗ Εάν δεν επιθυµείτε να χρησιµοποιείτε τις προσχεδιασµένες φόρµες εντύπων της Singular, η εργασία αυτή σας δίνει τη δυνατότητα να σχεδιάζετε φόρµες µε βάση τις οποίες επιθυµείτε
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
Συμβατικός προγραμματισμός CNC. κέντρα τόρνευσης
 Συμβατικός προγραμματισμός CNC κέντρα τόρνευσης Κέντρα τόρνευσης Δομή προγράμματος Αρχές προγραμματισμού Τυποποιημένες εντολές Παραδείγματα Γ.Βοσνιάκος-2013 Συμβατικός προγραμματισμός CNC Άδεια Χρήσης
Συμβατικός προγραμματισμός CNC κέντρα τόρνευσης Κέντρα τόρνευσης Δομή προγράμματος Αρχές προγραμματισμού Τυποποιημένες εντολές Παραδείγματα Γ.Βοσνιάκος-2013 Συμβατικός προγραμματισμός CNC Άδεια Χρήσης
