ΤΡΟΠΟΙ ΕΚΦΡΑΣΗΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ
|
|
|
- Κλυμένη Παππάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΣΤΑ ΙΑΛΥΜΑΤΑ ιάλυµα ονοµάζουµε το οµογενές µίγµα δύο ή περισσοτέρων ουσιών. Στο Γυµνάσιο εξετάζουµε µόνο τα διαλύµατα εκείνα που αποτελούνται από δύο ουσίες. Η µία ουσία που βρίσκεται σε υγρή κατάσταση και σε µεγαλύτερη αναλογία λέγεται διαλύτης και η άλλη µπορεί να είναι στερεή, υγρή ή αέρια και ονοµάζεται διαλυµένη ουσία. Ο συνηθέστερος διαλύτης είναι το νερό. Η περιεκτικότητα ενός διαλύµατος εκφράζει την ποσότητα της διαλυµένης ουσίας που περιέχεται σε ορισµένη ποσότητα διαλύµατος. Μπορούµε να εκφράσουµε την περιεκτικότητα ενός διαλύµατος µε πολλούς τρόπους. Στην Β Γυµνασίου αντιµετωπίζουµε τρεις από αυτούς. ΤΡΟΠΟΙ ΕΚΦΡΑΣΗΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ Περιεκτικότητα στα εκατό βάρος προς βάρος. (Σύµβολο % w/w) ηλώνει πόσα γραµµάρια (g) διαλυµένης ουσίας υπάρχουν σε g διαλύµατος. Για παράδειγµα διάλυµα 10% w/w, σηµαίνει ότι αν είχαµε g του διαλύµατος αυτού θα περιείχαν 10 g διαλυµένης Περιεκτικότητα στα εκατό βάρος προς όγκο. (Σύµβολο % w/v) ηλώνει πόσα γραµµάρια (g) διαλυµένης ουσίας υπάρχουν σε χιλιοστόλιτρα (ml) δ/τος. Για παράδειγµα διάλυµα 12% w/v, σηµαίνει ότι σε ml του διαλύµατος αυτού περιέχονται 12 g δ/νης Περιεκτικότητα στα εκατό όγκο προς όγκο. (Σύµβολο % V/V) Περιεκτικότητα % V/V (σε µίγµατα αερίων) Χρησιµοποιείται σε µίγµατα αερίων και εκφράζει πόσα L ή ml συγκεκριµένου αερίου υπάρχουν σε L ή ml του µίγµατος των αερίων. π.χ. Η περιεκτικότητα του ατµοσφαιρικού αέρα σε οξυγόνο είναι περίπου 20% v/v, που σηµαίνει ότι σε L αέρα υπάρχουν 20 L οξυγόνο. Περιεκτικότητα % V/V ή αλκοολικοί βαθµοί Χρησιµοποιείται σε διαλύµατα αιθυλικής αλκοόλης (οινόπνευµα) και δηλώνει πόσα ml καθαρής αιθανόλης υπάρχουν σε ml δ/τος. π.χ. Η περιεκτικότητα ενός κρασιού είναι 12 (αλκοολικοί βαθµοί). Αυτό σηµαίνει ότι σε ml του κρασιού περιέχονται 12 ml καθαρό οινόπνευµα. ΠΑΡΑΤΗΡΗΣΕΙΣ - Ο ΗΓΙΕΣ ΜΑΖΑ Η µάζα ενός διαλύµατος µετριέται σε γραµµάρια (g) ή χιλιόγραµµα (kg) και είναι πάντοτε ίση µε το άθροισµα της µάζας του διαλύτη και της διαλυµένης Αν για παράδειγµα µας λένε ότι σε 200 g νερό διαλύουµε 40 g ζάχαρη τότε το διάλυµα που θα προκύψει θα έχει µάζα 240 g.
2 ΟΓΚΟΣ Ο όγκος που θα έχει ένα διάλυµα µετριέται σε λίτρα (L) ή χιλιοστόλιτρα (ml) και υπολογίζεται ως εξής : α) Όταν ο διαλύτης είναι υγρό και η διαλυµένη ουσία στερεό ή αέριο τότε ο όγκος του διαλύµατος είναι ίσος µε τον όγκο του διαλύτη. Για παράδειγµα όταν µας λένε ότι σε 1 L νερό διαλύουµε 20 g αλάτι τότε θα θεωρούµε ότι ο όγκος του διαλύµατος είναι 1 L. β) Όταν ο διαλύτης και η διαλυµένη ουσία είναι υγρά τότε ο όγκος του διαλύµατος είναι ίσος µε το άθροισµα των όγκων του διαλύτη και της διαλυµένης Για παράδειγµα αν διαλύσουµε σε 900 ml νερό ml καθαρό οινόπνευµα τότε το διάλυµα που θα προκύψει θα έχει όγκο 0 ml. ΠΥΚΝΟΤΗΤΑ Η πυκνότητα (ρ ή d) ενός διαλύµατος είναι το πηλίκο της µάζας προς τον όγκο του. Αν λοιπόν µας δίνεται η πυκνότητα του διαλύµατος τότε µπορεί να υπολογιστεί ο όγκος του από τη µάζα του και αντίστροφα. m ρ = m= ρ V V = V m ρ ΥΠΟΛΟΓΙΣΜΟΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΒΑΡΟΣ ΠΡΟΣ ΒΑΡΟΣ Για να υπολογίσουµε την περιεκτικότητα % w/w ενός δ/τος πρέπει να γνωρίζουµε την µάζα (g) της διαλυµένης ουσίας που περιέχεται σε ορισµένη µάζα (g) δ/τος. Αυτά δίνονται είτε άµεσα από την εκφώνηση της άσκησης είτε έµµεσα (π.χ. από τον όγκο του δ/τος και την πυκνότητά του µπορούµε να υπολογίσουµε την µάζα του). Παράδειγµα 1. Σε 400 g δ/τος αλατόνερου είναι διαλυµένα 8 g αλάτι. Ποια είναι η % w/w περιεκτικότητα; Στα 400 g δ/τος περιέχονται 8 g δ/νης ουσίας Αν είχαµε g δ/τος = 400 x= 8 x= = Άρα η περιεκτικότητα του διαλύµατος θα είναι 2% w/w ΒΑΡΟΣ ΠΡΟΣ ΟΓΚΟ Για να υπολογίσουµε την περιεκτικότητα % w/v ενός δ/τος πρέπει να γνωρίζουµε την µάζα της διαλυµένης ουσίας που περιέχεται σε ορισµένο όγκο (ml) δ/τος. Παράδειγµα 2. ιαλύουµε 16 g ζάχαρη σε νερό, οπότε το διάλυµα που προκύπτει έχει όγκο 500 ml. Να υπολογιστεί η περιεκτικότητα % w/v. Στα 500 ml δ/τος περιέχονται 16 g δ/νης ουσίας Αν είχαµε ml δ/τος
3 = 500 x= 16 x= = 3, Άρα η περιεκτικότητα του διαλύµατος θα είναι 3,2% w/v ΟΓΚΟ ΠΡΟΣ ΟΓΚΟ Για να υπολογίσουµε την περιεκτικότητα % v/v ενός δ/τος πρέπει να γνωρίζουµε τον όγκο (ml) της διαλυµένης ουσίας που περιέχεται σε ορισµένο όγκο (ml) δ/τος. Παράδειγµα 3. Σε ένα µπουκάλι κρασί που έχει όγκο 700 ml περιέχονται 77 ml καθαρή αλκοόλη. Να υπολογιστεί η περιεκτικότητα % v/v. Στα 700 ml δ/τος περιέχονται 77 ml δ/νης ουσίας Αν είχαµε ml δ/τος x; ml δ/νης ουσίας = 700 x= 77 x= = Άρα η περιεκτικότητα του διαλύµατος θα είναι 11% v/v ΜΕΤΑΤΡΟΠΕΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΕΝΟΣ ΙΑΛΥΜΑΤΟΣ Όταν δίνεται ένας τρόπος έκφρασης της περιεκτικότητας και ζητείται κάποιος άλλος τότε πρέπει: α) να αναλύσουµε την έκφραση περιεκτικότητας που µας δίνεται, β) να σκεφτούµε τι δηλώνει ο τρόπος έκφρασης περιεκτικότητας που ζητείται και τι θα χρειαστεί να µετατρέψουµε γ) να κάνουµε την αναγωγή (απλή µέθοδο των τριών). Παράδειγµα 4. Ένα διάλυµα έχει όγκο 500 ml και περιεκτικότητα 8% w/v. Αν η πυκνότητα του διαλύµατος είναι 1,2 g/ml να υπολογιστεί η περιεκτικότητα του διαλύµατος % w/w. Αν είχαµε ml δ/τος θα περιείχαν 8 g δ/νης ουσίας Τώρα που έχουµε 500 ml δ/τος = x= x= = x Άρα το διάλυµα περιέχει 40 g δ/νης Επειδή ζητάµε την περιεκτικότητα % w/w θα πρέπει να µετατρέψουµε τον όγκο του διαλύµατος σε µάζα µε την βοήθεια της πυκνότητας. m m ρ = 1, 2= m= 1, 2 500= 600 Η µάζα λοιπόν του διαλύµατος V 500 είναι 600 g. Η διαλυµένη ουσία είναι σε g άρα δεν χρειάζεται µετατροπή. Έτσι έχουµε :
4 Στα 600 g δ/τος περιέχονται 40 g δ/νης ουσίας Αν είχαµε g δ/τος = 600 x= 40 x= = = 6, Άρα η περιεκτικότητα του διαλύµατος θα είναι 6,66 % w/w ΑΝΑΜΙΞΗ ΙΑΛΥΜΑΤΩΝ Στις ασκήσεις, που αναφέρονται στην ανάµιξη διαλυµάτων, µας πληροφορούν ότι γίνεται ανάµιξη δύο ή περισσοτέρων διαλυµάτων της ίδιας διαλυµένης ουσίας και ζητούνται οι ποσότητες των διαλυµάτων (αρχικών ή τελικών), οι περιεκτικότητές τους ή οποιαδήποτε άλλη µεταβλητή σχετική µ' αυτά. Έτσι έχουµε δυο αρχικά διαλύµατα ( 1 και 2) τα οποία αναµιγνύονται και δίνουν ένα τελικό διάλυµα ( 3). Κατά την ανάµιξη ισχύουν: α) Η µάζα της δ/νης ουσίας στο τελικό διάλυµα είναι πάντα ίση µε το άθροισµα των µαζών των διαλυµένων ουσιών που υπάρχουν στα αρχικά διαλύµατα. β) Η µάζα του τελικού δ/τος είναι πάντα ίση µε το άθροισµα των µαζών των διαλυµάτων που αναµίχθηκαν. γ) Ο όγκος του τελικού δ/τος θα θεωρείται ότι είναι ίσος µε το άθροισµα των όγκων των διαλυµάτων που αναµίχθηκαν. Παράδειγµα 5. Ένα διάλυµα 1 που έχει µάζα 600 g και περιεκτικότητα 5% w/w αναµιγνύεται µε ένα δεύτερο διάλυµα 2 που έχει µάζα 400 g και περιεκτικότητα 10% w/w. Να υπολογιστεί η περιεκτικότητα % w/w του διαλύµατος 3 που θα προκύψει από την ανάµιξη. Αν είχαµε g δ/τος θα περιείχαν 5 g δ/νης ουσίας Τώρα που έχουµε 600 g δ/τος = x= x= = x περιέχει 30 g δ/νης Αν είχαµε g δ/τος θα περιείχαν 10 g δ/νης ουσίας Τώρα που έχουµε 400 g δ/τος = x= x= = x Άρα το διάλυµα 2 περιέχει 40 g δ/νης Το τελικό διάλυµα 3 θα έχει µάζα = 0 g ενώ η διαλυµένη ουσία που περιέχει θα είναι = 70 g. Έτσι λοιπόν θα έχουµε:
5 Στα 0 g δ/τος περιέχονται 70 g δ/νης ουσίας Αν είχαµε g δ/τος ιάλυµα = 0 x= 70 x= = 7 0 Άρα η περιεκτικότητα του διαλύµατος 3 θα είναι 7 % w/w ΑΡΑΙΩΣΗ ΙΑΛΥΜΑΤΟΣ (ΠΡΟΣΘΕΣΗ ΙΑΛΥΤΗ) Η πρόσθεση διαλύτη σε ένα διάλυµα (αραίωση διαλύµατος) µπορεί να θεωρηθεί σαν ειδική περίπτωση ανάµιξης διαλυµάτων, αν θεωρήσουµε ότι ο διαλύτης είναι ένα διάλυµα µε 0% περιεκτικότητα. Έτσι ισχύουν: α) Η µάζα της διαλυµένης ουσίας του αρχικού και του τελικού (αραιωµένου) δ/τος είναι η ίδια. β) Η µάζα του τελικού δ/τος είναι ίση µε το άθροισµα των µαζών του αρχικού δ/τος και του διαλύτη που προστέθηκε. γ) Ο όγκος του τελικού δ/τος είναι ίσος µε το άθροισµα των όγκων του αρχικού δ/τος και του διαλύτη που προστέθηκε. Παράδειγµα 6. Ένα διάλυµα 1 που έχει µάζα 800 g και περιεκτικότητα 5% w/w αραιώνεται µε 200 g νερό οπότε προκύπτει διάλυµα 2. Να υπολογιστεί η περιεκτικότητα % w/w του διαλύµατος 2 που θα προκύψει από την αραίωση. Αν είχαµε g δ/τος θα περιείχαν 5 g δ/νης ουσίας Τώρα που έχουµε 800 g δ/τος = x= x= = x περιέχει 40 g δ/νης Αφού για να κάνουµε την αραίωση προσθέτουµε 200 g νερό, το διάλυµα 2 που θα προκύψει θα έχει µάζα = 0 g. Η διαλυµένη ουσία όµως θα παραµείνει 40 g. Έτσι θα έχουµε: Στα 0 g δ/τος περιέχονται 40 g δ/νης ουσίας Αν είχαµε g δ/τος = 0 x= 40 x= = 4 0 Άρα η περιεκτικότητα του αραιωµένου διαλύµατος 2 θα είναι 4 % w/w.
6 ΣΥΜΠΥΚΝΩΣΗ ΙΑΛΥΜΑΤΟΣ (ΑΦΑΙΡΕΣΗ ΙΑΛΥΤΗ) Η αφαίρεση διαλύτη από ένα δ/µα γίνεται συνήθως µε βράσιµο οπότε εξατµίζεται ένα µέρος του διαλύτη αλλά η ποσότητα της διαλυµένης ουσίας δεν µεταβάλλεται. Έτσι το διάλυµα που προκύπτει είναι πιο πυκνό από το αρχικό διάλυµα (συµπύκνωση διαλύµατος). Έτσι ισχύουν: α) Η µάζα της διαλυµένης ουσίας του αρχικού και του τελικού (συµπυκνωµένου) δ/τος είναι η ίδια. β) Η µάζα του τελικού δ/τος είναι ίση µε τη διαφορά των µαζών του αρχικού δ/τος και του διαλύτη που αφαιρέθηκε. γ) Ο όγκος του τελικού δ/τος είναι ίσος µε τη διαφορά των όγκων του αρχικού δ/τος και του διαλύτη που αφαιρέθηκε. Παράδειγµα 7. Ένα διάλυµα 1 που έχει µάζα 1200 g και περιεκτικότητα 2% w/w θερµαίνεται µέχρι βρασµού οπότε ένα µέρος του διαλύτη εξατµίζεται και το τελικό διάλυµα 2 που προκύπτει έχει µάζα 800 g. Να υπολογιστεί η περιεκτικότητα % w/w του συµπυκνωµένου διαλύµατος 2 καθώς και η µάζα του διαλύτη που εξατµίστηκε. Αν είχαµε g δ/τος θα περιείχαν 2 g δ/νης ουσίας Τώρα που έχουµε 1200 g δ/τος = x= x= = x περιέχει 24 g δ/νης Αφού θα το βράσουµε θα εξατµιστεί ένα µέρος του διαλύτη και το διάλυµα που θα προκύψει θα έχει µάζα 800 g αλλά η διαλυµένη ουσία θα παραµείνει 24 g. Έτσι θα έχουµε: Στα 800 g δ/τος περιέχονται 24 g δ/νης ουσίας Αν είχαµε g δ/τος = 800 x= 24 x= = Άρα η περιεκτικότητα του συµπυκνωµένου διαλύµατος 2 θα είναι 3 % w/w. Η µάζα του διαλύτη που εξατµίστηκε θα είναι = 400 g. ΣΥΜΠΥΚΝΩΣΗ ΙΑΛΥΜΑΤΟΣ (ΠΡΟΣΘΗΚΗ ΙΑΛ/ΝΗΣ ΟΥΣΙΑΣ) Μπορούµε να πετύχουµε συµπύκνωση ενός διαλύµατος προσθέτοντας επιπλέον διαλυµένη ουσία. Στην περίπτωση αυτή ισχύουν: α) Η µάζα της διαλυµένης ουσίας του τελικού (συµπυκνωµένου) δ/τος είναι ίση µε το άθροισµα της διαλυµένης ουσίας του αρχικού διαλύµατος και της επιπλέον διαλυµένης ουσίας που προσθέσαµε.
7 β) Η µάζα του τελικού δ/τος είναι ίση µε το άθροισµα των µαζών του αρχικού δ/τος και της επιπλέον διαλυµένης ουσίας που προστέθηκε. γ) Ο όγκος του τελικού δ/τος είναι ίσος µε τον όγκο του αρχικού διαλύµατος αν η διαλυµένη ουσία που προστέθηκε επιπλέον, είναι στερεή ή αέρια. Στην περίπτωση που η διαλυµένη ουσία είναι υγρή, ο τελικός όγκος θα είναι ίσος µε το άθροισµα του όγκου του αρχικού διαλύµατος και του όγκου της διαλυµένης ουσίας που προσθέσαµε. Παράδειγµα 8. Σε ένα διάλυµα 1 που έχει µάζα 800 g και περιεκτικότητα 5% w/w προσθέτουµε επιπλέον ποσότητα διαλυµένης ουσίας και το διάλυµα 2 που προκύπτει έχει µάζα 810 g. Να υπολογιστεί η µάζα της διαλυµένης ουσίας που προσθέσαµε καθώς και η περιεκτικότητα % w/w του συµπυκνωµένου διαλύµατος 2. Αν είχαµε g δ/τος θα περιείχαν 5 g δ/νης ουσίας Τώρα που έχουµε 800 g δ/τος = x= x= = x περιέχει 40 g δ/νης Αφού το τελικό διάλυµα έχει µάζα 810 g η ποσότητα της διαλυµένης ουσίας που προσθέσαµε θα είναι = 10 g. Έτσι το συµπυκνωµένο διάλυµα θα περιέχει = 50 g διαλυµένης Οπότε θα έχουµε: Στα 810 g δ/τος περιέχονται 50 g δ/νης ουσίας Αν είχαµε g δ/τος = 810 x= 50 x= 6, Άρα η περιεκτικότητα του συµπυκνωµένου διαλύµατος 2 θα είναι περίπου 6,17 % w/w.
Χημεία Α Λυκείου. Διαλύματα
Διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποούν τα συστατικά του διαλύματος. Από τα συστατικά αυτά, εκείνο που έχει την ίδια φυσική κατάσταση με αυτή του διαλύματος
ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΙΑΛΥΜΑΤΑ
ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυµάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούµε ή να
2.3 Περιεκτικότητα διαλύματος Εκφράσεις περιεκτικότητας
1 Η θεωρία του μαθήματος με ερωτήσεις. 2.3 Περιεκτικότητα διαλύματος Εκφράσεις περιεκτικότητας Ερωτήσεις θεωρίας με απάντηση 3-1. Τι ονομάζεται περιεκτικότητα ενός διαλύματος; Είναι μία έκφραση που δείχνει
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
ΜΕΘΟ ΟΛΟΓΙΑ: ΙΑΛΥΜΑΤΑ
ΜΕΘΟ ΟΛΟΓΙΑ: ΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυµάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούµε ή να µετατρέψουµε διάφορες περιεκτικότητες.
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
Για την επίλυση αυτής της άσκησης, αλλά και όλων των παρόμοιων χρησιμοποιούμε ιδιότητες των αναλογιών (χιαστί)
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
Περιεκτικότητα διαλύματος ονομάζουμε την ποσότητα της διαλυμένης ουσίας που περιέχεται σε ορισμένη μάζα ή όγκο διαλύματος.
Διαλύματα Περιεκτικότητες 11 Αν ο καθηγητής Χημείας έδινε στους μαθητές του τη δυνατότητα να παρασκευάσουν στο Εργαστήριο Χημείας, ο καθένας χωριστά, ένα υδατικό διάλυμα ζάχαρης, είναι προφανές ότι το
Διάλυμα, είναι κάθε ομογενές μίγμα δύο ή περισσότερων ουσιών.
Διάλυμα, είναι κάθε ομογενές μίγμα δύο ή περισσότερων ουσιών. Διαλύτης: Είναι το συστατικό του διαλύματος που έχει την ίδια φυσική κατάσταση με το διάλυμα. Όταν περισσότερα από ένα συστατικά έχουν την
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει τα δοµικά σωµατίδια της ύλης (άτοµο - µόριο - ιόν).
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει τι είναι η µάζα, το βάρος, ο όγκος και η πυκνότητα ενός σώµατος και τις µονάδες µέτρησής τους. Να γνωρίζει
Συγκέντρωση ή μοριακότητα κατά όγκο ή Molarity διαλύματος
79 Συγκέντρωση ή μοριακότητα κατά όγκο ή Molarity διαλύματος Molarity ( Μ ) ή μοριακότητα κατ όγκο: μας δίνει τα mol της διαλυμένης ουσίας που περιέχονται σε 1000 ml ( = 1 L ) διαλύματος. Π.χ. υδατικό
Συγκέντρωση διαλύματος
Συγκέντρωση διαλύματος 22-1. SOS Ερώτηση: τι ονομάζουμε μοριακότητα κατ όγκο ή Molarity (Μολάριτι); Η μοριακότητα κατ' όγκο ή συγκέντρωση ή Molarity, εκφράζει τα mol διαλυμένης ουσίας που περιέχονται σε
χημεία Κατά βάρος (w/w %) επιμέλεια: Φόρης Μουρατίδης σελίδα 1 από 6 Βασίλης Συμεωνίδης, προσωπικός δικτυακός τόπος
Φύλλο Εργασίας ΠΕΡΙΕΚΤΙΚΟΤΗΤΕΣ ΙΑΛΥΜΑΤΩΝ - 1 Κατά βάρος (w/w %) 10gr καθαρής ουσίας 90gr διαλύτη 100 gr διαλύµατος 90 + 10 = 100 gr διαλύµατος περιέχουν 10 gr καθαρής ουσίας Έχουµε διάλυµα 10% w/w Η περιεκτικότητα
Σημειώσεις Χημείας Α Λυκείου - Κεφάλαιο 1 ο
ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΚΤΙΚΟΤΗΤΕΣ ΔΙΑΛΥΜΑΤΩΝ ΔΙΑΛΥΤΟΤΗΤΑ - ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ Γενικά για τα διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποτελούν τα συστατικά του διαλύματος.
Μίγματα - Διαλύματα:
ΧΗΜΕΙΑ: Εισαγωγή στην Χημεία - από το νερό στο άτομο- από το μακρόκοσμο στον μικρόκοσμο 49 Μίγματα - Διαλύματα: Μίγματα: Τι είναι τα μίγματα; Μίγματα ονομάζονται τα υλικά που αποτελούνται από δύο ή περισσότερες
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity)
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity) ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σημειώστε με Σωστό ή Λάθος. i) Η συγκέντρωση ενός διαλύματος είναι ίδια για ολόκληρο το διάλυμα ή για ένα μέρος αυτού. ii) Σε 50 ml διαλύματος
2.3 Περιεκτικότητα διαλύματος εκφράσεις περιεκτικότητας
2.3 Περιεκτικότητα διαλύματος εκφράσεις περιεκτικότητας 2.3.1 Περιεκτικότητα διαλύματος στα εκατό κατά βάρος προς βάρος (% w/w) 2.3.2 Περιεκτικότητα διαλύματος στα εκατό κατά βάρος προς όγκο (%w/v) 2.3.3
Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C.
4.1 Βασικές έννοιες Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C. Σχετική ατομική μάζα ή ατομικό βάρος λέγεται ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη
Ταξινόμηση της ύλης Διαλύματα Περιεκτικότητες διαλυμάτων. Χημεία Α Λυκείου Διδ. Εν. 1.5 π. Ευάγγελος Μαρκαντώνης 2 ο ΓΕΛ Αργυρούπολης
Ταξινόμηση της ύλης Διαλύματα Περιεκτικότητες διαλυμάτων Χημεία Α Λυκείου Διδ. Εν. 1.5 π. Ευάγγελος Μαρκαντώνης 2 ο ΓΕΛ Αργυρούπολης Μακροσκοπική ταξινόμηση της ύλης ΥΛΗ Καθορισµένη (καθαρή) ουσία όχι
Α = Ζ + Ν ΑΤΟΜΟ. ΙΣΟΤΟΠΑ είναι. ΝΕΤΡΟΝΙΑ (n) ΠΥΡΗΝΑΣ
ΚΕΦ.1: 3. ΔΟΜΗ ΑΤΟΜΟΥ ΑΤΟΜΟ ΠΥΡΗΝΑΣ ΠΡΩΤΟΝΙΑ (p + ) ΝΕΤΡΟΝΙΑ (n) 1.3.1 Να βρείτε τον αριθμό πρωτονίων νετρονίων και ηλεκτρονίων που υπάρχουν στα παρακάτω άτομα ή ιόντα: ΗΛΕΚΤΡΟΝΙΑ (e - ) ΠΡΟΣΟΧΗ 1) Στα
n V m M n = C V Με το γράµµα n συµβολίζουµε το πλήθος των mol µιας χηµικής ουσίας. Το m παριστάνει την µάζα της ουσίας σε g ενώ το M r
Για να εκφράσουµε την ποσότητα µιας χηµικής ουσίας χρησιµοποιούµε τρία φυσικάµεγέθη: Τηνµάζα (), τονόγκο () καιτοπλήθοςτων ol (). ΣτηΧηµείατηνµάζατηνµετράµεσυνήθωςσεγραµµάρια (g) καιτονόγκο σε χιλιοστόλιτραήλίτρα
1 C 8 H /2 O 2 8 CO H 2 O
ΧΗΜΕΙΙΑ Β ΛΥΚΕΙΙΟΥ 4 ο ΘΕΜΑ (από τράπεζα θεµάτων) ΑΣΚΗΣΗ 1 Σε εργαστήριο ελέγχου καυσίµων πραγµατοποιήθηκαν τα παρακάτω πειράµατα: α) Ένα δείγµα C 8 H 18 µε µάζα 1,14 g κάηκε πλήρως µε την απαιτούµενη
ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ. ΑΣΚΗΣΗ 1 Ο παρακάτω πίνακας δίνει µερικές πληροφορίες που αφορούν την δοµή τεσσάρων ατόµων Q, X, Ψ, R: Ζ Α p + n
ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΑΣΚΗΣΗ 1 Ο παρακάτω πίνακας δίνει µερικές πληροφορίες που αφορούν την δοµή τεσσάρων ατόµων Q, X, Ψ, R: Ζ Α p + n Ηλεκτρονιακή διαµόρφωση κατά στιβάδες Q 19 39 X 20 10 Ψ 6 6 R 8 Κ(2) L(4)
1 o ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ ΚΟΡΔΕΛΙΟΥ ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ, ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1. ΚΕΦΑΛΑΙΟ 1- ΒΑΣΙΚΑ ΜΕΓΕΘΗ-ΣΩΜΑΤΙΔΙΑ - Τι πρέπει να γνωρίζουμε
1 o ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ ΚΟΡΔΕΛΙΟΥ ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ, ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 ΚΕΦΑΛΑΙΟ 1- ΒΑΣΙΚΑ ΜΕΓΕΘΗ-ΣΩΜΑΤΙΔΙΑ - Τι πρέπει να γνωρίζουμε 1. Βασικά μεγέθη και μονάδες αυτών που θα χρησιμοποιηθούν
ΙΣΧΥΡΟΙ ΗΛΕΚΤΡΟΛΥΤΕΣ
ΙΣΧΥΡΟΙ ΗΛΕΚΤΡΟΛΥΤΕΣ 1. ΙΑΛΥΜΑ ΕΝΟΣ ΙΣΧΥΡΟΥ ΟΞΕΟΣ (Ή ΒΑΣΕΩΣ) π.χ.1 Να υπολογιστεί το pη δ/τος ΗΝΟ 3 εάν σε 250mL περιέχονται 0,01575g ΗΝΟ 3. [3] π.χ.2 Πόσα g Bα(ΟΗ) 2 χρειάζεται να διαλύσουµε στο νερό
( α πό τράπεζα θεµάτων) ΚΕΦΑΛΑΙΟ 1 : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ. 1. Να χαρακτηρίσετε τις επόµενες προτάσεις ως σωστές (Σ) ή λανθασµένες (Λ).
Χηµεία Α Λυκείου Φωτεινή Ζαχαριάδου 1 από 12 ( α πό τράπεζα θεµάτων) ΚΕΦΑΛΑΙΟ 1 : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 1. Να χαρακτηρίσετε τις επόµενες προτάσεις ως σωστές (Σ) ή λανθασµένες (Λ). α) Ένα µείγµα είναι πάντοτε
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων)
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων) 1. Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές. i. H σχετική ατομική μάζα μετριέται σε γραμμάρια. ii. H σχετική ατομική μάζα είναι
Τι ονομάζουμε χημικό στοιχείο; Δώστε ένα παράδειγμα. Ερώτηση θεωρίας. Τι ονομάζουμε χημική ένωση; Δώστε ένα παράδειγμα. Ερώτηση θεωρίας.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ Β ΓΥΜΝΑΣΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 23-04-2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΜΑΡΙΝΟΣ ΙΩΑΝΝΟΥ ΑΠΑΝΤΗΣΕΙΣ ο ΘΕΜΑ 1 1.1 Τα πρωτόνια που περιέχονται στον πυρήνα του στοιχείου Χ είναι κατά 1 λιγότερα
τι θα κάνουµε Παρασκευή50 ml διαλύµατος 5% w/v ζαχαρόνερου
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: Παρασκευή, αραίωση και ανάµιξη διαλυµάτων Για την Ασφάλειά µας: 1. Προσοχή-Ησυχία 2. Μαζεύουµε τα µαλλιά 3. Ελαφρά ρούχα-ευκινησία 4. Εναλλαγή µαθητών στην εκτέλεση κάθε πειράµατος
Xημεία β γυμνασίου. Ερωτήσεις πολλαπλής επιλογής
Xημεία β γυμνασίου Ερωτήσεις πολλαπλής επιλογής 1. Ένα υγρό βρέθηκε με τη βοήθεια του ζυγού ότι έχει μάζα 22g και με τη βοήθεια ογκομετρικού κυλίνδρου ότι έχει όγκο 20 ml. Η πυκνότητά του είναι: α. 1,1
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων Ιωάννης Πούλιος Ιωάννης Ζιώγας Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Κανόνες ασφαλείας-βασικοί μικροβιολογικοί χειρισμοί-συγκεντρώσεις διαλυμάτων Παναγούλιας Ιωάννης, MSc,PhD
Άσκηση «Κανόνες ασφαλείας-βασικοί μικροβιολογικοί χειρισμοί-συγκεντρώσεις διαλυμάτων» Eρωτήσεις Αυτοαξιολόγησης 1. Σε 380gr Η 2 Ο προσθέτουμε 20gr NaOH και προκύπτει διάλυμα όγκου 320mL. To % w/w του διαλύματος
mol L (µονάδες 10) ίνονται οι σχετικές ατοµικές µάζες: A r (Η)=1, A r (Ο)=16, A r (Νa)=23.
Σε νερό διαλύεται ορισµένη ποσότητα NaOH και το διάλυµα που παρασκευάζεται έχει συγκέντρωση 0,4 (διάλυµα 1). α) Να υπολογίσετε τη µάζα (σε g) του NaOH που περιέχεται σε 100 του διαλύµατος 1. β) 50 διαλύµατος
Εργαστηριακή άσκηση 4: ΠΑΡΑΣΚΕΥΗ ΙΑΛΥΜΑΤΟΣ ΟΡΙΣΜΕΝΗΣ ΣΥΓΚΕΝΤΡΩΣΗΣ - ΑΡΑΙΩΣΗ ΙΑΛΥΜΑΤΩΝ
ΧΗΜΕΙΑ Α ΛΥΚΕΙΟΥ Εργαστηριακή άσκηση 4: ΠΑΡΑΣΚΕΥΗ ΙΑΛΥΜΑΤΟΣ ΟΡΙΣΜΕΝΗΣ ΣΥΓΚΕΝΤΡΩΣΗΣ - ΑΡΑΙΩΣΗ ΙΑΛΥΜΑΤΩΝ ΣΤΟΧΟΙ Στο τέλος του πειράµατος αυτού θα πρέπει να µπορείς : 1. Να εφαρµόζεις το ζυγό. 2. Να µετράς
Δομικά σωματίδια - Καταστάσεις και ιδιότητες της ύλης
Δομικά σωματίδια - Καταστάσεις και ιδιότητες της ύλης 1. Πόσα πρωτόνια, νετρόνια και ηλεκτρόνια περιέχει καθένα από τα επόμενα άτομα: 7 26 112 3 12 47 Li, Mg, Ag. 7 3Li : Ο ατομικός αριθμός (Ζ) είναι 3
δ. g NaCl σε 00g διαλύµατος 7.Σε υδατικό διάλυµα ζάχαρης έχουµε α. 0 g ζάχαρης, L β. 0 g ζάχαρης, L γ. 0 g ζάχαρης, L δ. 0 g ζάχαρης, L 0 %/ (αν από τ
Σ Τ Ο Ι Χ Ε Ι Ο Μ Ε Τ Ρ Ι Α ηµήτρης Αθανασίου Φυσικός A.ΠΕΡΙΕΚΤΙΚΟΤΗΤΑ - ΙΑΛΥΤΟΤΗΤΑ Ερωτήσεις πολλαπλής επιλογής.tα διαλύµατα α.είναι ετερογενή µίγµατα β.είναι οµογενή µίγµατα που έχουν την ίδια σύσταση
ΕΡΩΤΗΣΕΙΣ ΧΗΜΕΙΑΣ Β ΕΝΟΤΗΤΑ 1 1.1, 1.2
ΕΡΩΤΗΣΕΙΣ ΧΗΜΕΙΑΣ Β ΕΝΟΤΗΤΑ 1 1.1, 1.2 1. Ερώτηση 3 σελίδα 13 2. Ερωτήσεις 2 και 3 σελίδα 19 3. Ποιες µετατροπές της φυσικής κατάστασης των υλικών περιγράφονται παρακάτω ; α. Έπλυνε τα χέρια και το πρόσωπό
Άσκηση 2η. Παρασκευή Αραίωση διαλύματος
Άσκηση 2η Παρασκευή Αραίωση διαλύματος 2 Θεωρητικό μέρος Η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις) Τα μίγματα (δύο ή περισσότερες καθαρές ουσίες) Τα μίγματα
Περιεκτικότητα στα εκατό κατά βάρος (% W/W): εκφράζει τα γραµµάρια της διαλυµένης ουσίας που περιέχονται σε 100 g διαλύµατος.
1 ΚΕΦΑΛΑΙΟ 1 ο 1. ΙΑΛΥΜΑΤΑ (ΠΕΡΙΕΚΤΙΚΟΤΗΤΑ - ΙΑΛΥΤΟΤΗΤΑ) Όπως νφέρµε διάλυµ είνι έν οµογενές µίγµ που ποτελείτι πό δύο ή περισσότερες χηµικές ουσίες. Περιεκτικότητ διλύµτος είνι η ποσότητ της διλυµένης
Παρασκευή διαλυµάτων µε περιεκτικότητα % v/v Οδηγίες για τον καθηγητή
Οδηγίες για τον καθηγητή Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος B Γυµνασίου - A Λυκείου Χηµεία Περιεκτικότητα διαλυµάτων v/v ιαλύµατα Από το νερό στο άτοµο Βασικές έννοιες
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανολόγων Μηχανικών. Χημεία. Ενότητα 15: Διαλύματα
Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 15: Διαλύματα Αν. Καθηγητής Γεώργιος Μαρνέλλος e-mail: gmarnellos@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΡΑΣΚΕΥΗ ΙΑΛΥΜΑΤΟΣ ΟΡΙΣΜΕΝΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΣΤΟ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΤΗΡΙΟ ΤΟΥ ΛΟΓΙΣΜΙΚΟΥ Β ΓΥΜΝΑΣΙΟΥ <<Ο ΘΑΥΜΑΣΤΟΣ ΚΟΣΜΟΣ ΤΗΣ ΧΗΜΕΙΑΣ>>
1.ΤΙΤΛΟΣ: ΠΑΡΑΣΚΕΥΗ ΙΑΛΥΜΑΤΟΣ ΟΡΙΣΜΕΝΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΣΤΟ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΤΗΡΙΟ ΤΟΥ ΛΟΓΙΣΜΙΚΟΥ Β ΓΥΜΝΑΣΙΟΥ 2.ΕΜΠΛΕΚΟΜΕΝΕΣ ΓΝΩΣΤΙΚΕΣ ΠΕΡΙΟΧΕΣ 3.ΓΝΩΣΕΙΣ ΚΑΙ ΑΝΤΙΛΗΨΕΙΣ
ΑΣΚΗΣΗ ΥΔΑΤΟΚΑΛΛΙΕΡΓΕΙΩΝ: Υπολογισμοί με διαλύματα- 1
ΑΣΚΗΣΗ ΥΔΑΤΟΚΑΛΛΙΕΡΓΕΙΩΝ: Υπολογισμοί με διαλύματα- 1 Επί τοις 100 (%) διαλύματα είναι αυτά που έχουν παρασκευαστεί στη βάση του πόσα «μέρη» διαλυτού υπάρχουν διαλυμένα σε 100 μέρη διαλύματος. Ονοματολογία:
ΚΕΦΑΛΑΙΟ 1: Διαμοριακές Δυνάμεις-Καταστάσεις της ύλης-προσθετικές ιδιότητες
ΚΕΦΑΛΑΙΟ 1: Διαμοριακές Δυνάμεις-Καταστάσεις της ύλης-προσθετικές ιδιότητες 1. Η τάση ατμών ενός υγρού εξαρτάται: i. Από την ποσότητα του υγρού ii. Τη θερμοκρασία iii. Τον όγκο του δοχείου iv. Την εξωτερική
Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ. Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ
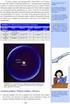ΑΕΝ / ΑΣΠΡΟΠΥΡΓΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ 2 Ογκομέτρηση προχοϊδα διάλυμα HCl ΕΔΩ ακριβώς μετράμε τον όγκο ( στην εφαπτομένη της καμπύλης
τα βιβλία των επιτυχιών
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα.
1. ΔΙΑΛΥΜΑ Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα. Ετερογενές σύστημα καλείται αυτό, το οποίο αποτελείται
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΠΡΟΗΓΟΥΜΕΝΩΝ ΕΤΩΝ ΜΕ ΑΠΑΝΤΗΣΕΙΣ
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΠΡΟΗΓΟΥΜΕΝΩΝ ΕΤΩΝ ΜΕ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο Στις επόµενες ερωτήσεις να επιλέξετε την σωστή απάντηση : 1. Το µικρότερο σωµατίδιο ενός στοιχείου που µπορεί να πάρει µέρος στον σχηµατισµό χηµικών
ΑΣΚΗΣΕΙΣ ΧΗΜΕΙΑΣ Β ΓΥΜΝΑΣΙΟΥ
ΑΣΚΗΣΕΙΣ ΧΗΜΕΙΑΣ Β ΓΥΜΝΑΣΙΟΥ 1. Να αντιστοιχίσετε το προϊόν της στήλης Ι με την πρώτη ύλη της στήλης ΙΙ. Ι ΙΙ Προϊόν Πρώτη ύλη 1. μακαρόνια α. ξύλο 2. πλαστικά β. λιγνίτης 3. ηλεκτρική ενέργεια γ. βωξίτης
Γενική Χημεία. Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής
Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Ασκήσεις διαλυμάτων. Επαναληπτικές ασκήσεις Α' Λυκείου 1
Επαναληπτικές ασκήσεις Α' Λυκείου 1 Ασκήσεις διαλυμάτων. 1. Διαλύουμε πλήρως 20 g σε 20 g H 2 O και προκύπτει διάλυμα Α. Να υπολογιστεί η % w/w περιεκτικότητα του διαλύματος. μάζα Δ/τος = 1 + 2 20 + 20
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Θεοδοσία Τσαβλίδου, Μαρίνος Ιωάννου
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 01 03 2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Θεοδοσία Τσαβλίδου, Μαρίνος Ιωάννου ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 1.1 Τι ονομάζουμε χημική αντίδραση; Πότε μια χημική αντίδραση
(Θεωρία-Λυμένες Ασκήσεις) Σπουδές στις Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας
ΕΙΣΑΓΩΓΗ ΣΤΑ ΔΙΑΛΥΜΑΤΑ (Θεωρία-Λυμένες Ασκήσεις) Εργαστηριακές Ασκήσεις Βιολογίας I Σπουδές στις Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία 1o ΜΕΡΟΣ ΘΕΩΡΙΑ Η ύλη μπορεί να
Σωματίδιο (σύμβολο) Θέση Σχετικό φορτίο
XHMEIA-NOTES Μάζα: είναι το μέτρο της αντίστασης που παρουσιάζει ένα σώμα ως προς την μεταβολή της ταχύτητάς του και εκφράζεται το ποσό της ύλης που περιέχεται σε μια ουσία. Όργανο μέτρησης: Ζυγός Όγκος:
1 η Εργαστηριακή άσκηση. Παρασκευή Αραίωση. διαλύματος. Δρ. Άρης Γιαννακάς - Ε.ΔΙ.Π.
1 η Εργαστηριακή άσκηση Παρασκευή Αραίωση διαλύματος 1 Θεωρητικό Μέρος Εισαγωγικές έννοιες Όπως είναι γνωστό η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις)
Λύνουµε περισσότερες ασκήσεις
Χηµεία Γ Λυκείου - Θετικής Κατεύθυνσης Βήµα 3 ο Λύνουµε περισσότερες ασκήσεις 61. Λύνουµε περισσότερες ασκήσεις 1. ιαθέτουµε 500 ml διαλύµατος ( ) NaOH µε ph = 13. α. Στο διάλυµα ( ) προσθέτουµε 1500 ml
Τράπεζα Χημεία Α Λυκείου
Τράπεζα Χημεία Α Λυκείου 1 ο Κεφάλαιο Όλα τα θέματα του 1 ου Κεφαλαίου από τη Τράπεζα Θεμάτων 25 ερωτήσεις Σωστού Λάθους 30 ερωτήσεις ανάπτυξης Επιμέλεια: Γιάννης Καλαμαράς, Διδάκτωρ Χημικός Ερωτήσεις
Κων/νος Θέος 1
Το παρόν φυλλάδιο περιέχει ορισµένα λυµένα παραδείγµατα ασκήσεων στο κεφάλαιο ώσµωση - ωσµωτική πίεση. Σε όλα τα παραδείγµατα δίνεται: R = 0, 082 L atm mol K Εφαρµογή της ωσµωµετρίας 1 ο παράδειγµα Κάνουµε
ΕΚΦΡΑΣΕΙΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΚΑΙ ΣΥΓΚΕΝΤΡΩΣΗΣ
ΕΚΦΡΑΣΕΙΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΚΑΙ ΣΥΓΚΕΝΤΡΩΣΗΣ Η συγκέντρωση συμβολίζεται γενικά με το σύμβολο C ή γράφοντας τον μοριακό τύπο της διαλυμένης ουσίας ανάμεσα σε αγκύλες, π.χ. [ΝΗ 3 ] ή [Η 2 SO 4 ]. Σε κάθε περίπτωση,
Παρασκευή διαλυµάτων µε περιεκτικότητα % w/w Οδηγίες για τον καθηγητή
Οδηγίες για τον καθηγητή Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος B Γυµνασίου - A Λυκείου Χηµεία Περιεκτικότητα διαλυµάτων w/w ιαλύµατα Από το νερό στο άτοµο Βασικές έννοιες
τα βιβλία των επιτυχιών
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
ΔΙΑΛΥΜΑΤΑ. Σγουρόπουλος Ιωάννης Συντονίστρια: Κ. Μήτκα Στέλλα
ΔΙΑΛΥΜΑΤΑ II Σγουρόπουλος Ιωάννης Συντονίστρια: Κ. Μήτκα Στέλλα Εκατοστιαία διαλύματα Δ/μα % στερεάς ουσίας κατά βάρος ανά μονάδα βάρους W/W Δ/μα % στερεάς ουσίας κατά βάρος ανά μονάδα όγκου W/V Δ/μα %
Εκπαιδευτικός Οργανισµός Ν. Ξυδάς 1
Εκπαιδευτικός Οργανισµός Ν. Ξυδάς 1 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1: ΜΕΛΕΤΑΜΕ ΤΑ ΜΕΙΓΜΑΤΑ Εισαγωγή Τα περισσότερα υλικά γύρω µας δεν είναι καθαρές ουσίες αλλά µείγµατα. Ο χρυσός και τα άλλα µέταλλα που παίρνουµε από
ΦΥΣΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ. Οι φυσικές καταστάσεις της ύλης είναι η στερεή, η υγρή και η αέρια.
ΦΥΣΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ Οι φυσικές καταστάσεις της ύλης είναι η στερεή, η υγρή και η αέρια. Οι μεταξύ τους μεταβολές εξαρτώνται από τη θερμοκρασία και την πίεση και είναι οι παρακάτω: ΣΗΜΕΙΟ ΤΗΞΗΣ ΚΑΙ ΣΗΜΕΙΟ
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους.
ΔΙΑΛΥΜΑΤΑ Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους. Διαλύτης: η ουσία που βρίσκεται σε μεγαλύτερη αναλογία
1.1 Ερωτήσεις πολλαπλής επιλογής Στις παρακάτω ερωτήσεις (1-24) να βάλετε σε κύκλο το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΚΕΦΑΛΑΙΟ 1o ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 1.1 Ερωτήσεις πολλαπλής επιλογής Στις παρακάτω ερωτήσεις (1-24) να βάλετε σε κύκλο το γράμμα που αντιστοιχεί στη σωστή απάντηση. 6. Τα ιόντα είναι: α. ηλεκτρικά φορτισμένα
Σύντομη περιγραφή του πειράματος
Σύντομη περιγραφή του πειράματος Παρασκευή διαλυμάτων ορισμένης περιεκτικότητας και συγκέντρωσης, καθώς επίσης και παρασκευή διαλυμάτων συγκεκριμένης συγκέντρωσης από διαλύματα μεγαλύτερης συγκέντρωσης
«Ανάπτυξη Ολοκληρωµένων Εκπαιδευτικών Πακέτων»
Ανάπτυξη Εκπαιδευτικού Λογισµικού και Ολοκληρωµένων Εκπαιδευτικών Πακέτων για τα Ελληνικά σχολεία της Πρωτοβάθµιας και ευτεροβάθµιας Εκπαίδευσης & ιάθεση Προϊόντων Εκπαιδευτικού Λογισµικού στα Σχολεία
Διαλυτότητα. Μάθημα 7
Διαλυτότητα 7.1. SOS: Τι ονομάζουμε διαλυτότητα μιας χημικής ουσίας σε ορισμένο διαλύτη; Διαλυτότητα είναι η μέγιστη ποσότητα της χημικής ουσίας που μπορεί να διαλυθεί σε ορισμένη ποσότητα του διαλύτη,
Προσδιορισμός της διαλυτότητας στο νερό στερεών ουσιών - Φύλλο εργασίας
Προσδιορισμός της διαλυτότητας στο νερό στερεών ουσιών - Φύλλο εργασίας Γνωστικό αντικείμενο: Τάξη Διδακτική ενότητα Απαιτούμενος χρόνος Διαλυτότητα ουσιών σε υγρούς διαλύτες B Γυμνασίου Ενότητα 2: ΑΠΟ
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Θεοδοσία Τσαβλίδου, Μαρίνος Ιωάννου ΑΠΑΝΤΗΣΕΙΣ
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Β ΓΥΜΝΑΣΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 26 04 2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Θεοδοσία Τσαβλίδου, Μαρίνος Ιωάννου ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 1.1 Στον επόμενο πίνακα δίνονται τα σημεία τήξης και τα
ΓΕΩΡΓΙΚΗ ΧΗΜΕΙΑ ΕΡΓΑΣΤΗΡΙΟ
ΓΕΩΡΓΙΚΗ ΧΗΜΕΙΑ ΕΡΓΑΣΤΗΡΙΟ ΔΙΑΛΥΜΑΤΑ Διάλυμα ονομάζεται κάθε ομοιογενές σύστημα, αποτελούμενο από δύο ή περισσότερες χημικές ουσίες, το οποίο έχει την ίδια σύσταση σε όλη τη μάζα του. Είναι δυνατό να υπάρχουν
Σχέση πυκνότητας και περιεκτικότητας σε αιθανόλη αλκοολούχων διαλυµάτων. Οδηγίες για τον καθηγητή
Σχέση πυκνότητας και περιεκτικότητας σε αιθανόλη αλκοολούχων διαλυµάτων. Τάξη Μάθηµα Γνωστικό αντικείµενο: ιδακτική ενότητα Απαιτούµενος χρόνος B Λυκείου Χηµεία (Γενικής Παιδείας) Αλκοόλες Οργανική Χηµεία
Α-1 Το στοιχείο Χ διαθέτει ιόν με φορτίο -2 έχει 10 ηλεκτρόνια και 16 νετρόνια να βρεθεί ο ατομικός αριθμός και ο μαζικός αριθμός του στοιχείου Χ.
. Ατομικός Μαζικός αριθμός και υποατομικά σωματίδια Α-1 Το στοιχείο Χ διαθέτει ιόν με φορτίο -2 έχει 10 ηλεκτρόνια και 16 νετρόνια να βρεθεί ο ατομικός αριθμός και ο μαζικός αριθμός του στοιχείου Χ. Α-2
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
Διαγώνισμα στο Πρώτο Κεφάλαιο 2/11/2014
Χημεία Α Λυκείου Διαγώνισμα στο Πρώτο Κεφάλαιο 2/11/2014 1 ο Θέμα.... Στις ερωτήσεις 1.1 έως 1.8 επιλέξτε τη σωστή απάντηση: 1.1. Ποιο από τα επόμενα σωματίδια δεν έχει ηλεκτρικό φορτίο; α)το πρωτόνιο,
Εργαστηριακές Ασκήσεις στις περιεκτικότητες των διαλυμάτων
Εργαστηριακές Ασκήσεις στις περιεκτικότητες των διαλυμάτων ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ 1 η Κατηγορία δραστηριοτήτων ΣΤΟΧΟΙ Να διαπιστώσουν οι μαθητές ότι πολλά υλικά καθημερινής χρήσης είναι διαλύματα. Να κατανοήσουν
ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΧΗΜΙΚΕΣ ΑΝΤΙ ΡΑΣΕΙΣ (ΣΤΟΙΧΕΙΟΜΕΤΡΙΚΑ)
ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΧΗΜΙΚΕΣ ΑΝΤΙ ΡΑΣΕΙΣ (ΣΤΟΙΧΕΙΟΜΕΤΡΙΚΑ) Κάθε χηµική εξίσωση εκτός από την ποιοτική µεταβολή δηλαδή την µετατροπή των αντιδρώντων σε προϊόντα παριστάνει και ποσοτική µεταβολή δηλαδή τις αναλογίες
AΝΑΛΟΓΙΑ ΜΑΖΩΝ ΣΤΟΧΕΙΩΝ ΧΗΜΙΚΗΣ ΕΝΩΣΗΣ
2 ο Γυμνάσιο Καματερού 1 ΦΥΣΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΗΣ ΥΛΗΣ 1. Πόσα γραμμάρια είναι: ι) 0,2 kg, ii) 5,1 kg, iii) 150 mg, iv) 45 mg, v) 0,1 t, vi) 1,2 t; 2. Πόσα λίτρα είναι: i) 0,02 m 3, ii) 15 m 3, iii) 12cm
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 8 ΥΔΑΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΑΣΘΕΝΩΝ ΗΛΕΚΤΡΟΛΥΤΩΝ
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 8 ΥΔΑΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΑΣΘΕΝΩΝ ΗΛΕΚΤΡΟΛΥΤΩΝ 1. Να βρεθεί το ph διαλύματος CH 3 COOH συγκέντρωσης 0,1Μ στους 25 ο C. Δίνεται για το CH 3 COOH στους 25 ο C Κ α =10-5.
ΓΗ_Α_ΧΗΜ_0_2215 ΓΗ_Α_ΧΗΜ_0_2530 ΓΗ_Α_ΧΗΜ_0_2532 ΓΗ_Α_ΧΗΜ_0_2742
Προβλήματα 1. ΓΗ_Α_ΧΗΜ_0_15 Σε νερό διαλύεται ορισμένη ποσότητα ΗNO 3. Το διάλυμα που παρασκευάστηκε έχει συγκέντρωση 0,7 Μ (διάλυμα Δ1). α) Να υπολογίσετε την περιεκτικότητα % w/v του διαλύματος Δ1 σε
2 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ
2 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ A. Παρασκευή Υδατικών Διαλυμάτων & μονάδες μέτρησης Για τη παρασκευή υδατικών διαλυμάτων στο εργαστήριο Βιοχημείας, χρησιμοποιείται ύδωρ τριών κατηγοριών. 1. Απιονισμένο (παραλαμβάνεται
7ο Μάθημα Η ΠΥΚΝΟΤΗΤΑ ΕΝΟΣ ΥΛΙΚΟΥ
7ο Μάθημα Η ΠΥΚΝΟΤΗΤΑ ΕΝΟΣ ΥΛΙΚΟΥ Συμβαίνει κι αυτό: ο όγκος ενός σώματος να 'ναι μεγάλος, αλλά η μάζα του να 'ναι μικρή Από την καθημερινή μας ζωή, ξέρουμε τι σημαίνει πυκνό και αραιό: πυκνό δάσος, αραιά
Εύρεση mol και συγκέντρωση από αριθμητικά δεδομένα Επανάληψη προηγούμενων τάξεων.
Εύρεση mol και συγκέντρωση από αριθμητικά δεδομένα Επανάληψη προηγούμενων τάξεων. A. Εύρεση συγκέντρωσης c. A. Δίνονται τα mol της διαλυμένης ουσίας και ο όγκος του διαλύματος: n C, C σε Μ, V σε λίτρα.
ΣΤΟΙΧΕΙΑ ΧΗΜΕΙΑΣ ΚΟΣΜΗΤΟΛΟΓΙΑ ΕΙΔΙΚΟΤΗΤΑ:ΕΙΔΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΑΙΣΘΗΤΙΚΗΣ Α ΕΞΑΜΗΝΟ
ΣΤΟΙΧΕΙΑ ΧΗΜΕΙΑΣ ΚΟΣΜΗΤΟΛΟΓΙΑ ΕΙΔΙΚΟΤΗΤΑ:ΕΙΔΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΑΙΣΘΗΤΙΚΗΣ Α ΕΞΑΜΗΝΟ ΙΕΚ ΒΑΡΗΣ ΦΙΩΤΑΚΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΤΑΞΙΝΟΜΗΣΗ ΤΗΣ ΥΛΗΣ ΔΙΑΛΥΜΑΤΑ Καθορισμένα ή καθαρά σώματα λέγονται εκείνα που έχουν την ίδια
«Ανάπτυξη Ολοκληρωµένων Εκπαιδευτικών Πακέτων»
Ανάπτυξη Εκπαιδευτικού Λογισµικού και Ολοκληρωµένων Εκπαιδευτικών Πακέτων για τα Ελληνικά σχολεία της Πρωτοβάθµιας και ευτεροβάθµιας Εκπαίδευσης & ιάθεση Προϊόντων Εκπαιδευτικού Λογισµικού στα Σχολεία
Enrico Fermi, Thermodynamics, 1937
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
2.2 Το νερό ως διαλύτης - μείγματα
1 2.2 Το νερό ως διαλύτης - μείγματα 2.2-1. Τι ονομάζεται μείγμα; Μείγμα ονομάζεται κάθε σύστημα που προκύπτει από την ανάμειξη δύο ή περισσότερων ουσιών. Τα περισσότερα υλικά στη φύση είναι μίγματα. 2.2-2.
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
ΚΕΦΑΛΑΙΟ 1: ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ
ΚΕΦΑΛΑΙΟ 1: ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Α' ΕΡΩΤΗΣΕΙΣ ΓΝΩΣΗΣ ΤΗΣ ΘΕΩΡΙΑΣ 1.1 Να συμπληρωθούν τα διάστικτα: α) Πυκνότητα d =.. β) Μονάδα μέτρησης της μάζας στο S.I. είναι το.., ενώ του βάρους στο ίδιο σύστημα είναι
1. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ. 19. Βλέπε θεωρία σελ. 9 και 10.
19. Βλέπε θεωρία σελ. 9 και 10. 7 1. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 20. Βλέπε θεωρία α) σελ. 8, β) σελ. 8, γ) σελ. 9. 21. α) ζυγού, β) I. προχοΐδας Π. ογκομετρικού κυλίνδρου. 22. Με το ζυγό υπολογίζουμε τη μάζα. O όγκος
1 Ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΜΕ ΑΠΑΝΤΗΣΗ
1 Ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΜΕ ΑΠΑΝΤΗΣΗ 1. Το στοιχείο Χ έχει 17 ηλεκτρόνια. Αν στον πυρήνα του περιέχει 3 νετρόνια περισσότερα από τα πρωτόνια, να υπολογισθούν ο ατομικός και ο μαζικός του
Εκπαιδευτικός Οργανισµός Ν. Ξυδάς 1
Εκπαιδευτικός Οργανισµός Ν. Ξυδάς 1 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1: ΟΓΚΟΣ Εισαγωγή Παρατήρησε τις δύο εικόνες. Σε τι διαφέρουν; Παρατηρείς ότι το δεύτερο αυτοκίνητο έχει περισσότερο χώρο για τις αποσκευές. Μια χαρακτηριστική
Γεωργική Χημεία Εργαστηριακές ασκήσεις
Γεωργική Χημεία Εργαστηριακές ασκήσεις Γεώργιος Παπαδόπουλος, Καθηγητής Τμ. Τεχνολόγων Γεωπόνων Τ.Ε. Άρτα, 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΕΚΦΩΝΗΣΕΙΣ. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
1 ΘΕΜΑ 1 Ο ΕΚΦΩΝΗΣΕΙΣ A ΛΥΚΕΙΟΥ ΧΗΜΕΙΑ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1) Το άτοµο του καλίου (Κ) έχει µαζικό
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
Επαναληπτικές Ασκήσεις
Επαναληπτικές Ασκήσεις Ενότητα 1: Εισαγωγή στη Χημεία 1.1 Στον επόμενο πίνακα δίνονται τα σημεία τήξης και τα σημεία ζέσης διαφόρων υλικών. Υλικό Σημείο Tήξης ( ο C) Σημείο Zέσης ( ο C) Α 0 100 Β 62 760
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΠΡΟΗΓΟΥΜΕΝΩΝ ΕΤΩΝ ΜΕ ΑΠΑΝΤΗΣΕΙΣ
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΠΡΟΗΓΟΥΜΕΝΩΝ ΕΤΩΝ ΜΕ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο 1. Η ένωση µε µοριακό τύπο C 6 H 6 ανήκει: 2. Η ένωση µε µοριακό τύπο C 11 H 20 ανήκει: 3. Η ένωση µε µοριακό τύπο C 10 H 20 ανήκει: 4. Η ένωση
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: XHMEIA A ΛΥΚΕΙΟΥ
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: XHMEIA A ΛΥΚΕΙΟΥ ΘΕΜΑ Α Να γράψετε στο τετράδιο σας τον αριθµό κάθε µίας από τις ερωτήσεις A1 έως A5 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. Α1. Το ιόν 56 Fe +2 περιέχει: