1 ΦΥΣΙΚΟ ΦΥΣΙΚ ΧΗΜΕΙΑ Ο ΣΥΣΤΗΜΑΤΩΝ
|
|
|
- Καλλιστράτης Παπάζογλου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 1 ΦΥΣΙΚΟΧΗΜΕΙΑ ΣΥΣΤΗΜΑΤΩΝ
2 Φυσικοχημεία συστημάτων 2 «Όμοιος Ό αρέσει όμοιο» Όσο συγγενέστερες από χημική άποψη είναι δύο ουσίες τόσο μεγαλύτερη είναι η αμοιβαία διαλυτότητά τους. Οι ανόργανες ενώσεις διαλύονται στο νερό Οι οργανικές ενώσεις είναι ευδιάλυτες σε οργανικούς διαλύτες Επιδιαλύτωση Κατά την διάλυση μιας ουσίας σε ένα διαλύτη, τα μόρια ή ιόντα της ουσίας περιβάλλονται από τα μόρια του διαλυτικού μέσου. Στην περίπτωση του νερού ως διαλύτη, το φαινόμενο ονομάζεται εφυδάτωση. Ο βαθμός εφυδάτωσης εξαρτάται από (α) την φύση, (β) το μέγεθος και (γ) το φορτίο των ιόντων. Στοιβάδα Α: σφιχτή στοιβάδα όπου τα μόρια του Η 2 Ο συγκρατούνται ισχυρά από τα ιόντα (Li +, Na +, F -, Cl - ). Στοιβάδα Β:χαλαρή στοιβάδα όπου τα μόρια του Η 2 Ο παρουσιάζουν μεγάλη κινητικότητα (Cs +, Br -, I - ). Υπάρχουν ιόντα που παρουσιάζουν και τις 2 στοιβάδες εφυδάτωσης (Mg 2+, Ca 2+, Sr 2+ ).
3 Φυσικοχημεία συστημάτων 3 Τα συστήματα α διακρίνονται αι ανάλογα με το μέγεθος των σωματιδίων της ουσίας που είναι σε διασπορά: Αδρομερή ή ετερογενή: > cm Κολλοειδή: cm Μοριακά ή ομογενή ή διαλύματα: <10 7 cm Χημικό δυναμικό Ως χημικό δυναμικό μια ουσίας σε ένα μίγμα ορίζεται η μερική μοριακή ενέργεια Gibbs: G i n ni PT,, n δηλαδή χημικό δυναμικό είναι η κλίση του διαγράμματος της ενέργειας Gibbs ως προς την ποσότητα της ουσίας I, για σταθερή πίεση, θερμοκρασία και συνολική σύσταση. Για μια καθαρή ουσία: μ i =G i Η συνολική ενέργεια Gibbs για ένα σύστημα είναι: G nii Για δυαδικό σύστημα: G=n A μ A +n B μ B
4 Φυσικοχημεία συστημάτων 4 Εξίσωση Gibbs-Duhem: Για ένα δυαδικό σύστημα, μια μικρή μεταβολή της σύστασης κατά dn A και dn B οδηγεί σε μεταβολή της G: dg=μμ A dn A +μμ B dn B +n A dμμ A +n B dμμ B Γενικότερα όμως: dg=vdp-sdt+μ Α dn Α +μ B dn B Άρα για σταθερή πίεση και θερμοκρασία: ή γενικότερα: n A dμ A +n B dμ B =0 nd i i 0 Το χημικό δυναμικό μιας ουσίας σε ένα μίγμα δεν μπορεί να αλλάξει ανεξάρτητα από το χημικό δυναμικό των άλλων συστατικών του μίγματος.
5 Φυσικοχημεία συστημάτων 5 Εφαρμογή: Ενέργεια Gibbs μίγματος ιδανικών αερίων P χημικό δυναμικό καθαρού αερίου: RT ln P o Η συνολική ενέργεια Gibbs για το σύστημα είναι: G n n i A A B B n ( RTln P ) n ( RTln P) A B B Μετά την ανάμιξη, οι μερικές πιέσεις των αερίων είναι P A και P B, με P A +P B =P: G n ( RTln P ) n ( RTln P ) f A A B B B
6 Φυσικοχημεία συστημάτων 6 Εφαρμογή: Ενέργεια Gibbs μίγματος ιδανικών αερίων Συνεπώς η ενέργεια Gibbs κατά την ανάμειξη (G f -G i ) είναι: PA PB G nartln nbrtln P P και επειδή: n i =x i n, P i /P=x i : G nrt( x lnx x ln x ) A A B B Επειδή x A,x B <1 ΔG<0
7 Διαλύματα αερίων σε υγρά 7 Παραδείγματα: Αέρας (Ν 2, Ο 2 ) διαλυμένος σε λίμνες, θάλασσες, πόσιμο νερό CO 2 σε αναψυκτικά Το περισσότερο διαλυτό αέριο είναι η αμμωνία: 1ml νερού διαλύει 1300cm 3 ΝΗ 3 Το λιγότερο διαλυτό αέριο είναι το ήλιο: 1ml νερού διαλύει 0.01cm 3 He Η διαλυτότητα αερίου σε υγρό εξαρτάται από την φύση του αερίου και του υγρού, την πίεση και την θερμοκρασία
8 Διαλύματα αερίων σε υγρά: Νόμος του Henry 8 Η διαλυτότητα α ενός αερίου σε ένα υγρό είναι ανάλογη της πίεσης και ελαττώνεται με την αύξηση της θερμοκρασίας: m m = μάζα αερίου στο υγρό V = όγκος του διαλύτη V kp k = συντελεστής που εξαρτάται από την φύση του αερίου, του διαλύτη και τη θερμοκρασία Ο νόμος του Henry ισχύει με την προϋπόθεση ότι δεν έχουμε διάσταση ή σύζευξη των μορίων του αερίου.
9 Διαλύματα αερίων σε υγρά: Εξίσωση Van t Hoff 9 Η διαλυτότητα α των αερίων στα υγρά ελαττώνεται αι με την αύξηση της θερμοκρασίας. Η διάλυση των αερίων σε υγρά συνοδεύεται με έκλυση θερμότητας (ΔΗ<0). Για ορισμένη εξωτερική πίεση αερίου σε κατάσταση θερμοδυναμικής ισορροπίας ισχύει η εξίσωση Van t Hoff: d ln S H dt RT S = συγκέντρωση του αερίου στο διάλυμα Τ = απόλυτη θερμοκρασία ΔΗ = γραμμομοριακή θερμότητα διάλυσης του αερίου 2 Σε περίπτωση που έχουμε σύζευξη ή διάσταση των μορίων του αερίου είναι δυνατόν να έχουμε ΔΗ>0 Η διαλυτότητα αυξάνεται με αύξηση της θερμοκρασίας Η διάλυση συνοδεύεται με απορρόφηση θερμότητας
10 Διαλύματα υγρών πλήρως αναμειγνυόμενων 10 Μέσα από μια σειρά πειραμάτων ιδανικά συμπεριφερόμενων διαλυμάτων δύο υγρών, ο Francois Raoult βρήκε ότι η μερική τάση ατμών κάθε ενός συστατικού: είναι απευθείας ανάλογη προς το γραμμομοριακό του κλάσμα στο διάλυμα ισούται με το γινόμενο της τάσης ατμών o o του καθαρού συστατικού (P A,P B ) επί το γραμμομοριακό του κλάσμα στην υγρή φάση (Ν Α, Ν Β ): o P N P, P N P o A A A B B B Με βάση το νόμο του Dalton (P ολ =P A +P B ), και επειδή Ν Α +Ν Β =1: o o o P P +Ν ( P P ) A B A
11 Διαλύματα υγρών πλήρως αναμειγνυόμενων 11 Με βάση τον νόμο του Raoult και το γεγονός ότι στην θερμοδυναμική ισορροπία το χημικό δυναμικό της κάθε ουσίας στην υγρή και στην αέρια φάση είναι το ίδιο, προκύπτει και η εξίσωση που ορίζει τα ιδανικά διαλύματα: RT ln x A A
12 Διαλύματα υγρών πλήρως αναμειγνυόμενων 12 Αποκλίσεις από τον νόμο του Raoult Στην ιδανική κατάσταση οι δυνάμεις μεταξύ των μορίων του διαλύτη (Α Α), της διαλυμένης ουσίας (Β Β) και μεταξύ των μορίων διαλύτη διαλυμένης ουσίας (Α Β) θεωρούνται μηδαμινές ή ίσες μεταξύ τους F F * F AB AA BB Θετικές αποκλίσεις: οι μερικές πιέσεις είναι μεγαλύτερες από τις προβλεπόμενες από το νόμο του Raoult. Δεσμοί Α Β ασθενέστεροι από τους δεσμούς Α Α και Β Β F F * F Η διάλυση είναι εξώθερμη AB AA BB Παραδείγματα: Μεθανόλη / νερό Αιθανόλη / κ εξάνιο
13 Διαλύματα υγρών πλήρως αναμειγνυόμενων 13 Αποκλίσεις από τον νόμο του Raoult Αρνητικές αποκλίσεις: οι μερικές πιέσεις είναι μικρότερες από τις προβλεπόμενες από το νόμο του Raoult. Δεσμοί Α Β ισχυρότεροι από τους δεσμούς Α Α και Β Β F F * F Η διάλυση είναι ενδώθερμη AB AA BB Παραδείγματα: Μεθανόλη / νερό Αιθανόλη / κ εξάνιο
14 Διαγράμματα σημείου ζέσεως σύστασης 14 Οι ατμοί είναι σχετικά πλουσιότεροι του υγρού διαλύματος ως προς εκείνο το συστατικό το οποίο όταν προστίθεται στην υγρή φάση του συστήματος επιφέρει αύξηση της ολικής τάσης των ατμών του όλου συστήματος (Konowaloff). Κλασματική απόσταξη Συμπυκνώνοντας την αέρια φάση παίρνουμε υγρό διάλυμα που έχει διαφορετική σύσταση από το πρώτο. Με διαδοχικούς κύκλους μπορούμε να καταλήξουμε σε τελικό συμπύκνωμα με σχεδόν καθαρό το Α.
15 Διαγράμματα σημείου ζέσεως σύστασης 15 Αζεοτροπικά μίγματα Συστήματα που παρουσιάζουν μέγιστο ή ελάχιστο σημείο ζέσεως. Μέγιστο εμφανίζουν τα συστήματα που η ανάμειξη είναι πιο εύκολη από τα ιδανικά διαλύματα (δεσμοί ία Β ισχυρότεροι από τους δεσμούς Α Α και Β Β) (νιτρικό οξύ/νερό : 20/80%wt) Ελάχιστο εμφανίζουν τα συστήματα που η ανάμειξη είναι λιγότερο εύκολη από τα ιδανικά διαλύματα (δεσμοί Α Β ασθενέστεροι από τους δεσμούς Α Α και Β Β) (αιθανόλη/νερό : 96/4%vol)
16 Μη αναμειγνυόμενα μ υγρά 16 Η αμοιβαία ύπαρξη δύο μη αναμειγνυόμενων υγρών δεν προκαλεί καμία αλλοίωση των φυσικοχημικών τους χαρακτηριστικών. Η συνολική τάση ατμών στο σύστημα, για παράδειγμα, δεν εξαρτάται από τις ποσότητες των δύο υγρών και επομένως είναι εντατική ιδιότητα: o o P P P Κάθε ένα από τα υγρά, ΑκαιΒ Β, βράζει στην θερμοκρασία που η τάση ατμών του γίνει ίση προς την εξωτερική πίεση (έστω 1atm ή 760 Torr). Επειδή όμως συνυπάρχουν, κάθε τάση ατμών δεν μπορεί να φτάσει στην τιμή των 760 Torr και επομένως το σύστημα βράζει όταν η συνολική και όχι η μερική πίεση φτάσει τα 760 Torr. Συνεπώς, το σύστημα βράζει σε θερμοκρασία χαμηλότερη από το σημείο βρασμού του πιο πτητικού υγρού. Αυτή είναι η αρχή της απόσταξης και της απόσταξη με υδρατμούς.
17 Μη αναμειγνυόμενα μ υγρά 17 Απόσταξη Αν απομακρύνουμε την αέρια φάση που περιέχει τους ατμούς των δύο μη αναμειγνυόμενων συστατικών, η οποία βρίσκεται σε ισορροπία με το διφασικό υγρό σύστημα, και την συμπυκνώσουμε θα εμφανιστούν δύο χωριστές στοιβάδες στο απόσταγμα σε αναλογία που εξαρτάται από την τάση ατμών των δύο συστατικών στη θερμοκρασία απόσταξης: w P M w P M A A A B B B w A, w B = ποσότητες ουσίας Α και Β στο απόσταγμα P A, P B = τάση ατμών ουσίας Α και Β στην θερμοκρασία απόσταξης Μ Α, Μ Β = μοριακά βάρη ουσία Α και Β Απόσταξη με υδρατμούς: Επιτρέπει την απόσταξη οργανικών ενώσεων, αδιάλυτων στο νερό, που είναι ευαίσθητες στην θερμοκρασία!
18 Μη αναμειγνυόμενα μ υγρά 18 Εκχύλιση διαλυμένης ουσίας από διάλυμα Προσθέτοντας μία ουσία διαλυτή σε δύο υγρά που δεν αναμειγνύονται μεταξύ τους, μετά από κάποιο χρόνο η ουσία κατανέμεται στα δύο υγρά με ορισμένη αναλογία, σύμφωνα με τον νόμο κατανομής του Nernst: K C C C 1, C 2 = συγκέντρωση της διαλυμένης ουσίας στο υγρό 1 και 2 Κ = συντελεστής κατανομής Εφαρμογή Έστω διάλυμα όγκου U με διαλυμένα W 0 gr ουσίας Γ. Προσθέτουμε L λίτρα άλλου υγρού που διαλύει την Γ αλλά δεν αναμειγνύεται με το πρώτο υγρό. Μετά την αποκατάσταση ισορροπίας: W1 C 1 KU K U W1 W0 C W 2 0 W1 K U L L Αν επαναλάβουμε την διαδικασία ν φορές: K U W W0 K U L Στην πρώτη φάση έχουν παραμείνει W ν gr ουσίας Γ και στα νl λίτρα του εκχυλιστικού υγρού έχουν μεταφερθεί (W 0 -W ν ) gr. 1 2
19 Διαλύματα μη πτητικών ουσιών σε υγρά 19 Στην περίπτωση αραιών διαλυμάτων μη πτητικών ηικώνή στερεών ουσιών σε υγρά διαλυτικά μέσα, ισχύει ο νόμος του Raoult για τον διαλύτη: P N P o ύ ύ ύ Η συνολική τάση ατμών του διαλύματος οφείλεται στην πίεση των ατμών του διαλύτη: o P P και P P P ύ ύ ύ ύ ύ Στα διαλύματα αυτά εμφανίζονται χαρακτηριστικές ιδιότητες που εξαρτώνται μόνο από την συγκέντρωση των σωματιδίων της διαλυμένης ουσίας και όχι από την φύση τους. Οι ιδιότητες αυτές λέγονται ωσμωτικές (ή αθροιστικές): Ελάττωση της τάσεως ατμών Ανύψωση του σημείου ζέσεως Ταπείνωση του σημείου πήξεως Ώσμωση Τα συστήματα πρέπει να είναι μη ηλεκτρολυτικά και πολύ αραιά!
20 Διαλύματα μη πτητικών ουσιών σε υγρά 20 Η βασική αρχή που διέπει τις ωσμωτικές ιδιότητες είναι ότι κατά την προσθήκη μια ουσίας ελαττώνεται το χημικό δυναμικό του υγρού διαλύτη (Α): lnx A <0 καθώς x A <1! * * RT ln x A
21 Ελάττωση της τάσεως ατμών 21 Εάν σε έναν διαλύτη που η τάση ατμών του είναι P o προσθέσω ποσότητα Ν 2 μη πτητικής ουσίας, η τάση ατμών ελαττώνεται σε P. Η σχέση που συνδέει ποσοτικά την μεταβολή της τάσεως ατμών με την ποσότητα της ουσίας διατυπώθηκε από τον Raoult: P o P N 2 ( P ) o P Ο λόγος (P o /P) / P o ονομάζεται σχετική ελάττωση της τάσεως ατμών.
22 Ανύψωση του σημείου ζέσεως 22 Εάν ο καθαρός διαλύτης βράζει σε μια θερμοκρασία Τ 1 (σε κανονική πίεση), το διάλυμα που προκύπτει με την προσθήκη μιας ουσία θα βράζει σε μια άλλη θερμοκρασία, έστω Τ 2. Επειδή η τάση ατμών του διαλύματος, P, είναι μικρότερη από αυτήν του διαλύτη, P o, το Τ 2 θα είναι μεγαλύτερο από το Τ 1 κατά ΔΤ b. H ΔΤ b εξαρτάται από την συγκέντρωση της b διαλυμένης μη πτητικής ή στερεάς ουσίας, σύμφωνα με την εξίσωση Clausius-Clapeyron: dln P 2 dt RT ΔΗ εξ = γραμμομοριακή ενθαλπία (θερμότητα) εξάτμισης Δεδομένου ότι dlnp=dp/p: dp P dt 2 RT και για μικρές μεταβολές των φυσικών μεγεθών: 2 P T P RT
23 Ανύψωση του σημείου ζέσεως 23 Λαμβάνοντας υπ όψιν την σχέση που δίνει την σχετική ελάττωση της τάσεως ατμών: P n N 2 2 P n n 1 2 (Ν 2 =γραμμομοριακό κλάσμα προστιθέμενης ουσίας, n 1 = moles διαλύτη και n 2 = moles προστιθέμενης ουσίας) η θερμοκρασία που βράζει το διάλυμα μετά την προσθήκη ποσότητας ουσίας Ν 2 πρέπει να ανεβεί κατά ΔΤ b : dp dt και T 2 2 b b P RT n1 n2 Για αραιά άδιαλύματα ισχύει n 1 >>n 2 : T b n2 n 1 RT n RT Εάν η μάζα του διαλύτη είναι 1000gr, τότε n 2 =γραμμομοριακή συγκέντρωση, m (molality) και n 1 =1000/Μ 1 (Μ 1 =μοριακό βάρος διαλύτη): 2 m RT mm RT Tb M
24 Ανύψωση του σημείου ζέσεως 24 Για δεδομένο δ διαλύτη το σημείο ζέσεώς του (Τ), το μοριακό του βάρος (Μ 1 ) και η γραμμομοριακή θερμότητα εξαέρωσής του (ΔΗ εξ ) είναι δεδομένα και σταθερά. Συνεπώς: όπου: K b T b 2 M1RT 1000 m b ζεσεοσκοπική σταθερά (χαρακτηριστική παράμετρος κάθε ηλεκτρολύτη) Για το νερό Κ =0 513: Για το νερό, Κ b =0.513: όταν 1 mole οποιασδήποτε μη πτητικής και μηηλεκτρολυτικής ουσίας διαλυθεί σε 1000 gr νερού, το διάλυμα βράζει στους 100,513 ο C (760 torr).
25 Ταπείνωση του σημείου πήξεως 25 Με αντίστοιχους συλλογισμούς καταλήγουμε στην σχέση που συνδέει την ταπείνωση του σημείου πήξεως με την συγκέντρωση της διαλυμένης ουσίας: T f m όπου: ΔΤ f = ταπείνωση του σημείου πήξεως 2 M1RT κρυοσκοπική σταθερά Kb 1000 f f Για το νερό, Κ f =1.86: όταν 1 mole οποιασδήποτε μη πτητικής και μηηλεκτρολυτικής ουσίας διαλυθεί σε 1000 gr νερού, το διάλυμα πήζει στους 1,86 ο C (760 torr).
26 Ώσμωση 26 Το φαινόμενο κατά το οποίο μόρια του διαλύτη διέρχονται αυθόρμητα από ένα αραιό διάλυμα σε άλλο πυκνότερο διάλυμα μέσω μιας ημιπερατής μεμβράνης. Η πίεση που πρέπει να ασκηθεί έτσι ώστε να σταματήσει το φαινόμενο της ώσμωσης λέγεται ωσμωτική πίεση (Π). Η ωσμωτική πίεση μπορεί να εκδηλωθεί ως υδροστατική πίεση ύψους.
27 Ώσμωση 27 O Van t Hoff παρατήρησε πειραματικά ότι : το γινόμενο της ωσμωτικής πίεσης (Π) επί τον όγκο (V) ορισμένης μάζας διαλυμένης ουσίας, σε ορισμένη θερμοκρασία, είναι σταθερό: V ό Η ωσμωτική πίεση (Π) είναι ανάλογη της απόλυτης θερμοκρασίας: K T και έτσι προέκυψε (εμπειρικά) ο νόμος του Van t Hoff αραιών διαλυμάτων: «Η ωσμωτική πίεση είναι ανάλογη της μοριακότητας, molarity (M), του διαλύματος και παρέχεται από την σχέση ανάλογη με την καταστατική εξίσωση των ιδανικών αερίων». m V nrt RT M Η θερμοδυναμική εύρεση της ωσμωτικής πίεσης στηρίζεται στην εξίσωση των χημικών δυναμικών (μ Α ) της διαλυμένης ουσίας στα δύο διαλύματα ως αποτέλεσμα της διαφορετικής πίεσης: Καθαρός διαλύτης: ( P A ) ( P ) Διάλυμα συγκέντρωσης x Α : ( x, P) ( p) RTlnx A A Στα πυκνά διαλύματα παρατηρούνται έντονες αποκλίσεις από τον νόμο του Στα πυκνά διαλύματα παρατηρούνται έντονες αποκλίσεις από τον νόμο του Vαn t Hoff. Στiς περιπτώσει αυτές πρέπει να αφαιρείται ο όγκος των μορίων της διαλυμένη ουσίας από τον συνολικό όγκο του διαλύματος. Ως όγκος του διαλύματος λαμβάνεται ο όγκος του διαλύτη (εξίσωση Morse).
28 Ώσμωση 28 Η ωσμωτική πίεση στο εσωτερικό ενός κυττάρου οφείλεται στην παρουσία ηλεκτρολυτικών και μη ηλεκτρολυτικών ουσιών, όπως άλατα, οργανικά οξέα, σάκχαρα. Το νερό που εισέρχεται στο εσωτερικό του κυττάρου περιέχει και μικρά θρεπτικά μόρια. Η ώσμωση βοηθάει στην διατήρηση της δομής των κυττάρων. Όταν το κύτταρο βρεθεί σε υποτονικό διάλυμα, ο όγκος του αυξάνει και η ωσμωτική του πίεση ελαττώνεται λόγω της εισόδου μορίων διαλύτη στο εσωτερικό του. Η διόγκωση αυτή ονομάζεται σπάργωση. Όταν το κύτταρο βρεθεί σε υπερτονικό διάλυμα οόγκοςτου Όταν το κύτταρο βρεθεί σε υπερτονικό διάλυμα, ο όγκος του συρρικνώνεται λόγω της απώλειας μορίων διαλύτη από το εσωτερικό του. Το φαινόμενο αυτό ονομάζεται πλασμόλυση.
29 Ώσμωση 29 Πριν και μετά την πλασμόλυση Η ωσμωτική πίεση στα φυτικά κύτταρα είναι μεταξύ 5 και 10 atm. Η ωσμωτική πίεση του αίματος είναι περίπου 7atm. Η πίεση των 5 atm οφείλεται στο NaCl που υπάρχει στο πλάσμα και η υπόλοιπη πίεση οφείλεται στις πρωτεΐνες και σε άλλες μεγαλομοριακές ενώσεις. Ενδοφλέβια ένεση υποτονικού υδατικού διαλύματος προκαλεί το φαινόμενο της αιμόλυσης (διάρρηξη ερυθρών αιμοσφαιρίων) στα κύτταρα του αίματος. Στην πράξη χρησιμοποιούνται ισότονα προς το αίμα διαλύματα, όπως το NaCl περιεκτικότητας 9. Δάκρυα: υπέρτονα Σάλιο, ιδρώτας: υπότονα
30 Ώσμωση 30 Εφαρμογή Να προσδιοριστούν τα γραμμάρια της γλυκόζης (C 6 H 12 O 6 ) που πρέπει να διαλυθούν σε 1000 gr νερού για να προκύψει ισότονο προς το αίμα διάλυμα. Χρησιμοποιώντας της εξίσωση Van t Hoff για Π=6.74 atm (ωσμωτική πίεση αίματος, στους 0 ο C): g CH O V M atm 1 lt 180 g / mol 54,19gr RT atm lt / K mol 273K Ο ίδιος υπολογισμός μπορεί να γίνει χρησιμοποιώντας την σχέση της ταπείνωσης του σημείου πήξεως των αραιών διαλυμάτων, γνωρίζοντας ότι το αίμα πήζει στους 0.56 ο C: m m 54.19gr f C H O C H O
31 Αντίστροφη ώσμωση 31 Αντίστροφη ώσμωση είναι το φαινόμενο κατά το οποίο αντιστρέφεται το φαινόμενο της ώσμωσης και τα μόρια του διαλύτη διέρχονται μέσω της ημιπερατής μεμβράνης από ένα πυκνότερο σε ένα αραιότερο διάλυμα. Η αντίστροφη ώσμωση επιτυγχάνεται με την άσκηση εξωτερικής πίεσης μεγαλύτερης της ωσμωτικής πίεσης. Εφαρμογές: καθαρισμός νερού, αφαλάτωση,
ΦΥΣΙΚΟΧΗΜΕΙΑ. Δημήτριος Τσιπλακίδης e-mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak. Φυσικοχημεία συστημάτων
 1 ΦΥΣΙΚΟΧΗΜΕΙΑ Δημήτριος Τσιπλακίδης e-mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak Φυσικοχημεία συστημάτων Φυσικοχημεία συστημάτων 2 «Όμοιος αρέσει όμοιο» Όσο συγγενέστερες από χημική άποψη
1 ΦΥΣΙΚΟΧΗΜΕΙΑ Δημήτριος Τσιπλακίδης e-mail: dtsiplak@chem.auth.gr url: users.auth.gr/~dtsiplak Φυσικοχημεία συστημάτων Φυσικοχημεία συστημάτων 2 «Όμοιος αρέσει όμοιο» Όσο συγγενέστερες από χημική άποψη
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Σε ένα διάλυμα η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη
 Διαλύματα 1 Διαδικασία διάλυσης Σε ένα διάλυμα η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται από
Διαλύματα 1 Διαδικασία διάλυσης Σε ένα διάλυμα η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται από
Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη
 Διαλύματα 1 Διαδικασία διάλυσης Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται
Διαλύματα 1 Διαδικασία διάλυσης Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται
Ανάλυση Τροφίμων. Ενότητα 6: Διαλύματα & οι ιδιότητές τους Τ.Ε.Ι. ΘΕΣΣΑΛΙΑΣ. Τμήμα Τεχνολογίας Τροφίμων. Ακαδημαϊκό Έτος
 Ανάλυση Τροφίμων Ενότητα 6: Διαλύματα & οι ιδιότητές τους Τμήμα Τεχνολογίας Τροφίμων Τ.Ε.Ι. ΘΕΣΣΑΛΙΑΣ Ακαδημαϊκό Έτος 2018-2019 Δημήτρης Π. Μακρής PhD DIC Αναπληρωτής Καθηγητής Διαλύματα Τα ομοιογενή μίγματα
Ανάλυση Τροφίμων Ενότητα 6: Διαλύματα & οι ιδιότητές τους Τμήμα Τεχνολογίας Τροφίμων Τ.Ε.Ι. ΘΕΣΣΑΛΙΑΣ Ακαδημαϊκό Έτος 2018-2019 Δημήτρης Π. Μακρής PhD DIC Αναπληρωτής Καθηγητής Διαλύματα Τα ομοιογενή μίγματα
Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη
 Διαλύματα 1 Διαδικασία διάλυσης Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται
Διαλύματα 1 Διαδικασία διάλυσης Σε ένα δάλ διάλυμα, η διαλυμένη ουσία διασπείρεται ομοιόμορφα σε όλη τη μάζα του διαλύτη 1. Τα μόρια του διαλύτη έλκονται από τα επιφανειακά ιόντα 2. Κάθε ιόν περιβάλλεται
w P M = Απόσταξη με υδρατμούς ουσ ίας ουσ ίας ουσ ίας νερου νερου ν έρου
 Απόσταξη με υδρατμούς Η απόσταξη υγρών ουσιών που δεν αναμιγνύονται με το νερό χρησιμοποιείται πολύ συχνά τόσο στο εργαστήριο όσο και στην βιομηχανία για τον διαχωρισμό και καθαρισμό υγρών που έχουν πολύ
Απόσταξη με υδρατμούς Η απόσταξη υγρών ουσιών που δεν αναμιγνύονται με το νερό χρησιμοποιείται πολύ συχνά τόσο στο εργαστήριο όσο και στην βιομηχανία για τον διαχωρισμό και καθαρισμό υγρών που έχουν πολύ
ΙΑΜΟΡΙΑΚΕΣ ΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ Ι ΙΟΤΗΤΕΣ
 ΙΑΜΟΡΙΑΚΕΣ ΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ Ι ΙΟΤΗΤΕΣ εσµός Υδρογόνου 1) Τι ονοµάζεται δεσµός υδρογόνου; εσµός ή γέφυρα υδρογόνου : είναι µια ειδική περίπτωση διαµοριακού δεσµού διπόλου-διπόλου,
ΙΑΜΟΡΙΑΚΕΣ ΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ Ι ΙΟΤΗΤΕΣ εσµός Υδρογόνου 1) Τι ονοµάζεται δεσµός υδρογόνου; εσµός ή γέφυρα υδρογόνου : είναι µια ειδική περίπτωση διαµοριακού δεσµού διπόλου-διπόλου,
Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας
 Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας ΙΣΟΡΡΟΠΙΑΙ ΙΔΑΝΙΚΟΥ ΔΙΑΛΥΜΑΤΟΣ ΜΕΘ ΕΤΕΡΑΣ ΦΑΣΕΩΣ ΕΚ ΚΑΘΑΡΟΥ ΔΙΑΛΥΤΟΥ Προσδιορισμός μοριακού βάρους κρυοσκοπικώς Γραμμομοριακή
Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας ΙΣΟΡΡΟΠΙΑΙ ΙΔΑΝΙΚΟΥ ΔΙΑΛΥΜΑΤΟΣ ΜΕΘ ΕΤΕΡΑΣ ΦΑΣΕΩΣ ΕΚ ΚΑΘΑΡΟΥ ΔΙΑΛΥΤΟΥ Προσδιορισμός μοριακού βάρους κρυοσκοπικώς Γραμμομοριακή
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανολόγων Μηχανικών. Χημεία. Ενότητα 15: Διαλύματα
 Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 15: Διαλύματα Αν. Καθηγητής Γεώργιος Μαρνέλλος e-mail: gmarnellos@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 15: Διαλύματα Αν. Καθηγητής Γεώργιος Μαρνέλλος e-mail: gmarnellos@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Συγκέντρωση διαλύματος
 Συγκέντρωση διαλύματος Συγκέντρωση διαλύματος: η ποσότητα της ουσίας που έχει διαλυθεί σε δεδομένη ποσότητα διαλύτη ή διαλύματος. Αραιό διάλυμα: όταν η συγκέντρωση της διαλυμένης ουσίας είναι χαμηλή Πυκνό
Συγκέντρωση διαλύματος Συγκέντρωση διαλύματος: η ποσότητα της ουσίας που έχει διαλυθεί σε δεδομένη ποσότητα διαλύτη ή διαλύματος. Αραιό διάλυμα: όταν η συγκέντρωση της διαλυμένης ουσίας είναι χαμηλή Πυκνό
ΚΕΦΑΛΑΙΟ 1: Διαμοριακές Δυνάμεις-Καταστάσεις της ύλης-προσθετικές ιδιότητες
 ΚΕΦΑΛΑΙΟ 1: Διαμοριακές Δυνάμεις-Καταστάσεις της ύλης-προσθετικές ιδιότητες 1. Η τάση ατμών ενός υγρού εξαρτάται: i. Από την ποσότητα του υγρού ii. Τη θερμοκρασία iii. Τον όγκο του δοχείου iv. Την εξωτερική
ΚΕΦΑΛΑΙΟ 1: Διαμοριακές Δυνάμεις-Καταστάσεις της ύλης-προσθετικές ιδιότητες 1. Η τάση ατμών ενός υγρού εξαρτάται: i. Από την ποσότητα του υγρού ii. Τη θερμοκρασία iii. Τον όγκο του δοχείου iv. Την εξωτερική
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 pulis@chem.auth.gr phtcatalysisgrup.web.auth.gr Διαλύματα και Συστήματα υγρών Διαμόρφωση μαθήματος Θεωρία/Ασκήσεις
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 pulis@chem.auth.gr phtcatalysisgrup.web.auth.gr Διαλύματα και Συστήματα υγρών Διαμόρφωση μαθήματος Θεωρία/Ασκήσεις
Γενική Χημεία. Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής
 Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα.
 1. ΔΙΑΛΥΜΑ Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα. Ετερογενές σύστημα καλείται αυτό, το οποίο αποτελείται
1. ΔΙΑΛΥΜΑ Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα. Ετερογενές σύστημα καλείται αυτό, το οποίο αποτελείται
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ
 1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
ΔΙΑΛΥΜΑΤΑ. Χρήστος Παππάς Επίκουρος Καθηγητής
 Χρήστος Παππάς Επίκουρος Καθηγητής 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 1. Γραμμομοριακή μάζα (γραμμομόριο) (M) Γραμμομόριο (M) = Μ r ή ΜΒ σε g ΠΑΡΑΔΕΙΓΜΑ M r,h2o =18 M H2O =18 g 2. Αριθμός mol ενός χημικού στοιχείου ή μιας
Χρήστος Παππάς Επίκουρος Καθηγητής 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 1. Γραμμομοριακή μάζα (γραμμομόριο) (M) Γραμμομόριο (M) = Μ r ή ΜΒ σε g ΠΑΡΑΔΕΙΓΜΑ M r,h2o =18 M H2O =18 g 2. Αριθμός mol ενός χημικού στοιχείου ή μιας
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 5 η - Α ΜΕΡΟΣ ΔΙΑΛΥΜΑΤΑ Όνομα καθηγητή: ΕΥΑΓΓΕΛΙΟΥ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟΥ ΜΑΘΗΜΑΤΟΣ Στόχος (1): Κατανόηση των εννοιών:
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 5 η - Α ΜΕΡΟΣ ΔΙΑΛΥΜΑΤΑ Όνομα καθηγητή: ΕΥΑΓΓΕΛΙΟΥ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟΥ ΜΑΘΗΜΑΤΟΣ Στόχος (1): Κατανόηση των εννοιών:
Τρόποι έκφρασης της συγκέντρωσης
 Τρόποι έκφρασης της συγκέντρωσης Συγκέντρωση διαλύματος: η ποσότητα της ουσίας (g ή moles) που έχει διαλυθεί σε δεδομένη ποσότητα διαλύτη ή διαλύματος (όγκο ή μάζα). Δημιουργούνται έτσι διάφοροι τρόποι
Τρόποι έκφρασης της συγκέντρωσης Συγκέντρωση διαλύματος: η ποσότητα της ουσίας (g ή moles) που έχει διαλυθεί σε δεδομένη ποσότητα διαλύτη ή διαλύματος (όγκο ή μάζα). Δημιουργούνται έτσι διάφοροι τρόποι
1. ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑ- ΜΕΙΣ - ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ - ΠΡΟΣΘΕ- ΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 27 1. ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑ- ΜΕΙΣ - ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ - ΠΡΟΣΘΕ- ΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ 28 29 ΔΙΔΑΚΤΙΚΗ ΩΡΑ: 1 ΔΙΔΑΚΤΙΚΗ ΕΝΟΤΗΤΑ: Διαμοριακές δυνάμεις - Καταστάσεις της ύλης - Προσθετικές ιδιότητες 1.1α Διαμοριακές
27 1. ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑ- ΜΕΙΣ - ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ - ΠΡΟΣΘΕ- ΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ 28 29 ΔΙΔΑΚΤΙΚΗ ΩΡΑ: 1 ΔΙΔΑΚΤΙΚΗ ΕΝΟΤΗΤΑ: Διαμοριακές δυνάμεις - Καταστάσεις της ύλης - Προσθετικές ιδιότητες 1.1α Διαμοριακές
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα
 Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΚΕΦΑΛΑΙΟ 1: ΔΙΑΜΟΡΙΑΚΕΣ ΑΥΝΑΜΕΙΣ-ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΑΗΣ -ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 ΚΕΦΑΛΑΙΟ 1: ΔΙΑΜΟΡΙΑΚΕΣ ΑΥΝΑΜΕΙΣ-ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΑΗΣ -ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ 1-15. βλέπε θεωρία. Ασκήσεις - προβλήματα α. Διαμοριακές δυνάμεις 16. Βλέπε θεωρία για τη συμπλήρωση των κενών. 17. To NaCl
ΚΕΦΑΛΑΙΟ 1: ΔΙΑΜΟΡΙΑΚΕΣ ΑΥΝΑΜΕΙΣ-ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΑΗΣ -ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ 1-15. βλέπε θεωρία. Ασκήσεις - προβλήματα α. Διαμοριακές δυνάμεις 16. Βλέπε θεωρία για τη συμπλήρωση των κενών. 17. To NaCl
Ποσοτική και Ποιoτική Ανάλυση
 Ποσοτική και Ποιoτική Ανάλυση ιδάσκων: Σπύρος Περγαντής Γραφείο: Α206 Τηλ. 2810 545084 E-mail: spergantis@chemistry.uoc.gr ΙΑΛΥΜΑΤΑ (Γενική Χημεία, Ebbing and Gammon κεφ. 12) Εισαγωγή: Γιατί διαλύματα;
Ποσοτική και Ποιoτική Ανάλυση ιδάσκων: Σπύρος Περγαντής Γραφείο: Α206 Τηλ. 2810 545084 E-mail: spergantis@chemistry.uoc.gr ΙΑΛΥΜΑΤΑ (Γενική Χημεία, Ebbing and Gammon κεφ. 12) Εισαγωγή: Γιατί διαλύματα;
Διάλυμα, είναι κάθε ομογενές μίγμα δύο ή περισσότερων ουσιών.
 Διάλυμα, είναι κάθε ομογενές μίγμα δύο ή περισσότερων ουσιών. Διαλύτης: Είναι το συστατικό του διαλύματος που έχει την ίδια φυσική κατάσταση με το διάλυμα. Όταν περισσότερα από ένα συστατικά έχουν την
Διάλυμα, είναι κάθε ομογενές μίγμα δύο ή περισσότερων ουσιών. Διαλύτης: Είναι το συστατικό του διαλύματος που έχει την ίδια φυσική κατάσταση με το διάλυμα. Όταν περισσότερα από ένα συστατικά έχουν την
Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ. Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ
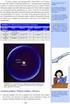 ΑΕΝ / ΑΣΠΡΟΠΥΡΓΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ 2 Ογκομέτρηση προχοϊδα διάλυμα HCl ΕΔΩ ακριβώς μετράμε τον όγκο ( στην εφαπτομένη της καμπύλης
ΑΕΝ / ΑΣΠΡΟΠΥΡΓΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ 2 Ογκομέτρηση προχοϊδα διάλυμα HCl ΕΔΩ ακριβώς μετράμε τον όγκο ( στην εφαπτομένη της καμπύλης
ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 Χημικός Διδάκτωρ Παν. Πατρών. ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Δεσμός υδρογόνου Κεφάλαιο 1ο 3 Χημικός Διδάκτωρ Παν. Πατρών 4 Δεσμο ς η γε φυρα υδρογο νου Παναγιώτης Αθανασόπουλος
Χημικός Διδάκτωρ Παν. Πατρών. ΔΙΑΜΟΡΙΑΚΕΣ ΔΥΝΑΜΕΙΣ ΚΑΤΑΣΤΑΣΕΙΣ ΤΗΣ ΥΛΗΣ ΠΡΟΣΘΕΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Δεσμός υδρογόνου Κεφάλαιο 1ο 3 Χημικός Διδάκτωρ Παν. Πατρών 4 Δεσμο ς η γε φυρα υδρογο νου Παναγιώτης Αθανασόπουλος
IΣΟΡΡΟΠΙΑ ΣΥΣΤΗΜΑΤΩΝ ΠΟΛΛΩΝ ΣΥΣΤΑΤΙΚΩΝ ΜΗ ΗΛΕΚΤΡΟΛΥΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΥΓΡΩΝ
 Ιωάννης Πούλιος Εργαστήριο Φυσικής Χημείας, Τμήμα Χημείας, ΑΠΘ IΣΟΡΡΟΠΙΑ ΣΥΣΤΗΜΑΤΩΝ ΠΟΛΛΩΝ ΣΥΣΤΑΤΙΚΩΝ ΜΗ ΗΛΕΚΤΡΟΛΥΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΥΓΡΩΝ ΘΕΣΣΑΛΟΝΙΚΗ 2018 ς Πούλιος Εργαστήριο Φυσικής Χημείας, Τμήμα Χημείας,
Ιωάννης Πούλιος Εργαστήριο Φυσικής Χημείας, Τμήμα Χημείας, ΑΠΘ IΣΟΡΡΟΠΙΑ ΣΥΣΤΗΜΑΤΩΝ ΠΟΛΛΩΝ ΣΥΣΤΑΤΙΚΩΝ ΜΗ ΗΛΕΚΤΡΟΛΥΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΥΓΡΩΝ ΘΕΣΣΑΛΟΝΙΚΗ 2018 ς Πούλιος Εργαστήριο Φυσικής Χημείας, Τμήμα Χημείας,
Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C.
 4.1 Βασικές έννοιες Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C. Σχετική ατομική μάζα ή ατομικό βάρος λέγεται ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη
4.1 Βασικές έννοιες Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C. Σχετική ατομική μάζα ή ατομικό βάρος λέγεται ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη
Παράγοντες που εξηγούν τη διαλυτότητα. Είδη διαλυμάτων
 Παράγοντες που εξηγούν τη διαλυτότητα 1. Η φυσική τάση των ουσιών να αναμιγνύονται μεταξύ τους. 2. Οι σχετικές ελκτικές δυνάμεις μεταξύ των χημικών οντοτήτων του διαλύματος Είδη διαλυμάτων Στα διαλύματα
Παράγοντες που εξηγούν τη διαλυτότητα 1. Η φυσική τάση των ουσιών να αναμιγνύονται μεταξύ τους. 2. Οι σχετικές ελκτικές δυνάμεις μεταξύ των χημικών οντοτήτων του διαλύματος Είδη διαλυμάτων Στα διαλύματα
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΔΥΑΔΙΚΑ ΣΥΣΤΗΜΑΤΑ ΜΕΛΕΤΗ ΤΩΝ ΔΙΑΓΡΑΜΜΑΤΩΝ ΤΟΥ ΣΗΜΕΙΟΥ ΖΕΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΔΥΑΔΙΚΑ ΣΥΣΤΗΜΑΤΑ ΜΕΛΕΤΗ ΤΩΝ ΔΙΑΓΡΑΜΜΑΤΩΝ ΤΟΥ ΣΗΜΕΙΟΥ ΖΕΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 8 η ΑΘΡΟΙΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Όνομα καθηγητή: ΕΥΑΓΓΕΛΙΟΥ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟΥ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των αθροιστικών
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 8 η ΑΘΡΟΙΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Όνομα καθηγητή: ΕΥΑΓΓΕΛΙΟΥ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟΥ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των αθροιστικών
M V n. nm V. M v. M v T P P S V P = = + = σταθερή σε παραγώγιση, τον ορισµό του συντελεστή διαστολής α = 1, κυκλική εναλλαγή 3
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
ΧΗΜΕΙΑ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ
 Θέματα Πανελλ. Εξετάσεων Χημείας Προσανατολισμού Β Λυκείου 1 ΧΗΜΕΙΑ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 1984 2004 (Περιέχει όσα από τα θέματα αναφέρονται στην ύλη της
Θέματα Πανελλ. Εξετάσεων Χημείας Προσανατολισμού Β Λυκείου 1 ΧΗΜΕΙΑ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 1984 2004 (Περιέχει όσα από τα θέματα αναφέρονται στην ύλη της
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα. Εισαγωγική Χημεία
 Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
ΦΥΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι
 ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
ΦΣΙΚΟΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ Ι Ενότητα 6 η - Β ΜΕΡΟΣ ΔΙΑΛΜΑΤΑ Όνομα καθηγητή: ΕΑΓΓΕΛΙΟ ΒΑΣΙΛΙΚΗ Τμήμα: Επιστήμης Τροφίμων και Διατροφής του Ανθρώπου ΣΤΟΧΟΙ ΤΟ ΜΑΘΗΜΑΤΟΣ Στόχος (): Κατανόηση των εννοιών: υγρά διαλύματα,
Ιδιότητες Μιγμάτων. Μερικές Μολαρικές Ιδιότητες
 Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
5. Εξώθερμο φαινόμενο είναι: α. ο βρασμός. β. η τήξη. γ. η εξάτμιση. δ. η εξουδετέρωση.
 ΔΙΑΓΩΝΙΜΑ: Μ Α Θ Η Μ Α : Β ΣΑΞΗ ΛΤΚΕΙΟΤ ΦΗΜΕΙΑ ΚΑΣΕΤΘΤΝΗ Ε Π Ω Ν Τ Μ Ο : < < < < < <
ΔΙΑΓΩΝΙΜΑ: Μ Α Θ Η Μ Α : Β ΣΑΞΗ ΛΤΚΕΙΟΤ ΦΗΜΕΙΑ ΚΑΣΕΤΘΤΝΗ Ε Π Ω Ν Τ Μ Ο : < < < < < <
Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους.
 ΔΙΑΛΥΜΑΤΑ Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους. Διαλύτης: η ουσία που βρίσκεται σε μεγαλύτερη αναλογία
ΔΙΑΛΥΜΑΤΑ Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους. Διαλύτης: η ουσία που βρίσκεται σε μεγαλύτερη αναλογία
Τράπεζα Χημεία Α Λυκείου
 Τράπεζα Χημεία Α Λυκείου 1 ο Κεφάλαιο Όλα τα θέματα του 1 ου Κεφαλαίου από τη Τράπεζα Θεμάτων 25 ερωτήσεις Σωστού Λάθους 30 ερωτήσεις ανάπτυξης Επιμέλεια: Γιάννης Καλαμαράς, Διδάκτωρ Χημικός Ερωτήσεις
Τράπεζα Χημεία Α Λυκείου 1 ο Κεφάλαιο Όλα τα θέματα του 1 ου Κεφαλαίου από τη Τράπεζα Θεμάτων 25 ερωτήσεις Σωστού Λάθους 30 ερωτήσεις ανάπτυξης Επιμέλεια: Γιάννης Καλαμαράς, Διδάκτωρ Χημικός Ερωτήσεις
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 11 η : Χημική ισορροπία. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 11 η : Χημική ισορροπία Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Η Κατάσταση Ισορροπίας 2 Πολλές αντιδράσεις δεν πραγματοποιούνται
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 11 η : Χημική ισορροπία Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Η Κατάσταση Ισορροπίας 2 Πολλές αντιδράσεις δεν πραγματοποιούνται
Συγκέντρωση διαλύματος
 Συγκέντρωση διαλύματος 22-1. SOS Ερώτηση: τι ονομάζουμε μοριακότητα κατ όγκο ή Molarity (Μολάριτι); Η μοριακότητα κατ' όγκο ή συγκέντρωση ή Molarity, εκφράζει τα mol διαλυμένης ουσίας που περιέχονται σε
Συγκέντρωση διαλύματος 22-1. SOS Ερώτηση: τι ονομάζουμε μοριακότητα κατ όγκο ή Molarity (Μολάριτι); Η μοριακότητα κατ' όγκο ή συγκέντρωση ή Molarity, εκφράζει τα mol διαλυμένης ουσίας που περιέχονται σε
ΠΑΡΑΡΤΗΜΑ A > ΛΕΞΙΛΟΓΙΟ OPΩΝ > ΕΥΡΕΤΗΡΙΟ >ΕΥΡΕΤΗΡΙΟΟΝΟΜΑΤΩΝ
 ΠΑΡΑΡΤΗΜΑ A > ΛΕΞΙΛΟΓΙΟ OPΩΝ > ΕΥΡΕΤΗΡΙΟ >ΕΥΡΕΤΗΡΙΟΟΝΟΜΑΤΩΝ A Αμφίδρομη αντίδραση: αυτή που πραγματοποιείται προς τις δύο κατευθύνσεις ταυτόχρονα και καταλήγει σε κατάσταση ισορροπίας. Αναγωγή: η ελάττωση
ΠΑΡΑΡΤΗΜΑ A > ΛΕΞΙΛΟΓΙΟ OPΩΝ > ΕΥΡΕΤΗΡΙΟ >ΕΥΡΕΤΗΡΙΟΟΝΟΜΑΤΩΝ A Αμφίδρομη αντίδραση: αυτή που πραγματοποιείται προς τις δύο κατευθύνσεις ταυτόχρονα και καταλήγει σε κατάσταση ισορροπίας. Αναγωγή: η ελάττωση
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων)
 ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων) 1. Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές. i. H σχετική ατομική μάζα μετριέται σε γραμμάρια. ii. H σχετική ατομική μάζα είναι
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων) 1. Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές. i. H σχετική ατομική μάζα μετριέται σε γραμμάρια. ii. H σχετική ατομική μάζα είναι
Καταστάσεις της ύλης. αέρια υγρή στερεά
 Καταστάσεις της ύλης αέρια υγρή στερεά Ύλη Καθαρή ουσία Μίγμα Στοιχείο Ένωση Ομογενές Ετερογενές Παράδειγμα: νάτριο, υδρογόνο Παράδειγμα: Αλάτι, νερό Παράδειγμα: αέρας, Αλάτι σε νερό Παράδειγμα: λάδι και
Καταστάσεις της ύλης αέρια υγρή στερεά Ύλη Καθαρή ουσία Μίγμα Στοιχείο Ένωση Ομογενές Ετερογενές Παράδειγμα: νάτριο, υδρογόνο Παράδειγμα: Αλάτι, νερό Παράδειγμα: αέρας, Αλάτι σε νερό Παράδειγμα: λάδι και
ΕΚΦΡΑΣΕΙΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΚΑΙ ΣΥΓΚΕΝΤΡΩΣΗΣ
 ΕΚΦΡΑΣΕΙΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΚΑΙ ΣΥΓΚΕΝΤΡΩΣΗΣ Η συγκέντρωση συμβολίζεται γενικά με το σύμβολο C ή γράφοντας τον μοριακό τύπο της διαλυμένης ουσίας ανάμεσα σε αγκύλες, π.χ. [ΝΗ 3 ] ή [Η 2 SO 4 ]. Σε κάθε περίπτωση,
ΕΚΦΡΑΣΕΙΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΚΑΙ ΣΥΓΚΕΝΤΡΩΣΗΣ Η συγκέντρωση συμβολίζεται γενικά με το σύμβολο C ή γράφοντας τον μοριακό τύπο της διαλυμένης ουσίας ανάμεσα σε αγκύλες, π.χ. [ΝΗ 3 ] ή [Η 2 SO 4 ]. Σε κάθε περίπτωση,
Περιεχόμενα. Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9. Κεφάλαιο 2 ΑΤΟΜΙΚΗ ΚΑΙ ΜΟΡΙΑΚΗ ΜΑΖΑ, ΓΡΑΜΜΟΜΟΡΙΑΚΗ ΜΑΖΑ... 25
 Περιεχόμενα Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9 Εισαγωγή. Μετρικά συστήματα. Διεθνές Σύστημα Μονάδων. Θερμοκρασία. Άλλες κλίμακες θερμοκρασιών. Ορθή και λανθασμένη χρήση των μονάδων. Μέθοδος του συντελεστή
Περιεχόμενα Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9 Εισαγωγή. Μετρικά συστήματα. Διεθνές Σύστημα Μονάδων. Θερμοκρασία. Άλλες κλίμακες θερμοκρασιών. Ορθή και λανθασμένη χρήση των μονάδων. Μέθοδος του συντελεστή
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων Ιωάννης Πούλιος Ιωάννης Ζιώγας Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων Ιωάννης Πούλιος Ιωάννης Ζιώγας Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Παρασκευαστικό διαχωρισμό πολλών ουσιών με κατανομή μεταξύ των δύο διαλυτών.
 1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
Περιεκτικότητα διαλύματος ονομάζουμε την ποσότητα της διαλυμένης ουσίας που περιέχεται σε ορισμένη μάζα ή όγκο διαλύματος.
 Διαλύματα Περιεκτικότητες 11 Αν ο καθηγητής Χημείας έδινε στους μαθητές του τη δυνατότητα να παρασκευάσουν στο Εργαστήριο Χημείας, ο καθένας χωριστά, ένα υδατικό διάλυμα ζάχαρης, είναι προφανές ότι το
Διαλύματα Περιεκτικότητες 11 Αν ο καθηγητής Χημείας έδινε στους μαθητές του τη δυνατότητα να παρασκευάσουν στο Εργαστήριο Χημείας, ο καθένας χωριστά, ένα υδατικό διάλυμα ζάχαρης, είναι προφανές ότι το
Τ, Κ Η 2 Ο(g) CΟ(g) CO 2 (g) Λύση Για τη συγκεκριμένη αντίδραση στους 1300 Κ έχουμε:
 ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΑΣΚΗΣΕΙΣ 5-6 (Α. Χημική Θερμοδυναμική) η Άσκηση Η αντίδραση CO(g) + H O(g) CO (g) + H (g) γίνεται σε θερμοκρασία 3 Κ. Να υπολογιστεί το κλάσμα των ατμών του
ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΕΙΑ - ΑΣΚΗΣΕΙΣ 5-6 (Α. Χημική Θερμοδυναμική) η Άσκηση Η αντίδραση CO(g) + H O(g) CO (g) + H (g) γίνεται σε θερμοκρασία 3 Κ. Να υπολογιστεί το κλάσμα των ατμών του
Χημεία Α Λυκείου. Διαλύματα
 Διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποούν τα συστατικά του διαλύματος. Από τα συστατικά αυτά, εκείνο που έχει την ίδια φυσική κατάσταση με αυτή του διαλύματος
Διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποούν τα συστατικά του διαλύματος. Από τα συστατικά αυτά, εκείνο που έχει την ίδια φυσική κατάσταση με αυτή του διαλύματος
1 η Εργαστηριακή άσκηση. Παρασκευή Αραίωση. διαλύματος. Δρ. Άρης Γιαννακάς - Ε.ΔΙ.Π.
 1 η Εργαστηριακή άσκηση Παρασκευή Αραίωση διαλύματος 1 Θεωρητικό Μέρος Εισαγωγικές έννοιες Όπως είναι γνωστό η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις)
1 η Εργαστηριακή άσκηση Παρασκευή Αραίωση διαλύματος 1 Θεωρητικό Μέρος Εισαγωγικές έννοιες Όπως είναι γνωστό η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις)
ΦΥΣΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ. Οι φυσικές καταστάσεις της ύλης είναι η στερεή, η υγρή και η αέρια.
 ΦΥΣΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ Οι φυσικές καταστάσεις της ύλης είναι η στερεή, η υγρή και η αέρια. Οι μεταξύ τους μεταβολές εξαρτώνται από τη θερμοκρασία και την πίεση και είναι οι παρακάτω: ΣΗΜΕΙΟ ΤΗΞΗΣ ΚΑΙ ΣΗΜΕΙΟ
ΦΥΣΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ Οι φυσικές καταστάσεις της ύλης είναι η στερεή, η υγρή και η αέρια. Οι μεταξύ τους μεταβολές εξαρτώνται από τη θερμοκρασία και την πίεση και είναι οι παρακάτω: ΣΗΜΕΙΟ ΤΗΞΗΣ ΚΑΙ ΣΗΜΕΙΟ
Περιεχόμενα. Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9. Κεφάλαιο 2 ΑΤΟΜΙΚΗ ΚΑΙ ΜΟΡΙΑΚΗ ΜΑΖΑ, ΓΡΑΜΜΟΜΟΡΙΑΚΗ ΜΑΖΑ... 25
 Περιεχόμενα Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9 Εισαγωγή. Μετρικά συστήματα. Διεθνές Σύστημα Μονάδων. Θερμοκρασία. Άλλες κλίμακες θερμοκρασιών. Ορθή και λανθασμένη χρήση των μονάδων. Μέθοδος του συντελεστή
Περιεχόμενα Κεφάλαιο 1 ΜΕΓΕΘΗ ΚΑΙ ΜΟΝΑΔΕΣ... 9 Εισαγωγή. Μετρικά συστήματα. Διεθνές Σύστημα Μονάδων. Θερμοκρασία. Άλλες κλίμακες θερμοκρασιών. Ορθή και λανθασμένη χρήση των μονάδων. Μέθοδος του συντελεστή
Α = Ζ + Ν ΑΤΟΜΟ. ΙΣΟΤΟΠΑ είναι. ΝΕΤΡΟΝΙΑ (n) ΠΥΡΗΝΑΣ
 ΚΕΦ.1: 3. ΔΟΜΗ ΑΤΟΜΟΥ ΑΤΟΜΟ ΠΥΡΗΝΑΣ ΠΡΩΤΟΝΙΑ (p + ) ΝΕΤΡΟΝΙΑ (n) 1.3.1 Να βρείτε τον αριθμό πρωτονίων νετρονίων και ηλεκτρονίων που υπάρχουν στα παρακάτω άτομα ή ιόντα: ΗΛΕΚΤΡΟΝΙΑ (e - ) ΠΡΟΣΟΧΗ 1) Στα
ΚΕΦ.1: 3. ΔΟΜΗ ΑΤΟΜΟΥ ΑΤΟΜΟ ΠΥΡΗΝΑΣ ΠΡΩΤΟΝΙΑ (p + ) ΝΕΤΡΟΝΙΑ (n) 1.3.1 Να βρείτε τον αριθμό πρωτονίων νετρονίων και ηλεκτρονίων που υπάρχουν στα παρακάτω άτομα ή ιόντα: ΗΛΕΚΤΡΟΝΙΑ (e - ) ΠΡΟΣΟΧΗ 1) Στα
2ο Σύνολο Ασκήσεων. Λύσεις 6C + 7H 2 C 6 H H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων καλείται
 1 2ο Σύνολο Ασκήσεων Λύσεις Άσκηση 1: 6C + 7H 2 C 6 H 14 H1 6C + 7H 2 ΔΗ αντίδρασης H2 C 6 + H 14 C + H 2 H αντίδραση είναι εξώθερμη Άσκηση 2 - H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων
1 2ο Σύνολο Ασκήσεων Λύσεις Άσκηση 1: 6C + 7H 2 C 6 H 14 H1 6C + 7H 2 ΔΗ αντίδρασης H2 C 6 + H 14 C + H 2 H αντίδραση είναι εξώθερμη Άσκηση 2 - H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων
Κων/νος Θέος 1
 Το παρόν φυλλάδιο περιέχει ορισµένα λυµένα παραδείγµατα ασκήσεων στο κεφάλαιο ώσµωση - ωσµωτική πίεση. Σε όλα τα παραδείγµατα δίνεται: R = 0, 082 L atm mol K Εφαρµογή της ωσµωµετρίας 1 ο παράδειγµα Κάνουµε
Το παρόν φυλλάδιο περιέχει ορισµένα λυµένα παραδείγµατα ασκήσεων στο κεφάλαιο ώσµωση - ωσµωτική πίεση. Σε όλα τα παραδείγµατα δίνεται: R = 0, 082 L atm mol K Εφαρµογή της ωσµωµετρίας 1 ο παράδειγµα Κάνουµε
Υδατική Χηµεία-Κεφάλαιο 3 1
 Υδατική Χηµεία-Κεφάλαιο 3 Δηµιουργία της σύστασης των φυσικών νερών Κεφάλαιο 3 Χηµικές Έννοιες:. Νόµος δράσεως των µαζών- Σταθερές ισορροπίας. Προσδιορισµός της αυθόρµητης κατεύθυνσης των αντιδράσεων 3.
Υδατική Χηµεία-Κεφάλαιο 3 Δηµιουργία της σύστασης των φυσικών νερών Κεφάλαιο 3 Χηµικές Έννοιες:. Νόµος δράσεως των µαζών- Σταθερές ισορροπίας. Προσδιορισµός της αυθόρµητης κατεύθυνσης των αντιδράσεων 3.
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
6.2. ΤΗΞΗ ΚΑΙ ΠΗΞΗ, ΛΑΝΘΑΝΟΥΣΕΣ ΘΕΡΜΟΤΗΤΕΣ
 45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
1 o ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ ΚΟΡΔΕΛΙΟΥ ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ, ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1. ΚΕΦΑΛΑΙΟ 1- ΒΑΣΙΚΑ ΜΕΓΕΘΗ-ΣΩΜΑΤΙΔΙΑ - Τι πρέπει να γνωρίζουμε
 1 o ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ ΚΟΡΔΕΛΙΟΥ ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ, ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 ΚΕΦΑΛΑΙΟ 1- ΒΑΣΙΚΑ ΜΕΓΕΘΗ-ΣΩΜΑΤΙΔΙΑ - Τι πρέπει να γνωρίζουμε 1. Βασικά μεγέθη και μονάδες αυτών που θα χρησιμοποιηθούν
1 o ΓΕΛ ΕΛΕΥΘΕΡΙΟΥ ΚΟΡΔΕΛΙΟΥ ΧΗΜΕΙΑ A ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ, ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 ΚΕΦΑΛΑΙΟ 1- ΒΑΣΙΚΑ ΜΕΓΕΘΗ-ΣΩΜΑΤΙΔΙΑ - Τι πρέπει να γνωρίζουμε 1. Βασικά μεγέθη και μονάδες αυτών που θα χρησιμοποιηθούν
ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ ΦΥΕ22 (ΦΥΣΙΚΟΧΗΜΕΙΑ) 2 ο Μέρος: ΑΣΚΗΣΕΙΣ (75 %) Διάρκεια: 3 ώρες και 45 λεπτά ( ) Α. Χημική Θερμοδυναμική
 ΘΕΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ ΦΥΕ22 (ΦΥΣΙΚΟΧΗΜΕΙΑ) 2 ο Μέρος: ΑΣΚΗΣΕΙΣ (75 %) Διάρκεια: 3 ώρες και 45 λεπτά (15.15 19.00) Α. Χημική Θερμοδυναμική Υπολογίστε την πρότυπη ελεύθερη ενέργεια Gibbs και τη σταθερά
ΘΕΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ ΦΥΕ22 (ΦΥΣΙΚΟΧΗΜΕΙΑ) 2 ο Μέρος: ΑΣΚΗΣΕΙΣ (75 %) Διάρκεια: 3 ώρες και 45 λεπτά (15.15 19.00) Α. Χημική Θερμοδυναμική Υπολογίστε την πρότυπη ελεύθερη ενέργεια Gibbs και τη σταθερά
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
Μοριακός Χαρακτηρισμός Πολυμερών
 Μοριακός Χαρακτηρισμός Πολυμερών Μοριακό Βάρος Πολυμερών Υψηλά όχι ακριβή ΜΒ λόγω τυχαιότητας πολυμερισμού Μίγμα αλυσίδων με διαφορετικό μήκος Μέσο ΜΒ ή κατανομή ΜΒ Βαθμός Πολυμερισμού (DP) = MB πολυμερούς
Μοριακός Χαρακτηρισμός Πολυμερών Μοριακό Βάρος Πολυμερών Υψηλά όχι ακριβή ΜΒ λόγω τυχαιότητας πολυμερισμού Μίγμα αλυσίδων με διαφορετικό μήκος Μέσο ΜΒ ή κατανομή ΜΒ Βαθμός Πολυμερισμού (DP) = MB πολυμερούς
2. ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΧΟΜΕΝΑ
 2. ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΧΟΜΕΝΑ Τύποι διαλυμάτων Διαλυτότητα και η διαδικασία διάλυσης Επιδράσεις θερμοκρασίας και πίεσης πάνω στη διαλυτότητα Τρόποι έκφρασης της συγκέντρωσης Τάση ατμών διαλύματος Ανύψωση σημείου
2. ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΧΟΜΕΝΑ Τύποι διαλυμάτων Διαλυτότητα και η διαδικασία διάλυσης Επιδράσεις θερμοκρασίας και πίεσης πάνω στη διαλυτότητα Τρόποι έκφρασης της συγκέντρωσης Τάση ατμών διαλύματος Ανύψωση σημείου
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
Για αραιά διαλύματα : x 1 0 : μ i = μ i 0 RTlnx i χ. όπου μ i φ =μ i 0 χ
 Για ιδανικά διαλύματα : μ i = μ i lnx i x= γ=1 Για αραιά διαλύματα : x 1 : μ i = μ i lnx i χ μ i = μ i φ lnx i όπου μ i φ =μ i χ Χημική Ισορροπία λ Από σελ. 7 Χημική Ισορροπία όταν ν i μ i = (T,P σταθερό)
Για ιδανικά διαλύματα : μ i = μ i lnx i x= γ=1 Για αραιά διαλύματα : x 1 : μ i = μ i lnx i χ μ i = μ i φ lnx i όπου μ i φ =μ i χ Χημική Ισορροπία λ Από σελ. 7 Χημική Ισορροπία όταν ν i μ i = (T,P σταθερό)
1 Ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΜΕ ΑΠΑΝΤΗΣΗ
 1 Ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΜΕ ΑΠΑΝΤΗΣΗ 1. Το στοιχείο Χ έχει 17 ηλεκτρόνια. Αν στον πυρήνα του περιέχει 3 νετρόνια περισσότερα από τα πρωτόνια, να υπολογισθούν ο ατομικός και ο μαζικός του
1 Ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΜΕ ΑΠΑΝΤΗΣΗ 1. Το στοιχείο Χ έχει 17 ηλεκτρόνια. Αν στον πυρήνα του περιέχει 3 νετρόνια περισσότερα από τα πρωτόνια, να υπολογισθούν ο ατομικός και ο μαζικός του
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. Ενότητα 10: Ισορροπίες φάσεων. Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 0: Ισορροπίες φάσεων Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η παρουσίαση και η εξέταση της ισορροπίας ανάμεσα
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 0: Ισορροπίες φάσεων Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η παρουσίαση και η εξέταση της ισορροπίας ανάμεσα
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity)
 ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity) ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σημειώστε με Σωστό ή Λάθος. i) Η συγκέντρωση ενός διαλύματος είναι ίδια για ολόκληρο το διάλυμα ή για ένα μέρος αυτού. ii) Σε 50 ml διαλύματος
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity) ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σημειώστε με Σωστό ή Λάθος. i) Η συγκέντρωση ενός διαλύματος είναι ίδια για ολόκληρο το διάλυμα ή για ένα μέρος αυτού. ii) Σε 50 ml διαλύματος
Σημειώσεις Χημείας Α Λυκείου - Κεφάλαιο 1 ο
 ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΚΤΙΚΟΤΗΤΕΣ ΔΙΑΛΥΜΑΤΩΝ ΔΙΑΛΥΤΟΤΗΤΑ - ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ Γενικά για τα διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποτελούν τα συστατικά του διαλύματος.
ΔΙΑΛΥΜΑΤΑ ΠΕΡΙΕΚΤΙΚΟΤΗΤΕΣ ΔΙΑΛΥΜΑΤΩΝ ΔΙΑΛΥΤΟΤΗΤΑ - ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ Γενικά για τα διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποτελούν τα συστατικά του διαλύματος.
ΧΗΜΕΙΑ Ι Ενότητα 12: Διαλύματα
 ΧΗΜΕΙΑ Ι Ενότητα 12: Διαλύματα Χρυσή Κ. Καραπαναγιώτη Τμήμα Χημείας Ορολογία Ε Δημοτικού, σελ. 23 Μίγματα Διαλύματα Διαλύτης Διαλυμένες ουσίες Ετερογενή Ίζημα Κατηγορίες της ύλης σύμφωνα με τα συστατικά
ΧΗΜΕΙΑ Ι Ενότητα 12: Διαλύματα Χρυσή Κ. Καραπαναγιώτη Τμήμα Χημείας Ορολογία Ε Δημοτικού, σελ. 23 Μίγματα Διαλύματα Διαλύτης Διαλυμένες ουσίες Ετερογενή Ίζημα Κατηγορίες της ύλης σύμφωνα με τα συστατικά
ΘΕΡΜΟΧΗΜΕΙΑ. Είδη ενέργειας ΘΕΡΜΟΔΥΝΑΜΙΚΟΙ ΟΡΙΣΜΟΙ
 ΘΕΡΜΟΧΗΜΕΙΑ Όλες οι χημικές αντιδράσεις περιλαμβάνουν έκλυση ή απορρόφηση ενέργειας υπό μορφή θερμότητας. Η γνώση του ποσού θερμότητας που συνδέεται με μια χημική αντίδραση έχει και πρακτική και θεωρητική
ΘΕΡΜΟΧΗΜΕΙΑ Όλες οι χημικές αντιδράσεις περιλαμβάνουν έκλυση ή απορρόφηση ενέργειας υπό μορφή θερμότητας. Η γνώση του ποσού θερμότητας που συνδέεται με μια χημική αντίδραση έχει και πρακτική και θεωρητική
Συνοπτική Θεωρία Χημείας Α Λυκείου. Στοιχειομετρία. Σχετική ατομική μάζα σχετική μοριακή μάζα- mole- γραμμομοριακός όγκος
 1 Web page www.a8eno.gr e-ail vrentzou@a8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή a8eno.gr Συνοπτική Θεωρία Χημείας Α Λυκείου Στοιχειομετρία Σχετική ατομική μάζα σχετική μοριακή
1 Web page www.a8eno.gr e-ail vrentzou@a8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή a8eno.gr Συνοπτική Θεωρία Χημείας Α Λυκείου Στοιχειομετρία Σχετική ατομική μάζα σχετική μοριακή
Για την επίλυση αυτής της άσκησης, αλλά και όλων των παρόμοιων χρησιμοποιούμε ιδιότητες των αναλογιών (χιαστί)
 ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ
 ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ 1. Σε δοχείο σταθερού όγκου και σε σταθερή θερμοκρασία, εισάγονται κάποιες ποσότητες των αερίων Η 2(g) και Ι 2(g) τα οποία αντιδρούν σύμφωνα με
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 6-ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ 1. Σε δοχείο σταθερού όγκου και σε σταθερή θερμοκρασία, εισάγονται κάποιες ποσότητες των αερίων Η 2(g) και Ι 2(g) τα οποία αντιδρούν σύμφωνα με
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
Θερμόχήμεία Κεφάλαιό 2 ό
 Θερμόχήμεία Κεφάλαιό 2 ό Επιμέλεια: Χημικός Διδάκτωρ Πανεπιστημίου Πατρών 11 12 Τι είναι η χημική ενέργεια των χημικών ουσιών; Που οφείλεται; Μπορεί να αποδοθεί στο περιβάλλον; Πότε μεταβάλλεται η χημική
Θερμόχήμεία Κεφάλαιό 2 ό Επιμέλεια: Χημικός Διδάκτωρ Πανεπιστημίου Πατρών 11 12 Τι είναι η χημική ενέργεια των χημικών ουσιών; Που οφείλεται; Μπορεί να αποδοθεί στο περιβάλλον; Πότε μεταβάλλεται η χημική
Ταξινόμηση της ύλης Διαλύματα Περιεκτικότητες διαλυμάτων. Χημεία Α Λυκείου Διδ. Εν. 1.5 π. Ευάγγελος Μαρκαντώνης 2 ο ΓΕΛ Αργυρούπολης
 Ταξινόμηση της ύλης Διαλύματα Περιεκτικότητες διαλυμάτων Χημεία Α Λυκείου Διδ. Εν. 1.5 π. Ευάγγελος Μαρκαντώνης 2 ο ΓΕΛ Αργυρούπολης Μακροσκοπική ταξινόμηση της ύλης ΥΛΗ Καθορισµένη (καθαρή) ουσία όχι
Ταξινόμηση της ύλης Διαλύματα Περιεκτικότητες διαλυμάτων Χημεία Α Λυκείου Διδ. Εν. 1.5 π. Ευάγγελος Μαρκαντώνης 2 ο ΓΕΛ Αργυρούπολης Μακροσκοπική ταξινόμηση της ύλης ΥΛΗ Καθορισµένη (καθαρή) ουσία όχι
Στοιχειμετρικοί υπολογισμοί σε διαλύματα
 Στοιχειμετρικοί υπολογισμοί σε διαλύματα 23-1. Τι εκφράζουν οι συντελεστές μιας χημικής αντίδρασης; Οι συντελεστές σε μία χημική εξίσωση καθορίζουν την αναλογία mol των αντιδρώντων και προϊόντων στην αντίδραση.
Στοιχειμετρικοί υπολογισμοί σε διαλύματα 23-1. Τι εκφράζουν οι συντελεστές μιας χημικής αντίδρασης; Οι συντελεστές σε μία χημική εξίσωση καθορίζουν την αναλογία mol των αντιδρώντων και προϊόντων στην αντίδραση.
έχει μια σταθερή τιμή που συμβολίζεται με K c.
 Χημικός Διδάκτωρ Παν. Πατρών 4.3 Σταθερα χημικη ς ισορροπι ας Κ - Kp Τι ονομάζεται σταθερά χημικής ισορροπίας Κ και τι νόμο χημικής ισορροπίας; Ποιες χημικές ουσίες δεν συμπεριλαμβάνοντ αι στο νόμο της
Χημικός Διδάκτωρ Παν. Πατρών 4.3 Σταθερα χημικη ς ισορροπι ας Κ - Kp Τι ονομάζεται σταθερά χημικής ισορροπίας Κ και τι νόμο χημικής ισορροπίας; Ποιες χημικές ουσίες δεν συμπεριλαμβάνοντ αι στο νόμο της
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
13. ΔΙΑΛΥΤΟΤΗΤΑ ΚΑΙ ΙΣΟΡΡΟΠΙΕΣ ΣΥΜΠΛΟΚΩΝ
 13. ΔΙΑΛΥΤΟΤΗΤΑ ΚΑΙ ΙΣΟΡΡΟΠΙΕΣ ΣΥΜΠΛΟΚΩΝ ΠΕΡΙΕΧΟΜΕΝΑ Η σταθερά γινομένου διαλυτότητας Διαλυτότητα και επίδραση κοινού ιόντος Υπολογισμοί καθίζησης Επίδραση του ph στη διαλυτότητα Σχηματισμός συμπλόκων
13. ΔΙΑΛΥΤΟΤΗΤΑ ΚΑΙ ΙΣΟΡΡΟΠΙΕΣ ΣΥΜΠΛΟΚΩΝ ΠΕΡΙΕΧΟΜΕΝΑ Η σταθερά γινομένου διαλυτότητας Διαλυτότητα και επίδραση κοινού ιόντος Υπολογισμοί καθίζησης Επίδραση του ph στη διαλυτότητα Σχηματισμός συμπλόκων
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία. Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η ανάπτυξη μαθηματικών
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 8: Θερμοχωρητικότητα Χημικό δυναμικό και ισορροπία Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η ανάπτυξη μαθηματικών
ΔΙΑΛΥΜΑΤΑ ΓΙΝΟΜΕΝΟ ΔΙΑΛΥΤΟΤΗΤΑΣ
 ΔΙΑΛΥΜΑΤΑ ΓΙΝΟΜΕΝΟ ΔΙΑΛΥΤΟΤΗΤΑΣ (K sp ) Έστω ότι σε ένα διαλύτη διαλύεται µια στερεά ουσία Α Χ Β Ψ ενώ µέρος της παραµένει αδιάλυτο. Τότε προκύπτει ένα κορεσµένο διάλυµα και επικρατεί η ισορροπία: Α Χ
ΔΙΑΛΥΜΑΤΑ ΓΙΝΟΜΕΝΟ ΔΙΑΛΥΤΟΤΗΤΑΣ (K sp ) Έστω ότι σε ένα διαλύτη διαλύεται µια στερεά ουσία Α Χ Β Ψ ενώ µέρος της παραµένει αδιάλυτο. Τότε προκύπτει ένα κορεσµένο διάλυµα και επικρατεί η ισορροπία: Α Χ
Στοιχειομετρικοί Υπολογισμοί στη Χημεία
 Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
2.2 Το νερό ως διαλύτης - μείγματα
 1 2.2 Το νερό ως διαλύτης - μείγματα 2.2-1. Τι ονομάζεται μείγμα; Μείγμα ονομάζεται κάθε σύστημα που προκύπτει από την ανάμειξη δύο ή περισσότερων ουσιών. Τα περισσότερα υλικά στη φύση είναι μίγματα. 2.2-2.
1 2.2 Το νερό ως διαλύτης - μείγματα 2.2-1. Τι ονομάζεται μείγμα; Μείγμα ονομάζεται κάθε σύστημα που προκύπτει από την ανάμειξη δύο ή περισσότερων ουσιών. Τα περισσότερα υλικά στη φύση είναι μίγματα. 2.2-2.
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ - ΠΑΡΑΔΕΙΓΜΑ
 ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ - ΠΑΡΑΔΕΙΓΜΑ ΘΕΜΑ 1ο Για τις παρακάτω ερωτήσεις Α1-Α3 να μεταφέρετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα μόνο το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ - ΠΑΡΑΔΕΙΓΜΑ ΘΕΜΑ 1ο Για τις παρακάτω ερωτήσεις Α1-Α3 να μεταφέρετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα μόνο το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Κεφάλαιο 5 Διαλύματα
 Κεφάλαιο 5 Διαλύματα Σύνοψη Τα διαλύματα είναι ομογενή μείγματα τα οποία βρίσκουν σημαντικές εφαρμογές σχεδόν σε όλους τους τομείς της ζωής. Κάθε διάλυμα περιέχει μία ή περισσότερες διαλυμένες ουσίες σε
Κεφάλαιο 5 Διαλύματα Σύνοψη Τα διαλύματα είναι ομογενή μείγματα τα οποία βρίσκουν σημαντικές εφαρμογές σχεδόν σε όλους τους τομείς της ζωής. Κάθε διάλυμα περιέχει μία ή περισσότερες διαλυμένες ουσίες σε
Εργαστήριο Φυσιολογίας Ι Εργαστηριακός Συνεργάτης: Ρήγας Παύλος. Ωσμωτικότητα
 Ωσμωτικότητα Στόχοι κατανόησης: Τί είναι ωσμωτικότητα, ωσμωτική πίεση και ώσμωση; Σε τι διαφέρει η συγκέντρωση από την ωσμωτικότητα ενός διαλύματος και πώς υπολογίζουμε την κάθε μία; Ωσμωτική πίεση: Το
Ωσμωτικότητα Στόχοι κατανόησης: Τί είναι ωσμωτικότητα, ωσμωτική πίεση και ώσμωση; Σε τι διαφέρει η συγκέντρωση από την ωσμωτικότητα ενός διαλύματος και πώς υπολογίζουμε την κάθε μία; Ωσμωτική πίεση: Το
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 7: Κατανομή ουσίας μεταξύ δύο διαλυτών και προσδιορισμός σταθεράς ισορροπίας αντιδράσεως Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 5 3. Επεξεργασία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 7: Κατανομή ουσίας μεταξύ δύο διαλυτών και προσδιορισμός σταθεράς ισορροπίας αντιδράσεως Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 5 3. Επεξεργασία
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
ΑΣΕΠ ΕΚΠΑΙΔΕΥΤΙΚΩΝ 2009. Κλάδος: ΠΕ 04.02 Χημικών ΑΠΑΝΤΗΣΕΙΣ ΕΙΔΙΚΗΣ ΔΙΔΑΚΤΙΚΗΣ
 ΑΣΕΠ ΕΚΠΑΙΔΕΥΤΙΚΩΝ 2009 Κλάδος: ΠΕ 04.02 Χημικών Λίγα λόγια για τα θέματα.. ΑΠΑΝΤΗΣΕΙΣ ΕΙΔΙΚΗΣ ΔΙΔΑΚΤΙΚΗΣ Τα θέματα σε γενικές γραμμές κρίνονται βατά και σχετικά πιο εύκολα από τα θέματα που τέθηκαν στον
ΑΣΕΠ ΕΚΠΑΙΔΕΥΤΙΚΩΝ 2009 Κλάδος: ΠΕ 04.02 Χημικών Λίγα λόγια για τα θέματα.. ΑΠΑΝΤΗΣΕΙΣ ΕΙΔΙΚΗΣ ΔΙΔΑΚΤΙΚΗΣ Τα θέματα σε γενικές γραμμές κρίνονται βατά και σχετικά πιο εύκολα από τα θέματα που τέθηκαν στον
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Βαθμός ιοντισμού. Για ισχυρούς ηλεκτρολύτες ισχύει α = 1. Για ασθενής ηλεκτρολύτες ισχύει 0 < α < 1.
 Βαθμός ιοντισμού Ο ιοντισμός μιας ομοιοπολικής ένωσης στο νερό μπορεί να είναι πλήρης ή μερικώς. Ένα μέτρο έκφρασης της ισχύος των ηλεκτρολυτών, κάτω από ορισμένες συνθήκες είναι ο βαθμός ιοντισμού (α).
Βαθμός ιοντισμού Ο ιοντισμός μιας ομοιοπολικής ένωσης στο νερό μπορεί να είναι πλήρης ή μερικώς. Ένα μέτρο έκφρασης της ισχύος των ηλεκτρολυτών, κάτω από ορισμένες συνθήκες είναι ο βαθμός ιοντισμού (α).
Αλληλεπίδραση ρύπων εδάφους
 Αλληλεπίδραση ρύπων εδάφους Παρουσίαση 1 από 4 Περιεχόμενα 1) Kίνητρο μελέτης αλληλεπίδρασης 2) Έννοιες και όροι 3) Προαπαιτούμενα από φυσικοχημεία & εδαφομηχανική Πώς κατανέμεται ο ρύπος στις εδαφικές
Αλληλεπίδραση ρύπων εδάφους Παρουσίαση 1 από 4 Περιεχόμενα 1) Kίνητρο μελέτης αλληλεπίδρασης 2) Έννοιες και όροι 3) Προαπαιτούμενα από φυσικοχημεία & εδαφομηχανική Πώς κατανέμεται ο ρύπος στις εδαφικές
Ομογενής και Ετερογενής Ισορροπία
 Ομογενής και Ετερογενής Ισορροπία Ομογενής ισορροπία : N 2(g) + O 2(g) 2NO (g) Ετερογενής ισορροπία : Zn (s) + 2H (aq) + Zn (aq) ++ + H 2(g) Σταθερά χηµικής ισορροπίας Kc: Για την αµφίδροµη χηµική αντίδραση:
Ομογενής και Ετερογενής Ισορροπία Ομογενής ισορροπία : N 2(g) + O 2(g) 2NO (g) Ετερογενής ισορροπία : Zn (s) + 2H (aq) + Zn (aq) ++ + H 2(g) Σταθερά χηµικής ισορροπίας Kc: Για την αµφίδροµη χηµική αντίδραση:
