Πανεπιστήµιο Πατρών Πολυτεχνική Σχολή Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής
|
|
|
- Βαρνάβας Βλαστός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πανεπιστήµιο Πατρών Πολυτεχνική Σχολή Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής ιπλωµατική Εργασία Στα πλαίσια του µεταπτυχιακού προγράµµατος ειδίκευσης: Επιστήµη και Τεχνολογία Των Υπολογιστών ροµολόγηση Και Ανάθεση Μήκους Κύµατος Σε Οπτικά ίκτυα Βασισµένη Στα Φυσικά Χαρακτηριστικά Του ικτύου Μανουσάκης Κων/νος Α.Μ.: 402 Επιβλέπων: Βαρβαρίγος Εµµανουήλ Τριµελής Επιτροπή: Βαρβαρίγος Εµµανουήλ Βλάχος Κυριάκος Κακλαµάνης Χρήστος Πάτρα, Ιούλιος 2007
2
3 Περίληψη Ο πιο σύγχρονος και περισσότερα υποσχόµενος τύπος οπτικών δικτύων, είναι τα οπτικά δίκτυα πολυπλεξίας διαίρεσης µήκους κύµατος (Wavelength Division Multiplexing WDM). Τα δίκτυα αυτά διαθέτουν τεράστια χωρητικότητα και αναµένεται να αποτελέσουν τα µελλοντικά δίκτυα κορµού για τη µεταφορά µεγάλου όγκου δεδοµένων. Η πλήρης αξιοποίηση της χωρητικότητας των WDM δικτύων, όµως, απαιτεί την επίλυση ειδικών θεµάτων που σχετίζονται µε τις ιδιαιτερότητες και τη φύση των WDM οπτικών δικτύων. Το σηµαντικότερο ίσως από αυτά είναι το πρόβληµα της δροµολόγησης και ανάθεσης µήκους κύµατος (Routing and Wavelength Assignment RWA) θέµα πάνω στο οποίο έχει αναπτυχθεί έντονη ερευνητική δραστηριότητα τα τελευταία χρόνια. Ένα άλλο θέµα που χρήζει ιδιαίτερης προσοχής είναι οι εξασθενήσεις που υφίσταται ένα σήµα µέσα στο οπτικό δίκτυο. Όταν λοιπόν κάποιο σήµα διαδίδεται κατά µήκος ενός οπτικού µονοπατιού πέφτει η ποιότητα του εξαιτίας των φυσικών επιδράσεων που δέχεται. Οι φυσικές επιδράσεις κατά κανόνα µειώνουν τον λόγο σήµατος προς θόρυβο (SNR), µε αποτέλεσµα να αυξηθεί σηµαντικά και η συχνότητα εµφάνισης λαθών (BER) στον κόµβο προορισµού. Αν η παραπάνω συχνότητα εµφάνισης λαθών είναι µεγαλύτερη από ένα καθορισµένο όριο, τότε το αίτηµα δροµολόγησης θα πρέπει να απορριφθεί. Εποµένως κατά την επίλυση του RWA προβλήµατος θα πρέπει να ληφθούν υπόψη οι επιδράσεις που προκαλούνται στο σήµα λόγω των φυσικών χαρακτηριστικών του δικτύου. Στην παρούσα διπλωµατική εργασία έχει µελετηθεί το πρόβληµα της δροµολόγησης και ανάθεσης µήκους κύµατος λαµβάνοντας υπόψη τις πιο σηµαντικές επιδράσεις, όπως η χρωµατική διασπορά (Chromatic Dispersion CD), η διασπορά τρόπου πόλωσης (Polarization Mode Dispersion PMD), η ενισχυµένη αυθόρµητη εκποµπή (Amplifier Spontaneous Emission ASE) και η αλληλεπίδραση γειτονικών καναλιών (crosstalk). Η επίδραση των τριών πρώτων παραµέτρων εξαρτάται αποκλειστικά από τα χαρακτηριστικά των συνδέσµων, ενώ η επίδραση του crosstalk εξαρτάται από τον αριθµό οπτικών µονοπατιών που διατρέχουν ένα σύνδεσµο. Εποµένως η αλληλεπίδραση των ανοιχτών καναλιών σε ένα σύνδεσµο θα πρέπει να εξεταστεί ταυτόχρονα µε την δροµολόγηση και ανάθεση µήκους κύµατος. Αντικείµενο της έρευνας είναι η επίλυση του στατικού προβλήµατος δροµολόγησης και ανάθεσης µήκους κύµατος βασισµένη στις ιδιαιτερότητες και τις φυσικές εξασθενήσεις που εµφανίζονται σε ένα οπτικό δίκτυο, µέσω διαφόρων προσεγγίσεων. Το κυριότερο µέτρο σύγκρισης των προσεγγίσεων που θα παρουσιαστούν είναι η blocking probability των αιτήσεων που χρειάζονται δροµολόγηση. Προτείνεται επίσης µία συνάρτηση βελτιστοποίησης που µειώνει την blocking probability σε σχέση µε τις προσεγγίσεις που υπάρχουν στην βιβλιογραφία.
4 Ευχαριστίες Πριν την παρουσίαση της παρούσας διπλωµατικής εργασίας θα ήθελα να ευχαριστήσω τους ανθρώπους που µε βοήθησαν και µε στήριξαν σ αυτήν την προσπάθεια. Αρχικά θα ήθελα να ευχαριστήσω θερµά τον καθηγητή µου κ. Μάνο Βαρβαρίγο που µου έδωσε την δυνατότητα να ασχοληθώ µε αυτό το ενδιαφέρον θέµα και υπήρξε σύµβουλός µου καθ όλη τη διάρκεια των µεταπτυχιακών µου σπουδών. Η συνεργασία υπήρξε άριστη όπως και στην εκπόνηση της προπτυχιακής µου εργασίας. Αυτή η δουλειά οφείλεται κατά µεγάλο ποσοστό στην καθοδήγηση και επιµονή του για συστηµατική δουλειά. Μέσα από συζητήσεις µας προέκυψαν οι ιδέες που παρουσιάζονται παρακάτω. Οµοίως θα ήθελα να ευχαριστήσω τον καθηγητή µου κ. Κυριάκο Βλάχο για τις συµβουλές του και την υποµονή που επέδειξε για να λύσει κάθε µου απορία. Με τις παροτρύνσεις του και τις συζητήσεις µας, µε οδήγησε στην κατανόηση θεµάτων γύρω από τα οπτικά δίκτυα. Θα ήθελα επίσης να ευχαριστήσω τον καθηγητή κ. Χρήστο Κακλαµάνη για την τιµή που µου έκανε να είναι µέλος της τριµελούς επιτροπής. Θα ήθελα να ευχαριστήσω τον φίλο και συνάδελφό µου Βασίλη Σούρλα για την συνεργασία µας όλα αυτά τα χρόνια κατά τη διάρκεια των σπουδών µας. Ευχαριστώ τον συνάδελφο Γιάννη Λακουµέντα για την συνεργασία και την βοήθειά του σε θέµατα που αφορούν το RWA πρόβληµα. Ένα ευχαριστώ επίσης στα παιδιά του εργαστηρίου δικτύων. Θέλω να ευχαριστήσω την Σκεύη γιατί είναι πάντα εκεί, κάθε στιγµή. Με τον δικό της τρόπο µου δείχνει ποια πράγµατα αξίζουν στη ζωή. Με την στήριξή της κατάφερα να ολοκληρώσω την διπλωµατική εργασία και µε συµβούλευσε για το πως θα γίνει κατανοητή η παρουσίασή της. Τέλος ένα µεγάλο ευχαριστώ στην αδερφή µου Βαλεντίνα και στους γονείς µου Σταύρο και Τσαµπίκα για την πίστη που δείχνουν στο πρόσωπό µου. Για το κουράγιο που µου δίνουν και τις θυσίες που κάνουν για να µου προσφέρουν ό,τι χρειάζοµαι.
5 Περιεχόµενα 1 WDM Αρχιτεκτονική WDM ικτύου Οπτικά ίκτυα Οπτικές Ίνες Ενισχυτές Φυσική Τοπολογία Ενός WDM ικτύου Κόµβοι Πρόσβασης Κόµβοι Μεταγωγής Lightpaths Μετατροπή Μήκους Κύµατος Το Πρόβληµα ροµολόγησης Και Ανάθεσης Μήκους Κύµατος Περιορισµοί Στη ροµολόγηση Ενός Συνόλου Από Lightpaths υναµική ροµολόγηση Και Ανάθεση Μήκους Κύµατος υναµική ροµολόγηση Σταθερή-Εναλλακτική ροµολόγηση Προσαρµοστική ροµολόγηση Ανάθεση Μήκους Κύµατος Ευριστικοί Αλγόριθµοι Στατική ροµολόγηση Και Ανάθεση Μήκους Κύµατος ροµολόγηση Kαι Ανάθεση Μήκους Κύµατος Mε Μετατροπή Μήκους Κύµατος Τεχνικές ιαχωρισµού Του RWA Για Την Στατική Περίπτωση ροµολόγηση Ανάθεση Μήκους Κύµατος Στατική Περίπτωση Μείωση Μεγέθους Του Προβλήµατος Μείωση Του Χώρου Μείωση Του Χρόνου Πρακτική Προσέγγιση Του RWA Εγκατάσταση Ενός Lightpath Σε WDM ίκτυο ροµολόγηση Και Ανάθεση Μήκους Κύµατος Η Προσέγγιση Μας LP1: Στατική ροµολόγηση Και Ανάθεση Μήκους Κύµατος Συνάρτηση Κόστους Ροής Τµηµατικά Γραµµική Συνάρτηση Κόστους Ροής Η Συνάρτηση Της Μοντελοποίησης Περιγραφή Του Αλγορίθµου LP2: Η Συµφόρηση Του Μονοπατιού Ως Objective Της Μοντελοποίησης Σύγκριση Αλγορίθµων Φυσικές Εξασθενήσεις ιασπορά Τρόπου Πόλωσης Χρωµατική ιασπορά NRZ ιαµόρφωση RZ ιαµόρφωση LPF ιαµόρφωση Θόρυβος ASE...52
6 4.3.1 ASE Amplifier Spontaneous Emission Ωφέλιµο Μήκος (Effective Length) Σε Ενισχυµένα Συστήµατα Crosstalk ροµολόγηση Βάση Των Φυσικών Εξασθενήσεων Αναπαράσταση ικτύου Με Φυσικές Εξασθενήσεις Απόρριψη Αιτήσεων Λόγω Φυσικών Εξασθενήσεων Τοποθέτηση Περιορισµών Μετά Την Επίλυση Του RWA Τοποθέτηση Περιορισµών Πριν Την Επίλυση Του RWA Τοποθέτηση Περιορισµών Μέσα Στην LP Μοντελοποίηση Τοποθέτηση Των Περιορισµών Με Τη Μορφή Μεταβλητών Μοντελοποίηση Του Crosstalk Αποτελέσµατα Προσοµοίωσης Σύγκριση LP1 Και LP Επίδραση Φυσικών Εξασθενήσεων Στην Απόδοση Του ικτύου Μελέτη Της PMD Μελέτη Της CD Μελέτη Του Θορύβου ASE Μελέτη Του Crosstalk Βιβλιογραφία... 80
7 1 WDM Η πολυπλεξία διαίρεσης µήκους κύµατος (Wavelength Division Multiplexing - (WDM)) είναι µία υποσχόµενη τεχνολογία για ταχύτερα και πιο αξιόπιστα δίκτυα επικοινωνιών [19]. Παραδοσιακά µόνο ένα µικρό µέρος της χωρητικότητας της ίνας χρησιµοποιείται, αλλά χρησιµοποιώντας τα WDM οπτικά δίκτυα έχουν ένα µεγάλο πλεονέκτηµα [13]. Να εκµεταλλεύονται πλήρως το πολύ µεγάλο εύρος ζώνης του οπτικού συνδέσµου. Αυτό επιτυγχάνεται ως εξής: Το εύρος ζώνης χωρίζεται σε n µη επικαλυπτόµενα διαστήµατα, κάθε ένα από τα οποία εκτείνεται γύρω από ένα βασικό µήκος κύµατος (wavelength). Στο πεδίο των συχνοτήτων, το εύρος συχνοτήτων που ορίζει το συγκεκριµένο εύρος ζώνης, χωρίζεται σε n ανεξάρτητα κανάλια, κάθε ένα από τα οποία αντιστοιχεί σε ένα συγκεκριµένο µήκος κύµατος. Κάθε ένα από τα κανάλια αυτά διαµορφώνεται ανεξάρτητα το ένα από το άλλο. Με άλλα λόγια, n πηγές εκποµπής σήµατος µπορούν να συνδυαστούν µεταξύ τους και εκπέµποντας η κάθε µία µε διαφορετικό ρυθµό που αντιστοιχεί στο συγκεκριµένο µήκος κύµατος που της έχει ανατεθεί, να µεταδώσουν ανεξάρτητα η µία από την άλλη πάνω από τον ίδιο σύνδεσµο. Τα n διαµορφωµένα µήκη κύµατος, πολυπλέκονται µεταξύ τους στον κόµβο πρόσβασης (access node) και στέλνονται στο δίκτυο. Σε κάθε κόµβο προορισµού υπάρχει ένα φίλτρο που είναι συντονισµένο στο αντίστοιχο µήκος κύµατος. Το λαµβανόµενο σήµα στη συνέχεια αποδιαµορφώνεται και ανακτάται το αρχικό σήµα. Σχήµα 1.1: Πολυπλεξία ιαίρεσης Μήκους Κύµατος (WDM) Στην WDM τεχνική, πολλαπλά σήµατα πληροφορίας προσαρµόζονται σε οπτικά σήµατα διαφορετικού µήκους κύµατος, µε τα προκύπτοντα µήκη κύµατος να συνδυάζονται και να εκπέµπονται ταυτόχρονα πάνω στην ίδια οπτική ίνα (σχήµα 1.1). 1.1 Αρχιτεκτονική WDM ικτύου Η επιτυχία των WDM οπτικών δικτύων στηρίζεται σε µεγάλο ποσοστό στα διαθέσιµα οπτικά στοιχεία. Ένα διάγραµµα ενός WDM συστήµατος επικοινωνίας παρουσιάζεται στο σχήµα 1.2. Το µέσο µετάδοσης (network medium ή transmission medium) µπορεί
8 να είναι µία απλή οπτική ίνα, ένας συζεύκτης παθητικού αστέρα (passive star coupler) για ένα δίκτυο εκποµπής και επιλογής (broadcast and select), ή ένα δίκτυο από οπτικούς ή ηλεκτρονικούς µεταγωγείς και οπτικές ίνες. Ο ποµπός (transmitter) αποτελείται από έναν ή περισσότερους οπτικούς ποµπούς, που µπορούν είτε να καθοριστούν σε ένα µόνο µήκος κύµατος, είτε µπορούν να ρυθµιστούν σε ένα εύρος από µήκη κύµατος. Κάθε οπτικός ποµπός αποτελείται από ένα laser και ένα διαµορφωτή laser και µπορεί επίσης να περιλαµβάνει ένα οπτικό φίλτρο για ρυθµιστικούς (tuning) σκοπούς. Εάν χρησιµοποιούνται πολλαπλοί οπτικοί ποµποί τότε χρειάζεται ένας πολυπλέκτης ή συζεύκτης για να συνδυάζει τα σήµατα από τους διαφορετικούς ποµπούς laser σε µία οπτική ίνα. Ο δέκτης αποτελείται από ένα ρυθµιζόµενο φίλτρο το οποίο ακολουθείται από έναν φωτοανιχνευτή ή έναν αποπολυπλέκτη που ακολουθείται από µία συστοιχία από φωτοανιχνευτές [3], [5]. Σχήµα 1.2: Σχηµατικό διάγραµµα ενός WDM συστήµατος µετάδοσης Παραδείγµατα µερικών WDM ποµπών και δεκτών παρουσιάζονται στο σχήµα 1.3. Οι ενισχυτές µπορεί να χρειάζονται σε διάφορες θέσεις σε όλο το δίκτυο για να διατηρήσουν την ισχύ των οπτικών σηµάτων. Σχήµα1.3: οµές ποµπού και δέκτη Οπτικά ίκτυα Τα οπτικά δίκτυα είναι ταχύτερα από τα παραδοσιακά δίκτυα, γιατί σε αντίθεση µε την µεταφορά ηλεκτρονίων στα καλώδια χαλκού, στις οπτικές ίνες έχουµε µεταφορά φωτονίων. Τα φωτόνια είναι ελαφρύτερα από τα ηλεκτρόνια και επιπλέον τα φωτόνια δεν αλληλεπιδρούν µεταξύ τους επειδή δεν έχουν φορτίο. Επίσης δεν επηρεάζονται από φωτόνια εκτός ίνας. Το φως χαρακτηρίζεται από υψηλότερες συχνότητες και συνεπώς από χαµηλότερα µήκη κύµατος, µε αποτέλεσµα περισσότερα bits
9 πληροφορίας µπορούν να µεταφερθούν µέσω της οπτικής ίνας έναντι του καλωδίου χαλκού Οπτικές Ίνες Η οπτική ίνα αποτελείται από ένα πολύ λεπτό γυάλινο κύλινδρο (πυρήνας), µέσω του οποίου µεταφέρεται το φως. Ο πυρήνας περικλείεται από ένα οµόκεντρο επίπεδο γυαλιού (επικάλυψη), το οποίο προστατεύεται από ένα λεπτό πλαστικό περίβληµα (Σχήµα 1.4α). Ο πυρήνας χαρακτηρίζεται από ένα ελαφρώς µεγαλύτερο δείκτη διάθλασης σε σχέση µε την επικάλυψη. Ο λόγος των δεικτών διάθλασης καθορίζει την κριτική γωνία θ c. Η λειτουργία της οπτικής ίνας στηρίζεται στην ολική εσωτερική ανάκλαση. Όταν µία ακτίνα φωτός απ τον πυρήνα πλησιάσει στην επιφάνεια µεταξύ του πυρήνα και της επικάλυψης µε γωνία µικρότερη από θ c, η ακτίνα φωτός ανακλάται πλήρως στον πυρήνα (Σχήµα 1.4β). Σχήµα 1.4: α) Οπτική ίνα, β) ανάκλαση στην οπτική ίνα Εφόσον κάθε ακτίνα φωτός που προσπίπτει στην επιφάνεια µεταξύ του πυρήνα και της επικάλυψης µε γωνία µικρότερη από θ c ανακλάται εσωτερικά, πολλές διαφορετικές ακτίνες φωτός στον πυρήνα θα ανακλώνται µε διαφορετικές γωνίες. Κάθε ακτίνα χαρακτηρίζεται από έναν τρόπο και η ίνα µε αυτή την ιδιότητα λέγεται πολυτροπική ίνα (Σχήµα 1.5α). Οι διαφορετικοί τρόποι αναγκάζουν τις ακτίνες να αλληλεπιδρούν µεταξύ τους, µε αποτέλεσµα να περιορίζεται ο µέγιστος ρυθµός από bits σε µία τέτοια ίνα. Στην περίπτωση που η διάµετρος του πυρήνα είναι πολύ µικρή, η ίνα δρα σαν κατευθυντής φωτονίων και το φως µπορεί να ταξιδέψει σε ευθεία γραµµή. Μία τέτοια ίνα καλείται µονοτροπική ίνα (Σχήµα 1.5β). Οι µονοτροπικές ίνες είναι πιο γρήγορες και πιο ακριβές από τις πολυτροπικές.
10 Σχήµα 1.5: α) πολυτροπική ίνα β) µονοτροπική ίνα Το σχήµα 1.6 δείχνει τις δύο περιοχές χαµηλής εξασθένησης της ίνας. Με κέντρο περίπου τα 1300 nm υπάρχει ένα εύρος 200 nm στο οποίο η εξασθένηση είναι µικρότερη από 0.5 db ανά km. Με κέντρο περίπου τα 1550 nm υπάρχει ένα εύρος περίπου ίσου µεγέθους στο οποίο η εξασθένηση είναι µικρότερη από 0.2 db ανά km. Όταν συνδυαστούν οι δύο αυτές περιοχές παρέχουν ένα θεωρητικό άνω όριο από 50 THz εύρος ζώνης [14]. Σχήµα 1.6: Οι περιοχές χαµηλής εξασθένησης µιας οπτικής ίνας Ενισχυτές Σε ένα σύστηµα οπτικών επικοινωνιών, τα οπτικά σήµατα από τον ποµπό εξασθενούν από την οπτική ίνα καθώς µεταδίδονται µέσω αυτής. Πριν από την εµφάνιση των οπτικών ενισχυτών, η µόνη επιλογή ήταν να αναπαραχθεί το σήµα και να αναµεταδοθεί. Αυτή η διαδικασία πραγµατοποιείται από τους αναγεννητές. Ένας αναγεννητής µετατρέπει το οπτικό σήµα σε ηλεκτρικό σήµα, το καθαρίζει, και το
11 µετατρέπει πάλι σε οπτικό σήµα για την µετάδοση του. Οι οπτικοί ενισχυτές δεν επηρεάζονται από τον ρυθµό µετάδοσης ή τη διαµόρφωση του σήµατος. Παρόλο που ένα οπτικό σήµα µπορεί να διαδοθεί µια µεγάλη απόσταση προτού χρειαστεί ενίσχυση, τα δίκτυα µεγάλης απόστασης (long haul) και τα τοπικά οπτικά δίκτυα (local lightwave) µπορούν να ωφεληθούν από τους οπτικούς ενισχυτές. Η ολική-οπτική ενίσχυση µπορεί να διαφέρει από την οπτικό-ηλεκτρονική ενίσχυση δεδοµένου ότι µπορεί να ενεργήσει µόνο για να αυξήσει την ενέργεια ενός σήµατος, και όχι να αποκαταστήσει τη µορφή ή το συγχρονισµό του σήµατος. Αυτός ο τύπος ενίσχυσης είναι γνωστός ως 1R (αναγέννηση), και παρέχει συνολική διαφάνεια δεδοµένων. Σε ένα WDM σύστηµα, κάθε µήκος κύµατος θα πρέπει να χωριστεί πριν να ενισχυθεί ηλεκτρονικά, και να επανασυνδεθεί πριν αναµεταδοθεί. Κατά συνέπεια, προκειµένου να εξαλειφτεί η ανάγκη για τον οπτικούς πολυπλέκτες και αποπολυπλέκτες στους ενισχυτές, οι οπτικοί ενισχυτές πρέπει να ενισχύσουν τη ισχύ των οπτικών σηµάτων χωρίς να πρώτα να µετατραπούν σε ηλεκτρικά σήµατα. Ένα µειονέκτηµα είναι ότι ο θόρυβος, όπως και το σήµα, θα ενισχυθούν. Η οπτική ενίσχυση χρησιµοποιεί την ιδιότητα της υποκινούµενης εκποµπής. Οι δύο βασικοί τύποι οπτικών ενισχυτών είναι οι ενισχυτές ηµιαγωγών λέιζερ και οι ενισχυτές εµποτισµένοι µε ιόντα ερβίου. Οι οπτικοί εµποτισµένοι ενισχυτές είναι οπτικές ίνες εµποτισµένες µε ένα στοιχείο που µπορεί να ενισχύσει το φως (σχήµα 1.7). Το πιο συνηθισµένο στοιχείο είναι το έρβιο, το οποίο παρέχει κέρδος για τα µήκη κύµατος µεταξύ 1525nm και 1560nm. Στο τέλος της οπτικής ίνας, ένα λέιζερ µεταδίδει ένα ισχυρό σήµα σε ένα χαµηλότερο µήκος κύµατος (το οποίο αναφέρεται ως µήκος κύµατος άντλησης pump wavelength) ενισχύοντας την ίνα. Αυτό το σήµα άντλησης διεγείρει τα εµποτισµένα άτοµα σε ένα υψηλότερο ενεργειακό επίπεδο. Αυτό επιτρέπει το σήµα των δεδοµένων να παρακινήσει τα διεγερµένα άτοµα να απελευθερώσουν φωτόνια. Οι περισσότεροι ενισχυτές ιόντων ερβίου (EDFAs) αντλούνται από λέιζερ µε µήκος κύµατος 980nm ή 1480nm. Το µήκος κύµατος άντλησης στα 980nm έχει κέρδος γύρω στα 10dB/mW, ενώ το µήκος κύµατος άντλησης στα 1480nm έχει κέρδος γύρω στα 5dB/mW. Τυπικά κέρδη είναι της τάξης των 25 db. Πειραµατικά, οι EDFAs έχει δειχθεί ότι πετυχαίνουν κέρδος µέχρι 51 db. Σχήµα 1.7: Ενισχυτής εµποτισµένος µε ιόντα ερβίου. Το φυσικό µήκος (physical length) ενός lightlink ορίζεται ως το µήκος της αντίστοιχης οπτικής ίνας. Το µήκος ενίσχυσης (amplifier length) ενός lightlink ορίζεται ως ο αριθµός των ενισχυτών κατά µήκος του lightlink. Το φυσικό και µήκος ενίσχυσης ενός οπτικού µονοπατιού, ορίζεται ως το άθροισµα των αντίστοιχων φυσικών και µηκών ενίσχυσης των lightlinks που απαρτίζουν το συγκεκριµένο οπτικό µονοπάτι. Το φαινόµενο της διασποράς (dispersion) και άλλοι παράγοντες θέτουν ένα άνω όριο στο µέγιστο επιτρεπτό φυσικό µήκος ενός οπτικού µονοπατιού. Υπάρχει
12 επίσης και ένα άνω όριο και στο µήκος ενίσχυσης ενός οπτικού µονοπατιού, πριν το σήµα υποστεί οπτοηλεκτρονική µετατροπή. Το µήκος ενίσχυσης ενός οπτικού µονοπατιού είναι συνήθως ανάλογο µε το φυσικό του µήκος, δεδοµένου ότι οι ενισχυτές συνήθως τοποθετούνται σε ίσες αποστάσεις µεταξύ τους. Στην περίπτωση αυτή, τα δύο παραπάνω είδη περιορισµών θα µπορούσαν να αντιµετωπιστούν σαν ένας, µειώνοντας έτσι την πολυπλοκότητα του προβλήµατος της δροµολόγησης και ανάθεσης µήκους κύµατος. 1.2 Φυσική Τοπολογία Ενός WDM ικτύου Κόµβοι Πρόσβασης Οι κόµβοι πρόσβασης (access nodes) είναι οι κόµβοι στους οποίους συγκεντρώνεται η κίνηση και οι αιτήσεις των χρηστών, συνδέονται µε τους διακόπτες του υπόλοιπου οπτικού δικτύου, µέσω κάποιων από τις ίνες εισόδου και εξόδου. Κάθε access node συνδέεται µε κάποιο routing node µέσω µιας συγκεκριµένης ίνας εισόδου σε ένα συγκεκριµένο µήκος κύµατος. Αν απαιτείται διαφορετικό µήκος κύµατος, τότε θα πρέπει να χρησιµοποιηθεί µετατροπή µήκους κύµατος (wavelength conversion). Οι κόµβοι πρόσβασης των WDM δικτύων διαθέτουν lasers και φίλτρα, για την εκποµπή και λήψη αντίστοιχα του οπτικού σήµατος, τα οποία ρυθµίζονται κατάλληλα ώστε να λειτουργούν στην επιθυµητή συχνότητα που αντιστοιχεί στο µήκος κύµατος που έχει ανατεθεί στην κάθε σύνδεση. Ένας κόµβος πρόσβασης µπορεί να µεταδίδει ταυτόχρονα σε πολλά µήκη κύµατος. Τα διαφορετικά αυτά σήµατα πολυπλέκονται µε τη βοήθεια κατάλληλων πολυπλεκτών µήκους κύµατος (wavelength multiplexers) και µεταδίδονται µαζί πάνω από την ίδια οπτική ίνα Κόµβοι Μεταγωγής Στους ενδιάµεσους κόµβους µεταγωγής (routing/switching nodes), χρησιµοποιούνται οπτοηλεκτρονικά switches (optical cross connects OXCs) για τη δροµολόγηση του σήµατος στον τελικό προορισµό. Ένα OXC παίρνει σαν είσοδο ένα οπτικό σήµα σε κάθε ένα από τα µήκη κύµατος σε µία από τις εισόδους του και µπορεί να το κάνει µεταγωγή σε µία συγκεκριµένη έξοδο, ανεξάρτητα από άλλα µήκη κύµατος. Ένα OXC µε N εισόδους και N εξόδους ικανό να χειρίζεται W µήκη κύµατος για κάθε port είναι ισοδύναµος µε W ανεξάρτητους N N µεταγωγείς. Αυτοί οι µεταγωγείς πρέπει να βρίσκονται µετά από έναν αποπολυπλέκτη µήκους κύµατος και να ακολουθούνται από έναν πολυπλέκτη µήκους κύµατος για να υλοποιούν έναν OXC όπως φαίνεται στο σχήµα 1.8. Εποµένως ένας OXC µπορεί να συνδέσει τα διαφορετικά µήκη κύµατος από την είσοδο στη έξοδο, όπου ο τύπος σύνδεσης του κάθε µήκους κύµατος είναι ανεξάρτητο µε τα άλλα. Με κατάλληλη διαµόρφωση των OXC κατά µήκος ενός φυσικού µονοπατιού, λογικές συνδέσεις (lightpaths) µπορούν να εγκατασταθούν µεταξύ οποιουδήποτε ζευγαριού από υποδίκτυα.
13 Σχήµα 1.8: Οπτικοί µεταγωγείς µε δύο µήκη κύµατος ανά ίνα Lightpaths Lightpath καλείται µία σύνδεση που εγκαθίσταται από έναν κόµβο αφετηρίας σε έναν κόµβο προορισµού προκειµένου να µεταφέρει circuit switched κίνηση. Ένα lightpath είναι στην ουσία µια ακολουθία από unidirectional lightlinks από έναν κόµβο αφετηρίας s σε έναν κόµβο προορισµού d (σχήµα 1.9). Το lightpath αποτελείται από ένα συγκεκριµένο wavelength της οπτικής ίνας εισόδου του κόµβου µεταγωγής s, ένα συγκεκριµένο wavelength της οπτικής ίνας εξόδου του κόµβου µεταγωγής d και τα ενδιάµεσα lightlinks που χρησιµοποιούνται για την επικοινωνία των ενδιάµεσων κόµβων. Κάθε lightpath που χρησιµοποιείται για µια σύνδεση θεωρείται ότι έχει χωρητικότητα c = 1 µονάδα, που αντιστοιχεί στη χωρητικότητα ενός lightlink (wavelength), δηλαδή τη ροή που µπορεί να µεταφέρει το wavelength αυτό. Αν κανένας κόµβος του δικτύου δεν έχει τη δυνατότητα για wavelength conversion, τότε το lightpath θα πρέπει να υπακούει στον περιορισµό της διατήρησης του µήκους κύµατος (wavelength continuity constraint), που υπαγορεύει ότι το lightpath θα πρέπει να καταλαµβάνει το ίδιο wavelength κατά µήκος όλων των συνδέσµων από τους οποίους διέρχεται µέχρι να φτάσει στον τελικό προορισµό. Ένα lightpath µπορεί να είναι all-optical ή όχι, ανάλογα µε το αν κατά µήκος του µονοπατιού το σήµα µεταδίδεται εξολοκλήρου στον οπτικό τοµέα, ή σε κάποιους κόµβους µεταγωγής υφίσταται οπτοηλεκτρονική µετατροπή.
14 Σχήµα 1.9: Ένα οπτικό WDM δίκτυο µε εγκατεστηµένα lightpaths. 1.3 Μετατροπή Μήκους Κύµατος Στα WDM οπτικά δίκτυα, είναι σηµαντική η λειτουργία της µετατροπής µήκους κύµατος (wavelength conversion). Το οπτικό σήµα φτάνοντας σε έναν ενδιάµεσο κόµβο από έναν σύνδεσµο εισόδου και µήκος κύµατος λ i, είναι δυνατόν κατά την έξοδο του από τον κόµβο, να φύγει σε ένα άλλο µήκος κύµατος λ j του συνδέσµου εξόδου, µε λi λ j. Για να γίνει η µετάβαση αυτή από το ένα µήκος κύµατος στο άλλο, θα πρέπει ο κόµβος να είναι εφοδιασµένος µε έναν µετατροπέα µήκους κύµατος (wavelength conversion) που να υποστηρίζει τη µετατροπή από το µήκος κύµατος i στο µήκος κύµατος j. Υπάρχουν διαφορετικά είδη µετατροπής µήκους κύµατος (σχήµα 1.10). Η πλήρης δυνατότητα µετατροπής µήκους κύµατος (full wavelength conversion) σηµαίνει ότι κάθε µήκος κύµατος εισόδου µπορεί να µετατραπεί σε οποιοδήποτε µήκος κύµατος εξόδου. Η περιορισµένη µετατροπή µήκους κύµατος (limited wavelength conversion) σηµαίνει ότι κάθε µήκος κύµατος εισόδου µπορεί να µετατραπεί σε ένα µόνο υποσύνολο των µηκών κύµατος εξόδου. Μία ειδική περίπτωση της περιορισµένης µετατροπής είναι σταθερή µετατροπή µήκους κύµατος (fixed wavelength conversion), όπου κάθε µήκος κύµατος εισόδου µπορεί να µετατραπεί σε ακριβώς ένα άλλο µήκος κύµατος. Η µετατροπή µήκους κύµατος αυξάνει της επιλογές δροµολόγησης για ένα οπτικό µονοπάτι και αυτό έχει σαν αποτέλεσµα να οδηγούµαστε σε µικρότερη blocking probability του δικτύου. Όταν δεν υπάρχει δυνατότητα για µετατροπή µήκους κύµατος (no wavelength conversion), το µήκος κύµατος εισόδου θα πρέπει να είναι το ίδιο µε το µήκος κύµατος εξόδου.
15 Σχήµα 1.10: a) Χωρίς Μετατροπή, b) Σταθερή Μετατροπή, c) Περιορισµένη Μετατροπή, d) Πλήρης Μετατροπή. Η µετατροπή του µήκους κύµατος σε έναν κόµβο µπορεί να απαιτείται για µια σύνδεση που φτάνει από έναν κόµβο µεταγωγής του δικτύου και θα πρέπει να κατευθυνθεί σε έναν άλλο (continuing connection), ή για µία σύνδεση που φτάνει από έναν κόµβο πρόσβασης (originating connection), ή για µία σύνδεση που καταλήγει σε έναν κόµβο πρόσβασης (terminating connection). H µετατροπή µήκους κύµατος µπορεί να επιτελέσει σπουδαίο ρόλο για καλύτερη και αποδοτικότερη χρησιµοποίηση (utilization) των διαθέσιµων µηκών κύµατος του δικτύου. Παράλληλα µε την κατάλληλη µετατροπή κύµατος σε ένα WDM δίκτυο, είναι δυνατό να µειωθεί ο ρυθµός blocking ή η blocking probability της εξυπηρέτησης µιας αίτησης για σύνδεση. Η µετατροπή µήκους κύµατος είναι γενικά µία πολύπλοκη και ακριβή επεξεργασία. Γενικά, όσον αφορά την πολυπλοκότητα, το πιο εύκολο ως προς την υλοποίηση είναι η no wavelength conversion και κατόπιν κατά αύξουσα σειρά πολυπλοκότητας, η fixed wavelength conversion, η limited wavelength conversion και η full wavelength conversion. Ειδικά για την περίπτωση που η µετατροπή µήκους κύµατος γίνεται αµιγώς οπτικά (all-optical), κάθε µετατροπή και ειδικά η full wavelength conversion, είναι εξαιρετικά πολύπλοκη και δαπανηρή. Υπάρχει µια στενή συσχέτιση του αριθµού των µεταγωγών που απαιτούνται για τη δροµολόγηση και της δυνατότητας για µετατροπή του µήκους κύµατος που διαθέτουν οι κόµβοι του δικτύου. Στη γενική περίπτωση, ένας ορισµένος βαθµός µετατροπής µπορεί να επιτευχθεί µε έναν κατάλληλο συνδυασµό από µεταγωγείς και µετατροπείς µήκους κύµατος. Αποτελέσµατα ερευνών και έχουνε δείξει ότι γενικά δεν υπάρχει πολύ µεγαλύτερο κέρδος όταν χρησιµοποιείται πλήρης µετατροπή µήκους κύµατος στους κόµβους ενός δικτύου. Έτσι λοιπόν η περιορισµένη µετατροπή µήκους κύµατος δίνει τη δυνατότητα να περιορίσει τον αριθµό των µεταγωγών, να µειώσει τον αριθµό των wavelength converters σε σχέση µε την πλήρη µετατροπή µήκους κύµατος και συνεπώς µειωθεί και το κόστος της υλοποίησης. Αξίζει να σηµειωθεί ότι έστω και η περιορισµένη χρήση της µετατροπής µήκους κύµατος αυξάνει το κόστος υλοποίησης, τις απαιτήσεις του δικτύου σε υλικό και την πολυπλοκότητα υπολογισµού σε σχέση µε τη no wavelength conversion. Στην περίπτωση που και η µεταγωγή και η ενίσχυση και η µετατροπή µήκους κύµατος γίνονται αµιγώς στον οπτικό τοµέα, τότε αναφερόµαστε στα αµιγώς οπτικά (all-optical) WDM οπτικά δίκτυα, που σαν αποτέλεσµα έχουν την εξασφάλιση της διαφάνειας (transparency) της λειτουργίας του δικτύου και τη σηµαντική αύξηση της
16 ταχύτητάς του. Αυτό συµβαίνει γιατί τα ηλεκτρονικά στοιχεία ενός οπτικού δικτύου, λειτουργούν σε πολύ µικρότερους ρυθµούς από την ταχύτητα µετάδοσης του σήµατος µέσα στον σύνδεσµο. Όταν υπάρχει λοιπόν οπτοηλεκτρονική µετατροπή µέσα στο δίκτυο, η καθυστέρηση οφείλεται περισσότερο στην επεξεργασία του σήµατος στους ενδιάµεσους κόµβους και λιγότερο στην ίδια τη µετάδοση του σήµατος. Η τεχνολογία βέβαια δεν έχει φτάσει ακόµα σε σηµείο που να υποστηρίζει εξολοκλήρου και σε ικανοποιητικό βαθµό την all-optical µετάδοση του σήµατος, αλλά ερευνητικές και εργαστηριακές µελέτες δείχνουν ότι κάτι τέτοιο δε θα αργήσει να επιτευχθεί.
17 2 ΤΟ ΠΡΟΒΛΗΜΑ ΡΟΜΟΛΟΓΗΣΗΣ ΚΑΙ ΑΝΑΘΕΣΗΣ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ Σε ένα WDM δίκτυο η δροµολόγηση δεν αφορά µόνο την εύρεση ενός µονοπατιού από την πηγή στον προορισµό, αλλά και στον καθορισµό των µηκών κύµατος κατά µήκος των συνδέσµων (Routing and wavelength Assignment), που θα καταλαµβάνει το σήµα [18], [21]. εδοµένου µιας τοπολογίας λοιπόν, ενός WDM δικτύου και ενός συνόλου αιτήσεων προς εξυπηρέτηση, το πρόβληµα του καθορισµού των µονοπατιών και τα µηκών κύµατος όλων των συνδέσεων που θα πρέπει να εγκατασταθούν για να ικανοποιηθούν οι αιτήσεις ονοµάζεται πρόβληµα ροµολόγησης και Ανάθεσης Μήκους Κύµατος [20],[27]. Τυπικά, οι τύποι κίνησης µπορεί να είναι τριών ειδών: Στατικός (Static), Αυξανόµενος (Incremental) και υναµικός (Dynamic). Στον στατικό τύπο, το σύνολο των αιτήσεων είναι γνωστό εκ των προτέρων. Γνωρίζουµε δηλαδή για το χρονικό διάστηµα στο οποίο θέλουµε να κάνουµε τη δροµολόγηση, τον πίνακα ροής (trafficmatrix) Λ sd, ο οποίος είναι ένας ακέραιος πίνακας που δίνει τον αριθµό των συνδέσεων που θα πρέπει να εγκατασταθούν για κάθε ζεύγος πηγής-προορισµού. Το πρόβληµα είναι τότε να εγκαταστήσουµε τα lightpaths για αυτές τις αιτήσεις µε έναν καθολικό τρόπο κάνοντας ελαχιστοποίηση των πόρων του δικτύου, όπως είναι ο αριθµός των µηκών κύµατος στο δίκτυο. Εναλλακτικά, είναι ισοδύναµο µε το να εγκατασταθούν όσες περισσότερες αιτήσεις γίνεται για έναν σταθερό αριθµό από µήκη κύµατος. Το RWA πρόβληµα για τον στατικό τύπο είναι γνωστό ως Static Lightpath Establishment (SLA) πρόβληµα. Στον Αυξανόµενο τύπο, οι αιτήσεις προς εξυπηρέτηση φτάνουν ακολουθιακά, ένα lightpath εγκαθίσταται για κάθε αίτηση και το lightpath παραµένει επ άπειρο. Για τον δυναµικό τύπο, ένα lightpath εγκαθίσταται για κάθε αίτηση καθώς έρχεται στο δίκτυο και το lightpath ελευθερώνεται µετά από πεπερασµένο διάστηµα. Ο αντικειµενικός σκοπός (Objective) στον Αυξανόµενο και στον υναµικό τύπο είναι να εγκατασταθούν µονοπάτια και να ανατεθούν µήκη κύµατος µε τρόπο που ελαχιστοποιείται η blocking probability ή µεγιστοποιείται ο αριθµός των συνδέσεων στο δίκτυο κάθε στιγµή. Αυτό το πρόβληµα αναφέρεται ως Dynamic Lightpath Establishment (DLE) πρόβληµα [28]. Το SLE πρόβληµα µπορεί να µοντελοποιηθεί ως ένα πρόγραµµα µικτού-ακέραιου γραµµικού προγραµµατισµού, που είναι NP-complete. Λόγω της πολυπλοκότητας του προβλήµατος, συχνά συνηθίζεται να διαχωρίζεται το RWA πρόβληµα σε δύο επιµέρους υποπροβλήµατα. Αυτό της ανεύρεσης ενός κατάλληλου µονοπατιού µεταξύ δύο κόµβων (routing) και της ανάθεσης των κατάλληλων µηκών κύµατος (wavelength assignment). Η επίλυση του προβλήµατος της δροµολόγησης ανεξάρτητα από εκείνο της ανάθεσης του κατάλληλου µήκους κύµατος, δε δίνει πάντα τα πιο βέλτιστα αποτελέσµατα. Συχνά όµως, στις περισσότερες προσεγγίσεις χρησιµοποιείται αυτή η τεχνική, γιατί απαιτεί µικρότερη υπολογιστική δύναµη και δίνει σε πολλές περιπτώσεις ικανοποιητικά αποτελέσµατα αναφορικά µε τους στόχους και τις ανάγκες που θέλουµε να ικανοποιήσουµε. Το DLE πρόβληµα είναι πιο δύσκολο να επιλυθεί και εποµένως χρησιµοποιούνται ευριστικές µέθοδοι. Ευριστικές µέθοδοι υπάρχουν και για τα δύο υποπροβλήµατα. Για το routing πρόβληµα, υπάρχουν τρεις βασικές προσεγγίσεις στην βιβλιογραφία: fixed routing,
18 fixed-alternate και adaptive routing. Ανάµεσα στις τρεις προσεγγίσεις το fixed routing είναι το πιο απλό, ενώ το adaptive routing οδηγεί σε καλύτερη απόδοση. Το alternate routing προσφέρει έναν ανταγωνισµό ανάµεσα στην πολυπλοκότητα και την απόδοση. Για το wavelength assignment πρόβληµα υπάρχουν αρκετοί ευριστικοί αλγόριθµοι έχουν προταθεί. Αυτοί είναι οι ακόλουθοι: Random Wavelength Assignment, First Fit, Least-Used/SPREAD, Most Used/PACK, Min-Product, Least Loaded, MAX-SUM, Relative Capacity Loss, Wavelength Reservation και Protection Threshold. 2.1 Περιορισµοί Στη ροµολόγηση Ενός Συνόλου Από Lightpaths Η λύση του RWA προβλήµατος είναι ένα σύνολο από lightpaths. Τα lightpaths αυτά θα πρέπει να πληρούν ένα σύνολο από περιορισµούς. Θα πρέπει λοιπόν να ισχύουν τα παρακάτω: 1. ιαδοχικοί σύνδεσµοι στο lightpath είτε θα πρέπει να καταλαµβάνουν το ίδιο µήκος (wavelength-continuity constraint) κύµατος είτε θα πρέπει να υπάρχει στον ενδιάµεσο κόµβο ένας κατάλληλος µετατροπέας µήκους κύµατος για τη µετατροπή από το µήκος κύµατος εισόδου σε ένα άλλο µήκος κύµατος εξόδου. 2. ύο διαφορετικά lightpaths δεν µπορούν να χρησιµοποιούν το ίδιο µήκος κύµατος στην ίδια οπτική ίνα (disjoint lightpaths). 3. Όταν ένας σταθµός πρόσβασης µεταδίδει/λαµβάνει δεδοµένα προς/από έναν κόµβο µεταγωγής, το µήκος κύµατος εισόδου/εξόδου θα πρέπει ή να είναι το ίδιο µε το µήκος κύµατος εξόδου/εισόδου του κόµβου µεταγωγής, ή θα πρέπει να χρησιµοποιείται κάποιος κατάλληλος µετατροπέας µήκους κύµατος. 4. Το φυσικό µήκος και το µήκος ενίσχυσης ενός lightpath θα πρέπει να είναι µικρότερα από τα αντίστοιχα άνω όρια που θέτουν τα χαρακτηριστικά της οπτικής ίνας και του ενισχυτή (π.χ. crosstalk, ASE). 2.2 υναµική ροµολόγηση Και Ανάθεση Μήκους Κύµατος Η κίνηση που θα εξυπηρετήσει το δίκτυο δεν είναι εκ των προτέρων γνωστή. Κάθε φορά που έρχεται µία αίτηση για σύνδεση, το δίκτυο προσπαθεί να την ικανοποιήσει µε τον καλύτερο δυνατό τρόπο. Τα κριτήρια που χρησιµοποιούνται κάθε φορά για τη λήψη της καλύτερης απόφασης µπορεί να είναι διαφορετικά και πάνω σε αυτό έχουν προταθεί διαφορετικές προσεγγίσεις και έχει αναπτυχθεί έντονο ερευνητικό ενδιαφέρον [15],[26]. Αν µε κανένα τρόπο το δίκτυο δε µµπορεί να διεκπεραιώσει τη δροµολόγηση, η ζητούµενη σύνδεση µπλοκάρεται. Το πρόβληµα αυτό είναι γνωστό ως dynamic RWA [12]. Παρόλο που το RWA πρόβληµα είναι δύσκολο (hard), µπορεί να απλοποιηθεί χωρίζοντας το σε δύο υποπροβήµατα: το routing υποπρόβληµα και το wavelength assignment υποπρόβληµα..
19 2.2.1 υναµική ροµολόγηση Ο πιο απλός τρόπος για την δροµολόγηση µιας σύνδεσης είναι να επιλέγουµε πάντα την ίδια σταθερή διαδροµή για ένα δοσµένο ζευγάρι πηγής προορισµού. Ένα παράδειγµα µιας τέτοιας προσέγγισης είναι το σταθερή δροµολόγηση συντοµότερου µονοπατιού (fixed shortest-path routing). Το συντοµότερο µονοπάτι για κάθε ζεύγος πηγής-προορισµού υπολογίζεται off-line χρησιµοποιώντας γνωστούς αλγορίθµους συντοµότερου µονοπατιού, όπως ο Dijkstra ή ο Bellman-Ford και κάθε σύνδεση µεταξύ ενός ζεύγους κόµβων εγκαθίσταται χρησιµοποιώντας την προκαθορισµένη διαδροµή. Στο σχήµα 2.1 απεικονίζεται το σταθερό συντοµότερο µονοπάτι από τον κόµβο 0 στον κόµβο 2. Σχήµα 2.1: Fixed routing, συντοµότερο µονοπάτι από τον κόµβο 0 στον κόµβο 2. Αυτή η προσέγγιση είναι πολύ απλή, εντούτοις το µειονέκτηµα µιας τέτοιας προσέγγισης είναι ότι, εάν οι πόροι (µήκη κύµατος) κατά µήκος του µονοπατιού καταναλωθούν θα οδηγήσει σε µεγάλη blocking probability. Επίσης το fixed routing ίσων να µην είναι ικανό να διαχειριστεί καταστάσεις όπως η πτώση κάποιου συνδέσµου στο δίκτυο. Για να διαχειριστεί µία τέτοια κατάσταση θα πρέπει είτε να χρησιµοποιηθούν εναλλακτικά µονοπάτια είτε να βρεθεί το µονοπάτι δυναµικά. Στο σχήµα 2.1 µία αίτηση για δροµολόγηση θα απορριφθεί εάν ένα κοινό µήκος κύµατος δεν είναι διαθέσιµο και στους δύο συνδέσµους στην σταθερή διαδροµή ή κάποιος από τους δύο συνδέσµους πέσει Σταθερή-Εναλλακτική ροµολόγηση Μία προσέγγιση στην δροµολόγηση που λαµβάνει υπόψη πολλαπλές διαδροµές είναι η σταθερή-εναλλακτική δροµολόγηση (fixed alternate routing). Στο fixed alternate routing, κάθε κόµβος στο δίκτυο χρειάζεται να διατηρεί έναν πίνακα δροµολόγησης που να περιέχει µία διατεταγµένη λίστα από σταθερές διαδροµές (fixed routes) σε κάθε κόµβο προορισµού. Για παράδειγµα, αυτές οι διαδροµές µπορεί να περιλαµβάνουν τις k-συντοµότερες διαδροµές. Μία κύρια διαδροµή µεταξύ ενός κόµβου πηγής s και ενός κόµβου προορισµού d ορίζεται ως η πρώτη διαδροµή στην λίστα των διαδροµών προς τον κόµβο d στον πίνακα δροµολόγησης του κόµβου s. Μία εναλλακτική διαδροµή µεταξύ του s και d είναι κάθε διαδροµή που δεν µοιράζεται κανέναν σύνδεσµο (link disjoint) µε την πρώτη διαδροµή στον πίνακα δροµολόγησης στον s. Ο όρος εναλλακτικές διαδροµές (alternate routes) χρησιµοποιείται για να περιγράψει όλες τις διαδροµές (περιλαµβάνοντας και την κύρια διαδροµή) από τον κόµβο πηγής στον κόσµο προορισµού. Το σχήµα 2.2
20 απεικονίζει µία κύρια διαδροµή από τον κόµβο 0 στον κόµβο 2 και µία εναλλακτική διαδροµή από τον κόµβο 0 στον κόµβο 2. Σχήµα 2.2: Κύριο και εναλλακτικό (διακεκοµµένη) µονοπάτι από τον κόµβο 0 στον κόµβο 2. Όταν µία αίτηση για δροµολόγηση φτάσει, ο κόµβος πηγή προσπαθεί να εγκαταστήσει την σύνδεση σε µία από τις διαδροµές που υπάρχουν στον πίνακα δροµολόγησης ακολουθιακά, µέχρι να βρεθεί µία διαδροµή µε κάποια έγκυρη ανάθεση µήκους κύµατος. Εάν δεν βρεθεί κάποια διαδροµή από το σύνολο των εναλλακτικών διαδροµών, τότε η αίτηση για δροµολόγηση απορρίπτεται και χάνεται. Στις περισσότερες περιπτώσεις, οι πίνακες δροµολόγησης σε κάθε κόµβο ταξινοµούνται σύµφωνα µε τον αριθµό των συνδέσµων (hops) προς τον προορισµό. Εποµένως το συντοµότερο µονοπάτι προς τον προορισµό είναι η πρώτη διαδροµή στον πίνακα δροµολόγησης. Όταν υπάρχουν συγκρούσεις για την απόσταση µεταξύ διαφορετικών διαδροµών, επιλέγεται τυχαία µία διαδροµή. Το fixed-alternate routing παρέχει απλότητα στην διαχείριση της εγκατάστασης και απεγκατάστασης των lightpaths και µπορεί να χρησιµοποιηθεί για να παρέχει κάποιο βαθµό ανοχής σε σφάλµατα, όπως η βλάβη κάποιου συνδέσµου. Ένα άλλο πλεονέκτηµα του fixedalternate routing είναι ότι µπορεί να µειώσει σηµαντικά την blocking probability συγκρινόµενο µε το fixed routing. Επίσης έχει δειχθεί ότι για ορισµένα δίκτυα έχοντας λίγα, ακόµη και δύο, εναλλακτικά µονοπάτια παρέχει σηµαντικά µικρότερη blocking probability από το να έχουν πλήρη µετατροπή µήκους κύµατος σε κάθε κόµβο µε fixed routing Προσαρµοστική ροµολόγηση Στην προσαρµοστική δροµολόγηση (adaptive routing), η διαδροµή από έναν κόµβο πηγής σε έναν κόµβο προορισµού επιλέγεται δυναµικά, ανάλογα µε την κατάσταση του δικτύου. Η κατάσταση του δικτύου καθορίζεται από το σύνολο όλο των συνδέσεων που είναι σε εξέλιξη. Μία µορφή του adaptive routing είναι το adaptive shortest-path routing, το οποίο είναι κατάλληλο για χρήση στα wavelength-converted δίκτυα. Σύµφωνα µε αυτή την προσέγγιση, κάθε σύνδεσµος που δεν χρησιµοποιείται έχει κόστος ίσο µε 1, κάθε σύνδεσµος που χρησιµοποιείται έχει κόστος και κάθε wavelength-converter σύνδεσµος έχει κόστος c µονάδες. Εάν το wavelength conversion δεν είναι διαθέσιµο, τότε c =. Όταν φτάσει µία σύνδεση, το συντοµότερο µονοπάτι επιλέγεται. Εάν υπάρχουν πολλά µονοπάτια µε το ίδιο κόστος, ένα από αυτά επιλέγεται τυχαία. Επιλέγοντας κατάλληλα το κόστος c wavelengthconversion, υπάρχει η εγγύηση ότι οι διαδροµές wavelength-converted επιλέγονται µόνο όταν wavelength-continuous µονοπάτια δεν είναι διαθέσιµα. Στο adaptive routing συντοµότερου µονοπατιού, µία σύνδεση απορρίπτεται µόνο όταν δεν υπάρχει
21 καµία διαδροµή (ούτε wavelength continuous ή wavelength converted), από τον κόµβο πηγή στον κόµβο προορισµού του δικτύου. Το adaptive routing χρειάζεται µεγάλη υποστήριξη από control και management πρωτόκολλα για να ανανεώνουν συνεχώς τους πίνακες δροµολόγησης στους κόµβους. Ένα πλεονέκτηµα του adaptive routing είναι ότι έχει µικρότερη blocking probability από το fixed και το fixedalternate routing. Για το δίκτυο του σχήµατος 2.3, εάν οι σύνδεσµοι του δικτύου ( 1, 2 ) και ( 4, 2) είναι απασχοληµένοι, τότε ο αλγόριθµος του adaptive routing µπορεί ακόµη να εγκαταστήσει µία σύνδεση µετξύ των κόµβων 0 και 2, ενώ οι άλλοι δύο αλγόριθµοι όπως φαίνεται στο σχήµα 2.3 θα απέρριπταν την σύνδεση. Μία άλλη µορφή του adaptive routing είναι το µονοπάτι ελάχιστης συµφόρησης (least-congested-path routing LCP). Παρόµοια µε το alternate routing, για κάθε ζεύγος πηγής-προορισµού, µία ακολουθία από διαδροµές επιλέγεται. Η συµφόρηση ενός συνδέσµου µετριέται από τον αριθµό των διαθέσιµων µηκών κύµατος στον σύνδεσµο. Η συµφόρηση ενός µονοπατιού είναι ανάλογη µε αυτή του συνδέσµου που έχει την µεγαλύτερη συµφόρηση. Μία εναλλακτική υλοποίηση είναι να δίνεται προτεραιότητα στα συντοµότερα µονοπάτια και όταν υπάρχει σύγκρουση να χρησιµοποιείται ο LCP. Ένα µειονέκτηµα του LCP είναι η υπολογιστική πολυπλοκότητα γιατί θα πρέπει να εξεταστούν όλα τα υποψήφια µονοπάτια. Μία παραλλαγή του LCP εξετάζει τους πρώτους k συνδέσµους για κάθε µονοπάτι. Σχήµα 2.3: Adaptive routing από τον κόµβο 0 στον κόµβο Ανάθεση Μήκους Κύµατος Ευριστικοί Αλγόριθµοι Για την περίπτωση που τα lightpaths φτάνουν ένα κάθε φορά (δυναµική περίπτωση), πρέπει να χρησιµοποιηθούν ευριστικοί αλγόριθµοι για την ανάθεση µήκους κύµατος. Για την δυναµική περίπτωση υποθέτουµε πως ο αριθµός των µηκών κύµατος είναι σταθερός και προσπαθούµε να ελαχιστοποιήσουµε την blocking probability. Οι ευριστικοί αλγόριθµοι που χρησιµοποιούνται για την ανάθεση µήκους κύµατος µπορούν να χρησιµοποιηθούν σε συνδυασµό µε όλους τους αλγορίθµους δροµολόγησης. Οι πιο συνηθισµένοι αλγόριθµοι για την ανάθεση µήκους κύµατος είναι οι παρακάτω: Random-1. Για µια αίτηση lightpath µεταξύ δύο κόµβων, επιλέγεται τυχαία ένα από τα διαθέσιµα µήκη κύµατος σε ένα προκαθορισµένο συντοµότερο µονοπάτι µεταξύ των κόµβων. Random-2. Καθορίζονται δύο συντοµότερα µονοπάτια µεταξύ κάθε ζεύγους κόµβων. Για µια αίτηση lightpath µεταξύ δύο κόµβων επιλέγεται τυχαία ένα από τα διαθέσιµα
22 µήκη κύµατος στο πρώτο συντοµότερο µονοπάτι µεταξύ των κόµβων. Εάν δεν υπάρχει διαθέσιµο τέτοιο µήκος κύµατος, επιλέγεται τυχαία ένα από τα διαθέσιµα µήκη κύµατος στο δεύτερο συντοµότερο µονοπάτι. Max-used-1. Για κάθε αίτηση lightpath µεταξύ δύο κόµβων, ανάµεσα στα διαθέσιµα µήκη κύµατος σε ένα προκαθορισµένο συντοµότερο µονοπάτι µεταξύ των κόµβων, επιλέγεται αυτό που χρησιµοποιείται τις περισσότερες φορές στο δίκτυο εκείνη τη στιγµή. Max-used-2. Καθορίζονται δύο συντοµότερα µονοπάτια µεταξύ κάθε ζεύγους κόµβων. Για κάθε αίτηση lightpath µεταξύ δύο κόµβων, ανάµεσα στα διαθέσιµα µήκη κύµατος του πρώτου συντοµότερου µονοπατιού µεταξύ των κόµβων, επιλέγεται αυτό που χρησιµοποιείται τις περισσότερες φορές εκείνη τη στιγµή στο δίκτυο. Εάν δεν υπάρχει διαθέσιµο µήκος κύµατος, τότε επιλέγεται ανάµεσα από τα διαθέσιµα µήκη κύµατος του δεύτερου µονοπατιού µεταξύ των κόµβων αυτό που χρησιµοποιείται τις περισσότερες φορές στο δίκτυο εκείνη τη στιγµή. Ο παράγοντας επαναχρησιµοποίησης βελτιώνεται ουσιαστικά όταν χρησιµοποιούµε ένα εναλλακτικό µονοπάτι. Ιδανικά θα θέλαµε περισσότερες εναλλακτικές διαδροµές για τις µεγαλύτερες διαδροµές και λιγότερες για τις συντοµότερες διαδροµές. Αυτό βοηθά στη µείωση της πιθανότητας µπλοκαρίσµατος στις µεγαλύτερες διαδροµές και εξασφαλίζει περισσότερη δικαιοσύνη συνολικά. ιαφορετικά, οι συντοµότερες διαδροµές τείνουν να έχουν πολύ λιγότερο µπλοκάρισµα από τις µεγαλύτερες. Έχοντας περισσότερες διαδροµές συνήθως αυξάνουµε τον έλεγχο της κυκλοφορίας στο δίκτυο και οδηγούµαστε σε ένα επιπρόσθετο υπολογιστικό φορτίο στους κόµβους του δικτύου. Αυτό όµως δεν είναι σηµαντικό σε δίκτυα µε µέτριο αριθµό κόµβων όπου τα lightpaths δηµιουργούνται και καταστρέφονται µε µικρό ρυθµό. Μαζί µε την επιλογή των διαδροµών, ο αλγόριθµος ανάθεσης µήκους κύµατος παίζει σηµαντικό ρόλο στον καθορισµό του παράγοντα επαναχρησιµοποίησης. Να σηµειωθεί ότι για τον ίδιο αριθµό διαθέσιµων διαδροµών, οι max-used αλγόριθµοι έχουν ευδιάκριτο πλεονέκτηµα έναντι των random αλγορίθµων. Ο διαισθητικός λόγος για αυτό το φαινόµενο είναι ότι η max-used στρατηγική παρέχει µεγαλύτερη πιθανότητα να βρούµε το ίδιο ελεύθερο µήκος κύµατος σε όλους τους συνδέσµους, κατά µήκος µιας συγκεκριµένης διαδροµής. Ένα µειονέκτηµα του max-used αλγορίθµου, είναι ότι απαιτεί να γνωρίζουµε τα µήκη κύµατος που χρησιµοποιούνται σε όλους τους άλλους συνδέσµους στο δίκτυο. Όταν η δροµολόγηση και η ανάθεση των µηκών κύµατος πραγµατοποιείται µε ένα κατανεµηµένο τρόπο, τέτοια πληροφορία τυπικά λαµβάνεται µέσα από περιοδικές µεταδόσεις για κάθε κόµβο. Αυτό επίσης αυξάνει το φορτίο ελέγχου της κυκλοφορίας στο δίκτυο. 2.3 Στατική ροµολόγηση Και Ανάθεση Μήκους Κύµατος Σε αυτή την παράγραφο παρουσιάζουµε την στατική δροµολόγηση και ανάθεση µήκους κύµατος (static routing and wavelength Assignment) [2], το οποίο είναι γνωστό ως Static Lightpath Establishment (SLE) πρόβληµα. Στο SLE οι αιτήσεις για τα lightpaths είναι γνωστά εκ των προτέρων και οι λειτουργίες της δροµολόγησης και ανάθεσης µήκους κύµατος γίνονται off-line. Το objective είναι να ελαχιστοποιηθεί ο αριθµός των µηκών κύµατος που χρειάζονται για να εγκατασταθεί ένα σύνολο από lightpaths για µία δεδοµένη φυσική τοπολογία. Ως εναλλακτική λύση στην
23 ελαχιστοποίηση του αριθµού των µηκών κύµατος του δικτύου, το δυικό πρόβληµα είναι να µεγιστοποιηθεί ο αριθµός των συνδέσεων που µπορούν να εγκατασταθούν (µείωση του blocking) για ένα δοσµένο αριθµό από µήκη κύµατος και ένα σύνολο από αιτήσεις προς εξυπηρέτηση. Αυτό το δυικό SLE πρόβληµα αυξάνει το πρόβληµα της δικαιοσύνης, στο ότι οι λύσεις του προβλήµατος τείνουν να εγκαταστήσουν περισσότερες µικρές (short) συνδέσεις που χρησιµοποιούν λιγότερους συνδέσµους από τις µεγάλες (long) συνδέσεις που χρησιµοποιούν µεγάλο αριθµό από συνδέσµους. Το SLE µε το wavelength-continuity constraint, µπορεί να µοντελοποιηθεί ως ένα πρόγραµµα ακέραιου γραµµικού προγραµµατισµού (Integer Linear Program-ILP) στο οποίο η objective function είναι να γίνει ελαχιστοποίηση της ροής σε κάθε σύνδεσµο, που είναι ισοδύναµο µε την ελαχιστοποίηση του αριθµού των lightpaths που διατρέχουν ένα συγκεκριµένο σύνδεσµο. Έστω το λ swd αναπαριστά την κίνηση (τον αριθµό αιτήσεων προς εξυπηρέτηση) από κάθε πηγή s σε κάθε προορισµό d σε κάθε µήκος κύµατος w. Υποθέτουµε πως δύο η περισσότερα lightpaths µπορεί να ενεργοποιηθούν µεταξύ του ίδιου ζευγαριού πηγής-προορισµού, εάν είναι απαραίτητο, αλλά κάθε ένα από αυτά θα πρέπει να καταλαµβάνει ένα διαφορετικό µήκος κύµατος. sdw Εποµένως λswd 1. Έστω το F ij αναπαριστά την κίνηση (τον αριθµό αιτήσεων προς εξυπηρέτηση) από την πηγή s στον προορισµό d, στον σύνδεσµο ij και µήκος sdw κύµατος w. Fij 1, αφού ένα µήκος κύµατος σε έναν σύνδεσµο µπορεί να ανατεθεί σε µόνο ένα µονοπάτι. εδοµένου µιας φυσικής τοπολογίας δικτύου, ενός συνόλου από µήκη κύµατος και ένα πίνακα κίνησης (traffic matrix) Λ στο οποίο Λ sd αναπαριστά των αριθµό των συνδέσεων που χρειάζονται µεταξύ της πηγής s και του προορισµού d, το πρόβληµα µπορεί να µοντελοποιηθεί ως ακολούθως (το οποίο είναι ένα ILP): Ελαχιστοποίηση : F max Έτσι ώστε F F ij i max sdw,, sdw max λsdw if s = j sdw sdw Fij Fjk = λsdw if s = j k 0 otherwise λ =Λ sdw w sdw F ij = sdw Fij sd, 0,1 1 sd Αυτή η προσέγγιση µπορεί να χρησιµοποιηθεί για να ληφθεί ο ελάχιστος αριθµός από µήκη κύµατος που χρειάζονται για ένα σύνολο από αιτήσεις προς εξυπηρέτηση. Για ένα δοσµένο αριθµό από µήκη κύµατος, µπορούµε να εφαρµόσουµε το ILP για να διαπιστώσουµε εάν µία λύση µπορεί να βρεθεί. Εάν δεν βρεθεί δεν βρεθεί λύση, τότε µεγαλύτερος αριθµός από µήκη κύµατος. Αυτή η διαδικασία επαναλαµβάνεται µέχρι να βρεθεί ο απαιτούµενος αριθµός από µήκη κύµατος. Το πρόβληµα όπως µοντελοποιείται είναι NP-complete. Το πρόβληµα µπορεί να επιλυθεί µε ευκολότερο
24 τρόπο µειώνοντας το µέγεθος του προβλήµατος και χαλαρώνοντας τους ακέραιους περιορισµούς. Το πρόβληµα της µεγιστοποίησης του αριθµού των συνδέσεων που θα εγκατασταθούν για ένα σταθερό αριθµό από µήκη κύµατος και ένα δοσµένο σύνολο από αιτήσεις σύνδεσης µπορεί να µοντελοποιηθεί ως ακολούθως. Έστω N sd : Αριθµός των ζευγαριών πηγής-προορισµού. L : Αριθµός των συνδέσµων. W : Αριθµός µηκών κύµατος κάθε συνδέσµου. m= { mi}, i = 1, 2,..., Nsd: Αριθµός των εγκαταστηµένων συνδέσµων για το ζεύγος πηγής-προορισµού i. ρ : Φορτίο προς εξυπηρέτηση (συνολικός αριθµός των αιτήσεων προς εξυπηρέτηση). q = { qi}, i = 1, 2,..., Nsd : Κλάσµα του συνολικού φορτίου για το ζευγάρι πηγής προορισµού i (κατά συνέπεια, qiρ = αριθµός των συνδέσεων προς εγκατάσταση για το ζευγάρι πηγής-προορισµού i ). (Στατική περίπτωση). P : Σύνολο από µονοπάτια στα οποία η σύνδεση θα δροµολογηθεί. A = ( aij ): P Nsd πίνακας στον οποίο a ij = 1 εάν το µονοπάτι i είναι µεταξύ του ζευγαριού πηγής προορισµού j, και a i = 0 διαφορετικά. B = ( bij ): P L πίνακας στον οποίο b ij = 1εάν ο σύνδεσµος j είναι στο µονοπάτι i, και b ij = 0 διαφορετικά. C = ( c ): P W πίνακας δροµολόγησης και ανάθεσης µήκους κύµατος, έτσι ώστε ij c ij = 1 εάν το µήκος κύµατος j ανατίθεται στο µονοπάτι i και c ij = 0 διαφορετικά. Το objective της δροµολόγησης και ανάθεσης µήκους κύµατος είναι να µεγιστοποιηθεί ο αριθµός των εγκαταστηµένων συνδέσεων, C0 ( ρ, q). Το ILP γίνεται: Μεγιστοποίηση : ( ρ, ) συνδέσεων στο δίκτυο) Έτσι ώστε 0 N sd C q = m (συνολικός αριθµός των εγκαταστηµένων i= 1 m 0, ακεραιος, i = 1, 2,..., N i { } c 0,1 i = 1, 2,..., P, j = 1, 2,..., W ij sd i T C B 1W L (ένα µήκος κύµατος µπορεί να χρησιµοποιηθεί το πολύ µία φορά σε έναν συγκεκριµένο σύνδεσµο) T m 1W C A mi qiρ, i = 1, 2,..., Nsd (ο αριθµός των εγκαταστηµένων συνδέσεων είναι µικρότερος από τον αριθµό των αιτήσεων προς εξυπηρέτηση) 1 W L είναι ο W Lπίνακας του οποίου τα στοιχεία είναι µονάδα. 1 W είναι ο 1 W πίνακας του οποίου τα στοιχεία είναι µονάδα.
25 2.4 ροµολόγηση Kαι Ανάθεση Μήκους Κύµατος Mε Μετατροπή Μήκους Κύµατος Σε ένα wavelength-routed WDM δίκτυο, ο περιορισµός του wavelength-continuity µπορεί να παραληφθεί εάν χρησιµοποιηθεί ένας µετατροπέας µήκους κύµατος (wavelength converter) για να µετατρέπει τα δεδοµένα που φτάνουν σε ένα µήκος κύµατος σε κάποιο σύνδεσµο σε άλλο µήκος κύµατος σε κάποιον ενδιάµεσο κόµβο πριν προωθηθεί στον επόµενο σύνδεσµο. Μία τέτοια τεχνική είναι εφικτή και αναφέρεται ως µετατροπή µήκους κύµατος (wavelength conversion). Wavelength routed δίκτυα µε αυτή τη δυνατότητα λέγονται wavelength-convertible δίκτυα. Εάν ένας wavelength converter διαθέτει την ικανότητα να µετατρέπει από κάθε wavelength σε οποιοδήποτε άλλο (τέτοιοι wavelength converters έχουν full range capacity), και εάν υπάρχει ένας wavelength converter σε κάθε οπτική ίνα σε κάθε κόµβο του δικτύου, τότε το δίκτυο έχει full wavelength-conversion ικανότητες). Ένα wavelength-convertible δίκτυο µε full wavelength-conversion ικανότητες σε κάθε κόµβο είναι ισοδύναµο µε ένα circuit-switched τηλεφωνικό δίκτυο. Να σηµειωθεί ότι ένα lightpath σε τέτοια wavelength-convertible δίκτυα µπορεί να χρησιµοποιεί διαφορετικό µήκος κύµατος κατά µήκος των συνδέσµων του µονοπατιού. Εποµένως, η µετατροπή µήκους κύµατος µπορεί να βελτιώνει την απόδοση του δικτύου αποτρέποντας τις συγκρούσεις των µηκών κύµατος των lightpaths. Συνήθως, για ένα δοσµένο σήµα δροµολόγησης, η µετατροπή µήκους κύµατος εξασφαλίζει ένα χαµηλότερο όριο στην blocking probability για ένα δοσµένο wavelength assignment σχήµα. Έστω το λ sd αναπαριστά την κίνηση (αριθµός των αιτήσεων προς εξυπηρέτηση) από sdw κάθε πηγή s προς κάθε προορισµό d. Έστω F ij αναπαριστά την κίνηση (αριθµός των αιτήσεων προς εξυπηρέτηση) από την πηγή s προς τον προορισµό d στον σύνδεσµο ij. Η µοντελοποίηση του RWA προβλήµατος χωρίς τον περιορισµό του wavelength-continuity είναι: Ελαχιστοποίηση: F max Έτσι ώστε F F ij i max sd, sdw max λsdw if s = j sdw sdw Fij Fjk = λsdw if s= j k 0 διαφορετικα Σε πολλές περιπτώσεις, η full wavelength conversion µπορεί να µην προτιµάται και µπορεί να µην είναι απαραίτητη εξαιτίας του µεγάλου κόστους και του περιορισµένου κέρδους απόδοσης. Είναι πιθανόν ένα υποσύνολο των κόµβων του δικτύου να επιτρέπουν wavelength conversion ή να χρησιµοποιούνται wavelength converters που επιτρέπουν µετατροπή σε ορισµένα µόνο µήκη κύµατος. Αυτό το πρόβληµα είναι γνωστό ως RWA µε περιορισµένο wavelength conversion.
26 2.5 Τεχνικές ιαχωρισµού Του RWA Για Την Στατική Περίπτωση Πολλοί αποδοτικοί ευριστικοί αλγόριθµοι έχουν δείξει ότι το RWA πρόβληµα µπορεί να διαχωριστεί σε δύο υποπροβλήµατα: Το υποπρόβληµα της δροµολόγησης και το υποπρόβληµα της ανάθεσης µήκους κύµατος (όπως και στην δυναµική περίπτωση). Και τα δύο υποπροβλήµατα είναι πιο απλά από το συνολικό RWA πρόβληµα και µπορούν να λυθούν ανεξάρτητα και ακολουθιακά ροµολόγηση Το υποπρόβληµα της δροµολόγησης στη γενική του µορφή είναι ένα πρόβληµα βελτιστοποίησης ισοδύναµο µε αυτό του RWA χωρίς τον περιορισµό συνέχειας µήκους κύµατος (wavelength continuity). Είναι δηλαδή η δροµολόγηση ενός δοθέντος συνόλου από αιτήµατα συνδέσεων έτσι ώστε να βελτιστοποιείται µία συνάρτηση κόστους χωρίς την απαίτηση της ανάθεσης µήκους κύµατος στα υπολογισµένα lightpaths. Το πρόβληµα της δροµολόγησης µπορεί να µοντελοποιηθεί ακριβώς όπως το πρόβληµα δροµολόγησης και ανάθεσης µήκους κύµατος µε ολική µετατροπή µήκους κύµατος (full wavelength conversion), αφού στην ουσία η µοντελοποίηση δεν θέτει περιορισµό για την διατήρηση του ίδιου µήκους κύµατος από ένα lightpath. Το πρόβληµα της δροµολόγηση µπορεί συνεπώς να λυθεί ως ένα ILP πρόβληµα, το οποίο όµως είναι πιο εύκολο υπολογιστικά από το πρόβληµα ILP χωρίς µετατροπή µήκους κύµατος. Αυτό το πρόβληµα µπορεί να µην επιλύνεται σε πολυωνυµικό χρόνο. Υπάρχουν µορφές όµως του προβλήµατος που λύνονται σε πολυωνιµικό χρόνο, όπως είναι η δροµολόγηση συντοµότερου µονοπατιού χρησιµοποιώντας γνωστούς αλγορίθµους (π.χ. Dijkstra, Bellman-Ford). Σε µία απλή περίπτωση το υποπρόβληµα της δροµολόγησης θα είχε την λειτουργία της εύρεσης του συντοµότερου µονοπατιού και θα ακολουθούσε το υποπρόβληµα της ανάθεσης µήκους κύµατος µόνο σε αυτό το µονοπάτι για µία σύνδεση Ανάθεση Μήκους Κύµατος Στατική Περίπτωση Η ανάθεση µήκους κύµατος για την στατική περίπτωση, δεδοµένου για παράδειγµα ενός συνόλου από lightpaths και τις διαδροµές τους, να βρεθεί η ανάθεση µήκους κύµατος για κάθε lightpath έτσι ώστε δύο lightpaths να µην έχουν το ίδιο µήκος κύµατος σε µία οπτική ίνα. Μία προσέγγιση αυτού του προβλήµατος είναι να µοντελοποιηθεί σαν πρόβληµα χρωµατισµού γράφου (graph coloring). Το πρόβληµα WA της ανάθεσης µήκους κύµατος, είναι στενά συσχετισµένο µε το πρόβληµα του χρωµατισµού των κορυφών ενός γράφου (graph coloring problem) και είναι εποµένως ένα δύσκολο υπολογιστικά (NP-complete) πρόβληµα. Προκειµένου να το κατανοήσουµε καλύτερα, ας θεωρήσουµε την αναπαράσταση ενός δικτύου G από έναν γράφο, όπου οι κορυφές του γράφου αναπαριστούν τους κόµβους του δικτύου, µε µια µη κατευθυνόµενη ακµή µεταξύ δυο κορυφών του γράφου να αντιστοιχεί σε ένα σύνδεσµο οπτικής ίνας µεταξύ των αντίστοιχων κόµβων. Ένα τέτοιο παράδειγµα φαίνεται στο σχήµα 2.4(α). Η διαδροµή για κάθε ένα µονοπάτι αντιστοιχεί σε ένα µονοπάτι στο G, και έτσι το σύνολο των διαδροµών που έχουν
27 καθοριστεί για τα µονοπάτια αντιστοιχίζεται µε ένα σύνολο µονοπατιών το οποίο ονοµάζουµε P. Ας θεωρήσουµε τώρα έναν άλλο γράφο, τον γράφο µονοπατιών του G, τον P(G), τον οποίο κατασκευάζουµε ως εξής. Κάθε ένα από τα µονοπάτια στο P αντιστοιχεί σε ένα κόµβο στο P(G) και δυο κόµβοι στο P(G) ενώνονται από µια (µη κατευθυνόµενη) ακµή εάν τα αντίστοιχα µονοπάτια στο P έχουν µια κοινή κορυφή στο G. Το σχήµα 2.4(β) δείχνει το γράφο µονοπατιών του γράφου του σχήµατος 1(α). Η επίλυση του WA προβλήµατος ισοδυναµεί µε την επίλυση του κλασσικού προβλήµατος χρωµατισµού του γράφου P(G), το οποίο ουσιαστικά είναι, η ανάθεση ενός χρώµατος σε κάθε ένα από τους κόµβους του P(G) έτσι ώστε οι γειτονικοί κόµβοι να έχουν διαφορετικά χρώµατα καθώς και ο συνολικός αριθµός των χρωµάτων να είναι ο ελάχιστος. Αυτά τα χρώµατα αντιστοιχούν στα µήκη κύµατος τα οποία χρησιµοποιούνται στο γράφο G. Ο ελάχιστος αριθµός των χρωµάτων που απαιτούνται για τον χρωµατισµό των κόµβων ενός γράφου µε αυτό τον τρόπο καλείται χρωµατικός αριθµός του γράφου. Έτσι, ο ελάχιστος αριθµός των µηκών κύµατος που απαιτούνται προκειµένου να λύσουµε το WA πρόβληµα είναι ο χρωµατικός αριθµός του γράφου P(G). Παράδειγµα: Ας θεωρήσουµε το γράφο G, ο οποίος αναπαριστά το δίκτυο όπως φαίνεται στο σχήµα 2.4. Αφού υπάρχει µόνο ένα µονοπάτι µεταξύ οποιουδήποτε ζεύγους κόµβων στο G, δοθέντος του συνόλου των ζευγών των κόµβων τα οποία συνδέονται µε µονοπάτια, οι διαδροµές καθορίζονται µε µοναδικό τρόπο. Άρα, έχουµε να λύσουµε µόνο το WA πρόβληµα. Ας υποθέσουµε ότι χρειάζεται να οργανώσουµε µονοπάτια µεταξύ των κόµβων 1 και 2, 2 και 3 και 1 και 3. Ο γράφος µονοπατιών P(G) που προκύπτει, φαίνεται στο ίδιο σχήµα. Ο χρωµατικός αριθµός του γράφου P(G) είναι 3, και ο χρωµατισµός του P(G) φαίνεται επίσης στο σχήµα. Κατά συνέπεια, χρειαζόµαστε τρία µήκη κύµατος προκειµένου να λύσουµε το WA πρόβληµα σε αυτό το παράδειγµα. Ο χρωµατισµός ενός τυχαίου γράφου είναι ένα αρκετά δύσκολο πρόβληµα το οποίο έχει µελετηθεί εντατικά εδώ και πολλές δεκαετίες NP-complete. Εν τούτοις, υπάρχουν αρκετές ειδικές κατηγορίες γράφων για τις οποίες έχουν βρεθεί αρκετά γρήγοροι αλγόριθµοι για τον χρωµατισµό τους. Εάν το P(G) για το οποίο ενδιαφερόµαστε, ανήκει σε µια τέτοια κατηγορία, τότε µπορούµε να βρούµε µια ακριβή λύση στο WA πρόβληµα. Σε διαφορετική περίπτωση, εκτός αν το P(G) έχει λίγους κόµβους, θα πρέπει να αρκεστούµε σε µια κατά προσέγγιση λύση του WA προβλήµατος. Αρκετοί γρήγοροι αλλά προσεγγιστικοί (ευριστικοί) αλγόριθµοι έχουν σχεδιαστεί για το πρόβληµα χρωµατισµού γράφων, και αυτοί οι αλγόριθµοι µπορούν να χρησιµοποιηθούν προκειµένου να βρίσκουµε καλές αλλά προσεγγιστικές λύσεις στο WA πρόβληµα. Παρόλο που αυτή η µετατροπή επεξηγεί την σχέση µε το χρωµατισµό γράφων, δεν αποδεικνύει ότι το WA πρόβληµα είναι από µόνο του δύσκολο ή πιο συγκεκριµένα NP-πλήρες. Προκειµένου να δείξουµε κάτι τέτοιο, θα πρέπει να κάνουµε την µετατροπή από την αντίθετη κατεύθυνση, δηλαδή, να πάρουµε ένα παράδειγµα προβλήµατος χρωµατισµού γράφου και να το µετατρέψουµε σε ένα παράδειγµα του WA προβλήµατος.
28 Σχήµα 2.4: Σχέση µε το χρωµατισµό γράφων. 2.6 Μείωση Μεγέθους Του Προβλήµατος Μείωση Του Χώρου Η µείωση του χώρου µπορεί να επιτευχθεί µε τον αρχικό καθορισµό ενός περιορισµένου υποσυνόλου από εναλλακτικά µονοπάτια ανάµεσα σε κάθε ζεύγος πηγής προορισµού. Η δροµολόγηση ανάµεσα σε κάθε ζεύγος πηγής προορισµού θα ακολουθήσει αποκλειστικά ένα από αυτά τα µονοπάτια. Με αυτό τον τρόπο το πρόβληµα του χώρου του προβλήµατος µειώνεται από εκθετικός σε γραµµικό. Τα υποψήφια µονοπάτια που θα εξεταστούν τελικά µειώνονται σε µεγάλο βαθµό. Για τον σκοπό αυτό, µπορούν να χρησιµοποιηθούν διάφοροι γενικευµένοι αλγόριθµοι συντοµότερου µονοπατιού (π.χ. γενικευµένος Dijkstra). Η µείωση του αριθµού των εναλλακτικών µονοπατιών γίνεται µε την επιλογή ενός αριθµού k, που ορίζει τον αριθµό των εναλλακτικών µονοπατιών που θα εξάγει ο γενικευµένος αλγόριθµος και θα τερµατίσει. Για παράδειγµα η µεταβλητή F χρειάζεται να λαµβάνεται υπόψη, µόνο αν ο σύνδεσµος ij ανήκει σε κάποιο από τα k εναλλακτικά µονοπάτια ανάµεσα στους κόµβους s και d. Με µία πρώτη µατιά ο αλγόριθµος φαίνεται ότι χωρίζεται σε δύο υποπροβλήµατα. Το ένα είναι η εύρεση των k µονοπατιών και το άλλο η ανάθεση µήκους κύµατος. Με αυτό τον τρόπο επίλυσης, υπάρχει όµως το πρόβληµα εάν η λύση που θα προκύψει είναι η ολική βέλτιστη του RWA προβλήµατος. Μπορεί δηλαδή η βέλτιστη λύση να υπάρχει σε κάποιο µονοπάτι εκτός των k που υπολογίστηκαν. Στην κατασκευή όµως του χώρου των k µονοπατιών, η επιλογή µιας αρκετά µεγάλης τιµής για το k εξασφαλίζει έναν αντιπροσωπευτικό χώρο, στον οποίο υπάρχει σχεδόν βέβαιη πιθανότητα ότι βρίσκεται η βέλτιστη λύση. Η ανάθεση µήκους κύµατος έχει να επιλέξει ανάµεσα στα k συντοµότερα µονοπάτια, γεγονός που µειώνει σηµαντικά τον χώρο του προβλήµατος, ενώ διατηρεί το πρόβληµα της δροµολόγησης και ανάθεσης µήκους κύµατος ενιαίο, µε σχεδόν βέβαιη πιθανότητα να βρίσκεται µέσα η βέλτιστη λύση Μείωση Του Χρόνου sdw ij Το πρόβληµα της δροµολόγησης και ανάθεσης µήκους κύµατος είναι NP-πλήρες, αφού είναι ένα πρόβληµα ακέραιου γραµµικού προγραµµατισµού. Η ακεραιότητα που οδηγεί στη NP-πληρότητα οφείλεται στην ακεραιότητα των µεταβλητών. Η χαλάρωση των περιορισµών ακεραιότητας µετατρέπει το πρόβληµα σε πρόβληµα
29 γραµµικού προγραµµατισµού (Linear Program-LP), το οποίο επιλύνεται αποδοτικά µε χρήση αλγορίθµων γραµµικού προγραµµατισµού (π.χ. Simplex). Στην περίπτωση του RWA προβλήµατος, οι µεταβλητές της ροής επιτρέπεται να παίρνουν και κλασµατικές τιµές και όχι µόνο ακέραιες. Για παράδειγµα οι µεταβλητές F και λ swd από τις µοντελοποιήσεις που παρουσιάστηκαν µπορούν να παίρνουν κλασµατικές τιµές και όχι µόνο ακέραιες. εν υπάρχει δηλαδή ο περιορισµός ακεραιότητας. Οι κλασµατικές ροές όµως που µπορεί να προκύψουν, δεν είναι υλοποιήσιµες στα WDM οπτικά δίκτυα. Οι κλασµατικές ροές θα πρέπει εποµένως να µετατραπούν σε ακέραιες µε τρόπο που να οδηγούν πιο κοντά στη βέλτιστη λύση του objective του προβλήµατος. 2.7 Πρακτική Προσέγγιση Του RWA sdw ij Μία από τις βασικές και θεµελιώδεις εργασίες που έγιναν σχετικά µε το RWA πρόβληµα και αποτέλεσαν τη βάση και την απαρχή για µια πιο εντατική µελέτη και έρευνα πάνω στο πρόβληµα της δροµολόγησης και της ανάθεσης µήκους κύµατος σε WDM οπτικά δίκτυα είχε ως στόχο την ελαχιστοποίηση του αριθµού των µηκών κύµατος για τη δροµολόγηση ενός σταθερού συνόλου συνδέσεων. Το RWA πρόβληµα τµηµατοποιείται σε επιµέρους µικρότερα υποπροβλήµατα, τα οποία λύνονται ανεξάρτητα µεταξύ τους χρησιµοποιώντας κατάλληλες και αποδοτικές προσεγγιστικές τεχνικές. Για τον προσδιορισµό των µονοπατιών για κάθε σύνδεση χρησιµοποιείται µία µοντελοποίηση multicommodity flow σε συνδυασµό µε κατάλληλες τεχνικές προσεγγιστικής στρογγυλοποίησης (randomized rounding techniques). Οι αναθέσεις µήκους κύµατος γίνονται µε τη βοήθεια τεχνικών που χρησιµοποιούνται για την επίλυση του προβλήµατος χρωµατισµού γράφου Εγκατάσταση Ενός Lightpath Σε WDM ίκτυο Από τη στιγµή που το RWA πρόβληµα έχει επιλυθεί, η εγκατάσταση µιας οπτικής σύνδεσης σε ένα WDM δίκτυο περιλαµβάνει κυρίως δύο βήµατα: 1. ηµιουργία του οπτικού µονοπατιού µε την κατάλληλη ρύθµιση των switches και ενδεχοµένως των wavelength converters κατά µήκος του µονοπατιού. 2. Ρύθµιση της πηγής εκποµπής (laser) του κόµβου αφετηρίας και του φίλτρου του κόµβου δέκτη στις συχνότητες λειτουργίας που αντιστοιχούν στα επιλεγµένα, από τον αλγόριθµο δροµολόγησης, µήκη κύµατος.
30 3 ΡΟΜΟΛΟΓΗΣΗ ΚΑΙ ΑΝΑΘΕΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ Η ΠΡΟΣΕΓΓΙΣΗ ΜΑΣ Όπως έχει αναφερθεί και σε προηγούµενο κεφάλαιο, δεδοµένου ενός συνόλου από συνδέσεις, το πρόβληµα της εγκατάστασης οπτικών µονοπατιών µε την δροµολόγηση και ανάθεση ενός µήκους κύµατος σε κάθε σύνδεση ονοµάζεται ροµολόγηση και Ανάθεση Μήκους Κύµατος (Routing and Wavelength Assignment RWA). Υπάρχουν διάφορα είδη αιτήσεων. Στην παρούσα εργασία θα ασχοληθούµε µε την περίπτωση της στατικής δροµολόγησης και ανάθεσης µήκους κύµατος. Στην στατική κίνηση, ολόκληρο το σύνολο των αιτήσεων προς δροµολόγηση είναι γνωστό εκ των προτέρων και το πρόβληµα είναι να εγκαταστήσουµε τα οπτικά µονοπάτια γι αυτές τις αιτήσεις, µειώνοντας τους πόρους του δικτύου. Αρχικά θα παρουσιάσουµε την στατική περίπτωση, όπου έχοντας σταθερό αριθµό από διαθέσιµα µήκη κύµατος προσπαθούµε να µειώσουµε την ροή του κάθε συνδέσµου. Αυτό θα έχει σαν αποτέλεσµα την δροµολόγηση περισσότερων συνδέσεων. Σε επόµενο κεφάλαιο θα παρουσιάσουµε τον ίδιο πρόβληµα, αλλά µε την παρουσία φυσικών περιορισµών (physical constraints) που θέτει ένα οπτικό δίκτυο. Η στατική δροµολόγηση και ανάθεση µήκους κύµατος µπορεί να µοντελοποιηθεί ως ένα πρόβληµα ακέραιου γραµµικού προγραµµατισµού (Integer Linear Programming ILP), το οποίο είναι NP-πλήρες. Η NP-πληρότητα γνωστών ILP προβληµάτων συχνά ξεπερνιέται χαλαρώνοντας τους περιορισµούς ακεραιότητας. Στην περίπτωσή µας, αυτό σηµαίνει ότι επιτρέπουµε στις µεταβλητές ροής να παίρνουν κλασµατικές τιµές αντί για τις ακέραιες που είναι απαραίτητες. Συνεπώς, αυτά τα προβλήµατα µοντελοποιούνται ως προβλήµατα γραµµικού προγραµµατισµού (Linear Programming LP) και µπορεί να λυθούν αποδοτικά γενικές µεθόδους γραµµικού προγραµµατισµού, όπως είναι ο αλγόριθµος Simplex που χρησιµοποιήσαµε στην υλοποίηση. Ακολουθεί η µοντελοποίηση του LP προβλήµατος [25] µε στόχο την ελαχιστοποίηση της ροής του κάθε συνδέσµου. Σε επόµενη παράγραφο, σε συνδυασµό µε τη συνάρτηση ελαχιστοποίησης της ροής του κάθε συνδέσµου, ο στόχος είναι η µείωση της συµφόρησης κατά µήκος του κάθε µονοπατιού. 3.1 LP1: Στατική ροµολόγηση Και Ανάθεση Μήκους Κύµατος Μία σταθερή τοπολογία δικτύου αναπαρίσταται από ένα συνεκτικό γράφο GVE (, ). Το V αναπαριστά το σύνολο των κόµβων του δικτύου, έστω N αναπαριστά το σύνολο των συνδέσµων του δικτύου, έστω L = V. Το E = E. Κάθε σύνδεσµος περιλαµβάνει µία οπτική ίνα και κάθε οπτική ίνα υποστηρίζει W διαφορετικά µήκη κύµατος. Τα ακόλουθα ορίζονται: k : Ο συνολικός αριθµός των µονοπατιών (κύριο και εναλλακτικά) που υπολογίζεται για κάθε αίτηση σύνδεσης
31 Λ N N: Ο πίνακας κίνησης (traffic matrix) σε µονάδες από οπτικά µονοπάτια (lightpaths), όπου το Λ sd είναι ο αριθµός των συνδέσεων που απαιτούν δροµολόγηση µεταξύ της πηγής s και του προορισµού d Λ total : Ο συνολικός αριθµός των αιτήσεων K = k Λ total : Ο συνολικός αριθµός των µονοπατιών που υπολογίζεται για όλες τις συνδέσεις C : Το σύνολο των διαθέσιµων µηκών κύµατος W = C : Ο συνολικός αριθµός των διαθέσιµων µηκών κύµατος P : Το σύνολο όλων των µονοπατιών όλων των συνδέσεων Παράµετροι: w C : ένα διαθέσιµο µήκος κύµατος p P : ένα υποψήφιο µονοπάτι l E: ένας σύνδεσµος του δικτύου Μεταβλητές: λ plw : µία δείκτρια µεταβλητή η οποία έχει την τιµή 1 όταν το µονοπάτι p καταλαµβάνει τον σύνδεσµο l και το µήκος κύµατος c και 0 σε όλες τις άλλες περιπτώσεις Fl = f λ plw = f λ plw : η συνολική ροή στον σύνδεσµο l p P p P w C w C Το πρόβληµα µπορεί να µοντελοποιηθεί ως εξής: ΜΟΝΤΕΛΟΠΟΙΗΣΗ I Ελαχιστοποίηση : Fl l E Έτσι ώστε 1. λ 1 l E, w C p plw ' 2. λplw = λ ' p P pl w ( l l ) 3. l και, ειναι διαδοχικοι συνδεσµοι στο p λplw =Λsd l που είναι ο πρώτος σύνδεσµος στο p w p Psd λplw =Λsd l που είναι ο τελευταίος σύνδεσµος στο p w p Psd
32 4. Fl f λplw p w Η πρώτη γραµµή της µοντελοποίησης περιλαµβάνει το αντικείµενο της βελτιστοποίησης (objective). Το πρώτο σύνολο των περιορισµών αναπαριστά τον περιορισµό διακριτής ανάθεσης µήκους κύµατος. Αυτό σηµαίνει πως το κάθε µήκος κύµατος σε έναν συγκεκριµένο σύνδεσµο µπορεί να χρησιµοποιηθεί µόνο µία φορά. Το δεύτερο και τρίτο σύνολο αναπαριστούν τον τύπο των περιορισµών που περιγράφουν τη διατήρηση της ροής. Στο δεύτερο σύνολο και σε κόµβους που δεν υπάρχει δυνατότητα για µετατροπή µήκους κύµατος, το οπτικό µονοπάτι θα πρέπει κατά την έξοδο να χρησιµοποιηθεί το ίδιο µήκος κύµατος µε αυτό που χρησιµοποίησε στην είσοδο προκειµένου να ισχύει ο περιορισµός του wavelength continuity constraint και γενικά θα πρέπει το οπτικό µονοπάτι να καταλαµβάνει το ίδιο µήκος κύµατος σε όλους τους συνδέσµους που καταλαµβάνει. Ο τρίτος περιορισµός δηλώνει πως το άθροισµα όλων των οπτικών µονοπατιών που ξεκινάνε από τον κόµβο s προς τον κόµβο d πρέπει να είναι ίσο µε την αντίστοιχη τιµή Λ sd του πίνακα κίνησης. Επίσης το άθροισµα όλων των οπτικών µονοπατιών που καταλήγουν στον τον κόµβο d από τον κόµβο s πρέπει να είναι ίσο µε την αντίστοιχη τιµή Λ sd του πίνακα κίνησης. Τέλος ο τελευταίος περιορισµός καθορίζει την τιµή της συνάρτησης κόστους ροής σε κάθε σύνδεσµο του δικτύου. Η συνάρτηση κόστους ροής χρησιµοποιείται για να εκφράσει το ποσό της συµφόρησης που υπάρχει σε κάθε σύνδεσµο του δικτύου. Στη δική µας προσέγγιση αρχικά ορίζουµε την παρακάτω συνάρτηση κόστους ροής. F l ( Wl ) = W W l + 1 W l. 3.2 Συνάρτηση Κόστους Ροής Ως συνάρτηση κόστους ροής στον σύνδεσµο l µπορεί να χρησιµοποιηθεί µια οποιαδήποτε κατάλληλα επιλεγµένη συνάρτηση, που θα έχει κάποια συγκεκριµένα χαρακτηριστικά γνωρίσµατα. Το σηµαντικότερο από αυτά είναι ότι θα πρέπει να είναι γνησίως αύξουσα. Ο βαθµός αυτής της συνάρτησης, αυτή θα µπορούσε να είναι πρώτου βαθµού, δηλαδή γραµµική. Αν χρησιµοποιηθεί µία γραµµική συνάρτηση η επίδραση που έχει η αύξηση του αριθµού των µηκών κύµατος που καταλαµβάνονται κατά µήκος ενός συνδέσµου είναι πολύ µµεγαλύτερη όσο τα χρησιµοποιούµενα µήκη κύµατος γίνονται περισσότερα. Γι αυτό προτιµάται µία µη γραµµική, συνήθως δευτέρου βαθµού, παραβολική συνάρτηση που έχει την επιθυµητή αυτή ιδιότητα και προσεγγίζει και ποσοτικοποιεί καλύτερα το κόστος από τη ροή της κίνησης κατά µήκος ενός συνδέσµου. Μια συνάρτηση δευτέρου βαθµού όµως έχει το εξής µειονέκτηµα. Επειδή δεν είναι γραµµική η χρησιµοποίηση της σε ένα πρόβληµα γραµµικού προγραµµατισµού θα µετέτρεπε το πρόβληµα σε ένα µη γραµµικό πρόβληµα προγραµµατισµού. Το γεγονός αυτό καθιστά εξαιρετικά ανεπιθύµητη την επιλογή µιας µη γραµµικής συνάρτησης σαν συνάρτηση κόστους ροής σε έναν σύνδεσµο.
33 Η δευτεροβάθµια συνάρτηση που έχει τις επιθυµητές ιδιότητες, µπορεί να προσεγγιστεί από µία τµηµατικά γραµµική συνάρτηση και έτσι µπορούµε να την εντάξουµε στη µοντελοποίηση του προβλήµατός µας Τµηµατικά Γραµµική Συνάρτηση Κόστους Ροής α) Η συνάρτηση κόστους σε κάθε σύνδεσµο είναι κυρτή, γνησίως αύξουσα και τµηµατικά γραµµική. Εποµένως η συνάρτηση κόστους µπορεί να εκφραστεί χρησιµοποιώντας ένα σύνολο από γραµµικούς περιορισµούς. Επιπλέον το κόστος για ένα νέο οπτικό µονοπάτι σε έναν σύνδεσµο αυξάνεται καθώς αυξάνεται και η κίνηση σε αυτόν τον σύνδεσµο. Η βέλτιστη λύση στο πρόγραµµα τείνει να επιλέγει µονοπάτια µε συνδέσµους που δεν χρησιµοποιούνται συχνά και να αφήνει χώρο για µελλοντικά οπτικά µονοπάτια. β) Τα σηµεία διαχωρισµού της κάθε συνάρτησης κόστους ροής του συνδέσµου είναι τα ακέραια σηµεία 0,1,..., C. Το κόστος για ροές µεγαλύτερες από C είναι. Εποµένως, η βέλτιστη λύση που προκύπτει τείνει να είναι ακέραιη, εξαλείφοντας έτσι την ανάγκη για τεχνικές ακέραιου προγραµµατισµού που απαιτούν µεγάλο χρόνο για επίλυση. Σχήµα 3.1: Εξαιτίας του χαρακτηριστικού (α), η βέλτιστη λύση που προκύπτει από το γραµµικό πρόγραµµα, επιλέγει µονοπάτια µε συνδέσµους που δεν χρησιµοποιούνται πολύ και τείνει να αφήνει χώρο για µελλοντικά οπτικά µονοπάτια. Εξαιτίας του δεύτερου χαρακτηριστικού (β), η βέλτιστη λύση που προκύπτει τείνει να είναι ακέραια, και έτσι δεν υπάρχει ανάγκη για τεχνικές ακέραιου γραµµικού προγραµµατισµού Η Συνάρτηση Της Μοντελοποίησης Η συνάρτηση κόστους ροής χρησιµοποιείται για να εκφράσει το ποσό της συµφόρησης που υπάρχει σε έναν σύνδεσµο. Αρκετές µαθηµατικές συναρτήσεις είναι κατάλληλες, αρκεί να είναι αύξουσες στον αριθµός των µηκών κύµατος που καταλαµβάνονται από κάποιον σύνδεσµο. Η πιο προφανής λύση είναι η χρησιµοποίηση µια γραµµικής συνάρτησης. Οι γραµµικές συναρτήσεις
34 χαρακτηρίζονται από τη απλότητά τους και το πλεονέκτηµα να χρησιµοποιούνται αµέσως στην LP µοντελοποίηση του προβλήµατος. Έστω Wl W είναι υποσύνολο των µηκών κύµατος που καταλαµβάνονται από τον σύνδεσµο l. Τότε ο αριθµός των οπτικών µονοπατιών που χρησιµοποιούν τον σύνδεσµο l είναι ίσος µε W l. Στην µοντελοποίηση Wl = λplw. Τότε µία αύξουσα γραµµική συνάρτηση είναι της µορφής F ( W ) W, 0 l l l p = α + β α >. Παρόλο που οι γραµµικές συναρτήσεις είναι αρκετά απλές, δεν χρησιµοποιούνται γενικά ως συναρτήσεις κόστους ροής στα δίκτυα, κυρίως επειδή δεν έχουν την ακόλουθη ιδιότητα: Οι συναρτήσεις κόστους ροής χρησιµοποιούνται για να εκφράσουν το γεγονός του πόσο ανεπιθύµητο είναι να προστίθεται κίνηση σε έναν σύνδεσµο. Η πρόσθεση µιας µονάδας ροής σε έναν κενό σύνδεσµο αποτελεί αµελητέο γεγονός σε σχέση µε την πρόσθεση µιας µονάδας ροής που είναι ήδη συµφορηµένο µε w 1 µονάδες ροής, όπου w είναι η χωρητικότητα του συνδέσµου. Αυτός ο τύπος εξάρτησης δεν µοιάζει γραµµικός. Οι συναρτήσεις κόστους ροής θα πρέπει να είναι γνησίως αύξουσες και επίσης κυρτές µε τον αριθµό των µηκών κύµατος που διαρρέουν έναν σύνδεσµο. Στην προσέγγισή µας χρησιµοποιούµε την παρακάτω συνάρτηση κόστους ροής: w F l ( Wl ) = W W l + 1 W l Για µηδενική ροή στο σύνδεσµο w = 0, το κόστος είναι 0, πράγµα που είναι και λογικό, ενώ για w= W, το κόστος γίνεται µέγιστο και ίσο µε W. Είναι προφανές ότι το κόστος αυξάνεται κατακόρυφα στην περίπτωση που w= W. Μέχρι την τιµή w= W 1, το κόστος έχει τιµή ( W 1/2 ), µικρότερη δηλαδή από το µισό της µέγιστης. Με τη δέσµευση όµως του τελευταίου µήκους κύµατος το κόστος πηγαίνει στη µέγιστη τιµή του και γίνεται ίσο µε W. Το χαρακτηριστικό αυτό θα µπορούσε να θεωρηθεί λογικό και εποµένως επιθυµητό, αφού η µετάβαση από το w= W 1 στο w= W σε έναν σύνδεσµο, σηµαίνει ότι ο συγκεκριµένος σύνδεσµος θα γίνει πλήρως συµφορηµένος, γεγονός που µπορεί να οδηγήσει σε µεγάλη συµφόρηση του δικτύου αφού καµία σύνδεση δε θα µπορεί πλέον να δροµολογηθεί µέσω αυτού. Γι αυτό το τίµηµα από τη χρήση και δέσµευση και του τελευταίου µήκους κύµατος θα πρέπει να είναι µεγάλο. 3.3 Περιγραφή Του Αλγορίθµου Βήµα 1 Είσοδος αλγορίθµου Ένας γράφος GVE (, ), ο οποίος αναπαριστά το υπό µελέτη δίκτυο και αποτελείται από N κόµβους και L συνδέσµους Το πλήθος των µηκών κύµατος του δικτύου σε κάθε σύνδεσµο W Ένας πίνακας Λ N Nδιαστάσεων N N που περιγράφει τις αιτήσεις σύνδεσης
35 Ένας θετικός ακέραιος k, που δηλώνει το πλήθος των υποψηφίων µονοπατιών για κάθε αίτηση σύνδεσης Οι παραπάνω παράµετροι καθορίζουν ένα στιγµιότυπο στου προβλήµατος δροµολόγησης και ανάθεσης µήκους κύµατος. Στο πρώτο βήµα, ο αλγόριθµος υπολογίζονται k εναλλακτικά µονοπάτια για κάθε σύνδεση. Η επιλογή των k µονοπατιών γίνεται µε έναν γενικευµένο Dijkstra αλγόριθµο. Επιλέγονται τα k συντοµότερα µονοπάτια µε την εξής διαδικασία: Έστω ότι έχουµε µία αίτηση για σύνδεση από τον κόµβο s στον κόµβο d. Αρχικά υπολογίζεται το συντοµότερο µονοπάτι από τον s στον d µε τον αλγόριθµο Dijkstra. Όλοι οι σύνδεσµοι θεωρείται ότι έχουν µοναδιαίο κόστος. Στην συνέχεια οι σύνδεσµοι που χρησιµοποιούνται από το συντοµότερο µονοπάτι θεωρείται ότι έχουν µεγαλύτερο κόστος (δύο φορές µεγαλύτερη από την αρχική τιµή τους). Υπολογίζεται πάλι το συντοµότερο µονοπάτι µε τις νέες τιµές στους συνδέσµους. Αυτό είναι το συντοµότερο µονοπάτι. Αυτή η διαδικασία επαναλαµβάνεται εωσότου υπολογιστούν τα k συντοµότερα µονοπάτια. Τα µονοπάτια που θα προκύψουν, θα είναι όσο το δυνατό ανεξάρτητα µεταξύ τους γιατί σε κάθε υπολογισµό επιλέγονται περισσότερο µονοπάτια που δεν έχουν χρησιµοποιηθεί, αφού έχουν µεγαλύτερο κόστος. Το σύνολο των µονοπατιών που προκύπτουν δίνεται σαν είσοδος στο επόµενο βήµα του αλγορίθµου. Αυτή η διαδικασία υπολογισµού των k µονοπατιών γίνεται σε πολυωνυµικό χρόνο, αφού ο αλγόριθµος Dijkstra είναι πολυωνυµικού χρόνου. Μπορεί να µην προκύψουν k µονοπάτια για κάθε αίτηση σύνδεσης, επειδή δεν υπάρχουν τόσα εναλλακτικά µονοπάτια. Βήµα 2 Είσοδος Τα k εναλλακτικά µονοπάτια της κάθε σύνδεσης Όλες οι παράµετροι εισόδου που δόθηκαν στον αλγόριθµο Χρησιµοποιώντας τα χαρακτηριστικά του δικτύου και τα k εναλλακτικά µονοπάτια της κάθε σύνδεσης το πρόβληµα της δροµολόγησης και ανάθεσης µήκους κύµατος διαµορφώνεται ως ένα πρόβληµα γραµµικού προγραµµατισµού LP. Στην συνέχεια, αφού το πρόβληµα πάρει την κατάλληλη µορφή, επιλύνεται µε τη χρήση του αλγορίθµου Simplex. Εάν υπάρχουν εφικτές λύσεις, ο αλγόριθµος τερµατίζει επιστρέφοντας την βέλτιστη λύση σύµφωνα µε την συνάρτηση βελτιστοποίησης. Η έξοδος αυτού του βήµατος είναι δηλαδή ένα σύνολο από δροµολογηµένα οπτικά µονοπάτια µε µήκη κύµατος να έχουν ανατεθεί σε αυτά. Εφικτές λύσεις υπάρχουν, µόνο εάν όλες οι αιτήσεις µπορούν να ικανοποιηθούν ταυτόχρονα. Τότε ο ρυθµός απόδοσης του δικτύου θα είναι 100% (blocking probability ίση µε µηδέν) και ο αλγόριθµος τερµατίζει. Σε περίπτωση που δεν υπάρχει εφικτή λύση, αν δεν υπάρχουν για παράδειγµα αρκετά διαθέσιµα για να δροµολογηθούν όλες οι αιτήσεις, το πρόβληµα είναι ανέφικτο και ακολουθεί ένα τρίτο βήµα Βήµα 3 Είσοδος Είσοδος του βήµατος 2 µε W = W + 1 Το τρίτο βήµα του αλγορίθµου χρησιµοποιείται για να διαχειριστεί τις περιπτώσεις που ο αλγόριθµος του RWA προβλήµατος δεν επιστρέφει εφικτή λύση. Έστω W το σύνολο των διαθέσιµων µηκών κύµατος. Μη εφικτές λύσεις προκύπτουν επειδή το σύνολο των W µηκών κύµατος δεν επαρκεί για να δροµολογηθούν ταυτόχρονα όλες οι αιτήσεις σύνδεσης. Σ αυτό το βήµα, ο αριθµός των διαθέσιµων µηκών κύµατος
36 αυξάνεται κατά ένα και στην συνέχεια λύνεται το γραµµικό πρόβληµα µε το νέο σύνολο από µήκη κύµατος. Αυτή η διαδικασία επαναλαµβάνεται εωσότου βρεθεί εφικτή λύση ή το πλήθος των επαναλήψεων είναι αρκετά µεγάλο. Εάν βρεθεί εφικτή λύση, τότε ανάγεται σε µία άλλη λύση η οποία χρησιµοποιεί µόνο το αρχικό σύνολο των µηκών κύµατος. Θα πρέπει δηλαδή στην τελική λύση να κρατήσουµε µόνο ένα υποσύνολο από τα οπτικά µονοπάτια που δροµολογήθηκαν. Ο τρόπος µε τον οποίο επιλέγονται τα οπτικά µονοπάτια που θα δροµολογηθούν είναι τέτοιος ώστε να έχουµε την µικρότερη blocking probability. 3.4 LP2: Η Συµφόρηση Του Μονοπατιού Ως Objective Της Μοντελοποίησης Σε αυτή την παράγραφο, επικεντρώνουµε την προσοχή µας στην ελαχιστοποίηση ενός διαφορετικού objective και να εξετάσουµε την συµπεριφορά του. Αρχικά, παρουσιάζεται ένα απλό σχηµατικό παράδειγµα, για να περιγραφούν διαισθητικά οι µεταβλητές που θα υποστούν ελαχιστοποίηση. Ας θεωρήσουµε λοιπόν ότι ο RWA αλγόριθµος έχει ολοκληρωθεί και ένα µέρος της λύσης του αλγορίθµου (µε την µορφή ενεργών µηκών κύµατος) απεικονίζεται στο σχήµα 3.2. Ένα lightpath έχει εγκατασταθεί από τον κόµβο s στον κόµβο d. Αυτό το lightpath χρησιµοποιεί το µήκος κύµατος λ 1 και καταλαµβάνει 4 συνδέσµους. Σύµφωνα µε το σχήµα, το lightpath ενεργοποιεί 4 κανάλια. Επιπλέον, υπάρχουν 4 ακόµη ενεργοποιηµένα µήκη κύµατος τα οποία χρησιµοποιούνται από άλλες συνόδους. Λαµβάνοντας τα όλα υπόψη, σε αυτούς τους συνδέσµους υπάρχουν 8 ενεργά κανάλια. Το objective του RWA που υλοποιήθηκε ήταν η ελαχιστοποίηση αυτού του αριθµού των καναλιών. Σχήµα 3.2: Υπάρχουν 5 ενεργά κανάλια κατά µήκος του lightpath s-d. Με τον όρο ενεργό κανάλι εννοούµε ένα µήκος κύµατος που χρησιµοποιείται µεταξύ δύο γειτονικών κόµβων. Η φιλοσοφία του αλγορίθµου περιγράφεται παρακάτω. Έστω µία αίτηση από την πηγή s στον προορισµό d όπως φαίνεται στο σχήµα 3.3. Έστω επίσης k = 3, ο αριθµός τον υποψήφιων µονοπατιών για την αίτηση σύνδεσης s d. Τότε τα υποψήφια µονοπάτια είναι: P = s a d, 1 2 { } { } { } P = s b e d και P = s c d. 3
37 Μεταξύ αυτών των µονοπατιών µόνο ένα µπορεί να εγκατασταθεί. Τα άλλα θα,,,, be, απορριφθούν. Θεωρούµε ότι στους συνδέσµους ( sa ),( ad ),( sc ),( cd ) και ( ) υπάρχει ένα ενεργό κανάλι. Σχήµα 3.3: Οι αριθµοί στους συνδέσµους αναπαριστούν τα ενεργά κανάλια Εποµένως, στα µονοπάτια P 1 και P 3 υπάρχουν 2 ενεργά κανάλια και στο µονοπάτι P 2 ένα ενεργό κανάλι. Βασιζόµενοι στο objective, τα lightpaths θα εγκατασταθούν κατά µήκος του µονοπατιού P 2. Αυτή η προσέγγιση χρησιµοποιείται για να µοιράσει την κίνηση σε όλο το δίκτυο, οδηγώντας έτσι σε µικρή blocking probability. Παράµετροι: w C : ένα διαθέσιµο µήκος κύµατος p P : ένα υποψήφιο µονοπάτι l E: ένας σύνδεσµος του δικτύου Μεταβλητές: λ plw : µία δείκτρια µεταβλητή η οποία έχει την τιµή 1 όταν το µονοπάτι p καταλαµβάνει τον σύνδεσµο l και το µήκος κύµατος c και 0 σε όλες τις άλλες περιπτώσεις Fl = f λ plw = f λ plw : η συνολική ροή στον σύνδεσµο l p P p P w C w C D : ο συνολικός αριθµός των ενεργών καναλιών του δικτύου κατά µήκος του p i p i πλην τον αριθµό των συνδέσµων που αποτελείται το µονοπάτι. µονοπατιού Με άλλα λόγια η µεταβλητή των άλλων συνόδων που επηρεάζουν το µονοπάτι To Dp i ορίζεται ως ακολούθως: Έστω pi P, 1 i K λplw= D j p p i i P, w C, j E, l Ei, wl,, j j i D p i είναι ο αριθµός των ενεργών καναλιών όλων p i. : To i-στο υποψήφιο µονοπάτι P= { p,..., p,..., p } όπου E = { συνδεσµοι p} i i 1 i K
38 Το D p i είναι δηλαδή ο αριθµός των ενεργών καναλιών κατά µήκος των συνδέσµων του p i που οφείλονται σε όλες τις συνόδους εκτός αυτής που θα εγκατασταθεί στο µονοπάτι που εξετάζουµε. Αυτό που ουσιαστικά επιδιώκουµε είναι η µείωση της επίδρασης των µονοπατιών µεταξύ τους. Ελαχιστοποιώντας το D p i αποθαρρύνουµε να ενεργοποιηθούν µήκη κύµατος κατά µήκος των συνδέσµων ενός lightpath που θα εγκατασταθεί (ελαχιστοποίηση της συµφόρησης µονοπατιού- path congestion minimization). Το πρόβληµα που συνδυάζει την ελαχιστοποίηση της συµφόρησης µονοπατιού (path congestion-) και ροής του συνδέσµου (flow link-) µπορεί να µοντελοποιηθεί ως ακολούθως: ΜΟΝΤΕΛΟΠΟΙΗΣΗ II Ελαχιστοποίηση : m D + F l E, p P Έτσι ώστε pi 1. λ 1 l E, w C p plw ' 2. λplw = λ ' p P pl w ( l l ) 3. pi l i l και, ειναι διαδοχικοι συνδεσµοι στο p λplw =Λsd l που είναι ο πρώτος σύνδεσµος στο p w p Psd λplw =Λsd l που είναι ο τελευταίος σύνδεσµος στο p w p Psd λplw= D j p p i i P, w C, j E, l Ei 4. Fl f λplw p w 5. wl,, j j i Η συνάρτηση κόστους ροής χρησιµοποιείται για να εκφράσει το ποσόν της συµφόρησης κατά µήκος ενός µονοπατιού. Σε αυτή την περίπτωση, το objective είναι η ελαχιστοποίηση του φορτίου σε έναν σύνδεσµο και της συµφόρησης του µονοπατιού κατά µήκος ενός οπτικού µονοπατιού. Μία αρκετά µεγάλη τιµή της σταθεράς m επιλέγεται για να δώσουµε έµφαση στην ελαχιστοποίηση της συµφόρησης του µονοπατιού εφόσον η D p κυριαρχεί. Μία µικρή τιµή της m (όχι αρνητική) χρησιµοποιείται για να δώσουµε έµφαση στην ελαχιστοποίηση της ροής του συνδέσµου.
39 3.5 Σύγκριση Αλγορίθµων Με τον όρο ιδανικό δίκτυο εννοούµε το δίκτυο στο οποίο τα σήµατα δεν υφίστανται φυσικές εξασθενήσεις λόγω των οπτικών µέσων που µπορεί να χρησιµοποιούνται. Το σχήµα 3.4 αναπαριστά την blocking probability του δικτύου χρησιµοποιώντας τα γραµµικά προγράµµατα LP1 και LP2. Είναι ξεκάθαρο πως η υλοποίηση σου LP2 υπερτερεί έναντι της LP1. Το δίκτυο που χρησιµοποιήθηκε για την εξαγωγή των πειραµάτων είναι αυτό του παρακάτω σχήµατος. Σχήµα 3.4: Ιδανικό δίκτυο (χωρίς φυσικές εξασθενήσεις). Στο σχήµα παρουσιάζεται η blocking probability συναρτήσει του φορτίου που υπάρχει στο δίκτυο (traffic load). Είναι λογικό όσο αυξάνεται η κίνηση στο δίκτυο να αυξάνεται και η blocking probability ανεξάρτητα από ποιες µεταβλητές υφίστανται ελαχιστοποίηση. Η χρήση του γραµµικού προγράµµατος LP2 έδειξε πως έχει καλύτερη απόδοση ως προς το throughput του δικτύου σε σχέση µε το πρόγραµµα LP1. Αυτό συµβαίνει γιατί στην περίπτωση του LP2 προγράµµατος, ο αλγόριθµος εκτός του ότι ελαχιστοποιεί την ροή σε κάθε σύνδεσµο, προσπαθεί να εγκαταστήσει τα lightpaths όσο πιο αποµακρυσµένα γίνεται µεταξύ τους. Αυτό έχει σαν αποτέλεσµα το άπλωµα της κίνησης στο δίκτυο και έτσι γίνεται καλύτερη χρησιµοποίηση των πόρων. Σχήµα 3.5: Blocking probability συναρτήσει του φορτίου για διαφορετικά objectives
40 Το objective του LP2 είναι η ελαχιστοποίηση της συµφόρησης µονοπατιού. Αυτό, σε συνδυασµό µε την προαναφερόµενη συνάρτηση κόστους ροής (ελαχιστοποίηση της συνολικής ροής ενός συνδέσµου), έχει αποτέλεσµα την χρησιµοποίηση ενός µεγάλου µέρους του δικτύου και τα οπτικά µονοπάτια εγκαθίστανται µε τρόπο που να µην επηρεάζει το ένα το άλλο. Η κεντρική ιδέα της ελαχιστοποίησης της συµφόρησης του µονοπατιού είναι η ίδια µε την δροµολόγηση ελάχιστης αλληλεπίδρασης, δηλαδή η επιλογή ενός µονοπατιού που αλληλεπιδρά λιγότερο µε τα άλλα µονοπάτια. Σχήµα 3.6: Ακέραιες ροές εναντίων δεκαδικών. Στο σχήµα 3.6 έστω ότι υπάρχει µία αίτηση σύνδεσης από τον κόµβο s στον κόµβο d και µία αίτηση από τον κόµβο d στον κόµβο s. Η κύρια ιδέα για το objective D είναι πως εάν υπάρχει ένα σπασµένο µονοπάτι (δεκαδικές ροές, έστω ' p λ i 1 = 0.5) pi ' ' τότε το λ 1 αλληλεπιδρά µε το λ 2 γεγονός που είναι ανεπιθύµητο από το objective γιατί τότε το objective για την συµφόρηση µονοπατιού είναι D p = = 4.5. i Στην άλλη περίπτωση, αν υπάρχουν ακέραιες ροές τότε το objective της συµφόρησης µονοπατιού είναι ίσο µε µηδέν D p = 0. i pi pi
41 4 ΦΥΣΙΚΕΣ ΕΞΑΣΘΕΝΗΣΕΙΣ Οι φυσικές εξασθενήσεις µπορούν να ταξινοµηθούν σε δύο κατηγορίες, τις γραµµικές και τις µη γραµµικές. Οι γραµµικές επιδράσεις είναι ανεξάρτητες από την ισχύ του σήµατος και επηρεάζουν τα µήκη κύµατος ανεξάρτητα. Ο θόρυβος αυθόρµητης εκποµπής ενισχυτή (amplifier spontaneous emission ASE), η διασπορά τρόπου πόλωσης (polarization mode dispersion PMD) [22] και η χρωµατική διασπορά (chromatic dispersion CD) είναι παραδείγµατα. Η έννοια της διασποράς αναφέρεται σε κάθε περίπτωση όπου διαφορετικά κοµµάτια του µεταδιδόµενου σήµατος, κινούνται µε διαφορετικές ταχύτητες µέσα στην ίνα και φτάνουν διαφορετικές χρονικές στιγµές στο δέκτη. Έτσι εξαιτίας της διασποράς, ένας παλµός σήµατος που κινείται µέσα στην ίνα, φτάνει αλλοιωµένος στο δέκτη. Αυτή η αλλοίωση προκαλεί µε την σειρά της διασυµβολική παρεµβολή (intersymbol interference) η οποία οδηγεί σε σφάλµατα που έχουν να κάνουν µε την ενέργεια. Η διασπορά έχει συσωρευτική επίδραση: όσο µακρύτερος είναι ο σύνδεσµος τόσο µεγαλύτερη ποσότητα διασποράς έχουµε. Οι µη γραµµικές εξασθενήσεις είναι πιο πολύπλοκες. εν δηµιουργούν µόνο εξασθενήσεις σε κάθε κανάλι, αλλά αλληλεπιδρούν µεταξύ των καναλιών. Ένας στενός παλµός που ταξιδεύει σε µία οπτική ίνα τείνει να ανοίγει καθώς διαδίδεται µέσα σε αυτή και το εύρος του µεγαλώνει. Όταν ένας παλµός ανοίγει σε τέτοιο βαθµό που να επικαλύπτει γειτονικούς παλµούς, η διασυµβολική παρεµβολή που προκύπτει αυξάνει τον ρυθµό µετάδοσης λαθών (Bit Error Rate BER). Αυτό το φαινόµενο της διασποράς της ίνας βάζει ένα όριο στον ρυθµό µετάδοσης που µπορεί να υποστηρίξει µία ίνα διασποράς ενός δεδοµένου µήκους. Ο ρυθµός λαθών είναι επίσης µία συνάρτηση της εξασθένησης του σήµατος στον σύνδεσµο και κατά συνέπεια του λόγου σήµατος προς θόρυβο (Signal to Noise Ratio SNR) στον δέκτη.
42 Σχήµα 4.1: Κάθε παλµός απλώνεται και επιδρά µε τους γειτονικούς και τελικά γίνεται δυσδιάκριτος στην είσοδο του δέκτη. 4.1 ιασπορά Τρόπου Πόλωσης Η διασπορά τρόπου πόλωσης (polarization-mode dispersion-pmd) προκύπτει επειδή ο πυρήνας της οπτικής ίνας δεν είναι απόλυτα στρογγυλός ιδιαίτερα όταν µιλάµε για παλιότερης τεχνολογίας οπτικές ίνες. Επίσης διαφορετικές πολώσεις κατά τη µετάδοση του σήµατος µε διαφορετικές ταχύτητες δηµιουργούν αυτή τη διασπορά. Το PMD αποδεικνύεται να είναι ένα σοβαρό εµπόδιο σε συστήµατα υψηλών ταχυτήτων µε ρυθµούς µετάδοσης δεδοµένων 10Gb/s και περισσότερο [17]. Οι δύο τρόποι πόλωσης του βασικού τρόπου µπορεί να διαδίδονται µε λίγο διαφορετικές ταχύτητες λόγω ασυµµετριών στην ίνα. Αυτό είναι γνωστό ως διασπορά τρόπου πόλωσης. Σχήµα 4.2: Απεικόνιση της διεύρυνσης του παλµού εξαιτίας του PMD. Η ενέργεια του παλµού υποθέτουµε ότι είναι χωρισµένη µεταξύ των δύο ορθογωνίων πόλωσης, η οποία φαίνεται από τον οριζόντιο και κάθετο παλµό στο (a). Εξαιτίας της διπλής διάθλασης (birefringence), µία από αυτές τις συνισταµένες ταξιδεύει πιο αργά από την άλλη. Υποθέτοντας ότι η οριζόντια συνισταµένη ταξιδεύει πιο αργά από την κάθετη, οι σχετικές θέσεις των οριζόντιων και κάθετων παλµών φαίνονται στο (b). Ο παλµός έχει διευρυνθεί εξαιτίας του PMD επειδή η ενέργεια του έχει απλωθεί σε µεγαλύτερη χρονική περίοδο. Η προέλευση της διασποράς PMD αναφέρεται στο γεγονός ότι διαφορετικές πολικότητες µεταδίδονται µε διαφορετικές ταχύτητες, εξαιτίας του ελλειπτικού σχήµατος του πυρήνα της οπτικής ίνας. Επίσης, η διανοµή της ενέργειας του σήµατος πάνω στις διαφορετικές καταστάσεις πολικότητας (State of polarizations SOPs) µεταβάλλεται αργά µε το χρόνο, για παράδειγµα εξαιτίας των αλλαγών στη θερµοκρασία του µέσου. Το γεγονός αυτό κάνει το σφάλµα της διασποράς να ποικίλλει επίσης µε το χρόνο. Εκτός εξαιτίας της ίδιας της ίνας, το PMD µπορεί να προκύψει και από άλλα συστατικά του δικτύου.
43 Η χρονική-µέση διαφορική χρονοκαθυστέρηση, ανάµεσα στα δύο ορθογώνια SOP s πάνω στο σύνδεσµο, είναι γνωστό ότι υπακούει τη σχέση τ = DPMD L όπου τ είναι η διαφορική οµαδική καθυστέρηση (Differential Group Delay DGD), L είναι το µήκος του συνδέσµου και η D είναι η παράµετρος PMD της ίνα, η οποία PMD µετριέται σε ps/ km. Το PMD για τυπική ίνα, κυµαίνεται από 0.5 και 2 ps/ km. Οι προσεκτικά κατασκευασµένοι νέοι σύνδεσµοι µπορούν να έχουν χαµηλό PMD όπως 0.1 ps/ km. Στη πραγµατικότητα, τα SOPs µεταβάλλονται αργά µε το χρόνο, και το πραγµατικό DGD τ είναι µια τυχαία µεταβλητή. Σχήµα 4.3. Οι περιορισµοί των ταυτόχρονα επιτεύξιµων bit rate και αποστάσεων, που προκαλούνται από το PMD. Αυτό σηµαίνει ότι το τετράγωνο του DGD µπορεί να µοντελοποιηθεί από µία πιο οικεία κατανοµή, την εκθετική κατανοµή. Όσο µεγαλύτερο είναι το DGD τόσο µεγαλύτερο είναι το σφάλµα ισχύος εξαιτίας του PMD. Επίσης το σφάλµα ισχύος εξαιτίας του PMD ποικίλλει ανάλογα µε το χρόνο, και αποδυκνείεται ότι είναι ανάλογο του τ 2 και ότι επίσης υπακούει στην εκθετική διανοµή. Εάν το σφάλµα ισχύος εξαιτίας του PMD είναι µεγάλο (PMD outage), ο σύνδεσµος έχει αποτύχει. Για DGD 0.3T, όπου T είναι η διάρκεια του bit, το σφάλµα ισχύος είναι περίπου 0.5dB για ένα δέκτη που περιορίζεται από θερµικό θόρυβο, και 1dB για ένα δέκτη µε εξαρτηµένο από το σήµα θόρυβο. Χρησιµοποιώντας την Μάξγουελ (Maxwellian) κατανοµή, η πιθανότητα ότι η πραγµατική καθυστέρηση θα είναι µεγαλύτερη περισσότερες από τρεις φορές από τη µέση, είναι περίπου Αν λάβουµε υπόψη την προηγούµενη αιτιολόγηση, αυτό σηµαίνει ότι για να µειώσουµε τη πιθανότητα του PMD (PMD 1dB) στο , πρέπει το µέσο DGD να είναι λιγότερο από 0.1Τ. ηλαδή τ = D L < 0.1T PMD
44 Το όριο αυτό φαίνεται στo σχήµα 4.3. Αξίζει να παρατηρήσουµε ότι για µια κακή ίνα µε PMD 2 ps/ km το όριο είναι 25km. Αυτό είναι µια υπερβολική κατάσταση αλλά τονίζει ότι το PMD µπορεί να επιφέρει σηµαντικούς περιορισµούς. Στο παραπάνω παράδειγµα, το DGD µπορεί να υπερβαίνει τρεις φορές τη µέση καθυστέρηση και επίσης µπορεί να έχουµε µια υπέρβαση του PMD (PMD outage) µε µέση διάρκεια µία µέρα για κάθε 70 χρόνια, ή µε µέση διάρκεια ένα λεπτό κάθε 17 µέρες. Αυτό εξαρτάται από το καλώδιο της ίνας και τις υπερβάσεις (outages) που διαρκούν για µερικά λεπτά. Επίσης µία πιθανότητα υπέρβασης (outage) της τάξης µπορεί να ερµηνευτεί ως τη σωρευµένη υπέρβαση 20 λεπτών κάθε χρόνο. Αυτοί οι περιορισµοί εξαιτίας της ενδοτροπικής διασποράς (intermodal dispersion), της χρωµατικής διασποράς και του PMD, συγκρίνονται στο παρακάτω σχήµα 4.4 Σχήµα 4.4. Οι περιορισµοί των ταυτόχρονα επιτεύξιµων bit rate και αποστάσεων, που προκαλούνται από ενδοτροπική διασπορά, χρωµατική διασπορά µε φασµατικό εύρος πηγής 1nm, χρωµατική διασπορά µε φασµατικό εύρος ανάλογο του εύρους ζώνης διαµόρφωσης, και PMD µε D PMD =0.5.Υποθέτουµε NRZ διαµόρφωση µετάδοσης πάνω από πρότυπη µονοτροπική ίνα µε χρωµατική διασπορά 17ps/nm-km. Το φαινόµενο PMD αυξάνει τη διασυµβολική παρεµβολή (ISI) εξαιτίας της εξάπλωσης του φάσµατος παλµού, όπως και µε τις άλλες κατηγορίες διασποράς. Η παραδοσιακή (ηλεκτρονική) τεχνική για να ξεπεράσουµε το φαινόµενο του ISI στα ψηφιακά συστήµατα είναι η τεχνική της ισοστάθµισης (equalization). Η τεχνική της ισοστάθµισης για την αντιστάθµιση του φαινόµενου του PMD, µπορεί να διεκπεραιωθεί ηλεκτρονικά. Όµως η τεχνική της ηλεκτρονικής ισοστάθµισης, γίνεται πιο δύσκολη όσο ο ρυθµός bit αυξάνεται, και σήµερα δεν είναι εφικτή για 40Gb/s συστήµατα. Για τέτοιους ρυθµούς bit πρέπει να χρησιµοποιηθεί οπτική PMD αντιστάθµιση. Για να γίνει αντιληπτό πως το PMD µπορεί να αντισταθµιστεί οπτικά, το PMD προκύπτει εξαιτίας της παραµόρφωσης που προκαλεί η ίνα. Ο µεταδιδόµενος παλµός αποτελείται από «γρήγορα» και «αργά» πολωτικά µέρη. Η αρχή της αντιστάθµισης
45 του PMD είναι ο διαχωρισµός του λαµβανόµενου σήµατος σε γρήγορα και αργά πολωτικά µέρη, και η καθυστέρηση του γρήγορου µέρους, έτσι ώστε το φαινόµενο DGD ανάµεσα στα δύο µέρη να αντισταθµίζεται. Από τη στιγµή που το DGD µεταβάλλεται µε το χρόνο η καθυστέρηση που πρέπει να εισάγεται στο «γρήγορο» µέρος για την αντιστάθµιση του PMD, πρέπει να εκτιµηθεί σε πραγµατικό χρόνο από τις ιδιότητες του συνδέσµου. Οι συνέπειες του PMD φαινόµενου που αναφέρθηκαν ονοµάζονται διασπορά πόλωσης 1 ης τάξης. Το PMD 1 ης τάξης είναι συνέπεια του γεγονότος ότι δύο ορθογώνιες τάξεις πόλωσης στην οπτική ίνα, ταξιδεύουν µε ελαφρώς διαφορετικές ταχύτητες, πράγµα το οποίο οδηγεί σε µια διαφοροποίηση στη χρονική καθυστέρηση ανάµεσα σε αυτές τις δύο τάξεις. Όµως η διαφοροποίηση αυτή στη χρονική καθυστέρηση είναι εξαρτηµένη από τη συχνότητα και ποικίλλει ανάλογα µε το εύρος ζώνης του µεταδιδόµενου παλµού. Αυτή η συνέπεια καλείτε PMD 2 ης τάξης. Το PMD 2 ης τάξης είναι µια επίδραση η οποία είναι όµοια µε τη χρωµατική διασπορά και επίσης µπορεί να οδηγήσει σε εξάπλωση του παλµού. Το φαινόµενο PMD εξαρτάται επίσης από το εάν χρησιµοποιείται RZ ή NRZ διαµόρφωση. Για την RZ διαµόρφωση, η χρήση µικρών παλµών κάνει δυνατή την ανοχή σε µεγαλύτερο PMD από τη στιγµή που ο παλµός εξόδου έχει περισσότερο χώρο να εξαπλωθεί, όπως και στη περίπτωση της χρωµατικής διασποράς. Όµως το 2 ης τάξης PMD εξαρτάται και από το φασµατικό εύρος του παλµού. Στενότερη παλµοί µεγαλύτερα φασµατικά εύρη. Αυτό είναι επίσης παρόµοιο µε την περίπτωση της χρωµατικής διασποράς. Πάλι, όπως στη περίπτωση της χρωµατικής διασποράς, υπάρχει ένα βέλτιστο εύρος παλµού εισόδου για την RZ διαµόρφωση που ελαχιστοποιεί το εύρος του παλµού εξόδου. Εκτός από το PMD, υπάρχουν συνέπειες που έχουν να κάνουν µε τη πόλωση και επηρεάζουν τη λειτουργία του συστήµατος. Μία από αυτές προκύπτει από το γεγονός ότι πολλά µέρη του συστήµατος παρουσιάζουν απώλειες εξαιτίας της πόλωσης (PDL) και επίσης η απώλεια αυτή εξαρτάται από τη κατάσταση της πόλωσης. Αυτές οι απώλειες συσσωρεύονται στο σύστηµα σε πολλά σηµεία στο µονοπάτι µετάδοσης. Έτσι από τη στιγµή που η κατάσταση της πόλωσης κυµαίνεται µε το χρόνο, ο λόγος σήµατος προς θόρυβο στο τέλος του µονοπατιού θα κυµαίνεται µε το χρόνο, και για αυτό το λόγο χρειάζεται µεγάλη προσοχή στη διατήρηση του συνολικού PDL στο µονοπάτι στα επιτρεπτά όρια. Ένα παράδειγµα για αυτό είναι ένας απλός γωνιακής όψης connector που χρησιµοποιείται σε κάποια συστήµατα για µειώσει τις ανακλάσεις. Αυτό ο connector µπορεί να έχει PDL περίπου 0.1dB, αλλά όµως εκατοντάδες τέτοιοι connectors µπορούν να υπάρχουν στο µονοπάτι µετάδοσης. Ο περιορισµός που επιβάλει το PMD µπορεί να εκφραστεί ως εξής: M k = 1 PMD 2 ( ) ( ) B D k L k < a Ως διαφανές τµήµα (span) σε ένα transparent δίκτυο ορίζουµε το κοµµάτι µεταξύ δύο οπτικών ενισχυτών. Το k ο span έχει µήκος L( k ), k = 1,2,..., M. Όταν όλα τα span της ίνας έχουν την ίδια παράµετρο PMD, για παράδειγµα D k = D, το άνω όριο του συνολικού µήκους των M-span, το οποίο PMD ( ) PMD συµβολίζεται µε L, είναι a 2 / ( BD ) 2 PMD.
46 Θέτοντας a = 0.1, για τυπικές ίνες µε DPMD = 0.5 ps/ km, σύµφωνα µε τον παραπάνω περιορισµό το µέγιστο µήκος δεν µπορεί να ξεπερνά τα 400km και 25km για bit rates 10 Gb / s και,40 Gb / s αντίστοιχα. Με τις καινούριες οπτικές ίνες και υποθέτοντας DPMD = 0.1 ps/ km, το µέγιστο µήκος L δεν πρέπει να ξεπερνά τα 10,000km και 625km για bit rates 10 Gb / s και, 40 Gb / s αντίστοιχα. 4.2 Χρωµατική ιασπορά Η πιο σοβαρή µορφή διασποράς είναι η χρωµατική διασπορά (chromatic dispersion), η οποία και έχει ένα προφανές αντίκτυπο στο σχεδιασµό µονοτροπικών συστηµάτων µετάδοσης (τόσο ώστε καµιά φορά µε τον όρο διασπορά να υπονοείται η χρωµατική διασπορά) και κυρίως σε συστήµατα που λειτουργούν µε ρυθµούς πάνω από 2.5 Gb / s. Η χρωµατική διασπορά (chromatic dispersion) προκύπτει επειδή τα διαφορετικά τµήµατα συχνότητας ενός παλµού (και επίσης σήµατα διαφορετικών µηκών κύµατος) ταξιδεύουν µε διαφορετικές ταχύτητες στην ίνα και έτσι φτάνουν διαφορετικές χρονικές στιγµές στους δέκτες. Η χρωµατική διασπορά είναι χαρακτηριστικό της ίνας και έτσι διαφορετικού τύπου ίνες έχουν διαφορετική χρωµατική διασπορά. Η χρωµατική συσσωρεύεται όσο αυξάνει το µήκος του συνδέσµου. Γενικά η χρωµατική διασπορά (chromatic dispersion) µπορεί επαρκώς (όχι βέλτιστα) να εξουδετερωθεί (compensate) σε κάθε σύνδεσµο και/ή στον χρόνο αρχικοποίησης του συστήµατος. Σήµερα οι συσκευές εξουδετέρωσης (compensation) βασίζονται στην ίνα εξουδετέρωσης διασποράς (Dispersion Compensation Fiber DCF). Η DCF παρέχει εξουδετέρωση ανά ίνα που σηµαίνει ότι κάθε ίνα είναι εφοδιασµένη µε έναν παράγοντα αντίθετο µε την ίνα. Λόγω του ατελούς ταιριάσµατος µεταξύ του CD της ίνας και του DCF µερικά µήκη κύµατος µπορεί να εξουδετερωθούν περισσότερο ενώ άλλα µπορεί να εξουδετερωθούν λιγότερο. Επιπλέον τα DCF κοµµάτια µπορεί να είναι διαθέσιµα µόνο σε σταθερά µήκη της ίνας εξουδετέρωσης. Αυτό σηµαίνει ότι µερικές φορές είναι αδύνατο να βρεθεί ένα κοµµάτι DCF που να εξουδετερώνει ακριβώς το CD που εισάγεται από την ίνα. Αυτές οι επιδράσεις εισάγουν αυτό που είναι γνωστό ως υπόλοιπο (residual) CD. Το υπόλοιπο CD ποικίλλει µε τη συχνότητα του µήκους κύµατος. Ξέροντας τα χαρακτηριστικά και της ίνας και των DCF κοµµατιών κατά µήκος του µονοπατιού, αυτό µπορεί να υπολογιστεί µε έναν ικανοποιητικό βαθµό ακρίβειας. Εντούτοις αυτό είναι αποτελεί µία πρόκληση. Στην πραγµατικότητα το υπόλοιπο διασποράς ανά-µήκος κύµατος πρέπει να συνδυαστεί µε άλλες πληροφορίες στο σύστηµα για να λάβει την καθαρή επίδραση του CD είτε από την προσοµοίωση είτε από κάποια αναλυτική προσέγγιση. Φαίνεται ότι το πλάνο δροµολόγησης/ελέγχου δεν πρέπει να φορτωθεί από ένα τέτοιο µεγάλο σύνολο πληροφοριών όταν µπορεί να αντιµετωπιστεί στο επίπεδο σχεδιασµού συστηµάτων. Για υψηλούς ρυθµούς µετάδοσης, µπορεί να χρειάζεται στο δέκτη η δυναµική αντιστάθµιση διασποράς για να εξαλείψει οποιοδήποτε υπόλοιπο διασποράς. Για ένα διαφανές τµήµα ίνας, η απαίτηση είναι ότι δεν πρέπει η τιµή της επαγόµενης από διασπορά ποινής P να βρίσκεται πιο χαµηλά από ένα καθορισµένο κατώφλι, τυπικά ίσο µε 2dB. Αυτή η ποινή εξαρτάται από διάφορες παραµέτρους, όπως το ρυθµό bit, την παράµετρο CD και τη διάταξη διαµόρφωσης που χρησιµοποιείται.
47 Συνήθεις διατάξεις διαµόρφωσης που χρησιµοποιούνται είναι η non-return to zero (NRZ) η return to zero (RZ) και η low-pass filter-based duobinary (LPF) NRZ ιαµόρφωση Σε αυτή τη παράγραφο, θα συζητήσουµε τις συνέπειες της χρωµατικής διασποράς σε NRZ διαµορφωµένα σήµατα [17]. Οι περιορισµοί µετάδοσης που επιβάλλονται από τη χρωµατική διασπορά µπορούν να µοντελοποιηθούν µε την υπόθεση ότι η εξάπλωση του παλµού εξαιτίας της χρωµατικής διασποράς πρέπει να είναι µικρότερη από ένα φράγµα ε για µια περίοδο bit και για µία συγκεκριµένη «ποινή» χρωµατικής διασποράς. Για παράδειγµα όταν η διασπορά είναι 1dB έχουµε ε =0.306 ενώ για διασπορά 2dB έχουµε ε = Εάν D είναι η χρωµατική διασπορά στο ισχύον µήκος κύµατος, Β είναι το bit rate, λ το φασµατικό εύρος του µεταδιδόµενου σήµατος και L το µήκος του συνδέσµου ο περιορισµός που αναφέραµε µπορεί να εκφρασθεί από τη σχέση D LB( λ) < ε Το D συνήθως καθορίζεται σε µονάδες ps/nm-km. Εδώ το ps αναφέρεται στη χρονική διασπορά του παλµού, το nm στο φασµατικό εύρος του παλµού και τα km αναφέρονται στο µήκος του συνδέσµου. Για την πρότυπη µονοτροπική ίνα, η τυπική τιµή του D είναι στη C µπάντα 17ps/nm-km. Για αυτή τη τιµή του D, το λ=155µm και επίσης έχουµε ε =0.491 (2 db διασπορά), έτσι από τη σχέση που αναφέραµε παραπάνω ισχύει BL<30(Gb/s)-km. Αυτό το όριο φαίνεται στο σχήµα 4.5. Επίσης ακόµα και µε ένα ρυθµό µετάδοσης 1Gb/s το µήκος του συνδέσµου είναι µικρότερο από 30 km πράγµα που είναι ένας σοβαρός περιορισµός. Αυτό επιδεικνύει την σηµασία της χρήσης µονοχρωµατικών πηγών όπως DFB laser και υψηλής ταχύτητας οπτικά επικοινωνιακά συστήµατα καθώς επίσης και την εύρεση µεθόδων που θα υπερνικούν την χρωµατική διασπορά. Ας θεωρήσουµε τη περίπτωση όπου χρησιµοποιούµε πηγές µε στενά φασµατικά εύρη. Ακόµα και για µία τέτοια πηγή, το φασµατικό εύρος του µεταδιδόµενου σήµατος εξαρτάται από το αν αυτό διαµορφώνεται άµεσα ή από το εάν χρησιµοποιείται ένας εξωτερικός διαµορφωτής. Τα SLM DFB laser έχουν αδιαµόρφωτα φασµατικά εύρη τυπικά λιγότερο από 50MHz. H άµεση διαµόρφωση ενός DFB laser, ιδανικά θα προκαλούσε το φασµατικό εύρος να ανταποκρίνεται στο εύρος ζώνης διαµόρφωσης (για παράδειγµα, περίπου 2.5 GHz για ένα on-off διαµορφωµένο σήµα). Πρακτικά όµως το φασµατικό εύρος µπορεί να αυξηθεί εξαιτίας της τεχνικής chirp. Αφού ο τύπος διαµόρφωσης ποικίλλει (όπως και η οπτική ισχύς), έτσι συνοδεύεται από αλλαγές στην πυκνότητα µεταφοράς µέσα στη κοιλότητα του laser η οποία µε τη σειρά της αλλάζει το διαθλώµενο περιεχόµενο αυτής της κοιλότητας και έτσι προκαλεί αποκλίσεις συχνότητας στη έξοδο. Το µέγεθος αυτής της επίδρασης εξαρτάται από την απόκλιση του ρεύµατος (ενέργειας), αλλά δεν είναι καθόλου ασυνήθιστο να παρατηρήσουµε φασµατικά εύρη µεγαλύτερα από 10 GHz σα συνέπεια του chirp.
48 Σχήµα 4.5. Το όριο της χρωµατικής διασποράς µε την απόσταση και το bit rate της µετάδοσης πάνω από µία πρότυπη µονοτροπική ίνα µε τι µη χρωµατικής διασποράς D=17ps/nm-km. Έχει παρατηρηθεί ένα σφάλµα χρωµατικής διασποράς των 2 db στη περίπτωση του NRZ. Αυτό δείχνει ότι το εύρος του διευρυµένου παλµού κυµαίνεται µε ένα κλάσµα της περιόδου bit. Για πηγές µε στενό φασµατικό εύρος, το φασµατικό εύρος του διαµορφωµένου σήµατος σε GHz υπολογίζεται να είναι 2.5 φορές µεγαλύτερο του bit rate σε Gb/s. Για µετάδοση RZ το εύρος του παλµού εξόδου υπολογίζεται να είναι λιγότερο από το διάστηµα µεταξύ bit. Η επίδραση του chirp µπορεί να µειωθεί µε την ελλάτωση τους ρυθµούς απώλειας. Το φασµατικό εύρος µπορεί να αυξηθεί εξαιτίας των πίσω-ανακλάσεων από τους connectors, τα συγκολλητικά στοιχεία ή καλύτερα splices καθώς και άλλα στοιχεία του οπτικού µονοπατιού. Για να εµποδίσουµε αυτήν την επίδραση, τα υψηλής ταχύτητας laser συνήθως πακετάρονται µε built-in αποµονωτές. Για εξωτερικά διαµορφωµένες πηγές το φασµατικό εύρος είναι ανάλογο στο bit rate. Υποθέτοντας ότι το φασµατικό εύρος είναι περίπου 2.5 φορές το bit rate, τότε ένα 10Gb/s εξωτερικά διαµορφωµένο σήµα έχει φασµατικό εύρος 25 GHz, το οποίο και είναι σήµερα ένας πρακτικός αριθµός. Στα 1.55µm, αυτό αντιστοιχεί σε ένα φασµατικό εύρος τον 0.2 nm χρησιµοποιώντας 2 2 τη σχέση λ = ( c/ f ) f = ( λ / c) f 2 Αντικαθιστώντας λ = ( λ / c)2.5b στη σχέση που προαναφέρθηκε παίρνουµε 2 2 λ / c 0.4 D LB < ε, ή Β λ D L/ c < 0.4ε. Για D=17ps/nm-km, λ=1.55km και ε=0.491 (2dB ποινής), η παραπάνω σχέση δίνει τη 2 2 συνθήκη Β L< 8327( Gb/ s) km. Αυτό το όριο φαίνεται και στο σχήµα. 4.5.
49 Οι περιορισµοί της χρωµατικής διασποράς είναι πολύ πιο χαλαροί από το φασµατικό εύρος στενής πηγής. Αυτό µπορεί να γίνει κατανοητό αν θεωρήσουµε την µεγάλη εξάπλωση των στενών φασµατικού εύρους SLM laser για high bit rate επικοινωνία. Επίσης, οι εξωτερικοί διαµορφωτές χρησιµοποιούνται για µετάδοση µακρινής απόστασης (περισσότερα από µερικές εκατοντάδες χιλιόµετρα) στα 2.5Gb/s και στα περισσότερα 10Gb/s συστήµατα RZ ιαµόρφωση Σε αυτή τη παράγραφο, µελετάµε τους περιορισµούς που υπάρχουν στα συστήµατα και οι οποίοι απορρέουν από τη χρωµατική διασπορά για γκαουσιανούς παλµούς που δεν χρησιµοποιούν την τεχνική chirp και οι οποίοι χρησιµοποιούνται σε συστήµατα που χρησιµοποιούν RZ διαµόρφωση [17]. Τα αποτελέσµατα µπορούν άµεσα να επεκταθούν και στην περίπτωση γκαουσιανών παλµών µε τη τεχνική chirp. Ας θεωρήσουµε µία ίνα µήκους L. Το εύρος του παλµού εξόδου βρίσκεται από τον τύπο: T L β L = T + ( ) T0 Αυτό είναι το µέσο εύρος του παλµού σε 1/e µέγεθος έντασης. Ένα διαφορετικό και πιο σύνηθες µέγεθος του εύρους του παλµού είναι το root-mean square ή (rms) εύρος του Τ rms. Για ένα παλµό A(t) το Τ rms ορίζεται ως T rms = 2 2 t A( t) dt 2 At ( ) dt Για γκαούσιαν παλµούς των οποίων το µέσο εύρος σε κλίµακα έντασης 1/e είναι Τ 0, ισχύει T = T / 2 rms 0 Αν επικοινωνούµε µε ένα bit rate των B bits/s η περίοδος του bit είναι (1/Β) s. Θα θεωρήσουµε ότι η ικανοποιητική επικοινωνία είναι εφικτή µόνο εάν το εύρος του παλµού που µετριέται µε το εύρος rms T rms είναι µικρότερο από µία περίοδο bit.( Ικανοποιητική επικοινωνία µπορεί να είναι εφικτή ακόµα και αν το εύρος του παλµού εξόδου είναι µεγαλύτερο από την περίοδο bit, µε µία σχετική ενεργειακή απόκλιση στη περίπτωση των NRZ συστηµάτων). Έτσι, BT < 2. L T = T / 2 < 1/ B ή ιαµέσου της παραπάνω συνθήκης, η χρωµατική διασπορά θέτει περιορισµό στο µήκος του συνδέσµου επικοινωνίας που µπορούµε να χρησιµοποιήσουµε για ένα bit rate B χωρίς συνέπειες διασποράς. Το T L είναι συνάρτηση του T 0 και έτσι µπορεί να rms L L
50 ελαχιστοποιηθεί µε τη κατάλληλη επιλογή του T 0. Η βέλτιστη επιλογή του T 0 είναι: opt T = β L. 0 2 opt Για τη συγκεκριµένη επιλογή του T 0 η τοµή του T L είναι: TL = 2 β2 L. Ο λόγος για την ύπαρξη ενός βέλτιστου εύρους παλµού είναι ο ακόλουθος. Εάν ο παλµός γίνεται πολύ «στενός» µε το χρόνο, τότε θα έχει ένα µεγάλο φασµατικό εύρος και έτσι µεγαλύτερη διασπορά και εξάπλωση. Το βέλτιστο εύρος παλµού προκύπτει από µία «συναλλαγή» µεταξύ δύο παραγόντων. Για τη βέλτιστη επιλογή του T 0, η συνθήκη BT L < 2 γίνεται B 2 β 2 L < 2. Συνήθως η τιµή του β 2 καθορίζεται έµµεσα από τη παράµετρο διασποράς D, που σχετίζεται µε το β 2 από την ισότητα: 2π c D = 2 β 2 λ Επίσης: D L Bλ 2π c < Για D=17ps/nm-km, προκύπτει Β L< 46152( Gb/ s) km. Αυτό το όριο φαίνεται στο σχήµα 4.5. Το όριο είναι µεγαλύτερο από το όριο της NRZ διαµόρφωσης όταν το φασµατικό εύρος καθορίζεται από το εύρος ζώνης διαµόρφωσης (για παράδειγµα για εξωτερική διαµόρφωση ενός SLM laser). Όµως και για την RZ και την NRZ µετάδοση, το bit rate Β κλιµακώνεται σε σχέση µε το 1/ L. Τα όρια διασποράς και για παλµούς που δεν χρησιµοποιούν την τεχνική chirp. Μία τυπική τιµή της chirp παραµέτρου κ για ένα άµεσα διαµορφώσιµο ηµιαγωγικό laser στα 1.55µm είναι -6 και επίσης το β2 είναι αρνητικό έτσι ώστε να γίνονται πιο ευρείς οι µονοτονικοί παλµοί. Εάν όµως η Chirp τεχνική υπάρχει θετικό πρόσηµο, τότε µπορεί να αλληλεπιδράσει µε την διασπορά και να προκαλέσει συµπίεση παλµού. Οι RZ παλµοί που χρησιµοποιούν τη τεχνική chirp µπορούν να εκµεταλλευτούν τις συνέπειες του παραπάνω γεγονότος LPF ιαµόρφωση Έστω l i το µήκος του τµήµατος ίνας i (σε χιλιόµετρα). Η τιµή της επαγόµενης από τη 1 διασπορά ποινής (σε db) υπολογίζεται µε βάση την έκφραση P = 10log 1 2, γ li 4( ) 2 2 λ DCD B όπου γ. 2 c
51 Σχήµα 4.6: Η τιµή της επαγόµενης από τη διασπορά ποινής ως συνάρτηση του µήκους τµήµατος της ίνας για D CD ίση µε 17 ps/ nm km, ρυθµούς µετάδοσης των 2.5 και 10 Gb / s και µε διάταξη διαµόρφωσης NRZ. Η ακριβής τιµή της παραµέτρου γ επιλέγεται µε τρόπο ώστε να ταιριάζει στα πειραµατικά αποτελέσµατα [1]. Για παράδειγµα, το πειραµατικό αποτέλεσµα του σχήµατος 4.6. Στην εξίσωση της τιµής της επαγόµενης από τη διασπορά ποινής, το B είναι ο ρυθµός bit, το λ είναι η ζώνη µήκους κύµατος και το c είναι η ταχύτητα του φωτός. Θεωρείται πως για Β ίσο µε 10Gb/s και για τυπικά τµήµατα ίνας µε D CD ίση µε 17 ps/nm km, το κατώφλι των 2dB εµφανίζεται περίπου στα 50km αν χρησιµοποιείται διάταξη διαµόρφωσης NRZ (προσεγγίζοντας έτσι το αντίστοιχο αποτέλεσµα της εικόνας 4.1) και περίπου στα 140km αν χρησιµοποιείται διάταξη διαµόρφωσης LPF. Όταν το κατώφλι ποινής και ο ρυθµός bit είναι σταθερά, η εξίσωση της τιµής της επαγόµενης από τη διασπορά ποινής οδηγεί σε µια αντιστρόφως ανάλογη σχέση ανάµεσα στην παράµετρο D CD και το l i. Έτσι υπολογίζεται και το κριτικό µήκος τµήµατος ίνας (αυτό στο οποίο εµφανίζεται το κατώφλι ποινής των 2dB) για διαφορετικές τιµές της D CD. Ας θεωρηθούν, για παράδειγµα, ρυθµοί δεδοµένων των 10Gb/s και νεότερες ίνες µε παράµετρο D CD ίση µε 8 ps/ nm km. Το κατώφλι ποινής των 2dB, τότε, εµφανίζεται στο αυξηµένο 17 µήκος τµήµατος ίνας των περίπου 50 = 106 km αν χρησιµοποιείται διάταξη 8 17 διαµόρφωσης NRZ και των περίπου 140 = 297 km αν χρησιµοποιείται διάταξη 8 διαµόρφωσης LPF. Το ίδιο εφαρµόζεται και στους ρυθµούς bit, αφού µε σταθερή την παράµετρο D CD το κριτικό µήκος τµήµατος ίνας αυξάνεται αντιστρόφως ανάλογα µε το Β 2. Ας θεωρηθούν, για παράδειγµα, ρυθµοί δεδοµένων των 2.5Gb/s και ίνες µε µια τυπική παράµετρο D των 17 ps/nm km. Το κατώφλι ποινής των 2dB, τότε, CD 10 εµφανίζεται στο αυξηµένο µήκος τµήµατος ίνας των περίπου 50 = 800 αν 2.5 χρησιµοποιείται διάταξη διαµόρφωσης NRZ (προσεγγίζοντας έτσι το αντίστοιχο αποτέλεσµα της εικόνας 4.1) και των περίπου = km αν
52 χρησιµοποιείται διάταξη διαµόρφωσης LPF. Τα παραπάνω οδηγούν στον ακόλουθο περιορισµό για το µέγιστο επιτρεπτό µήκος διαφανούς µονοπατιού, που αποτελείται από Μ τµήµατα ίνας (σε χιλιόµετρα), εξαιτίας της εξασθένησης CD: M d li < 2 D B i= 1 CD Όπου d = αν χρησιµοποιείται διάταξη διαµορφωσης NRZ και d = αν χρησιµοποιείται διάταξη διαµόρφωσης LPF. Αν η παράµετρος CD διαφέρει από τµήµα ίνας σε τµήµα ίνας, προκύπτει ένας πιο γενικευµένος περιορισµός. Έστω D CD, i η παράµετρος CD του τµήµατος ίνας i. Τότε, M d DCD, ili < 2 B i= 1 Σε υψηλότερους ρυθµούς bit, η εξασθένηση CD αρχίζει να αποτελεί τεράστιο πρόβληµα, ακόµα και για τυπικές µητροπολιτικές αποστάσεις. Ας θεωρηθούν, για παράδειγµα, ρυθµοί bit των 20, 30 και 40Gb/s, λόγω του παραπάνω περιορισµού, το κριτικό µήκος τµήµατος ίνας µειώνεται σε 74, 33 και 19km αντίστοιχα, στην περίπτωση (του καλύτερου δυνατού σεναρίου) των νεότερων ινών µε παράµετρο D CD ίση µε 8 ps/nm km και της χρησιµοποίησης διάταξης διαµόρφωσης LPF. Στην πράξη, οι σχεδιαστές των MANs ξεπερνούν αυτό το εµπόδιο µε το να χρησιµοποιούν µονάδες εξουδετέρωσης διασποράς (Dispersion Compensation Modules DCMs) σε όλους τους κόµβους του δικτύου. Οι DCMs είναι συσκευές που µπορούν και ακυρώνουν τη συγκεντρωµένη CD στο τέλος µιας ίνας. Στη περίπτωση αυτή, ο περιορισµός είναι να µην υπάρχει καµία ίνα σε κάθε µονοπάτι των Μ τµηµάτων ίνας, στην οποία να ξεπερνιέται το προκαθορισµένο κατώφλι ποινής. ηλαδή, max i= 1: M d < ή (αν η CD D B {} l i 2 CD D διαφέρει από ίνα σε ίνα) max { DCD i, li} i= 1: M d < B, 2 Σε κάθε περίπτωση, η µόνη πληροφορία εξαρτώµενη απ τους συνδέσµους που απαιτεί ένας RWA λογάριθµος για να θέσει το αντίστοιχο σύνολο περιορισµών, είναι το µήκος και η τιµή τη παραµέτρου CD του κάθε τµήµατος ίνας. 4.3 Θόρυβος ASE ASE Amplifier Spontaneous Emission Οι ενισχυτές χρησιµοποιούνται σε τρεις διαφορετικές διατάξεις. Ένας οπτικός προενισχυτής χρησιµοποιείται µπροστά από το δέκτη για να βελτιώσει την ευαισθησία του. Ένας ενισχυτής ισχύος χρησιµοποιείται µετά από τον ποµπό για να αυξήσει την ισχύ της εξόδου. Ένας ενισχυτής χρησιµοποιείται τυπικά στη µέση ενός συνδέσµου για να εξουδετερώσει τις απώλειες του συνδέσµου. Ο ενισχυτής δεν είναι µια τέλεια συσκευή. Υπάρχουν διάφορες ατέλειες που πρέπει να ληφθούν υπόψη, όταν
53 χρησιµοποιούνται ενισχυτές σε ένα σύστηµα. Ο ενισχυτής εισάγει θόρυβο, µαζί µε το κέρδος που παρέχει. Το κέρδος του ενισχυτή εξαρτάται από τη συνολική ισχύ εισόδου. Στο σύστηµα µε οπτικούς ενισχυτές, το σήµα ενισχύεται σε κάθε στάδιο ενίσχυσης χωρίς επαναπροσδιορισµό των αποτελεσµάτων λόγω των µη γραµµικοτήτων από το προηγούµενο τµήµα (span). Κατά συνέπεια το αποδοτικό µήκος σε ένα τέτοιο σύστηµα είναι το άθροισµα των αποδοτικών µηκών κάθε τµήµατος. Ο θόρυβος ASE (Amplifier Spontaneous Emission) υποβιβάζει τον λόγο του οπτικού σήµατος προς θόρυβο (Optical Signal to Noise Ratio OSNR). Ένα αποδεκτό οπτικό επίπεδο SNR (SNRmin), που εξαρτάται από τον ρυθµό µετάδοσης, την τεχνολογία ποµπού-δέκτη, και τα περιθώρια που διατίθενται για τις εξασθενήσεις, πρέπει να διατηρηθούν στο δέκτη. Προκειµένου να ικανοποιηθεί αυτή η απαίτηση, οι προµηθευτές παρέχουν συχνά κάποιο γενικό κανόνα από την άποψη του µέγιστου µήκους του διάφανου (transparent) τµήµατος και του αριθµού των τµηµάτων (spans). Για παράδειγµα, τα συστήµατα µετάδοσης περιορίζονται συχνά σε 6 τµήµατα µε κάθε τµήµα ίσο µε 80km. Για µεγαλύτερες περιοχές, απαιτούνται πιο λεπτοµερείς υπολογισµοί OSNR για να καθορίσουν εάν το επίπεδο OSNR είναι αποδεκτό. Αυτό θα παρείχε ευελιξία στην εγκατάσταση ή την αποκατάσταση ενός lightpath µέσω ενός διαφανούς υποδικτύου (transparent subnetwork). Υποθέτοντας ότι το lightpath από τον ποµπό στο δέκτη περνά από M οπτικούς ενισχυτές, µε κάθε έναν από αυτούς να εισάγει κάποια ισχύ θορύβου και ότι κάθε οπτικός ενισχυτής έχει το ίδιο κέρδος ισχύος G, µπορούµε να λάβουµε έναν άνω όριο για το Μ, δηλ., ο µέγιστος αριθµός των spans, ο περιορισµός του OSNR δίνεται ως εξής: M P L 2SNRminnsphv( G 1) Bo όπου P L είναι η µέση οπτική ισχύς του ποµπού, n sp είναι ο παράγοντας αυθόρµητης 34 εκποµπής, h= J / Hz είναι η σταθερά του Planck, v είναι η συχνότητα του φέροντος και B o είναι το οπτικό εύρος ζώνης. Όταν χρησιµοποιούνται διαφορετικοί τύποι οπτικών ενισχυτών για να αντιµετωπίσουν διαφορετικές απώλειες ισχύος στα επιµέρους τµήµατα ίνας (spans), το κέρδος ενισχυτή και ο παράγοντας αυθόρµητης εκποµπής µπορεί να ποικίλουν και συµβολίζονται ως G( k) και nsp ( k ), αντίστοιχα k = 1,2,..., M. Θεωρώντας ότι όλοι οι ενισχυτές εκπέµπουν την ίδια ισχύ, ο περιορισµός γίνεται: M L nsp ( k) ( G( k) 1) k = 1 2hvBoSNRmin P Σε ένα πραγµατικό δίκτυο ένα τυπικό παράδειγµα έχει ως εξής: P = 4dBm, SNR = db (όταν δεν χρησιµοποιείται Forward Error Correction FEC), min 20 n sp = 2.5, G = 25dB µε hvbo = 58dBm, χρησιµοποιώντας τον παραπάνω περιορισµό, ο µέγιστος αριθµός από spans είναι το πολύ ίσος µε 10. Εάν η απαίτηση για το SNR min είναι ίσο µε 25dB (δεν χρησιµοποιείται FEC), ο µέγιστος αριθµός από spans γίνεται ίσος µε 3. L
54 Σχήµα 4.7. Ωφέλιµο µήκος (effective length) µετάδοσης σα συνάρτηση του µήκους l Ωφέλιµο Μήκος (Effective Length) Σε Ενισχυµένα Συστήµατα Σε συστήµατα µε οπτικούς ενισχυτές, το σήµα ενισχύεται σε κάθε στάδιο ενίσχυσης, χωρίς όµως να απαλλάσσεται από τις συνέπειες της µη-γραµµικότητας που συνέβησαν στο προηγούµενο διάστηµα της ίνας. Έτσι το ωφέλιµο µήκος (effective length) σε ένα τέτοιο σύστηµα είναι το άθροισµα των ωφέλιµων µηκών (effective length) κάθε διαστήµατος της ίνας. Σε ένα σύνδεσµο µήκους L, µε ενισχυτές να έχουν τοποθετηθεί ανά l km, το ωφέλιµο µήκος (effective length) δίνεται από τον τύπο L e 1 e = a αl L l Στο σχήµα 4.7 φαίνεται η γραφική παράσταση του ωφέλιµου µήκους (effective length) έναντι του πραγµατικού µήκους (actual length) του συνδέσµου µετάδοσης συστηµάτων ενισχυµένων και µη. Από αυτό το σχήµα λοιπόν φαίνεται ότι για να µειώσουµε το ωφέλιµο µήκος (effective length), είναι καλύτερα να χρησιµοποιούµε λιγότερους ενισχυτές τοποθετηµένους περισσότερο αραιά. Όµως το ότι συµβαίνει στο σύστηµα σχετικό µε τις µη-γραµµικότητες δεν έχει να κάνει µόνο µε το ωφέλιµο µήκος (effective length). Ουσιαστικά είναι το γινόµενο της ισχύος P και του ωφέλιµου µήκους (effective length) L e. Τώρα λοιπόν, αυτό που µας ενδιαφέρει είναι πως το γινόµενο PL e αυξάνεται µε το l. Αυτό φαίνεται καλύτερα στο σχήµα 4.8. Στο σχήµα αυτό φαίνεται ότι οι επιδράσεις της µη-γραµµικότητας µπορούν να ελαττωθούν ελαττώνοντας το διάστηµα µεταξύ των ενισχυτών. Αν και το γεγονός
55 αυτό µπορεί να κάνει πιο εύκολη τη σχεδίαση των ενισχυτών (χρειάζονται λιγότερο κέρδος), χρειαζόµαστε όµως περισσότερους ενισχυτές αυξάνοντας το κόστος του συστήµατος. Οι συνέπειες µίας διασπαρµένης µη-γραµµικότητας, εξαρτάται από το PL e και επίσης αυξάνεται µε την αύξηση της ισχύος εισόδου και µε το µήκος του συνδέσµου. Όσο µακρύτερος είναι ο σύνδεσµος τόσο µεγαλύτερη είναι η ενέργεια που χάνεται από το σήµα (pump ενέργεια) και διοχετεύεται στο κύµα Stokes. Για ένα δοσµένο µήκος συνδέσµου, ένα προσεγγιστικό µέγεθος του επιπέδου ενέργειας στο οποίο η επίδραση της µη-γραµµικότητας αρχίζει να γίνεται πολύ σηµαντική είναι το κατώφλι ενέργειας (threshold power). Για ένα δοσµένο µήκος ίνας, το κατώφλι ενέργειας µίας διασπαρµένης µη-γραµµικότητας ορίζεται ως η οπτική ενέργεια ανά κανάλι µέσα στην ίνα όπου οι ενέργεια Stokes και η pump ενέργεια είναι ισοδύναµες. Στα συστήµατα που υπάρχουν ενισχυτές, το κατώφλι ενέργειας ελαττώνεται εξαιτίας της αύξησης του ωφέλιµου µήκους (effective length). Αυτό κάνει τα συστήµατα που διαθέτουν ενισχυτές πιο ευάλωτα σε εξασθενίσεις εξαιτίας µη-γραµµικοτήτων. Σχήµα 4.8. Η σχετική τιµή PL e σε αντιδιαστολή µε το διάστηµα µεταξύ ενισχυτών. Ο κατακόρυφος άξονας είναι η τιµή που έχει να κάνει µε τα διαστήµατα µεταξύ ενισχυτών. α=0.22 db/km.
56 4.4 Crosstalk Το οπτικό crosstalk αναφέρεται στην επίδραση των άλλων σηµάτων στο επιθυµητό σήµα. Περιλαµβάνει τόσο το συµφασικό crosstalk όσο και το µη συµφασικό crosstalk. Βασικοί συνεισφορείς του crosstalk είναι οι τοποθεσίες των WXC και WADM που χρησιµοποιούν MUX/DEMUX ζεύγη. Για ένα σχετικά αραιό δίκτυο όπου το πλήθος των κόµβων των WXCs και WADMs είναι χαµηλό, το crosstalk µπορεί να αντιµετωπιστεί µε ένα χαµηλό περιθώριο στο OSNR, χωρίς να αποτελεί σοβαρό δεσµευτικό περιορισµό. Για κάποιο σχετικά πυκνό δίκτυο όπου το crosstalk µπορεί να αποτελέσει δεσµευτικό περιορισµό, χρειάζεται κάθε φορά να διαδίδεται η πληροφορία του ανά συνδέσµου crosstalk για να εξασφαλιστεί το γεγονός ότι το συνολικό crosstalk του µονοπατιού, που αποτελεί το άθροισµα των crosstalks σε όλους τους αντίστοιχους συνδέσµους, βρίσκεται µέσα σε κάποιο αποδεκτό όριο. Ένας άλλος τρόπος να αντιµετωπιστεί το crosstalk χωρίς να απαιτηθεί διάδοση πληροφορίας, είναι να εκτιµηθεί από το σύστηµα ο µέγιστος αριθµός από κόµβους WXC και WADM για το χειρότερο δροµολόγιο στο διαφανές πεδίο για ένα χαµηλό ενσωµατωµένο περιθώριο. Η λύση αυτή αναµένεται να δουλεύει καλά, αν όλοι οι κόµβοι WXC και WADM έχουν παρόµοιο επίπεδο crosstalk.
57 5 ΡΟΜΟΛΟΓΗΣΗ ΒΑΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΕΞΑΣΘΕΝΗΣΕΩΝ Σε ένα wavelength routed δίκτυο η ποιότητα του σήµατος εξαρτάται από ένα πλήθος από εξασθενήσεις που εισάγονται από τη γραµµή µετάδοσης ή από τα switches. Αυτό µπορεί να αποφευχθεί χρησιµοποιώντας αναγεννητές ανά κανάλι σε επιλεγµένους κόµβους του δικτύου. Αυτή η επιλογή έχει όµως µεγάλο κόστος. Οι σχεδιαστές δικτύων µπορούν να χρησιµοποιήσουν κατάλληλους αλγορίθµους RWA που λαµβάνουν υπόψη τις εξασθενήσεις του σήµατος [4]. Τέτοιοι αλγόριθµοι περιορίζουν τη δροµολόγηση των καναλιών µήκους κύµατος έτσι ώστε είναι σε συµφωνία µε τα φυσικά χαρακτηριστικά και τους περιορισµούς των οπτικών µονοπατιών. Σε transparent δίκτυα η δροµολόγηση που λαµβάνει υπόψη τις φυσικές εξασθενήσεις (impairment constrained based routing ICBR) [16], [23], [24] µπορεί να χρησιµοποιηθεί ως εργαλείο για performance engineering µε στόχο την επιλογή feasible µονοπατιών ενώ µειώνεται η blocking probability για νέες αιτήσεις σύνδεσης. Το ICBR µπορεί να χρησιµοποιηθεί για να παρέχει QoS (Quality of Service) [10] στο δίκτυο. ιαφορετικές συνδέσεις µπορεί να έχουν διαφορετικές απαιτήσεις σε ότι αφορά την ποιότητα του λαµβανόµενου σήµατος. Εφόσον αυτό συνδέεται στενά µε τους περιορισµούς που κάθε εξασθένηση επιβάλει, είναι προφανές ότι το ICBR µπορεί να συµπεριληφθεί στον µηχανισµό δροµολόγησης για να παρέχει εξυπνότερη δροµολόγηση και να παρέχονται διάφορα επίπεδα QoS. Οι δυσκολίες της προσέγγισης ICBR πηγάζουν από την ετερογενή φύση και ένα σύνολο από περιορισµούς που πρέπει να ληφθούν υπόψη για να µειωθεί η blocking probability. Από τη µία πλευρά υπάρχουν φυσικές εξασθενήσεις (π.χ. chromatic dispersion, polarization mode dispersion, amplifier spontaneous emission, crosstalk), από την άλλη πλευρά υπάρχουν παράµετροι που σχετίζονται µε την απόδοση του δικτύου (π.χ. blocking probability, end-to-end delay, throughput) που περιγράφουν τη συνολική απόδοση των WDM οπτικών δικτύων. Οι ICBR αλγόριθµοι που έχουν προταθεί [7], [9], χωρίζονται σε κάποιες φάσεις. Αρχικά υπάρχει µία φάση προεπεξεργασίας όπου όλες οι πληροφορίες που σχετίζονται µε τα χαρακτηριστικά του δικτύου και απαιτήσεις κίνησης συγκεντρώνονται. Οι πληροφορίες δικτύου περιλαµβάνει την τοπολογία του δικτύου, εξοπλισµό (τύπος των κόµβων, ικανότητες µετατροπής µήκους κύµατος κτλ.), το modulation format, την χωρητικότητα του συνδέσµου, τα χαρακτηριστικά της ίνας. Τα χαρακτηριστικά της κίνησης περιλαµβάνουν πληροφορίες όπως είναι ο αριθµός των αιτήσεων, οι τελικοί κόµβοι και ο ρυθµός µετάδοσης. Ο υπολογισµός των link costs εξαρτάται από τους τύπους εξασθένησης που θέλουµε να λάβουµε υπόψη κάθε φορά. Η επόµενη φάση περιλαµβάνει την εκτέλεση του RWA αλγορίθµου. Για κάθε αίτηση σύνδεσης ένα σύνολο από k ελάχιστα µονοπάτια επιλέγεται και ένα γραµµικό πρόβληµα βελτιστοποίησης µε σκοπό την ελαχιστοποίηση του κόστους που παράγεται από όλες τις ροές στο δίκτυο. Η φάση impairment constraint routing ελέγχει την εγκυρότητα των lightpaths που παραδίδονται από την προηγούµενη φάση (RWA). Ένα µονοπάτι εγκαθίσταται αν το προτεινόµενο lightpath ικανοποιεί όλους τους περιορισµούς που καθορίζονται από τις εξασθενήσεις που λαµβάνονται υπόψη κάθε φορά. Εάν το προτεινόµενο lightpath δεν ικανοποιεί τις απαιτήσεις εξασθένησης, το µονοπάτι διαγράφεται από το σύνολο των k ελάχιστων και επιλέγεται ένα νέο µονοπάτι από αυτό το σύνολο. Αν κανένα από τα k µονοπάτια δεν ικανοποιεί τους περιορισµούς εξασθένησης, η σύνδεση µπλοκάρεται.
58 Άλλοι αλγόριθµοι RWA µε περιορισµούς στην ποιότητα του σήµατος για να βελτιώσουν την blocking probability, επεκτείνουν κλασσικούς αλγόριθµους RWA. Σε αντιστοιχία µε τους αλγορίθµους shortest path (SP), first fit (FF) και random (RAND) προτείνονται οι impairment based αλγόριθµοι IBSP, IBFF, IBRAND. IBSP Step1: Για µία νέα αίτηση σύνδεσης, βρες το διαθέσιµο συντοµότερο µονοπάτι για κάθε µήκος κύµατος. Αν δεν βρεθεί κανένα µονοπάτι για κάθε µήκος κύµατος η αίτηση µπλοκάρεται, λόγω έλλειψης µηκών κύµατος. Step 2: Επέλεξε ένα µήκος κύµατος, του οποίου το αντίστοιχο µονοπάτι έχει τη µικρότερη απόσταση. Step 3: Υπολόγισε την ποιότητα του σήµατος π.χ. BER για το µονοπάτι που επιλέχθηκε στο Step 2 στον κόµβο προορισµού. Step 4: Αν το BER ικανοποιεί την απαίτηση, χρησιµοποίησε αυτό το µήκος κύµατος και το αντίστοιχο µονοπάτι για να γίνει set up η κλήση (lightpath). ιαφορετικά, επανέλαβε τα βήµατα 2 µε 4 για τον έλεγχο των µονοπατιών για τα εναποµείναντα µήκη κύµατος. Αν κανένα µήκος κύµατος δεν µπορεί να ικανοποιήσει την απαίτηση για BER, τότε η προσπάθεια για εγκατάσταση αυτής της κλήσης αποτυγχάνει. Ο αλγόριθµος τερµατίζει και το σύστηµα είναι έτοιµο να επεξεργαστεί την επόµενη εισερχόµενη κλήση. Όµοια λειτουργούν και οι άλλοι δύο αλγόριθµοι. 5.1 Αναπαράσταση ικτύου Με Φυσικές Εξασθενήσεις Όπως έχει αναφερθεί σε προηγούµενο κεφάλαιο µία σταθερή τοπολογία δικτύου αναπαρίσταται από ένα συνεκτικό γράφο GVE (, ). Το V αναπαριστά το σύνολο των κόµβων του δικτύου, έστω N = V. Το E αναπαριστά το σύνολο των συνδέσµων του δικτύου, έστω L= E. Κάθε σύνδεσµος περιλαµβάνει µία οπτική ίνα και κάθε οπτική ίνα υποστηρίζει W διαφορετικά µήκη κύµατος. Επίσης ένας σύνδεσµος από τον, uv, κόµβο u στον κόµβο v αναπαρίσταται µε ( uv ). Κάθε σύνδεσµος ( ) συσχετίζεται µε n προσθετικά βάρη w ( u, v) 0, i = 1,..., n. Κάθε βάρος w ( u, v) 0 i αναπαριστά µία φυσική εξασθένηση του συνδέσµου. Ένα µονοπάτι από τον s στον d συµβολίζεται µε p ( sd, ) = su, 1,..., uj, d, όπου..., u1,..., u j,... είναι οι ενδιάµεσοι κόµβοι. Κάθε σύνδεσµος l συσχετίζεται µε ένα κόστος I l, το οποίο εξαρτάται από το µήκος του συνδέσµου και από την φυσική παράµετρο-εξασθένηση που λαµβάνεται υπόψη κάθε φορά. Όσον αφορά το µονοπάτι, το συνολικό κόστος του µονοπατιού ορίζεται ως το άθροισµα των εξασθενήσεων των επιµέρους συνδέσµων. Μία φυσική εξασθένηση µπορεί να είναι µία από τις παρακάτω: I = { CD PMD ASE} Η παράµετρος εξασθένησης στον σύνδεσµο i αναπαρίσταται ως < CD, PMD, ASE >. Εποµένως για κάθε σύνδεσµο έχουµε i i i wl ( i) CDi, PMDi, ASEi προορισµό d συµβολίζεται µε path [ weight, weight,..., weight ] =< > και κατά συνέπεια ένα µονοπάτι από την πηγή s στον =, ή sd 1 2 n sd i
59 (,, ),(,, ),...,(,, ) path = CD PMD ASE CD PMD ASE CD PMD ASE, όπου n sd n n n sd είναι ο αριθµός των συνδέσµων κατά µήκος του µονοπατιού. Το συνολικό κόστος του µονοπατιού θα πρέπει να είναι τελικά µικρότερο από ένα δοσµένο άνω όριο. Έστω ότι το D CD αναπαριστά την χρωµατική διασπορά, το D PMD την διασπορά τρόπου πόλωσης, το ASE τον θόρυβο ASE και l είναι το µήκος του συνδέσµου. Η τιµή του κόστους I l είναι ίση µε: l ( PMD) 2 PMD D l =, όταν αναφέρεται η PMD παράµετρος CDl = DCD l, όταν αναφέρεται η CD παράµετρος ASE l, ο συνολικός αριθµός των ενισχυτών που υπάρχουν στον σύνδεσµο l, όταν αναφέρεται η παράµετρος του θορύβου ASE. Ο αριθµός των ενισχυτών που τοποθετούνται σε κάθε ίνα εξαρτάται από το κέρδος του ενισχυτή G, το µήκος και τον συντελεστή εξασθένησης στην ίνα. Εφόσον όλες οι εξασθενήσεις είναι γραµµικές, η εισαγωγή τους στην LP µοντελοποίηση είναι σχετικά απλό θέµα. 5.2 Απόρριψη Αιτήσεων Λόγω Φυσικών Εξασθενήσεων Τοποθέτηση Περιορισµών Μετά Την Επίλυση Του RWA Ο αλγόριθµος RWA επιλύεται όπως περιγράφεται στην παράγραφο 3.4 σύµφωνα µε την µοντελοποίηση ΙΙ (LP2). Στην συνέχεια τα οπτικά µονοπάτια τα οποία δεν ικανοποιούν τους φυσικούς περιορισµούς απορρίπτονται. Αυτό συµβαίνει στην περίπτωση που δεν υπάρχουν αναγεννητές σήµατος. Η παραµόρφωση του σήµατος συσσωρεύεται σε κάθε σύνδεσµο κατά µήκος ενός αµιγώς-οπτικού µονοπατιού. Το πόσο µακριά µπορεί να δροµολογηθεί µία σύνδεση πλήρως οπτικά, εξαρτάται από το πόσο συσσωρεύονται οι φυσικές εξασθενήσεις χωρίς να ξεπερνούν ένα κατώφλι. Το συνολικό κόστος ενός µονοπατιού p είναι το άθροισµα του κόστους όλων των συνδέσµων που χρησιµοποιεί το µονοπάτι. ( ) N p wl ( i ), N( p): i= 1 αριθµός των συνδέσµων στο µονοπάτι Υποθέτουµε το κάθε αίτηση σύνδεσης έχει την ακόλουθη µορφή. max request =< i, j, weight >, where i = πηγη, j = προορισµος και ij ij max max max max weight =< CD, PMD, ASE > είναι οι µέγιστες τιµές των εξασθενήσεων ij ij ij ij που µία σύνοδος µπορεί να διαχειριστεί. Θεωρώντας ότι έχουµε αυτές τις τρεις φυσικές εξασθενήσεις κάθε µονοπάτι θα ικανοποιεί το όριο των φυσικών εξασθενήσεων εάν ικανοποιεί τις παρακάτω ανισότητες.
60 n max CDi < CD και i= 1 ή i I i n max PMDi < PMD και i= 1 threshold n i= 1 < impairment φυσική εξασθένηση ASE i < ASE Όπου i = i ος σύνδεσµος του οπτικού µονοπατιού. Αν δεν ισχύουν οι παραπάνω ανισότητες, τότε η αίτηση σύνδεσης απορρίπτεται. Οι µέγιστες τιµές που µπορούν να λάβουν οι φυσικές εξασθενήσεις είναι αυτές που παρουσιάστηκαν στο προηγούµενο κεφάλαιο. Συνοπτικά αφού εκτελεστεί ο αλγόριθµος RWA, υπολογίζεται η ποιότητα του σήµατος για κάθε οπτικό µονοπάτι, σύµφωνα µε τα παραπάνω κριτήρια. Εάν το BER δεν ικανοποιεί τις απαιτήσεις (παραβιάζονται οι ανισότητες), τότε το οπτικό µονοπάτι και κατά συνέπεια οι σύνδεση απορρίπτεται. Αυτός ο απλός αλγόριθµος που εισάγει τις φυσικές εξασθενήσεις εκτελείται για να αντιληφθούµε πως αυτές οι εξασθενήσεις επηρεάζουν την blocking probability. max Τοποθέτηση Περιορισµών Πριν Την Επίλυση Του RWA Για κάθε αίτηση σύνδεσης υπολογίζεται ένα σύνολο από k εναλλακτικά µονοπάτια χρησιµοποιώντας κάποιον αλγόριθµος δροµολόγησης συντοµότερου µονοπατιού, για παράδειγµα τον αλγόριθµο Dijkstra όπως παρουσιάστηκε σε προηγούµενο κεφάλαιο. Λαµβάνοντας υπόψη τις φυσικές εξασθενήσεις, ένα σύνολο παραµένει στο σύνολο των k µονοπατιών, εάν ικανοποιεί όλους τους φυσικούς περιορισµούς. Εάν το µονοπάτι δεν ικανοποιεί αυτές τις απαιτήσεις, τότε διαγράφεται από το σύνολο των k συντοµότερων µονοπατιών [11]. Τέλος λύνεται το πρόβληµα LP, χρησιµοποιώντας το σύνολο των υποψήφιων µονοπατιών που παραµένει από αυτή τη διαδικασία. Έστω { µονοπατια απο τον s στον d} K = και sd sd p K sd i, 1 i k. for 1 i k sd έλεγχος εάν το µονοπάτι p έχει επιθυµητή ποιότητα σήµατος i (όπως παρουσιάστηκε στο προηγούµενο κεφάλαιο) sd if η ποιότητα του σήµατος του p είναι αποδεκτή i Ksd = Ksd else sd K = K p end end { } sd sd i Τελικά το σύνολο K sd περιέχει µόνο µονοπάτια από τον κόµβο s στον κόµβο d που έχουν αποδεκτή ποιότητα σήµατος. Το BER είναι κάτω από ένα προκαθορισµένο κατώφλι.
61 Αυτό το σύνολο χρησιµοποιείται και το επιλύεται το πρόβληµα του γραµµικού προγραµµατισµού. Τα οπτικά µονοπάτια που θα προκύψουν τελικά από την επίλυση του RWA προβλήµατος, θα ικανοποιούν όλους τους φυσικούς περιορισµούς που λήφθηκαν υπόψη Τοποθέτηση Περιορισµών Μέσα Στην LP Μοντελοποίηση Εφόσον οι περιορισµοί είναι γραµµικοί, η εισαγωγή τους στην LP µοντελοποίηση είναι ένα σχετικά απλό θέµα. Οι περιορισµοί είναι: wl, I λ impairment, p P max l plw p ή max CDlλ plw CDp, wl, max PMDlλ plw PMDp και wl, max ASElλ plw ASEp p P wl, max όπου impairment p αναπαριστά την µέγιστη αποδεκτή τιµή του περιορισµού εξασθένησης για ένα µονοπάτι p. Για κάθε αίτηση σύνδεσης όµως επιλέγεται µόνο ένα µονοπάτι, ανεξάρτητα από τον αριθµό υποψηφίων µονοπατιών k (όταν το Λsd παίρνει µοναδιαίες τιµές), κατά συνέπεια ο παραπάνω περιορισµός µπορεί να µετατραπεί σε περιορισµό για κάθε αίτηση σύνδεσης. Μόνο ένα από τα k υποψήφια µονοπάτια επιλέγεται και τα άλλα απορρίπτονται. Λαµβάνοντας αυτό υπόψη, στην LP µοντελοποίηση για κάθε αίτηση σύνδεσης θα έχουµε µία ανισότητα (για κάθε φυσική εξασθένηση) και όχι k. Έστω Psd = { p1,..., pk}, είναι το σύνολο των k υποψηφίων µονοπατιών για την αίτηση σύνδεσης req από τον s στον d όπου P= P. Παράµετροι: w C : ένα διαθέσιµο µήκος κύµατος p P : ένα υποψήφιο µονοπάτι l E: ένας σύνδεσµος του δικτύου P P: µονοπάτια µία αίτησης σύνδεσης sd s d sd
62 Σταθερές: I l : η τιµή της φυσικής εξασθένησης για τον σύνδεσµο l 2 PMD = D l, όταν αναφέρεται η PMD παράµετρος o l ( PMD) o CDl = DCD l, όταν αναφέρεται η CD παράµετρος o ASE l, ο συνολικός αριθµός των ενισχυτών που υπάρχουν στον σύνδεσµο l, όταν αναφέρεται η παράµετρος του θορύβου ASE. Ο αριθµός των ενισχυτών που τοποθετούνται σε κάθε ίνα εξαρτάται από το κέρδος του ενισχυτή G, το µήκος και τον συντελεστή εξασθένησης στην ίνα. impairment Μεταβλητές: max p : η µέγιστη επιτρεπτή τιµή εξασθένησης για το µονοπάτι p λ plw : µία δείκτρια µεταβλητή η οποία έχει την τιµή 1 όταν το µονοπάτι p καταλαµβάνει τον σύνδεσµο l και το µήκος κύµατος c και 0 σε όλες τις άλλες περιπτώσεις Fl = f λ plw = f λ plw : η συνολική ροή στον σύνδεσµο l p P p P w C w C D : ο συνολικός αριθµός των ενεργών καναλιών του δικτύου κατά µήκος του p i µονοπατιού Με άλλα λόγια η µεταβλητή των άλλων συνόδων που επηρεάζουν το µονοπάτι p i πλην τον αριθµό των συνδέσµων που αποτελείται το µονοπάτι. D p i είναι ο αριθµός των ενεργών καναλιών όλων p i. Το πρόβληµα µπορεί να µοντελοποιηθεί ως ακολούθως: ΜΟΝΤΕΛΟΠΟΙΗΣΗ III pi Ελαχιστοποίηση : m D + F l E, p P Έτσι ώστε 1. λ 1 l E, w C p plw ' 2. λplw = λ ' p P pl w ( l l ) 3. sd p i l l και, ειναι διαδοχικοι συνδεσµοι στο p λplw =Λsd l που είναι ο πρώτος σύνδεσµος στο p w p Psd λplw =Λsd l που είναι ο τελευταίος σύνδεσµος στο p w p P
63 λplw= D j p p i i P, w C, j E, l Ei 4. Fl f λplw p w wl,, j j i max Ilλplw impairmentreq, p Psd, Psd wl,, p P Ο περιορισµός 6 χρησιµοποιείται για να αποφύγουµε την εγκατάσταση οπτικών µονοπατιών, τα οποία δεν έχουν αποδεκτά όρια φυσικών εξασθενήσεων. Η παραπάνω µοντελοποίηση οδηγεί όµως σε µεγάλο blocking probability κάθε φορά που κάθε ένα από τα k υποψήφια µονοπάτια, για τουλάχιστον µία από τις αιτήσεις σύνδεσης, δεν ικανοποιεί τον παραπάνω περιορισµό και αυτό συµβαίνει αρκετά συχνά όσο οι παράµετροι εξασθένησης γίνονται µεγαλύτεροι. Στην περίπτωση δηλαδή που έχουµε µία αίτηση και κανένα από τα k υποψήφια µονοπάτια δεν ικανοποιεί τους περιορισµούς εξασθένησης, τότε από την µοντελοποίηση III δεν θα προκύπτει εφικτή λύση Τοποθέτηση Των Περιορισµών Με Τη Μορφή Μεταβλητών Μία πιθανή λύση µπορεί να προκύψει, παίρνοντας τους φυσικούς περιορισµούς ως µεταβλητές. Για να ξεπεράσουµε το πρόβληµα που προκύπτει από το προηγούµενο κεφάλαιο, οι φυσικές εξασθενήσεις δεν χρησιµοποιούνται ως hard constraints. Παράµετροι: w C : ένα διαθέσιµο µήκος κύµατος p P : ένα υποψήφιο µονοπάτι l E: ένας σύνδεσµος του δικτύου P P: µονοπάτια µία αίτησης σύνδεσης sd Σταθερές: I l : η τιµή της φυσικής εξασθένησης για τον σύνδεσµο l 2 PMD = D l, όταν αναφέρεται η PMD παράµετρος o l ( PMD) o CDl = DCD l, όταν αναφέρεται η CD παράµετρος o ASE l, ο συνολικός αριθµός των ενισχυτών που υπάρχουν στον σύνδεσµο l, όταν αναφέρεται η παράµετρος του θορύβου ASE. Ο αριθµός των ενισχυτών που τοποθετούνται σε κάθε ίνα εξαρτάται από
64 το κέρδος του ενισχυτή G, το µήκος και τον συντελεστή εξασθένησης στην ίνα. impairment : η µέγιστη επιτρεπτή τιµή εξασθένησης για το µονοπάτι p max p Μεταβλητές: λ plw : µία δείκτρια µεταβλητή η οποία έχει την τιµή 1 όταν το µονοπάτι p καταλαµβάνει τον σύνδεσµο l και το µήκος κύµατος c και 0 σε όλες τις άλλες περιπτώσεις Fl = f λ plw = f λ plw : η συνολική ροή στον σύνδεσµο l p P p P w C w C D : ο συνολικός αριθµός των ενεργών καναλιών του δικτύου κατά µήκος του p i µονοπατιού Με άλλα λόγια η µεταβλητή των άλλων συνόδων που επηρεάζουν το µονοπάτι D P sd p i πλην τον αριθµό των συνδέσµων που αποτελείται το µονοπάτι. D p i είναι ο αριθµός των ενεργών καναλιών όλων p i. : Κάθε µονοπάτι µπορεί να διαχειριστεί µία εξασθένηση µέχρι ένα όριο. Το επιπλέον της φυσικής εξασθένησης που επιβάλλεται σε ένα µονοπάτι από αυτό που µπορεί να διαχειριστεί περιγράφεται από την µεταβλητή D. req Το σύνολο των περιορισµών λόγω φυσικών εξασθενήσεων για κάθε αίτηση µπορεί να εκφραστεί ως εξής: max Ilλplw DP impairment, sd req p Psd, Psd wl,, p P Το πρόβληµα µπορεί να µοντελοποιηθεί ως ακολούθως: ΜΟΝΤΕΛΟΠΟΙΗΣΗ IV i Ελαχιστοποίηση : m1 D + F + m2 D l E, p P, P P Έτσι ώστε 1. λ 1 l E, w C p plw ' 2. λplw = λ ' p P pl w ( l l ) 3. p l Psd i sd p l P i sd και, ειναι διαδοχικοι συνδεσµοι στο p λplw =Λsd l που είναι ο πρώτος σύνδεσµος στο p w p Psd
65 λplw =Λsd l που είναι ο τελευταίος σύνδεσµος στο p w p Psd λplw= D j p p i i P, w C, j E, l Ei 4. Fl f λplw p w wl,, j j i max Ilλplw DP impairment, sd req p Psd, Psd wl,, p P Το επιπρόσθετο objective είναι να ελαχιστοποιηθεί το άθροισµα των τιµών του κόστους των µονοπατιών λόγω των φυσικών εξασθενήσεων που επιλέγονται για να εξυπηρετηθεί το σύνολο των αιτήσεων σύνδεσης. Το objective είναι να ελαχιστοποιηθούν οι µεταβλητές D P sd. Για την αίτηση σύνδεσης req i από τον κόµβο s στον κόµβο d υπάρχουν k υποψήφια µονοπάτια. Ελαχιστοποιώντας την µεταβλητή D P sd επιλέγεται ένα µονοπάτι από τα k υποψήφια, το οποίο έχει το ελάχιστο κόστος λόγω εξασθενήσεων. Αυτή η επίλυση του προβλήµατος είναι βέλτιστη και εφόσον δεν χρησιµοποιούµε τους περιορισµούς ως hard constraints δεν προκύπτουν λύσεις που να είναι µη εφικτές όπως στην προηγούµενη παράγραφο. Στην περίπτωση που η µεταβλητή D P sd δεν είναι µηδέν, τότε το αντίστοιχο µονοπάτι δεν ικανοποιεί τις φυσικές εξασθενήσεις. Στην περίπτωση που αυτή η µεταβλητή είναι µηδέν, τότε το αντίστοιχο µονοπάτι ικανοποιεί τις φυσικές εξασθενήσεις. Εποµένως τα µονοπάτια που προκύπτουν µε DP sd 0 θα πρέπει να απορριφθούν. Η νέα µοντελοποίηση έχει το πλεονέκτηµα ότι έχει λύση ακόµη και όταν το αρχικό δεν έχει λύση. Η λύση που προκύπτει από αυτή την µοντελοποίηση µπορεί να χρησιµοποιηθεί στον σχεδιασµό δικτύων για την τοποθέτηση στοιχείων στο δίκτυο για την βελτιστοποίηση την ποιότητα του σήµατος ενός µονοπατιού. Τέλος τα οπτικά µονοπάτια που προκύπτουν από την επίλυση του RWA προβλήµατος και δεν ικανοποιούν τους φυσικούς περιορισµούς απορρίπτονται. 5.3 Μοντελοποίηση Του Crosstalk Στα WDM δίκτυα το σήµα καθώς µεταδίδεται χάνει την ποιότητά του εξαιτίας φυσικών ατελειών οι οποίες εξαρτώνται από την τοπολογία του δικτύου και τις φυσικές εξασθενήσεις. Σε αυτή την παράγραφο λαµβάνουµε υπόψη την παρεµβολή µεταξύ διαφορετικών ενεργών καναλιών (µήκη κύµατος που χρησιµοποιούνται) στην ίδια οπτική ίνα. Η διασυµβολική παρεµβολή εξαρτάται από τα ενεργά κανάλια που υπάρχουν στην ίνα και κυρίως από τα γειτονικά. Στην δυναµική περίπτωση του RWA µπορούµε να υπολογίσουµε την επίδραση των ενεργών καναλιών επειδή τα µήκη κύµατος έχουν ήδη εγκατασταθεί. Στην στατική περίπτωση όµως το πρόβληµα θα πρέπει να θεωρηθεί ως ενιαίο πρόβληµα επειδή τα οπτικά µονοπάτια δεν είναι
66 γνωστά εκ των προτέρων. Εισάγουµε λοιπόν τον περιορισµό που επιβάλει η παρεµβολή καναλιών στο RWA πρόβληµα να µην ξεπερνάει ένα άνω όριο. Σχήµα 5.1: Γειτονικά µήκη κύµατος. Ορισµοί Απόσταση µεταξύ δύο µηκών κύµατος d w, w d w w =, w { i} απόσταση: ( i i+ 1) ( i i+ 1 ) i =, wi C. Γειτονικά µήκη κύµατος ύο µήκη κύµατος λέγονται γειτονικά αν η απόσταση µεταξύ τους είναι d w, w + = 1. ( ) i i 1 Παρεµβολή δύο µηκών κύµατος στον ίδιο σύνδεσµο: ύο µήκη κύµατος αλληλεπιδρούν εάν η απόσταση µεταξύ τους είναι ίση µε 1. Σχήµα 5.2: Παρεµβολή µεταξύ δύο γειτονικών µηκών κύµατος, όπου c 1 είναι το σήµα και c 2 ο παρεµβολέας (crosstalk interferer). Το οπτικό crosstalk αναφέρεται στην επίδραση άλλων σηµάτων στο επιθυµητό σήµα. Το παραπάνω σχήµα απεικονίζει την παρεµβολή µεταξύ δύο διαφορετικών µηκών κύµατος, Τα σήµατα ταξιδεύοντας σε διαφορετικά κανάλια διαρρέουν στα διπλανά εξαιτίας µη γραµµικότητας στην ίνα. Ένα αποδεκτό οπτικό επίπεδο SNR (SNRmin) χρειάζεται να διατηρηθεί στον δέκτη. Εισάγουµε τον περιορισµό του crosstalk στο RWA να είναι κάτω από ένα προκαθορισµένο άνω όριο για κάθε οπτικό µονοπάτι για να διασφαλίσουµε ένα αποδεκτό OSNR στον προορισµό. Για να εξετάσουµε την επίδραση του interchannel crosstalk στην blocking probability του RWA προβλήµατος υλοποιούµε τον παρακάτω hard constraint. λ + λ + aλ D + a, p P l plw i 1 plw i+ 1 pl w j i ISI l όπου a : σταθερά, w C
67 D ISI, είναι η µέγιστη επιθυµητή παρεµβολή µεταξύ µηκών κύµατος που µπορεί να διαχειριστεί ένα µονοπάτι. l j : ο πρώτος σύνδεσµος του µονοπατιού p. a, if wi = 1 ( ενεργο) aλpl jw = i, 0, διαφορετικα o Στην περίπτωση όπου aλ pl jw = a i (Σχήµα 5.3α) ο παραπάνω περιορισµός γίνεται λ + λ D και υπολογίζεται ο l plwi 1 plwi+ 1 ISI l αριθµός των µηκών κύµατος που επηρεάζουν το σήµα (Σχήµα 5.3α) w o Στην περίπτωση όπου aλ i pl, = l = 0 (το µονοπάτι θα απορριφθεί και ο start περιορισµός του crosstalk δεν θα πρέπει να ληφθεί υπόψη) ο παραπάνω περιορισµός γίνεται λ + λ D + a. Με l plwi 1 plwi+ 1 ISI l µία σχετικά µεγάλη σταθερά, η ανισότητα είναι αληθής και δεν επηρεάζει το RWA πρόβληµα (Σχήµα 5.3β). λ + λ : το άθροισµα των µηκών κύµατος που επηρεάζουν το plwi 1 plwi+ 1 l l σήµα. Μόνο γειτονικά µήκη κύµατος αυξάνουν το crosstalk. Ας υποθέσουµε ότι υπάρχει µία αίτηση σύνδεσης από τον κόµβο Α στον κόµβο Ε. Ένα ενδεχόµενο µονοπάτι είναι το { ABCDE,,,, }. Το σχήµα α) δείχνει την περίπτωση όπου ένα οπτικό µονοπάτι από τον Α στον Ε υπολογίζεται και χρησιµοποιεί το µήκος κύµατος 2. Σε αυτή την περίπτωση πρέπει να υπολογίσουµε το crosstalk για αυτό το οπτικό µονοπάτι. Το σχήµα β) δείχνει ότι το µονοπάτι { A, BCDE,,, } δεν χρησιµοποιείται και το crosstalk γι αυτό το µονοπάτι δεν θα πρέπει να ληφθεί υπόψη. Σχήµα 5.3 α: Ένα ενεργό µήκος κύµατος αναπαρίσταται µε µία γραµµή. Το οπτικό µονοπάτι από τον Α στον Ε χρησιµοποιεί το µήκος κύµατος 2. Το crosstalk υπολογίζεται ως το άθροισµα των γειτονικών ενεργών µηκών κύµατος. aλ = a και ο περιορισµός γίνεται λ + λ D pl w j i l plwi 1 plwi+ 1 ISI l
68 Σχήµα 5.3β: Το µήκος κύµατος 2 είναι ανενεργό. Το crosstalk υπολογίζεται όπως το σχήµα 5.3α). aλ pl 0 jw = και ο περιορισµός γίνεται i λplw + λ i 1 plw D i 1 ISI a +. Όταν το a είναι + l l αρκετά µεγάλο, η ανισότητα είναι αληθής. Είναι το ίδιο µε το να γνωρίζαµε εκ των προτέρων ότι το µήκος κύµατος 2 στο µονοπάτι { A, BCDE,,, } δεν θα χρησιµοποιηθεί και δεν θα χρειαζόταν κάποιος περιορισµός. ΜΟΝΤΕΛΟΠΟΙΗΣΗ V Ελαχιστοποίηση : m1 D + F + m2 D l E, p P, P P Έτσι ώστε 1. λ 1 l E, w C p plw ' 2. λplw = λ ' p P pl w ( l l ) 3. pi l Psd i sd pi l Psd και, ειναι διαδοχικοι συνδεσµοι στο p λplw =Λsd l που είναι ο πρώτος σύνδεσµος στο p w p Psd λplw =Λsd l που είναι ο τελευταίος σύνδεσµος στο p w p Psd λplw= D j p p i i P, w C, j E, l Ei 4. Fl f λplw p w wl,, j j i max Ilλplw DP impairment, sd req p Psd, Psd wl,, p l plw i 1 plw i+ 1 pl w j i ISI l P λ + λ + aλ D + a, p P, w C
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής
 Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στατικοί αλγόριθμοι δρομολόγησης και ανάθεσης μηκών κύματος για ημιδιαφανή οπτικά δίκτυα
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στατικοί αλγόριθμοι δρομολόγησης και ανάθεσης μηκών κύματος για ημιδιαφανή οπτικά δίκτυα
Οπτικά Δίκτυα. Εγκατάσταση Οπτικών Διαδρομών (Lightpath Setup) και δρομολόγηση
 Οπτικά Δίκτυα Εγκατάσταση Οπτικών Διαδρομών (Lightpath Setup) και δρομολόγηση Εισαγωγή Στα αμιγώς οπτικά δίκτυα παρέχονται συνδέσεις στους πελάτες με τη μορφή των lightpahts. Η μεταγωγή των lightpaths
Οπτικά Δίκτυα Εγκατάσταση Οπτικών Διαδρομών (Lightpath Setup) και δρομολόγηση Εισαγωγή Στα αμιγώς οπτικά δίκτυα παρέχονται συνδέσεις στους πελάτες με τη μορφή των lightpahts. Η μεταγωγή των lightpaths
Τηλεπικοινωνιακά Δίκτυα Ευρείας Ζώνης Ενότητα 10: Οπτικές Τηλεπικοινωνίες Διατάξεις και Τεχνολογίες Δικτύου
 Δίκτυα Ευρείας Ζώνης Ενότητα 10: Οπτικές Τηλεπικοινωνίες Διατάξεις και Τεχνολογίες Δικτύου Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σύντομη
Δίκτυα Ευρείας Ζώνης Ενότητα 10: Οπτικές Τηλεπικοινωνίες Διατάξεις και Τεχνολογίες Δικτύου Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σύντομη
Πολύπλεξη μήκους κύματος Wavelength Division Multiplexing
 Πολύπλεξη μήκους κύματος Wavelength Division Multiplexing Η πολυπλεξία μήκους κύματος (WDM) επιτρέπει την παράλληλη μετάδοση πολλών υψίρυθμων ψηφιακών σημάτων (TDM) δια μέσου του ίδιου ζεύγους οπτικών
Πολύπλεξη μήκους κύματος Wavelength Division Multiplexing Η πολυπλεξία μήκους κύματος (WDM) επιτρέπει την παράλληλη μετάδοση πολλών υψίρυθμων ψηφιακών σημάτων (TDM) δια μέσου του ίδιου ζεύγους οπτικών
ιαδίκτυα & Ενδοδίκτυα Η/Υ
 ιαδίκτυα & Ενδοδίκτυα Η/Υ (Kεφ. 10) ΡΟΜΟΛΟΓΗΣΗ Χαρακτηριστικά Στρατηγικές ροµολόγησης Παραδείγµατα Βιβλίο Μαθήµατος: Επικοινωνίες Υπολογιστών & εδοµένων, William Stallings, 6/e, 2000. ΕΥ - κεφ.10 (2/3)
ιαδίκτυα & Ενδοδίκτυα Η/Υ (Kεφ. 10) ΡΟΜΟΛΟΓΗΣΗ Χαρακτηριστικά Στρατηγικές ροµολόγησης Παραδείγµατα Βιβλίο Μαθήµατος: Επικοινωνίες Υπολογιστών & εδοµένων, William Stallings, 6/e, 2000. ΕΥ - κεφ.10 (2/3)
(Light Emitting Diodes)
 ΕξαρτήµαταΟπτικών ικτύων Πηγές Φωτεινής δέσµης ίοδοι Εκϖοµϖής Φωτός(LED) Συσκευές Laser ίοδοι Εκποµπής Φωτός (LED) (Light Emitting Diodes) - Παράγουν δεδοµένα µε χαµηλό ρυθµό (Ταχύτητα
ΕξαρτήµαταΟπτικών ικτύων Πηγές Φωτεινής δέσµης ίοδοι Εκϖοµϖής Φωτός(LED) Συσκευές Laser ίοδοι Εκποµπής Φωτός (LED) (Light Emitting Diodes) - Παράγουν δεδοµένα µε χαµηλό ρυθµό (Ταχύτητα
Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η. Αρχές Δικτύων Επικοινωνιών
 Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η Αρχές Δικτύων Επικοινωνιών Τι είναι επικοινωνία; Είναι η διαδικασία αποστολής πληροφοριών από ένα πομπό σε κάποιο δέκτη. Η Τηλεπικοινωνία είναι η επικοινωνία από απόσταση (τηλε-).
Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η Αρχές Δικτύων Επικοινωνιών Τι είναι επικοινωνία; Είναι η διαδικασία αποστολής πληροφοριών από ένα πομπό σε κάποιο δέκτη. Η Τηλεπικοινωνία είναι η επικοινωνία από απόσταση (τηλε-).
Ολοκληρωµένα ικτυακά ΣυστήµαταΚορµού (Backbone Networks)
 Ολοκληρωµένα ικτυακά ΣυστήµαταΚορµού (Backbone Networks) Βασικές τεχνολογίες για δίκτυα κορµού (backbone networks) ο συνδυασµός της οπτικής τεχνολογίας WDM µε δικτυακές τεχνολογικές βαθµίδες υψηλοτέρων
Ολοκληρωµένα ικτυακά ΣυστήµαταΚορµού (Backbone Networks) Βασικές τεχνολογίες για δίκτυα κορµού (backbone networks) ο συνδυασµός της οπτικής τεχνολογίας WDM µε δικτυακές τεχνολογικές βαθµίδες υψηλοτέρων
1η Οµάδα Ασκήσεων. Τµήµα επεξεργασίας σήµατος του αναγεννητή
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΡΙΑΚΟ ΠΑΝΕΠΙΣΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΙΚΩΝ ΕΠΙΣΗΜΩΝ ΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΥΑ ΟΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης 1η Οµάδα Ασκήσεων Άσκηση 1η Εγκατεστηµένη ζεύξη συνολικού
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΡΙΑΚΟ ΠΑΝΕΠΙΣΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΙΚΩΝ ΕΠΙΣΗΜΩΝ ΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΥΑ ΟΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης 1η Οµάδα Ασκήσεων Άσκηση 1η Εγκατεστηµένη ζεύξη συνολικού
Κεφάλαιο 3 Πολυπλεξία
 Κεφάλαιο 3 Πολυπλεξία Μάθημα 3.1: Μάθημα 3.2: Μάθημα 3.3: Πολυπλεξία επιμερισμού συχνότητας χρόνου Συγκριτική αξιολόγηση τεχνικών πολυπλεξίας Στατιστική πολυπλεξία Μετάδοση Δεδομένων Δίκτυα Υπολογιστών
Κεφάλαιο 3 Πολυπλεξία Μάθημα 3.1: Μάθημα 3.2: Μάθημα 3.3: Πολυπλεξία επιμερισμού συχνότητας χρόνου Συγκριτική αξιολόγηση τεχνικών πολυπλεξίας Στατιστική πολυπλεξία Μετάδοση Δεδομένων Δίκτυα Υπολογιστών
Αρχές Δικτύων Επικοινωνιών. Επικοινωνίες Δεδομένων Μάθημα 4 ο
 Αρχές Δικτύων Επικοινωνιών Επικοινωνίες Δεδομένων Μάθημα 4 ο Τα επικοινωνιακά δίκτυα και οι ανάγκες που εξυπηρετούν Για την επικοινωνία δύο συσκευών απαιτείται να υπάρχει μεταξύ τους σύνδεση από σημείο
Αρχές Δικτύων Επικοινωνιών Επικοινωνίες Δεδομένων Μάθημα 4 ο Τα επικοινωνιακά δίκτυα και οι ανάγκες που εξυπηρετούν Για την επικοινωνία δύο συσκευών απαιτείται να υπάρχει μεταξύ τους σύνδεση από σημείο
Πρωτόκολλα Ελέγχου προσπέλασης μέσου
 Πρωτόκολλα Ελέγχου προσπέλασης μέσου Πρόβλημα: ταυτόχρονη μετάδοση δύο ή περισσότερων κόμβων στο ίδιο κανάλι (μήκος κύματος). Ένα τέτοιο γεγονός ονομάζεται σύγκρουση. Ένα πρωτόκολλο MAC έχει συνήθως ως
Πρωτόκολλα Ελέγχου προσπέλασης μέσου Πρόβλημα: ταυτόχρονη μετάδοση δύο ή περισσότερων κόμβων στο ίδιο κανάλι (μήκος κύματος). Ένα τέτοιο γεγονός ονομάζεται σύγκρουση. Ένα πρωτόκολλο MAC έχει συνήθως ως
Μάθηµα 9 ο : Συστήµατα πολλαπλής πρόσβασης
 Μάθηµα 9 ο : Συστήµατα πολλαπλής πρόσβασης Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Τι είναι οι τεχνικές πολλαπλής πρόσβασης και ποια η ανάγκη χρήσης τους στις δορυφορικές επικοινωνίες
Μάθηµα 9 ο : Συστήµατα πολλαπλής πρόσβασης Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Τι είναι οι τεχνικές πολλαπλής πρόσβασης και ποια η ανάγκη χρήσης τους στις δορυφορικές επικοινωνίες
ADAPTIVE DISTRIBUTED ROUTING AND TRAFFIC CONTROL IN OPTICAL NETWORKS
 University of Macedonia Master Information Systems Networking Technologies Professor: A.A. Economides economid@uom.gr ADAPTIVE DISTRIBUTED ROUTING AND TRAFFIC CONTROL IN OPTICAL NETWORKS LEONIDAS OXOUZOGLOU
University of Macedonia Master Information Systems Networking Technologies Professor: A.A. Economides economid@uom.gr ADAPTIVE DISTRIBUTED ROUTING AND TRAFFIC CONTROL IN OPTICAL NETWORKS LEONIDAS OXOUZOGLOU
ίκτυα Υπολογιστών και Επικοινωνία ίκτυα Υπολογιστών & Επικοινωνία ΙΑΛΕΞΗ 8 Η Παντάνο Ρόκου Φράνκα 1 ιάλεξη 8: Το Φυσικό Επίπεδο
 ίκτυα Υπολογιστών & Επικοινωνία ΙΑΛΕΞΗ 8 Η ιδάσκουσα: Παντάνο Ρόκου Φράνκα Παντάνο Ρόκου Φράνκα 1 ιάλεξη 8 η : Το Φυσικό Επίπεδο Το Φυσικό Επίπεδο ιάδοση Σήµατος Ηλεκτροµαγνητικά Κύµατα Οπτικές Ίνες Γραµµές
ίκτυα Υπολογιστών & Επικοινωνία ΙΑΛΕΞΗ 8 Η ιδάσκουσα: Παντάνο Ρόκου Φράνκα Παντάνο Ρόκου Φράνκα 1 ιάλεξη 8 η : Το Φυσικό Επίπεδο Το Φυσικό Επίπεδο ιάδοση Σήµατος Ηλεκτροµαγνητικά Κύµατα Οπτικές Ίνες Γραµµές
Τηλεπικοινωνιακά Δίκτυα Ευρείας Ζώνης Ενότητα 11: Οπτικά Δίκτυα Πρόσβασης Διατάξεις και Τεχνολογίες Δικτύου
 Τηλεπικοινωνιακά Δίκτυα Ευρείας Ζώνης Ενότητα 11: Οπτικά Δίκτυα Πρόσβασης Διατάξεις και Τεχνολογίες Δικτύου Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί
Τηλεπικοινωνιακά Δίκτυα Ευρείας Ζώνης Ενότητα 11: Οπτικά Δίκτυα Πρόσβασης Διατάξεις και Τεχνολογίες Δικτύου Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί
Περιεχόμενα. Πρόλογος 9. Ευχαριστίες 15
 1 Περιεχόμενα Πρόλογος 9 Ευχαριστίες 15 1 Εισαγωγή 17 1.1 Πλεονεκτήματα της Οπτικής Ίνας ως Μέσο Μετάδοσης 21 1.2 Βασικές Τεχνικές Πολύπλεξης 24 1.3 Ιστορική Εξέλιξη των Οπτικών Δικτύων Βασικοί Σταθμοί
1 Περιεχόμενα Πρόλογος 9 Ευχαριστίες 15 1 Εισαγωγή 17 1.1 Πλεονεκτήματα της Οπτικής Ίνας ως Μέσο Μετάδοσης 21 1.2 Βασικές Τεχνικές Πολύπλεξης 24 1.3 Ιστορική Εξέλιξη των Οπτικών Δικτύων Βασικοί Σταθμοί
8 η ιάλεξη: σε δίκτυα δεδομένων
 Εργαστήριο ικτύων Υπολογιστών 8 η ιάλεξη: Βασικές αρχές δρομολόγησης Βασικές αρχές δρομολόγησης σε δίκτυα δεδομένων ρομολόγηση (Routing) Μεταφορά μηνυμάτων μέσω του διαδικτύου από μία πηγή σε ένα προορισμό
Εργαστήριο ικτύων Υπολογιστών 8 η ιάλεξη: Βασικές αρχές δρομολόγησης Βασικές αρχές δρομολόγησης σε δίκτυα δεδομένων ρομολόγηση (Routing) Μεταφορά μηνυμάτων μέσω του διαδικτύου από μία πηγή σε ένα προορισμό
Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η
 Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η Αρχές Δικτύων Επικοινωνιών Σελ. 9-50 Γεώργιος Γιαννόπουλος ΠΕ19, ggiannop (at) sch.gr http://diktya-epal-b.ggia.info/ Creative Commons License 3.0 Share-Alike Σύνδεση από σημείο
Κεφάλαιο 1 Ε Π Α Ν Α Λ Η Ψ Η Αρχές Δικτύων Επικοινωνιών Σελ. 9-50 Γεώργιος Γιαννόπουλος ΠΕ19, ggiannop (at) sch.gr http://diktya-epal-b.ggia.info/ Creative Commons License 3.0 Share-Alike Σύνδεση από σημείο
Κεφάλαιο 4ο: Δικτυωτή Ανάλυση
 Κεφάλαιο ο: Δικτυωτή Ανάλυση. Εισαγωγή Η δικτυωτή ανάλυση έχει παίξει σημαντικό ρόλο στην Ηλεκτρολογία. Όμως, ορισμένες έννοιες και τεχνικές της δικτυωτής ανάλυσης είναι πολύ χρήσιμες και σε άλλες επιστήμες.
Κεφάλαιο ο: Δικτυωτή Ανάλυση. Εισαγωγή Η δικτυωτή ανάλυση έχει παίξει σημαντικό ρόλο στην Ηλεκτρολογία. Όμως, ορισμένες έννοιες και τεχνικές της δικτυωτής ανάλυσης είναι πολύ χρήσιμες και σε άλλες επιστήμες.
7.9 ροµολόγηση. Ερωτήσεις
 7.9 ροµολόγηση Ερωτήσεις 1. Να δώσετε τον ορισµό της δροµολόγησης; 2. Από τι εξαρτάται η χρονική στιγµή στην οποία λαµβάνονται οι αποφάσεις δροµολόγησης; Να αναφέρετε ποια είναι αυτή στην περίπτωση των
7.9 ροµολόγηση Ερωτήσεις 1. Να δώσετε τον ορισµό της δροµολόγησης; 2. Από τι εξαρτάται η χρονική στιγµή στην οποία λαµβάνονται οι αποφάσεις δροµολόγησης; Να αναφέρετε ποια είναι αυτή στην περίπτωση των
«ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ»
 ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ
 ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής
 Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στα πλαίσια του μεταπτυχιακού προγράμματος ειδίκευσης: Επιστήμη και Τεχνολογία Των Υπολογιστών
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στα πλαίσια του μεταπτυχιακού προγράμματος ειδίκευσης: Επιστήμη και Τεχνολογία Των Υπολογιστών
Bασική διάταξη τηλεπικοινωνιακού συστήµατος οπτικών ινών
 ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ - διαφάνεια 1 - Bασική διάταξη τηλεπικοινωνιακού συστήµατος οπτικών ινών ιαµορφωτής Ηλεκτρικό Σήµα Ποµπός Οπτικό Σήµα Οπτική Ίνα διαµορφωτής: διαµορφώνει τη φέρουσα συχνότητα
ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ - διαφάνεια 1 - Bασική διάταξη τηλεπικοινωνιακού συστήµατος οπτικών ινών ιαµορφωτής Ηλεκτρικό Σήµα Ποµπός Οπτικό Σήµα Οπτική Ίνα διαµορφωτής: διαµορφώνει τη φέρουσα συχνότητα
Οπτικά Δίκτυα Επικοινωνιών
 Οπτικά Δίκτυα Επικοινωνιών Ενότητα 2: Δίκτυα Πολυπλεξίας Μήκους Κύματος (WDM Δίκτυα) Βλάχος Κυριάκος Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Ο σκοπός της ενότητας είναι η
Οπτικά Δίκτυα Επικοινωνιών Ενότητα 2: Δίκτυα Πολυπλεξίας Μήκους Κύματος (WDM Δίκτυα) Βλάχος Κυριάκος Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Ο σκοπός της ενότητας είναι η
ΟΠΤΙΚΕΣ ΙΝΕΣ ΕΡΓΑΣΙΑ ΣΤΗ ΧΗΜΕΙΑ ΣΥΝΤΕΛΕΣΤΕΣ:ΝΙΚΟΛΑΣ ΚΙΜΠΙΖΗΣ ΝΙΚΟΛΑΣ ΠΑΞΙΝΟΣ
 ΟΠΤΙΚΕΣ ΙΝΕΣ ΕΡΓΑΣΙΑ ΣΤΗ ΧΗΜΕΙΑ ΣΥΝΤΕΛΕΣΤΕΣ:ΝΙΚΟΛΑΣ ΚΙΜΠΙΖΗΣ ΝΙΚΟΛΑΣ ΠΑΞΙΝΟΣ ΤΙ ΕΙΝΑΙ ΟΙ ΟΠΤΙΚΕΣ ΙΝΕΣ Τι είναι οι οπτικές ίνες λοιπόν; Οι οπτικές ίνες, είναι πολύ λεπτά νήματα από πλαστικό ή γυαλί, όπου
ΟΠΤΙΚΕΣ ΙΝΕΣ ΕΡΓΑΣΙΑ ΣΤΗ ΧΗΜΕΙΑ ΣΥΝΤΕΛΕΣΤΕΣ:ΝΙΚΟΛΑΣ ΚΙΜΠΙΖΗΣ ΝΙΚΟΛΑΣ ΠΑΞΙΝΟΣ ΤΙ ΕΙΝΑΙ ΟΙ ΟΠΤΙΚΕΣ ΙΝΕΣ Τι είναι οι οπτικές ίνες λοιπόν; Οι οπτικές ίνες, είναι πολύ λεπτά νήματα από πλαστικό ή γυαλί, όπου
2η Οµάδα Ασκήσεων. 250 km db/km. 45 km 0.22 db/km 1:2. T 75 km 0.22 db/km 1:2. 75 km db/km. 1:2 225 km 0.22 db/km
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η Στη ζεύξη που φαίνεται
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η Στη ζεύξη που φαίνεται
1 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. / 2. Οι όροι Eb. και Ec
 Τµήµα Μηχανικών Υπολογιστών, Τηλεπικοινωνιών και ικτύων ΗΥ 44: Ασύρµατες Επικοινωνίες Εαρινό Εξάµηνο -3 ιδάσκων: Λέανδρος Τασιούλας η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Θεωρήστε ένα κυψελωτό σύστηµα, στο οποίο ισχύει το
Τµήµα Μηχανικών Υπολογιστών, Τηλεπικοινωνιών και ικτύων ΗΥ 44: Ασύρµατες Επικοινωνίες Εαρινό Εξάµηνο -3 ιδάσκων: Λέανδρος Τασιούλας η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Θεωρήστε ένα κυψελωτό σύστηµα, στο οποίο ισχύει το
Αστικά δίκτυα και δίκτυα κορμού. Αλέξανδρος Σταυδάς Tέταρτος Κύκλος
 Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Tέταρτος Κύκλος Προστασία στa SONET/SDH Οπτικές ίνες σε χρήση και οπτικές ίνες προστασίας Γραμμικές τοπολογίες προστασίας Δύο κόμβοι συνδέονται με δύο
Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Tέταρτος Κύκλος Προστασία στa SONET/SDH Οπτικές ίνες σε χρήση και οπτικές ίνες προστασίας Γραμμικές τοπολογίες προστασίας Δύο κόμβοι συνδέονται με δύο
Σύνθετες Ασκήσεις για ιάδοση, ιασπορά και Αντιστάθµισή της
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης Σύνθετες Ασκήσεις για ιάδοση, ιασπορά και Αντιστάθµισή
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης Σύνθετες Ασκήσεις για ιάδοση, ιασπορά και Αντιστάθµισή
Φυσικό Επίπεδο ΕνσύρµαταΜέσαΜετάδοσης. Ενότητα Γ
 Ιόνιο Πανεπιστήµιο Τµήµα Αρχειονοµίας - Βιβλιοθηκονοµίας ίκτυα Η/Υ Φυσικό Επίπεδο ΕνσύρµαταΜέσαΜετάδοσης Ενότητα Γ ρ. Ε. Μάγκος Φυσικά Μέσα Μετάδοσης bit: Ηλεκτροµαγνητικό κύµα που µεταδίδεται σε ένα.
Ιόνιο Πανεπιστήµιο Τµήµα Αρχειονοµίας - Βιβλιοθηκονοµίας ίκτυα Η/Υ Φυσικό Επίπεδο ΕνσύρµαταΜέσαΜετάδοσης Ενότητα Γ ρ. Ε. Μάγκος Φυσικά Μέσα Μετάδοσης bit: Ηλεκτροµαγνητικό κύµα που µεταδίδεται σε ένα.
ιαδίκτυα & Ενδοδίκτυα Η/Υ
 ιαδίκτυα & Ενδοδίκτυα Η/Υ ρ Θεοδώρου Παύλος pavlos@aegean.gr Βιβλίο Μαθήµατος: Επικοινωνίες Υπολογιστών & εδοµένων, William Stallings, 6/e, 2000. ΕΥ - κεφ.9 (1/2) ρ Παύλος Θεοδώρου 1 Εισαγωγή Εισαγωγή
ιαδίκτυα & Ενδοδίκτυα Η/Υ ρ Θεοδώρου Παύλος pavlos@aegean.gr Βιβλίο Μαθήµατος: Επικοινωνίες Υπολογιστών & εδοµένων, William Stallings, 6/e, 2000. ΕΥ - κεφ.9 (1/2) ρ Παύλος Θεοδώρου 1 Εισαγωγή Εισαγωγή
Ερώτηση 1 η μεταγωγής κυκλώματος? : Ποια είναι τα κύρια χαρακτηριστικά της. Ερώτηση 2 η : Ποια είναι τα κύρια χαρακτηριστικά της μεταγωγής μηνύματος?
 Μετάδοση Δεδομένων Δίκτυα Υπολογιστών 68 Ερώτηση 1 η μεταγωγής κυκλώματος? : Ποια είναι τα κύρια χαρακτηριστικά της Απάντηση : Στα δίκτυα μεταγωγής κυκλώματος (circuit switching networks), η μετάδοση των
Μετάδοση Δεδομένων Δίκτυα Υπολογιστών 68 Ερώτηση 1 η μεταγωγής κυκλώματος? : Ποια είναι τα κύρια χαρακτηριστικά της Απάντηση : Στα δίκτυα μεταγωγής κυκλώματος (circuit switching networks), η μετάδοση των
Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης
 Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης Τα περισσότερα δίκτυα σήµερα είναι γραµµικά µε κωδικοποίηση γραµµής NRZ Τα µη γραµµικά συστήµατα στηρίζονται στα σολιτόνια µε κωδικοποίηση RZ. Οπτικό σύστηµα
Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης Τα περισσότερα δίκτυα σήµερα είναι γραµµικά µε κωδικοποίηση γραµµής NRZ Τα µη γραµµικά συστήµατα στηρίζονται στα σολιτόνια µε κωδικοποίηση RZ. Οπτικό σύστηµα
T R T R L 2 L 3 L 4 Αναγεννητής α 1 = 0.18 db/km α 2 = 0.45 db/km α 3 = 0.55 db/km α 4 = 0.34 db/km
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η ίνεται η
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η ίνεται η
ΙΑΛΕΞΗ 6 Η. ίκτυα Υπολογιστών & Επικοινωνία. ιδάσκουσα: : ρ. Παντάνο Ρόκου Φράνκα. ίκτυα Υπολογιστών και Επικοινωνία. ιάλεξη 6: H Πολύπλεξη
 ίκτυα Υπολογιστών & Επικοινωνία ΙΑΛΕΞΗ 6 Η ιδάσκουσα: : ρ. Παντάνο Ρόκου Φράνκα ρ. Παντάνο Ρόκου Φράνκα 1 Πολύπλεξη ΗΠολύπλεξηείναι η µετάδοση διαφορετικών ρευµάτων πληροφορίας µέσα από την ίδια φυσική
ίκτυα Υπολογιστών & Επικοινωνία ΙΑΛΕΞΗ 6 Η ιδάσκουσα: : ρ. Παντάνο Ρόκου Φράνκα ρ. Παντάνο Ρόκου Φράνκα 1 Πολύπλεξη ΗΠολύπλεξηείναι η µετάδοση διαφορετικών ρευµάτων πληροφορίας µέσα από την ίδια φυσική
Κουτσιούμπας Αχιλλέας U. Adamy, C. Ambuehl, R. Anand, T. Erlebach
 Κουτσιούμπας Αχιλλέας ΕΛΕΓΧΟΣ ΚΛΗΣΕΩΝ ΣΕ ΑΚΤΥΛΙΟ U. Adamy, C. Ambuehl, R. Anand, T. Erlebach ΜΠΛΑ 1 Δομή παρουσίασης Γενικά Ορισμός προβλήματος Σχετιζόμενη δουλειά Εισαγωγικά Αλγόριθμος Παράδειγμα εκτέλεσης
Κουτσιούμπας Αχιλλέας ΕΛΕΓΧΟΣ ΚΛΗΣΕΩΝ ΣΕ ΑΚΤΥΛΙΟ U. Adamy, C. Ambuehl, R. Anand, T. Erlebach ΜΠΛΑ 1 Δομή παρουσίασης Γενικά Ορισμός προβλήματος Σχετιζόμενη δουλειά Εισαγωγικά Αλγόριθμος Παράδειγμα εκτέλεσης
Η μονάδα db χρησιμοποιείται για να εκφράσει λόγους (κλάσματα) ομοειδών μεγεθών, αντιστοιχεί δηλαδή σε καθαρούς αριθμούς.
 0. ΥΠΟΛΟΓΙΣΜΟΣ ΣΤΑΘΜΗΣ ΣΗΜΑΤΟΣ 0.. Γενικά Στα τηλεπικοινωνιακά συστήματα, η μέτρηση στάθμης σήματος περιλαμβάνει, ουσιαστικά, τη μέτρηση της ισχύος ή της τάσης (ρεύματος) ενός σήματος σε διάφορα «κρίσιμα»
0. ΥΠΟΛΟΓΙΣΜΟΣ ΣΤΑΘΜΗΣ ΣΗΜΑΤΟΣ 0.. Γενικά Στα τηλεπικοινωνιακά συστήματα, η μέτρηση στάθμης σήματος περιλαμβάνει, ουσιαστικά, τη μέτρηση της ισχύος ή της τάσης (ρεύματος) ενός σήματος σε διάφορα «κρίσιμα»
Εισαγωγικές Ασκήσεις για Απώλειες και ιασπορά
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΡΙΑΚΟ ΠΑΝΕΠΙΣΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΙΚΩΝ ΕΠΙΣΗΜΩΝ ΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΥΑ ΟΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης Εισαγωγικές Ασκήσεις για Απώλειες και ιασπορά Άσκηση 1
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΡΙΑΚΟ ΠΑΝΕΠΙΣΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΙΚΩΝ ΕΠΙΣΗΜΩΝ ΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΥΑ ΟΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης Εισαγωγικές Ασκήσεις για Απώλειες και ιασπορά Άσκηση 1
1η Οµάδα Ασκήσεων. Τµήµα επεξεργασίας σήµατος του αναγεννητή
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης η Οµάδα Ασκήσεων Άσκηση η Εγκατεστηµένη ζεύξη
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής. Συβρίδης η Οµάδα Ασκήσεων Άσκηση η Εγκατεστηµένη ζεύξη
ΔΙΑΣΥΝΔΕΣΗ ΔΙΚΤΥΩΝ (INTERNETWORKING)
 ΔΙΑΣΥΝΔΕΣΗ ΔΙΚΤΥΩΝ (INTERNETWORKING) Α. Α. Οικονομίδης Πανεπιστήμιο Μακεδονίας Διασυνδεδεμένο δίκτυο διασύνδεση δικτύων που το καθένα διατηρεί την ταυτότητά του χρησιμοποιώντας ειδικούς μηχανισμούς διασύνδεσης
ΔΙΑΣΥΝΔΕΣΗ ΔΙΚΤΥΩΝ (INTERNETWORKING) Α. Α. Οικονομίδης Πανεπιστήμιο Μακεδονίας Διασυνδεδεμένο δίκτυο διασύνδεση δικτύων που το καθένα διατηρεί την ταυτότητά του χρησιμοποιώντας ειδικούς μηχανισμούς διασύνδεσης
Τηλεφωνικό Σύστημα και Μετάδοση Δεδομένων Μάνος Ρουμελιώτης Πανεπιστήμιο Μακεδονίας
 Τηλεφωνικό Σύστημα και Μετάδοση Δεδομένων Μάνος Ρουμελιώτης Πανεπιστήμιο Μακεδονίας http://www.etl.uom.gr/mr/ 18/10/2004 1 Μέσα Μετάδοσης Διαφόρων τύπων χάλκινα καλώδια Οπτικές ίνες Ασύρματη μετάδοση 18/10/2004
Τηλεφωνικό Σύστημα και Μετάδοση Δεδομένων Μάνος Ρουμελιώτης Πανεπιστήμιο Μακεδονίας http://www.etl.uom.gr/mr/ 18/10/2004 1 Μέσα Μετάδοσης Διαφόρων τύπων χάλκινα καλώδια Οπτικές ίνες Ασύρματη μετάδοση 18/10/2004
Οπτικά Δίκτυα. Δομή των Τηλεπικοινωνιακών Δικτύων. Εισαγωγή
 Οπτικά Δίκτυα Εισαγωγή University of Patras, GREECE, contact: kvlachos@ceid.upatras.gr Δομή των Τηλεπικοινωνιακών Δικτύων University of Patras, GREECE, contact: kvlachos@ceid.upatras.gr 2 1 Τυπική αρχιτεκτονική
Οπτικά Δίκτυα Εισαγωγή University of Patras, GREECE, contact: kvlachos@ceid.upatras.gr Δομή των Τηλεπικοινωνιακών Δικτύων University of Patras, GREECE, contact: kvlachos@ceid.upatras.gr 2 1 Τυπική αρχιτεκτονική
NRZ Non return to zero: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό Bandwidth)
 ιαµόρφωση Αποδιαµόρφωση ) Μορφές Σηµάτων NRZ No rtur to zro: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό adwidth) RZ Rtur to zro : Ανάµεσα σε δύο άσσους µεσολαβεί ένα κενό διάστηµα (Μεγαλύτερο
ιαµόρφωση Αποδιαµόρφωση ) Μορφές Σηµάτων NRZ No rtur to zro: Οι άσσοι καταλαµβάνουν ολόκληρη τη διάρκεια bit. (Μικρό adwidth) RZ Rtur to zro : Ανάµεσα σε δύο άσσους µεσολαβεί ένα κενό διάστηµα (Μεγαλύτερο
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
Κεφάλαιο 12. Πρότυπα. Ανακεφαλαίωση Ερωτήσεις
 Κεφάλαιο 12 Πρότυπα Μάθηµα 12.1: Μάθηµα 12.2: Μάθηµα 12.3: Μάθηµα 12.4: Μάθηµα 12.5: Πρότυπα FDDI-I και FDDI-II Πρότυπο 100 Mbps Ethernet Πρότυπο 100Base-VGAnyLAN Πρότυπο Gigabit Ethernet Πρότυπο LATM
Κεφάλαιο 12 Πρότυπα Μάθηµα 12.1: Μάθηµα 12.2: Μάθηµα 12.3: Μάθηµα 12.4: Μάθηµα 12.5: Πρότυπα FDDI-I και FDDI-II Πρότυπο 100 Mbps Ethernet Πρότυπο 100Base-VGAnyLAN Πρότυπο Gigabit Ethernet Πρότυπο LATM
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Σύνθετη Άσκηση για Απώλειες και ιασπορά
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής. Συβρίδης Σύνθετη Άσκηση για Απώλειες και ιασπορά
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής. Συβρίδης Σύνθετη Άσκηση για Απώλειες και ιασπορά
ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΡΩΤΗΣΕΙΣ & ΘΕΜΑΤΑ ΠΕΡΑΣΜΕΝΩΝ ΕΞΕΤΑΣΤΙΚΩΝ ΠΕΡΙΟ ΩΝ
 ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΡΩΤΗΣΕΙΣ & ΘΕΜΑΤΑ ΠΕΡΑΣΜΕΝΩΝ ΕΞΕΤΑΣΤΙΚΩΝ ΠΕΡΙΟ ΩΝ α. Τι ονοµάζουµε διασπορά οπτικού παλµού σε µια οπτική ίνα; Ποια φαινόµενα παρατηρούνται λόγω διασποράς; (Αναφερθείτε σε
ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΕΡΩΤΗΣΕΙΣ & ΘΕΜΑΤΑ ΠΕΡΑΣΜΕΝΩΝ ΕΞΕΤΑΣΤΙΚΩΝ ΠΕΡΙΟ ΩΝ α. Τι ονοµάζουµε διασπορά οπτικού παλµού σε µια οπτική ίνα; Ποια φαινόµενα παρατηρούνται λόγω διασποράς; (Αναφερθείτε σε
ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΣΤΟΥΣ ΟΠΤΙΚΟΥΣ ΕΝΙΣΧΥΤΕΣ ΚΑΙ ΣΤΑ ΟΠΤΙΚΑ ΦΙΛΤΡΑ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΜΑΘΗΜΑ: ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΣΤΟΥΣ ΟΠΤΙΚΟΥΣ ΕΝΙΣΧΥΤΕΣ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΜΑΘΗΜΑ: ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΣΤΟΥΣ ΟΠΤΙΚΟΥΣ ΕΝΙΣΧΥΤΕΣ
ΤΕΙ Κρήτης, Παράρτηµα Χανίων
 ΠΣΕ, Τµήµα Τηλεπικοινωνιών & ικτύων Η/Υ Εργαστήριο ιαδίκτυα & Ενδοδίκτυα Η/Υ ( ηµιουργία συστήµατος µε ροint-tο-ροint σύνδεση) ρ Θεοδώρου Παύλος Χανιά 2003 Περιεχόµενα 1 ΕΙΣΑΓΩΓΗ...2 2 ΤΟ ΚΑΝΑΛΙ PΟINT-TΟ-PΟINT...2
ΠΣΕ, Τµήµα Τηλεπικοινωνιών & ικτύων Η/Υ Εργαστήριο ιαδίκτυα & Ενδοδίκτυα Η/Υ ( ηµιουργία συστήµατος µε ροint-tο-ροint σύνδεση) ρ Θεοδώρου Παύλος Χανιά 2003 Περιεχόµενα 1 ΕΙΣΑΓΩΓΗ...2 2 ΤΟ ΚΑΝΑΛΙ PΟINT-TΟ-PΟINT...2
Κεφάλαιο 5: Τοπικά ίκτυα
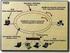 Κεφάλαιο 5: Τοπικά ίκτυα 5.1 ΤοΠρωτόκολλο ALOHA Αλγόριθµοι επίλυσης συγκρούσεων µε βάση το δυαδικό δένδρο 5.2 ίκτυα Ethernet Πρότυπο ΙΕΕΕ 802.3 5.3 ίκτυα Token Ring - Πρότυπο ΙΕΕΕ 802.5 Τοπικά ίκτυα 5-1
Κεφάλαιο 5: Τοπικά ίκτυα 5.1 ΤοΠρωτόκολλο ALOHA Αλγόριθµοι επίλυσης συγκρούσεων µε βάση το δυαδικό δένδρο 5.2 ίκτυα Ethernet Πρότυπο ΙΕΕΕ 802.3 5.3 ίκτυα Token Ring - Πρότυπο ΙΕΕΕ 802.5 Τοπικά ίκτυα 5-1
ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για το φυσικό στρώμα. λ από τον ρυθμό μετάδοσής της. Υποθέτοντας ότι ο κόμβος A
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για το φυσικό στρώμα 1. Στο δίκτυο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για το φυσικό στρώμα 1. Στο δίκτυο
Δίκτυα Θεωρία
 Δίκτυα Θεωρία 2016-17 Κεφάλαιο 5 1. Τι γνωρίζετε για τα Δίκτυα Ευρείας Περιοχής; Τα τοπικά δίκτυα αποτελούν πολύ καλή λύση για επικοινωνία με περιορισμένη, όμως, απόσταση κάλυψης. Για να ικανοποιηθεί η
Δίκτυα Θεωρία 2016-17 Κεφάλαιο 5 1. Τι γνωρίζετε για τα Δίκτυα Ευρείας Περιοχής; Τα τοπικά δίκτυα αποτελούν πολύ καλή λύση για επικοινωνία με περιορισμένη, όμως, απόσταση κάλυψης. Για να ικανοποιηθεί η
ΕΝΟΤΗΤΑ 3 3.0 ΜΕΣΑ ΜΕΤΑΔΟΣΗΣ ΕΙΣΑΓΩΓΗ
 ΕΝΟΤΗΤΑ 3 3.0 ΜΕΣΑ ΜΕΤΑΔΟΣΗΣ ΕΙΣΑΓΩΓΗ Όπως είναι ήδη γνωστό, ένα σύστημα επικοινωνίας περιλαμβάνει τον πομπό, το δέκτη και το κανάλι επικοινωνίας. Στην ενότητα αυτή, θα εξετάσουμε τη δομή και τα χαρακτηριστικά
ΕΝΟΤΗΤΑ 3 3.0 ΜΕΣΑ ΜΕΤΑΔΟΣΗΣ ΕΙΣΑΓΩΓΗ Όπως είναι ήδη γνωστό, ένα σύστημα επικοινωνίας περιλαμβάνει τον πομπό, το δέκτη και το κανάλι επικοινωνίας. Στην ενότητα αυτή, θα εξετάσουμε τη δομή και τα χαρακτηριστικά
Πώς γίνεται η µετάδοση των δεδοµένων µέσω οπτικών ινών:
 1 ΔΟΜΗ ΟΠΤΙΚΗΣ ΙΝΑΣ Κάθε οπτική ίνα αποτελείται από τρία μέρη: Την κεντρική γυάλινη κυλινδρική ίνα, που ονομάζεται πυρήνας(core core) και είναι το τμήμα στο οποίο διαδίδεται το φως. Την επικάλυψη (απλή
1 ΔΟΜΗ ΟΠΤΙΚΗΣ ΙΝΑΣ Κάθε οπτική ίνα αποτελείται από τρία μέρη: Την κεντρική γυάλινη κυλινδρική ίνα, που ονομάζεται πυρήνας(core core) και είναι το τμήμα στο οποίο διαδίδεται το φως. Την επικάλυψη (απλή
ΚΕΦΑΛΑΙΟ 7 ΕΠΕΞΕΡΓΑΣΙΑ ΚΑΙ ΜΕΤΑΔΟΣΗ ΨΗΦΙΑΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ΚΕΦΑΛΑΙΟ 7 ΕΠΕΞΕΡΓΑΣΙΑ ΚΑΙ ΜΕΤΑΔΟΣΗ ΨΗΦΙΑΚΩΝ ΔΕΔΟΜΕΝΩΝ 1 ΕΙΣΑΓΩΓΗ Ο πραγματικός κόσμος είναι ένας αναλογικός κόσμος. Όλα τα μεγέθη παίρνουν τιμές με άπειρη ακρίβεια. Π.χ. το ηλεκτρικό σήμα τάσης όπου κάθε
ΚΕΦΑΛΑΙΟ 7 ΕΠΕΞΕΡΓΑΣΙΑ ΚΑΙ ΜΕΤΑΔΟΣΗ ΨΗΦΙΑΚΩΝ ΔΕΔΟΜΕΝΩΝ 1 ΕΙΣΑΓΩΓΗ Ο πραγματικός κόσμος είναι ένας αναλογικός κόσμος. Όλα τα μεγέθη παίρνουν τιμές με άπειρη ακρίβεια. Π.χ. το ηλεκτρικό σήμα τάσης όπου κάθε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Τμήμα Πληροφορικής- Πρόγραμμα Μεταπτυχιακών Σπουδών Επικοινωνιακά Συστήματα και Τεχνολογίες
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Τμήμα Πληροφορικής- Πρόγραμμα Μεταπτυχιακών Σπουδών Επικοινωνιακά Συστήματα και Τεχνολογίες Δυναμική δρομολόγηση και ανάθεση μήκους κύματος για τη δημιουργία πράσινων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Τμήμα Πληροφορικής- Πρόγραμμα Μεταπτυχιακών Σπουδών Επικοινωνιακά Συστήματα και Τεχνολογίες Δυναμική δρομολόγηση και ανάθεση μήκους κύματος για τη δημιουργία πράσινων
Ιόνιο Πανεπιστήµιο Τµήµα Πληροφορικής. Φυσικά Μέσα Μετάδοσης. Φυσικό Επίπεδο Ενσύρµατα και ΑσύρµαταΜέσαΜετάδοσης. Ενότητα Γ. ΕνσύρµαταΜέσαΜετάδοσης
 Ιόνιο Πανεπιστήµιο Τµήµα Πληροφορικής ίκτυα Η/Υ Φυσικό Επίπεδο Ενσύρµατα και ΑσύρµαταΜέσαΜετάδοσης Φυσικά Μέσα Μετάδοσης bit: Ηλεκτροµαγνητικό κύµα που µεταδίδεται σε ένα. ΦΥΣΙΚΟ ΜΕΣΟ (Κατευθυνόµενα -Guided):
Ιόνιο Πανεπιστήµιο Τµήµα Πληροφορικής ίκτυα Η/Υ Φυσικό Επίπεδο Ενσύρµατα και ΑσύρµαταΜέσαΜετάδοσης Φυσικά Μέσα Μετάδοσης bit: Ηλεκτροµαγνητικό κύµα που µεταδίδεται σε ένα. ΦΥΣΙΚΟ ΜΕΣΟ (Κατευθυνόµενα -Guided):
Πολυπλεξία. http://diktya-epal-b.ggia.info Creative Commons License 3.0 Share-Alike
 Πολυπλεξία Ανάλυση σημάτων στο πεδίο χρόνου, συχνότητας, πολυπλεξία διαίρεσης συχνότητας, πολυπλεξία διαίρεσης χρόνου (1.6 ενότητα σελ 19-20, 29-30 και στοιχεία από 2.1 ενότητα σελ. 52-58). http://diktya-epal-b.ggia.info
Πολυπλεξία Ανάλυση σημάτων στο πεδίο χρόνου, συχνότητας, πολυπλεξία διαίρεσης συχνότητας, πολυπλεξία διαίρεσης χρόνου (1.6 ενότητα σελ 19-20, 29-30 και στοιχεία από 2.1 ενότητα σελ. 52-58). http://diktya-epal-b.ggia.info
Γ. Κορίλη Αλγόριθµοι ροµολόγησης
 - Γ. Κορίλη Αλγόριθµοι ροµολόγησης http://www.seas.upenn.edu/~tcom50/lectures/lecture.pdf ροµολόγηση σε ίκτυα εδοµένων Αναπαράσταση ικτύου µε Γράφο Μη Κατευθυνόµενοι Γράφοι Εκτεταµένα έντρα Κατευθυνόµενοι
- Γ. Κορίλη Αλγόριθµοι ροµολόγησης http://www.seas.upenn.edu/~tcom50/lectures/lecture.pdf ροµολόγηση σε ίκτυα εδοµένων Αναπαράσταση ικτύου µε Γράφο Μη Κατευθυνόµενοι Γράφοι Εκτεταµένα έντρα Κατευθυνόµενοι
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
ΕΠΙΚΟΙΝΩΝΙΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΕΣ INTERNET
 ΕΠΙΚΟΙΝΩΝΙΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΕΣ INTERNET Κεφάλαιο 4: Τεχνικές Μετάδοσης ΜΕΤΑΓΩΓΗ Τεχνική µεταγωγής ονομάζεται ο τρόπος µε τον οποίο αποκαθίσταται η επικοινωνία ανάµεσα σε δύο κόµβους με σκοπό την
ΕΠΙΚΟΙΝΩΝΙΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΕΣ INTERNET Κεφάλαιο 4: Τεχνικές Μετάδοσης ΜΕΤΑΓΩΓΗ Τεχνική µεταγωγής ονομάζεται ο τρόπος µε τον οποίο αποκαθίσταται η επικοινωνία ανάµεσα σε δύο κόµβους με σκοπό την
Γενική εικόνα τι είναι σήµα - Ορισµός. Ταξινόµηση σηµάτων. Βασικές ιδιότητες σηµάτων. Μετατροπές σήµατος ως προς το χρόνο. Στοιχειώδη σήµατα.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Εισαγωγή στα Σήµατα Εισαγωγή στα Συστήµατα Ανάπτυγµα - Μετασχηµατισµός Fourier Μετασχηµατισµός Laplace Μετασχηµατισµός Z Εφαρµογές 1. ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΗΜΑΤΑ Γενική εικόνα τι
ΜΑΘΗΜΑ: ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ - ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΟΠΤΙΚΩΝ ΖΕΥΞΕΩΝ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΜΑΘΗΜΑ: ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ - ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΟΠΤΙΚΩΝ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΜΑΘΗΜΑ: ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ - ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΟΠΤΙΚΩΝ
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Οι βασικές βαθμίδες του συστήματος των δορυφορικών επικοινωνιών δίνονται στο παρακάτω σχήμα :
 Εισαγωγικά Τα δορυφορικά δίκτυα επικοινωνίας αποτελούν ένα σημαντικό τμήμα των σύγχρονων τηλεπικοινωνιακών συστημάτων. Οι δορυφόροι παρέχουν τη δυνατότητα κάλυψης μεγάλων γεωγραφικών περιοχών. Η δυνατότητα
Εισαγωγικά Τα δορυφορικά δίκτυα επικοινωνίας αποτελούν ένα σημαντικό τμήμα των σύγχρονων τηλεπικοινωνιακών συστημάτων. Οι δορυφόροι παρέχουν τη δυνατότητα κάλυψης μεγάλων γεωγραφικών περιοχών. Η δυνατότητα
Ασκήσεις στα Συστήµατα Ηλεκτρονικών Επικοινωνιών Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ
 Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ 1. Ποµπός ΑΜ εκπέµπει σε φέρουσα συχνότητα 1152 ΚΗz, µε ισχύ φέροντος 10KW. Η σύνθετη αντίσταση της κεραίας είναι
Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ 1. Ποµπός ΑΜ εκπέµπει σε φέρουσα συχνότητα 1152 ΚΗz, µε ισχύ φέροντος 10KW. Η σύνθετη αντίσταση της κεραίας είναι
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής
 Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στα πλαίσια του μεταπτυχιακού προγράμματος ειδίκευσης: Επιστήμη και Τεχνολογία Των Υπολογιστών
Πανεπιστήμιο Πατρών Πολυτεχνική Σχολή Τμήμα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Διπλωματική Εργασία Στα πλαίσια του μεταπτυχιακού προγράμματος ειδίκευσης: Επιστήμη και Τεχνολογία Των Υπολογιστών
Τα ηλεκτρονικά σήματα πληροφορίας διακρίνονται ανάλογα με τη μορφή τους σε δύο κατηγορίες : Αναλογικά σήματα Ψηφιακά σήματα
 ΕΝΟΤΗΤΑ 2 2.0 ΗΛΕΚΤΡΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΑΡΧΕΣ ΕΠΙΚΟΙΝΩΝΙΑΣ ΕΙΣΑΓΩΓΗ Ηλεκτρικό σήμα ονομάζεται η τάση ή το ρεύμα που μεταβάλλεται ως συνάρτηση του χρόνου. Στα ηλεκτρονικά συστήματα επικοινωνίας, οι πληροφορίες
ΕΝΟΤΗΤΑ 2 2.0 ΗΛΕΚΤΡΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΑΡΧΕΣ ΕΠΙΚΟΙΝΩΝΙΑΣ ΕΙΣΑΓΩΓΗ Ηλεκτρικό σήμα ονομάζεται η τάση ή το ρεύμα που μεταβάλλεται ως συνάρτηση του χρόνου. Στα ηλεκτρονικά συστήματα επικοινωνίας, οι πληροφορίες
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης και Βέλτιστου Σχεδιασμού Δικτύων - NETMODE
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης και Βέλτιστου Σχεδιασμού Δικτύων - NETMODE
Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών
 1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
Οπτικά Δίκτυα Επικοινωνιών
 EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Η/Υ Οπτικά Δίκτυα Επικοινωνιών Καθ. Η Αβραμόπουλος Δρ. Δ. Αποστολόπουλος www.photonics.ntua.gr Περιεχόµενα Ηµέρας Οπτικοί συζεύκτες
EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Η/Υ Οπτικά Δίκτυα Επικοινωνιών Καθ. Η Αβραμόπουλος Δρ. Δ. Αποστολόπουλος www.photonics.ntua.gr Περιεχόµενα Ηµέρας Οπτικοί συζεύκτες
ΟΠΤΙΚΟΙ ΣΥΖΕΥΚΤΕΣ. ιαχωριστές Ισχύος Πολυπλέκτες/Αποπολυπλέκτες Μήκους Κύµατος (WDM) Πολλαπλές θύρες εισόδων-εξόδων
 ΟΠΤΙΚΟΙ ΣΥΖΕΥΚΤΕΣ ιαχωριστές Ισχύος Πολυπλέκτες/Αποπολυπλέκτες Μήκους Κύµατος (WDM) Πολλαπλές θύρες εισόδων-εξόδων Τεχνικές Κατασκευής Συζευκτών ΣΥΝΤΗΓΜΕΝΩΝ ΣΥΖΕΥΚΤΩΝ ΙΚΩΝΙΚΗΣ ΕΚΛΕΠΤΥΝΣΗΣ Χαρακτηριστικά
ΟΠΤΙΚΟΙ ΣΥΖΕΥΚΤΕΣ ιαχωριστές Ισχύος Πολυπλέκτες/Αποπολυπλέκτες Μήκους Κύµατος (WDM) Πολλαπλές θύρες εισόδων-εξόδων Τεχνικές Κατασκευής Συζευκτών ΣΥΝΤΗΓΜΕΝΩΝ ΣΥΖΕΥΚΤΩΝ ΙΚΩΝΙΚΗΣ ΕΚΛΕΠΤΥΝΣΗΣ Χαρακτηριστικά
Κεφάλαιο 3 ο : ΕΙΣΑΓΩΓΗ στις ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ. ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ και ΤΕΧΝΙΚΕΣ ΙΑΜΟΡΦΩΣΗΣ
 Μάθηµα 1ο Θέµα Εισαγωγή στις τηλεπικοινωνίες 1. Τι ορίζουµε µε τον όρο τηλεπικοινωνία; 2. Ποιες οι βασικότερες ανταλλασσόµενες πληροφορίες, ανάλογα µε τη φύση και το χαρακτήρα τους; 3. Τι αποκαλούµε ποµπό
Μάθηµα 1ο Θέµα Εισαγωγή στις τηλεπικοινωνίες 1. Τι ορίζουµε µε τον όρο τηλεπικοινωνία; 2. Ποιες οι βασικότερες ανταλλασσόµενες πληροφορίες, ανάλογα µε τη φύση και το χαρακτήρα τους; 3. Τι αποκαλούµε ποµπό
Τηλεπικοινωνίες οπτικών ινών
 Τηλεπικοινωνίες οπτικών ινών Ενότητα 1: Εισαγωγικά θέματα Βλάχος Κυριάκος Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Ο σκοπός της ενότητας είναι να εισάγει το σπουδαστή στα
Τηλεπικοινωνίες οπτικών ινών Ενότητα 1: Εισαγωγικά θέματα Βλάχος Κυριάκος Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Ο σκοπός της ενότητας είναι να εισάγει το σπουδαστή στα
Περίληψη. Ethernet Δίκτυα Δακτυλίου, (Token Ring) Άλλα Δίκτυα Σύνδεση Τοπικών Δικτύων.
 Τοπικά Δίκτυα Περίληψη Ethernet Δίκτυα Δακτυλίου, (Token Ring) Άλλα Δίκτυα Σύνδεση Τοπικών Δικτύων. Αναµεταδότες, Γέφυρες, Μεταγωγείς, δροµολογητές και Πύλες (repeaters, hubs, bridges, switches, routers,
Τοπικά Δίκτυα Περίληψη Ethernet Δίκτυα Δακτυλίου, (Token Ring) Άλλα Δίκτυα Σύνδεση Τοπικών Δικτύων. Αναµεταδότες, Γέφυρες, Μεταγωγείς, δροµολογητές και Πύλες (repeaters, hubs, bridges, switches, routers,
LAYER 3 ( NETWORΚ LEVEL ) - ΣΤΡΩΜΑ 3 ( ΕΠΙΠΕ Ο ΙΚΤΥΟΥ)
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 6 LAYER 3 ( NETWORΚ LEVEL ) - ΣΤΡΩΜΑ 3 ( ΕΠΙΠΕ Ο ΙΚΤΥΟΥ) Αυτή η ενότητα του δευτέρου κεφαλαίου περιέχει τα ακόλουθα: - που βρίσκεται το επίπεδο δικτύου - ποιός είναι ο ρόλος του - ποιά
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 6 LAYER 3 ( NETWORΚ LEVEL ) - ΣΤΡΩΜΑ 3 ( ΕΠΙΠΕ Ο ΙΚΤΥΟΥ) Αυτή η ενότητα του δευτέρου κεφαλαίου περιέχει τα ακόλουθα: - που βρίσκεται το επίπεδο δικτύου - ποιός είναι ο ρόλος του - ποιά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ
 ΘΕΜΑ ο 2.5 µονάδες ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 2 Σεπτεµβρίου 2005 5:00-8:00 Σχεδιάστε έναν αισθητήρα ercetro
ΘΕΜΑ ο 2.5 µονάδες ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 2 Σεπτεµβρίου 2005 5:00-8:00 Σχεδιάστε έναν αισθητήρα ercetro
7.3 Πρωτόκολλο TCP. 1. Το TCP πρωτόκολλο παρέχει υπηρεσίες προσανατολισµένες σε σύνδεση. Σ Λ
 Ερωτήσεις 7.3 Πρωτόκολλο TCP 1. Τι είναι το τµήµα (segment) στο πρωτόκολλο TCP; Από ποια µέρη αποτελείται; 2. Για ποιο σκοπό χρησιµοποιείται ο Αριθµός ειράς στην επικεφαλίδα ενός segment TCP; 3. την περίπτωση
Ερωτήσεις 7.3 Πρωτόκολλο TCP 1. Τι είναι το τµήµα (segment) στο πρωτόκολλο TCP; Από ποια µέρη αποτελείται; 2. Για ποιο σκοπό χρησιµοποιείται ο Αριθµός ειράς στην επικεφαλίδα ενός segment TCP; 3. την περίπτωση
Αλγόριθµοι Εκτίµησης Καθυστέρησης και
 Αλγόριθµοι Εκτίµησης Καθυστέρησης και Βελτιστοποίησης Εισαγωγή Το κύριο πρόβληµα στην σχεδίαση κυκλωµάτων είναι η επίτευξη της µέγιστης απόδοσης για την δεδοµένη τεχνολογία. Μεγιστοποίηση απόδοσης: (α)
Αλγόριθµοι Εκτίµησης Καθυστέρησης και Βελτιστοποίησης Εισαγωγή Το κύριο πρόβληµα στην σχεδίαση κυκλωµάτων είναι η επίτευξη της µέγιστης απόδοσης για την δεδοµένη τεχνολογία. Μεγιστοποίηση απόδοσης: (α)
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος. Ε. Μαρκάκης. Επικ. Καθηγητής
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
Σύνθεση Data Path. ιασύνδεσης. Μονάδες. Αριθµό Μονάδων. Τύπο Μονάδων. Unit Selection Unit Binding. λειτουργιών σε. Μονάδες. Αντιστοίχιση µεταβλητών &
 Data Path Allocation Σύνθεση Data Path Το DataPath είναι ένα netlist που αποτελείται από τρεις τύπους µονάδων: (α) Λειτουργικές Μονάδες, (β) Μονάδες Αποθήκευσης και (γ) Μονάδες ιασύνδεσης Αριθµό Μονάδων
Data Path Allocation Σύνθεση Data Path Το DataPath είναι ένα netlist που αποτελείται από τρεις τύπους µονάδων: (α) Λειτουργικές Μονάδες, (β) Μονάδες Αποθήκευσης και (γ) Μονάδες ιασύνδεσης Αριθµό Μονάδων
ιάθεση ασύρµατων πόρων
 ιάθεση ασύρµατων πόρων Μεταγωγή (Handover ή Handoff) ιαδικασία µεταγωγής µιας κλήσης από µια κυψέλη σε γειτονική κυψέλη Η κλήση από την συχνότητα f 1 της κυψέλης C 1 µεταφέρεται στη συχνότητα f 2 της κυψέλης
ιάθεση ασύρµατων πόρων Μεταγωγή (Handover ή Handoff) ιαδικασία µεταγωγής µιας κλήσης από µια κυψέλη σε γειτονική κυψέλη Η κλήση από την συχνότητα f 1 της κυψέλης C 1 µεταφέρεται στη συχνότητα f 2 της κυψέλης
Διάρθρωση. Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α. Διάρθρωση. Δίκτυα άμεσου συνδέσμου και μοντέλο OSI (1/2) Ευάγγελος Παπαπέτρου
 Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου 2 Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων 3 Δίκτυα Slotted Reservation Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα
Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου 2 Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων 3 Δίκτυα Slotted Reservation Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: Δρομολόγηση
 Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: Δρομολόγηση Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών Διαφάνεια 1 Δρομολόγηση Εισαγωγή Ιεραρχική δρομολόγηση
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: Δρομολόγηση Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών Διαφάνεια 1 Δρομολόγηση Εισαγωγή Ιεραρχική δρομολόγηση
Δίκτυα Υπολογιστών I
 Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα Υπολογιστών Ι 1 / 36 Διάρθρωση
Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα Υπολογιστών Ι 1 / 36 Διάρθρωση
Εισαγωγή - ορολογία. Προώθηση (forwarding): Δρομολόγηση (routing):
 Δρομολόγηση Ι Εισαγωγή - ορολογία Προώθηση (forwarding): Οι συσκευές διαδικτύωσης (γέφυρες, δρομολογητές, κ.τ.λ.) προωθούν πακέτα δεδομένων στα κατάλληλα μονοπάτια βάσει των πινάκων δρομολόγησης (routing
Δρομολόγηση Ι Εισαγωγή - ορολογία Προώθηση (forwarding): Οι συσκευές διαδικτύωσης (γέφυρες, δρομολογητές, κ.τ.λ.) προωθούν πακέτα δεδομένων στα κατάλληλα μονοπάτια βάσει των πινάκων δρομολόγησης (routing
Μέθοδοι Βελτιστοποίησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # : Επιχειρησιακή έρευνα Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # : Επιχειρησιακή έρευνα Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
Νέες Επικοινωνιακές Τεχνολογίες
 Νέες Επικοινωνιακές Τεχνολογίες Λύσεις Θεμάτων http://nop33.wordpress.com Τι ορίζουμε ως Τοπικό Δίκτυο Υπολογιστών; Ποια είναι τα βασικά χαρακτηριστικά των Τοπικών Δικτύων; Ποιες οι βασικές τοπολογίες
Νέες Επικοινωνιακές Τεχνολογίες Λύσεις Θεμάτων http://nop33.wordpress.com Τι ορίζουμε ως Τοπικό Δίκτυο Υπολογιστών; Ποια είναι τα βασικά χαρακτηριστικά των Τοπικών Δικτύων; Ποιες οι βασικές τοπολογίες
Μάθημα 5: To Μοντέλο Αναφοράς O.S.I.
 Μάθημα 5: To Μοντέλο Αναφοράς O.S.I. 5.1 Γενικά Τα πρώτα δίκτυα χαρακτηρίζονταν από την «κλειστή» αρχιτεκτονική τους με την έννοια ότι αυτή ήταν γνωστή μόνο στην εταιρία που την είχε σχεδιάσει. Με τον
Μάθημα 5: To Μοντέλο Αναφοράς O.S.I. 5.1 Γενικά Τα πρώτα δίκτυα χαρακτηρίζονταν από την «κλειστή» αρχιτεκτονική τους με την έννοια ότι αυτή ήταν γνωστή μόνο στην εταιρία που την είχε σχεδιάσει. Με τον
5.1.4 Τεχνολογίες Ψηφιακής Συνδρομητικής Γραμμής (xdsl)
 5.1.4 Τεχνολογίες Ψηφιακής Συνδρομητικής Γραμμής (xdsl) 1 / 36 Το DSL προέρχεται από τα αρχικά των λέξεων Digital Subscriber Line (Ψηφιακή Συνδρομητική Γραμμή) και στην ουσία αποτελεί μια τεχνολογία που
5.1.4 Τεχνολογίες Ψηφιακής Συνδρομητικής Γραμμής (xdsl) 1 / 36 Το DSL προέρχεται από τα αρχικά των λέξεων Digital Subscriber Line (Ψηφιακή Συνδρομητική Γραμμή) και στην ουσία αποτελεί μια τεχνολογία που
Εισαγωγή Στοιχεία Θεωρίας
 Εισαγωγή Σκοπός της άσκησης αυτής είναι η εισαγωγή στην τεχνογνωσία των οπτικών ινών και η μελέτη τους κατά τη διάδοση μιας δέσμης laser. Συγκεκριμένα μελετάται η εξασθένιση που υφίσταται το σήμα στην
Εισαγωγή Σκοπός της άσκησης αυτής είναι η εισαγωγή στην τεχνογνωσία των οπτικών ινών και η μελέτη τους κατά τη διάδοση μιας δέσμης laser. Συγκεκριμένα μελετάται η εξασθένιση που υφίσταται το σήμα στην
ΤΕΧΝΟΛΟΓΙΑ ΔΙΚΤΥΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ 1 ο ΚΕΦΑΛΑΙΟ
 ΤΕΧΝΟΛΟΓΙΑ ΔΙΚΤΥΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ 1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ 1. Έστω ότι θέλετε να συνδέσετε 20 υπολογιστές με συνδέσεις από σημείο σε σημείο (point-to-point), ώστε να είναι δυνατή η επικοινωνία όλων
ΤΕΧΝΟΛΟΓΙΑ ΔΙΚΤΥΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ 1 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ 1. Έστω ότι θέλετε να συνδέσετε 20 υπολογιστές με συνδέσεις από σημείο σε σημείο (point-to-point), ώστε να είναι δυνατή η επικοινωνία όλων
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΔΙΚΤΥΑ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΔΙΚΤΥΑ Καθηγητής Δ. Συβρίδης 1η Ομάδα Ασκήσεων Άσκηση 1η Έστω
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΔΙΚΤΥΑ Καθηγητής Δ. Συβρίδης 1η Ομάδα Ασκήσεων Άσκηση 1η Έστω
Λύσεις 1ης Ομάδας Ασκήσεων
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΔΙΚΤΥΑ Καθηγητής Δ. Συβρίδης Λύσεις ης Ομάδας Ασκήσεων Άσκηση
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΔΙΚΤΥΑ Καθηγητής Δ. Συβρίδης Λύσεις ης Ομάδας Ασκήσεων Άσκηση
Διάρθρωση. Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α. Διάρθρωση. Δίκτυα άμεσου συνδέσμου και μοντέλο OSI (1/2) Ευάγγελος Παπαπέτρου
 Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων 3 Δίκτυα Slotted Reservation Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα
Δίκτυα Υπολογιστών I Δίκτυα άμεσου συνδέσμου: Μέρος Α Ευάγγελος Παπαπέτρου Τμ. Μηχ. Η/Υ & Πληροφορικής, Παν. Ιωαννίνων 3 Δίκτυα Slotted Reservation Ε.Παπαπέτρου (Τμ.Μηχ. Η/Υ & Πληροφορικής) ΜΥΥ703: Δίκτυα
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου 2015 1 / 45 Εισαγωγή Ο δυναµικός
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 28 Μαΐου 2015 1 / 45 Εισαγωγή Ο δυναµικός
