ανατολή ή τη δύση, με άξονα περιστροφής τον άξονα βορρά νότου, δημιουργεί τους ανατολικούς και δυτικούς μεσημβρινούς της γης.
|
|
|
- Εὐνίκη Μαυρίδης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΗΛΙΑΣΜΟΣ Εισαγωγή Σ αυτή την ενότητα θα γνωρίσουμε μερικά στοιχεία για τον ηλιασμό, με στόχο να βρεθούμε σε θέση να διαχειριστούμε και εκμεταλλευτούμε το φυσικό φως προς όφελος του αρχιτεκτονικού σχεδιασμού. Γεωγραφικές συντεταγμένες της γης Από το κέντρο της γης θεωρούμε ένα οριζόντιο επίπεδο τομής, κάθετο στον άξονα βορρά νότου. Το επίπεδο τέμνει τη σφαίρα της γης 1 κατά έναν οριζόντιο κύκλο, που ονομάζουμε ισημερινό (σχ. 2). Ο ισημερινός είναι ο κύκλος με τη μεγαλύτερη περιφέρεια και χωρίζει τη γη στο βόρειο και νότιο ημισφαίριο. Παράλληλα προς τον ισημερινό, προς το βορρά και προς το νότο, θεωρούμε περισσότερους οριζόντιους κύκλους, τους παραλλήλους. Αν ενώσουμε οποιοδήποτε σημείο ενός παραλλήλου με το κέντρο της γης σχηματίζεται μία γωνία με τον ισημερινό, η γωνία του παραλλήλου (σχ. 1). Θεωρούμε επίσης ένα κατακόρυφο επίπεδο τομής, παράλληλο δηλαδή στον άξονα βορρά νότου, που τέμνει στην επιφάνεια της γης έναν κατακόρυφο κύκλο 2, που ονομάζουμε μεσημβρινό. Για λόγους σύμβασης θεωρούμε ότι ο πρώτος μεσημβρινός της γης διέρχεται από την πόλη Greenwich, κοντά στο Λονδίνο, γι αυτό συχνά ο 1 ος μεσημβρινός ονομάζεται και μεσημβρινός Greenwich (σχ. 2). Κάθε περιστροφική μετατόπιση του 1 ου μεσημβρινού προς την ανατολή ή τη δύση, με άξονα περιστροφής τον άξονα βορρά νότου, δημιουργεί τους ανατολικούς και δυτικούς μεσημβρινούς της γης. Το πλέγμα των παραλλήλων και μεσημβρινών δημιουργεί στην επιφάνεια της γης ένα θεωρητικό σύστημα συντεταγμένων. Κάθε τόπος στην επιφάνεια της γης ορίζεται από το γεωγραφικό του πλάτος (latitude), που αντιστοιχεί στη γωνία που σχηματίζει η ακτίνα της γης που περνά από τον τόπο αυτό με την ακτίνα προς τον ισημερινό και από το γεωγραφικό του μήκος (longitude), που αντιστοιχεί στη γωνία που σχηματίζει ο μεσημβρινός του τόπου με τον μεσημβρινό Greenwich. σχ. 1 σχ Στην πραγματικότητα η γη έχει σχήμα ελλειψοειδούς εκ περιστροφής 2. Σχηματίζεται μία πολύ ελαφρά πεπλατυσμένη έλλειψη 187
2 Το γεωγραφικό πλάτος παίρνει τιμές από 0 Ο έως 90 Ο βόρειο ή νότιο και το γεωγραφικό μήκος 0 Ο έως 180 Ο ανατολικό ή δυτικό. Η Αθήνα, για παράδειγμα έχει γεωγραφικό πλάτος 37 Ο 58 βόρειο και γεωγραφικό μήκος 23 Ο 43 ανατολικό. Οι μεσημβρινοί εκτός από το στίγμα κάθε τόπου σχετίζονται, όπως θα δούμε, και με την ώρα του τόπου. Οι κινήσεις της γης Η γη κινείται γύρω από τον ήλιο σε ελλειπτική τροχιά, με τον ήλιο να καταλαμβάνει τη θέση της μίας εστίας της έλλειψης (σχ. 3). Μία πλήρης περιστροφή της γης γύρω από τον ήλιο διαρκεί 365,256 ημέρες. Το επίπεδο της τροχιάς της γης γύρω από τον ήλιο σχηματίζει με το επίπεδο του ισημερινού του ήλιου γωνία 23 Ο 45 (σχ. 4). Αυτή η απόκλιση έχει σαν αποτέλεσμα οι ακτίνες του ήλιου να μη φτάνουν σε ένα δεδομένο σημείο της γης με την ίδια γωνία κατά τη διάρκεια ενός έτους. Στο ψηλότερο σημείο της τροχιάς της, η γη δέχεται στο βόρειο ημισφαίριο τις ακτίνες του ήλιου με τη μεγαλύτερη κλίση και κάθετα στο νότιο ημισφαίριο. Στη θέση αυτή η διάρκεια της ημέρας στο βόρειο ημισφαίριο είναι η μικρότερη όλου του έτους, συμβαίνει στις 21 εκεμβρίου και ονομάζεται χειμερινό ηλιοστάσιο (σχ. 5). Στο χαμηλότερο σημείο της τροχιάς της η γη δέχεται στο βόρειο ημισφαίριο τις ακτίνες του ήλιου κάθετα και στο νότιο ημισφαίριο με τη μεγαλύτερη κλίση. Στη χαμηλότερη θέση η γη βρίσκεται στις 21 Ιουνίου κάθε έτους και η ημέρα ονομάζεται θερινό ηλιοστάσιο (σχ. 6). Η διάρκεια της ημέρας είναι η μεγαλύτερη όλου του έτους στο βόρειο ημισφαίριο και η μικρότερη στο νότιο. Στο μέσο περίπου της διαδρομής της γης από το χειμερινό στο θερινό ηλιοστάσιο όπως και από το θερινό στο χειμερινό ηλιοστάσιο, η γη περνά από δύο θέσεις όπου οι ακτίνες του ήλιου πέφτουν κάθετα στον ισημερινό της γης. Τις ημέρες αυτές η διάρκεια της ημέρας και της νύχτας είναι ίσες, ονομάζονται εαρινή και φθινοπωρινή ισημερία και συμβαίνουν στις 20 Μαρτίου και 22 Σεπτεμβρίου αντίστοιχα. Παρατηρούμε ότι, καθώς η γη περιστρέφεται γύρω από τον άξονα βορρά νότου κατά τη διάρκεια του χειμερινού ηλιοστασίου, οι ηλιακές ακτίνες πέφτουν κάθετα και «χαράσσουν» τον παράλληλο κύκλο που ονομάζουμε τροπικό του Αιγόκερω στο νότιο ημισφαίριο και εφάπτονται στη σφαίρα της γης χαράσσοντας τον παράλληλο που ονομάζουμε Αρκτικό κύκλο στο βόρειο ημισφαίριο. Αντίστοιχα, κατά το θερινό ηλιοστάσιο «χαράσσονται» ο τροπικός του Καρκίνου στο βόρειο ημισφαίριο και ο Ανταρκτικός κύκλος στο νότιο ημισφαίριο (σχ. 5,6). σχ. 3 σχ
3 σχ. 5 σχ. 6 Εκλειπτική και ζωδιακός κύκλος 3 «Προκειμένου να μελετήσουμε ευκολότερα την κίνηση των ουρανίων σωμάτων, χρησιμοποιούμε μια πανάρχαια αντίληψη για ένα γεωκεντρικό συμπαντικό μοντέλο, που ασφαλώς γνωρίζουμε πια πως δεν είναι σωστό, αλλά η χρήση του δεν δημιουργεί προβλήματα στη συνέχεια των συλλογισμών μας. Σύμφωνα με το μοντέλο αυτό η γη βρίσκεται ακίνητη στο κέντρο ενός σφαιρικού σύμπαντος και γύρω της τα άστρα είναι τοποθετημένα στην εσωτερική κοίλη επιφάνεια της ουράνιας αυτής συμπαντικής σφαίρας (σχ. 7). Πάνω στη σφαίρα αυτή ο ήλιος φαίνεται να κινείται κατά τη διάρκεια ενός έτους, διαγράφοντας έναν μέγιστο ουράνιο κύκλο. Αυτός ο μέγιστος κύκλος που απεικονίζει τη φαινόμενη ετήσια τροχιά του ήλιου πάνω στην ουράνια σφαίρα ονομάζεται εκλειπτική, ΕγΕ γ. Όπως είναι φανερό, το επίπεδο της εκλειπτικής, απεικονίζοντας μια πλαστή κίνηση του ήλιου, αντί της αληθινής γήινης περιφοράς γύρω από το άστρο της μέρας, συμπίπτει με το επίπεδο της τροχιάς της γης γύρω από τον ήλιο.» Αν αντί του πρωινού ουρανού παρατηρούμε τον νυχτερινό ουρανό, βλέπουμε ότι η εκλειπτική διέρχεται από 12 αστερισμούς (συμπλέγματα άστρων), που είναι γνωστοί ως οι 12 αστερισμοί του ζωδιακού κύκλου. «Ο ουράνιος ισημερινός ΙγΙ γ, ο μέγιστος δηλαδή κύκλος που τέμνει καθέτως τον άξονα της φαινόμενης περιστροφής της ουράνιας σφαίρας (άξονας του κόσμου ΠΠ ), τέμνει την εκλειπτική σε δύο αντιδιαμετρικά σημεία τα γ και γ - που ονομάζονται ισημερινά σημεία. Το σημείο γ ονομάζεται εαρινό ισημερινό σημείο ή αναβιβάζων σύνδεσμος της ηλιακής τροχιάς, γιατί από το σημείο αυτό διέρχεται ο ήλιος στις 21 Μαρτίου, ανερχόμενος από το νότιο ημισφαίριο στο βόρειο. Η 21 η Μαρτίου (εαρινή ισημερία) οριοθετεί την έναρξη της εποχής της άνοιξης. Το σημείο γ ονομάζεται φθινοπωρινό ισημερινό σημείο ή καταβιβάζων σύνδεσμος της ηλιακής τροχιάς. Από το σημείο αυτό διέρχεται ο ήλιος στις 22 Σεπτεμβρίου (φθινοπωρινή ισημερία), κατερχόμενος από το βόρειο ημισφαίριο στο νότιο. Η 22 α Σεπτεμβρίου οριοθετεί την έναρξη της εποχής του φθινοπώρου. Τα ηλιακά ημερολόγια αναφέρονται στη φαινόμενη ετήσια περιφορά του ήλιου πάνω στην ουράνια σφαίρα. 3. Στράτος Θεοδοσίου Μάνος ανέζης, Η οδύσσεια των ημερολογίων, τόμος Α: Αναζητώντας τις ρίζες της γνώσης, εκδόσεις ίαυλος, Αθήνα 1995, κεφ. Τροπικό, αστρικό και πολικό έτος, σελ
4 Έτσι, ως αστρικό έτος ορίζουμε τον χρόνο που χρειάζεται το κέντρο του ηλιακού δίσκου για να διαγράψει ολόκληρη την εκλειπτική και να επιστρέψει στο αυτό σημείο, από το οποίο αρχίσαμε τη μέτρηση. Ομοίως, ως τροπικό ή εποχιακό έτος ορίζουμε το χρονικό διάστημα που μεσολαβεί μεταξύ δύο διαδοχικών διαβάσεων του κέντρου του ηλιακού δίσκου από το ηλιακό ισημερινό σημείο γ. Όπως είναι φανερό, λόγω ορισμού, εάν το εαρινό ισημερινό σημείο γ ήταν σταθερό σημείο πάνω στην εκλειπτική, τότε το αστρικό έτος θα ταυτιζόταν με το τροπικό. Όμως, όπως γνωρίζουμε σήμερα, το γ δεν παραμένει σταθερό, αλλά: σχ. 7 α) Υφίσταται μια μετάπτωση, μετακινείται δηλαδή πάνω στην εκλειπτική κατά dλ=50,24 ετησίως (ανάδρομη φορά) και β) Κλονίζεται περί τη μέση αρχική του θέση 4. Λόγω, λοιπόν, της μη σταθερότητας του γ, το κέντρο του ηλιακού δίσκου, κατά την ετήσια περιφορά του ήλιου θα καθυστερήσει να συναντήσει το εαρινό ισημερινό σημείο που θα βρίσκεται στη νέα του θέση- κατά 0, μέσες ηλιακές ημέρες, ή 20,38608 πρώτα λεπτά μέσου χρόνου. Το χρονικό αυτό διάστημα της καθυστέρησης αποτελεί τη διαφορά μεταξύ του αστρικού και τροπικού έτους. ηλαδή: 1 τροπικό έτος = 365, μέσες ηλιακές ημέρες, ενώ 1 αστρικό έτος = 365, μέσες ηλιακές ημέρες Τέλος, θα πρέπει να σημειώσουμε ότι για διάφορους λόγους ούτε η διάρκεια του τροπικού έτους παραμένει σταθερή, αλλά ελαττώνεται κατά 0,53 δευτερόλεπτα ανά αιώνα. Επειδή όμως η μεταβολή αυτή θεωρείται πολύ μικρή (σχεδόν αμελητέα), μπορούμε για μια μεγάλη χρονική περίοδο να θεωρούμε ότι το τροπικό έτος διαρκεί κατά μέσο όρο 365, πολιτικές ημέρες ή 365 ημέρες, 5 ώρες, 48 πρώτα λεπτά και 45,96 δευτερόλεπτα. Τέλος, για την ιστορία αναφέρουμε ότι η ονομασία του τροπικού έτους οφείλεται στο ότι όχι μόνον η γγ, η ισημερινή γραμμή, αλλά και η ΕΕ, η γραμμή των τροπών, μετατοπίζεται συνεχώς, έτσι ώστε να παραμένει πάντα κάθετη στη γγ. Επομένως η επάνοδος του ήλιου σε μια από τις τροπές (θερινή τροπή 21 Ιουνίου ή χειμερινή τροπή 22 εκεμβρίου) γίνεται μετά ένα τροπικό έτος. Τόσο όμως το τροπικό, όσο και το αστρικό έτος είναι ακατάλληλα για την κατασκευή ημερολογίων, επειδή, εκτός από τον ακέραιο αριθμό ημερών τους, περιέχουν και κλάσματα της ημέρας αρκετών δεκαδικών ψηφίων. 4. Ιδ. Παράρτημα IV: Μετάπτωση και κλόνηση 190
5 Εξαιτίας αυτού του γεγονότος, επινοήθηκε το «πολιτικό έτος», το έτος δηλαδή που περιέχει ακέραιο αριθμό ημερών, και ως εκ τούτου δεν δημιουργείται το φαινόμενο μία και η αυτή ημέρα να κατανέμεται μεταξύ δύο διαδοχικών ετών. Επιπλέον, το πολιτικό έτος βασίζεται στο τροπικό έτος και αυτό προκειμένου να εξασφαλίζεται η κανονική διαδοχή των τεσσάρων κλιματολογικών εποχών. Το πολιτικό έτος, όμως, διατηρεί μόνο τον ακέραιο αριθμό των ημερών του τροπικού έτους συνεπώς αριθμητικά είναι μικρότερο από αυτό κατά το δεκαδικό του μέρος, δηλαδή κατά 0,25 ηλιακές ημέρες περίπου. Η διαφορά αυτή με την πάροδο των αιώνων θα μεγάλωνε συνεχώς αθροιστικά, με αποτέλεσμα να μεταφέρονται ημερολογιακά οι κλιματολογικές εποχές του έτους. Γι αυτό, μετά από πάρα πολλά χρόνια, όταν το αθροιστικό σφάλμα θα είχε πάρει μια αναγκαία τιμή, ο μήνας Ιούνιος για παράδειγμα- δεν θα αντιστοιχούσε στην κλιματολογική εποχή του θέρους, αλλά του φθινοπώρου ή και του χειμώνα. Άμεσο αποτέλεσμα ενός τέτοιου γεγονότος θα ήταν η αδυναμία του προγραμματισμού των κοινωνικών και παραγωγικών διαδικασιών του ανθρώπου (π.χ. γεωργικές και κτηνοτροφικές εργασίες). Προκειμένου να ξεπεραστεί το πρόβλημα αυτό, κάθε ημερολογιακό σύστημα προβλέπει μια σειρά διορθώσεων, με πιο γνωστή την πρόσθεση μιας επιπλέον ημέρας κάθε τέσσερα έτη με τρόπο ώστε κάθε τετραετία να περιέχει ένα δίσεκτο έτος με διάρκεια 366 ημερών. Γενικά, λοιπόν, ως ημερολόγιο θεωρούμε κάθε σύστημα διαίρεσης του έτους, το οποίο προσπαθεί να επιτύχει, με τον καλύτερο δυνατό τρόπο, την εναρμόνιση της φυσικής διαίρεσης των κλιματολογικών εποχών με την κατά συνθήκη διάρκεια του εκάστοτε πολιτικού έτους». Ιστορία των ημερολογίων Από πολύ νωρίς στην ιστορία του ο άνθρωπος παρατήρησε τον ουρανό και κατανόησε ότι η διαδοχή της ημέρας και της νύχτας, η διαδοχή των εποχών του έτους, αλλά και η διαδοχή των «εποχών», με την έννοια μεγάλων χρονικών περιόδων, είχε να κάνει με τις κινήσεις του ήλιου, της γης και της σελήνης. Όλοι οι πολιτισμοί της αρχαιότητας είχαν κάνει προσπάθειες για τη μέτρηση του χρόνου και λίγο πολύ όλοι εναρμόνισαν τις θρησκευτικές τους τελετές και δοξασίες με τις κινήσεις των τριών αυτών κύριων (για τη ζωή στη γη) ουρανίων σωμάτων. Η μέτρηση του χρόνου ήταν θέμα ζωτικής σημασίας, διότι με τους σωστούς υπολογισμούς- μπορούσε εικ. 8 Το λίθινο ημερολόγιο των Αζτέκων ή Πέτρα του Ήλιου 191
6 να προβλεφθεί η αλληλουχία των εποχών κι επομένως οργανώνονταν οι αγροτικές εργασίες. Με την πρόοδο του πολιτισμού οι αστρονομικές παρατηρήσεις έγιναν απαραίτητες και στη ναυσιπλοΐα. Οι αστρονομικές παρατηρήσεις των αρχαίων λαών ήταν δύσκολο ν απομνημονευθούν, ακόμη και να καταγραφούν, ειδικά αν αναφερόμαστε σε λαούς που δε χρησιμοποιούσαν τη γραφή, όπως οι Μάγια στη χερσόνησο του Γιουκατάν της Κεντρικής Αμερικής. Οι μύθοι των θεών στους οποίους κάθε λαός πίστευε, πολύ συχνά αναφέρονται σε αστρονομικές παρατηρήσεις. Με άλλα λόγια, μια θεότητα συχνά απεικονίζεται σ ένα λαμπρό άστρο ή αστερισμό και με βάση τις αστρονομικές παρατηρήσεις του αστερισμού αυτού, δημιουργείται ένας μύθος, που αναφέρεται στη θεότητα. Αυτός ήταν για πολλούς λαούς και για πολλούς αιώνες ο πιο συνηθισμένος τρόπος απομνημόνευσης των αστρονομικών παρατηρήσεων κι αποτελούσε ασφαλή τρόπο κληροδότησης της γνώσης από τη μια γενιά στην άλλη. Παράλληλα εξυπηρετούσε την απομνημόνευση των παρατηρήσεων κι από τους «κοινούς θνητούς», τους απλούς ανθρώπους των αρχαίων κοινωνιών, που δεν μορφώνονταν ποτέ κι ανήκαν σε κατώτερες κάστες ή κοινωνικές ομάδες, οι οποίοι όμως μάθαιναν εύκολα κι απλά την αλληλουχία των εποχών και προετοίμαζαν τις αγροτικές εργασίες. Γίνονταν κι αυτοί (με τον τρόπο τους) φορείς των γνώσεων των αστρονομικών παρατηρήσεων. Ο συνδυασμός της θρησκείας με την επιστήμη είναι προφανής. ημιουργήθηκε πλήθος συμβολισμών που «έκρυβαν» και «φανέρωναν» τις γνώσεις κάθε λαού, με πιο σημαντικό εκείνο του φιδιού, που μάλιστα τείνει να είναι κοινός, σχεδόν για όλους τους αρχαίους πολιτισμούς. Είναι πιθανό η λατρεία των ερπετών να στηρίζεται στο γεγονός ότι το δέρμα του φιδιού είναι ατελείωτο, εφ όσον περιοδικά απορρίπτεται και συνεχώς ανανεώνεται, όπως ακριβώς κι ο χρόνος. Βέβαια οι ιερατικές κάστες κάθε αρχαίου λαού από νωρίς συνειδητοποίησαν ότι δεν μπορούσαν να στηριχτούν στις προφορικές παραδόσεις και τους μύθους των θεών τους για τη διατήρηση της γνώσης και τη συνέχιση των παρατηρήσεων. Το γεγονός δε ότι η περιφορά της γης γύρω από τον ήλιο δεν είναι ακέραιος αριθμός, δεν αντιστοιχεί δηλαδή σε ακέραιο, αλλά σε κλασματικό πλήθος ημερών, ήταν γνωστό σε όλους τους αρχαίους λαούς και μόνο η συνεχής παρατήρηση του φαινομένου μπορούσε να καταστήσει δυνατή τη διόρθωση των ημερολογίων. εικ. 9 Πρόπλασμα αναπαράστασης του θρησκευτικού κέντρου της πόλης Tenochtitlan των Αζτέκων, με σχεδιασμό σε απόλυτη συμμετρία και τάξη 192
7 Σχεδόν όλοι οι αρχαίοι πολιτισμοί στρογγυλοποιούν την περίοδο των 365,25 περίπου ημερών του έτους στις 360 και «διορθώνουν» τη διαφορά με εμβόλιμες ημέρες. Είναι λοιπόν προφανές γιατί ο αριθμός 360 και οι υποδιαιρέσεις του είναι τόσο σημαντικός και μέχρι σήμερα χρησιμοποιείται στη μέτρηση του κύκλου κι επομένως στη μέτρηση του χρόνου. Είναι επίσης προφανής ο λόγος που τα υποπολλαπλάσια του 360, όπως οι αριθμοί 3, 4, (3+4=)7, (3x4=)12, (3x12=)36 ήταν κι ακόμη είναι ιεροί αριθμοί. Το «όπλο» ενάντια στη λήθη ήταν η αρχιτεκτονική. Χτίστηκαν θρησκευτικά μνημεία όπου «καταγράφονταν» αστρονομικές παρατηρήσεις αφ ενός, αφ ετέρου δε λειτουργούσαν και σαν αστεροσκοπεία. Το πιο γνωστό και χαρακτηριστικό παράδειγμα είναι η πυραμίδα του Χέοπα, που μάλιστα έχει χαρακτηριστεί ως η «πέτρινη βίβλος» της ανθρωπότητας (εικ. 10). Πέρα από την παραφιλολογία που έχει πλαστεί πάνω στον μυστικισμό των αριθμών και των διαστάσεών της, είναι γεγονός ότι η πυραμίδα του Χέοπα κατασκευάστηκε υπό την επίβλεψη και καθοδήγηση των αρχαίων Αιγυπτίων ιερέων αστρονόμων. Αποτελεί το μεγαλύτερο μεσημβρινό αστρονομικό όργανο του κόσμου και η δίοδός της (πριν κλειστεί) ήταν στραμμένη προς τον πολικό αστέρα, που εκείνη την εποχή αντιστοιχούσε στο άστρο Τουμπάν, το λαμπρότερο άστρο του αστερισμού του ράκοντα (σχ. 11). Για κάποιο ανεξήγητο λόγο οι πυραμίδες της Γκίζας του Χέοπα (Χουφού ή Κνεφού), του Χεφρήνου (Χαφρ ή Κχαφρά) και του Μυκερίνου (Μενάκουρ ή Μενκερά)- βρίσκονται στον παράλληλο με γεωγραφικό πλάτος 30 Ο (για την ακρίβεια 29 Ο ) και είναι προσανατολισμένες προς τα τέσσερα σημεία του ορίζοντα. Μάλιστα η διαγώνιος της πυραμίδας του Χέοπα από τα Β προς τα ΝΑ αν προεκταθεί, αποτελεί διαγώνιο της πυραμίδας του Χεφρήνου (εικ. 12). Στην άλλη άκρη του Ατλαντικού οι Ίνκας τοποθετούσαν στις κορυφές των βουνών και στις πόλεις τους λίθινες κατασκευές, γνωστές ως Intihuatana (πέτρες που δένουν τον Ήλιο). Οι κατασκευές χρησίμευαν μάλλον για την παρακολούθηση της ετήσιας κίνησης του ήλιου, κάτι σαν τα ηλιακά ρολόγια. Ένας από τους πιο μυστηριώδεις λαούς της Κεντρικής Αμερικής, οι Μάγια, είχαν βρει το ακριβέστερο σύστημα μέτρησης του χρόνου και όσες από τις αστρονομικές τους παρατηρήσεις έχουν σωθεί 5, αποδεικνύουν ότι ο λαός αυτός κατείχε αστρονομικές γνώσεις που ακόμη και σήμερα προκαλούν έκπληξη. Οι Μάγια λάτρευαν τον Ήλιο, τη Σελήνη, τη Βροχή και κυρίως τον θεό Kukulcan, που τον παρίσταναν σαν ένα μεγάλο φτερωτό φίδι. Σύμφωνα με το μύθο, ο Kukulcan ήταν αυτός που είχε διδάξει εικ. 10 Οι τρεις πυραμίδες της Γκίζας 5. Έχουν διασωθεί μόνο τρία χειρόγραφα των Μάγια, όλα με αστρονομικές παρατηρήσεις, που σήμερα ονομάζονται: 1) Codex Tro-cortesianus (Ισπανία), 2) Codex Peresianus (Παρίσι), 3) Codex Dresdensis ( ρέσδη) 193
8 σχ. 11 εικ. 12 Αεροφωτογραφία της περιοχής των πυραμίδων της Γκίζας. Σημειώνεται η νοητή διαγώνιος των δύο μεγαλύτερων πυραμίδων 194
9 όλους τους νόμους που κυβερνούσαν τη ζωή τους. Όλες οι πυραμίδες των Μάγια έχουν ακριβή αστρονομικό προσανατολισμό και χτίστηκαν για τις ανάγκες ενός ημερολογίου (εικ. 14). Από τον ψηλότερο εξώστη της πυραμίδας του Ουαξακτούν (Β. Γουατεμάλα) ο ήλιος στις 21 Ιουνίου (θερινό ηλιοστάσιο) ανατέλλει πίσω από τη βόρεια γωνία του ναού Ι. Κατά τη φθινοπωρινή και εαρινή ισημερία, στις 22 Σεπτεμβρίου και 21 Μαρτίου αντίστοιχα, ο ήλιος ανατέλλει ακριβώς πίσω από το μέσο του ναού ΙΙ και τέλος κατά το χειμερινό ηλιοστάσιο στις 22 εκεμβρίου ο ήλιος ανατέλλει πίσω από τη νότια γωνία του ναού ΙΙΙ (σχ 15). Η πυραμίδα του Γιουκατάν, ή όπως είναι γνωστή σήμερα η «πυραμίδα του Πολεμιστή» είναι στην ουσία ναός αφιερωμένος στη λατρεία του ημερολογίου(!), με πλήθος αριθμητικών συμβολισμών σχετικών με το ημερολόγιο των Μάγια, τις μυθοπλασίες γύρω απ αυτό και την «τάξη» που αντιπροσώπευε. Μελετητές ισχυρίζονται ότι οι Μάγια όχι μόνο ασχολούνταν με τη μέτρηση του χρόνου και την αστρονομία, αλλά είχαν υποτάξει την τέχνη και την αρχιτεκτονική τους στην ημερολογιακή «μανία» που τους είχε καταλάβει! Αξίζει να σημειωθεί ότι οι Μάγια είχαν ένα ακριβέστατο ημερολόγιο, αλλά δεν γνώριζαν το ρολόι, που είναι η απαραίτητη προϋπόθεση (μαζί με το μεσημβρινό όργανο) για τον υπολογισμό του ηλιακού έτους! Στην Κίνα έχουμε αρχαιότατες καταγραφές αστρονομικών παρατηρήσεων, όχι τόσο σε έργα αρχιτεκτονικής όμως. Οι Κινέζοι δεν αρκέστηκαν στην παρατήρηση των κινήσεων του ήλιου και της σελήνης μόνο, αλλά προχώρησαν σε παρατηρήσεις της περιοδικότητας των εκλείψεων του ήλιου και της σελήνης, των εξάρσεων των ηλιακών κηλίδων και της κίνησης των κομητών. Είναι οι πρώτοι που χρησιμοποίησαν τα συστήματα των ισημερινών και ουρανογραφικών συντεταγμένων (που χρησιμοποιούμε και σήμερα). Όλες οι παρατηρήσεις τους είχαν καταγραφεί μ εξαιρετική ακρίβεια στα «Χρονικά της Σινίκης», στα οποία ακόμη και σήμερα ανατρέχουν οι αστρονόμοι 6. εικ. 13 Ηλιακό ρολόι (;) των Μάγια στο Machu Picchu 6. Στα «Χρονικά της Σινίκης» ο Κινέζος αστρονόμος Γιάνγκ Βέι Τεκ κατέγραψε στις 4 Ιουλίου 1056 μ.χ. την εμφάνιση ενός «επισκέπτη αστέρα» supernova (υπερκενοφανούς) στον αστερισμό του Ταύρου, που ήταν τόσο λαμπρός, που φαινόταν ακόμη και το πρωί για τρεις εβδομάδες και εύκολα αντιληπτός τη νύχτα, μέχρι τις 17 Απριλίου 1056, οπότε έπαψε να είναι ορατός με γυμνό μάτι. Η αναφορά αυτή βοήθησε στα 1942 τους αστρονόμους Mayall και Oort να καταλήξουν στο συμπέρασμα ότι το νεφέλωμα του Καρκίνου (Crab Nebula), που βρίσκεται στον αστερισμό του Ταύρου, είναι το υπόλειμμα της έκρηξης εκείνου του supernova. Η παρατήρηση αυτής της έκρηξης supernova είναι η μοναδική στ αστρονομικά χρονικά 195
10 σχ. 15 εικ. 14 Η πυραμίδα των Μάγια στο Palenque, ο ναός των αφιερωμάτων εικ. 16 Ηλιακό ρολόι στην Απαγορευμένη πόλη, Πεκίνο, Κίνα 196
11 σχ. 17 Σχηματική αναπαράσταση των τριών φάσεων κατασκευής του Stonehenge εικ. 18 Η ανατολή του ήλιου στις 21 Ιουνίου 2006 (θερινό ηλιοστάσιο) στο Stonehenge 197
12 Η πολύ προηγμένη κινεζική αστρονομία είχε σαν κύριο σκοπό την πρόγνωση μελλοντικών γεγονότων και για το λόγο αυτό οι αστρονόμοι είχαν επιδοθεί στη σύνταξη ημερολογίων. Ήταν κρατικοί υπάλληλοι επιφορτισμένοι με την παρακολούθηση των ουρανίων φαινομένων και των κινήσεων του ήλιου και της σελήνης, ώστε να προαναγγέλλουν τις μελλοντικές αλλαγές των κλιματολογικών συνθηκών και να υποδεικνύουν τις αναγκαίες θυσίες για τον εξευμενισμό των θεών. Στην Ευρώπη ένα από τα αρχαιότερα δείγματα αρχιτεκτονικού έργου στην υπηρεσία αστρονομικών παρατηρήσεων είναι το Stonehenge, το μεγαλιθικό μνημείο της Νότιας Αγγλίας, που χρονολογείται (στην 1 η φάση της κατασκευής του) στα 2950π.Χ. Πολύ λίγα είναι γνωστά για το καταπληκτικό αυτό μνημείο, κυρίως επειδή για πολλά χρόνια θεωρούνταν από τους μελετητές ως ρωμαϊκός ναός. Σήμερα πιστεύεται ότι το Stonehenge ήταν Κελτικός ναός αφιερωμένος στον ήλιο (σχ. 17). Έχει μάλιστα υπολογιστεί ότι το πρωινό της θερινής ισημερίας ο ήλιος ανέτειλε κατ ευθείαν πάνω από τη Heel Stone (ακρογωνιαίος λίθος) και οι πρώτες ακτίνες του φώτιζαν το κέντρο του μνημείου (εικ. 18), στο μεταξόνιο 7 των λίθων του πεταλωτού σχηματισμού. Πιο πρόσφατα ο αστρονόμος Gerard Hawkins αμφισβήτησε ότι το Stonehenge είναι απολύτως ευθυγραμμισμένο με τη θερινή ισημερία και άλλα ηλιακά και σεληνιακά φαινόμενα και ισχυρίστηκε ότι κατασκευάστηκε για να προβλέπει αστρονομικά φαινόμενα, όπως οι εκλείψεις. Με άλλα λόγια το Stonehenge είναι πιθανόν κάτι παραπάνω από ναός ή αστεροσκοπείο, είναι ένας αστρονομικός υπολογιστής! Περίπου 4000 χρόνια μεταγενέστερο ( μ.Χ.) είναι το κτίσμα Ram Yantra στο συγκρότημα Jantar Mantar στη Jaipur της Ινδίας (εικ. 19). Έχει σχεδόν την ίδια μορφολογία με το Stonehenge, αλλά διαφορετική χρήση. Το ύψος της περιμετρικής κιονοστοιχίας και της κεντρικής ράβδου είναι ίσο με την ακτίνα της κυκλικής κιονοστοιχίας και κατασκευάστηκε για να υπολογίζεται η γωνία ύψους ηλίου (altitude) τις διαφορετικές ημέρες του έτους (σχ. 20). Γενικά το συγκρότημα της Jantar Mantar της Jaipur και των άλλων πόλεων της Ινδίας κατασκευάστηκε ευθύς εξ αρχής ως συγκρότημα αστρονομικών οργάνων. Το ίδιο το όνομα του συγκροτήματος σε ελεύθερη μετάφραση σημαίνει: όργανα για τη μέτρηση της αρμονίας των ουρανών. Στο συγκρότημα περιλαμβάνεται το εικ. 19 Jantar Mantar, Jaipur, Ινδία 7. Μεταξόνιο είναι το διάστημα μεταξύ των αξόνων δύο διαδοχικών κιόνων ή πεσών ενός κτίσματος 198
13 Samrat Yantra, το μεγαλύτερο στον κόσμο ηλιακό ρολόι. Αυτό που είναι αξιοσημείωτο σ αυτό το μνημείο, το μόνο που έχει διατηρηθεί σε τόσο καλή κατάσταση 8, είναι ότι λόγω της μεγάλης κλίμακας των κατασκευών από άποψη μεγέθους, έγινε δυνατό να μετρηθεί το λεγόμενο σκιόφως. Ο ήλιος δεν είναι μια σημειακή πηγή φωτισμού, αλλά ένας δίσκος με αρκετά μεγάλο φαινόμενο μέγεθος. Από δύο (σχεδόν) αντιδιαμετρικά σημεία του δίσκου του ήλιου και τα ενδιάμεσά τους ξεκινά ένα πλήθος φωτεινών ακτίνων (σχ. 22), που δημιουργεί ένα «σύνολο» σκιών κι αυτό ισχύει για οποιοδήποτε αντικείμενο πάνω στη γη. Η γωνία που σχηματίζουν δύο (σχεδόν) αντιδιαμετρικά σημεία του δίσκου του ήλιου μ ένα σημείο στην επιφάνεια της γης είναι κατά μέσο όρο 30 Ο. Αποτέλεσμα του φαινομένου είναι ότι το όριο σχ. 20 εικ. 21 Το επίπεδο ηλιακό ρολόι στο Jantar Mantar εικ. 23 Το σκιόφως στο Ram Yantra σχ Αστεροσκοπεία σαν το Jantar Mantar χτίστηκαν σε αρκετές πόλεις της Ινδίας, όπως το ελχί, η Mathura, η Ujjain και η Varanassi, για να επιτυγχάνεται στατιστική ανάλυση των αστρονομικών παρατηρήσεων και συγκρίσεις των αποτελεσμάτων 199
14 ανάμεσα στο φως και τη σκιά, είτε πρόκειται για ερριμμένη σκιά, είτε γι αυτοσκιά (κι αυτό είναι πιο έκδηλο σε καμπύλα αντικείμενα), να μην είναι μια γραμμή, αλλά μια μικρή περιοχή, όπου η ένταση τη σκιά μειώνεται προς το φως και αντίστροφα. Αυτό το φαινόμενα στο Samrat Yantra δημιουργεί μια απροσδιοριστία στη μέτρηση του χρόνου της τάξης των 15, αλλά βοήθησε στον προσδιορισμό της απόστασης του ήλιου από τη γη και στη μέτρηση της ακτίνας του ισημερινού του ήλιου. σχ. 24 Γωνίες πρόσπτωσης ηλιακού φωτός Εάν υποθέσουμε ότι η γη είναι ακίνητη με τον ήλιο να κινείται γύρω της, τότε σε κάθε τόπο ο ήλιος ρίχνει τις ακτίνες του με διαφορετική γωνία κάθε χρονική στιγμή. Τοποθετώντας έναν παρατηρητή να κοιτά σταθερά προς το βορρά, τότε παρατηρούμε ότι από την ανατολή (στα δεξιά του παρατηρητή) μέχρι τη δύση του (στ αριστερά του παρατηρητή) ο ήλιος διαγράφει ένα τόξο, που μπορούμε να θεωρήσουμε κυκλικό. Αν ο παρατηρητής δεν βρίσκεται κοντά στον Αρκτικό ή τον Ανταρκτικό παράλληλο, τότε σχ. 25 παρατηρούμε ότι κατά τη διάρκεια μιας ημέρας ο ήλιος σχηματίζει με τον ορίζοντα του τόπου μια γωνία που συνεχώς αυξάνεται μέχρι τη μεσουράνηση του ήλιου και από κει και μετά μειώνεται, μέχρι τη δύση του ήλιου. Η γωνία που μας δίνει το ύψος του ήλιου από τη γραμμή του ορίζοντα (σχ. 24) ονομάζεται γωνία ύψους ηλίου (altitude angle). Η γωνία που μας δίνει την απόκλιση του ήλιου σε σχέση με το βορρά (σχ. 25) ονομάζεται γωνία αζιμουθίου (azimuth angle). Συνήθως η γωνία αζιμουθίου έχει θετικές τιμές κινούμενη δεξιόστροφα, με τις 0 Ο να ορίζονται στο βορρά. Στους παράπλευρους πίνακες παρουσιάζονται οι γωνίες ύψους ηλίου και αζιμουθίου για το στίγμα της Αθήνας στις 30 Ιανουαρίου 2004 και στην εαρινή ισημερία του Σημειώνεται ότι η ώρα αναφοράς είναι η UTC. Για να βρούμε την ώρα της Αθήνας, θα πρέπει να μετατρέψουμε σε μοίρες τη γωνία του γεωγραφικού μήκους της Αθήνας και να την προσθέσουμε στην UTC (περίπου 2:25). 200
15 πίνακας 1 πίνακας 2 201
16 Μέτρηση του χρόνου Ο υπολογισμός του χρόνου σ ένα τόπο έχει άμεση σχέση με το γεωγραφικό του μήκος, με τη διαφορά ότι το γεωγραφικό μήκος μετριέται σε μοίρες άλλοτε ανατολικές κι άλλοτε δυτικές (και μέχρι 180 Ο ), ενώ οι γωνίες του χρόνου μετριούνται μόνο προς τη δύση και φτάνουν τις 360 Ο. Κατά τη διάρκεια μίας ημέρας η γη κάνει μία πλήρη περιστροφή γύρω από τον άξονά της, δηλαδή διαγράφει πλήρη κύκλο 360 Ο, σε διάστημα 24 ωρών. Η παραπάνω αντιστοιχία μας επιτρέπει να υπολογίσουμε: 360 Ο = 24 ώρες 15 Ο = 1 ώρα 1 Ο = 4 λεπτά της ώρας 1/60 Ο = 4 δευτερόλεπτα της ώρας Αρχή μέτρησης του χρόνου της γης θεωρείται η χρονική στιγμή κατά την οποία ο μεσημβρινός Greenwich δέχεται κάθετα τις ηλιακές ακτίνες, κατά τη διάρκεια μιας ισημερίας. Τότε η ώρα στο Greenwich είναι 12:00 το μεσημέρι. Σ έναν άλλο τόπο στον ίδιο παράλληλο, που ο μεσημβρινός του σχηματίζει με τον μεσημβρινό Greenwich γωνία 15 Ο δυτικά, η ώρα είναι 11:00 το πρωί. Η ώρα Greenwich λέγεται αλλιώς GMT (Greenwich Mean Time) ή UTC (Coordinated Universal Time) ή πιο απλά UT (Universal Time) και δίνεται σε τιμή ρολογιού 24 ωρών, δηλαδή 22:19 (συχνά γράφεται 2219) αντί για 10:19μμ. Η ώρα Greenwich υπολογίζεται πολλές φορές κάθε μέρα, με βάση τα στοιχεία θέσης της γης, που δίνουν τα διάφορα ανά τον κόσμο εργαστήρια μέτρησης του χρόνου. Η μέτρηση του χρόνου φτάνει έτσι να παρουσιάζει απόκλιση 1 νανοδευτερολέπτου ανά ημέρα. Μεσημβρινός ενός τόπου Ένας πρακτικός τρόπος, αν και όχι ιδιαίτερα ακριβής, για να προσδιορίσουμε τη θέση του βορρά ενός τόπου, χωρίς να χρησιμοποιήσουμε πυξίδα, είναι ο εξής: Σε οριζόντιο και επίπεδο έδαφος στήνουμε κατακόρυφα έναν στύλο και χαράζουμε στο έδαφος ημικύκλια προς την πλευρά του βορρά (σχ. 26). Σε κάποια πρωινή ώρα η σκιά του στύλου θα βρεθεί σε κάποιο σημείο ενός από τα ημικύκλια. Σημαδεύουμε το σημείο α και περιμένουμε μέχρι η σκιά του στύλου να πέσει στο ίδιο με το πρώτο ημικύκλιο, κάποια απογευματινή ώρα. Σημαδεύουμε και το δεύτερο σημείο β. Η θέση του βορρά βρίσκεται στη διχοτόμο της γωνίας αοβ. Η χρήση της πυξίδας μοιάζει πιο απλή, αλλά πρέπει να συνυπολογίζουμε τη γωνία απόκλισης του γεωγραφικού από τον μαγνητικό βορρά, η οποία εξαρτάται από το στίγμα του τόπου. Για το στίγμα της Αθήνας η απόκλιση του μαγνητικού βορρά είναι περίπου 3 Ο 7 ανατολικά, με ρυθμό απόκλισης 3,8 /έτος. σχ
17 Ηλιακά ρολόγια Τα ηλιακά ρολόγια είναι διατάξεις που προσδιορίζουν τον ακριβή ηλιακό χρόνο και συνήθως αποτελούνται από μια ράβδο ή γνώμονα και μια πλάκα με εγχάρακτες γραμμές (εικ. 27), που αντιστοιχούν στις ερριμμένες σκιές της ράβδου σε ακέραιες ωριαίες γωνίες του ήλιου. Τα ηλιακά ρολόγια δείχνουν τον αληθή ηλιακό χρόνο ενός τόπου, που διαφέρει από τον επίσημο (πολιτικό). Η ιστορία των ηλιακών ρολογιών φαίνεται να είναι τόσο παλιά, όσο και η ιστορία του πολιτισμού του ανθρώπου. Σήμερα πιστεύεται από τους αρχαιολόγους ότι ήδη από την εποχή των σπηλαίων οι άνθρωποι είχαν προσέξει ότι οι σκιές των αντικειμένων μετέβαλλαν το μήκος τους κατά τη διάρκεια της ημέρας. Πιστεύεται επίσης ότι είχαν τοποθετήσει κάθετα σε μια τρύπα στη γη κάποιο ίσιο ξύλο και παρατηρούσαν τη διαφοροποίηση του μήκους της σκιάς του κι ακόμη ότι η περιοχή στην οποία δημιουργούνταν η σκιά ήταν συγκεκριμένη, περιορισμένη, αλλά και μεταβαλλόμενη από εποχή σε εποχή. εικ. 27 σχ. 28 Σχηματισμοί που πολύ πιθανό να είναι ηλιακά ρολόγια έχουν βρεθεί στην Αίγυπτο και χρονολογούνται από το 1500π.Χ. (σχ. 28). Η ορθότητα των χαράξεων όμως είναι τέτοια, που δηλώνει ότι οι παρατηρήσεις για την κίνηση του ήλιου και τη μέτρηση του χρόνου είναι πολύ προγενέστερες. Είναι λοιπόν πολύ πιθανό τα ηλιακά ρολόγια να είναι όργανα μέτρησης του χρόνου κατά πολύ αρχαιότερα, κατασκευασμένα όμως από υλικά που δεν άντεξαν στο χρόνο. Στην Ελλάδα το ηλιακό ρολόι παρουσιάστηκε για πρώτη φορά από τον φυσικό φιλόσοφο, μαθηματικό, γεωμέτρη και αστρονόμο Αναξίμανδρο από τη Μίλητο ( π.Χ.). Από τότε μέχρι σήμερα τα ηλιακά ρολόγια έχουν βρεθεί σε όλους τους τόπους της γης, όπου υπάρχουν ανθρώπινες κοινωνίες κι έχουν τη δική τους συμμετοχή ως μορφολογικά (εκτός από εικ. 29 Παλιό ημαρχείο, Πράγα, Τσεχία. Το αστρονομικό ρολόι, εκτός από την ώρα, δείχνει τις κινήσεις των πλανητών γύρω από τη γη, τον κύκλο των ζωδίων και περιλαμβάνει σεληνιακό ημερολόγιο 203
18 εικ. 30 Ηλιακό ρολόι, Milton Keynes, Αγγλία χρηστικά) στοιχεία της αρχιτεκτονικής κάθε τόπου και κάθε εποχής. Σήμερα τα ηλιακά ρολόγια είναι οι ξεχασμένοι θεματοφύλακες του χρόνου και λίγοι είναι εκείνοι που γνωρίζουν την ιστορία, τη χρήση τους και τη σκοπιμότητά τους. Τα ηλιακά ρολόγια χωρίζονται σε δύο μεγάλες οικογένειες: α) τα επίπεδα και β) τα καμπύλα ηλιακά ρολόγια. Α. Επίπεδα ηλιακά ρολόγια Επίπεδα ονομάζονται διότι η επιφάνεια πάνω στην οποία «γράφεται» ο χρόνος είναι επίπεδη πλάκα, τοποθετημένη σε διάφορες θέσεις. Τα οριζόντια ηλιακά ρολόγια αποτελούνται από μια πλάκα τοποθετημένη απολύτως οριζόντια και μια ράβδο ή γνώμονα που σχηματίζει με το επίπεδο της πλάκας γωνία φ ίση με το γεωγραφικό πλάτος του τόπου στον οποίο το ρολόι βρίσκεται, είναι δηλαδή παράλληλη με τον άξονα του κόσμου. Για τη χάραξη των διαιρέσεων του ρολογιού είναι απαραίτητο να είναι γνωστή η διεύθυνση της μεσημβρινής γραμμής (η διεύθυνση του βορρά) και οι γεωγραφικές συντεταγμένες του τόπου. Ξεκινώντας από τη βάση Β της ράβδου η γραμμή που αντιστοιχεί στη 12 η μεσημβρινή ώρα είναι η παράλληλη στη μεσημβρινή γραμμή. Επομένως η 6 η πρωινή και η 6 η απογευματινή βρίσκονται στην ευθεία ανατολής δύσης 9. Οι υπόλοιπες υποδιαιρέσεις δεν δημιουργούν στην πλάκα του ρολογιού (στο οριζόντιο επίπεδο) ίσες γωνίες, διότι ο ήλιος κινείται φαινομενικά κυκλικά και ανοδικά από την ανατολή στο ζενίθ και κατόπιν στη δύση του. Για τον προσδιορισμό των υποδιαιρέσεων των ωρών, θεωρούμε ένα επίπεδο που είναι κάθετο στη ράβδο του ηλιακού ρολογιού σε κάποιο σημείο της Κ. Το επίπεδο στο σχήμα 31 είναι πρόσθιο και σχηματίζουμε την 9. Οι θέσεις αυτές προκύπτουν από τις ισημερίες, οπότε ο ήλιος μεσουρανεί (βρίσκεται στο ζενίθ του) στις 12 το μεσημέρι και μέσα σε 12 ώρες διανύει τις 180 Ο από το σημείο της ανατολής στο σημείο της δύσης. 204
19 σχ. 31 εικ. 32 Ηλιακό ρολόι με ανατολικό προσανατολισμό, Doubs, Γαλλία. Το ρολόι δεν δέχεται ακτίνες του ήλιου μετά το μεσημέρι εικ. 33 Το ρολόι του Ανδρόνικου Κυρρήστου, Αγορά των Αθηνών 205
20 κατάκλισή του στο επίπεδο της πλάκας. Με κέντρο το Κ Ο γράφουμε κύκλο και τον διαιρούμε σε 24 ίσα τόξα, όσες και οι ώρες της ημέρας, ή ανά 15 Ο (1 ώρα=15 Ο ). Προεκτείνουμε τις ακτίνες μέχρι να τμήσουν το ίχνος του επιπέδου κι ενώνουμε με τη βάση Β(Β,Β ) της ράβδου. Έχοντας σαν βάση το οριζόντιο ηλιακό ρολόι, μπορούμε να μεταβάλλουμε το επίπεδο της πλάκας σε πλάγιο ή κατακόρυφο. Οποιοδήποτε επίπεδο του χώρου είναι δυνατό να παραλάβει ηλιακό ρολόι, αρκεί να μην περιέχουν τη ράβδο του. Τα ηλιακά ρολόγια σε μη οριζόντιες πλάκες δεν μπορούν (στη γενική περίπτωση) να λειτουργήσουν όλες τις ώρες της ημέρας (ώρες με ηλιοφάνεια), διότι οι πλάκες τους κάποιες ώρες αυτοσκιάζονται (εικ. 32). Για ν αντιμετωπιστεί αυτό το μειονέκτημα, γίνονται συνήθως κατασκευές με περισσότερα ρολόγια, καθένα από τα οποία έχει τη δική του πλάκα και συχνά και ράβδο, ώστε κάθε στιγμή κάποιο απ αυτά να λειτουργεί. Το ρωμαϊκό κτίσμα στην αγορά των Αθηνών, το ρολόι του Ανδρόνικου Κυρρήστου (εικ. 33) είναι ένα τέτοιο παράδειγμα ηλιακών ρολογιών σε κατακόρυφες πλάκες 10. Β. Καμπύλα ηλιακά ρολόγια Στα ηλιακά αυτά ρολόγια αντί της επίπεδης πλάκας χρησιμοποιείται τμήμα καμπύλης επιφάνειας (εικ. 34). Πιο συχνά έχει χρησιμοποιηθεί το εσωτερικό τμήμα ορθής κυλινδρικής επιφάνειας, με άξονα την ίδια τη ράβδο του ρολογιού. Έτσι, κάθε γενέτειρα της κυλινδρικής επιφάνειας αποτελεί υποδιαίρεση του ηλιακού ρολογιού. Και σ αυτά τα ρολόγια η κύρια γενέτειρα (12 η μεσημβρινή) είναι εκείνη που ταυτίζεται με τη σκιά της ράβδου στην ισημερία και στο ζενίθ του ήλιου. Οι υπόλοιπες εικ. 34 Το μεγαλύτερο ηλιακό ρολόι Ram Yantra, Jaipur, Ινδία 10. Το κτίσμα είναι οκταγωνικό σε κάτοψη και προσανατολισμένο και κάθε πλευρά του αντιστοιχεί στα τέσσερα κύρια και τέσσερα δευτερεύοντα σημεία του ορίζοντα. Σε κάθε πλευρά υπάρχει η ανάγλυφη παράσταση ανέμου και υπήρχε ανεμοδείκτης στην κορυφή. Για τον λόγο αυτό το ρολόι του Κυρρήστου είχε αρχικά θεωρηθεί ναός του Αιόλου, του θεού των ανέμων και από εκεί πήρε την κοινή ονομασία του «πύργος των Ανέμων» ή πιο απλά «Αέρηδες» 206
21 υποδιαιρέσεις προσδιορίζονται αν θεωρήσουμε ένα επίπεδο κάθετο στη ράβδο (στον άξονα του κόσμου), που τέμνει από την κυλινδρική επιφάνεια κύκλο. ιαιρούμε τον κύκλο σε 24 ίσα μέρη ή ανά 15 Ο (=1 ώρα) και από κάθε σημείο σχηματίζουμε μια γενέτειρα (σχ. 36,37). εικ. 35 Ηλιακό ρολόι της Αναγέννησης, βρέθηκε στην Ιταλία σχ. 36 σχ
22 εικ. 38 Ηλιακό ρολόι στον τοίχο του Astronomy Auditorium, University of Washington s Physics, Seattle, ΗΠΑ εικ. 39 Ηλιακό ρολόι στο Λονδίνο, Αγγλία 208
23 εικ. 40 Sandiago Calatrava, Sundial bridge, Redding, California, ΗΠΑ,
24
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Σφαιρικό Τρίγωνο Σφαιρικό τρίγωνο λέγεται το μέρος της σφαίρας, το οποίο περικλείεται μεταξύ των τόξων τριών μέγιστων κύκλων, με την προϋπόθεση
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Σφαιρικό Τρίγωνο Σφαιρικό τρίγωνο λέγεται το μέρος της σφαίρας, το οποίο περικλείεται μεταξύ των τόξων τριών μέγιστων κύκλων, με την προϋπόθεση
Η κατακόρυφη ενός τόπου συναντά την ουράνια σφαίρα σε δύο υποθετικά σηµεία, που ονοµάζονται. Ο κατακόρυφος κύκλος που περνά. αστέρα Α ονοµάζεται
 Sfaelos Ioannis Τα ουράνια σώµατα φαίνονται από τη Γη σαν να βρίσκονται στην εσωτερική επιφάνεια µιας γιγαντιαίας σφαίρας, απροσδιόριστης ακτίνας, µε κέντρο τη Γη. Τη φανταστική αυτή σφαίρα τη λέµε "ουράνια
Sfaelos Ioannis Τα ουράνια σώµατα φαίνονται από τη Γη σαν να βρίσκονται στην εσωτερική επιφάνεια µιας γιγαντιαίας σφαίρας, απροσδιόριστης ακτίνας, µε κέντρο τη Γη. Τη φανταστική αυτή σφαίρα τη λέµε "ουράνια
Να το πάρει το ποτάµι;
 Να το πάρει το ποτάµι; Είναι η σκιά ενός σώµατος που το φωτίζει ο Ήλιος. Όπως η σκιά του γνώµονα ενός ηλιακού ρολογιού που µε το αργό πέρασµά της πάνω απ τα σηµάδια των ωρών και µε το ύφος µιας άλλης εποχής
Να το πάρει το ποτάµι; Είναι η σκιά ενός σώµατος που το φωτίζει ο Ήλιος. Όπως η σκιά του γνώµονα ενός ηλιακού ρολογιού που µε το αργό πέρασµά της πάνω απ τα σηµάδια των ωρών και µε το ύφος µιας άλλης εποχής
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κύρια σημεία του μαθήματος Το σχήμα και οι κινήσεις της Γης Μετάπτωση και κλόνιση του άξονα της Γης Συστήματα χρόνου και ορισμοί: αστρικός χρόνος,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Κύρια σημεία του μαθήματος Το σχήμα και οι κινήσεις της Γης Μετάπτωση και κλόνιση του άξονα της Γης Συστήματα χρόνου και ορισμοί: αστρικός χρόνος,
ΗΛΙΑΚΟ ΡΟΛΟΙ. Ρώτησε τη φύση, θα σου απαντήσει! Παρατηρώντας την, κάτι το σημαντικό θα βρεις.
 ΕΙΣΑΓΩΓΗ Στα πλαίσια του προγράμματος περιβαλλοντικής Αγωγής, τη σχολική χρονιά 2012-2013, αποφασίσαμε με τους μαθητές του τμήματος Β 3 να ασχοληθούμε με κάτι που θα τους κέντριζε το ενδιαφέρον. Έτσι καταλήξαμε
ΕΙΣΑΓΩΓΗ Στα πλαίσια του προγράμματος περιβαλλοντικής Αγωγής, τη σχολική χρονιά 2012-2013, αποφασίσαμε με τους μαθητές του τμήματος Β 3 να ασχοληθούμε με κάτι που θα τους κέντριζε το ενδιαφέρον. Έτσι καταλήξαμε
Β.Π. Ουράνιος Ισηµερινός Ν.Π.
 Β.Π. Ουράνιος Ισηµερινός Ν.Π. Ανάδροµη Φορά Ορθή Φορά Η ορθή και ανάδροµη φορά περιστροφής της Ουράνιας Σφαίρας, όπως φαίνονται από το Βόρειο και το Νότιο ηµισφαίριο, αντίστοιχα Κύκλος Απόκλισης Μεσηµβρινός
Β.Π. Ουράνιος Ισηµερινός Ν.Π. Ανάδροµη Φορά Ορθή Φορά Η ορθή και ανάδροµη φορά περιστροφής της Ουράνιας Σφαίρας, όπως φαίνονται από το Βόρειο και το Νότιο ηµισφαίριο, αντίστοιχα Κύκλος Απόκλισης Μεσηµβρινός
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ 1 η ΟΜΑΔΑ ΑΣΚΗΣΕΩΝ Κεφάλαιο 2 ο Συστήματα αστρονομικών συντεταγμένων και χρόνος ΑΣΚΗΣΗ 1 η (α) Να εξηγηθεί γιατί το αζιμούθιο της ανατολής και της δύσεως του Ηλίου σε ένα τόπο,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ 1 η ΟΜΑΔΑ ΑΣΚΗΣΕΩΝ Κεφάλαιο 2 ο Συστήματα αστρονομικών συντεταγμένων και χρόνος ΑΣΚΗΣΗ 1 η (α) Να εξηγηθεί γιατί το αζιμούθιο της ανατολής και της δύσεως του Ηλίου σε ένα τόπο,
Αναρτήθηκε από τον/την Βασιλειάδη Γεώργιο Τρίτη, 26 Μάρτιος :23 - Τελευταία Ενημέρωση Τρίτη, 26 Μάρτιος :25
 Στη μία το μεσημέρι της Τετάρτης 20 Μαρτίου άρχισε και επίσημα η Άνοιξη του 2013 στο βόρειο ημισφαίριο, στο οποίο ανήκει και η χώρα μας. Η αρχή της άνοιξης, από αστρονομική πλευρά, συμπίπτει με την εαρινή
Στη μία το μεσημέρι της Τετάρτης 20 Μαρτίου άρχισε και επίσημα η Άνοιξη του 2013 στο βόρειο ημισφαίριο, στο οποίο ανήκει και η χώρα μας. Η αρχή της άνοιξης, από αστρονομική πλευρά, συμπίπτει με την εαρινή
Διδάσκοντας Φυσικές Επιστήμες στο Γυμνάσιο και στο Λύκειο
 Ο Γνώμονας, ένα απλό αστρονομικό όργανο και οι χρήσεις του στην εκπαίδευση Σοφία Γκοτζαμάνη και Σταύρος Αυγολύπης Ο Γνώμονας Ο Γνώμονας είναι το πιο απλό αστρονομικό όργανο και το πρώτο που χρησιμοποιήθηκε
Ο Γνώμονας, ένα απλό αστρονομικό όργανο και οι χρήσεις του στην εκπαίδευση Σοφία Γκοτζαμάνη και Σταύρος Αυγολύπης Ο Γνώμονας Ο Γνώμονας είναι το πιο απλό αστρονομικό όργανο και το πρώτο που χρησιμοποιήθηκε
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ Μάθημα 3 ο (Κεφ. 2 ο ) Ν. Στεργιούλας Τα 3 πρώτα ορίζονται με βάση περιοδικές κινήσεις ουρανίων σωμάτων. ΣΥΣΤΗΜΑΤΑ ΧΡΟΝΟΥ Τα κυριότερα συστήματα χρόνου στην Αστρονομία: (α) Αστρικός
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΣΤΡΟΝΟΜΙΑ Μάθημα 3 ο (Κεφ. 2 ο ) Ν. Στεργιούλας Τα 3 πρώτα ορίζονται με βάση περιοδικές κινήσεις ουρανίων σωμάτων. ΣΥΣΤΗΜΑΤΑ ΧΡΟΝΟΥ Τα κυριότερα συστήματα χρόνου στην Αστρονομία: (α) Αστρικός
15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο
 15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο 1.- Από τα πρώτα σχολικά µας χρόνια µαθαίνουµε για το πλανητικό µας σύστηµα. Α) Ποιος είναι ο πρώτος και
15 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας και Διαστηµικής 2010 Θέµατα για το Γυµνάσιο 1.- Από τα πρώτα σχολικά µας χρόνια µαθαίνουµε για το πλανητικό µας σύστηµα. Α) Ποιος είναι ο πρώτος και
ΦΩΣ ΚΑΙ ΣΚΙΑ. Πως δημιουργείτε η σκιά στη φυσική ;
 ΦΩΣ ΚΑΙ ΣΚΙΑ Πως δημιουργείτε η σκιά στη φυσική ; Λόγω της ευθύγραμμης διάδοσης του φωτός, όταν μεταξύ μιας φωτεινής πηγής και ενός περάσματος παρεμβάλλεται ένα αδιαφανές σώμα, δημιουργείτε στο πέρασμα
ΦΩΣ ΚΑΙ ΣΚΙΑ Πως δημιουργείτε η σκιά στη φυσική ; Λόγω της ευθύγραμμης διάδοσης του φωτός, όταν μεταξύ μιας φωτεινής πηγής και ενός περάσματος παρεμβάλλεται ένα αδιαφανές σώμα, δημιουργείτε στο πέρασμα
Κεφάλαιο 5: Ηλιακή γεωμετρία και ακτινοβολία Εισαγωγή
 Κεφάλαιο 5: 5.1. Εισαγωγή Η ηλιακή γεωμετρία περιγράφει τη σχετική κίνηση γης και ήλιου και αποτελεί ένα σημαντικό παράγοντα που υπεισέρχεται στον ενεργειακό ισολογισμό κτηρίων. Ανάλογα με τη γεωμετρία
Κεφάλαιο 5: 5.1. Εισαγωγή Η ηλιακή γεωμετρία περιγράφει τη σχετική κίνηση γης και ήλιου και αποτελεί ένα σημαντικό παράγοντα που υπεισέρχεται στον ενεργειακό ισολογισμό κτηρίων. Ανάλογα με τη γεωμετρία
Ηλιακήενέργεια. Ηλιακή γεωµετρία. Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης. ηµήτρης Αλ. Κατσαπρακάκης
 Ηλιακήενέργεια Ηλιακή γεωµετρία Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Ηλιακήγεωµετρία Ηλιακήγεωµετρία Η Ηλιακή Γεωµετρία αναφέρεται στη µελέτη της θέσης του ήλιου σε σχέση
Ηλιακήενέργεια Ηλιακή γεωµετρία Εργαστήριο Αιολικής Ενέργειας Τ.Ε.Ι. Κρήτης ηµήτρης Αλ. Κατσαπρακάκης Ηλιακήγεωµετρία Ηλιακήγεωµετρία Η Ηλιακή Γεωµετρία αναφέρεται στη µελέτη της θέσης του ήλιου σε σχέση
4/11/2018 ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ. ΘΕΜΑ 1 ο
 ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ 4/11/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι
ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΓΈΠΑΛ 4/11/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ. Αστρονομία. Ενότητα # 3: Συστήματα Χρόνου. Νικόλαος Στεργιούλας Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 3: Συστήματα Χρόνου Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 3: Συστήματα Χρόνου Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης Το παρόν
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3 Yπενθύμιση: Ισημερινές συντεταγμένες Βασικός κύκλος: ο ουράνιος ισημερινός Πρώτος κάθετος: o μεσημβρινός
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3 Yπενθύμιση: Ισημερινές συντεταγμένες Βασικός κύκλος: ο ουράνιος ισημερινός Πρώτος κάθετος: o μεσημβρινός
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1 Γεωκεντρικό σύστημα παρατήρησης Με εξαίρεση έναν αριθμό από διαστημικές αποστολές, οι παρατηρήσεις των ουράνιων αντικειμένων
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1 Γεωκεντρικό σύστημα παρατήρησης Με εξαίρεση έναν αριθμό από διαστημικές αποστολές, οι παρατηρήσεις των ουράνιων αντικειμένων
Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ. Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός
 Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός ρ. Ε. Λυκούδη Αθήνα 2005 Γεωγραφικά στοιχεία της Γης Η Φυσική Γεωγραφία εξετάζει: τον γήινο
Η ΓΗ ΣΑΝ ΠΛΑΝΗΤΗΣ Γεωγραφικά στοιχεία της Γης Σχήµα και µέγεθος της Γης - Κινήσεις της Γης Βαρύτητα - Μαγνητισµός ρ. Ε. Λυκούδη Αθήνα 2005 Γεωγραφικά στοιχεία της Γης Η Φυσική Γεωγραφία εξετάζει: τον γήινο
ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών
 ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών Συντεταγμένες του τόπου (γεωγραφικό μήκος και πλάτος) Π.χ. το Google Maps δίνει για το Παν. Πατρών 38.3, 21.8. Προσοχή, το πρώτο είναι το γεωγραφικό πλάτος
ΗΛΙΑΚΗ ΓΕΩΜΕΤΡΙΑ Δ. Κουζούδης Πανεπιστήμιο Πατρών Συντεταγμένες του τόπου (γεωγραφικό μήκος και πλάτος) Π.χ. το Google Maps δίνει για το Παν. Πατρών 38.3, 21.8. Προσοχή, το πρώτο είναι το γεωγραφικό πλάτος
Τεύχος B - Διδακτικών Σημειώσεων
 Τεύχος B - Διδακτικών Σημειώσεων ΟΙ ΚΙΝΗΣΕΙΣ ΤΗΣ ΓΗΣ ΚΑΙ ΟΙ ΕΠΙΠΤΩΣΕΙΣ ΣΤΑ ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ Δημήτρης Δεληκαράογλου Αναπλ. Καθ., Σχολή Αγρονόμων και Τοπογράφων Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Επισκ.
Τεύχος B - Διδακτικών Σημειώσεων ΟΙ ΚΙΝΗΣΕΙΣ ΤΗΣ ΓΗΣ ΚΑΙ ΟΙ ΕΠΙΠΤΩΣΕΙΣ ΣΤΑ ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ Δημήτρης Δεληκαράογλου Αναπλ. Καθ., Σχολή Αγρονόμων και Τοπογράφων Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Επισκ.
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3 Εφαρμογή: Μεταβολή των ουρανογραφικών συντεταγμένων λόγω της μετάπτωσης του άξονα του κόσμου (προηγούμενο
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων- Συστήματα Χρόνου Μάθημα 3 Εφαρμογή: Μεταβολή των ουρανογραφικών συντεταγμένων λόγω της μετάπτωσης του άξονα του κόσμου (προηγούμενο
ΝΑΥΣΙΠΛΟΪΑ. 1 o ΔΙΑΓΩΝΙΣΜΑ
 ΝΑΥΣΙΠΛΟΪΑ 1 o ΔΙΑΓΩΝΙΣΜΑ α. Τι είναι έξαρμα του πόλου υπέρ τον ορίζοντα και γιατί ενδιαφέρει τον ναυτιλλόμενο. β. Να ορίσετε τα είδη των αστέρων (αειφανείς, αφανείς και Αμφιφανείς)και να γράψετε τις συνθήκες
ΝΑΥΣΙΠΛΟΪΑ 1 o ΔΙΑΓΩΝΙΣΜΑ α. Τι είναι έξαρμα του πόλου υπέρ τον ορίζοντα και γιατί ενδιαφέρει τον ναυτιλλόμενο. β. Να ορίσετε τα είδη των αστέρων (αειφανείς, αφανείς και Αμφιφανείς)και να γράψετε τις συνθήκες
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 1
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 1 Σύστημα γήινων συντεταγμένων Γήινος μεσημβρινός του τόπου Ο Μεσημβρινός του Greenwich (πρώτος κάθετος) Γεωγραφικό μήκος 0
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 1 Σύστημα γήινων συντεταγμένων Γήινος μεσημβρινός του τόπου Ο Μεσημβρινός του Greenwich (πρώτος κάθετος) Γεωγραφικό μήκος 0
ΗλιακήΓεωµετρία. Γιάννης Κατσίγιαννης
 ΗλιακήΓεωµετρία Γιάννης Κατσίγιαννης ΗηλιακήενέργειαστηΓη Φασµατικήκατανοµήτηςηλιακής ακτινοβολίας ΗκίνησητηςΓηςγύρωαπότονήλιο ΗκίνησητηςΓηςγύρωαπότονήλιοµπορεί να αναλυθεί σε δύο κύριες συνιστώσες: Περιφορά
ΗλιακήΓεωµετρία Γιάννης Κατσίγιαννης ΗηλιακήενέργειαστηΓη Φασµατικήκατανοµήτηςηλιακής ακτινοβολίας ΗκίνησητηςΓηςγύρωαπότονήλιο ΗκίνησητηςΓηςγύρωαπότονήλιοµπορεί να αναλυθεί σε δύο κύριες συνιστώσες: Περιφορά
Επειδή ο μεσημβρινός τέμνει ξανά τον παράλληλο σε αντιδιαμετρικό του σημείο θα θεωρούμε μεσημβρινό το ημικύκλιο και όχι ολόκληρο τον κύκλο.
 ΝΑΥΣΙΠΛΟΪΑ Η ιστιοπλοΐα ανοιχτής θαλάσσης δεν διαφέρει στα βασικά από την ιστιοπλοΐα τριγώνου η οποία γίνεται με μικρά σκάφη καi σε προκαθορισμένο στίβο. Όταν όμως αφήνουμε την ακτή και ανοιγόμαστε στο
ΝΑΥΣΙΠΛΟΪΑ Η ιστιοπλοΐα ανοιχτής θαλάσσης δεν διαφέρει στα βασικά από την ιστιοπλοΐα τριγώνου η οποία γίνεται με μικρά σκάφη καi σε προκαθορισμένο στίβο. Όταν όμως αφήνουμε την ακτή και ανοιγόμαστε στο
Έκλειψη Ηλίου 20ης Μαρτίου 2015
 Έκλειψη Ηλίου 20ης Μαρτίου 2015 Πληροφοριακό υλικό Κέντρο Επισκεπτών Ινστιτούτο Αστρονομίας Αστροφυσικής Διαστημικών Εφαρμογών και Τηλεπισκόπησης (ΙΑΑΔΕΤ) Εθνικό Αστεροσκοπείο Αθηνών Την Παρασκευή 20 Μαρτίου
Έκλειψη Ηλίου 20ης Μαρτίου 2015 Πληροφοριακό υλικό Κέντρο Επισκεπτών Ινστιτούτο Αστρονομίας Αστροφυσικής Διαστημικών Εφαρμογών και Τηλεπισκόπησης (ΙΑΑΔΕΤ) Εθνικό Αστεροσκοπείο Αθηνών Την Παρασκευή 20 Μαρτίου
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 2
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 2 Ανατολή-δύση αστέρων Από την σχέση αυτή προκύπτουν δυο τιμές για την ωριαία γωνία Η Δ για την οποία ο αστέρας βρίσκεται στον
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: Συστήματα συντεταγμένων Μάθημα 2 Ανατολή-δύση αστέρων Από την σχέση αυτή προκύπτουν δυο τιμές για την ωριαία γωνία Η Δ για την οποία ο αστέρας βρίσκεται στον
Τα όργανα του Πτολεμαίου
 Ο Πτολεμαίος και η Αστρονομία. Ο Πτολεμαίος παρατηρεί με το τεταρτοκύκλιο το ύψος της σελήνης. Πρόκειται για μεταγενέστερη μορφή του οργάνου. Στο έδαφος και ο σφαιρικός αστρολάβος. Τα όργανα του Πτολεμαίου
Ο Πτολεμαίος και η Αστρονομία. Ο Πτολεμαίος παρατηρεί με το τεταρτοκύκλιο το ύψος της σελήνης. Πρόκειται για μεταγενέστερη μορφή του οργάνου. Στο έδαφος και ο σφαιρικός αστρολάβος. Τα όργανα του Πτολεμαίου
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ
 ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΗΛΙΑΚΗ ΕΝΕΡΓΕΙΑ ΑΚΤΙΝΟΒΟΛΙΑ ΗΛΙΑΚΗ ΜΗΧΑΝΙΚΗ Μάθημα 2o Διδάσκων: Επ. Καθηγητής Ε. Αμανατίδης ΔΕΥΤΕΡΑ 6/3/2017 Τμήμα Χημικών Μηχανικών Πανεπιστήμιο Πατρών Περίληψη Ηλιακή
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΗΛΙΑΚΗ ΕΝΕΡΓΕΙΑ ΑΚΤΙΝΟΒΟΛΙΑ ΗΛΙΑΚΗ ΜΗΧΑΝΙΚΗ Μάθημα 2o Διδάσκων: Επ. Καθηγητής Ε. Αμανατίδης ΔΕΥΤΕΡΑ 6/3/2017 Τμήμα Χημικών Μηχανικών Πανεπιστήμιο Πατρών Περίληψη Ηλιακή
Παρατηρησιακή Αστροφυσική Μέρος Α. Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1
 Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1 Γεωκεντρικό σύστημα παρατήρησης Με εξαίρεση έναν αριθμό από διαστημικές αποστολές, οι παρατηρήσεις των ουράνιων αντικειμένων
Παρατηρησιακή Αστροφυσική Μέρος Α Κεφάλαιο 1: ΓΕΩΚΕΝΤΡΙΚΟ ΣΥΣΤΗΜΑ ΠΑΡΑΤΗΡΗΣΗΣ Μάθημα 1 Γεωκεντρικό σύστημα παρατήρησης Με εξαίρεση έναν αριθμό από διαστημικές αποστολές, οι παρατηρήσεις των ουράνιων αντικειμένων
Η Λ Ι Α Κ Α Ρ Ο Λ Ο Γ Ι Α
 Η Λ Ι Α Κ Α Ρ Ο Λ Ο Γ Ι Α Αναγνωστοπούλου Στρατηγούλα (5553), Σταυρίδη Δήμητρα (5861) 1 ΛΙΓΗ ΑΣΤΡΟΝΟΜΙΑ 1.1 Η κίνηση της Γης Η Γη κινείται με τρεις τρόπους: περιστρέφεται γύρω από τον άξονά της σε 24h,
Η Λ Ι Α Κ Α Ρ Ο Λ Ο Γ Ι Α Αναγνωστοπούλου Στρατηγούλα (5553), Σταυρίδη Δήμητρα (5861) 1 ΛΙΓΗ ΑΣΤΡΟΝΟΜΙΑ 1.1 Η κίνηση της Γης Η Γη κινείται με τρεις τρόπους: περιστρέφεται γύρω από τον άξονά της σε 24h,
Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι:
 ΗΛΙΑΚΑ ΩΡΟΛΟΓΙΑ Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι: Οριζόντια Κατακόρυφα Ισημερινά Το παρακάτω άρθρο αναφέρεται στον τρόπο λειτουργίας αλλά και κατασκευής
ΗΛΙΑΚΑ ΩΡΟΛΟΓΙΑ Υπάρχουν πολλά είδη Ηλιακών Ρολογιών. Τα σημαντικότερα και συχνότερα απαντόμενα είναι: Οριζόντια Κατακόρυφα Ισημερινά Το παρακάτω άρθρο αναφέρεται στον τρόπο λειτουργίας αλλά και κατασκευής
ΝΑΥΣΙΠΛΟΙΑ ΙΙ ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ
 ΝΑΥΣΙΠΛΟΙΑ ΙΙ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
ΝΑΥΣΙΠΛΟΙΑ ΙΙ 3/02/2019 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή
Αστρονομία. Ενότητα # 1: Ουράνια Σφαίρα Συστήματα Συντεταγμένων. Νικόλαος Στεργιούλας Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 1: Ουράνια Σφαίρα Συστήματα Συντεταγμένων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 1: Ουράνια Σφαίρα Συστήματα Συντεταγμένων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης
5. ΔΙΑΤΑΡΑΧΕΣ ΤΩΝ ΚΙΝΗΣΕΩΝ ΤΗΣ ΓΗΣ
 37 5. ΔΙΑΤΑΡΑΧΕΣ ΤΩΝ ΚΙΝΗΣΕΩΝ ΤΗΣ ΓΗΣ 5.1 Εισαγωγή Οι κύριες κινήσεις της Γης είναι: μια τροχιακή κίνηση του κέντρου μάζας γύρω από τον Ήλιο και μια περιστροφική κίνηση γύρω από τον άξονα που περνά από
37 5. ΔΙΑΤΑΡΑΧΕΣ ΤΩΝ ΚΙΝΗΣΕΩΝ ΤΗΣ ΓΗΣ 5.1 Εισαγωγή Οι κύριες κινήσεις της Γης είναι: μια τροχιακή κίνηση του κέντρου μάζας γύρω από τον Ήλιο και μια περιστροφική κίνηση γύρω από τον άξονα που περνά από
Η γωνία υπό την οποία φαίνονται από κάποιον παρατηρητή δύο αστέρες ονοµάζεται
 ΚΕΦΑΛΑΙΟ 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΧΡΟΝΟΣ 2.1 Ουράνια σφαίρα-βασικοί ορισµοί Για να ορίσουµε τις θέσεις των αστέρων, τους θεωρούµε να προβάλλονται σαν σηµεία στην εσωτερική επιφάνεια µιας σφαίρας µε αυθαίρετη
ΚΕΦΑΛΑΙΟ 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΧΡΟΝΟΣ 2.1 Ουράνια σφαίρα-βασικοί ορισµοί Για να ορίσουµε τις θέσεις των αστέρων, τους θεωρούµε να προβάλλονται σαν σηµεία στην εσωτερική επιφάνεια µιας σφαίρας µε αυθαίρετη
7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ
 63 7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ Υπενθυμίζεται ότι αστρονομικό αζιμούθιο Α D μιας διεύθυνσης D, ως προς το σημείο (τόπο) Ο, ονομάζεται το μέτρο της δίεδρης γωνίας που σχηματίζεται μεταξύ του επιπέδου του
63 7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ Υπενθυμίζεται ότι αστρονομικό αζιμούθιο Α D μιας διεύθυνσης D, ως προς το σημείο (τόπο) Ο, ονομάζεται το μέτρο της δίεδρης γωνίας που σχηματίζεται μεταξύ του επιπέδου του
Κεφάλαιο 5. 5 Συστήματα συντεταγμένων
 Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
Φύλλα Εργασίας για την Υλοποίηση του Πειράματος του Ερατοσθένη
 Φύλλα Εργασίας για την Υλοποίηση του Πειράματος του Ερατοσθένη Υπεύθυνοι Καθηγητές Παντελοπούλου Σταυρούλα (ΠΕ 19) Τζώρτζης Κωνσταντίνος (ΠΕ03) Πηγές: http://www.astro.noa.gr/gr/eratosthenes/experiment.html
Φύλλα Εργασίας για την Υλοποίηση του Πειράματος του Ερατοσθένη Υπεύθυνοι Καθηγητές Παντελοπούλου Σταυρούλα (ΠΕ 19) Τζώρτζης Κωνσταντίνος (ΠΕ03) Πηγές: http://www.astro.noa.gr/gr/eratosthenes/experiment.html
β. ίιος πλανήτης γ. Ζωδιακό φως δ. ορυφόρος ε. Μετεωρίτης στ. Μεσοπλανητική ύλη ζ. Αστεροειδής η. Μετέωρο
 1. Αντιστοίχισε τα χαρακτηριστικά, που καταγράφονται στη αριστερή στήλη με τα αντικείμενα ή φαινόμενα, που παρατηρούνται στο ηλιακό σύστημα και περιέχονται στην δεξιά στήλη Α. Κινείται σε ελλειπτική τροχιά.
1. Αντιστοίχισε τα χαρακτηριστικά, που καταγράφονται στη αριστερή στήλη με τα αντικείμενα ή φαινόμενα, που παρατηρούνται στο ηλιακό σύστημα και περιέχονται στην δεξιά στήλη Α. Κινείται σε ελλειπτική τροχιά.
ΤΑ ΧΡΙΣΤΙΑΝΙΚΑ ΗΜΕΡΟΛΟΓΙΑ ΚΑΙ Ο ΚΑΝΩΝ ΤΟΥ ΠΑΣΧΑ
 ΤΑ ΧΡΙΣΤΙΑΝΙΚΑ ΗΜΕΡΟΛΟΓΙΑ ΚΑΙ Ο ΚΑΝΩΝ ΤΟΥ ΠΑΣΧΑ Στράτος Θεοδοσίου Αναπληρωτής καθηγητής Τμήμα Φυσικής Πανεπιστήμιο Αθηνών Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Tο ημερολογιακό ζήτημα από την άποψη
ΤΑ ΧΡΙΣΤΙΑΝΙΚΑ ΗΜΕΡΟΛΟΓΙΑ ΚΑΙ Ο ΚΑΝΩΝ ΤΟΥ ΠΑΣΧΑ Στράτος Θεοδοσίου Αναπληρωτής καθηγητής Τμήμα Φυσικής Πανεπιστήμιο Αθηνών Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Tο ημερολογιακό ζήτημα από την άποψη
ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. Ηρακλή, καθώς και στην κίνηση του γαλαξία
 Sfaelos Ioannis 1. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΗΣ Η Γη είναι ο τρίτος στη σειρά πλανήτης του ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. έ θ Η μέση απόστασή της από τον Ήλιο είναι 149.600.000 km.
Sfaelos Ioannis 1. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΗΣ Η Γη είναι ο τρίτος στη σειρά πλανήτης του ηλιακού μας συστήματος και ο πέμπτος σε μέγεθος. έ θ Η μέση απόστασή της από τον Ήλιο είναι 149.600.000 km.
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ
 ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
ΓΕΩΛΟΓΙΑ - ΓΕΩΓΡΑΦΙΑ Α ΓΥΜΝΑΣΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2018 2019 ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΕ ΕΡΩΤΗΣΕΙΣ- ΑΠΑΝΤΗΣΕΙΣ 1 Περιεχόμενα ΕΝΟΤΗΤΑ Α : ΧΑΡΤΕΣ Α1.4 Ποιον χάρτη να διαλέξω;. 3 Α1.3 Η χρήση των χαρτών στην καθημερινή
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΣΕΛΗΝΗΣ Η τροχιά της Σελήνης γύρω από τη Γη δεν είναι κύκλος αλλά έλλειψη. Αυτό σηµαίνει πως η Σελήνη δεν απέχει πάντα το
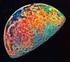 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΣΕΛΗΝΗΣ Η τροχιά της Σελήνης γύρω από τη Γη δεν είναι κύκλος αλλά έλλειψη. Αυτό σηµαίνει πως η Σελήνη δεν απέχει πάντα το ίδιο από τη Γη. Τα δύο σηµεία που έχουν ενδιαφέρον
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΤΗΣ ΣΕΛΗΝΗΣ Η τροχιά της Σελήνης γύρω από τη Γη δεν είναι κύκλος αλλά έλλειψη. Αυτό σηµαίνει πως η Σελήνη δεν απέχει πάντα το ίδιο από τη Γη. Τα δύο σηµεία που έχουν ενδιαφέρον
ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ
 ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ Χαρτογραφία Ι 1 Το σχήμα και το μέγεθος της Γης [Ι] Σφαιρική Γη Πυθαγόρεια & Αριστοτέλεια αντίληψη παρατηρήσεις φυσικών φαινομένων Ομαλότητα γεωμετρικού σχήματος (Διάμετρος
ΤΟ ΣΧΗΜΑ ΚΑΙ ΤΟ ΜΕΓΕΘΟΣ ΤΗΣ ΓΗΣ Χαρτογραφία Ι 1 Το σχήμα και το μέγεθος της Γης [Ι] Σφαιρική Γη Πυθαγόρεια & Αριστοτέλεια αντίληψη παρατηρήσεις φυσικών φαινομένων Ομαλότητα γεωμετρικού σχήματος (Διάμετρος
Η Μεγάλη Νύχτα. Το Χειμερινό Ηλιοστάσιο και τα Χριστούγεννα. Η Μεγάλη Νύχτα του Διονύση Π. Σιμόπουλου 1/5
 Η Μεγάλη Νύχτα του Διονύση Π. Σιμόπουλου 1/5 Το Χειμερινό Ηλιοστάσιο και τα Χριστούγεννα Η Μεγάλη Νύχτα Του Διονύση Π. Σιμόπουλου Διευθυντή Ευγενιδείου Πλανηταρίου Η νύχτα της ερχόμενης Πέμπτης, 22 Δεκεμβρίου,
Η Μεγάλη Νύχτα του Διονύση Π. Σιμόπουλου 1/5 Το Χειμερινό Ηλιοστάσιο και τα Χριστούγεννα Η Μεγάλη Νύχτα Του Διονύση Π. Σιμόπουλου Διευθυντή Ευγενιδείου Πλανηταρίου Η νύχτα της ερχόμενης Πέμπτης, 22 Δεκεμβρίου,
1. ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ ΣΤΗΝ ΟΥΡΑΝΙΑ ΣΦΑΙΡΑ
 3 1. ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ ΣΤΗΝ ΟΥΡΑΝΙΑ ΣΦΑΙΡΑ 1.1 Βασικές έννοιες Για τις εφαρμογές της Γεωδαιτικής Αστρονομίας είναι απαραίτητος ο ορισμός συστημάτων συντεταγμένων, στα οποία περιγράφονται οι θέσεις και
3 1. ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ ΣΤΗΝ ΟΥΡΑΝΙΑ ΣΦΑΙΡΑ 1.1 Βασικές έννοιες Για τις εφαρμογές της Γεωδαιτικής Αστρονομίας είναι απαραίτητος ο ορισμός συστημάτων συντεταγμένων, στα οποία περιγράφονται οι θέσεις και
ΣΚΙΑΓΡΑΦΙΑ. Γενικές αρχές και έννοιες
 ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
ΔÔ Û Ì Î È ÔÈ ÎÈÓ ÛÂÈ ÙË Ë
 ΚΕΦΑΛΑΙΟ 1 ΔÔ Û Ì Î È ÔÈ ÎÈÓ ÛÂÈ ÙË Ë Tα βασικά σημεία του μαθήματος Η Γη είναι ένα ουράνιο σώμα, που κινείται συνεχώς στο διάστημα. Το σχήμα της είναι γεωειδές, δηλαδή είναι ελαφρά συμπιεσμένο στις κορυφές
ΚΕΦΑΛΑΙΟ 1 ΔÔ Û Ì Î È ÔÈ ÎÈÓ ÛÂÈ ÙË Ë Tα βασικά σημεία του μαθήματος Η Γη είναι ένα ουράνιο σώμα, που κινείται συνεχώς στο διάστημα. Το σχήμα της είναι γεωειδές, δηλαδή είναι ελαφρά συμπιεσμένο στις κορυφές
7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ
 61 7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ Υπενθυμίζεται ότι αστρονομικό αζιμούθιο Α D μιας διεύθυνσης D, ως προς το σημείο (τόπο) Ο, ονομάζεται το μέτρο της δίεδρης γωνίας που σχηματίζεται μεταξύ του επιπέδου του
61 7. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΑΖΙΜΟΥΘΙΟΥ Υπενθυμίζεται ότι αστρονομικό αζιμούθιο Α D μιας διεύθυνσης D, ως προς το σημείο (τόπο) Ο, ονομάζεται το μέτρο της δίεδρης γωνίας που σχηματίζεται μεταξύ του επιπέδου του
Δρ. Απόστολος Ντάνης. Σχολικός Σύμβουλος Φυσικής Αγωγής
 Δρ. Απόστολος Ντάνης Σχολικός Σύμβουλος Φυσικής Αγωγής *Βασικές μορφές προσανατολισμού *Προσανατολισμός με τα ορατά σημεία προορισμού στη φύση *Προσανατολισμός με τον ήλιο *Προσανατολισμός από τη σελήνη
Δρ. Απόστολος Ντάνης Σχολικός Σύμβουλος Φυσικής Αγωγής *Βασικές μορφές προσανατολισμού *Προσανατολισμός με τα ορατά σημεία προορισμού στη φύση *Προσανατολισμός με τον ήλιο *Προσανατολισμός από τη σελήνη
Άλλοι χάρτες λαμβάνουν υπόψη και το υψόμετρο του αντικειμένου σε σχέση με ένα επίπεδο αναφοράς
 ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Ένας χάρτης είναι ένας τρόπος αναπαράστασης της πραγματικής θέσης ενός αντικειμένου ή αντικειμένων σε μια τεχνητά δημιουργουμένη επιφάνεια δύο διαστάσεων Πολλοί χάρτες (π.χ. χάρτες
ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ Ένας χάρτης είναι ένας τρόπος αναπαράστασης της πραγματικής θέσης ενός αντικειμένου ή αντικειμένων σε μια τεχνητά δημιουργουμένη επιφάνεια δύο διαστάσεων Πολλοί χάρτες (π.χ. χάρτες
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ).
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ). Ονοματεπώνυμο: Ημερομηνία... Ατομική εργασία: Παρατήρησε την υδρόγειο σφαίρα καθώς και τον παγκόσμιο χάρτη που βρίσκεται κρεμασμένος στον τοίχο
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΓΕΩΓΡΑΦΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ (ΤΑΞΗ Α ΓΥΜΝΑΣΙΟΥ). Ονοματεπώνυμο: Ημερομηνία... Ατομική εργασία: Παρατήρησε την υδρόγειο σφαίρα καθώς και τον παγκόσμιο χάρτη που βρίσκεται κρεμασμένος στον τοίχο
39 40'13.8"N 20 51'27.4"E ή , καταχωρουνται στο gps ως
 ΣΥΝΤΕΤΑΓΜΕΝΕΣ,ΑΝΑΛΥΣΗ ΕΝΝΟΙΩΝ &ΤΡΟΠΟΙ ΚΑΤΑΓΡΑΦΗΣ ΣΕ GPS Το γεωγραφικό πλάτος (latitude) είναι ένα από τα δύο μεγέθη των γεωγραφικών συντεταγμένων με τα οποία προσδιορίζεται η θέση των διαφόρων τόπων και
ΣΥΝΤΕΤΑΓΜΕΝΕΣ,ΑΝΑΛΥΣΗ ΕΝΝΟΙΩΝ &ΤΡΟΠΟΙ ΚΑΤΑΓΡΑΦΗΣ ΣΕ GPS Το γεωγραφικό πλάτος (latitude) είναι ένα από τα δύο μεγέθη των γεωγραφικών συντεταγμένων με τα οποία προσδιορίζεται η θέση των διαφόρων τόπων και
β. Το τρίγωνο που σχηματίζεται στην επιφάνεια της σφαίρας, του οποίου οι πλευρές αποτελούν τόξα μεγίστων κύκλων, ονομάζεται σφαιρικό τρίγωνο.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 19/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 19/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΝΑΥΣΙΠΛΟΪΑ ΙΙ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ 1 ο 1) Να χαρακτηρίσετε
Εισαγωγή στην Αστρονομία
 Παπαδόπουλος Μιλτιάδης ΑΕΜ: 13134 Εξάμηνο: 7 ο Ασκήσεις: 12-1 Εισαγωγή στην Αστρονομία 1. Ο αστέρας Βέγας στον αστερισμό της Λύρας έχει απόκλιση δ=+38 ο 47. α) Σχεδιάστε την φαινόμενη τροχιά του Βέγα στην
Παπαδόπουλος Μιλτιάδης ΑΕΜ: 13134 Εξάμηνο: 7 ο Ασκήσεις: 12-1 Εισαγωγή στην Αστρονομία 1. Ο αστέρας Βέγας στον αστερισμό της Λύρας έχει απόκλιση δ=+38 ο 47. α) Σχεδιάστε την φαινόμενη τροχιά του Βέγα στην
2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα.
 2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα. Ομάδα εργασίας : Παπαγεωργίου Κριστίνα, Σπύρου Μάρθα, Χαρδαλούπα Ελένη, Χαρδαλούπα Μαριάννα. Αρχαίοι
2ο ΕΡΕΥΝΗΤΙΚΟ ΠΕΔΙΟ: Πρακτικοί τρόποι και μέσα προσανατολισμού από την αρχαιότητα μέχρι και την πυξίδα. Ομάδα εργασίας : Παπαγεωργίου Κριστίνα, Σπύρου Μάρθα, Χαρδαλούπα Ελένη, Χαρδαλούπα Μαριάννα. Αρχαίοι
18 ος Πανελλήνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικής 2013 Φάση 3 η : «ΙΠΠΑΡΧΟΣ»
 Θέμα 1 ο (Σύντομης ανάπτυξης): 18 ος Πανελλήνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικής 2013 Φάση 3 η : «ΙΠΠΑΡΧΟΣ» Θέματα του Γυμνασίου (Α) Ποιοι πλανήτες ονομάζονται Δίιοι; (Β) Αναφέρατε και
Θέμα 1 ο (Σύντομης ανάπτυξης): 18 ος Πανελλήνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικής 2013 Φάση 3 η : «ΙΠΠΑΡΧΟΣ» Θέματα του Γυμνασίου (Α) Ποιοι πλανήτες ονομάζονται Δίιοι; (Β) Αναφέρατε και
3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ τρίγωνο θέσης position triangle astronomical triangle
 21 3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ Ως τώρα είδαμε πως ορίζονται διάφορα συστήματα αναφοράς και πως οι συντεταγμένες, σε κάθε σύστημα, αλλάζουν ανάλογα με την διεύθυνση παρατήρησης, τον τόπο και τον χρόνο. Για να γίνουν
21 3. ΤΟ ΤΡΙΓΩΝΟ ΘΕΣΗΣ Ως τώρα είδαμε πως ορίζονται διάφορα συστήματα αναφοράς και πως οι συντεταγμένες, σε κάθε σύστημα, αλλάζουν ανάλογα με την διεύθυνση παρατήρησης, τον τόπο και τον χρόνο. Για να γίνουν
Μεθοδολογία Έλλειψης
 Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
Μεθοδολογία Έλλειψης Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων το άθροισμα των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερό και μεγαλύτερο από την απόσταση (ΕΕ ). Στη Φύση
Ίωνες Φιλόσοφοι. Οι σημαντικότεροι Ίωνες φιλόσοφοι επιστήμονες
 Ίωνες Φιλόσοφοι Η απλή ενατένιση του ουρανού, με το πλήθος των εντυπωσιακών φαινομένων, ικανών να προσελκύσουν την προσοχή και το ενδιαφέρον των πρωτόγονων ανθρώπων, άρχισε να σημειώνει τα πρώτα εξελικτικά
Ίωνες Φιλόσοφοι Η απλή ενατένιση του ουρανού, με το πλήθος των εντυπωσιακών φαινομένων, ικανών να προσελκύσουν την προσοχή και το ενδιαφέρον των πρωτόγονων ανθρώπων, άρχισε να σημειώνει τα πρώτα εξελικτικά
Μάθηµα 4 ο : ορυφορικές τροχιές
 Μάθηµα 4 ο : ορυφορικές τροχιές Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Tις σηµαντικότερες κατηγορίες δορυφορικών τροχιών Τους παράγοντες που οδηγούν στην επιλογή συγκεκριµένης
Μάθηµα 4 ο : ορυφορικές τροχιές Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Tις σηµαντικότερες κατηγορίες δορυφορικών τροχιών Τους παράγοντες που οδηγούν στην επιλογή συγκεκριµένης
ΟΙ ΚΙΝΗΣΕΙΣ ΤΗΣ ΓΗΣ. www.meteo.gr - 1 -
 ΟΙ ΚΙΝΗΣΕΙΣ ΤΗΣ ΓΗΣ H Γη είναι ένας πλανήτης από τους οκτώ συνολικά του ηλιακού μας συστήματος, το οποίο αποτελεί ένα από τα εκατοντάδες δισεκατομμύρια αστρικά συστήματα του Γαλαξία μας, ο οποίος με την
ΟΙ ΚΙΝΗΣΕΙΣ ΤΗΣ ΓΗΣ H Γη είναι ένας πλανήτης από τους οκτώ συνολικά του ηλιακού μας συστήματος, το οποίο αποτελεί ένα από τα εκατοντάδες δισεκατομμύρια αστρικά συστήματα του Γαλαξία μας, ο οποίος με την
Μετρώντας τη γη με μαθητές γυμνασίου
 Μετρώντας τη γη με μαθητές γυμνασίου Ξενοφών Φανουρίου Γεωλόγος-Ωκεανογράφος 17 Σεπτεμβρίου 2015 Περίληψη Ο υπολογισμός του μεγέθους της γης αλλά και των άλλων σταθερών της, απασχόλησε από τα αρχαία χρόνια
Μετρώντας τη γη με μαθητές γυμνασίου Ξενοφών Φανουρίου Γεωλόγος-Ωκεανογράφος 17 Σεπτεμβρίου 2015 Περίληψη Ο υπολογισμός του μεγέθους της γης αλλά και των άλλων σταθερών της, απασχόλησε από τα αρχαία χρόνια
ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΩΦΥΣΙΚΗ 24.11.2005 Η ΘΕΩΡΙΑ ΤΟΥ MILANKOVITCH
 TZΕΜΟΣ ΑΘΑΝΑΣΙΟΣ Α.Μ. 3507 ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΩΦΥΣΙΚΗ 24.11.2005 Η ΘΕΩΡΙΑ ΤΟΥ MILANKOVITCH Όλοι γνωρίζουμε ότι η εναλλαγή των 4 εποχών οφείλεται στην κλίση που παρουσιάζει ο άξονας περιστροφής
TZΕΜΟΣ ΑΘΑΝΑΣΙΟΣ Α.Μ. 3507 ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΩΦΥΣΙΚΗ 24.11.2005 Η ΘΕΩΡΙΑ ΤΟΥ MILANKOVITCH Όλοι γνωρίζουμε ότι η εναλλαγή των 4 εποχών οφείλεται στην κλίση που παρουσιάζει ο άξονας περιστροφής
ΕΙΣΑΓΩΓΗ Γεωδαιτική Αστρονομία (Geodetic Astronomy) τρεις δύο γεωειδούς ουράνια σφαίρα
 1 ΕΙΣΑΓΩΓΗ Η Γεωδαιτική Αστρονομία (Geodetic Astronomy) είναι ο κλάδος της Αστρονομίας Θέσης (Positional Astronomy) που ασχολείται με τον προσδιορισμό διευθύνσεων στον χώρο, από σημεία πάνω ή κοντά στην
1 ΕΙΣΑΓΩΓΗ Η Γεωδαιτική Αστρονομία (Geodetic Astronomy) είναι ο κλάδος της Αστρονομίας Θέσης (Positional Astronomy) που ασχολείται με τον προσδιορισμό διευθύνσεων στον χώρο, από σημεία πάνω ή κοντά στην
Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ
 Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Γεωδαιτικό σύστημα Χάρτης Πυξίδα Χάραξη
Εισηγητής: Καραγιώργος Θωμάς, MSc, PhD candidate in Sport Management & Recreation ΤΜΗΜΑ ΕΠΙΣΤΙΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ & ΑΘΛΗΤΙΣΜΟΥ ΑΡΙΣΤOΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Γεωδαιτικό σύστημα Χάρτης Πυξίδα Χάραξη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ 1: ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ ΔΙΔΑΣΚΩΝ : Ι. ΖΑΧΑΡΙΑΣ ΑΓΡΙΝΙΟ, 2015 ΕΡΓΑΣΤΗΡΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΙ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ 1: ΤΟΠΟΓΡΑΦΙΚΟΙ ΧΑΡΤΕΣ ΔΙΔΑΣΚΩΝ : Ι. ΖΑΧΑΡΙΑΣ ΑΓΡΙΝΙΟ, 2015 ΕΡΓΑΣΤΗΡΙΟ
Να υπολογισθεί ο αστρικός χρόνος της ανατολής του Ήλιου στη Θεσσαλονίκη (φ = 40º 37') κατά την 21η Μαρτίου.
 Ενότητα 1 Να υπολογισθεί ο αστρικός χρόνος της ανατολής του Ήλιου στη Θεσσαλονίκη (φ = 40º 37') κατά την 21η Μαρτίου. Την 21η Μαρτίου οι ουρανογραφικές συντεταγμένες του Ήλιου είναι α = 0 h, δ = 0 ενώ
Ενότητα 1 Να υπολογισθεί ο αστρικός χρόνος της ανατολής του Ήλιου στη Θεσσαλονίκη (φ = 40º 37') κατά την 21η Μαρτίου. Την 21η Μαρτίου οι ουρανογραφικές συντεταγμένες του Ήλιου είναι α = 0 h, δ = 0 ενώ
Πρόγραμμα Παρατήρησης
 Πρόγραμμα Παρατήρησης Η αναζήτηση του ζοφερού ουρανού Άγγελος Κιοσκλής Οκτώβριος 2005 ΒΑΣΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ * η παρατήρηση πραγματοποιείται κατά προτίμηση όταν η Σελήνη δεν εμφανίζεται στον ουρανό, διότι
Πρόγραμμα Παρατήρησης Η αναζήτηση του ζοφερού ουρανού Άγγελος Κιοσκλής Οκτώβριος 2005 ΒΑΣΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ * η παρατήρηση πραγματοποιείται κατά προτίμηση όταν η Σελήνη δεν εμφανίζεται στον ουρανό, διότι
ΤΠΟΛΟΓΙΜΟ ΣΗ ΑΠΟΣΑΗ ΕΝΟ ΠΛΟΙΟΤ ΑΠΟ ΣΗ ΣΕΡΙΑ
 ΤΠΟΛΟΓΙΜΟ ΣΗ ΑΠΟΣΑΗ ΕΝΟ ΠΛΟΙΟΤ ΑΠΟ ΣΗ ΣΕΡΙΑ ΠΩ Ο ΘΑΛΗ ΜΕΣΡΗΕ ΣΟ ΤΨΟ ΣΗ ΠΤΡΑΜΙΔΑ Η πυραμίδα του Φέoπα (2ου Υαραώ της 4ης δυναστείας), ένα από τα 7 θαύματα της αρχαιότητας, άρχιζε να κτίζεται γύρω στο 2.600
ΤΠΟΛΟΓΙΜΟ ΣΗ ΑΠΟΣΑΗ ΕΝΟ ΠΛΟΙΟΤ ΑΠΟ ΣΗ ΣΕΡΙΑ ΠΩ Ο ΘΑΛΗ ΜΕΣΡΗΕ ΣΟ ΤΨΟ ΣΗ ΠΤΡΑΜΙΔΑ Η πυραμίδα του Φέoπα (2ου Υαραώ της 4ης δυναστείας), ένα από τα 7 θαύματα της αρχαιότητας, άρχιζε να κτίζεται γύρω στο 2.600
Ειδικά κεφάλαια παραγωγής ενέργειας
 Πανεπιστήμιο Δυτικής Μακεδονίας Τμήμα Μηχανολόγων Μηχανικών Ειδικά κεφάλαια παραγωγής ενέργειας Ενότητα 3 (β): Μη Συμβατικές Πηγές Ενέργειας Αν. Καθηγητής Γεώργιος Μαρνέλλος (Γραφείο 208) Τηλ.: 24610 56690,
Πανεπιστήμιο Δυτικής Μακεδονίας Τμήμα Μηχανολόγων Μηχανικών Ειδικά κεφάλαια παραγωγής ενέργειας Ενότητα 3 (β): Μη Συμβατικές Πηγές Ενέργειας Αν. Καθηγητής Γεώργιος Μαρνέλλος (Γραφείο 208) Τηλ.: 24610 56690,
P. E. QristopoÔlou - N. Galanˆkhc. Ergasthriak AstronomÐa. Ergasthriakèc Ask seic
 Πανεπιστήμιο Πατρών Σχολή Θετικών Επιστημών - Τμήμα Φυσικής Τομέας Θεωρητικής & Μαθηματικής Φυσικής, Αστρονομίας & Αστροφυσικής P. E. QristopoÔlou - N. Galanˆkhc Ergasthriak AstronomÐa Ergasthriakèc Ask
Πανεπιστήμιο Πατρών Σχολή Θετικών Επιστημών - Τμήμα Φυσικής Τομέας Θεωρητικής & Μαθηματικής Φυσικής, Αστρονομίας & Αστροφυσικής P. E. QristopoÔlou - N. Galanˆkhc Ergasthriak AstronomÐa Ergasthriakèc Ask
10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ
 77 10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Ολοκληρώνοντας την συνοπτική παρουσίαση των εννοιών και μεθόδων της Γεωδαιτικής Αστρονομίας θα κάνουμε μια σύντομη αναφορά στην αξιοποίηση των μεγεθών που προσδιορίστηκαν,
77 10. ΓΕΩΔΑΙΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ Ολοκληρώνοντας την συνοπτική παρουσίαση των εννοιών και μεθόδων της Γεωδαιτικής Αστρονομίας θα κάνουμε μια σύντομη αναφορά στην αξιοποίηση των μεγεθών που προσδιορίστηκαν,
Tοπογραφικά Σύμβολα. Περιγραφή Χάρτη. Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής:
 Tοπογραφικά Σύμβολα Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής: Κεντρική Αρτηρία Ρέμα Δευτερεύουσα Αρτηρία Πηγάδι Χωματόδρομος Πηγή Μονοπάτι
Tοπογραφικά Σύμβολα Συνήθως στους χάρτες υπάρχει υπόμνημα με τα σύμβολα που χρησιμοποιούνται. Τα πιο συνηθισμένα είναι τα εξής: Κεντρική Αρτηρία Ρέμα Δευτερεύουσα Αρτηρία Πηγάδι Χωματόδρομος Πηγή Μονοπάτι
Η Γη είναι ένας πλανήτης που κατοικούν εκατομμύρια άνθρωποι, αλλά και ο μοναδικός πλανήτης στον οποίο γνωρίζουμε ότι υπάρχει ζωή.
 Το Ηλιακό Σύστημα. Ήλιος Ο Ήλιος είναι ο αστέρας του Ηλιακού μας Συστήματος και το λαμπρότερο σώμα του ουρανού. Είναι μια τέλεια σφαίρα με διάμετρο 1,4 εκατομμύρια χμ. Η σημασία του Ήλιου στην εξέλιξη
Το Ηλιακό Σύστημα. Ήλιος Ο Ήλιος είναι ο αστέρας του Ηλιακού μας Συστήματος και το λαμπρότερο σώμα του ουρανού. Είναι μια τέλεια σφαίρα με διάμετρο 1,4 εκατομμύρια χμ. Η σημασία του Ήλιου στην εξέλιξη
2.1. Κυκλική κίνηση Κυκλική κίνηση. Ομάδα Β.
 2.1.. 2.1.. Ομάδα Β. 2.1.Σχέσεις μεταξύ γραμμικών και γωνιακών μεγεθών στην ΟΚΚ. Κινητό κινείται σε περιφέρεια κύκλου ακτίνας 40m με ταχύτητα μέτρου 4m/s. i) Ποια είναι η περίοδος και ποια η συχνότητά
2.1.. 2.1.. Ομάδα Β. 2.1.Σχέσεις μεταξύ γραμμικών και γωνιακών μεγεθών στην ΟΚΚ. Κινητό κινείται σε περιφέρεια κύκλου ακτίνας 40m με ταχύτητα μέτρου 4m/s. i) Ποια είναι η περίοδος και ποια η συχνότητά
1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης
 1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης Απαραίτητο όλων των ωκεανογραφικών ερευνών και μελετών Προσδιορισμός θέσης & πλοήγηση σκάφους Σε αυτό το εργαστήριο.. Τι περιλαμβάνει
1o ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑΤΟΣ «ΜΗΧΑΝΙΚΗ ΤΩΝ ΩΚΕΑΝΩΝ» Χάρτες: Προσδιορισμός θέσης Απαραίτητο όλων των ωκεανογραφικών ερευνών και μελετών Προσδιορισμός θέσης & πλοήγηση σκάφους Σε αυτό το εργαστήριο.. Τι περιλαμβάνει
Απαντήσεις πανελληνίων θεμάτων στην. Ναυσιπλοΐα ΙΙ 12/06/2018
 Απαντήσεις πανελληνίων θεμάτων στην Ναυσιπλοΐα ΙΙ 12/06/2018 ΘΕΜΑ Α Α1. α. Λ β. Σ γ. Λ δ. Λ ε. Σ Α2. 1 ε 2 στ 3 - β 4 α 5 - γ ΘΕΜΑ Β Β1. α)(σελ 13) Το επίπεδο κάθετο προς τη κατακόρυφο που διέρχεται από
Απαντήσεις πανελληνίων θεμάτων στην Ναυσιπλοΐα ΙΙ 12/06/2018 ΘΕΜΑ Α Α1. α. Λ β. Σ γ. Λ δ. Λ ε. Σ Α2. 1 ε 2 στ 3 - β 4 α 5 - γ ΘΕΜΑ Β Β1. α)(σελ 13) Το επίπεδο κάθετο προς τη κατακόρυφο που διέρχεται από
Κεφάλαιο 6 ο : Φύση και
 Κεφάλαιο 6 ο : Φύση και Διάδοση του Φωτός Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Η εξέλιξη ξ των αντιλήψεων για την όραση Ορισμένοι αρχαίοι Έλληνες φιλόσοφοι ερμήνευαν την
Κεφάλαιο 6 ο : Φύση και Διάδοση του Φωτός Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Η εξέλιξη ξ των αντιλήψεων για την όραση Ορισμένοι αρχαίοι Έλληνες φιλόσοφοι ερμήνευαν την
Αφροδίτη, Κρόνος, Ερμής, Ουρανός, Δίας, Ποσειδώνας, Άρης
 Αφροδίτη, Κρόνος, Ερμής, Ουρανός, Δίας, Ποσειδώνας, Άρης Το χρώμα της Αφροδίτη είναι κίτρινο προς κόκκινο. Το μέγεθός της είναι 9,38-10 χλ. Η απόσταση από τη γη είναι 41.400.000 χλ. Δεν είναι αρκετή απόσταση
Αφροδίτη, Κρόνος, Ερμής, Ουρανός, Δίας, Ποσειδώνας, Άρης Το χρώμα της Αφροδίτη είναι κίτρινο προς κόκκινο. Το μέγεθός της είναι 9,38-10 χλ. Η απόσταση από τη γη είναι 41.400.000 χλ. Δεν είναι αρκετή απόσταση
Γ ΛΥΚΕΙΟΥ ΟΙ ΚΙΝΗΣΕΙΣ ΤΩΝ ΣΤΕΡΕΩΝ ΣΩΜΑΤΩΝ
 Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
Όποτε χρησιμοποιείτε το σταυρό ή το κλειδί της εργαλειοθήκης σας για να ξεσφίξετε τα μπουλόνια ενώ αντικαθιστάτε ένα σκασμένο λάστιχο αυτοκινήτου, ολόκληρος ο τροχός αρχίζει να στρέφεται και θα πρέπει
ΗΛΙΑΚΟ ΡΟΛΟΙ ΓΥΜΝΑΣΙΟΥ ΝΙΚΗΦΟΡΟΥ
 ΗΛΙΑΚΟ ΡΟΛΟΙ ΓΥΜΝΑΣΙΟΥ ΝΙΚΗΦΟΡΟΥ Το ρολόι αυτό είναι κατασκευασµένο από λευκό µάρµαρο Θάσου. Βρίσκεται στην αυλή του Γυµνασίου Νικηφόρου ράµας σε 41 0 10' 12'' βόρειο πλάτος και 24 0 18' 49.83'' ανατολικό
ΗΛΙΑΚΟ ΡΟΛΟΙ ΓΥΜΝΑΣΙΟΥ ΝΙΚΗΦΟΡΟΥ Το ρολόι αυτό είναι κατασκευασµένο από λευκό µάρµαρο Θάσου. Βρίσκεται στην αυλή του Γυµνασίου Νικηφόρου ράµας σε 41 0 10' 12'' βόρειο πλάτος και 24 0 18' 49.83'' ανατολικό
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
Εισαγωγή στην Αστρονοµική Παρατήρηση. Ανδρέας Παπαλάμπρου Αστρονομική Εταιρεία Πάτρας Ωρίων 20/5/2009
 Εισαγωγή στην Αστρονοµική Παρατήρηση Ανδρέας Παπαλάμπρου Αστρονομική Εταιρεία Πάτρας Ωρίων 20/5/2009 1 Ερασιτεχνική Αστρονομία Μια ενασχόληση που αρχίζει από απλό χόμπι... & φτάνει έως συμβολή σε επιστημονικές
Εισαγωγή στην Αστρονοµική Παρατήρηση Ανδρέας Παπαλάμπρου Αστρονομική Εταιρεία Πάτρας Ωρίων 20/5/2009 1 Ερασιτεχνική Αστρονομία Μια ενασχόληση που αρχίζει από απλό χόμπι... & φτάνει έως συμβολή σε επιστημονικές
Κων/νος Χριστόπουλος Κων/νος Παράσογλου Γιάννης Παπαϊωάννου Μάριος Φλωράκης Χρήστος Σταματούλης
 Κων/νος Χριστόπουλος Κων/νος Παράσογλου Γιάννης Παπαϊωάννου Μάριος Φλωράκης Χρήστος Σταματούλης Οι αρχαίοι Έλληνες ήταν οι πρώτοι που εφάρμοσαν τα μαθηματικά στην αστρονομία Κατέκτησαν σημαντικές γνώσεις
Κων/νος Χριστόπουλος Κων/νος Παράσογλου Γιάννης Παπαϊωάννου Μάριος Φλωράκης Χρήστος Σταματούλης Οι αρχαίοι Έλληνες ήταν οι πρώτοι που εφάρμοσαν τα μαθηματικά στην αστρονομία Κατέκτησαν σημαντικές γνώσεις
Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth.
 Μια εικονική εκδρομή με το Google Earth Αγαπητέ μαθητή, Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth. Εσύ
Μια εικονική εκδρομή με το Google Earth Αγαπητέ μαθητή, Η εργασία που επέλεξες θα σου δώσει τη δυνατότητα να συνεργαστείς με συμμαθητές σου και να σχεδιάσετε μια εικονική εκδρομή με το Google Earth. Εσύ
2. Η παρακάτω φωτογραφία δείχνει (επιλέξτε τη µοναδική σωστή απάντηση):
 1 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας για µαθητές Δηµοτικού 1. Το διαστηµικό τηλεσκόπιο Χάµπλ (Hubble) πήρε πρόσφατα αυτή την φωτογραφία όπου µπορείτε να διακρίνετε ένα «χαµογελαστό πρόσωπο».
1 ος Πανελλήνιος Μαθητικός Διαγωνισµός Αστρονοµίας για µαθητές Δηµοτικού 1. Το διαστηµικό τηλεσκόπιο Χάµπλ (Hubble) πήρε πρόσφατα αυτή την φωτογραφία όπου µπορείτε να διακρίνετε ένα «χαµογελαστό πρόσωπο».
Οι Κινήσεις της Γης. Eπιπτώσεις. Η κίνηση της Γης. στα Συστήματα Αναφοράς για τη ορυφορική Γεωδαισία. Η περιστροφή της Γης
 Οι Κινήσεις της Γης. Eπιπτώσεις στα Συστήματα για τη ορυφορική Γεωδαισία Οι αρχαίοι θεωρούσαν τη Γη ακίνητη και κέντρο του σύμπαντος Η κίνηση της Γης TEPAK ορυφορική Γεωδαισία 6 ο Εξάμηνο 2011-12 Στην
Οι Κινήσεις της Γης. Eπιπτώσεις στα Συστήματα για τη ορυφορική Γεωδαισία Οι αρχαίοι θεωρούσαν τη Γη ακίνητη και κέντρο του σύμπαντος Η κίνηση της Γης TEPAK ορυφορική Γεωδαισία 6 ο Εξάμηνο 2011-12 Στην
8. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΛΑΤΟΥΣ
 69 8. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΛΑΤΟΥΣ 8.1 Εισαγωγή Υπενθυμίζεται ότι το αστρονομικό πλάτος ενός τόπου είναι η γωνία μεταξύ της διεύθυνσης της κατακορύφου του τόπου και του επιπέδου του ουράνιου Ισημερινού. Ο προσδιορισμός
69 8. ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΛΑΤΟΥΣ 8.1 Εισαγωγή Υπενθυμίζεται ότι το αστρονομικό πλάτος ενός τόπου είναι η γωνία μεταξύ της διεύθυνσης της κατακορύφου του τόπου και του επιπέδου του ουράνιου Ισημερινού. Ο προσδιορισμός
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Καμπυλόγραμμες Κινήσεις Επιμέλεια: Αγκανάκης Α. Παναγιώτης, Φυσικός http://phyiccore.wordpre.com/ Βασικές Έννοιες Μέχρι στιγμής έχουμε μάθει να μελετάμε απλές κινήσεις,
ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 7 ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΘΕΜΑΤΑ Α Α. ΚΙΝΗΣΗ - ΜΕΤΑΤΟΠΙΣΗ ΧΡΟΝΟΣ ΤΑΧΥΤΗΤΑ Στις ακόλουθες προτάσεις να διαλέξετε την σωστή απάντηση: 1. Ένα σημειακό αντικείμενο κινείται σε ευθύγραμμο δρόμο ο οποίος
7 ΚΕΦΑΛΑΙΟ 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΘΕΜΑΤΑ Α Α. ΚΙΝΗΣΗ - ΜΕΤΑΤΟΠΙΣΗ ΧΡΟΝΟΣ ΤΑΧΥΤΗΤΑ Στις ακόλουθες προτάσεις να διαλέξετε την σωστή απάντηση: 1. Ένα σημειακό αντικείμενο κινείται σε ευθύγραμμο δρόμο ο οποίος
Ο χώρος. 1.Μονοδιάστατη κίνηση
 Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
Ο χώρος Τα χελιδόνια έρχονται και ξανάρχονται. Κάθε χρόνο βρίσκουν μια γωνιά για να χτίσουν τη φωλιά, που θα γίνει το επίκεντρο του χώρου τους. Ο χώρος είναι ένας οργανικός χώρος, όπως εκείνος που αφορά
ΣΤΑΤΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΙΔΕΩΝ ΤΩΝ ΠΡΩΤΟΕΤΩΝ ΦΟΙΤΗΤΩΝ ΦΥΣΙΚΗΣ
 ΣΤΑΤΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΙΔΕΩΝ ΤΩΝ ΠΡΩΤΟΕΤΩΝ ΦΟΙΤΗΤΩΝ ΦΥΣΙΚΗΣ Πτυχιακή Εργασία Πέτρου Μαρία Επιβλέπων Καθηγητής Βλάχος Λουκάς «Ο πιο σπουδαίος απλός παράγοντας που επηρεάζει τη μάθηση είναι
ΣΤΑΤΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΙΔΕΩΝ ΤΩΝ ΠΡΩΤΟΕΤΩΝ ΦΟΙΤΗΤΩΝ ΦΥΣΙΚΗΣ Πτυχιακή Εργασία Πέτρου Μαρία Επιβλέπων Καθηγητής Βλάχος Λουκάς «Ο πιο σπουδαίος απλός παράγοντας που επηρεάζει τη μάθηση είναι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΤΡΙΤΗ 31
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΤΡΙΤΗ 31
Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ
 0 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ 0 1 Στρατηγική επίλυσης προβλημάτων Α. Κάνε κατάλληλο σχήμα,τοποθέτησε τα δεδομένα στο σχήμα και ονόμασε
0 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΑΣΚΗΣΕΙΣ Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η - Α Σ Κ Η Σ Ε Ι Σ 0 1 Στρατηγική επίλυσης προβλημάτων Α. Κάνε κατάλληλο σχήμα,τοποθέτησε τα δεδομένα στο σχήμα και ονόμασε
Επιλεγμένες Ασκήσεις Φυλλαδίου 1 8/3/2017
 Επιλεγμένες Ασκήσεις Φυλλαδίου 1 8/3/2017 19) Ποια είναι η περιοχή τιμών των ουρανογραφικών συντεταγμένων των ουράνιων αντικειμένων που είναι (i) αειφανή και (ii) αφανή για το Αστεροσκοπείο του Χελμού.
Επιλεγμένες Ασκήσεις Φυλλαδίου 1 8/3/2017 19) Ποια είναι η περιοχή τιμών των ουρανογραφικών συντεταγμένων των ουράνιων αντικειμένων που είναι (i) αειφανή και (ii) αφανή για το Αστεροσκοπείο του Χελμού.
