Pripreme za predavanja iz Fizike 1 doc. dr. sc. Sanda Pleslić
|
|
|
- Ίσις Πολίτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 . Mehanika tekućina: statika.. Tlak. Pascalov zakon. Hidrostatski tlak Tvar može ostojati u 3 agregatna stanja: čvrstom, tekućem i linovitom. Čvrsta tijela zadržavaju određeni volumen i oblik zbog relativno jakih kohezionih sila među atomima. Tekućine orimaju oblik osude u kojoj se nalaze, ali teško mijenjaju svoj volumen. U linovima su molekule relativno daleko mjedna od druge a je linove lako stlačiti i oni lako mijenjaju svoj volumen i orimaju oblik osude u kojoj se nalaze. Tekućine i linove nazivamo luidima. To su tvari koje lako mijenjaju oblik, odnosno mogu teći. Mehanika luida ili hidromehanika se dijeli na: - hidrostatiku oisuje luide u mirovanju - hidrodinamiku oisuje luide u gibanju... Tlak Čestice u luidu djeluju jedna na drugu i djeluju na stijenke osude u kojoj se nalazi luid. U luidima u mirovanju sile su uvijek okomite na ovršinu s kojom je luid u kontaktu. Sile koje djeluju okomito na ovršinu zovemo ritisnim silama. Tlak se deinira kao omjer sile i ovršine na koju ta sila djeluje okomito: F S Ako sila nije jednaka u svim točkama ovršine S, tada nam gornji omjer daje srednju vrijednost tlaka, a tlak u određenoj točki se deinira kao: F df lim S 0 S ds Tlak je skalarna veličina. Možemo isati i: na element ovršine ds. r r d F ds, gdje je d S r vektor u smjeru normale U svakoj točki mirnog luida tlak je isti u svim smjerovima. Jedinica tlaka je ascal: [ ] [ F] [ ] S N m Pa Može se uotrebljavati i jedinica bar: bar 0 5 Pa Fluidi lako mijenjaju oblik i orimaju oblik osude u kojoj se nalaze. Međutim, da bismo im romijenili volumen, otrebno je djelovati silom. Pri tom je linove lako stlačiti. Stlačivost tekućina je vrlo malena i otrebne su velike sile da bi se oazila romjena volumena tekućine, a tekućine smatramo nestlačivim.
2 Stlačivost luida ri izotermnoj komresiji deinira se kao: dv κ V d T Budući je romjena volumena uvijek surotnog redznaka od romjene tlaka, redznak minus čini stlačivost ozitivnom. Jedinica stlačivosti je Pa -. No obično je romjena volumena tekućina s tlakom malena a ćemo je većinom zanemariti. Za razliku od tekućina, linovi lakše mijenjaju obujam. Pri izotermnoj komresiji je umnožak volumena i tlaka konstantan (Boyle-Mariotteov zakon) i stlačivost linova je κ dv V d Često se zove i koeicijent izotermne komresibilnosti.... Pascalov zakon Djelujemo li na tekućinu u ravnoteži izvana nekom silom F, tada se taj vanjski tlak širi u tekućini jednako na sve strane. SLIKA: HIDRAULIČKI TLAK Kulišić slika 0.. str. 47 Nr. ako na osudu naunjenu vodom reko klia ovršine S djelujemo vanjskom silom F, sila se luidom renosi u svim smjerovima tako da se tlak, koji stvara vanjska sila, ojavljuje u svim točkama luida a vrijedi: F S F S F S To je Pascalov zakon za vanjski (ili hidraulički) tlak: U svakoj točki nestlačivog, mirnog luida je tlak jednak. U razmatranjima nismo uzeli u obzir djelovanje sile teže na čestice luida. Primjer: hidraulički tijesak Na tom rinciu se temelje hidraulički uređaji: tijesak (reša), kočnice, dizalice...
3 SLIKA: HIDRAULIČKI TIJESAK Kulišić slika 0.. str. 48 Ako na kli manje ovršine S djelujemo silom F, tlak F / S, renosit će se jednako u svim smjerovima a i na kli veće ovršine S na drugom kraju tijeska (reše) a je: F F S S, odnosno: F F S S Budući je S > S, bit će veća i sila F. Rad koji izvrše te sile jednak je: dw F s F s V Tako se hidrauličkim tijeskom (rešom) omoću manjih sila dobivaju veće sile te je tijesak rimjer mehaničkog stroja kojim se korisni rad, koji bi se bez stroja morao izvršiti velikom silom, može izvršiti manjom silom. Sličan rimjer je kod hidrauličke kočnice gdje se djelovanjem sile na aučicu hidrauličke kočnice reko klia u glavnom cilindru automobila tlak renosi na sve dijelove nestlačive tekućine a tako i na kli cilindra u kotačima. Tako je kod kočnica s reda veličine centimetra, a mala sila F odgovara sili vozačeve noge. Pomak s je reda veličine milimetra, a velika sila F djeluje na kočione loče i lako zaustavlja automobil...3. Hidrostatski tlak Na luid djeluje i sila teža. To je volumna sila koja, za razliku od ovršinskih sila, djeluje na sve čestice luida. Tlak uzrokovan težinom samog luida nazivamo hidrostatskim tlakom. Na rimjer, tlak na dno osude naunjene vodom uzrokuje težina stuca vode iznad dna. Zamislimo tekućinu u osudi kao na slici i izračunajmo koliki tlak djeluje na ovršinu S na dubini h. SLIKA: HIDROSTATSKI TLAK Kulišić slika 0.3. str.48 3
4 Neka je ta ovršina baza zamisljenog valjka unutar tekućine. Pretostavimo da je gustoća konstantna, a tekućina nestlačiva. Na gornju bazu djeluje sila: F a S gdje je a atmoserski tlak. Na donju bazu djeluje sila: F S gdje je tlak na mjestu gdje se nalazi ovršina te težina stuca tekućine nad tom ovršinom: G mg ρ g V ρgh S S na dubini h, Budući je zamišljeni volumen u ravnoteži, te se sile oništavaju: S a S ρ gh S 0 Odatle je ukuni tlak koji djeluje u svim točkama tekućine na dubini h: a + ρgh Dio ρ gh uzrokuje težina tekućine i zove se hidrostatski tlak. Na slici je rikazan okus kojim možemo okazati da sila hidrostatskog tlaka na dno ovisi o ovršini dna S i visini stuca vode h, a ne i o obliku osude. SLIKA: HIDROSTATSKI PARADOKS: TLAK NA DNO POSUDE NE OVISI O OBLIKU POSUDE Kulišić slika 0.4. str. 49 To je oznati hidrostatski aradoks koji zaravo i nije aradoks već osljedica zakona za hidrostatski tlak. 4
5 .. Atmoserski tlak. Torricelijev okus. Zemlja svojom rivlačnom silom drži oko sebe zračni omotač, Zemljinu atmoseru. Atmoserski tlak nastaje zbog vlastite težine zračnog stuca iznad Zemljine ovršine. Tlak zraka možemo izmjeriti omoću Torricellijeva okusa: - staklenu cijev (eruvetu) duljine oko m, zatvorenu na jednom kraju, isunimo živom - vrh joj zatvorimo, reokrenemo je i uronimo u osudu sa živom, te odčeimo - živa će se u cijevi sustiti do određene visine h ovisne o vanjskom tlaku - iznad žive u gornjem dijelu cijevi nema zraka, već imamo samo nešto živinih ara i tlak je 0 - na vanjsku ovršinu žive u osudi djeluje atmoserski tlak a SLIKA: TORRICELLIJEV POKUS (ŽIVIN BAROMETAR) Kulišić slika 0.7. str.50 Hidrostatski tlak za točke u horizontalnoj ravnini koja rolazi ovršinom žive u osudi: a ρ gh + ρgh ρ je gustoća žive, a h visina živina stuca. Pri normiranom atmoserskom tlaku, koji iznosi 035 Pa, visina stuca žive u živinu barometru je 0,76 m. Budući je gustoća žive ri 0ºC jednaka 3, kg/m 3, iz zadnje relacije dobijemo: 3 N a ρ gh 3, , ,76 035Pa m Kao rezultat Torricellijevog okusa je naravljen mjerni instrument barometar, koji mjeri tlak. Zbog toga se dugo koristila jedinica milimetri žive koja je danas zamijenjena ascalima. Osim jedinice bar koji se također i danas koristi, u uorabi je ostala i jedinica atmosera, to jest: atm 035 Pa 5
6 .3. Pokusi s U-cijevima. Manometar. Barometarska ormula.3.. Pokusi s U-cijevima U međusobno sojenim osudama razina tekućine u svim osudama nalazi se na istoj visini bez obzira na oblik osuda. SLIKA: SPOJENE POSUDE Kulišić slika 0.5. str. 49 To izlazi iz činjenice da je hidrostatski tlak jednak u svim točkama na jednakoj dubini (retostavljamo da nema kailarnih ojava). Ako se u sojenim osudama nalaze dvije različite tekućine, gustoća ρ i ρ, tada je razina tekućina različita. Budući da u svim točkama određenog horizontalnog resjeka ukuni tlak mora biti jednak, slijedi: a + ρ + gh a ρ gh Ovdje su h i h visine stuca jedne i druge tekućine, mjerene od granice između njih. Mjereći te dvije visine, ako znamo ρ, možemo odrediti neoznatu gustoću: ρ ρ h / h.3.. Manometar Na rinciu sojenih osuda rade uređaji za mjerenje tlaka, hidraulički manometri (tlakomjeri). Ako su vanjski tlakovi i različiti, razlika tekućine u obje osude je različita. SLIKA: MANOMETRI Kulišić slika 0.6. str. 50 6
7 Primjenom zakon za hidrostatski tlak dobijemo: ρg h Mjerenjem razlike razina tekućine.3.3. Barometarska ormula h može se mjeriti razlika tlaka Atmoserski tlak se mijenja s nadmorskom visinom i ada o takozvanoj barometarskoj ormuli.. SLIKA: UZ IZVOD BAROMETARSKE FORMULE Kulišić slika 0.8. str. 5 Neka je na visini h atmoserski tlak jednak, a na visini h+dh tlak +d. Ako je dh ozitivan, tada je d negativan jer tlak ada s visinom. Razlika u tlaku d između ta dva sloja nastaje zbog težine stuca zraka resjeka m i visine dh, a iznosi: d ρgdh gdje je ρ gustoća zraka na toj visini. Da bismo iz te jednadžbe odredili kao unkciju h, moramo znati romjenu gustoće zraka s tlakom. Gustoća zraka unkcija je tlaka i temerature. Pretostavimo li da je atmosera izotermna (T konst), tada iz Boyle-Mariotteova zakona slijedi: ρ0 ρ ( h) 0 ( h) Ovdje su 0 i ρ 0 tlak i gustoća zraka na nadmorskoj visini h 0. d ρ( h) gdh ρ 0 ( h) gdh 0 Slijedi: 0d dh ρ g 0 7
8 Odnosno: h dh 0 g ρ d Rješenje je: 0 ex( ρ0 gh / 0 ) Pri normiranoj temeraturi i tlaku (0ºC i 035 Pa) gustoća zraka ρ 0 je,93 kg/m 3 a zadnju ormulu možemo isati i u obliku: 0 ex( h / 7990) Ovdje h izražavamo u metrima i ormula nam govori da ribližno svakih 8000 m tlak ada za aktor e (,78). To je barometarska ormula izvedena uz retostavku da je g konst i da je veza tlaka i ρ0 gustoće dana s ρ ( h) ( h). 0 Točniju ormulu bismo dobili uzevši u obzir adanje temerature s visinom: 0,0065h 88 5,55 0 ( ) Ovdje je h nadmorska visina u metrima, a 88 K (5ºC) temeratura na nadmorskoj visini h 0. Ovisnost tlaka o visini za izotermnu atmoseru rikazana je na slici: SLIKA: PROMJENA TLAKA S NADMORSKOM VISINOM U IZOTERMNOJ ATMOSFERI (BAROMETARSKA FORMULA) Kulišić slika 0.9. str. 5 8
9 .4. Arhimedov zakon. Uzgon. Kad je tijelo uronjeno u luid (tekućinu ili lin), javlja se rezultantna sila rema gore kao osljedica hidrostatskog tlaka. Tu silu nazivamo uzgonom. Ilustracija uzgona: kada tijelo koje visi na dinamometru uronimo u vodu, dinamometar okazuje manje jer uzgon rividno smanjuje težinu tijela. SLIKA: UZGON Kulišić slika 0.0. str. 5 Zamislimo tijelo volumena V uronjeno u luid gustoće ρ kao na slici a). SLIKA: UZ IZVOD FORMULE ZA UZGON Kulišić slika 0.. str. 53 Radi jednostavnosti ćemo retostaviti da je tijelo oblika valjka ili kocke no svako tijelo, bilo kojeg oblika, možemo odijeliti na valjke ili kocke s dovoljno malim bazama tako da će dobiveni rezultat vrijediti oćenito. Sile ritiska, koje djeluju na bočne strane kocke, oništavaju se jer su na istoj horizontalnoj ravnini jednake o iznosu, a surotnog smjera. Na mjestu gdje je gornja baza tlak je: a + ρgh Na donjoj bazi je tlak: a + ρgh Sila na donju bazu je: Sila na gornju bazu je: F S F S S je ovršina baze. Sila F ima smjer rema gore, a sila F ima smjer rema dolje. 9
10 Budući je hidrostatski tlak na nivou h veći nego na nivou h, sila F bit će veća nego sila F. Kao rezultat će se ojaviti sila rema gore zvana uzgon: Fu F F ρ gh S ρ ghs ρ Vg m Masa istisnutog luida je m. g Isti rezultat možemo dobiti i na drugi način. Zamislimo dio luida volumena V kao na slici b). Težina tog dijela tekućine djeluje rema dolje i iznosi: G ρ gv Budući da tekućina miruje, tu težinu uravnotežuje druga sila, koja je jednaka o iznosu, ali je surotnog smjera i ta sila je uzgon. Uzgon na taj volumen tekućine je: F u ρ gv Ako je umjesto tekućine na tom mjestu neko drugo tijelo istog oblika ili volumena, hidrostatski tlakovi i njihove sile se neće romijeniti a će uzgon biti isti kao i rije: F u ρ gv Uzgon je sila koja djeluje vertikalno rema gore i o iznosu je jednak težini istisnutog luida. To je oznati Arhimedov rinci (Arhimed, grčki matematičar, izičar i izumitelj): Težina tijela uronjenog u luid smanjuje se za iznos težine istisnutog luida. SLIKA: UVJET PLIVANJA Kulišić slika 0.. str. 54 ) Tijelo lebdi u luidu ako je težina tijela uravnotežena uzgonom (slika a). Ako je tijelo homogeno, tada uvjet lebdenja možemo isati u obliku: ρ gv gv ρtijelo Ili: ρ ρtijelo ) Ako je uzgon veći od težine, tijelo se ubrzano diže (Primjer toga je dizanje balona u zraku.) a će tijelo uronjeno u tekućinu djelomično izroniti iz tekućine i livati (slika b). Tijelo, koje liva, bit će toliko uronjeno da će uzgon na uronjeni dio (volumen V ) biti jednak ukunoj težini tijela: G ρ gv Za homogena tijela vrijedi: ρ tijelogv ρ gv Odnosno: V ρ V / ρ tijelo 3) Ako je težine tijela veća od uzgona, tijelo se ubrzano giba rema dolje i tone (slika c). 0
11 AREOMETAR: To je uređaj za mjerenje gustoće i osniva se na ojavi uzgona. To je staklena cijev otežana na donjem kraju, na kojoj se nalazi baždarena skala. Što je gustoća tekućine veća, to će areometar manje uroniti u tekućinu, te se uranjanjem areometra vertikalno u tekućinu može direktno očitati njezina gustoća. SLIKA: AREOMETAR Kulišić slika 0.3. str. 54
12 .5. Površinska naetost..5.. Sile ovršinske naetosti. Koeicijent ovršinske naetosti U čvrstom tijelu atomi su oredani u kristalnoj rešetki i ne mogu se slobodno translacijski gibati već samo titrati oko oložaja ravnoteže. U linovima atomi (ili molekule) nisu vezani jedan za drugog i gibaju se kaotično u osudi u kojoj se nalazi lin. U tekućini su molekule relativno blizu jedna drugoj što znači da nisu vezane jedna za drugu kao u čvrstom stanju i nisu slobodne kao u linovima. Privlačne međumolekulske sile su dosta jake do određene udaljenosti, koju zovemo radijus molekulskog djelovanja, a onda naglo adnu na nulu. Možemo smatrati da svaka molekula djeluje na sve ostale koje se nalaze unutar kugle koja ima radijus molekulskog djelovanja. Polumjer takve kugle je desetak uta veći od razmaka molekula u tekućinama. Međumolekulske sile među istovrsnim molekulama zovu se kohezione sile, a sile među molekulama različitih tvari zovu se adhezione sile. Pojavu naetosti ovršine tekućina možemo objasniti navedenim svojstvima međumolekulskih sila. Površina tekućina se onaša kao rastegnuta ili naeta ona. Primjeri:. Vidjeli smo da aluminijsku ločicu možemo oložiti na ovršinu vode tako da na njoj liva.. Kukci mogu trčati o ovršini vode. 3. Ako na kolut od žice, u kojem se nalazi končić, uhvatimo onu od saunice (slika) i robušimo je s jedne strane konca, reostali dio one slegne se na najmanju ovršinu i konac dobije oblik kružnog luka. SLIKA: NAPETOST POVRŠINE OPNE OD SAPUNICE Kulišić slika 0.4. str. 56 Da bismo odredili naetost ovršine, zamislimo okus s ravokutnim okvirom od žice na kojem je ona od saunice. SLIKA: UZ DEFINICIJU KOEFICIJENTA POVRŠINSKE NAPETOSTI Kulišić slika 0.5. str. 56
13 Jedna stranica ravokutnika je omična i nju će ona u svom nastojanju da smanji ovršinu ovući. Kažemo da na stranicu AB djeluje sila ovršinske naetosti. Tu silu možemo uravnotežiti vanjskom silom F koja je o iznosu jednaka sili naetosti ovršine. Da bismo ovećali ovršinu one, omični dio AB djelovanjem sile F olako omaknemo za x. Pri tom se izvrši rad: W F x Budući da se ona sastoji od dvije ovršine između kojih je tanak sloj tekućine, ovećanje ovršine je: S l x W Koeicijent ovršinske naetosti σ se deinira kao: σ S W je rad otreban za ovećanje ovršine S. σ W S F x l x F l Koeicijent ovršinske naetosti se deinira omoću rada otrebnog za ovećanje ovršine ili omoću sile ovršinske naetosti. Jedinica koeicijenta ovršinske naetosti je J/m ili N/m. U unutrašnjosti tekućine molekula je sa svih strana okružena drugim, susjednim molekulama s kojima međudjeluje tako da je rezultantna sila jednaka nula (slika a). SLIKA: REZULTANTNA SILA NA MOLEKULU U UNUTRAŠNJOSTI (a) I NA POVRŠINI TEKUĆINE (b) Kulišić slika 0.6. str. 57 U ovršinskom sloju molekula nije sa svih strana okružena jednakim brojem molekula jer je unutar kugle olumjera R s donje strane veći broj molekula nego s gornje strane. Površinski sloj je debljine manje od radijusa međumolekulskog djelovanja R. Zato će na molekule na ovršini djelovati rezultantna sila F usmjerena rema unutrašnjosti tekućine (slika b). Da bi se molekule iz unutrašnjosti dovele na ovršinu, otreban je određeni rad a molekule na ovršini imaju veću otencijalnu energiju nego one u unutrašnjosti tekućine. Da bi bio isunjen uvjet ravnoteže, a to je minimum otencijalne energije, tekućina nastoji smanjiti slobodnu ovršinu i zato se javlja ovršinska naetost. 3
14 Povećanjem ovršine molekule se iz unutrašnjosti renose na ovršinu i ovećava im se otencijalna energija na račun izvršenog rada. Koeicijent ovršinske naetosti ovisi o vrsti tekućine, temeraturi tekućine i sredstvu s kojim tekućina graniči. TABLICA KOEFICIJENT POVRŠINSKE NAPETOSTI NEKIH TEKUĆINA KAD JE IZNAD POVRŠINE ZRAK Kulišić tablica 0.3. str Ekserimentalno određivanje koeicijenta ovršinske naetosti SLIKA: EKSPERIMENTALNO ODREĐIVANJE KOEFICIJENTA POVRŠINSKE NAPETOSTI Horvat slika 8.9. str. 8- Izmjerimo težinu rstena očitavanjem dinamometra. Podižemo odlogu dok rsten ne uhvati ovršinu vode. Zatim ostuno suštamo ostolje dok se rsten ne odvoji od ovršine tekućine i tada očitamo silu na dinamometru. Mjerenjem osega rstena i sile dobijemo koeicijent ovršinske naetosti. 4
15 .5.3. Nadtlak zbog zakrivljenosti slobodnih i graničnih ovršina U mjehuriću saunice (ili mjehuriću zraka u vodi) tlak je veći od vanjskog tlaka za neki dodatni nadtlak. Lalaceova ormula za razliku tlakova koja nastaje zbog zakrivljene ovršine: unutarnji vanjski σ ( + ) r r Ako je zakrivljena ovršina kuglasta, onda je r r a je Lalaceova ormula: σ unutarnji vanjski σ ( + ) r r r Površinska naetost u mjehuriću nastoji stegnuti mjehurić sve dok se ne usostavi ravnoteža zbog tlaka unutar mjehurića. Da bi se ovećao mjehurić s olumjera r na olumjer (r + dr), mora se izvršiti rad: dw σds σ 8rπdr Uzima se aktor jer mjehurić ima ovršine, a ovršina je dana s: S 4r π Slijedi: ds 8rπdr Unutar mjehurića je nadtlak je S. i sila koja zbog toga djeluje na unutrašnju ovršinu mjehurića Pri ovećanju mjehurića rad te sile je: dw Sdr 4r πdr Izjednačavanjem dw mjehuriću saunice: σds σ 8rπdr i dw Sdr 4r πdr dobijemo nadtlak u σ 8rπdr 4r πdr 4σ / r Nadtlak u mjehuriću saunice roorcionalan je ovršinskoj naetosti, a obrnuto roorcionalan olumjeru mjehurića. To je oseban oblik Lalaceove ormule za tlak isod zakrivljene ovršine tekućine. Ako dva mjehurića saunice međusobno sojimo staklenom cijevi, tada će zrak iz manjeg mjehurića relaziti u veći tako da će se manji mjehurić još više smanjivati, a veći će rasti dok manji ne nestane. Zadnja ormula je izvedena za mjehurić s dvije ovršine. U slučaju mjehurića zraka u tekućini ili kaljice tekućine dodatni je tlak unutar takve jednostruke serne ovršine: σ / r 5
16 .6. Kailarne ojave Promatrat ćemo ojave na granici tekućine i čvrstog tijela (nr. stijenke osude). Između molekula tekućine i molekula materijala stijenke osude djeluju međumolekulske sile a onašanje tekućine uz stijenku osude ovisi o odnosu kohezionih i adhezionih sila, F K i F A. Kohezija je sila koja se javlja između istovrsnih molekula i koja tekućinu onemogućava da se slobodno roširi o rostoru (kao lin). Kohezija djeluje rema luidu i ne da stijenki da rivuče luid. Adhezija je sila koja se javlja između različitih molekula i ima horizontalni smjer. Rezultanta sila okomita je na zakrivljenu ovršinu, odnosno s vertikalnom stijenkom zatvara kut (θ + 90º). Površina tekućine ostavlja se okomito na rezultantu svih tih međumolekulskih sila. Ako su adhezione sile veće od kohezionih sila (kao na rimjer na granici voda-staklo), ovršina tekućine orima konkavni oblik i kažemo da tekućina kvasi stijenke osude. SLIKA: TEKUĆINA KVASI STIJENKU POSUDE Kulišić slika 0.7. str. 58 F K < F A Ako su kohezione sile veće od adhezionih sila (kao na rimjer na granici živa-staklo), ovršina tekućine orima konveksni oblik i ne kvasi stijenku osude. SLIKA: TEKUĆINA NE KVASI STIJENKU POSUDE Kulišić slika 0.8. str. 58 F K > F A Kut što ga zatvara stijenka osude i tangenta na ovršinu tekućine zove se okrajnji kut. Ako je θ < 90º, tekućina kvasi stijenku osude. Ako je 90º < θ < 80º, tekućina ne kvasi stijenku osude. 6
17 TABLICA: VRIJEDNOST ZA OKRAJNJI KUT IZMEĐU STIJENKE POSUDE I NEKIH TEKUĆINA Kulišić tablica 0.4. str. 58 Ako na čistu odlogu (metalnu ili staklenu ločicu) kanemo ka neke tekućine, oblik kai ovisit će o ovršinskoj naetosti za granicu čvrsto tijelo-tekućina, tekućina-lin i čvrsto tijelolin, odnosno o okrajnjem kutu koji je unkcija tih ovršinskih naetosti. Primjer: - kaljica žive bit će gotovo serna - etrolej će teći reko ovršine ne ormirajući kaljice Ako usku cjevčicu (kailaru) uronimo u osudu s vodom (slika), oazit ćemo da će se voda u njoj odići do neke visine h (koja ovisi o olumjeru kailare i o vrsti tekućine) i da će meniskus vode u kailari biti konkavan. Slično vrijedi i za ostale tekućine koje kvase stijenku kailare. To je kailarna elevacija. SLIKA: KAPILARNA ELEVACIJA Kulišić slika 0.9. str. 59 Razina žive u staklenoj kailari niža je od razine žive u širokoj osudi i meniskus žive je konveksan. To je kailarna deresija. SLIKA: KAPILARNA DEPRESIJA Kulišić slika 0.0. str. 59 Kailarna elevacija i deresija osljedica su naetosti ovršine. 7
18 Izračunat ćemo visinu tekućine u kailari u slučaju kailarne elevacije. Slično razmatranje za kailarnu deresiju bi dovelo do istog rezultata. SLIKA: VISINA STUPCA TEKUĆINE U KAPILARI Kulišić slika 0.. str. 59 Zbog konkavnog meniskusa tekućine u kailari tlak isod meniskusa manji je nego atmoserski tlak iznad. Tekućina se odiže sve dok se ta razlika tlaka uzrokovan težinom stuca tekućine u kailari: ρgh ne izjednači s hidrostatskim tlakom, koji je Budući je σ / R uz R kao olumjer meniskusa, σ cosθ / r, uz r Rcosθ kao olumjer kailare, θ okrajnji kut, σ ovršinska naetost, slijedi: σ cosθ / r ρgh σ cosθ Odnosno: h ρgr Isti rezultat dobijemo ako vertikalnu komonentu ovršinske naetosti, koja odiže tekućinu u kailari, izjednačimo s težinom stuca tekućine. Sila zbog ovršinske naetosti na graničnoj liniji (kružnici) između ovršine tekućine i osude je: σl σ rπ rπ je oseg te kružnice. σ r π cosθ je njena vertikalna komonenta (vertikalna komonenta sile). Težina stuca tekućine je: r πhρg. Vertikalna komonenta sile ovršinske naetosti odiže tekućinu u kailari sve dok težina stuca tekućine ne ostane jednaka toj sili: rπσ cosθ r πhρg σ cosθ Slijedi: h ρgr 8
10. STATIKA FLUIDA Uvod. -ionizirani plin (visoka temperatura) kvantnomehanički. -odreñen oblik i volumen. -poprimaju oblik posude
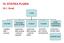 10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
U Z G O N. Iz iskustva je poznato da je tijela (npr., kamen) lakše podizati u vodi ili nekoj drugoj tekućini nego u zraku.
 U Z G O N Iz iskustva je poznato da je tijela (npr., kamen) lakše podizati u vodi ili nekoj drugoj tekućini nego u zraku. U to se možemo lako uvjeriti izvodeći sljedeći pokus. POKUS: Mjerenje težine utega
U Z G O N Iz iskustva je poznato da je tijela (npr., kamen) lakše podizati u vodi ili nekoj drugoj tekućini nego u zraku. U to se možemo lako uvjeriti izvodeći sljedeći pokus. POKUS: Mjerenje težine utega
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
VOLUMEN ILI OBUJAM TIJELA
 VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Unutarnji je volumen čaše V 1. Budući da je do polovice napunjena vodom masa te vode iznosi: 2 Ukupna masa čaše i vode u njoj je 1 kg
 Zadatak 6 (Josi, ginazija) Staklena čaša nalazi se u sudoeru naunjena vodo. Čaša je do olovice naunjena vodo. Unutarnji voluen čaše je 5 c, a njezina asa kada je razna iznosi 9 g. Ako oduzeo sao alo vode
Zadatak 6 (Josi, ginazija) Staklena čaša nalazi se u sudoeru naunjena vodo. Čaša je do olovice naunjena vodo. Unutarnji voluen čaše je 5 c, a njezina asa kada je razna iznosi 9 g. Ako oduzeo sao alo vode
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
( ) ( ) Količinu tekućine I koja prođe u jedinici vremena s nekim presjekom cijevi površine S zovemo jakost struje. Ona iznosi
 Zadatak 0 (Mario, ginazija) Razlika tlakova izeđu širokog i uskog dijela cijevi iznosi 9.8 0 4 Pa. Presjek šireg dijela cijevi je 0 d, a užeg 5 d. Koliko litara vode rotječe cjevovodo u sekundi? (gustoća
Zadatak 0 (Mario, ginazija) Razlika tlakova izeđu širokog i uskog dijela cijevi iznosi 9.8 0 4 Pa. Presjek šireg dijela cijevi je 0 d, a užeg 5 d. Koliko litara vode rotječe cjevovodo u sekundi? (gustoća
Gravitacija. Gravitacija. Newtonov zakon gravitacije. Odredivanje gravitacijske konstante. Keplerovi zakoni. Gravitacijsko polje. Troma i teška masa
 Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
T O P L I N A P l i n s k i z a k o n i
 1. Da bi mogli matematički oisati lin uvodimo ojam tzv. idealnog lina. Koji odgovor nije točan? Idealni lin o retostavci je onaj lin kod kojeg: a) možemo zanemariti međudjelovanje između molekula, tj.
1. Da bi mogli matematički oisati lin uvodimo ojam tzv. idealnog lina. Koji odgovor nije točan? Idealni lin o retostavci je onaj lin kod kojeg: a) možemo zanemariti međudjelovanje između molekula, tj.
( ) ρ = ρ. Zadatak 141 (Ron, gimnazija) Gustoća leda je 900 kg/m 3, a gustoća morske vode 1000 kg/m 3. Koliki dio ledene sante
 Zadatak 4 (Ron, ginazija) Gustoća leda je 900 /, a gustoća orske vode 00 /. Koliki dio ledene sante voluena viri iznad orske površine? (g = 9.8 /s ) Rješenje 4 ρ l = 900 /, ρ v = 000 /,, =? Akceleracija
Zadatak 4 (Ron, ginazija) Gustoća leda je 900 /, a gustoća orske vode 00 /. Koliki dio ledene sante voluena viri iznad orske površine? (g = 9.8 /s ) Rješenje 4 ρ l = 900 /, ρ v = 000 /,, =? Akceleracija
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
Primjeri zadataka iz Osnova fizike
 Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Neka je a 3 x 3 + a 2 x 2 + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka.
 Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
PITANJA IZ MEHANIKE FLUIDA
 PITANJA IZ MEHANIKE FLUIDA 1. Što su fluidi i koja su njihova najvaţnija obiljeţja? 2. Kako se definira tlak? Kojim ga jedinicama iskazujemo? Je li tlak skalarna ili vektorska veličina? 3. Kakva je veza
PITANJA IZ MEHANIKE FLUIDA 1. Što su fluidi i koja su njihova najvaţnija obiljeţja? 2. Kako se definira tlak? Kojim ga jedinicama iskazujemo? Je li tlak skalarna ili vektorska veličina? 3. Kakva je veza
Fizika 1. Auditorne vježbe 5. Dunja Polić. Dinamika: Newtonovi zakoni. Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva
 Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Školska godina 2006/2007 Fizika 1 Auditorne vježbe 5 Dinamika: Newtonovi zakoni 12. prosinca 2008. Dunja Polić (dunja.polic@fesb.hr)
Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Školska godina 2006/2007 Fizika 1 Auditorne vježbe 5 Dinamika: Newtonovi zakoni 12. prosinca 2008. Dunja Polić (dunja.polic@fesb.hr)
Studij racunarstva, Fizika 1, Predavanje siječnja Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva
 Školska godina 2007./2008. Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Fizika 1 Predavanje 10 Statika fluida. Dr. sc. Ivica Puljak (Ivica.Puljak@fesb.hr) Danas ćemo raditi: Tlak
Školska godina 2007./2008. Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Fizika 1 Predavanje 10 Statika fluida. Dr. sc. Ivica Puljak (Ivica.Puljak@fesb.hr) Danas ćemo raditi: Tlak
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Kolegij: Konstrukcije Rješenje zadatka 2. Okno Građevinski fakultet u Zagrebu. Efektivna. Jedinična težina. 1. Glina 18,5 21,
 Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika
 1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
12. SKUPINA ZADATAKA IZ FIZIKE I 6. lipnja 2016.
 12 SKUPIN ZDK IZ FIZIKE I 6 linja 2016 Zadatak 121 U osudi - sremniku očetnog volumena nalazi se n molova dvoatomnog lina na temeraturi rema slici) Plin izobarno ugrijemo na temeraturu, adijabatski ga
12 SKUPIN ZDK IZ FIZIKE I 6 linja 2016 Zadatak 121 U osudi - sremniku očetnog volumena nalazi se n molova dvoatomnog lina na temeraturi rema slici) Plin izobarno ugrijemo na temeraturu, adijabatski ga
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Fluidi. fluid je bilo koja tvar koja može teći. plinovi i tekućine razlika: plinovi su stlačivi, tekućine nisu (u većini slučajeva)
 MEHANIKA FLUIDA Fluidi fluidi igraju vitalnu ulogu u raznim aspektima naših života pijemo ih, dišemo, plivamo u njima oni cirkuliraju našim tijelima i kontroliraju meteorološke uvjete zrakoplovi lete kroz
MEHANIKA FLUIDA Fluidi fluidi igraju vitalnu ulogu u raznim aspektima naših života pijemo ih, dišemo, plivamo u njima oni cirkuliraju našim tijelima i kontroliraju meteorološke uvjete zrakoplovi lete kroz
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
MEHANIKA FLUIDA HIDROSTATIKA 5. Osnovna jednadžba gibanja (II. Newtonov zakon) čestice idealnog fluida i realnog fluida u relativnom mirovanju
 MENIK LUID IDTTIK 5. IDTTIK snovna jednadžba ibanja (II. Newtonov akon) čestice idealno fluida i realno fluida u relativnom mirovanju σ d av d fdv+ σd n V V t av d fdv+ ( pn+ σ ) V V d U anemarenje viskoni
MENIK LUID IDTTIK 5. IDTTIK snovna jednadžba ibanja (II. Newtonov akon) čestice idealno fluida i realno fluida u relativnom mirovanju σ d av d fdv+ σd n V V t av d fdv+ ( pn+ σ ) V V d U anemarenje viskoni
Statika fluida Oblast koja proučava stanje fluida u mirovanju.
 Oblast koja roučava stanje fluida u mirovanju. Agregatna stanja (AP ) Hidrostatički ritisak (AP 4-7) Paskalov zakon (AP -4) Zemljina atmosfera i atmosferski ritisak (AP 7-3) ila otiska i Arhimedov zakon.
Oblast koja roučava stanje fluida u mirovanju. Agregatna stanja (AP ) Hidrostatički ritisak (AP 4-7) Paskalov zakon (AP -4) Zemljina atmosfera i atmosferski ritisak (AP 7-3) ila otiska i Arhimedov zakon.
INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave
 ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave 1.MEHANIKA FLUIDA 1.1 Uvod Fluidima nazivamo tečnosti i gasove (plinove): to su supstance koje lako mijenaju oblik,
ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave 1.MEHANIKA FLUIDA 1.1 Uvod Fluidima nazivamo tečnosti i gasove (plinove): to su supstance koje lako mijenaju oblik,
Repetitorij-Dinamika. F i Zakon očuvanja impulsa (ZOI): i p i = j p j. Zakon očuvanja energije (ZOE):
 Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Zadatak 003 (Vesna, osnovna škola) Kolika je težina tijela koje savladava silu trenja 30 N, ako je koeficijent trenja 0.5?
 Zadata 00 (Jasna, osnovna šola) Kolia je težina tijela ase 400 g? Rješenje 00 Masa tijela izražava se u ilograia pa najprije orao 400 g pretvoriti u ilograe. Budući da g = 000 g, orao 400 g podijeliti
Zadata 00 (Jasna, osnovna šola) Kolia je težina tijela ase 400 g? Rješenje 00 Masa tijela izražava se u ilograia pa najprije orao 400 g pretvoriti u ilograe. Budući da g = 000 g, orao 400 g podijeliti
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
šupanijsko natjecanje iz zike 2017/2018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova)
 šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
( ) ( ) Zadatak 001 (Ines, hotelijerska škola) Ako je tg x = 4, izračunaj
 Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
Statika fluida. Tehnička fizika 1 15/12/2017 Tehnološki fakultet
 Tehnička fizika 1 15/12/2017 Tehnološki fakultet Oblast koja proučava stanje fluida u mirovanju Hidrostatički pritisak Paskalov zakon Zemljina atmosfera i atmosferski pritisak Sila potiska i arhimedov
Tehnička fizika 1 15/12/2017 Tehnološki fakultet Oblast koja proučava stanje fluida u mirovanju Hidrostatički pritisak Paskalov zakon Zemljina atmosfera i atmosferski pritisak Sila potiska i arhimedov
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Rad, energija i snaga
 Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA JEDNADŽBA KONTINUITETA. s1 =
 HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA Hidrodinamika proučava fluide (tekućine i plinove) u gibanju. Gibanje fluida naziva se strujanjem. Ovdje ćemo razmatrati strujanje tekućina.
HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA Hidrodinamika proučava fluide (tekućine i plinove) u gibanju. Gibanje fluida naziva se strujanjem. Ovdje ćemo razmatrati strujanje tekućina.
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
=1), što znači da će duljina cijevi L odgovarati kritičnoj duljini Lkr. koji vlada u ulaznom presjeku, tako da vrijedi
 Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Primjer. Zrak (R=87 J/(kg K), κ=,4) se iz atmosfere ( =, bar, T =88 K) usisava oz cijev romjera D = mm, duljine L = m, rema slici. Treba odrediti maksimalno mogući maseni rotok m max oz cijev uz retostavku
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
