ΑΛΓΟΡΙΘΜΙΚΕΣ ΜΕΘΟΔΟΙ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ

Transcript

1 ΑΛΓΟΡΙΘΜΙΚΕΣ ΜΕΘΟΔΟΙ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ ΚΟΥΛΙΝΑΣ ΓΕΩΡΓΙΟΣ Δρ. Μηχανικός Παραγωγής & Διοίκησης ΔΠΘ

2 ΜΕΤΑΕΥΡΕΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ METAHEURISTIC ALGORITHMS Ευφυείς διαδικασίες επαναληπτικής βελτίωσης Χρησιμοποιούν απλές κινήσεις στο χώρο των λύσεων Ανεξάρτητες από το πρόβλημα που αντιμετωπίζεται κάθε φορά

3 ΜΕΤΑΕΥΡΕΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ METAHEURISTIC ALGORITHMS Στόχος ενός Μεταευρετικού Αλγορίθμου: Γρήγορη εύρεση περιοχών με «καλές λύσεις» Μέσω της ισορροπημένης χρήσης «Διαφοροποίησης» & «Εντατικοποίησης» της αναζήτησης στο χώρο των λύσεων

4 ΜΕΤΑΕΥΡΕΤΙΚΟΙ ΑΛΓΟΡΙΘΜΟΙ METAHEURISTIC ALGORITHMS Εντατικοποίηση της ερευνας στο χώρο των λύσεων (Intensification) Εστιασμένη αναζήτηση σε μικρές περιοχές με υψηλής ποιότητας λύσεις για να βρεθεί το τοπικά βέλτιστο σημείο Διαφοροποίηση της ερευνας στο χώρο των λύσεων (Diversification) Απεγκλωβισμός από τοπικά βέλτιστα και μετακίνηση σε άλλες περιοχές

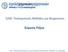
5 ΕΝΤΑΤΙΚΟΠΟΙΗΣΗ ΔΙΑΦΟΡΟΠΟΙΗΣΗ ΣΤΟ ΧΩΡΟ ΤΩΝ ΛΥΣΕΩΝ INTENSIFICATION - DIVERSIFICATION Z(x) Οι μεταευρετικοί αλγόριθμοι εφαρμόζουν στρατηγικές απεγλωβισμού της αναζήτησης από τοπικά βέλτιστα Τοπικό Ελάχιστο (Local minimum) Ολικό Ελάχιστο (Global minimum) x

6 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΑΝΟΠΤΗΣΗΣ The Simulated Annealing Algorithm (SA Metaheuristic Algorithm ή SA Algorithm ) Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by Simulated Annealing. Science, 220(4598), 671 LP-680. Retrieved from

7 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Ανεξάρτητος από το πρόβλημα που αντιμετωπίζει Ευφυής διαδικασία επαναληπτικής βελτίωσης Καθοδηγεί απλούς «τελεστές» - ευρετικούς

8 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Νέα χαρακτηριστικά: Αξιοποίηση του «ιστορικού» της αναζήτησης δηλ. της πορείας της έως τώρα Αποδοχή λύσεων με χειρότερη τιμή αντικειμενικής συνάρτησης προκειμένου να γίνει «απεγλωβισμός» από τοπικά βέλτιστα

9 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Η ιδέα λειτουργίας προέρχεται από την Ανόπτηση (Annealing) των μετάλλων από την υγρή στην στερεά κρυσταλλική κατάσταση Σε υψηλές θερμοκρασίες τα άτομα του μετάλλου βρίσκονται σε κατάσταση υψυλότερης ενέργειας με μεγαλύτερη «κινητικότητα» Με τη μείωση της θερμοκρασίας τα άτομα γίνονται περισσότερο «στατικά» μέχρι που τελικά θα λάβουν τις τελικές θέσεις τους στη στέρεη κατάσταση

10 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Εάν το υγρό μέταλλο «ψύχεται» αρκετά αργά τότε σχηματίζεται τέλειος κρύσταλλος καθώς τα άτομα είχαν το χρόνο και την ενέργεια να τακτοποιηθούν σωστά Εάν η θερμοκρασία μειώνεται γρήγορα, θα σχηματιστεί κρύσταλλος με ατέλειες καθώς τα άτομα δεν πρόλαβαν να τακτοποιηθούν όπως έπρεπε

11 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM (ΕΛΑΧΙΣΤΟΠΟΙΗΣΗ) Ο Simulated Annealing (SA) δεν ψάχνει για την καλύτερη λύση στην γειτονία λύσεων της τρέχουσας λύσης (x) όπως κάνουν οι local search αλγόριθμοι Ξεκινά σε κάθε επανάληψη από μια λύση x, επιλέγει στοχαστικά μια γειτονική λύση κι εφαρμόζει τον τελεστή κίνησης στη γειτονιά των λύσεων Θεωρούμε x την τρέχουσα λύση και x τη γειτονική της : Εάν z(x )-z(x) 0 τότε η x γίνεται αποδεκτή και θεωρείται ως η «νέα» τρέχουσα

12 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM (ΠΡΟΒΛΗΜΑ ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ) Εάν z(x )-z(x) > 0 τότε η x είτε: Γίνεται αποδεκτή και ορίζεται ως νέα τρέχουσα με πιθανότητα: Pt=exp-([z(x )-z(x))]/tt) Δεν γίνεται αποδεκτή και παραμένει τρέχουσα η x, με πιθανότητα: 1-Pt z(x ): αντικειμενική συνάρτηση της γειτονικής λύσης x z(x): αντικειμενική συνάρτηση της λύσης x Tt: «θερμοκρασία» του αλγορίθμου σε κάθε επανάληψη (ορίζεται από τον κατασκευαστή του αλγορίθμου)

13 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Η αποδοχή της χειρότερης λύσης x με μια πιθανότητα γίνεται με σκοπό να μπορέσει ο αλγόριθμος να απεγκλωβιστεί από το πιθανό τοπικό ελάχιστο Η θερμοκρασία Tt: Αρχικά θεωρείται μια πολύ υψηλή τιμή (έτσι ώστε να γίνονται αποδεκτές λύσεις με χειρότερη αντικειμενική συνάρτηση από την τρέχουσα) Σε κάθε επανάληψη, η θερμοκρασία πολλαπλασιάζεται με ένα συντελεστή (0 < s < 1) που ορίζει ο κατασκευαστής του αλγορίθμου Μειώνεται σταδιακά μέχρι στις τελευταίες επαναλήψεις- να μηδενιστεί Αποτέλεσμα: από εκείνο το σημείο της αναζήτησης γίνονται αποδεκτές μόνο καλύτερες λύσεις

14 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM - (ΠΡΟΒΛΗΜΑ ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ) Όρισε αρχική λύση x, και αρχική θερμοκρασία T0 Βρόχος 1: Για όσο η συνθήκη τερματισμού ΔΕΝ ικανοποιείται επανέλαβε Βρόχος 2: Για όσο η συνθήκη τερματισμού του Βρόχου 2 ΔΕΝ ικανοποιείται επανέλαβε 1. Φτιάξε μια λύση x G(x), όπου G(x) η γειτονιά της τρέχουσας λύσης x 2. Όρισε Δz = z(x ) z(x) 3. Εάν Δz<0, θέσε x=x. Έλεγξε εάν είναι z(x)<z(xbest). Εάν ναι, τότε xbest = x = x 4. Εάν Δz 0, θέσε x = x με μια πιθανότητα exp (-Δ/Tt) Επανέλαβε το Βρόχο 2 Μείωσε τη θερμοκρασία Tt Επανέλαβε τον Βρόχο 1 Τύπωσε την καλύτερη λύση xbest που βρέθηκε, καθώς και την zbest που αντιστοιχεί

15 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Οι τιμές που ορίζει ο κατασκευαστής του αλγορίθμου είναι: Η τιμή της αρχικής θερμοκρασίας T0 Ο τρόπος μείωσης της θερμοκρασίας Tt με την πάροδο των επαναλήψεων t Το κριτήριο τερματισμού του Βρόχου 1 και του Βρόχου 2

16 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Η αργή σύγκλιση του αλγορίθμου εξασφαλίζεται: Είτε μέσω του συντελεστή μείωσης της θερμοκρασίας Είτε μέσω της αύξησης των επαναλήψεων εκτέλεσης του Βρόχου 2

17 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Η τιμή της αρχικής θερμοκρασίας πρέπει να εξασφαλίζει ότι: 1. Θα γίνονται αποδεκτές «χειρότερες λύσεις» (για να μην παγιδευτεί σε τοπικό βέλτιστο) 2. Ο αλγόριθμος δεν θα τερματιστεί σύντομα (καθώς τότε μεταπίπτει σε κατάσταση πλήρως τυχαίας διαδικασίας) Στόχος είναι η σχετικά αργή πτώση της θερμοκρασίας καθώς διαφορετικά ο αλγόριθμος θα συγκλίνει γρήγορα σε τοπικό βέλτιστο

18 Ο ΑΛΓΟΡΙΘΜΟΣ ΠΡΟΣΟΜΟΙΩΜΕΝΗΣ ΒΕΛΤΙΩΣΗΣ SIMULATED ANNEALING ALGORITHM Συνήθεις συνθήκες τερματισμού αλγορίθμου ή / και βρόχων: 1. Η zbest δεν έχει μειωθεί για τουλάχιστον e επαναλήψεις 2. Η zbest δεν έχει μειωθεί κατά τουλάχιστον - v% - για τουλάχιστον e επαναλήψεις 3. Συμπλήρωση δεδομένου αριθμού επαναλήψεων 4. Συμπλήρωση δεδομένου χρονικού ορίου συνεχόμενης εκτέλεσης του αλγορίθμου

19 ΑΣΚΗΣΗ 1 Μια εταιρία επενδύσεων διαχειρίζεται κεφάλαια ύψους 100 μονάδων και μπορεί να εντάξει μόνο μία φορά στο χαρτοφυλάκιό της, κάποιες από τις μετοχές εταιριών του Πίνακα 1: Η εφαρμογή ενός στοχαστικού κατασκευαστικού ευρετικού αλγορίθμου είχε σαν αποτέλεσμα την κατασκευή της παρακάτω εφικτής λύσης s1: Να πραγματοποιηθεί εφαρμογή μεταευρετικού αλγορίθμου Προσομοιωμένης Ανόπτησης για 6 επαναλήψεις Η θερμοκρασία του SA θα μειώνεται από την T0 = 100 κατά έναν συντελεστή m=0.7, μετά τη συμπλήρωση 3 επανάληψεων του μεταευρετικού Ο μεταευρετικός SA θα εφαρμόζει τελεστή αντικατάστασης M4 M9 M3 M10 M7 Σύνολο Κόστος Μέρισμα Πίνακας 1 ΟΝΟΜΑ ΑΞΙΑ ΕΤΗΣΙΟ ΜΕΡΙΣΜΑ M M M M M M M M M M

20 ΑΣΚΗΣΗ 1 ΕΠΙΛΥΣΗ LOOP Μετοχές στην S M4 M9 M3 M10 M7 Σύνολο Κόστος Μέρισμα zs= 7.95 Zbest= 7.95 Μετοχές εκτός S Μ1 Μ2 Μ5 Μ6 Μ8 T0=100 Τυχαίες τιμές από rand() η τυχαία τιμή = 0,32887 άρα επιλέγεται να αντικατασταθεί η μετοχή της θέσης 2 που είναι η Μ9 2 η τυχαία τιμή = 0, άρα επιλέγεται να «μπεί» στην S1 η μετοχή της θέσης 5 που είναι η Μ8 Άρα Με: Μετοχές στην S1 M4 M8 M3 M10 M7 Σύνολο Κόστος Μέρισμα zs1=zcurrent= 8.25 Zbest= 8.25

21 ΑΣΚΗΣΗ 1 ΕΠΙΛΥΣΗ LOOP Μετοχές στην S1 M4 M8 M3 M10 M Μετοχές εκτός S1 Μ1 Μ2 Μ5 Μ6 Μ9 Τυχαίες τιμές από rand() η τυχαία τιμή = 0, άρα επιλέγεται να αντικατασταθεί η μετοχή της θέσης 3 στην S1, που είναι η Μ3 4 η τυχαία τιμή = 0, άρα επιλέγεται να «μπεί» στην S2 η μετοχή της θέσης 3 που είναι η Μ5 Άρα Με: Μετοχές στην S2 M4 M8 M5 M10 M7 Σύνολο Κόστος Μέρισμα zs2=zcurrent= 8.35 Zbest= 8.35

22 ΑΣΚΗΣΗ 1 ΕΠΙΛΥΣΗ LOOP Μετοχές στην S2 M4 M8 M5 M10 M Μετοχές εκτός S2 Μ1 Μ2 M3 Μ6 Μ9 Τυχαίες τιμές από rand() η τυχαία τιμή = 0, άρα επιλέγεται να αντικατασταθεί η μετοχή της θέσης 1 στην S2, που είναι η Μ4 6 η τυχαία τιμή = 0, άρα επιλέγεται να «μπεί» στην S3 η μετοχή της θέσης 4 που είναι η Μ6 Άρα Με: Μετοχές στην S3 Μ6 M8 M5 M10 M7 Σύνολο Κόστος Μέρισμα zs3=zcurrent= 8.5 Zbest= 8.5

23 ΑΣΚΗΣΗ 1 ΕΠΙΛΥΣΗ LOOP 4 Τυχαίες τιμές από rand() Μετοχές στην S3 Μ6 M8 M5 M10 M Μετοχές εκτός S3 Μ1 Μ2 M3 M4 Μ9 T0=0.7*100= η τυχαία τιμή = 0, άρα επιλέγεται να αντικατασταθεί η μετοχή της θέσης 3 στην S3, που είναι η Μ5 8 η τυχαία τιμή = 0, άρα επιλέγεται να «μπεί» στην S4 η μετοχή της θέσης 5που είναι η M9 Άρα Με: Μετοχές στην S4 Μ6 M8 M9 M10 M7 Σύνολο Κόστος Μέρισμα zs4=zcurrent= 10.2 Zbest= 10.2 Μή εφικτή

24 ΑΣΚΗΣΗ 1 ΕΠΙΛΥΣΗ LOOP 5 Τυχαίες τιμές από rand() Μετοχές στην S3 Μ6 M8 M5 M10 M Μετοχές εκτός S3 Μ1 Μ2 M3 M4 Μ9 T0=0.7*100= η τυχαία τιμή = 0, άρα επιλέγεται να αντικατασταθεί η μετοχή της θέσης 2 στην S3, που είναι η Μ8 10 η τυχαία τιμή = 0, άρα επιλέγεται να «μπεί» στην S4 η μετοχή της θέσης 4 που είναι η Μ4 Άρα Με: Μετοχές στην S5 Μ6 Μ4 M9 M10 M7 Σύνολο T Κόστος Μέρισμα Δz= P επιλογής zs1=zcurrent= 7.65 Zbest= η τυχαία τιμή, το 0,661667<0, άρα η χειρότερη λύση αποδεκτή

25 ΕΥΧΑΡΙΣΤΩ ΓΙΑ ΤΗΝ ΠΡΟΣΟΧΗ ΣΑΣ oερωτήσεις? ΕΠΙΚΟΙΝΩΝΙΑ oγραφειο 305 ΚΤΙΡΙΟ Ι, ΠΡΟΚΑΤ ΔΕΥΤΕΡΑ & oτηλεφωνο: o