v laboratorijski stomatološki protetiki Tehnologija CAD/CAM je raëunalniπko podprto naërtovanje in izdelava protetiënih konstrukcij.
|
|
|
- Ζακχαῖος Μαλαξός
- 6 χρόνια πριν
- Προβολές:
Transcript
1 CAD/CAM v laboratorijski stomatološki protetiki Tehnologija CAD/CAM je raëunalniπko podprto naërtovanje in izdelava protetiënih konstrukcij. Dentalna tehnologija CAD/CAM sloni na tem, da iz osnovnega mavënega delovnega modela pridobimo digitalizirani virtualni model, na katerem z dentalnim raëunalniπkim programom oblikujemo protetiëne konstrukcije. Te oblike raëunalnik preraëuna v poti bruπenja in tako vodi rezkalni stroj. 141 Sodobni programi CAD omogoëajo prostoroëno oblikovanje razliënih mostovnih ogrodij, gredi, implantatnih nazidkov, konusov, prevlek, faset, inlejev, onlejev kot tudi ustreznih okluzalnih povrπin pri keramiënih restavracijah. Tehnologija CAD/CAM se v zadnjih nekaj letih moëno razvija. Prevzema vodilno vlogo v izdelovanju keramiënih konstrukcij, πe posebno iz cirkonijevega dioksida, ki se vse bolj uveljavlja kot standardno protetiëno gradivo.
2 142 Sirona CEREC inlab
3 Z nekaj posnetki individualnega delovnega modela (IDM) in v vosku registriranega griza s skenerjem Sirona ineos dobimo na ekranu virtualni IDM, na katerem oblikujemo keramiëno restavracijo. 143
4 144 Najprej oznaëimo rob preparacije. Zunanje oblike inleja se pojavijo samodejno. Z raëunalniπkim orodjem prostoroëno oblikujemo inlej v odnosu do sosednjih in nasprotnih zob.
5 145
6 Prevleko prostorsko individualno pozicioniramo v tri polja barvne nasiëenosti keramiënega bloka VITABLOCS TriLuxe for CEREC. 146 Povrπinsko obarvana in glazirana prevleka iz keramike TriLuxe zagotavlja zaradi narave materiala naravni videz.
7 Prevleki na zobeh 11, 21 izdelani iz keramike VITA TriLuxe, ponazarjata barvna polja sosednjih zob. Barva prevlek se v svetlosti, nasiëenosti in barvnem tonu ne razlikuje od barve naravnih zob. 147
8 148 Prevleka s transparentnim ogrodjem VITA In-Ceram SPINELL je indicirana na svetli zobovini.
9 Litijevodisilikatno ogrodje (IPS e.max CAD) postane med postopkom kristalizacije transparentno. 149
10 DD3+TI1 TI 1 TI 3 TI 2 OE V OE 5 OE 1 DA2 OE 3 DDA3 DDA3.5+MMs 150 Transparentna prevleka z litijevodisilikatnim ogrodjem, fasetirana s keramiko IPS e.max Ceram.
11 Prevleka z delno transparentnim keramiënim ogrodjem VITA In Ceram ALUMINA zakrije potemnjen dentin. Ogrodje VITA In-Ceram ALUMINA lahko uporabimo za krajπi mostiëek v vidnem podroëju. 151
12 152 Temen dentin ali kovinski nazidek zakrijemo z netransparentnim ogrodjem, izdelanim iz keramike VITA In-Ceram ZIRCONIA. Tudi v tem primeru In-Ceram ZIRCONIA prekrije temno podlago.
13 Preparacija zob 21 in 22. Zob 11 je transparenten z zanimivimi barvnimi polji. Prevleka na zobu 12 ne skriva pomanjkljivosti zastarele kovinsko-porcelanske tehnike. KolorimetriËno preverjanje barvnih odtenkov naravnega zoba 11 (A) in prevleke 21 (B). Primerjava barvnih polj zagotavlja dober izid. A B 153 Obdelani prevleki 21 in 22 sta pripravljeni za kliniëno preverjanje barve in oblike. ShadeScanov primerjalni program zrcalne slike prevleke in zoba pokaæe z zelenim poljem stopnjo uspeπnosti ponovitve barve.
14 Naravni videz prevlek, fasetiranih s keramiko VITA VM 7 na zobeh 21 in Prevleka, fasetirana s keramiko VITA VM 9 na cirkonijevem ogrodju, lahko pokrije raznolika barvna polja obrušenih zob.
15 Prevleke iz cirkonije, fasetirane s keramiko VITA VM
16 156 Pri sistemu SIRONA lahko za analogno-digitalni prenos delovnega modela uporabimo laserski skener v rezkalniku CEREC inlab ali skener CEREC ineos.
17 Ogrodje VITA InCeram ZIRCONIA dokonëno obdelamo pred utrjevanjem z infiltracijo stekla. VeËkratni nanos infiltracijskega stekla zagotavlja enakomerno obarvanje in popolno utrditev ogrodja. 157
18 KeramiËne cirkonijeve bloke brusimo v nepopolno sintrani, tako imenovani zeleni fazi. Ogrodje je bruπeno toliko veëje, kolikor se bo med sintranjem skrëilo, kar dosega veëjo natanënost v primerjavi z ogrodji, bruπenimi v merilu 1 : Za ulivanje dentalnih zlitin lahko namesto voskovnih konstrukcij uporabimo zbrušena ogrodja iz zgorljive plastike VITA CAD-Waxx po tehnologiji CAD/CAM.
19 Pred sintranjem lahko ogrodja potopimo za minuto ali veë v tekoëa barvila in jim z razliënimi koncentracijami barvil in Ëasi doloëamo barvne odtenke. Zaradi omejene dolžine cirkonijevih blokov za CEREC inlab lahko izdelamo dvodelni most. 159
20 Primer izdelave triëlenskega mostiëka po tehnologiji IPS e.max ZirCAD. 160 tevilo, ki je vtisnjeno v vsak cirkonijev blok, pove, kolikπna bo skrëitev med sintranjem, in tako raëunalnik temu sorazmerno poveëa obliko predsintranega ogrodja.
21 Ogrodja, pripravljena iz keramiënih blokov VITA In-Cream YZ in IPS e.max ZirCAD, sintramo v peëeh VITA ZYrcomat oziroma IVOCLAR Sintramat na keramiënih kroglicah. 161
22 162 Na površino cirkonijevih ogrodij nanesemo fluorescentni barvni premaz, na primer IPS e.max Ceram ZirLiner.
23 DA1 DA2 DA3 163 OE1 TI1 TI2 TI3
24 164
25 Sistem CAD/CAM ZENO WIELAND 165
26 166 Dvo- in tridimenzionalno doloëanje meje preparacije s tanko zeleno Ërto omogoëa natanëno izvedbo robne zapore prevleke.
27 167
28 168
29 Wielandov naëin horizontalne stabilizacije cirkonijevih ogrodij med sintranjem na podpornikih na ravni keramiëni ploπëi omogoëa izdelavo daljπih mostovnih konstrukcij. 169
30 170 Sintranje ogrodja s polno sredico bloka prepreëuje, da bi se podkvasta ogrodja pri sintranju razprla.
31 ZL2 IZLy+IZLo 171 DD3
32 DA3,5 MMI 172 DA2 DA2+Tn
33 TI2 173
34 174
35 175
36 Za kliniëni prispevek h knjigi se najlepπe zahvaljujem zobozdravnikom: Alenka BrkiË, dr. dent. med. Asist. mag. Peter Jevnikar, dr. dent. med. Doc. dr. Igor KopaË, dr. dent. med. Jurka Korenini, dr. dent. med. Andrej KovaËiË, dr. dent. med. 176 Prof. dr. Ljubo Marion, dr. dent. med. Asist. mag.»edo Oblak, dr. dent. med. Joæe Pungerπek, dr. dent. med. Darja uπterπië, dr. dent. med Samo Trost, dr. dent. med. Slavko BrkiË Sodobne tehnologije dentalne keramike Uredili: Slavko BrkiË Jezikovni pregled: Irena Androjna Mencinger Oblikovanje: Samo Jarc Tisk:»ukgraf Naklada: 500 izvodov Knjiga je izšla v samozaložbi. Ljubljana 2007
37 177
38
39
40 odobne ehnologije entalne eramike
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Tretja vaja iz matematike 1
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Kotne in krožne funkcije
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
8. Diskretni LTI sistemi
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Zgodba vaše hiše
1022 1040 Zgodba vaše hiše B-panel strani 8-11 Osnovni enobarvni 3020 3021 3023 paneli 3040 3041 Zasteklitve C-panel strani 12-22 S-panel strani 28-35 1012 1010 1013 2090 2091 1022 1023 1021 1020 1040
Booleova algebra. Izjave in Booleove spremenljivke
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
-27% -25% -20% ΑΓΟΡΑΣΤΕ 4 -28% -27% -20% IPS e.max. IPS e.max Ceram. 1 x IPS PressVEST Premium Powder, 5kg AN (Τιµή τιµοκαταλόγου 198.
The service company 3 x IPS e.max Press Refill, 5 τµχ.* (Τιµή τιµοκαταλόγου 86.75) IPS e.max 1 x IPS PressVEST Premium Powder, 5kg 685586AN (Τιµή τιµοκαταλόγου 198.00) + 1 x IPS PressVEST Premium Liquid,
Kratka navodila za uporabo. IPS Style Ceram
Kratka navodila za uporabo IPS Style Ceram Vsebina 3 Oblikovanje ogrodja 4 Peka opakerja 6 Plastenje keramike IPS Style Ceram Standardna tehnika plastenja Individualna tehnika plastenja Dlesen Fasete oz.
IZPIT IZ ANALIZE II Maribor,
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Delovna točka in napajalna vezja bipolarnih tranzistorjev
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Prozorni in prosojni akustični zasloni
Prozorni in prosojni akustični zasloni Opis in uporaba: Samostoječi prozorni ali prosojni akustični zasloni iz materiala s strukturo satovja omogočajo visoko absorbcijo zvoka in zaščito pred hrupom. Obenem
13. Jacobijeva metoda za računanje singularnega razcepa
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
ARHITEKTURA DETAJL 1, 1:10
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
B-panel. C-panel. S-panel. Osnovni enobarvni paneli. Zasteklitve. strani strani strani
Zgodba vaše hiše B-panel strani 8-11 Osnovni enobarvni 3020 3021 3023 paneli 3040 3041 Zasteklitve C-panel strani 12-20 S-panel strani 28-35 1012 1010 1013 2090 2091 1022 1023 1021 1020 1040 1041 1042
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
POPIS DEL IN PREDIZMERE
POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Gimnazija Krˇsko. vektorji - naloge
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
PROCESIRANJE SIGNALOV
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Osnove elektrotehnike uvod
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
ΑΝΟΙΞΗ - ΚΑΛΟΚΑΙΡΙ ΠΡΟΣΦΟΡΕΣ ΟΔΟΝΤΙΑΤΡΙΚΩΝ. The service company
ΠΡΟΣΦΟΡΕΣ ΟΔΟΝΤΙΑΤΡΙΚΩΝ ΑΝΟΙΞΗ - ΚΑΛΟΚΑΙΡΙ 201 8 The service company ΑΘΗΝΑ: Μάγερ 13, ΤΚ: 10438, Τηλ.: 2107755900 ΘEΣΣAΛONIKH: Τσιμισκή 34, ΤΚ: 54623 Τηλ.: 2310253800 ΠΑΙΑΝΙΑ: 1 χλμ Λεώφ.Μαρκοπούλου, ΤΚ:
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
1. Trikotniki hitrosti
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
IZVODI ZADACI (I deo)
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
p 1 ENTROPIJSKI ZAKON
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg "matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):")
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Ολοκεραμικές αποκαταστάσεις διπυριτικού λιθίου, αλουμίνας και ζιρκονίας. Μέρος Α Εργαστηριακά δεδομένα
Προσθετική ΣΤΟΜΑ 2018; 46: 3 8 Βιβλιογραφική Ανασκόπηση Ολοκεραμικές αποκαταστάσεις διπυριτικού λιθίου, αλουμίνας και ζιρκονίας. Μέρος Α Εργαστηριακά δεδομένα ΙΦ. ΕΛΕΥΘΕΡΙΑΔΟΥ 1, Μ. ΡΑΠΤΟΠΟΥΛΟΣ 1, Μ. ΚΟΚΟΤΗ
Elementi spektralne teorije matrica
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
ΠΡΟΣΦΟΡΕΣ ΟΔΟΝΤOTEXNΙΚΩΝ EIΔΩΝ ΑΝΟΙΞΗ - ΚΑΛΟΚΑΙΡΙ
ΠΡΟΣΦΟΡΣ ΟΔΟΝOTEXNΙΚΩΝ EIΔΩΝ ΝΟΙΞΗ - ΚΛΟΚΙΡΙ 2018 The service company ΘΗΝ: Μάγερ 13,.Κ.: 10438, ηλ.: 2107755900 ΘEΣΣAΛONIKH: σιµισκ 34,.Κ.: 54623, ηλ.: 2310253800 e-mail: dental@oralvision.gr ΠΙΝΙ: 1 χλµ
Okna sistem kbe 76 mm
Okna sistem KBE 76 mm Odkrijte nove potenciale NOVA GENERACIJA OKEN SISTEM KBE 76 MM Individualne rešitve po meri strank, odliëna servisna mreæa in tehniëne inovacije to so odlike podjetja Arcont IP. Da
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Linearna algebra 2 prvi kolokvij,
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Numerično reševanje. diferencialnih enačb II
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
ΠΡΟΪΟΝΤΑ ΓΙΑ ΟΔΟΝΤΟΤΕΧΝΙΤΕΣ ΜΆΡΤΙΟΣ / ΑΎΓΟΥΣΤΟΣ Exceed expectations All ceramic, all you need. The service company
ΠΡΟΪΟΝΤΑ ΓΙΑ ΟΔΟΝΤΟΤΕΧΝΙΤΕΣ ΜΆΡΤΙΟΣ / ΑΎΓΟΥΣΤΟΣ 2019 Exceed expectations All ceramic, all you need. The service company Οι αισθητικές και ανθεκτικές οδοντικές αποκαταστάσεις είναι αυτό που επιθυμούν οι
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
ΠΡΟΣΦΟΡΕΣ ΟΔΟΝΤΟΤΕΧΝΙΚΩΝ ΠΡΟΙΟΝΤΩΝ Ivoclar Vivadent 4 Σεπτεμβρίου 2015 30 Νοεμβρίου 2015
Φούρνοι * Αγοράζοντας τον φούρνο όπτησης & press Programat EP3010 με το Vacuum pump VP5 συνολικής αξίας 8.979,10, παίρνετε δώρο το IPS e.max Press Multi Intro Kit A-D αξίας 406,25 Αγοράζοντας τον φούρνο
Operacije s matricama
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Moguća i virtuelna pomjeranja
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
INTELIGENTNO UPRAVLJANJE
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Sistem sučeljnih sila
Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
primer reševanja volumskega mehanskega problema z MKE
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
7. Κρημνός για την αφαίρεση οστού.
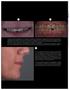1 2 1. Ασθενής ετών 30, προσήλθε με την επιθυμία να αλλάξει και να βελτιώσει το χαμόγελό της. Μετά από κλινική και ακτινογραφική εξέταση βρέθηκε ότι οι 2 μεταλλοκεραμικές στεφάνες στα #11, 21 ήταν μη αποδεκτές
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
5.2. Orientacija. Aleš Glavnik in Bojan Rotovnik
Orietacija Aleš Glavik i Boja Rotovik 52 Izvleček: Pred stav lje e so iz bra e te me iz orie ti ra ja v a ra vi, ki jih mo ra poz a ti vsak vod ik PZS, da lah ko var o vo di ude le `e ce a tu ri Pred stav
Splošno o interpolaciji
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA Poožaj težišta vozia predstavja jednu od bitnih konstruktivnih karakteristika vozia s obzirom da ova konstruktivna karakteristika ima veiki uticaj na vučne karakteristike
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE)
Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
ΣΥΝΕΔΡΙΟ ΠΡΟΣΘΕΤΙΚΗΣ
8-9 ΣΕΠΤΕΜΒΡΙΟΥ 2017 στο πολυχώρο COSMOPOLIS στον Κόρνο ΣΥΝΕΔΡΙΟ ΠΡΟΣΘΕΤΙΚΗΣ Το Θεωρητικό μέρος του Συνεδρίου θα μοριοδοτηθεί με 11,5 Μόρια Επιμόρφωσης (ΜΕ) και Το κάθε Πρακτικό μέρος μοριοδοτείται με
Poglavje 5. Poglavje 5. Poglavje 5. c = 1! SPOMNIMO SE!!! Regulacijski sistemi. Regulacijski sistemi
Reglacjsk ssem lka 5. : Vekorja saorskega n roorskega oka v prosor Faklea za elekroehnko Reglacjsk ssem POMNIMO E!!! lka. 5: Kompleksn vekor saorskega oka γ jγ ( e ) j0 j ( ) c ( ) e ( ) e ( ) c! Faklea
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
PONOVITEV SNOVI ZA 4. TEST
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
8. Posplošeni problem lastnih vrednosti
8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
Periodičke izmjenične veličine
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
- Geodetske točke in geodetske mreže
- Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
3.1 Granična vrednost funkcije u tački
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Termovizijski sistemi MS1TS
Termovizijski sistemi MS1TS Vežbe 02 primer 1 MATLAB funkcija conv. f x = rect x rect x 2 ( ) ( ) ( ) y=conv(rectangle_function(x),rectangle_function(x-2)); figure,subplot(3,1,1),plot(x,rectangle_function(x)),xlabel('\itx'),ylabel('rect({\itx})');
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp