ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ. Επιβλέπων Καθηγητής: Γεώργιος Σταυρουλάκης
|
|
|
- Πάνθηρας Θεοδοσίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ Επιβλέπων Καθηγητής: Γεώργιος Σταυρουλάκης Μεταπτυχιακή Διατριβή με Θέμα: Μελέτη Αυξητικών Κατασκευών με πεπερασμένα στοιχεία Συντζανάκης Αντώνιος Α.Μ.:
2 ΕΥΧΑΡΙΣΤΙΕΣ Οφείλω να ευχαριστήσω θερμά για τη βοήθεια που μου προσέφεραν στα πλαίσια της εκπόνησης της παρούσας μεταπτυχιακής διατριβής: Τον κύριο Γεώργιο Σταυρουλάκη, ως επιβλέποντα καθηγητή της παρούσας διπλωματικής εργασίας, για την άψογη συνεργασία που είχαμε και την πολύτιμη βοήθεια που μου προσέφερε. Λόγω της πολύχρονης εμπειρίας του μου έδωσε πολλές γνώσεις που σχετίζονται με την μέθοδο πεπερασμένων στοιχείων στην μελέτη στατικών και δυναμικών προβλημάτων. Επίσης τον ευχαριστώ για την συνεχή υποστήριξη του που συνετέλεσε στην ολοκλήρωση της παρούσας εργασίας. Όλους τους καθηγητές του Τμήματος Μηχανικών Παραγωγής και Διοίκησης του Πολυτεχνείου Κρήτης, για το αμείωτο ενδιαφέρον τους, τις πολύτιμες γνώσεις και συμβουλές πάσης φύσεως που μου προσέφεραν κατά τη διάρκεια των χρόνων φοίτησης μου στην προκειμένη πολυτεχνική σχολή. Την οικογένειά μου, τους φίλους μου, για την ψυχολογική και υλική υποστήριξη και συμπαράσταση που μου παρείχαν καθ όλη τη διάρκεια των σπουδών μου και ιδιαιτέρως, κατά τη διάρκεια της εκπόνησης της συγκεκριμένης διπλωματικής εργασίας.
3 Περίληψη Στην σχεδιαστική διαδικασία μηχανικών στοιχείων η επιλογή υλικού αποτελεί ένα από τα πιο σημαντικά στάδια καθώς δίνει στο προϊόν καθορισμένο σχήμα, μέγεθος, κόστος καθώς και τις μηχανικές του ιδιότητες. Η απόδοση του στοιχείου σε μια συγκεκριμένη εφαρμογή εξαρτάται από τις μηχανικές ιδιότητες του υλικού από το οποίο έχει κατασκευαστεί. Στις περισσότερες εφαρμογές, ένα στοιχείο σχεδιάζεται έτσι ώστε να έχουμε ελαχιστοποίηση του βάρους χωρίς αστοχία κάτω από συγκεκριμένες συνθήκες φόρτισης. Τα περισσότερα υλικά που χρησιμοποιούνται σε μηχανολογικές εφαρμογές έχουν θετικό λόγο poisson (τα περισσότερα μέταλλά έχουν λόγο poisson κοντά στο 1/3 ενώ τα ελαστικά έχουν κοντά στο ½). Ένα νέο αρκετά ενδιαφέρον πεδίο αφορά υλικά που επιδεικνύουν αρνητικό λόγο poisson ή αλλιώς τα λεγόμενα αυξητικά υλικά. Τα αυξητικά υλικά επιδεικνύουν την αρκετά ασυνήθιστη ιδιότητα του να διογκώνονται πλευρικά όταν υπόκεινται σε εφελκυστική τάση και να συστέλλονται όταν συμπιέζονται, αυτό οφείλεται στο γεγονός ότι έχουν αρνητικό λόγο poisson. Εκτός από το επιστημονικό ενδιαφέρον της ύπαρξης υλικών που επιδεικνύουν μια τόσο ασυνήθιστη ιδιότητα, ο αρνητικός λόγος poisson δίνει σε ένα υλικό αρκετές ενισχυμένες ιδιότητες όπως αυξημένη διατμητική δυσκαμψία, αυξημένη αντοχή σε θραύση και ελαστικότητα. Αυτές οι ιδιότητες κάνουν τα αυξητικά υλικά να πλεονεκτούν έναντι των συμβατικών υλικών σε αρκετές πρακτικές εφαρμογές. Στην παρούσα μεταπτυχιακή διατριβή χρησιμοποιείται μια μέθοδος πεπερασμένων στοιχείων για να προσομοιώσει την επίδραση διεγέρσεων σε σύνθετα υλικά συγκρίνοντας τις περιπτώσεις μεταξύ συμβατικών και αυξητικών δομών.
4 Περιεχόμενα ΕΥΧΑΡΙΣΤΙΕΣ... 2 Περίληψη... 3 Εισαγωγή... 6 Μηχανισμός, δομή και τις λειτουργίες των Υλικών Γενικά Μηχανισμός και δομή Κατάταξη και τύποι Ιδιότητες των Υλικών Μέτρο Young και Μέτρο Διάτμησης Συμπεριφορά στην εντομή Συμπεριφορά Παραμόρφωσης Αντοχή σε Ρηγμάτωση Συμπεριφορά σε ρηγμάτωση Μορφολογία μικροδομής Αντίσταση στην ρηγμάτωση Απόσβεση και Απορρόφηση ήχου Υλικά και γεωμετρικές ιδιότητες κυψελοειδών κατασκευών τύπου σάντουιτς ΕΙΣΑΓΩΓΗ Ιδιότητες υλικών Μοντέλο πάνελ τύπου σάντουιτς Εντός επιπέδου Μοντέλο Μοντέλο Πεπερασμένων Στοιχείων Μοντέλο πεπερασμένων στοιχείων για εντός επιπέδου φόρτιση Διακριτοποίηση Περιορισμοί Συνοριακές συνθήκες και Φορτίσεις ΠΕΡΙΠΤΩΣΗ ΠΕΡΙΠΤΩΣΗ ΠΕΡΙΠΤΩΣΗ Θεωρητικός υπολογισμός λόγου Poisson για συμβατική και αυξητική δομή Θεωρητικό μοντέλο Μοντέλο πεπερασμένων στοιχείων για εντός επιπέδου φόρτιση Διακριτοποίηση Συνοριακές συνθήκες και Φορτίσεις Δυναμική ανάλυση... 45
5 7.1 Εισαγωγή Μελέτη Περιπτώσεων Συμπεράσματα & Προτάσεις Διερεύνησης Σχολιασμός και Σύγκριση Αποτελεσμάτων Προτάσεις Διερεύνησης... 57
6 Εισαγωγή Η σύγχρονη τεχνολογία απαιτεί νέα υλικά ειδικών ιδιοτήτων. Ένας από τους λόγους για τον οποίο υπάρχει ενδιαφέρον για υλικά με ασυνήθιστες μηχανικές ιδιοτήτες προέρχεται από το γεγονός ότι μπορούν να χρησιμοποιηθούν ως μήτρες για να σχηματίσουν σύνθετα με άλλα υλικά τα οποία έχουν κάποιες επιθυμητές ιδιότητες, π.χ. ηλεκτρικές, μαγνητικές, και άλλου τύπου ιδιότητες. Ένα νέο πεδίο δραστηριότητας είναι η μελέτη υλικών που παρουσιάζουν αρνητικό λόγο Poisson (NPR). Μεγάλης κλίμακας κυτταρικές δομές με ιδιότητες αρνητικού λόγου Poisson NPR εισήχθησαν για πρώτη φορά το 1982 με τη μορφή δισδιάστατων κυψελών από ελαστική σιλικόνη ή αλουμίνιο τα οποία παραμορφώθηκαν με την κάμψη των νευρώσεων (Gibson, et al, 1982 & 1988). Το 1987, ο Lakes ανέπτυξε για πρώτη φορά τον αφρό πολυουρεθάνης με αρνητικό λόγο Poisson με αυξητική δομή (Lakes, 1987a and 1987b). Αυτός ο πολυμερής αφρός είχε λόγο Poisson -0,7. Αυτά τα νέου τύπου υλικά ονομάστηκαν αυξητικά από τον Evans (Evans, et al, 1991), τα οποία σε αντίθεση με τα συμβατικά υλικά (όπως το καουτσούκ, γυαλί, μέταλλα, κ.λπ.) έχουν την ιδιότητα να γίνονται παχύτερα όταν τεντώνονται, ή να γίνονται λεπτότερα όταν συμπιέζονται. Ο όρος αυξητικά "Auxetics" προέρχεται από την Ελληνική λέξη αυξητικός, που σημαίνει «εκείνο το οποίο μπορεί να αυξηθεί». Τα αυξητικά υλικά είναι γνωστά για πάνω από 100 χρόνια, παρόλα αυτά ειδικά στην αρχή δεν δόθηκε αρκετή προσοχή σε αυτά καθώς και σε εφαρμογές που θα μπορούσαν να έχουν. Αυτός ο τύπος υλικών μπορεί να βρεθεί στην φύση σε μερικά είδη πετρωμάτων και ορυκτά καθώς και σε ζώα, χαρακτηριστικό παράδειγμα είναι το δέρμα που καλύπτει την θηλή των αγελάδων. Μέχρι σήμερα, μεγάλη ποικιλία αυξητικών υλικών έχει κατασκευαστεί, σε αυτά περιλαμβάνονται πολυμερείς και μεταλλικοί αφροί, μικροπορώδη πολυμερή, ελάσματα ανθρακονημάτων καθώς και δομές κυψελών. Ένα τυπικό παράδειγμά είναι το ευρέως γνωστό τεφλόν (συνθετικό πολυμερές- πολυτετραφθοροαιθυλενίο PTFE), το οποίο χρησιμοποιείται εδώ και πολλά χρόνια. Άλλα παραδείγματα υλικών τα οποία έχουν την ιδιότητα αρνητικού λόγου Poisson είναι το μικροπορώδες, εξαιρετικά υψηλού μοριακού βάρους πολυαιθυλένιο (UHMWPE), το πολυπροπυλένιο (PP) (Caddock & Evans, 1989; Picklrs, et al, 1996; Alderson, et al, 2000), καθώς και αρκετοί τύποι πετρωμάτων (Nur & Simmons, 1969). Παρόλα αυτά, τα ειδικά χαρακτηριστικά δεν είχαν γίνει ευρέως γνωστά μέχρι σχετικά πρόσφατα, όπου η δουλειά του Lakes, τoυ Evans και άλλων επιστημόνων προσέλκυσαν την προσοχή στα αυξητικά υλικά. Τα αυξητικά υλικά τυγχάνουν ενδιαφέροντος λόγω του γεγονότος ότι παρουσιάζουν βελτιωμένες μηχανικές ιδιότητες, όπως διατμητική αντοχή, αντίσταση στην παραμόρφωση και αντοχή σε θραύση (Lakes, 1987a; Evans, 1990), σε σύγκριση με τα συμβατικά υλικά από τα οποία κατασκευάζονται. Συνεπώς, η μελέτη τέτοιου τύπου μη συμβατικών υλικών είναι πραγματικά σημαντική από την σκοπιά στοιχειώδους έρευνας καθώς και πιθανών πρακτικών εφαρμογών, ιδιαίτερα στο πεδίο της ιατρικής, της αεροδιαστημικής καθώς και της αμυντικής βιομηχανίας. Στην πραγματικότητα, μερικά υλικά με τέτοιου είδους ασυνήθιστες (π.χ. NPR) ιδιότητες έχουν χρησιμοποιηθεί σε εφαρμογές, όπως είναι ο πυρολιθικός γραφίτης που χρησιμοποιείται για θερμική προστασία στην αεροδιαστημική καθώς και δομή κρυστάλλων Ni 3Al σε βάνες στροβιλοκινητήρων αεροσκαφών.
7 Μηχανισμός, δομή και τις λειτουργίες των Υλικών 2.1 Γενικά Είναι γνωστό ότι ό λόγος Poisson που ορίζεται από το λόγο της εγκάρσιας συστολής προς τον διαμήκη επέκταση σε μια απλή κατάσταση έντασης (Fung, 1968; Beer,et al, 2001). (1) Δεδομένου ότι τα περισσότερα υλικά κατασκευών γίνονται λεπτότερα σε εγκάρσια τομή, όταν τεντώνονται, όπως φαίνεται στο Σχήμα 1 (α), ο λόγος Poisson σε αυτή την κατάσταση είναι θετικός, τυπικά παίρνει τιμές γύρω στο Ο λόγος είναι ότι οι ενδο-ατομικοί δεσμοί ανασχηματίζονται λόγω της παραμόρφωσης. Ωστόσο, ορισμένα υλικά ή δομές συστέλλονται κατά την εγκάρσια κατεύθυνση υπό μονοαξονική θλίψη, ή εκτείνονται εγκάρσια, όταν τεντώνονται, βλέπε Σχήμα 1 (β). Αυτά τα υλικά ή οι δομές λέγεται ότι έχουν αρνητικό λόγο Poisson (NPR). Ένα τυπικό παράδειγμα είναι μία νέα δομή αφρού ή ένα αυξητικό υλικό, όπου το υλικό γίνεται παχύτερο όταν τεντώνεται. Αυτή η συμπεριφορά δεν έρχεται σε αντίθεση με την κλασσική θεωρία της ελαστικότητας: βασιζόμενοι στις θερμοδυναμικές θεωρήσεις της ενέργειας παραμόρφωσης, οι λόγοι Poisson των ισοτροπικών υλικών όχι μόνο μπορούν να πάρουν αρνητικές τιμές, αλλά μπορούν να έχουν ένα εύρος αρνητικών τιμών διπλάσιο από αυτό των θετικών (Fung, 1968). Αυτό οφείλεται στο γεγονός ότι ο λόγος του Poisson που οριοθετείται από δύο θεωρητικά όρια: πρέπει να είναι μεγαλύτερός από -1, και μικρότερος ή ίσος με 0,5, δηλαδή, Το ανώτερο όριο του λόγου του Poisson αντιστοιχεί σε ελαστικά υλικά με ένα άπειρο συντελεστή όγκου (Lakes, 1987), ενώ το κατώτερο όριο αντιπροσωπεύει ένα άπειρο μέτρο διάτμησης. (2) Σχήμα 1: (a) Παραμόρφωση υλικού με θετικό λόγο Poisson και (b) Παραμόρφωση υλικού με αρνητικό λόγο Poisson όταν τεντώνεται.
8 2.2 Μηχανισμός και δομή Όπως αναφέρθηκε παραπάνω, ένα υλικό με αρνητικό λόγο Poisson NPR διαστέλλεται (γίνεται παχύτερο) όταν τεντώνεται, σε αντίθεση με τα περισσότερα υλικά τα οποία τείνουν να γίνουν λεπτότερα. Ένας τυπικός μηχανισμός φαίνεται στο Σχήμα 2. Όταν μια δύναμη τραβά την δομή σε μία κατεύθυνση (π.χ., εδώ κατακόρυφα), η δομή ανοίγει προς τα πάνω ή επεκτείνεται στην κάθετη κατεύθυνση (εδώ, οριζόντια), δηλαδή, η κατασκευή γίνεται παχυτερη. Με βάση αυτόν το απλό μηχανισμό, μια δομή που μοιάζει με δίκτυο μπορεί να δημιουργηθεί, όπως φαίνεται στο Σχήμα 3, όπου μια δισδιάστατη δομή (2D) από ένα τέτοιο υλικό αποτελείται από μια κανονική σειρά ορθογώνιων κόμβων που συνδέονται με ινίδια (Burke, 1997). Η παραμόρφωση της δομής προκύπτει από την στρέψη των ινιδίων. Για την «ανοικτή» γεωμετρία, τα κύτταρα επιμηκύνονται κατά μήκος της κατεύθυνσης της δύναμης και να συρρικνώνονται στην κάθετη διεύθυνση ως απόκριση στον εφελκυσμό του δικτύου, δίνοντας έναν θετικό λόγο Poisson ν, όπως φαίνεται στο Σχήμα 3 (α). Ωστόσο, η δομή έχει τροποποιηθεί για να υιοθετήσει μια νέα γεωμετρία, Σχήμα 3 (β), και το δίκτυο υποβάλλεται σε επιμήκυνση τόσο κατά μήκος όσο και εγκάρσια προς το κατεύθυνση του εφαρμοζόμενου φορτίου. Με άλλα λόγια, πρόκειται για μια αυξητική δομή. Σχήμα 2: Σχηματική απεικόνιση βασικού μηχανισμού παραμόρφωσης στα αυξητικά υλικά. Το Σχήμα 4 απεικονίζει την μεταβολή στο πλάτος συναρτήσει της μεταβολής μήκους για δύο ίνες πολυπροπυλένιού (ΡΡ) οι οποίες τεντώνονται αξονικά. Η ίνα 1 είναι μια συμβατική ίνα PP και δείχνει μια συρρίκνωση στο πλάτος καθώς τεντώνεται, που αντιστοιχεί σε θετικό λόγο Poisson (ν). Η ίνα 2 υποβάλλεται σε επεξεργασία με τη χρήση θερμοκρασιών εξωθητή, η οποία οδηγεί στην μικροδομή κόμβων-ινιδίων. Το πλάτος του σε αυτή την περίπτωση αυξάνει μετά το τέντωμα και συνεπώς παρουσιάζει αυξητική συμπεριφορά. Για αυξητικές κυψέλες, οι οποίες αποτελούν ένα ειδικό υποσύνολο των αυξητικών υλικών, η επίδραση του NPR οφείλεται στην γεωμετρική διάταξη της μονάδας κυττάρου της μικροδομής, οδηγώντας σε μια συνολική σκλήρηνση σε πολλές μηχανικές ιδιότητες, όπως η εντός επιπέδου αντίσταση σε παραμόρφωση, δυσκαμψία όσον αφορά το εγκάρσιο μέτρο διάτμησης και την κάμψη. Το Σχήμα 5 δείχνει τον μηχανισμό παραμόρφωσης κατά μήκος για αυξητική κυψέλη και για συμβατική κυψελοειδή δομή. Για μια συμβατική εξαγωνική γεωμετρία (Σχήμα 5 (α)), κάτω υπό εφελκυστική τάση στην κατεύθυνση Υ, τα κύτταρα επιμηκύνονται κατά μήκος του άξονα Y και συρρικνώνονται στην κατεύθυνση Χ, γεγονός που οδηγεί σε θετικό λόγο του Poisson. Ωστόσο, για μια αυξητική δομή, τα κύτταρα
9 υποβάλλονται σε επιμήκυνση τόσο στην παράλληλη όσο και στην κάθετη προς την κατεύθυνση του εφαρμοζόμενου φορτίου. Σχήμα 3: Σύγκρισή συμπεριφοράς παραμόρφωσης: (a) Συμβατικό Υλικό (b) Αυξητικό Υλικό (Alderson, 1999; Evans & Alderson, 2000; Lakes, 2001). Σχήμα 4: Πλάτος συναρτήσει του μήκους για ίνες πολυπροπυλενίου (Scott, et al,2000).
10 Σχήμα 5: Δισδιάστατοι μηχανισμοί παραμόρφωσης οι οποίοι υπόκεινται σε φόρτιση κατά την y διεύθυνση (a) Δομή συμβατικής κυψέλης (b) Δομή αυξητικής κυψέλης (Evans & Alderson, 2000a; Evans & Alderson, 2000b). Για αυξητικό μικροπορώδες πολυμερές, τα χαρακτηριστικά της μικροδομής μπορούν να αναπαρασταθούν από ένα απλό δισδιάστατο μοντέλο, όπως φαίνεται στο Σχήμα 6. Αυτό το μοντέλο αποτελείται από ένα διασυνδεδεμένο δίκτυο κόμβων ινιδίων. Εάν μια εφελκυστική τάση εφαρμοστεί, τα ινίδια προκαλούν πλευρική μετακίνηση των κόμβων, οδηγώντας σε έναν εξαρτώμενο από την παραμόρφωση αρνητικό λόγο Poisson. Σχήμα 6: σχηματική απεικόνιση της μικροδομής ενός τυπικού αυξητικού πολυμερούς. (a) το πολυμερές σε ηρεμία, (b) το πολυμερές υπό εφελκυστική τάση (Caddock & Evans, 1989 ; Evans & Caddock, 1989). 2.3 Κατάταξη και τύποι Υλικά με αρνητικό λόγο Poisson διογκώνονται σε όλες τις κατευθύνσεις όταν τεντώνονται σε μία κατεύθυνση, συνεπώς συμπεριφέρονται με αντίστροφο τρόπο συγκριτικά με τα συμβατικά υλικά. Αφροί και κυψέλες αποτελούν ένα ειδικό υποσύνολο των αυξητικών υλικών. Οι επιδόσεις του αρνητικού λόγου Poisson, οφείλονται στο γεωμετρικό σχέδιο της
11 μονάδας κελιού της μικροδομής και οδηγούν σε ένα αποτέλεσμα συνολικής ακαμψίας σε πολλές μηχανικές ιδιότητες, όπως είναι η εντός επιπέδου αντίσταση σε παραμόρφωση, το εγκάρσιο μέτρο διάτμησης και η καμπτική ακαμψία. Υπό θλιπτική φόρτιση, η αύξηση της σχετικής πυκνότητας οδηγεί επίσης, σε ενισχυμένη μηχανική συμπεριφορά. Οι πυρήνες αυξητικών κυψελών, επίσης μπορούν να χρησιμοποιηθούν αποτελεσματικά στην κατασκευή κυρτών πάνελ τύπου σάντουιτς, λόγου του καμπυλωτού συνκλαστικού χαρακτήρα τους που οφείλεται στη επίδραση του αρνητικού λόγου Poisson. Ποικιλία αυξητικών υλικών και δομών, έχουν ανακαλυφθεί, κατασκευαστεί ή συντεθεί μέσα στα τελευταία είκοσι χρόνια, τα οποία κατατάσσονται από το μοριακό επίπεδο στο μικροσκοπικό εως κυριολεκτικά το μακροσκοπικό επίπεδο. Το Σχήμα 7, απεικονίζει τις κύριες κατηγορίες των υλικών (πολυμερή, σύνθετα, μέταλλα και κεραμικά) που πλέον υπάρχουν σε αυξητική μορφή, αυτά τα φυσικά και συνθετικά αυξητικά υλικά είναι γνωστά για πολλές τάξεις μεγέθους ακαμψίας ή συντελεστή όγκου Young, Ε. Λεπτομέρειες της επισκόπησης από φυσικά σε τεχνητά αυξητικά υλικά μπορούμε να δούμε στην δημοσίευση των Evans & Alderson(2000b). Σχήμα 7: Τάξεις υλικών σε αυξητική μορφή(stott, et al,2000). Σχεδόν όλα τα συμβατικά υλικά, συμπεριλαμβανομένων των αφρών επιδεικνύουν θετικό λόγο Poisson. Ο Lakes δημιούργησε έναν νέο τύπο αφρώδους υλικού που επιδεικνύει αρνητικό λόγο Poisson (Lakes, 1987a & b). Αυτό το υλικό παράχθηκε από την μετατροπή μιας συμβατικής δομής κελιών ( Σχήμα 8(a)), έτσι ώστε οι νευρώσεις των κυττάρων να προεξέχουν προς τα μέσα και όχι προς τα έξω, παράδειγμα αυξητικής δομής παρουσιάζεται στο Σχήμα 8(b). Όταν οι νευρώσεις που προεξέχουν στην κάθετη διεύθυνση είναι υπό εφελκυσμό, οι νευρώσεις στις πλευρικές διευθύνσεις θα τείνουν να κινηθούν προς τα έξω, οδηγώντας σε πλευρική διόγκωση. Ωστόσο, όταν εφαρμόζεται θλιπτική φόρτιση οι νευρώσεις θα λυγίσουν περισσότερο προς τα μέσα και αυτό θα έχει ως αποτέλεσμα την
12 πλευρική συστολή σαν απόκριση στην αξονική συμπίεση. Βασιζόμενοι σε αυτό το μοντέλο, πολυμερείς αφροί με αρνητικό λόγο Poisson θα μπορούσαν να κατασκευαστούν. Σχήμα 8: Εξιδανικευμένα μοντέλα για κελιά αφρών. (a) Συμβατικό κελί (b) Αυξητικό κελί (Lakes & Witt,2002).
13 Ιδιότητες των Υλικών Υλικά με αρνητικό λόγο Poisson έχουν τις ακόλουθες ειδικές ιδιότητες: Υψηλή εντός επιπέδου αντίσταση σημειακής παραμόρφωσης Καλή δυσθραυστότητα Υψηλό εγκάρσιο μέτρο διάτμησης Υψηλές δυναμικές ιδιότητες 3.1 Μέτρο Young και Μέτρο Διάτμησης Άλλο ένα ειδικό χαρακτηριστικό των αυξητικών υλικών είναι ότι έχουν υψηλότερη αντίσταση στην διατμητική παραμόρφωση το οποίο οφείλεται στην συστροφή των δυνάμεων ρήξης. Η αντίσταση στην διάτμηση είναι ιδιαίτερα σημαντική στα δομικά στοιχεία όπως είναι τα ελάσματα ή οι δοκοί σε κτήρια, αυτοκίνητα και αεροσκάφη. Αυτό το χαρακτηριστικό μπορεί να επεξηγηθεί ποιοτικά από τις σχέσεις μεταξύ του συντελεστή δίατμησης (G), του συντελεστή Young (Ε), και του μέτρου ελαστικότητας όγκου (Κ) (το αντίστροφο της συμπιεστότητας) και του λόγου Poisson (ν). Για ισοτροπικά υλικά, ισχύουν οι ακόλουθες σχέσεις (Fung, 1968; Beer, et al, 2001): (3) και (4) Για συμβατικά ισοτροπικά υλικά, ο συντελεστής Young (Ε) είναι τουλάχιστον διπλάσιος από τον συντελεστή διάτμησης (G). Παρόλα αυτά όταν ο λόγος Poisson γίνεται αρνητικός, οι δυο συντελεστές πλησιάζουν μέχρι την τιμή ν = - 0,5 όπου γίνονται ίσοι. Με άλλα λόγια, το υλικό γίνεται υψηλά συμπιέσιμο αλλά είναι δύσκολο να διατμηθεί. Το μέτρο ελαστικότητας όγκου και ο συντελεστής Young του υλικού είναι αρκετά μικρότερα από τον συντελεστή διάτμησης. Πέρα από την τιμή ν= - 0,5, ο συντελεστής διάτμησης υπερβαίνει τον συντελεστή ελαστικότητας (Choi & Lakes, 1992). Για παράδειγμα, ένα στερεό με ν=-1 είναι δύσκολο να διατμηθεί αλλά εύκολο να παραμορφωθεί ογκομετρικά: G>>K. Παρόλα αυτά, αν ο λόγος Poisson προσεγγίσει την τιμή ν= 0,5, όπως συμβαίνει στα ελαστικά στερεά, το μέτρο ελαστικότητας όγκου (Κ) υπερβαίνει κατά πολύ τον συντελεστή διάτμησης (G) και το υλικό αναφέρεται ως ασυμπίεστο: G<<K. Για τέτοιο τύπο υλικού, ο συντελεστής Young επηρεάζεται από τον μόνιμο ογκομετρικό λόγο συμπίεσης. Γενικά, ο συντελεστής Young μειώνεται μονότονα με μόνιμη ογκομετρική
14 συμπίεση όταν βρίσκεται υπό φόρτιση, όπως απείκονείζεται στο Σχήμα 9. Η επίδραση του λόγου ογκομετρικής συμπίεσης στον συντελεστή Young υπό διαφορετική φόρτιση (εφελκυσμό-θλίψη) είναι διαφορετική, όπως φαίνεται και στο Σχήμα 10. Υπο θλιπτική φόρτιση, ο συντελεστής Young αυξάνεται μαζί με τον λόγο ογκομετρικής συμπίεσης. Σχήμα 9: Συντελεστής Young εξαρτώμενος από την αρχική σχετική πυκνότητα και από τον λόγο ογκομετρικής συμπίεσης; Αρχική σχετική πυκνότητα. Συμπαγή τετράγωνα -0,1; Ανοιχτά διαμάντια -0,09; Συμπαγή διαμάντια -0,08; Ανοιχτά τετράγωνα -0,04 (Choi & Lakes,1992). Σχήμα 10: Συντελεστής Young ως συνάρτηση του μόνιμου ογκομετρικού λόγου συμπίεσης για ανοπτημένο και μη ανοπτημένο αφρό χαλκού για μια παραμόρφωση της τάξης του 0,5%; Μη-επεξεργασμένος, μη-ανοπτημένος; Θερμικά επεξεργασμένος, ανοπτημένος (Choi & Lakes,1992).
15 3.2 Συμπεριφορά στην εντομή Τα αυξητικά υλικά δεν βαθουλώνουν τόσο εύκολα όσο τα μη αυξητικά υλικά και συνεπώς έχουν μεγαλύτερη αντίσταση στην εντομή. Όταν ένα μη-αυξητικό υλικό υπόκεινται σε δυναμικό φορτίο, η δύναμη συμπιέζει το υλικό και το υλικό συμπεριφέρεται απλώνοντάς στην κάθετη διεύθυνση και μακριά από την διεύθυνση της κρούσης ( Σχήμα 11(α)). Από την άλλη πλευρά, όταν ένα αντικείμενο χτυπά ένα αυξητικό υλικό και το συμπιέζει σε μια διεύθυνση, το αυξητικό υλικό συστέλλεται κάθετα- το υλικό ρέει προς την γειτονία της κρούσης, όπως φαίνεται και στο Σχήμα 11(β). Αυτό δημιουργεί μια περιοχή πυκνότερου υλικού, η οποία είναι ανθεκτικότερη στην εντομή. Η έρευνα έχει δείξει ότι αυξητικοί αφροί έχουν υψηλότερο όριο θραύσης (σ y) και λιγότερή ακαμψία (Ε) σε σχέση με συμβατικούς αφρούς με την ίδια σχετική πυκνότητα. Επίσης, έχει αποδειχθεί ότι όντως οι αυξητικοί αφροί αυξάνουν την πυκνότητα τους υπό εντομή εξαιτίας της αύξησης στον συντελεστή διάτμησης (Smith, et al, 1999). Σχήμα 11: Απεικόνιση της συμπεριφοράς παραμόρφωσης για συμβατικό και αυξητικό υλικό που υπόκεινται σε δυναμική θλιπτική φόρτιση (Alderson, 1999; Evans & Alderson, 2000). Βασιζόμενοι στην κλασσική θεωρία ελαστικότητας (Timoshenko & Goodier, 1970), η αντίσταση στην εντομή ή αλλιώς σκληρότητα ενός ισοτροπικού υλικού είναι αντιστρόφως ανάλογη προς το (1-ν2), το οποίο είναι: (5) Όπου γ=1 για ομοιόμορφη κατανομή πίεσης και γ=2/3 για ερτζιανή εντομή. Για μια δοσμένη τιμή του Ε, η αντίσταση σε εντομή αυξάνεται με αρνητικό λόγο Poisson(ν). Εάν η τιμή του ν προσεγγίζει το -1, η σκληρότητα γίνεται άπειρη. Η σκληρότητα έχει διερευνηθεί για πολλά από τα συνθετικά αυξητικά υλικά που έχουν παραχθεί μέχρι σήμερα και έχουν βρεθεί βελτιώσεις σε όλους τους τομείς των υλικών τόσο διαφορετικές όσο οι πολυμερείς μεταλλικοί αφροί (Chan & Evens, 1998; Lakes & Elms, 1993), συνθετικά ελάσματα από ανθρακονήματα (Coenen, et al, 2001b) και μικροπορώδη πολυμερή (Alderson, et al, 2000). Για παράδειγμα, η σκληρότητα ενός αυξητικού μικροπορώδους υπερύψηλού μοριακού βάρους πολυαιθυλενίου (UHMWPE) βελτιώθηκε ως έναν συντελεστή 2 πάνω από το συμβατικό UHMWPE (Alderson,et al, 1994 & 2000). Επιπλέον, για χαμηλότερες φορτίσεις (π.χ Ν) η δοκιμή εντομής έδειξε ότι είναι δυσκολότερο να βαθουλωθεί και η σκληρότητα είχε αυξηθεί ως έναν συντελεστή 8, εφόσον ο συντελεστής Poisson άλλαζε από την τιμή 0 σε περίπου -0,8 (Alderson, 1994; Yang, et al, 2004).
16 3.3 Συμπεριφορά Παραμόρφωσης Πολύ πρόσφατες έρευνες που αφορούν την κρούση χαμηλής ταχύτητας σε συνθετικά ελάσματα από ανθρακονήματα έχουν δείξει βελτιώσεις στην απορρόφηση ενέργειας μέχρι και ένα τρίτο για το πρώτο σημείο αστοχίας (Coenen, et al, 2001a). Η ψυχρή κατεργασία σε ένα αυξητικό αφρώδες υλικό έχει κάποιες επιπτώσεις λόγω της τριαξονικής συμπίεσης κατά τη διάρκεια της κατασκευής. Όμως, η θερμική κατεργασία (ανόπτηση) επιδρά εμφανώς στο συντελεστή Young. To Σχήμα 12 δείχνει τις σχέσεις τάσης- παραμόρφωσης των συμβατικών και των αυξητικών αφρωδών υλικών. Η ανόπτηση λογικά μειώνει το συντελεστή Young σε ένα δοσμένο λόγο ογκομετρικής συμπίεσης (βλέπε Σχήμα 10). Με άλλα λόγια, το υλικό γίνεται λιγότερο άκαμπτο. Ως αποτέλεσμα, ο αυξητικός αφρός χαλκού είναι λιγότερο άκαμπτος από τον συμβατικό αφρό από τον οποίο προήλθε. Στους συμβατικούς αφρούς χαλκού οι ιδιότητες υπο εφελκυσμό και συμπίεση είναι παρόμοιες. Όμως, οι αυξητικοί αφροί δείχνουν διαφορετικές συμπεριφορές στον εφελκυσμό και τη συμπίεση. Επίσης, τόσο στον εφελκυσμό όσο και στην συμπίεση και τα δύο είδη αφρών παρουσιάζουν μία σχετικά μακριά σταθεροποίηση πάνω από το όριο αναλογίας. Αυτή η συμπεριφορά αποδίδεται στην πλαστική μόρφωση αρθρώσεων των πλευρών κελιού (Choi & Lakes, 1992). Από το Σχήμα 12 μπορούμε επίσης να δούμε ότι ο συμβατικός αφρός έχει μια τάση δυσκολίας στην παραμόρφωση σε αντίθεση με τον αυξητικό αφρό που δεν την έχει. Επομένως, αυτό το υλικό στην μοντελοποίηση μπορεί λογικά να θεωρηθεί ως απολύτως ελαστικό και τέλεια πλαστικό υλικό. Σχήμα 12: Σχέσεις εφελκυσμού παραμόρφωσης συμβατικών και αυξητικών αφρών. Αρχική σχετική πυκνότητα: 0,08. Κλειστά σύμβολα: ανοπτημένα. Ανοιχτά σύμβολα: μη ανοπτημένα Τετράγωνα: συμβατικός αφρός, ογκομετρική συμπίεση 1. Τρίρωνα: αυξητικός αφρός, ογκομετρική συμπίεση 2.0. Κύκλοι: αυξητικός αφρός, ογκομετρική συμπίεση 2.5. Διαμάντια: αυξητικός αφρός, ογκομετρική συμπίεση 3.0 (Choi & Lakes, 1992).
17 3.4 Αντοχή σε Ρηγμάτωση Συμπεριφορά σε ρηγμάτωση Η συμπεριφορά ρηγμάτωσης τόσο των συμβατικών όσο και των αυξητικών αφρών στον εφελκυσμό είναι όπως στην brittle. Η αστοχία συμβαίνει ξαφνικά χωρίς την εμφάνιση λαιμού (Gibson & Ashby, 1988; Choi & Lakes, 1992). Από την άποψη της διάστασης των κελιών ένα ράγισμα διαδίδεται σταδιακά, κάθε βήμα του οποίου ενισχύει την ρηγμάτωση κατά ένα εύρος κελιού (Maiti, et al, 1984). Όταν η τάση στην άκρη της ρωγμής είναι αρκετά υψηλή στην ακμή ή στο τοίχωμα του κελιού, μια τοπική ρηγμάτωση συμβαίνει και το ράγισμα επεκτείνεται. Όμως, η διάδοση της ρηγμάτωσης γίνεται με δυο διαφορετικούς τρόπους (Ashby, 1983): Μέσω της αστοχίας λυγισμού το μη-κάθετου τοιχώματος ή της άκρης κελιού (Σχήμα 13(α)). Από την ρηγμάτωση κάθετων στοιχείων υπο τον συνδυασμό εφελκυσμού και ροπής κάμψης (Σχήμα 13(β)). Σχήμα 13: Σχηματική απεικόνιση της διάδοσης ρωγμής που συμβαίνει σε κυττάρικο στερεό (a) Μέσω της αστοχίας λυγισμού των μη-κάθετων στοιχείων κελιού και (b) Μέσω της εφελκυστικής ρηγμάτωσης των κάθετων στοιχείων κελιού (Maiti, et al, 1984). Αφού τα κελιά σε μη-συμβατικούς αφρούς έχουν μη-μηδενικό μέγεθος, τα ραγίσματα στο υλικό δεν μπορούν να έχουν τελείως οξεία μορφή (Σχήμα 14). Το μη μεμονωμένο πεδίο τάσεων σε απόσταση r ( για r>r tip/2) για μια ρωγμή της τάξης 2α με ακτίνα άκρης ρωγμής, rtip, δίνεται από την σχέση (Ewards & Wanhill, 1986): (6) Όπου Κ l είναι ό συντελεστής τάσεων καταπόνησης. Η δύναμη που επιδρά στην πλευρά του κελιού μπορεί να ανακτηθεί όταν το ολοκλήρωμα είναι πάνω από το πάχος μιας πλευράς, αυτό είναι,
18 (7) όπου το t είναι το πάχος της πλευράς. Χρησιμοποιώντας το ανάπτυγμα Taylor και μια πρώτη προσέγγιση διάταξης, η παραπάνω εξίσωση μπορεί να εκφραστεί: (8) όπου Κ l * είναι ο συντελεστής τάσεων καταπόνησης των συμβατικών αφρών και το l είναι το μήκος πλευρών (σχήμα 13 (α)). Σχήμα 14: Δομικές και συνεχείς όψεις μιας ρωγμής σε αφρό, που προτείνουν τη χρήση μιας μη μηδενικής κυρτότητας άκρης της ρωγμής. (Choi & Lakes, 1996). Δεδομένου ότι ο εφελκυστική τάση στις πλευρές των κελιών δεν είναι σημαντική σε σύγκριση με την κάμπτική, η καμπτική ροπή κρίνεται ως η κύρια δύναμη που εφαρμόζεται στις πλευρές των κελιών (Choi & Lakes, 1996). Αυτό δεν ισχύει για αφρούς με πολύ υψηλή πυκνότητα. Η τάση που οφείλεται στην καμπτική ροπή δίνεται από την σχέση: (9) Αντικαθιστώντας την Εξίσωση (8) στην παραπάνω εξίσωση, η τάση γίνεται: (10) Η ρωγμή θα αυξηθεί εάν σ =σ f, όπου σ το σ f είναι η αντοχή σε ρηγμάτωση της πλευράς κελιού. Κατά συνέπεια, η αντοχή σε θραύση των συμβατικών αφρών, K l*, μπορεί να υπολογιστεί από την σχέση:
19 (11) Από ρ*/ρ s α(t/l) n, επομένως, ο συντελεστής τάσεων καταπόνησης των συμβατικών αφρών είναι ανάλογος προς την ομαλοποιημένη πυκνότητα, δηλ., (12) Όπου ρ* είναι η πυκνότητα του αφρού, ρ s η πυκνότητα του στερεού από το οποίο είναι φτιαγμένος ο αφρός, α και n είναι σταθερές. Για την αντοχή σε θραύση αυξητικών αφρών, μπορούν να ανακτηθούν οι παρόμοιες σχέσεις υπό την μορφή των εξισώσεων (11) και (12) εφόσον έχει αποφασιστεί η ειδική δομή για αυτόν τον τύπο υλικού. Η αντοχή σε θραύση στους μη-συμβατικούς αφρούς (π.χ. αυξητικούς) μπορεί να εκφραστεί από την σχέση (Choi & Lakes, 1996) (13) Όπου Κ IC είναι η αντοχή σε θραύση για αυξητικούς αφρούς και φ είναι η γωνία πλευράς που σχετίζεται με το σχήμα του κελιού. Οι λεπτομέρειες της προέλευσης της εξίσωσης (12) είναι στην εργασία του Choi & Lakes (1996). Από τις σχέσεις (11) και (13), ό λόγος της αντοχής σε θραύση αυξητικών αφρών προς την αντοχή σε θραύση συμβατικών αφρών δίνεται από την ακόλουθη σχέση (14) Από τότε που το παραπάνω μοντέλο καθιερώθηκε στο απλοποιημένο μοντέλο, για λόγο ογκομετρικής συμπίεσης με τιμή 2.5 η μεγαλύτερη, τα αποτελέσματα μπόρεσαν να βελτιστοποιηθούν περαιτέρω, αυτό οφείλεται στο γεγονός ότι οι αυξητικοί αφροί έχουν μια σύνθετη ανώμαλη μικροδομή. Συνεπώς, το αποτέλεσμα του λόγου ογκομετρικής συμπίεσης στην αντοχή είναι ελαφρώς περίπλοκη, εξαρτάται από την κατάσταση ανόπτησης του υλικού (Σχήμα 15). Εν συγκρίσει με αυτό των υλικών συμβατικών αφρών, η αντοχή αυξάνεται από παράγοντες της τάξης 1.4, 1.5, και 1.7 με αύξηση του λόγου ογκομετρικής συμπίεσης 2.0, 2.5, 3.0 αναλογικά (Choi & Lakes, 1992). Για μη ανοπτημένα υλικά, η αντοχή αυξάνεται μαζί με τον λόγο ογκομετρικής συμπίεσης, αλλά κάτω από συνθήκες ανόπτησης, η αντοχή αυξάνεται εως τον λόγο ογκομετρικής συμπίεσης περίπου 2.0. Περαιτέρω αύξηση στον λόγο ογκομετρικής συμπίεσης οδηγεί σε μείωση αντοχής.
20 Σχήμα 15: Αντοχή ως εξίσωση της μόνιμης ογκομετρικής συμπίεσης για συμβατικούς και αυξητικούς αφρούς: ανοιχτά σύμβολα, μη-ανοπτημένα; συμπαγή σύμβολα, ανοπτημένα (Choi & Lakes, 1992) Μορφολογία μικροδομής Η μικροδομή του αφρού είναι περίπλοκη. Το Σχήμα 16 παρουσιάζει τις μικροδομές ανοιχτού κελιού και κλειστού κελιού πολυεστερικών αφρών πολυουρεθάνης. (Chan & Evans, 1997). Στον αφρό κλειστού κελιού, τα περισσότερα από τα μέτωπα των κελιών είναι κλειστά από λεπτές μεμβράνες. Οι πορώδεις ανοιχτού κελιού αφροί επιτρέπουν την ελεύθερη κίνηση του αέρα μέσα από το υλικό όταν τεντώνονται. Οι αυξητικοί αφροί έχουν μια πιο σύνθετη γεωμετρία ( Σχήμα 17(α)). Ως εκ τούτου, είναι πολύ πιο πιθανό να παραμορφωθούν από στρέψη και κάμψη παρά να εκταθούν σε εφελκυσμό (Σχήμα 17(β)) και θλίψη (Σχήμα 17( γ)). Υπο εφελκυσμό, τα κελιά εκτείνονται εγκάρσια υπο την διαμήκη εφελκυστική δύναμη (Chan & Evans, 1997). Αυτό οφείλεται στο γεγονός ότι οι αυξητικοί αφροί αποτελούνται από κόμβους που διασυνδέονται από ινίδια (Caddock & Evans, 1989). Επίσης, οι συμβατικοί αφροί αποτελούνται από συμβατικά πολυεδρικά κελιά, ενώ οι αυξητικοί αφροί αποτελούνται από αρκετά πιο μπερδεμένες κυτταρικές δομές (Choi & Lakes, 1995; Chan & Evans,1997), όπως φαίνεται και στο Σχήμα 18. Ένα παράδειγμα είναι η μικροδομή του UHMWPE που απεικονίζεται στο Σχήμα 19 (Alderson & Evans, 1992) Αντίσταση στην ρηγμάτωση Συγκρινόμενα με τα μη αυξητικά υλικά, τα αυξητικά υλικά έχουν κάποιες επιθυμητές μηχανικές ιδιότητες. Για παράδειγμά, αν το υλικό έχει μια ρωγμή και τραβιέται ώστε να διαχωριστεί, αυτό διαστέλλεται με αποτέλεσμα να κλείνει η ρωγμή. Με άλλα λόγια, αυτός ο τύπος υλικού επιδεικνύει μεγαλύτερη αντοχή στην ρηγμάτωση. Επίσης, έχει μεγάλη αντοχή υλικού στην διατμητική παραμόρφωση. Η διατμητική αντοχή είναι αρκετά σημαντική σε δομικά υλικά όπως φύλλα ή δοκοί σε κτήρια, αυτοκίνητα και αεροσκάφη.
21 (α) (β) Σχήμα 16: Μικροδομές του συμβατικού αφρού πολυουρεθάνης: (α) Κλειστού κελιού (οπτική μικρογραφία) και (β)ανοιχτού κελιού (Choi & Lakes, 1997) (α) (β) Σχήμα 17: (α) και (β) (Chan & Evans, 1997) Σχήμα 17: Μικρογραφίες των αυξητικών αφρών πολυουρεθάνης παρουσιάζοντας τις ελαστικές παραμορφώσεις υπο διαφορετικούς τύπους φορτίσεων (α) Ελεύθερο (β) Υπο εφελκυσμό (γ) Υπο συμπίεση (Chan & Evans, 1997)
22 (α) (β) Σχήμα 18: Πολυμερείς αφροί ανοιχτού κελιού: (α) Μη-αυξητικοί (β) Αυξητικοί (Choi & Lakes, 1995; Chan & Evans, 1997) Σχήμα 19: Μικρογραφία της μικροδομής του αυξητικού UHMWPE (Alderson & Evans, 1992) 3.5 Απόσβεση και Απορρόφηση ήχου Οι αφροί αρνητικού λόγου Poisson που παρουσιάζονται επιδεικνύουν μια συνολική υπεροχή όσον αφορά τις ιδιότητες απόσβεσης και απορρόφησης ήχου εν συγκρίσει με τους συμβατικούς αφρούς (Scarpa, et al, 2004). Οι αυξητικοί αφροί μπορούν να έχουν καλύτερη ικανότητα απορρόφησης ήχου σε σχέση με τους συμβατικούς αφρούς σε όλα τα επίπεδα των συχνοτήτων. Οι αυξητικοί αφροί με μικρότερο μέγεθος πόρων απορροφούν τον ήχο πιο αποτελεσματικά από αυτούς με μεγαλύτερους πόρους για συχνότητες άνω των 630 Hz (Howell, et al, 1994).
23 Υλικά και γεωμετρικές ιδιότητες κυψελοειδών κατασκευών τύπου σάντουιτς ΕΙΣΑΓΩΓΗ Η ιδέα για την κατασκευή στοιχείων τύπου σάντουιτς αναπτύχθηκε στις αρχές του 19 ου αιώνα, ωστόσο η ανάπτυξη τους αυτή ολοκληρώθηκε τον 20 ο αιώνα. Η χρήση κατασκευών τύπου σάντουιτς επικράτησε σε πολλές κατασκευές χάρη στα ποικίλα πλεονεκτήματα που προσφέρει όσον αφορά την εξοικονόμηση βάρους και την υψηλή ακαμψία. Γενικά, τα πάνελ τύπου σάντουιτς αποτελούνται από τον πυρήνα που βρίσκεται στην μέση και είναι από ελαφρύ υλικό και έχει ως κύριο σκοπό την μεταφορά των διατμητικών τάσεων μεταξύ των δύο επιστρώσεων, οι οποίες με την σειρά τους είναι από ισχυρότερο υλικό ανθεκτικό στις τάσεις εφελκυσμού και θλίψης που εφαρμόζονται στο επίπεδο τους. Οι επιστρώσεις είναι κολλημένες στις κύριες επιφάνειες του πυρήνα με κατάλληλο τρόπο που εξαρτάται από τον τύπο του στρωματοειδούς. Κάθε μέρος αυτής δομής από μόνο του είναι αδύναμο και εύκαμπτο, όταν λειτουργεί όμως ως σύνολο παρέχει μια άκαμπτη, ισχυρή και ελαφριά δομή. Τέτοιου είδους σάντουιτς πάνελ προσφέρουν πολλαπλές εφαρμογές στον τομέα της αεροδιαστημικής και της αυτοκινητοβιομηχανίας. Στις περισσότερες περιπτώσεις ο πυρήνας κατασκευάζεται από αφρώδη υλικά, δικτυώματα και κυψέλες. Πολλές μελέτες έχουν προσπαθήσει να μοντελοποιήσουν τις μηχανικές ιδιότητες δομών τύπου σάντουιτς με χρήση μαθηματικής μοντελοποίησης και ανάλυσης πεπερασμένων στοιχείων (FEA). Συμβατικές εξαγωνικές κυψέλες χρησιμοποιούνται στην κατασκευή του πυρήνα κατασκευών σάντουιτς. Ένα πλεονέκτημα της κυψελοειδούς δομής είναι η αντίσταση της στη κόπωση, στο Σχήμα 20 παρουσιάζονται τα αποτελέσματα από δοκιμή ηχητικής κόπωσης μεταξύ κυψελοειδούς πάνελ και δομής με ενισχυμένη επιφάνεια. Επισημαίνεται, ότι η κυψελοειδής δομή άντεξε 460 ώρες στα 167db ενώ η άλλη δομή άντεξε μόνο 3 λεπτά στα ίδια db. Ο λόγος για την μεγαλύτερη αντίσταση σε κόπωση της κυψελοειδούς δομής είναι ότι τα πάνελ είναι συνεχώς ενωμένα με τον πυρήνα και έτσι δεν έχουμε συγκεντρώσεις τάσεων. Ένας επιπλέον λόγος που χρησιμοποιούνται σάντουιτς κατασκευές με κυψελοειδή πυρήνα είναι ότι προσφέρουν υψηλή ακαμψία με παράλληλη εξοικονόμηση βάρους. Σχήμα 20: Σύγκριση ηχητικής κόπωσης μεταξύ δομής τύπου σάντουιτς και δομής με ενισχυμένη επιφάνεια.
24 Οι αυξητικές κυψέλες είναι κυτταρικές δομές στις οποίες αντιστρέφεται η γωνιά μιας μονάδας κελιού σε αρνητική. Στην αυξητική δομή με την αντιστροφή της γωνίας μεταβάλλεται και ο λόγος Poisson σε αρνητικές τιμές. Στο Σχήμα 21 απεικονίζεται η διαφορά μεταξύ συμβατικής και αυξητικής δομής όσον αφορά τις κυτταρικές μονάδες. Σχήμα 21: Γεωμετρία κυτταρικών μονάδων συμβατικής και αυξητικής κυψέλης. 4.1 Ιδιότητες υλικών Ως βασικό υλικό του κυψελοειδούς πάνελ τύπου σάντουιτς επιλέχθηκε κράμα αλουμινίου (Α5052-H34) καθώς είναι άκαμπτο. Material Young s Modulus Poisson s Ratio, ν Density, ρ (Kg/m 3 ) E(Gpa) A5052-H Πίνακας 1: Ιδιότητες κράματος αλουμινίου που χρησιμοποιείται για το σύνθετο πάνελ τύπου σάντουιτς. Οι Ashby και Gibson που έδωσαν δραστικές ιδιότητες της κυψέλης βασιζόμενοι στην θεωρία της δοκού. Σύμφωνα με τον Ashby και Gibson μια μοναδιαία κυψέλη μιας κυψελοειδούς δομής χρησιμοποιείται στην πρόβλεψη της συμπεριφοράς του πάνελ τύπου σάντουιτς. Μια μοναδιαία κυψέλη της συμβατικής και αυξητικής δομής απεικονίζονται στο Σχήμα 22, μαζί με τις παραμέτρους που καθορίζουν την γεωμετρία κελιού της κυψέλης. Οι παράμετροι είναι οι ακόλουθες: h (ύψος κελιού), l ( μήκος του τοιχώματος κελιού), d (βάθος του τοιχώματος κελιού) και θ (γωνία μεταξύ οριζόντιου και κεκλιμένου τοιχώματος κελιού). Επιπλέον, ως α ορίζεται ο λόγος που ισούται με h/l, ενώ ως β ορίζεται ο λόγος πάχους προς το μήκος t/l. Για την συμβατική κυψέλη, θ=30 και α=1, ενώ για την αυξητική ορίζεται ως θ=-30 και α=2. Με αυτήν την επιλογή παραμέτρων της αυξητικής μονάδας κελιού, ο ενεργός συντελεστής εντός του επιπέδου είναι το ίδιο στις δύο κάθετες διευθύνσεις, όπως είναι στην συμπεριφορά μιας συμβατικής κυψέλης. Οι παράμετροι του μοναδιαίου κελιού του πυρήνα της συμβατικής και της αυξητικής κυψέλης παρουσιάζονται στον Πίνακα 2.
25 Γεωμετρικές παράμετροι Συμβατική Κυψέλη Αυξητική Κυψέλη Ύψος του τοιχώματος κελιού(mm) 4,23 8,46 Κεκλιμένο μήκος τοιχώματος κελιού (mm) 4,23 4,23 Πάχος του τοιχώματος κελιού 0,423 0,423 Γωνία κελιού (θ) Συντελεστής αναλογίας κελιού (α) 1 2 Αναλογία πάχους προς μήκος 0,1 0,05 Πίνακας 2: Γεωμετρικοί παράμετροι συμβατικής και αυξητικής κυψέλης. Οι συνολικές διαστάσεις μιας συμβατικής μονάδας κυψέλης δίνεται από τις σχέσεις: Το συνολικό πλάτος μονάδας κελιού: L=2l cosθ Το συνολικό ύψος μονάδας κελιού: H=2(h+l sinθ) Ενώ οι συνολικές διαστάσεις της αυξητικής μονάδας κελιού δίνονται από: Το συνολικό πλάτος της μονάδας κελιού: L=2l cosθ Το συνολικό ύψος μονάδας κελιού: H=2(h-l sinθ) Σχήμα 22: Διαστάσεις συμβατικής και αυξητικής μονάδας κελιού. 4.2 Μοντέλο πάνελ τύπου σάντουιτς Για την μοντελοποίηση του σύνθετου αλουμινένιου πάνελ τύπου σάντουιτς χρησιμοποιήθηκε το λογισμικό προσομοίωσης Abaqus Δημιουργήθηκε ένα σύνθετο μοντέλο τύπου σάντουιτς για τις δυο διαφορετικές επιλογές πυρήνα. Το εντός επιπέδου μοντέλο αναπαριστά ένα μοντέλο το οποίο δέχεται φόρτιση κατά μήκος της Χ1 ή της Χ2 διεύθυνσης.
26 Εντός επιπέδου Μοντέλο Σε αυτήν την περίπτωση έχουμε φόρτιση μόνο κατά μήκος της Χ1 και Χ2 διεύθυνσης. Ως εκ τούτου ο αριθμός των μονάδων κελιών κατά μήκος της Χ1 διεύθυνσης επιλέχθηκε να είναι 10 και κατά μήκος της Χ2 είναι 3. Σύμφωνα με τις διαστάσεις της μονάδας κελιού και των εξισώσεων που προαναφέρθηκαν, οι συνολικές διαστάσεις της κυψέλης είναι 73,20 στην Χ1 διεύθυνση και 25,38 στην Χ2 διεύθυνση. Το βασικό χαρακτηριστικό επιλέχθηκε να είναι παραμορφώσιμο κέλυφος με σκοπό να μειωθεί ο υπολογιστικός χρόνος. Η κρίσιμης σημασίας διαμόρφωση της κυψέλης όσον αφορά το υλικό και το πάχος έγινε στο βήμα της ανάθεσης τμήματος (section assignment). Το Σχήμα 23 απεικονίζει τον συμβατικό και τον αυξητικό πυρήνα κυψέλης. Σχήμα 23: Συνολικές διαστάσεις συμβατικού και αυξητικού πυρήνα για εντός επιπέδου μοντέλο Για την φόρτιση στην Χ1 διεύθυνση δημιουργήθηκε ένα μετωπικό φύλο με διαστάσεις 73,27mm στο μήκος και 25,38mm στο πλάτος. Για την εντός επιπέδου φόρτιση στην Χ2 διεύθυνση, οι διαστάσεις του μετωπικού φύλλου είναι 73,27mm στο μήκος και 73,21mm στο πλάτος. Ο τύπος κέλυφός επιλέχθηκε για τα επιφανειακά φύλλα και ως υλικό προσδιορίστηκε το αλουμίνιο. Ο κυψελοειδής πυρήνας εσωκλείστηκε μεταξύ των μετωπικών φύλλων. Στο Σχήμα 24 και Σχήμα 25 βλέπουμε τις πλήρως συναρμολογημένες σύνθετες πλάκες σάντουιτς. Σχήμα 24: Απεικόνιση πλήρως συναρμολογημένης σύνθετης πλάκας τύπου σάντουιτς για εντός επιπέδου μοντέλο (Φόρτιση στην Χ1 διεύθυνση)
27 Σχήμα 25: Απεικόνιση πλήρως συναρμολογημένης σύνθετης πλάκας τύπου σάντουιτς για εντός επιπέδου μοντέλο (Φόρτιση στην Χ2 διεύθυνση)
28 Μοντέλο Πεπερασμένων Στοιχείων 5.1 Μοντέλο πεπερασμένων στοιχείων για εντός επιπέδου φόρτιση Μετά την δημιουργία της γεωμετρίας του μοντέλου για την εντός επιπέδου φόρτιση, το μοντέλο καθορίστηκε και διακριτοποιήθηκε για την ανάλυση φόρτισης που θα προσομοιωθεί στο λογισμικό Abaqus. Σε αυτό το κεφάλαιο αναλύονται οι λεπτομέρειες των βημάτων που χρησιμοποιήθηκαν στην ανάπτυξη των μοντέλων για την στατική, μη γραμμική ανάλυση πεπερασμένων στοιχείων. 5.2 Διακριτοποίηση Για το προαναφερθέν εντός επιπέδου μοντέλο φόρτισης χρησιμοποιήθηκαν S4R τα οποία αναπαρίστανται από στοιχεία 4 κόμβων τύπου κελύφους τόσο στον πυρήνα της κυψέλης όσο και στα μετωπικά φύλλα. Ο κάθε κόμβος στοιχείου έχει 3 μεταφορικούς και 3 περιστροφικούς βαθμούς ελευθερίας. Το σχετικό ολικό μέγεθος στοιχείου είναι 1 mm. Το Σχήμα 26 (α) και Σχήμα 26 (β) παρουσιάζει τον πλεγματοποιημένο πυρήνα και μετωπικά φύλλα για τα δύο μοντέλα. Σχήμα 26 (α): Πλεγματοποιημένος συμβατικός και Αυξητικός πυρήνας για το εντός επιπέδου μοντέλο. Σχήμα 26 (β): Πλεγματοποιημένο μετωπικό φύλλο για εντός επιπέδου μοντέλο.
29 5.3 Περιορισμοί Μετά την διαδικασία της συναρμολόγησης, τα επιμέρους κομμάτια (πυρήνας και τα δύο επιφανειακά φύλλα) συναρμολογούνται μαζί για να αποτελέσουν ένα μεμονωμένο κομμάτι. Περιορισμοί βασισμένοι στις επιφάνειες χρησιμοποιούνται για τα δυο μετωπικά φύλλα και τον πυρήνα του κάθε μοντέλου. Γενικά, η επιφάνεια με την μεγαλύτερη δυσκαμψία αποφασίστηκε να είναι η κύρια επιφάνεια. Οι περιορισμοί δένουν τον πυρήνα ως δευτερεύουσα επιφάνεια και τα μετωπικά φύλλα ως κύριες επιφάνειες. Η κύρια επιφάνεια έχει κοινή κίνηση περιορίζοντας κάθε κόμβο στην δευτερεύουσα επιφάνεια. Το Σχήμα 27 απεικονίζει τα μετωπικά φύλλα ως κύριες επιφάνειές συνδέονται στους δευτερεύοντες κόμβους του πυρήνα και από τις δύο πλευρές. Σχήμα 27: Σύνδεση πυρήνα με μετωπικά φύλλα για εντός επιπέδου μοντέλο. 5.4 Συνοριακές συνθήκες και Φορτίσεις Για τα εντός επιπέδου μοντέλα, χρησιμοποιήθηκαν διαφορετικοί συνδυασμοί φορτίσεων και περιορισμών όσον αφορά τους 6 βαθμούς ελευθερίας (U1,U2,U3,UR1,UR2,UR3). ΠΕΡΙΠΤΩΣΗ 1 ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι άκρες του πίσω μετωπικού φύλλου της σύνθετης κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα.
30 Σχήμα 28: Συνοριακές συνθήκες που επιβάλλονται στο εντός επιπέδου μοντέλο για συμβατική και αυξητική δομή (Φόρτιση στην Χ1 διεύθυνση). ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε φόρτιση με μέτρο 10KN υπό μορφή πίεσης στην επιφάνειά του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Σχήμα 29: Θλιπτική φόρτιση που επιβάλλεται στο εντός επιπέδου μοντέλο για συμβατική και αυξητική δομή (Φόρτιση στην Χ1 διεύθυνση).
31 ΑΠΟΤΕΛΕΣΜΑΤΑ Από το Visualisation Module μπορούμε να επιβλέψουμε τα αποτελέσματα και συγκεκριμένα την κατανομή των τάσεων von Mises όπως και την παραμόρφωση, με τους αντίστοιχους χρωματισμούς, πάνω στο μοντέλο καθώς και την έγχρωμη κλίμακα όπου φαίνεται στις ακόλουθες εικόνες. Σχήμα 30: Ισοδύναμη τάση κατά Von Mises για πυρήνα με συμβατική όσο και για αυξητική κυψέλη. Σχήμα 31: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη.
32 Σχήμα 32: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Χ- άξονα. Σχήμα 33: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Υ- άξονα. Σχήμα 34: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Ζ-άξονα.
33 ΠΕΡΙΠΤΩΣΗ 2 ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι άκρες του κάτω μετωπικού φύλλου της σύνθετης κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα. ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε φόρτιση με μέτρο 1KN υπό μορφή πίεσης στην επιφάνειά του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Σχήμα 35 : Θλιπτική φόρτιση που επιβάλλεται στο εντός επιπέδου μοντέλο για συμβατική και αυξητική δομή (Φόρτιση στην X2 διεύθυνση).
34 ΑΠΟΤΕΛΕΣΜΑΤΑ Ισοδύναμη τάση κατά Von Mises για πυρήνα με συμβατική όσο και για αυξητική κυψέλη. Σχήμα 36: Ισοδύναμη τάση κατά Von Mises για πυρήνα με συμβατική όσο και για αυξητική κυψέλη. Σχήμα 37: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη.
35 Σχήμα 38: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Χ- άξονα. Σχήμα 39: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Υ- άξονα. Σχήμα 40: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Ζ-άξονα.
36 ΠΕΡΙΠΤΩΣΗ 3 ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι δύο απέναντι άκρες του κάτω μετωπικού φύλλου της σύνθετης κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα. Σχήμα 41: Συνοριακές συνθήκες που επιβάλλονται στο εντός επιπέδου μοντέλο για συμβατική και αυξητική δομή (Φόρτιση στην Χ2 διεύθυνση). ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε καμπτική φόρτιση με μέτρο 1KN υπό μορφή πίεσης στο κέντρο της επιφάνειάς του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Σχήμα 42 : Καμπτική φόρτιση που επιβάλλεται στο εντός επιπέδου μοντέλο για συμβατική και αυξητική δομή (Φόρτιση στην X2 διεύθυνση).
37 ΑΠΟΤΕΛΕΣΜΑΤΑ Ισοδύναμη τάση κατά Von Mises για πυρήνα με συμβατική όσο και για αυξητική κυψέλη. Σχήμα 43: Ισοδύναμη τάση κατά Von Mises για πυρήνα με συμβατική όσο και για αυξητική κυψέλη. Σχήμα 44: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη. Σχήμα 45: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Χ- άξονα.
38 Σχήμα 46: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Υ- άξονα. Σχήμα 47: Συνολικές παραμορφώσεις για συμβατική και αυξητική κυψέλη κατά τον Z-άξονα.
39 Θεωρητικός υπολογισμός λόγου Poisson για συμβατική και αυξητική δομή 6.1 Θεωρητικό μοντέλο Όταν μια κυψέλη φορτίζεται είτε στην Χ1 είτε στην Χ2 διεύθυνση, παραμορφώνεται με έναν γραμμικό ελαστικό τρόπο, τα τοιχώματα των κελιών κάμπτονται (Patel and Finnie, 1970; Abd El-Sayed, 1976; Abd El Sayed et al., 1979; Gibson et al., 1982; Warren and Kraynik, 1987). Η απόκριση περιγράφεται από πέντε συντελεστές: δύο συντελεστές Young Ε 1 * και Ε 2 *, ένα μέτρο διάτμησης G 12 * και δύο λόγους Poisson ν 12 * και ν 21 *. Για τις δύο διαφορετικές περιπτώσεις πυρήνα κυψέλης, την συμβατική εξαγωνική κυψέλη με θετικό λόγο Poisson και την αυξητική κυψέλη με αρνητικό λόγο Poisson, σύμφωνα με την κυτταρική θεωρία υλικών (Gibson L.J., Ashby M.F., 1997) οι μηχανικές ιδιότητες της κυψελοειδούς δομής μπορούν να καθοριστούν από τις γεωμετρικές ιδιότητες της μονάδας κελιού και την μηχανική συμπεριφορά του υλικού της κυψέλης. Μονάδες κελιού για τις δύο διαφορετικές περιπτώσεις που εξετάζουμε απεικονίζονται στο Σχήμα 49, όπου l είναι το μήκος τής κεκλιμένης πλευράς του κελιού, h είναι το μήκος της οριζόντιας πλευράς κελιού, θ είναι η κεκλιμένη γωνιά, τα α και β καθορίζουν το σχετικό μήκος τοιχώματος κελιού και τον λόγο λεπτότητας. Οι προαναφερθείσες παράμετροι είναι σημαντικές όσον αφορά τις ιδιότητες κυψέλης. Οι σχέσεις που υιοθετούνται για τον θεωρητικό υπολογισμό ιδιοτήτων υλικού πυρήνα κυψέλης αναφέρονται στην συνέχεια. Σχήμα 48: Πυρήνας κυψέλης σε πλάκα τύπου σάντουιτς (α) Μοντέλο συμβατικής εξαγωνικής κυψέλης (β) Μοντέλο αυξητικής εξαγωνικής κυψέλης.
40 Σχήμα 49: Γεωμετρικά χαρακτηριστικά κελιού του πυρήνα κυψέλης. (15) (16) (17) (18) (19) οπου το σύμβολο c αντιπροσωπεύει το υλικό του πυρήνα, το Ε, το G και το ρ είναι ο συντελεστής Young, ο συντελεστής διάτμησης και η πυκνότητα μάζας του υλικού. Βάση των γεωμετρικών χαρακτηριστικών για τις δυο διαφορετικές περιπτώσεις πυρήνα, στον πίνακα 3 υπολογίζουμε την θεωρητική τιμή του λόγου Poisson για την κάθε περίπτωση. THEORITICAL CALCULATION OF POISSON RATIO DESIGN H(mm) L(mm) Θ(RAD) tv tr V 12 V 21 α E(Gpa) G(Gpa) θ(deg) AUXETIC 8,46 4,23-0, , CONVENTIONAL 4,23 4,23 0, , Πίνακας 3: Υπολογισμός λόγου Poisson βάση των γεωμετρικών χαρακτηριστικών κελιού κυψέλης. Δημιουργήθηκε λοιπόν ένα μοντέλο στο οποίο δόθηκαν οι ιδιότητες που προκύπτουν βάση των γεωμετρικών χαρακτηριστικών για τις δυο διαφορετικές επιλογές πυρήνα. Στην συνέχεα θα γίνει σύγκριση των αποτελεσμάτων που προκύπτουν από την προσομοίωση του θεωρητικού μοντέλου εν συγκρίσει με το μοντέλο που προσομοιώσαμε στο προηγούμενο κεφάλαιο. Το εντός επιπέδου μοντέλο αναπαριστά ένα μοντέλο το οποίο δέχεται φόρτιση κατά μήκος της Χ1 ή της Χ2 διεύθυνσης.
41 6.2 Μοντέλο πεπερασμένων στοιχείων για εντός επιπέδου φόρτιση Σύμφωνα με τις διαστάσεις της μονάδας κελιού και των εξισώσεων που προαναφέρθηκαν στο Κεφάλαιο 4, οι συνολικές διαστάσεις της κυψέλης είναι 73,20 στην Χ1 διεύθυνση και 25,38 στην Χ2 διεύθυνση και 73,27 στην Χ3 διεύθυνση. Δίνουμε λοιπόν τις παραπάνω διαστάσεις στο δοκίμιο μας. Στην συνέχεια ορίζουμε τις υπολογισμένες ιδιότητες του υλικού πού προκύπτουν για την κάθε γεωμετρία. Θα επικεντρωθούμε στην περίπτωση του αυξητικού πυρήνα κυψέλης καθώς στην περίπτωση του συμβατικού πυρήνα το θεωρητικό μοντέλο μας δίνει τιμή για τον λόγο Poisson εκτός των αποδεκτών ορίων. Μετά την δημιουργία της γεωμετρίας του μοντέλου για την εντός επιπέδου φόρτιση, το μοντέλο καθορίστηκε και διακριτοποιήθηκε για την ανάλυση φόρτισης που θα προσομοιωθεί στο λογισμικό Abaqus. 6.3 Διακριτοποίηση Για το προαναφερθέν εντός επιπέδου μοντέλο φόρτισης χρησιμοποιήθηκαν HEX στοιχεία τα οποία αναπαρίστανται από εξάεδρα στοιχεία. Ο κάθε κόμβος στοιχείου έχει 3 μεταφορικούς και 3 περιστροφικούς βαθμούς ελευθερίας. 6.4 Συνοριακές συνθήκες και Φορτίσεις ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι άκρες του κάτω μετωπικού φύλλου της κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα. Σχήμα 50: Συνοριακές συνθήκες που επιβάλλονται στο εντός επιπέδου μοντέλο για αυξητική δομή (Φόρτιση στην Χ2 διεύθυνση).
42 ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε φόρτιση με μέτρο 1KN υπό μορφή πίεσης στην επιφάνειά του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Σχήμα 51 : Θλιπτική φόρτιση που επιβάλλεται στο εντός επιπέδου μοντέλο για αυξητική δομή (Φόρτιση στην X2 διεύθυνση). ΑΠΟΤΕΛΕΣΜΑΤΑ ΚΑΙ ΣΥΓΚΡΙΣΗ ΘΕΩΡΗΤΙΚΟΥ ΜΕ ΓΕΩΜΕΤΡΙΚΟ ΜΟΝΤΕΛΟ Ισοδύναμη τάση κατά Von Mises για πυρήνα με αυξητική κυψέλη. Σχήμα 52: Ισοδύναμη τάση κατά Von Mises για αυξητική κυψέλη.
43 Σχήμα 53: Συνολικές παραμορφώσεις για αυξητική κυψέλη. Σχήμα 54: Συνολικές παραμορφώσεις για αυξητική κυψέλη κατά τον Χ-άξονα. Σχήμα 55: Συνολικές παραμορφώσεις για αυξητική κυψέλη κατά τον Υ-άξονα.
44 Σχήμα 56: Συνολικές παραμορφώσεις για αυξητική κυψέλη κατά τον Ζ-άξονα.
45 Δυναμική ανάλυση 7.1 Εισαγωγή Η σταθερής κατάστασης δυναμική ανάλυση μας παρέχει ένα σταθερής κατάστασης εύρος καθώς και την φάση της απόκρισης ενός συστήματος εξαιτίας μιας αρμονικής διέγερσης σε μια συγκεκριμένη συχνότητα. Συνήθως, αυτού του είδους η ανάλυση γίνεται ως μια εναλλαγή συχνοτήτων εφαρμόζοντας την φόρτιση σε μια σειρά διαφορετικών συχνοτήτων και καταγράφοντας την απόκριση. Σε μια βασισμένη στις ιδιομορφές δυναμική ανάλυση σταθερής κατάστασης η απόκριση βασίζεται σε τεχνικές υπέρθεσης ιδιομορφών, επομένως πρέπει πρώτα να εξαχθούν οι ιδιομορφές του συστήματος χρησιμοποιώντας την διαδικασία εξαγωγής ιδιομορφών. Ο αριθμός των ιδιομορφών που θα εξαχθούν πρέπει να είναι επαρκής έτσι ώστε να είναι δυνατή η επαρκής μοντελοποίηση της δυναμικής απόκρισης του συστήματος. Στον καθορισμό ενός σταθερής κατάστασης δυναμικού βήματος το οποίο βασίζεται σε ιδιομορφές, προσδιορίζουμε τα εύρη συχνοτήτων που μας ενδιαφέρουν και τον αριθμό συχνοτήτων στις οποίες ζητούνται αποτελέσματα σε κάθε εύρος (συμπεριλαμβανομένων των ακραίων συχνοτήτων του εύρους). Επιπλέον, μπορούμε να καθορίσουμε τον τύπο διαμοιρασμού των συχνοτήτων που θα χρησιμοποιηθεί (γραμμικός ή λογαριθμικός), ως προεπιλογή χρησιμοποιείται ο λογαριθμικός. Οι συχνότητες δίνονται σε κύκλους/χρόνο. 7.2 Μελέτη Περιπτώσεων Οι δύο υπό μελέτη δομές (Συμβατική και Αυξητική) υπόκεινται σε δυναμική διέγερση. Ως προκαταρκτική ανάλυση διενεργείται ανάλυση δονήσεων με σκοπό την ανάκτηση δεκαπέντε ιδιόμορφών και των φυσικών συχνοτήτων τους. Αναλυτικότερα τα βήματα που ακολουθούνται καθώς και οι παράμετροι της ανάλυσης περιγράφονται παρακάτω. Βήμα 1: Εξαγωγή ιδιόμορφών συστήματος Σχηματική απεικόνιση χαρακτηριστικών ιδιόμορφών που εξάχθηκαν για τις δύο διαφορετικές γεωμετρίες.
46
47
48 Βήμα 2: Modal dynamics Στο δεύτερο βήμα της δυναμικής ανάλυσης εφαρμόζουμε τόσο στο συμβατικό όσο και στο αυξητικό μοντέλο δύναμη υπό μορφή παλμού όπως περιγράφεται παρακάτω. Χρονική περίοδος: 0.05 Χρονικό βήμα: Δηλαδή έχουμε στην διάθεση μας 125 data points. Damping start mode-end mode-critical damping fraction ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι άκρες του κάτω μετωπικού φύλλου της κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα.
49 Σχήμα 57: Συνοριακές συνθήκες που επιβάλλονται στο εντός επιπέδου μοντέλο για αυξητική δομή (Φόρτιση στην Χ2 διεύθυνση). ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε σημειακή φόρτιση στο κέντρο της επιφάνειάς του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Για το παρόν βήμα της ανάλυσης Modal Dynamics έχουμε δύναμη υπό μορφή παλμού που περιγράφεται από τον ακόλουθο πίνακα 4. ΧΡΟΝΟΣ ΔΥΝΑΜΗ 0 0 0, , ,004 0 Πίνακας 4: Περιγραφή εφαρμοζόμενης δύναμης. Σχήμα 58 : Σημείο εφαρμογής δύναμης που επιβάλλεται στο εντός επιπέδου μοντέλο για αυξητική δομή (Φόρτιση στην Χ2 διεύθυνση). ΑΠΟΤΕΛΕΣΜΑΤΑ Συμπεριφορά (μετατόπιση ως προς τον χρόνο) του κόμβου στης ακμή αριστερά σύμφωνα με την παρούσα σχηματική απεικόνιση για τις δύο διαφορετικές δομές.
50 Σχήμα 59: Απεικόνιση σε γραμμική κλίμακα μετατόπισης ως προς τον χρόνο για το συμβατικό μοντέλο. Σχήμα 60: Απεικόνιση σε γραμμική κλίμακα μετατόπισης ως προς τον χρόνο για το αυξητικό μοντέλο.
51 Συμπεριφορά (μετατόπιση ως προς τον χρόνο) του κόμβου στο κέντρο πάνω πλάκας όπου αποτελεί και σημείο εφαρμογής της δύναμης για τις δύο διαφορετικές δομές. Σχήμα 61: Απεικόνιση σε γραμμική κλίμακα μετατόπισης ως προς τον χρόνο για το συμβατικό μοντέλο. Σχήμα 62: Απεικόνιση σε γραμμική κλίμακα μετατόπισης ως προς τον χρόνο για το αυξητικό μοντέλο.
52 Βήμα 3: Steady state dynamics ΣΥΝΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ Σε αυτήν την περίπτωση οι άκρες του κάτω μετωπικού φύλλου της κατασκευής περιορίζονται στους 6 βαθμούς ελευθερίας, όπως φαίνεται και στο ακόλουθο σχήμα. Σχήμα 63: Συνοριακές συνθήκες που επιβάλλονται στο εντός επιπέδου μοντέλο για αυξητική δομή (Φόρτιση στην Χ2 διεύθυνση). ΦΟΡΤΙΣΗ Στην παρούσα περίπτωση έχουμε σημειακή φόρτιση στο κέντρο της επιφάνειάς του μπροστινού μετωπικού φύλλου, όπως απεικονίζεται και στο ακόλουθο σχήμα. Για αυτό το βήμα της ανάλυσης έχουμε σταθερή σημειακή δύναμη μέτρου 100ΚΝ. ΑΠΟΤΕΛΕΣΜΑΤΑ o Συμπεριφορά (μετατόπιση ως προς την συχνότητα) του κόμβου στης ακμή αριστερά σύμφωνα με την παρούσα σχηματική απεικόνιση για τις δύο διαφορετικές δομές.
53 Σχήμα 64: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το συμβατικό μοντέλο για εύρος συχνοτήτων από 0-200Hz. Σχήμα 65: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το αυξητικό μοντέλο για εύρος συχνοτήτων από 0-200Hz. Για να έχουμε περισσότερη πληροφόρηση μειώνουμε το εύρος των υπο εξέταση συχνοτήτων για το διάστημα από 0-20 Hz.
54 Σχήμα 66: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το συμβατικό μοντέλο για εύρος συχνοτήτων από 0-20Hz. Σχήμα 67: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το αυξητικό μοντέλο για εύρος συχνοτήτων από 0-20Hz. o Συμπεριφορά (μετατόπιση ως προς την συχνότητα) του κόμβου στο κέντρο πάνω πλάκας όπου αποτελεί και σημείο εφαρμογής της δύναμης για τις δύο διαφορετικές δομές.
55 Σχήμα 68: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το συμβατικό μοντέλο για εύρος συχνοτήτων από 0-200Hz. Σχήμα 69: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το αυξητικό μοντέλο για εύρος συχνοτήτων από 0-200Hz. Για να έχουμε περισσότερη πληροφόρηση μειώνουμε το εύρος των υπο εξέταση συχνοτήτων για το διάστημα από 0-20 Hz.
56 Σχήμα 70: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το συμβατικό μοντέλο για εύρος συχνοτήτων από 0-20Hz. Σχήμα 71: Απεικόνιση σε ημιλογαριθμική κλίμακα μετατόπισης ως προς την συχνότητα για το αυξητικό μοντέλο για εύρος συχνοτήτων από 0-20Hz.
ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ. Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας
 ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας Αντοχή και Δυσκαμψία (Strength and Stiffness) Η τάση (stress) εφαρμόζεται σ ένα υλικό μέσω της φόρτισής του Παραμόρφωση
ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΣΤΗΝ ΑΝΑΠΤΥΞΗ ΠΡΟΪΟΝΤΩΝ Δυσκαμψία & βάρος: πυκνότητα και μέτρα ελαστικότητας Αντοχή και Δυσκαμψία (Strength and Stiffness) Η τάση (stress) εφαρμόζεται σ ένα υλικό μέσω της φόρτισής του Παραμόρφωση
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
Σχήμα 1 Εξαιτίας της συνιστώσας F X αναπτύσσεται εντός του υλικού η ορθή τάση σ: N σ = A N 2 [ / ] Εξαιτίας της συνιστώσας F Υ αναπτύσσεται εντός του υλικού η διατμητική τάση τ: τ = mm Q 2 [ N / mm ] A
ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I
 ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I 1. ΕΙΣΑΓΩΓΗ Μηχανική συμπεριφορά αντανακλά την σχέση παραμόρφωση ασκούμενο φορτίο/δύναμη Να γνωρίζουμε τα χαρακτηριστικά του υλικού - να αποφευχθεί υπερβολική παραμόρφωση,
ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΜΕΤΑΛΛΩΝ I 1. ΕΙΣΑΓΩΓΗ Μηχανική συμπεριφορά αντανακλά την σχέση παραμόρφωση ασκούμενο φορτίο/δύναμη Να γνωρίζουμε τα χαρακτηριστικά του υλικού - να αποφευχθεί υπερβολική παραμόρφωση,
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κεραμικών και Πολυμερικών Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Εισαγωγή Όπως ήδη είδαμε, η μηχανική συμπεριφορά των υλικών αντανακλά
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κεραμικών και Πολυμερικών Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Εισαγωγή Όπως ήδη είδαμε, η μηχανική συμπεριφορά των υλικών αντανακλά
Δομικά Υλικά. Μάθημα ΙΙ. Μηχανικές Ιδιότητες των Δομικών Υλικών (Αντοχές, Παραμορφώσεις)
 Δομικά Υλικά Μάθημα ΙΙ Μηχανικές Ιδιότητες των Δομικών Υλικών (Αντοχές, Παραμορφώσεις) Μηχανικές Ιδιότητες Υλικών Τάση - Παραμόρφωση Ελαστική Συμπεριφορά Πλαστική Συμπεριφορά Αντοχή και Ολκιμότητα Σκληρότητα
Δομικά Υλικά Μάθημα ΙΙ Μηχανικές Ιδιότητες των Δομικών Υλικών (Αντοχές, Παραμορφώσεις) Μηχανικές Ιδιότητες Υλικών Τάση - Παραμόρφωση Ελαστική Συμπεριφορά Πλαστική Συμπεριφορά Αντοχή και Ολκιμότητα Σκληρότητα
3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΤΕΧΝΙΚΑ ΥΛΙΚΑ 3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Ε. Βιντζηλαίου (Συντονιστής), Ε. Βουγιούκας, Ε. Μπαδογιάννης Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΤΕΧΝΙΚΑ ΥΛΙΚΑ 3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Ε. Βιντζηλαίου (Συντονιστής), Ε. Βουγιούκας, Ε. Μπαδογιάννης Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
Σχήμα 1 Η εντατική κατάσταση στην οποία βρίσκεται μία δοκός, που υποβάλλεται σε εγκάρσια φόρτιση, λέγεται κάμψη. Αμφιέριστη δοκός Πρόβολος Κατά την καταπόνηση σε κάμψη αναπτύσσονται καμπτικές ροπές, οι
Πολυτεχνείο Κρήτης Σχολή Μηχανικών Παραγωγής και Διοίκησης
 Πολυτεχνείο Κρήτης Σχολή Μηχανικών Παραγωγής και Διοίκησης Διπλωματική εργασία Mελέτη δυναμικής απόκρισης κλασσικού και αυξητικού υλικού με τη μέθοδο πεπερασμένων στοιχείων Γεωργέλλης Αλέξανδρος Επιβλέπων
Πολυτεχνείο Κρήτης Σχολή Μηχανικών Παραγωγής και Διοίκησης Διπλωματική εργασία Mελέτη δυναμικής απόκρισης κλασσικού και αυξητικού υλικού με τη μέθοδο πεπερασμένων στοιχείων Γεωργέλλης Αλέξανδρος Επιβλέπων
10,2. 1,24 Τυπική απόκλιση, s 42
 Ασκηση 3.1 (a) Αν μία ράβδος οπλισμού θεωρηθεί ότι λυγίζει μεταξύ δύο διαδοχικών συνδετήρων με μήκος λυγισμού το μισό της απόστασης, s w, των συνδετήρων, να υπολογισθεί η απόσταση συνδετήρων, s w, πέραν
Ασκηση 3.1 (a) Αν μία ράβδος οπλισμού θεωρηθεί ότι λυγίζει μεταξύ δύο διαδοχικών συνδετήρων με μήκος λυγισμού το μισό της απόστασης, s w, των συνδετήρων, να υπολογισθεί η απόσταση συνδετήρων, s w, πέραν
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ. Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ. 1.
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΤΟΧΗΣ ΥΛΙΚΩΝ Γεώργιος Κ. Μπαράκος Διπλ. Αεροναυπηγός Μηχανικός Καθηγητής Τ.Ε.Ι. ΚΑΜΨΗ 1. Γενικά Με τη δοκιμή κάμψης ελέγχεται η αντοχή σε κάμψη δοκών από διάφορα
Μάθημα: Πειραματική Αντοχή Υλικών Πείραμα εφελκυσμού
 Μάθημα: Πειραματική Αντοχή Υλικών Πείραμα εφελκυσμού Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Περιεχόμενα Σχήμα 1 οκίμια εφελκυσμού
Μάθημα: Πειραματική Αντοχή Υλικών Πείραμα εφελκυσμού Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Περιεχόμενα Σχήμα 1 οκίμια εφελκυσμού
4/11/2017. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ
 105 Κεφάλαιο 5 ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ 5.1 Εισαγωγή Στα προηγούμενα κεφάλαια αναλύσαμε την εντατική κατάσταση σε δομικά στοιχεία τα οποία καταπονούνται κατ εξοχήν αξονικά (σε εφελκυσμό ή θλίψη) ή πάνω
105 Κεφάλαιο 5 ΘΕΩΡΙΕΣ ΑΣΤΟΧΙΑΣ ΥΛΙΚΩΝ 5.1 Εισαγωγή Στα προηγούμενα κεφάλαια αναλύσαμε την εντατική κατάσταση σε δομικά στοιχεία τα οποία καταπονούνται κατ εξοχήν αξονικά (σε εφελκυσμό ή θλίψη) ή πάνω
Εργαστήριο Τεχνολογίας Υλικών
 Εργαστήριο Τεχνολογίας Υλικών Εργαστηριακή Άσκηση 07 Εφελκυσμός Διδάσκοντες: Δρ Γεώργιος Ι. Γιαννόπουλος Δρ Θεώνη Ασημακοπούλου Δρ Θεόδωρος Λούτας Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών Πάτρα 2011 1 Μηχανικές
Εργαστήριο Τεχνολογίας Υλικών Εργαστηριακή Άσκηση 07 Εφελκυσμός Διδάσκοντες: Δρ Γεώργιος Ι. Γιαννόπουλος Δρ Θεώνη Ασημακοπούλου Δρ Θεόδωρος Λούτας Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών Πάτρα 2011 1 Μηχανικές
Γεωγραφική κατανομή σεισμικών δονήσεων τελευταίου αιώνα. Πού γίνονται σεισμοί?
 Τι είναι σεισμός? Γεωγραφική κατανομή σεισμικών δονήσεων τελευταίου αιώνα Πού γίνονται σεισμοί? h
Τι είναι σεισμός? Γεωγραφική κατανομή σεισμικών δονήσεων τελευταίου αιώνα Πού γίνονται σεισμοί? h
5. Θερμικές τάσεις και παραμορφώσεις
 5. Θερμικές τάσεις και παραμορφώσεις Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 5. Θερμικές Τάσεις και Παραμορφώσεις/ Μηχανική Υλικών 2015 1 Περιεχόμενα ενότητας Επίδραση ορθών τάσεων στη μεταβολή
5. Θερμικές τάσεις και παραμορφώσεις Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 5. Θερμικές Τάσεις και Παραμορφώσεις/ Μηχανική Υλικών 2015 1 Περιεχόμενα ενότητας Επίδραση ορθών τάσεων στη μεταβολή
20/10/2016. Δρ. Σωτήρης Δέμης. Εργαστηριακές Σημειώσεις Κάμψη Ξυλινης Δοκού. Πανεπιστημιακός Υπότροφος
 Εργαστηριακές Σημειώσεις Κάμψη Ξυλινης Δοκού Δρ. Σωτήρης Δέμης Πανεπιστημιακός Υπότροφος Τσιμεντοπολτός Περιλαμβάνονται διαγράμματα από τα βιβλία «Μηχανική των Υλικών» και «Δομικά Υλικά» του Αθανάσιου
Εργαστηριακές Σημειώσεις Κάμψη Ξυλινης Δοκού Δρ. Σωτήρης Δέμης Πανεπιστημιακός Υπότροφος Τσιμεντοπολτός Περιλαμβάνονται διαγράμματα από τα βιβλία «Μηχανική των Υλικών» και «Δομικά Υλικά» του Αθανάσιου
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Εισαγωγή στο Μάθημα Μηχανική των Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Εισαγωγή/ Μηχανική Υλικών 1 Χρονοδιάγραμμα 2017 Φεβρουάριος
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Εισαγωγή στο Μάθημα Μηχανική των Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Εισαγωγή/ Μηχανική Υλικών 1 Χρονοδιάγραμμα 2017 Φεβρουάριος
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Εφελκυσμού. ΕργαστηριακήΆσκηση2 η
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Εφελκυσμού ΕργαστηριακήΆσκηση2 η Κατηγορίες υλικών Μέταλλα Σιδηρούχαµέταλλα (ατσάλι, ανθρακούχοι, κραµατούχοι και ανοξείγωτοιχάλυβες, κ.α. Πολυµερικά υλικά Πλαστικά Ελαστοµερή Μη
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Εφελκυσμού ΕργαστηριακήΆσκηση2 η Κατηγορίες υλικών Μέταλλα Σιδηρούχαµέταλλα (ατσάλι, ανθρακούχοι, κραµατούχοι και ανοξείγωτοιχάλυβες, κ.α. Πολυµερικά υλικά Πλαστικά Ελαστοµερή Μη
Μηχανικές ιδιότητες συνθέτων υλικών: Θραύση. Άλκης Παϊπέτης Τμήμα Επιστήμης & Τεχνολογίας Υλικών
 Μηχανικές ιδιότητες συνθέτων υλικών: Θραύση Άλκης Παϊπέτης Τμήμα Επιστήμης & Τεχνολογίας Υλικών Μηχανική της θραύσης: Εισαγωγή Υποθέσεις: Τα υλικά συμπεριφέρονται γραμμικώς ελαστικά Οι ρωγμές (ή τα ελαττώματα)
Μηχανικές ιδιότητες συνθέτων υλικών: Θραύση Άλκης Παϊπέτης Τμήμα Επιστήμης & Τεχνολογίας Υλικών Μηχανική της θραύσης: Εισαγωγή Υποθέσεις: Τα υλικά συμπεριφέρονται γραμμικώς ελαστικά Οι ρωγμές (ή τα ελαττώματα)
Μάθημα: Πειραματική Αντοχή των Υλικών Πείραμα Κάμψης
 Μάθημα: Πειραματική Αντοχή των Υλικών Πείραμα Κάμψης Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Περιεχόμενα Σχήμα 1 Α. Ασημακόπουλος
Μάθημα: Πειραματική Αντοχή των Υλικών Πείραμα Κάμψης Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Περιεχόμενα Σχήμα 1 Α. Ασημακόπουλος
ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΥΝΑΜΙΚΗ ΣΥΣΤΗΜΑΤΩΝ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ έκδοση DΥΝI-DCMB_2016b Copyright
ΣΥΓΚΡΙΣΗ ΑΝΑΛΥΤΙΚΩΝ ΠΡΟΒΛΕΨΕΩΝ ΚΑΝΕΠΕ ΜΕ ΠΕΙΡΑΜΑΤΙΚΑ ΔΕΔΟΜΕΝΑ ΑΠΟ ΕΝΙΣΧΥΣΕΙΣ ΔΟΚΩΝ ΜΕ ΙΟΠ
 ΣΥΓΚΡΙΣΗ ΑΝΑΛΥΤΙΚΩΝ ΠΡΟΒΛΕΨΕΩΝ ΚΑΝΕΠΕ ΜΕ ΠΕΙΡΑΜΑΤΙΚΑ ΔΕΔΟΜΕΝΑ ΑΠΟ ΕΝΙΣΧΥΣΕΙΣ ΔΟΚΩΝ ΜΕ ΙΟΠ ΜΠΕΡΝΑΚΟΣ ΑΝΤΩΝΙΟΣ Περίληψη Στόχος της παρούσας εργασίας είναι η πρακτική εφαρμογή αναλυτικών προβλέψεων του ΚΑΝΕΠΕ
ΣΥΓΚΡΙΣΗ ΑΝΑΛΥΤΙΚΩΝ ΠΡΟΒΛΕΨΕΩΝ ΚΑΝΕΠΕ ΜΕ ΠΕΙΡΑΜΑΤΙΚΑ ΔΕΔΟΜΕΝΑ ΑΠΟ ΕΝΙΣΧΥΣΕΙΣ ΔΟΚΩΝ ΜΕ ΙΟΠ ΜΠΕΡΝΑΚΟΣ ΑΝΤΩΝΙΟΣ Περίληψη Στόχος της παρούσας εργασίας είναι η πρακτική εφαρμογή αναλυτικών προβλέψεων του ΚΑΝΕΠΕ
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2018 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα
5/14/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80)
 Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) 1 Βασική αρχή εργαστηριακής άσκησης Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία
Στοιχεία Μηχανών. Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά
 Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
Στοιχεία Μηχανών Εαρινό εξάμηνο 2017 Διδάσκουσα: Σωτηρία Δ. Χουλιαρά Ύλη μαθήματος -ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΜΗΧΑΝΙΚΗΣ ΥΛΙΚΩΝ -ΑΞΟΝΕΣ -ΚΟΧΛΙΕΣ -ΙΜΑΝΤΕΣ -ΟΔΟΝΤΩΤΟΙ ΤΡΟΧΟΙ ΒΑΘΜΟΛΟΓΙΑ ΜΑΘΗΜΑΤΟΣ: 25% πρόοδος 15% θέμα
4/26/2016. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία. Βασική αρχή εργαστηριακής άσκησης
 Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
Βασική αρχή εργαστηριακής άσκησης Σημειώσεις Εργαστηριακής Άσκησης Διάτμηση Κοχλία Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Αξονικό φορτίο Ανάπτυξη διατμητικών τάσεων σε στοιχεία σύνδεσης
ΚΕΦΑΛΑΙΟ. Οι γραμμικοί φορείς. 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων
 ΚΕΦΑΛΑΙΟ 1 Οι γραμμικοί φορείς 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων 2 1. Οι γραμμικοί φορείς 1.1 Εισαγωγή 3 1.1 Εισαγωγή Για να γίνει ο υπολογισμός μιας κατασκευής, θα πρέπει ο μελετητής μηχανικός
ΚΕΦΑΛΑΙΟ 1 Οι γραμμικοί φορείς 1.1 Εισαγωγή 1.2 Συστήματα συντεταγμένων 2 1. Οι γραμμικοί φορείς 1.1 Εισαγωγή 3 1.1 Εισαγωγή Για να γίνει ο υπολογισμός μιας κατασκευής, θα πρέπει ο μελετητής μηχανικός
6/5/2017. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Θλίψη Σκυροδέματος. Πολιτικός Μηχανικός (Λέκτορας Π.Δ.
 Σημειώσεις Εργαστηριακής Άσκησης Θλίψη Σκυροδέματος Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Έως τώρα Καταστατικός νόμος όλκιμων υλικών (αξονική καταπόνιση σε μία διεύθυνση) σ ε Συμπεριφορά
Σημειώσεις Εργαστηριακής Άσκησης Θλίψη Σκυροδέματος Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Λέκτορας Π.Δ. 407/80) Έως τώρα Καταστατικός νόμος όλκιμων υλικών (αξονική καταπόνιση σε μία διεύθυνση) σ ε Συμπεριφορά
ΜΕΤΑΛΛΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ (602)
 Τ.Ε.Ι. Θεσσαλίας Σχολή Τεχνολογικών Εφαρμογών (Σ.Τ.ΕΦ.) ΜΕΤΑΛΛΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ (602) 3 η Διάλεξη Δημήτριος Ν. Χριστοδούλου Δρ. Πολιτικός Μηχανικός, M.Sc. Τ.Ε.Ι. Θεσσαλίας - Σχολή Τεχνολογικών Εφαρμογών
Τ.Ε.Ι. Θεσσαλίας Σχολή Τεχνολογικών Εφαρμογών (Σ.Τ.ΕΦ.) ΜΕΤΑΛΛΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ (602) 3 η Διάλεξη Δημήτριος Ν. Χριστοδούλου Δρ. Πολιτικός Μηχανικός, M.Sc. Τ.Ε.Ι. Θεσσαλίας - Σχολή Τεχνολογικών Εφαρμογών
Γεωμετρικές Μέθοδοι Υπολογισμού Μετακινήσεων. Εισαγωγή ΜέθοδοςΔιπλήςΟλοκλήρωσης
 Γεωμετρικές Μέθοδοι Υπολογισμού Μετακινήσεων Εισαγωγή ΜέθοδοςΔιπλήςΟλοκλήρωσης Εισαγωγή Παραμορφώσεις Ισοστατικών Δοκών και Πλαισίων: Δ22-2 Οι κατασκευές, όταν υπόκεινται σε εξωτερική φόρτιση, αναπτύσσουν
Γεωμετρικές Μέθοδοι Υπολογισμού Μετακινήσεων Εισαγωγή ΜέθοδοςΔιπλήςΟλοκλήρωσης Εισαγωγή Παραμορφώσεις Ισοστατικών Δοκών και Πλαισίων: Δ22-2 Οι κατασκευές, όταν υπόκεινται σε εξωτερική φόρτιση, αναπτύσσουν
20/3/2016. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου. Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος)
 Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος) Εργαστηριακή Άσκηση 1 Εισαγωγή στη Δοκιμή Εφελκυσμού Δοκίμιο στερεωμένο ακλόνητα
Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος) Εργαστηριακή Άσκηση 1 Εισαγωγή στη Δοκιμή Εφελκυσμού Δοκίμιο στερεωμένο ακλόνητα
Περιεχόμενα Ευχαριστίες...3 Περίληψη Εισαγωγή Γενικά στοιχεία Σκοπός εργασίας Αυξητικά υλικά
 1 Περιεχόμενα Ευχαριστίες...3 Περίληψη...4 1. Εισαγωγή...5 1.1 Γενικά στοιχεία...5 1.2 Σκοπός εργασίας...6 2.Αυξητικά υλικά...7 2.1 Γενική περιγραφή...7 2.2 Αρνητικός λόγος Poisson...8 2.3 Εφαρμογές αυξητικών
1 Περιεχόμενα Ευχαριστίες...3 Περίληψη...4 1. Εισαγωγή...5 1.1 Γενικά στοιχεία...5 1.2 Σκοπός εργασίας...6 2.Αυξητικά υλικά...7 2.1 Γενική περιγραφή...7 2.2 Αρνητικός λόγος Poisson...8 2.3 Εφαρμογές αυξητικών
ΣYMMIKTEΣ KATAΣKEYEΣ KAI OPIZONTIA ΦOPTIA
 ΣYMMIKTEΣ KATAΣKEYEΣ KAI OPIZONTIA ΦOPTIA Άρης Αβδελάς, Καθηγητής Εργαστήριο Μεταλλικών Κατασκευών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τα δομικά συστήματα στις σύμμικτες κτιριακές κατασκευές, αποτελούνται
ΣYMMIKTEΣ KATAΣKEYEΣ KAI OPIZONTIA ΦOPTIA Άρης Αβδελάς, Καθηγητής Εργαστήριο Μεταλλικών Κατασκευών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τα δομικά συστήματα στις σύμμικτες κτιριακές κατασκευές, αποτελούνται
7. Στρέψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών. 7. Στρέψη/ Μηχανική Υλικών
 7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
7. Στρέψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 7. Στρέψη/ Μηχανική Υλικών 2015 1 Εισαγωγή Σε προηγούμενα κεφάλαια μελετήσαμε πώς να υπολογίζουμε τις ροπές και τις τάσεις σε δομικά μέλη τα
Επιστήμη των Υλικών. Πανεπιστήμιο Ιωαννίνων. Τμήμα Φυσικής
 Επιστήμη των Υλικών Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής 2017 Α. Δούβαλης Μηχανικές ιδιότητες των στερεών (μεταλλικά στερεά) Τάση και παραμόρφωση Τάση (stress): αίτιο (δύναμη/ροπή) που προκαλεί παραμόρφωση
Επιστήμη των Υλικών Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής 2017 Α. Δούβαλης Μηχανικές ιδιότητες των στερεών (μεταλλικά στερεά) Τάση και παραμόρφωση Τάση (stress): αίτιο (δύναμη/ροπή) που προκαλεί παραμόρφωση
ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΣΤΡΕΨΗ ΕΠΙΜΕΛΕΙΑ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Μηχανικές ιδιότητες Στρέψη κυλινδρικών ράβδων Ελαστική περιοχή Πλαστική
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΣΤΡΕΨΗ ΕΠΙΜΕΛΕΙΑ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Μηχανικές ιδιότητες Στρέψη κυλινδρικών ράβδων Ελαστική περιοχή Πλαστική
Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές
 Παράρτηµα Γ Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές 1. Εισαγωγή Το σύνολο των προγραµµάτων ALGOR είναι ένα εργαλείο µελέτης (σχεδιασµού και ανάλυσης) κατασκευών και βασίζεται στη µέθοδο
Παράρτηµα Γ Το πρόγραµµα ALGOR και εφαρµογές σε ναυπηγικές κατασκευές 1. Εισαγωγή Το σύνολο των προγραµµάτων ALGOR είναι ένα εργαλείο µελέτης (σχεδιασµού και ανάλυσης) κατασκευών και βασίζεται στη µέθοδο
«Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής»
 ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Β5. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Β5. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Παραµόρφωση σε Σηµείο Σώµατος. Μεταβολή του σχήµατος του στοιχείου (διατµητική παραµόρφωση)
 Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
Επιστήμη και Τεχνολογία Συγκολλήσεων. Ενότητα 9: Θραύση και κόπωση συγκολλήσεων Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών
 Επιστήμη και Τεχνολογία Συγκολλήσεων Ενότητα 9: Θραύση και κόπωση συγκολλήσεων Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Επιστήμη και Τεχνολογία Συγκολλήσεων Ενότητα 9: Θραύση και κόπωση συγκολλήσεων Γρηγόρης Ν. Χαϊδεμενόπουλος Πολυτεχνική Σχολή Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Μάθημα: Πειραματική αντοχή των υλικών Σύνθετη καταπόνηση
 Μάθημα: Πειραματική αντοχή των υλικών Σύνθετη καταπόνηση Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχήμα 1 Μέσω των πειραμάτων
Μάθημα: Πειραματική αντοχή των υλικών Σύνθετη καταπόνηση Κατασκευαστικός Τομέας Τμήμα Μηχανολόγων Μηχανικών Σχολή Τεχνολογικών Εφαρμογών Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Σχήμα 1 Μέσω των πειραμάτων
ΕΠΙΡΡΟΗ ΔΙΑΦΟΡΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΑ ΠΑΡΑΜΟΡΦΩΣΙΑΚΑ ΜΕΓΕΘΗ ΔΟΜΙΚΟΥ ΣΤΟΙΧΕΙΟΥ ΚΑΙ ΣΥΓΚΡΙΣΗ ΜΕ ΤΥΠΟΥΣ ΚΑΝ.ΕΠΕ
 Επιρροή διαφόρων παραγόντων στα παραμορφωσιακά μεγέθη δομικού στοιχείου και σύγκριση με τύπους ΚΑΝ.ΕΠΕ ΕΠΙΡΡΟΗ ΔΙΑΦΟΡΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΑ ΠΑΡΑΜΟΡΦΩΣΙΑΚΑ ΜΕΓΕΘΗ ΔΟΜΙΚΟΥ ΣΤΟΙΧΕΙΟΥ ΚΑΙ ΣΥΓΚΡΙΣΗ ΜΕ ΤΥΠΟΥΣ ΚΑΝ.ΕΠΕ
Επιρροή διαφόρων παραγόντων στα παραμορφωσιακά μεγέθη δομικού στοιχείου και σύγκριση με τύπους ΚΑΝ.ΕΠΕ ΕΠΙΡΡΟΗ ΔΙΑΦΟΡΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΑ ΠΑΡΑΜΟΡΦΩΣΙΑΚΑ ΜΕΓΕΘΗ ΔΟΜΙΚΟΥ ΣΤΟΙΧΕΙΟΥ ΚΑΙ ΣΥΓΚΡΙΣΗ ΜΕ ΤΥΠΟΥΣ ΚΑΝ.ΕΠΕ
Ευστάθεια μελών μεταλλικών κατασκευών
 Ευστάθεια μελών μεταλλικών κατασκευών Χάρης Ι. Γαντές Αναπληρωτής Καθηγητής Χαλύβδινες και Σύμμικτες Κατασκευές Επιστημονικό Σεμινάριο Μυτιλήνη 9-10 Οκτωβρίου 009 Περιεχόμενα παρουσίασης Εισαγωγή Μορφές
Ευστάθεια μελών μεταλλικών κατασκευών Χάρης Ι. Γαντές Αναπληρωτής Καθηγητής Χαλύβδινες και Σύμμικτες Κατασκευές Επιστημονικό Σεμινάριο Μυτιλήνη 9-10 Οκτωβρίου 009 Περιεχόμενα παρουσίασης Εισαγωγή Μορφές
Σχήμα 1: Διάταξη δοκιμίου και όργανα μέτρησης 1 BUILDNET
 Παραμετρική ανάλυση κοχλιωτών συνδέσεων με μετωπική πλάκα χρησιμοποιώντας πεπερασμένα στοιχεία Χριστόφορος Δημόπουλος, Πολιτικός Μηχανικός, Υποψήφιος Διδάκτωρ ΕΜΠ Περίληψη Η εν λόγω εργασία παρουσιάζει
Παραμετρική ανάλυση κοχλιωτών συνδέσεων με μετωπική πλάκα χρησιμοποιώντας πεπερασμένα στοιχεία Χριστόφορος Δημόπουλος, Πολιτικός Μηχανικός, Υποψήφιος Διδάκτωρ ΕΜΠ Περίληψη Η εν λόγω εργασία παρουσιάζει
Διεπιφανειακοί Δεσμοί
 Διεπιφανειακοί Δεσμοί (a) Διάφοροι τύποι μοριακή διάχυση (b) (c) ηλεκτροστατική έλξη δευτερογενής πρόσφυση (d) (e) χημικός (ομοιοπολικός) δεσμός μηχανική πρόσφυση 1 Είδη Διεπιφανειακών Δεσμών Yπάρχουν
Διεπιφανειακοί Δεσμοί (a) Διάφοροι τύποι μοριακή διάχυση (b) (c) ηλεκτροστατική έλξη δευτερογενής πρόσφυση (d) (e) χημικός (ομοιοπολικός) δεσμός μηχανική πρόσφυση 1 Είδη Διεπιφανειακών Δεσμών Yπάρχουν
ΠΑΡΑΜΕΝΟΥΣΕΣ ΤΑΣΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΣΕ ΣΥΓΚΟΛΛΗΣΕΙΣ ΤΗΞΕΩΣ
 ΠΑΡΑΜΕΝΟΥΣΕΣ ΤΑΣΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΣΕ ΣΥΓΚΟΛΛΗΣΕΙΣ ΤΗΞΕΩΣ Τοπική θέρμανση συγκολλούμενων τεμαχίων Ανομοιόμορφη κατανομή θερμοκρασιών, πουμεαβάλλεταιμετοχρόνο Θερμικές παραμορφώσεις στο μέταλλο προσθήκης
ΠΑΡΑΜΕΝΟΥΣΕΣ ΤΑΣΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΕΙΣ ΣΕ ΣΥΓΚΟΛΛΗΣΕΙΣ ΤΗΞΕΩΣ Τοπική θέρμανση συγκολλούμενων τεμαχίων Ανομοιόμορφη κατανομή θερμοκρασιών, πουμεαβάλλεταιμετοχρόνο Θερμικές παραμορφώσεις στο μέταλλο προσθήκης
ΕΛΑΣΤΙΚΟΣ ΛΥΓΙΣΜΟΣ ΥΠΟΣΤΥΛΩΜΑΤΩΝ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΛΑΣΤΙΚΟΣ ΛΥΓΙΣΜΟΣ ΥΠΟΣΤΥΛΩΜΑΤΩΝ Λυγισμός - Ευστάθεια Κρίσιμο φορτίο λυγισμού Δρ. Σ. Π. Φιλόπουλος Εισαγωγή Μέχρι στιγμής στην ανάλυση των κατασκευών επικεντρώσαμε
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΛΑΣΤΙΚΟΣ ΛΥΓΙΣΜΟΣ ΥΠΟΣΤΥΛΩΜΑΤΩΝ Λυγισμός - Ευστάθεια Κρίσιμο φορτίο λυγισμού Δρ. Σ. Π. Φιλόπουλος Εισαγωγή Μέχρι στιγμής στην ανάλυση των κατασκευών επικεντρώσαμε
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΟΧΗΜΑΤΩΝ
 2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
2. ΣΤΑΤΙΚΗ Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στη δοκό του σχήματος: Να χαραχθούν τα διαγράμματα [Ν], [Q], [M] στον φορέα του σχήματος: Ασκήσεις υπολογισμού τάσεων Άσκηση 1 η (Αξονικός εφελκυσμός
ΕΝΙΣΧΥΣΗ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΣΕ ΔΙΑΤΜΗΣΗ
 49 ΚΕΦΑΛΑΙΟ 5 ΕΝΙΣΧΥΣΗ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΣΕ ΔΙΑΤΜΗΣΗ 5.1 Γενικά Η ενίσχυση στοιχείων οπλισμένου σκυροδέματος σε διάτμηση με σύνθετα υλικά επιτυγχάνεται μέσω της επικόλλησης υφασμάτων ή, σπανιότερα,
49 ΚΕΦΑΛΑΙΟ 5 ΕΝΙΣΧΥΣΗ ΟΠΛΙΣΜΕΝΟΥ ΣΚΥΡΟΔΕΜΑΤΟΣ ΣΕ ΔΙΑΤΜΗΣΗ 5.1 Γενικά Η ενίσχυση στοιχείων οπλισμένου σκυροδέματος σε διάτμηση με σύνθετα υλικά επιτυγχάνεται μέσω της επικόλλησης υφασμάτων ή, σπανιότερα,
Φυσικές & Μηχανικές Ιδιότητες
 Μάθημα 5 ο Ποιες είναι οι Ιδιότητες των Υλικών ; Φυσικές & Μηχανικές Ιδιότητες Κατεργαστικότητα & Αναφλεξιμότητα Εφελκυσμός Θλίψη Έλεγχοι των Υλικών Φορτίσεις -1 ιάτμηση Στρέψη Έλεγχοι των Υλικών Φορτίσεις
Μάθημα 5 ο Ποιες είναι οι Ιδιότητες των Υλικών ; Φυσικές & Μηχανικές Ιδιότητες Κατεργαστικότητα & Αναφλεξιμότητα Εφελκυσμός Θλίψη Έλεγχοι των Υλικών Φορτίσεις -1 ιάτμηση Στρέψη Έλεγχοι των Υλικών Φορτίσεις
16/4/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου. Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος)
 Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος) Το υλικό «πονάει». Πως; Πόσο; P P Εξωτερικό εφελκυστικό φορτίο P N = P N
Σημειώσεις Εργαστηριακής Άσκησης Εφελκυσμός χαλύβδινης ράβδου Δρ. Σωτήρης Δέμης Πολιτικός Μηχανικός (Πανεπιστημιακός Υπότροφος) Το υλικό «πονάει». Πως; Πόσο; P P Εξωτερικό εφελκυστικό φορτίο P N = P N
Εργαστήριο Συνθέτων Υλικών
 Εργαστήριο Συνθέτων Υλικών Εργαστηριακή Άσκηση 04 ΥΛΙΚΑ ΕΝΙΣΧΥΣΗΣ Διδάσκων Δρ Κατσιρόπουλος Χρήστος Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών 2014-15 1 Ταξινόμηση ΣΥ 2 Διάφοροι Τύποι ινών 3 Ίνες Άνθρακα -υψηλές ειδικές
Εργαστήριο Συνθέτων Υλικών Εργαστηριακή Άσκηση 04 ΥΛΙΚΑ ΕΝΙΣΧΥΣΗΣ Διδάσκων Δρ Κατσιρόπουλος Χρήστος Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών 2014-15 1 Ταξινόμηση ΣΥ 2 Διάφοροι Τύποι ινών 3 Ίνες Άνθρακα -υψηλές ειδικές
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Πειραματική Αντοχή Υλικών. Ενότητα: Μονοαξονική Θλίψη
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πειραματική Αντοχή Υλικών Ενότητα: Μονοαξονική Θλίψη Κωνσταντίνος Ι.Γιαννακόπουλος Τμήμα Μηχανολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πειραματική Αντοχή Υλικών Ενότητα: Μονοαξονική Θλίψη Κωνσταντίνος Ι.Γιαννακόπουλος Τμήμα Μηχανολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό
6. Κάμψη. Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών
 6. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας Ακτίνα καμπυλότητας 2 Εισαγωγή (1/2) Μελετήσαμε
6. Κάμψη Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενα ενότητας Ανάλυση της κάμψης Κατανομή ορθών τάσεων Ουδέτερη γραμμή Ροπές αδρανείας Ακτίνα καμπυλότητας 2 Εισαγωγή (1/2) Μελετήσαμε
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης. ΕργαστηριακήΆσκηση 3 η
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης ΕργαστηριακήΆσκηση 3 η Σκοπός Σκοπός του πειράµατος είναι ηκατανόησητωνδιαδικασιώνκατάτηκαταπόνησηστρέψης, η κατανόηση του διαγράµµατος διατµητικής τάσης παραµόρφωσης η ικανότητα
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Στρέψης ΕργαστηριακήΆσκηση 3 η Σκοπός Σκοπός του πειράµατος είναι ηκατανόησητωνδιαδικασιώνκατάτηκαταπόνησηστρέψης, η κατανόηση του διαγράµµατος διατµητικής τάσης παραµόρφωσης η ικανότητα
Σιδηρές Κατασκευές Ι. Άσκηση 7: Δικτύωμα πεζογέφυρας (εφελκυσμός, κάμψη και διάτμηση κάτω πέλματος) Δρ. Χάρης Γαντές, Καθηγητής ΕΜΠ
 Σιδηρές Κατασκευές Ι Άσκηση 7: Δικτύωμα πεζογέφυρας (εφελκυσμός, κάμψη και διάτμηση κάτω πέλματος) Δρ. Χάρης Γαντές, Καθηγητής ΕΜΠ Σχολή Πολιτικών Μηχανικών Εργαστήριο Μεταλλικών Κατασκευών Άδειες Χρήσης
Σιδηρές Κατασκευές Ι Άσκηση 7: Δικτύωμα πεζογέφυρας (εφελκυσμός, κάμψη και διάτμηση κάτω πέλματος) Δρ. Χάρης Γαντές, Καθηγητής ΕΜΠ Σχολή Πολιτικών Μηχανικών Εργαστήριο Μεταλλικών Κατασκευών Άδειες Χρήσης
ΠΡΟΣΟΜΟΙΩΜΑΤΑ ΚΤΙΡΙΩΝ ΑΠΌ ΦΕΡΟΥΣΑ ΤΟΙΧΟΠΟΙΙΑ ΓΙΑ ΣΕΙΣΜΙΚΕΣ ΔΡΑΣΕΙΣ Προσομοίωση κτιρίων από τοιχοποιία με : 1) Πεπερασμένα στοιχεία 2) Γραμμικά στοιχεί
 ΠΡΟΣΟΜΟΙΩΜΑΤΑ ΚΤΙΡΙΩΝ ΑΠΌ ΦΕΡΟΥΣΑ ΤΟΙΧΟΠΟΙΙΑ ΓΙΑ ΣΕΙΣΜΙΚΕΣ ΔΡΑΣΕΙΣ Η σεισμική συμπεριφορά κτιρίων από φέρουσα τοιχοποιία εξαρτάται κυρίως από την ύπαρξη ή όχι οριζόντιου διαφράγματος. Σε κτίρια από φέρουσα
ΠΡΟΣΟΜΟΙΩΜΑΤΑ ΚΤΙΡΙΩΝ ΑΠΌ ΦΕΡΟΥΣΑ ΤΟΙΧΟΠΟΙΙΑ ΓΙΑ ΣΕΙΣΜΙΚΕΣ ΔΡΑΣΕΙΣ Η σεισμική συμπεριφορά κτιρίων από φέρουσα τοιχοποιία εξαρτάται κυρίως από την ύπαρξη ή όχι οριζόντιου διαφράγματος. Σε κτίρια από φέρουσα
Διατμητική αστοχία τοιχώματος ισογείου. Διατμητική αστοχία υποστυλώματος λόγω κλιμακοστασίου
 Διατμητική αστοχία τοιχώματος ισογείου Διατμητική αστοχία υποστυλώματος λόγω κλιμακοστασίου Ανάλογα με τη στατική φόρτιση δημιουργούνται περιοχές στο φορέα όπου έχουμε καθαρή κάμψη ή καμπτοδιάτμηση. m(x)
Διατμητική αστοχία τοιχώματος ισογείου Διατμητική αστοχία υποστυλώματος λόγω κλιμακοστασίου Ανάλογα με τη στατική φόρτιση δημιουργούνται περιοχές στο φορέα όπου έχουμε καθαρή κάμψη ή καμπτοδιάτμηση. m(x)
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Κρούσης. ΕργαστηριακήΆσκηση 6 η
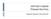 ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Κρούσης ΕργαστηριακήΆσκηση 6 η Σκοπός Σκοπός του πειράµατος είναι να κατανοηθούν οι αρχές του πειράµατος κρούσης οπροσδιορισµόςτουσυντελεστήδυσθραυστότητας ενόςυλικού. Η δοκιµή, είναι
ΑΝΤΟΧΗ ΥΛΙΚΩΝ Πείραμα Κρούσης ΕργαστηριακήΆσκηση 6 η Σκοπός Σκοπός του πειράµατος είναι να κατανοηθούν οι αρχές του πειράµατος κρούσης οπροσδιορισµόςτουσυντελεστήδυσθραυστότητας ενόςυλικού. Η δοκιµή, είναι
Βασικές Αρχές Σχεδιασμού Υλικά
 Βασικές Αρχές Σχεδιασμού Υλικά Δομική Μηχανική ΙΙΙ Χρ. Ζέρης Σχολή Πολιτικών Μηχανικών, ΕΜΠ Το Ευρωπαϊκό πλαίσιο Μελετών και Εκτέλεσης έργων ΕΝ 10080 Χάλυβας οπλισμού Νοέμ. 2013 Χ. Ζέρης 2 ΕΚΩΣ, ΕΝ1992:
Βασικές Αρχές Σχεδιασμού Υλικά Δομική Μηχανική ΙΙΙ Χρ. Ζέρης Σχολή Πολιτικών Μηχανικών, ΕΜΠ Το Ευρωπαϊκό πλαίσιο Μελετών και Εκτέλεσης έργων ΕΝ 10080 Χάλυβας οπλισμού Νοέμ. 2013 Χ. Ζέρης 2 ΕΚΩΣ, ΕΝ1992:
Φυσικές ιδιότητες οδοντικών υλικών
 Φυσικές ιδιότητες οδοντικών υλικών Η γνώση των µηχανικών ιδιοτήτων των υλικών είναι ουσιώδης για την επιλογή ενδεδειγµένης χρήσης και την µακρόχρονη λειτουργικότητά τους. Στη στοµατική κοιλότητα διαµορφώνεται
Φυσικές ιδιότητες οδοντικών υλικών Η γνώση των µηχανικών ιδιοτήτων των υλικών είναι ουσιώδης για την επιλογή ενδεδειγµένης χρήσης και την µακρόχρονη λειτουργικότητά τους. Στη στοµατική κοιλότητα διαµορφώνεται
ιάλεξη 7 η, 8 η και 9 η
 ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι ιάλεξη 7 η, 8 η και 9 η Ανάλυση Ισοστατικών οκών και Πλαισίων Τρίτη,, 21, Τετάρτη,, 22 και Παρασκευή 24 Σεπτεµβρίου,, 2004 Πέτρος Κωµοδρόµος komodromos@ucy.ac.cy
ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι ιάλεξη 7 η, 8 η και 9 η Ανάλυση Ισοστατικών οκών και Πλαισίων Τρίτη,, 21, Τετάρτη,, 22 και Παρασκευή 24 Σεπτεµβρίου,, 2004 Πέτρος Κωµοδρόµος komodromos@ucy.ac.cy
AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) 371 AΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ΑΥΤΟΑΞΙΟΛΟΓΗΣΗΣ (ΚΕΦ. 6-11) ΑΣΚΗΣΗ 1 Το µηκυνσιόµετρο στο σηµείο Α της δοκού του σχήµατος καταγράφει θλιπτική παραµόρφωση ίση µε 0.05. Πόση
Δυναμική Αντοχή. Σύνδεση με προηγούμενο μάθημα. Περιεχόμενα F = A V = M r = J. Δυναμική καταπόνηση κόπωση. Καμπύλη Woehler.
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Δυναμική Αντοχή Σύνδεση με προηγούμενο μάθημα Καμπύλη τάσης παραμόρφωσης Βασικές φορτίσεις A V y A M y M x M I
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Μάθημα: ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΩΝ Δυναμική Αντοχή Σύνδεση με προηγούμενο μάθημα Καμπύλη τάσης παραμόρφωσης Βασικές φορτίσεις A V y A M y M x M I
Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών
 Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ- 2015 1. Εισαγωγικές έννοιες στην μηχανική των υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών 1 Περιεχόμενο μαθήματος Μηχανική των Υλικών: τμήμα των θετικών επιστημών που
Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία
 1 Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία 2 Μετωπικό φραιζάρισμα: Χρησιμοποιείται κυρίως στις αρχικές φάσεις της κατεργασίας (φάση εκχόνδρισης) Μεγάλη διάμετρο Μεγάλες προώσεις μείωση
1 Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία 2 Μετωπικό φραιζάρισμα: Χρησιμοποιείται κυρίως στις αρχικές φάσεις της κατεργασίας (φάση εκχόνδρισης) Μεγάλη διάμετρο Μεγάλες προώσεις μείωση
Έλεγχος Ποιότητας και Τεχνολογία Δομικών Υλικών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Έλεγχος Ποιότητας και Τεχνολογία Δομικών Υλικών Ενότητα 4: Δοκιμή Εφελκυσμού Χάλυβα Οπλισμού Σκυροδέματος Ευάγγελος Φουντουκίδης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Έλεγχος Ποιότητας και Τεχνολογία Δομικών Υλικών Ενότητα 4: Δοκιμή Εφελκυσμού Χάλυβα Οπλισμού Σκυροδέματος Ευάγγελος Φουντουκίδης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ. Αντοχή Υλικού
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ Αντοχή Υλικού Ερρίκος Μουρατίδης (BSc, MSc) Σεπτέμβριος 015 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ Αντοχή Υλικού Ερρίκος Μουρατίδης (BSc, MSc) Σεπτέμβριος 015 Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τελική γραπτή εξέταση διάρκειας 2,5 ωρών
 τηλ: 410-74178, fax: 410-74169, www.uth.gr Τελική γραπτή εξέταση διάρκειας,5 ωρών Ονοματεπώνυμο: Αριθμός Μητρώου Φοιτητή: Μάθημα: Εδαφομηχανική Ι, 5 ο εξάμηνο. Διδάσκων: Ιωάννης-Ορέστης Σ. Γεωργόπουλος,
τηλ: 410-74178, fax: 410-74169, www.uth.gr Τελική γραπτή εξέταση διάρκειας,5 ωρών Ονοματεπώνυμο: Αριθμός Μητρώου Φοιτητή: Μάθημα: Εδαφομηχανική Ι, 5 ο εξάμηνο. Διδάσκων: Ιωάννης-Ορέστης Σ. Γεωργόπουλος,
Η ΑΝΤΟΧΗ ΤΟΥ ΠΛΟΙΟΥ. Αντικείμενο της αντοχής του πλοίου. Έλεγχος της κατασκευής του πλοίου
 Η ΑΝΤΟΧΗ ΤΟΥ ΠΛΟΙΟΥ Αντικείμενο της αντοχής του πλοίου Αντικείμενο της αντοχής του πλοίου είναι η μελέτη της κατασκευής του πλοίου σε σχέση με την ικανότητα της να φέρει ασφαλώς τις κάθε είδους δράσεις
Η ΑΝΤΟΧΗ ΤΟΥ ΠΛΟΙΟΥ Αντικείμενο της αντοχής του πλοίου Αντικείμενο της αντοχής του πλοίου είναι η μελέτη της κατασκευής του πλοίου σε σχέση με την ικανότητα της να φέρει ασφαλώς τις κάθε είδους δράσεις
ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ ΠΑΡΑΔΕΙΓΜΑ 1: Ο κύλινδρος που φαίνεται στο σχήμα είναι από χάλυβα που έχει ένα ειδικό βάρος 80.000 N/m 3. Υπολογίστε την θλιπτική τάση που ενεργεί στα σημεία Α και
ΠΑΡΑΔΕΙΓΜΑΤΑ ΑΞΟΝΙΚΟΣ ΕΦΕΛΚΥΣΜΟΣ, ΘΛΙΨΗ ΠΑΡΑΔΕΙΓΜΑ 1: Ο κύλινδρος που φαίνεται στο σχήμα είναι από χάλυβα που έχει ένα ειδικό βάρος 80.000 N/m 3. Υπολογίστε την θλιπτική τάση που ενεργεί στα σημεία Α και
Γενικευμένα Mονοβάθμια Συστήματα
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
ιαλέξεις Παρασκευή 8 Οκτωβρίου,, Πέτρος Κωµοδρόµος Στατική Ανάλυση των Κατασκευών Ι 1
 ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι ιαλέξεις 13-15 Εισαγωγή στις Παραµορφώσεις και Μετακινήσεις Τρίτη, 5, και Τετάρτη, 6 και Παρασκευή 8 Οκτωβρίου,, 2004 Πέτρος Κωµοδρόµος komodromos@ucy.ac.cy http://www.ucy.ac.cy/~petrosk
ΠΠΜ 220: Στατική Ανάλυση των Κατασκευών Ι ιαλέξεις 13-15 Εισαγωγή στις Παραµορφώσεις και Μετακινήσεις Τρίτη, 5, και Τετάρτη, 6 και Παρασκευή 8 Οκτωβρίου,, 2004 Πέτρος Κωµοδρόµος komodromos@ucy.ac.cy http://www.ucy.ac.cy/~petrosk
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
ΣΧΕΔΙΑΣΗ ΑΤΡΑΚΤΩΝ. Λειτουργικές Παράμετροι
 Άτρακτος: περιστρεφόμενο στοιχείο κυκλικής (συνήθως) διατομής (πλήρους ή σωληνωτής) που χρησιμοποιείται για να μεταφέρει ισχύ ή κίνηση Άξονας: μη περιστρεφόμενο στοιχείο που δεν μεταφέρει ροπή και χρησιμοποιείται
Άτρακτος: περιστρεφόμενο στοιχείο κυκλικής (συνήθως) διατομής (πλήρους ή σωληνωτής) που χρησιμοποιείται για να μεταφέρει ισχύ ή κίνηση Άξονας: μη περιστρεφόμενο στοιχείο που δεν μεταφέρει ροπή και χρησιμοποιείται
Γ. ΥΠΟΛΟΓΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M)
 . ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
. ΥΠΟΛΟΙΣΜΟΣ ΦΟΡΤΙΩΝ ΔΙΑΤΟΜΗΣ (N, Q, M). Ορισμοί φορτίσεων μίας δοκού Οι φορτίσεις που μπορεί να εμφανισθούν σ'ένα σώμα είναι ο εφελκυσμός (ή η θλίψη με κίνδυνο λογισμού), η διάτμηση, η κάμψη και η στρέψη.
Οριακή κατάσταση αστοχίας έναντι ιάτµησης-στρέψης- ιάτρησης
 Σχεδιασµός φορέων από σκυρόδεµα µε βάση τον Ευρωκώδικα 2 Οριακή κατάσταση αστοχίας έναντι ιάτµησης-στρέψης- ιάτρησης Καττής Μαρίνος, Αναπληρωτής Καθηγητής ΕΜΠ Λιβαδειά, 26 Σεπτεµβρίου 2009 1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ
Σχεδιασµός φορέων από σκυρόδεµα µε βάση τον Ευρωκώδικα 2 Οριακή κατάσταση αστοχίας έναντι ιάτµησης-στρέψης- ιάτρησης Καττής Μαρίνος, Αναπληρωτής Καθηγητής ΕΜΠ Λιβαδειά, 26 Σεπτεµβρίου 2009 1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ
ΕΡΩΤΗΣΕΙΣ ΕΜΒΑΘΥΝΣΗΣ
 ΕΡΩΤΗΣΕΙΣ ΕΜΒΑΘΥΝΣΗΣ Α. ΔΙΑΜΟΡΦΩΣΕΙΣ ΠΛΑΣΤΙΚΗ ΠΑΡΑΜΟΡΦΩΣΗ ΣΤΗΝ ΕΥΣΤΑΘΗ ΠΕΡΙΟΧΗ Α.1. Ποια οικογένεια υλικών αφορά η μορφοποίησή τους με διαμόρφωση; Χρησιμοποιώντας ένα τυπικό διάγραμμα εφελκυσμού, αναφέρετε
ΕΡΩΤΗΣΕΙΣ ΕΜΒΑΘΥΝΣΗΣ Α. ΔΙΑΜΟΡΦΩΣΕΙΣ ΠΛΑΣΤΙΚΗ ΠΑΡΑΜΟΡΦΩΣΗ ΣΤΗΝ ΕΥΣΤΑΘΗ ΠΕΡΙΟΧΗ Α.1. Ποια οικογένεια υλικών αφορά η μορφοποίησή τους με διαμόρφωση; Χρησιμοποιώντας ένα τυπικό διάγραμμα εφελκυσμού, αναφέρετε
Παραδείγματα μελών υπό αξονική θλίψη
 Παραδείγματα μελών υπό αξονική θλίψη Παραδείγματα μελών υπό αξονική θλίψη Η έννοια του λυγισμού Λυγισμός είναι η ξαφνική, μεγάλη αύξηση των παραμορφώσεων ενός φορέα για μικρή αύξηση των επιβαλλόμενων φορτίων.
Παραδείγματα μελών υπό αξονική θλίψη Παραδείγματα μελών υπό αξονική θλίψη Η έννοια του λυγισμού Λυγισμός είναι η ξαφνική, μεγάλη αύξηση των παραμορφώσεων ενός φορέα για μικρή αύξηση των επιβαλλόμενων φορτίων.
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΕΠΙΛΟΓΗΣ ΥΛΙΚΟΥ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΕΠΙΛΟΓΗΣ ΥΛΙΚΟΥ Τελική Χρήση/ Περιβάλλον λειτουργίας* Σχεδιασµός Μηχανολογική σχεδίαση Μεµονωµένα εξαρτήµατα Συνολική κατασκευή Επιλογή υλικού Κατασκευή Μορφοποίηση µερών Μηχανουργική κατεργασία
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΕΠΙΛΟΓΗΣ ΥΛΙΚΟΥ Τελική Χρήση/ Περιβάλλον λειτουργίας* Σχεδιασµός Μηχανολογική σχεδίαση Μεµονωµένα εξαρτήµατα Συνολική κατασκευή Επιλογή υλικού Κατασκευή Μορφοποίηση µερών Μηχανουργική κατεργασία
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ. Ασκήσεις προηγούμενων εξετάσεων ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΚΑΙ ΑΓΡΟΤΙΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ασκήσεις προηγούμενων
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2016 Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr 1 Περιεχόμενα ενότητας Α Βασικές έννοιες Στατική υλικού σημείου Αξιωματικές αρχές Νόμοι Νεύτωνα Εξισώσεις
Ενότητα: Υπολογισμός διατμητικών τάσεων
 ΔΙΑΜΗΚΗΣ ΑΝΤΟΧΗ ΠΛΟΙΟΥ Ενότητα: Υπολογισμός διατμητικών τάσεων Α. Θεοδουλίδης Υπολογισμός διατμητικών τάσεων Η ύπαρξη διατμητικών τάσεων οφείλεται στην διατμητική δύναμη Q(x): Κατανομή διατμητικών τάσεων
ΔΙΑΜΗΚΗΣ ΑΝΤΟΧΗ ΠΛΟΙΟΥ Ενότητα: Υπολογισμός διατμητικών τάσεων Α. Θεοδουλίδης Υπολογισμός διατμητικών τάσεων Η ύπαρξη διατμητικών τάσεων οφείλεται στην διατμητική δύναμη Q(x): Κατανομή διατμητικών τάσεων
Η σκληρότητα των πετρωμάτων ως γνωστόν, καθορίζεται από την αντίσταση που αυτά παρουσιάζουν κατά τη χάραξή τους
 Η σκληρότητα των πετρωμάτων ως γνωστόν, καθορίζεται από την αντίσταση που αυτά παρουσιάζουν κατά τη χάραξή τους σφυρί αναπήδησης Schmidt τύπου L (Schmidt rebound hammer) Κατηγορία πετρωμάτων Μέση ένδειξη
Η σκληρότητα των πετρωμάτων ως γνωστόν, καθορίζεται από την αντίσταση που αυτά παρουσιάζουν κατά τη χάραξή τους σφυρί αναπήδησης Schmidt τύπου L (Schmidt rebound hammer) Κατηγορία πετρωμάτων Μέση ένδειξη
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σχήμα 1 Τεχνικής Μηχανικής Διαγράμματα Ελευθέρου Σώματος (Δ.Ε.Σ.) Υπολογισμός Αντιδράσεων Διαγράμματα Φορτίσεων Διατομών (MNQ) Αντοχή Φορέα? Αντικείμενο Τεχνικής Μηχανικής Σχήμα 2 F Y A Γ B A Y B Y 1000N
Σεισμολογία. Ελαστική Τάση, Παραμόρφωση (Κεφ.2, Σύγχρονη Σεισμολογία) Σώκος Ευθύμιος
 Σεισμολογία Μάθημα 2: Ελαστική Τάση, Παραμόρφωση (Κεφ.2, Σύγχρονη Σεισμολογία) Σώκος Ευθύμιος Τάση (τι έχουμε πει έως τώρα?) Η τάση μπορεί να αναλυθεί σε κάθετη στην επιφάνεια (ορθή) και σε εφαπτομενική,
Σεισμολογία Μάθημα 2: Ελαστική Τάση, Παραμόρφωση (Κεφ.2, Σύγχρονη Σεισμολογία) Σώκος Ευθύμιος Τάση (τι έχουμε πει έως τώρα?) Η τάση μπορεί να αναλυθεί σε κάθετη στην επιφάνεια (ορθή) και σε εφαπτομενική,
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ - 2017 Β3. Κόπωση Υλικών Κώστας Γαλιώτης, καθηγητης Τμήματος Χημικών Μηχανικών galiotis@chemeng.upatras.gr Β3. Κόπωση/Μηχανική Υλικών 1 Εισαγωγή (1/2) Η κόπωση είναι μία μορφή αστοχίας
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ - 2017 Β3. Κόπωση Υλικών Κώστας Γαλιώτης, καθηγητης Τμήματος Χημικών Μηχανικών galiotis@chemeng.upatras.gr Β3. Κόπωση/Μηχανική Υλικών 1 Εισαγωγή (1/2) Η κόπωση είναι μία μορφή αστοχίας
11. Χρήση Λογισμικού Ανάλυσης Κατασκευών
 ΠΠΜ 325: Ανάλυση Κατασκευών με Η/Υ 11. Χρήση Λογισμικού Ανάλυσης Κατασκευών Εαρινό εξάμηνο 2015 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Μοντελοποίηση κατασκευής
ΠΠΜ 325: Ανάλυση Κατασκευών με Η/Υ 11. Χρήση Λογισμικού Ανάλυσης Κατασκευών Εαρινό εξάμηνο 2015 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Μοντελοποίηση κατασκευής
προς τον προσδιορισμό εντατικών μεγεθών, τα οποία μπορούν να υπολογιστούν με πολλά εμπορικά λογισμικά.
 ΜΕΤΑΛΛΟΝ [ ΑΝΤΟΧΗ ΑΜΦΙΑΡΘΡΩΤΩΝ ΚΥΚΛΙΚΩΝ ΤΟΞΩΝ ΚΟΙΛΗΣ ΚΥΚΛΙΚΗΣ ΔΙΑΤΟΜΗΣ ΥΠΟ ΟΜΟΙΟΜΟΡΦΑ ΚΑΤΑΝΕΜΗΜΕΝΟ ΚΑΤΑΚΟΡΥΦΟ ΦΟΡΤΙΟ ΚΑΤΑ ΤΟΝ ΕΚ3 Χάρης Ι. Γαντές Δρ. Πολιτικός Μηχανικός, Αναπληρωτής Καθηγητής & Χριστόφορος
ΜΕΤΑΛΛΟΝ [ ΑΝΤΟΧΗ ΑΜΦΙΑΡΘΡΩΤΩΝ ΚΥΚΛΙΚΩΝ ΤΟΞΩΝ ΚΟΙΛΗΣ ΚΥΚΛΙΚΗΣ ΔΙΑΤΟΜΗΣ ΥΠΟ ΟΜΟΙΟΜΟΡΦΑ ΚΑΤΑΝΕΜΗΜΕΝΟ ΚΑΤΑΚΟΡΥΦΟ ΦΟΡΤΙΟ ΚΑΤΑ ΤΟΝ ΕΚ3 Χάρης Ι. Γαντές Δρ. Πολιτικός Μηχανικός, Αναπληρωτής Καθηγητής & Χριστόφορος
9. Χρήση Λογισμικού Ανάλυσης Κατασκευών
 9. Χρήση Λογισμικού Ανάλυσης Κατασκευών Χειμερινό εξάμηνο 2016 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Μοντελοποίηση κατασκευής Κατανομή φορτίων πλακών
9. Χρήση Λογισμικού Ανάλυσης Κατασκευών Χειμερινό εξάμηνο 2016 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Μοντελοποίηση κατασκευής Κατανομή φορτίων πλακών
ΔΙΑΤΑΡΑΧΕΣ (DISLOCATIONS )
 ΔΙΑΤΑΡΑΧΕΣ (DISLOCATIONS ) 1. ΕΙΣΑΓΩΓΉ Η αντοχή και η σκληρότητα είναι μέτρα της αντίστασης ενός υλικού σε πλαστική παραμόρφωση Σε μικροσκοπική κλίμακα, πλαστική παραμόρφωση : - συνολική κίνηση μεγάλου
ΔΙΑΤΑΡΑΧΕΣ (DISLOCATIONS ) 1. ΕΙΣΑΓΩΓΉ Η αντοχή και η σκληρότητα είναι μέτρα της αντίστασης ενός υλικού σε πλαστική παραμόρφωση Σε μικροσκοπική κλίμακα, πλαστική παραμόρφωση : - συνολική κίνηση μεγάλου
Επιστήμη των Υλικών. Πανεπιστήμιο Ιωαννίνων. Τμήμα Φυσικής
 Επιστήμη των Υλικών Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής 2017 Α. Δούβαλης Ατέλειες, διαταραχές και σχέση τους με τις μηχανικές ιδιότητες των στερεών (μεταλλικά στερεά) μικτή διαταραχή διαταραχή κοχλία
Επιστήμη των Υλικών Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής 2017 Α. Δούβαλης Ατέλειες, διαταραχές και σχέση τους με τις μηχανικές ιδιότητες των στερεών (μεταλλικά στερεά) μικτή διαταραχή διαταραχή κοχλία
ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΔΟΚΙΜΗ ΕΦΕΛΚΥΣΜΟΥ ΔΙΔΑΣΚΩΝ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Δοκιμή Εφελκυσμού Βασικές Αρχές Ορολογία Στόχοι εργαστηριακής
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΝΑΥΠΗΓΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΙΙ ΔΟΚΙΜΗ ΕΦΕΛΚΥΣΜΟΥ ΔΙΔΑΣΚΩΝ: ΔΡ Σ. Π. ΦΙΛΟΠΟΥΛΟΣ ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή Δοκιμή Εφελκυσμού Βασικές Αρχές Ορολογία Στόχοι εργαστηριακής
6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ
 6-1 6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ 6.1. ΙΑ ΟΣΗ ΤΗΣ ΘΕΡΜΟΤΗΤΑΣ Πολλές βιοµηχανικές εφαρµογές των πολυµερών αφορούν τη διάδοση της θερµότητας µέσα από αυτά ή γύρω από αυτά. Πολλά πολυµερή χρησιµοποιούνται
6-1 6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ 6.1. ΙΑ ΟΣΗ ΤΗΣ ΘΕΡΜΟΤΗΤΑΣ Πολλές βιοµηχανικές εφαρµογές των πολυµερών αφορούν τη διάδοση της θερµότητας µέσα από αυτά ή γύρω από αυτά. Πολλά πολυµερή χρησιµοποιούνται
(συνδέσεις τοίχων, κρυμμένα ανοίγματα, τρίστρωτη τοιχοποιία; κ.λπ.) Επιτόπου αντοχές υλικών Περιγραφή του δομητικού συστήματος κ.λπ.
 1. Τεκμηρίωση του Μνημείου Συνοπτική ιστορία Αρχιτεκτονική τεκμηρίωση Καταγραφή α βλαβών (αποτύπωση, ο ύ εν χρόνω εξέλιξη) Προγενέστερες επεμβάσεις Περιγραφή και κατάσταση υλικών Πειραματικές μετρήσεις
1. Τεκμηρίωση του Μνημείου Συνοπτική ιστορία Αρχιτεκτονική τεκμηρίωση Καταγραφή α βλαβών (αποτύπωση, ο ύ εν χρόνω εξέλιξη) Προγενέστερες επεμβάσεις Περιγραφή και κατάσταση υλικών Πειραματικές μετρήσεις
