Αρχή διατήρηςησ τησ μηχανικήσ ενζργειασ
|
|
|
- Οἰνεύς Ζάρκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Αρχή διατήρηςησ τησ μηχανικήσ ενζργειασ Φφλλο εργαςίασ Α. Όργανα και υλικά που απαιτοφνται Βάςθ παραλλθλόγραμμθ φιγκτιρασ τφπου G Μία (1) ράβδοσ μεταλλικι 80 cm Δφο () ράβδοι μεταλλικζσ 30 cm Δφο () απλοί ςφνδεςμοι Δακτφλιοσ ορειχάλκινοσ με άγκιςτρο Φωτοφράκτθσ (Διαφανισ χάρακασ 30 cm που φζρει πάνω του 7 αδιαφανείσ ταινίεσ) Λεπτά χάλκινα ςφρματα μικουσ 1 cm περίπου Αναπτιρασ Μία φωτοπφλθ (με τον κατάλλθλο πλαςτικό ςυνδετιρα) Ηλεκτρονικό χρονόμετρο Ρ/Ν 1460 Ηλεκτρονικι ηυγαριά Β. Συναρμολόγηςη διάταξησ 1. Ο «φωτοφράκτθσ» (Εικόνα 1) που ςασ δίνεται αποτελείται από ζνα διαφανι χάρακα μικουσ 30 cm, πάνω ςτον οποίο -ςε ίςεσ μεταξφ τουσ αποςτάςεισ- είναι κολλθμζνεσ επτά ίςου πλάτουσ αδιαφανείσ ταινίεσ. Για το φωτοφράκτθ ςασ δίνονται τα εξισ καταςκευαςτικά ςτοιχεία: το πλάτοσ d κάκε αδιαφανοφσ ταινίασ είναι: d = 15,0 mm = m θ απόςταςθ α μεταξφ των διαδοχικϊν αδιαφανϊν ταινιϊν είναι: α = 4,0 cm = m Εικόνα 1: Ο προετοιμαςμζνοσ χάρακασ «φωτοφράκτησ» -1-
2 . Ζυγίςτε τον προετοιμαςμζνο χάρακα με τθν θλεκτρονικι ηυναριά που ςασ δίνεται και ςθμειϊςτε τθ μάηα του: Είναι: m =.... g = kg 3. υναρμολογιςτε τθν πειραματικι διάταξθ, όπωσ φαίνεται ςτθν Εικόνα. Εικόνα : Η πειραματική διάταξη Η φωτοπφλθ κα ςτερεωκεί ςτθν κατϊτερθ μεταλλικι ράβδο των 30 cm τθσ διάταξθσ με τθ βοικεια του κατάλλθλου πλαςτικοφ ςυνδετιρα που ςασ δίνεται, ϊςτε θ δζςμθ τθσ να είναι οριηόντια. Σο βφςμα τφπου jack τθσ φωτοπφλθσ κα ςυνδεκεί ςτθν είςοδο (1) του θλεκτρονικοφ χρονομετρθτι. Η διάταξθ κα ςτερεωκεί ςτον πάγκο εργαςίασ με τθ βοικεια ενόσ ςφιγκτιρα τφπου G. Με ζνα πολφ λεπτό χάλκινο ςφρμα κα αναρτιςετε το χάρακα ςτο γάντηο τθσ διάταξθσ, ϊςτε να κρζμεται κατακόρυφοσ κάτω από το γάντηο και με το κάτω άκρο του να βρίςκεται ςε απόςταςθ 3 5 cm από τθν επάνω οριηόντια όψθ τθσ φωτοπφλθσ. Προςζξετε ϊςτε κατά τθν πτϊςθ του χάρακα οι αδιαφανείσ ταινίεσ να τζμνουν κάκετα τθ δζςμθ τθσ φωτοπφλθσ. Για το ςκοπό αυτό μπορείτε να περιςτρζψετε ελαφρά το γάντηο του ορειχάλκινου δακτυλίου ο οποίοσ μζςω του χάλκινου ςφρματοσ κα ςτρζψει αντίςτοιχα και το χάρακα. Φροντίςτε να ρυκμίςετε τθ κζςθ του δακτυλίου με το γάντηο ϊςτε θ δζςμθ τθσ φωτοπφλθσ να μη τέμνει το τμιμα του χάρακα που φζρει τθ γράμμωςθ και τουσ αρικμοφσ. --
3 4. υνδζςτε το θλεκτρονικό χρονόμετρο ςτθν τάςθ τροφοδοςίασ και επιλζξτε τρόπο λειτουργίασ «F1». Ενϊ ο χάρακασ κρζμεται ακίνθτοσ πάνω από τθ φωτοπφλθ, κάψτε προςεκτικά με τον αναπτιρα το χάλκινο ςφρμα (χωρίσ να το αγγίξετε και αναταράξετε το ςφςτθμα). Ο χάρακασ πζφτει τότε κατακόρυφα, οι αδιαφανείσ του ταινίεσ διακόπτουν διαδοχικά τθ δζςμθ τθσ φωτοπφλθσ και ο θλεκτρονικόσ χρονομετρθτισ καταγράφει τουσ χρόνουσ διζλευςθσ των αδιαφανϊν ταινιϊν από τθ φωτοπφλθ. τον Πίνακα (1): τθ δεφτερθ ςτιλθ ςθμειϊςτε τθν απόςταςθ h μεταξφ των αντιςτοίχων άκρων (ι των μζςων) τθσ πρϊτθσ και όλων των επόμενων αδιαφανϊν ταινιϊν του χάρακα, απόςταςθ που είναι ίςθ με τθν κάκε φορά μετατόπιςθ του χάρακα κατά τθν πτϊςθ του. τθν τρίτθ ςτιλθ ςθμειϊςτε τουσ χρόνουσ διζλευςθσ Δt των αδιαφανϊν ταινιϊν από τθ φωτοπφλθ. Κακϊσ ο χρόνοσ διζλευςθσ Δt μιασ αδιαφανοφσ ταινίασ από τθ φωτοπφλθ αντιςτοιχεί ςε μετατόπιςθ του χάρακα κατά απόςταςθ ίςθ με το πλάτοσ dτθσ αδιαφανοφσ ταινίασ, μπορείτε να υπολογίςετε τθν αντίςτοιχθ ταχφτθτα του χάρακα μζςω τθσ εξίςωςθσ:. t d Θεωροφμε πωσ αυτι θ μζςθ τιμι τθσ ταχφτθτασ διζλευςθσ κατά προςζγγιςθ ταυτίηεται με τθ ςτιγμιαία ταχφτθτα του χάρακα ςτο μζςο τθσ αντίςτοιχθσ αδιαφανοφσ ταινίασ. Πίνακασ 1: Πειραματικά δεδομζνα και αποτελζςματα τησ επεξεργαςίασ τουσ α/α h (m) Δt (s) υ 1 (m/s) υ (m/s) ΔU (J) ΔΚ (J) Με ακρίβεια τεςςάρων δεκαδικϊν ψθφίων (εκτόσ από τισ δφο τελευταίεσ ςτιλεσ που κα χρθςιμοποιιςετε ακρίβεια δεκαδικϊν ψθφίων) ςυμπλθρϊςτε και τισ υπόλοιπεσ ςτιλεσ του Πίνακα 1 ωσ εξισ: τθν τζταρτθ ςτιλθ ςθμειϊςτε ςε όλα τα κελιά τθν ταχφτθτα διζλευςθσ (υ 1 ) τθσ πρϊτθσ αδιαφανοφσ ταινίασ από τθ φωτοπφλθ. τθν πζμπτθ ςτιλθ ςθμειϊςτε τθν ταχφτθτα διζλευςθσ (υ ) κάκε αδιαφανοφσ ταινίασ από τθ φωτοπφλθ. τθν ζκτθ ςτιλθ ςθμειϊςτε τθν κατ απόλυτθ τιμι μεταβολι τθσ δυναμικισ ενζργειασ του χάρακα όταν το μζςο κάκε αδιαφανοφσ ταινίασ διζρχεται από τθ φωτοπφλθ. Οι υπολογιςμοί να γίνουν μζςω τθσ εξίςωςθσ: U m g h. Να κεωριςτε -3-
4 ότι: g = 9,80 m/s. τθν ζβδομθ ςτιλθ ςθμειϊςτε τθ μεταβολι τθσ κινθτικισ ενζργειασ του χάρακα 1 1 μζςω τθσ εξίςωςθσ: K m m1. 5. Με βάςθ τα αποτελζςματα των υπολογιςμϊν ςασ όπωσ αποτυπϊκθκαν ςτον Πίνακα 1 ςχεδιάςτε ςτο μιλιμετρζ χαρτί που ςασ δίνεται τθ γραφικι παράςταςθ ΔK = f(δu), και αφοφ διαπιςτϊςετε τθ γραμμικότθτα τθσ ςχζςθσ που ςυνδζει τθν (απόλυτθ τιμι) μεταβολι τθσ δυναμικισ ενζργειασ και τθ μεταβολι τθσ κινθτικισ ενζργειασ του χάρακα, ςχεδιάςτε και τθν ευκεία που προςεγγίηει καλφτερα τα πειραματικά ςθμεία που ζχετε ιδθ τοποκετιςει ςτο διάγραμμα. Σζλοσ υπολογίςτε τθν κλίςθ λ τθσ καλφτερθσ ευκείασ που ςχεδιάςατε: Προκφπτει: λ =.... Εναλλακτικά: Η γραφικι παράςταςθ μπορεί να ςχεδιαςτεί με τθ βοικεια του Excel που μασ προςφζρει επιπλζον τθ δυνατότθτα προςδιοριςμοφ τθσ εξίςωςθσ τθσ καλφτερθσ ευκείασ προςζγγιςθσ των πειραματικϊν δεδομζνων. 7. Απαντιςτε -δίνοντασ τισ απαραίτθτεσ εξθγιςεισ- ςτισ παρακάτω ερωτιςεισ: α. Ποια θ κεωρθτικι τιμι του λόγου χάρακα κατά τθν πτϊςθ του είναι το βάροσ του; K, αν δεχκοφμε πωσ θ μόνθ δφναμθ που δρα ςτο U β. Μπορείτε να καταγράψετε οριςμζνα από τα ςφάλματα που πιςτεφετε ότι μπορεί να ζγιναν τόςο κατά το ςχεδιαςμό όςο και κατά τθν υλοποίθςθ τθσ πειραματικισ διαδικαςίασ; γ. Ποιο ςκοπό νομίηετε ότι εξυπθρετεί θ ανάρτθςθ του χάρακα μζςω του λεπτοφ χάλκινου ςφρματοσ και θ καφςθ του; Δε κα ιταν απλοφςτερο να χρθςιμοποιθκεί λεπτό νιμα και ψαλίδι για να το κόβουμε ϊςτε να απελευκερϊνεται ο χάρακασ; -4-
5 δ. Για κάκε γραμμι των πειραματικϊν δεδομζνων του Πίνακα 1 (εκτόσ από τθ πρϊτθ), υπολογίςτε τθν τιμι του λόγου λ =, και ςυμπλθρϊςτε τον Πίνακα. K U Πίνακασ : Τιμζσ του λόγου ΔK/ΔU α/α λ = U Δϊςτε μια εκτίμθςθ του ςφάλματοσ ςτθ μζτρθςθ του λόγου λ, ωσ: max min... ε. Μποροφμε να ιςχυριςτοφμε, λαμβάνοντασ υπόψθ και τα ςφάλματα που ζγιναν, ότι κατά τθν πτϊςθ του χάρακα διατθρείται θ μθχανικι του ενζργεια; -5-
23 Ιανουαρίου 2016 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 3 Ιανουαρίου 016 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1....... 3..... ΜΟΝΑΔΕΣ: Α. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - Η ΙΔΕΑ Εικόνα 1: Ελεύθερη πτώση Ελεύθερη πτώση ονομάζεται η κίνηση
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 3 Ιανουαρίου 016 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1....... 3..... ΜΟΝΑΔΕΣ: Α. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - Η ΙΔΕΑ Εικόνα 1: Ελεύθερη πτώση Ελεύθερη πτώση ονομάζεται η κίνηση
όπου θ ςτακερά k εξαρτάται από το μζςο και είναι για το κενό
 Φυςικι [1] ΔΤΝΑΜΙΚΟ ΗΛΕΚΣΡΟΣΑΣΙΚΟΤ ΠΕΔΙΟΤ Ειςαγωγή. Γφρω από θλεκτρικά φορτιςμζνα ςώματα δθμιουργείται θλεκτροςτατικό πεδίο. Η μελζτθ του θλεκτρικοφ πεδίου γίνεται με τθ βοικεια των μεγεκών: ζνταςη E (διανυςματικό)
Φυςικι [1] ΔΤΝΑΜΙΚΟ ΗΛΕΚΣΡΟΣΑΣΙΚΟΤ ΠΕΔΙΟΤ Ειςαγωγή. Γφρω από θλεκτρικά φορτιςμζνα ςώματα δθμιουργείται θλεκτροςτατικό πεδίο. Η μελζτθ του θλεκτρικοφ πεδίου γίνεται με τθ βοικεια των μεγεκών: ζνταςη E (διανυςματικό)
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις
 Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Κατευ θυνσής Γ Λυκει ου - Ταλαντώσεις Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε) περιςτροφισ του δίςκου;
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΡΩΝΥMΟ: ΗΜΕΟΜΗΝΙΑ: 1/3/2015 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΚΥΜΑΤΑ ΚΑΙ ΣΤΕΕΟ ΣΩΜΑ ΘΕΜΑ Α Α1. Ροιεσ από τισ δυνάμεισ του ςχιματοσ ζχουν μθδενικι ροπι ωσ προσ τον άξονα (ε)
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια
 Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
Διαγώνισμα Φυσική ς Α Λυκει ου Έργο και Ενε ργεια Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:.
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ ΜΕΛΕΣΗ ΣΗ ΚΙΝΗΗ ΩΜΑΣΟ Ε ΠΛΑΓΙΟ ΕΠΙΠΕΔΟ - ΜΕΣΡΗΗ ΣΟΤ ΤΝΣΕΛΕΣΗ ΣΡΙΒΗ ΟΛΙΘΗΗ ΕΚΦΕ Α & Β ΑΝΑΣΟΛΙΚΗ ΑΣΣΙΚΗ τόχοι Μετά το πζρασ τθσ εργαςτθριακισ άςκθςθσ, οι μακθτζσ κα πρζπει να είναι ςε κζςθ:.
Τάξη Β. Φυςικθ Γενικθσ Παιδείασ. Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ. Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά
 Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Δ Για όλεσ τισ αςκθςεισ δίνεται η ηλεκτρικθ ςταιερά k 2 9 9 10 Nm 2 1. Δφο ακίνθτα ςθμειακά θλεκτρικά φορτία q 1 = - 2 μq και q 2 = + 3 μq, βρίςκονται
ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ
 ΕΚΦΕ ΑΧΑΡΝΩΝ ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ Η άςκηςη αποτελεί τροποποιημζνη εκδοχή του θζματοσ τησ Ευρωπαϊκήσ Ολυμπιάδασ Φυςικών Επιςτημών EUSO 2014_Επιμζλεια Παπαμιχάλησ Κ.
ΕΚΦΕ ΑΧΑΡΝΩΝ ΔΙΑΘΛΑΗ - ΠΕΙΡΑΜΑΣΙΚΟ ΤΠΟΛΟΓΙΜΟ ΔΕΙΚΣΗ ΔΙΑΘΛΑΗ ΕΛΑΙΟΛΑΔΟΤ Η άςκηςη αποτελεί τροποποιημζνη εκδοχή του θζματοσ τησ Ευρωπαϊκήσ Ολυμπιάδασ Φυςικών Επιςτημών EUSO 2014_Επιμζλεια Παπαμιχάλησ Κ.
ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ
 ΜΑΘΗΜΑ /ΣΑΞΗ: ΦΤΙΚΗ ΚΑΣΕΤΘΤΝΗ / Β ΛΤΚΕΙΟΤ ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ ΘΕΜΑ Α 1. Δφο ςθμειακά φορτία απζχον μεταξφ τοσ απόςταςθ r και θ δναμικι
ΜΑΘΗΜΑ /ΣΑΞΗ: ΦΤΙΚΗ ΚΑΣΕΤΘΤΝΗ / Β ΛΤΚΕΙΟΤ ΟΝΟΜΑΣΕΠΩΝΤMΟ: ΗΜΕΡΟΜΗΝΙΑ: ΕΙΡΑ: 3 ΕΞΕΣΑΣΕΑ ΤΛΗ: ΗΛΕΚΣΡΙΚΟ ΠΕΔΙΟ- ΜΑΓΝΗΣΙΚΟ ΠΕΔΙΟ- ΕΠΑΓΩΓΗ ΘΕΜΑ Α 1. Δφο ςθμειακά φορτία απζχον μεταξφ τοσ απόςταςθ r και θ δναμικι
ΚΥΚΛΩΜΑΤΑ VLSI. Ασκήσεις Ι. Γ. Τσιατούχας. Πανεπιςτιμιο Ιωαννίνων. Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18
 ΚΥΚΛΩΜΑΤΑ LSI Πανεπιςτιμιο Ιωαννίνων Ασκήσεις Ι Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18 Γ. Τσιατούχας Άσκηση 1 1) Σχεδιάςτε τισ ςφνκετεσ COS λογικζσ πφλεσ (ςε επίπεδο τρανηίςτορ) που υλοποιοφν τισ
ΚΥΚΛΩΜΑΤΑ LSI Πανεπιςτιμιο Ιωαννίνων Ασκήσεις Ι Τμιμα Μθχανικϊν Η/Υ και Πλθροφορικισ 8/11/18 Γ. Τσιατούχας Άσκηση 1 1) Σχεδιάςτε τισ ςφνκετεσ COS λογικζσ πφλεσ (ςε επίπεδο τρανηίςτορ) που υλοποιοφν τισ
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό. μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ
 Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
ΧΗΥΙΑΚΟ ΔΚΠΑΙΔΔΤΣΙΚΟ ΒΟΗΘΗΜΑ «ΥΤΙΚΗ ΘΔΣΙΚΗ ΚΑΙ ΣΔΦΝΟΛΟΓΙΚΗ ΚΑΣΔΤΘΤΝΗ» ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΑΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΑΤΔΥΘΥΝΣΗΣ ΘΔΜΑ Α ΘΔΜΑ Β
 4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
Αν η ςυνάρτηςη ƒ είναι ςυνεχήσ ςτο να προςδιορίςετε το α.
 1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
1 AΣΚΗΣΕΙΣ 1. Να υπολογιςθοφν τα παρακάτω όρια Ι. ΙΙ. ΙΙΙ. Ιν. ν. νι. νιι. νιιι. 2. Να βρεθοφν τα όρια Ι. ΙΙ. 3. Αν ƒ(χ)= α. Να βρείτε το πεδίο οριςμοφ Β. Να βρείτε τα όρια Ι. ΙΙ. 4. Δίνεται η ςυνάρτηςη
Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 2009_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ
 ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
ΕΚΦΕ Αχαρνών Η άςκθςθ αποτελεί τροποποιθμζνθ εκδοχι του κζματοσ φυςικισ, τθσ Ευρωπαϊκισ Ολυμπιάδασ Φυςικών Επιςτθμών 9_επιμζλεια κζματοσ: Κώςτασ Παπαμιχάλθσ Εφαρμογζσ τθσ Αρχισ του Αρχιμιδθ & τθσ ςυνκικθσ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Α2. το ςτιγμιότυπο αρμονικοφ μθχανικοφ κφματοσ του χιματοσ 1, παριςτάνονται οι ταχφτθτεσ ταλάντωςθσ δφο ςθμείων του.
 ΘΕΜΑ Α. Στισ ερωτήςεισ Α1-Α4 να γράψετε ςτο τετράδιό ςασ τον αριθμό τησ ερϊτηςησ και, δίπλα, το γράμμα που αντιςτοιχεί ςτην επιλογή η οποία ςυμπληρϊνει ςωςτά την ημιτελή πρόταςη. Α1. τθ ςφνκεςθ δφο απλϊν
ΘΕΜΑ Α. Στισ ερωτήςεισ Α1-Α4 να γράψετε ςτο τετράδιό ςασ τον αριθμό τησ ερϊτηςησ και, δίπλα, το γράμμα που αντιςτοιχεί ςτην επιλογή η οποία ςυμπληρϊνει ςωςτά την ημιτελή πρόταςη. Α1. τθ ςφνκεςθ δφο απλϊν
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο
 Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Διαγώνισμα Φυσική ς Α Λυκει ου Δυναμική σε μι α δια στασή και στο επι πεδο Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα
Διάδοση θερμότητας σε μία διάσταση
 Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Η ζννοια της δφναμης. 1.Nα αντιςτοιχίςετε τουσ όρουσ τθσ ςτιλθσ-ι με τουσ όρουσ τθσ ςτιλθσ-ιι Στιλθ-Ι
 1 Η ζννοια της δφναμης. 1.Nα αντιςτοιχίςετε τουσ όρουσ τθσ ςτιλθσ-ι με τουσ όρουσ τθσ ςτιλθσ-ιι Στιλθ-Ι Στιλθ-ΙΙ Είδοσ δφναμθσ 1. Η δφναμθ που αςκοφμε με ζνα ςκοινί κακώσ τραβάμε μία βάρκα 2. Η δφναμθ
1 Η ζννοια της δφναμης. 1.Nα αντιςτοιχίςετε τουσ όρουσ τθσ ςτιλθσ-ι με τουσ όρουσ τθσ ςτιλθσ-ιι Στιλθ-Ι Στιλθ-ΙΙ Είδοσ δφναμθσ 1. Η δφναμθ που αςκοφμε με ζνα ςκοινί κακώσ τραβάμε μία βάρκα 2. Η δφναμθ
Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά;
 ; Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά; 30/1/ 2 Η φυςικι τθσ ςθμαςία είναι ότι προςδιορίηει τθ ςτροφικι κίνθςθ ενόσ ςτερεοφ ωσ
; Η ίδια κατά μζτρο δφναμθ όταν εφαρμοςκεί ςε διαφορετικά ςθμεία τθσ πόρτασ προκαλεί διαφορετικά αποτελζςματα Ροιά; 30/1/ 2 Η φυςικι τθσ ςθμαςία είναι ότι προςδιορίηει τθ ςτροφικι κίνθςθ ενόσ ςτερεοφ ωσ
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ
 Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ ΚΑΜΠΤΛΟΓΡΑΜΜΕ ΚΙΝΗΕΙ 1.1 ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ 1. Τα ςκαλοπάτια μιασ ςκάλασ είναι όλα όμοια μεταξφ τουσ και ζχουν φψοσ h = 20 cm και πλάτοσ d = 40 cm. Από
Σράπεζα θεμάτων Θετικού Προςανατολιςμού Κεφ. 1 Θέμα Δ ΚΑΜΠΤΛΟΓΡΑΜΜΕ ΚΙΝΗΕΙ 1.1 ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ 1. Τα ςκαλοπάτια μιασ ςκάλασ είναι όλα όμοια μεταξφ τουσ και ζχουν φψοσ h = 20 cm και πλάτοσ d = 40 cm. Από
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ.
 Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Επαναληπτικό Διαγώνισμα Φυσικη ς Α Λυκει όυ Ε.Ο.Κ. και Ε.Ο.Μ.Κ. Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και δίπλα το γράμμα
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Πνομα Ομάδασ: Προγραμματιςμόσ ενόσ κινοφμενου ρομπότ
 Φφλλο Εργαςίασ : Ακολοφθηςε τισ εντολζσ μου! Τάξθ: Β Γυμναςίου Ενότθτα: Λφνω προβλιματα με υπολογιςτικά φφλλα Εμπλεκόμενεσ ζννοιεσ: ρομποτικι, Lego Mindstorms, υπολογιςτικά φφλλα, ςυναρτιςεισ, γραφιματα
Φφλλο Εργαςίασ : Ακολοφθηςε τισ εντολζσ μου! Τάξθ: Β Γυμναςίου Ενότθτα: Λφνω προβλιματα με υπολογιςτικά φφλλα Εμπλεκόμενεσ ζννοιεσ: ρομποτικι, Lego Mindstorms, υπολογιςτικά φφλλα, ςυναρτιςεισ, γραφιματα
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Απάντηση ΘΕΜΑ1 ΘΕΜΑ2. t=t 1 +T/2. t=t 1 +3T/4. t=t 1 +T ΔΙΑΓΩΝΙΣΜΑ ΣΕ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ).
 Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ
 Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Λφκειο Ακρόπολθσ 2015 Επιμζλεια Μάριοσ Πουργουρίδθσ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΑΠΟ ΘΕΜΑΤΑ ΤΕΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 1. Η πιο κάτω μπάλα αφινεται να πζςει από το ςθμείο Α,κτυπά ςτο ζδαφοσ ςτο ςθμείο Ε και αναπθδά ςε μικρότερο
Ενδεικτικζσ Λφςεισ Θεμάτων
 c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
Φσσική Γ Λσκείοσ 37 Θετ. και Τετν. Κατεύθσνση
 Φσσική Γ Λσκείοσ 37 Θετ. και Τετν. Κατεύθσνση 4.43. Η ταχφτθτα του κζντρου μάηασ μιασ ςυμπαγοφσ ςφαίρασ που κυλίεται ςε οριηόντιο επίπεδο είναι υ = 0 m/s ενϊ θ ακτίνα τθσ R = 0, m. Η ςφαίρα ςτθν πορεία
Φσσική Γ Λσκείοσ 37 Θετ. και Τετν. Κατεύθσνση 4.43. Η ταχφτθτα του κζντρου μάηασ μιασ ςυμπαγοφσ ςφαίρασ που κυλίεται ςε οριηόντιο επίπεδο είναι υ = 0 m/s ενϊ θ ακτίνα τθσ R = 0, m. Η ςφαίρα ςτθν πορεία
Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ. Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes
 Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes Στόχοι 1. Ανάλυςθ τθσ λειτουργίασ τθσ πειραματικισ διάταξθσ 2. Εφαρμογι των νόμων τθσ κερμοδυναμικισ
Α ΕΚΦΕ ΑΝ. ΑΤΤΙΚΗΣ Υπ. Κ. Παπαμιχάλθσ Μζτρηςη του λόγου γ=c P /C V των αερίων με τη μζθοδο Clement Desormes Στόχοι 1. Ανάλυςθ τθσ λειτουργίασ τθσ πειραματικισ διάταξθσ 2. Εφαρμογι των νόμων τθσ κερμοδυναμικισ
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων. (v.1.0.7)
 Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Άπειρεσ κροφςεισ. Τθ χρονικι ςτιγμι. t, ο δακτφλιοσ ςυγκροφεται με τον τοίχο με ταχφτθτα (κζντρου μάηασ) μζτρου
 Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
Άπειρεσ κροφςεισ Δακτφλιοσ ακτίνασ κυλάει ςε οριηόντιο δάπεδο προσ ζνα κατακόρυφο τοίχο όπωσ φαίνεται ςτο ςχιμα. Ο ςυντελεςτισ τριβισ ίςκθςθσ του δακτυλίου με το δάπεδο είναι, ενϊ ο τοίχοσ είναι λείοσ.
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Electronics μαηί με τα ςυνοδευτικά καλϊδια και το αιςκθτιριο κερμοκραςίασ LM335 που περιζχονται
 Σομζασ: Ηλεκτρονικόσ Εκπαιδευτικόσ: Μπουλταδάκθσ τζλιοσ Μάθημα: υλλογι και μεταφορά δεδομζνων μζςω Η/Τ, Αιςκθτιρεσ-Ενεργοποιθτζσ Αντικείμενο: α) Μζτρθςθ κερμοκραςίασ με το αιςκθτιριο LM335 και μεταφορά
Σομζασ: Ηλεκτρονικόσ Εκπαιδευτικόσ: Μπουλταδάκθσ τζλιοσ Μάθημα: υλλογι και μεταφορά δεδομζνων μζςω Η/Τ, Αιςκθτιρεσ-Ενεργοποιθτζσ Αντικείμενο: α) Μζτρθςθ κερμοκραςίασ με το αιςκθτιριο LM335 και μεταφορά
Η γραφικι παράςταςθ τθσ ςυνάρτθςθσ f(x)=αx+β είναι μια ευκεία με εξίςωςθ y=αx+β θ οποία τζμνει τον άξονα των y ςτο ςθμείο Β(0,β) και ζχει κλίςθ λ=α.
 ε καρτεςιανό ςφςτθμα ςυντεταγμζνων Οxy δίνεται ευκεία ε. Σί ονομάηουμε : α) γωνία που ςχθματίηει θ ευκεία ε με τον άξονα xϋx; β) ςυντελεςτι διευκφνςεωσ τθσ ευκείασ ε; ΑΠΑΝΤΗΣΗ α) Παρατιρθςθ β) Παρατιρθςθ
ε καρτεςιανό ςφςτθμα ςυντεταγμζνων Οxy δίνεται ευκεία ε. Σί ονομάηουμε : α) γωνία που ςχθματίηει θ ευκεία ε με τον άξονα xϋx; β) ςυντελεςτι διευκφνςεωσ τθσ ευκείασ ε; ΑΠΑΝΤΗΣΗ α) Παρατιρθςθ β) Παρατιρθςθ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ
 ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
ΝΟΜΟΙ ΚΙΝΗΗ ΠΛΑΝΗΣΩΝ ΣΟΤ ΚΕΠΛΕΡ 1. Νόμοσ των ελλειπτικών τροχιών Η τροχιζσ των πλανθτϊν είναι ελλείψεισ, των οποίων τθ μία εςτία κατζχει ο Ήλιοσ. Προφανϊσ όλοι οι πλανιτεσ του ίδιου πλανθτικοφ ςυςτιματοσ
Επαναληπτικές Ασκήσεις στα κευ 1 και 2
 Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
Επαναληπτικές Ασκήσεις στα κευ 1 και 2 1. Αζριο με όγκο 0,004 m 3 κερμαίνεται με ςτακερι πίεςθ p =1,2 atm μζχρι ο όγκοσ του να γίνει 0,006 m 3. Τπολογίςτε το ζργο που παράγει το αζριο. Δίνεται 1 atm =
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Α ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ IMC (Key Stage II) 9 Μαρτίου 2016 ΧΡΟΝΟΣ: 2 ΩΡΕΣ Λύςεισ : Πρόβλημα 1 (α) Να βρείτε τθν τιμι του για να ιςχφει θ πιο κάτω ςχζςθ: (β) Ο Ανδρζασ τελειϊνει
CP VIOLATION in b system ΜΑΑΝΤΗΣ ΑΛΕΞΑΝΔΟΣ --ΣΑΒΒΙΔΗΣ ΓΙΩΓΟΣ
 CP VIOLATION in b system ΜΑΑΝΤΗΣ ΑΛΕΞΑΝΔΟΣ --ΣΑΒΒΙΔΗΣ ΓΙΩΓΟΣ PARITY (ΟΜΟΤΙΜΙΑ) P & ΣΥΖΥΓΙΑ ΦΟΤΙΟΥ C Τι είναι θ parity; Τι είναι θ ςυηυγία φορτίου; Το C αντιςτρζφει και τον λεπτονικό και βαρυονικό αρικμό.
CP VIOLATION in b system ΜΑΑΝΤΗΣ ΑΛΕΞΑΝΔΟΣ --ΣΑΒΒΙΔΗΣ ΓΙΩΓΟΣ PARITY (ΟΜΟΤΙΜΙΑ) P & ΣΥΖΥΓΙΑ ΦΟΤΙΟΥ C Τι είναι θ parity; Τι είναι θ ςυηυγία φορτίου; Το C αντιςτρζφει και τον λεπτονικό και βαρυονικό αρικμό.
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ2018
 Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
Διαγώνιςμα Γ Λυκείου Ιανουάριοσ08 Διάρκεια Εξζταςησ 3ώρεσ Ονοματεπώνυμο. ΘΕΜΑ Α: Στισ ερωτήςεισ Α ωσ και Α4 επιλζξτε την ςωςτή απάντηςη: Α.Αν το πλάτοσ Α μιασ φκίνουςασ ταλάντωςθσ μεταβάλλεται με το χρόνο
ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών. Στόχοσ. Θεωρητικό υπόβαθρο. Εκτζλεςη τησ άςκηςησ. Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό.
 ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών Στόχοσ Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό. Οι πυκνωτζσ αποκθκεφουν ενζργεια με τθν μορφι θλεκτρικοφ πεδίου. Το θλεκτρικό πεδίο δθμιουργείται ανάμεςα ςε
ΑΣΚΗΣΗ 2: Μελζτη πυκνωτών Στόχοσ Θα μελετιςουμε επίπεδουσ πυκνωτζσ με και χωρίσ διθλεκτρικό. Οι πυκνωτζσ αποκθκεφουν ενζργεια με τθν μορφι θλεκτρικοφ πεδίου. Το θλεκτρικό πεδίο δθμιουργείται ανάμεςα ςε
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ. ΚΕΦΑΛΑΙΟ 3: Εργονομία
 ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΑΚΗΕΙ ΡΕΤΣΩΝ. 2. Σωλινασ ςχιματοσ U περιζχει νερό πυκνότθτασ ρ ςε ιςορροπία. Τα
 ΑΚΗΕΙ ΡΕΤΣΩΝ 1. Το κλειςτό δοχείο του ςχιματοσ περιζχει ακίνθτο υγρό πυκνότθτασ ρ και φψουσ h και βρίςκεται εντόσ πεδίου βαρφτθτασ και εντόσ ατμόςφαιρασ. Το δοχείο κλείνεται πλευρικά με εφαρμοςτό ζμβολο
ΑΚΗΕΙ ΡΕΤΣΩΝ 1. Το κλειςτό δοχείο του ςχιματοσ περιζχει ακίνθτο υγρό πυκνότθτασ ρ και φψουσ h και βρίςκεται εντόσ πεδίου βαρφτθτασ και εντόσ ατμόςφαιρασ. Το δοχείο κλείνεται πλευρικά με εφαρμοςτό ζμβολο
ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο)
 ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο) χήμα Κφκλωμα RLC ςε ςειρά χήμα 2 Διανυςματικι παράςταςθ τάςεων και ρεφματοσ Ζςτω ότι ςτο κφκλωμα του ςχιματοσ που περιλαμβάνει ωμικι, επαγωγικι και χωρθτικι
ΚΤΚΛΩΜΑ RLC Ε ΕΙΡΑ (Απόκριςη ςε ημιτονοειδή είςοδο) χήμα Κφκλωμα RLC ςε ςειρά χήμα 2 Διανυςματικι παράςταςθ τάςεων και ρεφματοσ Ζςτω ότι ςτο κφκλωμα του ςχιματοσ που περιλαμβάνει ωμικι, επαγωγικι και χωρθτικι
3. Να υπολογίςετε τθ ροι θλιακισ ακτινοβολίασ ςε μια απόςταςθ R=1.5x10 11 m από τον ιλιο (απόςταςθ θλίου-γθσ). Δίνεται θ ροι τθσ εκπεμπόμενθσ ακτινοβο
 1. Υποκζτουμε ότι θ κερμοκραςία ςτο ζδαφοσ είναι 38 o C και αντίςτοιχα θ κερμοκραςία δρόςου είναι 30 o C. Έςτω ότι επικρατοφν αςτακείσ ατμοςφαιρικζσ ςυνκικεσ και ότι θ μεταβολι τθσ κερμοκραςίασ ακολουκεί
1. Υποκζτουμε ότι θ κερμοκραςία ςτο ζδαφοσ είναι 38 o C και αντίςτοιχα θ κερμοκραςία δρόςου είναι 30 o C. Έςτω ότι επικρατοφν αςτακείσ ατμοςφαιρικζσ ςυνκικεσ και ότι θ μεταβολι τθσ κερμοκραςίασ ακολουκεί
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9. ΑΝΩΣΗ Η αρχή του Αρχιμήδη
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΑΝΩΣΗ Η αρχή του Αρχιμήδη Όργανα Τλικά: Δυναμόμετρο 2 ι 2,5Ν Δοκιμαςτικόσ ςωλινασ Βαρίδι 50g Βάςθ Ράβδοι ςτιριξθσ Δοχείο με νερό κοπόσ τθσ άςκθςθσ: Οι μακθτζσ να κατανοιςουν ότι θ
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 ΑΝΩΣΗ Η αρχή του Αρχιμήδη Όργανα Τλικά: Δυναμόμετρο 2 ι 2,5Ν Δοκιμαςτικόσ ςωλινασ Βαρίδι 50g Βάςθ Ράβδοι ςτιριξθσ Δοχείο με νερό κοπόσ τθσ άςκθςθσ: Οι μακθτζσ να κατανοιςουν ότι θ
ΑΚΗΕΙ ΠΡΟΒΛΕΨΕΩΝ ΠΡΟΒΛΕΨΕΙ
 ΑΚΗΕΙ ΠΡΟΒΛΕΨΕΩΝ ΠΡΟΒΛΕΨΕΙ 1 Άσκηση 1 Μια βιομησανική επισείπηση έσει καταγπάτει τιρ μηνιαίερ πυλήσειρ τυν πποφόντυν τηρ, πος ήσαν οι εξήρ (σε εκατ. εςπώ): Μήναρ Πυλήσειρ 1 50 2 54 3 61 4 68 5 76 6 87
ΑΚΗΕΙ ΠΡΟΒΛΕΨΕΩΝ ΠΡΟΒΛΕΨΕΙ 1 Άσκηση 1 Μια βιομησανική επισείπηση έσει καταγπάτει τιρ μηνιαίερ πυλήσειρ τυν πποφόντυν τηρ, πος ήσαν οι εξήρ (σε εκατ. εςπώ): Μήναρ Πυλήσειρ 1 50 2 54 3 61 4 68 5 76 6 87
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ. ΕΝΟΤΗΤΑ: ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Τάξη : Β ΛΥΚΕΙΟΥ
 ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΕΝΟΤΗΤΑ: ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Τάξη : Β ΛΥΚΕΙΟΥ Α) ΔΙΔΑΚΣΙΚΟΙ ΣΟΧΟΙ Οι μακθτζσ, μετά το τζλοσ τθσ διδαςκαλίασ, να είναι ςε κζςθ : α) Γνώςεισ: 1. Να διατυπϊνουν τθν αρχι διατιρθςθσ
ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΕΝΟΤΗΤΑ: ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Τάξη : Β ΛΥΚΕΙΟΥ Α) ΔΙΔΑΚΣΙΚΟΙ ΣΟΧΟΙ Οι μακθτζσ, μετά το τζλοσ τθσ διδαςκαλίασ, να είναι ςε κζςθ : α) Γνώςεισ: 1. Να διατυπϊνουν τθν αρχι διατιρθςθσ
1 Εγκατϊςταςη λογαριαςμού email
 1 Εγκατϊςταςη λογαριαςμού email 1.1 Εγκατϊςταςη λογαριαςμού ςε Microsoft Office Outlook 2003 1.1.1 Αν δεν χρηςιμοποιεύτε όδη το Outlook. ε περίπτωςθ που δεν ζχετε εγκαταςτιςει άλλο λογαριαςμό ςτο Microsoft
1 Εγκατϊςταςη λογαριαςμού email 1.1 Εγκατϊςταςη λογαριαςμού ςε Microsoft Office Outlook 2003 1.1.1 Αν δεν χρηςιμοποιεύτε όδη το Outlook. ε περίπτωςθ που δεν ζχετε εγκαταςτιςει άλλο λογαριαςμό ςτο Microsoft
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Πωσ δθμιουργώ φακζλουσ;
 Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
1. Αν θ ςυνάρτθςθ είναι ΠΟΛΤΩΝΤΜΙΚΗ τότε το πεδίο οριςμοφ είναι το διότι για κάκε x θ f(x) δίνει πραγματικό αρικμό.
 ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΝΑ ΒΡΙΚΟΤΜΕ ΣΟ ΠΕΔΙΟ ΟΡΙΜΟΤ ΤΝΑΡΣΗΗ Για να οριςκεί μια ςυνάρτθςθ πρζπει να δοκοφν δφο ςτοιχεία : Σο πεδίο οριςμοφ τθσ Α και Η τιμι τθσ f() για κάκε Α. Οριςμζνεσ φορζσ μασ δίνουν μόνο τον
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΝΑ ΒΡΙΚΟΤΜΕ ΣΟ ΠΕΔΙΟ ΟΡΙΜΟΤ ΤΝΑΡΣΗΗ Για να οριςκεί μια ςυνάρτθςθ πρζπει να δοκοφν δφο ςτοιχεία : Σο πεδίο οριςμοφ τθσ Α και Η τιμι τθσ f() για κάκε Α. Οριςμζνεσ φορζσ μασ δίνουν μόνο τον
ΘΕΜΑ Α Να γράψετε ςτο τετράδιό ςασ τον αριθμό καθεμιάσ από τισ παρακάτω ερωτήςεισ 1-4 και δίπλα το γράμμα που αντιςτοιχεί ςτη ςωςτή απάντηςη.
 ΣΤΠΟΤ ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ (ΚΡΟΤΕΙ-ΣΑΛΑΝΣΩΕΙ-ΚΤΜΑΣΑ) ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΕΣΑΡΣΗ 6 ΙΑΝΟΤΑΡΙΟΤ 2016 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΤΙΚΗ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ (ΚΑΙ ΣΩΝ ΔΤΟ
ΣΤΠΟΤ ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ (ΚΡΟΤΕΙ-ΣΑΛΑΝΣΩΕΙ-ΚΤΜΑΣΑ) ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΣΕΣΑΡΣΗ 6 ΙΑΝΟΤΑΡΙΟΤ 2016 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΤΙΚΗ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ (ΚΑΙ ΣΩΝ ΔΤΟ
Μθχανολογικό Σχζδιο, από τθ κεωρία ςτο πρακτζο Χριςτοσ Καμποφρθσ, Κων/νοσ Βαταβάλθσ
 Λεπτζσ Αξονικζσ γραμμζσ χρθςιμοποιοφνται για να δθλϊςουν τθν φπαρξθ ςυμμετρίασ του αντικειμζνου. Υπενκυμίηουμε ότι οι άξονεσ ςυμμετρίασ χρθςιμοποιοφνται μόνον όταν το ίδιο το εξάρτθμα είναι πραγματικά
Λεπτζσ Αξονικζσ γραμμζσ χρθςιμοποιοφνται για να δθλϊςουν τθν φπαρξθ ςυμμετρίασ του αντικειμζνου. Υπενκυμίηουμε ότι οι άξονεσ ςυμμετρίασ χρθςιμοποιοφνται μόνον όταν το ίδιο το εξάρτθμα είναι πραγματικά
Διαγώνισμα Φυσικής Γενικής Παιδείας Β Λυκείου Κεφάλαιο 2 - υνεχές Ηλεκτρικό Ρεύμα
 Διαγώνισμα Φυσικής Γενικής Παιδείας Β Λυκείου Κεφάλαιο 2 - υνεχές Ηλεκτρικό Ρεύμα Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και
Διαγώνισμα Φυσικής Γενικής Παιδείας Β Λυκείου Κεφάλαιο 2 - υνεχές Ηλεκτρικό Ρεύμα Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-4 και
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4
 Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
Διαγώνισμα Χημείας Γ Λυκείου στα Κεφάλαια 1-4 Επιμέλεια: Σ. Ασημέλλης Θέμα Α Να γράψετε ςτο φφλλο απαντιςεϊν ςασ τον αρικμό κακεμιάσ από τισ παρακάτω ερωτιςεισ 1-5 και δίπλα το γράμμα που αντιςτοιχεί ςτθ
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών
 Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
Το καλωςόριςμα των μαθητών ςτο Εργαςτήριο Φυςικών Επιςτημών Η ΟΡΙΖΟΝΣΙΑ ΒΟΛΗ ΜΕΑ ΑΠΟ ΣΙ ΝΕΕ ΣΕΧΝΟΛΟΓΙΕ Εισαγωγή Ο καταλλθλότεροσ χϊροσ για ζνα επιτυχθμζνο μάκθμα φυςικισ είναι το εργαςτιριο φυςικϊν επιςτθμϊν.
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ
 ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
ΑΔΡΑΝΕΙΑ ΜΑΘΗΣΕ: ΜΑΡΙΑΝΝΑ ΠΑΡΑΘΤΡΑ ΑΝΑΣΑΗ ΠΟΤΛΙΟ ΠΑΝΑΓΙΩΣΗ ΠΡΟΔΡΟΜΟΤ ΑΝΑΣΑΙΑ ΠΟΛΤΧΡΟΝΙΑΔΟΤ ΙΩΑΝΝΑ ΠΕΝΓΚΟΤ Οριςμόσ: Με τον όρο αδράνεια ςτθ Φυςικι ονομάηεται θ χαρακτθριςτικι ιδιότθτα των ςωμάτων να αντιςτζκονται
Δίκτυα Υπολογιςτϊν 2-Rooftop Networking Project
 Ονοματεπώνυμα και Α.Μ. μελών ομάδασ Κοφινάσ Νίκοσ ΑΜ:2007030111 Πζρροσ Ιωακείμ ΑΜ:2007030085 Site survey Τα κτιρια τθσ επιλογισ μασ αποτελοφν το κτιριο επιςτθμϊν και το κτιριο ςτο οποίο ςτεγάηεται θ λζςχθ
Ονοματεπώνυμα και Α.Μ. μελών ομάδασ Κοφινάσ Νίκοσ ΑΜ:2007030111 Πζρροσ Ιωακείμ ΑΜ:2007030085 Site survey Τα κτιρια τθσ επιλογισ μασ αποτελοφν το κτιριο επιςτθμϊν και το κτιριο ςτο οποίο ςτεγάηεται θ λζςχθ
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
ΑΝΣΙΣΡΟΦΗ ΤΝΑΡΣΗΗ. f y x y f A αντιςτοιχίηεται ςτο μοναδικό x A για το οποίο. Παρατθριςεισ Ιδιότθτεσ τθσ αντίςτροφθσ ςυνάρτθςθσ 1. Η. f A τθσ f.
 .. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
.. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Εργαςτιριο 1
 Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Εργαςτιριο 1 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Τμήμα Μησανικών Πληποφοπικήρ, Τ.Ε.Ι. Ηπείπος Ακαδημαϊκό Έτορ 2016-2017, 6 ο Εξάμηνο Τυπικζσ Γλϊςςεσ Περιγραφισ Υλικοφ Εργαςτιριο 1 Διδάςκων Τςιακμάκθσ Κυριάκοσ, Phd MSc in Electronic Physics (Radioelectrology)
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Βάςεισ Δεδομζνων Ι. Ενότητα 12: Κανονικοποίηςη. Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ
 Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
ΟΜΑΔΑ: ΘΕΟΚΛΗΣΩ-ΑΝΣΡΕΑ-ΝΕΦΕΛΗ
 29/9/2014 το μάκθμα τθσ ευζλικτθσ ηϊνθσ,τα παιδιά χωρίςτθκαν ςε ομάδεσ και ζφτιαξαν τθν δικι τουσ ηωγραφιά χρθςιμοποιϊντασ γεωμετρικά ςχιματα. ΟΜΑΔΑ: ΘΕΟΚΛΗΣΩ-ΑΝΣΡΕΑ-ΝΕΦΕΛΗ ΤΜΜΕΣΡΙΑ: 10 ΚΑΙ 13 ΟΚΣΩΒΡΙΟΤ
29/9/2014 το μάκθμα τθσ ευζλικτθσ ηϊνθσ,τα παιδιά χωρίςτθκαν ςε ομάδεσ και ζφτιαξαν τθν δικι τουσ ηωγραφιά χρθςιμοποιϊντασ γεωμετρικά ςχιματα. ΟΜΑΔΑ: ΘΕΟΚΛΗΣΩ-ΑΝΣΡΕΑ-ΝΕΦΕΛΗ ΤΜΜΕΣΡΙΑ: 10 ΚΑΙ 13 ΟΚΣΩΒΡΙΟΤ
ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ
 ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
ΧΕΔΙΑΜΟ ΠΡΟΪΟΝΣΩΝ ΜΕ Η/Τ ΚΑΜΠΤΛΕ ΕΛΕΤΘΕΡΗ ΜΟΡΦΗ Χριςιμεσ για τθν περιγραφι ομαλών και ελεφκερων ςχθμάτων Αμάξωμα αυτοκινιτου, πτερφγια αεροςκαφών, ςκελετόσ πλοίου χιματα χαρακτιρων κινουμζνων ςχεδίων Περιγραφι
Τάξη Β. Φυςικθ Γενικθσ Παιδείασ. Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Β. 1.1 Νόμοσ Coulomb
 Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Β 1.1 Νόμοσ Coulomb 1. Δφο ίςα κετικά ςθμειακά θλεκτρικά φορτία q 1 και q βρίςκονται πάνω ςτθν ίδια ευκεία. Τα φορτία q 1 και q είναι ςτακερά
Τάξη Β Φυςικθ Γενικθσ Παιδείασ Τράπεζα ιεμάτων Κεφ.1 ο ΘΕΜΑ Β 1.1 Νόμοσ Coulomb 1. Δφο ίςα κετικά ςθμειακά θλεκτρικά φορτία q 1 και q βρίςκονται πάνω ςτθν ίδια ευκεία. Τα φορτία q 1 και q είναι ςτακερά
Είςοδοσ/Εγγραφή ςτη διαχειριςτική ςελίδα του Σχολείου
 Είςοδοσ/Εγγραφή ςτη διαχειριςτική ςελίδα του Σχολείου Ανοίγουμε τον Browser μασ και πλθκτρολογοφμε τθν ςελίδα http://bontime.gr/ Από τθν αρχικι ςελίδα και κάνοντασ scroll down βλζπουμε τισ επιλογζσ εγγραφισ
Είςοδοσ/Εγγραφή ςτη διαχειριςτική ςελίδα του Σχολείου Ανοίγουμε τον Browser μασ και πλθκτρολογοφμε τθν ςελίδα http://bontime.gr/ Από τθν αρχικι ςελίδα και κάνοντασ scroll down βλζπουμε τισ επιλογζσ εγγραφισ
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
GNSS Solutions guide. 1. Create new Project
 GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
Η διαδικαςία επιλογήσ μαθημάτων
 Η διαδικαςία επιλογήσ μαθημάτων 1. Ηθτιςτε από τθν Κοςμθτεία τθσ χολισ Οικονομικϊν Επιςτθμϊν και Διοίκθςθσ (Κτιριο ΟΕΔ02, 0 όροφοσ, γραφείο 027Α) τθν λίςτα με τα μακιματα αντιςτοιχίασ που ιδθ υπάρχουν
Η διαδικαςία επιλογήσ μαθημάτων 1. Ηθτιςτε από τθν Κοςμθτεία τθσ χολισ Οικονομικϊν Επιςτθμϊν και Διοίκθςθσ (Κτιριο ΟΕΔ02, 0 όροφοσ, γραφείο 027Α) τθν λίςτα με τα μακιματα αντιςτοιχίασ που ιδθ υπάρχουν
Δείκτεσ απόδοςθσ υλικών
 Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ
 Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
ΑΝΩΣΕΡΑ ΜΑΘΗΜΑΣΙΚΑ. Διαφορικόσ και Ολοκληρωτικόσ Λογιςμόσ Δφο ή Περιςςοτζρων Μεταβλητϊν
 ΑΝΩΣΕΡΑ ΜΑΘΗΜΑΣΙΚΑ Διαφορικόσ και Ολοκληρωτικόσ Λογιςμόσ Δφο ή Περιςςοτζρων Μεταβλητϊν 1 υναρτιςεισ Περιςςοτζρων Μεταβλθτϊν Παράδειγμα.(E.F. Dbois S =επιφάνεια ςϊματοσ W =βάροσ ςϊματοσ H =φψοσ ςϊματοσ
ΑΝΩΣΕΡΑ ΜΑΘΗΜΑΣΙΚΑ Διαφορικόσ και Ολοκληρωτικόσ Λογιςμόσ Δφο ή Περιςςοτζρων Μεταβλητϊν 1 υναρτιςεισ Περιςςοτζρων Μεταβλθτϊν Παράδειγμα.(E.F. Dbois S =επιφάνεια ςϊματοσ W =βάροσ ςϊματοσ H =φψοσ ςϊματοσ
Ο ήχοσ ωσ φυςικό φαινόμενο
 Ο ήχοσ ωσ φυςικό φαινόμενο Φφλλο Εργαςίασ Ονοματεπώνυμο. Παραγωγή και διάδοςη του ήχου Ήχοσ παράγεται όταν τα ςωματίδια κάποιου υλικοφ μζςου αναγκαςκοφν να εκτελζςουν ταλάντωςθ. Για να διαδοκεί ο ιχοσ
Ο ήχοσ ωσ φυςικό φαινόμενο Φφλλο Εργαςίασ Ονοματεπώνυμο. Παραγωγή και διάδοςη του ήχου Ήχοσ παράγεται όταν τα ςωματίδια κάποιου υλικοφ μζςου αναγκαςκοφν να εκτελζςουν ταλάντωςθ. Για να διαδοκεί ο ιχοσ
Πλαγιογώνια Συςτήματα Συντεταγμζνων Γιϊργοσ Καςαπίδθσ
 Πρόλογοσ το άρκρο αυτό κα δοφμε πωσ διαμορφϊνονται κάποιεσ ζννοιεσ όπωσ το εςωτερικό γινόμενο διανυςμάτων, οι ςυνκικεσ κακετότθτασ και παραλλθλίασ διανυςμάτων και ευκειϊν, ο ςυντελεςτισ διευκφνςεωσ διανφςματοσ
Πρόλογοσ το άρκρο αυτό κα δοφμε πωσ διαμορφϊνονται κάποιεσ ζννοιεσ όπωσ το εςωτερικό γινόμενο διανυςμάτων, οι ςυνκικεσ κακετότθτασ και παραλλθλίασ διανυςμάτων και ευκειϊν, ο ςυντελεςτισ διευκφνςεωσ διανφςματοσ
Ενδεικτική Οργάνωςη Ενοτήτων. Α Σάξη. Διδ. 1 ΕΝΟΣΗΣΑ 1. 6 Ομαδοποίθςθ, Μοτίβα,
 Ενδεικτική Οργάνωςη Ενοτήτων Α Σάξη Α/ Μαθηματικό περιεχόμενο Δείκτεσ Επιτυχίασ Ώρεσ Α Διδ. 1 ΕΝΟΣΗΣΑ 1 Αλ1.1 υγκρίνουν και ταξινομοφν αντικείμενα ςφμφωνα με κάποιο χαρακτθριςτικό/κριτιριο/ιδιότθτά Ομαδοποίθςθ,
Ενδεικτική Οργάνωςη Ενοτήτων Α Σάξη Α/ Μαθηματικό περιεχόμενο Δείκτεσ Επιτυχίασ Ώρεσ Α Διδ. 1 ΕΝΟΣΗΣΑ 1 Αλ1.1 υγκρίνουν και ταξινομοφν αντικείμενα ςφμφωνα με κάποιο χαρακτθριςτικό/κριτιριο/ιδιότθτά Ομαδοποίθςθ,
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
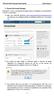 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων
 Πανελλόνιεσ εξετϊςεισ Γ Τϊξησ 2011 Ανϊπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβϊλλον ΘΕΜΑ Α Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων Α1. Σ/Λ 1. Σωςτι 2. Σωςτι 3. Λάκοσ 4. Λάκοσ 5. Λάκοσ Α2. Σ/Λ 1. Σωςτι 2.
Πανελλόνιεσ εξετϊςεισ Γ Τϊξησ 2011 Ανϊπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβϊλλον ΘΕΜΑ Α Α) Ενδεικτικϋσ απαντόςεισ των θεμϊτων Α1. Σ/Λ 1. Σωςτι 2. Σωςτι 3. Λάκοσ 4. Λάκοσ 5. Λάκοσ Α2. Σ/Λ 1. Σωςτι 2.
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ. ΚΕΦΑΛΑΙΟ 2: Σο Τλικό του Τπολογιςτι
 ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ ΚΕΦΑΛΑΙΟ 2: Σο Τλικό του Τπολογιςτι Τλικό υπολογιςτι (Hardware), Προςωπικόσ Τπολογιςτισ (ΡC), υςκευι ειςόδου, υςκευι εξόδου, Οκόνθ (Screen), Εκτυπωτισ (Printer), αρωτισ
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ ΚΕΦΑΛΑΙΟ 2: Σο Τλικό του Τπολογιςτι Τλικό υπολογιςτι (Hardware), Προςωπικόσ Τπολογιςτισ (ΡC), υςκευι ειςόδου, υςκευι εξόδου, Οκόνθ (Screen), Εκτυπωτισ (Printer), αρωτισ
Slide 1. Εισαγωγή στη ψυχρομετρία
 Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Μάθημα 9 ο ΤΕΧΝΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΕΙΚΟΝΙΚΗΣ ΜΝΗΜΗΣ
 Μάθημα 9 ο ΤΕΧΝΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΕΙΚΟΝΙΚΗΣ ΜΝΗΜΗΣ Ειςαγωγό Όπωσ είδαμε, ο χϊροσ εικονικϊν διευκφνςεων μνιμθσ που χρθςιμοποιεί κάκε διεργαςία, είναι αρκετά μεγαλφτεροσ από το χϊρο των φυςικϊν διευκφνςεων.
Μάθημα 9 ο ΤΕΧΝΙΚΕΣ ΔΙΑΧΕΙΡΙΣΗΣ ΕΙΚΟΝΙΚΗΣ ΜΝΗΜΗΣ Ειςαγωγό Όπωσ είδαμε, ο χϊροσ εικονικϊν διευκφνςεων μνιμθσ που χρθςιμοποιεί κάκε διεργαςία, είναι αρκετά μεγαλφτεροσ από το χϊρο των φυςικϊν διευκφνςεων.
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Epsilon Cloud Services
 1 Περίλθψθ Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ λειτουργίασ και παραμετροποίηςησ του Epsilon Cloud Services ςτην εφαρμογή extra Λογιςτική Διαχείριςη. 2 2 Περιεχόμενα
1 Περίλθψθ Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ λειτουργίασ και παραμετροποίηςησ του Epsilon Cloud Services ςτην εφαρμογή extra Λογιςτική Διαχείριςη. 2 2 Περιεχόμενα
ΜΗΝΙΑΙΑ ΕΚΘΕΗ ΠΑΡΑΓΩΓΗ ΕΡΓΟΤ. ΜΑΪΟ 2017
 Η ζκκεςθ αυτι ςυνοψίηει δεδομζνα παραγωγισ και μετεωρολογικά δεδομζνα από το ζργο.., εγκατεςτθμζνθσ ιςχφοσ 1.472,94kW ςτθ κζςθ, Δ.Δ.., Νομοφ.., ιδιοκτθςίασ τθσ Παρουςιάηονται ςυγκεντρωτικά διαγράμματα
Η ζκκεςθ αυτι ςυνοψίηει δεδομζνα παραγωγισ και μετεωρολογικά δεδομζνα από το ζργο.., εγκατεςτθμζνθσ ιςχφοσ 1.472,94kW ςτθ κζςθ, Δ.Δ.., Νομοφ.., ιδιοκτθςίασ τθσ Παρουςιάηονται ςυγκεντρωτικά διαγράμματα
lim x και lim f(β) f(β). (β > 0)
 . Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
. Δίνεται θ παραγωγίςιμθ ςτο * α, β + ( 0 < α < β ) ςυνάρτθςθ f για τθν οποία ιςχφουν: f(α) lim (-) a και lim ( f(β)) = Να δείξετε ότι: α. f(α) < α και f(β) > β β. Αν g() = τότε θ C f και C g ζχουν ζνα
Διδάσκοντας Φυσικές Επιστήμες στο Γυμνάσιο και στο Λύκειο
 Μελέτη της αρχής διατήρησης της μηχανικής ενέργειας με τη μέθοδο του «φωτοφράκτη» Βασίλης Νούσης Αντί της σχετικής προτεινόμενης εργαστηριακής άσκησης με χρήση δύο φωτοπυλών και μπίλιας που πέφτει ελεύθερα,
Μελέτη της αρχής διατήρησης της μηχανικής ενέργειας με τη μέθοδο του «φωτοφράκτη» Βασίλης Νούσης Αντί της σχετικής προτεινόμενης εργαστηριακής άσκησης με χρήση δύο φωτοπυλών και μπίλιας που πέφτει ελεύθερα,
Κροφςεισ Αν ζνα κινοφμενο ςϊμα ςυγκρουςτεί μετωπικά και ελαςτικά με άλλο ακίνθτο ίςθσ μάηασ, τότε θ ταχφτθτά
 Κροφςεισ - - Ερωτθςεισ πολλαπλθσ επιλογθσ Οδηγία: Για να απαντιςετε ςτισ παρακάτω ερωτιςεισ πολλαπλισ επιλογισ αρκεί να γράψετε ςτο φφλλο απαντιςεων τον αρικμό τθσ ερϊτθςθσ και δεξιά από αυτόν το γράμμα
Κροφςεισ - - Ερωτθςεισ πολλαπλθσ επιλογθσ Οδηγία: Για να απαντιςετε ςτισ παρακάτω ερωτιςεισ πολλαπλισ επιλογισ αρκεί να γράψετε ςτο φφλλο απαντιςεων τον αρικμό τθσ ερϊτθςθσ και δεξιά από αυτόν το γράμμα
assessment.gr USER S MANUAL (users)
 assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
assessment.gr USER S MANUAL (users) Human Factor January 2010 Περιεχόμενα 1. Γενικζσ οδθγίεσ ςυςτιματοσ... 3 1.1 Αρχικι ςελίδα... 3 1.2 Ερωτθματολόγια... 6 1.2.1 Τεςτ Γνϊςεων Γενικοφ Ρεριεχομζνου... 6
Σο θλεκτρικό κφκλωμα
 Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Σο θλεκτρικό κφκλωμα Για να είναι δυνατι θ ροι των ελεφκερων θλεκτρονίων, για να ζχουμε θλεκτρικό ρεφμα, απαραίτθτθ προχπόκεςθ είναι θ φπαρξθ ενόσ κλειςτοφ θλεκτρικοφ κυκλϊματοσ. Είδθ κυκλωμάτων Σα κυκλϊματα
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ ΔΗΜΙΟΤΡΓΙΑ
 ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ Επεξεργαςτισ Κειμζνου, Μορφοποίθςθ κειμζνου, Αποκικευςθ -Ανάκτθςθ εργαςίασ, Αντιγραφι - Μεταφορά κειμζνου, Γραμματοςειρά (Font), Ειςαγωγι εικόνασ ςε κείμενο Μία από
ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ Επεξεργαςτισ Κειμζνου, Μορφοποίθςθ κειμζνου, Αποκικευςθ -Ανάκτθςθ εργαςίασ, Αντιγραφι - Μεταφορά κειμζνου, Γραμματοςειρά (Font), Ειςαγωγι εικόνασ ςε κείμενο Μία από
