ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
|
|
|
- Νῶε Μήτζου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 5: Το CMOS transistor και κυκλώµατα CMOS ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ
2 Περίληψη q Κυκλώµατα CMOS Τρανζίστορ και µοντέλα διακόπτη Δίκτυα CMOS - Δίκτυα σε σειρά - Παράλληλα δίκτυα Πλήρως συµπληρωµατικά CMOS - Αντιστροφέας CMOS - CMOS NAND και CMOS NOR - Σύνθετες πύλες CMOS Πύλες µετάδοσης CMOS CMOS Three-state Buffer ΗΜΥ210 Δ05 CMOS Κυκλώµατα 2
3 Κυκλώµατα CMOS q Υλοποίηση λογικών πυλών και άλλων δοµών χρησιµοποιώντας τεχνολογία CMOS. q Βασικό στοιχείο: τρανζίστορ q Υπάρχουν 2 τύποι τρανζίστορ: n-κανάλι (n-channel): τρανζίστορ nmos p-κανάλι (p-channel): τρανζίστορ pmos Ο τύπος εξαρτάται από τα υλικά του ηµιαγωγού που χρησιµοποιήθηκαν για την υλοποίηση του τρανζίστορ (πέραν των στόχων του µαθήµατος ). Μοντελοποιούµε την συµπεριφορά του τρανζίστορ σε λογικό επίπεδο για να µπορέσουµε να µελετήσουµε τη συµπεριφορά κυκλωµάτων CMOS à Θεωρούµε τα τρανζίστορ pmos και nmos ως διακόπτες. ΗΜΥ210 Δ05 CMOS Κυκλώµατα 3
4 p-n Junctions (Διασταυρώσεις) q Μια «σύνδεση» ή διαστάυρωση µεταξύ ενός p-type και n- type ηµιαγωγού, διαµορφώνει µια δίοδο. q Το ρεύµα κινείται ΜΟΝΟ προς µια κατεύθυνση. p-type n-type anode cathode ΗΜΥ210 Δ05 CMOS Κυκλώµατα 4
5 Tο Metal Oxide Semiconductor Transistor Polysilicon Aluminum ΗΜΥ210 Δ05 CMOS Κυκλώµατα 5
6 nmos FET (Field-Effect Transistor) ΗΜΥ210 Δ05 CMOS Κυκλώµατα 6
7 Το Tranzistor First transistor Bell Labs, 1948 ΗΜΥ210 Δ05 CMOS Κυκλώµατα 7
8 ΗΜΥ210 Δ05 CMOS Κυκλώµατα 8
9 Ψηφιακά Κυκλώµατα ΗΜΥ210 Δ05 CMOS Κυκλώµατα 9
10 nmos Transistor q Τέσσερα τερµατικά: gate, source, drain, body q Gate oxide body στίβη σαν πυκνωτή! Gate και το body είναι ΚΑΛΟΙ αγωγοί! SiO 2 (oxide) είναι ΠΟΛΥ ΚΑΛΟ ΜΩΝΟΤΙΚΟ! Ονοµάζεται δηλαδή metal oxide semiconductor (MOS) capacitor (αν και η πύλη δεν κατασκευάζεται από µέταλλο πλέον) Source Gate Drain Polysilicon SiO 2 n+ n+ p bulk Si ΗΜΥ210 Δ05 CMOS Κυκλώµατα 10
11 nmos Λειτουργία q Το Body συνήθως συνδέεται στο ground (0 V) q Όταν η πύλη συνδέεται µε χαµηλή τάση (0V) : To P-type body είναι σε χαµηλή τάση Το Source-body και το drain-body διόδοι είναι OFF ΔΕΝ ΠΕΡΝΑ ΡΕΥΜΑ, άρα το transistor είναι OFF Source Gate Drain Polysilicon SiO 2 n+ p n+ bulk Si S 0 D ΗΜΥ210 Δ05 CMOS Κυκλώµατα 11
12 nmos Λειτουργία q Όταν η πύλη είναι σε high voltage (υψηλή τάση): Θετικό φορτίο στο gate του MOS capacitor Το αρνητικό φορτίο ελκύεται στο σώµα (Negative charge attracted to body) Δηµιουργεί ένα κανάλι κάτω από την πύλη (n-type) Άρα, όταν υπάρχει ΘΕΤΙΚΗ τάση από το ένα τερµατικό (π.χ. drain) στο άλλο (π.χ. source) τότε έχουµε ρεύµα να διαπερνά ΜΕΣΑ από το κανάλι και το τρανζίστορ είναι ON! Source Gate Drain Polysilicon SiO 2 n+ p n+ bulk Si S 1 D ΗΜΥ210 Δ05 CMOS Κυκλώµατα 12
13 pmos Transistor q Το ΙΔΙΟ απλώς µε τις αντίθετες τάσεις! Body tied to high voltage (V DD ) Gate low: transistor ON Gate high: transistor OFF Bubble indicates inverted behavior Polysilicon Source Gate Drain SiO 2 p+ p+ n bulk Si ΗΜΥ210 Δ05 CMOS Κυκλώµατα 13
14 CMOS Inverter - Αντιστροφέας CMOS A 0 1 Y V DD A Y A Y GND ΗΜΥ210 Δ05 CMOS Κυκλώµατα 14
15 CMOS Inverter A Y A Y V DD OFF A=1 Y=0 ON GND ΗΜΥ210 Δ05 CMOS Κυκλώµατα 15
16 CMOS Inverter A Y A Y V DD ON A=0 Y=1 OFF GND ΗΜΥ210 Δ05 CMOS Κυκλώµατα 16
17 Πλήρως Συµπληρωµατικά CMOS q Κάθε πλήρως συµπληρωµατικό δίκτυο CMOS ακολουθεί τη δοµή στα δεξιά. q Το κάθε ένα από τα δύο υπoδίκτυα υλοποιεί τη συνάρτηση δυϊσµού του άλλου. Pull-up δίκτυο (τραβά από +V) q Στατική CMOS (static CMOS): υλοποιεί την F() (όλους τους συνδυασµούς που δίνουν 1) και το συµπλήρωµά της F () (όλους τους συνδυασµούς που δίνουν 0). q Υπάρχει πάντα ένα µονοπάτι που οδηγεί στην έξοδο (F), είτε από την πηγή +V (λογικό 1) είτε από τη γείωση (λογικό 0). q Γιατί; Pull-down δίκτυο (τραβά από GRD) ΗΜΥ210 Δ05 CMOS Κυκλώµατα 17
18 Πλήρως Συµπληρωµατικά CMOS Παράδειγµα - Αντιστροφέας X F = X Λογικό σύµβολο + V X F = X GRD Σχηµατικό σε επίπεδο τρανζίστορ Λειτουργία: q X=1 à ο διακόπτης nmos κλείνει (pmos παραµένει ανοικτός) και η έξοδος άγει από το GRD à F = 0 q X=0 à ο διακόπτης pmos κλείνει (nmos παραµένει ανοικτός) και η έξοδος άγει από το +V à F = 1 ΗΜΥ210 Δ05 CMOS Κυκλώµατα 18
19 CMOS Inverter ΑΝΤΙΣΤΡΟΦΕΑΣ Απο σχηµατικό σε κύκλωµα! N Well The image cannot be displayed. Your computer may not have enough memory to open the image, or the image may have been corrupted. Restart your computer, and then open the file again. If the red x still appears, you may have to delete the image and then insert it again. V DD V DD PMOS 2l PMOS Contacts In Out In Out Metal 1 NMOS Polysilicon NMOS GND ΗΜΥ210 Δ05 CMOS Κυκλώµατα 19
20 CMOS Process - Επεξεργασία ΗΜΥ210 Δ05 CMOS Κυκλώµατα 20
21 Σύγχρονη Επεξεργασία CMOS gate-oxide TiSi 2 AlCu Tungsten SiO 2 n+ p-well p-epi poly n-well p+ SiO 2 p+ Dual-Well Trench-Isolated CMOS Process ΗΜΥ210 Δ05 CMOS Κυκλώµατα 21
22 Το κύκλωµα σε ΣΥΜΒΟΛΑ! V DD V DD M2 M4 V in V out V out2 M1 M3 ΗΜΥ210 Δ05 CMOS Κυκλώµατα 22
23 Και σε ΥΛΟΠΟΙΗΣΗ ΗΜΥ210 Δ05 CMOS Κυκλώµατα 23
24 Καλωδίωση! ΗΜΥ210 Δ05 CMOS Κυκλώµατα 24
25 Τρισδιάστατη Τοµή! Polysilicon Aluminum ΗΜΥ210 Δ05 CMOS Κυκλώµατα 25
26 Τρανζίστορ CMOS ως διακόπτες 3 άκρα (terminals) στα τρανζίστορ CMOS: G: Πύλη (Gate) D: Ακροδέκτης MOSFET (Drain) S: Πηγή (Source) nmos τρανζίστορ/διακόπτης X=1, διακόπτης κλείνει (ON) X=0, διακόπτης ανοίγει (OFF) pmos τρανζίστορ/διακόπτης X=0, διακόπτης κλείνει (ON) X=1, διακόπτης ανοίγει (OFF) ΗΜΥ210 Δ05 CMOS Κυκλώµατα 26
27 Τρανζίστορ CMOS ως διακόπτες q Στην ουσία, είναι ΗΛΕΚΤΡΟΝΙΚΑ ΕΛΕΓΧΟΜΕΝΟΙ ΔΙΑΚΟΠΤΕΣ! q Η τάση που τροφοδοτεί την πύλη, ελέγχει την λειτουργία τους (σαν το κουµπί του διακόπτη!) g = 0 g = 1 nmos g d s d s OFF d s ON pmos g d s d s ON d s OFF ΗΜΥ210 Δ05 CMOS Κυκλώµατα 27
28 Δίκτυα διακόπτων q Χρησιµοποιούµε διακόπτες για τη δηµιουργία δικτύων που αναπαριστάνουν λογικά κυκλώµατα CMOS. q Για να υλοποιήσουµε µια συνάρτηση F, δηµιουργούµε ένα δίκτυο έτσι ώστε να υπάρχει ένα µονοπάτι δια µέσου του δικτύου όταν το F = 1, και να µην υπάρχει όταν το F = 0. q Δύο βασικές δοµές: Τρανζίστορ σε σειρά Παράλληλα τρανζίστορ ΗΜΥ210 Δ05 CMOS Κυκλώµατα 28
29 Τρανζίστορ σε Σειρά/Παράλληλα nmos σε σειρά a a X Y b X:X Y:Y b υπάρχει µονοπάτι µεταξύ των σηµείων a και b εάν Χ και Y είναι 1 à X Y X παράλληλο nmos Y a b X:X a Y:Y b υπάρχει µονοπάτι µεταξύ των σηµείων a και b εάν το X ή το Y είναι 1 à X+Y pmos σε σειρά a a X X:X Y Y:Y b b υπάρχει µονοπάτι µεταξύ των σηµείων a και b εάν το Χ και Y είναι 0 à X Y παράλληλο pmos a a X Y X:X Y:Y b b υπάρχει µονοπάτι µεταξύ των σηµείων a και b εάν το X ή το Y είναι 0 à X +Y ΗΜΥ210 Δ05 CMOS Κυκλώµατα 29
30 Δίκτυα διακόπτων (συν.) q q Γενικά: 1. Το nmos σε σειρά υλοποιεί την λογική πύλη AND 2. Το pmos σε σειρά υλοποιεί την λογική πύλη NOR 3. Το παράλληλο nmos υλοποιεί την λογική πύλη OR 4. Το παράλληλο pmos υλοποιεί την λογική πύλη NAND Παρατηρήστε ότι: Το 1 είναι ο δυϊσµός του 3, και αντίστροφα Το 2 είναι ο δυϊσµός του 4, και αντίστροφα ΗΜΥ210 Δ05 CMOS Κυκλώµατα 30
31 Στατικά Κυκλώµατα CMOS q Pull-up network (PUN) και pull-down network (PDN) In 1 In 2 In N In 1 In 2 In N V DD PUN PDN PMOS transistors only pull-up: Συνδέει το V DD µε το F όταν το F(In 1,In 2, In N ) = 1 F(In 1,In 2, In N ) pull-down: Συνδέει το F µε το GND όταν το F(In 1,In 2, In N ) = 0 NMOS transistors only PUN and PDN are dual logic networks διϋσµός! ΗΜΥ210 Δ05 CMOS Κυκλώµατα 31
32 Ηλεκτρονικά Κυκλώµατα - ΒΑΣΙΚΑ PUN V DD S D 0 V OUT C L PDN V DD D C L V OUT 0 S ΗΜΥ210 Δ05 CMOS Κυκλώµατα 32
33 Πώς δηµιουργούµε το PDN και το PUN q NMOS in series à NAND function - ΣΕΙΡΙΑΚΑ A A B B q NMOS in parallel à NOR function - ΠΑΡΑΛΛΗΛΑ A B A + B ΗΜΥ210 Δ05 CMOS Κυκλώµατα 33
34 Δυϊσµός PUN και PDN q Το PUN και PDN είναι dual (δυϊσµός) DeMorgan s theorems A + B = A B [!(A + B) =!A!B or!(a B) =!A &!B] A B = A + B [!(A B) =!A +!B or!(a & B) =!A!B] Μια ΠΑΡΑΛΛΗΛΗ parallel διασύνδεση των transistors στο PUN αντιστοιχεί σε ΣΕΙΡΙΑΚΗ series διασύνδεση του PDN q Complementary gate - naturally inverting (NAND, NOR) q Για κάθε N-input logic gate χρειαζόµαστε 2N tranzistors ΗΜΥ210 Δ05 CMOS Κυκλώµατα 34
35 CMOS NAND A B A B F A B A B A B ΗΜΥ210 Δ05 CMOS Κυκλώµατα 35
36 CMOS NOR A B A B A + B A B F A B ΗΜΥ210 Δ05 CMOS Κυκλώµατα 36
37 Πλήρως ολοκληρωµένα δίκτυα CMOS Βασικές Πύλες (NOR, NAND, NOT) ΗΜΥ210 Δ05 CMOS Κυκλώµατα 37
38 CMOS NAND and NOR ΗΜΥ210 Δ05 CMOS Κυκλώµατα 38
39 Πλήρως ολοκληρωµένα CMOS q Γιατί τα δίκτυα pmos είναι συνδεδεµένα στο +V και τα nmos στο GRD? Τα στοιχεία pmos είναι σχεδόν ιδανικά όταν τα διαπερνά υψηλή τάση (Η) και αδύνατα όταν τα διαπερνά χαµηλή τάση (L). Τα στοιχεία nmos είναι σχεδόν ιδανικά όταν τα διαπερνά χαµηλή τάση και αδύνατα όταν τα διαπερνά υψηλή τάση (Η). Η δοµή του CMOS εξασφαλίζει την παραµονή των τιµών των διαφόρων σηµάτων στα κατάλληλα υψηλά και χαµηλά λογικά επίπεδα, όταν µεταδίδονται δια µέσω του δικτύου και φθάνουν στην έξοδο. ΗΜΥ210 Δ05 CMOS Κυκλώµατα 39
40 Πλήρως ολοκληρωµένα δίκτυα CMOS Σύνθετες Πύλες (Complex Gates) Δεδοµένης µιας συνάρτησης F(): 1. Βρείτε και απλοποιήστε την F (). Βεβαιωθείτε ότι θα προχωρήσετε µέχρι που τα συµπληρώµατα να φτάσουν στο επίπεδο παραγόντων (literal). 2. Υλοποιήστε την F () σαν ένα nmos δίκτυο και ακολούθως συνδέστε το µε το GRD και την έξοδο F() à δίκτυο pull-down 3. Βρείτε το δυϊσµό της F (), υλοποιήστε την ως ένα pmos δίκτυο και ακολούθως συνδέστε το µε το +V και την έξοδο F() à δίκτυο pull-up 4. Συνδέστε τις εισόδους σε κάθε ένα από τα δίκτυα pullup και pull-down. ΗΜΥ210 Δ05 CMOS Κυκλώµατα 40
41 Πλήρως ολοκληρωµένα δίκτυα CMOS: Σύνθετες Πύλες - Παράδειγµα F = AB +AC+BC ΗΜΥ210 Δ05 CMOS Κυκλώµατα 41
42 «Πολύπλοκη» Πύλη CMOS A B C D D B A C OUT =!(D + A (B + C)) ΗΜΥ210 Δ05 CMOS Κυκλώµατα 42
43 Πύλη Μετάδοσης CMOS ΗΜΥ210 Δ05 CMOS Κυκλώµατα 43
44 MUX 2-εισόδων και XOR µε πύλες µετάδοσης CMOS MUX (= multiplexer) = Πολυπλέκτης: Επιλέγει να περάσει την τιµή µίας από τις εισόδους βάση της τιµής του C ΗΜΥ210 Δ05 CMOS Κυκλώµατα 44
ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο Κυκλώματα CMOS. Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο 2005 Κυκλώματα CMOS Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κυκλώματα CMOS Περίληψη Τρανζίστορ και μοντέλα διακόπτη ίκτυα CMOS
ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο 2005 Κυκλώματα CMOS Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κυκλώματα CMOS Περίληψη Τρανζίστορ και μοντέλα διακόπτη ίκτυα CMOS
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
Εισαγωγή στα κυκλώµατα CMOS 2
 1 η Θεµατική Ενότητα : Εισαγωγή στα κυκλώµατα CMOS Επιµέλεια διαφανειών:. Μπακάλης Εισαγωγή Τεχνολογία CMOS = Complementary Metal Oxide Semiconductor Συµπληρωµατικού Ηµιαγωγού Μετάλλου Οξειδίου Αποτελείται
1 η Θεµατική Ενότητα : Εισαγωγή στα κυκλώµατα CMOS Επιµέλεια διαφανειών:. Μπακάλης Εισαγωγή Τεχνολογία CMOS = Complementary Metal Oxide Semiconductor Συµπληρωµατικού Ηµιαγωγού Μετάλλου Οξειδίου Αποτελείται
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφική Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφική Σχεδίαση Ενότητα 4: Υλοποίηση Κυκλωμάτων με πύλες NOT AND και NOR, περιττή συνάρτηση, συνάρτηση ισοτιμίας. Δρ. Μηνάς Δασυγένης @ieee.ormdasygg Εργαστήριο
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφική Σχεδίαση Ενότητα 4: Υλοποίηση Κυκλωμάτων με πύλες NOT AND και NOR, περιττή συνάρτηση, συνάρτηση ισοτιμίας. Δρ. Μηνάς Δασυγένης @ieee.ormdasygg Εργαστήριο
Υλοποίηση λογικών πυλών µε τρανζίστορ MOS. Εισαγωγή στην Ηλεκτρονική
 Υλοποίηση λογικών πυλών µε τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Λογική MOS Η αναπαράσταση των λογικών µεταβλητών 0 και 1 στα ψηφιακά κυκλώµατα γίνεται µέσω κατάλληλων επιπέδων τάσης, όπου κατά σύµβαση
Υλοποίηση λογικών πυλών µε τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Λογική MOS Η αναπαράσταση των λογικών µεταβλητών 0 και 1 στα ψηφιακά κυκλώµατα γίνεται µέσω κατάλληλων επιπέδων τάσης, όπου κατά σύµβαση
Ψηφιακά Ηλεκτρονικά. Μάθηµα 5ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
ECE 407 Computer Aided Design for Electronic Systems. CMOS Logic. Instructor: Maria K. Michael. Overview
 407 Computer Aided Design for Electronic Systems CMOS Logic Instructor: Maria K. Michael 1 Overview MOS transistors (nmos, pmos) CMOS processing technology CMOS design/layout rules MOS transistors as ideal
407 Computer Aided Design for Electronic Systems CMOS Logic Instructor: Maria K. Michael 1 Overview MOS transistors (nmos, pmos) CMOS processing technology CMOS design/layout rules MOS transistors as ideal
Ψηφιακή Λογική και Σχεδίαση
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
Κεφάλαιο Τρία: Ψηφιακά Ηλεκτρονικά
 Κεφάλαιο Τρία: 3.1 Τι είναι αναλογικό και τι ψηφιακό µέγεθος Αναλογικό ονοµάζεται το µέγεθος που µπορεί να πάρει οποιαδήποτε τιµή σε µια συγκεκριµένη περιοχή τιµών π.χ. η ταχύτητα ενός αυτοκινήτου. Ψηφιακό
Κεφάλαιο Τρία: 3.1 Τι είναι αναλογικό και τι ψηφιακό µέγεθος Αναλογικό ονοµάζεται το µέγεθος που µπορεί να πάρει οποιαδήποτε τιµή σε µια συγκεκριµένη περιοχή τιµών π.χ. η ταχύτητα ενός αυτοκινήτου. Ψηφιακό
Εισαγωγή στις κρυσταλλολυχνίες (Transistors)
 Εισαγωγή στις κρυσταλλολυχνίες (Transistors) Dr. Petros Panayi Διακόπτες Ένας διακόπτης είναι μια συσκευή που αλλάζει τη ροή ενός κυκλώματος. Το πρότυπο είναι μια μηχανική συσκευή (παραδείγματος χάριν
Εισαγωγή στις κρυσταλλολυχνίες (Transistors) Dr. Petros Panayi Διακόπτες Ένας διακόπτης είναι μια συσκευή που αλλάζει τη ροή ενός κυκλώματος. Το πρότυπο είναι μια μηχανική συσκευή (παραδείγματος χάριν
4.2 Αναπαράσταση δυαδικών τιμών στα ψηφιακά κυκλώματα
 ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 6: Συνδυαστική Λογική / Ολοκληρωµένα Κυκλώµατα (Συν.) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Συνέχεια
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 6: Συνδυαστική Λογική / Ολοκληρωµένα Κυκλώµατα (Συν.) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Συνέχεια
i Το τρανζίστορ αυτό είναι τύπου NMOS. Υπάρχει και το συμπληρωματικό PMOS. ; Τι συμβαίνει στο τρανζίστορ PMOS; Το τρανζίστορ MOS(FET)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ.
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Γιάννης Λιαπέρδος 2 ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΔΙΑΛΕΞΗΣ Άλγεβρα Διακοπτών Κυκλωματική Υλοποίηση Λογικών Πυλών με Ηλεκτρονικά
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Γιάννης Λιαπέρδος 2 ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΔΙΑΛΕΞΗΣ Άλγεβρα Διακοπτών Κυκλωματική Υλοποίηση Λογικών Πυλών με Ηλεκτρονικά
4/10/2008. Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης. Πραγματικά τρανζίστορ. Ψηφιακή λειτουργία. Κανόνες ψηφιακής λειτουργίας
 2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.2: Συνδυαστική Λογική - Σύνθετες Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.2: Συνδυαστική Λογική - Σύνθετες Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
Πολυσύνθετες πύλες. Διάλεξη 11
 Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων
 Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΒΑΣΙΚΕΣ ΠΥΛΕΣ ΨΗΦΙΑΚΗΣ ΛΟΓΙΚΗΣ. Τι σημαίνει
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΒΑΣΙΚΕΣ ΠΥΛΕΣ ΨΗΦΙΑΚΗΣ ΛΟΓΙΚΗΣ. Τι σημαίνει
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ CMOS. Εαρινό Εξάμηνο ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ
 ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2017 ΔΙΑΛΕΞΗ 6: ΚΥΚΛΩΜΑΤΑ CMOS ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002, J. Rabaey et
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2017 ΔΙΑΛΕΞΗ 6: ΚΥΚΛΩΜΑΤΑ CMOS ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002, J. Rabaey et
ΔΙΑΛΕΞΗ 2: Technology and Historical Progress of FPGAs
 ΗΜΥ 408 ΨΗΦΙΑΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΕ FPGAs Εαρινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 2: Technology and Historical Progress of FPGAs ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής ΗΜΜΥ (ttheocharides@ucy.ac.cy) Some slides adopted from
ΗΜΥ 408 ΨΗΦΙΑΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΕ FPGAs Εαρινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 2: Technology and Historical Progress of FPGAs ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής ΗΜΜΥ (ttheocharides@ucy.ac.cy) Some slides adopted from
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.3: Συνδυαστική Λογική - Δυναμικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.3: Συνδυαστική Λογική - Δυναμικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS
 ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ
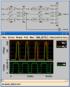 Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
V Vin $N PULSE 1.8V p 0.1p 1n 2n M M1 $N 0002 $N 0001 Vout $N 0002 MpTSMC180 + L=180n + W=720n + AD=0.324p + AS=0.
 Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
ΜΑΘΗΜΑ 5 Ο. Η Λειτουργία της Οργάνωσης. Ι. Η Έννοια και η Φύση της Οργάνωσης 05/04/2016
 ΜΑΘΗΜΑ 5 Ο Η Λειτουργία της Οργάνωσης Ι. Η Έννοια και η Φύση της Οργάνωσης Με τον όρο οργάνωση εννοούµε την εξεύρεση τρόπων και µεθόδων που θα συνενώσουν τα διαφορετικά ενδιαφέροντα των µελών ενός οργανισµού
ΜΑΘΗΜΑ 5 Ο Η Λειτουργία της Οργάνωσης Ι. Η Έννοια και η Φύση της Οργάνωσης Με τον όρο οργάνωση εννοούµε την εξεύρεση τρόπων και µεθόδων που θα συνενώσουν τα διαφορετικά ενδιαφέροντα των µελών ενός οργανισµού
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 17: Αναδιατασσόµενη Λογική Προγραµµατιζόµενο Υλικό
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 17: Αναδιατασσόµενη Λογική Προγραµµατιζόµενο Υλικό ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Προγραµµατιζόµενες
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 17: Αναδιατασσόµενη Λογική Προγραµµατιζόµενο Υλικό ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Προγραµµατιζόµενες
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino)
 Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
3. Βασικές αρχές ψηφιακών κυκλωμάτων και συστημάτων
 3. Βασικές αρχές ψηφιακών κυκλωμάτων και συστημάτων Σύνοψη Στο προηγούμενο κεφάλαιο συζητήσαμε για τα λειτουργικά συστήματα, τα οποία αποτελούν τη βάση του λογισμικού των υπολογιστικών συστημάτων, αλλά
3. Βασικές αρχές ψηφιακών κυκλωμάτων και συστημάτων Σύνοψη Στο προηγούμενο κεφάλαιο συζητήσαμε για τα λειτουργικά συστήματα, τα οποία αποτελούν τη βάση του λογισμικού των υπολογιστικών συστημάτων, αλλά
Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους
 3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
Η αντιστοιχία των παραπάνω επαφών με αυτές του διπολικού τρανζίστορ είναι (προφανώς) η εξής: S E, D C, G B.
 3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Οι λογικές πύλες (ή απλά πύλες) είναι οι θεμελιώδεις δομικές μονάδες των ψηφιακών κυκλωμάτων. Όπως φαίνεται και από την ονομασία
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Οι λογικές πύλες (ή απλά πύλες) είναι οι θεμελιώδεις δομικές μονάδες των ψηφιακών κυκλωμάτων. Όπως φαίνεται και από την ονομασία
Ψηφιακά Κυκλώματα (1 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
Ψηφιακά Κυκλώματα ( ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ψηφιακά κυκλώματα Οι δύο λογικές τιμές, αντιστοιχούν σε ηλεκτρικές τάσεις Υλοποιούνται με τρανζίστορ ή διόδους: ελεγχόμενοι διακόπτες
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ
 ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ 1η: ΜΕΛΕΤΗ ΤΟΥ MOSFET Σκοπός της άσκησης Στην άσκηση αυτή θα μελετήσουμε το τρανζίστορ τύπου MOSFET και τη λειτουργία
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ 1η: ΜΕΛΕΤΗ ΤΟΥ MOSFET Σκοπός της άσκησης Στην άσκηση αυτή θα μελετήσουμε το τρανζίστορ τύπου MOSFET και τη λειτουργία
Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Εκτέλεση πράξεων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Εκτέλεση πράξεων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 4: Ελαχιστοποίηση και Λογικές Πύλες ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Βελτιστοποίηση
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 4: Ελαχιστοποίηση και Λογικές Πύλες ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Βελτιστοποίηση
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Κεφάλαιο 1 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. CMOS Κυκλώματα 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων MOS Ψηφιακά Κυκλώματα Κεφάλαιο 1 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Άλγεβρα oole Χάρτης Karnaugh 2. MOS τρανζίστορ 3.
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων MOS Ψηφιακά Κυκλώματα Κεφάλαιο 1 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Άλγεβρα oole Χάρτης Karnaugh 2. MOS τρανζίστορ 3.
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 2: Το Τρανζίστορ Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 2: Το Τρανζίστορ Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων
 Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων Βασικές έννοιες και τεχνικές Γιώργος Δημητρακόπουλος Δημοκριτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Τι χρειαζόμαστε για να φτιάξουμε
Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων Βασικές έννοιες και τεχνικές Γιώργος Δημητρακόπουλος Δημοκριτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Τι χρειαζόμαστε για να φτιάξουμε
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 2 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 26 ΔΙΑΛΕΞΗ 8: Σχεδιασµός Συνδυαστικών Κυκλωµάτων Ι (Κεφάλαιο 4) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Συναρτήσεις
ΗΜΥ 2 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 26 ΔΙΑΛΕΞΗ 8: Σχεδιασµός Συνδυαστικών Κυκλωµάτων Ι (Κεφάλαιο 4) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Συναρτήσεις
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΤΕΧΝΟΛΟΓΙΑΣ MOS KAI CMOS
 Εισαγωγή στη Μικροηλεκτρονική (ΕΤΥ-482) 1 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΤΕΧΝΟΛΟΓΙΑΣ MOS KAI CMOS Α. Αναστροφέας MOSFET. Α.1 Αναστροφέας MOSFET µε φορτίο προσαύξησης. Ο αναστροφέας MOSFET (πύλη NOT) αποτελείται από
Εισαγωγή στη Μικροηλεκτρονική (ΕΤΥ-482) 1 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ ΤΕΧΝΟΛΟΓΙΑΣ MOS KAI CMOS Α. Αναστροφέας MOSFET. Α.1 Αναστροφέας MOSFET µε φορτίο προσαύξησης. Ο αναστροφέας MOSFET (πύλη NOT) αποτελείται από
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
Τρανζίστορ Επίδρασης Πεδίου Field-effect transistors (FET)
 Τρανζίστορ Επίδρασης Πεδίου Field-effect transistors (FET) Χρησιµοποιούνται σε κλίµακα υψηλής ολοκλήρωσης VLSI Χρησιµοποιούνται και σε αναλογικούς ενισχυτές καθώς και στο στάδιο εξόδου ενισχυτών Ισχύος-
Τρανζίστορ Επίδρασης Πεδίου Field-effect transistors (FET) Χρησιµοποιούνται σε κλίµακα υψηλής ολοκλήρωσης VLSI Χρησιµοποιούνται και σε αναλογικούς ενισχυτές καθώς και στο στάδιο εξόδου ενισχυτών Ισχύος-
ΗΛΕΚΤΡΟΝΙΚΗ Ι ΤΡΑΝΖΙΣΤΟΡ ΕΠΙΔΡΑΣΗΣ ΠΕΔΙΟΥ. Eλεγχος εσωτερικού ηλεκτρικού πεδίου με την εφαρμογή εξωτερικού δυναμικού στην πύλη (gate, G).
 ΗΛΕΚΤΡΟΝΙΚΗ Ι 1. Ημιαγωγική δίοδος Ένωση pn 2. Τρανζίστορ FET 3. Πόλωση των FET - Ισοδύναμα κυκλώματα 4. Ενισχυτές με FET 5. Διπολικό τρανζίστορ (BJT) 6. Πόλωση των BJT - Ισοδύναμα κυκλώματα 7. Ενισχυτές
ΗΛΕΚΤΡΟΝΙΚΗ Ι 1. Ημιαγωγική δίοδος Ένωση pn 2. Τρανζίστορ FET 3. Πόλωση των FET - Ισοδύναμα κυκλώματα 4. Ενισχυτές με FET 5. Διπολικό τρανζίστορ (BJT) 6. Πόλωση των BJT - Ισοδύναμα κυκλώματα 7. Ενισχυτές
Η αντιστοιχία των παραπάνω επαφών με αυτές του διπολικού τρανζίστορ είναι (προφανώς) η εξής: S E, D C, G B.
 3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
3. ΤΡΑΝΖΙΣΤΟΡ ΕΓΚΑΡΣΙΟΥ ΠΕΔΙΟΥ (Field Effect Transistor FET) 3.1. Γενικά Σε αντίθεση με τα διπολικά τρανζίστορ, που στηρίζουν τη λειτουργία τους σε δύο τύπους φορέων (ηλεκτρόνια και οπές), τα τρανζίστορ
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
Βασικές αρχές ηµιαγωγών και τρανζίστορ MOS. Εισαγωγή στην Ηλεκτρονική
 Βασικές αρχές ηµιαγωγών και τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Ηµιαγώγιµα υλικά και πυρίτιο Η κατασκευή ενός ολοκληρωµένου κυκλώµατος γίνεται µε βάση ένα υλικό ηµιαγωγού (semiconductor), το οποίο
Βασικές αρχές ηµιαγωγών και τρανζίστορ MOS Εισαγωγή στην Ηλεκτρονική Ηµιαγώγιµα υλικά και πυρίτιο Η κατασκευή ενός ολοκληρωµένου κυκλώµατος γίνεται µε βάση ένα υλικό ηµιαγωγού (semiconductor), το οποίο
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2018
 ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2018 ΔΙΑΛΕΞΗ 4: CMOS Αντιστροφέας (Inverter) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002,
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2018 ΔΙΑΛΕΞΗ 4: CMOS Αντιστροφέας (Inverter) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002,
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2017
 ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2017 ΔΙΑΛΕΞΗ 4: CMOS Αντιστροφέας (Inverter) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002,
ΗΜΥ 307 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Εαρινό Εξάμηνο 2017 ΔΙΑΛΕΞΗ 4: CMOS Αντιστροφέας (Inverter) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Rabaey s Digital Integrated Circuits, 2002,
 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Διαδικασία CMOS 2 1 Μια σύγχρονη διαδικασία CMOS gate-oxide
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Διαδικασία CMOS 2 1 Μια σύγχρονη διαδικασία CMOS gate-oxide
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 ΛΟΓΙΚΕΣ ΠΥΛΕΣ OR, NOR, XOR
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 ΛΟΓΙΚΕΣ ΠΥΛΕΣ OR, NOR, XOR Σκοπός: Να επαληθευτούν πειραµατικά οι πίνακες αληθείας των λογικών πυλών OR, NOR, XOR. Να δειχτεί ότι η πύλη NOR είναι οικουµενική.
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 ΛΟΓΙΚΕΣ ΠΥΛΕΣ OR, NOR, XOR Σκοπός: Να επαληθευτούν πειραµατικά οι πίνακες αληθείας των λογικών πυλών OR, NOR, XOR. Να δειχτεί ότι η πύλη NOR είναι οικουµενική.
Εκτέλεση πράξεων. Ψηφιακά Ηλεκτρονικά και Δυαδική Λογική. Πράξεις με δυαδικούς αριθμούς. Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 24-5 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης ; Ποιες κατηγορίες
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 24-5 Πράξεις με δυαδικούς αριθμούς (λογικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης ; Ποιες κατηγορίες
ΑΣΚΗΣΗ 7. ΘΕΜΑ 1ο MINORITY A B C. C out
 ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 3
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 3: Τρανζίστορ FET Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 3: Τρανζίστορ FET Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν
Χρήση διακοπτών για την κατασκευή λογικών πυλών Εισαγωγή στις οικογένειες πυλών nmos, CMOS, κα.
 Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής και Συστημάτων Πληροφορικής Εισαγωγή στη Σχεδίαση VLSI Χρήση διακοπτών για την κατασκευή
Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής και Συστημάτων Πληροφορικής Εισαγωγή στη Σχεδίαση VLSI Χρήση διακοπτών για την κατασκευή
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Δίοδοι, BJT και MOSFET ως Διακόπτες 2
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2018-2019 Ροή Σχεδίασης Κυκλωμάτων και Εργαλεία CAD ΗΥ220 - Βασίλης Παπαευσταθίου 1 Transistor: Δομική μονάδα κυκλωμάτων Τα ολοκληρωμένα κυκλώματα
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2018-2019 Ροή Σχεδίασης Κυκλωμάτων και Εργαλεία CAD ΗΥ220 - Βασίλης Παπαευσταθίου 1 Transistor: Δομική μονάδα κυκλωμάτων Τα ολοκληρωμένα κυκλώματα
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
Τα τρανζίστορ επίδρασης πεδίου (FET) Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής
 Τα τρανζίστορ επίδρασης πεδίου (FET) Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Τα τρανζίστορ επίδρασης πεδίου Τα πιο βασικά στοιχεία δομής των ηλεκτρονικών κυκλωμάτων
Τα τρανζίστορ επίδρασης πεδίου (FET) Σπύρος Νικολαΐδης Αναπληρωτής Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Τα τρανζίστορ επίδρασης πεδίου Τα πιο βασικά στοιχεία δομής των ηλεκτρονικών κυκλωμάτων
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Ροή Σχεδίασης Κυκλωμάτων και Εργαλεία CAD ΗΥ220 - Γιώργος Καλοκαιρινός & Βασίλης Παπαευσταθίου 1 Transistor: Δομική μονάδα κυκλωμάτων Τα
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Ροή Σχεδίασης Κυκλωμάτων και Εργαλεία CAD ΗΥ220 - Γιώργος Καλοκαιρινός & Βασίλης Παπαευσταθίου 1 Transistor: Δομική μονάδα κυκλωμάτων Τα
ΕΥΕΛΙΚΤΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΑΣ ΗΜΥ 499
 ΕΥΕΛΙΚΤΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΑΣ ΗΜΥ 499 ΟΜΗ ΙΑΚΟΠΤΙΚΩΝ ΜΕΤΑΤΡΟΠΕΩΝ ρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέµατα Επιλογή διακοπτών
ΕΥΕΛΙΚΤΑ ΣΥΣΤΗΜΑΤΑ ΜΕΤΑΦΟΡΑΣ ΗΜΥ 499 ΟΜΗ ΙΑΚΟΠΤΙΚΩΝ ΜΕΤΑΤΡΟΠΕΩΝ ρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέµατα Επιλογή διακοπτών
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων
 Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών The MOS Transistor Polysilicon Aluminum 2 N-MOS Τρανζίστορ Διάταξη τριών
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Αγγελική Αραπογιάννη Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών The MOS Transistor Polysilicon Aluminum 2 N-MOS Τρανζίστορ Διάταξη τριών
Καθυστέρηση στατικών πυλών CMOS
 Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν
1.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΛΟΓΙΚΕΣ ΠΥΛΕΣ NOT, AND, NAND Σκοπός: Να εξοικειωθούν οι φοιτητές µε τα ολοκληρωµένα κυκλώµατα της σειράς 7400 για τη σχεδίαση και υλοποίηση απλών λογικών συναρτήσεων.
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΛΟΓΙΚΕΣ ΠΥΛΕΣ NOT, AND, NAND Σκοπός: Να εξοικειωθούν οι φοιτητές µε τα ολοκληρωµένα κυκλώµατα της σειράς 7400 για τη σχεδίαση και υλοποίηση απλών λογικών συναρτήσεων.
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε αναστροφείς CMOS VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 3: Εισαγωγή στη Διαδικασία Κατασκευής (CMOS Processing) Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 3: Εισαγωγή στη Διαδικασία Κατασκευής (CMOS Processing) Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ
 ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Άλγεβρα Boole και Λογικές Πύλες 2. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Άλγεβρα Boole και Λογικές Πύλες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αξιωματικός Ορισμός Άλγεβρας Boole Άλγεβρα Boole: είναι μία
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Άλγεβρα Boole και Λογικές Πύλες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Αξιωματικός Ορισμός Άλγεβρας Boole Άλγεβρα Boole: είναι μία
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Ηλεκτρονική Μάθημα VIΙΙ Ψηφιακά Κυκλώματα Υλοποίηση Λογικών Συναρτήσεων
 Ηλεκτρονική Μάθημα VIΙΙ Ψηφιακά Κυκλώματα Υλοποίηση Λογικών Συναρτήσεων Καθηγητής Αντώνιος Γαστεράτος Τμήμα Ε.ΔΙ.Π. Μηχανικών Δρ. Αθανάσιος Παραγωγής Ψωμούλης και Διοίκησης, Δ.Π.Θ. Τμήμα Μηχανικών Παραγωγής
Ηλεκτρονική Μάθημα VIΙΙ Ψηφιακά Κυκλώματα Υλοποίηση Λογικών Συναρτήσεων Καθηγητής Αντώνιος Γαστεράτος Τμήμα Ε.ΔΙ.Π. Μηχανικών Δρ. Αθανάσιος Παραγωγής Ψωμούλης και Διοίκησης, Δ.Π.Θ. Τμήμα Μηχανικών Παραγωγής
Ακίνητα Μηχανήματα - Στήριξη
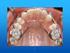 Ακίνητα Μηχανήματα - Στήριξη Στόχοι Μαθήματος Ο φοιτητής θα πρέπει: Να περιγράφει και αναγνωρίζει τα μέρη των ακινήτων ορθοδοντικών μηχανημάτων. Να επεξηγεί τις βασικές αρχές λειτουργίας τους. Να επεξηγεί
Ακίνητα Μηχανήματα - Στήριξη Στόχοι Μαθήματος Ο φοιτητής θα πρέπει: Να περιγράφει και αναγνωρίζει τα μέρη των ακινήτων ορθοδοντικών μηχανημάτων. Να επεξηγεί τις βασικές αρχές λειτουργίας τους. Να επεξηγεί
Low Power. Οργάνωση Παρουσίασης. ηµήτρης Μητροβγένης ηµήτρης Κασερίδης Μαρίνος Σαµψών VLSI II ΠΑΤΡΑ 2004
 Low Power ηµήτρης Μητροβγένης ηµήτρης Κασερίδης Μαρίνος Σαµψών VLSI II ΠΑΤΡΑ 004 Low Power 1 Οργάνωση Παρουσίασης Ηανάγκη για χαµηλή ισχύ (Low Power) Πηγές Κατανάλωσης ισχύος Τεχνικές Βελτιστοποίησης Κατανάλωσης
Low Power ηµήτρης Μητροβγένης ηµήτρης Κασερίδης Μαρίνος Σαµψών VLSI II ΠΑΤΡΑ 004 Low Power 1 Οργάνωση Παρουσίασης Ηανάγκη για χαµηλή ισχύ (Low Power) Πηγές Κατανάλωσης ισχύος Τεχνικές Βελτιστοποίησης Κατανάλωσης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. Σταθερές Μνήμες Αρχιτεκτονικές Μνήμης RAM
 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 ΗΥ330 - Διάλεξη 12η - Κυκλώματα Μνήμης Περιεχόμενα Είδη
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 ΗΥ330 - Διάλεξη 12η - Κυκλώματα Μνήμης Περιεχόμενα Είδη
ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες
 ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΕΙΣΑΓΩΓΗ στους Η/Υ Διδάσκουσα Δρ. Β. Σγαρδώνη 2013-14 ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες Α. ΑΛΓΕΒΡΑ Boole Η Άλγεβρα Boole (Boolean algebra) πήρε
ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΕΙΣΑΓΩΓΗ στους Η/Υ Διδάσκουσα Δρ. Β. Σγαρδώνη 2013-14 ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες Α. ΑΛΓΕΒΡΑ Boole Η Άλγεβρα Boole (Boolean algebra) πήρε
2. ΛΟΓΙΚΕΣ ΠΥΛΕΣ. e-book ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ΑΣΗΜΑΚΗΣ-ΒΟΥΡΒΟΥΛΑΚΗΣ- ΚΑΚΑΡΟΥΝΤΑΣ-ΛΕΛΙΓΚΟΥ 1
 2. ΛΟΓΙΚΕΣ ΠΥΛΕΣ e-book ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ΑΣΗΜΑΚΗΣ-ΒΟΥΡΒΟΥΛΑΚΗΣ- ΚΑΚΑΡΟΥΝΤΑΣ-ΛΕΛΙΓΚΟΥ 1 ΟΙ ΛΟΓΙΚΕΣ ΠΥΛΕΣ NOT, AND ΚΑΙ OR Οι βασικές πράξεις της Άλγεβρας Boole είναι οι πράξεις NOT, ANDκαι OR. Στα ψηφιακά
2. ΛΟΓΙΚΕΣ ΠΥΛΕΣ e-book ΛΟΓΙΚΗ ΣΧΕ ΙΑΣΗ ΑΣΗΜΑΚΗΣ-ΒΟΥΡΒΟΥΛΑΚΗΣ- ΚΑΚΑΡΟΥΝΤΑΣ-ΛΕΛΙΓΚΟΥ 1 ΟΙ ΛΟΓΙΚΕΣ ΠΥΛΕΣ NOT, AND ΚΑΙ OR Οι βασικές πράξεις της Άλγεβρας Boole είναι οι πράξεις NOT, ANDκαι OR. Στα ψηφιακά
Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο Περίληψη
 ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 27 Οκτ-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Συνδυαστική Λογική / Ολοκληρωμένα Κυκλώματα (Μέρος Γ) Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο
ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 27 Οκτ-7 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 27 Συνδυαστική Λογική / Ολοκληρωμένα Κυκλώματα (Μέρος Γ) Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο
3 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα. Επιµέλεια διαφανειών: Χρ. Καβουσιανός
 3 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Επιµέλεια διαφανειών: Χρ. Καβουσιανός Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων
3 η Θεµατική Ενότητα : Σύγχρονα Ακολουθιακά Κυκλώµατα Επιµέλεια διαφανειών: Χρ. Καβουσιανός Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωµα Έξοδοι Στοιχεία Μνήµης Κατάσταση Ακολουθιακού Κυκλώµατος : περιεχόµενα στοιχείων
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Οδυσσέας Κουφοπαύλου, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Οδυσσέας Κουφοπαύλου, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Το μάθημα συνοπτικά (1) Το μάθημα συνοπτικά (2) Τι είναι ένα υπολογιστικό σύστημα ;
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2016-17 Εισαγωγή στην Αρχιτεκτονική (θεμελιώδεις αρχές λειτουργίας των υπολογιστών) http://mxstef.gthub.o/courses/comparch/ Μ.Στεφανιδάκης
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2016-17 Εισαγωγή στην Αρχιτεκτονική (θεμελιώδεις αρχές λειτουργίας των υπολογιστών) http://mxstef.gthub.o/courses/comparch/ Μ.Στεφανιδάκης
10. Χαρακτηριστικά στοιχεία λογικών κυκλωμάτων
 10. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΛΟΓΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 10.1 Εισαγωγή στο Ολοκληρωμένο Κύκλωμα (integrated circuit) IC Ένα IC αποτελείται από ένα κομμάτι ημιαγώγιμου υλικού (σιλικόνης) ονομαζόμενο
10. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΤΟΙΧΕΙΑ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΛΟΓΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ 10.1 Εισαγωγή στο Ολοκληρωμένο Κύκλωμα (integrated circuit) IC Ένα IC αποτελείται από ένα κομμάτι ημιαγώγιμου υλικού (σιλικόνης) ονομαζόμενο
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
Ψηφιακά Ηλεκτρονικά. Μάθηµα 4ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 4ο. Λιούπης Λογική συζευγµένου εκποµπού Emitter-coupled logic (ECL) Χρησιµοποιούνται BJT transistor, µόνο στην ενεργή περιοχή Εµφανίζονται µικρές αλλαγές δυναµικού µεταξύ των
Ψηφιακά Ηλεκτρονικά Μάθηµα 4ο. Λιούπης Λογική συζευγµένου εκποµπού Emitter-coupled logic (ECL) Χρησιµοποιούνται BJT transistor, µόνο στην ενεργή περιοχή Εµφανίζονται µικρές αλλαγές δυναµικού µεταξύ των
Κεφάλαιο 9 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. CMOS Λογικές ομές 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Συνδυαστική Λογική Κεφάλαιο 9 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Στατική CMOS λογική και λογική 2. Διαφορική λογική 3.
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Συνδυαστική Λογική Κεφάλαιο 9 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Στατική CMOS λογική και λογική 2. Διαφορική λογική 3.
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
Εισαγωγή στην Αρχιτεκτονική Η/Υ
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2017-18 Εισαγωγή στην Αρχιτεκτονική (θεμελιώδεις αρχές λειτουργίας των υπολογιστών) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 2017-18 Εισαγωγή στην Αρχιτεκτονική (θεμελιώδεις αρχές λειτουργίας των υπολογιστών) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης
K15 Ψηφιακή Λογική Σχεδίαση 6: Λογικές πύλες και λογικά κυκλώματα
 K15 Ψηφιακή Λογική Σχεδίαση 6: Λογικές πύλες και λογικά κυκλώματα Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Λογικές πύλες Περιεχόμενα 1 Λογικές πύλες
K15 Ψηφιακή Λογική Σχεδίαση 6: Λογικές πύλες και λογικά κυκλώματα Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Λογικές πύλες Περιεχόμενα 1 Λογικές πύλες
Βασικές(αρχές(στη(θεραπευτική(αντιμετώπιση(του( μικροκυτταρικού(καρκίνου(του(πνεύμονα(
 Βασικές(αρχές(στη(θεραπευτική(αντιμετώπιση(του( μικροκυτταρικού(καρκίνου(του(πνεύμονα( ( ( ΣτέφανοςΔημούδης,ΟγκολόγοςΠαθολόγος ΓενικόΝομαρχιακόΝοσοκομείοΚαβάλας Περιβάλλον,ΚάπνισμακαιΚαρκίνοςΠνεύμονα Δράμα,29831Μαρτίου2013
Βασικές(αρχές(στη(θεραπευτική(αντιμετώπιση(του( μικροκυτταρικού(καρκίνου(του(πνεύμονα( ( ( ΣτέφανοςΔημούδης,ΟγκολόγοςΠαθολόγος ΓενικόΝομαρχιακόΝοσοκομείοΚαβάλας Περιβάλλον,ΚάπνισμακαιΚαρκίνοςΠνεύμονα Δράμα,29831Μαρτίου2013
Σχεδίαση Αναλογικών Κυκλωμάτων VLSI
 Σχεδίαση Αναλογικών Κυκλωμάτων VLSI «Τρανζίστορ και Απλά Κυκλώματα» (επανάληψη βασικών γνώσεων) Φώτης Πλέσσας fplessas@inf.uth.gr Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ 1 Δομή Παρουσίασης MOSFET
Σχεδίαση Αναλογικών Κυκλωμάτων VLSI «Τρανζίστορ και Απλά Κυκλώματα» (επανάληψη βασικών γνώσεων) Φώτης Πλέσσας fplessas@inf.uth.gr Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ 1 Δομή Παρουσίασης MOSFET
Δυναμική Τιμολόγηση στο Λιανεμπόριο Τροφίμων
 Δυναμική Τιμολόγηση στο Λιανεμπόριο Τροφίμων Πωλήσεις ή Μάρκετινγκ ; Αριστείδης Θεοτόκης Ερευνητής, ELTRUN Οικονομικό Πανεπιστήμιο Αθηνών Κατερίνα Πραμτάρη Επικ. Καθηγήτρια, Οικονομικό Πανεπιστήμιο Αθηνών
Δυναμική Τιμολόγηση στο Λιανεμπόριο Τροφίμων Πωλήσεις ή Μάρκετινγκ ; Αριστείδης Θεοτόκης Ερευνητής, ELTRUN Οικονομικό Πανεπιστήμιο Αθηνών Κατερίνα Πραμτάρη Επικ. Καθηγήτρια, Οικονομικό Πανεπιστήμιο Αθηνών
