Στοιχειώδης Διαφορική Γεωμετρία
|
|
|
- Εὐριπίδης Αποστόλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1
2 Στοιχειώδης Διαφορική Γεωμετρία Συγγραφή Ανδρέας Αρβανιτογεώργος Κριτικός αναγνώστης Βασίλης Παπαντωνίου Συντελεστές έκδοσης ΓΛΩΣΣΙΚΗ ΕΠΙΜΕΛΕΙΑ: Ουρανία Γυφτοπούλου ΓΡΑΦΙΣΤΙΚΗ ΕΠΙΜΕΛΕΙΑ: Μαρίνα Σταθά ΤΕΧΝΙΚΗ ΕΠΕΞΕΡΓΑΣΙΑ: Ηλίας Χριστοδουλόπουλος Copyright ΣΕΑΒ, 2015 Το παρόν έργο αδειοδοτείται υπό τους όρους της άδειας Creative Commons Αναφορά Δημιουργού - Μη Εμπορική Χρήση - Όχι Παράγωγα Έργα 3.0. Για να δείτε ένα αντίγραφο της άδειας αυτής επισκεφτείτε τον ιστότοπο ΣΥΝΔΕΣΜΟΣ ΕΛΛΗΝΙΚΩΝ ΑΚΑΔΗΜΑΪΚΩΝ ΒΙΒΛΙΟΘΗΚΩΝ Εθνικό Μετσόβιο Πολυτεχνείο Ηρώων Πολυτεχνείου 9, Ζωγράφου ISBN:
3 Περιεχόμενα Πρόλογος 4 Εισαγωγή 5 1 Καμπύλες στο επίπεδο και στον χώρο Καμπύλες στο επίπεδο R Εφαπτομένη καμπύλης Καμπύλες στον χώρο R Εξωτερικό και μικτό γινόμενο Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Κανονικές επιφάνειες Λείες απεικονίσεις Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Ο εφαπτόμενος χώρος Το διαφορικό μιας διαφορίσιμης απεικόνισης Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Η πρώτη θεμελιώδης μορφή Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Η απεικόνιση Gauss και καμπυλότητα Παράλληλες επιφάνειες Λυμένα παραδείγματα
4 5.3 Ασκήσεις Βιβλιογραφία Το Θαυμαστό Θεώρημα Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Οι εξισώσεις Codazzi και Gauss Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Συναλλοίωτη παράγωγος και παραλληλία Ασκήσεις Βιβλιογραφία Γεωδαισιακές καμπύλες Γεωδαισιακή καμπυλότητα Το Θεώρημα Clairaut Γεωδαισιακές μέσω λογισμού μεταβολών Η εκθετική απεικόνιση Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Το Θεώρημα Gauss-Bonnet Λυμένα παραδείγματα Ασκήσεις Βιβλιογραφία Επιφάνειες σταθερής καμπυλότητας Gauss Κλειστές επιφάνειες σταθερής καμπυλότητας Gauss Επιφάνειες με θετική καμπυλότητα Gauss Επιφάνειες με μηδενική καμπυλότητα Gauss Επιφάνειες με αρνητική καμπυλότητα Gauss Μη κλειστές επιφάνειες σταθερής καμπυλότητας Gauss Ασκήσεις Βιβλιογραφία
5 Πρόλογος Το βιβλίο αυτό αποτελεί μια εισαγωγή στη θεωρία των καμπυλών και των επιφανειών του Ευκλείδειου χώρου R 3. Απευθύνεται σε προπτυχιακούς φοιτητές μαθηματικών, αλλά και σε όσους χρησιμοποιούν τη διαφορική γεωμετρία ως εργαλείο (φυσικούς, μηχανικούς, κ.ά.). Το περιεχόμενο είναι δυνατόν να παρουσιαστεί κατά τη διάρκεια ενός εξαμηνιαίου μαθήματος, ανάλογα και με την έμφαση σε θέματα που επιθυμεί να δώσει ο διδάσκων. Ο αναγνώστης αναμένεται να έχει γνώσεις γραμμικής άλγεβρας και λογισμού πολλών μεταβλητών. Εχει γίνει προσπάθεια ώστε η γλώσσα που χρησιμοποιείται, καθώς και ο τρόπος παραρουσίασης, να προετοιμάζει τον αναγνώστη για την επέκταση της θεωρίας επιφανειών, στις πολλαπλότητες Riemann. Για το θέμα αυτό παραπέμπω στο βιβλίο μου Γεωμετρία Πολλαπλοτήτων. Πολλαπλότητες Riemann και Ομάδες Lie, Σύνδεσμος Ελληνικών Ακαδημαϊκών Βιβλιοθηκών, Αθήνα Θα ήθελα να ευχαριστήσω τον Ομότιμο Καθηγητή Βασίλη Παπαντωνίου, ο οποίος ως κριτικός αναγνώστης, βοήθησε με τα λεπτομερή σχόλιά του στη βελτίωση της συγγραφής του βιβλίου. Επίσης, ευχαριστώ ιδιαίτερα την υποψήφια διδάκτορα Μαρίνα Σταθά, η οποία, πέραν της δακτυλογράφησης του κειμένου και της κατασκευής των σχημάτων, είχε ευπρόσδεκτο ενεργό ρόλο στη διαμόρφωση του περιεχομένου, τον υ- ποψήφιο διδάκτορα Ηλία Χριστοδουλόπουλο για τη συμβολή του στην τεχνική επεξεργασία και τη φιλόλογο Ουρανία Γυφτοπούλου για τη φιλολογική επιμέλεια. Πάτρα, Σεπτέμβριος 2015 Ανδρέας Αρβανιτογεώργος
6 Εισαγωγή Η Ευκλείδεια γεωμετρία, πέραν της αξίας της ως το πρώτο σημαντικό μαθηματικό αξιωματικό σύστημα, είχε μια σημαντική αδυναμία, η οποία ήταν να περιγράψει ικανοποιητικά καμπύλες και επιφάνειες στο επίπεδο και στον χώρο (εκτός βέβαια της περίπτωσης των ευθειών και των επιπέδων). Η μόνη εξαίρεση ήταν οι κωνικές τομές, οι οποίες αποτέλεσαν σημαντική συνεισφορά της αρχαιοελληνικής περιόδου στη γεωμετρία. Πέραν αυτών όμως, και ίσως κάποιων εξαιρέσεων ειδικών καμπυλών και ασυνήθιστων επιφανειών, δεν υπήρχε ίχνος κάποιας γενικότερης θεωρίας καμπυλών και επιφανειών. Η αιτία της αδυναμίας αυτής ήταν ότι οι αρχαίοι Ελληνες γεωμέτρες δεν είχαν αναπτύξει την κατάλληλη γλώσσα προκειμένου να περιγράψουν τις έννοιες των καμπυλών και των επιφανειών και, κατ επέκταση, πιο περίπλοκες έννοιες, όπως αυτή της καμπυλότητας. Κατά τη διάρκεια των αιώνων που ακολούθησαν, οι μαθηματικοί της Αλεξανδρινής περιόδου, καθώς και σημαντικοί Αιγύπτιοι και Άραβες μαθηματικοί, μελέτησαν επαρκώς διάφορες απλές εξισώσεις, έως τη σημαντική συνεισφορά των Ιταλών αλγεβριστών (Cardano κ.ά.) στις αλγεβρικές εξισώσεις τρίτου και τέταρτου βαθμού. Το σημαντικό επιστημονικό άλμα επιτυγχάνεται με τον Καρτέσιο (Descartes) στις αρχές του 1600 με την ανακάλυψη των ομωνύμων καρτεσιανών συντεταγμένων. Οι καμπύλες και οι επιφάνειες μελετώνται πλέον με πολύ πιο αποτελεσματικά εργαλεία, μια και αντιμετωπίζονται ως σύνολα (γεωμετρικοί τόποι) μηδενισμού συναρτήσεων εκφραζόμενες σε καρτεσιανές συντεταγμένες. Ετσι δίνεται η ευκαιρία να μελετηθούν μεγάλες οικογένειες καμπυλών και επιφανειών (λημνίσκοι, αστεροειδείς κ.λπ.). Παρόλες τις παραπάνω σημαντικές συνεισφορές, το κεντρικό μαθηματικό πρόβλημα που παρέμενε ανοικτό, ήταν η εύρεση ενός μαθηματικού τρόπου εξήγησης με ακρίβεια της διαφοράς μεταξύ καμπύλης γραμμής από ευθεία και επιφάνειας από επίπεδο. Τι ακριβώς σημαίνει καμπυλότητα μιας καμπύλης ή μιας επιφάνειας και πώς μπορεί αυτή να μετρηθεί; Οι πρώτοι σπόροι της απάντησης τέθηκαν περί το δεύτερο μισό του 17 oυ αιώνα με την ανακάλυψη του διαφορικού και ολοκληρωτικού λογισμού από τον Νεύτωνα και τον Leibnitz. Ο απειροστικός λογισμός προσέφερε σημαντικά εργαλεία για την αποτελεσματική μελέτη, μέτρηση και καθορισμό της συμπεριφοράς κινούμενων αντικειμένων. Για παράδειγμα, η τροχιά που ακολουθεί ένα αντικείμενο το οποίο κινείται σε ένα επίπεδο ή στο χώρο, παρίσταται από μια καμπύλη. Ενα σημείο κινείται σε μια ευθεία εάν και μόνο εάν το διάνυσμα της ταχύτητάς του δεν αλλάζει διεύθυνση. Επιπλέον, όσο πιο γρήγορα μεταβάλλεται η διεύθυνση του εφαπτόμενου διανύσματος της ταχύτητας τόσο πιο πολύ η καμπύλη καμπυλώνεται, δηλαδή 5
7 6 διαφέρει από την ευθεία γραμμή. Ως γνωστόν, ο διαφορικός λογισμός οφείλει την ύπαρξή του στην ανάγκη να μετρηθούν μεταβολές, άρα έχουμε μπροστά μας μια σημαντική εφαρμογή, το μήκος του διανύσματος της επιτάχυνσης μια καμπύλης. Εδώ υποθέτουμε ότι το σημείο κινείται επί μιας καμπύλης της οποίας το μέτρο του διανύσματος της ταχύτητας είναι σταθερό, υπόθεση που, όπως θα δούμε, είναι πάντα δυνατόν να κάνουμε. Η ανάπτυξη της διαφορικής γεωμετρίας των καμπυλών και επιφανειών κατά τον 18 o και 19 o αιώνα ήταν πλέον ραγδαία. Ολες οι σημαντικές τεχνικές του απειροστικού λογισμού χρησιμοποιούνται πλέον αποτελεσματικά από την Γαλλική σχολή γεωμετρών (Clairaut, κ.ά.) προκειμένου να αποδειχθούν τα ονομαζόμενα θεμελιώδη θεωρήματα της τοπικής θεωρίας των καμπυλών και επιφανειών, τα οποία αναφέρουν ότι τα καινούργια μαθηματικά εργαλεία μπορούν να καθορίσουν πλήρως όλες τις τοπικές (local) ιδιότητες των καμπυλών και επιφανειών. Παρόλα αυτά, αν και η θεωρία υποστηρίζει ικανοποιητικά τη μελέτη των καμπυλών στο χώρο, παρουσιάζει διάφορα μειονεκτήματα στην ολική (global) μελέτη των επιφανειών. Με άλλα λόγια, αν και σε μακροκλίμακα θα μπορούσαμε να πούμε ότι οι καμπύλες είναι ουσιαστικά ευθείες και τμήματα κύκλων που έχουν συστραφεί στο χώρο, το να λέγαμε ότι μια επιφάνεια προέρχεται από μια λεία παραμόρφωση ενός επιπέδου, αν και επαρκές για υπολογισμούς σε τοπικό επίπεδο, σε καμμία περίπτωση δεν μας επιτρέπει να μελετήσουμε τις βαθύτερες ιδιότητες των επιφανειών, πέραν μιας απλής μέτρησης της καμπυλότητάς τους σε ένα σημείο. Ο μαθηματικός ο οποίος είχε πρώτος κατανοήσει τις δυσκολίες αυτές ήταν ο Carl Friedrich Gauss, ο οποίος με δύο από τα πιό σημαντικά θεωρήματα της κλασικής διαφορικής γεωμετρίας όχι μόνο συνεισέφερε στη θεωρία επιφανειών το μέγιστο δυνατό, αλλά έθεσε και τις βάσεις για τη μελλοντική ερευνητική ανάπτυξη του κλάδου. Με το πρώτο θεώρημα, το ονομαζόμενο Θαυμαστό Θεώρημα (Theorema Egregium), ο Gauss απέδειξε το εξής σημαντικό αποτέλεσμα: Αν και για την περίπτωση των καμπυλών, ένας παρατηρητής που βρίσκεται επάνω σε μια καμπύλη δεν μπορεί να αναγνωρίσει αν βρίσκεται σε ευθεία ή σε καμπύλη (δηλαδή θεωρεί ότι όλες οι καμπύλες είναι ίδιες), δεν συμβαίνει το ίδιο για την περίπτωση των επιφανειών. Υπάρχει ένα είδος καμπυλότητας (καμπυλότητα Gauss), η οποία μπορεί να μετρηθεί αποκλειστικά από έναν παρατηρητή επάνω στην επιφάνεια και η οποία ενδεχομένως διαφέρει από επιφάνεια σε επιφάνεια. Με άλλα λόγια, είναι δυνατόν να καταλάβουμε ότι η γη είναι σφαιρική χωρίς να ταξιδέψουμε στο διάστημα. Το δεύτερο θεώρημα, γνωστό ως Θεώρημα των Gauss-Bonnet, επειδή συμπληρώθηκε από τον μαθητή του Gauss τον Pierre Bonnet, αναφέρει ότι η μελέτη τοπικών ιδοτήτων μιας επιφάνειας δεν επαρκεί για την κατανόηση φαινομένων που σχετίζονται με την επιφάνεια σε ολικό επίπεδο. Μια συνέπεια του θεωρήματος Gauss-Bonnet είναι ότι, όσο και να παραμορφώσουμε στο χώρο μια επιφάνεια (χωρίς να την σκίσουμε) ώστε να μεταβάλεται τοπικά η καμπυλότητα Gauss, το ολοκλήρωμα της καμπυλότητας Gauss επί ολόκληρης της επιφάνειας παραμένει σταθερό. Ενα άλλο σημαντικό σημείο, όπου αναδεικνύεται η σύνδεση μεταξύ τοπικών και ολικών ιδιοτήτων μιας επιφάνειας, είναι στη μελέτη καμπυλών επάνω στην επιφάνεια. Ενα σημαντικό πρόβλημα της κλασικής διαφορικής γεωμετρίας (με άμεσες πρακτικές εφαρμογές) είναι η αναζήτηση καμπυλών σε μια επιφάνεια οι οποίες ελαχιστοποιούν το μήκος μεταξύ δύο σημείων της (γεωδαισιακές καμπύλες). Σημαντικά ερωτήματα εδώ είναι κατά πόσον οι γεωδαισιακές καμπύλες υπάρχουν, ή αν είναι δυνατόν δύο κοντινά μεταξύ τους
8 Εισαγωγή 7 σημεία σε μια επιφάνεια, να συνδεθούν με μια και μοναδική γεωδαισιακή. Αν τα σημεία βρίκονται μακριά το ένα από το άλλο, τότε μπορεί να υπάρχουν άπειρες γεωδαισιακές που να τα συνδέουν ή και καμία. Ο απειροστικός λογισμός δεν προσφέρεται ιδιαίτερα για τη μελέτη τέτοιων προβλημάτων. Ετσι, φτάνουμε στον 20 o αιώνα και την ανάπτυξη της τοπολογίας (Poincaré κ.ά.), η οποία αποδεικνύεται ως το τέλειο μαθηματικό πλαίσιο για τη μελέτη ολικών ιδιοτήτων μιας επιφάνειας. Για παράδειγμα, το θεώρημα των Hopf-Rinow αποτελεί ένα τέτοιο αποτέλεσμα. Στο σημείο αυτό αρχίζει μια άλλη ενδιαφέρουσα ιστορία (την οποία δεν θα αναπτύξουμε εδώ) με πρωταγωνιστή τον Bernhard Riemann, ο οποίος χρησιμοποίησε τις βασικές ιδέες του Gauss από τη θεωρία επιφανειών για να τις επεκτείνει σε n-διάστατα αντικείμενα γνωστά ως πολλαπλότητες (manifolds). Οι πολλαπλότητες αποτελούν την γλώσσα της σύγχρονης διαφορικής γεωμετρίας, με εφαρμογές και σε άλλους κλάδους των μαθηματικών όπως μαθηματική φυσική (π.χ. γενική θεωρία σχετικότητας), αρμονική ανάλυση, αλλά και σε άλλες επιστήμες, όπως οικονομικά, στατιστική, θεωρία ελέγχου, επιχειρησιακή έρευνα, κ.ά. Επιπλέον, ο Riemann απέδειξε ότι οι ονομαζόμενες μη Ευκλείδειες γεωμετρίες μπορούν να θεωρηθούν ως ιδιαίτερες γεωμετρίες επιφανειών, οι οποίες δεν εμφυτεύονται απαραίτητα σε κάποιον Ευκλείδειο χώρο (π.χ. προβολικός χώρος). Τα θέματα αυτά παρουσιάζονται στο βιβλίο μου Γεωμετρία Πολλαπλοτήτων: Πολλαπλότητες Riemann και Ομάδες Lie, Σύνδεσμος Ελληνικών Ακαδημαϊκών Βιβλιοθηκών, Αθήνα Η δομή του παρόντος βιβλίου έχει ως εξής: Το Κεφάλαιο 1 ασχολείται με τη θεωρία των καμπυλών στο επίπεδο και στον τρισδιάστατο Ευκλείδειο χώρο. Στο Κεφάλαιο 2 δίνουμε τον ορισμό της κανονικής επιφάνειας στον τρισδιάστατο Ευκλείδειο χώρο. Δίνουμε τοπικό ορισμό της επιφάνειας (μέσω μιας τοπικής παραμέτρησης), καθώς και ολικό ορισμό αυτής (υποσύνολο του R 3 το οποίο τοπικά είναι ομοιμορφικό με ανοικτο υποσύνολο του R 3 ). Ο εφαπτόμενος χώρος σε ένα σημείο μιας επιφάνειας μελετάται στο Κεφάλαιο 3, όπου ορίζουμε και το διαφορικό μιας λείας απεικόνισης μεταξύ επιφανειών. Το γνωστό θεώρημα αντίστροφης απεικόνισης για Ευκλείδειους χώρους μεταφέρεται στις επιφάνειες σχετικά εύκολα. Από το Κεφάλαιο 4 αρχίζει το καθαρά γεωμετρικό μέρος του βιβλίου, όπου ορίζουμε την πρώτη θεμελιώδη μορφή, δηλαδή ένα εσωτερικό γινόμενο στον εφαπτόμενο χώρο σε ένα σημείο μιας επιφάνειας, το οποίο επάγεται από το Ευκλείδειο εσωτερικό γινόμενο του R 3. Η κεντρική έννοια της θεωρίας επιφανειών, η καμπυλότητα Gauss, ορίζεται στο Κεφάλαιο 5 μέσω της απεικόνισης Gauss, το διαφορικό της οποίας σε ένα σημείο μιας επιφάνειας ονομάζεται τελεστής σχήματος. Το πρώτο σημαντικό αποτέλεσμα της θεωρίας επιφανειών, το Θαυμαστό Θεώρημα (Theorema Egregium) του Gauss, παρουσιάζεται στο Κεφάλαιο 6 και οι εξισώσεις δομής (Codazzi και Gauss) στο Κεφάλαιο 7. Στο Κεφάλαιο 8 ασχολούμαστε με το θέμα της παραλληλίας ενός εφαπτόμενου διανύσματος σε μια επιφάνεια, ορίζοντας τη συναλλοίωτη παράγωγο ενός διανυσματικού πεδίου. Στο Κεφάλαιο 9 μελετάμε γεωδαισιακές καμπύλες σε μια επιφάνεια, δηλαδή καμπύλες οι οποίες τοπικά ελαχιστοποιούν την απόσταση μεταξύ δύο σημείων αυτής. Στο Κεφάλαιο 10 παρουσιάζουμε το δεύτερο σημαντικό αποτέλεσμα της θεωρίας επιφανειών, το Θεώρημα των Gauss-Bonnet, το οποίο συνδέει τη γεωμετρία με την τοπολογία μιας επιφάνειας. Το θεώρημα αυτό γενικεύεται σε περισσότερες διαστάσεις και αποτελεί κλειδί για πολλές σημαντικές κατευθύνσεις στη σύγχρονη διαφορική γεωμετρία. Τέλος, στο Κεφάλαιο 11 παρουσιάζουμε κάποια θεωρήματα (χωρίς απόδειξη) σχετικά με την ταξινόμηση των κλειστών επιφανειών σταθερής καμπυλότητας Gauss (θετική, μηδέν, ή αρνητική), καθώς και την ταξινόμηση των εκ περιστροφής επιφανειών με σταθερή καμπυλότητα Gauss. Τα θεωρήματα αυτά είναι από τα πιο δύσκολα θεωρήματα της διαφορικής
9 8 γεωμετρίας.
10 Κεφάλαιο 1 Καμπύλες στο επίπεδο και στον χώρο Σύνοψη Μελετάμε ιδιότητες παραμετρημένων καμπυλών στο επίπεδο και στον χώρο. Το συνοδεύον τρίεδρο του Frenet είναι μια ορθοκανονική βάση του R 3 προσαρτημένη σε κάθε σημείο μιας καμπύλης στον χώρο, μέσω της οποίας πραγματοποιείται η μελέτη της. Η βασική αναλλοίωτη ποσότητα μιας επίπεδης καμπύλης είναι η καμπυλότητά της. Μια καμπύλη στον χώρο έχει δύο αναλλοίωτες ποσότητες, την καμπυλότητα και την στρέψη της. Οι συναρτήσεις αυτές καθορίζουν πλήρως τη θέση μιας καμπύλης ως προς μια στερεά κίνηση. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7]. Προαπαιτούμενη γνώση Αναλυτική Γεωμετρία, Απειροστικός Λογισμός, Εισαγωγή στη Γραμμική Άλγεβρα. 1.1 Καμπύλες στο επίπεδο R 2 Θεωρούμε τον n-διάστατο πραγματικό χώρο R n = {(x 1,..., x n ) : x i R} εφοδιασμένον με το συνηθισμένο Ευκλείδειο εσωτερικό γινόμενο, : R n R n R + 0 x, y = x 1 y x n y n. Αυτό ορίζει τη νόρμα (μέτρο) : R n R + 0 στον Rn, με τιμή x = x x2 n. Αναφέρουμε στη συνέχεια κάποιες ιδιότητες του εσωτερικού γινομένου: (1) x, y = y, x (2) x + z, y = x, y + z, y (3) λx, y = λ x, y για κάθε λ R. Για δύο συναρτήσεις γ, β : I R n, ορίζουμε τη συνάρτηση: f : I R n, f(t) = γ(t), β(t). Τότε προκύπτει εύκολα ο παρακάτω κανόνας παραγώγισης: df dt = d dt ( γ(t), β(t) ) = dγ(t) dt 9, β(t) + γ(t), dβ(t). dt
11 10 Καμπύλες στο επίπεδο και στον χώρο Ορισμός 1.1. Μια παραμετρημένη καμπύλη (parametrized curve) στον R n είναι μια διαφορίσιμη (λεία) απεικόνιση γ : I R n, όπου I οποιοδήποτε ανοικτό διάστημα της πραγματικής ευθείας R. Η εικόνα γ(i) R n της απεικόνισης γ ονομάζεται ίχνος ή τροχιά της καμπύλης. Παρατηρήσεις. 1. Πολλές φορές χρησιμοποιούμε τον όρο καμπύλη τόσο για την απεικόνιση γ : I R n όσο και για το ίχνος της. 2. Λέμε ότι η καμπύλη γ : I R n αποτελεί μια παραμέτρηση (parametrization) του ίχνους γ(i). 3. Επειδή γ(t) R n, θα είναι γ(t) = (γ 1 (t),..., γ n (t)), όπου γ i : I R είναι διαφορίσιμες συναρτήσεις. Ορισμός Το εφαπτόμενο διάνυσμα (tangent vector) της καμπύλης γ : I R n στο σημείο γ(t) είναι η παράγωγος γ (t). 2. Το μήκος τόξου (arclength) της καμπύλης γ ορίζεται ως L(γ) = γ (t) dt. 3. Μια καμπύλη ονομάζεται κανονική (ή ομαλή)(regular) εάν γ (t) 0 για κάθε t I. I Σχήμα 1.1: Κανονικές και μη κανονικές καμπύλες. Από εδώ και στο εξής, όταν γράφουμε καμπύλη, θα εννοούμε κανονική καμπύλη. Παραδείγματα. 1. Εστω p q δύο σημεία του R 2. Η απεικόνιση γ : R R 2, γ(t) = (1 t)p + tq αποτελεί μια παραμέτρηση της ευθείας που διέρχεται απο τα σημεία p = γ(0) και q = γ(1). 2. Η εικόνα της καμπύλης γ : I R 2 με γ (t) 0, για κάθε t I, περιέχεται σε κύκλο με κέντρο το (0, 0) αν και μόνο αν το διάνυσμα γ(t) είναι κάθετο στο γ (t) για κάθε t I. Πράγματι, η γ(i) περιέχεται σε κύκλο με κέντρο το (0, 0) αν και μόνο αν η συνάρτηση f(t) = γ(t), γ(t) = γ(t) 2 είναι σταθερή. Αυτό ισχύει αν και μόνο αν f (t) = 0 για κάθε t I. Αλλά f (t) = 0 αν και μόνο αν γ (t), γ(t) = 0 το οποίο ισοδυναμεί με το ότι γ (t) γ(t). 3. Η απεικόνιση γ : R R 2, γ(t) = (t, t ) δεν είναι μια παραμετρημένη καμπύλη στο R 2. (Σχήμα 1.1) 4. Η απεικόνιση γ : R R 2, γ(t) = (t 3 4t, t 2 4) ορίζει μια λεία καμπύλη στο επίπεδο. Η απεικόνιση αυτή δεν είναι 1-1 (γ(2) = γ( 2) = 0), αλλά αυτό δεν μας δημιουργεί πρόβλημα. (Σχήμα 1.2) 5. Η καμπύλη γ : R R 2, γ(t) = (t 3, t 2 ) δεν είναι κανονική, επειδή γ (0) = (0, 0).
12 Καμπύλες στο επίπεδο R 2 11 Σχήμα 1.2: Η καμπύλη γ(t) = (t, t ). Σχήμα 1.3: Η καμπύλη γ(t) = (t 3 4t, t 2 4). 6. Εστω p R 2 και r > 0. Τότε η απεικόνιση γ : R R 2, γ(t) = p + r(cos t, sin t) αποτελεί μια παραμέτρηση του κύκλου με κέντρο το σημείο p και ακτίνα r. Το μήκος της γ στο διάστημα [0, 2π) είναι L(γ [0,2π) ) = 2π 0 2π γ (t) dt = r dt = 2πr Οι απεικονίσεις γ 1, γ 2 : R R 2, γ 1 (t) = (cos t, sin t), γ 2 (t) = (cos(2t), sin(2t)), αποτελούν δύο παραμετρήσεις του κύκλου με κέντρο (0, 0) και ακτίνα 1, αλλά το διάνυσμα ταχύτητας της γ 2 έχει διπλάσιο μέτρο από αυτό της γ Εφαπτομένη καμπύλης Λέγοντας εφαπτομένη μιας καμπύλης γ στο σημείο γ(t 0 ) αυτής, εννοούμε την ευθεία που διέρχεται από το σημείο γ(t 0 ) και είναι παράλληλη προς το διάνυσμα γ (t 0 ). Αυτή δίνεται από τη διανυσματική παραμετρική
13 12 Καμπύλες στο επίπεδο και στον χώρο Σχήμα 1.4: Διαφορετικές παραμετρήσεις κύκλου με διπλάσια ταχύτητα. εξίσωση ɛ(λ) = γ(t 0 ) + λγ (t 0 ), λ R. (1.1) Είναι φανερό πως με λ = 0 έχουμε ɛ(0) = γ(t 0 ). Ας υποθέσουμε τώρα ότι ɛ(λ) = (x 1 (λ), x 2 (λ), x 3 (λ)), γ(t 0 ) = (x 1 (t 0 ), x 2 (t 0 ), x 3 (t 0 )) και γ (t 0 ) = (x 1 (t 0), x 2 (t 0), x 3 (t 0)). Τότε από την (1.1) προκύπτουν εύκολα οι ακόλουθες παραμετρικές εξισώσεις της εφαπτομένης: x 1 (λ) = x 1 (t 0 ) + λx 1(t 0 ) x 2 (λ) = x 2 (t 0 ) + λx 2(t 0 ) x 3 (λ) = x 3 (t 0 ) + λx 3(t 0 ). (1.2) Αν τώρα μεταξύ των (1.2) απαλείψουμε την παράμετρο λ, τότε προκύπτουν οι χωρίς παράμετρο εξισώσεις της εφαπτομένης της καμπύλης. Πράγματι, έχουμε εύκολα: x 1 x 1 (t 0 ) x 1 (t 0) = x 2 x 2 (t 0 ) x 2 (t 0) = x 3 x 3 (t 0 ) x 3 (t. 0) Από την γραφή αυτή της εφαπτομένης φαίνεται αμέσως ότι η εφαπτομένη περνάει από το σημείο γ(t 0 ) = (x 1 (t 0 ), x 2 (t 0 ), x 3 (t 0 )) και είναι παράλληλη προς το διάνυσμα γ (t 0 ) = (x 1 (t 0), x 2 (t 0), x 3 (t 0)). Παράδειγμα 1.1. Θα προσδιορίσουμε την εφαπτόμενη της κυκλικής έλικας γ(t) = (α cos t, α sin t, βt), α, β R \ {0}, t R στο σημείο t 0 = π/4. Είναι γ (t) = ( α sin t, α cos t, β), οπότε γ (π/4) = ( α 2/2,, α 2/2, β). Αλλά είναι και γ(π/4) = (α 2/2, α 2/2, βπ/4). Η εξίσωση λοιπόν (1.1) της εφαπτομένης της καμπύλης γίνεται: ɛ(λ) = ( 2 2 α (1 λ), α 2 2 (1 + λ), β(π/4 + λ)).
14 Καμπύλες στο επίπεδο R 2 13 Οι παραμετρικές εξισώσεις της εφαπτομένης είναι: 2 x 1 (λ) = α (1 λ) 2 2 x 2 (λ) = α (1 + λ) 2 x 3 (λ) = β(π/4 + λ), όπου λ η παράμετρος. Οι χωρίς παράμετρο εξισώσεις, της εφαπτομένης της καμπύλης στο σημείο t 0 = π/4 είναι x 1 α 2/2 α 2/2 = x 2 α 2/2 α 2/2 = x 3 βπ/4. β Ορισμός 1.3. Εστω γ : I R n και γ : J R n δύο λείες καμπύλες. Θα λέμε ότι η καμπύλη γ αποτελεί μια αναπαραμέτρηση (reparametrization) της γ, εάν υπάρχει μια αμφιδιαφόριση h : J I, τέτοια ώστε γ = γ h. Στον παραπάνω ορισμό η έκφραση η h είναι αμφιδιαφόριση σημαίνει ότι η απεικόνιση h είναι διαφορίσιμη, 1-1, επί, καθώς και η αντίστροφή της είναι διαφορίσιμη. Είναι προφανές ότι κάθε αναπαραμέτρηση μιας καμπύλης γ έχει την ίδια εικόνα με αυτήν. Ετσι στο Παράδειγμα 7 η καμπύλη γ 2 αποτελεί μια αναπαραμέτρηση της γ 1, διότι γ 2 (t) = (γ 1 h)(t), όπου h : R R είναι η αμφιδιαφόριση με τιμή h(t) = 2t. Επίσης, αν η καμπύλη γ είναι κανονική τότε και η αναπαραμέτρησή της θα είναι κανονική. Στη συνέχεια, θα αποδείξουμε ότι το μήκος τόξου μιας καμπύλης είναι ανεξάρτητο από την αναπαραμέτρηση αυτής. Πρόταση 1.1. Εστω γ μια αναπαραμέτρηση της γ. Τότε L( γ) = L(γ). Απόδειξη. Εστω γ : [a, b] R 3 και γ : [a, b ] R 3 μια αναπαραμέτρηση της γ με γ = γ h, όπου h : [a, b ] [a, b] μια αμφιδιαφόριση. Εχουμε L( γ) = b a γ (s) ds = b a (γ h) (s) ds = b Για h > 0, δηλαδή όταν η απεικόνιση h είναι γνησίως αύξουσα, έχουμε L( γ) = b a γ (h(s)) h (s)ds = h(b ) h(a ) a γ (h(s)) dh(s) = Για h < 0, δηλαδή όταν η απεικόνιση h είναι γνησίως φθίνουσα τότε b L( γ) = = a a b γ (h(s)) h (s)ds = γ (t) dt = L(γ). h(b ) h(a ) γ (h(s)) h (s) ds. b a γ (t) dt = L(γ). γ (h(s)) dh(s)
15 14 Καμπύλες στο επίπεδο και στον χώρο Εστω γ : I R n μια κανονική καμπύλη, t 0 I. Για δοθέν t I θεωρούμε το μήκος τόξου s(t) = L(γ (t0,t)) = t t 0 γ (u) du. (1.3) Ας υποθέσουμε ότι έχουμε την (βολική) περίπτωση, όπου η παράμετρος t της καμπύλης είναι η ίδια το μήκος τόξου από το σταθερό σημείο t 0, δηλαδή να ισχύει s(t) = t t 0. Τότε λόγω της (1.3) προκύπτει ότι 1 = ds dt = γ (t), δηλαδή το διάνυσμα της ταχύτητας της γ έχει μοναδιαίο μέτρο. Αντίστροφα, εάν υποθέσουμε ότι για μια καμπύλη γ : I R n ισχύει γ (t) = 1, τότε πάλι λόγω της (1.3) έχουμε ότι s(t) = t t 0 1du = t t 0, δηλαδή η παράμετρος t είναι το μήκος της γ από κάποιο αρχικό σημείο t 0. Λόγω της ιδιαίτερης αυτής περίπτωσης οδηγούμαστε στον παρακάτω ορισμό. Ορισμός 1.4. Μια λεία καμπύλη γ : I R n έχει παραμέτρηση ως προς το μήκος τόξου εάν γ(s) = 1, για κάθε s I. Παρατηρήσεις. 1. Οταν η γ έχει παραμέτρηση ως προς το μήκος τόξου, θα γράφουμε γ(s) αντί γ (s). Στην περίπτωση αυτή θα συμβολίζουμε την παράμετρο της γ με s αντί με t. 2. Το μέτρο γ (t) ονομάζεται ταχύτητα της γ, οπότε μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου έχει μοναδιαία ταχύτητα. 3. Αν S n 1 = {(x 1,..., x n ) R n : x x2 n = 1} είναι η μοναδιαία σφαίρα στον R n, τότε για μια καμπύλη γ αυτής με παραμέτρηση ως προς το μήκος τόξου οι εφαπτόμενες γ(s) είναι στοιχεία της S n 1 (αντί απλώς του R n ). Ισχύει η εξής πρόταση από τη διανυσματική ανάλυση: Πρόταση 1.2. Εστω f : I R n μια διανυσματική συνάρτηση τέτοια ώστε f(t) = c, σταθερό. Τότε ισχύει f (t), f(t) = 0, δηλαδή είτε f (t) = 0 είτε το διάνυσμα f (t) είναι κάθετο στο f(t) για κάθε t I. Απόδειξη. Επειδή f(t) = c προκύπτει ότι f(t) 0, επίσης έχουμε: f(t) = c f(t), f(t) = c και παραγωγίζοντας και τα δύο μέλη, παίρνουμε f (t), f(t) + f(t), f (t) = 0 από (1.1) 2 f (t), f(t) = 0, οπότε είτε f (t) = 0 είτε το f (t) είναι κάθετο στο f(t), για κάθε t I. Συμπέρασμα. Αν μια καμπύλη γ : I R n έχει παραμέτρηση ως προς το μήκος τόξου, τότε είτε γ(s) = 0 είτε το διάνυσμα γ(s) είναι κάθετο στο γ(s). Το ενδιαφέρον είναι ότι κάθε κανονική καμπύλη επιδέχεται μια παραμέτρηση ως προς το μήκος τόξου.
16 Καμπύλες στο επίπεδο R 2 15 Θεώρημα 1.1. Εστω γ : (α, β) R n μια κανονική καμπύλη του R n. Τότε το ίχνος γ((α, β)) της γ είναι δυνατόν να παραμετροποιηθεί ως προς το μήκος τόξου. Απόδειξη. Ορίζουμε τη συνάρτηση μήκους τόξου σ : (a, b) R +, σ(t) = t a γ (u) du. Τότε σ (t) = γ (t) > 0, δηλαδή η συνάρτηση σ είναι γνησίως αύξουσα και σ((a, b)) = (0, L(γ)). Εστω τ : (0, L(γ)) (a, b) η αντίστροφη συνάρτηση της σ, δηλαδή σ(τ(s)) = s για κάθε s (0, L(γ)). Παραγωγίζοντας την προηγούμενη σχέση, παίρνουμε: d ds (σ(τ(s))) = σ (τ(s)) τ(s) = 1. Ορίζουμε την καμπύλη α : (0, L(γ)) R n ως α = γ τ. Τότε από τον κανόνα της αλυσίδας είναι α(s) = γ (τ(s)) τ(s), επομένως α(s) = γ (τ(s)) τ(s) = σ (τ(s)) τ(s) = 1. Η συνάρτηση τ είναι 1-1, οπότε η α παραμετρικοποιεί την γ((a, b)) ως προς το μήκος τόξου. Συμβολίζουμε με M n n (R) το σύνολο όλων των πραγματικών n n πινάκων. Ορισμός 1.5. Μια απεικόνιση Φ : R n R n ονομάζεται Ευκλείδεια (ή στερεά) κίνηση (rigit motion) εάν έχει τη μορφή Φ(x) = Ax + b, όπου b R n και A O(n) = {X M n n (R) : XX t = I n }. 1 Μια Ευκλείδεια κίνηση Φ διατηρεί τον προσανατολισμό εάν A SO(n) = {X O(n) : detx = 1}. Τα σύνολα O(n) και SO(n) έχουν δομή ομάδας και ονομάζονται ορθογώνια και ειδική ορθογώνια ομάδα αντίστοιχα. Άσκηση. Γράψτε αναλυτικά τα στοιχεία των ομάδων O(2) και SO(2). Περιοριζόμαστε τώρα σε καμπύλες του επιπέδου R 2. Εστω γ : I R 2 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Ορίζουμε το εφαπτόμενο διάνυσμα κατά μήκος της γ ως T : I R 2, T (s) = γ(s) και το κάθετο διάνυσμα κατά μήκος της γ ως N : I R 2, N(s) = R T (s), όπου R : R 2 S 2 η (γραμμική) απεικόνιση στροφής κατά γωνία π 2 που δίνεται ως ( ) ( ) ( ) ( ) α 0 1 α α R =, R 2. β 1 0 β β Αποδεικνύεται εύκολα ότι για κάθε s I το σύνολο {T (s), N(s)} αποτελεί μια ορθοκανονική βάση του R 2, η οποία ονομάζεται πλαίσιο του Frenet κατά μήκος της καμπύλης γ. Θα ορίσουμε τώρα ένα σημαντικό μέτρο της κύρτωσης μιας επίπεδης καμπύλης. 1 Εδώ με I n συμβολίζουμε τον n n ταυτοτικό πίνακα.
17 16 Καμπύλες στο επίπεδο και στον χώρο Σχήμα 1.5: Πλαίσιο Frenet. Ορισμός 1.6. Εστω γ : I R 2 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Καμπυλότητα (curvature) της γ λέγεται η συνάρτηση κ : I R + 0, με τιμή κ(s) = T (s), N(s) = γ(s), N(s). Παρατηρήσεις. 1. Η καμπυλότητα, όπως ορίστηκε παραπάνω, αποτελεί ένα μέτρο του πόσο γρήγορα το μοναδιαίο εφαπτόμενο διάνυσμα T (s) = γ(s) στρέφεται προς τη διεύθυνση του κάθετου διανύσματος N(s) ή ισοδύναμα απομακρύνεται από τον φορέα του T (s). 2. Για κ(s) 0 η ακτίνα καμπυλότητας της γ στο σημείο γ(s) ορίζεται ως ρ(s) = 1 κ(s). Θεώρημα 1.2. Εστω γ : I R 2 καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε το πλαίσιο Frenet ικανοποιεί το παρακάτω σύστημα συνήθων διαφορικών εξισώσεων. ( T (s) Ṅ(s) ) = ( 0 κ(s) κ(s) 0 ) ( T (s) N(s) ). (1.4) Απόδειξη. Η καμπύλη γ έχει παράμετρο το μήκος τόξου της, οπότε τα διανύσματα T (s) και N(s) ορίζουν μια ορθοκανονική βάση του R 2. Συνεπώς T (s), N(s) = 0, επομένως θα έχουμε 0 = d T (s), N(s) = T (s), N(s) + T (s), Ṅ(s). ds Επειδή T (s), N(s) = κ(s) θα είναι T (s), Ṅ(s) = T (s), N(s) = κ(s), δηλαδή T (s) = T (s), N(s) N(s) = κ(s)n(s). και Ṅ(s) = Ṅ(s), T (s) T (s) = κ(s)t (s)
18 Καμπύλες στο επίπεδο R 2 17 Θεώρημα 1.3. Εστω γ : I R 2 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε η καμπυλότητα κ : I R είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(i) της καμπύλης είναι τμήμα ευθείας (ή και ολόκληρη ευθεία). Απόδειξη. Εστω κ(s) = 0 για κάθε s, δηλαδή T (s), N(s) = 0. Τότε, επειδή N(s) 0, θα έχουμε ότι T (s) = 0 για κάθε s I. Ολοκληρώνοντας παίρνουμε T (s) = c 1 ή γ (s) = c 1, όπου το c 1 είναι ένα τυχαίο διάνυσμα του R 2. Αν ολοκληρώσουμε την τελευταία εξίσωση θα έχουμε γ(s) = c 1 s + c 2, όπου c 2 τυχαίο διάνυσμα του R 2. (1.5) Η εξίσωση (1.5) παριστάνει μια ευθεία γραμμή. Αντίστροφα, αν η καμπύλη δίνεται απο την (1.5), τότε εύκολα προκύπτει ότι κ(s) = 0, για κάθε s I. Κάθε επίπεδη καμπύλη καθορίζεται πλήρως (μη λαμβάνοντας υπόψη προσανατολισμένες στερεές κινήσεις του επιπέδου) από την καμπυλότητά της, όπως αναφέρεται στο παρακάτω θεώρημα. Θεώρημα 1.4. Εστω κ : I R μια διαφορίσιμη απεικόνιση. Τότε υπάρχει μια κανονική καμπύλη γ : I R 2 με παραμέτρηση κατά μήκος τόξου, η οποία να έχει καμπυλότητα κ. Επιπλέον, εάν γ : I R 2 είναι μια άλλη τέτοια καμπύλη, τότε υπάρχει πίνακας A SO(2) και διάνυσμα b R 2 τέτοια ώστε γ(s) = A γ(s) + b. Στη διαφορική γεωμετρία το ενδιαφέρον μας εστιάζεται σε εκείνες τις ιδιότητες γεωμετρικών αντικειμένων, οι οποίες δεν εξαρτώνται από την παραμέτρηση. Συνεπώς, η καμπυλότητα μιας καμπύλης δεν θα πρέπει να εξαρτάται από την επιλογή της παραμέτρησης. Ορισμός 1.7. Εστω γ : I R 2 μια κανονική καμπύλη (όχι απαραίτητα με παραμέτρηση κατά μήκος τόξου). Εστω γ = γ h : J R 2 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια αμφιδιαφόριση h : J I και έστω κ : J R η καμπυλότητα της γ. Για κάθε t I η καμπυλότητα της καμπύλης γ στο σημείο t είναι ο αριθμός κ(t) = κ(h 1 (t)). Πρόταση 1.3. Εστω γ : I R 2 μια κανονική καμπύλη. Τότε η καμπυλότητα δίνεται από την σχέση κ(t) = det(γ (t), γ (t)) γ (t) 3. 2 Απόδειξη. Εστω γ = γ h : J R 2 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s 1 και s η συνάρτηση μήκους τόξου. Εστω T, Ñ το πλαίσιο Frenet κατά μήκος της καμπύλης γ και κ η καμπυλότητα αυτής. Τότε γ = γ h 1 ή ισοδύναμα γ = γ s, οπότε για κάθε t I, έχουμε: γ (t) = ( γ s) (t) = γ(s(t))s (t) = T (s(t))s (t), γ (t) = T (s(t))s (t) 2 + T (s(t))s (t) = s (t) 2 κ(s(t))ñ(s(t)) + s (t) T (s(t)). ( ) 2 α 1 α 2 Για δύο διανύσματα α = (α 1, α 2), β = (β 1, β 2) συμβολίζουμε det(α, β) = det. β 1 β 2
19 18 Καμπύλες στο επίπεδο και στον χώρο Παρατηρούμε ότι det(γ (t), γ s (t) 0 (t)) = s (t) κ(s(t))s (t) 2 = κ(s(t))s (t) 3, δηλαδή κ(s(t)) = det(γ (t), γ (t)) s (t) 3. Ομως s(t) = t t 0 γ (u) du οπότε s (t) = γ (t). Άρα Επομένως, απο τον Ορισμό 1.7, θα έχουμε κ(s(t)) = det(γ (t), γ (t)) γ (t) 3. κ(t) = κ(s(t)) = det(γ (t), γ (t)) γ (t) 3. Ειδικότερα, αν γ(t) = (x(t), y(t)) τότε για κάθε t I θα έχουμε x (t) y (t) κ(t) = det(γ (t), γ (t)) x (t) y (t) γ (t) 3 = ( x (t) 2 + y (t) 2 ). 3 Πόρισμα 1.1. Εστω γ : I R 2 μια κανονική καμπύλη. Τότε το ίχνος γ(i) της γ είναι τμήμα ευθείας εάν και μόνο εάν τα διανύσματα γ (t) και γ (t) είναι γραμμικώς εξαρτημένα για κάθε t I. Μια ενδιαφέρουσα εφαρμογή της θεωρίας των επίπεδων καμπυλών αποτελεί η ισοπεριμετρική ανισότητα. Η ανισότητα αυτή απαντά στο εξής απλό πρόβλημα, το οποίο είχε διατυπωθεί στην αρχαιότητα και η λύση του ήταν γνωστή στους αρχαίους Ελληνες: ποιό είναι το σχήμα που πρέπει να λάβει ένα κλειστό σχοινί στο επίπεδο, ώστε το εμβαδό που περικλείει να είναι το μέγιστο δυνατό;. Η πρώτη αυστηρή απόδειξη της ισοπεριμετρικής ανισότητας δόθηκε τον 19 o αιώνα. Αυτή έχει πολλές σύγχρονες διατυπώσεις και εξακολουθεί να ελκύει το ενδιαφέρον των μαθηματικών από διάφορες σκοπιές. Προκειμένου να τη διατυπώσουμε, χρειαζόμαστε τα εξής εισαγωγικά. Ορισμός 1.8. Μια συνεχής απεικόνιση γ : R R 2 αποτελεί παραμέτρηση μιας απλής κλειστής καμπύλης, εάν η γ είναι περιοδική με περίοδο L > 0 και ο περιορισμός γ [0,L) : R R 2 είναι απεικόνιση 1-1. (Ισοδύναμα γ(t) = γ(t ) εάν και μόνο εάν t t = kl για k Z). Σχήμα 1.6: Μορφές καμπυλών. Το παρακάτω θεώρημα είναι απλό στη διατύπωσή του, αλλά δύσκολο στην απόδειξη.
20 Καμπύλες στο επίπεδο R 2 19 Θεώρημα 1.5. (Κλειστής καμπύλης του Jordan) Εστω ότι η συνεχής απεικόνιση γ : R R 2 αποτελεί παραμέτρηση μιας απλής, κλειστής καμπύλης. Τότε το υποσύνολο R 2 \ γ(r) του επιπέδου αποτελείται ακριβώς από δύο συνεκτικές συνιστώσες. Η μια συνιστώσα είναι φραγμένη και ονομάζεται εσωτερικό Int(γ) της γ και η άλλη δεν είναι φραγμένη και ονομάζεται εξωτερικό Ext(γ) της γ. Ορισμός 1.9. Μια συνεχής απεικόνιση γ : R R 2 η οποία αποτελεί παραμέτρηση μιας απλής κλειστής καμπύλης έχει θετικό προσανατολισμό, εάν το κάθετο διάνυσμα ( ) N(t) = R γ 0 1 (t) = γ (t) 1 0 έχει φορά προς το εσωτερικό Int(γ) της γ για κάθε t R. Διαφορετικά, η γ έχει αρνητικό προσανατολισμό. Σχήμα 1.7: Προσανατολισμός καμπυλών. Θα χρειαστούμε το παρακάτω λήμμα, η απόδειξη του οποίου προκύπτει ως εφαρμογή του θεωρήματος Green από τη διανυσματική ανάλυση. Λήμμα 1.1. Εστω γ : R R 2 μια κανονική θετικά προσανατολισμένη απεικόνιση η οποία παραμετρικοποιεί μια επίπεδη, απλή κλειστή καμπύλη. Αν A είναι το εμβαδόν του εσωτερικού Int(γ) της γ, τότε A = 1 2 = ( x(t)y (t) y(t)x (t) ) dt γ(r) γ(r) x(t)y (t)dt = γ(r) x (t)y(t)dt. Θεώρημα 1.6. (Ισοπεριμετρική Ανισότητα) Εστω C μια κανονική, απλή και κλειστή καμπύλη του επιπέδου με μήκος L. περιοχής που περικλείεται από την C. Τότε ισχύει η σχέση Εστω A το εμβαδό της 4πA L 2. Η ισότητα ισχύει εάν και μόνο εάν η καμπύλη C είναι κύκλος.
21 20 Καμπύλες στο επίπεδο και στον χώρο Σχήμα 1.8: Ισοπεριμετρική ανισότητα. Απόδειξη. Εστω l 1 και l 2 δύο παράλληλες ευθείες οι οποίες εφάπτονται στην καμπύλη C, με τρόπο τέτοιο ώστε η C να βρίσκεται εντός τις λωρίδας που σχηματίζουν οι δύο ευθείες (βλ. Σχήμα 1.8). Εισάγουμε ένα σύστημα συντεταγμένων στο επίπεδο τέτοιο ώστε οι l 1 και l 2 να είναι κάθετες στον άξονα των x και άρα να περιγράφονται ως εξής: l 1 = {(x, y) R 2 x = r} και l 2 = {(x, y) R 2 x = r}, όπου 2r είναι η απόσταση μεταξύ των l 1 και l 2. Εστω γ = (x, y) : R R 2 μια παραμέτρηση ως προς το μήκος τόξου της καμπύλης C κατά τη θετική φορά τέτοια ώστε x(0) = r και x(s 1 ) = r για κάποιο s 1 (0, L). Ορίζουμε την καμπύλη α : R R 2 με τύπο α(s) = (x(s), ỹ(s)), όπου + r 2 x 2 (s), αν s [0, s 1 ) ỹ(s) = r 2 x 2 (s), αν s [s 1, L). Τότε η νέα αυτή καμπύλη παραμτρικοποιεί τον κύκλο με εξίσωση x 2 + y 2 = r 2. Ως άμεση συνέπεια του Λήμματος 1.1 έχουμε ότι A = L 0 x(s)y (s)ds και πr 2 = L 0 ỹ(s)x (s)ds.
22 1.2. ΚΑΜΠ ΥΛΕΣ ΣΤΟΝ Χ ΩΡΟ R 3 21 Εφαρμόζοντας την ανισότητα Cauchy-Schwartz, παίρνουμε ότι A + πr 2 = = L 0 L 0 L 0 L 0 ( x(s)y (s) ỹ(s)x (s) ) ds (x(s)y (s) ỹ(s)x (s)) 2 ds (x(s) 2 + ỹ(s) 2 ) (x (s) 2 + y (s) 2 )ds x(s) 2 + ỹ(s) 2 ds = Lr, αφού 2x(s)x (s)ỹ(s)y (s) x(s) 2 x (s) + ỹ(s) 2 y (s) 2 και x (s) 2 + y (s) 2 = 1. 0 ( A r π) 2 = A 2r A π + πr 2 προκύπτει ότι Λόγω της ανισότητας r A π A + πr2 2 Lr, δηλαδή ο γεωμετρικός μέσος των θετικών αριθμών A και πr 2 είναι μικρότερος του αριθμητικού μέσου αυτών. Συνεπώς 4Aπr 2 L 2 r 2 άρα τελικά 4πA L 2. Στην περίπτωση της ισότητας 4πA = L 2 προκύπτει ότι A = πr 2. Στην παραπάνω απόδειξη ο πραγματικός αριθμός r εξαρτάται από τη διεύθυνση των δύο παράλληλων ευθειών l 1 και l 2. Επειδή όμως το εμβαδό A είναι ανεξάρτητο από τη διεύθυνση των l 1, l 2, το ίδιο θα ισχύει και για το r. Συνεπώς, στην περίπτωση της ισότητας 4πA = L 2 η καμπύλη C είναι ένας κύκλος. 1.2 Καμπύλες στον χώρο R 3 Θα μελετήσουμε τώρα καμπύλες γ : I R 3 στον τρισδιάστατο χώρο R 3. Θα ορίσουμε την καμπυλότητα και την στρέψη τέτοιων καμπυλών και θα δείξουμε ότι οι ποσότητες αυτές καθορίζουν τις καμπύλες αυτές ως προς τις στερεές κινήσεις του χώρου στον οποίο διατηρούν τον προσανατολισμό. Θυμίζουμε το εξωτερικό και το μικτό γινόμενο στον χώρο R Εξωτερικό και μικτό γινόμενο Ορισμός Εστω u = (x 1, y 1, z 1 ), v = (x 2, y 2, z 2 ) δύο διανύσματα του R 3. Το εξωτερικό γινόμενο του u με το v είναι το διάνυσμα u v R 3 το οποίο είναι κάθετο στο επίπεδο που ορίζουν τα διανύσματα u και v και δίνεται ως εξής: u v = e 1 e 2 e 3 x 1 y 1 z 1 = (y 1 z 2 y 2 z 1 )e 1 (z 1 x 2 z 2 x 1 )e 2 + (x 1 y 2 x 2 y 1 ))e 3 x 2 y 2 z 2 = (y 1 z 2 y 2 z 1, z 1 x 2 z 2 x 1, x 1 y 2 x 2 y 1 ), όπου {e 1, e 2, e 3 } είναι η κανονική βάση του R 3. Η φορά του διανύσματος u v είναι τέτοια ώστε τα διανύσματα u, v, u v να αποτελούν δεξιόστροφο σύστημα.
23 22 Καμπύλες στο επίπεδο και στον χώρο Το μέτρο του εξωτερικού γινομένου δύο μη μηδενικών διανυσμάτων u, v είναι ίσο με το εμβαδόν του παραλληλογράμμου που ορίζεται από τα διανύσματα αυτά. Από τον ορισμό του εξωτερικού γινομένου, προκύπτουν εύκολα οι ακόλουθες ιδιότητες. u, v, z R 3 έχουμε (1) u v = v u (2) (au + bv) z = a(u z) + b(v z) = (au) z + (bv) z, a, b R (3) u u = 0. Για κάθε Εστω f, g : I R R 3 δύο λείες καμπύλες. Τότε η απεικόνιση f g : I R R 3, t (f g)(t) = f(t) g(t) είναι λεία και ισχύει ο παρακάτω κανόνας παραγώγισης d dt (f g)(t) = d df(t) (f(t) g(t)) = dt dt g(t) + f(t) dg(t). dt Ορισμός Εστω τρία διανύσματα u, v, z του χώρου R 3. Ο πραγματικός αριθμός (u v), z ονομάζεται μικτό γινόμενο των διανυσμάτων u, v, z και συμβολίζεται με [uvz], δηλαδή (u v), z = [uvz]. Η απόλυτη τιμή του μικτού γινομένου τριών μη συνεπίπεδων διανυσμάτων είναι ίση με τον όγκο του παραλληλεπιπέδου, που ορίζεται από τα τρία διανύσματα. Από τον ορισμό του μικτού γινομένου προκύπτουν εύκολα οι παρακάτω ιδιότητες. Για κάθε u, v, z R 3 : (1) [uvz] = [vzu] = [zuv], (2) [uvz] = [vuz] = [uzv] = [zvu], (3) [uvz] = 0 αν και μόνο αν τα διανύσματα u, v, z είναι συνεπίπεδα. Αρχίζουμε με μερικά παραδείγματα καμπυλών στον Ευκλείδειο χώρο R 3. Παραδείγματα 1. Εστω p q δύο σημεία στον R 3. Τότε η απεικόνιση γ : R R 3, με τιμή γ(t) = (1 t)p + tq είναι μια παραμέτρηση της ευθείας που διέρχεται από τα σημεία p = γ(0) και q = γ(1). 2. Εστω {Z, W } μια ορθοκανονική βάση ενός επιπέδου V του R 3, r > 0 και p V R 3. Τότε η απεικόνιση γ : R R 3, γ(t) = p + r ( (cos t)z + (sin t)w ) αποτελεί μια παραμέτρηση του κύκλου ο οποίος βρίσκεται στο (υπερ)επίπεδο p + V και έχει κέντρο το p και ακτίνα r. 3. Εστω r, a, b > 0. Η απεικόνιση γ : R R 3, γ(t) = (r cos(at), r sin(at), bt) αποτελεί παραμέτρηση της έλικας. Επειδή γ 1 (t) 2 + γ 2 (t) 2 = x 2 + y 2 = r 2, η εικόνα γ(r) της έλικας βρίσκεται επάνω στην επιφάνεια του κυλίνδρου {(x, y, z) R 3 : x 2 + y 2 = r 2 }
24 Καμπύλες στον χώρο R 3 23 Σχήμα 1.9: Η κυκλική έλικα. ακτίνας r, γι αυτό και η έλικα αυτή ονομάζεται κυκλική έλικα. Ο αριθμός 2πb ονομάζεται βήμα της έλικας (και αντιστοιχεί στην απόσταση επί του άξονα των z, όταν γίνει μια πλήρης διαγραφή της καμπύλης στο διάστημα [0, 2π)). Ορισμός Εστω γ : I R 3 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Καμπυλότητα της γ λέγεται η συνάρτηση κ : I R + 0 με τιμή κ(s) = γ(s). Θεώρημα 1.7. Εστω γ : I R 3 μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Τότε η καμπυλότητα κ : I R + 0 της γ είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(i) της καμπύλης είναι τμήμα ευθείας (ή ολόκληρη ευθεία). Απόδειξη. (Σκιαγράφηση) Η καμπυλότητα κ(s) = γ(s) είναι ταυτοτικά μηδέν εάν και μόνο εάν υπάρχει μοναδιαίο διάνυσμα Z S 2 και σημείο p R 3 τέτοια ώστε γ(s) = p + sz, δηλαδή το ίχνος γ(i) είναι τμήμα ευθείας. Το αντίστροφο είναι άμεσο. Ορισμός Μια καμπύλη γ : I R 3 με παραμέτρηση ως προς το μήκος τόξου ονομάζεται καμπύλη Frenet (καμιά φορά και ομαλή ή κανονική) εάν η καμπυλότητα κ είναι παντού μη μηδενική, δηλαδή κ(s) 0 για κάθε s I.
25 24 Καμπύλες στο επίπεδο και στον χώρο Εστω γ : I R 3 μια καμπύλη Frenet. Ορίζουμε τις παρακάτω σημαντικές διανυσματικές συναρτήσεις. Το εφαπτόμενο διάνυσμα (tangent vector) κατά μήκος της γ T : I R 3, T (s) = γ(s). Το διάνυσμα της πρώτης (ή κύριας) καθέτου (principal normal vector) κατά μήκος της γ N : I R 3, N(s) = γ(s) γ(s) = γ(s) κ(s). Το διάνυσμα της δεύτερης καθέτου (binormal vector) κατά μήκος της γ B : I R 3, B(s) = T (s) N(s). Για κάθε s I το σύνολο {T (s), N(s), B(s)} αποτελεί μια ορθοκανονική βάση του R 3 στο σημείο γ(s). Πράγματι, επειδή η γ : I R 3 έχει παραμέτρηση κατά μήκος τόξου, είναι Επομένως, προκύπτουν οι σχέσεις 0 = d ds( γ(s), γ(s) ) = 2 γ(s), γ(s) = 2κ(s) N(s), T (s). T (s) = N(s) B(s), N(s) = B(s) T (s), B(s) = T (s) N(s). Η βάση αυτή ονομάζεται συνοδεύον τρίεδρο (ή πλαίσιο) του Frenet κατά μήκος της γ. Μέσω των παραπάνω διανυσμάτων ορίζουμε τρία χαρακτηριστικά επίπεδα, τα οποία συνοδεύουν την καμπύλη. Ειδικότερα, για κάθε σημείο s I τα διανύσματα της εφαπτομένης και της πρώτης καθέτου ορίζουν την εφαπτομένη και την πρώτη κάθετο, οι οποίες ορίζουν το εγγύτατο επίπεδο της καμπύλης. Η πρώτη και η δεύτερη κάθετος ορίζουν τις ευθείες πρώτης και δεύτερης καθέτου, οι οποίες ορίζουν το κάθετο επίπεδο της καμπύλης και τέλος η δεύτερη κάθετος με την εφαπτομένη ευθεία ορίζουν το ευθειοποιούν επίπεδο της καμπύλης. Στη συνέχεια θα ορίσουμε ένα άλλο βασικό, για τη μελέτη μιας καμπύλης μέγεθος. Ορισμός Εστω γ : I R 3 μια καμπύλη Frenet. Ορίζουμε την στρέψη (torsion) της γ ως τη συνάρτηση τ : I R, τ(s) = Ṅ(s), B(s). Παρατήρηση. Η στρέψη αποτελεί ένα μέτρο του κάτα πόσο γρήγορα η πρώτη κάθετος N(s) = γ(s) στρέφεται προς γ(s) τη διεύθυνση της δεύτερης καθέτου B(s) ή ισοδύναμα απομακρύνεται από το εγγύτατο επίπεδο. Πρόταση 1.4. Εστω γ : I R 3 καμπύλη Frenet. παραγώγων της από την σχέση τ(s) = [ γ(s) γ(s)... γ (s)] κ(s) 2. Τότε η στρέψη της γ δίνεται συναρτήσει των
26 Καμπύλες στον χώρο R 3 25 Σχήμα 1.10: Πλαίσιο Frenet. Απόδειξη. Η στρέψη της καμπύλης γ δίνεται από τον τύπο τ(s) = Ṅ(s), B(s), όπου Η παράγωγος του N(s) = γ(s) κ(s) Επομένως, θα έχουμε B(s) = T (s) N(s) = γ(s) γ(s) κ(s) = 1 γ(s) γ(s). κ(s) θα μας δώσει: Ṅ(s) =... γ (s)κ(s) γ(s) κ(s) κ(s) 2. τ(s) = Ṅ(s), B(s) =... γ (s)κ(s) γ(s) κ(s) κ(s) 2, = 1 (... γ κ(s) 2 (s), γ(s) γ(s) γ(s) κ(s) κ(s) 2, 1 = κ(s) 2 [... γ (s) γ(s) γ(s)] [ κ(s) κ(s) 2 γ(s) 1 κ(s) γ(s) γ(s)] = [ γ(s) γ(s)... γ (s)] κ(s) 2, 1 γ(s) γ(s) κ(s) 1 γ(s) γ(s) ) κ(s) όπου στην τέταρτη ισότητα ο δεύτερος όρος (μικτό γινόμενο) είναι μηδέν αφού τα διανύσματα και γ(s) είναι συνεπίπεδα. κ(s) κ(s) 2 γ(s)
27 26 Καμπύλες στο επίπεδο και στον χώρο Θεώρημα 1.8. Εστω γ : I R 3 μια καμπύλη Frenet. Τότε το τρίεδρο Frenet ικανοποιεί το παρακάτω σύστημα συνήθων διαφορικών εξισώσεων: T (s) Ṅ(s) Ḃ(s) = 0 κ(s) 0 T (s) κ(s) 0 τ(s) N(s). 0 τ(s) 0 Απόδειξη. Η καμπύλη γ έχει παράμετρο το μήκος τόξου της s, επομένως η κύρια κάθετος θα δίνεται από τον τύπο N(s) = γ(s). Ομως T (s) = γ(s), οπότε T (s) = γ(s) άρα κ(s) B(s) N(s) = T (s) κ(s) δηλαδή T (s) = κ(s)n(s). Για τη δεύτερη εξίσωση πρέπει να δείξουμε ότι Ṅ(s) = κ(s)t (s) + τ(s)b(s). Γνωρίζουμε ότι τα διανύσματα T (s), N(s), B(s) αποτελούν μια βάση του χώρου R 3. Επομένως, κάθε διάνυσμα του R 3 (άρα και το Ṅ(s)) θα εκφράζεται ως γραμμικός συνδυασμός αυτών. Άρα Ṅ(s) = λ 1 T (s) + λ 2 N(s) + λ 3 B(s). (1.6) Για να προσιορίσουμε τα λ 1, λ 2, λ 3, θα πάρουμε το εσωτερικό γινόμενο του διανύσματος (1.6) διαδοχικά με τα διανύσματα T (s), N(s) και B(s). Εχουμε Ṅ(s), T (s) = λ 1 T (s), T (s) + λ 2 N(s), T (s) + λ 3 B(s), T (s) = λ 1. Ομως N(s), T (s) = 0, οπότε παραγωγίζοντας την σχέση αυτή, θα πάρουμε: d N(s), T (s) = 0 Ṅ(s), T (s) + N(s), T (s) = 0 ds και αφού αποδείξαμε ότι T (s) = κ(s)n(s), θα έχουμε Ṅ(s), T (s) + N(s), T (s) = 0 Ṅ(s), T (s) = κ(s). Ṅ(s), T (s) = κ(s) N(s), N(s) Επομένως λ 1 = κ(s). Στη συνέχεια θα προσδιορίσουμε το λ 2. Επειδή το διάνυσμα N(s) είναι μοναδιαίο, δηλαδή σταθερού μέτρου, σύμφωνα με την Πρόταση 1.2 θα είναι κάθετο στην παράγωγό του, οπότε 0 = Ṅ(s), N(s) = λ 1 T (s), N(s) + λ 2 N(s), N(s) + λ 3 B(s), N(s) = λ 2. Άρα η (1.6) θα έχει τη μορφή Ṅ(s) = κ(s)t (s) + λ 3B(s). Επομένως Ṅ(s), B(s) = κ(s) T (s), B(s) + λ 3 B(s), B(s) = λ 3. Ομως Ṅ(s), B(s) = τ(s), οπότε λ 3 = τ(s), δηλαδή Ṅ(s) = κ(s)t (s) + τ(s)b(s)
28 Καμπύλες στον χώρο R 3 27 και έτσι αποδείχθηκε η δεύτερη εξίσωση. Για την τελευταία εξίσωση Ḃ(s) = τ(s)n(s), θα παραγωγίσουμε την σχέση B(s) = T (s) N(s) λαμβάνοντας υπόψη τις δύο προηγούμενες εξισώσεις, που αποδείξαμε. Εχουμε: Ḃ(s) = T (s) N(s) + T (s) Ṅ(s) Ḃ(s) = κ(s)n(s) N(s) + T (s) ( κ(s)t (s) + τ(s)b(s)) Ḃ(s) = κ(s) 0 κ(s)t (s) T (s) + τ(s)t (s) B(s) Ḃ(s) = κ(s) 0 + τ(s)t (s) B(s) Ḃ(s) = τ(s)n(s), και έτσι έχει ολοκληρωθεί η απόδειξη του θεωρήματος. Αξίζει σε αυτό το σημείο να σημειώσουμε ότι οι τύποι του Frenet μπορούν να επαναδιατυπωθούν πιο απλά χρησιμοποιώντας το διάνυσμα περιστροφής του Darboux που ορίζεται από την σχέση ω(s) = τ(s)t (s) + κ(s)b(s). Στην περίπτωση αυτή, οι τύποι αποκτούν τις ακόλουθες συμμετρικές μορφές dt ds = ω(s) T (s), dn ds = ω(s) N(s), db ds = ω(s) B(s) Θεώρημα 1.9. Εστω γ : I R 3 καμπύλη Frenet. Τότε η στρέψη τ : I R είναι ταυτοτικά μηδέν εάν και μόνο εάν το ίχνος γ(i) της γ περιέχεται σε ένα επίπεδο. Απόδειξη. Υποθέτουμε πρώτα ότι η εικόνα της γ περιέχεται στο επίπεδο c, M = d, όπου M είναι ένα σταθερό μοναδιαίο διάνυσμα του R 3, d είναι μια αριθμητική σταθερά και το c R 3 ένα μη μηδενικό διάνυσμα. Μπορούμε να υποθέσουμε ότι το M είναι μοναδιαίο διάνυσμα. Παραγωγίζοντας δύο φορές την γ(s), M = d, ως προς s, παίρνουμε: γ(s), M = 0 ή T (s), M = 0, (1.7) γ(s), M = 0 T (s), M = 0 κ(s)n(s), M = 0. (1.8) Επειδή η καμπύλη είναι καμπύλη Frenet, θα είναι κ(s) 0 για κάθε s I, οπότε από την σχέση (1.5) παίρνουμε N(s), M = 0. (1.9) Από τις εξισώσεις (1.4) και (1.9) βλέπουμε ότι τα διανύσματα T (s) και N(s) είναι κάθετα στο M, οπότε το διάνυσμα B(s) = T (s) N(s) είναι παράλληλο με το M. Επειδή τα διανύσματα B(s) και M είναι μοναδιαία και η απεικόνιση B : I S 2, s B(s) είναι λεία (άρα συνεχής) συνάρτηση του s, πρέπει να έχουμε είτε B(s) = M για όλα τα s I είτε B(s) = M για όλα τα s I. Σε κάθε περίπτωση, το B(s) είναι σταθερό διάνυσμα, οπότε Ḃ(s) = 0, άρα τ = 0. Αντίστροφα, υποθέτουμε ότι η στρέψη τ της γ είναι παντού μηδέν. Επειδή ισχύει Ḃ(s) = τ(s)n(s), τότε Ḃ(s) = 0 άρα το B(s) είναι ένα σταθερό διάνυσμα έστω B(s) = M.
29 28 Καμπύλες στο επίπεδο και στον χώρο Τότε όμως για κάθε σημείο της καμπύλης είναι τ(s), B(s) = 0 τ(s), M = 0 γ(s), M = 0 d γ(s), M = 0 ds γ(s), M = d δηλαδή η γ περιέχεται στο επίπεδο c, M = d. Από την απόδειξη του παραπάνω θεωρήματος συνεπάγεται ότι η εφαπτομένη και η πρώτη κάθετος βρίσκονται στο επίπεδο της καμπύλης, οπότε το εγγύτατο επίπεδο σε κάθε σημείο της καμπύλης ταυτίζεται με το επίπεδό της. Ορισμός Η καμπύλη γ : I R 3 λέγεται γενικευμένη έλικα ή ισοκλινής καμπύλη, όταν οι εφαπτόμενές της σχηματίζουν σταθερή γωνία με σταθερό διάνυσμα του χώρου. Παραδείγματα γενικευμένων ελίκων είναι όλες οι επίπεδες καπμύλες, αρκεί ως σταθερό διάνυσμα να θεωρείται το διάνυσμα το κάθετο στο επίπεδο της καμπύλης, οπότε η σταθερή γωνία θα είναι π/2. Πρόταση 1.5. Μια καμπύλη γ : I R 3 με κ > 0, είναι γενικευμένη έλικα, αν και μόνο αν τ κ = σταθερό. Απόδειξη. Εστω ότι η γ είναι γενικευμένη έλικα μοναδιαίας ταχύτητας. Εστω M το σταθερό διάνυσμα στον χώρο, που σχηματίζει σταθερή γωνία ω με το εφαπτόμενο διάνυσμα T της καμπύλης και χωρίς βλάβη της γενικότητας, υποθέτουμε ότι M = 1. Εχουμε M, T (s) = cos ω (σταθερό), για κάθε s I. Παραγωγίζοντας και λαμβάνοντας υπόψη τους τύπους του Frenet, έχουμε ότι M, T (s) = 0, ή M, κ(s)n(s) = 0. Από την υπόθεση είναι κ(s) 0, άρα M, N(s) = 0. Επομένως το M ανήκει στο ευθειοποιούν επίπεδο της καμπύλης, οπότε M = λt (s) + µb(s), (1.10) για κάποια λ, µ R. Παίρνοντας το εσωτερικό γινόμενο της τελευταίας σχέσης διαδοχικά με τα διανύσματα T (s) και B(s), βρίσκουμε ότι λ = M, T (s) = cos ω και µ = M, B(s) = cos(π/2 ω) = sin ω. Άρα η (1.10) παίρνει τη μορφή M = cos ωt (s) + sin ωb(s), η παραγώγιση της οποίας δίνει ότι 0 = cos ωt (s) + sin ωḃ(s) = cos ωκ(s)n(s) sin ωτ(s)n(s) = ( cos ωκ(s) sin ωτ(s) ) N(s), απ όπου cos ωκ(s) sin ωτ(s) = 0 και τ(s) κ(s) = cos ω τ(s) = cot ω = c (σταθερά). Αντίστροφα, έστω sin ω κ(s) = c. Εφόσον η συνάρτηση cot ω παίρνει τιμές στο (, + ), μπορούμε να βρούμε ω, ώστε c = cot ω.
30 Καμπύλες στον χώρο R 3 29 Επομένως, έχουμε κ(s) cos ω = τ(s) sin ω κ(s) cos ωn(s) τ(s) sin ωn(s) = 0 cos ω T (s) + sin ωḃ(s) = 0 cos ωt (s) + sin ωb(s) = M = σταθερό διάνυσμα του R 3 cos ω T (s), T (s) + sin ω B(s), T (s) = M, T (s) cos ω = M, T (s) = σταθερό. Πρόταση 1.6. Εστω γ : I R 3 μια επίπεδη καμπύλη μοναδιαίας ταχύτητας. Τότε η γ είναι τμήμα κύκλου εάν και μόνο εάν έχει σταθερή καμπυλότητα. Απόδειξη. Αν η γ είναι τμήμα κύκλου κέντρου (x 0, y 0 ) και ακτίνας r, τότε δίνεται από την σχέση γ(s) = ( x 0 + r cos(s/r) y 0 + r sin(s/r) ), s I [0, 2π), Τότε θα έχουμε T (s) = γ(s) = ( sin(s/r), cos(s/r) ), T (s) = γ(s) = 1 r ( cos(s/r), sin(s/r) ), επομένως κ(s) = T (s) = 1 r, δηλαδή σταθερή. Αντίστροφα, έστω ότι η καμπυλότητα είναι σταθερή, κ(s) = κ για κάθε s I. Θεωρούμε την καμπύλη β(s) = γ(s) + 1 κ N(s). Τότε β (s) = T (s) + κṅ(s) 1 = T (s) + 1 κ ( κt (s)) = 0. Επομένως, η β(s) είναι σταθερή, δηλαδή β(s) = (x 0, y 0 ) και γ(s) (x 0, y 0 ) = γ(s) β(s) = 1 κ N(s) = 1 κ, άρα τα σημεία γ(s) ανήκουν στον κύκλο με κέντρο το (x 0, y 0 ) και ακτίνα 1 κ. Παράδειγμα 1.2. Εστω γ : I R 3 μια κανονική καμπύλη μοναδιαίας ταχύτητας με αντίστοιχο τρίεδρο Frenet {T, N, B}, τέτοιο ώστε για κάθε s I το διάνυσμα sin(2s)t (s) + cos(2s)n(s) + B(s) όπου cos(2s) 0 να είναι σταθερό. Τότε η γ είναι τμήμα κύκλου. Πράγματι, για κάθε s I έχουμε sin(2s)t (s) + cos(2s)n(s) + B(s) = c, c σταθερό διάνυσμα. Παραγωγίζουμε την προηγούμενη σχέση ως προς s και έχουμε ότι d ( ) sin(2s)t (s) + cos(2s)n(s) + B(s) = 0. ds Μετά από πράξεις προκύπτει ότι ( 2 cos(2s) κ(s) cos(2s) ) T (s) + ( sin(2s)κ(s) 2 sin(2s) τ(s) ) N(s) + cos(2s)τ(s)b(s) = 0.
31 30 Καμπύλες στο επίπεδο και στον χώρο Επειδή τα διανύσματα T (s), N(s), B(s) είναι γραμμικώς ανεξάρτητα, έχουμε 2 cos(2s) κ(s) cos(2s) = 0, sin(2s)κ(s) 2 sin(2s) τ(s) = 0, cos(2s)τ(s) = 0. Από την τελευταία εξίσωση παίρνουμε τ(s) = 0, άρα η γ είναι επίπεδη. Από την πρώτη εξίσωση έχουμε κ(s) = 2, άρα η γ σύμφωνα με την Πρόταση 1.6 είναι τμήμα κύκλου ακτίνας r = 1 κ = 1 2. Θα δούμε τώρα ότι μια καμπύλη Frenet στον χώρο R 3 καθορίζεται από την καμπυλότητά της και την στρέψη της (μη λαμβάνοντας υπόψη στερεές κινήσεις του R 3 που διατηρούν τον προσανατολισμό). Χρειαζόμαστε πρώτα τον εξής ορισμό: Ορισμός Μια απεικόνιση Φ : R 3 R 3 ονομάζεται Ευκλείδεια (ή στερεά) κίνηση του R 3 (rigid motion), εάν έχει τη μορφή Φ(X) = AX + b, όπου b R 3 και A O(3) = {X M 3 3 (R) : XX t = I 3 }. Η Φ διατηρεί τον προσανατολισμό, εάν A SO(3) = {X O(3) : detx = 1}. Θεώρημα (Θεμελιώδες Θεώρημα της Θεωρίας καμπυλών) Εστω κ : I R + και τ : I R διαφορίσιμες συναρτήσεις. Τότε υπάρχει μια καμπύλη Frenet γ : I R 3 η οποία να έχει καμπυλότητα κ και στρέψη τ. Επιπλέον, εάν γ : I R 3 είναι μια άλλη τέτοια καμπύλη, τότε υπάρχει πίνακας A SO(3) και διάνυσμα b R 3 τέτοια ώστε γ(s) = A γ(s) + b. Η απόδειξη στηρίζεται στο θεμελιώδες θεώρημα ύπαρξης και μοναδικότητας λύσης συνήθων διαφορικών εξισώσεων με αρχική συνθήκη. Παράδειγμα 1.3. (α) Δικαιολογήστε ότι υπάρχει καμπύλη γ με παράμετρο το μήκος τόξου της s, τέτοια ώστε κ(s) = e s και τ(s) = 2e s. (β) Για την προηγούμενη καμπύλη βρείτε όλα τα s R για τα οποία ισχύει N(s) = Ṅ(s) 10N(s). Για το (α), παρατηρούμε ότι κ(s) > 0 για κάθε s R και οι συναρτήσεις κ(s), τ(s) είναι διαφορίσιμες. Επομένως, από το προηγούμενο θεώρημα, υπάρχει καμπύλη γ με παραμέτρηση ως προς το μήκος τόξου για την οποία η καμπυλότητα και η στρέψη δίνονται από τους τύπους κ(s) = e s και τ(s) = 2e s. Για το (β) έχουμε Ṅ(s) = κ(s)t (s) + τ(s)b(s) = es T (s) + 2e s B(s). Παραγωγίζοντας την προηγούμενη σχέση, παίρνουμε N(s) = e s T (s) e s T (s) + 2e s B(s) + 2e s Ḃ(s) από του τύπους του Frenet = e s T (s) e s (e s N(s)) + 2e s B(s) + 2e s ( 2e s N(s)) = e s T (s) 5e 2s N(s) + 2e s B(s). Επομένως με αντικατάσταση στη δοσμένη σχέση N(s) = Ṅ(s) 10N(s) θα έχουμε: N(s) = Ṅ(s) 10N(s) N(s) Ṅ(s) + 10N(s) = 0 e s T (s) 5e 2s N(s) + 2e s B(s) ( e s T (s) + 2e s B(s) ) + 10N(s) = 0 (10 5e 2s )N(s) = 0 Άρα θα πρέπει e 2s = 2 δηλαδή s = ln 2/2.
32 Καμπύλες στον χώρο R 3 31 Ορισμός Εστω γ : I R 3 μια κανονική καμπύλη του R 3 (όχι απαραίτητα με παραμέτρηση ως προς το μήκος τόξου). Εστω γ = γ h : J R 3 μια μοναδιαίας ταχύτητας αναπαραμέτρηση της γ για κάποια αμφιδιαφόριση h : J I και έστω κ : J R η καμπυλότητα της γ. Για κάθε t I η καμπυλότητα της καμπύλης γ στο σημείο t είναι ο αριθμός Παρόμοια, ορίζουμε την στρέψη τ : I R της γ ως όπου τ : J R η στρέψη της γ. κ(t) = κ(h 1 (t)). τ(t) = τ(h 1 (t)), Χρησιμοποιώντας τους παραπάνω ορισμούς, είναι δυνατόν να προκύψουν τύποι για την καμπυλότητα και στρέψη καμπύλης αναφερομένης σε τυχαία παράμετρο. Πρόταση 1.7. Εστω γ : I R 3 μια κανονική καμπύλη του R 3 με καμπυλότητα κ και στρέψη τ. Τότε κ(t) = γ (t) γ (t) γ (t) 3, τ(t) = [γ (t)γ (t)γ (t)] γ (t) γ (t) 2. Απόδειξη. Εστω γ = γ h : J R 3 η αναπαραμέτρηση της γ μέσω του μήκους τόξου της, δηλαδή h = s 1 και s η συνάρτηση μήκους τόξου. Εστω T, Ñ, B το τρίεδρο Frenet της γ. Τότε γ = γ h 1 ή γ = γ s, οπότε για κάθε t I έχουμε: επομένως γ (t) = ( γ s) (t) = γ(s(t))s (t) = T (s(t))s (t) γ (t) = T (s(t))s (t) 2 + T (s(t))s (t) = s (t) 2 κ(s(t))ñ(s(t)) + s (t) T (s(t)), γ (t) γ (t) = s (t) T (s(t)) ( s (t) T (s(t)) + s (t) 2 κ(s(t))ñ(s(t))) = s (t)s (t) T (s(t)) T (s(t)) + s (t) 3 κ(s(t)) T (s(t)) Ñ(s(t)) = s (t) 3 κ(s(t)) B(s(t)). (1.11) Ομως s(t) = t t 0 γ (u) du, οπότε s (t) = γ (t). Άρα η σχέση (1.11) γίνεται Επομένως γ (t) γ (t) = γ (t) 3 κ(s(t)) B(s(t)). γ (t) γ (t) = γ (t) 3 κ(s(t)) B(s(t)) = γ (t) 3 κ(s(t)), δηλαδή κ(s(t)) = γ (t) γ (t) γ (t) 3, άρα απο τον Ορισμό 1.17 έχουμε τον ζητούμενο τύπο για την καμπυλότητα της γ: κ(t) = κ(s(t)) = γ (t) γ (t) γ (t) 3.
33 32 Καμπύλες στο επίπεδο και στον χώρο Για την στρέψη της καμπύλης γ θα υπολογίσουμε την τρίτη παράγωγο της γ. Οπως και προηγουμένως και μετά από πράξεις έχουμε: γ (t) = Ñ(s(t))s (t) 3 κ(s(t)) + Ñ(s(t)) κ (s(t))s (t) 3 + 3Ñ(s(t)) κ(s(t))s (t) 2 s (t) +s (t) T (s(t)) + s (t)s (t) T ( (s(t)) = κ(s(t)) 2 s (t) 3 + s (t)) T (s(t)) ( + κ(s(t))s (t) κ(s(t))s (t) 2 s (t) + s (t)s (t) κ(s(t)))ñ(s(t)) ( 3 τ(s(t))) + κ(s(t))s (t) B(s(t)) = f(t) T (s(t)) + g(t)ñ(s(t)) + w(t) B(s(t)). Επομένως, επειδή det(γ (t), γ (t), γ (t)) = [γ (t)γ (t)γ (t)] = γ (t) γ (t), γ (t), λαμβάνοντας υπόψη και την σχέση (1.11), θα πάρουμε: γ (t) γ (t), γ (t) = ( 0, 0, s (t) κ(s(t)) ), ( f(t), g(t), w(t) ) = s (t) 3 κ(s(t))w(t) = s (t) 3 κ(s(t)) ( κ(s(t))s (t) 3 τ(s(t)) ). (1.12) Ομως s (t) = γ (t) και δεδομένου ότι έχουμε δείξει κ(s(t)) = γ (t) γ (t) γ (t) 3, οπότε με αντικατάσταση στη σχέση (1.12) θα πάρουμε τ(s(t)) = γ (t) γ (t), γ (t) γ (t) γ (t) 2 = [γ (t)γ (t)γ (t)] γ (t) γ (t) 2. Με το ίδιο σκεπτικό που αναπτύξαμε για την καμπυλότητα της καμπύλης γ, ο ζητούμενος τύπος για την στρέψη της θα είναι τ(t) = τ(s(t)) = [γ (t)γ (t)γ (t)] γ (t) γ (t) 2. Εύκολα αποδεικνύεται ότι για μια κανονική καμπύλη γ : I R 3 θετικής καμπυλότητας και τυχαία παράμετρο, τα διανύσματα του τριέδρου Frenet σε κάποιο σημείο t I δίνονται από τους παρακάτω τύπους: ( T (t) = γ (t) γ γ (t), N(t) = (t) γ (t) ) γ (t) γ (t) γ (t) γ (t), B(t) = γ (t) γ (t) γ (t) γ (t). Πρόταση 1.8. Εστω γ : I R 3 μια κανονική καμπύλη με τυχαία παράμετρο και θετική καμπυλότητα. Εστω {T (t), N(t), B(t)} το τρίεδρο Frenet της γ. Τότε οι παράγωγοι των T, N, B δίνονται ως όπου v η ταχύτητα της γ. T (t) N (t) B (t) Η απόδειξη αφήνεται ως άσκηση. = 0 κ(t)v 0 T (t) κ(t)v 0 τ(t)v N(t) 0 τ(t)v 0 Πόρισμα 1.2. Εστω γ : I R 3 κανονική καμπύλη του R 3. Τότε: B(t),
34 Καμπύλες στον χώρο R Το ίχνος γ(i) είναι τμήμα ευθείας εάν και μόνο εάν τα διανύσματα γ (t), γ (t) είναι γραμμικώς εξαρτημένα για κάθε t I. 2. Το ίχνος γ(i) περιέχεται σε ένα επίπεδο εάν και μόνο εάν τα διανύσματα γ (t), γ (t), γ (t) είναι γραμμικώς εξαρτημένα για κάθε t I. 1.3 Λυμένα παραδείγματα Παράδειγμα 1.4. Θεωρούμε την κυκλοειδή καμπύλη του επιπέδου με παραμέτρηση γ(t) = α(t, 1) + α( sin t, cos t) (α > 0). 1. Περιγράψτε την καμπύλη γεωμετρικά. 2. Υπολογίστε το μήκος τόξου σ(t) = t 0 γ (u) du. 3. Είναι η καμπύλη κανονική; Λύση 1. Θέτοντας γ(t) = (x(t), y(t)), παίρνουμε τις εξισώσεις x(t) = α(t sin t) t x α = sin t y(t) = α(1 cos t) 1 y α = cos t. Άρα ( t x ) 2 ( α + 1 y 2 α) = 1 και (αt x) 2 + (α y) 2 = α 2. Η εξίσωση αυτή είναι οικογένεια κύκλου με κέντρο τα σημεία K(αt, α) και σταθερής ακτίνας α > 0. Η εικόνα της φαίνεται στο Σχήμα Σχήμα 1.11: Η κυκλοειδής καμπύλη. 2. Είναι γ (t) = α(1 cos t, sin t) άρα γ (t) = α 2 (1 cos t) 2 + α 2 sin 2 t = α 2 1 cos t = α 2 2 sin 2 t 2 = 2α sin( t 2 ). Για 0 t/2 π παίρνουμε σ(t) = t 0 2α sin u 2 du = 4α(1 cos t 2 ). 3. Η καμπύλη είναι κανονική εκτός εάν γ (t) = 0 δηλαδή cos t = 1 και sin t = 0, δηλαδή για t = 2kπ (k Z).
35 34 Καμπύλες στον χώρο R 3 Παράδειγμα 1.5. Εστω γ : I R 2 η καμπύλη γ(t) = (sin t, sin(2t)). Είναι η γ κανονική, απλή ή κλειστή; Λύση Η γ είναι κανονική, επειδή γ (t) = (cos t, 2 cos(2t)) (0, 0) για κάθε t. Η καμπύλη δεν είναι απλή, επειδή γ(0) = γ(π) = (0, 0) (δηλαδή η γ έχει αυτοτομές). Τέλος, η γ είναι κλειστή, διότι για I = [0, 2π] γ(0) = γ(2π) = (0, 0). Το ίχνος της φαίνεται παρακάτω: Σχήμα 1.12: Η καμπύλη γ(t) = (sin t, sin(2t)). Παράδειγμα 1.6. Θεωρούμε την καμπύλη γ(t) = (t, cosh t), t > 0. Βρείτε την ταχύτητα γ (t) της γ και χρησιμοποιήστε την για να κάνετε αναπαραμέτρηση της γ ως προς το μήκος τόξου. Λύση Είναι γ (t) = (1, sinh t) άρα γ (t) = s = t sinh 2 t = cosh t. Εστω γ (u) du = t 0 cosh udu = sinh t. Τότε t = sinh 1 s (αντίστροφη συνάρτηση του sinh s) και cosh t = αναπαραμέτρηση της γ ως προς το μήκος τόξου είναι η 1 + sinh 2 t = 1 + s 2. Συνεπώς, η β(s) = γ ( t(s) ) = ( sinh 1 s, 1 + s 2). Παράδειγμα 1.7. α) Υπολογίστε τις καμπυλότητες κ 1, κ 2 και τις στρέψεις τ 1, τ 2 των ελίκων γ 1, γ 2 : R R 3 γ 1 (t) = ( r cos(αt), r sin(αt), bt ) γ 2 (t) = ( r cos( αt), r sin( αt), bt ) (r, α, b > 0). β) Βρείτε μια στερεά κίνηση Φ : R 3 R 3 τέτοια ώστε γ 2 = Φ γ 1. Διατηρεί η Φ τον προσανατολισμό;
36 Καμπύλες στον χώρο R 3 35 Λύση α) Για τις καμπυλότητες θα χρησιμοποιήσουμε τον τύπο και για τις στρέψεις κ(t) = γ (t) γ (t) γ (t) 3 τ(t) = det( γ (t), γ (t), γ (t) ) γ (t) γ (t) 2. Προτρέπουμε τον αναγνώστη να επαληθεύσει τους παρακάτω υπολογισμούς: Άρα κ 1 (t) = γ 1(t) = ( rα sin(αt), rα cos(αt), b) γ 1 (t) = ( rα 2 cos(αt), rα 2 sin(αt), 0) γ 1(t) γ 1 (t) = rα 2 b 2 + r 2 α 2, γ 1(t) = r 2 α 2 + b 2. rα 2 r 2 α 2 + b 2 = r( α) 2 ( α) 2 r 2 + b 2 = κ 2(t). Επίσης, τ 1 (t) = αb r 2 α 2 + b 2 = τ 2(t). β) Εστω A είναι ο πίνακας της γραμμικής απεικόνισης Φ : R 3 R 3. Αρκεί να λύσουμε την εξίσωση r cos( αt) r cos(αt) r sin( αt) = A r sin(αt) ως προς A. Με απλή παρατήρηση προκύπτει ότι η λύση είναι A = bt bt έχει τύπο Φ(x, y, z) = (x, y, z). Επειδή det(a) = 1, η Φ δεν διατηρεί τον πρασανατολισμό.. Άρα η Φ : R 3 R 3 Παράδειγμα 1.8. Αποδείξτε ότι η καμπύλη γ : ( π/2, π/2) R 3, γ(t) = (2 cos 2 t 3, sin t 8, 3 sin 2 t+ 4) είναι κανονική. Ελέξτε κατά πόσον το ίχνος της γ είναι (α) τμήμα μιας ευθείας του R 3, (β) επίπεδη καμπύλη του R 3. Λύση Είναι γ (t) = ( 4 cos t sin t, cos t, 6 sin t cos t) (0, 0, 0) για κάθε t ( π/2, π/2) (επειδή cos t 0). Άρα η γ είναι κανονική καμπύλη. Υπολογίζουμε ότι det ( γ (t), γ (t), γ (t) ) = 0 άρα τ(t) = 0, συνεπώς η καμπύλη είναι επίπεδη. Τα διανύσματα γ (t) και γ (t) είναι γραμμικώς ανεξάρτητα (δείχνοντας π.χ. ότι γ (t) γ (t) 0 ) άρα κ(t) 0, οπότε η γ δεν είναι τμήμα ευθείας. Παράδειγμα 1.9. Να βρεθεί η εξίσωση του εγγύτατου επιπέδου σε ένα σημείο μιας κανονικής καμπύλης. Λύση (I) Εστω ότι έχουμε την καμπύλη γ : I R 3 με παράμετρο το μήκος τόξου της. Ενα σημείο (x, y, z) R 3 είναι σημείο του εγγύτατου επιπέδου στο σημείο γ(s 0 ) εάν και μόνο εάν η διαφορά (x, y, z) γ(s 0 ) ανήκει
37 36 Καμπύλες στον χώρο R 3 στον υπόχωρο που παράγουν τα διανύσματα T (s 0 ) και N(s 0 ), δηλαδή είναι κάθετη στο B(s 0 ). Άρα τα σημεία (x, y, z) του εγγύτατου επιπέδου στο γ(s 0 ) ικανοποιούν την σχέση (x, y, z) γ(s 0 ), B(s 0 ) = 0 (1.13) T Επειδή B(s 0 ) = T (s 0 ) N(s 0 ) = γ(s 0 ) (s 0 ) κ(s 0 ) = γ(s 0) γ(s 0), η σχέση (1.13) ισοδυναμεί με την κ(s 0 ) (x, y, z) γ(s 0 ), γ(s 0 ) γ(s 0 ) = 0. (II) Εστω τώρα ότι έχουμε μια κανονική καμπύλη a : I R 3 όχι κατ αναγκή μοναδιαίας ταχύτητας. Τα σημεία (x, y, z) του εγγύτατου επιπέδου στο a(t 0 ) ικανοποιούν την αντίστοιχη σχέση (1.13) δηλαδή (x, y, z) a(t 0 ), B(t 0 ) = 0, επειδή B(t 0 ) = a (t 0 ) a (t 0 ) a (t 0 ) a, παίρνουμε τη συνθήκη (t 0 ) (x, y, z) a(t 0 ), a (t 0 ) a (t 0 ) a (t 0 ) a (t 0 ) = 0 (x, y, z) a(t 0), a (t 0 ) a (t 0 ) = 0 Παράδειγμα Αν η καμπύλη γ : I R 3 έχει παράμετρο το μήκος τόξου της και σταθερή στρέψη τ 0, να δείξετε ότι η καμπύλη έχει σταθερή καμπυλότητα ίση με τ. Λύση β(s) = N(s) τ + B(s)ds Εχουμε β (s) = Ṅ(s) + B(s) και επειδή τ Ṅ(s) = κ(s)t (s) + τb(s), θα είναι β (s) = κ(s) τ T (s). Παρατηρούμε ότι β (s) = κ(s) 1 δηλαδή η παράμετρος s για την καμπύλη β είναι τυχαία, οπότε η τ καμπυλότητα θα δίνεται από τον τύπο Είναι β (s) = κ (s) τ και T (s) + κ(s) τ T (s), οπότε β (s) β (s) = κ (s)κ(s) τ 2 = κ(s)2 τ 2 κ(s) = β (s) β (s) β (s) 3. (T (s) T (s)) + κ(s)2 τ 2 (T (s) T (s)) T (s) (κ(s)n(s)) = κ(s)3 τ 2 B(s) β (s) β (s) = κ(s)3 τ 2 B(s) = κ(s) 3 τ 2. Επομένως, αντικαθιστώντας στον τύπο για την καμπυλότητα, θα πάρουμε κ(s) = κ(s) 3 τ 2 1 κ(s) 3 τ 3 = τ.
38 Καμπύλες στον χώρο R 3 37 Παράδειγμα Εστω β : R R 3 κανονική καμπύλη μοναδιαίας ταχύτητας τέτοια ώστε η εφαπτομένη σε κάθε σημείο β(s) περνά από σταθερό σημείο p R 3. Δείξτε ότι η καμπύλη β είναι ευθεία. Λύση Η εφαπτομένη στο σημείο β(s) δίνεται από την εξίσωση β(s) + t β(s). Αφού το σημείο p ανήκει σε αυτήν την ευθεία για κάθε s R, υπάρχει συνάρτηση f(s) τέτοια ώστε p = β(s) + f(s) β(s). Θα δείξουμε ότι η f είναι διαφορίσιμη. Εχουμε f(s) β(s) = p β(s) f(s) = p β(s), β(s) άρα η f διαφορίσιμη αφού η β είναι διαφορίσιμη. Παραγωγίζουμε στη συνέχεια την σχέση p = β(s) + f(s) β(s) και έχουμε 0 = T (s) + f (s)t (s) + f(s)κ(s)n(s) 1 + f (s) = 0 και f(s)κ(s) = 0 άρα f (s) = 1 και f(s) = s + c, c R. Αφού f(s)κ(s) = 0 έχουμε ότι κ(s) = 0 για κάθε s R άρα η καμπύλη β είναι ευθεία. 1.4 Ασκήσεις 1. Η αστεροειδής καμπύλη είναι η καμπύλη του επιπέδου με παραμέτρηση γ : R R 2, γ(t) = (4α cos 3 t, 4α sin 3 t) = 3α(cos t, sin t)+ α(cos(3t), sin(3t)), α > 0. a. Περιγράψτε την καμπύλη γεωμετρικά. b. Υπολογίστε το μήκος τόξου σ(t) = t 0 c. Είναι η καμπύλη κανονική; γ (u) du. 2. Δίνεται η καμπύλη γ(t) = (e t cos t, e t sin t), t R. a. Να αποδειχθεί ότι lim t + γ(t) = lim t + γ (t) = (0, 0). b. Να υπολογιστεί το t 0 γ (u) du. c. Να υπολογιστεί η καμπυλότητα της γ. 3. Δίνονται οι καμπύλες γ 1, γ 2 : R R 2 με γ 1 = r(cos(αt), sin(αt)), γ 2 = r(cos( αt), sin( αt)). Υπολογίστε τις καμπυλότητες κ 1, κ 2 των γ 1, γ 2 αντίστοιχα. Βρείτε μια στερεά κίνηση Φ : R 2 R 2 τέτοια ώστε γ 2 = Φ γ 1. Διατηρεί η Φ τον προσανατολισμό; 4. Εστω γ : I R 2 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου και με πλαίσιο Frenet {T (s), N(s)}. Για λ R ορίζουμε την παράλληλη καμπύλη γ λ (t) = γ(t) + λn(t).
39 38 Καμπύλες στον χώρο R 3 Σχήμα 1.13: Η αστεροειδής καμπύλη. Υποθέτουμε ότι ισχύει λκ < 1. Εκφράστε την καμπυλότητα κ λ της καμπύλης γ λ συναρτήσει της καμπυλότητας κ της καμπύλης γ. 5. Εστω γ : I R 2 μια κανονική καμπύλη του R 2. Αποδείξτε ότι η καμπυλότητα ικανοποιεί την σχέση κ(t) = det(γ (t), γ (t)) γ (t) Εστω γ : I R 2 η καμπύλη του R 2 με γ(t) = (sin t, sin(2t)). Είναι η γ κανονική, απλή και κλειστή; 7. Εστω ότι η απεικόνιση γ : R R 2 είναι μια παραμέτρηση ως προς το μήκος τόξου μιας θετικά προσανατολισμένης, απλής και κλειστής καμπύλης. Δείξτε ότι αν η περίοδος της γ είναι L > 0, τότε η καμπυλότητα κ(s) της γ ικανοποιεί την σχέση L 0 κ(s)ds = 2π. Το ολοκλήρωμα στο αριστερό μέλος ονομάζεται ολική καμπυλότητα της γ. 8. Υπολογίστε τις καμπυλότητες κ 1, κ 2 και τις στρέψεις τ 1, τ 2 των ελίκων γ 1, γ 2 : R R 3 με γ 1 (t) = (r cos(at), r sin(at), bt) και γ 2 (t) = (r cos( at), r sin( at), bt), (r, a, b > 0). Βρείτε μια στερεά κίνηση Φ : R 3 R 3 τέτοια ώστε γ 2 = Φ γ 1. Διατηρεί η Φ τον προσανατολισμό; 9. Βρείτε μια κανονική καμπύλη γ : R R 3 με σταθερή καμπυλότητα k > 0 και σταθερή στρέψη τ R. 10. Αποδείξτε ότι η στρέψη τ μιας κανονικής καμπύλης γ : R R 3 ικανοποιεί την σχέση τ(t) = [γ (t), γ (t), γ (t)] γ (t) γ (t) 2.
40 Καμπύλες στον χώρο R Αποδείξτε ότι η καμπύλη γ : ( π 2, π 2 ) R3 με γ(t) = (2 cos 2 t 3, sin t 8, 3 sin 2 t+4) είναι κανονική. Ελέγξτε κατά πόσον το ίχνος της γ περιέχεται σε: α) μια ευθεία του R 3, β) ένα επίπεδο του R Το ίδιο ερώτημα όπως στην Άσκηση 4 για την καμπύλη γ : R R 3, γ(t) = (t 3 + t 2 + 3, t 3 t + 1, t 2 + t + 1). 13. Αναζητήστε στη βιβλιογραφία μια απόδειξη του θεωρήματος του Fenchel: Εστω ότι η απεικόνιση γ : R R 3 είναι μια κανονική παραμέτρηση μιας κλειστής καμπύλης στον R 3 με παράμετρο το μήκος τόξου. Τότε ισχύει όπου P η περίοδος της γ. L( γ) = P 0 κ(s)ds 2π, 14. Αναζητήστε στην βιβλιογραφία μια απόδειξη του Θεμελιώδους Θεωρήματος της Θεωρίας Καμπυλών. 15. Εστω γ : R R 3 μια κανονική καμπύλη με παράμετρο το μήκος τόξου της, για την οποία υπάρχει παραγωγίσιμη απεικόνιση ϕ : R R, ώστε γ(s) = s 2 T (s) + ϕ(s)n(s) + s B(s), s R. 2 Αν γ(0) = ( 2 2, 0, 0), να υπολογίσετε την καμπυλότητα, την στρέψη της γ καθώς και τη συνάρτηση ϕ. 16. Εστω α : R R 3 κανονική καμπύλη μοναδιαίας ταχύτητας τέτοια ώστε κ(s) 0 για κάθε s R. Να δείξετε ότι η καμπύλη α είναι επίπεδη εάν και μόνο έαν όλα τα εγγύτατα επίπεδά της περνούν από σταθερό σημείο p.
41 40 Καμπύλες στον χώρο R3
42 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, Μετάφραση 3 ης εκδ. Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, [5] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [6] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [7] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
43 42 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
44 Κεφάλαιο 2 Κανονικές επιφάνειες Σύνοψη Προκειμένου να ορίσουμε την έννοια της επιφάνειας στον R 3, έχουμε δύο δυνατές προσεγγίσεις. Με την πρώτη μπορούμε να ορίσουμε μια επιφάνεια ως ένα υποσύνολο του R 3, ώστε για κάθε σημείο του να υπάρχει ένα ανοικτό υποσύνολο, το οποίο να είναι ομοιομορφικό με ένα ανοικτό υποσύνολο του R 2. Με τη δεύτερη προσέγγιση μια επιφάνεια (ή καλύτερα τμήμα επιφάνειας) ορίζεται ως εικόνα μιας απεικόνισης από ένα ανοικτό υποσύνολο του επιπέδου στον R 3, η οποία και αυτή ικανοποιεί συγκεκριμένες ιδιότητες. Η δεύτερη προσέγγιση είναι γενίκευση της περιγραφής των καμπυλών στον R 3. Αν και είναι χρήσιμη στην περιγραφή τοπικών ιδιοτήτων μιας επιφάνειας, έχει παρόλα αυτά περιορισμένη χρησιμότητα για πιο δύσκολα προβλήματα. Για τον λόγο αυτό, θα χρησιμοποιήσουμε και τον εναλλακτικό ορισμό μιας επιφάνειας ως ένα υποσύνολο του Ευκλείδειου χώρου R 3 το οποίο τοπικά να μοιάζει με ένα ανοικτό υποσύνολο του επιπέδου. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6]. Προαπαιτούμενη γνώση Αναλυτική Γεωμετρία, Απειροστικός Λογισμός μιας και πολλών μεταβλητών, Εισαγωγή στη Γραμμική Άλγεβρα. Ορισμός 2.1. Ενα μη κενό συνεκτικό υποσύνολο M του R 3 ονομάζεται κανονική επιφάνεια (regular surface) (ή τοπικά εμφυτευμένη (embedded) επιφάνεια) εάν για κάθε p M υπάρχουν ανοικτές περιοχές V R 3, U R 2 με p V και μια 1-1 απεικόνιση X : U R 2 V M R 3, X = X(u, v) τέτοια ώστε 1. Η X να είναι ομοιομορφισμός 2. Να είναι X u (q) X v (q) 0 για κάθε q U. Η απεικόνιση X ονομάζεται τοπική παραμέτρηση (local parametrization) της M και η δυάδα (V M, X 1 ), όπου X 1 : V M U, ονομάζεται τοπικός χάρτης (local chart) ή τοπικό σύστημα συντεταγμένων της M στο σημείο p = X(q). Παρατηρήσεις 1. Η απεικόνιση X ως προς ένα σύστημα συντεταγμένων O xyz του R 3 έχει τη μορφή X(u, v) = (x(u, v), y(u, v), z(u, v)), όπου x, y, z : U R 2 R είναι πραγματικές διαφορίσιμες απεικονίσεις, των u, v U. 43
45 44 Κανονικές επιφάνειες Κατόπιν αυτού, η συνθήκη 2 ισοδυναμεί με το ότι τα διανύσματα X u (q) = ( x u (q), y u (q), z u (q) ), X v (q) = ( x v (q), y v (q), z v (q) ) είναι γραμμικώς ανεξάρτητα. Ισοδύναμα, το διαφορικό dx q : R 2 R 3 είναι 1-1, δηλαδή η τάξη του πίνακα είναι Η συλλογή A = M, εάν ( x u (q) y u (q) z u (q) x v (q) y v (q) z v (q) { (Vα M, Xα 1 ) } : α I από τοπικούς χάρτες της M ονομάζεται άτλαντας της M = α I ( Vα M ) ) Εάν π i : R 3 R, (i = 1, 2) είναι οι κανονικές προβολές, τότε προκύπτει το παρακάτω διάγραμμα: Τότε η συνθήκη 2 ισοδυναμεί με το ότι Σχήμα 2.1: Τοπικό σύστημα συντεταγμένων. det X 1 u (q) X 1 v (q) X 2 u (q) X 2 v (q) Παράδειγμα 2.1. Το επίπεδο Π = {(x, y, z) R 3 0. : Ax + By + Γz + = 0} είναι μια κανονική επεφάνεια η οποία καλύπτεται με έναν μόνο χάρτη. Πράγματι, γνωρίζουμε ότι, για να ορίζεται ένα επίπεδο, θα πρέπει ένα τουλάχιστον από τα A, B, Γ να είναι διάφορο του μηδενός. Οπότε χωρίς βλάβη της γενικότητας
46 Κανονικές επιφάνειες 45 υποθέτουμε ότι Γ 0, άρα z = Θεωρούμε τώρα την απεικόνιση Ax By. Θέτουμε x = u, y = v, συνεπώς είναι z = z(u, v). Γ X : R 2 Π R 3 (u, v) X(u, v) = ( x(u, v), y(u, v), z(u, v) ) ( Au Bv ) = u, v,. Γ Προφανώς η X είναι 1-1, επί και συνεχής, οπότε υπάρχει η αντίστροφη X 1 : Π R 3 R 2, X 1 (x, y, z) = (x, y), η οποία είναι συνεχής, επομένως η απεικόνιση X είναι ομοιομορφισμός. Επίσης η X είναι διαφορίσιμη (διότι υπάρχουν και είναι συνεχείς όλες οι μερικές παράγωγοι των απεικονίσεων x, y, z : R 2 R). Τέλος, θα δείξουμε ότι X u (q) X v (q) 0 για κάθε q = (u, v) R 2. Είναι X u = (1, 0, A Γ ) και X v = (0, 1, B Γ ), οπότε e 1 e 2 e 3 X u X v = 1 0 A Γ = ( A 0 1 B Γ, B Γ, 1) Γ απ όπου παίρνουμε ότι X u X v = 0, άρα X u X v (0, 0, 0). Επομένως, σύμφωνα με τον Ορισμό 2.1, το επίπεδο Π είναι μια κανονική επιφάνεια η οποία καλύπτεται από έναν μόνο χάρτη (Π, X 1 ), όπου X 1 : Π R 3 R 2. Παράδειγμα 2.2. Εστω U ανοικτό υποσύνολο του R 2 και f : U R μια διαφορίσιμη συνάρτηση. Τότε η απεικόνιση X : U M με τιμή αποτελεί μια τοπική παραμέτρηση του γραφήματος X(u, v) = ( u, v, f(u, v) ) M = { (u, v, f(u, v)) : (u, v) U } της f. Ο αντίστοιχος τοπικός χάρτης (M, X 1 ) όπου X 1 : M U είναι X 1 (x, y, z) = (x, y). Συνεπώς το σύνολο M είναι μια κανονική επιφάνεια. Στο παραπάνω παράδειγμα το σύνολο M είναι το γράφημα της απεικόνισης f : R 2 R με f(x, y) = z. Ανάλογα, το γράφημα μιας απεικόνισης g : R 2 R με g(x, z) = y είναι το σύνολο {(u, g(u, v), v) : (u, v) R 2 } με παραμέτρηση Y (u, v) = (u, g(u, v), v), ενώ το γράφημα της απεικόνισης h : R 2 R με h(y, z) = x είναι το σύνολο {(h(u, v), u, v) : (u, v) R 2 } με παραμέτρηση W (u, v) = (h(u, v), u, v). Οι πραμετρήσεις αυτής της μορφής καλούνται παραμετρήσεις τύπου Monge. Εύκολα βλέπουμε ότι η παραμέτρηση του επιπέδου στο Παράδειγμα 2.1 είναι παραμέτρηση τύπου Monge. Παράδειγμα 2.3. Εστω S 2 = { (x, y, z) R 3 : x 2 + y 2 + z 2 = 1 } η μοναδιαία σφαίρα του R 3. Εστω N = (0, 0, 1), S = (0, 0, 1) ο βόρειος και ο νότιος πόλος αντίστοιχα. Θέτουμε U N = S 2 \ {N}, U S = S 2 \ {S} και ορίζουμε τις απεικονίσεις X N : U N R 2, X S : U S R 2 (στερεογραφικές προβολές) ως X N (x, y, z) = 1 (x, y), 1 z X S (x, y, z) = 1 (x, y). 1 + z
47 46 Κανονικές επιφάνειες Τότε το σύνολο A = { (U N, X N ), (U S, X S ) } αποτελεί έναν άτλαντα της σφαίρας S 2. Άσκηση Να γίνει αναλυτικός έλεγχος ότι ικανοποιείται ο Ορισμός 1.1. Σχήμα 2.2: Στερεογραφική προβολή. Ο παραπάνω ορισμός μιας επιφάνειας παρουσιάζει τεχνικές δυσκολίες στην εφαρμογή του. Θα δούμε τώρα έναν εναλλακτικό τρόπο κατασκευής επιφανειών στον R 3 μέσω του θεωρήματος πεπλεγμένης συνάρτησης. Χρειαζόμαστε κατ αρχάς να υπενθυμίσουμε τα εξής: Εστω F = (F 1,..., F m ) : U R n R m μια διαφορίσιμη απεικόνιση στο ανοικτό υποσύνολο U του R n και p U. Τότε το διαφορικό DF (p) : R n R m στο p είναι μια γραμμική απεικόνιση της οποίας ο m n πίνακας (ως προς τις κανονικές βάσεις των R n, R m ) είναι ο [DF (p)] = F 1 x 1 (p). F m (p) x 1 F 1 (p) x n. F. m (p) x n Συχνά θα γράφουμε τον παραπάνω πίνακα απλά ως DF (p). Στην ειδική περίπτωση όπου F : U R n R, τότε ο πίνακας του διαφορικού DF (p) : R n R είναι ο 1 n πίνακας [DF (p)] = [ F (p),..., F ] (p). x 1 x n ( F Το αντίστοιχο διάνυσμα (p),..., F ) (p) λέγεται κλίση (grand) της F και συμβολίζεται με gradf x 1 x n ή F, με άλλα λόγια η κλίση της απεικόνισης F στο σημείο p είναι ο πίνακας του διαφορικού [DF (p)] γραμμένος ως διάνυσμα. Εστω τώρα γ : R U R n μια διαφορίσιμη καμπύλη με γ(0) = p, γ (0) = Z R. Τότε η σύνθεση F γ : R R m είναι μια καμπύλη στον R m και από τον κανόνα της αλυσίδας προκύπτει ότι το εφαπτόμενο διάνυσμά της στο σημείο F (p) R m είναι d ( ) F γ(t) t=0 dt = DF (γ(0))γ (0) = DF (p)z.
48 Κανονικές επιφάνειες 47 Σημειώνουμε ότι η τελευταία ισότητα είναι ένα διάνυσμα του R m, που η παράστασή του προκύπτει ως το γινόμενο ενός m n και ενός n 1 πίνακα. Συνεπώς, το διαφορικό DF (p) μιας απεικόνισης F : R n R m μπορεί να θεωρηθεί ως μια γραμμική απεικόνιση, η οποία απεικονίζει εφαπτόμενα διανύσματα στο p U R n σε εφαπτόμενα διανύσματα στο F (p) R m. αποτέλεσμα: Από τον λογισμό πολλών μεταβλητών ισχύει το εξής Πρόταση 2.1. Το διαφορικό DF (p) μιας απεικόνισης F : R n R m δεν εξαρτάται από την επιλογή της καμπύλης γ. Το παρακάτω θεώρημα είναι ίσως το πιο κεντρικό θεώρημα της κλασικής Ανάλυσης. Θεώρημα 2.1. (Θεώρημα Αντίστροφης Απεικόνισης) Εστω U R n ανοικτό και F : U R n R n διαφορίσιμη. Υποθέτουμε ότι στο p U το διαφορικό DF (p) : R n R n της F στο p είναι αντιστρέψιμη (ως γραμμική απεικόνιση). Τότε υπάρχουν ανοικτές περιοχές U p p, V q q = F (p) έτσι ώστε η f = F Up : U p V q να είναι 1-1, επί και η αντίστροφή της f 1 : V q U p να είναι διαφορίσιμη. Επιπλέον, για το διαφορικό της f 1 ισχύει: Df 1 (q) = ( DF (p) ) 1. Ορισμός 2.2. Εστω U R n ανοικτό και F : U R m διαφορίσιμη. 1. Ενα σημείο p U ονομάζεται κρίσιμο σημείο (critical point) της F, εάν το διαφορικό DF (p) : R n R m δεν είναι επί. Διαφορετικά, το p ονομάζεται κανονικό σημείο (regular point). 2. Ενα σημείο q F (U) ονομάζεται κανονική τιμή (regular value) της F, εάν κάθε σημείο της αντίστροφης εικόνας F 1 ({q}) του q είναι κανονικό. Διαφορετικά, το q ονομάζεται κρίσιμη τιμή (critical value) της F. Εστω f : U R 3 R μια διαφορίσιμη απεικόνιση και U ένα ανοικτό υποσύνολο του R 3. Τότε ο πίνακας του διαφορικού Df(p) της f στο σημείο p είναι ο 1 3 πίνακας ( ) f f f [Df(p)] = (p), (p), x y z (p). Για να είναι η απεικόνιση Df(p) : R 3 R επί (δεδομένου ότι έχει πεδίο τιμών διάστασης 1) πρέπει και αρκεί τουλάχιστον ένα από τα f f f (p), (p), (p) να είναι διαφορετικό από το μηδέν. Συνεπώς, το x y z q f(u) είναι κανονική τιμή της απεικόνισης f : U R 3 R εάν και μόνο εάν οι μερικές παράγωγοι f f f (p), (p), x y z (p) δεν μηδενίζονται ταυτόχρονα στο f 1 (q), ή ισοδύναμα το f 1 (q) δεν περιέχει κρίσιμα σημεία. Χρησιμοποιώντας τώρα το παραπάνω Θεώρημα Αντίστροφης Απεικόνισης, μπορούμε να αποδείξουμε το επόμενο θεώρημα κατασκευής επιφανειών στον R 3. Πολλές φορές το θεώρημα αυτό αναφέρεται και ως Θεώρημα Πεπλεγμένης Συνάρτησης (για τη θεωρία επιφανειών).
49 48 Κανονικές επιφάνειες Θεώρημα 2.2. Εστω U R 3 ανοικτό, f : U R διαφορίσιμη απεικόνιση και q μια κανονική τιμή της f, δηλαδή ισχύει ( ) ( f f f ) f (p) = (p), (p), x y z (p) 0, για κάθε p M = f 1( {q} ). Τότε το σύνολο M είναι μια κανονική επιφάνεια του R 3. Απόδειξη. Εστω p ένα τυχαίο σημείο του συνόλου M. Η κλίση ( f)(p) στο p δεν είναι μηδέν, οπότε χωρίς βλάβη της γενικότητας, υποθέτουμε ότι f z (p) 0. Ορίζουμε την απεικόνιση F : U R3 R 3 με τιμή Ο πίνακας του διαφορικού DF (p) στο σημείο p είναι F (x, y, z) = (x, y, f(x, y, z)). [DF (p)] = f f f x y z η ορίζουσα του οποίου είναι ίση με det([df (p)]) = f 0. Από το Θεώρημα Αντίστροφης Απεικόνισης z p υπάρχουν ανοικτές περιοχές U p p, W l l = F (p), έτσι ώστε η απεικόνιση f = F Up : U p W l να είναι 1-1, επί και η αντίστροφή της p, f 1 : W l U p, (u, v, t) (u, v, g(u, v, t)) να είναι διαφορίσιμη, όπου g : W l R 3 R. Επεται ότι ο περιορισμός X = f 1 W l : Wl R 3 στο σύνολο (συγκεκριμένα το επίπεδο) W l = {(u, v, t) W l : t = q} είναι διαφορίσιμη συνάρτηση. Άρα η απεικόνιση X : Wl U p M είναι μια τοπική παραμέτρηση. Επειδή το σημείο p είναι τυχαίο, το σύνολο M είναι μια κανονική επιφάνεια του R 3. Παράδειγμα 2.4. Εστω f : R 3 R η διαφορίσιμη απεικόνιση f(x, y, z) = x 2 + y 2 + z 2 και p = (x, y, z) R 3. Η κλίση f(p) είναι f(p) = ( 2x, 2y, 2z ) p = 2p, συνεπώς κάθε θετικός πραγματικός αριθμός r είναι μια κανονική τιμή της f. Άρα η σφαίρα ακτίνας r είναι μια κανονική επιφάνεια του R 3. S 2 r = {(x, y, z) R 3 : x 2 + y 2 + z 2 = r 2 } = f 1( {r 2 } ) Παράδειγμα 2.5. Εστω r, R R με 0 < r < R. Θεωρούμε τη διαφορίσιμη συνάρτηση f : U = {(x, y, z) R 3 : x 2 + y 2 0} R
50 Κανονικές επιφάνειες 49 με τιμή Θεωρούμε την αντίστροφη εικόνα αυτής f(x, y, z) = z 2 + ( x 2 + y 2 R ) 2. T 2 = f 1( {r 2 } ) = {(x, y, z) R 3 : z 2 + ( x 2 + y 2 R ) 2 = r 2 }. Τότε η κλίση της f στο p = (x, y, z) είναι f(p) = 2 ( x( x 2 + y 2 R), y( x 2 + y 2 R), z x 2 + y ). 2 x 2 + y 2 Ισχυριζόμαστε ότι το r 2 είναι μια κανονική τιμή της f. Πράγματι, αν το p T 2 ήταν τέτοιο ώστε f(p) = 0, τότε z = 0, άρα θα ήταν f(p) = 2r (x, y, 0) 0, x 2 + y2 άτοπο. Συνεπώς, το σύνολο T 2 είναι μια κανονική επιφάνεια του R 3, η οποία ονομάζεται δακτύλιος ή τόρος (torus) Σχήμα 2.3: Ο τόρος T 2. Με την ίδια μέθοδο των Παραδειγμάτων 8.1 και 2.5 μπορούμε εύκολα να αποδείξουμε ότι οι επόμενες εξισώσεις ορίζουν κανονικές επιφάνειες: για a, b, c 0. Ελλειψοειδές x 2 a 2 + y2 b 2 + z2 c 2 = 1 Μονόχωνο υπερβολοειδές Δίχωνο υπερβολοειδές Υπερβολικό παραβολοειδές x 2 a 2 + y2 b 2 z2 c 2 = 1 x 2 a 2 y2 b 2 z2 c 2 = 1 x 2 a 2 y2 b 2 z = 0, Ερχόμαστε τώρα σε μια εναλλακτική περιγραφή μιας επιφάνειας (ή καλύτερα τμήματος επιφάνειας). Η διαδικασία αυτή αποτελεί γενίκευση της περιγραφής μιας καμπύλης μέσω απεικονίσεων παραμέτρησης. Ορισμός 2.3. Μια κανονική παραμετρημένη επιφάνεια (regular parametrized surface) είναι μια απεικόνιση X : U R 2 R 3 (U ανοικτό υποσύνολο του R 2 ) τέτοια ώστε για κάθε q U να ισχύει X u (q) X v (q) 0. ( )
51 50 Κανονικές επιφάνειες Παρατηρήσεις 1. Η εικόνα X(U) ονομάζεται και τμήμα επιφάνειας. 2. Η συνθήκη ( ) είναι ισοδύναμη με το ότι το διαφορικό DX(q) : R 2 R 3 είναι Μια κανονική παραμετρημένη επιφάνεια ονομάζεται και εμβαπτισμένη (immersed) επιφάνεια του R 3. Ορισμός 2.4. Εστω M μια κανονική επιφάνεια του R 3. Μια διαφορίσιμη απεικόνιση X : U R 2 M (U ανοικτό) αποτελεί μια παραμέτρηση (parametrization) της M εάν: 1. η X είναι επί. 2. Για κάθε p U υπάρχει ανοικτή περιοχή U p p τέτοια ώστε η απεικόνιση X Up : U p X(U p ) να είναι μια τοπική παραμέτρηση της M. Εστω X(U) ένα τμήμα μιας επιφάνειας η οποία να ορίζεται απο την απεικόνιση X : U R 2 R 3. Ας θεωρήσουμε το σημείο q = (u 0, v 0 ) U. Τότε η εικόνα της ευθείας v = v 0 μέσω της απεικόνισης X θα είναι η καμπύλη γ(u) X(u, v 0 ) στην επιφάνεια X(U), η οποία θα διέρχεται από την εικόνα X(q) του σημείου q. Η επιφανειακή αυτή καμπύλη θα ονομάζεται u-καμπύλη. Εντελώς ανάλογα, η εικόνα της ευθείας u = u 0 του επιπέδου U R 2 μέσω της απεικόνισης X, είναι η καμπύλη με εξίσωση γ(v) X(u 0, v) στην επιφάνεια X(U), η οποία θα διέρχεται επίσης, από την είκονα X(q) του σημείου q και ονομάζεται v-καμπύλη. Αν τώρα επιτρέψουμε τις μεταβλητές u, v να πάρουν όλες τις τιμές από το πεδίο ορισμού U, τότε ορίζεται ένα πλέγμα ευθειών οριζοντίων και καθέτων, τέτοιο ώστε από κάθε σημείο q του U να διέρχεται μοναδικό ζεύγος τέτοιων ευθειών. Η εικόνα αυτού του πλέγματος μέσω της X ορίζει ένα πλέγμα επιφανειακών καμπυλών της X(U) που την καλύπτουν. Δηλαδή από κάθε σημείο q = (u 0, v 0 ) της X(U) διέρχεται μία και μοναδική u-καμπύλη, η v = v 0 και μία και μοναδική v-καμπύλη, η u = u 0. Το ζεύγος (u 0, v 0 ) λέγεται ζεύγος καμπυλόγραμμων συντεταγμένων του σημείου q. Ορισμός 2.5. Εστω X : U R 2 M μια τοπική παραμέτρηση της επιφάνειας M. Τότε για κάθε σημείο (u 0, v 0 ) του U: (1) Το διάνυσμα της ταχύτητας της u-παραμετρικής καμπύλης, v = v 0, συμβολίζεται με X u (u 0, v 0 ). (2) Το διάνυσμα της ταχύτητας της v-παραμετρικής καμπύλης, u = u 0, συμβολίζεται με X v (u 0, v 0 ). Παράδειγμα 2.6. Θα δώσουμε δύο διαφορετικές παραμετρήσεις του επιπέδου O xy και θα ορίσουμε τις παραμετρικές καμπύλες αυτού. Θεωρούμε την εξίσωση X(u, v) = (u, v, 0). Η συνάρτηση αυτή είναι διαφορίσιμη και επιπλέον X u X v 0, άρα είναι πράγματι μια παραμέτρηση του επιπέδου z = 0. Το πλέγμα των παραμετρικών γραμμών αυτού, ορίζεται από τις ευθείες u = u 0, v = v 0, όπου (u 0, v 0 ) R 2, που είναι ευθείες παράλληλες προς τους άξονες των συντεταγμένων. Ας θεωρήσουμε τώρα την εξίσωση
52 Κανονικές επιφάνειες 51 X(u, v) = (u cos v, u sin v, 0). Η παράσταση αυτή είναι επίσης, όπως εύκολα αναγνωρίζεται, μια παραμέτρηση του επιπέδου, εκτός του σημείου (0, 0, 0). Το πλέγμα των παραμετρικών γραμμών στην περίπτωση αυτή αποτελείται από τις ακόλουθες καμπύλες: (α) Τις u-καμπύλες (v = v 0 ) που ορίζονται από την εξίσωση X(u, v 0 ) = (u cos v 0, u sin v 0, 0). Οι παραμετρικές εξισώσεις αυτών των καμπυλών (για τα διάφορα v 0 ) είναι x = u cos v 0 και y = u sin v 0. Απαλείφοντας την παράμετρο u μεταξύ αυτών των εξισώσεων, έχουμε y = x tan v 0. Αλλά η τελευταία εξίσωση για τα διάφορα v 0 [0, 2π] εκφράζει οικογένεια ευθειών οι οποίες διέρχονται από την αρχή O(0, 0) των συνταταγμένων. (β) Τις v-καμπύλες (u = u 0 ), που ορίζονται από την εξίσωση X(u 0, v) = (u 0 cos v, u 0 sin v, 0). Οι παραμετρικές εξισώσεις αυτών των καμπυλών είναι x = u 0 cos v και y = u 0 sin v. Απαλείφοντας την παράμετρο v μεταξύ αυτών, έχουμε x 2 + y 2 = u 2 0. Η εξίσωση όμως αυτή για τα διάφορα u 0 R \ {0} εκφράζει μια οικογένεια κύκλων κέντρου (0, 0). Ετσι κάθε σημείο του επιπέδου (u 0, v 0 ) ορίζεται από την τομή της ευθείας y = x tan v 0 και του κύκλου x 2 + y 2 = u 2 0. Παράδειγμα 2.7. Ο δακτύλιος T 2 του Παραδείγματος 2.5 προκύπτει με περιστροφή του κύκλου {(x, 0, z) R 3 : z 2 + (x R) 2 = r 2 } του επιπέδου (x, z), περί τον άξονα z (βλ. Σχήμα 2.4). Συνεπώς, μπορούμε να παραμετρήσουμε τοπικά τον δακτύλιο μέσω της απεικόνισης (τοπική παραμέτρηση) Σχήμα 2.4: Ο δακτύλιος T 2 ως επιφάνεια εκ περιστροφής. X : R 2 T 2 cos v sin v 0 X(u, v) = sin v cos v R + r cos u 0 r sin u.
53 52 Κανονικές επιφάνειες Παράδειγμα 2.8. Θεωρούμε τη μοναδιαία σφαίρα S 2 του R 3. Μια τοπική παραμέτρηση της σφαίρας S 2 με γεωγραφικές συντεταγμένες είναι η απεικόνιση X : U = {(θ, φ) : π/2 < θ < π/2, 0 < φ < 2π} S 2 X(θ, φ) = ( cos θ cos φ, cos θ sin φ, sin θ ). Σημειώστε ότι X(U) = S 2 \ C, όπου C = {(x, 0, z) S 2 : x 0} είναι ένας μέγιστος κύκλος της S 2. Παράδειγμα 2.9. Εστω γ = (r, 0, z) : I R 2 μια κανονική καμπύλη στο επίπεδο (x, z) τέτοια ώστε r(s) > 0 και ṙ(s) 2 + ż(s) 2 = 1 για κάθε s I. Περιστρέφοντας την καμπύλη αυτή περί τον άξονα z, προκύπτει μια κανονική επιφάνεια εκ περιστροφής (surface of revolution), η οποία παραμετροποιείται μέσω της απεικόνισης X : R 2 R 3 cos v sin v 0 X(u, v) = sin v cos v r(u) 0 z(u) = r(u) cos v r(u) sin v z(u). Σχήμα 2.5: Επειφάνειες εκ περιστροφής. Παρατήρηση Η καμπύλη γ ονομάζεται γενέτειρα (generating curve) και ο άξονας z καλείται άξονας περιστροφής της επιφάνειας. Τα σημεία της γ, κατά την περιστροφή της, διαγράφουν κύκλους, τους οποίους καλούμε παραλλήλους της επιφάνειας, ενώ η καμπύλη γ και οι νέες θέσεις της (κατά την περιστροφή) αποτελούν τους μεσημβρινούς της επιφάνειας. Ορισμός 2.6. Εστω M μια κανονική επιφάνεια του R 3. Μια συνεχής απεικόνιση γ : I M (I R ανοικτό) ονομάζεται λεία (ή διαφορίσιμη) καμπύλη στην M, εάν η γ είναι διαφορίσιμη ως απεικόνιση με τιμές στο R 3.
54 Λείες απεικονίσεις 53 Εστω γ 1 : I M και γ 2 : J M δύο επιφανειακές καμπύλες οι οποίες τέμνονται στο σημείο p M, δηλαδή υπάρχει t 0 I και s 0 J τέτοια ώστε γ 1 (t 0 ) = γ 2 (s 0 ) = p. Η γωνία των δύο καμπυλών είναι ίση με τη γωνία που σχηματίζουν τα εφαπτόμενα διανύσματα στο σημείο τομής αυτών, δηλαδή cos θ = γ 1 (t 0), γ 2 (s 0) γ 1 (t 0) γ 2 (s 0) Θα κλείσουμε το κεφάλαιο αυτό ορίζοντας την έννοια της διαφορίσιμης απεικόνισης μεταξύ επιφανειών. 2.1 Λείες απεικονίσεις Θέλουμε να ορίσουμε την έννοια της λείας απεικόνισης f : M 1 M 2, όπου M 1 και M 2 είναι κανονικές επιφάνειες. Δεν είναι προφανές πώς μπορούμε να το κάνουμε αυτό, διότι ως τώρα γνωρίζουμε πώς να ορίζουμε λείες απεικονίσεις μεταξύ ανοικτών υποσυνόλων Ευκλείδειων χώρων. Αρχίζουμε με μια ειδική περίπτωση. Ορισμός 2.7. Εστω M μια κανονική επιφάνεια του R 3. Μια πραγματική συνάρτηση f : M R ονομάζεται λεία ή διαφορίσιμη (smooth or differentiable), εάν για κάθε τοπική αναπαράσταση X : U M της M, η σύνθεση f X : U R 2 R είναι διαφορίσιμη. Σχήμα 2.6: Η απεικόνιση f X : U R 2 R. Πρόταση 2.2. Εστω M μια κανονική επιφάνεια του R 3 και f : M R. Η απεικόνιση f είναι λεία εάν και μόνο εάν, για κάθε τοπική παραμέτρηση X : U R 2 M, η απεικόνιση f X είναι λεία. Απόδειξη. Υποθέτουμε πρώτα ότι η απεικόνιση f είναι λεία. Σύμφωνα με τον Ορισμό 2.7, υπάρχει τοπική αναπαράσταση Y : V M της M τέτοια ώστε η f Y : V R
55 54 Κανονικές επιφάνειες να είναι λεία. Συνεπώς, η απεικόνιση f X = f Y Y 1 X : U V R είναι λεία ως σύνθεση των λείων απεικονίσεων f Y και Y 1 X. Το αντίστροφο είναι προφανές. Ορισμός 2.8. Μια απεικόνιση φ : M 1 M 2 μεταξύ δύο κανονικών επιφανειών του R 3 ονομάζεται λεία ή διαφορίσιμη, εάν για κάθε δύο τοπικές παραμετρήσεις (U 1, X 1 ) της M 1 και (U 2, X 2 ) της M 2 η απεικόνιση X2 1 φ X U 1 : U R 2 R 2, ( που ορίζεται στο ανοικτό U = X1 1 X 1 (U 1 ) φ 1( X 2 (U 2 ) )) R 2, είναι διαφορίσιμη. Σχήμα 2.7: Η απεικόνιση X 1 2 φ X 1 U : U R 2 R 2. Πρόταση 2.3. Εστω φ 1 : M 1 M 2 και φ 2 : M 2 M 3 δύο λείες απεικονίσεις μεταξύ κανονικών επιφανειών του R 3. Τότε η σύνθεση φ 2 φ 1 : M 1 M 3 είναι λεία. Απόδειξη. Επειδή η απεικόνιση φ 1 είναι λεία μεταξύ δύο κανονικών επιφανειών του R 3, τότε από τον Ορισμό 2.8, για κάθε δύο παραμετρήσεις X 1 : U 1 M 1 και X 2 : U 2 M 2 η σύνθεση X2 1 φ 1 X 1 : X1 1 ( X1 (U 1 ) φ 1 (X 2 (U 2 )) ) R 2 R 2 θα είναι λεία. Ομοίως, για τη λεία απεικόνιση φ 2, για κάθε δύο τοπικές παραμετρήσεις θα έχουμε ότι η απεικόνιση X3 1 φ 2 X 2 : X2 1 ( X2 (U 2 ) φ 1 2 (X 3(U 3 )) ) R 2 R 2 θα είναι λεία. Για τη σύνθεση φ 2 φ 1 : M 1 M 3 παρατηρούμε ότι, αν επιλέξουμε τις παραμετρήσεις X 1 : U 1 R 2 R και X 3 : U 3 R 2 R, τότε η απεικόνιση είναι λεία στο ανοικτό σύνολο W = X 1 1 X3 1 (φ 2 φ 1 ) X 1 : W R 2 R 2 ( X1 (U 1 ) (φ 2 φ 1 ) 1 (X 3 (U 3 )) ), ως σύνθεση των λείων απεικονίσεων X 1 3 φ 2 X 2 και X 1 2 φ 1 X 1.
56 Λυμένα παραδείγματα 55 Πρόταση 2.4. Εστω M 1, M 2 κανονικές επιφάνειες του R 3 και φ : U R 3 R 3 διαφορίσιμη απεικόνιση στο ανοικτό U, τέτοια ώστε M 1 U και φ(m 1 ) M 2. Τότε ο περιορισμός φ M1 απεικόνιση μεταξύ των δύο επιφανειών. : M 1 M 2 είναι λεία Απόδειξη. Εστω p τυχαίο σημείο της M 1 και X 1 : U 1 R 2 M 1, X 2 : U 2 R 2 M 2 δύο παραμετρήσεις, γύρω από τα σημεία p και φ(p) αντίστοιχα, τέτοιες ώστε p X 1 (U 1 ), φ(x 1 (U 1 )) X 2 (U 2 ). Τότε όμως, η απεικόνιση X 1 2 φ X 1 : U 1 R 2 U 2 R 2 είναι διαφορίσιμη στο X 1 (p), ως σύνθεση των διαφορίσιμων απεικονίσεων X 1 2 και φ X 1. Αλλά είναι X 1 2 φ X 1 = X 1 2 φ M1 X 1, οπότε η απεικόνιση φ M1 είναι διαφορίσιμη στο σημείο p. Επειδή όμως το σημείο p είναι ένα τυχαίο σημείο της M 1, η απεικόνιση φ M1 : M 1 M 2 θα είναι διαφορίσιμη. Παράδειγμα Εστω f : R 3 R 3, f(x, y, z) = (ax, by, cz) με abc > 0. Προφανώς η f είναι διαφορίσιμη. Ο περιορισμός της f στη σφαίρα S 2 είναι μια διαφορίσιμη απεικόνιση από την σφαίρα σε ένα ελλειψοειδές, όπου η σφαίρα είναι το σύνολο και το ελλειψοειδές είναι το σύνολο S 2 = {(x, y, z) R 3 : x 2 + y 2 + z 2 = 1} E = {(x, y, z) R 3 : x2 a 2 + y2 b 2 + z2 c 2 = 1}. Ορισμός 2.9. Μια διαφορίσιμη απεικόνιση φ : M 1 M 2 μεταξύ δύο κανονικών επιφανειών του R 3 ονομάζεται αμφιδιαφόριση (diffeomorphism), εάν είναι 1-1, επί και η αντίστροφη φ 1 : M 2 M 1 είναι διαφορίσιμη. Τότε οι επιφάνειες M 1 και M 2 ονομάζονται αμφιδιαφορικές. Παράδειγμα Η απεικόνιση f : S 2 S 2 με f(x, y, z) = ( x, y, z) είναι αμφιδιαφόριση. Πράγματι, παρατηρούμε ότι η f είναι 1-1 και επί με f 1 = f. Επίσης, η f είναι ο περιορισμός (επί της S 2 ) της διαφορίσιμης απεικόνισης F : R 3 R 3, (x, y, z) ( x, y, z). Άρα σύμφωνα με την Πρόταση 2.4, η f είναι επίσης διαφορίσιμη Πρόταση 2.5. Εστω f : M 1 M 2 μια αμφιδιαφόριση. Εάν X 1 είναι μια τοπική παραμέτρηση της επιφάνειας M 1, τότε η f X 1 είναι μια τοπική παραμέτρηση της επιφάνειας M 2. Μερικές φορές θα φανεί χρήσιμο αντί των αμφιδιαφορίσεων να θεωρούμε λείες απεικονίσεις που ι- κανοποιούν μια ελαφρώς ασθενέστερη συνθήκη. Μια λεία απεικόνιση f : M 1 M 2 καλείται τοπική αμφιδιαφόριση, εάν για κάθε σημείο p M 1 υπάρχει ανοικτό υποσύνολο U της M 1, τέτοιο ώστε το f(u) να είναι ανοικτό υποσύνολο της M 2 και η f U : U f(u) να είναι αμφιδιαφόριση. Είναι προφανές ότι κάθε αμφιδιαφόριση είναι τοπική αμφιδιαφόριση (αρκεί να πάρουμε U = M 1 ). Επιπλέον, η Πρόταση 2.5 ισχύει αν η f είναι τοπική αμφιδιαφόριση, υπό τον όρο ότι ο περιορισμός της στην εικόνα του X 1 είναι 1-1.
57 56 Κανονικές επιφάνειες 2.2 Λυμένα παραδείγματα Παράδειγμα Εστω X : U R 3, X(u, v) = (u cosh v, u sinh v, u 2 ) όπου U = {(u, v) R 2 : u > 0}. Αποδείξτε ότι η X αποτελεί μια κανονική παραμέτρηση (του τμήματος) της επιφάνειας του υπερβολικού παραβολοειδούς M = {(x, y, z) R 3 : z = x 2 y 2 }. Λύση Εστω X(u, v) = (x, y, z). Τότε x 2 y 2 = u 2( cosh 2 v sinh 2 v ) = u 2, άρα X(u, v) M για κάθε (u, v) U. Εστω V = X(U). Πρέπει να δείξουμε τα εξής: α) η X είναι 1 1 β) η X είναι διαφορίσιμη (άρα συνεχής) γ) η X 1 : V U είναι συνεχής δ) ισχύει X u X v 0 για κάθε (u, v) U. Πράγματι, α) Εστω X(u 1, v 1 ) = X(u 2, v 2 ). Τότε προκύπτει το σύστημα u 1 cosh v 1 = u 2 cosh v 2 u 1 sinh v 1 = u 2 sinh v 2 u 2 1 = u 2 2. Η τρίτη εξίσωση δίνει u 1 = ±u 2 και επειδή u 1, u 2 > 0 παίρνουμε u 1 = u 2. Λόγω του ότι η συνάρτηση sinh είναι 1-1 προκύπτει ότι v 1 = v 2, άρα η X είναι 1-1. β) Η X είναι διαφορίσιμη επειδή οι συνιστώσες συναρτήσεις της είναι διαφορίσιμες πραγματικές συναρτήσεις. γ) Για να βρούμε την αντίστροφη X 1 : V U πρέπει να λύσουμε το σύστημα των εξισώσεων x = u cosh v, y = u sinh v, z = u 2 ως προς u, v. Είναι u = z, v = tanh 1 y x άρα η αντίστροφη είναι X 1 : V U, (x, y, z) (u, v) = ( z, tanh 1 x) y, η οποία είναι συνεχής. Συνεπώς, η X είναι ομοιομορφισμός. δ) Είναι X u = ( cosh v, sinh v, 2u ), X v = ( u sinh v, u sinh v, 0 ), άρα X u X v = ( 2u 2 cosh v, 2u 2 sinh v, u ) (0, 0, 0) για κάθε (u, v) U. Παράδειγμα Να δείξετε ότι η συνάρτηση X : (0, ) (0, ) R 3, X(u, v) = (u, 2u, uv 2 ) αποτελεί παραμέτρηση επιφάνειας.
58 Λυμένα παραδείγματα 57 Λύση Η X είναι λεία, αφού οι μερικές παράγωγοι των u, 2u, uv 2 είναι συνεχείς και επίσης είναι 1-1, επειδή X(u 1, v 1 ) = X(u 2, v 2 ) (u 1, v 1 ) = (u 2, v 2 ). Η αντίστροφη απεικόνιση δίνεται ως X 1 (x, y, z) = ( ) z x,, x η οποία είναι συνεχής, αφού για κάθε (x, y, z) X(U) ισχύει ότι x 0 (και x, z > 0). Τέλος, με απλούς υπολογισμούς βρίσκουμε ότι X u X v = (4uv, 2uv, 0) (0, 0, 0), οπότε η απεικόνιση X αποτελεί μια παραμέτρηση μιας επιφάνειας. Παράδειγμα Εξετάστε εάν το σύνολο M = {(x, y, z) R 3 : x z+f(y z) = 0}, όπου f : R R μια διαφορίσιμη συνάρτηση, είναι μια κανονική επιφάνεια. Λύση Θεωρούμε την απεικόνιση F : R 3 R με F (x, y, z) = x z + f(y z). Εχουμε ότι M = F 1 ({0}). Η απεικόνιση F είναι διαφορίσιμη και F (x, y, z) = (1, f (y z), 1 f (y z)). Παρατηρούμε ότι για κάθε (x, y, z) M είναι F (x, y, z) (0, 0, 0), άρα όλα τα σημεία του συνόλου M = F 1 ({0}) είναι κανονικά, επομένως το M είναι μια κανονική επιφάνεια. Παράδειγμα Να δειχθεί ότι το σύνολο M = {(x, y, z) R 3 : xy + xz zy + y 2 = 2} είναι μια κανονική επιφάνεια και να βρείτε μια παραμέτρηση αυτής σε μια περιοχή του σημείου (1, 1, 1). Λύση Θέτουμε F (x, y, z) = xy + xz zy + y 2 2, οπότε M = F 1 ({0}). Αρκεί να δείξουμε ότι το σύνολο M δεν περιέχει κρίσιμα σημεία. Είναι F (x, y, z) = (y + z, x z + 2y, x y). Τα κρίσιμα σημεία της F είναι τα σημεία για τα οποία ισχύει F (x, y, z) = (0, 0, 0), δηλαδή y + z = 0, x z + 2y = 0, x y = 0 x = y = z = 0. Το (0, 0, 0) δεν ανήκει στο σύνολο M, οπότε το M αποτελεί μια κανονική επιφάνεια του R 3. Προκειμένου να βρούμε μια παραμέτρηση θα λύσουμε ως προς y. Επειδή είναι y 2 + y(x z) 2 + xz = 0 παίρνουμε y = (x z) ± (z x) 2 4(xz 2). 2 Το σημείο (1, 1, 1) ικανοποιεί την παραπάνω εξίσωση μόνο όταν πάρουμε το +. Άρα θέτοντας X(u, v) = ( u, u + v + (u v) uv, v ) 2 έχουμε μια παραμέτρηση της επιφάνειας M σε μια περιοχή του σημείου (1, 1, 1).
59 58 Κανονικές επιφάνειες Παράδειγμα Να βρεθούν οι τιμές του c R για τις οποίες το σύνολο είναι μια κανονική επιφάνεια του R 3 Λύση S = {(x, y, z) R 3 : 4x 5 + 2y 3 y + 3z 2 = c} Εστω f : R 3 R με f(x, y, z) = 4x 5 + 2y 3 y + 3z 2. Τότε S = f 1 (c). Για να είναι το σύνολο S κανονική επιφάνεια, θα πρέπει να μην περιέχει κρίσιμα σημεία. Εχουμε f(x, y, z) = 0 ( f x, f y, f ) = (0, 0, 0) z (20x 4, 6y 2 1, 6z) = (0, 0, 0) (x, y, z) = (0, ± 1, 0), 6 1 άρα τα κρίσιμα σημεία της f είναι τα (0, 6, 0), (0, 1 1 6, 0). Εάν (0, 6, 0) f 1 1 (c) τότε f((0, 6, 0)) = c δηλαδή c = 2 3. Παρόμοια, εάν (0, 1 6 6, 0) f 1 (c) τότε θα είναι c = 2 3. Επομένως το σύνολο 6 S = f 1 (c) ορίζει μια κανονική επιφάνεια για κάθε c R \ {± }. Παράδειγμα Ποιό από τα παρακάτω υποσύνολα του R 3 αποτελεί μια κανονική επιφάνεια; α) M 1 = {(x, y, z) R 3 : x 2 + y 2 = z} β) M 2 = {(x, y, z) R 3 : x 2 + y 2 = z 2 }. Σε θετική περίπτωση βρείτε μια παραμέτρηση της επιφάνειας. Λύση α) Θεωρούμε τη συνάρτηση f : R 3 R, f(x, y, z) = x 2 + y 2 z. Τότε M 1 = f 1 (0) και f = (2x, 2y, 1) (0, 0, 0) για κάθε (x, y, z) R 3. Μια παραμέτρηση της M 1 είναι η X(u, v) = (u, v, u 2 + v 2 ). β) Θεωρούμε τη συνάρτηση f : R 3 R, f(x, y, z) = x 2 + y 2 z 2. Τότε M 2 = f 1 (0) και f = (2x, 2y, 2z) το οποίο είναι μη μηδενικό διάνυσμα για κάθε (x, y, z) M 2 \{(0, 0, 0)}. Άρα η M 2 είναι κανονική επιφάνεια σε κάθε σημείο, εκτός από το (0, 0, 0) όπου δεν είναι κανονική. Παραπέμπουμε στη βιβλιογραφία για πλήρη απόδειξη του σημείου αυτού. Μια παραμέτρηση των δύο κανονικών τμημάτων της M 2 είναι X ± : R 2 \ {(0, 0)} R 3, X ± (u, v) = ( u, v, ± u 2 + v 2). Παράδειγμα Να κατασκευαστεί μια αμφιδιαφόριση μεταξύ του ελλειψοειδούς E = {(x, y, z) R 3 : x2 a 2 + y2 b 2 + z2 = 1}, abc 0 c2 και της μοναδιαίας σφαίρας με κέντρο το 0, δηλαδή S 2 = {(x, y, z) R 3 : x 2 + y 2 + z 2 = 1}.
60 Ασκήσεις 59 Λύση Θεωρούμε την απεικόνιση F : R 3 R 3 με F (x, y, z) = ( x a, y b, z ), η οποία είναι, προφανώς αμφιδιαφόριση, c με αντίστροφη την F 1 : R 3 R 3, (x, y, z) (ax, by, cz). Εύκολα προκύπτει ότι F (E) S 2 και F 1 (S 2 ) E. Επομένως, η απεικόνιση είναι μια αμφιδιαφόριση. f = F S : E S Ασκήσεις 1. Ποιό από τα παρακάτω υποσύνολα του R 3 αποτελεί μια κανονική επιφάνεια; M 1 = { (x, y, z) R 3 : x 2 + y 2 = z } M 2 = { (x, y, z) R 3 : x 2 + y 2 = z 2} M 3 = { (x, y, z) R 3 : x 2 + y 2 z 2 = 1 } M 4 = { (x, y, z) R 3 : x sin z = y cos z }. Για τα σύνολα τα οποία αποτελούν μια κανονική επιφάνεια του R 3, βρείτε μια παραμέτρηση. 2. Βρείτε μια παραμέτρηση του επιπέδου ax + by + cz = d του R Κατασκευάστε μια αμφιδιαφόριση ϕ : S 2 M μεταξύ της μοναδιαίας σφαίρας S 2 και του ελλειψοειδούς M = { (x, y, z) R 3 : x 2 + 2y 2 + 3z 2 = 1 }. 4. Εστω U = { (u, v) R 2 : π < u < π, 0 < v < 1 } και X : U R 3 με X(u, v) = (sin u, sin(2u), v). Εστω M = X(U). Σχεδιάστε το γράφημα του συνόλου M και δείξτε ότι η X είναι διαφορίσιμη, 1-1 και ότι είναι μια κανονική παραμέτρηση, παρόλα αυτά δείξτε ότι η X 1 δεν είναι συνεχής. Είναι η M μια κανονική επιφάνεια του R 3 ; 5. Εργαστείτε όπως στο Παράδειγμα 2.6, για τις επιφάνειες που ορίζονται ως ακολούθως: (1) Την σφαίρα X(u, v) = (r cos u sin v, r sin u sin v, r cos v), 0 u 2π, π 2 v π 2 (2) Τον κώνο X(u, v) = (u cos v, u sin v, αu) (3) Τον κύλινδρο X(u, v) = (α cos u, α sin v, βv) (4) Το ελλειψοειδές X(u, v) = (α cos u cos v, β sin u cos v, γ sin v) (5) Το υπερβολικό παραβολοειδές X(u, v) = (αu cosh u, βu sinh v, u 2 ) 6. Εστω f(x, y, z) = (x+y +z 1) 1 και g(x, y, z) = xyz 2. Να βρεθούν τα κρίσιμα σημεία και οι κρίσιμες τιμές των f, g. Για ποιές τιμές του c είναι τα σύνολα f 1 ({c}) και g 1 ({c}) κανονικές επιφάνειες του R 3 ; 7. Να δικαιολογηθεί γιατί το ελλειπτικό παραβολοειδές, που καθορίζεται από την εξίσωση z = x 2 + y 2, είναι αμφιδιαφορικό με ένα επίπεδο.
61 60 Κανονικές επιφάνειες 8. Να αποδειχθεί ότι η απεικόνιση X : U R 3 με X(u, v) = (a cos u sin v, b sin u sin v, c cos v), όπου U = R (0, π), είναι παραμέτρηση του ελλειψοειδούς. Να περιγραφούν οι u- και v-καμπύλες. 9. Εστω a, b 0. Αποδείξτε ότι οι εξισώσεις x 2 + y 2 + z 2 = ay και x 2 + y 2 + z 2 = bz ορίζουν κανονικές επιφάνειες του R 3. Στη συνέχεια, αποδείξτε ότι οι επιφάνειες αυτές τέμνονται κάθετα.
62 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
63 62 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
64 Κεφάλαιο 3 Ο εφαπτόμενος χώρος Σύνοψη Ο εφαπτόμενος χώρος μιας κανονικής επιφάνειας αποτελεί τη βέλτιση γραμμική προσέγγιση της επιφάνειας σε ένα σημείο της. Αποτελείται από όλα τα εφαπτόμενα διανύσματα σε ένα σημείο της. Αποδεικνύουμε ότι ο εφαπτόμενος χώρος είναι ένας διανυσματικός χώρος διάστασης 2. Από γεωμετρικής απόψεως ο εφαπτόμενος χώρος είναι το εφαπτόμενο επίπεδο σε ένα σημείο της επιφάνειας, του οποίου μπορούμε να γράψουμε την καρτεσιανή εξίσωση. Ενας χρήσιμος τρόπος περιγραφής του εφαπτόμενου επιπέδου είναι όταν θεωρήσουμε την επιφάνεια ως αντίστροφη εικόνα μιας κανονικής τιμής μιας διαφορίσιμης απεικόνισης. Στα πλαίσια αυτά, μπορούμε να γενικεύουμε το κλασικό θεώρημα της αντίστροφης απεικόνισης για την περίπτωση των επιφανειών. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6]. Προαπαιτούμενη γνώση Αναλυτική Γεωμετρία, Απειροστικός Λογισμός μιας και πολλών μεταβλητών, Εισαγωγή στη Γραμμική Άλγεβρα. Ορισμός 3.1. Εστω M μια κανονική επιφάνεια του R 3, p M. Ο εφαπτόμενος χώρος (tangent space) T p M της M στο p είναι το σύνολο όλων των εφαπτόμενων διανυσμάτων γ (0) σε κάθε λεία (ή κλάσης C 1 ) καμπύλη γ : I M, τέτοια ώστε γ(0) = p. Ισοδύναμα, T p M = { Z R 3 : υπάρχει καμπύλη γ : I M κλάσης C 1, ώστε γ(0) = p, γ (0) = Z }. Πρόταση 3.1. Ο εφαπτόμενος χώρος της επιφάνειας M στο σημείο p είναι ένας πραγματικός διανυσματικός χώρος διάστασης 2. Απόδειξη. Εστω X : U R 2 M μια τοπική παραμέτρηση της M στο σημείο p, τέτοια ώστε 0 U και X(0) = p. Εστω γ : I X(U) M μια λεία καμπύλη στο X(U) με γ(0) = p. Επειδή η απεικόνιση X : U X(U) είναι ομοιομορφισμός, η καμπύλη β : X 1 γ : I U είναι λεία στο U R 2 με β(0) = 0, 63
65 64 Ο εφαπτόμενος χώρος Σχήμα 3.1: Ο εφαπτόμενος χώρος. άρα γ = X β. Τότε γ (0) = DX(β(0))β (0) = DX(0, 0)β (0) = DX(0, 0)(ae 1 + be 2 ) = adx(0, 0)e 1 + bdx(0, 0)e 2 = ax u (0, 0) + bx v (0, 0). Συνεπώς, το διάνυσμα γ (0) είναι γραμμικός συνδυασμός των X u και X v. Αντίστροφα, έστω w = DX(0, 0)(Z) για κάποιο Z R 2. Θεωρούμε την καμπύλη β : I U R 2 με β(t) = tz. Τότε β(0) = 0, β (0) = Z και έστω γ = X β. Εχουμε γ(0) = X(β(0)) = X(0) = p και γ (0) = DX(0, 0)β (0) = DX(0, 0)Z = w, δηλαδή το διάνυσμα w το οποίο παράγεται από τα X u και X v είναι το εφαπτόμενο διάνυσμα στο p για κάποια καμπύλη γ της επιφάνειας M. Πόρισμα 3.1. Εστω M R 3 μια επιφάνεια και X : U R 2 M μια τοπική παραμέτρηση στο σημείο p, με X(q) = p. Τότε η απεικόνιση DX(q) : R 2 T p (M) είναι γραμμικός ισομορφισμός. Παρατήρηση Ο αναγνώστης ίσως θα αναρωτιέται, ανακαλώντας γνώση γραμμικής άλγεβρας, κατά πόσον ο εφαπτόμενος χώρος περιέχει το μηδέν. Στην προκειμένη περίπτωση το μηδενικό στοιχείο του εφαπτόμενου χώρου είναι το σημείο γ(0) = p. Τακτικά χρησιμοποιείται και ο όρος ἑφαπτόμενο επίπεδο που είναι πιο κοντά στην γεωμετρική μας εποπτεία. Ουσιαστικά, αυτό το οποίο προκύπτει από την απόδειξη του παραπάνω θεωρήματος είναι ότι T p M = span { X u (α, β), X v (α, β) }, όπου X : U R 2 M R 3 είναι μια τοπική παραμέτρηση της M στο σημείο p τέτοια ώστε (α, β) U και X(α, β) = p. Ως γνωστόν, επειδή η επιφάνεια είναι κανονική, τα διανύσματα X u (α, β), X v (α, β) είναι γραμμικώς ανεξάρτητα. Ειδικότερα, το διάνυσμα X u (α, β) X v (α, β) είναι κάθετο στα διανύσματα X u (α, β) και X v (α, β), οπότε θα είναι κάθετο και στο εφαπτόμενο επίπεδο το οποίο παράγεται από αυτά τα διανύσματα. Παράδειγμα 3.1. Να βρεθεί ο εφαπτόμενος χώρος του ελλειπτικού παραβολοειδούς M = {(x, y, z) R 3 : z = x 2 + y 2 } στο σημείο p = (1, 2, 5). Μια παραμέτρηση της επιφάνειας M είναι η X : R 2 M, X(u, v) = (u, v, u 2 + v 2 ). Τότε X u (u, v) = (1, 0, 2u) X v (u, v) = (0, 1, 2v)
66 Ο εφαπτόμενος χώρος 65 και X(1, 2) = (1, 2, 5) = p. Συνεπώς, T p M = span{x u (1, 2), X v (1, 2)} = span{(1, 0, 2), (0, 1, 4)}. Αξίζει να σημειώσουμε ότι, αν ζητούσαμε να βρούμε την καρτεσιανή εξίσωση του εφαπτόμενου επιπέδου (ως πρόβλημα αναλυτικής γεωμετρίας), τότε εργαζόμαστε ως εξής: Ενα κάθετο διάνυσμα στο ε- φαπτόμενο επίπεδο T p M είναι το (1, 2, 1/2) (το βρίσκουμε λύνοντας το σύστημα (a, b, c), (1, 0, 2) = (a, b, c), (0, 1, 4) = 0 ως προς a, b, c), συνεπώς η εξίσωση του επιπέδου είναι x + 2y 1 2z = d. Επειδή το επίπεδο διέρχεται από το σημείο p = (1, 2, 5), παίρνουμε τελικά ότι η εξίσωση του εφαπτόμενου επιπέδου είναι 2x + 4y z = 5. Πρόταση 3.2. Εστω U R ανοικτό, f : U R μια διαφορίσιμη συνάρτηση και έστω M = f 1 (q), όπου q μια κανονική τιμή της f, δηλαδή f(p) 0 για κάθε p M. Τότε ισχύει T p M = ( f(p) ). Εδώ X συμβολίζει το ορθογώνιο συμπλήρωμα του διανύσματος X στον χώρο R 3, ως προς το κανονικό εσωτερικό γινόμενο. Απόδειξη. Εστω Z T p M και έστω γ : I M μια διαφορίσμη καμπύλη με γ(0) = p και γ (0) = Z. Τότε είναι (f γ)(t) = q για κάθε t I. Παραγωγίζοντας ως προς t, προκύπτει ότι 0 = d dt (f γ) t=0 = f(γ(0)), γ (0) = f(p), Z, συνεπώς το διάνυσμα Z είναι κάθετο στο f(p), οπότε δείξαμε ότι T p M ( f(p) ). Επειδή και οι δύο υπόχωροι T p M, ( f(p) ) του R 3 έχουν διάσταση 2, προκύπτει ότι T p M = ( f(p) ). Εύρεση του εφαπτόμενο επιπέδου μιας επιφάνειας Γενικά όταν μας ζητείται να βρούμε το εφαπτόμενο επίπεδο μια επιφάνειας M σε ένα τυχαίο σημείο p = (x 0, y 0, z 0 ) M, εργαζόμαστε ως εξής: Πρώτη περίπτωση. Εστω X : U R 2 M R 3 μια τοπική παραμέτρηση στο σημείο p M με X(u, v) = (x(u, v), y(u, v), z(u, v)) και X(q) = p, όπου q = (u 0, v 0 ) U Γνωρίζουμε ότι ο εφαπτόμενος χώρος T p M της επιφάνειας στο σημείο p παράγεται από τα διανύσματα X u (q) και X v (q). Επίσης, το διάνυσμα X u (q) X v (q) είναι κάθετο στο εφαπτόμενο επίπεδο στο σημείο p. Συνεπώς, η εξίσωση του εφαπτόμενου επιπέδου για το τυχαίο σημείο (x, y, z) T p M θα είναι (x, y, z) (x 0, y 0, z 0 ), X u (q) X v (q) = 0 (3.1) Παράδειγμα 3.2. Θεωρούμε τη μοναδιαία σφαίρα M = S 2 (R) ακτίνας R με παραμέτρηση σε γεωγραφικές συντεταγμένες X(u, v) = (R cos u cos v, R sin u cos v, R sin v).
67 66 Ο εφαπτόμενος χώρος Τότε X u X v = (R 2 cos u cos 2 v, R 2 sin u cos 2 v, R 2 sin v cos v). Παρατηρείστε ότι X u X v = (R cos v)p, δηλαδή πολλαπλάσιο ενός σημείο p της σφαίρας. Από αυτό προκύπτει ότι το διάνυσμα με αρχή το (0, 0, 0) και πέρας τα σημείο p, τέμνει την σφαίρα κάθετα. Εστω ότι p = (R, 0, 0), άρα u = v = 0. Τότε στο σημείο p είναι X u X v = (R 2, 0, 0), συνεπώς ο εφαπτόμενος χώρος (επίπεδο) T p M έχει εξίσωση (x, y, z) (R, 0, 0), X u X v = 0 (x R, y, z), (R 2, 0, 0) = 0 R 2 x = R 3 x = R. Η παραπάνω εξίσωση ορίζει το εφαπτόμενο επίπεδο της σφαίρας στο σημείο p = (R, 0, 0). Δεύτερη περίπτωση. Η εξίσωση της επιφάνειας δίνεται στη μορφή f(x, y, z) = 0 με f : R 3 R. Τότε θα βρούμε την εξίσωση του εφαπτόμενου επιπέδου στο σημείο p ως εξής: Εστω Z T p M. Τότε από τον ορισμό του εφαπτόμενου χώρου, υπάρχει καμπύλη γ : I M με γ(t) = (x(t), y(t), z(t)) τέτοια ώστε γ(0) = (x(0), y(0), z(0)) = (x 0, y 0, z 0 ) = p και γ (0) = (x (0), y (0), z (0)) = Z. Επειδή η καμπύλη βρίσκεται πάνω στην επιφάνεια, θα ισχύει από τον κανόνα της αλυσίδας θα πάρουμε f(γ(t)) = f(x(t), y(t), z(t)) = 0, f dx x dt + f dy y dt + f dz z dt = 0 και για t = 0 θα είναι f x (p)x (0) + f y (p)y (0) + f z (p)z (0) = 0. Παρατηρούμε ότι όλα τα εφαπτόμενα διανύσματα Z = (x (0), y (0), z (0)) T p M είναι κάθετα στο διάνυσμα (f x (p), f y (p), f z (p)) f(p), άρα για το τυχαίο σημείο (x, y, z) T p M θα είναι f x (p)(x x 0 ) + f y (p)(y y 0 ) + f z (p)(z z 0 ) = 0. (3.2) Παράδειγμα 3.3. Η εξίσωση του εφαπτόμενου επιπέδου της επιφάνειας x 2 + 4y 2 z = 0 στο σημείο p = (2, 1, 8) αν θέσουμε f(x, y, z) = x 2 + 4y 2 z = 0, σύμφωνα με την σχέση (3.2) θα είναι: f x (2, 1, 8)(x 2) + f y (2, 1, 8)(y 1) + f z (2, 1, 8)(z 8) = 0 4(x 2) + 8(y 1) z + 8 = 0 4x + 8y z = 8. Το επόμενο παράδειγμα θα το χειριστούμε με έναν πιο ειδικό τρόπο. Δεν θα χρησιμοποιήσουμε κάποια παραμέτρηση της σφαίρας, κάτι που ούτως ή άλλως θα μπορούσαμε να κάνουμε. Παράδειγμα 3.4. Να βρεθεί ο εφαπτόμενος χώρος T p S 2 σε ένα σημείο p της μοναδιαίας σφαίρας S 2 του R 3.
68 Το διαφορικό μιας διαφορίσιμης απεικόνισης 67 Εστω γ : I S 2 R 3 μια καμπύλη της σφαίρας με γ(0) = p, γ (0) = Z, όπου Z R 3. Τότε επειδή γ(i) S 2 ισχύει ότι γ(t), γ(t) = 1, άρα με παραγώγιση προκύπτει ότι d dt ( γ(t), γ(t) ) = 0 γ (t), γ(t) + γ(t), γ (t) = 0 ή 2 γ (t), γ(t) = 0. Για t = 0 παίρνουμε γ (0), γ(0) = 0 άρα Z, p = 0. Συνεπώς, αν θέσουμε A = {Z R 3 : Z, p = 0} (το σύνολο όλων των κάθετων διανυσμάτων στην σφαίρα στο σημείο p), τότε δείξαμε ότι T p S 2 A. Αντίστροφα, έστω Z 0 με Z, p = 0. Τότε η καμπύλη γ : R S 2 με τιμή γ(t) = cos(t Z )p + sin(t Z ) Z Z είναι μια καμπύλη στην σφαίρα S 2 με γ(0) = p, γ (0) = Z (κάντε έλεγχο). Ουσιαστικά η καμπύλη αυτή είναι ένας μέγιστος κύκλος της S 2 που διέρχεται από το p). αναμενόμενο γεωμετρικώς αποτέλεσμα ότι T p S 2 = {Z R 3 : Z, p = 0}. Άρα A T p S 2 και τελικά παίρνουμε το 3.1 Το διαφορικό μιας διαφορίσιμης απεικόνισης Στο προηγούμενο κεφάλαιο επεκτείναμε την έννοια της διαφορίσιμης απεικόνισης μεταξύ Ευκλειδείων χώρων σε απεικονίσεις μεταξύ επιφανειών. Από την κλασική ανάλυση η επόμενη σχετική έννοια είναι αυτή του διαφορικού μιας διαφορίσιμης απεικόνισης σε ένα σημείο του πεδίου ορισμού της, την οποία θα ορίσουμε τώρα. Ορισμός 3.2. Εστω M 1, M 2 κανονικές επιφάνειες, p M 1 και φ : M 1 M 2 μια λεία απεικόνιση. Το διαφορικό (differential) dφ p : T p M 1 T φ(p) M 2 της φ στο p ορίζεται ως εξής: Εστω Z T p M 1 και γ : I M 1 με γ(0) = p, γ (0) = Z. Τότε dφ p (Z) = dt( d ) φ γ(t) t=0 T φ(p) M 2. Πρόταση 3.3. Η παραπάνω απεικόνιση είναι καλώς ορισμένη (δηλαδή η τιμή dφ p (Z) εξαρτάται μόνο από το διάνυσμα Z και όχι από την επιλογή της καμπύλης γ). Επιπλέον, η dφ p είναι γραμμική απεικόνιση. Απόδειξη. Εστω X : U M 1, Y : V M 2 τοπικές παραμετρήσεις των M 1, M 2 αντίστοιχα τέτοιες ώστε X(0) = p, Y (0) = φ(p) και έτσι ώστε φ(x(u)) Y (V ). Θέτουμε F = Y 1 φ X : U R 2. Θεωρούμε την καμπύλη γ : I M 1 τέτοια ώστε γ(0) = p, γ (0) = Z και επιπλέον γ(i) X(U) (με ενδεχόμενη μείωση του διαστήματος I). Θέτουμε α = X 1 γ : I U (επίπεδη καμπύλη). Τότε επειδή X α = γ, θα είναι D(X α)(0) = γ (0), συνεπώς από τον κανόνα αλυσίδας προκύπτει ότι DX(0)α (0) = Z (3.3)
69 68 Ο εφαπτόμενος χώρος (αλλά και απευθείας από τον απειροστικό λογισμό: Συνεπώς, χρησιμοποιώντας την (3.3) παίρνουμε ότι DX(0)(α (0)) = d dt (X α(t)) t=0 = d dt γ(t) t=0 = Z). dφ p (Z) = d dt (φ γ) t=0 = d dt (φ X α) t=0 = d dt (Y Y 1 φ X α) t=0 = d dt (Y F α) t=0 = D(Y F )(0)(α (0)) = D(Y F )(0)(DX 1 (0))Z. Η παραπάνω έκφραση του διαφορικού δεν εξαρτάται από την επιλογή της καμπύλης γ. Τέλος, η απεικόνιση dφ p είναι γραμμική ως σύνθεση γραμμικών απεικονίσεων. Παράδειγμα 3.5. Εστω f : M 1 M 2 μια σταθερή απεικόνιση. Τότε για κάθε σημείο p M 1 το διαφορικό df p είναι ίσο με 0. Πράγματι, έστω X T p M 1 ένα τυχαίο εφαπτόμενο διάνυσμα. Τότε από τον ορισμό του εφαπτόμενου χώρου υπάρχει καμπύλη α : I M 1 τέτοια ώστε α(0) = p και α (0) = X. Επομένως, είναι df p X = d dt (f α) t=0 = d dt (f(α(t))) t=0 = f (α(t)) α (t) t=0 = f (α(0)) α (0) = 0 α (0) = 0. Παράδειγμα 3.6. Εστω A : R 3 R 3 ένας ορθογώνιος τελεστής, δηλαδή A O(3) και έστω f : S 2 S 2 με τύπο f = A S 2. Εστω p S 2. Θα υπολογίσουμε το διαφορικό της f στο σημείο p. Εστω γ : I S 2 μια λεία καμπύλη με γ(0) = p, γ (0) = X T p S 2. Λόγω της γραμμικότητας του A έχουμε Συνεπώς, df p = A TpS 2 : T ps 2 T A(p) S 2. Πρόταση 3.4. d dt (f γ) t=0 = d dt (A γ) t=0 = A d dt γ t=0 = A(X). (1) Εστω M 1, M 2, M 3 κανονικές επιφάνειες και f : M 1 M 2, g : M 2 M 3 διαφορίσιμες απεικονίσεις. Τότε η σύνθεση g f : M 1 M 3 είναι διαφορίσιμη απεικόνιση και για κάθε p M 1. d(g f) p = (dg) f(p) df p, (2) Αν η απεικόνιση f : M 1 M 2 είναι αμφιδιαφόριση, τότε η απεικόνιση df p : T p M 1 T f(p) M 2 είναι αντιστρέψιμη και (df p ) 1 = d(f 1 ) f(p) για κάθε p M 1. Το κλασικό Θεώρημα Αντίστροφης Απεικόνισης γενικεύεται στην περίπτωση των επιφανειών ως εξής: Θεώρημα 3.1. (Αντίστροφης Απεικόνισης) Εστω f : M 1 M 2 μια λεία απεικόνιση μεταξύ επιφανειών του R 3 και έστω p M 1, q = φ(p). Υποθέτουμε ότι το διαφορικό df p : T p M 1 T φ(p) M 2 είναι 1-1 και επί (άρα αντιστρέφεται). Τότε υπάρχουν ανοικτές περιοχές U p p, V q q τέτοιες ώστε η απεικόνιση f Up : U p V q να είναι 1-1 και επί και η αντίστροφη ( ) 1 f Up : Vq U p να είναι λεία (δηλαδή η f είναι τοπική αμφιδιαφόριση).
70 Λυμένα παραδείγματα 69 Απόδειξη. Εστω X : U R 2 M 1 R 3, Y : V R 2 M 2 R 3 δύο τοπικοί χάρτες (παραμετρήσεις) των M 1 και M 2 στα σημεία p και q αντίστοιχα, με X(u 0, v 0 ) = p. Υποθέτουμε (ενδεχομένως λαμβάνοντας ένα υποσύνολο του U) ότι f(x(u)) Y (V ). Επειδή η f είναι διαφορίσιμη, θα υπάρχουν διαφορίσιμες συναρτήσεις α : U R, β : U R τέτοιες ώστε f(x(u, v)) = Y (α(u, v), β(u, v)). Πιο συγκεκριμένα, ορίζεται η διαφορίσιμη απεικόνιση χ : U V της μορφής χ(u, v) = (α(u, v), β(u, v)) ώστε f X = Y χ. Ο πίνακας του διαφορικού df p : T p M 1 T q M 2 ως προς τις βάσεις {X u, X v }, {Y u, Y v } των εφαπτόμενων χώρων T p M 1 και T q M 2 αντίστοιχα είναι ο Ιακωβιανός πίνακας ( ) α u α v J =. β u Επειδή το διαφορικό df p αντιστρέφεται, ο πίνακας J έχει και αυτός αντίστροφο. Από το κλασικό θεώρημα αντίστροφης απεικόνισης, η διαφορίσιμη συνάρτηση β v χ : U R 2 V R 2, (u, v) (α(u, v), β(u, v)) είναι τοπική αμφιδιαφόριση, από κάποιο ανοικτό υποσύνολο W U με (u 0, v 0 ) W σε ένα ανοικτό W V. Τότε θέτοντας U p = X(W ) και U q = Y ( W ) η απεικόνιση f Up : U p U q είναι αμφιδιαφόριση (προτρέπουμε τον αναγνώστη να κάνει ένα διάγραμμα της απόδειξης). 3.2 Λυμένα παραδείγματα Παράδειγμα 3.7. Να βρεθεί η εξίσωση του εφαπτόμενου επιπέδου της επιφάνειας M του υπερβολικού παραβολοειδούς με τοπική παραμέτρηση X(u, v) = (u, v, u 2 v 2 ), στο σημείο p = (1, 1, 0). Λύση Είναι X(1, 1) = (1, 1, 0) = p. Γνωρίζουμε ότι ο εφαπτόμενος χώρος T p M στο σημείο p παράγεται από τα διανύσματα {X u (1, 1), X v (1, 1)}. Ζητάμε την καρτεσιανή εξίσωση του εφαπτόμενου χώρου, ως επίπεδο στον R 3. Είναι X u (u, v) = (1, 0, 2u), X v (u, v) = (0, 1, 2v), άρα X u (1, 1) = (1, 0, 2) και X v (1, 1) = (0, 1, 2). Υπάρχουν διάφοροι εναλλακτικοί τρόποι να προχωρήσουμε. Για παράδειγμα, ένα διάνυσμα κάθετο στο ζητούμενο επίπεδο είναι το n = X u (1, 1) X v (1, 1) = ( 2, 2, 1). Συνεπώς, αν (x, y, z) είναι ένα τυχαίο σημείο του επιπέδου αυτού, τότε η καρτεσιανή εξίσωσή του είναι n, (x 1, y 1, z) = 0 ή 2x 2y z = 0. Παράδειγμα 3.8. Εστω M η επιφάνεια με εξίσωση z = x 2 + 3xy 5y 2.
71 70 Ο εφαπτόμενος χώρος (α) Δείξτε ότι τα μοναδιαία διανύσματα u 1 = (1, 0, 0) και u 2 = (0, 1, 0) αποτελούν βάση του εφαπτόμενου χώρου της M στο σημείο p = (0, 0, 0). (β) Αποδείξτε ότι οι απεικονίσεις γ 1, γ 2 : R 2 R 3 με γ 1 (t) = (t, 0, t 2 ), γ 2 (t) = (0, t, 5t 2 ) ορίζουν καμπύλες επί της M, οι οποίες διέρχονται από το p και έχουν ως εφαπτόμενα διανύσματα στο σημείο p τα u 1 και u 2 αντίστοιχα. (γ) Βρείτε ένα μοναδιαίο κάθετο διάνυσμα της επιφάνειας M σε μια περιοχή ενός τυχαίου σημείου της. Λύση (α) Επειδή η επιφάνεια είναι της μορφής z = f(x, y), όπου f : R 2 R με f(x, y) = x 2 + 3xy 5y 2, θέτουμε x = u, y = v τότε z = z(u, v). Τότε μια παραμέτρηση αυτής θα είναι η X(u, v) = (u, v, u 2 + 3uv 5v 2 ), οπότε θα έχουμε T p M = {λx u (q) + µx v (q) : λ, µ R}, όπου q = X 1 (p) = (0, 0) = {λ(1, 0, 2u + 3v) q + µ(0, 1, 3u 10v) q : λ, µ R} = {λ(1, 0, 0) + µ(0, 1, 0) : λ, µ R} = {λu 1 + µu 2 : λ, µ R} (β) Εστω F : R 3 R με F (x, y, z) = x 2 +3xy 5y 2 z. Αρκεί να δείξουμε ότι F (γ 1 (t)) = F (γ 2 (t)) = 0. Εχουμε F (γ 1 (t)) = F (t, 0, t 2 ) = t 2 + 3t t 2 = 0 F (γ 2 (t)) = F (0, t, 5t 2 ) = 0 + 3t 0 5t 2 + 5t 2 = 0 άρα γ 1, γ 2 M. Παρατηρούμε ότι για t = 0 είναι γ 1 (0) = γ 2 (0) = p, οπότε οι καμπύλες διέρχονται από το σημείο p. Τα εφαπτόμενα διανύσματα των δύο αυτών καμπυλών είναι αντίστοιχα: γ 1(t) = (1, 0, 2t) για t = 0 : γ 1(0) = (1, 0, 0) = u 1 γ 2(t) = (0, 1, 10t) για t = 0 : γ 2(0) = (0, 1, 0) = u 2. (γ) Ενα μοναδιαίο κάθετο διάνυσμα της επιφάνειας M σε ένα τυχαίο σημείο αυτής είναι το N = X u X v X u X v = 1 ( 2u 3v, 3u + 10v, 1). ( 2u 3v) 2 + ( 3u + 10v) Παράδειγμα 3.9. Δείξτε ότι το εφαπτόμενο επίπεδο της επιφάνειας x2 a 2 + y2 b 2 + z2 = 1 στο σημείο p = c2 (x 0, y 0, z 0 ) δίνεται από την εξίσωση xx 0 a 2 + yy 0 b 2 + zz 0 c 2 = 1. Λύση Εστω f : R 3 R με τιμή f(x, y, z) = x2 a 2 + y2 b 2 + z2 1. Τότε θα είναι c2 f x (p) = 2x a 2 p = 2x 0 a 2, f y(p) = 2y b 2 p = 2y 0 b 2, f z(p) = 2z c 2 p = 2z 0 c 2.
72 Ο εφαπτόμενος χώρος 71 Σύμφωνα με την εξίσωση (3.2) το εφαπτόμενο επίπεδο στο σημείο p = (x 0, y 0, z 0 ) δίνεται ως εξής: f x (p)(x x 0 ) + f y (p)(y y 0 ) + f z (p)(z z 0 ) = 0 xx 0 a 2 + yy 0 b 2 + zz 0 c 2 = x2 0 a 2 + y2 0 b 2 + z2 0 c 2 xx 0 a 2 + yy 0 b 2 + zz 0 c 2 = 1, όπου λάβαμε υπόψη ότι το σημείο p είναι σημείο της επιφάνειας (άρα ικανοποιεί την εξίσωσή αυτής). Παράδειγμα Εστω M μια κανονική επιφάνεια, v R 3 ένα μοναδιαίο διάνυσμα και έστω η συνάρτηση f : M R με τιμή f(p) = v, p. Να υπολογίσετε το διαφορικό df p (X), όπου X T p M. Λύση Εστω γ : R M μια καμπύλη με γ(0) = p και γ (0) = X. Τότε df p (X) = d dt (f γ(t)) t=0 = d dt (f(γ(t))) t=0 = d dt ( v, γ(t) ) t=0 = dv dt, γ(t) t=0 + v, dγ dt t=0 = v, γ (t) t=0 = v, γ (0) = v, X. Άρα df p (X) = v, X. Παράδειγμα Εστω S 2 R 3 η μοναδιαία σφαίρα και έστω R z,θ : R 3 R 3 η απεικόνιση στροφής κατά γωνία θ περί τον άξονα z. Τότε ο περιορισμός f = R z,θ S 2 : S 2 S 2 είναι λεία απεικόνιση. Να υπολογίσεται το διαφορικό df p : T p S 2 T f(p) S 2. Λύση Εστω γ : I S 2 λεία καμπύλη με γ(0) = p, γ (0) = Z. Λόγω της γραμμικότητας της R z,θ έχουμε df p (Z) = d dt (R z,θ γ(t)) t=0 = R z,θ (γ (0)) = R z,θ (Z). Παρατηρείστε ότι η R z,θ διατηρεί τον βόρειο πόλο N(0, 0, 1) σταθερό και ότι η απεικόνιση df N : T N S 2 T N S 2 παριστά στροφή κατά γωνία θ στο επίπεδο T N S 2. (Το παράδειγμα αυτό είναι ειδική περίπτωση του Παραδείγματος 3.6). 3.3 Ασκήσεις 1. Να βρεθεί η εξίσωση του εφαπτόμενου επιπέδου για κάθε μία από τις παρακάτω παραμετρημένες επιφάνειες στο αντίστοιχο σημείο: (α) X(u, v) = (u, v, u 2 v 2 ), p = (1, 1, 0). (β) X(r, θ) = (r cosh θ, r sinh θ, r 2 ), p = (1, 0, 1). 2. Να αποδειχθεί ότι σε κάθε σημείο μιας γενέτειρας του κυλίνδρου το εφαπτόμενο επίπεδο μένει σταθερό.
73 72 Ο εφαπτόμενος χώρος 3. Να βρεθεί η καρτεσιανή εξίσωση του εφαπτόμενου επιπέδου T p M της επιφάνειας M που ορίζει η παραμέτρηση X(u, v) = (u + v, u v, uv), (u, v) R 2 στο σημείο p = (0, 2, 1). 4. Να δειχθεί ότι οι επιφάνειες M 1, M 2 οι οποίες ορίζονται από τις εξισώσεις x 2 +y 2 +z 2 = αx, x 2 +y 2 +z 2 = βy, όπου α, β R τέμνονται κατά σταθερή γωνία. 5. Δείξτε ότι το ελλειψοειδές 3x 2 + 2y 2 + z 2 = 9 και η σφαίρα x 2 + y 2 + z 2 8x 6y 8z + 24 = 0 εφάπτονται στο σημείο p = (1, 1, 2). 6. Εστω M μια κανονική επιφάνεια, p 0 R 3 \ M και f : M R η συνάρτηση f(p) = p p 0 2. Δείξτε ότι df p (Z) = 2 Z, p p 0, για κάθε Z T p M. (Εδώ, είναι το κανονικό εσωτερικό γινόμενο του R 3 και x = x, x 1/2 ). 7. Αποδείξτε ότι αν μια κανονική επιφάνεια M τέμνει ένα επίπεδο Π σε ένα και μοναδικό σημείο p, τότε το επίπεδο Π είναι το εφαπτόμενο επίπεδο της M στο σημείο p. 8. (α) Εστω M μια κανονική επιφάνεια, p M και Id M : M M η ταυτοτική απεικόνιση. Αποδείξτε ότι (did M ) p = Id TpM : T p M T p M. (β) Αποδείξτε την Πρόταση 3.4. (γ) Εστω f : M 1 M 2 μια αμφιδιαφόριση μεταξύ κανονικών επιφανειών. Αποδείξτε ότι για κάθε p M 1 η γραμμική απεικόνιση df p : T p M 1 T f(p) M 2 είναι αντιστρέψιμη (άρα ισομορφισμός διανυσματικών χώρων). 9. Εστω M μια κανονική και συνεκτική 1 επιφάνεια. Εστω f : M R μια λεία απεικόνιση τέτοια ώστε df p = 0 για κάθε p M. Δείξτε ότι η f είναι σταθερή στην M. 1 Συνεκτική επιφάνεια ως συνεκτικό υποσύνολο του R 3.
74 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
75 74 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
76 Κεφάλαιο 4 Η πρώτη θεμελιώδης μορφή Σύνοψη Ενας από τους κεντρικούς στόχους της διαφορικής γεωμετρίας είναι η ανάπτυξη ενός αποτελεσματικού τρόπου μέτρησης της καμπυλότητας γεωμετρικών αντικειμένων τα οποία δεν είναι επίπεδα (π.χ. επιφάνειες στον χώρο R 3 ). Για τον σκοπό αυτό θα χρειαστούμε νέα εργαλεία και ένα από αυτά είναι η εισαγωγή μιας θετικά ορισμένης τετραγωνικής μορφής σε κάθε εφαπτόμενο επίπεδο μιας επιφάνειας. Με τον τρόπο αυτό θα είμαστε σε θέση να ορίσουμε μήκη καμπυλών στην επιφάνεια, μήκη και γωνίες διανυσμάτων στον εφαπτόμενο χώρο, καθώς και εμβαδά επάνω στην επιφάνεια. Οι ποσότητες αυτές αποτελούν εσωτερικές (intrinsic) ποσότητες μιας επιφάνειας, δηλαδή ο υπολογισμός τους προκύπτει από μετρήσεις επάνω στην επιφάνεια και όχι θεωρώντας την επιφάνεια ως υποσύνολο του R 3. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6]. Προαπαιτούμενη γνώση Αναλυτική Γεωμετρία, Απειροστικός Λογισμός, Γραμμική Άλγεβρα. Ορισμός 4.1. Εστω M μια κανονική επιφάνεια του R 3, p M και έστω, p το εσωτερικό γινόμενο στον εφαπτόμενο χώρο T p M το οποίο επαγεται από το κανονικό εσωτερικό γινόμενο, του R 3. Η πρώτη θεμελιώδης μορφή (first fundmental form) είναι η (θετικά ορισμένη) τετραγωνική μορφή I p : T p M R +, I p (Z) = Z, Z p = Z 2. Θυμίζουμε από την γραμμική άλγεβρα τα εξής: Εστω V ένας διανυσματικός χώρος. Μια διγραμμική μορφή στον V είναι μια απεικόνιση f : V V R τέτοια ώστε f(λ 1 u 1 + λ 2 u 2, u) = λ 1 f(u 1, u) +λ 2 f(u 2, u) και f(u, λ 1 u 1 +λ 2 u 2 ) = λ 1 f(u, u 1 ) +λ 2 f(u, u 2 ), για κάθε λ 1, λ 2 R και u 1, u 2, u V. Η διγραμμική μορφή f λέγεται συμμετρική, εάν ισχύει f(u, v) = f(v, u) για κάθε u, v V. Μια συνάρτηση Q : V R καλείται τετραγωνική μορφή εάν μπορεί να γραφτεί στη μορφή Q(u) = f(u, u), για κάποια συμμετρική διγραμμική μορφή f : V V R. Παρατηρήσεις. 1. Από εδώ και στο εξής θα γράφουμε, για το επαγόμενο εσωτερικό γινόμενο του R 3 στον T p M, αντί, p. 75
77 76 Η πρώτη θεμελιώδης μορφή 2. Η πρώτη θεμελιώδης μορφή καθορίζει πλήρως (αποδείξτε το) το εσωτερικό γινόμενο, p στον T p M, μέσω της ταυτότητας πολικότητας: Z, W p = 1 ( ) I p (Z + W ) I p (Z) I p (W ), για κάθε Z, W T p M Οι ιδιότητες μιας επιφάνειας οι οποίες εξαρτώνται μόνο από την πρώτη θεμελιώδη μορφή ονομάζονται εσωτερικές ιδιότητες της επιφάνειας. Η πρώτη θεμελιώδης μορφή μάς επιτρέπει να ορίσουμε το μήκος μιας καμπύλης σε μια επιφάνεια. Ορισμός 4.2. Εστω M μια κανονική επιφάνεια και γ : I M μια καμπύλη κλάσης C 1. Το μήκος της γ ορίζεται ως L(γ) = I γ (t), γ (t) dt. Επιπλέον, μπορούμε να ορίσουμε μια συνάρτηση απόστασης d στην M, ώστε το ζεύγος (M, d) να είναι ένας μετρικός χώρος (metric space). Πρόταση 4.1. Εστω M μια κανονική επιφάνεια και p, q δύο σημεία της M. Θεωρούμε το σύνολο C pq όλων των καμπυλών γ : [0, 1] M κλάσης C 1 με την ιδιότητα γ(0) = p, γ(1) = q. Ορίζουμε τη συνάρτηση d : M M R + 0, d(p, q) = inf{ } L(γ) : γ C pq. Τότε το σύνολο (M, d) είναι ένας μετρικός χώρος, δηλαδή για κάθε p, q, r M ισχύουν τα εξής: i. d(p, q) 0 ii. d(p, q) = 0 p = q iii. d(p, q) = d(q, p) iv. d(p, q) d(p, r) + d(r, q). Για κάθε λοιπόν επιφάνεια M έχουμε ορίσει σε κάθε εφαπτόμενο χώρο T p M (p M) ένα εσωτερικό γινόμενο, το οποίο επάγεται από το συνηθισμένο εσωτερικό γινόμενο του R 3. Το εσωτερικό αυτό γινόμενο μεταβάλλεται με την επιλογή του σημείου p (άρα και την επιλογή του εφαπτόμενου χώρου T p M). Προκειμένου να ποσοτικοποιήσουμε αυτή τη μεταβολή, θα χρησιμοποιήσουμε μια τοπική παραμέτρηση της επιφάνειας και θα ορίσουμε κάποιες σημαντικές συναρτήσεις, τα θεμελιώδη ποσά πρώτης τάξης. Εστω M μια κανονική επιφάνεια και X : U R 2 M R 3 μια τοπική παραμέτρηση της M. Τότε σε κάθε σημείο p = X(u, v) X(q) X(U) ο εφαπτόμενος χώρος T p M = T X(u,v) X(U) παράγεται από τα διανύσματα X u (u, v), X v (u, v). Θα δούμε στη συνέχεια πώς εκφράζεται η πρώτη θεμελιώδης μορφή σε αυτή τη βάση. Εστω w T p M. Τότε w = λ 1 X u (q) + λ 2 X v (q), άρα w, w = λ 2 1 X u (q), X u (q) + 2λ 1 λ 2 X u (q), X v (q) + λ 2 2 X v (q), X v (q). Θέτουμε E(q) = X u (q), X u (q) = X u (q) 2, F (q) = X u (q), X v (q), G(q) = X v (q), X v (q) = X v (q) 2.
78 Η πρώτη θεμελιώδης μορφή 77 Οι ποσότητες E(q), F (q), G(q) ονομάζονται θεμελιώδη ποσά πρώτης τάξης της επιφάνειας M στο σημείο p. Καθώς το q U μεταβάλεται ορίζονται οι συναρτήσεις E(u, v), F (u, v), G(u, v). Ειδικότερα, Ορισμός 4.3. Οι πραγματικές (διαφορίσιμες) συναρτήσεις E, F, G : U R E(u, v) = X u (u, v), X u (u, v), F (u, v) = X u (u, v), X v (u, v), G(u, v) = X v (u, v), X v (u, v) ονομάζονται θεμελιώδη ποσά πρώτης τάξης της επιφάνειας M για την παραμέτρηση X : U M. Παράδειγμα 4.1. Εστω M R 3 το επίπεδο του R 3 που διέρχεται από το σημείο p 0 R 3 και είναι παράλληλο με τα γραμμικώς αναξάρτητα διανύσματα v 1, v 2 R 3. Μια τοπική παραμέτρηση του M δίνεται ως X(u, v) = p 0 + u v 1 + v v 2. Για κάθε p M μια βάση του T p M είναι η { X u = v 1, X v = } v 2, συνεπώς τα θεμελιώδη ποσά πρώτης τάξης είναι E = v 1, v 1, F = v 1, v 2, G = v 2, v 2. Αν v 1, v 2 επιλεγούν ως ορθοκανονικά διανύσματα, τότε E = G = 1, F = 0. Παράδειγμα 4.2. Εστω M ο ορθός κυκλικός κύλινδρος ακτίνας 1 και με διαμήκη άξονα τον άξονα z. Μια τοπική παραμέτρηση του M δίνεται ως X : (0, 2π) R R 3, X(u, v) = (cos u, sin u, v), από όπου προκύπτει ότι E = G = 1, F = 0. Παρατηρήστε ότι τα θεμελιώδη ποσά πρώτης τάξης είναι τα ίδια με αυτά του επιπέδου, συμβάν όχι τυχαίο. Θα προσπαθήσουμε στη συνέχεια να εντοπίσουμε τον γεωμετρικό λόγο που συμβαίνει αυτό. Ενα επίπεδο κομμάτι χαρτιού μπορεί να τυλιχθεί επάνω σε έναν κύλινδρο με τον προφανή τρόπο χωρίς να τσαλακωθεί. Εάν σχεδιάσουμε μια καμπύλη επάνω στο επίπεδο, τότε μετά το τύλιγμα γίνεται μια καμπύλη του κυλίνδρου. Επειδή δεν υπάρχει τσαλάκωμα, τα μήκη αυτών των δύο καμπυλών θα είναι ίσα. Εφόσον τα μήκη υπολογίζονται ως το ολοκλήρωμα της πρώτης θεμελιώδους μορφής, είναι εύλογο το συμπέρασμα ότι οι πρώτες θεμελιώδεις μορφές αυτών των δύο επιφανειών είναι ίσες. Από την άλλη, είναι αδύνατον να τυλίξουμε ένα επίπεδο φύλλο χαρτιού γύρω από μια σφαίρα χωρίς να το τσαλακώσουμε. Συνεπώς, αναμένουμε το επίπεδο και η σφαίρα να μην έχουν την ίδια πρώτη θεμελιώδη μορφή (όποια και να είναι η επιλογή της παραμέτρησης). Ο ακόλουθος ορισμός δίνει με μαθηματικό τρόπο το τι σημαίνει να τυλίγουμε μια επιφάνεια επάνω σε μια άλλη χωρίς να την τσαλακώσουμε. Ορισμός 4.4. Εστω M 1 και M 2 κανονικές επιφάνειες, μια λεία απεικόνιση f : M 1 M 2 καλείται τοπική ισομετρία εάν απεικονίζει καμπύλες της M 1 σε καμπύλες ίδιου μήκους στην M 2. Εάν υπάρχει τοπική ισομετρία f : M 1 M 2, λέμε ότι οι επιφάνειες M 1, M 2 είναι τοπικά ισομετρικές. Κάθε τοπική ισομετρία είναι τοπική αμφιδιαφόριση και μια τοπική ισομετρία που είναι αμφιδιαφόριση καλείται ισομετρία. Εύκολα βλέπουμε ότι οποιαδήποτε σύνθεση τοπικών ισομετριών είναι τοπική ισομετρία και η αντίστροφη κάθε τοπικής ισομετρίας είναι τοπική ισομετρία.
79 78 Η πρώτη θεμελιώδης μορφή Ορισμός 4.5. Μια αμφιδιαφόριση φ : M 1 M 2 μεταξύ δύο κανονικών επιφανειών του R 3 ονομάζεται ισομετρία (isometry) εάν για κάθε p M 1 το διαφορικό dφ p : T p M 1 T φ(p) M 2 διατηρεί τις πρώτες θεμελιώδεις μορφές των αντίστοιχων επιφανειών, δηλαδή dφ p (Z), dφ p (W ) = Z, W για κάθε Z, W T p M 1. Στην περίπτωση αυτή οι επιφάνειες M 1, M 2 ονομάζονται ισομετρικές (isometric). Με όρους τμημάτων επιφανειών ισχύει το εξής αποτέλεσμα Πρόταση 4.2. Μια τοπική αμφιδιαφόριση f : M 1 M 2 είναι τοπική ισομετρία εάν και μόνο εάν, για κάθε τμήμα επιφάνειας X 1 (u, v) της M 1, τα τμήματα X 1 (u, v) και f X 1 (u, v) των M 1 και M 2 αντίστοιχα, έχουν την ίδια πρώτη θεμελιώδη μορφή. Παράδειγμα 4.3. Εστω X : U R 3 η τοπική παραμέτρηση X(u, v) = (u, v, 1 u 2 v 2 ) της σφαίρας S 2 και p = ( u, v, X(u, v) ) S 2. Τότε μια βάση του εφαπτόμενου χώρου T p S 2 είναι η { Xu (u, v), X v (u, v) } {( ) ( )} u v = 1, 0,, 0, 1,, 1 u 2 v 2 1 u 2 v 2 από όπου προκύπτει ότι E = X u, X u = 1 v2 1 u 2 v 2, F = X u, X v = uv 1 u 2 v 2, G = X v, X v = 1 u2 1 u 2 v 2. Ας χρησιμοποιήσουμε τώρα την εξής τοπική παραμέτρηση της σφαίρας S 2. Εστω U = {(θ, φ) R 2 : 0 < θ < π, 0 < φ < 2π} και Y : U R 3 με Y (θ, φ) = ( sin θ cos φ, sin θ sin φ, cos θ ). Τότε μια βάση του εφαπτόμενου χώρου T p S 2 στο σημείο p = (θ, φ, Y (θ, φ)) είναι η { } { } Yθ, Y φ = (cos θ cos φ, cos θ sin φ, sin θ), ( sin θ sin φ, sin θ cos φ, 0), απ όπου προκύπτουν τα πιο χρηστικά θεμελιώδη ποσά πρώτης τάξης E = 1, F = 0, G = sin 2 θ. Παρατηρήσεις. 1. Είναι χρήσιμο και θα το κάνουμε τακτικά, να εκφράζουμε τα θεμελιώδη ποσά πρώτης τάξης ως εξής: Θεωρούμε το διαφορικό dx(u, v) : R 2 R 3 και τον πίνακά του ως την απεικόνιση [dx] : U R 2 M 2 3 (R), [dx](u, v) = ( ) t, X u, X v όπου A t συμβολίζουμε τον ανάστροφο του πίνακα A. Τα διανύσματα X u, X v τα θεωρούμε ως διανύσματα-στήλη, συνεπώς το δεξί μέλος παραπάνω είναι ένας πραγματικός 2 3 πίνακας. Τότε τα θεμελιώδη ποσά πρώτης τάξης περιγράφονται μέσω της ακόλουθης ισότητας πινάκων ( ) E F = [dx][dx] t. F G
80 Η πρώτη θεμελιώδης μορφή 79 Εναλλακτικά, ο παραπάνω πίνακας στο δεξί μέλος συμβολίζεται και ως ( ) ( ) ( ) g 11 g 12 E F gij (u, v) =. g 21 g 22 F G 2. Το επαγόμενο εσωτερικό γινόμενο, p στον T p M μπορεί πλέον να εκφραστεί με χρήση των συναρτήσεων E, F, G ως εξής: Εστω Z = ax u + bx v, W = cx u + dx v δύο διανύσματα του T p M. Τότε Z, W p = ax u + bx v, cx u + dx v p = ac X u, X u p + (ad + bc) X u, X v p + bd X v, X v p = abe + (ad + bc)f + bdg. Συνεπώς, η πρώτη θεμελιώδης μορφή δίνεται ως I p (Z) = E(u, v)a 2 + 2F + G(u, v)b 2 ( ) (u, v)ab ) ( = (a, b) E F a F G b. (4.1) Η παραπάνω έκφραση γράφεται σε σύγχρονη γλώσσα ds 2 = Edu 2 + 2F dudv + Gdv 2, ( ) αλλά δεν θα επεκταθούμε εδώ στην πλήρη μαθηματικής της ερμηνεία 1. Η έκφραση ( ) ορίζει μια μετρική στην περιοχή παραμέτρησης U ως εξής: Για q U ορίζουμε το εσωτερικό γινόμενο ds 2 q : R 2 R 2 R, με τιμή: ds 2 ( ) q Z, W = Z t ( Αποδεικνύεται ότι η αμφιδιαφόριση X : U X(U) M διατηρεί τα εσωτερικά γινόμενα ds 2 q και, p=x(q), συνεπώς είναι μια (τοπική) ισομετρία. Συμπέρασμα. Η πρώτη θεμελιώδης μορφή στο (τμήμα) της επιφάνειας X(U) M επάγει μια μετρική στο U R 2. Κατόπιν αυτού, όπως θα φανεί αργότερα, η κύρτωση της M επάγει τοπικά μια γεωμετρία στον R 2 (ενδεχομένως μη Ευκλείδεια). E(q) F (q) Μέσω των θεμελιωδών μεγεθών μπορούμε να υπολογίσουμε μήκη, γωνίες και εμβαδά πάνω σε επιφάνειες. F (q) G(q) Εστω X : U M ένα τμήμα επιφάνειας και γ : I M μια καμπύλη επί της M, δηλαδή γ(t) = X(u(t), v(t)) για κάθε t I. Επειδή η καμπύλη βρίσκεται επάνω στην επιφάνεια, τα εφαπτόμενα διανύσματά της γράφονται ως γραμμικός συνδυασμός των διανύσματων της βάσης του εφαπτόμενου χώρου της επιφάνειας M, {X u, X v }. Ειδικότερα ισχύει ) W. γ (t) = X u (u(t), v(t))u (t) + X v (u(t), v(t))v (t). 1 Δηλαδή ότι πρόκειτα για ισότητα δύο διαφορικών μορφών (differential forms).
81 80 Η πρώτη θεμελιώδης μορφή Άρα το μήκος της γ (Ορισμός 4.2) γράφεται συναρτήσει των E, F, G ως εξής L(γ) = γ (t), γ (t) dt I = E(u(t), v(t))u (t) 2 + 2F (u(t), v(t))u (t)v (t) + G(u(t), v(t))v (t) 2 dt. I Σε προηγούμενο κεφάλαιο είδαμε ότι η γωνία δύο επιφανειακών καμπυλών γ 1, γ 2 είναι ίση με τη γωνία που σχηματίζουν τα εφπτόμενα διανύσματα στο σημείο τομής αυτών. Αξίζει να σημειώσουμε εδώ πως, όταν οι καμπύλες είναι οι παραμετρικές καμπύλες γ 1 (u) = X(u, v 0 ), γ 2 (v) = X(u 0, v), τότε η γωνία ϕ που σχηματίζουν δίνεται από την σχέση cos ϕ = X u(q), X v (q) X u (q) X v (q) = όπου p = X(q) είναι το σημείο τομής των γ 1 και γ 2. F (q) E(q)G(q) Παρατηρούμε ότι οι παραμετρικές καμπύλες της παραμέτρησης X είναι ορθογώνιες εάν και μόνο εάν F (u, v) = 0 για κάθε (u, v) U. περίπτωση η παραμέτρηση καλείται ορθωγώνια. Σε αυτή την Ορισμός 4.6. Εστω M 1 και M 2 κανονικές επιφάνειες του R 3. Λέγοντες σύμμορφη απεικόνιση f : M 1 M 2 εννοούμε μια τοπική αμφιδιαφόριση τέτοια ώστε, εάν γ 1 και γ 1 είναι δύο τεμνόμενες καμπύλες της M 1 στο σημείο p M 1 και εάν γ 2 και γ 2 είναι οι εικόνες τους μέσω της f, τότε η γωνία τομής των γ 1 και γ 1 είναι ίση με τη γωνία τομής των γ 2 και γ 2 στο σημείο f(p). Ο παραπάνω ορισμός μάς λέει ουσιαστικά ότι η απεικόνιση f : M 1 M 2 είναι σύμμορφη, εάν διατηρεί της γωνίες. Είναι προφανές ότι κάθε σύνθεση σύμμορφων απεικονίσεων είναι σύμμορφη και ότι η αντίστροφη κάθε σύμμορφης απεικόνισης είναι σύμμορφη απεικόνιση. Θεώρημα 4.1. Μια τοπική αμφιδιαφόριση f : M 1 M 2 είναι σύμμορφη εάν και μόνο εάν υπάρχει συνάρτηση λ : M 1 R τέτοια ώστε df p (Z), df p (W ) = λ(p) Z, W, για κάθε p M 1 και Z, W T p M 1. Αναδιατυπώνοντας αυτό το αποτέλεσμα με όρους τμημάτων επιφανειών παίρνουμε το εξής: Πόρισμα 4.1. Μια αμφιδιαφόριση f : M 1 M 2 είναι σύμμορφη, εάν και μόνο εάν, για κάθε τμήμα επιφάνειας X 1 της M 1, οι πρώτες θεμελιώδεις μορφές του X 1 και του f X 1 είναι ανάλογες. Ειδικότερα, ένα τμήμα επιφάνειας X(u, v) είναι σύμμορφο με επίπεδη επιφάνεια εάν και μόνο εάν η πρώτη θεμελιώδης μορφή του είναι λ(du 2 + dv 2 ) για κάποια λεία συνάρτηση λ(u, v). Παράδειγμα 4.4. Δίνεται η επιφάνεια με παραμέτρηση X(u, v) = (u cos v, u sin v, ϕ(v)). Να προσδιορισθεί η συνάρτηση ϕ(v), ώστε η παραμέτρηση X να είναι σύμμορφη με επίπεδο. Για να είναι η παραμέτρηση X σύμμορφη, θα πρέπει η πρώτη θεμελιώδης μορφή της επιφάνειας να γράφεται στη μορφή I = λ(u, v)(du 2 + dv 2 ). (4.2)
82 Η πρώτη θεμελιώδης μορφή 81 Εχουμε X u (u, v) = (cos v, sin v, 0) και X v (u, v) = ( u sin v, u cos v, ϕ (v)), οπότε E(u, v) = X u (u, v), X u (u, v) = 1, F (u, v) = X u (u, v), X v (u, v) = 0, G(u, v) = X v (u, v), X v (u, v) = u 2 + (ϕ ) 2. Άρα η πρώτη θεμελιώδης μορφή θα είναι I = E(u, v)du 2 + 2F (u, v)dudv + G(u, v)dv 2 = du 2 + (u 2 + ϕ 2 )dv 2 (4.3) Για να παίρνει η σχέση (4.3) τη μορφή (4.2), θα πρέπει να έχουμε προφανώς u 2 + ϕ 2 = 1, ή ακόμη ϕ (v) = ± 1 u 2, οπότε ϕ(v) = ±v 1 u 2 + c, c R, u 1. Ορισμός 4.7. Εστω M μια κανονική επιφάνεια, X : U X(U) M μια τοπική παραμέτρηση και έστω ότι το U είναι μετρήσιμο (measurable) υποσύνολο του R 2. Τότε, το εμβαδό (area) του τμήματος επιφάνειας X(U) ορίζεται ως A ( X(U) ) = Xu (q) X v (q) dudv, q U. U Παρατηρούμε ότι X u (q) X v (q) 2 = X u, X u X v (q), X v (q) X u (q), X v (q) 2 = E(q)G(q) F 2 (q). Επομένως ο τύπος για το εμβαδό, χρησιμοποιώντας τα θεμελιώδη ποσά πρώτης τάξης γράφεται A ( X(U) ) = U E(q)G(q) F 2 (q)dudv. Αποδεικνύεται ότι το εμβαδό δεν εξαρτάται από την επιλογή της παραμέτρησης του τμήματος X(U) της επιφάνειας M. Ορισμός 4.8. Εστω M 1 και M 2 δύο κανονικές επιφάνειες του R 3. Μια τοπική αμφιδιαφόριση f : M 1 M 2 λέγεται ισεμβαδική, εάν απεικονίζει κάθε χωρίο της M 1 σε χωρίο ίσου εμβαδού της M 2 (υποθέτουμε ότι κάθε ένα από τα χωρία είναι αρκετά μικρό, ώστε να περιέχεται στην εικόνα κάποιου τμήματος επιφάνειας). Δίνουμε στη συνέχεια το ανάλογο του Θεωρήματος 4.1 Θεώρημα 4.2. Μια αμφιδιαφόριση f : M 1 M 2 είναι ισεμβαδική εάν και μόνο εάν, για κάθε τμήμα επιφάνειας X(u, v) της M 1, οι πρώτες θεμελιώδεις μορφές E 1 du 2 + 2F 1 dudv + G 1 dv 2, E 2 du 2 + 2F 2 dudv + G 2 dv 2 των τμημάτων X της M 1 και f X της M 2 ικανοποιούν την σχέση E 1 G 1 F 2 1 = E 2 G 2 F 2 2.
83 82 Η πρώτη θεμελιώδης μορφή Παράδειγμα 4.5. Το εμβαδόν του δακτυλίου T 2 με παραμέτρηση X(u, v) = ( (R + r cos u) cos v, (R + r cos u) sin v, r sin u ) (u [0, 2π), v [0, 2π)) ισούται με 4π 2 rr. Πράγματι, έχουμε X u = ( r sin u cos v, r sin u sin v, r cos u), X v = ( (R + r cos u) sin v, (R + r cos u) cos v, 0 ) και E(u, v) = r 2, F (u, v) = 0, G(u, v) = (R + r cos u) 2, επομένως A(T 2 ) = = 2π 2π 0 2π 0 E(u, v)g(u, v) F 2 (u, v)dvdu = 2π 2π πr(R + r cos u)du = 4π 2 rr. r(r + r cos u)dvdu 4.1 Λυμένα παραδείγματα Παράδειγμα 4.6. Εστω M μια επιφάνεια εκ περιστροφής με παραμέτρηση X(u, v) = ( f(u) cos v, f(u) sin v, g(u) ). Αποδείξτε ότι οι στροφές περί τον άξονα περιστροφής της M είναι ισομετρίες της M ή ισοδύναμα, ότι διατηρούν τα θεμελιώδη ποσά πρώτης τάξης. Λύση Η επιφάνεια M γράφεται από την καμπύλη γ(u) = ( f(u), 0, g(u) ), όταν αυτή περιστρέφεται περί τον άξονα των z. Αποδεικνύεται ότι για μια τέτοια επιφάνεια ισχύει E = 1, F = 0, G = f(u) 2 (άσκηση). Εστω R θ μια στροφή κατά σταθερή γωνία θ περί τον άξονα των z. Τότε ως προς την κανονική βάση του R 3 είναι R θ = cos θ sin θ 0 sin θ cos θ άρα X θ (u, v) = (R θ X)(u, v) = ( f(u) cos(v + θ), f(u) sin(v + θ), g(u) ), είναι η νέα παραμέτρηση της M, μετά τη στροφή κατά γωνία θ. Για την παραμέτρηση αυτή προκύπτει ότι E θ = 1, F θ = 0, G θ = f(u) 2 απ όπου προκύπτει το αποτέλεσμα. Παράδειγμα 4.7. Εστω X : U R 2 X(U) R 3, X(u, v) = (u, v, u 2 + v 2 ) μια παραμέτρηση μιας κανονικής επιφάνειας του R 3. (1) Βρείτε τα θεμελιώδη ποσά πρώτης τάξης. (2) Να γράψετε την εξίσωση της επιφάνειας σε καρτεσιανές συντεταγμένες. Πώς λέγεται αυτή η επιφάνεια; (3) Να βρεθεί το εμβαδό του τμήματος K της επιφάνειας που καθορίζεται από τις συνθήκες x, y 0 και z [0, 1].
84 Λυμένα παραδείγματα 83 Λύση (1) Για τα θεμελιώδη ποσά πρώτης τάξης έχουμε X u = (1, 0, 2u) και X v = (0, 1, 2v), οπότε E(u, v) = X u 2 = 1 + 4u 2, F (u, v) = X u, X v = 4uv, G(u, v) = X v 2 = 1 + 4v 2. (2) Η εξίσωση της επιφάνειας σε καρτεσιανές συντεταγμένες είναι: z = x 2 + y 2. Η επιφάνεια αυτή λέγεται παραβολοειδές εκ περιστροφής. (3) Ζητάμε το εμβαδό A(K) = U E(u, v)g(u, v) F 2 (u, v)dudv, όπου U = X 1 (K) = {(u, v) R 2 : 0 u 2 + v 2 1, u, v 0}. Είναι A(K) = U 1 + 4v 2 + 4u 2 dudv. Για τον υπολογισμό αυτού του ολοκληρώματος θα χρησιμοποιήσουμε πολικές συντεταγμένες. Θέτουμε οπότε θα είναι όπου A(K) = D(u, v) D(ρ, θ) = u(ρ, θ) = ρ cos θ, v(ρ, θ) = ρ sin θ, 0 θ π/2 1 π/2 0 u ρ v ρ ρ 2 cos 2 θ + 4ρ 2 sin 2 θ u θ cos θ v = sin θ θ Συνεπώς, η σχέση (4.4) απλουστεύεται ως εξής: A(K) = 1 π/2 0 = π/2 0 ρ sin θ ρ cos θ = ρ cos2 θ + ρ sin 2 θ = ρ ρ 2 ρ dθdρ = ρ 1 + 4ρ 2 π/2dρ [ 1 12 (1 + 4ρ2 ) 3/2 ] = π 24 (5 5 1). D(u, v) dθdρ, (4.4) D(ρ, θ) Παράδειγμα 4.8. Δείξτε ότι το εμβαδόν ενός φραγμένου χωρίου U της επιφάνειας z = f(x, y) είναι A(K) = 1 + fu + f v dudv, όπου K είναι η προβολή του U στο xy επίπεδο. Λύση K Θεωρούμε την παραμέτρηση της επιφάνειας z = f(x, y) με X(u, v) = (u, v, f(u, v)). Υπολογίζουμε τα θεμελιώδη ποσά πρώτης τάξης και έχουμε οπότε είναι X u = (1, 0, f u ), X v = (0, 1, f v ), E = X u, X u = 1 + f 2 u, F = X u, X v = f u f v, G = X v, X v = 1 + f 2 v. Αν K είναι η ορθογώνια προβολή του U στο xy επίπεδο, έχουμε: A(K) = E(u, v)g(u, v) F 2 (u, v) dudv = K K 1 + f 2 u + f 2 v dudv.
85 84 Η πρώτη θεμελιώδης μορφή Παράδειγμα 4.9. Εστω X : U R 3 παραμέτρηση μιας επιφάνειας με θεμελιώδη ποσά πρώτης τάξης E(u, v) = 1 + v 2, F (u, v) = 2uv, G(u, v) = 1 + u 2. Υπολογίστε τη γωνία ανάμεσα στις u, v-παραμετρικές καμπύλες σε τυχαίο σημείο της επιφάνειας. Λύση Αν θ η γωνία που σχηματίζουν οι καμπύλες X(u, v 0 ), X(u 0, v) στο σημείο (u 0, v 0 ), τότε cos θ = X u(u, v 0 ), X v (u 0, v) X u (u, v 0 ) X v (u 0, v) = F (u 0, v 0 ) E(u0, v 0 )G(u 0, v 0 ) = 2u 0 v u v u2 0 v Ασκήσεις 1. Υπολογίστε την πρώτη θεμελιώδη μορφή της επιφάνειας M με παραμέτρηση X : R + R M, θ θ X a (r, θ) = (r sin a cos( ), r sin a sin( ), r cos a). sin a sin a Βρείτε την εξίσωση της μορφής f(x, y, z) = 0 που να περιγράφει την επιφάνεια αυτή. 2. Υπολογίστε τα θεμελιώδη ποσά πρώτης τάξης των παρακάτω επιφανειών: (1) Της σφαίρας με ακτίνα α: X(u, v) = α(sin u cos v, sin u sin v, cos u) (2) Του δακτυλίου: X(u, v) = ( R + r cos u) cos v, (R + r cos u) sin v, r sin u ) (0 < r < R) (3) Της ελικοειδούς: X(u, v) = (u cos v, u sin v, bv) (4) Της αλυσοειδούς: X(u, v) = α(cosh u cos v, cosh u sin v, u). 3. Βρείτε μια ισομετρική παραμέτρηση (ως προς το επίπεδο) X : R 2 M του ορθού κυλίνδρου M = {(x, y, z) R 3 : x 2 + y 2 = 1}. 4. Αποδείξτε ότι η παραμέτρηση του Mercator X : R 2 S 2 της σφαίρας S 2 με είναι σύμμορφη. X(u, v) = ( cos v cosh u, sin v cosh u, sinh u ) cosh u 5. Αποδείξτε ότι η πρώτη θεμελιώδης μορφή μιας κανονικής επιφάνειας M του R 3 παραμένει αναλλοίωτη κάτω απο στερεές κινήσεις 6. Εστω X, Y : R 2 R 3 παραμετρήσεις δύο κανονικών επιφανειών που δίνονται ως εξής: X(u, v) = (cosh u cos v, cosh u sin v, u), Y (u, v) = (sinh u cos v, sinh u sin v, v).
86 Ασκήσεις 85 Υπολογίστε τις πρώτες θεμελιώδεις μορφές των X και Y. Στη συνέχεια, βρείτε εξισώσεις της μορφής f(x, y, z) = 0, που να περιγράφουν τις επιφάνειες αυτές. 7. Υπολογίστε το εμβαδό του τμήματος του παραβολοειδούς εκ περιστροφής z = x 2 + y 2 με z 1 και να το συγκρίνετε με το εμβαδό του ημισφαιρίου x 2 + y 2 + z 2 = 1, z Εστω M R 3 μια κανονική επιφάνεια και X μια παραμέτρηση αυτής για την οποία ισχύει E = 1 και F = 0. Να αποδειχθεί ότι οι v-παραμετρικές καιμπύλες αποκόπτουν τις u-παραμετρικές καμπύλες σε ίσα τμήματα. 9. Εστω M η επιφάνεια με παραμέτρηση X : R + R + R 3, X(u, v) = (u cos v, u sin v, u). Αποδείξτε ότι οι παραμετρικές καμπύλες της X είναι ορθογώνιες σε κάθε σημείο. 10. Εστω γ(s) μια καμπύλη μοναδιαίας ταχύτητας στον R 3 με πρώτο κάθετο διάνυσμα N(s) και δεύτερο κάθετο διάνυσμα B(s). Ο σωλήνας ακτίνας α (α > 0) γύρω από την γ είναι η επιφάνεια που έχει παραμέτρηση X(s, θ) = γ(s) + α(n(s) cos θ + B(s) sin θ). Σχεδιάστε αυτή την επιφάνεια. Υποθέστε ότι η X είναι 1-1 και δείξτε ότι είναι κανονική επιφάνεια εάν η καμπυλότητα της γ είναι μικρότερη από 1 α για κάθε s. Δείξτε ότι το εμβαδόν του τμήματος της επιφάνειας που δίνεται από s 0 < s < s 1, 0 < θ < 2π, όπου s 0, s 1 σταθερές, είναι 2πα(s 1 s 0 ).
87 86 Η πρώτη θεμελιώδης μορφή
88 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
89 88 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
90 Κεφάλαιο 5 Η απεικόνιση Gauss και καμπυλότητα Σύνοψη Ενας από τους κεντρικούς στόχους της διαφορικής γεωμετρίας είναι η εύρεση ενός φυσικού και αποτελεσματικού τρόπου, προκειμένου να μετρηθεί η κύρτωση μη επίπεδων αντικειμένων (καμπύλες, επιφάνειες αλλά και άλλων). Υπάρχουν τουλάχιστον δύο τρόποι προκειμένου να οριστεί η καμπυλότητα μιας επιφάνειας. Εδώ θα ακολουθήσουμε τη διαδικασία μέσω της απεικόνισης Gauss, δηλαδή ουσιαστικά μιας απεικόνισης που σε κάθε σημείο μιας επιφάνειας αντιστοιχεί ένα μοναδιαίο κάθετο διάνυσμα στον αντίστοιχο εφαπτόμενο χώρο. Η προσέγγιση αυτή δεν είναι ο ιστορικός ορισμός που είχε δοθεί από τον Gauss, ο οποίος είναι λίγο πιο περίπλοκος. Οπως και να έχει, η καμπυλότητα Gauss μιας επιφάνειας θα οριστεί ως ένα μέγεθος η μέτρηση του οποίου απαιτεί να βλέπουμε την επιφάνεια ως υποσύνολο του R 3. Το Θαυμαστό Θεώρημα (Theorema Egregium) του Gauss το οποίο θα δούμε στο επόμενο κεφάλαιο, αναφέρει ότι η καμπυλότητα είναι ένα μέγεθος που μπορεί να μετρηθεί (ή να αναγνωριστεί) από έναν παρατηρητή ο οποίος βρίσκεται επάνω στην επιφάνεια και όχι εκτός αυτής. Είναι δηλαδή ένα εσωτερικό μέγεθος της επιφάνειας. Με πιο απλοϊκό τρόπο, ο καπετάνιος ενός πλοίου που ταξιδεύει σε μεγάλη απόσταση, είναι δυνατόν να διαπιστώσει με δικές του μετρήσεις ότι η γη είναι σφαιρική και δεν χρειάζεται να επικοινωνήσει με πιλότο αεροπλάνου για τον σκοπό αυτό! Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6]. Προαπαιτούμενη γνώση Αναλυτική Γεωμετρία, Απειροστικός Λογισμός, Εισαγωγή στη Γραμμική Άλγεβρα. Ορισμός 5.1. Εστω M μια κανονική επιφάνεια. Μια λεία απεικόνιση N : M S 2 ονομάζεται απεικόνιση Gauss της M εάν για κάθε p M η εικόνα N(p) έχει διάνυσμα θέσης ίσο με το μοναδιαίο διάνυσμα κάθετο της M στο p. Εάν μια τέτοια απεικόνιση υπάρχει, τότε η επιφάνεια M ονομάζεται προσανατολίσιμη (orientable). Η επιφάνεια M εφοδιασμένη με μια τέτοια απεικόνιση Gauss ονομάζεται προσανατολισμένη (oriented) επιφάνεια. Παραδείγματα. 1. Εστω M = {(x, y, 0) R 3 : x, y R} το επίπεδο xy. Τότε μια απεικόνιση Gauss είναι η N(x, y, 0) = 89
91 90 Η απεικόνιση Gauss και καμπυλότητα Σχήμα 5.1: Η απεικόνιση Gauss. (0, 0, 1). 2. Εστω M = S 2. Τότε μια απεικόνιση Gauss είναι η N = Id S 2, όπου Id : S 2 S 2, Id(p) = p η ταυτοτική απεικόνιση της M. 3. Εστω M = S 1 R ο ορθός μοναδιαίος κύλινδρος. Τότε N(x, y, z) = (x, y, 0) είναι μια απεικόνιση Gauss. 4. Η ταινία του Möbius (αναζητήστε τοπική παραμέτρηση και περιγραφή στην βιβλιογραφια) δεν επιδέχεται απεικόνιση Gauss, δηλαδή είναι μια μη προσανατολίσιμη επιφάνεια. Σχήμα 5.2: Η ταινία του Möbius. Παρατηρήσεις 1. Κάθε κανονική επιφάνεια είναι τοπικά προσανατολισμένη. Πράγματι, αν X : U X(U) M είναι μια τοπική παραμέτρηση της M με X( 0 ) = p, τότε για κάθε q = X(u, v) X(U) η απεικόνιση είναι μια (τοπική) απεικόνιση Gauss της M. N(q) = N(X(u, v)) = X u(u, v) X v (u, v) X u (u, v) X v (u, v) 2. Αν N : M S 2 είναι μια απεικόνιση Gauss της M, τότε το διάνυσμα N(p) είναι κάθετο ταυτόχρονα στα εφαπτόμενα επίπεδα T p M και T N(p) S 2. Συνεπώς, μπορούμε να ταυτίσουμε T p M = T N(p) S 2
92 Η απεικόνιση Gauss και καμπυλότητα 91 (ισομορφισμός διανυσματικών χώρων). Μέσω αυτής της ταύτισης το διαφορικό dn p : T p M T N(p) S 2 της απεικόνισης N τελικά γράφεται ως dn p : T p M T p M. Το προηγούμενο διαφορικό ουσιαστικά εκφράζει έναν τρόπο μεταβολής του διανύσματος N, άρα κατά κάποιο τρόπο, δίνει μια εικόνα για το σχήμα της επιφάνειας. Ορισμός 5.2. Εστω M μια κανονική προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2. Ο τελεστής σχήματος (shape operator) της M (απεικόνιση Weingarten) στο p M είναι η γραμμική απεικόνιση S p : T p M T p M, S p (Z) = dn p (Z), για κάθε Z T p M. Το παρακάτω θεώρημα γενικεύει τον χαρακτηρισμό της ευθείας ως καμπύλης με μηδενική καμπυλότητα στις δύο διαστάσεις: μια συνεκτική επιφάνεια περιέχεται σε επίπεδο εάν και μόνο εάν ο τελεστής σχήματος της επιφάνειας είναι μηδενικός. Υπενθυμίζουμε ότι ένα ανοικτό υποσύνολο U του επιπέδου είναι συνεκτικό, εάν δεν είναι ένωση μη κενών ανοικτών συνόλων, ξένων μεταξύ τους. Θεώρημα 5.1. Εστω M μια συνεκτική, προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2. Τότε ο τελεστής σχήματος S p : T p M T p M είναι ο μηδενικός τελεστής για κάθε p M, εάν και μόνο εάν η M είναι τμήμα ενός επιπέδου. Απόδειξη. Αν η επιφάνεια M περιέχεται σε ένα επίπεδο, τότε η απεικόνιση Gauss είναι σταθερή, επομένως ο τελεστής σχήματος θα είναι ο μηδενικός τελεστής, δηλαδή S p = dn p = 0, για κάθε p M. Αντίστροφα, σταθεροποιούμε ένα σημείο p M, έστω q ένα τυχαίο σημείο της M και γ : I M μια καμπύλη τέτοια ώστε γ(0) = q και γ(1) = p. Τότε η απεικόνιση f q : I R με τιμή f q (t) = q γ(t), N(γ(t)) ικανοποιεί την σχέση f q (0) = 0 και f q(t) = γ (t), N(γ(t)) + q γ(t), dn p γ (t) = 0. Αυτό σημαίνει ότι q γ(t), N(γ(t)) = 0 για κάθε t I. Επομένως, για t = 1 είναι (q p), N(p) = 0 για κάθε q M. Άρα η επιφάνεια περιέχεται στο επίπεδο που διέρχεται από το σημείο p και είναι κάθετη στο διάνυσμα N(p). Παραδείγματα. 1. Εστω M = S 2, N(p) = p. Τότε S p = Id : T p S 2 T p S Εστω M το επίπεδο O xy, N(x, y, 0) = (0, 0, 1). Τότε N = σταθερή, άρα S p = 0 για κάθε p M. 3. Εστω M = S 1 R ο ορθός μοναδιαίος κύλινδρος, N(x, y, z) = (x, y, 0). Θα υπολογίσουμε τον τελεστή σχήματος S p της M στο τυχαίο p = (x, y, z) M, βρίσκοντας τον αντίστοιχο πίνακα [S p ] της
93 92 Η απεικόνιση Gauss και καμπυλότητα γραμμικής απεικόνισης S p (ως προς κατάλληλη επιλογή της βάσης του T p M). Παρατηρούμε κατ αρχάς ότι T p M = span{( y, x, 0), (0, 0, 1)}. Τότε S p (0, 0, 1) = dn p (0, 0, 1) = d dt N(x, y, z + t) t=0 = d dt (x, y, 0) t=0 = (0, 0, 0). Θα υπολογίσουμε τώρα την τιμή S p ( y, x, 0). Εστω γ(t) = ( cos(t + t 0 ), sin(t + t 0 ), z ), όπου t 0 R είναι τέτοιο ώστε (cos t 0, sin t 0 ) = (x, y). Τότε για την καμπύλη αυτή ισχύουν ότι γ(0) = (cos t 0, sin t 0, z) = (x, y, z) = p γ (0) = ( sin t 0, cos t 0, 0) = ( y, x, 0). Άρα S p ( y, x, 0) = dn p ( y, x, 0) = d dt N( cos(t + t 0 ), sin(t + t 0 ), z ) t=0 = d dt( cos(t + t0 ), sin(t + t 0 ), 0 ) t=0 = (sin t 0, cos t 0, 0) = ( y, x, 0). Συνεπώς, ο πίνακας του τελεστή σχήματος ως προς τη βάση {( y, x, 0), (0, 0, 1)} είναι ( ) 1 0 [S p ] =. 0 0 Πρόταση 5.1. Εστω M μια κανονική, προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2 και p M. Τότε ο τελεστής σχήματος είναι αυτοσυζυγής τελεστής ως προς την πρώτη θεμελιώδη μορφή, δηλαδή ισχύει για κάθε Z, W T p M. S p (Z), W = Z, S p (W ), Απόδειξη. Εστω X : U M μια τοπική παραμέτρηση της M τέτοια ώστε X(0, 0) = p και έστω N : X(U) S 2 η απεικόνιση Gauss στο X(U), η οποία δίνεται ως N(X(u, v)) = X u(u, v) X v (u, v) X u (u, v) X v (u, v). Το διάνυσμα N X(u, v) είναι κάθετο στο εφαπτόμενο επίπεδο T p M οπότε έιναι 0 = d dv N X, X u = dn p X v, X u + N X, X uv και 0 = d du N X, X v = dn p X u, X v + N X, X vu. Αφαιρώντας τη δεύτερη από την πρώτη εξίσωση και χρησιμοποιώντας το γεγονός ότι X uv = X vu παίρνουμε: dn p X v, X u = X v, dn p X u.
94 Η απεικόνιση Gauss και καμπυλότητα 93 Η συμμετρικότητα του γραμμικού ενδομορφισμού dn p : T p M T p M είναι άμεση συνέπεια της τελευταίας σχέσης και των ακόλουθων σχέσεων dn p X u, X u = X u, dn p X u, dn p X v, X v = X v, dn p X v. Επομένως από τον ορισμό του τελεστή σχήματος έχουμε το ζητούμενο. Σημείωση. Επειδή ο τελεστής σχήματος S p είναι αυτοσυζυγής ο πίνακάς του είναι συμμετρικός, άρα είναι διαγωνιοποήσιμος με πραγματικές ιδιοτιμές. Πόρισμα 5.1. Εστω M κανονική και προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2, p M. Τότε υπάρχει ορθοκανονική βάση {Z 1, Z 2 } ιδιοδιανυσμάτων της απεικόνισης S p του εφαπτόμενου χώρου T p M τέτοια ώστε S p (Z 1 ) = λ 1 Z 1, S p (Z 2 ) = λ 2 Z 2 για κάποιους πραγματικούς αριθμούς λ 1, λ 2, οι οποίοι είναι οι αντίστοιχες ιδιοτιμές της S p. Ορισμός 5.3. Εστω M μια κανονική και προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2, p M. Η δεύτερη θεμελιώδης μορφή της M στο p είναι η συμμετρική, διγραμμική απεικόνιση II p : T p M T p M R, II p (Z, W ) = S p (Z), W. Οπως και στην περίπτωση της πρώτης θεμελιώδους μορφής, μάς ενδιαφέρει να βρούμε μια τοπική έκφραση της δεύτερης θεμελιώδους μορφής (δηλαδή έκφραση αυτής χρησιμοποιώντας μια τοπική παραμέτρηση της επιφάνειας). Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2. Εστω X : U R 2 M μια τοπική παραμέτρηση της M τέτοια ώστε X(0) = p M (είναι πάντα δυνατό να επιλέγουμε την απεικόνιση X με την ιδιότητα αυτή, απλώς κάνουμε μια μεταφορά). Ως γνωστόν, ο εφαπτόμενος χώρος T p M = T N(p) S 2 παράγεται από τα διανύσματα X u, X v. Εστω ( ) a 11 a 12 A = M 2 2 (R) a 21 a 22 ο πίνακας του γραμμικού τελεστή S p : T p M T p M ως προς τη βάση {X u, X v } (γνωστός και ως πίνακας του Weingarten). Τότε ισχύει S p (X u ) = a 11 X u + a 21 X v S p (X v ) = a 12 X u + a 22 X v. (5.1) Επίσης, από τον ορισμό του τελεστή σχήματος είναι S p = dn p, όπου dn p : T p M T N(p) S 2. Τότε ισχυριζόμαστε ότι ισχύει dn p (X u ) = N u, dn p (X v ) = N v. (5.2) (Πράγματι, έστω α : I U η καμπύλη α = (t, 0) (δηλαδή ο άξονας x) του U R 2 με α(0) = (0, 0) και α (0) = (1, 0) e 1. Τότε η α = X α : I M είναι μια καμπύλη στην επιφάνεια M, η οποία ικανοποιεί
95 94 Η απεικόνιση Gauss και καμπυλότητα α(0) = X ( α(0) ) = X(0, 0) = p και α (0) = X ( α(0) ) α (0) = X(0, 0)e 1 = X u. Συνεπώς, από τον ορισμό του διαφορικού απεικόνισης μεταξύ επιφανειών έχουμε ότι Παρόμοια προκύπτει και η άλλη ισότητα). dn p (X u ) = d ( ) N α t=0 = d ( ) N X α t=0 dt dt = D(N X)(0, 0)α (0) = u (N X) (0,0) = N u. Συνεπώς από τις (5.1) και (5.2) προκύπτει το σύστημα a 11 X u + a 21 X v = N u a 12 X u + a 22 X v = N v, (5.3) το οποίο σε μορφή πινάκων εκφράζεται ως A[dX] = [dn], όπου [dx] = (X u, X v ) t, [dn] = (N u, N v ) t. Ορίζουμε τώρα τις συναρτήσεις e, f, g : U R από την ισότητα πινάκων ( ) ( e f = [dn][dx] t = A[dX][dX] t E F = A f g F G ). (5.4) Ορισμός 5.4. Οι παραπάνω συναρτήσεις e, f, g : U R ονομάζονται θεμελιώδη ποσά δεύτερης τάξης. Παραδοσιακά η δεύτερη θεμελιώδης μορφή γράφεται και II = edu 2 + 2fdudv + gdv 2, αλλά δεν δίνουμε περισσότερες εξηγήσεις για το πώς ερμηνεύεται η έκφραση αυτή. Λαμβάνοντας υπόψη την ισότητα (5.4) και το γεγονός ότι N span{x u, X v }, προκύπτουν οι χρήσιμες σχέσεις: e = N u, X u = N, X uu = [X ux v X uu ] X u X v = [X ux v X uu ] EG F 2 f = N u, X v = N, X vu = [X ux v X uv ] X u X v = [X ux v X uv ] EG F 2 g = N v, X v = N, X vv = [X ux v X vv ] X u X v = [X ux v X vv ] EG F 2. Παρατηρούμε στους παραπάνω τύπους ότι το εσωτερικό γινόμενο της πρώτης ισότητας περιέχει τις μερικές παραγώγους (πρώτης τάξης) του N και της παραμέτρησης X, ενώ οι τελευταίες σχέσεις περιέχουν τις μερικές παραγώγους (πρώτης και δεύτερης τάξης) μόνο της X. Η προτίμηση για την χρήση της μιας ή της άλλης εκ των παραπάνω σχέσεων εξαρτάται από το πόσο πολύπλοκη είναι η μορφή του N και των X u, X v (οπότε και ο υπολογισμός των αντιστοίχων παραγώγων τους είναι επίσης πολύπλοκος). Επομένως, θα επιλέξουμε τους τύπους εκείνους, που προκύπτουν με την ευκολότερη δυνατή παραγώγιση.
96 Η απεικόνιση Gauss και καμπυλότητα 95 Οι θεμελιώδης μορφές προσδιορίζουν τοπικά την επιφάνεια. Πιο συγκεκριμένα ισχύει το θεμελιώδες θεώρημα των επιφανειών, σύμφωνα με το οποίο αν δίνονται τρείς συναρτήσεις E, F, G τάξης τουλάχιστον C 3 και τρείς συναρτήσεις e, f, g τάξης τουλάχιστον C 1, με πεδίο ορισμού ένα ανοικτό U υποσύνολο του R 2, έτσι ώστε να ισχύουν (1) EG F 2 > 0, E > 0, G > 0 (2) τα E, F, G, e, f, g ικανοποιούν κατάλληλες σχέσεις συμβατότητας (το θεώρημα Egregium του Gauss και τις εξισώσεις Mainardi - Codazzi), τότε υπάρχει παραμέτρηση X : U X(U) με X τάξης τουλάχιστον C 3, τέτοια ώστε τα E, F, G e, f, g να είναι τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης αντιστοίχως, που ορίζονται από την X. Η εικόνα X(U) είναι μονοσήμαντα ορισμένη, εκτός από τη θέση της στο χώρο. Ενα από τα θεμελιώδη ερωτήματα της διαφορικής γεωμετρίας είναι με ποιόν τρόπο μπορούμε να μετρήσουμε την καμπυλότητα μιας επιφάνειας. Μια σημαντική παρατήρηση είναι ότι η καμπυλότητα μιας επιφάνειας (με όποιον τρόπο και αν αυτή οριστεί) δεν είναι σταθερή προς όλες τις διευθύνσεις. Για παράδειγμα, ο κυκλικός κύλινδρος ακτίνας r δεν καμπυλώνεται κατά τη διεύθυνση μιας γεννέτειρας, αλλά καμπυλώνεται κατά τη διεύθυνση των εφαπτομένων στις παράλληλες τομές του. Συνεπώς, είναι λογικό να πούμε ότι η καμπυλότητα του κυλίνδρου είναι μηδέν κατά τη διεύθυνση των γεννητόρων του, ενώ στη διεύθυνση των παραλλήλων τομών η καμπυλότητα ισούται με αυτή των ίδιων των τομών, δηλαδή 1/r. Σχήμα 5.3: Η καμπυλότητα του κυλίνδρου. Άρα λοιπόν, ένας τρόπος μέτρησης της καμπυλότητας μιας επιφάνειας, είναι το να μελετηθούν κατάλληλες καμπύλες επί της επιφάνειας. Θα προσπαθήσουμε να κάνουμε την παραπάνω ιδέα πιο συγκεκριμένη. Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2 και έστω γ : I M μια καμπύλη με παραμέτρηση ως προς το μήκος τόξου τέτοια, ώστε γ(0) = p, γ (0) = Z T p M. Αναλύουμε τη δεύτερη παράγωγο γ(0) στο p ως εξής: γ(0) = γ(0) tan + γ(0) norm,
97 96 Η απεικόνιση Gauss και καμπυλότητα όπου γ(0) tan T p M είναι η εφαπτομενική συνιστώσα και γ(0) norm ( T p M ) η κάθετη συνιστώσα. Σχήμα 5.4: Η εφαπτομενική και η κάθετη συνιστώσα. Το κάθετο διάνυσμα N(γ(s)) κατά μήκος της καμπύλης γ είναι κάθετο στην εφαπτομένη γ(s), συνεπώς για την κάθετη συνιστώσα του διανύσματος γ(0) ισχύει ότι γ(0) norm = γ(0), N(p) N(p) = γ(0), dn(p) γ(0) N(p) = Z, dn(p)z N(p), το οποίο σημαίνει ότι η κάθετη συνοστώσα γ(0) norm του διανύσματος γ(0) καθορίζεται πλήρως από την τιμή γ(0) και τις τιμές της απεικόνισης Gauss κατά μήκος οποιασδήποτε καμπύλης, που διέρχεται από το σημείο p, και με εφαπτόμενο διάνυσμα γ(0) = Z T p M. Άρα ο ορισμός που δίνουμε στη συνέχεια είναι καλός. Ορισμός 5.5. Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2, p M και Z T p M. Η κάθετη καμπυλότητα (normal curvature) κ p (Z) της M στο p ως προς τη διεύθυνση του διανύσματος Z είναι ο αριθμός κ n (Z) = γ(0), N(p), όπου γ : I M οποιδήποτε λεία καμπύλη με παραμέτρηση ως προς το μήκος τόξου με γ(0) = p, γ (0) = Z. Προκειμένου να δώσουμε μια γεωμετρική περιγραφή της κάθετης καμπυλότητας, εργαζόμαστε ως εξής: Ως καμπύλη στον χώρο R 3 γ(s) η γ έχει καμπυλότητα κ(s) και κάθετο διάνυσμα Ñ(s) = κ(s), συνεπώς γ(0) = κ(0)ñ(0). Το διάνυσμα Ñ(0) αναλύεται ως Ñ(0) = Ñ(0)tan + Ñ(0)norm = Ñ(0)tan + Ñ(0), N(p) N(p),
98 Η απεικόνιση Gauss και καμπυλότητα 97 άρα γ(0) = κ(0)ñ(0) = κ(0)ñ(0)tan + κ(0) Ñ(0), N(p) N(p). Ο πρώτος όρος της σχέσης αυτής σχετίζεται με τη γεωδαισιακή καμπυλότητα (η έννοια αυτή θα ορισθεί σε επόμενο κεφάλαιο) της καμπύλης γ, ενώ για τον δεύτερο όρο ισχύει κ n (Z) = γ(0), N(p) = κ(0) Ñ(0), N(p). (Αν κ(0) = 0, τότε κ p (Z) = 0). Αν θ είναι η γωνία των διανυσμάτων N(p) και Ñ(0) τότε κ n (Z) = κ(0) cos θ. Σχήμα 5.5: Η κάθετη καμπυλότητα. Επιπλέον, ισχύει κ p (Z) κ(0). Είναι λοιπόν σαφές ότι η κάθετη καμπυλότητα καθορίζει την κύρτωση της επιφάνειας, οπότε αναμένεται να σχετίζεται με τον τελεστή σχήματος, όπως φαίνεται στην παρακάτω πρόταση: Πρόταση 5.2. (Θεώρημα Meusnier) Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2, p M και Z T p M. Τότε η κάθετη καμπυλότητα της M στο p ως προς τη διεύθυνση του διανύσματος Z ικανοποιεί την σχέση κ n (Z) = S p (Z), Z = II p (Z, Z). Απόδειξη. Εστω γ μια καμπύλη με παράμετρο το μήκος τόξου, τέτοια ώστε γ(0) = p και γ(0) = Z. Κατά μήκος της καμπύλης αυτής το διάνυσμα N(γ(s)) είναι κάθετο στο εφαπτόμενο διάνυσμα γ(s), δηλαδή έχουμε Επομένως, θα είναι 0 = d ( γ(s), N(γ(s)) ) = γ(s), N(γ(s)) + γ(s), dn(γ(s)) γ(s). ds κ n (Z) = γ(0), N(p) = Z, dn p Z = S p (Z), Z = II p (Z).
99 98 Η απεικόνιση Gauss και καμπυλότητα Θεωρούμε τώρα μια κανονική, προσανατολισμένη επιφάνεια M με απεικόνιση Gauss N : M S 2 και έστω Tp 1 M = { Z T p M : Z = 1 } ο μοναδιαίος κύκλος στον εφαπτόμενο χώρο T p M. Επειδή ο κύκλος Tp 1 M είναι συμπαγής, η συνεχής συνάρτηση κ n : Tp 1 M R, κ n (Z) = κ n (Z) παίρνει μέγιστη και ελάχιστη τιμή. Άρα υπάρχουν δύο διευθύνσεις Z 1, Z 2 Tp 1 M τέτοιες ώστε κ 1 (p) κ n (Z 1 ) = max Z T 1 p M κ n (Z), κ 2 (p) κ n (Z 2 ) = min Z T 1 p M κ n (Z). Οι διευθύνσεις Z 1, Z 2 ονομάζονται κύριες διευθύνσεις (principal directions) στο p και οι τιμές κ 1 (p), κ 2 (p) κύριες καμπυλότητες (principal curvatures) της M στο p. Εάν κ 1 (p) = κ 2 (p) το σημείο p ονομάζεται ομφαλικό (umbilic). Το παρακάτω θεώρημα δίνει έναν ιδιαιτέρως χρήσιμο αλγεβρικό χαρακτηρισμό των κύριων διευθύνσεων. Θεώρημα 5.2. Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2 και έστω p M. Τότε το διάνυσμα Z Tp 1 M είναι μια κύρια διεύθυνση στο p εάν και μόνο εάν το Z είναι ένα ιδιοδιάνυσμα του τελεστή σχήματος S p : T p M T p M. Απόδειξη. Εστω {Z 1, Z 2 } μια ορθοκανονική βάση του T p M από ιδιοδιανύσματα του S p, δηλαδή S p (Z 1 ) = λ 1 Z 1, S p (Z 2 ) = λ 2 Z 2, (λ 1, λ 2 R). Κάθε μοναδιαίο διάνυσμα Z Tp 1 M γράφεται ως Z(θ) = cos θz 1 + sin θz 2 και με υπολογισμό προκύπτει ότι ( ) κ n Z(θ) = Sp (cos θz 1 + sin θz 2 ), cos θz 1 + sin θz 2 = cos 2 θ S p (Z 1 ), Z 1 + sin 2 θ S p (Z 2 ), Z 2 + cos θ sin θ( S p (Z 1 ), Z 2 + S p (Z 2 ), Z 1 ) = λ 1 cos 2 θ + λ 2 sin 2 θ. Από την παραπάνω έκφραση προκύπτει ότι οι αριθμοί λ 1, λ 2 αποτελούν τη μέγιστη και την ελάχιστη τιμή ( ) ( ) της συνάρτησης κ n Z(θ) = IIp Z(θ), Z(θ). Συνεπώς θα είναι λ1 = κ 1, λ 2 = κ 2, άρα τελικά κ n (Z) = κ 1 cos 2 θ + κ 2 sin 2 θ, όπου κ 1, κ 2 οι κύριες καμπυλότητες της M στο p. Από την παραπάνω σχέση, γνωστή και ως τύπος του Euler, 1 προκύπτει ουσιαστικά το αποτέλεσμα. Συμπερασματικά, οι κύριες καμπυλότητες κ 1, κ 2 της M στο p είναι οι ιδιοτιμές του τελεστή σχήματος S p : T p M T p M, ο οποίος, όπως δείξαμε, είναι αυτοσυζυγής. Συνεπώς απο την γραμμική άλγεβρα 1 Ενας από την πλειάδα τύπων του Leonard Euler.
100 Παράλληλες επιφάνειες 99 γνωρίζουμε ότι υπάρχει μια ορθοκανονική βάση απο ιδιοδιανύσματα {Z 1, Z 2 } του T p M, ώστε ο πίνακας του τελεστή S p ως προς αυτή τη βάση να είναι διαγώνιος, δηλαδή ( ) κ 1 0 [S p ] =. 0 κ 2 Ο επόμενος σημαντικός ορισμός προκύπτει τώρα φυσιολογικά από τα προηγούμενα. Ορισμός 5.6. Εστω M προσανατολισμένη κανονική επιφάνεια του R 3 με απεικόνιση Gauss N : M S 2. Η καμπυλότητα Gauss (Gauss curvature) K και η μέση καμπυλότητα (mean curvature) H της M είναι οι συναρτήσεις K : M R, H : M R K(p) = det[s p ] = κ 1 κ 2, H(p) = 1 2 tr[s p] = 1 2 (κ 1 + κ 2 ). Μια επιφάνεια M ονομάζεται επίπεδη (flat), εάν K(p) = 0 για κάθε p M, και ελαχιστική (ή ελάχιστης έκτασης) (minimal), εάν H(p) = 0 για κάθε p M. (Υπάρχει εξήγηση για τον όρο ελάχιστης έκτασης, αλλά δεν θα μας απασχολήσει αυτή την στιγμή). Παράδειγμα 5.1. Στο παράδειγμα αυτό θα δείξουμε ότι για τυχαία επιφάνεια ισχύει η σχέση H 2 K, όπου H, K η μέση καμπυλότητα και η καμπυλότητα Gauss αντίστοιχα και ότι η ισότητα ισχύει μόνο για τα ομφαλικά σημεία αυτής. Γνωρίζουμε ότι K = κ 1 κ 2, H = 1 2 (κ 1 + κ 2 ) όπου κ 1, κ 2 είναι οι κύριες καμπυλότητες της επιφάνειας σε τυχαίο σημείο αυτής. Τότε έχουμε ότι (κ 1 κ 2 ) 2 0 κ 2 1 2κ 1 κ 2 + κ κ κ 1 κ 2 + κ 2 2 4κ 1 κ 2 ( ) 1 2 (κ 1 + κ 2 ) 2 4κ 1 κ 2 2 (κ 1 + κ 1 ) κ 1 κ 2 H 2 K. Αν είναι H 2 = K, τότε προφανώς θα έχουμε κ 1 = κ 2 και αν λάβουμε υπόψη μας και τον τύπο του Euler, θα έχουμε κ n (Z) = κ 1 cos 2 θ + κ 1 sin 2 θ = κ 1, οπότε θα έχουμε κ n (Z) = κ 1 = κ 2, δηλαδή το σημείο p είναι πράγματι ένα ομφαλικό σημείο της επιφάνειας (Z T 1 p M). Ορισμός 5.7. Ενα σημείο p M μιας κανονικής επιφάνειας του R 3 ονομάζεται (1) ελλειπτικό αν K(p) > 0, (2) υπερβολικό αν K(p) < 0, (3) παραβολικό αν K(p) = 0 και dn p 0, (4) επίπεδο αν dn p = 0.
101 100 Η απεικόνιση Gauss και καμπυλότητα 5.1 Παράλληλες επιφάνειες Ορισμός 5.8. Παράλληλη επιφάνεια της επιφάνειας M ονομάζεται η επιφάνεια M η οποία παράγεται από την κίνηση κάθε σημείου της M κατά μήκος της καθέτου της M στο σημείο αυτό και σε σταθερή απόσταση α, α R \ {0}. Σύμφωνα με τον παραπάνω ορισμό, μια παραμετρική εξίσωση της παράλληλης επιφάνειας θα είναι X (u, v) = X(u, v) + αn(u, v). Πρόταση 5.3. Οι παράλληλες επιφάνειες M και M έχουν στα αντίστοιχα σημεία τους, κάθετα διανύσματα τα οποία είτε ταυτίζονται, αν είναι ομόρροπα, είτε είναι αντίρροπα Απόδειξη. Εστω X : U M μια παραμέτρηση της M. Τότε η X = X(u, v) + αn(u, v) (α = 0) θα είναι η παραμέτρηση της M. Από την σχέση αυτή παραγωγίζοντας ως προς u, v έχουμε Xu = X u + αn u, Xv = X v + αn v. Παίρνοντας το εξωτερικό γινόμενο των παραπάνω σχέσεων παίρνουμε ότι Xu Xv = (X u + αn u ) (X v + αn v ) = X u X v + α(x u N v + N u X v ) + α 2 (N u N v ). Η σχέση αυτή, αν ληφθούν υπόψη οι σχέσεις του Παραδείγματος 5.8 της τελευταίας ενότητας του κεφαλαίου, γράφεται ως εξής Xu Xv = X u X v + α( 2H(X u X v )) + α 2 K(X u X v ) = (1 2αH + α 2 K)X u X v. Επειδή όμως είναι X u X v = EG F 2 N, θα πάρουμε τελικά ότι Xu Xv = (1 2αH + α 2 K) EG F 2 N. Συνεπώς, το κάθετο διάνυσμα στην επιφάνεια M ταυτίζεται με το κάθετο διάνυσμα ή με το αντίθετο του κάθετου διανύσματος της M στα αντίστοιχα σημεία. Ακριβέστερα, το κάθετο διάνυσμα στην επιφάνεια M ταυτίζεται με το διάνυσμα ɛn όπου ɛ = sgn(1 2αH + α 2 K) και το σύμβολο sgn σημαίνει το πρόσημο της παράστασης που ακολουθεί. Από την παραπάνω πρόταση συμπεραίνουμε πως οι παράλληλες επιφάνειες έχουν στα αντίστοιχα σημεία τους εφαπτόμενα επίπεδα παράλληλα. Για το λόγο αυτό η επιφάνεια M λέγεται και παράλληλη επιφάνεια της M σε απόσταση α. Υστερα από τις παραπάνω διαπιστώσεις, για τις παράλληλες επιφάνειες, είναι φυσικό να αναρωτηθεί κανείς αν υπάρχουν σχέσεις που να συνδέουν τα θεμελιώδη μεγέθη των επιφανειών αυτών. Στη συνέχεια συμβολίζουμε με αστερίσκο τα θεμελιώδη ποσά της επιφάνειας M. Ισχύει η ακόλουθη πρόταση:
102 Παράλληλες επιφάνειες 101 Πρόταση 5.4. Αν M και M είναι δύο παράλληλες επιφάνειες τότε (1) E G (F ) 2 = (1 2αH + α 2 K) 2 (EG F 2 ) (2) Οι καμπυλότητες K και H της επιφάνειας M, δίνονται από τις σχέσεις K = K 1 2αH + α 2 K, H = Τα ακόλουθα ενδιαφέροντα θεωρήματα οφείλονται στον Bonnet 2 : ±(H αk) 1 2αH + α 2 K. Θεώρημα 5.3. (Bonnet) Αν η καμπυλότητα Gauss K της επιφάνειας M είναι σταθερή και θετική, τότε υπάρχουν δύο παράλληλες επιφάνειες της M εκ των οποίων η μέση καμπυλότητα της μιας ισούται με K/2 και της άλλης με K/2. Απόδειξη. Σύμφωνα με την υπόθεση είναι K > 0 και η καμπυλότητα αυτή είναι σταθερή. Γνωρίζουμε ότι η μέση καμπυλότητα της επιφάνειας M παραλλήλου της M σε απόσταση α δίνεται από την σχέση Ας θεωρήσουμε την επιφάνεια M 1 Τότε η σχέση (5.5) γίνεται H = H αk 1 2αH + α 2 K. (5.5) που βρίσκεται σε απόσταση α = 1 K > 0. (5.6) H 1 = H K K 1 2H 1 K + 1 K K = H K 2 2H K = K( K H) 2( K H) = K 2, δηλαδή K H1 = 2. Δείξαμε λοιπόν ότι υπάρχει επιφάνεια M1 παράλληλη της M της οποίας η μέση καμπυλότητα ισούται με K/2. Ας θεωρήσουμε τώρα την επιφάνεια M 2 που βρίσκεται σε απόσταση α = 1 K < 0 από την επιφάνεια M. Το αρνητικό πρόσημο σημαίνει ότι τα διανύσματα N και N είναι αντίρροπα. Στην περίπτωση αυτήν η σχέση (5.5) γίνεται H 2 = H + K K 1 + 2H 1 K + 1 K K = H + K 2(1 + H K ) = K 2, δηλαδή K H2 = 2. Δείξαμε και εδώ ότι υπάρχει επιφάνεια M2 παράλληλη της M και συμμετρική της M 1, της οποίας η μέση καμπυλότητα ισούται με K/2. 2 Pierre Ossian Bonnet.
103 102 Η απεικόνιση Gauss και καμπυλότητα Αντίστοιχα για τις καμπυλότητες Gauss εύκολα έχουμε (αποδείξτε το) K 1 = K K 2( K H) < 0 και K 2 = K K 2( K + H) > 0. Θεώρημα 5.4. Αν η μέση καμπυλότητα H μιας επιφάνειας M είναι σταθερή και μη μηδενική, τότε υπάρχει παράλληλη επιφάνεια M της M με σταθερή καμπυλότητα Gauss ίση με 4H 2. Απόδειξη. Γνωρίζουμε ότι αν M είναι μια παράλληλη επιφάνεια της M σε απόσταση α, τότε η καμπυλότητα Gauss της M δίνεται από την σχέση K = Θεωρούμε την επιφάνεια M που βρίσκεται σε απόσταση από την M. Τότε η σχέση (5.7) γράφεται K 1 2αH + α 2 K. (5.7) α = 1 2H 0 (5.8) δηλαδή K = K 1 2H 1 2H + 1 4H 2 K = 4H2, K = 4H. Δείξαμε λοιπόν ότι υπάρχει επιφάνεια M παράλληλη της M της οποίας η καμπυλότητα Gauss είναι σταθερή και ίση με 4H 2. Η καμπυλότητα Gauss, η πιο σημαντική έννοια του παρόντος μαθήματος, δεν είχε οριστεί ιστορικά από τον Gauss με τον τρόπο που δώσαμε (ο οποίος είναι ιδιαιτέρως λειτουργικός). Η πραγματική γεωμετρική ερμηνεία της καμπυλότητας από τον Gauss περιγράφεται από την παρακάτω πρόταση: Πρόταση 5.5. Εστω M μια προσανατολισμένη κανονική επιφάνεια του R 3 K(p) 0 σε ένα σημείο της p M. Εστω V η συνεκτική περιοχή του σημείου p όπου η καμπυλότητα K δεν αλλάζει πρόσημο. Τότε με καμπυλότητα Gauss K(p) = lim A 0 A A, όπου A είναι το εμβαδόν μιας περιοχής B V με p B και A το εμβαδόν της εικόνας της B μέσω της απεικόνισης Gauss N : M S 2. Το όριο λαμβάνεται για μια ακολουθία περιοχών {B n } η οποία συγκλίνει στο p υπό την έννοια ότι για μεγάλο n κάθε σφαίρα με κέντρο το p περιέχει όλα τα B n. Θα εκφράσουμε τώρα την καμπυλότητα Gauss και τη μέση καμπυλότητα συναρτήσει των θεμελιωδών ποσών πρώτης και δεύτερης τάξης, χρησιμοποιώντας μια τοπική παραμέτρηση X : U M της επιφάνειας M.
104 Παράλληλες επιφάνειες 103 Θυμίζουμε ότι τα παραπάνω συνδέονται με την σχέση ( ) ( e f E = A f g F F G ), όπου A είναι ο πίνακας του τελεστή σχήματος S p : T p M T p M ως προς τη βάση {X u, X v }. Από την παραπάνω σχέση προκύπτει ότι A = ( e f f g ) ( E F F G ) 1 = ( 1 EG F 2 Επειδή η καμπυλότητα Gauss και η μέση καμπυλότητα ισούνται με την ορίζουσα και το ίχνος αντίστοιχα του πίνακα A, τότε προκύπτουν οι εκφράσεις: και K = det(a) = det = ( e det f ( E det F ) f g F G ( e f e f ) ( f det E g F ) = eg f 2 EG F 2 f g ) ( H = 1 2 tr(a) = 1 eg 2fF + ge 2 EG F 2. G F ) 1 F G Επιπλέον, οι κύριες καμπυλότητες κ 1, κ 2 προκύπτουν ως οι ρίζες της εξίσωσης det(a κi) = 0. F E ). Αφού είναι γνωστή η μορφή των α ij, μπορούμε να επανέλθουμε στο σύστημα (5.3) από το οποίο θα πάρουμε τις σχέσεις N u = ff eg α 11 X u + α 21 X v = EG F 2 X ef fe u + EG F 2 X v N v = gf fg α 12 X u + α 22 X v = EG F 2 X ff ge u + EG F 2 X v Οι τελευταίες είναι γνωστές ως εξισώσεις του Weingarten 3. Αξίζει να σημειώσουμε εδώ ότι, αν είναι γνωστές οι K και H, οι κύριες καμπυλότητες μπορούν να υπολογιστούν ως οι ρίζες της δευτεροβάθμιας εξίσωσης 3 Julius Weingarten. x 2 2Hx + K = 0.
105 104 Η απεικόνιση Gauss και καμπυλότητα Παράδειγμα 5.2. Εστω γ = (r, 0, z) : I R 3 μια λεία καμπύλη (με παράμετρο το μήκος τόξου) στο επίπεδο O xz με r(u) > 0 και ṙ(u) 2 + ż(u) 2 = 1 για κάθε su I. Τότε η απεικόνιση X : I R R 3 με τιμή cos v sin v 0 r(u) X(u, v) = sin v cos v z(u) = r(u) cos v r(u) sin v είναι μια παραμέτρηση μιας κανονικής επιφάνειας εκ περιστροφής (surface of revolution) M (περί τον άξονα z). Τα γραμμικώς ανεξάρτητα διανύσματα ṙ(u) cos v X u = ṙ(u) sin v ż(u), X v = r(u) sin v r(u) cos v 0 z(u) καθορίζουν μια (τοπική) απεικόνιση Gauss cos v sin v 0 N(u, v) = sin v cos v ż(u) 0 ṙ(u) = ż(u) cos v ż(u) sin v ṙ(u). Ελέξτε ότι X u, N = X v, N = 0. Επιπλέον, έχουμε ότι ( [dx] = (X u, X v ) t ṙ(u) cos v ṙ(u) sin v ż(u) = r(u) sin v r(u) cos v 0 ), άρα ( και ότι ( e f f g ) E F F G ) = [dn][dx] t = = [dx][dx] t = ( ( r(u) 2 ) r(u)ż(u) + z(u)ṙ(u) 0 0 ż(u)r(u) Επειδή η καμπύλη γ = (r, 0, z) έχει παραμέτρηση ως προς το μήκος τόξου λαμβάνουμε ότι (μετά από προσεκτικές πράξεις) K = eg f 2 EG F 2 = r(u) r(u). Θα κάνουμε μια διερεύνηση της παραπάνω έκφρασης της καμπυλότητας. Ας πάρουμε την περίπτωση όπου η επιφάνεια M είναι η μοναδιαία σφαίρα S 2, άρα r(u) = cos u, z(u) = sin u και έστω ότι π/2 < u < π/2. Τότε E = 1, F = 0, G = cos 2 u και e = 1, f = 0, g = cos 2 u, άρα K = cos2 u cos 2 u = 1 = κ 1κ 2, H = 1 cos 2 u + cos 2 u 2 cos 2 = 1 = 1 ) κ1 + κ 2, u 2( άρα για τις κύριες καμπυλότητες ισχύει κ 1 = κ 2 = 1. Αν η επιφάνεια είναι ο μοναδιαίος κύλινδρος r(u) = 1, z(u) = u, τότε E = 1, F = 0, G = 1 και e = f = 0, g = 1, συνεπώς K = 0 και H = 1 2. ). ( )
106 Παράλληλες επιφάνειες 105 Ερχόμαστε πάλι στην γενική εξίσωση ( ) και την γράφουμε ισοδύναμα ως τη διαφορική εξίσωση r(s) + K(s)r(s) = 0. Λύνοντας την εξίσωση αυτή για K = 1 (σταθερά αρνητική καμπυλότητα Gauss) προκύπτει η γενική λύση r(s) = αe s + be s, (α, b R). Για α = 0, b = 1 παίρνουμε r(s) = e s και z(s) = s 0 1 e 2t dt. Για τις επιλογές αυτές των συναρτήσεων r, z : R + R παίρνουμε την παραμέτρηση X : R + R M της ψευδοσφαίρας (είναι μια συμπαγής επιφάνεια με σταθερή καμπυλότητα Gauss K = 1). Σχήμα 5.6: Η ψευδόσφαιρα. Η αντίστοιχη πρώτη θεμελιώδης μορφή είναι ( ) ( Ẽ F F G = [d X][d X] t = e 2s ). Εισάγουμε μια νέα μεταβλητή u > 0 μέσω της s(u) = ln u, οπότε λαμβάνουμε μια νέα παραμέτρηση X : R + R M της ψευδοσφαίρας όπου X(u, v) = X ( s(u), v ). Από τον κανόνα αλυσίδας είναι X u = s u Xs = 1 u X s, οπότε παίρνουμε την πρώτη θεμελιώδη μορφή της παραμέτρησης X ( ) ( ) E F = [dx][dx] t = 1u F G 0 1 Με τον τρόπο αυτό επάγεται η μετρική (τοπική ισομετρία) ds 2 = 1 ( du 2 u 2 + dv 2)
107 106 Η απεικόνιση Gauss και καμπυλότητα στο άνω ημιεπίπεδο H 2 = {(v, u) R 2 : u > 0}. Το ζεύγος (H 2, ds 2 ) ονομάζεται υπερβολικός χώρος (hyperbolic space) και η μετρική ds 2 υπερβολική μετρική. Ο υπερβολικός χώρος αποτελεί ένα μοντέλο μη Ευκλείδειας γεωμετρίας (δηλαδή μιας γεωμετρίας όπου δεν ισχύει το πέμπτο αίτημα (των παραλλήλων) του Ευκλείδη). Κλείνουμε το κεφάλαιο αυτό με δύο ενδιαφέροντα αποτελέσματα ὁλικού χαρακτήρα για μια επιφάνεια M. Πρώτα θυμίζουμε το παρακάτω λήμμα από τον λογισμό συναρτήσεων πολλών μεταβλητών Λήμμα 5.1. Εστω U ανοικτό και συνεκτικό υποσύνολο του επιπέδου. Αν f : U R 2 είναι μια λεία απεικόνιση τέτοια ώστε f x = f y = 0, τότε η f είναι η σταθερή απεικόνιση. Θεώρημα 5.5. Εστω M μια συνεκτική προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2. Εάν κάθε σημείο p M είναι ομφαλικό, τότε η M είναι τμήμα είτε ενός επιπέδου είτε μιας σφαίρας. Απόδειξη. Εστω X : U M μια παραμέτρηση της επιφάνειας M με το U να είναι συνεκτικό υποσύνολο του R 2. Επειδή κάθε σημείο του τμήματος της επιφάνειας X(U) είναι ομφαλικό, υπάρχει μια λεία απεικόνιση f : U R τέτοια ώστε ο τελεστής σχήματος να δίνεται ως S p : T p M T p M (ax u + bx v ) f(u, v)(ax u + bx v ), οπότε έχουμε ότι (N X) u = fx u και (N X) v = fx v. Ειδικότερα, είναι 0 = (N X) uv (N X) vu = ( fx u ) v ( fx v ) u = f v X u fx uv + f u X v + fx vu = f v X u + f u X v. Τα διανύσματα X u και X v είναι γραμμικώς ανεξάρτητα, οπότε θα είναι f u = f v = 0. Επειδή το πεδίο ορισμού U της f είναι συνεκτικό, η f είναι σταθερή στο U και άρα σε όλη την επιφάνεια M, αφού η M είναι συνεκτική. Αν f = 0, τότε ο τελεστής σχήματος είναι ο μηδενικός τελεστής, οπότε από Θεώρημα 5.1 η επιφάνεια περιέχεται σε ένα επίπεδο. Αν f 0, τότε ορίζουμε Y : U R 3 με τιμή Y (u, v) = X(u, v) + 1 N(u, v). f Τότε dy = dx + 1 f dn = dx 1 fdx = 0, f
108 Παράλληλες επιφάνειες 107 άρα η Y είναι σταθερή και X Y 2 = 1. Αυτό σημαίνει ότι το τμήμα της επιφάνειας X(U) περιέχεται f 2 σε μια σφαίρα με κέντρο το Y και ακτίνα 1. Επειδή η M είναι συνεκτική, όλη η επιφάνεια θα περιέχεται f στην ίδια σφαίρα. Θεώρημα 5.6. Εστω M μια συμπαγής κανονική επιφάνεια. Τότε υπάρχει τουλάχιστον ένα σημείο p M με θετική καμπυλότητα Gauss K(p). Απόδειξη. Θεωρούμε τη συνάρτηση f : M R με τύπο f(p) = p 2. Η f είναι συνεχής και επειδή η επιφάνεια M είναι συμπαγής, τότε θα λαμβάνει μέγιστη και ελάχιστη τιμή. Εστω p 0 το σημείο της M, όπου η f λαμβάνει τη μέγιστη τιμή. Επειδή f(p 0 ) = p 0 2, το σημείο p 0 M έχει τη μέγιστη απόσταση από την αρχή τον αξόνων. Εστω r = p 0. Τότε η M περιέχεται σε μια σφαίρα S 2 r ακτίνας r. Ισχυρισμός. K(p 0 ) 1 r 2. Εστω Z T p0 M και γ : I M καμπύλη στην επιφάνεια M με γ(0) = p 0 και γ (0) = Z. Τότε η σύνθεση f γ : I R λαμβάνει και αυτή μέγιστη τιμή για t = 0. Συνεπώς θα έχουμε Επίσης, ισχύει d dt (f γ) t=0 = 0, d 2 dt 2 (f γ) t=0 0. f γ(t) = γ(t) 2 = γ(t), γ(t), άρα d dt (f γ(t)) t=0 = 2 γ(t), γ (t) t=0 0 = 2 γ(0), γ (0) = 2 p 0, Z. Άρα p 0, Z = 0 για κάθε Z T p0 M μοναδιαίο, συνεπώς, p 0 T p0 M. Επιπλέον, έχουμε ότι d 2 dt 2 (f γ(t)) t=0 = 2 γ (t), γ (t) t=0 + γ(t), γ (t) t=0 0 d2 dt 2 (f γ(t)) t=0 = 2 γ (0), γ (0) + 2 γ(0), γ (0) = 2 Z, Z + 2 p 0, γ (0) = p o, γ (0) 1 p 0, γ (0). Υπολογίζουμε τώρα τις κύριες καμπυλότητες της M στο σημείο p 0. Επειδή το p 0 r = 1 p 0 p 0 είναι μοναδιαίο διάνυσμα κάθετο στην M, υπολογίζουμε πρώτα την κάθετη καμπυλότητα ως κ p0 (Z) = N(p 0 ), γ (0) = p 0 r, γ (0) 1 r. Ειδικότερα, οι κύριες καμπυλότητες κ 1, κ 2 είναι μικρότερες από 1. Άρα για την καμπυλότητα Gauss στο r σημειο p 0 θα έχουμε ότι K(p 0 ) = κ 1 (p 0 )κ 2 (p 0 ) 1 r 1 r = 1 r 2 > 0. Πόρισμα 5.2. Δεν υπάρχουν συμπαγείς επιφάνειες στον R 3 με K 0. συμπαγείς επιφάνειες του R 3 ελάχιστης έκτασης. Ειδικότερα, δεν υπάρχουν
109 108 Η απεικόνιση Gauss και καμπυλότητα Το παρακάτω θεώρημα αποτελεί ένα σημαντικό αποτέλεσμα της ολικής διαφορικής γεωμετρίας. Θεώρημα 5.7. (Liebmann) Εστω M συμπαγής επιφάνεια με σταθερή καμπυλότητα Gauss K. Τότε η 1 M είναι μια σφαίρα ακτίνας. K 5.2 Λυμένα παραδείγματα Παράδειγμα 5.3. Δείξτε ότι το παραβολοειδές z = x 2 + y 2 είναι μια προσανατολισμένη επιφάνεια Λύση Μια παραμέτρηση του παραβολοειδούς είναι η X(u, v) = (u, v, u 2 + v 2 ). Θεωρούμε το μοναδιαίο κάθετο διάνυσμα που παίρνουμε από την παραμέτρηση N(u, v) = X u(u, v) X v (u, v) X u (u, v) X v (u, v) = 1 ( 2u, 2v, 1) u 2 + 4v2 Το N είναι μοναδιαίο, λείο κάθετο διανυσματικό πεδίο του παραβολοειδούς, επομένως το παραβολοειδές είναι προσανατολισμένη επιφάνεια. Παράδειγμα 5.4. Δίνεται η επιφάνεια του Enneper M με παραμέτρηση X : R R + R 3 X(u, v) = ( u u3 3 + uv2, v v3 3 + vu2, u 2 v 2). Σημειώνουμε ότι η επιφάνεια αυτή έχει αυτοτομές (κάντε γράφημα με Mathematica) και η παραπάνω παραμέτρηση αποτελεί τον μοναδικό χάρτη της. Βρείτε τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης, την απεικόνιση Gauss, τον τελεστή σχήματος την καμπυλότητα Gauss, τη μέση καμπυλότητα και τις κύριες καμπυλότητες. Λύση Είναι X u = (1 u 2 + v 2, 2uv, 2u), X v = (2uv, 1 v 2 + u 2, 2v), ( E F F G ) = [dx][dx] t, άρα E(u, v) = X u, X u = ( u 2 + v ) 2 F (u, v) = X u, X v = 0 G(u, v) = X v, X v = ( u 2 + v ) 2 (ελέγξτε τις πράξεις). Η μετρική ds 2 που επάγεται στην περιοχή παραμέτρησης U = R R 3 είναι ds 2 = Edu 2 + 2F dudv + Gdv 2 και συγκεκριμένα ( ) ds 2 (u,v) (Z, W ) = E(u, v) F (u, v) Zt W F (u, v) G(u, v) ( ( u = Z t 2 + v ) 2 0 ( 0 u 2 + v ) 2 ) W
110 Λυμένα παραδείγματα 109 για κάθε (u, v) U R 2 και Z, W R 2. Η απεικόνιση Gauss είναι N : M S 2 N(u, v) = X u X v X u X v = (κάντε τις πράξεις είναι αρκετές!). X u X v = 1 ( 2u, 2v, 1 u 2 EG F 2 (u 2 + v 2 + v 2) + 1) Για τα θεμελιώδη ποσά δεύτερης τάξης χρησιμοποιούμε τους τύπους 1 ( e = N, X uu = 4u 2 u 2 + v 2 + 4v u 2 2v 2) = f = N, X uv = 0 g = N, X vv = 2. Ο τελεστής σχήματος στο τυχαίο σημείο p = X(u, v) M είναι S p : T p M T p M, S p (Z) = dn p (Z) και γνωρίζουμε ότι ο πίνακάς του είναι [S p ] = = ( ) ( ) 1 ( ) ( ) e f E F 1 e f G F = f g F G EG F 2 f g F E ( ) ( ) ( 1 ( u 2 + v ) = ( u 2 + v ) ). Ο τελεστής σχήματος (ως γραμμική απεικόνιση) καθορίζεται πλήρως από τον παραπάνω πίνακα. Οι ιδιοτιμές του τελεστή σχήματος είναι οι κύριες καμπυλότητες, άρα κ 1 = κ 2 = 2 ( u 2 + v ) 2. Τέλος, η καμπυλότητα Gauss είναι K(u, v) = det[s p ] = 4 ( u 2 + v ) 4 και η μέση καμπυλότητα είναι H = 1 2 tr[s p] = 1 2( κ1 + κ 2 ) = 0, δηλαδή η επιφάνεια M είναι ελάχιστης έκτασης. Παράδειγμα 5.5. Θεωρούμε την κανονική επιφάνεια M R 3 με (ολική) παραμέτρηση X : R 2 M, X(u, v) = (u, v, u 2 v 2 ). α) Υπολογίστε τα θεμελιώδη ποσά πρώτης τάξης της M ως προς την παραμέτρηση αυτή. β) Βρείτε μια απεικόνιση Gauss της M. γ) Βρείτε τη δεύτερη θεμελιώδη μορφή και την καμπυλότητα Gauss της M.
111 110 Η απεικόνιση Gauss και καμπυλότητα δ) Εστω γ : I M μια καμπύλη στην M με γ(0) = X(0, 0) M. Αποδείξτε ότι η κάθετη καμπυλότητα Λύση της M στο σημείο γ(0) ως προς τη διεύθυνση του διανύσματος γ(0) = ax u + bx v παίρνει πάντα τιμές στο διάστημα [ 2, 2]. α) Είναι X u = (1, 0, 2u), X v = (0, 1, 2v). Άρα E = X u, X u = 1 + 4u 2, F = X u, X v = 4uv G = X v, X v = 1 + 4v 2. β) Μια απεικόνιση Gauss είναι N ( X(u, v) ) = X u X v X u X v = 1 ) 2u, 2v, 1. 4u 2 + 4v 2 + 1( γ) Υπολογίζουμε X uu = (0, 0, 2), X uv = (0, 0, 0), X vv = (0, 0, 2) άρα τα θεμελιώδη ποσά δεύτερης τάξης είναι e = N, X uu = f = N, X uv = 0 g = N, X vv = 2 4u 2 + 4v u 2 + 4v Η δεύτερη θεμελιώδης μορφή είναι II = 2 2 4u 2 + 4v du2 4u 2 + 4v dv2. Τέλος, είναι K = eg f 2 EG F 2 = 4 ( 4u 2 + 4v ) 2 (μονίμως αρνητική). δ) Είναι γ(0) 2 = a 2 + b 2 το οποίο πρέπει να είναι μοναδιαίο διάνυσμα, άρα a = cos θ, b = sin θ. Συνεπώς, η κάθετη καμπυλότητα στο σημείο p = γ(0) ως προς τη διεύθυνση του Z = γ(0) είναι κ γ(0) ( γ(0) ) = IIp (Z, Z) = 2 cos2 θ sin 2 θ 1 = 2 cos 2θ [ 2, 2]. Εδώ λάβαμε υπόψη από το γ) ότι II X(u,v) (ax u + bx v ) = ea 2 + 2fab + gb 2 = 2(a 2 b 2 ) 4u 2 + 4v Παράδειγμα 5.6. Δείξτε ότι η μέση καμπυλότητα μιας κανονικής επιφάνειας στο σημείο p δίνεται από την σχέση H = 1 2π κ p (θ)dθ, 2π 0 όπου κ p (θ) είναι η κάθετη καμπυλότητα στο p ως προς μια κατεύθυνση που σχηματίζει γωνία θ με σταθερό διάνυσμα.
112 Λυμένα παραδείγματα 111 Λύση Από τον τύπο του Euler κ p (θ) = κ 1 cos 2 θ + κ 2 sin 2 θ, όπου κ 1, κ 2 είναι οι κύριες καμπυλότητες στο p. Επομένως, έχουμε Άρα 2π 0 κ p (θ)dθ = 2π 0 = κ 1 2π 2π 2π (κ 1 cos 2 θ + κ 2 sin 2 θ)dθ = κ 1 cos 2 θdθ + κ 2 sin 2 θdθ 0 cos 2θ dθ + κ 2 2π 1 2π κ p (θ)dθ = κ 1π + κ 2 π 2π 0 2π cos 2θ 2 = κ 1 + κ dθ = κ 1 π + κ 2 π. Παράδειγμα 5.7. Εστω μια κανονική επιφάνεια M και p M. Αν w 1, w 2 T p M είναι γραμμικώς ανεξάρτητα διανύσματα τα οποία ικανοποιούν τις σχέσεις S p (w 1 ) = 3w 1 2w 2 και S p (w 2 ) = w 1, όπου S p = dn p είναι ο τελεστής σχήματος της M στο p, να υπολογιστούν οι κύριες καμπυλότητες της επιφάνειας M στο σημείο p. Λύση Για να υπολογίσουμε τις κύριες καμπυλοτητες, πρέπει να υπολογίσουμε τις ιδιοτιμές του τελεστή σχήματος S p : T p M T p M. Εστω λ μια ιδιοτιμή του S p και u ένα ιδιοδιάνυσμα που αντιστοιχεί σε αυτήν. Επειδή = H. τα w 1, w 2 είναι γραμμικώς ανεξάρτητα, θα έχουμε u = aw 1 + bw 2. Επειδή S p (u) = λu και S p (u) = S p (aw 1 + bw 2 ) = as p (w 1 ) + bs p (w 2 ) = a(3w 1 2w 2 ) + bw 1 = (3a + b)w 1 + ( 2a)w 2, έχουμε ότι (3a + b)w 1 + ( 2a)w 2 = λ(aw 1 + bw 2 ), δηλαδή (3a + b λa)w 1 + ( 2a λb)w 2 = 0. Από την τελευταία εξίσωση και αφού τα w 1, w 2 είναι γραμμικώς ανεξάρτητα θα έχουμε Επειδή το u είναι ένα ιδιοδιάνυσμα, θα είναι u 0, οπότε ( ) ( ) a 0. b 0 (3 λ)a + b = 0, 2a + λb = 0. (5.9) Το γραμμικό και ομογενές σύστημα (5.9) πρέπει να έχει μη μηδενική λύση. Άρα ( ) 3 λ 1 det = 0 λ 2 3λ + 2 = 0. 2 λ Απο την τελευταία εξίσωση παίρνουμε λ = 1 και λ = 2. Αφού οι ιδιοτιμές του S p είναι το 1 και 2, οι κύριες καμπυλότητες της επιφάνειας στο σημείο p είναι το 1 και 2.
113 112 Η απεικόνιση Gauss και καμπυλότητα Παράδειγμα 5.8. Δίνεται μια κανονική επιφάνεια M και ο εφαπτόμενος χώρος της T p M στο σημείο p M. Αν υποθέσουμε ότι w 1, w 2 T p M είναι γραμμικώς ανεξάρτητα διανύσματα, τότε ισχύουν οι σχέσεις (1) S p (w 1 ) S p (w 2 ) = K(p)(w 1 w 2 ), (2) S p (w 1 ) w 2 + w 1 S p (w 2 ) = 2H(p)(w 1 w 2 ). Λύση Τα διανύσματα w 1, w 2 αποτελούν βάση του εφαπτόμενου χώρου T p M, οπότε μπορούμε να γράψουμε ότι S p (w 1 ) = λ 1 w 1 + µ 1 w 2, S p (w 2 ) = λ 2 w 1 + µ 2 w 2, οπότε ο πίνακας του τελεστή σχήματος S p : T p M T p M (ως προς τη βάση αυτή) είναι ο ( ) [S p ] = λ 1 λ 2 µ 1 µ 2. Επομένως, θα είναι K(p) = det([s p ]) = λ 1 µ 2 λ 2 µ 1 H(p) = 1 2 tr([s p]) = 1 2 (λ 1 + µ 2 ), οπότε S p (w 1 ) S p (w 2 ) = (λ 1 w 1 + µ 1 w 2 ) (λ 2 w 1 + µ 2 w 2 ) = λ 1 λ 2 (w 1 w 1 ) + λ 1 µ 2 (w 1 w 2 ) + λ 2 µ 1 (w 2 w 1 ) + µ 1 µ 2 (w 2 w 2 ) = (λ 1 µ 2 λ 2 µ 1 )(w 1 w 2 ) = K(p)(w 1 w 2 ). Ανάλογα, έχουμε ότι S p (w 1 ) w 2 + w 1 S p (w 2 ) = (λ 1 w 1 + µ 1 w 2 ) w 2 + w 1 (λ 2 w 1 + µ 2 w 2 ) = (λ 1 + µ 2 )(w 1 w 2 ) = 2H(p)(w 1 w 2 ). 5.3 Ασκήσεις 1. Υπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της επιφάνειας X(u, v) = (u+v, u v, uv) στο σημείο (2, 0, 1.) 2. Εστω U ανοικτό υποσύνολο του R 3 και q R μια κανονική τιμή της διαφορίσιμης συνάρτησης f : U R. Αποδείξτε ότι η κανονική επιφάνεια M = f 1 ({q}) του R 3 είναι προσανατολίσιμη. 3. Υπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της σφαίρας Sr 2 = { (x, y, z) R 3 : x 2 + y 2 + z 2 = r 2}. 4. Δίνεται η επιφάνεια του Enneper με παραμέτρηση X : R R + R 3 X(u, v) = (3u u 3 + 3uv 2, 3v v 3 + 3vu 2, 3u 2 3v 2 ). Υπολογίστε:
114 Ασκήσεις 113 (α) την πρώτη θεμελιώδη μορφή (β) τη δεύτερη θεμελιώδη μορφή (γ) τις κύριες καμπυλότητες (δ) την καμπυλότητα Gauss και τη μέση καμπυλότητα. Σχήμα 5.7: Η επιφάνεια του Enneper. 5. Υπολογίστε την καμπυλότητα Gauss και τη μέση καμπυλότητα της αλυσοειδούς επιφάνειας (catenoid) M με παραμέτρηση X : R R + R 3 ( 1 + r 2 X(θ, r) = 2r cos θ, 1 + r2 2r ) sin θ, log r. Βρείτε μια εξίσωση της μορφής f(x, y, z) = 0 που να περιγράφει την M. Σχήμα 5.8: Αλυσοειδής επιφάνεια. 6. Εστω X, Y : R 2 R 3 με X(u, v) = (cosh u cos v, cosh u sin v, u) Y (u, v) = (sinh u cos v, sinh u sin v, v) οι παραμετρήσεις της αλυσοειδούς και ελικοειδούς επιφάνειας αντίστοιχα. Υπολογίστε τις κύριες καμπυλότητες κ 1, κ 2 των X, Y.
115 114 Η απεικόνιση Gauss και καμπυλότητα Σχήμα 5.9: Ελικοειδής επιφάνεια. 7. Αποδείξτε ότι η δεύτερη θεμελιώδης μορφή μιας κανονικής επιφάνειας M του R 3 παραμένει αναλλοίωτη κάτω από στερεές κινήσεις. 8. Εστω γ : R R 3 μια κανονική καμπύλη με παραμέτρηση ως προς το μήκος τόξου και με καμπυλότητα μη μηδενική. Εστω n, b τα διανύσματα της πρώτης καθέτου και της δεύτερης καθέτου της γ αντίστοιχα. Για r > 0 υποθέτουμε ότι ο σωλήνας (tube) M ακτίνας r περί την γ με παραμέτριση X : R 2 R 3, X(s, θ) = γ(s) + r(cos θ n(s) + sin θ b(s)) είναι μια κανονική επιφάνεια του R 3. καμπυλότητα Gauss K της επιφάνειας M ως προς s, θ, r, k(s) και τ(s). Υπολογίστε την 9. Εστω X : U R 3 παραμέτρηση μιας επιφάνειας M του R 3 με απεικόνιση Gauss N : M S 2 και με κύριες καμπυλότητες k 1 = 1 r 1, k 2 = 1 r 2. Εστω r R τέτοιο ώστε η X r : U R 3 με X r (u, v) = X(u, v) + rn(u, v) να είναι παραμέτρηση μιας επιφάνειας του R 3. Αποδείξτε ότι οι κύριες καμπυλότητες της X r ικανοποιούν τις σχέσεις k 1 (r) = 1 r 1 r και k 2(r) = 1 r 2 r. 10. Υπολογίστε την καμπυλότητα Gauss της επιφάνειας με παραμέτρηση X : R R M, X a (r, θ) = ( ( ) ( ) ) θ θ r sin a cos, r sin a sin, r cos a. sin a sin a 11. Εφοδιάζουμε τους χώρους R 2 και R 4 με τα κανονικά εσωτερικά γινόμενα. Αποδείξτε ότι η παραμέτρηση X : R 2 R 4 με X(u, v) = (cos u, sin u, cos v, sin v) του συμπαγούς δακτυλίου (torus) M στον R 4 είναι ισομετρική. Τί μας λέει αυτό για την καμπυλότητα Gauss του M; 12. Εστω α(s) μια καμπύλη μοναδιαίας ταχύτητα με στρέψη τ(s) 0 και διάνυσμα δεύτερης κάθετης B(s). Θεωρούμε την επιφάνεια M με τοπική παραμέτρηση X(s, u) = α(s) + ub(s),
116 Ασκήσεις 115 γνωστή ως ευθειογενής επιφάνεια. Αποδείξτε ότι η καμπυλότητα Gauss της M στο σημείο X(s, u) δίνεται από την σχέση τ(s) 2 K(s, u) = (1 + u 2 τ(s) 2 ) (a) Εξηγήστε (χωρίς ιδιαίτερους υπολογισμούς) γιατί οι παρακάτω επιφάνειες δεν είναι ανα δύο τοπικά ισομετρικές (1) Η σφαίρα, (2) Ο κύλινδρος, (3) Το υπερβολικό παραβολοειδές z = x 2 y 2. (b) Δώστε παράδειγμα επιφάνειας με σταθερή καμπυλότητα Gauss K = 1. Γράψτε την πρώτη θεμελιώδη μορφή αυτής. 14. Αναζητήστε στη βιβλιογραφία μια απόδειξη του Θεωρήματος 5.7.
117 116 Η απεικόνιση Gauss και καμπυλότητα
118 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
119 118 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
120 Κεφάλαιο 6 Το Θαυμαστό Θεώρημα Σύνοψη Στο Κεφάλαιο αυτό αποδεικνύουμε ένα από τα δύο κεντρικά θεωρήματα της θεωρίας επιφανειών (το άλλο είναι το Θεώρημα των Gauss-Bonnet). Το θεώρημα αυτό είναι γνωστό ως Θαυμαστό Θεώρημα (Theorema Egregium) και αποδείχτηκε απο τον Johann Carl Friedrich Gauss το Ο Gauss εντυπωσιάστηκε από το γεγονός ότι η καμπυλότητα μιας επιφάνειας, αν και ορίζεται ως μέγεθος το οποίο εξαρτάται από τον τρόπο που βλέπουμε την επιφάνεια εξωτερικά, τελικά εξαρτάται μόνο από την εσωτερική γεωμετρία της επιφάνειας, δηλαδή τη μετρική. Με άλλα λόγια, η καμπυλότητα Gauss είναι μια ισομετρική αναλλοίωτη. Στο Κεφάλαιο 5 είδαμε ότι η καμπυλότητα Gauss σε οποιοδήποτε σημείο μιας επιφάνειας M δίνεται από την σχέση K = eg f 2, δηλαδή εξαρτάται τόσο από την πρώτη όσο και από τη δεύτερη θεμελιώδη EG F 2 μορφή. Γεωμετρικά, αυτό σημαίνει ότι για να διαπιστώσουμε την κύρτωση μιας επιφάνειας, πρέπει να την παρατηρήσουμε από μακριά. Αυτό το οποίο απέδειξε ο Gauss και το θεώρησε ως Θαυμαστό Θεώρημα (Theorema Egregium) είναι ότι η ποσότητα eg f 2 είναι δυνατόν να εκφραστεί συναρτήσει των ποσοτήτων E, F, G (εσωτερικές ποσότητες της επιφάνειας), αν και από μόνες τους οι ποσότητες e, f, g δεν είναι εσωτερικές ποσότητες της επιφάνειας. Συνεπώς, η καμπυλότητα Gauss μιας επιφάνειας μπορεί να πιστοποιηθεί (μετρηθεί) από έναν παρατηρητή ο οποίος βρίσκεται επάνω στην επιφάνεια και όχι εκτός αυτής. Το αποτέλεσμα αυτό του Gauss χρησιμοποίησε αρκετά αργότερα ο μαθητής του Georg Friedrich Bernhard Riemann, προκειμένου να ορίσει έννοια καμπυλότητας σε έναν χώρο οποιασδήποτε διάστασης, γνωστός σήμερα ως λεία πολλαπλότητα. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7], [8], [9]. Προαπαιτούμενη γνώση Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα. Η διατύπωση του θεωρήματος έχει ως εξής: Θεώρημα 6.1. (Θαυμαστό Θεώρημα Theorema Egregium) Εστω M μια κανονική επιφάνεια του R 3. Τότε η καμπυλότητα Gauss K της M καθορίζεται πλήρως από την πρώτη θεμελιώδη μορφή. Ισοδύναμα, η καμπυλότητα Gauss παραμένει αναλλοίωτη, όταν η επιφάνεια παραμορφώνεται χωρίς τέντωμα. Κάποια άμεσα συμπεράσματα είναι τα εξής: 119
121 120 Το θαυμαστό Θεώρημα Πόρισμα 6.1. Εάν δύο επιφάνειες είναι τοπικά ισομετρικές, τότε οι καμπυλότητες Gauss στα αντίστοιχα σημεία τους είναι ίσες. Πόρισμα 6.2. Δεν υπάρχει τοπική παραμέτρηση της σφαίρας S 2 η οποία να διατηρεί τις αποστάσεις. Ισοδύναμα, δεν είναι δυνατόν να γίνει ένα κομμάτι της σφαίρας επίπεδο, ώστε τα μήκη να διατηρούνται. Απόδειξη. Εστω ότι υπάρχει μια τοπική παραμέτρηση X : U R 2 S 2 η οποία να είναι ισομετρία. Τότε η καμπυλότητα Gauss του επιπέδου και της σφαίρας θα ήταν ίσες. Αλλά γνωρίζουμε ότι για την σφαίρα η καμπυλότητα Gauss είναι σταθερή K = 1 0, που είναι η καμπυλότητα του επιπέδου. Απόδειξη του Θεωρήματος 6.1. Θυμίζουμε ότι η καμπυλότητα Gauss ορίζεται ως η ορίζουσα του τελεστή σχήματος της επιφάνειας, άρα θα πρέπει να εκφράσουμε την ορίζουσα αυτή συναρτήσει των E, F, G. Εστω X : U M μια τοπική παραμέτρηση της επιφάνειας M. Τότε η πρώτη θεμελιώδης μορφή καθορίζεται από τον πίνακα ( E F ) ( ) F = [DX][DX] t X u, X u X u, X v =. G X u, X v X v, X v Είναι γνωστό ότι το σύνολο {X u, X v } αποτελεί μια βάση του εφαπτόμενου χώρου της M στο σημείο X(u, v) X(U). Χρησιμοποιούμε τη διαδικασία Gram-Schmidt, προκειμένου να πάρουμε μια ορθοκανονική βάση {Z, W } του εφαπτόμενου χώρου ως εξής: Θέτουμε και και τελικά είναι Z = X u E W = X v X v, Z Z = X v X v, X u X u X u, X u W = W W = E EG F 2 (X v F E X u). = X v F E X u, Από τις παραπάνω εκφράσεις των διανυσμάτων Z και W προκύπτει ότι υπάρχουν συναρτήσεις a, b, c : U R, οι οποίες εξαρτώνται μόνο από τις συναρτήσεις E, F, G, έτσι ώστε Z = ax u, W = bx u + cx v. Ορίζουμε μια τοπική απεικόνιση Gauss N : X(U) S 2 ως N = X u X v X u X v = Z W. Τότε το σύνολο {Z, W, N} αποτελεί μια (θετικά προσανατολισμένη) ορθοκανονική βάση του R 3 επί του ανοικτού X(U) M (δηλαδή για κάθε (u, v) U είναι N(X(u, v)) X(U)). Συνεπώς, τα διανύσματα Z u, Z v, W u, W v θα γράφονται ως γραμμικός συνδυασμός των στοιχείων της βάσης αυτής ως εξής: Z u = Z u, Z Z + Z u, W W + Z u, N N Z v = Z v, Z Z + Z v, W W + Z v, N N W u = W u, Z Z + W u, W W + W u, N N W v = W v, Z Z + W v, W W + W v, N N.
122 Το θαυμαστό Θεώρημα 121 (Ελέγξτε τις παραπάνω ισότητες παίρνοντας διαδοχικά τα εσωτερικά γινόμενα των διανυσμάτων στο αριστερό μέλος με τα Z, W, N). Επειδή τα διανύσματα Z, W έχουν μέτρο 1, παραγωγίζουμε τις ισότητες Z, Z = W, W = 1 διαδοχικά ως προς u και v και παίρνουμε ότι Z u, Z = Z v, Z = W u, W = W v, W = 0, συνεπώς οι παραπάνω εκφράσεις των διανυσμάτων Z u, Z v, W u, W v απλουστεύονται ως εξής: Z u = Z u, W W + Z u, N N (6.1) Z v = Z v, W W + Z v, N N (6.2) W u = W u, Z Z + W u, N N (6.3) W v = W v, Z Z + W v, N N. (6.4) Στη συνέχεια, ο παρακάτω υπολογισμός δείχνει ότι η ποσότητα Z u, W είναι συνάρτηση των E, F, G : U R και ανάλογα αποδεικνύεται και για την ποσότητα Z v, W (άσκηση): Z u, W = (ax u ) u, W = a u X u + ax uu, bx u + cx v = a u be + a u cf + ab X uu, X v + ac X uu, X v = a u be + a u cf abe u + ac(f u 1 2 E v). Η απόδειξη θα τελειώσει εκφράζοντας την ποσότητα Z u, W v Z v, W u συναρτήσει της καμπυλότητας Gauss K και των E, F, G. Πράγματι, είναι Z u, W v Z v, W u = Z uv, W + Z u, W v Z vu, W Z v, W u = Z u, W v Z v, W u = K EG F 2, όπου στην τελευταία ισότητα χρησιμοποιήσαμε το παρακάτω λήμμα. Συπεπώς, η καμπυλότητα Gauss της επιφάνειας M εκφράζεται ως K = Z u, W v Z v, W u, EG F 2 δηλαδή εξαρτάται μόνο από τις συναρτήσεις E, F, G και τις παραγώγους αυτών και το θεώρημα αποδείχτηκε. Λήμμα 6.1. Με τις παραπάνω υποθέσεις ισχύει η ισότητα Z u, W v Z v, W u = K EG F 2. ( ) a 11 a 12 Απόδειξη. Εστω A = ο πίνακας του τελεστή σχήματος S X(u,v) ως προς τη βάση {X u, X v }, a 21 a 22 όπου det(a) = a 11 a 22 a 12 a 21 = K. Τότε έχουμε ότι N u = a 11 X u + a 21 X v και N v = a 12 X u + a 22 X v,
123 122 Το θαυμαστό Θεώρημα (όπου θυμίζουμε ότι e = N u, X u = N, X uu κλπ). Επίσης, είναι N u N v, N = (a 11 X u + a 21 X v ) (a 12 X u + a 22 X v ), N = (a 11 a 22 a 12 a 21 ) X u X v, N = K ( EG F 2 )N, N = K EG F 2. Ταυτόχρονα όμως, παραγωγίζοντας κατάλληλα την ισότητα N, Z = N, W = 0 ως προς u και v και λαμβάνοντας υπόψη τις σχέσεις (6.1) (6.4) προκύπτει ότι N u N v, N = N u N v, Z W = N u, Z N v, W N u, W N v, Z = Z u, N N, W v W u, N N, Z v = Z u, W v Z v, W u, και το λήμμα αποδείχτηκε. Από την απόδειξη του θαυμαστού θεωρήματος προκύπτει και η εξής (αναμενόμενη πλέον) έκφραση της καμπυλότητας K συναρτήσει των E, F, G και των μερικών παραγώγων τους: K = det 1 2 E vv + F uv 1 2 G 1 uu 2 E u F u 1 2 E v F v 1 2 G u E F det 1 2 G v F G ( ) EG F E v 1 2 G u 1 2 E v E F 1 2 G u F G Ο Frobenius 1 έδωσε στον τύπο αυτό την ακόλουθη συμμετρικότερη μορφή E E u E v [ ( ) 1 K = 4( EG F 2 ) det 1 4 F F u F v 2 Ev F u ( )] Fv G u EG F 2 v EG F 2 u EG F 2 G G u G v Τέλος, στην ειδική περίπτωση που το δίκτυο των παραμετρικών γραμμών επί της επιφάνειας είναι ορθογώνιο (δηλαδή η παραμέτρηση της επιφάνειας είναι ορθογώνια), οπότε F = F u = F v = 0, η παραπάνω σχέση γίνεται [ ( K = 1 1 ) ( G + 1 )] E EG u E u v G v Ολες οι προηγούμενες εκφράσεις είναι χρήσιμες για υπολογισμούς, ιδιαιτέρως όταν γίνεται χρήση υπολογιστή. Το παρακάτω (δύσκολο) θεώρημα απαντά στο ερώτημα πώς σχετίζονται δύο επιφάνειες με ίσες την πρώτη και δεύτερη θεμελιώδη μορφή. 1 Ferdinand Georg Frobenius (6.5)
124 Λυμένα παραδείγματα 123 Θεώρημα 6.2. Εστω M 1, M 2 δύο κανονικές επιφάνειες του R 3 και έστω φ : M 1 M 2 μια αμφιδιαφόριση που διατηρεί την πρώτη και δεύτερη θεμελιώδη μορφή των M 1 και M 2 αντίστοιχα, δηλαδή ισχύει I p (X, Y ) = ( I φ(p) dφp (X), dφ p (Y ) ) II p (X, Y ) = ( II p dφp (X), dφ p (Y ) ) για κάθε p M 1, X, Y T p M 1. Τότε η φ : M 1 M 2 είναι ο περιορισμός φ = Φ M1 στερεάς κίνησης Φ : R 3 R 3 περιορισμένη στην επιφάνεια M 1. : M 1 M 2 μιας Ερώτημα-Προβληματισμός. Θα θέλαμε να προσκαλέσουμε τον αναγνώστη να προβληματιστεί κατά πόσον το αποτέλεσμα του Θαυμαστού Θεωρήματος είναι απόρροια κάποιων τυχαίων ακροβασιών με παραγωγίσεις, ή υπάρχει κάποια βαθύτερη μαθηματική αιτιολόγηση πίσω από αυτό. 6.1 Λυμένα παραδείγματα Παράδειγμα 6.1. Αν η πρώτη θεμελιώδης μορφή μιας επιφάνειας M δίνεται ως I(u, v) = 1 (u 2 + v 2 c 2 ) 2 (du2 + dv 2 ), όπου c R, αποδείξτε ότι η καμπυλότητα Gauss K αυτής είναι σταθερή. Λύση Από τη δοθείσα έκφραση της πρώτης θεμελιώδους μορφής έχουμε E = G = 1 (u 2 + v 2 c 2 ) 2, F = 0. Άρα το παραμετρικό δίκτυο της επιφάνειας είναι ορθογώνιο, κατά συνέπεια η θεμελιώδης εξίσωση του Gauss θα έχει τη μορφή (6.5), δηλαδή [ ( K = 1 1 ) ( G + 1 )] E. EG u E u v G v Αλλά είναι E = G, επομένως θα έχουμε [ ( K = 1 1 ) ( E + 1 )] E. (6.6) E u E u v E v Είναι όμως, άρα, και E = 1 u 2 + v 2 c 2 1 E = u 2 + v 2 c 2 E u = 2u (u 2 + v 2 c 2 ) 2, E v 1 E E u = 2u u 2 + v 2 c 2, 1 E E v 2v = (u 2 + v 2 c 2 ) 2 2v = u 2 + v 2 c 2.
125 124 Το θαυμαστό Θεώρημα Επομένως, ( 1 ) E u E u ( = 2u2 2v 2 + 2c 2 (u 2 + v 2 c 2 ), v 1 E E v ) = 2v2 2u 2 + 2c 2 (u 2 + v 2 c 2 ) 2. (6.7) Η σχέση (6.6), λόγω των σχέσεων (6.7) γίνεται ( 2u K = (u 2 + v 2 c 2 ) 2 2 2v 2 + 2c 2 (u 2 + v 2 c 2 ) 2 + 2v2 2u 2 + 2c 2 ) (u 2 + v 2 c 2 ) 2 = (u 2 + v 2 c 2 ) 2 4c 2 (u 2 + v 2 c 2 ) 2 = 4c2 = σταθερό, οπότε η επιφάνεια M είναι πράγματι σταθερής καμπυλότητας Gauss. Παράδειγμα 6.2. Να βρεθούν οι τιμές της σταθεράς λ, ώστε η επιφάνεια της οποίας η πρώτη θεμελιώδης μορφή παίρνει την έκφραση να έχει μηδενική καμπυλότητα. Λύση ds 2 = v λ du 2 + u λ dv 2, Από την έκφραση της πρώτης θεμελιώδους μορφής συμπεραίνουμε άμεσα ότι E = v λ, F = 0, G = u λ. (6.8) Επομένως η εξίσωση της καμπυλότητας του Gauss θα δίνεται από την σχέση Από τις σχέσεις (7.1) τώρα εύκολα έχουμε ότι [ ( K = 1 1 ) ( G + 1 )] E. (6.9) EG u E u v G v οπότε άρα Επίσης, είναι EG = u λ 2 v λ 2, E v = λ 2 v λ 2 1, 1 G E u = λ 2 u λ 2 1 v λ 2, ( 1 ) G u E u ( v 1 E G v 1 E G v ) = λ 2 G u = λ 2 u λ 2 2, ( ) λ 2 1 u λ 2 1 v λ 2. (6.10) = λ 2 u λ 2 v λ 2 1 = λ 2 ( ) λ 2 1 u λ λ 2 v 2 2. (6.11)
126 Ασκήσεις 125 Η σχέση (6.9) λοιπόν λόγω των (6.10), (6.11) και του γεγονότος ότι K = 0, γίνεται ( ) λ λ ( u λ 2 2 v λ 2 + u λ λ 2 v 1) 2 = 0. (6.12) Η σχέση αυτή όμως ικανοποιείται για κάθε u, v, δηλαδή είναι ταυτότητα ως προς τα u, v. Κατά συνέπεια, έχουμε ότι οπότε ( ) λ λ = 0, λ = 0 ή λ = 2. Στην πρώτη περίπτωση (λ = 0) τα θεμελιώδη ποσά πρώτης τάξης γίνονται E = 1, F = 0, G = 1, οπότε η πρώτη θεμελιώδης μορφή γράφεται ds 2 = du 2 + dv 2, ενώ στη δεύτερη περίπτωση (λ = 2) τα αντίστοιχα θεμελιώδη ποσά πρώτης τάξης είναι E = v 2, F = 0, G = u 2 και η πρώτη θεμελιώδης μορφή γράφεται ds 2 = v 2 du 2 + u 2 dv Ασκήσεις 1. Εκφράστε την ποσότητα Z v, W στην απόδειξη του Θεωρήματος 6.1 ως συνάρτηση των E, F, G : U R. 2. Εστω α (0, π 2 ) και έστω M α η επιφάνεια με τοπική παραμέτρηση X α : R + R M, με τιμή θ θ X α (r, θ) = (r sin α cos( ), r sin α sin( ), r cos α). sin α sin α Υπολογίστε την καμπυλότητα Gauss K της M α. 3. Εστω M μια κανονική επιφάνεια και έστω X : U M μια ορθογώνια παραμέτρηση, δηλαδή τέτοια ώστε F = 0. Αποδείξτε ότι η καμπυλότητα Gauss δίνεται από την έκφραση K = 1 ( ( ) 2 Ev + ( )) Gu. EG v EG u EG 4. Εστω M μια κανονική επιφάνεια και έστω X : U M μια ισοθερμική παραμέτρηση, δηλαδή τέτοια ώστε F = 0 και E = G. Αποδείξτε ότι η καμπυλότητα Gauss δίνεται από την έκφραση K = 1 ( 2 2E u Εναλλακτικά, η παραπάνω έκφραση γράφεται ως 2 (ln E) + 2 v K = 1 2E 2 (ln E), ) (ln E) 2.
127 126 Το θαυμαστό Θεώρημα όπου η συνάρτηση 2 f ονομάζεται ο τελεστής Laplace της f. Κάντε εφαρμογή για τις περιπτώσεις όπου E = 4 (1 + u 2 + v 2 ) 2, E = 4 (1 u 2 v 2 ) 2, E = 1 u Αποδείξτε ότι η καμπυλότητες Gauss των επιφανειών M 1, M 2 με αντίστοιχες παραμετρήσεις X(u, v) = (u cos v, u sin v, v) Y (u, v) = (u cos v, u sin v, ln u) είναι ίσες, εντούτοις οι επιφάνειες έχουν διαφορετικές πρώτες θεμελιώδεις μορφές. Συνεπώς, το αντίστροφο του Πορίσματος 6.1 δεν ισχύει. 6. Εξετάστε αν υπάρχει παραμετρημένη επιφάνεια με E = G = 1, F = 0, e = 1 = g, f = 0.
128 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [5] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [6] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη [7] C. F. Gauss, General Investigations of Curved Surfaces of 1827 and 1825, The Princeton University Library, [8] C. F. Gauss, General Investigations Of Curved Surfaces Unabridged, Wexford College Press, [9] C. F. Gauss, General Investigations of Curved Surfaces, Dover Publications,
129 128 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
130 Κεφάλαιο 7 Οι εξισώσεις Codazzi και Gauss Σύνοψη Στο κεφάλαιο αυτό θα ασχοληθούμε με μια βαθύτερη κατανόηση της καμπυλότητας Gauss. Θα ορίσουμε τα σύμβολα του Christoffel, τα οποία είναι πραγματικές συναρτήσεις Γ k ij : U R σε μια περιοχή παραμέτρησης X : U M μιας επιφάνειας M. Οι συναρτήσεις αυτές θα οριστούν ως οι συντελεστές γραμμικών εκφράσεων των μερικών παραγώγων X uu, X uv, X vv ως προς τη βάση {X u, X v, N} του R 3. Θα καταλήξουμε σε δύο σημαντικές ομάδες εξισώσεων, τις εξισώσεις Codazzi και τις εξισώσεις Gauss, οι οποίες συνδέουν τα θεμελιώδη ποσά πρώτης τάξης E, F, G με την καμπυλότητα K και τα σύμβολα Christoffel Γ k ij. φανεί επίσης ότι τα σύμβολα Christoffel εξαρτώνται μόνο από τα E, F, G, άρα θα έχουμε μια εναλλακτική απόδειξη του Θαυμαστού Θεωρήματος του Gauss. Στη συνέχεια θα δούμε κάποια σημαντικά αποτελέσματα ολικού χαρακτήρα για μια επιφάνεια (όπως για παράδειγμα το Θεώρημα του Liebmann). Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7], [8]. Προαπαιτούμενη γνώση Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα. Εστω M μια κανονική επιφάνεια του R 3 με απεικόνιση Gauss N : M S 2 και έστω X : U R 2 M μια τοπική παραμέτρηση της M. Σε κάθε σημείο του X(U) M ορίζουμε τη βάση του R 3 που αποτελείται από τα διανύσματα {X u, X v, N} και θα μελετήσουμε τις εκφράσεις των παραγώγων των διανυσμάτων X u, X v και των N u, N v ως προς τη βάση αυτή (η μελέτη αυτή είναι ουσιαστικά το ανάλογο των τύπων Frenet στη θεωρία καμπυλών). Θυμίζουμε ότι σε οποιοδήποτε σημείο X(u, v) = p, (u, v) U είναι T p M = span{x u (u, v), X v (u, v)} και το διάνυσμα N(X(u, v)) = X u(u, v) X v (u, v) X u (u, v) X v (u, v) είναι κάθετο στον T pm. Επίσης, θυμίζουμε ότι για τα θεμελιώδη ποσά δεύτερης τάξης, ισχύουν οι σχέσεις e = N, X uu, f = N, X vu, g = N, X vv. (7.1) Προκειμένου να χρησιμοποιήσουμε τον ιστορικά καθιερωμένο συμβολισμό, θέτουμε u 1 και v 2. Ε- πειδή το σύνολο {X u, X v, N} αποτελεί βάση του R 3, υπάρχουν συναρτήσεις Γ 1 11, Γ2 11, Γ1 12, Γ2 12, Γ1 22 και Γ Θα
131 130 Οι εξισώσεις Codazzi και Gauss τέτοιες ώστε X uu = Γ 1 11X u + Γ 2 11X v + en X uv = Γ 1 12X u + Γ 2 12X v + fn X vu = Γ 1 21X u + Γ 2 21X v + fn X vv = Γ 1 22X u + Γ 2 22X v + gn, (7.2) όπου λάβαμε υπόψη τις σχέσεις (7.1). Οι πραγματικές συναρτήσεις Γ k ij (i, j, k {1, 2}) επί του U R2 ονομάζονται σύμβολα του Christoffel (δεύτερου είδους). Λόγω της σχέσης X uv = X vu προκύπτει ότι Γ 1 12 = Γ 1 21, Γ 2 12 = Γ Παράδειγμα 7.1. Θεωρούμε την σφαίρα S 2 με τοπική παραμέτρηση Είναι X(u, v) = (sin u cos v, sin u sin v, cos u). X u = (cos u cos v, cos u sin v, sin u) X v = ( sin u sin v, sin u cos v, 0) X uu = ( sin u cos v, sin u sin v, cos u) = X(u, v) X uv = ( cos u sin v, cos u cos v, 0) X vv = ( sin u cos v, sin u sin v, 0) = sin u(cos v, sin v, 0). Επειδή το διάνυσμα X uu βρίσκεται στη διεύθυνση του διανύσματος N, είναι Γ 1 11 = Γ2 11 = 0. Επιπλέον, παρατηρούμε ότι X uv = cot ux v, άρα Γ 1 12 = 0 και Γ2 12 = cot u. Τέλος, λόγω του ότι X vv = sin u cos ux u sin 2 un παίρνουμε ότι Γ 1 22 = sin u cos u και Γ2 22 = 0. Με παρόμοιες πράξεις βρίσκουμε ότι τα σύμβολα του Cristoffel για την τοπική παραμέτρηση του άνω ημισφαιρίου της σφαίρας S 2, Y (x, y) = (x, y, 1 x 2 y 2 ) είναι τα εξής: ότι Γ 1 11 = x 1 x 2 y 2, Γ1 12 = Γ 1 21 = x 2 y 1 x 2 y 2 Γ 1 22 = x(1 x2 ) 1 x 2 y 2, Γ2 11 = y(1 y2 ) 1 x 2 y 2 Γ 2 12 = Γ 2 xy 2 21 = 1 x 2 y 2, Γ2 22 = y(1 x2 ) 1 x 2 y 2. Στη συνέχεια, παίρνουμε τα εσωτερικά γινόμενα στις εξισώσεις (7.2) με τα X u και X v και λαμβάνουμε X uu, X u = Γ 1 11E + Γ 2 11F X uu, X v = Γ 1 11F + Γ 2 11G X uv, X u = Γ 1 12E + Γ 2 12F X uv, X v = Γ 1 12F + Γ 2 12G X vv, X u = Γ 1 22E + Γ 2 22F X vv, X v = Γ 1 22F + Γ 2 22G. (7.3)
132 Οι εξισώσεις Codazzi και Gauss 131 Παρατηρούμε τώρα ότι ισχύουν οι εξής σχέσεις: X uu, X u = 1 2 X u, X u u = 1 2 E u X uv, X u = 1 2 X u, X u v = 1 2 E v X uv, X v = 1 2 X v, X v u = 1 2 G u X uu, X v = X u, X v u X u, X uv = F u 1 2 E v Παρατηρήσεις. X vv, X u = X u, X v v X uv, X v = F v 1 2 G u X vv, X v = 1 2 X v, X v v = 1 2 G v. (7.4) 1. Τα πρώτα μέλη των σχέσεων (7.4) ονομάζονται σύμβολα του Christoffel πρώτου είδους και συμβολίζονται με Γ ijk, i, j, k = 1, 2. Εύκολα βλέπουμε ότι Γ ijk = Γ jik. Επίσης, από τις σχέσεις (7.4) φαίνεται ότι τα σύμβολα Christoffel πρώτου είδους εκφράζονται συναρτήσει των παραγώγων των θεμελιωδών ποσών πρώτης τάξης. 2. Αν θέσουμε u = x 1, v = x 2 και E = g 11, F = g 12, G = g 22, τότε υπάρχει ο αντίστροφος του πίνακα 1 g = (g ij ), i, j = 1, 2 και αν συμβολίσουμε με g ij,k την παράγωγο του g ij ως προς x k, τότε οι εξισώσεις (7.4) γράφονται Γ ijk = 1 2 (g ik,j + g jk,i g ij,k ). Συνεπώς, λόγω των σχέσεων (7.4) οι σχέσεις (7.3) μπορούν να ξαναγραφτούν ως εξής: ( ) ( ) 1 E F Γ 1 11 F G Γ 2 = 2 E u 11 F u 1 2 E v ( ) ( ) 1 E F Γ 1 12 F G Γ 2 = 2 E v G u ( ) ( ) E F Γ 1 22 F v 1 F G Γ 2 = 2 G u G. v Από τις παραπάνω ισότητες προκύπτουν οι εξής: ( ) ( ) 1 1 Γ 1 11 E F Γ 2 = 2 E u 11 F G F u 1 2 E v ( Γ 1 12 Γ 2 12 ) = ( E F F G ) E v 1 2 G u 1 Ο πίνακας g = (g ij) καλείται και μετρικός τανυστής. = = ( 1 EG F 2 ( 1 EG F 2 G F G F F E F E ) 1 2 E u F u 1 2 E v ) 1 2 E v 1 2 G u (7.5) (7.6)
133 132 Οι εξισώσεις Codazzi και Gauss ( Γ 1 22 Γ 2 22 ) = ( E F F G ) 1 F v 1 2 G u 1 2 G v = ( 1 EG F 2 Από τις σχέσεις (7.5), (7.6), (7.7) παίρνουμε αντίστοιχα ότι Γ 1 11 = Γ 1 22 = Παρατήρηση. 1 (GE u EG F 2 2 Γ 1 12 = 1 (GE v EG F ( GFv EG F 2 GG u 2 F F u + F E v ) 2 ) F G u 2 F G v 2 ) G F F E ) F v 1 2 G u 1 2 G v. (7.7) Γ 2 1 ( F E u 11 = EG F 2 + EF u EE v ), 2 2 Γ 2 1 ( F E v 12 = EG F 2 + EG u ), 2 2 Γ 2 1 ( 22 = F Fv EG F 2 + F G u + EG v ). (7.8) 2 2 Σύμφωνα με την παραπάνω Παρατήρηση 2, αν θέσουμε g 1 = (g kl ) τον αντίστροφο του πίνακα g, οι σχέσεις (7.8) γράφονται ως εξής: Γ k ij = g kl Γ ijk, i, j, k, l {1, 2}. Αυτό το οποίο είναι αξιοσημείωτο από τους παραπάνω τύπους είναι ότι τα σύμβολα του Christoffel, τα οποία καθορίζουν τις εφαπτομενικές συνιστώσες των δεύτερων παραγώγων X.., μπορούν να υπολογιστούν μόνο από τα θεμελιώδη ποσά πρώτης τάξης E, F, G, δηλαδή εξαρτώνται μόνο από την πρώτη θεμελιώδη μορφή της επιφάνειας. Παράδειγμα 7.2. Θα υπολογίσουμε εκ νέου τα σύμβολα Christoffel για την σφαίρα S 2 και θα συγκρίνουμε τα αποτελέσματα με αυτά του Παραδείγματος 7.1. Για την παραμέτρηση που χρησιμοποιήσαμε είναι E = 1, F = 0 και G = sin 2 u. Χρησιμοποιώντας τις σχέσεις (7.8) παίρνουμε ότι 2 ( ) ( ) ( ) ( ) Γ Γ 2 = 11 0 csc 2 = u 0 0 ( ) ( ) ( ) ( ) Γ Γ 2 = 12 0 csc 2 = u sin u cos u cot u ( ) ( ) ( ) ( ) Γ sin u cos u sin u cos u = 0 csc 2 =. u 0 0 Γ 2 22 Συνεπώς, τα μόνα μη μηδενικά σύμβολα Christoffel είναι τα Γ 2 12 = Γ2 21 = cot u και Γ1 22 όπως βρήκαμε στο Παράδειγμα 7.1. = sin u cos u, Προκειμένου να προχωρήσουμε, θυμίζουμε ότι αν S p : T p M ( T p M, ) S p = dn p είναι ο τελεστής a b σχήματος της επιφάνειας M σε ένα σημείο p M με πίνακα A = ως προς τη βάση {X u, X v }, c d τότε ( ) ( ) ( ) 1 ( ) a b e f E F 1 eg ff ef + fe = = c d f g F G EG F 2. (7.9) fg gf ff + ge 2 Θυμίζουμε ότι cscx = 1 1 ονομάζεται συντέμνουσα του x. Παρόμοια secx = ονομάζεται τέμνουσα του x. sin x cos x
134 Οι εξισώσεις Codazzi και Gauss 133 Από την προηγούμενη ισότητα προκύπτει ότι οι μερικές παραγώγοι του N ως προς τα u και v θα είναι N u = dn p (X u ) = S p (X u ) = (ax u + bx v ) N v = dn p (X v ) = S p (X v ) = (cx u + dx v ). (7.10) Παραγωγίζουμε τώρα τις εξισώσεις (7.2), χρησιμοποιούμε την ισότητα των μικτών παραγώγων καθώς και την (7.10) και παίρνουμε: X uuv = (Γ 1 11) v X u + Γ 1 11X uv + (Γ 2 11) v X v + Γ 2 11X vv + e v N + en v = (Γ 1 11) v X u + Γ 1 11( Γ 1 12 X u + Γ 2 12X v + fn ) + (Γ 2 11) v X v ( Γ 1 22 X u + Γ 2 22X v + gn ) + e v N e ( ) cx u + dx v +Γ 2 11 = ( (Γ 1 11) v + Γ 1 11Γ Γ 2 11Γ 1 22 ec ) X u + ( (Γ 2 11) v + Γ 1 11Γ Γ 2 11Γ 2 22 ed ) X v + ( Γ 1 11f + Γ 2 ) 11g + e v N. Επίσης, με παρόμοιο τρόπο προκύπτει ότι X uvu = ( (Γ 1 12) u + Γ 1 12Γ Γ 2 12Γ 1 12 fa ) X u + ( (Γ 2 12) u + Γ 1 12Γ Γ 2 12Γ 2 12 fb ) X v + ( eγ 1 12fΓ 2 ) 12 + f u N. Επειδή X uuv = X uvu, εξισώνουμε τις συνιστώσες των αντίστοιχων διανυσμάτων, όπως φαίνονται παρακάτω: (X u ) : (Γ 1 11) v + Γ 2 11Γ 1 22 ec = (Γ 1 12) u + Γ 1 12Γ Γ 2 12Γ 2 12 fa (X v ) : (Γ 2 11) v + Γ 1 11Γ Γ 2 11Γ 2 22 eb = (Γ 2 12) u + Γ 1 12Γ Γ 2 12Γ 2 12 fb (N) : e v + fγ gγ 2 11 = f u + eγ fγ 2 12 (7.11) Με ανάλογο τρόπο λαμβάνοντας υπόψη ότι X uvv = X vvu, παίρνουμε τις ισότητες των αντίστοιχων παρακάτω συνιστωσών: (X u ) : (Γ 1 12) v + Γ 1 12Γ Γ 2 12Γ 1 22 fb = (Γ 1 22) u + Γ 1 22Γ Γ 2 22Γ 1 12 ga (X v ) : (Γ 2 12) v + Γ 1 12Γ 2 12 fd = (Γ 2 22) u + Γ 1 22Γ 2 11 gc (N) : f v + fγ gγ 2 12 = g u + eγ fγ (7.12) Οι δύο εξισώσεις που προκύπτουν από την ισότητα των κάθετων συνιστωσών είναι γνωστές ως Εξισώσεις Codazzi 3 e v f u = eγ f( Γ 2 12 Γ1 11) gγ 2 11 f v g u = eγ f( Γ 2 22 Γ1 12) gγ 2 12 Χρησιμοποιώντας τώρα τον τύπο για την καμπυλότητα Gauss K = eg f 2 καθώς και ότι τα στοιχεία EG F 2 του πίνακα του τελεστή σχήματος δίνονται από τις εξισώσεις ( ) ( ) ( ) 1 ( ) ( ) a b e f E F 1 e f G F = = c d f g F G EG F 2 ( ) f g F E 3 Καμιά φορά αναφέρονται και ως εξισώσεις των Codazzi - Mainardi
135 134 Οι εξισώσεις Codazzi και Gauss και τις τέσσερεις από τις εξισώσεις (7.11) που αντιστοιχούν στις συνιστώσες X u και X v, λαμβάνουμε τις παρακάτω Εξισώσεις Gauss 4 EK = (Γ 2 11 ) v (Γ 2 12 ) u + Γ 1 11 Γ Γ2 11 Γ2 22 Γ1 12 Γ2 11 (Γ2 12 )2 F K = (Γ 1 12 ) u (Γ 1 11 ) v + Γ 2 12 Γ1 12 Γ2 11 Γ1 22 F K = (Γ 2 12 ) v (Γ 2 22 ) u + Γ 1 12 Γ2 12 Γ1 22 Γ2 11 GK = (Γ 1 22 ) u (Γ 1 12 ) v + Γ 1 22 Γ Γ2 22 Γ1 12 (Γ1 12 )2 Γ 2 12 Γ1 22. Άσκηση 1. Αποδείξτε αναλυτικά τις παραπάνω εξισώσεις του Gauss. Αποδεικνύουμε ενδεικτικά την πρώτη σχέση, χρησιμοποιώντας την δεύτερη εξίσωση από την σχέση (7.11), ειδικότερα είναι: (Γ 2 11) v + Γ 1 11Γ Γ 2 11Γ 2 22 ed = (Γ 2 12) u + Γ 1 12Γ Γ 2 12Γ 2 12 fb (Γ 2 11) v (Γ 2 12) u + Γ 1 11Γ Γ 2 11Γ 2 22 Γ 1 12Γ 2 11 (Γ 2 12) 2 = ed fb = 1 ( ) e( ff + ge) f( ef + fe) EG F 2 όπου στην τρίτη ισότητα χρησιμοποιήσαμε την σχέση ( ). 1 = EG F 2 ( eff + gee + eff f 2 E) 1 = EG F 2 (eg f 2 )E = EK, Άσκηση 2. Αποδείξτε ότι, αν F = 0, τότε η καμπυλότητα Gauss δίνεται από την σχέση K = 1 (( ) ( ) ) 2 Ev Gu +. EG EG v EG u Ως αποτέλεσμα των εξισώσεων Gauss έχουμε μια άλλη απόδειξη του Θαυμαστού Θεωρήματας (Therema Egregium) του Gauss. Θεώρημα 7.1. (Θαυμαστό Θεώρημα του Gauss) Η καμπυλότητα Gauss καθορίζεται πλήρως από την πρώτη θεμελιώδη μορφή, δηλαδή από τα θεμελιώδη ποσά πρώτης τάξης και τις μερικές παραγώγους αυτών. Απόδειξη. Από οποιαδήποτε από τις εξισώσεις του Gauss προκύπτει ότι η καμπυλότητα K εκφράζεται μόνο συναρτήσει των E, F, G, των συμβόλων του Christoffel και των παραγώγων τους, συνεπώς εκφράζεται μόνο συναρτήσει των E, F, G και των παραγώγων τους. Ειδικότερα, η καμπυλότητα Gauss δίνεται από τον τύπο K = 1 G 4 Απεδείχθηκαν από τον Gauss στην εργασία του [4] ( Γ u Γ1 12 v + ( Γ s 22 Γ 1 1s Γ s 12Γ 1 ) ) 2s. s=1
136 Οι εξισώσεις Codazzi και Gauss 135 Παρατήρηση. Ενας παρατηρητής ο οποίος βρίσκεται σε μια επιφάνεια χωρίς να έχει την αίσθηση της τρίτης διάστασης και ο οποίος μπορεί να μετρά τοπικά μήκη και γωνίες, μπορεί να υπολογίσει τα θεμελιώδη ποσά πρώτης τάξης E, F, G, άρα σύμφωνα με το Θαυμαστό Θεώρημα του Gauss μπορεί να υπολογίσει την καμπυλότητα K = κ 1 κ 2. Παρόλα αυτά έχει όμως τη δυνατότητα να υπολογίσει χωριστά τις κύριες καμπυλότητες κ 1 και κ 2, πράγμα που θα απαιτούσε τη γνώση της μεταβολής του κάθετου διανύσματος N. Αυτό σημαίνει ότι, για παράδειγμα, με γνώση μόνο της καμπυλότητας Gauss δεν μπορεί να διακρίνει αν βρίσκεται σε έναν κύλινδρο (κ 1 = 0, κ 2 = 1 r ) ή σε ένα επίπεδο (κ 1 = 0, κ 2 = 0), αφού οι δύο αυτές επιφάνειες έχουν την ίδια πρώτη θεμελιώδη μορφή και K = 0. Πόρισμα 7.1. Αν δύο επιφάνειες είναι τοπικά ισομετρικές, τότε οι αντίστοιχες καμπυλότητες Gauss είναι ίσες. Παράδειγμα 7.3. Εστω X : R R + M μια παραμέτρηση μιας επιφάνεια M με θεμελιώδη ποσά πρώτης τάξης E(u, v) = G(u, v) = v και F (u, v) = 0. Τότε η επιφάνεια M δεν είναι δυνατόν να είναι τοπικά ισομετρική με μια σφαίρα. Πράγματι, από την σχέση (7.8) παίρνουμε ότι Γ 1 11 = 0, Γ2 11 = 1 2v, Γ 1 12 = 1 2v, Γ2 12 = 0, Γ 1 22 = 0, Γ2 22 = 1. Από το Θαυμαστό Θεώρημα θα είναι: 2v K = 1 G ( Γ 1 22 u Γ1 12 v + 2 s=1 ( Γ s 22 Γ 1 1s Γ s 12Γ 1 2s) ) = 1 2v 3. Άρα η καμπυλότητα Gauss K δεν είναι σταθερή, οπότε από το προηγούμενο πόρισμα η επιφάνεια M δεν είναι δυνατόν να είναι (τοπικά) ισομετρική με σφαίρα. Οι εξισώσεις Codazzi μαζί με οποιαδήποτε από τις εξισώσεις Gauss ονομάζονται εξισώσεις συμβατότητας της θεωρίας επιφανειών. Ενα ερώτημα είναι κατά πόσον υπάρχουν και άλλες εξισώσεις συμβατότητας μεταξύ των θεμελιωδών ποσών πρώτης και δεύτερης τάξης για μια επιφάνεια εκτός από τις παραπάνω. Η απάντηση είναι αρνητική. Με άλλα λόγια, διαδοχικές παραγωγίσεις ή άλλες πράξεις δεν είναι δυνατόν να δώσουν επιπλέον σχέσεις μεταξύ των συναρτήσεων E, F, G, e, f, g και των παραγώγων τους. Το παρακάτω θεώρημα δίνει ακριβώς την απάντηση. Θεώρημα 7.2. (Bonnet) Εστω E, F, G, e, f, g : V R 2 R διαφορίσιμες συναρτήσεις στο ανοικτό σύνολο V με E > 0 και G > 0. Υποθέτουμε ότι οι συναρτήσεις αυτές ικανοποιούν τις εξισώσεις Codazzi και Gauss (μία από αυτές) και ότι EG F 2 > 0. Τότε για κάθε q V υπάρχει ανοικτό U V με q U και αμφιδιαφόριση X : U X(U) R 3, τέτοια ώστε η κανονική επιφάνεια X(U) R 3 να έχει τις συναρτήσεις E, F, G, e, f και g ως τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης. Στην περίπτωση που το U είναι συνεκτικό, η αμφιδιαφόριση X είναι μοναδική, μη λαμβάνοντας υπόψη στερεές κινήσεις του R 3. Ουσιαστικά το θεώρημα αυτό είναι ανάλογο της θεωρίας καμπυλών, διότι μας εξασφαλίζει την ύπαρξη επιφάνειας με δεδομένα τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης. Η απόδειξη δεν είναι ιδιαίτερα απλή. Χρειαζόμαστε αποτελέσματα θεωρίας διαφορικών εξισώσεων με μερικές παραγώγους (βλ. [1], [3])
137 136 Οι εξισώσεις Codazzi και Gauss Οι εξισώσεις Coodazzi και Gauss είναι ιδαίτερα δύσκολες στη χρήση τους στη γενική τους μορφή, αλλά κάποιες ειδικές περιπτώσεις έχουν ενδιαφέρουσες εφαρμογές και ταυτόχρονα αναδεικνύουν την αξία τους. Παρακάτω θα παρουσιάσουμε κάποιες από αυτές. Θυμίζουμε πρώτα κάποιους ορισμούς. Ορισμός 7.1. Εστω M R 3 μια προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2. Μια γραμμή καμπυλότητας (line of curvature) στην M είναι μια καμπύλη γ : I M, τέτοια ώστε το διάνυσμα γ (t) να είναι πάντα μια κύρια διεύθυνση. Ορισμός 7.2. Εστω X : U R 2 M μια τοπική παραμέτρηση μιας επιφάνειας M και (u, v) οι συντεταγμένες στο U. Μια u-καμπύλη (αντίστοιχα v-καμπύλη) στην M είναι μια καμπύλη της μορφής u X(u, v 0 ) (αντίστοιχα v X(u 0, v)). Αν τώρα οι μεταβλητές u, v παίρνουν όλες τις τιμές στο U, τότε ορίζεται ένα πλέγμα επιφανειακών καμπύλων στην M που την καλύπτουν. Το πλέγμα αυτό ονομάζεται γραμμές συντεταγμένων (coordinate lines) της M. Το ερώτημα είναι πότε οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας. Ισχύει το εξής: Πρόταση 7.1. Εστω X : U M R 3 μια τοπική παραμέτρηση μιας κανονικής επιφάνειας M και έστω ότι το σύνολο X(U) δεν περιέχει ομφαλικά σημεία (δηλαδή με ίσες κύριες καμπυλότητες). Τότε μια γραμμή συντεταγμένων είναι και γραμμή καμπυλότητας εάν και μόνο εάν ισχύει F f 0. Απόδειξη. Το γεγονός ότι οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας ισοδυναμεί με το ότι οι διευθύνσεις των γραμμών συντεταγμένων είναι πάντα κύριες διευθύνσεις. Αυτό με τη σειρά του ισοδυναμεί με το ότι ο πίνακας A του τελεστή σχήματος ως προς τη βάση {X u, X v } είναι πάντα διαγώνιος. Λαμβάνοντας τώρα υπόψη την έκφραση ( ), προκύπτει ότι αν F f 0, τότε ο πίνακας A είναι διαγώνιος, άρα οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας. Αντίστροφα, υποθέτουμε ότι οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας. Αυτό σημαίνει ότι τα διανύσματα X u, X v είναι κύριες διευθύνσεις. Επειδή δεν υπάρχουν ομφαλικά σημεία, τα διανύσματα X u, X v είναι κάθετα, άρα F = X u, X v = 0. Συνεπώς, τα f εκτός διαγωνίου στοιχεία του πίνακα A στην έκφραση ( ) είναι G και f και επειδή αυτά πρέπει να είναι E μηδέν παίρνουμε ότι f 0. Σημειώστε ότι στα ομφαλικά σημεία όλες οι διευθύνσεις είναι κύριες διεθύνσεις, άρα σε αυτά οι γραμμές συντεταγμένων είναι πάντα γραμμές καμπυλότητας. Λήμμα 7.1. Υποθέτουμε ότι X είναι μια παραμέτρηση, για την οποία οι γραμμές συντεταγμένων (δηλαδή οι u-καμπύλες και οι v-καμπύλες) είναι γραμμές καμπυλότητας με αντίστοιχες κύριες καμπυλότητες k 1 και k 2. Τότε ισχύουν οι σχέσεις (k 1 ) v = E v 2E (k 2 k 1 ) και (k 2 ) u = G u 2G (k 1 k 2 ). Απόδειξη. Λόγω της Πρότασης 7.1 είναι F 0 f. Τότε οι εξισώσεις Codazzi απλουστεύονται ως ( ) e v = eγ 1 12 gγ 2 11, g u = gγ 2 12 eγ Λόγω του ότι F = 0 οι σχέσεις (7.5), (7.6) και (7.7) δίνουν ότι Γ 2 11 = 1 E v 2 G, Γ1 12 = 1 E v 2 G Γ 1 22 = 1 G u 2 E, Γ2 12 = 1 G u 2 G.
138 Οι εξισώσεις Codazzi και Gauss 137 Συνεπώς, οι εξισώσεις Codazzi παίρνουν τη μορφή e v = E v 2 ( e E G) + g, g u = G ( u e 2 E G) + g (7.13) Λαμβάνοντας υπόψη τη μορφή του πίνακα του τελεστή σχήματος ( ) και ότι F = 0 = f, προκύπτει ότι k 1 = e E και k 2 = g G. Παραγωγίζοντας τις παραπάνω σχέσεις ως προς v και u αντίστοιχα και λαμβάνοντας υπόψη τις σχέσεις (7.13), προκύπτουν οι ζητούμενες σχέσεις. Ερχόμαστε τώρα στην πρώτη ενδιαφέρουσα εφαρμογή των εξισώσεων Codazzi, όπου K 0. Πρόταση 7.2. Εστω M μια αναπτυκτή επιφάνεια (δηλαδή K 0) χωρίς επίπεδα σημεία (δηλαδή σημεία p όπου k 1 (p) = k 2 (p) = 0). Τότε η M είναι ένας γενικευμένος κύλινδρος, του οποίου το εφαπτόμενο επίπεδο παραμένει σταθερό κατά μήκος των γεννητόρων. Απόδειξη. Επειδή η M είναι επίπεδη και δεν περιέχει επίπεδα σημεία, μπορούμε να υποθέσουμε ότι k 1 = 0 και k 2 0 παντού. Συνεπώς, υπάρχει μια τοπική παραμέτρηση X της M, για την οποία οι γραμμές συντεταγμένων είναι γραμμές καμπυλότητας (οι u-καμπύλες να αντιστοιχούν στην k 1 και οι v-καμπύλες στην k 2 ). (Αυτό δεν είναι εντελώς προφανές, ανάγεται σε θέμα διαφορικών εξισώσεων βλ. Shifrin σελ ). Αυτό σημαίνει ότι μπορούμε να επιλέξουμε την παραμέτρηση X, ώστε F = f = 0. Επειδή k 1 = 0, τότε για κάθε p M θα είναι S p (X u ) = 0, άρα N u = 0 παντού. Συνεπώς, το διάνυσμα N θα είναι σταθερό κατά μήκος των u-καμπυλών. Επίσης, παρατηρούμε ότι e = S p (X u ), X u = 0. Θέλουμε τώρα να δείξουμε ότι οι u-καμπύλες είναι ουσιαστικά ευθείες. Επειδή k 1 = 0 παντού, θα είναι και (k 1 ) v = 0 και δεδομένου ότι k 2 k 1, λόγω του Λήμματος 7.1 προκύπτει ότι E v = 0. Τότε η εξίσωση (7.5) δίνει ότι Γ 2 11 = 0, συνεπώς X uu = Γ 1 11X u + Γ 2 11X v + en = Γ 1 11X u, δηλαδή είναι παράλληλο του διανύσματος X u. Αυτό σημαίνει ότι το εφαπτόμενο διάνυσμα X u δεν αλλάζει διεύθυνση κατά μήκος των u-καμπύλων, άρα οι u-καμπύλες είναι ευθείες. Συνεπώς, η επιφάνεια είναι ένας γενικευμένος κύλινδρος, του οποίου το εφαπτόμενο επίπεδο παραμένει σταθερό κατά μήκος των γεννητόρων. Οι επίπεδοι γενικευμένοι κύλινδροι συχνά ονομάζονται και αναπτυκτές επιφάνειες (developable surfaces). Το όνομα αυτό οφείλεται στο γεγονός ότι αυτές οι επιφάνειες μπορούν να απεικονιστούν ισομετρικά πάνω σε ένα επίπεδο. Δύο άλλες κατηγορίες αναπτυκτών επιφανειών είναι οι επιφάνειες που σχηματίζονται από τις εφαπτόμενες μιας καμπύλης του R 3 και οι κωνικές επιφάνειες. Στη συνέχεια, θα αποδείξουμε ένα ολικό αποτέλεσμα για συμπαγείς επιφάνειες. Θεώρημα 7.3. (Liebmann) Εστω M μια συμπαγής κανονική επιφάνεια με σταθερή καμπυλότητα Gauss K. Τότε K > 0 και η M θα είναι μια σφαίρα ακτίνας 1/ K. Χρειαζόμαστε πρώτα το εξής:
139 138 Οι εξισώσεις Codazzi και Gauss Λήμμα 7.2. (Hilbert) Εστω p ένα σημείο μιας επιφάνειας το οποίο δεν είναι ομφαλικό και ότι k 1 (p) > k 2 (p). Υποθέτουμε ότι η k 1 έχει τοπικό μέγιστο στο p και η k 2 τοπικό ελάχιστο στο p. Τότε K(p) 0. Απόδειξη. Επειδή k 1 (p) k 2 (p), υπάρχει τοπική παραμέτρηση στο p, ώστε οι u-καμπύλες να είναι γραμμές καμπυλότητας με κύρια καμπυλότητα k 1 και οι v-καμπύλες να είναι γραμμές καμπυλότητας με κύρια καμπυλότητα k 2. Επειδή k 1 k 2 και (k 1 ) v = (k 2 ) u = 0, στο σημείο p, από το Λήμμα 2.1 προκύπτει ότι E v = G u = 0 στο p. Παραγωγίζοντας τις σχέσεις ( ) και λαμβάνοντας υπόψη ότι (k 1 ) u = (k 2 ) v = 0, προκύπτει ότι στο σημείο p ισχύουν οι σχέσεις (k 1 ) vv = E vv 2E (k 2 k 1 ) 0 (επειδή k 1 (p) τοπικό μέγιστο) (k 2 ) uu = G uu 2E (k 1 k 2 ) 0 (επειδή k 2 (p) τοπικό ελάχιστο), συνεπώς E vv 0 και G uu 0 στο p. Χρησιμοποιώντας τον τύπο για την καμπυλότητα Gauss, από την Άσκηση 2 προκύπτει ότι 2KEG = E vv + G uu + α(u, v)e v + β(u, v)g u για κάποιες συναρτήσεις α(u, v), β(u, v), συνεπώς K(p) 0. Απόδειξη. (του Θεωρήματος 2.3). Επειδή η M είναι συμπαγής, υπάρχει ένα σημείο με θετική καμπυλότητα Gauss και επειδή από υπόθεση αυτή είναι σταθερή στην M, τότε θα είναι K > 0, άρα αποδείχτηκε το πρώτο μέρος του θεωρήματος. Εάν όλα τα σημεία της M είναι ομφαλικά, τότε η M είναι μια σφαίρα. Εάν υπάρχει τουλάχιστον ένα μη ομφαλικό σημείο, τότε επειδή η M είναι συμπαγής, η μεγαλύτερη κύρια καμπυλότητα k 1 λαμβάνει μέγιστη τιμή σε κάποιο p M. Επειδή η K = k 1 k 2 είναι σταθερή, η συνάρτηση k 2 = K/k 1 πρέπει να λαμβάνει ελάχιστη τιμή στο σημείο p. Δεδομένου ότι το σημείο p δεν μπορεί να είναι ομφαλικό, (γιατί;) τότε λόγω του Λήμματος 7.2 θα είναι K(p) 0, πράγμα άτοπο. Άσκηση 3. Αποδείξτε ότι αν M είναι μια συμπαγής και συνεκτική (προσανατολισμένη) επιφάνεια με K > 0 και H σταθερή, τότε η M είναι μια σφαίρα ακτίνας 1/ K. (Υπόδειξη. Θεωρήστε τη συνάρτηση H 2 K = (k 1 k 2 ) 2 /4 και έστω p M ένα σημείο μεγίστου. Εξετάστε τις περιπτώσεις H 2 K(p) = 0 και H 2 K(p) > 0 και χρησιμοποιείστε το Θεώρημα Liebmann και το Λήμμα του Hilbert αντίστοιχα.) 7.1 Λυμένα παραδείγματα Παράδειγμα 7.4. Αν ϕ είναι η γωνία των παραμετρικών γραμμών u =σταθερό, v =σταθερό, της επιφάνειας M, τότε ισχύουν οι σχέσεις (1) ϕ u = N E Γ2 11 N G Γ2 12, (2) ϕ v = N E Γ2 12 N G Γ1 22, όπου N = EG F 2. Λύση
140 Λυμένα παραδείγματα 139 (1) Είναι γνωστό ότι η γωνία των παραμετρικών γραμμών u =σταθερό και v =σταθερό δίνεται από την σχέση Παραγωγίζουμε την σχέση αυτή ως προς u: cos ϕ = F EG. (7.14) sin ϕ 1 cos 2 ϕ ( ) ϕ u ( ) ϕ u = = F u EG F u ( EG) EG F u EG F E u G + EG u 2 EG EG και αν λάβουμε υπόψη μας την (7.14), έχουμε ή ακόμη 1 F 2 EG ( ) ϕ = 2EGF u F (E u G + EG u ) u 2EG EG Αλλά το δεύτερο μέρος της προς απόδειξη σχέσης γράφεται ϕ u = 2EGF u F GE u EF G u. (7.15) 2EGN N E Γ2 11 N G Γ1 12 = NGΓ NEΓ1 12 EG και αν λάβουμε υπόψη μας τις σχέσεις (7.5), (7.6), (7.6), έχουμε NG F E u + 2EF u EE v N E Γ2 11 N G Γ1 12 = 2(EG F 2 ) EG + NE GE v F G u 2(EG F 2 ) = 2EGF u F GE u EF G u. (7.16) 2EGN Αν τώρα συγκρίνουμε τα δεύτερα μέλη των (7.15) και (7.16), βλέπουμε πως είναι ίσα, επομένως θα είναι ίσα και τα πρώτα και άρα η σχέση έχει αποδειχθεί. Για την σχέση (2) εργαζόμαστε ανάλογα. Παράδειγμα 7.5. Αν N = N(u, v) είναι το μέτρο του κάθετου διανυσματικού πεδίου της επιφάνειας M με τοπική παραμέτρηση X : U R 2 M, τότε ισχύουν οι ακόλουθες σχέσεις (1) u ln N = Γ Γ 2 12 (2) v ln N = Γ Γ Λύση (1) Γνωρίζουμε ότι N = N(u, v) = EG F 2 (7.17)
141 140 Οι εξισώσεις Codazzi και Gauss όπου E, F και G είναι τα θεμελιώδη ποσά πρώτης τάξης της επιφάνειας M. Το πρώτο μέρος της προς απόδειξη σχέσης λόγω της (7.17) γράφεται u ln N = u ( EG F 2 ) = = = = 1 EG F 2 u ( EG F 2 ) 1 1 EG F 2 2 EG F 2 u (EG F 2 ) 1 2(EG F 2 ) (GE u + EG u 2F F u ) 1 ( (GEu 2(EG F 2 2F F u + F E v ) + (EG u F E v ) ) ) = GE u 2F F u + F E v 2(EG F 2 ) = Γ Γ (2) Εργαζόμαστε όπως και στην προηγούμενη περίπτωση. + EG u F E v 2(EG F 2 ) Παράδειγμα 7.6. Δίνεται η τετραγωνική μορφή A = du 2 + cos 2 udv 2. Να εξετασθεί εαν υπάρχει επιφάνεια του R 3 για την οποία ισχύει η σχέση I = II = A. Σε καταφατική περίπτωση να βρεθεί μια τοπική παραμέτρηση αυτής. Λύση Εφόσον I = A, θα είναι E = 1, F = 0, G = cos 2 u. (7.18) Επίσης από την σχέση II = A έπεται ότι e = 1, f = 0, g = cos 2 u. (7.19) Παρατηρούμε λοιπόν ότι E > 0, G > 0, EG F 2 = cos 2 u > 0. (7.20) Για να υπάρχει επιφάνεια που να έχει ως θεμελιώδη ποσά τις συναρτήσεις που δίνονται από τις (8.1) και (8.2), θα πρέπει επιπλέον να ικανοποιείται η θεμελιώδης εξίσωση του Gauss και οι εξισώσεις Codazzi. Θα δείξουμε πρώτα το Θεώρημα Egregium. Κατ αρχάς είναι Ομως K = eg f 2 = 1. (7.21) EG F 2 ( ( K = 1 1 ) ( G + 1 )) G EG u E u v E v = 1 ( cos u u ( sin u) + ) v ( 1 cos u 0) = 1. (7.22) Άρα ισχύει το θεώρημα Egregium. Θα εξετάσουμε τώρα την ισχύ των εξισώσεων Codazzi. Αφού όμως F = f = 0, αρκεί να δειχθούν οι εξισώσεις αυτές στη μορφή e v = E ( v e 2 E G) + g, g u = G ( u e 2 E G) + g. (7.23)
142 Ασκήσεις 141 Αλλά από τις (8.1) και (8.2) είναι προφανές ότι e v = E v = 0 και επομένως η πρώτη εκ των σχέσεων είναι αληθής. Επίσης οπότε g u = 2 sin u cos u, G u = 2 sin u cos u, G u 2 ( e E G) + g = 1 2 ( 2 sin u cos u)2 = g u e E + g G = 1 + cos2 u cos 2 u = 2, και έτσι αποδεικνύεται και η ισχύς της δεύτερης των συνθηκών Codazzi. Επομένως, σύμφωνα με το Θεώρημα 7.2 του Bonnet, υπάρχει επιφάνεια του τρισδιάστατου χώρου και μάλιστα μοναδική ως προς το σχήμα που έχει τη δοθείσα τετραγωνική μορφή, ως πρώτη και δεύτερη μορφή αντίστοιχα. Σχετικά με το δεύτερο μέρος του ερωτήματος, έστω X : U R 2 M μια τοπική παραμέτρηση της ζητούμενης επιφάνειας για την οποία ισχύουν E = 1 = X u, X u, F = 0 = X u, X v, G = cos 2 u = X v, X v. Από τις δύο τελευταίες σχέσεις μπορούμε να υποθέσουμε ότι Ως εκ τούτου η σχέση E = 1 παίρνει τη μορφή και η σχέση G = cos 2 u τη μορφή f(u) 2 = cos 2 u, άρα είναι Εύκολα όμως από την (7.24) προκύπτει ότι X(u, v) = (f(u) cos v, f(u) sin v, h(u)). (7.24) f (u) 2 + h (u) 2 = 1 (7.25) f(u) = ± cos u. (7.26) e = f(f h f h ) f 2 ((f ) 2 + (h ) 2 ), f = 0, g = f 2 h f 2 ((f ) 2 + (h ) 2 ) (7.27) και λόγω των σχέσεων (8.2) οι εξισώσεις αυτές ισοδύναμα γράφονται ως εξής f h f h = 1, hh = cos 2 u. (7.28) Πράγματι, από την (7.25) συνεπάγεται ότι h (u) 2 = cos 2 u, οπότε h(u) = ± sin u. (7.29) Η πρώτη εκ των (7.28), λόγω των (7.26) και (7.29) γίνεται f h f h = (± sin u)(± sin u) (± cos u)(± cos u) = sin 2 + cos 2 u = 1 (7.30) και η δεύτερη fh = cos 2 u. Οι ζητούμενες λοιπόν συναρτήσεις f(u) και h(u) ορίζονται από τις σχέσεις (7.26) και (7.29) και επομένως η ζητούμενη τελικά επιφάνεια θα ορίζεται από την ακόλουθη παραμέτρηση X(u, v) = (cos u sin v, cos u sin v, sin u).
143 142 Οι εξισώσεις Codazzi και Gauss 7.2 Ασκήσεις 1. Για την επιφάνεια εκ περιστροφής X(u, v) = (f(v) cos u, f(v) sin u, g(v)), f(v) 0 να αποδειχθεί ότι Γ 1 11 = Γ 1 12 = 0, Γ 1 12 = f Γ 2 ff 11 = (f ) 2 + (g ) 2 f, Γ2 22 = f f + g g (f ) 2 + (g ) Δίνεται η επιφάνεια M με εξίσωση z = z(x, y). Εστω p = z x, q = z y, r = z xx, s = z xy, t = z yy και N = EG F 2. Να αποδειχθεί ότι ισχύουν οι σχέσεις (1) Γ 1 11 = pr N 2, (4) Γ 2 11 = pr N 2, (2) Γ1 12 = ps N 2, (5) Γ2 12 = ps N 2, (3) Γ1 22 = pt N 2 (6) Γ2 22 = pt N 2 3. Δίνεται η τετραγωνική μορφή A = du 2 + sin 2 udv 2. Να εξετασθεί εάν υπάρχει επιφάνεια του R 3, για την οποία I = II = A. 4. Να εξετασθεί εάν υπάρχει επιφάνεια της οποίας τα θεμελιώδη ποσά να είναι E = 1 + 2u 2, F = 2uv, G = 1 + 2v 2 e = (1 + 2u 2 + 2v 2 ) 1/2, f = 0, g = (1 + 2u 2 + 2v 2 ) 1/2. 5. Να βρεθεί η επιφάνεια του R 3 της οποίας τα θεμελιώδη ποσά είναι E = G = 1, F = 0, e = 1, f = g = Δείξτε ότι δεν υπάρχει τμήμα επιφάνειας του οποίου η πρώτη και η δεύτερη θεμελιώδης μορφή είναι η αντίστοιχα. du 2 + cos 2 udv 2 και cos 2 udu 2 + dv 2 7. Αποδείξτε ότι τα σύμβολα του Cristoffel δίνονται από τον παρακάτω τύπο Γ k ij = l=1 ( g kl gil + g lj g ) ij, x j x i x l όπου g 11 = E, g 12 = F, g 22 = G και ο (g ij ) είναι ο αντίστροφος του πίνακα (g ij ).
144 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [4] K. F. Gauss, Disqusitiones generales circa suporhcies curves, Comm. Soc. Göttingen Bd 6, [5] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, Μετάφραση 3 ης εκδ. Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, [6] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [7] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [8] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
145 144 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
146 Κεφάλαιο 8 Συναλλοίωτη παράγωγος και παραλληλία Σύνοψη Ορίζουμε την έννοια του διανυσματικού πεδίου σε μια επιφάνεια και τη συναλλοίωτη παράγωγο αυτού κατά μήκος μιας λείας καμπύλης. Ενα διανυσματικό πεδίο σε μια επιφάνεια ονομάζεται παράλληλο κατά μηκος μιας καμπύλης στην επιφάνεια, εάν η συναλλοίωτη παράγωγος είναι μηδέν. Περιγράφουμε διάφορες ιδιότητες της συναλλοίωτης παραγώγου και κάνουμε εφαρμογή της παράλληλης μεταφοράς στη σφαίρα καθώς και στην κίνηση του εκκρεμούς του Foucault. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11]. Προαπαιτούμενη γνώση Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα, Συνήθεις Διαφορικές Εξισώσεις. Είναι γνωστό ότι η έννοια της παραλληλίας είναι ίσως η πιο σημαντική έννοια στην Ευκλείδεια γεωμετρία. Άλλωστε, οι μη Ευκλείδειες γεωμετρίες προκύπτουν από την άρνηση του αξιώματος των παραλλήλων του Ευκλείδη, το οποίο αναφέρει ότι δοθέντος ενός σημείου p εκτός ευθείας L του επιπέδου, υπάρχει μοναδική ευθεία η οποία διέρχεται απο το p και είναι παράλληλη με την L. Είναι λοιπόν φυσικό να ονομάζουμε δύο διανύσματα V και W του R 3 με σημεία εφαρμογής p, q R 3 (άρα V T p R 3, W T q R 3 ) παράλληλα, εάν το W προκύπτει με παράλληλη μετατόπιση του V από το σημείο p στο σημείο q. Το ερώτημα όμως που τίθεται είναι το εξής: Πώς θα μπορούμε να συγκρίνουμε ένα εφαπτόμενο διάνυσμα σε ένα σημείο της σφαίρας S 2 με ένα εφαπτόμενο διάνυσμα σε ένα άλλο σημείο αυτής και να αποφανθούμε εάν αυτά είναι παράλληλα ; (βλ. Σχήμα 8.1). Ισως ένα σαφέστερο ερώτημα (ιδαιτέρως αν επιθυμούμε γενικεύσεις σε αντικείμενα πέραν των επιφανειών) είναι το εξής: Δοθείσης μιας καμπύλης γ σε μια επιφάνεια M και ενός διανυσματικού πεδίου X (θα το γράφουμε X) κατα μήκος της καμπύλης γ, είναι δυνατόν να ορίσουμε το X ως παράλληλο διανυσματικό πεδίο εάν η παράγωγός του κατά μήκος της γ είναι μηδέν; Άρα χρειαζόμαστε κάποια έννοια παραγώγισης διανυσματικών πεδίων κατά μήκος μιας καμπύλης. Ορισμός 8.1. Ενα λείο διανυσματικό πεδίο (vector field) σε μια επιφάνεια M είναι μια συνάρτηση X : M R 3 με τις ιδιότητες: 145
147 146 Συναλλοίωτη παράγωγος και παραλληλία Σχήμα 8.1: Ενα διανυσματικό πεδίο στη σφαίρα S2. ~ 1. X(p) Tp M για κάθε p M. ~ X : U R3 είναι διαφορίσιμη. 2. Για κάθε τοπική παραμέτρηση X : U M η συνάρτηση X Σχήμα 8.2: Παράλληλα διανυσματικά πεδία. ~ σε μια επιφάνεια M γενικεύοντας την έννοια της Μπορούμε να παραγωγίσουμε ένα διανυσματικό πεδίο X παραγώγου κατά κατεύθυνση V f μιας πραγματικής συνάρτησης f : R3 R, όπου V R3. Θυμίζουμε ότι η παράγωγος κατά κατεύθυνση V f σε ένα σημείο p R3 ορίζεται από την τιμή του ορίου (αν υπάρχει) d f (γ(t)) dt t=0, όπου γ είναι μια καμπύλη του χώρου R3 τέτοια, ώστε γ(0) = p και γ 0 (0) = V. Αξίζει να σημειώσουμε τα εξής:
148 Συναλλοίωτη παράγωγος και παραλληλία 147 (1) Η τελευταία συνθήκη δείχει ότι ο ορισμός δεν εξαρτάται από την επιλογή της καμπύλης. (2) Η V f μπορεί να υπάρχει ως προς την κατεύθυνση του V, αλλά να μην υπάρχει ως προς την κατεύθυνση άλλου διανύσματος. (3) Για την παράγωγο κατά κατεύθυνση ισχύει ο κανόνας του Leibniz: V (fg) = ( V f)g + f( V g). Εστω f : R 3 R μια πραγματική συνάρτηση, για την οποία υπάρχουν οι μερικές παράγωγοι πρώτης τάξης και έστω γ : I R R 3 μια καμπύλη στην M με γ(t) = (γ 1 (t), γ 2 (t), γ 3 (t)). Τότε η παράγωγος της f στο σημείο γ(0) = p ως προς τη διεύθυνση του γ (0) = V είναι ίση με όπου V = (v 1, v 2, v 3 ). V f(p) = f x (p)v 1 + f y (p)v 2 + f z (p)v 3 = f(p), V, Εστω X ένα λείο διανυσματικό πεδίο στην επιφάνεια M, V T p M και γ : I M μια λεία καμπύλη της M με γ(0) = p, γ (0) = V. Η παράγωγος του X ως προς τη διεύθυνση του διανύσματος V είναι το διάνυσμα του R 3 DV X = d dt ( X γ) t=0. Καμιά φορά συμβολίζεται και ως dx X ή. Δεδομένου ότι ένας παρατηρητής επάνω στην επιφάνεια M dt μπορεί να διαπιστώσει μόνο τη συνιστώσα του διανύσματος D V X που βρίσκεται στον εφαπτόμενο χώρο T p M, οδηγούμαστε στον εξής σημαντικό ορισμό: Ορισμός ) Εστω M R 3 μια κανονική επιφάνεια με απεικόνιση Gauss N : M S 2, X ένα διανυσματικό πεδίο της M και V T p M. Η συναλλοίωτη παράγωγος (covariant derivative) του X ως προς τη διεύθυνση του V είναι το διάνυσμα V X = (DV X) tan = D V X DV X, N N, δηλαδή είναι η προβολη του διανύσματος D V X στον εφαπτόμενο χώρο Tp M. 2) Το διανυσματικό πεδίο X ονομάζεται παράλληλο κατά μήκος της καμπύλης γ (parallel along γ), εάν γ (t) X = 0 για κάθε t I. Αυτό σημαίνει ότι το διάνυσμα D γ (t) X είναι ένα πολλαπλάσιο του N(γ(t)) ή ισοδύναμα κάθετο στον T p M, (βλ. Σχήμα 8.3). Αποδεικνύεται εύκολα ότι ο ορισμός δεν εξαρτάται από την επιλογή της καμπύλης γ με γ (0) = V. Η συναλλοίωτη παράγωγος συμβολίζεται τακτικά και ως D X dt ή dt X
149 148 Συναλλοίωτη παράγωγος και παραλληλία Σχήμα 8.3: Συναλλοίωτη παράγωγος. Παράδειγμα 8.1. Εστω M = R 2 {0} το επίπεδο xy και γ : I M γ(t) = (γ 1 (t), γ 2 (t), 0) μια επίπεδη καμπύλη. Ενα διανυσματικό πεδίο X στην M κατά μήκος της γ (δηλαδή X(t) T γ(t) M για κάθε t I) έχει τη μορφή X(t) = (x 1 (t), x 2 (t), 0). Τότε γ (t) X = (D γ (t) X) tan = (x 1(t), x 2(t), 0), άρα στην περίπτωση αυτή η συναλλοίωτη παράγωγος συμφωνεί με τη συνήθη παράγωγο του X. Παράδειγμα 8.2. Εστω M = S 2 η μοναδιαία σφαίρα. Θεωρούμε το διανυσματικό πεδίο ταχυτήτων της καμπύλης γ : R S 2 γ(t) = (cos t, sin t, 0). Η καμπύλη διέρχεται από τον ισημερινό της S 2, δηλαδή την τομή της S 2 με το επίπεδο xy. Είναι γ(t) = ( cos t, sin t, 0) = γ(t), άρα το διάνυσμα γ(t) είναι κάθετο στον T γ(t) S 2. Συνεπώς, γ (t)γ (t) = 0. Παράδειγμα 8.3. Εστω X : U M μια τοπική παραμέτρηση της M. Τότε έχουμε ότι Xu X u = (X uu ) tan = Γ 1 11X u + Γ 2 11X v Xv X u = (X uv ) tan = Γ 1 12X u + Γ 2 12X v Xv X v = (X vv ) tan = Γ 1 22X u + Γ 2 22X v. Με τον τρόπο αυτό προκύπτει ένας εναλλακτικός τρόπος ορισμού των συμβόλων του Christoffel. Η ύπαρξη ενός παράλλληλου διανυσματικού πεδίου με αρχική συνθήκη εξασφαλίζεται από την παρακάτω πρόταση. Πρόταση 8.1. Εστω γ : [0, 1] M μια καμπύλη με γ(0) = p, X 0 T p M. Τότε υπάρχει μοναδικό παράλληλο διανυσματικό πεδίο X κατά μήκος της γ με την ιδιότητα X(p) = X 0. Απόδειξη. Εστω X : U R 2 M μια τοπική παραμέτρηση της M και γ : I R M μια λεία καμπύλη στην επιφάνεια τέτοια ώστε γ(t) = X(u(t), v(t)). Τότε γ (t) = u (t)x u + v (t)x v. Εστω ότι το πεδίο X
150 Συναλλοίωτη παράγωγος και παραλληλία 149 (κατά μήκος της καμπύλης) εκφράζεται ως X(γ(t)) = α(t)x u (u(t), v(t)) + β(t)x v (u(t), v(t)). Από τον κανόνα της παραγώγισησ-αλυσίδας θα έχουμε: γ (t) X ( ( = ( X tan d γ) (t)) = dt (α(t)x u(u(t), v(t)) + β(t)x v (u(t), v(t))) ( d = α (t)x u + β (t)x v + α(t) dt X u(u(t), v(t)) ( ) d tan +β(t) dt X v(u(t), v(t)) ) tan ) tan = α (t)x u + β (t)x v + α(t) ( u (t)x uu + v (t)x uv ) tan +β(t) ( u (t)x vu + v (t)x vv ) tan = α (t)x u + β (t)x v + α(t)(u (t)(γ 1 11X u + Γ 2 11X v ) +v (t)(γ 1 12X u + Γ 2 12X v )) +β(t) ( u (t)(γ 1 21X u + Γ 2 21X v ) + v (t)(γ 1 22X u + Γ 2 22X v ) ) = ( α (t) + α(t)(γ 1 11u (t) + Γ 1 12v (t)) + β(t)(γ 1 21u (t) + Γ 1 22v (t)) ) X u + ( β (t) + α(t)(γ 2 11u (t) + Γ 2 12v (t)) + β(t)(γ 2 21u (t) + Γ 2 22v (t)) ) X v. Συνεπώς, το X είναι παράλληλο κατά μήκος της καμπύλης γ εάν και μόνο εάν οι συναρτησεις α(t) και β(t) είναι λύσεις του γραμμικού συστήματος διαφορικών εξισώσεων πρώτης τάξης: α (t) + α(t) ( Γ 1 11u (t) + Γ 1 12v (t) ) + β(t) ( Γ 1 12u (t) + Γ 1 22v (t) ) = 0 (8.1) β (t) + α(t) ( Γ 2 11u (t) + Γ 2 12v (t) ) + β(t) ( Γ 2 12u (t) + Γ 2 22v (t) ) = 0. (8.2) Σύμφωνα με τη θεωρία των διαφορικών εξισώσεων το παραπάνω σύστημα έχει μοναδική λύσει στο διάστημα [0, 1], οπότε υπάρχει μοναδικό διανυσματικό πεδίο X με X(p) = X 0. Από την απόδειξη της παραπάνω πρότασης προκύπτει ότι η παράλληλη μεταφορά εξαρτάται μόνο από την πρώτη θεμελιώδη μορφή της M, άρα είναι εσωτερικό μέγεθος της επιφάνειας. Εστω X ένα διανυσματικό πεδίο, όπως στην παραπάνω πρόταση. Αν γ είναι μια καμπύλη που εννώνει τα σημεία p και q, τότε το διάνυσμα X(q) ονομάζεται παράλληλη μεταφορά (parallel translation) του διανύσματος X(p) = X 0 T p M κατά μήκος της γ. Πρόταση 8.2. Η παράλληλη μεταφορά διατηρεί τα μήκη και τις γωνίες διανυσματικών πεδίων. Συγκεκριμένα, αν X και Y είναι παράλληλα διανυσματικά πεδία κατά μήκος της καμπύλης γ από το σημείο p στο σημείο q, τότε X(p) = X(q) και η γωνία μεταξύ των X(p) και Y (p) ισούται με τη γωνία των X(q) και Y (q). Απόδειξη. Θεωρούμε τη συνάρτηση f(t) = X(γ(t)), Y (γ(t)). Τότε f (t) = ( X γ) (t), ( Y γ)(t) + ( X γ)(t), ( Y γ) (t) = D γ (t) X, Y + X, D γ (t) Y = γ (t), Y + X, γ (t) Y = 0.
151 150 Συναλλοίωτη παράγωγος και παραλληλία Η δεύτερη ισότητα ισχύει, επειδή τα διανυσματικά πεδία X και Y είναι εφαπτομενικά στην επιφάνεια M, συνεπώς το εσωτερικό γινόμενο με οποιοδήποτε κάθετο διάνυσμα στην επιφάνεια θα είναι μηδέν. Η τρίτη ισότητα ισχύει, επειδή τα πεδία X και Y είναι παράλληλα κατά μήκος της καμπύλης γ. Επομένως, το εσωτερικό γινόμενο X, Y παραμένει σταθερό κατά μήκος της γ. Θέτοντας X = Y συμπεραίνουμε ότι το μέτρο X (ομοίως το Y ) είναι σταθερό. Για τη γωνία θ μεταξύ των X και Y ισχύει ο τύπος cos θ = X, Y X Y και σύμφωνα με τα προηγούμενα αυτή είναι σταθερή. Παράδειγμα 8.4. Θεωρούμε τη μοναδιαία σφαίρα S 2 με τοπική παραμέτρηση X(u, v) = (sin u cos v, sin u sin v, cos u). Θα μελετήσουμε το αποτέλεσμα της παράλληλης μεταφοράς του διανύσματος X 0 = X v κατά μήκος του παράλληλου κύκλου u(t) = u 0, v(t) = t, με αρχή το σημείο p = X(u 0, 0). Τα θεμελιώδη ποσά πρώτης τάξης είναι E = 1, F = 0, G = sin 2 u και τα μη μηδενικά σύμβολα Christoffel είναι Γ 2 12 = cot u και Γ 1 22 = sin u cos u. Το σύστημα των διαφορικών εξισώσεων (8.1)-(8.2) παίρνει τη μορφή α (t) = sin u 0 cos u 0 β(t), α(0) = 0 β (t) = cot u 0 α(t), β(0) = 1. Παραγωγίζουμε τη δεύτερη εξίσωση και χρησιμοποιούμε την πρώτη οπότε παίρνουμε: β (t) = cot u 0 α (t) = cos 2 u 0 β(t), β(0) = 1. Από αυτήν προκύπτει ότι η λύση του συστήματος είναι 1 α(t) = sin u 0 sin ((cos u 0 )t), β(t) = cos ((cos u 0 )t). Συνεπώς, η ζητούμενη παράλληλη μεταφορά του διανύσματος X 0 είναι το διάνυσμα X(γ(t)) = sin u 0 sin ((cos u 0 )t) X u + cos ((cos u 0 )t) X v. Επειδή X(γ(t)) = Eα(t) 2 + 2F α(t)β(t) + Gb(t) 2 = sin 2 u 0 για κάθε t, η παράλληλη μεταφορά του διανύσματος X 0 διατηρεί το μήκος του. Επιπλέον, παρατηρούμε ότι το διάνυσμα X(γ(t)) δεν είναι γενικά εφαπτομενικό στην καμπύλη γ, παρά μόνο όταν u 0 = 0. Τότε το X(γ(t)) είναι εφαπτόμενο στον ισημερινό (για τον οποίον u(t) = 0, v(t) = 0, άρα α(t) = 0, β(t) = cos t). διάνυσμα X 0 στρέφεται κατα γωνία 2π cos u 0. μήκος της καμπύλης γ. Επειδή β(2π) = cos(2π cos u 0 ), το Η γωνία αυτή ονομάζεται ολονομία (holonomy) κατά Η έννοια της παραλληλίας μπορεί να χρησιμοποιηθεί, προκειμένου να δώσουμε έναν πρώτο ορισμό μιας γεωδαισιακής καμπύλης. Αναλυτικότερη μελέτη των γεωδαισιακών θα γίνει στο επόμενο κεφάλαιο. Ορισμός 8.3. Μια καμπύλη γ σε μια επιφάνεια M ονομάζεται γεωδαισιακή (geodesic) εάν το εφαπτόμενο διάνυσμά της είναι παράλληλο κατά μήκος της καμπύλης, δηλαδή γ γ = 0. Στο προηγούμενο παράδειγμα, το διάνυσμα X 0 θα παραμείνει κατά την παράλληλη μεταφορά του εφαπτομενικό στον ισημερινό, επειδή ο ισημερινός είναι μια γεωδαισιακή καμπύλη της σφαίρας. 1 Λαμβάνοντας υπόψη ότι η γενική λύση της διαφορικής εξίσωσης y (t) + k 2 y(t) = 0, είναι y(t) = c 1 cos(kt) + c 2 sin(kt), c 1, c 2 R.
152 Ασκήσεις 151 Σχήμα 8.4: Παράλληλη μεταφορά του διανύσματος X 0 κατά μήκος του παραλλήλου u(t) = u 0, v(t) = t της μοναδιαίας σφαίρας. Παράδειγμα 8.5. Το εκκρεμές του Foucault. Το 1851 ο Jean Foucault κατασκεύασε ένα εκκρεμές, προκειμένου να αποδείξει την κίνηση της γης. Με το πείραμα αυτό παρατήρησε ότι, αν το εκκρεμές βρίσκεται σε γεωγραφικό πλάτος u = u 0, τότε η περίοδος ενός πλήρους κύκλου του επιπέδου ταλάντωσης είναι T = 24 cos u 0 ώρες. Η συνήθης εξήγηση αυτού είναι μέσω της δύναμης Coriolis (βλ. Arnol d, Symon). Μια εναλλακτική εξήγηση μπορεί να δοθεί μέσω του Παραδείγματος Υποθέτουμε ότι η γη είναι ακίνητη και μεταφέρουμε το κινούμενο εκκρεμές παράλληλα κατά μήκος του κύκλου u = u 0 με σταθερή ταχύτητα, σε διάστημα 24 ωρών. Εάν το μήκος του νήματος του εκκρεμούς είναι αρκετά μεγάλο και το πλάτος της ταλάντωσης αρκετά μικρό, τότε η κίνηση του εκκρεμούς είναι σχεδόν εφαπτομενική με την επιφάνεια της γης. Ετσι δημιουργείται ένα διανυσματικό πεδίο από τις διάφορες διευθύνσεις του επιπέδου ταλάντωσης. Επειδή η εφαπτομενική συνιστώσα της κεντρομόλου επιτάχυνσης είναι αμελητέα 3, μπορούμε να υποθέσουμε ότι το διανυσματικό αυτό πεδίο είναι παράλληλο κατά μήκος της καμπύλης. Συνεπώς, μετά από μία πλήρη στροφή του εκκρεμούς περί τον κύκλο u = u 0, το πεδίο αυτό στρέφεται κατά γωνία 2π cos u 0, άρα το εκκρεμές επανέρχεται στο αρχικό επίπεδο ταλάντωσης μετά από 2π (2π cos u 0 )/24 = 24 ώρες. cos u Ασκήσεις 1. Μελετήστε την παράλληλη μεταφορά του διανύσματος (0, 0, 1) κατά μήκος του κύκλου x 2 + y 2 = 1, z = 0 στον ορθό κύλινδρο x 2 + y 2 = 1. 2 Και γενικότερα στα πλαίσια της θεωρίας της μαθηματικής φυσικής που ονομάζεται γεωμετρική θεωρία φάσεων. 3 Αν R = 2960mi είναι η ακτίνα της γης, τότε αποδεικνύεται ότι η εφαπτομενική συνιστώσα της κεντρομόλου επιτάχυνσης ( είναι R sin u 0 cos u 2π ) 2 0 2π2 R = 135, 7 mi/hr 2 = 0, 0553 ft/sec 2 = 0, 17g, όπου g η επιτάχυνση βαρύτητας. 2
153 152 Συναλλοίωτη παράγωγος και παραλληλία 2. Εστω V ένα παράλληλο διανυσματικό πεδίο κατά μήκος μιας καμπύλης γ της επιφάνειας M. Δείξτε ότι ένα διανυσματικό πεδίο W κατά μήκος της γ είναι παράλληλο εάν και μόνο εάν έχει σταθερό μήκος και η γωνία μεταξύ του V και του W είναι σταθερή. 3. Εστω X, Y λεία διανυσματικα πεδία σε μια επιφάνεια M και γ, δ λείες καμπύλες στην M. Αποδείξτε ότι για κάθε f, g λείες συναρτησεις στην M ισχύουν οι παρακάτω ιδιότητες της συναλλοίωτης παραγώγου: (1) fγ +gδ X = f γ X + g δ X. (2) γ ( X + Y ) = γ X + γ Y. (3) γ (f X) = d(f γ) dt X + f γ X. 4. Εστω M μια κανονική επιφάνεια και p, q M. Συμβολίζουμε με Pγ pq : T p M T q M την παράλληλη μεταφορά από το σημείο p στο σημείο q. Απδείξτε ότι η απεικόνιση Pγ pq είναι γραμμική. (Επιπλέον, είναι και ισομετρία, όπως αποδείχτηκε στην Πρόταση 8.2). 5. Θεωρούμε τον κώνο z 2 = a 2 (x 2 + y 2 ) με παραμέτρηση ( ( v X(u, v) = u sin φ cos sin φ ), u sin φ sin ( ) ) v, u cos φ, sin φ όπου φ η γωνία της γεννέτηρας του κώνου με sin φ = 1/ 1 + a 2, cos φ = a/ 1 + a 2. Αποδείξτε ότι η ολονομία κατά μήκος του παράλληλου ( γ(v) = u 0 sin φ cos είναι 2π sin φ. ( v sin φ ) ( ) ) v, u 0 sin φ sin, u 0 cos φ, 0 v 2π, sin φ 6. Θεωρούμε ένα τρίγωνο στην μοναδιαία σφαίρα με πλευρές τόξα μέγιστων κύκλων και με κορυφές p, q, r. Εστω X 0 ένα εφαπτόμενο διάνυσμα στο σημείο p του τόξου pq που εννώνει τα p και q. Δείξτε ότι η διαδοχική παράλληλη μεταφορά του X 0 κατά μήκος των τόξων pq, qr και rp, έχει ως αποτέλεσμα την στροφή του διανύσματος X 0 κατα γωνία 2π A, όπου A το εμβαδό του σφαιρικού τριγώνου pqr.
154 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] V. I. Arnol d, Mathematical Methods of Classical Mechanics, Springer-Verlag, [3] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [4] W. E. Boyce and R. C. DiPrima, Elementary Differential Equations, Ninth Edition, John Wiley and Sons, [5] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [6] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, Μετάφραση 3 ης εκδ. Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, [7] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [8] J. Oprea, Geometry and the Foucault pendulum, Amer. Math. Monthly 102 (6) (1995) [9] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [10] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη [11] K. Symon: Mechanics, Addison-Wesley,
155 154 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
156 Κεφάλαιο 9 Γεωδαισιακές καμπύλες Σύνοψη Ως γνωστόν οι ευθείες γραμμές παίζουν καθοριστικό ρόλο στη γεωμετρία του επιπέδου. Σκοπός του κεφαλαίου αυτού είναι να ορίσουμε εκείνες τις καμπύλες σε μια επιφάνεια, οι οποίες θα έχουν τον αντίστοιχο ρόλο των ευθειών στο επίπεδο. Στο κεφάλαιο αυτό δίνουμε τον ορισμό της γεωδαισιακής καμπύλης και της γεωδαισιακής καμπυλότητας. Η εξεύρεση γεωδαισιακών ανάγεται σε ένα σύστημα διαφορικών εξισώσεων, γενικά δύσκολο στην επίλυσή του. Το Θεώρημα Clairaut δίνει μια μέθοδο εύρεσης γεωδαισιακών σε επιφάνειες εκ περιστροφής. Επίσης, δίνουμε χαρακτηρισμό των γεωδαισικών ως κρίσιμα σημεία του συναρτησοειδούς ενέργειας και ορίζουμε την εκθετική απεικόνιση σε μια επιφάνεια. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [2], [3], [4], [5], [6], [7], [8]. Προαπαιτούμενη γνώση Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα, Συνήθεις Διαφορικές Εξισώσεις. Υπάρχουν (τουλάχιστον) δύο τρόποι χαρακτηρισμού των ευθειών (ή πιο γενικά ευθυγράμμων τμημάτων) στο σύνολο όλων των επίπεδων καμπυλών: ο πρώτος είναι γεωμετρικός (ολικός) και ο δεύτερος είναι αναλυτικός (τοπικός). Ενα ευθύγραμμο τμήμα είναι η ελάχιστη απόσταση μεταξύ δύο σταθερών σημείων του επιπέδου (γεωμετρική ή ολική περιγραφή). Ταυτόχρονα, είναι εκείνη η καμπύλη της οποίας το διάνυσμα ταχύτητας είναι σταθερό, υπό την έννοια ότι η διεύθυνσή του είναι σταθερή ή ότι παραμένει παράλληλο με τον εαυτό του (αναλυτική ή τοπική περιγραφή). Ο πρώτος τρόπος χαρακτηρισμού (γεωμετρικός - ολικός) δεν είναι ο πλέον ενδεδειγμένος, προκειμένου να γενικευθεί στις επιφάνειες. Ο λόγος είναι ότι, όπως θα δούμε, καμπύλες που ελαχιστοποιούν το μήκος μεταξύ δύο σημείων σε μια επιφάνεια μπορεί να μην υπάρχουν καθόλου. Επιπλέον, ακόμα και αν υπάρχουν μπορεί αυτές να μην είναι μοναδικές. Ο δεύτερος χαρακτηρισμός (αναλυτικός - τοπικός) θα δούμε ότι είναι πιο πρόσφορος, προκειμένου να γενικευθεί σε μια επιφάνεια, αλλά σίγουρα απαιτεί να αντιμετωπίσουμε ένα ευθύγραμμο τμήμα με μια διαφορετική οπτική από αυτή που το γνωρίζαμε από τα σχολικά μαθήματα γεωμετρίας. Η προσέγγιση αυτή απαιτεί την έννοια της παραλληλίας κατά μήκος μιας καμπύλης (βλ. Κεφάλαιο 8) Εστω M μια κανονική επιφάνεια του R 3 και έστω γ : I M μια καμπύλη της M με παραμέτρηση ως προς το μήκος τόξου, τέτοια ώστε γ(0) = p M. Εχουμε δει ότι το διάνυσμα γ(0) της δεύτερης 155
157 156 Γεωδαισιακές καμπύλες παραγώγου ( ἑπιτάχυνση ) στο σημείο p αναλύεται ως γ(0) = γ(0) tan + γ(0) norm, στην εφαπτομενική συνιστώσα γ(0) tan T p M και στην κάθετη συνιστώσα γ(0) norm (T p M) R 3. Ορισμός 9.1. Εστω M μια κανονική επιφάνεια του R 3. Μια καμπύλη γ : M (με παραμέτρηση ως προς το μήκος τόξου) στην M ονομάζεται γεωδαισιακή (geodesic), εάν η εφαπτομενική συνιστώσα της δεύτερης παραγώγου γ(t) μηδενίζεται, δηλαδή ισχύει γ(t) tan = 0 (9.1) για κάθε t I. Η σχέση (9.1) ισοδυναμεί με το ότι για κάθε t I, είτε το διάνυσμα γ(t) της επιτάχυνσης είναι κάθετο στον T p M, δηλαδή παράλληλο στο μοναδιαίο κάθετο διάνυσμα της επιφάνειας, είτε γ(t) = 0. Ισοδύναμα, η γ είναι μια γεωδαισιακή εάν και μόνο εάν το εφαπτόμενο διάνυσμα γ(t) είναι παράλληλο κατά μήκος της γ, δηλαδή γ γ = 0. Πράγματι, εξ ορισμού το γ γ είναι η προβολή του D γ γ = d dt ( γ γ) t=0 = γ στον T γ(t) M. Παρατηρήσεις. 1) Η σχέση (9.1) ισοδυναμεί με το ότι το διάνυσμα ταχύτητας γ(t) είναι παράλληλο κατά μήκος της γ, αλλά όπως εξηγήσαμε στην εισαγωγή του κεφαλαίου δεν θα αναπτύξουμε προς το παρόν την έννοια αυτή. 2) Η έννοια της γεωδαισιακής έχει την εξής φυσική ερμηνεία. Η τροχιά γ(t) ενός σωματιδίου, το οποίο κινείται σε μια επιφάνεια και στο οποίο δεν δρα καμμιά δύναμη παρά μόνο αυτή η οποία κρατά το σωματίδιο στην επιφάνεια (κάθετη δύναμη), είναι μια γεωδαισιακή. Πράγματι, από τον δεύτερο νόμο του Νεύτωνα είναι F (t) = k γ(t) και η F είναι κάθετη στον εφαπτόμενο χώρο T p M, συνεπώς το διάνυσμα γ(t) είναι κάθετο στον T p M άρα η τροχιά γ(t) είναι μια γεωδαισιακή. Παράδειγμα 9.1. Θεωρούμε τη μοναδιαία σφαίρα S 2, p S 2 και Z T p S 2 ένα μοναδιαίο εφαπτόμενο διάνυσμα στο p. Επειδή p, Z = 0 1, το σύνολο {p, Z} αποτελεί μια ορθοκανονική βάση ενός επιπέδου του R 3 (διερχόμενο από την αρχή των αξόνων), το οποίο τέμνει την σφαίρα κατά έναν μέγιστο κύκλο. Μια παραμέτρηση του κύκλου αυτού είναι η γ : R S 2 γ(s) = (cos s)p + (sin s)z. Τότε προκύπτει άμεσα ότι γ(s) = γ(s) για κάθε s R, συνεπώς γ tan = 0 (γιατί;). Άρα ο μέγιστος αυτός κύκλος είναι μια γεωδαισιακή της σφαίρας που διέρχεται από το σημείο γ(0) = p. Το ερώτημα που τίθεται αμέσως εδώ είναι αν υπάρχουν άλλες γεωδαισιακές στην σφαίρα. Αυτό θα απαντηθεί στη συνέχεια. Πρόταση 9.1. Εστω M μια κανονική επιφάνεια και γ : I M μια γεωδαισιακή της M. Τότε η ταχύτητα γ : I R της γ είναι σταθερή, δηλαδή η καμπύλη έχει παραμέτρηση ανάλογη του μήκους τόξου. 1 Ταυτίζουμε το σημείο p με το διάνυσμα θέσης του
158 Γεωδαισιακή καμπυλότητα 157 Απόδειξη. Προκύπτει άμεσα από τον εξής υπολογισμό: d dt ( γ(t) 2 ) = d dt γ(t), γ(t) = 2 γ(t), γ(t) = 2 γ(t) tan, γ(t) = 0. Από την παραπάνω πρόταση ουσιαστικά προκύπτει (κάτι που χρήζει αποδείξεως) ότι μια αναπαραμέτρηση μιας γεωδαισιακής καμπύλης γ, η οποία να είναι μοναδιαίας ταχύτητας, είναι γεωδαισιακή. Άρα μπορούμε να υποθέσουμε ότι οι γεωδαισιακές έχουν μοναδιαία ταχύτητα. Πριν προχωρήσουμε, θα εισαγάγουμε την έννοια της γεωδαισιακής καμπυλότητας μιας επιφανειακής καμπύλης και θα αποδείξουμε ότι μια καμπύλη γ : I R M είναι γεωδαισιακή εάν και μόνο εάν η γεωδαισιακή καμπυλότητα αυτής είναι μηδέν. 9.1 Γεωδαισιακή καμπυλότητα Γενικά το σχήμα μιας επιφάνειας επηρεάζει την καμπυλότητα των επιφανειακών καμπυλών. Συνεπώς, η κύρτωση μιας επιφάνειας μπορεί να μελετηθεί μέσω της καμπυλότητας των καμπυλών που βρίσκονται επάνω σε αυτή. Εστω γ : I R M μια καμπύλη μοναδιαίας ταχύτητας. Τότε το διάνυσμα γ(s) είναι μοναδιαίο και εφαπτόμενο στην M. Άρα γ(s) N(γ(s)), οπότε τα διανύσματα γ(s), N(γ(s)) και N(γ(s)) γ(s) είναι κάθετα μεταξύ τους και μοναδιαία. Το διάνυσμα N(γ(s)) γ(s) ονομάζεται γεωδαισιακή κάθετος και συμβολίζεται με n g. Επειδή η γ είναι μοναδιαίας ταχύτητας, το γ(s) είναι κάθετο στο γ(s), οπότε το γ(s) είναι γραμμικός συνδυασμός των N(γ(s)) και n g : γ(s) = κ n (Z)N + κ g (0)n g = γ(0) perp + γ(0) tan (9.2) όπου k n (Z) = γ(0), N(p) είναι η κάθετη καμπυλότητα της M. Ο αριθμός κ g (0) ονομάζεται γεωδαισιακή καμπυλότητα της γ, ειδικότερα Ορισμός 9.2. Εστω M μια κανονική προσανατολισμένη επιφάνεια με απεικόνιση Gauss N : M S 2 και έστω γ : I M μια καμπύλη στην M με παραμέτρηση ως προς το μήκος τόξου. Η γεωδαισιακή καμπυλότητα (geodesic curvature) k g : I R της γ ορίζεται ως k g (s) = N(γ(s)) γ(s), γ(s) = n g, γ(s). Θεώρημα 9.1. Η γεωδαισιακή καμπυλότητα μιας επιφανειακής καμπύλης σε τυχαίο σημείο αυτής μπορεί να εκφραστεί συναρτήσει των θεμελιωδών ποσών πρώτης τάξης της επιφάνειας, των παραγώγων αυτών και των παραγώγων των παραμέτρων της επιφάνειας.
159 158 Γεωδαισιακές καμπύλες Απόδειξη. Εχουμε κ g (s) = N γ, γ και N = X u X v EG F 2. Επομένως κ g (s) = = = = = ( ) Xu X v γ, γ = EG F 2 1 EG F 2 (X u γ)x v (X v γ)x u, γ 1 EG F 2 (X u X v ) γ, γ 1 EG F 2 ( (X u γ)x v, γ (X v γ)x u, γ ) 1 ( X u, γ X v, γ X v, γ X u, γ ) EG F 2 1 X u, γ X u, γ EG F 2 X v, γ X v, γ. (9.3) Επειδή η καμπύλη γ βρίσκεται πάνω στην επιφάνεια M με τοπική παραμέτρηση X : U R 2 M, θα ικανοποιεί την εξίσωση γ(s) = X(u(s), v(s)). Επομένως θα είναι γ = X u u + X v v (9.4) και γ = X uu u 2 + X uv v u + X u ü + X vu u v + X vv v 2 + X v v = X uu u 2 + 2X uv u v + X vv v 2 + X u ü + X v v. (9.5) Από τις σχέσεις (9.4) και (9.5) έχουμε X u, γ = X u, X u u + X v v = u X u, X u + v X u, X v = ue + vf (9.6) X v, γ = X v, X u u + X v v = u X v, X u + v X v, X v = uf + vg (9.7) X u, γ = X u, X uu u 2 + 2X uv u v + X vv v 2 + X u ü + X v v = u 2 X u, X uu + 2 u v X u, X uv + v 2 X u, X vv + üe + vf X v, γ = X v, X uu u 2 + 2X uv u v + X vv v 2 + X u ü + X v v = u 2 X v, X uu + 2 u v X v, X uv + v 2 X v, X vv + üf + vg. Αν τώρα λάβουμε υπόψη μας τους τύπους για τα σύμβολα του Christoffel πρώτου είδους από το Κεφάλαιο 7, τότε οι δύο τελευταίες σχέσεις γράφονται: X u, γ = u 2 Γ u vγ v 2 Γ üe + vf (9.8) X v, γ = u 2 Γ u vγ v 2 Γ üf + vg. (9.9)
160 Γεωδαισιακή καμπυλότητα 159 Η σχέση (9.3) λόγω των (9.6), (9.7), (9.8) και (9.9) γίνεται 1 ue + vf u 2 Γ u vγ v 2 Γ üe + vf κ g (s) = EG F 2 ue + vg u 2 Γ u vγ v 2 Γ üf + vg. (9.10) Η σχέση (9.10) μπορεί να γίνει απλούστερη, αν χρησιμοποιήσουμε τα σύμβολα του Christoffel δευτέρου είδους. Πράγματι, αν αναπτύξουμε την παραπάνω ορίζουσα, την οποία ας συμβολίσουμε με, έχουμε = ( u v ü v)(eg F 2 ) + u 3 (EΓ 211 F Γ 111 ) + 2 u 2 v(eγ 212 F Γ 112 ) + u v 2 (EΓ 222 F Γ 122 ) v 3 (GΓ 122 F Γ 222 ) 2 u v 2 (GΓ 112 F Γ 212 ) u 2 v(gγ 111 F Γ 211 ). Αν τώρα διαιρέσουμε και τα δύο μέλη αυτής της σχέσης με EG F 2 > 0 και λάβουμε υπόψη μας τις εκφράσεις για τα σύμβολα του Christoffel δευτέρου είδους (βλ. Κεφάλαιο 7), έχουμε EG F 2 = u v ü v + u 3 Γ u 2 vγ u v 2 Γ 2 22 v 3 Γ v 2 uγ 1 12 v u 2 Γ 1 11 = u( u 2 Γ u vγ v 2 Γ v) v( v 2 Γ u vγ u 2 Γ ü). Αντικαθιστώντας την παραπάνω σχέση στη σχέση (9.10), προκύπτει ο ακόλουθος τύπος για τη γεωδαισιακή καμπυλότητα κ g (s) = EG F 2 u ü + u 2 Γ u vγ v2 Γ 1 22 v v + v 2 Γ u vγ u2 Γ (9.11) Από την σχέση αυτή βλέπουμε ότι η γεωδαισιακή καμπυλότητα εξαρτάται από τα θεμελιώδη ποσά πρώτης τάξης, τις παραγώγους αυτών ως προς u, v, αφού τα σύμβολα Γ k ij, i, j, k = 1, 2 έχουν τέτοια εξάρτηση, και τέλος, από τις παραγώγους των παραμέτρων u, v ως προς την παράμετρο s και το θεώρημα έχει αποδειχθεί. Από τον τύπο (9.11) προκύπτουν, ως ειδικές περιπτώσεις, οι γεωδαισιακές καμπυλότητες (κ g (s)) u και (κ g (s)) v των παραμετρικών γραμμών v = σταθερό, u = σταθερό, στο τυχαίο σημείο αυτών: EG F (κ g (s)) u = Γ 2 2 EG F 11 E E, (κ g(s)) v = Γ G (9.12) G Παρατηρήσεις. 1) Οι παραπάνω τύποι είναι δυνατόν να εκφραστούν συναρτήσει της γωνίας ϕ των παραμετρικών γραμμών v = σταθερό, u = σταθερό, ως εξής: ( (κ g (s)) u = 1 ) ϕ E E u + Γ1 12 sin ϕ (9.13) G (κ g (s)) v = ( ) 1 ϕ G G + Γ2 12 sin ϕ. (9.14) E 2) Οταν οι παραμετρικές γραμμές της επιφάνειας M είναι ορθογώνιες, δηλαδή F = 0, τότε sin ϕ = 1, ϕ u = ϕ v = 0, Γ1 22 = G u 2E, Γ2 11 = E v 2G.
161 160 Γεωδαισιακές καμπύλες Στην περίπτωση αυτή οι τύποι (9.13) και (9.14) παίρνουν τη μορφή: E v (κ g (s)) u = 1 2 E G G u (κ g (s)) v = 1 2 G E. 3) Αν η επιφανειακή καμπύλη γ : I R M έχει τυχαία παράμετρο t, τότε η γεωδαισιακή καμπυλότητα αυτής δίνεται από τον τύπο: κ g (t) = EG F 2 u u + (u ) 2 Γ 1 11 γ (t) 3 + 2u v Γ (v ) 2 Γ 1 22 v v + (v ) 2 Γ u v Γ (u ) 2 Γ 2 11 (9.15) Εχοντας υπόψη τις σχέσεις (9.11) και (9.15), εύκολα συνάγεται ότι το πρόβλημα της εύρεσης γεωδαισιακών σε μια επιφάνεια ανάγεται στην επίλυση του παρακάτω συστήματος διαφορικών εξισώσεων: ü + Γ 1 11 u 2 + 2Γ 1 12 u v + Γ 1 22 v 2 = 0 v + Γ 2 11 u 2 + 2Γ 2 12 u v + Γ 2 22 v 2 = 0, (9.16) οπότε η γεωδαισιακή θα ορίζεται παραμετρικά από τις εξισώσεις u = u(s), v = v(s), όπου s το μήκος τόξου της καμπύλης. Αντίστοιχα στην επίλυση του παρακάτω συστήματος: u + Γ 1 11(u ) 2 + 2Γ 1 12u v + Γ 1 22(v ) 2 = 0 v + Γ 2 11(u ) 2 + 2Γ 2 12u v + Γ 2 22(v ) 2 = 0, (9.17) οπότε η γεωδαισιακή θα ορίζεται παραμετρικά από τις εξισώσεις u = u(t), v = v(t) όπου t τυχαία παράμετρος. Τέλος, αν κάνουμε απαλοιφή της παραμέτρου s ή t στις παραπάνω δύο περιπτώσεις των γεωδαισιακών, δηλαδή αν η ζητούμενη γεωδαισιακή είναι της μορφής v = v(u), τότε αυτή ικανοποιεί την ακόλουθη διαφορική εξίσωση v (u) = Γ 1 22(v (u)) 3 + (2Γ 1 12 Γ 2 22)(v (u)) 2 + (Γ Γ 2 12)v (u) Γ Πρόταση 9.2. Μια επιφανειακή καμπύλη είναι γεωδαισιακή εάν και μόνο εάν η γεωδαισιακή καμπυλότητά της είναι παντού μηδέν. Απόδειξη. Αν η γ είναι γεωδαισιακή, τότε γ(s) tan = 0, οπότε το διάνυσμα γ(s) είναι παράλληλο στο N(γ(s)) και κάθετο στο N(γ(s)) γ(s), άρα k g (s) = 0. Αντίστροφα, αν k g (s) = 0 τότε το διάνυσμα γ(s) είναι κάθετο στο N(γ(s)) γ(s). Συνεπώς, τα γ(s), N(γ(s)) και N(γ(s)) γ(s) είναι μοναδιαία διανύσματα του R 3 κάθετα μεταξύ τους και επειδή τα διανύσματα γ(s), γ(s) είναι και αυτά κάθετα μεταξύ τους, προκύπτει ότι το γ(s) είναι παράλληλο με το N(γ(s)), απ όπου προκύπτει ότι γ(s) tan = 0. Συνεπώς, η γ είναι μια γεωδαισιακή. Πρόταση 9.3. Οι παραμετρικές γραμμές v = σταθερό μιας επιφάνειας M με τοπική παραμέτρηση X : U R 2 M, X = X(u, v) είναι γεωδαισιακές αυτής, εάν και μόνο εάν ισχύουν οι σχέσεις E = E(u), αν F = 0, ή F E u + EE v = 2EF u αν F 0.
162 Γεωδαισιακή καμπυλότητα 161 Απόδειξη. Επειδή οι καμπύλες v = σταθερό είναι γεωδαισιακές της επιφάνειας M, θα έχουμε dv ds = 0, du ds = 1. (9.18) E Από τη δεύτερη εξίσωση των διαφορικών εξισώσεων (9.16) έχουμε Γ 2 11 = 0 ή ισοδύναμα F E u + EE v = 2EF u. (9.19) Η πρώτη εξίσωση των διαφορικών εξισώσεων (9.16) λόγω των (9.18) γίνεται οπότε τελικά έχουμε ( d 1 ds ) + Γ E E = 0 ή E u 2E E 1 + Γ E E = 0, Δεδομένου όμως ότι Γ 1 11 = GE u 2F F u + F E v 2(EG F 2, η σχέση (9.20) γίνεται: ) Γ 1 11 = E u 2E. (9.20) F (F E u + EE v 2EF u ) = 0. (9.21) Αν λοιπόν είναι F = 0, τότε από την (9.19) έχουμε ότι E v = 0, δηλαδή E = E(u). Αν όμως F 0, τότε η (9.21) ανάγεται στην (9.19) και η πρόταση έχει αποδειχθεί. Πρόταση 9.4. Εστω M μια προσανατολισμένη κανονική επιφάνεια με απεικόνιση Gauss N : M S 2 και έστω γ : I M μια καμπύλη στην M με παραμέτρηση κατά μήκος τόξου. Εστω k : I R η καμπυλότητα της γ ως καμπύλης στον R 3 και έστω k n, k g : I R η κάθετη και η γεωδαισιακή καμπυλότητα αντίστοιχα. Τότε ισχύει η σχέση k(s) 2 = k g (s) 2 + k n (s) 2. Απόδειξη. Τα διανύσματα N(γ(s)) και N(γ(s)) γ(s) είναι μοναδιαία και κάθετα μεταξύ τους, οπότε από την σχέση (9.2) έχουμε γ, γ = κ n N + κ g (N γ), κ n N + κ g (N γ) = κ n N + κ g (N γ), κ n N + κ n N + κ g (N γ), κ g (N γ) = κ 2 n + κ 2 g κ 2 = κ 2 n + κ 2 g, όπου κ = γ η καμπυλότητα της γ. Παράδειγμα 9.2. Κάθε (τμήμα) ευθείας σε μια επιφάνεια είναι γεωδαισιακή. Συγκεκριμένα, κάθε ευθεία σε μια επιφάνεια επιδέχεται μια παραμέτρηση ώστε να είναι γεωδαισιακή. Παράδειγμα 9.3. Οι γεννήτορες ενός γενικευμένου κυλίνδρου είναι γεωδαισιακές. Παράδειγμα 9.4. Κάθε κάθετη τομή μιας επιφάνειας M είναι γεωδαισιακή.
163 162 Γεωδαισιακές καμπύλες Σχήμα 9.1: Κάθετη τομή. Μια κάθετη τομή (normal section) της M είναι η τομή C της M με ένα επίπεδο Π, τέτοιο ώστε το Π να είναι κάθετο στο εφαπτόμενο επίπεδο της M σε κάθε σημείο της C. Αυτό προκύπτει από το Θεώρημα Meusnier (βλ. Κεφάλαιο 5). Παράδειγμα 9.5. Κάθε μέγιστος κύκλος μιας σφαίρας είναι γεωδαισιακή καμπύλη. Αυτό είναι άμεσο από το προηγούμενο παράδειγμα, επειδή οι μέγιστοι κύκλοι προκύπτουν από κάθετες τομές της σφαίρας από επίπεδα που διέρχονται από το κέντρο της σφαίρας. Παράδειγμα 9.6. Εστω γ = (r, 0, z) : I R 3 μια λεία καμπύλη στο επίπεδο xz, τέτοια ώστε r(s) > 0 και ṙ(s) 2 + ż(s) 2 = 1 για κάθε s I. Τότε η απεικόνιση X : I R R 3 cos v sin v 0 r(u) X(u, v) = sin v cos v z(u) = r(u) cos v r(u) sin v αποτελεί παραμέτρηση μιας επιφάνειας εκ περιστροφής M. Ο εφαπτόμενος χώρος σε ένα σημείο X(u, v) M παράγεται από τα διανύσματα ṙ(u) cos v X u = ṙ(u) sin v ż(u), X v = Διατηρώντας το v R σταθερό, η καμπύλη γ 1 : I M με τύπο r(u) cos v γ 1 (u) = r(u) sin v r(u) sin v r(u) cos v αποτελεί μια παραμέτρηση ως προς το μήκος τόξου ενός μεσημβρινού (meridian) της M. Εύκολα βλέπουμε ότι γ 1, X u = γ 1, X v = 0, δηλαδή γ 1 span{x u, X v }, οπότε ( γ 1 ) tan = 0, άρα η γ 1 : I M είναι μια z(u) 0 z(u).
164 Γεωδαισιακή καμπυλότητα 163 γεωδαισιακή της M. Παρόμοια, διατηρώντας το u R σταθερό (έστω u = u 0 ), η καμπύλη γ 2 : I M με τιμή γ 2 (v) = r(u) cos v r(u) sin v αποτελεί μια παραμέτρηση ενός παραλλήλου (parallel) της M. Με έναν απλό υπολογισμό προκύπτει ότι z(u) γ 2, X u = ṙ(u 0 )r(u 0 ), γ 2, X v = 0. Αυτό σημαίνει ότι η καμπύλη γ 2 : I M είναι μια γεωδαισιακή της M εάν και μόνο εάν ṙ(u 0 ) = 0, δηλαδή το u 0 είναι ένα κρίσιμο σημείο της συνάρτησης r : I R. Και σε αυτό το παράδειγμα, τίθεται το ερώτημα αν η M έχει και άλλες γεωδαισιακές (βλ. στη συνέχεια το Θεώρημα Clairaut). Από τα προηγούμενα παραδείγματα φαίνεται ότι το πρόβλημα εύρεσης των γεωδαισιακών καμπυλών σε μια επιφάνεια δεν είναι ιδιαιτέρως εύκολο. Στο επόμενο θεώρημα θα δούμε ότι το πρόβλημα αυτό ισοδυναμεί με την επίλυση ενός μη γραμμικού συστήματος συνήθων διαφορικών εξισώσεων, το οποίο όμως και αυτό στην πλήρη γενικότητά του δεν είναι πάντα εύκολο να επιλυθεί. Θεώρημα 9.2. Εστω M μια κανονική επιφάνεια και X : U R 2 M μια τοπική παραμέτρηση της M με θεμελιώδη ποσά πρώτης τάξης ( E F F G ) = [dx][dx] t. Αν γ : I M είναι μια καμπύλη της επιφάνειας M κλάσης C 2 τότε το τμήμα γ(s) = X(u(s), v(s)) : I X(U) M είναι μια γεωδαισιακή της M εάν και μόνο εάν ισχύουν οι εξής διαφορικές εξισώσεις: d ( ) 1( E u + F v = Eu u 2 + 2F u u v + G u v 2) dt 2 d ( ) 1( F u + G v = Ev u 2 + 2F v u v + G v v 2), (9.22) dt 2 όπου Edu 2 + 2F dudv + Gdv 2 είναι η πρώτη θεμελιώδης μορφή του X. Οι διαφορικές εξισώσεις (9.22) ονομάζονται γεωδαισιακές εξισώσεις. Απόδειξη. Επειδή το σύνολο {X u, X v } αποτελεί βάση του εφαπτόμενου επιπέδου του T X(u,v) M, η γ είναι γεωδαισιακή εάν και μόνο εάν η επιτάχυνση γ είναι ορθογώνια στο X u και στο X v. Επειδή γ = ux u + vx v, αυτό είναι ισοδύναμο με τις εξισώσεις d ds ( ux u + vx v ), X u = 0 και d ds ( ux u + vx v ), X v. (9.23)
165 164 Γεωδαισιακές καμπύλες Θα δείξουμε ότι αυτό το ζεύγος των εξισώσεων είναι ισοδύναμο με τις γεωδαισιακές εξισώσεις. Η αριστερή από τις εξίσωσεις (9.23) είναι ισοδύναμη με την d ds (( ux u + vx v )X u ) ( ux u + vx v ) dx u ds = d ds (E u + F v) ( ux u + vx v )( ux uu + vx uv ) = d ds (E u + F v) ( u2 (X u X uu ) + u v(x u X uv +X v X uu ) + v 2 (X v X uv )). (9.24) Επιπλέον, επειδή E u = X u, X u u = X uu, X u + X u, X uu = 2 X u, X uu, θα είναι X u, X uu = 1 2 E u και παρόμοια X u, X uv = 1 2 G u. Τέλος, είναι ότι X u, X uv + X v, X uu = X u, X v u = F u. Αντικαθιστώντας τις τελευταίες σχέσεις στην (9.24), παίρνουμε ( ) d ds ( ux u + vx v ) X u = d ds (E u + F v) 1 2 (E u u 2 + 2F u u v + G u v 2 ). Από εδώ φαίνεται ότι η πρώτη εξίσωση (9.23) είναι ισοδύναμη με την πρώτη γεωδαισιακή εξίσωση (9.22). Παρόμοια αποδεικνύεται η ισοδυναμία των δύο άλλων εξισώσεων. Παράδειγμα 9.7. Θα βρούμε τις γεωδαισιακές καμπύλες του ορθού κυκλικού κυλίνδρου ακτίνας 1 με τοπική παραμέτρηση X : U R 2 M R 3, X(u, v) = (cos u, sin u, v), όπου U = [0, 2π) R, χρησιμοποιώντας τις γεωδαισιακές εξισώσεις. Τα θεμελιώδη ποσά πρώτης τάξης είναι E = 1, F = 0 και G = 1. Αντικαθιστώντας στις εξισώσεις (9.22), έχουμε d ( u(s)) = 0 ü(s) = 0 u(s) = α u(s) = αs + β ds d ( v(s)) = 0 v(s) = 0 v(s) = c v(s) = cs + d, ds όπου α, β, c, d R. Άρα η καμπύλη γ : I R M με εξίσωση γ(s) = X(u(s), v(s)) = (cos(αs + β), sin(αs + β), cs + d) είναι γεωδαισιακή της επιφάνειας M. Αν α = 0, η παραπάνω είναι μια ευθεία παράλληλη στον άξονα των z, ένω, αν α 0, τότε η γεωδαισιακή είναι μια κυκλική έλικα. Στο ερώτημα κατά πόσον από κάθε σημείο μιας επιφάνειας διέρχεται μια γεωδαισιακή καμπύλη με δοσμένη αρχική ταχύτητα απαντά το παρακάτω θεώρημα. Θεώρημα 9.3. Εστω M μια κανονική επιφάνεια, p M και Z T p M. γεωδαισιακή γ : ( ɛ, ɛ) M Τότε υπάρχει μοναδική τοπικά ορισμένη που ικανοποιεί τις συνθήκες γ(0) = p και γ(0) = Z. Η απόδειξη του θεωρήματος αυτού ουσιαστικά βασίζεται στο θεμελιώδες θεώρημα των Picard - Lindelöf σχετικά με την ύπαρξη και μοναδικότητα λύσης ενός προβλήματος διαφορικών εξισώσεων αρχικών τιμών. Οι γεωδαισιακές διατηρούνται μέσω τοπικών ισομετριών. Αφήνουμε την απόδειξη της παρακάτω πρότασης ως άσκηση.
166 Γεωδαισιακή καμπυλότητα 165 Πρόταση 9.5. Εστω M 1, M 2 δύο κανονικές επιφάνειες και ϕ : M 1 M 2 μια τοπική ισομετρία. Τότε η καμπύλη γ 1 : I M 1 είναι μια γεωδαισιακή της M 1 εάν και μόνο εάν η σύνθεση γ 2 = ϕ γ 1 : I M 2 είναι μια γεωδαισιακή της M 2. Σχήμα 9.2: Γεωδαισιακή στον κύλινδρο. Εφαρμογή. Θα χρησιμοποιήσουμε την παραπάνω πρόταση για να βρούμε όλες τις γεωδαισιακές του ορθού κυκλικού κυλίνδρου M = S 1 I, I = [0, 1]. Γνωρίζουμε ήδη ότι οι κύκλοι x 2 + y 2 = 1 είναι γεωδαισιακές του M ως κάθετες τομές. Θεωρούμε την απεικόνιση X : R 2 M με X(u, v) = (cos u, sin u, v) από το επίπεδο xy στον κύλινδρο. Η απεικόνιση αυτή είναι μια τοπική ισομετρία (γιατί;) Γνωρίζουμε ότι οι γεωδαισιακές καμπύλες του επιπέδου είναι οι ευθείες. Παίρνουμε τις εικόνες μέσω της X των ευθειών y = mx + c που δεν είναι παράλληλες με τον άξονα x. Αυτές έχουν τη μορφή γ(u) = (cos u, sin u, mu + c) (όπου θέσαμε x = u, y = v), οι οποίες είναι κυκλικές έλικες βήματος 2π m. Για m = 0 παίρνουμε τις ήδη γνωστές κυκλικές γεωδαισιακές. Τέλος, μια άλλη κλάση γεωδαισιακών προκύπτει αν πάρουμε τις εικόνες μέσω της X των ευθειών του επιπέδου που είναι παράλληλες με τον άξονα y. Αυτές είναι οι γεννήτορες του κυλίνδρου. Παράδειγμα 9.8. Θα βρούμε τις γεωδαισιακές της σφαίρας S 2. Θεωρούμε την παραμέτρηση της σφαίρας με γεωγραφικές συντεταγμένες X(θ, ϕ) = (cos θ cos ϕ, cos θ sin ϕ, sin θ) (θ = γεωγραφικό πλάτος, ϕ = γεωγραφικό μήκος). Γνωρίζουμε ότι η πρώτη θεμελιώδης μορφή της σφαίρας για την παραμέτρηση αυτή είναι ds 2 = dθ 2 + cos 2 θdϕ 2, άρα E = 1, F = 0, G = cos 2 θ. Θα αναζητήσουμε γεωδαισιακές γ(t) = X ( θ(t), ϕ(t) ) μοναδιαίας ταχύτητας γ(t) = 1. Η σχέση αυτή δίνει θx θ + ϕx ϕ = 1, από όπου μετά από πράξεις παίρνουμε ότι θ 2 + ϕ 2 cos 2 θ = 1. (9.25) Από τη δεύτερη διαφορική εξίσωση των γεωδαισιακών του Θεωρήματος 9.2 προκύπτει ότι d dt ( ϕ cos2 θ) = 0 ϕ cos 2 θ = Ω
167 166 Γεωδαισιακές καμπύλες για μια σταθερά Ω, συνεπώς ϕ 2 = Ω2 cos 4 θ. Αν Ω = 0, τότε ϕ2 = 0, δηλαδή η ϕ είναι σταθερή, οπότε η γ είναι τμήμα ενός μεσημβρινού. Εστω ότι Ω 0, άρα ϕ 0. Τότε η συνθήκη (9.25) δίνει θ2 = 1 ϕ 2 cos 2 θ = 1 Ω2 cos 2 θ. Άρα ή από όπου παίρνουμε Συνεπώς, θ 2 1 ϕ 2 = Ω 2 cos 2 θ Ω 2 cos 4 θ = cos 2 θ(ω 2 cos 2 θ 1) (dθ ) 2 dt (dϕ) = cos 2 θ(ω 2 cos 2 θ 1), 2 dt ( ) dθ 2 = cos 2 θ(ω 2 cos 2 θ 1). dϕ ( ) dθ dϕ = ± cos θ Ω 2 cos 2 1 θ 1 dϕ = ± cos θ dθ Ω 2 cos 2 θ 1 dθ ±(ϕ ϕ 0 ) = cos θ Ω 2 cos 2 θ 1, ϕ 0 σταθερά. Θέτουμε u = tan θ, άρα du = 1 cos 2 dθ. Συνεπώς, προκύπτει τελικά ότι θ ( ) du ±(ϕ ϕ 0 ) = Ω 2 1 u = u 2 sin 1 Ω 2 1 άρα ± sin(ϕ ϕ 0 ) = tan θ Ω 2 1 άρα tan θ = ± Ω 2 1 sin(ϕ ϕ 0 ). Από αυτό προκύπτει ότι οι συντεταγμένες x = cos θ cos ϕ, y = cos θ sin ϕ, z = sin θ της γ(t) ικανοποιούν την εξίσωση z = ax + by, όπου a = ± Ω 2 1 sin ϕ 0 και b = ± Ω 2 1 cos ϕ 0. Με άλλα λόγια η γ προκύπτει από την τομή της σφαίρας S 2 με ένα επίπεδο που διέρχεται από την αρχή των αξόνων. Σε κάθε περίπτωση λοιπόν, η γ είναι τμήμα ενός μέγιστου κύκλου. 9.2 Το Θεώρημα Clairaut Οι γεωδαισιακές εξισώσεις για επιφάνειες εκ περιστροφής είναι συνήθως δύσκολο να επιλυθούν ακριβώς, ωστόσο μπορούν να χρησιμοποιηθούν, ώστε να έχουμε μια καλή ποσοτική κατανόηση των γεωδαισιακών για τέτοιου είδους επιφάνειες.
168 Το Θεώρημα Clairaut 167 Εστω X(u, v) = (f(u) cos v, f(u) sin v, g(u)) παραμέτρηση μιας εκ περιστροφής επιφάνειας, για την ( ) df 2 ( ) dg 2 οποία υποθέτουμε ότι f > 0 και + = 1. Από την (9.22) βλέπουμε ότι οι γεωδαισιακές du du εξισώσεις είναι οι ü = f(u) df du v2, Με βάση τα προηγούμενα αποδεικνύεται η εξής πρόταση (άσκηση). d dt (f 2 (u) v) = 0. (9.26) Πρόταση 9.6. Για την επιφάνεια εκ περιστροφής X(u, v) = (f(u) cos v, f(u) sin v, g(u)) ισχύουν τα εξής: (1) Κάθε μεσημβρινός είναι γεωδαισιακή. (2) Ο παράλληλος, για παράδειγμα u = u 0, είναι γεωδιασιακή εάν και μόνο εάν το u 0 είναι κρίσιμο σημείο της f, δηλαδή εάν df du = 0. u=u0 Η παραπάνω πρόταση δίνει κάποιες από τις γεωδαισιακές της επιφάνειας εκ περιστροφής. Ενας εναλλακτικός τρόπος εντοπισμού γεωδαισιακών για τέτοιου είδους επιφάνειες είναι χρησιμοποιώντας το παρακάτω ενδιαφέρον θεώρημα. Θεώρημα 9.4. (Clairaut) Εστω M μια κανονική επιφάνεια εκ περιστροφής και γ : I M μια γεωδαισιακή με παραμέτρηση ως προς το μηκός τόξου. Εστω ρ : M R + η συνάρτηση απόστασης ενός σημείου γ(t) M από τον άξονα περιστροφής και έστω ϕ : I M η γωνία μεταξύ του διανύσματος γ(t) και ένος μεσημβρινού που διέρχεται από το γ(t). Τότε το γινόμενο ρ(t) sin ϕ(t) είναι σταθερό κατά μήκος της γεωδαισιακής γ. Το αντίστροφο ισχύει, εάν η καμπύλη γ είναι τμήμα κάποιου παραλλήλου της M. Απόδειξη. Εστω M μια επιφάνεια εκ περιστροφής με την παραμέτρηση X(u, v) = (f(u) cos v, f(u) sin v, g(u)), όπου ρ = f(u). Επειδή ρ 2 (u) + ġ 2 X u (u) = 1, τα διανύσματα X u = X u και Xv X v X v = ρ 1 X v είναι μοναδιαία και εφαπτόμενα στους παράλληλους και στους μεσημβρινούς αντίστοιχα. Επειδή F = X u, X v = 0, τα διανύσματα αυτά είναι και κάθετα. Υποθέτουμε ότι η καμπύλη γ(t) = X(u(t), v(t)) είναι μοναδιαίας ταχύτητας. Τότε το εφαπτόμενο διάνυσμα γ(t) = X u u + X v v θα γράφεται ως γραμμικώς συνδυασμός ως προς τη βάση {X u, X v } με τον εξής τρόπο: γ(t) = X u u + X v v = cos ϕx u + sin ϕ X v = cos ϕx u + ρ 1 sin ϕx v. Από την παραπάνω ισότητα παίρνουμε ( u cos ϕ)x u + ( v ρ 1 sin ϕ)x v = 0. Επειδή τα X u και X v είναι γραμμικώς ανεξάρτητα, θα είναι u cos ϕ = 0 (9.27) v ρ 1 sin ϕ = 0. (9.28)
169 168 Γεωδαισιακές καμπύλες Σχήμα 9.3: Εκ περιστροφής επιφάνεια και το θεώρημα Clairaut. Η σχέση (9.28) δίνει ρ 2 v = ρ sin ϕ, οπότε από τη δεύτερη εξίσωση της σχέσης (9.26), προκύπτει ότι ρ sin ϕ = Ω, Ω R. Για το αντίστροφο, εάν το ρ sin ϕ είναι μια σταθερά Ω πάνω σε μια μοναδιαίας ταχύτητας καμπύλη γ της επιφάνειας M, από τα προηγούμενα προκύπτει εύκολα ότι ικανοποιείται η δεύτερη εξίσωση της σχέσης (9.26). Πρέπει να αποδείξουμε ότι ικανοποιείται και η πρώτη εξίσωση της (9.26). Είναι ρ v = sin ϕ v = ρ sin ϕ ρ 2 v = Ω ρ 2. (9.29) Επειδή η καμπύλη γ(t) = X(u(t), v(t)) είναι μοναδιαίας ταχύτητας θα έχουμε γ(t) = 1 u 2 + f 2 (u) v 2 = 1 u 2 = 1 Ω2 ρ 2. Παραγωγίζοντας την προηγούμενη σχέση ως προς t και μετά από πράξεις έχουμε: 2 uü = 2Ω ( 2Ω dρ ρ = ρ3 ρ 3 u u ü ρ dρ ) du du v2 = 0. Εάν η ποσότητα στην παραπάνω παρένθεση δεν μηδενίζεται σε κάποιο σημείο της καμπύλης, έστω γ(t 0 ) = X(u(t 0 ), v(t 0 )), θα υπάρχει ένας αριθμός ɛ > 0, τέτοιος ώστε η ποσότητα να μην μηδενίζεται και για t t 0 < ɛ. Αλλά τότε, u = 0 όταν t t 0 < ɛ. Επομένως, η γ ταυτίζεται με τον παράλληλο u = u 0 όταν t t 0 < ɛ, πράγμα αντίθετο με την υπόθεση. Άρα, η ποσότητα μέσα στην παρένθεση πρέπει να μηδενίζεται παντού πάνω στην γ, δηλαδή ü = ρ dρ du v2, το οποίο δείχνει ότι η πρώτη εξίσωση στην (9.26) ικανοποείται.
170 Γεωδαισιακές μέσω λογισμού μεταβολών 169 Σύμφωνα με το παραπάνω θεώρημα για τις επιφάνειες εκ περιστροφής ισχύει ότι u 2 = 1 Ω2 ρ 2 v = sin θ ρ Η σταθερά Ω παίρνει διαφορετικές τιμές για κάθε γεωδαισιακή και έχει την εξής γεωμετρική ερμηνεία: = Ω ρ 2 (1) Αν Ω = 0, τότε v =σταθερό και οι γεωδαισιακές είναι οι μεσημβρινοί. (2) Αν Ω > 0, τότε από την εξίσωση u 2 = 1 Ω2 ρ 2 βλέπουμε ότι οι γεωδαισιακές βρίσκονται στο μέρος της επιφάνειας M που απέχει απόσταση 0 Ω ρ από τον άξονα περιστροφής. 9.3 Γεωδαισιακές μέσω λογισμού μεταβολών Θα συζητήσουμε τη βασική ιδιότητα των γεωδαισιακών που είναι ότι τοπικά ελαχιστοποιούν την απόσταση μεταξύ δύο σημείων σε μια επιφάνεια. Η άποψη αυτή γενικεύει την ιδιότητα των ευθειών στο επίπεδο ως καμπύλες που ελαχιστοποιούν την Ευκλείδεια απόσταση μεταξύ δύο σημείων. Για την προσέγγιση αυτή θα χρησιμοποιήσουμε στοιχεία λογισμού μεταβολών, μια από τις πιο παλαιές περιοχές των μαθηματικών. Ορισμός 9.3. Εστω M μια κανονική επιφάνεια και γ : I M μια καμπύλη κλάσης C 2. Εστω [a, b] ένα συμπαγές υποδιάστημα του I. 1. Το συναρτησοειδές μήκους (length functional) L [a,b] ορίζεται ως L [a,b] (γ) = b a γ(t) dt. 2. Το συναρτησοειδές ενέργειας (energy functional) E [a,b] ορίζεται ως E [a,b] (γ) = 1 2 b a γ(t) 2 dt. Ορισμός 9.4. Εστω M μια κανονική επιφάνεια, γ : I M μια καμπύλη κλάσης C Μια μεταβολή (variation) της γ είναι μια απεικόνιση κλάσης C 2 της μορφής Φ : ( ɛ, ɛ) I M, Φ = Φ(t, s) = Φ t (s), τέτοια ώστε Φ 0 (s) = Φ(0, s) = γ(s) για κάθε s I. Εάν το διάστημα I είναι συμπαγές (I = [a, b]), τότε μια μεταβολή Φ ονομάζεται γνήσια (proper), εάν για κάθε t ( ɛ, ɛ) ισχύουν οι σχέσεις Φ t (a) = γ(a) και Φ t (b) = γ(b). 2. Μια καμπύλη γ : I M κλάσης C 2 ονομάζεται κρίσιμο σημείο του συναρτησοειδούς μήκους, εάν κάθε γνήσια μεταβολή Φ της γ [a,b] ικανοποιεί την σχέση d ( L[a,b] (Φ t ) ) dt t=0 = 0.
171 170 Γεωδαισιακές καμπύλες Το παρακάτω θεώρημα αναφέρει ότι οι γεωδαισιακές καμπύλες σε μια επιφάνεια χαρακτηρίζονται ως κρίσιμα σημεία του συναρτησοειδούς μήκους τα οποία, όπως αποδεικνύεται, είναι τα ίδια με αυτά του συναρτησοειδούς ενέργειας. Θεώρημα 9.5. Εστω γ : I = [a, b] M μια καμπύλη κλάσης C 2 με παραμέτρηση ως προς το μήκος τόξου. Τότε η γ είναι ένα κρίσιμο σημείο του συναρτησοειδούς μήκους εάν και μόνο εάν η γ είναι μια γεωδαισιακή της M Απόδειξη. Εστω Φ : ( ɛ, ɛ) I M με (t, s) Φ(t, s) μια γνήσια μεταβολή της γ : I M. Τότε d ( L[a,b] (Φ t ) ) t=0 dt = d ( b γ t (s) ds) dt a t=0 b d = Φ a dt s, Φ s ds t=0 ( b d = 2 Φ dt t s, Φ s / = = a b a b Επειδή η μεταβολή είναι γνήσια, θα ισχύει Επιπλέον, επειδή προκύπτει ότι d dt a d dt 2 Φ s t, Φ s ds t=0 ( d ds Φ t, Φ s Φ = ( Φ Φ (0, s), t s (0, s) ) b a Φ t Φ s, Φ s t, 2 Φ Φ (0, a) = (0, b) = 0. t 2 Φ (0, s) = γ(s), s2 ( L[a,b] (Φ t ) ) t=0 = b a ) ds ) s 2 ds b a t=0 t=0 Φ t (0, s), γ(s)tan ds. Φ t (0, s), 2 Φ (0, s) ds. s2 Το τελευταίο ολοκλήρωμα μηδενίζεται για κάθε γνήσια κύμανση Φ της γ, εάν και μόνο εάν η γ είναι μια γεωδαισιακή. Θα συζητήσουμε τώρα τις ελαχιστικές ιδιότητες των γεωδαισιακών. Θα αρχίσουμε με μερικές ενδιαφέρουσες παρατηρήσεις. 1. Αν η γ : I M είναι μια καμπύλη με ελάχιστο μήκος που ενώνει δύο σημεία γ(a), γ(b) M, τότε το συναρτησοειδές L [a,b] ελαχιστοποιείται για t = 0, άρα d ( L[a,b] (Φ t ) ) t=0 dt = 0, συνεπώς η γ είναι μια γεωδαισιακή της επιφάνειας M.
172 Η εκθετική απεικόνιση Αν η γ : I M είναι μια γεωδαισιακή που ενώνει τα γ(a), γ(b), τότε η γ είναι μεν ένα κρίσιμο σημείο του συναρτησοειδούς L [a,b], αλλά δεν είναι απαραίτητα μια καμπύλη ελάχιστου μήκους μεταξύ των γ(a), γ(b). Πάρτε για παράδειγμα την σφαίρα S 2 και τα σημεία της γ(a), γ(b) επί του ισημερινού γ, ο οποίος είναι μια γεωδαισιακή, όπως φαίνεται στο σχήμα. Το τμήμα της γ που ελαχιστοποιεί την απόσταση μεταξύ των γ(a), γ(b) είναι το μικρό τμήμα της γ μεταξύ των γ(a), γ(b) και όχι το μεγάλο. Σχήμα 9.4: Ελάχιστη απόσταση. 3. Μια καμπύλη ελάχιστου μήκους μεταξύ δύο σημείων μιας επιφάνειας M μπορεί και να μην υπάρχει καθόλου. Πάρτε για παράδειγμα M = R 2 \ {(0, 0)} R 3. Τότε δεν υπάρχει καμπύλη ελάχιστου μήκους, που να ενώνει τα σημεία p = ( 1, 0) και q = (1, 0). Παρόλα αυτά, αποδεικνύεται το εξής: αν δύο σημεία p, q σε μια κλειστή επιφάνεια M μπορούν να ενωθούν με μια καμπύλη στην M, τότε υπάρχει καμπύλη ελάχιστου μήκους που να τα ενώνει. Για παράδειγμα, το επίπεδο Π R 3 και η σφαίρα S 2 είναι κλειστές επιφάνειες, ενώ η M = R 2 \ {(0, 0)} R 3 δεν είναι κλειστή. 9.4 Η εκθετική απεικόνιση Θα προχωρήσουμε τώρα σε κάποια ελαφρώς πιο εξειδικευμένα θέματα. Εστω M μια κανονική επιφάνεια, p M και έστω T 1 p M = {W T p M : W = 1} η μοναδιαία σφαίρα (μοναδιαίος κύκλος) στον εφαπτόμενο χώρο T p M. Τότε κάθε μη μηδενικό διάνυσμα Z T p M μπορεί να γραφτεί ως Z = r Z e Z, όπου r Z = Z και e Z = 1 Z Z T p 1 M. Για κάθε W Tp 1 M έστω γ W : ( a W, b W ) M η μέγιστη γεωδαισιακή καμπύλη, τέτοια ώστε a W, b W R + { }, γ W (0) = p, γ W (0) = W (τέτοια γεωδαισιακή
173 172 Γεωδαισιακές καμπύλες υπάρχει). Αποδεικνύεται ότι ο πραγματικός αριθμός ɛ p = inf{a W, b W : W Tp 1 M} είναι θετικός, συνεπώς το σύνολο (ανοικτή μπάλα) B ɛp (0) = {Z T p M : Z < ɛ p } είναι μη κενό. Ορισμός 9.5. Η εκθετική απεικόνιση (exponetial map) exp p : B ɛp (0) T p M M στο σημείο p ορίζεται ως p, αν Z = 0 exp p (Z) = γ ɛz (r Z ), αν Z 0. Παρατηρήσεις. 1) Ο όρος ἑκθετική απεικόνιση εξηγείται καλύτερα μελετώντας διαφορική γεωμετρία σε μεγαλύτερες διαστάσεις, δηλαδή σε πολλαπλότητες. Εκεί είναι δυνατόν να οριστεί κατά φυσικό τρόπο η έννοια της γεωδαισιακής σε συμπαγείς ομάδες πινάκων, όπως για παράδειγμα η ορθογώνια ομάδα O(n). Τότε αποδεικνύεται ότι η αντίστοιχη εκθετική απεικόνιση στο ουδέτερο σημείο I O(n) (ταυτοτικός πίνακας) είναι η συνηθισμένη εκθετική απεικόνιση πινάκων, δηλαδή exp I (A) = e A, A T I O(n). 2) Αν W Tp 1 M, τότε η ευθεία λ W : ( ɛ p, ɛ p ) T p M, λ W (t) = tw απεικονίζεται μέσω της εκθετικής απεικόνισης στη γεωδαισιακή γ W, δηλαδή τοπικά ισχύει γ W = exp p λ W. Συνεπώς, τοπικά η εκθετική απεικόνιση απεικονίζει ευθείες σε γεωδαισιακές. Αποδεικνύεται ότι η απεικόνιση exp p είναι διαφορίσιμη. Επιπλέον, ισχύει το εξής: Πρόταση 9.7. Το διαφορικό d(exp p ) 0 : T p M T p M της εκθετικής απεικόνισης ισούται με την ταυτοτική απεικόνιση Id TpM στον εφαπτόμενο χώρο T p M. Απόδειξη. Εστω v T p M. Χρησιμοποιώντας την παραπάνω Παρατήρηση 2) υπολογίζουμε: d(exp p ) 0 (v) = d dt exp p(tv) = d t=0 dt γ tv ( tv ) = d t=0 dt γ tv(1) = d t=0 dt t=0 (tv) = v. tv Συνεπώς, από το θεώρημα αντίστροφης απεικόνισης υπάρχει r p R +, έτσι ώστε αν U p = B rp (0) και V p = exp p (U p ), τότε η απεικόνιση exp p Up : U p V p είναι μια αμφιδιαφόριση, η οποία παραμετρικοποιεί το ανοικτό υποσύνολο V p της επιφάνειας M. Το σύνολο αυτό (χάρτης της M) έχει ιδαίτερη σημασία στη διαφορική γεωμετρία και ονομάζεται κανονική περιοχή (normal neighborhood) του p M. Παράδειγμα 9.9. Εστω S 2 η μοναδιαία σφαίρα του R 3 και p = (1, 0, 0) ο βόρειος πόλος. μοναδιαίος κύκλος στον εφαπτόμενο χώρο T p S 2 δίνεται ως Τότε ο T 1 p S 2 = {(0, cos θ, sin θ) : θ R}.
174 Λυμένα παραδείγματα 173 Η εκθετική απεικόνιση exp p : T p S 2 S 2 της S 2 στο p δίνεται από την σχέση exp p (s(0, cos θ, sin θ)) = (cos s)(1, 0, 0) + (sin s)(0, cos θ, sin θ). Είναι σαφές ότι η εκθετική απεικόνιση περιορισμένη στην ανοικτή μπάλα B π (0) = {Z T p S 2 : Z < π} είναι 1 1, συνεπώς η γεωδαισιακή γ(s) = exp p (s(0, cos θ, sin θ)) αποτελεί την ελάχιστη απόσταση μεταξύ των σημείων p και γ(r), για κάθε r < π. Προτρέπουμε τον αναγνώστη να κάνει ένα σχήμα του παραδείγματος αυτού. Ερχόμαστε τώρα στο κεντρικό αποτέλεσμα του κεφαλαίου αυτού. Θεώρημα 9.6. Εστω M μια κανονική επιφάνεια. Τότε οι γεωδαισιακές καμπύλες ελαχιστοποιούν τοπικά την απόσταση μεταξύ των άκρων τους. Απόδειξη. Εστω p M, U = B r (0) T p M και V = exp p (U), έτσι ώστε ο περιορισμός ϕ = exp p U : U V της εκθετικής απεικόνισης στο p να είναι αμφιδιαφόριση. Ορίζουμε μια μετρική ds 2 στην περιοχή U ως ds 2 (Z, W ) = dϕ(z), dϕ(w ) για κάθε Z, W διανυσματικά πεδία στο U. Με τη μετρική αυτή η απεικόνιση ϕ γίνεται ισομετρία. Από τον τρόπο ορισμού της εκθετικής απεικόνισης προκύπτει ότι οι γεωδαισιακές στο U που διέρχονται από το σημείο 0 = ϕ 1 (p) είναι ακριβώς οι ευθείες λ Z : t tz (Z T p M). Εστω q B r (0) \ {0} και λ q : [0, 1] B r (0) η καμπύλη λ q (t) = tq. Θεωρούμε σ : [0, 1] U οποιαδήποτε καμπύλη του U, τέτοια ώστε σ(0) = 0, σ(1) = q. Ορίζουμε δύο διανυσματικά πεδία X και X rad κατά μήκος της σ ως εξής: X : t σ(t) και Τότε προκύπτει ότι και X rad : t ds2 ( σ(t), X(t)) ds 2 (X(t), X(t)) σ(t). X rad (t) = ds2 ( σ(t), X(t)) ds 2 (X(t), X(t)) d dt X(t) = d ds dt 2 (X(t), X(t)) = ds2 ( σ(t), X(t)), X(t) από τις οποίες παίρνουμε ότι X rad (t) d X(t). Συνεπώς dt L(σ) = 1 0 σ(t) dt 1 0 X rad (t) dt = X(1) X(0) = q = L(λ q ). 1 0 d dt X(t) dt Η παραπάνω ανισότητα αποδεικνύει ότι η καμπύλη λ q είναι η καμπύλη ελάχιστου μήκους που ενώνει τα σημεία p και q.
175 174 Γεωδαισιακές καμπύλες 9.5 Λυμένα παραδείγματα Παράδειγμα Να εξετασθεί αν οι καμπύλες που ορίζονται από τις εξισώσεις u = αt 2, v = αt 3, α R, είναι γεωδαισιακές της επιφάνειας της οποίας η πρώτη θεμελιώδης μορφή είναι I = 2v 2 du 2 2uvdudv + u 2 dv 2, u > 0, v > 0. Λύση Για να είναι μια καμπύλη γεωδαισιακή της επιφάνειας θα πρέπει κ g = 0, οπότε θα πρέπει να ισχύει η σχέση u v u v + Γ 2 11(u ) 3 + (2Γ 2 12 Γ 1 11)(u ) 2 v (2Γ 1 12 Γ 2 22)u (v ) 2 Γ 1 22(v ) 3 = 0. (9.30) Είναι όμως, u = 2αt, u = 2α, v = 3αt 2, v = 6αt (9.31) οπότε τα σύμβολα Christoffel θα είναι E = 2v 2, F = uv, G = u 2, EG F 2 = u 2 v 2, (9.32) Γ 2 11 = 6v u 2, Γ2 12 = 4 u, Γ1 11 = 3 u, Γ1 12 = 3 v, Γ2 22 = 2 v, Γ1 22 = 2u v 2. (9.33) Το πρώτο μέλος της σχέσης (9.30) λόγω των (9.32) και (9.33) γίνεται 12α 2 t 2 6α 2 t 2 6αt3 α 2 t 4 8α3 t αt 2 4α2 t 2 3αt 2 8 αt 3 18α3 t 5 + 2αt2 α 2 t 6 27α3 t 6 = 12α 2 t 2 6α 2 t 2 48α 2 t α 2 t 2 144α 2 t α 2 t 2 = 0. Από την παραπάνω εξίσωση βλέπουμε ότι ικανοποιείται η σχέση (9.30) κατά συνέπεια οι δοσμένες καμπύλες είναι γεωδαισιακές της επιφάνειας, εφοδιασμένη με την πρώτη θεμελιώδη μορφή I. Παράδειγμα Εστω M μια επιφάνεια με παραμέτρηση X : U R 2 M για την οποία ισχύει E = E(u), F = 0, G = G(u). Αν γ(s) = X(u(s), v(s)) είναι μια γεωδαισιακή, αναφερόμενη στη φυσική παράμετρό της, να δειχθεί ότι G cos θ =σταθερό, όπου θ είναι η γωνία μεταξύ της γεωδαισιακής και των v-παραμετρικών καμπυλών u =σταθερό. Λύση Υπολογίζουμε αρχικώς τα σύμβολα Christoffel Γ 2 11 = Γ 2 22 = 0, Επομένως η δεύτερη από τις εξισώσεις (9.16) γίνεται: Γ 2 12 = G u 2G. (9.34) v(s) + G u u(s) v(s) = 0 G G v(s) + G u u(s) v(s) = 0 ( d G dv ) = 0 ds ds
176 Λυμένα παραδείγματα 175 οπότε ολοκληρώνοντας έχουμε G dv = G v(s) = c, c R. (9.35) ds Αν θέσουμε T (s) το εφαπτόμενο διάνυσμα της γεωδαισιακής στο τυχαίο σημείο αυτής, θα έχουμε T (s) = X u u(s) + X v v(s). Παίρνοντας το εσωτερικό γινόμενο με X v και λαμβάνοντας υπόψη ότι F = X u, X v = 0, έχουμε Λόγω της (9.35) είναι T (s), X v = c, άρα T (s), X v = X v, X v v(s) T (s), X v = G v(s). T (s) X v cos θ = c. Επειδή όμως T (s) = 1 και X v = G, έχουμε τελικά ότι G cos θ = c, c R που είναι η ζητούμενη σχέση. Παράδειγμα Οι γεωδαισιακές καμπύλες του υπερβολικού επιπέδου. Λύση Θα αρχίουμε με κάποιους γενικότερους χρήσιμους υπολογισμούς. Εστω M μια επιφάνεια εκ περιστροφής με παραμέτρηση X : I R M cos v sin v 0 r(s) X(s, v) = sin v cos v z(s) = r(s) cos v r(s) sin v όπου (r, 0, z) : I R 3 μια διαφορίσιμη καμπύλη στο επίπεδο xz, τέτοια ώστε r(s) > 0 και ṙ(s) 2 +ż(s) 2 = 1 για κάθε s I. Γνωρίζουμε ότι (βλ. Κεφάλαιο 5) ότι η καμπυλότητα Gauss K της M ικανοποιεί τη διαφορική εξίσωση r(s) + K(s)r(s) = 0. Αν υποθέσουμε ότι K 1 (μονίμως αρνητική) και λύσουμε τη διαφορική αυτή εξίσωση, προκύπτει η γενική λύση r(s) = ae s + be s. Επιλέγοντας τις συναρτήσεις r, z : R + R να ικανοποιούν τις r(s) = e s, z(s) = s 0 1 e 2t dt λαμβάνουμε την παραμέτρηση X : R + R R 3 της ψευδοσφαίρας (pseudosphere), με θεμελιώδη ποσά πρώτης τάξης ( ) ( ) Ẽ F = [d F G X][d X] t 1 0 = 0 e 2s. z(s),
177 176 Γεωδαισιακές καμπύλες Εισάγουμε τώρα μια νέα μεταβλητή u > 0 από την σχέση s(u) = ln u και έτσι παίρνουμε μια νέα παραμέτρηση X : R + R M της ψευδοσφαίρας, όπου X(u, v) = X(s(u), v). Τότε από τον κανόνα της αλυσίδας προκύπτει ότι X u = s u X s = 1 u X s από όπου προκύπτουν τα θεμαλιώδη ποσά πρώτης τάξης της παραμέτρησης X: ( ) ( ) E F = [dx][dx] t = 1u F G 0 1 Η πρώτη θεμελιώδης μορφή ορίζει (επάγει) τη μετρική ds 2 = 1 u 2 (dv2 + du 2 ) στο άνω ημιεπίπεδο H 2 = {(v, u) R 2 : u > 0}. Η μετρική αυτή ονομάζεται υπερβολική μετρική του άνω ημιεπιπέδου. Ο υπερβολικός χώρος (ή επίπεδο) (hyperbolic space) (H 2, ds 2 ) έχει ιδιαίτερη γεωμετρική και ιστορική σημασία μια και είναι ένα μοντέλο μη Ευκλείδειας γεωμετρίας. Θα βρούμε τώρα τις γεωδαισιακές καμπύλες του υπερβολικού επιπέδου. Εστω γ = (v, u) : I H 2 μια γεωδαισιακή με παραμέτρηση ως προς το μήκος τόξου. Τότε γ = ( v, u) και γ 2 H 2 = ds 2 ( γ, γ) = 1 u 2 ( v2 + u 2 ) = 1 ή ισοδύναμα v 2 + u 2 = u 2. Από το Θεώρημα Clairaut ισχύει ότι η ποσότητα r(s) sin θ(s) = 1 u 2 ṙ R είναι σταθερή (πραγματικός αριθμός) κατά μήκος της γεωδαισιακής. Τότε προκύπτει ότι v = dv dt = u2 R. a) Αν R = 0, τότε v = 0 άρα η συνάρτηση v είναι σταθερή. Αυτό σημαίνει ότι οι κάθετες ευθείες v = v 0 του άνω ημιεπιπέδου H 2 είναι γεωδαισιακές. b) Αν R 0 τότε από τις παραπάνω σχέσεις παίρνουμε ότι u 4 R 2 + u 2 = u 2 και ισοδύναμα ότι u = ±u 1 R 2 u 2. Αυτό σημαίνει ότι και ισοδύναμα ότι dv du = v u = ± Ru 1 R 2 u 2 Ru dv = ± 1 R 2 u du. 2 du dt = Ολοκληρώνοντας παίρνουμε R(v v 0 ) = ± 1 R 2 u 2 άρα (v v 0 ) 2 + u 2 = γεωδαισιακή είναι ένα ημικύκλιο στο H 2 με κέντρο (v 0, 0) και ακτίνα 1 R. 1, το οποίο σημαίνει ότι η R2
178 Ασκήσεις 177 Σχήμα 9.5: Το υπερβολικό επίπεδο. Παράδειγμα Εστω M = {(x, y, z) R 3 : z = x 2 + y 2 ελλειπτικό παραβολοειδές εκ περιστροφής με τοπική παραμέτρηση X : R + (0, 2π) R 3, X(u, v) = (u cos v, u sin v, u 2 ). Θα υπολογίσουμε τη γεωδαισιακή καμπυλότητα των παραλλήλων. Λύση Είναι Για τον παράλληλο u = u 0 έχουμε ότι X u = (cos v, sin v, 2u), X v = ( u sin v, u cos v, 0), E = X u, X u = 1 + 4u 2, F = X u, X v = 0, G = X v, X v = u 2, 1 N = ( 2u cos v, 2u sin v, 1) u 2 γ = X v 1 = ( sin v, cos v, 0), γ = X v X vv X vv = 1 ( cos v, sin v, 0), u 0 1 N(γ(t)) γ = ( cos v, sin v, 2u 1 + 4u 2 0 ), 0 Συνεπώς, k g = γ, N(γ) γ = 1 u u Ασκήσεις 1. Εστω γ(t) μια τυχαία γεωδαισιακή καμπύλη σε μια επιφάνεια και έστω γ = λ. Αποδείξτε ότι η καμπύλη γ = γ(t/λ) είναι μια αναπαραμέτρηση της γ με μοναδιαία ταχύτητα, η οποία είναι και αυτή γεωδαισιακή καμπύλη. 2. Αποδείξτε ότι η γεωδαισιακή καμπυλότητα ικανοποιεί την σχέση k g (s) 2 = γ(s) tan Εστω T 2 R 3 ο δακτύλιος (torus) ο οποίος προκύπτει με περιστροφή του κύκλου με κέντρο (0, 2, 0) και ακτίνα 1 του επιπέδου yz, περί τον άξονα z.
179 178 Γεωδαισιακές καμπύλες (α) Αποδείξτε ότι η απεικόνιση X : ( π/2, 3π/2) (0, 2π) R 3 με τύπο X(u, v) = ((2 + cos u) cos v, (2 + cos u) sin v, sin u) είναι μια τοπική παραμέτρηση του T 2. (β) Υπολογίστε τη γεωδαισιακή καμπυλότητα του παραλλήλου X u : (0, 2π) T με X u (t) = ((2 + cos u) cos t, (2 + cos u) sin t, sin u), ως συνάρτηση του u ( π/2, 3π/2). 4. Να βρεθούν οι γεωδαισιακές καμπύλες του ορθού κυκλικού κώνου, που ορίζεται από την εξίσωση όπου θ = σταθερά, u > Αποδείξτε την Πρόταση Αποδείξτε την Πρόταση 9.6. X(u, v) = (u sin θ cos v, u sin θ sin v, u cos θ), 7. Αν X = X(u, v) είναι μια παραμέτρηση μιας επιφάνειας M, τέτοια ώστε E = E(u), F = 0 και G = G(u), τότε (1) Οι u-παραμετρικές καμπύλες (v =σταθερό) είναι γεωδαισιακές. (2) Οι v-παραμετρικές καμπύλες (u =σταθερό) είναι γεωδαισιακές εάν και μόνα εάν G u (u 0 ) = 0. (3) Μια καμπύλη γ(u) = X(u, v(u)) είναι γεωδαισιακή της επιφάνειας εάν και μόνο εάν v = ± c E du, c R. G(G c 2 ) 8. Μια επιφάνεια με παραμέτρηση X = X(u, v) λέγεται επιφάνεια του Liouville αν E = G = U(u) + V (v) και F = 0. Αν γ είναι μια γεωδαισιακή της επιφάνειας με εξίσωση γ(s) = X(u(s), v(s)), να δειχθεί ότι U sin 2 θ V cos 2 θ = c, c R, όπου θ είναι η γωνία της γ και των u-παραμετρικών καμπυλών. 9. Εστω M μια επιφάνεια του R 3 με τοπική παραμέτρηση X = X(u, v), τέτοια ώστε F = 0 και E = 1. Αποδείξτε ότι οι u-παραμετρικές καμπύλες είναι γεωδαισιακές. 10. Εστω X : U R 2 M μια παραμέτρηση μιας επιφάνειας M, τέτοια ώστε G v Δείξτε ότι οι v-παραμετρικές καμπύλες είναι γεωδαισιακές της επιφάνειας. = 0 και G u = 2 F v. 11. Βρείτε όλες τις γεωδαισιακές καμπύλες των επιφανειών του R 3 οι οποίες ορίζονται από τις εξισώσεις x 2 + 2y 2 = 2, x 2 + y 2 z 2 = 1 και x 2 + y 2 = z
180 Ασκήσεις Αν η πρώτη θεμελιώδης μορφή μιας επιφάνειας M είναι η I = du 2 + Gdv 2, δείξτε ότι η εξίσωση των γεωδαισιακών αυτής, ανάγεται στη μορφή dθ G dv =, όπου θ είναι η γωνία κατά την οποία οι u γεωδαισιακές τέμνουν τις καμπύλες v =σταθερό. 13. Εστω γ(s) μια καμπύλη μοναδιαίας ταχύτητας του ελικοειδούς με παραμέτρηση X(u, v) = (u cos v, u sin v, v). Δείξτε ότι u 2 + (1 + u 2 ) v 2 = 1. Δείξτε επίσης ότι, εάν η γ είναι γεωδαισιακή της επιφάνειας, τότε u = α 1 + u 2, όπου α είναι σταθερά. Βρείτε τις γεωδαισιακές που αντιστοιχούν στα α = 0 και α = Θεωρούμε την κανονική επιφάνεια M με τοπική παραμέτρηση X : R 2 R 3 X(u, v) = (u, v, sin u sin v). Βρείτε τις τιμές του θ R για τις οποίες η καμπύλη γ θ : R M με τύπο είναι μια γεωδαισιακή της M. γ θ (t) = X(t cos θ, t sin θ) 15. Βρείτε μερικές γεωδαισιακές καμπύλες οι οποίες να διέρχονται από το σημείο (0, 0, 0), της επιφάνειας M = {(x, y, z) R 3 : xy(x 2 y 2 ) = z}. 16. Αναζητήστε στην βιβλιογραφία την έννοια των γεωδαισιακών συντεταγμένων και του Λήμματος του Gauss.
181 180 Γεωδαισιακές καμπύλες
182 Βιβλιογραφία [1] M. Abate and F. Torena, Curves and Surfaces, Springer [2] C. Bär, Elementary Differential Geometry, Cambridge Univ. Press [3] W. E. Boyce and R. C. DiPrima, Elementary Differential Equation, Ninth Edition, John Wiley and Sons, [4] M. P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall [5] J. E. Marsden and M. J. Tromba, Vector Calculus, 6th ed., Macmillan Higher Edition, Μετάφραση 3 ης εκδ. Διανυσματικός Λογισμός, Πανεπιστημιακές Εκδόσεις Κρήτης, [6] J. Oprea, Differential Geometry and Its Applications, The Mathematical Assocation of America, [7] Β. Ι. Παπαντωνίου, Διαφορική Γεωμετρία, Εκδ. Πανεπιστ. Πατρών, Πάτρα, [8] A. Pressley, Elementary Differential Geometry, Second Edition, Springer Μετάφραση: Στοιχειώδης Διαφορική Γεωμετρία, Πανεπιστημιακές Εκδόσεις Κρήτης, Κρήτη
183 182 ΒΙΒΛΙΟΓΡΑΦ ΙΑ
184 Κεφάλαιο 10 Το Θεώρημα Gauss-Bonnet Σύνοψη Το Θεώρημα των Gauss - Bonnet αποτελεί ένα από τα πιο σημαντικά (αν όχι το πιο σημαντικό) αποτελέσματα της διαφορικής γεωμετρίας των επιφανειών. Μέσω του θεωρήματος αυτού, αναδεικνύεται μια απρόσμενη και βαθιά σχέση μεταξύ τοπικών ποσοτήτων μιας επιφάνειας, όπως η καμπυλότητα Gauss και η γεωδαισιακή καμπυλότητα και της τοπολογίας της επιφάνειας (ολική έννοια). Επιπλέον, το θεώρημα αυτό έχει σημαντικές γενικεύσεις σε μεγαλύτερες διαστάσεις, δίνοντας ώθηση στη γεωμετρία και τοπολογία του εικοστού αιώνα. Το Θεώρημα των Gauss - Bonnet διατυπώνεται σε δύο εκδοχές, μια τοπική και μια ολική. Η τοπική εκδοχή αφορά κανονικές περιοχές οι οποίες είναι απλές (δηλαδή ομοιομορφικές με έναν κλειστό δίσκο) και μικρές (δηλαδή βρίσκονται στην εικόνα μιας τοπικής παραμέτρησης της επιφάνειας). Η ολική εκδοχή του θεωρήματος αφορά οποιαδήποτε κανονική περιοχή σε μια επιφάνεια και ανάγεται μέσω μιας διαδικασίας τεμαχισμού της περιοχής αυτής, σε απλές και μικρές περιοχές, ώστε να εφαρμοστεί η τοπική εκδοχή του θεωρήματος Gauss - Bonnet. Η διαδικασία αυτή χρησιμοποιεί την έννοια της τριγωνοποίησης μιας επιφάνειας, όπου εδώ εισάγεται μια σημαντική τοπολογική αναλλοίωτη, η χαρακτηριστική των Euler - Poincaré. Η τριγωνοποίηση μιας επιφάνειας είναι μια μη τετριμμένη μαθηματική διαδικασία και μας οδηγεί στον σημαντικό κλάδο των μαθηματικών, την αλγεβρική τοπολογία. Σκοπός του κεφαλαίου αυτού είναι η παρουσίαση του θεωρήματος των Gauss - Bonnet και κάποιων σημαντικών εφαρμογών που προκύπτουν από αυτό. Για περισσότερες πληροφορίες προτείνουμε τα βιβλία [1], [4], [5], [8], [9] και [10]. Προαπαιτούμενη γνώση Διαφορικός Λογισμός μιας και πολλών μεταβλητών, Γραμμική Άλγεβρα, Συνήθεις Διαφορικές Εξισώσεις. Πριν διατυπώσουμε την πρώτη εκδοχή του θεωρήματος Gauss - Bonnet, χρειαζόμαστε να θυμίσουμε από την ανάλυση, την έννοια του ολοκληρώματος μιας πραγματικής συνάρτησης επί ενός ανοικτού χωρίου (βλ. για παράδειγμα [7]), προσαρμοσμένη στην περίπτωση των επιφανειών. Εστω M ένα τμήμα μιας κανονικής επιφάνειας με παραμέτρηση X : U R 2 X(U) M, X(u, v) = (x(u, v), y(u, v), z(u, v)) και έστω f : M R μια πραγματική συνάρτηση. (Στην περίπτωσή μας θα είναι f = K : M R, η καμπυλότητα Gauss της M). Θέλουμε να ορίσουμε την έννοια ενός ολοκληρώματος 183
185 184 Το Θεώρημα Gauss-Bonnet της μορφής M fda, όπου da το στοιχειώδες εμβαδό στο U. Γνωρίζουμε ότι X u X v 2 = X u 2 X v 2 (1 cos 2 θ) = X u 2 X v 2 X u, X v 2 = EG F 2, συνεπώς da = X u X v dudv = EG F 2 dudv. Εναλλακτικά, έχουμε ότι ( (x, ) y) 2 ( ) (x, z) 2 ( ) (y, z) 2 da = + +, (u, v) (u, v) (u, v) (x, y) όπου (u, v) είναι μια από τις τρείς ελάσσονες Ιακωβιανές ορίζουσες του 3 2 πίνακα [dx]t = (X u, X v ). Θεωρούμε τη σύνθεση ˆf = f X : U R 2 R και ορίζουμε fda = ˆf(u, v) X u X v dudv. M Αποδεικνύεται ότι το παραπάνω ολοκλήρωμα δεν εξαρτάται από την παραμέτρηση X. U Το παρακάτω θεώρημα, το οποίο είχε αποδειχθεί από τον Gauss, μπορούμε να πούμε ότι αποτελεί τον πρόγονο του θεωρήματος Gauss - Bonnet. Αφορά γεωδαισιακά τρίγωνα σε μια επιφάνεια, δηλαδή τρίγωνα των οποίων οι πλευρές είναι τμήματα γεωδαισιακών καμπυλών. Θεώρημα (Gauss) Εστω T ένα γεωδαισιακό τρίγωνο σε μια κανονική επιφάνεια M με εσωτερικές γωνίες α, β, γ. Αν K είναι η καμπυλότητα Gauss της M, τότε KdA = (α + β + γ) π. T Σχήμα 10.1: Παράλληλα διανυσματικά πεδία. Παρατήρηση. Είναι προφανές ότι για την περίπτωση όπου M = R 2 R 3 τότε K = 0, απ όπου προκύπτει η γνωστή ισότητα α + β + γ = π για επίπεδο τρίγωνο. Συνεπώς, η καμπυλότητα δημιουργεί μια μη Ευκλείδεια γεωμετρία. Πριν διατυπώσουμε την τοπική εκδοχή του θεωρήματος Gauss - Bonnet θα χρειαστούμε κάποιες προκαταρκτικές έννοιες.
186 Το Θεώρημα Gauss-Bonnet 185 Προκαταρκτική ορολογία. Ολες οι παρακάτω έννοιες είναι δυνατόν να οριστούν αυστηρά. Εδώ δίνουμε απλώς μια διαισθητική περιγραφή. 1) Προσανατολίσιμη επιφάνεια. Την έννοια αυτή την έχουμε χρησιμοποιήσει αρκετές φορές σε προηγούμενο κεφάλαιο. Σημαίνει ότι η επιφάνεια M επιδέχεται μια απεικόνιση Gauss N : M S 2. 2) Απλά συνεκτικό χωρίο του R 3. Είναι ένα συνεκτικό υποσύνολο M του R 3 το οποίο χαρακτηρίζεται από την ιδιότητα ότι δεν έχει οπές. Ισοδύναμα, κάθε απλή, και κλειστή καμπύλη του M μπορεί να συρρικνωθεί σε ένα σημείο. Για παράδειγμα, η σφαίρα M = S 2 είναι ένα απλά συνεκτικό σύνολο, ενώ ο δακτύλιος (torus) M = T 2 δεν είναι απλά συνεκτικό. Σχήμα 10.2: Μη απλά συνεκτικό χωρίο. 3) Απλή καμπύλη. Είναι μια καμπύλη η οποία δεν έχει αυτοτομές. Σχήμα 10.3: Απλή και μη απλή καμπύλη. 4) Κλειστή καμπύλη. Είναι μια καμπύλη γ : [a, b] M, τέτοια ώστε γ(a) = γ(b). Σχήμα 10.4: Κλειστή και ανοικτή καμπύλη.
187 186 Το Θεώρημα Gauss-Bonnet 5) Θετικά προσανατολισμένη καμπύλη σε επιφάνεια. Ο προσανατολισμός αναφέρεται ως προς τη συγκεκριμένη παραμέτρηση X της επιφάνειας. Σχετίζεται με τον δείκτη στροφής (rotation index) της καμπύλης, έννοια που δεν έχουμε χρησιμοποιήσει. Για τις ανάγκες μας αρκεί η έννοια του προσανατολισμού καμπύλης όπως έχει χρησιμοποιηθεί στη διανυσματική ανάλυση (π.χ. Θεώρημα Stokes κ.λπ.). Εκεί, μια καμπύλη γ σε μια επιφάνεια M ονομάζεται θετικά προσανατολισμένη όταν εφαρμόζοντας τον κανόνα των τριών δακτύλων το κάθετο διάνυσμα N της επιφάνειας δείχνει στην κατεύθυνση του αντίχειρα. 6) Περίοδος της καμπύλης. Δηλώνει πόσες φορές διαγράφουμε το ίχνος της καμπύλης. Θεώρημα (Gauss - Bonnet, πρώτη τοπική εκδοχή) Εστω M μια προσανατολίσιμη κανονική επιφάνεια με τοπική παραμέτρηση X : U M, τέτοια ώστε το σύνολο X(U) να είναι απλά συνεκτικό. Εστω γ : R M μια κανονική, απλή, κλειστή και θετικά προσανατολισμένη καμπύλη στο X(U), με παραμέτρηση ως προς το μήκος τόξου. Εστω Int(γ) X(U) M το εσωτερικό της γ και k g : R R η γεωδαισιακή καμπυλότητά της. Αν K είναι η καμπυλότητα Gauss της M και L R + η περίοδος της γ, τότε ισχύει L 0 k g (s)ds = 2π KdA. Int(γ) Απόδειξη. Εστω {Z, W } μια ορθοκανονική βάση του εφαπτόμενου χώρου T X(u,v) M, η οποία προκύπτει από τη βάση {X u, X v }, μέσω της διαδικασίας Gram-Schmidt. Κατά μήκος της γ : R X(U) ορίζουμε τη συνάρτηση θ : R R, για την οποία το διάνυσμα ταχύτητας γ(s) ικανοποιεί την σχέση γ(s) = cos θ(s)z(s) + sin θ(s)w (s). Τότε έχουμε ότι N γ = N (cos θz + sin θw ) = cos θ(n Z) + sin θ(n W ) = cos θw sin θz. Για τη δεύτερη παράγωγο γ έχουμε: γ = θ( sin θz + cos θw ) + cos θż + sin θẇ, οπότε η γεωδαιασιακή καμπυλότητα δίνεται ως κ g = N γ, γ = θ sin θz + cos θw, sin θz + cos θw + sin θz + cos θw, cos θż + sin θẇ = θ Z, Ẇ.
188 Το Θεώρημα Gauss-Bonnet 187 Ολοκληρώνοντας τη συνάρτηση γεωδαιασιακής καμπυλότητας κ g : R R για μια περίοδο, θα πάρουμε ότι L 0 κ g (s)ds = L 0 θ(s)ds = θ(l) θ(0) = 2π L 0 L 0 L 0 Z(s), Ẇ (s) ds Z(s), Ẇ (s) ds. Z(s), Ẇ (s) ds Εστω α = X 1 γ : R U η αντίστροφη εικόνα της καμπύλης γ στην απλά συνεκτική περιοχή U. Η καμπύλη α είναι απλή, κλειστή και θετικά ορισμένη. Χρησιμοποιώντας την σχέση Z u, W v Z u, W u = K EG F 2 (βλ. Λήμμα 6.1) και το Θεώρημα του Green ([7]), προκύπτει ότι L 0 Z(s), Ẇ (s) ds = = = = = = = γ α Z, uw u + vw v ds Z, W u du + Z, W v dv Int(α) Int(α) Int(α) Int(α) Int(γ) ( Z, W v u Z, W u v )dudv ( Zu, W v + Z, W uv Z v, W u Z, W vu ) dudv ( Z u, W v Z v, W u )dudv K EG F 2 dudv KdA. Πόρισμα Εστω γ : R R 2 μια κανονική, απλή, κλειστή και θετικά προσανατολισμένη (επίπεδη) καμπύλη με παραμέτρηση ως προς το μήκος τόξου. Αν L R + είναι η περίοδος της γ και k g : R R η γεωδαισιακή της καμπυλότητα, τότε L 0 k g (s)ds = 2π. Ορισμός Εστω M μια κανονική επιφάνεια. Μια συνεχής περιοδική συνάρτηση γ : R M με περίοδο L R + αποτελεί παραμέτρηση μιας κατά τμήματα κανονικής καμπύλης (ή ενός καμπυλόγραμμου πολυγώνου) στην M, εάν υπάρχει μια διαμέριση 0 = t 0 < t 1 < t 2 < < t n 1 < t n = L του διαστήματος [0, L], τέτοια ώστε να ισχύουν τα εξής: 1. γ(t) = γ(t ), εάν και μόνο εάν (t t ) = kl, k Z,
189 188 Το Θεώρημα Gauss-Bonnet 2. η συνάρτηση γ είναι διαφορίσιμη σε κάθε ανοικτό διάστημα (t 0, t 1 ), (t 1, t 2 ),..., (t n 1, t n ). 3. οι μονόπλευρες παράγωγοι γ (t i ) = lim t t i γ(t) γ(t i ) t t i, γ + (t i ) = lim t t + i γ(t) γ(t i ) t t i υπάρχουν, είναι μη μηδενικές και δεν είναι παράλληλες (ως διανύσματα). Για μια τέτοια καμπύλη ορίζονται οι εσωτερικές γωνίες ως οι γωνίες που σχηματίζουν οι εφαπτόμενες σε κάθε κορυφή της καμπύλης. Αντίστοιχα, ορίζονται οι εξωτερικές γωνίες. Θεώρημα (Gauss - Bonnet, δεύτερη τοπική εκδοχή) Εστω M μια κανονική προσανατολίσιμη επιφάνεια με τοπική παραμέτρηση X : U M, τέτοια ώστε το σύνολο X(U) M να είναι συνεκτικό και απλά συνεκτικό. Εστω γ : R M μια κατά τμήματα κανονική, απλή, κλειστή και θετικά προσανατολισμένη καμπύλη στην M, με παραμέτρηση ως προς το μήκος τόξου. Εστω Int(γ) το εσωτερικό της γ και k g : R R η γεωδαισιακή καμπυλότητα της γ, σε κάθε κανονικό (λείο) τμήμα της. Αν L R + είναι η περίοδος της γ, K η καμπυλότητα Gauss της M και α 1,..., α n οι εσωτερικές γωνίες των κορυφών της γ, τότε ισχύει L 0 k g (s)ds = n i=1 α i (n 2)π KdA. Int(γ) Απόδειξη. Εστω {Z, W } μια ορθοκανονική βάση, η οποία προκύπτει από την {X u, X v } μέσω της διαδικασίας Gram-Schmidt. Εστω D το διακριτό υποσύνολο του R, το οποίο αποτελείται από τις ακμές του πολυγώνου γ(r). Κατά μήκος των κανονικών τόξων της καμπύλης γ : R X(U), ορίζουμε τη συνάρτηση θ : R \ D R, έτσι ώστε το μοναδιαίο διάνυσμα ταχύτητας γ να ικανοποιεί την σχέση γ(s) = cos θ(s)z(s) + sin θ(s)w (s). Στην απόδειξη του προηγούμενου θεωρήματος είδαμε ότι σε αυτή την περίπτωση η γεωδαισιακή καμπυλότητα δίνεται ως κ g (s) = θ Z, Ẇ και το ολοκλήρωμα αυτής για μια περίοδο είναι L 0 κ g (s)ds = L 0 θ(s)ds L 0 Z(s), Ẇ (s) ds. Από το Θεώρημα του Green θα έχουμε ότι L 0 Z(s), Ẇ (s) ds = Int(γ) KdA. Το ολοκλήρωμα της παραγώγου θ ισούται με το άθροισμα των ολοκληρωμάτων σε κάθε ομαλό τόξο, δηλαδή L θ(s)ds = n si θ(s)ds. 0 i=1 s i 1 Το ολοκλήρωμα αυτό μετράει τη μεταβολή της γωνίας κατά μήκος κάθε τόξου, ως προς την ορθοκανονική βάση {Z, W }. Σε κάθε ακμή του πολυγώνου, η εφαπτομένη στρέφεται κατά γωνία (π α i ), όπου α i είναι η
190 Το Θεώρημα Gauss-Bonnet 189 αντίστοιχη εσωτερική γωνία. Σε μια πλήρη διαδρομή κατά μήκος της καμπύλης, το άθροισμα της μεταβολής των γωνιών κατά μήκος των τόξων και των αντίστοιχων μεταβολών στις ακμές, ισούται με 2π. Συνεπώς, προκύπτει ότι 2π = L 0 θ(s)ds + Από τις παραπάνω ισότητες, προκύπτει το ζητούμενο. n (π α i ). Παρατήρηση. Αν οι εσωτερικές γωνίες αντικατασταθούν με τις εξωτερικές γωνίες, τότε το δεξί μέλος της ισότητας στο Θεώρημα 10.3 παίρνει τη μορφή 2π n i=1 i=1 α i KdA. D Το θεώρημα αυτό έχει ενδιαφέροντα πορίσματα όπως θα δούμε στη συνέχεια. Πόρισμα (Θεώρημα Gauss). Αν γ : R M είναι ένα γεωδαισιακό τρίγωνο σε μια επιφάνεια M με εσωτερικές γωνίες α 1, α 2, α 3, τότε T KdA = α 1 + α 2 + α 3 π, όπου T το εσωτερικό του τριγώνου και K η καμπυλότητα Gauss της M. Απόδειξη. Στο προηγούμενο θεώρημα είναι n = 3 και σε κάθε τμήμα της γ η γεωδαισιακή καμπυλότητα είναι k g = 0. Πόρισμα Εστω ένα κανονικό n-γωνο του επιπέδου, του οποίου οι ακμές είναι ευθύγραμμα τμήματα και με εσωτερικές του γωνίες α 1,..., α n. Τότε ισχύει n α i = (n 2)π. i=1 Απόδειξη. Είναι K = 0 και k g = 0, άρα το αποτέλεσμα προκύπτει από το Θεώρημα Πόρισμα Εστω D ένα καμπυλόγραμμο n-γωνο στη σφαίρα S 2, του οποίου οι πλευρές είναι τόξα μέγιστων κύκλων (δηλαδή ένα γεωδαισιακό n-γωνο). Τότε ισχύει n α i > (n 2)π i=1 Απόδειξη. Είναι K = 1 για την σφαίρα S 2 και k g = 0, άρα από το Θεώρημα 10.3 προκύπτει ότι n i=1 από όπου προκύπτει η ζητούμενη ανισότητα. α i = (n 2)π + 1dA = (n 2)π + Εμβαδό(D), D
191 190 Το Θεώρημα Gauss-Bonnet Πόρισμα Το εμβαδό E ενός σφαιρικού τριγώνου με εσωτερικές γωνίες α, β, γ ισούται με α + β + γ π. Απόδειξη. Εφαρμόζουμε το Πόρισμα 10.2 για n = 3 και προκύπτει ότι α + β + γ = π + E, άρα E = α + β + γ π. Η προηγούμενη σχέση για το εμβαδό σφαιρικού τριγώνου είναι χαρακτηριστική ισότητα της σφαιρικής (ή ελλειπτικής) γεωμετρίας. Θυμίζουμε ότι, αν το τρίγωνο είναι επίπεδο, τότε ισχύει α + β + γ = E. Πόρισμα Για ένα γεωδαισιακό n-γωνο της ψευδοσφαίρας (K = 1), ισχύει ότι n α i < (n 2)π. i=1 Συνεπώς, το εμβαδό E ενός n-γωνου της ψευδοσφαίρας ισούται με E = (n 2)π α 1 α 2 α n. Για n = 3 προκύπτει η κλασική σχέση E = π (α + β + γ), η οποία χαρακτηρίζει το εμβαδό ενός τριγώνου στην υπερβολική γεωμετρία. Ερχόμαστε τώρα στην ολική εκδοχή του θεωρήματος Gauss - Bonnet. Οπως και προηγουμένως, θα δώσουμε αρχικά κάποιες εξηγήσεις για την ορολογία που θα χρησιμοποιηθεί. Προκαταρκτική ορολογία. 1) Συμπαγής επιφάνεια M είναι ένα κλειστό και φραγμένο υποσύνολο του R 3, δηλαδή η M περιέχεται σε μια μπάλα του R 3. Καμιά φορά χρησιμοποιείται στη βιβλιογραφία ο παραπλανητικός όρος κλειστή επιφάνεια χωρίς σύνορο. 2) Αν f : M R είναι μια λεία συνάρτηση επί της συμπαγούς επιφάνειας (και όχι απλώς επί ενός τμήματος X(U) M, όπου X : U M μια τοπική παραμέτρηση), τότε είναι δυνατόν να οριστεί το ολοκλήρωμα fda. Δεν θα παρουσιάσουμε εδώ αυτή τη διαδικασία. Στην ειδική όμως περίπτωση, όπου η f : M R M ικανοποιεί τη συνθήκη f M\X(U) 0, μπορούμε να ορίσουμε fda = M U f(x(u, v)) X u X v dudv. 3) Η πιο σημαντική έννοια είναι η χαρακτηριστική του Euler για μια τριγωνοποίηση μιας επιφάνειας. Μια τριγωνοποίηση (triangulation) μιας επιφάνειας M είναι μια κάλυψη της M με εικόνες τριγώνων, οι οποίες έχουν την εξής ιδιότητα: Αν δύο τρίγωνα τέμνονται, τότε η τομή τους είναι είτε μια κοινή ακμή, είτε μια κοινή κορυφή και μόνο. Ισχύει το εξής: Θεώρημα Κάθε συμπαγής επιφάνεια επιδέχεται μια τριγωνοποίηση, με πεπερασμένο αριθμό τριγώνων.
192 Το Θεώρημα Gauss-Bonnet 191 Σχήμα 10.5: Η αριστερή κάλυψη μιας επιφάνειας αποτελεί μια τριγωνοποίηση, ενώ η δεξιά όχι. Εστω K ο αριθμός των κορυφών, A ο αριθμός των ακμών και E ο αριθμός των εδρών μιας τριγωνοποίησης της συμπαγούς επιφάνειας M. Η χαρακτηριστική του Euler (ή των Euler - Poincaré) της M είναι ο αριθμός X (M) = E A + K. Παράδειγμα Παρακάτω, δίνονται δύο διαφορετικές τριγωνοποιήσεις της σφαίρας. Για την πρώτη τριγωνοποίηση είναι K = 6, A = 12, E = 8, άρα X (S 2 ) = K A + E = = 2. Για τη δεύτερη τριγωνοποίηση είναι K = 4, A = 6, E = 4, άρα X (S 2 ) = = 2. Σχήμα 10.6: Τριγωνοποιήσεις της σφαίρας. Το αποτέλεσμα δεν είναι τυχαίο. Πράγματι, ισχύει το εξής σημαντικό θεώρημα: Θεώρημα ) Η χαρακτηριστική του Euler είναι ανεξάρτητη της τριγωνοποίησης της επιφάνειας. 2) Αν M, M είναι δύο ομοιομορφικές επιφάνειες, τότε X (M) = X (M ). Συνεπώς, η χαρακτηριστική του Euler είναι μια τοπολογική αναλλοίωτη. Παρατηρήστε ότι στο παραπάνω παράδειγμα, οι δύο τριγωνοποιήσεις της σφαίρας έγιναν με τριγωνοποιήσεις, οι οποίες είναι ομοιομορφικές με ένα κυρτό πολύτοπο (γενίκευση του κανονικού πολυέδρου). Θυμίζουμε ότι γενικά για ένα κυρτό πολύτοπο ισχύει ο τύπος του Euler K + E = A + 2, ο οποίος μνημονεύεται για ευκολία με την φράση Κωνσταντίνος και Ελένη Άγιοι και οι δύο.
193 192 Το Θεώρημα Gauss-Bonnet Παράδειγμα Για τον δακτύλιο (torus) T 2 ισχύει X (T 2 ) = 0. Αυτό είναι λίγο πιο δύσκολο να αποδειχθεί. Θεώρημα (Gauss - Bonnet, ολική εκδοχή) Εστω M μια προσανατολίσιμη, συμπαγής, κανονική επιφάνεια του R 3, με καμπυλότητα Gauss K και χαρακτηριστική του Euler X (M). Τότε ισχύει KdA = 2πX (M). M Το αριστερό μέλος της παραπάνω ισότητας ονομάζεται ολική καμπυλότητα (total curvature) της M. Απόδειξη. Εστω T = {T 1,... T m } μια τριγωνοποιήση της επιφάνειας M, τέτοια ώστε κάθε T k να είναι ένα γεωδαισιακό τρίγωνο, το οποίο να περιέχεται στην εικόνα X k (U k ) της τοπικής παραμέτρησης X k : U k M. Τότε το ολοκλήρωμα της καμπυλότητας Gauss K της M γράφεται ως M KdA = m k=1 T k KdA, για κάθε T k T. Σύμφωνα με το Θεώρημα 10.3 θα έχουμε ότι n k KdA = α ki + (2 n k )π, T k για κάθε τρίγωνο T k. Συνδυάζοντας τις δύο παραπάνω σχέσεις προκύπτει ότι M i=1 m n k KdA = ((2 n k )π + α ki ) k=1 = 2πE 2πA + = 2π(E A + K). i=1 n k α k1 m k=1 i=1 Παράδειγμα Για την σφαίρα S 2 με K = 1 είδαμε ότι X (S 2 ) = 2. Τότε από το Θεώρημα 10.6, προκύπτει ότι Εμβαδό(S 2 ) = KdA = 4π. S 2 Αυτό δεν είναι ιδιαίτερα αξιοσημείωτο, αλλά το ενδιαφέρον είναι ότι, αν παραμορφώσουμε την σφαίρα S 2 κατά συνεχή τρόπο (δηλαδή προκύψει μια επιφάνεια M ομοιομορφική με τη σφαίρα S 2 ), τότε ισχύει KdA = 4π. M Με άλλα λόγια, η καμπυλότητα της νέας επιφάνειας M αλλάζει, αλλά η ολική καμπυλότητα παραμένει σταθερή.
194 Το Θεώρημα Gauss - Bonnet 193 Θα κλείσουμε με τη διατύπωση του σημαντικού θεωρήματος ταξινόμησης των προσανατολίσιμων συμπαγών επιφανειών. Ορισμός Ενα χερούλι (handle) σε μια επιφάνεια M είναι μια κανονική περιοχή H M ομοιομορφική με έναν κλειστό (πεπερασμένο) κυκλικό κύλινδρο και τέτοια ώστε το σύνολο M \ H να είναι συνεκτικό. Εστω g N 0. Μια σφαίρα με g το πλήθος χερούλια είναι μια επιφάνεια M, η οποία περιέχει g το πλήθος ξένα ανά δύο χερούλια H 1,..., H g, έτσι ώστε το σύνολο M \ (H 1 H g ), να είναι ομοιομορφικό με μια σφαίρα, από την οποία έχουν αφαιρεθεί 2g το πλήθος ξένες ανά δύο γεωδαισιακές μπάλλες. Σημείωση. 1) Μια γεωδαισιακή μπάλλα (geodesic ball) είναι το σύνολο B ɛp (p) = exp p (B ɛp (0)) (βλ. σχετικά με εκθετική απεικόνιση Κεφάλαιο 9). 2) Ο αριθμός g των χερουλιών ισούται με τον αριθμό των οπών μιας επιφάνειας M και ονομάζεται γένος (genus) της M. Θεώρημα (Ταξινόμηση των προσανατολίσιμων συμπαγών επιφανειών) Κάθε προσανατολίσιμη συμπαγής και συνεκτική επιφάνεια είναι ομοιομορφική με μια σφαίρα με g 0 χερούλια και της οποίας η χαρακτηριστική του Euler ισούται με 2 2g. Ειδικότερα: 1. Δύο προσανατολίσιμες συμπαγείς επιφάνειες είναι ομοιομορφικές εάν και μόνο εάν έχουν την ίδια χαρακτηριστική του Euler. 2. Η σφαίρα είναι η μόνη προσανατολίσιμη συμπαγής επιφάνεια με θετική χαρακτηριστική του Euler. 3. Ο δακτύλιος (torus) είναι η μόνη προσανατολίσιμη συμπαγής επιφάνεια με χαρακτηριστική του Euler ίση με το μηδέν. Παρατήρηση. Στον R 3 δεν υπάρχουν συμπαγείς επιφάνειες οι οποίες να μην είναι προσανατολίσιμες. Υπάρχουν πολλές πηγές όπου μπορεί να αναζητηθεί η απόδειξη του παραπάνω θεωρήματος, ανάλογα με τις λεπτομέρειες που επιθυμεί να δει ο αναγνώστης. Για παράδειγμα, [2], [3], [6], [11] Λυμένα παραδείγματα Σημειώνουμε ότι οι παρακάτω λύσεις είναι σε κάποια σημεία συνοπτικές. Παράδειγμα Να βρεθεί η ολική καμπυλότητα του ελλειψοειδούς Λύση x 2 α 2 + y2 β 2 + z2 γ 2 = 1. Γνωρίζουμε ότι ολική καμπυλότητα της σφαίρας S 2 KdA ισούται με 4π. Επίσης, γνωρίζουμε ότι το ελλειψοειδές είναι επιφάνεια ομοιομορφική με την σφαίρα και ότι οι ομοιομορφικές επιφάνειες έχουν την ίδια ολική καμπυλότητα. Από το Θεώρημα 10.6, η ολική καμπυλότητα κάθε κλειστής επιφάνειας M δίνεται από την σχέση M KdA = 2πX (M),
195 194 Λυμένα παραδείγματα όπου X (M) η χαρακτηριστική του Euler. επίσης με 4π. Επομένως, η ολική καμπυλότητα του ελλειψοειδούς ισούται Παράδειγμα Εστω M μια συμπαγής και συνεκτική επιφάνεια γένους g 1. υπάρχει ένα σημείο της M στο οποίο η καμπυλότητα Gauss να μηδενίζεται. Αποδείξτε ότι Λύση Από το Θεώρημα Gauss - Bonnet (ολική εκδοχή) έχουμε ότι KdA = 2πX (M) = 4π(1 g) 0. M Λόγω της συμπάγειας της M, υπάρχει ένα σημείο p M, τέτοιο ώστε K(p) > 0. Συνεπώς, λόγω της συνέχειας της K : M R, υπάρχει μια περιοχή U του p, έτσι ώστε K U > 0. Επιπλέον, ισχυριζόμαστε ότι υπάρχει και ένα άλλο σημείο q M, ώστε K(q) < 0. Πράγματι, αν αυτό δεν συνέβαινε, τότε θα είχαμε 0 KdA KdA > 0, άτοπο. M U Συνεπώς, λόγω της συνεκτικότητας της M, η συνεχής συνάρτηση K πρέπει να μηδενίζεται σε κάποιο σημείο της M. Παράδειγμα Θεωρούμε τον δακτύλιο (torus) T 2 ως επιφάνεια εκ περιστροφής, η οποία προκύπτει περιστρέφοντας τον κύκλο (x α) 2 + z 2 = r 2 περί τον άξονα z: T 2 = {(x, y, z) : (x 2 + y 2 + z 2 + α 2 r 2 ) 2 4α 2 (x 2 + y 2 ) = 0}. Περιγράψτε μια παραμέτρηση του δακτυλίου T 2, υπολογίστε την καμπυλότητα Gauss και επιβεβαιώστε αναλυτικά ότι T KdA = 0. Λύση Αρχικά παρατηρούμε ότι η τιμή του ολοκληρώματος προκύπτει άμεσα από το Θεώρημα Gauss - Bonnet, επειδή για τον δακτύλιο, το γένος ισούται με g = 1. Άρα X (T 2 ) = 2 2g = 0, οπότε KdA = 2πX (T 2 ) = 0. T Θα υπολογίσουμε το ολοκλήρωμα αυτό και χωρίς την χρήση του Θεωρήματος Gauss - Bonnet. Μια τοπική παραμέτρηση του δακτυλίου T 2 είναι η X(u, v) = ( (α + r cos u) cos v, (α + r cos u) sin v, r sin u ), 0 < u, v < 2π. Με έναν υπολογισμό προκύπτει ότι τα θεμελιώδη ποσά πρώτης και δεύτερης τάξης είναι Συνεπώς, η καμπυλότητα Gauss K : T 2 R είναι E = r 2, F = 0, G = (α + r cos u) 2 e = r, f = 0, g = cos u(α + r cos u). K = eg f 2 EG F 2 = cos u r(α + r cos u).
196 Το Θεώρημα Gauss - Bonnet 195 Το στοιχείο εμβαδού στον T 2 είναι da = EG F 2 dudv = r(α + r cos u)dudv, άρα 2π 2π KdA = cos ududv = 0. T Παράδειγμα Δώστε ένα παράδειγμα συνεκτικής επιφάνειας M, η οποία να περιέχει δύο σημεία, τα οποία να μην μπορούν να συνδεθούν με μια γεωδαισιακή. Ποιά είναι μια τοπολογική υπόθεση για την M, ώστε να αποφεύγεται αυτό το πρόβλημα; Λύση Εστω Π ένα επίπεδο στον R 3 και p, q δύο σημεία του Π. Θεωρούμε ένα εσωτερικό σημείο r του ευθύγραμμου τμήματος pq. Τότε η επιφάνεια Π \ {r} R 3 είναι το ζητούμενο παράδειγμα. Η συνηθισμένη τοπολογική υπόθεση προκειμένου να αποφεύγεται το παραπάνω πρόβλημα είναι η πληρότητα της (M, d), όπου d : M M R + η συνάρτηση που επάγεται από τη μετρική της M. Το σημαντικό θεώρημα των Hopf - Rinow αναφέρει ότι η συνθήκη αυτή ισοδυναμεί με τα εξής: 1. Για κάθε p M η εκθετική απεικόνιση exp p : T p M M ορίζεται σε όλον τον εφαπτόμενο χώρο T p M, 2. Κάθε ζεύγος σημείων της M μπορεί να συνδεθεί με μια γεωδαισιακή καμπύλη που ελαχιστοποιεί το μήκος. 3. Κάθε κλειστό και φραγμένο υποσύνολο της M είναι συμπαγές. Παράδειγμα Εστω M μια συμπαγής επιφάνεια, της οποίας η καμπυλότητα Gauss είναι παντού θετική. Αποδείξτε ότι η M είναι αμφιδιαφορική με την σφαίρα. Λύση Είναι K > 0 παντού, άρα M KdA > 0. Συνεπώς από το Θεώρημα Gauss - Bonnet είναι KdA = 4π(1 g) > 0, M από όπου προκύπτει ότι g < 1. Επειδή οι δυνατές τιμές του γένους g μιας επιφάνειας είναι g = 0, 1, 2,..., προκύπτει ότι g = 0, συνεπώς η M είναι αμφιδιαφορική με την σφαίρα. Το αντίστροφο δεν ισχύει. Η κυλινδρική επιφάνεια πούρο είναι αμφιδιαφορική με την σφαίρα, αλλά στο κυλινδρικό της κομμάτι είναι K = 0. Παράδειγμα Εστω M μια προσανατολίσιμη επιφάνεια με καμπυλότητα Gauss K 0 και έστω γ 1, γ 2 δύο γεωδαισιακές με αρχή ένα σημείο p M. Αποδείξτε ότι οι γ 1, γ 2 δεν μπορούν να ξανασυναντηθούν σε ένα σημείο q M, έτσι ώστε τα ίχνη τους να περικλείουν ένα απλά συνεκτικό χωρίο D της M. Λύση Υποθέτουμε το αντίθετο του συμπεράσματος και έστω α 1, α 2 οι εξωτερικές γωνίες των σημείων τομής των γ 1, γ 2. Τότε από τη δεύτερη εκδοχή του τοπικού Θεωρήματος Gauss - Bonnet έχουμε ότι KdA = 2π α 1 α 2. D Αλλά α 1, α 2 < π, συνεπώς α 1 + α 2 < 2π, οπότε 2π α 1 α 2 > 0. Επειδή όμως K 0 παντού, είναι KdA 0, πράγμα άτοπο. D
197 196 Ασκήσεις 10.2 Ασκήσεις Σχήμα 10.7: Επιφάνεια πούρο. 1. Εστω M μια κανονική επιφάνεια του R 3 αμφιδιαφορική με τον τόρο. Δείξτε ότι υπάρχει ένα σημείο p M για το οποίο η καμπυλότητα Gauss K(p) είναι αρνητική. 2. Εστω η κανονική επιφάνεια M του R 3 η οποία δίνεται ως M = {(x, y, z) R 3 : x 2 + y 2 z 2 = 1 και 1 < z < 1}. Υπολογίστε την τιμή του ολοκληρώματος KdA, M όπου K είναι η καμπυλότητα Gauss της M. 3. Για r R + θεωρούμε την επιφάνεια Σ r η οποία δίνεται ως Σ r = {(x, y, z) R 3 : z = cos x 2 + y 2, x 2 + y 2 < r 2, x, y > 0}. Υπολογίστε την τιμή του ολοκληρώματος KdA, Σ r όπου K η καμπυλότητα Gauss της Σ r. 4. Για n 1 έστω M n μια κανονική επιφάνεια του R 3 η οποία δίνεται ως M n = {(x, y, z) R 3 : x 2 + y 2 = (1 + z 2n ) 2, 0 < z < 1}. Υπολογίστε την τιμή του ολοκληρώματος KdA, M n όπου K η καμπυλότητα Gauss της M n. 5. Εστω M μια προσανατολισμένη συμπαγής επιφάνεια του R 3, η οποία δεν είναι ομοιομορφική με μια σφαίρα. Αποδείξτε ότι η M περιέχει σημεία ελλειπτικά, υπερβολικά και σημεία στα οποία η καμπυλότητα Gauss είναι μηδέν. 6. Εστω M μια προσανατολισμένη επιφάνεια του R 3 με καμπυλότητα Gauss K 0 παντού. Εστω R M ένα απλά συνεκτικό χωρίο, το σύνορο του οποίου είναι ένα γεωδαισιακό πολύγωνο. Αποδείξτε ότι το πολύγωνο αυτό έχει τουλάχιστον τρείς κορυφές.
x, y = x 1 y x n y n. x = x x2 n. df dt = d dt
 Κεφάλαιο 1 Καμπύλες στο επίπεδο και στον χώρο Σύνοψη Μελετάμε ιδιότητες παραμετρημένων καμπυλών στο επίπεδο και στον χώρο. Το συνοδεύον τρίεδρο του Frenet είναι μια ορθοκανονική βάση του R 3 προσαρτημένη
Κεφάλαιο 1 Καμπύλες στο επίπεδο και στον χώρο Σύνοψη Μελετάμε ιδιότητες παραμετρημένων καμπυλών στο επίπεδο και στον χώρο. Το συνοδεύον τρίεδρο του Frenet είναι μια ορθοκανονική βάση του R 3 προσαρτημένη
Τίτλος Μαθήματος: Διαφορική Γεωμετρία
 71 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Λσμένα Παραδείγματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 71 72 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
71 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Λσμένα Παραδείγματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 71 72 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών.
 14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών. 13 η εβδομάδα (16/01/2017 & 19/01/2017) Ασυμπτωτική διεύθυνση και ασυμπτωτικό
14 η εβδομάδα (26/01/2017) Έγιναν οι ασκήσεις 28, 29 και 30. Έγινε επανάληψη στη Θεωρία Καμπυλών και στη Θεωρία Επιφανειών. 13 η εβδομάδα (16/01/2017 & 19/01/2017) Ασυμπτωτική διεύθυνση και ασυμπτωτικό
Ημερολόγιο μαθήματος
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Α.Π.Θ. ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤPΙΑ Ι ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018 19 Τμήμα Α Διδάσκων: Kαθηγητής Στυλιανός Σταματάκης Website URL: http://stamata.webpages.auth.gr/geometry/ Ημερολόγιο
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Α.Π.Θ. ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤPΙΑ Ι ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018 19 Τμήμα Α Διδάσκων: Kαθηγητής Στυλιανός Σταματάκης Website URL: http://stamata.webpages.auth.gr/geometry/ Ημερολόγιο
X u, X u. Z = X u. W EG F 2 (X v F E X u). X u, X v X v, X v
 Κεφάλαιο 6 Το Θαυμαστό Θεώρημα Σύνοψη Στο Κεφάλαιο αυτό αποδεικνύουμε ένα από τα δύο κεντρικά θεωρήματα της θεωρίας επιφανειών το άλλο είναι το Θεώρημα των auss-bonnet. Το θεώρημα αυτό είναι γνωστό ως
Κεφάλαιο 6 Το Θαυμαστό Θεώρημα Σύνοψη Στο Κεφάλαιο αυτό αποδεικνύουμε ένα από τα δύο κεντρικά θεωρήματα της θεωρίας επιφανειών το άλλο είναι το Θεώρημα των auss-bonnet. Το θεώρημα αυτό είναι γνωστό ως
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT
 ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II
 Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Σσναλλοίωτη παράγωγος και παράλληλη μεταφορά Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 17 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Σσναλλοίωτη παράγωγος και παράλληλη μεταφορά Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 17 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Διαφορική Γεωμετρία
 33 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Ο εφαπτόμενος χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 33 34 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
33 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Ο εφαπτόμενος χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 33 34 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΣΚΗΣΕΙΣ. 4. Να βρεθεί η κάθετη καμπυλότητα του υπερβολικού παραβολειδούς. 5. Να βρεθεί η κάθετη καμπυλότητα της ελικοειδούς επιφάνειας.
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Α.Π.Θ. ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΙΙ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018 19 Kαθηγητής Στυλιανός Σταματάκης URL: http://stamata.webpages.auth.gr/geometry/ ΑΣΚΗΣΕΙΣ 1. Να εξεταστεί πώς αλλάζει
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Α.Π.Θ. ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΙΙ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018 19 Kαθηγητής Στυλιανός Σταματάκης URL: http://stamata.webpages.auth.gr/geometry/ ΑΣΚΗΣΕΙΣ 1. Να εξεταστεί πώς αλλάζει
= DX(0, 0)(ae 1 + be 2 ) = adx(0, 0)e 1 + bdx(0, 0)e 2 = ax u (0, 0) + bx v (0, 0).
 Κεφάλαιο 3 Ο εφαπτόμενος χώρος Σύνοψη Ο εφαπτόμενος χώρος μιας κανονικής επιφάνειας αποτελεί τη βέλτιση γραμμική προσέγγιση της επιφάνειας σε ένα σημείο της. Αποτελείται από όλα τα εφαπτόμενα διανύσματα
Κεφάλαιο 3 Ο εφαπτόμενος χώρος Σύνοψη Ο εφαπτόμενος χώρος μιας κανονικής επιφάνειας αποτελεί τη βέλτιση γραμμική προσέγγιση της επιφάνειας σε ένα σημείο της. Αποτελείται από όλα τα εφαπτόμενα διανύσματα
ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ
 ΜΑΘΗΜΑ : ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Πρώτα απ όλα θέλουμε να βρούμε και να εξηγήσουμε έναν ορισμό που να ταιριάζει όσο το δυνατό καλύτερα στα φυσικά φαινόμενα Και η πεποίθησή μας θα ενισχυθεί
ΜΑΘΗΜΑ : ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Πρώτα απ όλα θέλουμε να βρούμε και να εξηγήσουμε έναν ορισμό που να ταιριάζει όσο το δυνατό καλύτερα στα φυσικά φαινόμενα Και η πεποίθησή μας θα ενισχυθεί
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II
 Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Γεωδαιζιακές καμπύλες Όνομα Καθηγηηή: Ανδρέας Αρβανιηογεώργος Τμήμα: Μαθημαηικών 23 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Γεωδαιζιακές καμπύλες Όνομα Καθηγηηή: Ανδρέας Αρβανιηογεώργος Τμήμα: Μαθημαηικών 23 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
1 C k 1 = 1 C 2 sin 2 t, k 2 =
 Κεφάλαιο 11 Επιφάνειες σταθερής καμπυλότητας Gauss Σύνοψη Παρουσιάζουμε χωρίς απόδειξη την ταξινόμηση των επιφανειών του R 3 με σταθερή καμπυλότητα Gauss, θετική, μηδέν, ή αρνητική. Εξετάζουμε χωριστά
Κεφάλαιο 11 Επιφάνειες σταθερής καμπυλότητας Gauss Σύνοψη Παρουσιάζουμε χωρίς απόδειξη την ταξινόμηση των επιφανειών του R 3 με σταθερή καμπυλότητα Gauss, θετική, μηδέν, ή αρνητική. Εξετάζουμε χωριστά
Η μέθοδος του κινουμένου τριάκμου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Πρόγραμμα Μεταπτυχιακών Σπουδών Ειδίκευση Θεωρητικών Μαθηματικών Σ Σταματάκη Η μέθοδος του κινουμένου τριάκμου Σημειώσεις
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Πρόγραμμα Μεταπτυχιακών Σπουδών Ειδίκευση Θεωρητικών Μαθηματικών Σ Σταματάκη Η μέθοδος του κινουμένου τριάκμου Σημειώσεις
ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ
 ΜΑΘΗΜΑ 4: ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Στη φύση δεν υπάρχει ίσως τίποτε παλαιότερο από την κίνηση και οι φιλόσοφοι έχουν γράψει για αυτήν βιβλία που δεν είναι ούτε λίγα ούτε μικρά ΓΑΛΙΛΑΪΚΟΙ
ΜΑΘΗΜΑ 4: ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Στη φύση δεν υπάρχει ίσως τίποτε παλαιότερο από την κίνηση και οι φιλόσοφοι έχουν γράψει για αυτήν βιβλία που δεν είναι ούτε λίγα ούτε μικρά ΓΑΛΙΛΑΪΚΟΙ
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 ΚΕΦΑΛΑΙΟ 2: ΣΥΝΑΡΤΗΣΕΙΣ ΙΣΟΣΤΑΘΜΙΚΕΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ 35
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 1. Γενικά.. 15 Επιφάνεια 15 Ευθειογενεί επιφάνειε. 15 Επιφάνειε δευτέρου βαθμού.. 16 2. Μερικέ επιφάνειε δευτέρου
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 1. Γενικά.. 15 Επιφάνεια 15 Ευθειογενεί επιφάνειε. 15 Επιφάνειε δευτέρου βαθμού.. 16 2. Μερικέ επιφάνειε δευτέρου
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ
 ΜΑΘΗΜΑ 4: ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Στη φύση δεν υπάρχει ίσως τίποτε παλαιότερο από την κίνηση και οι φιλόσοφοι έχουν γράψει για αυτήν βιβλία που δεν είναι ούτε λίγα ούτε μικρά ΓΑΛΙΛΑΪΚΟΙ
ΜΑΘΗΜΑ 4: ΚΙΝΗΣΗ ΣΤΟ ΧΩΡΟ ΚΑΙ ΕΞΕΛΙΞΗ ΣΤΟ ΧΩΡΟ-ΧΡΟΝΟ Στη φύση δεν υπάρχει ίσως τίποτε παλαιότερο από την κίνηση και οι φιλόσοφοι έχουν γράψει για αυτήν βιβλία που δεν είναι ούτε λίγα ούτε μικρά ΓΑΛΙΛΑΪΚΟΙ
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II
 Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Επαναληπτικά θέματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών x Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τίτλος Μαθήματος: Διαφορική Γεωμετρία II Ενότητα: Επαναληπτικά θέματα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών x Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ds ds ds = τ b k t (3)
 Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Κλασικη ιαφορικη Γεωµετρια
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Πρώτη Εργασία, 2018-19 1 Προαπαιτούµενες γνώσεις και ϐασική προετοιµασία
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Πρώτη Εργασία, 2018-19 1 Προαπαιτούµενες γνώσεις και ϐασική προετοιµασία
ΣΗΜΕΙΩΣΕΙΣ 4. bt (γιατί;).
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 1 Τμήμα Α Ακ.Έτος: 6-7 Διδάσκων Σ.Ε.Π. : Τρύφων Δάρας ΣΗΜΕΙΩΣΕΙΣ 4 ΚΑΜΠΥΛΕΣ ΣΤΟ ΧΩΡΟ Μία συνάρτηση της μορφής r ():[ aβ, ] (αντίστοιχα r ():[, ] aβ ) λέμε ότι παριστάνει
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 1 Τμήμα Α Ακ.Έτος: 6-7 Διδάσκων Σ.Ε.Π. : Τρύφων Δάρας ΣΗΜΕΙΩΣΕΙΣ 4 ΚΑΜΠΥΛΕΣ ΣΤΟ ΧΩΡΟ Μία συνάρτηση της μορφής r ():[ aβ, ] (αντίστοιχα r ():[, ] aβ ) λέμε ότι παριστάνει
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
 ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
1. Κινηµατική. x dt (1.1) η ταχύτητα είναι. και η επιτάχυνση ax = lim = =. (1.2) Ο δεύτερος νόµος του Νεύτωνα παίρνει τη µορφή: (1.
 1. Κινηµατική Βιβλιογραφία C. Kittel W. D. Knight M. A. Rueman A. C. Helmholz και B. J. Moe Μηχανική. Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π. 1998. Κεφ.. {Μαθηµατικό Συµπλήρωµα Μ1 Παράγωγος} {Μαθηµατικό Συµπλήρωµα
1. Κινηµατική Βιβλιογραφία C. Kittel W. D. Knight M. A. Rueman A. C. Helmholz και B. J. Moe Μηχανική. Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π. 1998. Κεφ.. {Μαθηµατικό Συµπλήρωµα Μ1 Παράγωγος} {Μαθηµατικό Συµπλήρωµα
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Ανασκόπηση-Μάθημα 12 Συναρτήσεις πολλών μεταβλητών-καμπύλες-πολικές συντεταγμένες
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 12 Συναρτήσεις πολλών μεταβλητών-καμπύλες-πολικές συντεταγμένες Στο δωδέκατο μάθημα (24/10/2018)
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 12 Συναρτήσεις πολλών μεταβλητών-καμπύλες-πολικές συντεταγμένες Στο δωδέκατο μάθημα (24/10/2018)
ΣΧΕΤΙΚΑ ΠΑΡΑΛΛΗΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΣΤΟΝ ΕΥΚΛΕΙΔΕΙΟ ΧΩΡΟ Ε 3
 11 ο Πανελλήνιο Συνέδριο Γεωμετρίας Πανεπιστήμιο Αθηνών 31 Μαΐου Ιουνίου 013 ΣΧΕΤΙΚΑ ΠΑΡΑΛΛΗΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΣΤΟΝ ΕΥΚΛΕΙΔΕΙΟ ΧΩΡΟ Ε 3 Δρ. Δεληβός Ιωάννης Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 1 1. ΣΧΕΤΙΚΑ
11 ο Πανελλήνιο Συνέδριο Γεωμετρίας Πανεπιστήμιο Αθηνών 31 Μαΐου Ιουνίου 013 ΣΧΕΤΙΚΑ ΠΑΡΑΛΛΗΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΣΤΟΝ ΕΥΚΛΕΙΔΕΙΟ ΧΩΡΟ Ε 3 Δρ. Δεληβός Ιωάννης Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 1 1. ΣΧΕΤΙΚΑ
 = 1 A A = A A. A A + A2 y. A = (A x, A y ) = A x î + A y ĵ. z A. 2 A + A2 z
 Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
< F ( σ(h(t))), σ (h(t)) > h (t)dt.
 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ, ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ IV, /6/9 Θέμα 1. Εστω : a 1, β 1 ] R μια C 1 καμπύλη. Μια C 1 καμπύλη ρ : a, β] R λέγεται αναπαραμετρικοποίηση της αν υπάρχει h : a, β] a 1, β 1 ], 1 1 επί και
ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ, ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ IV, /6/9 Θέμα 1. Εστω : a 1, β 1 ] R μια C 1 καμπύλη. Μια C 1 καμπύλη ρ : a, β] R λέγεται αναπαραμετρικοποίηση της αν υπάρχει h : a, β] a 1, β 1 ], 1 1 επί και
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ
 ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2018 2 Περιεχόμενα 1 Καμπύλες του Ευκλειδείου χώρου R 2 7 1.1 Κανονικές καμπύλες................... 8 1.2 Αναπαραμετρήσεις
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2018 2 Περιεχόμενα 1 Καμπύλες του Ευκλειδείου χώρου R 2 7 1.1 Κανονικές καμπύλες................... 8 1.2 Αναπαραμετρήσεις
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ẋ = f(x), x = x 0 όταν t = t 0,
 Κεφάλαιο 2 ΤΟ ΘΕΩΡΗΜΑ ΥΠΑΡΞΗΣ ΚΑΙ ΜΟΝΑΔΙΚΟΤΗΤΑΣ 2.1 Πρόβλημα αρχικών τιμών Στο κεφάλαιο αυτό θα δούμε ότι το πρόβλημα αρχικών τιμών (ΑΤ) ẋ = f(x), x = x 0 όταν t = t 0, έχει λύση και μάλιστα μοναδική για
Κεφάλαιο 2 ΤΟ ΘΕΩΡΗΜΑ ΥΠΑΡΞΗΣ ΚΑΙ ΜΟΝΑΔΙΚΟΤΗΤΑΣ 2.1 Πρόβλημα αρχικών τιμών Στο κεφάλαιο αυτό θα δούμε ότι το πρόβλημα αρχικών τιμών (ΑΤ) ẋ = f(x), x = x 0 όταν t = t 0, έχει λύση και μάλιστα μοναδική για
Καµπύλες στον R. σ τελικό σηµείο της σ. Το σ. σ =. Η σ λέγεται διαφορίσιµη ( αντιστοίχως
 Καµπύλες στον R 9. Ορισµός Μια καµπύλη στον R είναι µια συνεχής συνάρτηση σ : Ι R R όπου Ι διάστηµα ( συνήθως κλειστό και φραγµένο ) στον R. Συνήθως φανταζόµαστε την µεταβλητή t Ι ως τον χρόνο και την
Καµπύλες στον R 9. Ορισµός Μια καµπύλη στον R είναι µια συνεχής συνάρτηση σ : Ι R R όπου Ι διάστηµα ( συνήθως κλειστό και φραγµένο ) στον R. Συνήθως φανταζόµαστε την µεταβλητή t Ι ως τον χρόνο και την
Λογισμός 4 Ενότητα 13
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΣΠΟΥΔΕΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΚΑΙ ΕΠΙΦΑΝΕΙΕΣ ΕΛΑΧΙΣΤΗΣ ΕΚΤΑΣΗΣ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΣΠΟΥΔΕΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΚΑΙ ΕΠΙΦΑΝΕΙΕΣ ΕΛΑΧΙΣΤΗΣ ΕΚΤΑΣΗΣ ΟΝΟΜΑ ΦΟΙΤΗΤΗ ΠΑΤΕΡΑΣ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΕΤΑΠΤΥΧΙΑΚΕΣ ΣΠΟΥΔΕΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΚΑΙ ΕΠΙΦΑΝΕΙΕΣ ΕΛΑΧΙΣΤΗΣ ΕΚΤΑΣΗΣ ΟΝΟΜΑ ΦΟΙΤΗΤΗ ΠΑΤΕΡΑΣ
Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις
 Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις ẋ 1 f 1 (x 1 x 2 ) ẋ 2 f 2 (x 1 x 2 ) (501) Το σύστημα αυτό γράφεται σε διανυσματική
Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις ẋ 1 f 1 (x 1 x 2 ) ẋ 2 f 2 (x 1 x 2 ) (501) Το σύστημα αυτό γράφεται σε διανυσματική
ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΟ ΣΥΝΕΧΕΙΑ Ορισμός. Αν τα και είναι τα μοναδιαία διανύσματα των αξόνων και αντίστοιχα η συνάρτηση που ορίζεται από τη σχέση όπου (συνιστώσες) είναι
ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΟ ΣΥΝΕΧΕΙΑ Ορισμός. Αν τα και είναι τα μοναδιαία διανύσματα των αξόνων και αντίστοιχα η συνάρτηση που ορίζεται από τη σχέση όπου (συνιστώσες) είναι
1.2 Συντεταγμένες στο Επίπεδο
 1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης. Λογισμός 3 Ασκήσεις. Μιχάλης Μαριάς Τμήμα Α.Π.Θ.
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Λογισμός 3 Μιχάλης Μαριάς Τμήμα Α.Π.Θ. Θεσσαλονίκη, 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Λογισμός 3 Μιχάλης Μαριάς Τμήμα Α.Π.Θ. Θεσσαλονίκη, 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
[4], [5], [6], [7], [8], [9], [10], [11].
![[4], [5], [6], [7], [8], [9], [10], [11]. [4], [5], [6], [7], [8], [9], [10], [11].](/thumbs/66/55331296.jpg) Κεφάλαιο 8 Συναλλοίωτη παράγωγος και παραλληλία Σύνοψη Ορίζουμε την έννοια του διανυσματικού πεδίου σε μια επιφάνεια και τη συναλλοίωτη παράγωγο αυτού κατά μήκος μιας λείας καμπύλης. Ενα διανυσματικό πεδίο
Κεφάλαιο 8 Συναλλοίωτη παράγωγος και παραλληλία Σύνοψη Ορίζουμε την έννοια του διανυσματικού πεδίου σε μια επιφάνεια και τη συναλλοίωτη παράγωγο αυτού κατά μήκος μιας λείας καμπύλης. Ενα διανυσματικό πεδίο
ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΙΙΙ Χειμερινό εξάμηνο Ασκήσεις 1.
 ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΙΙΙ Χειμερινό εξάμηνο -7 Ασκήσεις Αποδείξτε την ανισότητα Cuch-Schwr Για R Δείξτε ότι η ισότητα ισχύει αν και μόνο αν τα διανύσματα και είναι συγγραμμικά Αποδείξτε την τριγωνική ανισότητα
ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΙΙΙ Χειμερινό εξάμηνο -7 Ασκήσεις Αποδείξτε την ανισότητα Cuch-Schwr Για R Δείξτε ότι η ισότητα ισχύει αν και μόνο αν τα διανύσματα και είναι συγγραμμικά Αποδείξτε την τριγωνική ανισότητα
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
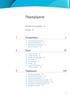 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
X v (q) = ( x v (q), y v (q), z v (q) ) x u (q) y u (q) z u (q) x v (q) y v (q) z v (q) X 1 u (q) X 1. det. X 2 u (q) X 2. v (q)
 Κεφάλαιο 2 Κανονικές επιφάνειες Σύνοψη Προκειμένου να ορίσουμε την έννοια της επιφάνειας στον R 3, έχουμε δύο δυνατές προσεγγίσεις. Με την πρώτη μπορούμε να ορίσουμε μια επιφάνεια ως ένα υποσύνολο του
Κεφάλαιο 2 Κανονικές επιφάνειες Σύνοψη Προκειμένου να ορίσουμε την έννοια της επιφάνειας στον R 3, έχουμε δύο δυνατές προσεγγίσεις. Με την πρώτη μπορούμε να ορίσουμε μια επιφάνεια ως ένα υποσύνολο του
ΘΕΜΕΛΙΩΔΕΙΣ ΑΡΧΕΣ ΤΗΣ ΚΛΑΣΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδημαϊκό έτος 010-11 Μάθημα: ΜΗΧΑΝΙΚΗ Καθηγητές: Σ Πνευματικός Α Μπούντης ΑΣΚΗΣΕΙΣ ΦΡΟΝΤΙΣΤΗΡΙΩΝ Α ΚΕΦΑΛΑΙΟΥ Τα φροντιστήρια γίνονται κάθε Δευτέρα 1100-100 και κάθε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδημαϊκό έτος 010-11 Μάθημα: ΜΗΧΑΝΙΚΗ Καθηγητές: Σ Πνευματικός Α Μπούντης ΑΣΚΗΣΕΙΣ ΦΡΟΝΤΙΣΤΗΡΙΩΝ Α ΚΕΦΑΛΑΙΟΥ Τα φροντιστήρια γίνονται κάθε Δευτέρα 1100-100 και κάθε
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1
 ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
(2) Θεωρούµε µοναδιαία διανύσµατα α, β, γ R 3, για τα οποία γνωρίζουµε ότι το διάνυσµα
 Πανεπιστηµιο Ιωαννινων σχολη θετικων επιστηµων τµηµα µαθηµατικων τοµεας αλγεβρας και γεωµετριας αναλυτικη γεωµετρια διδασκων : χρηστος κ. τατακης υποδειξεις λυσεων των θεµατων της 7.06.016 ΘΕΜΑ 1. µονάδες
Πανεπιστηµιο Ιωαννινων σχολη θετικων επιστηµων τµηµα µαθηµατικων τοµεας αλγεβρας και γεωµετριας αναλυτικη γεωµετρια διδασκων : χρηστος κ. τατακης υποδειξεις λυσεων των θεµατων της 7.06.016 ΘΕΜΑ 1. µονάδες
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ
 ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2017 2 Περιεχόμενα 1 Καμπύλες του Ευκλειδείου χώρου R 2 7 1.1 Κανονικές καμπύλες................... 8 1.2 Αναπαραμετρήσεις
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2017 2 Περιεχόμενα 1 Καμπύλες του Ευκλειδείου χώρου R 2 7 1.1 Κανονικές καμπύλες................... 8 1.2 Αναπαραμετρήσεις
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ
 ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2017 2 Περιεχόμενα 1 Καμπύλες του R 2 5 1.1 Κανονικές καμπύλες.................... 6 1.2 Αναπαραμετρήσεις καμπυλών..............
ΔΙΑΦΟΡΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΜΠΥΛΩΝ ΚΑΙ ΕΠΙΦΑΝΕΙΩΝ ΘΕΟΔΩΡΟΣ ΒΛΑΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΙΩΑΝΝΙΝΑ 2017 2 Περιεχόμενα 1 Καμπύλες του R 2 5 1.1 Κανονικές καμπύλες.................... 6 1.2 Αναπαραμετρήσεις καμπυλών..............
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Λύσεις στο επαναληπτικό διαγώνισμα 3
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ. Μερικές βασικές έννοιες διανυσματικού λογισμού
 ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ
 Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών. Διανυσματική Ανάλυση. Δρ. Θεόδωρος Ζυγκιρίδης
 Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Διανυσματική Ανάλυση Δρ. Θεόδωρος Ζυγκιρίδης 9 Ιουνίου 2011 2 Περιεχόμενα 1 Διανυσματικές συναρτήσεις 1 1.1 Γενικά στοιχεία.....................................
Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Διανυσματική Ανάλυση Δρ. Θεόδωρος Ζυγκιρίδης 9 Ιουνίου 2011 2 Περιεχόμενα 1 Διανυσματικές συναρτήσεις 1 1.1 Γενικά στοιχεία.....................................
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ
 Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
1 ΔΙΑΝΥΣΜΑΤΑ. Εισαγωγή
 1 ΙΝΥΣΜΤ Εισαγωγή Το διάνυσμα είναι ένα χαρακτηριστικό παράδειγμα έννοιας που αναπτύχθηκε μέσα από τη στενή αλληλεπίδραση Μαθηματικών και Φυσικής. κανόνας του παραλληλόγραμμου, σύμφωνα με τον οποίο το
1 ΙΝΥΣΜΤ Εισαγωγή Το διάνυσμα είναι ένα χαρακτηριστικό παράδειγμα έννοιας που αναπτύχθηκε μέσα από τη στενή αλληλεπίδραση Μαθηματικών και Φυσικής. κανόνας του παραλληλόγραμμου, σύμφωνα με τον οποίο το
ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
{(x, y) R 2 : f (x, y) = 0}
 ΜΕΜ 102 Γεωμετρία και Γραμμική Άλγεβρα Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης Οκτ 2014 Χ.Κουρουνιώτης (Παν.Κρήτης) ΜΕΜ 102-13 Οκτ 2014 1 / 10 Ενα θεμελιώδες πρόβλημα της Αναλυτικής Γεωμετρίας
ΜΕΜ 102 Γεωμετρία και Γραμμική Άλγεβρα Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης Οκτ 2014 Χ.Κουρουνιώτης (Παν.Κρήτης) ΜΕΜ 102-13 Οκτ 2014 1 / 10 Ενα θεμελιώδες πρόβλημα της Αναλυτικής Γεωμετρίας
Κλασικη ιαφορικη Γεωµετρια
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια εύτερη Εργασία, 2018-19 1 Καµπύλες στον χώρο και στο επίπεδο 1.1 Καµπύλες
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια εύτερη Εργασία, 2018-19 1 Καµπύλες στον χώρο και στο επίπεδο 1.1 Καµπύλες
Ερωτήσεις-Απαντήσεις Θεωρίας
 1 ΓΙΑΝΝΗΣ ΚΑΡΑΓΙΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΡΟΣ Β 2 ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ
1 ΓΙΑΝΝΗΣ ΚΑΡΑΓΙΑΝΝΗΣ Σχολικός Σύμβουλος Μαθηματικών ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕΡΟΣ Β 2 ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
σ (9) = i + j + 3 k, σ (9) = 1 6 k.
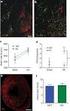 Ασκήσεις από το Διανυσματικός Λογισμός των Marsden - romba και από το alculus του Apostol. 1. Βρείτε τα διανύσματα της ταχύτητας και της επιτάχυνσης και την εξίσωση της εφαπτομένης για κάθε μία από τις
Ασκήσεις από το Διανυσματικός Λογισμός των Marsden - romba και από το alculus του Apostol. 1. Βρείτε τα διανύσματα της ταχύτητας και της επιτάχυνσης και την εξίσωση της εφαπτομένης για κάθε μία από τις
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 3 Μαρτίου 2019 1 Τανυστής Παραμόρφωσης Συνοδεύον σύστημα ονομάζεται το σύστημα συντεταγμένων ξ i το οποίο μεταβάλλεται
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 3 Μαρτίου 2019 1 Τανυστής Παραμόρφωσης Συνοδεύον σύστημα ονομάζεται το σύστημα συντεταγμένων ξ i το οποίο μεταβάλλεται
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΠΕΙΚΟΝΙΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΠΕΙΚΟΝΙΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ...23 ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...15 ΚΕΦΑΛΑΙΟ 3 ΕΥΘΕΙΕΣ...32 ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...43
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ
 Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Κλασικη ιαφορικη Γεωµετρια
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Τρίτη Εργασία, 2018-19 Επιφάνειες Εξάσκηση µε ϐασικούς υπολογισµούς κινούµενης
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Σχολη Θετικων Επιστηµων, Τµηµα Μαθηµατικων, Τοµεας Γεωµετριας Κλασικη ιαφορικη Γεωµετρια Τρίτη Εργασία, 2018-19 Επιφάνειες Εξάσκηση µε ϐασικούς υπολογισµούς κινούµενης
Λογισμός 4 Ενότητα 11
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Θεώρημα αλλαγής μεταβλητών. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Θεώρημα αλλαγής μεταβλητών. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Κεφάλαιο Χώρος, Διανύσματα, Διανυσματικές εξισώσεις, Συστήματα Συντεταγμένων.
 Χώρος Διανύσματα Κεφάλαιο Χώρος, Διανύσματα, Διανυσματικές εξισώσεις, Συστήματα Συντεταγμένων. Καρτεσιανές συντεταγμένες και διανύσματα στο χώρο. Στο σύστημα καρτεσιανών (ή ορθογώνιων) συντεταγμένων κάθε
Χώρος Διανύσματα Κεφάλαιο Χώρος, Διανύσματα, Διανυσματικές εξισώσεις, Συστήματα Συντεταγμένων. Καρτεσιανές συντεταγμένες και διανύσματα στο χώρο. Στο σύστημα καρτεσιανών (ή ορθογώνιων) συντεταγμένων κάθε
Ανασκόπηση-Μάθημα 32 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού πεδίου
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 3 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 3 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 2 0 Κεφάλαιο
 Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
Φυσική Θετικών Σπουδών Γ τάξη Ενιαίου Λυκείου 0 Κεφάλαιο Περιέχει: Αναλυτική Θεωρία Ερωτήσεις Θεωρίας Ερωτήσεις Πολλαπλής Επιλογής Ερωτήσεις Σωστού - λάθους Ασκήσεις ΘΕΩΡΙΑ 4- ΕΙΣΑΓΩΓΗ Στην μέχρι τώρα
Μεθοδική Επανα λήψή. Επιμέλεια Κων/νος Παπασταματίου. Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.
 Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Διαφορικός Λογισμός. Κεφάλαιο Συναρτήσεις. Κατανόηση εννοιών - Θεωρία. 1. Τι ονομάζουμε συνάρτηση;
 Κεφάλαιο 1 Διαφορικός Λογισμός 1.1 Συναρτήσεις Κατανόηση εννοιών - Θεωρία 1. Τι ονομάζουμε συνάρτηση; 2. Πως ορίζονται οι πράξεις της πρόσθεσης, της διαφοράς, του γινομένου και του πηλίκου μεταξύ δύο συναρτήσεων;
Κεφάλαιο 1 Διαφορικός Λογισμός 1.1 Συναρτήσεις Κατανόηση εννοιών - Θεωρία 1. Τι ονομάζουμε συνάρτηση; 2. Πως ορίζονται οι πράξεις της πρόσθεσης, της διαφοράς, του γινομένου και του πηλίκου μεταξύ δύο συναρτήσεων;
Μαθηματικά Κατεύθυνσης (Προσανατολισμού)
 Θέματα ενδοσχολικών εξετάσεων στα Μαθηματικά Προσανατολισμού Β Λυκείου Σχ έτος 03-04, Ν Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Μαθηματικά Κατεύθυνσης (Προσανατολισμού) ΣΧΟΛΙΚΟ
Θέματα ενδοσχολικών εξετάσεων στα Μαθηματικά Προσανατολισμού Β Λυκείου Σχ έτος 03-04, Ν Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Μαθηματικά Κατεύθυνσης (Προσανατολισμού) ΣΧΟΛΙΚΟ
ΑΝΑΛΥΤΙΚΗ ΥΛΗ ΤΟΥ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ RIEMANN
 ΑΝΑΛΥΤΙΚΗ ΥΛΗ ΤΟΥ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ RIEMANN Ι. Διαφορίσιμες Πολλαπλότητες 1. Διαφορίσιμες πολλαπλότητες και απεικονίσεις 2. Ο εφαπτόμενος χώρος και η εφαπτομένη δέσμη 3. Υποπολλαπλότητες
ΑΝΑΛΥΤΙΚΗ ΥΛΗ ΤΟΥ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ RIEMANN Ι. Διαφορίσιμες Πολλαπλότητες 1. Διαφορίσιμες πολλαπλότητες και απεικονίσεις 2. Ο εφαπτόμενος χώρος και η εφαπτομένη δέσμη 3. Υποπολλαπλότητες
t : (x, y) x 2 +y 2 y x
 Σύνοψη Κεφαλαίου 5: Αντιστροφική Γεωμετρία Αντιστροφή 1. Η ανάκλαση σε μία ευθεία l στο επίπεδο απεικονίζει ένα σημείο A σε ένα σημείο A που απέχει ίση απόσταση από την l αλλά βρίσκεται στην άλλη πλευρά
Σύνοψη Κεφαλαίου 5: Αντιστροφική Γεωμετρία Αντιστροφή 1. Η ανάκλαση σε μία ευθεία l στο επίπεδο απεικονίζει ένα σημείο A σε ένα σημείο A που απέχει ίση απόσταση από την l αλλά βρίσκεται στην άλλη πλευρά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ ΜΑΘΗΜΑ: ΚΛΑΣΙΚΗ ΜΗΧΑΝΙΚΗ. Καθηγητής: Σ. Πνευματικός ΜΕΡΟΣ Β.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0- ΜΑΘΗΜΑ: Καθηγητής: Σ. Πνευματικός ΜΕΡΟΣ Β ΠΕΔΙΑ ΔΥΝΑΜΕΩΝ ΣΤΗΝ Μάθημα ο Στην Κλασική Μηχανική, ένα πεδίο δυνάμεων ορίζεται στον τρισδιάστατο ευκλείδειο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0- ΜΑΘΗΜΑ: Καθηγητής: Σ. Πνευματικός ΜΕΡΟΣ Β ΠΕΔΙΑ ΔΥΝΑΜΕΩΝ ΣΤΗΝ Μάθημα ο Στην Κλασική Μηχανική, ένα πεδίο δυνάμεων ορίζεται στον τρισδιάστατο ευκλείδειο
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ. και σε κάθε γειτονιά του z
 7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Τίτλος Μαθήματος: Διαφορική Γεωμετρία
 48 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Καμπσλότητα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 48 49 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
48 Τίτλος Μαθήματος: Διαφορική Γεωμετρία Ενότητα: Καμπσλότητα Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών 48 49 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
